On the Theory of Metals.
|
|
|
- Kathleen Carr
- 6 years ago
- Views:
Transcription
1 On the Theory of Metals. I. Eigenvalues and eigenfunctions of a linear chain of atoms H. Bethe in Rome Zeitschrift für Physik 71 (1931) June 1931 Original title: Zur Theorie der Metalle. I. Eigenwerte und Eigenfunktionen der linearen Atomkette. (Translation by T. C. Dorlas, DIAS, 9 ovember 009.) Abstract A method is described for calculating, to zeroth and first order respectively (in the sense of London and Heitler), the eigenfunctions and eigenvalues for a one-dimensional metal consisting of a linear chain of very many atoms, each of which has a single s-electron with spin. Besides Bloch s spin waves, there exist eigenfunctions where the spins pointing in one direction tend to reside on neighbouring atoms. These eigenfunctions might be of importance for the theory of ferromagnetism. 1. In the theory of metals, one has so far considered only the movement of single conduction electrons in the field of the metal atoms (Sommerfeld, Bloch). The interaction between the electrons has been ignored, at least to the extent that it could not be included in the potential acting on the electrons. This approach has been very fruitful in treating the problem of metallic conduction (with the exception of superconduction). However, it has not allowed a deeper understanding of the problem of ferromagnetism for example 1, and it has made the calculation of cohesion forces in metals a virtually hopeless task: The exchange forces between the electrons, which are relevant for the size of the first-order terms in the perturbation series 1 F. Bloch, Zs. f. Phys. 57, 545 (199) showed that under certain circumstances, free electrons can also exhibit ferromagnetism. 1
2 for the energy, are of the same order of magnitude as the zero-point energy of the electron gas, and one can estimate that the second order is again of this magnitude, etc. This behaviour makes one somewhat sceptical about the entire approximation, in which the movement of the individual electrons (the kinetic zero-point energy) is considered to be of greater importance than the interaction (or exchange) energy. Therefore, Slater and Bloch 3 have recently attempted to approximate the problem from the opposite side, i.e. assuming that the atoms are fixed and considering the interaction as a perturbation, just as in the London-Heitler approximation for molecules. Slater was especially interested in the cohesion forces in non-ferromagnetic materials, where the London-Heitler exchange integral J is in general negative 4, and he developed an interesting method for the approximate calculation of the ground state energy of such metals, for which the total spin obviously vanishes. Bloch, for the purpose of ferromagnetism, calculated approximately the lowest terms in a systematic fashion in the opposite case where J > 0. However, in his method, he obtained too many eigenvalues. It is the aim of the present work to demonstrate, at first in the case of a linear chain of atoms, a method for calculating all eigenvalues of a one-dimensional crystal to arbitrary precision. This arbitrary precision, of course, has to be understood in the framework of the first approximation of the London-Heitler method, so that the problem has the same status as the H molecule in the work of London and Heitler. We obtain, in addition to modified versions of the solutions found by Bloch, a set of solutions of a different type, in such a way that the total number of eigenvalues is exactly the correct one.. Our problem is therefore as follows: Given is a linear chain of very many () identical atoms. Each atom has, apart from closed shells, one conduction electron in an s-orbit. We assume that the eigenfunction of the free atoms is known. What are the eigenfunctions to zeroth, and the eigenvalues to first-order approximation of the total system including the interaction between the atoms? Disregarding the interaction, each atoms has two states with equal energy: the spin of the conduction electron can point to the right or to the left. To zeroth order, the eigenvalue of the chain is therefore -fold degenerate. A state of the chain can be fixed by indicating for which atoms the spin points to the right. Assume that this is the case at the atoms with numbers m 1,..., m r. Let the corresponding eigenfunction of the chain be ψ(m 1,..., m r ). The J. C. Slater, Phys. Rev. 35, 509 (1930). 3 F. Bloch, Zs. f. Phys. 61, 06 (1930) (in the following referred to as l.c.). 4 W. Heisenberg, Zs. f. Phys. 49, 619 (198).
3 correct eigenfunction, in zeroth-order approximation, can then be written in the form Ψ = a(m 1, m,..., m r ) ψ(m 1,..., m r ), m 1,m,...,m r where the numbers m 1,..., m r run through the values 1 to, and we will assume that m 1 < m < < m r. If we calculate the matrix elements of the interaction energy w.r.t. the states defined by the spin distributions m 1,..., m r, then we obtain the following 5 : Diagonal elements: If the spin distribution m 1,..., m r contains neighbouring pairs of parallel spins, then W m1,...m r, m 1...m r = E 0 J. E 0 is the interaction due to the charged clouds of the atoms; J is the London-Heitler exchange integral between neighbouring atoms. For nonnearest neighbour atoms we neglect the exchange integral because it decreases exponentially in the distance. on-diagonal elements: These occur between two states which can be obtained from one another by exchanging two nearest-neighbour spins with opposite spins. For example, in our notation, the states m 1... m i... m r, and m 1... m i m r, where it is assumed that m i + 1 is indeed a left-pointing spin, i.e. m i+1 m i + 1. All such off-diagonal elements of the interaction energy are equal to J. Using these matrix elements for the interaction energy, we obtain the following equations between the coefficients a(m 1... m r ) of the required eigenfunction Ψ: ɛa(m 1... m r ) + [a(m 1... m r) a(m 1... m r )] = 0. (1) Here m 1...m r ɛj = e E 0 + J, () e being the total perturbed energy to first approximation. The sum runs over all distributions m 1... m r that can be obtained from m 1... m r by exchanging neighbouring opposite spins 6. 5 F. Bloch, l.c. 6 The equation (1) is due to Bloch, l.c., more accurately derived [there Eqn. (5)]; the atoms are numbered with f i there instead of m i, and instead of ɛj, he writes simply ɛ. 3
4 Apart from the equation (1), the coefficients a should also satisfy the periodicity condition a(m 1... m i... m r ) = a(m 1... m i +... m r ). (3) 3. For r = 1, the solution of (1) reads, as is well-known, a(m) = e ikm, ɛ = 1 cos k, k = π λ, λ = integer. For r = we have to distinguish two cases: Either the two right-spins are separate from one another, in which case ɛ a(m 1 m ) = a(m 1 + 1, m ) + a(m 1 1, m ) + a(m 1, m + 1) or they are nearest neighbours: + a(m 1, m 1) 4a(m 1, m ) (m m 1 + 1), (4-a) ɛ a(m 1, m 1 + 1) = a(m 1 1, m 1 + 1) + a(m 1, m 1 + ) a(m 1, m 1 + 1). (4-b) The first group of equations is solved rigorously by setting a(m 1 m ) = c 1 e i(f 1m 1 +f m ) + c e i(f m 1 +f 1 m ), ɛ = 1 cos f cos f, (5) where the constants c 1, c, f 1, f are for the moment undetermined. The second group can be satisfied by choosing c 1 and c such that 0 = a(m 1 m ) + a(m 1 + 1, m 1 + 1) a(m 1, m 1 + 1). (6) Here, a(m 1, m 1 ) has no physical meaning, but is defined by (5). Clearly, by adding (6) to (4-b), it becomes of the form (4-a), which has already been solved. Inserting (5) into (6) gives e i(f 1+f )m 1 [c 1 (1 + e i(f 1+f ) e if ) + c (1 + e i(f 1+f ) e if 1 )] = 0, (7) c 1 c = f1+f cos e i f1 f cos f 1+f e i f1 f = sin f 1 f + i ( cos f 1+f cos f 1 f ) sin f 1 f i ( cos f 1+f cos f 1 f ). 4
5 We set c 1 = e iϕ/ and c = e iϕ/, so that cot ϕ = sin f 1 f cos f 1+f cos f 1 f, Correspondingly, cot ϕ = cot f 1 cot f. (8) a(m 1, m ) = e i(f 1m 1 +f m + 1 ϕ) + e i(f m 1 +f 1 m 1 ϕ). (9) Here it is assumed that m 1 and m are in the basic part of the chain, i.e. 1 m 1 < m. The periodicity condition requires: a(m 1, m ) = a(m, m 1 + ). (10) [The notation a(m, m 1 + ) is suggested by the fact that we want to order the m i according to their size; cf. above.] Inserting (9) into (10), e i(f 1m 1 +f m + 1 ϕ) + e i(f m 1 +f 1 m 1 ϕ) = e i(f 1m +f (m 1 +)+ 1 ϕ) + e i(f m +f 1 (m 1 +) 1 ϕ). Since this has to hold for all m 1 and m, the first summand on the left must equal the second on the right and vice versa, so that f 1 ϕ = πλ 1, f + ϕ = πλ, λ 1, λ = 0, 1,,..., 1. (11) The numbers f 1 and f do not have the usual form π λ, but their sum does: k = f 1 + f = π (λ 1 + λ ). (1) k is a true integration constant of the problem; the coefficient a(m 1, m ) is multiplied by e ik when both right-spins are moved one place to the right, which obviously does not affect the physics of the system. We presently discuss the behaviour of the phase ϕ as a function of f 1 and f, where we take the convention that π ϕ π. (13) Interchanging f 1 and f obviously leads to a change of sign for ϕ, while the coefficients a remain unchanged according to (9). If we keep f fixed and 5
6 let f 1 increase starting at zero, then cot(ϕ/) decreases from + to smaller positive values, reaching 0 when f 1 = f ; ϕ therefore increases from 0 to π. As f 1 becomes slightly bigger than f, ϕ jumps from +π to π, and then increases steadily back to 0 when f 1 increases further to π. If f 1 = f then either ϕ = +π, λ 1 = λ 1 = f 1 π 1, or ϕ = π, λ 1 = λ + 1 = f 1 π + 1. In both cases, we have, according to (9), for all m 1, m, a(m 1, m ) = e if 1(m 1 +m ) ( e i π + e i π ) = 0. Conclusion: f 1 = f does not lead to a meaningful solution of the problem, and for a given λ, λ 1 can only take the values λ 1 = 0, 1,..., λ, λ +,..., 1. Moreover, since f 1, f and f, f 1 yield the same solution, we may assume f 1 < f. Thus, for a given λ, there are λ 1 solutions λ 1 = 0, 1,..., λ, and λ runs from to 1, so the total number of solutions is 1 (λ 1) = λ = ( 1 However, there ( must clearly be as many solutions as there are spin distributions, i.e. ). With our more accurate discussion, we have have therefore come to the conclusion that the usual spin waves do not yield sufficiently many solutions, whereas Bloch (l.c.) suggested that the method yielded too many solutions, namely ( ) There must therefore be a further 1 solutions. These can be obtained if one allows the wave numbers f 1 and f to have conjugate complex values. Indeed, we will find that, for every arbitrary value of f 1 + f = k, one can find exactly one pair of conjugate complex solutions of (8) and (11). Let } f 1 = u + i v, (14) f = u i v; ). then cot f 1 = cos u cosh v i sin u sinh v sin u cosh v + i cos u sinh v = sin u i sinh v cosh u cos u. (15) 6
7 ow, by (11), (f 1 f ) = i v = π(λ 1 λ ) + ϕ, ϕ = ψ + i χ, ψ = π(λ λ 1 ), χ = v. (16) If v should take a finite value (i.e v > 0), then χ must be very large, and hence cot ϕ sin ψ 1 ieχ 1 eχ cos ψ i + e χ (sin ψ i cos ψ), To first approximation, therefore, cot ϕ i(1 + e χ+iψ ). (17) and cot ϕ = cot f 1 cot f = i sin u i sinh v sin u + i sinh v = cosh v cos u cosh v cos u, sinh v = cosh v cos u, e v = cos u (18) ɛ = cos(u + iv) cos(u iv) = cos u cosh v = cos u ( cos u + 1 ), cos u ɛ = sin u = 1 (1 cos u). (19) Apparently, we must have cos u 0, i.e. π u π. Therefore, if k = u + nπ (n integer) is given, and between 0 and π, thenu = k, between π and π, then u = k π. In the second approximation, we set v = v 0 + ɛ, (0) 7
8 where v 0 is the value just obtained to first approximation. Then, cot ϕ = i sinh v 4ie χ+iψ = i [ cosh ( v cos u )] sinh v 0 cosh v0 sinh v 0 = i 1 + ɛ cosh v 0 cos u sinh v 0 cosh v 0 cos u [ ( )] 1 + cos u = i 1 + ɛ 1 cos u 1 = i(1 + ɛ cot u), ɛ = tan u e χ+iψ. Since ɛ is in general very small, we can replace χ by v 0. ψ is then determined by the given value of k: If k = λ π 1 + λ = λ is even, and smaller than, then we can put λ 1 = λ = 1 λ, ψ = 0. Similarly, for λ and + λ even, λ 1 = λ = 1 ( + λ), ψ = 0. If λ resp. + λ is odd, we must write Correspondingly, we have λ = λ 1 + 1, ψ = π. ɛ = ± tan u e v 0. (1) For even λ (resp. + λ, positive sign), therefore, v > v 0 ; hence, if in the next approximation v 0 is replaced by v then the resulting ɛ is smaller than that in the second approximation; the scheme for calculating v therefore certainly always converges, and even very rapidly. However, if the negative sign has to be taken (for odd λ or + λ), then v < v 0 and ɛ increases (in absolute value) in subsequent higher approximations. This does not of course make a difference as long as v 0 is finite (i.e. v 0 > 0 (ed.)), since ɛ is then only a tiny correction. But if u becomes small, and hence cos u 1, then v 0 also becomes small, and in fact we have, to reasonable accuracy, v 0 = log cos u = 1 cos u = 1 u. 8
9 ow, if u is small of order 1, then v 0 is finite, and ɛ = u e v 0 is larger in absolute value than v 0 when 1.4 v 0 < log 0.7, u < 1.4. For u < and odd λ, therefore, v 1 = v 0 + ɛ becomes negative, and the scheme diverges. As a result, there is no solution with two conjugate complex wave numbers 7. [In its place there appears an additional solution with two real wave numbers. Again, we consider k as given, so that f = k f 1. Previously, in the discussion about real solutions, we tacidly assumed that with increasing f 1, F = f 1 ϕ also increases monotonically. For, this is rather probable since f 1 is multiplied by such a large factor, and ϕ only by 1. evertheless, for small k, this increase does not happen. Indeed, we have, using (8), df = df 1 and if we put f 1 = f = k, then 1 1 sin f sin k f ( 1 cot f 1 1 cot k f 1 df = 1. df 1 sin f 1 This is obviously only positive as long as sin f 1 > 1. For k < 4 arcsin 1 4, the rise of F = f 1 ϕ as a function of f 1 is interrupted by a drop in the neighbourhood of f 1 = k k. If π k π = πλ 1 = π λ 1, ), = λ is odd, then where λ 1 is an integer, and for λ 1 = λ 1, λ = λ+1 there are two solutions of the equations (8) and (11): Apart from f 1 = f, ϕ = π, there is a solution f 1 < f, ϕ π, for which, in contradistinction from the former, the coefficients (9) remain finite. 7 If actual fact, this case already occurs for u < : although the second approximation for v is then still positive, the higher approximations push it into the negative. 9
10 To actually obtain this solution, we set f 1 = f ɛ, and replace sin f = f, cos f = 1 and cot f = 1 because of the small size of f. Then we have f cot ϕ = f ɛ f + ɛ = 8ɛ f, ϕ = π(λ λ 1 ) (f f 1 ) = π 4ɛ, (8a) (11a) cot ϕ = tan ɛ, tan ɛ ɛ = 4 f. () This determines ɛ, where ɛ < π, and also ϕ > 0 and f 1 > πλ 1.] We have now determined, for each value of λ, an additional solution with real or complex wave numbers. The highest allowed value for λ is clearly with λ 1 = λ = 1; for λ = 1 we would have λ = which is outside the range of values for λ 8 i. The coefficients a(m 1, m ) become, for our complex solutions, according to (9), (1) and (16a), ) a(m 1, m ) = e iu(m 1+m ) (e v(m 1 m + 1 ) ± e v(m m 1 1 ), a(m 1, m ) = e iu(m 1+m ) cosh sinh [ v ( 1 (m m 1 ) )]. (3) Here cosh resp. sinh applies depending on whether λ (resp. + λ for λ > /) is even or odd. It is thus for these solutions most probable that the two right-spins are close together, as the probability a(m 1, m ) decreases exponentially in the distance m m 1. The most extreme case occurs for the solution λ = 1, u = 1 π, v = : Here, upon appropriate normalisation, a(m 1, m ) = { 0 if m m 1 + 1, ( 1) m 1 if m = m 1 + 1, so the right-spins are always direct neighbours. Each eigenvalue ɛ with two complex conjugate wave numbers is, as we shall see shortly, smaller than all eigenvalues with the same wave number k and real wave numbers. By (), the corresponding energy to first order lies deeper than all solutions with real wave numbers in case the exchange 8 The solution λ 1 = 1, λ = has already been counted as λ = 0, λ 1 = 1. 10
11 integral J is positive (ferromagnetic case), but higher when J is negative (normal case). Indeed, for the complex solutions, and for real solutions ɛ k = sin u, (19) ɛ k = 1 cos f cos(k f 1 ). (5) (5) is minimal for { f 1 = 1 k, if 0 k π, f 1 = 1 k + π if π k π, so in general for f 1 = f = u. The minimum is so that ɛ min = (1 cos u), ɛ k = 1 (1 + cos u) 1, (4) ɛ min where the equality sign only applies if u = 0 9. But this was exactly our claim. 5. We now turn to the general case of r right-oriented spins. The equations (1) again split into different types: If among the r spins m 1,..., m r there are no neighbours, then r ɛ a(m 1,..., m r ) = [a(m 1,..., m i + 1,..., m r ) i=1 + a(m 1,..., m i 1,..., m r ) a(m 1,..., m i,..., m r )]. (4-a) If there are two neighbours, say m i+1 = m i + 1, then we have instead, ɛ a(m 1,..., m i,..., m k, m k + 1,..., m r ) = a(... m k 1, m k + 1,... ) + a(... m k m k +... ) a(... m k m k ) + [a(... m i ) + a(... m i 1... ) a(... m i... )] (4-b) i k,k+1 9 In fact f 1 can never be exactly equal to f (cf. 3), so in truth the <-sign always applies. 11
12 and analogously for the case of more neighbouring spins. We now make the Ansatz (hypothesis) [ r! r a(m 1... m r ) = exp i f P k m k + 1 i ] ϕ P k,p l, (5) P =1 k=1 k<l ɛ = r [1 cos f k ]. (6) k=1 P is some permutation of the numbers 1,,..., r and P k denotes the number that this permutation puts in place of k. This hypothesis clearly satisfies the first set of equations (4-a). The remaining equations will be satisfied by requiring that a(m 1,..., m k m k + 1,..., m r ) = a(... m k m k... ) + a(... m k + 1 m k ), (7) where the terms on the right-hand side are defined by (5). (7) must hold for arbitrary multiplets of values m 1,..., m r, where arbitrary many m i are neighbours provided only that m 1 < m < < m r. Thus all equations (4-b) and those in which the distributions m 1,..., m r have more than two neighbouring right-spins are satisfied simultaneously. Indeed, these equations are reduced (by the substitution (7)) to the type (4-a), which has already been solved. The equations (7) themselves are satisfied by determining the phases ϕ from cot ϕ kl = cot f k cot f l ; π ϕ kl +π. (8) That this is the case can be seen completely analogously to 3. It remains to consider the periodicity condition a(m 1, m,..., m r ) = a(m,..., m r, m 1 + ) [ r exp i f P k m k + 1 i ] ϕ P k,p l P k=1 k<l = [ ( r exp i f P (k 1)m k + f P r(m 1 + ) + )] ϕ P k,p l. P k<l k= This must hold for all m 1,..., m r ; therefore each pair of terms on the left and right, which depend on the m k in the same way, must be equal individually. 1
13 For example, the term P on the left and the term P on the right, where P is defined by P (k 1) = P k (k =,..., r), P r = P 1. This yields f P r + 1 ϕ P k,p l 1 ϕ P k,p l = πλ = f P = f P 1 k<l k<l ϕ P (k+1),p (l+1) + 1 r 1 k<l r 1 ϕ P k,p l 1 k<l r ϕ P 1,P k, k= r k= ϕ P 1,P k k=1 ϕ P (k+1),p 1 where we used the fact that ϕ kl = ϕ lk. Since this holds for all P it follows that f i = πλ i + ϕ ik (9) k for all i. Completely analogously to 3, one can also show that any two f i can never be equal, as otherwise all coefficients a vanish, and hence that for real f i two subsequent λ i must differ by at least two. The number of solutions with real f i thus becomes ( ) r + 1 and is therefore much smaller than the required number of solutions ( r ). 6. If f k = u k + i v k is a complex wave number then it follows from r f k = πλ k + l ϕ kl that at least one of the ϕ kl must have a very large imaginary part of the order. This implies in first approximation ( 4) cot 1 ϕ kl = cot 1 f k cot 1 f l = i. There must therefore be a f l such that the real part of cot 1 f l is the same as that of cot 1 f k, while their imaginary parts differ by i (up to a quantity of 13
14 order e ). This leads to the following solution, which we shall refer to as a wave complex: n wave numbers are determined by the identities cot 1 f κ = a i κ; κ = (n 1), (n 3),..., n 1, (30) where a is a constant which is the same for each of the n wave numbers. We then clearly have ϕ κ,κ± = ψ i, while the other ϕ κ,λ have a finite imaginary part. ψ remains undetermined. Using (15) we obtain the solutions of which are { u κ = arctan arctanh v κ = sin u κ cosh v κ cos u κ = a, sinh v κ cosh v κ cos u κ = κ, a a = arc cot arc cot, κ+1 κ 1, (31) a +κ +1 a a +κ 1 κ e v κ = (κ + 1) + a (κ 1) + a. (3) Here sin u always has the same sign as a. We now claim that a can be expressed in terms of the total wave number of the wave complex in the simple form k = n 1 κ= (n 1) f κ = κ u κ (33) a = n cot 1 k. (34) For n = 1 this is evident, and for n = it follows by substitution of the previously obtained solution (18) (cf. 4): a = sin u cosh v cos u = e v = cos u, u = 1 k resp. 1 k + π, sin u ( cos u) cos u = cot u = cot 1k. cos u 14
15 On the other hand, at constant a, the wave numbers u κ for a complex of n waves are the same as those for n waves; there are simply two additional wave numbers u n 1 = u (n 1), so that 1 k n = 1k n + u n 1 (33a) If we now assume that (34) has been proven for n, then we have 1 k n = arc cot = arc cot a n. a n + arc cot a a arc cot n n We also claim: The eigenvalue corresponding to our wave complex is ɛ n = 1 (1 cos k). (35) n Again, this is obvious for n = 1, while it was proved in (19) for n =. In general, we have ɛ n = n 1 κ= (n 1) [1 cos(u κ + i v κ )] = ɛ n + cos(u n 1 + i v n 1 ) cos(u n 1 i v n 1 ) = ɛ n + (1 cos u n 1 cosh v n 1 ) ( ) = ɛ n + 1 [a + (n 1) 1][a + (n 1) + 1] [a + (n 1) + 1] 4(n 1) a n(n ) = ɛ n + 4 (a + n )(a + (n ) ), where we have used (31) and (3). If we now assume that (35) is valid for n, then we get, with the help of (34), 1 ɛ n = 1 a ( ) n(n ) + (n ) 1 + a (a + n )(a + (n ) ) (n ) = (n )(a + n ) + (a n(n )) (a + n )(a + (n ) ) n = a + n = 1 (1 cos k). n Finally, we want to prove, analogously to 4: Given the number of rightoriented spins r and the total wave number k of all spin waves, the smallest 15
16 eigenvalue ɛ is obtained when all r spin waves are combined in a single wave complex. The eigenvalue is then given by ɛ r = 1 (1 cos k). r If, instead, there are two wave complexes with n and p = r n wave resp., then ɛ p+n = 1 n (1 cos k 1) + 1 p (1 cos(k k 1)). The minimum of this expression is attained when It is ow, 1 n sin k 1 = 1 p = sin(k k 1), sin k 1 = n sin k n + np cos k + p. ɛ min = n + P n + p + np cos k. n p (n + p) n + p + np cos k < (n + p) np(1 cos k), as can be verified easily by squaring. This implies immediately that ɛ r < ɛ min. (36) If the spin waves constitute more than two wave complexes then ɛ lies even higher of course. The state of lowest energy in case of r right-spins is therefore, when J > 0 (ferromagnetic case): a single wave complex of r spins; when J < 0 (normal case): r separate waves with real wave numbers. Of course, in the latter case, this does not fully determine the lowest energy solution. It is easy to compute the second approximation for the wave numbers of a wave complex, where the u and v in the formulas (31) and (3) are slightly modified to satisfy the true periodicity condition (9). The calculation proceeds in an analogous fashion to 4, and one finds, in general, that for finite k, there is always a solution in the immediate neighbourhood 1 of (31) and (3), whereas for small k of the order, the solution changes its character when k is not divisible by n. Instead of a complex of three π spin waves one then finds, for example, a pair of complex conjugate waves as described in 4 (with even λ), together with a single wave with a real wavenumber in a very close neighbourhood. The total number of solutions is not affected by this transformation in appearance: There is precisely one 16
17 solution for each λ = 0, 1,,..., n; the latter value corresponding to λ (n 1) = λ (n 3) = = λ n 1 = 1. For higher values of λ, one or more λ κ are equal to, which is not allowed. From now on, however, we want to also exclude λ i = 0 in general. First of all, we gain in symmetry as a result. Moreover, this automatically separates the solutions for which the total spin equals m = 1 r from those in which only the left-oriented component of the spin has this value, while the total spin itself has a higher value. The latter states, namely, are given precisely by those solutions for which one or more among the r wave numbers equals zero. Thus there remain only n + 1 solutions with a wave complex of n spin waves: λ = n, n + 1,..., n. 7. We now assume that there are two wave complexes with n and p(> n) spin waves respectively, and investigate what number of solutions can be obtained this way. For this, we need to discuss the phases ϕ. Let the wavenumbers of the first complex be given by cot 1f κ = a i κ, κ = (n 1), (n 3),..., n 1 a = n cot 1k 1, k 1 = f κ, κ (37-a) and the second by cot 1 f µ = b i µ, µ = (p 1), (p 3),..., p 1 b = p cot 1 k, k = µ f µ. (37-b) Then we have, by (8), (9) and (31), k 1 = πλ 1 + κ k = πλ κ ϕ κ,µ, µ ϕ κ,µ, µ cot ϕ κ,µ = cot(ψ κ,µ + i χ κ,µ ) = 1 (a b) 1 i(κ µ), tan ψ κ,µ = a b 1 4 b) + 1(κ 4 µ) 1. (38) µ χ κ,µ = 0 since the f κ and f µ are arranged in Sign of ψ κ,µ = sign of a b, κ complex-conjugate pairs. The ψ κ,µ are zero when k 1 is very small, a large, and they become positive with increasing k 1 as long as a > b. We are particularly interested in its value when a approaches b and eventually becomes smaller 17
18 than b, so that we can determine how many values the integers λ 1, λ cannot have. To this end, we keep λ 0 = k π fixed10 and define λ by n cot πλ > p cot πλ 0 > n cot π(λ + 1). (39) For k 1 = πλ, a b is then clearly still positive, and small of order 1/. Hence tan ψ κ,µ is small and positive when κ µ >, small and negative when κ µ <, and very large and positive when κ µ. The latter follows from the fact that κ and µ only differ from integers by amount of order e 1/ (cf. 4), so that 1(κ 4 µ) 1 (a b) whenever κ µ is close to. We conclude that, up to quantities of order 1/, 0 for κ µ >, ψ κ,µ = π for κ µ <, (40) 1 π for κ µ =. If we first assume that p n is odd, then, for a given κ, there are exactly two values µ = κ + 1 and µ = κ 1, for which ψ κ,µ does not vanish, but has the value π. Hence, in this case ψ κ,µ = πn. (41) κ µ On the other hand, if p n is even, then, for each κ there exist three µ for which ψ κ,µ 0: µ = κ, ψ κ,µ = π, µ = κ +, ψ κ,µ = 1 π, µ = κ, ψ κ,µ = 1 π. In total, we have again Thus we have ψ κ,µ = πn. κ µ λ 1 = k 1 π n = λ n, λ = λ 0 + n. (4-a) 10 We shall see in the following that for a b, k 1 and k are indeed of the form π times an integer, so that λ 0 = an integer. 18
19 Similarly, for k 1 = π(λ + 1), ψ κ,µ = πn, κ µ λ 1 = λ n, λ = λ n. (4-b) The possible values for λ 1 are therefore λ 1 = n, n + 1,... λ n, λ + n + 1,..., n. (4-c) The n values λ n + 1,..., λ + n are forbidden due to the presence of the other spin complex. In the same way one can see that if λ 0 is small then, in general, b > a and hence λ = λ 0 n. But λ must be at least p (see the end of the previous section), so λ 0 > p + n. Similarly, λ 0 p n, and it follows that λ 0 can take exactly n p + 1 values. Once again, this is n values fewer than if the other complex were not present. Here it is important that in both cases it is the number n of waves in the smaller of the two complexes which appears. The total number of solutions is therefore ( n p + 1)( 4n + 1). It remains to consider the case n = p. In this case, for κ = n 1, one of the partners µ = κ + is absent, which yielded a contribution ψ κ,µ = 1π previously, and similarly, for κ = (n 1), the partner µ = κ is absent. In this case, therefore, ψ κ,µ = (n 1)π. (43) κ µ Moreover, there is now just one λ such that n cot πλ = p cot πλ 0, namely λ = λ 0. This does not lead to a solution, however, since f κ = f µ whenever κ = µ, and we know that the eigenfunction vanishes when two wave numbers are equal. At most, therefore, k 1 = π(λ 0 1), and that yields λ 1 = λ 0 1 n, λ = λ n. 19
20 Similarly, for k 1 = π(λ 0 + 1), ψ κ,µ = (n 1)π, κ µ λ 1 = λ n, λ = λ n. λ 0 is in this case clearly a half-integer number. In the collection of values for λ 1, n numbers are again missing: λ 0 n + 1,..., λ 0 + n 1, but in the collection of possible values for λ 0 only n 1: λ 0 must be at least n 1 (λ = n), and can be at most n+ 1 (λ = n), i.e. 4n+ values instead of the n + 1 possible values if there were only a single complex with n waves. Interchanging λ 1 and λ does not change the solution, so the total number of solutions is 1 ( 4n + )( 4n + 1). [The behaviour becomes perhaps even clearer if, for the moment, we normalise ψ differently: Let ψ be defined in such a way that it agrees with ψ for large a, but remains continuous at a = b. Then, in the case of two complexes with n waves, κ µ ψ κ,µ increases from zero to (n 1)π when k 1 increases from πn to π( n) at constant k. ow, if πλ 1 = k 1 ψ κ,µ κ µ then λ 1 obviously takes all values n to 3n + 1, i.e. 4n + values, whatever the value of λ. For λ, on the contrary, one more value has to be excluded, namely that which would lead to k 1 = k.] We now consider the general case, in which there are q n complexes, each with n waves, i.e. q 1 single waves with real wave numbers, q pairs with conjugate complex wave numbers, etc. The constant λ 1 of the first complex with n waves would have the possible values n, n + 1,..., n, a total of n+1 possible values, namely when no other wave complex were present. But, for every complex with p > n waves, this collection of values is reduced, as we have seen, by n numbers, and for each complex with p > n waves by p, and finally, for the q n 1 complexes with n waves, by n 1. There remain Q n = n + 1 p<n p q p p>n n q p (n 1)(q n 1) 0
21 possible values for λ 1. The constant λ of the second complex of n waves, must in addition avoid k being equal to k 1 and hence has one possibility less. For the last of the complexes of n waves, λ qn can take just values, where Q n (q n 1) = Q n + 1 Q n (, q 1, q,... ) = p<n p q p p n n q p. (44) We finally have to take into account that interchanging λ s for different wave complexes with equal numbers n of waves does not lead to a new solution. The total number of solutions therefore becomes z(, q 1, q,... ) = n=1 (Q n + q n )... (Q n + 1) q n! = n ( Qn + q n q n ). (45) 8. We shall now prove that we have found the right number of solutions. It is well-know that the number z(r) of eigenvalues with given total spin s = 1 r is equal to the number of eigenvalues with total spin-component of left-oriented spins m = s minus those with m = s + 1, i.e. ( ) ( ) z(, r) = = r + 1 ( ). (46) r r 1 r + 1 r We must therefore have q 1,q,... z(, q 1, q,... ) = z(, r), (47) where the sum on the right-hand side runs over all values q 1, q,... for which the total number of spin waves equals r, i.e. q 1 + q + 3q 3 + = n q n = r. In other words, we have to sum over all partitions of the number r; q n indicates how often the summand n occurs in the partition. We introduce the total number of spin complexes: q = n q n (48) 1
22 and rewrite (44): Q n (, q 1, q,... ) = q (p 1)q p 1)q p p<n p n(n = Q n 1 ( q, q, q 3,... ). (49) In particular, Q 1 (, q 1, q,... ) = q. (49a) Hence, using (45), ( ) q + q1 z(, q 1, q,... ) = z( q, q, q 3,... ). (50) q 1 In the right-hand side is, apart from the binomial coefficient, the number of solutions with q single-spin waves, and in general q n complexes of n 1 waves, in a chain of q atoms. These solutions obviously contain a total r = n q n (n 1) = r q (50-a) of right-spins, arranged in q = q n = q q 1 n= (50-b) wave complexes. We now also introduce a notation for the number of solutions in which r right-spins are organised in q wave complexes, irrespective of how many waves each complex contains: z(, r, q) = z(, q 1, q,... ). (51) q 1 +q +q 3 + =q q 1 +q +3q 3 + =r Then we have, from (50), (50a) and (50b), z(, r, q) = q 1 q 1 =0 ( q + q1 q 1 ) z( q, r q, q q 1 ), (5) and z(, r) = r z(, r, q). (53) q=1
23 From this point, we treat the problem using mathematical induction. We make the conjecture z(, r, q) = r + 1 ( )( ) r + 1 r 1. (54) r + 1 q q 1 For q = 1 this is certainly correct: We then have a single complex of r waves, whose wave number can take r + 1 values. It is also correct for q = r: then q 1 = r and q n = 0 for n > 1, and (54) is the same as (45). We now assume that (54) has been proven for q, r q, q q 1, and have, according to (5), so ow, z(, r, q) = z(, r, q) = q 1 q 1 =0 ( ) q + q1 = = = = = q 1 q 1 q 1 q 1 =0 s=0 ( )( ) q + q1 r q + 1 q 1 q q 1 ( ) r q 1 r + 1 q q 1 1 r + 1. q 1 s=0 ( )( ) r 1 q + q1 + 1 r, s q 1 s ( r q + 1)! ( r q + q 1 + 1)! (q q 1 )!( r q + q 1 + 1)! (q 1 s)!( r q + s + 1)! r + 1 ( )( ) r 1 r q 1 r + 1 s q q 1 1 q 1 r + 1 ( )( ) r 1 r q + 1 r q + 1 s q s s=0 q 1 ( )( ) q s r q 1 q 1 s q q 1 1 q = s r + 1 (r 1)! (r s 1)! r q + 1 s!(r s 1)! (q s 1)!(r q)! s ( ) r q + 1 q s ( ) r + 1 r 1 ( )( ) q 1 r q + 1 r q + 1 q 1 s q s s ( )( ) r + 1 r 1 r, r q + 1 q 1 q 3
24 which is identical to (54). Since (54) holds for q = 1 and for q =, r =, and trivially also for q =, r = 1, its validity can also be proved for q =, r = 3 or 4, then for q = and larger values of r, finally for q = 3, 4, etc. Inserting (54) into (53) gives z(, r) = r + 1 r + 1 = r + 1 r + 1 r ( r + 1 q=1 ( r ), q )( r 1 r q which corresponds with the required number of solutions (46). Our method therefore yields all solutions of the problem. In future work this method will be extended to spatial lattices, and the physical consequences vis-a-vis cohesion, ferromagnetism and conductivity will be derived. Acknowledgement. I thank Prof. Fermi very much for the many lively discussions. I also thank the Rockefeller Foundation for providing a stipendium, which enabled my visit to Rome. Rome, 13 June ) 4
The Quantum Heisenberg Ferromagnet
 The Quantum Heisenberg Ferromagnet Soon after Schrödinger discovered the wave equation of quantum mechanics, Heisenberg and Dirac developed the first successful quantum theory of ferromagnetism W. Heisenberg,
The Quantum Heisenberg Ferromagnet Soon after Schrödinger discovered the wave equation of quantum mechanics, Heisenberg and Dirac developed the first successful quantum theory of ferromagnetism W. Heisenberg,
ON ISING'S MODEL OF FERROMAGNETISM
 477 ON ISING'S MODEL OF FERROMAGNETISM BY MR R. PEIERLS [Communicated by M. BORN] [Received 16 May, read 26 October 1936] Ising* discussed the following model of a ferromagnetic body: Assume N elementary
477 ON ISING'S MODEL OF FERROMAGNETISM BY MR R. PEIERLS [Communicated by M. BORN] [Received 16 May, read 26 October 1936] Ising* discussed the following model of a ferromagnetic body: Assume N elementary
Electrons in a periodic potential
 Chapter 3 Electrons in a periodic potential 3.1 Bloch s theorem. We consider in this chapter electrons under the influence of a static, periodic potential V (x), i.e. such that it fulfills V (x) = V (x
Chapter 3 Electrons in a periodic potential 3.1 Bloch s theorem. We consider in this chapter electrons under the influence of a static, periodic potential V (x), i.e. such that it fulfills V (x) = V (x
Chapter 2 Ensemble Theory in Statistical Physics: Free Energy Potential
 Chapter Ensemble Theory in Statistical Physics: Free Energy Potential Abstract In this chapter, we discuss the basic formalism of statistical physics Also, we consider in detail the concept of the free
Chapter Ensemble Theory in Statistical Physics: Free Energy Potential Abstract In this chapter, we discuss the basic formalism of statistical physics Also, we consider in detail the concept of the free
Physics 221A Fall 1996 Notes 16 Bloch s Theorem and Band Structure in One Dimension
 Physics 221A Fall 1996 Notes 16 Bloch s Theorem and Band Structure in One Dimension In these notes we examine Bloch s theorem and band structure in problems with periodic potentials, as a part of our survey
Physics 221A Fall 1996 Notes 16 Bloch s Theorem and Band Structure in One Dimension In these notes we examine Bloch s theorem and band structure in problems with periodic potentials, as a part of our survey
Section 10: Many Particle Quantum Mechanics Solutions
 Physics 143a: Quantum Mechanics I Section 10: Many Particle Quantum Mechanics Solutions Spring 015, Harvard Here is a summary of the most important points from this week (with a few of my own tidbits),
Physics 143a: Quantum Mechanics I Section 10: Many Particle Quantum Mechanics Solutions Spring 015, Harvard Here is a summary of the most important points from this week (with a few of my own tidbits),
Consequently, the exact eigenfunctions of the Hamiltonian are also eigenfunctions of the two spin operators
 VI. SPIN-ADAPTED CONFIGURATIONS A. Preliminary Considerations We have described the spin of a single electron by the two spin functions α(ω) α and β(ω) β. In this Sect. we will discuss spin in more detail
VI. SPIN-ADAPTED CONFIGURATIONS A. Preliminary Considerations We have described the spin of a single electron by the two spin functions α(ω) α and β(ω) β. In this Sect. we will discuss spin in more detail
CHMY 564 Homework #3 2Feb17 Due Friday, 10Feb17
 564-17 Lec 11 Mon 6feb17 CHMY 564 Homework #3 2Feb17 Due Friday, 10Feb17 1. (a) Find the eigenfunctions and eigenvalues of the x component of linear momentum. (b) Why can a momentum eigenfunction never
564-17 Lec 11 Mon 6feb17 CHMY 564 Homework #3 2Feb17 Due Friday, 10Feb17 1. (a) Find the eigenfunctions and eigenvalues of the x component of linear momentum. (b) Why can a momentum eigenfunction never
2.3 Band structure and lattice symmetries: example of diamond
 2.2.9 Product of representaitons Besides the sums of representations, one can also define their products. Consider two groups G and H and their direct product G H. If we have two representations D 1 and
2.2.9 Product of representaitons Besides the sums of representations, one can also define their products. Consider two groups G and H and their direct product G H. If we have two representations D 1 and
LECTURE 3. RATIONAL NUMBERS: AN EXAMPLE OF MATHEMATICAL CONSTRUCT
 ANALYSIS FOR HIGH SCHOOL TEACHERS LECTURE 3. RATIONAL NUMBERS: AN EXAMPLE OF MATHEMATICAL CONSTRUCT ROTHSCHILD CAESARIA COURSE, 2011/2 1. Rational numbers: how to define them? Rational numbers were discovered
ANALYSIS FOR HIGH SCHOOL TEACHERS LECTURE 3. RATIONAL NUMBERS: AN EXAMPLE OF MATHEMATICAL CONSTRUCT ROTHSCHILD CAESARIA COURSE, 2011/2 1. Rational numbers: how to define them? Rational numbers were discovered
v(r i r j ) = h(r i )+ 1 N
 Chapter 1 Hartree-Fock Theory 1.1 Formalism For N electrons in an external potential V ext (r), the many-electron Hamiltonian can be written as follows: N H = [ p i i=1 m +V ext(r i )]+ 1 N N v(r i r j
Chapter 1 Hartree-Fock Theory 1.1 Formalism For N electrons in an external potential V ext (r), the many-electron Hamiltonian can be written as follows: N H = [ p i i=1 m +V ext(r i )]+ 1 N N v(r i r j
I. CSFs Are Used to Express the Full N-Electron Wavefunction
 Chapter 11 One Must be Able to Evaluate the Matrix Elements Among Properly Symmetry Adapted N- Electron Configuration Functions for Any Operator, the Electronic Hamiltonian in Particular. The Slater-Condon
Chapter 11 One Must be Able to Evaluate the Matrix Elements Among Properly Symmetry Adapted N- Electron Configuration Functions for Any Operator, the Electronic Hamiltonian in Particular. The Slater-Condon
The 3 dimensional Schrödinger Equation
 Chapter 6 The 3 dimensional Schrödinger Equation 6.1 Angular Momentum To study how angular momentum is represented in quantum mechanics we start by reviewing the classical vector of orbital angular momentum
Chapter 6 The 3 dimensional Schrödinger Equation 6.1 Angular Momentum To study how angular momentum is represented in quantum mechanics we start by reviewing the classical vector of orbital angular momentum
DIFFERENCE EQUATIONS
 Chapter 3 DIFFERENCE EQUATIONS 3.1 Introduction Differential equations are applicable for continuous systems and cannot be used for discrete variables. Difference equations are the discrete equivalent
Chapter 3 DIFFERENCE EQUATIONS 3.1 Introduction Differential equations are applicable for continuous systems and cannot be used for discrete variables. Difference equations are the discrete equivalent
The Gutzwiller Density Functional Theory
 The Gutzwiller Density Functional Theory Jörg Bünemann, BTU Cottbus I) Introduction 1. Model for an H 2 -molecule 2. Transition metals and their compounds II) Gutzwiller variational theory 1. Gutzwiller
The Gutzwiller Density Functional Theory Jörg Bünemann, BTU Cottbus I) Introduction 1. Model for an H 2 -molecule 2. Transition metals and their compounds II) Gutzwiller variational theory 1. Gutzwiller
PRINCIPLE OF MATHEMATICAL INDUCTION
 Chapter 4 PRINCIPLE OF MATHEMATICAL INDUCTION Analysis and natural philosopy owe their most important discoveries to this fruitful means, which is called induction Newton was indebted to it for his theorem
Chapter 4 PRINCIPLE OF MATHEMATICAL INDUCTION Analysis and natural philosopy owe their most important discoveries to this fruitful means, which is called induction Newton was indebted to it for his theorem
Origin of the first Hund rule in He-like atoms and 2-electron quantum dots
 in He-like atoms and 2-electron quantum dots T Sako 1, A Ichimura 2, J Paldus 3 and GHF Diercksen 4 1 Nihon University, College of Science and Technology, Funabashi, JAPAN 2 Institute of Space and Astronautical
in He-like atoms and 2-electron quantum dots T Sako 1, A Ichimura 2, J Paldus 3 and GHF Diercksen 4 1 Nihon University, College of Science and Technology, Funabashi, JAPAN 2 Institute of Space and Astronautical
Brief review of Quantum Mechanics (QM)
 Brief review of Quantum Mechanics (QM) Note: This is a collection of several formulae and facts that we will use throughout the course. It is by no means a complete discussion of QM, nor will I attempt
Brief review of Quantum Mechanics (QM) Note: This is a collection of several formulae and facts that we will use throughout the course. It is by no means a complete discussion of QM, nor will I attempt
0 belonging to the unperturbed Hamiltonian H 0 are known
 Time Independent Perturbation Theory D Perturbation theory is used in two qualitatively different contexts in quantum chemistry. It allows one to estimate (because perturbation theory is usually employed
Time Independent Perturbation Theory D Perturbation theory is used in two qualitatively different contexts in quantum chemistry. It allows one to estimate (because perturbation theory is usually employed
Lecture 5. Hartree-Fock Theory. WS2010/11: Introduction to Nuclear and Particle Physics
 Lecture 5 Hartree-Fock Theory WS2010/11: Introduction to Nuclear and Particle Physics Particle-number representation: General formalism The simplest starting point for a many-body state is a system of
Lecture 5 Hartree-Fock Theory WS2010/11: Introduction to Nuclear and Particle Physics Particle-number representation: General formalism The simplest starting point for a many-body state is a system of
PHYSICS 220 : GROUP THEORY FINAL EXAMINATION SOLUTIONS
 PHYSICS 0 : GROUP THEORY FINAL EXAMINATION SOLUTIONS This exam is due in my office, 5438 Mayer Hall, at 9 am, Monday, June 6. You are allowed to use the course lecture notes, the Lax text, and the character
PHYSICS 0 : GROUP THEORY FINAL EXAMINATION SOLUTIONS This exam is due in my office, 5438 Mayer Hall, at 9 am, Monday, June 6. You are allowed to use the course lecture notes, the Lax text, and the character
Magnets, 1D quantum system, and quantum Phase transitions
 134 Phys620.nb 10 Magnets, 1D quantum system, and quantum Phase transitions In 1D, fermions can be mapped into bosons, and vice versa. 10.1. magnetization and frustrated magnets (in any dimensions) Consider
134 Phys620.nb 10 Magnets, 1D quantum system, and quantum Phase transitions In 1D, fermions can be mapped into bosons, and vice versa. 10.1. magnetization and frustrated magnets (in any dimensions) Consider
The Hubbard model for the hydrogen molecule
 INSTITUTE OF PHYSICS PUBLISHING Eur. J. Phys. 3 (00) 11 16 EUROPEAN JOURNAL OF PHYSICS PII:S0143-0807(0)351-6 The Hubbard model for the hydrogen molecule B Alvarez-Fernández and J A Blanco Dpto. de Física,
INSTITUTE OF PHYSICS PUBLISHING Eur. J. Phys. 3 (00) 11 16 EUROPEAN JOURNAL OF PHYSICS PII:S0143-0807(0)351-6 The Hubbard model for the hydrogen molecule B Alvarez-Fernández and J A Blanco Dpto. de Física,
Answers Quantum Chemistry NWI-MOL406 G. C. Groenenboom and G. A. de Wijs, HG00.307, 8:30-11:30, 21 jan 2014
 Answers Quantum Chemistry NWI-MOL406 G. C. Groenenboom and G. A. de Wijs, HG00.307, 8:30-11:30, 21 jan 2014 Question 1: Basis sets Consider the split valence SV3-21G one electron basis set for formaldehyde
Answers Quantum Chemistry NWI-MOL406 G. C. Groenenboom and G. A. de Wijs, HG00.307, 8:30-11:30, 21 jan 2014 Question 1: Basis sets Consider the split valence SV3-21G one electron basis set for formaldehyde
d 1 µ 2 Θ = 0. (4.1) consider first the case of m = 0 where there is no azimuthal dependence on the angle φ.
 4 Legendre Functions In order to investigate the solutions of Legendre s differential equation d ( µ ) dθ ] ] + l(l + ) m dµ dµ µ Θ = 0. (4.) consider first the case of m = 0 where there is no azimuthal
4 Legendre Functions In order to investigate the solutions of Legendre s differential equation d ( µ ) dθ ] ] + l(l + ) m dµ dµ µ Θ = 0. (4.) consider first the case of m = 0 where there is no azimuthal
Chem 3502/4502 Physical Chemistry II (Quantum Mechanics) 3 Credits Spring Semester 2006 Christopher J. Cramer. Lecture 22, March 20, 2006
 Chem 350/450 Physical Chemistry II Quantum Mechanics 3 Credits Spring Semester 006 Christopher J. Cramer Lecture, March 0, 006 Some material in this lecture has been adapted from Cramer, C. J. Essentials
Chem 350/450 Physical Chemistry II Quantum Mechanics 3 Credits Spring Semester 006 Christopher J. Cramer Lecture, March 0, 006 Some material in this lecture has been adapted from Cramer, C. J. Essentials
Løsningsforslag Eksamen 18. desember 2003 TFY4250 Atom- og molekylfysikk og FY2045 Innføring i kvantemekanikk
 Eksamen TFY450 18. desember 003 - løsningsforslag 1 Oppgave 1 Løsningsforslag Eksamen 18. desember 003 TFY450 Atom- og molekylfysikk og FY045 Innføring i kvantemekanikk a. With Ĥ = ˆK + V = h + V (x),
Eksamen TFY450 18. desember 003 - løsningsforslag 1 Oppgave 1 Løsningsforslag Eksamen 18. desember 003 TFY450 Atom- og molekylfysikk og FY045 Innføring i kvantemekanikk a. With Ĥ = ˆK + V = h + V (x),
Lecture 4: Basic elements of band theory
 Phys 769 Selected Topics in Condensed Matter Physics Summer 010 Lecture 4: Basic elements of band theory Lecturer: Anthony J. Leggett TA: Bill Coish 1 Introduction Most matter, in particular most insulating
Phys 769 Selected Topics in Condensed Matter Physics Summer 010 Lecture 4: Basic elements of band theory Lecturer: Anthony J. Leggett TA: Bill Coish 1 Introduction Most matter, in particular most insulating
Basis 4 ] = Integration of s(t) has been performed numerically by an adaptive quadrature algorithm. Discretization in the ɛ space
![Basis 4 ] = Integration of s(t) has been performed numerically by an adaptive quadrature algorithm. Discretization in the ɛ space Basis 4 ] = Integration of s(t) has been performed numerically by an adaptive quadrature algorithm. Discretization in the ɛ space](/thumbs/92/110829637.jpg) 1 [NPHYS-007-06-00643] SUPPLEMENTARY MATERIAL for Spinons and triplons in spatially anisotropic frustrated antiferromagnets by Masanori Kohno, Oleg A. Starykh, and Leon Balents Basis The two-spinon states
1 [NPHYS-007-06-00643] SUPPLEMENTARY MATERIAL for Spinons and triplons in spatially anisotropic frustrated antiferromagnets by Masanori Kohno, Oleg A. Starykh, and Leon Balents Basis The two-spinon states
conventions and notation
 Ph95a lecture notes, //0 The Bloch Equations A quick review of spin- conventions and notation The quantum state of a spin- particle is represented by a vector in a two-dimensional complex Hilbert space
Ph95a lecture notes, //0 The Bloch Equations A quick review of spin- conventions and notation The quantum state of a spin- particle is represented by a vector in a two-dimensional complex Hilbert space
Electronic structure of correlated electron systems. Lecture 2
 Electronic structure of correlated electron systems Lecture 2 Band Structure approach vs atomic Band structure Delocalized Bloch states Fill up states with electrons starting from the lowest energy No
Electronic structure of correlated electron systems Lecture 2 Band Structure approach vs atomic Band structure Delocalized Bloch states Fill up states with electrons starting from the lowest energy No
26 Group Theory Basics
 26 Group Theory Basics 1. Reference: Group Theory and Quantum Mechanics by Michael Tinkham. 2. We said earlier that we will go looking for the set of operators that commute with the molecular Hamiltonian.
26 Group Theory Basics 1. Reference: Group Theory and Quantum Mechanics by Michael Tinkham. 2. We said earlier that we will go looking for the set of operators that commute with the molecular Hamiltonian.
How the Result of a Measurement of a Component of the Spin of a Spin- 1 2 Particle Can Turn Out to be 100
 How the Result of a Measurement of a Component of the Spin of a Spin- 1 2 Particle Can Turn Out to be 100 Aharonov, Albert and Vaidman April 4, 1988 PRL Abstract We have found that the usual measuring
How the Result of a Measurement of a Component of the Spin of a Spin- 1 2 Particle Can Turn Out to be 100 Aharonov, Albert and Vaidman April 4, 1988 PRL Abstract We have found that the usual measuring
2. The Schrödinger equation for one-particle problems. 5. Atoms and the periodic table of chemical elements
 1 Historical introduction The Schrödinger equation for one-particle problems 3 Mathematical tools for quantum chemistry 4 The postulates of quantum mechanics 5 Atoms and the periodic table of chemical
1 Historical introduction The Schrödinger equation for one-particle problems 3 Mathematical tools for quantum chemistry 4 The postulates of quantum mechanics 5 Atoms and the periodic table of chemical
Renormalization Group analysis of 2D Ising model
 Renormalization Group analysis of D Ising model Amir Bar January 7, 013 1 Introduction In this tutorial we will see explicitly how RG can be used to probe the phase diagram of d > 1 systems, focusing as
Renormalization Group analysis of D Ising model Amir Bar January 7, 013 1 Introduction In this tutorial we will see explicitly how RG can be used to probe the phase diagram of d > 1 systems, focusing as
On the Interaction of Elementary Particles
 H. Yukawa, PTP, 17, 48 1935 On the Interaction of Elementary Particles H. Yukawa (Received 1935) At the present stage of the quantum theory little is known about the nature of interaction of elementary
H. Yukawa, PTP, 17, 48 1935 On the Interaction of Elementary Particles H. Yukawa (Received 1935) At the present stage of the quantum theory little is known about the nature of interaction of elementary
Kern- und Teilchenphysik I Lecture 13:Quarks and QCD
 Kern- und Teilchenphysik I Lecture 13:Quarks and QCD (adapted from the Handout of Prof. Mark Thomson) Prof. Nico Serra Dr. Patrick Owen, Dr. Silva Coutinho http://www.physik.uzh.ch/de/lehre/phy211/hs2016.html
Kern- und Teilchenphysik I Lecture 13:Quarks and QCD (adapted from the Handout of Prof. Mark Thomson) Prof. Nico Serra Dr. Patrick Owen, Dr. Silva Coutinho http://www.physik.uzh.ch/de/lehre/phy211/hs2016.html
H 2 in the minimal basis
 H 2 in the minimal basis Alston J. Misquitta Centre for Condensed Matter and Materials Physics Queen Mary, University of London January 27, 2016 Overview H 2 : The 1-electron basis. The two-electron basis
H 2 in the minimal basis Alston J. Misquitta Centre for Condensed Matter and Materials Physics Queen Mary, University of London January 27, 2016 Overview H 2 : The 1-electron basis. The two-electron basis
Static Fields as Mass-Currents and Mercury's Perihelion Shift
 Static Fields as Mass-Currents and Mercury's Perihelion Shift by Paul R. Gerber Gerber Molecular Design, Forten 649, CH-8873 Amden Email: Paul.Gerber@moloc.ch 03.65.Pm 95.30.Sf 04.60.-m 98.80.Jk Relativistic
Static Fields as Mass-Currents and Mercury's Perihelion Shift by Paul R. Gerber Gerber Molecular Design, Forten 649, CH-8873 Amden Email: Paul.Gerber@moloc.ch 03.65.Pm 95.30.Sf 04.60.-m 98.80.Jk Relativistic
Chapter 11 - Sequences and Series
 Calculus and Analytic Geometry II Chapter - Sequences and Series. Sequences Definition. A sequence is a list of numbers written in a definite order, We call a n the general term of the sequence. {a, a
Calculus and Analytic Geometry II Chapter - Sequences and Series. Sequences Definition. A sequence is a list of numbers written in a definite order, We call a n the general term of the sequence. {a, a
Electrons in a weak periodic potential
 Electrons in a weak periodic potential Assumptions: 1. Static defect-free lattice perfectly periodic potential. 2. Weak potential perturbative effect on the free electron states. Perfect periodicity of
Electrons in a weak periodic potential Assumptions: 1. Static defect-free lattice perfectly periodic potential. 2. Weak potential perturbative effect on the free electron states. Perfect periodicity of
Page 404. Lecture 22: Simple Harmonic Oscillator: Energy Basis Date Given: 2008/11/19 Date Revised: 2008/11/19
 Page 404 Lecture : Simple Harmonic Oscillator: Energy Basis Date Given: 008/11/19 Date Revised: 008/11/19 Coordinate Basis Section 6. The One-Dimensional Simple Harmonic Oscillator: Coordinate Basis Page
Page 404 Lecture : Simple Harmonic Oscillator: Energy Basis Date Given: 008/11/19 Date Revised: 008/11/19 Coordinate Basis Section 6. The One-Dimensional Simple Harmonic Oscillator: Coordinate Basis Page
Discrete Applied Mathematics
 Discrete Applied Mathematics 194 (015) 37 59 Contents lists available at ScienceDirect Discrete Applied Mathematics journal homepage: wwwelseviercom/locate/dam Loopy, Hankel, and combinatorially skew-hankel
Discrete Applied Mathematics 194 (015) 37 59 Contents lists available at ScienceDirect Discrete Applied Mathematics journal homepage: wwwelseviercom/locate/dam Loopy, Hankel, and combinatorially skew-hankel
Checking Consistency. Chapter Introduction Support of a Consistent Family
 Chapter 11 Checking Consistency 11.1 Introduction The conditions which define a consistent family of histories were stated in Ch. 10. The sample space must consist of a collection of mutually orthogonal
Chapter 11 Checking Consistency 11.1 Introduction The conditions which define a consistent family of histories were stated in Ch. 10. The sample space must consist of a collection of mutually orthogonal
(1.1) In particular, ψ( q 1, m 1 ; ; q N, m N ) 2 is the probability to find the first particle
 Chapter 1 Identical particles 1.1 Distinguishable particles The Hilbert space of N has to be a subspace H = N n=1h n. Observables Ân of the n-th particle are self-adjoint operators of the form 1 1 1 1
Chapter 1 Identical particles 1.1 Distinguishable particles The Hilbert space of N has to be a subspace H = N n=1h n. Observables Ân of the n-th particle are self-adjoint operators of the form 1 1 1 1
Ground state and low excitations of an integrable. Institut fur Physik, Humboldt-Universitat, Theorie der Elementarteilchen
 Ground state and low excitations of an integrable chain with alternating spins St Meinerz and B - D Dorfelx Institut fur Physik, Humboldt-Universitat, Theorie der Elementarteilchen Invalidenstrae 110,
Ground state and low excitations of an integrable chain with alternating spins St Meinerz and B - D Dorfelx Institut fur Physik, Humboldt-Universitat, Theorie der Elementarteilchen Invalidenstrae 110,
Non-Fixed Point Renormalization Group Flow
 Non-Fixed Point Renormalization Group Flow Gilberto de la Peña May 9, 2013 Abstract: The renormalization group flow of most systems is characterized by attractive or repelling fixed points. Nevertheless,
Non-Fixed Point Renormalization Group Flow Gilberto de la Peña May 9, 2013 Abstract: The renormalization group flow of most systems is characterized by attractive or repelling fixed points. Nevertheless,
Chapter 2 Approximation Methods Can be Used When Exact Solutions to the Schrödinger Equation Can Not be Found.
 Chapter 2 Approximation Methods Can be Used When Exact Solutions to the Schrödinger Equation Can Not be Found. In applying quantum mechanics to 'real' chemical problems, one is usually faced with a Schrödinger
Chapter 2 Approximation Methods Can be Used When Exact Solutions to the Schrödinger Equation Can Not be Found. In applying quantum mechanics to 'real' chemical problems, one is usually faced with a Schrödinger
UNIT I SOLID STATE PHYSICS
 UNIT I SOLID STATE PHYSICS CHAPTER 1 CRYSTAL STRUCTURE 1.1 INTRODUCTION When two atoms are brought together, two kinds of forces: attraction and repulsion come into play. The force of attraction increases
UNIT I SOLID STATE PHYSICS CHAPTER 1 CRYSTAL STRUCTURE 1.1 INTRODUCTION When two atoms are brought together, two kinds of forces: attraction and repulsion come into play. The force of attraction increases
Introduction. Chapter The Purpose of Statistical Mechanics
 Chapter 1 Introduction 1.1 The Purpose of Statistical Mechanics Statistical Mechanics is the mechanics developed to treat a collection of a large number of atoms or particles. Such a collection is, for
Chapter 1 Introduction 1.1 The Purpose of Statistical Mechanics Statistical Mechanics is the mechanics developed to treat a collection of a large number of atoms or particles. Such a collection is, for
arxiv:math/ v1 [math.qa] 29 Dec 2003
![arxiv:math/ v1 [math.qa] 29 Dec 2003 arxiv:math/ v1 [math.qa] 29 Dec 2003](/thumbs/88/117522162.jpg) THE ENERGY OPERATOR FOR INFINITE STATISTICS SONIA STANCIU arxiv:math/0312488v1 [math.qa] 29 Dec 2003 Abstract. We construct the energy operator for particles obeying infinite statistics defined by a q-deformation
THE ENERGY OPERATOR FOR INFINITE STATISTICS SONIA STANCIU arxiv:math/0312488v1 [math.qa] 29 Dec 2003 Abstract. We construct the energy operator for particles obeying infinite statistics defined by a q-deformation
LS coupling. 2 2 n + H s o + H h f + H B. (1) 2m
 LS coupling 1 The big picture We start from the Hamiltonian of an atomic system: H = [ ] 2 2 n Ze2 1 + 1 e 2 1 + H s o + H h f + H B. (1) 2m n e 4πɛ 0 r n 2 4πɛ 0 r nm n,m Here n runs pver the electrons,
LS coupling 1 The big picture We start from the Hamiltonian of an atomic system: H = [ ] 2 2 n Ze2 1 + 1 e 2 1 + H s o + H h f + H B. (1) 2m n e 4πɛ 0 r n 2 4πɛ 0 r nm n,m Here n runs pver the electrons,
Lecture 9. = 1+z + 2! + z3. 1 = 0, it follows that the radius of convergence of (1) is.
 The Exponential Function Lecture 9 The exponential function 1 plays a central role in analysis, more so in the case of complex analysis and is going to be our first example using the power series method.
The Exponential Function Lecture 9 The exponential function 1 plays a central role in analysis, more so in the case of complex analysis and is going to be our first example using the power series method.
On the behavior of an electron in a homogeneous electrical field according to the relativistic Theory of Dirac
 On the behavior of an electron in a homogeneous electrical field according to the relativistic Theory of Dirac Fritz Sauter in Munich. With 6 Illustrations. April 21st, 1931 Abstract We give the solutions
On the behavior of an electron in a homogeneous electrical field according to the relativistic Theory of Dirac Fritz Sauter in Munich. With 6 Illustrations. April 21st, 1931 Abstract We give the solutions
A Class of Partially Ordered Sets: III
 A Class of Partially Ordered Sets: III by Geoffrey Hemion 1 Definitions To begin with, let us fix a certain notation. Let the pair (X, ) be a given poset. For a X, let a = {x X : x < a} and a = {x X :
A Class of Partially Ordered Sets: III by Geoffrey Hemion 1 Definitions To begin with, let us fix a certain notation. Let the pair (X, ) be a given poset. For a X, let a = {x X : x < a} and a = {x X :
NORMAL MODES, WAVE MOTION AND THE WAVE EQUATION. Professor G.G.Ross. Oxford University Hilary Term 2009
 NORMAL MODES, WAVE MOTION AND THE WAVE EQUATION Professor G.G.Ross Oxford University Hilary Term 009 This course of twelve lectures covers material for the paper CP4: Differential Equations, Waves and
NORMAL MODES, WAVE MOTION AND THE WAVE EQUATION Professor G.G.Ross Oxford University Hilary Term 009 This course of twelve lectures covers material for the paper CP4: Differential Equations, Waves and
On the remarkable Properties of the Coefficients which occur in the Expansion of the binomial raised to an arbitrary power *
 On the remarkable Properties of the Coefficients which occur in the Expansion of the binomial raised to an arbitrary power * Leonhard Euler THEOREM If for the power of the binomial raised to the exponent
On the remarkable Properties of the Coefficients which occur in the Expansion of the binomial raised to an arbitrary power * Leonhard Euler THEOREM If for the power of the binomial raised to the exponent
A guide to Proof by Induction
 A guide to Proof by Induction Adapted from L. R. A. Casse, A Bridging Course in Mathematics, The Mathematics Learning Centre, University of Adelaide, 1996. Inductive reasoning is where we observe of a
A guide to Proof by Induction Adapted from L. R. A. Casse, A Bridging Course in Mathematics, The Mathematics Learning Centre, University of Adelaide, 1996. Inductive reasoning is where we observe of a
Mathematics 324 Riemann Zeta Function August 5, 2005
 Mathematics 324 Riemann Zeta Function August 5, 25 In this note we give an introduction to the Riemann zeta function, which connects the ideas of real analysis with the arithmetic of the integers. Define
Mathematics 324 Riemann Zeta Function August 5, 25 In this note we give an introduction to the Riemann zeta function, which connects the ideas of real analysis with the arithmetic of the integers. Define
On the quantum theory of rotating electrons
 Zur Quantentheorie des rotierenden Elektrons Zeit. f. Phys. 8 (98) 85-867. On the quantum theory of rotating electrons By Friedrich Möglich in Berlin-Lichterfelde. (Received on April 98.) Translated by
Zur Quantentheorie des rotierenden Elektrons Zeit. f. Phys. 8 (98) 85-867. On the quantum theory of rotating electrons By Friedrich Möglich in Berlin-Lichterfelde. (Received on April 98.) Translated by
Contents. 1 Solutions to Chapter 1 Exercises 3. 2 Solutions to Chapter 2 Exercises Solutions to Chapter 3 Exercises 57
 Contents 1 Solutions to Chapter 1 Exercises 3 Solutions to Chapter Exercises 43 3 Solutions to Chapter 3 Exercises 57 4 Solutions to Chapter 4 Exercises 77 5 Solutions to Chapter 5 Exercises 89 6 Solutions
Contents 1 Solutions to Chapter 1 Exercises 3 Solutions to Chapter Exercises 43 3 Solutions to Chapter 3 Exercises 57 4 Solutions to Chapter 4 Exercises 77 5 Solutions to Chapter 5 Exercises 89 6 Solutions
Nordhaus-Gaddum Theorems for k-decompositions
 Nordhaus-Gaddum Theorems for k-decompositions Western Michigan University October 12, 2011 A Motivating Problem Consider the following problem. An international round-robin sports tournament is held between
Nordhaus-Gaddum Theorems for k-decompositions Western Michigan University October 12, 2011 A Motivating Problem Consider the following problem. An international round-robin sports tournament is held between
Chapter 6. Q. Suppose we put a delta-function bump in the center of the infinite square well: H = αδ(x a/2) (1)
 Tor Kjellsson Stockholm University Chapter 6 6. Q. Suppose we put a delta-function bump in the center of the infinite square well: where α is a constant. H = αδ(x a/ ( a Find the first-order correction
Tor Kjellsson Stockholm University Chapter 6 6. Q. Suppose we put a delta-function bump in the center of the infinite square well: where α is a constant. H = αδ(x a/ ( a Find the first-order correction
JUST THE MATHS UNIT NUMBER DIFFERENTIATION APPLICATIONS 5 (Maclaurin s and Taylor s series) A.J.Hobson
 JUST THE MATHS UNIT NUMBER.5 DIFFERENTIATION APPLICATIONS 5 (Maclaurin s and Taylor s series) by A.J.Hobson.5. Maclaurin s series.5. Standard series.5.3 Taylor s series.5.4 Exercises.5.5 Answers to exercises
JUST THE MATHS UNIT NUMBER.5 DIFFERENTIATION APPLICATIONS 5 (Maclaurin s and Taylor s series) by A.J.Hobson.5. Maclaurin s series.5. Standard series.5.3 Taylor s series.5.4 Exercises.5.5 Answers to exercises
Basic counting techniques. Periklis A. Papakonstantinou Rutgers Business School
 Basic counting techniques Periklis A. Papakonstantinou Rutgers Business School i LECTURE NOTES IN Elementary counting methods Periklis A. Papakonstantinou MSIS, Rutgers Business School ALL RIGHTS RESERVED
Basic counting techniques Periklis A. Papakonstantinou Rutgers Business School i LECTURE NOTES IN Elementary counting methods Periklis A. Papakonstantinou MSIS, Rutgers Business School ALL RIGHTS RESERVED
Substituting this into the differential equation and solving for u, we have. + u2. du = 3x + c. ( )
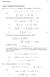 Worked Solutions 27 Chapter 6: Simplifying Through Substitution 6 a Let u = 3 + 3y + 2 Solving for y computing y we then see that 3y = u 3 2 y = u 3 2 3 = d [ u 3 2 3 = 3 Substituting this into the differential
Worked Solutions 27 Chapter 6: Simplifying Through Substitution 6 a Let u = 3 + 3y + 2 Solving for y computing y we then see that 3y = u 3 2 y = u 3 2 3 = d [ u 3 2 3 = 3 Substituting this into the differential
Skyrme model on S 3 and Harmonic maps
 Skyrme model on S 3 and Harmonic maps arxiv:hep-th/9810175v1 22 Oct 1998 Y. Brihaye and C. Gabriel Dep. of Mathematical Physics, University of Mons-Hainaut, Mons, Belgium Dep. of Mechanics and Gravitation,
Skyrme model on S 3 and Harmonic maps arxiv:hep-th/9810175v1 22 Oct 1998 Y. Brihaye and C. Gabriel Dep. of Mathematical Physics, University of Mons-Hainaut, Mons, Belgium Dep. of Mechanics and Gravitation,
Physics 221A Fall 2018 Notes 22 Bound-State Perturbation Theory
 Copyright c 2018 by Robert G. Littlejohn Physics 221A Fall 2018 Notes 22 Bound-State Perturbation Theory 1. Introduction Bound state perturbation theory applies to the bound states of perturbed systems,
Copyright c 2018 by Robert G. Littlejohn Physics 221A Fall 2018 Notes 22 Bound-State Perturbation Theory 1. Introduction Bound state perturbation theory applies to the bound states of perturbed systems,
arxiv: v1 [cond-mat.mes-hall] 26 Sep 2013
![arxiv: v1 [cond-mat.mes-hall] 26 Sep 2013 arxiv: v1 [cond-mat.mes-hall] 26 Sep 2013](/thumbs/83/88173709.jpg) Berry phase and the unconventional quantum Hall effect in graphene Jiamin Xue Microelectronic Research Center, The University arxiv:1309.6714v1 [cond-mat.mes-hall] 26 Sep 2013 of Texas at Austin, Austin,
Berry phase and the unconventional quantum Hall effect in graphene Jiamin Xue Microelectronic Research Center, The University arxiv:1309.6714v1 [cond-mat.mes-hall] 26 Sep 2013 of Texas at Austin, Austin,
Generating Permutations and Combinations
 Generating Permutations and Combinations March 0, 005 Generating Permutations We have learned that there are n! permutations of {,,, n} It is important in many instances to generate a list of such permutations
Generating Permutations and Combinations March 0, 005 Generating Permutations We have learned that there are n! permutations of {,,, n} It is important in many instances to generate a list of such permutations
Ahlswede Khachatrian Theorems: Weighted, Infinite, and Hamming
 Ahlswede Khachatrian Theorems: Weighted, Infinite, and Hamming Yuval Filmus April 4, 2017 Abstract The seminal complete intersection theorem of Ahlswede and Khachatrian gives the maximum cardinality of
Ahlswede Khachatrian Theorems: Weighted, Infinite, and Hamming Yuval Filmus April 4, 2017 Abstract The seminal complete intersection theorem of Ahlswede and Khachatrian gives the maximum cardinality of
1 One-dimensional lattice
 1 One-dimensional lattice 1.1 Gap formation in the nearly free electron model Periodic potential Bloch function x = n e iπn/ax 1 n= ψ k x = e ika u k x u k x = c nk e iπn/ax 3 n= Schrödinger equation [
1 One-dimensional lattice 1.1 Gap formation in the nearly free electron model Periodic potential Bloch function x = n e iπn/ax 1 n= ψ k x = e ika u k x u k x = c nk e iπn/ax 3 n= Schrödinger equation [
Lecture 4 Recap: normal metals and the clectron-phonon interaction *
 Phys. 598SC Fall 2015 Prof. A. J. Leggett Lecture 4 Recap: normal metals and the clectron-phonon interaction * 1. Normal metals: Sommerfeld-Bloch picture 2. Screening 3. Fermi liquid theory 4. Electron-phonon
Phys. 598SC Fall 2015 Prof. A. J. Leggett Lecture 4 Recap: normal metals and the clectron-phonon interaction * 1. Normal metals: Sommerfeld-Bloch picture 2. Screening 3. Fermi liquid theory 4. Electron-phonon
Section 3 Electronic Configurations, Term Symbols, and States
 Section 3 Electronic Configurations, Term Symbols, and States Introductory Remarks- The Orbital, Configuration, and State Pictures of Electronic Structure One of the goals of quantum chemistry is to allow
Section 3 Electronic Configurations, Term Symbols, and States Introductory Remarks- The Orbital, Configuration, and State Pictures of Electronic Structure One of the goals of quantum chemistry is to allow
Second Quantization Method for Bosons
 Second Quantization Method for Bosons Hartree-Fock-based methods cannot describe the effects of the classical image potential (cf. fig. 1) because HF is a mean-field theory. DFF-LDA is not able either
Second Quantization Method for Bosons Hartree-Fock-based methods cannot describe the effects of the classical image potential (cf. fig. 1) because HF is a mean-field theory. DFF-LDA is not able either
PRINCIPLE OF MATHEMATICAL INDUCTION
 Chapter 4 PRINCIPLE OF MATHEMATICAL INDUCTION 4.1 Overview Mathematical induction is one of the techniques which can be used to prove variety of mathematical statements which are formulated in terms of
Chapter 4 PRINCIPLE OF MATHEMATICAL INDUCTION 4.1 Overview Mathematical induction is one of the techniques which can be used to prove variety of mathematical statements which are formulated in terms of
Discrete Mathematics for CS Spring 2008 David Wagner Note 4
 CS 70 Discrete Mathematics for CS Spring 008 David Wagner Note 4 Induction Induction is an extremely powerful tool in mathematics. It is a way of proving propositions that hold for all natural numbers,
CS 70 Discrete Mathematics for CS Spring 008 David Wagner Note 4 Induction Induction is an extremely powerful tool in mathematics. It is a way of proving propositions that hold for all natural numbers,
1 Expansion in orthogonal functions
 Notes "orthogonal" January 9 Expansion in orthogonal functions To obtain a more useful form of the Green s function, we ll want to expand in orthogonal functions that are (relatively) easy to integrate.
Notes "orthogonal" January 9 Expansion in orthogonal functions To obtain a more useful form of the Green s function, we ll want to expand in orthogonal functions that are (relatively) easy to integrate.
Symmetry Groups conservation law quantum numbers Gauge symmetries local bosons mediate the interaction Group Abelian Product of Groups simple
 Symmetry Groups Symmetry plays an essential role in particle theory. If a theory is invariant under transformations by a symmetry group one obtains a conservation law and quantum numbers. For example,
Symmetry Groups Symmetry plays an essential role in particle theory. If a theory is invariant under transformations by a symmetry group one obtains a conservation law and quantum numbers. For example,
2.1 Calculation of the ground state energy via path integral
 Chapter 2 Instantons in Quantum Mechanics Before describing the instantons and their effects in non-abelian gauge theories, it is instructive to become familiar with the relevant ideas in the context of
Chapter 2 Instantons in Quantum Mechanics Before describing the instantons and their effects in non-abelian gauge theories, it is instructive to become familiar with the relevant ideas in the context of
Luttinger Liquid at the Edge of a Graphene Vacuum
 Luttinger Liquid at the Edge of a Graphene Vacuum H.A. Fertig, Indiana University Luis Brey, CSIC, Madrid I. Introduction: Graphene Edge States (Non-Interacting) II. III. Quantum Hall Ferromagnetism and
Luttinger Liquid at the Edge of a Graphene Vacuum H.A. Fertig, Indiana University Luis Brey, CSIC, Madrid I. Introduction: Graphene Edge States (Non-Interacting) II. III. Quantum Hall Ferromagnetism and
Abstract. 2. We construct several transcendental numbers.
 Abstract. We prove Liouville s Theorem for the order of approximation by rationals of real algebraic numbers. 2. We construct several transcendental numbers. 3. We define Poissonian Behaviour, and study
Abstract. We prove Liouville s Theorem for the order of approximation by rationals of real algebraic numbers. 2. We construct several transcendental numbers. 3. We define Poissonian Behaviour, and study
QM and Angular Momentum
 Chapter 5 QM and Angular Momentum 5. Angular Momentum Operators In your Introductory Quantum Mechanics (QM) course you learned about the basic properties of low spin systems. Here we want to review that
Chapter 5 QM and Angular Momentum 5. Angular Momentum Operators In your Introductory Quantum Mechanics (QM) course you learned about the basic properties of low spin systems. Here we want to review that
8.1 Bifurcations of Equilibria
 1 81 Bifurcations of Equilibria Bifurcation theory studies qualitative changes in solutions as a parameter varies In general one could study the bifurcation theory of ODEs PDEs integro-differential equations
1 81 Bifurcations of Equilibria Bifurcation theory studies qualitative changes in solutions as a parameter varies In general one could study the bifurcation theory of ODEs PDEs integro-differential equations
PHYSICS 721/821 - Spring Semester ODU. Graduate Quantum Mechanics II Midterm Exam - Solution
 PHYSICS 72/82 - Spring Semester 2 - ODU Graduate Quantum Mechanics II Midterm Exam - Solution Problem ) An electron (mass 5, ev/c 2 ) is in a one-dimensional potential well as sketched to the right (the
PHYSICS 72/82 - Spring Semester 2 - ODU Graduate Quantum Mechanics II Midterm Exam - Solution Problem ) An electron (mass 5, ev/c 2 ) is in a one-dimensional potential well as sketched to the right (the
Week 4-5: Generating Permutations and Combinations
 Week 4-5: Generating Permutations and Combinations February 27, 2017 1 Generating Permutations We have learned that there are n! permutations of {1, 2,...,n}. It is important in many instances to generate
Week 4-5: Generating Permutations and Combinations February 27, 2017 1 Generating Permutations We have learned that there are n! permutations of {1, 2,...,n}. It is important in many instances to generate
Chapter 1. Crystal structure. 1.1 Crystal lattices
 Chapter 1 Crystal structure 1.1 Crystal lattices We will concentrate as stated in the introduction, on perfect crystals, i.e. on arrays of atoms, where a given arrangement is repeated forming a periodic
Chapter 1 Crystal structure 1.1 Crystal lattices We will concentrate as stated in the introduction, on perfect crystals, i.e. on arrays of atoms, where a given arrangement is repeated forming a periodic
N E W S A N D L E T T E R S
 N E W S A N D L E T T E R S 74th Annual William Lowell Putnam Mathematical Competition Editor s Note: Additional solutions will be printed in the Monthly later in the year. PROBLEMS A1. Recall that a regular
N E W S A N D L E T T E R S 74th Annual William Lowell Putnam Mathematical Competition Editor s Note: Additional solutions will be printed in the Monthly later in the year. PROBLEMS A1. Recall that a regular
PUTNAM TRAINING NUMBER THEORY. Exercises 1. Show that the sum of two consecutive primes is never twice a prime.
 PUTNAM TRAINING NUMBER THEORY (Last updated: December 11, 2017) Remark. This is a list of exercises on Number Theory. Miguel A. Lerma Exercises 1. Show that the sum of two consecutive primes is never twice
PUTNAM TRAINING NUMBER THEORY (Last updated: December 11, 2017) Remark. This is a list of exercises on Number Theory. Miguel A. Lerma Exercises 1. Show that the sum of two consecutive primes is never twice
THE N-VALUE GAME OVER Z AND R
 THE N-VALUE GAME OVER Z AND R YIDA GAO, MATT REDMOND, ZACH STEWARD Abstract. The n-value game is an easily described mathematical diversion with deep underpinnings in dynamical systems analysis. We examine
THE N-VALUE GAME OVER Z AND R YIDA GAO, MATT REDMOND, ZACH STEWARD Abstract. The n-value game is an easily described mathematical diversion with deep underpinnings in dynamical systems analysis. We examine
Markov Chains CK eqns Classes Hitting times Rec./trans. Strong Markov Stat. distr. Reversibility * Markov Chains
 Markov Chains A random process X is a family {X t : t T } of random variables indexed by some set T. When T = {0, 1, 2,... } one speaks about a discrete-time process, for T = R or T = [0, ) one has a continuous-time
Markov Chains A random process X is a family {X t : t T } of random variables indexed by some set T. When T = {0, 1, 2,... } one speaks about a discrete-time process, for T = R or T = [0, ) one has a continuous-time
On Descents in Standard Young Tableaux arxiv:math/ v1 [math.co] 3 Jul 2000
![On Descents in Standard Young Tableaux arxiv:math/ v1 [math.co] 3 Jul 2000 On Descents in Standard Young Tableaux arxiv:math/ v1 [math.co] 3 Jul 2000](/thumbs/88/115824860.jpg) On Descents in Standard Young Tableaux arxiv:math/0007016v1 [math.co] 3 Jul 000 Peter A. Hästö Department of Mathematics, University of Helsinki, P.O. Box 4, 00014, Helsinki, Finland, E-mail: peter.hasto@helsinki.fi.
On Descents in Standard Young Tableaux arxiv:math/0007016v1 [math.co] 3 Jul 000 Peter A. Hästö Department of Mathematics, University of Helsinki, P.O. Box 4, 00014, Helsinki, Finland, E-mail: peter.hasto@helsinki.fi.
Vector Spaces in Quantum Mechanics
 Chapter 8 Vector Spaces in Quantum Mechanics We have seen in the previous Chapter that there is a sense in which the state of a quantum system can be thought of as being made up of other possible states.
Chapter 8 Vector Spaces in Quantum Mechanics We have seen in the previous Chapter that there is a sense in which the state of a quantum system can be thought of as being made up of other possible states.
Root systems and optimal block designs
 Root systems and optimal block designs Peter J. Cameron School of Mathematical Sciences Queen Mary, University of London Mile End Road London E1 4NS, UK p.j.cameron@qmul.ac.uk Abstract Motivated by a question
Root systems and optimal block designs Peter J. Cameron School of Mathematical Sciences Queen Mary, University of London Mile End Road London E1 4NS, UK p.j.cameron@qmul.ac.uk Abstract Motivated by a question
Phonons and lattice dynamics
 Chapter Phonons and lattice dynamics. Vibration modes of a cluster Consider a cluster or a molecule formed of an assembly of atoms bound due to a specific potential. First, the structure must be relaxed
Chapter Phonons and lattice dynamics. Vibration modes of a cluster Consider a cluster or a molecule formed of an assembly of atoms bound due to a specific potential. First, the structure must be relaxed
Lecture 4 Quantum mechanics in more than one-dimension
 Lecture 4 Quantum mechanics in more than one-dimension Background Previously, we have addressed quantum mechanics of 1d systems and explored bound and unbound (scattering) states. Although general concepts
Lecture 4 Quantum mechanics in more than one-dimension Background Previously, we have addressed quantum mechanics of 1d systems and explored bound and unbound (scattering) states. Although general concepts
129 Lecture Notes More on Dirac Equation
 19 Lecture Notes More on Dirac Equation 1 Ultra-relativistic Limit We have solved the Diraction in the Lecture Notes on Relativistic Quantum Mechanics, and saw that the upper lower two components are large
19 Lecture Notes More on Dirac Equation 1 Ultra-relativistic Limit We have solved the Diraction in the Lecture Notes on Relativistic Quantum Mechanics, and saw that the upper lower two components are large
So far we have limited the discussion to state spaces of finite dimensions, but it turns out that, in
 Chapter 0 State Spaces of Infinite Dimension So far we have limited the discussion to state spaces of finite dimensions, but it turns out that, in practice, state spaces of infinite dimension are fundamental
Chapter 0 State Spaces of Infinite Dimension So far we have limited the discussion to state spaces of finite dimensions, but it turns out that, in practice, state spaces of infinite dimension are fundamental
Solving ground eigenvalue and eigenfunction of spheroidal wave equation at low frequency by supersymmetric quantum mechanics method
 Chin. Phys. B Vol. 0, No. (0) 00304 Solving ground eigenvalue eigenfunction of spheroidal wave equation at low frequency by supersymmetric quantum mechanics method Tang Wen-Lin( ) Tian Gui-Hua( ) School
Chin. Phys. B Vol. 0, No. (0) 00304 Solving ground eigenvalue eigenfunction of spheroidal wave equation at low frequency by supersymmetric quantum mechanics method Tang Wen-Lin( ) Tian Gui-Hua( ) School
1 + lim. n n+1. f(x) = x + 1, x 1. and we check that f is increasing, instead. Using the quotient rule, we easily find that. 1 (x + 1) 1 x (x + 1) 2 =
 Chapter 5 Sequences and series 5. Sequences Definition 5. (Sequence). A sequence is a function which is defined on the set N of natural numbers. Since such a function is uniquely determined by its values
Chapter 5 Sequences and series 5. Sequences Definition 5. (Sequence). A sequence is a function which is defined on the set N of natural numbers. Since such a function is uniquely determined by its values
