Hilbert Transforms, Analytic Functions, and Analytic Signals
|
|
|
- Allan Hutchinson
- 6 years ago
- Views:
Transcription
1 Hilbrt Transorms Analtic Fnctions and Analtic Signals Cla S. Trnr 3//5 V. Introdction: Hilbrt transorms ar ssntial in ndrstanding man modrn modlation mthods. Ths transorms ctil phas shit a nction b 9 dgrs indpndnt o rqnc. O cors practical implmntations ha limitations. For ampl th phas shiting o a low rqnc implis a long dla which in trn implis a comptational procss that maintains a long histor o th signal. Hilbrt transorms ar sl in crating signals with on sidd Forir transorms. Also th concpts o analtic nctions and analtic signals will b shown to b rlatd throgh Hilbrt transorms. 9 Dgr Phas Shitrs: W will tak a spctral approach and start with an idal 9-dgr phas shitr. To do this w wold lik a nction that will transorm a sinsoid to anothr sinsoid with th sam amplitd and rqnc bt simpl phas shitd b 9 dgrs. So rcalling th trigonomtric idntitis: Thn w dsir or transorm to do th ollowing: Cos t 9 Sin Sin t 9 Cos Cos Sin Sin Cos Ths two conditions will also cas a sinsoid with arbitrar phas to b shitd 9 dgrs. This ollows sinc it ma b dcomposd into a sin and a cosin and ach o ths componnts will b shitd b 9 dgrs. To show this start with a sinsoid o arbitrar phas θ and dcompos it into a sin and a cosin componnts. Cos t θ Cos Cos θ Sin Sin θ 3 Nt transorm phas shi th two componnts and rdc. Cos t 9 Cos θ Sin t 9 Sin θ Sin Cos θ Cos Sin θ Sin t θ Cos t θ 9 4
2 So w can s th ct o th transormation is a 9-dgr phas shit rgardlss o th original phas. W also dsir th transorm to b prssibl as a linar conoltion. Ths th transorm will also ob sprposition. Th linarit proprt was sd abo in th arbitrar phas cas. B modling or transorm this wa w can thn s a powrl thorm rom Forir analsis that qats conoltion in on domain to mltiplication in th othr. So lt s look at th transorm in th rqnc domain. Rcalling th Forir pairs or sinsoids: Cos ω Sin ω δ ω ω δ ω ω / 5 δ ω ω δ ω ω / Thn or rqnc domain phas shit rqirmnts bcom atr cancling ot th twos and moing or: [ δ ω ω δ ω ω ] ω [ δ ω ω δ ω ω ] [ δ ω ω δ ω ω ] H ω [ δ ω ω δ ω ω ] H 6 Rcalling th Dirac Dlta nction is a distribtion whos non-ro spport is or an ininitl narrow rgion w thn onl ha to compar 4 points to sol this st o qations. It is hlpl to look at positi rqncis sparatl rom th ngati ons. Doing this w onl compar two points at a tim. So or ω ω > w ind δ H ω δ or simpl H ω. Likwis or ω ω < w ind H ω. Finall or ω ω w ind δ H hnc H. Atr ptting ths cass togthr w ind th rqnc domain soltion or th 9- dgr phas shitr is: Th Signm nction is dind as: H ω Sgn ω 7 Sgn ω ω > ω ω < 8
3 Hilbrt Transorms Analtic Fnctions and Analtic Signals Now w nd th tim domain rsion o th phas shitr so w can prss th phas shitr as a conoltion. This is achid st b inding th inrs Forir transorm o H ω. Th rslt is: ω ωt t ωt h sgn ω dω dω π π π dω π t 9 So whn w wish to phas shit a nction or ampl b 9 dgrs w st conol it with / π. Rcalling th standard intgral orm or th conoltion o two nctions h. ξ h t ξ dξ Sinc conoltion is commtati w also ha: h ξ t ξ dξ So in trms o conoltion or phas shitr has th ollowing intgral orms ξ t ξ dξ dξ π t ξ π ξ Now that w ha a dinition or th orward Hilbrt transorm w ind th dinition or th inrs transorm. Th inrs Hilbrt transorm ma b thoght o as Hilbrt transorming a nction thr tims. I.. shiting 7 dgrs is th sam as shiting ngati 9 dgrs. Two shits rslt in a 8-dgr phas shit which is simpl ngation. So a ngati 9-dgr phas shit is simpl th ngation o a 9-dgr phas shit! So or th inrs Hilbrt transorm w st conol with - / π. Hilbrt Transorm Dinitions: Som paprs start b dining a Hilbrt transorm is as an Intgral transorm. Sinc w startd rom a phas shitr point o iw and thn w modld it as a conoltion w immdiatl ha two rprsntations or th dirct and inrs transorms. O cors an lmntar chang o ariabl conrts on rprsntation into th othr. 3//5 Pag 3 o 3
4 Hilbrt Transorms Analtic Fnctions and Analtic Signals Gin a nction thn its Hilbrt transorm is: ξ t ξ P dξ P dξ π t ξ π ξ 3 Th inrs Hilbrt transorm is likwis similarl dind. ξ t ξ P dξ P dξ π t ξ π ξ 4 Sinc th basic intgrals ar impropr ths ar to b alatd as Cach Principal Val CPV Intgrals. This implis a carl limiting procss takn smmtricall abot th singlarit which rslts in act cancllation. This basicall mans or th st ariant o th transorm: P ε R ξ ξ ξ 5 dξ Lim ξ t R R ε ξ t dξ ξ t ε dξ ξ t Hr psilon is an incrasingl small distanc rom th singlarit. A similar limiting procss is also sd with th nd orm. Sinc intgration is a linar opration w s that Hilbrt transormation is also a linar opration. This mans an nction pandd into a sm o sinsoids can b asil Hilbrt transormd b doing th appropriat 9-dgr phas shits on ach o th componnts. Unlik othr tps o transorms Hilbrt transorms la th nction in th sam domain as th original th Hilbrt transorm o a tmporal nction is itsl tmporal. An ampl o alating a CPV intgral Lt s alat: P d 6 So sing th limit approach w ind: P Lim Lim Lim Lim d ε ε d ε d ε ε d d d d ε ε ε ε ε 7 3//5 Pag 4 o 3
5 Hilbrt Transorms Analtic Fnctions and Analtic Signals A chang o ariabl was mad in th middl stp. A simpl ampl o inding a Hilbrt transorm ia conoltion: Lt s ind th Hilbrt transorm o Cos. So insrting Cos into th nd orm o th Hilbrt transorm intgral w obtain: Cos t ξ P dξ π ξ 8 Using th trigonomtric idntit or th cosin o a sm o angls w now ind: Cos t ξ Cos ξ Sin ξ P dξ Cos Sin dξ π ξ π ξ ξ 9 Now sing or aorit intgral tabl or an adroit intgration tchniq [s appndi A] obtain th ollowing idntitis. So now th soltion is as. Cos ξ dξ ξ Sin ξ dξ π ξ Cos ξ Sin ξ Cos dξ Sin dξ Sin π ξ π ξ Ths w ind Sin. Hnc th Hilbrt transorm o Cos is Sin. Likwis a similar procss ma b sd to ind th Hilbrt transorm o Sin is Cos. So this riis that conoltion with th krnl π dos indd prorm a 9-dgr phas shit opration. 3//5 Pag 5 o 3
6 Hilbrt Transorms Analtic Fnctions and Analtic Signals 3//5 Pag 6 o 3 Analtic Fnctions Th thor o Hilbrt transormation is intimatl connctd with compl analsis so w will now look at a rqirmnt or isotropic dirntiation o compl nctions. W will s th standard paradigm o sing a compl ariabl composd o two ral componnts combind in th ollowing wa: Hr and ar ral als and rprsnts. Similarl w can compos a compl ald nction b combining two ral ald nctions also standard: 3 Nt w will tili th standard dinition o a driati rom ral analsis and tnd it to th compl cas. This driati limit is: Lim ' 4 A diiclt with th dinition is th rslt ma dpnd on th dirction that takn b hnc w wold lik to know ndr what conditions th driati is path indpndnt. So w will tak two orthogonal paths and rqir th rslting limits to b th sam. This will ild path indpndnc and ha a driati dinition that gis consistnt rslts. Rcall. So w will irst lt and mo along th -ais. Lim ' 5 Nt will mo along th -ais and lt. Lim ' 6
7 Hilbrt Transorms Analtic Fnctions and Analtic Signals 3//5 Pag 7 o 3 Th rqirmnt that th two limits ar to b th sam rslts in th Cach-Rimann rlations. Ths ar ond b stting th two limits qal to ach othr and qating th ral and imaginar parts. Th C-R rlations ar: 7 I a compl nction obs th C-R rlations and has dirntiabl componnts it is said to b analtic. A nction ma b analtic or st part o its domain. Howr a nction can t b analtic at st a singl point i it is analtic at a point thn it also mst b analtic in an opn nighborhood arond that point. Sinc w composd or compl nction b smming togthr two nctions on prl ral and th othr prl imaginar it wold sm that or compl nction has two dgrs o rdom. Howr th nction s bing analtic crats an intrsting rstriction. I w rcall that and and thn lt s look at th driati with rspct to. So sing th chain rl w ind th ollowing pansion: 8 Nt s 9 So or driati now has th orm: 3 I th nction obs th C-R rlations thn th partial driati is simpl ro! So in a sns analtic nctions ar indpndnt o. Anothr nat qalit o analtic nctions is th componnts and ach sol Laplac s qation. Spciicall and. Ths ollow dirctl rom dirntiating th C-R rlations. Starting with th C-R rlations:
8 Hilbrt Transorms Analtic Fnctions and Analtic Signals and 3 Atr dirntiating th irst rlation with rspct to and th scond rlation with rspct to w ind: 3 and Now qating th mid partials w ind so w s that Laplac s qation is satisid. A similar procss can b applid to mak th cas or. Sinc both componnts sol Laplac s qation thir sm will also so w ha th ollowing nat thorm or analtic nctions: 33 In or proo o this w assmd th qialnc o mid partials and th istnc o highr ordr driatis. In adancd tts on compl analsis ths will b shown to b alwas tr or analtic nctions. An Analtic Fnction Eampl Eampl: Show ind: is analtic. Using th ponnt addition rl and Elr s idntit w Cos Sin Cos Sin 34 So w ha: Cos Sin 35 Now ind th or partial driatis: Sin Sin Cos Cos 36 Plgging ths into th C-R rlations on inds th ar obd or all and. Sch a nction is analtic rwhr and is somtims calld an ntir nction. 3//5 Pag 8 o 3
9 Hilbrt Transorms Analtic Fnctions and Analtic Signals Analtic Signals Rlatd to th concpt o analtic nctions is th ida o an analtic signal. On wa to mak on is b alating an analtic nction along on o th as. For or ampl nction I will s th ral ais. Or abo analtic nction has th corrsponding analtic signal: Cos Sin 37 Th choic o ais dpnds on th analtic nction. I th wrong choic is mad th rslt will not b an analtic signal. How to chos which ais will b mad clar shortl. Analtic signals ha sral proprtis that pro important in signal procssing. Th irst proprt is analtic signals ha on-sidd Forir transorms. A scond proprt is analtic signals ob a gnraliation o Elr s idntit. A third proprt is th analtic signal s imaginar portion is th Hilbrt transorm o its ral portion. Assming or third proprt is tr thn gin an analtic signal ψ t its Forir transorm is Ψ ω U ω V ω. Nt s th spctral orm o th Hilbrt transormation to ind: Ψ ω U ω Sgn ω U ω Sgn ω U ω 38 And w can asil s that Ψ ω whn ω <. So this signal has no ngati rqnc componnts. Likwis starting with th congat ψ w ind its spctral rprsntation to b Ψ ω Sgn ω U ω which has no positi rqnc componnts. Th componnts o analtic signals also ob a gnraliation o Elr s idntit. For ampl: ψ ψ ψ ψ 39 And o cors: ψ t ψ 4 wt For Elr s idntit st lt ψ Cos ω Sin ω. 3//5 Pag 9 o 3
10 Hilbrt Transorms Analtic Fnctions and Analtic Signals To show th Hilbrt transorm proprt o analtic signals w will ha to alat a not so obios intgral. W want to alat th ollowing intgral or th 4-pic contor shown in igr : ψ 4 d τ C Figr Th or pics ar: th otr smicircl with radis R th lt horiontal lin sgmnt th right horiontal lin sgmnt and th innr smicircl with radis psilon. Sinc w ar assming ψ is analtic on and insid o c and th path taks a dtor arond th singlarit th Cach-Gorsat thorm sas this qals ro. So nt w pand this intgral into 4 path intgrals whos sm is ro. Ths w ha: ψ ψ ψ ψ d τ τ τ τ d d d A ε R R ε B 4 Sinc w will look at th limiting cas whr th limits ar sch that th otr smicircl bcoms ininitl larg and th innr smicircl likwis bcoms ininitl small w ar abl to combin th middl two intgrals into a CPV intgral. Hnc d P d A ψ ψ ψ d τ τ τ B 43 Earlir I mntiond how th choic o ais mattrs. This is whr w choos th ais so that Jordan s Lmma ma b applid to th st intgral to mak it ro. For som analtic nctions w will s th ais instad o th ais. Th last intgral somtims calld 3//5 Pag o 3
11 Hilbrt Transorms Analtic Fnctions and Analtic Signals a dtor intgral sinc it is sd to hop arond th singlarit alats to πψ τ. This intgral is ond b sing a ariation o Cach s intgral ormla whr in th limit o th path s radis going to ro th intgral s al is θψ τ whr θ is th angl masrd ccw sbtndd b th path rlati to th singlarit. So plgging in ths two rslts w ind: P ψ d τ πψ τ 44 Now rcalling ψ w ind: P d τ P d π τ τ τ 45 So b splitting this ot into two ral ald qations w ind: τ P π τ P π d τ d τ 46 Ths ar simpl th Hilbrt transorm rlations btwn τ and τ. Appndi A: Intgration tricks Itratd Intgration b Parts Lt s sa w wish to intgrat d. Sinc this is an intgral o a prodct o nctions w know that intgration b parts wold b th standard approach. Howr with this ampl w will ha to do this mltipl tims. Thr is an approach calld itratd intgration b parts that is asil applid. And th mthod is actall asir to rmmbr. Basicall w sparat th intgrand into two parts that bcom th hadings o two colmns. Each ntr in th lt colmn is ormd b taking th driati o th ntr right abo it. Similarl ach ntr in th right colmn is mad b taking th intgral o th ntr right abo it. Usall th colmns ar illd ntil th bottom lt hand ntr is 3//5 Pag o 3
12 Hilbrt Transorms Analtic Fnctions and Analtic Signals ro. Th intgral is mad p o th sm o diagonal ppr lt to lowr righ prodcts with altrnating sign pls th intgral o th prodct o th ntris on th bottom row takn with a contind altrnating sign. I th rows ar illd in ntil th bottom row is ro thn this last intgral is not ndd. An ampl will mak this itratd procss clar. For d w bild th ollowing tabl: So now combining trms with altrnating sign w ind: d d 4 C 48 So on can crtainl s this mthod s icac. Sinc this ampl is on whr th lt hand trm is a polnomial th rows ar illd in ntil th bottom row s prodct is ro. Howr som intgrals ha trms that will not go awa rgardlss o th nmbr o s tims a nction is dirntiatd. For ampl lt s ind: Sin d so w bild th tabl lik this: s s Sin 49 s s s Cos Sin So now w ind: s s s Cos s Sin s Sin s Sin d d C 5 This is on o th cass whr th intgration procss taks o arond a loop and nds p almost whr o bgan. Ecpt th bottom intgral works ot to b an indpndnt nction tims th original intgral. So simpliing th algbra w ind: 3//5 Pag o 3
13 Hilbrt Transorms Analtic Fnctions and Analtic Signals s s s Sin d Cos s Sin C 5 Which whn th intgral is ll rsold ilds: Cos s Sin C s 5 s Sin d s W will soon ha nd or th rlatd smi-ininit dinit intgral which w can asil alat sing th abo rslt. Sin s d s 53 / Sbstittion Now lt s look at a mthod or alating th intgral o a sinc nction. Spciicall Sin d. First raliing th intgrand is n w can rdc it to a smi-ininit intral and thn prorm th ollowing trick sbstittion. s how to do th intgral. st ds. So w can now s d d Sin dds Sin Sin s ds Tan s ] π 54 3//5 Pag 3 o 3
Computer Vision. Fourier Analysis. Computer Science Tripos Part II. Dr Christopher Town. Fourier Analysis. Fourier Analysis
 Comptr Vision Comptr Scinc Tripos Part II Dr Christophr Town orir Analsis An imag can b rprsntd b a linar combination of basis fnctions: In th cas of 2D orir analsis: orir Analsis orir Analsis Th transform
Comptr Vision Comptr Scinc Tripos Part II Dr Christophr Town orir Analsis An imag can b rprsntd b a linar combination of basis fnctions: In th cas of 2D orir analsis: orir Analsis orir Analsis Th transform
Differential Equations
 UNIT I Diffrntial Equations.0 INTRODUCTION W li in a world of intrrlatd changing ntitis. Th locit of a falling bod changs with distanc, th position of th arth changs with tim, th ara of a circl changs
UNIT I Diffrntial Equations.0 INTRODUCTION W li in a world of intrrlatd changing ntitis. Th locit of a falling bod changs with distanc, th position of th arth changs with tim, th ara of a circl changs
TMMI37, vt2, Lecture 8; Introductory 2-dimensional elastostatics; cont.
 Lctr 8; ntrodctor 2-dimnsional lastostatics; cont. (modifid 23--3) ntrodctor 2-dimnsional lastostatics; cont. W will now contin or std of 2-dim. lastostatics, and focs on a somwhat mor adancd lmnt thn
Lctr 8; ntrodctor 2-dimnsional lastostatics; cont. (modifid 23--3) ntrodctor 2-dimnsional lastostatics; cont. W will now contin or std of 2-dim. lastostatics, and focs on a somwhat mor adancd lmnt thn
Image Enhancement in the Spatial Domain
 s=tr Eampl PR3.: Eponntials of th form -ar a a positi constant ar sfl for constrcting smooth gra-ll transformation fnctions. Constrct th transformation fnctions haing th gnral shaps shown in th following
s=tr Eampl PR3.: Eponntials of th form -ar a a positi constant ar sfl for constrcting smooth gra-ll transformation fnctions. Constrct th transformation fnctions haing th gnral shaps shown in th following
Section 11.6: Directional Derivatives and the Gradient Vector
 Sction.6: Dirctional Drivativs and th Gradint Vctor Practic HW rom Stwart Ttbook not to hand in p. 778 # -4 p. 799 # 4-5 7 9 9 35 37 odd Th Dirctional Drivativ Rcall that a b Slop o th tangnt lin to th
Sction.6: Dirctional Drivativs and th Gradint Vctor Practic HW rom Stwart Ttbook not to hand in p. 778 # -4 p. 799 # 4-5 7 9 9 35 37 odd Th Dirctional Drivativ Rcall that a b Slop o th tangnt lin to th
NEW APPLICATIONS OF THE ABEL-LIOUVILLE FORMULA
 NE APPLICATIONS OF THE ABEL-LIOUVILLE FORMULA Mirca I CÎRNU Ph Dp o Mathmatics III Faculty o Applid Scincs Univrsity Polithnica o Bucharst Cirnumirca @yahoocom Abstract In a rcnt papr [] 5 th indinit intgrals
NE APPLICATIONS OF THE ABEL-LIOUVILLE FORMULA Mirca I CÎRNU Ph Dp o Mathmatics III Faculty o Applid Scincs Univrsity Polithnica o Bucharst Cirnumirca @yahoocom Abstract In a rcnt papr [] 5 th indinit intgrals
SECTION where P (cos θ, sin θ) and Q(cos θ, sin θ) are polynomials in cos θ and sin θ, provided Q is never equal to zero.
 SETION 6. 57 6. Evaluation of Dfinit Intgrals Exampl 6.6 W hav usd dfinit intgrals to valuat contour intgrals. It may com as a surpris to larn that contour intgrals and rsidus can b usd to valuat crtain
SETION 6. 57 6. Evaluation of Dfinit Intgrals Exampl 6.6 W hav usd dfinit intgrals to valuat contour intgrals. It may com as a surpris to larn that contour intgrals and rsidus can b usd to valuat crtain
DIFFERENTIAL EQUATION
 MD DIFFERENTIAL EQUATION Sllabus : Ordinar diffrntial quations, thir ordr and dgr. Formation of diffrntial quations. Solution of diffrntial quations b th mthod of sparation of variabls, solution of homognous
MD DIFFERENTIAL EQUATION Sllabus : Ordinar diffrntial quations, thir ordr and dgr. Formation of diffrntial quations. Solution of diffrntial quations b th mthod of sparation of variabls, solution of homognous
u x v x dx u x v x v x u x dx d u x v x u x v x dx u x v x dx Integration by Parts Formula
 7. Intgration by Parts Each drivativ formula givs ris to a corrsponding intgral formula, as w v sn many tims. Th drivativ product rul yilds a vry usful intgration tchniqu calld intgration by parts. Starting
7. Intgration by Parts Each drivativ formula givs ris to a corrsponding intgral formula, as w v sn many tims. Th drivativ product rul yilds a vry usful intgration tchniqu calld intgration by parts. Starting
Self-Adjointness and Its Relationship to Quantum Mechanics. Ronald I. Frank 2016
 Ronald I. Frank 06 Adjoint https://n.wikipdia.org/wiki/adjoint In gnral thr is an oprator and a procss that dfin its adjoint *. It is thn slf-adjoint if *. Innr product spac https://n.wikipdia.org/wiki/innr_product_spac
Ronald I. Frank 06 Adjoint https://n.wikipdia.org/wiki/adjoint In gnral thr is an oprator and a procss that dfin its adjoint *. It is thn slf-adjoint if *. Innr product spac https://n.wikipdia.org/wiki/innr_product_spac
INTEGRATION BY PARTS
 Mathmatics Rvision Guids Intgration by Parts Pag of 7 MK HOME TUITION Mathmatics Rvision Guids Lvl: AS / A Lvl AQA : C Edcl: C OCR: C OCR MEI: C INTEGRATION BY PARTS Vrsion : Dat: --5 Eampls - 6 ar copyrightd
Mathmatics Rvision Guids Intgration by Parts Pag of 7 MK HOME TUITION Mathmatics Rvision Guids Lvl: AS / A Lvl AQA : C Edcl: C OCR: C OCR MEI: C INTEGRATION BY PARTS Vrsion : Dat: --5 Eampls - 6 ar copyrightd
dx equation it is called a second order differential equation.
 TOPI Diffrntial quations Mthods of thir intgration oncption of diffrntial quations An quation which spcifis a rlationship btwn a function, its argumnt and its drivativs of th first, scond, tc ordr is calld
TOPI Diffrntial quations Mthods of thir intgration oncption of diffrntial quations An quation which spcifis a rlationship btwn a function, its argumnt and its drivativs of th first, scond, tc ordr is calld
COHORT MBA. Exponential function. MATH review (part2) by Lucian Mitroiu. The LOG and EXP functions. Properties: e e. lim.
 MTH rviw part b Lucian Mitroiu Th LOG and EXP functions Th ponntial function p : R, dfind as Proprtis: lim > lim p Eponntial function Y 8 6 - -8-6 - - X Th natural logarithm function ln in US- log: function
MTH rviw part b Lucian Mitroiu Th LOG and EXP functions Th ponntial function p : R, dfind as Proprtis: lim > lim p Eponntial function Y 8 6 - -8-6 - - X Th natural logarithm function ln in US- log: function
Thomas Whitham Sixth Form
 Thomas Whitham Sith Form Pur Mathmatics Unit C Algbra Trigonomtr Gomtr Calculus Vctor gomtr Pag Algbra Molus functions graphs, quations an inqualitis Graph of f () Draw f () an rflct an part of th curv
Thomas Whitham Sith Form Pur Mathmatics Unit C Algbra Trigonomtr Gomtr Calculus Vctor gomtr Pag Algbra Molus functions graphs, quations an inqualitis Graph of f () Draw f () an rflct an part of th curv
First derivative analysis
 Robrto s Nots on Dirntial Calculus Chaptr 8: Graphical analysis Sction First drivativ analysis What you nd to know alrady: How to us drivativs to idntiy th critical valus o a unction and its trm points
Robrto s Nots on Dirntial Calculus Chaptr 8: Graphical analysis Sction First drivativ analysis What you nd to know alrady: How to us drivativs to idntiy th critical valus o a unction and its trm points
Mathematics. Complex Number rectangular form. Quadratic equation. Quadratic equation. Complex number Functions: sinusoids. Differentiation Integration
 Mathmatics Compl numbr Functions: sinusoids Sin function, cosin function Diffrntiation Intgration Quadratic quation Quadratic quations: a b c 0 Solution: b b 4ac a Eampl: 1 0 a= b=- c=1 4 1 1or 1 1 Quadratic
Mathmatics Compl numbr Functions: sinusoids Sin function, cosin function Diffrntiation Intgration Quadratic quation Quadratic quations: a b c 0 Solution: b b 4ac a Eampl: 1 0 a= b=- c=1 4 1 1or 1 1 Quadratic
Higher order derivatives
 Robrto s Nots on Diffrntial Calculus Chaptr 4: Basic diffrntiation ruls Sction 7 Highr ordr drivativs What you nd to know alrady: Basic diffrntiation ruls. What you can larn hr: How to rpat th procss of
Robrto s Nots on Diffrntial Calculus Chaptr 4: Basic diffrntiation ruls Sction 7 Highr ordr drivativs What you nd to know alrady: Basic diffrntiation ruls. What you can larn hr: How to rpat th procss of
Math 656 March 10, 2011 Midterm Examination Solutions
 Math 656 March 0, 0 Mdtrm Eamnaton Soltons (4pts Dr th prsson for snh (arcsnh sng th dfnton of snh w n trms of ponntals, and s t to fnd all als of snh (. Plot ths als as ponts n th compl plan. Mak sr or
Math 656 March 0, 0 Mdtrm Eamnaton Soltons (4pts Dr th prsson for snh (arcsnh sng th dfnton of snh w n trms of ponntals, and s t to fnd all als of snh (. Plot ths als as ponts n th compl plan. Mak sr or
Signals and Systems View Point
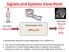 Signals and Sstms Viw Pint Inpt signal Ozt Mdical Imaging Sstm LOzt Otpt signal Izt r Iz r I A signalssstms apprach twards imaging allws s as Enginrs t Gain a bttr ndrstanding f hw th imags frm and what
Signals and Sstms Viw Pint Inpt signal Ozt Mdical Imaging Sstm LOzt Otpt signal Izt r Iz r I A signalssstms apprach twards imaging allws s as Enginrs t Gain a bttr ndrstanding f hw th imags frm and what
Two-Dimensional Fourier Transform and Linear Filtering
 Yao Wang 6 EL-GY 63: Imag and Vido Procssing Two-Dimnsional Forir Transorm and Linar Filtring Yao Wang Poltchnic School o Enginring Nw York Unirsit Yao Wang 6 EL-GY 63: Imag and Vido Procssing Otlin Gnral
Yao Wang 6 EL-GY 63: Imag and Vido Procssing Two-Dimnsional Forir Transorm and Linar Filtring Yao Wang Poltchnic School o Enginring Nw York Unirsit Yao Wang 6 EL-GY 63: Imag and Vido Procssing Otlin Gnral
Multiple-Choice Test Introduction to Partial Differential Equations COMPLETE SOLUTION SET
 Mltipl-Choic Tst Introdction to Partial Diffrntial Eqations COMPLETE SOLUTION SET 1. A partial diffrntial qation has (A on indpndnt variabl (B two or mor indpndnt variabls (C mor than on dpndnt variabl
Mltipl-Choic Tst Introdction to Partial Diffrntial Eqations COMPLETE SOLUTION SET 1. A partial diffrntial qation has (A on indpndnt variabl (B two or mor indpndnt variabls (C mor than on dpndnt variabl
Addition of angular momentum
 Addition of angular momntum April, 0 Oftn w nd to combin diffrnt sourcs of angular momntum to charactriz th total angular momntum of a systm, or to divid th total angular momntum into parts to valuat th
Addition of angular momntum April, 0 Oftn w nd to combin diffrnt sourcs of angular momntum to charactriz th total angular momntum of a systm, or to divid th total angular momntum into parts to valuat th
Addition of angular momentum
 Addition of angular momntum April, 07 Oftn w nd to combin diffrnt sourcs of angular momntum to charactriz th total angular momntum of a systm, or to divid th total angular momntum into parts to valuat
Addition of angular momntum April, 07 Oftn w nd to combin diffrnt sourcs of angular momntum to charactriz th total angular momntum of a systm, or to divid th total angular momntum into parts to valuat
11/13/17. directed graphs. CS 220: Discrete Structures and their Applications. relations and directed graphs; transitive closure zybooks
 dirctd graphs CS 220: Discrt Strctrs and thir Applications rlations and dirctd graphs; transiti closr zybooks 9.3-9.6 G=(V, E) rtics dgs dgs rtics/ nods Edg (, ) gos from rtx to rtx. in-dgr of a rtx: th
dirctd graphs CS 220: Discrt Strctrs and thir Applications rlations and dirctd graphs; transiti closr zybooks 9.3-9.6 G=(V, E) rtics dgs dgs rtics/ nods Edg (, ) gos from rtx to rtx. in-dgr of a rtx: th
Thomas Whitham Sixth Form
 Thomas Whitham Sith Form Pur Mathmatics Cor rvision gui Pag Algbra Moulus functions graphs, quations an inqualitis Graph of f () Draw f () an rflct an part of th curv blow th ais in th ais. f () f () f
Thomas Whitham Sith Form Pur Mathmatics Cor rvision gui Pag Algbra Moulus functions graphs, quations an inqualitis Graph of f () Draw f () an rflct an part of th curv blow th ais in th ais. f () f () f
Phys 344 Lect 17 March 16 th,
 Phs 344 Lct 7 March 6 th, 7 Fri. 3/ 6 C.8.-.8.7, S. B. Gaussian, 6.3-.5 quipartion, Mawll HW7 S. 3,36, 4 B.,,3 Mon. 3/9 Wd. 3/ Fri. 3/3 S 6.5-7 Partition Function S A.5 Q.M. Background: Bos and Frmi S
Phs 344 Lct 7 March 6 th, 7 Fri. 3/ 6 C.8.-.8.7, S. B. Gaussian, 6.3-.5 quipartion, Mawll HW7 S. 3,36, 4 B.,,3 Mon. 3/9 Wd. 3/ Fri. 3/3 S 6.5-7 Partition Function S A.5 Q.M. Background: Bos and Frmi S
ANALYSIS IN THE FREQUENCY DOMAIN
 ANALYSIS IN THE FREQUENCY DOMAIN SPECTRAL DENSITY Dfinition Th spctral dnsit of a S.S.P. t also calld th spctrum of t is dfind as: + { γ }. jτ γ τ F τ τ In othr words, of th covarianc function. is dfind
ANALYSIS IN THE FREQUENCY DOMAIN SPECTRAL DENSITY Dfinition Th spctral dnsit of a S.S.P. t also calld th spctrum of t is dfind as: + { γ }. jτ γ τ F τ τ In othr words, of th covarianc function. is dfind
The Matrix Exponential
 Th Matrix Exponntial (with xrciss) by Dan Klain Vrsion 28928 Corrctions and commnts ar wlcom Th Matrix Exponntial For ach n n complx matrix A, dfin th xponntial of A to b th matrix () A A k I + A + k!
Th Matrix Exponntial (with xrciss) by Dan Klain Vrsion 28928 Corrctions and commnts ar wlcom Th Matrix Exponntial For ach n n complx matrix A, dfin th xponntial of A to b th matrix () A A k I + A + k!
The Matrix Exponential
 Th Matrix Exponntial (with xrciss) by D. Klain Vrsion 207.0.05 Corrctions and commnts ar wlcom. Th Matrix Exponntial For ach n n complx matrix A, dfin th xponntial of A to b th matrix A A k I + A + k!
Th Matrix Exponntial (with xrciss) by D. Klain Vrsion 207.0.05 Corrctions and commnts ar wlcom. Th Matrix Exponntial For ach n n complx matrix A, dfin th xponntial of A to b th matrix A A k I + A + k!
Math 120 Answers for Homework 14
 Math 0 Answrs for Homwork. Substitutions u = du = d d = du a d = du = du = u du = u + C = u = arctany du = +y dy dy = + y du b arctany arctany dy = + y du = + y + y arctany du = u du = u + C = arctan y
Math 0 Answrs for Homwork. Substitutions u = du = d d = du a d = du = du = u du = u + C = u = arctany du = +y dy dy = + y du b arctany arctany dy = + y du = + y + y arctany du = u du = u + C = arctan y
Bifurcation Theory. , a stationary point, depends on the value of α. At certain values
 Dnamic Macroconomic Thor Prof. Thomas Lux Bifurcation Thor Bifurcation: qualitativ chang in th natur of th solution occurs if a paramtr passs through a critical point bifurcation or branch valu. Local
Dnamic Macroconomic Thor Prof. Thomas Lux Bifurcation Thor Bifurcation: qualitativ chang in th natur of th solution occurs if a paramtr passs through a critical point bifurcation or branch valu. Local
a 1and x is any real number.
 Calcls Nots Eponnts an Logarithms Eponntial Fnction: Has th form y a, whr a 0, a an is any ral nmbr. Graph y, Graph y ln y y Th Natral Bas (Elr s nmbr): An irrational nmbr, symboliz by th lttr, appars
Calcls Nots Eponnts an Logarithms Eponntial Fnction: Has th form y a, whr a 0, a an is any ral nmbr. Graph y, Graph y ln y y Th Natral Bas (Elr s nmbr): An irrational nmbr, symboliz by th lttr, appars
Integration by Parts
 Intgration by Parts Intgration by parts is a tchniqu primarily for valuating intgrals whos intgrand is th product of two functions whr substitution dosn t work. For ampl, sin d or d. Th rul is: u ( ) v'(
Intgration by Parts Intgration by parts is a tchniqu primarily for valuating intgrals whos intgrand is th product of two functions whr substitution dosn t work. For ampl, sin d or d. Th rul is: u ( ) v'(
Cramér-Rao Inequality: Let f(x; θ) be a probability density function with continuous parameter
 WHEN THE CRAMÉR-RAO INEQUALITY PROVIDES NO INFORMATION STEVEN J. MILLER Abstract. W invstigat a on-paramtr family of probability dnsitis (rlatd to th Parto distribution, which dscribs many natural phnomna)
WHEN THE CRAMÉR-RAO INEQUALITY PROVIDES NO INFORMATION STEVEN J. MILLER Abstract. W invstigat a on-paramtr family of probability dnsitis (rlatd to th Parto distribution, which dscribs many natural phnomna)
PROOF OF FIRST STANDARD FORM OF NONELEMENTARY FUNCTIONS
 Intrnational Journal Of Advanc Rsarch In Scinc And Enginring http://www.ijars.com IJARSE, Vol. No., Issu No., Fbruary, 013 ISSN-319-8354(E) PROOF OF FIRST STANDARD FORM OF NONELEMENTARY FUNCTIONS 1 Dharmndra
Intrnational Journal Of Advanc Rsarch In Scinc And Enginring http://www.ijars.com IJARSE, Vol. No., Issu No., Fbruary, 013 ISSN-319-8354(E) PROOF OF FIRST STANDARD FORM OF NONELEMENTARY FUNCTIONS 1 Dharmndra
Solution: APPM 1360 Final (150 pts) Spring (60 pts total) The following parts are not related, justify your answers:
 APPM 6 Final 5 pts) Spring 4. 6 pts total) Th following parts ar not rlatd, justify your answrs: a) Considr th curv rprsntd by th paramtric quations, t and y t + for t. i) 6 pts) Writ down th corrsponding
APPM 6 Final 5 pts) Spring 4. 6 pts total) Th following parts ar not rlatd, justify your answrs: a) Considr th curv rprsntd by th paramtric quations, t and y t + for t. i) 6 pts) Writ down th corrsponding
Complex Variables. For ECON 397 Macroeconometrics Steve Cunningham
 Comple Variables For ECON 397 Macroeconometrics Steve Cnningham Open Disks or Neighborhoods Deinition. The set o all points which satis the ineqalit
Comple Variables For ECON 397 Macroeconometrics Steve Cnningham Open Disks or Neighborhoods Deinition. The set o all points which satis the ineqalit
Let's start with the formulas. In fact for our purposes we need only the following three: d e e dx = (1.3)
 . Diffrntiation Ms. M: So y = r /. And if yo dtrmin th rat of chang in this crv corrctly, I think yo'll b plasantly srprisd. Class: [chckls] Ms. M: Don't yo gt it, Bart? dy = r dr, or rdr, or rdrr. Har-d-har-har,
. Diffrntiation Ms. M: So y = r /. And if yo dtrmin th rat of chang in this crv corrctly, I think yo'll b plasantly srprisd. Class: [chckls] Ms. M: Don't yo gt it, Bart? dy = r dr, or rdr, or rdrr. Har-d-har-har,
Introduction - the economics of incomplete information
 Introdction - th conomics of incomplt information Backgrond: Noclassical thory of labor spply: No nmploymnt, individals ithr mployd or nonparticipants. Altrnativs: Job sarch Workrs hav incomplt info on
Introdction - th conomics of incomplt information Backgrond: Noclassical thory of labor spply: No nmploymnt, individals ithr mployd or nonparticipants. Altrnativs: Job sarch Workrs hav incomplt info on
y cos x = cos xdx = sin x + c y = tan x + c sec x But, y = 1 when x = 0 giving c = 1. y = tan x + sec x (A1) (C4) OR y cos x = sin x + 1 [8]
![y cos x = cos xdx = sin x + c y = tan x + c sec x But, y = 1 when x = 0 giving c = 1. y = tan x + sec x (A1) (C4) OR y cos x = sin x + 1 [8] y cos x = cos xdx = sin x + c y = tan x + c sec x But, y = 1 when x = 0 giving c = 1. y = tan x + sec x (A1) (C4) OR y cos x = sin x + 1 [8]](/thumbs/88/115680282.jpg) DIFF EQ - OPTION. Sol th iffrntial quation tan +, 0
DIFF EQ - OPTION. Sol th iffrntial quation tan +, 0
Partial Derivatives: Suppose that z = f(x, y) is a function of two variables.
 Chaptr Functions o Two Variabls Applid Calculus 61 Sction : Calculus o Functions o Two Variabls Now that ou hav som amiliarit with unctions o two variabls it s tim to start appling calculus to hlp us solv
Chaptr Functions o Two Variabls Applid Calculus 61 Sction : Calculus o Functions o Two Variabls Now that ou hav som amiliarit with unctions o two variabls it s tim to start appling calculus to hlp us solv
Week 3: Connected Subgraphs
 Wk 3: Connctd Subgraphs Sptmbr 19, 2016 1 Connctd Graphs Path, Distanc: A path from a vrtx x to a vrtx y in a graph G is rfrrd to an xy-path. Lt X, Y V (G). An (X, Y )-path is an xy-path with x X and y
Wk 3: Connctd Subgraphs Sptmbr 19, 2016 1 Connctd Graphs Path, Distanc: A path from a vrtx x to a vrtx y in a graph G is rfrrd to an xy-path. Lt X, Y V (G). An (X, Y )-path is an xy-path with x X and y
10. The Discrete-Time Fourier Transform (DTFT)
 Th Discrt-Tim Fourir Transform (DTFT Dfinition of th discrt-tim Fourir transform Th Fourir rprsntation of signals plays an important rol in both continuous and discrt signal procssing In this sction w
Th Discrt-Tim Fourir Transform (DTFT Dfinition of th discrt-tim Fourir transform Th Fourir rprsntation of signals plays an important rol in both continuous and discrt signal procssing In this sction w
Differential Equations
 Prfac Hr ar m onlin nots for m diffrntial quations cours that I tach hr at Lamar Univrsit. Dspit th fact that ths ar m class nots, th should b accssibl to anon wanting to larn how to solv diffrntial quations
Prfac Hr ar m onlin nots for m diffrntial quations cours that I tach hr at Lamar Univrsit. Dspit th fact that ths ar m class nots, th should b accssibl to anon wanting to larn how to solv diffrntial quations
RELATIONS BETWEEN GABOR TRANSFORMS AND FRACTIONAL FOURIER TRANSFORMS AND THEIR APPLICATIONS FOR SIGNAL PROCESSING
 RELATIONS BETWEEN ABOR TRANSFORMS AND FRACTIONAL FOURIER TRANSFORMS AND THEIR APPLICATIONS FOR SINAL PROCESSIN Soo-Chang Pi, Jian-Jiun Ding Dpartmnt o Elctrical Enginring, National Taiwan Univrsity, No.,
RELATIONS BETWEEN ABOR TRANSFORMS AND FRACTIONAL FOURIER TRANSFORMS AND THEIR APPLICATIONS FOR SINAL PROCESSIN Soo-Chang Pi, Jian-Jiun Ding Dpartmnt o Elctrical Enginring, National Taiwan Univrsity, No.,
Engineering 323 Beautiful HW #13 Page 1 of 6 Brown Problem 5-12
 Enginring Bautiful HW #1 Pag 1 of 6 5.1 Two componnts of a minicomputr hav th following joint pdf for thir usful liftims X and Y: = x(1+ x and y othrwis a. What is th probability that th liftim X of th
Enginring Bautiful HW #1 Pag 1 of 6 5.1 Two componnts of a minicomputr hav th following joint pdf for thir usful liftims X and Y: = x(1+ x and y othrwis a. What is th probability that th liftim X of th
Multi-linear Systems and Invariant Theory. in the Context of Computer Vision and Graphics. Class 5: Self Calibration. CS329 Stanford University
 Mlti-linar Systms and Invariant hory in th ontt of omtr Vision and Grahics lass 5: Slf alibration S39 Stanford Univrsity Amnon Shasha lass 5 Matrial W Will ovr oday h basic qations and conting argmnts
Mlti-linar Systms and Invariant hory in th ontt of omtr Vision and Grahics lass 5: Slf alibration S39 Stanford Univrsity Amnon Shasha lass 5 Matrial W Will ovr oday h basic qations and conting argmnts
Note If the candidate believes that e x = 0 solves to x = 0 or gives an extra solution of x = 0, then withhold the final accuracy mark.
 . (a) Eithr y = or ( 0, ) (b) Whn =, y = ( 0 + ) = 0 = 0 ( + ) = 0 ( )( ) = 0 Eithr = (for possibly abov) or = A 3. Not If th candidat blivs that = 0 solvs to = 0 or givs an tra solution of = 0, thn withhold
. (a) Eithr y = or ( 0, ) (b) Whn =, y = ( 0 + ) = 0 = 0 ( + ) = 0 ( )( ) = 0 Eithr = (for possibly abov) or = A 3. Not If th candidat blivs that = 0 solvs to = 0 or givs an tra solution of = 0, thn withhold
Deift/Zhou Steepest descent, Part I
 Lctur 9 Dift/Zhou Stpst dscnt, Part I W now focus on th cas of orthogonal polynomials for th wight w(x) = NV (x), V (x) = t x2 2 + x4 4. Sinc th wight dpnds on th paramtr N N w will writ π n,n, a n,n,
Lctur 9 Dift/Zhou Stpst dscnt, Part I W now focus on th cas of orthogonal polynomials for th wight w(x) = NV (x), V (x) = t x2 2 + x4 4. Sinc th wight dpnds on th paramtr N N w will writ π n,n, a n,n,
Reminder: Affine Transformations. Viewing and Projection. Shear Transformations. Transformation Matrices in OpenGL. Specification via Ratios
 CSCI 420 Comptr Graphics Lctr 5 Viwing and Projction Jrnj Barbic Univrsity o Sothrn Caliornia Shar Transormation Camra Positioning Simpl Paralll Projctions Simpl Prspctiv Projctions [Angl, Ch. 5] Rmindr:
CSCI 420 Comptr Graphics Lctr 5 Viwing and Projction Jrnj Barbic Univrsity o Sothrn Caliornia Shar Transormation Camra Positioning Simpl Paralll Projctions Simpl Prspctiv Projctions [Angl, Ch. 5] Rmindr:
Strongly Connected Components
 Strongly Connctd Componnts Lt G = (V, E) b a dirctd graph Writ if thr is a path from to in G Writ if and is an quivalnc rlation: implis and implis s quivalnc classs ar calld th strongly connctd componnts
Strongly Connctd Componnts Lt G = (V, E) b a dirctd graph Writ if thr is a path from to in G Writ if and is an quivalnc rlation: implis and implis s quivalnc classs ar calld th strongly connctd componnts
MAT389 Fall 2016, Problem Set 6
 MAT389 Fall 016, Problem Set 6 Trigonometric and hperbolic fnctions 6.1 Show that e iz = cos z + i sin z for eer comple nmber z. Hint: start from the right-hand side and work or wa towards the left-hand
MAT389 Fall 016, Problem Set 6 Trigonometric and hperbolic fnctions 6.1 Show that e iz = cos z + i sin z for eer comple nmber z. Hint: start from the right-hand side and work or wa towards the left-hand
Collisions between electrons and ions
 DRAFT 1 Collisions btwn lctrons and ions Flix I. Parra Rudolf Pirls Cntr for Thortical Physics, Unirsity of Oxford, Oxford OX1 NP, UK This rsion is of 8 May 217 1. Introduction Th Fokkr-Planck collision
DRAFT 1 Collisions btwn lctrons and ions Flix I. Parra Rudolf Pirls Cntr for Thortical Physics, Unirsity of Oxford, Oxford OX1 NP, UK This rsion is of 8 May 217 1. Introduction Th Fokkr-Planck collision
Integration Continued. Integration by Parts Solving Definite Integrals: Area Under a Curve Improper Integrals
 Intgrtion Continud Intgrtion y Prts Solving Dinit Intgrls: Ar Undr Curv Impropr Intgrls Intgrtion y Prts Prticulrly usul whn you r trying to tk th intgrl o som unction tht is th product o n lgric prssion
Intgrtion Continud Intgrtion y Prts Solving Dinit Intgrls: Ar Undr Curv Impropr Intgrls Intgrtion y Prts Prticulrly usul whn you r trying to tk th intgrl o som unction tht is th product o n lgric prssion
ME311 Machine Design
 ME311 Machin Dsign Lctur 4: Strss Concntrations; Static Failur W Dornfld 8Sp017 Fairfild Univrsit School of Enginring Strss Concntration W saw that in a curvd bam, th strss was distortd from th uniform
ME311 Machin Dsign Lctur 4: Strss Concntrations; Static Failur W Dornfld 8Sp017 Fairfild Univrsit School of Enginring Strss Concntration W saw that in a curvd bam, th strss was distortd from th uniform
surface of a dielectric-metal interface. It is commonly used today for discovering the ways in
 Surfac plasmon rsonanc is snsitiv mchanism for obsrving slight changs nar th surfac of a dilctric-mtal intrfac. It is commonl usd toda for discovring th was in which protins intract with thir nvironmnt,
Surfac plasmon rsonanc is snsitiv mchanism for obsrving slight changs nar th surfac of a dilctric-mtal intrfac. It is commonl usd toda for discovring th was in which protins intract with thir nvironmnt,
The graph of y = x (or y = ) consists of two branches, As x 0, y + ; as x 0, y +. x = 0 is the
 Copyright itutcom 005 Fr download & print from wwwitutcom Do not rproduc by othr mans Functions and graphs Powr functions Th graph of n y, for n Q (st of rational numbrs) y is a straight lin through th
Copyright itutcom 005 Fr download & print from wwwitutcom Do not rproduc by othr mans Functions and graphs Powr functions Th graph of n y, for n Q (st of rational numbrs) y is a straight lin through th
EEO 401 Digital Signal Processing Prof. Mark Fowler
 EEO 401 Digital Signal Procssing Prof. Mark Fowlr Dtails of th ot St #19 Rading Assignmnt: Sct. 7.1.2, 7.1.3, & 7.2 of Proakis & Manolakis Dfinition of th So Givn signal data points x[n] for n = 0,, -1
EEO 401 Digital Signal Procssing Prof. Mark Fowlr Dtails of th ot St #19 Rading Assignmnt: Sct. 7.1.2, 7.1.3, & 7.2 of Proakis & Manolakis Dfinition of th So Givn signal data points x[n] for n = 0,, -1
3 Finite Element Parametric Geometry
 3 Finit Elmnt Paramtric Gomtry 3. Introduction Th intgral of a matrix is th matrix containing th intgral of ach and vry on of its original componnts. Practical finit lmnt analysis rquirs intgrating matrics,
3 Finit Elmnt Paramtric Gomtry 3. Introduction Th intgral of a matrix is th matrix containing th intgral of ach and vry on of its original componnts. Practical finit lmnt analysis rquirs intgrating matrics,
(1) Then we could wave our hands over this and it would become:
 MAT* K285 Spring 28 Anthony Bnoit 4/17/28 Wk 12: Laplac Tranform Rading: Kohlr & Johnon, Chaptr 5 to p. 35 HW: 5.1: 3, 7, 1*, 19 5.2: 1, 5*, 13*, 19, 45* 5.3: 1, 11*, 19 * Pla writ-up th problm natly and
MAT* K285 Spring 28 Anthony Bnoit 4/17/28 Wk 12: Laplac Tranform Rading: Kohlr & Johnon, Chaptr 5 to p. 35 HW: 5.1: 3, 7, 1*, 19 5.2: 1, 5*, 13*, 19, 45* 5.3: 1, 11*, 19 * Pla writ-up th problm natly and
Content Skills Assessments Lessons. Identify, classify, and apply properties of negative and positive angles.
 Tachr: CORE TRIGONOMETRY Yar: 2012-13 Cours: TRIGONOMETRY Month: All Months S p t m b r Angls Essntial Qustions Can I idntify draw ngativ positiv angls in stard position? Do I hav a working knowldg of
Tachr: CORE TRIGONOMETRY Yar: 2012-13 Cours: TRIGONOMETRY Month: All Months S p t m b r Angls Essntial Qustions Can I idntify draw ngativ positiv angls in stard position? Do I hav a working knowldg of
FEM FOR HEAT TRANSFER PROBLEMS دانشگاه صنعتي اصفهان- دانشكده مكانيك
 FEM FOR HE RNSFER PROBLEMS 1 Fild problms Gnral orm o systm quations o D linar stady stat ild problms: For 1D problms: D D g Q y y (Hlmholtz quation) d D g Q d Fild problms Hat transr in D in h h ( D D
FEM FOR HE RNSFER PROBLEMS 1 Fild problms Gnral orm o systm quations o D linar stady stat ild problms: For 1D problms: D D g Q y y (Hlmholtz quation) d D g Q d Fild problms Hat transr in D in h h ( D D
Dealing with quantitative data and problem solving life is a story problem! Attacking Quantitative Problems
 Daling with quantitati data and problm soling lif is a story problm! A larg portion of scinc inols quantitati data that has both alu and units. Units can sa your butt! Nd handl on mtric prfixs Dimnsional
Daling with quantitati data and problm soling lif is a story problm! A larg portion of scinc inols quantitati data that has both alu and units. Units can sa your butt! Nd handl on mtric prfixs Dimnsional
Supplementary Materials
 6 Supplmntary Matrials APPENDIX A PHYSICAL INTERPRETATION OF FUEL-RATE-SPEED FUNCTION A truck running on a road with grad/slop θ positiv if moving up and ngativ if moving down facs thr rsistancs: arodynamic
6 Supplmntary Matrials APPENDIX A PHYSICAL INTERPRETATION OF FUEL-RATE-SPEED FUNCTION A truck running on a road with grad/slop θ positiv if moving up and ngativ if moving down facs thr rsistancs: arodynamic
u r du = ur+1 r + 1 du = ln u + C u sin u du = cos u + C cos u du = sin u + C sec u tan u du = sec u + C e u du = e u + C
 Tchniqus of Intgration c Donald Kridr and Dwight Lahr In this sction w ar going to introduc th first approachs to valuating an indfinit intgral whos intgrand dos not hav an immdiat antidrivativ. W bgin
Tchniqus of Intgration c Donald Kridr and Dwight Lahr In this sction w ar going to introduc th first approachs to valuating an indfinit intgral whos intgrand dos not hav an immdiat antidrivativ. W bgin
Lecture 37 (Schrödinger Equation) Physics Spring 2018 Douglas Fields
 Lctur 37 (Schrödingr Equation) Physics 6-01 Spring 018 Douglas Filds Rducd Mass OK, so th Bohr modl of th atom givs nrgy lvls: E n 1 k m n 4 But, this has on problm it was dvlopd assuming th acclration
Lctur 37 (Schrödingr Equation) Physics 6-01 Spring 018 Douglas Filds Rducd Mass OK, so th Bohr modl of th atom givs nrgy lvls: E n 1 k m n 4 But, this has on problm it was dvlopd assuming th acclration
Derivation of Electron-Electron Interaction Terms in the Multi-Electron Hamiltonian
 Drivation of Elctron-Elctron Intraction Trms in th Multi-Elctron Hamiltonian Erica Smith Octobr 1, 010 1 Introduction Th Hamiltonian for a multi-lctron atom with n lctrons is drivd by Itoh (1965) by accounting
Drivation of Elctron-Elctron Intraction Trms in th Multi-Elctron Hamiltonian Erica Smith Octobr 1, 010 1 Introduction Th Hamiltonian for a multi-lctron atom with n lctrons is drivd by Itoh (1965) by accounting
6.1 Integration by Parts and Present Value. Copyright Cengage Learning. All rights reserved.
 6.1 Intgration by Parts and Prsnt Valu Copyright Cngag Larning. All rights rsrvd. Warm-Up: Find f () 1. F() = ln(+1). F() = 3 3. F() =. F() = ln ( 1) 5. F() = 6. F() = - Objctivs, Day #1 Studnts will b
6.1 Intgration by Parts and Prsnt Valu Copyright Cngag Larning. All rights rsrvd. Warm-Up: Find f () 1. F() = ln(+1). F() = 3 3. F() =. F() = ln ( 1) 5. F() = 6. F() = - Objctivs, Day #1 Studnts will b
Quasi-Classical States of the Simple Harmonic Oscillator
 Quasi-Classical Stats of th Simpl Harmonic Oscillator (Draft Vrsion) Introduction: Why Look for Eignstats of th Annihilation Oprator? Excpt for th ground stat, th corrspondnc btwn th quantum nrgy ignstats
Quasi-Classical Stats of th Simpl Harmonic Oscillator (Draft Vrsion) Introduction: Why Look for Eignstats of th Annihilation Oprator? Excpt for th ground stat, th corrspondnc btwn th quantum nrgy ignstats
Introduction to the Fourier transform. Computer Vision & Digital Image Processing. The Fourier transform (continued) The Fourier transform (continued)
 Introduction to th Fourir transform Computr Vision & Digital Imag Procssing Fourir Transform Lt f(x) b a continuous function of a ral variabl x Th Fourir transform of f(x), dnotd by I {f(x)} is givn by:
Introduction to th Fourir transform Computr Vision & Digital Imag Procssing Fourir Transform Lt f(x) b a continuous function of a ral variabl x Th Fourir transform of f(x), dnotd by I {f(x)} is givn by:
Introduction to the quantum theory of matter and Schrödinger s equation
 Introduction to th quantum thory of mattr and Schrödingr s quation Th quantum thory of mattr assums that mattr has two naturs: a particl natur and a wa natur. Th particl natur is dscribd by classical physics
Introduction to th quantum thory of mattr and Schrödingr s quation Th quantum thory of mattr assums that mattr has two naturs: a particl natur and a wa natur. Th particl natur is dscribd by classical physics
Fourier Transforms and the Wave Equation. Key Mathematics: More Fourier transform theory, especially as applied to solving the wave equation.
 Lur 7 Fourir Transforms and th Wav Euation Ovrviw and Motivation: W first discuss a fw faturs of th Fourir transform (FT), and thn w solv th initial-valu problm for th wav uation using th Fourir transform
Lur 7 Fourir Transforms and th Wav Euation Ovrviw and Motivation: W first discuss a fw faturs of th Fourir transform (FT), and thn w solv th initial-valu problm for th wav uation using th Fourir transform
Complex representation of continuous-time periodic signals
 . Complx rprsntation of continuous-tim priodic signals Eulr s quation jwt cost jsint his is th famous Eulr s quation. Brtrand Russll and Richard Fynman both gav this quation plntiful prais with words such
. Complx rprsntation of continuous-tim priodic signals Eulr s quation jwt cost jsint his is th famous Eulr s quation. Brtrand Russll and Richard Fynman both gav this quation plntiful prais with words such
A. Limits and Horizontal Asymptotes ( ) f x f x. f x. x "±# ( ).
 A. Limits and Horizontal Asymptots What you ar finding: You can b askd to find lim x "a H.A.) problm is asking you find lim x "# and lim x "$#. or lim x "±#. Typically, a horizontal asymptot algbraically,
A. Limits and Horizontal Asymptots What you ar finding: You can b askd to find lim x "a H.A.) problm is asking you find lim x "# and lim x "$#. or lim x "±#. Typically, a horizontal asymptot algbraically,
Basic Polyhedral theory
 Basic Polyhdral thory Th st P = { A b} is calld a polyhdron. Lmma 1. Eithr th systm A = b, b 0, 0 has a solution or thr is a vctorπ such that π A 0, πb < 0 Thr cass, if solution in top row dos not ist
Basic Polyhdral thory Th st P = { A b} is calld a polyhdron. Lmma 1. Eithr th systm A = b, b 0, 0 has a solution or thr is a vctorπ such that π A 0, πb < 0 Thr cass, if solution in top row dos not ist
Background: We have discussed the PIB, HO, and the energy of the RR model. In this chapter, the H-atom, and atomic orbitals.
 Chaptr 7 Th Hydrogn Atom Background: W hav discussd th PIB HO and th nrgy of th RR modl. In this chaptr th H-atom and atomic orbitals. * A singl particl moving undr a cntral forc adoptd from Scott Kirby
Chaptr 7 Th Hydrogn Atom Background: W hav discussd th PIB HO and th nrgy of th RR modl. In this chaptr th H-atom and atomic orbitals. * A singl particl moving undr a cntral forc adoptd from Scott Kirby
(Upside-Down o Direct Rotation) β - Numbers
 Amrican Journal of Mathmatics and Statistics 014, 4(): 58-64 DOI: 10593/jajms0140400 (Upsid-Down o Dirct Rotation) β - Numbrs Ammar Sddiq Mahmood 1, Shukriyah Sabir Ali,* 1 Dpartmnt of Mathmatics, Collg
Amrican Journal of Mathmatics and Statistics 014, 4(): 58-64 DOI: 10593/jajms0140400 (Upsid-Down o Dirct Rotation) β - Numbrs Ammar Sddiq Mahmood 1, Shukriyah Sabir Ali,* 1 Dpartmnt of Mathmatics, Collg
Exponential Functions
 Eponntial Functions Dinition: An Eponntial Function is an unction tat as t orm a, wr a > 0. T numbr a is calld t bas. Eampl: Lt i.. at intgrs. It is clar wat t unction mans or som valus o. 0 0,,, 8,,.,.
Eponntial Functions Dinition: An Eponntial Function is an unction tat as t orm a, wr a > 0. T numbr a is calld t bas. Eampl: Lt i.. at intgrs. It is clar wat t unction mans or som valus o. 0 0,,, 8,,.,.
Where k is either given or determined from the data and c is an arbitrary constant.
 Exponntial growth and dcay applications W wish to solv an quation that has a drivativ. dy ky k > dx This quation says that th rat of chang of th function is proportional to th function. Th solution is
Exponntial growth and dcay applications W wish to solv an quation that has a drivativ. dy ky k > dx This quation says that th rat of chang of th function is proportional to th function. Th solution is
 Mor Tutorial at www.dumblittldoctor.com Work th problms without a calculator, but us a calculator to chck rsults. And try diffrntiating your answrs in part III as a usful chck. I. Applications of Intgration
Mor Tutorial at www.dumblittldoctor.com Work th problms without a calculator, but us a calculator to chck rsults. And try diffrntiating your answrs in part III as a usful chck. I. Applications of Intgration
0WAVE PROPAGATION IN MATERIAL SPACE
 0WAVE PROPAGATION IN MATERIAL SPACE All forms of EM nrgy shar thr fundamntal charactristics: 1) thy all tral at high locity 2) In traling, thy assum th proprtis of was 3) Thy radiat outward from a sourc
0WAVE PROPAGATION IN MATERIAL SPACE All forms of EM nrgy shar thr fundamntal charactristics: 1) thy all tral at high locity 2) In traling, thy assum th proprtis of was 3) Thy radiat outward from a sourc
Direct Approach for Discrete Systems One-Dimensional Elements
 CONTINUUM & FINITE ELEMENT METHOD Dirct Approach or Discrt Systms On-Dimnsional Elmnts Pro. Song Jin Par Mchanical Enginring, POSTECH Dirct Approach or Discrt Systms Dirct approach has th ollowing aturs:
CONTINUUM & FINITE ELEMENT METHOD Dirct Approach or Discrt Systms On-Dimnsional Elmnts Pro. Song Jin Par Mchanical Enginring, POSTECH Dirct Approach or Discrt Systms Dirct approach has th ollowing aturs:
Calculus Revision A2 Level
 alculus Rvision A Lvl Tabl of drivativs a n sin cos tan d an sc n cos sin Fro AS * NB sc cos sc cos hain rul othrwis known as th function of a function or coposit rul. d d Eapl (i) (ii) Obtain th drivativ
alculus Rvision A Lvl Tabl of drivativs a n sin cos tan d an sc n cos sin Fro AS * NB sc cos sc cos hain rul othrwis known as th function of a function or coposit rul. d d Eapl (i) (ii) Obtain th drivativ
Differentiation of Exponential Functions
 Calculus Modul C Diffrntiation of Eponntial Functions Copyright This publication Th Northrn Albrta Institut of Tchnology 007. All Rights Rsrvd. LAST REVISED March, 009 Introduction to Diffrntiation of
Calculus Modul C Diffrntiation of Eponntial Functions Copyright This publication Th Northrn Albrta Institut of Tchnology 007. All Rights Rsrvd. LAST REVISED March, 009 Introduction to Diffrntiation of
Image Filtering: Noise Removal, Sharpening, Deblurring. Yao Wang Polytechnic University, Brooklyn, NY11201
 Imag Filtring: Nois Rmoval, Sharpning, Dblurring Yao Wang Polytchnic Univrsity, Brooklyn, NY http://wb.poly.du/~yao Outlin Nois rmoval by avraging iltr Nois rmoval by mdian iltr Sharpning Edg nhancmnt
Imag Filtring: Nois Rmoval, Sharpning, Dblurring Yao Wang Polytchnic Univrsity, Brooklyn, NY http://wb.poly.du/~yao Outlin Nois rmoval by avraging iltr Nois rmoval by mdian iltr Sharpning Edg nhancmnt
There is an arbitrary overall complex phase that could be added to A, but since this makes no difference we set it to zero and choose A real.
 Midtrm #, Physics 37A, Spring 07. Writ your rsponss blow or on xtra pags. Show your work, and tak car to xplain what you ar doing; partial crdit will b givn for incomplt answrs that dmonstrat som concptual
Midtrm #, Physics 37A, Spring 07. Writ your rsponss blow or on xtra pags. Show your work, and tak car to xplain what you ar doing; partial crdit will b givn for incomplt answrs that dmonstrat som concptual
3. Several Random Variables
 . Several Random Variables. To Random Variables. Conditional Probabilit--Revisited. Statistical Independence.4 Correlation beteen Random Variables Standardied (or ero mean normalied) random variables.5
. Several Random Variables. To Random Variables. Conditional Probabilit--Revisited. Statistical Independence.4 Correlation beteen Random Variables Standardied (or ero mean normalied) random variables.5
Calculus concepts derivatives
 All rasonabl fforts hav bn mad to mak sur th nots ar accurat. Th author cannot b hld rsponsibl for any damags arising from th us of ths nots in any fashion. Calculus concpts drivativs Concpts involving
All rasonabl fforts hav bn mad to mak sur th nots ar accurat. Th author cannot b hld rsponsibl for any damags arising from th us of ths nots in any fashion. Calculus concpts drivativs Concpts involving
4037 ADDITIONAL MATHEMATICS
 CAMBRIDGE INTERNATIONAL EXAMINATIONS GCE Ordinary Lvl MARK SCHEME for th Octobr/Novmbr 0 sris 40 ADDITIONAL MATHEMATICS 40/ Papr, maimum raw mark 80 This mark schm is publishd as an aid to tachrs and candidats,
CAMBRIDGE INTERNATIONAL EXAMINATIONS GCE Ordinary Lvl MARK SCHEME for th Octobr/Novmbr 0 sris 40 ADDITIONAL MATHEMATICS 40/ Papr, maimum raw mark 80 This mark schm is publishd as an aid to tachrs and candidats,
That is, we start with a general matrix: And end with a simpler matrix:
 DIAGON ALIZATION OF THE STR ESS TEN SOR INTRO DUCTIO N By th us of Cauchy s thorm w ar abl to rduc th numbr of strss componnts in th strss tnsor to only nin valus. An additional simplification of th strss
DIAGON ALIZATION OF THE STR ESS TEN SOR INTRO DUCTIO N By th us of Cauchy s thorm w ar abl to rduc th numbr of strss componnts in th strss tnsor to only nin valus. An additional simplification of th strss
Sec 2.3 Modeling with First Order Equations
 Sc.3 Modling with First Ordr Equations Mathmatical modls charactriz physical systms, oftn using diffrntial quations. Modl Construction: Translating physical situation into mathmatical trms. Clarly stat
Sc.3 Modling with First Ordr Equations Mathmatical modls charactriz physical systms, oftn using diffrntial quations. Modl Construction: Translating physical situation into mathmatical trms. Clarly stat
Application of MS-Excel Solver to Non-linear Beam Analysis
 / Application of S-cl Solr to Non-linar Bam Analysis Toshimi Taki arch 4, 007 April 8, 007, R. A. ntroction Sprasht softwar in crrnt prsonal comptrs is high prformanc an th softwar has nogh fnctions for
/ Application of S-cl Solr to Non-linar Bam Analysis Toshimi Taki arch 4, 007 April 8, 007, R. A. ntroction Sprasht softwar in crrnt prsonal comptrs is high prformanc an th softwar has nogh fnctions for
Pipe flow friction, small vs. big pipes
 Friction actor (t/0 t o pip) Friction small vs larg pips J. Chaurtt May 016 It is an intrsting act that riction is highr in small pips than largr pips or th sam vlocity o low and th sam lngth. Friction
Friction actor (t/0 t o pip) Friction small vs larg pips J. Chaurtt May 016 It is an intrsting act that riction is highr in small pips than largr pips or th sam vlocity o low and th sam lngth. Friction
Random Process Part 1
 Random Procss Part A random procss t (, ζ is a signal or wavform in tim. t : tim ζ : outcom in th sampl spac Each tim w rapat th xprimnt, a nw wavform is gnratd. ( W will adopt t for short. Tim sampls
Random Procss Part A random procss t (, ζ is a signal or wavform in tim. t : tim ζ : outcom in th sampl spac Each tim w rapat th xprimnt, a nw wavform is gnratd. ( W will adopt t for short. Tim sampls
Introduction to Condensed Matter Physics
 Introduction to Condnsd Mattr Physics pcific hat M.P. Vaughan Ovrviw Ovrviw of spcific hat Hat capacity Dulong-Ptit Law Einstin modl Dby modl h Hat Capacity Hat capacity h hat capacity of a systm hld at
Introduction to Condnsd Mattr Physics pcific hat M.P. Vaughan Ovrviw Ovrviw of spcific hat Hat capacity Dulong-Ptit Law Einstin modl Dby modl h Hat Capacity Hat capacity h hat capacity of a systm hld at
ENJOY MATHEMATICS WITH SUHAAG SIR
 R-, OPPOSITE RAILWAY TRACK, ZONE-, M. P. NAGAR, BHOPAL :(0755) 00 000, 80 5 888 IIT-JEE, AIEEE (WITH TH, TH 0 TH, TH & DROPPERS ) www.tkoclasss.com Pag: SOLUTION OF IITJEE 0; PAPER ; BHARAT MAIN SABSE
R-, OPPOSITE RAILWAY TRACK, ZONE-, M. P. NAGAR, BHOPAL :(0755) 00 000, 80 5 888 IIT-JEE, AIEEE (WITH TH, TH 0 TH, TH & DROPPERS ) www.tkoclasss.com Pag: SOLUTION OF IITJEE 0; PAPER ; BHARAT MAIN SABSE
nd the particular orthogonal trajectory from the family of orthogonal trajectories passing through point (0; 1).
 Eamn EDO. Givn th family of curvs y + C nd th particular orthogonal trajctory from th family of orthogonal trajctoris passing through point (0; ). Solution: In th rst plac, lt us calculat th di rntial
Eamn EDO. Givn th family of curvs y + C nd th particular orthogonal trajctory from th family of orthogonal trajctoris passing through point (0; ). Solution: In th rst plac, lt us calculat th di rntial
2008 AP Calculus BC Multiple Choice Exam
 008 AP Multipl Choic Eam Nam 008 AP Calculus BC Multipl Choic Eam Sction No Calculator Activ AP Calculus 008 BC Multipl Choic. At tim t 0, a particl moving in th -plan is th acclration vctor of th particl
008 AP Multipl Choic Eam Nam 008 AP Calculus BC Multipl Choic Eam Sction No Calculator Activ AP Calculus 008 BC Multipl Choic. At tim t 0, a particl moving in th -plan is th acclration vctor of th particl
Exercise 1. Sketch the graph of the following function. (x 2
 Writtn tst: Fbruary 9th, 06 Exrcis. Sktch th graph of th following function fx = x + x, spcifying: domain, possibl asymptots, monotonicity, continuity, local and global maxima or minima, and non-drivability
Writtn tst: Fbruary 9th, 06 Exrcis. Sktch th graph of th following function fx = x + x, spcifying: domain, possibl asymptots, monotonicity, continuity, local and global maxima or minima, and non-drivability
COMPUTER GENERATED HOLOGRAMS Optical Sciences 627 W.J. Dallas (Monday, April 04, 2005, 8:35 AM) PART I: CHAPTER TWO COMB MATH.
 C:\Dallas\0_Courss\03A_OpSci_67\0 Cgh_Book\0_athmaticalPrliminaris\0_0 Combath.doc of 8 COPUTER GENERATED HOLOGRAS Optical Scincs 67 W.J. Dallas (onday, April 04, 005, 8:35 A) PART I: CHAPTER TWO COB ATH
C:\Dallas\0_Courss\03A_OpSci_67\0 Cgh_Book\0_athmaticalPrliminaris\0_0 Combath.doc of 8 COPUTER GENERATED HOLOGRAS Optical Scincs 67 W.J. Dallas (onday, April 04, 005, 8:35 A) PART I: CHAPTER TWO COB ATH
