STUDY PACKAGE. Subject : Mathematics Topic : COMPLEX NUMBER Available Online :
|
|
|
- Walter Atkinson
- 6 years ago
- Views:
Transcription
1 fo/u fopkjr Hkh# tu] ugha vkjehks dke] fofr ns[k NksM+s rqjar e/;e eu dj ';kea q#"k flag lady dj] lgrs fofr vusd] ^cuk^ u NksM+s /;s; dks] j?kqcj jk[ks VsdAA jfpr% ekuo /kez.ksrk ln~xq# Jh j.knksm+nklth egkjkt STUDY PACKAGE Subject : Mathematcs Topc : COMPLEX NUMBER Avalable Onlne : R Index. Theory. Short Revson. Exercse (Ex. + 5 ) 4. Asserton & Reason 5. Que. from Compt. Exams. 9 Yrs. Que. from IIT-JEE(Advanced) 7. 5 Yrs. Que. from AIEEE (JEE Man) Student s Name : Class Roll No. : : Address : Plot No. 7, III- Floor, Near Patdar Studo, Above Bond Classes, Zone-, M.P. NAGAR, Bhopal : , , WhatsApp
2 Complex Numbers. The complex number system There s no real number x whch satsfes the polynomal equaton x + 0. To permt solutons of ths and smlar equatons, the set of complex numbers s ntroduced. We can consder a complex number as havng the form a + b where a and b are real number and, whch s called the magnary unt, has the property that. It s denoted by.e. a + b. a s called as real part of whch s denoted by (Re ) and b s called as magnary part of whch s denoted by (Im ). Any complex number s : () Purely real, f b 0 ; () Purely magnary, f a 0 () Imagnary, f b 0. NOTE : (a) The set R of real numbers s a proper subset of the Complex Numbers. Hence the complete number system s N W I Q R C. (b) Zero s purely real as well as purely magnary but not magnary. (c) s called the magnary unt. Also ² ; ; 4 etc. (d) a b a b only f atleast one of a or b s non - negatve. (e) s a + b, then a b s called complex conjugate of and wrtten as a b Self Practce Problems. Wrte the followng as complex number () () x, (x > 0) () b + 4ac, (a, c> 0) Ans. () 0 + () x + 0 () b + 4ac. Wrte the followng as complex number. () x (x < 0) () roots of x ( cos)x + 0 Algebrac Operatons: Fundamental operatons wth complex numbers In performng operatons wth complex numbers we can proceed as n the algebra of real numbers, replacng by when t occurs.. Addton (a + b) + (c + d) a + b + c + d (a + c) + (b + d).. Subtracton Multplcaton (a + b) c + d) a + b c d (a c) + (b d) (a + b) (c + d) ac + ad + bc + bd (ac bd) + (ad+ bc) 4. Dvson a b c d a b. c d c b c d ac ad bc bd c d ac bd (bc ad) ac bd bc ad + c d c d c d Inequaltes n complex numbers are not defned. There s no valdty f we say that complex number s postve or negatve. e.g. > 0, 4 + < + 4 are meanngless. In real numbers f a + b 0 then a 0 b however n complex numbers, + 0 does not mply 0. Example : Fnd multplcatve nverse of +. Soluton Let be the multplcatve nverse of +. then. ( + ) Ans. Self Practce Problem. Smplfy n+00 + n+50 + n+48 + n+4, n. Ans. 0. Equalty In Complex Number: Two complex numbers a + b & a + b are equal f and only f ther real and magnary parts are equal respectvely.e. Re( ) Re( ) and m ( ) m ( ). Teko Classes, Maths : Suhag R. Karya (S. R. K. Sr), Bhopal Phone : , page of 8
3 Fnd the value of x and y for whch ( + ) x ( ) y x y + 5 where x, y R. Soluton ( + )x ( )y x y + 5 x y x y x x 0 x 0, and x + y 5 Soluton. f x 0,y 5 and f x, y x 0, y 5 and x, y 5 are two solutons of the gven equaton whch can also be represented as 0, & (, ) 5 0,, (, ) Ans. Fnd the value of expresson x 4 4x + x x + when x + s a factor of expresson. x + x (x ) x x + 0 Now x 4 4x + x x + (x x + ) (x x ) 4x + 7 when x +.e. x x + 0 x 4 4x + x x ( + ) Ans. Solve for f + 0 Soluton. Let x + y (x + y) + x y 0 x y + x y 0 and xy 0 x 0 or y 0 when x 0 y + y 0 y 0,, 0,, when y 0 x + x 0 x 0 0 Ans. 0,, Fnd square root of Soluton. Let (x + y) x y 9...() and xy 0...() squng () and addng wth 4 tmes the square of () we get x 4 + y 4 x y + 4x y (x + y ) 8 x + y 4 from () + () we get...() x 5 x ± 5 and y y ± 4 from equaton () we can see that x & y are of same sgn x + y +(5 + 4) or (5 + 4) sq. roots of a + 40 ± (5 + 4) Self Practce Problem Ans. ± (5 + 4). Solve for : Ans. ±, 0, 4. Representaton Of A Complex Number: (a) Cartesan Form (Geometrc Representaton) : Every complex number x + y can be represented by a pont on the Cartesan plane known as complex plane (Argand dagram) by the ordered par (x, y). Length OP s called modulus of the complex number whch s denoted by & s called the argument or ampltude. Teko Classes, Maths : Suhag R. Karya (S. R. K. Sr), Bhopal Phone : , page of 8 x y & tan y x (angle made by OP wth postve xaxs)
4 NOTE : () Argument of a complex number s a many valued functon. If s the argument of a complex number then n+ ; n I wll also be the argument of that complex number. Any two arguments of a complex number dffer by n () The unque value of such that < s called the prncpal value of the argument. Unless otherwse stated, amp mples prncpal value of the argument. () By specfyng the modulus & argument a complex number s defned completely. For the complex number the argument s not defned and ths s the only complex number whch s only gven by ts modulus. (b) Trgnometrc/Polar Representaton : r (cos + sn ) where r; arg ; r (cos sn ) NOTE : cos + sn s also wrtten as CS or e. e x e x Also cos x e x e x & sn x (c) Euler's Representaton : re ; r; arg ; re are known as Euler's denttes. (d) Vectoral Representaton : Every complex number can be consdered as f t s the poston vector of a pont. If the pont P represents the complex number then, OP & OP Express the complex number + n polar form. Soluton. + ( ) Arg tan tan (say) (cos + sn ) where tan Self Practce Problems. Fnd the prncpal argument and (9 ) Ans. 7 tan, 8 5. Fnd the and prncpal argument of the complex number (cos 0º sn 0 ) 5. Ans., 50 Modulus of a Complex Number : If a + b, then t's modulus s denoted and defned by a b. Infact s the dstance of from orgn. Hence s the dstance between the ponts represented by and. Propertes of modulus (). () () + + (v) (provded 0) (Equalty n () and (v) holds f and only f orgn, and are collnear wth and on the same sde of orgn). If 5 7 9, then fnd the greatest and least values of. Soluton. We have 9 (5 + 7) dstance between and Thus locus of s the crcle of radus 9 and centre at For such a (on the crcle), we have to fnd ts greatest and least dstance as from +, whch obvously 4 and 4. Fnd the mnmum value of + +. Soluton (trangle nequalty) + + mnmum value of ( + + ) Geometrcally whch represents sum of dstances of from and t can be seen easly that mnmu (PA + PB) AB Ans. / 4 e n 8 Teko Classes, Maths : Suhag R. Karya (S. R. K. Sr), Bhopal Phone : , page 4 of 8
5 Soluton. then fnd the maxmum and mnmum value of Let r Self Practce Problem r r + r r + r + r r R +...() and r r r r r (, )...() from () and () r (, ) Ans. r (, ). < and 4 > M then fnd the postve real value of M for whch these exst at least one complex number satsfy both the equaton. Ans. M (0, ). Agrument of a Complex Number : Argument of a non-ero complex number P() s denoted and defned by arg() angle whch OP makes wth the postve drecton of real axs. If OP r and arg(), then obvously r(cos + sn), called the polar form of. In what follows, 'argument of ' would mean prncpal argument of (.e. argument lyng n (, ] unless the context requres otherwse. Thus argument of a complex number a + b r(cos + sn) s the value of satsfyng rcos a and rsn b. Thus the argument of,, +,, tan or V th quadrant. b a, accordng as a + b les n,, Propertes of arguments () arg( ) arg( ) + arg( ) + m for some nteger m. () arg( / ) arg ( ) arg( ) + m for some nteger m. () arg ( ) arg() + m for some nteger m. (v) arg() 0 s real, for any complex number 0 (v) arg() ± / s purely magnary, for any complex number 0 (v) arg( ) angle of the lne segment PQ PQ, where P les on real axs, wth the real axs. Solve for, whch satsfy Arg ( ) and Arg ( 4). Soluton From the fgure, t s clear that there s no, whch satsfy both ray Sketch the regon gven by () Arg ( ) / () 5 & Arg ( ) >/ Teko Classes, Maths : Suhag R. Karya (S. R. K. Sr), Bhopal Phone : , page 5 of 8
6 FREE Download Study Package from webste: & Soluton () () Self Practce Problems. Sketch the regon gven by () Arg ( ) < /4 () Arg ( + ) /. Consder the regon 5 0. Fnd the pont n the regon whch has () max () mn () max arg () (v) mn arg () 7. Conjugate of a complex Number Conjugate of a complex number a + b s denoted and defned by a b. In a complex number f we replace by, we get conjugate of the complex number. s the mrror mage of about real axs on Argand's Plane. Propertes of conjugate () () () ( ) ( ) + ( ) (v) ( ) ( ) ( ) (v) ) ( (v) (v) + ( + ) ( ) () ( ( ) 0) (v) ( ) (x) If w f(), then w f( ) (x) arg() + arg( ) 0 If s purely magnary, then prove that Soluton. Re Hence proved Self Practce Problem. If s unmodulus and s not unmodulus then fnd. Ans. 8. Rotaton theorem () () 0 If P( ) and Q( ) are two complex numbers such that, then e where POQ If P( ), Q( ) and R( ) are three complex numbers and PQR, then Teko Classes, Maths : Suhag R. Karya (S. R. K. Sr), Bhopal Phone : , page of 8 e
7 () If P( ), Q( ), R( ) and S( 4 ) are four complex numbers and STQ, then FREE Download Study Package from webste: & If arg then nterrupter the locus. Soluton arg Soluton. Self Practce Problems 4 e arg Here arg represents the angle between lnes jonng and and +. As ths angle s constant, the locus of wll be a of a crcle segment. (angle n a segment s count). It can be seen that locus s not the complete sde as n the major are arg wll be equal to. Now try to geometrcally fnd out radus and centre of ths crcle. centre 0, Radus Ans. If A( + ) and B( + 4) are two vertces of a square ABCD (take n antclock wse order) then fnd C and D. Let affx of C and D are + 4 respectvely Consderng DAB 90º + AD AB ( ) we get 4 ( 4 ) ( ) e AD AB 4 ( + ) ( + ) Z ( 4) ( ) ( 4) and e CB AB + 4 ( + ) ( ) ,,, 4 are the vertces of a square taken n antclockwse order then prove that ( + ) + ( ) Ans. ( + ) + ( ). Check that and 4 are parallel or, not where, Ans. Hence, and 4 are not parallel.. P s a pont on the argand dagram on the crcle wth OP as dameter two pont Q and R are taken such that POQ QOR If O s the orgn and P, Q, R are represented by complex,, respectvely then show that cos cos Ans. cos 9. Demovre s Theorem: Case Statement : If n s any nteger then () (cos + sn ) n cos n + sn n () (cos + sn ) (cos ) + sn ) (cos + sn ) (cos + sn )...(cos n + sn n ) cos ( n ) + sn ( n ) Case Statement : If p, q Z and q 0 then k p (cos + sn ) p/q cos k p + sn q q where k 0,,,,..., q Teko Classes, Maths : Suhag R. Karya (S. R. K. Sr), Bhopal Phone : , page 7 of 8
8 NOTE : Contnued product of the roots of a complex quantty should be determned usng theory of equatons. 0. Cube Root Of Unty : () The cube roots of unty are,,. () If s one of the magnary cube roots of unty then + + ² 0. In general + r + r 0; where r I but s not the multple of. () In polar form the cube roots of unty are : cos 0 + sn 0; cos sn, cos + sn (v) The three cube roots of unty when plotted on the argand plane consttute the vertes of an equlateral trangle. (v) The followng factorsaton should be remembered : (a, b, c R & s the cube root of unty) a b (a b) (a b) (a ²b) ; x + x + (x ) (x ) ; a + b (a + b) (a + b) (a + b) ; a + ab + b (a bw) (a bw ) a + b + c abc (a + b + c) (a + b + ²c) (a + ²b + c) Fnd the value of Soluton Ans. If,, are cube roots of unty prove () ( + ) ( + ) 4 () ( + ) 5 + ( + ) 5 () ( ) ( ) ( 4 ) ( 8 ) 9 (v) ( + ) ( + 4 ) ( )... to n factors n Soluton. () ( + ) ( + ) ( ) ( ) 4 Self Practce Problem 0 r. Fnd ( r0 Ans.. n th Roots of Unty : r ) If,,,.... n are the n, n th root of unty then : () They are n G.P. wth common rato e (/n) & () p + p + p n p 0 f p s not an ntegral multple of n n f p s an ntegral multple of n () ( ) ( )... ( n ) n & ( + ) ( + )... ( + n ) 0 f n s even and f n s odd. (v) n or accordng as n s odd or even. Fnd the roots of the equaton where real part s postve. Soluton. 4. e + (n + ) x (n ) e 5 e, e, e, e roots wth +ve real part are e e Ans. 7 e + e, e, e Teko Classes, Maths : Suhag R. Karya (S. R. K. Sr), Bhopal Phone : , page 8 of 8
9 k k Fnd the value sn cos 7 Soluton. k k 7 k k sn 7 cos 7 k k k sn 7 cos 7 + k0 Self Practce Problems k0 k Ans. k0 (Sum of magnary part of seven seventh roots of unty) (Sum of real part of seven seventh roots of unty) +. Resolve 7 nto lnear and quadratc factor wth real coeffcent. Ans. ( ) 4 cos. cos. cos Fnd the value of cos + cos + cos Ans.. The Sum Of The Followng Seres Should Be Remembered : sn n / () cos + cos + cos cos n sn / sn n / () sn + sn + sn sn n sn / sn NOTE : If (/n) then the sum of the above seres vanshes.. Logarthm Of A Complex Quantty : () Log e (+ ) Log e (² + ²) + () n represents a set of postve real numbers gven by e Fnd the value of cos n n tan where n. n, n. () log ( + ) Ans. log + (n + ) () log( ) Ans. () Ans. cos(ln) + sn(ln) e (ln) (4n). (v) Ans. e (8n). (v) ( + ) Ans. e 4 (v) arg (( + ) ) Ans. n(). n Soluton. () log ( + ) log e log + n () e n cos (n ) cos (n ) + sn (n ) ] Teko Classes, Maths : Suhag R. Karya (S. R. K. Sr), Bhopal Phone : , page 9 of 8
10 Self Practce Problem FREE Download Study Package from webste: & Fnd the real part of cos ( + ) Ans. e e 4. Geometrcal Propertes : Dstance formula : If and are affxes of the two ponts P and Q respectvely then dstance between P + Q s gven by. Secton formula If and are affxes of the two ponts P and Q respectvely and pont C devdes the lne jonng P and Q nternally n the rato m : n then affx of C s gven by m n m n If C devdes PQ n the rato m : n externally then m n m n (b) If a, b, c are three real numbers such that a + b + c 0 ; where a + b + c 0 and a,b,c are not all smultaneously ero, then the complex numbers, & are collnear. () If the vertces A, B, C of a represent the complex nos.,, respectvely and a, b, c are the length of sdes then, () Centrod of the ABC : () Orthocentre of the ABC asec A b sec B csecc tan A tanb tan C or aseca bsec B csecc tana tanb tanc () Incentre of the ABC (a + b + c ) (a + b + c). (v) Crcumcentre of the ABC : (Z sn A + Z sn B + Z sn C) (sn A + sn B + sn C). () amp() s a ray emanatng from the orgn nclned at an angle to the x axs. () a b s the perpendcular bsector of the lne jonng a to b. (4) The equaton of a lne jonng & s gven by, + t ( ) where t s a real parameter. (5) ( + t) where t s a real parameter s a lne through the pont & perpendcular to the lne jonng to the orgn. () The equaton of a lne passng through & can be expressed n the determnant form as 0. Ths s also the condton for three complex numbers to be collnear. The above equaton on manpulatng, takes the form r 0 where r s real and s a non ero complex constant. NOTE : If we replace by e and by e then we get equaton of a straght lne whch. Passes through the foot of the perpendcular from orgn to gven straght lne and makes an angle wth the gven straghtl lne. (7) The equaton of crcle havng centre 0 & radus s : 0 or ² 0 whch s of the form + k 0, k s real. Centre s & radus k. Crcle wll be real f k 0.. (8) The equaton of the crcle descrbed on the lne segment jonng & as dameter s arg ± or ( ) ( ) + ( ) ( ) 0. (9) Condton for four gven ponts,, & 4 to be concyclc s the number 4. should be real. Hence the equaton of a crcle through non collnear 4 Teko Classes, Maths : Suhag R. Karya (S. R. K. Sr), Bhopal Phone : , page 0 of 8
11 ponts, & can be taken as s real. (0) Arg represent () a lne segment f () Par of ray f 0 () a part of crcle, f 0 < < () Area of trangle formed by the ponts, & s () Perpendcular dstance of a pont 0 from the lne r 0 s () () Complex slope of a lne r 0 s () Complex slope of a lne jonng by the ponts & s () Complex slope of a lne makng angle wth real axs e (4) & are the compelx slopes of two lnes. () If lnes are parallel then () If lnes are perpendcular then + 0 (5) If + K > then locus of s an ellpse whose foc are & () If 0 (7) If r lne r 0 r then locus of s parabola whose focus s 0 and drectrx s the k, 0, then locus of s crcle. (8) If K < then locus of s a hyperbola, whose foc are &. Match the followng columns : Column - Column - () If + + 0, () crcle then locus of represents... () If arg, 4 () Straght lne then locus of represents... () f () Ellpse then locus of represents... (v) 4 If arg 5 5, (v) Hyperbola then locus of represents... (v) If (v) Major Arc then locus of represents... (v) + + (v) Mnor arc then locus of represents... (v) 5 (v) Perpendcular bsector of a lne segment 5 (v) arg (v) Lne segment Ans. () () () (v) (v) (v) (v) (v) (v) (v) (v) (v) () (v) () () Teko Classes, Maths : Suhag R. Karya (S. R. K. Sr), Bhopal Phone : , page of 8
12 5. (a) Reflecton ponts for a straght lne : Two gven ponts P & Q are the reflecton ponts for a gven straght lne f the gven lne s the rght bsector of the segment PQ. Note that the two ponts denoted by the complex numbers & wll be the reflecton ponts for the straght lne r 0 f and only f; r, where r s real and s non ero complex constant. 0 (b) Inverse ponts w.r.t. a crcle : Two ponts P & Q are sad to be nverse w.r.t. a crcle wth centre 'O' and radus, f: () the pont O, P, Q are collnear and P, Q are on the same sde of O. () OP. OQ. Note : that the two ponts & wll be the nverse ponts w.r.t. the crcle r 0 f and only f r. 0. Ptolemy s Theorem: It states that the product of the lengths of the dagonals of a convex quadrlateral nscrbed n a crcle s equal to the sum of the products of lengths of the two pars of ts opposte sdes..e If cos + cos + cos 0 and also sn + sn + sn 0, then prove that () cos + cos + cos sn + sn + sn 0 () sn + sn + sn sn () () cos + cos + cos cos () Soluton. Let cos + sn, cos + sn, cos + sn + + (cos + cos + cos ) + (sn + sn + sn ) () () Also (cos + sn ) cos sn cos sn, cos sn + (cos + cos + cos ) (sn + sn + sn ) () Now + + ( + + ) ( + + ) , usng () and () or (cos + sn ) + (cos + sn ) + (cos + sn ) 0 or cos + sn ) + cos + sn + cos + sn Equaton real and magnary parts on both sdes, cos + cos + cos 0 and sn + sn + sn 0 () + + ( + ) ( + ) + ( ) ( ) +, usng () (cos + sn ) + (cos + sn ) + (cos + sn ) (cos + sn ) (cos + sn ) (cos + sn ) or cos + sn + cos + sn + cos + sn {cos( + + ) + sn ( + + ) Equaton magnary parts on both sdes, sn + sn + sn sn ( + + ) Alternatve method Let C cos + cos + cos 0 S sn + sn + sn 0 C + S e + e + e 0 () C S e + e + e 0 () From () (e ) + (e ) + (e ) (e ) (e ) + (e ) (e ) + (e ) (e ) e + e + e e e e (e + e + e ) e () + e + e 0 (from ) Comparng the real and magnary parts we cos + cos + cos sn + sn + sn 0 Also from () (e ) + (e ) + (e ) e e e e + e + e e () Comparng the real and magnary parts we obtan the results. Teko Classes, Maths : Suhag R. Karya (S. R. K. Sr), Bhopal Phone : , page of 8 If and are two complex numbers and c > 0, then prove that
13 + (I + C) + (I +C ) Soluton. We have to prove : + ( + c) + ( + c ).e ( + c) + ( +c ) or + c + c or c + c 0 (usng Re ( ) ) or c c 0 whch s always true. If, [/, /],,,, 4, 5, and 4 cos + cos + cos. + cos 4 + cos 5, Soluton. Soluton. then show that > 4 Gven that cos. 4 + cos. + cos. + cos 4. + cos 5 or cos. 4 + cos. + cos. + cos 4. + cos 5 cos. 4 + cos. + cos. + cos 4. + cos 5 [/, /] cos < < e < 4 > > 4 + Two dfferent non parallel lnes cut the crcle r n pont a, b, c, d respectvely. Prove that a b c d these lnes meet n the pont gven by a b c d Snce pont P, A, B are collnear a a b b Smlarlym, snce ponts P, C, D are collnear b 0 b a (a b) + b ab a 0 () a (c d) c d (a b) c d cd (a b) b ab k k k r k (say) a, a b, b c etc. c From equaton () we get a (c d) () k k k k ck kd ak bk (c d) (a b) (a b) (c d) a b c d d c b a a b c d a b c d Teko Classes, Maths : Suhag R. Karya (S. R. K. Sr), Bhopal Phone : , page of 8
14 Short Revson. DEFINITION : Complex numbers are defnted as expressons of the form a + b where a, b R &. It s denoted by.e. a + b. a s called as real part of (Re ) and b s called as magnary part of (Im ). EVERY COMPLEX NUMBER CAN BE REGARDED AS Note : (a) (b) (c) Purely real Purely magnary Imagnary f b 0 f a 0 f b 0 The set R of real numbers s a proper subset of the Complex Numbers. Hence the Complete Number system s N W I Q R C. Zero s both purely real as well as purely magnary but not magnary. s called the magnary unt. Also ² l ; ; 4 etc. (d) a b a b only f atleast one of ether a or b s non-negatve.. CONJUGATE COMPLEX : If a + b then ts conjugate complex s obtaned by changng the sgn of ts magnary part & s denoted by..e. a b. Note that : () + Re() () Im() () a² + b² whch s real (v) If les n the st quadrant then les n the 4 th quadrant and les n the nd quadrant.. ALGEBRAIC OPERATIONS : The algebrac operatons on complex numbers are smlar to those on real numbers treatng as a polynomal. Inequaltes n complex numbers are not defned. There s no valdty f we say that complex number s postve or negatve. e.g. > 0, 4 + < + 4 are meanngless. However n real numbers f a + b 0 then a 0 b but n complex numbers, + 0 does not mply EQUALITY IN COMPLEX NUMBER : Two complex numbers a + b & a + b are equal f and only f ther real & magnary parts concde. 5. REPRESENTATION OF A COMPLEX NUMBER IN VARIOUS FORMS : (a) Cartesan Form (Geometrc Representaton) : Every complex number x + y can be represented by a pont on the cartesan plane known as complex plane (Argand dagram) by the ordered par (x, y). length OP s called modulus of the complex number denoted by & s called the argument or ampltude. eg. x y & tan y x (angle made by OP wth postve xaxs) f 0 NOTE :() s always non negatve. Unlke real numbers s not correct f 0 () Argument of a complex number s a many valued functon. If s the argument of a complex number then n+ ; n I wll also be the argument of that complex number. Any two arguments of a complex number dffer by n. () The unque value of such that < s called the prncpal value of the argument. (v) Unless otherwse stated, amp mples prncpal value of the argument. (v) By specfyng the modulus & argument a complex number s defned completely. For the complex number the argument s not defned and ths s the only complex number whch s gven by ts modulus. (v) There exsts a one-one correspondence between the ponts of the plane and the members of the set of complex numbers. Teko Classes, Maths : Suhag R. Karya (S. R. K. Sr), Bhopal Phone : , page 4 of 8
15 (b) Trgnometrc / Polar Representaton : r (cos + sn ) where r ; arg ; r (cos sn ) Note: cos + sn s also wrtten as CS. x x x x e e e e Also cos x & sn x are known as Euler's denttes. (c) Exponental Representaton : re ; r ; arg ; re. IMPORTANT PROPERTIES OF CONJUGATE / MODULI / AMPLITUDE : If,, C then ; (a) + Re () ; Im () ; ( ) ; + ; ;. ; 0 (b) 0 ; Re () ; Im () ; ;. ;, 0, n n ; + + ] [ ; + + [ TRIANGLE INEQUALITY ] (c) () amp (. ) amp + amp + k. k I () amp amp amp + k; k I () amp( n ) n amp() + k. where proper value of k must be chosen so that RHS les n (, ]. (7) VECTORIAL REPRESENTATION OF A COMPLEX : Every complex number can be consdered as f t s the poston vector of that pont. If the pont P represents the complex number then, OP & OP NOTE : () If OP r e then OQ r e ( + ). e. If OP and OQ are () () of unequal magntude then OQ OP e If A, B, C & D are four ponts representng the complex numbers,, & 4 then 4 4 AB CD f s purely real ; AB CD f s purely magnary ] If,, are the vertces of an equlateral trangle where 0 s ts crcumcentre then (a) (b) DEMOIVRE S THEOREM : Statement : cos n + sn n s the value or one of the values of (cos + sn ) n n Q. The theorem s very useful n determnng the roots of any complex quantty Note : Contnued product of the roots of a complex quantty should be determned usng theory of equatons. 9. CUBE ROOT OF UNITY :() The cube roots of unty are,,. () If w s one of the magnary cube roots of unty then + w + w² 0. In general + w r + w r 0 ; where r I but s not the multple of. () In polar form the cube roots of unty are : 4 4 cos 0 + sn 0 ; cos + sn, cos + sn (v) The three cube roots of unty when plotted on the argand plane consttute the vertes of an equlateral trangle. (v) The followng factorsaton should be remembered : (a, b, c R & s the cube root of unty) Teko Classes, Maths : Suhag R. Karya (S. R. K. Sr), Bhopal Phone : , page 5 of 8
COMPLEX NUMBERS AND QUADRATIC EQUATIONS
 COMPLEX NUMBERS AND QUADRATIC EQUATIONS INTRODUCTION We know that x 0 for all x R e the square of a real number (whether postve, negatve or ero) s non-negatve Hence the equatons x, x, x + 7 0 etc are not
COMPLEX NUMBERS AND QUADRATIC EQUATIONS INTRODUCTION We know that x 0 for all x R e the square of a real number (whether postve, negatve or ero) s non-negatve Hence the equatons x, x, x + 7 0 etc are not
STUDY PACKAGE. Subject : Mathematics Topic : INVERSE TRIGONOMETRY. Available Online :
 fo/u fopkjr Hkh# tu] ugha vkjehks dke] for ns[k NksM+s rqjar e/;e eu dj ';kea iq#"k flag ladyi dj] lgrs for vusd] ^cuk^ u NksM+s /;s; dks] j?kqcj jk[ks VsdAA jfpr% ekuo /kez iz.ksrk ln~q# Jh j.knksm+nklth
fo/u fopkjr Hkh# tu] ugha vkjehks dke] for ns[k NksM+s rqjar e/;e eu dj ';kea iq#"k flag ladyi dj] lgrs for vusd] ^cuk^ u NksM+s /;s; dks] j?kqcj jk[ks VsdAA jfpr% ekuo /kez iz.ksrk ln~q# Jh j.knksm+nklth
Section 8.3 Polar Form of Complex Numbers
 80 Chapter 8 Secton 8 Polar Form of Complex Numbers From prevous classes, you may have encountered magnary numbers the square roots of negatve numbers and, more generally, complex numbers whch are the
80 Chapter 8 Secton 8 Polar Form of Complex Numbers From prevous classes, you may have encountered magnary numbers the square roots of negatve numbers and, more generally, complex numbers whch are the
STUDY PACKAGE. Subject : Mathematics Topic : Trigonometric Ratio & Identity
 fo/u fopkjr Hkh# tu] ugha vkjehks dke] foifr ns[k NksMs rqjar e/;e eu dj ';ke iq#"k flag ladyi dj] lgrs foifr vusd] ^cuk^ u NksMs /;s; dks] j?kqcj jk[ks Vsd jfpr% ekuo /kez iz.ksrk ln~xq# Jh j.knksmnklth
fo/u fopkjr Hkh# tu] ugha vkjehks dke] foifr ns[k NksMs rqjar e/;e eu dj ';ke iq#"k flag ladyi dj] lgrs foifr vusd] ^cuk^ u NksMs /;s; dks] j?kqcj jk[ks Vsd jfpr% ekuo /kez iz.ksrk ln~xq# Jh j.knksmnklth
STUDY PACKAGE. Subject : PHYSICS Topic : OPTICAL INSTRUMENTS. Available Online :
 fo/u fopkjr Hkh# tu] ugha vkjehks dke] foifr ns[k NksM+s rqjar e/;e eu dj ';kea iq#"k flag ladyi dj] lgrs foifr vusd] ^cuk^ u NksM+s /;s; dks] j?kqcj jk[ks VsdAA jfpr% ekuo /kez iz.ksrk ln~xq# Jh j.knksm+nklth
fo/u fopkjr Hkh# tu] ugha vkjehks dke] foifr ns[k NksM+s rqjar e/;e eu dj ';kea iq#"k flag ladyi dj] lgrs foifr vusd] ^cuk^ u NksM+s /;s; dks] j?kqcj jk[ks VsdAA jfpr% ekuo /kez iz.ksrk ln~xq# Jh j.knksm+nklth
Subject : Mathematics Topic : Trigonometric Ratio & Identity
 fo/u fopkjr Hkh# tu] ugha vkjehks dke] foifr ns[k NksM+s rqjar e/;e eu dj ';ke iq#"k flag ladyi dj] lgrs foifr vusd] ^cuk^ u NksM+s /;s; dks] j?kqcj jk[ks Vsd jfpr% ekuo /kez iz.ksrk ln~xq# Jh j.knksm+nklth
fo/u fopkjr Hkh# tu] ugha vkjehks dke] foifr ns[k NksM+s rqjar e/;e eu dj ';ke iq#"k flag ladyi dj] lgrs foifr vusd] ^cuk^ u NksM+s /;s; dks] j?kqcj jk[ks Vsd jfpr% ekuo /kez iz.ksrk ln~xq# Jh j.knksm+nklth
For all questions, answer choice E) NOTA" means none of the above answers is correct.
 0 MA Natonal Conventon For all questons, answer choce " means none of the above answers s correct.. In calculus, one learns of functon representatons that are nfnte seres called power 3 4 5 seres. For
0 MA Natonal Conventon For all questons, answer choce " means none of the above answers s correct.. In calculus, one learns of functon representatons that are nfnte seres called power 3 4 5 seres. For
332600_08_1.qxp 4/17/08 11:29 AM Page 481
 336_8_.qxp 4/7/8 :9 AM Page 48 8 Complex Vector Spaces 8. Complex Numbers 8. Conjugates and Dvson of Complex Numbers 8.3 Polar Form and DeMovre s Theorem 8.4 Complex Vector Spaces and Inner Products 8.5
336_8_.qxp 4/7/8 :9 AM Page 48 8 Complex Vector Spaces 8. Complex Numbers 8. Conjugates and Dvson of Complex Numbers 8.3 Polar Form and DeMovre s Theorem 8.4 Complex Vector Spaces and Inner Products 8.5
Complex Numbers Alpha, Round 1 Test #123
 Complex Numbers Alpha, Round Test #3. Wrte your 6-dgt ID# n the I.D. NUMBER grd, left-justfed, and bubble. Check that each column has only one number darkened.. In the EXAM NO. grd, wrte the 3-dgt Test
Complex Numbers Alpha, Round Test #3. Wrte your 6-dgt ID# n the I.D. NUMBER grd, left-justfed, and bubble. Check that each column has only one number darkened.. In the EXAM NO. grd, wrte the 3-dgt Test
APPENDIX A Some Linear Algebra
 APPENDIX A Some Lnear Algebra The collecton of m, n matrces A.1 Matrces a 1,1,..., a 1,n A = a m,1,..., a m,n wth real elements a,j s denoted by R m,n. If n = 1 then A s called a column vector. Smlarly,
APPENDIX A Some Lnear Algebra The collecton of m, n matrces A.1 Matrces a 1,1,..., a 1,n A = a m,1,..., a m,n wth real elements a,j s denoted by R m,n. If n = 1 then A s called a column vector. Smlarly,
Complex Numbers. x = B B 2 4AC 2A. or x = x = 2 ± 4 4 (1) (5) 2 (1)
 Complex Numbers If you have not yet encountered complex numbers, you wll soon do so n the process of solvng quadratc equatons. The general quadratc equaton Ax + Bx + C 0 has solutons x B + B 4AC A For
Complex Numbers If you have not yet encountered complex numbers, you wll soon do so n the process of solvng quadratc equatons. The general quadratc equaton Ax + Bx + C 0 has solutons x B + B 4AC A For
Student s Name : Class Roll No. ADDRESS: R-1, Opp. Raiway Track, New Corner Glass Building, Zone-2, M.P. NAGAR, Bhopal
 fo/u fopkjr Hkh# tu] ugha vkjehks dke] foifr ns[k NksM+s rqjar e/;e eu dj ';kea iq#"k flag ladyi dj] lgrs foifr vusd] ^cuk^ u NksM+s /;s; dks] j?kqcj jk[ks VsdAA jfpr% ekuo /kez izksrk ln~q# Jh jknksm+nklth
fo/u fopkjr Hkh# tu] ugha vkjehks dke] foifr ns[k NksM+s rqjar e/;e eu dj ';kea iq#"k flag ladyi dj] lgrs foifr vusd] ^cuk^ u NksM+s /;s; dks] j?kqcj jk[ks VsdAA jfpr% ekuo /kez izksrk ln~q# Jh jknksm+nklth
Lectures - Week 4 Matrix norms, Conditioning, Vector Spaces, Linear Independence, Spanning sets and Basis, Null space and Range of a Matrix
 Lectures - Week 4 Matrx norms, Condtonng, Vector Spaces, Lnear Independence, Spannng sets and Bass, Null space and Range of a Matrx Matrx Norms Now we turn to assocatng a number to each matrx. We could
Lectures - Week 4 Matrx norms, Condtonng, Vector Spaces, Lnear Independence, Spannng sets and Bass, Null space and Range of a Matrx Matrx Norms Now we turn to assocatng a number to each matrx. We could
Formulas for the Determinant
 page 224 224 CHAPTER 3 Determnants e t te t e 2t 38 A = e t 2te t e 2t e t te t 2e 2t 39 If 123 A = 345, 456 compute the matrx product A adj(a) What can you conclude about det(a)? For Problems 40 43, use
page 224 224 CHAPTER 3 Determnants e t te t e 2t 38 A = e t 2te t e 2t e t te t 2e 2t 39 If 123 A = 345, 456 compute the matrx product A adj(a) What can you conclude about det(a)? For Problems 40 43, use
1. Estimation, Approximation and Errors Percentages Polynomials and Formulas Identities and Factorization 52
 ontents ommonly Used Formulas. Estmaton, pproxmaton and Errors. Percentages. Polynomals and Formulas 8. Identtes and Factorzaton. Equatons and Inequaltes 66 6. Rate and Rato 8 7. Laws of Integral Indces
ontents ommonly Used Formulas. Estmaton, pproxmaton and Errors. Percentages. Polynomals and Formulas 8. Identtes and Factorzaton. Equatons and Inequaltes 66 6. Rate and Rato 8 7. Laws of Integral Indces
Week3, Chapter 4. Position and Displacement. Motion in Two Dimensions. Instantaneous Velocity. Average Velocity
 Week3, Chapter 4 Moton n Two Dmensons Lecture Quz A partcle confned to moton along the x axs moves wth constant acceleraton from x =.0 m to x = 8.0 m durng a 1-s tme nterval. The velocty of the partcle
Week3, Chapter 4 Moton n Two Dmensons Lecture Quz A partcle confned to moton along the x axs moves wth constant acceleraton from x =.0 m to x = 8.0 m durng a 1-s tme nterval. The velocty of the partcle
Math1110 (Spring 2009) Prelim 3 - Solutions
 Math 1110 (Sprng 2009) Solutons to Prelm 3 (04/21/2009) 1 Queston 1. (16 ponts) Short answer. Math1110 (Sprng 2009) Prelm 3 - Solutons x a 1 (a) (4 ponts) Please evaluate lm, where a and b are postve numbers.
Math 1110 (Sprng 2009) Solutons to Prelm 3 (04/21/2009) 1 Queston 1. (16 ponts) Short answer. Math1110 (Sprng 2009) Prelm 3 - Solutons x a 1 (a) (4 ponts) Please evaluate lm, where a and b are postve numbers.
jfpr% ekuo /kez iz.ksrk ln~xq# Jh j.knksm+nklth egkjkt
 Phone : (0755) 00 000, 9890 5888 WhatsApp 9009 60 559 QUADRATIC EQUATIONS PART OF fo/u fopkjr Hkh# tu] ugha vkjehks dke] foifr ns[k NksM+s rqjar e/;e eu dj ';kea iq#"k flag ladyi dj] lgrs foifr vusd] ^cuk^
Phone : (0755) 00 000, 9890 5888 WhatsApp 9009 60 559 QUADRATIC EQUATIONS PART OF fo/u fopkjr Hkh# tu] ugha vkjehks dke] foifr ns[k NksM+s rqjar e/;e eu dj ';kea iq#"k flag ladyi dj] lgrs foifr vusd] ^cuk^
More metrics on cartesian products
 More metrcs on cartesan products If (X, d ) are metrc spaces for 1 n, then n Secton II4 of the lecture notes we defned three metrcs on X whose underlyng topologes are the product topology The purpose of
More metrcs on cartesan products If (X, d ) are metrc spaces for 1 n, then n Secton II4 of the lecture notes we defned three metrcs on X whose underlyng topologes are the product topology The purpose of
9. Complex Numbers. 1. Numbers revisited. 2. Imaginary number i: General form of complex numbers. 3. Manipulation of complex numbers
 9. Comple Numbers. Numbers revsted. Imagnar number : General form of comple numbers 3. Manpulaton of comple numbers 4. The Argand dagram 5. The polar form for comple numbers 9.. Numbers revsted We saw
9. Comple Numbers. Numbers revsted. Imagnar number : General form of comple numbers 3. Manpulaton of comple numbers 4. The Argand dagram 5. The polar form for comple numbers 9.. Numbers revsted We saw
Affine transformations and convexity
 Affne transformatons and convexty The purpose of ths document s to prove some basc propertes of affne transformatons nvolvng convex sets. Here are a few onlne references for background nformaton: http://math.ucr.edu/
Affne transformatons and convexty The purpose of ths document s to prove some basc propertes of affne transformatons nvolvng convex sets. Here are a few onlne references for background nformaton: http://math.ucr.edu/
8.6 The Complex Number System
 8.6 The Complex Number System Earler n the chapter, we mentoned that we cannot have a negatve under a square root, snce the square of any postve or negatve number s always postve. In ths secton we want
8.6 The Complex Number System Earler n the chapter, we mentoned that we cannot have a negatve under a square root, snce the square of any postve or negatve number s always postve. In ths secton we want
Problem Do any of the following determine homomorphisms from GL n (C) to GL n (C)?
 Homework 8 solutons. Problem 16.1. Whch of the followng defne homomomorphsms from C\{0} to C\{0}? Answer. a) f 1 : z z Yes, f 1 s a homomorphsm. We have that z s the complex conjugate of z. If z 1,z 2
Homework 8 solutons. Problem 16.1. Whch of the followng defne homomomorphsms from C\{0} to C\{0}? Answer. a) f 1 : z z Yes, f 1 s a homomorphsm. We have that z s the complex conjugate of z. If z 1,z 2
DEEPAWALI ASSIGNMENT
 fo/u fopkjr Hkh# tu] ugha vkjehks dke] foifr ns[k NksM+s rqjar e/;e eu dj ';kea iq#"k flag ladyi dj] lgrs foifr vusd] ^cuk^ u NksM+s /;s; dks] j?kqcj jk[ks VsdAA jfpr% ekuo /kez iz.ksrk ln~xq# Jh j.knksm+nklth
fo/u fopkjr Hkh# tu] ugha vkjehks dke] foifr ns[k NksM+s rqjar e/;e eu dj ';kea iq#"k flag ladyi dj] lgrs foifr vusd] ^cuk^ u NksM+s /;s; dks] j?kqcj jk[ks VsdAA jfpr% ekuo /kez iz.ksrk ln~xq# Jh j.knksm+nklth
Einstein Classes, Unit No. 102, 103, Vardhman Ring Road Plaza, Vikas Puri Extn., Outer Ring Road New Delhi , Ph. : ,
 MCN COMPLEX NUMBER C The complex number Complex number is denoted by ie = a + ib, where a is called as real part of (denoted by Re and b is called as imaginary part of (denoted by Im Here i =, also i =,
MCN COMPLEX NUMBER C The complex number Complex number is denoted by ie = a + ib, where a is called as real part of (denoted by Re and b is called as imaginary part of (denoted by Im Here i =, also i =,
(c) (cos θ + i sin θ) 5 = cos 5 θ + 5 cos 4 θ (i sin θ) + 10 cos 3 θ(i sin θ) cos 2 θ(i sin θ) 3 + 5cos θ (i sin θ) 4 + (i sin θ) 5 (A1)
 . (a) (cos θ + sn θ) = cos θ + cos θ( sn θ) + cos θ(sn θ) + (sn θ) = cos θ cos θ sn θ + ( cos θ sn θ sn θ) (b) from De Movre s theorem (cos θ + sn θ) = cos θ + sn θ cos θ + sn θ = (cos θ cos θ sn θ) +
. (a) (cos θ + sn θ) = cos θ + cos θ( sn θ) + cos θ(sn θ) + (sn θ) = cos θ cos θ sn θ + ( cos θ sn θ sn θ) (b) from De Movre s theorem (cos θ + sn θ) = cos θ + sn θ cos θ + sn θ = (cos θ cos θ sn θ) +
Unit 5: Quadratic Equations & Functions
 Date Perod Unt 5: Quadratc Equatons & Functons DAY TOPIC 1 Modelng Data wth Quadratc Functons Factorng Quadratc Epressons 3 Solvng Quadratc Equatons 4 Comple Numbers Smplfcaton, Addton/Subtracton & Multplcaton
Date Perod Unt 5: Quadratc Equatons & Functons DAY TOPIC 1 Modelng Data wth Quadratc Functons Factorng Quadratc Epressons 3 Solvng Quadratc Equatons 4 Comple Numbers Smplfcaton, Addton/Subtracton & Multplcaton
Complex Variables. Chapter 18 Integration in the Complex Plane. March 12, 2013 Lecturer: Shih-Yuan Chen
 omplex Varables hapter 8 Integraton n the omplex Plane March, Lecturer: Shh-Yuan hen Except where otherwse noted, content s lcensed under a BY-N-SA. TW Lcense. ontents ontour ntegrals auchy-goursat theorem
omplex Varables hapter 8 Integraton n the omplex Plane March, Lecturer: Shh-Yuan hen Except where otherwse noted, content s lcensed under a BY-N-SA. TW Lcense. ontents ontour ntegrals auchy-goursat theorem
U.C. Berkeley CS294: Beyond Worst-Case Analysis Luca Trevisan September 5, 2017
 U.C. Berkeley CS94: Beyond Worst-Case Analyss Handout 4s Luca Trevsan September 5, 07 Summary of Lecture 4 In whch we ntroduce semdefnte programmng and apply t to Max Cut. Semdefnte Programmng Recall that
U.C. Berkeley CS94: Beyond Worst-Case Analyss Handout 4s Luca Trevsan September 5, 07 Summary of Lecture 4 In whch we ntroduce semdefnte programmng and apply t to Max Cut. Semdefnte Programmng Recall that
n α j x j = 0 j=1 has a nontrivial solution. Here A is the n k matrix whose jth column is the vector for all t j=0
 MODULE 2 Topcs: Lnear ndependence, bass and dmenson We have seen that f n a set of vectors one vector s a lnear combnaton of the remanng vectors n the set then the span of the set s unchanged f that vector
MODULE 2 Topcs: Lnear ndependence, bass and dmenson We have seen that f n a set of vectors one vector s a lnear combnaton of the remanng vectors n the set then the span of the set s unchanged f that vector
Digital Signal Processing
 Dgtal Sgnal Processng Dscrete-tme System Analyss Manar Mohasen Offce: F8 Emal: manar.subh@ut.ac.r School of IT Engneerng Revew of Precedent Class Contnuous Sgnal The value of the sgnal s avalable over
Dgtal Sgnal Processng Dscrete-tme System Analyss Manar Mohasen Offce: F8 Emal: manar.subh@ut.ac.r School of IT Engneerng Revew of Precedent Class Contnuous Sgnal The value of the sgnal s avalable over
1 Matrix representations of canonical matrices
 1 Matrx representatons of canoncal matrces 2-d rotaton around the orgn: ( ) cos θ sn θ R 0 = sn θ cos θ 3-d rotaton around the x-axs: R x = 1 0 0 0 cos θ sn θ 0 sn θ cos θ 3-d rotaton around the y-axs:
1 Matrx representatons of canoncal matrces 2-d rotaton around the orgn: ( ) cos θ sn θ R 0 = sn θ cos θ 3-d rotaton around the x-axs: R x = 1 0 0 0 cos θ sn θ 0 sn θ cos θ 3-d rotaton around the y-axs:
Section 8.1 Exercises
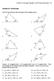 Secton 8.1 Non-rght Trangles: Law of Snes and Cosnes 519 Secton 8.1 Exercses Solve for the unknown sdes and angles of the trangles shown. 10 70 50 1.. 18 40 110 45 5 6 3. 10 4. 75 15 5 6 90 70 65 5. 6.
Secton 8.1 Non-rght Trangles: Law of Snes and Cosnes 519 Secton 8.1 Exercses Solve for the unknown sdes and angles of the trangles shown. 10 70 50 1.. 18 40 110 45 5 6 3. 10 4. 75 15 5 6 90 70 65 5. 6.
18.781: Solution to Practice Questions for Final Exam
 18.781: Soluton to Practce Questons for Fnal Exam 1. Fnd three solutons n postve ntegers of x 6y = 1 by frst calculatng the contnued fracton expanson of 6. Soluton: We have 1 6=[, ] 6 6+ =[, ] 1 =[,, ]=[,,
18.781: Soluton to Practce Questons for Fnal Exam 1. Fnd three solutons n postve ntegers of x 6y = 1 by frst calculatng the contnued fracton expanson of 6. Soluton: We have 1 6=[, ] 6 6+ =[, ] 1 =[,, ]=[,,
Important Instructions to the Examiners:
 Summer 0 Examnaton Subject & Code: asc Maths (70) Model Answer Page No: / Important Instructons to the Examners: ) The Answers should be examned by key words and not as word-to-word as gven n the model
Summer 0 Examnaton Subject & Code: asc Maths (70) Model Answer Page No: / Important Instructons to the Examners: ) The Answers should be examned by key words and not as word-to-word as gven n the model
International Mathematical Olympiad. Preliminary Selection Contest 2012 Hong Kong. Outline of Solutions
 Internatonal Mathematcal Olympad Prelmnary Selecton ontest Hong Kong Outlne of Solutons nswers: 7 4 7 4 6 5 9 6 99 7 6 6 9 5544 49 5 7 4 6765 5 6 6 7 6 944 9 Solutons: Snce n s a two-dgt number, we have
Internatonal Mathematcal Olympad Prelmnary Selecton ontest Hong Kong Outlne of Solutons nswers: 7 4 7 4 6 5 9 6 99 7 6 6 9 5544 49 5 7 4 6765 5 6 6 7 6 944 9 Solutons: Snce n s a two-dgt number, we have
STUDY PACKAGE. Available Online :
 fo/u fopkjr Hkh# tu] ugha vkjehks dke] foifr ns[k NksM+s rqjar e/;e eu dj ';kea iq#"k flag ladyi dj] lgrs foifr vusd] ^cuk^ u NksM+s /;s; dks] j?kqcj jk[ks VsdAA jfpr% ekuo /kez i.ksrk ln~q# Jh j.knksm+nklth
fo/u fopkjr Hkh# tu] ugha vkjehks dke] foifr ns[k NksM+s rqjar e/;e eu dj ';kea iq#"k flag ladyi dj] lgrs foifr vusd] ^cuk^ u NksM+s /;s; dks] j?kqcj jk[ks VsdAA jfpr% ekuo /kez i.ksrk ln~q# Jh j.knksm+nklth
of Nebraska - Lincoln
 Unversty of Nebraska - Lncoln DgtalCommons@Unversty of Nebraska - Lncoln MAT Exam Expostory Papers Math n the Mddle Insttute Partnershp 008 The Square Root of Tffany Lothrop Unversty of Nebraska-Lncoln
Unversty of Nebraska - Lncoln DgtalCommons@Unversty of Nebraska - Lncoln MAT Exam Expostory Papers Math n the Mddle Insttute Partnershp 008 The Square Root of Tffany Lothrop Unversty of Nebraska-Lncoln
The Order Relation and Trace Inequalities for. Hermitian Operators
 Internatonal Mathematcal Forum, Vol 3, 08, no, 507-57 HIKARI Ltd, wwwm-hkarcom https://doorg/0988/mf088055 The Order Relaton and Trace Inequaltes for Hermtan Operators Y Huang School of Informaton Scence
Internatonal Mathematcal Forum, Vol 3, 08, no, 507-57 HIKARI Ltd, wwwm-hkarcom https://doorg/0988/mf088055 The Order Relaton and Trace Inequaltes for Hermtan Operators Y Huang School of Informaton Scence
Lecture 5 Decoding Binary BCH Codes
 Lecture 5 Decodng Bnary BCH Codes In ths class, we wll ntroduce dfferent methods for decodng BCH codes 51 Decodng the [15, 7, 5] 2 -BCH Code Consder the [15, 7, 5] 2 -code C we ntroduced n the last lecture
Lecture 5 Decodng Bnary BCH Codes In ths class, we wll ntroduce dfferent methods for decodng BCH codes 51 Decodng the [15, 7, 5] 2 -BCH Code Consder the [15, 7, 5] 2 -code C we ntroduced n the last lecture
8.4 COMPLEX VECTOR SPACES AND INNER PRODUCTS
 SECTION 8.4 COMPLEX VECTOR SPACES AND INNER PRODUCTS 493 8.4 COMPLEX VECTOR SPACES AND INNER PRODUCTS All the vector spaces you have studed thus far n the text are real vector spaces because the scalars
SECTION 8.4 COMPLEX VECTOR SPACES AND INNER PRODUCTS 493 8.4 COMPLEX VECTOR SPACES AND INNER PRODUCTS All the vector spaces you have studed thus far n the text are real vector spaces because the scalars
Foundations of Arithmetic
 Foundatons of Arthmetc Notaton We shall denote the sum and product of numbers n the usual notaton as a 2 + a 2 + a 3 + + a = a, a 1 a 2 a 3 a = a The notaton a b means a dvdes b,.e. ac = b where c s an
Foundatons of Arthmetc Notaton We shall denote the sum and product of numbers n the usual notaton as a 2 + a 2 + a 3 + + a = a, a 1 a 2 a 3 a = a The notaton a b means a dvdes b,.e. ac = b where c s an
Lecture 3. Ax x i a i. i i
 18.409 The Behavor of Algorthms n Practce 2/14/2 Lecturer: Dan Spelman Lecture 3 Scrbe: Arvnd Sankar 1 Largest sngular value In order to bound the condton number, we need an upper bound on the largest
18.409 The Behavor of Algorthms n Practce 2/14/2 Lecturer: Dan Spelman Lecture 3 Scrbe: Arvnd Sankar 1 Largest sngular value In order to bound the condton number, we need an upper bound on the largest
Inner Product. Euclidean Space. Orthonormal Basis. Orthogonal
 Inner Product Defnton 1 () A Eucldean space s a fnte-dmensonal vector space over the reals R, wth an nner product,. Defnton 2 (Inner Product) An nner product, on a real vector space X s a symmetrc, blnear,
Inner Product Defnton 1 () A Eucldean space s a fnte-dmensonal vector space over the reals R, wth an nner product,. Defnton 2 (Inner Product) An nner product, on a real vector space X s a symmetrc, blnear,
Linear, affine, and convex sets and hulls In the sequel, unless otherwise specified, X will denote a real vector space.
 Lnear, affne, and convex sets and hulls In the sequel, unless otherwse specfed, X wll denote a real vector space. Lnes and segments. Gven two ponts x, y X, we defne xy = {x + t(y x) : t R} = {(1 t)x +
Lnear, affne, and convex sets and hulls In the sequel, unless otherwse specfed, X wll denote a real vector space. Lnes and segments. Gven two ponts x, y X, we defne xy = {x + t(y x) : t R} = {(1 t)x +
3.1 Expectation of Functions of Several Random Variables. )' be a k-dimensional discrete or continuous random vector, with joint PMF p (, E X E X1 E X
 Statstcs 1: Probablty Theory II 37 3 EPECTATION OF SEVERAL RANDOM VARIABLES As n Probablty Theory I, the nterest n most stuatons les not on the actual dstrbuton of a random vector, but rather on a number
Statstcs 1: Probablty Theory II 37 3 EPECTATION OF SEVERAL RANDOM VARIABLES As n Probablty Theory I, the nterest n most stuatons les not on the actual dstrbuton of a random vector, but rather on a number
Chapter 5. Solution of System of Linear Equations. Module No. 6. Solution of Inconsistent and Ill Conditioned Systems
 Numercal Analyss by Dr. Anta Pal Assstant Professor Department of Mathematcs Natonal Insttute of Technology Durgapur Durgapur-713209 emal: anta.bue@gmal.com 1 . Chapter 5 Soluton of System of Lnear Equatons
Numercal Analyss by Dr. Anta Pal Assstant Professor Department of Mathematcs Natonal Insttute of Technology Durgapur Durgapur-713209 emal: anta.bue@gmal.com 1 . Chapter 5 Soluton of System of Lnear Equatons
Section 3.6 Complex Zeros
 04 Chapter Secton 6 Comple Zeros When fndng the zeros of polynomals, at some pont you're faced wth the problem Whle there are clearly no real numbers that are solutons to ths equaton, leavng thngs there
04 Chapter Secton 6 Comple Zeros When fndng the zeros of polynomals, at some pont you're faced wth the problem Whle there are clearly no real numbers that are solutons to ths equaton, leavng thngs there
Solutions to exam in SF1811 Optimization, Jan 14, 2015
 Solutons to exam n SF8 Optmzaton, Jan 4, 25 3 3 O------O -4 \ / \ / The network: \/ where all lnks go from left to rght. /\ / \ / \ 6 O------O -5 2 4.(a) Let x = ( x 3, x 4, x 23, x 24 ) T, where the varable
Solutons to exam n SF8 Optmzaton, Jan 4, 25 3 3 O------O -4 \ / \ / The network: \/ where all lnks go from left to rght. /\ / \ / \ 6 O------O -5 2 4.(a) Let x = ( x 3, x 4, x 23, x 24 ) T, where the varable
SL n (F ) Equals its Own Derived Group
 Internatonal Journal of Algebra, Vol. 2, 2008, no. 12, 585-594 SL n (F ) Equals ts Own Derved Group Jorge Macel BMCC-The Cty Unversty of New York, CUNY 199 Chambers street, New York, NY 10007, USA macel@cms.nyu.edu
Internatonal Journal of Algebra, Vol. 2, 2008, no. 12, 585-594 SL n (F ) Equals ts Own Derved Group Jorge Macel BMCC-The Cty Unversty of New York, CUNY 199 Chambers street, New York, NY 10007, USA macel@cms.nyu.edu
Chapter Newton s Method
 Chapter 9. Newton s Method After readng ths chapter, you should be able to:. Understand how Newton s method s dfferent from the Golden Secton Search method. Understand how Newton s method works 3. Solve
Chapter 9. Newton s Method After readng ths chapter, you should be able to:. Understand how Newton s method s dfferent from the Golden Secton Search method. Understand how Newton s method works 3. Solve
STUDY PACKAGE. Subject : PHYSICS Topic : CURRENT ELECTRICITY. Available Online :
 fo/u fopkjr Hkh# tu] ugha vkjehks dke] foifr ns[k NksM+s rqjar e/;e eu dj ';kea iq#"k flag ladyi dj] lgrs foifr vusd] ^cuk^ u NksM+s /;s; dks] j?kqcj jk[ks VsdAA jfpr% ekuo /kez izksrk ln~xq# Jh jknksm+nklth
fo/u fopkjr Hkh# tu] ugha vkjehks dke] foifr ns[k NksM+s rqjar e/;e eu dj ';kea iq#"k flag ladyi dj] lgrs foifr vusd] ^cuk^ u NksM+s /;s; dks] j?kqcj jk[ks VsdAA jfpr% ekuo /kez izksrk ln~xq# Jh jknksm+nklth
Difference Equations
 Dfference Equatons c Jan Vrbk 1 Bascs Suppose a sequence of numbers, say a 0,a 1,a,a 3,... s defned by a certan general relatonshp between, say, three consecutve values of the sequence, e.g. a + +3a +1
Dfference Equatons c Jan Vrbk 1 Bascs Suppose a sequence of numbers, say a 0,a 1,a,a 3,... s defned by a certan general relatonshp between, say, three consecutve values of the sequence, e.g. a + +3a +1
Some Inequalities Between Two Polygons Inscribed One in the Other
 BULLETIN of the Malaysan Mathematcal Scences Socety http://math.usm.my/bulletn Bull. Malays. Math. Sc. Soc. () 8() (005), 73 79 Some Inequaltes Between Two Polygons Inscrbed One n the Other Aurelo de Gennaro
BULLETIN of the Malaysan Mathematcal Scences Socety http://math.usm.my/bulletn Bull. Malays. Math. Sc. Soc. () 8() (005), 73 79 Some Inequaltes Between Two Polygons Inscrbed One n the Other Aurelo de Gennaro
The equation of motion of a dynamical system is given by a set of differential equations. That is (1)
 Dynamcal Systems Many engneerng and natural systems are dynamcal systems. For example a pendulum s a dynamcal system. State l The state of the dynamcal system specfes t condtons. For a pendulum n the absence
Dynamcal Systems Many engneerng and natural systems are dynamcal systems. For example a pendulum s a dynamcal system. State l The state of the dynamcal system specfes t condtons. For a pendulum n the absence
First day August 1, Problems and Solutions
 FOURTH INTERNATIONAL COMPETITION FOR UNIVERSITY STUDENTS IN MATHEMATICS July 30 August 4, 997, Plovdv, BULGARIA Frst day August, 997 Problems and Solutons Problem. Let {ε n } n= be a sequence of postve
FOURTH INTERNATIONAL COMPETITION FOR UNIVERSITY STUDENTS IN MATHEMATICS July 30 August 4, 997, Plovdv, BULGARIA Frst day August, 997 Problems and Solutons Problem. Let {ε n } n= be a sequence of postve
CHAPTER 4. Vector Spaces
 man 2007/2/16 page 234 CHAPTER 4 Vector Spaces To crtcze mathematcs for ts abstracton s to mss the pont entrel. Abstracton s what makes mathematcs work. Ian Stewart The man am of ths tet s to stud lnear
man 2007/2/16 page 234 CHAPTER 4 Vector Spaces To crtcze mathematcs for ts abstracton s to mss the pont entrel. Abstracton s what makes mathematcs work. Ian Stewart The man am of ths tet s to stud lnear
3 Basic boundary value problems for analytic function in the upper half plane
 3 Basc boundary value problems for analytc functon n the upper half plane 3. Posson representaton formulas for the half plane Let f be an analytc functon of z throughout the half plane Imz > 0, contnuous
3 Basc boundary value problems for analytc functon n the upper half plane 3. Posson representaton formulas for the half plane Let f be an analytc functon of z throughout the half plane Imz > 0, contnuous
Lecture 12: Discrete Laplacian
 Lecture 12: Dscrete Laplacan Scrbe: Tanye Lu Our goal s to come up wth a dscrete verson of Laplacan operator for trangulated surfaces, so that we can use t n practce to solve related problems We are mostly
Lecture 12: Dscrete Laplacan Scrbe: Tanye Lu Our goal s to come up wth a dscrete verson of Laplacan operator for trangulated surfaces, so that we can use t n practce to solve related problems We are mostly
ˆ (0.10 m) E ( N m /C ) 36 ˆj ( j C m)
 7.. = = 3 = 4 = 5. The electrc feld s constant everywhere between the plates. Ths s ndcated by the electrc feld vectors, whch are all the same length and n the same drecton. 7.5. Model: The dstances to
7.. = = 3 = 4 = 5. The electrc feld s constant everywhere between the plates. Ths s ndcated by the electrc feld vectors, whch are all the same length and n the same drecton. 7.5. Model: The dstances to
NP-Completeness : Proofs
 NP-Completeness : Proofs Proof Methods A method to show a decson problem Π NP-complete s as follows. (1) Show Π NP. (2) Choose an NP-complete problem Π. (3) Show Π Π. A method to show an optmzaton problem
NP-Completeness : Proofs Proof Methods A method to show a decson problem Π NP-complete s as follows. (1) Show Π NP. (2) Choose an NP-complete problem Π. (3) Show Π Π. A method to show an optmzaton problem
Econ107 Applied Econometrics Topic 3: Classical Model (Studenmund, Chapter 4)
 I. Classcal Assumptons Econ7 Appled Econometrcs Topc 3: Classcal Model (Studenmund, Chapter 4) We have defned OLS and studed some algebrac propertes of OLS. In ths topc we wll study statstcal propertes
I. Classcal Assumptons Econ7 Appled Econometrcs Topc 3: Classcal Model (Studenmund, Chapter 4) We have defned OLS and studed some algebrac propertes of OLS. In ths topc we wll study statstcal propertes
MEM 255 Introduction to Control Systems Review: Basics of Linear Algebra
 MEM 255 Introducton to Control Systems Revew: Bascs of Lnear Algebra Harry G. Kwatny Department of Mechancal Engneerng & Mechancs Drexel Unversty Outlne Vectors Matrces MATLAB Advanced Topcs Vectors A
MEM 255 Introducton to Control Systems Revew: Bascs of Lnear Algebra Harry G. Kwatny Department of Mechancal Engneerng & Mechancs Drexel Unversty Outlne Vectors Matrces MATLAB Advanced Topcs Vectors A
C/CS/Phy191 Problem Set 3 Solutions Out: Oct 1, 2008., where ( 00. ), so the overall state of the system is ) ( ( ( ( 00 ± 11 ), Φ ± = 1
 C/CS/Phy9 Problem Set 3 Solutons Out: Oct, 8 Suppose you have two qubts n some arbtrary entangled state ψ You apply the teleportaton protocol to each of the qubts separately What s the resultng state obtaned
C/CS/Phy9 Problem Set 3 Solutons Out: Oct, 8 Suppose you have two qubts n some arbtrary entangled state ψ You apply the teleportaton protocol to each of the qubts separately What s the resultng state obtaned
Norms, Condition Numbers, Eigenvalues and Eigenvectors
 Norms, Condton Numbers, Egenvalues and Egenvectors 1 Norms A norm s a measure of the sze of a matrx or a vector For vectors the common norms are: N a 2 = ( x 2 1/2 the Eucldean Norm (1a b 1 = =1 N x (1b
Norms, Condton Numbers, Egenvalues and Egenvectors 1 Norms A norm s a measure of the sze of a matrx or a vector For vectors the common norms are: N a 2 = ( x 2 1/2 the Eucldean Norm (1a b 1 = =1 N x (1b
Solutions to Selected Exercises
 6 Solutons to Selected Eercses Chapter Secton.. a. f ( 0) b. Tons of garbage per week s produced by a cty wth a populaton of,000.. a. In 99 there are 0 ducks n the lake b. In 000 there are 0 ducks n the
6 Solutons to Selected Eercses Chapter Secton.. a. f ( 0) b. Tons of garbage per week s produced by a cty wth a populaton of,000.. a. In 99 there are 0 ducks n the lake b. In 000 there are 0 ducks n the
Spin-rotation coupling of the angularly accelerated rigid body
 Spn-rotaton couplng of the angularly accelerated rgd body Loua Hassan Elzen Basher Khartoum, Sudan. Postal code:11123 E-mal: louaelzen@gmal.com November 1, 2017 All Rghts Reserved. Abstract Ths paper s
Spn-rotaton couplng of the angularly accelerated rgd body Loua Hassan Elzen Basher Khartoum, Sudan. Postal code:11123 E-mal: louaelzen@gmal.com November 1, 2017 All Rghts Reserved. Abstract Ths paper s
Boundaries, Near-field Optics
 Boundares, Near-feld Optcs Fve boundary condtons at an nterface Fresnel Equatons : Transmsson and Reflecton Coeffcents Transmttance and Reflectance Brewster s condton a consequence of Impedance matchng
Boundares, Near-feld Optcs Fve boundary condtons at an nterface Fresnel Equatons : Transmsson and Reflecton Coeffcents Transmttance and Reflectance Brewster s condton a consequence of Impedance matchng
Problem Solving in Math (Math 43900) Fall 2013
 Problem Solvng n Math (Math 43900) Fall 2013 Week four (September 17) solutons Instructor: Davd Galvn 1. Let a and b be two nteger for whch a b s dvsble by 3. Prove that a 3 b 3 s dvsble by 9. Soluton:
Problem Solvng n Math (Math 43900) Fall 2013 Week four (September 17) solutons Instructor: Davd Galvn 1. Let a and b be two nteger for whch a b s dvsble by 3. Prove that a 3 b 3 s dvsble by 9. Soluton:
Advanced Circuits Topics - Part 1 by Dr. Colton (Fall 2017)
 Advanced rcuts Topcs - Part by Dr. olton (Fall 07) Part : Some thngs you should already know from Physcs 0 and 45 These are all thngs that you should have learned n Physcs 0 and/or 45. Ths secton s organzed
Advanced rcuts Topcs - Part by Dr. olton (Fall 07) Part : Some thngs you should already know from Physcs 0 and 45 These are all thngs that you should have learned n Physcs 0 and/or 45. Ths secton s organzed
Linear Algebra and its Applications
 Lnear Algebra and ts Applcatons 4 (00) 5 56 Contents lsts avalable at ScenceDrect Lnear Algebra and ts Applcatons journal homepage: wwwelsevercom/locate/laa Notes on Hlbert and Cauchy matrces Mroslav Fedler
Lnear Algebra and ts Applcatons 4 (00) 5 56 Contents lsts avalable at ScenceDrect Lnear Algebra and ts Applcatons journal homepage: wwwelsevercom/locate/laa Notes on Hlbert and Cauchy matrces Mroslav Fedler
Georgia Tech PHYS 6124 Mathematical Methods of Physics I
 Georga Tech PHYS 624 Mathematcal Methods of Physcs I Instructor: Predrag Cvtanovć Fall semester 202 Homework Set #7 due October 30 202 == show all your work for maxmum credt == put labels ttle legends
Georga Tech PHYS 624 Mathematcal Methods of Physcs I Instructor: Predrag Cvtanovć Fall semester 202 Homework Set #7 due October 30 202 == show all your work for maxmum credt == put labels ttle legends
princeton univ. F 17 cos 521: Advanced Algorithm Design Lecture 7: LP Duality Lecturer: Matt Weinberg
 prnceton unv. F 17 cos 521: Advanced Algorthm Desgn Lecture 7: LP Dualty Lecturer: Matt Wenberg Scrbe: LP Dualty s an extremely useful tool for analyzng structural propertes of lnear programs. Whle there
prnceton unv. F 17 cos 521: Advanced Algorthm Desgn Lecture 7: LP Dualty Lecturer: Matt Wenberg Scrbe: LP Dualty s an extremely useful tool for analyzng structural propertes of lnear programs. Whle there
Week 9 Chapter 10 Section 1-5
 Week 9 Chapter 10 Secton 1-5 Rotaton Rgd Object A rgd object s one that s nondeformable The relatve locatons of all partcles makng up the object reman constant All real objects are deformable to some extent,
Week 9 Chapter 10 Secton 1-5 Rotaton Rgd Object A rgd object s one that s nondeformable The relatve locatons of all partcles makng up the object reman constant All real objects are deformable to some extent,
2.3 Nilpotent endomorphisms
 s a block dagonal matrx, wth A Mat dm U (C) In fact, we can assume that B = B 1 B k, wth B an ordered bass of U, and that A = [f U ] B, where f U : U U s the restrcton of f to U 40 23 Nlpotent endomorphsms
s a block dagonal matrx, wth A Mat dm U (C) In fact, we can assume that B = B 1 B k, wth B an ordered bass of U, and that A = [f U ] B, where f U : U U s the restrcton of f to U 40 23 Nlpotent endomorphsms
Randić Energy and Randić Estrada Index of a Graph
 EUROPEAN JOURNAL OF PURE AND APPLIED MATHEMATICS Vol. 5, No., 202, 88-96 ISSN 307-5543 www.ejpam.com SPECIAL ISSUE FOR THE INTERNATIONAL CONFERENCE ON APPLIED ANALYSIS AND ALGEBRA 29 JUNE -02JULY 20, ISTANBUL
EUROPEAN JOURNAL OF PURE AND APPLIED MATHEMATICS Vol. 5, No., 202, 88-96 ISSN 307-5543 www.ejpam.com SPECIAL ISSUE FOR THE INTERNATIONAL CONFERENCE ON APPLIED ANALYSIS AND ALGEBRA 29 JUNE -02JULY 20, ISTANBUL
Complex Numbers Practice 0708 & SP 1. The complex number z is defined by
 IB Math Hgh Leel: Complex Nmbers Practce 0708 & SP Complex Nmbers Practce 0708 & SP. The complex nmber z s defned by π π π π z = sn sn. 6 6 Ale - Desert Academy (a) Express z n the form re, where r and
IB Math Hgh Leel: Complex Nmbers Practce 0708 & SP Complex Nmbers Practce 0708 & SP. The complex nmber z s defned by π π π π z = sn sn. 6 6 Ale - Desert Academy (a) Express z n the form re, where r and
Math 217 Fall 2013 Homework 2 Solutions
 Math 17 Fall 013 Homework Solutons Due Thursday Sept. 6, 013 5pm Ths homework conssts of 6 problems of 5 ponts each. The total s 30. You need to fully justfy your answer prove that your functon ndeed has
Math 17 Fall 013 Homework Solutons Due Thursday Sept. 6, 013 5pm Ths homework conssts of 6 problems of 5 ponts each. The total s 30. You need to fully justfy your answer prove that your functon ndeed has
Field and Wave Electromagnetic. Chapter.4
 Fel an Wave Electromagnetc Chapter.4 Soluton of electrostatc Problems Posson s s an Laplace s Equatons D = ρ E = E = V D = ε E : Two funamental equatons for electrostatc problem Where, V s scalar electrc
Fel an Wave Electromagnetc Chapter.4 Soluton of electrostatc Problems Posson s s an Laplace s Equatons D = ρ E = E = V D = ε E : Two funamental equatons for electrostatc problem Where, V s scalar electrc
Salmon: Lectures on partial differential equations. Consider the general linear, second-order PDE in the form. ,x 2
 Salmon: Lectures on partal dfferental equatons 5. Classfcaton of second-order equatons There are general methods for classfyng hgher-order partal dfferental equatons. One s very general (applyng even to
Salmon: Lectures on partal dfferental equatons 5. Classfcaton of second-order equatons There are general methods for classfyng hgher-order partal dfferental equatons. One s very general (applyng even to
The Multiple Classical Linear Regression Model (CLRM): Specification and Assumptions. 1. Introduction
 ECONOMICS 5* -- NOTE (Summary) ECON 5* -- NOTE The Multple Classcal Lnear Regresson Model (CLRM): Specfcaton and Assumptons. Introducton CLRM stands for the Classcal Lnear Regresson Model. The CLRM s also
ECONOMICS 5* -- NOTE (Summary) ECON 5* -- NOTE The Multple Classcal Lnear Regresson Model (CLRM): Specfcaton and Assumptons. Introducton CLRM stands for the Classcal Lnear Regresson Model. The CLRM s also
Linear Approximation with Regularization and Moving Least Squares
 Lnear Approxmaton wth Regularzaton and Movng Least Squares Igor Grešovn May 007 Revson 4.6 (Revson : March 004). 5 4 3 0.5 3 3.5 4 Contents: Lnear Fttng...4. Weghted Least Squares n Functon Approxmaton...
Lnear Approxmaton wth Regularzaton and Movng Least Squares Igor Grešovn May 007 Revson 4.6 (Revson : March 004). 5 4 3 0.5 3 3.5 4 Contents: Lnear Fttng...4. Weghted Least Squares n Functon Approxmaton...
Week 11: Chapter 11. The Vector Product. The Vector Product Defined. The Vector Product and Torque. More About the Vector Product
 The Vector Product Week 11: Chapter 11 Angular Momentum There are nstances where the product of two vectors s another vector Earler we saw where the product of two vectors was a scalar Ths was called the
The Vector Product Week 11: Chapter 11 Angular Momentum There are nstances where the product of two vectors s another vector Earler we saw where the product of two vectors was a scalar Ths was called the
The Minimum Universal Cost Flow in an Infeasible Flow Network
 Journal of Scences, Islamc Republc of Iran 17(2): 175-180 (2006) Unversty of Tehran, ISSN 1016-1104 http://jscencesutacr The Mnmum Unversal Cost Flow n an Infeasble Flow Network H Saleh Fathabad * M Bagheran
Journal of Scences, Islamc Republc of Iran 17(2): 175-180 (2006) Unversty of Tehran, ISSN 1016-1104 http://jscencesutacr The Mnmum Unversal Cost Flow n an Infeasble Flow Network H Saleh Fathabad * M Bagheran
THE CHINESE REMAINDER THEOREM. We should thank the Chinese for their wonderful remainder theorem. Glenn Stevens
 THE CHINESE REMAINDER THEOREM KEITH CONRAD We should thank the Chnese for ther wonderful remander theorem. Glenn Stevens 1. Introducton The Chnese remander theorem says we can unquely solve any par of
THE CHINESE REMAINDER THEOREM KEITH CONRAD We should thank the Chnese for ther wonderful remander theorem. Glenn Stevens 1. Introducton The Chnese remander theorem says we can unquely solve any par of
COMPLEX NUMBER & QUADRATIC EQUATION
 MCQ COMPLEX NUMBER & QUADRATIC EQUATION Syllus : Comple numers s ordered prs of rels, Representton of comple numers n the form + nd ther representton n plne, Argnd dgrm, lger of comple numers, modulus
MCQ COMPLEX NUMBER & QUADRATIC EQUATION Syllus : Comple numers s ordered prs of rels, Representton of comple numers n the form + nd ther representton n plne, Argnd dgrm, lger of comple numers, modulus
ON A DETERMINATION OF THE INITIAL FUNCTIONS FROM THE OBSERVED VALUES OF THE BOUNDARY FUNCTIONS FOR THE SECOND-ORDER HYPERBOLIC EQUATION
 Advanced Mathematcal Models & Applcatons Vol.3, No.3, 2018, pp.215-222 ON A DETERMINATION OF THE INITIAL FUNCTIONS FROM THE OBSERVED VALUES OF THE BOUNDARY FUNCTIONS FOR THE SECOND-ORDER HYPERBOLIC EUATION
Advanced Mathematcal Models & Applcatons Vol.3, No.3, 2018, pp.215-222 ON A DETERMINATION OF THE INITIAL FUNCTIONS FROM THE OBSERVED VALUES OF THE BOUNDARY FUNCTIONS FOR THE SECOND-ORDER HYPERBOLIC EUATION
Indeterminate pin-jointed frames (trusses)
 Indetermnate pn-jonted frames (trusses) Calculaton of member forces usng force method I. Statcal determnacy. The degree of freedom of any truss can be derved as: w= k d a =, where k s the number of all
Indetermnate pn-jonted frames (trusses) Calculaton of member forces usng force method I. Statcal determnacy. The degree of freedom of any truss can be derved as: w= k d a =, where k s the number of all
MTH 263 Practice Test #1 Spring 1999
 Pat Ross MTH 6 Practce Test # Sprng 999 Name. Fnd the area of the regon bounded by the graph r =acos (θ). Observe: Ths s a crcle of radus a, for r =acos (θ) r =a ³ x r r =ax x + y =ax x ax + y =0 x ax
Pat Ross MTH 6 Practce Test # Sprng 999 Name. Fnd the area of the regon bounded by the graph r =acos (θ). Observe: Ths s a crcle of radus a, for r =acos (θ) r =a ³ x r r =ax x + y =ax x ax + y =0 x ax
ACTM State Calculus Competition Saturday April 30, 2011
 ACTM State Calculus Competton Saturday Aprl 30, 2011 ACTM State Calculus Competton Sprng 2011 Page 1 Instructons: For questons 1 through 25, mark the best answer choce on the answer sheet provde Afterward
ACTM State Calculus Competton Saturday Aprl 30, 2011 ACTM State Calculus Competton Sprng 2011 Page 1 Instructons: For questons 1 through 25, mark the best answer choce on the answer sheet provde Afterward
PHYS 705: Classical Mechanics. Calculus of Variations II
 1 PHYS 705: Classcal Mechancs Calculus of Varatons II 2 Calculus of Varatons: Generalzaton (no constrant yet) Suppose now that F depends on several dependent varables : We need to fnd such that has a statonary
1 PHYS 705: Classcal Mechancs Calculus of Varatons II 2 Calculus of Varatons: Generalzaton (no constrant yet) Suppose now that F depends on several dependent varables : We need to fnd such that has a statonary
CALCULUS CLASSROOM CAPSULES
 CALCULUS CLASSROOM CAPSULES SESSION S86 Dr. Sham Alfred Rartan Valley Communty College salfred@rartanval.edu 38th AMATYC Annual Conference Jacksonvlle, Florda November 8-, 202 2 Calculus Classroom Capsules
CALCULUS CLASSROOM CAPSULES SESSION S86 Dr. Sham Alfred Rartan Valley Communty College salfred@rartanval.edu 38th AMATYC Annual Conference Jacksonvlle, Florda November 8-, 202 2 Calculus Classroom Capsules
Gravitational Acceleration: A case of constant acceleration (approx. 2 hr.) (6/7/11)
 Gravtatonal Acceleraton: A case of constant acceleraton (approx. hr.) (6/7/11) Introducton The gravtatonal force s one of the fundamental forces of nature. Under the nfluence of ths force all objects havng
Gravtatonal Acceleraton: A case of constant acceleraton (approx. hr.) (6/7/11) Introducton The gravtatonal force s one of the fundamental forces of nature. Under the nfluence of ths force all objects havng
Solutions to Problem Set 6
 Solutons to Problem Set 6 Problem 6. (Resdue theory) a) Problem 4.7.7 Boas. n ths problem we wll solve ths ntegral: x sn x x + 4x + 5 dx: To solve ths usng the resdue theorem, we study ths complex ntegral:
Solutons to Problem Set 6 Problem 6. (Resdue theory) a) Problem 4.7.7 Boas. n ths problem we wll solve ths ntegral: x sn x x + 4x + 5 dx: To solve ths usng the resdue theorem, we study ths complex ntegral:
The Quadratic Trigonometric Bézier Curve with Single Shape Parameter
 J. Basc. Appl. Sc. Res., (3541-546, 01 01, TextRoad Publcaton ISSN 090-4304 Journal of Basc and Appled Scentfc Research www.textroad.com The Quadratc Trgonometrc Bézer Curve wth Sngle Shape Parameter Uzma
J. Basc. Appl. Sc. Res., (3541-546, 01 01, TextRoad Publcaton ISSN 090-4304 Journal of Basc and Appled Scentfc Research www.textroad.com The Quadratc Trgonometrc Bézer Curve wth Sngle Shape Parameter Uzma
On the Multicriteria Integer Network Flow Problem
 BULGARIAN ACADEMY OF SCIENCES CYBERNETICS AND INFORMATION TECHNOLOGIES Volume 5, No 2 Sofa 2005 On the Multcrtera Integer Network Flow Problem Vassl Vasslev, Marana Nkolova, Maryana Vassleva Insttute of
BULGARIAN ACADEMY OF SCIENCES CYBERNETICS AND INFORMATION TECHNOLOGIES Volume 5, No 2 Sofa 2005 On the Multcrtera Integer Network Flow Problem Vassl Vasslev, Marana Nkolova, Maryana Vassleva Insttute of
WINTER 2017 EXAMINATION
 (ISO/IEC - 700-00 Certfed) WINTER 07 EXAMINATION Model wer ject Code: Important Instructons to Eamners: ) The answers should be eamned by key words and not as word-to-word as gven n the model answer scheme.
(ISO/IEC - 700-00 Certfed) WINTER 07 EXAMINATION Model wer ject Code: Important Instructons to Eamners: ) The answers should be eamned by key words and not as word-to-word as gven n the model answer scheme.
STUDY PACKAGE. Subject : Mathematics ENJOY MATHEMATICS WITH SUHAAG SIR. Student s Name : Class Roll No.
 fo/u fopkjr Hk# tu] uga vkjehks dke] foifr ns[k NksM+s rqjar e/;e eu dj ';kea iq#"k flag ladyi dj] lgrs foifr vusd] ^cuk^ u NksM+s /;s; dks] j?kqcj jk[ks VsdAA jfpr% ekuo /kez izksrk ln~q# J jknksm+nklt
fo/u fopkjr Hk# tu] uga vkjehks dke] foifr ns[k NksM+s rqjar e/;e eu dj ';kea iq#"k flag ladyi dj] lgrs foifr vusd] ^cuk^ u NksM+s /;s; dks] j?kqcj jk[ks VsdAA jfpr% ekuo /kez izksrk ln~q# J jknksm+nklt
Math 261 Exercise sheet 2
 Math 261 Exercse sheet 2 http://staff.aub.edu.lb/~nm116/teachng/2017/math261/ndex.html Verson: September 25, 2017 Answers are due for Monday 25 September, 11AM. The use of calculators s allowed. Exercse
Math 261 Exercse sheet 2 http://staff.aub.edu.lb/~nm116/teachng/2017/math261/ndex.html Verson: September 25, 2017 Answers are due for Monday 25 September, 11AM. The use of calculators s allowed. Exercse
The Number of Ways to Write n as a Sum of ` Regular Figurate Numbers
 Syracuse Unversty SURFACE Syracuse Unversty Honors Program Capstone Projects Syracuse Unversty Honors Program Capstone Projects Sprng 5-1-01 The Number of Ways to Wrte n as a Sum of ` Regular Fgurate Numbers
Syracuse Unversty SURFACE Syracuse Unversty Honors Program Capstone Projects Syracuse Unversty Honors Program Capstone Projects Sprng 5-1-01 The Number of Ways to Wrte n as a Sum of ` Regular Fgurate Numbers
