Quadratic Functions and Equations
|
|
|
- Roxanne Dana Ray
- 6 years ago
- Views:
Transcription
1 Quadratic Functions and Equations
2 Quadratic Graphs and Their Properties Objective: To graph quadratic functions of the form y = ax 2 and y = ax 2 + c.
3 Objectives I can identify a vertex. I can grapy y = ax 2. I can compare widths of parabolas. I can graph y = ax 2 + c. I can use the falling object model.
4 Vocabulary A quadratic function is a type of nonlinear function that models certain situations where the rate of change is not constant. The graph of a quadratic function is a symmetric curve with the highest or lowest point corresponding to a maximum or minimum value. Standard Form of a Quadratic Function: A quadratic function is a function that can be written in the form y = ax 2 + bx + c, where a 0. This form is called the standard form of a quadratic function. Examples: y = 3x 2 y = x y = x 2 x 2
5 Vocabulary The simplest quadratic function f x = x 2 or y = x 2 is the quadratic parent function. The graph of a quadratic function is a U-shaped curve called a parabola. You can fold a parabola so that the two sides match exactly. This property is called symmetry. The fold or line that divides the parabola into two matching halves is called the axis of symmetry.
6 Vocabulary The highest or lowest point of a parabola is its vertex, what is on the axis of symmetry. If a > 0 in y = ax 2 + bx + c, the parabola opens upward. The vertex is the minimum point, or lowest point, of the parabola. If a < 0 in y = ax 2 + bx + c, the parabola opens downward. The vertex is the maximum point, or highest point, of the parabola.
7 Identifying a Vertex
8 Practice Identify the vertex.
9 Practice
10 Vocabulary You can use the fact that a parabola is symmetric to graph it quickly. First, find the coordinates of the vertex and several points on one side of the vertex. Then reflect the points across the axis of symmetry. For graphs of functions of the form y = ax 2, the vertex is at the origin. The axis of symmetry is the y axis, or x = 0.
11 Graphing y = ax 2 Graph the function. Make a table of values. What are the domain and range? 1. y = 1 3 x2 2. y = 3x 2 3. y = 4x 2
12 Practice Graph each function. Then identify the domain and range of the function. 1. y = 4x 2 2. y = 1 3 x2 3. f x = 1.5x 2 4. f x = 2 3 x2
13 Vocabulary The coefficient of the x 2 term in a quadratic function affects the width of the parabola as well as the direction in which it opens. When m < n, the graph of y = mx 2 is wider than the graph of y = nx 2.
14 Comparing Widths of Parabolas Use your calculator to graph. What is the order, from widest to narrowest, of the graphs of the quadratic functions. f x = 4x 2, f x = 1 4 x2, f(x) = x 2 f x = x 2, f x = 3x 2, f x = 1 3 x2
15 Practice Order each group of quadratic functions from widest to narrowest graph. y = 3x 2, y = 2x 2, y = 4x 2 y = 1 2 x2, y = 5x 2, y = 1 4 x2 f x = 5x 2, f x = 3x 2, f x = x 2 f x = 2x 2, f x = 2 3 x2, f x = 4x 2
16 Vocabulary The y axis is the axis of symmetry for graphs of functions of the form y = ax 2 + c. The value of c translates the graph up or down.
17 Graphing y = ax 2 + c What is the relationship of the following graphs? 1. y = 2x and y = 2x 2 2. y = x 2 and y = x y = 1 2 x2 and y = 1 2 x2 + 1
18 Practice Graph each function. 1. f x = x f x = x f x = 1 2 x2 + 2
19 Vocabulary As an object falls, its speed continues to increase, so its height above the ground decreases at a faster and faster rate. Ignoring air resistance, you can model the object s height with the function h = 16t 2 + c. The height h is in feet, the time t is in seconds, and the object s initial height c is in feet.
20 Using the Falling Object Model An acorn drops from a tree branch 20 feet above the ground. The function h = 16t gives the height h of the acorn (in feet) after t seconds. What is the graph of this quadratic function? At what time does the the acorn hit the ground? t h = 16t
21 Using the Falling Object Model An acorn drops from a tree branch 70 feet above the ground. The function h = 16t gives the height h of the acorn (in feet) after t seconds. What is the graph of this quadratic function? At what time does the the acorn hit the ground? t h = 16t
22 Practice A person walking across a bridge accidentally drops an orange into the river below from a height of 40 feet. The function h = 16t gives the orange s approximate height h above the water, in feet, after t seconds. In how many seconds will the orange hit the water? A bird drops a stick to the ground from a height of 80 feet. The function h = 16t gives the stick s approximate height h above the ground, in feet, after t seconds. Graph the function. At about what time does the stick hit the ground?
23 Quadratic Functions Objective: To graph quadratic functions of the form y = ax 2 + bx + c.
24 Objectives I can graph y = ax 2 + bx + c. I can use the vertical motion model.
25 Vocabulary In the quadratic function y = ax 2 + bx + c, the value of b affects the position of the axis of symmetry. The axis of symmetry changes with each equation because of the change in the b-value. The equation of the axis of symmetry is related to the ratio b a. The equation of the axis of symmetry is x = 1 2 b a or x = b 2a. Graph of a Quadratic Function o The graph of y = ax 2 + bx + c, where a 0, has the line x = b The x coordinate of the vertex is b 2a. 2a as its axis of symmetry.
26 Vocabulary When you substitute x = 0 into the equation y = ax 2 + bx + c, you get y = c. So the y intercept of a quadratic function is c. You can use the axis of symmetry and the y intercept to help you graph a quadratic function.
27 Graphing y = ax 2 + bx + c What is the graph of the function? Show the axis of symmetry. 1. y = x 2 6x y = x 2 + 4x 2 3. y = 2x y = 3x x f x = x 2 + 4x 5 6. f x = 4x
28 Practice What is the graph of the function? Show the line of symmetry. 1. y = 2x 2 6x f x = 2x 2 + 4x 1 3. y = 6x 2 + 6x 5 4. f x = 5x 2 + 3x y = 2x 2 10x 6. y = 4x 2 16x 3
29 Vocabulary You have used h = 16t 2 + c to find the height h above the ground of an object falling from an initial height c at time t. If an object projected into the air given an initial upward velocity v continues with no additional force of its own, the formula h = 16t 2 + vt + c givens its approximate height above the ground.
30 Using a Vertical Motion Model During halftime of a basketball game, a sling shot launches T shirts at the crowd. A T shirt launched with an initial upward velocity of 72 feet per second. The T shirt is caught 35 feet above the court. The T shirt is launched from a height of 5 feet. a. How long will it take the T shirt to reach its maximum height? b. What is the maximum height? c. What is the range of the function that models the height of the T shirt over time?
31 Using a Vertical Motion Model During halftime of a basketball game, a sling shot launches T shirts at the crowd. A T shirt launched with an initial upward velocity of 64 feet per second. The T shirt is caught 35 feet above the court. The T shirt is launched from a height of 5 feet. a. How long will it take the T shirt to reach its maximum height? b. What is the maximum height? c. What is the range of the function that models the height of the T shirt over time?
32 Practice A baseball is thrown into the air with an upward velocity of 30 feet per second. Its height h, in feet, after t seconds is given by the function h = 16t t + 6. a. How long will it take the ball to reach its maximum height? b. What is the ball s maximum height? c. What is the range of the function?
33 Solving Quadratic Equations Objective: To solve quadratic equations by graphing and using square roots.
34 Objectives I can solve by graphing. I can solve using square roots. I can choose a reasonable solution.
35 Vocabulary Standard Form of a Quadratic Equation: A quadratic equation is an equation that can be written in the form ax 2 + bx + c = 0, where a 0. This form is called the standard form of a quadratic equation. Quadratic equations can be solved by a variety of methods, including graphing and finding square roots. One way to solve a quadratic equation ax 2 + bx + c = 0 is to graph the related quadratic function y = ax 2 +bx + c. The solutions of the equation are the x intercepts of the related function.
36 Vocabulary A quadratic equation can have two, one, or no real-number solutions. The solutions of a quadratic equation and the x intercepts of the graph of the related function are often called roots of the equation or zeros of the function.
37 Solving by Graphing What are the solutions of each equation? Use a graph of the related function. 1. x 2 1 = 0 2. x 2 = 0 3. x = 0 4. x 2 16 = x = 0 6. x 2 25 = 25
38 Practice Solve each equation by graphing the related function. If the equation has no real number solution, write no solution. 1. x 2 9 = x 2 = x2 3 = 0 4. x = 5 5. x 2 10 = x 2 18 = 0
39 Vocabulary You can solve equations of the form x 2 = k by finding the square roots of each side.
40 Solving Using Square Roots What are the solutions? 1. 3x 2 75 = 0 2. m 2 36 = x = d = t 2 = y = 0 7. x 2 25 = x 2 8 = 0
41 Practice Solve each equation by finding square roots. If the question has no real number solution, write no solution. 1. n 2 = w 2 36 = b 2 = q 2 20 = p 2 = a = 0 7. r = k = 0
42 Vocabulary You can solve some quadratic equations that model real world problems by finding square roots. In many cases, the negative square root may not be a reasonable solution.
43 Choosing a Reasonable Solution 1. An aquarium is designing a new exhibit to showcase tropical fish. The exhibit will include a tank that is a rectangular prism with a length l that is twice the width w. The volume of the tank is 420 ft 3. What is the width of the tank to the nearest tenth of a foot? (V = lwh), h = 3 ft 2. Suppose that the tank has a height of 4 feet and a volume of 500 ft 3. What is the width of the tank to the nearest tenth of a foot.
44 Practice You have enough paint to cover an area of 50 ft². What is the side length of the largest square that you could paint? Round your answer to the nearest tenth of a foot. Find the length of a square with an area of 75 ft². Round to your answer to the nearest tenth of a foot.
45 Factoring to Solve Quadratic Equations Objective: To solve quadratic equations by factoring.
46 Objectives I can use the zero-product property. I can solve by factoring. I can write in standard form first. I can use factoring to solve real-world problems.
47 Vocabulary In the previous lesson, you solved quadratic equations ax 2 + bx + c = 0 by finding square roots. This method works if b = 0. You can solve some quadratic equations, including equations where b 0, by using the Zero Product Property. The Multiplication Property of Zero states that for any real number a, a 0 = 0. This is equivalent to the following statement: For any real numbers a and b, if a = 0 or b = 0, then ab = 0. The Zero Product Property reverses this statement.
48 Vocabulary Zero Product Property For any real numbers a and b, if ab = 0, then a = 0 or b = 0. Example: If (x + 3)(x + 2) = 0, then x + 3 = 0 or x + 2 = 0.
49 Using the Zero Product Property What are the solutions of the equation? 1. (4t + 1)(t 2) = 0 2. (x + 1)(x 5) = 0 3. (2x + 3)(x 4) = 0 4. (2y + 1)(y + 14) = 0 5. (7n 2)(5n 4) = 0 6. (v 4)(v 7) = 0
50 Practice Use the Zero Product Property to solve each equation. 1. (x 9)(x 8) = 0 2. (4k + 5)(k + 7) = 0 3. n(n + 2) = n(2n 5) = 0 5. (7x + 2)(5x 4) = 0 6. (4a 7)(3a + 8) = 0
51 Vocabulary You can also use the Zero Product Property to solve equations of the form ax 2 + bx + c = 0 if the quadratic expression ax 2 + bx + c can be factored.
52 Solving by Factoring What is the solutions of the equations? 1. x 2 + 8x + 15 = 0 2. m 2 5m 14 = 0 3. p 2 + p 20 = a 2 15a + 18 = 0 5. t 2 + 3t 54 = y 2 17y + 24 = 0
53 Practice Solve by factoring. 1. x x + 10 = 0 2. g 2 + 4g 32 = q 2 + q 14 = 0 4. p 2 4p = w 2 11w = b 2 = 81
54 Vocabulary Before solving a quadratic equation, you may need to add or subtract terms from each side in order to write the equation in standard form. Then factor the quadratic expression.
55 Writing in Standard Form First What are the solutions? 1. 4x 2 21x = x x = p 2 4p = w 2 11w = h h = b 2 = 16
56 Practice Solve by factoring. 1. x x = c 2 = 5c 3. t 2 = 3t y 2 17y = n n + 15 = 2n q 2 + 3q = 3q 2 4q + 18
57 Using Factoring to Solve a Real World Problem You are constructing a frame for a rectangular photo (17 in by 11 in).you want the frame to be the same width all the way around and the total area of the frame and photo to be 315 in 2. What should the outer dimensions of the frame be?
58 Using Factoring to Solve a Real World Problem You are constructing a frame for a rectangular photo (17 in by 11 in).you want the frame to be the same width all the way around and the total area of the frame and photo to be 391 in 2. What should the outer dimensions of the frame be?
59 Practice A box shaped like a rectangular prism has a volume of 280 in³. Its dimensions are 4 in by (n + 2) in by (n + 5) in. Find n. You are building a rectangular deck. The area of the deck should be 250 ft 2. You want the length of the deck to be 5 feet longer than twice its width. What should the dimensions of the deck be?
60 Completing the Square Objective: To solve quadratic equations by completing the square.
61 Objective I can find c to complete the square. I can solve x 2 + bx + c = 0. I can find the vertex by completing the square. I can complete the square when a 1.
62 Vocabulary You can solve any quadratic equation by first writing it in the form m 2 = n. In general, you can change the expression x 2 + bx into a perfect square trinomial by adding ( b 2 )2 to x 2 + bx. This process is called completing the square. The process is the same whether b is positive or negative.
63 Finding c to Complete the Square What is the value of c so that it is a perfect square trinomial? 1. x 2 16x + c 2. x x + c 3. g g + c 4. q 2 4q + c 5. k 2 5k + c 6. x x + c
64 Practice Find the value of c such that each expression is a perfect square trinomial. 1. x 2 + 4x + c 2. a 2 7a + c 3. b b + c 4. w w + c 5. g 2 20g + c 6. n 2 9n + c
65 Vocabulary To solve an equation in the form x2 + bx + c = 0, first subtract the constant term c from each side of the equation.
66 Solving x 2 + bx + c = 0 What is the solution of the equation? 1. x 2 14x + 16 = 0 2. x 2 + 9x + 15 = 0 3. m 2 + 7m 294 = 0 4. m m = g 2 + 7g = z 2 2z = 323
67 Practice What are the solutions for the following? 1. x 2 + 6x = t 2 6t = r 2 4r = p 2 + 5p 7 = 0 5. m m + 19 = 0 6. w 2 14w + 13 = 0
68 Vocabulary The equation y = (x h) 2 +k represents a parabola with vertex (h, k). You can use the method of completing the square to find the vertex of quadratic functions of the form y = x 2 + bx + c.
69 Finding the Vertex by Completing the Square Find the vertex by completing the square. 1. y = x 2 + 6x y = x 2 + 4x y = x x y = x x y = x x 468
70 Practice Find the vertex of each parabola by completing the square. 1. y = x 2 + 4x y = x 2 + 6x 7 3. y = x 2 + 2x y = x 2 2x 323
71 Vocabulary The method of completing the square works when a = 1 in ax 2 + bx + c = 0. To solve an equation when a 1, divide each side by a before completing the square.
72 Completing the Square When a 1 You are planning a flower garden consisting of three square plots surrounded by a 1 foot border. The total area of the garden and the border is 100 ft 2. What is the side length x of each square? 1 x 1 1 x x 1 x
73 Completing the Square When a 1 You are planning a flower garden consisting of three square plots surrounded by a 1 foot border. The total area of the garden and the border is 150 ft 2. What is the side length x of each square? Round to the nearest hundredth. 1 1 x x x x
74 Practice Solve each equation by completing the square. If necessary, round to the nearest hundredth. 1. 4a 2 8a = y 2 8y 10 = n 2 3n 15 = w w 44 = r r = v 2 10v 20 = 8
75 The Quadratic Formula and the Discriminant Objective: To solve quadratic equations using the quadratic formula. To find the number of solutions of a quadratic equation.
76 Objectives I can use the quadratic formula. I can find approximate solutions. I can choose an appropriate method. I can use the discriminant.
77 Vocabulary You can find the solution(s) of any quadratic equation using the quadratic formula. Quadratic Formula: Algebra: If ax2 + bx + c = 0, and a 0, then x = b± b2 4ac. 2a Example: Suppose 2x 2 + 3x 5 = 0. Then a = 2, b = 3, and c = 5. Therefore x = (3)± (3)2 4(2)( 5) 2(2) Be sure to write a quadratic in standard form before using the quadratic formula.
78 Here s Why It Works: If you complete the square for the general equation ax 2 + bx + c = 0, you can derive the quadratic formula. Step 1: Write ax 2 + bx + c = 0 so that the coefficient of x 2 is 1. ax 2 + bx + c = 0 x 2 + b x + c = 0 Divide each side by a. a a Step 2: Complete the square. x 2 + b x = c a a x 2 + b b x + ( a 2a )2 = c + ( b a 2a )2 (x + b 2a )2 = c + b2 a 4a 2 (x + b 2a )2 = 4ac 4a 2 + b2 4a 2 (x + b 2a )2 = b2 4ac 4a 2 Step 3: Solve the equation for x. (x + b 2a )2 =± x + b = ± b2 4ac 2a 2a x = b ± b2 4ac 2a 2a x = b± b2 4ac 2a b2 4ac 4a 2 Subtract c from each side. a Add ( b 2a )2 to each side. Write the left side as a square. Multiply c a Simplify the right side. 4a by to get like denominators. 4a Take square roots of each side. Simplify the right side. Subtract b from each side. 2a Simplify
79 Using the Quadratic Formula What are the solutions using the quadratic formula? 1. x 2 8 = 2x 2. x 2 4x = x 2 + 5x + 3 = x x = x 2 45x 50 = 0
80 Practice Use the quadratic formula to solve each equation. 1. 3x 2 41x = x x 84 = x 2 x 120 = x x = x 2 47x = 156
81 Vocabulary When the radicand in the quadratic formula is not a perfect square, you can use a calculator to approximate the solutions of an equation.
82 Finding Approximate Solutions 1. In the shot put, an athlete throws a heavy metal ball through the air. The arc of the ball can be modeled by the equation y = 0.04x x + 2, where x is the horizontal distance, in meters, from the athlete and y is the height, in meters, of the ball. How far from the athlete will the ball land? 2. A batter strikes a baseball. The equation y = 0.005x x models its path, where x is the horizontal distance, in feet, the ball travels and y is the height, in feet, of the ball. How far from the batter will the ball land? Round to the nearest tenth of a foot.
83 Practice Use the quadratic formula to solve each equation. Round your answer to the nearest hundredth. 1. x 2 + 8x + 11 = x x 2 = x 2 16x = x 2 + 9x = 32
84 Vocabulary There are many methods for solving a quadratic equation. Method Graphing Square Roots Factoring Completing the Square Quadratic Formula When to Use Use if you have a graphing calculator handy Use if the equation has no x-terms Use if you can factor the equation easily Use if the coefficient of x 2 is 1, but you cannot easily factor the equation Use if the equation cannot be factored easily or at all
85 Choosing an Appropriate Method Which method(s) would you choose to solve each equation? Explain your reasoning. 1. 3x 2 9 = 0 2. x 2 x 30 = x x 17 = 0 4. x 2 5x + 3 = x 2 50x + 21 = 0 6. x 2 8x + 12 = x 2 = x x 1 = 0
86 Practice Which method(s) would you choose to solve each equation? Justify your reasoning. 1. x 2 + 4x 15 = x 2 49 = x 2 41x = x 2 7x + 3 = 0 5. x 2 + 4x 60 = x 2 + 8x + 1 = 0
87 Vocabulary Quadratic equations can have two, one, or no real-number solutions. Before you solve a quadratic equations, you can determine how many realnumber solutions it has by using the discriminant. The discriminant is the expression under the radical sign in the quadratic formula. The discriminant is b 2 4ac of x = b± b2 4ac 2a The discriminant of a quadratic equation can be positive, negative, or zero.
88 Using the Discriminant Discriminant b 2 4ac > 0 b 2 4ac = 0 b 2 4ac < 0 Example x 2 6x + 7 = 0 The discriminant (-6) 2 4(1)(7) = 8 which is positive x 2 6x + 9 = 0 The discriminant (-6) 2 4(1)(9) = 0 x 2 6x + 11 = 0 The discriminant (-6) 2 4(1)(11) = 8 which is negative Number of Solutions There are two real-number solutions There is one real-number solutions There are no real-number solutions
89 The Discriminant
90 Using the Discriminant How many real-number solutions does each have? 1. 2x 2 3x = x 2 5x = 7 3. x 2 + 3x + 11 = x x + 4 = 0 5. x 2 15 = 0
91 Practice Find the number of real number solutions of each equation. 1. x 2 2x + 3 = 0 2. x 2 + 7x 5 = 0 3. x 2 + 2x = p 2 + 4p = 10
Unit 5 Test: 9.1 Quadratic Graphs and Their Properties
 Unit 5 Test: 9.1 Quadratic Graphs and Their Properties Quadratic Equation: (Also called PARABOLAS) 1. of the STANDARD form y = ax 2 + bx + c 2. a, b, c are all real numbers and a 0 3. Always have an x
Unit 5 Test: 9.1 Quadratic Graphs and Their Properties Quadratic Equation: (Also called PARABOLAS) 1. of the STANDARD form y = ax 2 + bx + c 2. a, b, c are all real numbers and a 0 3. Always have an x
UNIT 2B QUADRATICS II
 UNIT 2B QUADRATICS II M2 12.1-8, M2 12.10, M1 4.4 2B.1 Quadratic Graphs Objective I will be able to identify quadratic functions and their vertices, graph them and adjust the height and width of the parabolas.
UNIT 2B QUADRATICS II M2 12.1-8, M2 12.10, M1 4.4 2B.1 Quadratic Graphs Objective I will be able to identify quadratic functions and their vertices, graph them and adjust the height and width of the parabolas.
Math 2 1. Lesson 4-5: Completing the Square. When a=1 in a perfect square trinomial, then. On your own: a. x 2 18x + = b.
 Math 1 Lesson 4-5: Completing the Square Targets: I can identify and complete perfect square trinomials. I can solve quadratic equations by Completing the Square. When a=1 in a perfect square trinomial,
Math 1 Lesson 4-5: Completing the Square Targets: I can identify and complete perfect square trinomials. I can solve quadratic equations by Completing the Square. When a=1 in a perfect square trinomial,
test corrections graphing calculator factoring test
 Warm-Up 1. Please turn in your test corrections to the inbox 2. You need your graphing calculator for today s lesson 3. If you need to take your factoring test, please come talk to Ms. Barger before class
Warm-Up 1. Please turn in your test corrections to the inbox 2. You need your graphing calculator for today s lesson 3. If you need to take your factoring test, please come talk to Ms. Barger before class
Objectives To solve quadratic equations using the quadratic formula To find the number of solutions of a quadratic equation
 9-6 The Quadratic Formula and the Discriminant Content Standards A.REI..a Use the method of completing the square to transform an quadratic equation in into an equation of the form ( p) 5 q... Derive the
9-6 The Quadratic Formula and the Discriminant Content Standards A.REI..a Use the method of completing the square to transform an quadratic equation in into an equation of the form ( p) 5 q... Derive the
Algebra I. Slide 1 / 175. Slide 2 / 175. Slide 3 / 175. Quadratics. Table of Contents Key Terms
 Slide 1 / 175 Slide 2 / 175 Algebra I Quadratics 2015-11-04 www.njctl.org Key Terms Table of Contents Click on the topic to go to that section Slide 3 / 175 Characteristics of Quadratic Equations Transforming
Slide 1 / 175 Slide 2 / 175 Algebra I Quadratics 2015-11-04 www.njctl.org Key Terms Table of Contents Click on the topic to go to that section Slide 3 / 175 Characteristics of Quadratic Equations Transforming
Algebra I. Key Terms. Slide 1 / 175 Slide 2 / 175. Slide 3 / 175. Slide 4 / 175. Slide 5 / 175. Slide 6 / 175. Quadratics.
 Slide 1 / 175 Slide / 175 Algebra I Quadratics 015-11-04 www.njctl.org Key Terms Slide 3 / 175 Table of Contents Click on the topic to go to that section Slide 4 / 175 Characteristics of Quadratic Equations
Slide 1 / 175 Slide / 175 Algebra I Quadratics 015-11-04 www.njctl.org Key Terms Slide 3 / 175 Table of Contents Click on the topic to go to that section Slide 4 / 175 Characteristics of Quadratic Equations
Algebra I Quadratics
 1 Algebra I Quadratics 2015-11-04 www.njctl.org 2 Key Terms Table of Contents Click on the topic to go to that section Characteristics of Quadratic Equations Transforming Quadratic Equations Graphing Quadratic
1 Algebra I Quadratics 2015-11-04 www.njctl.org 2 Key Terms Table of Contents Click on the topic to go to that section Characteristics of Quadratic Equations Transforming Quadratic Equations Graphing Quadratic
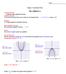
The x-coordinate of the vertex: The equation of the axis of symmetry:
 Algebra 2 Notes Section 4.1: Graph Quadratic Functions in Standard Form Objective(s): Vocabulary: I. Quadratic Function: II. Standard Form: III. Parabola: IV. Parent Function for Quadratic Functions: Vertex
Algebra 2 Notes Section 4.1: Graph Quadratic Functions in Standard Form Objective(s): Vocabulary: I. Quadratic Function: II. Standard Form: III. Parabola: IV. Parent Function for Quadratic Functions: Vertex
Chapter 5 Smartboard Notes
 Name Chapter 5 Smartboard Notes 10.1 Graph ax 2 + c Learning Outcome To graph simple quadratic functions Quadratic function A non linear function that can be written in the standard form y = ax 2 + bx
Name Chapter 5 Smartboard Notes 10.1 Graph ax 2 + c Learning Outcome To graph simple quadratic functions Quadratic function A non linear function that can be written in the standard form y = ax 2 + bx
4.1 Graphical Solutions of Quadratic Equations Date:
 4.1 Graphical Solutions of Quadratic Equations Date: Key Ideas: Quadratic functions are written as f(x) = x 2 x 6 OR y = x 2 x 6. f(x) is f of x and means that the y value is dependent upon the value of
4.1 Graphical Solutions of Quadratic Equations Date: Key Ideas: Quadratic functions are written as f(x) = x 2 x 6 OR y = x 2 x 6. f(x) is f of x and means that the y value is dependent upon the value of
3.1 Solving Quadratic Equations by Factoring
 3.1 Solving Quadratic Equations by Factoring A function of degree (meaning the highest exponent on the variable is ) is called a Quadratic Function. Quadratic functions are written as, for example, f(x)
3.1 Solving Quadratic Equations by Factoring A function of degree (meaning the highest exponent on the variable is ) is called a Quadratic Function. Quadratic functions are written as, for example, f(x)
9-8 Completing the Square
 In the previous lesson, you solved quadratic equations by isolating x 2 and then using square roots. This method works if the quadratic equation, when written in standard form, is a perfect square. When
In the previous lesson, you solved quadratic equations by isolating x 2 and then using square roots. This method works if the quadratic equation, when written in standard form, is a perfect square. When
Solving Quadratic Equations: Algebraically and Graphically Read 3.1 / Examples 1 4
 CC Algebra II HW #14 Name Period Row Date Solving Quadratic Equations: Algebraically and Graphically Read 3.1 / Examples 1 4 Section 3.1 In Exercises 3 12, solve the equation by graphing. (See Example
CC Algebra II HW #14 Name Period Row Date Solving Quadratic Equations: Algebraically and Graphically Read 3.1 / Examples 1 4 Section 3.1 In Exercises 3 12, solve the equation by graphing. (See Example
Chapter 9 Quadratic Functions and Equations
 Chapter 9 Quadratic Functions and Equations 1 9 1Quadratic Graphs and their properties U shaped graph such as the one at the right is called a parabola. A parabola can open upward or downward. A parabola
Chapter 9 Quadratic Functions and Equations 1 9 1Quadratic Graphs and their properties U shaped graph such as the one at the right is called a parabola. A parabola can open upward or downward. A parabola
CC Algebra Quadratic Functions Test Review. 1. The graph of the equation y = x 2 is shown below. 4. Which parabola has an axis of symmetry of x = 1?
 Name: CC Algebra Quadratic Functions Test Review Date: 1. The graph of the equation y = x 2 is shown below. 4. Which parabola has an axis of symmetry of x = 1? a. c. c. b. d. Which statement best describes
Name: CC Algebra Quadratic Functions Test Review Date: 1. The graph of the equation y = x 2 is shown below. 4. Which parabola has an axis of symmetry of x = 1? a. c. c. b. d. Which statement best describes
Common Core Algebra 2. Chapter 3: Quadratic Equations & Complex Numbers
 Common Core Algebra 2 Chapter 3: Quadratic Equations & Complex Numbers 1 Chapter Summary: The strategies presented for solving quadratic equations in this chapter were introduced at the end of Algebra.
Common Core Algebra 2 Chapter 3: Quadratic Equations & Complex Numbers 1 Chapter Summary: The strategies presented for solving quadratic equations in this chapter were introduced at the end of Algebra.
6.1 Solving Quadratic Equations by Factoring
 6.1 Solving Quadratic Equations by Factoring A function of degree 2 (meaning the highest exponent on the variable is 2), is called a Quadratic Function. Quadratic functions are written as, for example,
6.1 Solving Quadratic Equations by Factoring A function of degree 2 (meaning the highest exponent on the variable is 2), is called a Quadratic Function. Quadratic functions are written as, for example,
Algebra II Unit #2 4.6 NOTES: Solving Quadratic Equations (More Methods) Block:
 Algebra II Unit # Name: 4.6 NOTES: Solving Quadratic Equations (More Methods) Block: (A) Background Skills - Simplifying Radicals To simplify a radical that is not a perfect square: 50 8 300 7 7 98 (B)
Algebra II Unit # Name: 4.6 NOTES: Solving Quadratic Equations (More Methods) Block: (A) Background Skills - Simplifying Radicals To simplify a radical that is not a perfect square: 50 8 300 7 7 98 (B)
Quadratic Graphs and Their Properties
 - Think About a Plan Quadratic Graphs and Their Properties Physics In a physics class demonstration, a ball is dropped from the roof of a building, feet above the ground. The height h (in feet) of the
- Think About a Plan Quadratic Graphs and Their Properties Physics In a physics class demonstration, a ball is dropped from the roof of a building, feet above the ground. The height h (in feet) of the
MAT135 Review for Test 4 Dugopolski Sections 7.5, 7.6, 8.1, 8.2, 8.3, 8.4
 Sections 7.5, 7.6, 8.1, 8., 8., 8.4 1. Use the discriminant to determine the number and type(s) of solutions for 4x 8x 4 0. One real solution B. One complex solution Two real solutions Two complex solutions.
Sections 7.5, 7.6, 8.1, 8., 8., 8.4 1. Use the discriminant to determine the number and type(s) of solutions for 4x 8x 4 0. One real solution B. One complex solution Two real solutions Two complex solutions.
Chapter 1 Notes: Quadratic Functions
 19 Chapter 1 Notes: Quadratic Functions (Textbook Lessons 1.1 1.2) Graphing Quadratic Function A function defined by an equation of the form, The graph is a U-shape called a. Standard Form Vertex Form
19 Chapter 1 Notes: Quadratic Functions (Textbook Lessons 1.1 1.2) Graphing Quadratic Function A function defined by an equation of the form, The graph is a U-shape called a. Standard Form Vertex Form
Section 1.1. Chapter 1. Quadratics. Parabolas. Example. Example. ( ) = ax 2 + bx + c -2-1
 Chapter 1 Quadratic Functions and Factoring Section 1.1 Graph Quadratic Functions in Standard Form Quadratics The polynomial form of a quadratic function is: f x The graph of a quadratic function is a
Chapter 1 Quadratic Functions and Factoring Section 1.1 Graph Quadratic Functions in Standard Form Quadratics The polynomial form of a quadratic function is: f x The graph of a quadratic function is a
Name Class Date. Identify the vertex of each graph. Tell whether it is a minimum or a maximum.
 Practice Quadratic Graphs and Their Properties Identify the verte of each graph. Tell whether it is a minimum or a maimum. 1. y 2. y 3. 2 4 2 4 2 2 y 4 2 2 2 4 Graph each function. 4. f () = 3 2 5. f ()
Practice Quadratic Graphs and Their Properties Identify the verte of each graph. Tell whether it is a minimum or a maimum. 1. y 2. y 3. 2 4 2 4 2 2 y 4 2 2 2 4 Graph each function. 4. f () = 3 2 5. f ()
Quadratic Functions. Key Terms. Slide 1 / 200. Slide 2 / 200. Slide 3 / 200. Table of Contents
 Slide 1 / 200 Quadratic Functions Table of Contents Key Terms Identify Quadratic Functions Explain Characteristics of Quadratic Functions Solve Quadratic Equations by Graphing Solve Quadratic Equations
Slide 1 / 200 Quadratic Functions Table of Contents Key Terms Identify Quadratic Functions Explain Characteristics of Quadratic Functions Solve Quadratic Equations by Graphing Solve Quadratic Equations
Quadratic Functions. Key Terms. Slide 2 / 200. Slide 1 / 200. Slide 3 / 200. Slide 4 / 200. Slide 6 / 200. Slide 5 / 200.
 Slide 1 / 200 Quadratic Functions Slide 2 / 200 Table of Contents Key Terms Identify Quadratic Functions Explain Characteristics of Quadratic Functions Solve Quadratic Equations by Graphing Solve Quadratic
Slide 1 / 200 Quadratic Functions Slide 2 / 200 Table of Contents Key Terms Identify Quadratic Functions Explain Characteristics of Quadratic Functions Solve Quadratic Equations by Graphing Solve Quadratic
Slide 1 / 200. Quadratic Functions
 Slide 1 / 200 Quadratic Functions Key Terms Slide 2 / 200 Table of Contents Identify Quadratic Functions Explain Characteristics of Quadratic Functions Solve Quadratic Equations by Graphing Solve Quadratic
Slide 1 / 200 Quadratic Functions Key Terms Slide 2 / 200 Table of Contents Identify Quadratic Functions Explain Characteristics of Quadratic Functions Solve Quadratic Equations by Graphing Solve Quadratic
MAHS-DV Algebra 1-2 Q4
 MAHS-DV Algebra 1-2 Q4 Adrienne Wooten Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) www.ck12.org To access a customizable version of this book, as well as other interactive
MAHS-DV Algebra 1-2 Q4 Adrienne Wooten Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) www.ck12.org To access a customizable version of this book, as well as other interactive
Name Date Class California Standards 17.0, Quadratic Equations and Functions. Step 2: Graph the points. Plot the ordered pairs from your table.
 California Standards 17.0, 1.0 9-1 There are three steps to graphing a quadratic function. Graph y x 3. Quadratic Equations and Functions 6 y 6 y x y x 3 5 1 1 0 3 1 1 5 0 x 0 x Step 1: Make a table of
California Standards 17.0, 1.0 9-1 There are three steps to graphing a quadratic function. Graph y x 3. Quadratic Equations and Functions 6 y 6 y x y x 3 5 1 1 0 3 1 1 5 0 x 0 x Step 1: Make a table of
Algebra B Chapter 9 Unit Test Version 1 of 3
 Name Per. _ Date Algebra B Chapter 9 Unit Test Version 1 of 3 Instructions: 1. Reduce all radicals to simplest terms. Do not approximate square roots as decimals. 2. Place your name, period and the date
Name Per. _ Date Algebra B Chapter 9 Unit Test Version 1 of 3 Instructions: 1. Reduce all radicals to simplest terms. Do not approximate square roots as decimals. 2. Place your name, period and the date
Lesson 3.4 Exercises, pages
 Lesson 3. Exercises, pages 17 A. Identify the values of a, b, and c to make each quadratic equation match the general form ax + bx + c = 0. a) x + 9x - = 0 b) x - 11x = 0 Compare each equation to ax bx
Lesson 3. Exercises, pages 17 A. Identify the values of a, b, and c to make each quadratic equation match the general form ax + bx + c = 0. a) x + 9x - = 0 b) x - 11x = 0 Compare each equation to ax bx
Completing the Square
 5-7 Completing the Square TEKS FOCUS TEKS (4)(F) Solve quadratic and square root equations. TEKS (1)(A) Apply mathematics to problems arising in everyday life, society, and the workplace. Additional TEKS
5-7 Completing the Square TEKS FOCUS TEKS (4)(F) Solve quadratic and square root equations. TEKS (1)(A) Apply mathematics to problems arising in everyday life, society, and the workplace. Additional TEKS
Properties of Graphs of Quadratic Functions
 Properties of Graphs of Quadratic Functions y = ax 2 + bx + c 1) For a quadratic function given in standard form a tells us: c is the: 2) Given the equation, state the y-intercept and circle the direction
Properties of Graphs of Quadratic Functions y = ax 2 + bx + c 1) For a quadratic function given in standard form a tells us: c is the: 2) Given the equation, state the y-intercept and circle the direction
B. Complex number have a Real part and an Imaginary part. 1. written as a + bi some Examples: 2+3i; 7+0i; 0+5i
 Section 11.8 Complex Numbers I. The Complex Number system A. The number i = -1 1. 9 and 24 B. Complex number have a Real part and an Imaginary part II. Powers of i 1. written as a + bi some Examples: 2+3i;
Section 11.8 Complex Numbers I. The Complex Number system A. The number i = -1 1. 9 and 24 B. Complex number have a Real part and an Imaginary part II. Powers of i 1. written as a + bi some Examples: 2+3i;
Algebra 2 Honors. Unit 4, Day 1 Period: Date: Graph Quadratic Functions in Standard Form. (Three more problems on the back )
 Algebra Honors Name: Unit 4, Day 1 Period: Date: Graph Quadratic Functions in Standard Form 1. y = 3x. y = 5x + 1 3. y = x 5 4. y = 1 5 x 6. y = x + x + 1 7. f(x) = 6x 4x 5 (Three more problems on the
Algebra Honors Name: Unit 4, Day 1 Period: Date: Graph Quadratic Functions in Standard Form 1. y = 3x. y = 5x + 1 3. y = x 5 4. y = 1 5 x 6. y = x + x + 1 7. f(x) = 6x 4x 5 (Three more problems on the
6.1 Quadratic Expressions, Rectangles, and Squares. 1. What does the word quadratic refer to? 2. What is the general quadratic expression?
 Advanced Algebra Chapter 6 - Note Taking Guidelines Complete each Now try problem in your notes and work the problem 6.1 Quadratic Expressions, Rectangles, and Squares 1. What does the word quadratic refer
Advanced Algebra Chapter 6 - Note Taking Guidelines Complete each Now try problem in your notes and work the problem 6.1 Quadratic Expressions, Rectangles, and Squares 1. What does the word quadratic refer
Chapter 4: Quadratic Functions and Factoring 4.1 Graphing Quadratic Functions in Stand
 Chapter 4: Quadratic Functions and Factoring 4.1 Graphing Quadratic Functions in Stand VOCAB: a quadratic function in standard form is written y = ax 2 + bx + c, where a 0 A quadratic Function creates
Chapter 4: Quadratic Functions and Factoring 4.1 Graphing Quadratic Functions in Stand VOCAB: a quadratic function in standard form is written y = ax 2 + bx + c, where a 0 A quadratic Function creates
A. B. C. D. Quadratics Practice Test. Question 1. Select the graph of the quadratic function. g (x ) = 1 3 x 2. 3/8/2018 Print Assignment
 Question 1. Select the graph of the quadratic function. g (x ) = 1 3 x 2 C. D. https://my.hrw.com/wwtb2/viewer/printall_vs23.html?umk5tfdnj31tcldd29v4nnzkclztk3w8q6wgvr262aca0a5fsymn1tfv8j1vs4qotwclvofjr8xhs0cldd29v4
Question 1. Select the graph of the quadratic function. g (x ) = 1 3 x 2 C. D. https://my.hrw.com/wwtb2/viewer/printall_vs23.html?umk5tfdnj31tcldd29v4nnzkclztk3w8q6wgvr262aca0a5fsymn1tfv8j1vs4qotwclvofjr8xhs0cldd29v4
Name: Teacher: Per: Unit 1 Unit 2 Unit 3 Unit 4 Unit 5 Unit 6 Unit 7 Unit 8 Unit 9 Unit 10. Unit 9a. [Quadratic Functions] Unit 9 Quadratics 1
![Name: Teacher: Per: Unit 1 Unit 2 Unit 3 Unit 4 Unit 5 Unit 6 Unit 7 Unit 8 Unit 9 Unit 10. Unit 9a. [Quadratic Functions] Unit 9 Quadratics 1 Name: Teacher: Per: Unit 1 Unit 2 Unit 3 Unit 4 Unit 5 Unit 6 Unit 7 Unit 8 Unit 9 Unit 10. Unit 9a. [Quadratic Functions] Unit 9 Quadratics 1](/thumbs/82/86818253.jpg) Name: Teacher: Per: Unit 1 Unit 2 Unit 3 Unit 4 Unit 5 Unit 6 Unit 7 Unit 8 Unit 9 Unit 10 Unit 9a [Quadratic Functions] Unit 9 Quadratics 1 To be a Successful Algebra class, TIGERs will show #TENACITY
Name: Teacher: Per: Unit 1 Unit 2 Unit 3 Unit 4 Unit 5 Unit 6 Unit 7 Unit 8 Unit 9 Unit 10 Unit 9a [Quadratic Functions] Unit 9 Quadratics 1 To be a Successful Algebra class, TIGERs will show #TENACITY
2 P a g e. Essential Questions:
 NC Math 1 Unit 5 Quadratic Functions Main Concepts Study Guide & Vocabulary Classifying, Adding, & Subtracting Polynomials Multiplying Polynomials Factoring Polynomials Review of Multiplying and Factoring
NC Math 1 Unit 5 Quadratic Functions Main Concepts Study Guide & Vocabulary Classifying, Adding, & Subtracting Polynomials Multiplying Polynomials Factoring Polynomials Review of Multiplying and Factoring
2. Write each number as a power of 10 using negative exponents.
 Q Review 1. Simplify each expression. a. 1 0 b. 5 2 1 c. d. e. (7) 2 f. 6 1 g. 6 0 h. (12x) 2 i. 1 j. 6bc 0 0 8 k. (11x) 0 l. 2 2 9 m. m 8 p 0 n. 5a 2c k ( mn) o. p. 8 p 2m n q. 8 2 q r 5 r. (10a) b 0
Q Review 1. Simplify each expression. a. 1 0 b. 5 2 1 c. d. e. (7) 2 f. 6 1 g. 6 0 h. (12x) 2 i. 1 j. 6bc 0 0 8 k. (11x) 0 l. 2 2 9 m. m 8 p 0 n. 5a 2c k ( mn) o. p. 8 p 2m n q. 8 2 q r 5 r. (10a) b 0
Chapter 8 ~ Quadratic Functions and Equations In this chapter you will study... You can use these skills...
 Chapter 8 ~ Quadratic Functions and Equations In this chapter you will study... identifying and graphing quadratic functions transforming quadratic equations solving quadratic equations using factoring
Chapter 8 ~ Quadratic Functions and Equations In this chapter you will study... identifying and graphing quadratic functions transforming quadratic equations solving quadratic equations using factoring
Solving Quadratics Algebraically
 Solving Quadratics Algebraically Table of Contents 1. Introduction to Solving Quadratics. Solving Quadratic Equations using Factoring 3. Solving Quadratic Equations in Context 4. Solving Quadratics using
Solving Quadratics Algebraically Table of Contents 1. Introduction to Solving Quadratics. Solving Quadratic Equations using Factoring 3. Solving Quadratic Equations in Context 4. Solving Quadratics using
CHAPTER 1 QUADRATIC FUNCTIONS AND FACTORING
 CHAPTER 1 QUADRATIC FUNCTIONS AND FACTORING Big IDEAS: 1) Graphing and writing quadratic functions in several forms ) Solving quadratic equations using a variety of methods 3) Performing operations with
CHAPTER 1 QUADRATIC FUNCTIONS AND FACTORING Big IDEAS: 1) Graphing and writing quadratic functions in several forms ) Solving quadratic equations using a variety of methods 3) Performing operations with
2 If ax + bx + c = 0, then x = b) What are the x-intercepts of the graph or the real roots of f(x)? Round to 4 decimal places.
 Quadratic Formula - Key Background: So far in this course we have solved quadratic equations by the square root method and the factoring method. Each of these methods has its strengths and limitations.
Quadratic Formula - Key Background: So far in this course we have solved quadratic equations by the square root method and the factoring method. Each of these methods has its strengths and limitations.
3.1. QUADRATIC FUNCTIONS AND MODELS
 3.1. QUADRATIC FUNCTIONS AND MODELS 1 What You Should Learn Analyze graphs of quadratic functions. Write quadratic functions in standard form and use the results to sketch graphs of functions. Find minimum
3.1. QUADRATIC FUNCTIONS AND MODELS 1 What You Should Learn Analyze graphs of quadratic functions. Write quadratic functions in standard form and use the results to sketch graphs of functions. Find minimum
Section 5.4 Quadratic Functions
 Math 150 c Lynch 1 of 6 Section 5.4 Quadratic Functions Definition. A quadratic function is one that can be written in the form, f(x) = ax 2 + bx + c, where a, b, and c are real numbers and a 0. This if
Math 150 c Lynch 1 of 6 Section 5.4 Quadratic Functions Definition. A quadratic function is one that can be written in the form, f(x) = ax 2 + bx + c, where a, b, and c are real numbers and a 0. This if
AdvAlg6.4GraphingQuadratics.notebook. March 07, Newton s Formula h(t) = 1 gt 2 + v o t + h o 2. time. initial upward velocity
 Notes Lesson 6 4 Applications of Quadratic Functions Newton s Formula h(t) = 1 gt 2 + v o t + h o 2 Height of object time Constant (accel. due to gravity) *32 ft/sec 2 *9.8 m/sec 2 **MEMORIZE THESE** initial
Notes Lesson 6 4 Applications of Quadratic Functions Newton s Formula h(t) = 1 gt 2 + v o t + h o 2 Height of object time Constant (accel. due to gravity) *32 ft/sec 2 *9.8 m/sec 2 **MEMORIZE THESE** initial
( ) f ( x 1 ) . x 2. To find the average rate of change, use the slope formula, m = f x 2
 Common Core Regents Review Functions Quadratic Functions (Graphs) A quadratic function has the form y = ax 2 + bx + c. It is an equation with a degree of two because its highest exponent is 2. The graph
Common Core Regents Review Functions Quadratic Functions (Graphs) A quadratic function has the form y = ax 2 + bx + c. It is an equation with a degree of two because its highest exponent is 2. The graph
; Vertex: ( b. 576 feet above the ground?
 Lesson 8: Applications of Quadratics Quadratic Formula: x = b± b 2 4ac 2a ; Vertex: ( b, f ( b )) 2a 2a Standard: F.IF.7 Graph functions expressed symbolically and show key features of the graph, by hand
Lesson 8: Applications of Quadratics Quadratic Formula: x = b± b 2 4ac 2a ; Vertex: ( b, f ( b )) 2a 2a Standard: F.IF.7 Graph functions expressed symbolically and show key features of the graph, by hand
Quadratic Equations. Math 20-1 Chapter 4. General Outcome: Develop algebraic and graphical reasoning through the study of relations.
 Math 20-1 Chapter 4 Quadratic Equations General Outcome: Develop algebraic and graphical reasoning through the study of relations. Specific Outcomes: RF1. Factor polynomial expressions of the form: ax
Math 20-1 Chapter 4 Quadratic Equations General Outcome: Develop algebraic and graphical reasoning through the study of relations. Specific Outcomes: RF1. Factor polynomial expressions of the form: ax
Name I.D. Number. Select the response that best completes the statement or answers the question.
 Name I.D. Number Unit 4 Evaluation Evaluation 04 Second Year Algebra 1 (MTHH 039 059) This evaluation will cover the lessons in this unit. It is open book, meaning you can use your textbook, syllabus,
Name I.D. Number Unit 4 Evaluation Evaluation 04 Second Year Algebra 1 (MTHH 039 059) This evaluation will cover the lessons in this unit. It is open book, meaning you can use your textbook, syllabus,
Controlling the Population
 Lesson.1 Skills Practice Name Date Controlling the Population Adding and Subtracting Polynomials Vocabulary Match each definition with its corresponding term. 1. polynomial a. a polynomial with only 1
Lesson.1 Skills Practice Name Date Controlling the Population Adding and Subtracting Polynomials Vocabulary Match each definition with its corresponding term. 1. polynomial a. a polynomial with only 1
Chapter 2. Linear and Quadratic Function
 Chapter. Linear and Quadratic Function.1 Properties of Linear Functions and Linear Models.8 Equations and Inequalities Involving the Absolute Value.3 Quadratic Functions and Their Zeros.4 Properties of
Chapter. Linear and Quadratic Function.1 Properties of Linear Functions and Linear Models.8 Equations and Inequalities Involving the Absolute Value.3 Quadratic Functions and Their Zeros.4 Properties of
9.3 Using the Quadratic Formula to Solve Equations
 Name Class Date 9.3 Using the Quadratic Formula to Solve Equations Essential Question: What is the quadratic formula, and how can you use it to solve quadratic equations? Resource Locker Explore Deriving
Name Class Date 9.3 Using the Quadratic Formula to Solve Equations Essential Question: What is the quadratic formula, and how can you use it to solve quadratic equations? Resource Locker Explore Deriving
11.3 Finding Complex Solutions of Quadratic Equations
 Name Class Date 11.3 Finding Complex Solutions of Quadratic Equations Essential Question: How can you find the complex solutions of any quadratic equation? Resource Locker Explore Investigating Real Solutions
Name Class Date 11.3 Finding Complex Solutions of Quadratic Equations Essential Question: How can you find the complex solutions of any quadratic equation? Resource Locker Explore Investigating Real Solutions
Subtract 16 from both sides. Divide both sides by 9. b. Will the swing touch the ground? Explain how you know.
 REVIEW EXAMPLES 1) Solve 9x + 16 = 0 for x. 9x + 16 = 0 9x = 16 Original equation. Subtract 16 from both sides. 16 x 9 Divide both sides by 9. 16 x Take the square root of both sides. 9 4 x i 3 Evaluate.
REVIEW EXAMPLES 1) Solve 9x + 16 = 0 for x. 9x + 16 = 0 9x = 16 Original equation. Subtract 16 from both sides. 16 x 9 Divide both sides by 9. 16 x Take the square root of both sides. 9 4 x i 3 Evaluate.
Unit 7 Quadratic Functions
 Algebra I Revised 11/16 Unit 7 Quadratic Functions Name: 1 CONTENTS 9.1 Graphing Quadratic Functions 9.2 Solving Quadratic Equations by Graphing 9.1 9.2 Assessment 8.6 Solving x^2+bx+c=0 8.7 Solving ax^2+bx+c=0
Algebra I Revised 11/16 Unit 7 Quadratic Functions Name: 1 CONTENTS 9.1 Graphing Quadratic Functions 9.2 Solving Quadratic Equations by Graphing 9.1 9.2 Assessment 8.6 Solving x^2+bx+c=0 8.7 Solving ax^2+bx+c=0
PAP Algebra 2. Unit 4B. Quadratics (Part 2) Name Period
 PAP Algebra Unit 4B Quadratics (Part ) Name Period 1 After Test WS: 4.6 Solve by Factoring PAP Algebra Name Factor. 1. x + 6x + 8. 4x 8x 3 + + 3. x + 7x + 5 4. x 3x 1 + + 5. x + 7x + 6 6. 3x + 10x + 3
PAP Algebra Unit 4B Quadratics (Part ) Name Period 1 After Test WS: 4.6 Solve by Factoring PAP Algebra Name Factor. 1. x + 6x + 8. 4x 8x 3 + + 3. x + 7x + 5 4. x 3x 1 + + 5. x + 7x + 6 6. 3x + 10x + 3
MATH HIGH SCHOOL QUADRATIC FUNCTIONS EXERCISES
 MATH HIGH SCHOOL QUADRATIC FUNCTIONS CONTENTS LESSON 1: ZOOMING IN ON PARABOLAS... 5 LESSON : QUADRATIC FUNCTIONS... 7 LESSON 3: REAL-WORLD PROBLEMS... 13 LESSON 4: GRAPHING QUADRATICS... 15 LESSON 5:
MATH HIGH SCHOOL QUADRATIC FUNCTIONS CONTENTS LESSON 1: ZOOMING IN ON PARABOLAS... 5 LESSON : QUADRATIC FUNCTIONS... 7 LESSON 3: REAL-WORLD PROBLEMS... 13 LESSON 4: GRAPHING QUADRATICS... 15 LESSON 5:
Maintaining Mathematical Proficiency
 Chapter Maintaining Mathematical Proficiency Simplify the expression. 1. 8x 9x 2. 25r 5 7r r + 3. 3 ( 3x 5) + + x. 3y ( 2y 5) + 11 5. 3( h 7) 7( 10 h) 2 2 +. 5 8x + 5x + 8x Find the volume or surface area
Chapter Maintaining Mathematical Proficiency Simplify the expression. 1. 8x 9x 2. 25r 5 7r r + 3. 3 ( 3x 5) + + x. 3y ( 2y 5) + 11 5. 3( h 7) 7( 10 h) 2 2 +. 5 8x + 5x + 8x Find the volume or surface area
9.4 Start Thinking. 9.4 Warm Up. 9.4 Cumulative Review Warm Up. Use a graphing calculator to graph ( )
 9.4 Start Thinking Use a graphing calculator to graph ( ) f x = x + 4x 1. Find the minimum of the function using the CALC feature on the graphing calculator. Explain the relationship between the minimum
9.4 Start Thinking Use a graphing calculator to graph ( ) f x = x + 4x 1. Find the minimum of the function using the CALC feature on the graphing calculator. Explain the relationship between the minimum
Solving Multi-Step Equations
 1. Clear parentheses using the distributive property. 2. Combine like terms within each side of the equal sign. Solving Multi-Step Equations 3. Add/subtract terms to both sides of the equation to get the
1. Clear parentheses using the distributive property. 2. Combine like terms within each side of the equal sign. Solving Multi-Step Equations 3. Add/subtract terms to both sides of the equation to get the
Unit 3A: Factoring & Solving Quadratic Equations After completion of this unit, you will be able to
 Unit 3A: Factoring & Solving Quadratic Equations After completion of this unit, you will be able to Learning Target #1: Factoring Factor the GCF out of a polynomial Factor a polynomial when a = 1 Factor
Unit 3A: Factoring & Solving Quadratic Equations After completion of this unit, you will be able to Learning Target #1: Factoring Factor the GCF out of a polynomial Factor a polynomial when a = 1 Factor
30S Pre-Calculus Final Exam Review Chapters 1-4
 30S Pre-Calculus Final Exam Review Chapters 1 - Name: 30S Pre-Calculus Final Exam Formula Sheet 30S Pre-Calculus Exam Review- Chapter 1 Sequences and Series Multiple Choice Identify the choice that best
30S Pre-Calculus Final Exam Review Chapters 1 - Name: 30S Pre-Calculus Final Exam Formula Sheet 30S Pre-Calculus Exam Review- Chapter 1 Sequences and Series Multiple Choice Identify the choice that best
Ms. Peralta s IM3 HW 5.4. HW 5.4 Solving Quadratic Equations. Solve the following exercises. Use factoring and/or the quadratic formula.
 HW 5.4 HW 5.4 Solving Quadratic Equations Name: Solve the following exercises. Use factoring and/or the quadratic formula. 1. 2. 3. 4. HW 5.4 5. 6. 4x 2 20x + 25 = 36 7. 8. HW 5.4 9. 10. 11. 75x 2 30x
HW 5.4 HW 5.4 Solving Quadratic Equations Name: Solve the following exercises. Use factoring and/or the quadratic formula. 1. 2. 3. 4. HW 5.4 5. 6. 4x 2 20x + 25 = 36 7. 8. HW 5.4 9. 10. 11. 75x 2 30x
Ladies and Gentlemen: Please Welcome the Quadratic Formula!
 Lesson.1 Skills Practice Name Date Ladies and Gentlemen: Please Welcome the Quadratic Formula! The Quadratic Formula Vocabulary Complete the Quadratic Formula. Then, identify the discriminant and explain
Lesson.1 Skills Practice Name Date Ladies and Gentlemen: Please Welcome the Quadratic Formula! The Quadratic Formula Vocabulary Complete the Quadratic Formula. Then, identify the discriminant and explain
UNIT 3: MODELING AND ANALYZING QUADRATIC FUNCTIONS
 UNIT 3: MODELING AND ANALYZING QUADRATIC FUNCTIONS This unit investigates quadratic functions. Students study the structure of quadratic expressions and write quadratic expressions in equivalent forms.
UNIT 3: MODELING AND ANALYZING QUADRATIC FUNCTIONS This unit investigates quadratic functions. Students study the structure of quadratic expressions and write quadratic expressions in equivalent forms.
Name Teacher: Period: Date: ALGEBRA I FINAL REVIEW SPRING 2016
 Name Teacher: Period: Date: ALGEBRA I FINAL REVIEW SPRING 016 Solve each system of inequalities by graphing. (Book sections 4-5and 4-6) y x4 1.).) y x1 y x 4 4yx.) x y 14 x y0 4.) x y 4x y 10 5.) x y 1
Name Teacher: Period: Date: ALGEBRA I FINAL REVIEW SPRING 016 Solve each system of inequalities by graphing. (Book sections 4-5and 4-6) y x4 1.).) y x1 y x 4 4yx.) x y 14 x y0 4.) x y 4x y 10 5.) x y 1
9-4. Quadratics and Projectiles. Vocabulary. Equations for the Paths of Projectiles. Activity. Lesson
 Chapter 9 Lesson 9-4 Quadratics and Projectiles Vocabulary force of gravity initial upward velocity initial height BIG IDEA Assuming constant gravity, both the path of a projectile and the height of a
Chapter 9 Lesson 9-4 Quadratics and Projectiles Vocabulary force of gravity initial upward velocity initial height BIG IDEA Assuming constant gravity, both the path of a projectile and the height of a
More applications of quadratic functions
 Algebra More applications of quadratic functions Name: There are many applications of quadratic functions in the real world. We have already considered applications for which we were given formulas and
Algebra More applications of quadratic functions Name: There are many applications of quadratic functions in the real world. We have already considered applications for which we were given formulas and
Algebra 1. Math Review Packet. Equations, Inequalities, Linear Functions, Linear Systems, Exponents, Polynomials, Factoring, Quadratics, Radicals
 Algebra 1 Math Review Packet Equations, Inequalities, Linear Functions, Linear Systems, Exponents, Polynomials, Factoring, Quadratics, Radicals 2017 Math in the Middle 1. Clear parentheses using the distributive
Algebra 1 Math Review Packet Equations, Inequalities, Linear Functions, Linear Systems, Exponents, Polynomials, Factoring, Quadratics, Radicals 2017 Math in the Middle 1. Clear parentheses using the distributive
Unit 5: Quadratic Functions
 Unit 5: Quadratic Functions LESSON #2: THE PARABOLA APPLICATIONS AND WORD PROBLEMS INVERSE OF A QUADRATIC FUNCTION DO NOW: Review from Lesson #1 (a)using the graph shown to the right, determine the equation
Unit 5: Quadratic Functions LESSON #2: THE PARABOLA APPLICATIONS AND WORD PROBLEMS INVERSE OF A QUADRATIC FUNCTION DO NOW: Review from Lesson #1 (a)using the graph shown to the right, determine the equation
Using the Laws of Exponents to Simplify Rational Exponents
 6. Explain Radicals and Rational Exponents - Notes Main Ideas/ Questions Essential Question: How do you simplify expressions with rational exponents? Notes/Examples What You Will Learn Evaluate and simplify
6. Explain Radicals and Rational Exponents - Notes Main Ideas/ Questions Essential Question: How do you simplify expressions with rational exponents? Notes/Examples What You Will Learn Evaluate and simplify
1 P a g e Province Mathematics Department Southwest Tennessee Community College
 Chapter 10 Section 10.1 - Solving Quadratic Equations by the Square Root Property Objectives: 1. Review the zero-factor property. 2. Solve equations of the form x 2 = k, where k > 0. 3. Solve equations
Chapter 10 Section 10.1 - Solving Quadratic Equations by the Square Root Property Objectives: 1. Review the zero-factor property. 2. Solve equations of the form x 2 = k, where k > 0. 3. Solve equations
ALGEBRA UNIT 11-GRAPHING QUADRATICS THE GRAPH OF A QUADRATIC FUNCTION (DAY 1)
 ALGEBRA UNIT 11-GRAPHING QUADRATICS THE GRAPH OF A QUADRATIC FUNCTION (DAY 1) The Quadratic Equation is written as: ; this equation has a degree of. Where a, b and c are integer coefficients (where a 0)
ALGEBRA UNIT 11-GRAPHING QUADRATICS THE GRAPH OF A QUADRATIC FUNCTION (DAY 1) The Quadratic Equation is written as: ; this equation has a degree of. Where a, b and c are integer coefficients (where a 0)
Unit 6: Quadratics. Contents
 Unit 6: Quadratics Contents Animated gif Program...6-3 Setting Bounds...6-9 Exploring Quadratic Equations...6-17 Finding Zeros by Factoring...6-3 Finding Zeros Using the Quadratic Formula...6-41 Modeling:
Unit 6: Quadratics Contents Animated gif Program...6-3 Setting Bounds...6-9 Exploring Quadratic Equations...6-17 Finding Zeros by Factoring...6-3 Finding Zeros Using the Quadratic Formula...6-41 Modeling:
Solve Quadratic Equations by Completing the Square
 10.5 Solve Quadratic Equations by Completing the Square Before You solved quadratic equations by finding square roots. Now You will solve quadratic equations by completing the square. Why? So you can solve
10.5 Solve Quadratic Equations by Completing the Square Before You solved quadratic equations by finding square roots. Now You will solve quadratic equations by completing the square. Why? So you can solve
Chapter 5: Quadratic Functions
 Section 5.1: Square Root Property #1-20: Solve the equations using the square root property. 1) x 2 = 16 2) y 2 = 25 3) b 2 = 49 4) a 2 = 16 5) m 2 = 98 6) d 2 = 24 7) x 2 = 75 8) x 2 = 54 9) (x 3) 2 =
Section 5.1: Square Root Property #1-20: Solve the equations using the square root property. 1) x 2 = 16 2) y 2 = 25 3) b 2 = 49 4) a 2 = 16 5) m 2 = 98 6) d 2 = 24 7) x 2 = 75 8) x 2 = 54 9) (x 3) 2 =
The coordinates of the vertex of the corresponding parabola are p, q. If a > 0, the parabola opens upward. If a < 0, the parabola opens downward.
 Mathematics 10 Page 1 of 8 Quadratic Relations in Vertex Form The expression y ax p q defines a quadratic relation in form. The coordinates of the of the corresponding parabola are p, q. If a > 0, the
Mathematics 10 Page 1 of 8 Quadratic Relations in Vertex Form The expression y ax p q defines a quadratic relation in form. The coordinates of the of the corresponding parabola are p, q. If a > 0, the
Final Exam Review for DMAT 0310
 Final Exam Review for DMAT 010 MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Factor the polynomial completely. What is one of the factors? 1) x
Final Exam Review for DMAT 010 MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Factor the polynomial completely. What is one of the factors? 1) x
Unit 9: Quadratics Intercept Form
 For Teacher Use Packet Score: Name: Period: Algebra 1 Unit 9: Quadratics Intercept Form Note & Homework Packet Date Topic/Assignment HW Page 9-A Graphing Parabolas in Intercept Form 9-B Solve Quadratic
For Teacher Use Packet Score: Name: Period: Algebra 1 Unit 9: Quadratics Intercept Form Note & Homework Packet Date Topic/Assignment HW Page 9-A Graphing Parabolas in Intercept Form 9-B Solve Quadratic
Applied 30S Unit 1 Quadratic Functions
 Applied 30S Unit 1 Quadratic Functions Mrs. Kornelsen Teulon Collegiate Institute Learning checklist Quadratics Learning increases when you have a goal to work towards. Use this checklist as guide to track
Applied 30S Unit 1 Quadratic Functions Mrs. Kornelsen Teulon Collegiate Institute Learning checklist Quadratics Learning increases when you have a goal to work towards. Use this checklist as guide to track
Algebra 2/Trig Apps: Chapter 5 Quadratics Packet
 Algebra /Trig Apps: Chapter 5 Quadratics Packet In this unit we will: Determine what the parameters a, h, and k do in the vertex form of a quadratic equation Determine the properties (vertex, axis of symmetry,
Algebra /Trig Apps: Chapter 5 Quadratics Packet In this unit we will: Determine what the parameters a, h, and k do in the vertex form of a quadratic equation Determine the properties (vertex, axis of symmetry,
QUADRATIC FUNCTIONS AND MODELS
 QUADRATIC FUNCTIONS AND MODELS What You Should Learn Analyze graphs of quadratic functions. Write quadratic functions in standard form and use the results to sketch graphs of functions. Find minimum and
QUADRATIC FUNCTIONS AND MODELS What You Should Learn Analyze graphs of quadratic functions. Write quadratic functions in standard form and use the results to sketch graphs of functions. Find minimum and
y ax bx c OR 0 then either a = 0 OR b = 0 Steps: 1) if already factored, set each factor in ( ) = 0 and solve
 Algebra 1 SOL Review: Quadratics Name 67B Solving Quadratic equations using Zero-Product Property. Quadratic equation: ax bx c 0 OR y ax bx c OR f ( x ) ax bx c Zero-Product Property: if a b 0 then either
Algebra 1 SOL Review: Quadratics Name 67B Solving Quadratic equations using Zero-Product Property. Quadratic equation: ax bx c 0 OR y ax bx c OR f ( x ) ax bx c Zero-Product Property: if a b 0 then either
Study Guide and Intervention. The Quadratic Formula and the Discriminant. Quadratic Formula. Replace a with 1, b with -5, and c with -14.
 4-6 Study Guide and Intervention Quadratic Formula The Quadratic Formula can be used to solve any quadratic equation once it is written in the form ax 2 + bx + c = 0. Quadratic Formula The solutions of
4-6 Study Guide and Intervention Quadratic Formula The Quadratic Formula can be used to solve any quadratic equation once it is written in the form ax 2 + bx + c = 0. Quadratic Formula The solutions of
Mth 95 Module 4 Chapter 8 Spring Review - Solving quadratic equations using the quadratic formula
 Mth 95 Module 4 Chapter 8 Spring 04 Review - Solving quadratic equations using the quadratic formula Write the quadratic formula. The NUMBER of REAL and COMPLEX SOLUTIONS to a quadratic equation ( a b
Mth 95 Module 4 Chapter 8 Spring 04 Review - Solving quadratic equations using the quadratic formula Write the quadratic formula. The NUMBER of REAL and COMPLEX SOLUTIONS to a quadratic equation ( a b
Note: The zero function f(x) = 0 is a polynomial function. It has no degree and no leading coefficient. Sep 15 2:51 PM
 2.1 Linear and Quadratic Name: Functions and Modeling Objective: Students will be able to recognize and graph linear and quadratic functions, and use these functions to model situations and solve problems.
2.1 Linear and Quadratic Name: Functions and Modeling Objective: Students will be able to recognize and graph linear and quadratic functions, and use these functions to model situations and solve problems.
Solve for the variable by transforming equations:
 Cantwell Sacred Heart of Mary High School Math Department Study Guide for the Algebra 1 (or higher) Placement Test Name: Date: School: Solve for the variable by transforming equations: 1. y + 3 = 9. 1
Cantwell Sacred Heart of Mary High School Math Department Study Guide for the Algebra 1 (or higher) Placement Test Name: Date: School: Solve for the variable by transforming equations: 1. y + 3 = 9. 1
- a function that can be written in the standard form. - a form of a parabola where and (h, k) is the vertex
 4-1 Quadratic Functions and Equations Objectives A2.A.REI.D.6 (formerly A-REI.D.11) Explain why the x-coordinates of the points where the graphs of the equations y = f(x) and y = g(x) intersect are the
4-1 Quadratic Functions and Equations Objectives A2.A.REI.D.6 (formerly A-REI.D.11) Explain why the x-coordinates of the points where the graphs of the equations y = f(x) and y = g(x) intersect are the
Quadratic Functions. 5A Quadratic Functions and Complex Numbers. 5B Applying Quadratic Functions
 Quadratic Functions 5A Quadratic Functions and Complex Numbers Lab Explore Parameter Changes 5-1 Using Transformations to Graph Quadratic Functions 5- Properties of Quadratic Functions in Standard Form
Quadratic Functions 5A Quadratic Functions and Complex Numbers Lab Explore Parameter Changes 5-1 Using Transformations to Graph Quadratic Functions 5- Properties of Quadratic Functions in Standard Form
Additional Factoring Examples:
 Honors Algebra -3 Solving Quadratic Equations by Graphing and Factoring Learning Targets 1. I can solve quadratic equations by graphing. I can solve quadratic equations by factoring 3. I can write a quadratic
Honors Algebra -3 Solving Quadratic Equations by Graphing and Factoring Learning Targets 1. I can solve quadratic equations by graphing. I can solve quadratic equations by factoring 3. I can write a quadratic
Skills Practice Skills Practice for Lesson 3.1
 Skills Practice Skills Practice for Lesson. Name Date Lots and Projectiles Introduction to Quadratic Functions Vocabular Define each term in our own words.. quadratic function. vertical motion Problem
Skills Practice Skills Practice for Lesson. Name Date Lots and Projectiles Introduction to Quadratic Functions Vocabular Define each term in our own words.. quadratic function. vertical motion Problem
Mission 1 Factoring by Greatest Common Factor and Grouping
 Algebra Honors Unit 3 Factoring Quadratics Name Quest Mission 1 Factoring by Greatest Common Factor and Grouping Review Questions 1. Simplify: i(6 4i) 3+3i A. 4i C. 60 + 3 i B. 8 3 + 4i D. 10 3 + 3 i.
Algebra Honors Unit 3 Factoring Quadratics Name Quest Mission 1 Factoring by Greatest Common Factor and Grouping Review Questions 1. Simplify: i(6 4i) 3+3i A. 4i C. 60 + 3 i B. 8 3 + 4i D. 10 3 + 3 i.
Algebra II Honors Unit 3 Assessment Review Quadratic Functions. Formula Box. f ( x) 2 x 3 25 from the parent graph of
 Name: Algebra II Honors Unit 3 Assessment Review Quadratic Functions Date: Formula Box x = b a x = b ± b 4ac a h 6t h 0 ) What are the solutions of x 3 5? x 8or x ) Describe the transformation of f ( x)
Name: Algebra II Honors Unit 3 Assessment Review Quadratic Functions Date: Formula Box x = b a x = b ± b 4ac a h 6t h 0 ) What are the solutions of x 3 5? x 8or x ) Describe the transformation of f ( x)
Quadratic Equations Chapter Questions
 Quadratic Equations Chapter Questions 1. Describe the characteristics of a quadratic equation. 2. What are the steps for graphing a quadratic function? 3. How can you determine the number of solutions
Quadratic Equations Chapter Questions 1. Describe the characteristics of a quadratic equation. 2. What are the steps for graphing a quadratic function? 3. How can you determine the number of solutions
Unit four review. Name: Class: Date: Short Answer
 Name: Class: Date: ID: A Unit four review Short Answer 1. Graph the quadratic function y = 3x 2 6x + 5. Use the graph to determine the zeros of the function if they exist. 2. For what values of k does
Name: Class: Date: ID: A Unit four review Short Answer 1. Graph the quadratic function y = 3x 2 6x + 5. Use the graph to determine the zeros of the function if they exist. 2. For what values of k does
HONORS GEOMETRY Summer Skills Set
 HONORS GEOMETRY Summer Skills Set Algebra Concepts Adding and Subtracting Rational Numbers To add or subtract fractions with the same denominator, add or subtract the numerators and write the sum or difference
HONORS GEOMETRY Summer Skills Set Algebra Concepts Adding and Subtracting Rational Numbers To add or subtract fractions with the same denominator, add or subtract the numerators and write the sum or difference
= 9 = x + 8 = = -5x 19. For today: 2.5 (Review) and. 4.4a (also review) Objectives:
 Math 65 / Notes & Practice #1 / 20 points / Due. / Name: Home Work Practice: Simplify the following expressions by reducing the fractions: 16 = 4 = 8xy =? = 9 40 32 38x 64 16 Solve the following equations
Math 65 / Notes & Practice #1 / 20 points / Due. / Name: Home Work Practice: Simplify the following expressions by reducing the fractions: 16 = 4 = 8xy =? = 9 40 32 38x 64 16 Solve the following equations
