Quadratic Equations Chapter Questions
|
|
|
- Joy Baldwin
- 6 years ago
- Views:
Transcription
1 Quadratic Equations Chapter Questions 1. Describe the characteristics of a quadratic equation. 2. What are the steps for graphing a quadratic function? 3. How can you determine the number of solutions without graphing? NJ Center for Teaching and Learning ~ 1 ~
2 Quadratic Equations Chapter Questions Standard form and the axis of symmetry Find the axis of symmetry and rewrite in standard form if necessary. 1. y= x 2 +3x x 2 + 5x = 6 3. y= x 2-4x x 2-3 =6x 5. y= 3x 2-4x -2 Homework Find the axis of symmetry and rewrite in standard form if necessary. 6. y= x 2 +2x x 2-3x = 2 8. y= x 2-5x x - 4 = 2x y= 3x 2-2x Transforming Quadratic Functions Does the graph of the given equation open up or down? Is the graph wider or narrower than the parent equation of y=x 2? What is the y-intercept? 11. y = 2x 2 +3x y = -.7x 2-4x y = -1.2x y = 3x 2 +3x 15. y = -4x 2 Homework Does the graph of the given equation open up or down? Is the graph wider or narrower than the parent equation of y=x 2? What is the y-intercept? 16. y =-.6x 2 +3x y = 1.7x 2-4x y = -1.02x y = 1.3x 2 +4x 20. y = 5x 2 NJ Center for Teaching and Learning ~ 2 ~
3 Graphing to Find Zeros Find the zeros of the following quadratics: 21. y x y x y = x 2-4x y = -x 2 +3x y = -x 2-8x y = -x 2-8x y = x 2 +3x y = 2x 2 +4x y = -3x 2 +4x +4 NJ Center for Teaching and Learning ~ 3 ~
4 Homework 30. y x y x y = x 2-6x y = -x 2 +3x y = x 2 +6x y = x 2 +x y = x 2 +2x y = 2x 2 +5x y = -3x 2 +11x +4 Solving by Factoring Solve the following quadratics by factoring. 39. a 2 +4a +3= b 2-4b -5= c 2-6c = d 2 +8c = -12 NJ Center for Teaching and Learning ~ 4 ~
5 43. -e 2 +9 = f 2 +4f +4 = g 2 +5g = h 2 +7h +6= j 2-4j = A garden has a length of (x + 2) feet and a width of (2x - 1) feet. The garden s total area is 88 square feet. Find the length. Home Work Solve the following quadratics by factoring. 49. a 2 +6a +5= b 2 -b -6= c 2-6c = d 2 +7c = e = f 2 +6f +9 = g 2 +7g = h 2 +8h +6= j 2-7j = A garden has a length of (x - 4)feet and a width of (2x +3)feet. The garden s total area is 76 square feet. Find the length. Solving Using the Square Roots Method Solve the following quadratics using the square roots method 59. m 2 = n 2 = p 2 = q 2 = r 2-3 =6 64. s 2 +8 = t 2-6 = u 2 +5 = (v -7) 2-5 = (w -3) 2 +6 = 56 NJ Center for Teaching and Learning ~ 5 ~
6 69. The square of six less than a number is twenty-five. Write an equation that models this situation. Solve the equation. Homework Solve the following quadratics using the square roots method 70. m 2 = n 2 = p 2 = q 2 = r 2-3 = s 2 +8 = t 2-6 = u 2 +5 = (v -2) 2 +4 = (w +4) 2-4 = Two times the square of five more than a number is seventy-two. Write an equation that models this situation. Solve the equation. Solving by Completing the Square Fill in the blank to complete the square. 81. a 2 + 8a b b c 2-4c d 2-6d e 2 + 7e f 2-5f + Solve the following quadratics by completing the square. 87. h 2 + 6h = j 2-8j = k = -10k 90. m 2-13 = 12m n + 20 = -n p + p 2 = q 2-8q = r r = 12 NJ Center for Teaching and Learning ~ 6 ~
7 95. A toy rocket launched into the air has a height (h feet) at any given time (t seconds) as h = -16t t until it hits the ground. At what time(s) is it at a height of 7 feet above the ground? Homework Fill in the blank to complete the square. 96. a a b 2 + b c 2-14c d 2-16d e 2 + 9e f 2-1f + Solve the following quadratics by completing the square h 2 + 4h = j 2-10j = k = -14k 105. m 2-21 = 20m n + 80= -n p + p 2 = q 2-12q = r r = A toy rocket launched into the air has a height (h feet) at any given time (t seconds) as h = -16t t until it hits the ground. At what time(s) is it at a height of 9 feet above the ground? Solving Using the Quadratic Formula Solve the following using the quadratic formula. Round answers to the hundredth place x 2 +8x -6 = g 2-4g +2 = d 2 + 4d -3 = m 2 + 3m = w 2-8 = 5w z 9z 2 = An employee makes (2x + 3) dollars an hour for x hours. If the employer wants to pay no more than $120 a day, what is the maximum number of hours the employee can work? (Round to the nearest quarter hour) NJ Center for Teaching and Learning ~ 7 ~
8 Homework Solve the following using the quadratic formula. Round answers to the hundredth place x 2 +7x -5 = g 2-5g +3 = d 2 + 5d -3 = m 2 + 4m = w 2-2 = 5w z 6z 2 = An employee makes (3x - 5) dollars an hour for x hours. If the employer wants to pay no more than $200 a day, what is the maximum number of hours the employee can work? (Round to the nearest quarter hour) Discriminant Find the discriminant for each quadratic equation. State the number of real roots and then find the real solution(s), if any exist x 2-6x + 5 = x 2-4x - 6 = x + 4x = x 9 = x x 2 = 6x x 2-9x 2= x (2x 5) = A rock is thrown with a height equation of h = -16t t + 5 (where h is the height of the rock in feet at any given time of t in seconds). Will it reach a height of 30 feet? Explain your answer. Homework Find the discriminant for each quadratic equation. State the number of real roots and then find the real solution(s), if any exist x 2-9x + 7 = x 2-4x + 2 = x + 7x = x 6 = 2x x 2 = 7x 6 NJ Center for Teaching and Learning ~ 8 ~
9 138. 3x 2-7x 8= (x + 3)(2x + 6) = A rock is thrown with a height equation of h = -16t t + 5 (where h is the height of the rock in feet at any given time of t in seconds). Will it reach a height of 50 feet? Explain your answer. Mixed Application Problems Solve the following problems using any method The product of two consecutive positive integers is 272, find the integers The product of two consecutive positive even integers is 528, find the integers The product of two consecutive odd integers is 255, find the integers Two planes leave airport at the same time (from different runways). If three hours later they are 500 miles apart and the plane flying south has traveled 200 miles farther, how far did the one flying west travel? 145. Two cars leave a gas station at the same time, one traveling north and one traveling east. One hour later they are 80 miles apart and the one traveling east went 10 miles farther, how far is it from the gas station? 146. A square has its length increased by 4 feet and its width by 5 feet. If the resulting rectangle has an area of 132 square feet what was the perimeter of the original square? 147. A rectangular parking lot has a width 30 feet more than its length. The owners are able to increase the width by 20 feet and the length by 40. The new lot has an area of 27,200 square feet, what is the area of the original lot? Homework Solve the following problems using any method The product of two consecutive positive integers is 272, find the integers The product of two consecutive positive even integers is 342, find the integers The product of two consecutive odd integers is 483, find the integers Two planes leave airport at the same time (from different runways). If three hours later they are 600 miles apart and the plane flying south has traveled 100 miles farther, how far did the one flying west travel? 152. Two cars leave a gas station at the same time, one traveling north and one traveling east. One hour later they are 90 miles apart and the one traveling east went 15 miles farther, how far is it from the gas station? 153. A square has its length increased by 6 feet and its width by 8 feet. If the resulting rectangle has an area of square feet what was the perimeter of the original square? NJ Center for Teaching and Learning ~ 9 ~
10 154. A rectangular parking lot has a width 20 feet more than its length. The owners are able to increase the width by 20 feet and the length by 40. The new lot has an area of 7225 square feet, what is the area of the original lot? Unit Review Multiple Choice Choose the correct answer for each question. No partial credit will be given. 1. Comparing the graph of y = 5x 2 + 4x - 2 to its parent function, it: A) opens down and is wider than the parent function graph. B) opens down and is narrower than the parent function graph. C) opens up and is wider than the parent function graph. D) opens up and is narrower than the parent function graph. 2. What is the equation of the axis of symmetry of y = -3x 2-12x 5? A) x = -2 B) x = -4 C) x = 4 D) x = 2 3. What are the vertex and axis of symmetry of the parabola y = x 2 + 4x + 3? A) vertex: (2, 1); axis of symmetry: x = 2 B) vertex: (2,1); axis of symmetry: x = 2 C) vertex: ( 2, 1); axis of symmetry: x = 2 D) vertex: ( 2,1); axis of symmetry: x = 2 4.What is the y- intercept of y = -2x 2 + 2x 3? A) (0, 5) B) B (3, 0) C) C (0, -3) D) D (-3, 0) NJ Center for Teaching and Learning ~ 10 ~
11 5.Which graph(s) has more than one zero? 6.Which of the following is a step in solving y = 2x 2 - x - 3 by the Factoring Method? A) 2x + 1 = 0 or x + 3 = 0 B) 2x - 3 = 0 or x + 1 = 0 C) 2x + 3 = 0 or x - 1 = 0 D) 2x - 1 = 0 or x - 3 = 0 7.The solution to (x + 2) 2 = 16 is A) 14 and -18 B) -14 and 18 C) -6 and 2 D) -2 and 6 8.What value goes in the blank to complete the square: x 2-6x +? A) -9 B) -36 C) 36 D) 9 NJ Center for Teaching and Learning ~ 11 ~
12 9.What is the discriminant of 2x 2 + 6x + 2 = 0? A) 2 B) 6 C) 20 D) How many real zeros does an equation have if the discriminant is -4? A) 0 B) 1 C) 2 D) Not enough information 11. Solve 3x 2 + 5x + 1 =0 A) B) C) D) ± Simplify 2 A) -8 and -2 B) -3 and 1 C) -3 and -1 D) 3 and 2 NJ Center for Teaching and Learning ~ 12 ~
13 13. Given the height of a rocket as h = -16t t + 896, where t is in seconds. At what time t, does the rocket hit the ground? A) - 14 and 4 seconds B) 14 seconds C) - 4 seconds D) the rocket will not hit the ground 14. Solve 3x 2 + 7x + 4 = 0 A) - 1 and B) 1 and 4 3 C) -7 and - 6 D) 7 and 6 Short Constructed Response Write the correct answer for each question. 15. What value goes in the blank to complete the perfect square trinomial: x 2 + x + 36? 16. Solve 6x x + 6 = A square has its length increased by 4 feet and its width decreased by 3 feet; the resulting area is 144 square feet. What was the area of the original square? 18. Solve (3x- 7)(x+3)=0 Extended Constructed Response - Solve the problem, showing all work. 19. A rectangle has a length 6 more than its width. If the width is decreased by 2 and the length decreased by 4, the resulting rectangle has an area of 21 square units. What is the length of the original rectangle? What is ratio of the original rectangle s area to the new rectangle s area? What is the perimeter of the new rectangle? NJ Center for Teaching and Learning ~ 13 ~
14 Quadratic Equations CW HW Answer Key 1. axis of sym. = - 3/2 2. axis of sym. =5/2; y = x 2-5x axis of sym. =2 4. axis of sym. =- 3/2; y= 2x 2 + 6x axis of sym = 2/3 6. axis of sym. = axis of sym. =- 3/2;y = x 2 +3x axis of sym. =5/2; 9. axis of sym. = - 5/4; y = 2x 2 + 5x axis of sym. =1/3 11. Up ;narrower; Down; wider; Down;narrower; Up; narrower; Down; narrower; Down; wider; Up; narrower; Down; narrower; Up; narrower; Up; narrower; Zeros = 1 and Zeros = 1 and Zeros = 1 and Zeros = none 25. Zeros = -3 and Zeros = Zeros = -5 and Zeros = Zeros = 2 and -2/3 30. Zeros = 1 and Zeros = 3 and Zeros = 1 and Zeros = 5 and Zeros = Zeros = 3 and Zeros = none 37. Zeros = -2 and Zeros = - 1/3 and and and and and and and /2 and /3 and Length = 8 ft and and and and and and and and 4/3 58. Length = 4 ft. 59. ±4 60. ±5 61. ±2 62. ±4 63. ±3 64. ±3 65. ±1 66. ± and and (x 6) 2 = 25 x = 1 or m=±6 NJ Center for Teaching and Learning ~ 14 ~
15 71. n=±8 72. p=±3 73. q=±2 74. r=±4 75. s=±4 76. t=±3 77. u=±1 78. v=5 or w=0 or (x + 5) 2 = 72 x = 1 or h=2 or j = 1 or k = -9 or m = 13 or n 1.61 or p = 0 or q 6.9 or r.42 or t 5.93 sec h=2 or j=9 or k=-1 or m=21 or no solution 107. p=-6 or no solution 109. r=1 or t.06 sec. or 9.94 sec or or or m= 1 or 1/ or or hours or or or or or or hrs two solutions; x = 5 or two solutions; x = 3 or no solution 128. one solution; x= no solution 130. two solutions; 2.45 or two solutions; 3.81 or No, the max. ht. is about 11.2 ft no solutions 134. one solution ; x= no solutions 136. two solutions; x = 3/2 or no solutions 138. two solutions; 3.17 or two solutions; -.66 or Yes, max ht. is 69 ft & & & 17 NJ Center for Teaching and Learning ~ 15 ~
16 144. About mi About 61.4 mi ft ,000 sq ft & & & About 371 miles 152. About 70.7 miles ft ,925 sq ft. Review Answer Key 1. D 2. A 3. C 4. C 5. B, D 6. B 7. C 8. D 9. C 10. A 11. C 12. B 13. B 14. A and square feet 18. X = 7 and units; 55 ; 20 units 21 NJ Center for Teaching and Learning ~ 16 ~
Algebra I. Slide 1 / 175. Slide 2 / 175. Slide 3 / 175. Quadratics. Table of Contents Key Terms
 Slide 1 / 175 Slide 2 / 175 Algebra I Quadratics 2015-11-04 www.njctl.org Key Terms Table of Contents Click on the topic to go to that section Slide 3 / 175 Characteristics of Quadratic Equations Transforming
Slide 1 / 175 Slide 2 / 175 Algebra I Quadratics 2015-11-04 www.njctl.org Key Terms Table of Contents Click on the topic to go to that section Slide 3 / 175 Characteristics of Quadratic Equations Transforming
Algebra I. Key Terms. Slide 1 / 175 Slide 2 / 175. Slide 3 / 175. Slide 4 / 175. Slide 5 / 175. Slide 6 / 175. Quadratics.
 Slide 1 / 175 Slide / 175 Algebra I Quadratics 015-11-04 www.njctl.org Key Terms Slide 3 / 175 Table of Contents Click on the topic to go to that section Slide 4 / 175 Characteristics of Quadratic Equations
Slide 1 / 175 Slide / 175 Algebra I Quadratics 015-11-04 www.njctl.org Key Terms Slide 3 / 175 Table of Contents Click on the topic to go to that section Slide 4 / 175 Characteristics of Quadratic Equations
Algebra I Quadratics
 1 Algebra I Quadratics 2015-11-04 www.njctl.org 2 Key Terms Table of Contents Click on the topic to go to that section Characteristics of Quadratic Equations Transforming Quadratic Equations Graphing Quadratic
1 Algebra I Quadratics 2015-11-04 www.njctl.org 2 Key Terms Table of Contents Click on the topic to go to that section Characteristics of Quadratic Equations Transforming Quadratic Equations Graphing Quadratic
A. B. C. D. Quadratics Practice Test. Question 1. Select the graph of the quadratic function. g (x ) = 1 3 x 2. 3/8/2018 Print Assignment
 Question 1. Select the graph of the quadratic function. g (x ) = 1 3 x 2 C. D. https://my.hrw.com/wwtb2/viewer/printall_vs23.html?umk5tfdnj31tcldd29v4nnzkclztk3w8q6wgvr262aca0a5fsymn1tfv8j1vs4qotwclvofjr8xhs0cldd29v4
Question 1. Select the graph of the quadratic function. g (x ) = 1 3 x 2 C. D. https://my.hrw.com/wwtb2/viewer/printall_vs23.html?umk5tfdnj31tcldd29v4nnzkclztk3w8q6wgvr262aca0a5fsymn1tfv8j1vs4qotwclvofjr8xhs0cldd29v4
Chapter 5 Smartboard Notes
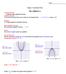 Name Chapter 5 Smartboard Notes 10.1 Graph ax 2 + c Learning Outcome To graph simple quadratic functions Quadratic function A non linear function that can be written in the standard form y = ax 2 + bx
Name Chapter 5 Smartboard Notes 10.1 Graph ax 2 + c Learning Outcome To graph simple quadratic functions Quadratic function A non linear function that can be written in the standard form y = ax 2 + bx
6.1 Quadratic Expressions, Rectangles, and Squares. 1. What does the word quadratic refer to? 2. What is the general quadratic expression?
 Advanced Algebra Chapter 6 - Note Taking Guidelines Complete each Now try problem in your notes and work the problem 6.1 Quadratic Expressions, Rectangles, and Squares 1. What does the word quadratic refer
Advanced Algebra Chapter 6 - Note Taking Guidelines Complete each Now try problem in your notes and work the problem 6.1 Quadratic Expressions, Rectangles, and Squares 1. What does the word quadratic refer
Name Date Class California Standards 17.0, Quadratic Equations and Functions. Step 2: Graph the points. Plot the ordered pairs from your table.
 California Standards 17.0, 1.0 9-1 There are three steps to graphing a quadratic function. Graph y x 3. Quadratic Equations and Functions 6 y 6 y x y x 3 5 1 1 0 3 1 1 5 0 x 0 x Step 1: Make a table of
California Standards 17.0, 1.0 9-1 There are three steps to graphing a quadratic function. Graph y x 3. Quadratic Equations and Functions 6 y 6 y x y x 3 5 1 1 0 3 1 1 5 0 x 0 x Step 1: Make a table of
Final Review. Intermediate Algebra / MAT135 S2014
 Final Review Intermediate Algebra / MAT135 S2014 1. Solve for. 2. Solve for. 3. Solve for. 4. Jenny, Abdul, and Frank sent a total of text messages during the weekend. Abdul sent more messages than Jenny.
Final Review Intermediate Algebra / MAT135 S2014 1. Solve for. 2. Solve for. 3. Solve for. 4. Jenny, Abdul, and Frank sent a total of text messages during the weekend. Abdul sent more messages than Jenny.
9-8 Completing the Square
 In the previous lesson, you solved quadratic equations by isolating x 2 and then using square roots. This method works if the quadratic equation, when written in standard form, is a perfect square. When
In the previous lesson, you solved quadratic equations by isolating x 2 and then using square roots. This method works if the quadratic equation, when written in standard form, is a perfect square. When
Name I.D. Number. Select the response that best completes the statement or answers the question.
 Name I.D. Number Unit 4 Evaluation Evaluation 04 Second Year Algebra 1 (MTHH 039 059) This evaluation will cover the lessons in this unit. It is open book, meaning you can use your textbook, syllabus,
Name I.D. Number Unit 4 Evaluation Evaluation 04 Second Year Algebra 1 (MTHH 039 059) This evaluation will cover the lessons in this unit. It is open book, meaning you can use your textbook, syllabus,
Math 2 1. Lesson 4-5: Completing the Square. When a=1 in a perfect square trinomial, then. On your own: a. x 2 18x + = b.
 Math 1 Lesson 4-5: Completing the Square Targets: I can identify and complete perfect square trinomials. I can solve quadratic equations by Completing the Square. When a=1 in a perfect square trinomial,
Math 1 Lesson 4-5: Completing the Square Targets: I can identify and complete perfect square trinomials. I can solve quadratic equations by Completing the Square. When a=1 in a perfect square trinomial,
3.4 Solving Quadratic Equations by Completing
 .4. Solving Quadratic Equations by Completing the Square www.ck1.org.4 Solving Quadratic Equations by Completing the Square Learning objectives Complete the square of a quadratic expression. Solve quadratic
.4. Solving Quadratic Equations by Completing the Square www.ck1.org.4 Solving Quadratic Equations by Completing the Square Learning objectives Complete the square of a quadratic expression. Solve quadratic
Exam 2 Review F15 O Brien. Exam 2 Review:
 Eam Review:.. Directions: Completely rework Eam and then work the following problems with your book notes and homework closed. You may have your graphing calculator and some blank paper. The idea is to
Eam Review:.. Directions: Completely rework Eam and then work the following problems with your book notes and homework closed. You may have your graphing calculator and some blank paper. The idea is to
9.4 Start Thinking. 9.4 Warm Up. 9.4 Cumulative Review Warm Up. Use a graphing calculator to graph ( )
 9.4 Start Thinking Use a graphing calculator to graph ( ) f x = x + 4x 1. Find the minimum of the function using the CALC feature on the graphing calculator. Explain the relationship between the minimum
9.4 Start Thinking Use a graphing calculator to graph ( ) f x = x + 4x 1. Find the minimum of the function using the CALC feature on the graphing calculator. Explain the relationship between the minimum
2 If ax + bx + c = 0, then x = b) What are the x-intercepts of the graph or the real roots of f(x)? Round to 4 decimal places.
 Quadratic Formula - Key Background: So far in this course we have solved quadratic equations by the square root method and the factoring method. Each of these methods has its strengths and limitations.
Quadratic Formula - Key Background: So far in this course we have solved quadratic equations by the square root method and the factoring method. Each of these methods has its strengths and limitations.
Quadratic Applications Name: Block: 3. The product of two consecutive odd integers is equal to 30 more than the first. Find the integers.
 Quadratic Applications Name: Block: This problem packet is due before 4pm on Friday, October 26. It is a formative assessment and worth 20 points. Complete the following problems. Circle or box your answer.
Quadratic Applications Name: Block: This problem packet is due before 4pm on Friday, October 26. It is a formative assessment and worth 20 points. Complete the following problems. Circle or box your answer.
Properties of Graphs of Quadratic Functions
 Properties of Graphs of Quadratic Functions y = ax 2 + bx + c 1) For a quadratic function given in standard form a tells us: c is the: 2) Given the equation, state the y-intercept and circle the direction
Properties of Graphs of Quadratic Functions y = ax 2 + bx + c 1) For a quadratic function given in standard form a tells us: c is the: 2) Given the equation, state the y-intercept and circle the direction
Completing the Square
 5-7 Completing the Square TEKS FOCUS TEKS (4)(F) Solve quadratic and square root equations. TEKS (1)(A) Apply mathematics to problems arising in everyday life, society, and the workplace. Additional TEKS
5-7 Completing the Square TEKS FOCUS TEKS (4)(F) Solve quadratic and square root equations. TEKS (1)(A) Apply mathematics to problems arising in everyday life, society, and the workplace. Additional TEKS
Algebra II Unit #2 4.6 NOTES: Solving Quadratic Equations (More Methods) Block:
 Algebra II Unit # Name: 4.6 NOTES: Solving Quadratic Equations (More Methods) Block: (A) Background Skills - Simplifying Radicals To simplify a radical that is not a perfect square: 50 8 300 7 7 98 (B)
Algebra II Unit # Name: 4.6 NOTES: Solving Quadratic Equations (More Methods) Block: (A) Background Skills - Simplifying Radicals To simplify a radical that is not a perfect square: 50 8 300 7 7 98 (B)
Unit 5: Quadratic Functions
 Unit 5: Quadratic Functions LESSON #2: THE PARABOLA APPLICATIONS AND WORD PROBLEMS INVERSE OF A QUADRATIC FUNCTION DO NOW: Review from Lesson #1 (a)using the graph shown to the right, determine the equation
Unit 5: Quadratic Functions LESSON #2: THE PARABOLA APPLICATIONS AND WORD PROBLEMS INVERSE OF A QUADRATIC FUNCTION DO NOW: Review from Lesson #1 (a)using the graph shown to the right, determine the equation
4.1 Graphical Solutions of Quadratic Equations Date:
 4.1 Graphical Solutions of Quadratic Equations Date: Key Ideas: Quadratic functions are written as f(x) = x 2 x 6 OR y = x 2 x 6. f(x) is f of x and means that the y value is dependent upon the value of
4.1 Graphical Solutions of Quadratic Equations Date: Key Ideas: Quadratic functions are written as f(x) = x 2 x 6 OR y = x 2 x 6. f(x) is f of x and means that the y value is dependent upon the value of
Algebra Quadratics Applications HW#54
 Algebra Quadratics Applications HW#54 1: A science class designed a ball launcher and tested it by shooting a tennis ball up and off the top of a 15-story building. They determined that the motion of the
Algebra Quadratics Applications HW#54 1: A science class designed a ball launcher and tested it by shooting a tennis ball up and off the top of a 15-story building. They determined that the motion of the
Math 521B Chapter 4 Test (33 marks) Name:
 Math 521B Chapter 4 Test (33 marks) Name: Multiple Choice Identify the choice that best completes the statement or answers the question. (10 marks) 1. What are the x-intercepts of the quadratic function
Math 521B Chapter 4 Test (33 marks) Name: Multiple Choice Identify the choice that best completes the statement or answers the question. (10 marks) 1. What are the x-intercepts of the quadratic function
My Math Plan Assessment #2 Study Guide
 My Math Plan Assessment #2 Study Guide 1. Find the x-intercept and the y-intercept of the linear equation. 8x y = 4 2. Use factoring to solve the quadratic equation. x 2 + 9x + 1 = 17. Multiply and simplify
My Math Plan Assessment #2 Study Guide 1. Find the x-intercept and the y-intercept of the linear equation. 8x y = 4 2. Use factoring to solve the quadratic equation. x 2 + 9x + 1 = 17. Multiply and simplify
ALGEBRA UNIT 11-GRAPHING QUADRATICS THE GRAPH OF A QUADRATIC FUNCTION (DAY 1)
 ALGEBRA UNIT 11-GRAPHING QUADRATICS THE GRAPH OF A QUADRATIC FUNCTION (DAY 1) The Quadratic Equation is written as: ; this equation has a degree of. Where a, b and c are integer coefficients (where a 0)
ALGEBRA UNIT 11-GRAPHING QUADRATICS THE GRAPH OF A QUADRATIC FUNCTION (DAY 1) The Quadratic Equation is written as: ; this equation has a degree of. Where a, b and c are integer coefficients (where a 0)
1. Graph (on graph paper) the following equations by creating a table and plotting points on a coordinate grid y = -2x 2 4x + 2 x y.
 1. Graph (on graph paper) the following equations by creating a table and plotting points on a coordinate grid y = -2x 2 4x + 2 x y y = x 2 + 6x -3 x y domain= range= -4-3 -2-1 0 1 2 3 4 domain= range=
1. Graph (on graph paper) the following equations by creating a table and plotting points on a coordinate grid y = -2x 2 4x + 2 x y y = x 2 + 6x -3 x y domain= range= -4-3 -2-1 0 1 2 3 4 domain= range=
Final Exam Review for DMAT 0310
 Final Exam Review for DMAT 010 MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Factor the polynomial completely. What is one of the factors? 1) x
Final Exam Review for DMAT 010 MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Factor the polynomial completely. What is one of the factors? 1) x
( ) f ( x 1 ) . x 2. To find the average rate of change, use the slope formula, m = f x 2
 Common Core Regents Review Functions Quadratic Functions (Graphs) A quadratic function has the form y = ax 2 + bx + c. It is an equation with a degree of two because its highest exponent is 2. The graph
Common Core Regents Review Functions Quadratic Functions (Graphs) A quadratic function has the form y = ax 2 + bx + c. It is an equation with a degree of two because its highest exponent is 2. The graph
Solve for the variable by transforming equations:
 Cantwell Sacred Heart of Mary High School Math Department Study Guide for the Algebra 1 (or higher) Placement Test Name: Date: School: Solve for the variable by transforming equations: 1. y + 3 = 9. 1
Cantwell Sacred Heart of Mary High School Math Department Study Guide for the Algebra 1 (or higher) Placement Test Name: Date: School: Solve for the variable by transforming equations: 1. y + 3 = 9. 1
Quadratic Functions and Equations
 Quadratic Functions and Equations Quadratic Graphs and Their Properties Objective: To graph quadratic functions of the form y = ax 2 and y = ax 2 + c. Objectives I can identify a vertex. I can grapy y
Quadratic Functions and Equations Quadratic Graphs and Their Properties Objective: To graph quadratic functions of the form y = ax 2 and y = ax 2 + c. Objectives I can identify a vertex. I can grapy y
1. The graph of a quadratic function is shown. Each square is one unit.
 1. The graph of a quadratic function is shown. Each square is one unit. a. What is the vertex of the function? b. If the lead coefficient (the value of a) is 1, write the formula for the function in vertex
1. The graph of a quadratic function is shown. Each square is one unit. a. What is the vertex of the function? b. If the lead coefficient (the value of a) is 1, write the formula for the function in vertex
Chapter 2 Polynomial and Rational Functions
 SECTION.1 Linear and Quadratic Functions Chapter Polynomial and Rational Functions Section.1: Linear and Quadratic Functions Linear Functions Quadratic Functions Linear Functions Definition of a Linear
SECTION.1 Linear and Quadratic Functions Chapter Polynomial and Rational Functions Section.1: Linear and Quadratic Functions Linear Functions Quadratic Functions Linear Functions Definition of a Linear
1) Solve the quadratic equation Y=5x*+3 where *=2 A. x = (Y-3) B. x = (3+Y) C. x = (3+Y) 2 D. x = (Y-3) 2
 TEST 13 REVIEW Quadratics 1) Solve the quadratic equation Y=5x*+3 where *=2 A. x = (Y-3) B. x = (3+Y) C. x = (3+Y) 2 D. x = (Y-3) 2 2) Explain in complete sentences how to solve the following equation
TEST 13 REVIEW Quadratics 1) Solve the quadratic equation Y=5x*+3 where *=2 A. x = (Y-3) B. x = (3+Y) C. x = (3+Y) 2 D. x = (Y-3) 2 2) Explain in complete sentences how to solve the following equation
CC Algebra Quadratic Functions Test Review. 1. The graph of the equation y = x 2 is shown below. 4. Which parabola has an axis of symmetry of x = 1?
 Name: CC Algebra Quadratic Functions Test Review Date: 1. The graph of the equation y = x 2 is shown below. 4. Which parabola has an axis of symmetry of x = 1? a. c. c. b. d. Which statement best describes
Name: CC Algebra Quadratic Functions Test Review Date: 1. The graph of the equation y = x 2 is shown below. 4. Which parabola has an axis of symmetry of x = 1? a. c. c. b. d. Which statement best describes
The x-coordinate of the vertex: The equation of the axis of symmetry:
 Algebra 2 Notes Section 4.1: Graph Quadratic Functions in Standard Form Objective(s): Vocabulary: I. Quadratic Function: II. Standard Form: III. Parabola: IV. Parent Function for Quadratic Functions: Vertex
Algebra 2 Notes Section 4.1: Graph Quadratic Functions in Standard Form Objective(s): Vocabulary: I. Quadratic Function: II. Standard Form: III. Parabola: IV. Parent Function for Quadratic Functions: Vertex
Word Problems Team Test KCATM 2014
 Word Problems Team Test KCATM 014 School 1) A right triangle has legs of length x and x + 4 and a hypotenuse of length x 4. Find the length of the triangle s longer leg. A) 4 B) 8 C) 1 D) 4 E) answer not
Word Problems Team Test KCATM 014 School 1) A right triangle has legs of length x and x + 4 and a hypotenuse of length x 4. Find the length of the triangle s longer leg. A) 4 B) 8 C) 1 D) 4 E) answer not
Algebra I End of Course Review
 Algebra I End of Course Review Properties and PEMDAS 1. Name the property shown: a + b + c = b + a + c (Unit 1) 1. Name the property shown: a(b) = b(a). Name the property shown: m + 0 = m. Name the property
Algebra I End of Course Review Properties and PEMDAS 1. Name the property shown: a + b + c = b + a + c (Unit 1) 1. Name the property shown: a(b) = b(a). Name the property shown: m + 0 = m. Name the property
Unit 1 Study Guide Answers. 1a. Domain: 2, -3 Range: -3, 4, -4, 0 Inverse: {(-3,2), (4, -3), (-4, 2), (0, -3)}
 Unit 1 Study Guide Answers 1a. Domain: 2, -3 Range: -3, 4, -4, 0 Inverse: {(-3,2), (4, -3), (-4, 2), (0, -3)} 1b. x 2-3 2-3 y -3 4-4 0 1c. no 2a. y = x 2b. y = mx+ b 2c. 2e. 2d. all real numbers 2f. yes
Unit 1 Study Guide Answers 1a. Domain: 2, -3 Range: -3, 4, -4, 0 Inverse: {(-3,2), (4, -3), (-4, 2), (0, -3)} 1b. x 2-3 2-3 y -3 4-4 0 1c. no 2a. y = x 2b. y = mx+ b 2c. 2e. 2d. all real numbers 2f. yes
Algebra I EOC Review (Part 3)
 1. Statement Reason 1. 2.5(6.25x + 0.5) = 11 1. Given 2. 15.625x + 1.25 = 11 2. Distribution Property 3. 15.625x = 9.75 3. Subtraction Property of Equality 4. x = 0.624 4. Division Property of Equality
1. Statement Reason 1. 2.5(6.25x + 0.5) = 11 1. Given 2. 15.625x + 1.25 = 11 2. Distribution Property 3. 15.625x = 9.75 3. Subtraction Property of Equality 4. x = 0.624 4. Division Property of Equality
Algebra II Honors Unit 3 Assessment Review Quadratic Functions. Formula Box. f ( x) 2 x 3 25 from the parent graph of
 Name: Algebra II Honors Unit 3 Assessment Review Quadratic Functions Date: Formula Box x = b a x = b ± b 4ac a h 6t h 0 ) What are the solutions of x 3 5? x 8or x ) Describe the transformation of f ( x)
Name: Algebra II Honors Unit 3 Assessment Review Quadratic Functions Date: Formula Box x = b a x = b ± b 4ac a h 6t h 0 ) What are the solutions of x 3 5? x 8or x ) Describe the transformation of f ( x)
3.4 Solving Quadratic Equations by Completing
 www.ck1.org Chapter 3. Quadratic Equations and Quadratic Functions 3.4 Solving Quadratic Equations by Completing the Square Learning objectives Complete the square of a quadratic expression. Solve quadratic
www.ck1.org Chapter 3. Quadratic Equations and Quadratic Functions 3.4 Solving Quadratic Equations by Completing the Square Learning objectives Complete the square of a quadratic expression. Solve quadratic
f(x) Determine whether each function has a maximum or minimum value, and find that value. Then state the domain and range of the function.
 NAME DATE PERID 4-1 Practice Graphing Quadratic Functions Complete parts a c for each quadratic function. a. Find the -intercept, the equation of the ais of smmetr, and the -coordinate of the verte. b.
NAME DATE PERID 4-1 Practice Graphing Quadratic Functions Complete parts a c for each quadratic function. a. Find the -intercept, the equation of the ais of smmetr, and the -coordinate of the verte. b.
Section 1.1. Chapter 1. Quadratics. Parabolas. Example. Example. ( ) = ax 2 + bx + c -2-1
 Chapter 1 Quadratic Functions and Factoring Section 1.1 Graph Quadratic Functions in Standard Form Quadratics The polynomial form of a quadratic function is: f x The graph of a quadratic function is a
Chapter 1 Quadratic Functions and Factoring Section 1.1 Graph Quadratic Functions in Standard Form Quadratics The polynomial form of a quadratic function is: f x The graph of a quadratic function is a
ALGEBRA II-GRAPHING QUADRATICS THE GRAPH OF A QUADRATIC FUNCTION
 ALGEBRA II-GRAPHING QUADRATICS THE GRAPH OF A QUADRATIC FUNCTION The Quadratic Equation is written as: ; this equation has a degree of. Where a, b and c are integer coefficients (where a 0) The graph of
ALGEBRA II-GRAPHING QUADRATICS THE GRAPH OF A QUADRATIC FUNCTION The Quadratic Equation is written as: ; this equation has a degree of. Where a, b and c are integer coefficients (where a 0) The graph of
!"#$%&'("$)*"+*,"--"$*,"./*0&'1*2*
 "#$%&'("$)*"+*,"--"$*,"./*0&'1** 3$('***4#&%.&'(5*0"%/66($7** "#$%&"""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""" Daily Plan Unit 3 FCC3 Day Class Lesson Homework Day 1: Thurs
"#$%&'("$)*"+*,"--"$*,"./*0&'1** 3$('***4#&%.&'(5*0"%/66($7** "#$%&"""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""" Daily Plan Unit 3 FCC3 Day Class Lesson Homework Day 1: Thurs
Chapter 9 Quadratic Functions and Equations
 Chapter 9 Quadratic Functions and Equations 1 9 1Quadratic Graphs and their properties U shaped graph such as the one at the right is called a parabola. A parabola can open upward or downward. A parabola
Chapter 9 Quadratic Functions and Equations 1 9 1Quadratic Graphs and their properties U shaped graph such as the one at the right is called a parabola. A parabola can open upward or downward. A parabola
Lesson 1: What is a Parabola?
 Lesson 1: What is a Parabola? Parabola Vocabulary Write the defintion of the given word. Label #3-6 on the graph. 1. Parabola: Name Class Date 2. Trajectory: 3. Zeros: 4. Axis of Symmetry: 5. Vertex: Online
Lesson 1: What is a Parabola? Parabola Vocabulary Write the defintion of the given word. Label #3-6 on the graph. 1. Parabola: Name Class Date 2. Trajectory: 3. Zeros: 4. Axis of Symmetry: 5. Vertex: Online
AdvAlg6.4GraphingQuadratics.notebook. March 07, Newton s Formula h(t) = 1 gt 2 + v o t + h o 2. time. initial upward velocity
 Notes Lesson 6 4 Applications of Quadratic Functions Newton s Formula h(t) = 1 gt 2 + v o t + h o 2 Height of object time Constant (accel. due to gravity) *32 ft/sec 2 *9.8 m/sec 2 **MEMORIZE THESE** initial
Notes Lesson 6 4 Applications of Quadratic Functions Newton s Formula h(t) = 1 gt 2 + v o t + h o 2 Height of object time Constant (accel. due to gravity) *32 ft/sec 2 *9.8 m/sec 2 **MEMORIZE THESE** initial
Name Class Date. Quadratic Functions and Transformations. 4 6 x
 - Quadratic Functions and Transformations For Eercises, choose the correct letter.. What is the verte of the function 53()? D (, ) (, ) (, ) (, ). Which is the graph of the function f ()5(3) 5? F 6 6 O
- Quadratic Functions and Transformations For Eercises, choose the correct letter.. What is the verte of the function 53()? D (, ) (, ) (, ) (, ). Which is the graph of the function f ()5(3) 5? F 6 6 O
Name: Teacher: Per: Unit 1 Unit 2 Unit 3 Unit 4 Unit 5 Unit 6 Unit 7 Unit 8 Unit 9 Unit 10. Unit 9a. [Quadratic Functions] Unit 9 Quadratics 1
![Name: Teacher: Per: Unit 1 Unit 2 Unit 3 Unit 4 Unit 5 Unit 6 Unit 7 Unit 8 Unit 9 Unit 10. Unit 9a. [Quadratic Functions] Unit 9 Quadratics 1 Name: Teacher: Per: Unit 1 Unit 2 Unit 3 Unit 4 Unit 5 Unit 6 Unit 7 Unit 8 Unit 9 Unit 10. Unit 9a. [Quadratic Functions] Unit 9 Quadratics 1](/thumbs/82/86818253.jpg) Name: Teacher: Per: Unit 1 Unit 2 Unit 3 Unit 4 Unit 5 Unit 6 Unit 7 Unit 8 Unit 9 Unit 10 Unit 9a [Quadratic Functions] Unit 9 Quadratics 1 To be a Successful Algebra class, TIGERs will show #TENACITY
Name: Teacher: Per: Unit 1 Unit 2 Unit 3 Unit 4 Unit 5 Unit 6 Unit 7 Unit 8 Unit 9 Unit 10 Unit 9a [Quadratic Functions] Unit 9 Quadratics 1 To be a Successful Algebra class, TIGERs will show #TENACITY
Secondary Math 2H Unit 3 Notes: Factoring and Solving Quadratics
 Secondary Math H Unit 3 Notes: Factoring and Solving Quadratics 3.1 Factoring out the Greatest Common Factor (GCF) Factoring: The reverse of multiplying. It means figuring out what you would multiply together
Secondary Math H Unit 3 Notes: Factoring and Solving Quadratics 3.1 Factoring out the Greatest Common Factor (GCF) Factoring: The reverse of multiplying. It means figuring out what you would multiply together
Ms. Peralta s IM3 HW 5.4. HW 5.4 Solving Quadratic Equations. Solve the following exercises. Use factoring and/or the quadratic formula.
 HW 5.4 HW 5.4 Solving Quadratic Equations Name: Solve the following exercises. Use factoring and/or the quadratic formula. 1. 2. 3. 4. HW 5.4 5. 6. 4x 2 20x + 25 = 36 7. 8. HW 5.4 9. 10. 11. 75x 2 30x
HW 5.4 HW 5.4 Solving Quadratic Equations Name: Solve the following exercises. Use factoring and/or the quadratic formula. 1. 2. 3. 4. HW 5.4 5. 6. 4x 2 20x + 25 = 36 7. 8. HW 5.4 9. 10. 11. 75x 2 30x
Intermediate Algebra Semester Summary Exercises. 1 Ah C. b = h
 . Solve: 3x + 8 = 3 + 8x + 3x A. x = B. x = 4 C. x = 8 8 D. x =. Solve: w 3 w 5 6 8 A. w = 4 B. w = C. w = 4 D. w = 60 3. Solve: 3(x ) + 4 = 4(x + ) A. x = 7 B. x = 5 C. x = D. x = 4. The perimeter of
. Solve: 3x + 8 = 3 + 8x + 3x A. x = B. x = 4 C. x = 8 8 D. x =. Solve: w 3 w 5 6 8 A. w = 4 B. w = C. w = 4 D. w = 60 3. Solve: 3(x ) + 4 = 4(x + ) A. x = 7 B. x = 5 C. x = D. x = 4. The perimeter of
Algebra I Quadratics Practice Questions
 1. Which is equivalent to 64 100? 10 50 8 10 8 100. Which is equivalent to 6 8? 4 8 1 4. Which is equivalent to 7 6? 4 4 4. Which is equivalent to 4? 8 6 From CCSD CSE S Page 1 of 6 1 5. Which is equivalent
1. Which is equivalent to 64 100? 10 50 8 10 8 100. Which is equivalent to 6 8? 4 8 1 4. Which is equivalent to 7 6? 4 4 4. Which is equivalent to 4? 8 6 From CCSD CSE S Page 1 of 6 1 5. Which is equivalent
Using the Laws of Exponents to Simplify Rational Exponents
 6. Explain Radicals and Rational Exponents - Notes Main Ideas/ Questions Essential Question: How do you simplify expressions with rational exponents? Notes/Examples What You Will Learn Evaluate and simplify
6. Explain Radicals and Rational Exponents - Notes Main Ideas/ Questions Essential Question: How do you simplify expressions with rational exponents? Notes/Examples What You Will Learn Evaluate and simplify
Algebra 2 Honors. Unit 4, Day 1 Period: Date: Graph Quadratic Functions in Standard Form. (Three more problems on the back )
 Algebra Honors Name: Unit 4, Day 1 Period: Date: Graph Quadratic Functions in Standard Form 1. y = 3x. y = 5x + 1 3. y = x 5 4. y = 1 5 x 6. y = x + x + 1 7. f(x) = 6x 4x 5 (Three more problems on the
Algebra Honors Name: Unit 4, Day 1 Period: Date: Graph Quadratic Functions in Standard Form 1. y = 3x. y = 5x + 1 3. y = x 5 4. y = 1 5 x 6. y = x + x + 1 7. f(x) = 6x 4x 5 (Three more problems on the
Subtract 16 from both sides. Divide both sides by 9. b. Will the swing touch the ground? Explain how you know.
 REVIEW EXAMPLES 1) Solve 9x + 16 = 0 for x. 9x + 16 = 0 9x = 16 Original equation. Subtract 16 from both sides. 16 x 9 Divide both sides by 9. 16 x Take the square root of both sides. 9 4 x i 3 Evaluate.
REVIEW EXAMPLES 1) Solve 9x + 16 = 0 for x. 9x + 16 = 0 9x = 16 Original equation. Subtract 16 from both sides. 16 x 9 Divide both sides by 9. 16 x Take the square root of both sides. 9 4 x i 3 Evaluate.
Quadratic Word Problems - Develop an Approach and Solve
 Name: Class: Date: ID: A Quadratic Word Problems - Develop an Approach and Solve Short Answer 1. Suppose you have 54 feet of fencing to enclose a rectangular dog pen. The function A = 7x x, where x = width,
Name: Class: Date: ID: A Quadratic Word Problems - Develop an Approach and Solve Short Answer 1. Suppose you have 54 feet of fencing to enclose a rectangular dog pen. The function A = 7x x, where x = width,
UNIT 3: MODELING AND ANALYZING QUADRATIC FUNCTIONS
 UNIT 3: MODELING AND ANALYZING QUADRATIC FUNCTIONS This unit investigates quadratic functions. Students study the structure of quadratic expressions and write quadratic expressions in equivalent forms.
UNIT 3: MODELING AND ANALYZING QUADRATIC FUNCTIONS This unit investigates quadratic functions. Students study the structure of quadratic expressions and write quadratic expressions in equivalent forms.
0115AI Common Core State Standards
 0115AI Common Core State Standards 1 The owner of a small computer repair business has one employee, who is paid an hourly rate of $22. The owner estimates his weekly profit using the function P(x) = 8600
0115AI Common Core State Standards 1 The owner of a small computer repair business has one employee, who is paid an hourly rate of $22. The owner estimates his weekly profit using the function P(x) = 8600
MAT135 Review for Test 4 Dugopolski Sections 7.5, 7.6, 8.1, 8.2, 8.3, 8.4
 Sections 7.5, 7.6, 8.1, 8., 8., 8.4 1. Use the discriminant to determine the number and type(s) of solutions for 4x 8x 4 0. One real solution B. One complex solution Two real solutions Two complex solutions.
Sections 7.5, 7.6, 8.1, 8., 8., 8.4 1. Use the discriminant to determine the number and type(s) of solutions for 4x 8x 4 0. One real solution B. One complex solution Two real solutions Two complex solutions.
Algebra 2/Trig Apps: Chapter 5 Quadratics Packet
 Algebra /Trig Apps: Chapter 5 Quadratics Packet In this unit we will: Determine what the parameters a, h, and k do in the vertex form of a quadratic equation Determine the properties (vertex, axis of symmetry,
Algebra /Trig Apps: Chapter 5 Quadratics Packet In this unit we will: Determine what the parameters a, h, and k do in the vertex form of a quadratic equation Determine the properties (vertex, axis of symmetry,
Final Exam Review Part 2 #1 Page 1 / 21
 Final Eam Review Part #1 Intermediate Algebra / MAT 135 Spring 017 Master ( Master Templates) Student Name/ID: v 1. Solve for, where is a real number. v v + 1 + =. Solve for, where is a real number. +
Final Eam Review Part #1 Intermediate Algebra / MAT 135 Spring 017 Master ( Master Templates) Student Name/ID: v 1. Solve for, where is a real number. v v + 1 + =. Solve for, where is a real number. +
Solve Quadratic Equations by Completing the Square
 10.5 Solve Quadratic Equations by Completing the Square Before You solved quadratic equations by finding square roots. Now You will solve quadratic equations by completing the square. Why? So you can solve
10.5 Solve Quadratic Equations by Completing the Square Before You solved quadratic equations by finding square roots. Now You will solve quadratic equations by completing the square. Why? So you can solve
2 nd Semester Final Exam Review Block Date
 Algebra 1B Name nd Semester Final Eam Review Block Date Calculator NOT Allowed Graph each function. 1 (10-1) 1. (10-1). (10-1) 3. (10-1) 4. 3 Graph each function. Identif the verte, ais of smmetr, and
Algebra 1B Name nd Semester Final Eam Review Block Date Calculator NOT Allowed Graph each function. 1 (10-1) 1. (10-1). (10-1) 3. (10-1) 4. 3 Graph each function. Identif the verte, ais of smmetr, and
L What are the properties that should be used to isolate the variable in the equation? 3x + 11 = 5
 lgebra Name: MITERM REVIEW Part Hour: ate: L... What are the properties that should be used to isolate the variable in the equation? x + = 5 additive identit and multiplicative identit additive inverse
lgebra Name: MITERM REVIEW Part Hour: ate: L... What are the properties that should be used to isolate the variable in the equation? x + = 5 additive identit and multiplicative identit additive inverse
11.3 Finding Complex Solutions of Quadratic Equations
 Name Class Date 11.3 Finding Complex Solutions of Quadratic Equations Essential Question: How can you find the complex solutions of any quadratic equation? Resource Locker Explore Investigating Real Solutions
Name Class Date 11.3 Finding Complex Solutions of Quadratic Equations Essential Question: How can you find the complex solutions of any quadratic equation? Resource Locker Explore Investigating Real Solutions
Unit 5 Test: 9.1 Quadratic Graphs and Their Properties
 Unit 5 Test: 9.1 Quadratic Graphs and Their Properties Quadratic Equation: (Also called PARABOLAS) 1. of the STANDARD form y = ax 2 + bx + c 2. a, b, c are all real numbers and a 0 3. Always have an x
Unit 5 Test: 9.1 Quadratic Graphs and Their Properties Quadratic Equation: (Also called PARABOLAS) 1. of the STANDARD form y = ax 2 + bx + c 2. a, b, c are all real numbers and a 0 3. Always have an x
My Math Plan Assessment #1 Study Guide
 My Math Plan Assessment #1 Study Guide 1. Find the x-intercept and the y-intercept of the linear equation. 8x y = 4. Use factoring to solve the quadratic equation. x + 9x + 1 = 17. Find the difference.
My Math Plan Assessment #1 Study Guide 1. Find the x-intercept and the y-intercept of the linear equation. 8x y = 4. Use factoring to solve the quadratic equation. x + 9x + 1 = 17. Find the difference.
Mini-Lecture 5.1 Exponents and Scientific Notation
 Mini-Lecture.1 Eponents and Scientific Notation Learning Objectives: 1. Use the product rule for eponents.. Evaluate epressions raised to the zero power.. Use the quotient rule for eponents.. Evaluate
Mini-Lecture.1 Eponents and Scientific Notation Learning Objectives: 1. Use the product rule for eponents.. Evaluate epressions raised to the zero power.. Use the quotient rule for eponents.. Evaluate
Date: Pd: Unit 4. GSE H Analytic Geometry EOC Review Name: Units Rewrite ( 12 3) 2 in simplest form. 2. Simplify
 GSE H Analytic Geometry EOC Review Name: Units 4 7 Date: Pd: Unit 4 1. Rewrite ( 12 3) 2 in simplest form. 2. Simplify 18 25 3. Which expression is equivalent to 32 8? a) 2 2 27 4. Which expression is
GSE H Analytic Geometry EOC Review Name: Units 4 7 Date: Pd: Unit 4 1. Rewrite ( 12 3) 2 in simplest form. 2. Simplify 18 25 3. Which expression is equivalent to 32 8? a) 2 2 27 4. Which expression is
Section 1.2 DOMAIN, RANGE, INTERCEPTS, SYMMETRY, EVEN/ODD
 Section 1.2 DOMAIN, RANGE, INTERCEPTS, SYMMETRY, EVEN/ODD zeros roots line symmetry point symmetry even function odd function Estimate Function Values A. ADVERTISING The function f (x) = 5x 2 + 50x approximates
Section 1.2 DOMAIN, RANGE, INTERCEPTS, SYMMETRY, EVEN/ODD zeros roots line symmetry point symmetry even function odd function Estimate Function Values A. ADVERTISING The function f (x) = 5x 2 + 50x approximates
LATE AND ABSENT HOMEWORK IS ACCEPTED UP TO THE TIME OF THE CHAPTER TEST ON
 Trig/Math Anal Name No LATE AND ABSENT HOMEWORK IS ACCEPTED UP TO THE TIME OF THE CHAPTER TEST ON HW NO. SECTIONS ASSIGNMENT DUE FS-1 4-4 Practice Set A #1-57 eoo 4-5 Practice Set B #1-45 eoo, 57, 59 FS-
Trig/Math Anal Name No LATE AND ABSENT HOMEWORK IS ACCEPTED UP TO THE TIME OF THE CHAPTER TEST ON HW NO. SECTIONS ASSIGNMENT DUE FS-1 4-4 Practice Set A #1-57 eoo 4-5 Practice Set B #1-45 eoo, 57, 59 FS-
MAT 107 College Algebra Fall 2013 Name. Final Exam, Version X
 MAT 107 College Algebra Fall 013 Name Final Exam, Version X EKU ID Instructor Part 1: No calculators are allowed on this section. Show all work on your paper. Circle your answer. Each question is worth
MAT 107 College Algebra Fall 013 Name Final Exam, Version X EKU ID Instructor Part 1: No calculators are allowed on this section. Show all work on your paper. Circle your answer. Each question is worth
5.4 - Quadratic Functions
 Fry TAMU Spring 2017 Math 150 Notes Section 5.4 Page! 92 5.4 - Quadratic Functions Definition: A function is one that can be written in the form f (x) = where a, b, and c are real numbers and a 0. (What
Fry TAMU Spring 2017 Math 150 Notes Section 5.4 Page! 92 5.4 - Quadratic Functions Definition: A function is one that can be written in the form f (x) = where a, b, and c are real numbers and a 0. (What
Unit four review. Name: Class: Date: Short Answer
 Name: Class: Date: ID: A Unit four review Short Answer 1. Graph the quadratic function y = 3x 2 6x + 5. Use the graph to determine the zeros of the function if they exist. 2. For what values of k does
Name: Class: Date: ID: A Unit four review Short Answer 1. Graph the quadratic function y = 3x 2 6x + 5. Use the graph to determine the zeros of the function if they exist. 2. For what values of k does
PART A CALCULATOR ACTIVE: Maximum Time: 35 Minutes
 Algebra II: Chapter 5 Unit Test 2 Name: PART A CALCULATOR ACTIVE: Maximum Time: 35 Minutes Fill in the blanks: Put answers in the space provided. 1. The value of k that makes x 2 + kx + 25 4 a perfect
Algebra II: Chapter 5 Unit Test 2 Name: PART A CALCULATOR ACTIVE: Maximum Time: 35 Minutes Fill in the blanks: Put answers in the space provided. 1. The value of k that makes x 2 + kx + 25 4 a perfect
PAP Algebra 2. Unit 4B. Quadratics (Part 2) Name Period
 PAP Algebra Unit 4B Quadratics (Part ) Name Period 1 After Test WS: 4.6 Solve by Factoring PAP Algebra Name Factor. 1. x + 6x + 8. 4x 8x 3 + + 3. x + 7x + 5 4. x 3x 1 + + 5. x + 7x + 6 6. 3x + 10x + 3
PAP Algebra Unit 4B Quadratics (Part ) Name Period 1 After Test WS: 4.6 Solve by Factoring PAP Algebra Name Factor. 1. x + 6x + 8. 4x 8x 3 + + 3. x + 7x + 5 4. x 3x 1 + + 5. x + 7x + 6 6. 3x + 10x + 3
Section 3.1 Quadratic Functions and Models
 Math 130 www.timetodare.com Section 3.1 Quadratic Functions and Models Quadratic Function: ( ) f x = ax + bx+ c ( a 0) The graph of a quadratic function is called a parabola. Graphing Parabolas: Special
Math 130 www.timetodare.com Section 3.1 Quadratic Functions and Models Quadratic Function: ( ) f x = ax + bx+ c ( a 0) The graph of a quadratic function is called a parabola. Graphing Parabolas: Special
MATH 121: EXTRA PRACTICE FOR TEST 2. Disclaimer: Any material covered in class and/or assigned for homework is a fair game for the exam.
 MATH 121: EXTRA PRACTICE FOR TEST 2 Disclaimer: Any material covered in class and/or assigned for homework is a fair game for the exam. 1 Linear Functions 1. Consider the functions f(x) = 3x + 5 and g(x)
MATH 121: EXTRA PRACTICE FOR TEST 2 Disclaimer: Any material covered in class and/or assigned for homework is a fair game for the exam. 1 Linear Functions 1. Consider the functions f(x) = 3x + 5 and g(x)
MATH 110: FINAL EXAM REVIEW
 MATH 0: FINAL EXAM REVIEW Can you solve linear equations algebraically and check your answer on a graphing calculator? (.) () y y= y + = 7 + 8 ( ) ( ) ( ) ( ) y+ 7 7 y = 9 (d) ( ) ( ) 6 = + + Can you set
MATH 0: FINAL EXAM REVIEW Can you solve linear equations algebraically and check your answer on a graphing calculator? (.) () y y= y + = 7 + 8 ( ) ( ) ( ) ( ) y+ 7 7 y = 9 (d) ( ) ( ) 6 = + + Can you set
Solve each equation by completing the square. Round to the nearest tenth if necessary. 5. x 2 + 4x = 6 ANSWER: 5.2, 1.2
 Find the value of c that makes each trinomial a perfect square. 1. x 2 18x + c 81 3. x 2 + 9x + c Solve each equation by completing the square. Round to the nearest tenth if necessary. 5. x 2 + 4x = 6
Find the value of c that makes each trinomial a perfect square. 1. x 2 18x + c 81 3. x 2 + 9x + c Solve each equation by completing the square. Round to the nearest tenth if necessary. 5. x 2 + 4x = 6
x 2 + x + x 2 x 3 b. x 7 Factor the GCF from each expression Not all may be possible. 1. Find two numbers that sum to 8 and have a product of 12
 Factor the GCF from each expression 4 5 1. 15x 3x. 16x 4 Name: a. b. 4 7 3 6 5 3. 18x y 36x y 4x y 5 4. 3x x 3 x 3 c. d. Not all may be possible. 1. Find two numbers that sum to 8 and have a product of
Factor the GCF from each expression 4 5 1. 15x 3x. 16x 4 Name: a. b. 4 7 3 6 5 3. 18x y 36x y 4x y 5 4. 3x x 3 x 3 c. d. Not all may be possible. 1. Find two numbers that sum to 8 and have a product of
The Quadratic Formula VOCABULARY
 - The Quadratic Formula TEKS FOCUS TEKS ()(F) Solve quadratic and square root equations. TEKS ()(G) Display, eplain, and justify mathematical ideas and arguments using precise mathematical language in
- The Quadratic Formula TEKS FOCUS TEKS ()(F) Solve quadratic and square root equations. TEKS ()(G) Display, eplain, and justify mathematical ideas and arguments using precise mathematical language in
MATH College Algebra Review for Test 2
 MATH 4 - College Algebra Review for Test Sections. and.. For f (x) = x + 4x + 5, give (a) the x-intercept(s), (b) the -intercept, (c) both coordinates of the vertex, and (d) the equation of the axis of
MATH 4 - College Algebra Review for Test Sections. and.. For f (x) = x + 4x + 5, give (a) the x-intercept(s), (b) the -intercept, (c) both coordinates of the vertex, and (d) the equation of the axis of
Skills Practice Skills Practice for Lesson 3.1
 Skills Practice Skills Practice for Lesson. Name Date Lots and Projectiles Introduction to Quadratic Functions Vocabular Define each term in our own words.. quadratic function. vertical motion Problem
Skills Practice Skills Practice for Lesson. Name Date Lots and Projectiles Introduction to Quadratic Functions Vocabular Define each term in our own words.. quadratic function. vertical motion Problem
In #1 and 2, use inverse operations to solve each equation. 2.
 In #1 and 2, use inverse operations to solve each equation. 1. 3x + 12 + 5x = 7 2. 1 (4x + 10) = x 5 2 3. Alex and Alyssa both have savings accounts. Alex has $515 and saves $23 per month. Alyssa has $725
In #1 and 2, use inverse operations to solve each equation. 1. 3x + 12 + 5x = 7 2. 1 (4x + 10) = x 5 2 3. Alex and Alyssa both have savings accounts. Alex has $515 and saves $23 per month. Alyssa has $725
In #8-11, Simplify the expression. Write your answer using only positive exponents. 11) 4
 Algebra 1 Summer Review 16-17 Name Directions: Do your best, this is a refresher from what you learned in Algebra 1. The more you review now, the easier it will be for you to jump back into Algebra Chapter
Algebra 1 Summer Review 16-17 Name Directions: Do your best, this is a refresher from what you learned in Algebra 1. The more you review now, the easier it will be for you to jump back into Algebra Chapter
1 P a g e Province Mathematics Department Southwest Tennessee Community College
 Chapter 10 Section 10.1 - Solving Quadratic Equations by the Square Root Property Objectives: 1. Review the zero-factor property. 2. Solve equations of the form x 2 = k, where k > 0. 3. Solve equations
Chapter 10 Section 10.1 - Solving Quadratic Equations by the Square Root Property Objectives: 1. Review the zero-factor property. 2. Solve equations of the form x 2 = k, where k > 0. 3. Solve equations
Fair Game Review. Chapter 9. Find the square root(s) ± Find the side length of the square. 7. Simplify Simplify 63.
 Name Date Chapter 9 Find the square root(s). Fair Game Review... 9. ±. Find the side length of the square.. s. s s Area = 9 ft s Area = 0. m 7. Simplif 0. 8. Simplif. 9. Simplif 08. 0. Simplif 88. Copright
Name Date Chapter 9 Find the square root(s). Fair Game Review... 9. ±. Find the side length of the square.. s. s s Area = 9 ft s Area = 0. m 7. Simplif 0. 8. Simplif. 9. Simplif 08. 0. Simplif 88. Copright
Math 150: Intermediate Algebra Spring 2012 Fall 2005 : Mock Exam 4 (z z
 Math 150: Intermediate Algebra Spring 01 Fall 005 : Mock Eam 4 (z 9. - z NAME 10.6) TICKET # [ 13 problems: 10 points each ] Answer problems and epress your answers appropriately, that is ; simply state
Math 150: Intermediate Algebra Spring 01 Fall 005 : Mock Eam 4 (z 9. - z NAME 10.6) TICKET # [ 13 problems: 10 points each ] Answer problems and epress your answers appropriately, that is ; simply state
MATH College Algebra Review for Test 2
 MATH 34 - College Algebra Review for Test 2 Sections 3. and 3.2. For f (x) = x 2 + 4x + 5, give (a) the x-intercept(s), (b) the -intercept, (c) both coordinates of the vertex, and (d) the equation of the
MATH 34 - College Algebra Review for Test 2 Sections 3. and 3.2. For f (x) = x 2 + 4x + 5, give (a) the x-intercept(s), (b) the -intercept, (c) both coordinates of the vertex, and (d) the equation of the
1. 4(x - 5) - 3(2x - 5) = 6-5(2x + 1) 2. 3(2x - 3) + 4(3-2x) = 5(3x - 2) - 2(x + 1) x + 6 x x + 6x
 Math 15 - Payne Blitzer Final Exam Review Solve for x: 1. 4(x - 5) - 3(x - 5) = 6-5(x + 1). 3(x - 3) + 4(3 - x) = 5(3x - ) - (x + 1) 3. x + 1 = 9 4. 3x - = 10 5. (x - 4)(x + 4) = 4x 6. (x - )(x + 3) =
Math 15 - Payne Blitzer Final Exam Review Solve for x: 1. 4(x - 5) - 3(x - 5) = 6-5(x + 1). 3(x - 3) + 4(3 - x) = 5(3x - ) - (x + 1) 3. x + 1 = 9 4. 3x - = 10 5. (x - 4)(x + 4) = 4x 6. (x - )(x + 3) =
Algebra I Practice Questions ? 1. Which is equivalent to (A) (B) (C) (D) 2. Which is equivalent to 6 8? (A) 4 3
 1. Which is equivalent to 64 100? 10 50 8 10 8 100. Which is equivalent to 6 8? 4 8 1 4. Which is equivalent to 7 6? 4 4 4. Which is equivalent to 4? 8 6 Page 1 of 0 11 Practice Questions 6 1 5. Which
1. Which is equivalent to 64 100? 10 50 8 10 8 100. Which is equivalent to 6 8? 4 8 1 4. Which is equivalent to 7 6? 4 4 4. Which is equivalent to 4? 8 6 Page 1 of 0 11 Practice Questions 6 1 5. Which
Pre-Calculus Midterm Practice Test (Units 1 through 3)
 Name: Date: Period: Pre-Calculus Midterm Practice Test (Units 1 through 3) Learning Target 1A I can describe a set of numbers in a variety of ways. 1. Write the following inequalities in interval notation.
Name: Date: Period: Pre-Calculus Midterm Practice Test (Units 1 through 3) Learning Target 1A I can describe a set of numbers in a variety of ways. 1. Write the following inequalities in interval notation.
Graphing Quadratic Functions 9.1
 Quadratic Functions - Graphing Quadratic Functions 9.1 f ( x) = a x + b x + c (also called standard form). The graph of quadratic functions is called a parabola. Axis of Symmetry a central line which makes
Quadratic Functions - Graphing Quadratic Functions 9.1 f ( x) = a x + b x + c (also called standard form). The graph of quadratic functions is called a parabola. Axis of Symmetry a central line which makes
Lesson 10.1 Solving Quadratic Equations
 Lesson 10.1 Solving Quadratic Equations 1. Sketch the graph of a quadratic equation with each set of conditions. a. One -intercept and all nonnegative y-values b. The verte in the third quadrant and no
Lesson 10.1 Solving Quadratic Equations 1. Sketch the graph of a quadratic equation with each set of conditions. a. One -intercept and all nonnegative y-values b. The verte in the third quadrant and no
0115AI Common Core State Standards
 0115AI Common Core State Standards 1 The owner of a small computer repair business has one employee, who is paid an hourly rate of $22. The owner estimates his weekly profit using the function P(x) = 8600
0115AI Common Core State Standards 1 The owner of a small computer repair business has one employee, who is paid an hourly rate of $22. The owner estimates his weekly profit using the function P(x) = 8600
Answer Key. Solve each equation x - 9 = (n + 2) = b - 6 = -3b + 48
 Solve each equation. 1. -3x - 9 = -27 2. 25 + 2(n + 2) = 30 3. -9b - 6 = -3b + 48 x = 6 n = 1 / 2 b = -9 4. 5 - (m - 4) = 2m + 3(m - 1) 5. -24-10k = -8(k + 4) - 2k 6. f - (-19) = 11f + 23-20f m = 2 no
Solve each equation. 1. -3x - 9 = -27 2. 25 + 2(n + 2) = 30 3. -9b - 6 = -3b + 48 x = 6 n = 1 / 2 b = -9 4. 5 - (m - 4) = 2m + 3(m - 1) 5. -24-10k = -8(k + 4) - 2k 6. f - (-19) = 11f + 23-20f m = 2 no
Algebra 1 Hour Final Exam Review Days. Complete and On Time 5 points
 Semester Final Exam Review Packet Name Algebra 1 Hour Final Exam Review Days Assigned on Assignment 6/1 Unit 5 and Unit 6, 1-39 Complete and On Time 5 points Complete and Late 4 points At Least 50% Complete.5
Semester Final Exam Review Packet Name Algebra 1 Hour Final Exam Review Days Assigned on Assignment 6/1 Unit 5 and Unit 6, 1-39 Complete and On Time 5 points Complete and Late 4 points At Least 50% Complete.5
