18.06 Problem Set 9 - Solutions Due Wednesday, 21 November 2007 at 4 pm in
|
|
|
- Margery Atkins
- 6 years ago
- Views:
Transcription
1 8.6 Problem Set 9 - Solutions Due Wednesday, 2 November 27 at 4 pm in 2-6. Problem : (5) When A = SΛS is a real-symmetric (or Hermitian) matrix, its eigenvectors can be chosen orthonormal and hence S = Q is orthogonal (or unitary). Thus, A = QΛQ T, which is called the spectral decomposition of A. ( ) 3 2 Find the spectral decomposition for A =, and check by explicit multiplication 2 3 that A = QΛQ T. Hence, find A 3 and cos(aπ/3). Solution The characteristic equation for A is λ 2 6λ + 5 =. ( Thus ) the eigenvalues of A are λ = and λ 2 = 5. For λ =, the eigenvector is v =. For λ 2 = 5, the ( ) eigenvector is v 2 =. Thus the spectral decomposition of A is A = ( ) ( ) ( ) 2/2 2/2 2/2 2/2 2/2. 2/2 5 2/2 2/2 We check the above decomposition by explicit multiplication: ( ) ( ) ( ) ( ) ( ) 2/2 2/2 2/2 2/2 2/2 2/2 5 2/2 = 2/2 5 2/2 2/2 2/2 5 2/2 2/2 2/2 2/2 2/2 ( ) 3 2 =. 2 3 and Now ( ) ( ) ( ) 2/2 2/2 A 3 = 2/2 2/2 2/2 2/ /2 2/2 ( ) ( + 5 = 3 )/2 ( )/2 ( )/2 ( )/2 ( ) ( ) ( ) 2/2 2/2 cos(aπ/3) = 2/2 cos(π/3) 2/2 2/2 2/2 cos(5π/3) 2/2 2/2 ( ) /2 =. /2
2 Problem 2: (=5+5) Suppose A is any n n real matrix. () If λ C is an eigenvalue of A, show that its complex conjugate λ is also an eigenvalue of A. (Hint: take the complex-conjugate of the eigen-equation.) Solution Let p(x) be the characteristic polynomial for A. Then p(λ) =. Take conjugate, we get p(λ) =. Since A is a real matrix, p is a polynomial of real coefficient, which implies have p(x) = p( x) for all x. Thus p( λ) =, i.e., λ is an eigenvalue of A. Another proof: Suppose Ax = λx, take conjugate, we get A x = λ x, so λ is an eigenvalue with eigenvector x. (2) Show that if n is odd, then A has at least one real eigenvalue. (Hint: think about the characteristic polynomial.) Solution We have seen above that if λ is an eigenvalue of A, then λ is also an eigenvalue of A. In fact, we can say more: if Av = λv, then by taking conjugate we have A v = λ v, where we used the property that A is a real matrix. This shows that if v is an eigenvector of A corresponding to eigenvalue λ, then v is an eigenvector of A corresponding to eigenvalue λ. So all complex eigenvalues of A can be paired (counting multiplicity) to be conjugated pairs (λ, λ). This implies that A has even number of complex eigenvalues. However, since n is odd, A has odd (=n) number of eigenvalues. Thus A has at least one real eigenvalue. Another proof: The leading term of the characteristic polynomial p(x) is λ n. When n is odd, p(x) will tend to ± when x tends to ±. So p(x) must has at least one real root. Problem 3: (2=6+6+8) In class, we showed that a Hermitian matrix (or its special case of a real-symmetric matrix) has real eigenvalues and that eigenvectors for distinct eigenvalues are always orthogonal. Now, we want to do a similar analysis of unitary matrices Q H = Q (including the special case of real orthogonal matrices). () The eigenvalues λ of Q are not real in general rather, they always satisfy λ 2 = λλ =. Prove this. (Hint: start with Qx = λx and consider the dot product (Qx) (Qx) = x H Q H Qx.) Solution Suppose λ is an eigenvalue of Q and x is an eigenvector of λ. Then one has (Qx) (Qx) = (λx) (λx) = λ 2 x x. On the other hand, since Q is unitary, we have (Qx) (Qx) = x H Q H Qx = x H x = x x. 2
3 Compare the above two equations, we get λ 2 x x = x x. Since x is an eigenvector, we have x, thus x x. So we must have λ 2 =. (2) Prove that eigenvectors with distinct eigenvalues are orthogonal. (Hint: consider (Qx) (Qy) for two eigenvectors x and y with different eigenvalues. You will also find useful the fact that, since λ 2 = = λλ, then λ = /λ.) Solution Suppose λ and λ 2 are distinct eigenvectors of A, with corresponding eigenvectors x and y respectively. Then as above, we have and Compare the above two equations, we have (Qx) (Qy) = (λ x) (λ 2 y) = λ λ 2 x y (Qx) (Qy) = x H Q H Qy = x H y = x y. λ λ 2 x y = x y. From part () we have already seen that λ 2 = λ λ =, thus λ = /λ. This implies λ λ 2 = λ 2 /λ, since λ are λ 2 are distinct. It follows that x y =, i.e. the eigenvectors x and y are orthogonal. (3) Give examples of and 2 2 unitary matrices and show that their eigensolutions have the above properties. (Give both a purely real and a complex example for each size. Don t pick a diagonal 2 2 matrix.) Solution For n =, A only has one entry which is its eigenvalue. Thus the only real examples are () and ( ), and complex examples are (cos θ + i sin θ) for any θ. For n = 2. The real example is given by any 2 ( 2 orthogonal ) matrix. For example, 2/2 2/2 we can take the matrix appeared in problem : 2/2. The eigenvalues of 2/2 this matrix are λ = 2 2 ± 2 2 i. We have λ 2 = for both of them. The corresponding eigenvectors are v = ( 2/2 2i/2 ) and v 2 = ( 2/2 2i/2 ). They are orthogonal: v v 2 = ( 2/2)( 2/2) + ( 2i/2)( 2i/2) =. To produce an complex example, we ( need) to find two orthogonal complex vectors. i For example, we may take the matrix. The eigenvalues are ±, both satisfies ( ) i ( ) i i λ 2 =. The eigenvectors are v = and v 2 =. They are orthogonal since we have v v 2 = ī ( i) + = + =. 3
4 Problem 4: (2= ) Consider the vector space of real twice-differentiable functions f(x) defined for x [, ] with f() = f() =, and the dot product f g = f(x)g(x)dx. Use the linear operator A defined by Af = d [ w(x) df ], dx dx where w(x) > is some positive differentiable function. () Show that A is Hermitian [use integration by parts to show f (Ag) = (Af) g] and positive-definite [by showing f (Af) > for f ]. What can you conclude about the eigenvalues and eigenfunctions (even though you can t calculate them explicitly)? Solution To show that A is Hermitian, we only need to show that f (Ag) = (Af) g for all f and g in this vector space. We compute By symmetry, we have f (Ag) = = f(x)(ag)(x)dx f(x) d dx = f(x)w(x) dg dx = [ w(x) dg dx + w(x) dg df dx dx dx. (Af) g = g (Af) = Thus f (Ag) = (Af) g, i.e. A is Hermitian. ] dx w(x) dg df dx dx dx w(x) df dg dx dx dx. Now suppose f. Since f() = f() =, we see that f is not constant, i.e. Take g = f in the above computation, we get f (Af) = since w(x) >. So A is positive definite. w(x) df df dx dx dx > df dx. So the eigenvalues of A are all positive real numbers, and eigenvectors corresponding to different eigenvalues are orthogonal to each other. 4
5 (2) To solve for the eigenfunctions of A for most functions w(x), we must do so numerically. The simplest approach is to replace the derivatives d/dx by approximate differences: f (x) [f(x + x) f(x x)]/2 x for some small x. In this way, we construct a finite n n matrix A (for n / x). This is done by the following Matlab code, given a number of points n > and a function w(x): dx = / (n - ); x = linspace(,,n); A = diag(w(x+dx/2)+w(x-dx/2)) - diag(w(x(:n-)+dx/2), ) - diag(w(x(2:n)-dx/2), -); A = A / (dx^2); Now, set n = and w(x) = : n = w ones(size(x)) and then type in the Matlab code above to initialize A. In this case, the problem f = λf is analytically solvable for the eigenfunctions f k (x) = sin(kπx) and eigenvalues λ k = (kπ) 2. Run [S,D] = eig(a) to find the eigenvectors (columns of S) and eigenvalues (diagonal of D) of your approximate matrix A from above, and compare the lowest 3 eigenvalues and the corresponding eigenvectors to the analytical solutions for k =, 2, 3. That is, do: [S,D] = eig(a); plot(x, S(:,:3), ro, x, [sin(pi*x);sin(2*pi*x);sin(3*pi*x)]*sqrt(2*dx), k- ) to plot the numerical eigenfunctions (red dots) and the analytical eigenfunctions (black lines). (The sqrt(2*dx) is there to make the normalizations the same. You might need to flip some of the signs to make the lines match up.) You can compare the eigenvalues (find their ratios) by running: lambda = diag(d); lambda(:3)./ ([:3] *pi).^2 Solution The commands are 5
6 >> ones(size(x)); >> dx=/(n-); >> x=linspace(,,n); >> A=diag(w(x+dx/2)+w(x-dx/2))-diag(w(x(:n-)+dx/2),)-diag(w(x(2:n)-dx/2),-); >> A=A/(dx^2); >> [S,D]=eig(A); >> plot(x,s(:,:3), ro,x,[-sin(pi*x);-sin(2*pi*x);-sin(3*pi*x)]*sqrt(2*dx), k- ) >> lambda=diag(d); >> lambda(:3)./([:3] *pi).^ The graph is Figure : Eigenfunctions 6
7 (3) Repeat the above process for n = 5 and show that the first three eigenvalues and eigenfunctions come closer to the analytical solutions as n increases. Solution The commands >> n=5;w=@(x) ones(size(x)); >> dx=/(n-); >> x=linspace(,,n); >> A=diag(w(x+dx/2)+w(x-dx/2))-diag(w(x(:n-)+dx/2),)-diag(w(x(2:n)-dx/2),-); >> A=A/(dx^2); >> [S,D]=eig(A); >> plot(x,s(:,:3), ro,x,[-sin(pi*x);-sin(2*pi*x);-sin(3*pi*x)]*sqrt(2*dx), k- ) >> lambda=diag(d); >> lambda(:3)./([:3] *pi).^ The graph is Figure 2: Eigenfunctions 7
8 (4) Try it for a different w(x) function, for example w(x) = cos(x) (which is positive for x [, ]), and n = : w cos(x) n = After you construct A with this new w(x) using the commands above, look at the upperleft corner to verify that it is symmetric: type A(:,:). Check that the eigenvalues satisfy your conditions from () by using the following commands to find the maximum imaginary part and the minimum real part of all the λ s, respectively: [S,D] = eig(a); lambda = diag(d); max(abs(imag(lambda))) min(real(lambda)) Plot the eigenvectors for the lowest three eigenvalues, as above, and compare them to the analytical solutions for the w(x) = case. You will need to make sure that the eigenvalues are sorted in increasing order, which can be done with the sort command: [lambda,order] = sort(diag(d)); Q = S(:,order); plot(x, Q(:,:3), r.-, x, [sin(pi*x);sin(2*pi*x);sin(3*pi*x)]*sqrt(2*dx), k- ) (Again, you may want to flip some of the signs to make the comparison easier.) Verify that the first three eigenvectors are still orthogonal (even though they are no longer simply sine functions) by computing the dot products: Q(:,) * Q(:,2) Q(:,) * Q(:,3) Q(:,2) * Q(:,3) The numbers should be almost zero, up to roundoff error (4 6 decimal places). Solution The commands >> n=;w=@(x) cos(x); >> dx=/(n-); >> x=linspace(,,n); >> A=diag(w(x+dx/2)+w(x-dx/2))-diag(w(x(:n-)+dx/2),)-diag(w(x(2:n)-dx/2),-); >> A=A/(dx^2); 8
9 >> A(:,:).e+4 * >> [S,D]=eig(A); >> lambda=diag(d); >> max(abs(imag(lambda))) >> min(real(lambda)) >> [lambda,order]=sort(diag(d)); >> Q=S(:,order); >> plot(x,q(:,:3), r.-,x,[-sin(pi*x);sin(2*pi*x);sin(3*pi*x)]*sqrt(2*dx), k- ) >> Q(:,) *Q(:,2).24e-4 9
10 >> Q(:,) *Q(:,3) >> e-5 >> Q(:,2) *Q(:,3) e-4 The graph Figure 3: Eigenfunctions
11 Problem 5: (5= ) True or False? Give reasons. () If A is real symmetric matrix, then any two linearly independent eigenvectors of A are perpendicular. Solution False. For a symmetric or Hermitian matrix, eigenvectors corresponds to different eigenvalues are orthogonal. But independent eigenvectors corresponds to the same eigenvalue may not be perpendicular. Counterexample: Take A to be the identity matrix. Then any vector is eigenvector. Two different vector don t have to be perpendicular. (2) Any n n complex matrix with n real eigenvalues and n orthonormal eigenvectors is a Hermitian matrix. Solution True. Let Λ be the diagonal matrix with diagonal entries the eigenvalues, and S be the matrix of corresponding eigenvectors. Then A = SΛS. Since S consists of orthonormal vectors, it is unitary. Thus A = SΛS H. Since Λ H = Λ, we see A H = SΛ H S H = SΛS H = A. So A is Hermitian. (3) If all entries of A are positive, then A is positive-definite matrix. Solution False. ( ) 2 Counterexample: Take A =. Then det(a) = 3 <, thus A must have 2 negative eigenvalue, and thus A is not positive-definite. (4) If A, B are positive definite matrices, then A + B is positive matrix. Solution True. Suppose A, B are positive definite, then for any x, x H Ax > and x H Bx >. Thus x H (A + B)x >. In other words, A + B is positive definite. (To graders: If a student thinks that this positive matrix means a matrix whose entries are positive, answers False and gives an correct counterexample, please give full score.) (5) If A is positive-definite matrix, then A is also a positive-definite matrix. Solution True. Since A is positive-definite, its eigenvalues λ,, λ n are all positive. Thus the eigenvalues of A, λ,, λ, are all positive. So A is positive-definite. n
12 Problem 6: () Find all 2 2 real matrices that are both symmetric and orthogonal. ( ) a b Solution Any symmetric 2 2 matrix is of the form A =. Since it is also b c orthogonal, two column vectors are perpendicular. So ab + bc =. In other words, b = or a + c =. ( ) a If b =, then the matrix has the form. It is orthogonal if and only if a = ± ( ) c ± and c = ±, i.e. A =. ± ( ) a b If a + c =, then the matrix has the form. It is orthogonal if and only if b a ( ) cos θ sin θ a 2 + b 2 =, i.e. a = cos θ and b = sin θ. So the matrix is A = for some sin θ cos θ θ. Problem 7: () For f = 2(x 2 + x x 2 3 x x 2 + x 2 x 3 ), find a 3 3 symmetric matrix A such that f = x T Ax, and check whether A is positive definite (hint: the easiest way is to use the pivots). Solution The matrix A is 2 A = 2. 2 To show that this is positive definite, we only need to find all the pivots: /2 3/ /3 The pivots are all positive, so A is positive definite. 2
18.06 Problem Set 8 - Solutions Due Wednesday, 14 November 2007 at 4 pm in
 806 Problem Set 8 - Solutions Due Wednesday, 4 November 2007 at 4 pm in 2-06 08 03 Problem : 205+5+5+5 Consider the matrix A 02 07 a Check that A is a positive Markov matrix, and find its steady state
806 Problem Set 8 - Solutions Due Wednesday, 4 November 2007 at 4 pm in 2-06 08 03 Problem : 205+5+5+5 Consider the matrix A 02 07 a Check that A is a positive Markov matrix, and find its steady state
Symmetric and anti symmetric matrices
 Symmetric and anti symmetric matrices In linear algebra, a symmetric matrix is a square matrix that is equal to its transpose. Formally, matrix A is symmetric if. A = A Because equal matrices have equal
Symmetric and anti symmetric matrices In linear algebra, a symmetric matrix is a square matrix that is equal to its transpose. Formally, matrix A is symmetric if. A = A Because equal matrices have equal
235 Final exam review questions
 5 Final exam review questions Paul Hacking December 4, 0 () Let A be an n n matrix and T : R n R n, T (x) = Ax the linear transformation with matrix A. What does it mean to say that a vector v R n is an
5 Final exam review questions Paul Hacking December 4, 0 () Let A be an n n matrix and T : R n R n, T (x) = Ax the linear transformation with matrix A. What does it mean to say that a vector v R n is an
MTH 102: Linear Algebra Department of Mathematics and Statistics Indian Institute of Technology - Kanpur. Problem Set
 MTH 102: Linear Algebra Department of Mathematics and Statistics Indian Institute of Technology - Kanpur Problem Set 6 Problems marked (T) are for discussions in Tutorial sessions. 1. Find the eigenvalues
MTH 102: Linear Algebra Department of Mathematics and Statistics Indian Institute of Technology - Kanpur Problem Set 6 Problems marked (T) are for discussions in Tutorial sessions. 1. Find the eigenvalues
A = 3 B = A 1 1 matrix is the same as a number or scalar, 3 = [3].
![A = 3 B = A 1 1 matrix is the same as a number or scalar, 3 = [3]. A = 3 B = A 1 1 matrix is the same as a number or scalar, 3 = [3].](/thumbs/78/77913594.jpg) Appendix : A Very Brief Linear ALgebra Review Introduction Linear Algebra, also known as matrix theory, is an important element of all branches of mathematics Very often in this course we study the shapes
Appendix : A Very Brief Linear ALgebra Review Introduction Linear Algebra, also known as matrix theory, is an important element of all branches of mathematics Very often in this course we study the shapes
Computational Methods CMSC/AMSC/MAPL 460. Eigenvalues and Eigenvectors. Ramani Duraiswami, Dept. of Computer Science
 Computational Methods CMSC/AMSC/MAPL 460 Eigenvalues and Eigenvectors Ramani Duraiswami, Dept. of Computer Science Eigen Values of a Matrix Recap: A N N matrix A has an eigenvector x (non-zero) with corresponding
Computational Methods CMSC/AMSC/MAPL 460 Eigenvalues and Eigenvectors Ramani Duraiswami, Dept. of Computer Science Eigen Values of a Matrix Recap: A N N matrix A has an eigenvector x (non-zero) with corresponding
4. Linear transformations as a vector space 17
 4 Linear transformations as a vector space 17 d) 1 2 0 0 1 2 0 0 1 0 0 0 1 2 3 4 32 Let a linear transformation in R 2 be the reflection in the line = x 2 Find its matrix 33 For each linear transformation
4 Linear transformations as a vector space 17 d) 1 2 0 0 1 2 0 0 1 0 0 0 1 2 3 4 32 Let a linear transformation in R 2 be the reflection in the line = x 2 Find its matrix 33 For each linear transformation
A VERY BRIEF LINEAR ALGEBRA REVIEW for MAP 5485 Introduction to Mathematical Biophysics Fall 2010
 A VERY BRIEF LINEAR ALGEBRA REVIEW for MAP 5485 Introduction to Mathematical Biophysics Fall 00 Introduction Linear Algebra, also known as matrix theory, is an important element of all branches of mathematics
A VERY BRIEF LINEAR ALGEBRA REVIEW for MAP 5485 Introduction to Mathematical Biophysics Fall 00 Introduction Linear Algebra, also known as matrix theory, is an important element of all branches of mathematics
Math 102, Winter Final Exam Review. Chapter 1. Matrices and Gaussian Elimination
 Math 0, Winter 07 Final Exam Review Chapter. Matrices and Gaussian Elimination { x + x =,. Different forms of a system of linear equations. Example: The x + 4x = 4. [ ] [ ] [ ] vector form (or the column
Math 0, Winter 07 Final Exam Review Chapter. Matrices and Gaussian Elimination { x + x =,. Different forms of a system of linear equations. Example: The x + 4x = 4. [ ] [ ] [ ] vector form (or the column
Quadratic forms. Here. Thus symmetric matrices are diagonalizable, and the diagonalization can be performed by means of an orthogonal matrix.
 Quadratic forms 1. Symmetric matrices An n n matrix (a ij ) n ij=1 with entries on R is called symmetric if A T, that is, if a ij = a ji for all 1 i, j n. We denote by S n (R) the set of all n n symmetric
Quadratic forms 1. Symmetric matrices An n n matrix (a ij ) n ij=1 with entries on R is called symmetric if A T, that is, if a ij = a ji for all 1 i, j n. We denote by S n (R) the set of all n n symmetric
Linear algebra II Homework #1 due Thursday, Feb A =
 Homework #1 due Thursday, Feb. 1 1. Find the eigenvalues and the eigenvectors of the matrix [ ] 3 2 A =. 1 6 2. Find the eigenvalues and the eigenvectors of the matrix 3 2 2 A = 2 3 2. 2 2 1 3. The following
Homework #1 due Thursday, Feb. 1 1. Find the eigenvalues and the eigenvectors of the matrix [ ] 3 2 A =. 1 6 2. Find the eigenvalues and the eigenvectors of the matrix 3 2 2 A = 2 3 2. 2 2 1 3. The following
18.06 Problem Set 10 - Solutions Due Thursday, 29 November 2007 at 4 pm in
 86 Problem Set - Solutions Due Thursday, 29 November 27 at 4 pm in 2-6 Problem : (5=5+5+5) Take any matrix A of the form A = B H CB, where B has full column rank and C is Hermitian and positive-definite
86 Problem Set - Solutions Due Thursday, 29 November 27 at 4 pm in 2-6 Problem : (5=5+5+5) Take any matrix A of the form A = B H CB, where B has full column rank and C is Hermitian and positive-definite
6 EIGENVALUES AND EIGENVECTORS
 6 EIGENVALUES AND EIGENVECTORS INTRODUCTION TO EIGENVALUES 61 Linear equations Ax = b come from steady state problems Eigenvalues have their greatest importance in dynamic problems The solution of du/dt
6 EIGENVALUES AND EIGENVECTORS INTRODUCTION TO EIGENVALUES 61 Linear equations Ax = b come from steady state problems Eigenvalues have their greatest importance in dynamic problems The solution of du/dt
Spectral Theorem for Self-adjoint Linear Operators
 Notes for the undergraduate lecture by David Adams. (These are the notes I would write if I was teaching a course on this topic. I have included more material than I will cover in the 45 minute lecture;
Notes for the undergraduate lecture by David Adams. (These are the notes I would write if I was teaching a course on this topic. I have included more material than I will cover in the 45 minute lecture;
Linear algebra II Homework #1 solutions A = This means that every eigenvector with eigenvalue λ = 1 must have the form
 Linear algebra II Homework # solutions. Find the eigenvalues and the eigenvectors of the matrix 4 6 A =. 5 Since tra = 9 and deta = = 8, the characteristic polynomial is f(λ) = λ (tra)λ+deta = λ 9λ+8 =
Linear algebra II Homework # solutions. Find the eigenvalues and the eigenvectors of the matrix 4 6 A =. 5 Since tra = 9 and deta = = 8, the characteristic polynomial is f(λ) = λ (tra)λ+deta = λ 9λ+8 =
Math 224, Fall 2007 Exam 3 Thursday, December 6, 2007
 Math 224, Fall 2007 Exam 3 Thursday, December 6, 2007 You have 1 hour and 20 minutes. No notes, books, or other references. You are permitted to use Maple during this exam, but you must start with a blank
Math 224, Fall 2007 Exam 3 Thursday, December 6, 2007 You have 1 hour and 20 minutes. No notes, books, or other references. You are permitted to use Maple during this exam, but you must start with a blank
18.06 Problem Set 8 Solution Due Wednesday, 22 April 2009 at 4 pm in Total: 160 points.
 86 Problem Set 8 Solution Due Wednesday, April 9 at 4 pm in -6 Total: 6 points Problem : If A is real-symmetric, it has real eigenvalues What can you say about the eigenvalues if A is real and anti-symmetric
86 Problem Set 8 Solution Due Wednesday, April 9 at 4 pm in -6 Total: 6 points Problem : If A is real-symmetric, it has real eigenvalues What can you say about the eigenvalues if A is real and anti-symmetric
18.06 Problem Set 8 Due Wednesday, 23 April 2008 at 4 pm in
 18.06 Problem Set 8 Due Wednesday, 23 April 2008 at 4 pm in 2-106. Problem 1: Do problem 3 in section 6.5 (pg. 339) in the book. The matrix A encodes the quadratic f = x 2 + 4xy + 9y 2. Completing the
18.06 Problem Set 8 Due Wednesday, 23 April 2008 at 4 pm in 2-106. Problem 1: Do problem 3 in section 6.5 (pg. 339) in the book. The matrix A encodes the quadratic f = x 2 + 4xy + 9y 2. Completing the
Announcements Wednesday, November 01
 Announcements Wednesday, November 01 WeBWorK 3.1, 3.2 are due today at 11:59pm. The quiz on Friday covers 3.1, 3.2. My office is Skiles 244. Rabinoffice hours are Monday, 1 3pm and Tuesday, 9 11am. Section
Announcements Wednesday, November 01 WeBWorK 3.1, 3.2 are due today at 11:59pm. The quiz on Friday covers 3.1, 3.2. My office is Skiles 244. Rabinoffice hours are Monday, 1 3pm and Tuesday, 9 11am. Section
Review problems for MA 54, Fall 2004.
 Review problems for MA 54, Fall 2004. Below are the review problems for the final. They are mostly homework problems, or very similar. If you are comfortable doing these problems, you should be fine on
Review problems for MA 54, Fall 2004. Below are the review problems for the final. They are mostly homework problems, or very similar. If you are comfortable doing these problems, you should be fine on
ELLIPSES. Problem: Find the points on the locus. Q(x, y) = 865x 2 294xy + 585y 2 = closest to, and farthest from, the origin. Answer.
 ELLIPSES Problem: Find the points on the locus closest to, and farthest from, the origin. Answer. Q(x, y) 865x 2 294xy + 585y 2 1450 This is a Lagrange multiplier problem: we want to extremize f(x, y)
ELLIPSES Problem: Find the points on the locus closest to, and farthest from, the origin. Answer. Q(x, y) 865x 2 294xy + 585y 2 1450 This is a Lagrange multiplier problem: we want to extremize f(x, y)
LINEAR ALGEBRA QUESTION BANK
 LINEAR ALGEBRA QUESTION BANK () ( points total) Circle True or False: TRUE / FALSE: If A is any n n matrix, and I n is the n n identity matrix, then I n A = AI n = A. TRUE / FALSE: If A, B are n n matrices,
LINEAR ALGEBRA QUESTION BANK () ( points total) Circle True or False: TRUE / FALSE: If A is any n n matrix, and I n is the n n identity matrix, then I n A = AI n = A. TRUE / FALSE: If A, B are n n matrices,
EE5120 Linear Algebra: Tutorial 7, July-Dec Covers sec 5.3 (only powers of a matrix part), 5.5,5.6 of GS
 EE5 Linear Algebra: Tutorial 7, July-Dec 7-8 Covers sec 5. (only powers of a matrix part), 5.5,5. of GS. Prove that the eigenvectors corresponding to different eigenvalues are orthonormal for unitary matrices.
EE5 Linear Algebra: Tutorial 7, July-Dec 7-8 Covers sec 5. (only powers of a matrix part), 5.5,5. of GS. Prove that the eigenvectors corresponding to different eigenvalues are orthonormal for unitary matrices.
Math Spring 2011 Final Exam
 Math 471 - Spring 211 Final Exam Instructions The following exam consists of three problems, each with multiple parts. There are 15 points available on the exam. The highest possible score is 125. Your
Math 471 - Spring 211 Final Exam Instructions The following exam consists of three problems, each with multiple parts. There are 15 points available on the exam. The highest possible score is 125. Your
Math Matrix Algebra
 Math 44 - Matrix Algebra Review notes - (Alberto Bressan, Spring 7) sec: Orthogonal diagonalization of symmetric matrices When we seek to diagonalize a general n n matrix A, two difficulties may arise:
Math 44 - Matrix Algebra Review notes - (Alberto Bressan, Spring 7) sec: Orthogonal diagonalization of symmetric matrices When we seek to diagonalize a general n n matrix A, two difficulties may arise:
Review of Linear Algebra Definitions, Change of Basis, Trace, Spectral Theorem
 Review of Linear Algebra Definitions, Change of Basis, Trace, Spectral Theorem Steven J. Miller June 19, 2004 Abstract Matrices can be thought of as rectangular (often square) arrays of numbers, or as
Review of Linear Algebra Definitions, Change of Basis, Trace, Spectral Theorem Steven J. Miller June 19, 2004 Abstract Matrices can be thought of as rectangular (often square) arrays of numbers, or as
33AH, WINTER 2018: STUDY GUIDE FOR FINAL EXAM
 33AH, WINTER 2018: STUDY GUIDE FOR FINAL EXAM (UPDATED MARCH 17, 2018) The final exam will be cumulative, with a bit more weight on more recent material. This outline covers the what we ve done since the
33AH, WINTER 2018: STUDY GUIDE FOR FINAL EXAM (UPDATED MARCH 17, 2018) The final exam will be cumulative, with a bit more weight on more recent material. This outline covers the what we ve done since the
MATH 423 Linear Algebra II Lecture 33: Diagonalization of normal operators.
 MATH 423 Linear Algebra II Lecture 33: Diagonalization of normal operators. Adjoint operator and adjoint matrix Given a linear operator L on an inner product space V, the adjoint of L is a transformation
MATH 423 Linear Algebra II Lecture 33: Diagonalization of normal operators. Adjoint operator and adjoint matrix Given a linear operator L on an inner product space V, the adjoint of L is a transformation
Maths for Signals and Systems Linear Algebra in Engineering
 Maths for Signals and Systems Linear Algebra in Engineering Lecture 18, Friday 18 th November 2016 DR TANIA STATHAKI READER (ASSOCIATE PROFFESOR) IN SIGNAL PROCESSING IMPERIAL COLLEGE LONDON Mathematics
Maths for Signals and Systems Linear Algebra in Engineering Lecture 18, Friday 18 th November 2016 DR TANIA STATHAKI READER (ASSOCIATE PROFFESOR) IN SIGNAL PROCESSING IMPERIAL COLLEGE LONDON Mathematics
Class notes: Approximation
 Class notes: Approximation Introduction Vector spaces, linear independence, subspace The goal of Numerical Analysis is to compute approximations We want to approximate eg numbers in R or C vectors in R
Class notes: Approximation Introduction Vector spaces, linear independence, subspace The goal of Numerical Analysis is to compute approximations We want to approximate eg numbers in R or C vectors in R
Linear Algebra- Final Exam Review
 Linear Algebra- Final Exam Review. Let A be invertible. Show that, if v, v, v 3 are linearly independent vectors, so are Av, Av, Av 3. NOTE: It should be clear from your answer that you know the definition.
Linear Algebra- Final Exam Review. Let A be invertible. Show that, if v, v, v 3 are linearly independent vectors, so are Av, Av, Av 3. NOTE: It should be clear from your answer that you know the definition.
Math 113 Final Exam: Solutions
 Math 113 Final Exam: Solutions Thursday, June 11, 2013, 3.30-6.30pm. 1. (25 points total) Let P 2 (R) denote the real vector space of polynomials of degree 2. Consider the following inner product on P
Math 113 Final Exam: Solutions Thursday, June 11, 2013, 3.30-6.30pm. 1. (25 points total) Let P 2 (R) denote the real vector space of polynomials of degree 2. Consider the following inner product on P
Mathematical foundations - linear algebra
 Mathematical foundations - linear algebra Andrea Passerini passerini@disi.unitn.it Machine Learning Vector space Definition (over reals) A set X is called a vector space over IR if addition and scalar
Mathematical foundations - linear algebra Andrea Passerini passerini@disi.unitn.it Machine Learning Vector space Definition (over reals) A set X is called a vector space over IR if addition and scalar
Eigenvectors and Hermitian Operators
 7 71 Eigenvalues and Eigenvectors Basic Definitions Let L be a linear operator on some given vector space V A scalar λ and a nonzero vector v are referred to, respectively, as an eigenvalue and corresponding
7 71 Eigenvalues and Eigenvectors Basic Definitions Let L be a linear operator on some given vector space V A scalar λ and a nonzero vector v are referred to, respectively, as an eigenvalue and corresponding
[Disclaimer: This is not a complete list of everything you need to know, just some of the topics that gave people difficulty.]
![[Disclaimer: This is not a complete list of everything you need to know, just some of the topics that gave people difficulty.] [Disclaimer: This is not a complete list of everything you need to know, just some of the topics that gave people difficulty.]](/thumbs/82/86615903.jpg) Math 43 Review Notes [Disclaimer: This is not a complete list of everything you need to know, just some of the topics that gave people difficulty Dot Product If v (v, v, v 3 and w (w, w, w 3, then the
Math 43 Review Notes [Disclaimer: This is not a complete list of everything you need to know, just some of the topics that gave people difficulty Dot Product If v (v, v, v 3 and w (w, w, w 3, then the
Math 113 Homework 5. Bowei Liu, Chao Li. Fall 2013
 Math 113 Homework 5 Bowei Liu, Chao Li Fall 2013 This homework is due Thursday November 7th at the start of class. Remember to write clearly, and justify your solutions. Please make sure to put your name
Math 113 Homework 5 Bowei Liu, Chao Li Fall 2013 This homework is due Thursday November 7th at the start of class. Remember to write clearly, and justify your solutions. Please make sure to put your name
A Brief Outline of Math 355
 A Brief Outline of Math 355 Lecture 1 The geometry of linear equations; elimination with matrices A system of m linear equations with n unknowns can be thought of geometrically as m hyperplanes intersecting
A Brief Outline of Math 355 Lecture 1 The geometry of linear equations; elimination with matrices A system of m linear equations with n unknowns can be thought of geometrically as m hyperplanes intersecting
ACM 104. Homework Set 4 Solutions February 14, 2001
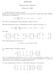 ACM 04 Homework Set 4 Solutions February 4, 00 Franklin Chapter, Problem 4, page 55 Suppose that we feel that some observations are more important or reliable than others Redefine the function to be minimized
ACM 04 Homework Set 4 Solutions February 4, 00 Franklin Chapter, Problem 4, page 55 Suppose that we feel that some observations are more important or reliable than others Redefine the function to be minimized
Practice Final Exam Solutions for Calculus II, Math 1502, December 5, 2013
 Practice Final Exam Solutions for Calculus II, Math 5, December 5, 3 Name: Section: Name of TA: This test is to be taken without calculators and notes of any sorts. The allowed time is hours and 5 minutes.
Practice Final Exam Solutions for Calculus II, Math 5, December 5, 3 Name: Section: Name of TA: This test is to be taken without calculators and notes of any sorts. The allowed time is hours and 5 minutes.
Maths for Signals and Systems Linear Algebra in Engineering
 Maths for Signals and Systems Linear Algebra in Engineering Lectures 13 15, Tuesday 8 th and Friday 11 th November 016 DR TANIA STATHAKI READER (ASSOCIATE PROFFESOR) IN SIGNAL PROCESSING IMPERIAL COLLEGE
Maths for Signals and Systems Linear Algebra in Engineering Lectures 13 15, Tuesday 8 th and Friday 11 th November 016 DR TANIA STATHAKI READER (ASSOCIATE PROFFESOR) IN SIGNAL PROCESSING IMPERIAL COLLEGE
GQE ALGEBRA PROBLEMS
 GQE ALGEBRA PROBLEMS JAKOB STREIPEL Contents. Eigenthings 2. Norms, Inner Products, Orthogonality, and Such 6 3. Determinants, Inverses, and Linear (In)dependence 4. (Invariant) Subspaces 3 Throughout
GQE ALGEBRA PROBLEMS JAKOB STREIPEL Contents. Eigenthings 2. Norms, Inner Products, Orthogonality, and Such 6 3. Determinants, Inverses, and Linear (In)dependence 4. (Invariant) Subspaces 3 Throughout
Linear Algebra - Part II
 Linear Algebra - Part II Projection, Eigendecomposition, SVD (Adapted from Sargur Srihari s slides) Brief Review from Part 1 Symmetric Matrix: A = A T Orthogonal Matrix: A T A = AA T = I and A 1 = A T
Linear Algebra - Part II Projection, Eigendecomposition, SVD (Adapted from Sargur Srihari s slides) Brief Review from Part 1 Symmetric Matrix: A = A T Orthogonal Matrix: A T A = AA T = I and A 1 = A T
Announcements Wednesday, November 01
 Announcements Wednesday, November 01 WeBWorK 3.1, 3.2 are due today at 11:59pm. The quiz on Friday covers 3.1, 3.2. My office is Skiles 244. Rabinoffice hours are Monday, 1 3pm and Tuesday, 9 11am. Section
Announcements Wednesday, November 01 WeBWorK 3.1, 3.2 are due today at 11:59pm. The quiz on Friday covers 3.1, 3.2. My office is Skiles 244. Rabinoffice hours are Monday, 1 3pm and Tuesday, 9 11am. Section
1. General Vector Spaces
 1.1. Vector space axioms. 1. General Vector Spaces Definition 1.1. Let V be a nonempty set of objects on which the operations of addition and scalar multiplication are defined. By addition we mean a rule
1.1. Vector space axioms. 1. General Vector Spaces Definition 1.1. Let V be a nonempty set of objects on which the operations of addition and scalar multiplication are defined. By addition we mean a rule
Math 520 Exam 2 Topic Outline Sections 1 3 (Xiao/Dumas/Liaw) Spring 2008
 Math 520 Exam 2 Topic Outline Sections 1 3 (Xiao/Dumas/Liaw) Spring 2008 Exam 2 will be held on Tuesday, April 8, 7-8pm in 117 MacMillan What will be covered The exam will cover material from the lectures
Math 520 Exam 2 Topic Outline Sections 1 3 (Xiao/Dumas/Liaw) Spring 2008 Exam 2 will be held on Tuesday, April 8, 7-8pm in 117 MacMillan What will be covered The exam will cover material from the lectures
Eigenvalues and Eigenvectors
 Eigenvalues and Eigenvectors week -2 Fall 26 Eigenvalues and eigenvectors The most simple linear transformation from R n to R n may be the transformation of the form: T (x,,, x n ) (λ x, λ 2,, λ n x n
Eigenvalues and Eigenvectors week -2 Fall 26 Eigenvalues and eigenvectors The most simple linear transformation from R n to R n may be the transformation of the form: T (x,,, x n ) (λ x, λ 2,, λ n x n
Linear Algebra Massoud Malek
 CSUEB Linear Algebra Massoud Malek Inner Product and Normed Space In all that follows, the n n identity matrix is denoted by I n, the n n zero matrix by Z n, and the zero vector by θ n An inner product
CSUEB Linear Algebra Massoud Malek Inner Product and Normed Space In all that follows, the n n identity matrix is denoted by I n, the n n zero matrix by Z n, and the zero vector by θ n An inner product
CS 143 Linear Algebra Review
 CS 143 Linear Algebra Review Stefan Roth September 29, 2003 Introductory Remarks This review does not aim at mathematical rigor very much, but instead at ease of understanding and conciseness. Please see
CS 143 Linear Algebra Review Stefan Roth September 29, 2003 Introductory Remarks This review does not aim at mathematical rigor very much, but instead at ease of understanding and conciseness. Please see
Linear Algebra. Workbook
 Linear Algebra Workbook Paul Yiu Department of Mathematics Florida Atlantic University Last Update: November 21 Student: Fall 2011 Checklist Name: A B C D E F F G H I J 1 2 3 4 5 6 7 8 9 10 xxx xxx xxx
Linear Algebra Workbook Paul Yiu Department of Mathematics Florida Atlantic University Last Update: November 21 Student: Fall 2011 Checklist Name: A B C D E F F G H I J 1 2 3 4 5 6 7 8 9 10 xxx xxx xxx
The Singular Value Decomposition
 The Singular Value Decomposition Philippe B. Laval KSU Fall 2015 Philippe B. Laval (KSU) SVD Fall 2015 1 / 13 Review of Key Concepts We review some key definitions and results about matrices that will
The Singular Value Decomposition Philippe B. Laval KSU Fall 2015 Philippe B. Laval (KSU) SVD Fall 2015 1 / 13 Review of Key Concepts We review some key definitions and results about matrices that will
MATH 431: FIRST MIDTERM. Thursday, October 3, 2013.
 MATH 431: FIRST MIDTERM Thursday, October 3, 213. (1) An inner product on the space of matrices. Let V be the vector space of 2 2 real matrices (that is, the algebra Mat 2 (R), but without the mulitiplicative
MATH 431: FIRST MIDTERM Thursday, October 3, 213. (1) An inner product on the space of matrices. Let V be the vector space of 2 2 real matrices (that is, the algebra Mat 2 (R), but without the mulitiplicative
Announcements Wednesday, November 7
 Announcements Wednesday, November 7 The third midterm is on Friday, November 16 That is one week from this Friday The exam covers 45, 51, 52 53, 61, 62, 64, 65 (through today s material) WeBWorK 61, 62
Announcements Wednesday, November 7 The third midterm is on Friday, November 16 That is one week from this Friday The exam covers 45, 51, 52 53, 61, 62, 64, 65 (through today s material) WeBWorK 61, 62
Math 291-2: Final Exam Solutions Northwestern University, Winter 2016
 Math 29-2: Final Exam Solutions Northwestern University, Winter 206 Determine whether each of the following statements is true or false f it is true, explain why; if it is false, give a counterexample
Math 29-2: Final Exam Solutions Northwestern University, Winter 206 Determine whether each of the following statements is true or false f it is true, explain why; if it is false, give a counterexample
Linear Algebra Primer
 Linear Algebra Primer David Doria daviddoria@gmail.com Wednesday 3 rd December, 2008 Contents Why is it called Linear Algebra? 4 2 What is a Matrix? 4 2. Input and Output.....................................
Linear Algebra Primer David Doria daviddoria@gmail.com Wednesday 3 rd December, 2008 Contents Why is it called Linear Algebra? 4 2 What is a Matrix? 4 2. Input and Output.....................................
HOMEWORK PROBLEMS FROM STRANG S LINEAR ALGEBRA AND ITS APPLICATIONS (4TH EDITION)
 HOMEWORK PROBLEMS FROM STRANG S LINEAR ALGEBRA AND ITS APPLICATIONS (4TH EDITION) PROFESSOR STEVEN MILLER: BROWN UNIVERSITY: SPRING 2007 1. CHAPTER 1: MATRICES AND GAUSSIAN ELIMINATION Page 9, # 3: Describe
HOMEWORK PROBLEMS FROM STRANG S LINEAR ALGEBRA AND ITS APPLICATIONS (4TH EDITION) PROFESSOR STEVEN MILLER: BROWN UNIVERSITY: SPRING 2007 1. CHAPTER 1: MATRICES AND GAUSSIAN ELIMINATION Page 9, # 3: Describe
18.06 Professor Strang Quiz 3 May 2, 2008
 18.06 Professor Strang Quiz 3 May 2, 2008 Your PRINTED name is: Grading 1 2 3 Please circle your recitation: 1) M 2 2-131 A. Ritter 2-085 2-1192 afr 2) M 2 4-149 A. Tievsky 2-492 3-4093 tievsky 3) M 3
18.06 Professor Strang Quiz 3 May 2, 2008 Your PRINTED name is: Grading 1 2 3 Please circle your recitation: 1) M 2 2-131 A. Ritter 2-085 2-1192 afr 2) M 2 4-149 A. Tievsky 2-492 3-4093 tievsky 3) M 3
Conceptual Questions for Review
 Conceptual Questions for Review Chapter 1 1.1 Which vectors are linear combinations of v = (3, 1) and w = (4, 3)? 1.2 Compare the dot product of v = (3, 1) and w = (4, 3) to the product of their lengths.
Conceptual Questions for Review Chapter 1 1.1 Which vectors are linear combinations of v = (3, 1) and w = (4, 3)? 1.2 Compare the dot product of v = (3, 1) and w = (4, 3) to the product of their lengths.
Math Homework 8 (selected problems)
 Math 102 - Homework 8 (selected problems) David Lipshutz Problem 1. (Strang, 5.5: #14) In the list below, which classes of matrices contain A and which contain B? 1 1 1 1 A 0 0 1 0 0 0 0 1 and B 1 1 1
Math 102 - Homework 8 (selected problems) David Lipshutz Problem 1. (Strang, 5.5: #14) In the list below, which classes of matrices contain A and which contain B? 1 1 1 1 A 0 0 1 0 0 0 0 1 and B 1 1 1
Examples and MatLab. Vector and Matrix Material. Matrix Addition R = A + B. Matrix Equality A = B. Matrix Multiplication R = A * B.
 Vector and Matrix Material Examples and MatLab Matrix = Rectangular array of numbers, complex numbers or functions If r rows & c columns, r*c elements, r*c is order of matrix. A is n * m matrix Square
Vector and Matrix Material Examples and MatLab Matrix = Rectangular array of numbers, complex numbers or functions If r rows & c columns, r*c elements, r*c is order of matrix. A is n * m matrix Square
LINEAR ALGEBRA BOOT CAMP WEEK 4: THE SPECTRAL THEOREM
 LINEAR ALGEBRA BOOT CAMP WEEK 4: THE SPECTRAL THEOREM Unless otherwise stated, all vector spaces in this worksheet are finite dimensional and the scalar field F is R or C. Definition 1. A linear operator
LINEAR ALGEBRA BOOT CAMP WEEK 4: THE SPECTRAL THEOREM Unless otherwise stated, all vector spaces in this worksheet are finite dimensional and the scalar field F is R or C. Definition 1. A linear operator
Linear Algebra (MATH ) Spring 2011 Final Exam Practice Problem Solutions
 Linear Algebra (MATH 4) Spring 2 Final Exam Practice Problem Solutions Instructions: Try the following on your own, then use the book and notes where you need help. Afterwards, check your solutions with
Linear Algebra (MATH 4) Spring 2 Final Exam Practice Problem Solutions Instructions: Try the following on your own, then use the book and notes where you need help. Afterwards, check your solutions with
DIAGONALIZATION. In order to see the implications of this definition, let us consider the following example Example 1. Consider the matrix
 DIAGONALIZATION Definition We say that a matrix A of size n n is diagonalizable if there is a basis of R n consisting of eigenvectors of A ie if there are n linearly independent vectors v v n such that
DIAGONALIZATION Definition We say that a matrix A of size n n is diagonalizable if there is a basis of R n consisting of eigenvectors of A ie if there are n linearly independent vectors v v n such that
MIT Final Exam Solutions, Spring 2017
 MIT 8.6 Final Exam Solutions, Spring 7 Problem : For some real matrix A, the following vectors form a basis for its column space and null space: C(A) = span,, N(A) = span,,. (a) What is the size m n of
MIT 8.6 Final Exam Solutions, Spring 7 Problem : For some real matrix A, the following vectors form a basis for its column space and null space: C(A) = span,, N(A) = span,,. (a) What is the size m n of
Lecture 10 - Eigenvalues problem
 Lecture 10 - Eigenvalues problem Department of Computer Science University of Houston February 28, 2008 1 Lecture 10 - Eigenvalues problem Introduction Eigenvalue problems form an important class of problems
Lecture 10 - Eigenvalues problem Department of Computer Science University of Houston February 28, 2008 1 Lecture 10 - Eigenvalues problem Introduction Eigenvalue problems form an important class of problems
Solutions to Second In-Class Exam: Math 401 Section 0201, Professor Levermore Friday, 16 April 2010
 Solutions to Second In-Class Exam: Math 4 Section, Professor Levermore Friday, 6 April No notes, books, or electrontics You must show your reasoning for full credit Good luck! [] Consider the polynomials
Solutions to Second In-Class Exam: Math 4 Section, Professor Levermore Friday, 6 April No notes, books, or electrontics You must show your reasoning for full credit Good luck! [] Consider the polynomials
HW #3 Solutions: M552 Spring (c)
 HW #3 Solutions: M55 Spring 6. (4.-Trefethen & Bau: parts (a), (c) and (e)) Determine the SVDs of the following matrices (by hand calculation): (a) [ 3 (c) (e) [ ANS: In each case we seek A UΣV. The general
HW #3 Solutions: M55 Spring 6. (4.-Trefethen & Bau: parts (a), (c) and (e)) Determine the SVDs of the following matrices (by hand calculation): (a) [ 3 (c) (e) [ ANS: In each case we seek A UΣV. The general
Symmetric matrices and dot products
 Symmetric matrices and dot products Proposition An n n matrix A is symmetric iff, for all x, y in R n, (Ax) y = x (Ay). Proof. If A is symmetric, then (Ax) y = x T A T y = x T Ay = x (Ay). If equality
Symmetric matrices and dot products Proposition An n n matrix A is symmetric iff, for all x, y in R n, (Ax) y = x (Ay). Proof. If A is symmetric, then (Ax) y = x T A T y = x T Ay = x (Ay). If equality
APPENDIX A. Background Mathematics. A.1 Linear Algebra. Vector algebra. Let x denote the n-dimensional column vector with components x 1 x 2.
 APPENDIX A Background Mathematics A. Linear Algebra A.. Vector algebra Let x denote the n-dimensional column vector with components 0 x x 2 B C @. A x n Definition 6 (scalar product). The scalar product
APPENDIX A Background Mathematics A. Linear Algebra A.. Vector algebra Let x denote the n-dimensional column vector with components 0 x x 2 B C @. A x n Definition 6 (scalar product). The scalar product
EXERCISES ON DETERMINANTS, EIGENVALUES AND EIGENVECTORS. 1. Determinants
 EXERCISES ON DETERMINANTS, EIGENVALUES AND EIGENVECTORS. Determinants Ex... Let A = 0 4 4 2 0 and B = 0 3 0. (a) Compute 0 0 0 0 A. (b) Compute det(2a 2 B), det(4a + B), det(2(a 3 B 2 )). 0 t Ex..2. For
EXERCISES ON DETERMINANTS, EIGENVALUES AND EIGENVECTORS. Determinants Ex... Let A = 0 4 4 2 0 and B = 0 3 0. (a) Compute 0 0 0 0 A. (b) Compute det(2a 2 B), det(4a + B), det(2(a 3 B 2 )). 0 t Ex..2. For
NOTES ON LINEAR ALGEBRA CLASS HANDOUT
 NOTES ON LINEAR ALGEBRA CLASS HANDOUT ANTHONY S. MAIDA CONTENTS 1. Introduction 2 2. Basis Vectors 2 3. Linear Transformations 2 3.1. Example: Rotation Transformation 3 4. Matrix Multiplication and Function
NOTES ON LINEAR ALGEBRA CLASS HANDOUT ANTHONY S. MAIDA CONTENTS 1. Introduction 2 2. Basis Vectors 2 3. Linear Transformations 2 3.1. Example: Rotation Transformation 3 4. Matrix Multiplication and Function
Math 205 A B Final Exam page 1 12/12/2012 Name
 Math 205 A B Final Exam page 1 12/12/2012 Name 1. Let F be the vector space of continuous functions f : R R that we have been using in class. Let H = {f F f has the same y-coordinate at x = 1 as it does
Math 205 A B Final Exam page 1 12/12/2012 Name 1. Let F be the vector space of continuous functions f : R R that we have been using in class. Let H = {f F f has the same y-coordinate at x = 1 as it does
MATRICES ARE SIMILAR TO TRIANGULAR MATRICES
 MATRICES ARE SIMILAR TO TRIANGULAR MATRICES 1 Complex matrices Recall that the complex numbers are given by a + ib where a and b are real and i is the imaginary unity, ie, i 2 = 1 In what we describe below,
MATRICES ARE SIMILAR TO TRIANGULAR MATRICES 1 Complex matrices Recall that the complex numbers are given by a + ib where a and b are real and i is the imaginary unity, ie, i 2 = 1 In what we describe below,
Linear algebra II Homework #1 due Thursday, Feb. 2 A =. 2 5 A = When writing up solutions, write legibly and coherently.
 Homework #1 due Thursday, Feb. 2 1. Find the eigenvalues and the eigenvectors of the matrix [ ] 4 6 A =. 2 5 2. Find the eigenvalues and the eigenvectors of the matrix 3 3 1 A = 1 1 1. 3 9 5 3. The following
Homework #1 due Thursday, Feb. 2 1. Find the eigenvalues and the eigenvectors of the matrix [ ] 4 6 A =. 2 5 2. Find the eigenvalues and the eigenvectors of the matrix 3 3 1 A = 1 1 1. 3 9 5 3. The following
University of British Columbia Math 307, Final
 1 University of British Columbia Math 37, Final April 29, 214 12.-2.3pm Name: Student Number: Signature: Instructor: Instructions: 1. No notes, books or calculators are allowed. A MATLAB/Octave formula
1 University of British Columbia Math 37, Final April 29, 214 12.-2.3pm Name: Student Number: Signature: Instructor: Instructions: 1. No notes, books or calculators are allowed. A MATLAB/Octave formula
Cheat Sheet for MATH461
 Cheat Sheet for MATH46 Here is the stuff you really need to remember for the exams Linear systems Ax = b Problem: We consider a linear system of m equations for n unknowns x,,x n : For a given matrix A
Cheat Sheet for MATH46 Here is the stuff you really need to remember for the exams Linear systems Ax = b Problem: We consider a linear system of m equations for n unknowns x,,x n : For a given matrix A
21 Symmetric and skew-symmetric matrices
 21 Symmetric and skew-symmetric matrices 21.1 Decomposition of a square matrix into symmetric and skewsymmetric matrices Let C n n be a square matrix. We can write C = (1/2)(C + C t ) + (1/2)(C C t ) =
21 Symmetric and skew-symmetric matrices 21.1 Decomposition of a square matrix into symmetric and skewsymmetric matrices Let C n n be a square matrix. We can write C = (1/2)(C + C t ) + (1/2)(C C t ) =
Maths for Signals and Systems Linear Algebra in Engineering
 Maths for Signals and Systems Linear Algebra in Engineering Lectures 13-14, Tuesday 11 th November 2014 DR TANIA STATHAKI READER (ASSOCIATE PROFFESOR) IN SIGNAL PROCESSING IMPERIAL COLLEGE LONDON Eigenvectors
Maths for Signals and Systems Linear Algebra in Engineering Lectures 13-14, Tuesday 11 th November 2014 DR TANIA STATHAKI READER (ASSOCIATE PROFFESOR) IN SIGNAL PROCESSING IMPERIAL COLLEGE LONDON Eigenvectors
Math 462: Homework 2 Solutions
 Math 46: Homework Solutions Paul Hacking /6/. Consider the matrix A = (a) Check that A is orthogonal. (b) Determine whether A is a rotation or a reflection / rotary reflection. [Hint: What is the determinant
Math 46: Homework Solutions Paul Hacking /6/. Consider the matrix A = (a) Check that A is orthogonal. (b) Determine whether A is a rotation or a reflection / rotary reflection. [Hint: What is the determinant
Final Review Written by Victoria Kala SH 6432u Office Hours R 12:30 1:30pm Last Updated 11/30/2015
 Final Review Written by Victoria Kala vtkala@mathucsbedu SH 6432u Office Hours R 12:30 1:30pm Last Updated 11/30/2015 Summary This review contains notes on sections 44 47, 51 53, 61, 62, 65 For your final,
Final Review Written by Victoria Kala vtkala@mathucsbedu SH 6432u Office Hours R 12:30 1:30pm Last Updated 11/30/2015 Summary This review contains notes on sections 44 47, 51 53, 61, 62, 65 For your final,
Linear algebra I Homework #1 due Thursday, Oct Show that the diagonals of a square are orthogonal to one another.
 Homework # due Thursday, Oct. 0. Show that the diagonals of a square are orthogonal to one another. Hint: Place the vertices of the square along the axes and then introduce coordinates. 2. Find the equation
Homework # due Thursday, Oct. 0. Show that the diagonals of a square are orthogonal to one another. Hint: Place the vertices of the square along the axes and then introduce coordinates. 2. Find the equation
I. Multiple Choice Questions (Answer any eight)
 Name of the student : Roll No : CS65: Linear Algebra and Random Processes Exam - Course Instructor : Prashanth L.A. Date : Sep-24, 27 Duration : 5 minutes INSTRUCTIONS: The test will be evaluated ONLY
Name of the student : Roll No : CS65: Linear Algebra and Random Processes Exam - Course Instructor : Prashanth L.A. Date : Sep-24, 27 Duration : 5 minutes INSTRUCTIONS: The test will be evaluated ONLY
Eigenvalues and Eigenvectors
 LECTURE 3 Eigenvalues and Eigenvectors Definition 3.. Let A be an n n matrix. The eigenvalue-eigenvector problem for A is the problem of finding numbers λ and vectors v R 3 such that Av = λv. If λ, v are
LECTURE 3 Eigenvalues and Eigenvectors Definition 3.. Let A be an n n matrix. The eigenvalue-eigenvector problem for A is the problem of finding numbers λ and vectors v R 3 such that Av = λv. If λ, v are
ft-uiowa-math2550 Assignment NOTRequiredJustHWformatOfQuizReviewForExam3part2 due 12/31/2014 at 07:10pm CST
 me me ft-uiowa-math2550 Assignment NOTRequiredJustHWformatOfQuizReviewForExam3part2 due 12/31/2014 at 07:10pm CST 1. (1 pt) local/library/ui/eigentf.pg A is n n an matrices.. There are an infinite number
me me ft-uiowa-math2550 Assignment NOTRequiredJustHWformatOfQuizReviewForExam3part2 due 12/31/2014 at 07:10pm CST 1. (1 pt) local/library/ui/eigentf.pg A is n n an matrices.. There are an infinite number
Linear algebra and applications to graphs Part 1
 Linear algebra and applications to graphs Part 1 Written up by Mikhail Belkin and Moon Duchin Instructor: Laszlo Babai June 17, 2001 1 Basic Linear Algebra Exercise 1.1 Let V and W be linear subspaces
Linear algebra and applications to graphs Part 1 Written up by Mikhail Belkin and Moon Duchin Instructor: Laszlo Babai June 17, 2001 1 Basic Linear Algebra Exercise 1.1 Let V and W be linear subspaces
This is a closed book exam. No notes or calculators are permitted. We will drop your lowest scoring question for you.
 Math 54 Fall 2017 Practice Final Exam Exam date: 12/14/17 Time Limit: 170 Minutes Name: Student ID: GSI or Section: This exam contains 9 pages (including this cover page) and 10 problems. Problems are
Math 54 Fall 2017 Practice Final Exam Exam date: 12/14/17 Time Limit: 170 Minutes Name: Student ID: GSI or Section: This exam contains 9 pages (including this cover page) and 10 problems. Problems are
MATH 31 - ADDITIONAL PRACTICE PROBLEMS FOR FINAL
 MATH 3 - ADDITIONAL PRACTICE PROBLEMS FOR FINAL MAIN TOPICS FOR THE FINAL EXAM:. Vectors. Dot product. Cross product. Geometric applications. 2. Row reduction. Null space, column space, row space, left
MATH 3 - ADDITIONAL PRACTICE PROBLEMS FOR FINAL MAIN TOPICS FOR THE FINAL EXAM:. Vectors. Dot product. Cross product. Geometric applications. 2. Row reduction. Null space, column space, row space, left
1. What is the determinant of the following matrix? a 1 a 2 4a 3 2a 2 b 1 b 2 4b 3 2b c 1. = 4, then det
 What is the determinant of the following matrix? 3 4 3 4 3 4 4 3 A 0 B 8 C 55 D 0 E 60 If det a a a 3 b b b 3 c c c 3 = 4, then det a a 4a 3 a b b 4b 3 b c c c 3 c = A 8 B 6 C 4 D E 3 Let A be an n n matrix
What is the determinant of the following matrix? 3 4 3 4 3 4 4 3 A 0 B 8 C 55 D 0 E 60 If det a a a 3 b b b 3 c c c 3 = 4, then det a a 4a 3 a b b 4b 3 b c c c 3 c = A 8 B 6 C 4 D E 3 Let A be an n n matrix
Linear Algebra Review. Fei-Fei Li
 Linear Algebra Review Fei-Fei Li 1 / 51 Vectors Vectors and matrices are just collections of ordered numbers that represent something: movements in space, scaling factors, pixel brightnesses, etc. A vector
Linear Algebra Review Fei-Fei Li 1 / 51 Vectors Vectors and matrices are just collections of ordered numbers that represent something: movements in space, scaling factors, pixel brightnesses, etc. A vector
18.06 Problem Set 1 - Solutions Due Wednesday, 12 September 2007 at 4 pm in
 18.6 Problem Set 1 - Solutions Due Wednesday, 12 September 27 at 4 pm in 2-16. Problem : from the book.(5=1+1+1+1+1) (a) problem set 1.2, problem 8. (a) F. A Counterexample: u = (1,, ), v = (, 1, ) and
18.6 Problem Set 1 - Solutions Due Wednesday, 12 September 27 at 4 pm in 2-16. Problem : from the book.(5=1+1+1+1+1) (a) problem set 1.2, problem 8. (a) F. A Counterexample: u = (1,, ), v = (, 1, ) and
University of Colorado Denver Department of Mathematical and Statistical Sciences Applied Linear Algebra Ph.D. Preliminary Exam January 22, 2016
 University of Colorado Denver Department of Mathematical and Statistical Sciences Applied Linear Algebra PhD Preliminary Exam January 22, 216 Name: Exam Rules: This exam lasts 4 hours There are 8 problems
University of Colorado Denver Department of Mathematical and Statistical Sciences Applied Linear Algebra PhD Preliminary Exam January 22, 216 Name: Exam Rules: This exam lasts 4 hours There are 8 problems
Linear Algebra Review
 Chapter 1 Linear Algebra Review It is assumed that you have had a course in linear algebra, and are familiar with matrix multiplication, eigenvectors, etc. I will review some of these terms here, but quite
Chapter 1 Linear Algebra Review It is assumed that you have had a course in linear algebra, and are familiar with matrix multiplication, eigenvectors, etc. I will review some of these terms here, but quite
Math 350 Fall 2011 Notes about inner product spaces. In this notes we state and prove some important properties of inner product spaces.
 Math 350 Fall 2011 Notes about inner product spaces In this notes we state and prove some important properties of inner product spaces. First, recall the dot product on R n : if x, y R n, say x = (x 1,...,
Math 350 Fall 2011 Notes about inner product spaces In this notes we state and prove some important properties of inner product spaces. First, recall the dot product on R n : if x, y R n, say x = (x 1,...,
Numerical Linear Algebra Homework Assignment - Week 2
 Numerical Linear Algebra Homework Assignment - Week 2 Đoàn Trần Nguyên Tùng Student ID: 1411352 8th October 2016 Exercise 2.1: Show that if a matrix A is both triangular and unitary, then it is diagonal.
Numerical Linear Algebra Homework Assignment - Week 2 Đoàn Trần Nguyên Tùng Student ID: 1411352 8th October 2016 Exercise 2.1: Show that if a matrix A is both triangular and unitary, then it is diagonal.
Mathematical foundations - linear algebra
 Mathematical foundations - linear algebra Andrea Passerini passerini@disi.unitn.it Machine Learning Vector space Definition (over reals) A set X is called a vector space over IR if addition and scalar
Mathematical foundations - linear algebra Andrea Passerini passerini@disi.unitn.it Machine Learning Vector space Definition (over reals) A set X is called a vector space over IR if addition and scalar
Math Linear Algebra II. 1. Inner Products and Norms
 Math 342 - Linear Algebra II Notes 1. Inner Products and Norms One knows from a basic introduction to vectors in R n Math 254 at OSU) that the length of a vector x = x 1 x 2... x n ) T R n, denoted x,
Math 342 - Linear Algebra II Notes 1. Inner Products and Norms One knows from a basic introduction to vectors in R n Math 254 at OSU) that the length of a vector x = x 1 x 2... x n ) T R n, denoted x,
MAT Linear Algebra Collection of sample exams
 MAT 342 - Linear Algebra Collection of sample exams A-x. (0 pts Give the precise definition of the row echelon form. 2. ( 0 pts After performing row reductions on the augmented matrix for a certain system
MAT 342 - Linear Algebra Collection of sample exams A-x. (0 pts Give the precise definition of the row echelon form. 2. ( 0 pts After performing row reductions on the augmented matrix for a certain system
Numerical Methods - Numerical Linear Algebra
 Numerical Methods - Numerical Linear Algebra Y. K. Goh Universiti Tunku Abdul Rahman 2013 Y. K. Goh (UTAR) Numerical Methods - Numerical Linear Algebra I 2013 1 / 62 Outline 1 Motivation 2 Solving Linear
Numerical Methods - Numerical Linear Algebra Y. K. Goh Universiti Tunku Abdul Rahman 2013 Y. K. Goh (UTAR) Numerical Methods - Numerical Linear Algebra I 2013 1 / 62 Outline 1 Motivation 2 Solving Linear
Announcements Wednesday, November 7
 Announcements Wednesday, November 7 The third midterm is on Friday, November 6 That is one week from this Friday The exam covers 45, 5, 52 53, 6, 62, 64, 65 (through today s material) WeBWorK 6, 62 are
Announcements Wednesday, November 7 The third midterm is on Friday, November 6 That is one week from this Friday The exam covers 45, 5, 52 53, 6, 62, 64, 65 (through today s material) WeBWorK 6, 62 are
Econ Slides from Lecture 8
 Econ 205 Sobel Econ 205 - Slides from Lecture 8 Joel Sobel September 1, 2010 Computational Facts 1. det AB = det BA = det A det B 2. If D is a diagonal matrix, then det D is equal to the product of its
Econ 205 Sobel Econ 205 - Slides from Lecture 8 Joel Sobel September 1, 2010 Computational Facts 1. det AB = det BA = det A det B 2. If D is a diagonal matrix, then det D is equal to the product of its
Linear Algebra: Matrix Eigenvalue Problems
 CHAPTER8 Linear Algebra: Matrix Eigenvalue Problems Chapter 8 p1 A matrix eigenvalue problem considers the vector equation (1) Ax = λx. 8.0 Linear Algebra: Matrix Eigenvalue Problems Here A is a given
CHAPTER8 Linear Algebra: Matrix Eigenvalue Problems Chapter 8 p1 A matrix eigenvalue problem considers the vector equation (1) Ax = λx. 8.0 Linear Algebra: Matrix Eigenvalue Problems Here A is a given
