SPHERICAL TRIGONOMETRY
|
|
|
- Stewart Mitchell
- 6 years ago
- Views:
Transcription
1 SPHERICAL TRIGONOMETRY THERE IS NO ROYAL ROAD TO GEOMETRY EUCLID BY KELLY LYNCH Saint May s College of Califonia Moaga 2016
2 Abstact The pupose of this pape is to deive vaious tigonometic fomulas fo spheical tiangles. The subject of spheical tigonomety has many navigational and astonomical applications. Histoy Geomety has been developing and evolving fo many centuies. Its uses ae vast and continue to affect ou evey day lives. The study of the sphee in paticula has its own unique stoy, and has two majo tuning points. This study fist began with the push of astonomy and was developed in depth by the Geeks. Thee is speculation that mathematical discoveies about the sphee wee made as ealy as the second centuy, but thee is no poof fo this.[1] The majo tansition fo the undestanding of spheical geomety was the wok of Menelaus of Alexanda. In his wok Spheica the autho delves deeply into the popeties of the sphee and the calculations elated to lengths and measues of a sphee s acs. Fo a long time the equations he discoveed, such as the measue of cicumfeence of a sphee and the measue of ac lengths, wee accepted and no futhe study was needed. The next majo motivation fo leaning spheical tigonomety was eligious mattes; the eligion of Islam equies that the diection of Mecca is always known fo daily paye. Menelaus findings wee futhe developed duing the Islamic Enlightenment peiod. Thee is some debate as to the discovey of the Law of Sines fo spheical tiangles. Possible souces of this discovey stem fom the debate ove the two Muslim scientists, Abū Nas o Abū ĺ-wafā. Who eve was esponsible fo the pogess in the Law of Sines allowed fo a moe concise poof to be developed late; as well as leading to othe theoems and identities on spheical tigonomety. Anothe majo name in geomety is Euclid. He made a big impact late in the thid centuy;
3 though the system of spheical tigonomety does not incopoate paallel lines, Euclidean geomety gave some insight to spheical behavio. In his wok Elements Euclid published equations which help lead us to the Pythagoean Theoem and the Law of Cosines. Though mathematicians bought insight to this aea of study, many influences on spheical tigonomety also came fom the field of science. Futhe discovey about the behavio of acs and angles became pominent in the late Renaissance peiod. John Napie, a Scottish scientist who lived aound the 17th centuy, was the fist to wok with ight spheical tiangles and the basic identities of these shapes. Using Napie s Rules, the law of cosines fo sphees was discoveed.[1] Definition On a sphee, a geat cicle is the intesection of the sphee with a plane passing though the cente, o oigin, of the sphee.[1] Example Geat Cicle
4 The solid line illustates a geat cicle which is the intesection of the plane X and the sphee A. The plane in the is the hoizontal plane; howeve, the plane can have any oientation that bisects the sphee. The cicle ceated by this intesection will have adius equal to the length of the adius of the sphee. It also follows that the length of the cicumfeence of the geat cicle will equal 2π whee is the length of the adius of the sphee. This is elevant because it enables us to calculate the length of a cicula segment by consideing the elation between the inne angle and the adius of the sphee. Theefoe, fo any sphee and any angle, the length of one ac segment will just equal θ whee θ is the measue of the angle in adians. This is tue because each cicula segment is just faction of the entie cicumfeence. We can show this elation of the angle and ac length in the example below. Example Geneal ac measue (whee a is the length of the ac This is a geneal example, but we can apply specific values as in the example on the following page.
5 Example Measue of Ac In this example we cut ou a segment of geat cicle by elating an inne angle. Fo this example let R = 4.69 and θ = adians, thus (4.69( = 4.39, which is the measue of the length of the ac. This example was ceated in a dynamic mathematics softwae pogam which gave these elated measuements. lune. The next definition equied in undestanding a spheical tiangle is that of a Definition Lune A lune is a pat of the sphee which is captued between two geat cicles.[1] This definition is elevant because it stated the ability to captue shapes on a sphee. This definition itself is not extemely significant, but it is though this shape which we can fom othe shapes on the sphee. The shape of a lune can also be seen in
6 the next figue. Example Lune Spheical tiangles can be defined in tems of lunes. Definition Spheical Tiangle A spheical tiangle is the intesection of thee distinct lunes.[1] In the figue above we can conside that thee ae two lunes which ae the on opposite sides of the sphee, it is natual that anothe lune bisecting these two will be needed. A simple way to think about a spheical tiangle is the shape captued though the intesection of thee geat cicles. It is also inteesting to conside that any two
7 unique points, which ae not diametic on the sphees suface, lie on a geat cicle. This makes sense because a tiangle would have thee vetices and theefoe thee diffeent geat cicles which go though two diffeent points. Since the spheical tiangle s edges ae cuved, it is clea that the equations, sides, aea, and geneal popeties will be diffeent fom that of a plana tiangle. We also know that in some way we should be able to elate the functions that we do discove to the adius of the sphee, because it seems natual that the fomulas would change in elation to the sphee s adius.we know that the behavio of a spheical tiangle will be vey diffeent fom the plana tiangles, thee ae even some definitions which can illustate this fo us. Example Spheical Tiangle Definition Spheical Excess is the amount by which the sum of the angles (in the spheical plane only exceed 180. This definition tells us about the behavio of the sphee and its edges. We know that the length of the edges on a spheical tiangle will be geate the edges on a coesponding plana tiangle, since they ae cuved. This definition allows fo a spheical tiangle to have multiple ight angles.
8 Example Spheical tiangle with thee ight angles Definition [3] Spheical Coodinates is a coodinate system in thee dimentions. The coodinate values stated below equie to be the length of the adius to the point P on the sphee. The value ϕ the angle between the z-axis, and the vecto fom the oigin to point P, and θ the angle between the x-axis, and the same vecto as in the figue Then we can say the x, y, z coodinates ae defined: os(θsin(ϕ, sin(θsin(ϕ, cos(ϕ Example Spheical Coodinates in the xyz plane
9 Theoem The Spheical Pythagoean Theoem[3] Fo a ight tiangle, ABC on a sphee of adius, with ight angle at vetex C and sides length a, b, c is defined: adius is 1. ( a ( b cos = cos cos This equation can equivalently be witten as cos(c = cos(acos(b when the Poof. Conside a spheical tiangle on the suface of a sphee with adius, and sides a, b, c. Let vetex C in the spheical tiangle be a ight angle, as in the diagam below.[3] Without loss of geneality, suppose C is defined by spheical coodinates C = (0, 0,. Now conside the othe vetices on the spheical tiangle. Call one of these A and let it be defined using spheical coodinates defined above A = ( sin ( b, 0, cos ( b whee b is equal to the measue of the ac length along the geat cicle between A and C. Note b is necessaily also equal the inteio angle between the vecto which goes fom the O to C and the vecto fom O to A, since the adius is equal to. Let the othe vetex called B be defined B = (0, sin ( a, cos ( a whee a is the ac length
10 between B to C, by the same easoning. Thus A = sin ( b ˆx + cos ( b ẑ and B = sin ( a ŷ + cos ( a ẑ. Now conside A B ( A B b = ( sin ˆx + cos ( b ( a = 2 cos cos ( b ( a ( a ẑ sin ŷ + cos ẑ Theefoesince the dot poduct of two vectos esults in a scala then A B = 2 cos ( b cos ( a. Now conside the magnitude of A B. Conside A B = A B cos A = since the adius is B = since the adius is A B = 2 cos Recall that the cosine of the angle between two vectos is just equal to the dot poduct of each vecto, ove the magnitude of each vecto. We know that the sign will not matte since the magnitude takes the absolute value so the signs will be equal, now using this infomation in elation to the equations above we can conclude that ( a ( b cos = cos cos
11 Theoem Law of Cosines The Law of Cosines states that if a,b,c ae the sides and A,B,C ae the angles of a spheical tiangle, then[1] ( a cos = cos cos ( b ( a + sin sin ( b cos(c Poof. Let thee be a spheical tiangle with sides denoted a, b, c. Let thei opposing angles be labeled A, B, C, whee A 90, B 90, and C 90. Let us call the cente of the sphee to be S. Theefoe we know fom any single vetex, A, B, C, to the point S is exactly equal to the adius,. If we abitay let A be the lagest angle(since we can abitaily name any angle then we can that thee is a point somewhee between the vetices B and C which ceates a ight angle, since A is the lagest angle and we must have spheical excess, it follows that ceating a ight angle is possible. Call this vetex N. This patition will ceate two ight spheical tiangles. Now we know that N some distance n fom B and is the distance (a n fom vetex C to N. Thee will also be some distance we shall call y fom the vetex N to point A. With this infomation we can use the spheical Pythagoean equation. So now applying the equation we ae left with two equations cos(b = cos(ncos(y cos(c = cos(a ncos(y Equation I Equation II
12 Now we can solve fo cos(y in equation I so theefoe we have: cos(y = cos(c cos(a n Now we need to solve using the same pocess fo equation II so we have: cos(y = cos(b cos(n cos(c cos(a n = cos(b cos(n cos(ccos(n = cos(bcos(a n combining equations coss multiply cos(ccos(n = cos(b(cos(acos(n + sin(asin(n cos(ccos(n = cos(bcos(acos(n + cos(bsin(asin(n cos(c = cos(bcos(a + sin(asin(b sin(n cos(n divide by cos(n cos(c = cos(acos(b + sin(acos(btan(n Napie 1 [1] cos(c = cos(acos(b + sin(asin(bcos(c which gives the law of cosines as desied. Also we can put this in tems of the adius of the sphee since we know that θ = x R whee x is the ac length and R is the adius of the sphee so if we substitute fo the sides and angles with espect to the adius we have 1 Napie discoveed the substitution fo this poof that cos(btan(n = sin(bcos(c
13 ( a cos = cos cos ( b ( a + sin sin ( b cos(c By equivalence we know that ( a cos = cos cos cos ( b + sin sin ( b cos(a ( b ( a ( a ( b = cos cos + sin sin cos(b This substitution can be made in any equation since the elation of inne angles to the ac length and will always be consistent fo that paticula sphee. Example Flight Routes Spheical tigonomety is vey applicable to ou evey day life. One of these applications is discoveing the length and diections needed fo navigation. The fomulas easily apply to the eath because the latitude and longitude lines ae actually examples of geat cicles. The law of cosines can be used on the example below, in which we want to find the distance between two cities. Given: Eath s adius: 6,371 km Distance fom San Fancisco, Califonia to Dublin, Ieland: 8198 km Distance fom San Fancisco, Califonia to Seattle, Washington: 1094 km
14 Angle between these two acs: (adians Now let us say we wish to find the distance fom Dublin to Seattle. To find this we use the equation below and then substitute the numeical values. ( ( a c = accos cos cos ( b ( a + sin sin ( b cos(c ( c = 6371 accos cos ( 1094 cos 6371 ( sin 6371 ( 1094 sin 6371 ( 8850 cos( c = 7232 km This value is an estimation because it assumes the eath is a pefect sphee with no dips o iegulaities which is not tue. This estimation is useful, howeve; since it was so quick and easy to find. Now we at least have some idea of the distance between two places that would othewise be impossible to diectly measue. Theoem Law of Sines[4] Whee a,b,c ae the sides of a spheical tiangle and A,B,C ae the angles opposing these sides, the Law of Sines states the following sin ( a sin(a = sin ( b sin(b = sin sin(c
15 Poof. Let thee be a spheical tiangle ABC, with adius. Let A be the vecto which goes fom the oigin of the sphee to the vetex A, B be the vecto which goes fom the oigin of the sphee to the vetex B, and C be the vecto which goes fom the oigin of the sphee to the vetex C Now conside x 1 = x 2 = C B 2 sin ( a A C 2 sin ( b x 3 = B A 2 sin ( c Each of these ae unit vectos and they also must be pependicula to the especting geat cicles, because of the ight hand ule. So x 1 is othogonal to the entie plane of secto COB. Then x 2 is othogonal to the entie plane coesponding to secto COA. Also x 3 is othogonal to the plane lying on secto BOA.
16 Conside the vecto identity below. ( A C ( C B = ( C ( B A C Fist note that, ( A C ( C B = ( ( b ( ( a 2 sin x 2 2 sin x 1 Thus, by we ae left with ( A C ( C B ( a ( b = 4 sin sin ( x 1 x 2 To detemine the value of ( x 1 x 2, fist conside that x 1 = x 2 = 1, since x 1 and x 2 ae unit vectos. Also note that C =. Next we need to conside the angle between x 1 and x 2, ecall that each of these angles is pependicula to its especting geat cicles.
17 Suppose we conside these unit vectos when they ae each lying exactly at point C. Because these unit vectos ae pependicula to the whole geat cicle we can abitaily place them at a specific point on that geat cicle without loss of geneality.we can abitaily place the unit vectos at a point because they do not depend on location, since they ae pependicula at any place on thei especting planes. Since x 1 is pependicula to the geat cicle coesponding to COB, then we know at vetex C, x 1 will be exactly tangent to the geat cicle ceated by vetices C and A. Note also that x 2 is pependicula to the geat cicle coesponding to AOC. Theefoe by simila logic x 2 will be exactly tangent at vetex C to the geat cicle which goes though vetices B and C. Theefoe these two vectos ceate an angle that must coespond to the angle ceated at vetex C. Thus ( x 1 x 2 = (1(1 sin(c C Substituting this value in ou pevious equation we get, ( A C ( C B ( a ( b = 3 sin sin sin(c C So theefoe by the oiginal vecto identity we have C ( B A ( a ( b = 3 sin sin sin(c Fom this the following is equivalent, A ( C B = 3 sin ( b sin sin(a B ( A C ( a = 3 sin sin sin(b
18 Also note that the tiple poduct of vectos coesponds to the deteminant. Fom popeites in linea algeba we know that deteminants do not change when two pais of ows ae swapped, which means it is invaiant. Theefoe, since we ae only swapping two pais of vectos; we know that the equations above all equivalent. ( a sin sin ( b sin(c = sin ( b ( a sin sin(a = sin sin sin(b Then dividing this whole expession by sin ( a sin ( b sin, we have which equivalently esults in sin(c sin ( = sin(a c sin ( = sin(b a sin ( b sin ( a sin(a = sin ( b sin(b = sin sin(c as desied. Now that we have the Pythagoean Theoem, Law of Cosines, and the Law of Sines fo a sphee, we can compae these to thei plana countepats. We can conside the following compaison. Spheical (Let =1 Pythagoean Theoem: Cosines: cos(c = cos(acos(b+sin(asin(bcos(c cos(c = cos(acos(b
19 Sines: sin(a sin(a = sin(b sin(b = sin(c sin(c Plana Pythagoean Theoem: c 2 = a 2 + b 2 Cosines: c 2 = a 2 + b 2 2abcos(C Sines: a sin(a = b sin(b = c sin(c Now it is inteesting to see that the Law of Sines is quite simila fo both plana and spheical. In contast the Pythagoean Theoem and Law of Cosines ae quite diffeent.it is also inteesting to note that in both plana and spheical the Pythagoean Theoem is a limit of the Law of Cosines. Fo the spheical equations this seems natual since we must use the Pythagoean Theoem in ode to pove the Law of Cosines; as shown in the poof above. It is impotant that we ecognize the fact that spheical tiangles and plana tiangles ae vey diffeent and the compaison of these equations help to show us the diffeences. Example Law of Sines Application Thee ae many examples we can use fo the application fo the Law of Sines. To keep vaiety I will including an example which elates to astonomy. Suppose that we have thee luna oves, call them A,B, and C espectively. Now suppose we wish
20 to find the distance between two of these such oves. We can use the following given infomation and the Law of Sines to discove a paticula length. Radius of moon:1737 km Distance between ove C and B (length a: 10 km Angle ceated at ove B: 3π 4 Angle ceated at ove A: π 6 How fa ae oves A and C (length of b? sin( a sin(a = sin( b sin(b Now we can substitute the numeical values and solve fo b so we have, b = 1737 acsin ( sin( 3π 10 sin( 4 sin( π b = km Thus the distance between ove A and ove C is aound 14 km. This value does not take into account any vaiation, such as dips o holes on the moon s suface so it is best used as a ough estimation. Again it was quite simple to find and gives some idea of how fa these luna oves ae fom eachothe. Theses ae just a few of the many examples spheical tigonomety has in ou wold. It is vey useful in the study of astonomy and in any navigational poblems on ou Eath. Having the ability to elate the spheical Phythagoeam Theoem, Law of Cosines, and Law of Sines to the adius of a sphee allows us use these equations on sphees of diffeent sizes. This also gives us moe feedom in the use of these equations as a whole, ove vaious disciplines such as math, physics, and astomony. Deiving the
21 spheical tigonometic fomulas in tems of the adius, was influential in histoy and its applications and uses continue to the moden day.
22 Bibliogaphy [1] Bummelen, Glen Van. Heavenly Mathematics: The Fogotten At of Spheical Tigonomety. Pinceton: Pinceton UP, Pint. [2] Clak, C. E. Poofs of the Fundamental Theoems of Spheical Tigonomety. Mathematics Magazine 21.3 (1948: 151. Web. [3] McCleay, John. Geomety fom a Diffeentiable Viewpoint. Cambidge: Cambidge UP, Pint. [4] Wilson, P. M. H. Cuved Spaces: Fom Classical Geometies to Elementay Diffeential Geomety. Cambidge: Cambidge UP, Pint. 22
Physics 2B Chapter 22 Notes - Magnetic Field Spring 2018
 Physics B Chapte Notes - Magnetic Field Sping 018 Magnetic Field fom a Long Staight Cuent-Caying Wie In Chapte 11 we looked at Isaac Newton s Law of Gavitation, which established that a gavitational field
Physics B Chapte Notes - Magnetic Field Sping 018 Magnetic Field fom a Long Staight Cuent-Caying Wie In Chapte 11 we looked at Isaac Newton s Law of Gavitation, which established that a gavitational field
Euclidean Figures and Solids without Incircles or Inspheres
 Foum Geometicoum Volume 16 (2016) 291 298. FOUM GEOM ISSN 1534-1178 Euclidean Figues and Solids without Incicles o Insphees Dimitis M. Chistodoulou bstact. ll classical convex plana Euclidean figues that
Foum Geometicoum Volume 16 (2016) 291 298. FOUM GEOM ISSN 1534-1178 Euclidean Figues and Solids without Incicles o Insphees Dimitis M. Chistodoulou bstact. ll classical convex plana Euclidean figues that
B. Spherical Wave Propagation
 11/8/007 Spheical Wave Popagation notes 1/1 B. Spheical Wave Popagation Evey antenna launches a spheical wave, thus its powe density educes as a function of 1, whee is the distance fom the antenna. We
11/8/007 Spheical Wave Popagation notes 1/1 B. Spheical Wave Popagation Evey antenna launches a spheical wave, thus its powe density educes as a function of 1, whee is the distance fom the antenna. We
RECTIFYING THE CIRCUMFERENCE WITH GEOGEBRA
 ECTIFYING THE CICUMFEENCE WITH GEOGEBA A. Matín Dinnbie, G. Matín González and Anthony C.M. O 1 Intoducction The elation between the cicumfeence and the adius of a cicle is one of the most impotant concepts
ECTIFYING THE CICUMFEENCE WITH GEOGEBA A. Matín Dinnbie, G. Matín González and Anthony C.M. O 1 Intoducction The elation between the cicumfeence and the adius of a cicle is one of the most impotant concepts
Graphs of Sine and Cosine Functions
 Gaphs of Sine and Cosine Functions In pevious sections, we defined the tigonometic o cicula functions in tems of the movement of a point aound the cicumfeence of a unit cicle, o the angle fomed by the
Gaphs of Sine and Cosine Functions In pevious sections, we defined the tigonometic o cicula functions in tems of the movement of a point aound the cicumfeence of a unit cicle, o the angle fomed by the
KEPLER S LAWS OF PLANETARY MOTION
 EPER S AWS OF PANETARY MOTION 1. Intoduction We ae now in a position to apply what we have leaned about the coss poduct and vecto valued functions to deive eple s aws of planetay motion. These laws wee
EPER S AWS OF PANETARY MOTION 1. Intoduction We ae now in a position to apply what we have leaned about the coss poduct and vecto valued functions to deive eple s aws of planetay motion. These laws wee
working pages for Paul Richards class notes; do not copy or circulate without permission from PGR 2004/11/3 10:50
 woking pages fo Paul Richads class notes; do not copy o ciculate without pemission fom PGR 2004/11/3 10:50 CHAPTER7 Solid angle, 3D integals, Gauss s Theoem, and a Delta Function We define the solid angle,
woking pages fo Paul Richads class notes; do not copy o ciculate without pemission fom PGR 2004/11/3 10:50 CHAPTER7 Solid angle, 3D integals, Gauss s Theoem, and a Delta Function We define the solid angle,
7.2. Coulomb s Law. The Electric Force
 Coulomb s aw Recall that chaged objects attact some objects and epel othes at a distance, without making any contact with those objects Electic foce,, o the foce acting between two chaged objects, is somewhat
Coulomb s aw Recall that chaged objects attact some objects and epel othes at a distance, without making any contact with those objects Electic foce,, o the foce acting between two chaged objects, is somewhat
Phys 201A. Homework 5 Solutions
 Phys 201A Homewok 5 Solutions 3. In each of the thee cases, you can find the changes in the velocity vectos by adding the second vecto to the additive invese of the fist and dawing the esultant, and by
Phys 201A Homewok 5 Solutions 3. In each of the thee cases, you can find the changes in the velocity vectos by adding the second vecto to the additive invese of the fist and dawing the esultant, and by
Geometry of the homogeneous and isotropic spaces
 Geomety of the homogeneous and isotopic spaces H. Sonoda Septembe 2000; last evised Octobe 2009 Abstact We summaize the aspects of the geomety of the homogeneous and isotopic spaces which ae most elevant
Geomety of the homogeneous and isotopic spaces H. Sonoda Septembe 2000; last evised Octobe 2009 Abstact We summaize the aspects of the geomety of the homogeneous and isotopic spaces which ae most elevant
Section 8.2 Polar Coordinates
 Section 8. Pola Coodinates 467 Section 8. Pola Coodinates The coodinate system we ae most familia with is called the Catesian coodinate system, a ectangula plane divided into fou quadants by the hoizontal
Section 8. Pola Coodinates 467 Section 8. Pola Coodinates The coodinate system we ae most familia with is called the Catesian coodinate system, a ectangula plane divided into fou quadants by the hoizontal
MODULE 5a and 5b (Stewart, Sections 12.2, 12.3) INTRO: In MATH 1114 vectors were written either as rows (a1, a2,..., an) or as columns a 1 a. ...
 MODULE 5a and 5b (Stewat, Sections 2.2, 2.3) INTRO: In MATH 4 vectos wee witten eithe as ows (a, a2,..., an) o as columns a a 2... a n and the set of all such vectos of fixed length n was called the vecto
MODULE 5a and 5b (Stewat, Sections 2.2, 2.3) INTRO: In MATH 4 vectos wee witten eithe as ows (a, a2,..., an) o as columns a a 2... a n and the set of all such vectos of fixed length n was called the vecto
AST 121S: The origin and evolution of the Universe. Introduction to Mathematical Handout 1
 Please ead this fist... AST S: The oigin and evolution of the Univese Intoduction to Mathematical Handout This is an unusually long hand-out and one which uses in places mathematics that you may not be
Please ead this fist... AST S: The oigin and evolution of the Univese Intoduction to Mathematical Handout This is an unusually long hand-out and one which uses in places mathematics that you may not be
Physics 2A Chapter 10 - Moment of Inertia Fall 2018
 Physics Chapte 0 - oment of netia Fall 08 The moment of inetia of a otating object is a measue of its otational inetia in the same way that the mass of an object is a measue of its inetia fo linea motion.
Physics Chapte 0 - oment of netia Fall 08 The moment of inetia of a otating object is a measue of its otational inetia in the same way that the mass of an object is a measue of its inetia fo linea motion.
Math Section 4.2 Radians, Arc Length, and Area of a Sector
 Math 1330 - Section 4. Radians, Ac Length, and Aea of a Secto The wod tigonomety comes fom two Geek oots, tigonon, meaning having thee sides, and mete, meaning measue. We have aleady defined the six basic
Math 1330 - Section 4. Radians, Ac Length, and Aea of a Secto The wod tigonomety comes fom two Geek oots, tigonon, meaning having thee sides, and mete, meaning measue. We have aleady defined the six basic
Electrostatics (Electric Charges and Field) #2 2010
 Electic Field: The concept of electic field explains the action at a distance foce between two chaged paticles. Evey chage poduces a field aound it so that any othe chaged paticle expeiences a foce when
Electic Field: The concept of electic field explains the action at a distance foce between two chaged paticles. Evey chage poduces a field aound it so that any othe chaged paticle expeiences a foce when
Describing Circular motion
 Unifom Cicula Motion Descibing Cicula motion In ode to undestand cicula motion, we fist need to discuss how to subtact vectos. The easiest way to explain subtacting vectos is to descibe it as adding a
Unifom Cicula Motion Descibing Cicula motion In ode to undestand cicula motion, we fist need to discuss how to subtact vectos. The easiest way to explain subtacting vectos is to descibe it as adding a
Math 2263 Solutions for Spring 2003 Final Exam
 Math 6 Solutions fo Sping Final Exam ) A staightfowad appoach to finding the tangent plane to a suface at a point ( x, y, z ) would be to expess the cuve as an explicit function z = f ( x, y ), calculate
Math 6 Solutions fo Sping Final Exam ) A staightfowad appoach to finding the tangent plane to a suface at a point ( x, y, z ) would be to expess the cuve as an explicit function z = f ( x, y ), calculate
Flux. Area Vector. Flux of Electric Field. Gauss s Law
 Gauss s Law Flux Flux in Physics is used to two distinct ways. The fist meaning is the ate of flow, such as the amount of wate flowing in a ive, i.e. volume pe unit aea pe unit time. O, fo light, it is
Gauss s Law Flux Flux in Physics is used to two distinct ways. The fist meaning is the ate of flow, such as the amount of wate flowing in a ive, i.e. volume pe unit aea pe unit time. O, fo light, it is
PDF Created with deskpdf PDF Writer - Trial ::
 A APPENDIX D TRIGONOMETRY Licensed to: jsamuels@bmcc.cun.edu PDF Ceated with deskpdf PDF Wite - Tial :: http://www.docudesk.com D T i g o n o m e t FIGURE a A n g l e s Angles can be measued in degees
A APPENDIX D TRIGONOMETRY Licensed to: jsamuels@bmcc.cun.edu PDF Ceated with deskpdf PDF Wite - Tial :: http://www.docudesk.com D T i g o n o m e t FIGURE a A n g l e s Angles can be measued in degees
ω = θ θ o = θ θ = s r v = rω
 Unifom Cicula Motion Unifom cicula motion is the motion of an object taveling at a constant(unifom) speed in a cicula path. Fist we must define the angula displacement and angula velocity The angula displacement
Unifom Cicula Motion Unifom cicula motion is the motion of an object taveling at a constant(unifom) speed in a cicula path. Fist we must define the angula displacement and angula velocity The angula displacement
Physics 235 Chapter 5. Chapter 5 Gravitation
 Chapte 5 Gavitation In this Chapte we will eview the popeties of the gavitational foce. The gavitational foce has been discussed in geat detail in you intoductoy physics couses, and we will pimaily focus
Chapte 5 Gavitation In this Chapte we will eview the popeties of the gavitational foce. The gavitational foce has been discussed in geat detail in you intoductoy physics couses, and we will pimaily focus
. Using our polar coordinate conversions, we could write a
 504 Chapte 8 Section 8.4.5 Dot Poduct Now that we can add, sutact, and scale vectos, you might e wondeing whethe we can multiply vectos. It tuns out thee ae two diffeent ways to multiply vectos, one which
504 Chapte 8 Section 8.4.5 Dot Poduct Now that we can add, sutact, and scale vectos, you might e wondeing whethe we can multiply vectos. It tuns out thee ae two diffeent ways to multiply vectos, one which
Analysis of simple branching trees with TI-92
 Analysis of simple banching tees with TI-9 Dušan Pagon, Univesity of Maibo, Slovenia Abstact. In the complex plane we stat at the cente of the coodinate system with a vetical segment of the length one
Analysis of simple banching tees with TI-9 Dušan Pagon, Univesity of Maibo, Slovenia Abstact. In the complex plane we stat at the cente of the coodinate system with a vetical segment of the length one
DonnishJournals
 DonnishJounals 041-1189 Donnish Jounal of Educational Reseach and Reviews. Vol 1(1) pp. 01-017 Novembe, 014. http:///dje Copyight 014 Donnish Jounals Oiginal Reseach Pape Vecto Analysis Using MAXIMA Savaş
DonnishJounals 041-1189 Donnish Jounal of Educational Reseach and Reviews. Vol 1(1) pp. 01-017 Novembe, 014. http:///dje Copyight 014 Donnish Jounals Oiginal Reseach Pape Vecto Analysis Using MAXIMA Savaş
CALCULUS II Vectors. Paul Dawkins
 CALCULUS II Vectos Paul Dawkins Table of Contents Peface... ii Vectos... 3 Intoduction... 3 Vectos The Basics... 4 Vecto Aithmetic... 8 Dot Poduct... 13 Coss Poduct... 21 2007 Paul Dawkins i http://tutoial.math.lama.edu/tems.aspx
CALCULUS II Vectos Paul Dawkins Table of Contents Peface... ii Vectos... 3 Intoduction... 3 Vectos The Basics... 4 Vecto Aithmetic... 8 Dot Poduct... 13 Coss Poduct... 21 2007 Paul Dawkins i http://tutoial.math.lama.edu/tems.aspx
EM Boundary Value Problems
 EM Bounday Value Poblems 10/ 9 11/ By Ilekta chistidi & Lee, Seung-Hyun A. Geneal Desciption : Maxwell Equations & Loentz Foce We want to find the equations of motion of chaged paticles. The way to do
EM Bounday Value Poblems 10/ 9 11/ By Ilekta chistidi & Lee, Seung-Hyun A. Geneal Desciption : Maxwell Equations & Loentz Foce We want to find the equations of motion of chaged paticles. The way to do
e.g: If A = i 2 j + k then find A. A = Ax 2 + Ay 2 + Az 2 = ( 2) = 6
 MOTION IN A PLANE 1. Scala Quantities Physical quantities that have only magnitude and no diection ae called scala quantities o scalas. e.g. Mass, time, speed etc. 2. Vecto Quantities Physical quantities
MOTION IN A PLANE 1. Scala Quantities Physical quantities that have only magnitude and no diection ae called scala quantities o scalas. e.g. Mass, time, speed etc. 2. Vecto Quantities Physical quantities
OSCILLATIONS AND GRAVITATION
 1. SIMPLE HARMONIC MOTION Simple hamonic motion is any motion that is equivalent to a single component of unifom cicula motion. In this situation the velocity is always geatest in the middle of the motion,
1. SIMPLE HARMONIC MOTION Simple hamonic motion is any motion that is equivalent to a single component of unifom cicula motion. In this situation the velocity is always geatest in the middle of the motion,
4.3 Area of a Sector. Area of a Sector Section
 ea of a Secto Section 4. 9 4. ea of a Secto In geomety you leaned that the aea of a cicle of adius is π 2. We will now lean how to find the aea of a secto of a cicle. secto is the egion bounded by a cental
ea of a Secto Section 4. 9 4. ea of a Secto In geomety you leaned that the aea of a cicle of adius is π 2. We will now lean how to find the aea of a secto of a cicle. secto is the egion bounded by a cental
Magnetic Field. Conference 6. Physics 102 General Physics II
 Physics 102 Confeence 6 Magnetic Field Confeence 6 Physics 102 Geneal Physics II Monday, Mach 3d, 2014 6.1 Quiz Poblem 6.1 Think about the magnetic field associated with an infinite, cuent caying wie.
Physics 102 Confeence 6 Magnetic Field Confeence 6 Physics 102 Geneal Physics II Monday, Mach 3d, 2014 6.1 Quiz Poblem 6.1 Think about the magnetic field associated with an infinite, cuent caying wie.
Chapter 2: Introduction to Implicit Equations
 Habeman MTH 11 Section V: Paametic and Implicit Equations Chapte : Intoduction to Implicit Equations When we descibe cuves on the coodinate plane with algebaic equations, we can define the elationship
Habeman MTH 11 Section V: Paametic and Implicit Equations Chapte : Intoduction to Implicit Equations When we descibe cuves on the coodinate plane with algebaic equations, we can define the elationship
arxiv: v1 [physics.pop-ph] 3 Jun 2013
![arxiv: v1 [physics.pop-ph] 3 Jun 2013 arxiv: v1 [physics.pop-ph] 3 Jun 2013](/thumbs/89/100795062.jpg) A note on the electostatic enegy of two point chages axiv:1306.0401v1 [physics.pop-ph] 3 Jun 013 A C Tot Instituto de Física Univesidade Fedeal do io de Janeio Caixa Postal 68.58; CEP 1941-97 io de Janeio,
A note on the electostatic enegy of two point chages axiv:1306.0401v1 [physics.pop-ph] 3 Jun 013 A C Tot Instituto de Física Univesidade Fedeal do io de Janeio Caixa Postal 68.58; CEP 1941-97 io de Janeio,
THE LAPLACE EQUATION. The Laplace (or potential) equation is the equation. u = 0. = 2 x 2. x y 2 in R 2
 THE LAPLACE EQUATION The Laplace (o potential) equation is the equation whee is the Laplace opeato = 2 x 2 u = 0. in R = 2 x 2 + 2 y 2 in R 2 = 2 x 2 + 2 y 2 + 2 z 2 in R 3 The solutions u of the Laplace
THE LAPLACE EQUATION The Laplace (o potential) equation is the equation whee is the Laplace opeato = 2 x 2 u = 0. in R = 2 x 2 + 2 y 2 in R 2 = 2 x 2 + 2 y 2 + 2 z 2 in R 3 The solutions u of the Laplace
To Feel a Force Chapter 7 Static equilibrium - torque and friction
 To eel a oce Chapte 7 Chapte 7: Static fiction, toque and static equilibium A. Review of foce vectos Between the eath and a small mass, gavitational foces of equal magnitude and opposite diection act on
To eel a oce Chapte 7 Chapte 7: Static fiction, toque and static equilibium A. Review of foce vectos Between the eath and a small mass, gavitational foces of equal magnitude and opposite diection act on
MATH Non-Euclidean Geometry Exercise Set 3: Solutions
 MATH 68090 NonEuclidean Geomety Execise Set : Solutions Pove that the opposite angles in a convex quadilateal inscibed in a cicle sum to 80º Convesely, pove that if the opposite angles in a convex quadilateal
MATH 68090 NonEuclidean Geomety Execise Set : Solutions Pove that the opposite angles in a convex quadilateal inscibed in a cicle sum to 80º Convesely, pove that if the opposite angles in a convex quadilateal
B da = 0. Q E da = ε. E da = E dv
 lectomagnetic Theo Pof Ruiz, UNC Asheville, doctophs on YouTube Chapte Notes The Maxwell quations in Diffeential Fom 1 The Maxwell quations in Diffeential Fom We will now tansfom the integal fom of the
lectomagnetic Theo Pof Ruiz, UNC Asheville, doctophs on YouTube Chapte Notes The Maxwell quations in Diffeential Fom 1 The Maxwell quations in Diffeential Fom We will now tansfom the integal fom of the
Math Notes on Kepler s first law 1. r(t) kp(t)
 Math 7 - Notes on Keple s fist law Planetay motion and Keple s Laws We conside the motion of a single planet about the sun; fo simplicity, we assign coodinates in R 3 so that the position of the sun is
Math 7 - Notes on Keple s fist law Planetay motion and Keple s Laws We conside the motion of a single planet about the sun; fo simplicity, we assign coodinates in R 3 so that the position of the sun is
Physics 2212 GH Quiz #2 Solutions Spring 2016
 Physics 2212 GH Quiz #2 Solutions Sping 216 I. 17 points) Thee point chages, each caying a chage Q = +6. nc, ae placed on an equilateal tiangle of side length = 3. mm. An additional point chage, caying
Physics 2212 GH Quiz #2 Solutions Sping 216 I. 17 points) Thee point chages, each caying a chage Q = +6. nc, ae placed on an equilateal tiangle of side length = 3. mm. An additional point chage, caying
Physics 11 Chapter 3: Vectors and Motion in Two Dimensions. Problem Solving
 Physics 11 Chapte 3: Vectos and Motion in Two Dimensions The only thing in life that is achieved without effot is failue. Souce unknown "We ae what we epeatedly do. Excellence, theefoe, is not an act,
Physics 11 Chapte 3: Vectos and Motion in Two Dimensions The only thing in life that is achieved without effot is failue. Souce unknown "We ae what we epeatedly do. Excellence, theefoe, is not an act,
1.6. Trigonometric Functions. 48 Chapter 1: Preliminaries. Radian Measure
 48 Chapte : Peliminaies.6 Tigonometic Functions Cicle B' B θ C A Unit of cicle adius FIGURE.63 The adian measue of angle ACB is the length u of ac AB on the unit cicle centeed at C. The value of u can
48 Chapte : Peliminaies.6 Tigonometic Functions Cicle B' B θ C A Unit of cicle adius FIGURE.63 The adian measue of angle ACB is the length u of ac AB on the unit cicle centeed at C. The value of u can
Physics 181. Assignment 4
 Physics 181 Assignment 4 Solutions 1. A sphee has within it a gavitational field given by g = g, whee g is constant and is the position vecto of the field point elative to the cente of the sphee. This
Physics 181 Assignment 4 Solutions 1. A sphee has within it a gavitational field given by g = g, whee g is constant and is the position vecto of the field point elative to the cente of the sphee. This
SMT 2013 Team Test Solutions February 2, 2013
 1 Let f 1 (n) be the numbe of divisos that n has, and define f k (n) = f 1 (f k 1 (n)) Compute the smallest intege k such that f k (013 013 ) = Answe: 4 Solution: We know that 013 013 = 3 013 11 013 61
1 Let f 1 (n) be the numbe of divisos that n has, and define f k (n) = f 1 (f k 1 (n)) Compute the smallest intege k such that f k (013 013 ) = Answe: 4 Solution: We know that 013 013 = 3 013 11 013 61
Trigonometry Standard Position and Radians
 MHF 4UI Unit 6 Day 1 Tigonomety Standad Position and Radians A. Standad Position of an Angle teminal am initial am Angle is in standad position when the initial am is the positive x-axis and the vetex
MHF 4UI Unit 6 Day 1 Tigonomety Standad Position and Radians A. Standad Position of an Angle teminal am initial am Angle is in standad position when the initial am is the positive x-axis and the vetex
Physics 111. Ch 12: Gravity. Newton s Universal Gravity. R - hat. the equation. = Gm 1 m 2. F g 2 1. ˆr 2 1. Gravity G =
 ics Announcements day, embe 9, 004 Ch 1: Gavity Univesal Law Potential Enegy Keple s Laws Ch 15: Fluids density hydostatic equilibium Pascal s Pinciple This week s lab will be anothe physics wokshop -
ics Announcements day, embe 9, 004 Ch 1: Gavity Univesal Law Potential Enegy Keple s Laws Ch 15: Fluids density hydostatic equilibium Pascal s Pinciple This week s lab will be anothe physics wokshop -
9.1 POLAR COORDINATES
 9. Pola Coodinates Contempoay Calculus 9. POLAR COORDINATES The ectangula coodinate system is immensely useful, but it is not the only way to assign an addess to a point in the plane and sometimes it is
9. Pola Coodinates Contempoay Calculus 9. POLAR COORDINATES The ectangula coodinate system is immensely useful, but it is not the only way to assign an addess to a point in the plane and sometimes it is
When two numbers are written as the product of their prime factors, they are in factored form.
 10 1 Study Guide Pages 420 425 Factos Because 3 4 12, we say that 3 and 4 ae factos of 12. In othe wods, factos ae the numbes you multiply to get a poduct. Since 2 6 12, 2 and 6 ae also factos of 12. The
10 1 Study Guide Pages 420 425 Factos Because 3 4 12, we say that 3 and 4 ae factos of 12. In othe wods, factos ae the numbes you multiply to get a poduct. Since 2 6 12, 2 and 6 ae also factos of 12. The
Chapter 5: Trigonometric Functions of Angles
 Chapte 5: Tigonometic Functions of Angles In the pevious chaptes we have exploed a vaiety of functions which could be combined to fom a vaiety of shapes. In this discussion, one common shape has been missing:
Chapte 5: Tigonometic Functions of Angles In the pevious chaptes we have exploed a vaiety of functions which could be combined to fom a vaiety of shapes. In this discussion, one common shape has been missing:
Math 259 Winter Handout 6: In-class Review for the Cumulative Final Exam
 Math 259 Winte 2009 Handout 6: In-class Review fo the Cumulative Final Exam The topics coveed by the cumulative final exam include the following: Paametic cuves. Finding fomulas fo paametic cuves. Dawing
Math 259 Winte 2009 Handout 6: In-class Review fo the Cumulative Final Exam The topics coveed by the cumulative final exam include the following: Paametic cuves. Finding fomulas fo paametic cuves. Dawing
History of Astronomy - Part II. Tycho Brahe - An Observer. Johannes Kepler - A Theorist
 Histoy of Astonomy - Pat II Afte the Copenican Revolution, astonomes stived fo moe obsevations to help bette explain the univese aound them Duing this time (600-750) many majo advances in science and astonomy
Histoy of Astonomy - Pat II Afte the Copenican Revolution, astonomes stived fo moe obsevations to help bette explain the univese aound them Duing this time (600-750) many majo advances in science and astonomy
Chapter 5 Force and Motion
 Chapte 5 Foce and Motion In Chaptes 2 and 4 we have studied kinematics, i.e., we descibed the motion of objects using paametes such as the position vecto, velocity, and acceleation without any insights
Chapte 5 Foce and Motion In Chaptes 2 and 4 we have studied kinematics, i.e., we descibed the motion of objects using paametes such as the position vecto, velocity, and acceleation without any insights
Uniform Circular Motion
 Unifom Cicula Motion constant speed Pick a point in the objects motion... What diection is the velocity? HINT Think about what diection the object would tavel if the sting wee cut Unifom Cicula Motion
Unifom Cicula Motion constant speed Pick a point in the objects motion... What diection is the velocity? HINT Think about what diection the object would tavel if the sting wee cut Unifom Cicula Motion
Math 124B February 02, 2012
 Math 24B Febuay 02, 202 Vikto Gigoyan 8 Laplace s equation: popeties We have aleady encounteed Laplace s equation in the context of stationay heat conduction and wave phenomena. Recall that in two spatial
Math 24B Febuay 02, 202 Vikto Gigoyan 8 Laplace s equation: popeties We have aleady encounteed Laplace s equation in the context of stationay heat conduction and wave phenomena. Recall that in two spatial
The Archimedean Circles of Schoch and Woo
 Foum Geometicoum Volume 4 (2004) 27 34. FRUM GEM ISSN 1534-1178 The Achimedean Cicles of Schoch and Woo Hioshi kumua and Masayuki Watanabe Abstact. We genealize the Achimedean cicles in an abelos (shoemake
Foum Geometicoum Volume 4 (2004) 27 34. FRUM GEM ISSN 1534-1178 The Achimedean Cicles of Schoch and Woo Hioshi kumua and Masayuki Watanabe Abstact. We genealize the Achimedean cicles in an abelos (shoemake
3.6 Applied Optimization
 .6 Applied Optimization Section.6 Notes Page In this section we will be looking at wod poblems whee it asks us to maimize o minimize something. Fo all the poblems in this section you will be taking the
.6 Applied Optimization Section.6 Notes Page In this section we will be looking at wod poblems whee it asks us to maimize o minimize something. Fo all the poblems in this section you will be taking the
2 E. on each of these two surfaces. r r r r. Q E E ε. 2 2 Qencl encl right left 0
 Ch : 4, 9,, 9,,, 4, 9,, 4, 8 4 (a) Fom the diagam in the textbook, we see that the flux outwad though the hemispheical suface is the same as the flux inwad though the cicula suface base of the hemisphee
Ch : 4, 9,, 9,,, 4, 9,, 4, 8 4 (a) Fom the diagam in the textbook, we see that the flux outwad though the hemispheical suface is the same as the flux inwad though the cicula suface base of the hemisphee
Math 451: Euclidean and Non-Euclidean Geometry MWF 3pm, Gasson 204 Homework 9 Solutions
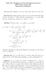 Math 451: Euclidean and Non-Euclidean Geomety MWF 3pm, Gasson 04 Homewok 9 Solutions Execises fom Chapte 3: 3.3, 3.8, 3.15, 3.19, 3.0, 5.11, 5.1, 5.13 Execise 3.3. Suppose that C and C ae two cicles with
Math 451: Euclidean and Non-Euclidean Geomety MWF 3pm, Gasson 04 Homewok 9 Solutions Execises fom Chapte 3: 3.3, 3.8, 3.15, 3.19, 3.0, 5.11, 5.1, 5.13 Execise 3.3. Suppose that C and C ae two cicles with
AY 7A - Fall 2010 Section Worksheet 2 - Solutions Energy and Kepler s Law
 AY 7A - Fall 00 Section Woksheet - Solutions Enegy and Keple s Law. Escape Velocity (a) A planet is obiting aound a sta. What is the total obital enegy of the planet? (i.e. Total Enegy = Potential Enegy
AY 7A - Fall 00 Section Woksheet - Solutions Enegy and Keple s Law. Escape Velocity (a) A planet is obiting aound a sta. What is the total obital enegy of the planet? (i.e. Total Enegy = Potential Enegy
Contact impedance of grounded and capacitive electrodes
 Abstact Contact impedance of gounded and capacitive electodes Andeas Hödt Institut fü Geophysik und extateestische Physik, TU Baunschweig The contact impedance of electodes detemines how much cuent can
Abstact Contact impedance of gounded and capacitive electodes Andeas Hödt Institut fü Geophysik und extateestische Physik, TU Baunschweig The contact impedance of electodes detemines how much cuent can
Determining solar characteristics using planetary data
 Detemining sola chaacteistics using planetay data Intoduction The Sun is a G-type main sequence sta at the cente of the Sola System aound which the planets, including ou Eath, obit. In this investigation
Detemining sola chaacteistics using planetay data Intoduction The Sun is a G-type main sequence sta at the cente of the Sola System aound which the planets, including ou Eath, obit. In this investigation
Lecture 8 - Gauss s Law
 Lectue 8 - Gauss s Law A Puzzle... Example Calculate the potential enegy, pe ion, fo an infinite 1D ionic cystal with sepaation a; that is, a ow of equally spaced chages of magnitude e and altenating sign.
Lectue 8 - Gauss s Law A Puzzle... Example Calculate the potential enegy, pe ion, fo an infinite 1D ionic cystal with sepaation a; that is, a ow of equally spaced chages of magnitude e and altenating sign.
! E da = 4πkQ enc, has E under the integral sign, so it is not ordinarily an
 Physics 142 Electostatics 2 Page 1 Electostatics 2 Electicity is just oganized lightning. Geoge Calin A tick that sometimes woks: calculating E fom Gauss s law Gauss s law,! E da = 4πkQ enc, has E unde
Physics 142 Electostatics 2 Page 1 Electostatics 2 Electicity is just oganized lightning. Geoge Calin A tick that sometimes woks: calculating E fom Gauss s law Gauss s law,! E da = 4πkQ enc, has E unde
Liquid gas interface under hydrostatic pressure
 Advances in Fluid Mechanics IX 5 Liquid gas inteface unde hydostatic pessue A. Gajewski Bialystok Univesity of Technology, Faculty of Civil Engineeing and Envionmental Engineeing, Depatment of Heat Engineeing,
Advances in Fluid Mechanics IX 5 Liquid gas inteface unde hydostatic pessue A. Gajewski Bialystok Univesity of Technology, Faculty of Civil Engineeing and Envionmental Engineeing, Depatment of Heat Engineeing,
transformation Earth V-curve (meridian) λ Conical projection. u,v curves on the datum surface projected as U,V curves on the projection surface
 . CONICAL PROJECTIONS In elementay texts on map pojections, the pojection sufaces ae often descibed as developable sufaces, such as the cylinde (cylindical pojections) and the cone (conical pojections),
. CONICAL PROJECTIONS In elementay texts on map pojections, the pojection sufaces ae often descibed as developable sufaces, such as the cylinde (cylindical pojections) and the cone (conical pojections),
Related Rates - the Basics
 Related Rates - the Basics In this section we exploe the way we can use deivatives to find the velocity at which things ae changing ove time. Up to now we have been finding the deivative to compae the
Related Rates - the Basics In this section we exploe the way we can use deivatives to find the velocity at which things ae changing ove time. Up to now we have been finding the deivative to compae the
Uniform Circular Motion
 Unifom Cicula Motion Intoduction Ealie we defined acceleation as being the change in velocity with time: a = v t Until now we have only talked about changes in the magnitude of the acceleation: the speeding
Unifom Cicula Motion Intoduction Ealie we defined acceleation as being the change in velocity with time: a = v t Until now we have only talked about changes in the magnitude of the acceleation: the speeding
Auchmuty High School Mathematics Department Advanced Higher Notes Teacher Version
 The Binomial Theoem Factoials Auchmuty High School Mathematics Depatment The calculations,, 6 etc. often appea in mathematics. They ae called factoials and have been given the notation n!. e.g. 6! 6!!!!!
The Binomial Theoem Factoials Auchmuty High School Mathematics Depatment The calculations,, 6 etc. often appea in mathematics. They ae called factoials and have been given the notation n!. e.g. 6! 6!!!!!
Physics 111 Lecture 5 (Walker: 3.3-6) Vectors & Vector Math Motion Vectors Sept. 11, 2009
 Physics 111 Lectue 5 (Walke: 3.3-6) Vectos & Vecto Math Motion Vectos Sept. 11, 2009 Quiz Monday - Chap. 2 1 Resolving a vecto into x-component & y- component: Pola Coodinates Catesian Coodinates x y =
Physics 111 Lectue 5 (Walke: 3.3-6) Vectos & Vecto Math Motion Vectos Sept. 11, 2009 Quiz Monday - Chap. 2 1 Resolving a vecto into x-component & y- component: Pola Coodinates Catesian Coodinates x y =
Hopefully Helpful Hints for Gauss s Law
 Hopefully Helpful Hints fo Gauss s Law As befoe, thee ae things you need to know about Gauss s Law. In no paticula ode, they ae: a.) In the context of Gauss s Law, at a diffeential level, the electic flux
Hopefully Helpful Hints fo Gauss s Law As befoe, thee ae things you need to know about Gauss s Law. In no paticula ode, they ae: a.) In the context of Gauss s Law, at a diffeential level, the electic flux
MODULE 5 ADVANCED MECHANICS GRAVITATIONAL FIELD: MOTION OF PLANETS AND SATELLITES VISUAL PHYSICS ONLINE
 VISUAL PHYSICS ONLIN MODUL 5 ADVANCD MCHANICS GRAVITATIONAL FILD: MOTION OF PLANTS AND SATLLITS SATLLITS: Obital motion of object of mass m about a massive object of mass M (m
VISUAL PHYSICS ONLIN MODUL 5 ADVANCD MCHANICS GRAVITATIONAL FILD: MOTION OF PLANTS AND SATLLITS SATLLITS: Obital motion of object of mass m about a massive object of mass M (m
3 Celestial Mechanics
 3 Celestial Mechanics 3.1 Keple s Laws Assign: Read Chapte 2 of Caol and Ostlie (2006) OJTA: 3. The Copenican Revolution/Keple (4) Keple s Fist Law b ' εa θ a C 0 D 2a b 2 D a 2.1 2 / (1) D a.1 2 / Aea
3 Celestial Mechanics 3.1 Keple s Laws Assign: Read Chapte 2 of Caol and Ostlie (2006) OJTA: 3. The Copenican Revolution/Keple (4) Keple s Fist Law b ' εa θ a C 0 D 2a b 2 D a 2.1 2 / (1) D a.1 2 / Aea
Chapter 5 Force and Motion
 Chapte 5 Foce and Motion In chaptes 2 and 4 we have studied kinematics i.e. descibed the motion of objects using paametes such as the position vecto, velocity and acceleation without any insights as to
Chapte 5 Foce and Motion In chaptes 2 and 4 we have studied kinematics i.e. descibed the motion of objects using paametes such as the position vecto, velocity and acceleation without any insights as to
Physics 11 Chapter 20: Electric Fields and Forces
 Physics Chapte 0: Electic Fields and Foces Yesteday is not ous to ecove, but tomoow is ous to win o lose. Lyndon B. Johnson When I am anxious it is because I am living in the futue. When I am depessed
Physics Chapte 0: Electic Fields and Foces Yesteday is not ous to ecove, but tomoow is ous to win o lose. Lyndon B. Johnson When I am anxious it is because I am living in the futue. When I am depessed
MATH 415, WEEK 3: Parameter-Dependence and Bifurcations
 MATH 415, WEEK 3: Paamete-Dependence and Bifucations 1 A Note on Paamete Dependence We should pause to make a bief note about the ole played in the study of dynamical systems by the system s paametes.
MATH 415, WEEK 3: Paamete-Dependence and Bifucations 1 A Note on Paamete Dependence We should pause to make a bief note about the ole played in the study of dynamical systems by the system s paametes.
Rotational Motion. Every quantity that we have studied with translational motion has a rotational counterpart
 Rotational Motion & Angula Momentum Rotational Motion Evey quantity that we have studied with tanslational motion has a otational countepat TRANSLATIONAL ROTATIONAL Displacement x Angula Position Velocity
Rotational Motion & Angula Momentum Rotational Motion Evey quantity that we have studied with tanslational motion has a otational countepat TRANSLATIONAL ROTATIONAL Displacement x Angula Position Velocity
rt () is constant. We know how to find the length of the radius vector by r( t) r( t) r( t)
 Cicula Motion Fom ancient times cicula tajectoies hae occupied a special place in ou model of the Uniese. Although these obits hae been eplaced by the moe geneal elliptical geomety, cicula motion is still
Cicula Motion Fom ancient times cicula tajectoies hae occupied a special place in ou model of the Uniese. Although these obits hae been eplaced by the moe geneal elliptical geomety, cicula motion is still
15 Solving the Laplace equation by Fourier method
 5 Solving the Laplace equation by Fouie method I aleady intoduced two o thee dimensional heat equation, when I deived it, ecall that it taes the fom u t = α 2 u + F, (5.) whee u: [0, ) D R, D R is the
5 Solving the Laplace equation by Fouie method I aleady intoduced two o thee dimensional heat equation, when I deived it, ecall that it taes the fom u t = α 2 u + F, (5.) whee u: [0, ) D R, D R is the
$ i. !((( dv vol. Physics 8.02 Quiz One Equations Fall q 1 q 2 r 2 C = 2 C! V 2 = Q 2 2C F = 4!" or. r ˆ = points from source q to observer
 Physics 8.0 Quiz One Equations Fall 006 F = 1 4" o q 1 q = q q ˆ 3 4" o = E 4" o ˆ = points fom souce q to obseve 1 dq E = # ˆ 4" 0 V "## E "d A = Q inside closed suface o d A points fom inside to V =
Physics 8.0 Quiz One Equations Fall 006 F = 1 4" o q 1 q = q q ˆ 3 4" o = E 4" o ˆ = points fom souce q to obseve 1 dq E = # ˆ 4" 0 V "## E "d A = Q inside closed suface o d A points fom inside to V =
Newton s Laws, Kepler s Laws, and Planetary Orbits
 Newton s Laws, Keple s Laws, and Planetay Obits PROBLEM SET 4 DUE TUESDAY AT START OF LECTURE 28 Septembe 2017 ASTRONOMY 111 FALL 2017 1 Newton s & Keple s laws and planetay obits Unifom cicula motion
Newton s Laws, Keple s Laws, and Planetay Obits PROBLEM SET 4 DUE TUESDAY AT START OF LECTURE 28 Septembe 2017 ASTRONOMY 111 FALL 2017 1 Newton s & Keple s laws and planetay obits Unifom cicula motion
(n 1)n(n + 1)(n + 2) + 1 = (n 1)(n + 2)n(n + 1) + 1 = ( (n 2 + n 1) 1 )( (n 2 + n 1) + 1 ) + 1 = (n 2 + n 1) 2.
 Paabola Volume 5, Issue (017) Solutions 151 1540 Q151 Take any fou consecutive whole numbes, multiply them togethe and add 1. Make a conjectue and pove it! The esulting numbe can, fo instance, be expessed
Paabola Volume 5, Issue (017) Solutions 151 1540 Q151 Take any fou consecutive whole numbes, multiply them togethe and add 1. Make a conjectue and pove it! The esulting numbe can, fo instance, be expessed
New problems in universal algebraic geometry illustrated by boolean equations
 New poblems in univesal algebaic geomety illustated by boolean equations axiv:1611.00152v2 [math.ra] 25 Nov 2016 Atem N. Shevlyakov Novembe 28, 2016 Abstact We discuss new poblems in univesal algebaic
New poblems in univesal algebaic geomety illustated by boolean equations axiv:1611.00152v2 [math.ra] 25 Nov 2016 Atem N. Shevlyakov Novembe 28, 2016 Abstact We discuss new poblems in univesal algebaic
, the tangent line is an approximation of the curve (and easier to deal with than the curve).
 114 Tangent Planes and Linea Appoimations Back in-dimensions, what was the equation of the tangent line of f ( ) at point (, ) f ( )? (, ) ( )( ) = f Linea Appoimation (Tangent Line Appoimation) of f at
114 Tangent Planes and Linea Appoimations Back in-dimensions, what was the equation of the tangent line of f ( ) at point (, ) f ( )? (, ) ( )( ) = f Linea Appoimation (Tangent Line Appoimation) of f at
Between any two masses, there exists a mutual attractive force.
 YEAR 12 PHYSICS: GRAVITATION PAST EXAM QUESTIONS Name: QUESTION 1 (1995 EXAM) (a) State Newton s Univesal Law of Gavitation in wods Between any two masses, thee exists a mutual attactive foce. This foce
YEAR 12 PHYSICS: GRAVITATION PAST EXAM QUESTIONS Name: QUESTION 1 (1995 EXAM) (a) State Newton s Univesal Law of Gavitation in wods Between any two masses, thee exists a mutual attactive foce. This foce
1 Spherical multipole moments
 Jackson notes 9 Spheical multipole moments Suppose we have a chage distibution ρ (x) wheeallofthechageiscontained within a spheical egion of adius R, as shown in the diagam. Then thee is no chage in the
Jackson notes 9 Spheical multipole moments Suppose we have a chage distibution ρ (x) wheeallofthechageiscontained within a spheical egion of adius R, as shown in the diagam. Then thee is no chage in the
Physics 107 TUTORIAL ASSIGNMENT #8
 Physics 07 TUTORIAL ASSIGNMENT #8 Cutnell & Johnson, 7 th edition Chapte 8: Poblems 5,, 3, 39, 76 Chapte 9: Poblems 9, 0, 4, 5, 6 Chapte 8 5 Inteactive Solution 8.5 povides a model fo solving this type
Physics 07 TUTORIAL ASSIGNMENT #8 Cutnell & Johnson, 7 th edition Chapte 8: Poblems 5,, 3, 39, 76 Chapte 9: Poblems 9, 0, 4, 5, 6 Chapte 8 5 Inteactive Solution 8.5 povides a model fo solving this type
The Derivative of the Sine and Cosine. A New Derivation Approach
 The Deivative of the Sine and Cosine. A New Deivation Appoach By John T. Katsikadelis Scool of Civil Engineeing, National Technical Univesity of Athens, Athens 15773, Geece. e-mail: jkats@cental.ntua.g
The Deivative of the Sine and Cosine. A New Deivation Appoach By John T. Katsikadelis Scool of Civil Engineeing, National Technical Univesity of Athens, Athens 15773, Geece. e-mail: jkats@cental.ntua.g
Geometry Unit 4b - Notes Triangle Relationships
 Geomety Unit 4b - Notes Tiangle Relationships This unit is boken into two pats, 4a & 4b. test should be given following each pat. quidistant fom two points the same distance fom one point as fom anothe.
Geomety Unit 4b - Notes Tiangle Relationships This unit is boken into two pats, 4a & 4b. test should be given following each pat. quidistant fom two points the same distance fom one point as fom anothe.
From Gravitational Collapse to Black Holes
 Fom Gavitational Collapse to Black Holes T. Nguyen PHY 391 Independent Study Tem Pape Pof. S.G. Rajeev Univesity of Rocheste Decembe 0, 018 1 Intoduction The pupose of this independent study is to familiaize
Fom Gavitational Collapse to Black Holes T. Nguyen PHY 391 Independent Study Tem Pape Pof. S.G. Rajeev Univesity of Rocheste Decembe 0, 018 1 Intoduction The pupose of this independent study is to familiaize
PHYS 301 HOMEWORK #10 (Optional HW)
 PHYS 301 HOMEWORK #10 (Optional HW) 1. Conside the Legende diffeential equation : 1 - x 2 y'' - 2xy' + m m + 1 y = 0 Make the substitution x = cos q and show the Legende equation tansfoms into d 2 y 2
PHYS 301 HOMEWORK #10 (Optional HW) 1. Conside the Legende diffeential equation : 1 - x 2 y'' - 2xy' + m m + 1 y = 0 Make the substitution x = cos q and show the Legende equation tansfoms into d 2 y 2
PHYS 110B - HW #7 Spring 2004, Solutions by David Pace Any referenced equations are from Griffiths Problem statements are paraphrased
 PHYS 0B - HW #7 Sping 2004, Solutions by David Pace Any efeenced euations ae fom Giffiths Poblem statements ae paaphased. Poblem 0.3 fom Giffiths A point chage,, moves in a loop of adius a. At time t 0
PHYS 0B - HW #7 Sping 2004, Solutions by David Pace Any efeenced euations ae fom Giffiths Poblem statements ae paaphased. Poblem 0.3 fom Giffiths A point chage,, moves in a loop of adius a. At time t 0
Thomas J. Osler Mathematics Department, Rowan University, Glassboro NJ 08028,
 1 Feb 6, 001 An unusual appoach to Keple s fist law Ameican Jounal of Physics, 69(001), pp. 106-8. Thomas J. Osle Mathematics Depatment, Rowan Univesity, Glassboo NJ 0808, osle@owan.edu Keple s fist law
1 Feb 6, 001 An unusual appoach to Keple s fist law Ameican Jounal of Physics, 69(001), pp. 106-8. Thomas J. Osle Mathematics Depatment, Rowan Univesity, Glassboo NJ 0808, osle@owan.edu Keple s fist law
INTRODUCTION. 2. Vectors in Physics 1
 INTRODUCTION Vectos ae used in physics to extend the study of motion fom one dimension to two dimensions Vectos ae indispensable when a physical quantity has a diection associated with it As an example,
INTRODUCTION Vectos ae used in physics to extend the study of motion fom one dimension to two dimensions Vectos ae indispensable when a physical quantity has a diection associated with it As an example,
Force between two parallel current wires and Newton s. third law
 Foce between two paallel cuent wies and Newton s thid law Yannan Yang (Shanghai Jinjuan Infomation Science and Technology Co., Ltd.) Abstact: In this pape, the essence of the inteaction between two paallel
Foce between two paallel cuent wies and Newton s thid law Yannan Yang (Shanghai Jinjuan Infomation Science and Technology Co., Ltd.) Abstact: In this pape, the essence of the inteaction between two paallel
Chapter 5 Linear Equations: Basic Theory and Practice
 Chapte 5 inea Equations: Basic Theoy and actice In this chapte and the next, we ae inteested in the linea algebaic equation AX = b, (5-1) whee A is an m n matix, X is an n 1 vecto to be solved fo, and
Chapte 5 inea Equations: Basic Theoy and actice In this chapte and the next, we ae inteested in the linea algebaic equation AX = b, (5-1) whee A is an m n matix, X is an n 1 vecto to be solved fo, and
APPLICATION OF MAC IN THE FREQUENCY DOMAIN
 PPLICION OF MC IN HE FREQUENCY DOMIN D. Fotsch and D. J. Ewins Dynamics Section, Mechanical Engineeing Depatment Impeial College of Science, echnology and Medicine London SW7 2B, United Kingdom BSRC he
PPLICION OF MC IN HE FREQUENCY DOMIN D. Fotsch and D. J. Ewins Dynamics Section, Mechanical Engineeing Depatment Impeial College of Science, echnology and Medicine London SW7 2B, United Kingdom BSRC he
COLLAPSING WALLS THEOREM
 COLLAPSING WALLS THEOREM IGOR PAK AND ROM PINCHASI Abstact. Let P R 3 be a pyamid with the base a convex polygon Q. We show that when othe faces ae collapsed (otated aound the edges onto the plane spanned
COLLAPSING WALLS THEOREM IGOR PAK AND ROM PINCHASI Abstact. Let P R 3 be a pyamid with the base a convex polygon Q. We show that when othe faces ae collapsed (otated aound the edges onto the plane spanned
( ) Make-up Tests. From Last Time. Electric Field Flux. o The Electric Field Flux through a bit of area is
 Mon., 3/23 Wed., 3/25 Thus., 3/26 Fi., 3/27 Mon., 3/30 Tues., 3/31 21.4-6 Using Gauss s & nto to Ampee s 21.7-9 Maxwell s, Gauss s, and Ampee s Quiz Ch 21, Lab 9 Ampee s Law (wite up) 22.1-2,10 nto to
Mon., 3/23 Wed., 3/25 Thus., 3/26 Fi., 3/27 Mon., 3/30 Tues., 3/31 21.4-6 Using Gauss s & nto to Ampee s 21.7-9 Maxwell s, Gauss s, and Ampee s Quiz Ch 21, Lab 9 Ampee s Law (wite up) 22.1-2,10 nto to
Trigonometric Functions of Any Angle 9.3 (, 3. Essential Question How can you use the unit circle to define the trigonometric functions of any angle?
 9. Tigonometic Functions of An Angle Essential Question How can ou use the unit cicle to define the tigonometic functions of an angle? Let be an angle in standad position with, ) a point on the teminal
9. Tigonometic Functions of An Angle Essential Question How can ou use the unit cicle to define the tigonometic functions of an angle? Let be an angle in standad position with, ) a point on the teminal
= 4 3 π( m) 3 (5480 kg m 3 ) = kg.
 CHAPTER 11 THE GRAVITATIONAL FIELD Newton s Law of Gavitation m 1 m A foce of attaction occus between two masses given by Newton s Law of Gavitation Inetial mass and gavitational mass Gavitational potential
CHAPTER 11 THE GRAVITATIONAL FIELD Newton s Law of Gavitation m 1 m A foce of attaction occus between two masses given by Newton s Law of Gavitation Inetial mass and gavitational mass Gavitational potential
Use Properties of Tangents
 opeties of icles 1010.1 Use opeties of Tangents 10.2 Find c Measues 10.3 pply opeties of hods 10.4 Use Inscibed ngles and olygons 10.5 pply Othe ngle elationships in icles 10.6 Find egment Lengths in icles
opeties of icles 1010.1 Use opeties of Tangents 10.2 Find c Measues 10.3 pply opeties of hods 10.4 Use Inscibed ngles and olygons 10.5 pply Othe ngle elationships in icles 10.6 Find egment Lengths in icles
