SOLUTIONS FOR 2012 APMO PROBLEMS
|
|
|
- Ann Rich
- 6 years ago
- Views:
Transcription
1 Problem. SOLUTIONS FOR 0 APMO PROBLEMS Solution: Let us denote by XY Z the area of the triangle XY Z. Let x = P AB, y = P BC and z = P CA. From y : z = BCP : ACP = BF : AF = BP F : AP F = x : follows that zx = y, which yields z + x = x + y + z. Similarly, we get x+y = x+y +z and y +z = x+y +z. Thus, we obtain x+y = y +z = z + x. We may assume without loss of generality that x y, z. If we assume that y > z holds, then we get y + z > z + x, which is a contradiction. Similarly, we see that y < z leads to a contradiction x + y < y + z. Therefore, we must have y = z. Then, we also get from y + z = z + x that x = z must hold. We now obtain from x : = y : z = : that x = y = z = holds. Therefore, we conclude that the area of the triangle ABC equals x + y + z = 6. Problem. Solution: If we insert numbers as in the figure below 0 s are to be inserted in the remaining blank boxes, then we see that the condition of the problem is satisfied and the total number of all the numbers inserted is We will show that the sum of all the numbers to be inserted in the boxes of the given grid cannot be more than 5 if the distribution of the numbers has to satisfy the requirement of the problem. Let n = 0. Let us say that the row number the column number of a box in the given grid is i j, respectively if the box lies on the i-th row and the j-th column. For a pair of positive integers x and y, denote by Rx, y the sum of the numbers inserted in all of the boxes whose row number is greater than or equal to x and less than or equal to y assign the value 0 if x > y. First let a be the largest integer satisfying a n and R, a, and then choose the smallest integer c satisfying a c n and Rc +, n. It is possible to choose such a pair a, c since R, 0 = 0 and Rn +, n = 0. If a < c, then we have a < n and so, by the maximality of a, we must have R, a >, while from the minimality of c, we must have Ra+, n >. Then by splitting the grid into rectangles by means of the horizontal line bordering the a-th row and the a + -th row, we get the splitting contradicting the requirement of the problem. Thus, we must have a = c. Similarly, if for any pair of integers x, y we define Cx, y to be the sum of the numbers inserted in all of the boxes whose column number is greater than or equal to x and less than or equal to y Cx, y = 0 if x > y, then we get a number b for which C, b, Cb +, n, b n.
2 If we let r be the number inserted in the box whose row number is a and the column number is b, then since r, we conclude that the sum of the numbers inserted into all of the boxes is Problem 3. R, a + Ra +, n + C, b + Cb +, n + r 5. Solution For integers a, b and a positive integer m, let us write a b mod m if a b is divisible by m. Since np + p n + must be a positive integer, we see that pn n p must hold. This means that if p =, then n n must hold. As it is easy to show by induction that n > n holds if n 5, we conclude that if p =, then n 4 must be satisfied. And we can check that p, n =,,, 4 satisfy the condition of the problem, while, 3 does not. Next, we consider the case where p 3. Suppose s is an integer satisfying s p. If s p p s for such an s, then we have s + p = s p + p p s + p s p = p s p r=0 p s + pc r p r < ps p r= r < p s + p s+ Thus we have s + p < p s+, and by induction on n, we can conclude that if n > p, then n p < p n. This implies that we must have n p in order to satisfy our requirement p n n p. We note that since p n + is even, so is n p +, which, in turn implies that n must be odd and therefore, p n + is divisible by p +, and n p + is also divisible by p +. Thus we have n p mod p +, and therefore, n p mod p +. Now, let e be the smallest positive integer for which n e mod p+. Then, we can write p = ex + y, where x, y are non-negative integers and 0 y < e, and we have p r=0 r! n p = n e x n y n y mod p +, which implies, because of the minimality of e, that y = 0 must hold. This means that p is an integral multiple of e, and therefore, e must equal one of the numbers,, p, p. Now, if e =, p, then we get n p mod p +, which contradicts the fact that p is an odd prime. Since n and p + are relatively prime, we have by Euler s Theorem that n ϕp+ mod p+, where ϕm denotes the number of integers j j m which are relatively prime with m. From ϕp+ < p+ < p and the minimality of e, we can then conclude that e = must hold. From n mod p +, we get n p p = n + n mod p +,
3 3 which implies that p + divides n +. Therefore, we must have p n, which, together with the fact n p, show that p = n must hold. It is clear that the pair p, p for any prime p 3 satisfies the condition of the problem, and thus, we conclude that the pairs p, n which satisfy the condition of the problem must be of the form, 4 and p, p with any prime p. Alternate Solution. Let us consider the case where p 3. As we saw in the preceding solution, n must be odd if the pair p, n satisfy the condition of the problem. Now, let q be a prime factor of p +. Then, since p + divides p n +, q must be a prime factor of p n + and of n p + as well. Suppose q 3. Then, from n p mod q, it follows that n p mod q holds. If we let e be the smallest positive integer satisfying n e mod q, then by using the same argument as we used in the preceding solution, we can conclude that e must equal one of the numbers,, p, p. If e =, p, then we get n p mod q, which contradicts the assumption q 3. Since n is not a multiple of q, by Fermat s Little Theorem we get n q mod q, and therefore, we get by the minimality of e that e = must hold. From n mod q, we also get n p p = n + n mod q, and since n p mod q, we have n mod q as well. Now, if q = then since n is odd, we have n mod q as well. Thus, we conclude that for an arbitrary prime factor q of p +, n mod q must hold. Suppose, for a prime q, q k for some positive integer k is a factor of p +. Then q k must be a factor of n p + as well. But since n p + = n + n p n p + n + n p n p + n + p p mod q, we see that q k must divide n +. By applying the argument above for each prime factor q of p +, we can then conclude that n + must be divisible by p +, and as we did in the preceding proof, we can conclude that n = p must hold. Problem 4. Solution: If AB = AC, then we get BF = CF and the conclusion of the problem is clearly satisfied. So, we assume that AB AC in the sequel. Due to symmetry, we may suppose without loss of generality that AB > AC. Let K be the point on the circle Γ such that AK is a diameter of this circle. Then, we get BCK = ACK ACB = 90 ACB = CBH and CBK = ABK ABC = 90 ABC = BCH, from which we conclude that the triangles BCK and CBH are congruent. Therefore, the quadrilateral BKCH is a parallelogram, and its diagonal HK passes through the center M of the other diagonal BC. Therefore, the 3 points H, M, K lie on the same straight line, and we have AEM = AEK = 90. From AED = 90 = ADM, we see that the 4 points A, E, D, M lie on the circumference of the same circle, from which we obtain AMB = AED = AEF = ACF. Putting this fact together with the fact that ABM = AF C, we conclude that the triangles ABM and AF C are similar, and we get AM BM = AC F C. By a similar argument, we get that the triangles ACM and AF B are similar, and and
4 4 therefore, that AM CM = AB AC F B holds. Noting that BM = CM, we also get F C = AB F B, from which we can conclude that BF, proving the assertion of the problem. Problem 5. Solution: CF = AB AC Let us note first that if i j, then since a i +a j, we have n n a i + a j n n = n > 0. If we set b i = a i i =,,..., n, then we get b + b + + b n = n and n b ib j, which shows that it is enough to prove the assertion of the problem in the case where all of a, a,, a n are non-negative. Hence, we assume from now on that a, a,, a n are all non-negative. By multiplying by n the both sides of the desired inequality we get the inequality: i<jn n n n n and since = + aiaj, we obtain from the inequality above by subtracting nn from both sides the following inequality: i i<jn n n We will show that this inequality i holds. If for some i the equality a i = n is valid, then a j = 0 must hold for all j i and the inequality i is trivially satisfied. So, we assume from now on that a i < n is valid for each i. ai+a Let us assume that i j from now on. Since 0 j a i +a j holds, we have ii n n a i +a j ai+a j n a i +a j = a i + a j n a i + n a j. Since n a i > 0, n a j > 0, we also get from the Cauchy-Schwarz inequality that a j n a i + a i n a j n a i + n a j a i + a j, from which it follows that iii a i + a j a n a i + n a j j n a i + a i n a j
5 5 holds. Combining the inequalities ii and iii, we get a j n n a i i<jn = = = n, i<jn i j n i= a j n a i n a i n a i + a i n a j which establishes the desired inequality i.
1. Suppose that a, b, c and d are four different integers. Explain why. (a b)(a c)(a d)(b c)(b d)(c d) a 2 + ab b = 2018.
 New Zealand Mathematical Olympiad Committee Camp Selection Problems 2018 Solutions Due: 28th September 2018 1. Suppose that a, b, c and d are four different integers. Explain why must be a multiple of
New Zealand Mathematical Olympiad Committee Camp Selection Problems 2018 Solutions Due: 28th September 2018 1. Suppose that a, b, c and d are four different integers. Explain why must be a multiple of
2008 Euclid Contest. Solutions. Canadian Mathematics Competition. Tuesday, April 15, c 2008 Centre for Education in Mathematics and Computing
 Canadian Mathematics Competition An activity of the Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario 008 Euclid Contest Tuesday, April 5, 008 Solutions c 008
Canadian Mathematics Competition An activity of the Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario 008 Euclid Contest Tuesday, April 5, 008 Solutions c 008
Problems and Solutions
 46 th Canadian Mathematical Olympiad Wednesday, April 2, 204 Problems and Solutions. Let a, a 2,..., a n be positive real numbers whose product is. Show that the sum a a 2 + + a ( + a )( + a 2 ) + a 3
46 th Canadian Mathematical Olympiad Wednesday, April 2, 204 Problems and Solutions. Let a, a 2,..., a n be positive real numbers whose product is. Show that the sum a a 2 + + a ( + a )( + a 2 ) + a 3
The sum x 1 + x 2 + x 3 is (A): 4 (B): 6 (C): 8 (D): 14 (E): None of the above. How many pairs of positive integers (x, y) are there, those satisfy
 Important: Answer to all 15 questions. Write your answers on the answer sheets provided. For the multiple choice questions, stick only the letters (A, B, C, D or E) of your choice. No calculator is allowed.
Important: Answer to all 15 questions. Write your answers on the answer sheets provided. For the multiple choice questions, stick only the letters (A, B, C, D or E) of your choice. No calculator is allowed.
41st International Mathematical Olympiad
 41st International Mathematical Olympiad Taejon, Korea, July 2000 1 Two circles Γ 1 and Γ 2 intersect at M and N Let l be the common tangent to Γ 1 and Γ 2 so that M is closer to l than N is Let l touch
41st International Mathematical Olympiad Taejon, Korea, July 2000 1 Two circles Γ 1 and Γ 2 intersect at M and N Let l be the common tangent to Γ 1 and Γ 2 so that M is closer to l than N is Let l touch
1 Hanoi Open Mathematical Competition 2017
 1 Hanoi Open Mathematical Competition 017 1.1 Junior Section Question 1. Suppose x 1, x, x 3 are the roots of polynomial P (x) = x 3 6x + 5x + 1. The sum x 1 + x + x 3 is (A): 4 (B): 6 (C): 8 (D): 14 (E):
1 Hanoi Open Mathematical Competition 017 1.1 Junior Section Question 1. Suppose x 1, x, x 3 are the roots of polynomial P (x) = x 3 6x + 5x + 1. The sum x 1 + x + x 3 is (A): 4 (B): 6 (C): 8 (D): 14 (E):
IMO Training Camp Mock Olympiad #2 Solutions
 IMO Training Camp Mock Olympiad #2 Solutions July 3, 2008 1. Given an isosceles triangle ABC with AB = AC. The midpoint of side BC is denoted by M. Let X be a variable point on the shorter arc MA of the
IMO Training Camp Mock Olympiad #2 Solutions July 3, 2008 1. Given an isosceles triangle ABC with AB = AC. The midpoint of side BC is denoted by M. Let X be a variable point on the shorter arc MA of the
First selection test
 First selection test Problem 1. Let ABC be a triangle right at C and consider points D, E on the sides BC, CA, respectively such that BD = AE = k. Lines BE and AC CD AD intersect at point O. Show that
First selection test Problem 1. Let ABC be a triangle right at C and consider points D, E on the sides BC, CA, respectively such that BD = AE = k. Lines BE and AC CD AD intersect at point O. Show that
Putnam n +1 (1 P (O n 1)) 2n +1. 2n +1 (2 (n 1) + 1) 2n +1 = (2 (n 1) + 1) P (O n 1)+1. (2(n 2)+1)P (On 2 )+1 2(n 1)+1. O n (n 1) + n 1 2n +1
 Putnam 00 A. Consider a set S and a binary operation, i.e., for each a, b S, a b S. Assume (a b) a b for all a, b S. Provethata (b a) b for all a, b S. Solution. Wehaveb ((b a) b) (b a) a (b a). A. You
Putnam 00 A. Consider a set S and a binary operation, i.e., for each a, b S, a b S. Assume (a b) a b for all a, b S. Provethata (b a) b for all a, b S. Solution. Wehaveb ((b a) b) (b a) a (b a). A. You
SOLUTIONS FOR 2011 APMO PROBLEMS
 SOLUTIONS FOR 2011 APMO PROBLEMS Problem 1. Solution: Suppose all of the 3 numbers a 2 + b + c, b 2 + c + a and c 2 + a + b are perfect squares. Then from the fact that a 2 + b + c is a perfect square
SOLUTIONS FOR 2011 APMO PROBLEMS Problem 1. Solution: Suppose all of the 3 numbers a 2 + b + c, b 2 + c + a and c 2 + a + b are perfect squares. Then from the fact that a 2 + b + c is a perfect square
 Q 1 Find the square root of 729. 6. Squares and Square Roots Q 2 Fill in the blank using the given pattern. 7 2 = 49 67 2 = 4489 667 2 = 444889 6667 2 = Q 3 Without adding find the sum of 1 + 3 + 5 + 7
Q 1 Find the square root of 729. 6. Squares and Square Roots Q 2 Fill in the blank using the given pattern. 7 2 = 49 67 2 = 4489 667 2 = 444889 6667 2 = Q 3 Without adding find the sum of 1 + 3 + 5 + 7
2010 Shortlist JBMO - Problems
 Chapter 1 2010 Shortlist JBMO - Problems 1.1 Algebra A1 The real numbers a, b, c, d satisfy simultaneously the equations abc d = 1, bcd a = 2, cda b = 3, dab c = 6. Prove that a + b + c + d 0. A2 Determine
Chapter 1 2010 Shortlist JBMO - Problems 1.1 Algebra A1 The real numbers a, b, c, d satisfy simultaneously the equations abc d = 1, bcd a = 2, cda b = 3, dab c = 6. Prove that a + b + c + d 0. A2 Determine
Hanoi Open Mathematical Competition 2017
 Hanoi Open Mathematical Competition 2017 Junior Section Saturday, 4 March 2017 08h30-11h30 Important: Answer to all 15 questions. Write your answers on the answer sheets provided. For the multiple choice
Hanoi Open Mathematical Competition 2017 Junior Section Saturday, 4 March 2017 08h30-11h30 Important: Answer to all 15 questions. Write your answers on the answer sheets provided. For the multiple choice
2011 Olympiad Solutions
 011 Olympiad Problem 1 Let A 0, A 1, A,..., A n be nonnegative numbers such that Prove that A 0 A 1 A A n. A i 1 n A n. Note: x means the greatest integer that is less than or equal to x.) Solution: We
011 Olympiad Problem 1 Let A 0, A 1, A,..., A n be nonnegative numbers such that Prove that A 0 A 1 A A n. A i 1 n A n. Note: x means the greatest integer that is less than or equal to x.) Solution: We
8 th December th December 2018 Junior Category. a 2 + b + c = 1 a, b 2 + c + a = 1 b, c 2 + a + b = 1 c.
 7 th European Mathematical Cup 8 th December 018-16 th December 018 Junior Category MLADI NADARENI MATEMATIČARI Marin Getaldic Problems and Solutions Problem 1. Let a, b, c be non-zero real numbers such
7 th European Mathematical Cup 8 th December 018-16 th December 018 Junior Category MLADI NADARENI MATEMATIČARI Marin Getaldic Problems and Solutions Problem 1. Let a, b, c be non-zero real numbers such
2007 Shortlist JBMO - Problems
 Chapter 1 007 Shortlist JBMO - Problems 1.1 Algebra A1 Let a be a real positive number such that a 3 = 6(a + 1). Prove that the equation x + ax + a 6 = 0 has no solution in the set of the real number.
Chapter 1 007 Shortlist JBMO - Problems 1.1 Algebra A1 Let a be a real positive number such that a 3 = 6(a + 1). Prove that the equation x + ax + a 6 = 0 has no solution in the set of the real number.
Canadian Open Mathematics Challenge
 The Canadian Mathematical Society in collaboration with The CENTRE for EDUCATION in MATHEMATICS and COMPUTING presents the Canadian Open Mathematics Challenge Wednesday, November, 006 Supported by: Solutions
The Canadian Mathematical Society in collaboration with The CENTRE for EDUCATION in MATHEMATICS and COMPUTING presents the Canadian Open Mathematics Challenge Wednesday, November, 006 Supported by: Solutions
The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca Euclid Contest. Wednesday, April 15, 2015
 The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca 015 Euclid Contest Wednesday, April 15, 015 (in North America and South America) Thursday, April 16, 015 (outside of North America
The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca 015 Euclid Contest Wednesday, April 15, 015 (in North America and South America) Thursday, April 16, 015 (outside of North America
37th United States of America Mathematical Olympiad
 37th United States of America Mathematical Olympiad 1. Prove that for each positive integer n, there are pairwise relatively prime integers k 0, k 1,..., k n, all strictly greater than 1, such that k 0
37th United States of America Mathematical Olympiad 1. Prove that for each positive integer n, there are pairwise relatively prime integers k 0, k 1,..., k n, all strictly greater than 1, such that k 0
2007 Cayley Contest. Solutions
 Canadian Mathematics Competition An activity of the Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario 007 Cayley Contest (Grade 10) Tuesday, February 0, 007 Solutions
Canadian Mathematics Competition An activity of the Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario 007 Cayley Contest (Grade 10) Tuesday, February 0, 007 Solutions
Write down all the 3-digit positive integers that are squares and whose individual digits are non-zero squares. Answer: Relay
 A Write down all the 3-digit positive integers that are squares and whose individual digits are non-zero squares. A2 What is the sum of all positive fractions that are less than and have denominator 73?
A Write down all the 3-digit positive integers that are squares and whose individual digits are non-zero squares. A2 What is the sum of all positive fractions that are less than and have denominator 73?
NUMBER SYSTEMS. Number theory is the study of the integers. We denote the set of integers by Z:
 NUMBER SYSTEMS Number theory is the study of the integers. We denote the set of integers by Z: Z = {..., 3, 2, 1, 0, 1, 2, 3,... }. The integers have two operations defined on them, addition and multiplication,
NUMBER SYSTEMS Number theory is the study of the integers. We denote the set of integers by Z: Z = {..., 3, 2, 1, 0, 1, 2, 3,... }. The integers have two operations defined on them, addition and multiplication,
Solutions Best Student Exams Texas A&M High School Math Contest November 16, 2013
 Solutions Best Student Exams Texas A&M High School Math Contest November 6, 20. How many zeros are there if you write out in full the number N = 0 (6 0000) = 0 (6 00) so there are 6 0 0 or N = (000000)
Solutions Best Student Exams Texas A&M High School Math Contest November 6, 20. How many zeros are there if you write out in full the number N = 0 (6 0000) = 0 (6 00) so there are 6 0 0 or N = (000000)
The 33 rd Balkan Mathematical Olympiad Tirana, May 7, 2016
 Language: English The 33 rd Balkan Mathematical Olympiad Tirana, May 7, 2016 Problem 1. Find all injective functions f : R R such that for every real number x and every positive integer n, n i f(x + i
Language: English The 33 rd Balkan Mathematical Olympiad Tirana, May 7, 2016 Problem 1. Find all injective functions f : R R such that for every real number x and every positive integer n, n i f(x + i
SOLUTIONS FOR IMO 2005 PROBLEMS
 SOLUTIONS FOR IMO 005 PROBLEMS AMIR JAFARI AND KASRA RAFI Problem. Six points are chosen on the sides of an equilateral triangle AB: A, A on B; B, B on A;, on AB. These points are the vertices of a convex
SOLUTIONS FOR IMO 005 PROBLEMS AMIR JAFARI AND KASRA RAFI Problem. Six points are chosen on the sides of an equilateral triangle AB: A, A on B; B, B on A;, on AB. These points are the vertices of a convex
Olimpiada Matemática de Centroamérica y el Caribe
 Olimpiada Matemática de Centroamérica y el Caribe 1st Centromerican 1999 Problem A1 A, B, C, D, E each has a unique piece of news. They make a series of phone calls to each other. In each call, the caller
Olimpiada Matemática de Centroamérica y el Caribe 1st Centromerican 1999 Problem A1 A, B, C, D, E each has a unique piece of news. They make a series of phone calls to each other. In each call, the caller
Some Basic Logic. Henry Liu, 25 October 2010
 Some Basic Logic Henry Liu, 25 October 2010 In the solution to almost every olympiad style mathematical problem, a very important part is existence of accurate proofs. Therefore, the student should be
Some Basic Logic Henry Liu, 25 October 2010 In the solution to almost every olympiad style mathematical problem, a very important part is existence of accurate proofs. Therefore, the student should be
EGMO 2016, Day 1 Solutions. Problem 1. Let n be an odd positive integer, and let x1, x2,..., xn be non-negative real numbers.
 EGMO 2016, Day 1 Solutions Problem 1. Let n be an odd positive integer, and let x1, x2,..., xn be non-negative real numbers. Show that min (x2i + x2i+1 ) max (2xj xj+1 ), j=1,...,n i=1,...,n where xn+1
EGMO 2016, Day 1 Solutions Problem 1. Let n be an odd positive integer, and let x1, x2,..., xn be non-negative real numbers. Show that min (x2i + x2i+1 ) max (2xj xj+1 ), j=1,...,n i=1,...,n where xn+1
34 th United States of America Mathematical Olympiad
 34 th United States of America Mathematical Olympiad 1. Determine all composite positive integers n for which it is possible to arrange all divisors of n that are greater than 1 in a circle so that no
34 th United States of America Mathematical Olympiad 1. Determine all composite positive integers n for which it is possible to arrange all divisors of n that are greater than 1 in a circle so that no
IMO Training Camp Mock Olympiad #2
 IMO Training Camp Mock Olympiad #2 July 3, 2008 1. Given an isosceles triangle ABC with AB = AC. The midpoint of side BC is denoted by M. Let X be a variable point on the shorter arc MA of the circumcircle
IMO Training Camp Mock Olympiad #2 July 3, 2008 1. Given an isosceles triangle ABC with AB = AC. The midpoint of side BC is denoted by M. Let X be a variable point on the shorter arc MA of the circumcircle
PURPLE COMET MATH MEET April 2012 MIDDLE SCHOOL - SOLUTIONS
 PURPLE COMET MATH MEET April 2012 MIDDLE SCHOOL - SOLUTIONS Copyright c Titu Andreescu and Jonathan Kane Problem 1 Evaluate 5 4 4 3 3 2 2 1 1 0. Answer: 549 The expression equals 625 64 9 2 1 = 549. Problem
PURPLE COMET MATH MEET April 2012 MIDDLE SCHOOL - SOLUTIONS Copyright c Titu Andreescu and Jonathan Kane Problem 1 Evaluate 5 4 4 3 3 2 2 1 1 0. Answer: 549 The expression equals 625 64 9 2 1 = 549. Problem
CHMMC 2015 Individual Round Problems
 CHMMC 05 Individual Round Problems November, 05 Problem 0.. The following number is the product of the divisors of n. What is n? 6 3 3 Solution.. In general, the product of the divisors of n is n # of
CHMMC 05 Individual Round Problems November, 05 Problem 0.. The following number is the product of the divisors of n. What is n? 6 3 3 Solution.. In general, the product of the divisors of n is n # of
T-2 In the equation A B C + D E F = G H I, each letter denotes a distinct non-zero digit. Compute the greatest possible value of G H I.
 2016 ARML Local Problems and Solutions Team Round Solutions T-1 All the shelves in a library are the same length. When filled, two shelves side-by-side can hold exactly 12 algebra books and 10 geometry
2016 ARML Local Problems and Solutions Team Round Solutions T-1 All the shelves in a library are the same length. When filled, two shelves side-by-side can hold exactly 12 algebra books and 10 geometry
HANOI OPEN MATHEMATICAL COMPETITON PROBLEMS
 HANOI MATHEMATICAL SOCIETY NGUYEN VAN MAU HANOI OPEN MATHEMATICAL COMPETITON PROBLEMS HANOI - 2013 Contents 1 Hanoi Open Mathematical Competition 3 1.1 Hanoi Open Mathematical Competition 2006... 3 1.1.1
HANOI MATHEMATICAL SOCIETY NGUYEN VAN MAU HANOI OPEN MATHEMATICAL COMPETITON PROBLEMS HANOI - 2013 Contents 1 Hanoi Open Mathematical Competition 3 1.1 Hanoi Open Mathematical Competition 2006... 3 1.1.1
MIDDLE SCHOOL - SOLUTIONS. is 1. = 3. Multiplying by 20n yields 35n + 24n + 20 = 60n, and, therefore, n = 20.
 PURPLE COMET! MATH MEET April 208 MIDDLE SCHOOL - SOLUTIONS Copyright c Titu Andreescu and Jonathan Kane Problem Find n such that the mean of 7 4, 6 5, and n is. Answer: 20 For the mean of three numbers
PURPLE COMET! MATH MEET April 208 MIDDLE SCHOOL - SOLUTIONS Copyright c Titu Andreescu and Jonathan Kane Problem Find n such that the mean of 7 4, 6 5, and n is. Answer: 20 For the mean of three numbers
SMT 2011 General Test and Solutions February 19, F (x) + F = 1 + x. 2 = 3. Now take x = 2 2 F ( 1) = F ( 1) = 3 2 F (2)
 SMT 0 General Test and Solutions February 9, 0 Let F () be a real-valued function defined for all real 0, such that ( ) F () + F = + Find F () Answer: Setting =, we find that F () + F ( ) = Now take =,
SMT 0 General Test and Solutions February 9, 0 Let F () be a real-valued function defined for all real 0, such that ( ) F () + F = + Find F () Answer: Setting =, we find that F () + F ( ) = Now take =,
Proofs Not Based On POMI
 s Not Based On POMI James K. Peterson Department of Biological Sciences and Department of Mathematical Sciences Clemson University February 12, 2018 Outline 1 Non POMI Based s 2 Some Contradiction s 3
s Not Based On POMI James K. Peterson Department of Biological Sciences and Department of Mathematical Sciences Clemson University February 12, 2018 Outline 1 Non POMI Based s 2 Some Contradiction s 3
XIX Asian Pacific Mathematics Olympiad
 XIX Asian Pacific Mathematics Olympiad Problem 1. Let S be a set of 9 distinct integers all of whose prime factors are at most 3. Prove that S contains 3 distinct integers such that their product is a
XIX Asian Pacific Mathematics Olympiad Problem 1. Let S be a set of 9 distinct integers all of whose prime factors are at most 3. Prove that S contains 3 distinct integers such that their product is a
SEQUENCES, MATHEMATICAL INDUCTION, AND RECURSION
 CHAPTER 5 SEQUENCES, MATHEMATICAL INDUCTION, AND RECURSION Copyright Cengage Learning. All rights reserved. SECTION 5.4 Strong Mathematical Induction and the Well-Ordering Principle for the Integers Copyright
CHAPTER 5 SEQUENCES, MATHEMATICAL INDUCTION, AND RECURSION Copyright Cengage Learning. All rights reserved. SECTION 5.4 Strong Mathematical Induction and the Well-Ordering Principle for the Integers Copyright
Baltic Way 2003 Riga, November 2, 2003
 altic Way 2003 Riga, November 2, 2003 Problems and solutions. Let Q + be the set of positive rational numbers. Find all functions f : Q + Q + which for all x Q + fulfil () f ( x ) = f (x) (2) ( + x ) f
altic Way 2003 Riga, November 2, 2003 Problems and solutions. Let Q + be the set of positive rational numbers. Find all functions f : Q + Q + which for all x Q + fulfil () f ( x ) = f (x) (2) ( + x ) f
Baltic Way 2008 Gdańsk, November 8, 2008
 Baltic Way 008 Gdańsk, November 8, 008 Problems and solutions Problem 1. Determine all polynomials p(x) with real coefficients such that p((x + 1) ) = (p(x) + 1) and p(0) = 0. Answer: p(x) = x. Solution:
Baltic Way 008 Gdańsk, November 8, 008 Problems and solutions Problem 1. Determine all polynomials p(x) with real coefficients such that p((x + 1) ) = (p(x) + 1) and p(0) = 0. Answer: p(x) = x. Solution:
1. Prove that for every positive integer n there exists an n-digit number divisible by 5 n all of whose digits are odd.
 32 nd United States of America Mathematical Olympiad Proposed Solutions May, 23 Remark: The general philosophy of this marking scheme follows that of IMO 22. This scheme encourages complete solutions.
32 nd United States of America Mathematical Olympiad Proposed Solutions May, 23 Remark: The general philosophy of this marking scheme follows that of IMO 22. This scheme encourages complete solutions.
The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca Euclid Contest. Tuesday, April 12, 2016
 The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca 016 Euclid Contest Tuesday, April 1, 016 (in North America and South America) Wednesday, April 13, 016 (outside of North America
The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca 016 Euclid Contest Tuesday, April 1, 016 (in North America and South America) Wednesday, April 13, 016 (outside of North America
CCSU Regional Math Competition, 2012 Part I
 CCSU Regional Math Competition, Part I Each problem is worth ten points. Please be sure to use separate pages to write your solution for every problem.. Find all real numbers r, with r, such that a -by-r
CCSU Regional Math Competition, Part I Each problem is worth ten points. Please be sure to use separate pages to write your solution for every problem.. Find all real numbers r, with r, such that a -by-r
PUTNAM TRAINING NUMBER THEORY. Exercises 1. Show that the sum of two consecutive primes is never twice a prime.
 PUTNAM TRAINING NUMBER THEORY (Last updated: December 11, 2017) Remark. This is a list of exercises on Number Theory. Miguel A. Lerma Exercises 1. Show that the sum of two consecutive primes is never twice
PUTNAM TRAINING NUMBER THEORY (Last updated: December 11, 2017) Remark. This is a list of exercises on Number Theory. Miguel A. Lerma Exercises 1. Show that the sum of two consecutive primes is never twice
40th International Mathematical Olympiad
 40th International Mathematical Olympiad Bucharest, Romania, July 999 Determine all finite sets S of at least three points in the plane which satisfy the following condition: for any two distinct points
40th International Mathematical Olympiad Bucharest, Romania, July 999 Determine all finite sets S of at least three points in the plane which satisfy the following condition: for any two distinct points
UAB MATH TALENT SEARCH
 NAME: GRADE: SCHOOL NAME: 2011-2012 UAB MATH TALENT SEARCH This is a two hour contest. Answers are to be written in the spaces provided on the test sheet. There will be no credit if the answer is incorrect.
NAME: GRADE: SCHOOL NAME: 2011-2012 UAB MATH TALENT SEARCH This is a two hour contest. Answers are to be written in the spaces provided on the test sheet. There will be no credit if the answer is incorrect.
International Mathematics TOURNAMENT OF THE TOWNS
 International Mathematics TOURNAMENT OF THE TOWNS Senior A-Level Paper Fall 2008. 1. A standard 8 8 chessboard is modified by varying the distances between parallel grid lines, so that the cells are rectangles
International Mathematics TOURNAMENT OF THE TOWNS Senior A-Level Paper Fall 2008. 1. A standard 8 8 chessboard is modified by varying the distances between parallel grid lines, so that the cells are rectangles
The Alberta High School Mathematics Competition Solution to Part I, 2014.
 The Alberta High School Mathematics Competition Solution to Part I, 2014. Question 1. When the repeating decimal 0.6 is divided by the repeating decimal 0.3, the quotient is (a) 0.2 (b) 2 (c) 0.5 (d) 0.5
The Alberta High School Mathematics Competition Solution to Part I, 2014. Question 1. When the repeating decimal 0.6 is divided by the repeating decimal 0.3, the quotient is (a) 0.2 (b) 2 (c) 0.5 (d) 0.5
2013 Grade 9 Mathematics Set A
 2013 Grade 9 Mathematics Set A Copyright National Institute for Educational Policy Reserch All Right Reserved URL: https://www.nier.go.jp/english/index.html The English translation is prepared by the Project
2013 Grade 9 Mathematics Set A Copyright National Institute for Educational Policy Reserch All Right Reserved URL: https://www.nier.go.jp/english/index.html The English translation is prepared by the Project
A Readable Introduction to Real Mathematics
 Solutions to selected problems in the book A Readable Introduction to Real Mathematics D. Rosenthal, D. Rosenthal, P. Rosenthal Chapter 7: The Euclidean Algorithm and Applications 1. Find the greatest
Solutions to selected problems in the book A Readable Introduction to Real Mathematics D. Rosenthal, D. Rosenthal, P. Rosenthal Chapter 7: The Euclidean Algorithm and Applications 1. Find the greatest
2015 Canadian Team Mathematics Contest
 The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca 205 Canadian Team Mathematics Contest April 205 Solutions 205 University of Waterloo 205 CTMC Solutions Page 2 Individual Problems.
The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca 205 Canadian Team Mathematics Contest April 205 Solutions 205 University of Waterloo 205 CTMC Solutions Page 2 Individual Problems.
SOLUTIONS TO PROBLEM SET 1. Section = 2 3, 1. n n + 1. k(k + 1) k=1 k(k + 1) + 1 (n + 1)(n + 2) n + 2,
 SOLUTIONS TO PROBLEM SET 1 Section 1.3 Exercise 4. We see that 1 1 2 = 1 2, 1 1 2 + 1 2 3 = 2 3, 1 1 2 + 1 2 3 + 1 3 4 = 3 4, and is reasonable to conjecture n k=1 We will prove this formula by induction.
SOLUTIONS TO PROBLEM SET 1 Section 1.3 Exercise 4. We see that 1 1 2 = 1 2, 1 1 2 + 1 2 3 = 2 3, 1 1 2 + 1 2 3 + 1 3 4 = 3 4, and is reasonable to conjecture n k=1 We will prove this formula by induction.
Syllabus for Grade 7. More details on each of the topics is covered in the following pages.
 Syllabus for Grade 7 Chapter 1 Algebraic Reasoning Chapter 2 Integers and rational numbers Chapter 3 Number Theory Chapter 4 Rational number Chapter 5 Patterns and functions Chapter 6 Proportional Relationships
Syllabus for Grade 7 Chapter 1 Algebraic Reasoning Chapter 2 Integers and rational numbers Chapter 3 Number Theory Chapter 4 Rational number Chapter 5 Patterns and functions Chapter 6 Proportional Relationships
Basic Proof Examples
 Basic Proof Examples Lisa Oberbroeckling Loyola University Maryland Fall 2015 Note. In this document, we use the symbol as the negation symbol. Thus p means not p. There are four basic proof techniques
Basic Proof Examples Lisa Oberbroeckling Loyola University Maryland Fall 2015 Note. In this document, we use the symbol as the negation symbol. Thus p means not p. There are four basic proof techniques
COT 2104 Homework Assignment 1 (Answers)
 1) Classify true or false COT 2104 Homework Assignment 1 (Answers) a) 4 2 + 2 and 7 < 50. False because one of the two statements is false. b) 4 = 2 + 2 7 < 50. True because both statements are true. c)
1) Classify true or false COT 2104 Homework Assignment 1 (Answers) a) 4 2 + 2 and 7 < 50. False because one of the two statements is false. b) 4 = 2 + 2 7 < 50. True because both statements are true. c)
20th Bay Area Mathematical Olympiad. BAMO 2018 Problems and Solutions. February 27, 2018
 20th Bay Area Mathematical Olympiad BAMO 201 Problems and Solutions The problems from BAMO- are A E, and the problems from BAMO-12 are 1 5. February 27, 201 A Twenty-five people of different heights stand
20th Bay Area Mathematical Olympiad BAMO 201 Problems and Solutions The problems from BAMO- are A E, and the problems from BAMO-12 are 1 5. February 27, 201 A Twenty-five people of different heights stand
First selection test. a n = 3n + n 2 1. b n = 2( n 2 + n + n 2 n),
 First selection test Problem. Find the positive real numbers a, b, c which satisfy the inequalities 4(ab + bc + ca) a 2 + b 2 + c 2 3(a 3 + b 3 + c 3 ). Laurenţiu Panaitopol Problem 2. Consider the numbers
First selection test Problem. Find the positive real numbers a, b, c which satisfy the inequalities 4(ab + bc + ca) a 2 + b 2 + c 2 3(a 3 + b 3 + c 3 ). Laurenţiu Panaitopol Problem 2. Consider the numbers
Fundamentals of Pure Mathematics - Problem Sheet
 Fundamentals of Pure Mathematics - Problem Sheet ( ) = Straightforward but illustrates a basic idea (*) = Harder Note: R, Z denote the real numbers, integers, etc. assumed to be real numbers. In questions
Fundamentals of Pure Mathematics - Problem Sheet ( ) = Straightforward but illustrates a basic idea (*) = Harder Note: R, Z denote the real numbers, integers, etc. assumed to be real numbers. In questions
Solutions to CRMO-2003
 Solutions to CRMO-003 1. Let ABC be a triangle in which AB AC and CAB 90. Suppose M and N are points on the hypotenuse BC such that BM + CN MN. Prove that MAN 45. Solution: Draw CP perpendicular to CB
Solutions to CRMO-003 1. Let ABC be a triangle in which AB AC and CAB 90. Suppose M and N are points on the hypotenuse BC such that BM + CN MN. Prove that MAN 45. Solution: Draw CP perpendicular to CB
The Advantage Testing Foundation Olympiad Solutions
 The Advantage Testing Foundation 015 Olympiad Problem 1 Prove that every positive integer has a unique representation in the form d i i, where k is a nonnegative integer and each d i is either 1 or. (This
The Advantage Testing Foundation 015 Olympiad Problem 1 Prove that every positive integer has a unique representation in the form d i i, where k is a nonnegative integer and each d i is either 1 or. (This
32 nd United States of America Mathematical Olympiad Recommended Marking Scheme May 1, 2003
 32 nd United States of America Mathematical Olympiad Recommended Marking Scheme May 1, 23 Remark: The general philosophy of this marking scheme follows that of IMO 22. This scheme encourages complete solutions.
32 nd United States of America Mathematical Olympiad Recommended Marking Scheme May 1, 23 Remark: The general philosophy of this marking scheme follows that of IMO 22. This scheme encourages complete solutions.
Australian Intermediate Mathematics Olympiad 2014
 5. Let 1 a + 1 b = 1 20, where a and b are positive integers. Find the largest value of a + b. [4 marks] A u s t r a l i a n M at h e m at i c a l O ly m p i a d C o m m i t t e e a d e p a r t m e n t
5. Let 1 a + 1 b = 1 20, where a and b are positive integers. Find the largest value of a + b. [4 marks] A u s t r a l i a n M at h e m at i c a l O ly m p i a d C o m m i t t e e a d e p a r t m e n t
2003 AIME Given that ((3!)!)! = k n!, where k and n are positive integers and n is as large as possible, find k + n.
 003 AIME 1 Given that ((3!)!)! = k n!, where k and n are positive integers and n is as large 3! as possible, find k + n One hundred concentric circles with radii 1,, 3,, 100 are drawn in a plane The interior
003 AIME 1 Given that ((3!)!)! = k n!, where k and n are positive integers and n is as large 3! as possible, find k + n One hundred concentric circles with radii 1,, 3,, 100 are drawn in a plane The interior
PUTNAM TRAINING EASY PUTNAM PROBLEMS
 PUTNAM TRAINING EASY PUTNAM PROBLEMS (Last updated: September 24, 2018) Remark. This is a list of exercises on Easy Putnam Problems Miguel A. Lerma Exercises 1. 2017-A1. Let S be the smallest set of positive
PUTNAM TRAINING EASY PUTNAM PROBLEMS (Last updated: September 24, 2018) Remark. This is a list of exercises on Easy Putnam Problems Miguel A. Lerma Exercises 1. 2017-A1. Let S be the smallest set of positive
CANADIAN MATHEMATICAL OLYMPIAD 2010 PROBLEMS AND SOLUTIONS
 CANADIAN MATHEMATICAL OLYMPIAD 2010 PROBLEMS AND SOLUTIONS (1) For a positive integer n, an n-staircase is a figure consisting of unit squares, with one square in the first row, two squares in the second
CANADIAN MATHEMATICAL OLYMPIAD 2010 PROBLEMS AND SOLUTIONS (1) For a positive integer n, an n-staircase is a figure consisting of unit squares, with one square in the first row, two squares in the second
Know the Well-ordering principle: Any set of positive integers which has at least one element contains a smallest element.
 The first exam will be on Monday, June 8, 202. The syllabus will be sections. and.2 in Lax, and the number theory handout found on the class web site, plus the handout on the method of successive squaring
The first exam will be on Monday, June 8, 202. The syllabus will be sections. and.2 in Lax, and the number theory handout found on the class web site, plus the handout on the method of successive squaring
Proofs Not Based On POMI
 s Not Based On POMI James K. Peterson Department of Biological Sciences and Department of Mathematical Sciences Clemson University February 1, 018 Outline Non POMI Based s Some Contradiction s Triangle
s Not Based On POMI James K. Peterson Department of Biological Sciences and Department of Mathematical Sciences Clemson University February 1, 018 Outline Non POMI Based s Some Contradiction s Triangle
Individual Round CHMMC November 20, 2016
 Individual Round CHMMC 20 November 20, 20 Problem. We say that d k d k d d 0 represents the number n in base 2 if each d i is either 0 or, and n d k ( 2) k + d k ( 2) k + + d ( 2) + d 0. For example, 0
Individual Round CHMMC 20 November 20, 20 Problem. We say that d k d k d d 0 represents the number n in base 2 if each d i is either 0 or, and n d k ( 2) k + d k ( 2) k + + d ( 2) + d 0. For example, 0
BRITISH COLUMBIA SECONDARY SCHOOL MATHEMATICS CONTEST,
 BRITISH COLUMBIA SECONDARY SCHOOL MATHEMATICS CONTEST, 014 Solutions Junior Preliminary 1. Rearrange the sum as (014 + 01 + 010 + + ) (013 + 011 + 009 + + 1) = (014 013) + (01 011) + + ( 1) = 1 + 1 + +
BRITISH COLUMBIA SECONDARY SCHOOL MATHEMATICS CONTEST, 014 Solutions Junior Preliminary 1. Rearrange the sum as (014 + 01 + 010 + + ) (013 + 011 + 009 + + 1) = (014 013) + (01 011) + + ( 1) = 1 + 1 + +
40th Canadian Mathematical Olympiad
 40th Canadian Mathematical Olympiad Wednesday, March 26, 2008 Solutions - CMO 2008 1. ABCD is a convex quadrilateral in which AB is the longest side. Points M and N are located on sides AB and BC respectively,
40th Canadian Mathematical Olympiad Wednesday, March 26, 2008 Solutions - CMO 2008 1. ABCD is a convex quadrilateral in which AB is the longest side. Points M and N are located on sides AB and BC respectively,
Vermont Talent Search April 12, 2011 School Year Test 4 Solutions
 Vermont Talent Search April, 0 School Year 00-0 Test 4 Solutions Problem. Find the area of a triangle whose medians have lengths of 39, 4 and 45. Let M be the center of gravity or centroid of the triangle.
Vermont Talent Search April, 0 School Year 00-0 Test 4 Solutions Problem. Find the area of a triangle whose medians have lengths of 39, 4 and 45. Let M be the center of gravity or centroid of the triangle.
HMMT November 2015 November 14, 2015
 HMMT November 05 November, 05 Guts round. [5] Farmer Yang has a 05 05 square grid of corn plants. One day, the plant in the very center of the grid becomes diseased. Every day, every plant adjacent to
HMMT November 05 November, 05 Guts round. [5] Farmer Yang has a 05 05 square grid of corn plants. One day, the plant in the very center of the grid becomes diseased. Every day, every plant adjacent to
NAME: Mathematics 133, Fall 2013, Examination 3
 NAME: Mathematics 133, Fall 2013, Examination 3 INSTRUCTIONS: Work all questions, and unless indicated otherwise give reasons for your answers. If the problem does not explicitly state that the underlying
NAME: Mathematics 133, Fall 2013, Examination 3 INSTRUCTIONS: Work all questions, and unless indicated otherwise give reasons for your answers. If the problem does not explicitly state that the underlying
HANOI OPEN MATHEMATICS COMPETITON PROBLEMS
 HANOI MATHEMATICAL SOCIETY NGUYEN VAN MAU HANOI OPEN MATHEMATICS COMPETITON PROBLEMS 2006-2013 HANOI - 2013 Contents 1 Hanoi Open Mathematics Competition 3 1.1 Hanoi Open Mathematics Competition 2006...
HANOI MATHEMATICAL SOCIETY NGUYEN VAN MAU HANOI OPEN MATHEMATICS COMPETITON PROBLEMS 2006-2013 HANOI - 2013 Contents 1 Hanoi Open Mathematics Competition 3 1.1 Hanoi Open Mathematics Competition 2006...
Solutions to Practice Final
 s to Practice Final 1. (a) What is φ(0 100 ) where φ is Euler s φ-function? (b) Find an integer x such that 140x 1 (mod 01). Hint: gcd(140, 01) = 7. (a) φ(0 100 ) = φ(4 100 5 100 ) = φ( 00 5 100 ) = (
s to Practice Final 1. (a) What is φ(0 100 ) where φ is Euler s φ-function? (b) Find an integer x such that 140x 1 (mod 01). Hint: gcd(140, 01) = 7. (a) φ(0 100 ) = φ(4 100 5 100 ) = φ( 00 5 100 ) = (
2016 Canadian Intermediate Mathematics Contest
 The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca 2016 Canadian Intermediate Mathematics Contest Wednesday, November 23, 2016 (in North America and South America) Thursday, November
The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca 2016 Canadian Intermediate Mathematics Contest Wednesday, November 23, 2016 (in North America and South America) Thursday, November
MATH 271 Summer 2016 Practice problem solutions Week 1
 Part I MATH 271 Summer 2016 Practice problem solutions Week 1 For each of the following statements, determine whether the statement is true or false. Prove the true statements. For the false statement,
Part I MATH 271 Summer 2016 Practice problem solutions Week 1 For each of the following statements, determine whether the statement is true or false. Prove the true statements. For the false statement,
Number Theory Notes Spring 2011
 PRELIMINARIES The counting numbers or natural numbers are 1, 2, 3, 4, 5, 6.... The whole numbers are the counting numbers with zero 0, 1, 2, 3, 4, 5, 6.... The integers are the counting numbers and zero
PRELIMINARIES The counting numbers or natural numbers are 1, 2, 3, 4, 5, 6.... The whole numbers are the counting numbers with zero 0, 1, 2, 3, 4, 5, 6.... The integers are the counting numbers and zero
Math Day at the Beach 2017 Solutions
 Math Day at the Beach 07 Solutions Mike Bao, Brendan Brzycki, Benjamin Chen, Samuel Cui, Michael Diao, Ayush Kamat, Emma Qin, Jack Sun, Jason Ye, Xuyang Yu, Beckman Math Club Individual Round Problem.
Math Day at the Beach 07 Solutions Mike Bao, Brendan Brzycki, Benjamin Chen, Samuel Cui, Michael Diao, Ayush Kamat, Emma Qin, Jack Sun, Jason Ye, Xuyang Yu, Beckman Math Club Individual Round Problem.
REMARKS 7.6: Let G be a finite group of order n. Then Lagrange's theorem shows that the order of every subgroup of G divides n; equivalently, if k is
 FIRST-YEAR GROUP THEORY 7 LAGRANGE'S THEOREM EXAMPLE 7.1: Set G = D 3, where the elements of G are denoted as usual by e, a, a 2, b, ab, a 2 b. Let H be the cyclic subgroup of G generated by b; because
FIRST-YEAR GROUP THEORY 7 LAGRANGE'S THEOREM EXAMPLE 7.1: Set G = D 3, where the elements of G are denoted as usual by e, a, a 2, b, ab, a 2 b. Let H be the cyclic subgroup of G generated by b; because
NEW YORK CITY INTERSCHOLASTIC MATHEMATICS LEAGUE Senior A Division CONTEST NUMBER 1
 Senior A Division CONTEST NUMBER 1 PART I FALL 2011 CONTEST 1 TIME: 10 MINUTES F11A1 Larry selects a 13-digit number while David selects a 10-digit number. Let be the number of digits in the product of
Senior A Division CONTEST NUMBER 1 PART I FALL 2011 CONTEST 1 TIME: 10 MINUTES F11A1 Larry selects a 13-digit number while David selects a 10-digit number. Let be the number of digits in the product of
S Group Events G1 a 47 G2 a *2
 Answers: (003-0 HKMO Final Events) Created by: Mr. Francis Hung Last updated: 9 September 07 Individual Events I a 6 I P I3 a I a IS P 8 b + Q 6 b 9 b Q 8 c 7 R 6 c d S 3 d c 6 R 7 8 d *33 3 see the remark
Answers: (003-0 HKMO Final Events) Created by: Mr. Francis Hung Last updated: 9 September 07 Individual Events I a 6 I P I3 a I a IS P 8 b + Q 6 b 9 b Q 8 c 7 R 6 c d S 3 d c 6 R 7 8 d *33 3 see the remark
1) Exercise 1 In the diagram, ABC = AED, AD = 3, DB = 2 and AE = 2. Determine the length of EC. Solution:
 1) Exercise 1 In the diagram, ABC = AED, AD = 3, DB = 2 and AE = 2. Determine the length of EC. Solution: First, we show that AED and ABC are similar. Since DAE = BAC and ABC = AED, we have that AED is
1) Exercise 1 In the diagram, ABC = AED, AD = 3, DB = 2 and AE = 2. Determine the length of EC. Solution: First, we show that AED and ABC are similar. Since DAE = BAC and ABC = AED, we have that AED is
DISCUSSION CLASS OF DAX IS ON 22ND MARCH, TIME : 9-12 BRING ALL YOUR DOUBTS [STRAIGHT OBJECTIVE TYPE]
![DISCUSSION CLASS OF DAX IS ON 22ND MARCH, TIME : 9-12 BRING ALL YOUR DOUBTS [STRAIGHT OBJECTIVE TYPE] DISCUSSION CLASS OF DAX IS ON 22ND MARCH, TIME : 9-12 BRING ALL YOUR DOUBTS [STRAIGHT OBJECTIVE TYPE]](/thumbs/90/102188445.jpg) DISCUSSION CLASS OF DAX IS ON ND MARCH, TIME : 9- BRING ALL YOUR DOUBTS [STRAIGHT OBJECTIVE TYPE] Q. Let y = cos x (cos x cos x). Then y is (A) 0 only when x 0 (B) 0 for all real x (C) 0 for all real x
DISCUSSION CLASS OF DAX IS ON ND MARCH, TIME : 9- BRING ALL YOUR DOUBTS [STRAIGHT OBJECTIVE TYPE] Q. Let y = cos x (cos x cos x). Then y is (A) 0 only when x 0 (B) 0 for all real x (C) 0 for all real x
15th Bay Area Mathematical Olympiad. BAMO Exam. February 26, Solutions to BAMO-8 and BAMO-12 Problems
 15th Bay Area Mathematical Olympiad BAMO Exam February 26, 2013 Solutions to BAMO-8 and BAMO-12 Problems 1 How many different sets of three points in this equilateral triangular grid are the vertices of
15th Bay Area Mathematical Olympiad BAMO Exam February 26, 2013 Solutions to BAMO-8 and BAMO-12 Problems 1 How many different sets of three points in this equilateral triangular grid are the vertices of
CHAPTER 1 POLYNOMIALS
 1 CHAPTER 1 POLYNOMIALS 1.1 Removing Nested Symbols of Grouping Simplify. 1. 4x + 3( x ) + 4( x + 1). ( ) 3x + 4 5 x 3 + x 3. 3 5( y 4) + 6 y ( y + 3) 4. 3 n ( n + 5) 4 ( n + 8) 5. ( x + 5) x + 3( x 6)
1 CHAPTER 1 POLYNOMIALS 1.1 Removing Nested Symbols of Grouping Simplify. 1. 4x + 3( x ) + 4( x + 1). ( ) 3x + 4 5 x 3 + x 3. 3 5( y 4) + 6 y ( y + 3) 4. 3 n ( n + 5) 4 ( n + 8) 5. ( x + 5) x + 3( x 6)
Australian Intermediate Mathematics Olympiad 2016
 Australian Intermediate Mathematics Olympiad 06 Questions. Find the smallest positive integer x such that x = 5y, where y is a positive integer. [ marks]. A 3-digit number in base 7 is also a 3-digit number
Australian Intermediate Mathematics Olympiad 06 Questions. Find the smallest positive integer x such that x = 5y, where y is a positive integer. [ marks]. A 3-digit number in base 7 is also a 3-digit number
2018 LEHIGH UNIVERSITY HIGH SCHOOL MATH CONTEST
 08 LEHIGH UNIVERSITY HIGH SCHOOL MATH CONTEST. A right triangle has hypotenuse 9 and one leg. What is the length of the other leg?. Don is /3 of the way through his run. After running another / mile, he
08 LEHIGH UNIVERSITY HIGH SCHOOL MATH CONTEST. A right triangle has hypotenuse 9 and one leg. What is the length of the other leg?. Don is /3 of the way through his run. After running another / mile, he
Unofficial Solutions
 Canadian Open Mathematics Challenge 2016 Unofficial Solutions COMC exams from other years, with or without the solutions included, are free to download online. Please visit http://comc.math.ca/2016/practice.html
Canadian Open Mathematics Challenge 2016 Unofficial Solutions COMC exams from other years, with or without the solutions included, are free to download online. Please visit http://comc.math.ca/2016/practice.html
The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca Cayley Contest. (Grade 10) Tuesday, February 27, 2018
 The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca 018 Cayley Contest (Grade 10) Tuesday, February 7, 018 (in North America and South America) Wednesday, February 8, 018 (outside of
The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca 018 Cayley Contest (Grade 10) Tuesday, February 7, 018 (in North America and South America) Wednesday, February 8, 018 (outside of
the coordinates of C (3) Find the size of the angle ACB. Give your answer in degrees to 2 decimal places. (4)
 . The line l has equation, 2 4 3 2 + = λ r where λ is a scalar parameter. The line l 2 has equation, 2 0 5 3 9 0 + = µ r where μ is a scalar parameter. Given that l and l 2 meet at the point C, find the
. The line l has equation, 2 4 3 2 + = λ r where λ is a scalar parameter. The line l 2 has equation, 2 0 5 3 9 0 + = µ r where μ is a scalar parameter. Given that l and l 2 meet at the point C, find the
1 2n. i=1. 2m+1 i = m, while. 2m + 1 = 1. is the best possible for any odd n.
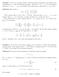 Problem 1. Let n be a positive integer. Find the largest nonnegative real number f(n) (depending on n) with the following property: whenever a 1, a,..., a n are real numbers such that a 1 + a + + a n is
Problem 1. Let n be a positive integer. Find the largest nonnegative real number f(n) (depending on n) with the following property: whenever a 1, a,..., a n are real numbers such that a 1 + a + + a n is
Proof 1: Using only ch. 6 results. Since gcd(a, b) = 1, we have
 Exercise 13. Consider positive integers a, b, and c. (a) Suppose gcd(a, b) = 1. (i) Show that if a divides the product bc, then a must divide c. I give two proofs here, to illustrate the different methods.
Exercise 13. Consider positive integers a, b, and c. (a) Suppose gcd(a, b) = 1. (i) Show that if a divides the product bc, then a must divide c. I give two proofs here, to illustrate the different methods.
2017 Canadian Team Mathematics Contest
 The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca 017 Canadian Team Mathematics Contest April 017 Solutions 017 University of Waterloo 017 CTMC Solutions Page Individual Problems
The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca 017 Canadian Team Mathematics Contest April 017 Solutions 017 University of Waterloo 017 CTMC Solutions Page Individual Problems
LAMC Beginners Circle November 10, Oleg Gleizer. Warm-up
 LAMC Beginners Circle November 10, 2013 Oleg Gleizer oleg1140@gmail.com Warm-up Problem 1 Can a power of two (a number of the form 2 n ) have all the decimal digits 0, 1,..., 9 the same number of times?
LAMC Beginners Circle November 10, 2013 Oleg Gleizer oleg1140@gmail.com Warm-up Problem 1 Can a power of two (a number of the form 2 n ) have all the decimal digits 0, 1,..., 9 the same number of times?
This class will demonstrate the use of bijections to solve certain combinatorial problems simply and effectively.
 . Induction This class will demonstrate the fundamental problem solving technique of mathematical induction. Example Problem: Prove that for every positive integer n there exists an n-digit number divisible
. Induction This class will demonstrate the fundamental problem solving technique of mathematical induction. Example Problem: Prove that for every positive integer n there exists an n-digit number divisible
a 2 + b 2 = (p 2 q 2 ) 2 + 4p 2 q 2 = (p 2 + q 2 ) 2 = c 2,
 5.3. Pythagorean triples Definition. A Pythagorean triple is a set (a, b, c) of three integers such that (in order) a 2 + b 2 c 2. We may as well suppose that all of a, b, c are non-zero, and positive.
5.3. Pythagorean triples Definition. A Pythagorean triple is a set (a, b, c) of three integers such that (in order) a 2 + b 2 c 2. We may as well suppose that all of a, b, c are non-zero, and positive.
2 13b + 37 = 54, 13b 37 = 16, no solution
 Answers: (999-00 HKMO Final Events) Created by: Mr. Francis Hung Last updated: 6 February 07 Individual Events SI P 6 I P 5 I P 6 I P I P I5 P Q 7 Q 8 Q 8 Q Q Q R R 7 R R 996 R R S 990 S 6 S S 666 S S
Answers: (999-00 HKMO Final Events) Created by: Mr. Francis Hung Last updated: 6 February 07 Individual Events SI P 6 I P 5 I P 6 I P I P I5 P Q 7 Q 8 Q 8 Q Q Q R R 7 R R 996 R R S 990 S 6 S S 666 S S
Chapter 8. Introduction to Number Theory
 Chapter 8 Introduction to Number Theory CRYPTOGRAPHY AND NETWORK SECURITY 1 Index 1. Prime Numbers 2. Fermat`s and Euler`s Theorems 3. Testing for Primality 4. Discrete Logarithms 2 Prime Numbers 3 Prime
Chapter 8 Introduction to Number Theory CRYPTOGRAPHY AND NETWORK SECURITY 1 Index 1. Prime Numbers 2. Fermat`s and Euler`s Theorems 3. Testing for Primality 4. Discrete Logarithms 2 Prime Numbers 3 Prime
