First selection test. a n = 3n + n 2 1. b n = 2( n 2 + n + n 2 n),
|
|
|
- Gwendoline Osborne
- 5 years ago
- Views:
Transcription
1 First selection test Problem. Find the positive real numbers a, b, c which satisfy the inequalities 4(ab + bc + ca) a 2 + b 2 + c 2 3(a 3 + b 3 + c 3 ). Laurenţiu Panaitopol Problem 2. Consider the numbers and for all n =, 2,..., 49. a n = 3n + n 2 b n = 2( n 2 + n + n 2 n), Prove that there are integers A, B so that a b + a 2 b a n b n = A + B 2. Titu Andreescu Problem 3. Consider a circle of center O and V a point outside the circle. The tangents from V touch the circle at points T, T 2. Let T be a point on the small arc T T 2 of the circle. The tangent at T intersects the line V T in the point A and the lines T T and V T 2 intersect in the point B. Let M be the intersection point of the lines OM and AB. Prove that lines OM and AB are perpendicular. Mircea Fianu Problem 4. Consider a cube and let M, N be two of its vertices. Assign the number to these vertices and 0 to the other six vertices. We are allowed to select a vertex and to increase with a unit the numbers assigned to the 3 adjiacent vertices - call this a movement. Prove that there is a sequence of movements after which all the numbers assigned to the vertices of the cube became equal if and only if MN is not a diagonal of a face of the cube. Marius Ghergu, Dinu Şerbănescu
2 2 Second selection test Problem 5. Let ABC be an acute triangle and let D be a point on the side BC. Points E and F are the projections of the point D on the sides AB and AC, respectively. Lines BF and CE meet at point P. Prove that AD is the bisector line of the angle BAC if and only if lines AP and BC are perpendicular. Sever Moldoveanu Problem 6. An array 8 8 consists of 64 unit squares. Inside each square are written the numbers or so that in any 2 2 subarray the sum of the four numbers equals 2 or 2. Prove that there exist two rows of the array which are equal. Marius Ghergu Problem 7. Consider a triangle ABC with the side lenghts a, b, c so that a is the greatest. Prove that the triangle is rightangled if and only if ( a + b + a b)( a + c + a c) = (a + b + c) 2. Virgil Nicula Problem 8. Find all positive integers n for which there are distinct integer numbers a, a 2,..., a n such that n = a + a a n. a a 2 a n 2 Dinu Şerbănescu
3 3 Third selection test Problem 9. In a chess tournament each of the players have played with all the others two games, one time with the white pieces and then with the black pieces. In each game the winners gets one point and both players receive 0.5 points if the game ends with a draw. At the end of the tournament, all the players end with the same number of points. a) Prove that there are two players with the same number of draws. b) Prove that there are two players with the same number of losses when playing the white. Marius Ghergu Problem 0. Consider the triangle ABC with AB = AC and a variable point M on the line BC so that B is between M and C. Prove that the sum between the inradius of AMB and the exradius of AMC corresponding to the angle M is constant. Problem. Let p, q, r be primes and let n be a positive integer such that Prove that n =. p n + q n = r 2. Problem 2. Let a < b c < d be positive integers so that ad = bc and d a. Prove that a is a square. Virgil Nicula Laurenţiu Panaitopol Dinu Şerbănescu
4 4 Fourth selection test Problem 3. Let ABC be a triangle inscribed in the circle K and consider a point M on the arc BC that do not contain A. The tangents from M to the incircle of ABC intersect the circle K at the points N and P. Prove that if BAC = N M P, then triangles ABC and M N P are congruent. Problem 4. The real numbers a, a 2,..., a n satisfy the relation Prove that a k 0, for all k =, 2, a 2 + a a (a + a a 00 ) 2 = 0. Valentin Vornicu Dinu Şerbănescu Problem 5. A finite set of positive integers is called isolated if the sum of the elements in any proper subset is a number relatively prime with the sum of the elements of the isolated set. Find all nonprime integers n for which there exist positive integers a, b so that the set A = {(a + b) 2, (a + 2b) 2,..., (a + nb) 2 } is isolated. Gabriel Dospinescu Problem 6. A regular polygon with 000 sides has the vertices colored in red, yellow or blue. A move consists in choosing to adjiacent vertices colored differently and coloring them in the third color. Prove that there is a sequence of moves after which all the vertices of the polygon will have the same color. Marius Ghergu
5 5 Problem 7. Consider the triangular array Fifth selection test defined by the conditions: i) on the first two rows, each element starting with the third is the sum of the two preceding elements; ii) on the other rows each element is the sum of the two elements placed above of the same column. a) Prove that all the rows are defined according to condition i). b) Consider 4 consecutive rows and let a, b, c, d be the first element in each of these rows, respectively. Find d in terms of a, b and c. Dinu Şerbănescu Problem 8. Let M, N, P be the midpoints of the sides BC, CA, AB of the triangle ABC, respectively, and let G be the centroid of the triangle. Prove that if BMGP is cyclic and 2BN = 3AB, then triangle ABC is equilateral. Problem 9. Let A be a set of positive integers with the properties: i) if a A, then all positive divisors of a are elements of A; ii) if a, b A and < a < b, then + ab A. Prove that if the set A has at least 3 elements, then A = N. BMO shortlist 2004 Valentin Vornicu Problem 20. Consider a convex polygon with n 5 sides. Prove that there are at most n(2n 5) 3 triangles of area with the vertices among the vertices of the polygon. Andrei Neguţ
6 6 FORMAL SOLUTIONS Solution to problem. Using the Chebyshev inequality we derive hence a + b + c. On the other hand, therefore ab + bc + ca. As (a + b + c)(a 2 + b 2 + c 2 ) 3(a 3 + b 3 + c 3 ), 4(ab + bc + ca) a 2 + b 2 + c 2 ab + bc + ca, 3(ab + bc + ca) (a + b + c) 2, we obtain a + b + c, thus a + b + c =. Consequently, a + b + c = and 3(ab + bc + ca) = (a + b + c) 2, which imply a = b = c = 3. Solution to problem 2. The key idea is to observe that a n b n = 2 ( n 2 n + n + ) 2. As 2 n n + n, it follows that the sum is Solution to problem 3. The approach of the problem is to see no circles in the figure. Instead, recall that a quadrilateral ABCD is orthogonal if and only if () AB 2 + CD 2 = AD 2 + BC 2. Using succesively the Pytagoras theorem we have BA 2 BT 2 2 = BA 2 (BO 2 OT 2 2 ) = BA 2 (BO 2 OT 2 ) = BA 2 (BA 2 AT 2 ) = AT 2 = AO 2 OT 2 = OA 2 OT 2 2, so the conclusion follows from the relation (). Solution to problem 4. Color the 8 vertices of the cube in black or white so that the 4 vertices of the 2 regular tetrahedrons have the same color; notice that the 3 vertices adjiacent to a vertex have its opposite color. Therefore, each movement increase the sum of the numbers assingned to the vertices sharing the same color by 3. Consider the cases: ) MN is a diagonal of a face of the cube. Then M and N have the same color, say black.assume by contradiction that there is a sequence of movements after which the same number n is assigned to all the vertices. Let k and k 2 be the number of white, respectively black vertices that were selected to perform the movements.then 4n = 3k + 2 = 3k 2, a contradiction.
7 7 2) MN is a diagonal of the cube. Selecting the vertices M, then N, and performing these 2 movements, to all the vertices the number will be assigned, as needed. 3) MN is a side of the cube. The same outcome as in the previous case will occur after 2 movements when selecting the diagonally opposite vertices of M and N. This provides us with a full solution. Solution to problem 5. Let a, b, c, x.y be the lengths of the sides BC, CA, AB, BD, DC, respectively and let A be the foot of the altitude from A in the triangle ABC. Notice that x + y = a. Due to Ceva theorem the claim is equivalent to BD DC CF F A AE EB = AB AC = BD DC. As CF = y cos C, F A = b y cos C, BE = x cos B, AE = c x cos B, BA = c cos B and A C = b cos C, the equivalence rewrites cy(c x cos B) = bx(b y cos C) xb = cy. Indeed, we have c 2 y cxy a2 + c 2 b 2 = b 2 x bxy a2 + b 2 c 2 2ac 2ab a(c 2 y b 2 x) = xy(c 2 b 2 ) c 2 y(a x) = b 2 x(a y) c 2 y 2 = b 2 x 2 cy = bx, as claimed. Solution to problem 6. The main idea is to observe that two consecutive rows have exactly 4 equal elements, namely those lying on the columns, 3, 5, 7 or 2, 4, 6, 8. Moreover, on the other 4 columns the elements are different. Wlog, assume that rows and 2 are equal with respect to the columns, 3, 5, 7 and different on the column 2, 4, 6, 8; we call these rows odd equal. If rows 2 and 3 are also odd equal, then rows and 3 are equal, as needed. If not, then rows 2 and 3 are even equal. Now consider the rows 3 and 4; we are done if the rows are even equal, so assume that they are odd equal. Finnaly, if rows 4 and 5 are odd equal,then rows 3 and 5 are equal, and if rows 4 and 5 are even equal, then rows and 5 are equal. This concludes the proof. Solution to problem 7. Squaring both sides of the equality yields 2(a + a 2 b 2 )(a + a 2 c 2 ) = (a + b + c) 2. It is easy to observe that the equality holds if a 2 = b 2 + c 2. To prove the converse statement, assume that a 2 > b 2 + c 2. Then a 2 b 2 > c and a 2 c 2 > b, hence 2(a + a 2 b 2 )(a + a 2 c 2 ) > 2(a + b)(a + c) = 2a 2 + 2(ab + bc + ca) > a 2 + b 2 + c 2 + 2(ab + bc + ca) = (a + b + c) 2, false. The case a 2 b 2 + c 2 leads similarily to a contradiction and we are done.
8 8 Solution to problem 8. Rearrange the numbers a, a 2,..., a n in ascending order: b < b 2 <... < b n. Obviously, k b k, and substituting b k with k, the left-hand side term increases. Futhermore, by the Rearrangements inequality we infer that the maximum value of the left-hand side term is n + 2 n + + n. On the other side, the right-hand side term is greater than or equal to We have = (n + ) n 2 = n + 2 n + + n = n k= For n > 6 we prove by induction on n that n(n + ). 4 n k= n k n = + (n + ) n+ n 4 k, k=2 k=2 n k + k n+ k = (n + ) which implies that the given equality cannot hold. Indeed, for n = 7 we have 7 4 = = If the inequality holds for n > 7 then it is true for n +, as 4 n+. We are left with the cases when n = 2, 3, 4, 5, 6. Clearly, the case case n = 2 is impossible. For n = 3 we have the numbers a =, a 2 = 2 and a 3 = 3., so n = 3 is a solution. If n = 4, then a + a 2 + a 3 + a 4 = 2( a + 2 a a a 4 ) 2( ) < 3, so a + a 2 + a 3 + a 4 2. By inspection, all the cases: {a, a 2, a 3, a 4 } = {, 2, 3, 4}, {, 2, 3, 5}, {, 2, 4, 5} and {, 2, 3, 6} fail to satisfy the required relation. If n = 5, then a + a 2 + a 3 + a 4 + a 5 = 2( a + 2 a a a a 5 ) 2( ) < 7.4, so a + a 2 + a 3 + a 4 + a 5 7. We study the cases {a, a 2, a 3, a 4, a 5 } = {, 2, 3, 4, 5}, {, 2, 3, 4, 6} and {, 2, 3, 5, 6} with no succes (for an easy argument, observe that 5 must be a 5 and so on). Finally, for n = 6 we obtain similarly a + a a 6 22, thus {a, a 2, a 3, a 4, a 5, a 6 } can be {, 2, 3, 4, 5, 6} or {, 2, 3, 4, 5, 7}. The last case fails immediately because of 7, and the same outcame is for the first one. Therefore n = 3. k=2 k.
9 9 Solution to problem 9. Let n be the number of players in the tournament. The total numbers of matches is n(n ), hence each player end up with n points. a) Assume by contradiction that each player has a different number of draws. As a draw gives 0.5 points, it follows that each player has an odd number of draws. Since the possible cases are: 0, 2, 4,..., 2(n ), we infer that each of these numbers is assigned to each of the players. Consider A the player with 0 draws and B the player with 2(n ) draws. Each player has played 2(n ) matches, hence B obtained a draw in each match played. The match A-B thus ended with a draw, a contradiction, since A has no draws. b) Suppose the contrary. Then each of the n players has 0,,..., n losses when playing the white. Let X and Y be the players with 0 and n losses, respectively. The player Y has no points when playing the white and n points, so he won all the matches with the black pieces. This implies that the match X-Y is won by Y, so is lost by X, a contradiction, since X has 0 losses with the white pieces. Solution to problem 0. The idea is to prove that the sum of the radii is equal to the altitude h from A of the triangle ABC; a hint is to think that line MA is parallel to BC. The Stewart relation gives AM 2 BC + AC 2 MB = AB 2 MC + MB MC BC, so AM 2 BC = AB 2 (MC MB) + MB MC BC, hence AM 2 = AB 2 + MB MC. Let r be the inradius of triangle AMB and R the exradius of triangle AMC corresponding to the angle M. Since and then and Thus so the claim holds. r = R = 2 areaamb AM + MB + AB, 2 areaamc MA + MB AB, r h = MB AM + MB + AB, R h = MC AM + MC AB. r + R = h MB(MA + MB AB) + MC(MA + MB + AB) = (MA + MB + AB)(MA + MB AB) MB(MA + MB AB) = (MA + MB + AB)(MA AB) MB MC + MB(MA AB) = MA 2 AB 2 + MB(MA AB) MA 2 = AB 2 + MB MC,
10 0 Solution to problem. Clearly one of the primes p, q or r is equal to 2. If r = 2 then p n + q n = 4, false, so assume that p > q = 2. Consider the case when n > is odd; we have (p + 2)(p n 2p n p n n ) = r 2. Notice that p n 2p n p n n = 2 n + (p 2)(p n 2 + p n 4 + ) > and p + 2 > hence both factors are equal to r. This rewrites as p n + 2 n = (p + 2) 2 = p 2 + 4p + 4, which is false for n 3. Consider the case when n > is even and let n = 2m. It follows that p m = a 2 b 2, 2 m = 2ab and r = a 2 + b 2, for some integers a, b with (a, b) =. Therefore, a and b are powers of 2, so b = and a = 2 m. This implies p m = 4 m < 4 m, so p must be equal to 3. The equality 3 m = 4 m fails for m = and also for m 2, as 4 m > 3 m +, by induction. Consequently n = - take for example p = 23, q = 2 and r = 5. Solution to problem 2. Consider the integers 0 < m n < p so that b = a+m, c = a+n and d = a+p. Then a(a+p) = (a+m)(a+n) and a + p a a. As p = m + n + mn a is an integer, then a mn and p m + n +. On the other hand, + 2 a n + m + a m+n 2 mn, hence a mn. Consequently, a = mn and m = n, so a is a square. Solution to problem 3. Let Q be the intersection point of the line segments AB and MP. The tangents from A and M to the incirle are equal (as they are r cot A 2 ). Moreover, the tangents from Q to the incircle are equal, so AQ = MQ. This implies QMA = QAM, so the arcs AP and BM are equal. In the trapezoid AP BM, the diagonals AB and MP are equal, and likewise AC = MN. This concludes the proof. Solution to problem 4. Assume by contradiction that a k > 0, for some k. Wlog, let k =. Then a 2 > 00 and a 2 2+a a 00 +s 2 <, where s = a + a a 00. On the other hand, the Cauchy-Schwarz inequality yields a contradiction. Solution to problem 5. a 2 = (s a 2 a 3... a 00 ) 2 00(a a a s 2 ) < 00, The sum of the elements of the set A is S = na 2 + n(n + )b + n(n+)(2n+) 6 b 2. Assume that n has a prime divisor p > 3. Then p S and p (a + b) 2 + (a + 2b) (a + pb) 2 = pa 2 + p(p + )b + p(p+)(2p+) 6 b 2, a contradiction. It remains n = 2 k 3 l, for some integers k, l. Suppose that k >. Then 2 S and so all elements of A must be odd. Taking the subset given by any pair we reach the contradiction. Finally, suppose that l >, so 3 S. If one of the numbers a + b, a + 2b, a + 3b is divisible by 3, then we have a contradiction; if not, then 3 b. Then 3 (a + b) 2 + (a + 2b) 2 + (a + 3b) 2 = 3a 2 + 2ab + 4b 2, again a contradiction. We are left with n = 6, which satisfies the claim: the set A = {4, 9, 6, 25, 36, 49} is isolated, because the sum of its elements is a prime number (39).
11 Solution to problem 6. Let A, A 2,... A 000 be the vertices of the polygon. We start with two lemmas. Lemma. Three of four consecutive vertices have the same color. Then after a sequence of moves all vertices will have the color of the fourth vertex. Proof. Let the colors be 0, and 2. We have two cases: a) b) Lemma 2. Any 4 consecutive vertices will turn after several moves in the same color. Proof. Form two pairs of consecutive vertices and change them in the same color - if they do not already have it. Then follow the sequence By the second lemma, after several moves the vertices A, A 2, A 3, A 4 will have the same color, say red. Likewise, A 5, A 6, A 7, A 8 will have the same color. Consider now the vertices A 4, A 5, A 6, A 7 ; the first is red and the other three have the same color. By the first lemma they all will turn red - of course, we do nothing if they were already red. We move on with this procedure until A, A 2,... A 997 turn red (note that 997 = , so this requires 332 steps). Now consider the vertices A 998, A 999, A 000, A ; by the second lemma they all will share the same color. If this is red, we are done. If not, say that they are blue, and taking the vertices A 997, A 998, A 999, A 000 we obtain - using the first lemma - all vertices to be red, except for A, which is blue. Now A, A 2, A 3, A 4 turn blue, then A 5, A 6, A 7, A 8 and so on. This time, after 333 steps, all the 000 vertices (000=+3 333) will be colored in blue. Comment. Substituting colors with digits, notice that all moves: 0 22, 02 and 2 00 preserve the sum (mod 3). This means that the final color is unique and, of course, is given by the sum of the digits assigned to the vertices of the initial configuration. Solution to problem 7. a) In the array below a b c d e f g h i where i is an element of the third row, observe that i = c + f = (a + b) + (d + e) = (a + d) + (b + c) = g + h. The same argument holds for all the other rows, by induction. b) We prove that d = 2b + 2c a. Indeed, from the array a x y z b t u c v d we derive d = u+v = b+t+(u+z) = 2(b+t)+(x+y)= 2b+2(t+y)+x y = 2b+2c+x (x+a) = 2b+2c a.
12 2 Solution to problem 8. By the Power of a point theorem we have AG AM = AP AB, so 4MA 2 = 3AB 2 and thus AM = 3 2 AB = BN. Then AG = GB, so the median GP is also an altitude in the triangle AGB. This implies BP G = 90, and since BMGP is cyclic, GMA = 90. It follows that BC = CA and AB = AC, so the triangle is equilateral. Solution to problem 9. It is obvious that A, since is a divisor of any integer. Consider a, b two elements of A with < a < b. Since at least one of a, b or + ab is even, then 2 is an element of A. We induct on n 6 to prove that n A. Assume that k A for all k =, 2,..., n. If n is odd, then n = 2p+ with < 2 < p A, hence n A. If n is even, then n = 2p. As above, 2p and 2p+ are elements ofa and consequently + (2p )(2p + ) = 4p 2 A. The first property implies n = 2p A, as needed. To complete the proof, we need to show that 3, 4, 5 A. For this, consider a > 2 an element of A. Then + 2 a A, + 2( + 2a) = 3 + 4a A and + ( + 2a)(3 + 4a) = 4 + 0a + 8a 2 A. If a is even, then a + 8a 2 and so 4 A. If a is odd, then choose a to be 4 + 0a + 8a 2 and again 4 A. Next, as < 2 < 4 A we have = 9 A and so 3 A. Finally, 7 = A, 5 = A, hence 5 A and we are done. Solution to problem 20. Let A, A 2,... A n be the vertices of the polygon. We start with the following Lemma:Each segment A i A j belongs to at most 2 triangle of area located on the same side of the line A i A j. Proof of the lemma. Indeed, suppose that on the same side of the line A i A j exist the vertices A m, A n, A p so that the triangles A i A j A m, A i A j A n and A i A j A p have the area. Then the points A m, A n, A p will be at the same distance to the line A i A j, hence colinear. This is a contradiction, since the polygon is convex. Consider first the n sides of the polygon. Each of them can form at most 2 triangles of area, as all the vertices lie on the same side, hence we have by now at most 2n such triangles. Consider now the n diagonals A i A i+2 - with the cyclic notations: A n+j = A j. Each of them can form at most 3 triangles of area, one with A i+ and two with the vertices lying on the other side. Thus we have at most 5n = 2n + 3n triangles. Finally, consider the other diagonals of the polygon. They are n(n 5) 2, and each of them can form at most 4 triangles. The final counting is 5n + 4 n(n 5) 2 = n(2n 5), except that we have counted each triangle three times, one time for each side. Therefore, there are at most n(2n 5) 2 triangles, as claimed.
First selection test
 First selection test Problem 1. Let ABC be a triangle right at C and consider points D, E on the sides BC, CA, respectively such that BD = AE = k. Lines BE and AC CD AD intersect at point O. Show that
First selection test Problem 1. Let ABC be a triangle right at C and consider points D, E on the sides BC, CA, respectively such that BD = AE = k. Lines BE and AC CD AD intersect at point O. Show that
INVERSION IN THE PLANE BERKELEY MATH CIRCLE
 INVERSION IN THE PLANE BERKELEY MATH CIRCLE ZVEZDELINA STANKOVA MILLS COLLEGE/UC BERKELEY SEPTEMBER 26TH 2004 Contents 1. Definition of Inversion in the Plane 1 Properties of Inversion 2 Problems 2 2.
INVERSION IN THE PLANE BERKELEY MATH CIRCLE ZVEZDELINA STANKOVA MILLS COLLEGE/UC BERKELEY SEPTEMBER 26TH 2004 Contents 1. Definition of Inversion in the Plane 1 Properties of Inversion 2 Problems 2 2.
IMO Training Camp Mock Olympiad #2 Solutions
 IMO Training Camp Mock Olympiad #2 Solutions July 3, 2008 1. Given an isosceles triangle ABC with AB = AC. The midpoint of side BC is denoted by M. Let X be a variable point on the shorter arc MA of the
IMO Training Camp Mock Olympiad #2 Solutions July 3, 2008 1. Given an isosceles triangle ABC with AB = AC. The midpoint of side BC is denoted by M. Let X be a variable point on the shorter arc MA of the
Baltic Way 2003 Riga, November 2, 2003
 altic Way 2003 Riga, November 2, 2003 Problems and solutions. Let Q + be the set of positive rational numbers. Find all functions f : Q + Q + which for all x Q + fulfil () f ( x ) = f (x) (2) ( + x ) f
altic Way 2003 Riga, November 2, 2003 Problems and solutions. Let Q + be the set of positive rational numbers. Find all functions f : Q + Q + which for all x Q + fulfil () f ( x ) = f (x) (2) ( + x ) f
The sum x 1 + x 2 + x 3 is (A): 4 (B): 6 (C): 8 (D): 14 (E): None of the above. How many pairs of positive integers (x, y) are there, those satisfy
 Important: Answer to all 15 questions. Write your answers on the answer sheets provided. For the multiple choice questions, stick only the letters (A, B, C, D or E) of your choice. No calculator is allowed.
Important: Answer to all 15 questions. Write your answers on the answer sheets provided. For the multiple choice questions, stick only the letters (A, B, C, D or E) of your choice. No calculator is allowed.
2007 Shortlist JBMO - Problems
 Chapter 1 007 Shortlist JBMO - Problems 1.1 Algebra A1 Let a be a real positive number such that a 3 = 6(a + 1). Prove that the equation x + ax + a 6 = 0 has no solution in the set of the real number.
Chapter 1 007 Shortlist JBMO - Problems 1.1 Algebra A1 Let a be a real positive number such that a 3 = 6(a + 1). Prove that the equation x + ax + a 6 = 0 has no solution in the set of the real number.
1 Hanoi Open Mathematical Competition 2017
 1 Hanoi Open Mathematical Competition 017 1.1 Junior Section Question 1. Suppose x 1, x, x 3 are the roots of polynomial P (x) = x 3 6x + 5x + 1. The sum x 1 + x + x 3 is (A): 4 (B): 6 (C): 8 (D): 14 (E):
1 Hanoi Open Mathematical Competition 017 1.1 Junior Section Question 1. Suppose x 1, x, x 3 are the roots of polynomial P (x) = x 3 6x + 5x + 1. The sum x 1 + x + x 3 is (A): 4 (B): 6 (C): 8 (D): 14 (E):
Baltic Way 2008 Gdańsk, November 8, 2008
 Baltic Way 008 Gdańsk, November 8, 008 Problems and solutions Problem 1. Determine all polynomials p(x) with real coefficients such that p((x + 1) ) = (p(x) + 1) and p(0) = 0. Answer: p(x) = x. Solution:
Baltic Way 008 Gdańsk, November 8, 008 Problems and solutions Problem 1. Determine all polynomials p(x) with real coefficients such that p((x + 1) ) = (p(x) + 1) and p(0) = 0. Answer: p(x) = x. Solution:
34 th United States of America Mathematical Olympiad
 34 th United States of America Mathematical Olympiad 1. Determine all composite positive integers n for which it is possible to arrange all divisors of n that are greater than 1 in a circle so that no
34 th United States of America Mathematical Olympiad 1. Determine all composite positive integers n for which it is possible to arrange all divisors of n that are greater than 1 in a circle so that no
Vectors - Applications to Problem Solving
 BERKELEY MATH CIRCLE 00-003 Vectors - Applications to Problem Solving Zvezdelina Stankova Mills College& UC Berkeley 1. Well-known Facts (1) Let A 1 and B 1 be the midpoints of the sides BC and AC of ABC.
BERKELEY MATH CIRCLE 00-003 Vectors - Applications to Problem Solving Zvezdelina Stankova Mills College& UC Berkeley 1. Well-known Facts (1) Let A 1 and B 1 be the midpoints of the sides BC and AC of ABC.
SMT 2018 Geometry Test Solutions February 17, 2018
 SMT 018 Geometry Test Solutions February 17, 018 1. Consider a semi-circle with diameter AB. Let points C and D be on diameter AB such that CD forms the base of a square inscribed in the semicircle. Given
SMT 018 Geometry Test Solutions February 17, 018 1. Consider a semi-circle with diameter AB. Let points C and D be on diameter AB such that CD forms the base of a square inscribed in the semicircle. Given
1998 IMO Shortlist BM BN BA BC AB BC CD DE EF BC CA AE EF FD
 IMO Shortlist 1998 Geometry 1 A convex quadrilateral ABCD has perpendicular diagonals. The perpendicular bisectors of the sides AB and CD meet at a unique point P inside ABCD. the quadrilateral ABCD is
IMO Shortlist 1998 Geometry 1 A convex quadrilateral ABCD has perpendicular diagonals. The perpendicular bisectors of the sides AB and CD meet at a unique point P inside ABCD. the quadrilateral ABCD is
2010 Shortlist JBMO - Problems
 Chapter 1 2010 Shortlist JBMO - Problems 1.1 Algebra A1 The real numbers a, b, c, d satisfy simultaneously the equations abc d = 1, bcd a = 2, cda b = 3, dab c = 6. Prove that a + b + c + d 0. A2 Determine
Chapter 1 2010 Shortlist JBMO - Problems 1.1 Algebra A1 The real numbers a, b, c, d satisfy simultaneously the equations abc d = 1, bcd a = 2, cda b = 3, dab c = 6. Prove that a + b + c + d 0. A2 Determine
2013 Sharygin Geometry Olympiad
 Sharygin Geometry Olympiad 2013 First Round 1 Let ABC be an isosceles triangle with AB = BC. Point E lies on the side AB, and ED is the perpendicular from E to BC. It is known that AE = DE. Find DAC. 2
Sharygin Geometry Olympiad 2013 First Round 1 Let ABC be an isosceles triangle with AB = BC. Point E lies on the side AB, and ED is the perpendicular from E to BC. It is known that AE = DE. Find DAC. 2
Olimpiada Matemática de Centroamérica y el Caribe
 Olimpiada Matemática de Centroamérica y el Caribe 1st Centromerican 1999 Problem A1 A, B, C, D, E each has a unique piece of news. They make a series of phone calls to each other. In each call, the caller
Olimpiada Matemática de Centroamérica y el Caribe 1st Centromerican 1999 Problem A1 A, B, C, D, E each has a unique piece of news. They make a series of phone calls to each other. In each call, the caller
11 th Philippine Mathematical Olympiad Questions, Answers, and Hints
 view.php3 (JPEG Image, 840x888 pixels) - Scaled (71%) https://mail.ateneo.net/horde/imp/view.php3?mailbox=inbox&inde... 1 of 1 11/5/2008 5:02 PM 11 th Philippine Mathematical Olympiad Questions, Answers,
view.php3 (JPEG Image, 840x888 pixels) - Scaled (71%) https://mail.ateneo.net/horde/imp/view.php3?mailbox=inbox&inde... 1 of 1 11/5/2008 5:02 PM 11 th Philippine Mathematical Olympiad Questions, Answers,
INTERNATIONAL MATHEMATICAL OLYMPIADS. Hojoo Lee, Version 1.0. Contents 1. Problems 1 2. Answers and Hints References
 INTERNATIONAL MATHEMATICAL OLYMPIADS 1990 2002 Hojoo Lee, Version 1.0 Contents 1. Problems 1 2. Answers and Hints 15 3. References 16 1. Problems 021 Let n be a positive integer. Let T be the set of points
INTERNATIONAL MATHEMATICAL OLYMPIADS 1990 2002 Hojoo Lee, Version 1.0 Contents 1. Problems 1 2. Answers and Hints 15 3. References 16 1. Problems 021 Let n be a positive integer. Let T be the set of points
Collinearity/Concurrence
 Collinearity/Concurrence Ray Li (rayyli@stanford.edu) June 29, 2017 1 Introduction/Facts you should know 1. (Cevian Triangle) Let ABC be a triangle and P be a point. Let lines AP, BP, CP meet lines BC,
Collinearity/Concurrence Ray Li (rayyli@stanford.edu) June 29, 2017 1 Introduction/Facts you should know 1. (Cevian Triangle) Let ABC be a triangle and P be a point. Let lines AP, BP, CP meet lines BC,
This class will demonstrate the use of bijections to solve certain combinatorial problems simply and effectively.
 . Induction This class will demonstrate the fundamental problem solving technique of mathematical induction. Example Problem: Prove that for every positive integer n there exists an n-digit number divisible
. Induction This class will demonstrate the fundamental problem solving technique of mathematical induction. Example Problem: Prove that for every positive integer n there exists an n-digit number divisible
1966 IMO Shortlist. IMO Shortlist 1966
 IMO Shortlist 1966 1 Given n > 3 points in the plane such that no three of the points are collinear. Does there exist a circle passing through (at least) 3 of the given points and not containing any other
IMO Shortlist 1966 1 Given n > 3 points in the plane such that no three of the points are collinear. Does there exist a circle passing through (at least) 3 of the given points and not containing any other
RMT 2013 Geometry Test Solutions February 2, = 51.
 RMT 0 Geometry Test Solutions February, 0. Answer: 5 Solution: Let m A = x and m B = y. Note that we have two pairs of isosceles triangles, so m A = m ACD and m B = m BCD. Since m ACD + m BCD = m ACB,
RMT 0 Geometry Test Solutions February, 0. Answer: 5 Solution: Let m A = x and m B = y. Note that we have two pairs of isosceles triangles, so m A = m ACD and m B = m BCD. Since m ACD + m BCD = m ACB,
Canadian Open Mathematics Challenge
 The Canadian Mathematical Society in collaboration with The CENTRE for EDUCATION in MATHEMATICS and COMPUTING presents the Canadian Open Mathematics Challenge Wednesday, November, 006 Supported by: Solutions
The Canadian Mathematical Society in collaboration with The CENTRE for EDUCATION in MATHEMATICS and COMPUTING presents the Canadian Open Mathematics Challenge Wednesday, November, 006 Supported by: Solutions
Hanoi Open Mathematical Competition 2017
 Hanoi Open Mathematical Competition 2017 Junior Section Saturday, 4 March 2017 08h30-11h30 Important: Answer to all 15 questions. Write your answers on the answer sheets provided. For the multiple choice
Hanoi Open Mathematical Competition 2017 Junior Section Saturday, 4 March 2017 08h30-11h30 Important: Answer to all 15 questions. Write your answers on the answer sheets provided. For the multiple choice
37th United States of America Mathematical Olympiad
 37th United States of America Mathematical Olympiad 1. Prove that for each positive integer n, there are pairwise relatively prime integers k 0, k 1,..., k n, all strictly greater than 1, such that k 0
37th United States of America Mathematical Olympiad 1. Prove that for each positive integer n, there are pairwise relatively prime integers k 0, k 1,..., k n, all strictly greater than 1, such that k 0
Calgary Math Circles: Triangles, Concurrency and Quadrilaterals 1
 Calgary Math Circles: Triangles, Concurrency and Quadrilaterals 1 1 Triangles: Basics This section will cover all the basic properties you need to know about triangles and the important points of a triangle.
Calgary Math Circles: Triangles, Concurrency and Quadrilaterals 1 1 Triangles: Basics This section will cover all the basic properties you need to know about triangles and the important points of a triangle.
2003 AIME Given that ((3!)!)! = k n!, where k and n are positive integers and n is as large as possible, find k + n.
 003 AIME 1 Given that ((3!)!)! = k n!, where k and n are positive integers and n is as large 3! as possible, find k + n One hundred concentric circles with radii 1,, 3,, 100 are drawn in a plane The interior
003 AIME 1 Given that ((3!)!)! = k n!, where k and n are positive integers and n is as large 3! as possible, find k + n One hundred concentric circles with radii 1,, 3,, 100 are drawn in a plane The interior
41st International Mathematical Olympiad
 41st International Mathematical Olympiad Taejon, Korea, July 2000 1 Two circles Γ 1 and Γ 2 intersect at M and N Let l be the common tangent to Γ 1 and Γ 2 so that M is closer to l than N is Let l touch
41st International Mathematical Olympiad Taejon, Korea, July 2000 1 Two circles Γ 1 and Γ 2 intersect at M and N Let l be the common tangent to Γ 1 and Γ 2 so that M is closer to l than N is Let l touch
IMO Training Camp Mock Olympiad #2
 IMO Training Camp Mock Olympiad #2 July 3, 2008 1. Given an isosceles triangle ABC with AB = AC. The midpoint of side BC is denoted by M. Let X be a variable point on the shorter arc MA of the circumcircle
IMO Training Camp Mock Olympiad #2 July 3, 2008 1. Given an isosceles triangle ABC with AB = AC. The midpoint of side BC is denoted by M. Let X be a variable point on the shorter arc MA of the circumcircle
45-th Moldova Mathematical Olympiad 2001
 45-th Moldova Mathematical Olympiad 200 Final Round Chişinǎu, March 2 Grade 7. Prove that y 3 2x+ x 3 2y x 2 + y 2 for any numbers x,y [, 2 3 ]. When does equality occur? 2. Let S(n) denote the sum of
45-th Moldova Mathematical Olympiad 200 Final Round Chişinǎu, March 2 Grade 7. Prove that y 3 2x+ x 3 2y x 2 + y 2 for any numbers x,y [, 2 3 ]. When does equality occur? 2. Let S(n) denote the sum of
HANOI OPEN MATHEMATICS COMPETITON PROBLEMS
 HANOI MATHEMATICAL SOCIETY NGUYEN VAN MAU HANOI OPEN MATHEMATICS COMPETITON PROBLEMS 2006-2013 HANOI - 2013 Contents 1 Hanoi Open Mathematics Competition 3 1.1 Hanoi Open Mathematics Competition 2006...
HANOI MATHEMATICAL SOCIETY NGUYEN VAN MAU HANOI OPEN MATHEMATICS COMPETITON PROBLEMS 2006-2013 HANOI - 2013 Contents 1 Hanoi Open Mathematics Competition 3 1.1 Hanoi Open Mathematics Competition 2006...
1. Suppose that a, b, c and d are four different integers. Explain why. (a b)(a c)(a d)(b c)(b d)(c d) a 2 + ab b = 2018.
 New Zealand Mathematical Olympiad Committee Camp Selection Problems 2018 Solutions Due: 28th September 2018 1. Suppose that a, b, c and d are four different integers. Explain why must be a multiple of
New Zealand Mathematical Olympiad Committee Camp Selection Problems 2018 Solutions Due: 28th September 2018 1. Suppose that a, b, c and d are four different integers. Explain why must be a multiple of
CHMMC 2015 Individual Round Problems
 CHMMC 05 Individual Round Problems November, 05 Problem 0.. The following number is the product of the divisors of n. What is n? 6 3 3 Solution.. In general, the product of the divisors of n is n # of
CHMMC 05 Individual Round Problems November, 05 Problem 0.. The following number is the product of the divisors of n. What is n? 6 3 3 Solution.. In general, the product of the divisors of n is n # of
International Mathematics TOURNAMENT OF THE TOWNS
 International Mathematics TOURNAMENT OF THE TOWNS Senior A-Level Paper Fall 2008. 1. A standard 8 8 chessboard is modified by varying the distances between parallel grid lines, so that the cells are rectangles
International Mathematics TOURNAMENT OF THE TOWNS Senior A-Level Paper Fall 2008. 1. A standard 8 8 chessboard is modified by varying the distances between parallel grid lines, so that the cells are rectangles
Winter Mathematical Competition Varna, February, 9-11, 2007
 Winter Mathematical Competition Varna, February, 9-11, 007 Problem 91 (Peter Boyvalenkov) Find all values of the real parameter p such that the equation x + (p + 1)x + p = has two real distinct roots x
Winter Mathematical Competition Varna, February, 9-11, 007 Problem 91 (Peter Boyvalenkov) Find all values of the real parameter p such that the equation x + (p + 1)x + p = has two real distinct roots x
1. Prove that for every positive integer n there exists an n-digit number divisible by 5 n all of whose digits are odd.
 32 nd United States of America Mathematical Olympiad Proposed Solutions May, 23 Remark: The general philosophy of this marking scheme follows that of IMO 22. This scheme encourages complete solutions.
32 nd United States of America Mathematical Olympiad Proposed Solutions May, 23 Remark: The general philosophy of this marking scheme follows that of IMO 22. This scheme encourages complete solutions.
40th International Mathematical Olympiad
 40th International Mathematical Olympiad Bucharest, Romania, July 999 Determine all finite sets S of at least three points in the plane which satisfy the following condition: for any two distinct points
40th International Mathematical Olympiad Bucharest, Romania, July 999 Determine all finite sets S of at least three points in the plane which satisfy the following condition: for any two distinct points
HANOI OPEN MATHEMATICAL COMPETITON PROBLEMS
 HANOI MATHEMATICAL SOCIETY NGUYEN VAN MAU HANOI OPEN MATHEMATICAL COMPETITON PROBLEMS HANOI - 2013 Contents 1 Hanoi Open Mathematical Competition 3 1.1 Hanoi Open Mathematical Competition 2006... 3 1.1.1
HANOI MATHEMATICAL SOCIETY NGUYEN VAN MAU HANOI OPEN MATHEMATICAL COMPETITON PROBLEMS HANOI - 2013 Contents 1 Hanoi Open Mathematical Competition 3 1.1 Hanoi Open Mathematical Competition 2006... 3 1.1.1
One Theorem, Six Proofs
 50/ ONE THEOREM, SIX PROOFS One Theorem, Six Proofs V. Dubrovsky It is often more useful to acquaint yourself with many proofs of the same theorem rather than with similar proofs of numerous results. The
50/ ONE THEOREM, SIX PROOFS One Theorem, Six Proofs V. Dubrovsky It is often more useful to acquaint yourself with many proofs of the same theorem rather than with similar proofs of numerous results. The
T-2 In the equation A B C + D E F = G H I, each letter denotes a distinct non-zero digit. Compute the greatest possible value of G H I.
 2016 ARML Local Problems and Solutions Team Round Solutions T-1 All the shelves in a library are the same length. When filled, two shelves side-by-side can hold exactly 12 algebra books and 10 geometry
2016 ARML Local Problems and Solutions Team Round Solutions T-1 All the shelves in a library are the same length. When filled, two shelves side-by-side can hold exactly 12 algebra books and 10 geometry
= 126 possible 5-tuples.
 19th Philippine Mathematical Olympiad 1 January, 017 JUDGES COPY EASY 15 seconds, points 1. If g (x) = x x 5 Answer: 14 Solution: Note that x x and f ( g ( x)) = x, find f (). x 6 = = x = 1. Hence f ()
19th Philippine Mathematical Olympiad 1 January, 017 JUDGES COPY EASY 15 seconds, points 1. If g (x) = x x 5 Answer: 14 Solution: Note that x x and f ( g ( x)) = x, find f (). x 6 = = x = 1. Hence f ()
Non-standard MMC problems
 Non-standard MMC problems Carl Joshua Quines 1 Algebra 1. (15S/9B/E6) A quadratic function f(x) satisfies f(0) = 30 and f(2) = 0. Determine all the zeros of f(x). [2 and 15] 2. (15S/IVB/E6) What is the
Non-standard MMC problems Carl Joshua Quines 1 Algebra 1. (15S/9B/E6) A quadratic function f(x) satisfies f(0) = 30 and f(2) = 0. Determine all the zeros of f(x). [2 and 15] 2. (15S/IVB/E6) What is the
2013 University of New South Wales School Mathematics Competition
 Parabola Volume 49, Issue (201) 201 University of New South Wales School Mathematics Competition Junior Division Problems and s Problem 1 Suppose that x, y, z are non-zero integers with no common factor
Parabola Volume 49, Issue (201) 201 University of New South Wales School Mathematics Competition Junior Division Problems and s Problem 1 Suppose that x, y, z are non-zero integers with no common factor
BRITISH COLUMBIA SECONDARY SCHOOL MATHEMATICS CONTEST,
 BRITISH COLUMBIA SECONDARY SCHOOL MATHEMATICS CONTEST, 014 Solutions Junior Preliminary 1. Rearrange the sum as (014 + 01 + 010 + + ) (013 + 011 + 009 + + 1) = (014 013) + (01 011) + + ( 1) = 1 + 1 + +
BRITISH COLUMBIA SECONDARY SCHOOL MATHEMATICS CONTEST, 014 Solutions Junior Preliminary 1. Rearrange the sum as (014 + 01 + 010 + + ) (013 + 011 + 009 + + 1) = (014 013) + (01 011) + + ( 1) = 1 + 1 + +
Indicate whether the statement is true or false.
 PRACTICE EXAM IV Sections 6.1, 6.2, 8.1 8.4 Indicate whether the statement is true or false. 1. For a circle, the constant ratio of the circumference C to length of diameter d is represented by the number.
PRACTICE EXAM IV Sections 6.1, 6.2, 8.1 8.4 Indicate whether the statement is true or false. 1. For a circle, the constant ratio of the circumference C to length of diameter d is represented by the number.
UNC Charlotte 2005 Comprehensive March 7, 2005
 March 7, 2005 1. The numbers x and y satisfy 2 x = 15 and 15 y = 32. What is the value xy? (A) 3 (B) 4 (C) 5 (D) 6 (E) none of A, B, C or D Solution: C. Note that (2 x ) y = 15 y = 32 so 2 xy = 2 5 and
March 7, 2005 1. The numbers x and y satisfy 2 x = 15 and 15 y = 32. What is the value xy? (A) 3 (B) 4 (C) 5 (D) 6 (E) none of A, B, C or D Solution: C. Note that (2 x ) y = 15 y = 32 so 2 xy = 2 5 and
Math Wrangle Practice Problems
 Math Wrangle Practice Problems American Mathematics Competitions November 19, 2010 1. Find the sum of all positive two-digit integers that are divisible by each of their digits. 2. A finite set S of distinct
Math Wrangle Practice Problems American Mathematics Competitions November 19, 2010 1. Find the sum of all positive two-digit integers that are divisible by each of their digits. 2. A finite set S of distinct
2016 AMC 12/AHSME. 3 The remainder can be defined for all real numbers x and y with y 0 by. x rem(x,y) = x y y
 AMC 12/AHSME 2016 A 1 What is the value of 11! 10!? 9! (A) 99 (B) 100 (C) 110 (D) 121 (E) 132 2 For what value of x does 10 x 100 2x = 1000 5? (A) 1 (B) 2 (C) 3 (D) 4 (E) 5 3 The remainder can be defined
AMC 12/AHSME 2016 A 1 What is the value of 11! 10!? 9! (A) 99 (B) 100 (C) 110 (D) 121 (E) 132 2 For what value of x does 10 x 100 2x = 1000 5? (A) 1 (B) 2 (C) 3 (D) 4 (E) 5 3 The remainder can be defined
Classical Theorems in Plane Geometry 1
 BERKELEY MATH CIRCLE 1999 2000 Classical Theorems in Plane Geometry 1 Zvezdelina Stankova-Frenkel UC Berkeley and Mills College Note: All objects in this handout are planar - i.e. they lie in the usual
BERKELEY MATH CIRCLE 1999 2000 Classical Theorems in Plane Geometry 1 Zvezdelina Stankova-Frenkel UC Berkeley and Mills College Note: All objects in this handout are planar - i.e. they lie in the usual
Organization Team Team ID#
 1. [4] A random number generator will always output 7. Sam uses this random number generator once. What is the expected value of the output? 2. [4] Let A, B, C, D, E, F be 6 points on a circle in that
1. [4] A random number generator will always output 7. Sam uses this random number generator once. What is the expected value of the output? 2. [4] Let A, B, C, D, E, F be 6 points on a circle in that
Figure 1: Problem 1 diagram. Figure 2: Problem 2 diagram
 Geometry A Solutions 1. Note that the solid formed is a generalized cylinder. It is clear from the diagram that the area of the base of this cylinder (i.e., a vertical cross-section of the log) is composed
Geometry A Solutions 1. Note that the solid formed is a generalized cylinder. It is clear from the diagram that the area of the base of this cylinder (i.e., a vertical cross-section of the log) is composed
VKR Classes TIME BOUND TESTS 1-7 Target JEE ADVANCED For Class XI VKR Classes, C , Indra Vihar, Kota. Mob. No
 VKR Classes TIME BOUND TESTS -7 Target JEE ADVANCED For Class XI VKR Classes, C-9-0, Indra Vihar, Kota. Mob. No. 9890605 Single Choice Question : PRACTICE TEST-. The smallest integer greater than log +
VKR Classes TIME BOUND TESTS -7 Target JEE ADVANCED For Class XI VKR Classes, C-9-0, Indra Vihar, Kota. Mob. No. 9890605 Single Choice Question : PRACTICE TEST-. The smallest integer greater than log +
Olympiad Correspondence Problems. Set 3
 (solutions follow) 1998-1999 Olympiad Correspondence Problems Set 3 13. The following construction and proof was proposed for trisecting a given angle with ruler and Criticizecompasses the arguments. Construction.
(solutions follow) 1998-1999 Olympiad Correspondence Problems Set 3 13. The following construction and proof was proposed for trisecting a given angle with ruler and Criticizecompasses the arguments. Construction.
chapter 1 vector geometry solutions V Consider the parallelogram shown alongside. Which of the following statements are true?
 chapter vector geometry solutions V. Exercise A. For the shape shown, find a single vector which is equal to a)!!! " AB + BC AC b)! AD!!! " + DB AB c)! AC + CD AD d)! BC + CD!!! " + DA BA e) CD!!! " "
chapter vector geometry solutions V. Exercise A. For the shape shown, find a single vector which is equal to a)!!! " AB + BC AC b)! AD!!! " + DB AB c)! AC + CD AD d)! BC + CD!!! " + DA BA e) CD!!! " "
LLT Education Services
 8. The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle. (a) 4 cm (b) 3 cm (c) 6 cm (d) 5 cm 9. From a point P, 10 cm away from the
8. The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle. (a) 4 cm (b) 3 cm (c) 6 cm (d) 5 cm 9. From a point P, 10 cm away from the
46th ANNUAL MASSACHUSETTS MATHEMATICS OLYMPIAD. A High School Competition Conducted by. And Sponsored by FIRST-LEVEL EXAMINATION SOLUTIONS
 46th ANNUAL MASSACHUSETTS MATHEMATICS OLYMPIAD 009 00 A High School Competition Conducted by THE MASSACHUSETTS ASSOCIATION OF MATHEMATICS LEAGUES (MAML) And Sponsored by THE ACTUARIES CLUB OF BOSTON FIRST-LEVEL
46th ANNUAL MASSACHUSETTS MATHEMATICS OLYMPIAD 009 00 A High School Competition Conducted by THE MASSACHUSETTS ASSOCIATION OF MATHEMATICS LEAGUES (MAML) And Sponsored by THE ACTUARIES CLUB OF BOSTON FIRST-LEVEL
Exercises for Unit V (Introduction to non Euclidean geometry)
 Exercises for Unit V (Introduction to non Euclidean geometry) V.1 : Facts from spherical geometry Ryan : pp. 84 123 [ Note : Hints for the first two exercises are given in math133f07update08.pdf. ] 1.
Exercises for Unit V (Introduction to non Euclidean geometry) V.1 : Facts from spherical geometry Ryan : pp. 84 123 [ Note : Hints for the first two exercises are given in math133f07update08.pdf. ] 1.
Q.1 If a, b, c are distinct positive real in H.P., then the value of the expression, (A) 1 (B) 2 (C) 3 (D) 4. (A) 2 (B) 5/2 (C) 3 (D) none of these
 Q. If a, b, c are distinct positive real in H.P., then the value of the expression, b a b c + is equal to b a b c () (C) (D) 4 Q. In a triangle BC, (b + c) = a bc where is the circumradius of the triangle.
Q. If a, b, c are distinct positive real in H.P., then the value of the expression, b a b c + is equal to b a b c () (C) (D) 4 Q. In a triangle BC, (b + c) = a bc where is the circumradius of the triangle.
XX Asian Pacific Mathematics Olympiad
 XX Asian Pacific Mathematics Olympiad March, 008 Problem 1. Let ABC be a triangle with A < 60. Let X and Y be the points on the sides AB and AC, respectively, such that CA + AX = CB + BX and BA + AY =
XX Asian Pacific Mathematics Olympiad March, 008 Problem 1. Let ABC be a triangle with A < 60. Let X and Y be the points on the sides AB and AC, respectively, such that CA + AX = CB + BX and BA + AY =
Australian Intermediate Mathematics Olympiad 2014
 5. Let 1 a + 1 b = 1 20, where a and b are positive integers. Find the largest value of a + b. [4 marks] A u s t r a l i a n M at h e m at i c a l O ly m p i a d C o m m i t t e e a d e p a r t m e n t
5. Let 1 a + 1 b = 1 20, where a and b are positive integers. Find the largest value of a + b. [4 marks] A u s t r a l i a n M at h e m at i c a l O ly m p i a d C o m m i t t e e a d e p a r t m e n t
BMT 2018 Team Test Solutions March 18, 2018
 . A circle with radius is inscribed in a right triangle with hypotenuse 4 as shown below. What is the area of the triangle? Note that the diagram is not to scale. 4 Answer: 9 Solution : We wish to use
. A circle with radius is inscribed in a right triangle with hypotenuse 4 as shown below. What is the area of the triangle? Note that the diagram is not to scale. 4 Answer: 9 Solution : We wish to use
32 nd United States of America Mathematical Olympiad Recommended Marking Scheme May 1, 2003
 32 nd United States of America Mathematical Olympiad Recommended Marking Scheme May 1, 23 Remark: The general philosophy of this marking scheme follows that of IMO 22. This scheme encourages complete solutions.
32 nd United States of America Mathematical Olympiad Recommended Marking Scheme May 1, 23 Remark: The general philosophy of this marking scheme follows that of IMO 22. This scheme encourages complete solutions.
2018 LEHIGH UNIVERSITY HIGH SCHOOL MATH CONTEST
 08 LEHIGH UNIVERSITY HIGH SCHOOL MATH CONTEST. A right triangle has hypotenuse 9 and one leg. What is the length of the other leg?. Don is /3 of the way through his run. After running another / mile, he
08 LEHIGH UNIVERSITY HIGH SCHOOL MATH CONTEST. A right triangle has hypotenuse 9 and one leg. What is the length of the other leg?. Don is /3 of the way through his run. After running another / mile, he
Singapore International Mathematical Olympiad 2008 Senior Team Training. Take Home Test Solutions. 15x 2 7y 2 = 9 y 2 0 (mod 3) x 0 (mod 3).
 Singapore International Mathematical Olympiad 2008 Senior Team Training Take Home Test Solutions. Show that the equation 5x 2 7y 2 = 9 has no solution in integers. If the equation has a solution in integer,
Singapore International Mathematical Olympiad 2008 Senior Team Training Take Home Test Solutions. Show that the equation 5x 2 7y 2 = 9 has no solution in integers. If the equation has a solution in integer,
2018 MOAA Gunga Bowl: Solutions
 08 MOAA Gunga Bowl: Solutions Andover Math Club Set Solutions. We pair up the terms as follows: +++4+5+6+7+8+9+0+ = (+)+(+0)+(+9)+(4+8)+(5+7)+6 = 5+6 = 66.. By the difference of squares formula, 6 x =
08 MOAA Gunga Bowl: Solutions Andover Math Club Set Solutions. We pair up the terms as follows: +++4+5+6+7+8+9+0+ = (+)+(+0)+(+9)+(4+8)+(5+7)+6 = 5+6 = 66.. By the difference of squares formula, 6 x =
14 th Annual Harvard-MIT Mathematics Tournament Saturday 12 February 2011
 14 th Annual Harvard-MIT Mathematics Tournament Saturday 1 February 011 1. Let a, b, and c be positive real numbers. etermine the largest total number of real roots that the following three polynomials
14 th Annual Harvard-MIT Mathematics Tournament Saturday 1 February 011 1. Let a, b, and c be positive real numbers. etermine the largest total number of real roots that the following three polynomials
(D) (A) Q.3 To which of the following circles, the line y x + 3 = 0 is normal at the point ? 2 (A) 2
 CIRCLE [STRAIGHT OBJECTIVE TYPE] Q. The line x y + = 0 is tangent to the circle at the point (, 5) and the centre of the circles lies on x y = 4. The radius of the circle is (A) 3 5 (B) 5 3 (C) 5 (D) 5
CIRCLE [STRAIGHT OBJECTIVE TYPE] Q. The line x y + = 0 is tangent to the circle at the point (, 5) and the centre of the circles lies on x y = 4. The radius of the circle is (A) 3 5 (B) 5 3 (C) 5 (D) 5
International Mathematics TOURNAMENT OF THE TOWNS: SOLUTIONS
 International Mathematics TOURNAMENT OF THE TOWNS: SOLUTIONS Juniors (Grades up to 10) A-Level Paper Spring 2003. 1 Answer: Yes. Example. Consider quadratic equation x 2 + 5x + 6 = 0. It could be transformed
International Mathematics TOURNAMENT OF THE TOWNS: SOLUTIONS Juniors (Grades up to 10) A-Level Paper Spring 2003. 1 Answer: Yes. Example. Consider quadratic equation x 2 + 5x + 6 = 0. It could be transformed
NEW YORK CITY INTERSCHOLASTIC MATHEMATICS LEAGUE Senior A Division CONTEST NUMBER 1
 Senior A Division CONTEST NUMBER 1 PART I FALL 2011 CONTEST 1 TIME: 10 MINUTES F11A1 Larry selects a 13-digit number while David selects a 10-digit number. Let be the number of digits in the product of
Senior A Division CONTEST NUMBER 1 PART I FALL 2011 CONTEST 1 TIME: 10 MINUTES F11A1 Larry selects a 13-digit number while David selects a 10-digit number. Let be the number of digits in the product of
NUMBER SYSTEM NATURAL NUMBERS
 NUMBER SYSTEM In Hindu Arabic System, we use ten symbols 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 called digits to represent any number. This is the decimal system where we use the numbers 0 to 9. 0 is called insignificant
NUMBER SYSTEM In Hindu Arabic System, we use ten symbols 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 called digits to represent any number. This is the decimal system where we use the numbers 0 to 9. 0 is called insignificant
So, eqn. to the bisector containing (-1, 4) is = x + 27y = 0
 Q.No. The bisector of the acute angle between the lines x - 4y + 7 = 0 and x + 5y - = 0, is: Option x + y - 9 = 0 Option x + 77y - 0 = 0 Option x - y + 9 = 0 Correct Answer L : x - 4y + 7 = 0 L :-x- 5y
Q.No. The bisector of the acute angle between the lines x - 4y + 7 = 0 and x + 5y - = 0, is: Option x + y - 9 = 0 Option x + 77y - 0 = 0 Option x - y + 9 = 0 Correct Answer L : x - 4y + 7 = 0 L :-x- 5y
PRACTICE QUESTIONS CLASS IX: CHAPTER 4 LINEAR EQUATION IN TWO VARIABLES
 PRACTICE QUESTIONS CLASS IX: CHAPTER 4 LINEAR EQUATION IN TWO VARIABLES 1. Find the value of k, if x =, y = 1 is a solution of the equation x + 3y = k.. Find the points where the graph of the equation
PRACTICE QUESTIONS CLASS IX: CHAPTER 4 LINEAR EQUATION IN TWO VARIABLES 1. Find the value of k, if x =, y = 1 is a solution of the equation x + 3y = k.. Find the points where the graph of the equation
1 Solution of Final. Dr. Franz Rothe December 25, Figure 1: Dissection proof of the Pythagorean theorem in a special case
 Math 3181 Dr. Franz Rothe December 25, 2012 Name: 1 Solution of Final Figure 1: Dissection proof of the Pythagorean theorem in a special case 10 Problem 1. Given is a right triangle ABC with angle α =
Math 3181 Dr. Franz Rothe December 25, 2012 Name: 1 Solution of Final Figure 1: Dissection proof of the Pythagorean theorem in a special case 10 Problem 1. Given is a right triangle ABC with angle α =
15th Bay Area Mathematical Olympiad. BAMO Exam. February 26, Solutions to BAMO-8 and BAMO-12 Problems
 15th Bay Area Mathematical Olympiad BAMO Exam February 26, 2013 Solutions to BAMO-8 and BAMO-12 Problems 1 How many different sets of three points in this equilateral triangular grid are the vertices of
15th Bay Area Mathematical Olympiad BAMO Exam February 26, 2013 Solutions to BAMO-8 and BAMO-12 Problems 1 How many different sets of three points in this equilateral triangular grid are the vertices of
QUESTION BANK ON STRAIGHT LINE AND CIRCLE
 QUESTION BANK ON STRAIGHT LINE AND CIRCLE Select the correct alternative : (Only one is correct) Q. If the lines x + y + = 0 ; 4x + y + 4 = 0 and x + αy + β = 0, where α + β =, are concurrent then α =,
QUESTION BANK ON STRAIGHT LINE AND CIRCLE Select the correct alternative : (Only one is correct) Q. If the lines x + y + = 0 ; 4x + y + 4 = 0 and x + αy + β = 0, where α + β =, are concurrent then α =,
UNCC 2001 Comprehensive, Solutions
 UNCC 2001 Comprehensive, Solutions March 5, 2001 1 Compute the sum of the roots of x 2 5x + 6 = 0 (A) (B) 7/2 (C) 4 (D) 9/2 (E) 5 (E) The sum of the roots of the quadratic ax 2 + bx + c = 0 is b/a which,
UNCC 2001 Comprehensive, Solutions March 5, 2001 1 Compute the sum of the roots of x 2 5x + 6 = 0 (A) (B) 7/2 (C) 4 (D) 9/2 (E) 5 (E) The sum of the roots of the quadratic ax 2 + bx + c = 0 is b/a which,
nx + 1 = (n + 1)x 13(n + 1) and nx = (n + 1)x + 27(n + 1).
 1. (Answer: 630) 001 AIME SOLUTIONS Let a represent the tens digit and b the units digit of an integer with the required property. Then 10a + b must be divisible by both a and b. It follows that b must
1. (Answer: 630) 001 AIME SOLUTIONS Let a represent the tens digit and b the units digit of an integer with the required property. Then 10a + b must be divisible by both a and b. It follows that b must
Higher Geometry Problems
 Higher Geometry Problems (1 Look up Eucidean Geometry on Wikipedia, and write down the English translation given of each of the first four postulates of Euclid. Rewrite each postulate as a clear statement
Higher Geometry Problems (1 Look up Eucidean Geometry on Wikipedia, and write down the English translation given of each of the first four postulates of Euclid. Rewrite each postulate as a clear statement
Circle and Cyclic Quadrilaterals. MARIUS GHERGU School of Mathematics and Statistics University College Dublin
 Circle and Cyclic Quadrilaterals MARIUS GHERGU School of Mathematics and Statistics University College Dublin 3 Basic Facts About Circles A central angle is an angle whose vertex is at the center of the
Circle and Cyclic Quadrilaterals MARIUS GHERGU School of Mathematics and Statistics University College Dublin 3 Basic Facts About Circles A central angle is an angle whose vertex is at the center of the
PUTNAM TRAINING EASY PUTNAM PROBLEMS
 PUTNAM TRAINING EASY PUTNAM PROBLEMS (Last updated: September 24, 2018) Remark. This is a list of exercises on Easy Putnam Problems Miguel A. Lerma Exercises 1. 2017-A1. Let S be the smallest set of positive
PUTNAM TRAINING EASY PUTNAM PROBLEMS (Last updated: September 24, 2018) Remark. This is a list of exercises on Easy Putnam Problems Miguel A. Lerma Exercises 1. 2017-A1. Let S be the smallest set of positive
Berkeley Math Circle, May
 Berkeley Math Circle, May 1-7 2000 COMPLEX NUMBERS IN GEOMETRY ZVEZDELINA STANKOVA FRENKEL, MILLS COLLEGE 1. Let O be a point in the plane of ABC. Points A 1, B 1, C 1 are the images of A, B, C under symmetry
Berkeley Math Circle, May 1-7 2000 COMPLEX NUMBERS IN GEOMETRY ZVEZDELINA STANKOVA FRENKEL, MILLS COLLEGE 1. Let O be a point in the plane of ABC. Points A 1, B 1, C 1 are the images of A, B, C under symmetry
Mathematics 2260H Geometry I: Euclidean geometry Trent University, Fall 2016 Solutions to the Quizzes
 Mathematics 2260H Geometry I: Euclidean geometry Trent University, Fall 2016 Solutions to the Quizzes Quiz #1. Wednesday, 13 September. [10 minutes] 1. Suppose you are given a line (segment) AB. Using
Mathematics 2260H Geometry I: Euclidean geometry Trent University, Fall 2016 Solutions to the Quizzes Quiz #1. Wednesday, 13 September. [10 minutes] 1. Suppose you are given a line (segment) AB. Using
EGMO 2016, Day 1 Solutions. Problem 1. Let n be an odd positive integer, and let x1, x2,..., xn be non-negative real numbers.
 EGMO 2016, Day 1 Solutions Problem 1. Let n be an odd positive integer, and let x1, x2,..., xn be non-negative real numbers. Show that min (x2i + x2i+1 ) max (2xj xj+1 ), j=1,...,n i=1,...,n where xn+1
EGMO 2016, Day 1 Solutions Problem 1. Let n be an odd positive integer, and let x1, x2,..., xn be non-negative real numbers. Show that min (x2i + x2i+1 ) max (2xj xj+1 ), j=1,...,n i=1,...,n where xn+1
13 th Annual Harvard-MIT Mathematics Tournament Saturday 20 February 2010
 13 th Annual Harvard-MIT Mathematics Tournament Saturday 0 February 010 1. [3] Suppose that x and y are positive reals such that Find x. x y = 3, x + y = 13. 3+ Answer: 17 Squaring both sides of x y =
13 th Annual Harvard-MIT Mathematics Tournament Saturday 0 February 010 1. [3] Suppose that x and y are positive reals such that Find x. x y = 3, x + y = 13. 3+ Answer: 17 Squaring both sides of x y =
International Mathematical Talent Search Round 26
 International Mathematical Talent Search Round 26 Problem 1/26. Assume that x, y, and z are positive real numbers that satisfy the equations given on the right. x + y + xy = 8, y + z + yz = 15, z + x +
International Mathematical Talent Search Round 26 Problem 1/26. Assume that x, y, and z are positive real numbers that satisfy the equations given on the right. x + y + xy = 8, y + z + yz = 15, z + x +
JBMO 2016 Problems and solutions
 JBMO 016 Problems and solutions Problem 1. A trapezoid ABCD (AB CD, AB > CD) is circumscribed. The incircle of the triangle ABC touches the lines AB and AC at the points M and N, respectively. Prove that
JBMO 016 Problems and solutions Problem 1. A trapezoid ABCD (AB CD, AB > CD) is circumscribed. The incircle of the triangle ABC touches the lines AB and AC at the points M and N, respectively. Prove that
Joe Holbrook Memorial Math Competition
 Joe Holbrook Memorial Math Competition 8th Grade Solutions October 9th, 06. + (0 ( 6( 0 6 ))) = + (0 ( 6( 0 ))) = + (0 ( 6)) = 6 =. 80 (n ). By the formula that says the interior angle of a regular n-sided
Joe Holbrook Memorial Math Competition 8th Grade Solutions October 9th, 06. + (0 ( 6( 0 6 ))) = + (0 ( 6( 0 ))) = + (0 ( 6)) = 6 =. 80 (n ). By the formula that says the interior angle of a regular n-sided
Higher Geometry Problems
 Higher Geometry Problems (1) Look up Eucidean Geometry on Wikipedia, and write down the English translation given of each of the first four postulates of Euclid. Rewrite each postulate as a clear statement
Higher Geometry Problems (1) Look up Eucidean Geometry on Wikipedia, and write down the English translation given of each of the first four postulates of Euclid. Rewrite each postulate as a clear statement
1. If two angles of a triangle measure 40 and 80, what is the measure of the other angle of the triangle?
 1 For all problems, NOTA stands for None of the Above. 1. If two angles of a triangle measure 40 and 80, what is the measure of the other angle of the triangle? (A) 40 (B) 60 (C) 80 (D) Cannot be determined
1 For all problems, NOTA stands for None of the Above. 1. If two angles of a triangle measure 40 and 80, what is the measure of the other angle of the triangle? (A) 40 (B) 60 (C) 80 (D) Cannot be determined
Solutions. cos ax + cos bx = 0. a sin ax + b sin bx = 0.
 Solutions 85. Find all pairs (a, b) of positive integers with a b for which the system cos ax + cos bx = 0 a sin ax + b sin bx = 0. Solution 1. Suppose that the system is solvable; note that x = 0 is not
Solutions 85. Find all pairs (a, b) of positive integers with a b for which the system cos ax + cos bx = 0 a sin ax + b sin bx = 0. Solution 1. Suppose that the system is solvable; note that x = 0 is not
1 2n. i=1. 2m+1 i = m, while. 2m + 1 = 1. is the best possible for any odd n.
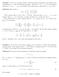 Problem 1. Let n be a positive integer. Find the largest nonnegative real number f(n) (depending on n) with the following property: whenever a 1, a,..., a n are real numbers such that a 1 + a + + a n is
Problem 1. Let n be a positive integer. Find the largest nonnegative real number f(n) (depending on n) with the following property: whenever a 1, a,..., a n are real numbers such that a 1 + a + + a n is
2007 Mathematical Olympiad Summer Program Tests
 2007 Mathematical Olympiad Summer Program Tests Edited by Zuming Feng Mathematics Olympiad Summer Program 2007 Tests 1 Practice Test 1 1.1. In triangle ABC three distinct triangles are inscribed, similar
2007 Mathematical Olympiad Summer Program Tests Edited by Zuming Feng Mathematics Olympiad Summer Program 2007 Tests 1 Practice Test 1 1.1. In triangle ABC three distinct triangles are inscribed, similar
2005 Palm Harbor February Invitational Geometry Answer Key
 005 Palm Harbor February Invitational Geometry Answer Key Individual 1. B. D. C. D 5. C 6. D 7. B 8. B 9. A 10. E 11. D 1. C 1. D 1. C 15. B 16. B 17. E 18. D 19. C 0. C 1. D. C. C. A 5. C 6. C 7. A 8.
005 Palm Harbor February Invitational Geometry Answer Key Individual 1. B. D. C. D 5. C 6. D 7. B 8. B 9. A 10. E 11. D 1. C 1. D 1. C 15. B 16. B 17. E 18. D 19. C 0. C 1. D. C. C. A 5. C 6. C 7. A 8.
Hanoi Open Mathematical Competition 2016
 Hanoi Open Mathematical Competition 2016 Junior Section Saturday, 12 March 2016 08h30-11h30 Question 1. If then m is equal to 2016 = 2 5 + 2 6 + + 2 m, (A): 8 (B): 9 (C): 10 (D): 11 (E): None of the above.
Hanoi Open Mathematical Competition 2016 Junior Section Saturday, 12 March 2016 08h30-11h30 Question 1. If then m is equal to 2016 = 2 5 + 2 6 + + 2 m, (A): 8 (B): 9 (C): 10 (D): 11 (E): None of the above.
1. Let g(x) and h(x) be polynomials with real coefficients such that
 1. Let g(x) and h(x) be polynomials with real coefficients such that g(x)(x 2 3x + 2) = h(x)(x 2 + 3x + 2) and f(x) = g(x)h(x) + (x 4 5x 2 + 4). Prove that f(x) has at least four real roots. 2. Let M be
1. Let g(x) and h(x) be polynomials with real coefficients such that g(x)(x 2 3x + 2) = h(x)(x 2 + 3x + 2) and f(x) = g(x)h(x) + (x 4 5x 2 + 4). Prove that f(x) has at least four real roots. 2. Let M be
Definitions, Axioms, Postulates, Propositions, and Theorems from Euclidean and Non-Euclidean Geometries by Marvin Jay Greenberg ( )
 Definitions, Axioms, Postulates, Propositions, and Theorems from Euclidean and Non-Euclidean Geometries by Marvin Jay Greenberg (2009-03-26) Logic Rule 0 No unstated assumptions may be used in a proof.
Definitions, Axioms, Postulates, Propositions, and Theorems from Euclidean and Non-Euclidean Geometries by Marvin Jay Greenberg (2009-03-26) Logic Rule 0 No unstated assumptions may be used in a proof.
2003 AIME2 SOLUTIONS (Answer: 336)
 1 (Answer: 336) 2003 AIME2 SOLUTIONS 2 Call the three integers a, b, and c, and, without loss of generality, assume a b c Then abc = 6(a + b + c), and c = a + b Thus abc = 12c, and ab = 12, so (a, b, c)
1 (Answer: 336) 2003 AIME2 SOLUTIONS 2 Call the three integers a, b, and c, and, without loss of generality, assume a b c Then abc = 6(a + b + c), and c = a + b Thus abc = 12c, and ab = 12, so (a, b, c)
Math Day at the Beach 2017 Solutions
 Math Day at the Beach 07 Solutions Mike Bao, Brendan Brzycki, Benjamin Chen, Samuel Cui, Michael Diao, Ayush Kamat, Emma Qin, Jack Sun, Jason Ye, Xuyang Yu, Beckman Math Club Individual Round Problem.
Math Day at the Beach 07 Solutions Mike Bao, Brendan Brzycki, Benjamin Chen, Samuel Cui, Michael Diao, Ayush Kamat, Emma Qin, Jack Sun, Jason Ye, Xuyang Yu, Beckman Math Club Individual Round Problem.
Mathematics 2260H Geometry I: Euclidean geometry Trent University, Winter 2012 Quiz Solutions
 Mathematics 2260H Geometry I: Euclidean geometry Trent University, Winter 2012 Quiz Solutions Quiz #1. Tuesday, 17 January, 2012. [10 minutes] 1. Given a line segment AB, use (some of) Postulates I V,
Mathematics 2260H Geometry I: Euclidean geometry Trent University, Winter 2012 Quiz Solutions Quiz #1. Tuesday, 17 January, 2012. [10 minutes] 1. Given a line segment AB, use (some of) Postulates I V,
SOLUTIONS. x 2 and BV 2 = x
 SOLUTIONS /3 SOLUTIONS No problem is ever permanently closed The editor is always pleased to consider new solutions or new insights on past problems Statements of the problems in this section originally
SOLUTIONS /3 SOLUTIONS No problem is ever permanently closed The editor is always pleased to consider new solutions or new insights on past problems Statements of the problems in this section originally
Objective Mathematics
 . In BC, if angles, B, C are in geometric seq- uence with common ratio, then is : b c a (a) (c) 0 (d) 6. If the angles of a triangle are in the ratio 4 : :, then the ratio of the longest side to the perimeter
. In BC, if angles, B, C are in geometric seq- uence with common ratio, then is : b c a (a) (c) 0 (d) 6. If the angles of a triangle are in the ratio 4 : :, then the ratio of the longest side to the perimeter
