A mathematical analysis of the motion of an in-flight soccer ball
|
|
|
- Sydney Harrell
- 6 years ago
- Views:
Transcription
1 Noname manuscript No. (will be inserted by the editor) A mathematical analysis of the motion of an in-flight soccer ball None given Received: date / Accepted: date Abstract In this paper an analytical and numerical study of the three-dimensional equations describing the motion through the air of a spinning ball is presented. The initial analysis involves constant drag coefficients but is later extended to involve drag varying with the spin ratio. Excellent agreement is demonstrated between numerical and analytical results. The analytical solution shows explicitly how the balls motion depends on parameters such as ball roughness, velocity and atmospheric conditions. The importance of applying three-dimensional models, rather than two-dimensional approximations, is demonstrated. Keywords aerodynamics soccer ball flight spinning soccer ball Magnus force perturbation solution 1 Introduction Over the years much work has been carried out on football design, moving from the traditional leather ball encasing an inflated pigs bladder to the most recent Jabulani which is constructed using polyurethane panels. The goal of the technological advances in football design has been to make the ball more reliable and better to play with, for the benefit of all players involved. Recently, at a mathematics in industry study group held in Johannesburg, the coach of a South African premiership team, Bidvest Wits, posed the question of whether amatchball couldbe chosento benefit the home side (oralternatively disadvantage the visiting team). This paper has evolved from that study and in the conclusions the question of whether the ball choice can indeed provide a home advantage will be discussed. In professional football matches in South Africa, and many other countries, the home team provides the ball. The choice of ball is of course restricted, primarily by Fifa law, which dictates the size, (dry) weight, pressure and Address(es) of author(s) should be given
2 None given material. Hence the main changes in ball design have entered through the material and shape of the panels [1]. A further restriction comes through the sponsor, in that the team must use one of their balls. In the case of Bidvest Wits the balls are provided by Nike. During the meeting in Johannesburg three Nike balls were presented, the balls had a very similar appearance, however there was one significant difference in that two balls were rough (with dimpled panels) while one ball had smooth panels (see, for example, close-up pictures of the Nike T9 Tracer and Catalyst on Nike.com). To answer the question on the choice of ball the following analysis will focus on its motion through the air and in particular from a free kick or corner. One reason for this is that these are relatively controlled situations and there is much data on a ball s motion through the air. A second reason is that free kicks are an important factor in scoring: in the 1998 world cup 4 of the 171 goals scored came from set-plays, with 5% of these from free kicks []. Consequently understanding the ball motion through the air from a free kick or corner could provide important information concerning the best ball choice. A final reason is that Johannesburg is located high above sea level (at around 18m). The air density is approximately % lower than that at sea level [11] and so it is expected that the greatest difference in ball motion between Johannesburg and cities located at a lower altitude will be when it moves through the air. Of course there has been much work carried out on the motion of balls and projectiles through the air. As early as the 16s Newton noted that a spinning tennis ball had a curved trajectory. A century later Robin showed there was a transverse aerodynamic force on a rotating sphere: this is what is now termed the Magnus effect (or more fairly the Robin-Magnus effect). In the late18staitwasthe firsttoapplythis notiontoasportsball(unfortunately a golfball rather than a football). All of this work involved frictionless fluids and so the correct explanation for the Magnus effect had to wait until Prandtl s boundary layer theory of 194. Specific analysis of the motion of an in-flight football came much later. Asai et al. [1] carried out an experimental study of the lift coefficients on a spinning and non-spinning football and showed a strong dependence on the lift coefficient with spin rate. The equations of motion for a football are provided in many papers, however, the convention of Goff and Carré [7] is used in this study, where the Magnus effect is split into lift and lateral components (Asai et al. also work with two components). Hörzer et al. [11] provide useful details of the differences in atmospheric conditions between World Cup venues in South Africa and demonstrate the effect of altitude on a ball s trajectory. Oggiano and Sætran [14] compare the trajectory of different footballs: this confirmed the belief that the ball choice could provide a home advantage. The organisation of this paper is as follows. In the three-dimensional mathematical model is given, this is well established and simply involves Newton s second law. Due to the nonlinearity of the governing equations all previous solutions have been obtained numerically. In an analysis of a simpler model than that considered in the present study, Bray and Kerwin [] state that the
3 Mathematics of soccer ball motion 3 governing equations have no closed form solution, although this is technically correct an accurate approximate solution is derived in 3. This clearly shows the effect of the model parameters on the ball s motion, which is not possible with a numerical solution. In 4 numerical solutions are calculated to verify the accuracy of the approximate solution. Experimental studies on drag and lift coefficients have demonstrated their dependence on spin, however theoretical studies generally set the coefficients as constant. In 5 the analysis is extended to deal with variable coefficients. Finally, the question of whether the choice of ball can really provide a home advantage is discussed. Mathematical model The motion of a football is described by Newton s second law F = mẍ, where the force F is comprised of gravity and drag due to the air. For a non-spinning ball the dragforceacts solelyin the directionopposite to the ball s motion. For a spinning ball the drag has two components, the resistance opposing forward motion and the Magnus force. The Magnus force acts perpendicular to the direction of motion and the spin axis. This force may be resolved into two components denoting lift and lateral motion, see [1,7]. If the ball moves in the direction defined by the velocity vector ˆv (where the hat indicates a unit vector) then a second vector ˆl may be defined which is perpendicular to ˆv but remains in the same plane as ˆv and the gravity vector, ĝ. Note that the z component of ˆl is positive (i.e. it points upwards). A right handed system is then defined through a third vector ˆl ˆv. The co-ordinate system and vectors are shown in Figure 1. So the drag force opposing motion, F d, acts in the direction ˆv, the lift F l acts in the ˆl direction and the lateral force F s acts in the ˆl ˆv direction. The total force is now defined as F = mg+f d +F l +F s. (1) Splitting the spin components requires two spin speeds to be defined: ω l is the spin rate about the ˆl axis and ω s is the spin rate about the ˆl ˆv axis. If a single spin axis is used (for example as defined in [11]), which is contained within the ˆl, ˆl ˆv plane, then the axis makes an angle Ω with the ˆl ˆv axis, where tanω = ω l /ω s. Note, the current problem is more general than that studied in [] where the spin axis is contained solely in the x-z plane. The signs of the forces depend on the convention used. The drag force F d of course acts in the opposite direction to the ball s forward motion. If pure side-spin is considered, then the z axis is the spin axis. Using standard polar co-ordinate notation as shown in Figure 1, with ψ contained in the x-y plane and measured from the x axis, and defining ψ = ω s, then the resultant force F s acts in the negative x direction. Pure top-spin has the x axis as the spin axis and then θ = ω l and the resultant force F l acts in the negativez direction.
4 4 None given z ˆl ˆv ˆl ˆv θ y x ψ ˆv p Fig. 1 Co-ordinate system. Consequently the following relationships hold: F d = 1 ρa v C dˆv, F l = 1 ρa v C lˆl, Fs = 1 ρa v C sˆl ˆv. () Here m is the mass of the ball, A is its cross-sectional area, ρ is the density of air, C i are the drag coefficients and v = (ẋ +ẏ +ż ), (3) where v = (ẋ,ẏ,ż) is the velocity vector. The product ˆl ˆv acts in the negative x direction so there is no minus sign in the expression for F s. The drag coefficients C i vary with Re = ρ v D/µ (where D is the ball diameter and µ the air viscosity) and the spin parameter Sp = Dω/( v ) [1,4]. The variation of C d with Re shows a radical change as the ball moves through the laminar-turbulent transition. The post-transition experimental results of [1] indicate C d,c l vary with Sp but have little variation with Re, see also [7]. Note, since C l, C s arise from the same effect they have the same behaviour. Since the Magnus force is resolved into two components there are two angular velocities, ω l, ω s. Then the variation of C l, C s with Sp means that they take different values if ω l ω s. The advantage of using two drag coefficients is that the different spin axes may be differentiated easily. In particular, for pure side-spin ω l, C l = and for pure top-spin ω s, C s = (the relation between ω and C will be discussed in more detail later).
5 Mathematics of soccer ball motion 5 The unit vectors may be defined in terms of the two angles ψ,θ by the following relations ˆv = sinθcosψi+sinθsinψj+cosθk (4) ˆl = cosθcosψi cosθsinψj+sinθk (5) ˆl ˆv = sinψi+cosψj. (6) Alternatively the angles in terms of the Cartesian velocity components can be expressed as sinθ = v p v, cosθ = ż v, sinψ = ẏ v p, cosψ = ẋ v p, (7) where v p = (ẋ,ẏ) is the projection of v on the x-y plane (see Figure 1). The equation of motion may now be written in component form v ẍ = k d v ẋ+k l v p ẋż +k v s v p ẏ, (8) v ÿ = k d v ẏ +k l v p ẏż k v s v p ẋ, (9) z = g k d v ż k l v v p. (1) The scaled drag coefficients are k i = ρac i /(m). This is a nonlinear set of second order ordinary differential equations with no analytical solution. They may easily be solved numerically however analytical progress can be made after applying certain sensible assumptions concerning the ball s motion: 1. The axes can be chosen so that the ball is kicked primarily in one direction (although due to swerve it will obviously deviate from this). Hence it is assumed that the ball is kicked mainly in the y direction.. The dominant swerve is in the sideways direction, that is, the ball is kicked mainly with side-spin. The first assumption means that the velocity in the y direction must be significantly higher than that in the x and z directions, ẏ ẋ,ż and also the ball travels furthest in the y direction. The second assumption holds in general for football motion, side-spin is usually greater than top-spin, for a golf ball one would expect a greater top-spin. The analysis is easily adapted to top-spin but, since the focus is on footballs, dominant side-spin is assumed. 3 Perturbation solution To make analytical progress the system is non-dimensionalised by setting X = x L 1, Y = y L, Z = z L 3, T = t τ. (11)
6 6 None given k d.13 k l.4 k s. 18 m.45 kg ρ 1 kg m 3 D. m A.39 m v 5 m/s C d.3 C s.5 C l.1 L m Table 1 Typical parameter values, see [1,5,15] where L is the distance in the y direction to the goal, τ = L /v is the timescale for the ball to reach the target where v is the initial velocity of the ball in the y direction and L 3 = gτ is the vertical length-scale. The capital letters X,Y,Z,T denote non-dimensional variables. The length-scale L 1 is, as yet, unknown but it is noted that due to assumption 1, L 1 L. First, consider the velocity vectors. Writing them in terms of non-dimensional quantities v = L τ Ẏ Ẋ Ż Ẏ = L τ Ẏr 1, v p = L τ Ẏ 1+ L 1 Ẋ L 1+ L 1 L Ẏ + L 3 L (1) where r 1,r denote the square roots. The factor L Ẏ/τ has been isolated since this is the largest term in the velocity expression and so r 1,r = O(1) (that is their size is of the order unity). The governing equations may now be written Ẏ = L τ Ẏr, L r 1 Ẍ = k d L ẊẎr r 1 1 +k l L 3 ẊŻ r +k s Ẏ L 1 r (13) Ÿ = k d L Ẏ r 1 r 1 +k l L 3 ẎŻ r k L 1 r1 s ẊẎ r (14) Z = 1 k d L r 1 ẎŻ k ll L 3 r 1 r Ẏ. (15) To determine L 1 it is noted that the motion in the x direction is caused by either an initial velocity or the spin component in the y direction. Since this study is focussed on the spin induced swerve, the initial velocity in the x direction is set to zero, ẋ() = Ẋ() =. The dominant term in equation (13) is clearly that involving Ẏ and since the velocity vectors are scaled so that r 1,r = O(1), L 1 = k s L. Using the parameter values of Table 1 this determines L 1 4m, that is, the ball is expected to travel of the order 4m laterally during its flight. The dominant term in equation (14) again involves Ẏ. With k d =.13, k d L =.6 and this is denoted as ǫ = k d L which is a small parameter (and ǫ.7). The square root terms r 1,r contain the ratios L 1 /L.4,L 3 /L.5 which are denoted c 1ǫ, c ǫ respectively (note, k s L 1 = L 1 /L ). Finally, k ll 3.3 = c 3 ǫ, k l L /L 3.7 = c 4 ǫ.
7 Mathematics of soccer ball motion 7 The governing equations are now [ ] Ẍ = Ẏr 1 ǫẋ c 3ǫ ẊŻ r Ẏ r 1 Ẏ r [ ] Ÿ = Ẏr 1 ǫẏ c 3ǫ Ż +c 1 ǫ r 1 Ẋ r r [ ] Z = 1 Ẏr 1 ǫż +c 4ǫr Ẏ (16) (17) (18) where r 1 = 1+c 1 ǫ Ẋ +cǫż Ẏ Ẏ, r = 1+c 1 ǫ Ẋ Ẏ. (19) Note the assumption that the ball is kicked primarily with side-spin means that the k l terms enter at lower order to the k s terms in the Ẍ,Ÿ equations (through the coefficient c 3 ). In the Z equation lift is the dominant force after gravity and so it enters at O(ǫ). With top-spin dominating the scaling would have to be changed accordingly. Written in non-dimensional form observations can be made about the solution behaviour, without solving the system. For example, all terms in (17) involve the small parameter ǫ indicating that the dominant motion in the Y direction is described by Ÿ = and that drag, represented by ǫ, has a relatively small effect. Since ǫ =.6 neglecting terms involving ǫ could lead to errors of around 6%. Motion in the Z direction is dominated by gravity. The X motion is dominated by the contribution of Ẏ (reflecting the fact that the Magnus force is due to the difference in equatorial velocities and the forward velocity, which is approximately Ẏ). However, the most interesting feature is that since r 1 contains the term ǫ(ż/ẏ) the velocity in the Z direction will contribute to all equations. Most importantly it will affect the X equation at order ǫ, i.e. for the current set of parameter values neglect of the Z motion may lead to errors of around 6%. Obviously this could have significant consequences for any experiment using a two-dimensional analysis to model the three dimensional ball motion. This is discussed further in the results section, 4. The initial conditions are that the ball starts at the origin and is kicked with (dimensional) velocity(, v, w). Note, the velocity in the x direction could always be chosen to be zero by simply defining the y axis as the direction of the kick in the x-y plane. In non-dimensional form these conditions are X() = Y() = Z() =, Ẋ() =, Ẏ() = 1, Ż() = W, where W = wτ/l 3. In order to determine a standard perturbation solution based on the small parameter ǫ write X = X +ǫx 1 +ǫ X +, Y = Y +ǫy 1 +ǫ Y +, Z = Z +ǫz 1 +ǫ Z + ()
8 8 None given To O(ǫ ) the solution is [ X = T +ǫ c W T (3+c W) T3 6 + c T 4 ] + (1) 1 ǫ [( 9 ) ( T c W 3 +3c 3 W c c 4 W 6 + 6c W + 11 c 3 c ) 1 T 4 +c c c T 5 ] 1 Y = T ǫ [ (c T +ǫ W c 3 W) T 4 +( c 1 +c W c 3 ) T3 6 c T 4 ] 4 () ] Z = WT [ (W T +ǫ +c 4 ) T + T3 + (3) 6 [ ǫ c W (W +c 4 ) T 4 +(4W +6c 4 +3c W +c c 4 W) T3 1 (3+3c W +c c 4 ) T4 4 + c T 5 ]. 4 Bray& Kerwin[3] study a simplified two-dimensional system. This analysis follows the line of equating the acceleration to the largest term on the right hand side of the equations. From equations (16, 17) this reduces the problem to Ẍ = Ẏ, Ÿ = ǫẏ, (4) where it is noted that r 1 r 1. Applying the initial conditions gives Y = 1 ǫ ln 1+ǫT, X = 1 (Y T). (5) ǫ To relate these solutions to equations (1,) the Taylor series expansion for ǫ 1 is used to find X = T ǫt3 3 +ǫt4 4 (6) Y = T ǫ T +ǫt3 3. (7) Setting W, c i = in (1,), to remove the Z dependence and make the solution appear two-dimensional, the x solutions differ at O(ǫ), while the y solutions differ at O(ǫ ). The simplification of only taking the largest terms on the right hand side will therefore correctly capture the dominant behaviour but, in the case of the sideways swerve, leads to errors in all subsequent terms. Consequently, this solution form will provide a reasonable approximation to the numerical result for y but a rather poorer one for x and the error increases with ǫ (for example if L is increased). Further deviation from the correct
9 Mathematics of soccer ball motion 9 solution will occur due to the neglect of the Z motion. This will be discussed later in the context of the solutions shown in 4. Now return to dimensional variables X = x/l 1, Y = y/l, Z = z/l 3, T = t/τ, where L 1 = k s L, L 3 = gτ, τ = L /v and L, v are the initial distance and velocity in the y direction. The constants must also be expressed in terms of the dimensional parameters ǫ = k d L, c 1 = k s kd, c = g L k d v 4, c 3 = k lg vkd L, c 4 = k lv, W = wv. gk d L gl (8) The dimensional solution is then given by x = k s(vt) [ 1 {k d vt g t 4gwt+6w }] 6v (9) [ { }] kd vt y = vt 1 (3) z = wt gt + { kd gvt 3 6 } (k d w+k l v) vt. (31) Note, since the expressions are rather cumbersome they are only written here to O(ǫ) (the O(ǫ) terms are given in the curly brackets). From these expressions the effect of the various parameters can be seen clearly. The y equation shows that the distance travelled is approximately proportional to the initial velocity and time but that drag reduces this and the effect of drag increases with time. In the z direction the distance travelled is determined primarily by the initial velocity and gravity but both drag and lift act to change this. Again these effects increase with time. However, since swerve due to side-spin is the main focus of this study the x equation is the most revealing. From this it is seen that, to leading order the distance travelled in the x direction is proportional to the sideways drag coefficient k s and also (vt). The ball design and atmospheric conditions contribute through k s hence ball design is very important for swerve. The product vt is the first approximation to the distance travelled in the y direction. The quadratic dependence then indicates the importance of taking a kick far from the goal. The further the ball travels the more it will swerve (this is obviously well known to free kick specialists in football who frequently attempt to move the ball away from the goal). Perhaps the most famous example is the free-kick of Roberto Carlos against France in 1997 which exhibited spectacular curve at the end of the flight. This free kick was taken approximately 35m from goal, see YouTube or [6]. The forward drag k d enters at first order and acts to reduce the swerve. An important feature of the solution is that the vertical motion, through g and w, also enters at first order. The quadratic g t 4gwt+6w is positive provided w (i.e. the ball is not kicked into the ground) and so acts to increase the swerve. A two-dimensional analysis will miss this effect and comparison with experiment would then lead to over-prediction of k s. Due to the differences in time dependence of the terms in equations (9-31) they will become less accurate as time increases. This is termed the secular
10 1 None given effect. The break down will occur when the O(ǫ) terms become O(1). In the case of the x equation this is when t 1/(k d v) 3s. The y and z equations indicate times around 9s. Given that the football flight is typically 1s these approximations should hold for all sensible kicks the secular effect is not considered. 4 Numerical and analytical results 4 3 z z x 15.5 y x y Fig. Left: Numerical solution showing a dimensional trajectory of a soccer ball being hit into the top corner of the goal. Right: plots of x and z against y. The numerical solution to equations (16-18) was carried out using MAT- LAB routine ODE45. In Figure a) the 3D trajectory of a ball kicked with initial conditions v = 5m/s, w = 8.76m/s and at a distance L = m from the target is shown. The choice of w was made so that the ball ended up near the top of the goal (since the centre of mass of the ball is tracked the top of the goal is taken at.34m, that is, the standard goal height minus the ball radius). Other parameters are given in Table 1. To travel m in the y direction takes.911s (without drag t = /5 =.8s). Figure b) demonstrates the x, z variation against y. From the x curve it can be seen that the ball moves around.3 m, with an approximately quadratic variation. In the z direction the ball height increases until quite close to the goal, reaching a maximum of only.4m above the goal. To show the trajectory clearly, Figure uses dimensional quantities. Whenever possible, in subsequent figures dimensionless quantities are preferred since these highlight the differences in motion better. They also allow results to be combined, such as in Figure 7, where x and y solutions are plotted on the same graph. In Figure 3 the variation of X, Y and Z against T is shown, for the same conditions as in Figure but now the various perturbation solutions are included. In non-dimensional units the time of flight is T =.911 5/
11 Mathematics of soccer ball motion 11 X Y Z T Fig. 3 Non-dimensional trajectories of X, Y and Z against T: full numerical solution (solid line), O(ǫ ) solution (dotted line), O(ǫ) solution (dot-dashed line) and O(ǫ ) solution (dashed line). Parameter values are C d =.3, C s =.5 and C l = The solid line is the numerical solution, the dotted line the leading order perturbation, dash-dot is the first order and dashed is the second order. In each case the leading order gives a reasonable approximation for small times but rapidly loses accuracy. To describe the full flight the perturbation solution for Y is reasonably accurate at first order, but the X and Z solutions are less accurate. All curves show excellent agreement at O(ǫ ). Since the second order solution involves neglecting terms O(ǫ 3 )., errors of the order of % is expected. In fact the error increases with time, obviously at T = the error is zero due to the imposition of the initial condition. In the X direction the maximum error between the numerical and second order solution is almost 3% and this occurs at the end of the flight. This is in agreement with the earlier discussion that the approximate solutions start to break down as time increases. Note, the same conclusion holds for the dimensional problem. In the previous section the apparent problem with neglecting vertical motion was discussed and, in particular, that this would be most apparent in the motion in the X direction. A two-dimensional model, with motion solely in the X-Y plane, is retrieved from this solution by setting c = c 3 = W = in equations (1,). Figure 4 compares numerical (solid line) and perturbation (dashed line) solutions in X up to second order. The two curves labelled (a) include motion in the Z direction and (b) neglect Z motion. If the Z motion is neglected the swerve is decreased by around 4.5%. This error increases nonlinearly with increasing w: if w is doubled the error increases to 3%. This observation has obvious consequences in the interpretation of experimental studies. For example, if the two-dimensional model of [3] is compared to experiments and used to calculate drag coefficients then to compensate for the
12 1 None given X (a) (b) T Fig. 4 Comparison of numerical (solid line) and second order perturbation (dashed line) solutions in X: (a) including vertical motion, (b) neglecting vertical motion. neglect of the Z motion it will predict higher values than in reality. In [], the mathematical model is simplified by assuming the spin axis remains in the X-Z plane and therefore the Ż term in equation (16) may be neglected, yet it is retained in the Y equation. This approximation appears rather inconsistent and will also affect predicted drag coefficients. It is therefore important to implement a full three-dimensional model when calculating experimental parameters. A two-dimensional study is possible but, since gravity cannot be avoided, this should be confined to the Y-Z plane and using only top-spin. 4.1 Comparison with experimental data In the paper of Carréet al [5] a number of results are presented for ball motion with and without spin. In their Figures 4a-c a typical trajectory is shown for a ball launched with no spin at approximately 15 to the ground and with a launch velocity in the range 17-31m/s. Taking the data from these figures it is a simple matter to curve fit (in this case the polyfit function of Matlab was used, which fits data using a least-squares criteria). A quadratic fit to the y(t) data of their Figure 4b leads to y a +a 1 t+a t, (3) where a =.1785, a 1 = , a = A cubic fit to the z(t) data of Figure 4c leads to z b +b 1 t+b t +b 3 t 3, (33)
13 Mathematics of soccer ball motion 13 where b =.53, b 1 = 6.87, b = 6.94, b 3 =.1. The appropriate data points are displayed on Figure 5 as asterisks. Finally, Figure 4a presents z(y) which takes the form z c +c 1 y +c y +c 3 y 3, (34) where c =.8, c 1 =.371, c =.3, c 3 = y (m) 6 4 t (s) z (m) t (s) Fig. 5 Comparison of experimental data of [5] (asterisks) and curve fits (solid line) The initial angle of the kick is easily determined from the curve fits by noting tanθ = ż() ẏ() = b (35) a Alternatively tanθ = dz/dy t= = c These two results indicate a launch angle of θ or.35, with an average of approximately (slightly higher than that quoted in the paper). The initial velocity in the y,z directions is (ẏ(),ż()) = (a 1,b 1 ) = (17.591,6.87) and so the initial speed v = a 1 +b m/s, which is within the quoted range.
14 14 None given Comparison of equations (3,33) and (3,31) allows us to determine additional information about the kick. First it may be noted that both y,z should start at the origin, which is the case with the perturbation solution, but the curvefit indicatessomeslighterror.however,both therelevanttermsb,c are small. The values for (v, w) are obtained from taking (ẏ(), ż()) in equations (3,31). The drag coefficient k d may be obtained by comparing the quadratic terms in the y expressions k dv = a k d =.8 (36) which is of a similar order of magnitude to that quoted in Table 1. The z expressions provide a means for verifying this value, comparing the cubic terms gives k d gv 6 = b 3 k d =.7 (37) which, allowing for experimental error and errors in curve fitting, appears to be in good agreement with the first estimate. In [5] it is stated that this trajectory is typical for a case with no-spin, consequently k l =. Comparison of the quadratic terms in the z expressions then determines k d.5, a result that is clearly at odds with the previous findings. Allowing k l the quadratic terms may be used with to determine k l =.61 when k d =.8 and k l =.65 when k d =.7. In Figure 5a) the experimental data is compared against the quadratic form given by equation (3) with the quoted values for a i. This is equivalent to plotting the approximate solution (3) with v = m/s, k d =.8. Clearly the agreement is excellent. In Figure 5b) the experimental data is compared against the cubic form given by equation(33) with the quoted values for b i. This is equivalent to plotting the approximate solution (31) with w = 6.87m/s, k d =.7. Clearly the agreement is excellent. In summary, the forms suggested by the perturbation solution can provide an excellent fit to the experimental data. Comparison between the coefficients of the fitted curve and the perturbation solutions then permits the calculation of the drag coefficients (and can also be used to determine initial velocities if these are unknown). As an example the data provided in [5] was used to determine flight parameters, indicating an initial angle of around, as opposed to the reported 15, a drag coefficient k d [.7,.8] and a lift coefficient k l [.61,.65]. The appearance of a non-zero lift coefficient for an experiment apparently with no spin is particularly interesting. Given that the equations provide three ways to calculate k d in the absence of spin and that two of these routes agree well it seems likely that the fault does not lie in the equations. Consequently we may infer that possibly the graphs have been misreported (they are in fact only presented as a typical solution) or that some spin was generated during the flight, perhaps due to the initial positioning of the seams or the valve?
15 Mathematics of soccer ball motion 15 5 Drag coefficients So far the analysis has dealt with constant drag coefficients. However, experimental studieshaveshownthat C d, C l, C s allvarywith spin ratesp = Rω/ v and, to a lesser extent, (provided the air flow is turbulent) the Reynolds number. During the flight of a ball the angular velocity decays very slowly [11]. This may also be observed in the experimental findings of [9] and so angular velocity may reasonably be taken as constant but the magnitude of v decreases due to the drag and so Sp increases. There exist numerous experimental studies showing the variation of C s (or C l ) with Sp, see [1,4,9,14] for example. Goff and Carré [7] summarise experimental results of Asai et al. [1] and Carré et al. [4]. They point out that since C l and C s arise from the same process they are equivalent (some authors do not split the lift coefficient into components, preferring to work with a single one defined on an appropriate spin axis, see [11] for example). The experimental results indicate that C s,c l increase with spin until levelling off around Sp =.3. The actual values vary between experiments and, as shown in [14], with different types of ball but typically range between and.35 as Sp increases from to.3 [1,5,9,15]. Since the focus of this study is on the effect of spin in these calculations the region where Sp is very small (below.1) is neglected and then a piecewise approximation is employed of the form ) C s (1+ ms C C s = s (Sp Sp ),.1 < Sp <.3 ) C s (1+ ms C s (.3 Sp ) = C sm, Sp >.3, (38) where the gradient m s =.8, C s =.5 is the coefficient when Sp = Sp =.15/.8 and C sm =.34 is the constant maximum value of C s. The drag coefficient k s = k s is now written k s = ρac s m. The linear form, without the cut-off, has also been employed by Hörzer et al. [11]. The drag coefficient C d shows a weaker dependence on Sp and so as a first attempt to model varying coefficients C s is allowed to vary and C d is left constant. Given the equivalence of C s, C l, only the effect of varying one of these quantities is studied. This is fortunate since, as pointed out in the previous section, the analysis should be three-dimensional (unless limited to the y-z plane with only top-spin imposed). If both C s and C l are allowed to vary then the perturbation will be extremely cumbersome. Instead the case of pure sidespin is studied by setting C l = k l = while C s is given by equation (38). The
16 16 None given non-dimensional model then reduces to [ Ẍ = Ẏr L 1 k d L Ẋ k s φ r ] 1 s Ẏ L 1 r [ ] Ÿ = Ẏr L 1 r 1 1 k d L Ẏ +k s φ s Ẋ where r (39) (4) Z = 1 k d L r 1 ẎŻ. (41) { 1+ m s C φ s = s (Sp Sp ),.1 < Sp <.3 C sm C s, Sp >.3, (4) and Sp = Dω v = Dω r 1 vẏ. (43) Defining φ s = φ 1 r 1 Ẏ +φ, φ 1 = m srω C s v, φ = 1 m ssp C s. (44) To retrieve the constant spin case the conditions set were φ 1 =, φ = 1. Retaining the previous definitions for the small parameters (but with k s replaced by k s ) the governing equations may be written as [ ( ) ] Ẍ = Ẏr 1 ǫẋ φ1 r 1 Ẏ +φ r1 Ẏ (45) r [ ( ) ] Ÿ = Ẏr 1 ǫẏ +c 1ǫ φ1 r 1 Ẏ +φ r1 Ẋ (46) r Z = 1 ǫr 1 ẎŻ. (47) Thevariablespinisrepresentedthroughtheterminvolvingφ 1 andthisappears at leading order in the Ẍ equation. Hence, variable spin is expected to have a significant effect on the X motion. However, φ 1 and X only appear in the Ÿ and Z equations at second order and so it is expected that variable spin has little effect on the Y, Z motion. Using a standard perturbation, to O(ǫ) the solutions are [ X = (φ 1 +φ ) T +ǫ c W (φ 1 +φ )T ( φ 1 (+c W)+φ (3+c W) ) T c (φ 1 +φ )T 4 ] 4 (48) Y = T ǫ T ] T, Z = WT [ +ǫ WT + T3. (49) 6
17 Mathematics of soccer ball motion (a) Y.4. Z X..4 T (b).6.4 Y X. Z T Fig. 6 Non-dimensional trajectories of X, Y and Z against T for variable C s (with ω = 5): full numerical solution (solid line), O(ǫ ) solution (dotted line) and O(ǫ) solution (dot-dashed line): a) L =, b) L = 3m. Noting that k l = leads to c 3 = c 4 = and then the Y and Z solutions above correspond to equations (1-3) to O(ǫ) while the X solution differs from equation (1) at leading order. Figure 6 shows a comparison of numerical and perturbation solutions for the model including variable spin. Figure 6a) has the same initial conditions as used in Figure 3 but now with C s varying according to equation (38) and
18 18 None given ω = 5rad/s. The solid line is the numerical solution and the broken lines indicate various levels of perturbation solution. The X curve shows that at the end of the trajectory the ball has moved slightly less than.6 non-dimensional units, which corresponds to a dimensional distance.6k s L.59m. Since the dimensional swerve is proportional to L, in Figure 6b) the same kick is shown but now taken from 3m away. The change in L results in an increase in ǫ = k d L and so it is expected that the perturbation solution will lose accuracy. This is clear from the figure, however the O(ǫ) solution is still relatively accurate (accuracy could be intcreased by finding the O(ǫ ) term). The dimensional swerve at the end of the kick is now around 4.86m. This is almost double that of the m kick and results from the approximately quadratic dependence on distance. In Figure 7a) four curves corresponding to ω = 3, 4, 5, 6rad/s and L = 3m are plotted (with other conditions as in Figure 3). As expected increasing ω increases the lateral motion such that X(1) ranges from.98 to.44 as ω increases from 3 to 6 (and dimensionally from.9m to 4.3m). Neglecting variable drag, equation (9) indicates that the increase should be approximately linear x k s. Including the variation in drag coefficient, with a cut-off, makes the increase nonlinear. For example, as ω increases from 3 to 4 X(1) increases by.5 (dimensionally.5m), but as increasing ω from 5 to 6 X(1) increases by only.4 (dimensionally.4 m). Increasing ω further will make very little difference to the motion. This may be understood through Figure7b)whichshowsthe variationofc s throughthetrajectory:with ω = 3 or 4 the value of C s is always increasing. When ω = 5 the value of C s becomes constant near the end of the flight and for ω = 6 it is constant half of the time. Consequently any kick with ω > 6 will provide a similar result as that with ω = 6. In carrying out this study the question arose as to what exactly is being presented by different research groups when plotting C s Sp curves. In particular it appears unclear how Sp = Rω/ v is interpreted. The experiments of Asai et al. and Passmore et al. [1,15] involve a ball fixed in a wind tunnel where both ω and v remain constant and so Sp takes a single value for each experiment. The drag and lateral force are measured directly, which then allows calculation of drag coefficients through the definitions of equation (). More realistic experiments involve actually kicking the ball in a controlled environment and then calculating coefficients by matching the data to some mathematical model. For example, Bray & Kerwin [] track a ball s flight with two cameras. The model equations are solved and iterated, using the drag coefficients as fitting parameters, until a good fit to the experimental data is achieved. By this method constant values for forward and lateral drag coefficients are determined for a given kick. However, since these values come from fitting to the full trajectory, where Sp is an increasing function, the coefficients must be some form of average for the specific kick. A similar technique is employed by Carré et al. [5] where drag coefficients are also averages, but plots are against the initial value of Sp (thus avoiding the confusion in the variation of Sp). Goff and Carré [7,8] fit drag coefficients to minimise the least-squares error between a numerical solution and experimental data but to
19 Mathematics of soccer ball motion ω s = 6 ω s = 5 ω s = 4 ω s = 3.5 X T C s.3.5. C s.3.5 ω s = 3. ω s = S p S p.35.3 C s.5. C s.5 ω s = 5. ω s = S p S p Fig. 7 a) Non-dimensional trajectories of x against t for variable C s, b) corresponding plots of C s against S p, dashed line represents equation (38) the thick solid line is the variation of C s over the trajectory. reduce variation in Sp they limit data to the first.7sof flight. Griffiths et al. [9] use an accurate ball tracking method but then calculate coefficients using the formula of Wesson [16] which assumes constant drag. Consequently, the various data presented may show actual C s and Sp values or may be average values over a given trajectory (with different methods of averaging). Figure 8 presents two sets of curves, the bottom curves correspond to variable C s with
20 None given L = 3m. The dashed line represents the ball trajectory up to t = 1.655s (to end at y 3m) the solid line ends at t =.693s (around y = 15m). The top curves use a constant value of C s =.37 which was chosen to match the variable C s result after 1.655s. The graph is presented dimensionally, since the non-dimensional scaling depends on the choice of C s. All other conditions are the same as in the ω = 5rad/s case of Figure 7. The important feature here is that for times not equal to 1.655s the constant C s curve has a different amount of swerve which indicates that if an average value is used for C s then its value will vary with the distance of the kick (in the figure the 15m kicks show a difference of 1cm in swerve). That is, if all other conditions are fixed fitting a constant C s value to experimental data will lead to range of C s values for kicks taken over different distances. 6 x (m) 5 4 Constant C s 3 Variable C s 1 y (m) Fig. 8 Comparison of trajectories for varying and constant C s. 6 Discussion In this study the three-dimensional equations of motion for a football in flight have been studied. The numerical solution is trivial but this does not show the dependence on the problem parameters. Consequently a perturbation solution was developed which proved highly accurate when compared to the numerical solution. In deriving this solution the scaling was based on the assumption that footballers impart more lateral than top spin. This could easily be changed, to study a golf ball for example, where top-spin dominates. The analysis allowed a number of observations to be made about the ball s motion. The analytical approximations show that at leading order the lateral motion is proportional to the lateral drag coefficient k s and the distance (vt). This indicates why free kicks taken from a large distance show greater swerve. To first order in the small parameter, the motion in each direction is at most described by a quartic equation in time. Experimental studies often approx-
21 Mathematics of soccer ball motion 1 imate data with a polynomial. For example, Carré et al. [5] show excellent agreement with data assuming x varies quadratically in t. This is in agreement with this study s leading order result x k s (vt) / and so will capture the dominant behaviour and small time solution well. Bray and Kerwin [] assume a quartic dependence for x, y, z: since a quartic contains more coefficients it can more accurately fit the data. This form agrees with the first order expression. For this reason the results presented here have not been compared with experimental data: numerous studies have shown that the data may be well approximated by quadratic or quartic functions. Since the results take this form equally good agreement can be obtained by simply choosing appropriate coefficients (and so inferring values for the drag coefficients). In fact this shows that in a sense the governing equations may be considered as rather forgiving in that an inaccurate model will still allow good agreement with experimental data. Missing out terms, for example by studying only the two-dimensional motion, will lead to the same form of solution as the three-dimensional system but the polynomial coefficients will be different. As a consequence a numerical study of a slightly incorrect set of governing equations will be able to provide excellent agreement with experimental data but the drag coefficients calculated from this solution will differ from the true values. To illustrate this, equations (9,3) are combined to determine an expression for x as a function of y, accurate to O(ǫ), x = k sy [ { w 1+ v gwy 3v 3 + g y }] 6v 4, (5) where the O(ǫ) terms are in the curly brackets. At leading order, the wellknown approximation that x varies quadratically with y is observed. As time, and so y, increases the O(ǫ) term grows in importance and causes the flight to deviate from the quadratic and this deviation is described by a quartic. The correct coefficient of y in the above equation is k s (1+w /v )/. Given a polynomial fit to experimentaldata and values of the initial velocities v, w it is then possible to calculate k s by simply comparing the appropriate polynomial coefficients. However, if the mathematical model neglects the z motion (so setting w = in (5)) then the prediction for k s will be a factor of approximately (1+w /v ) greater than the true value. Obviouslythen, careshould be taken in the choice of model to extract drag coefficients from three dimensional experimental data. If the ball is launched in a gravitational field (rather difficult to avoid) with side spin then the full three-dimensional equations should be used, since the vertical velocity has a marked effect on the lateral motion. The exception to this rule is when the ball is launched with zero velocity in the x direction and with only top (or bottom) spin, then a two-dimensional study in the y-z plane will suffice. Given that C s arises from the same effect as C l only one of these quantities actually needs to be determined and so the two-dimensional experiment would provide all necessary information. In the final section the effect of varying C s (or C l ) with spin during the flight was investigated. Numerical studies generally invoke a constant value,
22 None given often chosento providethe best fit againstdata. The resultsin this study show that varying C s does make a difference to the predicted trajectories. While it is possible to choose an average constant value this value will vary with the length of the trajectory. Since the drag coefficient is a function of the ball and air properties, not the distance of the flight, this is clearly a physically unrealistic result. An issue that arose during this part of the study involved the interpretation of spin. To determine C s in terms of Sp an experiment may be carried out where the trajectory of the football is tracked by some motion capturing equipment. Comparison with the results from a mathematical model then leads to a value of C s for a stated Sp for each experiment. However, since Sp actually increases through the flight it is not clear what is meant by the quoted value. Exceptions to this rule are experiments carried out with a fixed ball in a wind tunnel, when Sp can be kept constant, see [1,15] for example. The well-known jump in the drag coefficient, which can lead to reverse swing in other sports, was not considered in this paper since a football s flight normally occurs at values of the Reynolds number above the transition [11]. However, it is worth noting that the transition occurs at higher Re for smoother balls. Given the reduction in air density with altitude (and so Re) this could be an important factor in the motion of a smooth ball in high altitude stadiums, such as in Johannesburg. In fact, during the 1 World Cup where the Jabulani ball was used (a smooth ball with no seams), there was much criticism over the balls seemingly erratic flight. For example, the England coach Fabio Capello stated that the ball behaved oddly at altitude, Brazilian striker Fabiano stated that it unpredictably changed direction when traveling through the air, see [13]. The question of whether the choice of ball can provide an advantage for a team, and in particular does altitude make a difference, is now discussed. From equation (9) it may be seen that the swerve in the x direction is proportional to k s = ρac s /(m). The value of the air density ρ decreases with altitude. In high altitude stadiums, such as Johannesburg at 18m, ρ 1.4kg/m 3 is approximately % lower than at sea-level, ρ 1.9kg/m 3. Hence a team accustomed to playing at sea level will expect approximately % more swerve. To illustrate the difference more clearly in Figure 9 three trajectories are shown for identical kicks with ρ = 1.4,1.19,1.9kg/m 3 (the latter two values being appropriate for Madrid and Barcelona). The initial value of v = 36m/s and L = 35m, the drag coefficient is taken as constant, C s =.34, other conditions are the same as in earlier figures. If the ball is initially kicked at a level with a goalpost then a velocity in the x direction of 15.16m/s just leads to a goal at sea/level, when ρ = 1.9. (The numerical solution is used here since ẋ was not included in the perturbation and also this free kick rather tests the perturbation.) The same kick taken in Madrid misses the goal by around 1.3m while in Johannesburgit misses by around 3.3m. Hörzer et al. [11] found similar behaviour through their numerical simulations. The advantage of the analytical solution presented in this paper is that while it shows not only explicitly the effect of air density but it also shows the dependence on other variables. For example, since swerve is proportional
23 Mathematics of soccer ball motion 3 to ρac s the change in the ball s behaviour due to altitude can equally well be made by changing the drag coefficient. The trajectory for ρ = 1.9 in Figure 9 could be made identical to the ρ = 1.4 curve by setting C s = / This is currently an important issue for football manufacturers (prompted by the 1 South African world cup) who wish to develop balls that show the same behaviour at different altitudes. 1 ρ = 1.9 x t Fig. 9 Difference in trajectories at different altitudes. Finally, there remains the question of whether this analysis can make a practical difference. The analytical solution makes clear the factors affecting the balls flight. It shows that coastal teams expect more swerve than teams at high altitude, decreasing air density or the balls roughness both act to reduce swerve. Consequently, after the meeting held in Johannesburg in January 11 it was suggested that Bidvest Wits use a smooth ball in matches since this will behave in the manner furthest from that expected by teams that normally play at a lower altitude. When practising for away games they should use a rough ball. Coastal teams could apply the opposite argument and choose rough balls when playing high altitude teams. Of course one cannot say what factors affect a team s change in fortunes, but it should be noted that before the meeting, Wits had not won in 8 consecutive games. In their first home match after the meeting, played against a coastal team, they won 6-. Up to the end of the 11 season they subsequently lost only one home game which was a cup tie, where the home team do not provide the ball. Unfortunately they did not fare so well at away games.
24 4 None given Acknowledgements The research of TGM was supported by the Marie Curie International Reintegration Grant Industrial applications of moving boundary problems, grant no. FP and Ministerio de Ciencia e Innovación grant MTM SLM acknowledges the support of the Mathematics Applications Consortium for Science and Industry (MACSI, funded by the Science Foundation Ireland Mathematics Initiative Grant 6/MI/5. References 1. Asai, K. Seo, O. Kobayashi, and R. Sakashita, Fundamental aerodynamics of the soccer ball. Sports Eng. 1, 1111, (7). K. Bray and D. Kerwin. Modelling the flight of a soccer ball in a direct free kick, J. Sports Sci., 1(), 75-85, (3) 3. K. Bray and D. Kerwin. Simplified flight equations for a spinning soccer ball. Science and Football V: Proc. 5th world congress on sci. and football, (5) 4. M. J. Carré, S. R. Goodwill, and S. J. Haake, Understanding the effect of seams on the aerodynamics of an association football, J. Mech. Eng. Sci. 19, , (5) 5. M.J. Carré, T. Asai, T. Akatsuka and S.J Hakke. The Curve Kick of a Football ll: Flight through the air, Sports Engng., 193-, () 6. Dupeux G., Le Goff A., Qur D. and Clanet C. The spinning ball spiral. New J. Physics 1, 1, doi:1.188/ /1/9/ J.E. Goff and M.J. Carré. Trajectory analysis of a soccer ball, Am. J. Phys., 77(11), 1-17, (9) 8. J.E. Goff and M.J. Carré. Soccer ball lift coefficients via trajectory analysis, Eur. J. Phys., 31, , (1) 9. I. Griffiths, C. Evans and N. Griffiths. Tracking the flight of a spinning football in three dimensions, Meas. Sci. Technol., 16, 56-65, (5) 1. The history of soccer, last accessed 4th May S. Hörzer, C. Fuchs, R. Gastinger, A. Sabo, L. Mehnem, J. Martinek and M. Reichel. Simulation of spinning soccer ball trajectories influenced by altitude, 8th Conference of the Int. Sports Engng. Assoc. (ISEA), Procedia Engng., , (1) 1. Jabulani, last accessed 4th May Adidas Jabulani, last accessed 4th May L. Oggiano and L. Sætran. Aerodynamics of modern soccer balls, Procedia Engng,, , (1) 15. M. Passmore, S. Tuplin, A. Spencer and R. Jones. Experimental studies of the aerodynamics of spinning and stationary footballs, Proc. Inst. Mech. Engineers, Part C: J Mech. Engng. Sci., (), 195-5, (8) 16. J. Wesson The science of soccer. IoP Pub. Ltd., ()
T. G. Myers & S. L. Mitchell
 A mathematical analysis of the motion of an in-flight soccer ball T. G. Myers & S. L. Mitchell Sports Engineering ISSN 369-77 Volume 6 Number Sports Eng (3) 6:9-4 DOI.7/s83--5-8 3 Your article is protected
A mathematical analysis of the motion of an in-flight soccer ball T. G. Myers & S. L. Mitchell Sports Engineering ISSN 369-77 Volume 6 Number Sports Eng (3) 6:9-4 DOI.7/s83--5-8 3 Your article is protected
The application of simulation to the understanding of football flight
 Loughborough University Institutional Repository The application of simulation to the understanding of football flight This item was submitted to Loughborough University's Institutional Repository by the/an
Loughborough University Institutional Repository The application of simulation to the understanding of football flight This item was submitted to Loughborough University's Institutional Repository by the/an
Lab 1: Projectiles and Numerical Integration
 E91: DYNAMICS Lab 1: Projectiles and Numerical Integration 1 Introduction The goal of this project is to investigate the dynamics of projectiles (balls) used in sports and study their trajectories using
E91: DYNAMICS Lab 1: Projectiles and Numerical Integration 1 Introduction The goal of this project is to investigate the dynamics of projectiles (balls) used in sports and study their trajectories using
MEAM 211. Project 1. Department of Mechanical Engineering and Applied Mechanics University of Pennsylvania January 19, 2007
 MEAM 211 Project 1 Department of Mechanical Engineering and Applied Mechanics University of Pennsylvania January 19, 2007 1 Introduction The goal of this project is to investigate the dynamics of projectiles
MEAM 211 Project 1 Department of Mechanical Engineering and Applied Mechanics University of Pennsylvania January 19, 2007 1 Introduction The goal of this project is to investigate the dynamics of projectiles
Kick. Journal of Sport Science and Medicine 6.2 (2007); Academic One File. Web. 16 Mar
 The Physics of Soccer: Bounce and Ball Trajectory Jordan Grider and Professor Mari-Anne Rosario Department of Physics, Saint Marys College of Ca, 1928 St. Marys Rd Moraga, Ca The total trajectory of a
The Physics of Soccer: Bounce and Ball Trajectory Jordan Grider and Professor Mari-Anne Rosario Department of Physics, Saint Marys College of Ca, 1928 St. Marys Rd Moraga, Ca The total trajectory of a
Determining the Drag Coefficient from PITCHf/x Data
 Determining the Drag Coefficient from PITCHf/x Data Isaac N. Hall Michigan State University, East Lansing, Michigan 48824 Alan M. Nathan Department of Physics, University of Illinois, Urbana, IL 61801
Determining the Drag Coefficient from PITCHf/x Data Isaac N. Hall Michigan State University, East Lansing, Michigan 48824 Alan M. Nathan Department of Physics, University of Illinois, Urbana, IL 61801
Determining the 3D Spin Axis from TrackMan Data (updated, March 31, 2015)
 Determining the 3D Spin Axis from TrackMan Data (updated, March 31, 2015) Alan M. Nathan Department of Physics, University of Illinois, Urbana, IL 61801 A technique is developed to determine the direction
Determining the 3D Spin Axis from TrackMan Data (updated, March 31, 2015) Alan M. Nathan Department of Physics, University of Illinois, Urbana, IL 61801 A technique is developed to determine the direction
Footballs, phase change and nanotubes: practical applications of mathematics
 Footballs, phase change and nanotubes: practical applications of mathematics Tim Myers Centre de Recerca Matemàtica, Bellaterra, Barcelona, Spain May 20, 2012 Why... Freezing in gas flow channels of fuel
Footballs, phase change and nanotubes: practical applications of mathematics Tim Myers Centre de Recerca Matemàtica, Bellaterra, Barcelona, Spain May 20, 2012 Why... Freezing in gas flow channels of fuel
34.3. Resisted Motion. Introduction. Prerequisites. Learning Outcomes
 Resisted Motion 34.3 Introduction This Section returns to the simple models of projectiles considered in Section 34.1. It explores the magnitude of air resistance effects and the effects of including simple
Resisted Motion 34.3 Introduction This Section returns to the simple models of projectiles considered in Section 34.1. It explores the magnitude of air resistance effects and the effects of including simple
Fundamental aerodynamics of the soccer ball
 T. Asai,* K. Seo, O. Kobayashi and R. Sakashita *Comprehensive Human Sciences, Tsukuba University, Tsukuba, Japan Faculty of Education, Art & Science, Yamagata University, Yamagata, Japan Department of
T. Asai,* K. Seo, O. Kobayashi and R. Sakashita *Comprehensive Human Sciences, Tsukuba University, Tsukuba, Japan Faculty of Education, Art & Science, Yamagata University, Yamagata, Japan Department of
Available online at Procedia Engineering 200 (2010) (2009)
 Available online at www.sciencedirect.com Procedia Engineering 2 (21) (29) 2467 2472 Procedia Engineering www.elsevier.com/locate/procedia 8 th Conference of the International Sports Engineering Association
Available online at www.sciencedirect.com Procedia Engineering 2 (21) (29) 2467 2472 Procedia Engineering www.elsevier.com/locate/procedia 8 th Conference of the International Sports Engineering Association
Universities of Leeds, Sheffield and York
 promoting access to White Rose research papers Universities of Leeds, Sheffield and York http://eprints.whiterose.ac.uk/ This is an author produced version of a paper published in Computers & Fluids White
promoting access to White Rose research papers Universities of Leeds, Sheffield and York http://eprints.whiterose.ac.uk/ This is an author produced version of a paper published in Computers & Fluids White
Anders Florén PhiliPPe JeAnJAcquot dionysis KonstAntinou AndreAs Meier corina toma Zbigniew trzmiel
 5 A n de o n s ta n ionysis K tinou A n dr e a s M eie a Toma r Corin L L A B SCREW S C I S Y PH n Phil r s F lo r é ippe Je an jac quot D Zbignie w Tr zmie l Magnus effect, fluid dynamics physics, mathematics
5 A n de o n s ta n ionysis K tinou A n dr e a s M eie a Toma r Corin L L A B SCREW S C I S Y PH n Phil r s F lo r é ippe Je an jac quot D Zbignie w Tr zmie l Magnus effect, fluid dynamics physics, mathematics
3.2 Projectile Motion
 Motion in 2-D: Last class we were analyzing the distance in two-dimensional motion and revisited the concept of vectors, and unit-vector notation. We had our receiver run up the field then slant Northwest.
Motion in 2-D: Last class we were analyzing the distance in two-dimensional motion and revisited the concept of vectors, and unit-vector notation. We had our receiver run up the field then slant Northwest.
A Statistical Study of PITCHf/x Pitched Baseball Trajectories
 A Statistical Study of PITCHf/x Pitched Baseball Trajectories Alan M. Nathan Department of Physics, University of Illinois, Urbana, IL 6181 February 8, 28 A statistical study of PITCHf/x trajectories is
A Statistical Study of PITCHf/x Pitched Baseball Trajectories Alan M. Nathan Department of Physics, University of Illinois, Urbana, IL 6181 February 8, 28 A statistical study of PITCHf/x trajectories is
The aerodynamic performance of a range of FIFA-approved footballs
 Loughborough University Institutional Repository The aerodynamic performance of a range of FIFA-approved footballs This item was submitted to Loughborough University's Institutional Repository by the/an
Loughborough University Institutional Repository The aerodynamic performance of a range of FIFA-approved footballs This item was submitted to Loughborough University's Institutional Repository by the/an
Analysis of PITCHf/x Pitched Baseball Trajectories. Abstract
 Analysis of PTCHf/x Pitched Baseball Trajectories Alan M. Nathan Department of Physics, University of llinois, Urbana, L 6181 December 9, 27 Abstract An analysis is presented of 99 baseball trajectories
Analysis of PTCHf/x Pitched Baseball Trajectories Alan M. Nathan Department of Physics, University of llinois, Urbana, L 6181 December 9, 27 Abstract An analysis is presented of 99 baseball trajectories
Flow Visualisation around Spinning and Non- Spinning Soccer Balls Using the Lattice Boltzmann Method
 Proceedings Flow Visualisation around Spinning and Non- Spinning Soccer Balls Using the Lattice Boltzmann Method Takeshi Asai 1, *, Sungchan Hong 1, Kaoru Kimachi 2, Keiko Abe 3, Hisashi Kai 3 and Atsushi
Proceedings Flow Visualisation around Spinning and Non- Spinning Soccer Balls Using the Lattice Boltzmann Method Takeshi Asai 1, *, Sungchan Hong 1, Kaoru Kimachi 2, Keiko Abe 3, Hisashi Kai 3 and Atsushi
AH Mechanics Checklist (Unit 1) AH Mechanics Checklist (Unit 1) Rectilinear Motion
 Rectilinear Motion No. kill Done 1 Know that rectilinear motion means motion in 1D (i.e. along a straight line) Know that a body is a physical object 3 Know that a particle is an idealised body that has
Rectilinear Motion No. kill Done 1 Know that rectilinear motion means motion in 1D (i.e. along a straight line) Know that a body is a physical object 3 Know that a particle is an idealised body that has
Modeling Realistic Projectile Motion
 Modeling Realistic Projectile Motion Matthew Geske 1. Introduction The calculation of simple projectile motion is one of the most basic exercises in physics. Finding, for example, the range of a thrown
Modeling Realistic Projectile Motion Matthew Geske 1. Introduction The calculation of simple projectile motion is one of the most basic exercises in physics. Finding, for example, the range of a thrown
Distance travelled time taken and if the particle is a distance s(t) along the x-axis, then its instantaneous speed is:
 Chapter 1 Kinematics 1.1 Basic ideas r(t) is the position of a particle; r = r is the distance to the origin. If r = x i + y j + z k = (x, y, z), then r = r = x 2 + y 2 + z 2. v(t) is the velocity; v =
Chapter 1 Kinematics 1.1 Basic ideas r(t) is the position of a particle; r = r is the distance to the origin. If r = x i + y j + z k = (x, y, z), then r = r = x 2 + y 2 + z 2. v(t) is the velocity; v =
Kinesiology 201 Solutions Fluid and Sports Biomechanics
 Kinesiology 201 Solutions Fluid and Sports Biomechanics Tony Leyland School of Kinesiology Simon Fraser University Fluid Biomechanics 1. Lift force is a force due to fluid flow around a body that acts
Kinesiology 201 Solutions Fluid and Sports Biomechanics Tony Leyland School of Kinesiology Simon Fraser University Fluid Biomechanics 1. Lift force is a force due to fluid flow around a body that acts
8.01T Problem Set 2 Solutions Fall 2004
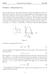 Problem 1. Measurement of g. a) The ball moves in the vertical direction under the influence of the constant force of gravity 1. Hence in our approximation the ball undergoes onedimensional motion with
Problem 1. Measurement of g. a) The ball moves in the vertical direction under the influence of the constant force of gravity 1. Hence in our approximation the ball undergoes onedimensional motion with
arxiv: v2 [physics.pop-ph] 18 Feb 2018
![arxiv: v2 [physics.pop-ph] 18 Feb 2018 arxiv: v2 [physics.pop-ph] 18 Feb 2018](/thumbs/83/87428285.jpg) An Aerodynamic Analysis of Recent FIFA World Cup Balls Adrian L. Kiratidis and Derek B. Leinweber Special Research Centre for the Subatomic Structure of Matter, Department of Physics, The University of
An Aerodynamic Analysis of Recent FIFA World Cup Balls Adrian L. Kiratidis and Derek B. Leinweber Special Research Centre for the Subatomic Structure of Matter, Department of Physics, The University of
3.4 Projectile Motion
 3.4 Projectile Motion Projectile Motion A projectile is anything launched, shot or thrown---i.e. not self-propelled. Examples: a golf ball as it flies through the air, a kicked soccer ball, a thrown football,
3.4 Projectile Motion Projectile Motion A projectile is anything launched, shot or thrown---i.e. not self-propelled. Examples: a golf ball as it flies through the air, a kicked soccer ball, a thrown football,
2-D Kinematics. In general, we have the following 8 equations (4 per dimension): Notes Page 1 of 7
 2-D Kinematics The problem we run into with 1-D kinematics, is that well it s one dimensional. We will now study kinematics in two dimensions. Obviously the real world happens in three dimensions, but
2-D Kinematics The problem we run into with 1-D kinematics, is that well it s one dimensional. We will now study kinematics in two dimensions. Obviously the real world happens in three dimensions, but
Projectile Motion B D B D A E A E
 Projectile Motion Projectile motion is motion under a constant unbalanced force. A projectile is a body that has been thrown or projected. No consideration is given to the force projecting the body, nor
Projectile Motion Projectile motion is motion under a constant unbalanced force. A projectile is a body that has been thrown or projected. No consideration is given to the force projecting the body, nor
PhysicsAndMathsTutor.com
 1. [In this question, the unit vectors i and j are horizontal vectors due east and north respectively.] At time t = 0, a football player kicks a ball from the point A with position vector (2i + j) m on
1. [In this question, the unit vectors i and j are horizontal vectors due east and north respectively.] At time t = 0, a football player kicks a ball from the point A with position vector (2i + j) m on
The Liapunov Method for Determining Stability (DRAFT)
 44 The Liapunov Method for Determining Stability (DRAFT) 44.1 The Liapunov Method, Naively Developed In the last chapter, we discussed describing trajectories of a 2 2 autonomous system x = F(x) as level
44 The Liapunov Method for Determining Stability (DRAFT) 44.1 The Liapunov Method, Naively Developed In the last chapter, we discussed describing trajectories of a 2 2 autonomous system x = F(x) as level
UNIVERSITY OF TORONTO Faculty of Arts and Science
 UNIVERSITY OF TORONTO Faculty of Arts and Science DECEMBER 2013 EXAMINATIONS PHY 151H1F Duration - 3 hours Attempt all questions. Each question is worth 10 points. Points for each part-question are shown
UNIVERSITY OF TORONTO Faculty of Arts and Science DECEMBER 2013 EXAMINATIONS PHY 151H1F Duration - 3 hours Attempt all questions. Each question is worth 10 points. Points for each part-question are shown
Aerodynamics of Sport Balls. 王啟川, PhD 國立交通大學機械工程系教授 Fellow ASME, Fellow ASHRAE Tel: ext
 Aerodynamics of Sport Balls 王啟川, PhD 國立交通大學機械工程系教授 Fellow ASME, Fellow ASHRAE Tel: 3-5712121 ext. 55105 E-mail:ccwang@mail.nctu.edu.tw Background Outline Basic Fluid Mechanics Non-spinning vs. spinning
Aerodynamics of Sport Balls 王啟川, PhD 國立交通大學機械工程系教授 Fellow ASME, Fellow ASHRAE Tel: 3-5712121 ext. 55105 E-mail:ccwang@mail.nctu.edu.tw Background Outline Basic Fluid Mechanics Non-spinning vs. spinning
3 Space curvilinear motion, motion in non-inertial frames
 3 Space curvilinear motion, motion in non-inertial frames 3.1 In-class problem A rocket of initial mass m i is fired vertically up from earth and accelerates until its fuel is exhausted. The residual mass
3 Space curvilinear motion, motion in non-inertial frames 3.1 In-class problem A rocket of initial mass m i is fired vertically up from earth and accelerates until its fuel is exhausted. The residual mass
(A) 10 m (B) 20 m (C) 25 m (D) 30 m (E) 40 m
 PSI AP Physics C Work and Energy (Algebra Based) Multiple Choice Questions (use g = 10 m/s 2 ) 1. A student throws a ball upwards from the ground level where gravitational potential energy is zero. At
PSI AP Physics C Work and Energy (Algebra Based) Multiple Choice Questions (use g = 10 m/s 2 ) 1. A student throws a ball upwards from the ground level where gravitational potential energy is zero. At
Kinematics and Dynamics
 AP PHYS 1 Test Review Kinematics and Dynamics Name: Other Useful Site: http://www.aplusphysics.com/ap1/ap1- supp.html 2015-16 AP Physics: Kinematics Study Guide The study guide will help you review all
AP PHYS 1 Test Review Kinematics and Dynamics Name: Other Useful Site: http://www.aplusphysics.com/ap1/ap1- supp.html 2015-16 AP Physics: Kinematics Study Guide The study guide will help you review all
First Year Physics: Prelims CP1. Classical Mechanics: Prof. Neville Harnew. Problem Set III : Projectiles, rocket motion and motion in E & B fields
 HT017 First Year Physics: Prelims CP1 Classical Mechanics: Prof Neville Harnew Problem Set III : Projectiles, rocket motion and motion in E & B fields Questions 1-10 are standard examples Questions 11-1
HT017 First Year Physics: Prelims CP1 Classical Mechanics: Prof Neville Harnew Problem Set III : Projectiles, rocket motion and motion in E & B fields Questions 1-10 are standard examples Questions 11-1
Non-textbook problem #I: The kinetic energy of a body depends on its mass and speed as. K = 1 2 mv2 (1) m 1 v 2 1 = 1 2 m 2v 2 2 (2)
 PHY 309 K. Solutions for Problem set # 7. Non-textbook problem #I: The kinetic energy of a body depends on its mass and speed as K = 1 mv (1) Therefore, two bodies of respective masses m 1 and m and speeds
PHY 309 K. Solutions for Problem set # 7. Non-textbook problem #I: The kinetic energy of a body depends on its mass and speed as K = 1 mv (1) Therefore, two bodies of respective masses m 1 and m and speeds
Thursday 12 June 2014 Afternoon
 Thursday June 4 Afternoon AS GCE MATHEMATICS (MEI) 476/ Mechanics QUESTION PAPER * 3 3 4 7 4 7 9 8 * Candidates answer on the Printed Answer Book. OCR supplied materials: Printed Answer Book 476/ MEI Examination
Thursday June 4 Afternoon AS GCE MATHEMATICS (MEI) 476/ Mechanics QUESTION PAPER * 3 3 4 7 4 7 9 8 * Candidates answer on the Printed Answer Book. OCR supplied materials: Printed Answer Book 476/ MEI Examination
1/3/2011. This course discusses the physical laws that govern atmosphere/ocean motions.
 Lecture 1: Introduction and Review Dynamics and Kinematics Kinematics: The term kinematics means motion. Kinematics is the study of motion without regard for the cause. Dynamics: On the other hand, dynamics
Lecture 1: Introduction and Review Dynamics and Kinematics Kinematics: The term kinematics means motion. Kinematics is the study of motion without regard for the cause. Dynamics: On the other hand, dynamics
Projectile Motion and 2-D Dynamics
 Projectile Motion and 2-D Dynamics Vector Notation Vectors vs. Scalars In Physics 11, you learned the difference between vectors and scalars. A vector is a quantity that includes both direction and magnitude
Projectile Motion and 2-D Dynamics Vector Notation Vectors vs. Scalars In Physics 11, you learned the difference between vectors and scalars. A vector is a quantity that includes both direction and magnitude
Motion Part 4: Projectile Motion
 Motion Part 4: Projectile Motion Last modified: 28/03/2017 CONTENTS Projectile Motion Uniform Motion Equations Projectile Motion Equations Trajectory How to Approach Problems Example 1 Example 2 Example
Motion Part 4: Projectile Motion Last modified: 28/03/2017 CONTENTS Projectile Motion Uniform Motion Equations Projectile Motion Equations Trajectory How to Approach Problems Example 1 Example 2 Example
AP Physics Laboratory #6.1: Analyzing Terminal Velocity Using an Interesting Version of Atwood s Machine
 AP Physics Laboratory #6.1: Analyzing Terminal Velocity Using an Interesting Version of Atwood s Machine Name: Date: Lab Partners: PURPOSE The purpose of this Laboratory is to study a system as it approaches
AP Physics Laboratory #6.1: Analyzing Terminal Velocity Using an Interesting Version of Atwood s Machine Name: Date: Lab Partners: PURPOSE The purpose of this Laboratory is to study a system as it approaches
STEP Support Programme. Mechanics STEP Questions
 STEP Support Programme Mechanics STEP Questions This is a selection of mainly STEP I questions with a couple of STEP II questions at the end. STEP I and STEP II papers follow the same specification, the
STEP Support Programme Mechanics STEP Questions This is a selection of mainly STEP I questions with a couple of STEP II questions at the end. STEP I and STEP II papers follow the same specification, the
UNIVERSITY OF MANITOBA
 PAGE NO.: 1 of 6 + Formula Sheet Equal marks for all questions. No marks are subtracted for wrong answers. Record all answers on the computer score sheet provided. USE PENCIL ONLY! Black pen will look
PAGE NO.: 1 of 6 + Formula Sheet Equal marks for all questions. No marks are subtracted for wrong answers. Record all answers on the computer score sheet provided. USE PENCIL ONLY! Black pen will look
ω = k/m x = A cos (ωt + ϕ 0 ) L = I ω a x = ω 2 x P = F v P = de sys J = F dt = p w = m g F G = Gm 1m 2 D = 1 2 CρAv2 a r = v2
 PHYS 2211 A & B Final Exam Formulæ & Constants Fall 2016 Unless otherwise directed, all problems take place on Earth, and drag is to be neglected. A v = d r ω = dθ a = d v α = d ω v sf = v si + a s t ω
PHYS 2211 A & B Final Exam Formulæ & Constants Fall 2016 Unless otherwise directed, all problems take place on Earth, and drag is to be neglected. A v = d r ω = dθ a = d v α = d ω v sf = v si + a s t ω
4 MOTION IN TWO AND THREE DIMENSIONS
 Chapter 4 Motion in Two and Three Dimensions 157 4 MOTION IN TWO AND THREE DIMENSIONS Figure 4.1 The Red Arrows is the aerobatics display team of Britain s Royal Air Force. Based in Lincolnshire, England,
Chapter 4 Motion in Two and Three Dimensions 157 4 MOTION IN TWO AND THREE DIMENSIONS Figure 4.1 The Red Arrows is the aerobatics display team of Britain s Royal Air Force. Based in Lincolnshire, England,
Lecture 17 - Gyroscopes
 Lecture 17 - Gyroscopes A Puzzle... We have seen throughout class that the center of mass is a very powerful tool for evaluating systems. However, don t let yourself get carried away with how useful it
Lecture 17 - Gyroscopes A Puzzle... We have seen throughout class that the center of mass is a very powerful tool for evaluating systems. However, don t let yourself get carried away with how useful it
Modelling of a Tennis Ball Server
 Mechanical Analysis and Design ME 2104 Lecture 6 Modelling of a Tennis Ball Server Prof Ahmed Kovacevic Department of Mechanical Engineering and Aeronautics Room CG25, Phone: 8780, E-Mail: a.kovacevic@city.ac.uk
Mechanical Analysis and Design ME 2104 Lecture 6 Modelling of a Tennis Ball Server Prof Ahmed Kovacevic Department of Mechanical Engineering and Aeronautics Room CG25, Phone: 8780, E-Mail: a.kovacevic@city.ac.uk
Bell Ringer. x- direction: Ball and car start with same position and velocity, a=0, so always have same position
 Objectives Students should be able to add, subtract, and resolve displacement and velocity vectors so they can: Determine the components of a vector along two specified, mutually perpendicular axes. Determine
Objectives Students should be able to add, subtract, and resolve displacement and velocity vectors so they can: Determine the components of a vector along two specified, mutually perpendicular axes. Determine
Physics. Practice Questions IEB
 Physics Practice Questions IEB Instructions Individual, eam-style questions The questions contained in this booklet match the style of questions that are typically asked in eams. This booklet is not however,
Physics Practice Questions IEB Instructions Individual, eam-style questions The questions contained in this booklet match the style of questions that are typically asked in eams. This booklet is not however,
161 Sp18 T1 grades (out of 40, max 100)
 Grades for test Graded out of 40 (scores over 00% not possible) o Three perfect scores based on this grading scale!!! o Avg = 57 o Stdev = 3 Scores below 40% are in trouble. Scores 40-60% are on the bubble
Grades for test Graded out of 40 (scores over 00% not possible) o Three perfect scores based on this grading scale!!! o Avg = 57 o Stdev = 3 Scores below 40% are in trouble. Scores 40-60% are on the bubble
Analytical Mechanics - Extra Problems
 Analytical Mechanics - Extra Problems Physics 105, F17 (R) are review problems. Review problems are those that have already been covered in prior courses, mostly Intro to Physics I and II. Some are math
Analytical Mechanics - Extra Problems Physics 105, F17 (R) are review problems. Review problems are those that have already been covered in prior courses, mostly Intro to Physics I and II. Some are math
Having a ball with science:
 Having a ball with science: Leveraging Sports for Science Education Professor Adedeji Badiru Air Force Institute of Technology (AFIT) Wright-Patterson Air Force Base Purpose of Workshop Shows how teaching
Having a ball with science: Leveraging Sports for Science Education Professor Adedeji Badiru Air Force Institute of Technology (AFIT) Wright-Patterson Air Force Base Purpose of Workshop Shows how teaching
Modeling the Motion of a Projectile in Air
 In this lab, you will do the following: Modeling the Motion of a Projectile in Air analyze the motion of an object fired from a cannon using two different fundamental physics principles: the momentum principle
In this lab, you will do the following: Modeling the Motion of a Projectile in Air analyze the motion of an object fired from a cannon using two different fundamental physics principles: the momentum principle
CHAPTER 6: Angular motion, projectile motion and fluid mechanics. Angular motion BIOMECHANICAL MOVEMENT. Three imaginary axes of rotation
 BIOMECHANICAL MOVEMENT CHAPTER 6: Angular motion, projectile motion and fluid mechanics Angular motion Axis A figure 6.1 planes and axes Sagittal Frontal Angular motion is defined as the motion of a body
BIOMECHANICAL MOVEMENT CHAPTER 6: Angular motion, projectile motion and fluid mechanics Angular motion Axis A figure 6.1 planes and axes Sagittal Frontal Angular motion is defined as the motion of a body
Resistance is Futile
 Resistance is Futile Joseph Hays 16 May 2014 Page 1 of 24 Abstract When introductory physics books consider projectile motion, they often suggest that the reader assume air resistance is negligible; an
Resistance is Futile Joseph Hays 16 May 2014 Page 1 of 24 Abstract When introductory physics books consider projectile motion, they often suggest that the reader assume air resistance is negligible; an
Pearson Edexcel International Advanced Subsidiary in Physics
 Scheme (SAM) Pearson Edexcel International Advanced Subsidiary in Physics Unit 1: Physics on the Go 31 All the material in this publication is copyright Pearson Education Ltd 2013 32 General marking guidance
Scheme (SAM) Pearson Edexcel International Advanced Subsidiary in Physics Unit 1: Physics on the Go 31 All the material in this publication is copyright Pearson Education Ltd 2013 32 General marking guidance
Acceleration Due to Gravity Lecture 2
 Acceleration Due to Gravity Lecture 2 ˆ This lecture covers the meat of Chapters 2 and 3 from the book. I am deliberately skipping vectors again you will have to bear with me. ˆ We will cover the basics
Acceleration Due to Gravity Lecture 2 ˆ This lecture covers the meat of Chapters 2 and 3 from the book. I am deliberately skipping vectors again you will have to bear with me. ˆ We will cover the basics
Wallace Hall Academy
 Wallace Hall Academy CfE Higher Physics Unit 1 - Dynamics Notes Name 1 Equations of Motion Vectors and Scalars (Revision of National 5) It is possible to split up quantities in physics into two distinct
Wallace Hall Academy CfE Higher Physics Unit 1 - Dynamics Notes Name 1 Equations of Motion Vectors and Scalars (Revision of National 5) It is possible to split up quantities in physics into two distinct
PHYS 211 Lecture 9 - Examples of 3D motion 9-1
 PHYS 211 Lecture 9 - Examples of 3D motion 9-1 Lecture 9 - Examples of 3D motion Text: Fowles and Cassiday, Chap. 4 In one dimension, the equations of motion to be solved are functions of only one position
PHYS 211 Lecture 9 - Examples of 3D motion 9-1 Lecture 9 - Examples of 3D motion Text: Fowles and Cassiday, Chap. 4 In one dimension, the equations of motion to be solved are functions of only one position
ENERGY CONSERVATION IN THE ONE-PHASE SUPERCOOLED STEFAN PROBLEM
 ENERGY CONSERVATION IN THE ONE-PHASE SUPERCOOLED STEFAN PROBLEM TIMOTHY MYERS, SARAH MITCHELL AND FRANCESC FONT Abstract. A one-phase reduction of the one-dimensional two-phase supercooled Stefan problem
ENERGY CONSERVATION IN THE ONE-PHASE SUPERCOOLED STEFAN PROBLEM TIMOTHY MYERS, SARAH MITCHELL AND FRANCESC FONT Abstract. A one-phase reduction of the one-dimensional two-phase supercooled Stefan problem
Aerodynamics of Spinning Sphere in Ideal Flow R. C. Mehta Department of Aeronautical Engineering, Noorul Islam University, Kumaracoil , India
 Scholars Journal of Engineering and Technology (SJET) Sch. J. Eng. Tech., 06; 4(5):5-9 Scholars Academic and Scientific Publisher (An International Publisher for Academic and Scientific Resources) www.saspublisher.com
Scholars Journal of Engineering and Technology (SJET) Sch. J. Eng. Tech., 06; 4(5):5-9 Scholars Academic and Scientific Publisher (An International Publisher for Academic and Scientific Resources) www.saspublisher.com
Proceedings The Behavior of Badminton Shuttlecocks from an Engineering Point of View
 Proceedings The Behavior of Badminton Shuttlecocks from an Engineering Point of View Christoffer Johansson 1, Kelken Chang 2, Christer Forsgren 3 and Magnus Karlsteen 1, * 1 Department of Physics, Chalmers
Proceedings The Behavior of Badminton Shuttlecocks from an Engineering Point of View Christoffer Johansson 1, Kelken Chang 2, Christer Forsgren 3 and Magnus Karlsteen 1, * 1 Department of Physics, Chalmers
PhysicsAndMathsTutor.com
 PhysicsAndMathsTutor.com January 2007 4. Figure 2 O θ T v P A (3ag) A particle P of mass m is attached to one end of a light inextensible string of length a. The other end of the string is attached to
PhysicsAndMathsTutor.com January 2007 4. Figure 2 O θ T v P A (3ag) A particle P of mass m is attached to one end of a light inextensible string of length a. The other end of the string is attached to
Available online at ScienceDirect. Procedia Engineering 147 (2016 )
 Available online at www.sciencedirect.com ScienceDirect Procedia Engineering 147 (016 ) 677 68 11th conference of the International Sports Engineering Association, ISEA 016 The effect of ball spin rate
Available online at www.sciencedirect.com ScienceDirect Procedia Engineering 147 (016 ) 677 68 11th conference of the International Sports Engineering Association, ISEA 016 The effect of ball spin rate
Physics 2211 A & B Quiz #2 Solutions Fall P sin θ = µ k P cos θ + mg
 Physics 2211 A & B Quiz #2 Solutions Fall 2016 I. (16 points) A block of mass m is sliding up a vertical wall at constant non-zero velocity v 0, due to an applied force P pushing against it at an angle
Physics 2211 A & B Quiz #2 Solutions Fall 2016 I. (16 points) A block of mass m is sliding up a vertical wall at constant non-zero velocity v 0, due to an applied force P pushing against it at an angle
Physics 202 Laboratory 3. Root-Finding 1. Laboratory 3. Physics 202 Laboratory
 Physics 202 Laboratory 3 Root-Finding 1 Laboratory 3 Physics 202 Laboratory The fundamental question answered by this week s lab work will be: Given a function F (x), find some/all of the values {x i }
Physics 202 Laboratory 3 Root-Finding 1 Laboratory 3 Physics 202 Laboratory The fundamental question answered by this week s lab work will be: Given a function F (x), find some/all of the values {x i }
Marble Launch Experiment
 Marble Launch Experiment Purpose The intent of this experiment is to numerically trace the path of a marble launched into the air at an angle in order to observe the parabolic nature of the trajectory.
Marble Launch Experiment Purpose The intent of this experiment is to numerically trace the path of a marble launched into the air at an angle in order to observe the parabolic nature of the trajectory.
Falling Objects and Projectile Motion
 Falling Objects and Projectile Motion Gravity influences motion in a particular way. How does a dropped object behave? accelerate, or speed constant? What if they have: different masses? different shapes?
Falling Objects and Projectile Motion Gravity influences motion in a particular way. How does a dropped object behave? accelerate, or speed constant? What if they have: different masses? different shapes?
Time: 1 hour 30 minutes
 Paper Reference(s) 6678/01 Edexcel GCE Mechanics M2 Silver Level S2 Time: 1 hour 30 minutes Materials required for examination Mathematical Formulae (Green) Items included with question papers Nil Candidates
Paper Reference(s) 6678/01 Edexcel GCE Mechanics M2 Silver Level S2 Time: 1 hour 30 minutes Materials required for examination Mathematical Formulae (Green) Items included with question papers Nil Candidates
Forces and Motion in One Dimension
 Nicholas J. Giordano www.cengage.com/physics/giordano Forces and Motion in One Dimension Applications of Newton s Laws We will learn how Newton s Laws apply in various situations We will begin with motion
Nicholas J. Giordano www.cengage.com/physics/giordano Forces and Motion in One Dimension Applications of Newton s Laws We will learn how Newton s Laws apply in various situations We will begin with motion
Physics *P43118A0128* Pearson Edexcel GCE P43118A. Advanced Subsidiary Unit 1: Physics on the Go. Tuesday 20 May 2014 Morning Time: 1 hour 30 minutes
 Write your name here Surname Other names Pearson Edexcel GCE Physics Advanced Subsidiary Unit 1: Physics on the Go Centre Number Candidate Number Tuesday 20 May 2014 Morning Time: 1 hour 30 minutes You
Write your name here Surname Other names Pearson Edexcel GCE Physics Advanced Subsidiary Unit 1: Physics on the Go Centre Number Candidate Number Tuesday 20 May 2014 Morning Time: 1 hour 30 minutes You
KINEMATICS. Challenging MCQ questions by The Physics Cafe. Compiled and selected by The Physics Cafe
 KINEMATICS Challenging MCQ questions by The Physics Cafe Compiled and selected by The Physics Cafe 1 Two diamonds begin free fall from rest from the same height 1.0 s apart. How long after the first diamond
KINEMATICS Challenging MCQ questions by The Physics Cafe Compiled and selected by The Physics Cafe 1 Two diamonds begin free fall from rest from the same height 1.0 s apart. How long after the first diamond
Circle on your answer sheet the ranking choice below that correctly ranks the situation above:
 For questions 1-5, use the information provided to rank the situations according to the instructions given. Remember that if two choices have the same rank that will be shown that with an equals sign.
For questions 1-5, use the information provided to rank the situations according to the instructions given. Remember that if two choices have the same rank that will be shown that with an equals sign.
Basic Ascent Performance Analyses
 Basic Ascent Performance Analyses Ascent Mission Requirements Ideal Burnout Solution Constant & Average Gravity Models Gravity Loss Concept Effect of Drag on Ascent Performance Drag Profile Approximation
Basic Ascent Performance Analyses Ascent Mission Requirements Ideal Burnout Solution Constant & Average Gravity Models Gravity Loss Concept Effect of Drag on Ascent Performance Drag Profile Approximation
 4754 Mark Scheme June 005 Mark Scheme 4754 June 005 4754 Mark Scheme June 005 1. (a) Please mark in red and award part marks on the right side of the script, level with the work that has earned them. (b)
4754 Mark Scheme June 005 Mark Scheme 4754 June 005 4754 Mark Scheme June 005 1. (a) Please mark in red and award part marks on the right side of the script, level with the work that has earned them. (b)
Bell Ringer: What is constant acceleration? What is projectile motion?
 Bell Ringer: What is constant acceleration? What is projectile motion? Can we analyze the motion of an object on the y-axis independently of the object s motion on the x-axis? NOTES 3.2: 2D Motion: Projectile
Bell Ringer: What is constant acceleration? What is projectile motion? Can we analyze the motion of an object on the y-axis independently of the object s motion on the x-axis? NOTES 3.2: 2D Motion: Projectile
2. FLUID-FLOW EQUATIONS SPRING 2019
 2. FLUID-FLOW EQUATIONS SPRING 2019 2.1 Introduction 2.2 Conservative differential equations 2.3 Non-conservative differential equations 2.4 Non-dimensionalisation Summary Examples 2.1 Introduction Fluid
2. FLUID-FLOW EQUATIONS SPRING 2019 2.1 Introduction 2.2 Conservative differential equations 2.3 Non-conservative differential equations 2.4 Non-dimensionalisation Summary Examples 2.1 Introduction Fluid
A-level MATHEMATICS. Paper 2. Exam Date Morning Time allowed: 2 hours SPECIMEN MATERIAL
 SPECIMEN MATERIAL Please write clearly, in block capitals. Centre number Candidate number Surname Forename(s) Candidate signature A-level MATHEMATICS Paper 2 Exam Date Morning Time allowed: 2 hours Materials
SPECIMEN MATERIAL Please write clearly, in block capitals. Centre number Candidate number Surname Forename(s) Candidate signature A-level MATHEMATICS Paper 2 Exam Date Morning Time allowed: 2 hours Materials
Control Volume. Dynamics and Kinematics. Basic Conservation Laws. Lecture 1: Introduction and Review 1/24/2017
 Lecture 1: Introduction and Review Dynamics and Kinematics Kinematics: The term kinematics means motion. Kinematics is the study of motion without regard for the cause. Dynamics: On the other hand, dynamics
Lecture 1: Introduction and Review Dynamics and Kinematics Kinematics: The term kinematics means motion. Kinematics is the study of motion without regard for the cause. Dynamics: On the other hand, dynamics
Lecture 1: Introduction and Review
 Lecture 1: Introduction and Review Review of fundamental mathematical tools Fundamental and apparent forces Dynamics and Kinematics Kinematics: The term kinematics means motion. Kinematics is the study
Lecture 1: Introduction and Review Review of fundamental mathematical tools Fundamental and apparent forces Dynamics and Kinematics Kinematics: The term kinematics means motion. Kinematics is the study
Game Physics. Game and Media Technology Master Program - Utrecht University. Dr. Nicolas Pronost
 Game and Media Technology Master Program - Utrecht University Dr. Nicolas Pronost Essential physics for game developers Introduction The primary issues Let s move virtual objects Kinematics: description
Game and Media Technology Master Program - Utrecht University Dr. Nicolas Pronost Essential physics for game developers Introduction The primary issues Let s move virtual objects Kinematics: description
Free-Body Diagrams: Introduction
 Free-Body Diagrams: Introduction Learning Goal: To learn to draw free-body diagrams for various real-life situations. Imagine that you are given a description of a real-life situation and are asked to
Free-Body Diagrams: Introduction Learning Goal: To learn to draw free-body diagrams for various real-life situations. Imagine that you are given a description of a real-life situation and are asked to
Gravity Pre-Lab 1. Why do you need an inclined plane to measure the effects due to gravity?
 Lab Exercise: Gravity (Report) Your Name & Your Lab Partner s Name Due Date Gravity Pre-Lab 1. Why do you need an inclined plane to measure the effects due to gravity? 2. What are several advantage of
Lab Exercise: Gravity (Report) Your Name & Your Lab Partner s Name Due Date Gravity Pre-Lab 1. Why do you need an inclined plane to measure the effects due to gravity? 2. What are several advantage of
PHY 1114: Physics I. Quick Question 1. Quick Question 2. Quick Question 3. Quick Question 4. Lecture 5: Motion in 2D
 PHY 1114: Physics I Lecture 5: Motion in D Fall 01 Kenny L. Tapp Quick Question 1 A child throws a ball vertically upward at the school playground. Which one of the following quantities is (are) equal
PHY 1114: Physics I Lecture 5: Motion in D Fall 01 Kenny L. Tapp Quick Question 1 A child throws a ball vertically upward at the school playground. Which one of the following quantities is (are) equal
Masters in Mechanical Engineering. Problems of incompressible viscous flow. 2µ dx y(y h)+ U h y 0 < y < h,
 Masters in Mechanical Engineering Problems of incompressible viscous flow 1. Consider the laminar Couette flow between two infinite flat plates (lower plate (y = 0) with no velocity and top plate (y =
Masters in Mechanical Engineering Problems of incompressible viscous flow 1. Consider the laminar Couette flow between two infinite flat plates (lower plate (y = 0) with no velocity and top plate (y =
On drag and lift forces acting at flow past rotating bodies
 On drag and lift forces acting at flow past rotating bodies Ing. Jan Dumek Vedoucí práce: Prof. Ing. Pavel Šafařík, CSc. Abstract Results of investigation of forces acting at flow past rotating sphere
On drag and lift forces acting at flow past rotating bodies Ing. Jan Dumek Vedoucí práce: Prof. Ing. Pavel Šafařík, CSc. Abstract Results of investigation of forces acting at flow past rotating sphere
Condensed. Mathematics. General Certificate of Education Advanced Subsidiary Examination January Unit Mechanics 1B.
 General Certificate of Education Advanced Subsidiary Examination January 2011 Mathematics MM1B Unit Mechanics 1B Wednesday 19 January 2011 1.30 pm to 3.00 pm For this paper you must have: the blue AQA
General Certificate of Education Advanced Subsidiary Examination January 2011 Mathematics MM1B Unit Mechanics 1B Wednesday 19 January 2011 1.30 pm to 3.00 pm For this paper you must have: the blue AQA
The Campion School P.E. Dept A Level PE Biomechanics
 Topic: Biomechanics Learning Objectives (What the teacher intends pupils to learn) Learners will be able to develop their knowledge and understanding of the underlying biomechanical principles related
Topic: Biomechanics Learning Objectives (What the teacher intends pupils to learn) Learners will be able to develop their knowledge and understanding of the underlying biomechanical principles related
2.1 Forces and Free-Body Diagrams
 2.1 Forces and Free-Body Diagrams A is a push or a pull. Forces act on objects, and can result in the acceleration, compression, stretching, or twisting of objects. Forces can also act to stabilize an
2.1 Forces and Free-Body Diagrams A is a push or a pull. Forces act on objects, and can result in the acceleration, compression, stretching, or twisting of objects. Forces can also act to stabilize an
POTENTIAL ENERGY AND ENERGY CONSERVATION
 7 POTENTIAL ENERGY AND ENERGY CONSERVATION 7.. IDENTIFY: U grav = mgy so ΔU grav = mg( y y ) SET UP: + y is upward. EXECUTE: (a) ΔU = (75 kg)(9.8 m/s )(4 m 5 m) = +6.6 5 J (b) ΔU = (75 kg)(9.8 m/s )(35
7 POTENTIAL ENERGY AND ENERGY CONSERVATION 7.. IDENTIFY: U grav = mgy so ΔU grav = mg( y y ) SET UP: + y is upward. EXECUTE: (a) ΔU = (75 kg)(9.8 m/s )(4 m 5 m) = +6.6 5 J (b) ΔU = (75 kg)(9.8 m/s )(35
PhysicsAndMathsTutor.com
 1. A ball is projected vertically upwards with a speed of 14.7 ms 1 from a point which is 49 m above horizontal ground. Modelling the ball as a particle moving freely under gravity, find (a) the greatest
1. A ball is projected vertically upwards with a speed of 14.7 ms 1 from a point which is 49 m above horizontal ground. Modelling the ball as a particle moving freely under gravity, find (a) the greatest
Vectors and Coordinate Systems
 Vectors and Coordinate Systems In Newtonian mechanics, we want to understand how material bodies interact with each other and how this affects their motion through space. In order to be able to make quantitative
Vectors and Coordinate Systems In Newtonian mechanics, we want to understand how material bodies interact with each other and how this affects their motion through space. In order to be able to make quantitative
Kinematics in Two-Dimensions
 Slide 1 / 92 Slide 2 / 92 Kinematics in Two-Dimensions www.njctl.org Slide 3 / 92 How to Use this File Each topic is composed of brief direct instruction There are formative assessment questions after
Slide 1 / 92 Slide 2 / 92 Kinematics in Two-Dimensions www.njctl.org Slide 3 / 92 How to Use this File Each topic is composed of brief direct instruction There are formative assessment questions after
Problem 05 Levitation
 Problem 05 Levitation reporter: Denise Sacramento Christovam Problem 05 Levitation A light ball (e.g. a Ping-Pong ball) can be supported on an upward airstream. The airstream can be tilted yet still support
Problem 05 Levitation reporter: Denise Sacramento Christovam Problem 05 Levitation A light ball (e.g. a Ping-Pong ball) can be supported on an upward airstream. The airstream can be tilted yet still support
Lecture 2. Lecture 1. Forces on a rotating planet. We will describe the atmosphere and ocean in terms of their:
 Lecture 2 Lecture 1 Forces on a rotating planet We will describe the atmosphere and ocean in terms of their: velocity u = (u,v,w) pressure P density ρ temperature T salinity S up For convenience, we will
Lecture 2 Lecture 1 Forces on a rotating planet We will describe the atmosphere and ocean in terms of their: velocity u = (u,v,w) pressure P density ρ temperature T salinity S up For convenience, we will
PHYSICS 221, FALL 2010 EXAM #1 Solutions WEDNESDAY, SEPTEMBER 29, 2010
 PHYSICS 1, FALL 010 EXAM 1 Solutions WEDNESDAY, SEPTEMBER 9, 010 Note: The unit vectors in the +x, +y, and +z directions of a right-handed Cartesian coordinate system are î, ĵ, and ˆk, respectively. In
PHYSICS 1, FALL 010 EXAM 1 Solutions WEDNESDAY, SEPTEMBER 9, 010 Note: The unit vectors in the +x, +y, and +z directions of a right-handed Cartesian coordinate system are î, ĵ, and ˆk, respectively. In
Old Dominion University Physics 811 Fall 2008
 Old Dominion University Physics 811 Fall 008 Projects Structure of Project Reports: 1 Introduction. Briefly summarize the nature of the physical system. Theory. Describe equations selected for the project.
Old Dominion University Physics 811 Fall 008 Projects Structure of Project Reports: 1 Introduction. Briefly summarize the nature of the physical system. Theory. Describe equations selected for the project.
Page 1. Name: Section This assignment is due at the first class in 2019 Part I Show all work!
 Name: Section This assignment is due at the first class in 2019 Part I Show all work! 7164-1 - Page 1 1) A car travels at constant speed around a section of horizontal, circular track. On the diagram provided
Name: Section This assignment is due at the first class in 2019 Part I Show all work! 7164-1 - Page 1 1) A car travels at constant speed around a section of horizontal, circular track. On the diagram provided
Paper Reference. Paper Reference(s) 6731/01 Edexcel GCE Physics Advanced Subsidiary Unit Test PHY1
 Centre No. Candidate No. Paper Reference(s) 6731/1 Edexcel GCE Physics Advanced Subsidiary Unit Test PHY1 Wednesday 16 January 28 Afternoon Time: 1 hour 15 minutes Materials required for examination Nil
Centre No. Candidate No. Paper Reference(s) 6731/1 Edexcel GCE Physics Advanced Subsidiary Unit Test PHY1 Wednesday 16 January 28 Afternoon Time: 1 hour 15 minutes Materials required for examination Nil
Version A (01) Question. Points
 Question Version A (01) Version B (02) 1 a a 3 2 a a 3 3 b a 3 4 a a 3 5 b b 3 6 b b 3 7 b b 3 8 a b 3 9 a a 3 10 b b 3 11 b b 8 12 e e 8 13 a a 4 14 c c 8 15 c c 8 16 a a 4 17 d d 8 18 d d 8 19 a a 4
Question Version A (01) Version B (02) 1 a a 3 2 a a 3 3 b a 3 4 a a 3 5 b b 3 6 b b 3 7 b b 3 8 a b 3 9 a a 3 10 b b 3 11 b b 8 12 e e 8 13 a a 4 14 c c 8 15 c c 8 16 a a 4 17 d d 8 18 d d 8 19 a a 4
