Estimating the predictability of an oceanic time series using linear and nonlinear methods
|
|
|
- Blanche Ward
- 6 years ago
- Views:
Transcription
1 JOURNAL OF GEOPHYSICAL RESEARCH, VOL. 109,, doi: /2003jc002148, 2004 Estimating the predictability of an oceanic time series using linear and nonlinear methods G.-C. Yuan, 1,2,3,4 M. S. Lozier, 3 L. J. Pratt, 2 C. K. R. T. Jones, 1,5 and K. R. Helfrich 2 Received 29 September 2003; revised 7 April 2004; accepted 5 May 2004; published 3 August [1] This study establishes a series of tests to examine the relative utility of nonlinear time series analysis for oceanic data. The performance of linear autoregressive models and nonlinear delay coordinate embedding methods are compared for three numerical and two observational data sets. The two observational data sets are (1) an hourly near-bottom pressure time series from the South Atlantic Bight and (2) an hourly current-meter time series from the Middle Atlantic Bight (MAB). The nonlinear methods give significantly better predictions than the linear methods when the underlying dynamics have low dimensionality. When the dimensionality is high, the utility of nonlinear methods is limited by the length and quality of the time series. On the application side we mainly focus on the MAB data set. We find that the slope velocities are much less predictable than shelf velocities. Predictability on the slope after several hours is no better than the statistical mean. On the other hand, significant predictability of shelf velocities can be obtained for up to at least 12 hours. INDEX TERMS: 3220 Mathematical Geophysics: Nonlinear dynamics; 4528 Oceanography: Physical: Fronts and jets; 9325 Information Related to Geographic Region: Atlantic Ocean; KEYWORDS: predictability, delay coordinate embedding, shelf break Citation: Yuan, G.-C., M. S. Lozier, L. J. Pratt, C. K. R. T. Jones, and K. R. Helfrich (2004), Estimating the predictability of an oceanic time series using linear and nonlinear methods, J. Geophys. Res., 109,, doi: /2003jc Introduction [2] Data available for even well-studied regions of the ocean are very sparse both temporally and spatially. For a host of applications, including those associated with navigation, resource management, weather forecasting, and national defense, we need, however, to be able to base predictions of changes in ocean properties on these data sets. Our work here is motivated by the desire to understand how much we can predict, and for how long, from such sparse data sets. [3] Coastal oceanographers are interested in predicting the strength and location of a shelf break front over the course of a few days. We address the dynamics of the shelf break front in the Middle Atlantic Bight (MAB). Many past studies have focused on the temporal and spatial variability of this front [e.g., Flagg and Beardsley, 1978; Gawarkiewicz, 1991; Lozier and Gawarkiewicz, 2001; Lozier et al., 2002; Fratantoni et al., 2000] in an effort to understand the underlying dynamics. The focus of our 1 Division of Applied Mathematics, Brown University, Providence, Rhode Island, USA. 2 Physical Oceanography Department, Woods Hole Oceanographic Institution, Woods Hole, Massachusetts, USA. 3 Division of Earth and Ocean Sciences, Duke University, Durham, North Carolina, USA. 4 Now at Bauer Laboratory, Harvard University, Cambridge, Massachusetts, USA. 5 Now at Division of Applied Mathematics, University of North Carolina at Chapel Hill, Chapel Hill, North Carolina, USA. Copyright 2004 by the American Geophysical Union /04/2003JC002148$09.00 investigation is to measure the predictability of the shelf break front, an analysis distinct from a description of its variability. We ascertain that the shelf velocities are more predictable than the corresponding slope velocities. [4] Standard methods of prediction are based on linear methods in the analyses of time series [e.g., Penland and Sardeshmukh, 1995; Emery and Thomson, 1998], and the basic technique here uses an autoregressive model. The real system is, however, nonlinear, being driven by an underlying fluid flow. We apply therefore a nonlinear prediction method based on phase space reconstruction and ask the question as to whether this offers any improvement over the standard linear prediction technique. As will be explained in section 5, the utility of such an approach is limited by the fact that it requires data length to be longer than the duration of most existing data records. This is borne out in the main case we consider of prediction around the shelf break front of the Middle Atlantic Bight. [5] Nonlinear techniques derive from recent advances in dynamical systems theories. These methods have proven to be effective in many scientific applications [Ott et al., 1994; Abarbanel, 1996; Kantz and Schreiber, 1997]. Such methods were used in a recent study of coastal water levels [Frison et al., 1999], where the underlying dynamics were well approximated by using a nonlinear deterministic model. This latter study, however, did not assess whether linear methods could yield comparable approximations, leaving open the question as to whether nonlinear methods are indeed superior (they are always more numerically costly). [6] The basis of nonlinear methods is to decode, purely from the data, the underlying rule governing their genera- 1of13
2 tion. As a simple example: Imagine that an observed variable is a sinusoidal function of time. Variability can be quantified as the amplitude of the sinusoidal function. If one uses this sinusoidal function to predict future values, however, the prediction errors would always be zero. Predictability is thus associated with skill at uncovering the rules governing the evolution of a time series. Ideally, an understanding of the local dynamics produces those governing rules. However, since we do not yet understand the dominant physical mechanisms that govern the shelf and slope waters of the Middle Atlantic Bight, past observations can provide an approximation to the rules, allowing for a measure of predictability. In order to isolate the limits and potential of past observations to predict future states, this study assesses predictability based solely on measurements. The measurements that are used for this assessment are from time series collected in the region, as will be detailed in section 3.4. [7] As a second consideration, aimed at understanding the usefulness of nonlinear techniques in geophysical prediction, we seek to obtain an idea of the cutoff at which nonlinear techniques cease to be useful. Two main variables are relevant here: length of time series available and dimension of the underlying system. In an observational data set the latter is most likely not known and cannot even be surmised. While the former is obviously known, a characteristic length for the time series from which the dynamics can be usefully deduced may not be known. Furthermore, it is important that the sampling rate of the data is not an inherent harmonic of the dynamics; otherwise, the subsequent analysis will be strongly subject to aliasing errors. To understand where, and why, nonlinear methods might be useful in a geophysical setting, we introduce a sequence of data sets with increasing complexity. These derive from a standard low-dimensional model, namely, the Lorenz system, a shallow water model, and an observational data set from the South Atlantic Bight. [8] We are not attempting here to use information from the underlying physics in any way. Data assimilation has emerged as a key technique for prediction that incorporates data into models to improve predictability. The predictive capability for data assimilation based schemes is, however, constrained not only by the quality and quantity of data but also by incomplete model physics, unknown initial and boundary conditions, and parameterizations. We are restricting ourselves here to the extreme case where only data are taken as a basis of prediction with the aim of addressing the question: What can be predicted purely from data, and under what circumstances? [9] An overview of our approach is given in section 2. This approach is applied to the data sets presented in section 3, with the methods detailed in section 4. Results are given in section 5, followed by a summary in section Approach [10] The purpose of estimating predictability is to infer the amount of uncertainty in the prediction of future values. To test the performance of prediction models, a subseries from a given time series is omitted for the model construction and then is compared to a model-generated subseries. We expect that the future evolution of a time series is a function of the current and past values. If we assume that this function is linear, we can use a linear autoregressive (AR) model for prediction [e.g., see Brockwell and Davis, 1991; Emery and Thomson, 1998]. On the other hand, if we have reason to believe that the function is nonlinear, it is difficult to select a global prediction model. However, a globally nonlinear model can be approximated by a model that has simple local structures. To construct such local models, we use the delay embedding technique that has recently been developed [e.g., see Ott et al., 1994; Abarbanel, 1996; Kantz and Schreiber, 1997]. Essentially, a delay vector is constructed by intelligently combining the current and past values in the time series, such that the evolution of the time series can be represented as a function of delay vectors. As an example of the basic concepts involved in the delay embedding technique, consider an (unforced) double pendulum system, in which the angles between the shafts of the two pendulums and the vertical are denoted by q 1 (t) and q 2 (t). The state of the system at any time t is uniquely specified by the two angles and the two angular velocities dq 1 /dt and dq 2 /dt. All future states are uniquely determined once the present state is specified. Now suppose that we have a time series of just one of the variables, say, q 1 (t), spanning 0 < t < T. We can construct a delay vector [q 1 (T), q 1 (T t),, q 1 (T (d 1)t)], where the time delay t is some multiple of the sampling interval in the time series and the embedding dimension d is an integer. It follows from the embedding theorem [Takens, 1981; Sauer et al., 1991] that for sufficiently large d the delay vectors uniquely specify the system state under a wide variety of conditions. This information can then be used for the prediction of future values. Details of this technique, such as the selection of the embedding dimension and the time delay, will be discussed in section 4. [11] One of the objectives of this paper is to gain insight into the utility and limitations of both linear and nonlinear methods in the construction of prediction models for observed time series. To achieve this goal, we address the following two questions: (1) Do observed time series contain structures that cannot be explained by linear models? (2) Can nonlinear models provide better predictions than linear models? To answer the first question, we test whether the observed time series can be differentiated from other time series that are generated with the same linear properties, a technique called surrogate data testing [Theiler et al., 1992; Smith, 1992; Schreiber and Schmitz, 2000]. The second question can be answered by applying both linear and nonlinear prediction models to the observed time series and then comparing their prediction errors. The methods used for the surrogate data testing and the computation of the prediction errors will be explained in section 4, following a discussion of the data used in this study. 3. Data [12] The approach outlined in section 2 is applied to four different systems: (1) the Lorenz system, which is a set of three ordinary differential equations, (2) a shallow water model, which contains an increasing number of degrees of freedom as the damping coefficient is reduced, (3) a pressure time series collected in the South Atlantic Bight, and (4) an array of velocity time series collected from the shelf and slope waters in the Middle Atlantic Bight. Though one of our 2of13
3 Figure 1. Representative time series from (a) data set A, (b) data set B, (c) data set C, and (d) data set D. In Figures 1a 1c, x n is unitless. primary goals is the application of these methods to time series from the Middle Atlantic Bight, considerable insight is gained from the application of these methods to less complicated systems and, for the Lorenz system and the shallow water model, systems that are known to be nonlinear. [13] Whereas the numerical data are noise-free, the observational signals are inevitably corrupted by instrument and other errors. An important and practical question is how sensitive the prediction methods are to measurement noise. For the Lorenz system (which is the underlying model for data set A to be discussed in section 3.1) it has been shown that the prediction methods are still valid when the noise level is 45% (M. Dodson et al., Noise sensitivity of simple deterministic prediction model tested on Lorenz attractor data, available at doc, 2004). For other systems the admissive noise level obviously can change depending on the details of the underlying dynamics. Statistical methods have been developed to incorporate the effects of observational noise and estimation error [Casdagli et al., 1991; Grassberger et al., 1993]. Typically, this requires some knowledge of some statistical properties of the noise. It is not a simple matter, however, to properly model the noise in the instrument: Is it pure error, or does it have a consistent bias, for instance? Too crude an addition of noise can be mistaken as a sign of high dimensionality in the nonlinear analysis. We have therefore decided to apply the techniques to the signals as they come, keeping in mind the obvious difference between the observational and computed signals Lorenz System: Data Set A [14] The Lorenz system is given by the following set of equations: dx dt ¼ sðy xþ ð1þ dy ¼ xz þ rx y dt ð2þ dz ¼ xy bz: dt ð3þ We numerically integrated these equations using the parameters s = 16, b = 4, and r = as was done by Abarbanel [1996] and a time step of Dt = The x coordinate was recorded after every time step. A time series of the x coordinate, containing 10,000 points, is referred to as data set A and is plotted in Figure 1a Shallow Water Model: Data Sets B and C [15] In a study by Helfrich and Pratt [2003], flow in a bounded basin that is drained through a strait is modeled by the nondimensional, reduced gravity, shallow water momentum and þ uru þ k u ¼ rðh þ ð4þ þrðuhþ ¼ w ð5þ equations on the f plane, where u =(u, v) is the horizontal velocity, h is layer depth, b defines the bottom topography, D = ru is the bottom drag with a linear coefficient r, w is the downwelling velocity, and M is the momentum flux due to downwelling. See Helfrich and Pratt [2003] for detailed information about the model and the choices for h, b, and w. For the initial state the flow is quiescent. After the flow is spun up, the mass flux across the strait is recorded after every dimensionless time unit, producing a time series of 3of13
4 10,000 data points. As r decreases, the time series changes from nearly steady to periodic and then to aperiodic. For sufficiently small r the time series appears irregular. In this paper, we consider two data sets, one obtained for r = (data set B, Figure 1b) and one for r = (data set C, Figure 1c). Although both time series are aperiodic, data set C appears more irregular than data set B. In section 5.1 we will show that data set B corresponds to a lowdimensional system, whereas data set C corresponds to a high-dimensional system South Atlantic Bight Data (Data Set D) [16] In an effort to gain experience in the application of our methods to observational data, we chose to analyze a record of near-bottom pressure from the continental shelf off Georgia, collected as part of the South Atlantic Bight Synoptic Offshore Observational Network (SABSOON) [Seim, 2000]. We chose this time series for two main reasons. First, we believed the dynamics of this region would be less complicated than the dynamics associated with the shelf break front in the Middle Atlantic Bight. We anticipated that the dynamics of these shelf waters would be tidally dominated and thus primarily linear. In this sense, the South Atlantic Bight (SAB) time series was used as a learning tool for the application of our methods to the shelf break front. The second reason we chose this time series was its record length and the anticipation of even longer records as the SABSOON program continues its operations. In our study we used a time series of near-bottom pressure collected from May 2000 to October The raw data, recorded in 6-min intervals, were hourly averaged to create our data set D (Figure 1d). Since nonlinear models can be constructed from consecutive data points only, gaps in the training subseries were filled by using Fourier interpolation, where the Fourier coefficients were estimated by least squares fitting with a 2-day window leading each gap Middle Atlantic Bight Data (Data Set E) [17] The main data set analyzed in this paper is a set of hourly averaged, high-quality current and temperature measurements collected during the Nantucket Shoals Flux Experiment (NSFE) from March 1979 to April 1980 [Beardsley et al., 1985]. Six moorings were deployed across the continental shelf and upper slope, south of Nantucket, near 70 W. A schematic cross section of the array is shown in Figure 2. A thorough description of the current and temperature data, with a focus on the low-frequency variability, was given by Beardsley et al. [1985]. Briefly, they found the mean current to be along-shelf toward the west, with energetic low-frequency fluctuations that were highly coherent over the shelf but were uncorrelated with fluctuations on the upper slope. An examination of the kinetic energy spectra reveals that most of the low-frequency variability occurs in the synoptic band that corresponds to 2- to 20-day periods. As mentioned in section 1, the source of this variability has been the focus of several studies over the past several decades [e.g., Flagg and Beardsley, 1978; Gawarkiewicz, 1991; Fratantoni et al., 2000; Lozier and Gawarkiewicz, 2001; Lozier et al., 2002]; however, no clear consensus has emerged. [18] In this paper, we use only the velocity time series from the NSFE array. Predicting temperature from the time Figure 2. Schematic cross section of the NSFE79 moored array. The locations of the moored instruments are marked by open (short time series) or solid (long time series) circles. The water depth (in meters) appears in parentheses next to the mooring number for the long time series. series is difficult because of the strong seasonality of the temperature record and the short length of the record relative to this dominant variability. Of the 18 velocity records available, 8 cover a period of more than 1 year. These eight relatively long records of both cross-shelf and along-shelf velocity (marked with solid circles in Figure 2) are investigated in this paper. The remaining records (at most about half of a year long) are of inadequate length for the application of our time series analysis. Four representative time series from the 16 selected for our study (eight cross-shelf and eight along-shelf ) are shown in Figure 3. We should also note that two of the eight long records contain gaps of approximately half a month. These gaps were not filled because they are too wide. Special treatment of these gaps will be discussed in section 5. Although there are no other gaps in these selected MAB time series, we note that these time series were prepared from raw data that contained many short gaps [Beardsley et al., 1985]. 4. Methods [19] In this section we give an overview of the fundamentals of linear and nonlinear prediction methods and comment on their utility and limitations. We also give an overview of surrogate data testing and detail how we quantify predictability Linear Versus Nonlinear Models [20] If consecutive values in a continuous time series are strongly correlated, a future value can be simply approximated by a linear combination of the preceding observations. This calculation forms the basis for the well-known autoregressive (AR) model, our choice for linear prediction. For a time series {x n }apth order AR model is given by x nþ1 ¼ Xp 1 a k x n k þ w n ; k¼0 ð6þ 4of13
5 Figure 3. Representative MAB time series: (a) N2(32) along-shelf velocity, (b) N2(32) cross-shelf velocity, (c) N5(28) along-shelf velocity, and (d) N5(28) cross-shelf velocity. where a k, k =1,..., p are constant coefficients and {w n }isa Gaussian white noise time series whose standard deviation is s. The noise term {w n } comes from random input from the background. The parameters a k are chosen such that the autocorrelation of the model matches with that for {x n }. Such matching is assured by the solution of the associated Yule-Walker equations [Brockwell and Davis, 1991]. [21] A time series satisfying equation (6) is a Gaussian random process, and the parameters a k are uniquely determined by the autocorrelation function. Another view is that these parameters are uniquely determined by the square of the Fourier amplitudes (i.e., the power spectrum), which can be converted from an autocorrelation by Fourier transform. A consequence is that the Fourier phases can be regarded as random. This important property is the basis for surrogate data testing to be discussed in section 4.2. [22] Linear methods are useful because they are very well understood and are straightforward to implement. Additionally, unlike the nonlinear methods to be discussed in section 4.1, constructing linear models does not require large amounts of data. However, when the underlying dynamics are nonlinear, it is possible that the evolution of the time series deviates significantly from that predicted by linear methods. Since stable linear dynamics can only lead to exponential decay or regular oscillations, a major concern with the use of linear models is that irregularity in a time series can only be attributed to random inputs, when it is well known that even simple nonlinear dynamics can generate quite irregular structures [Ott, 1993]. [23] It is hoped that by incorporating nonlinearity into time series analysis, predictions can be substantially improved. A recently developed nonlinear technique that has proven to be effective in many fields is delay coordinate embedding [e.g., Farmer and Sidorowich, 1987; Sugihara and May, 1990; Sauer, 1993], our choice for nonlinear prediction. This technique is based on the idea of phase space reconstruction. For example, a possible realization of the ocean field can be considered as a state in phase space. If the dynamics are deterministic, then all future phase states are unambiguously determined by the present phase state. Furthermore, if the present phase state can be determined with small uncertainty, then at least for a short time the future phase states can be determined quite accurately. If a time series consists of only one variable {x n }, then the phase state cannot be inversely determined. However, this task can be achieved by constructing delay vectors X n ={x n, x n t,, x n (d 1)t }, which involve two parameters: the time lag t and the embedding dimension d, provided d is sufficiently large, a property ensured by the embedding theorem [Takens, 1981; Sauer et al., 1991]. To predict a future value of x n+s, given the present delay vector X n, we search in the past record for its nearest neighbor, say, X m. The value of x n+s can then be approximately predicted as x m+s. Since observational data are generally contaminated with noise, the determination of the present state also involves uncertainty. Taking such uncertainty into account, prediction should be based not just on a single neighbor but rather on the average of an ensemble of close neighbors, each within a threshold level of uncertainty, resulting in a locally constant model. Furthermore, if there are enough close neighbors, then a linear map can be filled within each neighborhood in order to obtain more accurate predictions, resulting in a locally linear model. We note that an AR model can be viewed as a special case of locally linear models, for which the neighborhood is chosen to include all delay vectors. [24] As mentioned earlier, constructing delay embedding models involves the selection of the parameters t and d. While the optimal choice for these parameters depends on the details of the underlying dynamics and thus cannot be uniquely determined, we discuss some general criteria for their selection. The reader is referred to Kantz and Schreiber [1997] for a detailed discussion of the complicated issues 5of13
6 involved in making such selections. If t is too small, components in a delay vector are nearly identical, such that adding new components does not provide new information. On the other hand, if t is too large, successive components are totally unrelated. Popular choices for t include the first zero crossing of the autocorrelation function and the first minimum of mutual information function [Fraser and Swinney, 1986]. Typically, the effectiveness of a model is not highly sensitive to the choice of t [Kantz and Schreiber, 1997]. [25] Delay vectors can be viewed as projections from the full phase space of realizable states to a d-dimensional space. The embedding dimension d reflects how many degrees of freedom are being modeled. It should be chosen sufficiently large so that different states are truly represented by distinct delay vectors. The existence of d can be proven mathematically for purely deterministic systems of finite degrees of freedom [Takens, 1981; Sauer et al., 1991]. A too large choice of d, however, will introduce redundancy and thus will degrade the performance of the model. An appropriate choice of d can be identified by using the false nearest neighbor (FNN) technique [Kennel et al., 1992]. To choose d, one first assumes a provisional value for d, then locates the nearest neighbor of each delay vector using the d-dimensional metric. Next, the same pairs of vectors are both extended by adding one more delay coordinate and are compared using the d + 1-dimensional metric. If they become far apart, this nearest neighbor is judged false. The ratio (or percentage) of false nearest neighbors that is computed (the FNN ratio) can be viewed as a measure of determinism. By increasing d, the FNN ratio will decrease. If a d can be found for which there are no more FNNs, then determinism is established. This d is used for constructing delay embedding models. However, such a d may not always exist in application. When the data are too short or too noisy, estimates of the FNN ratio may contain significant uncertainty. In fact, we will show that in some cases the FNN ratio may appear to increase with d. As a result, determinism may not be established. In such cases, we choose d to be the dimension for which the FNN ratio either appears to saturate or achieves a minimum. [26] Nonlinear methods have a drawback when applied to high-dimensional systems since the length of data required for constructing nonlinear models increases rapidly with the dimension of the underlying dynamics. This requirement can be prohibitive for many observational time series, where data sufficiency is usually an issue. Unfortunately, it is difficult to determine how much data are needed for a given embedding dimension without strong simplifying assumptions. Different estimates have been given in the literature [e.g., see Eckmann and Ruelle, 1992; Smith, 1988; Procaccia, 1988]. Common to these studies is the supposition that the length of required data grows exponentially with increasing d Surrogate Data [27] To assess whether a nonlinear model is necessary for prediction, it is essential to understand the degree to which a simpler model (i.e., a linear model) captures the main predictable structures of a time series. An effective technique for this assessment is known as surrogate data testing [Theiler et al., 1992; Smith, 1992; Schreiber and Schmitz, 2000]. Following Theiler et al. [1992], the procedure for a surrogate data test contains the following steps. First, a null hypothesis (a potential explanation for the evolution of the time series) is specified. Second, a number of random realizations (called surrogate data) of the hypothesized process are generated numerically. Third, we select a discriminating statistic, denoted by h, and compute its value for the observed and surrogate time series. Finally, we determine whether the value for the observed data, h o, is significantly different (in a statistical sense) from the surrogate data h s i, i = 1,, m. If it is, then the null hypothesis is rejected. [28] The null hypothesis used in this paper is the following: The observed time series may not have a Gaussian distribution, but it can be derived from another time series originating from a linear Gaussian stochastic process by a nonlinear transform. The corresponding surrogate time series are generated by an iterative Fourier transform method [Hegger et al., 1999; Schreiber and Schmitz, 2000]. Notice that a Gaussian stochastic process is uniquely determined by its Fourier amplitudes. [29] After selecting h (discussed later in this section), we can compare h o and h s i. If the difference is unlikely to be due to chance only, then the null hypothesis is rejected. For example, if h is the nonlinear prediction error and we want to show that h o is less than h s i at a significance level of a = 0.05, then at least m =1/a = 20 surrogate time series need to be generated. If h o is less than h s i, for all i =1,, m, then the null hypothesis is rejected because the probability that such an event occurs by chance is less than [30] While the above analysis can distinguish between the surrogate and observed time series, it does not provide information about the magnitude of the discrepancy between h o and h s i. Such a quantification is necessary since the selection of a complex rather than a simple model is not worthwhile if the discrepancy is small. To quantify the relative magnitude of discrepancy, we select the following measure: g ¼ 1 X m h s i m h o 1 : ð7þ i¼1 If g is much less than 1, the relative discrepancy can be considered negligible. [31] We now discuss our choice of discriminating statistic h. Since our aim is to test whether nonlinear models contain extra predictable information compared with linear correlation, the discriminating statistic should reflect predictability. In particular, we consider the following two choices FNN Ratio (H F ) [32] The FNN ratio discussed in section 4.1 reflects degrees of determinism and therefore serves as a good choice for a discriminating statistic. The mathematical algorithm for computing the FNN ratio can be found in a study by Kennel et al. [1992]. We use a version implemented in the TISEAN software by Hegger et al. [1999] Nonlinear Prediction Error (H P ) [33] Another useful statistic to compute is the averaged nonlinear prediction error. Given a delay embedding model, the averaged relative error for an s-step prediction is h P i 1=2 1 N N n¼1 ð x nþs ^x nþs Þ 2 h P ¼ h P i 1=2 ; ð8þ 1 N N n¼1 ð x n x Þ 2 6of13
7 where ^x n+s is the predicted value for x n+s and x is the mean of x n estimated by x =(Sx n )/N. In equation (8) the RMS magnitude of x n is used as a normalizing factor; thus h P is a dimensionless measure. [34] Previous studies have shown that the statistic h P is a powerful discriminating statistic for detecting nonlinearity [Schreiber and Schmitz, 2000]. However, h F is also useful because it provides a guideline for the choice of the embedding dimension, which is important for the success of nonlinear prediction models. [35] To avoid statistical bias, the delay embedding model used for computing h F or h P should not be optimized for the original data. Therefore a different choice of embedding parameters could potentially improve predictions. In section 4.3, when we discuss in detail how to quantify predictability, we will search for an optimal model among a number of candidates. [36] What can we learn from a surrogate data test? We learn whether a time series contains predictable structures that cannot be modeled by linear methods, thereby gaining information about the utility of nonlinear methods. However, it may not determine whether the underlying system is nonlinear per se. In section 5 we present a time series that is nonlinear deterministic but is nevertheless indistinguishable from surrogate data. For this time series the use of nonlinear methods does not improve prediction skill because the available data are insufficient to uncover the deterministic dynamics. In fact, the results presented in section 5 suggest that surrogate data tests can detect low-dimensional nonlinear systems effectively, but not high-dimensional systems, unless, in theory, an extremely long time series is available. [37] Application of these methods to time series with strong periodicity has drawbacks that have been previously noted [Theiler et al., 1993]. In particular, positive surrogate data tests may result, not from nonlinearity, but from error induced by spectral estimation. In particular, this error may occur if the length of an interval used for spectral estimation is not a multiple of full cycles. In such a case, redundant frequencies are induced in the estimated spectrum, and, as a result, the surrogate time series appear noisier than the original data, even for linear systems. Such issues cause uncertainty for tests of the continental shelf data (data set D) and the MAB data set. However, we believe that such spectral errors compose only a small portion of prediction errors and thus do not seriously affect our results Prediction Errors [38] To test the accuracy of a prediction method, we pretend, tentatively, that we do not have knowledge of the true value at the time of prediction. After a prediction has been made, we compare the predicted value with the truth to identify a prediction error. We divide a time series under study into two parts: a training subseries, which is used to construct prediction models, and a testing subseries, which we attempt to predict by using the constructed models. We quantify predictability as the prediction error associated with the best model at hand. In other words, we use many different models, each optimized in its own class, to make predictions. The minimum prediction error is then regarded as an estimate of the predictability of the observed time series. The models we consider are AR models with various orders and nonlinear models with various embedding parameters, as specified in section 5. [39] As a final comment on our methods we note that we have purposely chosen not to employ a more advanced measure of predictability offered by dynamical systems theory, that is, the Lyapunov exponent [see, e.g., Ott, 1993], which measures the exponential growth rate of initial errors. Theoretically, this measure has the advantage in that it is a property of the underlying dynamical process. However, estimating Lyapunov exponents on the basis of time delay embedding is a very difficult task because of data limitations. Studies have shown that estimates are likely to be incorrect, even in relatively idealized situations [Ott et al., 1994; Kantz and Schreiber, 1997]. 5. Results [40] In this section we apply surrogate data tests to data sets A E. Additionally, we compute prediction errors for each of these data sets using linear and nonlinear methods, as discussed in section Testing Nonlinearity Using Surrogate Data [41] First, consider data sets A through C, all of which are generated from nonlinear, deterministic systems. We test the null hypothesis that the time series can be derived from a linear Gaussian stochastic process via a possibly nonlinear transform. In Figures 4a 4c h F is plotted as a function of d, with t at a fixed value of 4. The original data are plotted with the thick curve, while the distribution of the surrogate data is shaded. For data sets A and B, h F is initially large but drops to near zero as d increases to 3 or larger, reflecting the low dimensionality of data sets A and B. For the surrogates, h F decreases also with increasing d, but the values are substantially higher than the original time series. Clearly, the null hypothesis can be rejected with a significance level of 0.05 for both data sets A and B. For data set C, h F remains relatively high despite increasing d, suggesting that the underlying dynamics are highly dimensional. Additionally, h F for the original data falls within the cloud of the surrogate data sets; thus the null hypothesis cannot be rejected for data set C. The increase in h F past d = 4 for data set C is an artifact caused by data insufficiency. [42] The results of the surrogate data tests using h P as a discriminating statistic are shown in Figures 4d 4f, where h P is computed by using a locally constant model. The parameters d and t were each fixed at 4. The averaged prediction errors for data sets A, B, and C are plotted as a function of prediction time s in Figures 4d, 4e, and 4f, respectively. In agreement with the analysis of h F, the null hypothesis can be rejected for data sets A and B but not for data set C. While each of these data sets is nonlinear, only those which are low dimensional (A and B) are distinguishable from their linear surrogates. [43] The magnitude of the discrepancy for h F and h P is given by g F and g P, respectively, according to equation (7). The values of g F (averaged over d = 3, 4, 5) and g P (averaged over prediction time) are shown in Table 1. For data sets A and B, which are low dimensional, both g F and g P are greater than 1, indicating a significant difference between the surrogates and the original data. In contrast, for data set C, which is high dimensional, both g F and g P are 7of13
8 Figure 4. Surrogate data tests for data sets A C: (a c) h F and (d f ) h P. Values for the original data are shown as the thick solid curves, while the shaded region indicates the range of values for the surrogate data. much less than 1, suggesting that the difference between the original and the surrogates is not substantial. As with the analysis of h F and h P, these results suggest that surrogate data tests can detect low-dimensional nonlinear systems effectively but not high-dimensional systems. [44] The results of the surrogate data tests for the SAB shelf data are shown in Figure 5. The null hypothesis can be rejected using h P as the discriminating statistic but not when using h F. However, the evaluation of g P (Table 1) shows that the difference between the original data and the surrogate data is quite small. Thus, though the cloud of surrogates in Figure 5b is distinct from the original data, the difference is small enough such that the use of a nonlinear model would not be advisable. [45] The above results for the SAB data set (D) could suggest that the underlying dynamics are nonlinear and of high dimensionality, similar to data set C. However, unlike data set C, h F approaches zero when the embedding dimension is 4 or 5 (Figure 5a), suggesting a system of relatively low dimension. Additionally, the prediction errors for data set D are quite small relative to data set C, suggesting the existence of predictable structures. Given these indications, we favor an alternate interpretation for the surrogate data tests for the SAB data, namely, that the deviation is small because the original data set is close to linear. [46] For each of the selected velocity time series from the MAB (data set E, corresponding to the solid circles in Figure 2) we conducted surrogate data tests. For the two time series that contain wide gaps, we used the uninterrupted segment before the gaps, about 9 months long, for surrogate data testing. Results are shown in Figure 6 for a typical shelf time series, N2(32), and a typical slope time series, N5(28), for both the along-shelf and cross-shelf data. In all cases the original and surrogate data cannot be distinguished. This assessment is confirmed by the small values for g F and g P (Table 1). [47] As seen in Figures 6a and 6b, h F is significantly different from zero in all four cases, suggesting that the embedding dimension is not sufficient to uncover any determinism. Increasing the embedding dimension does not reduce h F significantly. In Figure 6b, h F at d =5is actually greater than at d = 4. As discussed in section 5.1, this artifact is due to data insufficiency. When the prediction errors for the surrogate time series saturate (Figures 6c and 6d), the prediction errors for the observed data are much larger than those for data sets A and B, also an indication that the system is not low dimensional. We add a cautionary note here that these prediction errors calculated in this section are not entirely indicative of the predictability of the system for two reasons. First, these errors represent only in sample errors, when out-of-sample errors should be used to quantify predictability. Second, no effort has been made to optimize the prediction models. With a different choice of Table 1. Measure of the Difference Between the Original Data and Surrogates g F (Averaged Over d = 3, 4, 5) and g P (Averaged Over Prediction Time) Data Set g F g P A B C D E N2(32) along-shelf N2(32) cross-shelf N5(28) along-shelf N5(28) cross-shelf of13
9 Figure 5. Surrogate data tests for data set D: (a) h F and (b) h P. Values for the original data are shown as thick solid curves, while the shaded region indicates the range of the surrogate data. embedding parameters, prediction errors are likely to be reduced, as will be seen in section Predictability [48] To quantify predictability, we divide a time series into a training subseries and a testing subseries, as explained in section 4.3. Linear and nonlinear models are constructed from the training subseries and are applied to the testing subseries. To test whether the prediction of nonlinear systems can be improved by using nonlinear models, we first consider data sets B and C. The order of AR models is increased from 1 until a further increase does not significantly improve prediction. This occurs when the order is about 6 in both cases. The minimum prediction error obtained from these 6 models is referred to as the linear prediction error. We vary the embedding parameters to optimize the nonlinear model. Our earlier computation of h F (see Figure 4) suggests that the embedding dimension should not exceed 5. Therefore we apply locally linear models using embedding dimensions from 3 up to 5, with the time delay varying from 1 through 6, for a total of 18 models. The same set of embedding parameters was also used to construct locally constant models, but we find that locally linear models are more accurate than locally constant models. The minimum prediction error obtained from these models is referred to as the nonlinear prediction error. [49] Linear and nonlinear prediction errors as a function of time for data sets B and C are shown in Figure 7. Nonlinear prediction errors are much smaller than linear prediction errors for data set B, suggesting that nonlinear prediction models are superior. On the other hand, nonlinear prediction errors are actually larger than linear prediction errors for data set C. Since an AR model can be viewed as a special case of locally linear models, the better performance of linear prediction errors for data set C indicates that none of the selected nonlinear models is Figure 6. Surrogate data tests for the N2(32) (solid curves, dark shading) and N5(28) (dashed curves, light shading) time series: (a) h F for the along-shelf velocity, (b) h P for the along-shelf velocity, (c) h F for the cross-shelf velocity, and (d) h P for the cross-shelf velocity. 9of13
10 Figure 7. Relative prediction errors as a function of time for (a) data set B and (b) data set C. Linear errors are shown by the thin curves, and nonlinear errors are shown by the thick curves. optimal. We note that the flexibility of nonlinear models makes it difficult to find the optimal one. Comparison of the two cases suggests that nonlinear models can improve prediction significantly if the system is low dimensional but not if the system is high dimensional. We believe this difference arises because the data are not sufficient for constructing high-dimensional models. [50] How much data are needed for nonlinear methods to be effective? Although in principle, data set C can be extended indefinitely, computational resources limited the regeneration of data set C to a tenfold increase, or 100,000 data points. For this longer time series the FNN ratio ceases to decay at around dimension 7. (As discussed in section 5.1, it is an artifact that the FNN ratio does not drop further for higher embedding dimension.) Thus we use embedding dimension from 3 up to 7. The testing subseries is chosen to be the same as for the shorter time series. Compared with the shorter time series, the magnitude of nonlinear prediction errors is smaller (see Figure 8), while linear prediction errors maintain the same magnitude. Nonetheless, nonlinear predictions are still no more effective than linear predictions. Furthermore, we find that the longer time series is also indistinguishable from the surrogate data. These results further suggest that highdimensional systems require very long duration data for the effectiveness of nonlinear methods. [51] For data sets D (the SAB data) and E (the MAB data) we use the same method to select the maximum order of AR models, which turns out to be about 12. Thus in total we consider 12 different models. As before, our nonlinear model is a locally linear model using embedding dimensions from 3 up to 5 and time delays from 1 hour up to 12 hours, for a total of 36 models. For the predictability of data set D, a year-long training subseries is used, and the length of the test subseries is chosen to be 1 month. The resulting prediction errors are plotted against prediction time in Figure 9. Both the nonlinear and the linear errors are quite small; however, linear models seem to outperform nonlinear models, which, as discussed earlier, is due to the suboptimal behavior of the selected nonlinear models. The fact that nonlinear models fail to outperform linear models could be due to the high dimensionality of the SAB data set, as suggested for data set C. However, for data set C both linear and nonlinear prediction errors are quite large, while for data set D they are both small. Therefore a more feasible explanation for why nonlinear models do not outperform linear models for data set D (the SAB data) may be that the underlying dynamics are close to linear, as postulated in Figure 8. Same as Figure 7b except that data set C has been extended tenfold. Figure 9. Relative prediction errors as a function of time for data set D. Linear errors are shown by the thin curve, and nonlinear errors are shown by the thick curve. 10 of 13
11 Figure 10. Relative prediction errors as a function of time for the N2(32) (solid curves) and N5(28) (dashed curves) time series: (a) along-shelf velocity and (b) cross-shelf velocity. Linear errors are shown by the thin curves, and nonlinear errors are shown by the thick curves. section 5.1. We note here that our results show that the pressure field in this region of the SAB is remarkably predictable out to 12 hours, with errors on the order of 10% of the RMS, a result consistent with our expectation of a tidally dominated regime. Data set E (the MAB data) is shorter than data set D, so a shorter training subseries is used. We use an 11-month training subseries for the six time series containing year-long consecutive records. For the two time series with wide gaps (at N2) we use the uninterrupted segments before the gaps as the training subseries. The length of the test subseries is again chosen to be 1 month. [52] Again, we use N2(32) and N5(28) to illustrate the typical time dependence of prediction errors for data set E (Figure 10). In all cases, prediction errors saturate at about 5 hours. Predictions are moderately good for N2(32) but rather poor after 5 hours for N5(28). Interestingly, crossshelf velocity is more predictable than along-shelf velocity at N2(32), but the opposite is found at N5(28). This difference might be due to the presence of the strong along-slope frontal current at N5(28), which would facilitate along-slope predictions. In general, this analysis shows that nonlinear predictions fail to outperform linear predictions, rendering their use unnecessary for this data, as suggested in section 5.1 by the surrogate data tests. [53] To examine the spatial structure of predictability, we show prediction errors at 1 hour, 3 hours, and 12 hours for all eight time series in Figure 11. In all cases, linear and nonlinear prediction errors have approximately the same magnitudes, again suggesting that there is no advantage in using nonlinear prediction models. Figures 11a and 11b show the magnitude of the absolute prediction errors, that is, without normalization. Although 1-hour prediction errors are typically only about 2 or 3 cm/s, errors for 12-hour predictions are about 3 or 4 times larger, reaching 10 cm/s. The greatest errors occur at N5(28), where the 12-hour prediction error is about 13 cm/s. Even on the shelf the 12-hour prediction error can reach 8 cm/s. To place these errors in context, relative prediction errors of the observed current velocity in that month are shown in Figures 11c and 11d. Relative prediction errors for both the cross-shelf and along-shelf velocities generally increase offshore, achieving a maximum at N5(28), then decreasing some at N6(10). Moorings N4 to N6 are located in the shelf break region, where the dynamics are dominated by a highly variable and unstable frontal current; therefore it is not surprising that prediction degenerates quickly for these time series. On the shelf the relative prediction errors are at most 0.5, suggesting there is significant predictability during this period, doubtless due to the dominance of the tides on the shelf, as was also noted for the SAB data set. On the other hand, on the slope the 12-hour prediction errors can be as large as the RMS magnitude of the velocity itself, which is no better than simply predicting the statistical mean. Hence predictability is lost almost completely. Prediction errors for crossshelf and along-shelf components are roughly the same order of magnitude, yet the difference between the two has significant spatial structures. In particular, the crossshelf velocity seems to be more predictable than the alongshelf components on the shelf, but the opposite is true on the slope. The greater predictability of the along-shelf component over the slope may be due to the downstream advective influence provided by the shelf break frontal current. 6. Summary [54] This analysis was designed with a twofold purpose: first, to establish procedures that would evaluate the effectiveness of nonlinear methods in the analysis of oceanic time series and second, to determine the predictability of the flow field in the shelf break region of the Middle Atlantic Bight. Subsumed by the first and second goals was another, namely, to determine whether nonlinear methods could improve on prediction estimates for the shelf break velocity field provided by linear methods. Regarding the first goal, this analysis has introduced the use of surrogate data tests to oceanic time series and has demonstrated the utility of comparing linear and nonlinear methods via measures of the false nearest neighbors and prediction errors. Additionally, measures have been introduced that allow for the quantification of the difference between the linear and nonlinear results. [55] Regarding the second goal, our study results reveal a sharp contrast between a fairly predictable shelf flow field and a fairly unpredictable slope flow field in the Middle Atlantic Bight. Predictability for both cross-shelf and along-shelf velocity has a cross-shelf dependence, with 11 of 13
The Behaviour of a Mobile Robot Is Chaotic
 AISB Journal 1(4), c SSAISB, 2003 The Behaviour of a Mobile Robot Is Chaotic Ulrich Nehmzow and Keith Walker Department of Computer Science, University of Essex, Colchester CO4 3SQ Department of Physics
AISB Journal 1(4), c SSAISB, 2003 The Behaviour of a Mobile Robot Is Chaotic Ulrich Nehmzow and Keith Walker Department of Computer Science, University of Essex, Colchester CO4 3SQ Department of Physics
Effects of data windows on the methods of surrogate data
 Effects of data windows on the methods of surrogate data Tomoya Suzuki, 1 Tohru Ikeguchi, and Masuo Suzuki 1 1 Graduate School of Science, Tokyo University of Science, 1-3 Kagurazaka, Shinjuku-ku, Tokyo
Effects of data windows on the methods of surrogate data Tomoya Suzuki, 1 Tohru Ikeguchi, and Masuo Suzuki 1 1 Graduate School of Science, Tokyo University of Science, 1-3 Kagurazaka, Shinjuku-ku, Tokyo
1 Random walks and data
 Inference, Models and Simulation for Complex Systems CSCI 7-1 Lecture 7 15 September 11 Prof. Aaron Clauset 1 Random walks and data Supposeyou have some time-series data x 1,x,x 3,...,x T and you want
Inference, Models and Simulation for Complex Systems CSCI 7-1 Lecture 7 15 September 11 Prof. Aaron Clauset 1 Random walks and data Supposeyou have some time-series data x 1,x,x 3,...,x T and you want
SIO 210: Data analysis methods L. Talley, Fall Sampling and error 2. Basic statistical concepts 3. Time series analysis
 SIO 210: Data analysis methods L. Talley, Fall 2016 1. Sampling and error 2. Basic statistical concepts 3. Time series analysis 4. Mapping 5. Filtering 6. Space-time data 7. Water mass analysis Reading:
SIO 210: Data analysis methods L. Talley, Fall 2016 1. Sampling and error 2. Basic statistical concepts 3. Time series analysis 4. Mapping 5. Filtering 6. Space-time data 7. Water mass analysis Reading:
SIO 210: Data analysis
 SIO 210: Data analysis 1. Sampling and error 2. Basic statistical concepts 3. Time series analysis 4. Mapping 5. Filtering 6. Space-time data 7. Water mass analysis 10/8/18 Reading: DPO Chapter 6 Look
SIO 210: Data analysis 1. Sampling and error 2. Basic statistical concepts 3. Time series analysis 4. Mapping 5. Filtering 6. Space-time data 7. Water mass analysis 10/8/18 Reading: DPO Chapter 6 Look
Algorithms for generating surrogate data for sparsely quantized time series
 Physica D 231 (2007) 108 115 www.elsevier.com/locate/physd Algorithms for generating surrogate data for sparsely quantized time series Tomoya Suzuki a,, Tohru Ikeguchi b, Masuo Suzuki c a Department of
Physica D 231 (2007) 108 115 www.elsevier.com/locate/physd Algorithms for generating surrogate data for sparsely quantized time series Tomoya Suzuki a,, Tohru Ikeguchi b, Masuo Suzuki c a Department of
Detection of Nonlinearity and Stochastic Nature in Time Series by Delay Vector Variance Method
 International Journal of Engineering & Technology IJET-IJENS Vol:10 No:02 11 Detection of Nonlinearity and Stochastic Nature in Time Series by Delay Vector Variance Method Imtiaz Ahmed Abstract-- This
International Journal of Engineering & Technology IJET-IJENS Vol:10 No:02 11 Detection of Nonlinearity and Stochastic Nature in Time Series by Delay Vector Variance Method Imtiaz Ahmed Abstract-- This
A benchmark test A benchmark test of accuracy and precision in estimating dynamical systems characteristics from a time series
 2 A benchmark test A benchmark test of accuracy and precision in estimating dynamical systems characteristics from a time series, SM Rispens, M Pijnappels, JH van Dieën, KS van Schooten, PJ Beek, A Daffertshofer
2 A benchmark test A benchmark test of accuracy and precision in estimating dynamical systems characteristics from a time series, SM Rispens, M Pijnappels, JH van Dieën, KS van Schooten, PJ Beek, A Daffertshofer
Separation of a Signal of Interest from a Seasonal Effect in Geophysical Data: I. El Niño/La Niña Phenomenon
 International Journal of Geosciences, 2011, 2, **-** Published Online November 2011 (http://www.scirp.org/journal/ijg) Separation of a Signal of Interest from a Seasonal Effect in Geophysical Data: I.
International Journal of Geosciences, 2011, 2, **-** Published Online November 2011 (http://www.scirp.org/journal/ijg) Separation of a Signal of Interest from a Seasonal Effect in Geophysical Data: I.
Testing for Chaos in Type-I ELM Dynamics on JET with the ILW. Fabio Pisano
 Testing for Chaos in Type-I ELM Dynamics on JET with the ILW Fabio Pisano ACKNOWLEDGMENTS B. Cannas 1, A. Fanni 1, A. Murari 2, F. Pisano 1 and JET Contributors* EUROfusion Consortium, JET, Culham Science
Testing for Chaos in Type-I ELM Dynamics on JET with the ILW Fabio Pisano ACKNOWLEDGMENTS B. Cannas 1, A. Fanni 1, A. Murari 2, F. Pisano 1 and JET Contributors* EUROfusion Consortium, JET, Culham Science
Predictability and Chaotic Nature of Daily Streamflow
 34 th IAHR World Congress - Balance and Uncertainty 26 June - 1 July 211, Brisbane, Australia 33 rd Hydrology & Water Resources Symposium 1 th Hydraulics Conference Predictability and Chaotic Nature of
34 th IAHR World Congress - Balance and Uncertainty 26 June - 1 July 211, Brisbane, Australia 33 rd Hydrology & Water Resources Symposium 1 th Hydraulics Conference Predictability and Chaotic Nature of
Bred vectors: theory and applications in operational forecasting. Eugenia Kalnay Lecture 3 Alghero, May 2008
 Bred vectors: theory and applications in operational forecasting. Eugenia Kalnay Lecture 3 Alghero, May 2008 ca. 1974 Central theorem of chaos (Lorenz, 1960s): a) Unstable systems have finite predictability
Bred vectors: theory and applications in operational forecasting. Eugenia Kalnay Lecture 3 Alghero, May 2008 ca. 1974 Central theorem of chaos (Lorenz, 1960s): a) Unstable systems have finite predictability
SIO 210 CSP: Data analysis methods L. Talley, Fall Sampling and error 2. Basic statistical concepts 3. Time series analysis
 SIO 210 CSP: Data analysis methods L. Talley, Fall 2016 1. Sampling and error 2. Basic statistical concepts 3. Time series analysis 4. Mapping 5. Filtering 6. Space-time data 7. Water mass analysis Reading:
SIO 210 CSP: Data analysis methods L. Talley, Fall 2016 1. Sampling and error 2. Basic statistical concepts 3. Time series analysis 4. Mapping 5. Filtering 6. Space-time data 7. Water mass analysis Reading:
Phase-Space Reconstruction. Gerrit Ansmann
 Phase-Space Reconstruction Gerrit Ansmann Reprise: The Need for Non-Linear Methods. Lorenz oscillator x = 1(y x), y = x(28 z) y, z = xy 8z 3 Autoregressive process measured with non-linearity: y t =.8y
Phase-Space Reconstruction Gerrit Ansmann Reprise: The Need for Non-Linear Methods. Lorenz oscillator x = 1(y x), y = x(28 z) y, z = xy 8z 3 Autoregressive process measured with non-linearity: y t =.8y
Modeling and Predicting Chaotic Time Series
 Chapter 14 Modeling and Predicting Chaotic Time Series To understand the behavior of a dynamical system in terms of some meaningful parameters we seek the appropriate mathematical model that captures the
Chapter 14 Modeling and Predicting Chaotic Time Series To understand the behavior of a dynamical system in terms of some meaningful parameters we seek the appropriate mathematical model that captures the
INTRODUCTION TO CHAOS THEORY T.R.RAMAMOHAN C-MMACS BANGALORE
 INTRODUCTION TO CHAOS THEORY BY T.R.RAMAMOHAN C-MMACS BANGALORE -560037 SOME INTERESTING QUOTATIONS * PERHAPS THE NEXT GREAT ERA OF UNDERSTANDING WILL BE DETERMINING THE QUALITATIVE CONTENT OF EQUATIONS;
INTRODUCTION TO CHAOS THEORY BY T.R.RAMAMOHAN C-MMACS BANGALORE -560037 SOME INTERESTING QUOTATIONS * PERHAPS THE NEXT GREAT ERA OF UNDERSTANDING WILL BE DETERMINING THE QUALITATIVE CONTENT OF EQUATIONS;
Is correlation dimension a reliable indicator of low-dimensional chaos in short hydrological time series?
 WATER RESOURCES RESEARCH, VOL. 38, NO. 2, 1011, 10.1029/2001WR000333, 2002 Is correlation dimension a reliable indicator of low-dimensional chaos in short hydrological time series? Bellie Sivakumar Department
WATER RESOURCES RESEARCH, VOL. 38, NO. 2, 1011, 10.1029/2001WR000333, 2002 Is correlation dimension a reliable indicator of low-dimensional chaos in short hydrological time series? Bellie Sivakumar Department
NONLINEAR TIME SERIES ANALYSIS, WITH APPLICATIONS TO MEDICINE
 NONLINEAR TIME SERIES ANALYSIS, WITH APPLICATIONS TO MEDICINE José María Amigó Centro de Investigación Operativa, Universidad Miguel Hernández, Elche (Spain) J.M. Amigó (CIO) Nonlinear time series analysis
NONLINEAR TIME SERIES ANALYSIS, WITH APPLICATIONS TO MEDICINE José María Amigó Centro de Investigación Operativa, Universidad Miguel Hernández, Elche (Spain) J.M. Amigó (CIO) Nonlinear time series analysis
Understanding the dynamics of snowpack in Washington State - part II: complexity of
 Understanding the dynamics of snowpack in Washington State - part II: complexity of snowpack Nian She and Deniel Basketfield Seattle Public Utilities, Seattle, Washington Abstract. In part I of this study
Understanding the dynamics of snowpack in Washington State - part II: complexity of snowpack Nian She and Deniel Basketfield Seattle Public Utilities, Seattle, Washington Abstract. In part I of this study
Complex system approach to geospace and climate studies. Tatjana Živković
 Complex system approach to geospace and climate studies Tatjana Živković 30.11.2011 Outline of a talk Importance of complex system approach Phase space reconstruction Recurrence plot analysis Test for
Complex system approach to geospace and climate studies Tatjana Živković 30.11.2011 Outline of a talk Importance of complex system approach Phase space reconstruction Recurrence plot analysis Test for
Chapter 6: Ensemble Forecasting and Atmospheric Predictability. Introduction
 Chapter 6: Ensemble Forecasting and Atmospheric Predictability Introduction Deterministic Chaos (what!?) In 1951 Charney indicated that forecast skill would break down, but he attributed it to model errors
Chapter 6: Ensemble Forecasting and Atmospheric Predictability Introduction Deterministic Chaos (what!?) In 1951 Charney indicated that forecast skill would break down, but he attributed it to model errors
Using modern time series analysis techniques to predict ENSO events from the SOI time series
 Nonlinear Processes in Geophysics () 9: 4 45 Nonlinear Processes in Geophysics c European Geophysical Society Using modern time series analysis techniques to predict ENSO events from the SOI time series
Nonlinear Processes in Geophysics () 9: 4 45 Nonlinear Processes in Geophysics c European Geophysical Society Using modern time series analysis techniques to predict ENSO events from the SOI time series
SINGAPORE RAINFALL BEHAVIOR: CHAOTIC?
 SINGAPORE RAINFALL BEHAVIOR: CHAOTIC? By Bellie Sivakumar, 1 Shie-Yui Liong, 2 Chih-Young Liaw, 3 and Kok-Kwang Phoon 4 ABSTRACT: The possibility of making short-term prediction of rainfall is studied
SINGAPORE RAINFALL BEHAVIOR: CHAOTIC? By Bellie Sivakumar, 1 Shie-Yui Liong, 2 Chih-Young Liaw, 3 and Kok-Kwang Phoon 4 ABSTRACT: The possibility of making short-term prediction of rainfall is studied
arxiv: v1 [nlin.ao] 21 Sep 2018
![arxiv: v1 [nlin.ao] 21 Sep 2018 arxiv: v1 [nlin.ao] 21 Sep 2018](/thumbs/89/98231389.jpg) Using reservoir computers to distinguish chaotic signals T L Carroll US Naval Research Lab, Washington, DC 20375 (Dated: October 11, 2018) Several recent papers have shown that reservoir computers are
Using reservoir computers to distinguish chaotic signals T L Carroll US Naval Research Lab, Washington, DC 20375 (Dated: October 11, 2018) Several recent papers have shown that reservoir computers are
ESTIMATING THE ATTRACTOR DIMENSION OF THE EQUATORIAL WEATHER SYSTEM M. Leok B.T.
 This paper was awarded in the I International Competition (99/9) First Step to Nobel Prize in Physics and published in the competition proceedings (Acta Phys. Pol. A 8 Supplement, S- (99)). The paper is
This paper was awarded in the I International Competition (99/9) First Step to Nobel Prize in Physics and published in the competition proceedings (Acta Phys. Pol. A 8 Supplement, S- (99)). The paper is
The Effects of Dynamical Noises on the Identification of Chaotic Systems: with Application to Streamflow Processes
 Fourth International Conference on Natural Computation The Effects of Dynamical Noises on the Identification of Chaotic Systems: with Application to Streamflow Processes Wen Wang, Pieter H.A.J.M. Van Gelder,
Fourth International Conference on Natural Computation The Effects of Dynamical Noises on the Identification of Chaotic Systems: with Application to Streamflow Processes Wen Wang, Pieter H.A.J.M. Van Gelder,
Quantitative Description of Robot-Environment Interaction Using Chaos Theory 1
 Quantitative Description of Robot-Environment Interaction Using Chaos Theory 1 Ulrich Nehmzow Keith Walker Dept. of Computer Science Department of Physics University of Essex Point Loma Nazarene University
Quantitative Description of Robot-Environment Interaction Using Chaos Theory 1 Ulrich Nehmzow Keith Walker Dept. of Computer Science Department of Physics University of Essex Point Loma Nazarene University
OTC Vertical current structures in the Deep Gulf using EOF analysis S.F. DiMarco, R.O. Reid, and W. D.Nowlin, Jr., Texas A&M University
 OTC 12994 Vertical current structures in the Deep Gulf using EOF analysis S.F. DiMarco, R.O. Reid, and W. D.Nowlin, Jr., Texas A&M University Copyright 21, Offshore Technology Conference This paper was
OTC 12994 Vertical current structures in the Deep Gulf using EOF analysis S.F. DiMarco, R.O. Reid, and W. D.Nowlin, Jr., Texas A&M University Copyright 21, Offshore Technology Conference This paper was
Stochastic Spectral Approaches to Bayesian Inference
 Stochastic Spectral Approaches to Bayesian Inference Prof. Nathan L. Gibson Department of Mathematics Applied Mathematics and Computation Seminar March 4, 2011 Prof. Gibson (OSU) Spectral Approaches to
Stochastic Spectral Approaches to Bayesian Inference Prof. Nathan L. Gibson Department of Mathematics Applied Mathematics and Computation Seminar March 4, 2011 Prof. Gibson (OSU) Spectral Approaches to
Application of Chaos Theory and Genetic Programming in Runoff Time Series
 Application of Chaos Theory and Genetic Programming in Runoff Time Series Mohammad Ali Ghorbani 1, Hossein Jabbari Khamnei, Hakimeh Asadi 3*, Peyman Yousefi 4 1 Associate Professor, Department of Water
Application of Chaos Theory and Genetic Programming in Runoff Time Series Mohammad Ali Ghorbani 1, Hossein Jabbari Khamnei, Hakimeh Asadi 3*, Peyman Yousefi 4 1 Associate Professor, Department of Water
Testing time series for nonlinearity
 Statistics and Computing 11: 257 268, 2001 C 2001 Kluwer Academic Publishers. Manufactured in The Netherlands. Testing time series for nonlinearity MICHAEL SMALL, KEVIN JUDD and ALISTAIR MEES Centre for
Statistics and Computing 11: 257 268, 2001 C 2001 Kluwer Academic Publishers. Manufactured in The Netherlands. Testing time series for nonlinearity MICHAEL SMALL, KEVIN JUDD and ALISTAIR MEES Centre for
Prof. Stephen G. Penny University of Maryland NOAA/NCEP, RIKEN AICS, ECMWF US CLIVAR Summit, 9 August 2017
 COUPLED DATA ASSIMILATION: What we need from observations and modellers to make coupled data assimilation the new standard for prediction and reanalysis. Prof. Stephen G. Penny University of Maryland NOAA/NCEP,
COUPLED DATA ASSIMILATION: What we need from observations and modellers to make coupled data assimilation the new standard for prediction and reanalysis. Prof. Stephen G. Penny University of Maryland NOAA/NCEP,
SURROGATE DATA PATHOLOGIES AND THE FALSE-POSITIVE REJECTION OF THE NULL HYPOTHESIS
 International Journal of Bifurcation and Chaos, Vol. 11, No. 4 (2001) 983 997 c World Scientific Publishing Company SURROGATE DATA PATHOLOGIES AND THE FALSE-POSITIVE REJECTION OF THE NULL HYPOTHESIS P.
International Journal of Bifurcation and Chaos, Vol. 11, No. 4 (2001) 983 997 c World Scientific Publishing Company SURROGATE DATA PATHOLOGIES AND THE FALSE-POSITIVE REJECTION OF THE NULL HYPOTHESIS P.
Dynamics of partial discharges involved in electrical tree growth in insulation and its relation with the fractal dimension
 Dynamics of partial discharges involved in electrical tree growth in insulation and its relation with the fractal dimension Daniela Contreras Departamento de Matemática Universidad Técnica Federico Santa
Dynamics of partial discharges involved in electrical tree growth in insulation and its relation with the fractal dimension Daniela Contreras Departamento de Matemática Universidad Técnica Federico Santa
Investigation of Chaotic Nature of Sunspot Data by Nonlinear Analysis Techniques
 American-Eurasian Journal of Scientific Research 10 (5): 272-277, 2015 ISSN 1818-6785 IDOSI Publications, 2015 DOI: 10.5829/idosi.aejsr.2015.10.5.1150 Investigation of Chaotic Nature of Sunspot Data by
American-Eurasian Journal of Scientific Research 10 (5): 272-277, 2015 ISSN 1818-6785 IDOSI Publications, 2015 DOI: 10.5829/idosi.aejsr.2015.10.5.1150 Investigation of Chaotic Nature of Sunspot Data by
Chaos, Complexity, and Inference (36-462)
 Chaos, Complexity, and Inference (36-462) Lecture 4 Cosma Shalizi 22 January 2009 Reconstruction Inferring the attractor from a time series; powerful in a weird way Using the reconstructed attractor to
Chaos, Complexity, and Inference (36-462) Lecture 4 Cosma Shalizi 22 January 2009 Reconstruction Inferring the attractor from a time series; powerful in a weird way Using the reconstructed attractor to
Complex Dynamics of Microprocessor Performances During Program Execution
 Complex Dynamics of Microprocessor Performances During Program Execution Regularity, Chaos, and Others Hugues BERRY, Daniel GRACIA PÉREZ, Olivier TEMAM Alchemy, INRIA, Orsay, France www-rocq.inria.fr/
Complex Dynamics of Microprocessor Performances During Program Execution Regularity, Chaos, and Others Hugues BERRY, Daniel GRACIA PÉREZ, Olivier TEMAM Alchemy, INRIA, Orsay, France www-rocq.inria.fr/
Wave Propagation Across Muddy Seafloors
 Wave Propagation Across Muddy Seafloors Steve Elgar Woods Hole Oceanographic Institution Woods Hole, MA 02543 phone: (508) 289-3614 fax: (508) 457-2194 email: elgar@whoi.edu Grant numbers: N00014-07-10461,
Wave Propagation Across Muddy Seafloors Steve Elgar Woods Hole Oceanographic Institution Woods Hole, MA 02543 phone: (508) 289-3614 fax: (508) 457-2194 email: elgar@whoi.edu Grant numbers: N00014-07-10461,
Time Series Analysis -- An Introduction -- AMS 586
 Time Series Analysis -- An Introduction -- AMS 586 1 Objectives of time series analysis Data description Data interpretation Modeling Control Prediction & Forecasting 2 Time-Series Data Numerical data
Time Series Analysis -- An Introduction -- AMS 586 1 Objectives of time series analysis Data description Data interpretation Modeling Control Prediction & Forecasting 2 Time-Series Data Numerical data
K. Pyragas* Semiconductor Physics Institute, LT-2600 Vilnius, Lithuania Received 19 March 1998
 PHYSICAL REVIEW E VOLUME 58, NUMBER 3 SEPTEMBER 998 Synchronization of coupled time-delay systems: Analytical estimations K. Pyragas* Semiconductor Physics Institute, LT-26 Vilnius, Lithuania Received
PHYSICAL REVIEW E VOLUME 58, NUMBER 3 SEPTEMBER 998 Synchronization of coupled time-delay systems: Analytical estimations K. Pyragas* Semiconductor Physics Institute, LT-26 Vilnius, Lithuania Received
SIMULATED CHAOS IN BULLWHIP EFFECT
 Journal of Management, Marketing and Logistics (JMML), ISSN: 2148-6670 Year: 2015 Volume: 2 Issue: 1 SIMULATED CHAOS IN BULLWHIP EFFECT DOI: 10.17261/Pressacademia.2015111603 Tunay Aslan¹ ¹Sakarya University,
Journal of Management, Marketing and Logistics (JMML), ISSN: 2148-6670 Year: 2015 Volume: 2 Issue: 1 SIMULATED CHAOS IN BULLWHIP EFFECT DOI: 10.17261/Pressacademia.2015111603 Tunay Aslan¹ ¹Sakarya University,
Delay Coordinate Embedding
 Chapter 7 Delay Coordinate Embedding Up to this point, we have known our state space explicitly. But what if we do not know it? How can we then study the dynamics is phase space? A typical case is when
Chapter 7 Delay Coordinate Embedding Up to this point, we have known our state space explicitly. But what if we do not know it? How can we then study the dynamics is phase space? A typical case is when
ESTIMATING CORRELATIONS FROM A COASTAL OCEAN MODEL FOR LOCALIZING AN ENSEMBLE TRANSFORM KALMAN FILTER
 ESTIMATING CORRELATIONS FROM A COASTAL OCEAN MODEL FOR LOCALIZING AN ENSEMBLE TRANSFORM KALMAN FILTER Jonathan Poterjoy National Weather Center Research Experiences for Undergraduates, Norman, Oklahoma
ESTIMATING CORRELATIONS FROM A COASTAL OCEAN MODEL FOR LOCALIZING AN ENSEMBLE TRANSFORM KALMAN FILTER Jonathan Poterjoy National Weather Center Research Experiences for Undergraduates, Norman, Oklahoma
Discrimination power of measures for nonlinearity in a time series
 PHYSICAL REVIEW E VOLUME 55, NUMBER 5 MAY 1997 Discrimination power of measures for nonlinearity in a time series Thomas Schreiber and Andreas Schmitz Physics Department, University of Wuppertal, D-42097
PHYSICAL REVIEW E VOLUME 55, NUMBER 5 MAY 1997 Discrimination power of measures for nonlinearity in a time series Thomas Schreiber and Andreas Schmitz Physics Department, University of Wuppertal, D-42097
Analysis of South China Sea Shelf and Basin Acoustic Transmission Data
 Analysis of South China Sea Shelf and Basin Acoustic Transmission Data Ching-Sang Chiu Department of Oceanography Naval Postgraduate School Monterey, CA 93943-5001 Phone: (831) 656-3239 Fax: (831) 656-7970
Analysis of South China Sea Shelf and Basin Acoustic Transmission Data Ching-Sang Chiu Department of Oceanography Naval Postgraduate School Monterey, CA 93943-5001 Phone: (831) 656-3239 Fax: (831) 656-7970
Analysis of South China Sea Shelf and Basin Acoustic Transmission Data
 DISTRIBUTION STATEMENT A: Approved for public release; distribution is unlimited. Analysis of South China Sea Shelf and Basin Acoustic Transmission Data Ching-Sang Chiu Department of Oceanography Naval
DISTRIBUTION STATEMENT A: Approved for public release; distribution is unlimited. Analysis of South China Sea Shelf and Basin Acoustic Transmission Data Ching-Sang Chiu Department of Oceanography Naval
Towards a more physically based approach to Extreme Value Analysis in the climate system
 N O A A E S R L P H Y S IC A L S C IE N C E S D IV IS IO N C IR E S Towards a more physically based approach to Extreme Value Analysis in the climate system Prashant Sardeshmukh Gil Compo Cecile Penland
N O A A E S R L P H Y S IC A L S C IE N C E S D IV IS IO N C IR E S Towards a more physically based approach to Extreme Value Analysis in the climate system Prashant Sardeshmukh Gil Compo Cecile Penland
Determination of fractal dimensions of solar radio bursts
 Astron. Astrophys. 357, 337 350 (2000) ASTRONOMY AND ASTROPHYSICS Determination of fractal dimensions of solar radio bursts A. Veronig 1, M. Messerotti 2, and A. Hanslmeier 1 1 Institute of Astronomy,
Astron. Astrophys. 357, 337 350 (2000) ASTRONOMY AND ASTROPHYSICS Determination of fractal dimensions of solar radio bursts A. Veronig 1, M. Messerotti 2, and A. Hanslmeier 1 1 Institute of Astronomy,
The tserieschaos Package
 Title Analysis of nonlinear time series Date 2007-10-09 Version 0.1-8 Author Depends R (>= 2.2.0), odesolve Suggests scatterplot3d LazyData yes LazyLoad yes The tserieschaos Package October 9, 2007 Routines
Title Analysis of nonlinear time series Date 2007-10-09 Version 0.1-8 Author Depends R (>= 2.2.0), odesolve Suggests scatterplot3d LazyData yes LazyLoad yes The tserieschaos Package October 9, 2007 Routines
Correction to Evaluation of the simulation of the annual cycle of Arctic and Antarctic sea ice coverages by 11 major global climate models
 JOURNAL OF GEOPHYSICAL RESEARCH, VOL. 111,, doi:10.1029/2006jc003949, 2006 Correction to Evaluation of the simulation of the annual cycle of Arctic and Antarctic sea ice coverages by 11 major global climate
JOURNAL OF GEOPHYSICAL RESEARCH, VOL. 111,, doi:10.1029/2006jc003949, 2006 Correction to Evaluation of the simulation of the annual cycle of Arctic and Antarctic sea ice coverages by 11 major global climate
Available online at AASRI Procedia 1 (2012 ) AASRI Conference on Computational Intelligence and Bioinformatics
 Available online at www.sciencedirect.com AASRI Procedia ( ) 377 383 AASRI Procedia www.elsevier.com/locate/procedia AASRI Conference on Computational Intelligence and Bioinformatics Chaotic Time Series
Available online at www.sciencedirect.com AASRI Procedia ( ) 377 383 AASRI Procedia www.elsevier.com/locate/procedia AASRI Conference on Computational Intelligence and Bioinformatics Chaotic Time Series
Internal Wave Generation in Straits
 DISTRIBUTION STATEMENT A. Approved for public release; distribution is unlimited. Internal Wave Generation in Straits David M. Farmer Graduate School of Oceanography (educational) University of Rhode Island
DISTRIBUTION STATEMENT A. Approved for public release; distribution is unlimited. Internal Wave Generation in Straits David M. Farmer Graduate School of Oceanography (educational) University of Rhode Island
Vulnerability of economic systems
 Vulnerability of economic systems Quantitative description of U.S. business cycles using multivariate singular spectrum analysis Andreas Groth* Michael Ghil, Stéphane Hallegatte, Patrice Dumas * Laboratoire
Vulnerability of economic systems Quantitative description of U.S. business cycles using multivariate singular spectrum analysis Andreas Groth* Michael Ghil, Stéphane Hallegatte, Patrice Dumas * Laboratoire
CHAPTER 8 MODEL DIAGNOSTICS. 8.1 Residual Analysis
 CHAPTER 8 MODEL DIAGNOSTICS We have now discussed methods for specifying models and for efficiently estimating the parameters in those models. Model diagnostics, or model criticism, is concerned with testing
CHAPTER 8 MODEL DIAGNOSTICS We have now discussed methods for specifying models and for efficiently estimating the parameters in those models. Model diagnostics, or model criticism, is concerned with testing
Commun Nonlinear Sci Numer Simulat
 Commun Nonlinear Sci Numer Simulat 16 (2011) 3294 3302 Contents lists available at ScienceDirect Commun Nonlinear Sci Numer Simulat journal homepage: www.elsevier.com/locate/cnsns Neural network method
Commun Nonlinear Sci Numer Simulat 16 (2011) 3294 3302 Contents lists available at ScienceDirect Commun Nonlinear Sci Numer Simulat journal homepage: www.elsevier.com/locate/cnsns Neural network method
SPARSE signal representations have gained popularity in recent
 6958 IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 57, NO. 10, OCTOBER 2011 Blind Compressed Sensing Sivan Gleichman and Yonina C. Eldar, Senior Member, IEEE Abstract The fundamental principle underlying
6958 IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 57, NO. 10, OCTOBER 2011 Blind Compressed Sensing Sivan Gleichman and Yonina C. Eldar, Senior Member, IEEE Abstract The fundamental principle underlying
Investigating volcanoes behaviour. With novel statistical approaches. UCIM-UNAM - CONACYT b. UCIM-UNAM. c. Colegio de Morelos
 Investigating volcanoes behaviour With novel statistical approaches Igor Barahona a, Luis Javier Alvarez b, Antonio Sarmiento b, Octavio Barahona c a UCIM-UNAM - CONACYT b UCIM-UNAM. c Colegio de Morelos
Investigating volcanoes behaviour With novel statistical approaches Igor Barahona a, Luis Javier Alvarez b, Antonio Sarmiento b, Octavio Barahona c a UCIM-UNAM - CONACYT b UCIM-UNAM. c Colegio de Morelos
Lennard-Jones as a model for argon and test of extended renormalization group calculations
 JOURNAL OF CHEMICAL PHYSICS VOLUME 111, NUMBER 2 22 NOVEMBER 1999 Lennard-Jones as a model for argon and test of extended renormalization group calculations John A. White Department of Physics, American
JOURNAL OF CHEMICAL PHYSICS VOLUME 111, NUMBER 2 22 NOVEMBER 1999 Lennard-Jones as a model for argon and test of extended renormalization group calculations John A. White Department of Physics, American
Applications of Hurst Coefficient Analysis to Chaotic Response of ODE Systems: Part 1a, The Original Lorenz System of 1963
 Applications of Hurst Coefficient Analysis to Chaotic Response of ODE Systems: Part 1a, The Original Lorenz System of 1963 Dan Hughes December 2008 Abstract I have coded the process for calculating Hurst
Applications of Hurst Coefficient Analysis to Chaotic Response of ODE Systems: Part 1a, The Original Lorenz System of 1963 Dan Hughes December 2008 Abstract I have coded the process for calculating Hurst
The minimisation gives a set of linear equations for optimal weights w:
 4. Interpolation onto a regular grid 4.1 Optimal interpolation method The optimal interpolation method was used to compute climatological property distributions of the selected standard levels on a regular
4. Interpolation onto a regular grid 4.1 Optimal interpolation method The optimal interpolation method was used to compute climatological property distributions of the selected standard levels on a regular
A. Windnagel M. Savoie NSIDC
 National Snow and Ice Data Center ADVANCING KNOWLEDGE OF EARTH'S FROZEN REGIONS Special Report #18 06 July 2016 A. Windnagel M. Savoie NSIDC W. Meier NASA GSFC i 2 Contents List of Figures... 4 List of
National Snow and Ice Data Center ADVANCING KNOWLEDGE OF EARTH'S FROZEN REGIONS Special Report #18 06 July 2016 A. Windnagel M. Savoie NSIDC W. Meier NASA GSFC i 2 Contents List of Figures... 4 List of
Ice-Core Data from Greenland and Near-Term Climate Prediction. Sergey R. Kotov
 Ice-Core Data from Greenland and Near-Term Climate Prediction Abstract Sergey R. Kotov Records from the GISP2 Greenland ice core are considered in terms of dynamical systems theory and nonlinear prediction.
Ice-Core Data from Greenland and Near-Term Climate Prediction Abstract Sergey R. Kotov Records from the GISP2 Greenland ice core are considered in terms of dynamical systems theory and nonlinear prediction.
Ensembles of Nearest Neighbor Forecasts
 Ensembles of Nearest Neighbor Forecasts Dragomir Yankov 1, Dennis DeCoste 2, and Eamonn Keogh 1 1 University of California, Riverside CA 92507, USA, {dyankov,eamonn}@cs.ucr.edu, 2 Yahoo! Research, 3333
Ensembles of Nearest Neighbor Forecasts Dragomir Yankov 1, Dennis DeCoste 2, and Eamonn Keogh 1 1 University of California, Riverside CA 92507, USA, {dyankov,eamonn}@cs.ucr.edu, 2 Yahoo! Research, 3333
Sensitivity Analysis of a Nuclear Reactor System Finite Element Model
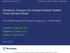 Westinghouse Non-Proprietary Class 3 Sensitivity Analysis of a Nuclear Reactor System Finite Element Model 2018 ASME Verification & Validation Symposium VVS2018-9306 Gregory A. Banyay, P.E. Stephen D.
Westinghouse Non-Proprietary Class 3 Sensitivity Analysis of a Nuclear Reactor System Finite Element Model 2018 ASME Verification & Validation Symposium VVS2018-9306 Gregory A. Banyay, P.E. Stephen D.
22/04/2014. Economic Research
 22/04/2014 Economic Research Forecasting Models for Exchange Rate Tuesday, April 22, 2014 The science of prognostics has been going through a rapid and fruitful development in the past decades, with various
22/04/2014 Economic Research Forecasting Models for Exchange Rate Tuesday, April 22, 2014 The science of prognostics has been going through a rapid and fruitful development in the past decades, with various
Interactive comment on Characterizing ecosystem-atmosphere interactions from short to interannual time scales by M. D. Mahecha et al.
 Biogeosciences Discuss., www.biogeosciences-discuss.net/4/s681/2007/ c Author(s) 2007. This work is licensed under a Creative Commons License. Biogeosciences Discussions comment on Characterizing ecosystem-atmosphere
Biogeosciences Discuss., www.biogeosciences-discuss.net/4/s681/2007/ c Author(s) 2007. This work is licensed under a Creative Commons License. Biogeosciences Discussions comment on Characterizing ecosystem-atmosphere
Sediment Transport at Density Fronts in Shallow Water: a Continuation of N
 DISTRIBUTION STATEMENT A. Approved for public release; distribution is unlimited. Sediment Transport at Density Fronts in Shallow Water: a Continuation of N00014-08-1-0846 David K. Ralston Applied Ocean
DISTRIBUTION STATEMENT A. Approved for public release; distribution is unlimited. Sediment Transport at Density Fronts in Shallow Water: a Continuation of N00014-08-1-0846 David K. Ralston Applied Ocean
Edward Lorenz. Professor of Meteorology at the Massachusetts Institute of Technology
 The Lorenz system Edward Lorenz Professor of Meteorology at the Massachusetts Institute of Technology In 1963 derived a three dimensional system in efforts to model long range predictions for the weather
The Lorenz system Edward Lorenz Professor of Meteorology at the Massachusetts Institute of Technology In 1963 derived a three dimensional system in efforts to model long range predictions for the weather
Theory and Practice of Data Assimilation in Ocean Modeling
 Theory and Practice of Data Assimilation in Ocean Modeling Robert N. Miller College of Oceanic and Atmospheric Sciences Oregon State University Oceanography Admin. Bldg. 104 Corvallis, OR 97331-5503 Phone:
Theory and Practice of Data Assimilation in Ocean Modeling Robert N. Miller College of Oceanic and Atmospheric Sciences Oregon State University Oceanography Admin. Bldg. 104 Corvallis, OR 97331-5503 Phone:
Treatment of Error in Experimental Measurements
 in Experimental Measurements All measurements contain error. An experiment is truly incomplete without an evaluation of the amount of error in the results. In this course, you will learn to use some common
in Experimental Measurements All measurements contain error. An experiment is truly incomplete without an evaluation of the amount of error in the results. In this course, you will learn to use some common
Wave number spectrum and mean square slope of intermediate-scale ocean surface waves
 JOURNAL OF GEOPHYSICAL RESEARCH, VOL. 110,, doi:10.1029/2005jc003002, 2005 Wave number spectrum and mean square slope of intermediate-scale ocean surface waves Paul A. Hwang Oceanography Division, Naval
JOURNAL OF GEOPHYSICAL RESEARCH, VOL. 110,, doi:10.1029/2005jc003002, 2005 Wave number spectrum and mean square slope of intermediate-scale ocean surface waves Paul A. Hwang Oceanography Division, Naval
Research Article Hidden Periodicity and Chaos in the Sequence of Prime Numbers
 Advances in Mathematical Physics Volume 2, Article ID 5978, 8 pages doi:.55/2/5978 Research Article Hidden Periodicity and Chaos in the Sequence of Prime Numbers A. Bershadskii Physics Department, ICAR,
Advances in Mathematical Physics Volume 2, Article ID 5978, 8 pages doi:.55/2/5978 Research Article Hidden Periodicity and Chaos in the Sequence of Prime Numbers A. Bershadskii Physics Department, ICAR,
NOTES AND CORRESPONDENCE. A Quantitative Estimate of the Effect of Aliasing in Climatological Time Series
 3987 NOTES AND CORRESPONDENCE A Quantitative Estimate of the Effect of Aliasing in Climatological Time Series ROLAND A. MADDEN National Center for Atmospheric Research,* Boulder, Colorado RICHARD H. JONES
3987 NOTES AND CORRESPONDENCE A Quantitative Estimate of the Effect of Aliasing in Climatological Time Series ROLAND A. MADDEN National Center for Atmospheric Research,* Boulder, Colorado RICHARD H. JONES
Backward Fokker-Planck equation for determining model valid prediction period
 JOURNAL OF GEOPHYSICAL RESEARCH, VOL. 107, NO. C6, 3058, 10.1029/2001JC000879, 2002 Backward Fokker-Planck equation for determining model valid prediction period Peter C. Chu, Leonid M. Ivanov, and Chenwu
JOURNAL OF GEOPHYSICAL RESEARCH, VOL. 107, NO. C6, 3058, 10.1029/2001JC000879, 2002 Backward Fokker-Planck equation for determining model valid prediction period Peter C. Chu, Leonid M. Ivanov, and Chenwu
Optimal Spectral Decomposition (OSD) for GTSPP Data Analysis
 Optimal Spectral Decomposition (OSD) for GTSPP Data Analysis Peter C Chu (1),Charles Sun (2), & Chenwu Fan (1) (1) Naval Postgraduate School, Monterey, CA 93943 pcchu@nps.edu, http://faculty.nps.edu/pcchu/
Optimal Spectral Decomposition (OSD) for GTSPP Data Analysis Peter C Chu (1),Charles Sun (2), & Chenwu Fan (1) (1) Naval Postgraduate School, Monterey, CA 93943 pcchu@nps.edu, http://faculty.nps.edu/pcchu/
Multiple-scale error growth and data assimilation in convection-resolving models
 Numerical Modelling, Predictability and Data Assimilation in Weather, Ocean and Climate A Symposium honouring the legacy of Anna Trevisan Bologna, Italy 17-20 October, 2017 Multiple-scale error growth
Numerical Modelling, Predictability and Data Assimilation in Weather, Ocean and Climate A Symposium honouring the legacy of Anna Trevisan Bologna, Italy 17-20 October, 2017 Multiple-scale error growth
Time-Dependent Statistical Mechanics 5. The classical atomic fluid, classical mechanics, and classical equilibrium statistical mechanics
 Time-Dependent Statistical Mechanics 5. The classical atomic fluid, classical mechanics, and classical equilibrium statistical mechanics c Hans C. Andersen October 1, 2009 While we know that in principle
Time-Dependent Statistical Mechanics 5. The classical atomic fluid, classical mechanics, and classical equilibrium statistical mechanics c Hans C. Andersen October 1, 2009 While we know that in principle
If we want to analyze experimental or simulated data we might encounter the following tasks:
 Chapter 1 Introduction If we want to analyze experimental or simulated data we might encounter the following tasks: Characterization of the source of the signal and diagnosis Studying dependencies Prediction
Chapter 1 Introduction If we want to analyze experimental or simulated data we might encounter the following tasks: Characterization of the source of the signal and diagnosis Studying dependencies Prediction
Testing for Regime Switching in Singaporean Business Cycles
 Testing for Regime Switching in Singaporean Business Cycles Robert Breunig School of Economics Faculty of Economics and Commerce Australian National University and Alison Stegman Research School of Pacific
Testing for Regime Switching in Singaporean Business Cycles Robert Breunig School of Economics Faculty of Economics and Commerce Australian National University and Alison Stegman Research School of Pacific
Coastal ocean wind fields gauged against the performance of an ocean circulation model
 GEOPHYSICAL RESEARCH LETTERS, VOL. 31, L14303, doi:10.1029/2003gl019261, 2004 Coastal ocean wind fields gauged against the performance of an ocean circulation model Ruoying He, 1 Yonggang Liu, 2 and Robert
GEOPHYSICAL RESEARCH LETTERS, VOL. 31, L14303, doi:10.1029/2003gl019261, 2004 Coastal ocean wind fields gauged against the performance of an ocean circulation model Ruoying He, 1 Yonggang Liu, 2 and Robert
A Preliminary Climatology of Extratropical Transitions in the Southwest Indian Ocean
 A Preliminary Climatology of Extratropical Transitions in the Southwest Indian Ocean Kyle S. Griffin Department of Atmospheric and Environmental Sciences, University at Albany, State University of New
A Preliminary Climatology of Extratropical Transitions in the Southwest Indian Ocean Kyle S. Griffin Department of Atmospheric and Environmental Sciences, University at Albany, State University of New
5. Two-layer Flows in Rotating Channels.
 5. Two-layer Flows in Rotating Channels. The exchange flow between a marginal sea or estuary and the open ocean is often approximated using two-layer stratification. Two-layer models are most valid when
5. Two-layer Flows in Rotating Channels. The exchange flow between a marginal sea or estuary and the open ocean is often approximated using two-layer stratification. Two-layer models are most valid when
No. 6 Determining the input dimension of a To model a nonlinear time series with the widely used feed-forward neural network means to fit the a
 Vol 12 No 6, June 2003 cfl 2003 Chin. Phys. Soc. 1009-1963/2003/12(06)/0594-05 Chinese Physics and IOP Publishing Ltd Determining the input dimension of a neural network for nonlinear time series prediction
Vol 12 No 6, June 2003 cfl 2003 Chin. Phys. Soc. 1009-1963/2003/12(06)/0594-05 Chinese Physics and IOP Publishing Ltd Determining the input dimension of a neural network for nonlinear time series prediction
Magnetic Case Study: Raglan Mine Laura Davis May 24, 2006
 Magnetic Case Study: Raglan Mine Laura Davis May 24, 2006 Research Objectives The objective of this study was to test the tools available in EMIGMA (PetRos Eikon) for their utility in analyzing magnetic
Magnetic Case Study: Raglan Mine Laura Davis May 24, 2006 Research Objectives The objective of this study was to test the tools available in EMIGMA (PetRos Eikon) for their utility in analyzing magnetic
meters, we can re-arrange this expression to give
 Turbulence When the Reynolds number becomes sufficiently large, the non-linear term (u ) u in the momentum equation inevitably becomes comparable to other important terms and the flow becomes more complicated.
Turbulence When the Reynolds number becomes sufficiently large, the non-linear term (u ) u in the momentum equation inevitably becomes comparable to other important terms and the flow becomes more complicated.
OPTIMAL PERTURBATION OF UNCERTAIN SYSTEMS
 Stochastics and Dynamics, Vol. 2, No. 3 (22 395 42 c World Scientific Publishing Company OPTIMAL PERTURBATION OF UNCERTAIN SYSTEMS Stoch. Dyn. 22.2:395-42. Downloaded from www.worldscientific.com by HARVARD
Stochastics and Dynamics, Vol. 2, No. 3 (22 395 42 c World Scientific Publishing Company OPTIMAL PERTURBATION OF UNCERTAIN SYSTEMS Stoch. Dyn. 22.2:395-42. Downloaded from www.worldscientific.com by HARVARD
arxiv:chao-dyn/ v1 9 Nov 1999
 1 Forecasting the SST space-time variability of the Alboran Sea with genetic algorithms Alberto Álvarez SACLANT Undersea Research Centre, La Spezia, Italy arxiv:chao-dyn/9911012v1 9 Nov 1999 Cristóbal
1 Forecasting the SST space-time variability of the Alboran Sea with genetic algorithms Alberto Álvarez SACLANT Undersea Research Centre, La Spezia, Italy arxiv:chao-dyn/9911012v1 9 Nov 1999 Cristóbal
Speculations About a Fourier Series Kicker for the TESLA Damping Ring
 1 Speculations About a Fourier Series Kicker for the TESLA Damping Ring George D. Gollin *, Thomas R. Junk Dept. of Physics, University of Illinois at Urbana-Champaign, Urbana, IL 61801 August 28, 2002
1 Speculations About a Fourier Series Kicker for the TESLA Damping Ring George D. Gollin *, Thomas R. Junk Dept. of Physics, University of Illinois at Urbana-Champaign, Urbana, IL 61801 August 28, 2002
Sensitivity of an Ocean Model to Details of Stochastic Forcing
 Sensitivity of an Ocean Model to Details of Stochastic Forcing Cécile Penland and Philip Sura NOAA-CIRES/Climate Diagnostics Center, Boulder CO 80305-3328 Abstract We review the sensitivity of a double-gyre
Sensitivity of an Ocean Model to Details of Stochastic Forcing Cécile Penland and Philip Sura NOAA-CIRES/Climate Diagnostics Center, Boulder CO 80305-3328 Abstract We review the sensitivity of a double-gyre
Modeling the Formation and Offshore Transport of Dense Water from High-Latitude Coastal Polynyas
 Modeling the Formation and Offshore Transport of Dense Water from High-Latitude Coastal Polynyas David C. Chapman Woods Hole Oceanographic Institution Woods Hole, MA 02543 phone: (508) 289-2792 fax: (508)
Modeling the Formation and Offshore Transport of Dense Water from High-Latitude Coastal Polynyas David C. Chapman Woods Hole Oceanographic Institution Woods Hole, MA 02543 phone: (508) 289-2792 fax: (508)
EEG- Signal Processing
 Fatemeh Hadaeghi EEG- Signal Processing Lecture Notes for BSP, Chapter 5 Master Program Data Engineering 1 5 Introduction The complex patterns of neural activity, both in presence and absence of external
Fatemeh Hadaeghi EEG- Signal Processing Lecture Notes for BSP, Chapter 5 Master Program Data Engineering 1 5 Introduction The complex patterns of neural activity, both in presence and absence of external
Experimental Characterization of Nonlinear Dynamics from Chua s Circuit
 Experimental Characterization of Nonlinear Dynamics from Chua s Circuit John Parker*, 1 Majid Sodagar, 1 Patrick Chang, 1 and Edward Coyle 1 School of Physics, Georgia Institute of Technology, Atlanta,
Experimental Characterization of Nonlinear Dynamics from Chua s Circuit John Parker*, 1 Majid Sodagar, 1 Patrick Chang, 1 and Edward Coyle 1 School of Physics, Georgia Institute of Technology, Atlanta,
Ingredients of statistical hypothesis testing and their significance
 Ingredients of statistical hypothesis testing and their significance Hans von Storch, Institute of Coastal Research, Helmholtz Zentrum Geesthacht, Germany 13 January 2016, New Orleans; 23rd Conference
Ingredients of statistical hypothesis testing and their significance Hans von Storch, Institute of Coastal Research, Helmholtz Zentrum Geesthacht, Germany 13 January 2016, New Orleans; 23rd Conference
RPSEA Hi-Res Environmental Data for Enhanced UDW Operations Safety (S&ES)
 RPSEA Hi-Res Environmental Data for Enhanced UDW Operations Safety (S&ES) Task 5: Bottom Current Measurements and Modeling Final Presentation Steve Morey, Dmitry Dukhovskoy, Eric Chassignet Florida State
RPSEA Hi-Res Environmental Data for Enhanced UDW Operations Safety (S&ES) Task 5: Bottom Current Measurements and Modeling Final Presentation Steve Morey, Dmitry Dukhovskoy, Eric Chassignet Florida State
Mesoscale Predictability of Terrain Induced Flows
 Mesoscale Predictability of Terrain Induced Flows Dale R. Durran University of Washington Dept. of Atmospheric Sciences Box 3516 Seattle, WA 98195 phone: (206) 543-74 fax: (206) 543-0308 email: durrand@atmos.washington.edu
Mesoscale Predictability of Terrain Induced Flows Dale R. Durran University of Washington Dept. of Atmospheric Sciences Box 3516 Seattle, WA 98195 phone: (206) 543-74 fax: (206) 543-0308 email: durrand@atmos.washington.edu
Characterization of normality of chaotic systems including prediction and detection of anomalies
 University of Iowa Iowa Research Online Theses and Dissertations Spring 2011 Characterization of normality of chaotic systems including prediction and detection of anomalies Joseph John Engler University
University of Iowa Iowa Research Online Theses and Dissertations Spring 2011 Characterization of normality of chaotic systems including prediction and detection of anomalies Joseph John Engler University
Bred Vectors: A simple tool to understand complex dynamics
 Bred Vectors: A simple tool to understand complex dynamics With deep gratitude to Akio Arakawa for all the understanding he has given us Eugenia Kalnay, Shu-Chih Yang, Malaquías Peña, Ming Cai and Matt
Bred Vectors: A simple tool to understand complex dynamics With deep gratitude to Akio Arakawa for all the understanding he has given us Eugenia Kalnay, Shu-Chih Yang, Malaquías Peña, Ming Cai and Matt
Global warming trend and multi-decadal climate
 Global warming trend and multi-decadal climate variability Sergey Kravtsov * and Anastasios A. Tsonis * Correspondence and requests for materials should be addressed to SK (kravtsov@uwm.edu) 0 Climate
Global warming trend and multi-decadal climate variability Sergey Kravtsov * and Anastasios A. Tsonis * Correspondence and requests for materials should be addressed to SK (kravtsov@uwm.edu) 0 Climate
( ) II. Why statistics? SIO 221B, Rudnick adapted from Davis!1
 SIO 221B, Rudnick adapted from Davis 1 II. Why statistics? This course addresses the analysis of oceanographic observations and, as they become more complex, ocean models. Much of the material involves
SIO 221B, Rudnick adapted from Davis 1 II. Why statistics? This course addresses the analysis of oceanographic observations and, as they become more complex, ocean models. Much of the material involves
Latest thoughts on stochastic kinetic energy backscatter - good and bad
 Latest thoughts on stochastic kinetic energy backscatter - good and bad by Glenn Shutts DARC Reading University May 15 2013 Acknowledgments ECMWF for supporting this work Martin Leutbecher Martin Steinheimer
Latest thoughts on stochastic kinetic energy backscatter - good and bad by Glenn Shutts DARC Reading University May 15 2013 Acknowledgments ECMWF for supporting this work Martin Leutbecher Martin Steinheimer
