Chapter 6 Differential Equations and Mathematical Modeling. 6.1 Antiderivatives and Slope Fields
|
|
|
- Veronica Edwards
- 6 years ago
- Views:
Transcription
1 Chapter 6 Differential Equations and Mathematical Modeling 6. Antiderivatives and Slope Fields Def: An equation of the form: = y ln x which contains a derivative is called a Differential Equation. In this equation, you are to find a function y in terms of x (i.e. y = f(x)) When we are given the derivative of a function and its value at a given point: Ex. = x f(4) = 0 This is called an initial value problem. o The value of f for one value of x is the initial condition of the problem. Finding ALL functions y that satisfy the differential equation is called solving the differential equation. Ex. Suppose $00 is invested in an account that pays 5.6% interest compounded continuously. Find a formula for the amount in the account at any time t. Because the interest is compounded on the original value, the equation would be: = 0.056y with y(0) = 00 How do you solve it? Well one way is to think of a function whose derivative is a multiple of itself. Another is to get the multiple of itself. o This would be the exponential function: 0.056x y( t) = Ce Proof: y = Ce 0.056x 0.056x = C(0.056e o Using the pre-existing condition: y( t) = Ce y(0) = Ce 00 = Ce 0.056x 00 = C o This leads to the equation: (0) ) = 0.056( Ce y = 00e 0.056x 0.056x ) = 0.056y( t) 0.056t The initial solution y( t) = Ce is called the family of solutions. Depending on the value of C. o Because of the pre-existing condition y(0) = 00, we could find the value of C. Is there a way to see the family of solutions for a particular integral?? Yes, it is called Slope Fields.
2 Def: Slope Field A slope field (or directional field) for a differential equation = f ( x, y) is a plot of short line segments with slopes f ( x, y) for a lattice (set) of points (x, y) in the plane. - Slope field for = x Same slope field with y = x x Each of the little lines in the slope field represent a tangent line to one of the family of curves for the differential equation. Here is the same slope field with two curves: y = x x and y = x x + This leads to the following: The result of an integral is a family of curves. o Each curve is the exact same shape but only differ by where the occurrences are This difference is only a vertical location. This results in the Indefinite Integral
3 Def: Indefinite Integral The set of all antiderivatives of a function f(x) is the indefinite integral of f with respect to x and is denoted by: f ( x) And if F(x) is an antiderivative of f(x) as defined in the Fundamental Theorem, then f ( x) = F( x) + C where F (x) = f(x) and C is ANY constant value. o C is called the constant of integration and is an arbitrary constant Ex. Evaluate:. x. cos x 3. ( x + 4x 5) 4. e x 5. x Below is a list of some Indefinite Integrals: n+ n x. (a) x = + C, n n + (b) = ln x + C x kx kx e. e = + C k coskx 3. sin kx = + C k sin kx 4. cos kx = + C k tan kx 5. sec kx = + C k ex. Evaluate: e 4 x cos x Homework: Pg. 3 #-0
4 6. Antiderivatives and Slope Fields (Day ) Properties of Indefinite Integrals: Let k be a real number:. Constant Multiple Rule: ( x) k If k =, then, f ( x) = f ( x) kf = f ( x). Sum and Difference Rule: ( ( x) g( x)) = f ( x) ± f ± g( x) Ex. Evaluate (3x 4x + 5) We can use the two rules above to evaluate this: (3x 4x + 5) = 3x 4x + = 3 x 4 x x = 3 3 = x = x = x C x x x + C 4 x 4C + 5x + (3C + 5x + C 5 + C + 5x + 5C 4C + 5( x + C3 ) 3 + 5C ) 3 ex. A right cylindrical tank with radius 5 ft and height 6 ft was initially filled with water is being drained at a rate of 0.5 x ft 3 /min, where x is the depth of the water. Find a formula for the depth and the amount of water in the tank at any time t. How long will it take the tank to empty? V = πr h at any given height h, the volume of this tank would be: V = π 5 h = 5πh Taking the derivative with respect to time: V = 5πh dv dh = 5π dh 0.5 h = 5π Negative due to draining Solving for dh/: 0.5 h dh = 5π dh h = 50π Initial value: h(0) = 6
5 We can now solve this differential equation: dh h = 50π dh = h 50π dh h = 50π dh h = 50π h dh = 50π h + C = t + C 50π h = t + C 50π Using the initial condition: 6 = (0) + C 50π 8 = C Substituting back into the equation, we get: h = t π h = t π h = 4 t 00π Substituting back into the Volume formula: V = 5πh V = 5π 4 t 00π
6 Ex. A heavy projectile is fired straight up into the air from a platform 3 feet above the ground with an initial velocity of 60 m/sec. Assume that only the force affecting the projectile during its flight is gravity, which produces a downward acceleration of 9.8 m/sec. If t = 0 when the projectile is fired, find a formula for the projectile s (a) velocity as a function of time t (b) height above the ground as a function of time t. The acceleration function is a constant function defined above: a ( t) = 9.8 negative since it is a downward acceleration But, acceleration is the derivative of the velocity: a( t) = v' ( t) v( t) = v( t) = a( t) 9.8 = 9.8t + C Using the information above (initial velocity is 60): v(0) = 9.8(0) + C 60 = C We get the velocity function to be: v ( t) = 9.8t + 60 The velocity function is the derivative of the position function (the height of the projectile). v( t) = s' ( t) s( t) = = v( t) s( t) = 4.9t ( 9.8t + 60) + 60t + C Aside: 9.8t = 9.8 t t = t = = 4.9t + C Using the information above, s(0) = 4.9(0 ) + 690(0) + C 3 = C We get the position function to be: s ( t) = 4.9t + 60t + 3 Homework: Pg #3-36, 38-44, 50, 5, 53, 57
7 6. Integration by Substitution When u is a differentiable function of x and n is a real number not equal to, then the Chain Rule gives us: d Switch the direction, we get: n+ u = u n + n du n+ n du u u = + C n + for n A change in variable can often make an unfamiliar or difficult looking integral into one that we can evaluate. o This method is called substitution method of integration. 5 Ex. Evaluate ( x + ) In this one, we will use a substitution of: Let u = x + du = du = So we now have: 6 5 u u du = + C 6 but u = x +, so we get ( x + 6 ) 6 + C Ex. Evaluate 4 x Let u = 4x du = 4 du = 4 = du 4 Substituting back in, we get: 3 3 u du = u su = u + C = (4x ) + C
8 Ex. Evaluate: cos( 3x ) Ex. Evaluate cos x Ex. Evaluate tan x To evaluate integrals that are not simple : Let u = an expression whose derivative in also in the expression Take the derivative of the equation written in step, and solve for du It should be the other expression in the integrand and Make you substitutions and integrate with respect to u (this should be a simple integral). Substitute back into the u and add a +C if it is an indefinite integral. Ex. Evaluate: sin 3 x cos x ( x + x 3) ( x + )
9 What if it a definite integral? Same process, just plug the value of u back in then use the bounds. Ex. Evaluate 4 tan x sec π 0 x Let u = tan x 3 Ex. Evaluate 3x x + There are some people who think that when you make the u-substitution, that you change the bounds according the substitution. b f ( g( x)) g' ( x) = a g ( b) g ( a) f ( u) du Personally, I don t like this method and I don t use it Separable Differential Equations A differential equation y ' = f ( x, y) is separable if f can be expressed as a product of a function of x and a function of y. This means: = g( x) h( y) If h(y) 0, then we can separate the variables by dividing both sides of the equation by h(y): = g( x) h( y)
10 Integrating both sides of the equation with respect to x, we get: = g( x) h( y) = h( y) g( x) With the variables separated, we can integrate each side of the equation and write the function expressing y as a function of x. Ex. Solve the differential equation = x( + y ) e x Ex. Solve the differential equation = x y cos y Homework: Day : Pg 3 3 QR -0, Ex. 8, 9 9odd, 3, 33, 39, 4, 43 Day : Pg 3 33 Exercises #0-30 even, 3, 34-36, 4, 44, 49, 5
11 6.3 Integration by Parts There are some integrals that can t be done by a simple u-substitution. o So we need another way to find these integrals. Suppose we take the Product Rule and write it in integral form: d ( uv) = uv' + vu' d dv du ( uv) = u + v Integrating both sides with respect to x and rearranging: d dv du ( uv) = u + v d ( uv) = uv = udv + udv = uv dv u + vdu vdu v du This formula is called Integration by Parts o This formula expresses one integral udv in terms of another vdu Choosing the correct u and v may make the second integral ( vdu ) easier to evaluate. Ex. Evaluate x cos x To Set up Integration by Parts:. You want to split this integral up into a u and a dv. a. u should be easy to find the derivative b. dv should be an easy integral. Find the derivative of u and integrate dv 3. Plug into the formula udv = uv vdu 4. Simplify/evaluate You are trying to make the second integral easy to do. One method selecting a u is using the following Order of Selection :. Natural Log (ln) L. Inverse Trig Function I 3. Polynomial Function P L I P E T 4. Exponential Function E 5. Trigonometry Function T This is strictly a guide (works 95% of time). Ex. Find the area bounded by the curve x y = xe and the x-axis from x = 0 to x = 3
12 Ex. Evaluate: ln x Ex. Evaluate: 0 tan x Sometimes, you need to play around a little with the integral: Ex. Evaluate: e x cos x Homework: Pg QR #-0, Ex. 8
13 6.3 Integration by Parts (Part ) x Ex. Evaluate: x e Ex. Evaluate: 3 x sin x Tabular Integration o Many Integration by parts problems are of the form f ( x) g( x) in which f can be differentiated repeatedly to become ZERO and g can be integrated repeatedly without difficulty. o Integration by parts can result in many repetitions to get a solution o You can organize the calculation (derivatives/integrals) and save work. Ex. Evaluate: x e x Use f(x) = x and g(x) = e x f(x) and its derivatives g(x) and its integrals x (+) e x x ( ) e x (+) e x 0 e x Using this table and combining the products of the functions connected by the arrows and using the alternating signs we get: x x x x e = x e xe + e x + c
14 Ex. Evaluate 3 x sin x using Tabular Integration 4 Ex. Evaluate: x e z Homework Day : Pg. 39 #9-, 5-0,, 3 Day : Pg. 39 #5, 6a-d, 7, 8, 9, 3, 35
15 6.4 Exponential Growth and Decay Suppose we are interested in the quantity y, that increases or decreases at a rate proportional to the amount currently present o Population o Radioactive element o Money If we know the amount initially (time t=0), which we will call y 0 (pronounced Y naught ), we can find y as a function of t using the initial value of y: o Differential Equation to Solve: = ky o Initial Condition: y0 y = when t = 0 If y is positive and an increasing function, then k is positive and the rate of growth is proportional to the current value of y. If y is positive and decreasing, then k is negative and the rate of decay is proportion to the amount still left. o So what is the equation for y? = ky = k y ln y = kt + C e ln y y = e = e C y = ± Ae kt+ C e kt kt o Using the initial value: y = ± Ae = ± A ± y0 = A o So The Law of Exponential Change is: y y 0 0 kt = ± Ae k 0 If y changes at a rate proportional to the amount present ( = ky ) and y = y when t = 0, then 0 kt y = y0e If k > 0, then this is exponential growth If k < 0, then this is exponential decay k represents the RATE CONSTANT of the equation
16 Continuous Compound Interest o The formula for compound interest on an account with A 0 at a rate of r% over a time period of t years in which there are k times it is compounded is: kt r A ( t ) = A0 + k o This formula is used when you have a set number of times when the interest is compounded, k. The interest rate never changes so the interest is proportional on the amount that is in the account. If we were to compound it continuously, then it would be considered an exponential growth. Therefore the formula would be: kt ( t) = A e A 0 Ex. Suppose you have $5000 is an IRA that earns 6.5% annually. How much would you have after 8 years if the interest was compounded (a) quarterly (b) monthly (c) daily (d) continuously Radioactivity o Radioactivity works the exact same way as interest, except it is a decay. If you have an initial amount y 0 of a radioactive substance, then the amount still present at any later time t will be kt y = y 0 e o The half-life of a radioactive substance is the amount of time for half of the radioactive nuclei present in a sample it decay. Ex. Find the half-life formula of any radioactive substance as a function of k Homework: Pg. 338 #-0, 3,4
17 6.4 Exponential Growth and Decay (con t) Ex. Suppose that 0 grams of the plutonium isotope Pu-39 was released in the Chernobyl nuclear reactor accident in 986. How long will it take for the 0 grams to decay to gram if the half-life of Pu-39 is 4,360 yrs? Ex. Suppose an experimental population of fruit flies increases according to the law of exponential growth. There were 00 flies after the second day of the experiment and 300 flies after day 4. Approximately how many flies were in the original population? Ex. Scientists who do carbon-4 dating use 5700 yrs for its half-life. Find the age of a sample in which 0% of the radioactive nuclei originally present have decayed. Half-life is 5700 = ln k
18 Newton s Law of Cooling If T is the temperature of an object at time t, and T x, is the surrounding temperature, then dt = k( T Ts ) Since dt represents the change in temperature, then dt = d( T Ts ), we can rewrite the above equation: dt = k( T Ts ) d ( T T s ) = k( T T This new equation is of the form y = ky which is solved as follows: s ) ln y = kt + C e = ky = k y ln y y' = ky = e y = e kt+ C C e y = ± Ce kt kt Law of Exponential Change Therefore: d ( T T ) = k( T T ) s s kt T Ts = ( T0 Ts ) e where T 0 is the original temperature at t = 0. This is Newton s Law of Cooling Ex. Let y represent the temperature (in o F) of an object in a room whose temperature is kept at a constant 60 o. If the object cools from 00 o to 90 o in 0 minutes, how much longer will it take for its temperature to decrease to 80 o
19 ex. A deep dish apple pie whose internal temperature is 0 o F when removed from the oven, was set on a 40 o F porch to cool. Fifteen minutes later, the pie s internal temperature was 80 o F. How long did it take the pie to cool from there to 70 o F? Ex. A pan of warm water (46 o C) is put in the refrigerator. 0 minutes later, the water s temperature was 39 o C. 0 minutes later, it was 33 o C. Estimate the temperature of the refrigerator. Resistance Proportional to Velocity In Physics, the resistance encountered by a moving object (i.e. a car coasting to a stop) is proportional to the object s velocity. The slower the object moves, the less resistance against the forward progress Mathematically: Force = mass acceleration F = ma F = mv' dv F = m Since the resistance force is proportion to the velocity, then dv m = kv dv k = v m dv k = v m which when solved (just like we did earlier), results in: v = v e 0 ( k m) t
20 ex. For a 50-kg ice skater, k =.5 kg/sec. Answer the following: (a) How long will it take the skater to coast from 7 m/sec to m/sec? (b) How far will the skater coast before coming to a stop? Homework: Day : Pg #(a),, 8 0, 6 8 Day : Pg #4-7, -4, 9, 3, 35
6.1 Antiderivatives and Slope Fields Calculus
 6. Antiderivatives and Slope Fields Calculus 6. ANTIDERIVATIVES AND SLOPE FIELDS Indefinite Integrals In the previous chapter we dealt with definite integrals. Definite integrals had limits of integration.
6. Antiderivatives and Slope Fields Calculus 6. ANTIDERIVATIVES AND SLOPE FIELDS Indefinite Integrals In the previous chapter we dealt with definite integrals. Definite integrals had limits of integration.
Differential Equations & Separation of Variables
 Differential Equations & Separation of Variables SUGGESTED REFERENCE MATERIAL: As you work through the problems listed below, you should reference Chapter 8. of the recommended textbook (or the equivalent
Differential Equations & Separation of Variables SUGGESTED REFERENCE MATERIAL: As you work through the problems listed below, you should reference Chapter 8. of the recommended textbook (or the equivalent
Chapters 8.1 & 8.2 Practice Problems
 EXPECTED SKILLS: Chapters 8.1 & 8. Practice Problems Be able to verify that a given function is a solution to a differential equation. Given a description in words of how some quantity changes in time
EXPECTED SKILLS: Chapters 8.1 & 8. Practice Problems Be able to verify that a given function is a solution to a differential equation. Given a description in words of how some quantity changes in time
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
 Chapter Practice Test Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find the general solution to the eact differential equation. ) dy dt =
Chapter Practice Test Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find the general solution to the eact differential equation. ) dy dt =
Chapter 6: Messy Integrals
 Chapter 6: Messy Integrals Review: Solve the following integrals x 4 sec x tan x 0 0 Find the average value of 3 1 x 3 3 Evaluate 4 3 3 ( x 1), then find the area of ( x 1) 4 Section 6.1: Slope Fields
Chapter 6: Messy Integrals Review: Solve the following integrals x 4 sec x tan x 0 0 Find the average value of 3 1 x 3 3 Evaluate 4 3 3 ( x 1), then find the area of ( x 1) 4 Section 6.1: Slope Fields
7.1 Day 1: Differential Equations & Initial Value Problems (30L)
 A P 7.1 Day 1: Differential Equations & Initial Value Problems (30L) Calculus 30 & 30L I CAN SOLVE DIFFERENTIAL EQUATIONS AND INITIAL VALUE PROBLEMS VIDEO LINKS: a) http://bit.ly/2bxsc6r b) http://bit.ly/2sshyyh
A P 7.1 Day 1: Differential Equations & Initial Value Problems (30L) Calculus 30 & 30L I CAN SOLVE DIFFERENTIAL EQUATIONS AND INITIAL VALUE PROBLEMS VIDEO LINKS: a) http://bit.ly/2bxsc6r b) http://bit.ly/2sshyyh
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. D) u = - x15 cos (x15) + C
 AP Calculus AB Exam Review Differential Equations and Mathematical Modelling MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find the general solution
AP Calculus AB Exam Review Differential Equations and Mathematical Modelling MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find the general solution
6.5 Separable Differential Equations and Exponential Growth
 6.5 2 6.5 Separable Differential Equations and Exponential Growth The Law of Exponential Change It is well known that when modeling certain quantities, the quantity increases or decreases at a rate proportional
6.5 2 6.5 Separable Differential Equations and Exponential Growth The Law of Exponential Change It is well known that when modeling certain quantities, the quantity increases or decreases at a rate proportional
1 Antiderivatives graphically and numerically
 Math B - Calculus by Hughes-Hallett, et al. Chapter 6 - Constructing antiderivatives Prepared by Jason Gaddis Antiderivatives graphically and numerically Definition.. The antiderivative of a function f
Math B - Calculus by Hughes-Hallett, et al. Chapter 6 - Constructing antiderivatives Prepared by Jason Gaddis Antiderivatives graphically and numerically Definition.. The antiderivative of a function f
Honors Advanced Algebra Chapter 8 Exponential and Logarithmic Functions and Relations Target Goals
 Honors Advanced Algebra Chapter 8 Exponential and Logarithmic Functions and Relations Target Goals By the end of this chapter, you should be able to Graph exponential growth functions. (8.1) Graph exponential
Honors Advanced Algebra Chapter 8 Exponential and Logarithmic Functions and Relations Target Goals By the end of this chapter, you should be able to Graph exponential growth functions. (8.1) Graph exponential
MATH 1231 MATHEMATICS 1B Calculus Section 3A: - First order ODEs.
 MATH 1231 MATHEMATICS 1B 2010. For use in Dr Chris Tisdell s lectures. Calculus Section 3A: - First order ODEs. Created and compiled by Chris Tisdell S1: What is an ODE? S2: Motivation S3: Types and orders
MATH 1231 MATHEMATICS 1B 2010. For use in Dr Chris Tisdell s lectures. Calculus Section 3A: - First order ODEs. Created and compiled by Chris Tisdell S1: What is an ODE? S2: Motivation S3: Types and orders
AP Calculus Testbank (Chapter 6) (Mr. Surowski)
 AP Calculus Testbank (Chapter 6) (Mr. Surowski) Part I. Multiple-Choice Questions 1. Suppose that f is an odd differentiable function. Then (A) f(1); (B) f (1) (C) f(1) f( 1) (D) 0 (E). 1 1 xf (x) =. The
AP Calculus Testbank (Chapter 6) (Mr. Surowski) Part I. Multiple-Choice Questions 1. Suppose that f is an odd differentiable function. Then (A) f(1); (B) f (1) (C) f(1) f( 1) (D) 0 (E). 1 1 xf (x) =. The
Today: 5.4 General log and exp functions (continued) Warm up:
 Today: 5.4 General log and exp functions (continued) Warm up: log a (x) =ln(x)/ ln(a) d dx log a(x) = 1 ln(a)x 1. Evaluate the following functions. log 5 (25) log 7 p 7 log4 8 log 4 2 2. Di erentiate the
Today: 5.4 General log and exp functions (continued) Warm up: log a (x) =ln(x)/ ln(a) d dx log a(x) = 1 ln(a)x 1. Evaluate the following functions. log 5 (25) log 7 p 7 log4 8 log 4 2 2. Di erentiate the
DIFFERENTIATION RULES
 3 DIFFERENTIATION RULES DIFFERENTIATION RULES 3.8 Exponential Growth and Decay In this section, we will: Use differentiation to solve real-life problems involving exponentially growing quantities. EXPONENTIAL
3 DIFFERENTIATION RULES DIFFERENTIATION RULES 3.8 Exponential Growth and Decay In this section, we will: Use differentiation to solve real-life problems involving exponentially growing quantities. EXPONENTIAL
Chapter 5: Integrals
 Chapter 5: Integrals Section 5.5 The Substitution Rule (u-substitution) Sec. 5.5: The Substitution Rule We know how to find the derivative of any combination of functions Sum rule Difference rule Constant
Chapter 5: Integrals Section 5.5 The Substitution Rule (u-substitution) Sec. 5.5: The Substitution Rule We know how to find the derivative of any combination of functions Sum rule Difference rule Constant
dx. Ans: y = tan x + x2 + 5x + C
 Chapter 7 Differential Equations and Mathematical Modeling If you know one value of a function, and the rate of change (derivative) of the function, then yu can figure out many things about the function.
Chapter 7 Differential Equations and Mathematical Modeling If you know one value of a function, and the rate of change (derivative) of the function, then yu can figure out many things about the function.
Math Applied Differential Equations
 Math 256 - Applied Differential Equations Notes Basic Definitions and Concepts A differential equation is an equation that involves one or more of the derivatives (first derivative, second derivative,
Math 256 - Applied Differential Equations Notes Basic Definitions and Concepts A differential equation is an equation that involves one or more of the derivatives (first derivative, second derivative,
Calculus II. Philippe Rukimbira. Department of Mathematics Florida International University PR (FIU) MAC / 1
 Calculus II Philippe Rukimbira Department of Mathematics Florida International University PR (FIU) MAC 2312 1 / 1 5.4. Sigma notation; The definition of area as limit Assignment: page 350, #11-15, 27,
Calculus II Philippe Rukimbira Department of Mathematics Florida International University PR (FIU) MAC 2312 1 / 1 5.4. Sigma notation; The definition of area as limit Assignment: page 350, #11-15, 27,
2. (12 points) Find an equation for the line tangent to the graph of f(x) =
 November 23, 2010 Name The total number of points available is 153 Throughout this test, show your work Throughout this test, you are expected to use calculus to solve problems Graphing calculator solutions
November 23, 2010 Name The total number of points available is 153 Throughout this test, show your work Throughout this test, you are expected to use calculus to solve problems Graphing calculator solutions
Chapter 2 Notes, Kohler & Johnson 2e
 Contents 2 First Order Differential Equations 2 2.1 First Order Equations - Existence and Uniqueness Theorems......... 2 2.2 Linear First Order Differential Equations.................... 5 2.2.1 First
Contents 2 First Order Differential Equations 2 2.1 First Order Equations - Existence and Uniqueness Theorems......... 2 2.2 Linear First Order Differential Equations.................... 5 2.2.1 First
Differential Equations
 Math 181 Prof. Beydler 9.1/9.3 Notes Page 1 of 6 Differential Equations A differential equation is an equation that contains an unknown function and some of its derivatives. The following are examples
Math 181 Prof. Beydler 9.1/9.3 Notes Page 1 of 6 Differential Equations A differential equation is an equation that contains an unknown function and some of its derivatives. The following are examples
Math 370 Exam 2 Review Name
 Math 70 Exam 2 Review Name Be sure to complete these problems before the review session. 10 of these questions will count as a quiz in Learning Catalytics. Round 1 will be individual. Round 2 will be in
Math 70 Exam 2 Review Name Be sure to complete these problems before the review session. 10 of these questions will count as a quiz in Learning Catalytics. Round 1 will be individual. Round 2 will be in
LECTURE 4-1 INTRODUCTION TO ORDINARY DIFFERENTIAL EQUATIONS
 130 LECTURE 4-1 INTRODUCTION TO ORDINARY DIFFERENTIAL EQUATIONS DIFFERENTIAL EQUATIONS: A differential equation (DE) is an equation involving an unknown function and one or more of its derivatives. A differential
130 LECTURE 4-1 INTRODUCTION TO ORDINARY DIFFERENTIAL EQUATIONS DIFFERENTIAL EQUATIONS: A differential equation (DE) is an equation involving an unknown function and one or more of its derivatives. A differential
Math 2250 Final Exam Practice Problem Solutions. f(x) = ln x x. 1 x. lim. lim. x x = lim. = lim 2
 Math 5 Final Eam Practice Problem Solutions. What are the domain and range of the function f() = ln? Answer: is only defined for, and ln is only defined for >. Hence, the domain of the function is >. Notice
Math 5 Final Eam Practice Problem Solutions. What are the domain and range of the function f() = ln? Answer: is only defined for, and ln is only defined for >. Hence, the domain of the function is >. Notice
Chapter1. Ordinary Differential Equations
 Chapter1. Ordinary Differential Equations In the sciences and engineering, mathematical models are developed to aid in the understanding of physical phenomena. These models often yield an equation that
Chapter1. Ordinary Differential Equations In the sciences and engineering, mathematical models are developed to aid in the understanding of physical phenomena. These models often yield an equation that
Math 113 Final Exam Practice Problem Solutions. f(x) = ln x x. lim. lim. x x = lim. = lim 2
 Math 3 Final Eam Practice Problem Solutions. What are the domain and range of the function f() = ln? Answer: is only defined for, and ln is only defined for >. Hence, the domain of the function is >. Notice
Math 3 Final Eam Practice Problem Solutions. What are the domain and range of the function f() = ln? Answer: is only defined for, and ln is only defined for >. Hence, the domain of the function is >. Notice
Solving differential equations (Sect. 7.4) Review: Overview of differential equations.
 Solving differential equations (Sect. 7.4 Previous class: Overview of differential equations. Exponential growth. Separable differential equations. Review: Overview of differential equations. Definition
Solving differential equations (Sect. 7.4 Previous class: Overview of differential equations. Exponential growth. Separable differential equations. Review: Overview of differential equations. Definition
Extra Practice Recovering C
 Etra Practice Recovering C 1 Given the second derivative of a function, integrate to get the first derivative, then again to find the equation of the original function. Use the given initial conditions
Etra Practice Recovering C 1 Given the second derivative of a function, integrate to get the first derivative, then again to find the equation of the original function. Use the given initial conditions
A) 13 B) 9 C) 22 D) log 9
 Math 70 Exam 2 Review Name Be sure to complete these problems before the review session. Participation in our review session will count as a quiz grade. Please bring any questions you have ready to ask!
Math 70 Exam 2 Review Name Be sure to complete these problems before the review session. Participation in our review session will count as a quiz grade. Please bring any questions you have ready to ask!
Applications of First Order Differential Equation
 Dr Mansoor Alshehri King Saud University MATH204-Differential Equations Center of Excellence in Learning and Teaching 1 / 39 Orthogonal Trajectories How to Find Orthogonal Trajectories Growth and Decay
Dr Mansoor Alshehri King Saud University MATH204-Differential Equations Center of Excellence in Learning and Teaching 1 / 39 Orthogonal Trajectories How to Find Orthogonal Trajectories Growth and Decay
Mathematics 134 Calculus 2 With Fundamentals Exam 4 Solutions for Review Sheet Sample Problems April 26, 2018
 Mathematics 3 Calculus 2 With Fundamentals Exam Solutions for Review Sheet Sample Problems April 26, 28 Sample problems Note: The actual exam will be considerably shorter than the following list of questions
Mathematics 3 Calculus 2 With Fundamentals Exam Solutions for Review Sheet Sample Problems April 26, 28 Sample problems Note: The actual exam will be considerably shorter than the following list of questions
Basic Theory of Differential Equations
 page 104 104 CHAPTER 1 First-Order Differential Equations 16. The following initial-value problem arises in the analysis of a cable suspended between two fixed points y = 1 a 1 + (y ) 2, y(0) = a, y (0)
page 104 104 CHAPTER 1 First-Order Differential Equations 16. The following initial-value problem arises in the analysis of a cable suspended between two fixed points y = 1 a 1 + (y ) 2, y(0) = a, y (0)
MAC Find the x-value that maximizes the area of the shaded rectangle inscribed in a right triangle below.
 MAC 23. Find the x-value that maximizes the area of the shaded rectangle inscribed in a right triangle below. (x, y) y = 3 x + 4 a. x = 6 b. x = 4 c. x = 2 d. x = 5 e. x = 3 2. Consider the area of the
MAC 23. Find the x-value that maximizes the area of the shaded rectangle inscribed in a right triangle below. (x, y) y = 3 x + 4 a. x = 6 b. x = 4 c. x = 2 d. x = 5 e. x = 3 2. Consider the area of the
Chapter 5: Integrals
 Chapter 5: Integrals Section 5.3 The Fundamental Theorem of Calculus Sec. 5.3: The Fundamental Theorem of Calculus Fundamental Theorem of Calculus: Sec. 5.3: The Fundamental Theorem of Calculus Fundamental
Chapter 5: Integrals Section 5.3 The Fundamental Theorem of Calculus Sec. 5.3: The Fundamental Theorem of Calculus Fundamental Theorem of Calculus: Sec. 5.3: The Fundamental Theorem of Calculus Fundamental
Purdue University Study Guide for MA Credit Exam
 Purdue University Study Guide for MA 16010 Credit Exam Students who pass the credit exam will gain credit in MA16010. The credit exam is a two-hour long exam with multiple choice questions. No books or
Purdue University Study Guide for MA 16010 Credit Exam Students who pass the credit exam will gain credit in MA16010. The credit exam is a two-hour long exam with multiple choice questions. No books or
DIFFERENTIAL EQUATIONS
 Mr. Isaac Akpor Adjei (MSc. Mathematics, MSc. Biostats) isaac.adjei@gmail.com April 7, 2017 ORDINARY In many physical situation, equation arise which involve differential coefficients. For example: 1 The
Mr. Isaac Akpor Adjei (MSc. Mathematics, MSc. Biostats) isaac.adjei@gmail.com April 7, 2017 ORDINARY In many physical situation, equation arise which involve differential coefficients. For example: 1 The
Announcements. Topics: Homework:
 Announcements Topics: - sections 7.3 (the definite integral +area), 7.4 (FTC), 7.5 (additional techniques of integration) * Read these sections and study solved examples in your textbook! Homework: - review
Announcements Topics: - sections 7.3 (the definite integral +area), 7.4 (FTC), 7.5 (additional techniques of integration) * Read these sections and study solved examples in your textbook! Homework: - review
Chapter 3 Exponential and Logarithmic Functions
 Chapter 3 Exponential and Logarithmic Functions Overview: 3.1 Exponential Functions and Their Graphs 3.2 Logarithmic Functions and Their Graphs 3.3 Properties of Logarithms 3.4 Solving Exponential and
Chapter 3 Exponential and Logarithmic Functions Overview: 3.1 Exponential Functions and Their Graphs 3.2 Logarithmic Functions and Their Graphs 3.3 Properties of Logarithms 3.4 Solving Exponential and
CALCULUS I. Practice Problems. Paul Dawkins
 CALCULUS I Practice Problems Paul Dawkins Table of Contents Preface... iii Outline... iii Review... Introduction... Review : Functions... Review : Inverse Functions... 6 Review : Trig Functions... 6 Review
CALCULUS I Practice Problems Paul Dawkins Table of Contents Preface... iii Outline... iii Review... Introduction... Review : Functions... Review : Inverse Functions... 6 Review : Trig Functions... 6 Review
Exponential and Logarithmic Functions. 3. Pg #17-57 column; column and (need graph paper)
 Algebra 2/Trig Unit 6 Notes Packet Name: Period: # Exponential and Logarithmic Functions 1. Worksheet 2. Worksheet 3. Pg 483-484 #17-57 column; 61-73 column and 76-77 (need graph paper) 4. Pg 483-484 #20-60
Algebra 2/Trig Unit 6 Notes Packet Name: Period: # Exponential and Logarithmic Functions 1. Worksheet 2. Worksheet 3. Pg 483-484 #17-57 column; 61-73 column and 76-77 (need graph paper) 4. Pg 483-484 #20-60
Tangent Lines Sec. 2.1, 2.7, & 2.8 (continued)
 Tangent Lines Sec. 2.1, 2.7, & 2.8 (continued) Prove this Result How Can a Derivative Not Exist? Remember that the derivative at a point (or slope of a tangent line) is a LIMIT, so it doesn t exist whenever
Tangent Lines Sec. 2.1, 2.7, & 2.8 (continued) Prove this Result How Can a Derivative Not Exist? Remember that the derivative at a point (or slope of a tangent line) is a LIMIT, so it doesn t exist whenever
Section Exponential Functions
 121 Section 4.1 - Exponential Functions Exponential functions are extremely important in both economics and science. It allows us to discuss the growth of money in a money market account as well as the
121 Section 4.1 - Exponential Functions Exponential functions are extremely important in both economics and science. It allows us to discuss the growth of money in a money market account as well as the
Practice Final Exam Solutions
 Important Notice: To prepare for the final exam, study past exams and practice exams, and homeworks, quizzes, and worksheets, not just this practice final. A topic not being on the practice final does
Important Notice: To prepare for the final exam, study past exams and practice exams, and homeworks, quizzes, and worksheets, not just this practice final. A topic not being on the practice final does
Math 112 Section 10 Lecture notes, 1/7/04
 Math 11 Section 10 Lecture notes, 1/7/04 Section 7. Integration by parts To integrate the product of two functions, integration by parts is used when simpler methods such as substitution or simplifying
Math 11 Section 10 Lecture notes, 1/7/04 Section 7. Integration by parts To integrate the product of two functions, integration by parts is used when simpler methods such as substitution or simplifying
Write the equation of the given line in slope-intercept form and match with the correct alternate form. 10. A
 Slope & y-intercept Class Work Identify the slope and y-intercept for each equation 1. y = 3x 4 2. y = 2x 3. y = 7 m = 3 b = 4 m = 2 b = 0 m = 0 b = 7 4. x = 5 5. y = 0 6. y 3 = 4(x + 6) m = undef b =
Slope & y-intercept Class Work Identify the slope and y-intercept for each equation 1. y = 3x 4 2. y = 2x 3. y = 7 m = 3 b = 4 m = 2 b = 0 m = 0 b = 7 4. x = 5 5. y = 0 6. y 3 = 4(x + 6) m = undef b =
Practice Exam 1 Solutions
 Practice Exam 1 Solutions 1a. Let S be the region bounded by y = x 3, y = 1, and x. Find the area of S. What is the volume of the solid obtained by rotating S about the line y = 1? Area A = Volume 1 1
Practice Exam 1 Solutions 1a. Let S be the region bounded by y = x 3, y = 1, and x. Find the area of S. What is the volume of the solid obtained by rotating S about the line y = 1? Area A = Volume 1 1
MATH 18.01, FALL PROBLEM SET #5 SOLUTIONS (PART II)
 MATH 8, FALL 7 - PROBLEM SET #5 SOLUTIONS (PART II (Oct ; Antiderivatives; + + 3 7 points Recall that in pset 3A, you showed that (d/dx tanh x x Here, tanh (x denotes the inverse to the hyperbolic tangent
MATH 8, FALL 7 - PROBLEM SET #5 SOLUTIONS (PART II (Oct ; Antiderivatives; + + 3 7 points Recall that in pset 3A, you showed that (d/dx tanh x x Here, tanh (x denotes the inverse to the hyperbolic tangent
Chapter 3 Exponential and Logarithmic Functions
 Chapter 3 Exponential and Logarithmic Functions Overview: 3.1 Exponential Functions and Their Graphs 3.2 Logarithmic Functions and Their Graphs 3.3 Properties of Logarithms 3.4 Solving Exponential and
Chapter 3 Exponential and Logarithmic Functions Overview: 3.1 Exponential Functions and Their Graphs 3.2 Logarithmic Functions and Their Graphs 3.3 Properties of Logarithms 3.4 Solving Exponential and
Math Applied Differential Equations
 Math 256 - Applied Differential Equations Notes Existence and Uniqueness The following theorem gives sufficient conditions for the existence and uniqueness of a solution to the IVP for first order nonlinear
Math 256 - Applied Differential Equations Notes Existence and Uniqueness The following theorem gives sufficient conditions for the existence and uniqueness of a solution to the IVP for first order nonlinear
Practice Questions for Final Exam - Math 1060Q - Fall 2014
 Practice Questions for Final Exam - Math 1060Q - Fall 01 Before anyone asks, the final exam is cumulative. It will consist of about 50% problems on exponential and logarithmic functions, 5% problems on
Practice Questions for Final Exam - Math 1060Q - Fall 01 Before anyone asks, the final exam is cumulative. It will consist of about 50% problems on exponential and logarithmic functions, 5% problems on
First Order Differential Equations
 Chapter 2 First Order Differential Equations Introduction Any first order differential equation can be written as F (x, y, y )=0 by moving all nonzero terms to the left hand side of the equation. Of course,
Chapter 2 First Order Differential Equations Introduction Any first order differential equation can be written as F (x, y, y )=0 by moving all nonzero terms to the left hand side of the equation. Of course,
Lecture : The Indefinite Integral MTH 124
 Up to this point we have investigated the definite integral of a function over an interval. In particular we have done the following. Approximated integrals using left and right Riemann sums. Defined the
Up to this point we have investigated the definite integral of a function over an interval. In particular we have done the following. Approximated integrals using left and right Riemann sums. Defined the
Math 2250 Final Exam Practice Problem Solutions. f(x) = ln x x. 1 x. lim. lim. x x = lim. = lim 2
 Math 5 Final Eam Practice Problem Solutions. What are the domain and range of the function f() = ln? Answer: is only defined for, and ln is only defined for >. Hence, the domain of the function is >. Notice
Math 5 Final Eam Practice Problem Solutions. What are the domain and range of the function f() = ln? Answer: is only defined for, and ln is only defined for >. Hence, the domain of the function is >. Notice
Announcements. Topics: Homework:
 Announcements Topics: - sections 7.4 (FTC), 7.5 (additional techniques of integration), 7.6 (applications of integration) * Read these sections and study solved examples in your textbook! Homework: - review
Announcements Topics: - sections 7.4 (FTC), 7.5 (additional techniques of integration), 7.6 (applications of integration) * Read these sections and study solved examples in your textbook! Homework: - review
Calculus II Practice Test Problems for Chapter 7 Page 1 of 6
 Calculus II Practice Test Problems for Chapter 7 Page of 6 This is a set of practice test problems for Chapter 7. This is in no way an inclusive set of problems there can be other types of problems on
Calculus II Practice Test Problems for Chapter 7 Page of 6 This is a set of practice test problems for Chapter 7. This is in no way an inclusive set of problems there can be other types of problems on
Section 5.6. Integration By Parts. MATH 126 (Section 5.6) Integration By Parts The University of Kansas 1 / 10
 Section 5.6 Integration By Parts MATH 126 (Section 5.6) Integration By Parts The University of Kansas 1 / 10 Integration By Parts Manipulating the Product Rule d dx (f (x) g(x)) = f (x) g (x) + f (x) g(x)
Section 5.6 Integration By Parts MATH 126 (Section 5.6) Integration By Parts The University of Kansas 1 / 10 Integration By Parts Manipulating the Product Rule d dx (f (x) g(x)) = f (x) g (x) + f (x) g(x)
AP Calculus Multiple Choice Questions - Chapter 7
 Find the general solution to the eact differential equation dy/d = t cos(t ) a y = cos(6t) + b y = sin(6t) + c y = cos(t ) + d y = sin(t ) + Find the general solution to the eact differential equation
Find the general solution to the eact differential equation dy/d = t cos(t ) a y = cos(6t) + b y = sin(6t) + c y = cos(t ) + d y = sin(t ) + Find the general solution to the eact differential equation
Example. Evaluate. 3x 2 4 x dx.
 3x 2 4 x 3 + 4 dx. Solution: We need a new technique to integrate this function. Notice that if we let u x 3 + 4, and we compute the differential du of u, we get: du 3x 2 dx Going back to our integral,
3x 2 4 x 3 + 4 dx. Solution: We need a new technique to integrate this function. Notice that if we let u x 3 + 4, and we compute the differential du of u, we get: du 3x 2 dx Going back to our integral,
Exponential Functions
 Exponential Functions MATH 160, Precalculus J. Robert Buchanan Department of Mathematics Fall 2011 Objectives In this lesson we will learn to: recognize and evaluate exponential functions with base a,
Exponential Functions MATH 160, Precalculus J. Robert Buchanan Department of Mathematics Fall 2011 Objectives In this lesson we will learn to: recognize and evaluate exponential functions with base a,
7.1. Calculus of inverse functions. Text Section 7.1 Exercise:
 Contents 7. Inverse functions 1 7.1. Calculus of inverse functions 2 7.2. Derivatives of exponential function 4 7.3. Logarithmic function 6 7.4. Derivatives of logarithmic functions 7 7.5. Exponential
Contents 7. Inverse functions 1 7.1. Calculus of inverse functions 2 7.2. Derivatives of exponential function 4 7.3. Logarithmic function 6 7.4. Derivatives of logarithmic functions 7 7.5. Exponential
3.4 The Chain Rule. F (x) = f (g(x))g (x) Alternate way of thinking about it: If y = f(u) and u = g(x) where both are differentiable functions, then
 3.4 The Chain Rule To find the derivative of a function that is the composition of two functions for which we already know the derivatives, we can use the Chain Rule. The Chain Rule: Suppose F (x) = f(g(x)).
3.4 The Chain Rule To find the derivative of a function that is the composition of two functions for which we already know the derivatives, we can use the Chain Rule. The Chain Rule: Suppose F (x) = f(g(x)).
Write the equation of the given line in slope-intercept form and match with the correct alternate form. 10. A
 Slope & y-intercept Class Work Identify the slope and y-intercept for each equation 1. y = 3x 4 2. y = 2x 3. y = 7 4. x = 5 5. y = 0 6. y 3 = 4(x + 6) 7. y + 2 = 1 (x + 6) 8. 2x + 3y = 9 9. 4x 7y = 14
Slope & y-intercept Class Work Identify the slope and y-intercept for each equation 1. y = 3x 4 2. y = 2x 3. y = 7 4. x = 5 5. y = 0 6. y 3 = 4(x + 6) 7. y + 2 = 1 (x + 6) 8. 2x + 3y = 9 9. 4x 7y = 14
MATH165 Homework 7. Solutions
 MATH165 Homework 7. Solutions March 23. 2010 Problem 1. 3.7.9 The stone is thrown with speed of 10m/s, and height is given by h = 10t 0.83t 2. (a) To find the velocity after 3 seconds, we first need to
MATH165 Homework 7. Solutions March 23. 2010 Problem 1. 3.7.9 The stone is thrown with speed of 10m/s, and height is given by h = 10t 0.83t 2. (a) To find the velocity after 3 seconds, we first need to
Drill Exercise Differential equations by abhijit kumar jha DRILL EXERCISE - 1 DRILL EXERCISE - 2. e x, where c 1
 DRILL EXERCISE -. Find the order and degree (if defined) of the differential equation 5 4 3 d y d y. Find the order and degree (if defined) of the differential equation n. 3. Find the order and degree
DRILL EXERCISE -. Find the order and degree (if defined) of the differential equation 5 4 3 d y d y. Find the order and degree (if defined) of the differential equation n. 3. Find the order and degree
Solutions. .5 = e k k = ln(.5) Now that we know k we find t for which the exponential function is = e kt
 MATH 1220-03 Exponential Growth and Decay Spring 08 Solutions 1. (#15 from 6.5.) Cesium 137 and strontium 90 were two radioactive chemicals released at the Chernobyl nuclear reactor in April 1986. The
MATH 1220-03 Exponential Growth and Decay Spring 08 Solutions 1. (#15 from 6.5.) Cesium 137 and strontium 90 were two radioactive chemicals released at the Chernobyl nuclear reactor in April 1986. The
3. On the grid below, sketch and label graphs of the following functions: y = sin x, y = cos x, and y = sin(x π/2). π/2 π 3π/2 2π 5π/2
 AP Physics C Calculus C.1 Name Trigonometric Functions 1. Consider the right triangle to the right. In terms of a, b, and c, write the expressions for the following: c a sin θ = cos θ = tan θ =. Using
AP Physics C Calculus C.1 Name Trigonometric Functions 1. Consider the right triangle to the right. In terms of a, b, and c, write the expressions for the following: c a sin θ = cos θ = tan θ =. Using
m(x) = f(x) + g(x) m (x) = f (x) + g (x) (The Sum Rule) n(x) = f(x) g(x) n (x) = f (x) g (x) (The Difference Rule)
 Chapter 3 Differentiation Rules 3.1 Derivatives of Polynomials and Exponential Functions Aka The Short Cuts! Yay! f(x) = c f (x) = 0 g(x) = x g (x) = 1 h(x) = x n h (x) = n x n-1 (The Power Rule) k(x)
Chapter 3 Differentiation Rules 3.1 Derivatives of Polynomials and Exponential Functions Aka The Short Cuts! Yay! f(x) = c f (x) = 0 g(x) = x g (x) = 1 h(x) = x n h (x) = n x n-1 (The Power Rule) k(x)
Problem Set. Assignment #1. Math 3350, Spring Feb. 6, 2004 ANSWERS
 Problem Set Assignment #1 Math 3350, Spring 2004 Feb. 6, 2004 ANSWERS i Problem 1. [Section 1.4, Problem 4] A rocket is shot straight up. During the initial stages of flight is has acceleration 7t m /s
Problem Set Assignment #1 Math 3350, Spring 2004 Feb. 6, 2004 ANSWERS i Problem 1. [Section 1.4, Problem 4] A rocket is shot straight up. During the initial stages of flight is has acceleration 7t m /s
Solutions to the Review Questions
 Solutions to the Review Questions Short Answer/True or False. True or False, and explain: (a) If y = y + 2t, then 0 = y + 2t is an equilibrium solution. False: This is an isocline associated with a slope
Solutions to the Review Questions Short Answer/True or False. True or False, and explain: (a) If y = y + 2t, then 0 = y + 2t is an equilibrium solution. False: This is an isocline associated with a slope
The above statement is the false product rule! The correct product rule gives g (x) = 3x 4 cos x+ 12x 3 sin x. for all angles θ.
 Math 7A Practice Midterm III Solutions Ch. 6-8 (Ebersole,.7-.4 (Stewart DISCLAIMER. This collection of practice problems is not guaranteed to be identical, in length or content, to the actual exam. You
Math 7A Practice Midterm III Solutions Ch. 6-8 (Ebersole,.7-.4 (Stewart DISCLAIMER. This collection of practice problems is not guaranteed to be identical, in length or content, to the actual exam. You
Write each expression as a sum or difference of logarithms. All variables are positive. 4) log ( ) 843 6) Solve for x: 8 2x+3 = 467
 Write each expression as a single logarithm: 10 Name Period 1) 2 log 6 - ½ log 9 + log 5 2) 4 ln 2 - ¾ ln 16 Write each expression as a sum or difference of logarithms. All variables are positive. 3) ln
Write each expression as a single logarithm: 10 Name Period 1) 2 log 6 - ½ log 9 + log 5 2) 4 ln 2 - ¾ ln 16 Write each expression as a sum or difference of logarithms. All variables are positive. 3) ln
in terms of p, q and r.
 Logarithms and Exponents 1. Let ln a = p, ln b = q. Write the following expressions in terms of p and q. ln a 3 b ln a b 2. Let log 10 P = x, log 10 Q = y and log 10 R = z. Express P log 10 QR 3 2 in terms
Logarithms and Exponents 1. Let ln a = p, ln b = q. Write the following expressions in terms of p and q. ln a 3 b ln a b 2. Let log 10 P = x, log 10 Q = y and log 10 R = z. Express P log 10 QR 3 2 in terms
Calculus II Practice Test 1 Problems: , 6.5, Page 1 of 10
 Calculus II Practice Test Problems: 6.-6.3, 6.5, 7.-7.3 Page of This is in no way an inclusive set of problems there can be other types of problems on the actual test. To prepare for the test: review homework,
Calculus II Practice Test Problems: 6.-6.3, 6.5, 7.-7.3 Page of This is in no way an inclusive set of problems there can be other types of problems on the actual test. To prepare for the test: review homework,
Solutions for homework 1. 1 Introduction to Differential Equations
 Solutions for homework 1 1 Introduction to Differential Equations 1.1 Differential Equation Models The phrase y is proportional to x implies that y is related to x via the equation y = kx, where k is a
Solutions for homework 1 1 Introduction to Differential Equations 1.1 Differential Equation Models The phrase y is proportional to x implies that y is related to x via the equation y = kx, where k is a
+ i sin. + i sin. = 2 cos
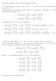 Math 11 Lesieutre); Exam review I; December 4, 017 1. a) Find all complex numbers z for which z = 8. Write your answers in rectangular non-polar) form. We are going to use de Moivre s theorem. For 1, r
Math 11 Lesieutre); Exam review I; December 4, 017 1. a) Find all complex numbers z for which z = 8. Write your answers in rectangular non-polar) form. We are going to use de Moivre s theorem. For 1, r
APPLICATIONS OF DIFFERENTIATION
 4 APPLICATIONS OF DIFFERENTIATION APPLICATIONS OF DIFFERENTIATION 4.9 Antiderivatives In this section, we will learn about: Antiderivatives and how they are useful in solving certain scientific problems.
4 APPLICATIONS OF DIFFERENTIATION APPLICATIONS OF DIFFERENTIATION 4.9 Antiderivatives In this section, we will learn about: Antiderivatives and how they are useful in solving certain scientific problems.
1 Introduction; Integration by Parts
 1 Introduction; Integration by Parts September 11-1 Traditionally Calculus I covers Differential Calculus and Calculus II covers Integral Calculus. You have already seen the Riemann integral and certain
1 Introduction; Integration by Parts September 11-1 Traditionally Calculus I covers Differential Calculus and Calculus II covers Integral Calculus. You have already seen the Riemann integral and certain
Section 5.6. Applications and Models: Growth and Decay; Compound
 Section 5.6 Applications and Models: Growth and Decay; Compound Interest Exponential Growth A quantity that experiences exponential growth will increase according to the equation P(t) = P 0 e kt t is the
Section 5.6 Applications and Models: Growth and Decay; Compound Interest Exponential Growth A quantity that experiences exponential growth will increase according to the equation P(t) = P 0 e kt t is the
Methods of Integration
 Methods of Integration Professor D. Olles January 8, 04 Substitution The derivative of a composition of functions can be found using the chain rule form d dx [f (g(x))] f (g(x)) g (x) Rewriting the derivative
Methods of Integration Professor D. Olles January 8, 04 Substitution The derivative of a composition of functions can be found using the chain rule form d dx [f (g(x))] f (g(x)) g (x) Rewriting the derivative
Chapter 11 Logarithms
 Chapter 11 Logarithms Lesson 1: Introduction to Logs Lesson 2: Graphs of Logs Lesson 3: The Natural Log Lesson 4: Log Laws Lesson 5: Equations of Logs using Log Laws Lesson 6: Exponential Equations using
Chapter 11 Logarithms Lesson 1: Introduction to Logs Lesson 2: Graphs of Logs Lesson 3: The Natural Log Lesson 4: Log Laws Lesson 5: Equations of Logs using Log Laws Lesson 6: Exponential Equations using
AP Calculus Summer Homework MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
 AP Calculus Summer Homework 2015-2016 Part 2 Name Score MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find the distance d(p1, P2) between the points
AP Calculus Summer Homework 2015-2016 Part 2 Name Score MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find the distance d(p1, P2) between the points
1.1. BASIC ANTI-DIFFERENTIATION 21 + C.
 .. BASIC ANTI-DIFFERENTIATION and so e x cos xdx = ex sin x + e x cos x + C. We end this section with a possibly surprising complication that exists for anti-di erentiation; a type of complication which
.. BASIC ANTI-DIFFERENTIATION and so e x cos xdx = ex sin x + e x cos x + C. We end this section with a possibly surprising complication that exists for anti-di erentiation; a type of complication which
= π + sin π = π + 0 = π, so the object is moving at a speed of π feet per second after π seconds. (c) How far does it go in π seconds?
 Mathematics 115 Professor Alan H. Stein April 18, 005 SOLUTIONS 1. Define what is meant by an antiderivative or indefinite integral of a function f(x). Solution: An antiderivative or indefinite integral
Mathematics 115 Professor Alan H. Stein April 18, 005 SOLUTIONS 1. Define what is meant by an antiderivative or indefinite integral of a function f(x). Solution: An antiderivative or indefinite integral
1.3 Exponential Functions
 22 Chapter 1 Prerequisites for Calculus 1.3 Exponential Functions What you will learn about... Exponential Growth Exponential Decay Applications The Number e and why... Exponential functions model many
22 Chapter 1 Prerequisites for Calculus 1.3 Exponential Functions What you will learn about... Exponential Growth Exponential Decay Applications The Number e and why... Exponential functions model many
Math 1501 Calc I Fall 2013 Lesson 9 - Lesson 20
 Math 1501 Calc I Fall 2013 Lesson 9 - Lesson 20 Instructor: Sal Barone School of Mathematics Georgia Tech August 19 - August 6, 2013 (updated October 4, 2013) L9: DIFFERENTIATION RULES Covered sections:
Math 1501 Calc I Fall 2013 Lesson 9 - Lesson 20 Instructor: Sal Barone School of Mathematics Georgia Tech August 19 - August 6, 2013 (updated October 4, 2013) L9: DIFFERENTIATION RULES Covered sections:
Chapter 4 Integration
 Chapter 4 Integration SECTION 4.1 Antiderivatives and Indefinite Integration Calculus: Chapter 4 Section 4.1 Antiderivative A function F is an antiderivative of f on an interval I if F '( x) f ( x) for
Chapter 4 Integration SECTION 4.1 Antiderivatives and Indefinite Integration Calculus: Chapter 4 Section 4.1 Antiderivative A function F is an antiderivative of f on an interval I if F '( x) f ( x) for
D1.3 Separable Differential Equations
 Section 5.3 Separable Differential Equations D.3 Separable Differential Equations Sketching solutions of a differential equation using its direction field is a powerful technique, and it provides a wealth
Section 5.3 Separable Differential Equations D.3 Separable Differential Equations Sketching solutions of a differential equation using its direction field is a powerful technique, and it provides a wealth
9.1 Solving Differential Equations
 9.1 Solving Differential Equations What is a differential equation? Real-world examples: The order of a differential equation is the order of the that occurs in the equation. A differential equation is
9.1 Solving Differential Equations What is a differential equation? Real-world examples: The order of a differential equation is the order of the that occurs in the equation. A differential equation is
First Order Differential Equations Chapter 1
 First Order Differential Equations Chapter 1 Doreen De Leon Department of Mathematics, California State University, Fresno 1 Differential Equations and Mathematical Models Section 1.1 Definitions: An equation
First Order Differential Equations Chapter 1 Doreen De Leon Department of Mathematics, California State University, Fresno 1 Differential Equations and Mathematical Models Section 1.1 Definitions: An equation
Displacement and Total Distance Traveled
 Displacement and Total Distance Traveled We have gone over these concepts before. Displacement: This is the distance a particle has moved within a certain time - To find this you simply subtract its position
Displacement and Total Distance Traveled We have gone over these concepts before. Displacement: This is the distance a particle has moved within a certain time - To find this you simply subtract its position
HW#1. Unit 4B Logarithmic Functions HW #1. 1) Which of the following is equivalent to y=log7 x? (1) y =x 7 (3) x = 7 y (2) x =y 7 (4) y =x 1/7
 HW#1 Name Unit 4B Logarithmic Functions HW #1 Algebra II Mrs. Dailey 1) Which of the following is equivalent to y=log7 x? (1) y =x 7 (3) x = 7 y (2) x =y 7 (4) y =x 1/7 2) If the graph of y =6 x is reflected
HW#1 Name Unit 4B Logarithmic Functions HW #1 Algebra II Mrs. Dailey 1) Which of the following is equivalent to y=log7 x? (1) y =x 7 (3) x = 7 y (2) x =y 7 (4) y =x 1/7 2) If the graph of y =6 x is reflected
1.4 Techniques of Integration
 .4 Techniques of Integration Recall the following strategy for evaluating definite integrals, which arose from the Fundamental Theorem of Calculus (see Section.3). To calculate b a f(x) dx. Find a function
.4 Techniques of Integration Recall the following strategy for evaluating definite integrals, which arose from the Fundamental Theorem of Calculus (see Section.3). To calculate b a f(x) dx. Find a function
dy dx dx = 7 1 x dx dy = 7 1 x dx e u du = 1 C = 0
 1. = 6x = 6x = 6 x = 6 x x 2 y = 6 2 + C = 3x2 + C General solution: y = 3x 2 + C 3. = 7 x = 7 1 x = 7 1 x General solution: y = 7 ln x + C. = e.2x = e.2x = e.2x (u =.2x, du =.2) y = e u 1.2 du = 1 e u
1. = 6x = 6x = 6 x = 6 x x 2 y = 6 2 + C = 3x2 + C General solution: y = 3x 2 + C 3. = 7 x = 7 1 x = 7 1 x General solution: y = 7 ln x + C. = e.2x = e.2x = e.2x (u =.2x, du =.2) y = e u 1.2 du = 1 e u
Practice Midterm 1 Solutions Written by Victoria Kala July 10, 2017
 Practice Midterm 1 Solutions Written by Victoria Kala July 10, 2017 1. Use the slope field plotter link in Gauchospace to check your solution. 2. (a) Not linear because of the y 2 sin x term (b) Not linear
Practice Midterm 1 Solutions Written by Victoria Kala July 10, 2017 1. Use the slope field plotter link in Gauchospace to check your solution. 2. (a) Not linear because of the y 2 sin x term (b) Not linear
3.8 Exponential Growth and Decay
 3.8 Exponential Growth and Decay Suppose the rate of change of y with respect to t is proportional to y itself. So there is some constant k such that dy dt = ky The only solution to this equation is an
3.8 Exponential Growth and Decay Suppose the rate of change of y with respect to t is proportional to y itself. So there is some constant k such that dy dt = ky The only solution to this equation is an
Calculus AB Topics Limits Continuity, Asymptotes
 Calculus AB Topics Limits Continuity, Asymptotes Consider f x 2x 1 x 3 1 x 3 x 3 Is there a vertical asymptote at x = 3? Do not give a Precalculus answer on a Calculus exam. Consider f x 2x 1 x 3 1 x 3
Calculus AB Topics Limits Continuity, Asymptotes Consider f x 2x 1 x 3 1 x 3 x 3 Is there a vertical asymptote at x = 3? Do not give a Precalculus answer on a Calculus exam. Consider f x 2x 1 x 3 1 x 3
Handout 1. Research shows that students learn when they MAKE MISTAKES and not when they get it right. SO MAKE MISTAKES, because MISTAKES ARE GOOD!
 Handout Research shows that students learn when they MAKE MISTAKES and not when they get it right. SO MAKE MISTAKES, because MISTAKES ARE GOOD! Review:. The Substitution Rule Indefinite f (g()) g ()d =
Handout Research shows that students learn when they MAKE MISTAKES and not when they get it right. SO MAKE MISTAKES, because MISTAKES ARE GOOD! Review:. The Substitution Rule Indefinite f (g()) g ()d =
7.5. Exponential Growth and Decay. 502 Chapter 7: Transcendental Functions. The Law of Exponential Change
 502 Chapter 7: Transcendental Functions 7.5 Exponential Growth and Decay Exponential functions increase or decrease very rapidly with changes in the independent variable. They describe growth or decay
502 Chapter 7: Transcendental Functions 7.5 Exponential Growth and Decay Exponential functions increase or decrease very rapidly with changes in the independent variable. They describe growth or decay
Logarithmic, Exponential, and Other Transcendental Functions. Copyright Cengage Learning. All rights reserved.
 5 Logarithmic, Exponential, and Other Transcendental Functions Copyright Cengage Learning. All rights reserved. 5.5 Bases Other Than e and Applications Copyright Cengage Learning. All rights reserved.
5 Logarithmic, Exponential, and Other Transcendental Functions Copyright Cengage Learning. All rights reserved. 5.5 Bases Other Than e and Applications Copyright Cengage Learning. All rights reserved.
