A Dilatonic Alternative
|
|
|
- Scott Hardy
- 6 years ago
- Views:
Transcription
1 A Dilatonic Alternative Thesis For the degree Master of Science in Physics - research profile Jens F. C. Krog Supervisors: Francesco Sannino and Claudio Pica CP 3 -Origins, September 2012
2 Abstract We put forth the conjecture that the recent findings at the LHC might indicate that the Higgs particle of electroweak physics is a so-called dilaton; a pseudo-goldstone boson of a broken conformal symmetry. We then go on to show how the onset of symmetry breaking appears in massless theories of any number of scalars from quantum corrections where we through the effective potential and the balancing of gauge or quartic couplings may ensure spontaneous symmetry breaking. An additional analysis using the renormalization group equations and the improved couplings is discussed, and the possibility of a geometrical picture to investigate the phase structure of a theory is presented. A specific near conformal theory featuring nontrivial fixed point structure is investigated, and a light scalar is shown to be a dilaton, which can be tuned to have arbitrarily small mass without making the theory noninteracting. We then investigate which effects an electroweak SU (2) U (1) sector has on the features of the theory. We find that if the number of flavors and colors in the theory are chosen carefully, then the theory will be virtually unaffected by the new interactions, but if parameters are chosen differently the conformal phase of the original theory becomes hidden, because the theory can never reach a fixed point. We show that this specific implementation of the electroweak sector renders it difficult to reach a realistic spectrum and inside the perturbative region. We relate the theory discussed to technicolor theories and review recent phenomenological studies of LHC data in this context.
3 Acknowledgements During this work I have had the pleasure to be a part of the very active research environment of CP 3 -Origins, which has given me rich opportunities for discussion and assistance with both specifics and questions of more philosophical nature. I am very grateful to the staff of CP 3 and in particular I would like to thank my advisors Francesco Sannino and Claudio Pica as well as Oleg Antipin, Matin Mojaza, and Esben Mølgaard which without I would not have gotten nearly as far. In addition I would like to thank my friends and family for the strong support they have shown me through these last stressful months.
4 CONTENTS Contents 4 1 Electroweak symmetry breaking and the unknown nature of the Higgs 7 2 The Coleman-Weinberg analysis of radiative corrections Symmetry breaking in massless theories Massless φ 4 theory Massless scalar electrodynamics Higgs physics with the Coleman-Weinberg Mechanism The Gildener-Weinberg potential analysis Coupling constant constraints Appearance of a nontrivial minimum Spectrum analysis Phase transitions in the linear sigma model The model Beta function analysis The CW mechanism in the effective potential Patterns of symmetry breaking Coupling-constant flows and dynamical symmetry breaking Solving the Callan-Symanzik equation Conditions for symmetry breaking Geometrical example A near-conformal model featuring the dilaton The theory, its beta functions and their fixed points Gildener-Weinberg analysis of the effective potential Enter: "The dilaton" Geometrical analysis and phase transitions Gildener-Weinberg vs. Yamagishi Ultra light scale supersymmetry Where to go from here
5 CONTENTS 7 Coupling the dilaton to the standard model Introducing the SU(2) U(1) gauge Electroweak corrections to the beta functions and their fixed points Adjusting the notation The corrected beta functions Fixed point analysis The phase diagram Gildener-Weinberg analysis with massive vector bosons Satisfaction of the Callan-Symanzik equation Dilatonic stability and further extension Technicolor, dilatons, and the LHC Technicolor Walking Technicolor Technidilaton at the LHC? Conclusion 85 A Identities for the T A generators 87 B Identities for the S r matrices 89 Bibliography 91 Jens F. C. Krog 5
6
7 CHAPTER 1 ELECTROWEAK SYMMETRY BREAKING AND THE UNKNOWN NATURE OF THE HIGGS The description of the electromagnetic and weak interactions have been discussed thoroughly since the middle of the last century. Many theories and ideas have been presented, but the most prominent description was presented in the works of Glashow [1], S. Weinberg [2] and Salam [3], and relies on a SU (2) U (1) gauge theory. Below we review the basic structure in the notation of Peskin [4]. The purpose of this gauge theory is the introduction of vector bosons, which will make up the electroweak force mediators, the W and Z bosons, along with the photon, known from nature. The procedure of generating the masses of the massive vector bosons is a very simple and economical one. If we include a scalar doublet φ = that transforms under the fundamental representation of SU (2) ( ) φ1 and φ 2 has hypercharge +1/2 under the U (1) transformations, then the covariant derivative of this field is given D µ φ = ( µ i g A a µ τa 1 2 i g B µ )φ, (1.1) where τ a = σ a /2, which corresponds to the gauge transformation φ e αa τ a e iβ/2 φ. (1.2) If now, in the Lagrangian, we include a potential for the scalar field of the form V = µ 2 φ 2 + λ 2 ( φ 2 ) 2 (1.3) then, in the case of µ 2 > 0 the potential develops nontrivial global minima as seen in Figure 1.1. As the theory has a continuum of nontrivial global minima, spontaneous symmetry breaking occurs, as the theory chooses a specific direction. The usual choice for the minimum is the one where we assign a vacuum expectation value (vev) to φ, which is written as φ = 1 ( ) 0. (1.4) 2 v 7
8 CHAPTER 1. ELECTROWEAK SYMMETRY BREAKING AND THE UNKNOWN NATURE OF THE HIGGS Figure 1.1: The potential (1.3) showing degenerate minima in a circle around the origin. If this is done, then a gauge transformation like (1.2) with α 1 = α 2 = 0 and α 3 = β will leave the vev invariant, and we are left with just one combination of generators that leave the vacuum invariant, corresponding to a single massless vector boson. With this choice, we may write up the part of the kinetic terms involving (1.1), that contain squares of the gauge fields A a µ,b µ; L = 1 2 v 2 4 [g 2 (A 1µ )2 + g 2 (A 2µ )2 + ( g A 3µ + 12 g B µ ) 2 ]. (1.5) Rearranging the vector boson fields, we may then from this see that we obtain three massive vector bosons, where we notate W µ ± = 1 (A 1 µ i A2 µ ) with mass m W = g v (1.6) 2 2 Zµ 0 = 1 g 2 + g (g 2 A3 µ g B µ ) with mass m Z = g 2 + g 2 v 2. (1.7) The final vector field is then given A µ = 1 g 2 + g 2 (g A3 µ + g B µ ) with mass m A = 0 (1.8) corresponding to the massless photon. Thus we see that the insertion of a scalar doublet with a negative squared mass in the Lagrangian may produce the spontaneous symmetry breaking that make distinct the weak force and the electromagnetic, while producing masses of the gauge bosons. The discovery of such a particle would therefore be a great development for the description of the electroweak theory and unification of the weak and electromagnetic forces. The search for such a particle has been going on for the last couple of years at the Large Hadron Collider (LHC) at CERN, and the most recent (July 2012) reports 8 Jens F. C. Krog
9 from the ATLAS and CMS detector indicate that a boson with mass about 125 GeV and consistent with the standard model Higgs has been discovered. In Figure 1.2 a sample of data from the ATLAS collaboration showing events emitting two photons. The difference between the expected values for the no-particle hypothesis indicated by the dotted line and the statistical fit to data, indicated by the solid line, at around 125 GeV points to the existence of a new particle. This is obviously Figure 1.2: Mass distribution of events from the two photon channel. The dotted line depicts events expected from processes involving known particles, while the black dots and the solid line shows the data and a statistical fit to data respectively. The discrepancy around 125 GeV is indication of the existence of an unknown particle. a huge development for high energy physics and the description of electroweak physics. Indeed it is consistent with the electroweak theory of the 60 s described above - the observed particles might be the elementary Higgs scalar with a negative squared bare mass. However, this is not the only option, which is the basic conjecture of this work. Many different theories have been proposed that all include a Higgs-like particle, but besides from that are very different. Some propose that the Higgs particle should be composite, rendering the standard model without any elementary scalars, and others propose the existence of multiple scalar particles. For now though, we will motivate a specific effective description instead of trying to supply a fundamental theory. The line of thought will be as follows: If we assume that the standard model with a Higgs is an effective theory, which is only valid below a certain energy scale, we might try to compare the spectrum with a relevant energy scale and see if this gives any hints to the nature of the Higgs. If this is done in the low energy case of the effective description of strong in- Jens F. C. Krog 9
10 CHAPTER 1. ELECTROWEAK SYMMETRY BREAKING AND THE UNKNOWN NATURE OF THE HIGGS teraction, where we compare the pion mass to its decay constant, we find m π 4πF π 0.1, (1.9) i.e the pions seem a little light compared to relevant scale of the theory. This may be seen as support to the conjecture that the pions are Goldstone bosons of the breaking of the global SU (2) L SU (2) R symmetry of QCD, which protects their masses from getting large. In the case of the electroweak theory, the relevant scale is the vev of the Higgs v 246 GeV, which when assuming m H = 125 GeV yields m H 0.04, (1.10) 4πv giving us an even smaller ratio. Once again we may assume that some symmetry, which is only softly broken, protects the mass of the Higgs from being larger [5]. One such symmetry might be a conformal symmetry, which implies that the theory is scale invariant, and therefore does not have any nonzero dimensionful couplings. If such a symmetry was present before the electroweak symmetry breaking, and remained an approximate symmetry, it might be responsible for a light scalar particle, such that the Higgs is a pseudo-goldstone boson of conformal invariance. The first problem one encounters is that in a massless theory, we would have to set µ 2 = 0 in (1.3), giving us only a quartic interaction, which means that no nontrivial minimum can arise at this level. In order to create the electroweak symmetry breaking, we therefore need another mechanism to give the scalar field a vev. 10 Jens F. C. Krog
11 CHAPTER 2 THE COLEMAN-WEINBERG ANALYSIS OF RADIATIVE CORRECTIONS The Glashow-Weinberg-Salam (GWS) theory provides a very intuitive way of describing how the spontaneous breaking of the electroweak symmetries occur, however this is not the only way of producing this sort of symmetry breaking. Where the breaking in the GWS theory occurs due to an insertion of a imaginary tree level mass for the Higgs doublet, it may occur even in the absense of any tree level masses. In such theories symmetry breaking may arise due to radiative corrections as was first shown by Coleman and Weinberg [6]. 2.1 SYMMETRY BREAKING IN MASSLESS THEORIES The analysis of Coleman and Weinberg (CW), relies on the computation of the effective potential, which is simply put the potential where all diagrams with external scalar legs are included, corresponding to including all quantum corrections. For a scalar field φ this will produce terms in the effective potential with arbitrary high powers of φ. As argued by CW, it is sensible to do an expansion in loops, and the original analysis is therefore done at one loop. This, however, will still produce an infinite number of diagrams to sum, but the sum is calculable and the theory is renormalizable. The formulation of an effective potential that takes into account quantum corrections can be seen as a direct analogy of the formulation of the thermodynamic potentials which handle thermal fluctuations, for example the Gibbs free energy of a magnetic system [4]. If we define an energy functional E(J) for a theory with a scalar field φ by Z (J) = e ie(j) = [ Dφexp ] d 4 x(l (φ) + Jφ), (2.1) where J = J(x) is an external source in analogy to an external field, and the integrals are functional integrals, then we may take the derivative of the energy functional with respect to the external source, which in the magnetic system gives us 11
12 CHAPTER 2. THE COLEMAN-WEINBERG ANALYSIS OF RADIATIVE CORRECTIONS the magnetization; δe(j) δj(x) = i δ Dφe d 4 x (L (φ)+jφ) φ(x) ln Z (J) = δj(x) Dφe d 4 x (L (φ)+jφ) = Ω φ(x) Ω φ c (2.2) then φ c, which is called the classical field, is the analogy of the magnetization of the magnetic system of spins, only in a quantum field theory. As is done in thermodynamics, we will now define the Legendre transform of E(J) Γ(φ c ) E(J) d 4 y J(y)φ c (y) (2.3) where Γ(φ c ) is called the effective action. If we now look for an extremum in this action, we find δ δφ c (x) Γ(φ c) = δ δφ c x E(J) d 4 y δj(y) δφ c x φ c(y) J(x) = d 4 y δj(y) δe(j) δφ c x δj(y) d 4 y δj(y) δφ c x φ c(y) J(x) = J(x) (2.4) Thus, in the absence of an external source, the effective action will satisfy δ δφ c (x) Γ(φ c) = 0 (2.5) meaning that solutions of this equations are field configurations φ c (x) corresponding to a vacuum expectation value φ(x) giving stable vacuum states. If a nonzero field distribution of the classical field satisfies (2.5), then a nonzero vacuum expectation value will be a stable state. If we now assume that the theory is Lorentz and translation invariant, then a stable state will have φ c independent of x, and the action will just be the space time volume, V where the functional integral is taken times the effective potential Γ(φ c ) = V V e f f (φ c ) (2.6) such that all stable states that satisfy (2.5) will also satisfy V e f f φ c = 0 (2.7) and the classical φ c that satisfies this will correspond to the vacuum expectation value φ which minimizes the potential. The most important feature of an effective potential is that if the classical field, develops a nonzero vacuum expectation value, coming from a nontrivial minimum of the potential, then the quantum field theory it describes will have spontaneously broken symmetry [6]. 12 Jens F. C. Krog
13 2.2. MASSLESS φ 4 THEORY 2.2 MASSLESS φ 4 THEORY The outset of the CW analysis is a theory of only one self-interacting massless field φ, and the Lagrangian is given L = 1 2 ( µφ) 2 λ 4! φ A( µφ) Bφ2 1 4! Cφ4 (2.8) where the A,B, and C terms are counter terms used to enforce renormalization conditions and remove divergences. At the tree level, we therefore have the effective potential corresponding to tree level quartic interaction, shown in Figure 2.1: V 0 = λ 4! φ4 c (2.9) where the change from φ φ c indicates that we consider the classical background field. At one loop however, an infinite series of diagrams need to be included, of which some are shown in Figure 2.2 Figure 2.1: The tree level Figure 2.2: The first diagrams contributing to the potential at one effective potential loop Summing the series and evaluating the momentum integral with a large cutoff Λ then leads to the result for the 1 loop effective potential of the theory V = λ 4! φ4 c Bφ2 c 1 4! Cφ4 c + λλ2 64π 2 φ2 c + λ2 φ 4 ( c 256π 2 ln λφ2 c 2Λ 1 ) 2 (2.10) where we may now determine the counter terms by imposing renormalization conditions. As the goal is to investigate theories with massless particles, it is natural to enforce zero renormalized mass of the scalar field. we therefore require d 2 V = 0 (2.11) dφ 2 c 0 which then fixes B = λλ2 32π 2 (2.12) Jens F. C. Krog 13
14 CHAPTER 2. THE COLEMAN-WEINBERG ANALYSIS OF RADIATIVE CORRECTIONS The next natural step would be to require that the quartic coupling equals the fourth derivative at the origin, however this is not possible, since the fourth derivative is ill defined there because of the divergence of the logarithm. Instead, we define the coupling constant at a distance from the origin at the scale M, such that d 4 V dφ 4 c M = λ. (2.13) As will be shown, the choice of M is completely arbitrary and only affects the definition of the coupling but not the physics of the theory. Enforcing (2.13) we then find C = (ln 3λ2 λm 2 32π 2 2Λ 2 11 ) 3 and we have the complete expression for the effective potential at one loop V = λ 4! φ4 c + λ2 φ 4 ( c 256π 2 ln φ2 c M 2 25 ) 6 (2.14) (2.15) where we see that all dependence on the cutoff has vanished. An important feature of this result is that the effective potential only depends polynomially on the coupling constant, and has no inconvenient logarithmic dependence. This is true to higher orders as well [6]. Now we may investigate how the coupling constant depends on the choice of the scale M and see whether it affects the physics of the theory or not. If we instead chose a scale M, we can find the redefined coupling constant λ from (2.15) λ = d 4 V dφ 4 c = λ + 3λ2 2 M ln M 32π2 M 2 (2.16) and we may then rewrite (2.15) in terms of the new coupling V = λ 4! φ4 c + λ 2 φ 4 ( c 256π 2 ln φ2 c M 2 25 ) + O (λ 3 ) (2.17) 6 which to the order in which we are working is no different from the original expression. The choice of the renormalization scale M is therefore totally arbitrary, and will not affect the physics of the theory. A last interesting fact about the resulting effective potential is that, where the tree level potential has a minimum at the origin, the logarithm in the one loop potential will give negative values for small values of the field corresponding to a maximum at the origin and opens up the possibility that spontaneous symmetry breaking has already occured. However, the new minimum of the potential is at a vacuum expectation value φ given by λln φ 2 M 2 = 32 3 π2 + O (λ) (2.18) 14 Jens F. C. Krog
15 2.3. MASSLESS SCALAR ELECTRODYNAMICS which means that, since higher order terms will be of a higher power in λln(φ 2 c /M 2 ), we are far from the limit where we can trust the one loop approximation to be accurate, which is in the region where φ c M. The problem is that we must balance terms of order λ and λ 2 ln(φ 2 c /M 2 ) to find a minimum, resulting in a large logarithm. Even though we did not accomplish a spontaneous symmetry breaking for the simple interacting scalar model, the apparatus developed here may serve to show that the phenomena occurs in slightly more advanced models. The next few pages will show that the features may be improved just by including photons in the theory. 2.3 MASSLESS SCALAR ELECTRODYNAMICS In order to introduce couplings to a photon field, we instead use a charged scalar field, which means that we will have to introduce two scalar fields instead of one; a scalar particle and its antiparticle, φ 1 and φ 2. The Lagrangian of the theory is written L = 1 4 (F µν ) ( µφ 1 e A µ φ 2 ) ( µφ 2 +e A µ φ 1 ) 2 λ 4! (φ2 1 +φ2 2 )2 + CT (2.19) where F µν is the regular field strength tensor for the vector field A µ. The extra interactions lead to a larger amount of diagrams to compute, like the ones shown in Figure 2.3, but when the dust has settled the effective potential at one loop now reads where φ 2 c = φ2 1c + φ2 2c. V = λ 4! φ4 c + ( 5λ 2 ) ( 1152π 2 + 3e4 64π 2 φ 4 c ln φ2 c M 2 25 ) 6 (2.20) Figure 2.3: The diagrams containing the new interactions contributing to the potential at one loop Although this looks a lot like the result in the previous section, it does have some advantages over the simple massless scalar theory. This potential has a minimum away from the origin, but the minimum need not arise from balancing terms Jens F. C. Krog 15
16 CHAPTER 2. THE COLEMAN-WEINBERG ANALYSIS OF RADIATIVE CORRECTIONS of order λ and λ 2, which are by definition hard to balance without a large logarithm. In the new case we may simply balance terms in λ and e 4, where we have made no assumptions on the size of e. Although the term proportional to e 4 ln(φ c /M) does not appear until the first order in the loop expansion, and therefore intuitively should be small compared to the tree level potential, we have no constraints in the model that tell us that e 4 should not be of order λ. Indeed this assumption would enable us to find a minimum inside the trustable regime even for very small quartic couplings. This is perhaps the most interesting aspect of the work of Coleman and Weinberg, because it shows that radiative corrections not only may be of the same order as the tree level potential, but they may in fact induce spontaneous symmetry breaking. Working with the assumption that e 4 λ, we may discard the λ 2 term in (2.20), which is also justified by the fact that it is of the same order as e 8, which would come from the two loop radiative corrections. In addition to this simplification, as M was shown to be arbitrary, we will choose it to be the location of the minimum of the potential φ. The effective potential now reads V = λ 4! φ4 c + 3e4 64π 2 since φ is the minimum, we then have such that 0 = V ( φ ) = φ 3 c ( ln φ2 c φ ( ) λ 6 11e4 16π 2 ) (2.21) (2.22) λ = 33e4 8π 2 (2.23) which means that the quartic coupling is fixed when we choose a renormalization scale, which was also mentioned in the previous section. Coleman and Weinberg call this procedure of replacing the dimensionless quartic coupling by another free parameter, the dimensional φ, dimensional transmutation.this inevitably happens in a massless field theory when spontaneous symmetry breaking occurs, since the choice of renormalization scale defines the dimensionless couplings. Inserting (2.23) into (2.20) we find the final expression for the potential V = 3e4 64π 2 φ4 c ( ln φ2 c φ 1 2 ) (2.24) where the λ dependance is absorbed in φ. As spontaneous symmetry breaking has occurred in a trustable region we may now continue to calculate the spectrum of the theory, just as is done in the GWS model. The mass of the scalar is given m 2 φ = V ( φ ) = 3e4 8π 2 φ 2 (2.25) 16 Jens F. C. Krog
17 2.3. MASSLESS SCALAR ELECTRODYNAMICS and just as in the GWS model, we find that the mass of the vector, which is now no longer a photon, is given m 2 A = e2 φ (2.26) and we may calculate the mass ratio m 2 φ m 2 A = 3e2 8π 2. (2.27) With the assumption that e is small, which it had to be for the expansion to be trustable, although the constrains on λ are more strict, we then see that the scalar is relatively light compared to the vector boson of the theory. Although this is most likely not the case for the Higgs boson and the massive vector bosons of the standard model, it still shows that theories with this sort of symmetry breaking may produce relatively light scalar masses, which will become very important in the discussions later on. In their work CW also investigated what would happen if the mechanism of radiatively induces symmetry breaking was applied to the GWS model. Their approach was basically to calculate the effective potential from the known masses of the W and Z bosons, and what they obtained was a relation for the mass of the scalar m 2 s = 3 32π 2 [2g 2 m 2 W + (g 2 + g 2 )m 2 Z ] (2.28) where m W,Z is the mass of the W and Z bosons respectively, and g, g are the SU (2) and U (1) couplings. Coleman and Weinberg were very unimpressed by the amount of information that was extractable from enforcing a massless theory at tree level, since the only information that was obtained was a constraint on the mass of the scalar. This is natural, however, as they remark, because they have effectively just added one assumption of the system and therefore gain one relation. This was viewed as being mostly useless, because the available theories of the electroweak sector had either enough free parameters to always be able to match a mass constraint like this or not enough to ever be able to do so [6]. Now that we have seen a different mechanism for spontaneous symmetry breaking including massless fields, we will move on to investigations of more complicated models that behave similarly, but more closely resembles the dilatonic models that are the scope of this work. These models do not rely on the introduction of a gauge field with a weak coupling, bringing along radiative corrections, but instead that multiple scalar couplings, which are naturally of the same order, may be included in such a way that a nontrivial minimum appears. Jens F. C. Krog 17
18
19 CHAPTER 3 HIGGS PHYSICS WITH THE COLEMAN-WEINBERG MECHANISM Although Sidney Coleman and Erick Weinberg were not convinced that the mechanism they had analyzed was usable for electroweak phenomenology, Eldad Gildener and another Weinberg named Steven were [7]. Their reasons to suspect that the CW mechanism might be responsible for the breaking of electroweak symmetry, that Gildener and Weinberg (GW) offer, has their roots in the conjecture that the semi simple gauge group that constitutes the standard model is in fact embedded in a larger simple group. In this case, to explain why only a few of the gauge bosons of such a large group have been observed, one would naturally argue that the simple group has been broken down at a large energy scale and that the gauge bosons for the broken symmetries have therefore acquired so large masses, that they are unobservable to us. In this kind of theory, the physics of energies close enough to the reach of our experiments would be described by an effective theory, containing all the particles that have not acquired super large masses. It is reasonable to think that the gauge bosons associated with unbroken symmetries are among these, and to explain the observed leptons and quarks one could argue that other symmetries have protected them from getting large masses as well. Actually it is preferable that there are no large mass ratios in the original Lagrangian, so it is then reasonable to think that the observed particles are massless after the super strong symmetry breaking, and obtain their masses from a second symmetry breaking. If only the quarks, leptons and gauge bosons survive this super strong symmetry breaking, and the theory does not contain any elementary scalar fields, the masses of these particles must come from a so-called dynamical spontaneous breakdown, involving some sort of bound states. These bound states should be held together by some force that becomes strong around the electroweak scale. Indeed this is the essence of the technicolor models, originally presented in [8], which are still being investigated [9]. However this idea does not seem appealling to GW, since the normal strong force is much too weak at the electroweak scale, and theories with new strong 19
20 CHAPTER 3. HIGGS PHYSICS WITH THE COLEMAN-WEINBERG MECHANISM couplings at the time, often had problems with leftover massless scalar particles, which are not observed in nature. Additionally, a theory of strong interaction around the electroweak scale makes perturbative calculations of, for example, mass ratios impossible. In this work GW argue instead, that introducing an elementary scalar field, left massless by the super strong symmetry breaking, is the way to go. Even though they give no explanation to why the scalars should be protected from getting large masses by the super strong breaking, they argue that we have no idea of the nature of this symmetry breaking, and can at least imagine that it leaves some scalars massless. The massless scalars could then, in a manner like the one described by CW be responsible for the electroweak symmetry breaking, and the masses of the observed particles. An advantage of this is of course, that perturbative calculations of mass ratios are possible, since we require the scalar couplings to be weak, in order to do a loop expansion. What GW go on to do, is to try and generalize the work of CW to gauge theories of massless scalars and fermions, instead of just the one scalar and one vector field in the work described previously. 3.1 THE GILDENER-WEINBERG POTENTIAL ANALYSIS The outset of the GW analysis is to consider a general renormalizable gauge theory with a multiplet of real scalar fields, which are singlet under color, such that they cannot produce mass for the gluons. Once again an effective potential V (Φ) is considered, which is a function of the scalar multiplet Φ i. The potential is defined such that V (0) = 0 (3.1) and, just as in the case of the CW analysis, we assume the fields to be massless, so 2 V Φ i Φ j Φ=0 = 0 (3.2) In the CW analysis we could not define the quartic coupling at the origin, and here we will likewise define the quartic couplings 4 V Φ i Φ j Φ k Φ l Φ Λ = f i j kl (3.3) where it is assumed that cubic terms are excluded by some symmetry. Just as before, the couplings are then defined by an renormalization energy scale Λ, which will be chosen carefully as seen below. Furthermore it is assumed that a generic scale Λ, the nonzero components of f i j kl will be of order e 2, where e is a typical gauge coupling and e 1. With this assumption, an expansion in e 2 is the same as a loop expansion, and an analysis similar to the one of the previous section is possible. Note that in the CW case we 20 Jens F. C. Krog
21 3.2. COUPLING CONSTANT CONSTRAINTS put the quartic coupling of order e 4 instead, such that the one loop term was of the same order as the tree level potential. In this case, such a match is not possible, so something will have to happen to the tree level potential. As we saw in the previous section, a one loop expansion will introduce terms of the form ln(φ/λ), so if Φ Λ the potential will be dominated by the tree level term V 0 (Φ) = 1 4! f i j kl Φ i Φ j Φ k Φ l (3.4) In general, this term only has a stationary point at Φ = 0, and the one loop terms are of order e 4 Φ 4 ln(φ/λ), so to balance the two terms and find a new minimum we would require ln(φ/λ) to be of order 1/e 2, which puts us well outside of the perturbative regime. Thus, without modifications, we are unable to find a trustable minimum using perturbation theory. Luckily, we may modify our theory because the scalar couplings are defined from the energy scale at which we choose to renormalize our theory, and we can therefore change the couplings by redefining this scale. We will therefore choose a renormalization scale Λ GW, where the tree level potential (3.4) has a nontrivial minimum along a ray Φ i = φn i. This is done by adjusting the renormalization scale, so that the minimum of the tree level potential on the unit sphere in field space, denoted by the set of vectors N i where N i N i = 1, vanishes min (f i j kl N i N j N k N l ) = 0. (3.5) N i N i =1 For a given minimum that is a unit vector n i = N i, all field configurations along the ray Φ i = n i φ will be minima of the potential. In other words the, a rescaling of the configuration is always a minima, such that the potential is in fact scale invariant along a certain direction in field space. 3.2 COUPLING CONSTANT CONSTRAINTS In the analysis of CW, the constraint that allowed for a perturbative nontrivial minimum was that the quartic coupling λ e 4. Here this constraint has been relaxed, such that the quartic coupling can be a lot larger, with the result that a different constraint such as (3.5) must be enforced. The strength of this strategy is that there is now still a lot of free parameters in the f i j kl s, where as the scalar coupling was totally fixed by the scale in the CW case. To demonstrate the effects that these constraints have on a theory, we will consider the linear sigma model with a global SU (N f ) SU (N f ) symmetry, which will become the main subject of the rest of this work anyway. The original work was done by Gildener in his Ph.D thesis but was also published [10], and reviewed later by Paterson [11] because this model will be used extensively beyond this point, the notation will be slightly altered. We will assume that we work with a linear sigma model, where we have a complex scalar bifundamental with an SU (N f ) SU (N f ) global symmetry, and in the Jens F. C. Krog 21
22 CHAPTER 3. HIGGS PHYSICS WITH THE COLEMAN-WEINBERG MECHANISM Lagrangian the scalar fields are contained in a complex matrix H. The tree level potential of this theory is [ V 0 = u 1 (Tr H H ]) 2 + u2 Tr[(H H ) 2 ] (3.6) with the two quartic scalar couplings u 1,u 2. We may now, because of the symmetry of the theory, transform H to a diagonal matrix such that H = diag(h 1,h 2,...,h N f ). In this case the potential simplifies to V 0 = u 1 ( i ) 2 + u 2 h 4 i. (3.7) h 2 i i where we now have to find a scale Λ g w, with a given configuration h i where the tree level potential vanishes and is a minimum, i.e V 0 (h i,λ g w ) = 0 (3.8) V 0 (h i + δh i,λ g w ) 0 (3.9) for some shift δh i. As mentioned before, a vanishing of the tree level potential along a direction h i, means that it will vanish for any rescaled φh i, so we may, in our search for an extremum, restrict our configuration to be on the unit hypersphere, where i h 2 i = 1. If we add a Lagrange multiplier, λ, to enforce this condition, we find the extremum condition V 0 = 4h j (u 1 h 2 i h + u 2h j λ) = 0 h j = 0 h j = λ u 1 (3.10) j u 2 i which means that all the nonzero entries in h i must be of equal value, and since h i is on the unit sphere, in the case of n nonzero entries, these will all be h 2 i = 1 n (3.11) If this is inserted back into the potential (3.7) we then find that at the extremum V extremum 0 = u 1 + u 2 n. (3.12) As we are looking for a minimum, that has to satisfy (3.9), we may infer two possibilities for the number of nonzero entries n: A: n = N f, u 2 > 0, and u 1 + u 2 N f = 0 B: n = 1, u 2 < 0, and u 1 + u 2 = 0 22 Jens F. C. Krog
23 3.3. APPEARANCE OF A NONTRIVIAL MINIMUM where we have the restrictions on our quartic couplings. Here is also hints of the possibility of different symmetry breaking patterns, which we will return to comment on later. In the general case, the requirement (3.5), where we require that n i is a unit vector, guarantees that f i j kl n j n k n l = 0 (3.13) which is just an expression of stationarity. However, this only ensures us that, we are at a vanishing extremum. For the point to be a minimum, we need, for an arbitrary vector u i (not to be confused with the couplings from before) This means that all eigenvalues of the matrix f i j kl u i u j n k n l 0 (3.14) should be positive or zero. P i j = 1 2 f i j kl n k n l (3.15) 3.3 APPEARANCE OF A NONTRIVIAL MINIMUM As we have now established a vanishing minimum of the tree level potential along the ray Φ i = n i φ, we may investigate what happens when we turn on the higher order terms, δv (Φ). As in the CW case, we expect the potential to develop a new minimum, at definite value of the field φ,which is at a lower energy than the trivial minimum at the origin. The corrections produce a curvature in the direction of the ray of the minimum, thus breaking scale invariance along the ray. Besides from this, the loop corrections may produce a shift in the direction of the direction of the minimum, which should be small, such that the new minimum is at a point n i φ + δφ i. The stationary point will then satisfy the condition 0 = (V 0 (Φ) + δv (Φ)) Φ (3.16) i n φ +δφ which can be expanded to first order in small parameters δv, δφ 0 = P i j δφ i φ 2 δv (Φ) + Φ (3.17) i n φ with P i j defined above. From this we can determine the shift of the minimum δφ up to directions which are eigenvectors of the matrix P with eigenvalue zero. As we have already seen from (3.13) and (3.15), the direction of the ray n i is such an eigenvector. In addition, if the potential has some continuous symmetries for a shift δφ i = ɛθ i j Φ j, (3.18) Jens F. C. Krog 23
24 CHAPTER 3. HIGGS PHYSICS WITH THE COLEMAN-WEINBERG MECHANISM where ɛ is an infinitesimal number and Θ i j a generator of the continuus symmetry, these directions will also have eigenvalue zero. Thus all the eigenvalues of P are either zero or of order e 2, since P is of order f. We may expand our knowledge on the position of the minimum of the potential, by using the fact that the ray, along which the tree level potential vanishes, is an eigenvector of P with eigenvalue zero, such that if we contract (3.17) with n i, we find 0 = δv (Φ) δv (nφ) Φ = i n φ φ (3.19) φ which gives us the position of the new minimum φ. For a closer inspection of this minimum, and to see that it is in fact of lower energy than the minimum at the origin, we turn to the analysis general renormalizable gauge theory. For this section, we will modify the notation of GW slightly, to the one of Stephen Martin [12], since this will be reused for similar analysis later on. According to Martin, the one loop potential of such a theory can be written, in the MS scheme, in the Landau gauge, as V = V π 2 V 1 (3.20) where V 1, which is our higher order corrections δv, is given by ( [ ] [ ] 1 V 1 = (m 2 i 4 )2 ln m2 i i Λ (m 2 i 2 2 )2 ln m2 I I Λ [ (ma 2 4 )2 ln m2 a Λ 2 5 ]) 6 a (3.21) where the indexes, i, I, a correspond to the different scalars, fermions, and vector bosons of the theory, respectively. Λ is the renormalization scale. As we work in a massless theory, the only scale is the field φ, such that the squared masses m 2 i,m2 I,m2 a are all of proportional to φ2. At the scale Λ GW the tree level potential should vanish along the ray Φ i = n i φ, so we can write the total one loop potential on the form V = Aφ 4 + Bφ 4 ln(φ 2 /Λ 2 ) (3.22) where A and B both arise at the one loop level, and therefore are of order e 4. We now see that this potential has a nontrivial stationary point, which is defined at a value φ satisfying ln φ 2 Λ 2 GW = 1 2 A B. (3.23) As A and B are both of order e 4, this extremum is inside the perturbative regime. The reason that A is not of order e 2 is precisely that we have chosen a renormalization scale, where the tree level potential vanishes. 24 Jens F. C. Krog
25 3.4. SPECTRUM ANALYSIS From (3.22) we see that for the extremum to be a minimum, we must require B > 0, since the potential would be unstable for large φ otherwise. If B = 0 then the potential has exactly the form of the original quartic potential, except with a weaker coupling. For the theory to be interesting, we therefore need B to be positive, which is guaranteed if there is no fermions in the theory, or if the fermion couplings are very weak, as seen from (3.21). For further considerations the theory is defined such that the scalar and vector couplings and numbers are such, that the fermions do not dominate B. If we insert the extremum solution into (3.22) we see that the value of the potential at the minimum V (n φ ) = 1 2 B φ 4 (3.24) which means that the extremum is in fact of lower energy than the one at the origin, and this should imply spontaneous symmetry breaking. With this knowledge of the minimum of the theory, we go on to discuss the scalar masses. Even though the analysis above has produced a nontrivial minimum, one should remember that there might be several scales Λ where (3.5) is satisfied. In this case the true minimum of the theory is the one produced at a specific scale, where the energy is lowest. However, as we have seen, since the energy at such a minimum with broken symmetry is lower than the one at the origin, we can be guaranteed that the true minimum of the theory will be of broken symmetry. One should note here, that contrary to the work of CW [6], it has not been necessary to include any gauge fields to be able to obtain a symmetry breaking mechanism. 3.4 SPECTRUM ANALYSIS As we have found that symmetry is spontaneously broken, we may evaluate the zero order squared mass matrix (m 2 ) i j = 2 V 0 (Φ) Φ i Φ j n φ = P i j φ 2 (3.25) where P is the matrix from before. As already discussed, at the tree level, we will have a set of scalar particles with mass squared e 2 φ 2 corresponding to the directions of positive eigenvalues for P and a set of massless particles, corresponding to directions of the continuous symmetry (3.18) aswell as a massless particle along the eigenvector n i. The eigenvectors with zero eigenvalue and eigenvectors θn i correspond to Goldstone bosons [7], so we have a set of scalars with large mass of the order of the gauge bosons, a set of Goldstone bosons, and a massless particle corresponding to the zero order scale invariance. This last particle is therefore termed a "scalon" by Gildener and Weinberg, and is basically what will be called the "dilaton" in later sections. Jens F. C. Krog 25
26 CHAPTER 3. HIGGS PHYSICS WITH THE COLEMAN-WEINBERG MECHANISM As we turn on the higher order corrections, we shift the mass matrix as well as the position of the minimum, such that (m 2 + δm 2 2 ) i j = [V 0 (Φ) + δ(φ)] Φ i Φ j n φ +δφ which can, once more, be expanded to first order in small quantities, yielding (δm) i j = 2 δv Φ Φ i Φ j n φ (3.26) + f i j kl n k δφ l φ (3.27) For the heavy scalars, we need more information in order calculate their masses. However, as they have positive definite masses already at tree level, we expect their masses to stay approximately the same, since the one loop corrections should be a small perturbation. For the Goldstone bosons and the scalon, however, the story is different, since they have vanishing mass at the tree level. For the Goldstone bosons, GW assume that the only symmetry that is broken by the higher order corrections is the scale invariance corresponding to the scalon [7]. This means that the Goldstone bosons remain massless, and that the scalon develops a mass from the loop corrections. They remark that in a realistic model, one would need the Higgs mechanism to eliminate the Goldstone bosons, but offer no recipe for such a theory. For the scalon, we can evaluate its mass by contracting (3.27) with the scalon direction n i twice, which yields, by remembering (3.13) m 2 s = n i n j (δm 2 ) i j = n i n j 2 δv (Φ) Φ i Φ j n φ = d 2 V (nφ) dφ 2 (3.28) φ so if we return to our generalized theory, we may calculate the mass from the second derivative of (3.22) at the new minimum specified in (3.23), which yields m 2 s = 8B φ 2. (3.29) Summed up: the assumption that fermions do not dominate the one loop potential, it is clear that B > 0 and that the extremum is a minimum with negative energy and a positive mass for the scalon. With this information, it is clear that the matrix P has positive definite eigenvalues, and that the found extremum is a minimum. Note that the scalon has a lower squared mass than the other massive scalars of the theory, since its mass only becomes nonzero at higher order corrections, and therefore is, at most, of order e 4. As mentioned previously, this is a feature often shown in these kinds of theories, and we once again produce a mass which is substantially smaller than the scale of the theory, defined by φ. With this machinery set up GW set out to see whether they can deduce some implications on the mass of a scalon that plays the role of the Higgs boson. The general procedure is to divide the many scalar fields into a number doublets, to 26 Jens F. C. Krog
27 3.4. SPECTRUM ANALYSIS gauge under the electroweak SU (2) U (1) gauge, such that an expectation value of the scalon field gives mass to the W and Z bosons. These masses can of course be inserted into (3.28), and the fermion masses are ignored, based on the fact that the, at the time known, standard model fermions are much lighter than the vector bosons(the top quark was not discovered until more than 20 years later). As the unknown scalar masses only contribute positively to the mass of the scalon, GW are able to set a lower bound of ms 2 5.3GeV, while their best bet for the value of the weak mixing angle would give a lower bound of about 7 GeV. Both of these numbers are subject to large corrections from the inclusion of the heavier scalar particles, which would make it possible to get to the 125 GeV which seems to be a good bet today. As should now be obvious, the phenomenological implications of the Gildener- Weinberg analysis are not that much greater than what Coleman and Weinberg obtain a couple of years earlier, although they claim to be able to give a lower bound on the mass of the Higgs boson, which is possible only because they assume that fermions are negligible. In summation, the assumption of a massless theory before symmetry breaking yields a constraint on the mass of the light scalar, and assuming negligible fermion contributions, this becomes a lower bound. As we have seen some results for the case of general renormalizable gauge theories, we will turn our attention once again to the linear sigma model and see how the symmetry breaking mechanism of Coleman and Weinberg takes place here, and especially see that there are different symmetry breaking patterns that can occur, such that these theories have different phases. Jens F. C. Krog 27
28
29 CHAPTER 4 PHASE TRANSITIONS IN THE LINEAR SIGMA MODEL As the scope of this work is to deal with models containing the linear sigma model along with a set of fermions, it is worthwhile to consider a deeper analysis of how the CW phenomenon occurs in such a model, which has been done by A.J. Paterson [11]. In this section we will discuss different symmetry breaking patterns, and see how the general work of GW can be used in a specific linear sigma model, by invoking a nontrivial but useful notation. The reasons, submitted by Paterson, for studying the CW phenomenon such models is partly, what we have already seen, that the CW mechanism may provide a lower bound for the mass of the Higgs. People fond of linear sigma models for the description of electroweak theory may then be able to constrain the Higgs mass if the model exhibits the CW mechanism. Also, the SU (N ) SU (N ) model was thought to be able to describe the origins of composite scalar fields that could break the electroweak symmetry. The SU (N ) SU (N ) symmetry of some N new fermions would be broken by a new strong force, which should then bind composite states together to be the needed Goldstone bosons for electroweak symmetry breaking [8]. Paterson calls the force that binds such composite states together "Heavy Color", and it may readily be identified with the technicolor force of the recently discussed theories of the same name [13]. 4.1 THE MODEL The essence of the SU (N ) SU (N ) linear sigma model is that it is constructed from a matrix of complex scalar fields, constructed from the matrices M ab and M ab in the notation of Paterson. If one then invokes a SU (N ) SU (N ) transformation, the fields M, M will transform as M M = U MV M M = V M U (4.1) 29
30 CHAPTER 4. PHASE TRANSITIONS IN THE LINEAR SIGMA MODEL where U,V SU (N ). From here on we will always work in the case of N > 2, and we may then write M = (σ a + iφ a )T a (4.2) where σ a,φ a are scalar fields and T a are the generators of SU (N ) where we include T 0 = 1 2N Note that in [11] the indices are capitalized, but we have changed the notation as well as the normalization for future convenience. With this normalization we deviate from the notation of Paterson, such that the numeric factors in our expressions will be different from the results of [11] but the structure the same. The most general SU (N ) SU (N ) invariant Lagrangian we may write is then given, in d = 4 ɛ < 4 dimensions (as is the preferred description for Paterson), in the form L =Tr[ µ M µ M ] + m 2 Tr[MM ] + kɛ 4! u 1(Tr[MM ]) 2 + kɛ 4! u 2(Tr[MM MM ]) + CT (4.3) where CT are counter terms, and k is an arbitrary renormalization mass. As it is now the trend in these theories, we will set the mass m = 0. As will become important later, this Lagrangian is actually also invariant under an arbitrary global U (N ) U (N ) transformation, where the U,V from the transformations (4.1) now belong to U (N ). 4.2 BETA FUNCTION ANALYSIS In order to discuss the CW symmetry breaking and the different phases of symmetry breaking Paterson starts by obtaining the beta functions for the scalar couplings. As it is not entirely trivial to obtain the beta functions for quartic couplings of the sort u 1,u 2 presented in (4.3) we will briefly review the strategy of Paterson for future reference. The general idea is to convert the contracted Lagrangian (4.3) to one of the standard form L = 1 2 µψ i µ ψ i + kɛ 4! u i j kl ψ i ψ j ψ k ψ l + CT (4.4) where u i j kl is totally symmetric in its indices, since this yields the beta functions [11] β i j kl = k u i j kl = ɛu i j kl + 1 [ ui j pq u pqkl + 2perms ] (4.5) k 16 The task is now to convert the trace terms of the quartic couplings in (4.3) to a contraction of some tensors and the scalar multiplet φ a. Paterson thus defines two tensors P (1),P (2) for this task such that (Tr[M M ]) 2 = P (1) ABCD φ Aφ B φ C φ D (4.6) Tr[MM MM ] = P (2) ABCD φ Aφ B φ C φ D (4.7) 30 Jens F. C. Krog
31 4.3. THE CW MECHANISM IN THE EFFECTIVE POTENTIAL where we once again deviate from the notation of [11]. The capital indexes here correspond to the combination of the two indexes used by Paterson, such that A runs from 0 to 2N 2 1, double the range of a, to include both the the σ and iφ in the bifundamental scalars. The details of this will be presented, when needed, in Chapter 7. With this notation we may write the Lagrangian of the theory as L = 1 2 µφ A µ φ A + kɛ 4! R ABCDφ A φ B φ C φ D + CT (4.8) where the quartic coupling tensor R ABCD = ( u 1 P (1) + u 2 P (2)) ABCD, and we may calculate the beta functions β ABCD = k ( u1 P (1) + u 2 P (2)) ABCD k = β 1P (1) ABCD + β 2P (2) (4.9) ABCD where β 1,β 2 are the beta functions for u 1,u 2 respectively, and Paterson obtains from (4.5) β 1 = ɛu [ 1 8π 2 3 (N 2 + 4)u ] 3 Nu 1u 2 + u 2 (4.10) β 2 = ɛu [ 8π 2 2u 1 u ] 3 Nu2 2 (4.11) These beta functions only have fixed points in the trivial point (u 1,u 2 ) = (0,0) and in (u 1,u 2 ) = (8π 2 3ɛ/(N 2 + 4),0), and neither of these are all direction IR stable [11], as will also be clear from plots of the coupling constant flows later on. The absence of all directions stable IR fixed points are interpreted by Paterson as a hint that the symmetry breaking in the theory is first order, as will be confirmed later. From here Paterson turns to an analysis of the effective potential to see what kind of symmetry breaking patterns may be observed depending on the starting conditions for the couplings u 1,u THE CW MECHANISM IN THE EFFECTIVE POTENTIAL With the beta functions, and thereby the running of the couplings, in place, we now turn our attention to the question of whether symmetry breaking occurs in the model. Just as CW argue in their original paper [6], Paterson sets out to use the effective potential in order to investigate whether the model will exhibit spontaneous symmetry breaking. His recipe for calculating this potential is the expansion V (φ c ) = N=1 1 N! ΓN A 1 A 2...A N (0)φ c A 1 φ c A 2...φ c A N (4.12) where Γ N A 1 A 2...A N (0) is the N -point 1PI vertex function evaluated at zero external momentum, like it is in the CW paper, and φ c A are the classical fields. Note that Jens F. C. Krog 31
32 CHAPTER 4. PHASE TRANSITIONS IN THE LINEAR SIGMA MODEL this expression covers both the loop expansion and summation over the infinite number of diagrams with equal number of loops. As noted before, if one finds a vacuum expectation value φ c A 0, then spontaneous symmetry breaking has occurred, assuming that the theory is source free, translational invariant and that there was a symmetry to begin with. As Paterson is also concerned with the order of the phase transition, he remarks that in the CW mechanism the vacuum expectation value (vev) persists to be nonzero, even though the masses have been set to zero, such that it is a first order transition. This is contrary to the GWS model, where the vev of the scalar field goes to zero along with the mass. Paterson then goes on to calculate effective potential at one loop, to be able investigate the symmetries and size of the perturbations of it, and obtains [11] V (1) (φ c,u i,k) = 1 4! Rφ4 c + 1 ( [(Rφ 256π 2 Tr 2c )(Rφ2c ) ln Rφ2 c 2k 2 1 )] (4.13) 2 As the potential is now known, we may begin to investigate the nature of the symmetry breaking, if it occurs at all. For this, we must recall the analysis by GW, and especially the conditions (3.5) and (3.14). Paterson now reviews the procedure of [10] and finds the two possibilities, from before, that satisfy the constraint that the tree level potential vanishes and is a minimum, heralding the onset of the CW mechanism; M is set to be diagonal with n nonzero values in the diagonal which all equal 1/ n A: n = N, u 2 > 0, and u 1 + u 2 N = 0 B: n = 1, u 2 < 0, and u 1 + u 2 = 0 If we can show that we can always choose our initial couplings u 1,u 2 such that either A or B will arise, then the CW mechanism will induce spontaneous symmetry breaking. In Figure 4.1 the flows of the coupling constants, calculated from the beta functions (4.10),(4.11) are plotted along with lines corresponding to u 1 + u 2 N = 0 for u 2 > 0 and, u 1 + u 2 = 0 for u 2 < 0 for two values of N. As is seen from the figure, all of the coupling constant flows will eventually run into one of the two boundaries where the CW mechanism will set in, besides from the flow at u 2 = 0. If we start at a scale k = k 1, where the tree level potential does not have a nontrivial minimum, i.e where the value of V 0 at the extremum is larger than 0, meaning that we are on the right-hand side of the two boundaries where the potential will vanish at the extremum, then we will always flow into a region where V 0 = 0 by decreasing the scale k. Hence CW symmetry breaking will always be possible in this model, if one chooses the right scale k 0 where one of the conditions above are satisfied. 4.4 PATTERNS OF SYMMETRY BREAKING As already mentioned, the field configuration that minimizes the potential depends on the sign of the u 2 coupling, which means that different symmetry break- 32 Jens F. C. Krog
33 4.4. PATTERNS OF SYMMETRY BREAKING u u Figure 4.1: The coupling constant flows for the quartic couplings of the SU (N ) SU (N ) linear sigma model, for N = 3 to the left and N = 10 to the right. The conditions for the onset of the CW mechanism, u 2 > 0 u 1 + u 2 N = 0 (u 2 < 0 u 1 +u 2 = 0) have been marked in red (green) 1 ing patterns may arise depending on the value of this coupling, as a coupling constant flow reaches the region of spontaneous symmetry breaking. In order to use the remaining analysis from GW, Paterson shows that the one loop corrections to the effective potential are invariant under a generic SU (N ) SU (N ) transformation, such that the Goldstone bosons of the broken symmetries remain massless at one loop. He then goes on to calculate the eigenvalues for the zero mass matrix corresponding to (3.25). In the case of A above, Paterson finds that there are N 2 1 heavy massive fields, corresponding to σ a, a = 1,2,... N 2 1 in the notation of (4.2), aswell as N massless fields, corresponding to the N 2 Goldstone fields, φ a, and σ 0 in the same notation. The σ 0 field is exactly the in direction of the ray that minimized the tree level potential, and obtains a small mass from one loop effects. In the case of B, Paterson finds 2(N 1) 2 fields with zero order masses and 4N 3 goldstone fields aswell as one pseudo goldstone field which once again does not obtain a mass until the one loop effects are taken into account. The two symmetry breaking patterns break the theory down to the diagonal U (N ) and the U (N 1) U(N 1) U(1) subgroups of the original U (N ) U N symmetry, respectively [11]. For future reference, we will mainly be concerned with symmetry breaking patterns of the first type, as we would like to be in the large N limit, but this will be clarified as we go on. It is worthwhile, however, to note that already in the pure scalar theory, there are different phases in the model, and in models considered later on, we will see that there can be conformal phases besides the ones of broken symmetry. Thus we have seen that if we renormalize our theory at a scale k 1 where the SU (N ) SU (N ) symmetry is unbroken, then spontaneous symmetry breaking will occur by the CW mechanism as we move along the renormalization flow to a lower Jens F. C. Krog 33
34 CHAPTER 4. PHASE TRANSITIONS IN THE LINEAR SIGMA MODEL energy scale k 0. Before we begin working on the so-called Dilaton model that are the scope of this work we will examine how evidence of symmetry breaking can be inferred from the coupling constants and their beta functions alone, which will provide us with some useful tools for future analysis. 34 Jens F. C. Krog
35 CHAPTER 5 COUPLING-CONSTANT FLOWS AND DYNAMICAL SYMMETRY BREAKING is exactly the title of a paper by H. Yamagishi, which shows, very briefly, how the Coleman-Weinberg theory can be investigated directly from the coupling constants and their beta functions for scalars in a gauge theory [14], where Paterson only considered a pure scalar theory. The theory leads to a very nice geometrical way of investigating the phase diagrams of such theories, which will be shown below. 5.1 SOLVING THE CALLAN-SYMANZIK EQUATION By following the procedure of Yamagishi, we will once again consider the effective potential V (φ) (the c from before has been dropped, such that φ is the classical field) of the theory. This time we will enforce the fact that the potential should remain invariant under renormalization, such that if the scale of renormalization is changed, the explicit scale dependence in the potential is compensated by a rescaling of the coupling constants and the anomalous dimension. This is contained, in an elegant fashion, in what is called the renormalization group equation or the Callan-Symanzik equation, [ M M + i β i ] + γφ V (φ) = 0 (5.1) λ i φ where β i is the beta function for the coupling λ i, γ is the anomalous dimension, and M is now (as in the paper by CW) the renormalization scale. For the case of massless electrodynamics, which is considered by Yamagishi, i β i = β λ i λ + β e e (5.2) such that β is the beta function for the quartic scalar coupling λ, and β e is the beta function for the electric coupling e, and these are all the couplings of the theory. 35
36 CHAPTER 5. COUPLING-CONSTANT FLOWS AND DYNAMICAL SYMMETRY BREAKING As V /φ 4 is dimensionless it must be given by some dimensionless function, and Yamagishi gives us the general solution, which was also presented in [6]; ( t ) V (φ) = f (λ(t),e(t))φ 4 γ(t) exp 4 dt (5.3) 1 γ(t) where the function f and anomalous dimension γ, are functions of the running couplings λ(t),e(t) and they all depend on t = ln(φ/m). To gain some understanding of how the formalism changes when the parameter t is introduced, it is worthwhile to check that this a solution, and what it says about the parameters of the theory. If we differentiate the potential (5.3) with respect to the scale M and φ respectively, we find M V M = M ( [ t ]) f φ 4 γ exp 4 dt M 0 1 γ ( λ = t λ + e t e + 4 γ ) V (5.4) 1 γ and φγ V φ = φγ φ ( λ = γ t ( [ f φ 4 exp 4 λ + e t 0 t 0 e γ ]) γ dt 1 γ ) V (5.5) If we now define our beta functions such that the running couplings they satisfy the differential equations λ t = β 1 γ e t = β e 1 γ we find, as expected, that ( M M + φγ ) ( V = β φ λ + β e e (5.6) ) V (5.7) and V satisfies the Callan-Symanzik (CS) equation (5.1). We will define our coupling constants to be solutions to the differential equations (5.6), with the initial conditions, λ(0) = λ e(0) = e (5.8) which basically correspond to our renormalization conditions at φ = M; V (M) = λ 4! M 4 (5.9) such that we obtain from (5.3) V (φ) = λ(t) ( φ 4 exp 4 4! t 0 ) γ(t) dt 1 γ(t) (5.10) 36 Jens F. C. Krog
37 5.2. CONDITIONS FOR SYMMETRY BREAKING 5.2 CONDITIONS FOR SYMMETRY BREAKING From this expression for the effective potential, we may now investigate what the conditions for spontaneous symmetry breaking are. To begin with, the potential must have a nontrivial extremum at φ 0 0 such that 0 = V φ = φ3 0 β(t 0 ) + 4λ(t 0 ) φ0 4! 1 γ(t 0 ) ( exp 4 t0 0 ) γ(t) dt 1 γ(t) (5.11) Furthermore it must be a minimum, so the second derivative should be positive; where we have the rather ugly ( 0 < 2 V φ 2 = φ2 0 κ(t 0 ) φ0 4! [1 γ(t 0 )] 2 exp 4 t0 0 ) γ(t) dt 1 γ(t) κ = β e β e + β β + 4β + (β + 4λ)(1 γ) + 4(β + 4λ)γ λ which however simplifies, since β(t 0 ) + 4λ(t 0 ) = 0 from (5.11), such that the last two terms vanish and κ(t 0 ) = β e β e + β β + 4β. (5.12) λ Last, we see that for the φ 0 to be a global minimum, we need 0 > V (φ 0 ) = λ(t) φ 4 0 (4 4! exp t 0 ) γ(t) dt 1 γ(t) (5.13) The combined constraints on the couplings and their beta functions for a nontrivial global minimum to appear is then that for a given value of the coupling t 0 β + 4λ = 0 (5.14) and κ > 0 λ < 0 (5.15) where the first constraint specifies a specific line in coupling space and the last two are regions. Thus if a renormalization flow crosses the curve (5.14) in the region (5.15), then spontanenous symmetry breaking will occur. With knowledge of the beta functions and thereby of the flows of coupling constants in a given theory, by doing a similar analysis of the potential, it becomes easy to visualize the conditions for symmetry breaking, which will be shown below. Jens F. C. Krog 37
38 CHAPTER 5. COUPLING-CONSTANT FLOWS AND DYNAMICAL SYMMETRY BREAKING 5.3 GEOMETRICAL EXAMPLE For demonstration of the use of the geometrical interpretation, we will return (almost) to the model considered by Coleman & Weinberg, the massless electrodynamics, although with an added N fermions. The beta functions for the two couplings are then β = 1 24π 2 (5λ2 18λe e 4 ) (5.16) β e = 1 + 4N 48π 2 e3 (5.17) For the current illustrative purposes, we will not go into rigorous detail concerning the specific points of phase transitions in coupling space, but the interested reader may go on to study the analysis of [14]. In the simplest analysis, we should note that there is only one fixed point for these beta functions, which is the trivial one at e = λ = 0, since at one loop, the beta function for the electric coupling β e e 3. This fixed point is IR unstable in the λ direction. The fate of the system should therefore depend on the starting position in coupling space relative to this fixpoint. 2 1 Λ e Figure 5.1: The coupling constant flows for massless electrodynamics with 4 fermions. Marked in blue is the region in coupling space where (5.15) is satisfied, and the dashed line corresponds to the curve (5.14). If the flow for a given theory crosses the dashed line inside the blue region, the improved one loop potential will have a nontrivial global minimum, and spontaneous symmetry breaking will occur by the CW mechanism. The green line indicates a specific region in coupling constant space, that separates a nearly noninterating phase with an interacting one. 38 Jens F. C. Krog
39 5.3. GEOMETRICAL EXAMPLE The flows for the two couplings e,λ are shown in Figure 5.1. The region where (5.15) is satisfied is indicated by the blue shading, and the curve (5.14) is marked in red. As is indicated in the Figure 5.1 the region where (5.15) is satisfied is basically just everywhere where λ < 0, since κ is positive in the whole, at one loop, trustable perturbative region. (Solving κ = 0 analytically in Mathematica, results in solutions around (e, λ) = (7, 100), which is well outside the perturbative region, and in the region where are considering, numerical evaluation shows that κ is positive) As it appears, all RG flows will at some point cross into a region of spontaneous symmetry breaking, although the resulting spectrum will depend on the starting point. Around λ = 0, the evolution of the theory is mainly in the e direction, and flows with a low e will end up with a very small e value when symmetry breaking occurs, resulting in a very light spectrum. It would seem that moving closer and closer to the e = 0 starting point will decrease the mass of resulting spectrum correspondingly, as expected. The behavior is not entirely trivial though, as the phase structure seems to hold a nearly noninteracting phase, and one with stronger interaction, separated by the green line (which is only a qualitative marking, as no flows with e 0 will run directly into the fixed point). This form of symmetry breaking is said to be of the CW kind by Yamagishi [14], even though the analysis is quite different than the one done in their original paper [6]. The difference here is that, instead of calculating the effective potential and balancing terms from different orders in perturbation theory or simply ensuring that the tree level contributions vanish, the coupling constants themselves evolve with the renormalization theory and the potential acquires a new minimum through these improved couplings. Where Paterson used the beta functions to show that one could define the theory such that it would flow into a region where the tree level potential satisfied the requirements for the CW mechanism, the work of Yamagishi reads of symmetry breaking directly from the beta functions and the couplings. This new geometrical way of investigating the phase diagram of a theory will be deployed for the more complex theories that will be the subject of the next sections. Jens F. C. Krog 39
40
41 CHAPTER 6 A NEAR-CONFORMAL MODEL FEATURING THE DILATON The work of the previous sections has enabled us to engage in the analysis of a specific model, presented in [15]. The model is basically a Bank-Zaks model [16], an SU (X ) gauge theory with 2N f fermion flavors transforming under the fundamental representation of the gauge group, but with the addition of a scalar sector of the form of [11] along with an extra adjoint fermion. The addition of a Bank- Zaks sector aswell as an adjoint fermion will be shown to produce a fixed point structure with some highly interesting features. 6.1 THE THEORY, ITS BETA FUNCTIONS AND THEIR FIXED POINTS The theory that we investigate is an SU (X ) gauge theory with 2N f fermion flavors q, q and a SU (N f ) SU (N f ) scalar bifundamental H, like the one in [11], which is singlet under the gauge group, as well as an adjoint fermion λ m. The Lagrangian of the theory is thus L =L K (G µ,λ m, q, q, H) + y H qh q + h.c 2 [ u 1 (Tr[H H ]) u2 Tr (H H ) 2] (6.1) where L K contains the kinetic terms of the Lagrangian, including the covariant derivatives for the fermions (D µ λ m ) a = µ λ a + i f abc G b µ λc (6.2) (D µ q) i = µ q i i gg a µ T a i j q j (6.3) ( D µ q) i = µ q i + i gg a µ T a i j q j (6.4) where the indexes a,b,c = 1,..., X 2 1, T a are the generators of SU (X ), and the indexes i, j = 1,..., N f are the flavor indexes. The explicit forms of these derivatives are shown here, since we would like to modify the theory by including electroweak interactions later. 41
42 CHAPTER 6. A NEAR-CONFORMAL MODEL FEATURING THE DILATON The Bank-Zaks sector of this theory has a nontrivial fixed point if N 9 2 X, and because of authors interest in near conformal dynamics we will stay close to this limit, by defining x = N f /X = 9 2 (1 ɛ), where we now have a small expansion parameter in ɛ. The possibility for a nontrivial fixed point emerges because the first coefficient of the beta function for the gauge coupling vanishes when x = 9 2, such that by tuning x we may set it to be of the order of the assumed small gauge coupling g in the second coefficient. As we would like to be able to tune x continuously, while N f and X are integers, we will go to the large N limit where N f, X, but where x stays fixed and may now be tuned virtually continuously. Working in this limit, we will redefine our couplings for convenience, such that a g = g 2 X (4π) 2, a H = y 2 h X u 1 N 2 (4π) 2, z f 1 = (4π) 2, z 2 = u 2N f (4π) 2 (6.5) The beta functions are then given [15] β(a g ) = 2ag [3 2 2x3 ( x ) ] a g + x 2 a H 3 [ ] β(a H ) = 2a H (1 + x)ah 3a g (6.6) (6.7) β(z 1 ) = 4(z z 1z 2 + 3z z 1a H ) (6.8) β(z 2 ) = 4(2z z 2a H x 2 a2 H ) (6.9) where the explicit dependence on N f and X has vanished, and all terms 1/X have been dropped. In these calculations, the gauge beta function has been calculated to two loops, as the first coefficient is being tuned to be small here. The coefficients of the other beta functions are not tuned in this fashion, so in the perturbative regime we only need to consider the one loop expressions. As the quartic scalar couplings do not contribute to the runnings of the Yukawaand gauge couplings, the fixed points are not hard to find, and indeed, to the lowest order in ɛ, we find the fixed point values of the couplings a g = 11 9 ɛ, a H = 2 3 ɛ, z 1 = 2 19 ± 2( ) 6 ɛ, z 2 = ɛ (6.10) 6 The fixed point corresponding to the upper sign in z 1 is all directions IR stable, while the other is unstable in the z 1 direction only. This means that it is meaningful to assume that the gauge and Yukawa couplings are set at their fixed points and to examine the renormalization group(rg) flows in z 1 and z 2 which is done in Figure 6.1 for ɛ = 0.1. As seen in Chapter 5 the knowledge of the flows of the coupling constants may show us the phase space of the theory if coupled to knowledge of the effective potential, which is what we will seek in the next sections. 42 Jens F. C. Krog
43 6.2. GILDENER-WEINBERG ANALYSIS OF THE EFFECTIVE POTENTIAL z Figure 6.1: The RG flow of the quartic couplings displaying the two fixed points for ɛ = GILDENER-WEINBERG ANALYSIS OF THE EFFECTIVE PO- TENTIAL As we now know the dynamics of the theory, we might investigate the phase diagram by finding the proper conditions for symmetry breaking to occur, which requires knowledge of the effective potential. The analysis of the effective potential will follow the trail of thought presented in Chapter 3, where we will write the effective potential at one loop on the form V (1) = V 0 +V 1 (6.11) where we assume that there is a scale M 0, at which the tree level potential V 0 vanishes and is a minimum in some direction in scalar field space χ i = χn i. We then know that the effective potential equals the one loop contribution, and can be put on the form V (1) = φ 4 c (A + B ln(φ c/m 0 )), where φ c is the classical field. As mentioned in Chapter 3, this means that we develop a global minimum as long as B > 0, producing a vacuum expectation value for the φ c 0. This leads to a mass of, what Gildener and Weinberg called the "scalon", but which will from now on be named the dilaton, of m 2 d = 8B φ c 2. As B is simply extracted from (3.21), we see that the mass of the dilaton (in this specific model without vector bosons) is given, m 2 d = 1 8π 2 φ c ( ) (m 4 scal ar ) i (m 4 f er mion ) i. (6.12) i As is noted in [15], just as in the paper by CW, the masses at the order of the cutoff, which arise from quantum corrections are subtracted away, leaving it to some- Jens F. C. Krog 43
44 CHAPTER 6. A NEAR-CONFORMAL MODEL FEATURING THE DILATON one else to solve the hierarchy problem. We should note, however, that because we assume that B > 0, we impose some conditions on the relations between the numbers and masses of the scalar and fermion particles. As for the masses of the particles in the theory, they depend on the the symmetry breaking pattern, and how the matrix of the bifundamental Higgs field H i j will acquire a vev. As we saw in Chapter 4, two symmetry breaking patterns are available to the pure scalar sector of this theory; the conditions A and B from above, corresponding to a vev along the diagonal of H or along just one position in the diagonal, respectively. With the rescaled couplings, the conditions can be rewritten such that A: z 0 2 > 0, and z0 1 + z0 2 = 0 B: z 0 2 < 0, and z0 1 + z0 2 N f = 0 where it is made clear by the superscript 0 that this is true at the scale M 0. As we would like to set N f, it is clear that B will never be satisfied, so we will assume that the symmetry breaking pattern is the one of condition A, the diagonal SU (N f ) SU (N f ) SU (N f ), and we will only consider the coupling space for z 2 > 0. In this case we will denote the vev of H i j H i j = v 2N f δ i j (6.13) where v is a real constant, and the denominator takes care of canonical normalization. The scalar spectrum is now straightforward computable, by inserting the vev in the Lagrangian, and expanding around it. As the scalar sector is a SU (N f ) SU (N f ) linear sigma model, we may expand around the vev such that H = v + φ + iψ 2N f 1 + (h a + iπ a )T a, (6.14) much as it is done in [11] although with the normalization Tr[T a T b ] = δab 2. Along expanding about the diagonal value, at the scale M 0, we find the tree level masses for the scalar fields presented in Table 6.1, where we have used the convenient rewritings a φ = (4π) 2 3(z0 1 + z0 2 ) N 2 f a h = (4π) 2 z z0 2 N 2 f a ψ = a π = (4π) 2 z0 1 + z0 2 N 2 f (6.15) (6.16) (6.17) 44 Jens F. C. Krog
45 6.2. GILDENER-WEINBERG ANALYSIS OF THE EFFECTIVE POTENTIAL The expansion around the diagonal also produces a mass term for the fermions m 2 q q = (4π)2 a0 H xv2 2N 2 f (6.18) which now enables us to calculate the effective potential from (3.21) and the dilaton mass from (6.12). scalar m 2 i (v) φ a φ v 2 ψ a ψ v 2 h a h v 2 π a π v 2 Table 6.1: The tree level masses of the scalars, where we have expanded around a diagonal background vev. To begin with, we can easily see that the constraint z1 0 + z0 2 = 0 renders the diagonal direction, to be identified with the dilaton, massless along with the ψ and π directions. This should not be surprising, as it was already stated by Paterson in [11]. We therefore remain with N 2 1 massive h scalars, which we will call "heavy f Higgses". Combining the scalar and fermion masses in (6.12) then leads to the dilaton mass [ m 2 d = 2(4π)2 v 2 N 2 f 1 ] N 2 N 2 4(z2 0 )2 (a 0 H )2 x 2(4π)2 v 2 N 2 f f f [ 4(z 0 2 ) 2 (a 0 H )2 x ] (6.19) where we have dropped the 1/N f terms. The important features about this is that, by tuning the scalar and quartic couplings, we may make the dilaton arbitrarily light without turning off interactions, as well as the fact that there is a bound on the relations of the couplings z2 0 and a 0 H, since the dilaton mass needs to be positive for the nontrivial extremum to be a minimum. The solution to the latter, adopted by CW and GW, was to assume that the fermions played no essential role, which made sense because the fermions in their models were the, at the time, known quarks which were very light compared to the vector bosons which were also included. Here the fermions that enter in the theory will not be identified with known fermions, so their masses can only be assumed to not violate the criteria given above. The careful reader might have observed that all of the masses given so far have been inversely proportional to N 2, which might lead to a massless theory in the f large N limit. However, as we shall show, v N 2, such that all physical masses in f the theory, which are not exactly zero, have finite nonzero values. Given the tree level masses mentioned above, the effective potential in the diagonal direction, at Jens F. C. Krog 45
46 CHAPTER 6. A NEAR-CONFORMAL MODEL FEATURING THE DILATON the scale M 0, where z 1 + z 2 = 0, is given from (3.21) to be ( V = 4π2 φ 4 c N 2 f 4(z 0 2 )2 ln(2z 0 2 ) (a0 H )2 x ln(a 0 H x) + [ 4(z 0 2 )2 (a 0 H )2 x ] ln 8π2 φ 2 c M 2 0 N 2 f ) (6.20) where we can easily identify A and B from (3.22) and find the minimum through (3.23) generating the vev v = φ c M v 2 0 2N 2 f = 8π 2 e 1 2 4(z0 2 )2 ln(4z 2 0) x(a0 H )2 ln(xa 0 H ) 4(z 2 0)2 x(a h 0 )2 (6.21) hence the masses defined above are independent on N f. From here it is also obvious that the vev is directly given from the scale M 0, where the tree level potential vanishes. This gives us the necessary information to begin the geometrical analysis to see how which phases exist in the theory in the spirit of [14]. However, we will first take a small detour to justify renaming the pseudo-goldstone boson, which acquires a mass from broken scale invariance, the dilaton. 6.3 ENTER: "THE DILATON" The name "dilaton" always comes along with the definition of a Goldstone boson originating in spontaneously broken scale invariance [17], [15], [18]. However, as noted in [17], a theory may have multiple massless or light spinless fields that could be identified with the dilaton, so a more rigorous definition is needed, which will be given below. If a theory has scale invariance at the classical level, which theories without dimensionful couplings do, meaning that the Lagrangian is unaltered by a scale transformation, which acting on a scalar field χ(x) with canonical mass dimension 1 gives χ(x) e σ χ(e σ x). (6.22) As the theory has a symmetry, a corresponding conserved current must be given µ D µ = 0 (6.23) which is called the dilatation current. This current is simply related to the so-called improved energy-momentum tensor Θ µν, which is basically just the regular energy-momentum tensor converted to a symmetric and gauge invariant version that does not depend on the renormalization cutoff of the theory. [4], [19] µ D µ = Θ µ µ (6.24) such that as long as the trace of the improved energy momentum tensor vanishes, the theory remains scale invariant. 46 Jens F. C. Krog
47 6.3. ENTER: "THE DILATON" As quantum corrections are introduced however, the couplings of the theory will depend on the scale, such that under scale transformations, the couplings are shifted g i g i + σβ(g i ) (6.25) which means that the Lagrangian is shifted L = L + σ i β(g i ) g i L (6.26) and the dilatation current equation, for a theory which classically is scale-invariant, is now µ D µ = Θ µ µ = β(g i ) L, (6.27) i g i and a nonzero value of this trace is appropriately called a trace anomaly. While the latter equations are not needed to define the dilaton state, they will become very useful when computing which state it is in our theory later on. We will use the following definition for the dilaton: The dilaton is the state D that is created from the vacuum from the spontaneously broken dilatation current D µ. The dilaton mass m D and decay constant f D are defined from 0 µ D µ D = f D m 2 D (6.28) Now, as already stated, coupling to the improved energy-momentum tensor may occur for numerous scalar particles, and as we have quite a few at our disposal in this theory, we would need to distinguish the dilaton from the rest of them. The following requirements are given for the dilaton in [17]: 1: It must be a state that couples most strongly to the the energy-momentum tensor 2: It must be the lightest particles that does so. where by most strongly, we will adopt the convention that by expansion of Θ µ µ around the vev of the theory, we will consider the field that appears at the lowest order to be the one coupling most strongly. As noted earlier, we would like to work in the sector, where we are very close to the fixed point for the Yukawa and gauge couplings, such that the beta functions β(a g ),β(a h ) 0, and we may neglect these terms when doing the calculations for (6.27). At tree level we therefore only consider the contributions from the quartic terms 2 [ u 1 (Tr[H H ]) + u2 Tr (H H ) 2], while expanding about the vev (6.13), where we will now look for the fields that contribute linearly. As seen from the expansion (6.14) the ψ,π will not contribute at this level, because linear terms in φ,π will vanish due to the hermitian conjugation on half of Jens F. C. Krog 47
48 CHAPTER 6. A NEAR-CONFORMAL MODEL FEATURING THE DILATON the Hs. As for the h field, a term of order h would come from something proportional to Tr[h a T a ] but as the T a s are generators of SU (X ), and are therefore traceless, this term will vanish. Hence only the field φ may contribute linearly to the trace anomaly, and indeed, calculations show that ( ) Θ µ 4π 2 µ = [β(z 1 ) + β(z 2 )]v 3 φ + (6.29) N f where the ellipsis are terms that arise beyond tree level, and as such are of higher order in the couplings. As only our diagonal field φ contributes to the trace of the improved energy-momentum tensor, we can identify it with the dilaton. In order to identify the mass of the φ state with the mass of the dilaton from (6.28), we calculate the matrix element at the scale M 0 and find 0 µ D µ D M0 = 64π2 v 3 N 2 f = 2(4π)2 v 3 N 2 f ( z z z 1z 2 x ) 2 a2 H M0 ( 4(z 0 2 ) 2 x(a 0 H )2) = vm 2 d (6.30) such that we can identify m 2 d = m2 D and v = f D. The result is not surprising, since we have seen that in a massless theory, we may write the one loop potential on the form V = φ 4 c (A + Bt), and that the mass of the light scalar should be proportional to B as mentioned (again) in Chapter 6.2. The Callan-Symanzik equation requires that the change in the potential due to the scale of renormalization should be cancelled by the change in the beta functions as seen in (5.1), Hence it was needed that the product of the beta functions governing the quartic couplings should be proportional to the mass of the light scalar. As we have finally identified a dilaton, which is the subject of the thesis, in our model, we may now turn our attention back to the other features of the model; the phase diagram and whether or not conformal symmetry is actually broken. 6.4 GEOMETRICAL ANALYSIS AND PHASE TRANSITIONS In the spirit of [14], we will now need to find an expression for the improved one loop effective potential, in order to derive the conditions for spontaneous symmetry breaking. A similar analysis has been conducted in [20]. Just like Yamagishi, we will consider the dimensionless expression V /φ 4 c, which may then only depend on the parameter t = ln(φ c /M) and the dimensionless couplings. The potential, just as in the Yamagishi case, has to obey the Callan-Symanzik equation (5.1), and using the improved couplings λ i (t), the lowest order contribution comes from the improved tree level terms, giving { ( 2 V imp = u 1 (t) Tr[H H ]) + u2 (t)tr [(H H ) 2]} e 4 t 0 dt γ 1 γ (6.31) 48 Jens F. C. Krog
49 6.4. GEOMETRICAL ANALYSIS AND PHASE TRANSITIONS where the dependence of the u 1,2 on the other couplings is taken to be implicit through t. As has already been mentioned, we would like to set our model in the large N limit, where symmetry breaking may occur for z 2 > 0 and where the scalar bifundamental H i j will acquire a vev along the diagonal c φ δ i j. In the analysis of the 2N f conditions for symmetry breaking, we will need positive z 2 and therefore also u 2 yet a negative potential, such that the conditions for a new global minimum will be z 2 > 0 z 1 + z 2 < 0 (6.32) As we are searching along the diagonal, it is not hard to find the first derivatives of the potential (6.31), where we have changed to the rescaled couplings of (6.5) such that using that V imp φ c = (4π)2 4N 2 f ( dz1 dt + dz 2 dt + 4 z ) 1 + z 2 φ 3 t γ c 1 γ e4 0 1 γ (6.33) β(λ i ) = M dλ i dm = (1 γ)dλ i dt like it was done by Yamagishi, we find the condition for a nontrivial extremum (6.34) β(z 1 ) + β(z 2 ) + 4(z 1 + z 2 ) = 0 (6.35) Lastly, the second derivative of the improved potential can be found easily by imposing (6.35), such that 2 V imp φ 2 c [ > 0 β(λ i ) ] + 4 (β(z 1 ) + β(z 2 )) > 0. (6.36) λ i Now (6.32),(6.35), and (6.36) are the conditions that guarantee that we have a new global minimum, which means that the chiral SU (N f ) SU (N f ) symmetry will spontaneously break. For the condition that the extremum be a minimum, (6.36), we will discard the first terms on the grounds that in the perturbative regime, where we are working, such terms, which are of higher order in the couplings, will be negligible. This is consistent with the actual form of the beta functions (6.6), which are all squared in the couplings. When we examine the flows of the couplings we thus know that for spontaneous symmetry breaking to occur, we must intersect the so-called stability line, (6.35), corresponding to the appearance of a nontrivial extremum, in the desired region for stability β(z 1 ) + β(z 2 ) > 0 and where the minimum is global z 1 + z 2 < 0. The stability line and desired region of coupling constant space is shown in Figure 6.2. From Figure 6.2 it is evident, that at least two different opportunities are present in the model. For the flows that start out at z 1 + z 2 > 0 with positive z 2, flowing towards lower scale will either produce spontaneous symmetry breaking, if the Jens F. C. Krog 49
50 CHAPTER 6. A NEAR-CONFORMAL MODEL FEATURING THE DILATON z Figure 6.2: The RG flows of the quartic couplings displaying the two fixed points for ɛ = 0.1, with the conditions for spontaneous symmetry breaking displayed. The thick black line corresponds to the points where a nontrivial extremum appears (6.35). The blue region marks where this extremum is global minimum, i.e where V ( H ) < 0 and V ( H ) > 0. The dashed orange line marks where the tree level potential vanishes, which was the condition for spontaneous symmetry breaking used by Gildener-Weinberg [7] and Paterson [11]. The red RG flow separates the two phases in the theory, one with symmetry breaking and one conformal, and is called the separatrix. z 1 stability line is reached within the stabile region, or the flow will terminate in the fixed point, and the theory will be conformal. The region of initial coupling constant values may be split into two distinct phases, separated by a separatrix, which is exactly the RG flow that goes crosses the stability line at the boundary of the stabile region, the point where z 1 + z 2 = β(z 1 ) + β(z 2 ) = 0. (6.37) which is marked in red. As noted before, the sum of the two quartic beta functions is exactly proportional to the squared mass of the dilaton, so at this boundary the dilaton is exactly massless, and symmetry breaking does not take place. As one moves towards slightly smaller values of z 1, the stability line sits in the region where z 1 + z 2 < 0 50 Jens F. C. Krog
51 6.5. GILDENER-WEINBERG VS. YAMAGISHI and therefore β(z 1 ) + β(z 2 ) > 0, and the dilaton acquires a mass proportional to the "distance" from the boundary. One should note that the flows shown in the diagrams are only valid until spontaneous symmetry breaking occurs (if indeed it does). At this point, some particles will acquire masses that depend on the energy scale where the symmetries were broken, thus as one moves to lighter scales these particles will eventually decouple, which will alter the beta functions significantly and change the coupling constant flows. As was also the case in the previously considered cases, the RG flows can only be used to determine if spontaneous symmetry breaking occurs, but not what will happen once it has. The interesting part of Figure 6.2 is the upper rightmost part of the diagram, where the flows either end in conformality or spontaneous symmetry breaking. Most flows on the lower lefthand side are unrelevant, since they seem to either flow to strong coupling or cross the stability line where the extremum is a maximum and the potential is unstable in the perturbative regime. 6.5 GILDENER-WEINBERG VS. YAMAGISHI Having applied two different ways of analyzing the effective potential to the same theory, it is worthwhile to review the differences and similarities of the two methods. Of course, the two methods should yield the same conclusions about the theory, such that no ambiguities arise. That this is the case, even though seemingly different assumptions were made about the coupling constants is not, at least to this author, totally obvious, so we will investigate this. To reiterate, we recall that the strategy of GW was to find a scale M 0 where the tree level potential vanishes, such that one loop order corrections may induce spontaneous symmetry breaking. What is actually done is that the effective potential is calculated, and then counter terms are used to make sure that the theory remains massless (at vanishing vev) and that when the scalar field φ c = M such that t = 0, the four point function equals the bare quartic coupling. By this procedure a nontrivial minimum was found for a small value of t, where it was the bare couplings that entered into the potential, and the only thing that was required was that we could pick a renormalization scale where z 0 1 = z0 2. This corresponds to initiating the flow on a point on the dashed line in Figure 6.2. The flow then tells you what happens when quantum corrections are taken into account, which gives rise new terms in the effective potential. Introducing new terms then leads to spontaneous symmetry breaking, and one may consider these new terms as corrections to the bare couplings, such that the symmetry breaking does not happen at the original point of z 1 +z 2 = 0 but rather somewhere close, as described above. The distance between the starting point on the dashed line and the stability line, along the RG flow, then roughly corresponds to the size of the quantum corrections, and how far away from the original scale you have to go before the symmetries are broken. If this distance is too long, then the effective Jens F. C. Krog 51
52 CHAPTER 6. A NEAR-CONFORMAL MODEL FEATURING THE DILATON potential analysis incorporating factors of t = ln(φ c /M) breaks down, because t becomes so large that we are outside the perturbative regime. On the contrary, the scale dependence was included through the effective couplings by Yamagishi using the renormalization group equation. The advantage of this way of going about the analysis is that as long as the couplings stay small, the improved couplings are a good estimate and perturbation theory is still valid, no matter how far along a renormalization flow you go. In a sense then, this procedure is stronger, which is indeed the reason this potential is called the improved potential already in [6]. The consistency of the two different ways of conducting the analysis was shown through the Callan-Symanzik equation, from which we could infer the squared mass of the dilaton. In Chapter 6.3 we discussed how this had to be proportional to the sum of the two beta functions β(z 1 ) + β(z 2 ), since these are connected to the effective potential through the Callan-Symanzik equation. By examining the improved effective potential, we saw that it was proportional to z 1 + z 2, such that the dilaton mass should also be proportional to this, but indeed we saw that the requirement, (6.35) for symmetry breaking stated, that z 1 + z 2 = β(z 1 ) + β(z 2 ) so the analysis seems consistent. Before embarking on the voyage to the electroweak sector, to see whether it will destroy the nice dilatonic picture we have considered so far, we will include a short remark on the lighter part of the spectrum of the theory; the massless gluons and gluinos. 6.6 ULTRA LIGHT SCALE SUPERSYMMETRY Where much of the former considerations have been mostly with a single "light" scalar field, which could easily be identified with a Higgs field, and therefore would fit nicely into the standard model, we have yet to address the uncomfortable truth that the theories of [11] and [15] include a large amount of particles, that are not all that compatible with the data available at present time. The linear sigma models we have considered so far will, in addition to a light scalar and some heavy scalar that might be though to be too heavy to influence ongoing experiments, also contain an amount of massless Goldstone bosons, perhaps even a large amount. While some of these might be consumed by the Higgs mechanism, it would seem that some would survive, which means that the models so far are not great descriptions of nature. This issue will be forgotten for the present work. In addition, the latest model we investigated included a Bank-Zaks sector with an infinite amount of fermions in the fundamental representation, and an adjoint fermion transforming under the infinite dimensional representation of the gauge group. These numbers are of course, also a little unrealistic, but might be seen as an approximation of something not quite as infinite. It does, however, beg the question; "Why include them?" And additionally; "Wont they affect the picture?" These questions will be addressed shortly below. 52 Jens F. C. Krog
53 6.7. WHERE TO GO FROM HERE To the first question an answer comes easily; The Bank-Zaks sector is included in order to include a nontrivial perturbative fixed point for the gauge coupling. As a Yukawa coupling are included however, one needs to find a fixed point for the Yukawa coupling, if not to destroy the Bank-Zaks fixed point. If the adjoint fermion λ m was not included, there would be no fixed point for the Yukawa coupling, and the only fixed point for the gauge-yukawa beta functions would be the trivial noninteracting one. In order to do the geometrical analysis of the former section, one would then have to set the gauge- and Yukawa coupling equal to zero when doing the RG flow diagram for the quartic couplings, which would then be exactly the one depicted in Figure 4.1 in 4.Thus the adjoint fermion is responsible for the nontrivial dynamics of our model. Besides the Goldstone bosons the remaining particles in the theory are the mentioned adjoint fermion λ m and the gauge bosons of the SU (X ) gauge theory, which is exactly the constituents of N = 1 Super Yang Mills theory, and the low energy theory is a supersymmetric one. At lower scales this theory develops degenerate condensates, which could disturb the picture of the diagonal dilaton field φ, since we recall that the dilaton should be the lightest field that couples the most strongly to the improved energy momentum tensor. However, as supersymmetry is not broken and the trace of the energy momentum tensor is left untouched by the lower energy spectrum [15]. Hence, the inclusion of the many fermions does have significant consequences on the behavior of the theory, but does not threaten the identification or lightness of the dilaton. At most it makes the theory unnatural, since these particles have not been observed. 6.7 WHERE TO GO FROM HERE As we now have a fully computable model with near conformal behavior, perturbative interacting fixed points, a nice large N f, X limit and a light scalar state, which can be made as light as needed without turning off interactions, and which may even be identified with the dilaton, we might be content. However we are not. As noted on numerous occasions earlier, a scalar particle which is much lighter than the scale of symmetry breaking seems to be a good explanation of electroweak symmetry breaking. This requires, however, that the nice features found for the theory are not utterly destroyed if electroweak interaction is also taken into account. The next of this work will be dedicated to an attempt to couple the dilaton of this model with the electroweak sector, and see whether the analysis can be repeated and the results will make sense. Jens F. C. Krog 53
54
55 CHAPTER 7 COUPLING THE DILATON TO THE STANDARD MODEL Even though the model presented in the previous section is not the optimal solution for a fundamental theory of elementary particle interactions, some features displayed were desirable for the task. It is therefore worthwhile to try to extend the simple dilaton model from before, by introducing interactions and particles known from nature. The primary role of the Higgs field in the standard model is to break electroweak symmetry, thus giving masses to the vector bosons of weak interactions. The first step will therefore be to see if the coupling of the scalars of the SU (N f ) SU (N f ) multiplet to a semi simple SU (2) U (1) gauge group will preserve the features mentioned last in the former section (as in the standard model, the Higgs doublet is a singlet under the strong interaction, to preserve normal QCD). It is possible to think of a lot of different ways to introduce the electroweak gauge group into the scalar linear sigma model sector we have considered. The route we will take is one of [21], where the gauge group and covariant derivatives are included in a simple way. 7.1 INTRODUCING THE SU(2) U(1) GAUGE The electroweak interactions are introduced as an additional gauge group, which comes into play through appearance of covariant derivatives. To gauge the bifundamental H under the electroweak gauge group we will therefore introduce the covariant derivative (D µ H) i j = µ H i j i g A r µ S r ik H k j + i g B µ H ik S k j (7.1) where the SU (2) transformations are implemented through the coupling g and the S r matrices, where r = 1,2,3. Similarly the coupling g and the S matrices take care of the U (1) transformations. The matrices that generate the electroweak 55
56 CHAPTER 7. COUPLING THE DILATON TO THE STANDARD MODEL transformations are S r = σr 2 (1 N g 0 (N f /2 N g )) (7.2) S = σ3 2 (1 N g 0 (N f /2 N g )) (7.3) so basically these matrices are N f N f matrices with the Pauli matrices σ r in the diagonal. In [21], only two cases are considered; either there is only one Pauli matrix in the diagonal besides from zeros, or the diagonal is filled up. These cases are called the partial- and one-family- gauge respectively inspired by [22]. For this work we have tried the generalization to the case which any number of Pauli matrices N g = 1,..., N f /2 are allowed, letting us couple an arbitrary portion of the scalars to the electroweak sector, which also means that we assume that N f is even. We would also like to gauge the fundamental fermions under the electroweak gauge, which is done in a similar fashion. Because we would like to use the formalism of [23] to calculate the beta functions, we will rewrite the fundamental fermion covariant derivative to the form D µ ψ j = ψ j i g t a j k V a µ ψ k. (7.4) If we arrange the q, q fermions into one multiplet q i where the flavors as well as the colors are incorporated, such that i = 1,...,2N f X, and that q i { q, if i N f X. q, if i > N f X, (7.5) then we can write the covariant derivative of the SU (X ) SU (2) U (1) gauge as (D µ q) i = q i i g F a i j G a µ q j i g A r µ F r i j q j + i g B µ F i j q j (7.6) where the F a = T a 1 2N f, a rewriting of the SU (X ) generators from before. The matrices that generate electroweak transformations are of a similar nature, but once again we restrict ourselves to gauging the ratio κ = 2N g /N f of the fermion sector under the electroweak; F r = S r (1 X 0 X ) (7.7) F = S (0 X 1 X ). (7.8) The choice of gauging the q fermions will not play into the calculation of the effective potential, but it will however, affect the beta functions and the dynamics of the theory. Before investigating the dynamics of this extended theory, we will consider how the electroweak symmetry breaking will unfold, and which masses are given to the gauge bosons. As was done in the previous section, we will assume that 56 Jens F. C. Krog
57 7.2. ELECTROWEAK CORRECTIONS TO THE BETA FUNCTIONS AND THEIR FIXED POINTS Vector boson W Z m 2 i (v) N g g 2 2N f v 2 N g (g 2 +g 2 ) 2N f v 2 Table 7.1: The tree level masses of the weak vector bosons, assuming a diagonal vev. spontaneous symmetry breaking occurs, such that the H i j obtains a vev along the diagonal v H = 1 (7.9) 2N f then by inserting this vev in the covariant derivative term and introducing the usual linear combinations of gauge fields to make the gauge bosons W ±, Z we find the gauge boson masses presented in Table 7.1 In the following the idea will mainly be to assume the electroweak coupling to be fixed parameters, such that we always are close to the electroweak scale. In this case, if we set g, g to correspond to the regular electroweak couplings, and since the mass of the W and Z bosons are known, then the vev v must relate to Λ ew = 246 GeV in the way v = N f 2N g Λ ew = 1 κ Λ ew (7.10) in order to generate the correct masses for the weak force mediators. As the electroweak spectrum has been shown to not behave entirely bad, assuming symmetry breaking, it will now be the goal of the next section to see whether spontaneous symmetry breaking will actually occur as the new interactions have been included. The following sections will show that it is not entirely trivial to include a finite number of particles into a theory which, at the desired limit, has an infinite number of particles. 7.2 ELECTROWEAK CORRECTIONS TO THE BETA FUNCTIONS AND THEIR FIXED POINTS The first step in examining the dynamics of the theory will be to calculate the corrections from electroweak interactions to the already known beta functions. The work here will closely follow the formalism and results that are gathered in [23]. The main procedure will be to calculate the Casimir invariants of the theory and using the expressions given for the beta functions. Jens F. C. Krog 57
58 CHAPTER 7. COUPLING THE DILATON TO THE STANDARD MODEL Adjusting the notation As already mentioned, the procedure of [23] makes use of a specific notation for the covariant derivatives. The fermion part has already been rewritten to match this notation in (7.6). Similarly, we need to put the scalar covariant derivatives on the form D µ φ a = µ φ a i g θ r ab V r µ φ b, (7.11) but seeing as the scalars of our theory are in a bifundamental, this is not entirely trivial. The strategy, in the spirit of [11], will be to exploit the fact that we may write the SU (N f ) SU (N f ) scalar as a linear combination of the generators of SU (N f ), T a with the addition of T 0 = 1/ 2N f, such that we ensure the normalization Tr[T a T b ] = δ ab /2. However, as the convention of [23] is that the scalar covariant derivative is on the form of (7.11) with the scalars all being real, we will rewrite our scalar matrix on the form H = φ A T A (7.12) where the capitalized index A = 0,...,2N 2 f 1, and for A > N 2 f 1 we have T A = it A N 2 f. These redefined generators of SU (N f ) will play a central role in the calculations to follow, it is worthwhile to go over their properties. Naturally, the properties, which hold for the regular SU (N ) generators Tr[T a T b ] = 1 2 δab, T a T a = N f 2 1 (7.13) do not hold for the redefined generators. Specifically, since each generator T a will appear twice when going through the index A, the delta function of this first equation does not translate to the redefined case. The second expression is even more obvious to reject, since, by summing over all of A, all terms will be generated twice, with a different sign. The related properties for the T A s are as follows Tr[T A T B ] = 1 2 (δab iδ A(B N 2 f ) + iδ (A N 2 f )B ) (7.14) Tr[T A T B ] + Tr[T B T A ] = δ AB (7.15) T A T A = 0 (7.16) T A T A = N f 1 (7.17) which are derived in Appendix A. As we now have the scalars φ A on a vector like form, we may continue to rewrite the covariant derivative. The goal is to find an expression for the gauge generators θ r of (7.11). To do this we simply write down what the kinetic terms ab are for the (7.11) form and compare this to the corresponding terms in our Lagrangian. 58 Jens F. C. Krog
59 7.2. ELECTROWEAK CORRECTIONS TO THE BETA FUNCTIONS AND THEIR FIXED POINTS For a canonically normalized Lagrangian, the kinetic terms coming from (7.11) are 1 2 D µφ A D µ φ A = 1 2 µφ A µ φ A i g µ φ A θ r AB V µ r φ B 1 2 g 2 V r µ V µ s θ r AB θs AC φ B φ C. (7.18) If we only consider the SU (2) gauge then the kinetic terms in our theory are [ Tr D µ H(D µ H) ] SU (2) = Tr [( µ φ A T A i g A r µ S r φ A T A)( )] µ φ B T B i g A r µ T B S r φ B = 1 2 µφ A µ φ A i g A r µ φ B µ φ A Tr [S ] r T B T A T A T B S r [ + g 2 Aµ s Aµ r φ A φ B Tr S r T A T B S s] (7.19) where we have used the fact that the S r matrices are hermitian and that A,B Tr[T A T B ] = A,B δ AB 2. (7.20) We may now read off the generators for the SU (2) transformation by compairing (7.19) and (7.11) and we find ] θ r AB [S = Tr r (T B T A T A T B ) (7.21) If we instead look only at the U (1) covariant terms, we find [ Tr D µ H(D µ H) ] U (1) [ ( µ = Tr φ A T A + i g B µ φ A T A S )( )] µ φ B T B i g B µ S T B φ B = 1 2 µφ A µ φ A i g B µ φ B µ φ A Tr [T A S T B T B S T A ] + 1 [ 4 g 2 B µ B µ φ A φ B Tr T A T B ] (7.22) from which we may read off the U (1) generators ] θ AB [S = Tr (T B T A T A T B ). (7.23) We may now go on to calculate the Casimir invariants which determine the form of the beta functions, of which we will start with the beta function for the gauge couplings. From the form of the covariant derivatives depicted above, the needed Casimir invariants are C 2 (F ) = F a F a (7.24) C 2 (S) = θ a θ a (7.25) S 2 (F )δ ab = Tr[F a F b ] (7.26) S 2 (S)δ ab = Tr[θ a θ b ] (7.27) C 2 (G)δ ab = f acd f bcd (7.28) Jens F. C. Krog 59
60 CHAPTER 7. COUPLING THE DILATON TO THE STANDARD MODEL which must be evaluated for each gauge group independently. The S 2 invariants are not hard to calculate, due to the fact that the trace in either the fermion or scalar index is taken. For the fermions the C 2 invariant is also easy to calculate due to the simple nature of F r,f, but for the scalars the matter is more complicated. For C 2 (S) one finds for example for the SU (2) gauge group C AB 2 (S) SU (2) = Tr[S r (T C T A T A T C )]Tr[S r (T B T C T C T B )] [ ] = Tr S r S r (T B T A + T A T B ) (7.29) where the S r S r = N g 0 N f 2N g essentially cut off a part of matrix formed by the product of the T A s. In the case of a general N g this is nontrivial, but if we set κ = 1 such that N g = N f /2 and we are in the one family gauge, then C2 AB (S) SU (2) = 3 4 δab. Regrettably, we see that in the case of a general κ, each scalar φ A is coupled differently to the electroweak gauge group, i.e the couplings are of different "strength" corresponding to different eigenvalue of C 2 (S). In addition to the gauge invariants mentioned above, we need to calculate specific quantities that depend on the Yukawa couplings of the theory. To follow the notation of [23] we need the Yukawa terms of the Lagrangian to be on the form L Y = 1 2 (Y a j k ψ j ψ k φ a + h.c.) (7.30) if this is compared to our Lagrangian (6.1), we see that with the fermions put in a single vector q i as done in (7.5) and with the rewriting of the scalar field (7.12), we may write our Yukawa term on the form ( L Y = y H q i q j φ A 0 T A) T A 1 X, (7.31) 0 such that we may define T A ( Y A 0 = y H T A 0 ) 1 X (7.32) With this definition, we may calculate the last term needed for the gauge beta functions, which is the quantity Y 4 (F ) = 1 d(g) Tr[C 2(F )Y A Y A ] (7.33) where d(g) is the dimension of the group. When calculating this term for the SU (2) and U (1) gauge, we should remember that only 2N g X of the 2N f X fermions are gauged under each gauge group. In Table 7.2 the invariants of (7.24)-(7.28) are listed, where the C 2 (S) invariants are evaluated in the κ = 1 case. The two values for the C 2 (F ) invariants are for the fundamental and adjoint fermions in the SU (X ) case, and for the fermions that are gauged under the electroweak gauge and those who are not in the other cases. 60 Jens F. C. Krog
61 7.2. ELECTROWEAK CORRECTIONS TO THE BETA FUNCTIONS AND THEIR FIXED SU (X ) C 2 (G) C 2 (F ) C 2 (S) S 2 (F ) S 2 (S) Y 4 (F ) X SU (2) 2 U (1) 0 X 2 1 2X, X 0 N f + X 0 y 2 H N 2 f 3 4, X N 1 g N f N g 2 y 2 H N f N g X 1 4, X N 1 g N f N g 2 y 2 H N f N g X Table 7.2: Useful casimir invariants for the different gauge groups. casimirs are evaluated in the one family gauge POINTS The C 2 (S) The corrected beta functions We may now proceed to calculate the gauge beta function to two loops, which is given in a semi simple gauge theory [23] β(g k ) = g 3 k (4π) 2 + g 3 k (4π) 4 g 5 k (4π) 4 ( 11 3 C 2(G k ) 2 3 Sk 2 (F ) 1 6 Sk 2 (S) Y 4 k(f ) ) (4π) 2 ( l g 2 l (2C l 2 (F )Sk 2 (F ) + 2C l 2 (S)Sk 2 (S)) ) ( 34 3 [C 2(G k )] C 2(G k )S k 2 (F ) 1 3 C 2(G k )S k 2 (S) ) (7.34) where the k,l indices correspond to the simple gauge groups that compose the semi simple one. In this formulation it is implicit that the eigenvalues of C 2 (F,S) should be multiplied onto the trace argument of S 2 (F,S) before the trace is taken, such that for example for SU (X ), from Table 7.2, the factor (X 2 1)/(2X ) is multiplied with N f and X with X. With this in place, the calculation is a straightforward insertion of the factors of Table 7.2. For the SU (X ) gauge coupling the only new terms are from a new two loop term from the fermions (the first term of the second line in (7.34)) since the scalars are singlet under the SU (X ) gauge. The calculation yields, when remembering the notation x = N f /X and dropping two 1/X terms, β(a g ) = 2a 2 g ( 3 2x 3 κx ( a g + 1 ) ( 2 a g x ) ) a g + x 2 a H 3 where we have rescaled the g and g couplings as well, such that (7.35) a g ( ) = [g ( )] 2 (4π) 2. (7.36) Defining β(a g ) AMS as the beta function in the absence of electroweak interaction, we may write the corrected beta function β(a g ) = β(a g ) AMS ag 2 κx( 3 2 a g a g ) (7.37) Jens F. C. Krog 61
62 CHAPTER 7. COUPLING THE DILATON TO THE STANDARD MODEL Thus we get a term that will either contribute of the order of the Yukawa coupling, although with a different sign since x 9/2, or, if the electroweak couplings are fixed, a constant term that is of the other terms (remember that the other constant terms are tuned to be small). As we saw before, the Yukawa and gauge beta functions are unaffected by the running of the quartic scalar couplings, so in order to establish whether the theory remains the nontrivial fixed point in these couplings, we need only calculate the corrected beta function for the Yukawa coupling. At one loop, the beta function for the Yukawa coupling of the scalar φ A to the fermions q i,q j is given [23] β A i j = 1 [ 1 ( (4π) 2 Y 2 2 (F )Y A + Y A Y 2 (F ) ] g 2 l {C 2 l (F ),Y A } l i j ) + 2Y B Y A Y B + Y B Y AB 2 (S) (7.38) where Y AB 2 (S) = 1 2 Tr[Y A Y B + Y B Y A ] = y 2 H X δab as seen from (7.32) and (7.15). One should note here that this formula covers all of the possible Yukawa couplings, where our theory only has one at the moment. At one loop, however, the Yukawa coupling of those fermions which are gauged under the electroweak gauge will receive contributions to its beta function, which are absent for the couplings where the fermions are not gauged under the electroweak gauge. We should therefore expect to get two Yukawa couplings instead of just the one. Going through with the calculation then gives us β(a H ) = 2a H ( a H (1 + x) 3a g ξ( 9 2 a g a g ) ) (7.39) where ξ = 0, 1 depending on whether the fermions corresponding to the specific Yukawa coupling are untouched by the electroweak gauge or not. At this level, it therefore becomes clear that choosing κ 1 will break the chiral SU (N f ) SU (N f ) symmetry by introducing two different Yukawa couplings, already at one loop. Once again, though, we see that the correction to the beta function is not horribly large, and should be of the order of the other terms, and as before, the sign of the electro correction is opposite the sign of the Yukawa term. Investigation of the fixed point in the gauge and Yukawa sector is now possible, but for the sake of continuity, we will wait until the remaining interesting quantities, the beta functions for the quartic couplings, have been calculated. Moving on to the quartic couplings we encounter a somewhat harder round of calculations than the previous ones. First of all, our scalar multiplet φ A is represented in a nontrivial way in the Lagrangian, and we have chosen to engage in the investigation of a semisimple gauge group acting on these scalars. In [23], the quartic couplings are assumed to enter the Lagrangian as L φ 4 = 1 4! λ ABCDφ A φ B φ C φ D (7.40) 62 Jens F. C. Krog
63 7.2. ELECTROWEAK CORRECTIONS TO THE BETA FUNCTIONS AND THEIR FIXED where as in our case 2 L φ 4 = u 1 (Tr[H H ]) u2 Tr [(H H ) 2] = (u 1 Tr[T A T B ]Tr[T C T C ] + u 2 Tr[T A T B T C T D ])φ A φ B φ C φ D = 1 4! φa φ B φ C φ D per ms POINTS (u 1 Tr[T A T B ]Tr[T C T C ] + u 2 Tr[T A T B T C T D ]) (7.41) which identifies our coupling λ ABCD as the sum in (7.41). As the beta function for the quartic couplings in [23] are given as β(λ ABCD ) we may predict what the terms in our analysis will look like, since β(λ ABCD ) = dλ ABCD dlnµ = per ms = λ ABCD u 1 du 1 dlnµ + λ ABCD u 2 du 2 dlnµ ( β(u 1 )Tr[T A T B ]Tr[T C T C ] + β(u 2 )Tr[T A T B T C T D ] ) (7.42) such that terms contribute to the beta functions in the way that they are proportional to the summed terms in (7.42). The one loop terms in the beta function for the quartic couplings that involves the gauging of the scalars are given in [23] ( β I ABCD = 1 (4π 2 3 ) k + 3 g 2 k 4 g 2 l k,l g 2 k C 2 k (i )λ ABCD i per ms (Λ k AC,EF Λl EF,BD + Λk AE,F D Λl FC,BE ) ) (7.43) where the index i = A,B,C,D runs over the 4 involved scalars, and we have now introduced Λ k AC,EF = (θk ) r AE (θk ) r CF. The first term, as it is proportional to λ ABCD will contribute equally to both beta functions. As we need to be in the κ = 1 (one-family) gauge in order to calculate C 2 (S), this will be assumed for this analysis. The contribution is then 3 (4π) 2 k i ( 3 g 2 k C 2 k (i )λ ABCD = 6 2 a g + 1 ) 2 a g λ ABCD (7.44) which contributes to both β(u 1 ) and β(u 2 ). This was the easy part. We now move on to the second term in (7.43). To begin with, we observe that as the scalars are all real in this theory, and due to the form of the covariant derivative (7.11) the generators θ AB must be imaginary. As they are also hermitian, this means that they must be antisymmetric in A,B. This means specifically that Λ AB,CD = Λ AD,CB (7.45) Jens F. C. Krog 63
64 CHAPTER 7. COUPLING THE DILATON TO THE STANDARD MODEL along with similar rules for additional permutations. This means that per ms Λ k AC,EF Λl EF,BD + Λk AE,F D Λl FC,BE = 2 per ms Λ k AC,EF Λl EF,BD (7.46) since we sum over all permutations of the scalars φ A,B,C,D. For the contribution only from the U (1) gauge, with the generators defined in (7.23), we thus find Λ AC,EF Λ EF,BD per ms = per ms = per ms θ AE θ CF θ EB θ F D [ (Tr[S T E T A ]Tr[S T B T E ] + Tr[S T A T E ]Tr[S T E T B ]) ] (Tr[S T F T C ]Tr[S T D T F ] + Tr[S T C T F ]Tr[S T F T D ]) = 4 Tr[S T E T A ]Tr[S T B T E ]Tr[S T F T C ]Tr[S T D T F ] = 1 4 per ms per ms Tr[T A T B ]Tr[T C T D ] (7.47) where for the first second equality we use the identity T A i j T A = 0, and for the third kl the T A i j T A = δ kl il δ j k. These identities are similar to the Fierz identity, but hold for our redefined T A generators. Lastly we also use that we are in the one family gauge where S S = 1/4. This means that of the sum in (7.43) the term coming from only the pure U (1) term 3 2(4π) 2 g 4 per ms Λ AC,EF Λ EF,BD = (4π)2 3 8 a2 g per ms Tr[T A T B ]Tr[T C T D ] (7.48) and hence only contributes to β(u 1 ). 64 Jens F. C. Krog
65 7.2. ELECTROWEAK CORRECTIONS TO THE BETA FUNCTIONS AND THEIR FIXED In the case of the pure SU (2) terms we may follow a similar logic, and Λ AC,EF Λ EF,BD per ms = per ms = per ms θ r AE θ r CF θ s EB θ s F D ( ) Tr[S r T E T A ]Tr[S s T B T E ] + Tr[S r T A T E ]Tr[S s T E T B ] POINTS ( ) Tr[S r T F T C ]Tr[S s T D T F ] + Tr[S r T C T F ]Tr[S s T F T D ] = Tr[S r S s T B T A ]Tr[S r S s T D T C ] + Tr[S r S s T B T A ]Tr[S s S r T D T C ] per ms + Tr[S s S r T A T B ]Tr[S r S s T D T C ] + Tr[S s S r T A T B ]Tr[S r S s T D T C ] = 2 (S r ab S s bc S r de S s e f + S s ab S r bc S r de S s e f )T A cl T B l a T C f g T D g d = 3 4 per ms per ms Tr[T A T B ]Tr[T C T D ] (7.49) where the second equality uses T A i j T A A = 0, the third that T kl i j T A = δ kl il δ j k and the fifth uses the useful identity for the S matrices, derived in Appendix B; S r ab S s bc S r de S s e f + S s ab S r bc S r de S s e f = 3 8 δ acδ d f. (7.50) It is clear then that the pure SU (2) terms contribute as 3 2(4π) 2 g 4 per ms Λ AC,EF Λ EF,BD = (4π)2 9 8 a2 g per ms Tr[T A T B ]Tr[T C T D ] (7.51) and only affects β(u 1 ). As we have computed the pure terms, the only remaining thing to be done is the mixed terms of (7.43). These seem to be nontrivial to work out, however, and we find = Λ AC,EF Λ EF,BD = 4Tr[T A S r T B S ]Tr[T C S r T D S ] (7.52) per ms which we have not been able to put on the form of the terms in (7.42). From the Callan-Symanzik equation we know that the sum of the quartic beta functions should roughly equal the part of the effective potential proportional to t = ln(φ c /M 0 ). As this term is calculated from the sum of m 4 V, where m V is the mass of the vector bosons, we may see from the tree level masses of the vector bosons in Table 7.1, that mixed terms should arise, so we know that the sum of the contributions to the two beta functions should be nonzero. In order to go through with the analysis, we will therefore in the following follow the strategy of letting g tend to zero. This will make all of the beta functions known, and as it is the case in the gauge- and Yukawa beta function, will hopefully not make the quartic beta functions deviate much from the case of nonzero g. If Jens F. C. Krog 65
66 CHAPTER 7. COUPLING THE DILATON TO THE STANDARD MODEL this is indeed the case, the following analysis should yield close to the same results as if we had not let g 0. Letting g 0 leaves the quartic beta functions as β(z 1 ) = β(z 1 ) AMS 9a g z N 2 f a2 g (7.53) β(z 2 ) = β(z 1 ) AMS 9a g z 2 (7.54) where we, once again, see that the large N limit is no longer a reasonable way to work with, as it will render us unable to find a perturbative fixed point in z 1. A rescaling of the coupling with N f or N g, would make the last term in (7.53) the only nonvanishing correction to the beta functions, so this route will not be taken. Instead we will hope to choose an N f sufficiently high that the large N limit is still a good approximation, without having nonperturbative fixed points. Another thing to note is that we for computing β(z 1 ) we will need to specify N f as well as x, moving a little bit away from the formal regime and into pseudo model building. As the beta functions(or what is left of them) are finally in place, we may go on to see how the fixed point structure of [15] has been changed by the electroweak corrections Fixed point analysis In the following, we will, as mentioned above, assume that we are in close proximity to the electroweak scale, such that we can fix the electroweak couplings and ignore their dynamics. The fixed points will then be altered by these new constant corrections, but can be calculated as before. As we have seen that several issues arise whenever we are not in the one-family gauge, we will fix κ = 1 in the analysis of the beta functions and their fixed points. In this special case, the Yukawa- and gauge- coupling beta functions are β(a g ) = 2a 2 g ( 3 2x 3 x 2 ( 3 2 a g a g ) + ( 6 13x 3 β(a H ) = 2a H ( a H (1 + x) 3a g ( 9 2 a g a g ) ) ) a g + x 2 a H ) (7.55) (7.56) Normally, when looking for a perturbatively trustable fixed point, we just require that the parameter ɛ = 1 2x/9 is small, as this will keep the fixed point couplings small, such that higher order effects should be negligible. As we introduce a new parameter Ω = 3 2 a g a g, we must ensure that this is small as well, such that higher order contributions from this will also be negligible. To lowest order in ɛ, we find the nontrivial fixed point solutions for the Yukawaand gauge- coupling a H = 2 3 ɛ Ω (7.57) ag = 11 9 ɛ + 43 Ω. (7.58) Jens F. C. Krog
67 7.2. ELECTROWEAK CORRECTIONS TO THE BETA FUNCTIONS AND THEIR FIXED POINTS where setting Ω = 0 will return the fixed point values of [15], as is expected. As long as Ω 1, this fixed point is still perturbative, and the normal Bank- Zaks boundary at ɛ = 0 has been shifted. In order to include the analysis of the quartic couplings, we will let g tend to zero. If we set g = 0 and g = 0.6, the fixed point in the Yukawa and gauge couplings are as seen in Figure a g a h Figure 7.1: The fixed point values of the Yukawa and gauge couplings at a g = ( 0.6 4π and a g = 0 as a function of ɛ ) 2 As expected from (7.57) and(7.58), the electroweak interactions are only a small perturbation, and do not destroy the Bank-Zaks fixed point, but rather seem to moves the border of asymptotic freedom to a higher number of flavors. Moreover, the couplings move to zero at different rates, such that we are not able to tune the couplings to zero at the same ɛ. We may now move on to the fixed points of the quartic couplings, which, when g 0 have beta functions β(z 1 ) = 4(z z 1z 2 + 3z z 1a H 3 2 a g z 1 + 9N 2 f 32 a2 g ) (7.59) β(z 2 ) = 4(2z z 2a H x 2 a2 H 3 2 a g z 2) (7.60) where we will now have to specify N f as well as ɛ to be able to calculate the fixed point values. As mentioned above, we will have to set a finite N f in order to remain in the perturbative regime, which means that we are not in the large N limit. We would like to choose the largest value possible, which will not take us outside the perturbative regime, in order to suppress the omitted 1/N f terms. In Figure 7.2 and 7.3 we show how the fixed point values behave, while holding either ɛ or N f fixed while varying the other. The behavior of the quartic coupling fixed points is altered to a much greater extent than the ones of the Yukawa and gauge coupling fixed points. Where the two fixed points would previously merge at ɛ = 0 and Jens F. C. Krog 67
68 CHAPTER 7. COUPLING THE DILATON TO THE STANDARD MODEL z 2 1 z 1 2 z Figure 7.2: The fixed point values for the quartic couplings, where g = 0 and N f = 36 as a function of ɛ z 2 1 z 1 2 z Figure 7.3: The fixed point values for the quartic couplings for g = 0 and ɛ = 0.05 as a function of N f would be independent on N f, we now see a merging at a positive nonzero ɛ, that grows when N f is increased. Similarly, the fixed point values z (1,2) 1 now also depend on N f, and fixing ɛ will lead to merging of the fixed points at a critical N f. Besides from the already noted fact that the merging of fixed points are moved when including this new constant term, we have now also added an N f dependance to the fixed point structure, rendering it necessary to balance N f and ɛ to remain in the perturbative regime while trying to keep the large N limit a good approximation. From Figures 7.2 and 7.3, we would argue that is is still possible to find a region in N f,ɛ space where these requirements are still met, so it would seem that the fixed point structure need not be destroyed by the electroweak interactions. 68 Jens F. C. Krog
69 7.3. THE PHASE DIAGRAM We may now begin to investigate whether the corrections to the fixed points have altered the phase space of the theory. 7.3 THE PHASE DIAGRAM The phase space of the model without electroweak interactions, featured a conformal phase and a phase of spontaneous symmetry breaking, stemming from the Coleman-Weinberg mechanism as reviewed in Chapter 6. The investigation at hand will be concerned with the question of whether electroweak interactions disturb this structure or not. The requirements regarding the conditions for spontaneous symmetry breaking were presented in (6.32),(6.35), and (6.36), and are z 2 > 0, z 1 + z 2 < 0 β(z 1 ) + β(z 2 ) + 4(z 1 + z 2 ) = 0 [ β(λ i ) ] + 4 (β(z 1 ) + β(z 2 )) > 0 λ i which still applies to the model, as the tree level potential is unchanged. As discussed earlier, the first line ensures that the symmetry breaking is along the diagonal of H, and that the new minimum is lower than the trivial one at φ = 0. The second is the so-called stability line that marks that a nontrivial extremum exists, and the third that this extremum is a minimum. As done before, we will ignore the sum in the third line, as it will be of higher order in the couplings, even with the electroweak corrections. In Figure 7.4 the coupling constant flows of the model with the added electroweak interactions are shown for ɛ = 0.1 and N f = 36. Which should be compared with Figure 6.2, which has the same features. With the choice for N f we have here, it seems if though the dynamics of the system suffer only small perturbations. The theory still has a parameter space containing a conformal phase and a phase with spontaneous symmetry breaking, lying on each side of the separatrix marked in red. Now, as marked before, having a finite N f is in contradiction with the large N limit, used for calculating the gauge beta function (this is the only place in the analysis where the assumption has actually been used), so in order to get as close to consistency as possible, we would like to have a high N f. However, as seen from Figure 7.3, for a fixed ɛ, as we increase N f the z 1 value of the IR stable fixed point will decrease and at one point the fixed points will merge. Furthermore, if the z 1 value of the fixed point becomes too small, then the fixed point will be beyond the stability line, and the conformal phase on the right side of the separatrix in Figure 7.4 will become one of spontaneous symmetry breaking, as shown in Figure 7.5. Here it is seen that the addition of the electroweak interactions, through the influence of N f, may change the phases the system can be in, depending on where the fixed points are set. Of course, the fixed points could be moved by the tuning Jens F. C. Krog 69
70 CHAPTER 7. COUPLING THE DILATON TO THE STANDARD MODEL z z 1 Figure 7.4: The RG flows of the quartic couplings displaying the two fixed points for ɛ = 0.1 and N f = 36, with the added electroweak interactions, with the conditions for spontaneous symmetry breaking displayed. The thick black line corresponds to the points where a nontrivial extremum appears (6.35). The blue region marks where this extremum is global minimum, i.e where V ( H ) < 0 and V ( H ) > 0. The dashed orange line marks where the tree level potential vanishes, which was the condition for spontaneous symmetry breaking used by Gildener-Weinberg [7] and Paterson [11]. The red RG flow separates the two phases in the theory, one with symmetry breaking and one conformal, and is called the separatrix. of ɛ in the work reviewed in Chapter 6, but to low order in ɛ, the fixed points values where proportional to ɛ, and would therefore for decreasing ɛ move straight to the point of decoupling z 1 = z 2 = 0, without crossing the z 1 = z 2 line. In Figure 7.6 a contour plot of z 1 + z 2 as a function of ɛ and N f is shown. We see that there are both choices yielding no fixed points, some with a positive sum and some with a negative sum, meaning that the theory has three different phase diagrams. The addition of the electroweak interactions as a constant contribution thus may alter the theory radically, if the external parameters are not chosen carefully. If they are however, it seems that the phase space only receives minor corrections from the new dynamics. 70 Jens F. C. Krog
71 7.4. GILDENER-WEINBERG ANALYSIS WITH MASSIVE VECTOR BOSONS z Figure 7.5: As in 7.4, but with N f = 100. The IR stable fixed point has moved beyond the stability line, and the conformal phase has vanished. z GILDENER-WEINBERG ANALYSIS WITH MASSIVE VECTOR BOSONS Knowing that the H matrix may develop a vev along the diagonal, as has been described before, we will investigate how the potential is changed by the introduction of the vector bosons of electroweak theory. As the masses of these particles were given, at tree level, in Table 7.1, we may calculate the corrections to the one loop effective potential as in (3.21). We will return to the case of a general κ, as the potential analysis does not suffer any difficulties from this generalization. The part of the potential coming from the vector bosons is then V 1 V = 3 (ma 2 4 )2 (lnma ) = φ 4 c + φ 4 c i ( Ng N f ( Ng ) 2 ( 3 4 g (g 2 + g 2 ) 2) ln φ c M N f ) 2 ( ( 3 8 g 4 ln N ) g g 2 2N f (g 2 + g 2 ) ( ln N )) g (g 2 +g 2 ) 2N f 5 6. (7.61) As promised, the one loop potential has a term of the form g 2 g 2, so a similar term should arise in the sum of the quartic beta functions. Jens F. C. Krog 71
72 CHAPTER 7. COUPLING THE DILATON TO THE STANDARD MODEL N f Ε Figure 7.6: The behavior sum of the coupling constants z 1, z 2 as ɛ and N f are varied, shown in contour plots. The black line indicates, in each case, where z 1 + z 2 = 0. If we write up the total effective potential, having taking the vector bosons into account, we find, at the scale M 0 where z 1 + z 2 = 0 V = 4π2 φ 4 ( N 2 c f 1 N 2 N 2 4z2 2 ln2z 2 a 2 H xln[a H x] f f N g 2 a2 g ln[a g N g N f ] N g 2 (a g + a g )2 ln[(a g + a g )N g N f ] [ N 2 f 1 ] + N 2 4z2 2 a2 H x N g 2 a2 g N g 2 (a g + a g )2 ln 8π2 φ 2 ) c M 2 f 0 N 2 f (7.62) where we have not taken the large N limit. The reason for not taking this limit is that, with the chosen conventions, the large N limit is not perturbative. As already explained, in a theory where the effective potential may be put on the form V = A + Bt, we need A/B 1 for a nontrivial minimum to be perturbative. In (7.62) the first two lines make up what corresponds to the A and the last line B. We see that in the A terms for the vector bosons, logarithms in N f appear, which do not appear in the B term. This means that for the Gildener-Weinberg analysis, we may not use the large N limit, which is why we did not use this limit above. One might think that a solution to this issue could be to rescale the electroweak couplings such that a g g 2 N f. Even though the N g s in the terms above might be a problem, another problem arises. As we see from the contributions to the gauge and beta functions (7.35) and (7.39), this rescaling would make them of order 1/N f, thus making them vanish in the large N limit. In fact, the issue was 72 Jens F. C. Krog
Lecture 03. The Standard Model of Particle Physics. Part II The Higgs Boson Properties of the SM
 Lecture 03 The Standard Model of Particle Physics Part II The Higgs Boson Properties of the SM The Standard Model So far we talked about all the particles except the Higgs If we know what the particles
Lecture 03 The Standard Model of Particle Physics Part II The Higgs Boson Properties of the SM The Standard Model So far we talked about all the particles except the Higgs If we know what the particles
Lecture III: Higgs Mechanism
 ecture III: Higgs Mechanism Spontaneous Symmetry Breaking The Higgs Mechanism Mass Generation for eptons Quark Masses & Mixing III.1 Symmetry Breaking One example is the infinite ferromagnet the nearest
ecture III: Higgs Mechanism Spontaneous Symmetry Breaking The Higgs Mechanism Mass Generation for eptons Quark Masses & Mixing III.1 Symmetry Breaking One example is the infinite ferromagnet the nearest
Hunting New Physics in the Higgs Sector
 HS Hunting New Physics in the Higgs Sector SM Higgs Sector - Test of the Higgs Mechanism Oleg Kaikov KIT, Seminar WS 2015/16 Prof. Dr. M. Margarete Mühlleitner, Dr. Roger Wolf, Dr. Hendrik Mantler Advisor:
HS Hunting New Physics in the Higgs Sector SM Higgs Sector - Test of the Higgs Mechanism Oleg Kaikov KIT, Seminar WS 2015/16 Prof. Dr. M. Margarete Mühlleitner, Dr. Roger Wolf, Dr. Hendrik Mantler Advisor:
Gauge coupling unification without leptoquarks Mikhail Shaposhnikov
 Gauge coupling unification without leptoquarks Mikhail Shaposhnikov March 9, 2017 Work with Georgios Karananas, 1703.02964 Heidelberg, March 9, 2017 p. 1 Outline Motivation Gauge coupling unification without
Gauge coupling unification without leptoquarks Mikhail Shaposhnikov March 9, 2017 Work with Georgios Karananas, 1703.02964 Heidelberg, March 9, 2017 p. 1 Outline Motivation Gauge coupling unification without
The Standard Model Part. II
 Our Story Thus Far The Standard Model Part. II!!We started with QED (and!)!!we extended this to the Fermi theory of weak interactions! Adding G F!!Today we will extended this to Glashow-Weinberg-Salam
Our Story Thus Far The Standard Model Part. II!!We started with QED (and!)!!we extended this to the Fermi theory of weak interactions! Adding G F!!Today we will extended this to Glashow-Weinberg-Salam
The Higgs Boson and Electroweak Symmetry Breaking
 The Higgs Boson and Electroweak Symmetry Breaking 1. Minimal Standard Model M. E. Peskin Chiemsee School September 2014 The Higgs boson has an odd position in the Standard Model of particle physics. On
The Higgs Boson and Electroweak Symmetry Breaking 1. Minimal Standard Model M. E. Peskin Chiemsee School September 2014 The Higgs boson has an odd position in the Standard Model of particle physics. On
Electroweak and Higgs Physics
 Electroweak and Higgs Physics Lecture 2 : Higgs Mechanism in the Standard and Supersymmetric Models Alexei Raspereza DESY Summer Student Program Hamburg August 2017 Standard Model (Summary) Building blocks
Electroweak and Higgs Physics Lecture 2 : Higgs Mechanism in the Standard and Supersymmetric Models Alexei Raspereza DESY Summer Student Program Hamburg August 2017 Standard Model (Summary) Building blocks
Little Higgs Models Theory & Phenomenology
 Little Higgs Models Theory Phenomenology Wolfgang Kilian (Karlsruhe) Karlsruhe January 2003 How to make a light Higgs (without SUSY) Minimal models The Littlest Higgs and the Minimal Moose Phenomenology
Little Higgs Models Theory Phenomenology Wolfgang Kilian (Karlsruhe) Karlsruhe January 2003 How to make a light Higgs (without SUSY) Minimal models The Littlest Higgs and the Minimal Moose Phenomenology
Who is afraid of quadratic divergences? (Hierarchy problem) & Why is the Higgs mass 125 GeV? (Stability of Higgs potential)
 Who is afraid of quadratic divergences? (Hierarchy problem) & Why is the Higgs mass 125 GeV? (Stability of Higgs potential) Satoshi Iso (KEK, Sokendai) Based on collaborations with H.Aoki (Saga) arxiv:1201.0857
Who is afraid of quadratic divergences? (Hierarchy problem) & Why is the Higgs mass 125 GeV? (Stability of Higgs potential) Satoshi Iso (KEK, Sokendai) Based on collaborations with H.Aoki (Saga) arxiv:1201.0857
Vacuum Energy and Effective Potentials
 Vacuum Energy and Effective Potentials Quantum field theories have badly divergent vacuum energies. In perturbation theory, the leading term is the net zero-point energy E zeropoint = particle species
Vacuum Energy and Effective Potentials Quantum field theories have badly divergent vacuum energies. In perturbation theory, the leading term is the net zero-point energy E zeropoint = particle species
The mass of the Higgs boson
 The mass of the Higgs boson LHC : Higgs particle observation CMS 2011/12 ATLAS 2011/12 a prediction Higgs boson found standard model Higgs boson T.Plehn, M.Rauch Spontaneous symmetry breaking confirmed
The mass of the Higgs boson LHC : Higgs particle observation CMS 2011/12 ATLAS 2011/12 a prediction Higgs boson found standard model Higgs boson T.Plehn, M.Rauch Spontaneous symmetry breaking confirmed
Particle Physics I Lecture Exam Question Sheet
 Particle Physics I Lecture Exam Question Sheet Five out of these 16 questions will be given to you at the beginning of the exam. (1) (a) Which are the different fundamental interactions that exist in Nature?
Particle Physics I Lecture Exam Question Sheet Five out of these 16 questions will be given to you at the beginning of the exam. (1) (a) Which are the different fundamental interactions that exist in Nature?
Solutions to gauge hierarchy problem. SS 10, Uli Haisch
 Solutions to gauge hierarchy problem SS 10, Uli Haisch 1 Quantum instability of Higgs mass So far we considered only at RGE of Higgs quartic coupling (dimensionless parameter). Higgs mass has a totally
Solutions to gauge hierarchy problem SS 10, Uli Haisch 1 Quantum instability of Higgs mass So far we considered only at RGE of Higgs quartic coupling (dimensionless parameter). Higgs mass has a totally
The Gauge Principle Contents Quantum Electrodynamics SU(N) Gauge Theory Global Gauge Transformations Local Gauge Transformations Dynamics of Field Ten
 Lecture 4 QCD as a Gauge Theory Adnan Bashir, IFM, UMSNH, Mexico August 2013 Hermosillo Sonora The Gauge Principle Contents Quantum Electrodynamics SU(N) Gauge Theory Global Gauge Transformations Local
Lecture 4 QCD as a Gauge Theory Adnan Bashir, IFM, UMSNH, Mexico August 2013 Hermosillo Sonora The Gauge Principle Contents Quantum Electrodynamics SU(N) Gauge Theory Global Gauge Transformations Local
Introduction to Supersymmetry
 Introduction to Supersymmetry 1: Formalism of SUSY M. E. Peskin Maria Laach Herbstschule September, 2004 Among models of electroweak symmetry breaking and physics beyond the Standard Model Supersymmetry
Introduction to Supersymmetry 1: Formalism of SUSY M. E. Peskin Maria Laach Herbstschule September, 2004 Among models of electroweak symmetry breaking and physics beyond the Standard Model Supersymmetry
NTNU Trondheim, Institutt for fysikk
 FY3464 Quantum Field Theory II Final exam 0..0 NTNU Trondheim, Institutt for fysikk Examination for FY3464 Quantum Field Theory II Contact: Kåre Olaussen, tel. 735 9365/4543770 Allowed tools: mathematical
FY3464 Quantum Field Theory II Final exam 0..0 NTNU Trondheim, Institutt for fysikk Examination for FY3464 Quantum Field Theory II Contact: Kåre Olaussen, tel. 735 9365/4543770 Allowed tools: mathematical
Textbook Problem 4.2: We begin by developing Feynman rules for the theory at hand. The Hamiltonian clearly decomposes into Ĥ = Ĥ0 + ˆV where
 PHY 396 K. Solutions for problem set #11. Textbook Problem 4.2: We begin by developing Feynman rules for the theory at hand. The Hamiltonian clearly decomposes into Ĥ = Ĥ0 + ˆV where Ĥ 0 = Ĥfree Φ + Ĥfree
PHY 396 K. Solutions for problem set #11. Textbook Problem 4.2: We begin by developing Feynman rules for the theory at hand. The Hamiltonian clearly decomposes into Ĥ = Ĥ0 + ˆV where Ĥ 0 = Ĥfree Φ + Ĥfree
A Renormalization Group Primer
 A Renormalization Group Primer Physics 295 2010. Independent Study. Topics in Quantum Field Theory Michael Dine Department of Physics University of California, Santa Cruz May 2010 Introduction: Some Simple
A Renormalization Group Primer Physics 295 2010. Independent Study. Topics in Quantum Field Theory Michael Dine Department of Physics University of California, Santa Cruz May 2010 Introduction: Some Simple
Standard Model & Beyond
 XI SERC School on Experimental High-Energy Physics National Institute of Science Education and Research 13 th November 2017 Standard Model & Beyond Lecture III Sreerup Raychaudhuri TIFR, Mumbai 2 Fermions
XI SERC School on Experimental High-Energy Physics National Institute of Science Education and Research 13 th November 2017 Standard Model & Beyond Lecture III Sreerup Raychaudhuri TIFR, Mumbai 2 Fermions
Where are we heading? Nathan Seiberg IAS 2016
 Where are we heading? Nathan Seiberg IAS 2016 Two half-talks A brief, broad brush status report of particle physics and what the future could be like The role of symmetries in physics and how it is changing
Where are we heading? Nathan Seiberg IAS 2016 Two half-talks A brief, broad brush status report of particle physics and what the future could be like The role of symmetries in physics and how it is changing
The Higgs Mechanism and the Higgs Particle
 The Higgs Mechanism and the Higgs Particle Heavy-Ion Seminar... or the Anderson-Higgs-Brout-Englert-Guralnik-Hagen-Kibble Mechanism Philip W. Anderson Peter W. Higgs Tom W. B. Gerald Carl R. François Robert
The Higgs Mechanism and the Higgs Particle Heavy-Ion Seminar... or the Anderson-Higgs-Brout-Englert-Guralnik-Hagen-Kibble Mechanism Philip W. Anderson Peter W. Higgs Tom W. B. Gerald Carl R. François Robert
Double Higgs production via gluon fusion (gg hh) in composite models
 Double Higgs production via gluon fusion (gg hh) in composite models Ennio Salvioni CERN and University of Padova based on work in collaboration with C.Grojean (CERN), M.Gillioz (Zürich), R.Gröber and
Double Higgs production via gluon fusion (gg hh) in composite models Ennio Salvioni CERN and University of Padova based on work in collaboration with C.Grojean (CERN), M.Gillioz (Zürich), R.Gröber and
Theory toolbox. Chapter Chiral effective field theories
 Chapter 3 Theory toolbox 3.1 Chiral effective field theories The near chiral symmetry of the QCD Lagrangian and its spontaneous breaking can be exploited to construct low-energy effective theories of QCD
Chapter 3 Theory toolbox 3.1 Chiral effective field theories The near chiral symmetry of the QCD Lagrangian and its spontaneous breaking can be exploited to construct low-energy effective theories of QCD
Twin Higgs Theories. Z. Chacko, University of Arizona. H.S Goh & R. Harnik; Y. Nomura, M. Papucci & G. Perez
 Twin Higgs Theories Z. Chacko, University of Arizona H.S Goh & R. Harnik; Y. Nomura, M. Papucci & G. Perez Precision electroweak data are in excellent agreement with the Standard Model with a Higgs mass
Twin Higgs Theories Z. Chacko, University of Arizona H.S Goh & R. Harnik; Y. Nomura, M. Papucci & G. Perez Precision electroweak data are in excellent agreement with the Standard Model with a Higgs mass
Where are we heading?
 Where are we heading? PiTP 2013 Nathan Seiberg IAS Purpose of this talk A brief, broad brush status report of particle physics Where we are How we got here (some historical perspective) What are the problems
Where are we heading? PiTP 2013 Nathan Seiberg IAS Purpose of this talk A brief, broad brush status report of particle physics Where we are How we got here (some historical perspective) What are the problems
NTNU Trondheim, Institutt for fysikk
 NTNU Trondheim, Institutt for fysikk Examination for FY3464 Quantum Field Theory I Contact: Michael Kachelrieß, tel. 99890701 Allowed tools: mathematical tables Some formulas can be found on p.2. 1. Concepts.
NTNU Trondheim, Institutt for fysikk Examination for FY3464 Quantum Field Theory I Contact: Michael Kachelrieß, tel. 99890701 Allowed tools: mathematical tables Some formulas can be found on p.2. 1. Concepts.
STANDARD MODEL and BEYOND: SUCCESSES and FAILURES of QFT. (Two lectures)
 STANDARD MODEL and BEYOND: SUCCESSES and FAILURES of QFT (Two lectures) Lecture 1: Mass scales in particle physics - naturalness in QFT Lecture 2: Renormalisable or non-renormalisable effective electroweak
STANDARD MODEL and BEYOND: SUCCESSES and FAILURES of QFT (Two lectures) Lecture 1: Mass scales in particle physics - naturalness in QFT Lecture 2: Renormalisable or non-renormalisable effective electroweak
Week 3: Renormalizable lagrangians and the Standard model lagrangian 1 Reading material from the books
 Week 3: Renormalizable lagrangians and the Standard model lagrangian 1 Reading material from the books Burgess-Moore, Chapter Weiberg, Chapter 5 Donoghue, Golowich, Holstein Chapter 1, 1 Free field Lagrangians
Week 3: Renormalizable lagrangians and the Standard model lagrangian 1 Reading material from the books Burgess-Moore, Chapter Weiberg, Chapter 5 Donoghue, Golowich, Holstein Chapter 1, 1 Free field Lagrangians
Scale invariance and the electroweak symmetry breaking
 Scale invariance and the electroweak symmetry breaking ARC Centre of Excellence for Particle Physics at the Terascale, School of Physics, The University of Melbourne, VIC 3010 and School of Physics, The
Scale invariance and the electroweak symmetry breaking ARC Centre of Excellence for Particle Physics at the Terascale, School of Physics, The University of Melbourne, VIC 3010 and School of Physics, The
Genesis of Electroweak. Unification
 Unification Tom Kibble Imperial College London ICTP October 2014 1 Outline Development of the electroweak theory, which incorporates the idea of the Higgs boson as I saw it from my standpoint in Imperial
Unification Tom Kibble Imperial College London ICTP October 2014 1 Outline Development of the electroweak theory, which incorporates the idea of the Higgs boson as I saw it from my standpoint in Imperial
Discovery potential of toppartners in a realistic composite Higgs model with early LHC data
 Discovery potential of toppartners in a realistic composite Higgs model with early LHC data Günther Dissertori, Elisabetta Furlan, Filip Moortgat, JHEP09(20)019 Kick-off Meeting Of The LHCPhenoNet Initial
Discovery potential of toppartners in a realistic composite Higgs model with early LHC data Günther Dissertori, Elisabetta Furlan, Filip Moortgat, JHEP09(20)019 Kick-off Meeting Of The LHCPhenoNet Initial
Symmetries of the Two-Higgs Doublet Model (2HDM) Eddie Santos Final Presentation, Physics 251 6/8/11
 Symmetries of the Two-Higgs Doublet Model (2HDM) Eddie Santos Final Presentation, Physics 251 6/8/11 Outline Introduction to Higgs & Motivations for an Extended Higgs Sector Two-Higgs Doublet Model (2HDM)
Symmetries of the Two-Higgs Doublet Model (2HDM) Eddie Santos Final Presentation, Physics 251 6/8/11 Outline Introduction to Higgs & Motivations for an Extended Higgs Sector Two-Higgs Doublet Model (2HDM)
Electroweak Symmetry Breaking
 Electroweak Symmetry Breaking An enduring mystery of the standard model of particle physics and how we hope to solve it David Schaich Department of Physics and Center for Computational Science Boston University
Electroweak Symmetry Breaking An enduring mystery of the standard model of particle physics and how we hope to solve it David Schaich Department of Physics and Center for Computational Science Boston University
A model of the basic interactions between elementary particles is defined by the following three ingredients:
 I. THE STANDARD MODEL A model of the basic interactions between elementary particles is defined by the following three ingredients:. The symmetries of the Lagrangian; 2. The representations of fermions
I. THE STANDARD MODEL A model of the basic interactions between elementary particles is defined by the following three ingredients:. The symmetries of the Lagrangian; 2. The representations of fermions
Scale invariance and the electroweak symmetry breaking
 Scale invariance and the electroweak symmetry breaking Archil Kobakhidze School of Physics, University of Melbourne R. Foot, A.K., R.R. Volkas, Phys. Lett. B 655,156-161,2007 R. Foot, A.K., K.L. Mcdonald,
Scale invariance and the electroweak symmetry breaking Archil Kobakhidze School of Physics, University of Melbourne R. Foot, A.K., R.R. Volkas, Phys. Lett. B 655,156-161,2007 R. Foot, A.K., K.L. Mcdonald,
Donoghue, Golowich, Holstein Chapter 4, 6
 1 Week 7: Non linear sigma models and pion lagrangians Reading material from the books Burgess-Moore, Chapter 9.3 Donoghue, Golowich, Holstein Chapter 4, 6 Weinberg, Chap. 19 1 Goldstone boson lagrangians
1 Week 7: Non linear sigma models and pion lagrangians Reading material from the books Burgess-Moore, Chapter 9.3 Donoghue, Golowich, Holstein Chapter 4, 6 Weinberg, Chap. 19 1 Goldstone boson lagrangians
Symmetry Groups conservation law quantum numbers Gauge symmetries local bosons mediate the interaction Group Abelian Product of Groups simple
 Symmetry Groups Symmetry plays an essential role in particle theory. If a theory is invariant under transformations by a symmetry group one obtains a conservation law and quantum numbers. For example,
Symmetry Groups Symmetry plays an essential role in particle theory. If a theory is invariant under transformations by a symmetry group one obtains a conservation law and quantum numbers. For example,
+ µ 2 ) H (m 2 H 2
 I. THE HIGGS POTENTIAL AND THE LIGHT HIGGS BOSON In the previous chapter, it was demonstrated that a negative mass squared in the Higgs potential is generated radiatively for a large range of boundary
I. THE HIGGS POTENTIAL AND THE LIGHT HIGGS BOSON In the previous chapter, it was demonstrated that a negative mass squared in the Higgs potential is generated radiatively for a large range of boundary
Triplet Higgs Scenarios
 Triplet Higgs Scenarios Jack Gunion U.C. Davis Grenoble Higgs Workshop, March 2, 203 Higgs-like LHC Signal Fits with MVA CMS suggest we are heading towards the SM, but it could simply be a decoupling limit
Triplet Higgs Scenarios Jack Gunion U.C. Davis Grenoble Higgs Workshop, March 2, 203 Higgs-like LHC Signal Fits with MVA CMS suggest we are heading towards the SM, but it could simply be a decoupling limit
Simplified models in collider searches for dark matter. Stefan Vogl
 Simplified models in collider searches for dark matter Stefan Vogl Outline Introduction/Motivation Simplified Models for the LHC A word of caution Conclusion How to look for dark matter at the LHC? experimentally
Simplified models in collider searches for dark matter Stefan Vogl Outline Introduction/Motivation Simplified Models for the LHC A word of caution Conclusion How to look for dark matter at the LHC? experimentally
Mathematical Underpinnings of Fundamental Gauge Theories
 UNIVERSITY OF SOUTHERN DENMARK MASTER THESIS Mathematical Underpinnings of Fundamental Gauge Theories Author: Nicolai SANDAL BANKE Supervisor: Francesco SANNINO A thesis submitted in fulfillment of the
UNIVERSITY OF SOUTHERN DENMARK MASTER THESIS Mathematical Underpinnings of Fundamental Gauge Theories Author: Nicolai SANDAL BANKE Supervisor: Francesco SANNINO A thesis submitted in fulfillment of the
Birth of electroweak theory from an Imperial perspective
 Birth of electroweak theory from an Imperial perspective Tom Kibble King s College London 2 Oct 2012 Electroweak theory Oct 2012 1 Outline Story of spontaneous symmetry breaking in gauge theories and electro-weak
Birth of electroweak theory from an Imperial perspective Tom Kibble King s College London 2 Oct 2012 Electroweak theory Oct 2012 1 Outline Story of spontaneous symmetry breaking in gauge theories and electro-weak
Where are we heading? Nathan Seiberg IAS 2014
 Where are we heading? Nathan Seiberg IAS 2014 Purpose of this talk A brief, broad brush status report of particle physics Where we are How we got here (some historical perspective) Problems and challenges
Where are we heading? Nathan Seiberg IAS 2014 Purpose of this talk A brief, broad brush status report of particle physics Where we are How we got here (some historical perspective) Problems and challenges
The Strong Interaction and LHC phenomenology
 The Strong Interaction and LHC phenomenology Juan Rojo STFC Rutherford Fellow University of Oxford Theoretical Physics Graduate School course Lecture 2: The QCD Lagrangian, Symmetries and Feynman Rules
The Strong Interaction and LHC phenomenology Juan Rojo STFC Rutherford Fellow University of Oxford Theoretical Physics Graduate School course Lecture 2: The QCD Lagrangian, Symmetries and Feynman Rules
What We Really Know About Neutrino Speeds
 What We Really Know About Neutrino Speeds Brett Altschul University of South Carolina March 22, 2013 In particle physics, the standard model has been incredibly successful. If the Higgs boson discovered
What We Really Know About Neutrino Speeds Brett Altschul University of South Carolina March 22, 2013 In particle physics, the standard model has been incredibly successful. If the Higgs boson discovered
2.4 Parity transformation
 2.4 Parity transformation An extremely simple group is one that has only two elements: {e, P }. Obviously, P 1 = P, so P 2 = e, with e represented by the unit n n matrix in an n- dimensional representation.
2.4 Parity transformation An extremely simple group is one that has only two elements: {e, P }. Obviously, P 1 = P, so P 2 = e, with e represented by the unit n n matrix in an n- dimensional representation.
Outlook Post-Higgs. Fermilab. UCLA Higgs Workshop March 22, 2013
 Outlook Post-Higgs Christopher T. Hill Fermilab UCLA Higgs Workshop March 22, 2013 A dynamical Higgs mechanism was supposed to explain the origin of electroweak mass A dynamical Higgs mechanism was supposed
Outlook Post-Higgs Christopher T. Hill Fermilab UCLA Higgs Workshop March 22, 2013 A dynamical Higgs mechanism was supposed to explain the origin of electroweak mass A dynamical Higgs mechanism was supposed
PhD in Theoretical Particle Physics Academic Year 2017/2018
 July 10, 017 SISSA Entrance Examination PhD in Theoretical Particle Physics Academic Year 017/018 S olve two among the four problems presented. Problem I Consider a quantum harmonic oscillator in one spatial
July 10, 017 SISSA Entrance Examination PhD in Theoretical Particle Physics Academic Year 017/018 S olve two among the four problems presented. Problem I Consider a quantum harmonic oscillator in one spatial
Light-Cone Quantization of Electrodynamics
 Light-Cone Quantization of Electrodynamics David G. Robertson Department of Physics, The Ohio State University Columbus, OH 43210 Abstract Light-cone quantization of (3+1)-dimensional electrodynamics is
Light-Cone Quantization of Electrodynamics David G. Robertson Department of Physics, The Ohio State University Columbus, OH 43210 Abstract Light-cone quantization of (3+1)-dimensional electrodynamics is
The Standard Model of Electroweak Physics. Christopher T. Hill Head of Theoretical Physics Fermilab
 The Standard Model of Electroweak Physics Christopher T. Hill Head of Theoretical Physics Fermilab Lecture I: Incarnations of Symmetry Noether s Theorem is as important to us now as the Pythagorean Theorem
The Standard Model of Electroweak Physics Christopher T. Hill Head of Theoretical Physics Fermilab Lecture I: Incarnations of Symmetry Noether s Theorem is as important to us now as the Pythagorean Theorem
SM predicts massless neutrinos
 MASSIVE NEUTRINOS SM predicts massless neutrinos What is the motivation for considering neutrino masses? Is the question of the existence of neutrino masses an isolated one, or is connected to other outstanding
MASSIVE NEUTRINOS SM predicts massless neutrinos What is the motivation for considering neutrino masses? Is the question of the existence of neutrino masses an isolated one, or is connected to other outstanding
Gauge Theory of Electro-Weak Interactions. Following slides based among others on
 Gauge Theory of Electro-Weak Interactions Read Appendix D of Book Gauge Theories Following slides based among others on The ideas of particle physics: an introduction to scientists, by Coughlan, Dodd,
Gauge Theory of Electro-Weak Interactions Read Appendix D of Book Gauge Theories Following slides based among others on The ideas of particle physics: an introduction to scientists, by Coughlan, Dodd,
Lecture 7 SUSY breaking
 Lecture 7 SUSY breaking Outline Spontaneous SUSY breaking in the WZ-model. The goldstino. Goldstino couplings. The goldstino theorem. Reading: Terning 5.1, 5.3-5.4. Spontaneous SUSY Breaking Reminder:
Lecture 7 SUSY breaking Outline Spontaneous SUSY breaking in the WZ-model. The goldstino. Goldstino couplings. The goldstino theorem. Reading: Terning 5.1, 5.3-5.4. Spontaneous SUSY Breaking Reminder:
Symmetries, Groups Theory and Lie Algebras in Physics
 Symmetries, Groups Theory and Lie Algebras in Physics M.M. Sheikh-Jabbari Symmetries have been the cornerstone of modern physics in the last century. Symmetries are used to classify solutions to physical
Symmetries, Groups Theory and Lie Algebras in Physics M.M. Sheikh-Jabbari Symmetries have been the cornerstone of modern physics in the last century. Symmetries are used to classify solutions to physical
Masses and the Higgs Mechanism
 Chapter 8 Masses and the Higgs Mechanism The Z, like the W ± must be very heavy. This much can be inferred immediately because a massless Z boson would give rise to a peculiar parity-violating long-range
Chapter 8 Masses and the Higgs Mechanism The Z, like the W ± must be very heavy. This much can be inferred immediately because a massless Z boson would give rise to a peculiar parity-violating long-range
Higgs Boson Phenomenology Lecture I
 iggs Boson Phenomenology Lecture I Laura Reina TASI 2011, CU-Boulder, June 2011 Outline of Lecture I Understanding the Electroweak Symmetry Breaking as a first step towards a more fundamental theory of
iggs Boson Phenomenology Lecture I Laura Reina TASI 2011, CU-Boulder, June 2011 Outline of Lecture I Understanding the Electroweak Symmetry Breaking as a first step towards a more fundamental theory of
Lecture 39, 40 Supplement: Particle physics in the LHC era
 Lecture 39, 40 Supplement: Particle physics in the LHC era The Matter Particles (Fermions) plus their antiparticles... What is measured? quarks confined into hadrons A zoo of strongly interacting particles...
Lecture 39, 40 Supplement: Particle physics in the LHC era The Matter Particles (Fermions) plus their antiparticles... What is measured? quarks confined into hadrons A zoo of strongly interacting particles...
12.2 Problem Set 2 Solutions
 78 CHAPTER. PROBLEM SET SOLUTIONS. Problem Set Solutions. I will use a basis m, which ψ C = iγ ψ = Cγ ψ (.47) We can define left (light) handed Majorana fields as, so that ω = ψ L + (ψ L ) C (.48) χ =
78 CHAPTER. PROBLEM SET SOLUTIONS. Problem Set Solutions. I will use a basis m, which ψ C = iγ ψ = Cγ ψ (.47) We can define left (light) handed Majorana fields as, so that ω = ψ L + (ψ L ) C (.48) χ =
2T-physics and the Standard Model of Particles and Forces Itzhak Bars (USC)
 2T-physics and the Standard Model of Particles and Forces Itzhak Bars (USC) hep-th/0606045 Success of 2T-physics for particles on worldlines. Field theory version of 2T-physics. Standard Model in 4+2 dimensions.
2T-physics and the Standard Model of Particles and Forces Itzhak Bars (USC) hep-th/0606045 Success of 2T-physics for particles on worldlines. Field theory version of 2T-physics. Standard Model in 4+2 dimensions.
Particle physics today. Giulia Zanderighi (CERN & University of Oxford)
 Particle physics today Giulia Zanderighi (CERN & University of Oxford) Particle Physics Particle Physics is fundamental research, as opposed to many applied sciences (medicine, biology, chemistry, nano-science,
Particle physics today Giulia Zanderighi (CERN & University of Oxford) Particle Physics Particle Physics is fundamental research, as opposed to many applied sciences (medicine, biology, chemistry, nano-science,
(a) (b) Notes 6: The Higgs. Spontaneous symmetry breaking
 Notes 6: The Higgs This is a middle difficulty explaination. The text books are either much more detailed or simpler. This is a useful guide for those who want to look at HM, Griffiths or Burcham and Jobes
Notes 6: The Higgs This is a middle difficulty explaination. The text books are either much more detailed or simpler. This is a useful guide for those who want to look at HM, Griffiths or Burcham and Jobes
Physics at e + e - Linear Colliders. 4. Supersymmetric particles. M. E. Peskin March, 2002
 Physics at e + e - Linear Colliders 4. Supersymmetric particles M. E. Peskin March, 2002 In this final lecture, I would like to discuss supersymmetry at the LC. Supersymmetry is not a part of the Standard
Physics at e + e - Linear Colliders 4. Supersymmetric particles M. E. Peskin March, 2002 In this final lecture, I would like to discuss supersymmetry at the LC. Supersymmetry is not a part of the Standard
New Physics from Vector-Like Technicolor: Roman Pasechnik Lund University, THEP group
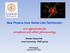 New Physics from Vector-Like Technicolor: Roman Pasechnik Lund University, THEP group CP3 Origins, September 16 th, 2013 At this seminar I will touch upon... σ 2 Issues of the Standard Model Dramatically
New Physics from Vector-Like Technicolor: Roman Pasechnik Lund University, THEP group CP3 Origins, September 16 th, 2013 At this seminar I will touch upon... σ 2 Issues of the Standard Model Dramatically
Theory of Elementary Particles homework VIII (June 04)
 Theory of Elementary Particles homework VIII June 4) At the head of your report, please write your name, student ID number and a list of problems that you worked on in a report like II-1, II-3, IV- ).
Theory of Elementary Particles homework VIII June 4) At the head of your report, please write your name, student ID number and a list of problems that you worked on in a report like II-1, II-3, IV- ).
Invariants and CP violation in the 2HDM and 3HDM
 Invariants and CP violation in the 2HDM and 3HDM Talk given at Workshop on the Standard Model and Beyond, Corfu September 5, 2017 Odd Magne Ogreid Based on work with B. Grzadkowski and P. Osland Motivations
Invariants and CP violation in the 2HDM and 3HDM Talk given at Workshop on the Standard Model and Beyond, Corfu September 5, 2017 Odd Magne Ogreid Based on work with B. Grzadkowski and P. Osland Motivations
QFT Dimensional Analysis
 QFT Dimensional Analysis In the h = c = 1 units, all quantities are measured in units of energy to some power. For example m = p µ = E +1 while x µ = E 1 where m stands for the dimensionality of the mass
QFT Dimensional Analysis In the h = c = 1 units, all quantities are measured in units of energy to some power. For example m = p µ = E +1 while x µ = E 1 where m stands for the dimensionality of the mass
The Dilaton/Radion and the 125 GeV Resonance
 The Dilaton/Radion and the 125 GeV Resonance Zackaria Chacko University of Maryland, College Park Introduction The discovery of a new Higgs-like particle with mass close to 125 GeV is a watershed in high
The Dilaton/Radion and the 125 GeV Resonance Zackaria Chacko University of Maryland, College Park Introduction The discovery of a new Higgs-like particle with mass close to 125 GeV is a watershed in high
Particle Physics 2018 Final Exam (Answers with Words Only)
 Particle Physics 2018 Final Exam (Answers with Words Only) This was a hard course that likely covered a lot of new and complex ideas. If you are feeling as if you could not possibly recount all of the
Particle Physics 2018 Final Exam (Answers with Words Only) This was a hard course that likely covered a lot of new and complex ideas. If you are feeling as if you could not possibly recount all of the
Lecture 23. November 16, Developing the SM s electroweak theory. Fermion mass generation using a Higgs weak doublet
 Lecture 23 November 16, 2017 Developing the SM s electroweak theory Research News: Higgs boson properties and use as a dark matter probe Fermion mass generation using a Higgs weak doublet Summary of the
Lecture 23 November 16, 2017 Developing the SM s electroweak theory Research News: Higgs boson properties and use as a dark matter probe Fermion mass generation using a Higgs weak doublet Summary of the
Gauge-Higgs Unification on Flat Space Revised
 Outline Gauge-Higgs Unification on Flat Space Revised Giuliano Panico ISAS-SISSA Trieste, Italy The 14th International Conference on Supersymmetry and the Unification of Fundamental Interactions Irvine,
Outline Gauge-Higgs Unification on Flat Space Revised Giuliano Panico ISAS-SISSA Trieste, Italy The 14th International Conference on Supersymmetry and the Unification of Fundamental Interactions Irvine,
The 1/N expansion method in quantum field theory
 III d International School Symmetry in Integrable Systems and Nuclear Physics Tsakhkadzor, Armenia, 3-13 July 2013 The 1/N expansion method in quantum field theory Hagop Sazdjian IPN, Université Paris-Sud,
III d International School Symmetry in Integrable Systems and Nuclear Physics Tsakhkadzor, Armenia, 3-13 July 2013 The 1/N expansion method in quantum field theory Hagop Sazdjian IPN, Université Paris-Sud,
Sreerup Raychaudhuri TIFR
 The Boson in the Model Sreerup Raychaudhuri TIFR What everyone knows What everyone knows Electroweak interactions are very accurately described by a local SU(2) U(1) gauge theory The gauge symmetry does
The Boson in the Model Sreerup Raychaudhuri TIFR What everyone knows What everyone knows Electroweak interactions are very accurately described by a local SU(2) U(1) gauge theory The gauge symmetry does
Is there a Scalar Sector?
 Is there a Scalar Sector? Roberto Peccei Cornwall Symposium UCLA November 2009 Is there a Scalar Sector? The Cornwall Norton Paper Technicolor and its Troubles Difficulties with CP Concluding Remarks The
Is there a Scalar Sector? Roberto Peccei Cornwall Symposium UCLA November 2009 Is there a Scalar Sector? The Cornwall Norton Paper Technicolor and its Troubles Difficulties with CP Concluding Remarks The
125 GeV Higgs Boson and Gauge Higgs Unification
 125 GeV Higgs Boson and Gauge Higgs Unification Nobuchika Okada The University of Alabama Miami 2013, Fort Lauderdale, Dec. 12 18, 2013 Discovery of Higgs boson at LHC! 7/04/2012 Standard Model Higgs boson
125 GeV Higgs Boson and Gauge Higgs Unification Nobuchika Okada The University of Alabama Miami 2013, Fort Lauderdale, Dec. 12 18, 2013 Discovery of Higgs boson at LHC! 7/04/2012 Standard Model Higgs boson
REVIEW REVIEW. Quantum Field Theory II
 Quantum Field Theory II PHYS-P 622 Radovan Dermisek, Indiana University Notes based on: M. Srednicki, Quantum Field Theory Chapters: 13, 14, 16-21, 26-28, 51, 52, 61-68, 44, 53, 69-74, 30-32, 84-86, 75,
Quantum Field Theory II PHYS-P 622 Radovan Dermisek, Indiana University Notes based on: M. Srednicki, Quantum Field Theory Chapters: 13, 14, 16-21, 26-28, 51, 52, 61-68, 44, 53, 69-74, 30-32, 84-86, 75,
Quantum Field Theory II
 Quantum Field Theory II PHYS-P 622 Radovan Dermisek, Indiana University Notes based on: M. Srednicki, Quantum Field Theory Chapters: 13, 14, 16-21, 26-28, 51, 52, 61-68, 44, 53, 69-74, 30-32, 84-86, 75,
Quantum Field Theory II PHYS-P 622 Radovan Dermisek, Indiana University Notes based on: M. Srednicki, Quantum Field Theory Chapters: 13, 14, 16-21, 26-28, 51, 52, 61-68, 44, 53, 69-74, 30-32, 84-86, 75,
1 Introduction. 1.1 The Standard Model of particle physics The fundamental particles
 1 Introduction The purpose of this chapter is to provide a brief introduction to the Standard Model of particle physics. In particular, it gives an overview of the fundamental particles and the relationship
1 Introduction The purpose of this chapter is to provide a brief introduction to the Standard Model of particle physics. In particular, it gives an overview of the fundamental particles and the relationship
Weak interactions and vector bosons
 Weak interactions and vector bosons What do we know now about weak interactions? Theory of weak interactions Fermi's theory of weak interactions V-A theory Current - current theory, current algebra W and
Weak interactions and vector bosons What do we know now about weak interactions? Theory of weak interactions Fermi's theory of weak interactions V-A theory Current - current theory, current algebra W and
Hidden two-higgs doublet model
 Hidden two-higgs doublet model C, Uppsala and Lund University SUSY10, Bonn, 2010-08-26 1 Two Higgs doublet models () 2 3 4 Phenomenological consequences 5 Two Higgs doublet models () Work together with
Hidden two-higgs doublet model C, Uppsala and Lund University SUSY10, Bonn, 2010-08-26 1 Two Higgs doublet models () 2 3 4 Phenomenological consequences 5 Two Higgs doublet models () Work together with
Physics 129 LECTURE 6 January 23, Particle Physics Symmetries (Perkins Chapter 3)
 Physics 129 LECTURE 6 January 23, 2014 Particle Physics Symmetries (Perkins Chapter 3) n Lagrangian Deductions n Rotations n Parity n Charge Conjugation Gauge Invariance and Charge Conservation The Higgs
Physics 129 LECTURE 6 January 23, 2014 Particle Physics Symmetries (Perkins Chapter 3) n Lagrangian Deductions n Rotations n Parity n Charge Conjugation Gauge Invariance and Charge Conservation The Higgs
SM, EWSB & Higgs. MITP Summer School 2017 Joint Challenges for Cosmology and Colliders. Homework & Exercises
 SM, EWSB & Higgs MITP Summer School 017 Joint Challenges for Cosmology and Colliders Homework & Exercises Ch!"ophe Grojean Ch!"ophe Grojean DESY (Hamburg) Humboldt University (Berlin) ( christophe.grojean@desy.de
SM, EWSB & Higgs MITP Summer School 017 Joint Challenges for Cosmology and Colliders Homework & Exercises Ch!"ophe Grojean Ch!"ophe Grojean DESY (Hamburg) Humboldt University (Berlin) ( christophe.grojean@desy.de
Lecture 03. The Standard Model of Particle Physics. Part III Extensions of the Standard Model
 Lecture 03 The Standard Model of Particle Physics Part III Extensions of the Standard Model Where the SM Works Excellent description of 3 of the 4 fundamental forces Explains nuclear structure, quark confinement,
Lecture 03 The Standard Model of Particle Physics Part III Extensions of the Standard Model Where the SM Works Excellent description of 3 of the 4 fundamental forces Explains nuclear structure, quark confinement,
Review of scalar field theory. Srednicki 5, 9, 10
 Review of scalar field theory Srednicki 5, 9, 10 2 The LSZ reduction formula based on S-5 In order to describe scattering experiments we need to construct appropriate initial and final states and calculate
Review of scalar field theory Srednicki 5, 9, 10 2 The LSZ reduction formula based on S-5 In order to describe scattering experiments we need to construct appropriate initial and final states and calculate
Reφ = 1 2. h ff λ. = λ f
 I. THE FINE-TUNING PROBLEM A. Quadratic divergence We illustrate the problem of the quadratic divergence in the Higgs sector of the SM through an explicit calculation. The example studied is that of the
I. THE FINE-TUNING PROBLEM A. Quadratic divergence We illustrate the problem of the quadratic divergence in the Higgs sector of the SM through an explicit calculation. The example studied is that of the
Introduction to Supersymmetry
 Introduction to Supersymmetry I. Antoniadis Albert Einstein Center - ITP Lecture 5 Grand Unification I. Antoniadis (Supersymmetry) 1 / 22 Grand Unification Standard Model: remnant of a larger gauge symmetry
Introduction to Supersymmetry I. Antoniadis Albert Einstein Center - ITP Lecture 5 Grand Unification I. Antoniadis (Supersymmetry) 1 / 22 Grand Unification Standard Model: remnant of a larger gauge symmetry
9 Quantum Field Theory for Children
 101 9 Quantum Field Theory for Children The theories (known and hypothetical) needed to describe the (very) early universe are quantum field theories (QFT). The fundamental entities of these theories are
101 9 Quantum Field Theory for Children The theories (known and hypothetical) needed to describe the (very) early universe are quantum field theories (QFT). The fundamental entities of these theories are
Lecture 8. September 21, General plan for construction of Standard Model theory. Choice of gauge symmetries for the Standard Model
 Lecture 8 September 21, 2017 Today General plan for construction of Standard Model theory Properties of SU(n) transformations (review) Choice of gauge symmetries for the Standard Model Use of Lagrangian
Lecture 8 September 21, 2017 Today General plan for construction of Standard Model theory Properties of SU(n) transformations (review) Choice of gauge symmetries for the Standard Model Use of Lagrangian
Patrick Kirchgaeßer 07. Januar 2016
 Patrick Kirchgaeßer 07. Januar 2016 INSTITUTE OF EXPERIMENTAL PARTICLE PHYSICS (IEKP) PHYSICS FACULTY KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft
Patrick Kirchgaeßer 07. Januar 2016 INSTITUTE OF EXPERIMENTAL PARTICLE PHYSICS (IEKP) PHYSICS FACULTY KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft
The bestest little Higgs
 The bestest little Higgs The MIT Faculty has made this article openly available. Please share how this access benefits you. Your story matters. Citation As Published Publisher Schmaltz, Martin, Daniel
The bestest little Higgs The MIT Faculty has made this article openly available. Please share how this access benefits you. Your story matters. Citation As Published Publisher Schmaltz, Martin, Daniel
Fundamental Forces. David Morrissey. Key Concepts, March 15, 2013
 Fundamental Forces David Morrissey Key Concepts, March 15, 2013 Not a fundamental force... Also not a fundamental force... What Do We Mean By Fundamental? Example: Electromagnetism (EM) electric forces
Fundamental Forces David Morrissey Key Concepts, March 15, 2013 Not a fundamental force... Also not a fundamental force... What Do We Mean By Fundamental? Example: Electromagnetism (EM) electric forces
SUSY Phenomenology & Experimental searches
 SUSY Phenomenology & Experimental searches Slides available at: Alex Tapper http://www.hep.ph.ic.ac.uk/~tapper/lecture.html Objectives - Know what Supersymmetry (SUSY) is - Understand qualitatively the
SUSY Phenomenology & Experimental searches Slides available at: Alex Tapper http://www.hep.ph.ic.ac.uk/~tapper/lecture.html Objectives - Know what Supersymmetry (SUSY) is - Understand qualitatively the
The Higgs discovery - a portal to new physics
 The Higgs discovery - a portal to new physics Department of astronomy and theoretical physics, 2012-10-17 1 / 1 The Higgs discovery 2 / 1 July 4th 2012 - a historic day in many ways... 3 / 1 July 4th 2012
The Higgs discovery - a portal to new physics Department of astronomy and theoretical physics, 2012-10-17 1 / 1 The Higgs discovery 2 / 1 July 4th 2012 - a historic day in many ways... 3 / 1 July 4th 2012
arxiv: v2 [hep-ph] 14 Aug 2017
![arxiv: v2 [hep-ph] 14 Aug 2017 arxiv: v2 [hep-ph] 14 Aug 2017](/thumbs/86/93479524.jpg) Minimal conformal extensions of the Higgs sector Alexander J. Helmboldt, Pascal Humbert, Manfred Lindner, and Juri Smirnov Max-Planck-Institut für Kernphysik, Saupfercheckweg 1, 69117 Heidelberg, Germany
Minimal conformal extensions of the Higgs sector Alexander J. Helmboldt, Pascal Humbert, Manfred Lindner, and Juri Smirnov Max-Planck-Institut für Kernphysik, Saupfercheckweg 1, 69117 Heidelberg, Germany
University of Illinois at Champaign Urbana Department of Physics
 University of Illinois at Champaign Urbana Department of Physics Electroweak Symmetry Breaking. Higgs Particle Discovery Potential within the ATLAS Experiment Hovhannes Khandanyan Abstract. One of the
University of Illinois at Champaign Urbana Department of Physics Electroweak Symmetry Breaking. Higgs Particle Discovery Potential within the ATLAS Experiment Hovhannes Khandanyan Abstract. One of the
A first trip to the world of particle physics
 A first trip to the world of particle physics Itinerary Massimo Passera Padova - 13/03/2013 1 Massimo Passera Padova - 13/03/2013 2 The 4 fundamental interactions! Electromagnetic! Weak! Strong! Gravitational
A first trip to the world of particle physics Itinerary Massimo Passera Padova - 13/03/2013 1 Massimo Passera Padova - 13/03/2013 2 The 4 fundamental interactions! Electromagnetic! Weak! Strong! Gravitational
THE STANDARD MODEL AND THE GENERALIZED COVARIANT DERIVATIVE
 THE STANDAD MODEL AND THE GENEALIZED COVAIANT DEIVATIVE arxiv:hep-ph/9907480v Jul 999 M. Chaves and H. Morales Escuela de Física, Universidad de Costa ica San José, Costa ica E-mails: mchaves@cariari.ucr.ac.cr,
THE STANDAD MODEL AND THE GENEALIZED COVAIANT DEIVATIVE arxiv:hep-ph/9907480v Jul 999 M. Chaves and H. Morales Escuela de Física, Universidad de Costa ica San José, Costa ica E-mails: mchaves@cariari.ucr.ac.cr,
Electroweak unification
 Electroweak unification Electroweak unification τ Experimental facts τ SU(2) L U(1) Y gauge theory τ Charged current interaction τ Neutral current interaction τ Gauge self-interactions III/1 Experimental
Electroweak unification Electroweak unification τ Experimental facts τ SU(2) L U(1) Y gauge theory τ Charged current interaction τ Neutral current interaction τ Gauge self-interactions III/1 Experimental
Elementary Particles, Flavour Physics and all that...
 Elementary Particles, Flavour Physics and all that... 1 Flavour Physics The term Flavour physics was coined in 1971 by Murray Gell-Mann and his student at the time, Harald Fritzsch, at a Baskin-Robbins
Elementary Particles, Flavour Physics and all that... 1 Flavour Physics The term Flavour physics was coined in 1971 by Murray Gell-Mann and his student at the time, Harald Fritzsch, at a Baskin-Robbins
The Phases of QCD. Thomas Schaefer. North Carolina State University
 The Phases of QCD Thomas Schaefer North Carolina State University 1 Motivation Different phases of QCD occur in the universe Neutron Stars, Big Bang Exploring the phase diagram is important to understanding
The Phases of QCD Thomas Schaefer North Carolina State University 1 Motivation Different phases of QCD occur in the universe Neutron Stars, Big Bang Exploring the phase diagram is important to understanding
July 2, SISSA Entrance Examination. PhD in Theoretical Particle Physics Academic Year 2018/2019. olve two among the three problems presented.
 July, 018 SISSA Entrance Examination PhD in Theoretical Particle Physics Academic Year 018/019 S olve two among the three problems presented. Problem I Consider a theory described by the Lagrangian density
July, 018 SISSA Entrance Examination PhD in Theoretical Particle Physics Academic Year 018/019 S olve two among the three problems presented. Problem I Consider a theory described by the Lagrangian density
