and right turns are selected independently with xed probabilities) and by dn(x) the
|
|
|
- Dwight Francis
- 6 years ago
- Views:
Transcription
1 BINOMIAL-COEFFICIENT MULTIPLES OF IRRATIONALS Terrence M. Adams and Karl E. Petersen Abstract. Denote by x a random innite path in the graph of Pascal's triangle (left and right turns are selected independently with xed probabilities) and by dn(x) the binomial coecient at the n'th level along the path x. Then for a dense G set of in the unit interval, fdn(x)g is almost surely dense but not uniformly distributed modulo.. Introduction The Pascal graph is the directed innite planar graph with vertices (n; k), for n = 0; ; : : : and k = 0; : : : ; n and two edges coming out of each vertex (n; k), one to (n + ; k) and one to (n + ; k + ). Labeling edges of the rst kind by 0 and of the second kind by produces a natural correspondence between innite sequences x 2 = f0; g N and innite paths in the Pascal graph which start at the root vertex (0; 0). We will denote by d n (x) the binomial coecient C(n; k n (x)) found at the n'th vertex of x, if the Pascal graph is superimposed on the Pascal triangle. The Pascal adic transformation on the space of innite paths (see [9,, 2, 6]) corresponds to the map T :! given by T ( p 0 q 0 : : : ) = 0 q p 0 : : : for p; q 0. Vershik [9] noted that the invariant ergodic measures for this map are exactly the Bernoulli measures = B(; ) on and conjectured [0] that they are weakly mixing. It was noted in [6] that if, for a xed Bernoulli measure on, is an eigenvalue of T, then d n(x)! for a.e. x. The question of whether or not there exist such, and its variants concerning the distribution of the points d n(x) on the unit circle for typical x or indeed for all x, some of them also mentioned in [6], lead to the study of the distribution modulo of binomial-coecient multiples of irrationals; answering many of these questions seems to demand deeper understanding of the divisibility properties of binomial coecients than we have at present. While we are not yet able to answer the question of weak mixing for the Pascal adic transformation, we do have some progress on related questions. First, we note that if x is a path in the Pascal graph which tracks a line of a xed slope, then the proportion of j's, 0 j n, for which d j (x) is divisible by a xed prime q tends to as n!. Using this, we construct an uncountable set of on the unit circle such that for a.e. path x in the Pascal graph (with respect to a xed Bernoulli measure) the points d n(x) are not uniformly distributed on the circle, since asymptotically too large a fraction of them are near. Thus these points might be candidates for eigenvalues of T but we construct such for which the d n(x) are 99 Mathematics Subject Classication. Primary 28D05, 28D99.. Key words and phrases. uniform distribution modulo, Pascal adic transformation, measurepreserving transformation, eigenvalue, weak mixing.
2 2 TERRENCE M. ADAMS AND KARL E. PETERSEN dense. We also list several further observations, questions, and conjectures about the distribution of these points; perhaps the strongest conjecture (also mentioned in [6]) is the following: If 2 C and there exists a path x in the Pascal graph for which d n(x)!, then =. The second author gratefully acknowledges the support of the Erwin Schrodinger Institute, Vienna, where part of this research was conducted. 2. Intersections of lines with Sierpinski's gasket Let E denote the triangle with vertices (0; 0), (; 0), and (0; ). In this section we construct Sierpinski's gasket as a subset of E. Then we prove that every straight line path (with slope strictly greater than 0) through Sierpinski's gasket intersects the gasket in a set with one-dimensional Lebesgue measure 0. (Since Sierpinski's gasket has two-dimensional Lebesgue measure 0, Fubini's theorem guarantees that almost every line with a specied slope intersects Sierpinski's gasket with one-dimensional Lebesgue measure 0, but this is not sucient for our purpose.) We give two lemmas which set up the general proof. Also we apply this to the generalized Sierpinski gasket dened at the end of this section. Given a natural number n, let E n denote the interior of the right triangle with vertices ((2 n )=2 n ; =2 n ), ((2 n )=2 n ; 0) and ((2 n )=2 n ; =2 n ) and let E 2 n be the interior of the triangle with vertices (=2 n ; (2 n )=2 n ), (0; (2 n )=2 n ) and (=2 n ; (2 n )=2 n ). We view the collection of E i n's contained in the larger triangle E with vertices (0; 0), (; 0) and (0; ). The next two lemmas concern the intersection of the E i n's with a straight line of slope > 0 (where corresponds to the invariant Bernoulli measure, with = =( + ) for the Pascal adic transformation). Lemma 2.3. Given > 0 there exists = () > 0 such that: for any straight line L of slope which intersects the interior of E, there exists n and i such that (L \ E i n ) (L \ E) : Before we prove Lemma 2.3 we state and prove the preliminary Lemma 2.2. Lemma 2.2. Given > 0 there exist positive real numbers = () and = () such that for all b 2 [ ; ( )=2] and L b = f(x; (x b)) : x 2 Rg we have (L b \ E ) (L b \ E) : Proof. First we nd the intersection of L b with the hypotenuse of E. Solving y = (x b) and y = =2 x simultaneously, we obtain x = (=2 + b)=( + ) and y = (=2 b)=( + ). Thus if we choose < =(2) our point of intersection will have positive x and y coordinates. Hence the function f(b) = (L b \ E )=(L b \ E) is positive and continuous on the closed interval [ ; ( )=2] and therefore achieves a positive minimum value. Proof of Lemma 2.3. Any line L which intersects the interior of E intersects either the line segment joining (0; 0) to (; 0) or the line segment joining (0; 0) to (0; ).
3 BINOMIAL-COEFFICIENT MULTIPLES OF IRRATIONALS 3 Without loss of generality let us consider line segments L intersecting the segment joining (0; 0) to (; 0). If we let I = f(x; 0) : 0 x < g, then I \ L 6= ;. In this case we may focus on the sets E n = En. Choose > 0 as in Lemma 2.2. (In particular < =(2) will work.) We may cover I with subintervals S I n = [(2 n )=2 n =2 n ; (2 n )=2 n =2 n ); so we have I = I n= n. For each b 2 I n dene L b = f(x; (x b)) : x 2 Rg and f n : I n! [0; ] as f n (b) = (L b \ E n )=(L b \ E). The self-similarity properties of the triangles E n imply that each f n : I n! [0; ] is continuous, and they all have the same image. Therefore by Lemma 2.2 there exists a single real number > 0 such that f n (b) = (L b \ E n ) (L b \ E) for all positive integers n and all b 2 I n. Now we construct Sierpinski's gasket as a closed nowhere dense subset of E. We call triangles in the plane lower triangles if we can label the vertices (a ; b ), (a 2 ; b 2 ) and (a 3 ; b 3 ) so that the right angle is at (a 2 ; b 2 ) and a 2 = minfa ; a 3 g and b 2 = minfb ; b 3 g. Upper triangles have right angle at (a 2 ; b 2 ) with a 2 = maxfa ; a 3 g and b 2 = maxfb ; b 3 g. Note that given a lower triangle R there is a unique upper triangle (inscribed in R) whose vertices are the midpoints of the sides of R. This upper triangle is denoted U(R); let L(R) = fr ; R 2 ; R 3 g be the collection of lower triangles remaining when we extract U(R) from R. Also given a collection C of lower triangles let U(C) = fu(r) : R 2 Cg and let L(C) = [ R2C L(R): We take the triangles in L(R) to be closed. The following proposition uses Lemma 2.3 to prove that (L \ G) = 0 for any line L with slope > 0. First note that Lemmas 2.2 and 2.3 can be extended to any lower triangle playing the role of the initial triangle E. Also note that En i 2 U(L n (E)) for positive integers n and i = ; 2. This implies that each R 2 L n (E) is disjoint from the interior of E i n. Let G n = [ Then G = T n= G n is Sierpinski's gasket. R2L n (E) Proposition 2.4. If > 0 and L = f(x; x) : x 2 Rg, then (G \ L) = lim n! (G n \ L) = 0. Proof. Choose = () > 0 as in Lemma 2.3. We construct inductively a sequence n j of natural numbers such that for all positive integers j we have (L \ G nj ) (L \ E) R: ( ) j :
4 4 TERRENCE M. ADAMS AND KARL E. PETERSEN For the primary case Lemma 2.3 ensures that there exists E i n 2 U(L n (E)) such that (L \ E i n )=(L \ E). (Actually n =.) Hence (L \ G n )=(L \ E) : For the general case suppose that n k satises (L \ G nk )=(L \ E) ( ) k : Now L n k (E) = fr ; : : : ; R p g is composed of a nite number of closed triangles. Let M = fm : m p; R m \L 6= ;g. Thus (R m \L) = 0 for m =2 M. For each m 2 M, by Lemma 2.3 there exists a positive integer e(m) and E(m) 2 U(L e(m) (R m )) such that (L \ E(m))=(L \ R m ). Let e = max m2m fe(m)g, and let n k+ = n k + e. Therefore we have (L \ G nk+ ) ( )(L \ G nk ) ( ) k+ : Now we dene the generalized Sierpinski gasket and give the analogous proposition which may be proved by the same method. Let E be the closed triangle described above. Given a positive integer q the lines y = p=q, x = p=q and y = p=q x partition E into q 2 triangles with q(q )=2 upper triangles and q(q + )=2 lower triangles. Let U q (E) be the collection of upper triangles and L q (E) be the collection lower triangles. (Take the members of U q (E) to be open and the members of L q (E) to be closed.) Dene U q (C) and L q (C) analogously for any collection C of lower triangles. We obtain G n q = [ R2L n q (E) R ; G q = Proposition 2.5. If > 0 and L = f(x; x) : x 2 Rg, then for all positive integers q (G q \ L) = lim n! (Gn q \ L) = 0: Proof. We explain how to choose sets E i n(q) analogous to the E i n above. Then the analogues of the previous lemmas and proposition follow in the same manner as before. Given a lower triangle R let L q (R) be the collection of two lower triangles: the top left, lower triangle from L q (R) and the bottom right, lower triangle from L q (R). Similarly we dene L n q (C). The sets E i n(q) are chosen in U q (L n q (E)). \ n= G n q : 3. Binomial coefficients modulo a prime along a random path in Pascal's triangle If Pascal's triangle is reduced modulo a prime q, a well-known self-similar pattern (which can be produced by a cellular automaton) results; this is a consequence of Kummer's Carry Theorem [4] and the resulting formula of Lucas [5]. The parts of the triangle that correspond to the upper triangles (which form (G q ) c ) (the `voids') consist of regions in which the binomial coecients are divisible by q. The following theorem says that since a line of slope spends most of its time outside of each G n q, a -typical path x, which eventually approaches a line of slope = ( )= in Pascal's triangle, spends most of its time on vertices which carry binomial coecients divisible by q.
5 BINOMIAL-COEFFICIENT MULTIPLES OF IRRATIONALS 5 Theorem 3.. If q is prime and 0 < <, then for -almost all x we have n lim n! n je 2id j (x)=q j = 0: Proof. Let > 0. Using Proposition 2.5, choose N so large that if n N then (G n q \ L ) <. Notice that since the complement of G N q is a union of nitely many triangles, if we move L just a small amount we cannot decrease the Lebesgue measure of its intersection with (G N q ) c by very much. Thus we may choose > 0 and then a large-enough natural number M such that if the part within our unit triangle E of the band of width about the line L is cut into M equally-spaced chunks by lines parallel to the hypotenuse of E, and if one point is chosen from each of those chunks, then the proportion of those points which are in G n q is still less than 2. Let S k (x) denote the number of 's along the path x (regarded as a sequence in = f0; g Z ). By the Ergodic Theorem, for -almost every x there is K = K(x) such that js k (x) kj < k for all k K: Choose a time M > K=, and consider Pascal's triangle down to that level, including subtriangles of rank up to N. When this part of Pascal's triangle is scaled down to lie over our unit triangle E, we see the subtriangles that form (G N q )c, and the scaled-down path x lies entirely inside the band of width about L, the line of slope = ( )= in the Sierpinski gasket. We have arranged that the proportion of vertices of the scaled-down path which are in (G N q ) c is at least 2, and hence the proportion of vertices of the path x at which the binomial coecients d j (x) are divisible by q is at least Main result: a construction of special irrationals In this section we use Theorem 3. to construct an uncountable dense set (in fact a G ) [0; ) such that for each 2 and for -almost every x 2 we have that the sequence fd j (x)g is not uniformly distributed modulo. In particular we obtain a result similar to Theorem 3., but with the limit replaced by lim inf. Theorem 4.. There exist a dense G set [0; ) and a set of full -measure Y so that for each 2 and x 2 Y we have lim inf n! n n je 2id j (x) j = 0: Proof. Let f n g be a sequence of positive real numbers satisfying P n= n <, and let fq n g be a sequence of primes increasing to. We will produce sequences R n of natural numbers and n > 0 so that if Y n = fx 2 : R n R n je 2id j (x)p=q n j < n for p = 0; ; : : : ; q n g;
6 6 TERRENCE M. ADAMS AND KARL E. PETERSEN then n = f 2 [0; ) : there exists p = 0; ; : : : ; q n with j p q n j < n g; = \ [ k= n=k lim inf n! n, and Y = n n [ \ k= n=k je 2id j (x) j = 0 for all 2 and all x 2 Y. For each n, by Theorem 3. we may choose R n so that (Y n ) > n. Then, since f R n R n je 2id j (x) j : x 2 Y n g is a nite collection of continuous functions of, we may choose n > 0 so that R n R n je 2id j(x) j < 2 n for all x 2 Y n and all 2 n. Then is a dense G with the usual topology, and P (Y ) = because n= n converges. To verify the outcome of the theorem, rst choose 2 and x 2 Y. Then there exists a sequence n m! such that 2 nm for all positive integers m. Also there exists k such that x 2 Y n for n k. Hence for n m k we have R nm R n m je 2id j(x) j < 2 n m : Y n ; 5. Density without uniform distribution In the previous section we constructed a dense G set [0; ) such that for each 2, fd j (x)g is not uniformly distributed modulo for -almost every x 2. Those 2, which are irrational, remain candidates for eigenvalues of the Pascal adic transformation. However in this section we will show that if the sequence f n g converges to zero suciently fast, then fd j (x)g is dense modulo for each 2 and for -almost every x 2. This excludes these as eigenvalues for the Pascal adic. We begin by considering Pascal's triangle modulo a prime q. Recall that for n 2 N and k q n, we have C(q n ; k) =q 0. Hence C(q n ; k) =q ( ) k for 0 k q n, which gives a `blocking line' on the triangle. It is this `blocking line' that yields total ergodicity of the Pascal adic. In Lemma 5. we note that
7 BINOMIAL-COEFFICIENT MULTIPLES OF IRRATIONALS 7 among the binomial coecients in the row numbered q n 2 one can nd all the congruence classes modulo q, and in fact they appear in a regular way. This allows us to show that along a random path in the triangle a hit of congruence class r at level q m and of congruence class p at level q n are approximately independent if m and n are far apart, and therefore with probability no congruence class modulo q can be avoided. Consequently, if is very well approximated by rationals p n =q n, then fd j (x)g must be dense modulo. Lemma 5.. Let q be prime and n a natural number. Then for k = 0; : : : ; q n 2 we have the following formula: () C(q n 2; k) =q ( ) k (k + ): Moreover, for natural numbers k and p satisfying 0 p q and 0 k q n 2q the set (2) fi : k i k + 2q ; C(q n 2; i) =q pg has exactly two elements. Proof. First we derive the formula inductively. The primary case is trivial: C(q n 2; 0) = = ( ) 0 (). Assume the formula holds for k = `. Thus for k = ` we have C(q n 2; `) = C(q n ; `) C(q n 2; ` ) = q ( )` ( )` ` = ( )`[ + `]: Now for the second part of the lemma, we note that our formula gives the following: if i even C(q n 2; i + 2) C(qn 2; i) + 2 =q C(q n 2; i) 2 if i odd: Hence if q = 2 we obtain C(q n 2; k) =q for k even and C(q n 2; k) =q 0 for k odd. For q 6= 2 we have that each of the maps j 7! C(q n 2; k + 2j) mod q and j 7! C(q n 2; k + + 2j) mod q gives a bijection of f0; : : : ; q g. Lemma 5.2. Suppose that for each n 2 N, we have a unimodal distribution f n on the set f0; : : : ; q n 2g. For each p satisfying 0 p q, let M p = fm : 0 m q n 2; C(q n 2; m) =q pg: If lim n! maxff n (m) : 0 m q n 2g = 0, then Proof. We will show that lim f n! n (m) = q : m2m p lim n! ( m2m p f n (m) m2m r f n (m)) = 0
8 8 TERRENCE M. ADAMS AND KARL E. PETERSEN for all p and r. Without loss of generality, assume that f n (m) m2m p m2m r f n (m): Partition f0; : : : ; q n 2g into subintervals of 2q consecutive numbers with one remaining subinterval of at most 2q consecutive numbers. Discard the subinterval which contains the peak of the distribution f n, as well as its two adjacent subintervals, from the set M p. Call the remaining set M p. Now for each m 2 M p there exists m 2 M r in the next interval of length 2q towards the peak of f n such that f n (m) f n (m ). Therefore f n (m) f n (m) f n (m) 6 maxff n (m) : 0 m q n 2g: m2m r m2m p m2m p Let F n (q; p) be the set of paths which pass through a vertex (q n 2; k) satisfying C(q n 2; k) =q p. Lemma 5.2 implies that the conditional probability of the set F n (q; p), given that the path passes through a xed vertex, converges to =q as n!. Therefore for each m 2 N (3) lim n! (F n (q; p) \ F m (q; r)) = q (F m (q; r)): A standard Hilbert space argument of A. Renyi and P. Revesz [8] implies that F n (q; p), n = ; 2; : : : is a mixing sequence of sets. In particular we have Lemma 5.3, which says F n (q; p) `sweeps out'. Finally we prove Theorem 5.4 using an approximation technique similar to that used in the previous section. Lemma 5.3. For 0 p < q with q prime and 0 < <, ( [ n= F n (q; p)) = : Theorem 5.4. There exist a dense G set [0; ) and a set of full -measure Y so that for each 2 and x 2 Y the set fe 2id j (x) : j 2 Ng is dense (but not uniformly distributed) in S. Proof. Let f n g P be a sequence of positive real numbers satisfying n= n <, and let fq n g be a sequence of primes increasing to. We will produce sequences R n of natural numbers and n > 0 so that if Y n = q n \ R[ n p=0 j= F j (q n ; p); n = f 2 [0; ) : there exists p n = 0; ; : : : ; q n with j p n q n j < n g;
9 BINOMIAL-COEFFICIENT MULTIPLES OF IRRATIONALS 9 = \ [ k= n=k n, and Y = [ \ k= n=k then fe 2id j(x) : j 2 Ng is dense but not uniformly distributed for all 2 and all x 2 Y. For each n, by Lemma 5.3 we may choose R n so that (Y n ) > n. Then choose n < n C(q R n n 2; (q R n n 2)=2) : As before, if 2 and x 2 Y, then we can nd arbitrarily large n such that 2 n and x 2 Y n. Now is very well approximated by a rational p n =q n, and as p runs through the congruence classes modulo q n, the points pp n =q n are =q n -dense modulo. Further, for each congruence class p modulo q n there is j = ; : : : ; R n such that at level s = qn j the path x has its binomial coecient d s(x) hit that congruence class. Since n has been chosen so small that all the points d s (x) under consideration are very close to the points d s (x)p n =q n, and the latter are =q n -dense, we are done. 6. Questions and Conjectures. Conjecture [0, 6]: For each Bernoulli measure, the Pascal adic transformation T is weakly mixing. This would follow if one could show that d n(x)! for a.e. x with respect to implies =. 2. Conjecture: If there is a path x such that d n(x)!, then =. 3. Does there exist any in the unit circle such that f d n(x) g is uniformly distributed in the circle for every x (except for the two paths down the edges)? For such a, the skew-product transformation Y n ; S(z ; z 2 ; z 3 ; : : : ) = (z ; z z 2 ; z 2 z 3 ; : : : ) on the innite torus, known to be uniquely ergodic by results of Weyl [3, 4], Furstenberg [], Hahn [3], and Postnikov [7], would have the very strong property that we would see a uniformly distributed sequence f(s j z) k g not only when we looked in a xed coordinate k at the orbit of a point z, but also when we allowed our view to shift one place to the right from time to time: f(s j z) kj g would be uniformly distributed for each z and each choice of fk j g N with k j+ k j 2 f0; g for each j. (The that we construct above are at another extreme from this property.) 4. From another theorem of Weyl and Tonelli's Theorem it follows that for almost every the sequence f d n(x) g is uniformly distributed for a.e. x, with respect to each Bernoulli measure. For which does this hold? Similarly, what paths x have the property that this sequence is uniformly distributed for each that is not a root of unity? (By Weyl's Theorem, this is the case for each path x that is eventually diagonal.) 5. Studies like these on divisibility of binomial coecients by primes suggest questions on simultaneous divisibility by several primes. For example, thinking about the central path in Pascal's triangle and divisibility by 2 and 3 leads to the
10 0 TERRENCE M. ADAMS AND KARL E. PETERSEN following Conjecture: The only solutions in nonnegative integers r and distinct s ; : : : ; s m of an equation 2 r = 3 s s m are =, 4 = +3, and 256 = We thank Charles Gien for pointing out that this conjecture was already made by Erdos see [2]. More generally, if for a prime p we dene an integer Cantor set H(p) to consist of all those expansions base p with coecients in the interval [0; p=2] (or subject to some other restriction), is H(p ) \ \ H(p n ) typically nite? References. H. Furstenberg, Strict ergodicity and transformations of the torus, Amer. J. Math. 83 (96), 573{ R. K. Guy, Unsolved Problems in Number Theory, Second Edition, Springer- Verlag, New York, 994, p F. J. Hahn, On ane transformations of compact abelian groups, Amer. J. Math. 85 (963), 428{ E. E. Kummer, Uber die Erganzungssatze zu den allgemeinen Reciprocitatsgesetzen, J. fur Math. 44 (852), 5{6. 5. E. Lucas, Theorie des fonctions numeriques simplement periodiques, Amer. J. Math. (878), 84{ K. Petersen and K. Schmidt, Symmetric Gibbs measures (to appear). 7. A. G. Postnikov, Ergodic problems in the theory of congruences and of Diophantine approximations, Proc. Steklov Inst. Math. 82 (966), 3{2. 8. A. Renyi, On mixing sequences of sets, Acad. Sci. Hung. 9 (958), A. M. Vershik, Description of invariant measures for actions of some innite groups, Dokl. Akad. Nauk SSSR 28 (974), ; Soviet Math. Dokl. 5 (974), 396{ , private communication.., Uniform algebraic approximation of shift and multiplication operators, Dokl. Akad. Nauk SSSR 259 (98), ; Soviet Math. Dokl. 24 (98), 97{ A. M. Vershik and A. N. Livshitz, Adic models of ergodic transformations, spectral theory, substitutions, and related topics, Adv. Soviet Math. 9 (992), 85{ H. Weyl, Uber ein Problem aus dem Gebiete der diophantischen Approximationen, Nach. Ges. Wiss. Gottingen (94), 234{ H. Weyl, Uber die Gleichverteilung von Zahlen mod. Eins, Math. Ann. 77 (96), 33{352. Department of Mathematics, CB 3250 Phillips Hall, University of North Carolina, Chapel Hill, NC , USA Current address: Department of Mathematics, Ohio State University, Columbus, OH 4320, USA address: tadams@math.ohio-state.edu Department of Mathematics, CB 3250 Phillips Hall, University of North Carolina, Chapel Hill, NC USA address: petersen@math.unc.edu
FACTOR MAPS BETWEEN TILING DYNAMICAL SYSTEMS KARL PETERSEN. systems which cannot be achieved by working within a nite window. By. 1.
 FACTOR MAPS BETWEEN TILING DYNAMICAL SYSTEMS KARL PETERSEN Abstract. We show that there is no Curtis-Hedlund-Lyndon Theorem for factor maps between tiling dynamical systems: there are codes between such
FACTOR MAPS BETWEEN TILING DYNAMICAL SYSTEMS KARL PETERSEN Abstract. We show that there is no Curtis-Hedlund-Lyndon Theorem for factor maps between tiling dynamical systems: there are codes between such
The Erwin Schrodinger International Boltzmanngasse 9. Institute for Mathematical Physics A-1090 Wien, Austria
 ESI The Erwin Schrodinger International Boltzmanngasse 9 Institute for Mathematical Physics A-1090 Wien, Austria Common Homoclinic Points of Commuting Toral Automorphisms Anthony Manning Klaus Schmidt
ESI The Erwin Schrodinger International Boltzmanngasse 9 Institute for Mathematical Physics A-1090 Wien, Austria Common Homoclinic Points of Commuting Toral Automorphisms Anthony Manning Klaus Schmidt
Real Analysis Math 131AH Rudin, Chapter #1. Dominique Abdi
 Real Analysis Math 3AH Rudin, Chapter # Dominique Abdi.. If r is rational (r 0) and x is irrational, prove that r + x and rx are irrational. Solution. Assume the contrary, that r+x and rx are rational.
Real Analysis Math 3AH Rudin, Chapter # Dominique Abdi.. If r is rational (r 0) and x is irrational, prove that r + x and rx are irrational. Solution. Assume the contrary, that r+x and rx are rational.
SUMS PROBLEM COMPETITION, 2000
 SUMS ROBLEM COMETITION, 2000 SOLUTIONS 1 The result is well known, and called Morley s Theorem Many proofs are known See for example HSM Coxeter, Introduction to Geometry, page 23 2 If the number of vertices,
SUMS ROBLEM COMETITION, 2000 SOLUTIONS 1 The result is well known, and called Morley s Theorem Many proofs are known See for example HSM Coxeter, Introduction to Geometry, page 23 2 If the number of vertices,
Balance properties of multi-dimensional words
 Theoretical Computer Science 273 (2002) 197 224 www.elsevier.com/locate/tcs Balance properties of multi-dimensional words Valerie Berthe a;, Robert Tijdeman b a Institut de Mathematiques de Luminy, CNRS-UPR
Theoretical Computer Science 273 (2002) 197 224 www.elsevier.com/locate/tcs Balance properties of multi-dimensional words Valerie Berthe a;, Robert Tijdeman b a Institut de Mathematiques de Luminy, CNRS-UPR
NATIONAL BOARD FOR HIGHER MATHEMATICS. Research Scholarships Screening Test. Saturday, February 2, Time Allowed: Two Hours Maximum Marks: 40
 NATIONAL BOARD FOR HIGHER MATHEMATICS Research Scholarships Screening Test Saturday, February 2, 2008 Time Allowed: Two Hours Maximum Marks: 40 Please read, carefully, the instructions on the following
NATIONAL BOARD FOR HIGHER MATHEMATICS Research Scholarships Screening Test Saturday, February 2, 2008 Time Allowed: Two Hours Maximum Marks: 40 Please read, carefully, the instructions on the following
Solutions to Tutorial 8 (Week 9)
 The University of Sydney School of Mathematics and Statistics Solutions to Tutorial 8 (Week 9) MATH3961: Metric Spaces (Advanced) Semester 1, 2018 Web Page: http://www.maths.usyd.edu.au/u/ug/sm/math3961/
The University of Sydney School of Mathematics and Statistics Solutions to Tutorial 8 (Week 9) MATH3961: Metric Spaces (Advanced) Semester 1, 2018 Web Page: http://www.maths.usyd.edu.au/u/ug/sm/math3961/
Notes for Math 290 using Introduction to Mathematical Proofs by Charles E. Roberts, Jr.
 Notes for Math 290 using Introduction to Mathematical Proofs by Charles E. Roberts, Jr. Chapter : Logic Topics:. Statements, Negation, and Compound Statements.2 Truth Tables and Logical Equivalences.3
Notes for Math 290 using Introduction to Mathematical Proofs by Charles E. Roberts, Jr. Chapter : Logic Topics:. Statements, Negation, and Compound Statements.2 Truth Tables and Logical Equivalences.3
CONGRUENT NUMBERS AND ELLIPTIC CURVES
 CONGRUENT NUMBERS AND ELLIPTIC CURVES JIM BROWN Abstract. In this short paper we consider congruent numbers and how they give rise to elliptic curves. We will begin with very basic notions before moving
CONGRUENT NUMBERS AND ELLIPTIC CURVES JIM BROWN Abstract. In this short paper we consider congruent numbers and how they give rise to elliptic curves. We will begin with very basic notions before moving
NAME: Mathematics 205A, Fall 2008, Final Examination. Answer Key
 NAME: Mathematics 205A, Fall 2008, Final Examination Answer Key 1 1. [25 points] Let X be a set with 2 or more elements. Show that there are topologies U and V on X such that the identity map J : (X, U)
NAME: Mathematics 205A, Fall 2008, Final Examination Answer Key 1 1. [25 points] Let X be a set with 2 or more elements. Show that there are topologies U and V on X such that the identity map J : (X, U)
64 Garunk»stis and Laurin»cikas can not be satised for any polynomial P. S. M. Voronin [10], [12] obtained the functional independence of the Riemann
![64 Garunk»stis and Laurin»cikas can not be satised for any polynomial P. S. M. Voronin [10], [12] obtained the functional independence of the Riemann 64 Garunk»stis and Laurin»cikas can not be satised for any polynomial P. S. M. Voronin [10], [12] obtained the functional independence of the Riemann](/thumbs/92/110999423.jpg) PUBLICATIONS DE L'INSTITUT MATHÉMATIQUE Nouvelle série, tome 65 (79), 1999, 63 68 ON ONE HILBERT'S PROBLEM FOR THE LERCH ZETA-FUNCTION R. Garunk»stis and A. Laurin»cikas Communicated by Aleksandar Ivić
PUBLICATIONS DE L'INSTITUT MATHÉMATIQUE Nouvelle série, tome 65 (79), 1999, 63 68 ON ONE HILBERT'S PROBLEM FOR THE LERCH ZETA-FUNCTION R. Garunk»stis and A. Laurin»cikas Communicated by Aleksandar Ivić
Name (please print) Mathematics Final Examination December 14, 2005 I. (4)
 Mathematics 513-00 Final Examination December 14, 005 I Use a direct argument to prove the following implication: The product of two odd integers is odd Let m and n be two odd integers Since they are odd,
Mathematics 513-00 Final Examination December 14, 005 I Use a direct argument to prove the following implication: The product of two odd integers is odd Let m and n be two odd integers Since they are odd,
Monomial Graphs and Generalized Quadrangles
 Monomial Graphs and Generalized Quadrangles Brian G. Kronenthal Department of Mathematical Sciences, Ewing Hall, University of Delaware, Newark, DE 19716, USA Abstract Let F q be a finite field, where
Monomial Graphs and Generalized Quadrangles Brian G. Kronenthal Department of Mathematical Sciences, Ewing Hall, University of Delaware, Newark, DE 19716, USA Abstract Let F q be a finite field, where
Lebesgue Measure and The Cantor Set
 Math 0 Final year project Lebesgue Measure and The Cantor Set Jason Baker, Kyle Henke, Michael Sanchez Overview Define a measure Define when a set has measure zero Find the measure of [0, ], I and Q Construct
Math 0 Final year project Lebesgue Measure and The Cantor Set Jason Baker, Kyle Henke, Michael Sanchez Overview Define a measure Define when a set has measure zero Find the measure of [0, ], I and Q Construct
PERIODICITY OF SOME RECURRENCE SEQUENCES MODULO M
 INTEGERS: ELECTRONIC JOURNAL OF COMBINATORIAL NUMBER THEORY 8 (2008), #A42 PERIODICITY OF SOME RECURRENCE SEQUENCES MODULO M Artūras Dubickas Department of Mathematics and Informatics, Vilnius University,
INTEGERS: ELECTRONIC JOURNAL OF COMBINATORIAL NUMBER THEORY 8 (2008), #A42 PERIODICITY OF SOME RECURRENCE SEQUENCES MODULO M Artūras Dubickas Department of Mathematics and Informatics, Vilnius University,
CDMTCS Research Report Series Explicit Denition of the Binary Reected Gray Codes Marston Conder Department of Mathematics University of Auckland Auckl
 CDMTCS Research Report Series Explicit Denition of the Binary Reected Gray Codes Marston Conder Department of Mathematics University of Auckland Auckland, New Zealand CDMTCS-041 June 1997 Centre for Discrete
CDMTCS Research Report Series Explicit Denition of the Binary Reected Gray Codes Marston Conder Department of Mathematics University of Auckland Auckland, New Zealand CDMTCS-041 June 1997 Centre for Discrete
GENERALIZED CANTOR SETS AND SETS OF SUMS OF CONVERGENT ALTERNATING SERIES
 Journal of Applied Analysis Vol. 7, No. 1 (2001), pp. 131 150 GENERALIZED CANTOR SETS AND SETS OF SUMS OF CONVERGENT ALTERNATING SERIES M. DINDOŠ Received September 7, 2000 and, in revised form, February
Journal of Applied Analysis Vol. 7, No. 1 (2001), pp. 131 150 GENERALIZED CANTOR SETS AND SETS OF SUMS OF CONVERGENT ALTERNATING SERIES M. DINDOŠ Received September 7, 2000 and, in revised form, February
NOTES Edited by William Adkins. On Goldbach s Conjecture for Integer Polynomials
 NOTES Edited by William Adkins On Goldbach s Conjecture for Integer Polynomials Filip Saidak 1. INTRODUCTION. We give a short proof of the fact that every monic polynomial f (x) in Z[x] can be written
NOTES Edited by William Adkins On Goldbach s Conjecture for Integer Polynomials Filip Saidak 1. INTRODUCTION. We give a short proof of the fact that every monic polynomial f (x) in Z[x] can be written
IRRATIONAL ROTATION OF THE CIRCLE AND THE BINARY ODOMETER ARE FINITARILY ORBIT EQUIVALENT
 IRRATIONAL ROTATION OF THE CIRCLE AND THE BINARY ODOMETER ARE FINITARILY ORBIT EQUIVALENT MRINAL KANTI ROYCHOWDHURY Abstract. Two invertible dynamical systems (X, A, µ, T ) and (Y, B, ν, S) where X, Y
IRRATIONAL ROTATION OF THE CIRCLE AND THE BINARY ODOMETER ARE FINITARILY ORBIT EQUIVALENT MRINAL KANTI ROYCHOWDHURY Abstract. Two invertible dynamical systems (X, A, µ, T ) and (Y, B, ν, S) where X, Y
Chapter 8. P-adic numbers. 8.1 Absolute values
 Chapter 8 P-adic numbers Literature: N. Koblitz, p-adic Numbers, p-adic Analysis, and Zeta-Functions, 2nd edition, Graduate Texts in Mathematics 58, Springer Verlag 1984, corrected 2nd printing 1996, Chap.
Chapter 8 P-adic numbers Literature: N. Koblitz, p-adic Numbers, p-adic Analysis, and Zeta-Functions, 2nd edition, Graduate Texts in Mathematics 58, Springer Verlag 1984, corrected 2nd printing 1996, Chap.
ALMOST DISJOINT AND INDEPENDENT FAMILIES. 1. introduction. is infinite. Fichtenholz and Kantorovich showed that there is an independent family
 ALMOST DISJOINT AND INDEPENDENT FAMILIES STEFAN GESCHKE Abstract. I collect a number of proofs of the existence of large almost disjoint and independent families on the natural numbers. This is mostly
ALMOST DISJOINT AND INDEPENDENT FAMILIES STEFAN GESCHKE Abstract. I collect a number of proofs of the existence of large almost disjoint and independent families on the natural numbers. This is mostly
An extension of the Pascal triangle and the Sierpiński gasket to finite words. Joint work with Julien Leroy and Michel Rigo (ULiège)
 An extension of the Pascal triangle and the Sierpiński gasket to finite words Joint work with Julien Leroy and Michel Rigo (ULiège) Manon Stipulanti (ULiège) FRIA grantee LaBRI, Bordeaux (France) December
An extension of the Pascal triangle and the Sierpiński gasket to finite words Joint work with Julien Leroy and Michel Rigo (ULiège) Manon Stipulanti (ULiège) FRIA grantee LaBRI, Bordeaux (France) December
MATH 202B - Problem Set 5
 MATH 202B - Problem Set 5 Walid Krichene (23265217) March 6, 2013 (5.1) Show that there exists a continuous function F : [0, 1] R which is monotonic on no interval of positive length. proof We know there
MATH 202B - Problem Set 5 Walid Krichene (23265217) March 6, 2013 (5.1) Show that there exists a continuous function F : [0, 1] R which is monotonic on no interval of positive length. proof We know there
Mathematics Course 111: Algebra I Part I: Algebraic Structures, Sets and Permutations
 Mathematics Course 111: Algebra I Part I: Algebraic Structures, Sets and Permutations D. R. Wilkins Academic Year 1996-7 1 Number Systems and Matrix Algebra Integers The whole numbers 0, ±1, ±2, ±3, ±4,...
Mathematics Course 111: Algebra I Part I: Algebraic Structures, Sets and Permutations D. R. Wilkins Academic Year 1996-7 1 Number Systems and Matrix Algebra Integers The whole numbers 0, ±1, ±2, ±3, ±4,...
Lebesgue Measure on R n
 CHAPTER 2 Lebesgue Measure on R n Our goal is to construct a notion of the volume, or Lebesgue measure, of rather general subsets of R n that reduces to the usual volume of elementary geometrical sets
CHAPTER 2 Lebesgue Measure on R n Our goal is to construct a notion of the volume, or Lebesgue measure, of rather general subsets of R n that reduces to the usual volume of elementary geometrical sets
ERGODIC DYNAMICAL SYSTEMS CONJUGATE TO THEIR COMPOSITION SQUARES. 0. Introduction
 Acta Math. Univ. Comenianae Vol. LXXI, 2(2002), pp. 201 210 201 ERGODIC DYNAMICAL SYSTEMS CONJUGATE TO THEIR COMPOSITION SQUARES G. R. GOODSON Abstract. We investigate the question of when an ergodic automorphism
Acta Math. Univ. Comenianae Vol. LXXI, 2(2002), pp. 201 210 201 ERGODIC DYNAMICAL SYSTEMS CONJUGATE TO THEIR COMPOSITION SQUARES G. R. GOODSON Abstract. We investigate the question of when an ergodic automorphism
Discrete dynamics on the real line
 Chapter 2 Discrete dynamics on the real line We consider the discrete time dynamical system x n+1 = f(x n ) for a continuous map f : R R. Definitions The forward orbit of x 0 is: O + (x 0 ) = {x 0, f(x
Chapter 2 Discrete dynamics on the real line We consider the discrete time dynamical system x n+1 = f(x n ) for a continuous map f : R R. Definitions The forward orbit of x 0 is: O + (x 0 ) = {x 0, f(x
Je Lagarias, University of Michigan. Workshop on Discovery and Experimentation in Number Theory Fields Institute, Toronto (September 25, 2009)
 Ternary Expansions of Powers of 2 Je Lagarias, University of Michigan Workshop on Discovery and Experimentation in Number Theory Fields Institute, Toronto (September 25, 2009) Topics Covered Part I. Erdős
Ternary Expansions of Powers of 2 Je Lagarias, University of Michigan Workshop on Discovery and Experimentation in Number Theory Fields Institute, Toronto (September 25, 2009) Topics Covered Part I. Erdős
ON AN INFINITE-DIMENSIONAL GROUP OVER A FINITE FIELD. A. M. Vershik, S. V. Kerov
 ON AN INFINITE-DIMENSIONAL GROUP OVER A FINITE FIELD A. M. Vershik, S. V. Kerov Introduction. The asymptotic representation theory studies the behavior of representations of large classical groups and
ON AN INFINITE-DIMENSIONAL GROUP OVER A FINITE FIELD A. M. Vershik, S. V. Kerov Introduction. The asymptotic representation theory studies the behavior of representations of large classical groups and
Master of Arts In Mathematics
 ESTIMATING THE FRACTAL DIMENSION OF SETS DETERMINED BY NONERGODIC PARAMETERS A thesis submitted to the faculty of San Francisco State University In partial fulllment of The Requirements for The Degree
ESTIMATING THE FRACTAL DIMENSION OF SETS DETERMINED BY NONERGODIC PARAMETERS A thesis submitted to the faculty of San Francisco State University In partial fulllment of The Requirements for The Degree
1 2n. i=1. 2m+1 i = m, while. 2m + 1 = 1. is the best possible for any odd n.
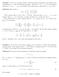 Problem 1. Let n be a positive integer. Find the largest nonnegative real number f(n) (depending on n) with the following property: whenever a 1, a,..., a n are real numbers such that a 1 + a + + a n is
Problem 1. Let n be a positive integer. Find the largest nonnegative real number f(n) (depending on n) with the following property: whenever a 1, a,..., a n are real numbers such that a 1 + a + + a n is
Contents Ordered Fields... 2 Ordered sets and fields... 2 Construction of the Reals 1: Dedekind Cuts... 2 Metric Spaces... 3
 Analysis Math Notes Study Guide Real Analysis Contents Ordered Fields 2 Ordered sets and fields 2 Construction of the Reals 1: Dedekind Cuts 2 Metric Spaces 3 Metric Spaces 3 Definitions 4 Separability
Analysis Math Notes Study Guide Real Analysis Contents Ordered Fields 2 Ordered sets and fields 2 Construction of the Reals 1: Dedekind Cuts 2 Metric Spaces 3 Metric Spaces 3 Definitions 4 Separability
ON A CLASS OF APERIODIC SUM-FREE SETS NEIL J. CALKIN PAUL ERD OS. that is that there are innitely many n not in S which are not a sum of two elements
 ON A CLASS OF APERIODIC SUM-FREE SETS NEIL J. CALKIN PAUL ERD OS Abstract. We show that certain natural aperiodic sum-free sets are incomplete, that is that there are innitely many n not in S which are
ON A CLASS OF APERIODIC SUM-FREE SETS NEIL J. CALKIN PAUL ERD OS Abstract. We show that certain natural aperiodic sum-free sets are incomplete, that is that there are innitely many n not in S which are
ON THE FRACTIONAL PARTS OF LACUNARY SEQUENCES
 MATH. SCAND. 99 (2006), 136 146 ON THE FRACTIONAL PARTS OF LACUNARY SEQUENCES ARTŪRAS DUBICKAS Abstract In this paper, we prove that if t 0,t 1,t 2,... is a lacunary sequence, namely, t n+1 /t n 1 + r
MATH. SCAND. 99 (2006), 136 146 ON THE FRACTIONAL PARTS OF LACUNARY SEQUENCES ARTŪRAS DUBICKAS Abstract In this paper, we prove that if t 0,t 1,t 2,... is a lacunary sequence, namely, t n+1 /t n 1 + r
MEASURE AND CATEGORY { Department of Mathematics, University of Tennessee, Chattanooga,
 Mathematica Pannonica 7/1 (1996), 69 { 78 MEASURE AND CATEGORY { SOME NON-ANALOGUES Harry I. Miller Department of Mathematics, University of Tennessee, Chattanooga, TN, 371403, USA Franz J. Schnitzer Institut
Mathematica Pannonica 7/1 (1996), 69 { 78 MEASURE AND CATEGORY { SOME NON-ANALOGUES Harry I. Miller Department of Mathematics, University of Tennessee, Chattanooga, TN, 371403, USA Franz J. Schnitzer Institut
3 hours UNIVERSITY OF MANCHESTER. 22nd May and. Electronic calculators may be used, provided that they cannot store text.
 3 hours MATH40512 UNIVERSITY OF MANCHESTER DYNAMICAL SYSTEMS AND ERGODIC THEORY 22nd May 2007 9.45 12.45 Answer ALL four questions in SECTION A (40 marks in total) and THREE of the four questions in SECTION
3 hours MATH40512 UNIVERSITY OF MANCHESTER DYNAMICAL SYSTEMS AND ERGODIC THEORY 22nd May 2007 9.45 12.45 Answer ALL four questions in SECTION A (40 marks in total) and THREE of the four questions in SECTION
5 Birkhoff s Ergodic Theorem
 5 Birkhoff s Ergodic Theorem Birkhoff s Ergodic Theorem extends the validity of Kolmogorov s strong law to the class of stationary sequences of random variables. Stationary sequences occur naturally even
5 Birkhoff s Ergodic Theorem Birkhoff s Ergodic Theorem extends the validity of Kolmogorov s strong law to the class of stationary sequences of random variables. Stationary sequences occur naturally even
ON DEVANEY S DEFINITION OF CHAOS AND DENSE PERIODIC POINTS
 ON DEVANEY S DEFINITION OF CHAOS AND DENSE PERIODIC POINTS SYAHIDA CHE DZUL-KIFLI AND CHRIS GOOD Abstract. We look again at density of periodic points and Devaney Chaos. We prove that if f is Devaney Chaotic
ON DEVANEY S DEFINITION OF CHAOS AND DENSE PERIODIC POINTS SYAHIDA CHE DZUL-KIFLI AND CHRIS GOOD Abstract. We look again at density of periodic points and Devaney Chaos. We prove that if f is Devaney Chaotic
2017 Harvard-MIT Mathematics Tournament
 Team Round 1 Let P(x), Q(x) be nonconstant polynomials with real number coefficients. Prove that if P(y) = Q(y) for all real numbers y, then P(x) = Q(x) for all real numbers x. 2 Does there exist a two-variable
Team Round 1 Let P(x), Q(x) be nonconstant polynomials with real number coefficients. Prove that if P(y) = Q(y) for all real numbers y, then P(x) = Q(x) for all real numbers x. 2 Does there exist a two-variable
NORMAL NUMBERS AND UNIFORM DISTRIBUTION (WEEKS 1-3) OPEN PROBLEMS IN NUMBER THEORY SPRING 2018, TEL AVIV UNIVERSITY
 ORMAL UMBERS AD UIFORM DISTRIBUTIO WEEKS -3 OPE PROBLEMS I UMBER THEORY SPRIG 28, TEL AVIV UIVERSITY Contents.. ormal numbers.2. Un-natural examples 2.3. ormality and uniform distribution 2.4. Weyl s criterion
ORMAL UMBERS AD UIFORM DISTRIBUTIO WEEKS -3 OPE PROBLEMS I UMBER THEORY SPRIG 28, TEL AVIV UIVERSITY Contents.. ormal numbers.2. Un-natural examples 2.3. ormality and uniform distribution 2.4. Weyl s criterion
ALMOST ODD RANDOM SUM-FREE SETS NEIL J. CALKIN AND P. J. CAMERON. 1. introduction
 ALMOST ODD RANDOM SUM-FREE SETS NEIL J. CALKIN AND P. J. CAMERON Abstract. We show that if S 1 is a strongly complete sum-free set of positive integers, and if S 0 is a nite sum-free set, then with positive
ALMOST ODD RANDOM SUM-FREE SETS NEIL J. CALKIN AND P. J. CAMERON Abstract. We show that if S 1 is a strongly complete sum-free set of positive integers, and if S 0 is a nite sum-free set, then with positive
What you learned in Math 28. Rosa C. Orellana
 What you learned in Math 28 Rosa C. Orellana Chapter 1 - Basic Counting Techniques Sum Principle If we have a partition of a finite set S, then the size of S is the sum of the sizes of the blocks of the
What you learned in Math 28 Rosa C. Orellana Chapter 1 - Basic Counting Techniques Sum Principle If we have a partition of a finite set S, then the size of S is the sum of the sizes of the blocks of the
1 The Local-to-Global Lemma
 Point-Set Topology Connectedness: Lecture 2 1 The Local-to-Global Lemma In the world of advanced mathematics, we are often interested in comparing the local properties of a space to its global properties.
Point-Set Topology Connectedness: Lecture 2 1 The Local-to-Global Lemma In the world of advanced mathematics, we are often interested in comparing the local properties of a space to its global properties.
University of California. Berkeley, CA fzhangjun johans lygeros Abstract
 Dynamical Systems Revisited: Hybrid Systems with Zeno Executions Jun Zhang, Karl Henrik Johansson y, John Lygeros, and Shankar Sastry Department of Electrical Engineering and Computer Sciences University
Dynamical Systems Revisited: Hybrid Systems with Zeno Executions Jun Zhang, Karl Henrik Johansson y, John Lygeros, and Shankar Sastry Department of Electrical Engineering and Computer Sciences University
On the classification of irrational numbers
 arxiv:506.0044v [math.nt] 5 Nov 07 On the classification of irrational numbers José de Jesús Hernández Serda May 05 Abstract In this note we make a comparison between the arithmetic properties of irrational
arxiv:506.0044v [math.nt] 5 Nov 07 On the classification of irrational numbers José de Jesús Hernández Serda May 05 Abstract In this note we make a comparison between the arithmetic properties of irrational
The Maximum Upper Density of a Set of Positive. Real Numbers with no solutions to x + y = kz. John L. Goldwasser. West Virginia University
 The Maximum Upper Density of a Set of Positive Real Numbers with no solutions to x + y = z John L. Goldwasser West Virginia University Morgantown, WV 6506 Fan R. K. Chung University ofpennsylvania Philadelphia,
The Maximum Upper Density of a Set of Positive Real Numbers with no solutions to x + y = z John L. Goldwasser West Virginia University Morgantown, WV 6506 Fan R. K. Chung University ofpennsylvania Philadelphia,
MORE ON CONTINUOUS FUNCTIONS AND SETS
 Chapter 6 MORE ON CONTINUOUS FUNCTIONS AND SETS This chapter can be considered enrichment material containing also several more advanced topics and may be skipped in its entirety. You can proceed directly
Chapter 6 MORE ON CONTINUOUS FUNCTIONS AND SETS This chapter can be considered enrichment material containing also several more advanced topics and may be skipped in its entirety. You can proceed directly
Rudiments of Ergodic Theory
 Rudiments of Ergodic Theory Zefeng Chen September 24, 203 Abstract In this note we intend to present basic ergodic theory. We begin with the notion of a measure preserving transformation. We then define
Rudiments of Ergodic Theory Zefeng Chen September 24, 203 Abstract In this note we intend to present basic ergodic theory. We begin with the notion of a measure preserving transformation. We then define
Part IA Numbers and Sets
 Part IA Numbers and Sets Theorems Based on lectures by A. G. Thomason Notes taken by Dexter Chua Michaelmas 2014 These notes are not endorsed by the lecturers, and I have modified them (often significantly)
Part IA Numbers and Sets Theorems Based on lectures by A. G. Thomason Notes taken by Dexter Chua Michaelmas 2014 These notes are not endorsed by the lecturers, and I have modified them (often significantly)
Test Codes : MIA (Objective Type) and MIB (Short Answer Type) 2007
 Test Codes : MIA (Objective Type) and MIB (Short Answer Type) 007 Questions will be set on the following and related topics. Algebra: Sets, operations on sets. Prime numbers, factorisation of integers
Test Codes : MIA (Objective Type) and MIB (Short Answer Type) 007 Questions will be set on the following and related topics. Algebra: Sets, operations on sets. Prime numbers, factorisation of integers
Real Analysis Notes. Thomas Goller
 Real Analysis Notes Thomas Goller September 4, 2011 Contents 1 Abstract Measure Spaces 2 1.1 Basic Definitions........................... 2 1.2 Measurable Functions........................ 2 1.3 Integration..............................
Real Analysis Notes Thomas Goller September 4, 2011 Contents 1 Abstract Measure Spaces 2 1.1 Basic Definitions........................... 2 1.2 Measurable Functions........................ 2 1.3 Integration..............................
ERGODIC AVERAGES FOR INDEPENDENT POLYNOMIALS AND APPLICATIONS
 ERGODIC AVERAGES FOR INDEPENDENT POLYNOMIALS AND APPLICATIONS NIKOS FRANTZIKINAKIS AND BRYNA KRA Abstract. Szemerédi s Theorem states that a set of integers with positive upper density contains arbitrarily
ERGODIC AVERAGES FOR INDEPENDENT POLYNOMIALS AND APPLICATIONS NIKOS FRANTZIKINAKIS AND BRYNA KRA Abstract. Szemerédi s Theorem states that a set of integers with positive upper density contains arbitrarily
 Max-Planck-Institut fur Mathematik in den Naturwissenschaften Leipzig Uniformly distributed measures in Euclidean spaces by Bernd Kirchheim and David Preiss Preprint-Nr.: 37 1998 Uniformly Distributed
Max-Planck-Institut fur Mathematik in den Naturwissenschaften Leipzig Uniformly distributed measures in Euclidean spaces by Bernd Kirchheim and David Preiss Preprint-Nr.: 37 1998 Uniformly Distributed
Constrained Leja points and the numerical solution of the constrained energy problem
 Journal of Computational and Applied Mathematics 131 (2001) 427 444 www.elsevier.nl/locate/cam Constrained Leja points and the numerical solution of the constrained energy problem Dan I. Coroian, Peter
Journal of Computational and Applied Mathematics 131 (2001) 427 444 www.elsevier.nl/locate/cam Constrained Leja points and the numerical solution of the constrained energy problem Dan I. Coroian, Peter
THE EULER ADIC DYNAMICAL SYSTEM AND PATH COUNTS IN THE EULER GRAPH. 1. Introduction
 THE EULER ADIC DYNAMICAL SYSTEM AND PATH COUNTS IN THE EULER GRAPH K. PETERSEN AND A. VARCHENKO Abstract. We give a formula for generalized Eulerian numbers, prove monotonicity of sequences of certain
THE EULER ADIC DYNAMICAL SYSTEM AND PATH COUNTS IN THE EULER GRAPH K. PETERSEN AND A. VARCHENKO Abstract. We give a formula for generalized Eulerian numbers, prove monotonicity of sequences of certain
van Rooij, Schikhof: A Second Course on Real Functions
 vanrooijschikhof.tex April 25, 2018 van Rooij, Schikhof: A Second Course on Real Functions Notes from [vrs]. Introduction A monotone function is Riemann integrable. A continuous function is Riemann integrable.
vanrooijschikhof.tex April 25, 2018 van Rooij, Schikhof: A Second Course on Real Functions Notes from [vrs]. Introduction A monotone function is Riemann integrable. A continuous function is Riemann integrable.
0 Sets and Induction. Sets
 0 Sets and Induction Sets A set is an unordered collection of objects, called elements or members of the set. A set is said to contain its elements. We write a A to denote that a is an element of the set
0 Sets and Induction Sets A set is an unordered collection of objects, called elements or members of the set. A set is said to contain its elements. We write a A to denote that a is an element of the set
Ergodic Theory and Topological Groups
 Ergodic Theory and Topological Groups Christopher White November 15, 2012 Throughout this talk (G, B, µ) will denote a measure space. We call the space a probability space if µ(g) = 1. We will also assume
Ergodic Theory and Topological Groups Christopher White November 15, 2012 Throughout this talk (G, B, µ) will denote a measure space. We call the space a probability space if µ(g) = 1. We will also assume
RANK AND PERIOD OF PRIMES IN THE FIBONACCI SEQUENCE. A TRICHOTOMY
 RANK AND PERIOD OF PRIMES IN THE FIBONACCI SEQUENCE. A TRICHOTOMY Christian Ballot Université de Caen, Caen 14032, France e-mail: ballot@math.unicaen.edu Michele Elia Politecnico di Torino, Torino 10129,
RANK AND PERIOD OF PRIMES IN THE FIBONACCI SEQUENCE. A TRICHOTOMY Christian Ballot Université de Caen, Caen 14032, France e-mail: ballot@math.unicaen.edu Michele Elia Politecnico di Torino, Torino 10129,
Some Results Concerning Uniqueness of Triangle Sequences
 Some Results Concerning Uniqueness of Triangle Sequences T. Cheslack-Postava A. Diesl M. Lepinski A. Schuyler August 12 1999 Abstract In this paper we will begin by reviewing the triangle iteration. We
Some Results Concerning Uniqueness of Triangle Sequences T. Cheslack-Postava A. Diesl M. Lepinski A. Schuyler August 12 1999 Abstract In this paper we will begin by reviewing the triangle iteration. We
Garrett: `Bernstein's analytic continuation of complex powers' 2 Let f be a polynomial in x 1 ; : : : ; x n with real coecients. For complex s, let f
 1 Bernstein's analytic continuation of complex powers c1995, Paul Garrett, garrettmath.umn.edu version January 27, 1998 Analytic continuation of distributions Statement of the theorems on analytic continuation
1 Bernstein's analytic continuation of complex powers c1995, Paul Garrett, garrettmath.umn.edu version January 27, 1998 Analytic continuation of distributions Statement of the theorems on analytic continuation
arxiv: v2 [math.ca] 4 Jun 2017
![arxiv: v2 [math.ca] 4 Jun 2017 arxiv: v2 [math.ca] 4 Jun 2017](/thumbs/76/73528053.jpg) EXCURSIONS ON CANTOR-LIKE SETS ROBERT DIMARTINO AND WILFREDO O. URBINA arxiv:4.70v [math.ca] 4 Jun 07 ABSTRACT. The ternary Cantor set C, constructed by George Cantor in 883, is probably the best known
EXCURSIONS ON CANTOR-LIKE SETS ROBERT DIMARTINO AND WILFREDO O. URBINA arxiv:4.70v [math.ca] 4 Jun 07 ABSTRACT. The ternary Cantor set C, constructed by George Cantor in 883, is probably the best known
The Erwin Schrodinger International Pasteurgasse 6/7. Institute for Mathematical Physics A-1090 Wien, Austria
 ESI The Erwin Schrodinger International Pasteurgasse 6/7 Institute for Mathematical Physics A-1090 Wien, Austria Invariant Cocycles, Random Tilings and the Super-K and Strong Markov Properties Klaus Schmidt
ESI The Erwin Schrodinger International Pasteurgasse 6/7 Institute for Mathematical Physics A-1090 Wien, Austria Invariant Cocycles, Random Tilings and the Super-K and Strong Markov Properties Klaus Schmidt
Probability and Measure
 Part II Year 2018 2017 2016 2015 2014 2013 2012 2011 2010 2009 2008 2007 2006 2005 2018 84 Paper 4, Section II 26J Let (X, A) be a measurable space. Let T : X X be a measurable map, and µ a probability
Part II Year 2018 2017 2016 2015 2014 2013 2012 2011 2010 2009 2008 2007 2006 2005 2018 84 Paper 4, Section II 26J Let (X, A) be a measurable space. Let T : X X be a measurable map, and µ a probability
NOTES ON DIOPHANTINE APPROXIMATION
 NOTES ON DIOPHANTINE APPROXIMATION Jan-Hendrik Evertse January 29, 200 9 p-adic Numbers Literature: N. Koblitz, p-adic Numbers, p-adic Analysis, and Zeta-Functions, 2nd edition, Graduate Texts in Mathematics
NOTES ON DIOPHANTINE APPROXIMATION Jan-Hendrik Evertse January 29, 200 9 p-adic Numbers Literature: N. Koblitz, p-adic Numbers, p-adic Analysis, and Zeta-Functions, 2nd edition, Graduate Texts in Mathematics
Immerse Metric Space Homework
 Immerse Metric Space Homework (Exercises -2). In R n, define d(x, y) = x y +... + x n y n. Show that d is a metric that induces the usual topology. Sketch the basis elements when n = 2. Solution: Steps
Immerse Metric Space Homework (Exercises -2). In R n, define d(x, y) = x y +... + x n y n. Show that d is a metric that induces the usual topology. Sketch the basis elements when n = 2. Solution: Steps
4. Ergodicity and mixing
 4. Ergodicity and mixing 4. Introduction In the previous lecture we defined what is meant by an invariant measure. In this lecture, we define what is meant by an ergodic measure. The primary motivation
4. Ergodicity and mixing 4. Introduction In the previous lecture we defined what is meant by an invariant measure. In this lecture, we define what is meant by an ergodic measure. The primary motivation
Disintegration into conditional measures: Rokhlin s theorem
 Disintegration into conditional measures: Rokhlin s theorem Let Z be a compact metric space, µ be a Borel probability measure on Z, and P be a partition of Z into measurable subsets. Let π : Z P be the
Disintegration into conditional measures: Rokhlin s theorem Let Z be a compact metric space, µ be a Borel probability measure on Z, and P be a partition of Z into measurable subsets. Let π : Z P be the
MATH31011/MATH41011/MATH61011: FOURIER ANALYSIS AND LEBESGUE INTEGRATION. Chapter 2: Countability and Cantor Sets
 MATH31011/MATH41011/MATH61011: FOURIER ANALYSIS AND LEBESGUE INTEGRATION Chapter 2: Countability and Cantor Sets Countable and Uncountable Sets The concept of countability will be important in this course
MATH31011/MATH41011/MATH61011: FOURIER ANALYSIS AND LEBESGUE INTEGRATION Chapter 2: Countability and Cantor Sets Countable and Uncountable Sets The concept of countability will be important in this course
On Distance Sets in the Triangular Lattice
 On Distance Sets in the Triangular Lattice Tanbir Ahmed Department of Computer Science and Software Engineering Concordia University, Montréal, Canada ta ahmed@cs.concordia.ca David Jacob Wildstrom Department
On Distance Sets in the Triangular Lattice Tanbir Ahmed Department of Computer Science and Software Engineering Concordia University, Montréal, Canada ta ahmed@cs.concordia.ca David Jacob Wildstrom Department
MATH 215 Sets (S) Definition 1 A set is a collection of objects. The objects in a set X are called elements of X.
 MATH 215 Sets (S) Definition 1 A set is a collection of objects. The objects in a set X are called elements of X. Notation 2 A set can be described using set-builder notation. That is, a set can be described
MATH 215 Sets (S) Definition 1 A set is a collection of objects. The objects in a set X are called elements of X. Notation 2 A set can be described using set-builder notation. That is, a set can be described
Ergodic Theory (Lecture Notes) Joan Andreu Lázaro Camí
 Ergodic Theory (Lecture Notes) Joan Andreu Lázaro Camí Department of Mathematics Imperial College London January 2010 Contents 1 Introduction 2 2 Measure Theory 5 2.1 Motivation: Positive measures and
Ergodic Theory (Lecture Notes) Joan Andreu Lázaro Camí Department of Mathematics Imperial College London January 2010 Contents 1 Introduction 2 2 Measure Theory 5 2.1 Motivation: Positive measures and
Multiple attractors in Newton's method
 Ergod. Th. & Dynam. Sys. (1986), 6, 561-569 Printed in Great Britain Multiple attractors in Newton's method MIKE HURLEY Department of Mathematics and Statistics, Case Western Reserve University, Cleveland,
Ergod. Th. & Dynam. Sys. (1986), 6, 561-569 Printed in Great Britain Multiple attractors in Newton's method MIKE HURLEY Department of Mathematics and Statistics, Case Western Reserve University, Cleveland,
Problems for Putnam Training
 Problems for Putnam Training 1 Number theory Problem 1.1. Prove that for each positive integer n, the number is not prime. 10 1010n + 10 10n + 10 n 1 Problem 1.2. Show that for any positive integer n,
Problems for Putnam Training 1 Number theory Problem 1.1. Prove that for each positive integer n, the number is not prime. 10 1010n + 10 10n + 10 n 1 Problem 1.2. Show that for any positive integer n,
Notes on Iterated Expectations Stephen Morris February 2002
 Notes on Iterated Expectations Stephen Morris February 2002 1. Introduction Consider the following sequence of numbers. Individual 1's expectation of random variable X; individual 2's expectation of individual
Notes on Iterated Expectations Stephen Morris February 2002 1. Introduction Consider the following sequence of numbers. Individual 1's expectation of random variable X; individual 2's expectation of individual
A ZERO ENTROPY T SUCH THAT THE [T,ID] ENDOMORPHISM IS NONSTANDARD
![A ZERO ENTROPY T SUCH THAT THE [T,ID] ENDOMORPHISM IS NONSTANDARD A ZERO ENTROPY T SUCH THAT THE [T,ID] ENDOMORPHISM IS NONSTANDARD](/thumbs/93/112888481.jpg) A ZERO ENTROPY T SUCH THAT THE [T,ID] ENDOMORPHISM IS NONSTANDARD CHRISTOPHER HOFFMAN Abstract. We present an example of an ergodic transformation T, a variant of a zero entropy non loosely Bernoulli map
A ZERO ENTROPY T SUCH THAT THE [T,ID] ENDOMORPHISM IS NONSTANDARD CHRISTOPHER HOFFMAN Abstract. We present an example of an ergodic transformation T, a variant of a zero entropy non loosely Bernoulli map
Nonarchimedean Cantor set and string
 J fixed point theory appl Online First c 2008 Birkhäuser Verlag Basel/Switzerland DOI 101007/s11784-008-0062-9 Journal of Fixed Point Theory and Applications Nonarchimedean Cantor set and string Michel
J fixed point theory appl Online First c 2008 Birkhäuser Verlag Basel/Switzerland DOI 101007/s11784-008-0062-9 Journal of Fixed Point Theory and Applications Nonarchimedean Cantor set and string Michel
Logical Connectives and Quantifiers
 Chapter 1 Logical Connectives and Quantifiers 1.1 Logical Connectives 1.2 Quantifiers 1.3 Techniques of Proof: I 1.4 Techniques of Proof: II Theorem 1. Let f be a continuous function. If 1 f(x)dx 0, then
Chapter 1 Logical Connectives and Quantifiers 1.1 Logical Connectives 1.2 Quantifiers 1.3 Techniques of Proof: I 1.4 Techniques of Proof: II Theorem 1. Let f be a continuous function. If 1 f(x)dx 0, then
DIMENSION OF SLICES THROUGH THE SIERPINSKI CARPET
 DIMENSION OF SLICES THROUGH THE SIERPINSKI CARPET ANTHONY MANNING AND KÁROLY SIMON Abstract For Lebesgue typical (θ, a), the intersection of the Sierpinski carpet F with a line y = x tan θ + a has (if
DIMENSION OF SLICES THROUGH THE SIERPINSKI CARPET ANTHONY MANNING AND KÁROLY SIMON Abstract For Lebesgue typical (θ, a), the intersection of the Sierpinski carpet F with a line y = x tan θ + a has (if
Glossary Common Core Curriculum Maps Math/Grade 9 Grade 12
 Glossary Common Core Curriculum Maps Math/Grade 9 Grade 12 Grade 9 Grade 12 AA similarity Angle-angle similarity. When twotriangles have corresponding angles that are congruent, the triangles are similar.
Glossary Common Core Curriculum Maps Math/Grade 9 Grade 12 Grade 9 Grade 12 AA similarity Angle-angle similarity. When twotriangles have corresponding angles that are congruent, the triangles are similar.
Introduction to Dynamical Systems
 Introduction to Dynamical Systems France-Kosovo Undergraduate Research School of Mathematics March 2017 This introduction to dynamical systems was a course given at the march 2017 edition of the France
Introduction to Dynamical Systems France-Kosovo Undergraduate Research School of Mathematics March 2017 This introduction to dynamical systems was a course given at the march 2017 edition of the France
arxiv: v1 [math.ds] 1 Oct 2014
![arxiv: v1 [math.ds] 1 Oct 2014 arxiv: v1 [math.ds] 1 Oct 2014](/thumbs/71/66050382.jpg) A NOTE ON THE POINTS WITH DENSE ORBIT UNDER AND MAPS arxiv:1410.019v1 [math.ds] 1 Oct 014 AUTHOR ONE, AUTHOR TWO, AND AUTHOR THREE Abstract. It was conjectured by Furstenberg that for any x [0,1]\Q, dim
A NOTE ON THE POINTS WITH DENSE ORBIT UNDER AND MAPS arxiv:1410.019v1 [math.ds] 1 Oct 014 AUTHOR ONE, AUTHOR TWO, AND AUTHOR THREE Abstract. It was conjectured by Furstenberg that for any x [0,1]\Q, dim
CMSC Discrete Mathematics FINAL EXAM Tuesday, December 5, 2017, 10:30-12:30
 CMSC-37110 Discrete Mathematics FINAL EXAM Tuesday, December 5, 2017, 10:30-12:30 Name (print): Email: This exam contributes 40% to your course grade. Do not use book, notes, scrap paper. NO ELECTRONIC
CMSC-37110 Discrete Mathematics FINAL EXAM Tuesday, December 5, 2017, 10:30-12:30 Name (print): Email: This exam contributes 40% to your course grade. Do not use book, notes, scrap paper. NO ELECTRONIC
DIVISIBILITY AND DISTRIBUTION OF PARTITIONS INTO DISTINCT PARTS
 DIVISIBILITY AND DISTRIBUTION OF PARTITIONS INTO DISTINCT PARTS JEREMY LOVEJOY Abstract. We study the generating function for (n), the number of partitions of a natural number n into distinct parts. Using
DIVISIBILITY AND DISTRIBUTION OF PARTITIONS INTO DISTINCT PARTS JEREMY LOVEJOY Abstract. We study the generating function for (n), the number of partitions of a natural number n into distinct parts. Using
ax 2 + bx + c = 0 where
 Chapter P Prerequisites Section P.1 Real Numbers Real numbers The set of numbers formed by joining the set of rational numbers and the set of irrational numbers. Real number line A line used to graphically
Chapter P Prerequisites Section P.1 Real Numbers Real numbers The set of numbers formed by joining the set of rational numbers and the set of irrational numbers. Real number line A line used to graphically
Lecture 1. Toric Varieties: Basics
 Lecture 1. Toric Varieties: Basics Taras Panov Lomonosov Moscow State University Summer School Current Developments in Geometry Novosibirsk, 27 August1 September 2018 Taras Panov (Moscow University) Lecture
Lecture 1. Toric Varieties: Basics Taras Panov Lomonosov Moscow State University Summer School Current Developments in Geometry Novosibirsk, 27 August1 September 2018 Taras Panov (Moscow University) Lecture
Congruences for Fishburn numbers modulo prime powers
 Congruences for Fishburn numbers modulo prime powers Armin Straub Department of Mathematics University of Illinois at Urbana-Champaign July 16, 2014 Abstract The Fishburn numbers ξ(n) are defined by the
Congruences for Fishburn numbers modulo prime powers Armin Straub Department of Mathematics University of Illinois at Urbana-Champaign July 16, 2014 Abstract The Fishburn numbers ξ(n) are defined by the
Maximal Independent Sets In Graphs With At Most r Cycles
 Maximal Independent Sets In Graphs With At Most r Cycles Goh Chee Ying Department of Mathematics National University of Singapore Singapore goh chee ying@moe.edu.sg Koh Khee Meng Department of Mathematics
Maximal Independent Sets In Graphs With At Most r Cycles Goh Chee Ying Department of Mathematics National University of Singapore Singapore goh chee ying@moe.edu.sg Koh Khee Meng Department of Mathematics
P-adic Functions - Part 1
 P-adic Functions - Part 1 Nicolae Ciocan 22.11.2011 1 Locally constant functions Motivation: Another big difference between p-adic analysis and real analysis is the existence of nontrivial locally constant
P-adic Functions - Part 1 Nicolae Ciocan 22.11.2011 1 Locally constant functions Motivation: Another big difference between p-adic analysis and real analysis is the existence of nontrivial locally constant
COM BIN ATOR 1 A L MATHEMATICS YEA R
 0 7 8 9 3 5 2 6 6 7 8 9 2 3 '" 5 0 5 0 2 7 8 9 '" 3 + 6 + 6 3 7 8 9 5 0 2 8 6 3 0 6 5 + 9 8 7 2 3 7 0 2 + 7 0 6 5 9 8 2 3 + 6 3 5 8 7 2 0 6 9 3 + 5 0 7 8 9 9 8 7 3 2 0 + 5 6 9 7 8 9 8 7 + 3 2 5 6 0 2 8
0 7 8 9 3 5 2 6 6 7 8 9 2 3 '" 5 0 5 0 2 7 8 9 '" 3 + 6 + 6 3 7 8 9 5 0 2 8 6 3 0 6 5 + 9 8 7 2 3 7 0 2 + 7 0 6 5 9 8 2 3 + 6 3 5 8 7 2 0 6 9 3 + 5 0 7 8 9 9 8 7 3 2 0 + 5 6 9 7 8 9 8 7 + 3 2 5 6 0 2 8
Maximal and Maximum Independent Sets In Graphs With At Most r Cycles
 Maximal and Maximum Independent Sets In Graphs With At Most r Cycles Bruce E. Sagan Department of Mathematics Michigan State University East Lansing, MI sagan@math.msu.edu Vincent R. Vatter Department
Maximal and Maximum Independent Sets In Graphs With At Most r Cycles Bruce E. Sagan Department of Mathematics Michigan State University East Lansing, MI sagan@math.msu.edu Vincent R. Vatter Department
1 I A Q E B A I E Q 1 A ; E Q A I A (2) A : (3) A : (4)
 Latin Squares Denition and examples Denition. (Latin Square) An n n Latin square, or a latin square of order n, is a square array with n symbols arranged so that each symbol appears just once in each row
Latin Squares Denition and examples Denition. (Latin Square) An n n Latin square, or a latin square of order n, is a square array with n symbols arranged so that each symbol appears just once in each row
Ergodicity of the adic transformation on the Euler graph
 Under consideration for publication in Math. Proc. Camb. Phil. Soc. Ergodicity of the adic transformation on the Euler graph By SARAH BAILEY Department of Mathematics, CB 250, Phillips Hall, University
Under consideration for publication in Math. Proc. Camb. Phil. Soc. Ergodicity of the adic transformation on the Euler graph By SARAH BAILEY Department of Mathematics, CB 250, Phillips Hall, University
ADDING MACHINES, ENDPOINTS, AND INVERSE LIMIT SPACES. 1. Introduction
 ADDING MACHINES, ENDPOINTS, AND INVERSE LIMIT SPACES LORI ALVIN AND KAREN BRUCKS Abstract. Let f be a unimodal map in the logistic or symmetric tent family whose restriction to the omega limit set of the
ADDING MACHINES, ENDPOINTS, AND INVERSE LIMIT SPACES LORI ALVIN AND KAREN BRUCKS Abstract. Let f be a unimodal map in the logistic or symmetric tent family whose restriction to the omega limit set of the
Fourier series, Weyl equidistribution. 1. Dirichlet s pigeon-hole principle, approximation theorem
 (October 4, 25) Fourier series, Weyl equidistribution Paul Garrett garrett@math.umn.edu http://www.math.umn.edu/ garrett/ [This document is http://www.math.umn.edu/ garrett/m/mfms/notes 25-6/8 Fourier-Weyl.pdf]
(October 4, 25) Fourier series, Weyl equidistribution Paul Garrett garrett@math.umn.edu http://www.math.umn.edu/ garrett/ [This document is http://www.math.umn.edu/ garrett/m/mfms/notes 25-6/8 Fourier-Weyl.pdf]
THE p-adic VALUATION OF LUCAS SEQUENCES
 THE p-adic VALUATION OF LUCAS SEQUENCES CARLO SANNA Abstract. Let (u n) n 0 be a nondegenerate Lucas sequence with characteristic polynomial X 2 ax b, for some relatively prime integers a and b. For each
THE p-adic VALUATION OF LUCAS SEQUENCES CARLO SANNA Abstract. Let (u n) n 0 be a nondegenerate Lucas sequence with characteristic polynomial X 2 ax b, for some relatively prime integers a and b. For each
Laboratoire de l Informatique du Parallélisme
 Laboratoire de l Informatique du Parallélisme Ecole Normale Supérieure de Lyon Unité de recherche associée au CNRS n 1398 An Algorithm that Computes a Lower Bound on the Distance Between a Segment and
Laboratoire de l Informatique du Parallélisme Ecole Normale Supérieure de Lyon Unité de recherche associée au CNRS n 1398 An Algorithm that Computes a Lower Bound on the Distance Between a Segment and
On divisibility of Narayana numbers by primes
 On divisibility of Narayana numbers by primes Miklós Bóna Department of Mathematics, University of Florida Gainesville, FL 32611, USA, bona@math.ufl.edu and Bruce E. Sagan Department of Mathematics, Michigan
On divisibility of Narayana numbers by primes Miklós Bóna Department of Mathematics, University of Florida Gainesville, FL 32611, USA, bona@math.ufl.edu and Bruce E. Sagan Department of Mathematics, Michigan
PARKING FUNCTIONS. Richard P. Stanley Department of Mathematics M.I.T Cambridge, MA
 PARKING FUNCTIONS Richard P. Stanley Department of Mathematics M.I.T. -75 Cambridge, MA 09 rstan@math.mit.edu http://www-math.mit.edu/~rstan Transparencies available at: http://www-math.mit.edu/~rstan/trans.html
PARKING FUNCTIONS Richard P. Stanley Department of Mathematics M.I.T. -75 Cambridge, MA 09 rstan@math.mit.edu http://www-math.mit.edu/~rstan Transparencies available at: http://www-math.mit.edu/~rstan/trans.html
The Ternary Expansions of Powers of 2
 The Ternary Expansions of Powers of 2 Jeffrey C. Lagarias Dept. of Mathematics University of Michigan Ann Arbor, MI 4809-09 arxiv:math/052006v [math.ds] Dec 2005 (To Mel Nathanson on his 60-th birthday)
The Ternary Expansions of Powers of 2 Jeffrey C. Lagarias Dept. of Mathematics University of Michigan Ann Arbor, MI 4809-09 arxiv:math/052006v [math.ds] Dec 2005 (To Mel Nathanson on his 60-th birthday)
