A Tractable, Parsimonious and Highly Flexible Model for Cylindrical Data, with Applications
|
|
|
- Shonda Garrison
- 6 years ago
- Views:
Transcription
1 A Tractable, Parsimonious and Highly Flexible Model for Cylindrical Data, with Applications Toshihiro Abe Nanzan University Christophe Ley SBS-EM, ECARES, Université libre de Bruxelles June 5 ECARES working paper 5- ECARES ULB - CP 4/4 5, F.D. Roosevelt Ave., B-5 Brussels BELGIUM
2 A tractable, parsimonious and highly flexible model for cylindrical data, with applications Toshihiro Abe and Christophe Ley Nanzan University, Nagoya, Japan Université libre de Bruxelles, Brussels, Belgium May 9, 5 Abstract In this paper, we propose cylindrical distributions obtained by combining the sine-skewed von Mises distribution (circular part) with the Weibull distribution (linear part). This new model, the WeiSSVM, enjoys numerous advantages: simple normalizing constant and hence very tractable density, parameter-parsimony and interpretability, good circular-linear dependence structure, easy random number generation thanks to known marginal/conditional distributions, flexibility illustrated via excellent fitting abilities, and a straightforward extension to the case of directional-linear data. Inferential issues, such as independence testing, can easily be tackled with our model, which we apply on two real data sets. We conclude the paper by discussing future applications of our model. Key words: Circular-linear data, directional-linear data, distributions on the cylinder, sineskewed von Mises distribution, Weibull distribution Introduction Cylindrical data are observations that consist of a directional part (a set of angles), which is often of a circular nature (a single angle), and a linear part (mostly a positive real number). This explains the alternative terminology of directional-linear or circular-linear data. Such data occur frequently in natural sciences; typical examples are wind direction and another climatological variable such as wind speed or air temperature, the direction an animal moves and the distance moved, or wave direction and wave height. Recent studies of cylindrical data include the exploration of wind direction and SO concentration ([7]), the analysis of Japanese earthquakes ([3]), the link between wildfire orientation and burnt area ([6]), and space-time modeling of sea currents in the Adriatic Sea ([], [5]). A non-trivial yet fundamental problem is the joint modeling of the directional/circular and linear variables via the construction of cylindrical probability distributions. The best known examples stem from the seminal papers Mardia and Sutton (978) [9], conditioning from a trivariate normal distribution, and Johnson and Wehrly (978) [], invoking maximum entropy principles. The latter also provide in their paper a general way, based on copulas, to construct circular-linear distributions with specified marginals. We refer to [3] for a thorough study of this construction and for references having put it to use. One such example is [4], who uses circular distributions based on nonnegative trigonometric sums. A more flexible generalization
3 of the Mardia-Sutton model is given in [4]. All these models shall be described in detail in the course of this paper. What desirable properties should a good cylindrical distribution possess? It should be able to model diverse shapes, in other words present good fitting aptitudes, yet it should ideally remain of a tractable form (this is crucial for stochastic properties, estimation purposes and for describing the circular-linear relationship) and be parsimonious in terms of parameters at play. The marginal and conditional distributions should optimally lead to popular and flexible directional resp. linear models (e.g., there is no reason for the circular component to be always symmetric), whilst the dependence structure has to take care of a reasonable joint behavior. Indeed, numerous examples of cylindrical data require that the circular concentration tends to increase with the linear component. All these conditions are well fulfilled by the new model we propose in the present paper. For the sake of simplicity and for the sake of comparison with the large majority of existing models from the literature, we shall present it and investigate its properties in the circular-linear setting (and discuss later the directional-linear extension), where the probability density function is of the form (θ, x) αβα π cosh(κ) { + λ sin(θ µ)} xα exp [ (βx) α { tanh(κ) cos(θ µ)}], () where (x, θ) [, ) [, π), α > is a (linear) shape parameter, β > a (linear) scale parameter, µ < π a (circular) location parameter, κ controls the (circular) concentration and λ is a (circular) skewing parameter. We term the distribution () WeiSSVM: Wei of course stands for the linear Weibull distribution with density x αβ α x α exp { (βx) α } over R +, which is a very popular distribution to model diverse natural phenomena, especially wind speed, whereas SSVM is an abbreviation for the sine-skewed von Mises distribution. This circular distribution, presented and studied in detail in [], is a tractable skew extension (simple multiplication by { + λ sin(θ µ)}, without altering the normalizing constant) of the von Mises density θ exp{κ cos(θ µ)} πi (κ) where I (κ) is the modified Bessel function of the first kind and order zero. This explains our motivation for (): a versatile linear distribution, combined with a flexible yet tractable circular one. D contour plots of the density () are given in Figure. The dependence structure is chosen in such a way that the normalizing constant is of an extremely simple form. Independence is attained when κ, in which case the density () becomes the product of the linear Weibull and the circular cardioid distribution. The numerous good properties of the WeiSSVM will be studied in detail in Section, and compared with the well-known models from the literature in Section 3. In that same section, we shall also present further new circular-linear densities having the same flavor as the WeiSSVM. Maximum likelihood estimation and the ensuing efficient likelihood ratio tests (including tests for circular-linear independence) are discussed in Section 4. We will study two distinct cylindrical data sets in Section 5, and show the excellent modeling capacities of the WeiSSVM compared with other models. In Section 6 we provide the straightforward extension of the WeiSSVM to the general directional-linear setting, and we conclude the paper by some final comments in Section 7.
4 3.4 (a) λ (b) λ.5 (c) λ Direction Direction Direction Length Length Length Figure : Contour plots of the WeiSSVM density () over [, π) [, 5) for (α, β, µ, κ) (,,, ) with (a) λ, (b) λ.5 and (c) λ. Properties of the WeiSSVM. The normalizing constant As can be seen from (), the normalizing constant is very simple, which is rather rare for cylindrical, or more generally, directional models. For a better understanding of the intricacies of our construction, we now briefly establish its expression: π π αβ α αβ α π π π cosh(κ) αβ α, { + λ sin(θ µ)} x α exp [ (βx) α { tanh(κ) cos(θ µ)}] dθdx x α exp [ (βx) α { tanh(κ) cos(θ µ)}] dθdx tanh(κ) cos(θ µ) dθ + tanh (κ/) + tanh (κ/) tanh(κ/) cos(θ µ) dθ where we have used the facts that { tanh (κ/)}/[π{+tanh (κ/) tanh(κ/) cos(θ µ)}] is the density of the wrapped Cauchy distribution and { + tanh (κ/)}/{ tanh (κ/)} cosh(κ).. Special cases and parameter interpretability When the circular skewness parameter λ, we obtain the Weibull von Mises distribution, which is to the best of the authors knowledge also new. If moreover α, that is, the linear Weibull is turned into the exponential distribution, () becomes β exp [ βx { tanh(κ) cos(θ µ)}], π cosh(κ) 3
5 which coincides with the first model in [] and could be termed exponential von Mises distribution and abbreviated ExpVM. When the circular concentration parameter κ, we re-write the WeiSSVM density under the product form π { + λ sin(θ µ)} αβα x α exp { (βx) α }, () which corresponds to the product of a Weibull with a cardioid density. Noting that sin(θ µ) cos(θ µ π/), the location parameter of the cardioid distribution here is µ + π/. Quoting [] about their first two distributions, A major limitation of the two previous densities is that if X and Θ are independent, then Θ is forced to be uniformly distributed on the circle. Thanks to the sine-skewed circular structure, the WeiSSVM does not suffer from this drawback. The preceding special cases also well illustrate the interpretations all parameters enjoy: α is the linear shape parameter, β is the linear scale parameter, µ is the circular location parameter and λ is the circular skewness parameter. The most interesting parameter in some sense is κ, which bears both the interpretation as circular concentration parameter and as parameter regulating the circular-linear dependence structure. In the independent setting (), it is to be noted that λ endorses the role of concentration parameter of the cardioid density..3 Marginal and conditional distributions The marginal density of the circular component Θ from pdf () is given by f(θ) { + λ sin(θ µ)} αβ α x α exp [ (βx) α { tanh(κ) cos(θ µ)}] dx π cosh(κ) + λ sin(θ µ) π cosh(κ) tanh(κ) cos(θ µ) tanh (κ/) π + λ sin(θ µ) + tanh (κ/) tanh(κ/) cos(θ µ), which is the sine-skewed wrapped Cauchy distribution ([]), a flexible extension of the symmetric wrapped Cauchy distribution. The marginal density of the linear component X from pdf () in turn corresponds to f(x) π π cosh(κ) αβα x α { + λ sin(θ µ)} exp [ (βx) α { tanh(κ) cos(θ µ)}] dθ π π cosh(κ) αβα x α exp{ (βx) α } exp {(βx) α tanh(κ) cos(θ µ)} dθ I (x α β α tanh(κ)) αβ α x α exp{ (βx) α }. cosh(κ) This is an extended version of the marginal density obtained for the ExpVM in []; as already noticed, it simplifies to the Weibull when κ. The conditional densities from () are now readily given by f(θ x) πi (x α β α tanh(κ)) { + λ sin(θ µ)} exp {(βx)α tanh(κ) cos(θ µ)} (3) In the original Johnson-Wehrly parameterization, we would write κ β tanh(κ) < β, and β/ cosh(κ) (β κ ) /, which is exactly their expression. 4
6 and f(x θ) α [ β{ tanh(κ) cos(θ µ)} /α] α [ { } α ] x α exp β ( tanh(κ) cos(θ µ)) /α x. (4) Both densities are quite common; (3) is the sine-skewed von Mises distribution with concentration (βx) α tanh(κ) (note how large values of x tend to increase concentration, as is often desirable) whereas (4) is the Weibull with shape parameter β ( tanh(κ) cos(θ µ)) /α..4 Random number generation Thanks to the results of the previous section, we can describe a simple random number generation algorithm by decomposing f(θ, x) into f(x θ)f(θ), in other words, by first generating Θ f(θ) and then X Θ θ f(x θ). The algorithm goes as follows. Step : Generate a random variable Θ following a (symmetric) wrapped Cauchy law with location µ and concentration tanh(κ/), and generate independently U U nif[, ]. Step : Define Θ as { Θ if U < { + λ sin(θ µ)}/ Θ if U { + λ sin(θ µ)}/; Θ then follows the sine-skewed wrapped Cauchy distribution. Step 3: Generate X from a Weibull with shape parameter β { tanh(κ) cos(θ µ)} /α. Random number generation from sine-skewed distributions follows from general skew-symmetric theory on R k ; see also []..5 Moment expressions As is known, the moments of the Weibull distribution and trigonometric moments of the sineskewed von Mises distribution are given explicitly. These nice properties are inherited to our model. For n,,... and m,,..., we have E[X n cos(mθ)] αβ α π x n cos(mθ) ( + λ sin θ) x α exp [ (βx) α { tanh(κ) cos θ}] dθdx π cosh(κ) π cos(mθ) αβ α x n x α exp { (βx) α ( tanh(κ) cos θ)} dxdθ π cosh(κ) π Γ( + n/α) cos(mθ) dθ π cosh(κ) β n n/α+ ( tanh(κ) cos θ) Γ(n/α + ){cosh(κ)}n/α+ cosh(κ)β n Γ(n/α + ){cosh(κ)}n/α β n π π cos(mθ) (cosh(κ) sinh(κ) cos θ) Γ(n/α + m)p m n/α (cosh(κ)) Γ(n/α + ) {cosh(κ)}n/α Γ(n/α + m) β n Pn/α m (cosh(κ)), n/α+ dθ 5
7 where Pν m (z) is the associated Legendre function of the first kind of degree ν and order m given by (equation 8.7. of [8], p. 969) P m ν (z) ( ν) m π π Here, we used the relation Similarly, cos mt (z + z cos t) dt Γ(ν + ) ν+ πγ(ν m + ) ( ν) m Γ(m ν) Γ( ν) m Γ(ν + ) ( ) Γ(ν m + ). cos mt (z z cos t) E[X n sin(mθ)] αβ α π x n sin(mθ) ( + λ sin θ) x α exp [ (βx) α { tanh(κ) cos θ}] dθdx π cosh(κ) λ π sin(mθ) sin θ αβ α x n x α exp [ (βx) α { tanh(κ) cos θ}] dxdθ π cosh(κ) λ π Γ(n/α + ) sin(mθ) sin θ dθ π cosh(κ) β n n/α+ { tanh(κ) cos θ} λγ(n/α + ){cosh(κ)}(n/α+) cosh(κ)β n λγ(n/α + ){cosh(κ)}n/α β n { λ{cosh(κ)}n/α β n π {cos((m )θ) cos((m + )θ)} π (cosh(κ) sinh(κ) cos θ) ( Γ(n/α + m) Γ(n/α + ) Γ(n/α + m)p m n/α n/α+ dθ ν+ dt. ) P m Γ(n/α m) n/α (cosh(κ)) Γ(n/α + ) P m+ n/α (cosh(κ)) } n/α (cosh(κ)) (cosh(κ)) Γ(n/α m)p m+ Specifying choices for m and n, and noting that the marginal of the circular part is the sine skewed wrapped Cauchy density, we obtain the following simple moment expressions (we write P ν (z) for P ν (z)) E[X] {cosh(κ)}/α Γ(/α + ) P β /α (cosh(κ)), ( κ ) E[cos(Θ)] tanh, E[sin(Θ)] λ { ( tanh κ )}, E[X cos(θ)] {cosh(κ)}/α Γ(/α) P/α β (cosh(κ)), } {Γ(/α + )P /α (cosh(κ)) Γ(/α )P/α (cosh(κ)) E[X sin(θ)] λ{cosh(κ)}/α β 3 Comparison with other new models and existing models For the sake of consistency with the original proposals in the literature, we shall use in what follows the same parameters as the authors of the diverse proposals. This entails, of course, that some of our parameters (e.g., the skewness parameter λ) will endorse different roles in the following models; this should however not raise any concerns, as we explain in detail the parameters for each model... 6
8 3. The Mardia-Sutton and Kato-Shimizu models Kato and Shimizu (8) [4] propose a cylindrical distribution as an extension of the distribution by Mardia and Sutton (978) [9]. Their model has as density ] {x µ(θ)} f KS (θ, x) C exp [ σ + κ cos(θ µ ) + κ cos{(θ µ )}, (5) where θ < π, < x <, σ >, κ, κ >, µ < π, / µ < π/, µ(θ) µ + λ cos(θ ν), < µ <, λ >, ν < π and its normalizing constant C is provided by C (π) 3/ σ I (κ )I (κ ) + I j (κ )I j (κ ) cos{j(µ µ )}. j The conditional distribution of X given Θ θ is a normal distribution and the marginal distribution of Θ is the generalized von Mises distribution ([7]). The conditional distribution of Θ given X x is also the generalized von Mises distribution, and the marginal distribution of X does not admit a simple form; see [4] for details. The dependence is obviously regulated via their parameter λ, independence occurring for λ, leading to the product of a normal and the generalized von Mises. A clear drawback of the Kato-Shimizu model is that the density involves an infinite sum in the normalizing constant which, in practice, must be approximated using a finite sum of central terms. The Mardia-Sutton model is obtained by setting κ in (5). The infinite sum in the normalizing constant then vanishes, resulting in a simpler density. All properties from above of course are the same, except that the generalized von Mises is replaced with the von Mises. 3. The Johnson-Wehrly- and Johnson-Wehrly-3 models Besides what we may now call ExpVM model, [] have also proposed the density f JW (θ, x) e κ /(4σ ) (x λ) C exp { πσ σ + κx } cos(θ µ) σ where θ < π, < x <, < λ <, κ, σ > and µ < π, and with normalizing constant ( ) ( ) κλ κ C ( ) ( ) κ κλ π I σ I 4σ + I j 4σ I j σ. As in the previous model, the conditional distribution of X given Θ θ is a normal distribution and the marginal distribution of Θ is the generalized von Mises, whereas the conditional distribution of Θ given X x is the von Mises distribution, and the marginal distribution of X is proportional to exp{ (x λ) /(σ )}I (κx/σ ); see [4], who have studied the Johnson- Wehrly- model, for more details. [] have noticed as drawback that, in case of independence (here, κ ), the circular component is forced to be uniform. In order to overcome the latter limitation, Johnson and Wehrly have further proposed the density f JW 3 (θ, x) C exp { λx + κx cos(θ µ ) + ν cos(θ µ )} (6) j 7
9 where θ < π, < x <, λ > κ > and µ, µ < π, and with normalizing constant C π κ I j I j (ν) cos{j(µ µ )} (ν) + λ κ (λ +. λ κ ) j j This density has as conditional circular distribution the von Mises and as conditional linear distribution an exponential; the circular marginal density is proportional to exp{ν cos(θ µ )}/{λ κ cos(θ µ )}, while the linear marginal is of a complicated form. Independence is attained at κ, with (6) becoming the product of an exponential and the von Mises density. 3.3 The Fernández-Durán model [] have further proposed a general, copula-like way of defining a cylindrical density, namely via the expression (θ, x) πg{π(f Θ (θ) + F X (x))}f Θ (θ)f X (x) (7) where g and f Θ are circular densities, f X is a linear density, and F Θ and F X stand for the corresponding cumulative distribution functions. As established in Theorem 5 of [], such a formulation ensures the marginal densities are f Θ and f X, respectively. When g is uniform, (7) becomes the simple product of both marginals. This nice construction, which does not underpin our model (), has been put to use by Fernández-Durán (7) [4] with the Weibull as linear component f X and both g and f Θ circular densities based on nonnegative trigonometric sums, of the form π + n π j (a j cos(jθ) + b j sin(jθ)) with a j ib j π n j ν c ν+j c ν for complex numbers c j such that n j c j (π) ; see [4] for details. The number n of terms in the sum is not fixed, hence figures as an additional parameter (n is the uniform, n the cardioid). Conditional densities are given by standard copula theory, but their forms are usually not known and of a complicated form for n >. 3.4 A new model: the generalized Gamma sine skewed von Mises distribution A natural generalization of our WeiSSVM model consists in replacing the linear Weibull part with the Generalized Gamma distribution ([]), resulting in the generalized Gamma sine skewed von Mises (GGSSVM) density (θ, x) C { + λ sin(θ µ)} x α exp [ (βx) γ { tanh(κ) cos(θ µ)}], (8) with α, γ, β, κ >, λ and µ < π. The normalizing constant is calculated as follows: π Γ(α/γ) γβ α { + λ sin(θ µ)}x α e (βx)γ { tanh(κ) cos(θ µ)} dxdθ π dθ { tanh(κ) cos θ} α/γ πγ(α/γ){cosh(κ)}α/γ P α/γ (cosh(κ)) γβ α. The WeiSSVM clearly corresponds to γ α in (8). An interesting submodel is the Gamma sine skewed von Mises (GamSSVM), obtained for γ, where, as the name suggests, the linear part is Gamma distributed. All properties of the GGSSVM and GamSSVM are easily obtained along the same lines as our developments in Section. It is to be noted that the 8
10 Table : Comparison, in terms of stochastic properties, of the different cylindrical densities: Weibull sine skewed von Mises (WeiSSVM), Mardia-Sutton (MS), Kato-Shimizu (KS), Johnson- Wehrly- (JW) or exponential von Mises, Johnson-Wehrly- (JW), Johnson-Wehrly-3 (JW3), Fernández-Durán (FD), generalized Gamma sine skewed von Mises (GGSSVM) and Gamma sine skewed von Mises (GamSSVM). means good, means medium, 3 means bad. WeiSSVM MS KS JW JW JW3 FD GGSSVM GamSSVM Simple density Independence 3 3 Marginal in Θ Marginal in X Conditional in Θ 3 Conditional in X 3 Overall circular marginal distribution for the GGSSVM is the sine skewed Jones Pewsey distribution (see [], and []). The WeiSSVM occupies a particular role within the GGSSVM, as it has a much simpler normalizing constant (no associated Legendre functions are required), especially compared with the GamSSVM. 3.5 Comparison In Table, we have drawn a comparison between the distinct proposed models, by having recourse to the following criteria: (i) is the density expressed in simple terms, hence tractable, (ii) is the independence structure good in the sense of [], (iii)-(vi) does the model give rise to reasonable (in the sense of well-known) marginal and conditional distributions. For each criterion, we have given points between and 3 ( means good, means medium, 3 means bad). These criteria are based on commonly recognized (from the literature) good properties a cylindrical model should exhibit; the ranking, of course, may be subject to criticism in the sense that one may disagree with some of our marks. As can be seen from this comparison, our WeiSSVM model comes out first, followed next by the Mardia-Sutton model. Now, clearly, this comparison lacks an important aspect, namely the inferential viewpoint (although, with regard to estimation purposes, criterion (i) is intimately related to reasonable estimation properties). We deliberately do not add the important criterion Flexibility/Fitting, as this issue will be treated in Section 5, where we compare several models in terms of their fitting properties. 4 Statistical inference 4. Parameter estimation Let (θ, x ),..., (θ n, x n ) be independent and identically distributed samples drawn from the distribution with density (). Then the log-likelihood function can be expressed as 9
11 l(α, β, µ, κ, λ) (α ) + log x i β α i x α i { tanh (κ) cos(θ i µ)} i log{ + λ sin(θ i µ)} + n{α log β + log α log(π cosh(κ))}. (9) i The elements of the score vector are just the first-order partial derivatives of (9) with respect to each of the parameters: l ( α log x i β α log(βx i )x α i { tanh (κ) cos(θ i µ)} + n log β + ), α i l β αβα i x α i { tanh(κ) cos(θ i µ)} + nα β, x α i sin(θ i µ) λ i l µ βα tanh(κ) l κ l λ β α {cosh(κ)} i i i x α i cos(θ i µ) n tanh(κ), i sin(θ i µ) + λ sin(θ i µ). cos(θ i µ) + λ sin(θ i µ), Any numerical root-finding algorithm can readily solve the associated likelihood equations and yield the maximum likelihood estimates of the five parameters at play. Quite conveniently, some elements of the expected Fisher information matrix I are zero, namely I αλ, I βλ and I κλ, implying that the maximum likelihood estimate of λ is asymptotically independent of the maximum likelihood estimates of α, β and κ. This property is especially important when performing hypothesis tests about λ under unspecified α, β, κ, as their estimation then does not affect the power of such tests. 4. Submodel and independence testing Testing for submodels of the WeiSSVM model is straightforward via likelihood ratio tests. For each parameter η {α, β, µ, κ, λ}, we denote ˆη the unconstrained maximum likelihood estimate and ˆη the maximum likelihood estimate under the respective null hypotheses. Two particular instances are of interest. On the one hand, testing for the Johnson-Wehrly-, or ExpVM, submodel, which is taken care of by the test statistic T JW {log l(, ˆβ, ˆµ, ˆκ, ) log l(ˆα, ˆβ, ˆµ, ˆκ, ˆλ)}, rejecting H : {α } {λ } at asymptotic level α whenever T JW exceeds χ ; α, the α-upper quantile of the chi-square distribution with degrees of freedom. On the other hand, we are interested in testing for circular-linear independence via the test statistic T Indep {log l(ˆα, ˆβ, ˆµ,, ˆλ ) log l(ˆα, ˆβ, ˆµ, ˆκ, ˆλ)}, to be compared with χ ; α. Such tests, or the goal of defining measures of angular-linear correlation, have a long-standing history in the statistical literature, initiated by [8] and [9]; see [6] for a recent proposal, based on directional-linear kernel density estimation, and for references.
12 5 Fitting two circular-linear real data sets In this section we shall illustrate the good fitting behavior of the WeiSSVM by analyzing two popular data sets from the literature. More concretely, we shall compare the WeiSSVM with the models Johnson-Wehrly- or ExpVM, Mardia-Sutton, Kato-Shimizu, the independence model (linear Weibull and circular sine skewed densities), and the alternative new models, GamSSVM and GGSSVM. From the more complicated (in terms of tractability) models described in Section 3, we have chosen the Kato-Shimizu model since it is the most recent and the authors have shown its good fitting abilities in [4]. Our means of comparison shall be the Akaike Information Criterion (AIC). 5. Periwinkle data We give an analysis of n 3 observations which consist of the movements of blue periwinkles after they had been transplanted downshore from the height at which they normally live. The data set was taken from Table of [5]; see that paper for details about the experience. A visual inspection of Figure in [5] or of Figure.a) in [4] reveals that the concentration of the circular part tends to increase with length, which is precisely one of the features that the WeiSSVM model can well incorporate. Moreover, [4] have shown that, on basis of the Pewsey test of symmetry (see []), the circular part of the data is asymmetric, which can well be captured by the sine skewed von Mises distribution. Table presents the maximum likelihood estimates, maximized log-likelihood and Akaike Information Criterion values obtained from all models under investigation. As we can see, the location parameters of the GGSSVM and its submodels are close (note that, as remarked in Section., the location of the Independence model is.97 + π/.4) and the WeiSSVM has the lowest AIC value. It clearly improves on Johnson-Wehrly- and Mardia-Sutton, and even on the flexible Kato-Shimizu model. It is quite remarkable to notice the tiny difference in the maximized log-likelihood between WeiSSVM and the embedding model, the GGSSVM. The likelihood ratio test for the Johnson-Wehrly- submodel (w.r.t. the WeiSSVM) takes value T JW ( ) 8.7, with p-value., which emphatically rejects the Johnson-Wehrly- model. Even stronger, the independence test yields T Indep ( ) 37.36, clearly stressing the dependence between the angular and the linear part. As a conclusion, our WeiSSVM model (with 5 parameters) is a good-fitting and parsimonious model for the periwinkle data set. For visual impression, we have superimposed the contour plot of the fitted WeiSSVM model on a list plot of the data in the panel making up Figure. 5. Wind direction and temperature data As second example, we consider the original data set from [9], consisting of 8 measurements of wind direction and temperature at Kew during the period The data are taken from Table in [9], whose Figure also provides a good idea of the distribution of the data. Although the effect noticed for the periwinkle data, namely high concentration for high linear values, is less marked here, Mardia and Sutton have noted (and established) a strong dependence between the circular and the linear component. It has been shown in [4] that the Mardia-Sutton model is extremely good for this data set; it is therefore very interesting to compare it with the WeiSSVM and related new models. Table 3 contains the maximum likelihood estimates, maximized log-likelihood and Akaike information criterion values. The (circular) location parameters of our proposed models are almost the same (again, the location of the Independence model is.6 + π/.95). We see that our
13 Table : Maximum likelihood estimates (MLEs), maximized log-likelihood, l max, and Akaike Information Criterion (AIC) values for the Weibull sine skewed von Mises (WeiSSVM) and its competitor models, the generalized Gamma sine skewed von Mises (GGSSVM), the Gamma sine skewed von Mises (GamSSVM), the exponential von Mises (ExpVM), the independence (Indep.), Mardia-Sutton (MS) and Kato-Shimizu (KS) models, fitted to the blue periwinkle data. MLEs Distributions ˆα ˆβ ˆγ ˆµ ˆκ ˆλ lmax AIC WeiSSVM GGSSVM GamSSVM JW/ExpVM Indep ˆµ ˆσ ˆλ ˆν ˆµ ˆµ ˆκ ˆκ l max AIC MS KS WeiSSVM model best incorporates the non-trivial behavior of this data set (its AIC value is clearly below that of the MS model), and again it is much better than the Johnson-Wehrly- model (which is clearly rejected as submodel). A contour plot of the fitted WeiSSVM model with a list plot of the data is provided in Figure 3. We finally note that the independence test of course heavily rejects (p-value.) the null of independence, hereby agreeing with [9]. 6 Extension to the directional-linear setting Yet another advantage of the WeiSSVM is its straightforward extension to the directionallinear setting. It is obtained by replacing the circular sine skewed von Mises density with its equivalent on unit spheres S k {v R k : v }, k 3, recently defined in [6]. The cosine part simply becomes the scalar product θ µ between θ S k and the location parameter µ S k, while λ sin(θ µ) is expressed as (θ µ) λ S µ (θ), λ S k, where S µ (θ (θ µ)µ)/ θ (θ µ)µ is the multivariate sign vector on the unit sphere. We refer to [6] for further information, and for more general skew-rotsymmetric distributions, as they are termed. The density of the Weibull sine skewed Fisher-von Mises-Langevin, in short WeiSSFVML, distribution on S k R +, for the directional part with respect to the usual surface area measure dσ k, is defined as (θ, x) f(θ, x) C k ( + ) (θ µ) λ S µ (θ) x α exp { (βx) α ( tanh(κ)θ µ) }. () The normalizing constant of the distribution () is simply given by C k αβ α {sinh(κ)} (k/) (π) k/ cosh(κ)p (k/) k/ (cosh(κ)). In higher dimensions, the VM is called Fisher-von Mises-Langevin and hence abbreviated FVML.
14 3 Direction Length Figure : Contour plot of the blue periwinkle data (in lengths and radians), together with the fitted WeiSSVM density. The data are plotted over [, π) [, 5). Indeed S k S k S k (µ ) ( + ) (θ µ) λ S µ (θ) x α e (βx)α ( tanh(κ)θ µ) dxdσ k (θ) x α e (βx)α ( tanh(κ)θ µ) dxdσ k (θ) π k/ αβ α Γ(k/)B(/, (k )/) x α e (βx)α ( tanh(κ)t) dxdσ k (v)( t ) (k 3)/ dt (π)k/ cosh(κ)p (k/) k/ (cosh(κ)) αβ α {sinh(κ)} (k/), ( t ) (k 3)/ tanh(κ)t dt where B(, ) denotes the beta function. We have used above the change of variables formula dσ k (θ) ( t ) (k 3)/ dσ k (v)dt where v S k (µ ) {v R k : v, v µ }, the equality ω k ω k /B(/, (k )/) (with ω k π k/ /Γ(k/) the surface area measure of S k ) as well as, like for the result of Section 5 in [], the following relationship of the associated Legendre function (equation 8.7. of [8], p. 969) Pν µ (z) (z ) µ µ πγ(µ + ) ( t ) µ (z + t z ) dt [Rµ >, arg(z ± ) < π]. µ ν Clearly, the distribution () reduces to () when k, and as in [], the distribution also has a simpler form when k 3, namely, f(θ, x) αβα tanh(κ) 4πκ ( + ) (θ µ) λ S µ (θ) x α exp { (βx) α ( tanh(κ)θ µ) }. 3
15 Table 3: Maximum likelihood estimates (MLEs), maximized log-likelihood, l max, and Akaike Information Criterion (AIC) values for the Weibull sine skewed von Mises (WeiSSVM) and its competitor models, the generalized Gamma sine skewed von Mises (GGSSVM), the Gamma sine skewed von Mises (GamSSVM), the exponential von Mises (ExpVM), the independence (Indep.), Mardia-Sutton (MS) and Kato-Shimizu (KS) models, fitted to the wind-temperature data. MLEs Distributions ˆα ˆβ ˆγ ˆµ ˆκ ˆλ lmax AIC WeiSSVM GGSSVM GamSSVM JW/ExpVM Indep ˆµ ˆσ ˆλ ˆν ˆµ ˆµ ˆκ ˆκ l max AIC MS KS The nice properties from Section extend to the directional-linear setting, with the circular distributions replaced with their higher-dimensional directional counterparts. Maximum likelihood estimators for the parameters α, β, µ, κ, λ can readily be derived, baring in mind that µ is constrained to lie on S k ; one way to overcome the latter issue consists in using spherical coordinates to express the location. 7 Discussion and future research In this paper, we have introduced a new distribution for circular-linear data, the WeiSSVM. We have presented its numerous good properties: tractable density expression (in particular, simple normalizing constant), a good dependence structure in the sense that, in case of independence, the circular part is not necessarily uniform but cardioid, nice expressions for the marginal and conditional circular and linear expressions (except for the marginal linear one, whose density is slightly more complex), much more flexibility than the first model in [] which is a special case of the WeiSSVM, and direct extension to the general directional-linear setting, yielding the WeiSSFVML distribution. Last but certainly not least, the WeiSSVM exhibits very good fitting properties (shown by means of two distinct data sets), improving in particular on the more complicated models from the literature. Thus, we can consider our model as a tractable, parsimonious (in terms of the number of parameters) and flexible model for cylindrical data. Given its fitting capacities and simple parameter interpretation, the WeiSSVM is a viable model to investigate in detail further data sets. Two concrete examples shall be elucidated in the future. The first concerns ecological data related to trees. Indeed, [] have only used the direction of fallen logs, hence a pure circular setting, to model the influence of neighborhood structure and directionality of radiation on crown asymmetry; a more detailed analysis can be obtained by adding as linear part the distance to each neighboring tree. The second data set concerns cylindrical data consisting of the burnt area and the direction of wildfires in Portugal, as analyzed in [3] and [6]. Our parametric model will be an interesting alternative especially to the non-parametric approach of the latter paper. Moreover, these data are both circular-linear 4
16 Direction Length Figure 3: Contour plot of the wind and temperature data (in lengths and radians), together with the fitted WeiSSVM density. The data are plotted over [, π) [3, 6). and directional-linear, requiring our extension from Section 6. Acknowledgement Toshihiro Abe was supported in part by JSPS KAKENHI Grant Number 5K7593. Christophe Ley thanks the Fonds National de la Recherche Scientifique, Communauté française de Belgique, for financial support via a Mandat de Chargé de Recherche. References [] T. Abe, Y. Kubota, K. Shimatani, T. Aakala, and T. Kuuluvainen. Circular distributions of fallen logs as an indicator of forest disturbance regimes. Ecological Indicators, 8: ,. [] T. Abe and A. Pewsey. Sine-skewed circular distributions. Statistical Papers, 5:683 77,. [3] A. M. G. Barros, J. M. C. Pereira, and U. J. Lund. Identifying geographical patterns of wildfire orientation: A watershed-based analysis. Forest Ecology and Management, 64:98 7,. [4] J. J. Fernández-Durán. Models for circular-linear and circular-circular data constructed from circular distributions based on nonnegative trigonometric sums. Biometrics, 63: , 7. [5] N. I. Fisher and A. J. Lee. Regression models for an angular response. Biometrics, 48: , 99. 5
17 [6] E. García-Portugués, A. M. G. Barros, R. M. Crujeiras, W. González-Manteiga, and J. M. C. Pereira. A test for directional-linear independence, with applications to wildfire orientation and size. Stochastic Environmental Research and Risk Assessment, 8:6 75, 4. [7] E. García-Portugués, R. M. Crujeiras, and W. González-Manteiga. Exploring wind direction and SO concentration by circular-linear density estimation. Stochastic Environmental Research and Risk Assessment, 7:55 67, 3. [8] I. S. Gradshteyn and I. M. Ryzhik. Tables of integrals, series, and products, 8th Edn. London: Academic Press, 5. [9] R. A. Johnson and T. E. Wehrly. Measures and models for angular correlation and angularlinear correlation. Journal of the Royal Statistical Society Series B, 39: 9, 977. [] R. A. Johnson and T. E. Wehrly. Some angular-linear distributions and related regression models. Journal of the American Statistical Association, 73:6 66, 978. [] M. C. Jones and A. Pewsey. A family of symmetric distributions on the circle. Journal of the American Statistical Association, :4 48, 5. [] M. C. Jones and A. Pewsey. Inverse Batschelet distributions. Biometrics, 68:83 93,. [3] M. C. Jones, A. Pewsey, and S. Kato. On a class of circulas: copulas for circular distributions. Annals of the Institute of Statistical Mathematics, DOI:.7/s , 4. [4] S. Kato and K. Shimizu. Dependent models for observations which include angular ones. Journal of Statistical Planning and Inference, 38: , 8. [5] F. Lagona, M. Picone, A. Maruotti, and S. Cosoli. A hidden Markov approach to the analysis of space-time environmental data with linear and circular components. Stochastic Environmental Research and Risk Assessment, 9:397 49, 5. [6] C. Ley and T. Verdebout. Skew-rotsymmetric distributions on unit spheres and related efficient inferential procedures. ECARES Working Paper 4-46, 4. [7] V. M. Maksimov. Necessary and sufficient statistics for a family of shifts of probability distributions on continuous bicompact groups. Rossiskaya Akademiya Nauk. Teor. Verojatnost. i Primenen., :37 3 (in Russian), English Translation: Theory of Probability and its Applications, 67 8, 967. [8] K. V. Mardia. Linear-circular correlation coefficients and rhythmometry. Biometrika, 63:43 45, 976. [9] K. V. Mardia and T. W. Sutton. A model for cylindrical variables with applications. Journal of the Royal Statistical Society Series B, 4:9 33, 978. [] A. Pewsey. Testing circular symmetry. Canadian Journal of Statistics, 3:59 6,. [] E. W. Stacy. A generalization of the Gamma distribution. Annals of Mathematical Statistics, 33:87 9, 96. [] F. Wang, A. E. Gelfand, and G. Jona-Lasinio. Joint spatio-temporal analysis of a linear and a directional variable: space-time modeling of wave heights and wave directions in the Adriatic Sea. Statistica Sinica, 5:5 39, 5. 6
18 [3] M.-Z. Wang, K. Shimizu, and K. Uesu. An analysis of earthquakes latitude, longitude and magnitude data by use of directional statistics. Japanese Journal of Applied Statistics, pages 9 44 (in Japanese), 3. 7
By Bhattacharjee, Das. Published: 26 April 2018
 Electronic Journal of Applied Statistical Analysis EJASA, Electron. J. App. Stat. Anal. http://siba-ese.unisalento.it/index.php/ejasa/index e-issn: 2070-5948 DOI: 10.1285/i20705948v11n1p155 Estimation
Electronic Journal of Applied Statistical Analysis EJASA, Electron. J. App. Stat. Anal. http://siba-ese.unisalento.it/index.php/ejasa/index e-issn: 2070-5948 DOI: 10.1285/i20705948v11n1p155 Estimation
Circular Distributions Arising from the Möbius Transformation of Wrapped Distributions
 isid/ms/05/09 August, 05 http://www.isid.ac.in/ statmath/index.php?module=preprint Circular Distributions Arising from the Möbius Transformation of Wrapped Distributions Yogendra P. Chaubey and N.N. Midhu
isid/ms/05/09 August, 05 http://www.isid.ac.in/ statmath/index.php?module=preprint Circular Distributions Arising from the Möbius Transformation of Wrapped Distributions Yogendra P. Chaubey and N.N. Midhu
Joint work with Nottingham colleagues Simon Preston and Michail Tsagris.
 /pgf/stepx/.initial=1cm, /pgf/stepy/.initial=1cm, /pgf/step/.code=1/pgf/stepx/.expanded=- 10.95415pt,/pgf/stepy/.expanded=- 10.95415pt, /pgf/step/.value required /pgf/images/width/.estore in= /pgf/images/height/.estore
/pgf/stepx/.initial=1cm, /pgf/stepy/.initial=1cm, /pgf/step/.code=1/pgf/stepx/.expanded=- 10.95415pt,/pgf/stepy/.expanded=- 10.95415pt, /pgf/step/.value required /pgf/images/width/.estore in= /pgf/images/height/.estore
Davy PAINDAVEINE Thomas VERDEBOUT
 2013/94 Optimal Rank-Based Tests for the Location Parameter of a Rotationally Symmetric Distribution on the Hypersphere Davy PAINDAVEINE Thomas VERDEBOUT Optimal Rank-Based Tests for the Location Parameter
2013/94 Optimal Rank-Based Tests for the Location Parameter of a Rotationally Symmetric Distribution on the Hypersphere Davy PAINDAVEINE Thomas VERDEBOUT Optimal Rank-Based Tests for the Location Parameter
SYMMETRIC UNIMODAL MODELS FOR DIRECTIONAL DATA MOTIVATED BY INVERSE STEREOGRAPHIC PROJECTION
 J. Japan Statist. Soc. Vol. 40 No. 1 010 45 61 SYMMETRIC UNIMODAL MODELS FOR DIRECTIONAL DATA MOTIVATED BY INVERSE STEREOGRAPHIC PROJECTION Toshihiro Abe*, Kunio Shimizu** and Arthur Pewsey*** In this
J. Japan Statist. Soc. Vol. 40 No. 1 010 45 61 SYMMETRIC UNIMODAL MODELS FOR DIRECTIONAL DATA MOTIVATED BY INVERSE STEREOGRAPHIC PROJECTION Toshihiro Abe*, Kunio Shimizu** and Arthur Pewsey*** In this
Discussion Paper No. 28
 Discussion Paper No. 28 Asymptotic Property of Wrapped Cauchy Kernel Density Estimation on the Circle Yasuhito Tsuruta Masahiko Sagae Asymptotic Property of Wrapped Cauchy Kernel Density Estimation on
Discussion Paper No. 28 Asymptotic Property of Wrapped Cauchy Kernel Density Estimation on the Circle Yasuhito Tsuruta Masahiko Sagae Asymptotic Property of Wrapped Cauchy Kernel Density Estimation on
Bootstrap Goodness-of-fit Testing for Wehrly Johnson Bivariate Circular Models
 Overview Bootstrap Goodness-of-fit Testing for Wehrly Johnson Bivariate Circular Models Arthur Pewsey apewsey@unex.es Mathematics Department University of Extremadura, Cáceres, Spain ADISTA14 (BRUSSELS,
Overview Bootstrap Goodness-of-fit Testing for Wehrly Johnson Bivariate Circular Models Arthur Pewsey apewsey@unex.es Mathematics Department University of Extremadura, Cáceres, Spain ADISTA14 (BRUSSELS,
Statistics - Lecture One. Outline. Charlotte Wickham 1. Basic ideas about estimation
 Statistics - Lecture One Charlotte Wickham wickham@stat.berkeley.edu http://www.stat.berkeley.edu/~wickham/ Outline 1. Basic ideas about estimation 2. Method of Moments 3. Maximum Likelihood 4. Confidence
Statistics - Lecture One Charlotte Wickham wickham@stat.berkeley.edu http://www.stat.berkeley.edu/~wickham/ Outline 1. Basic ideas about estimation 2. Method of Moments 3. Maximum Likelihood 4. Confidence
On Fisher Information Matrices and Profile Log-Likelihood Functions in Generalized Skew-Elliptical Models
 On Fisher Information Matrices and Profile Log-Likelihood Functions in Generalized Skew-Elliptical Models Christophe Ley and Davy Paindaveine E.C.A.R.E.S., Institut de Recherche en Statistique, and Département
On Fisher Information Matrices and Profile Log-Likelihood Functions in Generalized Skew-Elliptical Models Christophe Ley and Davy Paindaveine E.C.A.R.E.S., Institut de Recherche en Statistique, and Département
Maximum likelihood characterization of rotationally symmetric distributions on the sphere
 Sankhyā : The Indian Journal of Statistics 2012, Volume 74-A, Part 2, pp. 249-262 c 2012, Indian Statistical Institute Maximum likelihood characterization of rotationally symmetric distributions on the
Sankhyā : The Indian Journal of Statistics 2012, Volume 74-A, Part 2, pp. 249-262 c 2012, Indian Statistical Institute Maximum likelihood characterization of rotationally symmetric distributions on the
A CIRCULAR CIRCULAR REGRESSION MODEL
 Statistica Sinica 18(2008), 633-645 A CIRCULAR CIRCULAR REGRESSION MODEL Shogo Kato, Kunio Shimizu and Grace S. Shieh Institute of Statistical Mathematics, Keio University and Academia Sinica Abstract:
Statistica Sinica 18(2008), 633-645 A CIRCULAR CIRCULAR REGRESSION MODEL Shogo Kato, Kunio Shimizu and Grace S. Shieh Institute of Statistical Mathematics, Keio University and Academia Sinica Abstract:
SUPPLEMENT TO TESTING UNIFORMITY ON HIGH-DIMENSIONAL SPHERES AGAINST MONOTONE ROTATIONALLY SYMMETRIC ALTERNATIVES
 Submitted to the Annals of Statistics SUPPLEMENT TO TESTING UNIFORMITY ON HIGH-DIMENSIONAL SPHERES AGAINST MONOTONE ROTATIONALLY SYMMETRIC ALTERNATIVES By Christine Cutting, Davy Paindaveine Thomas Verdebout
Submitted to the Annals of Statistics SUPPLEMENT TO TESTING UNIFORMITY ON HIGH-DIMENSIONAL SPHERES AGAINST MONOTONE ROTATIONALLY SYMMETRIC ALTERNATIVES By Christine Cutting, Davy Paindaveine Thomas Verdebout
Wrapped Gaussian processes: a short review and some new results
 Wrapped Gaussian processes: a short review and some new results Giovanna Jona Lasinio 1, Gianluca Mastrantonio 2 and Alan Gelfand 3 1-Università Sapienza di Roma 2- Università RomaTRE 3- Duke University
Wrapped Gaussian processes: a short review and some new results Giovanna Jona Lasinio 1, Gianluca Mastrantonio 2 and Alan Gelfand 3 1-Università Sapienza di Roma 2- Università RomaTRE 3- Duke University
Graduate Econometrics I: Maximum Likelihood II
 Graduate Econometrics I: Maximum Likelihood II Yves Dominicy Université libre de Bruxelles Solvay Brussels School of Economics and Management ECARES Yves Dominicy Graduate Econometrics I: Maximum Likelihood
Graduate Econometrics I: Maximum Likelihood II Yves Dominicy Université libre de Bruxelles Solvay Brussels School of Economics and Management ECARES Yves Dominicy Graduate Econometrics I: Maximum Likelihood
BIO5312 Biostatistics Lecture 13: Maximum Likelihood Estimation
 BIO5312 Biostatistics Lecture 13: Maximum Likelihood Estimation Yujin Chung November 29th, 2016 Fall 2016 Yujin Chung Lec13: MLE Fall 2016 1/24 Previous Parametric tests Mean comparisons (normality assumption)
BIO5312 Biostatistics Lecture 13: Maximum Likelihood Estimation Yujin Chung November 29th, 2016 Fall 2016 Yujin Chung Lec13: MLE Fall 2016 1/24 Previous Parametric tests Mean comparisons (normality assumption)
is a Borel subset of S Θ for each c R (Bertsekas and Shreve, 1978, Proposition 7.36) This always holds in practical applications.
 Stat 811 Lecture Notes The Wald Consistency Theorem Charles J. Geyer April 9, 01 1 Analyticity Assumptions Let { f θ : θ Θ } be a family of subprobability densities 1 with respect to a measure µ on a measurable
Stat 811 Lecture Notes The Wald Consistency Theorem Charles J. Geyer April 9, 01 1 Analyticity Assumptions Let { f θ : θ Θ } be a family of subprobability densities 1 with respect to a measure µ on a measurable
Statement: With my signature I confirm that the solutions are the product of my own work. Name: Signature:.
 MATHEMATICAL STATISTICS Homework assignment Instructions Please turn in the homework with this cover page. You do not need to edit the solutions. Just make sure the handwriting is legible. You may discuss
MATHEMATICAL STATISTICS Homework assignment Instructions Please turn in the homework with this cover page. You do not need to edit the solutions. Just make sure the handwriting is legible. You may discuss
Extending circular distributions through transformation of argument
 Ann Inst Stat Math (203) 65:833 858 DOI 0.007/s0463-02-0394-5 Extending circular distributions through transformation of argument Toshihiro Abe Arthur Pewsey Kunio Shimizu Received: 20 July 20 / Revised:
Ann Inst Stat Math (203) 65:833 858 DOI 0.007/s0463-02-0394-5 Extending circular distributions through transformation of argument Toshihiro Abe Arthur Pewsey Kunio Shimizu Received: 20 July 20 / Revised:
STAT 730 Chapter 4: Estimation
 STAT 730 Chapter 4: Estimation Timothy Hanson Department of Statistics, University of South Carolina Stat 730: Multivariate Analysis 1 / 23 The likelihood We have iid data, at least initially. Each datum
STAT 730 Chapter 4: Estimation Timothy Hanson Department of Statistics, University of South Carolina Stat 730: Multivariate Analysis 1 / 23 The likelihood We have iid data, at least initially. Each datum
Stable Limit Laws for Marginal Probabilities from MCMC Streams: Acceleration of Convergence
 Stable Limit Laws for Marginal Probabilities from MCMC Streams: Acceleration of Convergence Robert L. Wolpert Institute of Statistics and Decision Sciences Duke University, Durham NC 778-5 - Revised April,
Stable Limit Laws for Marginal Probabilities from MCMC Streams: Acceleration of Convergence Robert L. Wolpert Institute of Statistics and Decision Sciences Duke University, Durham NC 778-5 - Revised April,
Mathematics Ph.D. Qualifying Examination Stat Probability, January 2018
 Mathematics Ph.D. Qualifying Examination Stat 52800 Probability, January 2018 NOTE: Answers all questions completely. Justify every step. Time allowed: 3 hours. 1. Let X 1,..., X n be a random sample from
Mathematics Ph.D. Qualifying Examination Stat 52800 Probability, January 2018 NOTE: Answers all questions completely. Justify every step. Time allowed: 3 hours. 1. Let X 1,..., X n be a random sample from
Frailty Models and Copulas: Similarities and Differences
 Frailty Models and Copulas: Similarities and Differences KLARA GOETHALS, PAUL JANSSEN & LUC DUCHATEAU Department of Physiology and Biometrics, Ghent University, Belgium; Center for Statistics, Hasselt
Frailty Models and Copulas: Similarities and Differences KLARA GOETHALS, PAUL JANSSEN & LUC DUCHATEAU Department of Physiology and Biometrics, Ghent University, Belgium; Center for Statistics, Hasselt
Discriminant Analysis with High Dimensional. von Mises-Fisher distribution and
 Athens Journal of Sciences December 2014 Discriminant Analysis with High Dimensional von Mises - Fisher Distributions By Mario Romanazzi This paper extends previous work in discriminant analysis with von
Athens Journal of Sciences December 2014 Discriminant Analysis with High Dimensional von Mises - Fisher Distributions By Mario Romanazzi This paper extends previous work in discriminant analysis with von
CHAPTER 1 INTRODUCTION
 CHAPTER 1 INTRODUCTION 1.0 Discrete distributions in statistical analysis Discrete models play an extremely important role in probability theory and statistics for modeling count data. The use of discrete
CHAPTER 1 INTRODUCTION 1.0 Discrete distributions in statistical analysis Discrete models play an extremely important role in probability theory and statistics for modeling count data. The use of discrete
arxiv: v3 [math.st] 10 Jan 2014
![arxiv: v3 [math.st] 10 Jan 2014 arxiv: v3 [math.st] 10 Jan 2014](/thumbs/71/66081468.jpg) The value at the mode in multivariate t distributions: a curiosity or not? Christophe Ley and Anouk Neven arxiv:.74v3 [math.st] 0 Jan 04 Université Libre de Bruxelles, ECARES and Département de Mathématique,
The value at the mode in multivariate t distributions: a curiosity or not? Christophe Ley and Anouk Neven arxiv:.74v3 [math.st] 0 Jan 04 Université Libre de Bruxelles, ECARES and Département de Mathématique,
Statistics 3858 : Maximum Likelihood Estimators
 Statistics 3858 : Maximum Likelihood Estimators 1 Method of Maximum Likelihood In this method we construct the so called likelihood function, that is L(θ) = L(θ; X 1, X 2,..., X n ) = f n (X 1, X 2,...,
Statistics 3858 : Maximum Likelihood Estimators 1 Method of Maximum Likelihood In this method we construct the so called likelihood function, that is L(θ) = L(θ; X 1, X 2,..., X n ) = f n (X 1, X 2,...,
Directional Statistics
 Directional Statistics Kanti V. Mardia University of Leeds, UK Peter E. Jupp University of St Andrews, UK I JOHN WILEY & SONS, LTD Chichester New York Weinheim Brisbane Singapore Toronto Contents Preface
Directional Statistics Kanti V. Mardia University of Leeds, UK Peter E. Jupp University of St Andrews, UK I JOHN WILEY & SONS, LTD Chichester New York Weinheim Brisbane Singapore Toronto Contents Preface
Some New Aspects of Dose-Response Models with Applications to Multistage Models Having Parameters on the Boundary
 Some New Aspects of Dose-Response Models with Applications to Multistage Models Having Parameters on the Boundary Bimal Sinha Department of Mathematics & Statistics University of Maryland, Baltimore County,
Some New Aspects of Dose-Response Models with Applications to Multistage Models Having Parameters on the Boundary Bimal Sinha Department of Mathematics & Statistics University of Maryland, Baltimore County,
A Bayesian perspective on GMM and IV
 A Bayesian perspective on GMM and IV Christopher A. Sims Princeton University sims@princeton.edu November 26, 2013 What is a Bayesian perspective? A Bayesian perspective on scientific reporting views all
A Bayesian perspective on GMM and IV Christopher A. Sims Princeton University sims@princeton.edu November 26, 2013 What is a Bayesian perspective? A Bayesian perspective on scientific reporting views all
Multivariate and Time Series Models for Circular Data with Applications to Protein Conformational Angles
 Multivariate and Time Series Models for Circular Data with Applications to Protein Conformational Angles Gareth Hughes Submitted in accordance with the requirements for the degree of Doctor of Philosophy
Multivariate and Time Series Models for Circular Data with Applications to Protein Conformational Angles Gareth Hughes Submitted in accordance with the requirements for the degree of Doctor of Philosophy
A General Overview of Parametric Estimation and Inference Techniques.
 A General Overview of Parametric Estimation and Inference Techniques. Moulinath Banerjee University of Michigan September 11, 2012 The object of statistical inference is to glean information about an underlying
A General Overview of Parametric Estimation and Inference Techniques. Moulinath Banerjee University of Michigan September 11, 2012 The object of statistical inference is to glean information about an underlying
Burr Type X Distribution: Revisited
 Burr Type X Distribution: Revisited Mohammad Z. Raqab 1 Debasis Kundu Abstract In this paper, we consider the two-parameter Burr-Type X distribution. We observe several interesting properties of this distribution.
Burr Type X Distribution: Revisited Mohammad Z. Raqab 1 Debasis Kundu Abstract In this paper, we consider the two-parameter Burr-Type X distribution. We observe several interesting properties of this distribution.
GARCH Models Estimation and Inference
 GARCH Models Estimation and Inference Eduardo Rossi University of Pavia December 013 Rossi GARCH Financial Econometrics - 013 1 / 1 Likelihood function The procedure most often used in estimating θ 0 in
GARCH Models Estimation and Inference Eduardo Rossi University of Pavia December 013 Rossi GARCH Financial Econometrics - 013 1 / 1 Likelihood function The procedure most often used in estimating θ 0 in
On Weighted Exponential Distribution and its Length Biased Version
 On Weighted Exponential Distribution and its Length Biased Version Suchismita Das 1 and Debasis Kundu 2 Abstract In this paper we consider the weighted exponential distribution proposed by Gupta and Kundu
On Weighted Exponential Distribution and its Length Biased Version Suchismita Das 1 and Debasis Kundu 2 Abstract In this paper we consider the weighted exponential distribution proposed by Gupta and Kundu
Testing Hypothesis. Maura Mezzetti. Department of Economics and Finance Università Tor Vergata
 Maura Department of Economics and Finance Università Tor Vergata Hypothesis Testing Outline It is a mistake to confound strangeness with mystery Sherlock Holmes A Study in Scarlet Outline 1 The Power Function
Maura Department of Economics and Finance Università Tor Vergata Hypothesis Testing Outline It is a mistake to confound strangeness with mystery Sherlock Holmes A Study in Scarlet Outline 1 The Power Function
Gaussian processes. Chuong B. Do (updated by Honglak Lee) November 22, 2008
 Gaussian processes Chuong B Do (updated by Honglak Lee) November 22, 2008 Many of the classical machine learning algorithms that we talked about during the first half of this course fit the following pattern:
Gaussian processes Chuong B Do (updated by Honglak Lee) November 22, 2008 Many of the classical machine learning algorithms that we talked about during the first half of this course fit the following pattern:
Lecture 3. Inference about multivariate normal distribution
 Lecture 3. Inference about multivariate normal distribution 3.1 Point and Interval Estimation Let X 1,..., X n be i.i.d. N p (µ, Σ). We are interested in evaluation of the maximum likelihood estimates
Lecture 3. Inference about multivariate normal distribution 3.1 Point and Interval Estimation Let X 1,..., X n be i.i.d. N p (µ, Σ). We are interested in evaluation of the maximum likelihood estimates
Speed and change of direction in larvae of Drosophila melanogaster
 CHAPTER Speed and change of direction in larvae of Drosophila melanogaster. Introduction Holzmann et al. (6) have described, inter alia, the application of HMMs with circular state-dependent distributions
CHAPTER Speed and change of direction in larvae of Drosophila melanogaster. Introduction Holzmann et al. (6) have described, inter alia, the application of HMMs with circular state-dependent distributions
Mathematics Qualifying Examination January 2015 STAT Mathematical Statistics
 Mathematics Qualifying Examination January 2015 STAT 52800 - Mathematical Statistics NOTE: Answer all questions completely and justify your derivations and steps. A calculator and statistical tables (normal,
Mathematics Qualifying Examination January 2015 STAT 52800 - Mathematical Statistics NOTE: Answer all questions completely and justify your derivations and steps. A calculator and statistical tables (normal,
7. Estimation and hypothesis testing. Objective. Recommended reading
 7. Estimation and hypothesis testing Objective In this chapter, we show how the election of estimators can be represented as a decision problem. Secondly, we consider the problem of hypothesis testing
7. Estimation and hypothesis testing Objective In this chapter, we show how the election of estimators can be represented as a decision problem. Secondly, we consider the problem of hypothesis testing
Solution. (i) Find a minimal sufficient statistic for (θ, β) and give your justification. X i=1. By the factorization theorem, ( n
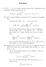 Solution 1. Let (X 1,..., X n ) be a simple random sample from a distribution with probability density function given by f(x;, β) = 1 ( ) 1 β x β, 0 x, > 0, β < 1. β (i) Find a minimal sufficient statistic
Solution 1. Let (X 1,..., X n ) be a simple random sample from a distribution with probability density function given by f(x;, β) = 1 ( ) 1 β x β, 0 x, > 0, β < 1. β (i) Find a minimal sufficient statistic
Space Telescope Science Institute statistics mini-course. October Inference I: Estimation, Confidence Intervals, and Tests of Hypotheses
 Space Telescope Science Institute statistics mini-course October 2011 Inference I: Estimation, Confidence Intervals, and Tests of Hypotheses James L Rosenberger Acknowledgements: Donald Richards, William
Space Telescope Science Institute statistics mini-course October 2011 Inference I: Estimation, Confidence Intervals, and Tests of Hypotheses James L Rosenberger Acknowledgements: Donald Richards, William
Multivariate Distributions
 IEOR E4602: Quantitative Risk Management Spring 2016 c 2016 by Martin Haugh Multivariate Distributions We will study multivariate distributions in these notes, focusing 1 in particular on multivariate
IEOR E4602: Quantitative Risk Management Spring 2016 c 2016 by Martin Haugh Multivariate Distributions We will study multivariate distributions in these notes, focusing 1 in particular on multivariate
3. Linear Regression With a Single Regressor
 3. Linear Regression With a Single Regressor Econometrics: (I) Application of statistical methods in empirical research Testing economic theory with real-world data (data analysis) 56 Econometrics: (II)
3. Linear Regression With a Single Regressor Econometrics: (I) Application of statistical methods in empirical research Testing economic theory with real-world data (data analysis) 56 Econometrics: (II)
where x and ȳ are the sample means of x 1,, x n
 y y Animal Studies of Side Effects Simple Linear Regression Basic Ideas In simple linear regression there is an approximately linear relation between two variables say y = pressure in the pancreas x =
y y Animal Studies of Side Effects Simple Linear Regression Basic Ideas In simple linear regression there is an approximately linear relation between two variables say y = pressure in the pancreas x =
Comparing measures of fit for circular distributions
 Comparing measures of fit for circular distributions by Zheng Sun B.Sc., Simon Fraser University, 2006 A Thesis Submitted in Partial Fulfillment of the Requirements for the Degree of MASTER OF SCIENCE
Comparing measures of fit for circular distributions by Zheng Sun B.Sc., Simon Fraser University, 2006 A Thesis Submitted in Partial Fulfillment of the Requirements for the Degree of MASTER OF SCIENCE
DISCRIMINATING BETWEEN THE NORMAL INVERSE GAUSSIAN AND GENERALIZED HYPERBOLIC SKEW-T DISTRIBUTIONS WITH A FOLLOW-UP THE STOCK EXCHANGE DATA
 Yugoslav Journal of Operations Research 8 (018), Number, 185 199 DOI: https://doi.org/10.98/yjor170815013p DISCRIMINATING BETWEEN THE NORMAL INVERSE GAUSSIAN AND GENERALIZED HYPERBOLIC SKEW-T DISTRIBUTIONS
Yugoslav Journal of Operations Research 8 (018), Number, 185 199 DOI: https://doi.org/10.98/yjor170815013p DISCRIMINATING BETWEEN THE NORMAL INVERSE GAUSSIAN AND GENERALIZED HYPERBOLIC SKEW-T DISTRIBUTIONS
Foundations of Statistical Inference
 Foundations of Statistical Inference Jonathan Marchini Department of Statistics University of Oxford MT 2013 Jonathan Marchini (University of Oxford) BS2a MT 2013 1 / 27 Course arrangements Lectures M.2
Foundations of Statistical Inference Jonathan Marchini Department of Statistics University of Oxford MT 2013 Jonathan Marchini (University of Oxford) BS2a MT 2013 1 / 27 Course arrangements Lectures M.2
STATISTICS SYLLABUS UNIT I
 STATISTICS SYLLABUS UNIT I (Probability Theory) Definition Classical and axiomatic approaches.laws of total and compound probability, conditional probability, Bayes Theorem. Random variable and its distribution
STATISTICS SYLLABUS UNIT I (Probability Theory) Definition Classical and axiomatic approaches.laws of total and compound probability, conditional probability, Bayes Theorem. Random variable and its distribution
Eco517 Fall 2004 C. Sims MIDTERM EXAM
 Eco517 Fall 2004 C. Sims MIDTERM EXAM Answer all four questions. Each is worth 23 points. Do not devote disproportionate time to any one question unless you have answered all the others. (1) We are considering
Eco517 Fall 2004 C. Sims MIDTERM EXAM Answer all four questions. Each is worth 23 points. Do not devote disproportionate time to any one question unless you have answered all the others. (1) We are considering
1 Degree distributions and data
 1 Degree distributions and data A great deal of effort is often spent trying to identify what functional form best describes the degree distribution of a network, particularly the upper tail of that distribution.
1 Degree distributions and data A great deal of effort is often spent trying to identify what functional form best describes the degree distribution of a network, particularly the upper tail of that distribution.
New Family of the t Distributions for Modeling Semicircular Data
 Communications of the Korean Statistical Society Vol. 15, No. 5, 008, pp. 667 674 New Family of the t Distributions for Modeling Semicircular Data Hyoung-Moon Kim 1) Abstract We develop new family of the
Communications of the Korean Statistical Society Vol. 15, No. 5, 008, pp. 667 674 New Family of the t Distributions for Modeling Semicircular Data Hyoung-Moon Kim 1) Abstract We develop new family of the
TESTING FOR NORMALITY IN THE LINEAR REGRESSION MODEL: AN EMPIRICAL LIKELIHOOD RATIO TEST
 Econometrics Working Paper EWP0402 ISSN 1485-6441 Department of Economics TESTING FOR NORMALITY IN THE LINEAR REGRESSION MODEL: AN EMPIRICAL LIKELIHOOD RATIO TEST Lauren Bin Dong & David E. A. Giles Department
Econometrics Working Paper EWP0402 ISSN 1485-6441 Department of Economics TESTING FOR NORMALITY IN THE LINEAR REGRESSION MODEL: AN EMPIRICAL LIKELIHOOD RATIO TEST Lauren Bin Dong & David E. A. Giles Department
Multivariate Distribution Models
 Multivariate Distribution Models Model Description While the probability distribution for an individual random variable is called marginal, the probability distribution for multiple random variables is
Multivariate Distribution Models Model Description While the probability distribution for an individual random variable is called marginal, the probability distribution for multiple random variables is
Stat 451 Lecture Notes Simulating Random Variables
 Stat 451 Lecture Notes 05 12 Simulating Random Variables Ryan Martin UIC www.math.uic.edu/~rgmartin 1 Based on Chapter 6 in Givens & Hoeting, Chapter 22 in Lange, and Chapter 2 in Robert & Casella 2 Updated:
Stat 451 Lecture Notes 05 12 Simulating Random Variables Ryan Martin UIC www.math.uic.edu/~rgmartin 1 Based on Chapter 6 in Givens & Hoeting, Chapter 22 in Lange, and Chapter 2 in Robert & Casella 2 Updated:
The formal relationship between analytic and bootstrap approaches to parametric inference
 The formal relationship between analytic and bootstrap approaches to parametric inference T.J. DiCiccio Cornell University, Ithaca, NY 14853, U.S.A. T.A. Kuffner Washington University in St. Louis, St.
The formal relationship between analytic and bootstrap approaches to parametric inference T.J. DiCiccio Cornell University, Ithaca, NY 14853, U.S.A. T.A. Kuffner Washington University in St. Louis, St.
GARCH Models Estimation and Inference
 Università di Pavia GARCH Models Estimation and Inference Eduardo Rossi Likelihood function The procedure most often used in estimating θ 0 in ARCH models involves the maximization of a likelihood function
Università di Pavia GARCH Models Estimation and Inference Eduardo Rossi Likelihood function The procedure most often used in estimating θ 0 in ARCH models involves the maximization of a likelihood function
Math 181B Homework 1 Solution
 Math 181B Homework 1 Solution 1. Write down the likelihood: L(λ = n λ X i e λ X i! (a One-sided test: H 0 : λ = 1 vs H 1 : λ = 0.1 The likelihood ratio: where LR = L(1 L(0.1 = 1 X i e n 1 = λ n X i e nλ
Math 181B Homework 1 Solution 1. Write down the likelihood: L(λ = n λ X i e λ X i! (a One-sided test: H 0 : λ = 1 vs H 1 : λ = 0.1 The likelihood ratio: where LR = L(1 L(0.1 = 1 X i e n 1 = λ n X i e nλ
If we want to analyze experimental or simulated data we might encounter the following tasks:
 Chapter 1 Introduction If we want to analyze experimental or simulated data we might encounter the following tasks: Characterization of the source of the signal and diagnosis Studying dependencies Prediction
Chapter 1 Introduction If we want to analyze experimental or simulated data we might encounter the following tasks: Characterization of the source of the signal and diagnosis Studying dependencies Prediction
Power and Sample Size Calculations with the Additive Hazards Model
 Journal of Data Science 10(2012), 143-155 Power and Sample Size Calculations with the Additive Hazards Model Ling Chen, Chengjie Xiong, J. Philip Miller and Feng Gao Washington University School of Medicine
Journal of Data Science 10(2012), 143-155 Power and Sample Size Calculations with the Additive Hazards Model Ling Chen, Chengjie Xiong, J. Philip Miller and Feng Gao Washington University School of Medicine
Pattern Recognition and Machine Learning. Bishop Chapter 2: Probability Distributions
 Pattern Recognition and Machine Learning Chapter 2: Probability Distributions Cécile Amblard Alex Kläser Jakob Verbeek October 11, 27 Probability Distributions: General Density Estimation: given a finite
Pattern Recognition and Machine Learning Chapter 2: Probability Distributions Cécile Amblard Alex Kläser Jakob Verbeek October 11, 27 Probability Distributions: General Density Estimation: given a finite
A Very Brief Summary of Statistical Inference, and Examples
 A Very Brief Summary of Statistical Inference, and Examples Trinity Term 2008 Prof. Gesine Reinert 1 Data x = x 1, x 2,..., x n, realisations of random variables X 1, X 2,..., X n with distribution (model)
A Very Brief Summary of Statistical Inference, and Examples Trinity Term 2008 Prof. Gesine Reinert 1 Data x = x 1, x 2,..., x n, realisations of random variables X 1, X 2,..., X n with distribution (model)
Testing Some Covariance Structures under a Growth Curve Model in High Dimension
 Department of Mathematics Testing Some Covariance Structures under a Growth Curve Model in High Dimension Muni S. Srivastava and Martin Singull LiTH-MAT-R--2015/03--SE Department of Mathematics Linköping
Department of Mathematics Testing Some Covariance Structures under a Growth Curve Model in High Dimension Muni S. Srivastava and Martin Singull LiTH-MAT-R--2015/03--SE Department of Mathematics Linköping
Testing Restrictions and Comparing Models
 Econ. 513, Time Series Econometrics Fall 00 Chris Sims Testing Restrictions and Comparing Models 1. THE PROBLEM We consider here the problem of comparing two parametric models for the data X, defined by
Econ. 513, Time Series Econometrics Fall 00 Chris Sims Testing Restrictions and Comparing Models 1. THE PROBLEM We consider here the problem of comparing two parametric models for the data X, defined by
1 Hypothesis Testing and Model Selection
 A Short Course on Bayesian Inference (based on An Introduction to Bayesian Analysis: Theory and Methods by Ghosh, Delampady and Samanta) Module 6: From Chapter 6 of GDS 1 Hypothesis Testing and Model Selection
A Short Course on Bayesian Inference (based on An Introduction to Bayesian Analysis: Theory and Methods by Ghosh, Delampady and Samanta) Module 6: From Chapter 6 of GDS 1 Hypothesis Testing and Model Selection
Bayesian Econometrics
 Bayesian Econometrics Christopher A. Sims Princeton University sims@princeton.edu September 20, 2016 Outline I. The difference between Bayesian and non-bayesian inference. II. Confidence sets and confidence
Bayesian Econometrics Christopher A. Sims Princeton University sims@princeton.edu September 20, 2016 Outline I. The difference between Bayesian and non-bayesian inference. II. Confidence sets and confidence
arxiv: v1 [math.st] 7 Nov 2017
![arxiv: v1 [math.st] 7 Nov 2017 arxiv: v1 [math.st] 7 Nov 2017](/thumbs/92/111014201.jpg) DETECTING THE DIRECTION OF A SIGNAL ON HIGH-DIMENSIONAL SPHERES: NON-NULL AND LE CAM OPTIMALITY RESULTS arxiv:1711.0504v1 [math.st] 7 Nov 017 By Davy Paindaveine and Thomas Verdebout Université libre de
DETECTING THE DIRECTION OF A SIGNAL ON HIGH-DIMENSIONAL SPHERES: NON-NULL AND LE CAM OPTIMALITY RESULTS arxiv:1711.0504v1 [math.st] 7 Nov 017 By Davy Paindaveine and Thomas Verdebout Université libre de
Chapter 2 Continuous Distributions
 Chapter Continuous Distributions Continuous random variables For a continuous random variable X the probability distribution is described by the probability density function f(x), which has the following
Chapter Continuous Distributions Continuous random variables For a continuous random variable X the probability distribution is described by the probability density function f(x), which has the following
Notes on the Multivariate Normal and Related Topics
 Version: July 10, 2013 Notes on the Multivariate Normal and Related Topics Let me refresh your memory about the distinctions between population and sample; parameters and statistics; population distributions
Version: July 10, 2013 Notes on the Multivariate Normal and Related Topics Let me refresh your memory about the distinctions between population and sample; parameters and statistics; population distributions
Noninformative Priors for the Ratio of the Scale Parameters in the Inverted Exponential Distributions
 Communications for Statistical Applications and Methods 03, Vol. 0, No. 5, 387 394 DOI: http://dx.doi.org/0.535/csam.03.0.5.387 Noninformative Priors for the Ratio of the Scale Parameters in the Inverted
Communications for Statistical Applications and Methods 03, Vol. 0, No. 5, 387 394 DOI: http://dx.doi.org/0.535/csam.03.0.5.387 Noninformative Priors for the Ratio of the Scale Parameters in the Inverted
Master s Written Examination
 Master s Written Examination Option: Statistics and Probability Spring 05 Full points may be obtained for correct answers to eight questions Each numbered question (which may have several parts) is worth
Master s Written Examination Option: Statistics and Probability Spring 05 Full points may be obtained for correct answers to eight questions Each numbered question (which may have several parts) is worth
Model comparison and selection
 BS2 Statistical Inference, Lectures 9 and 10, Hilary Term 2008 March 2, 2008 Hypothesis testing Consider two alternative models M 1 = {f (x; θ), θ Θ 1 } and M 2 = {f (x; θ), θ Θ 2 } for a sample (X = x)
BS2 Statistical Inference, Lectures 9 and 10, Hilary Term 2008 March 2, 2008 Hypothesis testing Consider two alternative models M 1 = {f (x; θ), θ Θ 1 } and M 2 = {f (x; θ), θ Θ 2 } for a sample (X = x)
Transformations The bias-variance tradeoff Model selection criteria Remarks. Model selection I. Patrick Breheny. February 17
 Model selection I February 17 Remedial measures Suppose one of your diagnostic plots indicates a problem with the model s fit or assumptions; what options are available to you? Generally speaking, you
Model selection I February 17 Remedial measures Suppose one of your diagnostic plots indicates a problem with the model s fit or assumptions; what options are available to you? Generally speaking, you
COM336: Neural Computing
 COM336: Neural Computing http://www.dcs.shef.ac.uk/ sjr/com336/ Lecture 2: Density Estimation Steve Renals Department of Computer Science University of Sheffield Sheffield S1 4DP UK email: s.renals@dcs.shef.ac.uk
COM336: Neural Computing http://www.dcs.shef.ac.uk/ sjr/com336/ Lecture 2: Density Estimation Steve Renals Department of Computer Science University of Sheffield Sheffield S1 4DP UK email: s.renals@dcs.shef.ac.uk
STAT 513 fa 2018 hw 5
 STAT 513 fa 2018 hw 5 assigned: Thursday, Oct 4th, 2018 due: Thursday, Oct 11th, 2018 1. Let X 11,..., X 1n1 and X 21,..., X 2n2 be independent random samples from the Normal(µ 1, σ 2 ) and Normal(µ 1,
STAT 513 fa 2018 hw 5 assigned: Thursday, Oct 4th, 2018 due: Thursday, Oct 11th, 2018 1. Let X 11,..., X 1n1 and X 21,..., X 2n2 be independent random samples from the Normal(µ 1, σ 2 ) and Normal(µ 1,
Regression and Statistical Inference
 Regression and Statistical Inference Walid Mnif wmnif@uwo.ca Department of Applied Mathematics The University of Western Ontario, London, Canada 1 Elements of Probability 2 Elements of Probability CDF&PDF
Regression and Statistical Inference Walid Mnif wmnif@uwo.ca Department of Applied Mathematics The University of Western Ontario, London, Canada 1 Elements of Probability 2 Elements of Probability CDF&PDF
The Expectation-Maximization Algorithm
 1/29 EM & Latent Variable Models Gaussian Mixture Models EM Theory The Expectation-Maximization Algorithm Mihaela van der Schaar Department of Engineering Science University of Oxford MLE for Latent Variable
1/29 EM & Latent Variable Models Gaussian Mixture Models EM Theory The Expectation-Maximization Algorithm Mihaela van der Schaar Department of Engineering Science University of Oxford MLE for Latent Variable
ASSESSING A VECTOR PARAMETER
 SUMMARY ASSESSING A VECTOR PARAMETER By D.A.S. Fraser and N. Reid Department of Statistics, University of Toronto St. George Street, Toronto, Canada M5S 3G3 dfraser@utstat.toronto.edu Some key words. Ancillary;
SUMMARY ASSESSING A VECTOR PARAMETER By D.A.S. Fraser and N. Reid Department of Statistics, University of Toronto St. George Street, Toronto, Canada M5S 3G3 dfraser@utstat.toronto.edu Some key words. Ancillary;
STATISTICAL METHODS FOR SIGNAL PROCESSING c Alfred Hero
 STATISTICAL METHODS FOR SIGNAL PROCESSING c Alfred Hero 1999 32 Statistic used Meaning in plain english Reduction ratio T (X) [X 1,..., X n ] T, entire data sample RR 1 T (X) [X (1),..., X (n) ] T, rank
STATISTICAL METHODS FOR SIGNAL PROCESSING c Alfred Hero 1999 32 Statistic used Meaning in plain english Reduction ratio T (X) [X 1,..., X n ] T, entire data sample RR 1 T (X) [X (1),..., X (n) ] T, rank
The Mixture Approach for Simulating New Families of Bivariate Distributions with Specified Correlations
 The Mixture Approach for Simulating New Families of Bivariate Distributions with Specified Correlations John R. Michael, Significance, Inc. and William R. Schucany, Southern Methodist University The mixture
The Mixture Approach for Simulating New Families of Bivariate Distributions with Specified Correlations John R. Michael, Significance, Inc. and William R. Schucany, Southern Methodist University The mixture
Model Selection for Semiparametric Bayesian Models with Application to Overdispersion
 Proceedings 59th ISI World Statistics Congress, 25-30 August 2013, Hong Kong (Session CPS020) p.3863 Model Selection for Semiparametric Bayesian Models with Application to Overdispersion Jinfang Wang and
Proceedings 59th ISI World Statistics Congress, 25-30 August 2013, Hong Kong (Session CPS020) p.3863 Model Selection for Semiparametric Bayesian Models with Application to Overdispersion Jinfang Wang and
DUBLIN CITY UNIVERSITY
 DUBLIN CITY UNIVERSITY SAMPLE EXAMINATIONS 2017/2018 MODULE: QUALIFICATIONS: Simulation for Finance MS455 B.Sc. Actuarial Mathematics ACM B.Sc. Financial Mathematics FIM YEAR OF STUDY: 4 EXAMINERS: Mr
DUBLIN CITY UNIVERSITY SAMPLE EXAMINATIONS 2017/2018 MODULE: QUALIFICATIONS: Simulation for Finance MS455 B.Sc. Actuarial Mathematics ACM B.Sc. Financial Mathematics FIM YEAR OF STUDY: 4 EXAMINERS: Mr
Some Approximations of the Logistic Distribution with Application to the Covariance Matrix of Logistic Regression
 Working Paper 2013:9 Department of Statistics Some Approximations of the Logistic Distribution with Application to the Covariance Matrix of Logistic Regression Ronnie Pingel Working Paper 2013:9 June
Working Paper 2013:9 Department of Statistics Some Approximations of the Logistic Distribution with Application to the Covariance Matrix of Logistic Regression Ronnie Pingel Working Paper 2013:9 June
13 Spherical Coordinates
 Utah State University DigitalCommons@USU Foundations of Wave Phenomena Library Digital Monographs 8-204 3 Spherical Coordinates Charles G. Torre Department of Physics, Utah State University, Charles.Torre@usu.edu
Utah State University DigitalCommons@USU Foundations of Wave Phenomena Library Digital Monographs 8-204 3 Spherical Coordinates Charles G. Torre Department of Physics, Utah State University, Charles.Torre@usu.edu
Ornstein-Uhlenbeck processes for geophysical data analysis
 Ornstein-Uhlenbeck processes for geophysical data analysis Semere Habtemicael Department of Mathematics North Dakota State University May 19, 2014 Outline 1 Introduction 2 Model 3 Characteristic function
Ornstein-Uhlenbeck processes for geophysical data analysis Semere Habtemicael Department of Mathematics North Dakota State University May 19, 2014 Outline 1 Introduction 2 Model 3 Characteristic function
Statistical Methods for Handling Incomplete Data Chapter 2: Likelihood-based approach
 Statistical Methods for Handling Incomplete Data Chapter 2: Likelihood-based approach Jae-Kwang Kim Department of Statistics, Iowa State University Outline 1 Introduction 2 Observed likelihood 3 Mean Score
Statistical Methods for Handling Incomplete Data Chapter 2: Likelihood-based approach Jae-Kwang Kim Department of Statistics, Iowa State University Outline 1 Introduction 2 Observed likelihood 3 Mean Score
Statistics: Learning models from data
 DS-GA 1002 Lecture notes 5 October 19, 2015 Statistics: Learning models from data Learning models from data that are assumed to be generated probabilistically from a certain unknown distribution is a crucial
DS-GA 1002 Lecture notes 5 October 19, 2015 Statistics: Learning models from data Learning models from data that are assumed to be generated probabilistically from a certain unknown distribution is a crucial
1 Mixed effect models and longitudinal data analysis
 1 Mixed effect models and longitudinal data analysis Mixed effects models provide a flexible approach to any situation where data have a grouping structure which introduces some kind of correlation between
1 Mixed effect models and longitudinal data analysis Mixed effects models provide a flexible approach to any situation where data have a grouping structure which introduces some kind of correlation between
Generalized Exponential Distribution: Existing Results and Some Recent Developments
 Generalized Exponential Distribution: Existing Results and Some Recent Developments Rameshwar D. Gupta 1 Debasis Kundu 2 Abstract Mudholkar and Srivastava [25] introduced three-parameter exponentiated
Generalized Exponential Distribution: Existing Results and Some Recent Developments Rameshwar D. Gupta 1 Debasis Kundu 2 Abstract Mudholkar and Srivastava [25] introduced three-parameter exponentiated
1 Isotropic Covariance Functions
 1 Isotropic Covariance Functions Let {Z(s)} be a Gaussian process on, ie, a collection of jointly normal random variables Z(s) associated with n-dimensional locations s The joint distribution of {Z(s)}
1 Isotropic Covariance Functions Let {Z(s)} be a Gaussian process on, ie, a collection of jointly normal random variables Z(s) associated with n-dimensional locations s The joint distribution of {Z(s)}
Modulation of symmetric densities
 1 Modulation of symmetric densities 1.1 Motivation This book deals with a formulation for the construction of continuous probability distributions and connected statistical aspects. Before we begin, a
1 Modulation of symmetric densities 1.1 Motivation This book deals with a formulation for the construction of continuous probability distributions and connected statistical aspects. Before we begin, a
MTH739U/P: Topics in Scientific Computing Autumn 2016 Week 6
 MTH739U/P: Topics in Scientific Computing Autumn 16 Week 6 4.5 Generic algorithms for non-uniform variates We have seen that sampling from a uniform distribution in [, 1] is a relatively straightforward
MTH739U/P: Topics in Scientific Computing Autumn 16 Week 6 4.5 Generic algorithms for non-uniform variates We have seen that sampling from a uniform distribution in [, 1] is a relatively straightforward
Lecture 4: Lower Bounds (ending); Thompson Sampling
 CMSC 858G: Bandits, Experts and Games 09/12/16 Lecture 4: Lower Bounds (ending); Thompson Sampling Instructor: Alex Slivkins Scribed by: Guowei Sun,Cheng Jie 1 Lower bounds on regret (ending) Recap from
CMSC 858G: Bandits, Experts and Games 09/12/16 Lecture 4: Lower Bounds (ending); Thompson Sampling Instructor: Alex Slivkins Scribed by: Guowei Sun,Cheng Jie 1 Lower bounds on regret (ending) Recap from
Boundary value problems for partial differential equations
 Boundary value problems for partial differential equations Henrik Schlichtkrull March 11, 213 1 Boundary value problem 2 1 Introduction This note contains a brief introduction to linear partial differential
Boundary value problems for partial differential equations Henrik Schlichtkrull March 11, 213 1 Boundary value problem 2 1 Introduction This note contains a brief introduction to linear partial differential
Laplace s Equation in Cylindrical Coordinates and Bessel s Equation (I)
 Laplace s Equation in Cylindrical Coordinates and Bessel s Equation I) 1 Solution by separation of variables Laplace s equation is a key equation in Mathematical Physics. Several phenomena involving scalar
Laplace s Equation in Cylindrical Coordinates and Bessel s Equation I) 1 Solution by separation of variables Laplace s equation is a key equation in Mathematical Physics. Several phenomena involving scalar
Illustration of the Varying Coefficient Model for Analyses the Tree Growth from the Age and Space Perspectives
 TR-No. 14-06, Hiroshima Statistical Research Group, 1 11 Illustration of the Varying Coefficient Model for Analyses the Tree Growth from the Age and Space Perspectives Mariko Yamamura 1, Keisuke Fukui
TR-No. 14-06, Hiroshima Statistical Research Group, 1 11 Illustration of the Varying Coefficient Model for Analyses the Tree Growth from the Age and Space Perspectives Mariko Yamamura 1, Keisuke Fukui
Cost Efficiency, Asymmetry and Dependence in US electricity industry.
 Cost Efficiency, Asymmetry and Dependence in US electricity industry. Graziella Bonanno bonanno@diag.uniroma1.it Department of Computer, Control, and Management Engineering Antonio Ruberti - Sapienza University
Cost Efficiency, Asymmetry and Dependence in US electricity industry. Graziella Bonanno bonanno@diag.uniroma1.it Department of Computer, Control, and Management Engineering Antonio Ruberti - Sapienza University
Optimum designs for model. discrimination and estimation. in Binary Response Models
 Optimum designs for model discrimination and estimation in Binary Response Models by Wei-Shan Hsieh Advisor Mong-Na Lo Huang Department of Applied Mathematics National Sun Yat-sen University Kaohsiung,
Optimum designs for model discrimination and estimation in Binary Response Models by Wei-Shan Hsieh Advisor Mong-Na Lo Huang Department of Applied Mathematics National Sun Yat-sen University Kaohsiung,
Analysis of the AIC Statistic for Optimal Detection of Small Changes in Dynamic Systems
 Analysis of the AIC Statistic for Optimal Detection of Small Changes in Dynamic Systems Jeremy S. Conner and Dale E. Seborg Department of Chemical Engineering University of California, Santa Barbara, CA
Analysis of the AIC Statistic for Optimal Detection of Small Changes in Dynamic Systems Jeremy S. Conner and Dale E. Seborg Department of Chemical Engineering University of California, Santa Barbara, CA
Statistics for scientists and engineers
 Statistics for scientists and engineers February 0, 006 Contents Introduction. Motivation - why study statistics?................................... Examples..................................................3
Statistics for scientists and engineers February 0, 006 Contents Introduction. Motivation - why study statistics?................................... Examples..................................................3
