Tzitzeica theory - opportunity for reflection in Mathematics
|
|
|
- Lynne Jenkins
- 5 years ago
- Views:
Transcription
1 Tzitzeica theory - opportunity for reflection in Mathematics Constantin Udrişte Abstract Our aim is to emphasize the topical interest, richness and vitality of Tzitzeica theory. Rather than aspiring to a comprehensive treatise, this Note contains the mathematical discussion of only those topics which are in connection with our concerns. That is why, we have in view four aspects : to recall the symmetry groups associated to Tzitzeica PDEs; to emphasize again that the Tzitzeica PDEs are Euler -Lagrange equations; to reveal some physical roots of Tzitzeica theory; to underline new properties of Tzitzeica PDEs and their connection to Painlevé ODEs. Mathematics Subject Classification: 58J70, 35A15, 53C99. Key words: Tzitzeica PDEs, symmetry groups, Tzitzeica Lagrangian, Tzitzeica geometric dynamics. 1 Introduction Gheorghe Tzitzeica is known as one of the founders of the centro-affine differential geometry. He introduced a class of surfaces and a class of curves that today carry his name. Also, he realized the curve net theory based on a partial derivative equation of Laplace type. The work of Gheorghe Tzitzeica is a permanent incitation to mathematical reflection. It inspired many mathematicians, but the most faithful continuers have been the Romanians Alexandru Myller, Octav Mayer, Gheorghe Theodor Gheorghiu and Gheorghe Călugăreanu. The Tzitzeica ideas have reappeared in recent times due to their relation with groups of symmetries, variational equations, electrons theory, soliton theory, etc. 2 PDEs of Tzitzeica type In 1907, Gheorghe Tzitzeica [9] introduced a famous class of surfaces, that now carries his name. Locally, these surfaces can be considered as graphs of functions u = u(x, y) which satisfy the partial derivative equation Balkan Journal of Geometry and Its Applications, Vol.10, No.1, 2005, pp c Balkan Society of Geometers, Geometry Balkan Press 2005.
2 Tzitzeica theory - opportunity for reflection in Mathematics 111 (2.1) u xx u yy u 2 xy = c(xu x + yu y u) 4, c = const 0. In 1923, still Gheorghe Tzitzeica [10] has described the surfaces that carry his name as solutions of a completely integrable PDEs system (2.2) r uu = ar u + br v, r uv = hr, r vv = a r u + b r v, where r = xī + y j + z k. More precisely: 1) the ruled Tzitzeica surfaces are defined as solutions of the PDEs system (2.3) r uu = h u h r u + ϕ(u) h r v, r uv = hr, r vv = h v h r v, where h is a solution of partial derivative equation (complete integrability condition) (2.4) (ln h) uv = h; 2) the non-ruled Tzitzeica surfaces are defined as solutions of the PDEs system (2.5) r uu = h u h r u + 1 h r v, r uv = hr, r vv = 1 h r u + h v h r v, where h is a solution of partial derivative equation (complete integrability condition) (2.6) (ln h) uv = h 1 h 2. With a change of function ln h = ω the equations (2.4) and (2.6) rewrite respectively (2.7) ω uv = e ω, and (2.8) ω uv = e ω e 2ω. Being impressed by the Tzitzeica genius and stimulated by the papers of Bobenko [2] and Wolf [18], as well as the debates with Romanian and foreigner [6], [8] geometers, together Nicoleta Bâlă, the author studied two problems [1],[11]: 1) the characterization of the symmetry groups associated to the equations (2.1)- (2.4); 2) showing that the equations (2.1), (2.3), (2.4) are equivalent to Euler-Lagrange equations. The surprises where in line with expectations: A. The symmetry group associated to the equation (2.1) is the unimodular subgroup of the centro-affine group. The Lie algebra of this group is generated by the vector fields X 1 = x x u u, X 2 = y y u u, X 3 = y x, X 4 = u x,
3 112 Constantin Udrişte (2.9) X 5 = x y, X 6 = u y, X 7 = x u, X 8 = y u. These infinitesimal generators have permitted the finding of group-invariant solutions of the equation (2.1). Also, we proved that the only partial derivative equation of Monge-Ampere-Tzitzeica type, invariant with respect to unimodular group (2.9), is the equation (2.1). The equation (2.1) is equivalent to an Euler-Lagrange equation produced by the second order Lagrangian L 1 (x, y, u (2) ) = u(u2 xy u xx u yy ) (xu x + yu y u) 4 cu. Automatically, it appears the variational symmetry group and adequate conservation laws. From this point of view, the problem is still open. Open problem. There exists or not a first order Lagrangian producing the Tzitzeica equation? B. The symmetry subgroup that acts on the space of independent variables and of the system (2.2) is generated by vector fields of the type Z = ζ(u) u + η(v) v, where the functions ζ(u), η(v) are solutions of a PDEs system. The symmetry subgroup which acts on the space of dependent variables x, y, z of the system (2.2) is the unimodular subgroup of the centro-affine group of generators X 1 = x x z z, X 2 = y y z z, X 3 = y x, X 4 = z x, X 5 = x y, X 6 = z y, X 7 = x z, X 8 = y z. In fact, the previous result is found. C. The general vector field which describes the infinitesimal symmetry algebra associated to the equation (2.7) is W = f(u) u + g(v) v + (f (u) + g (v)) u. The equation (2.7) is the Euler-Lagrange equation provided by the first order Lagrangian L 2 (u, v, ω (1) ) = 1 2 ω uω v e ω. The Lie algebra of the variational symmetries for the action produced by L 2 is generated by the vector fields W 1 = u u w, W 2 = v v w, W 3 = u, W 4 = v. Automatically, adequate conservation laws have appeared. Also the equation (2.7) is conservative in the sense that the divergence of the momentum-energy tensor field
4 Tzitzeica theory - opportunity for reflection in Mathematics 113 T α β = ω β L ω α Lδ α β, α, β = 1, 2, ω 1 = ω u, ω 2 = ω v vanishes on the solutions of the equation. D. The vector fields which generate the algebra of infinitesimal symmetries associated to the equation (2.8) are U 1 = u u v v, U 2 = u, U 3 = v. The equation (2.8) is the Euler-Lagrange equation produced by the first order Lagrangian L 3 (u, v, ω (1) ) = 1 2 ω uω v e ω e 2ω. The Lie algebra of variational symmetry group for the action produced by L 3 is the same with {U 1, U 2, U 3 }. Automatically, one writes adequate conservation laws. We prefer to add that the equation (2.8) is conservative in the sense that the divergence of the momentum-energy tensor field vanishes on the solutions of the equation. All the results underlined in the sections A-D confirm that Tzitzeica theory can be considered as essential part of variational principles on differential manifolds. It was a matter of course since the real world is governed, among other things, by optimum principles, and Gheorghe Tzitzeica realized indirectly that this is the clue of real problems. 3 Tzitzeica geometric dynamics We find of interest to present shortly the Tzitzeica geometric dynamics introduced by us in [15]. Also we point out its connections with physical theories. It is well-known that the most simple Tzitzeica surface is that described by the equation xyz = 1 (see Fig.1). If we denote the Tzitzeica potential by u(x, y, z) = xyz, then its gradient lines are solutions of the first order ODEs system dx dt = yz, dy dt = zx, dz dt = xy. Interpreting them as trajectories for the motion of a particle in R 3, we have well known properties: 1) if two of the numbers x(0), y(0), z(0) are null, then the particle does not move; 2) if at least two of the initial values x(0), y(0), z(0) are different from zero, then either the particle moves to infinity in a finite time (in future), or it comes from the infinity in a finite time (in the past). This differential system together with Euclidean metric determine a geometric dynamics of Tzitzeica type described by the second order ODEs system d 2 x dt 2 = x(z2 + y 2 ), d2 y dt 2 = y(x2 + z 2 ), d2 z dt 2 = z(y2 + x 2 ). This conservative dynamics is characterized by the density of energy 2f(x, y, z) = x 2 y 2 + y 2 z 2 + z 2 x 2
5 114 Constantin Udrişte Figure 1: Tzitzeica surface whose constant level sets are totally h-geodesic and hence h-minimal (see Fig.2). Surfaces with shapes similar to those in Fig. 2 were met as Fermi surfaces (surfaces of constant energy) in the theory of Wolfgang Pauli and Arnold Sommerfeld [7] for metal electrons (crystal meshes populated by electrons). For a complete theory of this type, see [12]-[17]. 4 Tzitzeica law in economics In the case of general economic equilibrium analysis the demand and the supply functions relative to each good are in principle functions of the prices of all goods, and not only of the price of the good to which they refer. That is why the problem of the static or dynamic stability of demand and supply requires the introduction of excess demand vector field E of components E i = E i (p 1,..., p n ), i = 1,..., n, where E i is the excess demand for the i th good, and p i are prices [3], [17]. From dynamical point of view, we must analyze the excess demand flow dp i dt = E i, i = 1,..., n. In this context, the Walras law δ ij p i E j = 0 means that δ ij p i p j is a first integral of the excess demand flow. This condition is used for normalization and the completeness of the field E, because the constant level surfaces are spheres. The Tzitzeica law p 1...p n 1 E n = 0 (summation by cyclic permutations), introduced in [3], [17], says that p 1...p n is a first integral of the excess demand flow. This reflects a constant volume of the prices since the tangent hyperplane to the hypersurface p 1...p n = C, at an arbitrary point, determines together with the coordinate hyperplanes a hyper-tetrahedron of constant volume. Since this last condition represents a multiplicative effect, the individual prices act in series: the effect of process i with price p i followed by process j with price p j will be the process of price p i p j.
6 Tzitzeica theory - opportunity for reflection in Mathematics 115 Figure 2: 0.5-Level set of energy density Open problem. A function f : R n R, (x 1,..., x n ) f(x 1,..., x n ) whose value remains unchanged under any permutation of its independent variables is called symmetric function. Any rational symmetric function is a rational function of elementary symmetric polynomials P 1 = x i, P 2 = x i x j, P 3 = x i x j x k,..., P n = x 1 x 2...x n, where the summations are extended over all distinct products of distinct factors. If X is a C vector field of components X i, then each condition of type Xi = 0, (x i X j + X i x j ) = 0, (X i x j x k + x i X j x k + x i x j X k ) = 0,..., (X 1 x 2...x n + x 1 X 2 x 3...x n x 1 x 2...x n 1 X n ) = 0 generates a first integral of the flow dx i dt = X i(x). If instead equalities we use the sign 0 or <, we obtain Lyapunov functions, respectively strong Lyapunov functions. Find the sense of such functions when the vector field X has a practical meaning. 5 Properties of Tzitzeica PDE Let us use MAPLE simulations (PDEtools package) to find new properties of Tzitzeica PDE (2.1). The main result relates the Tzitzeica PDE to the second order Painlevé equations, y (x) = f(x, y(x), y (x)), i.e., equations where f is a rational function of y, y with coefficients functions of x. The Painlevé equations have numerous applications to differential geometry, probability theory, soliton theory, topological field theory, and others [4], [5] [6], [8].
7 116 Constantin Udrişte 5.1 Decomposition of solutions Theorem. The Tzitzeica PDE (2.1) admits solutions of the form u(x, y) = a f(x)y or u(x, y) = f(x) y if and only if the function f is solution of a second order Painlevé ODE. Model 1, Proof. > P DE := diff(u(x, y), x, x) diff(u(x, y), y, y) diff(u(x, y), x, y) 2 = c (x diff(u(x, y), x) + y diff(u(x, y), y) u(x, y)) 4 ; > ansatz := u(x, y) = a/(f(x) y); Use pdetest to simplify the PDE with regard to this ansatz. ans 1 := pdetest(ansatz, P DE); ans 1 := a2 ( 3f 2 f 4 + 2f f 5 + cx 4 a 2 f 4 + 8cx 3 a 2 f 3 f) f 8 y 4 a2 (24cx 2 a 2 f 2 f cxa 2 f f ca 2 f 4 ) f 8 y 4 The ansatz above separated the variables, so the solution of the PDE is determined by the function f which is a solution of a Painlevé equation. > ans f := dsolve(ans 1, f(x)); ans f := f = ae (R b( a)d a+ C1) &where [{ b( a) = 3(27a2 c a 2 ) b( a) 3 + 2(27a2 c a 2 ) b( a) 2 2 a a 2 + 3(18a2 c a 2 ) b( a) 2 a 3 + 6a2 c a 4 + a 2 c 2 a 5 b( a) }, { a = f x, b( a) = x f x f } ] {f = ae (R b( a)d a+ C1), x = ae (R b( a)d a+ C1) } Model 2, Proof. Another particular result can be obtained by separating the variables by product. We can use HINT option to obtain the general solution, inspired by the solution above. > struc1 := solve(p DE, HINT = f(x)/y); struc1 := (u(x, y) = f/y) &where [{f = f 2 8cx 3 f 3 f + 24cx 2 f 2 f 2 + cx 4 f 4 32cxf f cf 4 ] } 2f
8 Tzitzeica theory - opportunity for reflection in Mathematics 117 > struc2 := solve(p DE, HINT = f(x)/xy); struc2 := (u(x, y) = f/xy) [ &where {f = 2ff x 3f 2 + f 2 x 2 12cx 3 f 3 f 2fx cx2 f 2 f 2 108cxf f 3 + cx 4 f cf 4 ] 2fx 2 } In these two cases, the solution of the Tzitzeica PDE is determined by the function f which is a solution of a Painlevé equation. Case c= -1: > ode := diff(f(x), $ (x, 2)) = 1/2 (diff(f(x), x) 2 x 4 diff(f(x), x) 4 16 f(x) x diff(f(x), x) f(x) 3 24 x 2 diff(f(x), x) 2 f(x) x 3 diff(f(x), x) 3 f(x))/f(x); > ans := dsolve({ode, f(0) = 1, D(f)(0) = 1}, f(x), type = series); ans := f = 1 + x 15 4 x2 8 3 x3 1 3 x x5 + O(x 6 ) Case c= 1: > ode1 := diff(f(x), $ (x, 2)) = 1/2 (diff(f(x), x) 2 + x 4 diff(f(x), x) f(x) 4 32 x diff(f(x), x) f(x) x 2 diff(f(x), x) 2 f(x) 2 8 x 3 diff(f(x), x) 3 f(x)/f(x); > ans := dsolve({ode1, f(0) = 1, D(f)(0) = 1}, f(x), type = series); ans := f = 1 + x x x x x5 + O(x 6 ) Now let us refer to a boundary value problem with curvature c as unknown parameter: > ode2 := diff(f(x), $ (x, 2)) = 1/2 (2 f(x) diff(f(x), x) x 3 f(x) 2 + diff(f(x), x) 2 x c x diff(f(x), x) f(x) c f(x) 4 12 c x 3 diff(f(x), x) 3 f(x) + 54 c x 2 diff(f(x), x) 2 f(x) 2 + c x 4 diff(f(x), x) 4 /f(x)/x 2, f(0.1) = 1, f(0.2) = 1.5, D(f)(0.1) = 2; > dsol := dsolve({ode2}, numeric); dsol := proc(x bvp )...endproc dsol(0.1); [x = 0.1, f = , f = , c = ] 5.2 DEtools[symgen] We look for a symmetry generator for previous ODEs. Case c = -1 > with(detools) : > P DEtools[declare](f(x), pime = x); > ode3 := diff(f(x), $ (x, 2)) = 1/2 (diff(f(x), x) 2 x 4 diff(f(x), x) 4 16 f(x) x diff(f(x), x) f(x) 3 24 x 2 diff(f(x), x) 2 f(x) x 3 diff(f(x), x) 3 f(x))/f(x); > odeadvisor(ode3); > symgen(ode3); [ ξ = x, η = f] Case c = 1 > with(detools) : > P DEtools[declare](f(x), pime = x);
9 118 Constantin Udrişte > ode4 := diff(f(x), $ (x, 2)) = 1/2 (diff(f(x), x) 2 +x 4 diff(f(x), x) f(x) 4 32 x diff(f(x), x) f(x) x 2 diff(f(x), x) 2 f(x) 2 8 x 3 diff(f(x), x) 3 f(x))/f(x); > odeadvisor(ode4); > symgen(ode4); [ ξ = x, η = f] 5.3 DEtools[buildsym] Let us build the symmetry generator given a solution of an ODE. > with(detools, bildsym, equinv, symtest); We start with a pair of infinitesimals: sym := [ ξ = x, η = f] ; The most general first order ODE invariant under the above flow is: > ODE := equinv(sym, f(x)); ODE := f = F 1(fx). This ODE can be solved using the following command: x 2 > ans := dsolve(ode, Lie); ln(x) R Z 1 a+ F 1( a) d a C1 ans := f = RootOf x The infinitesimals can be reobtained from this solution: [ > buildsym(ans, f(x)); ] ξ = 0, η = F 1(fx)+fx x 5.4 convert/ode Let us convert the previous ode3 to the other ODE of different type: > convert(ode3, y x); x f,f = 1 x(f) 4 2 x f f 4x(f)3 + 12x f fx(f) 2 16x 2 f f 2 x(f) + 8f 3 xf 3 1 x f 2 f Now, let us find the solution of a Cauchy problem attached to this second order ODE. > ode5 := diff(x(f), $ (f, 2)) = 1/2 x(f) 4 /(f diff(x(f), f)) 4 x(f) diff(x(f), f) f x(f) 2 16 diff(x(f), f) 2 f 2 x(f) + 8 f 3 diff(x(f), f) 3 1/2 diff(x(f), f)/f; > ans := dsolve({ode5, x(0) = 1, D(x)(0) = 1}, x(f), type = series); ans := x(f) = 1 + f 1 2 f f f f 5 + O(f 6 ) 5.5 Tzitzeica PDE as hypersurface in second order jet space Let us transpose the Tzitzeica PDE in the second order jet space of coordinates (x, y, z, p, q, r, s, t), i.e., c(xp + yq u) 4 = rt s 2. This represents a hypersurface of dimension 7 in an 8-dimensional space. To analyze this hypersurface we can use MAPLE: > f := c (x p + y q u) 4 (r t s 2 ); > f1 := diff(f, x); > f2 := diff(f, y); > f3 := diff(f, u);
10 Tzitzeica theory - opportunity for reflection in Mathematics 119 > f4 := diff(f, p); > f5 := diff(f, q); > f6 := diff(f, r); > f7 := diff(f, s); > f8 := diff(f, t); It follows the critical points: > solve({f1 = 0, f2 = 0, f3 = 0, f4 = 0, f5 = 0, f6 = 0, f7 = 0, f8 = 0}, {x, y, u, p, q, r, s, t}); {p = p, q = q, s = 0, r = 0, t = 0, u = xp + yq, x = x, y = y} To obtain information about the curvature, we can use: > with(linalg) : > H := hessian(f, [x, y, z, p, q, r, s, t]); > D := det(h); D := 6144 c 5 (x p + y q u) 14 Consequently the sign of the curvature of the hypersurface f = 0 is opposite to the sign of the curvature c of the Tzitzeica surface u = u(x, y). Acknowledgements. I want to express deep gratitude to Prof. Dr. Vladimir Balan, Prof. Dr. Gabriel Pripoae for helpful discussions, and to Prof. Dr. Iskander Taimanov, Prof. Dr. Serguei Tsarev for sending me three important references. All of these confirm the originality of my results in the last section because the connection spotlighted in the references [6], [8] between Tzitzeica and Painlevé theories is not the same with that discovered by us. References [1] N. Bâlă, Symmetry Groups and Conservation Laws of Some PDEs, PhD Thesis, University Politehnica of Bucharest, Department of Mathematics and Physics, [2] A. I. Bobenko, Surfaces in Terms of 2 by 2 Matrics: Old and New Integrable Cases, in Harmonic Maps and Integrable Systems, Aspects of Mathematics, vol. E 23, A. P. Fordy, J. C. Wood, Friedr. Vieweg&Sohn, Verlagsgesellschaft mbh, Braunsschweig, Wiesbaden, [3] M.T.Calapso, C. Udrişte, Tzitzeica and Walras Laws in Geometric Economics, Analele Universitaţii Bucureşti, 55, 1(2005), in print. [4] P. A. Clarkson, Connection Formulae for the Painlevé Equations, on INTER- NET. [5] A. S. Fokas, M. J. Ablowitz, On a Unified Approach to Transformations and Elementary Solutions of Painlevé Equations, J. Math. Phys. 23 (1982), [6] S. Meleshko, W. Schief, A Truncated Painleve Expansion Associated with Tzitzeica Equation: Consistency and General Solution, on INTERNET. [7] A. Sommerfeld, H. Bethe, Electronentheorie der Metalle, 2nd edn., Springer- Verlag, Berlin, [8] S. Tsarev, Classical Differential Geometry and Integrability of Systems of Hydrodynamic Type, Proc. NATO ARW, 1992, Exeter, UK; arxiv:hep-th/ v1, [9] G. Tzitzeica, Sur une Nouvelle Classe de Surfaces, Comptes Rendus, Acad.Sci.Paris, 144(1907),
11 120 Constantin Udrişte [10] G. Tzitzeica, Géométrie Différentielle Projective des Réseaux, Cultura Naţională, Bucureşti, [11] C. Udrişte, N. Bâlă, Symmetry Group of Tzitzeica Surfaces PDE, Balkan Journal of Geometry and Its Applications, 4, 2(1999), [12] C. Udrişte, Geometric Dynamics, Kluwer Academic Publishers, [13] C. Udrişte, Geometric Dynamics, Southeast Asian Bulletin of Mathematics, Springer - Verlag, 24 (2000), [14] C. Udrişte, Solutions of DEs and PDEs as Potential Maps Using First Order Lagrangians, Balkan Journal of Geometry and Its Applications, 6,1 (2001), [15] C. Udrişte, M. Postolache, Atlas of Magnetic Geometric Dynamics, Geometry Balkan Press, Bucharest, [16] C. Udrişte, Tools of Geometric Dynamics, Buletinul Institutului de Geodinamica, Academia Romana, Vol. 14, fasc. 4 (2003), [17] C. Udrişte, M. Ferrara, D. Opriş, Economic Geometric Dynamics, Geometry Balkan Press, Bucharest, [18] T. Wolf, A Comparison of Four Approaches to the Calculation of Conservation Laws, Eur. J. Appl. Math. 13, 2(2002), Constantin Udrişte University Politehnica of Bucharest Department of Mathematics Splaiul Independenţei Bucharest, Romania udriste@mathem.pub.ro
Linearized geometric dynamics of Tobin-Benhabib-Miyao economic flow
 Linearized geometric dynamics of Tobin-Benhabib-Miyao economic flow Constantin Udrişte and Armando Ciancio Abstract The aim of this paper is to study the influence of the Euclidean-Lagrangian structure
Linearized geometric dynamics of Tobin-Benhabib-Miyao economic flow Constantin Udrişte and Armando Ciancio Abstract The aim of this paper is to study the influence of the Euclidean-Lagrangian structure
H-convex Riemannian submanifolds
 H-convex Riemannian submanifolds Constantin Udrişte and Teodor Oprea Abstract. Having in mind the well known model of Euclidean convex hypersurfaces [4], [5] and the ideas in [1], many authors defined
H-convex Riemannian submanifolds Constantin Udrişte and Teodor Oprea Abstract. Having in mind the well known model of Euclidean convex hypersurfaces [4], [5] and the ideas in [1], many authors defined
Symmetry reductions for the Tzitzeica curve equation
 Fayetteville State University DigitalCommons@Fayetteville State University Math and Computer Science Working Papers College of Arts and Sciences 6-29-2012 Symmetry reductions for the Tzitzeica curve equation
Fayetteville State University DigitalCommons@Fayetteville State University Math and Computer Science Working Papers College of Arts and Sciences 6-29-2012 Symmetry reductions for the Tzitzeica curve equation
Palais-Smale condition for multi-time actions that produce Poisson-gradient PDEs
 Palais-Smale condition for multi-time actions that produce Poisson-gradient PDEs Iulian Duca Abstract. We study the Palais-Smale (P S) c -condition in the case of the multi-times actions ϕ that produces
Palais-Smale condition for multi-time actions that produce Poisson-gradient PDEs Iulian Duca Abstract. We study the Palais-Smale (P S) c -condition in the case of the multi-times actions ϕ that produces
Cylindrical Tzitzeica Curves Implies Forced Harmonic Oscillators
 Cylindrical Tzitzeica Curves Implies Forced Harmonic Oscillators Dedicated to Acad. Radu Miron on the occasion of his 75 birthday Mircea Crâşmăreanu Abstract Elliptic and hyperbolic cylindrical curves
Cylindrical Tzitzeica Curves Implies Forced Harmonic Oscillators Dedicated to Acad. Radu Miron on the occasion of his 75 birthday Mircea Crâşmăreanu Abstract Elliptic and hyperbolic cylindrical curves
Multitime sine-gordon solitons via geometric characteristics
 Multitime sine-gordon solitons via geometric characteristics Laura Gabriela Matei, Constantin Udrişte Abstract. Our paper introduces and studies the idea of multitime evolution in the context of solitons.
Multitime sine-gordon solitons via geometric characteristics Laura Gabriela Matei, Constantin Udrişte Abstract. Our paper introduces and studies the idea of multitime evolution in the context of solitons.
Module 2: First-Order Partial Differential Equations
 Module 2: First-Order Partial Differential Equations The mathematical formulations of many problems in science and engineering reduce to study of first-order PDEs. For instance, the study of first-order
Module 2: First-Order Partial Differential Equations The mathematical formulations of many problems in science and engineering reduce to study of first-order PDEs. For instance, the study of first-order
Research works of Romanian mathematicians on Centro-Affine Geometry
 Research works of Romanian mathematicians on Centro-Affine Geometry Vasile Cruceanu Abstract The aim of this paper is to review some Romanian researches in centro-affine geometry, field pioneered by Gh.
Research works of Romanian mathematicians on Centro-Affine Geometry Vasile Cruceanu Abstract The aim of this paper is to review some Romanian researches in centro-affine geometry, field pioneered by Gh.
William P. Thurston. The Geometry and Topology of Three-Manifolds
 William P. Thurston The Geometry and Topology of Three-Manifolds Electronic version 1.1 - March 00 http://www.msri.org/publications/books/gt3m/ This is an electronic edition of the 1980 notes distributed
William P. Thurston The Geometry and Topology of Three-Manifolds Electronic version 1.1 - March 00 http://www.msri.org/publications/books/gt3m/ This is an electronic edition of the 1980 notes distributed
Math 115 ( ) Yum-Tong Siu 1. Euler-Lagrange Equations for Many Functions and Variables and High-Order Derivatives
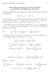 Math 115 006-007 Yum-Tong Siu 1 Euler-Lagrange Equations for Many Functions and Variables and High-Order Derivatives The Case of High-Order Derivatives. The context is to find the extremal for the functional
Math 115 006-007 Yum-Tong Siu 1 Euler-Lagrange Equations for Many Functions and Variables and High-Order Derivatives The Case of High-Order Derivatives. The context is to find the extremal for the functional
Fractal Magnetic Dynamics around a Koch Fractal Electric Circuit
 8th WSEAS International Conference on SYSTEMS THEORY and SCIENTIFIC COMPUTATION ISTASC 08 Fractal Magnetic Dynamics around a Koch Fractal Electric Circuit CONSTANTIN UDRISTE University Politehnica of Bucharest
8th WSEAS International Conference on SYSTEMS THEORY and SCIENTIFIC COMPUTATION ISTASC 08 Fractal Magnetic Dynamics around a Koch Fractal Electric Circuit CONSTANTIN UDRISTE University Politehnica of Bucharest
Classification of cubics up to affine transformations
 Classification of cubics up to affine transformations Mehdi Nadjafikah and Ahmad-Reza Forough Abstract. Classification of cubics (that is, third order planar curves in the R 2 ) up to certain transformations
Classification of cubics up to affine transformations Mehdi Nadjafikah and Ahmad-Reza Forough Abstract. Classification of cubics (that is, third order planar curves in the R 2 ) up to certain transformations
The symmetry structures of ASD manifolds
 The symmetry structures of ASD manifolds 1 1 School of Mathematics University of the Witatersrand, Johannesburg South Africa African Institute of Mathematics Outline 1 Introduction 2 3 The dispersionless
The symmetry structures of ASD manifolds 1 1 School of Mathematics University of the Witatersrand, Johannesburg South Africa African Institute of Mathematics Outline 1 Introduction 2 3 The dispersionless
RESEARCH STATEMENT YUHAO HU
 RESEARCH STATEMENT YUHAO HU I am interested in researching in differential geometry and the geometry of partial differential equations. Earlier in my PhD studies, I learned the theory of exterior differential
RESEARCH STATEMENT YUHAO HU I am interested in researching in differential geometry and the geometry of partial differential equations. Earlier in my PhD studies, I learned the theory of exterior differential
Conservation laws for the geodesic equations of the canonical connection on Lie groups in dimensions two and three
 Appl Math Inf Sci 7 No 1 311-318 (013) 311 Applied Mathematics & Information Sciences An International Journal Conservation laws for the geodesic equations of the canonical connection on Lie groups in
Appl Math Inf Sci 7 No 1 311-318 (013) 311 Applied Mathematics & Information Sciences An International Journal Conservation laws for the geodesic equations of the canonical connection on Lie groups in
THEODORE VORONOV DIFFERENTIABLE MANIFOLDS. Fall Last updated: November 26, (Under construction.)
 4 Vector fields Last updated: November 26, 2009. (Under construction.) 4.1 Tangent vectors as derivations After we have introduced topological notions, we can come back to analysis on manifolds. Let M
4 Vector fields Last updated: November 26, 2009. (Under construction.) 4.1 Tangent vectors as derivations After we have introduced topological notions, we can come back to analysis on manifolds. Let M
4.7 The Levi-Civita connection and parallel transport
 Classnotes: Geometry & Control of Dynamical Systems, M. Kawski. April 21, 2009 138 4.7 The Levi-Civita connection and parallel transport In the earlier investigation, characterizing the shortest curves
Classnotes: Geometry & Control of Dynamical Systems, M. Kawski. April 21, 2009 138 4.7 The Levi-Civita connection and parallel transport In the earlier investigation, characterizing the shortest curves
arxiv: v1 [math.ap] 25 Aug 2009
![arxiv: v1 [math.ap] 25 Aug 2009 arxiv: v1 [math.ap] 25 Aug 2009](/thumbs/89/99243941.jpg) Lie group analysis of Poisson s equation and optimal system of subalgebras for Lie algebra of 3 dimensional rigid motions arxiv:0908.3619v1 [math.ap] 25 Aug 2009 Abstract M. Nadjafikhah a, a School of
Lie group analysis of Poisson s equation and optimal system of subalgebras for Lie algebra of 3 dimensional rigid motions arxiv:0908.3619v1 [math.ap] 25 Aug 2009 Abstract M. Nadjafikhah a, a School of
Multivariable Calculus and Matrix Algebra-Summer 2017
 Multivariable Calculus and Matrix Algebra-Summer 017 Homework 4 Solutions Note that the solutions below are for the latest version of the problems posted. For those of you who worked on an earlier version
Multivariable Calculus and Matrix Algebra-Summer 017 Homework 4 Solutions Note that the solutions below are for the latest version of the problems posted. For those of you who worked on an earlier version
Non-Classical Lagrangian Dynamics and Potential Maps
 Non-Classical Lagrangian Dynamics and Potential Maps CONSTANTIN UDRISTE University Politehnica of Bucharest Faculty of Applied Sciences Department of Mathematics Splaiul Independentei 313 060042 BUCHAREST,
Non-Classical Lagrangian Dynamics and Potential Maps CONSTANTIN UDRISTE University Politehnica of Bucharest Faculty of Applied Sciences Department of Mathematics Splaiul Independentei 313 060042 BUCHAREST,
Applied Mathematics 505b January 22, Today Denitions, survey of applications. Denition A PDE is an equation of the form F x 1 ;x 2 ::::;x n ;~u
 Applied Mathematics 505b January 22, 1998 1 Applied Mathematics 505b Partial Dierential Equations January 22, 1998 Text: Sobolev, Partial Dierentail Equations of Mathematical Physics available at bookstore
Applied Mathematics 505b January 22, 1998 1 Applied Mathematics 505b Partial Dierential Equations January 22, 1998 Text: Sobolev, Partial Dierentail Equations of Mathematical Physics available at bookstore
Dispersionless integrable systems in 3D and Einstein-Weyl geometry. Eugene Ferapontov
 Dispersionless integrable systems in 3D and Einstein-Weyl geometry Eugene Ferapontov Department of Mathematical Sciences, Loughborough University, UK E.V.Ferapontov@lboro.ac.uk Based on joint work with
Dispersionless integrable systems in 3D and Einstein-Weyl geometry Eugene Ferapontov Department of Mathematical Sciences, Loughborough University, UK E.V.Ferapontov@lboro.ac.uk Based on joint work with
Getting started: CFD notation
 PDE of p-th order Getting started: CFD notation f ( u,x, t, u x 1,..., u x n, u, 2 u x 1 x 2,..., p u p ) = 0 scalar unknowns u = u(x, t), x R n, t R, n = 1,2,3 vector unknowns v = v(x, t), v R m, m =
PDE of p-th order Getting started: CFD notation f ( u,x, t, u x 1,..., u x n, u, 2 u x 1 x 2,..., p u p ) = 0 scalar unknowns u = u(x, t), x R n, t R, n = 1,2,3 vector unknowns v = v(x, t), v R m, m =
Market competition via geometric dynamics. M.Ferrara and A.Niglia
 Market competition via geometric dynamics M.Ferrara and A.Niglia Abstract. In this paper we use the Geometric Dynamics see [3], [4]) to analyse some economical problems concerning market competition. We
Market competition via geometric dynamics M.Ferrara and A.Niglia Abstract. In this paper we use the Geometric Dynamics see [3], [4]) to analyse some economical problems concerning market competition. We
Chapter 3 Second Order Linear Equations
 Partial Differential Equations (Math 3303) A Ë@ Õæ Aë áöß @. X. @ 2015-2014 ú GA JË@ É Ë@ Chapter 3 Second Order Linear Equations Second-order partial differential equations for an known function u(x,
Partial Differential Equations (Math 3303) A Ë@ Õæ Aë áöß @. X. @ 2015-2014 ú GA JË@ É Ë@ Chapter 3 Second Order Linear Equations Second-order partial differential equations for an known function u(x,
1 Eigenvalues and eigenvectors of the Laplacian on a parallelepiped
 Eigenvalues and eigenvectors of Laplacian on a parallelepiped I. Ţevy, C. Udrişte, F. Munteanu, D. Zugrăvescu, L. Petrescu Abstract. The purpose of this paper is threefold: (i) to prove new properties
Eigenvalues and eigenvectors of Laplacian on a parallelepiped I. Ţevy, C. Udrişte, F. Munteanu, D. Zugrăvescu, L. Petrescu Abstract. The purpose of this paper is threefold: (i) to prove new properties
On the classification of certain curves up to projective tranformations
 On the classification of certain curves up to projective tranformations Mehdi Nadjafikhah Abstract The purpose of this paper is to classify the curves in the form y 3 = c 3 x 3 +c 2 x 2 + c 1x + c 0, with
On the classification of certain curves up to projective tranformations Mehdi Nadjafikhah Abstract The purpose of this paper is to classify the curves in the form y 3 = c 3 x 3 +c 2 x 2 + c 1x + c 0, with
Alexei F. Cheviakov. University of Saskatchewan, Saskatoon, Canada. INPL seminar June 09, 2011
 Direct Method of Construction of Conservation Laws for Nonlinear Differential Equations, its Relation with Noether s Theorem, Applications, and Symbolic Software Alexei F. Cheviakov University of Saskatchewan,
Direct Method of Construction of Conservation Laws for Nonlinear Differential Equations, its Relation with Noether s Theorem, Applications, and Symbolic Software Alexei F. Cheviakov University of Saskatchewan,
SINGULAR CURVES OF AFFINE MAXIMAL MAPS
 Fundamental Journal of Mathematics and Mathematical Sciences Vol. 1, Issue 1, 014, Pages 57-68 This paper is available online at http://www.frdint.com/ Published online November 9, 014 SINGULAR CURVES
Fundamental Journal of Mathematics and Mathematical Sciences Vol. 1, Issue 1, 014, Pages 57-68 This paper is available online at http://www.frdint.com/ Published online November 9, 014 SINGULAR CURVES
Equivalence of multitime optimal control problems
 Equivalence of multitime optimal control problems Constantin Udrişte Abstract. Many science and engineering problems can be formulated as optimization problems that are governed by m-flow type P DEs (multitime
Equivalence of multitime optimal control problems Constantin Udrişte Abstract. Many science and engineering problems can be formulated as optimization problems that are governed by m-flow type P DEs (multitime
Definition 5.1. A vector field v on a manifold M is map M T M such that for all x M, v(x) T x M.
 5 Vector fields Last updated: March 12, 2012. 5.1 Definition and general properties We first need to define what a vector field is. Definition 5.1. A vector field v on a manifold M is map M T M such that
5 Vector fields Last updated: March 12, 2012. 5.1 Definition and general properties We first need to define what a vector field is. Definition 5.1. A vector field v on a manifold M is map M T M such that
On divergence representations of the Gaussian and the mean curvature of surfaces and applications
 Bull. Nov. Comp. Center, Math. Model. in Geoph., 17 (014), 35 45 c 014 NCC Publisher On divergence representations of the Gaussian and the mean curvature of surfaces and applications A.G. Megrabov Abstract.
Bull. Nov. Comp. Center, Math. Model. in Geoph., 17 (014), 35 45 c 014 NCC Publisher On divergence representations of the Gaussian and the mean curvature of surfaces and applications A.G. Megrabov Abstract.
Math512 PDE Homework 2
 Math51 PDE Homework October 11, 009 Exercise 1.3. Solve u = xu x +yu y +(u x+y y/ = 0 with initial conditon u(x, 0 = 1 x. Proof. In this case, we have F = xp + yq + (p + q / z = 0 and Γ parameterized as
Math51 PDE Homework October 11, 009 Exercise 1.3. Solve u = xu x +yu y +(u x+y y/ = 0 with initial conditon u(x, 0 = 1 x. Proof. In this case, we have F = xp + yq + (p + q / z = 0 and Γ parameterized as
Final Exam May 4, 2016
 1 Math 425 / AMCS 525 Dr. DeTurck Final Exam May 4, 2016 You may use your book and notes on this exam. Show your work in the exam book. Work only the problems that correspond to the section that you prepared.
1 Math 425 / AMCS 525 Dr. DeTurck Final Exam May 4, 2016 You may use your book and notes on this exam. Show your work in the exam book. Work only the problems that correspond to the section that you prepared.
V (r,t) = i ˆ u( x, y,z,t) + ˆ j v( x, y,z,t) + k ˆ w( x, y, z,t)
 IV. DIFFERENTIAL RELATIONS FOR A FLUID PARTICLE This chapter presents the development and application of the basic differential equations of fluid motion. Simplifications in the general equations and common
IV. DIFFERENTIAL RELATIONS FOR A FLUID PARTICLE This chapter presents the development and application of the basic differential equations of fluid motion. Simplifications in the general equations and common
MATH 19520/51 Class 5
 MATH 19520/51 Class 5 Minh-Tam Trinh University of Chicago 2017-10-04 1 Definition of partial derivatives. 2 Geometry of partial derivatives. 3 Higher derivatives. 4 Definition of a partial differential
MATH 19520/51 Class 5 Minh-Tam Trinh University of Chicago 2017-10-04 1 Definition of partial derivatives. 2 Geometry of partial derivatives. 3 Higher derivatives. 4 Definition of a partial differential
12. Stresses and Strains
 12. Stresses and Strains Finite Element Method Differential Equation Weak Formulation Approximating Functions Weighted Residuals FEM - Formulation Classification of Problems Scalar Vector 1-D T(x) u(x)
12. Stresses and Strains Finite Element Method Differential Equation Weak Formulation Approximating Functions Weighted Residuals FEM - Formulation Classification of Problems Scalar Vector 1-D T(x) u(x)
On the Linearization of Second-Order Dif ferential and Dif ference Equations
 Symmetry, Integrability and Geometry: Methods and Applications Vol. (006), Paper 065, 15 pages On the Linearization of Second-Order Dif ferential and Dif ference Equations Vladimir DORODNITSYN Keldysh
Symmetry, Integrability and Geometry: Methods and Applications Vol. (006), Paper 065, 15 pages On the Linearization of Second-Order Dif ferential and Dif ference Equations Vladimir DORODNITSYN Keldysh
Symmetry analysis of the cylindrical Laplace equation
 Symmetry analysis of the cylindrical Laplace equation Mehdi Nadjafikhah Seyed-Reza Hejazi Abstract. The symmetry analysis for Laplace equation on cylinder is considered. Symmetry algebra the structure
Symmetry analysis of the cylindrical Laplace equation Mehdi Nadjafikhah Seyed-Reza Hejazi Abstract. The symmetry analysis for Laplace equation on cylinder is considered. Symmetry algebra the structure
7a3 2. (c) πa 3 (d) πa 3 (e) πa3
 1.(6pts) Find the integral x, y, z d S where H is the part of the upper hemisphere of H x 2 + y 2 + z 2 = a 2 above the plane z = a and the normal points up. ( 2 π ) Useful Facts: cos = 1 and ds = ±a sin
1.(6pts) Find the integral x, y, z d S where H is the part of the upper hemisphere of H x 2 + y 2 + z 2 = a 2 above the plane z = a and the normal points up. ( 2 π ) Useful Facts: cos = 1 and ds = ±a sin
QUADRATIC EQUATIONS AND MONODROMY EVOLVING DEFORMATIONS
 QUADRATIC EQUATIONS AND MONODROMY EVOLVING DEFORMATIONS YOUSUKE OHYAMA 1. Introduction In this paper we study a special class of monodromy evolving deformations (MED). Chakravarty and Ablowitz [4] showed
QUADRATIC EQUATIONS AND MONODROMY EVOLVING DEFORMATIONS YOUSUKE OHYAMA 1. Introduction In this paper we study a special class of monodromy evolving deformations (MED). Chakravarty and Ablowitz [4] showed
On projective classification of plane curves
 Global and Stochastic Analysis Vol. 1, No. 2, December 2011 Copyright c Mind Reader Publications On projective classification of plane curves Nadiia Konovenko a and Valentin Lychagin b a Odessa National
Global and Stochastic Analysis Vol. 1, No. 2, December 2011 Copyright c Mind Reader Publications On projective classification of plane curves Nadiia Konovenko a and Valentin Lychagin b a Odessa National
Engg. Math. I. Unit-I. Differential Calculus
 Dr. Satish Shukla 1 of 50 Engg. Math. I Unit-I Differential Calculus Syllabus: Limits of functions, continuous functions, uniform continuity, monotone and inverse functions. Differentiable functions, Rolle
Dr. Satish Shukla 1 of 50 Engg. Math. I Unit-I Differential Calculus Syllabus: Limits of functions, continuous functions, uniform continuity, monotone and inverse functions. Differentiable functions, Rolle
ENGI Second Order Linear ODEs Page Second Order Linear Ordinary Differential Equations
 ENGI 344 - Second Order Linear ODEs age -01. Second Order Linear Ordinary Differential Equations The general second order linear ordinary differential equation is of the form d y dy x Q x y Rx dx dx Of
ENGI 344 - Second Order Linear ODEs age -01. Second Order Linear Ordinary Differential Equations The general second order linear ordinary differential equation is of the form d y dy x Q x y Rx dx dx Of
Magnetic geometric dynamics around one infinite rectilinear circuit
 Magnetic geometric dynamics around one infinite rectilinear circuit Adriana Calotă and Nona Crăciun Abstract. In this paper we compare the trajectories of particles described by the Lorentz Law and the
Magnetic geometric dynamics around one infinite rectilinear circuit Adriana Calotă and Nona Crăciun Abstract. In this paper we compare the trajectories of particles described by the Lorentz Law and the
Comparative Statics. Autumn 2018
 Comparative Statics Autumn 2018 What is comparative statics? Contents 1 What is comparative statics? 2 One variable functions Multiple variable functions Vector valued functions Differential and total
Comparative Statics Autumn 2018 What is comparative statics? Contents 1 What is comparative statics? 2 One variable functions Multiple variable functions Vector valued functions Differential and total
Lagrange Multipliers
 Optimization with Constraints As long as algebra and geometry have been separated, their progress have been slow and their uses limited; but when these two sciences have been united, they have lent each
Optimization with Constraints As long as algebra and geometry have been separated, their progress have been slow and their uses limited; but when these two sciences have been united, they have lent each
New methods of reduction for ordinary differential equations
 IMA Journal of Applied Mathematics (2001) 66, 111 125 New methods of reduction for ordinary differential equations C. MURIEL AND J. L. ROMERO Departamento de Matemáticas, Universidad de Cádiz, PO Box 40,
IMA Journal of Applied Mathematics (2001) 66, 111 125 New methods of reduction for ordinary differential equations C. MURIEL AND J. L. ROMERO Departamento de Matemáticas, Universidad de Cádiz, PO Box 40,
Contact and Symplectic Geometry of Monge-Ampère Equations: Introduction and Examples
 Contact and Symplectic Geometry of Monge-Ampère Equations: Introduction and Examples Vladimir Rubtsov, ITEP,Moscow and LAREMA, Université d Angers Workshop "Geometry and Fluids" Clay Mathematical Institute,
Contact and Symplectic Geometry of Monge-Ampère Equations: Introduction and Examples Vladimir Rubtsov, ITEP,Moscow and LAREMA, Université d Angers Workshop "Geometry and Fluids" Clay Mathematical Institute,
On a linear family of affine connections
 On a linear family of affine connections Liviu Nicolescu Dedicated to the memory of Radu Rosca (1908-2005) Abstract. The aim of this paper is to study some geometrical objects in the deformation algebra
On a linear family of affine connections Liviu Nicolescu Dedicated to the memory of Radu Rosca (1908-2005) Abstract. The aim of this paper is to study some geometrical objects in the deformation algebra
Symmetry Preserving Numerical Methods via Moving Frames
 Symmetry Preserving Numerical Methods via Moving Frames Peter J. Olver University of Minnesota http://www.math.umn.edu/ olver = Pilwon Kim, Martin Welk Cambridge, June, 2007 Symmetry Preserving Numerical
Symmetry Preserving Numerical Methods via Moving Frames Peter J. Olver University of Minnesota http://www.math.umn.edu/ olver = Pilwon Kim, Martin Welk Cambridge, June, 2007 Symmetry Preserving Numerical
3 Applications of partial differentiation
 Advanced Calculus Chapter 3 Applications of partial differentiation 37 3 Applications of partial differentiation 3.1 Stationary points Higher derivatives Let U R 2 and f : U R. The partial derivatives
Advanced Calculus Chapter 3 Applications of partial differentiation 37 3 Applications of partial differentiation 3.1 Stationary points Higher derivatives Let U R 2 and f : U R. The partial derivatives
Chapter 9: Differential Analysis of Fluid Flow
 of Fluid Flow Objectives 1. Understand how the differential equations of mass and momentum conservation are derived. 2. Calculate the stream function and pressure field, and plot streamlines for a known
of Fluid Flow Objectives 1. Understand how the differential equations of mass and momentum conservation are derived. 2. Calculate the stream function and pressure field, and plot streamlines for a known
On homogeneous Randers spaces with Douglas or naturally reductive metrics
 On homogeneous Randers spaces with Douglas or naturally reductive metrics Mansour Aghasi and Mehri Nasehi Abstract. In [4] Božek has introduced a class of solvable Lie groups with arbitrary odd dimension.
On homogeneous Randers spaces with Douglas or naturally reductive metrics Mansour Aghasi and Mehri Nasehi Abstract. In [4] Božek has introduced a class of solvable Lie groups with arbitrary odd dimension.
14 Divergence, flux, Laplacian
 Tel Aviv University, 204/5 Analysis-III,IV 240 4 Divergence, flux, Laplacian 4a What is the problem................ 240 4b Integral of derivative (again)........... 242 4c Divergence and flux.................
Tel Aviv University, 204/5 Analysis-III,IV 240 4 Divergence, flux, Laplacian 4a What is the problem................ 240 4b Integral of derivative (again)........... 242 4c Divergence and flux.................
Before you begin read these instructions carefully:
 NATURAL SCIENCES TRIPOS Part IB & II (General) Friday, 31 May, 2013 9:00 am to 12:00 pm MATHEMATICS (2) Before you begin read these instructions carefully: You may submit answers to no more than six questions.
NATURAL SCIENCES TRIPOS Part IB & II (General) Friday, 31 May, 2013 9:00 am to 12:00 pm MATHEMATICS (2) Before you begin read these instructions carefully: You may submit answers to no more than six questions.
Gauge Theory of Gravitation: Electro-Gravity Mixing
 Gauge Theory of Gravitation: Electro-Gravity Mixing E. Sánchez-Sastre 1,2, V. Aldaya 1,3 1 Instituto de Astrofisica de Andalucía, Granada, Spain 2 Email: sastre@iaa.es, es-sastre@hotmail.com 3 Email: valdaya@iaa.es
Gauge Theory of Gravitation: Electro-Gravity Mixing E. Sánchez-Sastre 1,2, V. Aldaya 1,3 1 Instituto de Astrofisica de Andalucía, Granada, Spain 2 Email: sastre@iaa.es, es-sastre@hotmail.com 3 Email: valdaya@iaa.es
BACKGROUND IN SYMPLECTIC GEOMETRY
 BACKGROUND IN SYMPLECTIC GEOMETRY NILAY KUMAR Today I want to introduce some of the symplectic structure underlying classical mechanics. The key idea is actually quite old and in its various formulations
BACKGROUND IN SYMPLECTIC GEOMETRY NILAY KUMAR Today I want to introduce some of the symplectic structure underlying classical mechanics. The key idea is actually quite old and in its various formulations
Summer 2017 MATH Solution to Exercise 5
 Summer 07 MATH00 Solution to Exercise 5. Find the partial derivatives of the following functions: (a (xy 5z/( + x, (b x/ x + y, (c arctan y/x, (d log((t + 3 + ts, (e sin(xy z 3, (f x α, x = (x,, x n. (a
Summer 07 MATH00 Solution to Exercise 5. Find the partial derivatives of the following functions: (a (xy 5z/( + x, (b x/ x + y, (c arctan y/x, (d log((t + 3 + ts, (e sin(xy z 3, (f x α, x = (x,, x n. (a
On local normal forms of completely integrable systems
 On local normal forms of completely integrable systems ENCUENTRO DE Răzvan M. Tudoran West University of Timişoara, România Supported by CNCS-UEFISCDI project PN-II-RU-TE-2011-3-0103 GEOMETRÍA DIFERENCIAL,
On local normal forms of completely integrable systems ENCUENTRO DE Răzvan M. Tudoran West University of Timişoara, România Supported by CNCS-UEFISCDI project PN-II-RU-TE-2011-3-0103 GEOMETRÍA DIFERENCIAL,
(a) The points (3, 1, 2) and ( 1, 3, 4) are the endpoints of a diameter of a sphere.
 MATH 4 FINAL EXAM REVIEW QUESTIONS Problem. a) The points,, ) and,, 4) are the endpoints of a diameter of a sphere. i) Determine the center and radius of the sphere. ii) Find an equation for the sphere.
MATH 4 FINAL EXAM REVIEW QUESTIONS Problem. a) The points,, ) and,, 4) are the endpoints of a diameter of a sphere. i) Determine the center and radius of the sphere. ii) Find an equation for the sphere.
ν(u, v) = N(u, v) G(r(u, v)) E r(u,v) 3.
 5. The Gauss Curvature Beyond doubt, the notion of Gauss curvature is of paramount importance in differential geometry. Recall two lessons we have learned so far about this notion: first, the presence
5. The Gauss Curvature Beyond doubt, the notion of Gauss curvature is of paramount importance in differential geometry. Recall two lessons we have learned so far about this notion: first, the presence
Chapter 9: Differential Analysis
 9-1 Introduction 9-2 Conservation of Mass 9-3 The Stream Function 9-4 Conservation of Linear Momentum 9-5 Navier Stokes Equation 9-6 Differential Analysis Problems Recall 9-1 Introduction (1) Chap 5: Control
9-1 Introduction 9-2 Conservation of Mass 9-3 The Stream Function 9-4 Conservation of Linear Momentum 9-5 Navier Stokes Equation 9-6 Differential Analysis Problems Recall 9-1 Introduction (1) Chap 5: Control
MA 201: Partial Differential Equations Lecture - 2
 MA 201: Partial Differential Equations Lecture - 2 Linear First-Order PDEs For a PDE f(x,y,z,p,q) = 0, a solution of the type F(x,y,z,a,b) = 0 (1) which contains two arbitrary constants a and b is said
MA 201: Partial Differential Equations Lecture - 2 Linear First-Order PDEs For a PDE f(x,y,z,p,q) = 0, a solution of the type F(x,y,z,a,b) = 0 (1) which contains two arbitrary constants a and b is said
MATH 31BH Homework 5 Solutions
 MATH 3BH Homework 5 Solutions February 4, 204 Problem.8.2 (a) Let x t f y = x 2 + y 2 + 2z 2 and g(t) = t 2. z t 3 Then by the chain rule a a a D(g f) b = Dg f b Df b c c c = [Dg(a 2 + b 2 + 2c 2 )] [
MATH 3BH Homework 5 Solutions February 4, 204 Problem.8.2 (a) Let x t f y = x 2 + y 2 + 2z 2 and g(t) = t 2. z t 3 Then by the chain rule a a a D(g f) b = Dg f b Df b c c c = [Dg(a 2 + b 2 + 2c 2 )] [
EFFECTS OF AVERAGING ON SODE MODELS OF DYNAMIC CELL PROCESSES
 U.P.B. Sci. Bull., Series A, Vol. 68, No. 3, 006 EFFECTS OF AVERAGING ON SODE MODELS OF DYNAMIC CELL PROCESSES V. BALAN, Simona-Mihaela BIBIC Lucrarea studiază efectele medierii directe şi ciclice asupra
U.P.B. Sci. Bull., Series A, Vol. 68, No. 3, 006 EFFECTS OF AVERAGING ON SODE MODELS OF DYNAMIC CELL PROCESSES V. BALAN, Simona-Mihaela BIBIC Lucrarea studiază efectele medierii directe şi ciclice asupra
ENGI Partial Differentiation Page y f x
 ENGI 3424 4 Partial Differentiation Page 4-01 4. Partial Differentiation For functions of one variable, be found unambiguously by differentiation: y f x, the rate of change of the dependent variable can
ENGI 3424 4 Partial Differentiation Page 4-01 4. Partial Differentiation For functions of one variable, be found unambiguously by differentiation: y f x, the rate of change of the dependent variable can
THE GAUSS MAP OF TIMELIKE SURFACES IN R n Introduction
 Chin. Ann. of Math. 16B: 3(1995),361-370. THE GAUSS MAP OF TIMELIKE SURFACES IN R n 1 Hong Jianqiao* Abstract Gauss maps of oriented timelike 2-surfaces in R1 n are characterized, and it is shown that
Chin. Ann. of Math. 16B: 3(1995),361-370. THE GAUSS MAP OF TIMELIKE SURFACES IN R n 1 Hong Jianqiao* Abstract Gauss maps of oriented timelike 2-surfaces in R1 n are characterized, and it is shown that
Übungen zu RT2 SS (4) Show that (any) contraction of a (p, q) - tensor results in a (p 1, q 1) - tensor.
 Übungen zu RT2 SS 2010 (1) Show that the tensor field g µν (x) = η µν is invariant under Poincaré transformations, i.e. x µ x µ = L µ νx ν + c µ, where L µ ν is a constant matrix subject to L µ ρl ν ση
Übungen zu RT2 SS 2010 (1) Show that the tensor field g µν (x) = η µν is invariant under Poincaré transformations, i.e. x µ x µ = L µ νx ν + c µ, where L µ ν is a constant matrix subject to L µ ρl ν ση
Module Two: Differential Calculus(continued) synopsis of results and problems (student copy)
 Module Two: Differential Calculus(continued) synopsis of results and problems (student copy) Srikanth K S 1 Syllabus Taylor s and Maclaurin s theorems for function of one variable(statement only)- problems.
Module Two: Differential Calculus(continued) synopsis of results and problems (student copy) Srikanth K S 1 Syllabus Taylor s and Maclaurin s theorems for function of one variable(statement only)- problems.
ENGI Partial Differentiation Page y f x
 ENGI 344 4 Partial Differentiation Page 4-0 4. Partial Differentiation For functions of one variable, be found unambiguously by differentiation: y f x, the rate of change of the dependent variable can
ENGI 344 4 Partial Differentiation Page 4-0 4. Partial Differentiation For functions of one variable, be found unambiguously by differentiation: y f x, the rate of change of the dependent variable can
Symmetry Reductions of (2+1) dimensional Equal Width. Wave Equation
 Authors: Symmetry Reductions of (2+1) dimensional Equal Width 1. Dr. S. Padmasekaran Wave Equation Asst. Professor, Department of Mathematics Periyar University, Salem 2. M.G. RANI Periyar University,
Authors: Symmetry Reductions of (2+1) dimensional Equal Width 1. Dr. S. Padmasekaran Wave Equation Asst. Professor, Department of Mathematics Periyar University, Salem 2. M.G. RANI Periyar University,
2xy 0 y = ln y 0. d(p 2 x p) =0. p = 1 ± p 1+Cx. 1 ± 1+Cx 1+Cx ln
 () Consider the di erential equation Find all solutions and the discriminant xy y = ln y Solution: Let F (x, y, p) = xp y ln p, where p = y Let us consider the surface M = {(x, y, p): F (x, y, p) =} in
() Consider the di erential equation Find all solutions and the discriminant xy y = ln y Solution: Let F (x, y, p) = xp y ln p, where p = y Let us consider the surface M = {(x, y, p): F (x, y, p) =} in
Generalized vector equilibrium problems on Hadamard manifolds
 Available online at www.tjnsa.com J. Nonlinear Sci. Appl. 9 (2016), 1402 1409 Research Article Generalized vector equilibrium problems on Hadamard manifolds Shreyasi Jana a, Chandal Nahak a, Cristiana
Available online at www.tjnsa.com J. Nonlinear Sci. Appl. 9 (2016), 1402 1409 Research Article Generalized vector equilibrium problems on Hadamard manifolds Shreyasi Jana a, Chandal Nahak a, Cristiana
MA102: Multivariable Calculus
 MA102: Multivariable Calculus Rupam Barman and Shreemayee Bora Department of Mathematics IIT Guwahati Differentiability of f : U R n R m Definition: Let U R n be open. Then f : U R n R m is differentiable
MA102: Multivariable Calculus Rupam Barman and Shreemayee Bora Department of Mathematics IIT Guwahati Differentiability of f : U R n R m Definition: Let U R n be open. Then f : U R n R m is differentiable
Boyce/DiPrima/Meade 11 th ed, Ch 1.1: Basic Mathematical Models; Direction Fields
 Boyce/DiPrima/Meade 11 th ed, Ch 1.1: Basic Mathematical Models; Direction Fields Elementary Differential Equations and Boundary Value Problems, 11 th edition, by William E. Boyce, Richard C. DiPrima,
Boyce/DiPrima/Meade 11 th ed, Ch 1.1: Basic Mathematical Models; Direction Fields Elementary Differential Equations and Boundary Value Problems, 11 th edition, by William E. Boyce, Richard C. DiPrima,
M E 320 Professor John M. Cimbala Lecture 10
 M E 320 Professor John M. Cimbala Lecture 10 Today, we will: Finish our example problem rates of motion and deformation of fluid particles Discuss the Reynolds Transport Theorem (RTT) Show how the RTT
M E 320 Professor John M. Cimbala Lecture 10 Today, we will: Finish our example problem rates of motion and deformation of fluid particles Discuss the Reynolds Transport Theorem (RTT) Show how the RTT
PARALLEL TRANSPORT AND MULTI-TEMPORAL CONTROLLABILITY
 U.P.B. Sci. Bull., Series A, Vol. 77, Iss. 2, 25 ISSN 22-727 PARALLEL TRANSPORT AND MULTI-TEMPORAL CONTROLLABILITY Cristian Ghiu, Constantin Udrişte 2 Our idea was to make a bridge between the parallel
U.P.B. Sci. Bull., Series A, Vol. 77, Iss. 2, 25 ISSN 22-727 PARALLEL TRANSPORT AND MULTI-TEMPORAL CONTROLLABILITY Cristian Ghiu, Constantin Udrişte 2 Our idea was to make a bridge between the parallel
MTH4101 CALCULUS II REVISION NOTES. 1. COMPLEX NUMBERS (Thomas Appendix 7 + lecture notes) ax 2 + bx + c = 0. x = b ± b 2 4ac 2a. i = 1.
 MTH4101 CALCULUS II REVISION NOTES 1. COMPLEX NUMBERS (Thomas Appendix 7 + lecture notes) 1.1 Introduction Types of numbers (natural, integers, rationals, reals) The need to solve quadratic equations:
MTH4101 CALCULUS II REVISION NOTES 1. COMPLEX NUMBERS (Thomas Appendix 7 + lecture notes) 1.1 Introduction Types of numbers (natural, integers, rationals, reals) The need to solve quadratic equations:
Symmetry Methods for Differential Equations and Conservation Laws. Peter J. Olver University of Minnesota
 Symmetry Methods for Differential Equations and Conservation Laws Peter J. Olver University of Minnesota http://www.math.umn.edu/ olver Santiago, November, 2010 Symmetry Groups of Differential Equations
Symmetry Methods for Differential Equations and Conservation Laws Peter J. Olver University of Minnesota http://www.math.umn.edu/ olver Santiago, November, 2010 Symmetry Groups of Differential Equations
Metrisability of Painleve equations and Hamiltonian systems of hydrodynamic type
 Metrisability of Painleve equations and Hamiltonian systems of hydrodynamic type Felipe Contatto Department of Applied Mathematics and Theoretical Physics University of Cambridge felipe.contatto@damtp.cam.ac.uk
Metrisability of Painleve equations and Hamiltonian systems of hydrodynamic type Felipe Contatto Department of Applied Mathematics and Theoretical Physics University of Cambridge felipe.contatto@damtp.cam.ac.uk
Sophus Lie s Approach to Differential Equations
 Sophus Lie s Approach to Differential Equations IAP lecture 2006 (S. Helgason) 1 Groups Let X be a set. A one-to-one mapping ϕ of X onto X is called a bijection. Let B(X) denote the set of all bijections
Sophus Lie s Approach to Differential Equations IAP lecture 2006 (S. Helgason) 1 Groups Let X be a set. A one-to-one mapping ϕ of X onto X is called a bijection. Let B(X) denote the set of all bijections
4 Divergence theorem and its consequences
 Tel Aviv University, 205/6 Analysis-IV 65 4 Divergence theorem and its consequences 4a Divergence and flux................. 65 4b Piecewise smooth case............... 67 4c Divergence of gradient: Laplacian........
Tel Aviv University, 205/6 Analysis-IV 65 4 Divergence theorem and its consequences 4a Divergence and flux................. 65 4b Piecewise smooth case............... 67 4c Divergence of gradient: Laplacian........
CORRESPONDENCE BETWEEN ELLIPTIC CURVES IN EDWARDS-BERNSTEIN AND WEIERSTRASS FORMS
 CORRESPONDENCE BETWEEN ELLIPTIC CURVES IN EDWARDS-BERNSTEIN AND WEIERSTRASS FORMS DEPARTMENT OF MATHEMATICS AND STATISTICS UNIVERSITY OF OTTAWA SUPERVISOR: PROFESSOR MONICA NEVINS STUDENT: DANG NGUYEN
CORRESPONDENCE BETWEEN ELLIPTIC CURVES IN EDWARDS-BERNSTEIN AND WEIERSTRASS FORMS DEPARTMENT OF MATHEMATICS AND STATISTICS UNIVERSITY OF OTTAWA SUPERVISOR: PROFESSOR MONICA NEVINS STUDENT: DANG NGUYEN
arxiv: v1 [math.ds] 27 Jul 2017
![arxiv: v1 [math.ds] 27 Jul 2017 arxiv: v1 [math.ds] 27 Jul 2017](/thumbs/96/128497858.jpg) POLYNOMIAL VECTOR FIELDS ON THE CLIFFORD TORUS arxiv:1707.08859v1 [math.ds] 27 Jul 2017 JAUME LLIBRE AND ADRIAN C. MURZA Abstract. First we characterize all the polynomial vector fields in R 4 which have
POLYNOMIAL VECTOR FIELDS ON THE CLIFFORD TORUS arxiv:1707.08859v1 [math.ds] 27 Jul 2017 JAUME LLIBRE AND ADRIAN C. MURZA Abstract. First we characterize all the polynomial vector fields in R 4 which have
ON THE PARALLEL PLANES IN VECTOR BUNDLES
 ON THE PARALLEL PLANES IN VECTOR BUNDLES Kostadin Trenčevski Abstract In this paper are found the necessary and sufficient conditions of local existence of parallel r-plane or which is equivalent with
ON THE PARALLEL PLANES IN VECTOR BUNDLES Kostadin Trenčevski Abstract In this paper are found the necessary and sufficient conditions of local existence of parallel r-plane or which is equivalent with
Hamiltonian partial differential equations and Painlevé transcendents
 The 6th TIMS-OCAMI-WASEDA Joint International Workshop on Integrable Systems and Mathematical Physics March 22-26, 2014 Hamiltonian partial differential equations and Painlevé transcendents Boris DUBROVIN
The 6th TIMS-OCAMI-WASEDA Joint International Workshop on Integrable Systems and Mathematical Physics March 22-26, 2014 Hamiltonian partial differential equations and Painlevé transcendents Boris DUBROVIN
Bäcklund transformations for fourth-order Painlevé-type equations
 Bäcklund transformations for fourth-order Painlevé-type equations A. H. Sakka 1 and S. R. Elshamy Department of Mathematics, Islamic University of Gaza P.O.Box 108, Rimae, Gaza, Palestine 1 e-mail: asakka@mail.iugaza.edu
Bäcklund transformations for fourth-order Painlevé-type equations A. H. Sakka 1 and S. R. Elshamy Department of Mathematics, Islamic University of Gaza P.O.Box 108, Rimae, Gaza, Palestine 1 e-mail: asakka@mail.iugaza.edu
Minimal timelike surfaces in a certain homogeneous Lorentzian 3-manifold II
 Minimal timelike surfaces in a certain homogeneous Lorentzian 3-manifold II Sungwook Lee Abstract The 2-parameter family of certain homogeneous Lorentzian 3-manifolds which includes Minkowski 3-space and
Minimal timelike surfaces in a certain homogeneous Lorentzian 3-manifold II Sungwook Lee Abstract The 2-parameter family of certain homogeneous Lorentzian 3-manifolds which includes Minkowski 3-space and
ON THE SYMMETRIES OF INTEGRABLE PARTIAL DIFFERENCE EQUATIONS
 Proceedings of the International Conference on Difference Equations, Special Functions and Orthogonal Polynomials, World Scientific (2007 ON THE SYMMETRIES OF INTEGRABLE PARTIAL DIFFERENCE EQUATIONS ANASTASIOS
Proceedings of the International Conference on Difference Equations, Special Functions and Orthogonal Polynomials, World Scientific (2007 ON THE SYMMETRIES OF INTEGRABLE PARTIAL DIFFERENCE EQUATIONS ANASTASIOS
b) The system of ODE s d x = v(x) in U. (2) dt
 How to solve linear and quasilinear first order partial differential equations This text contains a sketch about how to solve linear and quasilinear first order PDEs and should prepare you for the general
How to solve linear and quasilinear first order partial differential equations This text contains a sketch about how to solve linear and quasilinear first order PDEs and should prepare you for the general
Week 6: Differential geometry I
 Week 6: Differential geometry I Tensor algebra Covariant and contravariant tensors Consider two n dimensional coordinate systems x and x and assume that we can express the x i as functions of the x i,
Week 6: Differential geometry I Tensor algebra Covariant and contravariant tensors Consider two n dimensional coordinate systems x and x and assume that we can express the x i as functions of the x i,
B.7 Lie Groups and Differential Equations
 96 B.7. LIE GROUPS AND DIFFERENTIAL EQUATIONS B.7 Lie Groups and Differential Equations Peter J. Olver in Minneapolis, MN (U.S.A.) mailto:olver@ima.umn.edu The applications of Lie groups to solve differential
96 B.7. LIE GROUPS AND DIFFERENTIAL EQUATIONS B.7 Lie Groups and Differential Equations Peter J. Olver in Minneapolis, MN (U.S.A.) mailto:olver@ima.umn.edu The applications of Lie groups to solve differential
g(t) = f(x 1 (t),..., x n (t)).
 Reading: [Simon] p. 313-333, 833-836. 0.1 The Chain Rule Partial derivatives describe how a function changes in directions parallel to the coordinate axes. Now we shall demonstrate how the partial derivatives
Reading: [Simon] p. 313-333, 833-836. 0.1 The Chain Rule Partial derivatives describe how a function changes in directions parallel to the coordinate axes. Now we shall demonstrate how the partial derivatives
On universality of critical behaviour in Hamiltonian PDEs
 Riemann - Hilbert Problems, Integrability and Asymptotics Trieste, September 23, 2005 On universality of critical behaviour in Hamiltonian PDEs Boris DUBROVIN SISSA (Trieste) 1 Main subject: Hamiltonian
Riemann - Hilbert Problems, Integrability and Asymptotics Trieste, September 23, 2005 On universality of critical behaviour in Hamiltonian PDEs Boris DUBROVIN SISSA (Trieste) 1 Main subject: Hamiltonian
Math 4263 Homework Set 1
 Homework Set 1 1. Solve the following PDE/BVP 2. Solve the following PDE/BVP 2u t + 3u x = 0 u (x, 0) = sin (x) u x + e x u y = 0 u (0, y) = y 2 3. (a) Find the curves γ : t (x (t), y (t)) such that that
Homework Set 1 1. Solve the following PDE/BVP 2. Solve the following PDE/BVP 2u t + 3u x = 0 u (x, 0) = sin (x) u x + e x u y = 0 u (0, y) = y 2 3. (a) Find the curves γ : t (x (t), y (t)) such that that
Sec. 1.1: Basics of Vectors
 Sec. 1.1: Basics of Vectors Notation for Euclidean space R n : all points (x 1, x 2,..., x n ) in n-dimensional space. Examples: 1. R 1 : all points on the real number line. 2. R 2 : all points (x 1, x
Sec. 1.1: Basics of Vectors Notation for Euclidean space R n : all points (x 1, x 2,..., x n ) in n-dimensional space. Examples: 1. R 1 : all points on the real number line. 2. R 2 : all points (x 1, x
CALCULUS ON MANIFOLDS. 1. Riemannian manifolds Recall that for any smooth manifold M, dim M = n, the union T M =
 CALCULUS ON MANIFOLDS 1. Riemannian manifolds Recall that for any smooth manifold M, dim M = n, the union T M = a M T am, called the tangent bundle, is itself a smooth manifold, dim T M = 2n. Example 1.
CALCULUS ON MANIFOLDS 1. Riemannian manifolds Recall that for any smooth manifold M, dim M = n, the union T M = a M T am, called the tangent bundle, is itself a smooth manifold, dim T M = 2n. Example 1.
Computers and Mathematics with Applications
 Computers and Mathematics with Applications 60 (00) 3088 3097 Contents lists available at ScienceDirect Computers and Mathematics with Applications journal homepage: www.elsevier.com/locate/camwa Symmetry
Computers and Mathematics with Applications 60 (00) 3088 3097 Contents lists available at ScienceDirect Computers and Mathematics with Applications journal homepage: www.elsevier.com/locate/camwa Symmetry
On a Hamiltonian version of a 3D Lotka-Volterra system
 On a Hamiltonian version of a 3D Lotka-Volterra system Răzvan M. Tudoran and Anania Gîrban arxiv:1106.1377v1 [math-ph] 7 Jun 2011 Abstract In this paper we present some relevant dynamical properties of
On a Hamiltonian version of a 3D Lotka-Volterra system Răzvan M. Tudoran and Anania Gîrban arxiv:1106.1377v1 [math-ph] 7 Jun 2011 Abstract In this paper we present some relevant dynamical properties of
