Remarks concerning the Lyapunov exponents of linear cocycles
|
|
|
- Dennis Hopkins
- 5 years ago
- Views:
Transcription
1 Rend. Istit. Mat. Univ. Trieste Volume 44 (202), 89 6 Remarks concerning the Lyapunov exponents of linear cocycles Russell Johnson and Luca Zampogni Dedicated to Professor Fabio Zanolin on the occasion of his 60th birthday Abstract. We impose a condition of pointwise convergence on the Lyapunov exponents of a d-dimensional cocycle over a compact metric minimal flow. This condition turns out to have significant consequences for the dynamics of the cocycle. We make use of such classical ODE techniques as the Lyapunov-Perron triangularization method, and the ergodic-theoretical techniques of Krylov and Bogoliubov. Keywords: Lyapunov exponent, Sacker-Sell spectrum, discrete spectrum. MS Classification 200: 37B55, 34D08, 34D09. Introduction The question of the continuity properties of the Lyapunov exponents of a linear differential system under perturbation of the coefficient matrix is of intrinsic interest and is of importance in various applications. Many important results concerning this theme are due to the Moscow school centered around the Nemytskii seminar; we mention some representative papers ([3, 4, 26]) and refer especially to the book [5] by Bylov-Vinograd-Grobman-Nemytskii. In the works of the Moscow school, attention is not restricted to the Lyapunov exponents; other quantities such the upper and lower characteristic indexes and the Bohl exponent are also studied in a systematic way, both from the point of view of continuity and from that of intrinsic properties. More recent work of Bochi-Viana [2] and of Bessa [] permits one to make statements concerning the discontinuity of the Lyapunov exponents of certain topological/ergodic families of linear systems. The paper [] adapts to the continuous setting certain important results of [2] for discrete cocycles. The basic object of study in [, 2] is the set of Lyapunov exponents determined by the Oseledets theorem relative to a discrete or continuous cocycle and an ergodic measure defined on a compact metric flow. Generally speaking, it is shown that, if the cocycle does not admit a dominated splitting (a.k.a. an exponential separation), and if the Lyapunov exponents are not all equal, then
2 90 R. JOHNSON AND L. ZAMPOGNI those exponents do not vary continuously under C 0 -perturbation of the cocycle. See also ([28, 30]) for results in this vein. In a somewhat different vein, Furman [4] studied the case of a discrete cocycle over a strictly ergodic flow. He considered the time averages which define the maximal Lyapunov exponent of the cocycle; that exponent is welldefined by the subadditive ergodic theorem. He shows that, if the cocycle has dimension d = 2, and if the time averages converge uniformly with respect to the phase point of the flow, then the maximal Lyapunov exponent varies continuously if the cocycle is perturbed. If in addition the flow is equicontinuous, then the converse statement holds as well. In the present paper, our point of departure is similar to that of [4], though we work with the usual Lyapunov exponents and not with the maximal exponent. We assume that, for each phase point in the flow, each Lyapunov exponent is defined by a true limit (and not by a non-convergent limit superior). Let d 2 be the dimension of the cocycle. We show that, if the flow is minimal, and if the Oseledets spectrum of the cocycle is simple (i.e., consists of d distinct numbers), then the cocycle has the discrete spectrum property of Sacker and Sell. If d = 2, we do not need to assume that the Oseledets spectrum is simple (but need slightly more information concerning the limits defining the Lyapunov exponents). We are able to strengthen the continuity result of [4] in the sense that the compact metric flow is minimal but need not be strictly ergodic. We wish to emphasize that our results will be proved by using quite classical techniques in the theory of linear differential and discrete systems. These include the method of Krylov and Bogoliubov for constructing invariant measures, and the Lyapunov-Perron triangularization procedure. We will also adapt a small part of that proof of the Oseledets theorem which is based on those methods. Beyond that, we will apply some specific results, including an ergodic oscillation result of [6], and two statements of [0] which concern smoothing of real cocycles and the untwisting of invariant vector bundles. The paper is organized as follows. In Section 2 we prepare the ground by recalling the statement of the Oseledets theorem, and some elements of the spectral theory of Sacker and Sell for linear cocycles. In Section 3 we work out some consequences, regarding the continuity of Lyapunov exponents, of the hypothesis that a cocycle Φ have discrete spectrum. These results are (mostly) known, but perhaps not well -known.we also discuss a specific situation in which the results of [, 2] imply the discontinuity of the Lyapunov exponents under a C 0 -perturbation of the cycle. In Section 4 we present our main result. We show that, if Φ is a cocycle over a compact minimal flow of dimension d = 2, and if the time averages which define its Lyapunov exponents all converge, then Φ has discrete spectrum. If the dimension d of Φ is greater than two, we encounter technical problems
3 REMARKS CONCERNING LYAPUNOV EXPONENTS 9 when attempting to prove the above result. We are, however, able to prove a theorem which has the following corollary. Suppose that (, {τ t }) is strictly ergodic with unique ergodic measure µ. Suppose that the cocycle Φ has simple Oseledets spectrum with respect to µ. Finally, suppose that the time averages which define the Lyapunov exponents of Φ all converge. Then Φ has discrete spectrum, and in fact the Sacker-Sell spectrum of Φ is simple. In classical language, this means that Φ has the Lillo property [23]. We finish this Introduction by listing some notational conventions which will be in force throughout the paper. First, the brackets, will indicate the Euclidean inner product on R d. Second, the symbol will denote a norm whose significance will be clear from the context if it is not explicitly defined. Third, we let GL(R d ) denote the set of invertible d d matrices. Fourth, we let L(R d ) denote the set of all d d real matrices with the operator norm: if A L(R d ), then A = sup{ Ax x R d, x = }. 2. Preliminaries In this section, we introduce basic concepts and results, and express in a precise way the issue to be discussed in this paper. Let be a compact metric space, and let T be either the reals (T = R) or the integers (T = Z). For each t T, let τ t : be a continuous map. We say that the family {τ t t T } defines a topological flow on if the following conditions are satisfied: (i) τ 0 (ω) = ω for all ω ; (ii) τ t τ s = τ t+s for all t, s T ; (iii) the map τ : T : (t, ω) τ t (ω) is continuous. It is clear that, if these conditions are satisfied, then for each t T, the map τ t : is a homeomorphism and (τ t ) = τ t (t T ). If T = Z, then the topological flow {τ t t Z} is generated by τ, in the sense that τ n = (τ ) n if n > 0 and τ n = (τ ) n if n < 0. We will refer to a pair (, {τ t t T }) consisting of a compact metric space and a flow {τ t t T } on as a compact metric flow. Important examples of flows are obtained via the following construction. Let T g = R g /Z g be the g-dimensional torus, and let γ,..., γ g be rationally independent numbers. Let θ,..., θ g be -periodic coordinates on T g. If T = R or Z, set τ t (θ,..., θ g ) = (θ + tγ,..., θ g + tγ g ) (t T ). Then {τ t t T } is a flow on T g, called a Kronecker flow. A compact metric flow (, {τ t }) is called minimal or Birkhoff recurrent if is nonempty and for each ω, the orbit {τ t (ω) t T } is dense in. A Kronecker flow as defined above on = T g is minimal. Actually a Kronecker
4 92 R. JOHNSON AND L. ZAMPOGNI flow satisfies a stronger property, namely that of Bohr almost periodicity : thus, in addition to minimality, there is a metric d on, which is compatible with its topology, such that d(τ t (ω ), τ t (ω 2 )) = d(ω, ω 2 ) for all points ω, ω 2 and all t T. Clearly the Euclidean metric d on = T g satisfies this last condition. Let (, {τ t }) be a compact metric flow, and let µ be a regular Borel probability measure on (thus in particular µ() = ). The measure µ is called {τ t }-invariant if µ(τ t (B)) = µ(b) for each Borel set B and t T. An invariant measure µ is called ergodic if it satisfies the following indecomposibility condition: whenever B is a Borel set and µ(τ t (B) B) = 0 for all t T, there holds µ(b) = 0 or µ(b) = ( = symmetric difference of sets). A classical construction of Krylov and Bogoliubov ([20, 29]) shows that a compact metric flow (, {τ t }) always admits an ergodic measure µ. If (, {τ t }) is minimal and admits exactly one ergodic measure, then it is called strictly ergodic. A Kronecker flow {τ t } on = T g is strictly ergodic: the unique ergodic measure is the normalized Haar measure on T g. Next we discuss cocycles. A T -cocycle over a compact metric flow (, {τ t }) with values in the general linear group GL(R d ) is a continuous map Φ : T GL(R d ) such that: (i) Φ(ω, 0) = I= identity for all ω ; (ii) Φ(ω, t + s) = Φ(τ t (ω), s)φ(ω, t) for all ω and t, s T. One obtains an important class of real cocycles (T = R) from appropriate families of linear nonautonomous differential systems. Let (, {τ t }) be a compact metric real flow, and let A : L(R d ) be a continuous function. Let Φ(ω, t) be the fundamental matrix solution of the ODE dx dt = A(τ t(ω))x (x R d ); ( ω ) thus Φ(ω, 0) = I and d dt Φ(ω, t) = A(τ t(ω))φ(ω, t) for all ω and t T = R. It can be checked that Φ is a real cocycle. Actually the general real cocycle can be obtained in this way, up to cohomology. We explain this. Let (, {τ t }) be a compact metric real flow, and let Ψ : R GL(R d ) be a real cocycle. Then there exist continuous functions A : L(R d ) and F : GL(R d ) such that, if Φ(ω, t) is the cocycle generated by the family ( ω ) corresponding to A( ), then Ψ(ω, t) = F (τ t (ω))φ(ω, t)f (ω) (ω, t R). See [0] for a proof; in fact one defines F (ω) = Φ(ω, s)ds for sufficiently ε 0 small ε. The function F is called a cohomology between Ψ and Φ. It turns out ε
5 REMARKS CONCERNING LYAPUNOV EXPONENTS 93 that the properties of a real cocycle which are of interest to us are preserved under a cohomology. So we will always be able to assume that the real cocycles which we study are derived from a family ( ω ) of linear differential systems in the manner described above. An integer cocycle (T = Z) is obtained from a nonautonomous difference equation, as follows. Set A(ω) = Φ(ω, ), τ(ω) = τ (ω), and consider x n+ = A(τ n (ω))x n (n Z, x R d ). (2 ω ) Then the family of difference equations (2 ω ) generates the cocycle Φ in the sense that Φ(ω, n) = A(τ n (ω))... A(ω) n > 0, Φ(ω, 0) = I, Φ(ω, n) = A (τ n (ω))... A (τ (ω)) n < 0 for all ω. Note that an integer cocycle Φ(ω, n) is determined once Φ(ω, ) is known. Next let T = R or Z, and let (, {τ t }) be a compact metric flow. Let Φ : T GL(R d ) be a cocycle. We recall the definition and some basic properties of the Lyapunov exponents of Φ. Fix ω. For each 0 x R d, let β(ω, x) = lim sup ln Φ(ω, t)x. t The number β(ω, x) is called a Lyapunov exponent of Φ at ω. It is well-known that, as x varies over R d \ {0}, β(ω, x) takes on only finitely many values, say β (ω) β 2 (ω) β s (ω) where s d. Moreover, for each r s, one has that W r (ω) = {0} {0 x R d β(ω, x) β r (ω)} is a vector subspace of R d. One says that {0} = W 0 (ω) W (ω) W s (ω) = R d is the filtration associated to Φ at ω. Set d = dim W (ω),..., d r = dim W r (ω) dim W r (ω) (2 r s); the integer d r is called the multiplicity of β r (ω) ( r s). Continuing the discussion, we now define the upper Lyapunov exponent of Φ at ω to be β (ω) = lim sup ln Φ(ω, t). t It is clear that β s (ω) β (ω) for each ω. According to the regularity theory of Lyapunov [24], one has the following. Let d r be the multiplicity of β r (ω) ( r s), and suppose that d β (ω) + + d s β s (ω) = lim inf ln det Φ(ω, t). t Then β s (ω) = β (ω), and the limit lim ln Φ(ω, t)x exists for each 0 x t R d. One says that Φ is regular at ω. The regularity concept is important in the study of the stability of x = 0 relative to nonlinear perturbations of Φ.
6 94 R. JOHNSON AND L. ZAMPOGNI There is a considerable body of Russian literature concerning the theory of the Lyapunov exponents, as well as other exponents related to a T -cocycle, namely the central exponents and the Bohl exponents. We will not discuss these important concepts, but refer the reader to [5]. It is useful to consider the Lyapunov exponents associated with the exterior products of the cocycle Φ. For this, let Λ R d = R d, Λ 2 R d,..., Λ d R d = R be the exterior product spaces of R d. These spaces have natural inner products and norms induced by the Euclidean inner product and Euclidean norm in R d ; (see [3, Chapter ]). The cocycle Φ induces a cocycle with values in GL(R d ) for each k d, via the formula Λ k Φ(ω, t)(x x k ) = Φ(ω, t)x Φ(ω, t)x k. Each of these cocycles admits Lyapunov exponents which are analogues of these introduced above for Φ. In this paper, we will only make use of the upper Lyapunov exponents of these cocycles, which are determined as follows λ k (ω) = lim sup t ln Λ kφ(ω, t) (ω, k d). Of course, λ (ω) = β (ω) and λ k (ω) = lim sup ln det Φ(ω, t). t Let us state a corollary of a result of Ruelle ([36, Proposition.3]). Proposition 2.. Let T = R or Z, let (, {τ t }) be a compact metric flow, and let Φ : T GL(n, R) be a T -cocycle. Let ω. Suppose that, for each k =, 2,..., d, the following limit exists: lim t ln Λ k(ω, t) = λ k (ω). Let β (ω) <... < β s (ω) be the Lyapunov exponents of Φ at ω, and let {0} = W 0 (ω) W (ω) W s (ω) = R d be the corresponding filtration. Then if r s and if 0 x W r (ω) \ W r (ω), one has lim t ln Φ(ω, t)x = β r(ω) ( r s). Thus the limit lim t ln Φ(ω, t)x exists for each 0 x Rd. We now recall certain results concerning T -cocycles, namely the Oseledets theorem [3] and the spectral theorem of Sacker and Sell [38]. Theorem 2.2 (Oseledets). Let T = R or Z, let (, {τ t }) be a compact metric flow, and let µ be a {τ t }-ergodic measure on. Let Φ : T GL(R d ) be a T -cocycle over (, {τ t }). If ω, let β (ω),..., β s (ω) be the Lyapunov exponents of Φ at ω.
7 REMARKS CONCERNING LYAPUNOV EXPONENTS 95 There is a {τ t }-invariant µ-measurable subset with µ( ) =, such that, if ω, then R d admits a direct sum decomposition R d = V (m) (ω) V (m) 2 (ω) V s (m) (ω), such that the following statements are valid. First, if 0 x V r (m) (ω), then lim t ± t ln Φ(ω, t)x = β r(ω); note the two-sidedness of the limit. The dimension of V r (m) (ω) equals the multiplicity d r of β r (ω). Second, the number s and the multiplicities d,..., d s do not depend on ω, and moreover β r (ω) is constant on ( r s). Third, the correspondence ω V r (m) (ω) is µ-measurable in the Grassmann sense ( r s). Fourth, the measurable bundle V (m) r = ω { (ω, x) x V (m) r } (ω) is Φ invariant in the sense that, if ω, t T and x V r (m) (ω), then (τ t (ω), Φ(ω, t)x) V r (m). This is not the most general form of the Oseledets theorem but it will be sufficient for our purposes. We note that the µ-measurability of ω V r (m) (ω) has the following meaning. For each ω, V r (m) (ω) defines an element of the Grassmannian manifold Gr(d, d r ) of d r -dimensional subspaces of R d ; the mapping Gr(d, d r ) : ω V r (m) (ω) is µ-measurable. The numbers β <... < β s, which do not depend on ω, are collectively referred to as the Oseledets spectrum or µ-spectrum of Φ. The Oseledets theorem is a basic result in the theory of real or discrete cocycles. It has been proved using two distinct approaches. One method of proof uses the triangularization technique of Lyapunov-Perron; see [8, 3]. The other approach makes use of the subadditive ergodic theorem of Kingman [5, 36]. Both methods offer advantages and important information. Next we review some aspects of the Sacker-Sell spectral theory, which taken together can be thought of as a continuous analogue of the Oseledets theory. First recall that a T -cocycle Φ over a compact metric flow (, {τ t }) is said to have an exponential dichotomy if there are positive constants k > 0, γ > 0 and a continuous, projection-valued function ω P ω = Pω 2 : L(R d ) such that the following estimates hold: Φ(ω, t)p ω Φ(ω, s) ke γ(t s) Φ(ω, t)(i P ω )Φ(ω, s) ke γ(t s) t s t s
8 96 R. JOHNSON AND L. ZAMPOGNI for all ω and t, s T. The following basic theorem was proved by Sacker-Sell [37] and Selgrade [39]. Recall that a compact metric flow (, {τ t }) is said to be chain recurrent [7] if for each ω, ε > 0 and T > 0, there are points ω = ω 0, ω,..., ω N = ω and times t > T,..., t N > T such that d(τ ti (ω i ), ω i ) ε ( i N). A minimal flow (, {τ t }) is chain recurrent. Theorem 2.3. Suppose that the compact metric flow (, {τ t }) is chain recurrent, where t T = R or Z. Let Φ : T GL(R d ) be a T -cocycle. Suppose that, for each ω, the condition sup Φ(ω, t)x < implies that x = 0; t T i.e., the cocycle Φ admits no nontrivial bounded orbits. Then Φ admits an exponential dichotomy over. Let us define the dynamical (or Sacker-Sell ) spectrum σ Φ of the T -cocycle Φ over the compact metric flow (, {τ t }) to be {λ R the translated cocycle e λt Φ(ω, t) does not admit an exponential dichotomy over }. Let us also recall that a compact metric flow (, {τ t }) is said to be invariantly connected [2] if cannot be expressed as the union of two nonempty disjoint compact invariant subsets. We state the spectral theorem of Sacker-Sell. Theorem 2.4 ([38]). Let (, {τ t }) be a compact metric invariantly connected flow, where T = R or Z. Let Φ : T GL(R d ) be a T -cocycle. Then the dynamical spectrum σ Φ of Φ is a disjoint union of finitely many compact intervals: σ Φ = [a, b ] [a 2, b 2 ] [a q, b q ] where q d and < a b < a 2... < a q b q <. To each interval [a p, b p ] there corresponds a Φ-invariant topological vector subbundle V (c) p R d with the property that (ω, x) V p (c) and x 0 a p lim inf t ln Φ(ω, t)x lim sup t ln Φ(ω, t)x b p and a p lim inf t t ln Φ(ω, t)x lim sup t ( p q). One has further t ln Φ(ω, t)x b p R d = V (c) V (c) 2 V q (c) (Whitney sum).
9 REMARKS CONCERNING LYAPUNOV EXPONENTS 97 We will emphasize the following concept: Definition 2.5. Let T = R or Z, let (, {τ t }) be a compact metric flow, and let Φ be a T -cocycle over (, {τ t }). Suppose that (, {τ t }) is invariantly connected. Then Φ is said to have discrete spectrum if each spectral interval [a p, b p ] reduces to a point: a p = b p for each p q. The discrete spectrum concept is related to but weaker than that of the Lillo property [23]. See [9] in this regard. In Section 3, we will state and prove some results to the effect that, if a T -cocycle Φ has discrete spectrum, then its Lyapunov exponents vary continuously under perturbation of Φ. We claim no particular originality for these results as many statements of this type appear in the literature; e.g., [4, 26]. We do wish to emphasize our use of the Krylov-Bogoliubov method in our proofs, and the fact that one result (Proposition 3.4) appears to be more general than most. We also note that quite recent papers [, 2, 4] have taken up the theme of the continuity of Lyapunov exponents, so it may not be inappropriate if we do so as well. In Section 4, we give conditions which are sufficient in order that a cocycle Φ have discrete spectrum. One of our results (Theorem 4.4) generalizes a result of Furman [4] when d = 2. To our knowledge, the connection between the expressibility of β(ω, x) as a limit for all ω, 0 x R d, and the discrete spectrum property has not received much attention in the literature. However that may be, the said connection has turned out to be important in the spectral theory of quasicrystals. In this context d = 2. For example, in the paper [8] by Damanik- Lenz, the authors use the so-called avalance principle and detailed properties of certain strictly ergodic shift flows to verify that lim ln Φ(ω, t) exists for t all ω. One can then use Proposition 2. to show that β(ω, x) is expressible as a limit for all ω, 0 x R 2. In [8], the authors use the Furman result mentioned above to show that Φ has discrete spectrum; that result is subsumed in ours. They go on to show that, for certain quasicrystals, the spectrum of the associated Schrödinger operator has zero Lebesgue measure and is purely singular and continuous. Perhaps our results will be useful in the study of higher-dimensional spectral problems of Atkinson type. We plan to investigate this issue in future work. 3. Discrete spectrum and Lyapunov exponents In this section, we derive some continuity results for the Lyapunov exponents of a T -cocycle Φ (T = R or Z) when Φ has discrete spectrum. As stated above, we make no claims concerning the originality of these results, as there is a
10 98 R. JOHNSON AND L. ZAMPOGNI very substantial literature on the subject. On the other hand, we think it is appropriate to present them here since they generalize some theorems in the recent literature. Also our proofs differ from some others in our systematic use of the classical Krylov-Bogoliubov method. We begin the discussion with a simple consequence of Theorem 2.4. Proposition 3.. Let T = R or Z, let (, {τ t }) be a compact metric flow which is invariantly connected, and let Φ : T GL(R d ) be a T -cocycle. Suppose that the dynamical spectrum σ Φ of Φ is discrete: σ Φ = {a 0 < a 2 <... < a q } ( q d). Then for each ω and 0 x R d the limits lim ln Φ(ω, t)x exist. In fact, if (ω, x) V p (c) t ± t then lim t ± t ln Φ(ω, t)x = a p ( p q), while if x / V p (c) (ω) for all p =, 2,..., q, then lim lim t t ln Φ(ω, t)x = a l where l m and x V (c) l t ln Φ(ω, t)x = a m and (ω) V m (c) (ω).. Actually, if one restricts attention to the dynamics of Φ on a subbundle V p (c), then the limits defining the Lyapunov exponents converge uniformly, in a sense which we now make precise. We first consider real cocycles, and carry out a preliminary discussion concerning them. Let L be the usual projective space of lines through the origin in R d, so that L is a compact (d )-dimensional manifold. Let B = L. We assume that the R-cocycle Φ = Φ(ω, t) is defined by the family of linear ordinary differential equations x = A(τ t (ω))x ω, x R d (3 ω ) where A : L(R d ) is a continuous function. Define a flow {ˆτ t t R} on B by setting ˆτ t (ω, l) = (τ t (ω), Φ(ω, t)l) for ω, l L. Then define f : B R : f(ω, l) = A(ω)x, x / x, x where 0 x l. It is easy to check that, if x R d has norm, and if l L is the line containing x, then ln Φ(ω, t)x = t 0 f(ˆτ t (ω, l))ds. (4) This formula allows one to use ergodic theory (in particular the method of Krylov-Bogoliubov) to study the limiting expressions which define Lyapunov exponents. Proposition 3.2. Let (, {τ t, t R}) be a compact metric invariantly connected flow, and let Φ : R GL(R d ) be a real cocycle. Let [a p, b p ] be the p-th interval in the dynamical spectrum σ Φ of Φ, and let the corresponding
11 REMARKS CONCERNING LYAPUNOV EXPONENTS 99 spectral subbundle be V p (c) ( p q). Suppose that [a p, b p ] degenerates to a point for some p {, 2,..., q}: thus a p = b p. Then lim t ± t ln Φ(ω, t)x = a p where the limit is uniform with respect to pairs (ω, x) V p (c) with x =. Proof. It follows from (4) that it is sufficient to prove that f(ˆτ s (b))ds t 0 converges uniformly to a p with respect to b = (ω, l) B p = {(ω, l) l V p (c) (ω)}. We do this by using arguments of the classical Krylov-Bogoliubov type (see, e.g., [29]). Suppose for contradiction that, for some ε > 0, there exist a sequence {t n } R with t n and a sequence {b n = (ω n, l n )} B p such that tn f(ˆτ s (b n ))ds a p ε (n =, 2,... ). t n 0 Let C(B p ) be the space of continuous, real-valued functions on B p with the uniform norm. Let F C(B p ) be a countable dense set: F = {f, f 2,..., f k,... } with f = f. Using a Cantor diagonal argument, we can determine a subsequence {t m } of {t n } such that lim m t m tm 0 f k (ˆτ s (b m ))ds exists for k =, 2,.... Call the limit ν (f k ) ( k < ). One shows easily that ν extends to a bounded nonnegative linear functional on C(B p ), which we also denote by ν. It is clear that ν (c) = c for each constant function c on B p. This functional is {ˆτ t }-invariant in the sense that ν (g ˆτ t ) = ν (g) for each g C(B p ) and each t R. Using the Riesz representation theorem, one can find a {ˆτ t }-invariant measure ν on B p such that fdν a p B p ε. We claim that there exists a {ˆτ t }-ergodic measure e on B p such that fde a p B p ε. To see this, use the Krein-Mil man theorem to represent the weak- compact convex set I of {ˆτ t }-invariant linear functionals on B p as the closed convex hull t
12 00 R. JOHNSON AND L. ZAMPOGNI of its set E of extreme points. It is easy to see that e E if and only if its associated measure e is ergodic. By the Choquet representation theorem [35]: ( ) fdν = fde dm(e ) B p E B p where m is the representing measure of ν on E. It is now clear that e can be found. Changing notation, let ν be a {ˆτ t }-ergodic measure on B p such that fdν a p B p ε. By the Birkhoff ergodic theorem there is a set B B p of full ν-measure such that, if b B, then t t 0 f(ˆτ s (b ))ds fdν a p B p as t. This contradicts Proposition 3. and completes the proof of Proposition 3.2. Remark 3.3. (a) We can prove the T = Z-analogue of Proposition 3.2 in the following way. Set A(ω) = Φ(ω, ), then define f : B p R : f (ω, l) = 2 ln A(ω)x, A(ω)x for each (ω, l) B p and x l, x =. One can check that Proposition 3.2 and its proof remain valid if one considers an integer cocycle Φ and if f is substituted with the above function f. (b) Let T = R or Z, let (, {τ t }) be an invariantly connected compact metric flow, and let Φ : T GL(R d ) be a T -cocycle for which the hypotheses of Proposition 3.2 are valid. Let Φ (ω, t) be the restriction of Φ(ω, t) to, so that for each ω and t T one has the linear transformation Φ (ω, t) : V p (c) (ω) V p (c) (τ t (ω)). Define the norm Φ (ω, t) in the usual way. Then V (c) p lim t ± t ln Φ (ω, t) = a p, where the limit is uniform in ω. This statement is a consequence of Proposition 3.2, because for each ω and t R, there exists a unit vector x V (c) p (ω) such that Φ (ω, t) = Φ (ω, t)x. (c) By combining Propositions 3. and 3.2, one obtains a continuity result for the Lyapunov exponents of Φ with respect to variation of ω. In fact, let {β (ω),..., β s (ω)} be the Lyapunov exponents of Φ at ω, with
13 REMARKS CONCERNING LYAPUNOV EXPONENTS 0 multiplicities d,..., d s. If the hypotheses of Propositions 3. and 3.2 are valid, then the multiplicities and the exponents β r (ω) themselves do not depend on ω. Now we consider another type of continuity result for the Lyapunov exponents of a T -cocycle Φ. We will see that it is possible to vary the matrix function A(ω) in a non-uniform way, and still retain continuous variation of the exponents. We formulate a result along these lines which illustrate the power of a perturbation theorem due to Sacker and Sell ([38]; see also Palmer [34]). For this, let be the g-torus T g = R g /Z g. Let γ,..., γ g be rationally independent numbers. Consider the Kronecker flow {τ t } on T g defined by γ = (γ,..., γ g ). Thus if ω R g /Z g, then τ t (ω) = ω + γt (t R). Next, let A : T g L(R d ) be a continuous function. Let Φ(ω, t) be the cocycle defined by the family of differential systems ( ω ): x = A(τ t (ω))x. Suppose that Φ has discrete spectrum; σ Φ = {a < a 2 <... < a q }. Let γ (n) be a sequence in R g such that γ (n) γ. Each γ (n) defines a flow {τ (n) t } on T g via the formula τ (n) t (ω) = ω + γ (n) t. However these flows need not be minimal because we do not assume that the components γ (n),..., γ g (n) of γ (n) are rationally independent. Let Φ (n) (ω, t) be the cocycle generated by the family of linear systems x = A(τ (n) t (ω))x. Note that, if γ (n) γ for n =, 2,..., then A(τ (n) t (ω)) certainly does not converge uniformly in t R to A(τ t (ω)) (ω ). Nevertheless we have the following result. Proposition 3.4. For each ω and n, let {β r (n) (ω) r s = s(n)} be the Lyapunov exponents of Φ (n). Also let β (n) (ω) be the upper Lyapunov exponent of Φ (n) at ω (ω, n ). Given ε > 0, there exists n 0 such that, if n n 0, then each Lyapunov exponent β r (n) (ω) is in the ε-neighborhood of σ Φ (ω ) and β (n) (ω) is in the ε-neighborhood of a q. We sketch the proof of Proposition 3.4. Let C = {c : R L(R d ) c is continuous and bounded} with the the topology of uniform convergence on compact sets. Introduce the Bebutov (translation) flow {ˆτ t } on C: thus ˆτ t c( ) = c( + t) for each t R and c C. Next let U R g be a compact neighborhood of γ. For each ˆγ U and each ω, set c(t, ω, ˆγ) = A(ω+ˆγt) (t R). Set Cˆγ = {c(, ω, ˆγ) ω } C, and
14 02 R. JOHNSON AND L. ZAMPOGNI further set C = {Cˆγ ˆγ U} C. It can be checked that C is a compact, {ˆτ t }-invariant subset of C which is invariantly connected. Define a cocycle ˆΦ on C in the following way: ˆΦ(c, t) is the fundamental matrix solution of the linear differential equation x = c(t)x (c C, t R, x R d ). Let C γ = {t A(ω + γt) ω } C; it can be checked that the dynamical spectrum of the restriction ˆΦ γ = ˆΦ Cγ R equals σ Φ. Similarly, let C γn = {t A(ω + γ n t) ω }. Then the dynamical spectrum of the restriction ˆΦ n = ˆφ Cγn R of ˆΦ to C γn R equals σ Φ (n). We are now in a position to apply the perturbation Theorem 6 of [38]. According to this theorem, there is a neighborhood W C of C γ with the property that, if C is a {ˆτ t }-invariant subset of W, then the dynamical spectrum of ˆΦ C is contained in the ε-neighborhood of = σ σˆφγ Φ = {a < a 2 <... < a q }. Now if n is sufficiently large, then C γ W. So the remarks of the preceding paragraph and Proposition 3. imply that the thesis of Proposition 3.4 is true. Remark 3.5. Let T = Z, let A : = T g GL(R d ) be a continuous map, let γ R g have rationally independent components, and let Φ(ω, t) be the cocycle generated by the family of difference equations x t+ = A(ω + γt)x t (ω, t Z). Similarly, let Φ (n) (ω, t) be the cocycle generated by the family x t+ = A(ω + γ (n) t)x t (ω, t Z) where γ (n) R g (n =, 2,... ). Then Proposition 3.4 is true as stated for Φ and Φ (n). The proof is practically identical to that given above for real cocycles (one must introduce a discrete Bebutov flow, and one must note that [38, Theorem 6] holds also for integer cocycles). We have shown that the discrete spectrum condition has significant consequences for the convergence of the limits which define the Lyapunov exponents, and for the continuity of those Lyapunov exponents. Our results can be viewed as generalizations of [4, Theorem 3]. If the discrete spectrum condition does not hold, then one cannot expect the Lyapunov exponents of Φ to vary continuously when Φ is subjected to a C 0 -perturbation. We indicate a concrete result along these lines, the proof of which uses important theorems of Bochi-Viana [2] and Bessa []. These papers were motivated by a well-known conjecture of Mañe [25]. Let T = R or Z. Let (, {τ t }) be a compact metric flow which is strictly ergodic with unique ergodic measure µ. Thus for example it can be a Kronecker flow as defined in Section 2. Let Φ : T GL(R d ) be a cocycle over (, {τ t }). Suppose that the dynamical spectrum σ Φ of Φ is a single interval: σ Φ = [a, b]. Suppose that
15 REMARKS CONCERNING LYAPUNOV EXPONENTS 03 a < b. Let {β <... < β s } be the Oseledets spectrum of Φ with respect to µ, and let V (m),..., V s (m) be the corresponding Oseledets bundles. According to the results of [] and [2], there is a C 0 -residual set {Ψ} of GL(R d )-valued cocycles over (, {τ t }) for which one of the following alternatives holds. (i) The Oseledets spectrum of Ψ reduces to a single point; (ii) The Oseledets bundles give rise to a dominated splitting (or exponential separation) of Ψ over (, {τ t }). Moreover, it is shown that, if Ψ does not admit a dominated splitting, then an arbitrarily small C 0 -perturbation of Ψ has property (i). See also [28, 30] for related results. We will not define the concept of dominated splitting/exponential separation here. For this we refer to [, 2] or to the older literature on exponential separation (e.g., [3, 4, 5, 32, 33]). Now, one can use a Krylov-Bogoliubov argument to show that, if the Oseledets bundles of Ψ give rise to a dominated splitting, then the dynamical spectrum σ Ψ of Ψ consists of at least two disjoint intervals. We omit the proof, but note that it uses the hypothesis that (, {τ t }) admits just one ergodic measure. Returning to the cocycle Φ, one can use another Krylov-Bogoliubov argument to show that the endpoints a and b of σ Φ = [a, b] are in the Oseledets spectrum; see [8]. But an arbitrarily small C 0 -perturbation of Φ has the property that its Oseledets spectrum reduces to a single point. This implies that the Lyapunov exponents of Φ cannot vary continuously if Φ is varied in the C 0 -sense. 4. Consequences of convergence In this section, we consider a problem which is inverse to that taken up in Section 3. Namely, suppose that Φ is a cocycle over a compact metric flow (, {τ t }), and suppose that lim ln Φ(ω, t) exists for all ω and all 0 t x R d. We ask if the cocycle Φ has discrete spectrum. In general this is not true, as the following example shows. Example 4.. Let be the annulus 0 < α r β, 0 θ 2π in the plane R 2 with polar coordinates (r, θ). Let a : R be a continuous function such that the correspondence r 2π the family of one-dimensional ODEs 0 a(r, θ)d θ takes on more than one value. Consider x = a(r, θ + t)x x R (5 ω )
16 04 R. JOHNSON AND L. ZAMPOGNI where ω = (r, θ). The family (5 ω ) has the form of the family ( ω ) if we put τ t (r, θ) = (r, θ + t) for t R and (r, θ). It it clear that the cocycle Φ which is determined by equations (5 ω ) has the form ( t ) Φ(ω, t) = exp a(r, θ + s)ds (ω = (r, θ), t R). 0 We see that, if ω = (r, θ) and 0 x R, then lim ln Φ(ω, t)x exists t and equals 2π a(r, 2π θ)d θ. This integral traces out a nondegenerate interval 0 I as r varies from α to β. It turns out that I is the dynamical spectrum of the family (5 ω ). This example is in fact too simple and only indicates that we must specify our inverse problem in a more detailed way. So let us suppose that (, {τ t }) is minimal, and that, for each ω and each 0 x R d, the limit lim ln Φ(ω, t)x exists. We ask: does Φ have discrete spectrum? t This question has an affirmative answer if d =. It may well be that the answer is still affirmative if d 2. We have not been able to prove this, however. Here is what we can and will do. () If d 2, we suppose (in addition to the conditions already listed) that, for each ergodic measure µ on, the corresponding Oseledets spectrum {β (µ) < β 2 (µ) <... < β s (µ)} is simple. That is, s = d, or equivalently all the multiplicities d r are equal to ( r s = d: see Theorem 2.2). Under these conditions, we will show that Φ has discrete spectrum. In fact, it will turn out that the numbers β (µ) = β,..., β d (µ) = β d do not depend on the choice of the ergodic measure µ, and that σ Φ = {β < β 2 <... < β d }. Thus in particular Φ satisfies the classical Lillo property [23]. (2) If d = 2, we make no a priori hypothesis regarding the Oseledets spectrum: we suppose that (, {τ t }) is minimal, and that, for each ω and each 0 x R 2, the limits lim ln Φ(ω, t)x and t lim ln Φ(ω, t)x t t exist (they need not be equal). We will prove that, subject to these hypotheses, Φ has discrete spectrum. As noted in the Introduction, we generalize a result of Furman [4], who assumes that (, {τ t }) is strictly ergodic. He uses certain properties of the projective flow defined by Φ when d = 2. See also [7] in this regard. To our knowledge, our inverse problem has not been frequently discussed in the literature. We point out that the hypothesis concerning the existence of
17 REMARKS CONCERNING LYAPUNOV EXPONENTS 05 t the limits lim ln Φ(ω, t)x (and t lim ln Φ(ω, t)x in point (2)) is rather t delicate since no uniformity is assumed. We also remark that there are various results in the literature to the effect that the set of cocycles over a given compact metric flow which have simple Oseledets spectrum is dense in various topologies. See, e.g., [2, 27]. After these preliminary remarks, we express point () in a formal statement: Theorem 4.2. Let T = R or Z. Let (, {τ t }) be a compact metric minimal flow, and let Φ : T GL(R d ) be a T -cocycle over (, {τ t }). Suppose that, for every {τ t }-ergodic measure µ on, the Oseledets spectrum is simple. This means that it consists of d distinct points β <... < β d (which may depend on µ). Suppose that, for each ω and 0 x R d, the limit lim ln Φ(ω, t)x t exists. Then the dynamical spectrum σ Φ of Φ consists of d distinct points (and in particular is discrete). Note that, if (, {τ t }) is minimal, then it is invariantly connected and chain recurrent. So the results stated in Section 2 will be available to us in the proof of Theorem 4.2, to which we now turn. Before beginning the proof of Theorem 4.2, we describe several convenient constructions. Let Φ be a T -cocycle over (, {τ t }), let σ Φ = [a, b ] [a q, b q ], and let V (c),..., V q (c) be the corresponding spectral subbundles of Theorem 2.4. These are topological vector subbundles of R d, of fiber dimension d,..., d q where d + + d q = d. They need not be topologically trivial; i.e., they need not be equivalent to product bundles R dp, p q. However, it is explained in [0] how these bundles can be trivialized via an appropriate cohomology. We explain the relevant constructions of [0]. Let us recall that a minimal flow (ˆ, {ˆτ t }) is said to be an extension of the minimal flow (, {τ t }) if there is a continuous map π : ˆ such that π ˆτ t = τ t π for all t T (one says that π is a flow homomorphism). Using the minimality of (, {τ t }) one sees that π must be surjective. The cocycle Φ can be lifted to a cocycle ˆΦ on ˆ via the formula ˆΦ(ˆω, t) = Φ(π(ˆω), t) (ˆω ˆ, t T ). Moreover the bundles V (c),..., V q (c) lift to ˆ via (c) (c) the usual pullback construction. Call the lifted bundles ˆV,..., ˆV q ; they are ˆΦ-invariant and it is easy to see that they are the spectral subbundles of ˆΦ. (c) (c) Let us write ˆV p (ˆω) = ˆV p ({ˆω} R d ) for the fiber of ˆV p (c) at ˆω ˆ. Next let O(d) be the group of orthogonal d d matrices. According to [0, Theorem 4.5], one can find a minimal extension (ˆ, {ˆτ t }) of (, {τ t }) together with a continuous map F : ˆ O(d) such that, if Ṽ p (c) (c) (ˆω) = F (ˆω) ˆV p (ˆω), then the bundle Ṽ p (c) (ˆω) is a product bundle. In fact, let e,..., e d be = ˆω ˆ Ṽ (c) p the standard basis of R d. For each p {2, 3,..., q}, let us identify R dp with the
18 06 R. JOHNSON AND L. ZAMPOGNI span of the set of unit vectors {e d+...d p +,..., e d+ +d p }; if p = we identify R d with Span{e,..., e d }. Then F can be chosen so that Ṽ p (c) = R dp ( p q). Define the cocycle Φ by Φ(ˆω, t) = F ( τ t (ˆω))ˆΦ(ˆω, t)f (ˆω) (ˆω ˆ, t T ); thus Φ is cohomologous to the cocycle Φ via the cohomology F. We see that Φ admits the spectral decomposition Ṽ (c) = R d,..., Ṽ q (c) = R dq. We conclude that, to prove Theorem 4.2, there is no loss of generality in assuming that the spectral subbundles of Φ are product bundles: V p (c) = R dp ( p q). This is equivalent to saying that there is no loss of generality in assuming that: (i) Φ has block-diagonal form: Φ 0 Φ =... (6) 0 Φ q where Φ p is a T -cocycle over (, {τ t }) with values in GL(R d ), and (ii) the dynamical spectrum of Φ p is the single interval [a p, b p ] ( p q). (The reader is warned that, if (, {τ t }) is strictly ergodic, then the extension (ˆ, {ˆτ t }) of the above construction need not be strictly ergodic.) We pass to a second construction. Say that Φ is upper triangular if Φ = (Φ ij ) where Φ ij = 0 if i > j and Φ ii > 0 ( i d). Our construction will give rise to a cohomology between a suitable lifted version of Φ, and an upper triangular cocycle. Let O(d) be the group of orthogonal d d matrices. If u 0 O(d), then Φ(ω, t)u 0 can be uniquely decomposed in the form Φ(ω, t)u 0 = U(ω, u 0, t) (ω, u 0, t) (ω, t T ) where U O(d) and is upper triangular with positive diagonal elements. This follows from the Gram-Schmidt decomposition of Φ(ω, t)u 0. It turns out that, if one sets ˆτ t (ω, u 0 ) = (τ t (ω), U(ω, u 0, t)) then {ˆτ t t T } is a flow on O(d), and is a {ˆτ t }-cocycle. Note that, if Φ has a block diagonal structure as in (6), then U and have corresponding block-diagonal structures. Next let ˆ O(d) be a minimal {ˆτ t }-subflow (such a subflow exists by Zorn s Lemma). Then the projection π : ˆ : (ω, u0 ) ω is continuous, and π ˆτ t = τ t π. We introduce the lifted cocycle ˆΦ : ˆ T GL(R d ) : ˆΦ(ω, t) = Φ(π(ˆω), t) where ˆω = (ω, t) ˆ. Note that the map F : ˆ O(d) : F (ω, u 0 ) = u 0 defines a cohomology between ˆΦ and. In fact, F (ˆτ t (ˆω)) (ˆω)F (ˆω) = ˆΦ(ˆω, t) for ˆω = (ω, t) ˆ and t T.
19 REMARKS CONCERNING LYAPUNOV EXPONENTS 07 Our third and final construction was already discussed in Section 2. Namely, assume that T = R. Then there exists a continuous function A : L(R d ) such that Φ is cohomologous to the cocycle generated by the family of linear ODEs ( ω ): x = A(τ t (ω))x. We observe that, if a given cocycle Φ has a block-triangular form as in the first construction, then the coefficient matrix A( ) in ( ω ) may be chosen to have the corresponding block-diagonal form. Moreover, if Φ has an upper triangular from as in the second construction, then A( ) may be chosen to have the corresponding upper triangular form. We assume until further notice that T = R. Using the above constructions, we see that by introducing a suitable minimal extension of (, {τ t }), and by introducing a suitable cohomology, it can be arranged that Φ satisfies the following conditions. Hypotheses 4.3. (a) The cocycle Φ is generated by a family of linear ODEs x = A(τ t (ω))x ω, x R d (7 ω ) A 0 where the matrix function A( ) has block-diagonal form: A = A q (b) If Φ p is the cocycle over (, {τ t }) which is generated by the family x = A p (τ t (ω))x, then the dynamical spectrum σ p of Φ p is the single interval [a p, b p ] ( p q). (c) Each matrix function A p is upper triangular ( p q). It can be shown that, if Φ and Ψ are cohomologous cocycles, and if Φ satisfies the hypotheses of Theorem 4.2, then so does Ψ. It can also be shown that, if Φ and Ψ are cohomologous, and if Φ satisfies the thesis of Theorem 4.2, then so does Ψ. We pass to the proof of Theorem 4.2 in the case when T = R. According to the above constructions and remarks, we can assume that Φ satisfies any or all of Hypotheses 4.3 (a) (c), when it is appropriate to do so. We proceed by induction on the dimension d of the cocycle Φ. Suppose that d =. There is no loss of generality in assuming that Φ is generated by a family of one dimensional systems of the form ( ω ). The family ( ω ) has the form x = A(τ t (ω))x where A : R is a continuous scalar function. Using the hypothesis concerning the existence of the limits which define the Lyapunov t exponents of Φ, we see that lim A(τ s (ω))ds exists for all ω. t o Now the flow (, {τ t }) is by assumption minimal, so one can use an oscillation result of Johnson [6] to show that the quantity ā = lim A(τ s (ω))ds t t 0
20 08 R. JOHNSON AND L. ZAMPOGNI does not depend on ω, and the limit is uniform in ω. Moreover ā = t lim A(τ s (ω))ds, where again the limit is uniform in ω. One can t t 0 now check directly that the dynamical spectrum of Φ satisfies σ Φ = {ā}; i.e., it is discrete. Next, suppose that Theorem 4.2 is valid for all continuous R-cocycles of dimension d, over all minimal flows (, {τ t }). We suppose without loss of generality that our given cocycle Φ satisfies Hypotheses 4.3 (a) and (b). Suppose first that the number of diagonal blocks of the (d-dimensional) matrix function A( ) is at least 2. Each block A,..., A q then has dimension d. So by the induction hypothesis, the family x = A p (τ t (ω))x (ω, x R d ) has discrete spectrum ( p q). By Hypotheses 4.3 (2), this spectrum is the singleton {a p }, and it follows that the cocycle Φ has discrete spectrum: σ Φ = {a,..., a q }. So Theorem 4.2 is proved in this case. We now assume that q =, which means that the spectrum σ Φ of Φ consists of a single interval [a, b]. We must show that a = b. We assume w.l.o.g. that Hypotheses (a), (b) and (c) are valid. The matrix function A( ) has values in L(R d ) and is upper triangular. Let us write A(ω) = A (ω) a d (ω) 0 a dd (ω) where A takes values in L(R d ) and is upper triangular. Consider the family of subsystems y = A (τ t (ω))y ω, y R d. (8 ω ) ( ) y(t) Note that a solution y(t) of (8 ω ) determines a solution x(t) = of (7 x n (t) ω ) ( ) y(t) by setting x n (t) = 0; that is, x(t) = is a solution of (7 0 ω ) if and only if y(t) is a solution of (8 ω ). We see that the family (8 ω ) has the property that lim ln y(t) exists t whenever y(t) is a nonzero solution of equation (8 ω ) (ω ). By the induction hypothesis, the dynamical spectrum σ of the family (8 ω ) is discrete, say σ = {α < α 2 <... < α j } where j d. By Proposition 2.2, the set of Lyapunov exponents of (8 ω ) is exactly {α,..., α j } for each ω. Moreover, if d i is the multiplicity of α i for i j, then d + + d j = d.
21 REMARKS CONCERNING LYAPUNOV EXPONENTS 09 Now, for each ergodic measure µ on, the Oseledets spectrum of the family (8 ω ) is contained in the dynamical spectrum σ of that family. Moreover, the Oseledets spectrum equals the set of averages { } a ii (ω)dµ(ω) i d of the diagonal elements of A ; see [8, 3]. By hypothesis, the µ-oseledets spectrum of Φ is simple, and therefore the µ-oseledets spectrum of the cocycle Φ generated by equations (8 ω ) is also simple. Using the fact that σ = {α < α 2 <... < α j }, we see that each multiplicity d i =, and that σ = {α < α 2 <... < α d } consists of d distinct real numbers. { It is clear that these numbers } are just a reordered version of the numbers a ii (ω)dµ(ω) i d. One can show (by applying Proposition 3.2, or by carrying out a secondary induction on j, j d ) that a ii (ω)dµ(ω) does not depend on the choice of the {τ t }-ergodic measure µ, if j d. We must now study the significance of the numbers a dd (ω)dµ(ω) as µ ranges over the set of {τ t }-ergodic measures on. To do this, it is convenient to introduce a projective flow. The construction is quite similar to that carried out in the proof of Theorem 3.2 above. Let L be the (d )-dimensional manifold of lines through the origin in R d. Let B = L, and define a flow {ˆτ t } on B by setting ˆτ t (ω, l) = (τ t (ω), Φ(ω, t)l) (ω, l L). Define f : B R : f(ω, l) = A(ω)x, x / x, x if 0 x l. Then if x(t) is a solution of (7 ω ), and if l L is the line containing x(0) 0, then t 0 f(ˆτ s (ω, l))ds = ln x(t) x(0). (9) By the hypothesis concerning the existence of the limits defining the Lyapunov exponents, and by (9), one has that the limit lim t f(ˆτ s (b))ds exists t 0 for each b B. Let us denote the limit by f (b). Since f is the pointwise limit of a sequence of continuous functions, it admits a residual set of continuity points [6]. Let b be a point of continuity of f. For each ε > 0, there is an open neighborhood U = U(ε) L of b such that, if b U, then f (b) f (b ) < ε. There is no loss of generality in assuming that U = U U 2 where U and U 2 L are open sets. There is also no loss of generality in assuming that U does not intersect the {ˆτ t }-invariant set B = {(ω, l) B l R d R d }. For each ω, there is a real number β (ω) such that the set of Lyapunov exponents of equation (7 ω ) equals {α, α 2,..., α d, β (ω)}. Let β max (ω) = max{α,..., α d, β (ω)} be the largest Lyapunov exponent of (7 ω ). Write
22 0 R. JOHNSON AND L. ZAMPOGNI the continuity point b of f in the form b = (ω, l ). It follows from the continuity of f at b that f (b ) equals β max (ω ). In fact, this is a consequence of the observation that, if β(ω ) is the maximum { of the Lypunov exponents of (7 ω ) which are distinct from β max (ω ), then x R d x = 0 or lim t ln Φ(ω, t)x β(ω } ) is a proper vector subspace of R d, so its complement in R d is open and dense. This means that there is an open dense subset W L such that, if l W, then lim t 0 f(ˆτ s (ω, l)ds = β max (ω ). Recall that we are working under the hypothesis that σ Φ is a single interval [a, b]. Using Theorem 2.4, we see that the numbers α,..., α d all lie in [a, b]. Suppose for the time being that b is greater than α d. According to a result of [8], there is a {τ t }-ergodic measure µ on for which b is a Lyapunov exponent of Φ, for µ-a.a. ω. By Theorem 2.4, we have that β max (ω) = b for µ-a.a. ( ω). Fix a point ω such that β max ( ω) = b. If y x R d, we write x = where y R x d and x d R. Let x be a vector such d ( ) ( ) y y(t) that lim t ln Φ( ω, t)x = b. Writing Φ( ω, t)x = Φ( ω, t) =, and x d x d (t) using the fact that b > α d = max{α i i d }, we see that x d 0, and that lim lim t t t ln x d(t) = b. (For later use, we note that b = lim t ln x d(t) = a dd (τ s ( ω)ds.) 0 ( y One checks that, if is any vector with x xd) d 0, then lim ln Φ( ω, t)x = b. t Return to the continuity point (ω, l ) B of f which was introduced previously. Let ε > 0, and choose U(ε) = U = U U 2 as before. Let ω be the point of the preceding two paragraphs. Since (, {τ t }) is minimal, the positive semiorbit {τ t ( ω) t 0} is dense in, hence it enters U. Using the fact that U does not intersect B together with the result of the previous paragraph, we ( y can find a vector R xd) d, whose projective image l lies in U 2, such that lim t ln Φ(ω, t)x = b. This means that f (ω, l ) b ε. Since ε > 0 is arbitrary, we have that f (ω, l ) = b. Next, let ε > 0, and let ω be any point of. Again the positive ( semiorbit {τ t (ω) t 0} enters U. So there exists a vector x = y R xd) d with x d 0 such that lim t ln Φ(ω, t)x f (ω, l ) ε. Hence lim ln Φ(ω, t)x b t ε. At this point choose 0 < ε < 2 (b α d ), and
SYSTEMS. Russell Johnson
 NONAUTONOMOUS DYNAMICAL SYSTEMS Russell Johnson Università di Firenze Luca Zampogni Università di Perugia Thanks for collaboration to R. Fabbri, M. Franca, S. Novo, C. Núñez, R. Obaya, and many other colleagues.
NONAUTONOMOUS DYNAMICAL SYSTEMS Russell Johnson Università di Firenze Luca Zampogni Università di Perugia Thanks for collaboration to R. Fabbri, M. Franca, S. Novo, C. Núñez, R. Obaya, and many other colleagues.
THE MULTIPLICATIVE ERGODIC THEOREM OF OSELEDETS
 THE MULTIPLICATIVE ERGODIC THEOREM OF OSELEDETS. STATEMENT Let (X, µ, A) be a probability space, and let T : X X be an ergodic measure-preserving transformation. Given a measurable map A : X GL(d, R),
THE MULTIPLICATIVE ERGODIC THEOREM OF OSELEDETS. STATEMENT Let (X, µ, A) be a probability space, and let T : X X be an ergodic measure-preserving transformation. Given a measurable map A : X GL(d, R),
MET Workshop: Exercises
 MET Workshop: Exercises Alex Blumenthal and Anthony Quas May 7, 206 Notation. R d is endowed with the standard inner product (, ) and Euclidean norm. M d d (R) denotes the space of n n real matrices. When
MET Workshop: Exercises Alex Blumenthal and Anthony Quas May 7, 206 Notation. R d is endowed with the standard inner product (, ) and Euclidean norm. M d d (R) denotes the space of n n real matrices. When
Part V. 17 Introduction: What are measures and why measurable sets. Lebesgue Integration Theory
 Part V 7 Introduction: What are measures and why measurable sets Lebesgue Integration Theory Definition 7. (Preliminary). A measure on a set is a function :2 [ ] such that. () = 2. If { } = is a finite
Part V 7 Introduction: What are measures and why measurable sets Lebesgue Integration Theory Definition 7. (Preliminary). A measure on a set is a function :2 [ ] such that. () = 2. If { } = is a finite
Part III. 10 Topological Space Basics. Topological Spaces
 Part III 10 Topological Space Basics Topological Spaces Using the metric space results above as motivation we will axiomatize the notion of being an open set to more general settings. Definition 10.1.
Part III 10 Topological Space Basics Topological Spaces Using the metric space results above as motivation we will axiomatize the notion of being an open set to more general settings. Definition 10.1.
THEOREM OF OSELEDETS. We recall some basic facts and terminology relative to linear cocycles and the multiplicative ergodic theorem of Oseledets [1].
![THEOREM OF OSELEDETS. We recall some basic facts and terminology relative to linear cocycles and the multiplicative ergodic theorem of Oseledets [1]. THEOREM OF OSELEDETS. We recall some basic facts and terminology relative to linear cocycles and the multiplicative ergodic theorem of Oseledets [1].](/thumbs/95/124190157.jpg) THEOREM OF OSELEDETS We recall some basic facts and terminology relative to linear cocycles and the multiplicative ergodic theorem of Oseledets []. 0.. Cocycles over maps. Let µ be a probability measure
THEOREM OF OSELEDETS We recall some basic facts and terminology relative to linear cocycles and the multiplicative ergodic theorem of Oseledets []. 0.. Cocycles over maps. Let µ be a probability measure
Eilenberg-Steenrod properties. (Hatcher, 2.1, 2.3, 3.1; Conlon, 2.6, 8.1, )
 II.3 : Eilenberg-Steenrod properties (Hatcher, 2.1, 2.3, 3.1; Conlon, 2.6, 8.1, 8.3 8.5 Definition. Let U be an open subset of R n for some n. The de Rham cohomology groups (U are the cohomology groups
II.3 : Eilenberg-Steenrod properties (Hatcher, 2.1, 2.3, 3.1; Conlon, 2.6, 8.1, 8.3 8.5 Definition. Let U be an open subset of R n for some n. The de Rham cohomology groups (U are the cohomology groups
On the dynamics of strongly tridiagonal competitive-cooperative system
 On the dynamics of strongly tridiagonal competitive-cooperative system Chun Fang University of Helsinki International Conference on Advances on Fractals and Related Topics, Hong Kong December 14, 2012
On the dynamics of strongly tridiagonal competitive-cooperative system Chun Fang University of Helsinki International Conference on Advances on Fractals and Related Topics, Hong Kong December 14, 2012
CHAPTER 7. Connectedness
 CHAPTER 7 Connectedness 7.1. Connected topological spaces Definition 7.1. A topological space (X, T X ) is said to be connected if there is no continuous surjection f : X {0, 1} where the two point set
CHAPTER 7 Connectedness 7.1. Connected topological spaces Definition 7.1. A topological space (X, T X ) is said to be connected if there is no continuous surjection f : X {0, 1} where the two point set
9 Radon-Nikodym theorem and conditioning
 Tel Aviv University, 2015 Functions of real variables 93 9 Radon-Nikodym theorem and conditioning 9a Borel-Kolmogorov paradox............. 93 9b Radon-Nikodym theorem.............. 94 9c Conditioning.....................
Tel Aviv University, 2015 Functions of real variables 93 9 Radon-Nikodym theorem and conditioning 9a Borel-Kolmogorov paradox............. 93 9b Radon-Nikodym theorem.............. 94 9c Conditioning.....................
Integration on Measure Spaces
 Chapter 3 Integration on Measure Spaces In this chapter we introduce the general notion of a measure on a space X, define the class of measurable functions, and define the integral, first on a class of
Chapter 3 Integration on Measure Spaces In this chapter we introduce the general notion of a measure on a space X, define the class of measurable functions, and define the integral, first on a class of
A generic property of families of Lagrangian systems
 Annals of Mathematics, 167 (2008), 1099 1108 A generic property of families of Lagrangian systems By Patrick Bernard and Gonzalo Contreras * Abstract We prove that a generic Lagrangian has finitely many
Annals of Mathematics, 167 (2008), 1099 1108 A generic property of families of Lagrangian systems By Patrick Bernard and Gonzalo Contreras * Abstract We prove that a generic Lagrangian has finitely many
B 1 = {B(x, r) x = (x 1, x 2 ) H, 0 < r < x 2 }. (a) Show that B = B 1 B 2 is a basis for a topology on X.
 Math 6342/7350: Topology and Geometry Sample Preliminary Exam Questions 1. For each of the following topological spaces X i, determine whether X i and X i X i are homeomorphic. (a) X 1 = [0, 1] (b) X 2
Math 6342/7350: Topology and Geometry Sample Preliminary Exam Questions 1. For each of the following topological spaces X i, determine whether X i and X i X i are homeomorphic. (a) X 1 = [0, 1] (b) X 2
Topology. Xiaolong Han. Department of Mathematics, California State University, Northridge, CA 91330, USA address:
 Topology Xiaolong Han Department of Mathematics, California State University, Northridge, CA 91330, USA E-mail address: Xiaolong.Han@csun.edu Remark. You are entitled to a reward of 1 point toward a homework
Topology Xiaolong Han Department of Mathematics, California State University, Northridge, CA 91330, USA E-mail address: Xiaolong.Han@csun.edu Remark. You are entitled to a reward of 1 point toward a homework
Def. A topological space X is disconnected if it admits a non-trivial splitting: (We ll abbreviate disjoint union of two subsets A and B meaning A B =
 CONNECTEDNESS-Notes Def. A topological space X is disconnected if it admits a non-trivial splitting: X = A B, A B =, A, B open in X, and non-empty. (We ll abbreviate disjoint union of two subsets A and
CONNECTEDNESS-Notes Def. A topological space X is disconnected if it admits a non-trivial splitting: X = A B, A B =, A, B open in X, and non-empty. (We ll abbreviate disjoint union of two subsets A and
CHILE LECTURES: MULTIPLICATIVE ERGODIC THEOREM, FRIENDS AND APPLICATIONS
 CHILE LECTURES: MULTIPLICATIVE ERGODIC THEOREM, FRIENDS AND APPLICATIONS. Motivation Context: (Ω, P) a probability space; σ : Ω Ω is a measure-preserving transformation P(σ A) = P(A) for all measurable
CHILE LECTURES: MULTIPLICATIVE ERGODIC THEOREM, FRIENDS AND APPLICATIONS. Motivation Context: (Ω, P) a probability space; σ : Ω Ω is a measure-preserving transformation P(σ A) = P(A) for all measurable
Lebesgue Measure on R n
 8 CHAPTER 2 Lebesgue Measure on R n Our goal is to construct a notion of the volume, or Lebesgue measure, of rather general subsets of R n that reduces to the usual volume of elementary geometrical sets
8 CHAPTER 2 Lebesgue Measure on R n Our goal is to construct a notion of the volume, or Lebesgue measure, of rather general subsets of R n that reduces to the usual volume of elementary geometrical sets
Locally convex spaces, the hyperplane separation theorem, and the Krein-Milman theorem
 56 Chapter 7 Locally convex spaces, the hyperplane separation theorem, and the Krein-Milman theorem Recall that C(X) is not a normed linear space when X is not compact. On the other hand we could use semi
56 Chapter 7 Locally convex spaces, the hyperplane separation theorem, and the Krein-Milman theorem Recall that C(X) is not a normed linear space when X is not compact. On the other hand we could use semi
A VERY BRIEF REVIEW OF MEASURE THEORY
 A VERY BRIEF REVIEW OF MEASURE THEORY A brief philosophical discussion. Measure theory, as much as any branch of mathematics, is an area where it is important to be acquainted with the basic notions and
A VERY BRIEF REVIEW OF MEASURE THEORY A brief philosophical discussion. Measure theory, as much as any branch of mathematics, is an area where it is important to be acquainted with the basic notions and
MAT 570 REAL ANALYSIS LECTURE NOTES. Contents. 1. Sets Functions Countability Axiom of choice Equivalence relations 9
 MAT 570 REAL ANALYSIS LECTURE NOTES PROFESSOR: JOHN QUIGG SEMESTER: FALL 204 Contents. Sets 2 2. Functions 5 3. Countability 7 4. Axiom of choice 8 5. Equivalence relations 9 6. Real numbers 9 7. Extended
MAT 570 REAL ANALYSIS LECTURE NOTES PROFESSOR: JOHN QUIGG SEMESTER: FALL 204 Contents. Sets 2 2. Functions 5 3. Countability 7 4. Axiom of choice 8 5. Equivalence relations 9 6. Real numbers 9 7. Extended
Math 676. A compactness theorem for the idele group. and by the product formula it lies in the kernel (A K )1 of the continuous idelic norm
 Math 676. A compactness theorem for the idele group 1. Introduction Let K be a global field, so K is naturally a discrete subgroup of the idele group A K and by the product formula it lies in the kernel
Math 676. A compactness theorem for the idele group 1. Introduction Let K be a global field, so K is naturally a discrete subgroup of the idele group A K and by the product formula it lies in the kernel
Lebesgue Measure on R n
 CHAPTER 2 Lebesgue Measure on R n Our goal is to construct a notion of the volume, or Lebesgue measure, of rather general subsets of R n that reduces to the usual volume of elementary geometrical sets
CHAPTER 2 Lebesgue Measure on R n Our goal is to construct a notion of the volume, or Lebesgue measure, of rather general subsets of R n that reduces to the usual volume of elementary geometrical sets
Extreme points of compact convex sets
 Extreme points of compact convex sets In this chapter, we are going to show that compact convex sets are determined by a proper subset, the set of its extreme points. Let us start with the main definition.
Extreme points of compact convex sets In this chapter, we are going to show that compact convex sets are determined by a proper subset, the set of its extreme points. Let us start with the main definition.
Dynamics of Group Actions and Minimal Sets
 University of Illinois at Chicago www.math.uic.edu/ hurder First Joint Meeting of the Sociedad de Matemática de Chile American Mathematical Society Special Session on Group Actions: Probability and Dynamics
University of Illinois at Chicago www.math.uic.edu/ hurder First Joint Meeting of the Sociedad de Matemática de Chile American Mathematical Society Special Session on Group Actions: Probability and Dynamics
Topological vectorspaces
 (July 25, 2011) Topological vectorspaces Paul Garrett garrett@math.umn.edu http://www.math.umn.edu/ garrett/ Natural non-fréchet spaces Topological vector spaces Quotients and linear maps More topological
(July 25, 2011) Topological vectorspaces Paul Garrett garrett@math.umn.edu http://www.math.umn.edu/ garrett/ Natural non-fréchet spaces Topological vector spaces Quotients and linear maps More topological
Math 350 Fall 2011 Notes about inner product spaces. In this notes we state and prove some important properties of inner product spaces.
 Math 350 Fall 2011 Notes about inner product spaces In this notes we state and prove some important properties of inner product spaces. First, recall the dot product on R n : if x, y R n, say x = (x 1,...,
Math 350 Fall 2011 Notes about inner product spaces In this notes we state and prove some important properties of inner product spaces. First, recall the dot product on R n : if x, y R n, say x = (x 1,...,
DAVID DAMANIK AND DANIEL LENZ. Dedicated to Barry Simon on the occasion of his 60th birthday.
 UNIFORM SZEGŐ COCYCLES OVER STRICTLY ERGODIC SUBSHIFTS arxiv:math/052033v [math.sp] Dec 2005 DAVID DAMANIK AND DANIEL LENZ Dedicated to Barry Simon on the occasion of his 60th birthday. Abstract. We consider
UNIFORM SZEGŐ COCYCLES OVER STRICTLY ERGODIC SUBSHIFTS arxiv:math/052033v [math.sp] Dec 2005 DAVID DAMANIK AND DANIEL LENZ Dedicated to Barry Simon on the occasion of his 60th birthday. Abstract. We consider
Introduction to Real Analysis Alternative Chapter 1
 Christopher Heil Introduction to Real Analysis Alternative Chapter 1 A Primer on Norms and Banach Spaces Last Updated: March 10, 2018 c 2018 by Christopher Heil Chapter 1 A Primer on Norms and Banach Spaces
Christopher Heil Introduction to Real Analysis Alternative Chapter 1 A Primer on Norms and Banach Spaces Last Updated: March 10, 2018 c 2018 by Christopher Heil Chapter 1 A Primer on Norms and Banach Spaces
Finite-dimensional spaces. C n is the space of n-tuples x = (x 1,..., x n ) of complex numbers. It is a Hilbert space with the inner product
 Chapter 4 Hilbert Spaces 4.1 Inner Product Spaces Inner Product Space. A complex vector space E is called an inner product space (or a pre-hilbert space, or a unitary space) if there is a mapping (, )
Chapter 4 Hilbert Spaces 4.1 Inner Product Spaces Inner Product Space. A complex vector space E is called an inner product space (or a pre-hilbert space, or a unitary space) if there is a mapping (, )
16. Local theory of regular singular points and applications
 16. Local theory of regular singular points and applications 265 16. Local theory of regular singular points and applications In this section we consider linear systems defined by the germs of meromorphic
16. Local theory of regular singular points and applications 265 16. Local theory of regular singular points and applications In this section we consider linear systems defined by the germs of meromorphic
CHAPTER II THE HAHN-BANACH EXTENSION THEOREMS AND EXISTENCE OF LINEAR FUNCTIONALS
 CHAPTER II THE HAHN-BANACH EXTENSION THEOREMS AND EXISTENCE OF LINEAR FUNCTIONALS In this chapter we deal with the problem of extending a linear functional on a subspace Y to a linear functional on the
CHAPTER II THE HAHN-BANACH EXTENSION THEOREMS AND EXISTENCE OF LINEAR FUNCTIONALS In this chapter we deal with the problem of extending a linear functional on a subspace Y to a linear functional on the
Metric Spaces and Topology
 Chapter 2 Metric Spaces and Topology From an engineering perspective, the most important way to construct a topology on a set is to define the topology in terms of a metric on the set. This approach underlies
Chapter 2 Metric Spaces and Topology From an engineering perspective, the most important way to construct a topology on a set is to define the topology in terms of a metric on the set. This approach underlies
Lecture Notes Introduction to Ergodic Theory
 Lecture Notes Introduction to Ergodic Theory Tiago Pereira Department of Mathematics Imperial College London Our course consists of five introductory lectures on probabilistic aspects of dynamical systems,
Lecture Notes Introduction to Ergodic Theory Tiago Pereira Department of Mathematics Imperial College London Our course consists of five introductory lectures on probabilistic aspects of dynamical systems,
Chapter 1. Measure Spaces. 1.1 Algebras and σ algebras of sets Notation and preliminaries
 Chapter 1 Measure Spaces 1.1 Algebras and σ algebras of sets 1.1.1 Notation and preliminaries We shall denote by X a nonempty set, by P(X) the set of all parts (i.e., subsets) of X, and by the empty set.
Chapter 1 Measure Spaces 1.1 Algebras and σ algebras of sets 1.1.1 Notation and preliminaries We shall denote by X a nonempty set, by P(X) the set of all parts (i.e., subsets) of X, and by the empty set.
Functional Analysis. Franck Sueur Metric spaces Definitions Completeness Compactness Separability...
 Functional Analysis Franck Sueur 2018-2019 Contents 1 Metric spaces 1 1.1 Definitions........................................ 1 1.2 Completeness...................................... 3 1.3 Compactness......................................
Functional Analysis Franck Sueur 2018-2019 Contents 1 Metric spaces 1 1.1 Definitions........................................ 1 1.2 Completeness...................................... 3 1.3 Compactness......................................
Chapter 2 Metric Spaces
 Chapter 2 Metric Spaces The purpose of this chapter is to present a summary of some basic properties of metric and topological spaces that play an important role in the main body of the book. 2.1 Metrics
Chapter 2 Metric Spaces The purpose of this chapter is to present a summary of some basic properties of metric and topological spaces that play an important role in the main body of the book. 2.1 Metrics
here, this space is in fact infinite-dimensional, so t σ ess. Exercise Let T B(H) be a self-adjoint operator on an infinitedimensional
 15. Perturbations by compact operators In this chapter, we study the stability (or lack thereof) of various spectral properties under small perturbations. Here s the type of situation we have in mind:
15. Perturbations by compact operators In this chapter, we study the stability (or lack thereof) of various spectral properties under small perturbations. Here s the type of situation we have in mind:
THE RADON NIKODYM PROPERTY AND LIPSCHITZ EMBEDDINGS
 THE RADON NIKODYM PROPERTY AND LIPSCHITZ EMBEDDINGS Motivation The idea here is simple. Suppose we have a Lipschitz homeomorphism f : X Y where X and Y are Banach spaces, namely c 1 x y f (x) f (y) c 2
THE RADON NIKODYM PROPERTY AND LIPSCHITZ EMBEDDINGS Motivation The idea here is simple. Suppose we have a Lipschitz homeomorphism f : X Y where X and Y are Banach spaces, namely c 1 x y f (x) f (y) c 2
NECESSARY CONDITIONS FOR WEIGHTED POINTWISE HARDY INEQUALITIES
 NECESSARY CONDITIONS FOR WEIGHTED POINTWISE HARDY INEQUALITIES JUHA LEHRBÄCK Abstract. We establish necessary conditions for domains Ω R n which admit the pointwise (p, β)-hardy inequality u(x) Cd Ω(x)
NECESSARY CONDITIONS FOR WEIGHTED POINTWISE HARDY INEQUALITIES JUHA LEHRBÄCK Abstract. We establish necessary conditions for domains Ω R n which admit the pointwise (p, β)-hardy inequality u(x) Cd Ω(x)
Exercise Solutions to Functional Analysis
 Exercise Solutions to Functional Analysis Note: References refer to M. Schechter, Principles of Functional Analysis Exersize that. Let φ,..., φ n be an orthonormal set in a Hilbert space H. Show n f n
Exercise Solutions to Functional Analysis Note: References refer to M. Schechter, Principles of Functional Analysis Exersize that. Let φ,..., φ n be an orthonormal set in a Hilbert space H. Show n f n
Introduction to Dynamical Systems
 Introduction to Dynamical Systems France-Kosovo Undergraduate Research School of Mathematics March 2017 This introduction to dynamical systems was a course given at the march 2017 edition of the France
Introduction to Dynamical Systems France-Kosovo Undergraduate Research School of Mathematics March 2017 This introduction to dynamical systems was a course given at the march 2017 edition of the France
16 1 Basic Facts from Functional Analysis and Banach Lattices
 16 1 Basic Facts from Functional Analysis and Banach Lattices 1.2.3 Banach Steinhaus Theorem Another fundamental theorem of functional analysis is the Banach Steinhaus theorem, or the Uniform Boundedness
16 1 Basic Facts from Functional Analysis and Banach Lattices 1.2.3 Banach Steinhaus Theorem Another fundamental theorem of functional analysis is the Banach Steinhaus theorem, or the Uniform Boundedness
Lyapunov exponents of Teichmüller flows
 Lyapunov exponents ofteichmüller flows p 1/6 Lyapunov exponents of Teichmüller flows Marcelo Viana IMPA - Rio de Janeiro Lyapunov exponents ofteichmüller flows p 2/6 Lecture # 1 Geodesic flows on translation
Lyapunov exponents ofteichmüller flows p 1/6 Lyapunov exponents of Teichmüller flows Marcelo Viana IMPA - Rio de Janeiro Lyapunov exponents ofteichmüller flows p 2/6 Lecture # 1 Geodesic flows on translation
1 Topology Definition of a topology Basis (Base) of a topology The subspace topology & the product topology on X Y 3
 Index Page 1 Topology 2 1.1 Definition of a topology 2 1.2 Basis (Base) of a topology 2 1.3 The subspace topology & the product topology on X Y 3 1.4 Basic topology concepts: limit points, closed sets,
Index Page 1 Topology 2 1.1 Definition of a topology 2 1.2 Basis (Base) of a topology 2 1.3 The subspace topology & the product topology on X Y 3 1.4 Basic topology concepts: limit points, closed sets,
g 2 (x) (1/3)M 1 = (1/3)(2/3)M.
 COMPACTNESS If C R n is closed and bounded, then by B-W it is sequentially compact: any sequence of points in C has a subsequence converging to a point in C Conversely, any sequentially compact C R n is
COMPACTNESS If C R n is closed and bounded, then by B-W it is sequentially compact: any sequence of points in C has a subsequence converging to a point in C Conversely, any sequentially compact C R n is
The Lorentz group provides another interesting example. Moreover, the Lorentz group SO(3, 1) shows up in an interesting way in computer vision.
 190 CHAPTER 3. REVIEW OF GROUPS AND GROUP ACTIONS 3.3 The Lorentz Groups O(n, 1), SO(n, 1) and SO 0 (n, 1) The Lorentz group provides another interesting example. Moreover, the Lorentz group SO(3, 1) shows
190 CHAPTER 3. REVIEW OF GROUPS AND GROUP ACTIONS 3.3 The Lorentz Groups O(n, 1), SO(n, 1) and SO 0 (n, 1) The Lorentz group provides another interesting example. Moreover, the Lorentz group SO(3, 1) shows
II - REAL ANALYSIS. This property gives us a way to extend the notion of content to finite unions of rectangles: we define
 1 Measures 1.1 Jordan content in R N II - REAL ANALYSIS Let I be an interval in R. Then its 1-content is defined as c 1 (I) := b a if I is bounded with endpoints a, b. If I is unbounded, we define c 1
1 Measures 1.1 Jordan content in R N II - REAL ANALYSIS Let I be an interval in R. Then its 1-content is defined as c 1 (I) := b a if I is bounded with endpoints a, b. If I is unbounded, we define c 1
Some Background Material
 Chapter 1 Some Background Material In the first chapter, we present a quick review of elementary - but important - material as a way of dipping our toes in the water. This chapter also introduces important
Chapter 1 Some Background Material In the first chapter, we present a quick review of elementary - but important - material as a way of dipping our toes in the water. This chapter also introduces important
ON THE REGULARITY OF SAMPLE PATHS OF SUB-ELLIPTIC DIFFUSIONS ON MANIFOLDS
 Bendikov, A. and Saloff-Coste, L. Osaka J. Math. 4 (5), 677 7 ON THE REGULARITY OF SAMPLE PATHS OF SUB-ELLIPTIC DIFFUSIONS ON MANIFOLDS ALEXANDER BENDIKOV and LAURENT SALOFF-COSTE (Received March 4, 4)
Bendikov, A. and Saloff-Coste, L. Osaka J. Math. 4 (5), 677 7 ON THE REGULARITY OF SAMPLE PATHS OF SUB-ELLIPTIC DIFFUSIONS ON MANIFOLDS ALEXANDER BENDIKOV and LAURENT SALOFF-COSTE (Received March 4, 4)
B. Appendix B. Topological vector spaces
 B.1 B. Appendix B. Topological vector spaces B.1. Fréchet spaces. In this appendix we go through the definition of Fréchet spaces and their inductive limits, such as they are used for definitions of function
B.1 B. Appendix B. Topological vector spaces B.1. Fréchet spaces. In this appendix we go through the definition of Fréchet spaces and their inductive limits, such as they are used for definitions of function
s P = f(ξ n )(x i x i 1 ). i=1
 Compactness and total boundedness via nets The aim of this chapter is to define the notion of a net (generalized sequence) and to characterize compactness and total boundedness by this important topological
Compactness and total boundedness via nets The aim of this chapter is to define the notion of a net (generalized sequence) and to characterize compactness and total boundedness by this important topological
08a. Operators on Hilbert spaces. 1. Boundedness, continuity, operator norms
 (February 24, 2017) 08a. Operators on Hilbert spaces Paul Garrett garrett@math.umn.edu http://www.math.umn.edu/ garrett/ [This document is http://www.math.umn.edu/ garrett/m/real/notes 2016-17/08a-ops
(February 24, 2017) 08a. Operators on Hilbert spaces Paul Garrett garrett@math.umn.edu http://www.math.umn.edu/ garrett/ [This document is http://www.math.umn.edu/ garrett/m/real/notes 2016-17/08a-ops
2. The Concept of Convergence: Ultrafilters and Nets
 2. The Concept of Convergence: Ultrafilters and Nets NOTE: AS OF 2008, SOME OF THIS STUFF IS A BIT OUT- DATED AND HAS A FEW TYPOS. I WILL REVISE THIS MATE- RIAL SOMETIME. In this lecture we discuss two
2. The Concept of Convergence: Ultrafilters and Nets NOTE: AS OF 2008, SOME OF THIS STUFF IS A BIT OUT- DATED AND HAS A FEW TYPOS. I WILL REVISE THIS MATE- RIAL SOMETIME. In this lecture we discuss two
fy (X(g)) Y (f)x(g) gy (X(f)) Y (g)x(f)) = fx(y (g)) + gx(y (f)) fy (X(g)) gy (X(f))
 1. Basic algebra of vector fields Let V be a finite dimensional vector space over R. Recall that V = {L : V R} is defined to be the set of all linear maps to R. V is isomorphic to V, but there is no canonical
1. Basic algebra of vector fields Let V be a finite dimensional vector space over R. Recall that V = {L : V R} is defined to be the set of all linear maps to R. V is isomorphic to V, but there is no canonical
arxiv: v1 [math.fa] 14 Jul 2018
![arxiv: v1 [math.fa] 14 Jul 2018 arxiv: v1 [math.fa] 14 Jul 2018](/thumbs/82/85634312.jpg) Construction of Regular Non-Atomic arxiv:180705437v1 [mathfa] 14 Jul 2018 Strictly-Positive Measures in Second-Countable Locally Compact Non-Atomic Hausdorff Spaces Abstract Jason Bentley Department of
Construction of Regular Non-Atomic arxiv:180705437v1 [mathfa] 14 Jul 2018 Strictly-Positive Measures in Second-Countable Locally Compact Non-Atomic Hausdorff Spaces Abstract Jason Bentley Department of
NOTES ON LINEAR ODES
 NOTES ON LINEAR ODES JONATHAN LUK We can now use all the discussions we had on linear algebra to study linear ODEs Most of this material appears in the textbook in 21, 22, 23, 26 As always, this is a preliminary
NOTES ON LINEAR ODES JONATHAN LUK We can now use all the discussions we had on linear algebra to study linear ODEs Most of this material appears in the textbook in 21, 22, 23, 26 As always, this is a preliminary
Robustly transitive diffeomorphisms
 Robustly transitive diffeomorphisms Todd Fisher tfisher@math.byu.edu Department of Mathematics, Brigham Young University Summer School, Chengdu, China 2009 Dynamical systems The setting for a dynamical
Robustly transitive diffeomorphisms Todd Fisher tfisher@math.byu.edu Department of Mathematics, Brigham Young University Summer School, Chengdu, China 2009 Dynamical systems The setting for a dynamical
Contents Ordered Fields... 2 Ordered sets and fields... 2 Construction of the Reals 1: Dedekind Cuts... 2 Metric Spaces... 3
 Analysis Math Notes Study Guide Real Analysis Contents Ordered Fields 2 Ordered sets and fields 2 Construction of the Reals 1: Dedekind Cuts 2 Metric Spaces 3 Metric Spaces 3 Definitions 4 Separability
Analysis Math Notes Study Guide Real Analysis Contents Ordered Fields 2 Ordered sets and fields 2 Construction of the Reals 1: Dedekind Cuts 2 Metric Spaces 3 Metric Spaces 3 Definitions 4 Separability
Real Analysis Notes. Thomas Goller
 Real Analysis Notes Thomas Goller September 4, 2011 Contents 1 Abstract Measure Spaces 2 1.1 Basic Definitions........................... 2 1.2 Measurable Functions........................ 2 1.3 Integration..............................
Real Analysis Notes Thomas Goller September 4, 2011 Contents 1 Abstract Measure Spaces 2 1.1 Basic Definitions........................... 2 1.2 Measurable Functions........................ 2 1.3 Integration..............................
of the set A. Note that the cross-section A ω :={t R + : (t,ω) A} is empty when ω/ π A. It would be impossible to have (ψ(ω), ω) A for such an ω.
 AN-1 Analytic sets For a discrete-time process {X n } adapted to a filtration {F n : n N}, the prime example of a stopping time is τ = inf{n N : X n B}, the first time the process enters some Borel set
AN-1 Analytic sets For a discrete-time process {X n } adapted to a filtration {F n : n N}, the prime example of a stopping time is τ = inf{n N : X n B}, the first time the process enters some Borel set
ABSOLUTE CONTINUITY OF FOLIATIONS
 ABSOLUTE CONTINUITY OF FOLIATIONS C. PUGH, M. VIANA, A. WILKINSON 1. Introduction In what follows, U is an open neighborhood in a compact Riemannian manifold M, and F is a local foliation of U. By this
ABSOLUTE CONTINUITY OF FOLIATIONS C. PUGH, M. VIANA, A. WILKINSON 1. Introduction In what follows, U is an open neighborhood in a compact Riemannian manifold M, and F is a local foliation of U. By this
Commutative Banach algebras 79
 8. Commutative Banach algebras In this chapter, we analyze commutative Banach algebras in greater detail. So we always assume that xy = yx for all x, y A here. Definition 8.1. Let A be a (commutative)
8. Commutative Banach algebras In this chapter, we analyze commutative Banach algebras in greater detail. So we always assume that xy = yx for all x, y A here. Definition 8.1. Let A be a (commutative)
Math 215B: Solutions 1
 Math 15B: Solutions 1 Due Thursday, January 18, 018 (1) Let π : X X be a covering space. Let Φ be a smooth structure on X. Prove that there is a smooth structure Φ on X so that π : ( X, Φ) (X, Φ) is an
Math 15B: Solutions 1 Due Thursday, January 18, 018 (1) Let π : X X be a covering space. Let Φ be a smooth structure on X. Prove that there is a smooth structure Φ on X so that π : ( X, Φ) (X, Φ) is an
4.2. ORTHOGONALITY 161
 4.2. ORTHOGONALITY 161 Definition 4.2.9 An affine space (E, E ) is a Euclidean affine space iff its underlying vector space E is a Euclidean vector space. Given any two points a, b E, we define the distance
4.2. ORTHOGONALITY 161 Definition 4.2.9 An affine space (E, E ) is a Euclidean affine space iff its underlying vector space E is a Euclidean vector space. Given any two points a, b E, we define the distance
Loos Symmetric Cones. Jimmie Lawson Louisiana State University. July, 2018
 Louisiana State University July, 2018 Dedication I would like to dedicate this talk to Joachim Hilgert, whose 60th birthday we celebrate at this conference and with whom I researched and wrote a big blue
Louisiana State University July, 2018 Dedication I would like to dedicate this talk to Joachim Hilgert, whose 60th birthday we celebrate at this conference and with whom I researched and wrote a big blue
Math 396. Bijectivity vs. isomorphism
 Math 396. Bijectivity vs. isomorphism 1. Motivation Let f : X Y be a C p map between two C p -premanifolds with corners, with 1 p. Assuming f is bijective, we would like a criterion to tell us that f 1
Math 396. Bijectivity vs. isomorphism 1. Motivation Let f : X Y be a C p map between two C p -premanifolds with corners, with 1 p. Assuming f is bijective, we would like a criterion to tell us that f 1
HILBERT SPACES AND THE RADON-NIKODYM THEOREM. where the bar in the first equation denotes complex conjugation. In either case, for any x V define
 HILBERT SPACES AND THE RADON-NIKODYM THEOREM STEVEN P. LALLEY 1. DEFINITIONS Definition 1. A real inner product space is a real vector space V together with a symmetric, bilinear, positive-definite mapping,
HILBERT SPACES AND THE RADON-NIKODYM THEOREM STEVEN P. LALLEY 1. DEFINITIONS Definition 1. A real inner product space is a real vector space V together with a symmetric, bilinear, positive-definite mapping,
Analysis Comprehensive Exam Questions Fall 2008
 Analysis Comprehensive xam Questions Fall 28. (a) Let R be measurable with finite Lebesgue measure. Suppose that {f n } n N is a bounded sequence in L 2 () and there exists a function f such that f n (x)
Analysis Comprehensive xam Questions Fall 28. (a) Let R be measurable with finite Lebesgue measure. Suppose that {f n } n N is a bounded sequence in L 2 () and there exists a function f such that f n (x)
Generalized Pigeonhole Properties of Graphs and Oriented Graphs
 Europ. J. Combinatorics (2002) 23, 257 274 doi:10.1006/eujc.2002.0574 Available online at http://www.idealibrary.com on Generalized Pigeonhole Properties of Graphs and Oriented Graphs ANTHONY BONATO, PETER
Europ. J. Combinatorics (2002) 23, 257 274 doi:10.1006/eujc.2002.0574 Available online at http://www.idealibrary.com on Generalized Pigeonhole Properties of Graphs and Oriented Graphs ANTHONY BONATO, PETER
MATHS 730 FC Lecture Notes March 5, Introduction
 1 INTRODUCTION MATHS 730 FC Lecture Notes March 5, 2014 1 Introduction Definition. If A, B are sets and there exists a bijection A B, they have the same cardinality, which we write as A, #A. If there exists
1 INTRODUCTION MATHS 730 FC Lecture Notes March 5, 2014 1 Introduction Definition. If A, B are sets and there exists a bijection A B, they have the same cardinality, which we write as A, #A. If there exists
SENSITIVITY AND REGIONALLY PROXIMAL RELATION IN MINIMAL SYSTEMS
 SENSITIVITY AND REGIONALLY PROXIMAL RELATION IN MINIMAL SYSTEMS SONG SHAO, XIANGDONG YE AND RUIFENG ZHANG Abstract. A topological dynamical system is n-sensitive, if there is a positive constant such that
SENSITIVITY AND REGIONALLY PROXIMAL RELATION IN MINIMAL SYSTEMS SONG SHAO, XIANGDONG YE AND RUIFENG ZHANG Abstract. A topological dynamical system is n-sensitive, if there is a positive constant such that
1 Directional Derivatives and Differentiability
 Wednesday, January 18, 2012 1 Directional Derivatives and Differentiability Let E R N, let f : E R and let x 0 E. Given a direction v R N, let L be the line through x 0 in the direction v, that is, L :=
Wednesday, January 18, 2012 1 Directional Derivatives and Differentiability Let E R N, let f : E R and let x 0 E. Given a direction v R N, let L be the line through x 0 in the direction v, that is, L :=
Representations of moderate growth Paul Garrett 1. Constructing norms on groups
 (December 31, 2004) Representations of moderate growth Paul Garrett Representations of reductive real Lie groups on Banach spaces, and on the smooth vectors in Banach space representations,
(December 31, 2004) Representations of moderate growth Paul Garrett Representations of reductive real Lie groups on Banach spaces, and on the smooth vectors in Banach space representations,
(x, y) = d(x, y) = x y.
 1 Euclidean geometry 1.1 Euclidean space Our story begins with a geometry which will be familiar to all readers, namely the geometry of Euclidean space. In this first chapter we study the Euclidean distance
1 Euclidean geometry 1.1 Euclidean space Our story begins with a geometry which will be familiar to all readers, namely the geometry of Euclidean space. In this first chapter we study the Euclidean distance
On Equivariant Block Triangularization of Matrix Cocyles
 On Equivariant Block Triangularization of Matrix Cocyles Christopher Bose, Joseph Horan, Anthony Quas September 24, 24 Abstract The Multiplicative Ergodic Theorem shows that a real matrix cocycle is block
On Equivariant Block Triangularization of Matrix Cocyles Christopher Bose, Joseph Horan, Anthony Quas September 24, 24 Abstract The Multiplicative Ergodic Theorem shows that a real matrix cocycle is block
Topological properties of Z p and Q p and Euclidean models
 Topological properties of Z p and Q p and Euclidean models Samuel Trautwein, Esther Röder, Giorgio Barozzi November 3, 20 Topology of Q p vs Topology of R Both R and Q p are normed fields and complete
Topological properties of Z p and Q p and Euclidean models Samuel Trautwein, Esther Röder, Giorgio Barozzi November 3, 20 Topology of Q p vs Topology of R Both R and Q p are normed fields and complete
Compact operators on Banach spaces
 Compact operators on Banach spaces Jordan Bell jordan.bell@gmail.com Department of Mathematics, University of Toronto November 12, 2017 1 Introduction In this note I prove several things about compact
Compact operators on Banach spaces Jordan Bell jordan.bell@gmail.com Department of Mathematics, University of Toronto November 12, 2017 1 Introduction In this note I prove several things about compact
Chapter 3. Riemannian Manifolds - I. The subject of this thesis is to extend the combinatorial curve reconstruction approach to curves
 Chapter 3 Riemannian Manifolds - I The subject of this thesis is to extend the combinatorial curve reconstruction approach to curves embedded in Riemannian manifolds. A Riemannian manifold is an abstraction
Chapter 3 Riemannian Manifolds - I The subject of this thesis is to extend the combinatorial curve reconstruction approach to curves embedded in Riemannian manifolds. A Riemannian manifold is an abstraction
ERGODIC AVERAGES FOR INDEPENDENT POLYNOMIALS AND APPLICATIONS
 ERGODIC AVERAGES FOR INDEPENDENT POLYNOMIALS AND APPLICATIONS NIKOS FRANTZIKINAKIS AND BRYNA KRA Abstract. Szemerédi s Theorem states that a set of integers with positive upper density contains arbitrarily
ERGODIC AVERAGES FOR INDEPENDENT POLYNOMIALS AND APPLICATIONS NIKOS FRANTZIKINAKIS AND BRYNA KRA Abstract. Szemerédi s Theorem states that a set of integers with positive upper density contains arbitrarily
Rudiments of Ergodic Theory
 Rudiments of Ergodic Theory Zefeng Chen September 24, 203 Abstract In this note we intend to present basic ergodic theory. We begin with the notion of a measure preserving transformation. We then define
Rudiments of Ergodic Theory Zefeng Chen September 24, 203 Abstract In this note we intend to present basic ergodic theory. We begin with the notion of a measure preserving transformation. We then define
LINKED ALTERNATING FORMS AND LINKED SYMPLECTIC GRASSMANNIANS
 LINKED ALTERNATING FORMS AND LINKED SYMPLECTIC GRASSMANNIANS BRIAN OSSERMAN AND MONTSERRAT TEIXIDOR I BIGAS Abstract. Motivated by applications to higher-rank Brill-Noether theory and the Bertram-Feinberg-Mukai
LINKED ALTERNATING FORMS AND LINKED SYMPLECTIC GRASSMANNIANS BRIAN OSSERMAN AND MONTSERRAT TEIXIDOR I BIGAS Abstract. Motivated by applications to higher-rank Brill-Noether theory and the Bertram-Feinberg-Mukai
Semicontinuity of rank and nullity and some consequences
 Semicontinuity of rank and nullity and some consequences Andrew D Lewis 2009/01/19 Upper and lower semicontinuity Let us first define what we mean by the two versions of semicontinuity 1 Definition: (Upper
Semicontinuity of rank and nullity and some consequences Andrew D Lewis 2009/01/19 Upper and lower semicontinuity Let us first define what we mean by the two versions of semicontinuity 1 Definition: (Upper
Physical measures of discretizations of generic diffeomorphisms
 Ergod. Th. & Dynam. Sys. (2018), 38, 1422 1458 doi:10.1017/etds.2016.70 c Cambridge University Press, 2016 Physical measures of discretizations of generic diffeomorphisms PIERRE-ANTOINE GUIHÉNEUF Université
Ergod. Th. & Dynam. Sys. (2018), 38, 1422 1458 doi:10.1017/etds.2016.70 c Cambridge University Press, 2016 Physical measures of discretizations of generic diffeomorphisms PIERRE-ANTOINE GUIHÉNEUF Université
NAME: Mathematics 205A, Fall 2008, Final Examination. Answer Key
 NAME: Mathematics 205A, Fall 2008, Final Examination Answer Key 1 1. [25 points] Let X be a set with 2 or more elements. Show that there are topologies U and V on X such that the identity map J : (X, U)
NAME: Mathematics 205A, Fall 2008, Final Examination Answer Key 1 1. [25 points] Let X be a set with 2 or more elements. Show that there are topologies U and V on X such that the identity map J : (X, U)
3 (Due ). Let A X consist of points (x, y) such that either x or y is a rational number. Is A measurable? What is its Lebesgue measure?
 MA 645-4A (Real Analysis), Dr. Chernov Homework assignment 1 (Due ). Show that the open disk x 2 + y 2 < 1 is a countable union of planar elementary sets. Show that the closed disk x 2 + y 2 1 is a countable
MA 645-4A (Real Analysis), Dr. Chernov Homework assignment 1 (Due ). Show that the open disk x 2 + y 2 < 1 is a countable union of planar elementary sets. Show that the closed disk x 2 + y 2 1 is a countable
Spectrum for compact operators on Banach spaces
 Submitted to Journal of the Mathematical Society of Japan Spectrum for compact operators on Banach spaces By Luis Barreira, Davor Dragičević Claudia Valls (Received Nov. 22, 203) (Revised Jan. 23, 204)
Submitted to Journal of the Mathematical Society of Japan Spectrum for compact operators on Banach spaces By Luis Barreira, Davor Dragičević Claudia Valls (Received Nov. 22, 203) (Revised Jan. 23, 204)
SRB MEASURES FOR AXIOM A ENDOMORPHISMS
 SRB MEASURES FOR AXIOM A ENDOMORPHISMS MARIUSZ URBANSKI AND CHRISTIAN WOLF Abstract. Let Λ be a basic set of an Axiom A endomorphism on n- dimensional compact Riemannian manifold. In this paper, we provide
SRB MEASURES FOR AXIOM A ENDOMORPHISMS MARIUSZ URBANSKI AND CHRISTIAN WOLF Abstract. Let Λ be a basic set of an Axiom A endomorphism on n- dimensional compact Riemannian manifold. In this paper, we provide
Dynamical Systems 2, MA 761
 Dynamical Systems 2, MA 761 Topological Dynamics This material is based upon work supported by the National Science Foundation under Grant No. 9970363 1 Periodic Points 1 The main objects studied in the
Dynamical Systems 2, MA 761 Topological Dynamics This material is based upon work supported by the National Science Foundation under Grant No. 9970363 1 Periodic Points 1 The main objects studied in the
ASYMPTOTICALLY NONEXPANSIVE MAPPINGS IN MODULAR FUNCTION SPACES ABSTRACT
 ASYMPTOTICALLY NONEXPANSIVE MAPPINGS IN MODULAR FUNCTION SPACES T. DOMINGUEZ-BENAVIDES, M.A. KHAMSI AND S. SAMADI ABSTRACT In this paper, we prove that if ρ is a convex, σ-finite modular function satisfying
ASYMPTOTICALLY NONEXPANSIVE MAPPINGS IN MODULAR FUNCTION SPACES T. DOMINGUEZ-BENAVIDES, M.A. KHAMSI AND S. SAMADI ABSTRACT In this paper, we prove that if ρ is a convex, σ-finite modular function satisfying
FUNCTIONAL ANALYSIS LECTURE NOTES: COMPACT SETS AND FINITE-DIMENSIONAL SPACES. 1. Compact Sets
 FUNCTIONAL ANALYSIS LECTURE NOTES: COMPACT SETS AND FINITE-DIMENSIONAL SPACES CHRISTOPHER HEIL 1. Compact Sets Definition 1.1 (Compact and Totally Bounded Sets). Let X be a metric space, and let E X be
FUNCTIONAL ANALYSIS LECTURE NOTES: COMPACT SETS AND FINITE-DIMENSIONAL SPACES CHRISTOPHER HEIL 1. Compact Sets Definition 1.1 (Compact and Totally Bounded Sets). Let X be a metric space, and let E X be
MORE ON CONTINUOUS FUNCTIONS AND SETS
 Chapter 6 MORE ON CONTINUOUS FUNCTIONS AND SETS This chapter can be considered enrichment material containing also several more advanced topics and may be skipped in its entirety. You can proceed directly
Chapter 6 MORE ON CONTINUOUS FUNCTIONS AND SETS This chapter can be considered enrichment material containing also several more advanced topics and may be skipped in its entirety. You can proceed directly
Math 6455 Nov 1, Differential Geometry I Fall 2006, Georgia Tech
 Math 6455 Nov 1, 26 1 Differential Geometry I Fall 26, Georgia Tech Lecture Notes 14 Connections Suppose that we have a vector field X on a Riemannian manifold M. How can we measure how much X is changing
Math 6455 Nov 1, 26 1 Differential Geometry I Fall 26, Georgia Tech Lecture Notes 14 Connections Suppose that we have a vector field X on a Riemannian manifold M. How can we measure how much X is changing
REAL ANALYSIS LECTURE NOTES: 1.4 OUTER MEASURE
 REAL ANALYSIS LECTURE NOTES: 1.4 OUTER MEASURE CHRISTOPHER HEIL 1.4.1 Introduction We will expand on Section 1.4 of Folland s text, which covers abstract outer measures also called exterior measures).
REAL ANALYSIS LECTURE NOTES: 1.4 OUTER MEASURE CHRISTOPHER HEIL 1.4.1 Introduction We will expand on Section 1.4 of Folland s text, which covers abstract outer measures also called exterior measures).
JUHA KINNUNEN. Harmonic Analysis
 JUHA KINNUNEN Harmonic Analysis Department of Mathematics and Systems Analysis, Aalto University 27 Contents Calderón-Zygmund decomposition. Dyadic subcubes of a cube.........................2 Dyadic cubes
JUHA KINNUNEN Harmonic Analysis Department of Mathematics and Systems Analysis, Aalto University 27 Contents Calderón-Zygmund decomposition. Dyadic subcubes of a cube.........................2 Dyadic cubes
ALGEBRAICALLY TRIVIAL, BUT TOPOLOGICALLY NON-TRIVIAL MAP. Contents 1. Introduction 1
 ALGEBRAICALLY TRIVIAL, BUT TOPOLOGICALLY NON-TRIVIAL MAP HONG GYUN KIM Abstract. I studied the construction of an algebraically trivial, but topologically non-trivial map by Hopf map p : S 3 S 2 and a
ALGEBRAICALLY TRIVIAL, BUT TOPOLOGICALLY NON-TRIVIAL MAP HONG GYUN KIM Abstract. I studied the construction of an algebraically trivial, but topologically non-trivial map by Hopf map p : S 3 S 2 and a
COMMON COMPLEMENTS OF TWO SUBSPACES OF A HILBERT SPACE
 COMMON COMPLEMENTS OF TWO SUBSPACES OF A HILBERT SPACE MICHAEL LAUZON AND SERGEI TREIL Abstract. In this paper we find a necessary and sufficient condition for two closed subspaces, X and Y, of a Hilbert
COMMON COMPLEMENTS OF TWO SUBSPACES OF A HILBERT SPACE MICHAEL LAUZON AND SERGEI TREIL Abstract. In this paper we find a necessary and sufficient condition for two closed subspaces, X and Y, of a Hilbert
NOTES AND ERRATA FOR RECURRENCE AND TOPOLOGY. (τ + arg z) + 1
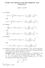 NOTES AND ERRATA FOR RECURRENCE AND TOPOLOGY JOHN M. ALONGI p.11 Replace ρ(t, z) = ρ(t, z) = p.11 Replace sin 2 z e τ ] 2 (τ + arg z) + 1 1 + z (e τ dτ. sin 2 (τ + arg z) + 1 z 2 z e τ ] 2 1 + z (e τ dτ.
NOTES AND ERRATA FOR RECURRENCE AND TOPOLOGY JOHN M. ALONGI p.11 Replace ρ(t, z) = ρ(t, z) = p.11 Replace sin 2 z e τ ] 2 (τ + arg z) + 1 1 + z (e τ dτ. sin 2 (τ + arg z) + 1 z 2 z e τ ] 2 1 + z (e τ dτ.
Measures. 1 Introduction. These preliminary lecture notes are partly based on textbooks by Athreya and Lahiri, Capinski and Kopp, and Folland.
 Measures These preliminary lecture notes are partly based on textbooks by Athreya and Lahiri, Capinski and Kopp, and Folland. 1 Introduction Our motivation for studying measure theory is to lay a foundation
Measures These preliminary lecture notes are partly based on textbooks by Athreya and Lahiri, Capinski and Kopp, and Folland. 1 Introduction Our motivation for studying measure theory is to lay a foundation
MATH 51H Section 4. October 16, Recall what it means for a function between metric spaces to be continuous:
 MATH 51H Section 4 October 16, 2015 1 Continuity Recall what it means for a function between metric spaces to be continuous: Definition. Let (X, d X ), (Y, d Y ) be metric spaces. A function f : X Y is
MATH 51H Section 4 October 16, 2015 1 Continuity Recall what it means for a function between metric spaces to be continuous: Definition. Let (X, d X ), (Y, d Y ) be metric spaces. A function f : X Y is
DEVELOPMENT OF MORSE THEORY
 DEVELOPMENT OF MORSE THEORY MATTHEW STEED Abstract. In this paper, we develop Morse theory, which allows us to determine topological information about manifolds using certain real-valued functions defined
DEVELOPMENT OF MORSE THEORY MATTHEW STEED Abstract. In this paper, we develop Morse theory, which allows us to determine topological information about manifolds using certain real-valued functions defined
