SYSTEMS. Russell Johnson
|
|
|
- Annabelle Bradford
- 5 years ago
- Views:
Transcription
1 NONAUTONOMOUS DYNAMICAL SYSTEMS Russell Johnson Università di Firenze Luca Zampogni Università di Perugia Thanks for collaboration to R. Fabbri, M. Franca, S. Novo, C. Núñez, R. Obaya, and many other colleagues. Dynamics and Differential Equations Dedicated to Prof. George R. Sell Minneapolis, 22 25/06 /
2 Introduction A nonautonomous dynamical system (NDS) can be of continuous or discrete type. Usually a continuous NDS is generated by the solutions of a nonautonomous differential equation x = f(t, x), t R, x B (1) where B is a Banach space. A discrete NDS is usually obtained by solving x n+1 = f n (x n ), n N, f n : B B. Let us consider the case (1) when B = R d. Suppose that each initial condition (t 0, x 0 ) gives rise to a unique global solution ϕ(t, t 0, x 0 ). For t R, set ˆτ t : R R d R R d : ˆτ t (t 0, x 0 ) = (t 0 +t, ϕ(t, t 0, x 0 )). Then {ˆτ t t R} is a one-parameter group of homeomorphisms, or dynamical system, on R R d. This is simple but already important. 2
3 If f satisfies recurrence conditions in t, one can often compactify time (Bebutov, Sell). That is, there exists a compact metric space Ω, a dynamical system {τ t } on Ω, and a function F : Ω R d R d such that the solutions ϕ(t, t 0, x 0 ) of x = F (τ t (ω), x) (1 ω ) define a dynamical system {ˆτ t } on Ω R d via ˆτ t (ω, x 0 ) = (τ t (ω), ϕ(t, ω, x 0 )). Moreover there is a point ω 0 Ω such that (1 ω0 ) coincides with (1 ω ). The upshot is that one can apply methods of dynamical systems theory to study the solutions of the family (1 ω ). 3
4 Topics of current interest include: Bifurcation Theory Oscillation Theory, Control Theory Spectral Theory of Ordinary Differential Equations Sturm-Liouville problems, Integrable systems Nonautonomous Functional Differential Equations Finite-Interval problems. 4
5 One needs a good linear theory to make inroads on these problems. In fact some are inherently linear, and one can study the others by the method of linearization along a solution. So, let us consider the linear nonautonomous system x = a(t)x, x R d. (2) Here a( ) takes values in the set M d of d d real matrices. Suppose that a( ) is bounded and uniformly continuous (for most purposes boundedness and measurability are enough). We assume that a( ) has some recurrence properties (e.g., almost periodicity, Birkhoff recurrence, chain recurrence,...). 5
6 One studies a constant coefficient system x = ax by making systematic use of the eigenvalues and generalized eigenspaces of a. Let us look for quantities which are related to the nonautonomous equation (2) and which are analogous to: (α) real parts of eigenvalues (β) generalized eigenspaces (γ) imaginary parts of eigenvalues. 6
7 Introduce the Bebutov hull (Ω, {τ t }) of a( ), and let A : Ω M d be the corresponding function. Consider the family x = A (τ t (ω)) x. (2 ω ) Let Φ ω (t) be the fundamental matrix solution of (2 ω ). One obtains a flow {ˆτ t } on Ω R d as follows: ˆτ t (ω, x) = (τ t (ω), Φ ω (t)x). This is a so-called skew-product flow. 7
8 (α) The notion of real part of an eigenvalue has two very useful generalizations to the nonautonomous case: Lyapunov exponents Dynamical (Sacker-Sell) spectrum. If ω Ω, the corresponding (maximal) Lyapunov exponent is β(ω) = lim sup t 1 t ln Φ ω(t). The existence of the limit and the properties of β( ) are studied in the Oseledets theory, of which more later. To define the dynamical spectrum, we introduce the concept of exponential dichotomy, or ED for short (Perron, Coppel, Palmer,...). 8
9 Definition 1 The family (2 ω ) admits an ED over Ω if there are constants K > 0, k > 0 and a continuous projection-valued function P : Ω M d : ω P ω = P 2 ω such that Φ ω (t)p ω Φ 1 ω (s) Ke k(t s), t s Φ ω (t)(i P ω )Φ 1 ω (s) Ke k(t s), t s. Thus an ED exists when the solution space Ω R d admits a hyperbolic splitting. Definition 2 A real number λ belongs to the dichotomy spectrum Σ of (2 ω ) if the translated family x = [ λi + A(τ t (ω))]x does not admit an ED over Ω. Clearly if A( ) reduces to a constant a, then Σ = {Rµ µ is an eigenvalue of a}. Sacker and Sell proved that, if (Ω, {τ t }) is chain recurrent, then Σ is a union of finitely many compact intervals. It is known that each Lyapunov exponent β(ω) lies in Σ. 9
10 (β) The concept of generalized eigenspace has two nonautonomous versions: the Oseledets bundles and the Sacker-Sell bundles (also Millionščikov and Selgrade). Oseledets Let µ be a {τ t }-ergodic measure on Ω (thus µ is indecomposable in a certain sense). Then Ω R d = W 1 W 2 W s where W 1,..., W s are µ-measurable, {ˆτ t }-invariant vector subbundles of Ω R d. Within each subbundle W i, all trajectories (τ t (ω), Φ ω (t)x 0 ) give rise to the same Lyapunov exponent (if x 0 0): β(ω, x 0 ) = β i = lim t ± 1 t ln Φ ω(t)x 0. 10
11 Sacker-Sell Let (Ω, {τ t }) be chain recurrent, and let Σ = [a 1, b 1 ]... [a r, b r ] be the spectrum. There is a decomposition Ω R d = W 1 W 2... W r where W 1,..., W r are continuous, {τ t }-invariant vector subbundles of Ω R d. For each i = 1, 2,..., r, the dynamical spectrum of ( W i, {ˆτ t }) is [a i, b i ]. An Oseledets bundles is always contained in a Sacker-Sell bundle; the reverse inclusion need not hold. 11
12 (γ) In the case of a constant-coefficient system, one views the imaginary part of an eigenvalue as the source of rotation of certain solutions of the system. This notion can be rendered concrete for certain types of families (2 ω ) via the concept of rotation number. Let us briefly discuss the rotation number in the context of two-dimensional families (2 ω ). Introduce polar coordinates r 2 = x x2 2, θ = arctan x 2 x 1 and write out the θ-equation θ = g(τ t (ω), θ) =... Definition 3 Let µ be an ergodic measure on Ω. The rotation number is α = lim t θ(t) t where θ(t) is the solution of the θ-equation. 12
13 It is known that the limit exists for µ-almost all ω Ω (it is easy to see that it is insensitive to the initial value θ(0)). One obtains a quantity which is very useful in the study of the spectral theory of ordinary differential operators, for example the Schrödinger operator (in one space dimension), Sturm-Liouville operators, the AKNS operator, and operators of Atkinson type. The initial work involved in applying the rotation number to these operators was carried out by J.-Moser, Kotani, and other scientists. A higher-dimensional version on the rotation number has been developed for linear Hamiltonian systems, and has been applied to spectral problems of Atkinson type and to control problems (J., J.-Nerurkar, Novo-Núñez- Obaya,... ). These matters have been studied by Fabbri, J., Novo, Núñez, Obaya; see the recent book of these authors. 13
14 Let us now consider an application of the basic tools of Nonautonomous Dynamics to the 1-D Schrödinger operator. We will discuss questions concerning the generalized reflectionless Schrödinger potentials (Lundina, Marchenko, Kotani). Let q : R R be a bounded continuous function. Introduce the differential expression L = d2 dx 2 + q(x). Then L determines an unbounded self-adjoint operator (Schrödinger operator) on L 2 (R). It also determines two half-line operators L ± defined on L 2 [0, ± ] respectively, via the Dirichlet boundary condition in x = 0: L ± ϕ = λϕ ϕ(0) = 0. 14
15 EXAMPLE. Consider the soliton potential q(x)=-2 d2 ln det(i + A(x)) (3) dx2 where A(x) = (A ij (x)) n i,j=1 and A ij (x) = li l j η i + η j e (η i+η j )x. Here l 1,..., l n and η 1,..., η n are positive numbers. If q(x) is of the form (3), then the spectrum of the operator L consists of the half-line [0, ) (where it is absolutely continuous) together with the finitely many eigenvalues η 2 1,..., η2 n.
16 A soliton potential has a very important property. Let g(x, y, λ) be the Green s function (integral kernel) of (L λ) 1 for λ in the resolvent of L. Then Rg(x, x, λ + i0) = 0 (λ > 0, x R), (4) where λ+i0 means the limit of g(x, x, λ+iε) as ε decreases to zero. One says that q (or L) is reflectionless. 15
17 To summarize: a soliton potential is reflectionless in (0, ), and has finitely many eigenvalues in (, 0). Let c < 0, and set { R c = cls q q is a soliton potential, and the eigenvalues of L = d2 + q(x) lie in (c, 0) dx2 Here the closure is taken in the topology of uniform convergence on compact subsets of R. One says that R c consists of generalized reflectionless Schrödinger potentials. Let GR = R c. c<0 }. Theorem (Lundina, 1985) The set R c is compact (in the compact-open topology). 16
18 There is a well-known connection between the Schrödinger operator L and the Korteweg-de Vries equation u t = 3u u x 1 3 u 2 x 3, u(0, x) = q(x). It was proved by Gardner-Green-Kruskal-Miura that a regular solution u(t, x) of the K-dV equation has the property that the family of Schrödinger operators L t = d2 + u(t, x) dx2 is isospectral (in L 2 (R)). This fact can be used to determine explicit solutions of the K- dv equation in certain cases (including that of soliton potentials). 17
19 Let q be a generalized reflectionless Schrödinger potential, that is q R c = GR. Marchenko c<0 tried to prove in 1991 that each such q gives rise to a regular solution of the K-dV equation. Along the way he worked out a nice parametrization of the elements in GR. About ten years later Kotani succeeded in proving that indeed each q GR gives rise to a solution u(t, x) of the K-dV equation, which in fact is meromorphic in the entire complex (t, x) space. He used the theory of the infinite-dimensional Grassmann-type space Gr 2, which is due to Sato-Segal-Wilson. 18
20 From now on we set c = 1 and unify R = R c = R 1. We will study certain compact subsets of R which are invariant under the natural translation flow, defined by τ x (q)( ) = q(x + ) (x R, q R). Let = a 0 < b 0 < a j < b j 0 (j 1), where b 0 1 and {(a j, b j ) j 1} are pairwise disjoint nonempty open intervals. Set then set E = R \ j=0 (a j, b j ), Q E = {q R L q = d2 dx 2 + q(x) has spectrum E and is reflectionless} By reflectionless we mean that the appropriate generalization of condition (2) holds, namely Rg q (x, x, λ + i0) = 0 (a.a λ E, all x R). (2 bis ) 19
21 Note: condition (2 bis ) holds on 0 < λ < for every q R. However if q R and L q has spectrum E, it need not be the case that (2 bis ) holds on the set E [ 1, 0]. Proposition Let E and Q E be as above. Suppose also that E has locally positive measure. Then Q E is compact and translation invariant. At this point the methods of Nonautonomous Dynamics become relevant. Introduce the set of divisors D E = {(y j, ε j ) y j [a j, b j ], ε j = ±1, 1 j < }. The points (a j, ±1) and (b j, ±1) are identified, so D E is a product of countably many circles. 20
22 Now we want to define a map π : Q E D E which will provide information about Q E and about the flow (Q E, {τ x }). To do this we need to carry out a preliminary discussion. Let q Q E. Consider the map g q : λ g g (0, 0, λ), which is defined and meromorphic on Ω E = C \ E. The map g q ( ) is strictly monotone increasing on each interval (a j, b j ). There are three cases to consider. (i) The map g q has a (unique) zero µ j (a j, b j ). (ii) The map g q is positive in (a j, b j ); in this case set µ j = a j. (iii) The map g q is negative in (a j, b j ); in this case set µ j = b j. 21
23 We define a divisor d q = {(µ 1, ε 1 ),..., (µ j, ε j ),... } D E where the signs ε j are determined using the Weyl m-functions m ± (λ). Recall that these functions are defined as follows: if λ C \ E, there are nonzero solutions ϕ ± (x, λ) L 2 [0, ± ) of Lϕ = λϕ. Set Then sign Im ±(λ) Iλ m ± (λ) = ϕ ± (0, λ) ϕ ± (0, λ). = ±1 if Iλ 0, and also sign dm ±(λ) = ±1 dλ if λ R \ E. (5) It turns out that 1 g q (λ) = m (λ) m + (λ). So if g q (λ) = 0 and a j < λ < b j then either m (λ) or m + (λ) has a pole at λ, and it follows from (5) that at most one of m ± (λ) has a pole at λ. 22
24 Now return to the definition of the divisor d q (the pole divisor). If µ j (a j, b j ), set ε j = 1 if m + ( ) has a pole at µ j, and ε j = 1 if m ( ) has a pole at µ j. If µ j = a j or µ j = b j then there is no need to worry about the sign ε j, since (a j, ±1) and (b j, ±1) are identified. So we obtain a map π : Q E D E : q d q = = {(µ j, ε j ) j 1}. We also obtain a pole motion : let τ x (q) = q(x+ ) be the translation, and set τ x (d q ) = {(µ j (x), ε j (x)) j 1} := d τx (q). It is not a priori clear that we obtain a flow on D E from this construction. This is because trajectories could conceivably cross, and in any case it is not clear that π is continuous. 23
25 The idea now is to produce examples via a study of the map π. The starting point is the following result. Theorem Let E R be a closed set of the form E = R \ j=0 (a j, b j ), where = a 0 < b 0 < a j < b j 0 (j 1), where b 0 1 and the closed intervals [a j, b j ] are pairwise disjoint. Suppose that E has locally positive measure. Then (a) The map π : Q E D E : q {(µ 1, ε 1 ),..., (µ j, ε j ),... } is continuous and surjective. (b) If the half-line operators L ± have purely absolutely continuous spectrum for all q Q E, then π is also injective, hence is a homeomorphism. 24
26 One can use this theorem to construct examples of sets E for which Q E has interesting structure. Example 1 There exists a closed set E R, which satisfies the hypotheses of the Theorem, such that Q E contains a minimal set M which is almost automorphic in the sense of Bochner-Veech, but is not Bohr almost periodic. We explain the terminology. A minimal flow {M, {τ x }) is Bohr almost periodic if there is a metric d on M, which is compatible with its topology, such that the flow {τ x } is isometric: d(τ x (q 1 ), τ x (q 2 )) = d(q 1, q 2 ) for all q 1, q 2 M and all x R. A minimal flow (M, {τ x }) is almost automorphic if there exists an almost periodic flow (M 0, {τ x }) and a flow homomorphism h : M M 0 such that h 1 (q 0 ) is a singleton for some q 0 M 0. The almost periodic minimal set of the example turns out to be the character group J E of the infinitely connected domain Ω E = C \ E. The domain Ω E is of Parreau-Widom (PW) type. 25
27 This example contradicts the Kotani-Last conjecture, according to which if the operators L ± all have purely a.c. spectrum for all q Q E, then Q E should consist entirely of Bohr almost periodic potentials. For other examples: Avila, Damanik-Yuditskii. 26
28 The Character Group of a Parreau-Widom domain The discussion is based on work by Sodin- Yuditskii, Volberg-Yuditskii. Let E = R \ j=0 (a j, b j ) where a 0 =, 1 b 0 < 0 and the nonempty open intervals (a j, b j ) are pairwise disjoint and contained in (b 0, 0). We define the character group J E of the domain Ω E = C \ E. For this, let c j (j = 1, 2,... ) be a closed simple curve in Ω E which contains λ 0 = 2, passes through (a j, b j ), and is orthogonal to R. Let c j be oriented clockwise. The fundamental group Γ E is generated by these closed curves. Let J E be the set of all characters on Γ E, that is, the set of all group homomorphisms from Γ E to the unit circle S 1 = R/Z. One puts a group operation on J E via pointwise addition of pairs α 1, α 2 J E : (α 1 + α 2 )(γ) = α 1 (γ) + α 2 (γ) R/Z. Then J E is a compact Abelian topological group. 27
29 Suppose now that E has locally positive measure. We define a particular character δ J E as follows. Let ν be an ergodic measure on Q E, and let w ν be the ν-floquet exponent. Set δ(c j ) = ρ j π R/Z where ρ j = ρ ν (aj,b j ) is the value of the ν- rotation number on (a j, b j ). This character defines a translation flow {ˆτ x } on J E, as follows: ˆτ x (α) = α + δx (α J E, x R). 28
30 Next, introduce an Abel map from the set of divisors D E to the character group J E, as follows. Let ω(λ, F ) be the harmonic measure of a subset F E with respect to the domain Ω E. This means that ω(, F ) solves the Laplace equation ω = 0 in Ω E, and has boundary value equal to the characteristic function of F. Let d = {(y 1, ε 1 ),..., (y j, ε j ),... } D E, and define A(d)(γ k ) = 1 2 bj ε j j=1 a j ω(dλ, E k ) R/Z (6) where E k is the part of E to the right of b k, that is E k = E [b k, ). There is no a priori reason to think that the series on the right-hand side of (6) converges. It does converge if Ω E is a Parreau-Widom domain. 29
31 To explain what this means, we introduce the Green s function G(λ, λ 0 ) of Ω E with logarithmic pole at λ 0 = 2. We assume that Ω E is regular for the Dirichlet problem, which means that G assumes continuously the boundary value zero at each point of E (which is the boundary of Ω E ). Further, let {c j j 1} be the points in Ω E where the gradient G(c j ) = 0; there is exactly one such point in each interval (a j, b j ) and there are no other such points in Ω E. One now says that Ω E is of Parreau-Widom type if j=1 G(c j ) <. 30
32 Theorem (Gesztesy-Yuditskii). Suppose that Ω E is of Parreau-Widom type. Then the Abel map A is well-defined, continuous and surjective, and maps {τ x }-orbits in D E onto {ˆτ x }-orbits in J E. Moreover, there is a right inverse I : J E D E, that is, a map such that A I(α) = α for all α J E. This map I need not be continuous (it is if E is homogeneous in the sense on Carlesen). 31
33 To create sets E and corresponding domains Ω E as in Example 1, we arrange that E satisfies all the hypotheses of the first theorem and is also of Parreau-Widom type. We arrange that the δ-translation flow ˆτ x (α) = α + δx is minimal on J E. We further arrange that the right inverse I : J E D E satisfies the following conditions I is not continuous; I(α + δx) = τ x (I(α)) (α J E, x R) I is of the first Baire class. The last condition means that I(α) = lim I N(α) N (α J E ) where each map I N : J E D E is continuous. This implies that I has a residual set of continuity points. This in turn implies that M = cls{i(α) α J E } D E is an almost automorphic, non-almost periodic minimal subset of D E. 32
34 Example 2 This example will consist of a set E of the the type under discussion for which the divisor map is not injective. Let E = [ 1, ) \ n=1 (a n, b n ), where a = a 0 = 3/4, b = b 0 = 1/2, 0 > b 1 > a 1 > a 2 > b 2 >... and where b j, a j b = 1/2. Note that the interval [ 1, 3/4] E. Let Q E be the corresponding set of potentials. Choose an ergodic measure ν on Q E. (i) One can choose the intervals (a j, b j ) so that b = 1/2 is irregular in the sense of potential theory. This implies that the ν-lyapunov exponent β ν (λ) > 0. (ii) Use the Oseledets Theorem to see that for ν-a.a. q Q E the equation L q ϕ = ( d 2 dx 2 + q(x) ) ϕ = bϕ admits solutions ϕ ± (x) which decay exponentially at x = ±. 33
35 Using the fact that L q ϕ = bϕ is oscillatory, we can find q Q E so that the Dirichlet problem L q ϕ = bϕ ϕ(0) = 0 admits a nonzero solution in L 2 [0, ). (iii) Introduce the spectral measures σ ± of L ± q : σ ± (dλ) = σ ±,ac (dλ) + σ ±,d (dλ) + r ± b λ Choose q Q E so that r + > 0, this is possible by point (ii). If r + 0, r 0, and r + + r = r + + r, then one can use the Marchenko parametrization of GR (and bypass the less informative Gel fand-levitan theory) to show that there exists q Q E with spectral measures σ ± (dλ) = σ ±,ac (dλ) + σ ±,d (dλ) + r ± b λ. Since r + > 0 one has that π is not injective. 34
Remarks concerning the Lyapunov exponents of linear cocycles
 Rend. Istit. Mat. Univ. Trieste Volume 44 (202), 89 6 Remarks concerning the Lyapunov exponents of linear cocycles Russell Johnson and Luca Zampogni Dedicated to Professor Fabio Zanolin on the occasion
Rend. Istit. Mat. Univ. Trieste Volume 44 (202), 89 6 Remarks concerning the Lyapunov exponents of linear cocycles Russell Johnson and Luca Zampogni Dedicated to Professor Fabio Zanolin on the occasion
Infinite gap Jacobi matrices
 Infinite gap Jacobi matrices Jacob Stordal Christiansen Centre for Mathematical Sciences, Lund University Spectral Theory of Orthogonal Polynomials Master class by Barry Simon Centre for Quantum Geometry
Infinite gap Jacobi matrices Jacob Stordal Christiansen Centre for Mathematical Sciences, Lund University Spectral Theory of Orthogonal Polynomials Master class by Barry Simon Centre for Quantum Geometry
ALMOST AUTOMORPHIC AND ALMOST PERIODIC DYNAMICS IN SKEW-PRODUCT SEMIFLOWS. Dedicated to Professor R. Ellis on the Occasion of His 70th Birthday
 ALMOST AUTOMORPHIC AND ALMOST PERIODIC DYNAMICS IN SKEW-PRODUCT SEMIFLOWS Dedicated to Professor R. Ellis on the Occasion of His 70th Birthday Part I. Almost Automorphy and Almost Periodicity by Yingfei
ALMOST AUTOMORPHIC AND ALMOST PERIODIC DYNAMICS IN SKEW-PRODUCT SEMIFLOWS Dedicated to Professor R. Ellis on the Occasion of His 70th Birthday Part I. Almost Automorphy and Almost Periodicity by Yingfei
On the dynamics of strongly tridiagonal competitive-cooperative system
 On the dynamics of strongly tridiagonal competitive-cooperative system Chun Fang University of Helsinki International Conference on Advances on Fractals and Related Topics, Hong Kong December 14, 2012
On the dynamics of strongly tridiagonal competitive-cooperative system Chun Fang University of Helsinki International Conference on Advances on Fractals and Related Topics, Hong Kong December 14, 2012
Dynamical Systems and Ergodic Theory PhD Exam Spring Topics: Topological Dynamics Definitions and basic results about the following for maps and
 Dynamical Systems and Ergodic Theory PhD Exam Spring 2012 Introduction: This is the first year for the Dynamical Systems and Ergodic Theory PhD exam. As such the material on the exam will conform fairly
Dynamical Systems and Ergodic Theory PhD Exam Spring 2012 Introduction: This is the first year for the Dynamical Systems and Ergodic Theory PhD exam. As such the material on the exam will conform fairly
Analysis Preliminary Exam Workshop: Hilbert Spaces
 Analysis Preliminary Exam Workshop: Hilbert Spaces 1. Hilbert spaces A Hilbert space H is a complete real or complex inner product space. Consider complex Hilbert spaces for definiteness. If (, ) : H H
Analysis Preliminary Exam Workshop: Hilbert Spaces 1. Hilbert spaces A Hilbert space H is a complete real or complex inner product space. Consider complex Hilbert spaces for definiteness. If (, ) : H H
16 1 Basic Facts from Functional Analysis and Banach Lattices
 16 1 Basic Facts from Functional Analysis and Banach Lattices 1.2.3 Banach Steinhaus Theorem Another fundamental theorem of functional analysis is the Banach Steinhaus theorem, or the Uniform Boundedness
16 1 Basic Facts from Functional Analysis and Banach Lattices 1.2.3 Banach Steinhaus Theorem Another fundamental theorem of functional analysis is the Banach Steinhaus theorem, or the Uniform Boundedness
A Biography of Russell A. Johnson
 J Dyn Diff Equat (2011) 23:397 404 DOI 10.1007/s10884-011-9221-6 A Biography of Russell A. Johnson George R. Sell Yingfei Yi Published online: 24 August 2011 Springer Science+Business Media, LLC 2011 Russell
J Dyn Diff Equat (2011) 23:397 404 DOI 10.1007/s10884-011-9221-6 A Biography of Russell A. Johnson George R. Sell Yingfei Yi Published online: 24 August 2011 Springer Science+Business Media, LLC 2011 Russell
Ergodic Theory. Constantine Caramanis. May 6, 1999
 Ergodic Theory Constantine Caramanis ay 6, 1999 1 Introduction Ergodic theory involves the study of transformations on measure spaces. Interchanging the words measurable function and probability density
Ergodic Theory Constantine Caramanis ay 6, 1999 1 Introduction Ergodic theory involves the study of transformations on measure spaces. Interchanging the words measurable function and probability density
Lecture Notes Introduction to Ergodic Theory
 Lecture Notes Introduction to Ergodic Theory Tiago Pereira Department of Mathematics Imperial College London Our course consists of five introductory lectures on probabilistic aspects of dynamical systems,
Lecture Notes Introduction to Ergodic Theory Tiago Pereira Department of Mathematics Imperial College London Our course consists of five introductory lectures on probabilistic aspects of dynamical systems,
ON ALMOST AUTOMORPHIC OSCILLATIONS
 ON ALMOST AUTOMORPHIC OSCILLATIONS YINGFEI YI Abstract. Almost automorphic dynamics have been given a notable amount of attention in recent years with respect to the study of almost periodically forced
ON ALMOST AUTOMORPHIC OSCILLATIONS YINGFEI YI Abstract. Almost automorphic dynamics have been given a notable amount of attention in recent years with respect to the study of almost periodically forced
Remarks on nonautonomous bifurcation theory
 Rend. Istit. Mat. Univ. Trieste Volume 49 (2017), 215 243 DOI: 10.13137/2464-8728/16214 Remarks on nonautonomous bifurcation theory Matteo Franca and Russell Johnson Dedicated to 75th birthday of Professor
Rend. Istit. Mat. Univ. Trieste Volume 49 (2017), 215 243 DOI: 10.13137/2464-8728/16214 Remarks on nonautonomous bifurcation theory Matteo Franca and Russell Johnson Dedicated to 75th birthday of Professor
A Minimal Uncertainty Product for One Dimensional Semiclassical Wave Packets
 A Minimal Uncertainty Product for One Dimensional Semiclassical Wave Packets George A. Hagedorn Happy 60 th birthday, Mr. Fritz! Abstract. Although real, normalized Gaussian wave packets minimize the product
A Minimal Uncertainty Product for One Dimensional Semiclassical Wave Packets George A. Hagedorn Happy 60 th birthday, Mr. Fritz! Abstract. Although real, normalized Gaussian wave packets minimize the product
Physical measures of discretizations of generic diffeomorphisms
 Ergod. Th. & Dynam. Sys. (2018), 38, 1422 1458 doi:10.1017/etds.2016.70 c Cambridge University Press, 2016 Physical measures of discretizations of generic diffeomorphisms PIERRE-ANTOINE GUIHÉNEUF Université
Ergod. Th. & Dynam. Sys. (2018), 38, 1422 1458 doi:10.1017/etds.2016.70 c Cambridge University Press, 2016 Physical measures of discretizations of generic diffeomorphisms PIERRE-ANTOINE GUIHÉNEUF Université
On SL(2, R) valued cocycles of Hölder class with zero exponent over Kronecker flows
 On SL(2, R) valued cocycles of Hölder class with zero exponent over Kronecker flows Russell Johnson Departimento di Sistemi e Informatica Universita di Firenze, Firenze 539, Italy and Mahesh Nerurkar Department
On SL(2, R) valued cocycles of Hölder class with zero exponent over Kronecker flows Russell Johnson Departimento di Sistemi e Informatica Universita di Firenze, Firenze 539, Italy and Mahesh Nerurkar Department
LECTURE 10: THE ATIYAH-GUILLEMIN-STERNBERG CONVEXITY THEOREM
 LECTURE 10: THE ATIYAH-GUILLEMIN-STERNBERG CONVEXITY THEOREM Contents 1. The Atiyah-Guillemin-Sternberg Convexity Theorem 1 2. Proof of the Atiyah-Guillemin-Sternberg Convexity theorem 3 3. Morse theory
LECTURE 10: THE ATIYAH-GUILLEMIN-STERNBERG CONVEXITY THEOREM Contents 1. The Atiyah-Guillemin-Sternberg Convexity Theorem 1 2. Proof of the Atiyah-Guillemin-Sternberg Convexity theorem 3 3. Morse theory
Spectrum for compact operators on Banach spaces
 Submitted to Journal of the Mathematical Society of Japan Spectrum for compact operators on Banach spaces By Luis Barreira, Davor Dragičević Claudia Valls (Received Nov. 22, 203) (Revised Jan. 23, 204)
Submitted to Journal of the Mathematical Society of Japan Spectrum for compact operators on Banach spaces By Luis Barreira, Davor Dragičević Claudia Valls (Received Nov. 22, 203) (Revised Jan. 23, 204)
Analysis Comprehensive Exam Questions Fall 2008
 Analysis Comprehensive xam Questions Fall 28. (a) Let R be measurable with finite Lebesgue measure. Suppose that {f n } n N is a bounded sequence in L 2 () and there exists a function f such that f n (x)
Analysis Comprehensive xam Questions Fall 28. (a) Let R be measurable with finite Lebesgue measure. Suppose that {f n } n N is a bounded sequence in L 2 () and there exists a function f such that f n (x)
NOTES AND ERRATA FOR RECURRENCE AND TOPOLOGY. (τ + arg z) + 1
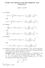 NOTES AND ERRATA FOR RECURRENCE AND TOPOLOGY JOHN M. ALONGI p.11 Replace ρ(t, z) = ρ(t, z) = p.11 Replace sin 2 z e τ ] 2 (τ + arg z) + 1 1 + z (e τ dτ. sin 2 (τ + arg z) + 1 z 2 z e τ ] 2 1 + z (e τ dτ.
NOTES AND ERRATA FOR RECURRENCE AND TOPOLOGY JOHN M. ALONGI p.11 Replace ρ(t, z) = ρ(t, z) = p.11 Replace sin 2 z e τ ] 2 (τ + arg z) + 1 1 + z (e τ dτ. sin 2 (τ + arg z) + 1 z 2 z e τ ] 2 1 + z (e τ dτ.
CHAPTER 6. Representations of compact groups
 CHAPTER 6 Representations of compact groups Throughout this chapter, denotes a compact group. 6.1. Examples of compact groups A standard theorem in elementary analysis says that a subset of C m (m a positive
CHAPTER 6 Representations of compact groups Throughout this chapter, denotes a compact group. 6.1. Examples of compact groups A standard theorem in elementary analysis says that a subset of C m (m a positive
Linear ODEs. Existence of solutions to linear IVPs. Resolvent matrix. Autonomous linear systems
 Linear ODEs p. 1 Linear ODEs Existence of solutions to linear IVPs Resolvent matrix Autonomous linear systems Linear ODEs Definition (Linear ODE) A linear ODE is a differential equation taking the form
Linear ODEs p. 1 Linear ODEs Existence of solutions to linear IVPs Resolvent matrix Autonomous linear systems Linear ODEs Definition (Linear ODE) A linear ODE is a differential equation taking the form
Ergodic Properties and Rotation Number for Linear Hamiltonian Systems*
 journal of differential equations 48, 4885 (998) article no. DE983469 Ergodic Properties and Rotation Number for Linear Hamiltonian Systems* Sylvia Novo, Carmen Nu n~ ez, and Rafael Obaya Departamento
journal of differential equations 48, 4885 (998) article no. DE983469 Ergodic Properties and Rotation Number for Linear Hamiltonian Systems* Sylvia Novo, Carmen Nu n~ ez, and Rafael Obaya Departamento
CHAPTER V DUAL SPACES
 CHAPTER V DUAL SPACES DEFINITION Let (X, T ) be a (real) locally convex topological vector space. By the dual space X, or (X, T ), of X we mean the set of all continuous linear functionals on X. By the
CHAPTER V DUAL SPACES DEFINITION Let (X, T ) be a (real) locally convex topological vector space. By the dual space X, or (X, T ), of X we mean the set of all continuous linear functionals on X. By the
THREE ZUTOT ELI GLASNER AND BENJAMIN WEISS
 THREE ZUTOT ELI GLASNER AND BENJAMIN WEISS Abstract. Three topics in dynamical systems are discussed. In the first two sections we solve some open problems concerning, respectively, Furstenberg entropy
THREE ZUTOT ELI GLASNER AND BENJAMIN WEISS Abstract. Three topics in dynamical systems are discussed. In the first two sections we solve some open problems concerning, respectively, Furstenberg entropy
8 Periodic Linear Di erential Equations - Floquet Theory
 8 Periodic Linear Di erential Equations - Floquet Theory The general theory of time varying linear di erential equations _x(t) = A(t)x(t) is still amazingly incomplete. Only for certain classes of functions
8 Periodic Linear Di erential Equations - Floquet Theory The general theory of time varying linear di erential equations _x(t) = A(t)x(t) is still amazingly incomplete. Only for certain classes of functions
The uniformization theorem
 1 The uniformization theorem Thurston s basic insight in all four of the theorems discussed in this book is that either the topology of the problem induces an appropriate geometry or there is an understandable
1 The uniformization theorem Thurston s basic insight in all four of the theorems discussed in this book is that either the topology of the problem induces an appropriate geometry or there is an understandable
An Inverse Problem for the Matrix Schrödinger Equation
 Journal of Mathematical Analysis and Applications 267, 564 575 (22) doi:1.16/jmaa.21.7792, available online at http://www.idealibrary.com on An Inverse Problem for the Matrix Schrödinger Equation Robert
Journal of Mathematical Analysis and Applications 267, 564 575 (22) doi:1.16/jmaa.21.7792, available online at http://www.idealibrary.com on An Inverse Problem for the Matrix Schrödinger Equation Robert
SYMPLECTIC GEOMETRY: LECTURE 5
 SYMPLECTIC GEOMETRY: LECTURE 5 LIAT KESSLER Let (M, ω) be a connected compact symplectic manifold, T a torus, T M M a Hamiltonian action of T on M, and Φ: M t the assoaciated moment map. Theorem 0.1 (The
SYMPLECTIC GEOMETRY: LECTURE 5 LIAT KESSLER Let (M, ω) be a connected compact symplectic manifold, T a torus, T M M a Hamiltonian action of T on M, and Φ: M t the assoaciated moment map. Theorem 0.1 (The
Research Statement. Jayadev S. Athreya. November 7, 2005
 Research Statement Jayadev S. Athreya November 7, 2005 1 Introduction My primary area of research is the study of dynamics on moduli spaces. The first part of my thesis is on the recurrence behavior of
Research Statement Jayadev S. Athreya November 7, 2005 1 Introduction My primary area of research is the study of dynamics on moduli spaces. The first part of my thesis is on the recurrence behavior of
Nonlinear Control Lecture 5: Stability Analysis II
 Nonlinear Control Lecture 5: Stability Analysis II Farzaneh Abdollahi Department of Electrical Engineering Amirkabir University of Technology Fall 2010 Farzaneh Abdollahi Nonlinear Control Lecture 5 1/41
Nonlinear Control Lecture 5: Stability Analysis II Farzaneh Abdollahi Department of Electrical Engineering Amirkabir University of Technology Fall 2010 Farzaneh Abdollahi Nonlinear Control Lecture 5 1/41
Tame definable topological dynamics
 Tame definable topological dynamics Artem Chernikov (Paris 7) Géométrie et Théorie des Modèles, 4 Oct 2013, ENS, Paris Joint work with Pierre Simon, continues previous work with Anand Pillay and Pierre
Tame definable topological dynamics Artem Chernikov (Paris 7) Géométrie et Théorie des Modèles, 4 Oct 2013, ENS, Paris Joint work with Pierre Simon, continues previous work with Anand Pillay and Pierre
B 1 = {B(x, r) x = (x 1, x 2 ) H, 0 < r < x 2 }. (a) Show that B = B 1 B 2 is a basis for a topology on X.
 Math 6342/7350: Topology and Geometry Sample Preliminary Exam Questions 1. For each of the following topological spaces X i, determine whether X i and X i X i are homeomorphic. (a) X 1 = [0, 1] (b) X 2
Math 6342/7350: Topology and Geometry Sample Preliminary Exam Questions 1. For each of the following topological spaces X i, determine whether X i and X i X i are homeomorphic. (a) X 1 = [0, 1] (b) X 2
Aliprantis, Border: Infinite-dimensional Analysis A Hitchhiker s Guide
 aliprantis.tex May 10, 2011 Aliprantis, Border: Infinite-dimensional Analysis A Hitchhiker s Guide Notes from [AB2]. 1 Odds and Ends 2 Topology 2.1 Topological spaces Example. (2.2) A semimetric = triangle
aliprantis.tex May 10, 2011 Aliprantis, Border: Infinite-dimensional Analysis A Hitchhiker s Guide Notes from [AB2]. 1 Odds and Ends 2 Topology 2.1 Topological spaces Example. (2.2) A semimetric = triangle
Spectral theory for compact operators on Banach spaces
 68 Chapter 9 Spectral theory for compact operators on Banach spaces Recall that a subset S of a metric space X is precompact if its closure is compact, or equivalently every sequence contains a Cauchy
68 Chapter 9 Spectral theory for compact operators on Banach spaces Recall that a subset S of a metric space X is precompact if its closure is compact, or equivalently every sequence contains a Cauchy
Estimates for the resolvent and spectral gaps for non self-adjoint operators. University Bordeaux
 for the resolvent and spectral gaps for non self-adjoint operators 1 / 29 Estimates for the resolvent and spectral gaps for non self-adjoint operators Vesselin Petkov University Bordeaux Mathematics Days
for the resolvent and spectral gaps for non self-adjoint operators 1 / 29 Estimates for the resolvent and spectral gaps for non self-adjoint operators Vesselin Petkov University Bordeaux Mathematics Days
Isomorphisms between pattern classes
 Journal of Combinatorics olume 0, Number 0, 1 8, 0000 Isomorphisms between pattern classes M. H. Albert, M. D. Atkinson and Anders Claesson Isomorphisms φ : A B between pattern classes are considered.
Journal of Combinatorics olume 0, Number 0, 1 8, 0000 Isomorphisms between pattern classes M. H. Albert, M. D. Atkinson and Anders Claesson Isomorphisms φ : A B between pattern classes are considered.
Dynamical Systems 2, MA 761
 Dynamical Systems 2, MA 761 Topological Dynamics This material is based upon work supported by the National Science Foundation under Grant No. 9970363 1 Periodic Points 1 The main objects studied in the
Dynamical Systems 2, MA 761 Topological Dynamics This material is based upon work supported by the National Science Foundation under Grant No. 9970363 1 Periodic Points 1 The main objects studied in the
Geometry 2: Manifolds and sheaves
 Rules:Exam problems would be similar to ones marked with! sign. It is recommended to solve all unmarked and!-problems or to find the solution online. It s better to do it in order starting from the beginning,
Rules:Exam problems would be similar to ones marked with! sign. It is recommended to solve all unmarked and!-problems or to find the solution online. It s better to do it in order starting from the beginning,
arxiv: v1 [math.ds] 20 Feb 2017
![arxiv: v1 [math.ds] 20 Feb 2017 arxiv: v1 [math.ds] 20 Feb 2017](/thumbs/74/70751481.jpg) Homoclinic tangencies and singular hyperbolicity for three-dimensional vector fields Sylvain Crovisier Dawei Yang arxiv:1702.05994v1 [math.ds] 20 Feb 2017 February 2017 Abstract We prove that any vector
Homoclinic tangencies and singular hyperbolicity for three-dimensional vector fields Sylvain Crovisier Dawei Yang arxiv:1702.05994v1 [math.ds] 20 Feb 2017 February 2017 Abstract We prove that any vector
ERGODIC JACOBI MATRICES AND CONFORMAL MAPS
 ERGODIC JACOBI MATRICES AND CONFORMAL MAPS INJO HUR AND CHRISTIAN REMLING Abstract. We study structural properties of the Lyapunov exponent γ and the density of states k for ergodic (or just invariant)
ERGODIC JACOBI MATRICES AND CONFORMAL MAPS INJO HUR AND CHRISTIAN REMLING Abstract. We study structural properties of the Lyapunov exponent γ and the density of states k for ergodic (or just invariant)
Topology. Xiaolong Han. Department of Mathematics, California State University, Northridge, CA 91330, USA address:
 Topology Xiaolong Han Department of Mathematics, California State University, Northridge, CA 91330, USA E-mail address: Xiaolong.Han@csun.edu Remark. You are entitled to a reward of 1 point toward a homework
Topology Xiaolong Han Department of Mathematics, California State University, Northridge, CA 91330, USA E-mail address: Xiaolong.Han@csun.edu Remark. You are entitled to a reward of 1 point toward a homework
AN EFFECTIVE METRIC ON C(H, K) WITH NORMAL STRUCTURE. Mona Nabiei (Received 23 June, 2015)
 NEW ZEALAND JOURNAL OF MATHEMATICS Volume 46 (2016), 53-64 AN EFFECTIVE METRIC ON C(H, K) WITH NORMAL STRUCTURE Mona Nabiei (Received 23 June, 2015) Abstract. This study first defines a new metric with
NEW ZEALAND JOURNAL OF MATHEMATICS Volume 46 (2016), 53-64 AN EFFECTIVE METRIC ON C(H, K) WITH NORMAL STRUCTURE Mona Nabiei (Received 23 June, 2015) Abstract. This study first defines a new metric with
Before you begin read these instructions carefully.
 MATHEMATICAL TRIPOS Part IB Tuesday, 5 June, 2012 9:00 am to 12:00 pm PAPER 1 Before you begin read these instructions carefully. Each question in Section II carries twice the number of marks of each question
MATHEMATICAL TRIPOS Part IB Tuesday, 5 June, 2012 9:00 am to 12:00 pm PAPER 1 Before you begin read these instructions carefully. Each question in Section II carries twice the number of marks of each question
SENSITIVITY AND REGIONALLY PROXIMAL RELATION IN MINIMAL SYSTEMS
 SENSITIVITY AND REGIONALLY PROXIMAL RELATION IN MINIMAL SYSTEMS SONG SHAO, XIANGDONG YE AND RUIFENG ZHANG Abstract. A topological dynamical system is n-sensitive, if there is a positive constant such that
SENSITIVITY AND REGIONALLY PROXIMAL RELATION IN MINIMAL SYSTEMS SONG SHAO, XIANGDONG YE AND RUIFENG ZHANG Abstract. A topological dynamical system is n-sensitive, if there is a positive constant such that
here, this space is in fact infinite-dimensional, so t σ ess. Exercise Let T B(H) be a self-adjoint operator on an infinitedimensional
 15. Perturbations by compact operators In this chapter, we study the stability (or lack thereof) of various spectral properties under small perturbations. Here s the type of situation we have in mind:
15. Perturbations by compact operators In this chapter, we study the stability (or lack thereof) of various spectral properties under small perturbations. Here s the type of situation we have in mind:
B. Appendix B. Topological vector spaces
 B.1 B. Appendix B. Topological vector spaces B.1. Fréchet spaces. In this appendix we go through the definition of Fréchet spaces and their inductive limits, such as they are used for definitions of function
B.1 B. Appendix B. Topological vector spaces B.1. Fréchet spaces. In this appendix we go through the definition of Fréchet spaces and their inductive limits, such as they are used for definitions of function
1. If 1, ω, ω 2, -----, ω 9 are the 10 th roots of unity, then (1 + ω) (1 + ω 2 ) (1 + ω 9 ) is A) 1 B) 1 C) 10 D) 0
 4 INUTES. If, ω, ω, -----, ω 9 are the th roots of unity, then ( + ω) ( + ω ) ----- ( + ω 9 ) is B) D) 5. i If - i = a + ib, then a =, b = B) a =, b = a =, b = D) a =, b= 3. Find the integral values for
4 INUTES. If, ω, ω, -----, ω 9 are the th roots of unity, then ( + ω) ( + ω ) ----- ( + ω 9 ) is B) D) 5. i If - i = a + ib, then a =, b = B) a =, b = a =, b = D) a =, b= 3. Find the integral values for
Part V. 17 Introduction: What are measures and why measurable sets. Lebesgue Integration Theory
 Part V 7 Introduction: What are measures and why measurable sets Lebesgue Integration Theory Definition 7. (Preliminary). A measure on a set is a function :2 [ ] such that. () = 2. If { } = is a finite
Part V 7 Introduction: What are measures and why measurable sets Lebesgue Integration Theory Definition 7. (Preliminary). A measure on a set is a function :2 [ ] such that. () = 2. If { } = is a finite
An introduction to random walks on groups
 An introduction to random walks on groups Jean-François Quint School on Information and Randomness, Puerto Varas, December 2014 Contents 1 Locally compact groups and Haar measure 2 2 Amenable groups 4
An introduction to random walks on groups Jean-François Quint School on Information and Randomness, Puerto Varas, December 2014 Contents 1 Locally compact groups and Haar measure 2 2 Amenable groups 4
DAVIS WIELANDT SHELLS OF NORMAL OPERATORS
 DAVIS WIELANDT SHELLS OF NORMAL OPERATORS CHI-KWONG LI AND YIU-TUNG POON Dedicated to Professor Hans Schneider for his 80th birthday. Abstract. For a finite-dimensional operator A with spectrum σ(a), the
DAVIS WIELANDT SHELLS OF NORMAL OPERATORS CHI-KWONG LI AND YIU-TUNG POON Dedicated to Professor Hans Schneider for his 80th birthday. Abstract. For a finite-dimensional operator A with spectrum σ(a), the
Ratner fails for ΩM 2
 Ratner fails for ΩM 2 Curtis T. McMullen After Chaika, Smillie and Weiss 9 December 2018 Contents 1 Introduction............................ 2 2 Unipotent dynamics on ΩE 4................... 3 3 Shearing
Ratner fails for ΩM 2 Curtis T. McMullen After Chaika, Smillie and Weiss 9 December 2018 Contents 1 Introduction............................ 2 2 Unipotent dynamics on ΩE 4................... 3 3 Shearing
Summary of topics relevant for the final. p. 1
 Summary of topics relevant for the final p. 1 Outline Scalar difference equations General theory of ODEs Linear ODEs Linear maps Analysis near fixed points (linearization) Bifurcations How to analyze a
Summary of topics relevant for the final p. 1 Outline Scalar difference equations General theory of ODEs Linear ODEs Linear maps Analysis near fixed points (linearization) Bifurcations How to analyze a
SYMPLECTIC MANIFOLDS, GEOMETRIC QUANTIZATION, AND UNITARY REPRESENTATIONS OF LIE GROUPS. 1. Introduction
 SYMPLECTIC MANIFOLDS, GEOMETRIC QUANTIZATION, AND UNITARY REPRESENTATIONS OF LIE GROUPS CRAIG JACKSON 1. Introduction Generally speaking, geometric quantization is a scheme for associating Hilbert spaces
SYMPLECTIC MANIFOLDS, GEOMETRIC QUANTIZATION, AND UNITARY REPRESENTATIONS OF LIE GROUPS CRAIG JACKSON 1. Introduction Generally speaking, geometric quantization is a scheme for associating Hilbert spaces
Locally convex spaces, the hyperplane separation theorem, and the Krein-Milman theorem
 56 Chapter 7 Locally convex spaces, the hyperplane separation theorem, and the Krein-Milman theorem Recall that C(X) is not a normed linear space when X is not compact. On the other hand we could use semi
56 Chapter 7 Locally convex spaces, the hyperplane separation theorem, and the Krein-Milman theorem Recall that C(X) is not a normed linear space when X is not compact. On the other hand we could use semi
NATIONAL BOARD FOR HIGHER MATHEMATICS. Research Awards Screening Test. February 25, Time Allowed: 90 Minutes Maximum Marks: 40
 NATIONAL BOARD FOR HIGHER MATHEMATICS Research Awards Screening Test February 25, 2006 Time Allowed: 90 Minutes Maximum Marks: 40 Please read, carefully, the instructions on the following page before you
NATIONAL BOARD FOR HIGHER MATHEMATICS Research Awards Screening Test February 25, 2006 Time Allowed: 90 Minutes Maximum Marks: 40 Please read, carefully, the instructions on the following page before you
On (h, k) trichotomy for skew-evolution semiflows in Banach spaces
 Stud. Univ. Babeş-Bolyai Math. 56(2011), No. 4, 147 156 On (h, k) trichotomy for skew-evolution semiflows in Banach spaces Codruţa Stoica and Mihail Megan Abstract. In this paper we define the notion of
Stud. Univ. Babeş-Bolyai Math. 56(2011), No. 4, 147 156 On (h, k) trichotomy for skew-evolution semiflows in Banach spaces Codruţa Stoica and Mihail Megan Abstract. In this paper we define the notion of
LECTURE 15: COMPLETENESS AND CONVEXITY
 LECTURE 15: COMPLETENESS AND CONVEXITY 1. The Hopf-Rinow Theorem Recall that a Riemannian manifold (M, g) is called geodesically complete if the maximal defining interval of any geodesic is R. On the other
LECTURE 15: COMPLETENESS AND CONVEXITY 1. The Hopf-Rinow Theorem Recall that a Riemannian manifold (M, g) is called geodesically complete if the maximal defining interval of any geodesic is R. On the other
Lecture 10. Theorem 1.1 [Ergodicity and extremality] A probability measure µ on (Ω, F) is ergodic for T if and only if it is an extremal point in M.
![Lecture 10. Theorem 1.1 [Ergodicity and extremality] A probability measure µ on (Ω, F) is ergodic for T if and only if it is an extremal point in M. Lecture 10. Theorem 1.1 [Ergodicity and extremality] A probability measure µ on (Ω, F) is ergodic for T if and only if it is an extremal point in M.](/thumbs/95/126112735.jpg) Lecture 10 1 Ergodic decomposition of invariant measures Let T : (Ω, F) (Ω, F) be measurable, and let M denote the space of T -invariant probability measures on (Ω, F). Then M is a convex set, although
Lecture 10 1 Ergodic decomposition of invariant measures Let T : (Ω, F) (Ω, F) be measurable, and let M denote the space of T -invariant probability measures on (Ω, F). Then M is a convex set, although
Short note on compact operators - Monday 24 th March, Sylvester Eriksson-Bique
 Short note on compact operators - Monday 24 th March, 2014 Sylvester Eriksson-Bique 1 Introduction In this note I will give a short outline about the structure theory of compact operators. I restrict attention
Short note on compact operators - Monday 24 th March, 2014 Sylvester Eriksson-Bique 1 Introduction In this note I will give a short outline about the structure theory of compact operators. I restrict attention
Banach Spaces V: A Closer Look at the w- and the w -Topologies
 BS V c Gabriel Nagy Banach Spaces V: A Closer Look at the w- and the w -Topologies Notes from the Functional Analysis Course (Fall 07 - Spring 08) In this section we discuss two important, but highly non-trivial,
BS V c Gabriel Nagy Banach Spaces V: A Closer Look at the w- and the w -Topologies Notes from the Functional Analysis Course (Fall 07 - Spring 08) In this section we discuss two important, but highly non-trivial,
MAS3706 Topology. Revision Lectures, May I do not answer enquiries as to what material will be in the exam.
 MAS3706 Topology Revision Lectures, May 208 Z.A.Lykova It is essential that you read and try to understand the lecture notes from the beginning to the end. Many questions from the exam paper will be similar
MAS3706 Topology Revision Lectures, May 208 Z.A.Lykova It is essential that you read and try to understand the lecture notes from the beginning to the end. Many questions from the exam paper will be similar
Lecture 5: Hodge theorem
 Lecture 5: Hodge theorem Jonathan Evans 4th October 2010 Jonathan Evans () Lecture 5: Hodge theorem 4th October 2010 1 / 15 Jonathan Evans () Lecture 5: Hodge theorem 4th October 2010 2 / 15 The aim of
Lecture 5: Hodge theorem Jonathan Evans 4th October 2010 Jonathan Evans () Lecture 5: Hodge theorem 4th October 2010 1 / 15 Jonathan Evans () Lecture 5: Hodge theorem 4th October 2010 2 / 15 The aim of
285K Homework #1. Sangchul Lee. April 28, 2017
 285K Homework #1 Sangchul Lee April 28, 2017 Problem 1. Suppose that X is a Banach space with respect to two norms: 1 and 2. Prove that if there is c (0, such that x 1 c x 2 for each x X, then there is
285K Homework #1 Sangchul Lee April 28, 2017 Problem 1. Suppose that X is a Banach space with respect to two norms: 1 and 2. Prove that if there is c (0, such that x 1 c x 2 for each x X, then there is
Stability of an abstract wave equation with delay and a Kelvin Voigt damping
 Stability of an abstract wave equation with delay and a Kelvin Voigt damping University of Monastir/UPSAY/LMV-UVSQ Joint work with Serge Nicaise and Cristina Pignotti Outline 1 Problem The idea Stability
Stability of an abstract wave equation with delay and a Kelvin Voigt damping University of Monastir/UPSAY/LMV-UVSQ Joint work with Serge Nicaise and Cristina Pignotti Outline 1 Problem The idea Stability
Functional Analysis. Franck Sueur Metric spaces Definitions Completeness Compactness Separability...
 Functional Analysis Franck Sueur 2018-2019 Contents 1 Metric spaces 1 1.1 Definitions........................................ 1 1.2 Completeness...................................... 3 1.3 Compactness......................................
Functional Analysis Franck Sueur 2018-2019 Contents 1 Metric spaces 1 1.1 Definitions........................................ 1 1.2 Completeness...................................... 3 1.3 Compactness......................................
DRIFT OF SPECTRALLY STABLE SHIFTED STATES ON STAR GRAPHS
 DRIFT OF SPECTRALLY STABLE SHIFTED STATES ON STAR GRAPHS ADILBEK KAIRZHAN, DMITRY E. PELINOVSKY, AND ROY H. GOODMAN Abstract. When the coefficients of the cubic terms match the coefficients in the boundary
DRIFT OF SPECTRALLY STABLE SHIFTED STATES ON STAR GRAPHS ADILBEK KAIRZHAN, DMITRY E. PELINOVSKY, AND ROY H. GOODMAN Abstract. When the coefficients of the cubic terms match the coefficients in the boundary
Introduction to Functional Analysis
 Introduction to Functional Analysis Carnegie Mellon University, 21-640, Spring 2014 Acknowledgements These notes are based on the lecture course given by Irene Fonseca but may differ from the exact lecture
Introduction to Functional Analysis Carnegie Mellon University, 21-640, Spring 2014 Acknowledgements These notes are based on the lecture course given by Irene Fonseca but may differ from the exact lecture
An introduction to Mathematical Theory of Control
 An introduction to Mathematical Theory of Control Vasile Staicu University of Aveiro UNICA, May 2018 Vasile Staicu (University of Aveiro) An introduction to Mathematical Theory of Control UNICA, May 2018
An introduction to Mathematical Theory of Control Vasile Staicu University of Aveiro UNICA, May 2018 Vasile Staicu (University of Aveiro) An introduction to Mathematical Theory of Control UNICA, May 2018
A Crash Course in Topological Groups
 A Crash Course in Topological Groups Iian B. Smythe Department of Mathematics Cornell University Olivetti Club November 8, 2011 Iian B. Smythe (Cornell) Topological Groups Nov. 8, 2011 1 / 28 Outline 1
A Crash Course in Topological Groups Iian B. Smythe Department of Mathematics Cornell University Olivetti Club November 8, 2011 Iian B. Smythe (Cornell) Topological Groups Nov. 8, 2011 1 / 28 Outline 1
CHAPTER I THE RIESZ REPRESENTATION THEOREM
 CHAPTER I THE RIESZ REPRESENTATION THEOREM We begin our study by identifying certain special kinds of linear functionals on certain special vector spaces of functions. We describe these linear functionals
CHAPTER I THE RIESZ REPRESENTATION THEOREM We begin our study by identifying certain special kinds of linear functionals on certain special vector spaces of functions. We describe these linear functionals
Propagation of longitudinal waves in a random binary rod
 Downloaded By: [University of North Carolina, Charlotte At: 7:3 2 May 28 Waves in Random and Complex Media Vol. 6, No. 4, November 26, 49 46 Propagation of longitudinal waves in a random binary rod YURI
Downloaded By: [University of North Carolina, Charlotte At: 7:3 2 May 28 Waves in Random and Complex Media Vol. 6, No. 4, November 26, 49 46 Propagation of longitudinal waves in a random binary rod YURI
Rotation set for maps of degree 1 on sun graphs. Sylvie Ruette. January 6, 2019
 Rotation set for maps of degree 1 on sun graphs Sylvie Ruette January 6, 2019 Abstract For a continuous map on a topological graph containing a unique loop S, it is possible to define the degree and, for
Rotation set for maps of degree 1 on sun graphs Sylvie Ruette January 6, 2019 Abstract For a continuous map on a topological graph containing a unique loop S, it is possible to define the degree and, for
Math Ordinary Differential Equations
 Math 411 - Ordinary Differential Equations Review Notes - 1 1 - Basic Theory A first order ordinary differential equation has the form x = f(t, x) (11) Here x = dx/dt Given an initial data x(t 0 ) = x
Math 411 - Ordinary Differential Equations Review Notes - 1 1 - Basic Theory A first order ordinary differential equation has the form x = f(t, x) (11) Here x = dx/dt Given an initial data x(t 0 ) = x
ẋ = f(x, y), ẏ = g(x, y), (x, y) D, can only have periodic solutions if (f,g) changes sign in D or if (f,g)=0in D.
 4 Periodic Solutions We have shown that in the case of an autonomous equation the periodic solutions correspond with closed orbits in phase-space. Autonomous two-dimensional systems with phase-space R
4 Periodic Solutions We have shown that in the case of an autonomous equation the periodic solutions correspond with closed orbits in phase-space. Autonomous two-dimensional systems with phase-space R
Two-sided multiplications and phantom line bundles
 Two-sided multiplications and phantom line bundles Ilja Gogić Department of Mathematics University of Zagreb 19th Geometrical Seminar Zlatibor, Serbia August 28 September 4, 2016 joint work with Richard
Two-sided multiplications and phantom line bundles Ilja Gogić Department of Mathematics University of Zagreb 19th Geometrical Seminar Zlatibor, Serbia August 28 September 4, 2016 joint work with Richard
Spectrum (functional analysis) - Wikipedia, the free encyclopedia
 1 of 6 18/03/2013 19:45 Spectrum (functional analysis) From Wikipedia, the free encyclopedia In functional analysis, the concept of the spectrum of a bounded operator is a generalisation of the concept
1 of 6 18/03/2013 19:45 Spectrum (functional analysis) From Wikipedia, the free encyclopedia In functional analysis, the concept of the spectrum of a bounded operator is a generalisation of the concept
CHAPTER VIII HILBERT SPACES
 CHAPTER VIII HILBERT SPACES DEFINITION Let X and Y be two complex vector spaces. A map T : X Y is called a conjugate-linear transformation if it is a reallinear transformation from X into Y, and if T (λx)
CHAPTER VIII HILBERT SPACES DEFINITION Let X and Y be two complex vector spaces. A map T : X Y is called a conjugate-linear transformation if it is a reallinear transformation from X into Y, and if T (λx)
Functional Analysis I
 Functional Analysis I Course Notes by Stefan Richter Transcribed and Annotated by Gregory Zitelli Polar Decomposition Definition. An operator W B(H) is called a partial isometry if W x = X for all x (ker
Functional Analysis I Course Notes by Stefan Richter Transcribed and Annotated by Gregory Zitelli Polar Decomposition Definition. An operator W B(H) is called a partial isometry if W x = X for all x (ker
Recall that any inner product space V has an associated norm defined by
 Hilbert Spaces Recall that any inner product space V has an associated norm defined by v = v v. Thus an inner product space can be viewed as a special kind of normed vector space. In particular every inner
Hilbert Spaces Recall that any inner product space V has an associated norm defined by v = v v. Thus an inner product space can be viewed as a special kind of normed vector space. In particular every inner
Section 3.9. Matrix Norm
 3.9. Matrix Norm 1 Section 3.9. Matrix Norm Note. We define several matrix norms, some similar to vector norms and some reflecting how multiplication by a matrix affects the norm of a vector. We use matrix
3.9. Matrix Norm 1 Section 3.9. Matrix Norm Note. We define several matrix norms, some similar to vector norms and some reflecting how multiplication by a matrix affects the norm of a vector. We use matrix
MET Workshop: Exercises
 MET Workshop: Exercises Alex Blumenthal and Anthony Quas May 7, 206 Notation. R d is endowed with the standard inner product (, ) and Euclidean norm. M d d (R) denotes the space of n n real matrices. When
MET Workshop: Exercises Alex Blumenthal and Anthony Quas May 7, 206 Notation. R d is endowed with the standard inner product (, ) and Euclidean norm. M d d (R) denotes the space of n n real matrices. When
A note on the σ-algebra of cylinder sets and all that
 A note on the σ-algebra of cylinder sets and all that José Luis Silva CCM, Univ. da Madeira, P-9000 Funchal Madeira BiBoS, Univ. of Bielefeld, Germany (luis@dragoeiro.uma.pt) September 1999 Abstract In
A note on the σ-algebra of cylinder sets and all that José Luis Silva CCM, Univ. da Madeira, P-9000 Funchal Madeira BiBoS, Univ. of Bielefeld, Germany (luis@dragoeiro.uma.pt) September 1999 Abstract In
ne varieties (continued)
 Chapter 2 A ne varieties (continued) 2.1 Products For some problems its not very natural to restrict to irreducible varieties. So we broaden the previous story. Given an a ne algebraic set X A n k, we
Chapter 2 A ne varieties (continued) 2.1 Products For some problems its not very natural to restrict to irreducible varieties. So we broaden the previous story. Given an a ne algebraic set X A n k, we
Connectedness. Proposition 2.2. The following are equivalent for a topological space (X, T ).
 Connectedness 1 Motivation Connectedness is the sort of topological property that students love. Its definition is intuitive and easy to understand, and it is a powerful tool in proofs of well-known results.
Connectedness 1 Motivation Connectedness is the sort of topological property that students love. Its definition is intuitive and easy to understand, and it is a powerful tool in proofs of well-known results.
An introduction to arithmetic groups. Lizhen Ji CMS, Zhejiang University Hangzhou , China & Dept of Math, Univ of Michigan Ann Arbor, MI 48109
 An introduction to arithmetic groups Lizhen Ji CMS, Zhejiang University Hangzhou 310027, China & Dept of Math, Univ of Michigan Ann Arbor, MI 48109 June 27, 2006 Plan. 1. Examples of arithmetic groups
An introduction to arithmetic groups Lizhen Ji CMS, Zhejiang University Hangzhou 310027, China & Dept of Math, Univ of Michigan Ann Arbor, MI 48109 June 27, 2006 Plan. 1. Examples of arithmetic groups
Course Description - Master in of Mathematics Comprehensive exam& Thesis Tracks
 Course Description - Master in of Mathematics Comprehensive exam& Thesis Tracks 1309701 Theory of ordinary differential equations Review of ODEs, existence and uniqueness of solutions for ODEs, existence
Course Description - Master in of Mathematics Comprehensive exam& Thesis Tracks 1309701 Theory of ordinary differential equations Review of ODEs, existence and uniqueness of solutions for ODEs, existence
Category O and its basic properties
 Category O and its basic properties Daniil Kalinov 1 Definitions Let g denote a semisimple Lie algebra over C with fixed Cartan and Borel subalgebras h b g. Define n = α>0 g α, n = α
Category O and its basic properties Daniil Kalinov 1 Definitions Let g denote a semisimple Lie algebra over C with fixed Cartan and Borel subalgebras h b g. Define n = α>0 g α, n = α
SYNCHRONIZATION OF NONAUTONOMOUS DYNAMICAL SYSTEMS
 Electronic Journal of Differential Equations, Vol. 003003, No. 39, pp. 1 10. ISSN: 107-6691. URL: http://ejde.math.swt.edu or http://ejde.math.unt.edu ftp ejde.math.swt.edu login: ftp SYNCHRONIZATION OF
Electronic Journal of Differential Equations, Vol. 003003, No. 39, pp. 1 10. ISSN: 107-6691. URL: http://ejde.math.swt.edu or http://ejde.math.unt.edu ftp ejde.math.swt.edu login: ftp SYNCHRONIZATION OF
Loos Symmetric Cones. Jimmie Lawson Louisiana State University. July, 2018
 Louisiana State University July, 2018 Dedication I would like to dedicate this talk to Joachim Hilgert, whose 60th birthday we celebrate at this conference and with whom I researched and wrote a big blue
Louisiana State University July, 2018 Dedication I would like to dedicate this talk to Joachim Hilgert, whose 60th birthday we celebrate at this conference and with whom I researched and wrote a big blue
MAT 570 REAL ANALYSIS LECTURE NOTES. Contents. 1. Sets Functions Countability Axiom of choice Equivalence relations 9
 MAT 570 REAL ANALYSIS LECTURE NOTES PROFESSOR: JOHN QUIGG SEMESTER: FALL 204 Contents. Sets 2 2. Functions 5 3. Countability 7 4. Axiom of choice 8 5. Equivalence relations 9 6. Real numbers 9 7. Extended
MAT 570 REAL ANALYSIS LECTURE NOTES PROFESSOR: JOHN QUIGG SEMESTER: FALL 204 Contents. Sets 2 2. Functions 5 3. Countability 7 4. Axiom of choice 8 5. Equivalence relations 9 6. Real numbers 9 7. Extended
Random Walks on Hyperbolic Groups III
 Random Walks on Hyperbolic Groups III Steve Lalley University of Chicago January 2014 Hyperbolic Groups Definition, Examples Geometric Boundary Ledrappier-Kaimanovich Formula Martin Boundary of FRRW on
Random Walks on Hyperbolic Groups III Steve Lalley University of Chicago January 2014 Hyperbolic Groups Definition, Examples Geometric Boundary Ledrappier-Kaimanovich Formula Martin Boundary of FRRW on
with spectral parameter E. Thisequationcanbewrittenas(1)with SL(2, R), 1 V (θ) E y(t)+v (θ + tω)y(t) = Ey(t)
 Doc. Math. J. DMV 779 L. H. Eliasson Abstract. We consider linear quasi-periodic skew-product systems on T d G where G is some matrix group. When the quasi-periodic frequencies are Diophantine such systems
Doc. Math. J. DMV 779 L. H. Eliasson Abstract. We consider linear quasi-periodic skew-product systems on T d G where G is some matrix group. When the quasi-periodic frequencies are Diophantine such systems
n [ F (b j ) F (a j ) ], n j=1(a j, b j ] E (4.1)
![n [ F (b j ) F (a j ) ], n j=1(a j, b j ] E (4.1) n [ F (b j ) F (a j ) ], n j=1(a j, b j ] E (4.1)](/thumbs/81/82707553.jpg) 1.4. CONSTRUCTION OF LEBESGUE-STIELTJES MEASURES In this section we shall put to use the Carathéodory-Hahn theory, in order to construct measures with certain desirable properties first on the real line
1.4. CONSTRUCTION OF LEBESGUE-STIELTJES MEASURES In this section we shall put to use the Carathéodory-Hahn theory, in order to construct measures with certain desirable properties first on the real line
Topics in Harmonic Analysis Lecture 1: The Fourier transform
 Topics in Harmonic Analysis Lecture 1: The Fourier transform Po-Lam Yung The Chinese University of Hong Kong Outline Fourier series on T: L 2 theory Convolutions The Dirichlet and Fejer kernels Pointwise
Topics in Harmonic Analysis Lecture 1: The Fourier transform Po-Lam Yung The Chinese University of Hong Kong Outline Fourier series on T: L 2 theory Convolutions The Dirichlet and Fejer kernels Pointwise
Lecture Notes in Advanced Calculus 1 (80315) Raz Kupferman Institute of Mathematics The Hebrew University
 Lecture Notes in Advanced Calculus 1 (80315) Raz Kupferman Institute of Mathematics The Hebrew University February 7, 2007 2 Contents 1 Metric Spaces 1 1.1 Basic definitions...........................
Lecture Notes in Advanced Calculus 1 (80315) Raz Kupferman Institute of Mathematics The Hebrew University February 7, 2007 2 Contents 1 Metric Spaces 1 1.1 Basic definitions...........................
Spectral theorems for bounded self-adjoint operators on a Hilbert space
 Chapter 10 Spectral theorems for bounded self-adjoint operators on a Hilbert space Let H be a Hilbert space. For a bounded operator A : H H its Hilbert space adjoint is an operator A : H H such that Ax,
Chapter 10 Spectral theorems for bounded self-adjoint operators on a Hilbert space Let H be a Hilbert space. For a bounded operator A : H H its Hilbert space adjoint is an operator A : H H such that Ax,
MATHS 730 FC Lecture Notes March 5, Introduction
 1 INTRODUCTION MATHS 730 FC Lecture Notes March 5, 2014 1 Introduction Definition. If A, B are sets and there exists a bijection A B, they have the same cardinality, which we write as A, #A. If there exists
1 INTRODUCTION MATHS 730 FC Lecture Notes March 5, 2014 1 Introduction Definition. If A, B are sets and there exists a bijection A B, they have the same cardinality, which we write as A, #A. If there exists
Notation. 0,1,2,, 1 with addition and multiplication modulo
 Notation Q,, The set of all natural numbers 1,2,3, The set of all integers The set of all rational numbers The set of all real numbers The group of permutations of distinct symbols 0,1,2,,1 with addition
Notation Q,, The set of all natural numbers 1,2,3, The set of all integers The set of all rational numbers The set of all real numbers The group of permutations of distinct symbols 0,1,2,,1 with addition
Math 249B. Nilpotence of connected solvable groups
 Math 249B. Nilpotence of connected solvable groups 1. Motivation and examples In abstract group theory, the descending central series {C i (G)} of a group G is defined recursively by C 0 (G) = G and C
Math 249B. Nilpotence of connected solvable groups 1. Motivation and examples In abstract group theory, the descending central series {C i (G)} of a group G is defined recursively by C 0 (G) = G and C
The Structure of C -algebras Associated with Hyperbolic Dynamical Systems
 The Structure of C -algebras Associated with Hyperbolic Dynamical Systems Ian F. Putnam* and Jack Spielberg** Dedicated to Marc Rieffel on the occasion of his sixtieth birthday. Abstract. We consider the
The Structure of C -algebras Associated with Hyperbolic Dynamical Systems Ian F. Putnam* and Jack Spielberg** Dedicated to Marc Rieffel on the occasion of his sixtieth birthday. Abstract. We consider the
