SOME SERIES IDENTITIES FOR SOME SPECIAL CLASSES OF APOSTOL-BERNOULLI AND APOSTOL-EULER POLYNOMIALS RELATED TO GENERALIZED POWER AND ALTERNATING SUMS
|
|
|
- Jade Hart
- 5 years ago
- Views:
Transcription
1 Bullet of Mthemtcl Alyss d Applctos ISSN: , URL: Volume 4 Issue 4 01, Pges SOME SERIES IDENTITIES FOR SOME SPECIAL CLASSES OF APOSTOL-BERNOULLI AND APOSTOL-EULER POLYNOMIALS RELATED TO GENERALIZED POWER AND ALTERNATING SUMS COMMUNICATED BY R.K. RAINA B.-J. FUGÈRE, S. GABOURY, R. TREMBLAY Astrct. The purpose of ths pper s to ot severl seres dettes volvg some clsses of geerlzed Apostol-Beroull d Apostol-Euler polyomls troduced ltely y Srvstv et l. 16, 17] s well s the geerlzed sum of teger powers, the geerlzed ltertg sum d the logues of the expsos of the hyperolc tget d the hyperolc cotget. The method used s tht of geertg fuctos. It c e foud tht my dettes recetly oted re specl cses of our results. 1. Itroducto, Deftos d Nottos The geerlzed Beroull polyomls B α x of order α C, the geerlzed Euler polyomls E α x of order α C d the geerlzed Geocch polyomls G α x of order α C, ech of degree s well s α, re defed respectvely y the followg geertg fuctos see,4, vol.3, p.53 et seq.], 8, Secto.8] d 10]: α t e t e xt B α 1 xt t < π; 1 α : 1, 1.1! 0 α e t e xt + 1 xt t < π; 1 α : 1 1.! d α t e t e xt G α xt! t < π; 1 α : The lterture cots lrge umer of terestg propertes d reltoshps volvg these polyomls 1,, 3, 4, 5, 15]. Q.-M. Luo d Srvstv 1, 14] troduced the geerlzed Apostol-Beroull polyomls B α x of order α, 1991 Mthemtcs Suject Clssfcto. Prmry 11B68; Secodry 11S80. Key words d phrses. Beroull umers d polyomls, Euler umers d polyomls, Geocch umers d polyomls, Apostol-Beroull polyomls, Apostol-Euler polyomls, Apostol-Geocch polyomls, Geerlzed power sums, Geerlzed ltertg sums. Sumtted Jue 19, 01. Pulshed Novemer 6,
2 Q.-M. Luo 9] vestgted the geerlzed Apostol-Euler polyomls x of order α d the geerlzed Apostol-Geocch polyomls G α x of order α see lso,10, 11, 13]. The geerlzed Apostol-Beroull polyomls B α x; λ of order α C, the geerlzed Apostol-Euler polyomls x; λ of order α C, the geerlzed Apostol-Geocch polyomls G α x; λ of order α C re defed respectvely y the followg geertg fuctos α t λe t e xt B α x; λt t + l λ < π; 1 α : ! d 0 α λe t e xt + 1 α t λe t e xt + 1 It s esy to see tht 0 0 G α x; λt! x; λt! 77 t + l λ < π; 1 α : t + l λ < π; 1 α : B α x B α x; 1, E α x x; 1 d G α x G α x; 1. Recetly, Srvstv et l. 16, 17] hve vestgted some ew clsses of Apostol-Beroull, Apostol-Euler d Apostol-Geocch polyomls wth prmeters, d c defed y the followg geertg fuctos. Defto 1.1. Let,, c R +, d N 0. The geerlzed Apostol- Beroull polyomls B α x; λ;,, c of order α, the geerlzed Apostol-Euler polyomls x; λ;,, c of order α d the geerlzed Apostol-Geocch polyomls G α x; λ;,, c of order α re defed respectvely y the followg geertg fuctos α t λ t t c xt B α x; λ;,, c t t!, l + l λ < π; 1 α : 1, 1.7 α λ t + t c xt x; λ;,, c t t!, l + l λ < π; 1 α : d α t λ t + t c xt G α x; λ;,, c t t!, l + l λ < π; 1 α : If we te 1, c e 1.7, 1.8 d 1.9 respectvely, we hve 1.4, 1.5 d 1.6. Ovously, whe we set λ 1, α 1, 1, c e 1.7, 1.8 d 1.9, we hve clsscl Beroull polyomls B x, clsscl Euler polyomls E x d clsscl Geocch polyomls G x.
3 78 For ech N 0, S defed y S j 1.10 s clled the sum of teger powers. The expoetl geertg fucto for S s gve y 19] S t! e+1t 1 e t We ow defe the geerlzed sum of teger powers s follows. Defto 1.. For rtrry rel or complex λ, the geerlzed sum of tegers powers S ; λ s defed y the geertg relto S ; λ t! λe+1t 1 λe t It s ovous tht 0 For N 0 d N, T defed y s clled the ltertg sum. gve y 0 S ; 1 S T The expoetl geertg fucto for T s T t! 1 1 e t 1 + e t The geerlzed ltertg sum of order α s defed 7] s follows. Defto 1.3. For y rtrry rel or complex prmeter λ, the geerlzed ltertg sum of order α, T α ; λ s defed y the followg geertg fucto: T α ; λ t 1 λ 1! e t α 1 + λe t It s esy to oserve tht T 1 ; 1 T I ths pper, we preset severl seres dettes volvg the geerlzed Apostol- Beroull d the geerlzed Apostol-Euler polyomls defed respectvely y 1.7 d 1.8. I Secto, we ot severl symmetry dettes for the geerlzed Apostol-Beroull polyomls relto etwee the these polyomls d the geerlzed sum of teger powers 1.1. I Secto 3, we prove severl dettes volvg the geerlzed Apostol-Euler, the geerlzed ltertg sum d the logues of the expsos of the hyperolc tget d the hyperolc cotget. Some dettes re lso oted y usg the reltoshps etwee the geerlzed Apostol-Beroull, Apostol-Euler d Apostol-Geocch polyomls.
4 79. Symmetry dettes for the geerlzed Apostol-Beroull polyomls I ths secto, we estlsh some symmetry dettes volvg the geerlzed Apostol-Beroull polyomls B α x; λ;,, c defed the frst secto d the geerlzed sum of teger powers defed y 1.1. Ths s doe y usg the method of geertg fuctos. These results provdes geerlzto of ow dettes 18, 1,, 3] Theorem.1. For ll tegers µ > 0, ν > 0, α 1, 0, for,, c R + d for λ C, we hve the followg detty: B α νx + µ 1ν l ; λ;,, c µ ν +1 S µ 1, λ B α 1 µy; λ;,, c l B α µx + ] ν 1µ l ; λ;,, c ν µ +1 S ν 1, λ B α 1 νy; λ;,, c l ]..1 Proof. Cosderg gt tα 1 c µνxt λ µνt µνt λ µt µt α λ νt νt α. We hve to expd the lst fucto to seres two wy to prove the theorem. We hve gt tα 1 c µνxt λ µνt µνt λ µt µt α λ νt νt α α 1 µt c νxµt λ µνt µνt α 1 νt µ α ν α 1 λ µt µt λ νt νt λ νt νt c νt l α l c µt c νxµt λ ν µt 1 α 1 µ α ν α 1 λ µt µt ν λ νt ν t 1 λ νt νt ν 1 µ α ν α 1 S µ 1, λ 0 1 µ α ν α B α νx ν l B α µ 1ν l µt ; λ;,, c! ] t νx +! 0 B α 1 µy; λ;,, c νt! µ 1ν l ; λ;,, c S µ 1, λ B α 1 µy; λ;,, c l µ ν +1 ] ] t!..
5 80 By expdg dfferet wy, we hve gt 1 B α ν α µ α µx S ν 1, λ B α 1 νy; λ;,, c ν 1µ l ; λ;,, c ν µ +1 l ] ] t!..3 By settg 1, c e Theorem 1, we ot oe of the results exhted y Zhg d Yg 3, Eq. 8]: Corollry.. For ll tegers µ > 0, ν > 0, α 1, 0 d for λ C, we hve B α νx; λ µ ν +1 S µ 1, λ B α 1 µy; λ 0 0 B α µx; λ ν µ Puttg x 0, y 0 d α 1 Theorem 1, we hve: 0 S ν 1, λ B α 1 νy; λ..4 Corollry.3. For ll tegers µ > 0, ν > 0, 0 d for,, c R + d λ C, we hve the followg relto: ] µ 1ν l B ; λ;,, c µ 1 ν S µ 1, λ l 0 ].5 ν 1µ l B ; λ;,, c ν 1 µ S ν 1, λ l. Flly, susttutg λ 1, 1, c e.5, we fd µ 1 ν B S µ 1 ν 1 µ B S ν result gve y Tueter 18]. 0 Theorem.4. For ll tegers µ > 0, ν > 0, α 1, 0, for,, c R +, d for λ C, we hve the followg detty: λ +j µ ν B α νx + ν l + µν ν µ l ; λ;,, c 0 0 B α µy + jµ l ; λ;,, c ν µ B α µx + µ l + µν ν µ l ; λ;,, c 0 0 λ +j B α νy + jν l ; λ;,, c..7
6 81 Proof. Let the fucto ht e gve y ht tα c µνxt λ µ µνt µνt λ ν µνt µνt λ µt µt α+1 λ νt νt α+1,.8 whch c e expded s follows: ht 1 α µt λ µν α λ µt µt c µνxt µ µνt µνt α νt λ νt νt λ νt νt λ ν µνt µνt λ µt µt α µνt νt µt µt µν α λ µt µt c µνxt λ µ e µνt l α 1 νt λe νt l 1 λ νt νt λ ν e νµt l 1 λe µt l 1 1 α µν α c µν ν µt l µt l c λ µt µt c µνxt λ e νt l 0 α νt λ νt νt λ j e jµt l c µνyt α c µνxt + νt l µν ν µt l + l c l c 1 µν α λ µt λ µt µt 0 α λ j νt λ νt νt + jµt l l c 1 µν α λ B α νx + ν l + µν ν µ l µt ; λ;,, c! 0 λ j B α µy + jµ l νt ; λ;,, c! 0 1 µν α λ +j µ ν B α µy + jµ l ; λ;,, c 0 0 B α νx + ν l ] + µν ν µ l t ; λ;,, c!..9 Sce ht s symmetrc µ d ν, we c lso expd ht s follows: ht 1 λ +j ν µ B α µν α νy + jν l ; λ;,, c 0 0 B α µx + µ l ].10 + µν ν µ l t ; λ;,, c!.
7 8 By equtg the coeffcet of t! o the rght-hd sdes of these lst two.9 d.10, we get the detty.7. Settg 1, c e Theorem yelds result gve recetly y Zhg d Yg 3, Eq. 18] : Corollry.5. For ll tegers µ > 0, ν > 0, α 1, 0 d for λ C, we hve λ +j µ ν B α νx + νµ ; λ B α µy + jµν ; λ λ +j ν µ B α µx + µν ; λ B α νy + jνµ ; λ. Puttg ν 1 d y 0 Theorem gves the ext corollry:.11 Corollry.6. For ll tegers µ > 0, α 1, 0, for,, c R +, d for λ C, we hve the followg detty: λ µ B α λ j µ B α µx + x + l + µ 1 l ; λ;,, c µ 1 l j l ; λ;,, c B α B α 0; λ;,, c ; λ;,, c..1 Theorem.7. For ll tegers µ > 0, ν > 0, α 1, 0, for,, c R +, d for λ C, we hve the followg detty: 0 B α B α λ +j µ ν B α µy; λ;,, c νx + ν l + µν ν µ l + jµ l λ +j ν µ B α νy; λ;,, c µx + µ l + µν ν µ l + jν l ; λ;,, c ; λ;,, c..13 Proof. The proof of Theorem 3 s smlr to tht of Theorems 1 d. I the proof of Theorem 3, we frst me use of 1.7 order to expd the fucto ht defed y.8 d the pply the symmetry of ht µ d ν to ot secod expso of ht. The detls volved re strghtforwrd d we leve them s exercse. If we set 1, c e Theorem 3, we recover result gve recetly y Zhg d Yg 3, Eq. 3] :
8 83 Corollry.8. For ll tegers µ > 0, ν > 0, α 1, 0 d for λ C, we hve λ +j µ ν B α νx + νµ + j; λ B α µy; λ 0 λ +j ν µ B α µx + µ ν + j; λ B α νy; λ. Puttg ν 1 d y 0 Theorem 3 gves the ext corollry:.14 Corollry.9. For ll tegers µ > 0, α 1, 0, for,, c R +, d for λ C, we hve the followg detty: λ µ B α λ j µ B α x + l + µ 1 l ; λ;,, c µx + µ 1 l + j l ; λ;,, c l c B α 0; λ;,, c B α 0; λ;,, c Some dettes relted to geerlzed Apostol-Euler polyomls I ths secto, we derve some dettes cocerg the geerlzed Apostol- Euler polyomls x; λ;,, c defed y 1.8, the geerlzed ltertg sum 1.16 d the logues of the expsos of hyperolc cotget d hyperolc tget troduced 0]. These results exted some ow formuls 6, 7, 1]. We coclude ths secto y gvg some dettes sed o reltoshps etwee the geerlzed Apostol-Euler polyomls x; λ;,, c d the geerlzed Apostol-Beroull polyomls B α x; λ;,, c d etwee the geerlzed Apostol-Beroull polyomls B α x; λ;,, c d the geerlzed Apostol- Geocch polyomls G α x; λ;,, c defed y 1.9. Theorem 3.1. For N 0, µ, ν N, α 1,,, c R +, d for λ C. If µ d ν hve the sme prty, the the followg detty holds true: µ ν l 0 ν µ l 0 νx µx αν l ; λ;,, c T α µ; λ αµ l ; λ;,, c T α ν; λ. 3.1 Proof. Let the fucto gt e gve y gt c µνxt 1 λ 1 µ e µνt l α λ µt + µt α λ νt + νt α 3.
9 84 Mg use of 1.8 d 1.16 to expd gt to ot frst: gt 1 α c ανt l α l c c νxµt 1 λ 1 µ e µνt l λ µt + µt 1 α 1 α 0 E α νx αν l µ ν l µt ; λ;,, c! λe νt l νx α T α µ; λ νt l! αν l ; λ;,, c T α µ; λ t!. 3.3 Now, sce µ d ν hve the sme prty, the the fucto gt s symmetrc µ d ν. Therefore, we c expd gt s follows: gt 1 α ν µ l 0 µx αµ l ; λ;,, c T α ν; λ t!. 3.4 By equtg the coeffcet of t! o the rght-hd sde of the lst two equtos 3.3 d 3.4, we thus recover the detty 3.1 sserted y Theorem 4. As specl cse, f we set 1, c e Theorem 4, we ot the followg corollry gve recetly y Lu d Srvstv 7, Eq. 30]. Corollry 3.. For N 0, µ, ν N, α 1 d for λ C. If µ d ν hve the sme prty, the the followg detty holds true: µ ν α νx ; λ T µ; λ ν µ α µx; λ T ν; λ Now, lettg α λ 1, we recover the result gve y Yg d Qo 1, Eq. 18]: Corollry 3.3. For N 0 d µ, ν N. If µ d ν hve the sme prty, the we hve µ ν E νx T µ ν µ E µx T ν Theorem 3.4. For N 0, µ, ν N, α 1,,, c R +, d for λ C. If µ d ν hve the sme prty, the the followg detty holds true: λ +j µ ν νx + ν + jµ l µ + ν l ; λ;,, c µy; λ;,, c λ +j ν µ 0 µx + µ + jν l µ + ν l ; λ;,, c νy; λ;,, c. 3.7
10 85 Proof. Let the fucto gt e gve y gt c µνxt c 1 µνyt νt µ ] 1 µt ν ] λ λ λ µt + µt α+1 λ νt + νt α whch c e expded, wth the help of 1.8, s follows: gt 1 α c µνxt 1 1 λ νt µ α λ µt + µt νt 1 µt µ+νt α 1 λ µt ν λ µt + 1 λ νt + νt λ νt + 1 α α νt c µνxt λ λ µt + µt 0 jµt α λ j λ νt + νt 1 α λ +j c µνxt + νt l l c α λ µt + µt 0 α λ νt + νt 1 α 1 α λ +j jµt l µ + νt l l c l c νx + ν + µj l µ + ν l ; λ;,, c νt µy; λ;,, c! λ +j µ ν µy; λ;,, c 0 νx + ν + µj l ] µ + ν l ; λ;,, c t!. µt! Usg the fct tht gt s symmetrc sce µ d ν hve the sme prty, we c lso expd gt the followg the wy: gt 1 α λ +j ν µ νy; λ;,, c 0 0 µx + µ + νj l ] µ + ν l ; λ;,, c t!. 3.9 Equtg coeffcets of t! the rght-hd sde of the lst two equtos gves the detty of the Theorem 5. Lettg 1, c e Theorem 5, we fd the followg corollry gve recetly y Lu d Srvstv 7, Eq. 43].
11 86 Corollry 3.5. For N 0, µ, ν N, α 1 d for λ C. If µ d ν hve the sme prty, the the followg detty holds true: λ +j µ ν νx + νµ + j; λ µy; λ λ +j ν µ µx + µ ν + j; λ νy; λ. 0 0 Accordg to 0], we hve the followg logues of the expsos of hyperolc cotget d hyperolc tget, respectvely: λe z + 1 λe z 1 λe z 1 λe z + 1 E 0; λ z! From 3.11, we c ot the followg theorem. B 0; λ + λb 1; λ z 1, 3.11! Theorem 3.6. For N 0, µ, ν N, α 1,,, c R +, d for λ C. Let δ,j deotes the Kroecer delt defed y δ, 1 d δ,j 0 for j. If µ s odd d ν s eve the the followg detty holds true: δ +1,1 + B +1 0; λ] µ µ ν µx µ l ; λ;,, c l j µ ν νx ν l ; λ;,, c l 0 E α 1 µy; λ;,, c. ] + j T 1 j ν; λeα 1 j νy; λ;,, c 0 ] T 1 µ; λ 3.13 Proof. Whe µ s odd d ν s eve, the fucto gt, gve elow, s ot symmetrc µ d ν, so we hve o the oe hd gt 1 α c µνxt 1 λ 1 ν e µνt l 1 λ 1 µ e µνt l α 1 λ νt + νt λ µt + µt 1 λ 1 ν e µνt l α 1 λ µt + µt 1 1 λ 1 µ e µνt l α µt l µνxt α 1 1 λ 1 ν e µνt l c l c λ νt + νt 1 λ 1 ν e µνt l α 1 λe µt l + 1 λ µt + µt 1 1 B 0; λ + λb 1; λ µνt l α 1! µx µ l νt ; λ;,, c! 0
12 µt l T 1 ν ; λ! 0 1 B α 1 0; λ + λb 1; λ] µ 1 0 µ ν 1 µx µ l ; λ;,, c 0 ] ] 1 + j l T 1 j ν; λeα 1 j νy; λ;,, c j E α 1 j νy; λ;,, c µtj j! 87 t ! O the other other hd, we c lso expd gt s follows: gt 1 α c µνxt 1 λ 1 µ e µνt l α 1 λ µt + µt λ νt + νt α 1 λ νt + νt 1 α νt l µνxt 1 λ 1 c l c µ e µνt l α 1 λ µt + µt 1 + λe νt l α 1 λ νt + νt 1 α 1 νx ν l µt νt l ] ; λ;,, c T 1! µ; λ! 0 E α 1 µy; λ;,, c νt! 0 1 µ ν α 1 νx ν l ; λ;,, c 0 0 l ] T 1 µ; λeα 1 µy; λ;,, c Sce λb x + 1; λ B x; λ x 1 see 14] the ] t!. B 0; λ + λb 1; λ δ,1 + B 0; λ Mg use of ths lst relto 3.15 volvg the Apostol-Beroull polyomls d umers d equtg the coeffcets of t! 3.14 d 3.15, we ot Susttutg 1, c e Theorem 6 furshes the followg corollry. Corollry 3.7. For N 0, µ, ν N, α 1 d for λ C. Let δ,j deotes the Kroecer delt defed y δ, 1 d δ,j 0 for j. If µ s odd d ν s eve the the followg detty holds true: δ +1,1 + B +1 0; λ] µ T 1 j ν; λeα 1 j νy; λ j µ ν µx; λ
13 88 µ ν νx; λ T 1 µ; λeα 1 µy; λ Lettg λ , we get the result oted y Lu d Wg 6, Theorem.4]. Corollry 3.8. For N 0, µ, ν N, α 1. If µ s odd d ν s eve the the followg detty holds true: B +1 0 µ µ ν + 1 µx T 1 j j νeα 1 j νy 0 0 µ ν νx T 1 µeα 1 µy We c proceed smlrly to Theorem 3.6, ut usg ths tme 3.1 to estlsh the ext result. 0 0 Theorem 3.9. For 1, µ, ν N, α 1,,, c R +, d for λ C. If µ s eve d ν s odd the the followg detty holds true: E 0; λµ µ ν µx µ l ; λ;,, c 0 0 ] + j l T 1 j ν; λeα 1 j νy; λ;,, c j ν µ µx µ l ; λ;,, c 0 ] 3.18 l T 1 ν; λeα 1 νy; λ;,, c 0 µ ν νx ν l ; λ;,, c 0 ] l T 1 µ; λeα 1 µy; λ;,, c. A terestg specl cse of Theorem 7 s oted y settg 1, c e d λ Corollry For 1, µ, ν N, α 1. If µ s eve d ν s odd the the followg detty holds true: 1 E 0µ µ ν µx T 1 j j νeα 1 j νy 0 0 µ ν νx T 1 µeα 1 µy result gve frst y Lu d Wg 6, Theorem.7].
14 89 Flly, we would le to meto tht my other dettes c e oted from those show ths pper. As exmple, t s esy to see tht the two followg reltoshps hold etwee the Apostol-Beroull d Apostol-Euler polyomls d the Apostol-Beroull d Apostol-Geocch polyomls. Respectvely, we hve for N 0, µ, ν N, α N,,, c R +, d for λ C, d x; λ;,, c α! B α +αx; λ;,, c + α! 3.0 B α x; λ;,, c Gα x; λ;,, c α. 3.1 Let us see two exmples of pplcto of these two results. Frst, comg 3.0 wth Theorem 4 yelds Theorem For N 0, µ, ν N, α N,,, c R +, d for λ C. If µ d ν hve the sme prty, the the followg detty holds true: µ ν! B α αν l +α νx ; λ;,, c l T α µ; λ + α! 0 ν µ! B α +α µx αµ l ; λ;,, c l T α ν; λ. + α! 0 3. Next, cosderg 3.1 wth Theorem 1 gves Theorem 3.1. For ll tegers µ > 0, ν > 0, α N, 0, for,, c R + d for λ C, we hve the followg detty: G α µ 1ν l νx + ; λ;,, c µ ν S µ 1, λ G α 1 µy; λ;,, c l G α µx + ] ν 1µ l ; λ;,, c ν µ +1 S ν 1, λ G α 1 νy; λ;,, c l Refereces ] M. Armowtz d I.A. Stegu, Hdoo of mthemtcl fuctos wth formuls, grphs d mthemtcl tles, Ntol Bureu of Stdrds, Wshgto, DC, Yu. A. Brychov, O multple sums of specl fuctos, Itegrl Trsform Spec. Fuct , L. Comtet, Advced comtorcs: The rt of fte d fte expsos, Trslted from frech y J.W. Nehuys, Redel, Dordrecht, A. Erdely, W. Mgus, F. Oerhettger, d F. Trcom, Hgher trscedetl fuctos, vols.1-3,, E.R. Hse, A tle of seres d products, Pretce-Hll, Eglewood Clffs, NJ, Hogme Lu d Wepg Wg, Some dettes o the Beroull, Euler d Geocch polyomls v power sums d lterte power sums, Dscrete Mthemtcs ,
15 90 7. D.-Q. Lu d H.M. Srvstv, Some seres dettes volvg the geerlzed Apostol type d relted polyomls, Comput. Mth. Appl. DOI: /j.cmw Y. Lue, The specl fuctos d ther pproxmtos, vols. 1-, Q.-M. Luo, Apostol-Euler polyomls of hgher order d guss hypergeometrc fuctos, Twese J. Mth , , q-extesos for the Apostol-Geocch polyomls, Ge. Mth , , Exteso for the geocch polyomls d ts fourer expsos d tegrl represettos, Os J. Mth , Q.-M. Luo d H.M. Srvstv, Some geerlztos of the Apostol-Beroull d Apostol- Euler polyomls, J. Mth.Al.Appl , Q.-M. Luo d H.M. Srvstv, Some geerlztos of the postol-geocch polyomls d the strlg umers of the secod d, Appl. Mth. Comput , Q.M. Luo d H.M. Srvstv, Some reltoshps etwee the Apostol-Beroull d Apostol-Euler polyomls, Comput. Mth. Appl , F. Mgus, W. Oerhettger d R.P. So, Formuls d theorems for the specl fuctos of mthemtcl physcs, Thrd elrged edto, Sprger-Verlg, New Yor, H.M. Srvstv, M. Grg, d S. Choudhry, A ew geerlzto of the Beroull d relted polyomls, Russ J. Mth. Phys , , Some ew fmles of geerlzed Euler d Geocch polyomls, Twese J. Mth , H.J.H. Tueter, A symmetry of power sum polyomls d Beroull umers, Amer.Mth.Mothly , , The Froeus prolem, sums of powers of tegers, d recurreces for the Beroull umers, J. Numer Theory , Wepg Wg d Wewe Wg, Some results o power sums d Apostol-type polyomls, Itegrl Trsform Spec. Fuct , S.-L. Yg d Z.-K. Qo, Some symmetry dettes for the Euler polyomls, J. Mth. Res. Exposto , S.L. Yg, A detty of symmetry for the Beroull polyomls, Dscrete Mth , Zhzheg Zhg d Hqg Yg, Severl dettes for the geerlzed Apostol-Beroull polyomls, Comput. Mth. Appl , B.-Je Fugère Deprtmet of Mthemtcs d Computer Scece, Royl Mltry College, Kgsto, Otro, Cd, K7K 5L0 E-ml ddress: fugerej@rmc.c Seste Goury Deprtmet of Mthemtcs d Computer Scece, Uversty of Queec t Chcoutm, Queec, Cd, G7H B1 E-ml ddress: s1gour@uqc.c Rchrd Tremly Deprtmet of Mthemtcs d Computer Scece, Uversty of Queec t Chcoutm, Queec, Cd, G7H B1 E-ml ddress: rtreml@uqc.c
SUM PROPERTIES FOR THE K-LUCAS NUMBERS WITH ARITHMETIC INDEXES
 Avlble ole t http://sc.org J. Mth. Comput. Sc. 4 (04) No. 05-7 ISSN: 97-507 SUM PROPERTIES OR THE K-UCAS NUMBERS WITH ARITHMETIC INDEXES BIJENDRA SINGH POOJA BHADOURIA AND OMPRAKASH SIKHWA * School of
Avlble ole t http://sc.org J. Mth. Comput. Sc. 4 (04) No. 05-7 ISSN: 97-507 SUM PROPERTIES OR THE K-UCAS NUMBERS WITH ARITHMETIC INDEXES BIJENDRA SINGH POOJA BHADOURIA AND OMPRAKASH SIKHWA * School of
On Several Inequalities Deduced Using a Power Series Approach
 It J Cotemp Mth Sceces, Vol 8, 203, o 8, 855-864 HIKARI Ltd, wwwm-hrcom http://dxdoorg/02988/jcms2033896 O Severl Iequltes Deduced Usg Power Seres Approch Lored Curdru Deprtmet of Mthemtcs Poltehc Uversty
It J Cotemp Mth Sceces, Vol 8, 203, o 8, 855-864 HIKARI Ltd, wwwm-hrcom http://dxdoorg/02988/jcms2033896 O Severl Iequltes Deduced Usg Power Seres Approch Lored Curdru Deprtmet of Mthemtcs Poltehc Uversty
On a class of analytic functions defined by Ruscheweyh derivative
 Lfe Scece Jourl ;9( http://wwwlfescecestecom O clss of lytc fuctos defed by Ruscheweyh dervtve S N Ml M Arf K I Noor 3 d M Rz Deprtmet of Mthemtcs GC Uversty Fslbd Pujb Pst Deprtmet of Mthemtcs Abdul Wl
Lfe Scece Jourl ;9( http://wwwlfescecestecom O clss of lytc fuctos defed by Ruscheweyh dervtve S N Ml M Arf K I Noor 3 d M Rz Deprtmet of Mthemtcs GC Uversty Fslbd Pujb Pst Deprtmet of Mthemtcs Abdul Wl
MTH 146 Class 7 Notes
 7.7- Approxmte Itegrto Motvto: MTH 46 Clss 7 Notes I secto 7.5 we lered tht some defte tegrls, lke x e dx, cot e wrtte terms of elemetry fuctos. So, good questo to sk would e: How c oe clculte somethg
7.7- Approxmte Itegrto Motvto: MTH 46 Clss 7 Notes I secto 7.5 we lered tht some defte tegrls, lke x e dx, cot e wrtte terms of elemetry fuctos. So, good questo to sk would e: How c oe clculte somethg
Sequences and summations
 Lecture 0 Sequeces d summtos Istructor: Kgl Km CSE) E-ml: kkm0@kokuk.c.kr Tel. : 0-0-9 Room : New Mleum Bldg. 0 Lb : New Egeerg Bldg. 0 All sldes re bsed o CS Dscrete Mthemtcs for Computer Scece course
Lecture 0 Sequeces d summtos Istructor: Kgl Km CSE) E-ml: kkm0@kokuk.c.kr Tel. : 0-0-9 Room : New Mleum Bldg. 0 Lb : New Egeerg Bldg. 0 All sldes re bsed o CS Dscrete Mthemtcs for Computer Scece course
In Calculus I you learned an approximation method using a Riemann sum. Recall that the Riemann sum is
 Mth Sprg 08 L Approxmtg Dete Itegrls I Itroducto We hve studed severl methods tht llow us to d the exct vlues o dete tegrls However, there re some cses whch t s ot possle to evlute dete tegrl exctly I
Mth Sprg 08 L Approxmtg Dete Itegrls I Itroducto We hve studed severl methods tht llow us to d the exct vlues o dete tegrls However, there re some cses whch t s ot possle to evlute dete tegrl exctly I
Available online through
 Avlble ole through wwwmfo FIXED POINTS FOR NON-SELF MAPPINGS ON CONEX ECTOR METRIC SPACES Susht Kumr Moht* Deprtmet of Mthemtcs West Begl Stte Uverst Brst 4 PrgsNorth) Kolt 76 West Begl Id E-ml: smwbes@yhoo
Avlble ole through wwwmfo FIXED POINTS FOR NON-SELF MAPPINGS ON CONEX ECTOR METRIC SPACES Susht Kumr Moht* Deprtmet of Mthemtcs West Begl Stte Uverst Brst 4 PrgsNorth) Kolt 76 West Begl Id E-ml: smwbes@yhoo
ICS141: Discrete Mathematics for Computer Science I
 Uversty o Hw ICS: Dscrete Mthemtcs or Computer Scece I Dept. Iormto & Computer Sc., Uversty o Hw J Stelovsy bsed o sldes by Dr. Be d Dr. Stll Orgls by Dr. M. P. Fr d Dr. J.L. Gross Provded by McGrw-Hll
Uversty o Hw ICS: Dscrete Mthemtcs or Computer Scece I Dept. Iormto & Computer Sc., Uversty o Hw J Stelovsy bsed o sldes by Dr. Be d Dr. Stll Orgls by Dr. M. P. Fr d Dr. J.L. Gross Provded by McGrw-Hll
Systems of second order ordinary differential equations
 Ffth order dgolly mplct Ruge-Kutt Nystrom geerl method solvg secod Order IVPs Fudzh Isml Astrct A dgolly mplct Ruge-Kutt-Nystróm Geerl (SDIRKNG) method of ffth order wth explct frst stge for the tegrto
Ffth order dgolly mplct Ruge-Kutt Nystrom geerl method solvg secod Order IVPs Fudzh Isml Astrct A dgolly mplct Ruge-Kutt-Nystróm Geerl (SDIRKNG) method of ffth order wth explct frst stge for the tegrto
Patterns of Continued Fractions with a Positive Integer as a Gap
 IOSR Jourl of Mthemtcs (IOSR-JM) e-issn: 78-578, -ISSN: 39-765X Volume, Issue 3 Ver III (My - Ju 6), PP -5 wwwosrjourlsorg Ptters of Cotued Frctos wth Postve Iteger s G A Gm, S Krth (Mthemtcs, Govermet
IOSR Jourl of Mthemtcs (IOSR-JM) e-issn: 78-578, -ISSN: 39-765X Volume, Issue 3 Ver III (My - Ju 6), PP -5 wwwosrjourlsorg Ptters of Cotued Frctos wth Postve Iteger s G A Gm, S Krth (Mthemtcs, Govermet
Chapter 7. Bounds for weighted sums of Random Variables
 Chpter 7. Bouds for weghted sums of Rdom Vrbles 7. Itroducto Let d 2 be two depedet rdom vrbles hvg commo dstrbuto fucto. Htczeko (998 d Hu d L (2000 vestgted the Rylegh dstrbuto d obted some results bout
Chpter 7. Bouds for weghted sums of Rdom Vrbles 7. Itroducto Let d 2 be two depedet rdom vrbles hvg commo dstrbuto fucto. Htczeko (998 d Hu d L (2000 vestgted the Rylegh dstrbuto d obted some results bout
Some identities involving the partial sum of q-binomial coefficients
 Some dettes volvg the partal sum of -bomal coeffcets Bg He Departmet of Mathematcs, Shagha Key Laboratory of PMMP East Cha Normal Uversty 500 Dogchua Road, Shagha 20024, People s Republc of Cha yuhe00@foxmal.com
Some dettes volvg the partal sum of -bomal coeffcets Bg He Departmet of Mathematcs, Shagha Key Laboratory of PMMP East Cha Normal Uversty 500 Dogchua Road, Shagha 20024, People s Republc of Cha yuhe00@foxmal.com
14.2 Line Integrals. determines a partition P of the curve by points Pi ( xi, y
 4. Le Itegrls I ths secto we defe tegrl tht s smlr to sgle tegrl except tht sted of tegrtg over tervl [ ] we tegrte over curve. Such tegrls re clled le tegrls lthough curve tegrls would e etter termology.
4. Le Itegrls I ths secto we defe tegrl tht s smlr to sgle tegrl except tht sted of tegrtg over tervl [ ] we tegrte over curve. Such tegrls re clled le tegrls lthough curve tegrls would e etter termology.
Analytical Approach for the Solution of Thermodynamic Identities with Relativistic General Equation of State in a Mixture of Gases
 Itertol Jourl of Advced Reserch Physcl Scece (IJARPS) Volume, Issue 5, September 204, PP 6-0 ISSN 2349-7874 (Prt) & ISSN 2349-7882 (Ole) www.rcourls.org Alytcl Approch for the Soluto of Thermodymc Idettes
Itertol Jourl of Advced Reserch Physcl Scece (IJARPS) Volume, Issue 5, September 204, PP 6-0 ISSN 2349-7874 (Prt) & ISSN 2349-7882 (Ole) www.rcourls.org Alytcl Approch for the Soluto of Thermodymc Idettes
A Technique for Constructing Odd-order Magic Squares Using Basic Latin Squares
 Itertol Jourl of Scetfc d Reserch Publctos, Volume, Issue, My 0 ISSN 0- A Techque for Costructg Odd-order Mgc Squres Usg Bsc Lt Squres Tomb I. Deprtmet of Mthemtcs, Mpur Uversty, Imphl, Mpur (INDIA) tombrom@gml.com
Itertol Jourl of Scetfc d Reserch Publctos, Volume, Issue, My 0 ISSN 0- A Techque for Costructg Odd-order Mgc Squres Usg Bsc Lt Squres Tomb I. Deprtmet of Mthemtcs, Mpur Uversty, Imphl, Mpur (INDIA) tombrom@gml.com
Area and the Definite Integral. Area under Curve. The Partition. y f (x) We want to find the area under f (x) on [ a, b ]
![Area and the Definite Integral. Area under Curve. The Partition. y f (x) We want to find the area under f (x) on [ a, b ] Area and the Definite Integral. Area under Curve. The Partition. y f (x) We want to find the area under f (x) on [ a, b ]](/thumbs/83/87614710.jpg) Are d the Defte Itegrl 1 Are uder Curve We wt to fd the re uder f (x) o [, ] y f (x) x The Prtto We eg y prttog the tervl [, ] to smller su-tervls x 0 x 1 x x - x -1 x 1 The Bsc Ide We the crete rectgles
Are d the Defte Itegrl 1 Are uder Curve We wt to fd the re uder f (x) o [, ] y f (x) x The Prtto We eg y prttog the tervl [, ] to smller su-tervls x 0 x 1 x x - x -1 x 1 The Bsc Ide We the crete rectgles
Integration by Parts for D K
 Itertol OPEN ACCESS Jourl Of Moder Egeerg Reserc IJMER Itegrto y Prts for D K Itegrl T K Gr, S Ry 2 Deprtmet of Mtemtcs, Rgutpur College, Rgutpur-72333, Purul, West Begl, Id 2 Deprtmet of Mtemtcs, Ss Bv,
Itertol OPEN ACCESS Jourl Of Moder Egeerg Reserc IJMER Itegrto y Prts for D K Itegrl T K Gr, S Ry 2 Deprtmet of Mtemtcs, Rgutpur College, Rgutpur-72333, Purul, West Begl, Id 2 Deprtmet of Mtemtcs, Ss Bv,
this is the indefinite integral Since integration is the reverse of differentiation we can check the previous by [ ]
![this is the indefinite integral Since integration is the reverse of differentiation we can check the previous by [ ] this is the indefinite integral Since integration is the reverse of differentiation we can check the previous by [ ]](/thumbs/78/76749440.jpg) Atervtves The Itegrl Atervtves Ojectve: Use efte tegrl otto for tervtves. Use sc tegrto rules to f tervtves. Aother mportt questo clculus s gve ervtve f the fucto tht t cme from. Ths s the process kow
Atervtves The Itegrl Atervtves Ojectve: Use efte tegrl otto for tervtves. Use sc tegrto rules to f tervtves. Aother mportt questo clculus s gve ervtve f the fucto tht t cme from. Ths s the process kow
02/15/04 INTERESTING FINITE AND INFINITE PRODUCTS FROM SIMPLE ALGEBRAIC IDENTITIES
 0/5/04 ITERESTIG FIITE AD IFIITE PRODUCTS FROM SIMPLE ALGEBRAIC IDETITIES Thomas J Osler Mathematcs Departmet Rowa Uversty Glassboro J 0808 Osler@rowaedu Itroducto The dfferece of two squares, y = + y
0/5/04 ITERESTIG FIITE AD IFIITE PRODUCTS FROM SIMPLE ALGEBRAIC IDETITIES Thomas J Osler Mathematcs Departmet Rowa Uversty Glassboro J 0808 Osler@rowaedu Itroducto The dfferece of two squares, y = + y
Union, Intersection, Product and Direct Product of Prime Ideals
 Globl Jourl of Pure d Appled Mthemtcs. ISSN 0973-1768 Volume 11, Number 3 (2015), pp. 1663-1667 Reserch Id Publctos http://www.rpublcto.com Uo, Itersecto, Product d Drect Product of Prme Idels Bdu.P (1),
Globl Jourl of Pure d Appled Mthemtcs. ISSN 0973-1768 Volume 11, Number 3 (2015), pp. 1663-1667 Reserch Id Publctos http://www.rpublcto.com Uo, Itersecto, Product d Drect Product of Prme Idels Bdu.P (1),
ITERATIVE METHODS FOR SOLVING SYSTEMS OF LINEAR ALGEBRAIC EQUATIONS
 Numercl Alyss for Egeers Germ Jord Uversty ITERATIVE METHODS FOR SOLVING SYSTEMS OF LINEAR ALGEBRAIC EQUATIONS Numercl soluto of lrge systems of ler lgerc equtos usg drect methods such s Mtr Iverse, Guss
Numercl Alyss for Egeers Germ Jord Uversty ITERATIVE METHODS FOR SOLVING SYSTEMS OF LINEAR ALGEBRAIC EQUATIONS Numercl soluto of lrge systems of ler lgerc equtos usg drect methods such s Mtr Iverse, Guss
Least Squares Method For Solving Integral Equations With Multiple Time Lags
 Eg. & Tech. Jourl, Vol.8, No., Lest Squres Method For Solvg Itegrl Equtos Wth Multple Tme Lgs Dr.Suh N. Sheh*, Hyt Adel Al* & Hl Mohmmed Ysee* Receved o:6//9 Accepted o:// Astrct The m purpose of ths work
Eg. & Tech. Jourl, Vol.8, No., Lest Squres Method For Solvg Itegrl Equtos Wth Multple Tme Lgs Dr.Suh N. Sheh*, Hyt Adel Al* & Hl Mohmmed Ysee* Receved o:6//9 Accepted o:// Astrct The m purpose of ths work
DERIVATIVES OF KRONECKER PRODUCTS THEMSELVES BASED ON KRONECKER PRODUCT AND MATRIX CALCULUS
 Jourl of heoretcl d ppled Iformto echology th Februry 3. Vol. 48 No. 5-3 JI & S. ll rghts reserved. ISSN: 99-8645 www.jtt.org E-ISSN: 87-395 DERIVIVES OF KRONECKER PRODUCS HEMSEVES SED ON KRONECKER PRODUC
Jourl of heoretcl d ppled Iformto echology th Februry 3. Vol. 48 No. 5-3 JI & S. ll rghts reserved. ISSN: 99-8645 www.jtt.org E-ISSN: 87-395 DERIVIVES OF KRONECKER PRODUCS HEMSEVES SED ON KRONECKER PRODUC
Neville Robbins Mathematics Department, San Francisco State University, San Francisco, CA (Submitted August 2002-Final Revision December 2002)
 Nevlle Robbs Mathematcs Departmet, Sa Fracsco State Uversty, Sa Fracsco, CA 943 (Submtted August -Fal Revso December ) INTRODUCTION The Lucas tragle s a fte tragular array of atural umbers that s a varat
Nevlle Robbs Mathematcs Departmet, Sa Fracsco State Uversty, Sa Fracsco, CA 943 (Submtted August -Fal Revso December ) INTRODUCTION The Lucas tragle s a fte tragular array of atural umbers that s a varat
Journal of Mathematical Analysis and Applications
 J. Math. Aal. Appl. 365 200) 358 362 Cotets lsts avalable at SceceDrect Joural of Mathematcal Aalyss ad Applcatos www.elsever.com/locate/maa Asymptotc behavor of termedate pots the dfferetal mea value
J. Math. Aal. Appl. 365 200) 358 362 Cotets lsts avalable at SceceDrect Joural of Mathematcal Aalyss ad Applcatos www.elsever.com/locate/maa Asymptotc behavor of termedate pots the dfferetal mea value
under the curve in the first quadrant.
 NOTES 5: INTEGRALS Nme: Dte: Perod: LESSON 5. AREAS AND DISTANCES Are uder the curve Are uder f( ), ove the -s, o the dom., Prctce Prolems:. f ( ). Fd the re uder the fucto, ove the - s, etwee,.. f ( )
NOTES 5: INTEGRALS Nme: Dte: Perod: LESSON 5. AREAS AND DISTANCES Are uder the curve Are uder f( ), ove the -s, o the dom., Prctce Prolems:. f ( ). Fd the re uder the fucto, ove the - s, etwee,.. f ( )
Advanced Algorithmic Problem Solving Le 3 Arithmetic. Fredrik Heintz Dept of Computer and Information Science Linköping University
 Advced Algorthmc Prolem Solvg Le Arthmetc Fredrk Hetz Dept of Computer d Iformto Scece Lköpg Uversty Overvew Arthmetc Iteger multplcto Krtsu s lgorthm Multplcto of polyomls Fst Fourer Trsform Systems of
Advced Algorthmc Prolem Solvg Le Arthmetc Fredrk Hetz Dept of Computer d Iformto Scece Lköpg Uversty Overvew Arthmetc Iteger multplcto Krtsu s lgorthm Multplcto of polyomls Fst Fourer Trsform Systems of
ON NILPOTENCY IN NONASSOCIATIVE ALGEBRAS
 Jourl of Algebr Nuber Theory: Advces d Applctos Volue 6 Nuber 6 ges 85- Avlble t http://scetfcdvces.co. DOI: http://dx.do.org/.864/t_779 ON NILOTENCY IN NONASSOCIATIVE ALGERAS C. J. A. ÉRÉ M. F. OUEDRAOGO
Jourl of Algebr Nuber Theory: Advces d Applctos Volue 6 Nuber 6 ges 85- Avlble t http://scetfcdvces.co. DOI: http://dx.do.org/.864/t_779 ON NILOTENCY IN NONASSOCIATIVE ALGERAS C. J. A. ÉRÉ M. F. OUEDRAOGO
The z-transform. LTI System description. Prof. Siripong Potisuk
 The -Trsform Prof. Srpog Potsuk LTI System descrpto Prevous bss fucto: ut smple or DT mpulse The put sequece s represeted s ler combto of shfted DT mpulses. The respose s gve by covoluto sum of the put
The -Trsform Prof. Srpog Potsuk LTI System descrpto Prevous bss fucto: ut smple or DT mpulse The put sequece s represeted s ler combto of shfted DT mpulses. The respose s gve by covoluto sum of the put
POWERS OF COMPLEX PERSYMMETRIC ANTI-TRIDIAGONAL MATRICES WITH CONSTANT ANTI-DIAGONALS
 IRRS 9 y 04 wwwrppresscom/volumes/vol9issue/irrs_9 05pdf OWERS OF COLE ERSERIC I-RIIGOL RICES WIH COS I-IGOLS Wg usu * Q e Wg Hbo & ue College of Scece versty of Shgh for Scece d echology Shgh Ch 00093
IRRS 9 y 04 wwwrppresscom/volumes/vol9issue/irrs_9 05pdf OWERS OF COLE ERSERIC I-RIIGOL RICES WIH COS I-IGOLS Wg usu * Q e Wg Hbo & ue College of Scece versty of Shgh for Scece d echology Shgh Ch 00093
10.2 Series. , we get. which is called an infinite series ( or just a series) and is denoted, for short, by the symbol. i i n
 0. Sere I th ecto, we wll troduce ere tht wll be dcug for the ret of th chpter. Wht ere? If we dd ll term of equece, we get whch clled fte ere ( or jut ere) d deoted, for hort, by the ymbol or Doe t mke
0. Sere I th ecto, we wll troduce ere tht wll be dcug for the ret of th chpter. Wht ere? If we dd ll term of equece, we get whch clled fte ere ( or jut ere) d deoted, for hort, by the ymbol or Doe t mke
Mu Sequences/Series Solutions National Convention 2014
 Mu Sequeces/Seres Solutos Natoal Coveto 04 C 6 E A 6C A 6 B B 7 A D 7 D C 7 A B 8 A B 8 A C 8 E 4 B 9 B 4 E 9 B 4 C 9 E C 0 A A 0 D B 0 C C Usg basc propertes of arthmetc sequeces, we fd a ad bm m We eed
Mu Sequeces/Seres Solutos Natoal Coveto 04 C 6 E A 6C A 6 B B 7 A D 7 D C 7 A B 8 A B 8 A C 8 E 4 B 9 B 4 E 9 B 4 C 9 E C 0 A A 0 D B 0 C C Usg basc propertes of arthmetc sequeces, we fd a ad bm m We eed
Fibonacci and Lucas Numbers as Tridiagonal Matrix Determinants
 Rochester Isttute of echology RI Scholr Wors Artcles 8-00 bocc d ucs Nubers s rdgol trx Deterts Nth D. Chll Est Kod Copy Drre Nry Rochester Isttute of echology ollow ths d ddtol wors t: http://scholrwors.rt.edu/rtcle
Rochester Isttute of echology RI Scholr Wors Artcles 8-00 bocc d ucs Nubers s rdgol trx Deterts Nth D. Chll Est Kod Copy Drre Nry Rochester Isttute of echology ollow ths d ddtol wors t: http://scholrwors.rt.edu/rtcle
Answer: First, I ll show how to find the terms analytically then I ll show how to use the TI to find them.
 . CHAPTER 0 SEQUENCE, SERIES, d INDUCTION Secto 0. Seqece A lst of mers specfc order. E / Fd the frst terms : of the gve seqece: Aswer: Frst, I ll show how to fd the terms ltcll the I ll show how to se
. CHAPTER 0 SEQUENCE, SERIES, d INDUCTION Secto 0. Seqece A lst of mers specfc order. E / Fd the frst terms : of the gve seqece: Aswer: Frst, I ll show how to fd the terms ltcll the I ll show how to se
arxiv:math/ v2 [math.co] 2 Oct 2001
![arxiv:math/ v2 [math.co] 2 Oct 2001 arxiv:math/ v2 [math.co] 2 Oct 2001](/thumbs/75/71507134.jpg) 000]Prmry 05A10, 05A19, 05A30, 11B65, 33D15; Secodry 11P8 THE WP BAILEY TREE AD ITS IMPLICATIOS rxv:mth/0109141v [mth.co] Oct 001 GEORGE ADREWS AD ALEXADER BERKOVICH Abstrct. Our object s thorough lyss
000]Prmry 05A10, 05A19, 05A30, 11B65, 33D15; Secodry 11P8 THE WP BAILEY TREE AD ITS IMPLICATIOS rxv:mth/0109141v [mth.co] Oct 001 GEORGE ADREWS AD ALEXADER BERKOVICH Abstrct. Our object s thorough lyss
ME 501A Seminar in Engineering Analysis Page 1
 Mtr Trsformtos usg Egevectors September 8, Mtr Trsformtos Usg Egevectors Lrry Cretto Mechcl Egeerg A Semr Egeerg Alyss September 8, Outle Revew lst lecture Trsformtos wth mtr of egevectors: = - A ermt
Mtr Trsformtos usg Egevectors September 8, Mtr Trsformtos Usg Egevectors Lrry Cretto Mechcl Egeerg A Semr Egeerg Alyss September 8, Outle Revew lst lecture Trsformtos wth mtr of egevectors: = - A ermt
Numerical Solution of Higher Order Linear Fredholm Integro Differential Equations.
 Amerc Jorl of Egeerg Reserch (AJER) 04 Amerc Jorl of Egeerg Reserch (AJER) e-iss : 30-0847 p-iss : 30-0936 Volme-03, Isse-08, pp-43-47 www.jer.org Reserch Pper Ope Access mercl Solto of Hgher Order Ler
Amerc Jorl of Egeerg Reserch (AJER) 04 Amerc Jorl of Egeerg Reserch (AJER) e-iss : 30-0847 p-iss : 30-0936 Volme-03, Isse-08, pp-43-47 www.jer.org Reserch Pper Ope Access mercl Solto of Hgher Order Ler
Applied Mathematics and Computation
 Aled Mtemtcs d Comutto 17 (011) 570 578 Cotets lsts vlble t SceceDrect Aled Mtemtcs d Comutto ourl omege: www.elsever.com/locte/mc Some geerlztos of te Aostol Geocc olyomls d te Strlg umbers of te secod
Aled Mtemtcs d Comutto 17 (011) 570 578 Cotets lsts vlble t SceceDrect Aled Mtemtcs d Comutto ourl omege: www.elsever.com/locte/mc Some geerlztos of te Aostol Geocc olyomls d te Strlg umbers of te secod
Roberto s Notes on Integral Calculus Chapter 4: Definite integrals and the FTC Section 2. Riemann sums
 Roerto s Notes o Itegrl Clculus Chpter 4: Defte tegrls d the FTC Secto 2 Rem sums Wht you eed to kow lredy: The defto of re for rectgle. Rememer tht our curret prolem s how to compute the re of ple rego
Roerto s Notes o Itegrl Clculus Chpter 4: Defte tegrls d the FTC Secto 2 Rem sums Wht you eed to kow lredy: The defto of re for rectgle. Rememer tht our curret prolem s how to compute the re of ple rego
On quaternions with generalized Fibonacci and Lucas number components
 Polatl Kesm Advaces Dfferece Equatos (205) 205:69 DOI 0.86/s3662-05-05-x R E S E A R C H Ope Access O quateros wth geeralzed Fboacc Lucas umber compoets Emrah Polatl * Seyhu Kesm * Correspodece: emrah.polatl@beu.edu.tr
Polatl Kesm Advaces Dfferece Equatos (205) 205:69 DOI 0.86/s3662-05-05-x R E S E A R C H Ope Access O quateros wth geeralzed Fboacc Lucas umber compoets Emrah Polatl * Seyhu Kesm * Correspodece: emrah.polatl@beu.edu.tr
An Alternative Method to Find the Solution of Zero One Integer Linear Fractional Programming Problem with the Help of -Matrix
 Itertol Jourl of Scetfc d Reserch Pulctos, Volue 3, Issue 6, Jue 3 ISSN 5-353 A Altertve Method to Fd the Soluto of Zero Oe Iteger Ler Frctol Progrg Prole wth the Help of -Mtr VSeeregsy *, DrKJeyr ** *
Itertol Jourl of Scetfc d Reserch Pulctos, Volue 3, Issue 6, Jue 3 ISSN 5-353 A Altertve Method to Fd the Soluto of Zero Oe Iteger Ler Frctol Progrg Prole wth the Help of -Mtr VSeeregsy *, DrKJeyr ** *
The Lucas and Babbage congruences
 The Lucas ad Baage cogrueces Dar Grerg Feruary 26, 2018 Cotets 01 Itroducto 1 1 The cogrueces 2 11 Bomal coeffcets 2 12 Negatve 3 13 The two cogrueces 4 2 Proofs 5 21 Basc propertes of omal coeffcets modulo
The Lucas ad Baage cogrueces Dar Grerg Feruary 26, 2018 Cotets 01 Itroducto 1 1 The cogrueces 2 11 Bomal coeffcets 2 12 Negatve 3 13 The two cogrueces 4 2 Proofs 5 21 Basc propertes of omal coeffcets modulo
Exercises for Square-Congruence Modulo n ver 11
 Exercses for Square-Cogruece Modulo ver Let ad ab,.. Mark True or False. a. 3S 30 b. 3S 90 c. 3S 3 d. 3S 4 e. 4S f. 5S g. 0S 55 h. 8S 57. 9S 58 j. S 76 k. 6S 304 l. 47S 5347. Fd the equvalece classes duced
Exercses for Square-Cogruece Modulo ver Let ad ab,.. Mark True or False. a. 3S 30 b. 3S 90 c. 3S 3 d. 3S 4 e. 4S f. 5S g. 0S 55 h. 8S 57. 9S 58 j. S 76 k. 6S 304 l. 47S 5347. Fd the equvalece classes duced
COMPLEX NUMBERS AND DE MOIVRE S THEOREM
 COMPLEX NUMBERS AND DE MOIVRE S THEOREM OBJECTIVE PROBLEMS. s equl to b d. 9 9 b 9 9 d. The mgr prt of s 5 5 b 5. If m, the the lest tegrl vlue of m s b 8 5. The vlue of 5... s f s eve, f s odd b f s eve,
COMPLEX NUMBERS AND DE MOIVRE S THEOREM OBJECTIVE PROBLEMS. s equl to b d. 9 9 b 9 9 d. The mgr prt of s 5 5 b 5. If m, the the lest tegrl vlue of m s b 8 5. The vlue of 5... s f s eve, f s odd b f s eve,
#A27 INTEGERS 13 (2013) SOME WEIGHTED SUMS OF PRODUCTS OF LUCAS SEQUENCES
 #A27 INTEGERS 3 (203) SOME WEIGHTED SUMS OF PRODUCTS OF LUCAS SEQUENCES Emrah Kılıç Mathematcs Departmet, TOBB Uversty of Ecoomcs ad Techology, Akara, Turkey eklc@etu.edu.tr Neşe Ömür Mathematcs Departmet,
#A27 INTEGERS 3 (203) SOME WEIGHTED SUMS OF PRODUCTS OF LUCAS SEQUENCES Emrah Kılıç Mathematcs Departmet, TOBB Uversty of Ecoomcs ad Techology, Akara, Turkey eklc@etu.edu.tr Neşe Ömür Mathematcs Departmet,
DATA FITTING. Intensive Computation 2013/2014. Annalisa Massini
 DATA FITTING Itesve Computto 3/4 Als Mss Dt fttg Dt fttg cocers the problem of fttg dscrete dt to obt termedte estmtes. There re two geerl pproches two curve fttg: Iterpolto Dt s ver precse. The strteg
DATA FITTING Itesve Computto 3/4 Als Mss Dt fttg Dt fttg cocers the problem of fttg dscrete dt to obt termedte estmtes. There re two geerl pproches two curve fttg: Iterpolto Dt s ver precse. The strteg
A Brief Introduction to Olympiad Inequalities
 Ev Che Aprl 0, 04 The gol of ths documet s to provde eser troducto to olympd equltes th the stdrd exposto Olympd Iequltes, by Thoms Mldorf I ws motvted to wrte t by feelg gulty for gettg free 7 s o problems
Ev Che Aprl 0, 04 The gol of ths documet s to provde eser troducto to olympd equltes th the stdrd exposto Olympd Iequltes, by Thoms Mldorf I ws motvted to wrte t by feelg gulty for gettg free 7 s o problems
Entropy ISSN by MDPI
 Etropy 2003, 5, 233-238 Etropy ISSN 1099-4300 2003 by MDPI www.mdp.org/etropy O the Measure Etropy of Addtve Cellular Automata Hasa Aı Arts ad Sceces Faculty, Departmet of Mathematcs, Harra Uversty; 63100,
Etropy 2003, 5, 233-238 Etropy ISSN 1099-4300 2003 by MDPI www.mdp.org/etropy O the Measure Etropy of Addtve Cellular Automata Hasa Aı Arts ad Sceces Faculty, Departmet of Mathematcs, Harra Uversty; 63100,
Lecture 12 APPROXIMATION OF FIRST ORDER DERIVATIVES
 FDM: Appromato of Frst Order Dervatves Lecture APPROXIMATION OF FIRST ORDER DERIVATIVES. INTRODUCTION Covectve term coservato equatos volve frst order dervatves. The smplest possble approach for dscretzato
FDM: Appromato of Frst Order Dervatves Lecture APPROXIMATION OF FIRST ORDER DERIVATIVES. INTRODUCTION Covectve term coservato equatos volve frst order dervatves. The smplest possble approach for dscretzato
GENERALIZED OPERATIONAL RELATIONS AND PROPERTIES OF FRACTIONAL HANKEL TRANSFORM
 S. Res. Chem. Commu.: (3 8-88 ISSN 77-669 GENERLIZED OPERTIONL RELTIONS ND PROPERTIES OF FRCTIONL NKEL TRNSFORM R. D. TYWDE *. S. GUDDE d V. N. MLLE b Pro. Rm Meghe Isttute o Teholog & Reserh Bder MRVTI
S. Res. Chem. Commu.: (3 8-88 ISSN 77-669 GENERLIZED OPERTIONL RELTIONS ND PROPERTIES OF FRCTIONL NKEL TRNSFORM R. D. TYWDE *. S. GUDDE d V. N. MLLE b Pro. Rm Meghe Isttute o Teholog & Reserh Bder MRVTI
On Solution of Min-Max Composition Fuzzy Relational Equation
 U-Sl Scece Jourl Vol.4()7 O Soluto of M-Mx Coposto Fuzzy eltol Equto N.M. N* Dte of cceptce /5/7 Abstrct I ths pper, M-Mx coposto fuzzy relto equto re studed. hs study s geerlzto of the works of Ohsto
U-Sl Scece Jourl Vol.4()7 O Soluto of M-Mx Coposto Fuzzy eltol Equto N.M. N* Dte of cceptce /5/7 Abstrct I ths pper, M-Mx coposto fuzzy relto equto re studed. hs study s geerlzto of the works of Ohsto
Numerical Solution of Second order Integro- Differential Equations(Ides) with Different Four Polynomials Bases Functions
 Numercl Soluto of Secod order Itegro- Dfferetl Equtos(Ides) wth Dfferet Four Polyomls Bses Fuctos wo O A R M Deprtmet of Mthemtcs Uersty of Ilor Deprtmet of Mthemtcs d Sttstcs he Poly Id Astrct: - I ths
Numercl Soluto of Secod order Itegro- Dfferetl Equtos(Ides) wth Dfferet Four Polyomls Bses Fuctos wo O A R M Deprtmet of Mthemtcs Uersty of Ilor Deprtmet of Mthemtcs d Sttstcs he Poly Id Astrct: - I ths
Asymptotic Dominance Problems. is not constant but for n 0, f ( n) 11. 0, so that for n N f
 Asymptotc Domce Prolems Dsply ucto : N R tht s Ο( ) ut s ot costt 0 = 0 The ucto ( ) = > 0 s ot costt ut or 0, ( ) Dee the relto " " o uctos rom N to R y g d oly = Ο( g) Prove tht s relexve d trstve (Recll:
Asymptotc Domce Prolems Dsply ucto : N R tht s Ο( ) ut s ot costt 0 = 0 The ucto ( ) = > 0 s ot costt ut or 0, ( ) Dee the relto " " o uctos rom N to R y g d oly = Ο( g) Prove tht s relexve d trstve (Recll:
h-analogue of Fibonacci Numbers
 h-aalogue of Fboacc Numbers arxv:090.0038v [math-ph 30 Sep 009 H.B. Beaoum Prce Mohammad Uversty, Al-Khobar 395, Saud Araba Abstract I ths paper, we troduce the h-aalogue of Fboacc umbers for o-commutatve
h-aalogue of Fboacc Numbers arxv:090.0038v [math-ph 30 Sep 009 H.B. Beaoum Prce Mohammad Uversty, Al-Khobar 395, Saud Araba Abstract I ths paper, we troduce the h-aalogue of Fboacc umbers for o-commutatve
Numerical Differentiation and Integration
 Numerl Deretto d Itegrto Overvew Numerl Deretto Newto-Cotes Itegrto Formuls Trpezodl rule Smpso s Rules Guss Qudrture Cheyshev s ormul Numerl Deretto Forwrd te dvded deree Bkwrd te dvded deree Ceter te
Numerl Deretto d Itegrto Overvew Numerl Deretto Newto-Cotes Itegrto Formuls Trpezodl rule Smpso s Rules Guss Qudrture Cheyshev s ormul Numerl Deretto Forwrd te dvded deree Bkwrd te dvded deree Ceter te
MATH2999 Directed Studies in Mathematics Matrix Theory and Its Applications
 MATH999 Drected Studes Mthemtcs Mtr Theory d Its Applctos Reserch Topc Sttory Probblty Vector of Hgher-order Mrkov Ch By Zhg Sho Supervsors: Prof. L Ch-Kwog d Dr. Ch Jor-Tg Cotets Abstrct. Itroducto: Bckgroud.
MATH999 Drected Studes Mthemtcs Mtr Theory d Its Applctos Reserch Topc Sttory Probblty Vector of Hgher-order Mrkov Ch By Zhg Sho Supervsors: Prof. L Ch-Kwog d Dr. Ch Jor-Tg Cotets Abstrct. Itroducto: Bckgroud.
Strategies for the AP Calculus Exam
 Strteges for the AP Clculus Em Strteges for the AP Clculus Em Strtegy : Kow Your Stuff Ths my seem ovous ut t ees to e metoe. No mout of cochg wll help you o the em f you o t kow the mterl. Here s lst
Strteges for the AP Clculus Em Strteges for the AP Clculus Em Strtegy : Kow Your Stuff Ths my seem ovous ut t ees to e metoe. No mout of cochg wll help you o the em f you o t kow the mterl. Here s lst
ON THE MIKI AND MATIYASEVICH IDENTITIES FOR BERNOULLI NUMBERS
 #A7 INTEGERS 4 (4) ON THE MIKI AND MATIYASEVICH IDENTITIES FOR BERNOULLI NUMBERS Takash Agoh Departmet of Mathematcs, Tokyo Uversty of Scece, Noda, Chba, Japa agoh takash@ma.oda.tus.ac.jp Receved: 3/9/3,
#A7 INTEGERS 4 (4) ON THE MIKI AND MATIYASEVICH IDENTITIES FOR BERNOULLI NUMBERS Takash Agoh Departmet of Mathematcs, Tokyo Uversty of Scece, Noda, Chba, Japa agoh takash@ma.oda.tus.ac.jp Receved: 3/9/3,
Bounds for the Connective Eccentric Index
 It. J. Cotemp. Math. Sceces, Vol. 7, 0, o. 44, 6-66 Bouds for the Coectve Eccetrc Idex Nlaja De Departmet of Basc Scece, Humates ad Socal Scece (Mathematcs Calcutta Isttute of Egeerg ad Maagemet Kolkata,
It. J. Cotemp. Math. Sceces, Vol. 7, 0, o. 44, 6-66 Bouds for the Coectve Eccetrc Idex Nlaja De Departmet of Basc Scece, Humates ad Socal Scece (Mathematcs Calcutta Isttute of Egeerg ad Maagemet Kolkata,
Bond Additive Modeling 5. Mathematical Properties of the Variable Sum Exdeg Index
 CROATICA CHEMICA ACTA CCACAA ISSN 00-6 e-issn -7X Crot. Chem. Act 8 () (0) 9 0. CCA-5 Orgl Scetfc Artcle Bod Addtve Modelg 5. Mthemtcl Propertes of the Vrble Sum Edeg Ide Dmr Vukčevć Fculty of Nturl Sceces
CROATICA CHEMICA ACTA CCACAA ISSN 00-6 e-issn -7X Crot. Chem. Act 8 () (0) 9 0. CCA-5 Orgl Scetfc Artcle Bod Addtve Modelg 5. Mthemtcl Propertes of the Vrble Sum Edeg Ide Dmr Vukčevć Fculty of Nturl Sceces
Linear Open Loop Systems
 Colordo School of Me CHEN43 Trfer Fucto Ler Ope Loop Sytem Ler Ope Loop Sytem... Trfer Fucto for Smple Proce... Exmple Trfer Fucto Mercury Thermometer... 2 Derblty of Devto Vrble... 3 Trfer Fucto for Proce
Colordo School of Me CHEN43 Trfer Fucto Ler Ope Loop Sytem Ler Ope Loop Sytem... Trfer Fucto for Smple Proce... Exmple Trfer Fucto Mercury Thermometer... 2 Derblty of Devto Vrble... 3 Trfer Fucto for Proce
Chapter 2 Intro to Math Techniques for Quantum Mechanics
 Wter 3 Chem 356: Itroductory Qutum Mechcs Chpter Itro to Mth Techques for Qutum Mechcs... Itro to dfferetl equtos... Boudry Codtos... 5 Prtl dfferetl equtos d seprto of vrbles... 5 Itroducto to Sttstcs...
Wter 3 Chem 356: Itroductory Qutum Mechcs Chpter Itro to Mth Techques for Qutum Mechcs... Itro to dfferetl equtos... Boudry Codtos... 5 Prtl dfferetl equtos d seprto of vrbles... 5 Itroducto to Sttstcs...
SOME IDENTITIES BETWEEN BASIC HYPERGEOMETRIC SERIES DERIVING FROM A NEW BAILEY-TYPE TRANSFORMATION
 SOME IDENTITIES BETWEEN BASIC HYPERGEOMETRIC SERIES DERIVING FROM A NEW BAILEY-TYPE TRANSFORMATION JAMES MC LAUGHLIN AND PETER ZIMMER Abstrct We prove ew Biley-type trsformtio reltig WP- Biley pirs We
SOME IDENTITIES BETWEEN BASIC HYPERGEOMETRIC SERIES DERIVING FROM A NEW BAILEY-TYPE TRANSFORMATION JAMES MC LAUGHLIN AND PETER ZIMMER Abstrct We prove ew Biley-type trsformtio reltig WP- Biley pirs We
Non-uniform Turán-type problems
 Joural of Combatoral Theory, Seres A 111 2005 106 110 wwwelsevercomlocatecta No-uform Turá-type problems DhruvMubay 1, Y Zhao 2 Departmet of Mathematcs, Statstcs, ad Computer Scece, Uversty of Illos at
Joural of Combatoral Theory, Seres A 111 2005 106 110 wwwelsevercomlocatecta No-uform Turá-type problems DhruvMubay 1, Y Zhao 2 Departmet of Mathematcs, Statstcs, ad Computer Scece, Uversty of Illos at
CS473-Algorithms I. Lecture 3. Solving Recurrences. Cevdet Aykanat - Bilkent University Computer Engineering Department
 CS473-Algorthms I Lecture 3 Solvg Recurreces Cevdet Aykt - Blket Uversty Computer Egeerg Deprtmet Solvg Recurreces The lyss of merge sort Lecture requred us to solve recurrece. Recurreces re lke solvg
CS473-Algorthms I Lecture 3 Solvg Recurreces Cevdet Aykt - Blket Uversty Computer Egeerg Deprtmet Solvg Recurreces The lyss of merge sort Lecture requred us to solve recurrece. Recurreces re lke solvg
ZETA REGULARIZATION METHOD APPLIED TO THE CALCULATION OF DIVERGENT DIVERGENT INTEGRALS
 ZETA REGULARIZATION METOD APPLIED TO TE CALCULATION OF DIVERGENT DIVERGENT INTEGRALS Jose Jver Grc Moret Grdute studet of Physcs t the UPV/EU (Uversty of Bsque coutry) I Sold Stte Physcs Addres: Prctctes
ZETA REGULARIZATION METOD APPLIED TO TE CALCULATION OF DIVERGENT DIVERGENT INTEGRALS Jose Jver Grc Moret Grdute studet of Physcs t the UPV/EU (Uversty of Bsque coutry) I Sold Stte Physcs Addres: Prctctes
APPLICATION OF THE CHEBYSHEV POLYNOMIALS TO APPROXIMATION AND CONSTRUCTION OF MAP PROJECTIONS
 APPLICATION OF THE CHEBYSHEV POLYNOMIALS TO APPROXIMATION AND CONSTRUCTION OF MAP PROJECTIONS Pweł Pędzch Jerzy Blcerz Wrsw Uversty of Techology Fculty of Geodesy d Crtogrphy Astrct Usully to pproto of
APPLICATION OF THE CHEBYSHEV POLYNOMIALS TO APPROXIMATION AND CONSTRUCTION OF MAP PROJECTIONS Pweł Pędzch Jerzy Blcerz Wrsw Uversty of Techology Fculty of Geodesy d Crtogrphy Astrct Usully to pproto of
Chapter Unary Matrix Operations
 Chpter 04.04 Ury trx Opertos After redg ths chpter, you should be ble to:. kow wht ury opertos mes,. fd the trspose of squre mtrx d t s reltoshp to symmetrc mtrces,. fd the trce of mtrx, d 4. fd the ermt
Chpter 04.04 Ury trx Opertos After redg ths chpter, you should be ble to:. kow wht ury opertos mes,. fd the trspose of squre mtrx d t s reltoshp to symmetrc mtrces,. fd the trce of mtrx, d 4. fd the ermt
AN EULER-MC LAURIN FORMULA FOR INFINITE DIMENSIONAL SPACES
 AN EULER-MC LAURIN FORMULA FOR INFINITE DIMENSIONAL SPACES Jose Javer Garca Moreta Graduate Studet of Physcs ( Sold State ) at UPV/EHU Address: P.O 6 890 Portugalete, Vzcaya (Spa) Phoe: (00) 3 685 77 16
AN EULER-MC LAURIN FORMULA FOR INFINITE DIMENSIONAL SPACES Jose Javer Garca Moreta Graduate Studet of Physcs ( Sold State ) at UPV/EHU Address: P.O 6 890 Portugalete, Vzcaya (Spa) Phoe: (00) 3 685 77 16
About k-perfect numbers
 DOI: 0.47/auom-04-0005 A. Şt. Uv. Ovdus Costaţa Vol.,04, 45 50 About k-perfect umbers Mhály Becze Abstract ABSTRACT. I ths paper we preset some results about k-perfect umbers, ad geeralze two equaltes
DOI: 0.47/auom-04-0005 A. Şt. Uv. Ovdus Costaţa Vol.,04, 45 50 About k-perfect umbers Mhály Becze Abstract ABSTRACT. I ths paper we preset some results about k-perfect umbers, ad geeralze two equaltes
A Series Illustrating Innovative Forms of the Organization & Exposition of Mathematics by Walter Gottschalk
 The Sgm Summto Notto #8 of Gottschlk's Gestlts A Seres Illustrtg Iovtve Forms of the Orgzto & Exposto of Mthemtcs by Wlter Gottschlk Ifte Vsts Press PVD RI 00 GG8- (8) 00 Wlter Gottschlk 500 Agell St #44
The Sgm Summto Notto #8 of Gottschlk's Gestlts A Seres Illustrtg Iovtve Forms of the Orgzto & Exposto of Mthemtcs by Wlter Gottschlk Ifte Vsts Press PVD RI 00 GG8- (8) 00 Wlter Gottschlk 500 Agell St #44
AN INEQUALITY OF GRÜSS TYPE FOR RIEMANN-STIELTJES INTEGRAL AND APPLICATIONS FOR SPECIAL MEANS
 RGMIA Reserch Report Collectio, Vol., No., 998 http://sci.vut.edu.u/ rgmi/reports.html AN INEQUALITY OF GRÜSS TYPE FOR RIEMANN-STIELTJES INTEGRAL AND APPLICATIONS FOR SPECIAL MEANS S.S. DRAGOMIR AND I.
RGMIA Reserch Report Collectio, Vol., No., 998 http://sci.vut.edu.u/ rgmi/reports.html AN INEQUALITY OF GRÜSS TYPE FOR RIEMANN-STIELTJES INTEGRAL AND APPLICATIONS FOR SPECIAL MEANS S.S. DRAGOMIR AND I.
Algorithms Theory, Solution for Assignment 2
 Juor-Prof. Dr. Robert Elsässer, Marco Muñz, Phllp Hedegger WS 2009/200 Algorthms Theory, Soluto for Assgmet 2 http://lak.formatk.u-freburg.de/lak_teachg/ws09_0/algo090.php Exercse 2. - Fast Fourer Trasform
Juor-Prof. Dr. Robert Elsässer, Marco Muñz, Phllp Hedegger WS 2009/200 Algorthms Theory, Soluto for Assgmet 2 http://lak.formatk.u-freburg.de/lak_teachg/ws09_0/algo090.php Exercse 2. - Fast Fourer Trasform
Section IV.6: The Master Method and Applications
 Sectio IV.6: The Mster Method d Applictios Defiitio IV.6.1: A fuctio f is symptoticlly positive if d oly if there exists rel umer such tht f(x) > for ll x >. A cosequece of this defiitio is tht fuctio
Sectio IV.6: The Mster Method d Applictios Defiitio IV.6.1: A fuctio f is symptoticlly positive if d oly if there exists rel umer such tht f(x) > for ll x >. A cosequece of this defiitio is tht fuctio
Keywords: Heptic non-homogeneous equation, Pyramidal numbers, Pronic numbers, fourth dimensional figurate numbers.
 [Gol 5: M 0] ISSN: 77-9655 IJEST INTENTIONL JOUNL OF ENGINEEING SCIENCES & ESECH TECHNOLOGY O the Hetc No-Hoogeeous Euto th Four Ukos z 6 0 M..Gol * G.Suth S.Vdhlksh * Dertet of MthetcsShrt Idr Gdh CollegeTrch
[Gol 5: M 0] ISSN: 77-9655 IJEST INTENTIONL JOUNL OF ENGINEEING SCIENCES & ESECH TECHNOLOGY O the Hetc No-Hoogeeous Euto th Four Ukos z 6 0 M..Gol * G.Suth S.Vdhlksh * Dertet of MthetcsShrt Idr Gdh CollegeTrch
A Study on New Sequence of Functions Involving the Generalized Contour Integral
 Globl Jourl of Scece Froter Reerch Mthetc d Deco Scece Volue 3 Iue Vero. Yer 23 Type : Double Bld Peer Revewed Itertol Reerch Jourl Publher: Globl Jourl Ic. (USA Ole ISS: 2249-4626 & Prt ISS: 975-5896
Globl Jourl of Scece Froter Reerch Mthetc d Deco Scece Volue 3 Iue Vero. Yer 23 Type : Double Bld Peer Revewed Itertol Reerch Jourl Publher: Globl Jourl Ic. (USA Ole ISS: 2249-4626 & Prt ISS: 975-5896
CHAPTER 4 RADICAL EXPRESSIONS
 6 CHAPTER RADICAL EXPRESSIONS. The th Root of a Real Number A real umber a s called the th root of a real umber b f Thus, for example: s a square root of sce. s also a square root of sce ( ). s a cube
6 CHAPTER RADICAL EXPRESSIONS. The th Root of a Real Number A real umber a s called the th root of a real umber b f Thus, for example: s a square root of sce. s also a square root of sce ( ). s a cube
Part 4b Asymptotic Results for MRR2 using PRESS. Recall that the PRESS statistic is a special type of cross validation procedure (see Allen (1971))
 art 4b Asymptotc Results for MRR usg RESS Recall that the RESS statstc s a specal type of cross valdato procedure (see Alle (97)) partcular to the regresso problem ad volves fdg Y $,, the estmate at the
art 4b Asymptotc Results for MRR usg RESS Recall that the RESS statstc s a specal type of cross valdato procedure (see Alle (97)) partcular to the regresso problem ad volves fdg Y $,, the estmate at the
Solving Constrained Flow-Shop Scheduling. Problems with Three Machines
 It J Cotemp Math Sceces, Vol 5, 2010, o 19, 921-929 Solvg Costraed Flow-Shop Schedulg Problems wth Three Maches P Pada ad P Rajedra Departmet of Mathematcs, School of Advaced Sceces, VIT Uversty, Vellore-632
It J Cotemp Math Sceces, Vol 5, 2010, o 19, 921-929 Solvg Costraed Flow-Shop Schedulg Problems wth Three Maches P Pada ad P Rajedra Departmet of Mathematcs, School of Advaced Sceces, VIT Uversty, Vellore-632
{ }{ ( )} (, ) = ( ) ( ) ( ) Chapter 14 Exercises in Sampling Theory. Exercise 1 (Simple random sampling): Solution:
 Chapter 4 Exercses Samplg Theory Exercse (Smple radom samplg: Let there be two correlated radom varables X ad A sample of sze s draw from a populato by smple radom samplg wthout replacemet The observed
Chapter 4 Exercses Samplg Theory Exercse (Smple radom samplg: Let there be two correlated radom varables X ad A sample of sze s draw from a populato by smple radom samplg wthout replacemet The observed
Level-2 BLAS. Matrix-Vector operations with O(n 2 ) operations (sequentially) BLAS-Notation: S --- single precision G E general matrix M V --- vector
 evel-2 BS trx-vector opertos wth 2 opertos sequetlly BS-Notto: S --- sgle precso G E geerl mtrx V --- vector defes SGEV, mtrx-vector product: r y r α x β r y ther evel-2 BS: Solvg trgulr system x wth trgulr
evel-2 BS trx-vector opertos wth 2 opertos sequetlly BS-Notto: S --- sgle precso G E geerl mtrx V --- vector defes SGEV, mtrx-vector product: r y r α x β r y ther evel-2 BS: Solvg trgulr system x wth trgulr
SUBCLASS OF HARMONIC UNIVALENT FUNCTIONS ASSOCIATED WITH SALAGEAN DERIVATIVE. Sayali S. Joshi
 Faculty of Sceces ad Matheatcs, Uversty of Nš, Serba Avalable at: http://wwwpfacyu/float Float 3:3 (009), 303 309 DOI:098/FIL0903303J SUBCLASS OF ARMONIC UNIVALENT FUNCTIONS ASSOCIATED WIT SALAGEAN DERIVATIVE
Faculty of Sceces ad Matheatcs, Uversty of Nš, Serba Avalable at: http://wwwpfacyu/float Float 3:3 (009), 303 309 DOI:098/FIL0903303J SUBCLASS OF ARMONIC UNIVALENT FUNCTIONS ASSOCIATED WIT SALAGEAN DERIVATIVE
X ε ) = 0, or equivalently, lim
 Revew for the prevous lecture Cocepts: order statstcs Theorems: Dstrbutos of order statstcs Examples: How to get the dstrbuto of order statstcs Chapter 5 Propertes of a Radom Sample Secto 55 Covergece
Revew for the prevous lecture Cocepts: order statstcs Theorems: Dstrbutos of order statstcs Examples: How to get the dstrbuto of order statstcs Chapter 5 Propertes of a Radom Sample Secto 55 Covergece
LINEAR RECURRENT SEQUENCES AND POWERS OF A SQUARE MATRIX
 INTEGERS: ELECTRONIC JOURNAL OF COMBINATORIAL NUMBER THEORY 6 2006, #A12 LINEAR RECURRENT SEQUENCES AND POWERS OF A SQUARE MATRIX Hacèe Belbachr 1 USTHB, Departmet of Mathematcs, POBox 32 El Ala, 16111,
INTEGERS: ELECTRONIC JOURNAL OF COMBINATORIAL NUMBER THEORY 6 2006, #A12 LINEAR RECURRENT SEQUENCES AND POWERS OF A SQUARE MATRIX Hacèe Belbachr 1 USTHB, Departmet of Mathematcs, POBox 32 El Ala, 16111,
2006 Jamie Trahan, Autar Kaw, Kevin Martin University of South Florida United States of America
 SOLUTION OF SYSTEMS OF SIMULTANEOUS LINEAR EQUATIONS Gauss-Sedel Method 006 Jame Traha, Autar Kaw, Kev Mart Uversty of South Florda Uted States of Amerca kaw@eg.usf.edu Itroducto Ths worksheet demostrates
SOLUTION OF SYSTEMS OF SIMULTANEOUS LINEAR EQUATIONS Gauss-Sedel Method 006 Jame Traha, Autar Kaw, Kev Mart Uversty of South Florda Uted States of Amerca kaw@eg.usf.edu Itroducto Ths worksheet demostrates
Chapter 2 - Free Vibration of Multi-Degree-of-Freedom Systems - II
 CEE49b Chapter - Free Vbrato of Mult-Degree-of-Freedom Systems - II We ca obta a approxmate soluto to the fudametal atural frequecy through a approxmate formula developed usg eergy prcples by Lord Raylegh
CEE49b Chapter - Free Vbrato of Mult-Degree-of-Freedom Systems - II We ca obta a approxmate soluto to the fudametal atural frequecy through a approxmate formula developed usg eergy prcples by Lord Raylegh
The Primitive Idempotents in
 Iteratoal Joural of Algebra, Vol, 00, o 5, 3 - The Prmtve Idempotets FC - I Kulvr gh Departmet of Mathematcs, H College r Jwa Nagar (rsa)-5075, Ida kulvrsheora@yahoocom K Arora Departmet of Mathematcs,
Iteratoal Joural of Algebra, Vol, 00, o 5, 3 - The Prmtve Idempotets FC - I Kulvr gh Departmet of Mathematcs, H College r Jwa Nagar (rsa)-5075, Ida kulvrsheora@yahoocom K Arora Departmet of Mathematcs,
PubH 7405: REGRESSION ANALYSIS REGRESSION IN MATRIX TERMS
 PubH 745: REGRESSION ANALSIS REGRESSION IN MATRIX TERMS A mtr s dspl of umbers or umercl quttes ld out rectgulr rr of rows d colums. The rr, or two-w tble of umbers, could be rectgulr or squre could be
PubH 745: REGRESSION ANALSIS REGRESSION IN MATRIX TERMS A mtr s dspl of umbers or umercl quttes ld out rectgulr rr of rows d colums. The rr, or two-w tble of umbers, could be rectgulr or squre could be
Analysis of Lagrange Interpolation Formula
 P IJISET - Iteratoal Joural of Iovatve Scece, Egeerg & Techology, Vol. Issue, December 4. www.jset.com ISS 348 7968 Aalyss of Lagrage Iterpolato Formula Vjay Dahya PDepartmet of MathematcsMaharaja Surajmal
P IJISET - Iteratoal Joural of Iovatve Scece, Egeerg & Techology, Vol. Issue, December 4. www.jset.com ISS 348 7968 Aalyss of Lagrage Iterpolato Formula Vjay Dahya PDepartmet of MathematcsMaharaja Surajmal
Rank One Update And the Google Matrix by Al Bernstein Signal Science, LLC
 Introducton Rnk One Updte And the Google Mtrx y Al Bernsten Sgnl Scence, LLC www.sgnlscence.net here re two dfferent wys to perform mtrx multplctons. he frst uses dot product formulton nd the second uses
Introducton Rnk One Updte And the Google Mtrx y Al Bernsten Sgnl Scence, LLC www.sgnlscence.net here re two dfferent wys to perform mtrx multplctons. he frst uses dot product formulton nd the second uses
Bivariate Vieta-Fibonacci and Bivariate Vieta-Lucas Polynomials
 IOSR Joural of Mathematcs (IOSR-JM) e-issn: 78-78, p-issn: 19-76X. Volume 1, Issue Ver. II (Jul. - Aug.016), PP -0 www.osrjourals.org Bvarate Veta-Fboacc ad Bvarate Veta-Lucas Polomals E. Gokce KOCER 1
IOSR Joural of Mathematcs (IOSR-JM) e-issn: 78-78, p-issn: 19-76X. Volume 1, Issue Ver. II (Jul. - Aug.016), PP -0 www.osrjourals.org Bvarate Veta-Fboacc ad Bvarate Veta-Lucas Polomals E. Gokce KOCER 1
v 1 -periodic 2-exponents of SU(2 e ) and SU(2 e + 1)
 Joural of Pure ad Appled Algebra 216 (2012) 1268 1272 Cotets lsts avalable at ScVerse SceceDrect Joural of Pure ad Appled Algebra joural homepage: www.elsever.com/locate/jpaa v 1 -perodc 2-expoets of SU(2
Joural of Pure ad Appled Algebra 216 (2012) 1268 1272 Cotets lsts avalable at ScVerse SceceDrect Joural of Pure ad Appled Algebra joural homepage: www.elsever.com/locate/jpaa v 1 -perodc 2-expoets of SU(2
Soo King Lim Figure 1: Figure 2: Figure 3: Figure 4: Figure 5: Figure 6: Figure 7: Figure 8: Figure 9: Figure 10: Figure 11:
 Soo Kg Lm 1.0 Nested Fctorl Desg... 1.1 Two-Fctor Nested Desg... 1.1.1 Alss of Vrce... Exmple 1... 5 1.1. Stggered Nested Desg for Equlzg Degree of Freedom... 7 1.1. Three-Fctor Nested Desg... 8 1.1..1
Soo Kg Lm 1.0 Nested Fctorl Desg... 1.1 Two-Fctor Nested Desg... 1.1.1 Alss of Vrce... Exmple 1... 5 1.1. Stggered Nested Desg for Equlzg Degree of Freedom... 7 1.1. Three-Fctor Nested Desg... 8 1.1..1
1 Onto functions and bijections Applications to Counting
 1 Oto fuctos ad bectos Applcatos to Coutg Now we move o to a ew topc. Defto 1.1 (Surecto. A fucto f : A B s sad to be surectve or oto f for each b B there s some a A so that f(a B. What are examples of
1 Oto fuctos ad bectos Applcatos to Coutg Now we move o to a ew topc. Defto 1.1 (Surecto. A fucto f : A B s sad to be surectve or oto f for each b B there s some a A so that f(a B. What are examples of
5 Short Proofs of Simplified Stirling s Approximation
 5 Short Proofs of Smplfed Strlg s Approxmato Ofr Gorodetsky, drtymaths.wordpress.com Jue, 20 0 Itroducto Strlg s approxmato s the followg (somewhat surprsg) approxmato of the factoral,, usg elemetary fuctos:
5 Short Proofs of Smplfed Strlg s Approxmato Ofr Gorodetsky, drtymaths.wordpress.com Jue, 20 0 Itroducto Strlg s approxmato s the followg (somewhat surprsg) approxmato of the factoral,, usg elemetary fuctos:
å 1 13 Practice Final Examination Solutions - = CS109 Dec 5, 2018
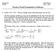 Chrs Pech Fal Practce CS09 Dec 5, 08 Practce Fal Examato Solutos. Aswer: 4/5 8/7. There are multle ways to obta ths aswer; here are two: The frst commo method s to sum over all ossbltes for the rak of
Chrs Pech Fal Practce CS09 Dec 5, 08 Practce Fal Examato Solutos. Aswer: 4/5 8/7. There are multle ways to obta ths aswer; here are two: The frst commo method s to sum over all ossbltes for the rak of
EVALUATION OF FUNCTIONAL INTEGRALS BY MEANS OF A SERIES AND THE METHOD OF BOREL TRANSFORM
 EVALUATION OF FUNCTIONAL INTEGRALS BY MEANS OF A SERIES AND THE METHOD OF BOREL TRANSFORM Jose Javer Garca Moreta Ph. D research studet at the UPV/EHU (Uversty of Basque coutry) Departmet of Theoretcal
EVALUATION OF FUNCTIONAL INTEGRALS BY MEANS OF A SERIES AND THE METHOD OF BOREL TRANSFORM Jose Javer Garca Moreta Ph. D research studet at the UPV/EHU (Uversty of Basque coutry) Departmet of Theoretcal
Department of Statistics, Dibrugarh University, Dibrugarh, Assam, India. Department of Statistics, G. C. College, Silchar, Assam, India.
 A Dscrete Power Dstruto Surt Chkrort * d Dhrujot Chkrvrt Dertet of Sttstcs Drugrh Uverst Drugrh Ass Id. Dertet of Sttstcs G. C. College Slchr Ass Id. *el: surt_r@hoo.co. Astrct A ew dscrete dstruto hs
A Dscrete Power Dstruto Surt Chkrort * d Dhrujot Chkrvrt Dertet of Sttstcs Drugrh Uverst Drugrh Ass Id. Dertet of Sttstcs G. C. College Slchr Ass Id. *el: surt_r@hoo.co. Astrct A ew dscrete dstruto hs
3. REVIEW OF PROPERTIES OF EIGENVALUES AND EIGENVECTORS
 . REVIEW OF PROPERTIES OF EIGENVLUES ND EIGENVECTORS. EIGENVLUES ND EIGENVECTORS We hll ow revew ome bc fct from mtr theory. Let be mtr. clr clled egevlue of f there et ozero vector uch tht Emle: Let 9
. REVIEW OF PROPERTIES OF EIGENVLUES ND EIGENVECTORS. EIGENVLUES ND EIGENVECTORS We hll ow revew ome bc fct from mtr theory. Let be mtr. clr clled egevlue of f there et ozero vector uch tht Emle: Let 9
Study of Correlation using Bayes Approach under bivariate Distributions
 Iteratoal Joural of Scece Egeerg ad Techolog Research IJSETR Volume Issue Februar 4 Stud of Correlato usg Baes Approach uder bvarate Dstrbutos N.S.Padharkar* ad. M.N.Deshpade** *Govt.Vdarbha Isttute of
Iteratoal Joural of Scece Egeerg ad Techolog Research IJSETR Volume Issue Februar 4 Stud of Correlato usg Baes Approach uder bvarate Dstrbutos N.S.Padharkar* ad. M.N.Deshpade** *Govt.Vdarbha Isttute of
