4.7 Case studies 175. tank 1 tank 2
|
|
|
- Blake Hardy
- 5 years ago
- Views:
Transcription
1 47 Case studies 75 s:47c 47 Case studies 47 Two-tank mixing problem s:563 g/lit ct g/lit V lit V lit tank tank 2 Fig 45 color online A cartoon which depicts a two-tank extension of the one-tank problem considered in Chapter 36 Here two identical tanks are connected, except that a solution flows into one tank, but fresh water flows into the other As for the one-tank problem, the incoming concentration ct is not necessarily constant f:twotankmix3 Consider the two-tank mixing problem illustrated in Figure 45 This system is a natural extension of the one-tank problem considered in Chapter 36 Following the same argument as that presented in Chapter 4, if we let x denote the grams of salt in tank and x 2 the grams of salt in tank 2, then the governing equation for the system is the IVP x = Ax + av ct x 2a a, x = ; A = 47 e:343 x 2 a 2a We will be interested in the concentrations in each tank for large time First consider the homogeneous system The eigenvalues and associated eigenvectors for the matrix A are λ = a, v = The homogeneous solution is then x h t = c e at ; λ 2 = 3a, v 2 = + c 2 e 3at Since both eigenvalues are negative, the homogeneous solution x h t satisfies x h t as t + Recalling the discussion leading to Theorem 442, we know that for the full problem the initial data is taken care of via an appropriate choice of the constants c,c 2
2 76 4 Systems of first-order linear differential equations Consequently, the concentration in each tank for large times will be described by the particular solution, and will not depend on the initial concentration in each tank First suppose that ct = c, ie, the incoming concentration is constant Using the method of undetermined coefficients we know that the particular solution will be of the form av c x p t = a Aa + = Solving the linear system yields x p t = 3 V c 2 Since the concentration in each tank is given by we see that after a long time c t = x t V, c 2 t = x 2t V, 472 e:defcab c t 2 3 c, c 2 t 3 c The tank which receives the mixed solution has a higher concentration than that which receives the fresh water Moreover, we have the physically plausible result that the sum of the asymptotic concentrations in each tank is equal to the incoming concentration Now, as in the one-tank problem of Chapter 36 suppose that the incoming concentration is sinusoidal with average c, ie, ct = c cosωt, ω > Using the above result we know that the particular solution will be of the form x p t = 3 V c 2 + cosωta + sinωta Plugging this guess into the system 47 and equating the cosine and sine terms yields the pair of linear systems Aa ωa = av c, ωa + A = In block matrix form this pair of linear systems can be rewritten as the system A ωi2 ωi 2 A a a av c = We will solve the algebraic system using WolframAlpha
3 47 Case studies 77 row reduce 2a,a, b,,a V c, a, 2a,, b,, b,, 2a,a,,,b,a, 2a, Input: row reduce 2 a a b a c V a 2 a b b 2 a a b a 2 a Result: 2 a2 c V 3 a 2 b 2 9 a 4 a 2 b 2 b 4 a2 c V 3 a 2 b 2 9 a 4 a 2 b 2 b 4 a c V 5 a2 b b 3 9 a 4 a 2 b 2 b 4 4 a 3 b c V 9 a 4 a 2 b 2 b 4 Step by step solution In the input Dimensions: we used the substitution b = ω The solution to the linear system is the last column The4 subscripts rows 5 columns for the coefficients were not used in the CAS computation, so we should read the output with c c and V V Upon setting 9a 4 + a 2 b 2 + b 4 = 9a 4 + a 2 ω 2 + ω 4 >, which as WolframAlpha will tell you is the determinant of the coefficient matrix, upon one final simplification the undetermined vectors are a = a2 V c 6a 2 + 2ω 2 3a 2 ω 2, a = av c ω 5a 2 + ω 2 4a 2 Upon collecting terms we see the particular solution is x p t = 2 3 V c a2 V c 6a 2 + 2ω 2 3a 2 ω 2 cosωt av c ω 5a 2 + ω 2 4a 2 sinωt In terms of the individual components we have x,p t = 2 3 V c av c x 2,p t = 3 V c av c [ a6a 2 + 2ω 2 cosωt + ω5a 2 + ω 2 sinωt ] [ a3a 2 ω 2 cosωt + 4ωa 2 sinωt ] Generated by Wolfram Alpha wwwwolframalphacom on March 27, 24 from Champaign, IL Wolfram Alpha LLC A Wolfram Research Company
4 78 4 Systems of first-order linear differential equations π 6 tank 3π/4 tank 2 A * ω 4 φ ω π/2 2 tank 2 π/4 tank ω ω Fig 46 color online A plot of the amplitudes A j ω left panel and φ j ω right panel for the variation about the mean concentration in each tank when a = 45 The curves for tank are given by a dashed blue curve, and those for tank 2 by a solid red curve Note that the variation about the mean in the first tank - that closest to the incoming solute - is always greater than that in the second tank However, there is more of a phase-lag for the concentration in the tank which is furthest from the incoming solute f:twotankamplitudephas In order to better interpret the solution, we will now use the identity c cosωt + c 2 sinωt = c 2 + c2 2 cosωt φ, tanφ = c 2 c After some simplification this identity yields av c av c with the amplitudes being and the phases satisfying [ a6a 2 + 2ω 2 cosωt + ω5a 2 + ω 2 sinωt ] = V c A ωcosωt φ ω [ a3a 2 ω 2 cosωt + 4ωa 2 sinωt ] = V c A 2 ωcosωt φ 2 ω, A ω a a 2 6a 2 + 2ω ω 2 5a 2 + ω 2 2 A 2 ω a a 2 3a 2 ω a 4 ω 2,
5 47 Case studies 79 tanφ ω ω5a2 + ω 2 a6a 2 + 2ω 2, tanφ 4ωa2 2 ω a3a 2 ω 2 It can be checked that A = 2 3, A 2 = 3, and moreover for fixed a each amplitude function is a strictly decreasing function of the frequency ω Using 472 it is that case that after a long time the concentration in each tank is c t 2 3 c c A cosωt φ, c 2t 3 c c A 2 cosωt φ 2 The mean concentration in each tank is the same as for the previous case of constant incoming concentration Just as in the one-tank example of Chapter 36 there is a variation about the mean; moreover, the variation decreases as the frequency increases 2c_ 5c_/3 4c_/3 tank 2 tank ct c_ 2c_/3 c_/ t Fig 47 color online A plot of the solution to 47 for large t when a = 45,ω = 3, and c = The incoming concentration is given by the thin green curve, the concentration in tank is given by the dashed blue curve, and the concentration in tank 2 is denoted by the solid red curve Note that the incoming concentration varies about its mean c, the concentration in tank varies about its mean 2c /3, and the concentration in tank 2 varies about its mean c /3 f:twotanksolution A sample plot of the amplitudes and phases is given in Figure 46 for the case that a = 45 Note that in tank there will more of a variation about the mean concentration in that tank, but that in tank 2 the larger phase value implies there will be more lag between the variation in the incoming solute and that in the tank A solution curve for the concentration in each tank for t is given in Figure 47 when a = 45,ω = 3, and c = Here we clearly see that the concentration in each tank varies about its mean, and that the amount of variation is markedly different for each tank Further note the phase lag: the maximum concentration in tank 2 occurs at a later time than that in tank, which in turn occurs at a later time than that for the incoming solute For large frequency
6 8 4 Systems of first-order linear differential equations the lag in tank is approximately T /4, whereas the lag for tank 2 is approximately T /2 Here T refers to the period of oscillation, ie, T = 2π/ω 472 Lead in the human body s:lead Lead poisoning is a medical condition which is caused by increased levels of the heavy metal lead in the body Lead interferes with a variety of body processes and is toxic to many organs and tissues including the heart, bones, intestines, kidneys, and reproductive and nervous systems It interferes with the development of the nervous system; therefore, it is particularly toxic to children, as it causes potentially permanent learning and behavior disorders Routes of exposure to lead include contaminated air, water, soil, food, and consumer products One of the largest threats to children is lead paint that exists in many homes, especially older ones No safe threshold for lead exposure has been discovered; in other words, as far as is known, any amount of lead whatsoever will cause harm to the body In Borelli and Coleman [5, Chapter 6] a mathematical model is derived for the ingestion and absorption of lead in the body for a healthy male volunteer in Los Angeles: x = 3 36 x ,875 x , x 3 + I L t x 2 = 9 x 35 x 2 x 3 = 7 8 x 7 2, x e:lead The variable x corresponds to the amount of lead in the blood, x 2 is the amount of lead in tissue, and x 3 is the amount of lead in the bones The amount is measured in micrograms, and the rate of change is in micrograms/day The forcing term I L represents the rate of ingestion of lead into the blood We wish to determine how the amount of lead in each component of the body changes as a function of time Written as a first-order system the ODEs become I L t x = Ax +, A = 3/36 272/2, 875 7/2, /9 /35 7/8 7/2, First consider the homogeneous system Using WolframAlpha the eigenvalues and associated eigenvectors of A are
7 47 Case studies 8 eigenvalues 3 36, ,7 2, 9, 35,, 7 8,, 7 2 Input: Eigenvalues Results: Λ Λ Λ More digits Corresponding eigenvectors: Exact forms More digits v 482, 79636, v , , v 3 237, 43667, In scientific Alternate notation form: the eigenvalues are root of x x x near x 44687, λ 447 2, λ 2 2 2, λ root of x x x near x 99998, Since all of the eigenvalues are negative, upon arguing as in the previous example of the two-tank mixing problem it will be the case that the homogeneous solution satisfies x h t as t + However, the smallness of the eigenvalues in absolute value implies 3 in this case that large means times of 2 O , which is2 on the 37order 8 of years recall that t is in terms of days! Thus, while it is mathematically the case that for large times the amount of lead in each part of the body will not depend upon the initial amount of lead in the body, from a practical perspective this is simply not true Now consider the particular solution under the assumption of a constant ingestion rate of I L t = 493 The particular solution will be of the form 493 x p t = a Aa + =, so that upon solving using WolframAlpha,, 848, 75/27, 84 x p t = 2, 56, 875/ , 25, /38 2, 623 Generated by Wolfram Alpha wwwwolframalphacom on April 4, 24 from Champaign, IL Wolfram Alpha LLC A Wolfram Research Company
8 82 4 Systems of first-order linear differential equations blood bone 5 tissue t years Fig 48 color online A plot of the solution to the system 473 with the initial condition x = x 2 = x 3 = The ingestion rate is given by I L = 493 for t < 365, and I L = for t 365; in other words, there is a steady intake of lead in the first year, and afterwards the environment is lead-free The amount of lead in the bone is given by the solid red curve, the amount of lead in the blood by the dashed blue curve, and the amount of lead in the tissue is given by the solid green curve Note that the lead in the blood and tissue clears out after a year or so of living in a lead-free environment, but that there is still a significant amount of lead in the bone f:leadbook From zero initial data, and after approximately one year, the amount of lead in the blood and tissue, respectively, is given by x t,57778, x 2 t 63 These values are relatively close to the equilibrium values On the other hand, after 8 years x 3 t 9,8627: the amount of lead in the blood at this time is roughly only 6% of the equilibrium value In other words, the amount of lead in the bones continually increases until death, and never reaches an equilibrium value Now let us briefly consider the problem of what happens to the amount of lead in the body after there is no more lead in the environment to be ingested In particular, suppose that 493, t < 365 I L t =,, 365 t and further suppose that at time t = the body contains no lead In other words, we are supposing that the body is continually exposed to lead for one year, and is afterward placed in a lead-free environment The solution is plotted in Figure 48 Here we see that after one year of living in a lead-free environment there will no longer be any significant amounts of lead in the blood or tissue On the other hand, there will still be a significant amount of lead in the bone Indeed, while it is not shown in this figure, there will be 93 micrograms of lead in the bone after 8 years of living in a lead-free environment Unfortunately, exposure to lead for a relatively short time means that according to this mathematical model you will carry that lead with you for the rest of your life Why does it take so long for the lead to clear out of the bones? The disparity in the size of the eigenvalues means that for large time the solution will approximately be
9 47 Case studies 83 In this case, since xt c 3 e λ 3t v 3, t t > 58 e λ 2t,e λ 3t < 5 large time is on the order of about two years Since an eigenvector is unique only up to scalar multiplication, we can rescale it so that each entry corresponds to a percentage this was done in Chapter 232 during our study of the Northern spotted owl We have 237, 43667, Input interpretation: 237, 43667, Result: 863, , ie, the rescaled Total: eigenvector is v Vector length: Thus, of the remaining lead in the body, approximately % is in the blood, 4% is in the tissue, and 9984% is in the bones As a final remark, the size of the eigenvalue λ 3 means that Normalized it will vector: take at least t = O 5 days which is O 3 years! before this final term becomes 237, negligible 43667, In other words, once the lead has been ingested, it will never really leave your body Exercises Spherical coordinates radial, polar, azimuthal : r , Θ , Φ 2273 Exercise 47 Consider the system of two interconnected tanks given below:
Solutions to Math 53 Math 53 Practice Final
 Solutions to Math 5 Math 5 Practice Final 20 points Consider the initial value problem y t 4yt = te t with y 0 = and y0 = 0 a 8 points Find the Laplace transform of the solution of this IVP b 8 points
Solutions to Math 5 Math 5 Practice Final 20 points Consider the initial value problem y t 4yt = te t with y 0 = and y0 = 0 a 8 points Find the Laplace transform of the solution of this IVP b 8 points
2.3 Oscillation. The harmonic oscillator equation is the differential equation. d 2 y dt 2 r y (r > 0). Its solutions have the form
 2. Oscillation So far, we have used differential equations to describe functions that grow or decay over time. The next most common behavior for a function is to oscillate, meaning that it increases and
2. Oscillation So far, we have used differential equations to describe functions that grow or decay over time. The next most common behavior for a function is to oscillate, meaning that it increases and
Solutions to the Homework Replaces Section 3.7, 3.8
 Solutions to the Homework Replaces Section 3.7, 3.8. Show that the period of motion of an undamped vibration of a mass hanging from a vertical spring is 2π L/g SOLUTION: With no damping, mu + ku = 0 has
Solutions to the Homework Replaces Section 3.7, 3.8. Show that the period of motion of an undamped vibration of a mass hanging from a vertical spring is 2π L/g SOLUTION: With no damping, mu + ku = 0 has
Understand the existence and uniqueness theorems and what they tell you about solutions to initial value problems.
 Review Outline To review for the final, look over the following outline and look at problems from the book and on the old exam s and exam reviews to find problems about each of the following topics.. Basics
Review Outline To review for the final, look over the following outline and look at problems from the book and on the old exam s and exam reviews to find problems about each of the following topics.. Basics
MATH 24 EXAM 3 SOLUTIONS
 MATH 4 EXAM 3 S Consider the equation y + ω y = cosω t (a) Find the general solution of the homogeneous equation (b) Find the particular solution of the non-homogeneous equation using the method of Undetermined
MATH 4 EXAM 3 S Consider the equation y + ω y = cosω t (a) Find the general solution of the homogeneous equation (b) Find the particular solution of the non-homogeneous equation using the method of Undetermined
V 1 V 2. r 3. r 6 r 4. Math 2250 Lab 12 Due Date : 4/25/2017 at 6:00pm
 Math 50 Lab 1 Name: Due Date : 4/5/017 at 6:00pm 1. In the previous lab you considered the input-output model below with pure water flowing into the system, C 1 = C 5 =0. r 1, C 1 r 5, C 5 r r V 1 V r
Math 50 Lab 1 Name: Due Date : 4/5/017 at 6:00pm 1. In the previous lab you considered the input-output model below with pure water flowing into the system, C 1 = C 5 =0. r 1, C 1 r 5, C 5 r r V 1 V r
Notes on the Periodically Forced Harmonic Oscillator
 Notes on the Periodically orced Harmonic Oscillator Warren Weckesser Math 38 - Differential Equations 1 The Periodically orced Harmonic Oscillator. By periodically forced harmonic oscillator, we mean the
Notes on the Periodically orced Harmonic Oscillator Warren Weckesser Math 38 - Differential Equations 1 The Periodically orced Harmonic Oscillator. By periodically forced harmonic oscillator, we mean the
Solutions to the Homework Replaces Section 3.7, 3.8
 Solutions to the Homework Replaces Section 3.7, 3.8 1. Our text (p. 198) states that µ ω 0 = ( 1 γ2 4km ) 1/2 1 1 2 γ 2 4km How was this approximation made? (Hint: Linearize 1 x) SOLUTION: We linearize
Solutions to the Homework Replaces Section 3.7, 3.8 1. Our text (p. 198) states that µ ω 0 = ( 1 γ2 4km ) 1/2 1 1 2 γ 2 4km How was this approximation made? (Hint: Linearize 1 x) SOLUTION: We linearize
1. (10 points) Find the general solution to the following second-order differential equation:
 Math 307A, Winter 014 Midterm Solutions Page 1 of 8 1. (10 points) Find the general solution to the following second-order differential equation: 4y 1y + 9y = 9t. To find the general solution to this nonhomogeneous
Math 307A, Winter 014 Midterm Solutions Page 1 of 8 1. (10 points) Find the general solution to the following second-order differential equation: 4y 1y + 9y = 9t. To find the general solution to this nonhomogeneous
The Kinetics of Lead Transfer in the Human Body
 The Kinetics of Lead Transfer in the Human Body Miyuki Shimokawa May 20, 2000 Abstract The kinetics of lead in the human body are described by a system of first order differential equations. Parameters
The Kinetics of Lead Transfer in the Human Body Miyuki Shimokawa May 20, 2000 Abstract The kinetics of lead in the human body are described by a system of first order differential equations. Parameters
Chapter 10: Sinusoidal Steady-State Analysis
 Chapter 10: Sinusoidal Steady-State Analysis 1 Objectives : sinusoidal functions Impedance use phasors to determine the forced response of a circuit subjected to sinusoidal excitation Apply techniques
Chapter 10: Sinusoidal Steady-State Analysis 1 Objectives : sinusoidal functions Impedance use phasors to determine the forced response of a circuit subjected to sinusoidal excitation Apply techniques
Math 322. Spring 2015 Review Problems for Midterm 2
 Linear Algebra: Topic: Linear Independence of vectors. Question. Math 3. Spring Review Problems for Midterm Explain why if A is not square, then either the row vectors or the column vectors of A are linearly
Linear Algebra: Topic: Linear Independence of vectors. Question. Math 3. Spring Review Problems for Midterm Explain why if A is not square, then either the row vectors or the column vectors of A are linearly
Exam 2 Study Guide: MATH 2080: Summer I 2016
 Exam Study Guide: MATH 080: Summer I 016 Dr. Peterson June 7 016 First Order Problems Solve the following IVP s by inspection (i.e. guessing). Sketch a careful graph of each solution. (a) u u; u(0) 0.
Exam Study Guide: MATH 080: Summer I 016 Dr. Peterson June 7 016 First Order Problems Solve the following IVP s by inspection (i.e. guessing). Sketch a careful graph of each solution. (a) u u; u(0) 0.
Work sheet / Things to know. Chapter 3
 MATH 251 Work sheet / Things to know 1. Second order linear differential equation Standard form: Chapter 3 What makes it homogeneous? We will, for the most part, work with equations with constant coefficients
MATH 251 Work sheet / Things to know 1. Second order linear differential equation Standard form: Chapter 3 What makes it homogeneous? We will, for the most part, work with equations with constant coefficients
APPLICATIONS The eigenvalues are λ = 5, 5. An orthonormal basis of eigenvectors consists of
 CHAPTER III APPLICATIONS The eigenvalues are λ =, An orthonormal basis of eigenvectors consists of, The eigenvalues are λ =, A basis of eigenvectors consists of, 4 which are not perpendicular However,
CHAPTER III APPLICATIONS The eigenvalues are λ =, An orthonormal basis of eigenvectors consists of, The eigenvalues are λ =, A basis of eigenvectors consists of, 4 which are not perpendicular However,
AC analysis. EE 201 AC analysis 1
 AC analysis Now we turn to circuits with sinusoidal sources. Earlier, we had a brief look at sinusoids, but now we will add in capacitors and inductors, making the story much more interesting. What are
AC analysis Now we turn to circuits with sinusoidal sources. Earlier, we had a brief look at sinusoids, but now we will add in capacitors and inductors, making the story much more interesting. What are
Module 6 : Solving Ordinary Differential Equations - Initial Value Problems (ODE-IVPs) Section 3 : Analytical Solutions of Linear ODE-IVPs
 Module 6 : Solving Ordinary Differential Equations - Initial Value Problems (ODE-IVPs) Section 3 : Analytical Solutions of Linear ODE-IVPs 3 Analytical Solutions of Linear ODE-IVPs Before developing numerical
Module 6 : Solving Ordinary Differential Equations - Initial Value Problems (ODE-IVPs) Section 3 : Analytical Solutions of Linear ODE-IVPs 3 Analytical Solutions of Linear ODE-IVPs Before developing numerical
Math 331 Homework Assignment Chapter 7 Page 1 of 9
 Math Homework Assignment Chapter 7 Page of 9 Instructions: Please make sure to demonstrate every step in your calculations. Return your answers including this homework sheet back to the instructor as a
Math Homework Assignment Chapter 7 Page of 9 Instructions: Please make sure to demonstrate every step in your calculations. Return your answers including this homework sheet back to the instructor as a
Math 312 Lecture Notes Linear Two-dimensional Systems of Differential Equations
 Math 2 Lecture Notes Linear Two-dimensional Systems of Differential Equations Warren Weckesser Department of Mathematics Colgate University February 2005 In these notes, we consider the linear system of
Math 2 Lecture Notes Linear Two-dimensional Systems of Differential Equations Warren Weckesser Department of Mathematics Colgate University February 2005 In these notes, we consider the linear system of
Properties of Linear Transformations from R n to R m
 Properties of Linear Transformations from R n to R m MATH 322, Linear Algebra I J. Robert Buchanan Department of Mathematics Spring 2015 Topic Overview Relationship between the properties of a matrix transformation
Properties of Linear Transformations from R n to R m MATH 322, Linear Algebra I J. Robert Buchanan Department of Mathematics Spring 2015 Topic Overview Relationship between the properties of a matrix transformation
Linear Algebra and ODEs review
 Linear Algebra and ODEs review Ania A Baetica September 9, 015 1 Linear Algebra 11 Eigenvalues and eigenvectors Consider the square matrix A R n n (v, λ are an (eigenvector, eigenvalue pair of matrix A
Linear Algebra and ODEs review Ania A Baetica September 9, 015 1 Linear Algebra 11 Eigenvalues and eigenvectors Consider the square matrix A R n n (v, λ are an (eigenvector, eigenvalue pair of matrix A
Lab #2 - Two Degrees-of-Freedom Oscillator
 Lab #2 - Two Degrees-of-Freedom Oscillator Last Updated: March 0, 2007 INTRODUCTION The system illustrated in Figure has two degrees-of-freedom. This means that two is the minimum number of coordinates
Lab #2 - Two Degrees-of-Freedom Oscillator Last Updated: March 0, 2007 INTRODUCTION The system illustrated in Figure has two degrees-of-freedom. This means that two is the minimum number of coordinates
Copyright (c) 2006 Warren Weckesser
 2.2. PLANAR LINEAR SYSTEMS 3 2.2. Planar Linear Systems We consider the linear system of two first order differential equations or equivalently, = ax + by (2.7) dy = cx + dy [ d x x = A x, where x =, and
2.2. PLANAR LINEAR SYSTEMS 3 2.2. Planar Linear Systems We consider the linear system of two first order differential equations or equivalently, = ax + by (2.7) dy = cx + dy [ d x x = A x, where x =, and
Physics 8 Monday, December 4, 2017
 Physics 8 Monday, December 4, 2017 HW12 due Friday. Grace will do a review session Dec 12 or 13. When? I will do a review session: afternoon Dec 17? Evening Dec 18? Wednesday, I will hand out the practice
Physics 8 Monday, December 4, 2017 HW12 due Friday. Grace will do a review session Dec 12 or 13. When? I will do a review session: afternoon Dec 17? Evening Dec 18? Wednesday, I will hand out the practice
Exercises Lecture 15
 AM1 Mathematical Analysis 1 Oct. 011 Feb. 01 Date: January 7 Exercises Lecture 15 Harmonic Oscillators In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium
AM1 Mathematical Analysis 1 Oct. 011 Feb. 01 Date: January 7 Exercises Lecture 15 Harmonic Oscillators In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium
Test #2 Math 2250 Summer 2003
 Test #2 Math 225 Summer 23 Name: Score: There are six problems on the front and back of the pages. Each subpart is worth 5 points. Show all of your work where appropriate for full credit. ) Show the following
Test #2 Math 225 Summer 23 Name: Score: There are six problems on the front and back of the pages. Each subpart is worth 5 points. Show all of your work where appropriate for full credit. ) Show the following
INHOMOGENEOUS LINEAR SYSTEMS OF DIFFERENTIAL EQUATIONS
 INHOMOGENEOUS LINEAR SYSTEMS OF DIFFERENTIAL EQUATIONS Definitions and a general fact If A is an n n matrix and f(t) is some given vector function, then the system of differential equations () x (t) Ax(t)
INHOMOGENEOUS LINEAR SYSTEMS OF DIFFERENTIAL EQUATIONS Definitions and a general fact If A is an n n matrix and f(t) is some given vector function, then the system of differential equations () x (t) Ax(t)
FINAL EXAM MAY 20, 2004
 18.034 FINAL EXAM MAY 20, 2004 Name: Problem 1: /10 Problem 2: /20 Problem 3: /25 Problem 4: /15 Problem 5: /20 Problem 6: /25 Problem 7: /10 Problem 8: /35 Problem 9: /40 Problem 10: /10 Extra credit
18.034 FINAL EXAM MAY 20, 2004 Name: Problem 1: /10 Problem 2: /20 Problem 3: /25 Problem 4: /15 Problem 5: /20 Problem 6: /25 Problem 7: /10 Problem 8: /35 Problem 9: /40 Problem 10: /10 Extra credit
Thursday, August 4, 2011
 Chapter 16 Thursday, August 4, 2011 16.1 Springs in Motion: Hooke s Law and the Second-Order ODE We have seen alrealdy that differential equations are powerful tools for understanding mechanics and electro-magnetism.
Chapter 16 Thursday, August 4, 2011 16.1 Springs in Motion: Hooke s Law and the Second-Order ODE We have seen alrealdy that differential equations are powerful tools for understanding mechanics and electro-magnetism.
Math 216 Second Midterm 16 November, 2017
 Math 216 Second Midterm 16 November, 2017 This sample exam is provided to serve as one component of your studying for this exam in this course. Please note that it is not guaranteed to cover the material
Math 216 Second Midterm 16 November, 2017 This sample exam is provided to serve as one component of your studying for this exam in this course. Please note that it is not guaranteed to cover the material
Name Solutions Linear Algebra; Test 3. Throughout the test simplify all answers except where stated otherwise.
 Name Solutions Linear Algebra; Test 3 Throughout the test simplify all answers except where stated otherwise. 1) Find the following: (10 points) ( ) Or note that so the rows are linearly independent, so
Name Solutions Linear Algebra; Test 3 Throughout the test simplify all answers except where stated otherwise. 1) Find the following: (10 points) ( ) Or note that so the rows are linearly independent, so
Identification Methods for Structural Systems
 Prof. Dr. Eleni Chatzi System Stability Fundamentals Overview System Stability Assume given a dynamic system with input u(t) and output x(t). The stability property of a dynamic system can be defined from
Prof. Dr. Eleni Chatzi System Stability Fundamentals Overview System Stability Assume given a dynamic system with input u(t) and output x(t). The stability property of a dynamic system can be defined from
This is the number of cycles per unit time, and its units are, for example,
 16 4. Sinusoidal solutions Many things in nature are periodic, even sinusoidal. We will begin by reviewing terms surrounding periodic functions. If an LTI system is fed a periodic input signal, we have
16 4. Sinusoidal solutions Many things in nature are periodic, even sinusoidal. We will begin by reviewing terms surrounding periodic functions. If an LTI system is fed a periodic input signal, we have
DIAGONALIZABLE LINEAR SYSTEMS AND STABILITY. 1. Algebraic facts. We first recall two descriptions of matrix multiplication.
 DIAGONALIZABLE LINEAR SYSTEMS AND STABILITY. 1. Algebraic facts. We first recall two descriptions of matrix multiplication. Let A be n n, P be n r, given by its columns: P = [v 1 v 2... v r ], where the
DIAGONALIZABLE LINEAR SYSTEMS AND STABILITY. 1. Algebraic facts. We first recall two descriptions of matrix multiplication. Let A be n n, P be n r, given by its columns: P = [v 1 v 2... v r ], where the
Wed Apr continued: solving x = A x when the eigenvalues and eigenvectors are complex. More examples. Announcements: Warm-up Exercise:
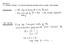 Wed Apr 18 7.3 continued: solving x = A x when the eigenvalues and eigenvectors are complex. More examples. Announcements: Warm-up Exercise: Consider this second order underdamped IVP for x t : x 2 x 5
Wed Apr 18 7.3 continued: solving x = A x when the eigenvalues and eigenvectors are complex. More examples. Announcements: Warm-up Exercise: Consider this second order underdamped IVP for x t : x 2 x 5
Differential equations
 Differential equations Math 7 Spring Practice problems for April Exam Problem Use the method of elimination to find the x-component of the general solution of x y = 6x 9x + y = x 6y 9y Soln: The system
Differential equations Math 7 Spring Practice problems for April Exam Problem Use the method of elimination to find the x-component of the general solution of x y = 6x 9x + y = x 6y 9y Soln: The system
Lecture Notes for Math 251: ODE and PDE. Lecture 16: 3.8 Forced Vibrations Without Damping
 Lecture Notes for Math 25: ODE and PDE. Lecture 6:.8 Forced Vibrations Without Damping Shawn D. Ryan Spring 202 Forced Vibrations Last Time: We studied non-forced vibrations with and without damping. We
Lecture Notes for Math 25: ODE and PDE. Lecture 6:.8 Forced Vibrations Without Damping Shawn D. Ryan Spring 202 Forced Vibrations Last Time: We studied non-forced vibrations with and without damping. We
Differential Equations 2280 Sample Midterm Exam 3 with Solutions Exam Date: 24 April 2015 at 12:50pm
 Differential Equations 228 Sample Midterm Exam 3 with Solutions Exam Date: 24 April 25 at 2:5pm Instructions: This in-class exam is 5 minutes. No calculators, notes, tables or books. No answer check is
Differential Equations 228 Sample Midterm Exam 3 with Solutions Exam Date: 24 April 25 at 2:5pm Instructions: This in-class exam is 5 minutes. No calculators, notes, tables or books. No answer check is
REVIEW PROBLEMS FOR MIDTERM II MATH 2373, FALL 2016 ANSWER KEY
 REVIEW PROBLEMS FOR MIDTERM II MATH 7, FALL 6 ANSWER KEY This list of problems is not guaranteed to be an absolutely complete review. For completeness you must also make sure that you know how to do all
REVIEW PROBLEMS FOR MIDTERM II MATH 7, FALL 6 ANSWER KEY This list of problems is not guaranteed to be an absolutely complete review. For completeness you must also make sure that you know how to do all
1 Review of simple harmonic oscillator
 MATHEMATICS 7302 (Analytical Dynamics YEAR 2017 2018, TERM 2 HANDOUT #8: COUPLED OSCILLATIONS AND NORMAL MODES 1 Review of simple harmonic oscillator In MATH 1301/1302 you studied the simple harmonic oscillator:
MATHEMATICS 7302 (Analytical Dynamics YEAR 2017 2018, TERM 2 HANDOUT #8: COUPLED OSCILLATIONS AND NORMAL MODES 1 Review of simple harmonic oscillator In MATH 1301/1302 you studied the simple harmonic oscillator:
4.5. Applications of Trigonometry to Waves. Introduction. Prerequisites. Learning Outcomes
 Applications of Trigonometry to Waves 4.5 Introduction Waves and vibrations occur in many contexts. The water waves on the sea and the vibrations of a stringed musical instrument are just two everyday
Applications of Trigonometry to Waves 4.5 Introduction Waves and vibrations occur in many contexts. The water waves on the sea and the vibrations of a stringed musical instrument are just two everyday
Second Order Linear ODEs, Part II
 Craig J. Sutton craig.j.sutton@dartmouth.edu Department of Mathematics Dartmouth College Math 23 Differential Equations Winter 2013 Outline Non-homogeneous Linear Equations 1 Non-homogeneous Linear Equations
Craig J. Sutton craig.j.sutton@dartmouth.edu Department of Mathematics Dartmouth College Math 23 Differential Equations Winter 2013 Outline Non-homogeneous Linear Equations 1 Non-homogeneous Linear Equations
Notes for CS542G (Iterative Solvers for Linear Systems)
 Notes for CS542G (Iterative Solvers for Linear Systems) Robert Bridson November 20, 2007 1 The Basics We re now looking at efficient ways to solve the linear system of equations Ax = b where in this course,
Notes for CS542G (Iterative Solvers for Linear Systems) Robert Bridson November 20, 2007 1 The Basics We re now looking at efficient ways to solve the linear system of equations Ax = b where in this course,
LS.5 Theory of Linear Systems
 LS.5 Theory of Linear Systems 1. General linear ODE systems and independent solutions. We have studied the homogeneous system of ODE s with constant coefficients, (1) x = Ax, where A is an n n matrix of
LS.5 Theory of Linear Systems 1. General linear ODE systems and independent solutions. We have studied the homogeneous system of ODE s with constant coefficients, (1) x = Ax, where A is an n n matrix of
Old Math 330 Exams. David M. McClendon. Department of Mathematics Ferris State University
 Old Math 330 Exams David M. McClendon Department of Mathematics Ferris State University Last updated to include exams from Fall 07 Contents Contents General information about these exams 3 Exams from Fall
Old Math 330 Exams David M. McClendon Department of Mathematics Ferris State University Last updated to include exams from Fall 07 Contents Contents General information about these exams 3 Exams from Fall
Linear Algebra Practice Problems
 Math 7, Professor Ramras Linear Algebra Practice Problems () Consider the following system of linear equations in the variables x, y, and z, in which the constants a and b are real numbers. x y + z = a
Math 7, Professor Ramras Linear Algebra Practice Problems () Consider the following system of linear equations in the variables x, y, and z, in which the constants a and b are real numbers. x y + z = a
Section 4.9; Section 5.6. June 30, Free Mechanical Vibrations/Couple Mass-Spring System
 Section 4.9; Section 5.6 Free Mechanical Vibrations/Couple Mass-Spring System June 30, 2009 Today s Session Today s Session A Summary of This Session: Today s Session A Summary of This Session: (1) Free
Section 4.9; Section 5.6 Free Mechanical Vibrations/Couple Mass-Spring System June 30, 2009 Today s Session Today s Session A Summary of This Session: Today s Session A Summary of This Session: (1) Free
10. Linear Systems of ODEs, Matrix multiplication, superposition principle (parts of sections )
 c Dr. Igor Zelenko, Fall 2017 1 10. Linear Systems of ODEs, Matrix multiplication, superposition principle (parts of sections 7.2-7.4) 1. When each of the functions F 1, F 2,..., F n in right-hand side
c Dr. Igor Zelenko, Fall 2017 1 10. Linear Systems of ODEs, Matrix multiplication, superposition principle (parts of sections 7.2-7.4) 1. When each of the functions F 1, F 2,..., F n in right-hand side
Math 216 Second Midterm 28 March, 2013
 Math 26 Second Midterm 28 March, 23 This sample exam is provided to serve as one component of your studying for this exam in this course. Please note that it is not guaranteed to cover the material that
Math 26 Second Midterm 28 March, 23 This sample exam is provided to serve as one component of your studying for this exam in this course. Please note that it is not guaranteed to cover the material that
Matrix Solutions to Linear Systems of ODEs
 Matrix Solutions to Linear Systems of ODEs James K. Peterson Department of Biological Sciences and Department of Mathematical Sciences Clemson University November 3, 216 Outline 1 Symmetric Systems of
Matrix Solutions to Linear Systems of ODEs James K. Peterson Department of Biological Sciences and Department of Mathematical Sciences Clemson University November 3, 216 Outline 1 Symmetric Systems of
Math Ordinary Differential Equations
 Math 411 - Ordinary Differential Equations Review Notes - 1 1 - Basic Theory A first order ordinary differential equation has the form x = f(t, x) (11) Here x = dx/dt Given an initial data x(t 0 ) = x
Math 411 - Ordinary Differential Equations Review Notes - 1 1 - Basic Theory A first order ordinary differential equation has the form x = f(t, x) (11) Here x = dx/dt Given an initial data x(t 0 ) = x
4. Linear Systems. 4A. Review of Matrices A-1. Verify that =
 4. Linear Systems 4A. Review of Matrices 0 2 0 0 0 4A-. Verify that 0 2 =. 2 3 2 6 0 2 2 0 4A-2. If A = and B =, show that AB BA. 3 2 4A-3. Calculate A 2 2 if A =, and check your answer by showing that
4. Linear Systems 4A. Review of Matrices 0 2 0 0 0 4A-. Verify that 0 2 =. 2 3 2 6 0 2 2 0 4A-2. If A = and B =, show that AB BA. 3 2 4A-3. Calculate A 2 2 if A =, and check your answer by showing that
4. Sinusoidal solutions
 16 4. Sinusoidal solutions Many things in nature are periodic, even sinusoidal. We will begin by reviewing terms surrounding periodic functions. If an LTI system is fed a periodic input signal, we have
16 4. Sinusoidal solutions Many things in nature are periodic, even sinusoidal. We will begin by reviewing terms surrounding periodic functions. If an LTI system is fed a periodic input signal, we have
Math 216 Final Exam 24 April, 2017
 Math 216 Final Exam 24 April, 2017 This sample exam is provided to serve as one component of your studying for this exam in this course. Please note that it is not guaranteed to cover the material that
Math 216 Final Exam 24 April, 2017 This sample exam is provided to serve as one component of your studying for this exam in this course. Please note that it is not guaranteed to cover the material that
Math Assignment 5
 Math 2280 - Assignment 5 Dylan Zwick Fall 2013 Section 3.4-1, 5, 18, 21 Section 3.5-1, 11, 23, 28, 35, 47, 56 Section 3.6-1, 2, 9, 17, 24 1 Section 3.4 - Mechanical Vibrations 3.4.1 - Determine the period
Math 2280 - Assignment 5 Dylan Zwick Fall 2013 Section 3.4-1, 5, 18, 21 Section 3.5-1, 11, 23, 28, 35, 47, 56 Section 3.6-1, 2, 9, 17, 24 1 Section 3.4 - Mechanical Vibrations 3.4.1 - Determine the period
MTH Linear Algebra. Study Guide. Dr. Tony Yee Department of Mathematics and Information Technology The Hong Kong Institute of Education
 MTH 3 Linear Algebra Study Guide Dr. Tony Yee Department of Mathematics and Information Technology The Hong Kong Institute of Education June 3, ii Contents Table of Contents iii Matrix Algebra. Real Life
MTH 3 Linear Algebra Study Guide Dr. Tony Yee Department of Mathematics and Information Technology The Hong Kong Institute of Education June 3, ii Contents Table of Contents iii Matrix Algebra. Real Life
Selected Solutions: 3.5 (Undetermined Coefficients)
 Selected Solutions: 3.5 (Undetermined Coefficients) In Exercises 1-10, we want to apply the ideas from the table to specific DEs, and solve for the coefficients as well. If you prefer, you might start
Selected Solutions: 3.5 (Undetermined Coefficients) In Exercises 1-10, we want to apply the ideas from the table to specific DEs, and solve for the coefficients as well. If you prefer, you might start
Identification Methods for Structural Systems. Prof. Dr. Eleni Chatzi System Stability - 26 March, 2014
 Prof. Dr. Eleni Chatzi System Stability - 26 March, 24 Fundamentals Overview System Stability Assume given a dynamic system with input u(t) and output x(t). The stability property of a dynamic system can
Prof. Dr. Eleni Chatzi System Stability - 26 March, 24 Fundamentals Overview System Stability Assume given a dynamic system with input u(t) and output x(t). The stability property of a dynamic system can
MTH 464: Computational Linear Algebra
 MTH 464: Computational Linear Algebra Lecture Outlines Exam 4 Material Prof. M. Beauregard Department of Mathematics & Statistics Stephen F. Austin State University April 15, 2018 Linear Algebra (MTH 464)
MTH 464: Computational Linear Algebra Lecture Outlines Exam 4 Material Prof. M. Beauregard Department of Mathematics & Statistics Stephen F. Austin State University April 15, 2018 Linear Algebra (MTH 464)
Elementary Linear Algebra Review for Exam 2 Exam is Monday, November 16th.
 Elementary Linear Algebra Review for Exam Exam is Monday, November 6th. The exam will cover sections:.4,..4, 5. 5., 7., the class notes on Markov Models. You must be able to do each of the following. Section.4
Elementary Linear Algebra Review for Exam Exam is Monday, November 6th. The exam will cover sections:.4,..4, 5. 5., 7., the class notes on Markov Models. You must be able to do each of the following. Section.4
21 Linear State-Space Representations
 ME 132, Spring 25, UC Berkeley, A Packard 187 21 Linear State-Space Representations First, let s describe the most general type of dynamic system that we will consider/encounter in this class Systems may
ME 132, Spring 25, UC Berkeley, A Packard 187 21 Linear State-Space Representations First, let s describe the most general type of dynamic system that we will consider/encounter in this class Systems may
Solutions for homework 5
 1 Section 4.3 Solutions for homework 5 17. The following equation has repeated, real, characteristic roots. Find the general solution. y 4y + 4y = 0. The characteristic equation is λ 4λ + 4 = 0 which has
1 Section 4.3 Solutions for homework 5 17. The following equation has repeated, real, characteristic roots. Find the general solution. y 4y + 4y = 0. The characteristic equation is λ 4λ + 4 = 0 which has
Homework 3 Solutions Math 309, Fall 2015
 Homework 3 Solutions Math 39, Fall 25 782 One easily checks that the only eigenvalue of the coefficient matrix is λ To find the associated eigenvector, we have 4 2 v v 8 4 (up to scalar multiplication)
Homework 3 Solutions Math 39, Fall 25 782 One easily checks that the only eigenvalue of the coefficient matrix is λ To find the associated eigenvector, we have 4 2 v v 8 4 (up to scalar multiplication)
4. Linear Systems. 4A. Review of Matrices ) , show that AB BA (= A A A).
 4A-. Verify that 4A-2. If A = 2 3 2 2 4A-3. Calculate A if A = and A A = I. 4. Linear Systems 4A. Review of Matrices 2 2 and B = = 3 2 6, show that AB BA. 2 2 2, and check your answer by showing that AA
4A-. Verify that 4A-2. If A = 2 3 2 2 4A-3. Calculate A if A = and A A = I. 4. Linear Systems 4A. Review of Matrices 2 2 and B = = 3 2 6, show that AB BA. 2 2 2, and check your answer by showing that AA
Recall the convention that, for us, all vectors are column vectors.
 Some linear algebra Recall the convention that, for us, all vectors are column vectors. 1. Symmetric matrices Let A be a real matrix. Recall that a complex number λ is an eigenvalue of A if there exists
Some linear algebra Recall the convention that, for us, all vectors are column vectors. 1. Symmetric matrices Let A be a real matrix. Recall that a complex number λ is an eigenvalue of A if there exists
Damped harmonic motion
 Damped harmonic motion March 3, 016 Harmonic motion is studied in the presence of a damping force proportional to the velocity. The complex method is introduced, and the different cases of under-damping,
Damped harmonic motion March 3, 016 Harmonic motion is studied in the presence of a damping force proportional to the velocity. The complex method is introduced, and the different cases of under-damping,
Dot Products. K. Behrend. April 3, Abstract A short review of some basic facts on the dot product. Projections. The spectral theorem.
 Dot Products K. Behrend April 3, 008 Abstract A short review of some basic facts on the dot product. Projections. The spectral theorem. Contents The dot product 3. Length of a vector........................
Dot Products K. Behrend April 3, 008 Abstract A short review of some basic facts on the dot product. Projections. The spectral theorem. Contents The dot product 3. Length of a vector........................
Math 216 Second Midterm 19 March, 2018
 Math 26 Second Midterm 9 March, 28 This sample exam is provided to serve as one component of your studying for this exam in this course. Please note that it is not guaranteed to cover the material that
Math 26 Second Midterm 9 March, 28 This sample exam is provided to serve as one component of your studying for this exam in this course. Please note that it is not guaranteed to cover the material that
Sinusoids. Amplitude and Magnitude. Phase and Period. CMPT 889: Lecture 2 Sinusoids, Complex Exponentials, Spectrum Representation
 Sinusoids CMPT 889: Lecture Sinusoids, Complex Exponentials, Spectrum Representation Tamara Smyth, tamaras@cs.sfu.ca School of Computing Science, Simon Fraser University September 6, 005 Sinusoids are
Sinusoids CMPT 889: Lecture Sinusoids, Complex Exponentials, Spectrum Representation Tamara Smyth, tamaras@cs.sfu.ca School of Computing Science, Simon Fraser University September 6, 005 Sinusoids are
CMPT 889: Lecture 2 Sinusoids, Complex Exponentials, Spectrum Representation
 CMPT 889: Lecture 2 Sinusoids, Complex Exponentials, Spectrum Representation Tamara Smyth, tamaras@cs.sfu.ca School of Computing Science, Simon Fraser University September 26, 2005 1 Sinusoids Sinusoids
CMPT 889: Lecture 2 Sinusoids, Complex Exponentials, Spectrum Representation Tamara Smyth, tamaras@cs.sfu.ca School of Computing Science, Simon Fraser University September 26, 2005 1 Sinusoids Sinusoids
Systems of Ordinary Differential Equations
 Systems of Ordinary Differential Equations Scott A. McKinley October 22, 2013 In these notes, which replace the material in your textbook, we will learn a modern view of analyzing systems of differential
Systems of Ordinary Differential Equations Scott A. McKinley October 22, 2013 In these notes, which replace the material in your textbook, we will learn a modern view of analyzing systems of differential
Linear Hyperbolic Systems
 Linear Hyperbolic Systems Professor Dr E F Toro Laboratory of Applied Mathematics University of Trento, Italy eleuterio.toro@unitn.it http://www.ing.unitn.it/toro October 8, 2014 1 / 56 We study some basic
Linear Hyperbolic Systems Professor Dr E F Toro Laboratory of Applied Mathematics University of Trento, Italy eleuterio.toro@unitn.it http://www.ing.unitn.it/toro October 8, 2014 1 / 56 We study some basic
Physics 142 AC Circuits Page 1. AC Circuits. I ve had a perfectly lovely evening but this wasn t it. Groucho Marx
 Physics 142 A ircuits Page 1 A ircuits I ve had a perfectly lovely evening but this wasn t it. Groucho Marx Alternating current: generators and values It is relatively easy to devise a source (a generator
Physics 142 A ircuits Page 1 A ircuits I ve had a perfectly lovely evening but this wasn t it. Groucho Marx Alternating current: generators and values It is relatively easy to devise a source (a generator
Solution: In standard form (i.e. y + P (t)y = Q(t)) we have y t y = cos(t)
 Math 380 Practice Final Solutions This is longer than the actual exam, which will be 8 to 0 questions (some might be multiple choice). You are allowed up to two sheets of notes (both sides) and a calculator,
Math 380 Practice Final Solutions This is longer than the actual exam, which will be 8 to 0 questions (some might be multiple choice). You are allowed up to two sheets of notes (both sides) and a calculator,
Extreme Values and Positive/ Negative Definite Matrix Conditions
 Extreme Values and Positive/ Negative Definite Matrix Conditions James K. Peterson Department of Biological Sciences and Department of Mathematical Sciences Clemson University November 8, 016 Outline 1
Extreme Values and Positive/ Negative Definite Matrix Conditions James K. Peterson Department of Biological Sciences and Department of Mathematical Sciences Clemson University November 8, 016 Outline 1
Homogeneous Constant Matrix Systems, Part II
 4 Homogeneous Constant Matrix Systems, Part II Let us now expand our discussions begun in the previous chapter, and consider homogeneous constant matrix systems whose matrices either have complex eigenvalues
4 Homogeneous Constant Matrix Systems, Part II Let us now expand our discussions begun in the previous chapter, and consider homogeneous constant matrix systems whose matrices either have complex eigenvalues
Final 09/14/2017. Notes and electronic aids are not allowed. You must be seated in your assigned row for your exam to be valid.
 Final 09/4/207 Name: Problems -5 are each worth 8 points. Problem 6 is a bonus for up to 4 points. So a full score is 40 points and the max score is 44 points. The exam has 6 pages; make sure you have
Final 09/4/207 Name: Problems -5 are each worth 8 points. Problem 6 is a bonus for up to 4 points. So a full score is 40 points and the max score is 44 points. The exam has 6 pages; make sure you have
Lab 11. Spring-Mass Oscillations
 Lab 11. Spring-Mass Oscillations Goals To determine experimentally whether the supplied spring obeys Hooke s law, and if so, to calculate its spring constant. To find a solution to the differential equation
Lab 11. Spring-Mass Oscillations Goals To determine experimentally whether the supplied spring obeys Hooke s law, and if so, to calculate its spring constant. To find a solution to the differential equation
9 - Matrix Methods for Linear Systems
 9 - Matrix Methods for Linear Systems 9.4 Linear Systems in Normal Form Homework: p. 523-526 # ü Introduction Consider a system of n linear differential equations given by x 1 x 2 x n = a 11 HtL x 1 HtL
9 - Matrix Methods for Linear Systems 9.4 Linear Systems in Normal Form Homework: p. 523-526 # ü Introduction Consider a system of n linear differential equations given by x 1 x 2 x n = a 11 HtL x 1 HtL
4. Complex Oscillations
 4. Complex Oscillations The most common use of complex numbers in physics is for analyzing oscillations and waves. We will illustrate this with a simple but crucially important model, the damped harmonic
4. Complex Oscillations The most common use of complex numbers in physics is for analyzing oscillations and waves. We will illustrate this with a simple but crucially important model, the damped harmonic
= 2e t e 2t + ( e 2t )e 3t = 2e t e t = e t. Math 20D Final Review
 Math D Final Review. Solve the differential equation in two ways, first using variation of parameters and then using undetermined coefficients: Corresponding homogenous equation: with characteristic equation
Math D Final Review. Solve the differential equation in two ways, first using variation of parameters and then using undetermined coefficients: Corresponding homogenous equation: with characteristic equation
Linearization of Differential Equation Models
 Linearization of Differential Equation Models 1 Motivation We cannot solve most nonlinear models, so we often instead try to get an overall feel for the way the model behaves: we sometimes talk about looking
Linearization of Differential Equation Models 1 Motivation We cannot solve most nonlinear models, so we often instead try to get an overall feel for the way the model behaves: we sometimes talk about looking
Math 1302, Week 8: Oscillations
 Math 302, Week 8: Oscillations T y eq Y y = y eq + Y mg Figure : Simple harmonic motion. At equilibrium the string is of total length y eq. During the motion we let Y be the extension beyond equilibrium,
Math 302, Week 8: Oscillations T y eq Y y = y eq + Y mg Figure : Simple harmonic motion. At equilibrium the string is of total length y eq. During the motion we let Y be the extension beyond equilibrium,
Seminar 6: COUPLED HARMONIC OSCILLATORS
 Seminar 6: COUPLED HARMONIC OSCILLATORS 1. Lagrangian Equations of Motion Let consider a system consisting of two harmonic oscillators that are coupled together. As a model, we will use two particles attached
Seminar 6: COUPLED HARMONIC OSCILLATORS 1. Lagrangian Equations of Motion Let consider a system consisting of two harmonic oscillators that are coupled together. As a model, we will use two particles attached
Date: 1 April (1) The only reference material you may use is one 8½x11 crib sheet and a calculator.
 PH1140: Oscillations and Waves Name: Solutions Conference: Date: 1 April 2005 EXAM #1: D2005 INSTRUCTIONS: (1) The only reference material you may use is one 8½x11 crib sheet and a calculator. (2) Show
PH1140: Oscillations and Waves Name: Solutions Conference: Date: 1 April 2005 EXAM #1: D2005 INSTRUCTIONS: (1) The only reference material you may use is one 8½x11 crib sheet and a calculator. (2) Show
Span and Linear Independence
 Span and Linear Independence It is common to confuse span and linear independence, because although they are different concepts, they are related. To see their relationship, let s revisit the previous
Span and Linear Independence It is common to confuse span and linear independence, because although they are different concepts, they are related. To see their relationship, let s revisit the previous
Investigating Springs (Simple Harmonic Motion)
 Investigating Springs (Simple Harmonic Motion) INTRODUCTION The purpose of this lab is to study the well-known force exerted by a spring The force, as given by Hooke s Law, is a function of the amount
Investigating Springs (Simple Harmonic Motion) INTRODUCTION The purpose of this lab is to study the well-known force exerted by a spring The force, as given by Hooke s Law, is a function of the amount
1. Diagonalize the matrix A if possible, that is, find an invertible matrix P and a diagonal
 . Diagonalize the matrix A if possible, that is, find an invertible matrix P and a diagonal 3 9 matrix D such that A = P DP, for A =. 3 4 3 (a) P = 4, D =. 3 (b) P = 4, D =. (c) P = 4 8 4, D =. 3 (d) P
. Diagonalize the matrix A if possible, that is, find an invertible matrix P and a diagonal 3 9 matrix D such that A = P DP, for A =. 3 4 3 (a) P = 4, D =. 3 (b) P = 4, D =. (c) P = 4 8 4, D =. 3 (d) P
Section 3: Complex numbers
 Essentially: Section 3: Complex numbers C (set of complex numbers) up to different notation: the same as R 2 (euclidean plane), (i) Write the real 1 instead of the first elementary unit vector e 1 = (1,
Essentially: Section 3: Complex numbers C (set of complex numbers) up to different notation: the same as R 2 (euclidean plane), (i) Write the real 1 instead of the first elementary unit vector e 1 = (1,
Date: 31 March (1) The only reference material you may use is one 8½x11 crib sheet and a calculator.
 PH1140: Oscillations and Waves Name: SOLUTIONS AT END Conference: Date: 31 March 2005 EXAM #1: D2006 INSTRUCTIONS: (1) The only reference material you may use is one 8½x11 crib sheet and a calculator.
PH1140: Oscillations and Waves Name: SOLUTIONS AT END Conference: Date: 31 March 2005 EXAM #1: D2006 INSTRUCTIONS: (1) The only reference material you may use is one 8½x11 crib sheet and a calculator.
1. Background: The SVD and the best basis (questions selected from Ch. 6- Can you fill in the exercises?)
 Math 35 Exam Review SOLUTIONS Overview In this third of the course we focused on linear learning algorithms to model data. summarize: To. Background: The SVD and the best basis (questions selected from
Math 35 Exam Review SOLUTIONS Overview In this third of the course we focused on linear learning algorithms to model data. summarize: To. Background: The SVD and the best basis (questions selected from
APPM 2360: Final Exam 10:30am 1:00pm, May 6, 2015.
 APPM 23: Final Exam :3am :pm, May, 25. ON THE FRONT OF YOUR BLUEBOOK write: ) your name, 2) your student ID number, 3) lecture section, 4) your instructor s name, and 5) a grading table for eight questions.
APPM 23: Final Exam :3am :pm, May, 25. ON THE FRONT OF YOUR BLUEBOOK write: ) your name, 2) your student ID number, 3) lecture section, 4) your instructor s name, and 5) a grading table for eight questions.
Mathematical Foundations -1- Difference equations. Systems of difference equations. Life cycle model 2. Phase diagram 4. Eigenvalue and eigenvector 5
 Mathematical Foundations -- Difference equations Systems of difference equations Life cycle model Phase diagram 4 Eigenvalue and eigenvector 5 The general two variable model 9 Complex eigenvalues 5 Stable
Mathematical Foundations -- Difference equations Systems of difference equations Life cycle model Phase diagram 4 Eigenvalue and eigenvector 5 The general two variable model 9 Complex eigenvalues 5 Stable
What is A + B? What is A B? What is AB? What is BA? What is A 2? and B = QUESTION 2. What is the reduced row echelon matrix of A =
 STUDENT S COMPANIONS IN BASIC MATH: THE ELEVENTH Matrix Reloaded by Block Buster Presumably you know the first part of matrix story, including its basic operations (addition and multiplication) and row
STUDENT S COMPANIONS IN BASIC MATH: THE ELEVENTH Matrix Reloaded by Block Buster Presumably you know the first part of matrix story, including its basic operations (addition and multiplication) and row
Resonance and response
 Chapter 2 Resonance and response Last updated September 20, 2008 In this section of the course we begin with a very simple system a mass hanging from a spring and see how some remarkable ideas emerge.
Chapter 2 Resonance and response Last updated September 20, 2008 In this section of the course we begin with a very simple system a mass hanging from a spring and see how some remarkable ideas emerge.
Linear Differential Equations. Problems
 Chapter 1 Linear Differential Equations. Problems 1.1 Introduction 1.1.1 Show that the function ϕ : R R, given by the expression ϕ(t) = 2e 3t for all t R, is a solution of the Initial Value Problem x =
Chapter 1 Linear Differential Equations. Problems 1.1 Introduction 1.1.1 Show that the function ϕ : R R, given by the expression ϕ(t) = 2e 3t for all t R, is a solution of the Initial Value Problem x =
Singular Value Decomposition
 Singular Value Decomposition Motivatation The diagonalization theorem play a part in many interesting applications. Unfortunately not all matrices can be factored as A = PDP However a factorization A =
Singular Value Decomposition Motivatation The diagonalization theorem play a part in many interesting applications. Unfortunately not all matrices can be factored as A = PDP However a factorization A =
Linear Systems of ODE: Nullclines, Eigenvector lines and trajectories
 Linear Systems of ODE: Nullclines, Eigenvector lines and trajectories James K. Peterson Department of Biological Sciences and Department of Mathematical Sciences Clemson University October 6, 203 Outline
Linear Systems of ODE: Nullclines, Eigenvector lines and trajectories James K. Peterson Department of Biological Sciences and Department of Mathematical Sciences Clemson University October 6, 203 Outline
u u + 4u = 2 cos(3t), u(0) = 1, u (0) = 2
 MATH HOMEWORK #6 PART A SOLUTIONS Problem 7..5. Transform the given initial value problem into an initial value problem for two first order equations. u + 4 u + 4u cost, u0, u 0 Solution. Let x u and x
MATH HOMEWORK #6 PART A SOLUTIONS Problem 7..5. Transform the given initial value problem into an initial value problem for two first order equations. u + 4 u + 4u cost, u0, u 0 Solution. Let x u and x
Linear Algebra- Final Exam Review
 Linear Algebra- Final Exam Review. Let A be invertible. Show that, if v, v, v 3 are linearly independent vectors, so are Av, Av, Av 3. NOTE: It should be clear from your answer that you know the definition.
Linear Algebra- Final Exam Review. Let A be invertible. Show that, if v, v, v 3 are linearly independent vectors, so are Av, Av, Av 3. NOTE: It should be clear from your answer that you know the definition.
