ON THE PARALLEL SURFACES IN GALILEAN SPACE
|
|
|
- Marshall Bryan
- 5 years ago
- Views:
Transcription
1 ON THE PARALLEL SURFACES IN GALILEAN SPACE Mustafa Dede 1, Cumali Ekici 2 and A. Ceylan Çöken 3 1 Kilis 7 Aral k University, Department of Mathematics, 79000, Kilis-TURKEY 2 Eskişehir Osmangazi University, Department of Mathematics and Computer Science, 26480, Eskişehir-TURKEY 3 Süleyman Demirel University, Department of Mathematics, 32260, Isparta-TURKEY August 11, 2012 Abstract In this paper, rst of all, the de nition of parallel surfaces in Galilean space is given. Then, the relationship between the curvatures of the parallel surfaces in Galilean space is determined. Moreover, the rst and second fundamental forms of parallel surfaces are found in Galilean space. Consequently, we obtained Gauss curvature and mean curvature of parallel surface in terms of those curvatures of the base surface. Key words: Parallel surfaces, Curvatures of surface, Galilean space. 1 Introduction It is known that two surfaces with a common normal are called parallel surfaces. A large number of papers and books have been published in the literature which deal with parallel surfaces in both Minkowski space and Euclidean space such as [1,6,10-11,14]. However, this paper presents the di erential properties of the parallel surfaces in three-dimensional Galilean space. There are nine related plane geometries including Euclidean geometry, hyperbolic geometry and elliptic geometry. Galilean geometry is one of these geometries whose motions are the Galilean transformations of classical kinematics [13]. Di erential geometry of the Galilean space G 3 and especially the geometry of ruled surfaces in this space have been largely developed in O. Röschel s paper [12]. Some more results about ruled surfaces in G 3 have been given in [7-9]. A. Ö¼grenmiş [15] obtained characterizations of helix for a curve with respect to the Frenet frame in Galilean space. Curves in pseudo-galilean space have 1
2 been explained in details in [2]. Recently, C. Cekici and M. Dede [4] investigated Darboux vectors of ruled surface in pseudo-galilean space. The Galilean space G 3 is a Cayley Klein space equipped with the projective metric of signature (0; 0; +; +). The absolute gure of the Galilean geometry consists of an ordered triple f!; f; Ig, where! is the real (absolute) plane, f is the real line (absolute line) in!. I is the xed elliptic involution of points of f. De nition 1.1. A plane is called Euclidean if it contains f, otherwise it is called isotropic. Planes x = constant are Euclidean and so is the plane!. Other planes are isotropic. A vector u = (u 1 ; u 2 ; u 3 ) is said to be non-isotropic if u 1 6= 0. All unit non-isotropic vectors are of the form u = (1; u 2 ; u 3 ). For isotropic vectors, u 1 = 0 holds [8]. Since x = 0 plane is Euclidean in Galilean space, it is easy to see that isotropic vectors are on the Euclidean plane. De nition 1.2. Let a = (x; y; z) and b = (x 1 ; y 1 ; z 1 ) be vectors in Galilean space. The scalar product is de ned by < a; b >= x 1 x (1) The norm of a is de ned by kak = jxj ; and a is called a unit vector if kak = 1: On the other hand, as a consequence of De nition 1.1, we de ne the scalar product of two isotropic vectors, p = (0; y; z) and q = (0; y 1 ; z 1 ); as < p; q > 1 = yy 1 + zz 1 (2) The orthogonality of isotropic vectors, p? 1 q; means that < p; q > 1 = 0: The norm of p is de ned by kpk 1 = p y 2 + z 2 ; and p is called a unit isotropic vector if kpk 1 = 1 [13]: De nition 1.3. Let u = (u 1 ; u 2 ; u 3 ) and v = (v 1 ; v 2 ; v 3 ) be vectors in Galilean space [8]. The cross product of the vectors u and v is de ned as follows: u ^ v = 0 e 2 e 3 u 1 u 2 u 3 v 1 v 2 v 3 = (0; u 3v 1 u 1 v 3 ; u 1 v 2 u 2 v 1 ) (3) De nition 1.4. Let " be a plane and f(") the intersection of the absolute line f and ": Figure 1 2
3 The point f(") is called the absolute point of ". Then f(")? = I(f(")) denotes the point on f orthogonal to f(") according to the elliptic involution I. This is an elliptic involution because there is no line perpendicular to itself [12]. The elliptic involution in homogeneous coordinates is given by (0 : 0 : x 2 : x 3 )! (0 : 0 : x 3 : x 2 ) (4) De nition 1.5. If an admisable curve C of the class C r (r 3) is given by the parametrization r(x) = (x; y(x); z(x)) then x is a Galilean invariant of the arc length on C [7]. associated invariant moving trihedron is given by t = (1; y 0 (x); z 0 (x)); In Figure 2, the n = 1 (0; y00 (x); z 00 (x)); (5) b = 1 (0; z00 (x); y 00 (x)) where = p y 00 (x) 2 + z 00 (x) 2 is the curvature and = 1 2 det[r0 (x); r 00 (x); r 000 (x)] is the torsion. Figure 2 Frenet formulas may be written as 2 d 4 t 3 2 n 5 = dx b t n b 2 Surface Theory in Galilean Space 3 5 Assume that M is a surface in G 3. parametrization The equation of M is given by the '(v 1 ; v 2 ) = (x(v 1 ; v 2 ); y(v 1 ; v 2 ); z(v 1 ; v 2 )); v 1 ; v 2 2 R (6) 3
4 where x(v 1 ; v 2 ); y(v 1 ; v 2 ); z(v 1 ; v 2 ) 2 C 3. The isotropic unit normal vector eld N, shown in Figure 3, is given by N = ' ;1 ^ ' ;2 (0; z ;2 x ;1 z ;1 x ;2 ; y ;1 x ;2 y ;2 x ;1 ) ';1 ^ ' 1 = p (7) ;2 (z;1 x ;2 z ;2 x ;1 ) 2 + (y ;2 x ;1 y ;1 x ;2 ) 2 where partial di erentiation with respect to v 1 and v 2 will be denoted by su xes 1 and 2 respectively, that ' ;1 ; v 2 1 and ' ;2 ; v 2 2 [12]. Figure 3 Using (4); we obtain the isotropic unit vector in the tangent plane of surface as = (0; y ;1x ;2 y ;2 x ;1 ; z ;1 x ;2 z ;2 x ;1 ) (8) w where hn; i 1 = 0; 2 = 1; w = ';1 ^ ' 1 ;2 (9) by means of Galilean geometry. Observe that a straightforward computation shows that can be expressed by = x ;2' ;1 x ;1 ' ;2 w (10) where x ;1 and x ;2 are the partial di erentiation of the rst component of the surface M with respect to v 1 and v 2, respectively. x ;1 ; v 2 1 ; x ;2 ; v 2 2 (11) Consequently to simplify the presentation (10), we may use Einstein summation convention, then may rewritten as follows = g i ' ;i = g 1 ' ;1 + g 2 ' ;2 (12) 4
5 where g 1 = x ;1 g 2 = x ;2 g ij = g i g j g 1 = x ;2 w g2 = x (13) ;1 w gij = g i g j From De nition 1.2, the rst fundamental form I of the surface is given by I = (g ij + h ij )dv i dv j (14) where h ij and g ij (i; j = 1; 2) are called induced metric on the surface given by h ij = ' ;i ; ' ; g ;j 1 ij = ' ;i ; ' ;j (15) and 8 < 0; dv 1 : dv 2 non-isotropic = : 1; dv 1 : dv 2 isotropic (16) Isotropic curves, shown in Figure 4, are the intersections of the surface M with Euclidean planes [12]. All other curves on the surface are called nonisotropic curves. Figure 4 Let (s) = '(v(s) 1 ; v(s) 2 ) be a non-isotropic curve in a surface patch '; parametrized by the arc length s: From (13) it follows that g i v i0 = 1 (17) where " 0 " refers to d ds : The coe cients L ij of second fundamental form are given by ';ij x ;1 x ;ij ' ;1 L ij = ; N x ;1 1 (18) 5
6 and the Christo el symbols of the surface are given by ';ij x 1 ;2 x ;ij ' ;2 ';ij x 2 ;1 x ;ij ' ;1 ij = ; ij = w w Theorem 2.1. Let M be a surface in Galilean space. ; 1 ; 1 (19) ' ;ij = k ij' ;k + L ij N (20) is called the Gauss equation of the surface [12]. Theorem 2.2. Let M be a surface in Galilean space. The Weingarten equation is given by N ;i = B i + C i N (21) where C i = 0; B i = g k L ki [12]. Moreover, from (9) and (21), we have ;i = g k L ki N (22) Theorem 2.3. Let (s) = '(v(s) 1 ; v(s) 2 ) be non-isotropic curve on the surface, parametrized by the arc length s: The equation of normal curvature k n and geodesic curvature k g of the surface are given by, respectively k n = L ij v i0 v j0 ; k g = k ij vi0 v j0 + v k00 g k (23) where " 0 " refers to d ds. In addition, let be the Euclidean angle between the isotropic vectors, the surface normal N and the curve normal n; we have cos = hn; '00 i 1 k' 00 k 1, sin = h; '00 i 1 k' 00 k 1 (24) Consequently, k n and k g are obtained by, respectively k n = cos, k g = sin (25) where = k' 00 k 1 is the curvature of (s) [12]. Corollary 2.4. The equation of the asymptotic lines are given by L ij v i0 v j0 = 0 (26) Corollary 2.5. Since K 1 corresponding value of the normal curvature may be found by making use of Lagrange s multipliers, we have This implies the following theorem. K 1 = L 11L 22 (L 12 ) 2 w 2 g ij L ij (27) 6
7 Theorem 2.6. Let M be a surface in G 3 [12]. The Gauss curvature K and the mean curvature H of the surface are given by, respectively K = det L ij w 2 ; 2H = g ij L ij (28) The following corollary is clear from (27) and (28). Corollary 2.7. K 1 can be expressed by K 1 = K 2H (29) 3 Parallel Surfaces in Galilean Space De nition 3.1. Let M and M be two surfaces in Galilean space G 3 and 2 R; 8p 2 M: The function f : '(v 1 ; v 2 )! ' (v 1 ; v 2 ) p! f(p) = [p 1 ; p 2 + a 2 (p); p 3 + a 3 (p)] is called the parallelization function between M and M where p = (p 1 ; p 2 ; p 3 ) and N = a i = (0; a 2 ; a 3 i i=2 is the isotropic unit normal vector eld on M and furthermore M is called parallel surface to M in G 3 where is a given positive real number. Figure 5 In Figure 5, T and T are the isotropic tangent planes of parallel surfaces M and M, respectively. 7
8 Note that from the de nition of parallel surfaces, we have N(p) = N (f(p)). Moreover this leads to the fact that (p) = (f(p)) in Galilean space: De nition 3.2. Let M and M be parallel surfaces in Galilean space. We de ne the parallel surface M to base surface M at distance as ' (v 1 ; v 2 ) = '(v 1 ; v 2 ) + N (30) where N is normal vector of the base surface. Theorem 3.3. Let M and M be parallel surfaces in Galilean space. The relationship between the w = ' ;1 ^ ' 1 ;2 and w = ' ;1 ^ ' ;2 1 can be given as follows: w = w(1 2H) (31) Proof: Taking the partial derivatives of M gives ' ;1 = ' ;1 + N ;1, ' ;2 = ' ;2 + N ;2 (32) Thus, by (3), we see N ;1 ^ N ;2 = 0. In addition, by (21), (28) and (32), we get ' ;1 ^ ' ;2 = (' ;1 ^ ' ;2 )(1 2H) Taking norm of the both sides, we have w = w(1 2H) Theorem 3.4. Let M and M be parallel surfaces in Galilean space. The rst fundamental form I of the parallel surface is given by 8 < I dv 1 : dv 2 non-isotropic I = : I (2L ij g k L ki g k L kj )dv i dv j dv 1 : dv 2 isotropic Proof: Let us now consider = 0 in (14), it follows that I = g ijdv i dv j From (7), (11) and (30), we obtained the partial di erentiation of the rst component of the surface M as which implies that By using (13), I is obtained by x ;1 = x ;1 ; x ;2 = x ;2 (33) g i = g i (34) I = g ij dv i dv j = I (35) We now consider = 1: In this case, the rst fundamental form I is I = h ijdv i dv j (36) 8
9 Di erentiating (30), then using (15) gives ' ;i ; ';j = h ij + 2 N ;i ; ' ;j hn ;i ; N ;j i 1 (37) 1 Finally, substituting, (12), (14), (20) and (21) into (37), we have I = I (2L ij g k L ki g k L kj )dv i dv j Theorem 3.5. Let M and M be two parallel surfaces. The coe cients L ij of second fundamental form of the parallel surface are given by Proof: Di erentiating (30), we get L ij = L ij g k L ki g k L kj (38) ' ;ij = ' ;ij + N ;ij (39) Substituting (33) and (39) into (18) and using hn ;ij ; Ni 1 = hn ;i ; N ;j i 1 implies that L ij = L ij hn ;i ; N ;j i 1 From (9) and (21), L ij is obtained by L ij = L ij g k L ki g k L kj (40) Corollary 3.6. Asymptotic lines of the parallel surface M are given by L ij = L ij g k L ki g k L kj = 0 (41) Theorem 3.7. Let M and M be two parallel surfaces in G 3 and (s) = ' (v(s) 1 ; v(s) 2 ) be a non-isotropic curve on the parallel surface; parametrized by the arc length s; given by g i v i0 = 1 (42) where " 0 " refers to d ds. The normal curvature k n of parallel surface is given by k n = k n (g k L ki g k L kj )v i0 v j0 (43) where k n is the normal curvature of M: Proof: Di erentiating (30) with respect to s gives and ' 0 = ' ;i v i0 + N ;i v i0 (44) ' 00 = ' ;ij v i0 v j0 + ' ;k v k00 + (N ;ij v i0 v j0 + N ;k v k00 ) (45) Substituting (20) into (45), we get ' 00 = ( k ijv i0 v j0 + v k00 )' ;k + L ij v i0 v j0 N + (N ;ij v i0 v j0 + N ;k v k00 ) (46) 9
10 Taking scalar product of both sides of (46) with N gives ' 00 ; N 1 = (L ij + hn; N ;ij i 1 )v i0 v j0 Using (21), (23) and hn ;ij ; Ni 1 = hn ;i ; N ;j i 1 implies that the relation between the normal curvatures of two parallel surfaces is k n = k n (g k L ki g k L kj )v i0 v j0 (47) Theorem 3.8. Let M and M be two parallel surfaces in G 3. The relation between the geodesic curvatures of two parallel surfaces is given by k g = k g g k L ki v k00 (48) Proof: Taking scalar product of both sides of (46) with gives ' 00 ; 1 = ( k ijv i0 v j0 + v k00 ) ' ;k ; 1 + (hn ;ij; i 1 v i0 v j0 + hn ;k ; i 1 v k00 ) (49) Substituting (21) and (23) into (49), we have k g = k g + (hn ;ij ; i 1 v i0 v j0 g k L ki v k00 ) (50) From (21) and (22) we have hn ;ij ; i 1 = 0 which implies that k g = k g g k L ki v k00 Theorem 3.9. Let M and M be two parallel surfaces in G 3 : The relations between the Gauss curvatures and the mean curvatures of two parallel surfaces are K K = (51) 1 2H and H = H 1 2H respectively. Proof: Substituting (31) and (38) into (28) gives Simple calculation implies that (52) K = det[l ij g k L ki g k L kj ] w 2 (1 2H) 2 (53) K = (L 11L 22 L 2 12)(1 (g 11 L g 12 L 12 + g 22 L 22 )) w 2 (1 2H) 2 (54) Combining (28) and (54), we have K = K 1 2H (55) 10
11 Using (13), (31) and (33) implies that (g ij ) = Taking account of (28), (38) and (56), we nd that 2H = g ij (1 2H) 2 (56) g ij (1 2H) 2 (L ij g k L ki g k L kj ) (57) Finally, substituting (28) into (57) then, H can be written as H = H 1 2H (58) Now we shall consider some particular cases of the results (55) and (58). Theorem Let M and M be two parallel surfaces in G 3 : If base surface is minimal, then parallel surface is minimal. Proof: Since M is minimal surface, H = 0: Therefore, from (58) we have H = 0 Theorem Let M and M be two parallel surfaces in G 3 : If base surface is Weingarten, then parallel surface is Weingarten. Proof: Since base surface is Weingarten, it satis es the following condition H ;1 K ;2 H ;2 K ;1 = 0 (59) On the other hand, di erentiating (55) and (58) with respect to v 1 and v 2 ; we get K ;1 = (1 2H)K ;1 + 2KH ;1 (1 2H) 2 ; H ;1 = (1 2H)H ;1 + 2HH ;1 (1 2H) 2 (60) K ;2 = (1 2H)K ;2 + 2KH ;2 (1 2H) 2 ; H ;2 = (1 2H)H ;2 + 2HH ;2 (1 2H) 2 (61) Thus, Combining (59) and (62) gives This completes the proof. H ;1K ;2 H ;2K ;1 = H ;1K ;2 H ;2 K ;1 (1 2H) 3 (62) H ;1K ;2 H ;2K ;1 = 0 11
12 References: [1] Çöken, A. C., Çiftçi, Ü. and Ekici, C. On parallel timelike ruled surfaces with timelike rulings, Kuwait Journal of Science & Engineering, 35(1A), 21-31, [2] Divjak, B. Curves in pseudo-galilean geometry, Annales Univ. Sci. Budapest, 41, , [3] Eisenhart, L. P. A treatise on the di erential geometry of curves and surfaces (Dover Publication, Inc., New York, 1960). [4] Ekici, C. and Dede, M. On the Darboux vector of ruled surfaces in pseudo- Galilean space, Mathematical and Computational Applications, 16(4), , [5] Guggenheimer, H. W. Di erential geometry (McGraw-Hill, New York, 1963). [6] Sa¼gel, M. K., and Hac saliho¼glu, H. H. On the parallel hypersurfaces with constant curvature, Commun. Fac. Sci. Univ. Ank. Series A, 40, [7] Kamenarovic, I. Existence theorems for ruled surfaces in the Galilean space G 3 ; Rad Hrvatske Akad. Znan. Umj. Mat., 456(10), , [8] Milin-Sipus, Z. Ruled Weingarten surfaces in Galilean space, Periodica Mathematica Hungarica, 56(2), , [9] Milin-Sipus, Z. Divjak, B. Special curves on ruled surfaces in Galilean and pseudo-galilean spaces, Acta Math. Hungar., 98(3), , [10] Roberts, S. On Parallel surfaces, Proc. London Math. Soc., 1-4(1), , [11] Roberts, S. On the parallel surfaces of developables and curves of double curvature, Proc. London Math. Soc., 1-5(1), 90-94, [12] Röschel, O. Die geometrie des Galileischen raumes (Habilitationsschrift, Leoben, 1984). [13] Yaglom, I. M. A simple non-euclidean geometry and its physical basis (Springer-Verlag, New York Inc., 1979). [14] Görgülü, A. and Çöken A. C. The Euler theorem for parallel pseudo- Euclidean hpersurfaces in pseudo-euclidean space E1 n+1, Journ. Inst. Math. and Comp. Sci. (Math. Series), 6.2, , [15 ] Ö¼grenmiş, A., Ergüt, M. and Bektaş, M. On the helices in the Galilean space G 3, Iranian Journal of Science & Technology, Transaction A, 31(A2), ,
On a family of surfaces with common asymptotic curve in the Galilean space G 3
 Available online at www.tjnsa.com J. Nonlinear Sci. Appl. 9 2016), 518 523 Research Article On a family of surfaces with common asymptotic curve in the Galilean space G 3 Zühal Küçükarslan Yüzbaşı Fırat
Available online at www.tjnsa.com J. Nonlinear Sci. Appl. 9 2016), 518 523 Research Article On a family of surfaces with common asymptotic curve in the Galilean space G 3 Zühal Küçükarslan Yüzbaşı Fırat
On T-slant, N-slant and B-slant Helices in Pseudo-Galilean Space G 1 3
 Filomat :1 (018), 45 5 https://doiorg/1098/fil180145o Published by Faculty of Sciences and Mathematics, University of Niš, Serbia Available at: http://wwwpmfniacrs/filomat On T-slant, N-slant and B-slant
Filomat :1 (018), 45 5 https://doiorg/1098/fil180145o Published by Faculty of Sciences and Mathematics, University of Niš, Serbia Available at: http://wwwpmfniacrs/filomat On T-slant, N-slant and B-slant
Determination of the Position Vectors of Curves from Intrinsic Equations in G 3
 Applied Mathematics Determination of the Position Vectors of Curves from Intrinsic Equations in G 3 Handan ÖZTEKIN * and Serpil TATLIPINAR Department of Mathematics, Firat University, Elazig, Turkey (
Applied Mathematics Determination of the Position Vectors of Curves from Intrinsic Equations in G 3 Handan ÖZTEKIN * and Serpil TATLIPINAR Department of Mathematics, Firat University, Elazig, Turkey (
Constant ratio timelike curves in pseudo-galilean 3-space G 1 3
 CREAT MATH INFORM 7 018, No 1, 57-6 Online version at http://creative-mathematicsubmro/ Print Edition: ISSN 1584-86X Online Edition: ISSN 1843-441X Constant ratio timelike curves in pseudo-galilean 3-space
CREAT MATH INFORM 7 018, No 1, 57-6 Online version at http://creative-mathematicsubmro/ Print Edition: ISSN 1584-86X Online Edition: ISSN 1843-441X Constant ratio timelike curves in pseudo-galilean 3-space
THE CHARACTERIZATIONS OF GENERAL HELICES IN THE 3-DIMEMSIONAL PSEUDO-GALILEAN SPACE
 SOOCHOW JOURNAL OF MATHEMATICS Volume 31, No. 3, pp. 441-447, July 2005 THE CHARACTERIZATIONS OF GENERAL HELICES IN THE 3-DIMEMSIONAL PSEUDO-GALILEAN SPACE BY MEHMET BEKTAŞ Abstract. T. Ikawa obtained
SOOCHOW JOURNAL OF MATHEMATICS Volume 31, No. 3, pp. 441-447, July 2005 THE CHARACTERIZATIONS OF GENERAL HELICES IN THE 3-DIMEMSIONAL PSEUDO-GALILEAN SPACE BY MEHMET BEKTAŞ Abstract. T. Ikawa obtained
The equiform differential geometry of curves in 4-dimensional galilean space G 4
 Stud. Univ. Babeş-Bolyai Math. 582013, No. 3, 393 400 The equiform differential geometry of curves in 4-dimensional galilean space G 4 M. Evren Aydin and Mahmut Ergüt Abstract. In this paper, we establish
Stud. Univ. Babeş-Bolyai Math. 582013, No. 3, 393 400 The equiform differential geometry of curves in 4-dimensional galilean space G 4 M. Evren Aydin and Mahmut Ergüt Abstract. In this paper, we establish
The equiform differential geometry of curves in the pseudo-galilean space
 Mathematical Communications 13(2008), 321-332 321 The equiform differential geometry of curves in the pseudo-galilean space Zlatko Erjavec and Blaženka Divjak Abstract. In this paper the equiform differential
Mathematical Communications 13(2008), 321-332 321 The equiform differential geometry of curves in the pseudo-galilean space Zlatko Erjavec and Blaženka Divjak Abstract. In this paper the equiform differential
Characterizations of a helix in the pseudo - Galilean space G
 International Journal of the Phsical ciences Vol 59), pp 48-44, 8 August, 00 Available online at http://wwwacademicjournalsorg/ijp IN 99-950 00 Academic Journals Full Length Research Paper Characterizations
International Journal of the Phsical ciences Vol 59), pp 48-44, 8 August, 00 Available online at http://wwwacademicjournalsorg/ijp IN 99-950 00 Academic Journals Full Length Research Paper Characterizations
Differential-Geometrical Conditions Between Geodesic Curves and Ruled Surfaces in the Lorentz Space
 Differential-Geometrical Conditions Between Geodesic Curves and Ruled Surfaces in the Lorentz Space Nihat Ayyildiz, A. Ceylan Çöken, Ahmet Yücesan Abstract In this paper, a system of differential equations
Differential-Geometrical Conditions Between Geodesic Curves and Ruled Surfaces in the Lorentz Space Nihat Ayyildiz, A. Ceylan Çöken, Ahmet Yücesan Abstract In this paper, a system of differential equations
The General Solutions of Frenet s System in the Equiform Geometry of the Galilean, Pseudo-Galilean, Simple Isotropic and Double Isotropic Space 1
 International Mathematical Forum, Vol. 6, 2011, no. 17, 837-856 The General Solutions of Frenet s System in the Equiform Geometry of the Galilean, Pseudo-Galilean, Simple Isotropic and Double Isotropic
International Mathematical Forum, Vol. 6, 2011, no. 17, 837-856 The General Solutions of Frenet s System in the Equiform Geometry of the Galilean, Pseudo-Galilean, Simple Isotropic and Double Isotropic
Existence Theorems for Timelike Ruled Surfaces in Minkowski 3-Space
 Existence Theorems for Timelike Ruled Surfaces in Minkowski -Space Mehmet Önder Celal Bayar University, Faculty of Science and Arts, Department of Mathematics, Muradiye Campus, 45047 Muradiye, Manisa,
Existence Theorems for Timelike Ruled Surfaces in Minkowski -Space Mehmet Önder Celal Bayar University, Faculty of Science and Arts, Department of Mathematics, Muradiye Campus, 45047 Muradiye, Manisa,
Smarandache Curves and Spherical Indicatrices in the Galilean. 3-Space
 arxiv:50.05245v [math.dg 2 Jan 205, 5 pages. DOI:0.528/zenodo.835456 Smarandache Curves and Spherical Indicatrices in the Galilean 3-Space H.S.Abdel-Aziz and M.Khalifa Saad Dept. of Math., Faculty of Science,
arxiv:50.05245v [math.dg 2 Jan 205, 5 pages. DOI:0.528/zenodo.835456 Smarandache Curves and Spherical Indicatrices in the Galilean 3-Space H.S.Abdel-Aziz and M.Khalifa Saad Dept. of Math., Faculty of Science,
On a Certain Class of Translation Surfaces in a Pseudo-Galilean Space
 International Mathematical Forum, Vol. 6,, no. 3, 3-5 On a Certain Class of Translation Surfaces in a Pseudo-Galilean Space Željka Milin Šipuš Department of Mathematics Universit of Zagreb Bijenička cesta
International Mathematical Forum, Vol. 6,, no. 3, 3-5 On a Certain Class of Translation Surfaces in a Pseudo-Galilean Space Željka Milin Šipuš Department of Mathematics Universit of Zagreb Bijenička cesta
A STUDY ON A RULED SURFACE WITH LIGHTLIKE RULING FOR A NULL CURVE WITH CARTAN FRAME
 Bull. Korean Math. Soc. 49 (), No. 3, pp. 635 645 http://dx.doi.org/.434/bkms..49.3.635 A STUDY ON A RULED SURFACE WITH LIGHTLIKE RULING FOR A NULL CURVE WITH CARTAN FRAME N ihat Ayyildiz and Tunahan Turhan
Bull. Korean Math. Soc. 49 (), No. 3, pp. 635 645 http://dx.doi.org/.434/bkms..49.3.635 A STUDY ON A RULED SURFACE WITH LIGHTLIKE RULING FOR A NULL CURVE WITH CARTAN FRAME N ihat Ayyildiz and Tunahan Turhan
T. Şahin, M. Yilmaz (Ondokuz Mayıs Univ., Turkey)
 UDC 517.9 T. Şahin, M. Yilmaz Ondokuz Mayıs Univ., Turkey ON SINGULARITIES OF THE GALILEAN SPHERICAL DARBOUX RULED SURFACE OF A SPACE CURVE IN G 3 ПРО ОСОБЛИВОСТI СФЕРИЧНО-ГАЛIЛЕЄВОЇ ЛIНIЙЧАТОЇ ПОВЕРХНI
UDC 517.9 T. Şahin, M. Yilmaz Ondokuz Mayıs Univ., Turkey ON SINGULARITIES OF THE GALILEAN SPHERICAL DARBOUX RULED SURFACE OF A SPACE CURVE IN G 3 ПРО ОСОБЛИВОСТI СФЕРИЧНО-ГАЛIЛЕЄВОЇ ЛIНIЙЧАТОЇ ПОВЕРХНI
CERTAIN CLASSES OF RULED SURFACES IN 3-DIMENSIONAL ISOTROPIC SPACE
 Palestine Journal of Mathematics Vol. 7(1)(2018), 87 91 Palestine Polytechnic University-PPU 2018 CERTAIN CLASSES OF RULED SURFACES IN 3-DIMENSIONAL ISOTROPIC SPACE Alper Osman Ogrenmis Communicated by
Palestine Journal of Mathematics Vol. 7(1)(2018), 87 91 Palestine Polytechnic University-PPU 2018 CERTAIN CLASSES OF RULED SURFACES IN 3-DIMENSIONAL ISOTROPIC SPACE Alper Osman Ogrenmis Communicated by
Inelastic Admissible Curves in the Pseudo Galilean Space G 3
 Int. J. Open Problems Compt. Math., Vol. 4, No. 3, September 2011 ISSN 1998-6262; Copyright ICSRS Publication, 2011 www.i-csrs.org Inelastic Admissible Curves in the Pseudo Galilean Space G 3 1 Alper Osman
Int. J. Open Problems Compt. Math., Vol. 4, No. 3, September 2011 ISSN 1998-6262; Copyright ICSRS Publication, 2011 www.i-csrs.org Inelastic Admissible Curves in the Pseudo Galilean Space G 3 1 Alper Osman
On the Dual Darboux Rotation Axis of the Timelike Dual Space Curve
 On the Dual Darboux Rotation Axis of the Timelike Dual Space Curve Ahmet Yücesan, A. Ceylan Çöken and Nihat Ayyildiz Abstract In this paper, the Dual Darboux rotation axis for timelike dual space curve
On the Dual Darboux Rotation Axis of the Timelike Dual Space Curve Ahmet Yücesan, A. Ceylan Çöken and Nihat Ayyildiz Abstract In this paper, the Dual Darboux rotation axis for timelike dual space curve
arxiv: v3 [math.gm] 5 Jan 2018
![arxiv: v3 [math.gm] 5 Jan 2018 arxiv: v3 [math.gm] 5 Jan 2018](/thumbs/74/70123547.jpg) Submitted to doi:10.1017/s... arxiv:1707.03930v3 [math.gm] 5 Jan 2018 POSITION VECTORS OF CURVES WITH RECPECT TO DARBOUX FRAME IN THE GALILEAN SPACE G 3 TEVFİK ŞAHİN and BUKET CEYLAN DİRİŞEN Abstract In
Submitted to doi:10.1017/s... arxiv:1707.03930v3 [math.gm] 5 Jan 2018 POSITION VECTORS OF CURVES WITH RECPECT TO DARBOUX FRAME IN THE GALILEAN SPACE G 3 TEVFİK ŞAHİN and BUKET CEYLAN DİRİŞEN Abstract In
Transversal Surfaces of Timelike Ruled Surfaces in Minkowski 3-Space
 Transversal Surfaces of Timelike Ruled Surfaces in Minkowski -Space Mehmet Önder Celal Bayar University, Faculty of Science and Arts, Department of Mathematics, Muradiye Campus, 45047, Muradiye, Manisa,
Transversal Surfaces of Timelike Ruled Surfaces in Minkowski -Space Mehmet Önder Celal Bayar University, Faculty of Science and Arts, Department of Mathematics, Muradiye Campus, 45047, Muradiye, Manisa,
BERTRAND CURVES IN GALILEAN SPACE AND THEIR CHARACTERIZATIONS. and Mahmut ERGÜT
 139 Kragujevac J. Math. 32 (2009) 139 147. BERTRAND CURVES IN GALILEAN SPACE AND THEIR CHARACTERIZATIONS Alper Osman ÖĞRENMİŞ, Handan ÖZTEKİN and Mahmut ERGÜT Fırat University, Faculty of Arts and Science,
139 Kragujevac J. Math. 32 (2009) 139 147. BERTRAND CURVES IN GALILEAN SPACE AND THEIR CHARACTERIZATIONS Alper Osman ÖĞRENMİŞ, Handan ÖZTEKİN and Mahmut ERGÜT Fırat University, Faculty of Arts and Science,
Abstract. In this paper we give the Euler theorem and Dupin indicatrix for surfaces at a
 MATEMATIQKI VESNIK 65, 2 (2013), 242 249 June 2013 originalni nauqni rad research paper THE EULER THEOREM AND DUPIN INDICATRIX FOR SURFACES AT A CONSTANT DISTANCE FROM EDGE OF REGRESSION ON A SURFACE IN
MATEMATIQKI VESNIK 65, 2 (2013), 242 249 June 2013 originalni nauqni rad research paper THE EULER THEOREM AND DUPIN INDICATRIX FOR SURFACES AT A CONSTANT DISTANCE FROM EDGE OF REGRESSION ON A SURFACE IN
Killing Magnetic Curves in Three Dimensional Isotropic Space
 Prespacetime Journal December l 2016 Volume 7 Issue 15 pp. 2015 2022 2015 Killing Magnetic Curves in Three Dimensional Isotropic Space Alper O. Öğrenmiş1 Department of Mathematics, Faculty of Science,
Prespacetime Journal December l 2016 Volume 7 Issue 15 pp. 2015 2022 2015 Killing Magnetic Curves in Three Dimensional Isotropic Space Alper O. Öğrenmiş1 Department of Mathematics, Faculty of Science,
INEXTENSIBLE FLOWS OF CURVES IN THE EQUIFORM GEOMETRY OF THE PSEUDO-GALILEAN SPACE G 1 3
 TWMS J. App. Eng. Math. V.6, N.2, 2016, pp. 175-184 INEXTENSIBLE FLOWS OF CURVES IN THE EQUIFORM GEOMETRY OF THE PSEUDO-GALILEAN SPACE G 1 3 HANDAN ÖZTEKIN 1, HÜLYA GÜN BOZOK 2, Abstract. In this paper,
TWMS J. App. Eng. Math. V.6, N.2, 2016, pp. 175-184 INEXTENSIBLE FLOWS OF CURVES IN THE EQUIFORM GEOMETRY OF THE PSEUDO-GALILEAN SPACE G 1 3 HANDAN ÖZTEKIN 1, HÜLYA GÜN BOZOK 2, Abstract. In this paper,
A new characterization of curves on dual unit sphere
 NTMSCI 2, No. 1, 71-76 (2017) 71 Journal of Abstract and Computational Mathematics http://www.ntmsci.com/jacm A new characterization of curves on dual unit sphere Ilim Kisi, Sezgin Buyukkutuk, Gunay Ozturk
NTMSCI 2, No. 1, 71-76 (2017) 71 Journal of Abstract and Computational Mathematics http://www.ntmsci.com/jacm A new characterization of curves on dual unit sphere Ilim Kisi, Sezgin Buyukkutuk, Gunay Ozturk
On The Volume Of The Trajectory Surface Under The Galilean Motions In The Galilean Space
 Applied Mathematics E-Notes, 17(2017), 297-306 c ISSN 1607-2510 Available free at mirror sites of http://www.math.nthu.edu.tw/ amen/ On The Volume Of The Trajectory Surface Under The alilean Motions In
Applied Mathematics E-Notes, 17(2017), 297-306 c ISSN 1607-2510 Available free at mirror sites of http://www.math.nthu.edu.tw/ amen/ On The Volume Of The Trajectory Surface Under The alilean Motions In
SOME NEW ASSOCIATED CURVES OF AN ADMISSIBLE FRENET CURVE IN 3-DIMENSIONAL AND 4-DIMENSIONAL GALILEAN SPACES
 ROMANIAN JOURNAL OF MAHEMAICS AND COMPUER SCIENCE 27 VOLUME 7 ISSUE 2 p.-22 SOME NEW ASSOCIAED CURVES OF AN ADMISSIBLE FRENE CURVE IN 3-DIMENSIONAL AND 4-DIMENSIONAL GALILEAN SPACES N. MACI M.AKBIYIK S.
ROMANIAN JOURNAL OF MAHEMAICS AND COMPUER SCIENCE 27 VOLUME 7 ISSUE 2 p.-22 SOME NEW ASSOCIAED CURVES OF AN ADMISSIBLE FRENE CURVE IN 3-DIMENSIONAL AND 4-DIMENSIONAL GALILEAN SPACES N. MACI M.AKBIYIK S.
Null Bertrand curves in Minkowski 3-space and their characterizations
 Note di Matematica 23, n. 1, 2004, 7 13. Null Bertrand curves in Minkowski 3-space and their characterizations Handan Balgetir Department of Mathematics, Firat University, 23119 Elazig, TURKEY hbalgetir@firat.edu.tr
Note di Matematica 23, n. 1, 2004, 7 13. Null Bertrand curves in Minkowski 3-space and their characterizations Handan Balgetir Department of Mathematics, Firat University, 23119 Elazig, TURKEY hbalgetir@firat.edu.tr
Warped Products. by Peter Petersen. We shall de ne as few concepts as possible. A tangent vector always has the local coordinate expansion
 Warped Products by Peter Petersen De nitions We shall de ne as few concepts as possible. A tangent vector always has the local coordinate expansion a function the di erential v = dx i (v) df = f dxi We
Warped Products by Peter Petersen De nitions We shall de ne as few concepts as possible. A tangent vector always has the local coordinate expansion a function the di erential v = dx i (v) df = f dxi We
GENERALIZED NULL SCROLLS IN THE n-dimensional LORENTZIAN SPACE. 1. Introduction
 ACTA MATHEMATICA VIETNAMICA 205 Volume 29, Number 2, 2004, pp. 205-216 GENERALIZED NULL SCROLLS IN THE n-dimensional LORENTZIAN SPACE HANDAN BALGETIR AND MAHMUT ERGÜT Abstract. In this paper, we define
ACTA MATHEMATICA VIETNAMICA 205 Volume 29, Number 2, 2004, pp. 205-216 GENERALIZED NULL SCROLLS IN THE n-dimensional LORENTZIAN SPACE HANDAN BALGETIR AND MAHMUT ERGÜT Abstract. In this paper, we define
On the Dual Quaternionic N 3 Slant Helices in D 4
 Vol. 132 2017 ACTA PHYSICA POLONICA A No. 3-II Special issue of the 3rd International Conference on Computational and Experimental Science and Engineering ICCESEN 2016 On the Dual Quaternionic N 3 Slant
Vol. 132 2017 ACTA PHYSICA POLONICA A No. 3-II Special issue of the 3rd International Conference on Computational and Experimental Science and Engineering ICCESEN 2016 On the Dual Quaternionic N 3 Slant
On Rectifying Dual Space Curves
 On Rectifying Dual Space Curves Ahmet YÜCESAN, NihatAYYILDIZ, anda.ceylançöken Süleyman Demirel University Department of Mathematics 32260 Isparta Turkey yucesan@fef.sdu.edu.tr ayyildiz@fef.sdu.edu.tr
On Rectifying Dual Space Curves Ahmet YÜCESAN, NihatAYYILDIZ, anda.ceylançöken Süleyman Demirel University Department of Mathematics 32260 Isparta Turkey yucesan@fef.sdu.edu.tr ayyildiz@fef.sdu.edu.tr
THE NATURAL LIFT CURVES AND GEODESIC CURVATURES OF THE SPHERICAL INDICATRICES OF THE TIMELIKE BERTRAND CURVE COUPLE
 International Electronic Journal of Geometry Volume 6 No.2 pp. 88 99 (213) c IEJG THE NATURAL LIFT CURVES AND GEODESIC CURVATURES OF THE SPHERICAL INDICATRICES OF THE TIMELIKE BERTRAND CURVE COUPLE SÜLEYMAN
International Electronic Journal of Geometry Volume 6 No.2 pp. 88 99 (213) c IEJG THE NATURAL LIFT CURVES AND GEODESIC CURVATURES OF THE SPHERICAL INDICATRICES OF THE TIMELIKE BERTRAND CURVE COUPLE SÜLEYMAN
ON OSCULATING, NORMAL AND RECTIFYING BI-NULL CURVES IN R 5 2
 Novi Sad J. Math. Vol. 48, No. 1, 2018, 9-20 https://doi.org/10.30755/nsjom.05268 ON OSCULATING, NORMAL AND RECTIFYING BI-NULL CURVES IN R 5 2 Kazım İlarslan 1, Makoto Sakaki 2 and Ali Uçum 34 Abstract.
Novi Sad J. Math. Vol. 48, No. 1, 2018, 9-20 https://doi.org/10.30755/nsjom.05268 ON OSCULATING, NORMAL AND RECTIFYING BI-NULL CURVES IN R 5 2 Kazım İlarslan 1, Makoto Sakaki 2 and Ali Uçum 34 Abstract.
THE DARBOUX TRIHEDRONS OF REGULAR CURVES ON A REGULAR SURFACE
 International lectronic Journal of eometry Volume 7 No 2 pp 61-71 (2014) c IJ TH DARBOUX TRIHDRONS OF RULAR CURVS ON A RULAR SURFAC MRAH TUNÇ AND MİN OZYILMAZ (Communicated by Levent KULA) Abstract In
International lectronic Journal of eometry Volume 7 No 2 pp 61-71 (2014) c IJ TH DARBOUX TRIHDRONS OF RULAR CURVS ON A RULAR SURFAC MRAH TUNÇ AND MİN OZYILMAZ (Communicated by Levent KULA) Abstract In
SPLIT QUATERNIONS AND SPACELIKE CONSTANT SLOPE SURFACES IN MINKOWSKI 3-SPACE
 INTERNATIONAL JOURNAL OF GEOMETRY Vol. (13), No. 1, 3-33 SPLIT QUATERNIONS AND SPACELIKE CONSTANT SLOPE SURFACES IN MINKOWSKI 3-SPACE MURAT BABAARSLAN AND YUSUF YAYLI Abstract. A spacelike surface in the
INTERNATIONAL JOURNAL OF GEOMETRY Vol. (13), No. 1, 3-33 SPLIT QUATERNIONS AND SPACELIKE CONSTANT SLOPE SURFACES IN MINKOWSKI 3-SPACE MURAT BABAARSLAN AND YUSUF YAYLI Abstract. A spacelike surface in the
CHARACTERIZATION OF SLANT HELIX İN GALILEAN AND PSEUDO-GALILEAN SPACES
 SAÜ Fen Edebiyat Dergisi (00-I) CHARACTERIZATION OF SLANT HELIX İN ALILEAN AND PSEUDO-ALILEAN SPACES Murat Kemal KARACAN * and Yılmaz TUNÇER ** *Usak University, Faculty of Sciences and Arts,Department
SAÜ Fen Edebiyat Dergisi (00-I) CHARACTERIZATION OF SLANT HELIX İN ALILEAN AND PSEUDO-ALILEAN SPACES Murat Kemal KARACAN * and Yılmaz TUNÇER ** *Usak University, Faculty of Sciences and Arts,Department
THE TAXICAB HELIX ON TAXICAB CYLINDER
 International Electronic Journal of Geometry Volume 5 No. 2 pp. 168 182 (2012) c IEJG THE TAXICAB HELIX ON TAXICAB CYLINDER CUMALİ EKİCİ, SİBEL SEVİNÇ, YASEMİN E. CENGİZ (Communicated by Kazım İLARSLAN)
International Electronic Journal of Geometry Volume 5 No. 2 pp. 168 182 (2012) c IEJG THE TAXICAB HELIX ON TAXICAB CYLINDER CUMALİ EKİCİ, SİBEL SEVİNÇ, YASEMİN E. CENGİZ (Communicated by Kazım İLARSLAN)
Fathi M. Hamdoon and A. K. Omran
 Korean J. Math. 4 (016), No. 4, pp. 613 66 https://doi.org/10.11568/kjm.016.4.4.613 STUDYING ON A SKEW RULED SURFACE BY USING THE GEODESIC FRENET TRIHEDRON OF ITS GENERATOR Fathi M. Hamdoon and A. K. Omran
Korean J. Math. 4 (016), No. 4, pp. 613 66 https://doi.org/10.11568/kjm.016.4.4.613 STUDYING ON A SKEW RULED SURFACE BY USING THE GEODESIC FRENET TRIHEDRON OF ITS GENERATOR Fathi M. Hamdoon and A. K. Omran
The Ruled Surfaces According to Type-2 Bishop Frame in E 3
 International Mathematical Forum, Vol. 1, 017, no. 3, 133-143 HIKARI Ltd, www.m-hikari.com https://doi.org/10.1988/imf.017.610131 The Ruled Surfaces According to Type- Bishop Frame in E 3 Esra Damar Department
International Mathematical Forum, Vol. 1, 017, no. 3, 133-143 HIKARI Ltd, www.m-hikari.com https://doi.org/10.1988/imf.017.610131 The Ruled Surfaces According to Type- Bishop Frame in E 3 Esra Damar Department
BÄCKLUND TRANSFORMATIONS ACCORDING TO BISHOP FRAME IN EUCLIDEAN 3-SPACE
 iauliai Math. Semin., 7 15), 2012, 4149 BÄCKLUND TRANSFORMATIONS ACCORDING TO BISHOP FRAME IN EUCLIDEAN 3-SPACE Murat Kemal KARACAN, Yilmaz TUNÇER Department of Mathematics, Usak University, 64200 Usak,
iauliai Math. Semin., 7 15), 2012, 4149 BÄCKLUND TRANSFORMATIONS ACCORDING TO BISHOP FRAME IN EUCLIDEAN 3-SPACE Murat Kemal KARACAN, Yilmaz TUNÇER Department of Mathematics, Usak University, 64200 Usak,
International Journal of Scientific & Engineering Research, Volume 5, Issue 11, November-2014 ISSN
 1522 Note on the Four Components of the Generalized Lorentz Group O(n; 1) Abstract In physics and mathematics, the generalized Lorentz group is the group of all Lorentz transformations of generalized Minkowski
1522 Note on the Four Components of the Generalized Lorentz Group O(n; 1) Abstract In physics and mathematics, the generalized Lorentz group is the group of all Lorentz transformations of generalized Minkowski
Geometric Modelling Summer 2016
 Geometric Modelling Summer 2016 Exercises Benjamin Karer M.Sc. http://gfx.uni-kl.de/~gm Benjamin Karer M.Sc. Geometric Modelling Summer 2016 1 Dierential Geometry Benjamin Karer M.Sc. Geometric Modelling
Geometric Modelling Summer 2016 Exercises Benjamin Karer M.Sc. http://gfx.uni-kl.de/~gm Benjamin Karer M.Sc. Geometric Modelling Summer 2016 1 Dierential Geometry Benjamin Karer M.Sc. Geometric Modelling
Index. Bertrand mate, 89 bijection, 48 bitangent, 69 Bolyai, 339 Bonnet s Formula, 283 bounded, 48
 Index acceleration, 14, 76, 355 centripetal, 27 tangential, 27 algebraic geometry, vii analytic, 44 angle at a corner, 21 on a regular surface, 170 angle excess, 337 angle of parallelism, 344 angular velocity,
Index acceleration, 14, 76, 355 centripetal, 27 tangential, 27 algebraic geometry, vii analytic, 44 angle at a corner, 21 on a regular surface, 170 angle excess, 337 angle of parallelism, 344 angular velocity,
TRANSLATION SURFACES IN THE GALILEAN SPACE. University of Zagreb, Croatia
 GLASNIK MATEMATIČKI Vol. 46(66)(11), 455 469 TRANSLATION SURFACES IN THE GALILEAN SPACE Željka Milin Šipuš and Blaženka Divjak University of Zagreb, Croatia Abstract. In this paper we describe, up to a
GLASNIK MATEMATIČKI Vol. 46(66)(11), 455 469 TRANSLATION SURFACES IN THE GALILEAN SPACE Željka Milin Šipuš and Blaženka Divjak University of Zagreb, Croatia Abstract. In this paper we describe, up to a
On the Differential Geometric Elements of Mannheim Darboux Ruled Surface in E 3
 Applied Mathematical Sciences, Vol. 10, 016, no. 6, 3087-3094 HIKARI Ltd, www.m-hiari.com https://doi.org/10.1988/ams.016.671 On the Differential Geometric Elements of Mannheim Darboux Ruled Surface in
Applied Mathematical Sciences, Vol. 10, 016, no. 6, 3087-3094 HIKARI Ltd, www.m-hiari.com https://doi.org/10.1988/ams.016.671 On the Differential Geometric Elements of Mannheim Darboux Ruled Surface in
THE BERTRAND OFFSETS OF RULED SURFACES IN R Preliminaries. X,Y = x 1 y 1 + x 2 y 2 x 3 y 3.
 ACTA MATHEMATICA VIETNAMICA 39 Volume 31, Number 1, 2006, pp. 39-48 THE BERTRAND OFFSETS OF RULED SURFACES IN R 3 1 E. KASAP AND N. KURUOĞLU Abstract. The problem of finding a curve whose principal normals
ACTA MATHEMATICA VIETNAMICA 39 Volume 31, Number 1, 2006, pp. 39-48 THE BERTRAND OFFSETS OF RULED SURFACES IN R 3 1 E. KASAP AND N. KURUOĞLU Abstract. The problem of finding a curve whose principal normals
A METHOD OF THE DETERMINATION OF A GEODESIC CURVE ON RULED SURFACE WITH TIME-LIKE RULINGS
 Novi Sad J. Math. Vol., No. 2, 200, 10-110 A METHOD OF THE DETERMINATION OF A GEODESIC CURVE ON RULED SURFACE WITH TIME-LIKE RULINGS Emin Kasap 1 Abstract. A non-linear differential equation is analyzed
Novi Sad J. Math. Vol., No. 2, 200, 10-110 A METHOD OF THE DETERMINATION OF A GEODESIC CURVE ON RULED SURFACE WITH TIME-LIKE RULINGS Emin Kasap 1 Abstract. A non-linear differential equation is analyzed
SPLIT QUATERNIONS and CANAL SURFACES. in MINKOWSKI 3-SPACE
 INTERNATIONAL JOURNAL OF GEOMETRY Vol. 5 (016, No., 51-61 SPLIT QUATERNIONS and CANAL SURFACES in MINKOWSKI 3-SPACE SELAHATTIN ASLAN and YUSUF YAYLI Abstract. A canal surface is the envelope of a one-parameter
INTERNATIONAL JOURNAL OF GEOMETRY Vol. 5 (016, No., 51-61 SPLIT QUATERNIONS and CANAL SURFACES in MINKOWSKI 3-SPACE SELAHATTIN ASLAN and YUSUF YAYLI Abstract. A canal surface is the envelope of a one-parameter
The Natural Lift of the Fixed Centrode of a Non-null Curve in Minkowski 3-Space
 Malaya J Mat 4(3(016 338 348 The Natural Lift of the Fixed entrode of a Non-null urve in Minkowski 3-Space Mustafa Çalışkan a and Evren Ergün b a Faculty of Sciences epartment of Mathematics Gazi University
Malaya J Mat 4(3(016 338 348 The Natural Lift of the Fixed entrode of a Non-null urve in Minkowski 3-Space Mustafa Çalışkan a and Evren Ergün b a Faculty of Sciences epartment of Mathematics Gazi University
A Note on Inextensible Flows of Partially & Pseudo Null Curves in E 4 1
 Prespacetime Journal April 216 Volume 7 Issue 5 pp. 818 827 818 Article A Note on Inextensible Flows of Partially & Pseudo Null Curves in E 4 1 Zühal Küçükarslan Yüzbaşı 1 & & Mehmet Bektaş Firat University,
Prespacetime Journal April 216 Volume 7 Issue 5 pp. 818 827 818 Article A Note on Inextensible Flows of Partially & Pseudo Null Curves in E 4 1 Zühal Küçükarslan Yüzbaşı 1 & & Mehmet Bektaş Firat University,
ON THE RULED SURFACES WHOSE FRAME IS THE BISHOP FRAME IN THE EUCLIDEAN 3 SPACE. 1. Introduction
 International Electronic Journal of Geometry Volume 6 No.2 pp. 110 117 (2013) c IEJG ON THE RULED SURFACES WHOSE FRAME IS THE BISHOP FRAME IN THE EUCLIDEAN 3 SPACE ŞEYDA KILIÇOĞLU, H. HILMI HACISALIHOĞLU
International Electronic Journal of Geometry Volume 6 No.2 pp. 110 117 (2013) c IEJG ON THE RULED SURFACES WHOSE FRAME IS THE BISHOP FRAME IN THE EUCLIDEAN 3 SPACE ŞEYDA KILIÇOĞLU, H. HILMI HACISALIHOĞLU
Classifications of Special Curves in the Three-Dimensional Lie Group
 International Journal of Mathematical Analysis Vol. 10, 2016, no. 11, 503-514 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/10.12988/ijma.2016.6230 Classifications of Special Curves in the Three-Dimensional
International Journal of Mathematical Analysis Vol. 10, 2016, no. 11, 503-514 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/10.12988/ijma.2016.6230 Classifications of Special Curves in the Three-Dimensional
SOME RESULTS ON THE GEOMETRY OF TRAJECTORY SURFACES. Basibuyuk, 34857, Maltepe, Istanbul, Turkey,
 SOME RESULTS ON THE GEOMETRY OF TRAJECTORY SURFACES Osman Gürsoy 1 Ahmet Küçük Muhsin ncesu 3 1 Maltepe University, Faculty of Science and Art, Department of Mathematics, Basibuyuk, 34857, Maltepe, stanbul,
SOME RESULTS ON THE GEOMETRY OF TRAJECTORY SURFACES Osman Gürsoy 1 Ahmet Küçük Muhsin ncesu 3 1 Maltepe University, Faculty of Science and Art, Department of Mathematics, Basibuyuk, 34857, Maltepe, stanbul,
SOME ASPECTS ON CIRCLES AND HELICES IN A COMPLEX PROJECTIVE SPACE. Toshiaki Adachi* and Sadahiro Maeda
 Mem. Fac. Sci. Eng. Shimane Univ. Series B: Mathematical Science 32 (1999), pp. 1 8 SOME ASPECTS ON CIRCLES AND HELICES IN A COMPLEX PROJECTIVE SPACE Toshiaki Adachi* and Sadahiro Maeda (Received December
Mem. Fac. Sci. Eng. Shimane Univ. Series B: Mathematical Science 32 (1999), pp. 1 8 SOME ASPECTS ON CIRCLES AND HELICES IN A COMPLEX PROJECTIVE SPACE Toshiaki Adachi* and Sadahiro Maeda (Received December
Dual Smarandache Curves of a Timelike Curve lying on Unit dual Lorentzian Sphere
 MATHEMATICAL SCIENCES AND APPLICATIONS E-NOTES 4 () -3 (06) c MSAEN Dual Smarandache Curves of a Timelike Curve lying on Unit dual Lorentzian Sphere Tanju Kahraman* and Hasan Hüseyin Uğurlu (Communicated
MATHEMATICAL SCIENCES AND APPLICATIONS E-NOTES 4 () -3 (06) c MSAEN Dual Smarandache Curves of a Timelike Curve lying on Unit dual Lorentzian Sphere Tanju Kahraman* and Hasan Hüseyin Uğurlu (Communicated
MINIMAL AFFINE TRANSLATION SURFACES IN HYPERBOLIC SPACE
 Palestine Journal of Mathematics Vol. 7(1)(018), 57 61 Palestine Polytechnic University-PPU 018 MINIMAL AFFINE TRANSLATION SURFACES IN HYPERBOLIC SPACE Hülya Gün Bozok Mahmut Ergüt Communicated by Ayman
Palestine Journal of Mathematics Vol. 7(1)(018), 57 61 Palestine Polytechnic University-PPU 018 MINIMAL AFFINE TRANSLATION SURFACES IN HYPERBOLIC SPACE Hülya Gün Bozok Mahmut Ergüt Communicated by Ayman
D Tangent Surfaces of Timelike Biharmonic D Helices according to Darboux Frame on Non-degenerate Timelike Surfaces in the Lorentzian Heisenberg GroupH
 Bol. Soc. Paran. Mat. (3s.) v. 32 1 (2014): 35 42. c SPM ISSN-2175-1188 on line ISSN-00378712 in press SPM: www.spm.uem.br/bspm doi:10.5269/bspm.v32i1.19035 D Tangent Surfaces of Timelike Biharmonic D
Bol. Soc. Paran. Mat. (3s.) v. 32 1 (2014): 35 42. c SPM ISSN-2175-1188 on line ISSN-00378712 in press SPM: www.spm.uem.br/bspm doi:10.5269/bspm.v32i1.19035 D Tangent Surfaces of Timelike Biharmonic D
Lie Algebra of Unit Tangent Bundle in Minkowski 3-Space
 INTERNATIONAL ELECTRONIC JOURNAL OF GEOMETRY VOLUME 12 NO. 1 PAGE 1 (2019) Lie Algebra of Unit Tangent Bundle in Minkowski 3-Space Murat Bekar (Communicated by Levent Kula ) ABSTRACT In this paper, a one-to-one
INTERNATIONAL ELECTRONIC JOURNAL OF GEOMETRY VOLUME 12 NO. 1 PAGE 1 (2019) Lie Algebra of Unit Tangent Bundle in Minkowski 3-Space Murat Bekar (Communicated by Levent Kula ) ABSTRACT In this paper, a one-to-one
On the Fundamental Forms of the B-scroll with Null Directrix and Cartan Frame in Minkowskian 3-Space
 Applied Mathematical Sciences, Vol. 9, 015, no. 80, 3957-3965 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/10.1988/ams.015.5330 On the Fundamental Forms of the B-scroll with Null Directrix and Cartan
Applied Mathematical Sciences, Vol. 9, 015, no. 80, 3957-3965 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/10.1988/ams.015.5330 On the Fundamental Forms of the B-scroll with Null Directrix and Cartan
On Natural Lift of a Curve
 Pure Mathematical Sciences, Vol. 1, 2012, no. 2, 81-85 On Natural Lift of a Curve Evren ERGÜN Ondokuz Mayıs University, Faculty of Arts and Sciences Department of Mathematics, Samsun, Turkey eergun@omu.edu.tr
Pure Mathematical Sciences, Vol. 1, 2012, no. 2, 81-85 On Natural Lift of a Curve Evren ERGÜN Ondokuz Mayıs University, Faculty of Arts and Sciences Department of Mathematics, Samsun, Turkey eergun@omu.edu.tr
SLANT HELICES IN MINKOWSKI SPACE E 3 1
 J. Korean Math. Soc. 48 (2011), No. 1, pp. 159 167 DOI 10.4134/JKMS.2011.48.1.159 SLANT HELICES IN MINKOWSKI SPACE E 3 1 Ahmad T. Ali and Rafael López Abstract. We consider a curve α = α(s) in Minkowski
J. Korean Math. Soc. 48 (2011), No. 1, pp. 159 167 DOI 10.4134/JKMS.2011.48.1.159 SLANT HELICES IN MINKOWSKI SPACE E 3 1 Ahmad T. Ali and Rafael López Abstract. We consider a curve α = α(s) in Minkowski
ON THE SCALAR AND DUAL FORMULATIONS OF THE CURVATURE THEORY OF LINE TRAJECTORIES IN THE LORENTZIAN SPACE. 1. Introduction
 J. Korean Math. Soc. 43 (2006), No. 6, pp. 1339 1355 ON THE SCALAR AND DUAL FORMULATIONS OF THE CURVATURE THEORY OF LINE TRAJECTORIES IN THE LORENTZIAN SPACE N ihat Ayyıldız and Ahmet Yücesan Abstract.
J. Korean Math. Soc. 43 (2006), No. 6, pp. 1339 1355 ON THE SCALAR AND DUAL FORMULATIONS OF THE CURVATURE THEORY OF LINE TRAJECTORIES IN THE LORENTZIAN SPACE N ihat Ayyıldız and Ahmet Yücesan Abstract.
Eikonal slant helices and eikonal Darboux helices in 3-dimensional pseudo-riemannian manifolds
 Eikonal slant helices and eikonal Darboux helices in -dimensional pseudo-riemannian maniolds Mehmet Önder a, Evren Zıplar b a Celal Bayar University, Faculty o Arts and Sciences, Department o Mathematics,
Eikonal slant helices and eikonal Darboux helices in -dimensional pseudo-riemannian maniolds Mehmet Önder a, Evren Zıplar b a Celal Bayar University, Faculty o Arts and Sciences, Department o Mathematics,
Classical differential geometry of two-dimensional surfaces
 Classical differential geometry of two-dimensional surfaces 1 Basic definitions This section gives an overview of the basic notions of differential geometry for twodimensional surfaces. It follows mainly
Classical differential geometry of two-dimensional surfaces 1 Basic definitions This section gives an overview of the basic notions of differential geometry for twodimensional surfaces. It follows mainly
94 CHAPTER 3. VECTORS AND THE GEOMETRY OF SPACE
 94 CHAPTER 3. VECTORS AND THE GEOMETRY OF SPACE 3.3 Dot Product We haven t yet de ned a multiplication between vectors. It turns out there are di erent ways this can be done. In this section, we present
94 CHAPTER 3. VECTORS AND THE GEOMETRY OF SPACE 3.3 Dot Product We haven t yet de ned a multiplication between vectors. It turns out there are di erent ways this can be done. In this section, we present
SELECTED SAMPLE FINAL EXAM SOLUTIONS - MATH 5378, SPRING 2013
 SELECTED SAMPLE FINAL EXAM SOLUTIONS - MATH 5378, SPRING 03 Problem (). This problem is perhaps too hard for an actual exam, but very instructional, and simpler problems using these ideas will be on the
SELECTED SAMPLE FINAL EXAM SOLUTIONS - MATH 5378, SPRING 03 Problem (). This problem is perhaps too hard for an actual exam, but very instructional, and simpler problems using these ideas will be on the
arxiv: v1 [math.dg] 12 Jun 2015
![arxiv: v1 [math.dg] 12 Jun 2015 arxiv: v1 [math.dg] 12 Jun 2015](/thumbs/72/67096922.jpg) arxiv:1506.03938v1 [math.dg] 1 Jun 015 NOTES ON W-DIRECTION CURVES IN EUCLIDEAN 3-SPACE İlkay Arslan Güven 1,, Semra Kaya Nurkan and İpek Ağaoğlu Tor 3 1,3 Department of Mathematics, Faculty of Arts and
arxiv:1506.03938v1 [math.dg] 1 Jun 015 NOTES ON W-DIRECTION CURVES IN EUCLIDEAN 3-SPACE İlkay Arslan Güven 1,, Semra Kaya Nurkan and İpek Ağaoğlu Tor 3 1,3 Department of Mathematics, Faculty of Arts and
THE NATURAL LIFT CURVE OF THE SPHERICAL INDICATRIX OF A TIMELIKE CURVE IN MINKOWSKI 4-SPACE
 Journal of Science Arts Year 5, o (, pp 5-, 5 ORIGIAL PAPER HE AURAL LIF CURVE OF HE SPHERICAL IDICARIX OF A IMELIKE CURVE I MIKOWSKI -SPACE EVRE ERGÜ Manuscript received: 65; Accepted paper: 55; Published
Journal of Science Arts Year 5, o (, pp 5-, 5 ORIGIAL PAPER HE AURAL LIF CURVE OF HE SPHERICAL IDICARIX OF A IMELIKE CURVE I MIKOWSKI -SPACE EVRE ERGÜ Manuscript received: 65; Accepted paper: 55; Published
k type partially null and pseudo null slant helices in Minkowski 4-space
 MATHEMATICAL COMMUNICATIONS 93 Math. Commun. 17(1), 93 13 k type partially null and pseudo null slant helices in Minkowski 4-space Ahmad Tawfik Ali 1, Rafael López and Melih Turgut 3, 1 Department of Mathematics,
MATHEMATICAL COMMUNICATIONS 93 Math. Commun. 17(1), 93 13 k type partially null and pseudo null slant helices in Minkowski 4-space Ahmad Tawfik Ali 1, Rafael López and Melih Turgut 3, 1 Department of Mathematics,
Solutions to Test #1 MATH 2421
 Solutions to Test # MATH Pulhalskii/Kawai (#) Decide whether the following properties are TRUE or FALSE for arbitrary vectors a; b; and c: Circle your answer. [Remember, TRUE means that the statement is
Solutions to Test # MATH Pulhalskii/Kawai (#) Decide whether the following properties are TRUE or FALSE for arbitrary vectors a; b; and c: Circle your answer. [Remember, TRUE means that the statement is
Relatively normal-slant helices lying on a surface and their characterizations
 Hacettepe Journal of Mathematics and Statistics Volume 46 3 017, 397 408 Relatively normal-slant helices lying on a surface and their characterizations Nesibe MAC T and Mustafa DÜLDÜL Abstract In this
Hacettepe Journal of Mathematics and Statistics Volume 46 3 017, 397 408 Relatively normal-slant helices lying on a surface and their characterizations Nesibe MAC T and Mustafa DÜLDÜL Abstract In this
On the Blaschke trihedrons of a line congruence
 NTMSCI 4, No. 1, 130-141 (2016) 130 New Trends in Mathematical Sciences http://dx.doi.org/10.20852/ntmsci.2016115659 On the Blaschke trihedrons of a line congruence Sadullah Celik Emin Ozyilmaz Department
NTMSCI 4, No. 1, 130-141 (2016) 130 New Trends in Mathematical Sciences http://dx.doi.org/10.20852/ntmsci.2016115659 On the Blaschke trihedrons of a line congruence Sadullah Celik Emin Ozyilmaz Department
1 The Classical Embedding Problem
 1 The Classical Embedding Problem 1.1 Surfaces vs Manifolds The currently accepted way to represent a non-euclidean geometry is to start with a manifold, de ned only in terms of overlapping coordinate
1 The Classical Embedding Problem 1.1 Surfaces vs Manifolds The currently accepted way to represent a non-euclidean geometry is to start with a manifold, de ned only in terms of overlapping coordinate
1-TYPE AND BIHARMONIC FRENET CURVES IN LORENTZIAN 3-SPACE *
 Iranian Journal of Science & Technology, Transaction A, ol., No. A Printed in the Islamic Republic of Iran, 009 Shiraz University -TYPE AND BIHARMONIC FRENET CURES IN LORENTZIAN -SPACE * H. KOCAYIGIT **
Iranian Journal of Science & Technology, Transaction A, ol., No. A Printed in the Islamic Republic of Iran, 009 Shiraz University -TYPE AND BIHARMONIC FRENET CURES IN LORENTZIAN -SPACE * H. KOCAYIGIT **
Curves. Contents. 1 Introduction 3
 Curves Danilo Magistrali and M. Eugenia Rosado María Departamento de Matemática Aplicada Escuela Técnica Superior de Arquitectura, UPM Avda. Juan de Herrera 4, 8040-Madrid, Spain e-mail: danilo.magistrali@upm.es
Curves Danilo Magistrali and M. Eugenia Rosado María Departamento de Matemática Aplicada Escuela Técnica Superior de Arquitectura, UPM Avda. Juan de Herrera 4, 8040-Madrid, Spain e-mail: danilo.magistrali@upm.es
N C Smarandache Curve of Bertrand Curves Pair According to Frenet Frame
 International J.Math. Combin. Vol.1(016), 1-7 N C Smarandache Curve of Bertrand Curves Pair According to Frenet Frame Süleyman Şenyurt, Abdussamet Çalışkan and Ünzile Çelik (Faculty of Arts and Sciences,
International J.Math. Combin. Vol.1(016), 1-7 N C Smarandache Curve of Bertrand Curves Pair According to Frenet Frame Süleyman Şenyurt, Abdussamet Çalışkan and Ünzile Çelik (Faculty of Arts and Sciences,
Timelike Rotational Surfaces of Elliptic, Hyperbolic and Parabolic Types in Minkowski Space E 4 with Pointwise 1-Type Gauss Map
 Filomat 29:3 (205), 38 392 DOI 0.2298/FIL50338B Published by Faculty of Sciences and Mathematics, University of Niš, Serbia Available at: http://www.pmf.ni.ac.rs/filomat Timelike Rotational Surfaces of
Filomat 29:3 (205), 38 392 DOI 0.2298/FIL50338B Published by Faculty of Sciences and Mathematics, University of Niš, Serbia Available at: http://www.pmf.ni.ac.rs/filomat Timelike Rotational Surfaces of
THE NATURAL GAUGE OF THE WORLD: WEYL S SCALE FACTOR c William O. Straub Astoria, California March 13, 2007
 THE NATURAL GAUGE OF THE WORLD: WEYL S SCALE FACTOR c William O. Straub Astoria, California March 13, 2007 We now aim at a nal synthesis. To be able to characterize the physical state of the world at a
THE NATURAL GAUGE OF THE WORLD: WEYL S SCALE FACTOR c William O. Straub Astoria, California March 13, 2007 We now aim at a nal synthesis. To be able to characterize the physical state of the world at a
Normal Curvature, Geodesic Curvature and Gauss Formulas
 Title Normal Curvature, Geodesic Curvature and Gauss Formulas MATH 2040 December 20, 2016 MATH 2040 Normal and Geodesic Curvature December 20, 2016 1 / 12 Readings Readings Readings: 4.4 MATH 2040 Normal
Title Normal Curvature, Geodesic Curvature and Gauss Formulas MATH 2040 December 20, 2016 MATH 2040 Normal and Geodesic Curvature December 20, 2016 1 / 12 Readings Readings Readings: 4.4 MATH 2040 Normal
ON HELICES AND BERTRAND CURVES IN EUCLIDEAN 3-SPACE. Murat Babaarslan 1 and Yusuf Yayli 2
 ON HELICES AND BERTRAND CURVES IN EUCLIDEAN 3-SPACE Murat Babaarslan 1 and Yusuf Yayli 1 Department of Mathematics, Faculty of Arts and Sciences Bozok University, Yozgat, Turkey murat.babaarslan@bozok.edu.tr
ON HELICES AND BERTRAND CURVES IN EUCLIDEAN 3-SPACE Murat Babaarslan 1 and Yusuf Yayli 1 Department of Mathematics, Faculty of Arts and Sciences Bozok University, Yozgat, Turkey murat.babaarslan@bozok.edu.tr
On constant isotropic submanifold by generalized null cubic
 On constant isotropic submanifold by generalized null cubic Leyla Onat Abstract. In this paper we shall be concerned with curves in an Lorentzian submanifold M 1, and give a characterization of each constant
On constant isotropic submanifold by generalized null cubic Leyla Onat Abstract. In this paper we shall be concerned with curves in an Lorentzian submanifold M 1, and give a characterization of each constant
A NEW CHARACTERIZATION FOR INCLINED CURVES BY THE HELP OF SPHERICAL REPRESENTATIONS
 International Electronic Journal of Geometry Volume 2 No. 2 pp. 71 75 (2009 c IEJG A NEW CHARACTERIZATION FOR INCLINED CURVES BY THE HELP OF SPHERICAL REPRESENTATIONS H. HILMI HACISALIHOĞLU (Communicated
International Electronic Journal of Geometry Volume 2 No. 2 pp. 71 75 (2009 c IEJG A NEW CHARACTERIZATION FOR INCLINED CURVES BY THE HELP OF SPHERICAL REPRESENTATIONS H. HILMI HACISALIHOĞLU (Communicated
Hilbert s Metric and Gromov Hyperbolicity
 Hilbert s Metric and Gromov Hyperbolicity Andrew Altman May 13, 2014 1 1 HILBERT METRIC 2 1 Hilbert Metric The Hilbert metric is a distance function defined on a convex bounded subset of the n-dimensional
Hilbert s Metric and Gromov Hyperbolicity Andrew Altman May 13, 2014 1 1 HILBERT METRIC 2 1 Hilbert Metric The Hilbert metric is a distance function defined on a convex bounded subset of the n-dimensional
Spherical Images and Characterizations of Time-like Curve According to New Version of the Bishop Frame in Minkowski 3-Space
 Prespacetime Journal January 016 Volume 7 Issue 1 pp. 163 176 163 Article Spherical Images and Characterizations of Time-like Curve According to New Version of the Umit Z. Savcı 1 Celal Bayar University,
Prespacetime Journal January 016 Volume 7 Issue 1 pp. 163 176 163 Article Spherical Images and Characterizations of Time-like Curve According to New Version of the Umit Z. Savcı 1 Celal Bayar University,
B is Galilean transformation group which
 Proceedins of IAM V.5 N. 06 pp.98-09 NORMAL AND RECTIFYING CURVES IN GALILEAN SPACE G Handan Öztekin Department of Mathematics Firat University Elazığ Turkey e-mail: handanoztekin@mail.com Abstract. In
Proceedins of IAM V.5 N. 06 pp.98-09 NORMAL AND RECTIFYING CURVES IN GALILEAN SPACE G Handan Öztekin Department of Mathematics Firat University Elazığ Turkey e-mail: handanoztekin@mail.com Abstract. In
C-partner curves and their applications
 C-partner curves and their applications O. Kaya and M. Önder Abstract. In this study, we define a new type of partner curves called C- partner curves and give some theorems characterizing C-partner curves.
C-partner curves and their applications O. Kaya and M. Önder Abstract. In this study, we define a new type of partner curves called C- partner curves and give some theorems characterizing C-partner curves.
An introduction to General Relativity and the positive mass theorem
 An introduction to General Relativity and the positive mass theorem National Center for Theoretical Sciences, Mathematics Division March 2 nd, 2007 Wen-ling Huang Department of Mathematics University of
An introduction to General Relativity and the positive mass theorem National Center for Theoretical Sciences, Mathematics Division March 2 nd, 2007 Wen-ling Huang Department of Mathematics University of
e 2 = e 1 = e 3 = v 1 (v 2 v 3 ) = det(v 1, v 2, v 3 ).
 3. Frames In 3D space, a sequence of 3 linearly independent vectors v 1, v 2, v 3 is called a frame, since it gives a coordinate system (a frame of reference). Any vector v can be written as a linear combination
3. Frames In 3D space, a sequence of 3 linearly independent vectors v 1, v 2, v 3 is called a frame, since it gives a coordinate system (a frame of reference). Any vector v can be written as a linear combination
arxiv: v1 [math.dg] 1 Feb 2018
![arxiv: v1 [math.dg] 1 Feb 2018 arxiv: v1 [math.dg] 1 Feb 2018](/thumbs/95/126121025.jpg) AFFINE FACTORABLE SURFACES IN ISOTROPIC SPACES arxiv:80.0040v [math.dg] Feb 08 MUHITTIN EVREN AYDIN AYLA ERDUR MAHMUT ERGUT 3 Abstract. In this paper we study the problem of finding the affine factorable
AFFINE FACTORABLE SURFACES IN ISOTROPIC SPACES arxiv:80.0040v [math.dg] Feb 08 MUHITTIN EVREN AYDIN AYLA ERDUR MAHMUT ERGUT 3 Abstract. In this paper we study the problem of finding the affine factorable
CHARACTERIZATIONS OF SPACE CURVES WITH 1-TYPE DARBOUX INSTANTANEOUS ROTATION VECTOR
 Commun. Korean Math. Soc. 31 016), No., pp. 379 388 http://dx.doi.org/10.4134/ckms.016.31..379 CHARACTERIZATIONS OF SPACE CURVES WITH 1-TYPE DARBOUX INSTANTANEOUS ROTATION VECTOR Kadri Arslan, Hüseyin
Commun. Korean Math. Soc. 31 016), No., pp. 379 388 http://dx.doi.org/10.4134/ckms.016.31..379 CHARACTERIZATIONS OF SPACE CURVES WITH 1-TYPE DARBOUX INSTANTANEOUS ROTATION VECTOR Kadri Arslan, Hüseyin
A local characterization for constant curvature metrics in 2-dimensional Lorentz manifolds
 A local characterization for constant curvature metrics in -dimensional Lorentz manifolds Ivo Terek Couto Alexandre Lymberopoulos August 9, 8 arxiv:65.7573v [math.dg] 4 May 6 Abstract In this paper we
A local characterization for constant curvature metrics in -dimensional Lorentz manifolds Ivo Terek Couto Alexandre Lymberopoulos August 9, 8 arxiv:65.7573v [math.dg] 4 May 6 Abstract In this paper we
102 CHAPTER 3. VECTORS AND THE GEOMETRY OF SPACE
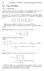 102 CHAPTER 3. VECTORS AND THE GEOMETRY OF SPACE 3.4 Cross Product 3.4.1 De nitions Unlike the dot product, the cross product is only de ned for 3-D vectors. In this section, when we use the word vector,
102 CHAPTER 3. VECTORS AND THE GEOMETRY OF SPACE 3.4 Cross Product 3.4.1 De nitions Unlike the dot product, the cross product is only de ned for 3-D vectors. In this section, when we use the word vector,
Available online at J. Math. Comput. Sci. 6 (2016), No. 5, ISSN:
 Available online at http://scik.org J. Math. Comput. Sci. 6 (2016), No. 5, 706-711 ISSN: 1927-5307 DARBOUX ROTATION AXIS OF A NULL CURVE IN MINKOWSKI 3-SPACE SEMRA KAYA NURKAN, MURAT KEMAL KARACAN, YILMAZ
Available online at http://scik.org J. Math. Comput. Sci. 6 (2016), No. 5, 706-711 ISSN: 1927-5307 DARBOUX ROTATION AXIS OF A NULL CURVE IN MINKOWSKI 3-SPACE SEMRA KAYA NURKAN, MURAT KEMAL KARACAN, YILMAZ
Coordinate Finite Type Rotational Surfaces in Euclidean Spaces
 Filomat 28:10 (2014), 2131 2140 DOI 10.2298/FIL1410131B Published by Faculty of Sciences and Mathematics, University of Niš, Serbia Available at: http://www.pmf.ni.ac.rs/filomat Coordinate Finite Type
Filomat 28:10 (2014), 2131 2140 DOI 10.2298/FIL1410131B Published by Faculty of Sciences and Mathematics, University of Niš, Serbia Available at: http://www.pmf.ni.ac.rs/filomat Coordinate Finite Type
Inextensible Flows of Curves in Lie Groups
 CJMS. 113, 3-3 Caspian Journal of Mathematical Sciences CJMS University of Mazandaran, Iran http://cjms.journals.umz.ac.ir ISSN: 1735-611 Inextensible Flows of Curves in Lie Groups Gökmen Yıldız a and
CJMS. 113, 3-3 Caspian Journal of Mathematical Sciences CJMS University of Mazandaran, Iran http://cjms.journals.umz.ac.ir ISSN: 1735-611 Inextensible Flows of Curves in Lie Groups Gökmen Yıldız a and
Unit Speed Curves. Recall that a curve Α is said to be a unit speed curve if
 Unit Speed Curves Recall that a curve Α is said to be a unit speed curve if The reason that we like unit speed curves that the parameter t is equal to arc length; i.e. the value of t tells us how far along
Unit Speed Curves Recall that a curve Α is said to be a unit speed curve if The reason that we like unit speed curves that the parameter t is equal to arc length; i.e. the value of t tells us how far along
UNIVERSITY OF DUBLIN
 UNIVERSITY OF DUBLIN TRINITY COLLEGE JS & SS Mathematics SS Theoretical Physics SS TSM Mathematics Faculty of Engineering, Mathematics and Science school of mathematics Trinity Term 2015 Module MA3429
UNIVERSITY OF DUBLIN TRINITY COLLEGE JS & SS Mathematics SS Theoretical Physics SS TSM Mathematics Faculty of Engineering, Mathematics and Science school of mathematics Trinity Term 2015 Module MA3429
On the Mannheim surface offsets
 NTMSCI 3, No. 3, 35-45 (25) 35 New Trends in Mathematical Sciences http://www.ntmsci.com On the Mannheim surface offsets Mehmet Önder and H. Hüseyin Uǧurlu 2 Celal Bayar University, Faculty of Arts and
NTMSCI 3, No. 3, 35-45 (25) 35 New Trends in Mathematical Sciences http://www.ntmsci.com On the Mannheim surface offsets Mehmet Önder and H. Hüseyin Uǧurlu 2 Celal Bayar University, Faculty of Arts and
Qing-Ming Cheng and Young Jin Suh
 J. Korean Math. Soc. 43 (2006), No. 1, pp. 147 157 MAXIMAL SPACE-LIKE HYPERSURFACES IN H 4 1 ( 1) WITH ZERO GAUSS-KRONECKER CURVATURE Qing-Ming Cheng and Young Jin Suh Abstract. In this paper, we study
J. Korean Math. Soc. 43 (2006), No. 1, pp. 147 157 MAXIMAL SPACE-LIKE HYPERSURFACES IN H 4 1 ( 1) WITH ZERO GAUSS-KRONECKER CURVATURE Qing-Ming Cheng and Young Jin Suh Abstract. In this paper, we study
