A NOTE ON BOUNDARY BLOW-UP PROBLEM OF u = u p
|
|
|
- Buck Hunt
- 5 years ago
- Views:
Transcription
1 A NOTE ON BOUNDARY BLOW-UP PROBLEM OF u = u p SEICK KIM Abstract. Assume that Ω is a bouded domai i R with 2. We study positive solutios to the problem, u = u p i Ω, u(x) as x Ω, where p > 1. Such solutios are called boudary blow-up solutios of u = u p. We show that a boudary blow-up solutio exists i ay bouded domai if 1 < p <. I particular, whe = 2, there exists a boudary blow-up solutio to u = u p for all p (1, ). We also prove the uiqueess uder the additioal assumptio that the domai satisfies the coditio Ω = Ω. 1. Itroductio Let Ω be a bouded domai of R with 2 ad let Ω deote its boudary. I this article we study the problem (1) (2) u(x) = f(u(x)) for x Ω, u(x) + as d(x) := dist(x, Ω) 0, where f(t) = t p + := {max(t, 0)} p with p > 1. Solutios to the problem (1), (2) are called boudary blow-up solutios. I 1957, Keller [5] ad Osserma [11] proved existece of solutios to problem (1), (2) for a rather geeral class of fuctios f; i.e., f : R [0, ) is a locally Lipschitz cotiuous fuctio which is icreasig ad satisfies the followig growth coditio called Keller-Osserma coditio: { t 1/2 (3) f(s) ds} dt < + for all t 0 > 0. t 0 0 It is easy to check that f(t) = t p + with p > 1 satisfies (3). They showed that (3) is a ecessary coditio for the existece of blow-up solutios. Ideed, if the domai Ω is regular eough, say Lipschitz, the the existece of a classical solutio to the problem (1), (2) is established by the method of supersolutios ad subsolutios together with the uiform estimates of Keller [5]. We will briefly review existece results i the ext sectio. The case f(t) = t p + with p > 1 is of special iterest, ad i this article oly this case will be treated. Loewer ad Nireberg [7] studied the case whe p = +2 with > 2, which is related to a problem i differetial geometry. The problem (1), (2) is also related to probability theory. The equatio u = u p +, 1 < p 2, appears i the aalytical theory of a Markov process called superdiffusio; see [2]. By meas of a probabilistic represetatio, a uiqueess result i domais with o-smooth boudary was established by Le Gall [6] i the case whe p = 2. Later, Marcus ad Véro [8, 9] exteded the uiqueess i very geeral domais for all 2000 Mathematics Subject Classificatio. Primary 35J65; Secodary 35B05. Key words ad phrases. Blow-up, semi-liear equatio, existece, uiqueess. 1
2 2 SEICK KIM p > 1, usig purely aalytical method; they proved uiqueess i a domai whose boudary is locally represeted as a graph of a cotiuous fuctio. However, it is ot clear whether a boudary blow-up solutio exists or ot i such a geeral domai. I [10], Matero costructed a boudary blow-up solutio of u = u p + with 1 < p <, i a two-dimesioal domai with fractal boudary called the vo Koch sowflake domai. His approach is based o the compariso with boudary blow-up solutios i a cut-off ope coe. We treat a special case whe p (1, ) for 3 ad p (1, ) for = 2. Some iterestig results are obtaied i that case. We will prove that a boudary blow-up solutio exists i every bouded domai. As a cosequece, it will imply a result of Matero [10] metioed above. We will also show the uiqueess if the domai satisfies a additioal assumptio, Ω = Ω. For example, if Ω ca be locally represeted as a graph of a cotiuous fuctio, the it satisfies the above coditio. I this case, uiqueess was earlier proved by Marcus ad Véro [8, 9]. 2. Prelimiaries I this sectio, we briefly discuss the existece results of Keller [5], Loewer ad Nireberg [7]. We also itroduce some termiology which will be used i the later parts of the paper. We begi with a simple lemma. Lemma 2.1 (Compariso priciple). Let Ω R be a bouded domai. Assume that f is icreasig. Let u, v C 2 (Ω) be solutios of u f(u) ad v f(v) respectively. If lim if x Ω (v u)(x) 0, the v u i Ω. Proof. Suppose, to the cotrary, that there exists x 0 Ω such that u(x 0 ) > v(x 0 ). The for sufficietly small ɛ > 0, Ω ɛ := {u v > ɛ} ad Ω ɛ Ω. Let w := u v ɛ. The w = 0 o Ω ɛ. Sice f is icreasig, Lw f(u) f(v) f(u) f(v + ɛ) 0 i Ω ɛ. The the maximum priciple implies w 0 i Ω ɛ. This cotradictio proves the lemma. Remark 2.2. Let Ω 1, Ω 2 R be bouded domais such that Ω 1 Ω 2, i.e., Ω 1 Ω 2. Suppose u i (i = 1, 2) are solutios to (1), (2) i Ω i. The, it follows from Lemma 2.1 that u 1 u 2 i Ω 1. The ext theorem is quoted from [5]; see also [11]. Theorem 2.3 (Keller [5, pp ]). Let u be a solutio of (1) i a bouded domai Ω. There exist a cotiuous, decreasig fuctio g : (0, ) R determied by f such that lim t 0 g(t) = + ad (4) u(x) g(d(x)), where d(x) := dist(x, Ω). Usig the above estimate (4), Keller proved the existece of a boudary blow-up solutio. Although he claimed the existece i arbitrary domais, his argumet seems to require certai smoothess assumptio o Ω. Let Ω be a regular domai, say a Lipschitz domai. By the method of supersolutios ad subsolutios (see e.g. [3, pp ]), oe ca show that, for each m 1, there exists a uique solutio u m C 0 (Ω) C 2 (Ω) of (1) such that u m = α m o Ω, where α m < α m+1 ad α m as m. The by the compariso priciple, {u m } m=1 is a icreasig sequece of fuctios. By (4), u m (x) g(d(x)) uiformly for m 1. Deote by u(x) the poitwise limit of {u m (x)} m=1. The by the stadard elliptic theory (see
3 A NOTE ON BOUNDARY BLOW-UP PROBLEM 3 e.g. [4]), u C 2 (Ω) ad u is a solutio of (1). As x approaches Ω, u(x) icreases idefiitely sice u m = α m becomes ifiite o Ω; thus u is a solutio of the problem (1), (2). The solutio u costructed above is called a miimal boudary blow-up solutio. Ideed, if v is a boudary blow-up solutio, the by the compariso priciple, u m v i Ω for all m 1 ad thus, u = lim m u m v follows. Loewer ad Nireberg [7] itroduced aother importat solutio of (1) called a maximal solutio which is ot ecessarily a blow-up solutio but ca be costructed i ay bouded domai Ω. Let {Ω m } m=1 be a exhaustig sequece of smooth subdomais of Ω; i.e., Ω m Ω m+1 Ω ad m=1 Ω m = Ω. Let u m be the miimal blow-up solutio i Ω m for each m 1, ad let v be the miimal blowup solutio i a ball cotaiig Ω. By Remark 2.2, {u m } m=1 is decreasig ad bouded below by v. Hece, the limit fuctio u exists ad by the stadard elliptic theory, it is a solutio to (1). This solutio u is maximal sice if v is a solutio of (1) i Ω, the by the compariso priciple, we see u m v for all m 1. I ext sectio, we will provide a example of maximal solutio which is ot a boudary blow-up solutio; see Remark 3.3 below. 3. Mai Results We cosider the problem (1), (2) with f(t) = t p +. Note that i this case, a solutio to the problem (1), (2) must be positive, which is a simple cosequece of the maximum priciple. Ideed, more geerally, let t 0 := sup {t : f(t) = 0}. If t 0, the by cotiuity, f(t 0 ) = 0 ad thus, u t 0 is a solutio to (1). By Lemma 2.1, we fid that ay blow-up solutio of (1) is bouded below by t 0. Hereafter, we always assume p (1, ) whe = 2, ad p (1, ) whe 3. We will show that i that case, a boudary blow-up solutio exists i ay bouded domai, which obviously iclude the domai cosidered by Matero i [10]. Also, by usig Safoov s iteratio techique i [12], we prove uiqueess provided that Ω satisfies the coditio Ω = Ω. For example, if Ω ca be locally represeted as a graph of a cotiuous fuctio, the it satisfies the above coditio Costructio of a barrier i R \ {0}. We will costruct a solutio of u = u p + i R \ {0} which blows up at the origi. We look for a solutio of the form v(x) = c p x γ, where c p, γ > 0. Sice v is positive ad radially symmetric, v(r) = c p r γ, where r = x, must solve the followig ODE: (5) v (r) + 1 v (r) = v p (r) i (0, ). r Hece, the ukow costats c p, γ should satisfy (6) c p γ(γ + 2 )r γ 2 = c p pr γp. Set γ = 2/(p 1) so that γ + 2 = γp. The assumptio c p > 0 requires a restrictio o p, amely 2/(p 1) > 2. It is satisfied for all p > 1 whe = 2 ad for p (1, ) whe 3. If we choose (7) { } 1/(p 1) c p = {γ(γ + 2 )} γ/2 2 2( 2)p = (p 1) 2, it follows c p p = c p γ(γ + 2 ).
4 4 SEICK KIM The, v(x) = c p x γ is a solutio of v = v p + o R \{0} such that v(x) + as x 0. We summarize the above result as a lemma. Lemma 3.1. Let p > 1 whe = 2, ad let p (1, ) whe 3. The, v(x) := c p x γ is a solutio of v = v p + i R \ {0} such that v(x) + as { } 1/(p 1) 2 2( 2)p x 0. Here, γ = 2/(p 1) ad c p = (p 1) Existece ad uiqueess of boudary blow-up solutio. Theorem 3.2. Let Ω R be a bouded domai. The, there exists a solutio u to the problem (1), (2). Proof. Let {Ω m } m=1 be a exhaustig sequece of smooth subdomais of Ω, ad let u m be the miimal blow-up solutio of (1) i Ω m. The, the limit u := lim m u m is a maximal solutio; see Sectio 2. We eed to show that u is ideed a boudary blow-up solutio. For ay y Ω, choose a poit y 0 Ω such that d(y) = y y 0. Let v(x) := c p x y 0 γ with c p, γ defied as i Lemma 3.1. Sice y 0 / Ω m for each m 1, wee fid v(x) < + for all x Ω m. Hece, we coclude by Lemma 2.1 that (8) u m (y) v(y) = c p d γ (y) provided m is large eough so that y Ω m. Therefore, by passig to the limit, we fid u(y) c p d γ (y) for ay y Ω. Clearly, u(y) + as d(y) 0, ad thus, u is a desired solutio. Remark 3.3. I Theorem 3.2, the restrictio that p < whe > 2 is essetial. Let Ω := {x R : 0 < x < 1}, where > 2. Brézis ad Véro [1] showed that if p, the ay positive solutio u of u = up i Ω satisfies lim x 0 u(x) < +. Cosequetly, there is o solutio of the problem (1), (2) i Ω. This also shows that i geeral, a maximal solutio is ot ecessarily a boudary blow-up solutio. Theorem 3.4. I additio, assume that Ω satisfies Ω = Ω. The, the solutio of the problem (1), (2) is uique. Proof. Let u 1, u 2 be two boudary blow-up solutios i Ω. followig estimate holds: (9) N 1 d γ (x) u i (x) N 2 d γ (x), for all x Ω; i = 1, 2, We claim that the where N 1, N 2 > 0 are costats depedig oly o ad p. Fix x 0 Ω ad deote r := d(x 0 ). Choose z 0 Ω such that x 0 z 0 = r. From the assumptio that Ω = Ω, there exists a poit y 0 B r (z 0 ) \ Ω. Note that r x 0 y 0 2r. Let v(x) := c p x y 0 γ. Sice Ω is bouded ad y 0 / Ω, we fid, by see Lemma 2.1, that u i (x) v(x), where i = 1, 2. I particular, (10) u i (x 0 ) c p x 0 y 0 γ c p 2 γ d γ (x 0 ); i = 1, 2. Also, by cosiderig a ball B r (x 0 ) ad the miimal boudary blow-up solutio i that ball as a compariso fuctio, it is ot hard to see u i (x 0 ) N 2 d(x 0 ) γ, i = 1, 2, for some costat N 2 > 0 depedig oly o ad p; see e.g. [5]. Therefore, we coclude that the estimate (9) holds. Oce we obtai the estimate (9), u 1 u 2 will follow from the iteratio techique of Safoov i [12]. For the reader s coveiece, we will reproduce his techique here.
5 A NOTE ON BOUNDARY BLOW-UP PROBLEM 5 Assume, to the cotrary, that u 2 (x 1 )/u 1 (x 1 ) > k > 1 for some x 1 Ω. Let Ω 0 := {u 2 > ku 1 } B r (x 1 ), where r = 1 2 d(x 1). The, we fid (u 2 ku 1 ) = u p 2 kup 1 > (kp k)u p 1 c 1kr γp, where c 1 = 2 γp N p 1 (kp 1 1). Therefore, (u 2 ku 1 + w) 0 i Ω 0, where w = c 1 2 kr γp (r 2 x x 1 2 ). By the maximum priciple w(x 1 ) < (u 2 ku 1 + w) (x 1 ) sup Ω 0 (u 2 ku 1 + w). Note that the maximum must be achieved o B r (x 1 ) Ω 0 Ω 0 ; otherwise, it is achieved o {u 2 = ku 1 } B r (x 1 ), where we have u 2 ku 1 + w w(x 1 ). Hece, w(x 1 ) < (u 2 ku 1 )(x 2 ), where x 2 B r (x 1 ) Ω 0 Ω. O the other had, by (9), we fid (recall x 2 B r (x 1 ) so that d(x 2 ) r) w(x 1 ) = c 1 2 kr γp r 2 = c 1 2 kr γ c 2 ku 1 (x 2 ), where c 2 = c 1 N p 1 = 2N 2 2 γp+1 (k p 1 1). Therefore, we coclude u 2 (x 2 )/u 1 (x 2 ) > N 2 (1 + c 2 )k. By iteratig the above process (both c 1 ad c 2 are mootoe icreasig i k), we obtai a sequece of poits {x j } j=1 i Ω satisfyig u 2(x j )/u 1 (x j ) > (1 + c 2 ) j k, which teds to ifiity as j. O the other had, by (9), u 2 (x) u 1 (x) < N 2d γ (x) N 1 d γ (x) = N 2 x Ω. N 1 This cotradictio proves the uiqueess. Remark 3.5. If Ω = { x R 2 : 0 < x < 1 }, the Ω Ω. The uiqueess fails i this case; see [13]. Ackowledgmet. This paper is based o a presetatio by the author at the 2001 AMS sectioal meetig, Williamstow, MA, ad was supported i part by NSF Grat No. DMS Refereces [1] Brézis, H. ad Véro, L.: Removable sigularities for some oliear elliptic equatios. Arch. Ratioal Mech. Aal. 75 (1980/81), o. 1, 1 6. [2] Dyki, E. B.: Diffusios, superdiffusios ad partial differetial equatios. America Mathematical Society Colloquium Publicatios, Vol. 50, America Mathematical Society, Providece, RI, [3] Evas, L. C.: Partial differetial equatios. America Mathematical Society, Providece, RI, 1998 [4] Gilbarg, D. ad Trudiger, N. S.: Elliptic partial differetial equatios of secod order. Secod editio (1983), Spriger-Verlag, Berli. [5] Keller, J. B.: O solutios of u = f(u). Comm. Pure Appl. Math. 10 (1957), [6] Le Gall, J. F.: A path-valued Markov process ad its coectios with partial differetial equatios. I First Europea Cogress of Mathematics, Vol. II (Paris, 1992), , Progr. Math., Vol. 120, Birkhäuser, Basel, [7] Loewer, C. ad Nireberg, L.: Partial differetial equatios ivariat uder coformal or projective trasformatios. I Cotributios to aalysis, Academic Press, New York, 1974, , [8] Marcus, M. ad Véro, L: Uiqueess of solutios with blowup at the boudary for a class of oliear elliptic equatios. C. R. Acad. Sci. Paris Sér. I Math. 317 (1993), o. 6,
6 6 SEICK KIM [9] Marcus, M ad Véro, L: Uiqueess ad asymptotic behavior of solutios with boudary blow-up for a class of oliear elliptic equatios. A. Ist. H. Poicaré Aal. No Liéaire 14 (1997), o. 2, [10] Matero, J.: Boudary-blow up problems i a fractal domai. Z. Aal. Aweduge 15 (1996), o. 2, [11] Osserma, R.: O the iequality u f(u). Pacific J. Math. 7 (1957) [12] Safoov, M. V.: O the uiqueess of blowup solutios for semiliear elliptic equatios. Preprit. [13] Véro, L.: Solutios sigulières d équatios elliptiques semiliéaires (Frech). C. R. Acad. Sci. Paris Sér. A-B 288 (1979), o. 18, A867 A869. School of Mathematics, Uiversity of Miesota, Mieapolis, Miesota address: skim@math.um.edu
Existence of viscosity solutions with asymptotic behavior of exterior problems for Hessian equations
 Available olie at www.tjsa.com J. Noliear Sci. Appl. 9 (2016, 342 349 Research Article Existece of viscosity solutios with asymptotic behavior of exterior problems for Hessia equatios Xiayu Meg, Yogqiag
Available olie at www.tjsa.com J. Noliear Sci. Appl. 9 (2016, 342 349 Research Article Existece of viscosity solutios with asymptotic behavior of exterior problems for Hessia equatios Xiayu Meg, Yogqiag
SINGLE-POINT CONDENSATION AND LEAST-ENERGY SOLUTIONS
 SINGLE-POINT CONDENSATION AND LEAST-ENERGY SOLUTIONS XIAOFENG REN AND JUNCHENG WEI Abstract. We prove a cojecture raised i our earlier paper which says that the least-eergy solutios to a two dimesioal
SINGLE-POINT CONDENSATION AND LEAST-ENERGY SOLUTIONS XIAOFENG REN AND JUNCHENG WEI Abstract. We prove a cojecture raised i our earlier paper which says that the least-eergy solutios to a two dimesioal
Chapter 7 Isoperimetric problem
 Chapter 7 Isoperimetric problem Recall that the isoperimetric problem (see the itroductio its coectio with ido s proble) is oe of the most classical problem of a shape optimizatio. It ca be formulated
Chapter 7 Isoperimetric problem Recall that the isoperimetric problem (see the itroductio its coectio with ido s proble) is oe of the most classical problem of a shape optimizatio. It ca be formulated
Sequences and Series of Functions
 Chapter 6 Sequeces ad Series of Fuctios 6.1. Covergece of a Sequece of Fuctios Poitwise Covergece. Defiitio 6.1. Let, for each N, fuctio f : A R be defied. If, for each x A, the sequece (f (x)) coverges
Chapter 6 Sequeces ad Series of Fuctios 6.1. Covergece of a Sequece of Fuctios Poitwise Covergece. Defiitio 6.1. Let, for each N, fuctio f : A R be defied. If, for each x A, the sequece (f (x)) coverges
b i u x i U a i j u x i u x j
 M ath 5 2 7 Fall 2 0 0 9 L ecture 1 9 N ov. 1 6, 2 0 0 9 ) S ecod- Order Elliptic Equatios: Weak S olutios 1. Defiitios. I this ad the followig two lectures we will study the boudary value problem Here
M ath 5 2 7 Fall 2 0 0 9 L ecture 1 9 N ov. 1 6, 2 0 0 9 ) S ecod- Order Elliptic Equatios: Weak S olutios 1. Defiitios. I this ad the followig two lectures we will study the boudary value problem Here
Chapter 6 Infinite Series
 Chapter 6 Ifiite Series I the previous chapter we cosidered itegrals which were improper i the sese that the iterval of itegratio was ubouded. I this chapter we are goig to discuss a topic which is somewhat
Chapter 6 Ifiite Series I the previous chapter we cosidered itegrals which were improper i the sese that the iterval of itegratio was ubouded. I this chapter we are goig to discuss a topic which is somewhat
Product measures, Tonelli s and Fubini s theorems For use in MAT3400/4400, autumn 2014 Nadia S. Larsen. Version of 13 October 2014.
 Product measures, Toelli s ad Fubii s theorems For use i MAT3400/4400, autum 2014 Nadia S. Larse Versio of 13 October 2014. 1. Costructio of the product measure The purpose of these otes is to preset the
Product measures, Toelli s ad Fubii s theorems For use i MAT3400/4400, autum 2014 Nadia S. Larse Versio of 13 October 2014. 1. Costructio of the product measure The purpose of these otes is to preset the
ON MEAN ERGODIC CONVERGENCE IN THE CALKIN ALGEBRAS
 PROCEEDINGS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 00, Number 0, Pages 000 000 S 0002-9939(XX0000-0 ON MEAN ERGODIC CONVERGENCE IN THE CALKIN ALGEBRAS MARCH T. BOEDIHARDJO AND WILLIAM B. JOHNSON 2
PROCEEDINGS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 00, Number 0, Pages 000 000 S 0002-9939(XX0000-0 ON MEAN ERGODIC CONVERGENCE IN THE CALKIN ALGEBRAS MARCH T. BOEDIHARDJO AND WILLIAM B. JOHNSON 2
Numerical Method for Blasius Equation on an infinite Interval
 Numerical Method for Blasius Equatio o a ifiite Iterval Alexader I. Zadori Omsk departmet of Sobolev Mathematics Istitute of Siberia Brach of Russia Academy of Scieces, Russia zadori@iitam.omsk.et.ru 1
Numerical Method for Blasius Equatio o a ifiite Iterval Alexader I. Zadori Omsk departmet of Sobolev Mathematics Istitute of Siberia Brach of Russia Academy of Scieces, Russia zadori@iitam.omsk.et.ru 1
LOWER BOUNDS FOR THE BLOW-UP TIME OF NONLINEAR PARABOLIC PROBLEMS WITH ROBIN BOUNDARY CONDITIONS
 Electroic Joural of Differetial Equatios, Vol. 214 214), No. 113, pp. 1 5. ISSN: 172-6691. URL: http://ejde.math.txstate.edu or http://ejde.math.ut.edu ftp ejde.math.txstate.edu LOWER BOUNDS FOR THE BLOW-UP
Electroic Joural of Differetial Equatios, Vol. 214 214), No. 113, pp. 1 5. ISSN: 172-6691. URL: http://ejde.math.txstate.edu or http://ejde.math.ut.edu ftp ejde.math.txstate.edu LOWER BOUNDS FOR THE BLOW-UP
lim za n n = z lim a n n.
 Lecture 6 Sequeces ad Series Defiitio 1 By a sequece i a set A, we mea a mappig f : N A. It is customary to deote a sequece f by {s } where, s := f(). A sequece {z } of (complex) umbers is said to be coverget
Lecture 6 Sequeces ad Series Defiitio 1 By a sequece i a set A, we mea a mappig f : N A. It is customary to deote a sequece f by {s } where, s := f(). A sequece {z } of (complex) umbers is said to be coverget
Common Coupled Fixed Point of Mappings Satisfying Rational Inequalities in Ordered Complex Valued Generalized Metric Spaces
 IOSR Joural of Mathematics (IOSR-JM) e-issn: 78-578, p-issn:319-765x Volume 10, Issue 3 Ver II (May-Ju 014), PP 69-77 Commo Coupled Fixed Poit of Mappigs Satisfyig Ratioal Iequalities i Ordered Complex
IOSR Joural of Mathematics (IOSR-JM) e-issn: 78-578, p-issn:319-765x Volume 10, Issue 3 Ver II (May-Ju 014), PP 69-77 Commo Coupled Fixed Poit of Mappigs Satisfyig Ratioal Iequalities i Ordered Complex
Riesz-Fischer Sequences and Lower Frame Bounds
 Zeitschrift für Aalysis ud ihre Aweduge Joural for Aalysis ad its Applicatios Volume 1 (00), No., 305 314 Riesz-Fischer Sequeces ad Lower Frame Bouds P. Casazza, O. Christese, S. Li ad A. Lider Abstract.
Zeitschrift für Aalysis ud ihre Aweduge Joural for Aalysis ad its Applicatios Volume 1 (00), No., 305 314 Riesz-Fischer Sequeces ad Lower Frame Bouds P. Casazza, O. Christese, S. Li ad A. Lider Abstract.
Math Solutions to homework 6
 Math 175 - Solutios to homework 6 Cédric De Groote November 16, 2017 Problem 1 (8.11 i the book): Let K be a compact Hermitia operator o a Hilbert space H ad let the kerel of K be {0}. Show that there
Math 175 - Solutios to homework 6 Cédric De Groote November 16, 2017 Problem 1 (8.11 i the book): Let K be a compact Hermitia operator o a Hilbert space H ad let the kerel of K be {0}. Show that there
Definition 4.2. (a) A sequence {x n } in a Banach space X is a basis for X if. unique scalars a n (x) such that x = n. a n (x) x n. (4.
 4. BASES I BAACH SPACES 39 4. BASES I BAACH SPACES Sice a Baach space X is a vector space, it must possess a Hamel, or vector space, basis, i.e., a subset {x γ } γ Γ whose fiite liear spa is all of X ad
4. BASES I BAACH SPACES 39 4. BASES I BAACH SPACES Sice a Baach space X is a vector space, it must possess a Hamel, or vector space, basis, i.e., a subset {x γ } γ Γ whose fiite liear spa is all of X ad
Approximation by Superpositions of a Sigmoidal Function
 Zeitschrift für Aalysis ud ihre Aweduge Joural for Aalysis ad its Applicatios Volume 22 (2003, No. 2, 463 470 Approximatio by Superpositios of a Sigmoidal Fuctio G. Lewicki ad G. Mario Abstract. We geeralize
Zeitschrift für Aalysis ud ihre Aweduge Joural for Aalysis ad its Applicatios Volume 22 (2003, No. 2, 463 470 Approximatio by Superpositios of a Sigmoidal Fuctio G. Lewicki ad G. Mario Abstract. We geeralize
Math 341 Lecture #31 6.5: Power Series
 Math 341 Lecture #31 6.5: Power Series We ow tur our attetio to a particular kid of series of fuctios, amely, power series, f(x = a x = a 0 + a 1 x + a 2 x 2 + where a R for all N. I terms of a series
Math 341 Lecture #31 6.5: Power Series We ow tur our attetio to a particular kid of series of fuctios, amely, power series, f(x = a x = a 0 + a 1 x + a 2 x 2 + where a R for all N. I terms of a series
6a Time change b Quadratic variation c Planar Brownian motion d Conformal local martingales e Hints to exercises...
 Tel Aviv Uiversity, 28 Browia motio 59 6 Time chage 6a Time chage..................... 59 6b Quadratic variatio................. 61 6c Plaar Browia motio.............. 64 6d Coformal local martigales............
Tel Aviv Uiversity, 28 Browia motio 59 6 Time chage 6a Time chage..................... 59 6b Quadratic variatio................. 61 6c Plaar Browia motio.............. 64 6d Coformal local martigales............
ON THE CLASSIFICATION OF STABLE SOLUTION TO BIHARMONIC PROBLEMS IN LARGE DIMENSIONS
 ON THE CLASSIFICATION OF STABLE SOLUTION TO BIHARMONIC PROBLEMS IN LARGE DIMENSIONS JUNCHENG WEI, XINGWANG XU, AND WEN YANG Abstract. We give a ew boud o the expoet for oexistece of stable solutios to
ON THE CLASSIFICATION OF STABLE SOLUTION TO BIHARMONIC PROBLEMS IN LARGE DIMENSIONS JUNCHENG WEI, XINGWANG XU, AND WEN YANG Abstract. We give a ew boud o the expoet for oexistece of stable solutios to
Convergence of random variables. (telegram style notes) P.J.C. Spreij
 Covergece of radom variables (telegram style otes).j.c. Spreij this versio: September 6, 2005 Itroductio As we kow, radom variables are by defiitio measurable fuctios o some uderlyig measurable space
Covergece of radom variables (telegram style otes).j.c. Spreij this versio: September 6, 2005 Itroductio As we kow, radom variables are by defiitio measurable fuctios o some uderlyig measurable space
PRELIM PROBLEM SOLUTIONS
 PRELIM PROBLEM SOLUTIONS THE GRAD STUDENTS + KEN Cotets. Complex Aalysis Practice Problems 2. 2. Real Aalysis Practice Problems 2. 4 3. Algebra Practice Problems 2. 8. Complex Aalysis Practice Problems
PRELIM PROBLEM SOLUTIONS THE GRAD STUDENTS + KEN Cotets. Complex Aalysis Practice Problems 2. 2. Real Aalysis Practice Problems 2. 4 3. Algebra Practice Problems 2. 8. Complex Aalysis Practice Problems
Poincaré Problem for Nonlinear Elliptic Equations of Second Order in Unbounded Domains
 Advaces i Pure Mathematics 23 3 72-77 http://dxdoiorg/4236/apm233a24 Published Olie Jauary 23 (http://wwwscirporg/oural/apm) Poicaré Problem for Noliear Elliptic Equatios of Secod Order i Ubouded Domais
Advaces i Pure Mathematics 23 3 72-77 http://dxdoiorg/4236/apm233a24 Published Olie Jauary 23 (http://wwwscirporg/oural/apm) Poicaré Problem for Noliear Elliptic Equatios of Secod Order i Ubouded Domais
University of Colorado Denver Dept. Math. & Stat. Sciences Applied Analysis Preliminary Exam 13 January 2012, 10:00 am 2:00 pm. Good luck!
 Uiversity of Colorado Dever Dept. Math. & Stat. Scieces Applied Aalysis Prelimiary Exam 13 Jauary 01, 10:00 am :00 pm Name: The proctor will let you read the followig coditios before the exam begis, ad
Uiversity of Colorado Dever Dept. Math. & Stat. Scieces Applied Aalysis Prelimiary Exam 13 Jauary 01, 10:00 am :00 pm Name: The proctor will let you read the followig coditios before the exam begis, ad
6.3 Testing Series With Positive Terms
 6.3. TESTING SERIES WITH POSITIVE TERMS 307 6.3 Testig Series With Positive Terms 6.3. Review of what is kow up to ow I theory, testig a series a i for covergece amouts to fidig the i= sequece of partial
6.3. TESTING SERIES WITH POSITIVE TERMS 307 6.3 Testig Series With Positive Terms 6.3. Review of what is kow up to ow I theory, testig a series a i for covergece amouts to fidig the i= sequece of partial
Mathematical Methods for Physics and Engineering
 Mathematical Methods for Physics ad Egieerig Lecture otes Sergei V. Shabaov Departmet of Mathematics, Uiversity of Florida, Gaiesville, FL 326 USA CHAPTER The theory of covergece. Numerical sequeces..
Mathematical Methods for Physics ad Egieerig Lecture otes Sergei V. Shabaov Departmet of Mathematics, Uiversity of Florida, Gaiesville, FL 326 USA CHAPTER The theory of covergece. Numerical sequeces..
Topics. Homework Problems. MATH 301 Introduction to Analysis Chapter Four Sequences. 1. Definition of convergence of sequences.
 MATH 301 Itroductio to Aalysis Chapter Four Sequeces Topics 1. Defiitio of covergece of sequeces. 2. Fidig ad provig the limit of sequeces. 3. Bouded covergece theorem: Theorem 4.1.8. 4. Theorems 4.1.13
MATH 301 Itroductio to Aalysis Chapter Four Sequeces Topics 1. Defiitio of covergece of sequeces. 2. Fidig ad provig the limit of sequeces. 3. Bouded covergece theorem: Theorem 4.1.8. 4. Theorems 4.1.13
MAS111 Convergence and Continuity
 MAS Covergece ad Cotiuity Key Objectives At the ed of the course, studets should kow the followig topics ad be able to apply the basic priciples ad theorems therei to solvig various problems cocerig covergece
MAS Covergece ad Cotiuity Key Objectives At the ed of the course, studets should kow the followig topics ad be able to apply the basic priciples ad theorems therei to solvig various problems cocerig covergece
Math 220B Final Exam Solutions March 18, 2002
 Math 0B Fial Exam Solutios March 18, 00 1. (1 poits) (a) (6 poits) Fid the Gree s fuctio for the tilted half-plae {(x 1, x ) R : x 1 + x > 0}. For x (x 1, x ), y (y 1, y ), express your Gree s fuctio G(x,
Math 0B Fial Exam Solutios March 18, 00 1. (1 poits) (a) (6 poits) Fid the Gree s fuctio for the tilted half-plae {(x 1, x ) R : x 1 + x > 0}. For x (x 1, x ), y (y 1, y ), express your Gree s fuctio G(x,
PAPER : IIT-JAM 2010
 MATHEMATICS-MA (CODE A) Q.-Q.5: Oly oe optio is correct for each questio. Each questio carries (+6) marks for correct aswer ad ( ) marks for icorrect aswer.. Which of the followig coditios does NOT esure
MATHEMATICS-MA (CODE A) Q.-Q.5: Oly oe optio is correct for each questio. Each questio carries (+6) marks for correct aswer ad ( ) marks for icorrect aswer.. Which of the followig coditios does NOT esure
Sequences and Limits
 Chapter Sequeces ad Limits Let { a } be a sequece of real or complex umbers A ecessary ad sufficiet coditio for the sequece to coverge is that for ay ɛ > 0 there exists a iteger N > 0 such that a p a q
Chapter Sequeces ad Limits Let { a } be a sequece of real or complex umbers A ecessary ad sufficiet coditio for the sequece to coverge is that for ay ɛ > 0 there exists a iteger N > 0 such that a p a q
McGill University Math 354: Honors Analysis 3 Fall 2012 Solutions to selected problems
 McGill Uiversity Math 354: Hoors Aalysis 3 Fall 212 Assigmet 3 Solutios to selected problems Problem 1. Lipschitz fuctios. Let Lip K be the set of all fuctios cotiuous fuctios o [, 1] satisfyig a Lipschitz
McGill Uiversity Math 354: Hoors Aalysis 3 Fall 212 Assigmet 3 Solutios to selected problems Problem 1. Lipschitz fuctios. Let Lip K be the set of all fuctios cotiuous fuctios o [, 1] satisfyig a Lipschitz
Periodic solutions for a class of second-order Hamiltonian systems of prescribed energy
 Electroic Joural of Qualitative Theory of Differetial Equatios 215, No. 77, 1 1; doi: 1.14232/ejqtde.215.1.77 http://www.math.u-szeged.hu/ejqtde/ Periodic solutios for a class of secod-order Hamiltoia
Electroic Joural of Qualitative Theory of Differetial Equatios 215, No. 77, 1 1; doi: 1.14232/ejqtde.215.1.77 http://www.math.u-szeged.hu/ejqtde/ Periodic solutios for a class of secod-order Hamiltoia
Seunghee Ye Ma 8: Week 5 Oct 28
 Week 5 Summary I Sectio, we go over the Mea Value Theorem ad its applicatios. I Sectio 2, we will recap what we have covered so far this term. Topics Page Mea Value Theorem. Applicatios of the Mea Value
Week 5 Summary I Sectio, we go over the Mea Value Theorem ad its applicatios. I Sectio 2, we will recap what we have covered so far this term. Topics Page Mea Value Theorem. Applicatios of the Mea Value
(A sequence also can be thought of as the list of function values attained for a function f :ℵ X, where f (n) = x n for n 1.) x 1 x N +k x N +4 x 3
 MATH 337 Sequeces Dr. Neal, WKU Let X be a metric space with distace fuctio d. We shall defie the geeral cocept of sequece ad limit i a metric space, the apply the results i particular to some special
MATH 337 Sequeces Dr. Neal, WKU Let X be a metric space with distace fuctio d. We shall defie the geeral cocept of sequece ad limit i a metric space, the apply the results i particular to some special
M17 MAT25-21 HOMEWORK 5 SOLUTIONS
 M17 MAT5-1 HOMEWORK 5 SOLUTIONS 1. To Had I Cauchy Codesatio Test. Exercise 1: Applicatio of the Cauchy Codesatio Test Use the Cauchy Codesatio Test to prove that 1 diverges. Solutio 1. Give the series
M17 MAT5-1 HOMEWORK 5 SOLUTIONS 1. To Had I Cauchy Codesatio Test. Exercise 1: Applicatio of the Cauchy Codesatio Test Use the Cauchy Codesatio Test to prove that 1 diverges. Solutio 1. Give the series
Advanced Stochastic Processes.
 Advaced Stochastic Processes. David Gamarik LECTURE 2 Radom variables ad measurable fuctios. Strog Law of Large Numbers (SLLN). Scary stuff cotiued... Outlie of Lecture Radom variables ad measurable fuctios.
Advaced Stochastic Processes. David Gamarik LECTURE 2 Radom variables ad measurable fuctios. Strog Law of Large Numbers (SLLN). Scary stuff cotiued... Outlie of Lecture Radom variables ad measurable fuctios.
Measure and Measurable Functions
 3 Measure ad Measurable Fuctios 3.1 Measure o a Arbitrary σ-algebra Recall from Chapter 2 that the set M of all Lebesgue measurable sets has the followig properties: R M, E M implies E c M, E M for N implies
3 Measure ad Measurable Fuctios 3.1 Measure o a Arbitrary σ-algebra Recall from Chapter 2 that the set M of all Lebesgue measurable sets has the followig properties: R M, E M implies E c M, E M for N implies
Local Approximation Properties for certain King type Operators
 Filomat 27:1 (2013, 173 181 DOI 102298/FIL1301173O Published by Faculty of Scieces ad athematics, Uiversity of Niš, Serbia Available at: http://wwwpmfiacrs/filomat Local Approimatio Properties for certai
Filomat 27:1 (2013, 173 181 DOI 102298/FIL1301173O Published by Faculty of Scieces ad athematics, Uiversity of Niš, Serbia Available at: http://wwwpmfiacrs/filomat Local Approimatio Properties for certai
Linear Elliptic PDE s Elliptic partial differential equations frequently arise out of conservation statements of the form
 Liear Elliptic PDE s Elliptic partial differetial equatios frequetly arise out of coservatio statemets of the form B F d B Sdx B cotaied i bouded ope set U R. Here F, S deote respectively, the flux desity
Liear Elliptic PDE s Elliptic partial differetial equatios frequetly arise out of coservatio statemets of the form B F d B Sdx B cotaied i bouded ope set U R. Here F, S deote respectively, the flux desity
Analytic Continuation
 Aalytic Cotiuatio The stadard example of this is give by Example Let h (z) = 1 + z + z 2 + z 3 +... kow to coverge oly for z < 1. I fact h (z) = 1/ (1 z) for such z. Yet H (z) = 1/ (1 z) is defied for
Aalytic Cotiuatio The stadard example of this is give by Example Let h (z) = 1 + z + z 2 + z 3 +... kow to coverge oly for z < 1. I fact h (z) = 1/ (1 z) for such z. Yet H (z) = 1/ (1 z) is defied for
The value of Banach limits on a certain sequence of all rational numbers in the interval (0,1) Bao Qi Feng
 The value of Baach limits o a certai sequece of all ratioal umbers i the iterval 0, Bao Qi Feg Departmet of Mathematical Scieces, Ket State Uiversity, Tuscarawas, 330 Uiversity Dr. NE, New Philadelphia,
The value of Baach limits o a certai sequece of all ratioal umbers i the iterval 0, Bao Qi Feg Departmet of Mathematical Scieces, Ket State Uiversity, Tuscarawas, 330 Uiversity Dr. NE, New Philadelphia,
Weighted Approximation by Videnskii and Lupas Operators
 Weighted Approximatio by Videsii ad Lupas Operators Aif Barbaros Dime İstabul Uiversity Departmet of Egieerig Sciece April 5, 013 Aif Barbaros Dime İstabul Uiversity Departmet Weightedof Approximatio Egieerig
Weighted Approximatio by Videsii ad Lupas Operators Aif Barbaros Dime İstabul Uiversity Departmet of Egieerig Sciece April 5, 013 Aif Barbaros Dime İstabul Uiversity Departmet Weightedof Approximatio Egieerig
ANSWERS TO MIDTERM EXAM # 2
 MATH 03, FALL 003 ANSWERS TO MIDTERM EXAM # PENN STATE UNIVERSITY Problem 1 (18 pts). State ad prove the Itermediate Value Theorem. Solutio See class otes or Theorem 5.6.1 from our textbook. Problem (18
MATH 03, FALL 003 ANSWERS TO MIDTERM EXAM # PENN STATE UNIVERSITY Problem 1 (18 pts). State ad prove the Itermediate Value Theorem. Solutio See class otes or Theorem 5.6.1 from our textbook. Problem (18
An alternative proof of a theorem of Aldous. concerning convergence in distribution for martingales.
 A alterative proof of a theorem of Aldous cocerig covergece i distributio for martigales. Maurizio Pratelli Dipartimeto di Matematica, Uiversità di Pisa. Via Buoarroti 2. I-56127 Pisa, Italy e-mail: pratelli@dm.uipi.it
A alterative proof of a theorem of Aldous cocerig covergece i distributio for martigales. Maurizio Pratelli Dipartimeto di Matematica, Uiversità di Pisa. Via Buoarroti 2. I-56127 Pisa, Italy e-mail: pratelli@dm.uipi.it
INVERSE THEOREMS OF APPROXIMATION THEORY IN L p,α (R + )
 Electroic Joural of Mathematical Aalysis ad Applicatios, Vol. 3(2) July 2015, pp. 92-99. ISSN: 2090-729(olie) http://fcag-egypt.com/jourals/ejmaa/ INVERSE THEOREMS OF APPROXIMATION THEORY IN L p,α (R +
Electroic Joural of Mathematical Aalysis ad Applicatios, Vol. 3(2) July 2015, pp. 92-99. ISSN: 2090-729(olie) http://fcag-egypt.com/jourals/ejmaa/ INVERSE THEOREMS OF APPROXIMATION THEORY IN L p,α (R +
Solutions to home assignments (sketches)
 Matematiska Istitutioe Peter Kumli 26th May 2004 TMA401 Fuctioal Aalysis MAN670 Applied Fuctioal Aalysis 4th quarter 2003/2004 All documet cocerig the course ca be foud o the course home page: http://www.math.chalmers.se/math/grudutb/cth/tma401/
Matematiska Istitutioe Peter Kumli 26th May 2004 TMA401 Fuctioal Aalysis MAN670 Applied Fuctioal Aalysis 4th quarter 2003/2004 All documet cocerig the course ca be foud o the course home page: http://www.math.chalmers.se/math/grudutb/cth/tma401/
Singular Continuous Measures by Michael Pejic 5/14/10
 Sigular Cotiuous Measures by Michael Peic 5/4/0 Prelimiaries Give a set X, a σ-algebra o X is a collectio of subsets of X that cotais X ad ad is closed uder complemetatio ad coutable uios hece, coutable
Sigular Cotiuous Measures by Michael Peic 5/4/0 Prelimiaries Give a set X, a σ-algebra o X is a collectio of subsets of X that cotais X ad ad is closed uder complemetatio ad coutable uios hece, coutable
62. Power series Definition 16. (Power series) Given a sequence {c n }, the series. c n x n = c 0 + c 1 x + c 2 x 2 + c 3 x 3 +
 62. Power series Defiitio 16. (Power series) Give a sequece {c }, the series c x = c 0 + c 1 x + c 2 x 2 + c 3 x 3 + is called a power series i the variable x. The umbers c are called the coefficiets of
62. Power series Defiitio 16. (Power series) Give a sequece {c }, the series c x = c 0 + c 1 x + c 2 x 2 + c 3 x 3 + is called a power series i the variable x. The umbers c are called the coefficiets of
Inverse Nodal Problems for Differential Equation on the Half-line
 Australia Joural of Basic ad Applied Scieces, 3(4): 4498-4502, 2009 ISSN 1991-8178 Iverse Nodal Problems for Differetial Equatio o the Half-lie 1 2 3 A. Dabbaghia, A. Nematy ad Sh. Akbarpoor 1 Islamic
Australia Joural of Basic ad Applied Scieces, 3(4): 4498-4502, 2009 ISSN 1991-8178 Iverse Nodal Problems for Differetial Equatio o the Half-lie 1 2 3 A. Dabbaghia, A. Nematy ad Sh. Akbarpoor 1 Islamic
Dirichlet s Theorem on Arithmetic Progressions
 Dirichlet s Theorem o Arithmetic Progressios Athoy Várilly Harvard Uiversity, Cambridge, MA 0238 Itroductio Dirichlet s theorem o arithmetic progressios is a gem of umber theory. A great part of its beauty
Dirichlet s Theorem o Arithmetic Progressios Athoy Várilly Harvard Uiversity, Cambridge, MA 0238 Itroductio Dirichlet s theorem o arithmetic progressios is a gem of umber theory. A great part of its beauty
MAT1026 Calculus II Basic Convergence Tests for Series
 MAT026 Calculus II Basic Covergece Tests for Series Egi MERMUT 202.03.08 Dokuz Eylül Uiversity Faculty of Sciece Departmet of Mathematics İzmir/TURKEY Cotets Mootoe Covergece Theorem 2 2 Series of Real
MAT026 Calculus II Basic Covergece Tests for Series Egi MERMUT 202.03.08 Dokuz Eylül Uiversity Faculty of Sciece Departmet of Mathematics İzmir/TURKEY Cotets Mootoe Covergece Theorem 2 2 Series of Real
Independence number of graphs with a prescribed number of cliques
 Idepedece umber of graphs with a prescribed umber of cliques Tom Bohma Dhruv Mubayi Abstract We cosider the followig problem posed by Erdős i 1962. Suppose that G is a -vertex graph where the umber of
Idepedece umber of graphs with a prescribed umber of cliques Tom Bohma Dhruv Mubayi Abstract We cosider the followig problem posed by Erdős i 1962. Suppose that G is a -vertex graph where the umber of
Assignment 5: Solutions
 McGill Uiversity Departmet of Mathematics ad Statistics MATH 54 Aalysis, Fall 05 Assigmet 5: Solutios. Let y be a ubouded sequece of positive umbers satisfyig y + > y for all N. Let x be aother sequece
McGill Uiversity Departmet of Mathematics ad Statistics MATH 54 Aalysis, Fall 05 Assigmet 5: Solutios. Let y be a ubouded sequece of positive umbers satisfyig y + > y for all N. Let x be aother sequece
Fall 2013 MTH431/531 Real analysis Section Notes
 Fall 013 MTH431/531 Real aalysis Sectio 8.1-8. Notes Yi Su 013.11.1 1. Defiitio of uiform covergece. We look at a sequece of fuctios f (x) ad study the coverget property. Notice we have two parameters
Fall 013 MTH431/531 Real aalysis Sectio 8.1-8. Notes Yi Su 013.11.1 1. Defiitio of uiform covergece. We look at a sequece of fuctios f (x) ad study the coverget property. Notice we have two parameters
Entire Functions That Share One Value with One or Two of Their Derivatives
 JOURNAL OF MATHEMATICAL ANALYSIS AND APPLICATIONS 223, 88 95 1998 ARTICLE NO. AY985959 Etire Fuctios That Share Oe Value with Oe or Two of Their Derivatives Gary G. Guderse* Departmet of Mathematics, Ui
JOURNAL OF MATHEMATICAL ANALYSIS AND APPLICATIONS 223, 88 95 1998 ARTICLE NO. AY985959 Etire Fuctios That Share Oe Value with Oe or Two of Their Derivatives Gary G. Guderse* Departmet of Mathematics, Ui
Lecture Notes for Analysis Class
 Lecture Notes for Aalysis Class Topological Spaces A topology for a set X is a collectio T of subsets of X such that: (a) X ad the empty set are i T (b) Uios of elemets of T are i T (c) Fiite itersectios
Lecture Notes for Aalysis Class Topological Spaces A topology for a set X is a collectio T of subsets of X such that: (a) X ad the empty set are i T (b) Uios of elemets of T are i T (c) Fiite itersectios
Math 140A Elementary Analysis Homework Questions 3-1
 Math 0A Elemetary Aalysis Homework Questios -.9 Limits Theorems for Sequeces Suppose that lim x =, lim y = 7 ad that all y are o-zero. Detarime the followig limits: (a) lim(x + y ) (b) lim y x y Let s
Math 0A Elemetary Aalysis Homework Questios -.9 Limits Theorems for Sequeces Suppose that lim x =, lim y = 7 ad that all y are o-zero. Detarime the followig limits: (a) lim(x + y ) (b) lim y x y Let s
SOME GENERALIZATIONS OF OLIVIER S THEOREM
 SOME GENERALIZATIONS OF OLIVIER S THEOREM Alai Faisat, Sait-Étiee, Georges Grekos, Sait-Étiee, Ladislav Mišík Ostrava (Received Jauary 27, 2006) Abstract. Let a be a coverget series of positive real umbers.
SOME GENERALIZATIONS OF OLIVIER S THEOREM Alai Faisat, Sait-Étiee, Georges Grekos, Sait-Étiee, Ladislav Mišík Ostrava (Received Jauary 27, 2006) Abstract. Let a be a coverget series of positive real umbers.
Chapter 3. Strong convergence. 3.1 Definition of almost sure convergence
 Chapter 3 Strog covergece As poited out i the Chapter 2, there are multiple ways to defie the otio of covergece of a sequece of radom variables. That chapter defied covergece i probability, covergece i
Chapter 3 Strog covergece As poited out i the Chapter 2, there are multiple ways to defie the otio of covergece of a sequece of radom variables. That chapter defied covergece i probability, covergece i
Sequences. A Sequence is a list of numbers written in order.
 Sequeces A Sequece is a list of umbers writte i order. {a, a 2, a 3,... } The sequece may be ifiite. The th term of the sequece is the th umber o the list. O the list above a = st term, a 2 = 2 d term,
Sequeces A Sequece is a list of umbers writte i order. {a, a 2, a 3,... } The sequece may be ifiite. The th term of the sequece is the th umber o the list. O the list above a = st term, a 2 = 2 d term,
MATH301 Real Analysis (2008 Fall) Tutorial Note #7. k=1 f k (x) converges pointwise to S(x) on E if and
 MATH01 Real Aalysis (2008 Fall) Tutorial Note #7 Sequece ad Series of fuctio 1: Poitwise Covergece ad Uiform Covergece Part I: Poitwise Covergece Defiitio of poitwise covergece: A sequece of fuctios f
MATH01 Real Aalysis (2008 Fall) Tutorial Note #7 Sequece ad Series of fuctio 1: Poitwise Covergece ad Uiform Covergece Part I: Poitwise Covergece Defiitio of poitwise covergece: A sequece of fuctios f
Oscillation and Property B for Third Order Difference Equations with Advanced Arguments
 Iter atioal Joural of Pure ad Applied Mathematics Volume 3 No. 0 207, 352 360 ISSN: 3-8080 (prited versio); ISSN: 34-3395 (o-lie versio) url: http://www.ijpam.eu ijpam.eu Oscillatio ad Property B for Third
Iter atioal Joural of Pure ad Applied Mathematics Volume 3 No. 0 207, 352 360 ISSN: 3-8080 (prited versio); ISSN: 34-3395 (o-lie versio) url: http://www.ijpam.eu ijpam.eu Oscillatio ad Property B for Third
1+x 1 + α+x. x = 2(α x2 ) 1+x
 Math 2030 Homework 6 Solutios # [Problem 5] For coveiece we let α lim sup a ad β lim sup b. Without loss of geerality let us assume that α β. If α the by assumptio β < so i this case α + β. By Theorem
Math 2030 Homework 6 Solutios # [Problem 5] For coveiece we let α lim sup a ad β lim sup b. Without loss of geerality let us assume that α β. If α the by assumptio β < so i this case α + β. By Theorem
Math 128A: Homework 1 Solutions
 Math 8A: Homework Solutios Due: Jue. Determie the limits of the followig sequeces as. a) a = +. lim a + = lim =. b) a = + ). c) a = si4 +6) +. lim a = lim = lim + ) [ + ) ] = [ e ] = e 6. Observe that
Math 8A: Homework Solutios Due: Jue. Determie the limits of the followig sequeces as. a) a = +. lim a + = lim =. b) a = + ). c) a = si4 +6) +. lim a = lim = lim + ) [ + ) ] = [ e ] = e 6. Observe that
2.4.2 A Theorem About Absolutely Convergent Series
 0 Versio of August 27, 200 CHAPTER 2. INFINITE SERIES Add these two series: + 3 2 + 5 + 7 4 + 9 + 6 +... = 3 l 2. (2.20) 2 Sice the reciprocal of each iteger occurs exactly oce i the last series, we would
0 Versio of August 27, 200 CHAPTER 2. INFINITE SERIES Add these two series: + 3 2 + 5 + 7 4 + 9 + 6 +... = 3 l 2. (2.20) 2 Sice the reciprocal of each iteger occurs exactly oce i the last series, we would
A NOTE ON INVARIANT SETS OF ITERATED FUNCTION SYSTEMS
 Acta Math. Hugar., 2007 DOI: 10.1007/s10474-007-7013-6 A NOTE ON INVARIANT SETS OF ITERATED FUNCTION SYSTEMS L. L. STACHÓ ad L. I. SZABÓ Bolyai Istitute, Uiversity of Szeged, Aradi vértaúk tere 1, H-6720
Acta Math. Hugar., 2007 DOI: 10.1007/s10474-007-7013-6 A NOTE ON INVARIANT SETS OF ITERATED FUNCTION SYSTEMS L. L. STACHÓ ad L. I. SZABÓ Bolyai Istitute, Uiversity of Szeged, Aradi vértaúk tere 1, H-6720
CANTOR SETS WHICH ARE MINIMAL FOR QUASISYMMETRIC MAPS
 CANTOR SETS WHICH ARE MINIMAL FOR QUASISYMMETRIC MAPS HRANT A. HAKOBYAN Abstract. We show that middle iterval Cator sets of Hausdorff dimesio are miimal for quasisymmetric maps of a lie. Combiig this with
CANTOR SETS WHICH ARE MINIMAL FOR QUASISYMMETRIC MAPS HRANT A. HAKOBYAN Abstract. We show that middle iterval Cator sets of Hausdorff dimesio are miimal for quasisymmetric maps of a lie. Combiig this with
Exponential Functions and Taylor Series
 MATH 4530: Aalysis Oe Expoetial Fuctios ad Taylor Series James K. Peterso Departmet of Biological Scieces ad Departmet of Mathematical Scieces Clemso Uiversity March 29, 2017 MATH 4530: Aalysis Oe Outlie
MATH 4530: Aalysis Oe Expoetial Fuctios ad Taylor Series James K. Peterso Departmet of Biological Scieces ad Departmet of Mathematical Scieces Clemso Uiversity March 29, 2017 MATH 4530: Aalysis Oe Outlie
A FIXED POINT THEOREM IN THE MENGER PROBABILISTIC METRIC SPACE. Abdolrahman Razani (Received September 2004)
 NEW ZEALAND JOURNAL OF MATHEMATICS Volume 35 (2006), 109 114 A FIXED POINT THEOREM IN THE MENGER PROBABILISTIC METRIC SPACE Abdolrahma Razai (Received September 2004) Abstract. I this article, a fixed
NEW ZEALAND JOURNAL OF MATHEMATICS Volume 35 (2006), 109 114 A FIXED POINT THEOREM IN THE MENGER PROBABILISTIC METRIC SPACE Abdolrahma Razai (Received September 2004) Abstract. I this article, a fixed
Rational Bounds for the Logarithm Function with Applications
 Ratioal Bouds for the Logarithm Fuctio with Applicatios Robert Bosch Abstract We fid ratioal bouds for the logarithm fuctio ad we show applicatios to problem-solvig. Itroductio Let a = + solvig the problem
Ratioal Bouds for the Logarithm Fuctio with Applicatios Robert Bosch Abstract We fid ratioal bouds for the logarithm fuctio ad we show applicatios to problem-solvig. Itroductio Let a = + solvig the problem
7.1 Convergence of sequences of random variables
 Chapter 7 Limit Theorems Throughout this sectio we will assume a probability space (, F, P), i which is defied a ifiite sequece of radom variables (X ) ad a radom variable X. The fact that for every ifiite
Chapter 7 Limit Theorems Throughout this sectio we will assume a probability space (, F, P), i which is defied a ifiite sequece of radom variables (X ) ad a radom variable X. The fact that for every ifiite
ON BLEIMANN, BUTZER AND HAHN TYPE GENERALIZATION OF BALÁZS OPERATORS
 STUDIA UNIV. BABEŞ BOLYAI, MATHEMATICA, Volume XLVII, Number 4, December 2002 ON BLEIMANN, BUTZER AND HAHN TYPE GENERALIZATION OF BALÁZS OPERATORS OGÜN DOĞRU Dedicated to Professor D.D. Stacu o his 75
STUDIA UNIV. BABEŞ BOLYAI, MATHEMATICA, Volume XLVII, Number 4, December 2002 ON BLEIMANN, BUTZER AND HAHN TYPE GENERALIZATION OF BALÁZS OPERATORS OGÜN DOĞRU Dedicated to Professor D.D. Stacu o his 75
Mi-Hwa Ko and Tae-Sung Kim
 J. Korea Math. Soc. 42 2005), No. 5, pp. 949 957 ALMOST SURE CONVERGENCE FOR WEIGHTED SUMS OF NEGATIVELY ORTHANT DEPENDENT RANDOM VARIABLES Mi-Hwa Ko ad Tae-Sug Kim Abstract. For weighted sum of a sequece
J. Korea Math. Soc. 42 2005), No. 5, pp. 949 957 ALMOST SURE CONVERGENCE FOR WEIGHTED SUMS OF NEGATIVELY ORTHANT DEPENDENT RANDOM VARIABLES Mi-Hwa Ko ad Tae-Sug Kim Abstract. For weighted sum of a sequece
Lecture 3 The Lebesgue Integral
 Lecture 3: The Lebesgue Itegral 1 of 14 Course: Theory of Probability I Term: Fall 2013 Istructor: Gorda Zitkovic Lecture 3 The Lebesgue Itegral The costructio of the itegral Uless expressly specified
Lecture 3: The Lebesgue Itegral 1 of 14 Course: Theory of Probability I Term: Fall 2013 Istructor: Gorda Zitkovic Lecture 3 The Lebesgue Itegral The costructio of the itegral Uless expressly specified
MASSACHUSETTS INSTITUTE OF TECHNOLOGY 6.436J/15.085J Fall 2008 Lecture 19 11/17/2008 LAWS OF LARGE NUMBERS II THE STRONG LAW OF LARGE NUMBERS
 MASSACHUSTTS INSTITUT OF TCHNOLOGY 6.436J/5.085J Fall 2008 Lecture 9 /7/2008 LAWS OF LARG NUMBRS II Cotets. The strog law of large umbers 2. The Cheroff boud TH STRONG LAW OF LARG NUMBRS While the weak
MASSACHUSTTS INSTITUT OF TCHNOLOGY 6.436J/5.085J Fall 2008 Lecture 9 /7/2008 LAWS OF LARG NUMBRS II Cotets. The strog law of large umbers 2. The Cheroff boud TH STRONG LAW OF LARG NUMBRS While the weak
NEW RESULTS ON THE ASYMPTOTIC BEHAVIOUR OF DIRICHLET PROBLEMS IN PERFORATED DOMAINS
 NEW RESULTS ON THE ASYMPTOTIC BEHAVIOUR OF DIRICHLET PROBLEMS IN PERFORATED DOMAINS GIANNI DAL MASO ad ADRIANA GARRONI S.I.S.S.A., via Beirut 4, 34014 Trieste, Italy Let A be a liear elliptic operator
NEW RESULTS ON THE ASYMPTOTIC BEHAVIOUR OF DIRICHLET PROBLEMS IN PERFORATED DOMAINS GIANNI DAL MASO ad ADRIANA GARRONI S.I.S.S.A., via Beirut 4, 34014 Trieste, Italy Let A be a liear elliptic operator
Solutions for Math 411 Assignment #8 1
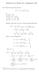 Solutios for Math Assigmet #8 A8. Fid the Lauret series of f() 3 2 + i (a) { < }; (b) { < < }; (c) { < 2 < 3}; (d) {0 < + < 2}. Solutio. We write f() as a sum of partial fractios: f() 3 2 + ( ) 2 ( + )
Solutios for Math Assigmet #8 A8. Fid the Lauret series of f() 3 2 + i (a) { < }; (b) { < < }; (c) { < 2 < 3}; (d) {0 < + < 2}. Solutio. We write f() as a sum of partial fractios: f() 3 2 + ( ) 2 ( + )
A 2nTH ORDER LINEAR DIFFERENCE EQUATION
 A 2TH ORDER LINEAR DIFFERENCE EQUATION Doug Aderso Departmet of Mathematics ad Computer Sciece, Cocordia College Moorhead, MN 56562, USA ABSTRACT: We give a formulatio of geeralized zeros ad (, )-discojugacy
A 2TH ORDER LINEAR DIFFERENCE EQUATION Doug Aderso Departmet of Mathematics ad Computer Sciece, Cocordia College Moorhead, MN 56562, USA ABSTRACT: We give a formulatio of geeralized zeros ad (, )-discojugacy
Solutions to Tutorial 3 (Week 4)
 The Uiversity of Sydey School of Mathematics ad Statistics Solutios to Tutorial Week 4 MATH2962: Real ad Complex Aalysis Advaced Semester 1, 2017 Web Page: http://www.maths.usyd.edu.au/u/ug/im/math2962/
The Uiversity of Sydey School of Mathematics ad Statistics Solutios to Tutorial Week 4 MATH2962: Real ad Complex Aalysis Advaced Semester 1, 2017 Web Page: http://www.maths.usyd.edu.au/u/ug/im/math2962/
5. Matrix exponentials and Von Neumann s theorem The matrix exponential. For an n n matrix X we define
 5. Matrix expoetials ad Vo Neuma s theorem 5.1. The matrix expoetial. For a matrix X we defie e X = exp X = I + X + X2 2! +... = 0 X!. We assume that the etries are complex so that exp is well defied o
5. Matrix expoetials ad Vo Neuma s theorem 5.1. The matrix expoetial. For a matrix X we defie e X = exp X = I + X + X2 2! +... = 0 X!. We assume that the etries are complex so that exp is well defied o
Council for Innovative Research
 ABSTRACT ON ABEL CONVERGENT SERIES OF FUNCTIONS ERDAL GÜL AND MEHMET ALBAYRAK Yildiz Techical Uiversity, Departmet of Mathematics, 34210 Eseler, Istabul egul34@gmail.com mehmetalbayrak12@gmail.com I this
ABSTRACT ON ABEL CONVERGENT SERIES OF FUNCTIONS ERDAL GÜL AND MEHMET ALBAYRAK Yildiz Techical Uiversity, Departmet of Mathematics, 34210 Eseler, Istabul egul34@gmail.com mehmetalbayrak12@gmail.com I this
A) is empty. B) is a finite set. C) can be a countably infinite set. D) can be an uncountable set.
 M.A./M.Sc. (Mathematics) Etrace Examiatio 016-17 Max Time: hours Max Marks: 150 Istructios: There are 50 questios. Every questio has four choices of which exactly oe is correct. For correct aswer, 3 marks
M.A./M.Sc. (Mathematics) Etrace Examiatio 016-17 Max Time: hours Max Marks: 150 Istructios: There are 50 questios. Every questio has four choices of which exactly oe is correct. For correct aswer, 3 marks
We are mainly going to be concerned with power series in x, such as. (x)} converges - that is, lims N n
 Review of Power Series, Power Series Solutios A power series i x - a is a ifiite series of the form c (x a) =c +c (x a)+(x a) +... We also call this a power series cetered at a. Ex. (x+) is cetered at
Review of Power Series, Power Series Solutios A power series i x - a is a ifiite series of the form c (x a) =c +c (x a)+(x a) +... We also call this a power series cetered at a. Ex. (x+) is cetered at
Sieve Estimators: Consistency and Rates of Convergence
 EECS 598: Statistical Learig Theory, Witer 2014 Topic 6 Sieve Estimators: Cosistecy ad Rates of Covergece Lecturer: Clayto Scott Scribe: Julia Katz-Samuels, Brado Oselio, Pi-Yu Che Disclaimer: These otes
EECS 598: Statistical Learig Theory, Witer 2014 Topic 6 Sieve Estimators: Cosistecy ad Rates of Covergece Lecturer: Clayto Scott Scribe: Julia Katz-Samuels, Brado Oselio, Pi-Yu Che Disclaimer: These otes
Random Walks on Discrete and Continuous Circles. by Jeffrey S. Rosenthal School of Mathematics, University of Minnesota, Minneapolis, MN, U.S.A.
 Radom Walks o Discrete ad Cotiuous Circles by Jeffrey S. Rosethal School of Mathematics, Uiversity of Miesota, Mieapolis, MN, U.S.A. 55455 (Appeared i Joural of Applied Probability 30 (1993), 780 789.)
Radom Walks o Discrete ad Cotiuous Circles by Jeffrey S. Rosethal School of Mathematics, Uiversity of Miesota, Mieapolis, MN, U.S.A. 55455 (Appeared i Joural of Applied Probability 30 (1993), 780 789.)
Multi parameter proximal point algorithms
 Multi parameter proximal poit algorithms Ogaeditse A. Boikayo a,b,, Gheorghe Moroşau a a Departmet of Mathematics ad its Applicatios Cetral Europea Uiversity Nador u. 9, H-1051 Budapest, Hugary b Departmet
Multi parameter proximal poit algorithms Ogaeditse A. Boikayo a,b,, Gheorghe Moroşau a a Departmet of Mathematics ad its Applicatios Cetral Europea Uiversity Nador u. 9, H-1051 Budapest, Hugary b Departmet
A NOTE ON SPECTRAL CONTINUITY. In Ho Jeon and In Hyoun Kim
 Korea J. Math. 23 (2015), No. 4, pp. 601 605 http://dx.doi.org/10.11568/kjm.2015.23.4.601 A NOTE ON SPECTRAL CONTINUITY I Ho Jeo ad I Hyou Kim Abstract. I the preset ote, provided T L (H ) is biquasitriagular
Korea J. Math. 23 (2015), No. 4, pp. 601 605 http://dx.doi.org/10.11568/kjm.2015.23.4.601 A NOTE ON SPECTRAL CONTINUITY I Ho Jeo ad I Hyou Kim Abstract. I the preset ote, provided T L (H ) is biquasitriagular
A REMARK ON A PROBLEM OF KLEE
 C O L L O Q U I U M M A T H E M A T I C U M VOL. 71 1996 NO. 1 A REMARK ON A PROBLEM OF KLEE BY N. J. K A L T O N (COLUMBIA, MISSOURI) AND N. T. P E C K (URBANA, ILLINOIS) This paper treats a property
C O L L O Q U I U M M A T H E M A T I C U M VOL. 71 1996 NO. 1 A REMARK ON A PROBLEM OF KLEE BY N. J. K A L T O N (COLUMBIA, MISSOURI) AND N. T. P E C K (URBANA, ILLINOIS) This paper treats a property
1.3 Convergence Theorems of Fourier Series. k k k k. N N k 1. With this in mind, we state (without proof) the convergence of Fourier series.
 .3 Covergece Theorems of Fourier Series I this sectio, we preset the covergece of Fourier series. A ifiite sum is, by defiitio, a limit of partial sums, that is, a cos( kx) b si( kx) lim a cos( kx) b si(
.3 Covergece Theorems of Fourier Series I this sectio, we preset the covergece of Fourier series. A ifiite sum is, by defiitio, a limit of partial sums, that is, a cos( kx) b si( kx) lim a cos( kx) b si(
Beyond simple iteration of a single function, or even a finite sequence of functions, results
 A Primer o the Elemetary Theory of Ifiite Compositios of Complex Fuctios Joh Gill Sprig 07 Abstract: Elemetary meas ot requirig the complex fuctios be holomorphic Theorem proofs are fairly simple ad are
A Primer o the Elemetary Theory of Ifiite Compositios of Complex Fuctios Joh Gill Sprig 07 Abstract: Elemetary meas ot requirig the complex fuctios be holomorphic Theorem proofs are fairly simple ad are
Some Common Fixed Point Theorems in Cone Rectangular Metric Space under T Kannan and T Reich Contractive Conditions
 ISSN(Olie): 319-8753 ISSN (Prit): 347-671 Iteratioal Joural of Iovative Research i Sciece, Egieerig ad Techology (A ISO 397: 7 Certified Orgaizatio) Some Commo Fixed Poit Theorems i Coe Rectagular Metric
ISSN(Olie): 319-8753 ISSN (Prit): 347-671 Iteratioal Joural of Iovative Research i Sciece, Egieerig ad Techology (A ISO 397: 7 Certified Orgaizatio) Some Commo Fixed Poit Theorems i Coe Rectagular Metric
PAijpam.eu ON DERIVATION OF RATIONAL SOLUTIONS OF BABBAGE S FUNCTIONAL EQUATION
 Iteratioal Joural of Pure ad Applied Mathematics Volume 94 No. 204, 9-20 ISSN: 3-8080 (prited versio); ISSN: 34-3395 (o-lie versio) url: http://www.ijpam.eu doi: http://dx.doi.org/0.2732/ijpam.v94i.2 PAijpam.eu
Iteratioal Joural of Pure ad Applied Mathematics Volume 94 No. 204, 9-20 ISSN: 3-8080 (prited versio); ISSN: 34-3395 (o-lie versio) url: http://www.ijpam.eu doi: http://dx.doi.org/0.2732/ijpam.v94i.2 PAijpam.eu
y X F n (y), To see this, let y Y and apply property (ii) to find a sequence {y n } X such that y n y and lim sup F n (y n ) F (y).
 Modica Mortola Fuctioal 2 Γ-Covergece Let X, d) be a metric space ad cosider a sequece {F } of fuctioals F : X [, ]. We say that {F } Γ-coverges to a fuctioal F : X [, ] if the followig properties hold:
Modica Mortola Fuctioal 2 Γ-Covergece Let X, d) be a metric space ad cosider a sequece {F } of fuctioals F : X [, ]. We say that {F } Γ-coverges to a fuctioal F : X [, ] if the followig properties hold:
On general Gamma-Taylor operators on weighted spaces
 It. J. Adv. Appl. Math. ad Mech. 34 16 9 15 ISSN: 347-59 Joural homepage: www.ijaamm.com IJAAMM Iteratioal Joural of Advaces i Applied Mathematics ad Mechaics O geeral Gamma-Taylor operators o weighted
It. J. Adv. Appl. Math. ad Mech. 34 16 9 15 ISSN: 347-59 Joural homepage: www.ijaamm.com IJAAMM Iteratioal Joural of Advaces i Applied Mathematics ad Mechaics O geeral Gamma-Taylor operators o weighted
Advanced Analysis. Min Yan Department of Mathematics Hong Kong University of Science and Technology
 Advaced Aalysis Mi Ya Departmet of Mathematics Hog Kog Uiversity of Sciece ad Techology September 3, 009 Cotets Limit ad Cotiuity 7 Limit of Sequece 8 Defiitio 8 Property 3 3 Ifiity ad Ifiitesimal 8 4
Advaced Aalysis Mi Ya Departmet of Mathematics Hog Kog Uiversity of Sciece ad Techology September 3, 009 Cotets Limit ad Cotiuity 7 Limit of Sequece 8 Defiitio 8 Property 3 3 Ifiity ad Ifiitesimal 8 4
Beurling Integers: Part 2
 Beurlig Itegers: Part 2 Isomorphisms Devi Platt July 11, 2015 1 Prime Factorizatio Sequeces I the last article we itroduced the Beurlig geeralized itegers, which ca be represeted as a sequece of real umbers
Beurlig Itegers: Part 2 Isomorphisms Devi Platt July 11, 2015 1 Prime Factorizatio Sequeces I the last article we itroduced the Beurlig geeralized itegers, which ca be represeted as a sequece of real umbers
BIRKHOFF ERGODIC THEOREM
 BIRKHOFF ERGODIC THEOREM Abstract. We will give a proof of the poitwise ergodic theorem, which was first proved by Birkhoff. May improvemets have bee made sice Birkhoff s orgial proof. The versio we give
BIRKHOFF ERGODIC THEOREM Abstract. We will give a proof of the poitwise ergodic theorem, which was first proved by Birkhoff. May improvemets have bee made sice Birkhoff s orgial proof. The versio we give
The Wasserstein distances
 The Wasserstei distaces March 20, 2011 This documet presets the proof of the mai results we proved o Wasserstei distaces themselves (ad ot o curves i the Wasserstei space). I particular, triagle iequality
The Wasserstei distaces March 20, 2011 This documet presets the proof of the mai results we proved o Wasserstei distaces themselves (ad ot o curves i the Wasserstei space). I particular, triagle iequality
The natural exponential function
 The atural expoetial fuctio Attila Máté Brookly College of the City Uiversity of New York December, 205 Cotets The atural expoetial fuctio for real x. Beroulli s iequality.....................................2
The atural expoetial fuctio Attila Máté Brookly College of the City Uiversity of New York December, 205 Cotets The atural expoetial fuctio for real x. Beroulli s iequality.....................................2
Real and Complex Analysis, 3rd Edition, W.Rudin
 Real ad Complex Aalysis, 3rd ditio, W.Rudi Chapter 6 Complex Measures Yug-Hsiag Huag 206/08/22. Let ν be a complex measure o (X, M ). If M, defie { } µ () = sup ν( j ) : N,, 2, disjoit, = j { } ν () =
Real ad Complex Aalysis, 3rd ditio, W.Rudi Chapter 6 Complex Measures Yug-Hsiag Huag 206/08/22. Let ν be a complex measure o (X, M ). If M, defie { } µ () = sup ν( j ) : N,, 2, disjoit, = j { } ν () =
