An Interpolation Process on Laguerre Polynomial
|
|
|
- Sheena Todd
- 5 years ago
- Views:
Transcription
1 Global Joural of Pure ad Applied Mathematics. ISSN Volume 13, Number 10 (2017), pp Research Idia Publicatios A Iterpolatio Process o Laguerre Polyomial R. Srivastava 1 ad Geeta Vishwakarma 2 Departmet of Mathematics ad Astroomy, Luckow Uiversity, Luckow , Idia. Abstract I the preset paper,we have cosidered the problem i which {ξ i } i=1 ad {ξ i } i=1 the two sets of iterscaled odal poits o the iterval [0, ). Here we deal with the problem i which fuctio values are prescribed at the zeros of L k (x) ad the first derivative values are prescribed o the zeros L k 1 (x). We ivestigate the existece, uiqueess explicit represetatio of iterpolatory polyomial. Estimatio of the fudametal polyomials leadig to a covergece theorem have also bee obtaied. Keywords: Lacuary iterpolatio, Pál - Type iterpolatio, Laguerre Polyomial MSC 2000: 41 A D INTRODUCTION Pál [10], Mathur P. ad Datta S. [8] ad may other authors [1][2][6][7] [12] [14] have discussed about various kid of iterpolatio problems.. I 1975 Pál [10] proved that whe the fuctio values are prescribed o oe set of poits ad derivative values o other set of -1 poits, the there exist o uique polyomial of degree 2-2, but prescribig fuctio value at oe more poit ot belogig to former set of poits there exists a uique polyomial of degree 2-1. Léárd M. [5] ivestigated the Pál type iterpolatio problem o the odes of Laguerre abscissas. I this paper we study Pál type iterpolatioal polyomial with ω +k (x) = x k L (k) (x).we have examied the existece, uiqueess,explicit
2 7090 R. Srivastava ad Geeta Vishwakarma represetatio ad estimatio of fudametal polyomials of such special kid of mixed type of iterpolatio o iterval [0, ). For this we have cosidered the problem i which {ξ i } i=1 ad {ξ i } i=1 the two sets of iterscaled odal poits. (1.1) 0 ξ 0 < ξ 1 < ξ 1 < < ξ 1 < ξ < ξ < o the iterval [0, ). We seek to determie a polyomial R (x) of miimal possible degree 3+k satisfyig the iterpolatory coditios : (1.2) R (ξ i ) = g i, R (ξ i ) = g i, R (ξ i ) = g i, for i = 1(1) (1.3) R (j) (ξ 0 ) = g 0 (j), j = 0,1,, k where g i, g i, g i ad g 0 (j) L (k) (x) ad L (k 1) (x) have zeroes {ξ i } i=1 are arbitrary real umbers. Here Laguerre polyomials ad {ξ i } i=1 respectively ad x 0 = 0. We prove existece, uiqueess, explicit represetatio ad estimatio of fudametal polyomials. 2. PRELIMINARIES I this sectio we shall give some well-kow results which are as follws : As we kow that the Laguerre polyomial is a costat multiple of a cofluet hypergeometric fuctio so the differetial equatio is give by (2.1) xd 2 L k (x) + (1 + k x)dl k (x) + L k (x) = 0 (k 1) (2.2) L (x) = L (k) 1 (x) Also usig the idetities (2.3) L (k) (k+1) (k+1) (x) = L (x) L 1 (x) (k) (2.4) xl (k) (k) (x) = L (x) ( + k)l 1(x) We ca easily fid a relatio d (2.5) dx [xk L k (x)] = ( + k)x k 1 (k 1) L (x) By the followig coditios of orthogoality ad ormalizatio we defie Laguerre polyomial L (k) (x), for k > 1
3 A Iterpolatio Process o Laguerre Polyomial (2.6) e x x k L (k) (x)l (k) m (x)dx = Γk + 1 ( +k )δ m, m = 0,1,2,.. (2.7) L (k) (x) = ( +k μ=0 ) ( x)μ μ! The fudametal polyomials of Lagrage iterpolatio are give by L (k) (x) (2.8) l j (x) = (k) L = δ i,j (x j )(x x j ) L (k 1) (x) (2.9) l j (x) = (k 1) L = δ i,j (x j )(x x j ) (2.10) l j (y j ) = { L (k 1) (y i ) L (k 1) (y j )(y i y j ) (k y j) 2y j i j i = j i, j = 1(1) (2.12) l j (y j ) = 1 (k) (k) (y j x j ) [L (y j ) (k) L L (yj ) (k) (x j ) L ] (x j )(y j x j ), j = 1(1) For the roots of L (k) (x) we have (2.13) x k 2 ~ k2 (2.14) η(x) S (l) (x) = О(1) where η(x) is the weight fuctio (2.15) L (k) (x j ) ~j k 3 2 k+1, (0 < x j Ω, = 1,2,3,. ) k (2.16) L k (x j ) = { x 2 1 4О ( k 2 1 4), c 1 x Ω О( k ), 0 x c 1 3 (2.17) l j (x) = О ( jk+ 2 ) (k+), for 0 x c 1 1 k = О ( jk+ 2x k (k+) ), c 1 x Ω
4 7092 R. Srivastava ad Geeta Vishwakarma 1 (2.18) l j (x) = О ( jk+ 2 ) (k+ 1), for 0 x c 1 1 k = О ( jk+ 2x k (k+ 1) ), for c 1 x Ω 3. NEW RESULT Theorem 1 : For >1 fixed iteger let {g i } i=1, {g i } i=1, {g i } i=1 ad, {g (j) k 0 } j=0 arbitrary real umbers the there exists a uique polyomial R (x) of miimal possible degree 3+k o the odal poits (1.1) satisfyig the coditio (1.2) ad (1.3). The polyomial R (x) ca be writte i the form (3.1) R (x) = U j (x)g j + V j (x)g j + W j (x)g k (j) j + C j (x)g 0 where U j (x), V j (x ), W j (x) ad C j (x) are fudametal polyomials of degree 3+k give by (3.2) U j (x) = x(k+1) l j (x)[l (k 1) (x)] 2 x j (k+1) [L (k 1) (xj )] 2 (3.3) V j (x) = xk+1 l j (x)l k (x) [L (k) (k+1) (k) y j [L (yj )] 2 (x) + y j 3k+2 L (k 1) (x)] 2y j j=0 are (3.4) W j (x) = xk+1 l j (x)l (k) (x)l (k 1) (x) y j k+1 L k (y j )L (k 1) (y j ) (3.5) C j (x) = p j (x)x j [L k (x)] 2 L (k 1) (x)+x k L (k) (x)l (k 1) (x)[cj L k (x)p j (x)+q j (x)l (k 1) (x) x k j ] vc, j = 0,1,, k 1 (3.6) C k (x) = 1 ( +k k )k!l (k 1) (0) x k L (k) (x)[l (k 1) (x)] 2 where p j (x) ad q j (x) are polyomials of degree at most k-j-1. c j is defied i (4.14)
5 A Iterpolatio Process o Laguerre Polyomial 7093 Theorem 2 Let the iterpolatory fuctio f: R R be cotiuously differetiable such that, C(m) = {f(x): f is cotiuous i[0, ), f(x) = О(x m )as x ; m 0 is a iteger} For every f C(m) ad α 0, The (3.7) R (x) = U j (x)g j + V j (x)g j + W j (x)g k (j) j + j=0 C j (x)g 0 satisfies the relatios 3k (3.8) R (x) f(x) = О ( jj (3.9) R (x) f(x) = О ( j k 2 1 j 2 (k+) 2 +1 x k k 2 (k+)(k+ 1) where ω is the modulus of cotiuity. ) ω (f, log ), for 0 x c 1 log ) ω (f, ), for c 1 x Ω 4. PROOF OF THEOREM 1 Let U j (x), V j (x), W j (x) ad C j (x) are polyomials of degree 3+k satisfyig coditios (4.1), (4.2), (4.3) ad (4.4) respectively. (4.1) U j (x i ) = 0 whe i j 1 whe i=j U j(x i ) = 0, U j (x i ) = 0 { U (l) j (0) = 0, i = 1(1) ad l = 0,1,, k (4.2) 0 whe i j V j (y i ) = 0 V j (y i ) = 1 whe i=j, V j (y i ) = 0 { V (l) j (0) = 0, i = 1(1) ad l = 0,1,, k (4.3) 0 whe i j 1 whe i=j W j (y i ) = 0 W j (y i ) = 0, W j (y i ) = { W (l) j (0) = 0, i = 1(1) ad l = 0,1,, k
6 7094 R. Srivastava ad Geeta Vishwakarma (4.4) { C k(x i ) = 0, C k (y i ) = 0, C k (y i ) = 0 C (l) k (0) = 0, i = 1(1) ad l = 0,1,, k To determie U j (x) let (4.5) U j (x) = C 1 x k+1 l j (x)[l (k 1) (x)] 2 where C 1 is a costat. l j (x) is defied i (2.8). U j (x) is a polyomial of degree 3+k By usig (2.8) we determie (4.6) C 1 = 1 x j (k+1) L (k 1) (xj ) Hece we fid the first fudametal polyomial U j (x)of degree 3+k To fid secod fudametal polyomial let ( 4.7) V j (x) = C 2 x k+1 l j (x)[l (k) (x)] 2 + C 3 x k+1 l j (x)l (k) (x)l (k 1) (x) where C 2 ad C 3 are arbitrary costats. By usig (2.9) ad (4.2) we determie (4.8) C 2 = 1 y j (k+1) [L k (y j )] 2 ad (4.9) C 3 = y j 3k+2 (k+1) (k) 2y j y j [L (yj )] 2 Hece we fid the first fudametal polyomial V j (x)of degree 3+k Agai let (4.10) W j (x) = C 4 x k+1 l j (x)l (k) (x)l (k 1) (x) where C 4 is a costat, l j (x) is defied i (2.8).W j (x) is polyomial of degree 3+k satisfyig the coditios (4.3) by which we obtai (4.11) C 4 = 1 (k+1) y j )L k (k 1) (y j )L (y j ) Hece we fid the third fudametal polyomial W j (x) of degree 3+k To fid C j (x), we assume C j (x) for fixed j ε {0,1,.., k 1} i the form
7 A Iterpolatio Process o Laguerre Polyomial 7095 (4.12) C j (x) = p j (x)x j [L k (x)] 2 L (k 1) (x) + x k L (k) (x)l (k 1) (x)g (x) Where p j (x) ad g (x) are polyomials of degree k-j-1 ad respectively. Now it is clear that C j (l) (0) = 0 for (l = 0,, j 1) ad sice L (k) (x i ) = 0 ad L (k 1) (y i ) = 0 we get C j (x i ) = 0 ad C j (y i ) = 0 for i = 1(1). The coefficiet of the polyomial p j (x) are calculated by the system (4.13) C j (l) (0) = dl dx l [p j(x)x j [L k (x)] 2 L (k 1) (x)]x=0 = δ i,j (l = j,, k 1) ow from the equatio C j (k) (0) = 0 we get (4.14) c j = g (0) = 1 d k ( +k k )k!l (k 1) (0) Now usig the coditio C j (y i ) = 0 of (4.7), we get dx k [p j(x)x j [L k (x)] 2 L (k 1) (x)]x=0 (4.15) g (y i ) = (y i ) j k L k (y i )p j (y i ) Which implies g (x) as follows (4.16) g (x) = L k (x)p j (x)+q j (x)l (k 1) (x) x k j Where q j (x) is a polyomial of degree k-j ad fuctio g (x) will be a polyomial iff for r = 0,1,, k j 1 (4.17) d r dx r [L k (x)p j (x) + q j (x)l (k 1) (x)]x=0 = 0 The coefficiets of q j (x) are uiquely calculated by this system (4.13) Usig (4.12) ad (4.14) we obtai C j (x) of degree 3+k satisfyig the coditios (4.4) 5. ESTIMATION OF THE FUNDAMENTAL POLYNOMIALS Lemma 5.1. For j = 1(1) ad [0, ), we have 3 2 ) (k+) (5.1) U j (x) О ( jk+, for 0 x c 1 k (5.2) U j (x) О ( j 2 +1 k x 2 1 k 42 ), for c 1 x Ω (k+)
8 7096 R. Srivastava ad Geeta Vishwakarma Wher U j (x) is give i equqtio (3.2) Proof : from (3.2) we have x(k+1) (k 1) 2 l j (x) L i=1 (k+1) (k 1) x j L (xj ) 2 (5.3) U j (x) where U j (x) is give i equqtio (3.2) usig equatios (4.1) (2.13) ad (2.17) we yield the result. Lemma 5.2. For j = 1(1) ad [0, ), we have 1 2 ) (k+ 1) ( 5.4) V j (x) О ( jk+, for 0 x c 1 5k (5.5) V j (x) О ( j2k+1 x k ), for c 1 x Ω (k+ 1) Where V j (x) is give i equqtio (3.3) Proof : from (3.3) we have (5.6) V j (x) x k+1 l j (x) L k (x) y j (k+1) L (k) (yj ) 2 [ L (k) (x) + y j 3k+2 L (k 1) 2y (x) ] j usig equatios (2.16) ad (2.18) we yield the result. Lemma 5.3. For j = 1(1) ad [0, ), we have 3k (5.7) W j (x) О ( j , for 0 x c 1 (k+ 1) ) 7 3k 4x 2 1 k (5.8) W j (x) О ( j2k+ ), for c 1 x Ω (k+ 1) where W j (x) is give i equqtio (3.4) Proof : from (3.3) we have (5.9) W j (x) = xk+1 l j (x) L (k) (x) L (k 1) (x) y j k+1 L k (y j ) L (k 1) (y j )
9 A Iterpolatio Process o Laguerre Polyomial 7097 By equatios (2.15), (2.16) ad (2.17) we yield the result. Lemma 5.4. For j = 0,1,2,, k ad [0, ), we have k (5.8) j=0 C j (x) O (j j 3k 2 j 2 ), for 0 x c 1 k (5.9) j=0 C j (x) O (j j x 3k (3k j) 7 4), for c 1 x Ω Proof : by usig equatio (3.5) dealig with similar method we get the result. 6. PROOF OF THEOREM 2 We prove theorem 2 with the help of certai theorem metioed as below Theorem (5.5): Let C(m) = {f(x): f is cotiuous i[0, ), f(x) = О(x m )as x ; m 0 is a iteger} The by Szego[12] is lim f(x) H (α) (f, x) = 0 I For every f C(s) ad (0, )for α 0, or I (0, )for 1 < α < 0. furthermore there exists a fuctio i C(m) such that {H (α) (f, x)} diverges for α 0 at x=0.as for thr rate of covergece the followig result is due to Vertesi (5.10) f(x) H (α) (f, x) I = О(ω(f, 1 α )); 1 < α < 0 { log О (ω (f, )) ; α 1 2 Proof of mai theorem 2 : Sice R (x) give by equatio (3.1) is exact for all polyomial S (x) of degree 3+k, we have (5.11) S (x) = S (x j )U j (x) + S (y j )V j (x) + S (y j )W j (x) + S (y i )C j (x) k j=0
10 7098 R. Srivastava ad Geeta Vishwakarma From equatio (5.11) ad (3.1) we get R (x) (x) = S (x) f(x) + f(x j ) S (x j ) U j (x) + f(y j ) S (y j ) V j (x) k + f (y j ) S (y j ) W j (x) + f l (y j ) S l (y j ) C j (x) l=1 Owig to equatios (2.14) ad lemmas (5.1), (5.2), (5.3), (5.4) we get the result. REFERENCES [1] Balázs, J. ad Turá.P., Notes o iterpolatio, II. Acta Math. Acad. Sci. Huger., 8 (1957), pp [2] Balázs, J., Weighted (0; 2)-iterpolatio o the roots of the ultraspherical polyomials, (i Hugaria: Súlyozott (0; 2)-iterpoláció ultraszférikus poliom gyökei), Mat. Fiz. Tud. Oszt. Közl., 11 (1961), [3] Balázs, J..P., Modified weighted (0,2) iterpolatio, Approx. Theory, Marcel Dekker Ic., New York, 1998, 1-73 [4] Chak, A.M. ad Szabados, J. : O (0,2) iterpolatio for Laguerre abscissas, Acta Math. Acad. Hug. 49 (1987) [5] Léárd, M. : Pál type- iterpolatio ad quadrature formulae o Laguerre abscissas, Mathematica Paoica 15/2 (2004), [6] Léárd, M., O weighted (0; 2)-type iterpolatio, Electro. Tras. Numer. Aal., 25 (2006), [7] Léárd, M., O weighted lacuary iterpolatio, Electro. Tras. Numer. Aal., 37 (2010), [8] Mathur, P. ad Datta S., O Pál -type weighted lacuary (0; 2; 0)- iterpolatio o ifiite iterval (-,+ ), Approx. Theor. Appl., 17 (4) (2001), [9] Mathur, K.K.ad Srivastava, R.: Pál type Hermite iterpolatio o ifiite iterval, J.Math. Aal.ad App. 192, (1995) [10] Pál L. G., A ew modificatio of the Hermite-Fejér iterpolatio, Aal.
11 A Iterpolatio Process o Laguerre Polyomial 7099 Math., 1 (1975), [11] Prasad, J. ad Jhujhuwala,N. : Some lacuary iterpolatio problems for the Laguerre abscissas, Demostratio Math. 32 (1999), o. 4, [12] Szegö G., Orthogoal polyomials,amer. Math. Soc.,Coll. Publ., 23, New York, 1939 (4th ed.1975). [13] Szili, L.,Weighted (0,2) iterpolatio o the roots of classical orthogoal polyomials, Bull. Of Allahabad Math. Soc., 8-9 ( ), [14] Srivastava, R.ad Mathur, K.K.:weighted (0;0,2)- iterpolatio o the roots of Hermite polyomials, Acta Math. Huger. 70 (1-2)(1996), [15] Xie,T.F., O ] Pál s problem, Chiese Quart. J. Math. 7 (1992), 48-2.
12 7100 R. Srivastava ad Geeta Vishwakarma
Inverse Nodal Problems for Differential Equation on the Half-line
 Australia Joural of Basic ad Applied Scieces, 3(4): 4498-4502, 2009 ISSN 1991-8178 Iverse Nodal Problems for Differetial Equatio o the Half-lie 1 2 3 A. Dabbaghia, A. Nematy ad Sh. Akbarpoor 1 Islamic
Australia Joural of Basic ad Applied Scieces, 3(4): 4498-4502, 2009 ISSN 1991-8178 Iverse Nodal Problems for Differetial Equatio o the Half-lie 1 2 3 A. Dabbaghia, A. Nematy ad Sh. Akbarpoor 1 Islamic
Sequences and Series of Functions
 Chapter 6 Sequeces ad Series of Fuctios 6.1. Covergece of a Sequece of Fuctios Poitwise Covergece. Defiitio 6.1. Let, for each N, fuctio f : A R be defied. If, for each x A, the sequece (f (x)) coverges
Chapter 6 Sequeces ad Series of Fuctios 6.1. Covergece of a Sequece of Fuctios Poitwise Covergece. Defiitio 6.1. Let, for each N, fuctio f : A R be defied. If, for each x A, the sequece (f (x)) coverges
It is often useful to approximate complicated functions using simpler ones. We consider the task of approximating a function by a polynomial.
 Taylor Polyomials ad Taylor Series It is ofte useful to approximate complicated fuctios usig simpler oes We cosider the task of approximatig a fuctio by a polyomial If f is at least -times differetiable
Taylor Polyomials ad Taylor Series It is ofte useful to approximate complicated fuctios usig simpler oes We cosider the task of approximatig a fuctio by a polyomial If f is at least -times differetiable
On polynomial and barycentric interpolations
 Special Issue for the 10 years of the Padua poits, Volume 8 2015 Pages 17 22 O polyomial ad barycetric iterpolatios László Szili a Péter Vértesi b Abstract The preset survey collects some recet results
Special Issue for the 10 years of the Padua poits, Volume 8 2015 Pages 17 22 O polyomial ad barycetric iterpolatios László Szili a Péter Vértesi b Abstract The preset survey collects some recet results
Chapter 6 Infinite Series
 Chapter 6 Ifiite Series I the previous chapter we cosidered itegrals which were improper i the sese that the iterval of itegratio was ubouded. I this chapter we are goig to discuss a topic which is somewhat
Chapter 6 Ifiite Series I the previous chapter we cosidered itegrals which were improper i the sese that the iterval of itegratio was ubouded. I this chapter we are goig to discuss a topic which is somewhat
62. Power series Definition 16. (Power series) Given a sequence {c n }, the series. c n x n = c 0 + c 1 x + c 2 x 2 + c 3 x 3 +
 62. Power series Defiitio 16. (Power series) Give a sequece {c }, the series c x = c 0 + c 1 x + c 2 x 2 + c 3 x 3 + is called a power series i the variable x. The umbers c are called the coefficiets of
62. Power series Defiitio 16. (Power series) Give a sequece {c }, the series c x = c 0 + c 1 x + c 2 x 2 + c 3 x 3 + is called a power series i the variable x. The umbers c are called the coefficiets of
Math 341 Lecture #31 6.5: Power Series
 Math 341 Lecture #31 6.5: Power Series We ow tur our attetio to a particular kid of series of fuctios, amely, power series, f(x = a x = a 0 + a 1 x + a 2 x 2 + where a R for all N. I terms of a series
Math 341 Lecture #31 6.5: Power Series We ow tur our attetio to a particular kid of series of fuctios, amely, power series, f(x = a x = a 0 + a 1 x + a 2 x 2 + where a R for all N. I terms of a series
Find quadratic function which pass through the following points (0,1),(1,1),(2, 3)... 11
 Adrew Powuk - http://www.powuk.com- Math 49 (Numerical Aalysis) Iterpolatio... 4. Polyomial iterpolatio (system of equatio)... 4.. Lier iterpolatio... 5... Fid a lie which pass through (,) (,)... 8...
Adrew Powuk - http://www.powuk.com- Math 49 (Numerical Aalysis) Iterpolatio... 4. Polyomial iterpolatio (system of equatio)... 4.. Lier iterpolatio... 5... Fid a lie which pass through (,) (,)... 8...
A collocation method for singular integral equations with cosecant kernel via Semi-trigonometric interpolation
 Iteratioal Joural of Mathematics Research. ISSN 0976-5840 Volume 9 Number 1 (017) pp. 45-51 Iteratioal Research Publicatio House http://www.irphouse.com A collocatio method for sigular itegral equatios
Iteratioal Joural of Mathematics Research. ISSN 0976-5840 Volume 9 Number 1 (017) pp. 45-51 Iteratioal Research Publicatio House http://www.irphouse.com A collocatio method for sigular itegral equatios
Shivley s Polynomials of Two Variables
 It. Joural of Math. Aalysis, Vol. 6, 01, o. 36, 1757-176 Shivley s Polyomials of Two Variables R. K. Jaa, I. A. Salehbhai ad A. K. Shukla Departmet of Mathematics Sardar Vallabhbhai Natioal Istitute of
It. Joural of Math. Aalysis, Vol. 6, 01, o. 36, 1757-176 Shivley s Polyomials of Two Variables R. K. Jaa, I. A. Salehbhai ad A. K. Shukla Departmet of Mathematics Sardar Vallabhbhai Natioal Istitute of
A note on the p-adic gamma function and q-changhee polynomials
 Available olie at wwwisr-publicatioscom/jmcs J Math Computer Sci, 18 (2018, 11 17 Research Article Joural Homepage: wwwtjmcscom - wwwisr-publicatioscom/jmcs A ote o the p-adic gamma fuctio ad q-chaghee
Available olie at wwwisr-publicatioscom/jmcs J Math Computer Sci, 18 (2018, 11 17 Research Article Joural Homepage: wwwtjmcscom - wwwisr-publicatioscom/jmcs A ote o the p-adic gamma fuctio ad q-chaghee
II. EXPANSION MAPPINGS WITH FIXED POINTS
 Geeralizatio Of Selfmaps Ad Cotractio Mappig Priciple I D-Metric Space. U.P. DOLHARE Asso. Prof. ad Head,Departmet of Mathematics,D.S.M. College Jitur -431509,Dist. Parbhai (M.S.) Idia ABSTRACT Large umber
Geeralizatio Of Selfmaps Ad Cotractio Mappig Priciple I D-Metric Space. U.P. DOLHARE Asso. Prof. ad Head,Departmet of Mathematics,D.S.M. College Jitur -431509,Dist. Parbhai (M.S.) Idia ABSTRACT Large umber
On the Variations of Some Well Known Fixed Point Theorem in Metric Spaces
 Turkish Joural of Aalysis ad Number Theory, 205, Vol 3, No 2, 70-74 Available olie at http://pubssciepubcom/tjat/3/2/7 Sciece ad Educatio Publishig DOI:0269/tjat-3-2-7 O the Variatios of Some Well Kow
Turkish Joural of Aalysis ad Number Theory, 205, Vol 3, No 2, 70-74 Available olie at http://pubssciepubcom/tjat/3/2/7 Sciece ad Educatio Publishig DOI:0269/tjat-3-2-7 O the Variatios of Some Well Kow
Numerical integration of analytic functions
 Numerical itegratio of aalytic fuctios Gradimir V. Milovaović, Dobrilo Ð Tošić, ad Miloljub Albijaić Citatio: AIP Cof. Proc. 1479, 146 212); doi: 1.163/1.4756325 View olie: http://dx.doi.org/1.163/1.4756325
Numerical itegratio of aalytic fuctios Gradimir V. Milovaović, Dobrilo Ð Tošić, ad Miloljub Albijaić Citatio: AIP Cof. Proc. 1479, 146 212); doi: 1.163/1.4756325 View olie: http://dx.doi.org/1.163/1.4756325
Section 5.5. Infinite Series: The Ratio Test
 Differece Equatios to Differetial Equatios Sectio 5.5 Ifiite Series: The Ratio Test I the last sectio we saw that we could demostrate the covergece of a series a, where a 0 for all, by showig that a approaches
Differece Equatios to Differetial Equatios Sectio 5.5 Ifiite Series: The Ratio Test I the last sectio we saw that we could demostrate the covergece of a series a, where a 0 for all, by showig that a approaches
Comparison Study of Series Approximation. and Convergence between Chebyshev. and Legendre Series
 Applied Mathematical Scieces, Vol. 7, 03, o. 6, 3-337 HIKARI Ltd, www.m-hikari.com http://d.doi.org/0.988/ams.03.3430 Compariso Study of Series Approimatio ad Covergece betwee Chebyshev ad Legedre Series
Applied Mathematical Scieces, Vol. 7, 03, o. 6, 3-337 HIKARI Ltd, www.m-hikari.com http://d.doi.org/0.988/ams.03.3430 Compariso Study of Series Approimatio ad Covergece betwee Chebyshev ad Legedre Series
Local Approximation Properties for certain King type Operators
 Filomat 27:1 (2013, 173 181 DOI 102298/FIL1301173O Published by Faculty of Scieces ad athematics, Uiversity of Niš, Serbia Available at: http://wwwpmfiacrs/filomat Local Approimatio Properties for certai
Filomat 27:1 (2013, 173 181 DOI 102298/FIL1301173O Published by Faculty of Scieces ad athematics, Uiversity of Niš, Serbia Available at: http://wwwpmfiacrs/filomat Local Approimatio Properties for certai
MAT1026 Calculus II Basic Convergence Tests for Series
 MAT026 Calculus II Basic Covergece Tests for Series Egi MERMUT 202.03.08 Dokuz Eylül Uiversity Faculty of Sciece Departmet of Mathematics İzmir/TURKEY Cotets Mootoe Covergece Theorem 2 2 Series of Real
MAT026 Calculus II Basic Covergece Tests for Series Egi MERMUT 202.03.08 Dokuz Eylül Uiversity Faculty of Sciece Departmet of Mathematics İzmir/TURKEY Cotets Mootoe Covergece Theorem 2 2 Series of Real
Best bounds for dispersion of ratio block sequences for certain subsets of integers
 Aales Mathematicae et Iformaticae 49 (08 pp. 55 60 doi: 0.33039/ami.08.05.006 http://ami.ui-eszterhazy.hu Best bouds for dispersio of ratio block sequeces for certai subsets of itegers József Bukor Peter
Aales Mathematicae et Iformaticae 49 (08 pp. 55 60 doi: 0.33039/ami.08.05.006 http://ami.ui-eszterhazy.hu Best bouds for dispersio of ratio block sequeces for certai subsets of itegers József Bukor Peter
(p, q)-type BETA FUNCTIONS OF SECOND KIND
 Adv. Oper. Theory 6, o., 34 46 http://doi.org/.34/aot.69. ISSN: 538-5X electroic http://aot-math.org p, q-type BETA FUNCTIONS OF SECOND KIND ALI ARAL ad VIJAY GUPTA Commuicated by A. Kamisa Abstract. I
Adv. Oper. Theory 6, o., 34 46 http://doi.org/.34/aot.69. ISSN: 538-5X electroic http://aot-math.org p, q-type BETA FUNCTIONS OF SECOND KIND ALI ARAL ad VIJAY GUPTA Commuicated by A. Kamisa Abstract. I
PROBLEMS AND RESULTS ON THE THEORY OF INTERPOLATION. I
 PROBLEMS AND RESULTS ON THE THEORY OF INTERPOLATION. I By P. ERDŐS (Budapest), correspodig member of the Academy X Let xp X ) be a triagular matrix of real umbers i (-,-}-), - X00 < X00
PROBLEMS AND RESULTS ON THE THEORY OF INTERPOLATION. I By P. ERDŐS (Budapest), correspodig member of the Academy X Let xp X ) be a triagular matrix of real umbers i (-,-}-), - X00 < X00
Arkansas Tech University MATH 2924: Calculus II Dr. Marcel B. Finan
 Arkasas Tech Uiversity MATH 94: Calculus II Dr Marcel B Fia 85 Power Series Let {a } =0 be a sequece of umbers The a power series about x = a is a series of the form a (x a) = a 0 + a (x a) + a (x a) +
Arkasas Tech Uiversity MATH 94: Calculus II Dr Marcel B Fia 85 Power Series Let {a } =0 be a sequece of umbers The a power series about x = a is a series of the form a (x a) = a 0 + a (x a) + a (x a) +
Ma 530 Introduction to Power Series
 Ma 530 Itroductio to Power Series Please ote that there is material o power series at Visual Calculus. Some of this material was used as part of the presetatio of the topics that follow. What is a Power
Ma 530 Itroductio to Power Series Please ote that there is material o power series at Visual Calculus. Some of this material was used as part of the presetatio of the topics that follow. What is a Power
THE REPRESENTATION OF THE REMAINDER IN CLASSICAL BERNSTEIN APPROXIMATION FORMULA
 Global Joural of Advaced Research o Classical ad Moder Geometries ISSN: 2284-5569, Vol.6, 2017, Issue 2, pp.119-125 THE REPRESENTATION OF THE REMAINDER IN CLASSICAL BERNSTEIN APPROXIMATION FORMULA DAN
Global Joural of Advaced Research o Classical ad Moder Geometries ISSN: 2284-5569, Vol.6, 2017, Issue 2, pp.119-125 THE REPRESENTATION OF THE REMAINDER IN CLASSICAL BERNSTEIN APPROXIMATION FORMULA DAN
A Fixed Point Result Using a Function of 5-Variables
 Joural of Physical Scieces, Vol., 2007, 57-6 Fixed Poit Result Usig a Fuctio of 5-Variables P. N. Dutta ad Biayak S. Choudhury Departmet of Mathematics Begal Egieerig ad Sciece Uiversity, Shibpur P.O.:
Joural of Physical Scieces, Vol., 2007, 57-6 Fixed Poit Result Usig a Fuctio of 5-Variables P. N. Dutta ad Biayak S. Choudhury Departmet of Mathematics Begal Egieerig ad Sciece Uiversity, Shibpur P.O.:
Additional Notes on Power Series
 Additioal Notes o Power Series Mauela Girotti MATH 37-0 Advaced Calculus of oe variable Cotets Quick recall 2 Abel s Theorem 2 3 Differetiatio ad Itegratio of Power series 4 Quick recall We recall here
Additioal Notes o Power Series Mauela Girotti MATH 37-0 Advaced Calculus of oe variable Cotets Quick recall 2 Abel s Theorem 2 3 Differetiatio ad Itegratio of Power series 4 Quick recall We recall here
NEW FAST CONVERGENT SEQUENCES OF EULER-MASCHERONI TYPE
 UPB Sci Bull, Series A, Vol 79, Iss, 207 ISSN 22-7027 NEW FAST CONVERGENT SEQUENCES OF EULER-MASCHERONI TYPE Gabriel Bercu We itroduce two ew sequeces of Euler-Mascheroi type which have fast covergece
UPB Sci Bull, Series A, Vol 79, Iss, 207 ISSN 22-7027 NEW FAST CONVERGENT SEQUENCES OF EULER-MASCHERONI TYPE Gabriel Bercu We itroduce two ew sequeces of Euler-Mascheroi type which have fast covergece
MATH4822E FOURIER ANALYSIS AND ITS APPLICATIONS
 MATH48E FOURIER ANALYSIS AND ITS APPLICATIONS 7.. Cesàro summability. 7. Summability methods Arithmetic meas. The followig idea is due to the Italia geometer Eresto Cesàro (859-96). He shows that eve if
MATH48E FOURIER ANALYSIS AND ITS APPLICATIONS 7.. Cesàro summability. 7. Summability methods Arithmetic meas. The followig idea is due to the Italia geometer Eresto Cesàro (859-96). He shows that eve if
2.4.2 A Theorem About Absolutely Convergent Series
 0 Versio of August 27, 200 CHAPTER 2. INFINITE SERIES Add these two series: + 3 2 + 5 + 7 4 + 9 + 6 +... = 3 l 2. (2.20) 2 Sice the reciprocal of each iteger occurs exactly oce i the last series, we would
0 Versio of August 27, 200 CHAPTER 2. INFINITE SERIES Add these two series: + 3 2 + 5 + 7 4 + 9 + 6 +... = 3 l 2. (2.20) 2 Sice the reciprocal of each iteger occurs exactly oce i the last series, we would
k-generalized FIBONACCI NUMBERS CLOSE TO THE FORM 2 a + 3 b + 5 c 1. Introduction
 Acta Math. Uiv. Comeiaae Vol. LXXXVI, 2 (2017), pp. 279 286 279 k-generalized FIBONACCI NUMBERS CLOSE TO THE FORM 2 a + 3 b + 5 c N. IRMAK ad M. ALP Abstract. The k-geeralized Fiboacci sequece { F (k)
Acta Math. Uiv. Comeiaae Vol. LXXXVI, 2 (2017), pp. 279 286 279 k-generalized FIBONACCI NUMBERS CLOSE TO THE FORM 2 a + 3 b + 5 c N. IRMAK ad M. ALP Abstract. The k-geeralized Fiboacci sequece { F (k)
Generating Functions for Laguerre Type Polynomials. Group Theoretic method
 It. Joural of Math. Aalysis, Vol. 4, 2010, o. 48, 257-266 Geeratig Fuctios for Laguerre Type Polyomials α of Two Variables L ( xy, ) by Usig Group Theoretic method Ajay K. Shula* ad Sriata K. Meher** *Departmet
It. Joural of Math. Aalysis, Vol. 4, 2010, o. 48, 257-266 Geeratig Fuctios for Laguerre Type Polyomials α of Two Variables L ( xy, ) by Usig Group Theoretic method Ajay K. Shula* ad Sriata K. Meher** *Departmet
Chapter 10: Power Series
 Chapter : Power Series 57 Chapter Overview: Power Series The reaso series are part of a Calculus course is that there are fuctios which caot be itegrated. All power series, though, ca be itegrated because
Chapter : Power Series 57 Chapter Overview: Power Series The reaso series are part of a Calculus course is that there are fuctios which caot be itegrated. All power series, though, ca be itegrated because
Some Common Fixed Point Theorems in Cone Rectangular Metric Space under T Kannan and T Reich Contractive Conditions
 ISSN(Olie): 319-8753 ISSN (Prit): 347-671 Iteratioal Joural of Iovative Research i Sciece, Egieerig ad Techology (A ISO 397: 7 Certified Orgaizatio) Some Commo Fixed Poit Theorems i Coe Rectagular Metric
ISSN(Olie): 319-8753 ISSN (Prit): 347-671 Iteratioal Joural of Iovative Research i Sciece, Egieerig ad Techology (A ISO 397: 7 Certified Orgaizatio) Some Commo Fixed Poit Theorems i Coe Rectagular Metric
SOME SEQUENCE SPACES DEFINED BY ORLICZ FUNCTIONS
 ARCHIVU ATHEATICU BRNO Tomus 40 2004, 33 40 SOE SEQUENCE SPACES DEFINED BY ORLICZ FUNCTIONS E. SAVAŞ AND R. SAVAŞ Abstract. I this paper we itroduce a ew cocept of λ-strog covergece with respect to a Orlicz
ARCHIVU ATHEATICU BRNO Tomus 40 2004, 33 40 SOE SEQUENCE SPACES DEFINED BY ORLICZ FUNCTIONS E. SAVAŞ AND R. SAVAŞ Abstract. I this paper we itroduce a ew cocept of λ-strog covergece with respect to a Orlicz
Zeros of Polynomials
 Math 160 www.timetodare.com 4.5 4.6 Zeros of Polyomials I these sectios we will study polyomials algebraically. Most of our work will be cocered with fidig the solutios of polyomial equatios of ay degree
Math 160 www.timetodare.com 4.5 4.6 Zeros of Polyomials I these sectios we will study polyomials algebraically. Most of our work will be cocered with fidig the solutios of polyomial equatios of ay degree
Generalized Little q-jacobi Polynomials as Eigensolutions of Higher-Order q-difference Operators
 Geeralized Little q-jacobi Polyomials as Eigesolutios of Higher-Order q-differece Operators Luc Viet Alexei Zhedaov CRM-2583 December 1998 Cetre de recherches mathématiques, Uiversité de Motréal, C.P.
Geeralized Little q-jacobi Polyomials as Eigesolutios of Higher-Order q-differece Operators Luc Viet Alexei Zhedaov CRM-2583 December 1998 Cetre de recherches mathématiques, Uiversité de Motréal, C.P.
6. Uniform distribution mod 1
 6. Uiform distributio mod 1 6.1 Uiform distributio ad Weyl s criterio Let x be a seuece of real umbers. We may decompose x as the sum of its iteger part [x ] = sup{m Z m x } (i.e. the largest iteger which
6. Uiform distributio mod 1 6.1 Uiform distributio ad Weyl s criterio Let x be a seuece of real umbers. We may decompose x as the sum of its iteger part [x ] = sup{m Z m x } (i.e. the largest iteger which
For a carefully chose system of odes := f ; ; :::; g; ; our results imply i particular, that the Lebesgue costat k (W k; ; )k L (R) satises uiformly f
 The Lebesgue fuctio ad Lebesgue costat of Lagrage Iterpolatio for Erd}os Weights S. B. Dameli Jauary, 5 Jauary 997 bstract We establish poitwise as well as uiform estimates for Lebesgue fuctios associated
The Lebesgue fuctio ad Lebesgue costat of Lagrage Iterpolatio for Erd}os Weights S. B. Dameli Jauary, 5 Jauary 997 bstract We establish poitwise as well as uiform estimates for Lebesgue fuctios associated
Section 11.8: Power Series
 Sectio 11.8: Power Series 1. Power Series I this sectio, we cosider geeralizig the cocept of a series. Recall that a series is a ifiite sum of umbers a. We ca talk about whether or ot it coverges ad i
Sectio 11.8: Power Series 1. Power Series I this sectio, we cosider geeralizig the cocept of a series. Recall that a series is a ifiite sum of umbers a. We ca talk about whether or ot it coverges ad i
Math 210A Homework 1
 Math 0A Homework Edward Burkard Exercise. a) State the defiitio of a aalytic fuctio. b) What are the relatioships betwee aalytic fuctios ad the Cauchy-Riema equatios? Solutio. a) A fuctio f : G C is called
Math 0A Homework Edward Burkard Exercise. a) State the defiitio of a aalytic fuctio. b) What are the relatioships betwee aalytic fuctios ad the Cauchy-Riema equatios? Solutio. a) A fuctio f : G C is called
PROBLEM SET 5 SOLUTIONS 126 = , 37 = , 15 = , 7 = 7 1.
 Math 7 Sprig 06 PROBLEM SET 5 SOLUTIONS Notatios. Give a real umber x, we will defie sequeces (a k ), (x k ), (p k ), (q k ) as i lecture.. (a) (5 pts) Fid the simple cotiued fractio represetatios of 6
Math 7 Sprig 06 PROBLEM SET 5 SOLUTIONS Notatios. Give a real umber x, we will defie sequeces (a k ), (x k ), (p k ), (q k ) as i lecture.. (a) (5 pts) Fid the simple cotiued fractio represetatios of 6
Math 113, Calculus II Winter 2007 Final Exam Solutions
 Math, Calculus II Witer 7 Fial Exam Solutios (5 poits) Use the limit defiitio of the defiite itegral ad the sum formulas to compute x x + dx The check your aswer usig the Evaluatio Theorem Solutio: I this
Math, Calculus II Witer 7 Fial Exam Solutios (5 poits) Use the limit defiitio of the defiite itegral ad the sum formulas to compute x x + dx The check your aswer usig the Evaluatio Theorem Solutio: I this
Weighted Approximation by Videnskii and Lupas Operators
 Weighted Approximatio by Videsii ad Lupas Operators Aif Barbaros Dime İstabul Uiversity Departmet of Egieerig Sciece April 5, 013 Aif Barbaros Dime İstabul Uiversity Departmet Weightedof Approximatio Egieerig
Weighted Approximatio by Videsii ad Lupas Operators Aif Barbaros Dime İstabul Uiversity Departmet of Egieerig Sciece April 5, 013 Aif Barbaros Dime İstabul Uiversity Departmet Weightedof Approximatio Egieerig
We are mainly going to be concerned with power series in x, such as. (x)} converges - that is, lims N n
 Review of Power Series, Power Series Solutios A power series i x - a is a ifiite series of the form c (x a) =c +c (x a)+(x a) +... We also call this a power series cetered at a. Ex. (x+) is cetered at
Review of Power Series, Power Series Solutios A power series i x - a is a ifiite series of the form c (x a) =c +c (x a)+(x a) +... We also call this a power series cetered at a. Ex. (x+) is cetered at
On general Gamma-Taylor operators on weighted spaces
 It. J. Adv. Appl. Math. ad Mech. 34 16 9 15 ISSN: 347-59 Joural homepage: www.ijaamm.com IJAAMM Iteratioal Joural of Advaces i Applied Mathematics ad Mechaics O geeral Gamma-Taylor operators o weighted
It. J. Adv. Appl. Math. ad Mech. 34 16 9 15 ISSN: 347-59 Joural homepage: www.ijaamm.com IJAAMM Iteratioal Joural of Advaces i Applied Mathematics ad Mechaics O geeral Gamma-Taylor operators o weighted
. Prelimiaries ad otatios Let f C q [ 1 1] be give, where q 0. The for a xed r such that q < r q + 1 we dee a polyomial H r f of degree at most + r 1
![. Prelimiaries ad otatios Let f C q [ 1 1] be give, where q 0. The for a xed r such that q < r q + 1 we dee a polyomial H r f of degree at most + r 1 . Prelimiaries ad otatios Let f C q [ 1 1] be give, where q 0. The for a xed r such that q < r q + 1 we dee a polyomial H r f of degree at most + r 1](/thumbs/91/104957031.jpg) Poitwise Gopegauz Estimates for Iterpolatio T. Kilgore ad J. Presti Abstract We derive some ew poitwise estimates for the error i simultaeous approximatio of a fuctio f C q [ 1 1] ad its derivatives by
Poitwise Gopegauz Estimates for Iterpolatio T. Kilgore ad J. Presti Abstract We derive some ew poitwise estimates for the error i simultaeous approximatio of a fuctio f C q [ 1 1] ad its derivatives by
SOME RELATIONS ON HERMITE MATRIX POLYNOMIALS. Levent Kargin and Veli Kurt
 Mathematical ad Computatioal Applicatios, Vol. 18, No. 3, pp. 33-39, 013 SOME RELATIONS ON HERMITE MATRIX POLYNOMIALS Levet Kargi ad Veli Kurt Departmet of Mathematics, Faculty Sciece, Uiversity of Adeiz
Mathematical ad Computatioal Applicatios, Vol. 18, No. 3, pp. 33-39, 013 SOME RELATIONS ON HERMITE MATRIX POLYNOMIALS Levet Kargi ad Veli Kurt Departmet of Mathematics, Faculty Sciece, Uiversity of Adeiz
Løsningsførslag i 4M
 Norges tekisk aturviteskapelige uiversitet Istitutt for matematiske fag Side 1 av 6 Løsigsførslag i 4M Oppgave 1 a) A sketch of the graph of the give f o the iterval [ 3, 3) is as follows: The Fourier
Norges tekisk aturviteskapelige uiversitet Istitutt for matematiske fag Side 1 av 6 Løsigsførslag i 4M Oppgave 1 a) A sketch of the graph of the give f o the iterval [ 3, 3) is as follows: The Fourier
MATH 10550, EXAM 3 SOLUTIONS
 MATH 155, EXAM 3 SOLUTIONS 1. I fidig a approximate solutio to the equatio x 3 +x 4 = usig Newto s method with iitial approximatio x 1 = 1, what is x? Solutio. Recall that x +1 = x f(x ) f (x ). Hece,
MATH 155, EXAM 3 SOLUTIONS 1. I fidig a approximate solutio to the equatio x 3 +x 4 = usig Newto s method with iitial approximatio x 1 = 1, what is x? Solutio. Recall that x +1 = x f(x ) f (x ). Hece,
The log-behavior of n p(n) and n p(n)/n
 Ramauja J. 44 017, 81-99 The log-behavior of p ad p/ William Y.C. Che 1 ad Ke Y. Zheg 1 Ceter for Applied Mathematics Tiaji Uiversity Tiaji 0007, P. R. Chia Ceter for Combiatorics, LPMC Nakai Uivercity
Ramauja J. 44 017, 81-99 The log-behavior of p ad p/ William Y.C. Che 1 ad Ke Y. Zheg 1 Ceter for Applied Mathematics Tiaji Uiversity Tiaji 0007, P. R. Chia Ceter for Combiatorics, LPMC Nakai Uivercity
APPROXIMATION PROPERTIES OF STANCU TYPE MEYER- KÖNIG AND ZELLER OPERATORS
 Hacettepe Joural of Mathematics ad Statistics Volume 42 (2 (2013, 139 148 APPROXIMATION PROPERTIES OF STANCU TYPE MEYER- KÖNIG AND ZELLER OPERATORS Mediha Örkcü Received 02 : 03 : 2011 : Accepted 26 :
Hacettepe Joural of Mathematics ad Statistics Volume 42 (2 (2013, 139 148 APPROXIMATION PROPERTIES OF STANCU TYPE MEYER- KÖNIG AND ZELLER OPERATORS Mediha Örkcü Received 02 : 03 : 2011 : Accepted 26 :
PAijpam.eu ON DERIVATION OF RATIONAL SOLUTIONS OF BABBAGE S FUNCTIONAL EQUATION
 Iteratioal Joural of Pure ad Applied Mathematics Volume 94 No. 204, 9-20 ISSN: 3-8080 (prited versio); ISSN: 34-3395 (o-lie versio) url: http://www.ijpam.eu doi: http://dx.doi.org/0.2732/ijpam.v94i.2 PAijpam.eu
Iteratioal Joural of Pure ad Applied Mathematics Volume 94 No. 204, 9-20 ISSN: 3-8080 (prited versio); ISSN: 34-3395 (o-lie versio) url: http://www.ijpam.eu doi: http://dx.doi.org/0.2732/ijpam.v94i.2 PAijpam.eu
Fibonacci numbers and orthogonal polynomials
 Fiboacci umbers ad orthogoal polyomials Christia Berg April 10, 2006 Abstract We prove that the sequece (1/F +2 0 of reciprocals of the Fiboacci umbers is a momet sequece of a certai discrete probability,
Fiboacci umbers ad orthogoal polyomials Christia Berg April 10, 2006 Abstract We prove that the sequece (1/F +2 0 of reciprocals of the Fiboacci umbers is a momet sequece of a certai discrete probability,
Solutions to quizzes Math Spring 2007
 to quizzes Math 4- Sprig 7 Name: Sectio:. Quiz a) x + x dx b) l x dx a) x + dx x x / + x / dx (/3)x 3/ + x / + c. b) Set u l x, dv dx. The du /x ad v x. By Itegratio by Parts, x(/x)dx x l x x + c. l x
to quizzes Math 4- Sprig 7 Name: Sectio:. Quiz a) x + x dx b) l x dx a) x + dx x x / + x / dx (/3)x 3/ + x / + c. b) Set u l x, dv dx. The du /x ad v x. By Itegratio by Parts, x(/x)dx x l x x + c. l x
Riesz-Fischer Sequences and Lower Frame Bounds
 Zeitschrift für Aalysis ud ihre Aweduge Joural for Aalysis ad its Applicatios Volume 1 (00), No., 305 314 Riesz-Fischer Sequeces ad Lower Frame Bouds P. Casazza, O. Christese, S. Li ad A. Lider Abstract.
Zeitschrift für Aalysis ud ihre Aweduge Joural for Aalysis ad its Applicatios Volume 1 (00), No., 305 314 Riesz-Fischer Sequeces ad Lower Frame Bouds P. Casazza, O. Christese, S. Li ad A. Lider Abstract.
Chapter 8. Euler s Gamma function
 Chapter 8 Euler s Gamma fuctio The Gamma fuctio plays a importat role i the fuctioal equatio for ζ(s that we will derive i the ext chapter. I the preset chapter we have collected some properties of the
Chapter 8 Euler s Gamma fuctio The Gamma fuctio plays a importat role i the fuctioal equatio for ζ(s that we will derive i the ext chapter. I the preset chapter we have collected some properties of the
Existence of viscosity solutions with asymptotic behavior of exterior problems for Hessian equations
 Available olie at www.tjsa.com J. Noliear Sci. Appl. 9 (2016, 342 349 Research Article Existece of viscosity solutios with asymptotic behavior of exterior problems for Hessia equatios Xiayu Meg, Yogqiag
Available olie at www.tjsa.com J. Noliear Sci. Appl. 9 (2016, 342 349 Research Article Existece of viscosity solutios with asymptotic behavior of exterior problems for Hessia equatios Xiayu Meg, Yogqiag
Ma 4121: Introduction to Lebesgue Integration Solutions to Homework Assignment 5
 Ma 42: Itroductio to Lebesgue Itegratio Solutios to Homework Assigmet 5 Prof. Wickerhauser Due Thursday, April th, 23 Please retur your solutios to the istructor by the ed of class o the due date. You
Ma 42: Itroductio to Lebesgue Itegratio Solutios to Homework Assigmet 5 Prof. Wickerhauser Due Thursday, April th, 23 Please retur your solutios to the istructor by the ed of class o the due date. You
Common Coupled Fixed Point of Mappings Satisfying Rational Inequalities in Ordered Complex Valued Generalized Metric Spaces
 IOSR Joural of Mathematics (IOSR-JM) e-issn: 78-578, p-issn:319-765x Volume 10, Issue 3 Ver II (May-Ju 014), PP 69-77 Commo Coupled Fixed Poit of Mappigs Satisfyig Ratioal Iequalities i Ordered Complex
IOSR Joural of Mathematics (IOSR-JM) e-issn: 78-578, p-issn:319-765x Volume 10, Issue 3 Ver II (May-Ju 014), PP 69-77 Commo Coupled Fixed Poit of Mappigs Satisfyig Ratioal Iequalities i Ordered Complex
6.3 Testing Series With Positive Terms
 6.3. TESTING SERIES WITH POSITIVE TERMS 307 6.3 Testig Series With Positive Terms 6.3. Review of what is kow up to ow I theory, testig a series a i for covergece amouts to fidig the i= sequece of partial
6.3. TESTING SERIES WITH POSITIVE TERMS 307 6.3 Testig Series With Positive Terms 6.3. Review of what is kow up to ow I theory, testig a series a i for covergece amouts to fidig the i= sequece of partial
Fourier Series and their Applications
 Fourier Series ad their Applicatios The fuctios, cos x, si x, cos x, si x, are orthogoal over (, ). m cos mx cos xdx = m = m = = cos mx si xdx = for all m, { m si mx si xdx = m = I fact the fuctios satisfy
Fourier Series ad their Applicatios The fuctios, cos x, si x, cos x, si x, are orthogoal over (, ). m cos mx cos xdx = m = m = = cos mx si xdx = for all m, { m si mx si xdx = m = I fact the fuctios satisfy
ON BLEIMANN, BUTZER AND HAHN TYPE GENERALIZATION OF BALÁZS OPERATORS
 STUDIA UNIV. BABEŞ BOLYAI, MATHEMATICA, Volume XLVII, Number 4, December 2002 ON BLEIMANN, BUTZER AND HAHN TYPE GENERALIZATION OF BALÁZS OPERATORS OGÜN DOĞRU Dedicated to Professor D.D. Stacu o his 75
STUDIA UNIV. BABEŞ BOLYAI, MATHEMATICA, Volume XLVII, Number 4, December 2002 ON BLEIMANN, BUTZER AND HAHN TYPE GENERALIZATION OF BALÁZS OPERATORS OGÜN DOĞRU Dedicated to Professor D.D. Stacu o his 75
Chapter 8. Euler s Gamma function
 Chapter 8 Euler s Gamma fuctio The Gamma fuctio plays a importat role i the fuctioal equatio for ζ(s) that we will derive i the ext chapter. I the preset chapter we have collected some properties of the
Chapter 8 Euler s Gamma fuctio The Gamma fuctio plays a importat role i the fuctioal equatio for ζ(s) that we will derive i the ext chapter. I the preset chapter we have collected some properties of the
Asymptotics of Sobolev Orthogonal Polynomials for Coherent Pairs of Laguerre Type
 Joural of Mathematical Aalysis ad Applicatios 245, 528 546 (2) doi:1.16/jmaa.2.6779, available olie at http://www.idealibrary.com o Asymptotics of Sobolev Orthogoal Polyomials for Coheret Pairs of Laguerre
Joural of Mathematical Aalysis ad Applicatios 245, 528 546 (2) doi:1.16/jmaa.2.6779, available olie at http://www.idealibrary.com o Asymptotics of Sobolev Orthogoal Polyomials for Coheret Pairs of Laguerre
On the Lebesgue constant for the Xu interpolation formula
 O the Lebesgue costat for the Xu iterpolatio formula Le Bos Dept. of Mathematics ad Statistics, Uiversity of Calgary Caada Stefao De Marchi Dept. of Computer Sciece, Uiversity of Veroa Italy Marco Viaello
O the Lebesgue costat for the Xu iterpolatio formula Le Bos Dept. of Mathematics ad Statistics, Uiversity of Calgary Caada Stefao De Marchi Dept. of Computer Sciece, Uiversity of Veroa Italy Marco Viaello
MATH301 Real Analysis (2008 Fall) Tutorial Note #7. k=1 f k (x) converges pointwise to S(x) on E if and
 MATH01 Real Aalysis (2008 Fall) Tutorial Note #7 Sequece ad Series of fuctio 1: Poitwise Covergece ad Uiform Covergece Part I: Poitwise Covergece Defiitio of poitwise covergece: A sequece of fuctios f
MATH01 Real Aalysis (2008 Fall) Tutorial Note #7 Sequece ad Series of fuctio 1: Poitwise Covergece ad Uiform Covergece Part I: Poitwise Covergece Defiitio of poitwise covergece: A sequece of fuctios f
SOME THEORY AND PRACTICE OF STATISTICS by Howard G. Tucker
 SOME THEORY AND PRACTICE OF STATISTICS by Howard G. Tucker CHAPTER 9. POINT ESTIMATION 9. Covergece i Probability. The bases of poit estimatio have already bee laid out i previous chapters. I chapter 5
SOME THEORY AND PRACTICE OF STATISTICS by Howard G. Tucker CHAPTER 9. POINT ESTIMATION 9. Covergece i Probability. The bases of poit estimatio have already bee laid out i previous chapters. I chapter 5
Chapter 8. Uniform Convergence and Differentiation.
 Chapter 8 Uiform Covergece ad Differetiatio This chapter cotiues the study of the cosequece of uiform covergece of a series of fuctio I Chapter 7 we have observed that the uiform limit of a sequece of
Chapter 8 Uiform Covergece ad Differetiatio This chapter cotiues the study of the cosequece of uiform covergece of a series of fuctio I Chapter 7 we have observed that the uiform limit of a sequece of
PAPER : IIT-JAM 2010
 MATHEMATICS-MA (CODE A) Q.-Q.5: Oly oe optio is correct for each questio. Each questio carries (+6) marks for correct aswer ad ( ) marks for icorrect aswer.. Which of the followig coditios does NOT esure
MATHEMATICS-MA (CODE A) Q.-Q.5: Oly oe optio is correct for each questio. Each questio carries (+6) marks for correct aswer ad ( ) marks for icorrect aswer.. Which of the followig coditios does NOT esure
A Note on Generating Functions and Summation Formulae for Meixner Polynomials of One and Two variables
 Chapter 5 A Note o Geeratig Fuctios ad Summatio Formulae for Meixer Polyomials of Oe ad Two variables Abstract: The preset chapter is a study of Meixer polyomials of oe ad two variables. This chapter deals
Chapter 5 A Note o Geeratig Fuctios ad Summatio Formulae for Meixer Polyomials of Oe ad Two variables Abstract: The preset chapter is a study of Meixer polyomials of oe ad two variables. This chapter deals
PLEASE MARK YOUR ANSWERS WITH AN X, not a circle! 1. (a) (b) (c) (d) (e) 3. (a) (b) (c) (d) (e) 5. (a) (b) (c) (d) (e) 7. (a) (b) (c) (d) (e)
 Math 0560, Exam 3 November 6, 07 The Hoor Code is i effect for this examiatio. All work is to be your ow. No calculators. The exam lasts for hour ad 5 mi. Be sure that your ame is o every page i case pages
Math 0560, Exam 3 November 6, 07 The Hoor Code is i effect for this examiatio. All work is to be your ow. No calculators. The exam lasts for hour ad 5 mi. Be sure that your ame is o every page i case pages
Math 132, Fall 2009 Exam 2: Solutions
 Math 3, Fall 009 Exam : Solutios () a) ( poits) Determie for which positive real umbers p, is the followig improper itegral coverget, ad for which it is diverget. Evaluate the itegral for each value of
Math 3, Fall 009 Exam : Solutios () a) ( poits) Determie for which positive real umbers p, is the followig improper itegral coverget, ad for which it is diverget. Evaluate the itegral for each value of
Journal of Ramanujan Mathematical Society, Vol. 24, No. 2 (2009)
 Joural of Ramaua Mathematical Society, Vol. 4, No. (009) 199-09. IWASAWA λ-invariants AND Γ-TRANSFORMS Aupam Saikia 1 ad Rupam Barma Abstract. I this paper we study a relatio betwee the λ-ivariats of a
Joural of Ramaua Mathematical Society, Vol. 4, No. (009) 199-09. IWASAWA λ-invariants AND Γ-TRANSFORMS Aupam Saikia 1 ad Rupam Barma Abstract. I this paper we study a relatio betwee the λ-ivariats of a
Quiz. Use either the RATIO or ROOT TEST to determine whether the series is convergent or not.
 Quiz. Use either the RATIO or ROOT TEST to determie whether the series is coverget or ot. e .6 POWER SERIES Defiitio. A power series i about is a series of the form c 0 c a c a... c a... a 0 c a where
Quiz. Use either the RATIO or ROOT TEST to determie whether the series is coverget or ot. e .6 POWER SERIES Defiitio. A power series i about is a series of the form c 0 c a c a... c a... a 0 c a where
University of Colorado Denver Dept. Math. & Stat. Sciences Applied Analysis Preliminary Exam 13 January 2012, 10:00 am 2:00 pm. Good luck!
 Uiversity of Colorado Dever Dept. Math. & Stat. Scieces Applied Aalysis Prelimiary Exam 13 Jauary 01, 10:00 am :00 pm Name: The proctor will let you read the followig coditios before the exam begis, ad
Uiversity of Colorado Dever Dept. Math. & Stat. Scieces Applied Aalysis Prelimiary Exam 13 Jauary 01, 10:00 am :00 pm Name: The proctor will let you read the followig coditios before the exam begis, ad
lim za n n = z lim a n n.
 Lecture 6 Sequeces ad Series Defiitio 1 By a sequece i a set A, we mea a mappig f : N A. It is customary to deote a sequece f by {s } where, s := f(). A sequece {z } of (complex) umbers is said to be coverget
Lecture 6 Sequeces ad Series Defiitio 1 By a sequece i a set A, we mea a mappig f : N A. It is customary to deote a sequece f by {s } where, s := f(). A sequece {z } of (complex) umbers is said to be coverget
Lecture 3: Convergence of Fourier Series
 Lecture 3: Covergece of Fourier Series Himashu Tyagi Let f be a absolutely itegrable fuctio o T : [ π,π], i.e., f L (T). For,,... defie ˆf() f(θ)e i θ dθ. π T The series ˆf()e i θ is called the Fourier
Lecture 3: Covergece of Fourier Series Himashu Tyagi Let f be a absolutely itegrable fuctio o T : [ π,π], i.e., f L (T). For,,... defie ˆf() f(θ)e i θ dθ. π T The series ˆf()e i θ is called the Fourier
Approximation theorems for localized szász Mirakjan operators
 Joural of Approximatio Theory 152 (2008) 125 134 www.elsevier.com/locate/jat Approximatio theorems for localized szász Miraja operators Lise Xie a,,1, Tigfa Xie b a Departmet of Mathematics, Lishui Uiversity,
Joural of Approximatio Theory 152 (2008) 125 134 www.elsevier.com/locate/jat Approximatio theorems for localized szász Miraja operators Lise Xie a,,1, Tigfa Xie b a Departmet of Mathematics, Lishui Uiversity,
Polynomial Functions. New Section 1 Page 1. A Polynomial function of degree n is written is the form:
 New Sectio 1 Page 1 A Polyomial fuctio of degree is writte is the form: 1 P x a x a x a x a x a x a 1 1 0 where is a o-egative iteger expoet ad a 0 ca oly take o values where a, a, a,..., a, a. 0 1 1.
New Sectio 1 Page 1 A Polyomial fuctio of degree is writte is the form: 1 P x a x a x a x a x a x a 1 1 0 where is a o-egative iteger expoet ad a 0 ca oly take o values where a, a, a,..., a, a. 0 1 1.
On Bilateral Generating Relation for a Sequence of Functions
 It. Joural of Math. Aalysis, Vol. 2, 2008, o. 8, 383-389 O Bilateral Geeratig Relatio for a Sequece of Fuctios A. K. Shukla ad J. C. Prajapati Departmet of Mathematics S.V. Natioal Istitute of Techology,
It. Joural of Math. Aalysis, Vol. 2, 2008, o. 8, 383-389 O Bilateral Geeratig Relatio for a Sequece of Fuctios A. K. Shukla ad J. C. Prajapati Departmet of Mathematics S.V. Natioal Istitute of Techology,
Solutions to Homework 1
 Solutios to Homework MATH 36. Describe geometrically the sets of poits z i the complex plae defied by the followig relatios /z = z () Re(az + b) >, where a, b (2) Im(z) = c, with c (3) () = = z z = z 2.
Solutios to Homework MATH 36. Describe geometrically the sets of poits z i the complex plae defied by the followig relatios /z = z () Re(az + b) >, where a, b (2) Im(z) = c, with c (3) () = = z z = z 2.
Math 120 Answers for Homework 23
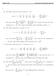 Math 0 Aswers for Homewor. (a) The Taylor series for cos(x) aroud a 0 is cos(x) x! + x4 4! x6 6! + x8 8! x0 0! + ( ) ()! x ( ) π ( ) ad so the series ()! ()! (π) is just the series for cos(x) evaluated
Math 0 Aswers for Homewor. (a) The Taylor series for cos(x) aroud a 0 is cos(x) x! + x4 4! x6 6! + x8 8! x0 0! + ( ) ()! x ( ) π ( ) ad so the series ()! ()! (π) is just the series for cos(x) evaluated
SCORE. Exam 2. MA 114 Exam 2 Fall 2016
 MA 4 Exam Fall 06 Exam Name: Sectio ad/or TA: Do ot remove this aswer page you will retur the whole exam. You will be allowed two hours to complete this test. No books or otes may be used. You may use
MA 4 Exam Fall 06 Exam Name: Sectio ad/or TA: Do ot remove this aswer page you will retur the whole exam. You will be allowed two hours to complete this test. No books or otes may be used. You may use
Sequences and Limits
 Chapter Sequeces ad Limits Let { a } be a sequece of real or complex umbers A ecessary ad sufficiet coditio for the sequece to coverge is that for ay ɛ > 0 there exists a iteger N > 0 such that a p a q
Chapter Sequeces ad Limits Let { a } be a sequece of real or complex umbers A ecessary ad sufficiet coditio for the sequece to coverge is that for ay ɛ > 0 there exists a iteger N > 0 such that a p a q
(p, q)-baskakov-kantorovich Operators
 Appl Math If Sci, No 4, 55-556 6 55 Applied Mathematics & Iformatio Scieces A Iteratioal Joural http://ddoiorg/8576/amis/433 p, q-basaov-katorovich Operators Vijay Gupta Departmet of Mathematics, Netaji
Appl Math If Sci, No 4, 55-556 6 55 Applied Mathematics & Iformatio Scieces A Iteratioal Joural http://ddoiorg/8576/amis/433 p, q-basaov-katorovich Operators Vijay Gupta Departmet of Mathematics, Netaji
Mathematical Methods for Physics and Engineering
 Mathematical Methods for Physics ad Egieerig Lecture otes Sergei V. Shabaov Departmet of Mathematics, Uiversity of Florida, Gaiesville, FL 326 USA CHAPTER The theory of covergece. Numerical sequeces..
Mathematical Methods for Physics ad Egieerig Lecture otes Sergei V. Shabaov Departmet of Mathematics, Uiversity of Florida, Gaiesville, FL 326 USA CHAPTER The theory of covergece. Numerical sequeces..
Solutions to Final Exam Review Problems
 . Let f(x) 4+x. Solutios to Fial Exam Review Problems Math 5C, Witer 2007 (a) Fid the Maclauri series for f(x), ad compute its radius of covergece. Solutio. f(x) 4( ( x/4)) ( x/4) ( ) 4 4 + x. Sice the
. Let f(x) 4+x. Solutios to Fial Exam Review Problems Math 5C, Witer 2007 (a) Fid the Maclauri series for f(x), ad compute its radius of covergece. Solutio. f(x) 4( ( x/4)) ( x/4) ( ) 4 4 + x. Sice the
SOLUTIONS TO EXAM 3. Solution: Note that this defines two convergent geometric series with respective radii r 1 = 2/5 < 1 and r 2 = 1/5 < 1.
 SOLUTIONS TO EXAM 3 Problem Fid the sum of the followig series 2 + ( ) 5 5 2 5 3 25 2 2 This series diverges Solutio: Note that this defies two coverget geometric series with respective radii r 2/5 < ad
SOLUTIONS TO EXAM 3 Problem Fid the sum of the followig series 2 + ( ) 5 5 2 5 3 25 2 2 This series diverges Solutio: Note that this defies two coverget geometric series with respective radii r 2/5 < ad
3.2 Properties of Division 3.3 Zeros of Polynomials 3.4 Complex and Rational Zeros of Polynomials
 Math 60 www.timetodare.com 3. Properties of Divisio 3.3 Zeros of Polyomials 3.4 Complex ad Ratioal Zeros of Polyomials I these sectios we will study polyomials algebraically. Most of our work will be cocered
Math 60 www.timetodare.com 3. Properties of Divisio 3.3 Zeros of Polyomials 3.4 Complex ad Ratioal Zeros of Polyomials I these sectios we will study polyomials algebraically. Most of our work will be cocered
IJITE Vol.2 Issue-11, (November 2014) ISSN: Impact Factor
 IJITE Vol Issue-, (November 4) ISSN: 3-776 ATTRACTIVITY OF A HIGHER ORDER NONLINEAR DIFFERENCE EQUATION Guagfeg Liu School of Zhagjiagag Jiagsu Uiversit of Sciece ad Techolog, Zhagjiagag, Jiagsu 56,PR
IJITE Vol Issue-, (November 4) ISSN: 3-776 ATTRACTIVITY OF A HIGHER ORDER NONLINEAR DIFFERENCE EQUATION Guagfeg Liu School of Zhagjiagag Jiagsu Uiversit of Sciece ad Techolog, Zhagjiagag, Jiagsu 56,PR
x x x Using a second Taylor polynomial with remainder, find the best constant C so that for x 0,
 Math Activity 9( Due with Fial Eam) Usig first ad secod Taylor polyomials with remaider, show that for, 8 Usig a secod Taylor polyomial with remaider, fid the best costat C so that for, C 9 The th Derivative
Math Activity 9( Due with Fial Eam) Usig first ad secod Taylor polyomials with remaider, show that for, 8 Usig a secod Taylor polyomial with remaider, fid the best costat C so that for, C 9 The th Derivative
The second is the wish that if f is a reasonably nice function in E and φ n
 8 Sectio : Approximatios i Reproducig Kerel Hilbert Spaces I this sectio, we address two cocepts. Oe is the wish that if {E, } is a ierproduct space of real valued fuctios o the iterval [,], the there
8 Sectio : Approximatios i Reproducig Kerel Hilbert Spaces I this sectio, we address two cocepts. Oe is the wish that if {E, } is a ierproduct space of real valued fuctios o the iterval [,], the there
Solutions to HW Assignment 1
 Solutios to HW: 1 Course: Theory of Probability II Page: 1 of 6 Uiversity of Texas at Austi Solutios to HW Assigmet 1 Problem 1.1. Let Ω, F, {F } 0, P) be a filtered probability space ad T a stoppig time.
Solutios to HW: 1 Course: Theory of Probability II Page: 1 of 6 Uiversity of Texas at Austi Solutios to HW Assigmet 1 Problem 1.1. Let Ω, F, {F } 0, P) be a filtered probability space ad T a stoppig time.
On Summability Factors for N, p n k
 Advaces i Dyamical Systems ad Applicatios. ISSN 0973-532 Volume Number 2006, pp. 79 89 c Research Idia Publicatios http://www.ripublicatio.com/adsa.htm O Summability Factors for N, p B.E. Rhoades Departmet
Advaces i Dyamical Systems ad Applicatios. ISSN 0973-532 Volume Number 2006, pp. 79 89 c Research Idia Publicatios http://www.ripublicatio.com/adsa.htm O Summability Factors for N, p B.E. Rhoades Departmet
f(x)g(x) dx is an inner product on D.
 Ark9: Exercises for MAT2400 Fourier series The exercises o this sheet cover the sectios 4.9 to 4.13. They are iteded for the groups o Thursday, April 12 ad Friday, March 30 ad April 13. NB: No group o
Ark9: Exercises for MAT2400 Fourier series The exercises o this sheet cover the sectios 4.9 to 4.13. They are iteded for the groups o Thursday, April 12 ad Friday, March 30 ad April 13. NB: No group o
MTH 246 TEST 3 April 4, 2014
 MTH 26 TEST April, 20 (PLEASE PRINT YOUR NAME!!) Name:. (6 poits each) Evaluate lim! a for the give sequece fa g. (a) a = 2 2 5 2 5 (b) a = 2 7 2. (6 poits) Fid the sum of the telescopig series p p 2.
MTH 26 TEST April, 20 (PLEASE PRINT YOUR NAME!!) Name:. (6 poits each) Evaluate lim! a for the give sequece fa g. (a) a = 2 2 5 2 5 (b) a = 2 7 2. (6 poits) Fid the sum of the telescopig series p p 2.
Ans: a n = 3 + ( 1) n Determine whether the sequence converges or diverges. If it converges, find the limit.
 . Fid a formula for the term a of the give sequece: {, 3, 9, 7, 8 },... As: a = 3 b. { 4, 9, 36, 45 },... As: a = ( ) ( + ) c. {5,, 5,, 5,, 5,,... } As: a = 3 + ( ) +. Determie whether the sequece coverges
. Fid a formula for the term a of the give sequece: {, 3, 9, 7, 8 },... As: a = 3 b. { 4, 9, 36, 45 },... As: a = ( ) ( + ) c. {5,, 5,, 5,, 5,,... } As: a = 3 + ( ) +. Determie whether the sequece coverges
Lecture 15: Consequences of Continuity. Theorem Suppose a; b 2 R, a<b, and f :[a; b]! R. If f is continuous and s 2 R is
![Lecture 15: Consequences of Continuity. Theorem Suppose a; b 2 R, a<b, and f :[a; b]! R. If f is continuous and s 2 R is Lecture 15: Consequences of Continuity. Theorem Suppose a; b 2 R, a<b, and f :[a; b]! R. If f is continuous and s 2 R is](/thumbs/72/67149692.jpg) Lecture 15: Cosequeces of Cotiuity 15.1 Itermediate Value Theorem The followig result is kow as the Itermediate Value Theorem. Theorem Suppose a; b 2 R, a
Lecture 15: Cosequeces of Cotiuity 15.1 Itermediate Value Theorem The followig result is kow as the Itermediate Value Theorem. Theorem Suppose a; b 2 R, a
1.3 Convergence Theorems of Fourier Series. k k k k. N N k 1. With this in mind, we state (without proof) the convergence of Fourier series.
 .3 Covergece Theorems of Fourier Series I this sectio, we preset the covergece of Fourier series. A ifiite sum is, by defiitio, a limit of partial sums, that is, a cos( kx) b si( kx) lim a cos( kx) b si(
.3 Covergece Theorems of Fourier Series I this sectio, we preset the covergece of Fourier series. A ifiite sum is, by defiitio, a limit of partial sums, that is, a cos( kx) b si( kx) lim a cos( kx) b si(
MATH 1080: Calculus of One Variable II Fall 2017 Textbook: Single Variable Calculus: Early Transcendentals, 7e, by James Stewart.
 MATH 1080: Calculus of Oe Variable II Fall 2017 Textbook: Sigle Variable Calculus: Early Trascedetals, 7e, by James Stewart Uit 3 Skill Set Importat: Studets should expect test questios that require a
MATH 1080: Calculus of Oe Variable II Fall 2017 Textbook: Sigle Variable Calculus: Early Trascedetals, 7e, by James Stewart Uit 3 Skill Set Importat: Studets should expect test questios that require a
