Recitation 2: Binding, Semantics, and Safety : Foundations of Programming Languages
|
|
|
- Cassandra Greene
- 5 years ago
- Views:
Transcription
1 Recitation 2: Binding, Semantics, and Safety : Foundations of Programming Languages Charles Yuan, Jeanne Luning Prak September 5, Abstract Binding Trees The abstract syntax trees we saw previously contained the concept of variables, but not the ability to give variables meaning. To do that, we need the concept of binding, which is provided by the abstract binding tree, or abt. Like ast s, abt s are characterized by variables and operators, but operators have notion of binding. In an abt, every operator may specify a number of variables that are bound within the scope of the operator. Operators accordingly have arities that reflect the number and sorts of variables they bind. For example, an operator let of arity (Exp, Exp.Exp)Exp takes a first abt argument that has no bound variables of sort Exp and a second argument with one bound variable of sort Exp and which is also of sort Exp. The notation x.e is used to indicate a binder, or an expression coupled with a named bound variable. We might use such an operator to represent a let-expression in ML: let(1, x.x + 2) for let x = 1 in x + 2 end Inside an operator that binds some variable x, x is considered bound, and a variable that is not inside a binding of its own name is considered free. The distinction between bound and free variables is significant when we consider the semantics of substitution. Binders themselves are not valid abt s but for convenience we often use notation that pretends they are. 2 Statics The statics of a language is the system of rules that govern the meaning of the language at expression-level before the expression is evaluated (updated) according to a different set of rules known as the dynamics. It usually consists of typing judgments that determine whether an expression is well-formed. Given a language, we introduce two sorts, Typ and Exp, corresponding to the types and expressions of the language respectively. When parsing of the program completes, we will have an abt that can be decomposed into subtrees falling into these sorts. 1
2 2 3 DYNAMICS Example of the syntax of a language: Typ τ ::= num number Exp e ::= x variable num[n] literal plus(e 1 ; e 2 ) addition times(e 1 ; e 2 ) multiplication let(e 1 ; x.e 2 ) definition We then define a judgment, typing, which relates an expression e with its type τ using the typing context Γ: Γ e : τ Example of our language s typing judgment definition: The rules state the following: Variables are given types by the context. Numeric literals are of type num. Γ, x : τ x : τ Γ num[n] : num Γ e 1 : num Γ e 2 : num Γ plus(e 1 ; e 2 ) : num Γ e 1 : num Γ e 2 : num Γ times(e 1 ; e 2 ) : num Γ e 1 : τ 1 Γ, x : τ 1 e 2 : τ 2 Γ let(e 1 ; x.e 2 ) : τ 2 Sums and products of two expressions of type num are of type num. Given that e 1 has some type τ 1, if substituting e 1 for x with type τ 1 in e 2 would give it type τ 2, then let x = e 1 in e 2 has type τ 2. A unicity of typing theorem ensures the consistency of a type system. It says: For all Γ and e, there is at most one τ such that Γ e : τ. 3 Dynamics The dynamics of a language describe how expressions evaluate. In this class we mainly focus on structural dynamics, which is given by a system of transitions from one expression to another, until final states called values are reached. The judgment e val states that e is a value. The judgment e e states that expression e steps to expression e. Example of our language s value and step judgment definitions: num[n] val n 1 + n 2 = n plus(num[n 1 ]; num[n 2 ]) num[n]
3 3 3 DYNAMICS e 1 e 1 plus(e 1 ; e 2 ) plus(e 1 ; e 2) e 1 val e 2 e 2 plus(e 1 ; e 2 ) plus(e 1 ; e 2 ) n 1 n 2 = n times(num[n 1 ]; num[n 2 ]) num[n] e 1 e 1 times(e 1 ; e 2 ) times(e 1 ; e 2) e 1 val e 2 e 2 times(e 1 ; e 2 ) times(e 1 ; e 2 ) e 1 e 1 let(e 1 ; x.e 2 ) let(e 1 ; x.e 2) e 1 val let(e 1 ; x.e 2 ) [e 1 /x]e 2 The rules state the following: Numeric literals are values. Sums and products evaluate their first argument, then their second, then evaluate to the arithmetic result. Note that this constitutes an eager, left-to-right dynamics, meaning that arguments are evaluated immediately from left to right. Most languages we study in this course will share this property. Let-expressions evaluate their substitute argument, then perform substitution to yield a new expression. This is eager as before, though there is discussion in Section 5.2 of PFPL as to how it might be lazy instead. Note what the dynamics does not do: account for free variables, or likewise ill-typed expressions. The intention is for the statics check to have already occurred, and for dynamics to purely describe evaluation. Here we also did not account for runtime errors, but you will do so in Assignment 1. A canonical forms lemma says that if we know the type of an expression, we already know what the values of the expression look like. It looks like this: If e val, then [for each type τ in the language,] if Γ e : τ then e = V [where V is the form of the value]. Example of our language s canonical forms lemma: If e val, then if Γ e : num, then e = num[n] for some n. Not all languages have canonical forms, as it depends on the definition of values. There are two other useful notions for a dynamics: finality, which says that a well-typed expression is either a value or can step (never both); and determinacy, which says that an expression always steps to a unique expression if it can step at all. Finality is usually assumed to hold in this course, and so is determinacy (until much later in the course!).
4 4 4 TYPE SAFETY 4 Type Safety A progress theorem guarantees our language does not get stuck during execution: If e : τ, then either e val, or there exists e such that e e. A preservation theorem guarantees our language never violates the type of an expression: If e : τ and e e, then e : τ. Notice that the progress and preservation theorems only apply to typing judgments where the context is empty. This means that they only applies to closed terms: there can be no free variables in e. Together, progress and preservation constitute the central property of a language: type safety. Progress and preservation can be proven about a language using rule induction. 4.1 Progress Proof A proof of progress proceeds by rule induction on the typing derivation. We can specialize the principle of rule induction for a proof of progress on the example language like so: Let P(e) be the property that either e val or there exists an e such that e e. To prove that if e : τ, then either e val, or there exists e such that e e, it is sufficient to prove the following: P(num[n]) If P(e 1 ), P(e 2 ), e 1 : num, and e 2 : num, then P(plus(e 1 ; e 2 )) If P(e 1 ), P(e 2 ), e 1 : num, and e 2 : num, then P(times(e 1 ; e 2 )) If P(e 1 ), e 1 : τ 1, and x : τ 1 e 2 : τ 2, then P(let(e 1 ; x.e 2 )) The proof itself is left as an exercise. 4.2 Preservation Proof A proof of preservation proceeds by rule induction on the transition judgment, because it hinges on examining all possible transitions from a given expression. A proof of preservation for the example language is given below. In the below proof, we make use of the following lemmas: 1. Inversion on Typing: If Γ plus(e 1 ; e 2 ) : τ then τ = num, Γ e 1 : num, and Γ e 2 : num. If Γ times(e 1 ; e 2 ) : τ then τ = num, Γ e 1 : num, and Γ e 2 : num. If Γ let(e 1 ; x.e 2 ) : τ then Γ e 1 : τ 1 s.t. Γ, x : τ 1 e 2 : τ. 2. Substitution Lemma: If Γ, x : τ e : τ and Γ e : τ then Γ [e/x]e : τ. Proof: Let P(e, e ) be the property that if e : τ, then e : τ. Proceed by rule induction on judgment e e.
5 4.2 Preservation Proof 4 TYPE SAFETY Case: If n 1 + n 2 = n, then P(plus(num[n 1 ]; num[n 2 ]), num[n]) I.H.: n 1 + n 2 = n Assume plus(num[n 1 ]; num[n 2 ]) : τ WTS: num[n] : τ plus(num[n 1 ]; num[n 2 ]) : num [Inversion on Typing] num[n] : num [Typing rule for num] num[n] : τ [Take τ = num] Case: If P(e 1, e 1 ) and e 1 e 1, then P(plus(e 1; e 2 ), plus(e 1 ; e 2)) I.H.: P(e 1, e 1 ) and e 1 e 1 Assume plus(e 1 ; e 2 ) : τ WTS: plus(e 1 ; e 2) : τ plus(e 1 ; e 2 ) : num [Inversion on Typing] e 1 : num [Inversion on Typing] e 1 : num [I.H.] e 2 : num [Inversion on Typing] plus(e 1; e 2 ) : num [Typing rule for plus] plus(e 1; e 2 ) : τ [Take τ = num] Case: If P(e 2, e 2 ) and e 1 val and e 2 e 2, then P(plus(e 1; e 2 ), plus(e 1 ; e 2 )) I.H.: P(e 2, e 2 ) and e 1 val and e 2 e 2 Assume plus(e 1 ; e 2 ) : τ WTS: plus(e 1 ; e 2 ) : τ plus(e 1 ; e 2 ) : num [Inversion on Typing] e 2 : num [Inversion on Typing] e 2 : num [I.H.] e 1 : num [Inversion on Typing] plus(e 1 ; e 2) : num [Typing rule for plus] plus(e 1 ; e 2) : τ [Take τ = num] Case: If n 1 n 2 = n, then P(times(num[n 1 ]; num[n 2 ]), num[n]) [Identical to the proof for plus. Left as exercise.] Case: If P(e 1, e 1 ) and e 1 e 1, then P(times(e 1; e 2 ), times(e 1 ; e 2)) [Identical to the proof for plus. Left as exercise.] Case: If P(e 2, e 2 ) and e 1 val and e 2 e 2, then P(times(e 1; e 2 ), times(e 1 ; e 2 )) [Identical to the proof for plus. Left as exercise.] Case: If P(e 1, e 1 ) and e 1 e 1, then P(let(e 1; x.e 2 ), let(e 1 ; x.e 2)) I.H.: P(e 1, e 1 ) and e 1 e 1 Assume let(e 1 ; x.e 2 ) : τ 5
6 4.2 Preservation Proof 4 TYPE SAFETY WTS: let(e 1 ; x.e 2) : τ e 1 : τ 1 s.t. x : τ 1 e 2 : τ [Inversion on Typing] e 1 : τ 1 s.t. x : τ 1 e 2 : τ [I.H.] let(e 1; x.e 2 ) : τ [Typing rule for let] Case: If e 1 val, then P(let(e 1 ; x.e 2 ), [e 1 /x]e 2 ) I.H.: e 1 val Assume let(e 1 ; x.e 2 ) : τ WTS: [e 1 /x]e 2 : τ e 1 : τ 1 s.t. x : τ 1 e 2 : τ [Inversion on Typing] [e 1 /x]e 2 : τ [Substitution Lemma] This completes the proof of preservation for the example language. 6
Models of Computation,
 Models of Computation, 2010 1 Induction We use a lot of inductive techniques in this course, both to give definitions and to prove facts about our semantics So, it s worth taking a little while to set
Models of Computation, 2010 1 Induction We use a lot of inductive techniques in this course, both to give definitions and to prove facts about our semantics So, it s worth taking a little while to set
Lectures Notes on Progress
 Lectures Notes on Progress 15-312: Foundations of Programming Languages Frank Pfenning Lecture 7 September 21, 2004 In this lecture we prove the progress property for MinML, discuss type safety, and consider
Lectures Notes on Progress 15-312: Foundations of Programming Languages Frank Pfenning Lecture 7 September 21, 2004 In this lecture we prove the progress property for MinML, discuss type safety, and consider
The L Machines are very high-level, in two senses:
 What is a Computer? State of the machine. CMPSCI 630: Programming Languages An Abstract Machine for Control Spring 2009 (with thanks to Robert Harper) Internal registers, memory, etc. Initial and final
What is a Computer? State of the machine. CMPSCI 630: Programming Languages An Abstract Machine for Control Spring 2009 (with thanks to Robert Harper) Internal registers, memory, etc. Initial and final
Simply Typed Lambda Calculus
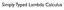 Simply Typed Lambda Calculus Language (ver1) Lambda calculus with boolean values t ::= x variable x : T.t abstraction tt application true false boolean values if ttt conditional expression Values v ::=
Simply Typed Lambda Calculus Language (ver1) Lambda calculus with boolean values t ::= x variable x : T.t abstraction tt application true false boolean values if ttt conditional expression Values v ::=
Lecture Notes on Data Abstraction
 Lecture Notes on Data Abstraction 15-814: Types and Programming Languages Frank Pfenning Lecture 14 October 23, 2018 1 Introduction Since we have moved from the pure λ-calculus to functional programming
Lecture Notes on Data Abstraction 15-814: Types and Programming Languages Frank Pfenning Lecture 14 October 23, 2018 1 Introduction Since we have moved from the pure λ-calculus to functional programming
COSE212: Programming Languages. Lecture 1 Inductive Definitions (1)
 COSE212: Programming Languages Lecture 1 Inductive Definitions (1) Hakjoo Oh 2017 Fall Hakjoo Oh COSE212 2017 Fall, Lecture 1 September 4, 2017 1 / 9 Inductive Definitions Inductive definition (induction)
COSE212: Programming Languages Lecture 1 Inductive Definitions (1) Hakjoo Oh 2017 Fall Hakjoo Oh COSE212 2017 Fall, Lecture 1 September 4, 2017 1 / 9 Inductive Definitions Inductive definition (induction)
Element x is R-minimal in X if y X. R(y, x).
 CMSC 22100/32100: Programming Languages Final Exam M. Blume December 11, 2008 1. (Well-founded sets and induction principles) (a) State the mathematical induction principle and justify it informally. 1
CMSC 22100/32100: Programming Languages Final Exam M. Blume December 11, 2008 1. (Well-founded sets and induction principles) (a) State the mathematical induction principle and justify it informally. 1
EDA045F: Program Analysis LECTURE 10: TYPES 1. Christoph Reichenbach
 EDA045F: Program Analysis LECTURE 10: TYPES 1 Christoph Reichenbach In the last lecture... Performance Counters Challenges in Dynamic Performance Analysis Taint Analysis Binary Instrumentation 2 / 44 Types
EDA045F: Program Analysis LECTURE 10: TYPES 1 Christoph Reichenbach In the last lecture... Performance Counters Challenges in Dynamic Performance Analysis Taint Analysis Binary Instrumentation 2 / 44 Types
Predicate Logic. Xinyu Feng 09/26/2011. University of Science and Technology of China (USTC)
 University of Science and Technology of China (USTC) 09/26/2011 Overview Predicate logic over integer expressions: a language of logical assertions, for example x. x + 0 = x Why discuss predicate logic?
University of Science and Technology of China (USTC) 09/26/2011 Overview Predicate logic over integer expressions: a language of logical assertions, for example x. x + 0 = x Why discuss predicate logic?
Predicate Logic. x. x + 0 = x. Predicate logic over integer expressions: a language of logical assertions, for example. Why discuss predicate logic?
 Predicate Logic Predicate logic over integer expressions: a language of logical assertions, for example x. x + 0 = x Why discuss predicate logic? It is an example of a simple language It has simple denotational
Predicate Logic Predicate logic over integer expressions: a language of logical assertions, for example x. x + 0 = x Why discuss predicate logic? It is an example of a simple language It has simple denotational
Introduction to Logic in Computer Science: Autumn 2006
 Introduction to Logic in Computer Science: Autumn 2006 Ulle Endriss Institute for Logic, Language and Computation University of Amsterdam Ulle Endriss 1 Plan for Today Today s class will be an introduction
Introduction to Logic in Computer Science: Autumn 2006 Ulle Endriss Institute for Logic, Language and Computation University of Amsterdam Ulle Endriss 1 Plan for Today Today s class will be an introduction
The Importance of Being Formal. Martin Henz. February 5, Propositional Logic
 The Importance of Being Formal Martin Henz February 5, 2014 Propositional Logic 1 Motivation In traditional logic, terms represent sets, and therefore, propositions are limited to stating facts on sets
The Importance of Being Formal Martin Henz February 5, 2014 Propositional Logic 1 Motivation In traditional logic, terms represent sets, and therefore, propositions are limited to stating facts on sets
COP-5555 PROGRAMMING LANGUAGEPRINCIPLES NOTES ON THE MECHANICAL EVALUATION OF APPLICATIVE EXPRESSSIONS
 COP-5555 PROGRAMMING LANGUAGEPRINCIPLES NOTES ON THE MECHANICAL EVALUATION OF APPLICATIVE EXPRESSSIONS The substitution mechanism for evaluating applicative expressions is convenient for humans, but inconvenient
COP-5555 PROGRAMMING LANGUAGEPRINCIPLES NOTES ON THE MECHANICAL EVALUATION OF APPLICATIVE EXPRESSSIONS The substitution mechanism for evaluating applicative expressions is convenient for humans, but inconvenient
Interoperation for Lazy and Eager Evaluation
 Interoperation for Lazy and Eager Evaluation 1 Matthews & Findler New method of interoperation Type safety, observational equivalence & transparency Eager evaluation strategies Lazy vs. eager 2 Lambda
Interoperation for Lazy and Eager Evaluation 1 Matthews & Findler New method of interoperation Type safety, observational equivalence & transparency Eager evaluation strategies Lazy vs. eager 2 Lambda
Typed Arithmetic Expressions
 Typed Arithmetic Expressions CS 550 Programming Languages Jeremy Johnson TAPL Chapters 3 and 5 1 Types and Safety Evaluation rules provide operational semantics for programming languages. The rules provide
Typed Arithmetic Expressions CS 550 Programming Languages Jeremy Johnson TAPL Chapters 3 and 5 1 Types and Safety Evaluation rules provide operational semantics for programming languages. The rules provide
Lecture Notes on Inductive Definitions
 Lecture Notes on Inductive Definitions 15-312: Foundations of Programming Languages Frank Pfenning Lecture 2 September 2, 2004 These supplementary notes review the notion of an inductive definition and
Lecture Notes on Inductive Definitions 15-312: Foundations of Programming Languages Frank Pfenning Lecture 2 September 2, 2004 These supplementary notes review the notion of an inductive definition and
High-Level Small-Step Operational Semantics for Transactions (Technical Companion)
 High-Level Small-Step Operational Semantics for Transactions (Technical Companion) Katherine F. Moore, Dan Grossman July 15, 2007 Abstract This document is the technical companion to our POPL 08 submission
High-Level Small-Step Operational Semantics for Transactions (Technical Companion) Katherine F. Moore, Dan Grossman July 15, 2007 Abstract This document is the technical companion to our POPL 08 submission
INTEROPERATION FOR LAZY AND EAGER EVALUATION. A Thesis. Presented to. the Faculty of California Polytechnic State University.
 INTEROPERATION FOR LAZY AND EAGER EVALUATION A Thesis Presented to the Faculty of California Polytechnic State University San Luis Obispo In Partial Fulfillment of the Requirements for the Degree Master
INTEROPERATION FOR LAZY AND EAGER EVALUATION A Thesis Presented to the Faculty of California Polytechnic State University San Luis Obispo In Partial Fulfillment of the Requirements for the Degree Master
Lecture Notes on Inductive Definitions
 Lecture Notes on Inductive Definitions 15-312: Foundations of Programming Languages Frank Pfenning Lecture 2 August 28, 2003 These supplementary notes review the notion of an inductive definition and give
Lecture Notes on Inductive Definitions 15-312: Foundations of Programming Languages Frank Pfenning Lecture 2 August 28, 2003 These supplementary notes review the notion of an inductive definition and give
Typing λ-terms. Types. Typed λ-terms. Base Types. The Typing Relation. Advanced Formal Methods. Lecture 3: Simply Typed Lambda calculus
 Course 2D1453, 200607 Advanced Formal Methods Lecture 3: Simply Typed Lambda calculus Mads Dam KTH/CSC Some material from B. Pierce: TAPL + some from G. Klein, NICTA Typing λterms The uptyped λcalculus
Course 2D1453, 200607 Advanced Formal Methods Lecture 3: Simply Typed Lambda calculus Mads Dam KTH/CSC Some material from B. Pierce: TAPL + some from G. Klein, NICTA Typing λterms The uptyped λcalculus
Propositional Logic. CS 3234: Logic and Formal Systems. Martin Henz and Aquinas Hobor. August 26, Generated on Tuesday 31 August, 2010, 16:54
 Propositional Logic CS 3234: Logic and Formal Systems Martin Henz and Aquinas Hobor August 26, 2010 Generated on Tuesday 31 August, 2010, 16:54 1 Motivation In traditional logic, terms represent sets,
Propositional Logic CS 3234: Logic and Formal Systems Martin Henz and Aquinas Hobor August 26, 2010 Generated on Tuesday 31 August, 2010, 16:54 1 Motivation In traditional logic, terms represent sets,
Induction on Failing Derivations
 Induction on Failing Derivations Technical Report PL-Sep13 September 2013, with addenda from Spring 2016 ay Ligatti Department of Computer Science and Engineering University of South Florida Abstract A
Induction on Failing Derivations Technical Report PL-Sep13 September 2013, with addenda from Spring 2016 ay Ligatti Department of Computer Science and Engineering University of South Florida Abstract A
Type Inference. For the Simply-Typed Lambda Calculus. Peter Thiemann, Manuel Geffken. Albert-Ludwigs-Universität Freiburg. University of Freiburg
 Type Inference For the Simply-Typed Lambda Calculus Albert-Ludwigs-Universität Freiburg Peter Thiemann, Manuel Geffken University of Freiburg 24. Januar 2013 Outline 1 Introduction 2 Applied Lambda Calculus
Type Inference For the Simply-Typed Lambda Calculus Albert-Ludwigs-Universität Freiburg Peter Thiemann, Manuel Geffken University of Freiburg 24. Januar 2013 Outline 1 Introduction 2 Applied Lambda Calculus
Programming Language Concepts, CS2104 Lecture 3
 Programming Language Concepts, CS2104 Lecture 3 Statements, Kernel Language, Abstract Machine 31 Aug 2007 CS2104, Lecture 3 1 Reminder of last lecture Programming language definition: syntax, semantics
Programming Language Concepts, CS2104 Lecture 3 Statements, Kernel Language, Abstract Machine 31 Aug 2007 CS2104, Lecture 3 1 Reminder of last lecture Programming language definition: syntax, semantics
Problem. Problem Given a dictionary and a word. Which page (if any) contains the given word? 3 / 26
 Binary Search Introduction Problem Problem Given a dictionary and a word. Which page (if any) contains the given word? 3 / 26 Strategy 1: Random Search Randomly select a page until the page containing
Binary Search Introduction Problem Problem Given a dictionary and a word. Which page (if any) contains the given word? 3 / 26 Strategy 1: Random Search Randomly select a page until the page containing
Intelligent Agents. First Order Logic. Ute Schmid. Cognitive Systems, Applied Computer Science, Bamberg University. last change: 19.
 Intelligent Agents First Order Logic Ute Schmid Cognitive Systems, Applied Computer Science, Bamberg University last change: 19. Mai 2015 U. Schmid (CogSys) Intelligent Agents last change: 19. Mai 2015
Intelligent Agents First Order Logic Ute Schmid Cognitive Systems, Applied Computer Science, Bamberg University last change: 19. Mai 2015 U. Schmid (CogSys) Intelligent Agents last change: 19. Mai 2015
Type Systems. Today. 1. What is the Lambda Calculus. 1. What is the Lambda Calculus. Lecture 2 Oct. 27th, 2004 Sebastian Maneth
 Today 1. What is the Lambda Calculus? Type Systems 2. Its Syntax and Semantics 3. Church Booleans and Church Numerals 4. Lazy vs. Eager Evaluation (call-by-name vs. call-by-value) Lecture 2 Oct. 27th,
Today 1. What is the Lambda Calculus? Type Systems 2. Its Syntax and Semantics 3. Church Booleans and Church Numerals 4. Lazy vs. Eager Evaluation (call-by-name vs. call-by-value) Lecture 2 Oct. 27th,
Types and Programming Languages (15-814), Fall 2018 Assignment 4: Data Representation (Sample Solutions)
 Types and Programming Languages (15-814), Fall 2018 Assignment 4: Data Representation (Sample Solutions) Contact: 15-814 Course Staff Due Tuesday, October 16, 2018, 10:30am This assignment is due by 10:30am
Types and Programming Languages (15-814), Fall 2018 Assignment 4: Data Representation (Sample Solutions) Contact: 15-814 Course Staff Due Tuesday, October 16, 2018, 10:30am This assignment is due by 10:30am
Homework 5: Parallelism and Control Flow : Types and Programming Languages Fall 2015 TA: Evan Cavallo
 Homework 5: Parallelism and Control Flow 15-814: Types and Programming Languages Fall 2015 TA: Evan Cavallo (ecavallo@cs.cmu.edu) Out: 11/5/15 Due: 11/17/15, 10:30am 1 Cost Dynamics In this section, we
Homework 5: Parallelism and Control Flow 15-814: Types and Programming Languages Fall 2015 TA: Evan Cavallo (ecavallo@cs.cmu.edu) Out: 11/5/15 Due: 11/17/15, 10:30am 1 Cost Dynamics In this section, we
CS522 - Programming Language Semantics
 1 CS522 - Programming Language Semantics Simply Typed Lambda Calculus Grigore Roşu Department of Computer Science University of Illinois at Urbana-Champaign 2 We now discuss a non-trivial extension of
1 CS522 - Programming Language Semantics Simply Typed Lambda Calculus Grigore Roşu Department of Computer Science University of Illinois at Urbana-Champaign 2 We now discuss a non-trivial extension of
Consequence Relations and Natural Deduction
 Consequence Relations and Natural Deduction Joshua D. Guttman Worcester Polytechnic Institute September 9, 2010 Contents 1 Consequence Relations 1 2 A Derivation System for Natural Deduction 3 3 Derivations
Consequence Relations and Natural Deduction Joshua D. Guttman Worcester Polytechnic Institute September 9, 2010 Contents 1 Consequence Relations 1 2 A Derivation System for Natural Deduction 3 3 Derivations
7 RC Simulates RA. Lemma: For every RA expression E(A 1... A k ) there exists a DRC formula F with F V (F ) = {A 1,..., A k } and
 7 RC Simulates RA. We now show that DRC (and hence TRC) is at least as expressive as RA. That is, given an RA expression E that mentions at most C, there is an equivalent DRC expression E that mentions
7 RC Simulates RA. We now show that DRC (and hence TRC) is at least as expressive as RA. That is, given an RA expression E that mentions at most C, there is an equivalent DRC expression E that mentions
An Introduction to Logical Relations Proving Program Properties Using Logical Relations
 An Introduction to Logical Relations Proving Program Properties Using Logical Relations Lau Skorstengaard lask@cs.au.dk July 27, 2018 Contents 1 Introduction 2 1.1 Simply Typed Lambda Calculus....................
An Introduction to Logical Relations Proving Program Properties Using Logical Relations Lau Skorstengaard lask@cs.au.dk July 27, 2018 Contents 1 Introduction 2 1.1 Simply Typed Lambda Calculus....................
Supplementary Notes on Inductive Definitions
 Supplementary Notes on Inductive Definitions 15-312: Foundations of Programming Languages Frank Pfenning Lecture 2 August 29, 2002 These supplementary notes review the notion of an inductive definition
Supplementary Notes on Inductive Definitions 15-312: Foundations of Programming Languages Frank Pfenning Lecture 2 August 29, 2002 These supplementary notes review the notion of an inductive definition
Lecture Notes on Subject Reduction and Normal Forms
 Lecture Notes on Subject Reduction and Normal Forms 15-814: Types and Programming Languages Frank Pfenning Lecture 4 September 13, 2018 1 Introduction In the last lecture we proved some key aspect of a
Lecture Notes on Subject Reduction and Normal Forms 15-814: Types and Programming Languages Frank Pfenning Lecture 4 September 13, 2018 1 Introduction In the last lecture we proved some key aspect of a
Notes on Proving Arithmetic Equations
 Massachusetts Institute of Technology Course Notes 1 6.844, Spring 03: Computability Theory of and with Scheme February 10 Prof. Albert Meyer revised February 25, 2003, 1300 minutes Notes on Proving Arithmetic
Massachusetts Institute of Technology Course Notes 1 6.844, Spring 03: Computability Theory of and with Scheme February 10 Prof. Albert Meyer revised February 25, 2003, 1300 minutes Notes on Proving Arithmetic
MAI0203 Lecture 7: Inference and Predicate Calculus
 MAI0203 Lecture 7: Inference and Predicate Calculus Methods of Artificial Intelligence WS 2002/2003 Part II: Inference and Knowledge Representation II.7 Inference and Predicate Calculus MAI0203 Lecture
MAI0203 Lecture 7: Inference and Predicate Calculus Methods of Artificial Intelligence WS 2002/2003 Part II: Inference and Knowledge Representation II.7 Inference and Predicate Calculus MAI0203 Lecture
COSE212: Programming Languages. Lecture 1 Inductive Definitions (1)
 COSE212: Programming Languages Lecture 1 Inductive Definitions (1) Hakjoo Oh 2018 Fall Hakjoo Oh COSE212 2018 Fall, Lecture 1 September 5, 2018 1 / 10 Inductive Definitions Inductive definition (induction)
COSE212: Programming Languages Lecture 1 Inductive Definitions (1) Hakjoo Oh 2018 Fall Hakjoo Oh COSE212 2018 Fall, Lecture 1 September 5, 2018 1 / 10 Inductive Definitions Inductive definition (induction)
Static Program Analysis
 Static Program Analysis Xiangyu Zhang The slides are compiled from Alex Aiken s Michael D. Ernst s Sorin Lerner s A Scary Outline Type-based analysis Data-flow analysis Abstract interpretation Theorem
Static Program Analysis Xiangyu Zhang The slides are compiled from Alex Aiken s Michael D. Ernst s Sorin Lerner s A Scary Outline Type-based analysis Data-flow analysis Abstract interpretation Theorem
Introduction to lambda calculus Part 2
 Introduction to lambda calculus Part 2 Antti-Juhani Kaijanaho 2017-01-24... 1 Untyped lambda calculus 1.1 Syntax... x, y, z Var t, u Term t, u ::= x t u λx t... In this document, I will be using the following
Introduction to lambda calculus Part 2 Antti-Juhani Kaijanaho 2017-01-24... 1 Untyped lambda calculus 1.1 Syntax... x, y, z Var t, u Term t, u ::= x t u λx t... In this document, I will be using the following
Predicate Logic. Xinyu Feng 11/20/2013. University of Science and Technology of China (USTC)
 University of Science and Technology of China (USTC) 11/20/2013 Overview Predicate logic over integer expressions: a language of logical assertions, for example x. x + 0 = x Why discuss predicate logic?
University of Science and Technology of China (USTC) 11/20/2013 Overview Predicate logic over integer expressions: a language of logical assertions, for example x. x + 0 = x Why discuss predicate logic?
INDUCTIVE DEFINITION
 1 INDUCTIVE DEFINITION OUTLINE Judgements Inference Rules Inductive Definition Derivation Rule Induction 2 META-VARIABLES A symbol in a meta-language that is used to describe some element in an object
1 INDUCTIVE DEFINITION OUTLINE Judgements Inference Rules Inductive Definition Derivation Rule Induction 2 META-VARIABLES A symbol in a meta-language that is used to describe some element in an object
Operational semantics for disintegration
 Operational semantics for disintegration Chung-chieh Shan (Indiana University) Norman Ramsey (Tufts University) Mathematical Foundations of Programming Semantics 2016-05-25 1 What is semantics for? 1.
Operational semantics for disintegration Chung-chieh Shan (Indiana University) Norman Ramsey (Tufts University) Mathematical Foundations of Programming Semantics 2016-05-25 1 What is semantics for? 1.
Consequence Relations and Natural Deduction
 Consequence Relations and Natural Deduction Joshua D Guttman Worcester Polytechnic Institute September 16, 2010 Contents 1 Consequence Relations 1 2 A Derivation System for Natural Deduction 3 3 Derivations
Consequence Relations and Natural Deduction Joshua D Guttman Worcester Polytechnic Institute September 16, 2010 Contents 1 Consequence Relations 1 2 A Derivation System for Natural Deduction 3 3 Derivations
CSE 505, Fall 2008, Midterm Examination 29 October Please do not turn the page until everyone is ready.
 CSE 505, Fall 2008, Midterm Examination 29 October 2008 Please do not turn the page until everyone is ready. Rules: The exam is closed-book, closed-note, except for one side of one 8.5x11in piece of paper.
CSE 505, Fall 2008, Midterm Examination 29 October 2008 Please do not turn the page until everyone is ready. Rules: The exam is closed-book, closed-note, except for one side of one 8.5x11in piece of paper.
TRUTH-THEORIES FOR FRAGMENTS OF PA
 TRUTH-THEORIES FOR FRAGMENTS OF PA RICHARD G. HECK, JR. The discussion here follows Petr Hájek and Pavel Pudlák, Metamathematics of First-order Arithmetic (Berlin: Springer-Verlag, 1993). See especially
TRUTH-THEORIES FOR FRAGMENTS OF PA RICHARD G. HECK, JR. The discussion here follows Petr Hájek and Pavel Pudlák, Metamathematics of First-order Arithmetic (Berlin: Springer-Verlag, 1993). See especially
Safety Analysis versus Type Inference
 Information and Computation, 118(1):128 141, 1995. Safety Analysis versus Type Inference Jens Palsberg palsberg@daimi.aau.dk Michael I. Schwartzbach mis@daimi.aau.dk Computer Science Department, Aarhus
Information and Computation, 118(1):128 141, 1995. Safety Analysis versus Type Inference Jens Palsberg palsberg@daimi.aau.dk Michael I. Schwartzbach mis@daimi.aau.dk Computer Science Department, Aarhus
Theory of Computation
 Theory of Computation (Feodor F. Dragan) Department of Computer Science Kent State University Spring, 2018 Theory of Computation, Feodor F. Dragan, Kent State University 1 Before we go into details, what
Theory of Computation (Feodor F. Dragan) Department of Computer Science Kent State University Spring, 2018 Theory of Computation, Feodor F. Dragan, Kent State University 1 Before we go into details, what
PART II QUANTIFICATIONAL LOGIC
 Page 1 PART II QUANTIFICATIONAL LOGIC The language m of part I was built from sentence letters, symbols that stand in for sentences. The logical truth of a sentence or the logical validity of an argument,
Page 1 PART II QUANTIFICATIONAL LOGIC The language m of part I was built from sentence letters, symbols that stand in for sentences. The logical truth of a sentence or the logical validity of an argument,
Online Appendix to: Types for Atomicity: Static Checking and Inference for Java
 Online Appendix to: Types for Atomicity: Static Checking and Inference for Java CORMAC FLANAGAN University of California at Santa Cruz STEPHEN N. FREUND and MARINA LIFSHIN Williams College and SHAZ QADEER
Online Appendix to: Types for Atomicity: Static Checking and Inference for Java CORMAC FLANAGAN University of California at Santa Cruz STEPHEN N. FREUND and MARINA LIFSHIN Williams College and SHAZ QADEER
BRICS. A Computational Formalization for Partial Evaluation. (Extended Version) Basic Research in Computer Science
 BRICS RS-96-34 Hatcliff & Danvy: A Computational Formalization for Partial Evaluation BRICS Basic Research in Computer Science A Computational Formalization for Partial Evaluation (Extended Version) John
BRICS RS-96-34 Hatcliff & Danvy: A Computational Formalization for Partial Evaluation BRICS Basic Research in Computer Science A Computational Formalization for Partial Evaluation (Extended Version) John
A Monadic Analysis of Information Flow Security with Mutable State
 A Monadic Analysis of Information Flow Security with Mutable State Karl Crary Aleksey Kliger Frank Pfenning July 2003 CMU-CS-03-164 School of Computer Science Carnegie Mellon University Pittsburgh, PA
A Monadic Analysis of Information Flow Security with Mutable State Karl Crary Aleksey Kliger Frank Pfenning July 2003 CMU-CS-03-164 School of Computer Science Carnegie Mellon University Pittsburgh, PA
Roy L. Crole. Operational Semantics Abstract Machines and Correctness. University of Leicester, UK
 Midlands Graduate School, University of Birmingham, April 2008 1 Operational Semantics Abstract Machines and Correctness Roy L. Crole University of Leicester, UK Midlands Graduate School, University of
Midlands Graduate School, University of Birmingham, April 2008 1 Operational Semantics Abstract Machines and Correctness Roy L. Crole University of Leicester, UK Midlands Graduate School, University of
Midterm Exam Types and Programming Languages Frank Pfenning. October 18, 2018
 Midterm Exam 15-814 Types and Programming Languages Frank Pfenning October 18, 2018 Name: Andrew ID: Instructions This exam is closed-book, closed-notes. You have 80 minutes to complete the exam. There
Midterm Exam 15-814 Types and Programming Languages Frank Pfenning October 18, 2018 Name: Andrew ID: Instructions This exam is closed-book, closed-notes. You have 80 minutes to complete the exam. There
Soundness Theorem for System AS1
 10 The Soundness Theorem for System AS1 1. Introduction...2 2. Soundness, Completeness, and Mutual Consistency...2 3. The Weak Soundness Theorem...4 4. The Strong Soundness Theorem...6 5. Appendix: Supporting
10 The Soundness Theorem for System AS1 1. Introduction...2 2. Soundness, Completeness, and Mutual Consistency...2 3. The Weak Soundness Theorem...4 4. The Strong Soundness Theorem...6 5. Appendix: Supporting
1 AC 0 and Håstad Switching Lemma
 princeton university cos 522: computational complexity Lecture 19: Circuit complexity Lecturer: Sanjeev Arora Scribe:Tony Wirth Complexity theory s Waterloo As we saw in an earlier lecture, if PH Σ P 2
princeton university cos 522: computational complexity Lecture 19: Circuit complexity Lecturer: Sanjeev Arora Scribe:Tony Wirth Complexity theory s Waterloo As we saw in an earlier lecture, if PH Σ P 2
ECONOMICS 207 SPRING 2006 LABORATORY EXERCISE 5 KEY. 8 = 10(5x 2) = 9(3x + 8), x 50x 20 = 27x x = 92 x = 4. 8x 2 22x + 15 = 0 (2x 3)(4x 5) = 0
 ECONOMICS 07 SPRING 006 LABORATORY EXERCISE 5 KEY Problem. Solve the following equations for x. a 5x 3x + 8 = 9 0 5x 3x + 8 9 8 = 0(5x ) = 9(3x + 8), x 0 3 50x 0 = 7x + 7 3x = 9 x = 4 b 8x x + 5 = 0 8x
ECONOMICS 07 SPRING 006 LABORATORY EXERCISE 5 KEY Problem. Solve the following equations for x. a 5x 3x + 8 = 9 0 5x 3x + 8 9 8 = 0(5x ) = 9(3x + 8), x 0 3 50x 0 = 7x + 7 3x = 9 x = 4 b 8x x + 5 = 0 8x
Analysis of Algorithms - Midterm (Solutions)
 Analysis of Algorithms - Midterm (Solutions) K Subramani LCSEE, West Virginia University, Morgantown, WV {ksmani@cseewvuedu} 1 Problems 1 Recurrences: Solve the following recurrences exactly or asymototically
Analysis of Algorithms - Midterm (Solutions) K Subramani LCSEE, West Virginia University, Morgantown, WV {ksmani@cseewvuedu} 1 Problems 1 Recurrences: Solve the following recurrences exactly or asymototically
3.2 Reduction 29. Truth. The constructor just forms the unit element,. Since there is no destructor, there is no reduction rule.
 32 Reduction 29 32 Reduction In the preceding section, we have introduced the assignment of proof terms to natural deductions If proofs are programs then we need to explain how proofs are to be executed,
32 Reduction 29 32 Reduction In the preceding section, we have introduced the assignment of proof terms to natural deductions If proofs are programs then we need to explain how proofs are to be executed,
Meta-programming & you
 Meta-programming & you Robin Message Cambridge Programming Research Group 10 th May 2010 What s meta-programming about? 1 result=somedb. customers. select 2 { first_name+ +last_name } 3 where name LIKE
Meta-programming & you Robin Message Cambridge Programming Research Group 10 th May 2010 What s meta-programming about? 1 result=somedb. customers. select 2 { first_name+ +last_name } 3 where name LIKE
CMSC 336: Type Systems for Programming Languages Lecture 10: Polymorphism Acar & Ahmed 19 February 2008
 CMSC 336: Type Systems for Programming Languages Lecture 10: Polymorphism Acar & Ahmed 19 February 2008 Contents 1 Polymorphism 1 2 Polymorphic λ-calculus: Syntax 1 3 Static Semantics 2 4 Dynamic Semantics
CMSC 336: Type Systems for Programming Languages Lecture 10: Polymorphism Acar & Ahmed 19 February 2008 Contents 1 Polymorphism 1 2 Polymorphic λ-calculus: Syntax 1 3 Static Semantics 2 4 Dynamic Semantics
Propositional and Predicate Logic
 Formal Verification of Software Propositional and Predicate Logic Bernhard Beckert UNIVERSITÄT KOBLENZ-LANDAU B. Beckert: Formal Verification of Software p.1 Propositional Logic: Syntax Special symbols
Formal Verification of Software Propositional and Predicate Logic Bernhard Beckert UNIVERSITÄT KOBLENZ-LANDAU B. Beckert: Formal Verification of Software p.1 Propositional Logic: Syntax Special symbols
PEANO AXIOMS FOR THE NATURAL NUMBERS AND PROOFS BY INDUCTION. The Peano axioms
 PEANO AXIOMS FOR THE NATURAL NUMBERS AND PROOFS BY INDUCTION The Peano axioms The following are the axioms for the natural numbers N. You might think of N as the set of integers {0, 1, 2,...}, but it turns
PEANO AXIOMS FOR THE NATURAL NUMBERS AND PROOFS BY INDUCTION The Peano axioms The following are the axioms for the natural numbers N. You might think of N as the set of integers {0, 1, 2,...}, but it turns
Foundations of Programming Languages. Paul Downen
 Foundations of Programming Languages Paul Downen July 3 8, 2018 2 Contents 1 Static and Dynamic Semantics of a Little Language 7 1.1 Syntax................................. 7 1.2 Static Scope..............................
Foundations of Programming Languages Paul Downen July 3 8, 2018 2 Contents 1 Static and Dynamic Semantics of a Little Language 7 1.1 Syntax................................. 7 1.2 Static Scope..............................
Lecture 2: Proof of Switching Lemma
 Lecture 2: oof of Switching Lemma Yuan Li June 25, 2014 1 Decision Tree Instead of bounding the probability that f can be written as some s-dnf, we estimate the probability that f can be computed by a
Lecture 2: oof of Switching Lemma Yuan Li June 25, 2014 1 Decision Tree Instead of bounding the probability that f can be written as some s-dnf, we estimate the probability that f can be computed by a
KRIPKE S THEORY OF TRUTH 1. INTRODUCTION
 KRIPKE S THEORY OF TRUTH RICHARD G HECK, JR 1. INTRODUCTION The purpose of this note is to give a simple, easily accessible proof of the existence of the minimal fixed point, and of various maximal fixed
KRIPKE S THEORY OF TRUTH RICHARD G HECK, JR 1. INTRODUCTION The purpose of this note is to give a simple, easily accessible proof of the existence of the minimal fixed point, and of various maximal fixed
Mathematical Foundations of Programming. Nicolai Kraus. Draft of February 15, 2018
 Very short lecture notes: Mathematical Foundations of Programming University of Nottingham, Computer Science, module code G54FOP, Spring 2018 Nicolai Kraus Draft of February 15, 2018 What is this? This
Very short lecture notes: Mathematical Foundations of Programming University of Nottingham, Computer Science, module code G54FOP, Spring 2018 Nicolai Kraus Draft of February 15, 2018 What is this? This
SKETCHY NOTES FOR WEEKS 7 AND 8
 SKETCHY NOTES FOR WEEKS 7 AND 8 We are now ready to start work on the proof of the Completeness Theorem for first order logic. Before we start a couple of remarks are in order (1) When we studied propositional
SKETCHY NOTES FOR WEEKS 7 AND 8 We are now ready to start work on the proof of the Completeness Theorem for first order logic. Before we start a couple of remarks are in order (1) When we studied propositional
Introduction to first-order logic:
 Introduction to first-order logic: First-order structures and languages. Terms and formulae in first-order logic. Interpretations, truth, validity, and satisfaction. Valentin Goranko DTU Informatics September
Introduction to first-order logic: First-order structures and languages. Terms and formulae in first-order logic. Interpretations, truth, validity, and satisfaction. Valentin Goranko DTU Informatics September
Principles of Program Analysis: Control Flow Analysis
 Principles of Program Analysis: Control Flow Analysis Transparencies based on Chapter 3 of the book: Flemming Nielson, Hanne Riis Nielson and Chris Hankin: Principles of Program Analysis. Springer Verlag
Principles of Program Analysis: Control Flow Analysis Transparencies based on Chapter 3 of the book: Flemming Nielson, Hanne Riis Nielson and Chris Hankin: Principles of Program Analysis. Springer Verlag
Type Systems. Lecture 2 Oct. 27th, 2004 Sebastian Maneth.
 Type Systems Lecture 2 Oct. 27th, 2004 Sebastian Maneth http://lampwww.epfl.ch/teaching/typesystems/2004 Today 1. What is the Lambda Calculus? 2. Its Syntax and Semantics 3. Church Booleans and Church
Type Systems Lecture 2 Oct. 27th, 2004 Sebastian Maneth http://lampwww.epfl.ch/teaching/typesystems/2004 Today 1. What is the Lambda Calculus? 2. Its Syntax and Semantics 3. Church Booleans and Church
Mathematical Logics. 12. Soundness and Completeness of tableaux reasoning in first order logic. Luciano Serafini
 12. Soundness and Completeness of tableaux reasoning in first order logic Fondazione Bruno Kessler, Trento, Italy November 14, 2013 Example of tableaux Example Consider the following formulas: (a) xyz(p(x,
12. Soundness and Completeness of tableaux reasoning in first order logic Fondazione Bruno Kessler, Trento, Italy November 14, 2013 Example of tableaux Example Consider the following formulas: (a) xyz(p(x,
Lecture Notes: Program Analysis Correctness
 Lecture Notes: Program Analysis Correctness 15-819O: Program Analysis Jonathan Aldrich jonathan.aldrich@cs.cmu.edu Lecture 5 1 Termination As we think about the correctness of program analysis, let us
Lecture Notes: Program Analysis Correctness 15-819O: Program Analysis Jonathan Aldrich jonathan.aldrich@cs.cmu.edu Lecture 5 1 Termination As we think about the correctness of program analysis, let us
Programming Languages and Types
 Programming Languages and Types Klaus Ostermann based on slides by Benjamin C. Pierce Where we re going Type Systems... Type systems are one of the most fascinating and powerful aspects of programming
Programming Languages and Types Klaus Ostermann based on slides by Benjamin C. Pierce Where we re going Type Systems... Type systems are one of the most fascinating and powerful aspects of programming
Logic I - Session 10 Thursday, October 15,
 Logic I - Session 10 Thursday, October 15, 2009 1 Plan Re: course feedback Review of course structure Recap of truth-functional completeness? Soundness of SD Thursday, October 15, 2009 2 The course structure
Logic I - Session 10 Thursday, October 15, 2009 1 Plan Re: course feedback Review of course structure Recap of truth-functional completeness? Soundness of SD Thursday, October 15, 2009 2 The course structure
Propositional Logic: Part II - Syntax & Proofs 0-0
 Propositional Logic: Part II - Syntax & Proofs 0-0 Outline Syntax of Propositional Formulas Motivating Proofs Syntactic Entailment and Proofs Proof Rules for Natural Deduction Axioms, theories and theorems
Propositional Logic: Part II - Syntax & Proofs 0-0 Outline Syntax of Propositional Formulas Motivating Proofs Syntactic Entailment and Proofs Proof Rules for Natural Deduction Axioms, theories and theorems
Well-foundedness of Countable Ordinals and the Hydra Game
 Well-foundedness of Countable Ordinals and the Hydra Game Noah Schoem September 11, 2014 1 Abstract An argument involving the Hydra game shows why ACA 0 is insufficient for a theory of ordinals in which
Well-foundedness of Countable Ordinals and the Hydra Game Noah Schoem September 11, 2014 1 Abstract An argument involving the Hydra game shows why ACA 0 is insufficient for a theory of ordinals in which
CSE 505, Fall 2009, Midterm Examination 5 November Please do not turn the page until everyone is ready.
 CSE 505, Fall 2009, Midterm Examination 5 November 2009 Please do not turn the page until everyone is ready Rules: The exam is closed-book, closed-note, except for one side of one 85x11in piece of paper
CSE 505, Fall 2009, Midterm Examination 5 November 2009 Please do not turn the page until everyone is ready Rules: The exam is closed-book, closed-note, except for one side of one 85x11in piece of paper
Introduction to Metalogic
 Introduction to Metalogic Hans Halvorson September 21, 2016 Logical grammar Definition. A propositional signature Σ is a collection of items, which we call propositional constants. Sometimes these propositional
Introduction to Metalogic Hans Halvorson September 21, 2016 Logical grammar Definition. A propositional signature Σ is a collection of items, which we call propositional constants. Sometimes these propositional
First-Order Logic. Chapter Overview Syntax
 Chapter 10 First-Order Logic 10.1 Overview First-Order Logic is the calculus one usually has in mind when using the word logic. It is expressive enough for all of mathematics, except for those concepts
Chapter 10 First-Order Logic 10.1 Overview First-Order Logic is the calculus one usually has in mind when using the word logic. It is expressive enough for all of mathematics, except for those concepts
1 Some loose ends from last time
 Cornell University, Fall 2010 CS 6820: Algorithms Lecture notes: Kruskal s and Borůvka s MST algorithms September 20, 2010 1 Some loose ends from last time 1.1 A lemma concerning greedy algorithms and
Cornell University, Fall 2010 CS 6820: Algorithms Lecture notes: Kruskal s and Borůvka s MST algorithms September 20, 2010 1 Some loose ends from last time 1.1 A lemma concerning greedy algorithms and
06 From Propositional to Predicate Logic
 Martin Henz February 19, 2014 Generated on Wednesday 19 th February, 2014, 09:48 1 Syntax of Predicate Logic 2 3 4 5 6 Need for Richer Language Predicates Variables Functions 1 Syntax of Predicate Logic
Martin Henz February 19, 2014 Generated on Wednesday 19 th February, 2014, 09:48 1 Syntax of Predicate Logic 2 3 4 5 6 Need for Richer Language Predicates Variables Functions 1 Syntax of Predicate Logic
Chapter 11: Automated Proof Systems
 Chapter 11: Automated Proof Systems SYSTEM RS OVERVIEW Hilbert style systems are easy to define and admit a simple proof of the Completeness Theorem but they are difficult to use. Automated systems are
Chapter 11: Automated Proof Systems SYSTEM RS OVERVIEW Hilbert style systems are easy to define and admit a simple proof of the Completeness Theorem but they are difficult to use. Automated systems are
arxiv: v1 [math.co] 28 Oct 2016
![arxiv: v1 [math.co] 28 Oct 2016 arxiv: v1 [math.co] 28 Oct 2016](/thumbs/92/108819504.jpg) More on foxes arxiv:1610.09093v1 [math.co] 8 Oct 016 Matthias Kriesell Abstract Jens M. Schmidt An edge in a k-connected graph G is called k-contractible if the graph G/e obtained from G by contracting
More on foxes arxiv:1610.09093v1 [math.co] 8 Oct 016 Matthias Kriesell Abstract Jens M. Schmidt An edge in a k-connected graph G is called k-contractible if the graph G/e obtained from G by contracting
Operationally-Based Theories of Program Equivalence
 Operationally-Based Theories of Program Equivalence Andrew Pitts Contents 1 Introduction : : : : : : : : : : : : : : : : : : : : : : : : : : : : 241 2 Contextual Equivalence : : : : : : : : : : : : : :
Operationally-Based Theories of Program Equivalence Andrew Pitts Contents 1 Introduction : : : : : : : : : : : : : : : : : : : : : : : : : : : : 241 2 Contextual Equivalence : : : : : : : : : : : : : :
INF3170 / INF4171 Notes on Resolution
 INF3170 / INF4171 Notes on Resolution Andreas Nakkerud Autumn 2015 1 Introduction This is a short description of the Resolution calculus for propositional logic, and for first order logic. We will only
INF3170 / INF4171 Notes on Resolution Andreas Nakkerud Autumn 2015 1 Introduction This is a short description of the Resolution calculus for propositional logic, and for first order logic. We will only
Propositional logic. First order logic. Alexander Clark. Autumn 2014
 Propositional logic First order logic Alexander Clark Autumn 2014 Formal Logic Logical arguments are valid because of their form. Formal languages are devised to express exactly that relevant form and
Propositional logic First order logic Alexander Clark Autumn 2014 Formal Logic Logical arguments are valid because of their form. Formal languages are devised to express exactly that relevant form and
Classical Program Logics: Hoare Logic, Weakest Liberal Preconditions
 Chapter 1 Classical Program Logics: Hoare Logic, Weakest Liberal Preconditions 1.1 The IMP Language IMP is a programming language with an extensible syntax that was developed in the late 1960s. We will
Chapter 1 Classical Program Logics: Hoare Logic, Weakest Liberal Preconditions 1.1 The IMP Language IMP is a programming language with an extensible syntax that was developed in the late 1960s. We will
CHAPTER 10. Gentzen Style Proof Systems for Classical Logic
 CHAPTER 10 Gentzen Style Proof Systems for Classical Logic Hilbert style systems are easy to define and admit a simple proof of the Completeness Theorem but they are difficult to use. By humans, not mentioning
CHAPTER 10 Gentzen Style Proof Systems for Classical Logic Hilbert style systems are easy to define and admit a simple proof of the Completeness Theorem but they are difficult to use. By humans, not mentioning
HOW DO ULTRAFILTERS ACT ON THEORIES? THE CUT SPECTRUM AND TREETOPS
 HOW DO ULTRAFILTERS ACT ON THEORIES? THE CUT SPECTRUM AND TREETOPS DIEGO ANDRES BEJARANO RAYO Abstract. We expand on and further explain the work by Malliaris and Shelah on the cofinality spectrum by doing
HOW DO ULTRAFILTERS ACT ON THEORIES? THE CUT SPECTRUM AND TREETOPS DIEGO ANDRES BEJARANO RAYO Abstract. We expand on and further explain the work by Malliaris and Shelah on the cofinality spectrum by doing
CSE505, Fall 2012, Final Examination December 10, 2012
 CSE505, Fall 2012, Final Examination December 10, 2012 Rules: The exam is closed-book, closed-notes, except for one side of one 8.5x11in piece of paper. Please stop promptly at 12:20. You can rip apart
CSE505, Fall 2012, Final Examination December 10, 2012 Rules: The exam is closed-book, closed-notes, except for one side of one 8.5x11in piece of paper. Please stop promptly at 12:20. You can rip apart
Axiomatic Semantics. Operational semantics. Good for. Not good for automatic reasoning about programs
 Review Operational semantics relatively l simple many flavors (small vs. big) not compositional (rule for while) Good for describing language implementation reasoning about properties of the language eg.
Review Operational semantics relatively l simple many flavors (small vs. big) not compositional (rule for while) Good for describing language implementation reasoning about properties of the language eg.
Part 2: First-Order Logic
 Part 2: First-Order Logic First-order logic formalizes fundamental mathematical concepts is expressive (Turing-complete) is not too expressive (e. g. not axiomatizable: natural numbers, uncountable sets)
Part 2: First-Order Logic First-order logic formalizes fundamental mathematical concepts is expressive (Turing-complete) is not too expressive (e. g. not axiomatizable: natural numbers, uncountable sets)
First-Order Logic First-Order Theories. Roopsha Samanta. Partly based on slides by Aaron Bradley and Isil Dillig
 First-Order Logic First-Order Theories Roopsha Samanta Partly based on slides by Aaron Bradley and Isil Dillig Roadmap Review: propositional logic Syntax and semantics of first-order logic (FOL) Semantic
First-Order Logic First-Order Theories Roopsha Samanta Partly based on slides by Aaron Bradley and Isil Dillig Roadmap Review: propositional logic Syntax and semantics of first-order logic (FOL) Semantic
Truth-Functional Logic
 Truth-Functional Logic Syntax Every atomic sentence (A, B, C, ) is a sentence and are sentences With ϕ a sentence, the negation ϕ is a sentence With ϕ and ψ sentences, the conjunction ϕ ψ is a sentence
Truth-Functional Logic Syntax Every atomic sentence (A, B, C, ) is a sentence and are sentences With ϕ a sentence, the negation ϕ is a sentence With ϕ and ψ sentences, the conjunction ϕ ψ is a sentence
The semantics of propositional logic
 The semantics of propositional logic Readings: Sections 1.3 and 1.4 of Huth and Ryan. In this module, we will nail down the formal definition of a logical formula, and describe the semantics of propositional
The semantics of propositional logic Readings: Sections 1.3 and 1.4 of Huth and Ryan. In this module, we will nail down the formal definition of a logical formula, and describe the semantics of propositional
Logic Part I: Classical Logic and Its Semantics
 Logic Part I: Classical Logic and Its Semantics Max Schäfer Formosan Summer School on Logic, Language, and Computation 2007 July 2, 2007 1 / 51 Principles of Classical Logic classical logic seeks to model
Logic Part I: Classical Logic and Its Semantics Max Schäfer Formosan Summer School on Logic, Language, and Computation 2007 July 2, 2007 1 / 51 Principles of Classical Logic classical logic seeks to model
Propositional Logic and Semantics
 Propositional Logic and Semantics English is naturally ambiguous. For example, consider the following employee (non)recommendations and their ambiguity in the English language: I can assure you that no
Propositional Logic and Semantics English is naturally ambiguous. For example, consider the following employee (non)recommendations and their ambiguity in the English language: I can assure you that no
First-Order Predicate Logic. Basics
 First-Order Predicate Logic Basics 1 Syntax of predicate logic: terms A variable is a symbol of the form x i where i = 1, 2, 3.... A function symbol is of the form fi k where i = 1, 2, 3... und k = 0,
First-Order Predicate Logic Basics 1 Syntax of predicate logic: terms A variable is a symbol of the form x i where i = 1, 2, 3.... A function symbol is of the form fi k where i = 1, 2, 3... und k = 0,
The length-ω 1 open game quantifier propagates scales
 The length-ω 1 open game quantifier propagates scales John R. Steel June 5, 2006 0 Introduction We shall call a set T an ω 1 -tree if only if T α
The length-ω 1 open game quantifier propagates scales John R. Steel June 5, 2006 0 Introduction We shall call a set T an ω 1 -tree if only if T α
