The Log-Kumaraswamy Generalized Gamma Regression Model with Application to Chemical Dependency Data
|
|
|
- Jack Charles
- 5 years ago
- Views:
Transcription
1 Journal of Daa Scence ), The Log-Kumaraswamy Generalzed Gamma Regresson Model wh Applcaon o Chemcal Dependency Daa Marcelno A. R. Pascoa 1, Clauda M. M. de Pava 2, Gauss M. Cordero 3 and Edwn M. M. Orega 4 1 Unversdade Federal de Mao Grosso, 2 Unversdade Federal de São João del Re, 3 Unversdade Federal de Pernambuco and 4 Unversdade de São Paulo Absrac: The fve parameer Kumaraswamy generalzed gamma model Pascoa e al., 2011) ncludes some mporan dsrbuons as specal cases and s very useful for modelng lfeme daa. We propose an exended verson of hs dsrbuon by assumng ha a shape parameer can ake negave values. The new dsrbuon can accommodae ncreasng, decreasng, bahub and unmodal shaped hazard funcons. A second advanage s ha also ncludes as specal models recprocal dsrbuons such as he recprocal gamma and recprocal Webull dsrbuons. A hrd advanage s ha can represen he error dsrbuon for he log-kumaraswamy generalzed gamma regresson model. We provde a mahemacal reamen of he new dsrbuon ncludng explc expressons for momens, generang funcon, mean devaons and order sascs. We oban he momens of he log-ransformed dsrbuon. The new regresson model can be used more effecvely n he analyss of survval daa snce ncludes as submodels several wdely-known regresson models. The mehod of maxmum lkelhood and a Bayesan procedure are used for esmang he model parameers for censored daa. Overall, he new regresson model s very useful o he analyss of real daa. Key words: Censored daa, generang funcon, Kumaraswamy generalzed gamma dsrbuon, log-gamma generalzed regresson, momen, survval funcon. 1. Inroducon Sandard lfeme dsrbuons usually presen very srong resrcons o produce bahub curves, and hus appear o be unapproprae for daa wh hs characersc. The gamma dsrbuon s he mos popular model for analyzng skewed daa. The generalzed gamma GG) Sacy, 1962) dsrbuon ncludes Correspondng auhor.
2 782 Pascoa, M. A. R., de Pava, C. M. M., Cordero, G. M. and Orega, E. M. M. as specal models he exponenal, Webull, gamma and Raylegh dsrbuons, among ohers. I s suable for modelng daa wh hazard rae funcon of dfferen forms ncreasng, decreasng, bahub and unmodal) and hen s useful for esmang ndvdual hazard funcons and boh relave hazards and relave mes Cox, 2008). The GG dsrbuon has been used n several research areas such as engneerng, hydrology and survval analyss. In fac, Orega e al. 2003) dscussed nfluence dagnoscs n GG regresson models, Nadarajah and Gupa 2007) appled hs dsrbuon o drough daa and Cox e al. 2007) presened a paramerc survval analyss and axonomy of GG hazard funcons. For X 1 and X 2 ndependen GG random varables, Al e al. 2008) derved he exac dsrbuons of he produc X 1 X 2 and quoen X 1 /X 2 and provded applcaons of her resuls o drough daa from Nebraska. Furher, Gomes e al. 2008) focused on parameer esmaon, Orega e al. 2008) compared hree ypes of devance componen resduals n GG regresson models under censored observaons, Cox 2008) dscussed and compared he F-generalzed famly wh he GG model, Almpands and Koropoulos 2008) presened a ex-ndependen auomac phone segmenaon algorhm based on hs dsrbuon and Nadarajah 2008a) analyzed some ncorrec references wh respec o s use n elecrcal and elecronc engneerng. More recenly, Barkauskas e al. 2009) suded he nose par of a specrum as an auoregressve movng average ARMA) model wh he nnovaons havng he GG dsrbuon and Malhora e al. 2009) provded a unfed analyss for wreless sysem over generalzed fadng channels ha s modeled by a wo parameer GG model. Also, Orega e al. 2009) proposed a modfed GG regresson model o allow he possbly ha long-erm survvors may be presened n he daa and Cordero e al. 2010) defned he exponenaed generalzed gamma EGG) dsrbuon. Ths dsrbuon due o s flexbly n accommodang many forms of he rsk funcon seems o be an mporan model ha can be used n a varey of problems n survval analyss. In he las years, new dsrbuons for modelng survval daa based on exensons of he Webull dsrbuon were developed. Mudholkar e al. 1995), Xe and La 1995), La e al. 2003) and Carrasco e al. 2008) nroduced he exponenaed Webull EW), addve Webull, modfed Webull MW) and generalzed modfed Webull GMW) dsrbuons, respecvely. Furher, he man movaon for he exponenaed generalzed gamma EGG) dsrbuon Cordero e al., 2010) s ha conans as specal cases he GG, EW, exponenaed exponenal EE) Gupa and Kundu, 1999) and generalzed Raylegh GR) Kundu and Raqab, 2005) dsrbuons. The Kumaraswamy generalzed gamma KGG) dsrbuon Pascoa e al., 2011) can model four ypes of he falure rae funcon.e. ncreasng, decreasng, unmodal and bahub) dependng on he values of s parameers. I s also
3 The Log-Kumaraswamy Generalzed Gamma Regresson Model 783 suable for esng goodness-of-f of some sub-models, such as he EGG, GG, EW, Webull and GR dsrbuons. In hs paper, we defne an exended form of he KGG dsrbuon o cope wh several recprocal ype dsrbuons and sudy some of s srucural properes. We exend he model by Pascoa e al. 2011), snce a shape parameer can ake negave values. The mehod of maxmum lkelhood s used for esmang he model parameers. Unless oherwse saed, all of he resuls presened n he paper are new and orgnal. I s expeced ha hey could encourage furher research on he new dsrbuon. Dfferen forms of regresson models have been proposed n survval analyss. Among hem, he locaon-scale regresson model Lawless, 2003) s dsngushed snce s frequenly used n clncal rals. Here, we propose a locaon-scale regresson model based on he new dsrbuon called he log-kumaraswamy generalzed gamma LKGG) regresson model, whch s a feasble alernave for modelng he four ypes of falure rae funcons. The res of he paper s organzed as follows. In Secon 2, we defne an exended verson of he KGG dsrbuon. In Secon 3, we derve s ordnary momens, momen generang funcon mgf), order sascs and her momens. In Secon 4, we defne he LKGG dsrbuon and derve an explc expresson for s momens. In Secon 5, we propose he LKGG regresson model for analyss of censored daa. We esmae he model parameers by maxmum lkelhood, derve he observed nformaon marx and dscuss a Bayesan mehodology o esmae he model parameers. In Secon 6, we llusrae he poenaly of he new regresson model by means of a real daa se n chemcal dependency. Secon 7 ends wh some concludng remarks. 2. The KGG Dsrbuon Pascoa e al. 2011) defned he KGG dsrbuon wh fve posve parameers, τ, k, λ and ϕ o exend he GG and EGG dsrbuons poneered by Sacy 1962) and Cordero e al. 2010), respecvely. The KGG probably densy funcon pdf) for > 0) s gven by f) = λ ϕ τ ) τk 1 exp Γk) γ 1 k, ) ] τ ) ]} τ λ 1 γ 1 k, ) ]} τ λ ) ϕ 1, 1) where Γk) = 0 w k 1 e w dw for k > 0) s he gamma funcon, γ 1 k, x) = γk, x)/γk) s he ncomplee gamma funcon rao and γk, x) = x 0 wk 1 e w dw s he ncomplee gamma funcon. The ncomplee gamma funcon defned here
4 784 Pascoa, M. A. R., de Pava, C. M. M., Cordero, G. M. and Orega, E. M. M. for posve real k and x can be developed no he conex of holomorphc funcons for any complex k and x. Complex analyss shows how properes of he real ncomplee gamma funcons exend o her holomorphc counerpars. In he densy funcon 1), s a scale parameer and τ, k, λ and ϕ are shape parameers. The Webull, GG and EGG dsrbuons are specal models of 1) when λ = k = 1, λ = ϕ = 1 and ϕ = 1, respecvely. The KGG dsrbuon approaches he log-normal dsrbuon when λ = ϕ = 1 and k. Now, we defne an exended form of he densy funcon 1) for > 0) gven by f) = λ ϕ τ ) τk 1 ) τ ) ]} τ λ 1 exp ]γ 1 k, Γk) γ 1 k, ) ]} τ λ ) ϕ 1, 2) where τ s no zero and he oher parameers are posve. The ermnology Kumaraswamy generalzed gamma KGG) dsrbuon s mananed for 2). For a random varable T havng hs densy, we wre T KGG, τ, k, λ, ϕ). For τ > 0, 2) reduces o 1) and for τ > 0 and λ = ϕ = 1, s dencal o he GG dsrbuon. For τ > 0 and λ = ϕ = k = 1, we oban he Webull dsrbuon. The case τ < 0 and λ = ϕ = k = 1 gves he recprocal Webull or nverse Webull) dsrbuon. For τ = 1 and λ = ϕ = k = 1, we oban he recprocal exponenal. If τ = 2 and λ = ϕ = k = 1, we have he recprocal Raylegh. For τ = 1 and λ = ϕ = 1, we oban he recprocal gamma. The case τ < 0 and λ = ϕ = 1 corresponds o he generalzed recprocal gamma. If = 1/2, τ = 1, k = p/2 and λ = ϕ = 1, we have he recprocal ch-square. The values = 1/ 2, τ = 2, k = p/2 and λ = ϕ = 1 yeld he recprocal-ch. If = 2, τ = 2, k = p/2 and λ = ϕ = 1, we oban he scaled recprocal-ch. The case τ < 0 and k = 1 gves he Kumaraswamy Kum for shor) recprocal Webull. For τ = 1 and k = 1, we have he Kum recprocal exponenal. If τ = 2 and k = 1, we oban he Kum recprocal Raylegh. The Kum recprocal gamma corresponds o τ < 0. Several specal models of 2) when τ > 0 are dscussed by Pascoa e al. 2011). Plos of he KGG densy funcon for seleced values of τ > 0 and τ < 0 are dsplayed n Fgure 1. The cumulave dsrbuon funcon cdf) correspondng o 2) becomes γ 1 k, )] } λ ϕ, )τ f τ > 0, F ) = γ 1 k, )] } 3) λ ϕ, )τ f τ < 0.
5 The Log-Kumaraswamy Generalzed Gamma Regresson Model 785 a) b) c) f) =1; τ=0.7; k=1; λ=1; ϕ=1 =1; τ=1.5; k=1; λ=1; ϕ=1 =1; τ=2; k=1; λ=1; ϕ=1 =1; τ=2.5; k=1; λ=1; ϕ=1 =1; τ=3; k=1; λ=1; ϕ=1 f) =1; τ= 0.7; k=1; λ=1; ϕ=1 =1; τ= 1.5; k=1; λ=1; ϕ=1 =1; τ= 2; k=1; λ=1; ϕ=1 =1; τ= 2.5; k=1; λ=1; ϕ=1 =1; τ= 3; k=1; λ=1; ϕ=1 f) =4.7; τ=7.2; k=2.8; λ=0.8; ϕ=1.5 =5; τ=2.3; k=3; λ=0.9; ϕ=2.5 =1.9; τ= 5; k=0.4; λ=2.1; ϕ=2 =1.2; τ= 0.6; k=0.4; λ=10; ϕ=0.8 =6; τ=3; k=1; λ=20; ϕ=0.9 =3.1; τ= 10.3; k=2; λ=0.1; ϕ= Fgure 1: The KGG densy curves: a) For some values of τ > 0. b) For some values of τ < 0. c) For some values of τ > 0 and τ < 0 Le g,τ,k ) be he GG, τ, k) densy funcon Sacy and Mhram, 1965) gven by for > 0) g,τ,k ) = τ ) τk 1 ) ] τ exp. 4) Γk) The generalzed bnomal expanson converges for z < 1 and any real b ) b z) b = 1) j z j, 5) j j=0 where b j) = Γb + 1)/Γb j + 1)j!]. Then, from 5), he densy funcon 2) can be expressed as f) = λ ϕ τ Γk) γ 1 ) τk 1 ) ] τ ) ]} τ λ 1 ) ϕ 1 exp γ 1 k, 1) j j j=0 k, ) ]} τ λj. Ths equaon holds for any ϕ > 0. From expanson 27) gven n Appendx A), we oban f) = λ ϕ τ ) τk 1 ) ] τ ) ϕ 1 exp 1) j s m λ 1) Γk) j m,j=0 ) ]} τ λj+m γ 1 k,. 6)
6 786 Pascoa, M. A. R., de Pava, C. M. M., Cordero, G. M. and Orega, E. M. M. For any real λj + m > 0, we can wre ) ]} τ jλ+m ) γ λj + m 1 k, = 1) l γ 1 l l=0 k, ) ]} τ l. Applyng he bnomal expanson, 6) can be rewren as f) = λ ϕ τ ) kτ 1 ) ] τ l exp 1) j+l+q s m λ 1) Γk) j,l,m=0 q=0 ) ) ) ) ]} ϕ 1 jλ + m l τ q γ 1 k,. j l q From 31) gven n Appendx A) and replacng l l=0 q=0 by q=0 l=q, he densy funcon f) can be expressed as a double lnear combnaon of GG densy funcons f) = d,q=0 w d,q g,τ,k1+q)+d ), > 0, 7) where g,τ,k1+q)+d ) s he GG, τ, k1 + q) + d) densy funcon gven by 4) and he coeffcens w d,q are w d,q = w d,q k, λ, ϕ) = λ ϕ ) ϕ 1 λj + m j l j,m=0 l=q ) l q 1) j+l+q Γk1 + q) + d] s m λ 1) c q,d Γk) q+1 ), 8) where he quany s m λ 1) s gven by 28) and he quanes c q,d can be deermned from he recurrence 30) see Appendx A). Clearly, d,q=0 w d,q = 1. 7) s he man resul of hs secon. Some KGG mahemacal properes for example, he ordnary, nverse, facoral and ncomplee momens and generang funcon can be obaned from 7) and hose GG properes. 3. General Properes Henceforh, le T and Y be random varables havng he denses 2) and 4), respecvely. 3.1 Momens Here, we oban an nfne represenaon for he rh ordnary momen of T,
7 The Log-Kumaraswamy Generalzed Gamma Regresson Model 787 say µ r = ET r ). The rh momen of he GG, τ, k) dsrbuon s Based on 7), µ r can be expressed as µ r,gg = r Γk + r/τ). Γk) µ r = r 1) j+l+q Γk1 + q) + d + r/τ] s m λ 1) c q,d λ ϕ Γk) q+1 d,q,j,m=0 l=q ) ) ) ϕ 1 λj + m l, j l q where he quany s m λ) s gven by 28) and he coeffcens c q,d can be deermned from 30). 3.2 Generang Funcon Here, we provde an explc expresson for he mgf of Y, say M,τ,k s) = Ee sy ), for τ > 1, based on he Wrgh funcon Wrgh, 1935). We are unable o oban a closed-form expresson for M,τ,k s) when τ < 0. We can wre M,τ,k s) = Seng u = /, we have M,τ,k s) = τ τk Γk) τ Γk) 0 0 exps) τk 1 exp /) τ }d. expsu) u τk 1 exp u τ )du. Now, we assume τ > 0. Expandng he frs exponenal n Taylor seres and usng 0 u kτ+m 1 e uτ du = τ 1 Γm/τ + k), we oban M,τ,k s) = sgnτ) Γk) m ) s) m Γ τ + k. 9) m! m=0 9) holds for any real τ > 0. However, for τ > 1, can be smplfed by consderng he Wrgh generalzed hypergeomerc funcon Wrgh, 1935) defned by ) ) ] 1, A 1,, p, A p pψ q ) β1, B 1,, βq, B q ) ; x = m=0 p Γ j + A j m) j=1 q Γβ j + B j m) j=1 x m m!.
8 788 Pascoa, M. A. R., de Pava, C. M. M., Cordero, G. M. and Orega, E. M. M. Ths funcon exss f 1 + q j=1 B j p j=1 A j > 0. By combnng he las wo equaons, we have M,τ,k s) = 1 k, τ 1 ) Γk) 1 Ψ 0 ] ; s. 10) Fnally, he mgf of T for τ > 1) can be wren from 7) and 10) as Ms) = d,q=0 w d,q k1 + q] + d, τ 1 ) Γk1 + q] + d) 1 Ψ 0 9)-11) are he man resul of hs secon. 3.3 Order Sascs ] ; s. 11) The densy funcon f :n ) of he h order sasc, say T :n, for = 1,, n, from random varables T 1,, T n havng densy 2), s gven by f :n ) = 1 B, n + 1) f) F ) 1 F )} n, where f) and F ) are he pdf and cdf of he KGG dsrbuon, respecvely and Bp, q) = Γp)Γq)/Γp + q) denoes he bea funcon. We readly oban usng he bnomal expanson f :n ) = n 1 B, n + 1) f) ) 1) j 1 n F ) +j1 1. j 1 =0 j 1 Now, we derve an expresson for he densy funcon of he KGG order sascs n erms of he baselne densy funcon mulpled by a power seres of G) = γ 1 k, /) τ ). Seng ϕ = λ = 1 n 3), s clear ha he cdf of he GG, τ, k) dsrbuon s G) = γ 1 k, /) τ ) for τ > 0 and G) = γ 1 k, /) τ ) for τ < 0. Ths resul enables us o oban he ordnary momens of he KGG order sascs as nfne weghed sums of convenen quanes defned by δ s,r = 0 ) τ ] r s γ 1 k, g,τ,k)d. These quanes δ s,r can be easly negraed numercally. They represen he probably weghed momens PWMs) of Y when τ > 0. We shall consder wo dsnc cases: τ > 0 and τ < 0.
9 For τ > 0 The Log-Kumaraswamy Generalzed Gamma Regresson Model 789 An expanson for F ) +j 1 1 follows from 3) as F ) +j 1 1 = +j 1 l 1 =0 1) l 1 ) + j 1 G) λ] l 1 ϕ. Usng he seres expanson for G) λ] l 1 ϕ, we oban F ) +j 1 1 = +j 1 l 1 =0 l 1 l 1 ) 1) l 1 + j 1 ) 1) m 1 l1 ϕ G) m1λ. m 1 =0 For m 1 λ > 0, we can wre G) m1λ = r=0 s rm 1 λ) G) r, where he coeffcens s r m 1 λ) can be obaned from 28) as s r m 1 λ) = for r = 0, 1,. Thus, F ) +j 1 1 = +j 1 l 1 =0 l 2 =r 1) l 2+r m1 λ l 2 ) ) l2, r m 1 ) 1) l 1 + j 1 υ r l 1, λ, ϕ) G) r, l 1 r=0 where υ r l 1, λ, ϕ) = ) 1) m 1 l1 ϕ s r m 1 λ). m 1 =0 m 1 Inerchangng he sums, we oban where p r,u λ, ϕ) = F ) +j 1 1 = p r,+j1λ, ϕ) G) r, r=0 u ) 1) l 1 u l 1 =0 l 1 m 1 =0 l 2 =r ) 1) m 1+r+l 2 l1 ϕ m1 λ m 1 for r, u = 0, 1,. The densy funcon of T :n becomes l 2 ) l2 r ), f :n ) = n 1 B, n + 1) f) ) 1) j 1 n p r,+j1λ, ϕ) G) r, j 1 =0 j 1 r=0
10 790 Pascoa, M. A. R., de Pava, C. M. M., Cordero, G. M. and Orega, E. M. M. and hen 1 n ) f :n ) = 1) j 1 n w d,q p r,+j1λ, ϕ) γ 1 B, n + 1) j d,q,r=0 j 1 =0 1 ) τ ] r k, g,τ,k1+q)+d). The las equaon can be rewren as where f :n ) = n d,q,r=0 j 1 =0 k, md, q,, j 1, n) p r,+j1λ, ϕ) τkq+d) γ 1 ) τ ] r g,τ,k), 12) λ ϕ 1) j+j1+l+q s m λ 1) c q,d md, q,, j 1, n) = B, n + 1) τkq+d) Γk) q j,m=0 l=q ) ) ) ) ϕ 1 n λj + m l. 13) j l q Then, for τ > 0, E T:n s ) can be expressed as E T s :n) = n d,q,r=0 j 1 =0 where δ s+τkq+d),r was defned before. For τ < 0 From 3), we can wre j 1 md, q,, j 1, n) p r,+j1λ, ϕ) δ s+τkq+d),r, F ) +j1 1 = G) λ] ϕ+j 1) ) = 1) m 1 ϕ + j 1) G) m1λ. m 1 =0 For m 1 λ > 0, we have G) m 1λ = r=0 s rm 1 λ) G) r, where s r m 1 λ) s gven by 28) for r = 0, 1,. Furher, F ) +j 1 1 = q r, j 1, λ, ϕ) G) r, r=0 m 1
11 where The Log-Kumaraswamy Generalzed Gamma Regresson Model 791 q r, j 1, λ, ϕ) = ) 1) m 1 ϕ + j 1) s r m 1 λ). m 1 =0 The densy funcon of he KGG order sascs becomes m 1 f :n ) = n 1 B, n + 1) f) ) 1) j 1 n q r, j 1, λ, ϕ) G) r, j 1 =0 j 1 r=0 and hen 1 n ) f :n ) = 1) j 1 n w d,q q r, j 1, λ, ϕ)γ 1 B, n + 1) j d,q,r=0 j 1 =0 1 ) τ ] r k, g,τ,k1+q)+d). The las equaon can be rewren as f :n ) = n d,q,r=0 j 1 =0 k, md, q,, j 1, n) τkq+d) q r, j 1, λ, ϕ)γ 1 ) τ ] r g,τ,k), 14) where md, q,, j 1, n) s gven by 13). So, he momens of he KGG order sascs for τ < 0 can be expressed as E T s :n) = n d,q,r=0 j 1 =0 12) and 14) are he man resuls of hs secon. 4. The LKGG Dsrbuon md, q,, j 1, n)q r, j 1, λ, ϕ) δ s+τkq+d),r. Henceforh, le T be a random varable followng he KGG densy funcon 2) and le Y = logt ). Seng k = q 2, τ = k) 1 and = exp µ τ 1 logk) ], he densy funcon of Y can be expressed as fy) = λ ϕ q q 2 ) q 2 Γq 2 exp q 1 y µ ) y µ γ 1 q 2, q 2 exp q )}]} λ 1 ) q 2 exp q y µ )]} γ 1 q 2, q 2 exp y µ )})] λ } ϕ 1, q
12 792 Pascoa, M. A. R., de Pava, C. M. M., Cordero, G. M. and Orega, E. M. M. where < y, µ <, > 0, λ > 0, ϕ > 0 and q s dfferen from zero. We consder an exended form ncludng he case q = 0 Lawless, 2003). Thus, he densy of Y can be expressed as ) )]} λ ϕ q q 2 ) q 2 exp q 1 y µ Γq 2 ) q 2 exp q y µ )}]} λ 1 γ 1 q 2, q 2 exp fy) = q γ 1 q 2, q 2 exp λ ϕ 2π exp 1 2 y µ y µ q y µ ) 2 }Φ λ 1) y µ )})] λ } ϕ 1, f q 0, ) Φ λ y µ )] ϕ 1, f q = 0, where Φ ) s he sandard normal cumulave dsrbuon. We refer o 15) as he log-kumaraswamy generalzed gamma LKGG) dsrbuon, say Y LKGGµ,, q, λ, ϕ), where µ R s he locaon parameer, > 0 s he scale parameer and q, λ and ϕ are shape parameers. For q = 0 and λϕ = 1 and q = 1, we have from 15) he skew normal and exreme value dsrbuons, respecvely. For ϕ = 1 and λ = ϕ = 1, we oban he log-exponenaed generalzed gamma Orega e al., 2012) and log-gamma generalzed dsrbuons, respecvely. The case λ = ϕ = 1 and q = 1 corresponds o he log-nverse Webull dsrbuon. Thus, f T KGG, τ, k, λ, ϕ) hen Y = logt ) LKGGµ,, q, λ, ϕ). Seng µ = 0 and = 1, he plos of he densy funcon 15) for seleced values of λ and ϕ, when q < 0, q > 0 and q = 0, are dsplayed n Fgure 2. These plos clearly ndcae ha he LKGG dsrbuon could be very flexble for modelng s kuross. 15) fy) q=0.4; λ=0.6; ϕ=0.9 q=4; λ=3; ϕ=0.5 q=0.2; λ=0.4; ϕ=1.2 q=0.5; λ=1.9; ϕ=0.8 q=0.1; λ=0.7; ϕ=5 fy) q= 0.4; λ=0.6; ϕ=0.9 q= 4; λ=3; ϕ=0.5 q= 0.2; λ=0.4; ϕ=1.2 q= 0.5; λ=1.9; ϕ=0.8 q= 0.1; λ=0.7; ϕ=5 fy) λ=0.6; ϕ=0.9 λ=3; ϕ=0.5 λ=0.4; ϕ=1.2 λ=1.9; ϕ=0.8 λ=0.7; ϕ= y Fgure 2: The LKGG densy curves: a) For some values of q > 0. b) For some values of q < 0. c) For some values of q = 0 y y
13 The Log-Kumaraswamy Generalzed Gamma Regresson Model 793 For q > 0, he survval funcon of Y s gven by Sy) = F y) = P Y > y) = P µ + Z > y) = P Z > z) γ1 = λϕqq 2 ) q 2 exp q 1 u q 2 expqu)} q 2, q 2 expqu) ]} λ 1 du Γq 2 ) γ1 q 2, q 2 expqu) ]} λ] ϕ 1) ; z For q < 0, he survval funcon of Y s gven by Sy) = F y) = P Y > y) = P µ + Z > y) = P Z > z) γ1 = λϕqq 2 ) q 2 exp q 1 u q 2 expqu)} q 2, q 2 expqu) ]} λ 1 du Γq 2 ) γ1 q 2, q 2 expqu) ]} λ] ϕ 1). z These negrals can be reduced o γ 1 q 2, q 2 exp } q y µ )])] λ ϕ, f q > 0, Sy) = γ 1 q 2, q 2 exp } q y µ )])] λ ϕ, f q < 0, 16) Φ λ y µ ) ] ϕ, f q = 0. Now, we derve he rh momen of Y LKGGµ,, q, λ, ϕ), say µ r. For q 0, we oban µ r = y r λϕ q q 2) q 2 Γq 2 exp q 2 y µ ) y µ )]}) q exp q ) y µ )]}) λ 1 γ 1 q 2, q 2 exp q y µ )]}) λ ] ϕ 1dy. γ 1 q 2, q 2 exp q Seng x = q 2 exp q y µ )] and usng 5), µ r reduces o µ λϕ sgnq) } r r = Γ q 2 logx) + 2 log q )] + µ x q 2 1 e x ) 0 q ) ϕ 1 γ1 1) j q 2, x )] λj+1) 1 dx. j j=0
14 794 Pascoa, M. A. R., de Pava, C. M. M., Cordero, G. M. and Orega, E. M. M. Applyng expanson 27) n Appendx A for γ 1 q 2, x )] λj+1) 1, we oban } µ λϕ sgnq) r r = 0 Γ q 2 logx) + 2 log q )] + µ x q 2 1 e x ) q ) ϕ 1 1) j s m λj + 1) 1) γ 1 q 2, x ) m dx. j j,m=0 Usng expanson 31) n Appendx A for γ 1 q 2, x ) m, we have } µ λϕ sgnq) r r = 0 Γ q 2 logx) + 2 log q )] + µ e x ) q 1) j ) s m λj + 1) 1) c m, ϕ 1 Γq 2 ) m x q 2 m+1)+ 1 dx. j j,m,=0 Noe ha 2 q log q ) + µ + } r q logx) = r ) ] r 2 r l ) l l q log q ) + µ l logx), q l=0 and hen µ λϕ sgnq) r 1) j ) ) s m λj + 1) 1) c m, ϕ 1 r r = Γq 2 ) Γ q 2 ) m j l j,m,=0 l=0 ] 2 r l ) l q log q ) + µ l logx)e x x q 2 m+1)+ 1 dx. q The las negral s gven n Prudnkov e al. 1986, Vol 1, Secon ) and hen µ λϕ sgnq) r 1) j ) ) s m λj + 1) 1) c m, ϕ 1 r r = Γq 2 ) Γ q 2 ) m j l j,m,=0 l=0 2 q log q ) + µ where Γp) = Γp)/ p. For q = 0, we can wre µ r = EY r ) = λϕ 2π Φ λ) y µ 0 ] r l Γq 2 m + 1) + )] q y r exp 1 2 )] ϕ 1dy. y µ ) 2 ] ) ll, Φ λ 1) y µ )
15 The Log-Kumaraswamy Generalzed Gamma Regresson Model 795 Usng 5), we have µ r = λϕ 2π y µ ) dy. y r exp 1 2 y µ ) 2 ] ) ϕ 1 1) m m m=0 Φ λm+1) 1) The PWM for j and p non-negave negers) of he sandardzed normal dsrbuon s ν j,p = z j φz) Φ p z)dz, where φz) s he sandard normal densy. Seng y = µ + z and usng 27) n Appendx A for Φ λm+1) 1) z), we oban µ r = λ ϕ r m,p=0 j=0 1) m ϕ 1 m ) r j ) s p λm + 1) 1) j µ r j ν j,p, 17) The sandard cumulave normal can be expressed as Φx) = 1 )} x 1 + erf, x R. 2 2 Usng he bnomal expanson and nerchangng erms, we oban ν j,p = 1 2 p 2π p l=0 ) p ) x p l x j e x2 /2 erf dx. l 2 From he power seres for he error funcon erf ) erfx) = 2 π m=0 1) m x 2m+1 2m + 1) m!, he las negral follows from 9)-11) of Nadarajah 2008b). When j +p l s even, we have ν j,p = 2 j/2 π p+1)/2 F p l) A p l=0 j+p l) even j + p l ) p 2 l π l/2 Γ l ) j + p l + 1 ; 1 2,, 1 2 ; 3 2,, 3 2 ; 1,, 1 ), 18) 2
16 796 Pascoa, M. A. R., de Pava, C. M. M., Cordero, G. M. and Orega, E. M. M. where F p l) A s gven n erms of he Laurcella funcon of ype A Exon, 1978; Aars, 2000) defned by F n) A a; b 1,, b n ; c 1,, c n ; x 1,, x n ) a) m1 + +m n b 1 ) = m1 b n ) mn x m1 1 x mn n c 1 ) m1 c n ) mn m 1! m n!, m 1 =0 m n=0 and a) = aa + 1) a + 1) s he ascendng facoral wh he convenon ha a) 0 = 1. Numercal rounes for he drec compuaon of he Laurcella funcon of ype A are avalable, see Exon 1978) and Mahemaca Tro, 2006). Plos of he skewness and kuross for seleced values of µ,, q, λ and ϕ are dsplayed n Fgures 3 and 4, respecvely. Skewness ϕ=0.5 ϕ=1 ϕ=1.5 ϕ=2 Kuross ϕ=0.5 ϕ=1 ϕ=1.5 ϕ= λ Fgure 3: Skewness and kuross of he LKGG dsrbuon as a funcon of λ for some values of ϕ wh µ = 1.5, = 2 and q = 0.5 λ Skewness λ=0.5 λ=1 λ=1.5 λ=2 Kuross λ=0.5 λ=1 λ=1.5 λ= ϕ Fgure 4: Skewness and kuross of he LKGG dsrbuon as a funcon of ϕ for some values of λ wh µ = 1.5, = 2 and q = 0.5 ϕ
17 The Log-Kumaraswamy Generalzed Gamma Regresson Model The LKGG Regresson Model In many praccal applcaons, he lfemes are affeced by explanaory varables such as he choleserol level, blood pressure, wegh and many ohers. Paramerc models o esmae unvarae survval funcons for censored daa regresson problems are wdely used. A paramerc model ha provdes a good f o lfeme daa ends o yeld more precse esmaes of he quanes of neres. If Y LKGGµ,, q, λ, ϕ), we defne he sandardzed random varable Z = Y µ)/ havng densy funcon gven by fz) = λ ϕ q Γq 2 ) q 2 ) q 2 exp q 1 z q 2 expqz) } γ 1 q 2, q 2 expqz) ]} λ 1 γ 1 q 2, q 2 expqz) ]) λ} ϕ 1, f q 0, λ ϕ 2π exp ) z2 Φ λ 1) z) Φ λ z)] ϕ 1, f q = 0. 2 We wre Z LKGG0, 1, q, λ, ϕ). Furher, we propose a lnear locaon-scale regresson model lnkng he response varable y and he explanaory varable vecor x T = x 1,, x p ) by 19) y = x T β + z, = 1,, n, 20) where he random error z has densy funcon 19), β = β 1,, β p ) T, > 0, λ > 0 and < q < are unknown parameers. The parameer µ = x T β s he locaon of y. The locaon parameer vecor µ = µ 1,, µ n ) T s defned by a lnear model µ = Xβ, where X = x 1,, x n ) T s a known model marx. The LKGG model 20) opens new possbles for fed many dfferen ypes of daa. I conans as specal models some well-known regresson models. For ϕ = 1, we oban he log-exponenaed generalzed gamma LEGG) regresson model Orega e al., 2012). The case λ = 1 leads o he log-exponenaed complemen generalzed gamma LECGG) regresson model, whereas ϕ = λ = 1 yelds he log-gamma generalzed LGG) regresson model. For ϕ = λ = q = 1, we oban he classcal log-webull or exreme value) regresson model see, Lawless, 2003). If = 1 and = 0.5, n addon o ϕ = λ = q = 1, he new regresson model reduces o he exponenal and Raylegh regresson models, respecvely. The case λ = ϕ = q = 1 refers o he log-exponenaed Webull LEW) regresson model Mudholkar e al., 1995). See, also, Cancho e al. 1999, 2009), Orega e al. 2006) and Hashmoo e al. 2010). If = 1, n addon o q = 1, concdes wh he log-exponenaed exponenal regresson model. If = 0.5, n addon o q = 1, gves he log-generalzed Raylegh regresson model. For λ = 1, we have he log-gamma generalzed LGG) regresson model Lawless, 2003). Recenly, he LGG dsrbuon has been used n several research areas.
18 798 Pascoa, M. A. R., de Pava, C. M. M., Cordero, G. M. and Orega, E. M. M. See, for example, Orega e al. 2003, 2008, 2009). For q = 1, we oban he log-generalzed nverse Webull regresson model. If λ = 1, n addon o q = 1, follows he log-nverse Webull regresson model. For q = 0, we have he logexponenaed normal regresson model. Fnally, for λ = 2, he LKGG regresson model reduces o he skew normal regresson model. 5.1 Maxmum Lkelhood Esmaon Consder a sample y 1, x 1 ),, y n, x n ) of n ndependen observaons, where each random response s defned by y = mnlog ), logc )}. We assume nonnformave censorng such ha he observed lfemes and censorng mes are ndependen. Le F and C be he ses of ndvduals for whch y s he log-lfeme or log-censorng, respecvely. Convenonal lkelhood esmaon echnques can be appled here. The log-lkelhood funcon for he vecor of parameers θ = q, λ, ϕ,, β T ) T from model 20) has he form lθ) = l θ) + C l c) θ), where l θ) = logfy )], l c) θ) = logsy )], fy ) s he densy funcon 15) and Sy ) s he survval funcon 16) of Y. The oal log-lkelhood funcon for θ can be paroned as lθ) = ] v log λ ϕ q q 2 ) q 2 + q 1 z Γq 2 ) q 2 expqz ) +λ 1) logγ 1 q 2, q 2 expqz )]} +ϕ 1) log γ 1 q 2, q 2 expqz )]} λ} +ϕ log γ 1 q 2, q 2 expqz )]} λ}, f q > 0, C ] v log λ ϕ q) q 2 ) q 2 + q 1 z Γq 2 ) q 2 expqz ) +λ 1) logγ 1 q 2, q 2 expqz )]} +ϕ 1) log γ 1 q 2, q 2 expqz )]} λ} + log γ 1 q 2, q 2 expqz )]} λ] ϕ}, f q < 0, C ] v log 1 2 z 2 + λ 1) logφz )] λϕ 2π +ϕ 1) log Φ λ z )] + ϕ C log Φ λ z )], f q = 0, 21) where v s he number of uncensored observaons falures) and z = y x T β)/. The maxmum lkelhood esmae MLE) θ of he vecor of he model parameers can be calculaed by maxmzng he log-lkelhood 21). Inal values for β and are obaned by fng he Webull regresson model wh λ = 1, ϕ = 1 and
19 The Log-Kumaraswamy Generalzed Gamma Regresson Model 799 q = 1. If ẑ = y x T ˆβ)/ˆ, he f of he LKGG model yelds he esmaed survval funcon for y Ŝy ; ˆλ, ˆϕ, ˆ, ˆq, β T ) = γ1 ˆq 2, ˆq 2 expˆqẑ )]}ˆλ } ˆϕ, f q > 0, γ 1 ˆq 2, ˆq 2 ) ˆϕ, expˆqẑ ]}ˆλ} f q < 0, 22) Φˆλẑ ) ] ˆϕ, f q = 0. Under condons ha are fulflled for he parameer vecor θ n he neror of he parameer space bu no on he boundary, he asympoc dsrbuon of n θ θ) s mulvarae normal Np+3 0, Kθ) 1 ), where Kθ) s he nformaon marx. The asympoc covarance marx Kθ) 1 of θ can be approxmaed by he nverse of he p + 3) p + 3) observed nformaon marx Lθ). The elemens of Lθ), namely L λλ, L λϕ, L λ, L λβj, L ϕϕ, L ϕ, L ϕβj, L, L βj and L βj β s for j, s = 1,, p, are gven n Appendx B. The approxmae mulvarae normal dsrbuon N p+3 0, Lθ) 1 ) for θ can be used n he classcal way o consruc approxmae confdence regons for some componens of θ. Furher, we can use he lkelhood rao LR) sasc for comparng some sub-models wh he LKGG model. We consder he paron θ = θ T 1, θ T 2 ) T, where θ 1 s a subse of parameers of neres and θ 2 s a subse of remanng parameers. The LR sasc for esng he null hypohess H 0 : θ 1 = θ 0) 1 versus he alernave hypohess H 1 : θ 1 θ 0) 1 s gven by w = 2l θ) l θ)}, where θ and θ are he esmaes under he null and alernave hypoheses, respecvely. The sasc w s asympocally as n ) dsrbued as χ 2 k, where k s he dmenson of he subse of parameers θ 1 of neres. 5.2 A Bayesan Analyss As an alernave analyss, we use he Bayesan mehod whch allows for he ncorporaon of prevous knowledge of he parameers hrough nformave pror densy funcons. When hs nformaon s no avalable, we can consder a nonnformave pror. In he Bayesan approach, he nformaon referrng o he model parameers s obaned hrough a poseror margnal dsrbuon. In hs way, wo dffcules usually arse. The frs refers o aanng margnal poseror dsrbuon, and he second o he calculaon of he momens of neres. Boh cases requre numercal negraon ha, many mes, do no presen an analycal soluon. Here, we use he smulaon mehod of Markov Chan Mone Carlo MCMC), such as he Gbbs sampler and Meropols-Hasngs algorhm.
20 800 Pascoa, M. A. R., de Pava, C. M. M., Cordero, G. M. and Orega, E. M. M. Snce we have no pror nformaon from hsorcal daa or from prevous expermen, we assgn conjugae bu weakly nformave pror dsrbuons o he parameers. Snce we assume nformave bu weakly) pror dsrbuon, he poseror dsrbuon s a well-defned proper dsrbuon. Here, we consder ha he elemens of he parameer vecor are ndependen and ha he jon pror dsrbuon of all unknown parameers has densy funcon gven by πλ, ϕ,, q, β) πλ) πϕ) π) πq) πβ). 23) Here, λ Γa 1, b 1 ), ϕ Γa 2, b 2 ), Γa 3, b 3 ), q N µ 1, 1 2) and β s N µ s, s), 2 where Γa, b ) denoes a gamma dsrbuon wh mean a /b, varance a /b 2 and densy funcon fυ; a, b ) = ba υa 1 exp υb ), Γa ) where υ > 0, a > 0 and b > 0, N µ s, 2 s) denoes he normal dsrbuon wh mean µ s, varance 2 s and densy funcon gven by fx; µ s, s ) = 1 2π 2 s exp x µ s) 2 where x, µ s R and s 2 > 0. All hyper-parameers are specfed. Combnng he lkelhood funcon 21) and he pror dsrbuon 23), he jon poseror dsrbuon for λ, ϕ,, q and βs T reduces o ] υ λϕ q)q 2 ) q 2 πλ, ϕ,, q, β y) exp Γq 2 q ] 1 y x T β) ) exp q ]}) 2 y x T exp q β) ]})] λ 1 γ 1 q 2, q 2 y x T exp q β) ]})] λ } ϕ 1 γ 1 q 2, q 2 y x T exp q β) ]})] λ } ϕ γ 1 q 2, q 2 y x T exp q β) C πλ, ϕ,, q, β). 2 2 s ],
21 The Log-Kumaraswamy Generalzed Gamma Regresson Model 801 The jon poseror densy above s analycally nracable because he negraon of he jon poseror densy s no easy o perform. So, he nference can be based on MCMC smulaon mehods such as he Gbbs sampler and Meropols-Hasngs algorhm, whch can be used o draw samples, from whch feaures of he margnal dsrbuons of neres can be nferred. In hs drecon, we frs oban he full condonal dsrbuons of he unknown parameers gven by πλ y, ϕ,, q, β) λ ]})] λ γ υ 1 q 2, q 2 y x T exp q β) ]})] λ } ϕ 1 γ 1 q 2, q 2 y x T exp q β) ]})] λ } ϕ γ 1 q 2, q 2 y x T exp q β) C πλ), πϕ y, λ,, q, β) ϕ υ π y, λ, ϕ, q, β) υ exp γ 1 C C πϕ), q 1 q 2, q 2 exp γ 1 γ 1 q 2, q 2 exp γ 1 q q 2, q 2 exp ]})] λ } ϕ y x T β) q ]})] λ } ϕ y x T β) ] y x T β) exp q ]}) 2 y x T exp q β) q q 2, q 2 exp γ 1 ]})] λ 1 y x T β) q q 2, q 2 exp ]})] λ } ϕ 1 y x T β) q ]})] λ } ϕ y x T β) π),
22 802 Pascoa, M. A. R., de Pava, C. M. M., Cordero, G. M. and Orega, E. M. M. ] υ q)q 2 ) q 2 πq y, λ, ϕ,, β) exp Γq 2 q ] 1 y x T β) ) exp q ]}) 2 y x T exp q β) ]})] λ 1 γ 1 q 2, q 2 y x T exp q β) ]})] λ } ϕ 1 γ 1 q 2, q 2 y x T exp q β) ]})] λ } ϕ γ 1 q 2, q 2 y x T exp q β) C πq) and πβ y, λ, ϕ,, q) exp q 1 ] ]}) y x T β) exp q 2 y x T exp q β) γ 1 C πβ). q 2, q 2 exp γ 1 q q 2, q 2 exp γ 1 ]})] λ 1 y x T β) q q 2, q 2 exp ]})] λ } ϕ 1 y x T β) q ]})] λ } ϕ y x T β) Snce he full condonal dsrbuons for λ, ϕ,, q and β do no have closedform, we requre he use of he Meropols-Hasngs algorhm. The jon poseror densy for q > 0 s defned analogously, consderng he lkelhood funcon 21) for q > 0 and he pror dsrbuon 23). Combnng he lkelhood funcon 21) and he pror dsrbuon 23), he jon poseror dsrbuon for λ, ϕ, and βs T for q = 0 reduces o
23 The Log-Kumaraswamy Generalzed Gamma Regresson Model 803 ) υ ) 2 ] )] λ 1 λϕ πλ, ϕ,, β y) exp 1 y x T β y x T Φ β 2π 2 )] λ } ϕ 1 )] λ } ϕ y x T Φ β y x T Φ β C πλ, ϕ,, β). The condonal dsrbuons for hese parameers akng q = 0 are gven by πλ y, ϕ,, β) λ )] λ )] λ } ϕ 1 υ y x T Φ β y x T Φ β )] λ } ϕ y x T Φ β πλ), C πϕ y, λ,, β) ϕ υ πϕ), Φ y x T β )] λ } ϕ Φ C )] λ } ϕ y x T β ) 2 ] )] λ 1 π y, λ, ϕ, β) exp 1 y x T β y x T Φ β 2 )] λ } ϕ 1 )] λ } ϕ y x T Φ β y x T Φ β C πλ), and ] )] λ 1 πβ y, λ, ϕ, ) exp 1 x T β 2y ) y x T 2 2 Φ β )] λ } ϕ 1 )] λ } ϕ y x T Φ β y x T Φ β C πβ). The MCMC compuaons were mplemened n he sascal sofware package R.
24 804 Pascoa, M. A. R., de Pava, C. M. M., Cordero, G. M. and Orega, E. M. M. 6. Applcaon: Chemcal Dependency Daa We demonsrae he poenaly of he LKGG regresson model appled o chemcal dependency paens as nvesgaed by Pascoa 2008). The daa were provded by he Assocaon Moher Brave, localzed n he cy of Caranga, MG, Brazl, where n = 141 resdens were consdered drug addcs from 2000 o The response varable was he me spen n he communy unl he whdraw of he reamen, consderng ha each resden remans n he communy for a maxmum perod of 270 days whou any conac wh drugs or free drugs. The resden who acheves hs goal was regarded as a censored observaon. Chemcal dependency s a chronc dsease of he bran Kalvas and Volkow, 2005). One of s man characerscs s he relapse phenomenon, whereby sufferers reurn o her consumpon of he problem subsance, followed by a renewed aemp o sop or reduce hs consumpon Brandon e al., 2007; Koob and Le Moal, 1997). Relapse does no mean falure of reamen. Raher s a par of he rehablaon process Marla, 2001). The paen s n relapse when he or she presens all or par of he dysfunconal behavor paerns ha were presen before reamen. Thus, relapse sars before acual renewed consumpon. I s marked by he occurrence of faclang smul wh cognve, emoonal, physcal and socal aspecs Maso e al., 2003). Behavoral changes and exposure o hgh-rsk suaons generally precede resumed consumpon of he subsance Mller e al., 1996). Even he mos movaed paens can presen relapse epsodes Baker e al., 2004). Neverheless, relapse s predcable and avodable Brandon e al., 2007). As he me of absnence ncreases, he chance of relapse decreases, alhough hs rsk s never oally elmnaed durng he lfeme of a person wh an addcon. Sudes of he rsk facors assocaed wh relapse n chemcal dependency are very mporan, because her fndngs can ncrease he probably of suable early clncal nervenons. Furhermore, rsk sudes allow denfcaon of proecve facors o reduce vulnerably and favor ressance o he empaon o relapse. The varables nvolved n he sudy are: : he me spen n he communy unl he whdrawal of reamen days); δ : he censorng ndcaor 0 = censorng, 1 = lfeme observed); x 1 : he maral saus 0 = sngle, 1 = marred); x 2 : schoolng 0 = no educaon or ncomplee bases, 1 = elemenary educaon and hgher educaon); x 3 : age 0 =< 30 years, 1 = 30 years).
25 The Log-Kumaraswamy Generalzed Gamma Regresson Model 805 We f he LKGG regresson model y = β 0 + β 1 x 1 + β 2 x 2 + β 3 x 3 + z, where he errors z 1,, z 141 are ndependen random varables havng densy funcon 19). Table 1 lss he MLEs of he parameers for he LKGG regresson model fed o he curren daa usng he NLMxed procedure n SAS. Ths model nvolves an exra parameer whch gves more flexbly o f hese daa. Inal values for β, q and are aken from he f of he LGG regresson model wh λ = 1 and ϕ = 1. The explanaory varables x 1, x 2 and x 3 are margnally sgnfcan for he LKGG model a he sgnfcance level of 5%. Table 1: MLEs of he parameers, sandard errors, p-values and 95% confdence nervals for he LKGG model fed o he chemcal dependency daa Parameer Esmae SE p-value CI 95% q ; ) λ ; ) ϕ ; ) ; ) β < ; ) β < ; ) β < ; ) β < ; ) Cox 1972) proposed a very useful regresson model for analyzng censorng falure mes, where he random varable of neres represens falure me and he falures mes are assumed dencally dsrbued n some specfed form. He noed ha f he proporonal hazards assumpon holds or, s assumed o hold) hen s possble o esmae he effec parameers) whou any consderaon of he hazard funcon non-paramerc approach). Ths approach o survval daa s called proporonal hazards model. The Cox model may be specalzed f a reason exss o assume ha he baselne hazard follows a paramerc form. In hs case, he baselne hazard can be replaced by a paramerc densy. Typcally, we can hen maxmze he full lkelhood whch grealy smplfes model-fng and provdes nerpreably a he cos of flexbly. Le R ) be he se of ndvduals a rsk a me. Condonally on he rsk ses, he requred lkelhood Lβ) can be expressed as Lβ) = n =1 ] expx T β) δ expx T β), 25) j R )
26 806 Pascoa, M. A. R., de Pava, C. M. M., Cordero, G. M. and Orega, E. M. M. where δ s he censorng ndcaor. The MLE ˆβ of β can be calculaed by maxmzng he lkelhood funcon 25) usng he R sofware. In Table 2, we ls he esmaes, correspondng sandard errors and p-values for he fed Cox regresson model. Explanaory varables x 2 and x 3 are margnally sgnfcan a he 5% sgnfcance level. Table 2: Esmaes of he Cox model fed o he daa of chemcal dependency and correspondng hazard raos HR j ) covarae Esmae SE p-value HR j CI 95% HR j ) β ; ) β ; ) β ; ) Furher, Table 3 gves he Akake Informaon Creron AIC), Conssen Akake Informaon Creron CAIC) and Bayesan Informaon Creron BIC) o compare he LKGG model and Cox proporonal hazard regresson models. The LKGG regresson model ouperforms he oher models rrespecve of he crera and can be used effecvely n he analyss of hese daa. So, he proposed model s a grea alernave o model survval daa. Table 3: The AIC, CAIC and BIC sascs for comparng he LKGG model and Cox proporonal hazard regresson models Model AIC CAIC BIC LKGG Cox In order o assess f he model s approprae, we f he LKGG regresson model for each explanaory varable. In Fgures 5a, b, c, d, we plo he emprcal survval funcon and he esmaed survval funcon 22) for each explanaory varable. We can conclude ha he LKGG regresson model provdes a good f o hese daa. Bayesan analyss The followng ndependen prors were consdered o perform he Meropols- Hasngs algorhm: λ Γ0.01, 0.01), ϕ Γ0.01, 0.01), Γ0.01, 0.01), q N 0, 10) and β s N 0, 10), so ha we have a vague pror dsrbuon. Consderng hese pror densy funcons, we generae wo parallel ndependen runs of he Meropols-Hasngs wh sze 100, 000 for each parameer, dsregardng he frs 10, 000 eraons o elmnae he effec of he nal values and, o avod correlaon problems, we consder a spacng of sze 10, obanng a sample of sze 9, 000 from each chan. To monor he convergence of he Meropols-Hasngs,
27 The Log-Kumaraswamy Generalzed Gamma Regresson Model 807 Sy;x) Kaplan Meer x1=0) Kaplan Meer x1=1) LKGG Regresson model x1=0) LKGG Regresson model x1=1) Sy;x) Kaplan Meer x2=0) Kaplan Meer x2=1) LKGG Regresson model x2=0) LKGG Regresson model x2=1) Sy;x) Kaplan Meer x3=0) Kaplan Meer x3=1) LKGG Regresson model x3=0) LKGG Regresson model x3=1) y Fgure 5: Kaplan-Meer curves srafed by explanaory varable and esmaed survval funcons o he chemcal dependency daa: a) The maral saus explanaory varable. b) Schoolng explanaory varable. c) Age explanaory varable we perform he mehods suggesed by Cowles and Carln 1996). We use he beween and whn sequence nformaon, followng he approach developed n Gelman and Rubn 1992), o oban he poenal scale reducon, R. In all cases, hese values were close o one, ndcang he convergence of he chan. The approxmae poseror margnal densy funcons for he parameers are presened n Fgure 6. In Table 4, we repor poseror summares for he parameers of he LKGG model. We noe ha he values for he means a poseror Table 4) are que close as expeced) o he MLEs gven n Table 1. SD denoes he sandard devaon from he poseror dsrbuons of he parameers and HPD represens he 95% hghes poseror densy HPD) nervals. Densy Densy Densy λ λ Densy Densy Densy y ϕ ϕ Densy Densy Densy y Densy Densy Densy λ q q Densy Densy Densy ϕ β β Densy Densy Densy β β Densy Densy Densy q β2 Densy Densy Densy β0 β β3 Fgure 6: Approxmae poseror margnal denses for he parameers from β β he LKGG model for he chemcal dependency daa β2 β3
28 808 Pascoa, M. A. R., de Pava, C. M. M., Cordero, G. M. and Orega, E. M. M. Table 4: Poseror summares for he parameers from he LKGG model for he chemcal dependency daa Parameer Mean SD HPD 95%) R q ; ) λ ; ) ϕ ; ) ; ) β ; ) β ; ) β ; ) β ; ) Concludng Remarks We nroduce an exended form of he Kumaraswamy generalzed gamma KGG) dsrbuon Pascoa e al., 2011) for whch he hazard rae funcon accommodaes he four ypes of shape forms,.e. ncreasng, decreasng, bahub and unmodal. The KGG model ncludes as specal cases several useful lfeme models. We derve explc expressons for s momens, generang funcon, order sascs and her momens. Furher, we also nroduce he called log- Kumaraswamy generalzed gamma LKGG) dsrbuon and oban explc expressons for s momens. Based on hs new dsrbuon, we defne he LKGG regresson model whch s very suable for modelng censored and uncensored lfeme daa. The new regresson model allow us o es as specal models he goodness of f of some wdely known regresson models. Hence, represens a good alernave for lfeme daa analyss. We esmae he model parameers usng maxmum lkelhood and a Bayesan approach. We demonsrae by means of an applcaon o real daa ha he LKGG model can produce beer fs han some well-known models. Acknowledgemens The auhors are graeful o he Assocae Edor and an anonymous referee and he Edor for very useful commens and suggesons. Ths work was suppored by CNPq and CAPES. Appendx A We derve an expanson for γ 1 k, x) λ 1 for any real λ > 0. We can wre
29 The Log-Kumaraswamy Generalzed Gamma Regresson Model 809 ) λ 1 γ 1 k, x) λ 1 = γ 1 k, x)}] λ 1 = 1) j γ 1 k, x)} j, j j=0 whch always converges snce 0 < γ 1 k, x) < 1. Hence, γ 1 k, x) λ 1 = j=0 m=0 j ) ) λ 1 j 1) j+m γ 1 k, x) m. 26) j m We can subsue j j=0 m=0 for m=0 j=m o oban where γ 1 k, x) λ 1 = s m λ 1) γ 1 k, x) m, 27) s m λ 1) = m=0 ) ) λ 1 j 1) j+m. 28) j m j=m We use he power seres for he ncomplee gamma rao funcon gven by γ 1 k, x) = xk Γk) d=0 x) d k + d) d!. By applcaon a resul by Gradsheyn and Ryzhk 2000, Secon 0.314) for a power seres rased o a posve neger q, we oban ) q a d x d = c q,d x d. 29) d=0 Here, he coeffcens c q,d for d = 1, 2, ) are deermned from he recurrence equaon c q,d = da 0 ) 1 d=0 d p q + 1) d] a p c q,d p, 30) p=1 where c q,0 = a q 0 and a p = 1) p /k + p)p!]. So, he coeffcen c q,d can be calculaed from c q,0,, c q,d 1, and hen can be expressed as a funcon of he quanes a 0,, a d, alhough s no necessary for programmng numercally he expansons. Furher, usng 29), we oban γ 1 k, x) q = xkq Γk) q c q,d x d. 31) d=0
30 810 Pascoa, M. A. R., de Pava, C. M. M., Cordero, G. M. and Orega, E. M. M. Appendx B: Marx of second dervaves Lθ) Here, we provde formulas for he second-order paral dervaves of he loglkelhood funcon. Afer some algebrac manpulaons, we oban L, = υ 2 q 1 2 z 2 expqz )] + qz expqz )} q 1 q 2 1) q 1 Γq 2 ) w q 2 1 z expqz w )γ 1 q 2, w )] z expqz ) w 1 z }) + q 1 Γq 1 ) wq 2 z exp w )γ 1 q 2, w )] 1 λ 1 + λ ϕ)γ 1 q 2, w )] λ γ 1 q 2, w )] λ} 1 + w q 2 1 z )} expqz w )γ 1 q 2, w )] q 1 2 Γq 2 ) C w q 2 1 z expqz w ) γ 1 q 2, w )] λ 1 γ 1 q 2, w )] λ} ϕ γ 1 q 2, w )] λ} ϕ) q 1 q 2 1)z expqz ) q z + wq 2 Γq 2 ) exp w ) γ 1 q 2, w )] 1 λ λγ 1 q 2, w )] λ γ 1 q 2, w )] λ} 2 ϕ 1 + ϕ γ 1 q 2, w )] λ} ϕ γ 1 q 2, w )] λ} )]}} ϕ) 1, L,λ = q 1 Γq 2 w q 2 1 z expqz w )γ 1 q 2, w )] 1 + ϕ) ) γ 1 q 2, w )] λ 1 γ 1 q 2, w )] λ} λ logγ 1 q 2, w )] 1 + γ 1 q 2, w )] λ γ 1 q 2, w )] λ} )]} 1 ϕq 1 Γq 2 w q 2 1 z ) expqz w )γ 1 q 2, w )] λ 1 γ 1 q 2, w )] λ} ϕ 1 γ 1 q 2, w )] λ} ϕ) λ logγ 1 q 2, w )] C
31 L,ϕ = The Log-Kumaraswamy Generalzed Gamma Regresson Model ϕ)γ 1 q 2, w )] λ γ 1 q 2, w )] λ} ) 1 λϕγ 1 q 2, w )] λ γ 1 q 2, w )] λ} 1 γ 1 q 2, w )] λ} } ϕ) 1, λq 1 Γq 2 ) w q 2 1 z expqz w )γ 1 q 2, w )] λ 1 γ 1 q 2, w )] λ} 1 λq 1 Γq 2 w q 2 1 z expqz w ) ) C γ 1 q 2, w )] λ 1 γ 1 q 2, w )] λ} ϕ 1 γ 1 q 2, w )] λ} ϕ) ϕ log γ 1 q 2, w )] λ} + γ 1 q 2, w )] λ} ϕ γ 1 q 2, w )] λ} )} ϕ) 1, L,βj = q 2 x j 1 + qz ) expqz ) 1] q 1 2 Γq 2 ) γ 1 q 2, w )] 1 + λ 1 + ϕ)γ 1 q 2, w )] λ x j w q 2 1 z expqz ) γ 1 q 2, w )] λ} )] 1 q 1 q 2 1)w 1 z expqz ) qz ) exp w ) + q 2 q 2 1)w q 2 1 expqz ) + q 1 expqz 2w )γ 1 q 2, w )] 1 ] 1 Γq 2 ) wq 2 z q 1 Γq 2 ) wq 2 1 z expqz w ) γ 1 q 2, w )] λ} λγ 1 q 2, w )] 2λ 1 γ 1 q 2, w )] λ} )} 1 λ2 ϕ q 2 ) 2 Γq 2 )] 2 x j w q 2 1 expqz w ) C γ 1 q 2, w )] λ 1 γ 1 q 2, w )] λ} ϕ 2 γ 1 q 2, w )] λ} ϕ) ϕ 1 + γ 1 q 2, w )] λ} ϕ γ 1 q 2, w )] λ} )} ϕ) 1,
32 812 Pascoa, M. A. R., de Pava, C. M. M., Cordero, G. M. and Orega, E. M. M. L λ,λ = υ λ 2 + ϕ) logγ1 q 2, w )] } 2 γ1 q 2, w )] λ γ 1 q 2, w )] λ} γ 1 q 2, w )] λ γ 1 q 2, w )] λ} } 1 + ϕ logγ1 q 2, w )] } 2 C γ 1 q 2, w )] λ γ 1 q 2, w )] λ} ϕ 1 γ 1 q 2, w )] λ} ϕ) γ 1 q 2, w )] λ γ 1 q 2, w )] λ} 1 ϕ 1 + γ 1 q 2, w )] λ} ϕ γ 1 q 2, w )] λ} )]} ϕ) 1, L λ,ϕ = logγ 1 q 2, w )]γ 1 q 2, w )] λ γ 1 q 2, w )] λ} 1 + logγ 1 q 2, w )]γ 1 q 2, w )] 1 λ + γ 1 q 2, w )] λ} ϕ 1 C γ 1 q 2, w )] λ} ϕ) 1 ϕ log γ 1 q 2, w )] } 1 + γ 1 q 2, w )] λ} ϕ γ 1 q 2, w )] λ} )]} ϕ) 1, L λ,βj = q 1 Γq 2 x j w q 2 1 expqz w )γ 1 q 2, w )] 1 + ϕ) ) γ 1 q 2, w )] λ γ 1 q 2, w )] λ} )} logγ 1 q 2, w )] q 1 Γq 2 x j w q 2 1 expqz w )γ 1 q 2, w )] λ 1 ) C γ 1 q 2, w )] λ} ϕ 1 γ 1 q 2, w )] λ} ϕ) logγ 1 q 2, w )] 1 + λγ 1 q 2, w )] λ γ 1 q 2, w )] λ} 1 ϕ 1 + γ 1 q 2, w )] λ} ϕ γ 1 q 2, w )] λ} })]} ϕ) 1, L ϕ,ϕ = υ ϕ 2 C log γ 1 q 2, w )] λ}) 2 γ 1 q 2, w )] λ} ϕ γ 1 q 2, w )] λ} ϕ) γ 1 q 2, w )] λ} ϕ γ 1 q 2, w )] λ} } ϕ) 1,
33 L ϕ,βj = The Log-Kumaraswamy Generalzed Gamma Regresson Model 813 λq 1 Γq 2 ) x j w q 2 1 expqz w )γ 1 q 2, w )] λ 1 γ 1 q 2, w )] λ} 1 λq 1 Γq 2 x j w q 2 1 expqz w ) ) γ 1 q 2, w )] λ 1 γ 1 q 2, w )] λ} ϕ 1 γ 1 q 2, w )] λ} ϕ) log γ 1 q 2, w )] λ} ϕ 1 + γ 1 q 2, w )] λ} ϕ C γ 1 q 2, w )] λ} )]} ϕ) 1, L βj,β s = 1 2 x j x s expqz ) q 1 2 Γq 2 ) γ 1 q 2, w )] q + q 1 expqz ) x j x s w q 2 1 expqz w ) q 2 1)w 1 wq Γq 2 ) }) exp w )γ 1 q 2, w )] λ 1 + ϕ)γ 1 q 2, w )] λ γ 1 q 2, w )] λ} }) 1 λq 1 Γq 2 ) wq 2 expqz w ) γ 1 q 2, w )] λ 1 γ 1 q 2, w )] λ} γ 1 q 2, w )] λ γ 1 q 2, w )] λ} )} 1 λϕq 1 2 Γq 2 ) C x j x s w q 2 1 expqz w ) γ 1 q 2, w )] λ 1 γ 1 q 2, w )] λ} ϕ 1 γ 1 q 2, w )] λ} ϕ) 1 q + q 1 expqz ) q 2 1)w 1 wq Γq 2 ) exp w ) γ 1 q 2, w )] λ 1 + γ 1 q 2, w )] λ γ 1 q 2, w )] λ} 1 ϕ 1 + γ 1 q 2, w )] λ} ϕ γ 1 q 2, w )] λ} )]})]} ϕ) 1, where z = y x T β)/ and w = q 2 expqz ).
34 814 Pascoa, M. A. R., de Pava, C. M. M., Cordero, G. M. and Orega, E. M. M. References Aars, R. M. 2000). Laurcella funcons. From MahWorld, A Wolfram Web Resource, creaed by Erc W. Wessen. hp://mahworld.wolfram.com/ LaurcellaFuncons.hml. Al, M. M., Woo, J. and Nadarajah, S. 2008). Generalzed gamma varables wh drough applcaon. Journal of he Korean Sascal Socey 37, Almpands, G. and Koropoulos, C. 2008). Phonemc segmenaon usng he generalzed gamma dsrbuon and small sample Bayesan nformaon creron. Speech Communcaon 50, Barkauskas, D. A., Kronewer, S. R., Lebrlla, C. B. and Rocke, D. M. 2009). Analyss of MALDI FT-ICR mass specromery daa: a me seres approach. Analyca Chmca Aca 648, Baker, T. B., Pper, M. E., McCarhy, D. E., Majeske, M. R. and Fore, M. C. 2004). Addcon movaon reformulaed: an effecve processng model of negave renforcemen. Psychologcal Bullen 111, Brandon, T. H., Vdrne, J. I. and Lvn, E. B. 2007). Relapse and relapse prevenon. Annual Revew of Psychology 3, Cancho, V. G., Bolfarne, H. and Achcar, J. A. 1999). A Bayesan analyss for he exponenaed Webull dsrbuon. Journal of Appled Sascs 8, Cancho, V. G., Orega, E. M. M. and Bolfarne, H. 2009). The exponenaed- Webull regresson models wh cure rae. Journal of Appled Probably & Sascs 4, Cowles, M. K. and Carln, B. P. 1996). Markov chan Mone Carlo convergence dagnoscs: a comparave revew. Journal of he Amercan Sascal Assocaon 91, Carrasco, J. M. F., Orega, E. M. M. and Cordero, G. M. 2008). A generalzed modfed Webull dsrbuon for lfeme modelng. Compuaonal Sascs and Daa Analyss 53, Cordero, G. M., Orega, E. M. M. and Slva, G. O. 2011). The exponenaed generalzed gamma dsrbuon wh applcaon o lfeme daa. Journal of Sascal Compuaon and Smulaon 81,
35 The Log-Kumaraswamy Generalzed Gamma Regresson Model 815 Cox, D. R. 1972) Regresson models and lfe-ables wh dscusson). Journal of he Royal Sascal Socey, Seres B 34, Cox, C. 2008). The generalzed F dsrbuon: an umbrella for paramerc survval analyss. Sascs n Medcne 27, Cox, C., Chu, H., Schneder, M. F. and Muñoz, A. 2007). Paramerc survval analyss and axonomy of hazard funcons for he generalzed gamma dsrbuon. Sascs n Medcne 26, Exon, H. 1978). Handbook of Hypergeomerc Inegrals: Theory, Applcaons, Tables, Compuer Programs. Halsed Press, New York. Gelman, A. and Rubn, D. B. 1992). Inference from erave smulaon usng mulple sequences wh dscusson). Sascal Scence 7, Gomes, O., Combes, C. and Dussauchoy, A. 2008). Parameer esmaon of he generalzed gamma dsrbuon. Mahemacs and Compuers n Smulaon 79, Gradsheyn, I. S. and Ryzhk, I. M. 2000). Table of Inegrals, Seres, and Producs, 6h edon. Eded by A. Jeffrey and D. Zwllnger. Academc Press, New York. Gupa, R. D. and Kundu, D. 1999). Generalzed exponenal dsrbuons. Ausralan & New Zealand Journal of Sascs 41, Hashmoo, E. M., Orega, E. M. M., Cancho, V. G. and Cordero, G. M. 2010). The log-exponenaed Webull regresson model for nerval-censored daa. Compuaonal Sascs & Daa Analyss 54, Kalvas, P. W. and Volkow, N. D. 2005). The neural bass of addcon: a pahology of movaon and choce. Amercan Journal Psycharc 162, Koob, G. F. and Le Moal, M. 1997). Drug abuse: hedonc homeosac dysregulaon. Scence 278, Kundu, D. and Raqab, M. Z. 2005). Generalzed Raylegh dsrbuon: dfferen mehods of esmaon. Compuaonal Sascs and Daa Analyss 49, La, C. D., Xe, M. and Murhy, D. N. P. 2003). A modfed Webull dsrbuon. IEEE Transacons on Relably 52,
( t) Outline of program: BGC1: Survival and event history analysis Oslo, March-May Recapitulation. The additive regression model
 BGC1: Survval and even hsory analyss Oslo, March-May 212 Monday May 7h and Tuesday May 8h The addve regresson model Ørnulf Borgan Deparmen of Mahemacs Unversy of Oslo Oulne of program: Recapulaon Counng
BGC1: Survval and even hsory analyss Oslo, March-May 212 Monday May 7h and Tuesday May 8h The addve regresson model Ørnulf Borgan Deparmen of Mahemacs Unversy of Oslo Oulne of program: Recapulaon Counng
Robustness Experiments with Two Variance Components
 Naonal Insue of Sandards and Technology (NIST) Informaon Technology Laboraory (ITL) Sascal Engneerng Dvson (SED) Robusness Expermens wh Two Varance Componens by Ana Ivelsse Avlés avles@ns.gov Conference
Naonal Insue of Sandards and Technology (NIST) Informaon Technology Laboraory (ITL) Sascal Engneerng Dvson (SED) Robusness Expermens wh Two Varance Componens by Ana Ivelsse Avlés avles@ns.gov Conference
Bayesian Estimation of the Kumaraswamy Inverse Weibull Distribution
 Journal of Sascal Theory and Applcaons, Vol 16, No 2 June 217) 248 26 Bayesan Esmaon of he Kumaraswamy Inverse Webull Dsrbuon Felpe R S de Gusmão Deparmen of Sascs, Federal Unversy of São Carlos, Brazl
Journal of Sascal Theory and Applcaons, Vol 16, No 2 June 217) 248 26 Bayesan Esmaon of he Kumaraswamy Inverse Webull Dsrbuon Felpe R S de Gusmão Deparmen of Sascs, Federal Unversy of São Carlos, Brazl
V.Abramov - FURTHER ANALYSIS OF CONFIDENCE INTERVALS FOR LARGE CLIENT/SERVER COMPUTER NETWORKS
 R&RATA # Vol.) 8, March FURTHER AALYSIS OF COFIDECE ITERVALS FOR LARGE CLIET/SERVER COMPUTER ETWORKS Vyacheslav Abramov School of Mahemacal Scences, Monash Unversy, Buldng 8, Level 4, Clayon Campus, Wellngon
R&RATA # Vol.) 8, March FURTHER AALYSIS OF COFIDECE ITERVALS FOR LARGE CLIET/SERVER COMPUTER ETWORKS Vyacheslav Abramov School of Mahemacal Scences, Monash Unversy, Buldng 8, Level 4, Clayon Campus, Wellngon
Solution in semi infinite diffusion couples (error function analysis)
 Soluon n sem nfne dffuson couples (error funcon analyss) Le us consder now he sem nfne dffuson couple of wo blocks wh concenraon of and I means ha, n a A- bnary sysem, s bondng beween wo blocks made of
Soluon n sem nfne dffuson couples (error funcon analyss) Le us consder now he sem nfne dffuson couple of wo blocks wh concenraon of and I means ha, n a A- bnary sysem, s bondng beween wo blocks made of
John Geweke a and Gianni Amisano b a Departments of Economics and Statistics, University of Iowa, USA b European Central Bank, Frankfurt, Germany
 Herarchcal Markov Normal Mxure models wh Applcaons o Fnancal Asse Reurns Appendx: Proofs of Theorems and Condonal Poseror Dsrbuons John Geweke a and Gann Amsano b a Deparmens of Economcs and Sascs, Unversy
Herarchcal Markov Normal Mxure models wh Applcaons o Fnancal Asse Reurns Appendx: Proofs of Theorems and Condonal Poseror Dsrbuons John Geweke a and Gann Amsano b a Deparmens of Economcs and Sascs, Unversy
New M-Estimator Objective Function. in Simultaneous Equations Model. (A Comparative Study)
 Inernaonal Mahemacal Forum, Vol. 8, 3, no., 7 - HIKARI Ld, www.m-hkar.com hp://dx.do.org/.988/mf.3.3488 New M-Esmaor Objecve Funcon n Smulaneous Equaons Model (A Comparave Sudy) Ahmed H. Youssef Professor
Inernaonal Mahemacal Forum, Vol. 8, 3, no., 7 - HIKARI Ld, www.m-hkar.com hp://dx.do.org/.988/mf.3.3488 New M-Esmaor Objecve Funcon n Smulaneous Equaons Model (A Comparave Sudy) Ahmed H. Youssef Professor
RELATIONSHIP BETWEEN VOLATILITY AND TRADING VOLUME: THE CASE OF HSI STOCK RETURNS DATA
 RELATIONSHIP BETWEEN VOLATILITY AND TRADING VOLUME: THE CASE OF HSI STOCK RETURNS DATA Mchaela Chocholaá Unversy of Economcs Braslava, Slovaka Inroducon (1) one of he characersc feaures of sock reurns
RELATIONSHIP BETWEEN VOLATILITY AND TRADING VOLUME: THE CASE OF HSI STOCK RETURNS DATA Mchaela Chocholaá Unversy of Economcs Braslava, Slovaka Inroducon (1) one of he characersc feaures of sock reurns
In the complete model, these slopes are ANALYSIS OF VARIANCE FOR THE COMPLETE TWO-WAY MODEL. (! i+1 -! i ) + [(!") i+1,q - [(!
 ANALYSIS OF VARIANCE FOR THE COMPLETE TWO-WAY MODEL The frs hng o es n wo-way ANOVA: Is here neracon? "No neracon" means: The man effecs model would f. Ths n urn means: In he neracon plo (wh A on he horzonal
ANALYSIS OF VARIANCE FOR THE COMPLETE TWO-WAY MODEL The frs hng o es n wo-way ANOVA: Is here neracon? "No neracon" means: The man effecs model would f. Ths n urn means: In he neracon plo (wh A on he horzonal
5th International Conference on Advanced Design and Manufacturing Engineering (ICADME 2015)
 5h Inernaonal onference on Advanced Desgn and Manufacurng Engneerng (IADME 5 The Falure Rae Expermenal Sudy of Specal N Machne Tool hunshan He, a, *, La Pan,b and Bng Hu 3,c,,3 ollege of Mechancal and
5h Inernaonal onference on Advanced Desgn and Manufacurng Engneerng (IADME 5 The Falure Rae Expermenal Sudy of Specal N Machne Tool hunshan He, a, *, La Pan,b and Bng Hu 3,c,,3 ollege of Mechancal and
January Examinations 2012
 Page of 5 EC79 January Examnaons No. of Pages: 5 No. of Quesons: 8 Subjec ECONOMICS (POSTGRADUATE) Tle of Paper EC79 QUANTITATIVE METHODS FOR BUSINESS AND FINANCE Tme Allowed Two Hours ( hours) Insrucons
Page of 5 EC79 January Examnaons No. of Pages: 5 No. of Quesons: 8 Subjec ECONOMICS (POSTGRADUATE) Tle of Paper EC79 QUANTITATIVE METHODS FOR BUSINESS AND FINANCE Tme Allowed Two Hours ( hours) Insrucons
Department of Economics University of Toronto
 Deparmen of Economcs Unversy of Torono ECO408F M.A. Economercs Lecure Noes on Heeroskedascy Heeroskedascy o Ths lecure nvolves lookng a modfcaons we need o make o deal wh he regresson model when some of
Deparmen of Economcs Unversy of Torono ECO408F M.A. Economercs Lecure Noes on Heeroskedascy Heeroskedascy o Ths lecure nvolves lookng a modfcaons we need o make o deal wh he regresson model when some of
Bayesian Inference of the GARCH model with Rational Errors
 0 Inernaonal Conference on Economcs, Busness and Markeng Managemen IPEDR vol.9 (0) (0) IACSIT Press, Sngapore Bayesan Inference of he GARCH model wh Raonal Errors Tesuya Takash + and Tng Tng Chen Hroshma
0 Inernaonal Conference on Economcs, Busness and Markeng Managemen IPEDR vol.9 (0) (0) IACSIT Press, Sngapore Bayesan Inference of he GARCH model wh Raonal Errors Tesuya Takash + and Tng Tng Chen Hroshma
( ) () we define the interaction representation by the unitary transformation () = ()
 Hgher Order Perurbaon Theory Mchael Fowler 3/7/6 The neracon Represenaon Recall ha n he frs par of hs course sequence, we dscussed he chrödnger and Hesenberg represenaons of quanum mechancs here n he chrödnger
Hgher Order Perurbaon Theory Mchael Fowler 3/7/6 The neracon Represenaon Recall ha n he frs par of hs course sequence, we dscussed he chrödnger and Hesenberg represenaons of quanum mechancs here n he chrödnger
GENERATING CERTAIN QUINTIC IRREDUCIBLE POLYNOMIALS OVER FINITE FIELDS. Youngwoo Ahn and Kitae Kim
 Korean J. Mah. 19 (2011), No. 3, pp. 263 272 GENERATING CERTAIN QUINTIC IRREDUCIBLE POLYNOMIALS OVER FINITE FIELDS Youngwoo Ahn and Kae Km Absrac. In he paper [1], an explc correspondence beween ceran
Korean J. Mah. 19 (2011), No. 3, pp. 263 272 GENERATING CERTAIN QUINTIC IRREDUCIBLE POLYNOMIALS OVER FINITE FIELDS Youngwoo Ahn and Kae Km Absrac. In he paper [1], an explc correspondence beween ceran
CS434a/541a: Pattern Recognition Prof. Olga Veksler. Lecture 4
 CS434a/54a: Paern Recognon Prof. Olga Veksler Lecure 4 Oulne Normal Random Varable Properes Dscrmnan funcons Why Normal Random Varables? Analycally racable Works well when observaon comes form a corruped
CS434a/54a: Paern Recognon Prof. Olga Veksler Lecure 4 Oulne Normal Random Varable Properes Dscrmnan funcons Why Normal Random Varables? Analycally racable Works well when observaon comes form a corruped
Econ107 Applied Econometrics Topic 5: Specification: Choosing Independent Variables (Studenmund, Chapter 6)
 Econ7 Appled Economercs Topc 5: Specfcaon: Choosng Independen Varables (Sudenmund, Chaper 6 Specfcaon errors ha we wll deal wh: wrong ndependen varable; wrong funconal form. Ths lecure deals wh wrong ndependen
Econ7 Appled Economercs Topc 5: Specfcaon: Choosng Independen Varables (Sudenmund, Chaper 6 Specfcaon errors ha we wll deal wh: wrong ndependen varable; wrong funconal form. Ths lecure deals wh wrong ndependen
On One Analytic Method of. Constructing Program Controls
 Appled Mahemacal Scences, Vol. 9, 05, no. 8, 409-407 HIKARI Ld, www.m-hkar.com hp://dx.do.org/0.988/ams.05.54349 On One Analyc Mehod of Consrucng Program Conrols A. N. Kvko, S. V. Chsyakov and Yu. E. Balyna
Appled Mahemacal Scences, Vol. 9, 05, no. 8, 409-407 HIKARI Ld, www.m-hkar.com hp://dx.do.org/0.988/ams.05.54349 On One Analyc Mehod of Consrucng Program Conrols A. N. Kvko, S. V. Chsyakov and Yu. E. Balyna
CHAPTER 10: LINEAR DISCRIMINATION
 CHAPER : LINEAR DISCRIMINAION Dscrmnan-based Classfcaon 3 In classfcaon h K classes (C,C,, C k ) We defned dscrmnan funcon g j (), j=,,,k hen gven an es eample, e chose (predced) s class label as C f g
CHAPER : LINEAR DISCRIMINAION Dscrmnan-based Classfcaon 3 In classfcaon h K classes (C,C,, C k ) We defned dscrmnan funcon g j (), j=,,,k hen gven an es eample, e chose (predced) s class label as C f g
Approximate Analytic Solution of (2+1) - Dimensional Zakharov-Kuznetsov(Zk) Equations Using Homotopy
 Arcle Inernaonal Journal of Modern Mahemacal Scences, 4, (): - Inernaonal Journal of Modern Mahemacal Scences Journal homepage: www.modernscenfcpress.com/journals/jmms.aspx ISSN: 66-86X Florda, USA Approxmae
Arcle Inernaonal Journal of Modern Mahemacal Scences, 4, (): - Inernaonal Journal of Modern Mahemacal Scences Journal homepage: www.modernscenfcpress.com/journals/jmms.aspx ISSN: 66-86X Florda, USA Approxmae
Fall 2010 Graduate Course on Dynamic Learning
 Fall 200 Graduae Course on Dynamc Learnng Chaper 4: Parcle Flers Sepember 27, 200 Byoung-Tak Zhang School of Compuer Scence and Engneerng & Cognve Scence and Bran Scence Programs Seoul aonal Unversy hp://b.snu.ac.kr/~bzhang/
Fall 200 Graduae Course on Dynamc Learnng Chaper 4: Parcle Flers Sepember 27, 200 Byoung-Tak Zhang School of Compuer Scence and Engneerng & Cognve Scence and Bran Scence Programs Seoul aonal Unversy hp://b.snu.ac.kr/~bzhang/
Ordinary Differential Equations in Neuroscience with Matlab examples. Aim 1- Gain understanding of how to set up and solve ODE s
 Ordnary Dfferenal Equaons n Neuroscence wh Malab eamples. Am - Gan undersandng of how o se up and solve ODE s Am Undersand how o se up an solve a smple eample of he Hebb rule n D Our goal a end of class
Ordnary Dfferenal Equaons n Neuroscence wh Malab eamples. Am - Gan undersandng of how o se up and solve ODE s Am Undersand how o se up an solve a smple eample of he Hebb rule n D Our goal a end of class
On computing differential transform of nonlinear non-autonomous functions and its applications
 On compung dfferenal ransform of nonlnear non-auonomous funcons and s applcaons Essam. R. El-Zahar, and Abdelhalm Ebad Deparmen of Mahemacs, Faculy of Scences and Humanes, Prnce Saam Bn Abdulazz Unversy,
On compung dfferenal ransform of nonlnear non-auonomous funcons and s applcaons Essam. R. El-Zahar, and Abdelhalm Ebad Deparmen of Mahemacs, Faculy of Scences and Humanes, Prnce Saam Bn Abdulazz Unversy,
2. SPATIALLY LAGGED DEPENDENT VARIABLES
 2. SPATIALLY LAGGED DEPENDENT VARIABLES In hs chaper, we descrbe a sascal model ha ncorporaes spaal dependence explcly by addng a spaally lagged dependen varable y on he rgh-hand sde of he regresson equaon.
2. SPATIALLY LAGGED DEPENDENT VARIABLES In hs chaper, we descrbe a sascal model ha ncorporaes spaal dependence explcly by addng a spaally lagged dependen varable y on he rgh-hand sde of he regresson equaon.
CHAPTER FOUR REPEATED MEASURES IN TOXICITY TESTING
 CHAPTER FOUR REPEATED MEASURES IN TOXICITY TESTING 4. Inroducon The repeaed measures sudy s a very commonly used expermenal desgn n oxcy esng because no only allows one o nvesgae he effecs of he oxcans,
CHAPTER FOUR REPEATED MEASURES IN TOXICITY TESTING 4. Inroducon The repeaed measures sudy s a very commonly used expermenal desgn n oxcy esng because no only allows one o nvesgae he effecs of he oxcans,
ABSTRACT KEYWORDS. Bonus-malus systems, frequency component, severity component. 1. INTRODUCTION
 EERAIED BU-MAU YTEM ITH A FREQUECY AD A EVERITY CMET A IDIVIDUA BAI I AUTMBIE IURACE* BY RAHIM MAHMUDVAD AD HEI HAAI ABTRACT Frangos and Vronos (2001) proposed an opmal bonus-malus sysems wh a frequency
EERAIED BU-MAU YTEM ITH A FREQUECY AD A EVERITY CMET A IDIVIDUA BAI I AUTMBIE IURACE* BY RAHIM MAHMUDVAD AD HEI HAAI ABTRACT Frangos and Vronos (2001) proposed an opmal bonus-malus sysems wh a frequency
Analysis And Evaluation of Econometric Time Series Models: Dynamic Transfer Function Approach
 1 Appeared n Proceedng of he 62 h Annual Sesson of he SLAAS (2006) pp 96. Analyss And Evaluaon of Economerc Tme Seres Models: Dynamc Transfer Funcon Approach T.M.J.A.COORAY Deparmen of Mahemacs Unversy
1 Appeared n Proceedng of he 62 h Annual Sesson of he SLAAS (2006) pp 96. Analyss And Evaluaon of Economerc Tme Seres Models: Dynamc Transfer Funcon Approach T.M.J.A.COORAY Deparmen of Mahemacs Unversy
TSS = SST + SSE An orthogonal partition of the total SS
 ANOVA: Topc 4. Orhogonal conrass [ST&D p. 183] H 0 : µ 1 = µ =... = µ H 1 : The mean of a leas one reamen group s dfferen To es hs hypohess, a basc ANOVA allocaes he varaon among reamen means (SST) equally
ANOVA: Topc 4. Orhogonal conrass [ST&D p. 183] H 0 : µ 1 = µ =... = µ H 1 : The mean of a leas one reamen group s dfferen To es hs hypohess, a basc ANOVA allocaes he varaon among reamen means (SST) equally
( ) [ ] MAP Decision Rule
![( ) [ ] MAP Decision Rule ( ) [ ] MAP Decision Rule](/thumbs/82/84970741.jpg) Announcemens Bayes Decson Theory wh Normal Dsrbuons HW0 due oday HW o be assgned soon Proec descrpon posed Bomercs CSE 90 Lecure 4 CSE90, Sprng 04 CSE90, Sprng 04 Key Probables 4 ω class label X feaure
Announcemens Bayes Decson Theory wh Normal Dsrbuons HW0 due oday HW o be assgned soon Proec descrpon posed Bomercs CSE 90 Lecure 4 CSE90, Sprng 04 CSE90, Sprng 04 Key Probables 4 ω class label X feaure
Survival Analysis and Reliability. A Note on the Mean Residual Life Function of a Parallel System
 Communcaons n Sascs Theory and Mehods, 34: 475 484, 2005 Copyrgh Taylor & Francs, Inc. ISSN: 0361-0926 prn/1532-415x onlne DOI: 10.1081/STA-200047430 Survval Analyss and Relably A Noe on he Mean Resdual
Communcaons n Sascs Theory and Mehods, 34: 475 484, 2005 Copyrgh Taylor & Francs, Inc. ISSN: 0361-0926 prn/1532-415x onlne DOI: 10.1081/STA-200047430 Survval Analyss and Relably A Noe on he Mean Resdual
Time-interval analysis of β decay. V. Horvat and J. C. Hardy
 Tme-nerval analyss of β decay V. Horva and J. C. Hardy Work on he even analyss of β decay [1] connued and resuled n he developmen of a novel mehod of bea-decay me-nerval analyss ha produces hghly accurae
Tme-nerval analyss of β decay V. Horva and J. C. Hardy Work on he even analyss of β decay [1] connued and resuled n he developmen of a novel mehod of bea-decay me-nerval analyss ha produces hghly accurae
HEAT CONDUCTION PROBLEM IN A TWO-LAYERED HOLLOW CYLINDER BY USING THE GREEN S FUNCTION METHOD
 Journal of Appled Mahemacs and Compuaonal Mechancs 3, (), 45-5 HEAT CONDUCTION PROBLEM IN A TWO-LAYERED HOLLOW CYLINDER BY USING THE GREEN S FUNCTION METHOD Sansław Kukla, Urszula Sedlecka Insue of Mahemacs,
Journal of Appled Mahemacs and Compuaonal Mechancs 3, (), 45-5 HEAT CONDUCTION PROBLEM IN A TWO-LAYERED HOLLOW CYLINDER BY USING THE GREEN S FUNCTION METHOD Sansław Kukla, Urszula Sedlecka Insue of Mahemacs,
Comparison of Weibayes and Markov Chain Monte Carlo methods for the reliability analysis of turbine nozzle components with right censored data only
 Comparson of Webayes and Markov Chan Mone Carlo mehods for he relably analyss of urbne nozzle componens wh rgh censored daa only Francesco Cannarle,2, Mchele Compare,2, Sara Maafrr 3, Fauso Carlevaro 3,
Comparson of Webayes and Markov Chan Mone Carlo mehods for he relably analyss of urbne nozzle componens wh rgh censored daa only Francesco Cannarle,2, Mchele Compare,2, Sara Maafrr 3, Fauso Carlevaro 3,
Robust and Accurate Cancer Classification with Gene Expression Profiling
 Robus and Accurae Cancer Classfcaon wh Gene Expresson Proflng (Compuaonal ysems Bology, 2005) Auhor: Hafeng L, Keshu Zhang, ao Jang Oulne Background LDA (lnear dscrmnan analyss) and small sample sze problem
Robus and Accurae Cancer Classfcaon wh Gene Expresson Proflng (Compuaonal ysems Bology, 2005) Auhor: Hafeng L, Keshu Zhang, ao Jang Oulne Background LDA (lnear dscrmnan analyss) and small sample sze problem
DEEP UNFOLDING FOR MULTICHANNEL SOURCE SEPARATION SUPPLEMENTARY MATERIAL
 DEEP UNFOLDING FOR MULTICHANNEL SOURCE SEPARATION SUPPLEMENTARY MATERIAL Sco Wsdom, John Hershey 2, Jonahan Le Roux 2, and Shnj Waanabe 2 Deparmen o Elecrcal Engneerng, Unversy o Washngon, Seale, WA, USA
DEEP UNFOLDING FOR MULTICHANNEL SOURCE SEPARATION SUPPLEMENTARY MATERIAL Sco Wsdom, John Hershey 2, Jonahan Le Roux 2, and Shnj Waanabe 2 Deparmen o Elecrcal Engneerng, Unversy o Washngon, Seale, WA, USA
Linear Response Theory: The connection between QFT and experiments
 Phys540.nb 39 3 Lnear Response Theory: The connecon beween QFT and expermens 3.1. Basc conceps and deas Q: ow do we measure he conducvy of a meal? A: we frs nroduce a weak elecrc feld E, and hen measure
Phys540.nb 39 3 Lnear Response Theory: The connecon beween QFT and expermens 3.1. Basc conceps and deas Q: ow do we measure he conducvy of a meal? A: we frs nroduce a weak elecrc feld E, and hen measure
Dynamic Team Decision Theory. EECS 558 Project Shrutivandana Sharma and David Shuman December 10, 2005
 Dynamc Team Decson Theory EECS 558 Proec Shruvandana Sharma and Davd Shuman December 0, 005 Oulne Inroducon o Team Decson Theory Decomposon of he Dynamc Team Decson Problem Equvalence of Sac and Dynamc
Dynamc Team Decson Theory EECS 558 Proec Shruvandana Sharma and Davd Shuman December 0, 005 Oulne Inroducon o Team Decson Theory Decomposon of he Dynamc Team Decson Problem Equvalence of Sac and Dynamc
Clustering (Bishop ch 9)
 Cluserng (Bshop ch 9) Reference: Daa Mnng by Margare Dunham (a slde source) 1 Cluserng Cluserng s unsupervsed learnng, here are no class labels Wan o fnd groups of smlar nsances Ofen use a dsance measure
Cluserng (Bshop ch 9) Reference: Daa Mnng by Margare Dunham (a slde source) 1 Cluserng Cluserng s unsupervsed learnng, here are no class labels Wan o fnd groups of smlar nsances Ofen use a dsance measure
THEORETICAL AUTOCORRELATIONS. ) if often denoted by γ. Note that
 THEORETICAL AUTOCORRELATIONS Cov( y, y ) E( y E( y))( y E( y)) ρ = = Var( y) E( y E( y)) =,, L ρ = and Cov( y, y ) s ofen denoed by whle Var( y ) f ofen denoed by γ. Noe ha γ = γ and ρ = ρ and because
THEORETICAL AUTOCORRELATIONS Cov( y, y ) E( y E( y))( y E( y)) ρ = = Var( y) E( y E( y)) =,, L ρ = and Cov( y, y ) s ofen denoed by whle Var( y ) f ofen denoed by γ. Noe ha γ = γ and ρ = ρ and because
Standard Error of Technical Cost Incorporating Parameter Uncertainty
 Sandard rror of echncal Cos Incorporang Parameer Uncerany Chrsopher Moron Insurance Ausrala Group Presened o he Acuares Insue General Insurance Semnar 3 ovember 0 Sydney hs paper has been prepared for
Sandard rror of echncal Cos Incorporang Parameer Uncerany Chrsopher Moron Insurance Ausrala Group Presened o he Acuares Insue General Insurance Semnar 3 ovember 0 Sydney hs paper has been prepared for
Data Collection Definitions of Variables - Conceptualize vs Operationalize Sample Selection Criteria Source of Data Consistency of Data
 Apply Sascs and Economercs n Fnancal Research Obj. of Sudy & Hypoheses Tesng From framework objecves of sudy are needed o clarfy, hen, n research mehodology he hypoheses esng are saed, ncludng esng mehods.
Apply Sascs and Economercs n Fnancal Research Obj. of Sudy & Hypoheses Tesng From framework objecves of sudy are needed o clarfy, hen, n research mehodology he hypoheses esng are saed, ncludng esng mehods.
e-journal Reliability: Theory& Applications No 2 (Vol.2) Vyacheslav Abramov
 June 7 e-ournal Relably: Theory& Applcaons No (Vol. CONFIDENCE INTERVALS ASSOCIATED WITH PERFORMANCE ANALYSIS OF SYMMETRIC LARGE CLOSED CLIENT/SERVER COMPUTER NETWORKS Absrac Vyacheslav Abramov School
June 7 e-ournal Relably: Theory& Applcaons No (Vol. CONFIDENCE INTERVALS ASSOCIATED WITH PERFORMANCE ANALYSIS OF SYMMETRIC LARGE CLOSED CLIENT/SERVER COMPUTER NETWORKS Absrac Vyacheslav Abramov School
Sampling Procedure of the Sum of two Binary Markov Process Realizations
 Samplng Procedure of he Sum of wo Bnary Markov Process Realzaons YURY GORITSKIY Dep. of Mahemacal Modelng of Moscow Power Insue (Techncal Unversy), Moscow, RUSSIA, E-mal: gorsky@yandex.ru VLADIMIR KAZAKOV
Samplng Procedure of he Sum of wo Bnary Markov Process Realzaons YURY GORITSKIY Dep. of Mahemacal Modelng of Moscow Power Insue (Techncal Unversy), Moscow, RUSSIA, E-mal: gorsky@yandex.ru VLADIMIR KAZAKOV
Variants of Pegasos. December 11, 2009
 Inroducon Varans of Pegasos SooWoong Ryu bshboy@sanford.edu December, 009 Youngsoo Cho yc344@sanford.edu Developng a new SVM algorhm s ongong research opc. Among many exng SVM algorhms, we wll focus on
Inroducon Varans of Pegasos SooWoong Ryu bshboy@sanford.edu December, 009 Youngsoo Cho yc344@sanford.edu Developng a new SVM algorhm s ongong research opc. Among many exng SVM algorhms, we wll focus on
Comb Filters. Comb Filters
 The smple flers dscussed so far are characered eher by a sngle passband and/or a sngle sopband There are applcaons where flers wh mulple passbands and sopbands are requred Thecomb fler s an example of
The smple flers dscussed so far are characered eher by a sngle passband and/or a sngle sopband There are applcaons where flers wh mulple passbands and sopbands are requred Thecomb fler s an example of
Math 128b Project. Jude Yuen
 Mah 8b Proec Jude Yuen . Inroducon Le { Z } be a sequence of observed ndependen vecor varables. If he elemens of Z have a on normal dsrbuon hen { Z } has a mean vecor Z and a varancecovarance marx z. Geomercally
Mah 8b Proec Jude Yuen . Inroducon Le { Z } be a sequence of observed ndependen vecor varables. If he elemens of Z have a on normal dsrbuon hen { Z } has a mean vecor Z and a varancecovarance marx z. Geomercally
Tools for Analysis of Accelerated Life and Degradation Test Data
 Acceleraed Sress Tesng and Relably Tools for Analyss of Acceleraed Lfe and Degradaon Tes Daa Presened by: Reuel Smh Unversy of Maryland College Park smhrc@umd.edu Sepember-5-6 Sepember 28-30 206, Pensacola
Acceleraed Sress Tesng and Relably Tools for Analyss of Acceleraed Lfe and Degradaon Tes Daa Presened by: Reuel Smh Unversy of Maryland College Park smhrc@umd.edu Sepember-5-6 Sepember 28-30 206, Pensacola
FTCS Solution to the Heat Equation
 FTCS Soluon o he Hea Equaon ME 448/548 Noes Gerald Reckenwald Porland Sae Unversy Deparmen of Mechancal Engneerng gerry@pdxedu ME 448/548: FTCS Soluon o he Hea Equaon Overvew Use he forward fne d erence
FTCS Soluon o he Hea Equaon ME 448/548 Noes Gerald Reckenwald Porland Sae Unversy Deparmen of Mechancal Engneerng gerry@pdxedu ME 448/548: FTCS Soluon o he Hea Equaon Overvew Use he forward fne d erence
Lecture 2 M/G/1 queues. M/G/1-queue
 Lecure M/G/ queues M/G/-queue Posson arrval process Arbrary servce me dsrbuon Sngle server To deermne he sae of he sysem a me, we mus now The number of cusomers n he sysems N() Tme ha he cusomer currenly
Lecure M/G/ queues M/G/-queue Posson arrval process Arbrary servce me dsrbuon Sngle server To deermne he sae of he sysem a me, we mus now The number of cusomers n he sysems N() Tme ha he cusomer currenly
Appendix H: Rarefaction and extrapolation of Hill numbers for incidence data
 Anne Chao Ncholas J Goell C seh lzabeh L ander K Ma Rober K Colwell and Aaron M llson 03 Rarefacon and erapolaon wh ll numbers: a framewor for samplng and esmaon n speces dversy sudes cology Monographs
Anne Chao Ncholas J Goell C seh lzabeh L ander K Ma Rober K Colwell and Aaron M llson 03 Rarefacon and erapolaon wh ll numbers: a framewor for samplng and esmaon n speces dversy sudes cology Monographs
Lecture 18: The Laplace Transform (See Sections and 14.7 in Boas)
 Lecure 8: The Lalace Transform (See Secons 88- and 47 n Boas) Recall ha our bg-cure goal s he analyss of he dfferenal equaon, ax bx cx F, where we emloy varous exansons for he drvng funcon F deendng on
Lecure 8: The Lalace Transform (See Secons 88- and 47 n Boas) Recall ha our bg-cure goal s he analyss of he dfferenal equaon, ax bx cx F, where we emloy varous exansons for he drvng funcon F deendng on
P R = P 0. The system is shown on the next figure:
 TPG460 Reservor Smulaon 08 page of INTRODUCTION TO RESERVOIR SIMULATION Analycal and numercal soluons of smple one-dmensonal, one-phase flow equaons As an nroducon o reservor smulaon, we wll revew he smples
TPG460 Reservor Smulaon 08 page of INTRODUCTION TO RESERVOIR SIMULATION Analycal and numercal soluons of smple one-dmensonal, one-phase flow equaons As an nroducon o reservor smulaon, we wll revew he smples
CH.3. COMPATIBILITY EQUATIONS. Continuum Mechanics Course (MMC) - ETSECCPB - UPC
 CH.3. COMPATIBILITY EQUATIONS Connuum Mechancs Course (MMC) - ETSECCPB - UPC Overvew Compably Condons Compably Equaons of a Poenal Vecor Feld Compably Condons for Infnesmal Srans Inegraon of he Infnesmal
CH.3. COMPATIBILITY EQUATIONS Connuum Mechancs Course (MMC) - ETSECCPB - UPC Overvew Compably Condons Compably Equaons of a Poenal Vecor Feld Compably Condons for Infnesmal Srans Inegraon of he Infnesmal
Should Exact Index Numbers have Standard Errors? Theory and Application to Asian Growth
 Should Exac Index umbers have Sandard Errors? Theory and Applcaon o Asan Growh Rober C. Feensra Marshall B. Rensdorf ovember 003 Proof of Proposon APPEDIX () Frs, we wll derve he convenonal Sao-Vara prce
Should Exac Index umbers have Sandard Errors? Theory and Applcaon o Asan Growh Rober C. Feensra Marshall B. Rensdorf ovember 003 Proof of Proposon APPEDIX () Frs, we wll derve he convenonal Sao-Vara prce
This document is downloaded from DR-NTU, Nanyang Technological University Library, Singapore.
 Ths documen s downloaded from DR-NTU, Nanyang Technologcal Unversy Lbrary, Sngapore. Tle A smplfed verb machng algorhm for word paron n vsual speech processng( Acceped verson ) Auhor(s) Foo, Say We; Yong,
Ths documen s downloaded from DR-NTU, Nanyang Technologcal Unversy Lbrary, Sngapore. Tle A smplfed verb machng algorhm for word paron n vsual speech processng( Acceped verson ) Auhor(s) Foo, Say We; Yong,
F-Tests and Analysis of Variance (ANOVA) in the Simple Linear Regression Model. 1. Introduction
 ECOOMICS 35* -- OTE 9 ECO 35* -- OTE 9 F-Tess and Analyss of Varance (AOVA n he Smple Lnear Regresson Model Inroducon The smple lnear regresson model s gven by he followng populaon regresson equaon, or
ECOOMICS 35* -- OTE 9 ECO 35* -- OTE 9 F-Tess and Analyss of Varance (AOVA n he Smple Lnear Regresson Model Inroducon The smple lnear regresson model s gven by he followng populaon regresson equaon, or
Performance Analysis for a Network having Standby Redundant Unit with Waiting in Repair
 TECHNI Inernaonal Journal of Compung Scence Communcaon Technologes VOL.5 NO. July 22 (ISSN 974-3375 erformance nalyss for a Nework havng Sby edundan Un wh ang n epar Jendra Sngh 2 abns orwal 2 Deparmen
TECHNI Inernaonal Journal of Compung Scence Communcaon Technologes VOL.5 NO. July 22 (ISSN 974-3375 erformance nalyss for a Nework havng Sby edundan Un wh ang n epar Jendra Sngh 2 abns orwal 2 Deparmen
Lecture 6: Learning for Control (Generalised Linear Regression)
 Lecure 6: Learnng for Conrol (Generalsed Lnear Regresson) Conens: Lnear Mehods for Regresson Leas Squares, Gauss Markov heorem Recursve Leas Squares Lecure 6: RLSC - Prof. Sehu Vjayakumar Lnear Regresson
Lecure 6: Learnng for Conrol (Generalsed Lnear Regresson) Conens: Lnear Mehods for Regresson Leas Squares, Gauss Markov heorem Recursve Leas Squares Lecure 6: RLSC - Prof. Sehu Vjayakumar Lnear Regresson
Cubic Bezier Homotopy Function for Solving Exponential Equations
 Penerb Journal of Advanced Research n Compung and Applcaons ISSN (onlne: 46-97 Vol. 4, No.. Pages -8, 6 omoopy Funcon for Solvng Eponenal Equaons S. S. Raml *,,. Mohamad Nor,a, N. S. Saharzan,b and M.
Penerb Journal of Advanced Research n Compung and Applcaons ISSN (onlne: 46-97 Vol. 4, No.. Pages -8, 6 omoopy Funcon for Solvng Eponenal Equaons S. S. Raml *,,. Mohamad Nor,a, N. S. Saharzan,b and M.
A NEW TECHNIQUE FOR SOLVING THE 1-D BURGERS EQUATION
 S19 A NEW TECHNIQUE FOR SOLVING THE 1-D BURGERS EQUATION by Xaojun YANG a,b, Yugu YANG a*, Carlo CATTANI c, and Mngzheng ZHU b a Sae Key Laboraory for Geomechancs and Deep Underground Engneerng, Chna Unversy
S19 A NEW TECHNIQUE FOR SOLVING THE 1-D BURGERS EQUATION by Xaojun YANG a,b, Yugu YANG a*, Carlo CATTANI c, and Mngzheng ZHU b a Sae Key Laboraory for Geomechancs and Deep Underground Engneerng, Chna Unversy
THE PREDICTION OF COMPETITIVE ENVIRONMENT IN BUSINESS
 THE PREICTION OF COMPETITIVE ENVIRONMENT IN BUSINESS INTROUCTION The wo dmensonal paral dfferenal equaons of second order can be used for he smulaon of compeve envronmen n busness The arcle presens he
THE PREICTION OF COMPETITIVE ENVIRONMENT IN BUSINESS INTROUCTION The wo dmensonal paral dfferenal equaons of second order can be used for he smulaon of compeve envronmen n busness The arcle presens he
Improvement in Estimating Population Mean using Two Auxiliary Variables in Two-Phase Sampling
 Rajesh ngh Deparmen of ascs, Banaras Hndu Unvers(U.P.), Inda Pankaj Chauhan, Nrmala awan chool of ascs, DAVV, Indore (M.P.), Inda Florenn marandache Deparmen of Mahemacs, Unvers of New Meco, Gallup, UA
Rajesh ngh Deparmen of ascs, Banaras Hndu Unvers(U.P.), Inda Pankaj Chauhan, Nrmala awan chool of ascs, DAVV, Indore (M.P.), Inda Florenn marandache Deparmen of Mahemacs, Unvers of New Meco, Gallup, UA
The Finite Element Method for the Analysis of Non-Linear and Dynamic Systems
 Swss Federal Insue of Page 1 The Fne Elemen Mehod for he Analyss of Non-Lnear and Dynamc Sysems Prof. Dr. Mchael Havbro Faber Dr. Nebojsa Mojslovc Swss Federal Insue of ETH Zurch, Swzerland Mehod of Fne
Swss Federal Insue of Page 1 The Fne Elemen Mehod for he Analyss of Non-Lnear and Dynamc Sysems Prof. Dr. Mchael Havbro Faber Dr. Nebojsa Mojslovc Swss Federal Insue of ETH Zurch, Swzerland Mehod of Fne
Additive Outliers (AO) and Innovative Outliers (IO) in GARCH (1, 1) Processes
 Addve Oulers (AO) and Innovave Oulers (IO) n GARCH (, ) Processes MOHAMMAD SAID ZAINOL, SITI MERIAM ZAHARI, KAMARULZAMMAN IBRAHIM AZAMI ZAHARIM, K. SOPIAN Cener of Sudes for Decson Scences, FSKM, Unvers
Addve Oulers (AO) and Innovave Oulers (IO) n GARCH (, ) Processes MOHAMMAD SAID ZAINOL, SITI MERIAM ZAHARI, KAMARULZAMMAN IBRAHIM AZAMI ZAHARIM, K. SOPIAN Cener of Sudes for Decson Scences, FSKM, Unvers
Chapter 6: AC Circuits
 Chaper 6: AC Crcus Chaper 6: Oulne Phasors and he AC Seady Sae AC Crcus A sable, lnear crcu operang n he seady sae wh snusodal excaon (.e., snusodal seady sae. Complee response forced response naural response.
Chaper 6: AC Crcus Chaper 6: Oulne Phasors and he AC Seady Sae AC Crcus A sable, lnear crcu operang n he seady sae wh snusodal excaon (.e., snusodal seady sae. Complee response forced response naural response.
An introduction to Support Vector Machine
 An nroducon o Suppor Vecor Machne 報告者 : 黃立德 References: Smon Haykn, "Neural Neworks: a comprehensve foundaon, second edon, 999, Chaper 2,6 Nello Chrsann, John Shawe-Tayer, An Inroducon o Suppor Vecor Machnes,
An nroducon o Suppor Vecor Machne 報告者 : 黃立德 References: Smon Haykn, "Neural Neworks: a comprehensve foundaon, second edon, 999, Chaper 2,6 Nello Chrsann, John Shawe-Tayer, An Inroducon o Suppor Vecor Machnes,
PhD/MA Econometrics Examination. January, 2019
 Economercs Comprehensve Exam January 2019 Toal Tme: 8 hours MA sudens are requred o answer from A and B. PhD/MA Economercs Examnaon January, 2019 PhD sudens are requred o answer from A, B, and C. The answers
Economercs Comprehensve Exam January 2019 Toal Tme: 8 hours MA sudens are requred o answer from A and B. PhD/MA Economercs Examnaon January, 2019 PhD sudens are requred o answer from A, B, and C. The answers
Relative controllability of nonlinear systems with delays in control
 Relave conrollably o nonlnear sysems wh delays n conrol Jerzy Klamka Insue o Conrol Engneerng, Slesan Techncal Unversy, 44- Glwce, Poland. phone/ax : 48 32 37227, {jklamka}@a.polsl.glwce.pl Keywor: Conrollably.
Relave conrollably o nonlnear sysems wh delays n conrol Jerzy Klamka Insue o Conrol Engneerng, Slesan Techncal Unversy, 44- Glwce, Poland. phone/ax : 48 32 37227, {jklamka}@a.polsl.glwce.pl Keywor: Conrollably.
Volatility Interpolation
 Volaly Inerpolaon Prelmnary Verson March 00 Jesper Andreasen and Bran Huge Danse Mares, Copenhagen wan.daddy@danseban.com brno@danseban.com Elecronc copy avalable a: hp://ssrn.com/absrac=69497 Inro Local
Volaly Inerpolaon Prelmnary Verson March 00 Jesper Andreasen and Bran Huge Danse Mares, Copenhagen wan.daddy@danseban.com brno@danseban.com Elecronc copy avalable a: hp://ssrn.com/absrac=69497 Inro Local
Inverse Joint Moments of Multivariate. Random Variables
 In J Conem Mah Scences Vol 7 0 no 46 45-5 Inverse Jon Momens of Mulvarae Rom Varables M A Hussan Dearmen of Mahemacal Sascs Insue of Sascal Sudes Research ISSR Caro Unversy Egy Curren address: Kng Saud
In J Conem Mah Scences Vol 7 0 no 46 45-5 Inverse Jon Momens of Mulvarae Rom Varables M A Hussan Dearmen of Mahemacal Sascs Insue of Sascal Sudes Research ISSR Caro Unversy Egy Curren address: Kng Saud
CHAPTER 5: MULTIVARIATE METHODS
 CHAPER 5: MULIVARIAE MEHODS Mulvarae Daa 3 Mulple measuremens (sensors) npus/feaures/arbues: -varae N nsances/observaons/eamples Each row s an eample Each column represens a feaure X a b correspons o he
CHAPER 5: MULIVARIAE MEHODS Mulvarae Daa 3 Mulple measuremens (sensors) npus/feaures/arbues: -varae N nsances/observaons/eamples Each row s an eample Each column represens a feaure X a b correspons o he
Robustness of DEWMA versus EWMA Control Charts to Non-Normal Processes
 Journal of Modern Appled Sascal Mehods Volume Issue Arcle 8 5--3 Robusness of D versus Conrol Chars o Non- Processes Saad Saeed Alkahan Performance Measuremen Cener of Governmen Agences, Insue of Publc
Journal of Modern Appled Sascal Mehods Volume Issue Arcle 8 5--3 Robusness of D versus Conrol Chars o Non- Processes Saad Saeed Alkahan Performance Measuremen Cener of Governmen Agences, Insue of Publc
CS286.2 Lecture 14: Quantum de Finetti Theorems II
 CS286.2 Lecure 14: Quanum de Fne Theorems II Scrbe: Mara Okounkova 1 Saemen of he heorem Recall he las saemen of he quanum de Fne heorem from he prevous lecure. Theorem 1 Quanum de Fne). Le ρ Dens C 2
CS286.2 Lecure 14: Quanum de Fne Theorems II Scrbe: Mara Okounkova 1 Saemen of he heorem Recall he las saemen of he quanum de Fne heorem from he prevous lecure. Theorem 1 Quanum de Fne). Le ρ Dens C 2
FI 3103 Quantum Physics
 /9/4 FI 33 Quanum Physcs Aleander A. Iskandar Physcs of Magnesm and Phooncs Research Grou Insu Teknolog Bandung Basc Conces n Quanum Physcs Probably and Eecaon Value Hesenberg Uncerany Prncle Wave Funcon
/9/4 FI 33 Quanum Physcs Aleander A. Iskandar Physcs of Magnesm and Phooncs Research Grou Insu Teknolog Bandung Basc Conces n Quanum Physcs Probably and Eecaon Value Hesenberg Uncerany Prncle Wave Funcon
Improvement in Estimating Population Mean using Two Auxiliary Variables in Two-Phase Sampling
 Improvemen n Esmang Populaon Mean usng Two Auxlar Varables n Two-Phase amplng Rajesh ngh Deparmen of ascs, Banaras Hndu Unvers(U.P.), Inda (rsnghsa@ahoo.com) Pankaj Chauhan and Nrmala awan chool of ascs,
Improvemen n Esmang Populaon Mean usng Two Auxlar Varables n Two-Phase amplng Rajesh ngh Deparmen of ascs, Banaras Hndu Unvers(U.P.), Inda (rsnghsa@ahoo.com) Pankaj Chauhan and Nrmala awan chool of ascs,
Lecture VI Regression
 Lecure VI Regresson (Lnear Mehods for Regresson) Conens: Lnear Mehods for Regresson Leas Squares, Gauss Markov heorem Recursve Leas Squares Lecure VI: MLSC - Dr. Sehu Vjayakumar Lnear Regresson Model M
Lecure VI Regresson (Lnear Mehods for Regresson) Conens: Lnear Mehods for Regresson Leas Squares, Gauss Markov heorem Recursve Leas Squares Lecure VI: MLSC - Dr. Sehu Vjayakumar Lnear Regresson Model M
Machine Learning Linear Regression
 Machne Learnng Lnear Regresson Lesson 3 Lnear Regresson Bascs of Regresson Leas Squares esmaon Polynomal Regresson Bass funcons Regresson model Regularzed Regresson Sascal Regresson Mamum Lkelhood (ML)
Machne Learnng Lnear Regresson Lesson 3 Lnear Regresson Bascs of Regresson Leas Squares esmaon Polynomal Regresson Bass funcons Regresson model Regularzed Regresson Sascal Regresson Mamum Lkelhood (ML)
Kayode Ayinde Department of Pure and Applied Mathematics, Ladoke Akintola University of Technology P. M. B. 4000, Ogbomoso, Oyo State, Nigeria
 Journal of Mahemacs and Sascs 3 (4): 96-, 7 ISSN 549-3644 7 Scence Publcaons A Comparave Sudy of he Performances of he OLS and some GLS Esmaors when Sochasc egressors are boh Collnear and Correlaed wh
Journal of Mahemacs and Sascs 3 (4): 96-, 7 ISSN 549-3644 7 Scence Publcaons A Comparave Sudy of he Performances of he OLS and some GLS Esmaors when Sochasc egressors are boh Collnear and Correlaed wh
Advanced time-series analysis (University of Lund, Economic History Department)
 Advanced me-seres analss (Unvers of Lund, Economc Hsor Dearmen) 3 Jan-3 Februar and 6-3 March Lecure 4 Economerc echnues for saonar seres : Unvarae sochasc models wh Box- Jenns mehodolog, smle forecasng
Advanced me-seres analss (Unvers of Lund, Economc Hsor Dearmen) 3 Jan-3 Februar and 6-3 March Lecure 4 Economerc echnues for saonar seres : Unvarae sochasc models wh Box- Jenns mehodolog, smle forecasng
M. Y. Adamu Mathematical Sciences Programme, AbubakarTafawaBalewa University, Bauchi, Nigeria
 IOSR Journal of Mahemacs (IOSR-JM e-issn: 78-578, p-issn: 9-765X. Volume 0, Issue 4 Ver. IV (Jul-Aug. 04, PP 40-44 Mulple SolonSoluons for a (+-dmensonalhroa-sasuma shallow waer wave equaon UsngPanlevé-Bӓclund
IOSR Journal of Mahemacs (IOSR-JM e-issn: 78-578, p-issn: 9-765X. Volume 0, Issue 4 Ver. IV (Jul-Aug. 04, PP 40-44 Mulple SolonSoluons for a (+-dmensonalhroa-sasuma shallow waer wave equaon UsngPanlevé-Bӓclund
Chapter Lagrangian Interpolation
 Chaper 5.4 agrangan Inerpolaon Afer readng hs chaper you should be able o:. dere agrangan mehod of nerpolaon. sole problems usng agrangan mehod of nerpolaon and. use agrangan nerpolans o fnd deraes and
Chaper 5.4 agrangan Inerpolaon Afer readng hs chaper you should be able o:. dere agrangan mehod of nerpolaon. sole problems usng agrangan mehod of nerpolaon and. use agrangan nerpolans o fnd deraes and
Computing Relevance, Similarity: The Vector Space Model
 Compung Relevance, Smlary: The Vecor Space Model Based on Larson and Hears s sldes a UC-Bereley hp://.sms.bereley.edu/courses/s0/f00/ aabase Managemen Sysems, R. Ramarshnan ocumen Vecors v ocumens are
Compung Relevance, Smlary: The Vecor Space Model Based on Larson and Hears s sldes a UC-Bereley hp://.sms.bereley.edu/courses/s0/f00/ aabase Managemen Sysems, R. Ramarshnan ocumen Vecors v ocumens are
SOME NOISELESS CODING THEOREMS OF INACCURACY MEASURE OF ORDER α AND TYPE β
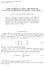 SARAJEVO JOURNAL OF MATHEMATICS Vol.3 (15) (2007), 137 143 SOME NOISELESS CODING THEOREMS OF INACCURACY MEASURE OF ORDER α AND TYPE β M. A. K. BAIG AND RAYEES AHMAD DAR Absrac. In hs paper, we propose
SARAJEVO JOURNAL OF MATHEMATICS Vol.3 (15) (2007), 137 143 SOME NOISELESS CODING THEOREMS OF INACCURACY MEASURE OF ORDER α AND TYPE β M. A. K. BAIG AND RAYEES AHMAD DAR Absrac. In hs paper, we propose
Let s treat the problem of the response of a system to an applied external force. Again,
 Page 33 QUANTUM LNEAR RESPONSE FUNCTON Le s rea he problem of he response of a sysem o an appled exernal force. Agan, H() H f () A H + V () Exernal agen acng on nernal varable Hamlonan for equlbrum sysem
Page 33 QUANTUM LNEAR RESPONSE FUNCTON Le s rea he problem of he response of a sysem o an appled exernal force. Agan, H() H f () A H + V () Exernal agen acng on nernal varable Hamlonan for equlbrum sysem
Bayes rule for a classification problem INF Discriminant functions for the normal density. Euclidean distance. Mahalanobis distance
 INF 43 3.. Repeon Anne Solberg (anne@f.uo.no Bayes rule for a classfcaon problem Suppose we have J, =,...J classes. s he class label for a pxel, and x s he observed feaure vecor. We can use Bayes rule
INF 43 3.. Repeon Anne Solberg (anne@f.uo.no Bayes rule for a classfcaon problem Suppose we have J, =,...J classes. s he class label for a pxel, and x s he observed feaure vecor. We can use Bayes rule
. The geometric multiplicity is dim[ker( λi. number of linearly independent eigenvectors associated with this eigenvalue.
 Lnear Algebra Lecure # Noes We connue wh he dscusson of egenvalues, egenvecors, and dagonalzably of marces We wan o know, n parcular wha condons wll assure ha a marx can be dagonalzed and wha he obsrucons
Lnear Algebra Lecure # Noes We connue wh he dscusson of egenvalues, egenvecors, and dagonalzably of marces We wan o know, n parcular wha condons wll assure ha a marx can be dagonalzed and wha he obsrucons
10. A.C CIRCUITS. Theoretically current grows to maximum value after infinite time. But practically it grows to maximum after 5τ. Decay of current :
 . A. IUITS Synopss : GOWTH OF UNT IN IUIT : d. When swch S s closed a =; = d. A me, curren = e 3. The consan / has dmensons of me and s called he nducve me consan ( τ ) of he crcu. 4. = τ; =.63, n one
. A. IUITS Synopss : GOWTH OF UNT IN IUIT : d. When swch S s closed a =; = d. A me, curren = e 3. The consan / has dmensons of me and s called he nducve me consan ( τ ) of he crcu. 4. = τ; =.63, n one
ESTIMATIONS OF RESIDUAL LIFETIME OF ALTERNATING PROCESS. COMMON APPROACH TO ESTIMATIONS OF RESIDUAL LIFETIME
 Srucural relably. The heory and pracce Chumakov I.A., Chepurko V.A., Anonov A.V. ESTIMATIONS OF RESIDUAL LIFETIME OF ALTERNATING PROCESS. COMMON APPROACH TO ESTIMATIONS OF RESIDUAL LIFETIME The paper descrbes
Srucural relably. The heory and pracce Chumakov I.A., Chepurko V.A., Anonov A.V. ESTIMATIONS OF RESIDUAL LIFETIME OF ALTERNATING PROCESS. COMMON APPROACH TO ESTIMATIONS OF RESIDUAL LIFETIME The paper descrbes
Discussion Paper No Multivariate Time Series Model with Hierarchical Structure for Over-dispersed Discrete Outcomes
 Dscusson Paper No. 113 Mulvarae Tme Seres Model wh Herarchcal Srucure for Over-dspersed Dscree Oucomes Nobuhko Teru and Masaaka Ban Augus, 213 January, 213 (Frs verson) TOHOKU MANAGEMENT & ACCOUNTING RESEARCH
Dscusson Paper No. 113 Mulvarae Tme Seres Model wh Herarchcal Srucure for Over-dspersed Dscree Oucomes Nobuhko Teru and Masaaka Ban Augus, 213 January, 213 (Frs verson) TOHOKU MANAGEMENT & ACCOUNTING RESEARCH
Outline. Probabilistic Model Learning. Probabilistic Model Learning. Probabilistic Model for Time-series Data: Hidden Markov Model
 Probablsc Model for Tme-seres Daa: Hdden Markov Model Hrosh Mamsuka Bonformacs Cener Kyoo Unversy Oulne Three Problems for probablsc models n machne learnng. Compung lkelhood 2. Learnng 3. Parsng (predcon
Probablsc Model for Tme-seres Daa: Hdden Markov Model Hrosh Mamsuka Bonformacs Cener Kyoo Unversy Oulne Three Problems for probablsc models n machne learnng. Compung lkelhood 2. Learnng 3. Parsng (predcon
Part II CONTINUOUS TIME STOCHASTIC PROCESSES
 Par II CONTINUOUS TIME STOCHASTIC PROCESSES 4 Chaper 4 For an advanced analyss of he properes of he Wener process, see: Revus D and Yor M: Connuous marngales and Brownan Moon Karazas I and Shreve S E:
Par II CONTINUOUS TIME STOCHASTIC PROCESSES 4 Chaper 4 For an advanced analyss of he properes of he Wener process, see: Revus D and Yor M: Connuous marngales and Brownan Moon Karazas I and Shreve S E:
Including the ordinary differential of distance with time as velocity makes a system of ordinary differential equations.
 Soluons o Ordnary Derenal Equaons An ordnary derenal equaon has only one ndependen varable. A sysem o ordnary derenal equaons consss o several derenal equaons each wh he same ndependen varable. An eample
Soluons o Ordnary Derenal Equaons An ordnary derenal equaon has only one ndependen varable. A sysem o ordnary derenal equaons consss o several derenal equaons each wh he same ndependen varable. An eample
Childhood Cancer Survivor Study Analysis Concept Proposal
 Chldhood Cancer Survvor Sudy Analyss Concep Proposal 1. Tle: Inverse probably censored weghng (IPCW) o adjus for selecon bas and drop ou n he conex of CCSS analyses 2. Workng group and nvesgaors: Epdemology/Bosascs
Chldhood Cancer Survvor Sudy Analyss Concep Proposal 1. Tle: Inverse probably censored weghng (IPCW) o adjus for selecon bas and drop ou n he conex of CCSS analyses 2. Workng group and nvesgaors: Epdemology/Bosascs
Machine Learning 2nd Edition
 INTRODUCTION TO Lecure Sldes for Machne Learnng nd Edon ETHEM ALPAYDIN, modfed by Leonardo Bobadlla and some pars from hp://www.cs.au.ac.l/~aparzn/machnelearnng/ The MIT Press, 00 alpaydn@boun.edu.r hp://www.cmpe.boun.edu.r/~ehem/mle
INTRODUCTION TO Lecure Sldes for Machne Learnng nd Edon ETHEM ALPAYDIN, modfed by Leonardo Bobadlla and some pars from hp://www.cs.au.ac.l/~aparzn/machnelearnng/ The MIT Press, 00 alpaydn@boun.edu.r hp://www.cmpe.boun.edu.r/~ehem/mle
ESTIMATION METHODS FOR DURATION MODELS. Brian P. McCall. University of Minnesota. and. John J. McCall. University of California, Los Angeles
 Draf: Commens Welcome ESTIMATION METHODS FOR DURATION MODELS by Bran P. McCall Unversy of Mnnesoa and John J. McCall Unversy of Calforna, Los Angeles and Unversy of Calforna, Sana Barbara JANUARY 25 24
Draf: Commens Welcome ESTIMATION METHODS FOR DURATION MODELS by Bran P. McCall Unversy of Mnnesoa and John J. McCall Unversy of Calforna, Los Angeles and Unversy of Calforna, Sana Barbara JANUARY 25 24
. The geometric multiplicity is dim[ker( λi. A )], i.e. the number of linearly independent eigenvectors associated with this eigenvalue.
![. The geometric multiplicity is dim[ker( λi. A )], i.e. the number of linearly independent eigenvectors associated with this eigenvalue. . The geometric multiplicity is dim[ker( λi. A )], i.e. the number of linearly independent eigenvectors associated with this eigenvalue.](/thumbs/78/77822798.jpg) Mah E-b Lecure #0 Noes We connue wh he dscusson of egenvalues, egenvecors, and dagonalzably of marces We wan o know, n parcular wha condons wll assure ha a marx can be dagonalzed and wha he obsrucons are
Mah E-b Lecure #0 Noes We connue wh he dscusson of egenvalues, egenvecors, and dagonalzably of marces We wan o know, n parcular wha condons wll assure ha a marx can be dagonalzed and wha he obsrucons are
NPTEL Project. Econometric Modelling. Module23: Granger Causality Test. Lecture35: Granger Causality Test. Vinod Gupta School of Management
 P age NPTEL Proec Economerc Modellng Vnod Gua School of Managemen Module23: Granger Causaly Tes Lecure35: Granger Causaly Tes Rudra P. Pradhan Vnod Gua School of Managemen Indan Insue of Technology Kharagur,
P age NPTEL Proec Economerc Modellng Vnod Gua School of Managemen Module23: Granger Causaly Tes Lecure35: Granger Causaly Tes Rudra P. Pradhan Vnod Gua School of Managemen Indan Insue of Technology Kharagur,
Bernoulli process with 282 ky periodicity is detected in the R-N reversals of the earth s magnetic field
 Submed o: Suden Essay Awards n Magnecs Bernoull process wh 8 ky perodcy s deeced n he R-N reversals of he earh s magnec feld Jozsef Gara Deparmen of Earh Scences Florda Inernaonal Unversy Unversy Park,
Submed o: Suden Essay Awards n Magnecs Bernoull process wh 8 ky perodcy s deeced n he R-N reversals of he earh s magnec feld Jozsef Gara Deparmen of Earh Scences Florda Inernaonal Unversy Unversy Park,
An Extended Gamma Function Involving a Generalized Hypergeometric Function
 World Appled cences Journal 8 (): 79-799, IN 88-495 IDOI Publcaons, DOI:.589/dos.wasj..8..366 An Exended Gamma Funcon Involvng a Generalzed Hypergeomerc Funcon Abdus aboor Deparmen of Mahemacs, Koha Unversy
World Appled cences Journal 8 (): 79-799, IN 88-495 IDOI Publcaons, DOI:.589/dos.wasj..8..366 An Exended Gamma Funcon Involvng a Generalzed Hypergeomerc Funcon Abdus aboor Deparmen of Mahemacs, Koha Unversy
Advanced Machine Learning & Perception
 Advanced Machne Learnng & Percepon Insrucor: Tony Jebara SVM Feaure & Kernel Selecon SVM Eensons Feaure Selecon (Flerng and Wrappng) SVM Feaure Selecon SVM Kernel Selecon SVM Eensons Classfcaon Feaure/Kernel
Advanced Machne Learnng & Percepon Insrucor: Tony Jebara SVM Feaure & Kernel Selecon SVM Eensons Feaure Selecon (Flerng and Wrappng) SVM Feaure Selecon SVM Kernel Selecon SVM Eensons Classfcaon Feaure/Kernel
