CSED233: Data Structures (2018F) Lecture13: Sorting and Selection
|
|
|
- Bryce Holland
- 5 years ago
- Views:
Transcription
1 (018F) Lecture13: Sortig ad Selectio Daiji Kim CSE, POSECH
2 Divide-ad-Coquer Divide-ad coquer a geeral algorithm desig paradigm: Divide: divide the iput data S i two djoit susets S 1 ad S Recur: solve the suprolems associated with S 1 ad S Coquer: comie the solutios or S 1 ad S ito a solutio or S he ase case or the recursio are suprolems o size 0 or 1 Merge-sort a sortig algorithm ased o the divide-ad-coquer paradigm Like heap-sort It has O( ) ruig time Ulike heap-sort It does ot use a auxiliary priority queue It accesses data i a sequetial maer (suitale to sort data o a dk) By Pro. Daiji Kim, Fall 018
3 Merge-Sort Merge-sort o a iput sequece S with elemets costs o three steps: Divide: partitio S ito two sequeces S 1 ad S o aout elemets each Recur: recursively sort S 1 ad S Coquer: merge S 1 ad S ito a uique sorted sequece Algorithm mergesort(s) Iput sequece S with elemets Output sequece S sorted accordig to C S.size() > 1 (S 1, S ) partitio(s, ) mergesort(s 1 ) mergesort(s ) S merge(s 1, S ) 3 By Pro. Daiji Kim, Fall 018
4 Mergig wo Sorted Sequeces he coquer step o merge-sort costs o mergig two sorted sequeces A ad B ito a sorted sequece S cotaiig the uio o the elemets o A ad B Mergig two sorted sequeces, each with elemets ad implemeted y meas o a douly liked lt, takes O() time Algorithm merge(a, B) Iput sequeces A ad B with elemets each Output sorted sequece o A B S empty sequece while A.Empty() B.Empty() A.irst().elemet() < B.irst().elemet() S.addLast(A.remove(A.irst())) else S.addLast(B.remove(B.irst())) while A.Empty() S.addLast(A.remove (A.irst())) while B.Empty() S.addLast(B.remove (B.irst())) retur S 4 By Pro. Daiji Kim, Fall 018
5 Java Merge Implemetatio 5 By Pro. Daiji Kim, Fall 018
6 Java Merge-Sort Implemetatio 6 By Pro. Daiji Kim, Fall 018
7 Merge-Sort ree A executio o merge-sort depicted y a iary tree each ode represets a recursive call o merge-sort ad stores usorted sequece eore the executio ad its partitio sorted sequece at the ed o the executio the root the iitial call the leaves are calls o susequeces o size 0 or By Pro. Daiji Kim, Fall 018
8 Executio Example Partitio By Pro. Daiji Kim, Fall 018
9 Executio Example (cot.) Recursive call, partitio By Pro. Daiji Kim, Fall 018
10 Executio Example (cot.) Recursive call, partitio By Pro. Daiji Kim, Fall 018
11 Executio Example (cot.) Recursive call, ase case By Pro. Daiji Kim, Fall 018
12 Executio Example (cot.) Recursive call, ase case By Pro. Daiji Kim, Fall 018
13 Executio Example (cot.) Merge By Pro. Daiji Kim, Fall 018
14 Executio Example (cot.) Recursive call,, ase case, merge By Pro. Daiji Kim, Fall 018
15 Merge Executio Example (cot.) By Pro. Daiji Kim, Fall 018
16 Executio Example (cot.) Recursive call,, merge, merge By Pro. Daiji Kim, Fall 018
17 Merge Executio Example (cot.) By Pro. Daiji Kim, Fall 018
18 Aalys o Merge-Sort he height h o the merge-sort tree O( ) at each recursive call we divide i hal the sequece, he overall amout or work doe at the odes o depth i O() we partitio ad merge i sequeces o size i we make i1 recursive calls hus, the total ruig time o merge-sort O( ) depth #seqs size i i i 18 By Pro. Daiji Kim, Fall 018
19 Summary o Sortig Algorithms Algorithm ime Notes selectio-sort O( ) ertio-sort O( ) heap-sort O( ) merge-sort O( ) slow i-place or small data sets (< 1K) slow i-place or small data sets (< 1K) ast i-place or large data sets (1K 1M) ast sequetial data access or huge data sets (> 1M) 19 By Pro. Daiji Kim, Fall 018
20 Divide-ad-Coquer Divide-ad coquer a geeral algorithm desig paradigm: Divide: divide the iput data S i two or more djoit susets S 1, S, Coquer: solve the suprolems recursively Comie: comie the solutios or S 1, S,, ito a solutio or S he ase case or the recursio are suprolems o costat size Aalys ca e doe usig recurrece equatios 0 By Pro. Daiji Kim, Fall 018
21 Merge-Sort Review Merge-sort o a iput sequece S with elemets costs o three steps: Divide: partitio S ito two sequeces S 1 ad S o aout elemets each Coquer: recursively sort S 1 ad S Comie: merge S 1 ad S ito a uique sorted sequece Algorithm mergesort(s) Iput sequece S with elemets Output sequece S sorted accordig to C S.size() > 1 (S 1, S ) partitio(s, ) mergesort(s 1 ) mergesort(s ) S merge(s 1, S ) 1 By Pro. Daiji Kim, Fall 018
22 Recurrece Equatio Aalys he coquer step o merge-sort costs o mergig two sorted sequeces, each with elemets ad implemeted y meas o a douly liked lt, takes at most steps, or some costat. Likewe, the as case ( < ) will take at most steps. hereore, we let () deote the ruig time o merge-sort: ( ) ( ) We ca thereore aalyze the ruig time o merge-sort y idig a closed orm solutio to the aove equatio. hat, a solutio that has () oly o the let-had side. By Pro. Daiji Kim, Fall 018
23 Iterative Sustitutio I the iterative sustitutio, or plug-ad-chug, techique, we iteratively apply the recurrece equatio to itsel ad see we ca id a patter: ( ) ( ) ( ( )) ( )) ( ) 3 ( 3 ) 3 4 ( 4 ) 4... Note that ase, ()=, case occurs whe i =. hat, i =. So, hus, () O( ). ( ) i ( i ) i 3 By Pro. Daiji Kim, Fall 018
24 he Recursio ree Draw the recursio tree or the recurrece relatio ad look or a patter: ( ) ( ) depth s size i i i time otal time = (last level plus all previous levels) 4 By Pro. Daiji Kim, Fall 018
25 Guess-ad-est Method I the guess-ad-test method, we guess a closed orm solutio a d the try to prove it true y iductio: ( ) ( Guess: () < c. ) ( ) ( ) ( c ( ) ( )) c ( ) c c Wrog: we caot make th last lie e less tha c 5 By Pro. Daiji Kim, Fall 018
26 Guess-ad-est Method, (cot.) Recall the recurrece equatio: ( ) ( ) Guess #: () < c. ( ) ( ) ( c ( ) ( )) c ( ) c c c c >. c So, () O( ). I geeral, to use th method, you eed to have a good guess ad you eed to e good at iductio proos. 6 By Pro. Daiji Kim, Fall 018
27 Master Method (Appedix) May divide-ad-coquer recurrece equatios have the orm: ( ) a ( c ) ( ) d d he Master heorem: 1. ( ) O ( a ), the ( ) ( a ). ( ) ( a k ), the ( ) ( a k 1 ) 3. ( ) ( a ), the ( ) ( ( )), provided a ( ) ( ) or some 1. 7 By Pro. Daiji Kim, Fall 018
28 Master Method, Example 1 he orm: ( ) a ( c ) ( ) d d he Master heorem: 1. ( ) O ( a ), the ( ) ( a ). ( ) ( a k ), the ( ) ( a k 1 ) 3. ( ) ( a ), the ( ) ( ( )), provided a ( ) ( ) or some 1. Example: ( ) 4 ( ) Solutio: a=, so case 1 says () O( ). 8 By Pro. Daiji Kim, Fall 018
29 Master Method, Example he orm: ( ) a ( c ) ( ) d d he Master heorem: 1. ( ) O ( a ), the ( ) ( a ). ( ) ( a k ), the ( ) ( a k 1 ) 3. ( ) ( a ), the ( ) ( ( )), provided a ( ) ( ) or some 1. Example: ( ) ( ) Solutio: a=1, so case says () O( ). 9 By Pro. Daiji Kim, Fall 018
30 Master Method, Example 3 he orm: ( ) a ( c ) ( ) d d he Master heorem: 1. ( ) O ( a ), the ( ) ( a ). ( ) ( a k ), the ( ) ( a k 1 ) 3. ( ) ( a ), the ( ) ( ( )), provided a ( ) ( ) or some 1. Example: ( ) ( 3) Solutio: a=0, so case 3 says () O( ). 30 By Pro. Daiji Kim, Fall 018
31 Master Method, Example 4 he orm: ( ) a ( c ) ( ) d d he Master heorem: 1. ( ) O ( a ), the ( ) ( a ). ( ) ( a k ), the ( ) ( a k 1 ) 3. ( ) ( a ), the ( ) ( ( )), provided a ( ) ( ) or some 1. Example: ( ) 8 ( ) Solutio: a=3, so case 1 says () O( 3 ). 31 By Pro. Daiji Kim, Fall 018
32 Master Method, Example 5 he orm: ( ) a ( c ) ( ) d d he Master heorem: 1. ( ) O ( a ), the ( ) ( a ). ( ) ( a k ), the ( ) ( a k 1 ) 3. ( ) ( a ), the ( ) ( ( )), provided a ( ) ( ) or some 1. Example: ( ) 9 ( 3) 3 Solutio: a=, so case 3 says () O( 3 ). 3 By Pro. Daiji Kim, Fall 018
33 Master Method, Example 6 he orm: ( ) a c ( ) ( ) d d he Master heorem: 1. ( ) O ( a ), the ( ) ( a ). ( ) ( a k ), the ( ) ( a k 1 ) 3. ( ) ( a ), the ( ) ( ( )), provided a ( ) ( ) or some 1. Example: ( ) ( ) 1 (iary search) Solutio: a=0, so case says () O( ). 33 By Pro. Daiji Kim, Fall 018
34 Master Method, Example 7 he orm: ( ) a ( c ) ( ) d d he Master heorem: 1. ( ) O ( a ), the ( ) ( a ). ( ) ( a k ), the ( ) ( a k 1 ) 3. ( ) ( a ), the ( ) ( ( )), provided a ( ) ( ) or some 1. Example: ( ) ( ) (heap costructio) Solutio: a=1, so case 1 says () O(). 34 By Pro. Daiji Kim, Fall 018
35 By Pro. Daiji Kim, Fall 018 Iterative Proo o the Master heorem Usig iterative sustitutio, let us see we ca id a patter: We the dtiguh the three cases as he irst term domiat Each part o the summatio equally domiat he summatio a geometric series 35 1 ) ( 0 1 ) ( ) ( (1) ) ( (1)... ) ( ) ( ) ( ) ( ) ( ) ( ) ( )) ( )) ( ( ) ( ) ( ) ( i i i a i i i a a a a a a a a a a a
36 By Pro. Daiji Kim, Fall 018 Iteger Multiplicatio Algorithm: Multiply two -it itegers I ad J. Divide step: Split I ad J ito high-order ad low-order its We ca the deie I*J y multiplyig the parts ad addig: So, () = 4(), which implies () O( ). But that o etter tha the algorithm we leared i grade s chool. 36 l h l h J J J I I I l l h l l h h h l h l h J I J I J I J I J J I I J I ) ( * ) ( *
37 By Pro. Daiji Kim, Fall 018 A Improved Iteger Multiplicatio Algorithm Algorithm: Multiply two -it itegers I ad J. Divide step: Split I ad J ito high-order ad low-order its Oserve that there a deret way to multiply parts: So, () = 3(), which implies () O( 3 ), y the Master heorem. hus, () O( ). 37 l h l h J J J I I I l l h l l h h h l l l l h h h l h h l l l h h h l l l l h h h l l h h h J I J I J I J I J I J I J I J I J I J I J I J I J I J I J I J J I I J I J I ) ( ] ) [( ] ) )( [( *
38 Quick-Sort Quick-sort a radomized sortig algorithm ased o the divide-ad-coquer paradigm: Divide: pick a radom elemet x (called pivot) ad partitio S ito L elemets less tha x E elemets equal x G elemets greater tha x Recur: sort L ad G Coquer: joi L, E ad G L E x x x G 38 By Pro. Daiji Kim, Fall 018
39 Partitio We partitio a iput sequece as ollows: We remove, i tur, each elemet y rom S ad We ert y ito L, E or G, depedig o the result o the comparo with the pivot x Each ertio ad removal at the egiig or at the ed o a sequece, ad hece takes O(1) time hus, the partitio step o quick-sort takes O() time Algorithm partitio(s, p) Iput sequece S, positio p o pivot Output susequeces L, E, G o the elemets o S less tha, equal to, or greater tha the pivot, resp. L, E, G empty sequeces x S.remove(p) while S.Empty() y S.remove(S.irst()) y < x L.addLast(y) else y = x E.addLast(y) else { y > x } G.addLast(y) retur L, E, G 39 By Pro. Daiji Kim, Fall 018
40 Java Implemetatio 40 By Pro. Daiji Kim, Fall 018
41 Quick-Sort ree A executio o quick-sort depicted y a iary tree Each ode represets a recursive call o quick-sort ad stores Usorted sequece eore the executio ad its pivot Sorted sequece at the ed o the executio he root the iitial call he leaves are calls o susequeces o size 0 or By Pro. Daiji Kim, Fall 018
42 Executio Example Pivot selectio By Pro. Daiji Kim, Fall 018
43 Executio Example (cot.) Partitio, recursive call, pivot selectio By Pro. Daiji Kim, Fall 018
44 Executio Example (cot.) Partitio, recursive call, ase case By Pro. Daiji Kim, Fall 018
45 Executio Example (cot.) Recursive call,, ase case, joi By Pro. Daiji Kim, Fall 018
46 Executio Example (cot.) Recursive call, pivot selectio By Pro. Daiji Kim, Fall 018
47 Executio Example (cot.) Partitio,, recursive call, ase case By Pro. Daiji Kim, Fall 018
48 Joi, joi Executio Example (cot.) By Pro. Daiji Kim, Fall 018
49 Worst-case Ruig ime he worst case or quick-sort occurs whe the pivot the uique miimum or maximum elemet Oe o L ad G has size 1 ad the other has size 0 he ruig time proportioal to the sum ( 1) 1 hus, the worst-case ruig time o quick-sort O( ) depth time By Pro. Daiji Kim, Fall 018
50 Expected Ruig ime Cosider a recursive call o quick-sort o a sequece o size s Good call: the sizes o L ad G are each less tha 3s4 Bad call: oe o L ad G has size greater tha 3s Good call A call good with proaility 1 1 o the possile pivots cause good calls: Bad call Bad pivots Good pivots Bad pivots 50 By Pro. Daiji Kim, Fall 018
51 Expected Ruig ime, Part Proailtic Fact: he expected umer o coi tosses required i order to get k heads k For a ode o depth i, we expect i acestors are good calls he size o the iput sequece or the curret call at most (34) i hereore, we have For a ode o depth 43, the expected iput size oe he expected height o the quick-sort tree O( ) he amout or work doe at the odes o the same depth O() hus, the expected ruig time o quick-sort O( ) expected height O( ) s(a) s(r) s() s(c) s(d) s(e) s() time per level O() O() O() total expected time: O( ) 51 By Pro. Daiji Kim, Fall 018
52 I-Place Quick-Sort Quick-sort ca e implemeted to ru i-place I the partitio step, we use replace operatios to rearrage the elemets o the iput sequece such that the elemets less tha the pivot have rak less tha h the elemets equal to the pivot have rak etwee h ad k the elemets greater tha the pivot have rak greater tha k he recursive calls cosider elemets with rak less tha h elemets with rak greater tha k Algorithm iplacequicksort(s, l, r) Iput sequece S, raks l ad r Output sequece S with the elemets o rak etwee l ad r rearraged i icreasig order l r retur i a radom iteger etwee l ad r x S.elemAtRak(i) (h, k) iplacepartitio(x) iplacequicksort(s, l, h 1) iplacequicksort(s, k 1, r) 5 By Pro. Daiji Kim, Fall 018
53 I-Place Partitioig Perorm the partitio usig two idices to split S ito L ad E U G (a similar method ca split E U G ito E ad G j k Repeat util j ad k cross: Sca j to the right util idig a elemet > x. Sca k to the let util idig a elemet < x. Swap elemets at idices j ad k (pivot = 6) j k By Pro. Daiji Kim, Fall 018
54 Java Implemetatio 54 By Pro. Daiji Kim, Fall 018
55 Summary o Sortig Algorithms Algorithm ime Notes selectio-sort O( ) i-place slow (good or small iputs) ertio-sort O( ) quick-sort O( ) expected heap-sort O( ) merge-sort O( ) i-place slow (good or small iputs) i-place, radomized astest (good or large iputs) i-place ast (good or large iputs) sequetial data access ast (good or huge iputs) 55 By Pro. Daiji Kim, Fall 018
56 Comparo-Based Sortig May sortig algorithms are comparo ased. hey sort y makig comparos etwee pairs o ojects Examples: ule-sort, selectio-sort, ertio-sort, heap-sort, merge-sort, quick-sort,... Let us thereore derive a lower oud o the ruig ti me o ay algorithm that uses comparos to sort el emets, x 1, x,, x. Is x i < x j? o yes 56 By Pro. Daiji Kim, Fall 018
57 Coutig Comparos Let us just cout comparos the. Each possile ru o the algorithm correspods to a root-to-lea path i a decio tree x i < x j? x a < x? x c < x d? x e < x? x k < x l? x m < x o? x p < x q? 57 By Pro. Daiji Kim, Fall 018
58 Decio ree Height he height o the decio tree a lower oud o the ruig time Every iput permutatio must lead to a separate lea output I ot, some iput 4 5 would have same output orderig as 5 4, which would e wrog Sice there are!=1 leaves, the height at least (!) miimum height (time) x i < x j? x a < x? x c < x d? (!) x e < x? x k < x l? x m < x o? x p < x q?! 58 By Pro. Daiji Kim, Fall 018
59 he Lower Boud Ay comparo-ased sortig algorithms takes at least (!) time hereore, ay such algorithm takes time at least (!) hat, ay comparo-ased sortig algorithm must ru i ( ) time. ( ) ( ). 59 By Pro. Daiji Kim, Fall 018
60 Bucket-Sort Let e S e a sequece o (key, elemet) items with keys i the rage [0, N 1] Bucket-sort uses the keys as idices I to a auxiliary array B o sequeces (uckets) Phase 1: Empty sequece S y movig each etry (k, o) ito its ucket B[k] Phase : For i 0,, N 1, move the etries o ucket B[i] to the ed o sequece S Aalys: Phase 1 takes O() time Phase takes O( N) time Bucket-sort takes O( N) time Algorithm ucketsort(s): Iput: Sequece S o etries with i teger keys i the rage [0, N 1] Output: Sequece S sorted i ode creasig order o the keys let B e a array o N sequeces, eac h o which iitially empty or each etry e i S do k = the key o e remove e rom S ert e at the ed o ucket B[k] or i = 0 to N 1 do or each etry e i B[i] do remove e rom B[i] ert e at the ed o S 60 By Pro. Daiji Kim, Fall 018
61 Example Key rage [0, 9] 7, d 1, c 3, a 7, g 3, 7, e Phase 1 1, c 3, a 3, 7, d 7, g 7, e B Phase 1, c 3, a 3, 7, d 7, g 7, e 61 By Pro. Daiji Kim, Fall 018
62 Properties ad Extesios Key-type Property he keys are used as idices ito a array ad caot e aritrary ojects No exteral comparator Stale Sort Property he relative order o ay two items with the same key preserved ater the executio o the algorithm Extesios Iteger keys i the rage [a, ] Put etry (k, o) ito ucket B[k a] Strig keys rom a set D o possile strigs, where D has costat size (e.g., ames o the 50 U.S. states) Sort D ad compute the rak r(k) o each strig k o D i the sorted sequece Put etry (k, o) ito ucket B[r(k)] 6 By Pro. Daiji Kim, Fall 018
63 Lexicographic Order A d-tuple a sequece o d keys (k 1, k,, k d ), where key k i said to e the i-th dimesio o the tuple Example: he Cartesia coordiates o a poit i space are a 3-tuple he lexicographic order o two d-tuples recursively deied as ollows (x 1, x,, x d ) (y 1, y,, y d ) x 1 y 1 x 1 y 1 (x,, x d ) (y,, y d ) I.e., the tuples are compared y the irst dimesio, the y the secod dimesio, etc. 63 By Pro. Daiji Kim, Fall 018
64 Lexicographic-Sort Let C i e the comparator that compares two tuples y their i-th dimesio Let stalesort(s, C) e a stale sorti g algorithm that uses comparator C Lexicographic-sort sorts a sequece o d-tuples i lexicographic order y executig d times algorithm stalesort, oe per dimesio Lexicographic-sort rus i O(d()) time, where () the ruig time o stalesort Algorithm lexicographicsort(s) Iput sequece S o d-tuples Output sequece S sorted i lexicographic order or i d dowto 1 stalesort(s, C i ) Example: (7,4,6) (5,1,5) (,4,6) (, 1, 4) (3,, 4) (, 1, 4) (3,, 4) (5,1,5) (7,4,6) (,4,6) (, 1, 4) (5,1,5) (3,, 4) (7,4,6) (,4,6) (, 1, 4) (,4,6) (3,, 4) (5,1,5) (7,4,6) 64 By Pro. Daiji Kim, Fall 018
65 Radix-Sort Radix-sort a specializatio o lexicographic-sort that uses ucketsort as the stale sortig algorithm i each dimesio Radix-sort applicale to tuples where the keys i each dimesio i are itegers i the rage [0, N 1] Radix-sort rus i time O(d( N)) Algorithm radixsort(s, N) Iput sequece S o d-tuples such that (0,, 0) (x 1,, x d ) ad (x 1,, x d ) (N 1,, N 1) or each tuple (x 1,, x d ) i S Output sequece S sorted i lexicographic order or i d dowto 1 ucketsort(s, N) 65 By Pro. Daiji Kim, Fall 018
66 Radix-Sort or Biary Numers Cosider a sequece o -it itegers x x 1 x 1 x 0 We represet each elemet as a -tuple o itegers i the rage [0, 1] ad apply radix-so rt with N h applicatio o the radixsort algorithm rus i O() time For example, we ca sort a sequece o 3-it itegers i liear time Algorithm iaryradixsort(s) Iput sequece S o -it itegers Output sequece S sorted replace each elemet x o S with the item (0, x) or i 0 to 1 replace the key k o each item (k, x) o S with it x i o x ucketsort(s, ) 66 By Pro. Daiji Kim, Fall 018
67 Example Sortig a sequece o 4-it itegers By Pro. Daiji Kim, Fall 018
68 he Selectio Prolem Give a iteger k ad elemets x 1, x,, x, take rom a total order, id the k-th smallest elemet i th set. O course, we ca sort the set i O( ) time ad the idex the k-th elemet. k= Ca we solve the selectio prolem aster? 68 By Pro. Daiji Kim, Fall 018
69 Quick-Select Quick-select a radomized selectio algorithm ased o the prue-ad-search paradigm: Prue: pick a radom elemet x(called pivot) ad partitio S ito L: elemets less tha x E: elemets equal x G: elemets greater tha x Search: depedig o k, either aswer i E, or we eed to recur i either L or G L k < L E x x G L < k < L E (doe) k > L E k = k - L - E 69 By Pro. Daiji Kim, Fall 018
70 Partitio We partitio a iput sequece as i the quick-sort algorithm: We remove, i tur, each elemet y rom S ad We ert y ito L, E or G, depedig o the result o the comparo with the pivot x Each ertio ad removal at the egiig or at the ed o a sequece, ad hece takes O(1) time hus, the partitio step o quick-select takes O() time Algorithm partitio(s, p) Iput sequece S, positio p o pivot Output susequeces L, E, G o the elemets o S less tha, equal to, or greater tha the pivot, resp. L, E, G empty sequeces x S.remove(p) while S.Empty() y S.remove(S.irst()) y < x L.addLast(y) else y = x E.addLast(y) else { y > x } G.addLast(y) retur L, E, G 70 By Pro. Daiji Kim, Fall 018
71 Quick-Select Vualizatio A executio o quick-select ca e vualized y a recursio path Each ode represets a recursive call o quick-select, ad stores k ad the remaiig sequece k=5, S=( ) k=, S=( ) k=, S=( ) k=1, S=(7 6 5) 5 71 By Pro. Daiji Kim, Fall 018
72 Expected Ruig ime Cosider a recursive call o quick-select o a sequece o size s Good call: the sizes o L ad G are each less tha 3s4 Bad call: oe o L ad G has size greater tha 3s Good call Bad call A call good with proaility 1 1 o the possile pivots cause good calls: Bad pivots Good pivots Bad pivots 7 By Pro. Daiji Kim, Fall 018
73 Expected Ruig ime, Part Proailtic Fact #1: he expected umer o coi tosses required i order to get oe head two Proailtic Fact #: Expectatio a liear uctio: E(X Y ) = E(X ) E(Y ) E(cX ) = ce(x ) Let () deote the expected ruig time o quick-select. By Fact #, () < (34) *(expected # o calls eore a good call) By Fact #1, () < (34) hat, () a geometric series: () < (34) (34) (34) 3 So () O(). We ca solve the selectio prolem i O() expected time. 73 By Pro. Daiji Kim, Fall 018
74 Determitic Selectio We ca do selectio i O() worst-case time. Mai idea: recursively use the selectio algorithm itsel to id a good pivot or quick-select: Divide S ito 5 sets o 5 each Fid a media i each set Recursively id the media o the ay medias. Mi size or L Mi size or G 74 By Pro. Daiji Kim, Fall 018
Data Structures Lecture 9
 Fall 2017 Fag Yu Software Security Lab. Dept. Maagemet Iformatio Systems, Natioal Chegchi Uiversity Data Structures Lecture 9 Midterm o Dec. 7 (9:10-12:00am, 106) Lec 1-9, TextBook Ch1-8, 11,12 How to
Fall 2017 Fag Yu Software Security Lab. Dept. Maagemet Iformatio Systems, Natioal Chegchi Uiversity Data Structures Lecture 9 Midterm o Dec. 7 (9:10-12:00am, 106) Lec 1-9, TextBook Ch1-8, 11,12 How to
Merge and Quick Sort
 Merge ad Quick Sort Merge Sort Merge Sort Tree Implemetatio Quick Sort Pivot Item Radomized Quick Sort Adapted from: Goodrich ad Tamassia, Data Structures ad Algorithms i Java, Joh Wiley & So (1998). Ruig
Merge ad Quick Sort Merge Sort Merge Sort Tree Implemetatio Quick Sort Pivot Item Radomized Quick Sort Adapted from: Goodrich ad Tamassia, Data Structures ad Algorithms i Java, Joh Wiley & So (1998). Ruig
CS 332: Algorithms. Linear-Time Sorting. Order statistics. Slide credit: David Luebke (Virginia)
 1 CS 332: Algorithms Liear-Time Sortig. Order statistics. Slide credit: David Luebke (Virgiia) Quicksort: Partitio I Words Partitio(A, p, r): Select a elemet to act as the pivot (which?) Grow two regios,
1 CS 332: Algorithms Liear-Time Sortig. Order statistics. Slide credit: David Luebke (Virgiia) Quicksort: Partitio I Words Partitio(A, p, r): Select a elemet to act as the pivot (which?) Grow two regios,
This Lecture. Divide and Conquer. Merge Sort: Algorithm. Merge Sort Algorithm. MergeSort (Example) - 1. MergeSort (Example) - 2
 This Lecture Divide-ad-coquer techique for algorithm desig. Example the merge sort. Writig ad solvig recurreces Divide ad Coquer Divide-ad-coquer method for algorithm desig: Divide: If the iput size is
This Lecture Divide-ad-coquer techique for algorithm desig. Example the merge sort. Writig ad solvig recurreces Divide ad Coquer Divide-ad-coquer method for algorithm desig: Divide: If the iput size is
Merge Sort. Outline and Reading. Divide-and-Conquer. Divide-and-conquer paradigm ( 4.1.1) Merge-sort ( 4.1.1)
 Merge Sort 7 2 9 4 2 4 7 9 7 2 2 7 9 4 4 9 7 7 2 2 9 9 4 4 Merge Sort versio 1.3 1 Outlie d Redig Divide-d-coquer prdigm ( 4.1.1 Merge-sort ( 4.1.1 Algorithm Mergig two sorted sequeces Merge-sort tree
Merge Sort 7 2 9 4 2 4 7 9 7 2 2 7 9 4 4 9 7 7 2 2 9 9 4 4 Merge Sort versio 1.3 1 Outlie d Redig Divide-d-coquer prdigm ( 4.1.1 Merge-sort ( 4.1.1 Algorithm Mergig two sorted sequeces Merge-sort tree
Sorting Algorithms. Algorithms Kyuseok Shim SoEECS, SNU.
 Sortig Algorithms Algorithms Kyuseo Shim SoEECS, SNU. Desigig Algorithms Icremetal approaches Divide-ad-Coquer approaches Dyamic programmig approaches Greedy approaches Radomized approaches You are ot
Sortig Algorithms Algorithms Kyuseo Shim SoEECS, SNU. Desigig Algorithms Icremetal approaches Divide-ad-Coquer approaches Dyamic programmig approaches Greedy approaches Radomized approaches You are ot
Design and Analysis of Algorithms
 Desig ad Aalysis of Algorithms CSE 53 Lecture 9 Media ad Order Statistics Juzhou Huag, Ph.D. Departmet of Computer Sciece ad Egieerig Dept. CSE, UT Arligto CSE53 Desig ad Aalysis of Algorithms Medias ad
Desig ad Aalysis of Algorithms CSE 53 Lecture 9 Media ad Order Statistics Juzhou Huag, Ph.D. Departmet of Computer Sciece ad Egieerig Dept. CSE, UT Arligto CSE53 Desig ad Aalysis of Algorithms Medias ad
Divide & Conquer. Divide-and-conquer algorithms. Conventional product of polynomials. Conventional product of polynomials.
 Divide-ad-coquer algorithms Divide & Coquer Strategy: Divide the problem ito smaller subproblems of the same type of problem Solve the subproblems recursively Combie the aswers to solve the origial problem
Divide-ad-coquer algorithms Divide & Coquer Strategy: Divide the problem ito smaller subproblems of the same type of problem Solve the subproblems recursively Combie the aswers to solve the origial problem
4.3 Growth Rates of Solutions to Recurrences
 4.3. GROWTH RATES OF SOLUTIONS TO RECURRENCES 81 4.3 Growth Rates of Solutios to Recurreces 4.3.1 Divide ad Coquer Algorithms Oe of the most basic ad powerful algorithmic techiques is divide ad coquer.
4.3. GROWTH RATES OF SOLUTIONS TO RECURRENCES 81 4.3 Growth Rates of Solutios to Recurreces 4.3.1 Divide ad Coquer Algorithms Oe of the most basic ad powerful algorithmic techiques is divide ad coquer.
Classification of problem & problem solving strategies. classification of time complexities (linear, logarithmic etc)
 Classificatio of problem & problem solvig strategies classificatio of time complexities (liear, arithmic etc) Problem subdivisio Divide ad Coquer strategy. Asymptotic otatios, lower boud ad upper boud:
Classificatio of problem & problem solvig strategies classificatio of time complexities (liear, arithmic etc) Problem subdivisio Divide ad Coquer strategy. Asymptotic otatios, lower boud ad upper boud:
CS / MCS 401 Homework 3 grader solutions
 CS / MCS 401 Homework 3 grader solutios assigmet due July 6, 016 writte by Jāis Lazovskis maximum poits: 33 Some questios from CLRS. Questios marked with a asterisk were ot graded. 1 Use the defiitio of
CS / MCS 401 Homework 3 grader solutios assigmet due July 6, 016 writte by Jāis Lazovskis maximum poits: 33 Some questios from CLRS. Questios marked with a asterisk were ot graded. 1 Use the defiitio of
Divide and Conquer II
 Algorithms Divide ad Coquer II Divide ad Coquer II Desig ad Aalsis of Algorithms Adrei Bulatov Algorithms Divide ad Coquer II 6- Closest Pair: The Problem The Closest Pair Problem Istace: poits i the plae
Algorithms Divide ad Coquer II Divide ad Coquer II Desig ad Aalsis of Algorithms Adrei Bulatov Algorithms Divide ad Coquer II 6- Closest Pair: The Problem The Closest Pair Problem Istace: poits i the plae
Analysis of Algorithms. Introduction. Contents
 Itroductio The focus of this module is mathematical aspects of algorithms. Our mai focus is aalysis of algorithms, which meas evaluatig efficiecy of algorithms by aalytical ad mathematical methods. We
Itroductio The focus of this module is mathematical aspects of algorithms. Our mai focus is aalysis of algorithms, which meas evaluatig efficiecy of algorithms by aalytical ad mathematical methods. We
CSE 4095/5095 Topics in Big Data Analytics Spring 2017; Homework 1 Solutions
 CSE 09/09 Topics i ig Data Aalytics Sprig 2017; Homework 1 Solutios Note: Solutios to problems,, ad 6 are due to Marius Nicolae. 1. Cosider the followig algorithm: for i := 1 to α log e do Pick a radom
CSE 09/09 Topics i ig Data Aalytics Sprig 2017; Homework 1 Solutios Note: Solutios to problems,, ad 6 are due to Marius Nicolae. 1. Cosider the followig algorithm: for i := 1 to α log e do Pick a radom
Divide-and-Conquer. Divide-and-Conquer 1
 Divide-d-Coquer 7 9 4 4 7 9 7 7 9 4 4 9 7 7 9 9 4 4 Divide-d-Coquer 1 Outie d Redig Divide-d-coquer prdigm 5. Review Merge-sort 4.1.1 Recurrece Equtios 5..1 tertive sustitutio Recursio trees Guess-d-test
Divide-d-Coquer 7 9 4 4 7 9 7 7 9 4 4 9 7 7 9 9 4 4 Divide-d-Coquer 1 Outie d Redig Divide-d-coquer prdigm 5. Review Merge-sort 4.1.1 Recurrece Equtios 5..1 tertive sustitutio Recursio trees Guess-d-test
CS 270 Algorithms. Oliver Kullmann. Growth of Functions. Divide-and- Conquer Min-Max- Problem. Tutorial. Reading from CLRS for week 2
 Geeral remarks Week 2 1 Divide ad First we cosider a importat tool for the aalysis of algorithms: Big-Oh. The we itroduce a importat algorithmic paradigm:. We coclude by presetig ad aalysig two examples.
Geeral remarks Week 2 1 Divide ad First we cosider a importat tool for the aalysis of algorithms: Big-Oh. The we itroduce a importat algorithmic paradigm:. We coclude by presetig ad aalysig two examples.
Matriculation number: You have 90 minutes to complete the exam of InformatikIIb. The following rules apply:
 Departmet of Iformatics Prof. Dr. Michael Böhle Bizmühlestrasse 14 8050 Zurich Phoe: +41 44 635 4333 Email: boehle@ifi.uzh.ch AlgoDat Midterm1 Sprig 016 08.04.016 Name: Matriculatio umber: Advice You have
Departmet of Iformatics Prof. Dr. Michael Böhle Bizmühlestrasse 14 8050 Zurich Phoe: +41 44 635 4333 Email: boehle@ifi.uzh.ch AlgoDat Midterm1 Sprig 016 08.04.016 Name: Matriculatio umber: Advice You have
CS583 Lecture 02. Jana Kosecka. some materials here are based on E. Demaine, D. Luebke slides
 CS583 Lecture 02 Jaa Kosecka some materials here are based o E. Demaie, D. Luebke slides Previously Sample algorithms Exact ruig time, pseudo-code Approximate ruig time Worst case aalysis Best case aalysis
CS583 Lecture 02 Jaa Kosecka some materials here are based o E. Demaie, D. Luebke slides Previously Sample algorithms Exact ruig time, pseudo-code Approximate ruig time Worst case aalysis Best case aalysis
CS 332: Algorithms. Quicksort
 CS 33: Aorithms Quicsort David Luebe //03 Homewor Assiged today, due ext Wedesday Will be o web page shortly after class Go over ow David Luebe //03 Review: Quicsort Sorts i place Sorts O( ) i the average
CS 33: Aorithms Quicsort David Luebe //03 Homewor Assiged today, due ext Wedesday Will be o web page shortly after class Go over ow David Luebe //03 Review: Quicsort Sorts i place Sorts O( ) i the average
Model of Computation and Runtime Analysis
 Model of Computatio ad Rutime Aalysis Model of Computatio Model of Computatio Specifies Set of operatios Cost of operatios (ot ecessarily time) Examples Turig Machie Radom Access Machie (RAM) PRAM Map
Model of Computatio ad Rutime Aalysis Model of Computatio Model of Computatio Specifies Set of operatios Cost of operatios (ot ecessarily time) Examples Turig Machie Radom Access Machie (RAM) PRAM Map
Algorithms and Data Structures Lecture IV
 Algorithms ad Data Structures Lecture IV Simoas Šalteis Aalborg Uiversity simas@cs.auc.dk September 5, 00 1 This Lecture Aalyzig the ruig time of recursive algorithms (such as divide-ad-coquer) Writig
Algorithms ad Data Structures Lecture IV Simoas Šalteis Aalborg Uiversity simas@cs.auc.dk September 5, 00 1 This Lecture Aalyzig the ruig time of recursive algorithms (such as divide-ad-coquer) Writig
CS:3330 (Prof. Pemmaraju ): Assignment #1 Solutions. (b) For n = 3, we will have 3 men and 3 women with preferences as follows: m 1 : w 3 > w 1 > w 2
 Shiyao Wag CS:3330 (Prof. Pemmaraju ): Assigmet #1 Solutios Problem 1 (a) Cosider iput with me m 1, m,..., m ad wome w 1, w,..., w with the followig prefereces: All me have the same prefereces for wome:
Shiyao Wag CS:3330 (Prof. Pemmaraju ): Assigmet #1 Solutios Problem 1 (a) Cosider iput with me m 1, m,..., m ad wome w 1, w,..., w with the followig prefereces: All me have the same prefereces for wome:
Chapter 22 Developing Efficient Algorithms
 Chapter Developig Efficiet Algorithms 1 Executig Time Suppose two algorithms perform the same task such as search (liear search vs. biary search). Which oe is better? Oe possible approach to aswer this
Chapter Developig Efficiet Algorithms 1 Executig Time Suppose two algorithms perform the same task such as search (liear search vs. biary search). Which oe is better? Oe possible approach to aswer this
COMP285 Midterm Exam Department of Mathematics
 COMP85 Midterm Exam Departmet of Mathematics Fall 010/011 - November 8, 010 Name: Studet Number: Please fiish withi 90 miutes. All poits above 100 are cosidered as bous poit. You ca reach maximal 1 poits.
COMP85 Midterm Exam Departmet of Mathematics Fall 010/011 - November 8, 010 Name: Studet Number: Please fiish withi 90 miutes. All poits above 100 are cosidered as bous poit. You ca reach maximal 1 poits.
Skip Lists. Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015 S 3 S S 1
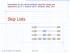 Presetatio for use with the textbook, Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 2015 Skip Lists S 3 15 15 23 10 15 23 36 Skip Lists 1 What is a Skip List A skip list for
Presetatio for use with the textbook, Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 2015 Skip Lists S 3 15 15 23 10 15 23 36 Skip Lists 1 What is a Skip List A skip list for
Department of Informatics Prof. Dr. Michael Böhlen Binzmühlestrasse Zurich Phone:
 Departmet of Iformatics Prof. Dr. Michael Böhle Bizmühlestrasse 14 8050 Zurich Phoe: +41 44 635 4333 Email: boehle@ifi.uzh.ch Iformatik II Midterm1 Sprig 018 3.03.018 Advice You have 90 miutes to complete
Departmet of Iformatics Prof. Dr. Michael Böhle Bizmühlestrasse 14 8050 Zurich Phoe: +41 44 635 4333 Email: boehle@ifi.uzh.ch Iformatik II Midterm1 Sprig 018 3.03.018 Advice You have 90 miutes to complete
CS270 Combinatorial Algorithms & Data Structures Spring Lecture 9:
 CS70 Comiatorial Algorithms & Data Structures Sprig 00 Lecture 9: 170 Lecturer: Satish Rao Scrie: Adam Chlipala Disclaimer: These otes have ot ee sujected to the usual scrutiy reserved for formal pulicatios
CS70 Comiatorial Algorithms & Data Structures Sprig 00 Lecture 9: 170 Lecturer: Satish Rao Scrie: Adam Chlipala Disclaimer: These otes have ot ee sujected to the usual scrutiy reserved for formal pulicatios
Model of Computation and Runtime Analysis
 Model of Computatio ad Rutime Aalysis Model of Computatio Model of Computatio Specifies Set of operatios Cost of operatios (ot ecessarily time) Examples Turig Machie Radom Access Machie (RAM) PRAM Map
Model of Computatio ad Rutime Aalysis Model of Computatio Model of Computatio Specifies Set of operatios Cost of operatios (ot ecessarily time) Examples Turig Machie Radom Access Machie (RAM) PRAM Map
CS161: Algorithm Design and Analysis Handout #10 Stanford University Wednesday, 10 February 2016
 CS161: Algorithm Desig ad Aalysis Hadout #10 Staford Uiversity Wedesday, 10 February 2016 Lecture #11: Wedesday, 10 February 2016 Topics: Example midterm problems ad solutios from a log time ago Sprig
CS161: Algorithm Desig ad Aalysis Hadout #10 Staford Uiversity Wedesday, 10 February 2016 Lecture #11: Wedesday, 10 February 2016 Topics: Example midterm problems ad solutios from a log time ago Sprig
Algorithm Analysis. Chapter 3
 Data Structures Dr Ahmed Rafat Abas Computer Sciece Dept, Faculty of Computer ad Iformatio, Zagazig Uiversity arabas@zu.edu.eg http://www.arsaliem.faculty.zu.edu.eg/ Algorithm Aalysis Chapter 3 3. Itroductio
Data Structures Dr Ahmed Rafat Abas Computer Sciece Dept, Faculty of Computer ad Iformatio, Zagazig Uiversity arabas@zu.edu.eg http://www.arsaliem.faculty.zu.edu.eg/ Algorithm Aalysis Chapter 3 3. Itroductio
) n. ALG 1.3 Deterministic Selection and Sorting: Problem P size n. Examples: 1st lecture's mult M(n) = 3 M ( È
 Algorithms Professor Joh Reif ALG 1.3 Determiistic Selectio ad Sortig: (a) Selectio Algorithms ad Lower Bouds (b) Sortig Algorithms ad Lower Bouds Problem P size fi divide ito subproblems size 1,..., k
Algorithms Professor Joh Reif ALG 1.3 Determiistic Selectio ad Sortig: (a) Selectio Algorithms ad Lower Bouds (b) Sortig Algorithms ad Lower Bouds Problem P size fi divide ito subproblems size 1,..., k
Math 475, Problem Set #12: Answers
 Math 475, Problem Set #12: Aswers A. Chapter 8, problem 12, parts (b) ad (d). (b) S # (, 2) = 2 2, sice, from amog the 2 ways of puttig elemets ito 2 distiguishable boxes, exactly 2 of them result i oe
Math 475, Problem Set #12: Aswers A. Chapter 8, problem 12, parts (b) ad (d). (b) S # (, 2) = 2 2, sice, from amog the 2 ways of puttig elemets ito 2 distiguishable boxes, exactly 2 of them result i oe
CSE 202 Homework 1 Matthias Springer, A Yes, there does always exist a perfect matching without a strong instability.
 CSE 0 Homework 1 Matthias Spriger, A9950078 1 Problem 1 Notatio a b meas that a is matched to b. a < b c meas that b likes c more tha a. Equality idicates a tie. Strog istability Yes, there does always
CSE 0 Homework 1 Matthias Spriger, A9950078 1 Problem 1 Notatio a b meas that a is matched to b. a < b c meas that b likes c more tha a. Equality idicates a tie. Strog istability Yes, there does always
Analysis of Algorithms -Quicksort-
 Aalysis of Algorithms -- Adreas Ermedahl MRTC (Mälardales Real-Time Research Ceter) adreas.ermedahl@mdh.se Autum 2004 Proposed by C.A.R. Hoare i 962 Worst- case ruig time: Θ( 2 ) Expected ruig time: Θ(
Aalysis of Algorithms -- Adreas Ermedahl MRTC (Mälardales Real-Time Research Ceter) adreas.ermedahl@mdh.se Autum 2004 Proposed by C.A.R. Hoare i 962 Worst- case ruig time: Θ( 2 ) Expected ruig time: Θ(
Math 155 (Lecture 3)
 Math 55 (Lecture 3) September 8, I this lecture, we ll cosider the aswer to oe of the most basic coutig problems i combiatorics Questio How may ways are there to choose a -elemet subset of the set {,,,
Math 55 (Lecture 3) September 8, I this lecture, we ll cosider the aswer to oe of the most basic coutig problems i combiatorics Questio How may ways are there to choose a -elemet subset of the set {,,,
Recursive Algorithms. Recurrences. Recursive Algorithms Analysis
 Recursive Algorithms Recurreces Computer Sciece & Egieerig 35: Discrete Mathematics Christopher M Bourke cbourke@cseuledu A recursive algorithm is oe i which objects are defied i terms of other objects
Recursive Algorithms Recurreces Computer Sciece & Egieerig 35: Discrete Mathematics Christopher M Bourke cbourke@cseuledu A recursive algorithm is oe i which objects are defied i terms of other objects
Divide and Conquer. 1 Overview. 2 Multiplying Bit Strings. COMPSCI 330: Design and Analysis of Algorithms 1/19/2016 and 1/21/2016
 COMPSCI 330: Desig ad Aalysis of Algorithms 1/19/2016 ad 1/21/2016 Lecturer: Debmalya Paigrahi Divide ad Coquer Scribe: Tiaqi Sog 1 Overview I this lecture, a importat algorithm desig techique called divide-ad-coquer
COMPSCI 330: Desig ad Aalysis of Algorithms 1/19/2016 ad 1/21/2016 Lecturer: Debmalya Paigrahi Divide ad Coquer Scribe: Tiaqi Sog 1 Overview I this lecture, a importat algorithm desig techique called divide-ad-coquer
Sequences, Mathematical Induction, and Recursion. CSE 2353 Discrete Computational Structures Spring 2018
 CSE 353 Discrete Computatioal Structures Sprig 08 Sequeces, Mathematical Iductio, ad Recursio (Chapter 5, Epp) Note: some course slides adopted from publisher-provided material Overview May mathematical
CSE 353 Discrete Computatioal Structures Sprig 08 Sequeces, Mathematical Iductio, ad Recursio (Chapter 5, Epp) Note: some course slides adopted from publisher-provided material Overview May mathematical
Data Structures and Algorithms
 Data Structures ad Algorithms Autum 2017-2018 Outlie 1 Sortig Algorithms (cotd) Outlie Sortig Algorithms (cotd) 1 Sortig Algorithms (cotd) Heapsort Sortig Algorithms (cotd) Have see that we ca build a
Data Structures ad Algorithms Autum 2017-2018 Outlie 1 Sortig Algorithms (cotd) Outlie Sortig Algorithms (cotd) 1 Sortig Algorithms (cotd) Heapsort Sortig Algorithms (cotd) Have see that we ca build a
Average-Case Analysis of QuickSort
 Average-Case Aalysis of QuickSort Comp 363 Fall Semester 003 October 3, 003 The purpose of this documet is to itroduce the idea of usig recurrece relatios to do average-case aalysis. The average-case ruig
Average-Case Aalysis of QuickSort Comp 363 Fall Semester 003 October 3, 003 The purpose of this documet is to itroduce the idea of usig recurrece relatios to do average-case aalysis. The average-case ruig
A Probabilistic Analysis of Quicksort
 A Probabilistic Aalysis of Quicsort You are assumed to be familiar with Quicsort. I each iteratio this sortig algorithm chooses a pivot ad the, by performig comparisios with the pivot, splits the remaider
A Probabilistic Aalysis of Quicsort You are assumed to be familiar with Quicsort. I each iteratio this sortig algorithm chooses a pivot ad the, by performig comparisios with the pivot, splits the remaider
Algorithm Analysis. Algorithms that are equally correct can vary in their utilization of computational resources
 Algorithm Aalysis Algorithms that are equally correct ca vary i their utilizatio of computatioal resources time ad memory a slow program it is likely ot to be used a program that demads too much memory
Algorithm Aalysis Algorithms that are equally correct ca vary i their utilizatio of computatioal resources time ad memory a slow program it is likely ot to be used a program that demads too much memory
Test One (Answer Key)
 CS395/Ma395 (Sprig 2005) Test Oe Name: Page 1 Test Oe (Aswer Key) CS395/Ma395: Aalysis of Algorithms This is a closed book, closed otes, 70 miute examiatio. It is worth 100 poits. There are twelve (12)
CS395/Ma395 (Sprig 2005) Test Oe Name: Page 1 Test Oe (Aswer Key) CS395/Ma395: Aalysis of Algorithms This is a closed book, closed otes, 70 miute examiatio. It is worth 100 poits. There are twelve (12)
CIS 121 Data Structures and Algorithms with Java Spring Code Snippets and Recurrences Monday, February 4/Tuesday, February 5
 CIS 11 Data Structures ad Algorithms with Java Sprig 019 Code Sippets ad Recurreces Moday, February 4/Tuesday, February 5 Learig Goals Practice provig asymptotic bouds with code sippets Practice solvig
CIS 11 Data Structures ad Algorithms with Java Sprig 019 Code Sippets ad Recurreces Moday, February 4/Tuesday, February 5 Learig Goals Practice provig asymptotic bouds with code sippets Practice solvig
Disjoint set (Union-Find)
 CS124 Lecture 7 Fall 2018 Disjoit set (Uio-Fid) For Kruskal s algorithm for the miimum spaig tree problem, we foud that we eeded a data structure for maitaiig a collectio of disjoit sets. That is, we eed
CS124 Lecture 7 Fall 2018 Disjoit set (Uio-Fid) For Kruskal s algorithm for the miimum spaig tree problem, we foud that we eeded a data structure for maitaiig a collectio of disjoit sets. That is, we eed
CSI 5163 (95.573) ALGORITHM ANALYSIS AND DESIGN
 CSI 5163 (95.573) ALGORITHM ANALYSIS AND DESIGN CSI 5163 (95.5703) ALGORITHM ANALYSIS AND DESIGN (3 cr.) (T) Topics of curret iterest i the desig ad aalysis of computer algorithms for graphtheoretical
CSI 5163 (95.573) ALGORITHM ANALYSIS AND DESIGN CSI 5163 (95.5703) ALGORITHM ANALYSIS AND DESIGN (3 cr.) (T) Topics of curret iterest i the desig ad aalysis of computer algorithms for graphtheoretical
CS537. Numerical Analysis and Computing
 CS57 Numerical Aalysis ad Computig Lecture Locatig Roots o Equatios Proessor Ju Zhag Departmet o Computer Sciece Uiversity o Ketucky Leigto KY 456-6 Jauary 9 9 What is the Root May physical system ca be
CS57 Numerical Aalysis ad Computig Lecture Locatig Roots o Equatios Proessor Ju Zhag Departmet o Computer Sciece Uiversity o Ketucky Leigto KY 456-6 Jauary 9 9 What is the Root May physical system ca be
CS 171 Lecture Outline October 09, 2008
 CS 171 Lecture Outlie October 09, 2008 The followig theorem comes very hady whe calculatig the expectatio of a radom variable that takes o o-egative iteger values. Theorem: Let Y be a radom variable that
CS 171 Lecture Outlie October 09, 2008 The followig theorem comes very hady whe calculatig the expectatio of a radom variable that takes o o-egative iteger values. Theorem: Let Y be a radom variable that
CS321. Numerical Analysis and Computing
 CS Numerical Aalysis ad Computig Lecture Locatig Roots o Equatios Proessor Ju Zhag Departmet o Computer Sciece Uiversity o Ketucky Leigto KY 456-6 September 8 5 What is the Root May physical system ca
CS Numerical Aalysis ad Computig Lecture Locatig Roots o Equatios Proessor Ju Zhag Departmet o Computer Sciece Uiversity o Ketucky Leigto KY 456-6 September 8 5 What is the Root May physical system ca
An Introduction to Randomized Algorithms
 A Itroductio to Radomized Algorithms The focus of this lecture is to study a radomized algorithm for quick sort, aalyze it usig probabilistic recurrece relatios, ad also provide more geeral tools for aalysis
A Itroductio to Radomized Algorithms The focus of this lecture is to study a radomized algorithm for quick sort, aalyze it usig probabilistic recurrece relatios, ad also provide more geeral tools for aalysis
CS 5150/6150: Assignment 1 Due: Sep 23, 2010
 CS 5150/6150: Assigmet 1 Due: Sep 23, 2010 Wei Liu September 24, 2010 Q1: (1) Usig master theorem: a = 7, b = 4, f() = O(). Because f() = log b a ε holds whe ε = log b a = log 4 7, we ca apply the first
CS 5150/6150: Assigmet 1 Due: Sep 23, 2010 Wei Liu September 24, 2010 Q1: (1) Usig master theorem: a = 7, b = 4, f() = O(). Because f() = log b a ε holds whe ε = log b a = log 4 7, we ca apply the first
CSE 5311 Notes 1: Mathematical Preliminaries
 Chapter 1 - Algorithms Computig CSE 5311 Notes 1: Mathematical Prelimiaries Last updated 1/20/18 12:56 PM) Relatioship betwee complexity classes, eg log,, log, 2, 2, etc Chapter 2 - Gettig Started Loop
Chapter 1 - Algorithms Computig CSE 5311 Notes 1: Mathematical Prelimiaries Last updated 1/20/18 12:56 PM) Relatioship betwee complexity classes, eg log,, log, 2, 2, etc Chapter 2 - Gettig Started Loop
Examples: data compression, path-finding, game-playing, scheduling, bin packing
 Algorithms - Basic Cocepts Algorithms so what is a algorithm, ayway? The dictioary defiitio: A algorithm is a well-defied computatioal procedure that takes iput ad produces output. This class will deal
Algorithms - Basic Cocepts Algorithms so what is a algorithm, ayway? The dictioary defiitio: A algorithm is a well-defied computatioal procedure that takes iput ad produces output. This class will deal
CSI 2101 Discrete Structures Winter Homework Assignment #4 (100 points, weight 5%) Due: Thursday, April 5, at 1:00pm (in lecture)
 CSI 101 Discrete Structures Witer 01 Prof. Lucia Moura Uiversity of Ottawa Homework Assigmet #4 (100 poits, weight %) Due: Thursday, April, at 1:00pm (i lecture) Program verificatio, Recurrece Relatios
CSI 101 Discrete Structures Witer 01 Prof. Lucia Moura Uiversity of Ottawa Homework Assigmet #4 (100 poits, weight %) Due: Thursday, April, at 1:00pm (i lecture) Program verificatio, Recurrece Relatios
Lecture 3: Asymptotic Analysis + Recurrences
 Lecture 3: Asymptotic Aalysis + Recurreces Data Structures ad Algorithms CSE 373 SU 18 BEN JONES 1 Warmup Write a model ad fid Big-O for (it i = 0; i < ; i++) { for (it j = 0; j < i; j++) { System.out.pritl(
Lecture 3: Asymptotic Aalysis + Recurreces Data Structures ad Algorithms CSE 373 SU 18 BEN JONES 1 Warmup Write a model ad fid Big-O for (it i = 0; i < ; i++) { for (it j = 0; j < i; j++) { System.out.pritl(
Lecture 16: Monotone Formula Lower Bounds via Graph Entropy. 2 Monotone Formula Lower Bounds via Graph Entropy
 15-859: Iformatio Theory ad Applicatios i TCS CMU: Sprig 2013 Lecture 16: Mootoe Formula Lower Bouds via Graph Etropy March 26, 2013 Lecturer: Mahdi Cheraghchi Scribe: Shashak Sigh 1 Recap Graph Etropy:
15-859: Iformatio Theory ad Applicatios i TCS CMU: Sprig 2013 Lecture 16: Mootoe Formula Lower Bouds via Graph Etropy March 26, 2013 Lecturer: Mahdi Cheraghchi Scribe: Shashak Sigh 1 Recap Graph Etropy:
Introduction to Algorithms 6.046J/18.401J LECTURE 3 Divide and conquer Binary search Powering a number Fibonacci numbers Matrix multiplication
 Itroductio to Algorithms 6.046J/8.40J LECTURE 3 Divide ad coquer Biary search Powerig a umber Fiboacci umbers Matrix multiplicatio Strasse s algorithm VLSI tree layout Prof. Charles E. Leiserso The divide-ad-coquer
Itroductio to Algorithms 6.046J/8.40J LECTURE 3 Divide ad coquer Biary search Powerig a umber Fiboacci umbers Matrix multiplicatio Strasse s algorithm VLSI tree layout Prof. Charles E. Leiserso The divide-ad-coquer
Recurrence Relations
 Recurrece Relatios Aalysis of recursive algorithms, such as: it factorial (it ) { if (==0) retur ; else retur ( * factorial(-)); } Let t be the umber of multiplicatios eeded to calculate factorial(). The
Recurrece Relatios Aalysis of recursive algorithms, such as: it factorial (it ) { if (==0) retur ; else retur ( * factorial(-)); } Let t be the umber of multiplicatios eeded to calculate factorial(). The
Chapter 6. Advanced Counting Techniques
 Chapter 6 Advaced Coutig Techiques 6.: Recurrece Relatios Defiitio: A recurrece relatio for the sequece {a } is a equatio expressig a i terms of oe or more of the previous terms of the sequece: a,a2,a3,,a
Chapter 6 Advaced Coutig Techiques 6.: Recurrece Relatios Defiitio: A recurrece relatio for the sequece {a } is a equatio expressig a i terms of oe or more of the previous terms of the sequece: a,a2,a3,,a
Advanced Course of Algorithm Design and Analysis
 Differet complexity measures Advaced Course of Algorithm Desig ad Aalysis Asymptotic complexity Big-Oh otatio Properties of O otatio Aalysis of simple algorithms A algorithm may may have differet executio
Differet complexity measures Advaced Course of Algorithm Desig ad Aalysis Asymptotic complexity Big-Oh otatio Properties of O otatio Aalysis of simple algorithms A algorithm may may have differet executio
Fast Sorting and Selection. A Lower Bound for Worst Case
 Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 0 Fast Sorting and Selection USGS NEIC. Public domain government image. A Lower Bound
Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 0 Fast Sorting and Selection USGS NEIC. Public domain government image. A Lower Bound
Recursive Algorithm for Generating Partitions of an Integer. 1 Preliminary
 Recursive Algorithm for Geeratig Partitios of a Iteger Sug-Hyuk Cha Computer Sciece Departmet, Pace Uiversity 1 Pace Plaza, New York, NY 10038 USA scha@pace.edu Abstract. This article first reviews the
Recursive Algorithm for Geeratig Partitios of a Iteger Sug-Hyuk Cha Computer Sciece Departmet, Pace Uiversity 1 Pace Plaza, New York, NY 10038 USA scha@pace.edu Abstract. This article first reviews the
COMP26120: More on the Complexity of Recursive Programs (2018/19) Lucas Cordeiro
 COMP26120: More o the Complexity of Recursive Programs (2018/19) Lucas Cordeiro lucas.cordeiro@machester.ac.uk Divide-ad-Coquer (Recurrece) Textbook: Algorithm Desig ad Applicatios, Goodrich, Michael T.
COMP26120: More o the Complexity of Recursive Programs (2018/19) Lucas Cordeiro lucas.cordeiro@machester.ac.uk Divide-ad-Coquer (Recurrece) Textbook: Algorithm Desig ad Applicatios, Goodrich, Michael T.
2.4 - Sequences and Series
 2.4 - Sequeces ad Series Sequeces A sequece is a ordered list of elemets. Defiitio 1 A sequece is a fuctio from a subset of the set of itegers (usually either the set 80, 1, 2, 3,... < or the set 81, 2,
2.4 - Sequeces ad Series Sequeces A sequece is a ordered list of elemets. Defiitio 1 A sequece is a fuctio from a subset of the set of itegers (usually either the set 80, 1, 2, 3,... < or the set 81, 2,
Problem Set 2 Solutions
 CS271 Radomess & Computatio, Sprig 2018 Problem Set 2 Solutios Poit totals are i the margi; the maximum total umber of poits was 52. 1. Probabilistic method for domiatig sets 6pts Pick a radom subset S
CS271 Radomess & Computatio, Sprig 2018 Problem Set 2 Solutios Poit totals are i the margi; the maximum total umber of poits was 52. 1. Probabilistic method for domiatig sets 6pts Pick a radom subset S
w (1) ˆx w (1) x (1) /ρ and w (2) ˆx w (2) x (2) /ρ.
 2 5. Weighted umber of late jobs 5.1. Release dates ad due dates: maximimizig the weight of o-time jobs Oce we add release dates, miimizig the umber of late jobs becomes a sigificatly harder problem. For
2 5. Weighted umber of late jobs 5.1. Release dates ad due dates: maximimizig the weight of o-time jobs Oce we add release dates, miimizig the umber of late jobs becomes a sigificatly harder problem. For
Data Structures and Algorithm. Xiaoqing Zheng
 Data Structures ad Algorithm Xiaoqig Zheg zhegxq@fudaeduc What are algorithms? A sequece of computatioal steps that trasform the iput ito the output Sortig problem: Iput: A sequece of umbers
Data Structures ad Algorithm Xiaoqig Zheg zhegxq@fudaeduc What are algorithms? A sequece of computatioal steps that trasform the iput ito the output Sortig problem: Iput: A sequece of umbers
Fundamental Algorithms
 Fudametal Algorithms Chapter 2b: Recurreces Michael Bader Witer 2014/15 Chapter 2b: Recurreces, Witer 2014/15 1 Recurreces Defiitio A recurrece is a (i-equality that defies (or characterizes a fuctio i
Fudametal Algorithms Chapter 2b: Recurreces Michael Bader Witer 2014/15 Chapter 2b: Recurreces, Witer 2014/15 1 Recurreces Defiitio A recurrece is a (i-equality that defies (or characterizes a fuctio i
1 Hash tables. 1.1 Implementation
 Lecture 8 Hash Tables, Uiversal Hash Fuctios, Balls ad Bis Scribes: Luke Johsto, Moses Charikar, G. Valiat Date: Oct 18, 2017 Adapted From Virgiia Williams lecture otes 1 Hash tables A hash table is a
Lecture 8 Hash Tables, Uiversal Hash Fuctios, Balls ad Bis Scribes: Luke Johsto, Moses Charikar, G. Valiat Date: Oct 18, 2017 Adapted From Virgiia Williams lecture otes 1 Hash tables A hash table is a
Design and Analysis of ALGORITHM (Topic 2)
 DR. Gatot F. Hertoo, MSc. Desig ad Aalysis of ALGORITHM (Topic 2) Algorithms + Data Structures = Programs Lessos Leared 1 Our Machie Model: Assumptios Geeric Radom Access Machie (RAM) Executes operatios
DR. Gatot F. Hertoo, MSc. Desig ad Aalysis of ALGORITHM (Topic 2) Algorithms + Data Structures = Programs Lessos Leared 1 Our Machie Model: Assumptios Geeric Radom Access Machie (RAM) Executes operatios
Randomized Algorithms I, Spring 2018, Department of Computer Science, University of Helsinki Homework 1: Solutions (Discussed January 25, 2018)
 Radomized Algorithms I, Sprig 08, Departmet of Computer Sciece, Uiversity of Helsiki Homework : Solutios Discussed Jauary 5, 08). Exercise.: Cosider the followig balls-ad-bi game. We start with oe black
Radomized Algorithms I, Sprig 08, Departmet of Computer Sciece, Uiversity of Helsiki Homework : Solutios Discussed Jauary 5, 08). Exercise.: Cosider the followig balls-ad-bi game. We start with oe black
ECEN 655: Advanced Channel Coding Spring Lecture 7 02/04/14. Belief propagation is exact on tree-structured factor graphs.
 ECEN 655: Advaced Chael Codig Sprig 014 Prof. Hery Pfister Lecture 7 0/04/14 Scribe: Megke Lia 1 4-Cycles i Gallager s Esemble What we already kow: Belief propagatio is exact o tree-structured factor graphs.
ECEN 655: Advaced Chael Codig Sprig 014 Prof. Hery Pfister Lecture 7 0/04/14 Scribe: Megke Lia 1 4-Cycles i Gallager s Esemble What we already kow: Belief propagatio is exact o tree-structured factor graphs.
ORIE 633 Network Flows September 27, Lecture 8
 ORIE 633 Network Flows September 7, 007 Lecturer: David P. Williamso Lecture 8 Scribe: Gema Plaza-Martíez 1 Global mi-cuts i udirected graphs 1.1 Radom cotractio Recall from last time we itroduced the
ORIE 633 Network Flows September 7, 007 Lecturer: David P. Williamso Lecture 8 Scribe: Gema Plaza-Martíez 1 Global mi-cuts i udirected graphs 1.1 Radom cotractio Recall from last time we itroduced the
Infinite Sequences and Series
 Chapter 6 Ifiite Sequeces ad Series 6.1 Ifiite Sequeces 6.1.1 Elemetary Cocepts Simply speakig, a sequece is a ordered list of umbers writte: {a 1, a 2, a 3,...a, a +1,...} where the elemets a i represet
Chapter 6 Ifiite Sequeces ad Series 6.1 Ifiite Sequeces 6.1.1 Elemetary Cocepts Simply speakig, a sequece is a ordered list of umbers writte: {a 1, a 2, a 3,...a, a +1,...} where the elemets a i represet
Discrete Mathematics Recurrences
 Discrete Mathematics Recurreces Saad Meimeh 1 What is a recurrece? It ofte happes that, i studyig a sequece of umbers a, a coectio betwee a ad a 1, or betwee a ad several of the previous a i, i
Discrete Mathematics Recurreces Saad Meimeh 1 What is a recurrece? It ofte happes that, i studyig a sequece of umbers a, a coectio betwee a ad a 1, or betwee a ad several of the previous a i, i
SEQUENCE AND SERIES NCERT
 9. Overview By a sequece, we mea a arragemet of umbers i a defiite order accordig to some rule. We deote the terms of a sequece by a, a,..., etc., the subscript deotes the positio of the term. I view of
9. Overview By a sequece, we mea a arragemet of umbers i a defiite order accordig to some rule. We deote the terms of a sequece by a, a,..., etc., the subscript deotes the positio of the term. I view of
Sums, products and sequences
 Sums, products ad sequeces How to write log sums, e.g., 1+2+ (-1)+ cocisely? i=1 Sum otatio ( sum from 1 to ): i 3 = 1 + 2 + + If =3, i=1 i = 1+2+3=6. The ame ii does ot matter. Could use aother letter
Sums, products ad sequeces How to write log sums, e.g., 1+2+ (-1)+ cocisely? i=1 Sum otatio ( sum from 1 to ): i 3 = 1 + 2 + + If =3, i=1 i = 1+2+3=6. The ame ii does ot matter. Could use aother letter
A recurrence equation is just a recursive function definition. It defines a function at one input in terms of its value on smaller inputs.
 CS23 Algorithms Hadout #6 Prof Ly Turbak September 8, 200 Wellesley College RECURRENCES This hadout summarizes highlights of CLRS Chapter 4 ad Appedix A (CLR Chapters 3 & 4) Two-Step Strategy for Aalyzig
CS23 Algorithms Hadout #6 Prof Ly Turbak September 8, 200 Wellesley College RECURRENCES This hadout summarizes highlights of CLRS Chapter 4 ad Appedix A (CLR Chapters 3 & 4) Two-Step Strategy for Aalyzig
Dynamic Programming. Sequence Of Decisions
 Dyamic Programmig Sequece of decisios. Problem state. Priciple of optimality. Dyamic Programmig Recurrece Equatios. Solutio of recurrece equatios. Sequece Of Decisios As i the greedy method, the solutio
Dyamic Programmig Sequece of decisios. Problem state. Priciple of optimality. Dyamic Programmig Recurrece Equatios. Solutio of recurrece equatios. Sequece Of Decisios As i the greedy method, the solutio
Dynamic Programming. Sequence Of Decisions. 0/1 Knapsack Problem. Sequence Of Decisions
 Dyamic Programmig Sequece Of Decisios Sequece of decisios. Problem state. Priciple of optimality. Dyamic Programmig Recurrece Equatios. Solutio of recurrece equatios. As i the greedy method, the solutio
Dyamic Programmig Sequece Of Decisios Sequece of decisios. Problem state. Priciple of optimality. Dyamic Programmig Recurrece Equatios. Solutio of recurrece equatios. As i the greedy method, the solutio
Lecture 4 Recursive Algorithm Analysis. Merge Sort Solving Recurrences The Master Theorem
 Lecture 4 Recursive Algorithm Alysis Merge Sort Solvig Recurreces The Mster Theorem Merge Sort MergeSortA, left, right) { if left < right) { mid = floorleft + right) / 2); MergeSortA, left, mid); MergeSortA,
Lecture 4 Recursive Algorithm Alysis Merge Sort Solvig Recurreces The Mster Theorem Merge Sort MergeSortA, left, right) { if left < right) { mid = floorleft + right) / 2); MergeSortA, left, mid); MergeSortA,
SECTION 1.5 : SUMMATION NOTATION + WORK WITH SEQUENCES
 SECTION 1.5 : SUMMATION NOTATION + WORK WITH SEQUENCES Read Sectio 1.5 (pages 5 9) Overview I Sectio 1.5 we lear to work with summatio otatio ad formulas. We will also itroduce a brief overview of sequeces,
SECTION 1.5 : SUMMATION NOTATION + WORK WITH SEQUENCES Read Sectio 1.5 (pages 5 9) Overview I Sectio 1.5 we lear to work with summatio otatio ad formulas. We will also itroduce a brief overview of sequeces,
( ) = p and P( i = b) = q.
 MATH 540 Radom Walks Part 1 A radom walk X is special stochastic process that measures the height (or value) of a particle that radomly moves upward or dowward certai fixed amouts o each uit icremet of
MATH 540 Radom Walks Part 1 A radom walk X is special stochastic process that measures the height (or value) of a particle that radomly moves upward or dowward certai fixed amouts o each uit icremet of
OPTIMAL ALGORITHMS -- SUPPLEMENTAL NOTES
 OPTIMAL ALGORITHMS -- SUPPLEMENTAL NOTES Peter M. Maurer Why Hashig is θ(). As i biary search, hashig assumes that keys are stored i a array which is idexed by a iteger. However, hashig attempts to bypass
OPTIMAL ALGORITHMS -- SUPPLEMENTAL NOTES Peter M. Maurer Why Hashig is θ(). As i biary search, hashig assumes that keys are stored i a array which is idexed by a iteger. However, hashig attempts to bypass
ALG 2.2 Search Algorithms
 Algorithms Professor Joh Reif ALG 2.2 Search Algorithms (a Biary Search: average case (b Biary Search with Errors (homework (c Iterpolatio Search (d Ubouded Search Biary Search Trees (i sorted Table of
Algorithms Professor Joh Reif ALG 2.2 Search Algorithms (a Biary Search: average case (b Biary Search with Errors (homework (c Iterpolatio Search (d Ubouded Search Biary Search Trees (i sorted Table of
Lecture 2: April 3, 2013
 TTIC/CMSC 350 Mathematical Toolkit Sprig 203 Madhur Tulsiai Lecture 2: April 3, 203 Scribe: Shubhedu Trivedi Coi tosses cotiued We retur to the coi tossig example from the last lecture agai: Example. Give,
TTIC/CMSC 350 Mathematical Toolkit Sprig 203 Madhur Tulsiai Lecture 2: April 3, 203 Scribe: Shubhedu Trivedi Coi tosses cotiued We retur to the coi tossig example from the last lecture agai: Example. Give,
The Basic Space Model
 The Basic Space Model Let x i be the ith idividual s (i=,, ) reported positio o the th issue ( =,, m) ad let X 0 be the by m matrix of observed data here the 0 subscript idicates that elemets are missig
The Basic Space Model Let x i be the ith idividual s (i=,, ) reported positio o the th issue ( =,, m) ad let X 0 be the by m matrix of observed data here the 0 subscript idicates that elemets are missig
Section 5.1 The Basics of Counting
 1 Sectio 5.1 The Basics of Coutig Combiatorics, the study of arragemets of objects, is a importat part of discrete mathematics. I this chapter, we will lear basic techiques of coutig which has a lot of
1 Sectio 5.1 The Basics of Coutig Combiatorics, the study of arragemets of objects, is a importat part of discrete mathematics. I this chapter, we will lear basic techiques of coutig which has a lot of
Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, Divide-and-Conquer
 Presettio for use with the textook, Algorithm Desig d Applictios, y M. T. Goodrich d R. Tmssi, Wiley, 25 Divide-d-Coquer Divide-d-Coquer Divide-d coquer is geerl lgorithm desig prdigm: Divide: divide the
Presettio for use with the textook, Algorithm Desig d Applictios, y M. T. Goodrich d R. Tmssi, Wiley, 25 Divide-d-Coquer Divide-d-Coquer Divide-d coquer is geerl lgorithm desig prdigm: Divide: divide the
6.3 Testing Series With Positive Terms
 6.3. TESTING SERIES WITH POSITIVE TERMS 307 6.3 Testig Series With Positive Terms 6.3. Review of what is kow up to ow I theory, testig a series a i for covergece amouts to fidig the i= sequece of partial
6.3. TESTING SERIES WITH POSITIVE TERMS 307 6.3 Testig Series With Positive Terms 6.3. Review of what is kow up to ow I theory, testig a series a i for covergece amouts to fidig the i= sequece of partial
Linear chord diagrams with long chords
 Liear chord diagrams with log chords Everett Sulliva Departmet of Mathematics Dartmouth College Haover New Hampshire, U.S.A. everett..sulliva@dartmouth.edu Submitted: Feb 7, 2017; Accepted: Oct 7, 2017;
Liear chord diagrams with log chords Everett Sulliva Departmet of Mathematics Dartmouth College Haover New Hampshire, U.S.A. everett..sulliva@dartmouth.edu Submitted: Feb 7, 2017; Accepted: Oct 7, 2017;
Seunghee Ye Ma 8: Week 5 Oct 28
 Week 5 Summary I Sectio, we go over the Mea Value Theorem ad its applicatios. I Sectio 2, we will recap what we have covered so far this term. Topics Page Mea Value Theorem. Applicatios of the Mea Value
Week 5 Summary I Sectio, we go over the Mea Value Theorem ad its applicatios. I Sectio 2, we will recap what we have covered so far this term. Topics Page Mea Value Theorem. Applicatios of the Mea Value
Algorithms. Elementary Sorting. Dong Kyue Kim Hanyang University
 Algorithms Elemetary Sortig Dog Kyue Kim Hayag Uiversity dqkim@hayag.a.kr Cotets Sortig problem Elemetary sortig algorithms Isertio sort Merge sort Seletio sort Bubble sort Sortig problem Iput A sequee
Algorithms Elemetary Sortig Dog Kyue Kim Hayag Uiversity dqkim@hayag.a.kr Cotets Sortig problem Elemetary sortig algorithms Isertio sort Merge sort Seletio sort Bubble sort Sortig problem Iput A sequee
Chapter 2. Asymptotic Notation
 Asyptotic Notatio 3 Chapter Asyptotic Notatio Goal : To siplify the aalysis of ruig tie by gettig rid of details which ay be affected by specific ipleetatio ad hardware. [1] The Big Oh (O-Notatio) : It
Asyptotic Notatio 3 Chapter Asyptotic Notatio Goal : To siplify the aalysis of ruig tie by gettig rid of details which ay be affected by specific ipleetatio ad hardware. [1] The Big Oh (O-Notatio) : It
Hand Out: Analysis of Algorithms. September 8, Bud Mishra. In general, there can be several algorithms to solve a problem; and one is faced
 Had Out Aalysis of Algorithms September 8, 998 Bud Mishra c Mishra, February 9, 986 Itroductio I geeral, there ca be several algorithms to solve a problem; ad oe is faced with the problem of choosig a
Had Out Aalysis of Algorithms September 8, 998 Bud Mishra c Mishra, February 9, 986 Itroductio I geeral, there ca be several algorithms to solve a problem; ad oe is faced with the problem of choosig a
Introduction to Algorithms
 Itroductio to Algorithms 6.046J/8.40J/SMA5503 Lecture 9 Pro. Charles E. Leiserso Biary-search-tree sort T Create a empty BST or i to do TREE-INSERT(T, A[i]) Perorm a iorder tree wal o T. Eample: A [3 8
Itroductio to Algorithms 6.046J/8.40J/SMA5503 Lecture 9 Pro. Charles E. Leiserso Biary-search-tree sort T Create a empty BST or i to do TREE-INSERT(T, A[i]) Perorm a iorder tree wal o T. Eample: A [3 8
CS 330 Discussion - Probability
 CS 330 Discussio - Probability March 24 2017 1 Fudametals of Probability 11 Radom Variables ad Evets A radom variable X is oe whose value is o-determiistic For example, suppose we flip a coi ad set X =
CS 330 Discussio - Probability March 24 2017 1 Fudametals of Probability 11 Radom Variables ad Evets A radom variable X is oe whose value is o-determiistic For example, suppose we flip a coi ad set X =
STAT 516 Answers Homework 6 April 2, 2008 Solutions by Mark Daniel Ward PROBLEMS
 STAT 56 Aswers Homework 6 April 2, 28 Solutios by Mark Daiel Ward PROBLEMS Chapter 6 Problems 2a. The mass p(, correspods to either o the irst two balls beig white, so p(, 8 7 4/39. The mass p(, correspods
STAT 56 Aswers Homework 6 April 2, 28 Solutios by Mark Daiel Ward PROBLEMS Chapter 6 Problems 2a. The mass p(, correspods to either o the irst two balls beig white, so p(, 8 7 4/39. The mass p(, correspods
5. Solving recurrences
 5. Solvig recurreces Time Complexity Alysis of Merge Sort T( ) 0 if 1 2T ( / 2) otherwise sortig oth hlves mergig Q. How to prove tht the ru-time of merge sort is O( )? A. 2 Time Complexity Alysis of Merge
5. Solvig recurreces Time Complexity Alysis of Merge Sort T( ) 0 if 1 2T ( / 2) otherwise sortig oth hlves mergig Q. How to prove tht the ru-time of merge sort is O( )? A. 2 Time Complexity Alysis of Merge
Divide and Conquer. 1 Overview. 2 Insertion Sort. COMPSCI 330: Design and Analysis of Algorithms 1/19/2016 and 1/21/2016
 COMPSCI 330: Desig ad Aalysis of Algorithms 1/19/2016 ad 1/21/2016 Divide ad Coquer Lecturer: Debmalya Paigrahi Scribe: Tiaqi Sog, Tiayu Wag 1 Overview This set of otes is orgaized as follows. We begi
COMPSCI 330: Desig ad Aalysis of Algorithms 1/19/2016 ad 1/21/2016 Divide ad Coquer Lecturer: Debmalya Paigrahi Scribe: Tiaqi Sog, Tiayu Wag 1 Overview This set of otes is orgaized as follows. We begi
