Introduction to Probability and Sample Spaces
|
|
|
- Carmel Watkins
- 5 years ago
- Views:
Transcription
1 Introduction to Probability and Sample Spaces Prof. Tesler Math 186 Winter 2019 Prof. Tesler Ch Intro to Probability Math 186 / Winter / 26
2 Course overview Probability: Determine likelihood of events Roll a die. The probability of rolling 1 is 1/6. Descriptive statistics: Summarize data Mean, median, standard deviation,... Inferential statistics: Infer a conclusion/prediction from data Test a drug to see if it is safe and effective, and at what dose. Poll to predict the outcome of an election. Repeatedly flip a coin or roll a die to determine if it is fair. Bioinformatics We ll apply these to biological data, such as DN sequences and microarrays. Prof. Tesler Ch Intro to Probability Math 186 / Winter / 26
3 Related courses Math 183: Usually uses the same textbook and chapters as Math 186. Focuses on the examples in the book. The mathematical content is the same, but Math 186 has extra material for bioinformatics. Math 180BC plus 181BC: More in-depth: a year of probability and a year of statistics. CSE 103, Econ 120, ECE 109: One quarter intro to probability and statistics, specialized for other areas. Math 283: Graduate version of this course. Review of basic probability and statistics, with a lot more applications in bioinformatics. Prof. Tesler Ch Intro to Probability Math 186 / Winter / 26
4 2.2 Sample spaces Flip a coin 3 times. The possible outcomes are HHH HHT HTH HTT THH THT TTH TTT The sample space is the set of all possible outcomes: S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT} The size of the sample space is N(S) = 8 Our book s notation S = 8 more common notation in other books We could count this by making a table: 2 choices for the first flip 2 choices for the second flip 2 choices for the third flip = 2 3 = 8 The number of strings x 1 x 2... x k or sequences (x 1, x 2,..., x k ) of length k with r choices for each entry is r k. Prof. Tesler Ch Intro to Probability Math 186 / Winter / 26
5 Rolling two dice Roll two six-sided dice, one red, one green: green red 1 (1, 1) (1, 2) (1, 3) (1, 4) (1, 5) (1, 6) 2 (2, 1) (2, 2) (2, 3) (2, 4) (2, 5) (2, 6) 3 (3, 1) (3, 2) (3, 3) (3, 4) (3, 5) (3, 6) 4 (4, 1) (4, 2) (4, 3) (4, 4) (4, 5) (4, 6) 5 (5, 1) (5, 2) (5, 3) (5, 4) (5, 5) (5, 6) 6 (6, 1) (6, 2) (6, 3) (6, 4) (6, 5) (6, 6) The sample space is S = {(1, 1), (1, 2),..., (6, 6)} = { (i, j) Z 2 : 1 i 6, 1 j 6 } where Z = integers N(S) = 6 2 = 36 Z 2 = ordered pairs of integers Prof. Tesler Ch Intro to Probability Math 186 / Winter / 26
6 DN sequences codon is a DN sequence of length 3, in the alphabet of nucleotides {, C, G, T }: S = {, C, G, T,..., TTT } How many codons are there? N(S) = 4 3 = 64 Prof. Tesler Ch Intro to Probability Math 186 / Winter / 26
7 continuous sample space Consider this disk (filled-in circle): y 3 3 C 2 x 3 Complications 3 S = { (x, y) R 2 : x 2 + y } The sample space is infinite and continuous. The choices of x and y are dependent. E.g.: at x = 0, we have 2 y 2; at x = 2, we have y = 0. Prof. Tesler Ch Intro to Probability Math 186 / Winter / 26
8 Events Flip a coin 3 times. The sample space is S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT} n event is a subset of the sample space ( S): = First flip is heads = {HHH, HHT, HTH, HTT} B = Two flips are heads = {HHT, HTH, THH} C = Four flips are heads = (empty set or null set) We can combine these using set operations. For example, The first flip is heads or two flips are heads = { HHH, HHT, HTH, HTT } B = { HHT, HTH, THH } B = { HHH, HHT, HTH, HTT, THH } Prof. Tesler Ch Intro to Probability Math 186 / Winter / 26
9 Using set operations to form new events = First flip is heads = {HHH, HHT, HTH, HTT} B = Two flips are heads THT = {HHT, HTH, THH} TTH Union: ll elements that are in or in B TTT HHH HTT HHT HTH B = {HHH, HHT, HTH, HTT, THH} or B : The first flip is heads or two flips are heads This is inclusive or: one or both conditions are true. Intersection: ll elements that are in both and in B THH B = {HHT, HTH} and B : The first flip is heads and two flips are heads Complement: ll elements of the sample space not in c = {THT, TTH, TTT, THH} Not : The first flip is not heads Prof. Tesler Ch Intro to Probability Math 186 / Winter / 26 B
10 Venn diagram and set sizes = {HHH, HHT, HTH, HTT} B = {HHT, HTH, THH} B = {HHH, HHT, HTH, HTT, THH} B = {HHT, HTH} THT TTH TTT HHH HTT Relation between sizes of union and intersection HHT HTH Notice that N( B) = N() + N(B) N( B) 5 = THH N() + N(B) counts everything in the union, but elements in the intersection are counted twice. Subtract N( B) to compensate. Size of complement N(B c ) = N(S) N(B) 5 = 8 3 B Prof. Tesler Ch Intro to Probability Math 186 / Winter / 26
11 lgebraic rules for set theory Commutative laws B = B B = B ssociative laws ( B) C = (B C) ( B) C = (B C) One may omit parentheses in B C or B C. But don t do that with a mix of and. Distributive laws (B C) = ( B) ( C) (B C) = ( B) ( C) These are like a(b + c) = ab + ac Complements De Morgan s laws c = S c = ( B) c = c B c ( B) c = c B c Prof. Tesler Ch Intro to Probability Math 186 / Winter / 26
12 Distributive laws Visualizing identities using Venn diagrams: (B C) = ( B) ( C) B C (B C) # B# # B# S# C# S# C# B C ( B) ( C) # B# # B# # B# S# C# S# C# S# C# Prof. Tesler Ch Intro to Probability Math 186 / Winter / 26
13 Mutually exclusive sets Two events are mutually exclusive if their intersection is. = First flip is heads = {HHH, HHT, HTH, HTT} B = Two flips are heads = {HHT, HTH, THH} C = One flip is heads = {HTT, THT, TTH} and B are not mutually exclusive, since B = {HHT, HTH}. B and C are mutually exclusive, since B C =. For mutually exclusive events, since N(B C) = 0, we get: N(B C) = N(B) + N(C) Events 1, 2,... are pairwise mutually exclusive when i j = for i j Prof. Tesler Ch Intro to Probability Math 186 / Winter / 26
14 2.3 Probability functions Historically, there have been several ways of defining probabilities. We ll start with Classical Probability: Classical probability Suppose the sample space has n outcomes (N(S) = n) and all of them are equally likely. Each outcome has a probability 1/n of occurring: P(s) = 1/n for each outcome s S n event S with m outcomes has probability m/n of occurring: P() = m n = N() N(S) Example: Rolling a pair of dice N(S) = n = 36 P(first die is 3) = P ( {(3, 1), (3, 2),..., (3, 6)} ) = 6 36 P(the sum is 8) = P ( {(2, 6), (3, 5), (4, 4), (5, 3), (6, 2)} ) = 5 36 Prof. Tesler Ch Intro to Probability Math 186 / Winter / 26
15 Classical probability Drawbacks What if outcomes are not equally likely? What if there are infinitely many outcomes? Prof. Tesler Ch Intro to Probability Math 186 / Winter / 26
16 Empirical probability Use long-term frequencies of different outcomes to estimate their probabilities. Flip a coin a lot of times. Use the fraction of times it comes up heads to estimate the probability of heads. 520 heads out of 1000 flips leads to estimating P(heads) = This estimate is only approximate because Due to random variation, the numerator will fluctuate. Precision is limited by the denominator flips can only estimate it to three decimals. More on this later in the course in Chapter 5.3. Prof. Tesler Ch Intro to Probability Math 186 / Winter / 26
17 Empirical probability E. coli has been sequenced: Position: Base: G C T T T T C T On the forwards strand: # s 1,142,136 P() = 1,142,136 4,639, # C s 1,179,433 P(C) # G s 1,176,775 P(G) # T s 1,140,877 P(T) Total 4,639,221 1 Sample space: set of positions S = {1, 2,..., } Event is the set of positions with nucleotide (similar for C, G, T). = {1, 9,...} C = {3, 8,...} G = {2,...} T = {4, 5, 6, 7, 10,...} Simplistic model: the sequence is generated from a biased 4-sided die with faces, C, G, T. Prof. Tesler Ch Intro to Probability Math 186 / Winter / 26
18 xiomatic probability definition of a probability function P based on events and the following axioms is the most useful. Each event S is assigned a probability that obeys these axioms: xioms for a finite sample space For any event S: P() 0 The total sample space has probability 1: P(S) = 1 For mutually exclusive events and B: dditional axiom for an infinite sample space P( B) = P() + P(B) If 1, 2,... (infinitely many) ( are pairwise mutually exclusive, then ) P i = P( i ) i=1 i=1 i=1 i = 1 2 is like notation, but for unions. Prof. Tesler Ch Intro to Probability Math 186 / Winter / 26
19 xiomatic probability additional properties dditional properties of the probability function follow from the axioms. P( c ) = 1 P() Example: P(die roll = 1) = 1 6 P(die roll 1) = = 5 6 Proof. and c are mutually exclusive, so P( c ) = P() + P( c ). lso, P( c ) = P(S) = 1. Thus, P( c ) = 1 P(). c P( ) = 0 Proof: P( ) = P(S c ) = 1 P(S) = 1 1 = 0 Prof. Tesler Ch Intro to Probability Math 186 / Winter / 26
20 xiomatic probability additional properties If B then P() P(B) Proof: Write B = ( c B). and c B are mutually exclusive, so P(B) = P() + P( c B). The first axiom gives P( c B) 0, so P(B) P(). B c U B P() 1 Proof: S so P() P(S) = 1. Prof. Tesler Ch Intro to Probability Math 186 / Winter / 26
21 xiomatic probability additional properties dditive Law If 1, 2,..., n are pairwise ( mutually exclusive, then n ) n P i = P( i ) n i=1 i=1 i=1 i = 1 2 n is like notation, but for unions. Prove for all integers n 1 using induction, based on: P ( ) ( 1 n ) n+1 = P(1 n ) + P( n+1 ) = ( P( 1 ) + + P( n ) ) + P( n+1 ). Prof. Tesler Ch Intro to Probability Math 186 / Winter / 26
22 xiomatic probability additional properties Induction proves the dditive Law for positive integers n = 1, 2,..., but not for n =, so we have to introduce an additional axiom for that: dditional axiom for an infinite sample space If 1, 2,... (infinitely many) are pairwise mutually exclusive, then ( ) P i = i=1 P( i ) i=1 Prof. Tesler Ch Intro to Probability Math 186 / Winter / 26
23 xiomatic probability additional properties c B U B B U U c U B B De Moivre s Law: P( B) = P() + P(B) P( B) Proof: P() = P( B) + P( B c ) P(B) = P( B) + P( c B) P() + P(B) = P( B) + ( P( B) + P( B c ) + P( c B) ) = P( B) + P( B) c U B c Prof. Tesler Ch Intro to Probability Math 186 / Winter / 26
24 xiomatic probability additional properties dditional properties of the probability function follow from the axioms: P( c ) = 1 P() P( ) = 0 If B then P() P(B) P() 1 dditive Law: If 1, 2,..., n are pairwise mutually exclusive ( i j = for all i j) then ( n ) P i = i=1 n P( i ) i=1 (The first three axioms only lead to a proof of this for finite n, but not n =, so n = has to be handled by an additional axiom.) De Moivre s Law: P( B) = P() + P(B) P( B) Prof. Tesler Ch Intro to Probability Math 186 / Winter / 26
25 Generalizing Sigma ( ) notation Sum over sets instead of over a range of consecutive integers Consider a biased n-sided die, with faces 1,..., n. The probability of face i is q i, with 0 q i 1, and q q n = 1: n q i = 1 i=1 For n = 8, the probability of an even number is: P(even number) = q s = q 2 + q 4 + q 6 + q 8 s {2,4,6,8} For a 26-sided die with faces,b,...,z, the total probability is P({, B,..., Z}) = q s = q + q B + + q Z = 1, s {,B,...,Z} and the probability of a vowel is P({, E, I, O, U}) = q s = q + q E + q I + q O + q U. s {,E,I,O,U} Prof. Tesler Ch Intro to Probability Math 186 / Winter / 26
26 Finite discrete sample space Each outcome has a probability between 0 and 1 and the probabilities add up to 1: 0 P(s) 1 for each s S P(s) = 1 For an event S, define P() = s P(s). Examples DN biased n-sided die (previous slide). s S For flipping a coin 3 times, P({HHT, HTH, THH}) = P(HHT) + P(HTH) + P(THH). Generate a random DN sequence by rolling a biased CGT-die. Deviations from what s expected from random rolls of a dice are used to detect structure in the DN sequence, like genes, codons, repeats, etc. Prof. Tesler Ch Intro to Probability Math 186 / Winter / 26
Lecture 1 : The Mathematical Theory of Probability
 Lecture 1 : The Mathematical Theory of Probability 0/ 30 1. Introduction Today we will do 2.1 and 2.2. We will skip Chapter 1. We all have an intuitive notion of probability. Let s see. What is the probability
Lecture 1 : The Mathematical Theory of Probability 0/ 30 1. Introduction Today we will do 2.1 and 2.2. We will skip Chapter 1. We all have an intuitive notion of probability. Let s see. What is the probability
Events A and B are said to be independent if the occurrence of A does not affect the probability of B.
 Independent Events Events A and B are said to be independent if the occurrence of A does not affect the probability of B. Probability experiment of flipping a coin and rolling a dice. Sample Space: {(H,
Independent Events Events A and B are said to be independent if the occurrence of A does not affect the probability of B. Probability experiment of flipping a coin and rolling a dice. Sample Space: {(H,
Mathematics. ( : Focus on free Education) (Chapter 16) (Probability) (Class XI) Exercise 16.2
 ( : Focus on free Education) Exercise 16.2 Question 1: A die is rolled. Let E be the event die shows 4 and F be the event die shows even number. Are E and F mutually exclusive? Answer 1: When a die is
( : Focus on free Education) Exercise 16.2 Question 1: A die is rolled. Let E be the event die shows 4 and F be the event die shows even number. Are E and F mutually exclusive? Answer 1: When a die is
Conditional Probability and Bayes Theorem (2.4) Independence (2.5)
 Conditional Probability and Bayes Theorem (2.4) Independence (2.5) Prof. Tesler Math 186 Winter 2019 Prof. Tesler Conditional Probability and Bayes Theorem Math 186 / Winter 2019 1 / 38 Scenario: Flip
Conditional Probability and Bayes Theorem (2.4) Independence (2.5) Prof. Tesler Math 186 Winter 2019 Prof. Tesler Conditional Probability and Bayes Theorem Math 186 / Winter 2019 1 / 38 Scenario: Flip
STAT 430/510 Probability
 STAT 430/510 Probability Hui Nie Lecture 3 May 28th, 2009 Review We have discussed counting techniques in Chapter 1. Introduce the concept of the probability of an event. Compute probabilities in certain
STAT 430/510 Probability Hui Nie Lecture 3 May 28th, 2009 Review We have discussed counting techniques in Chapter 1. Introduce the concept of the probability of an event. Compute probabilities in certain
Probability Pearson Education, Inc. Slide
 Probability The study of probability is concerned with random phenomena. Even though we cannot be certain whether a given result will occur, we often can obtain a good measure of its likelihood, or probability.
Probability The study of probability is concerned with random phenomena. Even though we cannot be certain whether a given result will occur, we often can obtain a good measure of its likelihood, or probability.
Introduction Probability. Math 141. Introduction to Probability and Statistics. Albyn Jones
 Math 141 to and Statistics Albyn Jones Mathematics Department Library 304 jones@reed.edu www.people.reed.edu/ jones/courses/141 September 3, 2014 Motivation How likely is an eruption at Mount Rainier in
Math 141 to and Statistics Albyn Jones Mathematics Department Library 304 jones@reed.edu www.people.reed.edu/ jones/courses/141 September 3, 2014 Motivation How likely is an eruption at Mount Rainier in
Axioms of Probability
 Sample Space (denoted by S) The set of all possible outcomes of a random experiment is called the Sample Space of the experiment, and is denoted by S. Example 1.10 If the experiment consists of tossing
Sample Space (denoted by S) The set of all possible outcomes of a random experiment is called the Sample Space of the experiment, and is denoted by S. Example 1.10 If the experiment consists of tossing
Probability: Terminology and Examples Class 2, Jeremy Orloff and Jonathan Bloom
 1 Learning Goals Probability: Terminology and Examples Class 2, 18.05 Jeremy Orloff and Jonathan Bloom 1. Know the definitions of sample space, event and probability function. 2. Be able to organize a
1 Learning Goals Probability: Terminology and Examples Class 2, 18.05 Jeremy Orloff and Jonathan Bloom 1. Know the definitions of sample space, event and probability function. 2. Be able to organize a
CSC Discrete Math I, Spring Discrete Probability
 CSC 125 - Discrete Math I, Spring 2017 Discrete Probability Probability of an Event Pierre-Simon Laplace s classical theory of probability: Definition of terms: An experiment is a procedure that yields
CSC 125 - Discrete Math I, Spring 2017 Discrete Probability Probability of an Event Pierre-Simon Laplace s classical theory of probability: Definition of terms: An experiment is a procedure that yields
Statistics Statistical Process Control & Control Charting
 Statistics Statistical Process Control & Control Charting Cayman Systems International 1/22/98 1 Recommended Statistical Course Attendance Basic Business Office, Staff, & Management Advanced Business Selected
Statistics Statistical Process Control & Control Charting Cayman Systems International 1/22/98 1 Recommended Statistical Course Attendance Basic Business Office, Staff, & Management Advanced Business Selected
324 Stat Lecture Notes (1) Probability
 324 Stat Lecture Notes 1 robability Chapter 2 of the book pg 35-71 1 Definitions: Sample Space: Is the set of all possible outcomes of a statistical experiment, which is denoted by the symbol S Notes:
324 Stat Lecture Notes 1 robability Chapter 2 of the book pg 35-71 1 Definitions: Sample Space: Is the set of all possible outcomes of a statistical experiment, which is denoted by the symbol S Notes:
MODULE 2 RANDOM VARIABLE AND ITS DISTRIBUTION LECTURES DISTRIBUTION FUNCTION AND ITS PROPERTIES
 MODULE 2 RANDOM VARIABLE AND ITS DISTRIBUTION LECTURES 7-11 Topics 2.1 RANDOM VARIABLE 2.2 INDUCED PROBABILITY MEASURE 2.3 DISTRIBUTION FUNCTION AND ITS PROPERTIES 2.4 TYPES OF RANDOM VARIABLES: DISCRETE,
MODULE 2 RANDOM VARIABLE AND ITS DISTRIBUTION LECTURES 7-11 Topics 2.1 RANDOM VARIABLE 2.2 INDUCED PROBABILITY MEASURE 2.3 DISTRIBUTION FUNCTION AND ITS PROPERTIES 2.4 TYPES OF RANDOM VARIABLES: DISCRETE,
Lecture Notes 1 Basic Probability. Elements of Probability. Conditional probability. Sequential Calculation of Probability
 Lecture Notes 1 Basic Probability Set Theory Elements of Probability Conditional probability Sequential Calculation of Probability Total Probability and Bayes Rule Independence Counting EE 178/278A: Basic
Lecture Notes 1 Basic Probability Set Theory Elements of Probability Conditional probability Sequential Calculation of Probability Total Probability and Bayes Rule Independence Counting EE 178/278A: Basic
Why should you care?? Intellectual curiosity. Gambling. Mathematically the same as the ESP decision problem we discussed in Week 4.
 I. Probability basics (Sections 4.1 and 4.2) Flip a fair (probability of HEADS is 1/2) coin ten times. What is the probability of getting exactly 5 HEADS? What is the probability of getting exactly 10
I. Probability basics (Sections 4.1 and 4.2) Flip a fair (probability of HEADS is 1/2) coin ten times. What is the probability of getting exactly 5 HEADS? What is the probability of getting exactly 10
Probability: Sets, Sample Spaces, Events
 Probability: Sets, Sample Spaces, Events Engineering Statistics Section 2.1 Josh Engwer TTU 01 February 2016 Josh Engwer (TTU) Probability: Sets, Sample Spaces, Events 01 February 2016 1 / 29 The Need
Probability: Sets, Sample Spaces, Events Engineering Statistics Section 2.1 Josh Engwer TTU 01 February 2016 Josh Engwer (TTU) Probability: Sets, Sample Spaces, Events 01 February 2016 1 / 29 The Need
Fundamentals of Probability CE 311S
 Fundamentals of Probability CE 311S OUTLINE Review Elementary set theory Probability fundamentals: outcomes, sample spaces, events Outline ELEMENTARY SET THEORY Basic probability concepts can be cast in
Fundamentals of Probability CE 311S OUTLINE Review Elementary set theory Probability fundamentals: outcomes, sample spaces, events Outline ELEMENTARY SET THEORY Basic probability concepts can be cast in
What is Probability? Probability. Sample Spaces and Events. Simple Event
 What is Probability? Probability Peter Lo Probability is the numerical measure of likelihood that the event will occur. Simple Event Joint Event Compound Event Lies between 0 & 1 Sum of events is 1 1.5
What is Probability? Probability Peter Lo Probability is the numerical measure of likelihood that the event will occur. Simple Event Joint Event Compound Event Lies between 0 & 1 Sum of events is 1 1.5
CS4705. Probability Review and Naïve Bayes. Slides from Dragomir Radev
 CS4705 Probability Review and Naïve Bayes Slides from Dragomir Radev Classification using a Generative Approach Previously on NLP discriminative models P C D here is a line with all the social media posts
CS4705 Probability Review and Naïve Bayes Slides from Dragomir Radev Classification using a Generative Approach Previously on NLP discriminative models P C D here is a line with all the social media posts
Sec$on Summary. Assigning Probabilities Probabilities of Complements and Unions of Events Conditional Probability
 Section 7.2 Sec$on Summary Assigning Probabilities Probabilities of Complements and Unions of Events Conditional Probability Independence Bernoulli Trials and the Binomial Distribution Random Variables
Section 7.2 Sec$on Summary Assigning Probabilities Probabilities of Complements and Unions of Events Conditional Probability Independence Bernoulli Trials and the Binomial Distribution Random Variables
Steve Smith Tuition: Maths Notes
 Maths Notes : Discrete Random Variables Version. Steve Smith Tuition: Maths Notes e iπ + = 0 a + b = c z n+ = z n + c V E + F = Discrete Random Variables Contents Intro The Distribution of Probabilities
Maths Notes : Discrete Random Variables Version. Steve Smith Tuition: Maths Notes e iπ + = 0 a + b = c z n+ = z n + c V E + F = Discrete Random Variables Contents Intro The Distribution of Probabilities
4/17/2012. NE ( ) # of ways an event can happen NS ( ) # of events in the sample space
 I. Vocabulary: A. Outcomes: the things that can happen in a probability experiment B. Sample Space (S): all possible outcomes C. Event (E): one outcome D. Probability of an Event (P(E)): the likelihood
I. Vocabulary: A. Outcomes: the things that can happen in a probability experiment B. Sample Space (S): all possible outcomes C. Event (E): one outcome D. Probability of an Event (P(E)): the likelihood
Probability. VCE Maths Methods - Unit 2 - Probability
 Probability Probability Tree diagrams La ice diagrams Venn diagrams Karnough maps Probability tables Union & intersection rules Conditional probability Markov chains 1 Probability Probability is the mathematics
Probability Probability Tree diagrams La ice diagrams Venn diagrams Karnough maps Probability tables Union & intersection rules Conditional probability Markov chains 1 Probability Probability is the mathematics
6.2 Introduction to Probability. The Deal. Possible outcomes: STAT1010 Intro to probability. Definitions. Terms: What are the chances of?
 6.2 Introduction to Probability Terms: What are the chances of?! Personal probability (subjective) " Based on feeling or opinion. " Gut reaction.! Empirical probability (evidence based) " Based on experience
6.2 Introduction to Probability Terms: What are the chances of?! Personal probability (subjective) " Based on feeling or opinion. " Gut reaction.! Empirical probability (evidence based) " Based on experience
 CHAPTER - 16 PROBABILITY Random Experiment : If an experiment has more than one possible out come and it is not possible to predict the outcome in advance then experiment is called random experiment. Sample
CHAPTER - 16 PROBABILITY Random Experiment : If an experiment has more than one possible out come and it is not possible to predict the outcome in advance then experiment is called random experiment. Sample
Notes 1 Autumn Sample space, events. S is the number of elements in the set S.)
 MAS 108 Probability I Notes 1 Autumn 2005 Sample space, events The general setting is: We perform an experiment which can have a number of different outcomes. The sample space is the set of all possible
MAS 108 Probability I Notes 1 Autumn 2005 Sample space, events The general setting is: We perform an experiment which can have a number of different outcomes. The sample space is the set of all possible
Deep Learning for Computer Vision
 Deep Learning for Computer Vision Lecture 3: Probability, Bayes Theorem, and Bayes Classification Peter Belhumeur Computer Science Columbia University Probability Should you play this game? Game: A fair
Deep Learning for Computer Vision Lecture 3: Probability, Bayes Theorem, and Bayes Classification Peter Belhumeur Computer Science Columbia University Probability Should you play this game? Game: A fair
SDS 321: Introduction to Probability and Statistics
 SDS 321: Introduction to Probability and Statistics Lecture 2: Conditional probability Purnamrita Sarkar Department of Statistics and Data Science The University of Texas at Austin www.cs.cmu.edu/ psarkar/teaching
SDS 321: Introduction to Probability and Statistics Lecture 2: Conditional probability Purnamrita Sarkar Department of Statistics and Data Science The University of Texas at Austin www.cs.cmu.edu/ psarkar/teaching
Conditional Probability
 Conditional Probability Idea have performed a chance experiment but don t know the outcome (ω), but have some partial information (event A) about ω. Question: given this partial information what s the
Conditional Probability Idea have performed a chance experiment but don t know the outcome (ω), but have some partial information (event A) about ω. Question: given this partial information what s the
Probability- describes the pattern of chance outcomes
 Chapter 6 Probability the study of randomness Probability- describes the pattern of chance outcomes Chance behavior is unpredictable in the short run, but has a regular and predictable pattern in the long
Chapter 6 Probability the study of randomness Probability- describes the pattern of chance outcomes Chance behavior is unpredictable in the short run, but has a regular and predictable pattern in the long
Econ 325: Introduction to Empirical Economics
 Econ 325: Introduction to Empirical Economics Lecture 2 Probability Copyright 2010 Pearson Education, Inc. Publishing as Prentice Hall Ch. 3-1 3.1 Definition Random Experiment a process leading to an uncertain
Econ 325: Introduction to Empirical Economics Lecture 2 Probability Copyright 2010 Pearson Education, Inc. Publishing as Prentice Hall Ch. 3-1 3.1 Definition Random Experiment a process leading to an uncertain
Mean, Median and Mode. Lecture 3 - Axioms of Probability. Where do they come from? Graphically. We start with a set of 21 numbers, Sta102 / BME102
 Mean, Median and Mode Lecture 3 - Axioms of Probability Sta102 / BME102 Colin Rundel September 1, 2014 We start with a set of 21 numbers, ## [1] -2.2-1.6-1.0-0.5-0.4-0.3-0.2 0.1 0.1 0.2 0.4 ## [12] 0.4
Mean, Median and Mode Lecture 3 - Axioms of Probability Sta102 / BME102 Colin Rundel September 1, 2014 We start with a set of 21 numbers, ## [1] -2.2-1.6-1.0-0.5-0.4-0.3-0.2 0.1 0.1 0.2 0.4 ## [12] 0.4
Chapter 2 PROBABILITY SAMPLE SPACE
 Chapter 2 PROBABILITY Key words: Sample space, sample point, tree diagram, events, complement, union and intersection of an event, mutually exclusive events; Counting techniques: multiplication rule, permutation,
Chapter 2 PROBABILITY Key words: Sample space, sample point, tree diagram, events, complement, union and intersection of an event, mutually exclusive events; Counting techniques: multiplication rule, permutation,
ELEG 3143 Probability & Stochastic Process Ch. 1 Experiments, Models, and Probabilities
 Department of Electrical Engineering University of Arkansas ELEG 3143 Probability & Stochastic Process Ch. 1 Experiments, Models, and Probabilities Dr. Jing Yang jingyang@uark.edu OUTLINE 2 Applications
Department of Electrical Engineering University of Arkansas ELEG 3143 Probability & Stochastic Process Ch. 1 Experiments, Models, and Probabilities Dr. Jing Yang jingyang@uark.edu OUTLINE 2 Applications
CS 441 Discrete Mathematics for CS Lecture 20. Probabilities. CS 441 Discrete mathematics for CS. Probabilities
 CS 441 Discrete Mathematics for CS Lecture 20 Probabilities Milos Hauskrecht milos@cs.pitt.edu 5329 Sennott Square CS 441 Discrete mathematics for CS Probabilities Three axioms of the probability theory:
CS 441 Discrete Mathematics for CS Lecture 20 Probabilities Milos Hauskrecht milos@cs.pitt.edu 5329 Sennott Square CS 441 Discrete mathematics for CS Probabilities Three axioms of the probability theory:
Lecture 3 - Axioms of Probability
 Lecture 3 - Axioms of Probability Sta102 / BME102 January 25, 2016 Colin Rundel Axioms of Probability What does it mean to say that: The probability of flipping a coin and getting heads is 1/2? 3 What
Lecture 3 - Axioms of Probability Sta102 / BME102 January 25, 2016 Colin Rundel Axioms of Probability What does it mean to say that: The probability of flipping a coin and getting heads is 1/2? 3 What
Chapter 7. Inclusion-Exclusion a.k.a. The Sieve Formula
 Chapter 7. Inclusion-Exclusion a.k.a. The Sieve Formula Prof. Tesler Math 184A Fall 2019 Prof. Tesler Ch. 7. Inclusion-Exclusion Math 184A / Fall 2019 1 / 25 Venn diagram and set sizes A = {1, 2, 3, 4,
Chapter 7. Inclusion-Exclusion a.k.a. The Sieve Formula Prof. Tesler Math 184A Fall 2019 Prof. Tesler Ch. 7. Inclusion-Exclusion Math 184A / Fall 2019 1 / 25 Venn diagram and set sizes A = {1, 2, 3, 4,
CMPSCI 240: Reasoning about Uncertainty
 CMPSCI 240: Reasoning about Uncertainty Lecture 2: Sets and Events Andrew McGregor University of Massachusetts Last Compiled: January 27, 2017 Outline 1 Recap 2 Experiments and Events 3 Probabilistic Models
CMPSCI 240: Reasoning about Uncertainty Lecture 2: Sets and Events Andrew McGregor University of Massachusetts Last Compiled: January 27, 2017 Outline 1 Recap 2 Experiments and Events 3 Probabilistic Models
Probability deals with modeling of random phenomena (phenomena or experiments whose outcomes may vary)
 Chapter 14 From Randomness to Probability How to measure a likelihood of an event? How likely is it to answer correctly one out of two true-false questions on a quiz? Is it more, less, or equally likely
Chapter 14 From Randomness to Probability How to measure a likelihood of an event? How likely is it to answer correctly one out of two true-false questions on a quiz? Is it more, less, or equally likely
Problems from Probability and Statistical Inference (9th ed.) by Hogg, Tanis and Zimmerman.
 Math 224 Fall 2017 Homework 1 Drew Armstrong Problems from Probability and Statistical Inference (9th ed.) by Hogg, Tanis and Zimmerman. Section 1.1, Exercises 4,5,6,7,9,12. Solutions to Book Problems.
Math 224 Fall 2017 Homework 1 Drew Armstrong Problems from Probability and Statistical Inference (9th ed.) by Hogg, Tanis and Zimmerman. Section 1.1, Exercises 4,5,6,7,9,12. Solutions to Book Problems.
27 Binary Arithmetic: An Application to Programming
 27 Binary Arithmetic: An Application to Programming In the previous section we looked at the binomial distribution. The binomial distribution is essentially the mathematics of repeatedly flipping a coin
27 Binary Arithmetic: An Application to Programming In the previous section we looked at the binomial distribution. The binomial distribution is essentially the mathematics of repeatedly flipping a coin
Probabilistic models
 Probabilistic models Kolmogorov (Andrei Nikolaevich, 1903 1987) put forward an axiomatic system for probability theory. Foundations of the Calculus of Probabilities, published in 1933, immediately became
Probabilistic models Kolmogorov (Andrei Nikolaevich, 1903 1987) put forward an axiomatic system for probability theory. Foundations of the Calculus of Probabilities, published in 1933, immediately became
Expected Value. Lecture A Tiefenbruck MWF 9-9:50am Center 212 Lecture B Jones MWF 2-2:50pm Center 214 Lecture C Tiefenbruck MWF 11-11:50am Center 212
 Expected Value Lecture A Tiefenbruck MWF 9-9:50am Center 212 Lecture B Jones MWF 2-2:50pm Center 214 Lecture C Tiefenbruck MWF 11-11:50am Center 212 http://cseweb.ucsd.edu/classes/wi16/cse21-abc/ March
Expected Value Lecture A Tiefenbruck MWF 9-9:50am Center 212 Lecture B Jones MWF 2-2:50pm Center 214 Lecture C Tiefenbruck MWF 11-11:50am Center 212 http://cseweb.ucsd.edu/classes/wi16/cse21-abc/ March
EE 178 Lecture Notes 0 Course Introduction. About EE178. About Probability. Course Goals. Course Topics. Lecture Notes EE 178
 EE 178 Lecture Notes 0 Course Introduction About EE178 About Probability Course Goals Course Topics Lecture Notes EE 178: Course Introduction Page 0 1 EE 178 EE 178 provides an introduction to probabilistic
EE 178 Lecture Notes 0 Course Introduction About EE178 About Probability Course Goals Course Topics Lecture Notes EE 178: Course Introduction Page 0 1 EE 178 EE 178 provides an introduction to probabilistic
ECE 340 Probabilistic Methods in Engineering M/W 3-4:15. Lecture 2: Random Experiments. Prof. Vince Calhoun
 ECE 340 Probabilistic Methods in Engineering M/W 3-4:15 Lecture 2: Random Experiments Prof. Vince Calhoun Reading This class: Section 2.1-2.2 Next class: Section 2.3-2.4 Homework: Assignment 1: From the
ECE 340 Probabilistic Methods in Engineering M/W 3-4:15 Lecture 2: Random Experiments Prof. Vince Calhoun Reading This class: Section 2.1-2.2 Next class: Section 2.3-2.4 Homework: Assignment 1: From the
(i) Given that a student is female, what is the probability of having a GPA of at least 3.0?
 MATH 382 Conditional Probability Dr. Neal, WKU We now shall consider probabilities of events that are restricted within a subset that is smaller than the entire sample space Ω. For example, let Ω be the
MATH 382 Conditional Probability Dr. Neal, WKU We now shall consider probabilities of events that are restricted within a subset that is smaller than the entire sample space Ω. For example, let Ω be the
Monty Hall Puzzle. Draw a tree diagram of possible choices (a possibility tree ) One for each strategy switch or no-switch
 Monty Hall Puzzle Example: You are asked to select one of the three doors to open. There is a large prize behind one of the doors and if you select that door, you win the prize. After you select a door,
Monty Hall Puzzle Example: You are asked to select one of the three doors to open. There is a large prize behind one of the doors and if you select that door, you win the prize. After you select a door,
Week 2. Section Texas A& M University. Department of Mathematics Texas A& M University, College Station 22 January-24 January 2019
 Week 2 Section 1.2-1.4 Texas A& M University Department of Mathematics Texas A& M University, College Station 22 January-24 January 2019 Oğuz Gezmiş (TAMU) Topics in Contemporary Mathematics II Week2 1
Week 2 Section 1.2-1.4 Texas A& M University Department of Mathematics Texas A& M University, College Station 22 January-24 January 2019 Oğuz Gezmiş (TAMU) Topics in Contemporary Mathematics II Week2 1
Probability Theory and Applications
 Probability Theory and Applications Videos of the topics covered in this manual are available at the following links: Lesson 4 Probability I http://faculty.citadel.edu/silver/ba205/online course/lesson
Probability Theory and Applications Videos of the topics covered in this manual are available at the following links: Lesson 4 Probability I http://faculty.citadel.edu/silver/ba205/online course/lesson
Term Definition Example Random Phenomena
 UNIT VI STUDY GUIDE Probabilities Course Learning Outcomes for Unit VI Upon completion of this unit, students should be able to: 1. Apply mathematical principles used in real-world situations. 1.1 Demonstrate
UNIT VI STUDY GUIDE Probabilities Course Learning Outcomes for Unit VI Upon completion of this unit, students should be able to: 1. Apply mathematical principles used in real-world situations. 1.1 Demonstrate
PERMUTATIONS, COMBINATIONS AND DISCRETE PROBABILITY
 Friends, we continue the discussion with fundamentals of discrete probability in the second session of third chapter of our course in Discrete Mathematics. The conditional probability and Baye s theorem
Friends, we continue the discussion with fundamentals of discrete probability in the second session of third chapter of our course in Discrete Mathematics. The conditional probability and Baye s theorem
Outline. 1. Define likelihood 2. Interpretations of likelihoods 3. Likelihood plots 4. Maximum likelihood 5. Likelihood ratio benchmarks
 Outline 1. Define likelihood 2. Interpretations of likelihoods 3. Likelihood plots 4. Maximum likelihood 5. Likelihood ratio benchmarks Likelihood A common and fruitful approach to statistics is to assume
Outline 1. Define likelihood 2. Interpretations of likelihoods 3. Likelihood plots 4. Maximum likelihood 5. Likelihood ratio benchmarks Likelihood A common and fruitful approach to statistics is to assume
Statistical Inference
 Statistical Inference Lecture 1: Probability Theory MING GAO DASE @ ECNU (for course related communications) mgao@dase.ecnu.edu.cn Sep. 11, 2018 Outline Introduction Set Theory Basics of Probability Theory
Statistical Inference Lecture 1: Probability Theory MING GAO DASE @ ECNU (for course related communications) mgao@dase.ecnu.edu.cn Sep. 11, 2018 Outline Introduction Set Theory Basics of Probability Theory
TA Qinru Shi: Based on poll result, the first Programming Boot Camp will be: this Sunday 5 Feb, 7-8pm Gates 114.
 TA Qinru Shi: Based on poll result, the first Programming Boot Camp will be: this Sunday 5 Feb, 7-8pm Gates 114. Prob Set 1: to be posted tomorrow. due in roughly a week Finite probability space S 1) a
TA Qinru Shi: Based on poll result, the first Programming Boot Camp will be: this Sunday 5 Feb, 7-8pm Gates 114. Prob Set 1: to be posted tomorrow. due in roughly a week Finite probability space S 1) a
Lecture Lecture 5
 Lecture 4 --- Lecture 5 A. Basic Concepts (4.1-4.2) 1. Experiment: A process of observing a phenomenon that has variation in its outcome. Examples: (E1). Rolling a die, (E2). Drawing a card form a shuffled
Lecture 4 --- Lecture 5 A. Basic Concepts (4.1-4.2) 1. Experiment: A process of observing a phenomenon that has variation in its outcome. Examples: (E1). Rolling a die, (E2). Drawing a card form a shuffled
LECTURE NOTES by DR. J.S.V.R. KRISHNA PRASAD
 .0 Introduction: The theory of probability has its origin in the games of chance related to gambling such as tossing of a coin, throwing of a die, drawing cards from a pack of cards etc. Jerame Cardon,
.0 Introduction: The theory of probability has its origin in the games of chance related to gambling such as tossing of a coin, throwing of a die, drawing cards from a pack of cards etc. Jerame Cardon,
Venn Diagrams; Probability Laws. Notes. Set Operations and Relations. Venn Diagram 2.1. Venn Diagrams; Probability Laws. Notes
 Lecture 2 s; Text: A Course in Probability by Weiss 2.4 STAT 225 Introduction to Probability Models January 8, 2014 s; Whitney Huang Purdue University 2.1 Agenda s; 1 2 2.2 Intersection: the intersection
Lecture 2 s; Text: A Course in Probability by Weiss 2.4 STAT 225 Introduction to Probability Models January 8, 2014 s; Whitney Huang Purdue University 2.1 Agenda s; 1 2 2.2 Intersection: the intersection
Marquette University MATH 1700 Class 5 Copyright 2017 by D.B. Rowe
 Class 5 Daniel B. Rowe, Ph.D. Department of Mathematics, Statistics, and Computer Science Copyright 2017 by D.B. Rowe 1 Agenda: Recap Chapter 3.2-3.3 Lecture Chapter 4.1-4.2 Review Chapter 1 3.1 (Exam
Class 5 Daniel B. Rowe, Ph.D. Department of Mathematics, Statistics, and Computer Science Copyright 2017 by D.B. Rowe 1 Agenda: Recap Chapter 3.2-3.3 Lecture Chapter 4.1-4.2 Review Chapter 1 3.1 (Exam
General Info. Grading
 Syllabus & Policies General Info Lecture 1: Introduction, Set Theory, and Boolean Algebra Classroom: Perkins 2-072 Time: Mon - Fri, 2:00-3:15 pm Wed, 3:30-4:30 pm Sta 111 Colin Rundel May 13, 2014 Professor:
Syllabus & Policies General Info Lecture 1: Introduction, Set Theory, and Boolean Algebra Classroom: Perkins 2-072 Time: Mon - Fri, 2:00-3:15 pm Wed, 3:30-4:30 pm Sta 111 Colin Rundel May 13, 2014 Professor:
AMS7: WEEK 2. CLASS 2
 AMS7: WEEK 2. CLASS 2 Introduction to Probability. Probability Rules. Independence and Conditional Probability. Bayes Theorem. Risk and Odds Ratio Friday April 10, 2015 Probability: Introduction Probability:
AMS7: WEEK 2. CLASS 2 Introduction to Probability. Probability Rules. Independence and Conditional Probability. Bayes Theorem. Risk and Odds Ratio Friday April 10, 2015 Probability: Introduction Probability:
Math 1313 Experiments, Events and Sample Spaces
 Math 1313 Experiments, Events and Sample Spaces At the end of this recording, you should be able to define and use the basic terminology used in defining experiments. Terminology The next main topic in
Math 1313 Experiments, Events and Sample Spaces At the end of this recording, you should be able to define and use the basic terminology used in defining experiments. Terminology The next main topic in
Introduction to Probability. Ariel Yadin. Lecture 1. We begin with an example [this is known as Bertrand s paradox]. *** Nov.
![Introduction to Probability. Ariel Yadin. Lecture 1. We begin with an example [this is known as Bertrand s paradox]. *** Nov. Introduction to Probability. Ariel Yadin. Lecture 1. We begin with an example [this is known as Bertrand s paradox]. *** Nov.](/thumbs/87/97208194.jpg) Introduction to Probability Ariel Yadin Lecture 1 1. Example: Bertrand s Paradox We begin with an example [this is known as Bertrand s paradox]. *** Nov. 1 *** Question 1.1. Consider a circle of radius
Introduction to Probability Ariel Yadin Lecture 1 1. Example: Bertrand s Paradox We begin with an example [this is known as Bertrand s paradox]. *** Nov. 1 *** Question 1.1. Consider a circle of radius
CHAPTER 1 SETS AND EVENTS
 CHPTER 1 SETS ND EVENTS 1.1 Universal Set and Subsets DEFINITION: set is a well-defined collection of distinct elements in the universal set. This is denoted by capital latin letters, B, C, If an element
CHPTER 1 SETS ND EVENTS 1.1 Universal Set and Subsets DEFINITION: set is a well-defined collection of distinct elements in the universal set. This is denoted by capital latin letters, B, C, If an element
Probability 1 (MATH 11300) lecture slides
 Probability 1 (MATH 11300) lecture slides Márton Balázs School of Mathematics University of Bristol Autumn, 2015 December 16, 2015 To know... http://www.maths.bris.ac.uk/ mb13434/prob1/ m.balazs@bristol.ac.uk
Probability 1 (MATH 11300) lecture slides Márton Balázs School of Mathematics University of Bristol Autumn, 2015 December 16, 2015 To know... http://www.maths.bris.ac.uk/ mb13434/prob1/ m.balazs@bristol.ac.uk
ECE 450 Lecture 2. Recall: Pr(A B) = Pr(A) + Pr(B) Pr(A B) in general = Pr(A) + Pr(B) if A and B are m.e. Lecture Overview
 ECE 450 Lecture 2 Recall: Pr(A B) = Pr(A) + Pr(B) Pr(A B) in general = Pr(A) + Pr(B) if A and B are m.e. Lecture Overview Conditional Probability, Pr(A B) Total Probability Bayes Theorem Independent Events
ECE 450 Lecture 2 Recall: Pr(A B) = Pr(A) + Pr(B) Pr(A B) in general = Pr(A) + Pr(B) if A and B are m.e. Lecture Overview Conditional Probability, Pr(A B) Total Probability Bayes Theorem Independent Events
Properties of Probability
 Econ 325 Notes on Probability 1 By Hiro Kasahara Properties of Probability In statistics, we consider random experiments, experiments for which the outcome is random, i.e., cannot be predicted with certainty.
Econ 325 Notes on Probability 1 By Hiro Kasahara Properties of Probability In statistics, we consider random experiments, experiments for which the outcome is random, i.e., cannot be predicted with certainty.
PROBABILITY CHAPTER LEARNING OBJECTIVES UNIT OVERVIEW
 CHAPTER 16 PROBABILITY LEARNING OBJECTIVES Concept of probability is used in accounting and finance to understand the likelihood of occurrence or non-occurrence of a variable. It helps in developing financial
CHAPTER 16 PROBABILITY LEARNING OBJECTIVES Concept of probability is used in accounting and finance to understand the likelihood of occurrence or non-occurrence of a variable. It helps in developing financial
Introduction to Probability 2017/18 Supplementary Problems
 Introduction to Probability 2017/18 Supplementary Problems Problem 1: Let A and B denote two events with P(A B) 0. Show that P(A) 0 and P(B) 0. A A B implies P(A) P(A B) 0, hence P(A) 0. Similarly B A
Introduction to Probability 2017/18 Supplementary Problems Problem 1: Let A and B denote two events with P(A B) 0. Show that P(A) 0 and P(B) 0. A A B implies P(A) P(A B) 0, hence P(A) 0. Similarly B A
Chapter 13, Probability from Applied Finite Mathematics by Rupinder Sekhon was developed by OpenStax College, licensed by Rice University, and is
 Chapter 13, Probability from Applied Finite Mathematics by Rupinder Sekhon was developed by OpenStax College, licensed by Rice University, and is available on the Connexions website. It is used under a
Chapter 13, Probability from Applied Finite Mathematics by Rupinder Sekhon was developed by OpenStax College, licensed by Rice University, and is available on the Connexions website. It is used under a
More on Distribution Function
 More on Distribution Function The distribution of a random variable X can be determined directly from its cumulative distribution function F X. Theorem: Let X be any random variable, with cumulative distribution
More on Distribution Function The distribution of a random variable X can be determined directly from its cumulative distribution function F X. Theorem: Let X be any random variable, with cumulative distribution
Conditional Probability
 Conditional Probability Conditional Probability The Law of Total Probability Let A 1, A 2,..., A k be mutually exclusive and exhaustive events. Then for any other event B, P(B) = P(B A 1 ) P(A 1 ) + P(B
Conditional Probability Conditional Probability The Law of Total Probability Let A 1, A 2,..., A k be mutually exclusive and exhaustive events. Then for any other event B, P(B) = P(B A 1 ) P(A 1 ) + P(B
First Digit Tally Marks Final Count
 Benford Test () Imagine that you are a forensic accountant, presented with the two data sets on this sheet of paper (front and back). Which of the two sets should be investigated further? Why? () () ()
Benford Test () Imagine that you are a forensic accountant, presented with the two data sets on this sheet of paper (front and back). Which of the two sets should be investigated further? Why? () () ()
MA : Introductory Probability
 MA 320-001: Introductory Probability David Murrugarra Department of Mathematics, University of Kentucky http://www.math.uky.edu/~dmu228/ma320/ Spring 2017 David Murrugarra (University of Kentucky) MA 320:
MA 320-001: Introductory Probability David Murrugarra Department of Mathematics, University of Kentucky http://www.math.uky.edu/~dmu228/ma320/ Spring 2017 David Murrugarra (University of Kentucky) MA 320:
Probability: Axioms, Properties, Interpretations
 Probability: Axioms, Properties, Interpretations Engineering Statistics Section 2.2 Josh Engwer TTU 03 February 2016 Josh Engwer (TTU) Probability: Axioms, Properties, Interpretations 03 February 2016
Probability: Axioms, Properties, Interpretations Engineering Statistics Section 2.2 Josh Engwer TTU 03 February 2016 Josh Engwer (TTU) Probability: Axioms, Properties, Interpretations 03 February 2016
CS206 Review Sheet 3 October 24, 2018
 CS206 Review Sheet 3 October 24, 2018 After ourintense focusoncounting, wecontinue withthestudyofsomemoreofthebasic notions from Probability (though counting will remain in our thoughts). An important
CS206 Review Sheet 3 October 24, 2018 After ourintense focusoncounting, wecontinue withthestudyofsomemoreofthebasic notions from Probability (though counting will remain in our thoughts). An important
Lecture notes for probability. Math 124
 Lecture notes for probability Math 124 What is probability? Probabilities are ratios, expressed as fractions, decimals, or percents, determined by considering results or outcomes of experiments whose result
Lecture notes for probability Math 124 What is probability? Probabilities are ratios, expressed as fractions, decimals, or percents, determined by considering results or outcomes of experiments whose result
Key Concepts. Key Concepts. Event Relations. Event Relations
 Probability and Probability Distributions Event Relations S B B Event Relations The intersection of two events, and B, is the event that both and B occur when the experient is perfored. We write B. S Event
Probability and Probability Distributions Event Relations S B B Event Relations The intersection of two events, and B, is the event that both and B occur when the experient is perfored. We write B. S Event
MATH MW Elementary Probability Course Notes Part I: Models and Counting
 MATH 2030 3.00MW Elementary Probability Course Notes Part I: Models and Counting Tom Salisbury salt@yorku.ca York University Winter 2010 Introduction [Jan 5] Probability: the mathematics used for Statistics
MATH 2030 3.00MW Elementary Probability Course Notes Part I: Models and Counting Tom Salisbury salt@yorku.ca York University Winter 2010 Introduction [Jan 5] Probability: the mathematics used for Statistics
Executive Assessment. Executive Assessment Math Review. Section 1.0, Arithmetic, includes the following topics:
 Executive Assessment Math Review Although the following provides a review of some of the mathematical concepts of arithmetic and algebra, it is not intended to be a textbook. You should use this chapter
Executive Assessment Math Review Although the following provides a review of some of the mathematical concepts of arithmetic and algebra, it is not intended to be a textbook. You should use this chapter
9/6/2016. Section 5.1 Probability. Equally Likely Model. The Division Rule: P(A)=#(A)/#(S) Some Popular Randomizers.
 Chapter 5: Probability and Discrete Probability Distribution Learn. Probability Binomial Distribution Poisson Distribution Some Popular Randomizers Rolling dice Spinning a wheel Flipping a coin Drawing
Chapter 5: Probability and Discrete Probability Distribution Learn. Probability Binomial Distribution Poisson Distribution Some Popular Randomizers Rolling dice Spinning a wheel Flipping a coin Drawing
Notes slides from before lecture. CSE 21, Winter 2017, Section A00. Lecture 15 Notes. Class URL:
 Notes slides from before lecture CSE 21, Winter 2017, Section A00 Lecture 15 Notes Class URL: http://vlsicad.ucsd.edu/courses/cse21-w17/ Notes slides from before lecture Notes March 6 (1) This week: Days
Notes slides from before lecture CSE 21, Winter 2017, Section A00 Lecture 15 Notes Class URL: http://vlsicad.ucsd.edu/courses/cse21-w17/ Notes slides from before lecture Notes March 6 (1) This week: Days
Origins of Probability Theory
 1 16.584: INTRODUCTION Theory and Tools of Probability required to analyze and design systems subject to uncertain outcomes/unpredictability/randomness. Such systems more generally referred to as Experiments.
1 16.584: INTRODUCTION Theory and Tools of Probability required to analyze and design systems subject to uncertain outcomes/unpredictability/randomness. Such systems more generally referred to as Experiments.
Expected Value 7/7/2006
 Expected Value 7/7/2006 Definition Let X be a numerically-valued discrete random variable with sample space Ω and distribution function m(x). The expected value E(X) is defined by E(X) = x Ω x m(x), provided
Expected Value 7/7/2006 Definition Let X be a numerically-valued discrete random variable with sample space Ω and distribution function m(x). The expected value E(X) is defined by E(X) = x Ω x m(x), provided
Independence Solutions STAT-UB.0103 Statistics for Business Control and Regression Models
 Independence Solutions STAT-UB.003 Statistics for Business Control and Regression Models The Birthday Problem. A class has 70 students. What is the probability that at least two students have the same
Independence Solutions STAT-UB.003 Statistics for Business Control and Regression Models The Birthday Problem. A class has 70 students. What is the probability that at least two students have the same
Topic 5 Basics of Probability
 Topic 5 Basics of Probability Equally Likely Outcomes and the Axioms of Probability 1 / 13 Outline Equally Likely Outcomes Axioms of Probability Consequences of the Axioms 2 / 13 Introduction A probability
Topic 5 Basics of Probability Equally Likely Outcomes and the Axioms of Probability 1 / 13 Outline Equally Likely Outcomes Axioms of Probability Consequences of the Axioms 2 / 13 Introduction A probability
Section 13.3 Probability
 288 Section 13.3 Probability Probability is a measure of how likely an event will occur. When the weather forecaster says that there will be a 50% chance of rain this afternoon, the probability that it
288 Section 13.3 Probability Probability is a measure of how likely an event will occur. When the weather forecaster says that there will be a 50% chance of rain this afternoon, the probability that it
ENGI 4421 Introduction to Probability; Sets & Venn Diagrams Page α 2 θ 1 u 3. wear coat. θ 2 = warm u 2 = sweaty! θ 1 = cold u 3 = brrr!
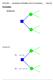 ENGI 4421 Introduction to Probability; Sets & Venn Diagrams Page 2-01 Probability Decision trees u 1 u 2 α 2 θ 1 u 3 θ 2 u 4 Example 2.01 θ 1 = cold u 1 = snug! α 1 wear coat θ 2 = warm u 2 = sweaty! θ
ENGI 4421 Introduction to Probability; Sets & Venn Diagrams Page 2-01 Probability Decision trees u 1 u 2 α 2 θ 1 u 3 θ 2 u 4 Example 2.01 θ 1 = cold u 1 = snug! α 1 wear coat θ 2 = warm u 2 = sweaty! θ
Business Statistics MBA Pokhara University
 Business Statistics MBA Pokhara University Chapter 3 Basic Probability Concept and Application Bijay Lal Pradhan, Ph.D. Review I. What s in last lecture? Descriptive Statistics Numerical Measures. Chapter
Business Statistics MBA Pokhara University Chapter 3 Basic Probability Concept and Application Bijay Lal Pradhan, Ph.D. Review I. What s in last lecture? Descriptive Statistics Numerical Measures. Chapter
Recap. The study of randomness and uncertainty Chances, odds, likelihood, expected, probably, on average,... PROBABILITY INFERENTIAL STATISTICS
 Recap. Probability (section 1.1) The study of randomness and uncertainty Chances, odds, likelihood, expected, probably, on average,... PROBABILITY Population Sample INFERENTIAL STATISTICS Today. Formulation
Recap. Probability (section 1.1) The study of randomness and uncertainty Chances, odds, likelihood, expected, probably, on average,... PROBABILITY Population Sample INFERENTIAL STATISTICS Today. Formulation
Standard & Conditional Probability
 Biostatistics 050 Standard & Conditional Probability 1 ORIGIN 0 Probability as a Concept: Standard & Conditional Probability "The probability of an event is the likelihood of that event expressed either
Biostatistics 050 Standard & Conditional Probability 1 ORIGIN 0 Probability as a Concept: Standard & Conditional Probability "The probability of an event is the likelihood of that event expressed either
Lecture 8: Probability
 Lecture 8: Probability The idea of probability is well-known The flipping of a balanced coin can produce one of two outcomes: T (tail) and H (head) and the symmetry between the two outcomes means, of course,
Lecture 8: Probability The idea of probability is well-known The flipping of a balanced coin can produce one of two outcomes: T (tail) and H (head) and the symmetry between the two outcomes means, of course,
Summary of basic probability theory Math 218, Mathematical Statistics D Joyce, Spring 2016
 8. For any two events E and F, P (E) = P (E F ) + P (E F c ). Summary of basic probability theory Math 218, Mathematical Statistics D Joyce, Spring 2016 Sample space. A sample space consists of a underlying
8. For any two events E and F, P (E) = P (E F ) + P (E F c ). Summary of basic probability theory Math 218, Mathematical Statistics D Joyce, Spring 2016 Sample space. A sample space consists of a underlying
ELEG 3143 Probability & Stochastic Process Ch. 1 Probability
 Department of Electrical Engineering University of Arkansas ELEG 3143 Probability & Stochastic Process Ch. 1 Probability Dr. Jingxian Wu wuj@uark.edu OUTLINE 2 Applications Elementary Set Theory Random
Department of Electrical Engineering University of Arkansas ELEG 3143 Probability & Stochastic Process Ch. 1 Probability Dr. Jingxian Wu wuj@uark.edu OUTLINE 2 Applications Elementary Set Theory Random
4. Probability of an event A for equally likely outcomes:
 University of California, Los Angeles Department of Statistics Statistics 110A Instructor: Nicolas Christou Probability Probability: A measure of the chance that something will occur. 1. Random experiment:
University of California, Los Angeles Department of Statistics Statistics 110A Instructor: Nicolas Christou Probability Probability: A measure of the chance that something will occur. 1. Random experiment:
P [(E and F )] P [F ]
![P [(E and F )] P [F ] P [(E and F )] P [F ]](/thumbs/90/102647023.jpg) CONDITIONAL PROBABILITY AND INDEPENDENCE WORKSHEET MTH 1210 This worksheet supplements our textbook material on the concepts of conditional probability and independence. The exercises at the end of each
CONDITIONAL PROBABILITY AND INDEPENDENCE WORKSHEET MTH 1210 This worksheet supplements our textbook material on the concepts of conditional probability and independence. The exercises at the end of each
STT When trying to evaluate the likelihood of random events we are using following wording.
 Introduction to Chapter 2. Probability. When trying to evaluate the likelihood of random events we are using following wording. Provide your own corresponding examples. Subjective probability. An individual
Introduction to Chapter 2. Probability. When trying to evaluate the likelihood of random events we are using following wording. Provide your own corresponding examples. Subjective probability. An individual
STAT 111 Recitation 1
 STAT 111 Recitation 1 Linjun Zhang January 20, 2017 What s in the recitation This class, and the exam of this class, is a mix of statistical concepts and calculations. We are going to do a little bit of
STAT 111 Recitation 1 Linjun Zhang January 20, 2017 What s in the recitation This class, and the exam of this class, is a mix of statistical concepts and calculations. We are going to do a little bit of
Random Variables. Statistics 110. Summer Copyright c 2006 by Mark E. Irwin
 Random Variables Statistics 110 Summer 2006 Copyright c 2006 by Mark E. Irwin Random Variables A Random Variable (RV) is a response of a random phenomenon which is numeric. Examples: 1. Roll a die twice
Random Variables Statistics 110 Summer 2006 Copyright c 2006 by Mark E. Irwin Random Variables A Random Variable (RV) is a response of a random phenomenon which is numeric. Examples: 1. Roll a die twice
What are the odds? Coin tossing and applications
 What are the odds? Coin tossing and applications Dr. Antal Járai Department of Mathematical Sciences University of Bath 19 July 2011 Please feel free to interrupt with questions at any time. Outline This
What are the odds? Coin tossing and applications Dr. Antal Járai Department of Mathematical Sciences University of Bath 19 July 2011 Please feel free to interrupt with questions at any time. Outline This
Chapter 2.5 Random Variables and Probability The Modern View (cont.)
 Chapter 2.5 Random Variables and Probability The Modern View (cont.) I. Statistical Independence A crucially important idea in probability and statistics is the concept of statistical independence. Suppose
Chapter 2.5 Random Variables and Probability The Modern View (cont.) I. Statistical Independence A crucially important idea in probability and statistics is the concept of statistical independence. Suppose
