A New Class of Generalized Modified Weibull Distribution with Applications
|
|
|
- Erika Montgomery
- 5 years ago
- Views:
Transcription
1 Georga Southern Unversty Dgtal Southern Mathematcal Scences Faculty Publcatons Mathematcal Scences, Department of A New Class of Generalzed Modfed Webull Dstrbuton wth Applcatons Broderck O. Oluyede Georga Southern Unversty, boluyede@georgasouthern.edu Shujao Huang Georga Southern Unversty Tantan Yang Georga Southern Unversty Follow ths and addtonal works at: Part of the Mathematcs Commons Recommended Ctaton Oluyede, Broderck O., Shujao Huang, Tantan Yang "A New Class of Generalzed Modfed Webull Dstrbuton wth Applcatons." Austran Journal of Statstcs, 44 (3): do: /ajs.v Ths artcle s brought to you for free and open access by the Mathematcal Scences, Department of at Dgtal Commons@Georga Southern. It has been accepted for ncluson n Mathematcal Scences Faculty Publcatons by an authorzed admnstrator of Dgtal Commons@Georga Southern. For more nformaton, please contact dgtalcommons@georgasouthern.edu.
2 Austran Journal of Statstcs October 215, Volume 44, AJS do: /ajs.v A New Class of Generalzed Modfed Webull Dstrbuton wth Applcatons Broderck O. Oluyede Georga Southern Unversty Shujao Huang Georga Southern Unversty Tantan Yang Georga Southern Unversty Abstract A new fve parameter gamma-generalzed modfed Webull (GGMW) dstrbuton whch ncludes exponental, Raylegh, Webull, modfed Webull, gamma-modfed Webull, gamma-modfed Raylegh, gamma-modfed exponental, gamma-webull, gamma-raylegh, gamma-lnear falure rate and gamma-exponental dstrbutons as specal cases s proposed and studed. Some mathematcal propertes of the new class of dstrbutons ncludng hazard functon, quantle functon, moments, dstrbuton of the order statstcs and Rény entropy are presented. Maxmum lkelhood estmaton technque s used to estmate the model parameters and applcatons to real datasets n order to llustrate the usefulness of the proposed class of models are presented. Keywords: Gamma dstrbuton, Modfed Webull dstrbuton, Maxmum lkelhood estmaton. 1. Introducton Webull dstrbuton has been wdely used for modelng data n a wde varety of areas ncludng relablty, engneerng, stochastc processes, survval analyss and renewal theory. In ths paper, we present and study the mathematcal propertes of the gamma-generalzed modfed Webull dstrbuton. Ths class of dstrbutons s flexble n accommodatng all forms of hazard rate functons and contans several well known and new sub-models such as Webull, Raylegh, exponental, modfed Webull, gamma-modfed Webull, gamma-modfed exponental, gamma-webull, gamma-raylegh, gamma-lnear falure rate, gamma-extreme value, gamma-addtve exponental and gamma-exponental dstrbutons. There are several extensons of the Webull dstrbuton and ts sub-models ncludng the exponentated Webull (Mudholkar, Srvastava, and Kolla 1996), whch s a specal case of the beta Webull dstrbuton proposed by (Lee, Famoye, and Olumolade 27), generalzed Raylegh (Kundu and Rakab 25), exponentated exponental (Gupta and Kundu 1999), (Gupta and Kundu 21), modfed Webull (Mudholkar, Srvastava, and Fremer 1995), exponentated modfed Webull (Sarhan and Zandn 29), and a host of other dstrbutons, some of whch are presented n secton 2 of ths paper. Addtonal generalzatons of Webull dstrbuton nclude (Famoye, Lee, and Olumolade 25) where the authors dscussed and presented results on the beta-webull dstrbuton. (Nadarajah 25) presented results on the modfed Webull
3 46 A New Class of Generalzed Modfed Webull Dstrbuton wth Applcatons dstrbuton. A host of researchers have also developed several parameter Webull, modfed Webull and flexble Webull dstrbutons over the years. The two parameter Webull extensons nclude (Bebbngton, La, and Ztks 27), (Zhang and Xe 211). The three parameter Webull extensons nclude (Marshall and Olkn 1997), (Xe, Tang, and Goh 22), (Nadarajah and Kotz 25). Some of these extensons enable the accommodaton of bathtub shape hazard rate functon. (Carrasco, Ortega, and Cordero 28) generalzed the modfed Webull dstrbuton of (La, Moore, and Xe 1998) to obtan the exponentated modfed Webull dstrbuton. The four parameter generalzatons nclude the addtve Webull dstrbuton of (Xe and La 1995), modfed Webull (Sarhan and Zandn 29), beta-webull proposed by (Famoye et al. 25) and Kumaraswamy Webull by (Cordero, Ortega, and Nadarajah 21). The fve parameter modfed Webull dstrbuton nclude those ntroduced by (Phan 1987), beta modfed Webull by (Slva, Ortega, and Cordero 21) and (Nadarajah, Cordero, and Ortega 211). Addtonal results on the generalzaton of the Webull dstrbuton nclude work by (Sngha, Jan, and Kumar 212), as well as (Almalk and Yuan 213) where results on a new modfed Webull dstrbuton was presented. (Barlow and Campo 1975) dscussed total tme on test processes wth applcaton to falure data analyss. (Choudhury 25) presented moments of the exponentated Webull dstrbuton. The exponentated Webull dstrbuton was also studed by (Nassar and Essa 23). (Haupt and Schabe 1992) presented a model for bathtub shaped falure rate functon. (Hjorth 198) studed a relablty functon wth ncreasng, decreasng and bathtub shaped falure rate functons, and (Rajarsh and Rajarsh 1988) gave a comprehensve revew of bathtub shaped dstrbutons. For any contnuous baselne cdf F (x), and x R, (Zografos and Balakrshnan 29) defned the dstrbuton (when ψ 1 n equaton (1)) wth pdf g(x) and cdf G(x) (for δ > ) as follows: 1 g(x) ψ δ [ log(f (x))]δ 1 (1 F (x)) 1/ψ 1 f(x), (1) and G(x) 1 ψ δ log(f (x)) t δ 1 e t/ψ dt γ(δ, ψ 1 log(f (x))), (2) respectvely, where g(x) dg(x)/dx, t δ 1 e t dt s the gamma functon, and γ(z, δ) z tδ 1 e t dt s the ncomplete gamma functon. The correspondng hazard rate functon (hrf) s h G (x) [ log(1 F (x))]δ 1 f(x)(1 F (x)) 1/ψ 1 ψ δ ( γ( ψ 1. (3) log(1 F (x)), δ)) When ψ 1, ths dstrbuton s referred to as the ZB-G famly of dstrbutons. Also, (when ψ 1), (Rstć and Balakrshnan 211) proposed an alternatve gamma-generator defned by the cdf and pdf and G 2 (x) 1 g 2 (x) 1 ψ δ log F (x) t δ 1 e t/ψ dt, x R, δ >, (4) 1 ψ δ [ log(f (x))]δ 1 (F (x)) 1/ψ 1 f(x), (5) respectvely. Note that f ψ 1 and δ n + 1, n equatons (1) and (2), we obtan the cdf and pdf of the upper record values U gven by G U (u) 1 n! log(1 F (u)) y n e y dy, (6) and g U (u) f(u)[ log(1 F (u))] n /n!. (7)
4 Austran Journal of Statstcs 47 Smlarly, from equatons (4) and (5), the pdf of the lower record values T s gven by g L (t) f(t)[ log(f (t))] n /n!. (8) In ths paper, we wll consder and present a generalzaton of the generalzed modfed Webull dstrbuton va the famly of dstrbutons gven n equaton (5). (Zografos and Balakrshnan 29) motvated the ZB-G model as follows. Let X (1), X (2),..., X (n) be upper record values from a sequence of ndependent and dentcally dstrbuted (..d.) random varables from a populaton wth pdf f(x). Then, the pdf of the n th upper record value s gven by equaton (1) when ψ 1. A logarthmc transformaton of the parent dstrbuton F transforms the random varable X wth densty (1) to a gamma dstrbuton. That s, f X has the densty (1), then the random varable Y log[1 F (X)] has a gamma dstrbuton GAM(δ; 1) wth densty k(y; δ) 1 yδ 1 e y, y >. The opposte s also true, f Y has a gamma GAM(δ; 1) dstrbuton, then the random varable X G 1 (1 e Y ) has a ZB-G dstrbuton. In addton to the motvatons provded by (Zografos and Balakrshnan 29), we are nterested n the generalzaton of the generalzed modfed Webull dstrbuton va the gamma-generator and establshng the relatonshp between weghted dstrbutons and equatons (1) and (5), respectvely. Weghted dstrbutons apples to a varety of areas and provdes an approach to dealng wth model specfcaton and data nterpretaton problems. It adjusts the probabltes of actual occurrence of events to arrve at a specfcaton of the probabltes when those events are recorded. (Fsher 1934) ntroduced the concept of weghted dstrbuton, n order to study the effect of ascertanment upon estmaton of frequences. (Patl and Rao 1978) used weghted dstrbuton as stochastc models n the study of harvestng and predaton. (Rao 1965) unfed concept of weghted dstrbuton and use t to dentfy varous samplng stuatons. The usefulness and applcatons of weghted dstrbuton to based samples n varous areas ncludng medcne, ecology, relablty, and branchng processes can also be seen n (Nanda and Jan 1999), (Gupta and Keatng 1985), (Oluyede 1999) and n references theren. Let Y be a non-negatve random varable wth ts natural pdf f(y; θ), where θ s a vector of parameters, then the pdf of the weghted random varable Y w s gven by: f w w(y, β)f(y; θ) (y; θ, β), (9) ω where the weght functon w(y, β) s a non-negatve functon, that may depend on the vector of parameters β, and < ω E(w(Y, β)) < s a normalzng constant. In general, consder the weght functon w(y) defned as follows: w(y) y k e ly F (y)f j (y). (1) Settng k ; k j ; l j ; k l ; 1; j n ; k l and k l j n ths weght functon, one at a tme, mples probablty weghted moments, moment-generatng functons, moments, order statstcs, proportonal hazards and proportonal reversed hazards, respectvely, where F (y) P (Y y) and F (y) 1 F (y). If w(y) y, then Y Y w s called the sze-based verson of Y. (Rstć and Balakrshnan 211) provded motvatons for the famly of dstrbutons gven n equaton (4) when ψ 1, that s for n N, equaton (4) s the pdf of the n th lower record value of a sequence of..d. varables from a populaton wth densty f(x). (Rstć and Balakrshnan 211) used the exponentated exponental (EE) dstrbuton wth cdf F (x) (1 e βx ) α, where α > and β >, to obtaned and study the gamma-exponentated exponental (GEE) model. See references theren for addtonal results on the GEE model. In ths note, we obtan a natural extenson of the generalzed modfed Webull dstrbuton, whch we refer to as gamma-generalzed modfed Webull (GGMW) dstrbuton. In secton 2, some basc results, the gamma-generalzed modfed Webull (GGMW) dstrbuton, seres expanson and ts sub-models, quantle functon, hazard and reverse hazard
5 48 A New Class of Generalzed Modfed Webull Dstrbuton wth Applcatons functons are presented. Moments and moment generatng functon are gven n secton 3. Secton 4 contans some addtonal useful results on the dstrbuton of order statstcs and Rény entropy. In secton 5, results on the estmaton of the parameters of the GGMW dstrbuton va the method of maxmum lkelhood are presented. Applcatons are gven n secton 6, and concludng remarks n secton GGMW dstrbuton, seres expanson and sub-models In ths secton, the GGMW dstrbuton and some of ts sub-models are presented. Frst consder the generalzed modfed Webull (GMW) dstrbuton (Sarhan and Zandn 29) gven by F GMW (x, α, β, θ, λ) 1 exp( αx βx θ e λx ), x, α, β, θ, λ. (11) We note that n (Sarhan and Zandn 29) paper, the parameter λ was taken to be zero. The parameters α and β control the scale of the dstrbuton, θ controls the shape, whereas λ can be consdered to be an acceleratng factor n the mperfecton tme and a factor of fraglty n the survval of the ndvdual as tme ncreases. By nsertng the GMW dstrbuton n equaton (4), the survval functon G GGMW (x) 1 G GGMW (x) of the GGMW dstrbuton s obtaned as follows: G GGMW (x) 1 ψ δ log(1 e αx βx θ e λx ) t δ 1 e t/ψ dt γ( ψ 1 log(1 e αx βxθ e λx ), δ), (12) where x >, α, β, θ, λ, δ >, ψ >, and γ(x, δ) x tδ 1 e t dt s the lower ncomplete gamma functon. The correspondng pdf s gven by g GGMW (x) 1 ψ δ [ log(1 e αx βxθ e λx )] δ 1 (α + βx θ 1 e λx [θ + λx])e αx βxθ e λx [1 e αx βxθ e λx ] (1/ψ) 1. (13) If F (x) [1 e αxη βx θ e λx ] φ, then the correspondng generalzed gamma-generalzed modfed Webull pdf s gven by g GGMW (x) φ ψ δ [ log(1 e αxη βx θ e λx ) φ ] δ 1 (αηx η 1 + βx θ 1 e λx [θ + λx])e αxη βx θ e λx [1 e αxη βx θ e λx ] φ+(1/ψ) 2. (14) In ths note, we take φ η ψ 1. The pdf n equaton (14) s now gven by g GGMW (x) 1 [ log(1 e αx βxθ e λx )] δ 1 (α + βx θ 1 e λx [θ + λx])e αx βxθ e λx. (15) If a random varable X has the GGMW densty gven n equaton (15), we wrte X GGMW (α, β, θ, λ, δ). The parameter δ s an extra shape parameter n the GGMW dstrbuton. Let y e αx βxθ e λx, < y < 1, α, β, θ, δ >, and λ, then usng the seres representaton log(1 y) y +1 +1, we have [ ] δ 1 [ log(1 y) y δ 1 m ( δ 1 m ) ( y m y s ) m ]. s + 2 s
6 Austran Journal of Statstcs 49 Applyng the result on power seres rased to a postve nteger, wth a s (s + 2) 1, that s, ( ) m a s y s s b s,m y s, (16) where b s,m (sa ) 1 s l1 [m(l + 1) s]a lb s l,m, and b,m a m, (Gradshteyn and Ryzhk 2), the GGMW pdf can be wrtten as g GGMW (x) 1 1 m s m s ( δ 1 m ( δ 1 m s ) b s,m y m+s+δ (α + βx θ 1 e λx [θ + λx]) ) b s,m e α(m+s+δ)x β(m+s+δ)xθ e λx m + s + δ m + s + δ (α + βxθ 1 e λx [θ + λx]) ( ) δ 1 b s,m m (m + s + δ) g (x; α(m + s + δ), β(m + s + δ), θ, λ), m s where g (x; α(m + s + δ), β(m + s + δ), θ, λ) s the generalzed modfed Webull pdf wth parameters α(m + s + δ) >, β(m + s + δ) >, θ >, and λ. Let C {(m, s) Z 2 +}, then the weghts n the GGMW pdf above are ( ) δ 1 b s,m w ν m (m + s + δ), and g GGMW (x) ν C w ν g (x; α(m + s + δ), β(m + s + δ), θ, λ), (17) for x >, δ >, α(m + s + δ), β(m + s + δ), θ >, and λ. It follows therefore that the GGMW densty s lnear combnaton of the generalzed modfed Webull (GMW) denstes. The statstcal and mathematcal propertes of the GGMW dstrbuton can be readly obtaned from those of the generalzed modfed Webull dstrbuton. For the convergence of equatons (16) and (17), as well as elsewhere n ths paper, note that for δ >, so that [ 1 + y [ log(1 y)] δ 1 k s convergent f and only f < y k ] δ 1 k + 2 [ ( y 1 + y ( δ 1 k k s y s )] δ 1 s + 2 ) y k ( s y s ) k s + 2 ( y k y k k k+2) < 1 y (, 1), snce < y e αx βxθ e λx < 1, for x >, α, β, θ >, and λ. Now, y y k k k+2 log(1 y) y 1, so we must have < log(1 y) y 1 < 1. Ths leads to 1 y > exp( 2y), and on the other hand exp( y) ( 1) k y k k k! > 1 y. Thus, we have the system of nequaltes 1 y > exp( 2y) and exp( y) > 1 y, whch s satsfed y (,.7968). The mplcaton here s that the nequalty ( < y k y k k k+2) < 1 s not vald for all values of < y e αx βxθ e λx < 1, and equatons (16) and (17), and elsewhere n ths paper are convergent only y (,.7968). The seres n equatons (16) and (17), and elsewhere n ths paper are not vald for all values of <
7 5 A New Class of Generalzed Modfed Webull Dstrbuton wth Applcatons Fgure 1: Graphs of GGMW pdf y e αx βxθ e λx < 1, but are convergent y (,.7968), and not vald (convergent) for y > Note that n general, g GGMW (x) s a weghted pdf wth the weght functon that s, w(x) [ log(1 F (x))] δ 1 [1 F (x)] 1 ψ 1, (18) g GGMW (x) [ log(1 F (x))]δ 1 [1 F (x)] 1 ψ 1 ψ δ f(x) w(x)f(x) E F (w(x)), (19) where < E F {[ log(1 F (x))] δ 1 [1 F (x)] 1 ψ 1 } ψ δ <, s the normalzng constant. Graphs of the pdf of GGMW dstrbuton are gven n the Fgure 1 for selected values of the parameters. The plots show that the GGMW pdf can be decreasng or rght skewed among several other possble shapes as seen n Fgure 1. The dstrbuton has postve asymmetry Quantle functon The quantle functon of the GGMW dstrbuton s gven by the soluton of the nonlnear equaton γ( log[1 e αx βxθ e λx ], δ) 1 u. (2) That s, log[1 e αx βxθ e λx ] γ 1 ((1 u), δ) and αx + βx θ e λx log(1 exp( γ 1 ((1 u), δ))). (21) We can smulate from the GGMW by solvng the nonlnear equaton αx + βx θ e λx + log(1 exp( γ 1 ((1 u), δ))), (22) where u s a unformly dstrbuted random varable on the nterval [, 1]. The nverse ncomplete gamma functon can be mplemented by usng numercal methods. Consequently, random numbers can be generated based the equaton above. Table 1 lsts the quantle for selected parameter values of the GGMW dstrbuton.
8 Austran Journal of Statstcs 51 Table 1: GGMW quantle for selected values (α, β, θ, λ, δ) u (1,1,1,1,1) (2,1,2,1,1) (6,4,3,6,1) (5,3,3,5,6) (.1,.3,.4,.2,.3) Some sub-models of the GGMW dstrbuton The proposed model has several new and well known sub-models. Some of the sub-models of the GGMW dstrbuton are lsted n Table 2. They nclude the gamma-generalzed modfed Raylegh (GGMR), gamma-generalzed modfed exponental (GGME), gamma-modfed Webull (GMW), gamma-modfed exponental (GME), gamma-addtve exponental (GAE), gamma-extreme value (GEV), gamma-webull (GW), modfed Webull (MW), Sardn and Zandn modfed Webull (S-ZMW), modfed Raylegh (MR), modfed exponental (ME), gamma-lnear falure rate (GLFR), lnear falure rate (LFR), extreme value (EV), Webull (W) and exponental (E) dstrbutons Hazard and reverse hazard functons In ths secton, we present the hazard and reverse hazard functons, as well as graphs of the hazard functon for selected values of the model parameters. Let X be a contnuous random varable wth dstrbuton functon G, and probablty densty functon (pdf) g, then the hazard functon, reverse hazard functon and mean resdual lfe functons are gven by h G (x) g(x)/g(x), τ G (x) g(x)/g(x), and δ G (x) x G(u)du/G(x), respectvely. The functons λ G (x), δ G (x), and G(x) are equvalent. (Shaked and Shanthkumar 1994). The hazard and reverse hazard functons are of the GGMW dstrbuton are gven by and h G (x) { log(1 e αx βxθ e λx )} δ 1 e αx βxθ e λx (α + βx θ 1 e λx [θ + λx]), (23) γ( log(1 e αx βxθ e λx ), δ) τ G (x) { log(1 e αx βxθ e λx )} δ 1 e αx βxθ e λx (α + βx θ 1 e λx [θ + λx]), (24) γ( log(1 e αx βxθ e λx ), δ) respectvely. Plots of the hazard rate functon for dfferent combnatons of the parameter values are gven n Fgure 2. The plot shows varous shapes ncludng monotoncally ncreasng, monotoncally ncreasng and bathtub shapes for fve combnatons of the values of the parameters. Ths flexblty makes the GGMW hazard rate functon sutable for both monotonc and non-monotonc emprcal hazard behavors that are lkely to be encountered n real lfe stuatons. 3. Moments and moment generatng functon In ths secton, we obtan moments and moment generatng functon of the GGMW dstrbuton. Let X GGMW (α, β, θ, λ, δ), and Y GMW (α, β, θ, λ). Note that the r th moment of the random varable Y s obtaned as follows. By Taylor seres expanson of the functons
9 52 A New Class of Generalzed Modfed Webull Dstrbuton wth Applcatons Table 2: Sub-models of the gamma generalzed modfed Webull dstrbuton Model α β θ λ δ G(x) Reference GGMR GGME GMW GME GAE GEV γ( log[1 e αx βx2 e λx ],δ) γ( log[1 e αx βxeλx ],δ) γ( log[1 e βxθ e λx ],δ) γ( log[1 e βxeλx ],δ) γ( log[1 e αx βx ],δ) γ( log[1 e eλx ],δ) GW γ( log[1 e βxθ ],δ) Pnho, Cordero, and Nobre (212) MW e βxθ e λx La, Xe, and Murthy (23) S-ZMW e αx βxθ e λx Sarhan and Zandn (29) LFR e αx βx2 Ban (1974) EV e eλx Ban (1974) Webull e βxθ Webull (1951) Exponental e αx Ban (1974) New New New New New New Fgure 2: Graphs of GGMW hazard functon
10 Austran Journal of Statstcs 53 e βxθ e λx and e kλx, we have: E(Y r ) k,n k,n y r d(1 e αy βxθ e λy ) ry r 1 e αy βyθ e λy dy r( β) n (nλ) k k!n! ry r+nθ+k 1 e αy dy r( β) n (nλ) k α (r+θn+k) Γ (r + θn + k). (25) k!n! Consequently, that the r th raw moment of GGMW dstrbuton s gven by: µ r E(X r ) ν C w ν E(Y r ), where Y GMW (α(m + s + δ), β(m + s + δ), θ, λ). Note that, snce r tr r! xr g GGMW (x) converges and each term s ntegrable for all t close to zero, say (for t < 1), the moment generatng functon (MGF) of the GGMW dstrbuton s gven by: M X (t) ν C ν C j k,n,j w ν t j j! E(Y j ) w ν t j j( β(k + s + δ)) n (nλ) k Γ (j + θn + k), (26) k!n!j!(α(k + s + δ)) (j+θn+k) where Γ (a) b a t a 1 e t dt s the gamma functon, and r 1, 2,... Table 3 lsts the frst sx moments for selected parameter values of GGMW dstrbuton, where V arance E(Y 2 ) E(Y ) 2, Skewness E(Y 3 ) 3E(Y )σ 2 E(Y ) 3, and Kurtoss E(Y 4 ) 3. σ 3 σ 4 Theorem 3.1. Proof: E{[ log(1 F (X))] r [(1 F (X)) s ]} ψr+δ Γ (r + δ) (sψ + 1) δ ψ δ. (27) E{[ log(1 F (X))] r [(1 F (X)) s ]} If s n equaton (28), then we have f(x) ψ δ [ log(1 F (x))]r+δ 1 [1 F (x)] s+(1/ψ) 1 dx ψ r+δ Γ (r + δ) (sψ + 1) δ ψ δ. (28) E[ log(1 F (X)) r ] ψr+δ Γ (r + δ) ψ δ. (29) Let ψ s + 1 ψ, then wth r n equaton (28), we obtan E[(1 F (X)) s ] ( ) 1 δ (ψ ) δ f(x) ψψ [ log(1 F (x))] δ 1 [1 F (x)] ψ 1 dx [sψ + 1] δ. (3)
11 54 A New Class of Generalzed Modfed Webull Dstrbuton wth Applcatons Table 3: GGMW moments for selected values (α, β, θ, λ, δ) Moments (1,2,.5,.5,1) (1,2,.5,1.5,2) (1,4,2,1,6) (1,1.5,2,1,2.5) (2,.9,1,1,3) E(Y ) E(Y 2 ) E(Y 3 ) E(Y 4 ) E(Y 5 ) E(Y 6 ) Varance Skewness Kurtoss Order statstcs and Rény entropy Order statstcs play an mportant role n probablty and statstcs. The concept of entropy plays a vtal role n nformaton theory. The entropy of a random varable s defned n terms of ts probablty dstrbuton and can be shown to be a good measure of randomness or uncertanty. In ths secton, we present Rény entropy and the dstrbuton of the order statstcs for the GGMW dstrbuton Rény entropy Rény entropy s an extenson of Shannon entropy. Rény entropy s defned to be I R (v) 1 ( ) 1 v log [g GGMW (x; α, β, θ, λ, δ)] v dx, v 1, v >. (31) Rény entropy tends to Shannon entropy as v 1. Note that ( ) 1 v g v (x)dx ((α + βx θ 1 e λx [θ + λx])e αx βxθ e λx ) v GGMW [ log(1 e αx βxθ e λx )] v(δ 1) dx. (32) Let < y e αx βxθ e λx < Note that ((α + βx θ 1 e λx [θ + λx])) v v j v ( ) v α v j β j x jθ j j j j r n ( v j )( j r n ( ) j (jλx) n r n! j θ j r (λx) r r )α v j β j θ j r λ r (jλ)n x n+r+jθ j. n! Now, for < e vβxθ e λx < 1, v >, and applyng Taylor seres expanson, we have e vβxθ e λx ( 1) l (vβ) l (lλ) w x lθ+w, (33) l!w! l w
12 Austran Journal of Statstcs 55 so that, g v (x) [] v v j j r n,l,w,m,s ( 1) l ( v j )( )( ) j δ(v 1) r m α v j β j θ j r λ r (jλ)n (vβ) l (lλ) w b s,m n! l! w! x n+r+jθ j+lθ+w e (m+s+vδ v)αx (m+s+vδ v)βxθ e λx e vαx v j ( )( v j [] v ( 1) l+k j r m j r n,l,w,m,s,k, α v j β j+l θ j r λ r+n+w (j)n (v) l (l) w n!l!w! )( δ(v 1) ) b s,m (m + s + vδ v)k β k (kλ) x n+r+jθ j+lθ+w+kθ+ e (m+s+vδ)αx. k!! Usng the fact that t a 1 e t dt Γ (a) b, we have a g v GGMW (x)dx [] v v j j r n,l,w,m,s,k, ( 1) l+k ( v j )( j r )( δ(v 1) α v j β j+l+ θ j r λ r+n+w+ (j)n (v) l (l) w k (m + s + vδ v) k n!l!w!k!! Γ (n + r + w + + θ(j + l + k) j + 1) (m + s + vδ) n+r+w++θ(j+l+k) j+1, for v >, v 1. Consequently, Rény entropy for the GGMW dstrbuton s gven by I R (v) [ 1 v 1 v log [] v j j r n,l,w,m,s,k, ( 1) l+k ( v j )( j r m )( δ(v 1) α v j β j+l+ θ j r λ r+n+w+ (j)n (v) l (l) w k (m + s + vδ v) k n!l!w!k!! ] Γ (n + r + w + + θ(j + l + k) j + 1) (m + s + vδ) n+r+w++θ(j+l+k) j+1, for v >, v 1. m ) b s,m ) b s,m 4.2. Order statstcs In ths secton, the pdf of the th order statstc and the correspondng moments are presented. Let X 1, X 2,..., X n be ndependent and dentcally dstrbuted GGMW random varables. The pdf of of the th order statstc for a random sample of sze n for any gamma G famly wth densty (5) can be expressed as an nfnte weghted sum of gamma G denstes. The pdf of the th order statstc from the GGMW pdf g GGMW (x) s gven by g :n (x) n!g(x) ( 1)!(n )! [G(x)] 1 [1 G(x)] n n!g(x) 1 ( 1 ( 1) j ( 1)!(n )! j j j ) [G(x)] n +j n!g(x) 1 ( )[ ] 1 γ( log(1 e ( 1) j αx βx θ e λx )) n +j. ( 1)!(n )! j where < y e αx βxθ e λx <.7968, x >, α, β, θ, δ >, and λ. Usng the fact that γ(x, δ) ( 1) m x m+δ m (m+δ)m!, and settng c m ( 1) m /((m + δ)m!), we can wrte the pdf of the
13 56 A New Class of Generalzed Modfed Webull Dstrbuton wth Applcatons th order statstc from the GGMW dstrbuton as follows: g :n (x) n!g(x) 1 ( ) 1 ( 1) j ( 1)!(n )! j [] n +j [ log(1 e λx e αx βxθ )] δ(n +j) j [ ( 1) m (log(1 e αx βxθ e λx )) m ] n +j (m + δ)m! m n!g(x) 1 ( ) 1 ( 1) j ( 1)!(n )! j [] n +j [ log(1 e λx e αx βxθ )] δ(n +j) j d m,n +j ( log(1 e αx βxθ e λx )) m, m where d c (n +j), d m,n +j (mc ) 1 m l1 [(n + j)l m + l]c ld m l,n +j. We note that g :n (x) where n!g(x) 1 ( 1)!(n )! j m ( n n![ log(1 e αx βxθ e λx )] δ 1 f(x) 1 ( 1)!(n )! j ) ( 1) j d m,+j 1 [] n +j [ log(1 e αx βxθ e λx )] δ(n +j)+m j m ( n [ log(1 e αx βxθ e λx )] δ(n +j)+m n! 1 ( ) 1 ( 1) j d m,n +j ( 1)!(n )! j [] n +j j m j ) ( 1) j d m,n +j [] n +j Γ (δ(n + j) + m + δ) [ log(1 e αx βxθ e λx )] δ(n +j)+m+δ 1 Γ (δ(n + j) + m + δ) (α + βx θ 1 e λx [θ + λx])e αx βxθ e λx n! 1 ( 1)!(n )! j m ( ) 1 ( 1)j d m,n +j Γ (δ(n + j) + m + δ) [] n +j+1 f GGMW (x), f GGMW (x) j 1 Γ (δ(n + j) + m + δ) [ log(1 e αx βxθ e λx )] δ(n +j)+m+δ 1 (α + βx θ 1 e λx [θ + λx])e αx βxθ e λx (34) s the GGMW pdf wth parameters α, β, θ >, λ, and shape parameter δ δ(n + j) + m + δ >. It follows therefore that the r th moment s gven by E(X j :n ) ν C 1 j m,k,n r( β) n (k + s + δ )(nλ) k w ν l,j,m k!n![α(k + s + δ ) r+nθ+k Γ (r + nθ + k), ] where l,j,m n! ( 1)!(n )! ( 1) j d m,n +j Γ (δ(n +j)+m+δ) [] n +j+1, and δ δ(n + j) + m + δ >. We note that these moments are often used n several areas ncludng relablty, survval analyss, bometry, engneerng, nsurance and qualty control for the predcton of future falures tmes from a set of past or prevous falures.
14 Austran Journal of Statstcs Maxmum lkelhood estmaton be the parameter vector. The log- Let X GGMW (α, β, θ, λ, δ) and (α, β, θ, λ, δ) T lkelhood for a sngle observaton x of X s gven by l l( ) (δ 1) log( log(1 e αx βxθ e λx )) + log(α + βx θ 1 e λx [θ + λx]) αx βx θ e λx log(). (35) The frst dervatve of the log-lkelhood functon wth respect to the parameters (α, β, θ, λ, δ) T are gven by l β l α x(δ 1)e αx βxθeλx (1 e αx βxθ e λx ) log(1 e αx βxθ e λx ) + 1 α + βx θ 1 e λx x, (36) [θ + λx] x θ e λx (δ 1)e αx βxθeλx (1 e αx βxθ e λx ) log(1 e αx βxθ e λx ) + xθ 1 e λx (θ + λx) α + βx θ 1 e λx [θ + λx] xθ e λx, (37) l θ (δ 1)x θ log(x)βe λx e αx βxθ e λx (1 e αx βxθ e λx ) log(1 e αx βxθ e λx ) + βxθ 1 e λx [(θ + λx) log(x) + 1] α + βx θ 1 e λx [θ + λx] βx θ e λx log(x), (38) l λ (δ 1)x θ+1 βe λx e αx βxθeλx (1 e αx βxθ e λx ) log(1 e αx βxθ e λx ) + βxθ e λx (θ + λx + 1) α + βx θ 1 e λx [θ + λx] βxθ+1 e λx, (39) and l δ log( log(1 e αx βxθ e λx )) Γ (δ). (4) The total log-lkelhood functon based on a random sample of n observatons: x 1, x 2,..., x n drawn from the GGMW dstrbuton s gven by l n l( ) n l ( ), where l ( ), 1, 2,..., n s gven by equaton (35). The equatons obtaned by settng the above partal dervatves to zero are not n closed form and the values of the parameters α, β, θ, λ, δ must be found by usng teratve methods. The maxmum lkelhood estmates of the parameters, denoted by ˆ s obtaned by solvng the nonlnear equatons ( l α, l β, l θ, l λ, l δ )T. It s convenent to apply or use nonlnear optmzaton algorthm such as quas-newton algorthm to numercally maxmze the log-lkelhood functon. We maxmze the lkelhood functon usng NLmxed n SAS as well as the functon nlm n R (The R Development Core Team (211)). These functons were appled and executed for wde range of ntal values. Ths process often results or lead to more than one maxmum, however, n these cases, we take the MLEs correspondng to the largest value of the maxma. In a few cases, no maxmum was dentfed for the selected ntal values. In these cases, a new ntal value was tred n order to obtan a maxmum. The ssues of exstence and unqueness of the MLEs are theoretcal nterest and has been studed by several authors for dfferent dstrbutons ncludng Seregn (21), Santos Slva and Tenreyro (21), Zhou (29), and Xa, M, and Zhou (29). At ths pont we are not able to address the theoretcal aspects (exstence, unqueness) of the MLE of the parameters of the GGMW dstrbuton. Note that for the fve parameters of the GGMW dstrbuton, all second order partal dervatves of the log-lkelhood functon ext, and are gven n appendx A. The Fsher nformaton matrx s gven by I( ) [I θ,θ j ] 5X5 E( 2 l θ θ j ),, j 1, 2, 3, 4, 5, can be numercally
15 58 A New Class of Generalzed Modfed Webull Dstrbuton wth Applcatons obtaned by MATHLAB, R or MAPLE software. The total Fsher nformaton matrx ni( ) can be approxmated by J n ( ˆ ) [ 2 l θ θ j ˆ ],, j 1, 2, 3, 4, 5. (41) 5X5 For a gven set of observatons, the matrx gven n equaton (41) s obtaned after the convergence of the Newton-Raphson procedure n MATHLAB or R software. Elements of the observed nformaton matrx are gven n the appendx Asymptotc confdence ntervals In ths secton, we present the asymptotc confdence ntervals for the parameters of the GGMW dstrbuton. The expectatons n the Fsher Informaton Matrx (FIM) can be obtaned numercally. Let ˆ (ˆα, ˆβ, ˆθ, ˆλ, ˆδ) be the maxmum lkelhood estmate of (α, β, θ, λ, δ). Under the usual regularty condtons and that the parameters are n the nteror of the parameter space, but not on the boundary, (Ferguson 1996) we have: n( ˆ d ) N 5 (, I 1 ( )), where I( ) s the expected Fsher nformaton matrx. The asymptotc behavor s stll vald f I( ) s replaced by the observed nformaton matrx evaluated at ˆ, that s J( ˆ ). The multvarate normal dstrbuton N 5 (, J( ˆ ) 1 ), where the mean vector (,,,, ) T, can be used to construct confdence ntervals and confdence regons for the ndvdual model parameters and for the survval and hazard rate functons. That s, the approxmate 1(1 η)% two-sded confdence ntervals for α, β, θ λ, and δ are gven by: and δ ± Z η 2 α ± Z η Iαα( 1 ˆ ), 2 β ± Z η I 1 2 ββ ( ˆ ), θ ± Z η I 1 2 θθ ( ˆ ), λ ± Z η I 1 2 λλ ( ˆ ), I 1 δδ ( ˆ ), respectvely, where I 1 αα( ˆ ), I 1 ββ ( ˆ ), I 1 θθ ( ˆ ), I 1 λλ ( ˆ ) and I 1 the dagonal elements of In 1 dstrbuton. ( ˆ ), and Z η 2 s the upper η 2 δδ ( ˆ ) are th percentle of a standard normal The maxmum lkelhood estmates (MLEs) of the GGMW parameters α, β, θ, λ, and δ are computed by maxmzng the objectve functon va the subroutne NLmxed n SAS and the functon nlm n R. The estmated values of the parameters (standard error n parenthess), -2log-lkelhood statstc, Akake Informaton Crteron, AIC 2p 2 ln(l), Bayesan Informaton Crteron, BIC p ln(n) 2 ln(l), and Consstent Akake Informaton Crteron, AICC AIC + 2 p(p+1) n p 1, where L L( ˆ ) s the value of the lkelhood functon evaluated at the parameter estmates, n s the number of observatons, and p s the number of estmated parameters are presented. In order to compare the models, we use the crtera stated above. Note that for the value of the log-lkelhood functon at ts maxmum (l n ), larger value s good and preferred, and for AIC, AICC and BIC, smaller values are preferred. GGMW dstrbuton s ftted to the data sets and these fts are compared to the fts of the GGME, GGMR, GMW, GW, beta exponentated Webull (BEW) and beta Webull (BW) dstrbutons. We can use the lkelhood rato (LR) test to compare the ft of the GGMW dstrbuton wth ts sub-models for a gven data set. For example, to test λ, δ 1, the LR statstc s ω 2[ln(L(ˆα, ˆβ, ˆθ, ˆλ, ˆδ)) ln(l( α, β, θ,, 1))], where ˆα, ˆβ, ˆλ, ˆθ and ˆδ, are the unrestrcted estmates, and α, β, and θ are the restrcted estmates. The LR test rejects the null hypothess f ω > χ 2, where ɛ χ2 denote the upper 1ɛ% pont of the ɛ χ2 dstrbuton wth 2 degrees of freedom. 6. Applcatons In ths secton, we present examples to llustrate the flexblty and applcablty of the GGMW dstrbuton and ts sub-models for data modelng. The GGMW dstrbuton s also compared
16 Austran Journal of Statstcs 59 Table 4: Estmaton of GGMW model for watng tmes data Estmates Statstcs Dstrbuton α β θ λ δ -2LogLkelhood AIC AICC BIC SS GGMW (.1679) (.2513) (.1642) (.178) (.1386) GGME (.292) (.2142) (.6622) (.2897) GMW (.7322) (.162) (.5437) (.1887) GME (.9978) (.6636) (.3738) GAE (.9663) (.9657) (.141) GEV (.96) (.2987) GW (.7656) (.8978) (.236) BW k λ a b (.18) (.4812) (.5264) (.1871) BEW k λ α a b (.2224) (1.4164) (1.3948) (.7837) (.2345) wth the non-nested beta exponentated Webull (BEW), and beta Webull (BW) dstrbutons. The pdf of the BEW dstrbuton (Cordero, Gomes, da Slva, and Ortega 213) s gven by g(x) αkλk B(a, b) xk 1 e (λx)k (1 e (λx)k ) aα 1 [1 (1 e (λx)k ) α ] b 1, x >. (42) When α 1, we have the BW dstrbuton. The frst data set s watng tmes (n mnutes) of 1 bank customers before servce. See (Ghtany, Ateh, and Nadarajah 28) for addtonal detals. The second data set s falure tmes of a sample of n 3 devces, see (Meeker and Escobar 1998). The thrd data set represent the survval tmes of 121 patents wth breast cancer obtaned from a large hosptal n a perod from 1929 to 1938, (Lee 1992). Estmates of the parameters of GGMW dstrbuton (standard error n parentheses), Akake Informaton Crteron (AIC), Consstent Akake Informaton Crteron (AICC) and Bayesan Informaton Crteron (BIC) are gven n Table 4 for the frst data set, n Table 5 for the second data set and n Table 6 for the thrd data set. The estmated covarance matrx for the GGMW dstrbuton (Watng Tmes Data) s gven by The 95% asymptotc confdence ntervals for the GGMW model (Watng Tmes Data) parameters are: α (.32,.3529), β (.69,.154), θ (1.2915, ), λ (.187,.235), and δ (.1415,.1959), respectvely. The estmated covarance matrx for the GGMW dstrbuton (Meeker Data) s gven by
17 6 A New Class of Generalzed Modfed Webull Dstrbuton wth Applcatons Fgure 3: Graphs for watng tmes data Table 5: Estmaton of GGMW model for meeker data Estmates Statstcs Dstrbuton α β θ λ δ -2LogLkelhood AIC AICC BIC SS GGMW (.392) (.2771) (.893) (.2629) (.123) GGME (.8775) (.2176) (.289) (.1758) GMW (.6536) (.5393) (.585) (.195) GAE (.3377) (.3435) (.4661) GEV (.1629) (.484) GW (.1258) (.672) (2.1364) BW k λ a b (.3331) (.4279) (1.1345) (.938) BEW k λ α a b (.3881) (1.1182) (.2485) (.5873) (.799) Fgure 4: Graphs for meeker data
18 Austran Journal of Statstcs 61 Table 6: Estmaton of GGMW model for breast cancer data Estmates Statstcs Dstrbuton α β θ λ δ -2LogLkelhood AIC AICC BIC SS GGMW (.6267) (.1812) (.8788) (.2297) (.6779) GGME (.1342) (.1374) (.2869) (.1646) GMW (.1335) (.1543) (.2969) (.3898) GME (.1223) (.1698) (.3784) GAE (.257) (.257) (.189) GEV (.181) (.2174) GW (.142) (.6238) (2.2681) BW k λ a b (.495) (.362) (.3752) (.6166) BEW k λ α a b (.741) (.2646) (.2518) (.694) (.6678) Fgure 5: Graphs for breast cancer data
19 62 A New Class of Generalzed Modfed Webull Dstrbuton wth Applcatons The estmated covarance matrx for the GGMW dstrbuton (Breast Cancer Data) s gven by E Plots of the ftted denstes, the hstogram of the data are gven n Fgure 3, Fgure 4 and Fgure 5. For the probablty plot, we plotted G GGMW (x (j) ; ˆα, ˆβ, ˆθ, ˆλ, ˆδ) aganst j.375 n +.25, j 1, 2,, n, where x (j) are the ordered values of the observed data. We also computed a measure of closeness of each plot to the dagonal lne. Ths measure of closeness s gven by the sum of squares SS j1 [ G GGMW (x (j) ; ˆα, ˆβ, ˆθ, ˆλ, ˆδ) ( )] j n +.25 For watng tmes data set, the LR test statstc of the hypothess H : GGME aganst H a : GGMW s ω 2.8. The p-value.94. Therefore, there s no sgnfcant dfference between GGMW and GGME dstrbutons at the 5% level. However, there s a sgnfcant dfference between GGME and GGMW dstrbutons at the 1% level. The LR statstc of the hypothess H : GEV aganst H a : GGMW for watng tmes data s ω 89.4 The p-value <.1, we can conclude that there s a sgnfcance dfference between GGMW and GEV dstrbutons. There s no sgnfcant dfference between the GGMW and GMW dstrbutons. Also, there s no sgnfcant dfference between the GW and GMW dstrbutons. The values of the statstcs AIC, AICC and BIC shows that the sub-model GW s a good ft for ths data. Based on these statstcs, the GW dstrbuton could be chosen as the best model among these dstrbutons. The values of the statstcs are comparable to those of the non-nested BW dstrbuton and those correspondng to the BEW dstrbuton. For Meeker data set, the LR test statstcs of the hypothess H : GGME aganst H a : GGMW s ω The p-value <.1. Therefore, there s sgnfcant dfference between GGMW and GGME dstrbutons. The LR statstc of the hypothess H : GMW aganst H a : GGMW s ω 1.6. The p-value.11, we can conclude that there s a sgnfcance dfference between GGMW and GMW dstrbutons. The values of the statstcs AIC, BIC, and AICC are smaller for the GGMW dstrbuton. The values of these statstcs ponts to the GGMW dstrbuton as the better ft for Meeker data. Also, the values of AIC, BIC and AICC are better for the GMW and GGMW dstrbutons when compared to the non-nested BW and BEW dstrbutons. For breast cancer data set, there s no sgnfcant dfference between GGMW, GGME, GMW, GW and GME dstrbutons based on the correspondng LR tests. The sub-models GME and GW seem to be the best fts for ths data. The values of the statstcs AIC, BIC and AICC are smaller for the GME dstrbuton. The values of SS from the probablty plots are.64 and.527 for the GME and GW dstrbutons, respectvely. The values of these statstcs ponts to and supports the GW as well as the GME dstrbutons as the better fts among the nested dstrbutons. Also, the values of the statstcs: AIC, BIC and AICC are far better for the GMW and GGMW dstrbutons when compared to those of the non-nested BW and BEW dstrbutons. The conclusons based on the LR tests, ftted pdfs, the hstograms of the data, and probablty plots are n agreement wth the statstcs AIC, AICC and BIC for the selected models. The GW dstrbuton provdes a better fts for the watng tmes data, whle the GGMW dstrbuton and GME as well as the GW dstrbutons provdes better fts for the Meeker and Escobar, and breast cancer data, respectvely.
20 Austran Journal of Statstcs Concludng remarks A new class of generalzed modfed Webull dstrbuton called the gamma-generalzed modfed Webull (GGMW) dstrbuton s proposed and studed. The GGMW dstrbuton has several sub-models such as the GGMR, GGME, GAE, GLFR, LFR, GMW, GME, MW, MR, ME, Webull, Ralegh and exponental dstrbutons as specal cases. The densty of ths new class of dstrbutons can be expressed as a lnear combnaton of GMW densty functons. The GGMW dstrbuton possesses hazard functon wth flexble behavor. We also obtan closed form expressons for the moments, dstrbuton of order statstcs and Reny entropy. Maxmum lkelhood estmaton technque was used to estmate the model parameters. Fnally, the GGMW dstrbuton and ts sub-models was ftted to real data sets to llustrate the applcablty and usefulness of ths class of dstrbutons. Acknowledgements The authors would lke to thank the edtor and the referee for carefully readng the paper and for ther valuable comments, whch greatly mproved the presentaton n ths paper. References Almalk SJ, Yuan J (213). A New Modfed Webull Dstrbuton. Relablty Engneerng and System Safety, 111, Ban L (1974). Analyss for the Lnear Falure Rate Lfe Testng Dstrbuton. Technometrcs, 16(4), Barlow R, Campo R (1975). Total Tme on Test Processes and Applcatons to Falure Data Analyss. Socety for Industral and Appled Mathematcs. Bebbngton M, La C, Ztks R (27). A Flexble Webull Extenson. Relablty Engneerng and System Safety, 92(6), Carrasco M, Ortega EM, Cordero G (28). A Generalzed Webull Dstrbuton for Lfetme Modelng. Computatonal Statstcs and Data Analyss, 53(2), Choudhury A (25). A Smple Dervaton of Moments of the Exponentated Webull Dstrbuton. Metrka, 62(1), Cordero G, Gomes A, da Slva C, Ortega M (213). The Beta Exponentated Webull Dstrbuton. Journal of Statstcal Computaton and Smulatons, 38(1), Cordero G, Ortega E, Nadarajah S (21). The Kumaraswamy Webull Dstrbuton wth Applcatons to Falure Data. Journal of Frankln Insttute, 347(8), Famoye F, Lee C, Olumolade O (25). The Beta-Webull Dstrbuton. Journal of Statstcal Theory and Applcatons, pp Ferguson T (1996). A Course n Large Sample Theory. Chapman and Hall. Fsher R (1934). The Effects of Methods of Ascertanment Upon the Estmaton of Frequences. Annals of Human Genetcs, 6(1), Ghtany M, Ateh B, Nadarajah S (28). Lndley Dstrbuton and Its Applcatons. Mathematcs and Computers n Smulatons, 78(4), Gradshteyn I, Ryzhk I (2). Tables of Integrals, Seres and Products. Academc Press. Gupta R, Keatng J (1985). Relaton for Relablty Measures under Length Based Samplng. Scandnavan Journal of Statstcs, 13,
21 64 A New Class of Generalzed Modfed Webull Dstrbuton wth Applcatons Gupta R, Kundu D (1999). Generalzed Exponental Dstrbutons. Australan and New Zealand Journal of Statstcs, 43, Gupta R, Kundu D (21). Exponentated Exponental Dstrbuton: An Alternatve to Gamma and Webull Dstrbutons. Bometrcal Journal, 43, Haupt E, Schabe H (1992). A New Model for A Lfetme Dstrbuton wth Bathtub Shaped Falure Rate. Mcroelectroncs and Relablty, 32, Hjorth U (198). A Relablty Dstrbuton wth Increasng, Decreasng, Constant and Bathtub Falure Rates. Technometrcs, 22, Kundu D, Rakab M (25). Generalzed Raylegh Dstrbuton: Dfferent Methods of Estmaton. Computatonal Statstcs and Data Analyss, 49, La C, Moore T, Xe M (1998). The Beta Integrated Model. Proceedngs Internatonal Workshop on Relablty Modelng and Analyss-From Theory to Practce, pp La C, Xe M, Murthy D (23). A Modfed Webull Dstrbuton. IEEE Transactons on Relablty, 52, Lee C, Famoye F, Olumolade O (27). Beta Webull Dstrbuton, Propertes and Applcatons to Censored Data. Journal of Mod. Appl. Statst. Meth, 6, Lee E (1992). Statstcal Methods for Survval Data Analyss. John Wley. Marshall AW, Olkn I (1997). A New Method for Addng a Parameter to a Famly of Dstrbutons wth Applcatons to the Exponental and Webull Famles. Bometrka, 84(3), Meeker W, Escobar L (1998). Statstcal Methods for Relablty Data. John Wley. Mudholkar G, Srvastava D, Fremer M (1995). The Exponentated Webull Famly: A Reanalyss of the Bus-motor-falure Data. Technometrcs, 37, Mudholkar G, Srvastava D, Kolla G (1996). A Generalzaton of the Webull Dstrbuton wth Applcaton to the Analyss of Survval Data. Journal of the Amercan Statstcal Assocaton, 91, Nadarajah S (25). On the Moments of the Modfed Webull Dstrbuton. Relablty Engneerng and System Safety, 9, Nadarajah S, Cordero GM, Ortega EMM (211). General Results for the beta-modfed Webull Dstrbuton. Journal of Statstcal Computaton and Smulaton, 81(1), Nadarajah S, Kotz S (25). On Some Recent Modfcatons of Webull Dstrbuton. IEEE Transactons Relablty, 54, Nanda K, Jan K (1999). Some Weghted Dstrbuton Results on Unvarate and Bvarate Cases. Journal of Statstcal Plannng and Inference, 77(2), Nassar M, Essa F (23). On the Exponentated Webull Dstrbuton. Communcatons n Statstcs - Theory and Methods, 32(7), Oluyede B (1999). On Inequaltes and Selecton of Experments for Length-Based Dstrbutons. Probablty n the Engneerng and Informatonal Scences, 13(2), Patl G, Rao C (1978). Weghted Dstrbutons and Sze-Based Samplng wth Applcatons to Wldlfe and Human Famles. Bometrcs, 34(6),
22 Austran Journal of Statstcs 65 Phan KK (1987). A New Modfed Webull Dstrbuton Functon. Communcatons of the Amercan Ceramc Socety, 7(8), Pnho L, Cordero G, Nobre J (212). The Gamma-Exponentated Webull Dstrbuton. Journal of Statstcal Theory and Applcatons, 11(4), Rajarsh S, Rajarsh M (1988). Bathtub Dstrbutons: A Revew. Communcatons n Statstcs-Theory and Methods, 17, Rao C (1965). On Dscrete Dstrbutons Arsng out of Methods of Ascertanment. The Indan Journal of Statstcs, 27(2), Rstć M, Balakrshnan N (211). The Gamma-Exponentated Exponental Dstrbuton. J. Statst. Comp. and Smulaton, 82(8), Santos Slva JMC, Tenreyro S (21). On the Exstence of Maxmum Lkelhood Estmates n Posson Regresson. Economcs Letters, 17, Sarhan AM, Zandn M (29). Modfed Webull Dstrbuton. Appled Scences, 11, Seregn A (21). Unqueness of the Maxmum Lkelhood Estmator for K-monotone Denstes. Proceedngs of the Amercan Mathematcal Socety, 138(12), Shaked M, Shanthkumar J (1994). Stochastc Orders and Ther Applcatons. Academc Press. Slva G, Ortega E, Cordero G (21). The Beta Modfed Webull Dstrbuton. Lfetme Data Analyss, 16, Sngha N, Jan K, Kumar SS (212). The Beta Generalzed Webull Dstrbuton: Propertes and Applcatons. Relablty Engneerng and System Safety, 12, The R Development Core Team (211). A Language and Envronment for Statstcal Computng. R Foundaton for Statstcal Computng. Webull WA (1951). Statstcal Dstrbuton Functon of Wde Applcablty. Journal of Appled Mechancs, 18, Xa J, M J, Zhou YY (29). On the Exstence and Unqueness of the Maxmum Lkelhood Estmators of Normal and Log-normal Populaton Parameters wth Grouped Data. Journal of Probablty and Statstcs. Xe M, La C (1995). Relablty Analyss Usng an Addtve Webull Model wth Bathtubshaped Falure Rate Functon. Relablty Engneerng and System Safety, 52, Xe M, Tang Y, Goh T (22). A Modfed Webull Extenson wth Bathtub Falure Rate Functon. Relablty Engneerng and System Safety, 76, Zhang T, Xe M (211). On the Upper Truncated Webull Dstrbuton and Its Relablty Implcatons. Relablty Engneerng and System Safety, 96(1), Zhou C (29). Exstence and Consstency of the Maxmum Lkelhood Estmator for the Extreme Index. J. Multvarate Analyss, 1, Zografos K, Balakrshnan N (29). On Famles of Beta- and Generalzed Gamma-Generated Dstrbuton and Assocated Inference. Stat. Method, 6,
23 66 A New Class of Generalzed Modfed Webull Dstrbuton wth Applcatons APPENDIX Let A(x ; α, β, θ, λ) (1 e αx βx θ eλx ) log(1 e αx βx θ eλx ), B(x ; α, β, θ, λ) e αx βx θ eλx + log(1 e αx βx θ eλx ), and C(x ; α, β, θ, λ) (1 e αx βx θ eλx βx θ eλx ) log(1 e αx βx θ eλx ) βx θ e (α λ)x βx θ eλx. Elements of the observed nformaton matrx of the GGMW dstrbuton are gven by α 2 (1 δ)x 2 e αx βx θ eλx B(x ; α, β, θ, λ) A 2 (x ; α, β, θ, λ) 1 [α + βx θ 1 e λx (θ + λx )]. (43) 2 α β (1 δ)x θ+1 e (α λ)x βx θ eλx B(x ; α, β, θ, λ) A 2 (x ; α, β, θ, λ) x θ 1 e λx (θ + λx ) [α + βx θ 1 e λx (θ + λx )] 2. (44) α θ (1 δ)βx θ+1 e (α λ)x βx θ eλx log(x )B(x ; α, β, θ, λ) A 2 (x ; α, β, θ, λ) βx θ 1 e λx [(θ + λx ) log(x ) + 1] [α + βx θ 1 e λx (θ + λx )] 2. (45) α λ (1 δ)βx θ+2 e (α λ)x βx θ eλx B(x ; α, β, θ, λ) A 2 (x ; α, β, θ, λ) βx θ eλx (θ + λx + 1) [α + βx θ 1 e λx (θ + λx )] 2. (46) α δ e αx βx θ eλx x A(x ; α, β, θ, λ). (47) β 2 (1 δ)x 2θ e (α 2λ)x βx θ eλx B(x ; α, β, θ, λ) A 2 (x ; α, β, θ, λ) x 2θ 2 e 2λx (θ + λx ) 2 [α + βx θ 1 e λx (θ + λx )] 2. (48) β θ + (δ 1)x θ e (α λ)x βx θ eλx log(x )C(x ; α, β, θ, λ) A 2 (x ; α, β, θ, λ) x θ 1 e λx [(θ + λx ) log(x ) + 1]α [α + βx θ 1 x θ e λx (θ + λx )] 2 e λx log(x ). (49)
24 Austran Journal of Statstcs 67 β λ + (δ 1)x θ+1 e (α λ)x βx θ eλx C(x ; α, β, θ, λ) A 2 (x ; α, β, θ, λ) x θ eλx (θ + λx + 1)α [α + βx θ 1 e λx (θ + λx )] 2 x θ+1 e λx. (5) β δ e (α λ)x βx θ eλx x θ A(x ; α, β, θ, λ). (51) θ 2 + (δ 1)βx θ e (α λ)x βx θ eλx (log(x )) 2 C(x ; α, β, θ, λ) A 2 (x ; α, β, θ, λ) { [(θ βx θ 1 e λx + λx )(log(x )) log(x ) ] } α βx θ 1 e λx β [α + βx θ 1 e λx (θ + λx )] 2 x θ e λx (log(x )) 2. (52) θ λ + β (δ 1)βx θ+1 e (α λ)x βx θ eλx log(x )C(x ; α, β, θ, λ) A 2 (x ; α, β, θ, λ) βx θ eλx { [(θ + λx + 1) log(x ) + 1] α βx θ 1 [α + βx θ 1 e λx (θ + λx )] 2 e λx x θ+1 e λx log(x ). (53) } θ δ βe (α λ)x βx θ eλx x θ log(x ). (54) A(x ; α, β, θ, λ) λ 2 + (δ 1)βx θ+2 e (α λ)x βx θ eλx C(x ; α, β, θ, λ) A 2 (x ; α, β, θ, λ) βx θ+1 e λx [(θ + λx + 2)α βx θ 1 e λx ] [α + βx θ 1 β e λx (θ + λx )] 2 x θ+2 e λx. (55) λ δ βe (α λ)x βx θ eλx x θ+1. (56) A(x ; α, β, θ, λ) δ 2 nψ d log() (δ), where Ψ(δ) Γ (δ) dδ. (57)
25 68 A New Class of Generalzed Modfed Webull Dstrbuton wth Applcatons ## defne GGMW pdf GGMW_pdf <- functon(alpha, beta, theta, lambda, delta, x){ (1/gamma(delta)) * ((-log(1-exp(-alpha * x - beta * (x^theta) * (exp(lambda * x)))))^(delta-1)) * (alpha + beta * (x^(theta - 1)) * (exp(lambda * x)) * (theta + lambda * x)) * (exp(-alpha * x - beta * (x^theta) * (exp(lambda * x)))) } ## defne GGMW cdf GGMW_cdf <- functon(alpha, beta, theta, lambda, delta, x){ 1 - pgamma(-log(1 - exp(-alpha * x - beta * (x^theta) * exp(lambda * x))), delta) } ## defne GGMW Hazard GGMW_hazard <- functon(alpha, beta, theta, lambda, delta, x){ GGMW_pdf(alpha, beta, theta, lambda, delta, x) / (1 - GGMW_cdf(alpha, beta, theta, lambda, delta, x)) } ## defne GGMW moments GGMW_moments <- functon(alpha, beta, theta, lambda, delta, k){ f <- functon(alpha, beta, theta, lambda, delta, k, x){ (x^k) * (GGMW_pdf(alpha, beta, theta, lambda, delta, x)) } y <- ntegrate(f, lower, upper Inf, subdvsons 1, alpha alpha, beta beta, theta theta, lambda lambda, delta delta, k k) return(y) } ## defne GGMW quantle GGMW_quantle <- functon(alpha, beta, theta, lambda, delta, u){ f <- functon(x){alpha * x + beta * (x^theta) * (exp(lambda * x)) + log(1 - exp(-qgamma(1 - u, delta))) } rc <- unroot(f, lower, upper1, tol 1e-9) result <- rc$root # check error <- GGMW_cdf(alpha, beta, theta, lambda, delta, result) - u return(lst("result" result, "error" error)) } Afflaton: Broderck O. Oluyede Department of Mathematcal Scences Georga Southern Unversty Statesboro, GA 346 E-mal: boluyede@georgasouthern.edu Austran Journal of Statstcs publshed by the Austran Socety of Statstcs Volume 44 Submtted: October 215 Accepted:
Parameters Estimation of the Modified Weibull Distribution Based on Type I Censored Samples
 Appled Mathematcal Scences, Vol. 5, 011, no. 59, 899-917 Parameters Estmaton of the Modfed Webull Dstrbuton Based on Type I Censored Samples Soufane Gasm École Supereure des Scences et Technques de Tuns
Appled Mathematcal Scences, Vol. 5, 011, no. 59, 899-917 Parameters Estmaton of the Modfed Webull Dstrbuton Based on Type I Censored Samples Soufane Gasm École Supereure des Scences et Technques de Tuns
Marshall-Olkin Log-Logistic Extended Weibull Distribution : Theory, Properties and Applications
 Journal of Data Scence 15(217), 691-722 Marshall-Olkn Log-Logstc Extended Webull Dstrbuton : Theory, Propertes and Applcatons Lornah Lepetu 1, Broderck O. Oluyede 2, Bokanyo Makubate 3, Susan Foya 4 and
Journal of Data Scence 15(217), 691-722 Marshall-Olkn Log-Logstc Extended Webull Dstrbuton : Theory, Propertes and Applcatons Lornah Lepetu 1, Broderck O. Oluyede 2, Bokanyo Makubate 3, Susan Foya 4 and
Computing MLE Bias Empirically
 Computng MLE Bas Emprcally Kar Wa Lm Australan atonal Unversty January 3, 27 Abstract Ths note studes the bas arses from the MLE estmate of the rate parameter and the mean parameter of an exponental dstrbuton.
Computng MLE Bas Emprcally Kar Wa Lm Australan atonal Unversty January 3, 27 Abstract Ths note studes the bas arses from the MLE estmate of the rate parameter and the mean parameter of an exponental dstrbuton.
On an Extension of Stochastic Approximation EM Algorithm for Incomplete Data Problems. Vahid Tadayon 1
 On an Extenson of Stochastc Approxmaton EM Algorthm for Incomplete Data Problems Vahd Tadayon Abstract: The Stochastc Approxmaton EM (SAEM algorthm, a varant stochastc approxmaton of EM, s a versatle tool
On an Extenson of Stochastc Approxmaton EM Algorthm for Incomplete Data Problems Vahd Tadayon Abstract: The Stochastc Approxmaton EM (SAEM algorthm, a varant stochastc approxmaton of EM, s a versatle tool
Parametric fractional imputation for missing data analysis. Jae Kwang Kim Survey Working Group Seminar March 29, 2010
 Parametrc fractonal mputaton for mssng data analyss Jae Kwang Km Survey Workng Group Semnar March 29, 2010 1 Outlne Introducton Proposed method Fractonal mputaton Approxmaton Varance estmaton Multple mputaton
Parametrc fractonal mputaton for mssng data analyss Jae Kwang Km Survey Workng Group Semnar March 29, 2010 1 Outlne Introducton Proposed method Fractonal mputaton Approxmaton Varance estmaton Multple mputaton
Estimation of the Mean of Truncated Exponential Distribution
 Journal of Mathematcs and Statstcs 4 (4): 84-88, 008 ISSN 549-644 008 Scence Publcatons Estmaton of the Mean of Truncated Exponental Dstrbuton Fars Muslm Al-Athar Department of Mathematcs, Faculty of Scence,
Journal of Mathematcs and Statstcs 4 (4): 84-88, 008 ISSN 549-644 008 Scence Publcatons Estmaton of the Mean of Truncated Exponental Dstrbuton Fars Muslm Al-Athar Department of Mathematcs, Faculty of Scence,
STAT 3008 Applied Regression Analysis
 STAT 3008 Appled Regresson Analyss Tutoral : Smple Lnear Regresson LAI Chun He Department of Statstcs, The Chnese Unversty of Hong Kong 1 Model Assumpton To quantfy the relatonshp between two factors,
STAT 3008 Appled Regresson Analyss Tutoral : Smple Lnear Regresson LAI Chun He Department of Statstcs, The Chnese Unversty of Hong Kong 1 Model Assumpton To quantfy the relatonshp between two factors,
x i1 =1 for all i (the constant ).
 Chapter 5 The Multple Regresson Model Consder an economc model where the dependent varable s a functon of K explanatory varables. The economc model has the form: y = f ( x,x,..., ) xk Approxmate ths by
Chapter 5 The Multple Regresson Model Consder an economc model where the dependent varable s a functon of K explanatory varables. The economc model has the form: y = f ( x,x,..., ) xk Approxmate ths by
Predictive Analytics : QM901.1x Prof U Dinesh Kumar, IIMB. All Rights Reserved, Indian Institute of Management Bangalore
 Sesson Outlne Introducton to classfcaton problems and dscrete choce models. Introducton to Logstcs Regresson. Logstc functon and Logt functon. Maxmum Lkelhood Estmator (MLE) for estmaton of LR parameters.
Sesson Outlne Introducton to classfcaton problems and dscrete choce models. Introducton to Logstcs Regresson. Logstc functon and Logt functon. Maxmum Lkelhood Estmator (MLE) for estmaton of LR parameters.
ANSWERS. Problem 1. and the moment generating function (mgf) by. defined for any real t. Use this to show that E( U) var( U)
 Econ 413 Exam 13 H ANSWERS Settet er nndelt 9 deloppgaver, A,B,C, som alle anbefales å telle lkt for å gøre det ltt lettere å stå. Svar er gtt . Unfortunately, there s a prntng error n the hnt of
Econ 413 Exam 13 H ANSWERS Settet er nndelt 9 deloppgaver, A,B,C, som alle anbefales å telle lkt for å gøre det ltt lettere å stå. Svar er gtt . Unfortunately, there s a prntng error n the hnt of
Double Acceptance Sampling Plan for Time Truncated Life Tests Based on Transmuted Generalized Inverse Weibull Distribution
 J. Stat. Appl. Pro. 6, No. 1, 1-6 2017 1 Journal of Statstcs Applcatons & Probablty An Internatonal Journal http://dx.do.org/10.18576/jsap/060101 Double Acceptance Samplng Plan for Tme Truncated Lfe Tests
J. Stat. Appl. Pro. 6, No. 1, 1-6 2017 1 Journal of Statstcs Applcatons & Probablty An Internatonal Journal http://dx.do.org/10.18576/jsap/060101 Double Acceptance Samplng Plan for Tme Truncated Lfe Tests
Exponentiated Kumaraswamy-Dagum distribution with applications to income and lifetime data
 Huang and Oluyede Journal of Statstcal Dstrbutons and Applcatons 2014 1:8 RESEARCH Open Access Exponentated Kumaraswamy-Dagum dstrbuton wth applcatons to ncome and lfetme data Shujao Huang and Broderck
Huang and Oluyede Journal of Statstcal Dstrbutons and Applcatons 2014 1:8 RESEARCH Open Access Exponentated Kumaraswamy-Dagum dstrbuton wth applcatons to ncome and lfetme data Shujao Huang and Broderck
First Year Examination Department of Statistics, University of Florida
 Frst Year Examnaton Department of Statstcs, Unversty of Florda May 7, 010, 8:00 am - 1:00 noon Instructons: 1. You have four hours to answer questons n ths examnaton.. You must show your work to receve
Frst Year Examnaton Department of Statstcs, Unversty of Florda May 7, 010, 8:00 am - 1:00 noon Instructons: 1. You have four hours to answer questons n ths examnaton.. You must show your work to receve
STAT 405 BIOSTATISTICS (Fall 2016) Handout 15 Introduction to Logistic Regression
 STAT 45 BIOSTATISTICS (Fall 26) Handout 5 Introducton to Logstc Regresson Ths handout covers materal found n Secton 3.7 of your text. You may also want to revew regresson technques n Chapter. In ths handout,
STAT 45 BIOSTATISTICS (Fall 26) Handout 5 Introducton to Logstc Regresson Ths handout covers materal found n Secton 3.7 of your text. You may also want to revew regresson technques n Chapter. In ths handout,
Simulated Power of the Discrete Cramér-von Mises Goodness-of-Fit Tests
 Smulated of the Cramér-von Mses Goodness-of-Ft Tests Steele, M., Chaselng, J. and 3 Hurst, C. School of Mathematcal and Physcal Scences, James Cook Unversty, Australan School of Envronmental Studes, Grffth
Smulated of the Cramér-von Mses Goodness-of-Ft Tests Steele, M., Chaselng, J. and 3 Hurst, C. School of Mathematcal and Physcal Scences, James Cook Unversty, Australan School of Envronmental Studes, Grffth
Econ107 Applied Econometrics Topic 3: Classical Model (Studenmund, Chapter 4)
 I. Classcal Assumptons Econ7 Appled Econometrcs Topc 3: Classcal Model (Studenmund, Chapter 4) We have defned OLS and studed some algebrac propertes of OLS. In ths topc we wll study statstcal propertes
I. Classcal Assumptons Econ7 Appled Econometrcs Topc 3: Classcal Model (Studenmund, Chapter 4) We have defned OLS and studed some algebrac propertes of OLS. In ths topc we wll study statstcal propertes
Statistical inference for generalized Pareto distribution based on progressive Type-II censored data with random removals
 Internatonal Journal of Scentfc World, 2 1) 2014) 1-9 c Scence Publshng Corporaton www.scencepubco.com/ndex.php/ijsw do: 10.14419/jsw.v21.1780 Research Paper Statstcal nference for generalzed Pareto dstrbuton
Internatonal Journal of Scentfc World, 2 1) 2014) 1-9 c Scence Publshng Corporaton www.scencepubco.com/ndex.php/ijsw do: 10.14419/jsw.v21.1780 Research Paper Statstcal nference for generalzed Pareto dstrbuton
Computation of Higher Order Moments from Two Multinomial Overdispersion Likelihood Models
 Computaton of Hgher Order Moments from Two Multnomal Overdsperson Lkelhood Models BY J. T. NEWCOMER, N. K. NEERCHAL Department of Mathematcs and Statstcs, Unversty of Maryland, Baltmore County, Baltmore,
Computaton of Hgher Order Moments from Two Multnomal Overdsperson Lkelhood Models BY J. T. NEWCOMER, N. K. NEERCHAL Department of Mathematcs and Statstcs, Unversty of Maryland, Baltmore County, Baltmore,
Comparison of the Population Variance Estimators. of 2-Parameter Exponential Distribution Based on. Multiple Criteria Decision Making Method
 Appled Mathematcal Scences, Vol. 7, 0, no. 47, 07-0 HIARI Ltd, www.m-hkar.com Comparson of the Populaton Varance Estmators of -Parameter Exponental Dstrbuton Based on Multple Crtera Decson Makng Method
Appled Mathematcal Scences, Vol. 7, 0, no. 47, 07-0 HIARI Ltd, www.m-hkar.com Comparson of the Populaton Varance Estmators of -Parameter Exponental Dstrbuton Based on Multple Crtera Decson Makng Method
Interval Estimation of Stress-Strength Reliability for a General Exponential Form Distribution with Different Unknown Parameters
 Internatonal Journal of Statstcs and Probablty; Vol. 6, No. 6; November 17 ISSN 197-73 E-ISSN 197-74 Publshed by Canadan Center of Scence and Educaton Interval Estmaton of Stress-Strength Relablty for
Internatonal Journal of Statstcs and Probablty; Vol. 6, No. 6; November 17 ISSN 197-73 E-ISSN 197-74 Publshed by Canadan Center of Scence and Educaton Interval Estmaton of Stress-Strength Relablty for
ECONOMETRICS II (ECO 2401S) University of Toronto. Department of Economics. Winter 2017 Instructor: Victor Aguirregabiria
 ECOOMETRICS II ECO 40S Unversty of Toronto Department of Economcs Wnter 07 Instructor: Vctor Agurregabra SOLUTIO TO FIAL EXAM Tuesday, Aprl 8, 07 From :00pm-5:00pm 3 hours ISTRUCTIOS: - Ths s a closed-book
ECOOMETRICS II ECO 40S Unversty of Toronto Department of Economcs Wnter 07 Instructor: Vctor Agurregabra SOLUTIO TO FIAL EXAM Tuesday, Aprl 8, 07 From :00pm-5:00pm 3 hours ISTRUCTIOS: - Ths s a closed-book
Linear Regression Analysis: Terminology and Notation
 ECON 35* -- Secton : Basc Concepts of Regresson Analyss (Page ) Lnear Regresson Analyss: Termnology and Notaton Consder the generc verson of the smple (two-varable) lnear regresson model. It s represented
ECON 35* -- Secton : Basc Concepts of Regresson Analyss (Page ) Lnear Regresson Analyss: Termnology and Notaton Consder the generc verson of the smple (two-varable) lnear regresson model. It s represented
Non-Mixture Cure Model for Interval Censored Data: Simulation Study ABSTRACT
 Malaysan Journal of Mathematcal Scences 8(S): 37-44 (2014) Specal Issue: Internatonal Conference on Mathematcal Scences and Statstcs 2013 (ICMSS2013) MALAYSIAN JOURNAL OF MATHEMATICAL SCIENCES Journal
Malaysan Journal of Mathematcal Scences 8(S): 37-44 (2014) Specal Issue: Internatonal Conference on Mathematcal Scences and Statstcs 2013 (ICMSS2013) MALAYSIAN JOURNAL OF MATHEMATICAL SCIENCES Journal
The Topp-Leone Generated Weibull Distribution: Regression Model, Characterizations and Applications
 Internatonal Journal of Statstcs and Probablty; Vol. 6, No. ; January 207 ISSN 927-7032 E-ISSN 927-7040 Publshed by Canadan Center of Scence and Educaton The Topp-Leone Generated Webull Dstrbuton: Regresson
Internatonal Journal of Statstcs and Probablty; Vol. 6, No. ; January 207 ISSN 927-7032 E-ISSN 927-7040 Publshed by Canadan Center of Scence and Educaton The Topp-Leone Generated Webull Dstrbuton: Regresson
On the Transmuted Additive Weibull Distribution
 AUSTRIAN JOURNAL OF STATISTICS Volume 42 213, Number 2, 117 132 On the Transmuted Addtve Webull Dstrbuton Ibrahm Elbatal 1 and Gokarna Aryal 2 1 Mathematcal Statstcs, Caro Unversty, Egypt 2 Mathematcs,
AUSTRIAN JOURNAL OF STATISTICS Volume 42 213, Number 2, 117 132 On the Transmuted Addtve Webull Dstrbuton Ibrahm Elbatal 1 and Gokarna Aryal 2 1 Mathematcal Statstcs, Caro Unversty, Egypt 2 Mathematcs,
3.1 Expectation of Functions of Several Random Variables. )' be a k-dimensional discrete or continuous random vector, with joint PMF p (, E X E X1 E X
 Statstcs 1: Probablty Theory II 37 3 EPECTATION OF SEVERAL RANDOM VARIABLES As n Probablty Theory I, the nterest n most stuatons les not on the actual dstrbuton of a random vector, but rather on a number
Statstcs 1: Probablty Theory II 37 3 EPECTATION OF SEVERAL RANDOM VARIABLES As n Probablty Theory I, the nterest n most stuatons les not on the actual dstrbuton of a random vector, but rather on a number
Chapter 11: Simple Linear Regression and Correlation
 Chapter 11: Smple Lnear Regresson and Correlaton 11-1 Emprcal Models 11-2 Smple Lnear Regresson 11-3 Propertes of the Least Squares Estmators 11-4 Hypothess Test n Smple Lnear Regresson 11-4.1 Use of t-tests
Chapter 11: Smple Lnear Regresson and Correlaton 11-1 Emprcal Models 11-2 Smple Lnear Regresson 11-3 Propertes of the Least Squares Estmators 11-4 Hypothess Test n Smple Lnear Regresson 11-4.1 Use of t-tests
Reliability Engineering and System Safety
 Relablty Engneerng and System Safety 111 (213) 164 17 Contents lsts avalable at ScVerse ScenceDrect Relablty Engneerng and System Safety journal homepage: www.elsever.com/locate/ress A new modfed Webull
Relablty Engneerng and System Safety 111 (213) 164 17 Contents lsts avalable at ScVerse ScenceDrect Relablty Engneerng and System Safety journal homepage: www.elsever.com/locate/ress A new modfed Webull
1. Inference on Regression Parameters a. Finding Mean, s.d and covariance amongst estimates. 2. Confidence Intervals and Working Hotelling Bands
 Content. Inference on Regresson Parameters a. Fndng Mean, s.d and covarance amongst estmates.. Confdence Intervals and Workng Hotellng Bands 3. Cochran s Theorem 4. General Lnear Testng 5. Measures of
Content. Inference on Regresson Parameters a. Fndng Mean, s.d and covarance amongst estmates.. Confdence Intervals and Workng Hotellng Bands 3. Cochran s Theorem 4. General Lnear Testng 5. Measures of
Using T.O.M to Estimate Parameter of distributions that have not Single Exponential Family
 IOSR Journal of Mathematcs IOSR-JM) ISSN: 2278-5728. Volume 3, Issue 3 Sep-Oct. 202), PP 44-48 www.osrjournals.org Usng T.O.M to Estmate Parameter of dstrbutons that have not Sngle Exponental Famly Jubran
IOSR Journal of Mathematcs IOSR-JM) ISSN: 2278-5728. Volume 3, Issue 3 Sep-Oct. 202), PP 44-48 www.osrjournals.org Usng T.O.M to Estmate Parameter of dstrbutons that have not Sngle Exponental Famly Jubran
The EM Algorithm (Dempster, Laird, Rubin 1977) The missing data or incomplete data setting: ODL(φ;Y ) = [Y;φ] = [Y X,φ][X φ] = X
![The EM Algorithm (Dempster, Laird, Rubin 1977) The missing data or incomplete data setting: ODL(φ;Y ) = [Y;φ] = [Y X,φ][X φ] = X The EM Algorithm (Dempster, Laird, Rubin 1977) The missing data or incomplete data setting: ODL(φ;Y ) = [Y;φ] = [Y X,φ][X φ] = X](/thumbs/94/122242296.jpg) The EM Algorthm (Dempster, Lard, Rubn 1977 The mssng data or ncomplete data settng: An Observed Data Lkelhood (ODL that s a mxture or ntegral of Complete Data Lkelhoods (CDL. (1a ODL(;Y = [Y;] = [Y,][
The EM Algorthm (Dempster, Lard, Rubn 1977 The mssng data or ncomplete data settng: An Observed Data Lkelhood (ODL that s a mxture or ntegral of Complete Data Lkelhoods (CDL. (1a ODL(;Y = [Y;] = [Y,][
Maximum Likelihood Estimation of Binary Dependent Variables Models: Probit and Logit. 1. General Formulation of Binary Dependent Variables Models
 ECO 452 -- OE 4: Probt and Logt Models ECO 452 -- OE 4 Maxmum Lkelhood Estmaton of Bnary Dependent Varables Models: Probt and Logt hs note demonstrates how to formulate bnary dependent varables models
ECO 452 -- OE 4: Probt and Logt Models ECO 452 -- OE 4 Maxmum Lkelhood Estmaton of Bnary Dependent Varables Models: Probt and Logt hs note demonstrates how to formulate bnary dependent varables models
The RS Generalized Lambda Distribution Based Calibration Model
 Internatonal Journal of Statstcs and Probablty; Vol. 2, No. 1; 2013 ISSN 1927-7032 E-ISSN 1927-7040 Publshed by Canadan Center of Scence and Educaton The RS Generalzed Lambda Dstrbuton Based Calbraton
Internatonal Journal of Statstcs and Probablty; Vol. 2, No. 1; 2013 ISSN 1927-7032 E-ISSN 1927-7040 Publshed by Canadan Center of Scence and Educaton The RS Generalzed Lambda Dstrbuton Based Calbraton
a. (All your answers should be in the letter!
 Econ 301 Blkent Unversty Taskn Econometrcs Department of Economcs Md Term Exam I November 8, 015 Name For each hypothess testng n the exam complete the followng steps: Indcate the test statstc, ts crtcal
Econ 301 Blkent Unversty Taskn Econometrcs Department of Economcs Md Term Exam I November 8, 015 Name For each hypothess testng n the exam complete the followng steps: Indcate the test statstc, ts crtcal
Economics 130. Lecture 4 Simple Linear Regression Continued
 Economcs 130 Lecture 4 Contnued Readngs for Week 4 Text, Chapter and 3. We contnue wth addressng our second ssue + add n how we evaluate these relatonshps: Where do we get data to do ths analyss? How do
Economcs 130 Lecture 4 Contnued Readngs for Week 4 Text, Chapter and 3. We contnue wth addressng our second ssue + add n how we evaluate these relatonshps: Where do we get data to do ths analyss? How do
Which estimator of the dispersion parameter for the Gamma family generalized linear models is to be chosen?
 STATISTICS Dalarna Unversty D-level Master s Thess 007 Whch estmator of the dsperson parameter for the Gamma famly generalzed lnear models s to be chosen? Submtted by: Juan Du Regstraton Number: 8096-T084
STATISTICS Dalarna Unversty D-level Master s Thess 007 Whch estmator of the dsperson parameter for the Gamma famly generalzed lnear models s to be chosen? Submtted by: Juan Du Regstraton Number: 8096-T084
Test for Intraclass Correlation Coefficient under Unequal Family Sizes
 Journal of Modern Appled Statstcal Methods Volume Issue Artcle 9 --03 Test for Intraclass Correlaton Coeffcent under Unequal Famly Szes Madhusudan Bhandary Columbus State Unversty, Columbus, GA, bhandary_madhusudan@colstate.edu
Journal of Modern Appled Statstcal Methods Volume Issue Artcle 9 --03 Test for Intraclass Correlaton Coeffcent under Unequal Famly Szes Madhusudan Bhandary Columbus State Unversty, Columbus, GA, bhandary_madhusudan@colstate.edu
ECONOMICS 351*-A Mid-Term Exam -- Fall Term 2000 Page 1 of 13 pages. QUEEN'S UNIVERSITY AT KINGSTON Department of Economics
 ECOOMICS 35*-A Md-Term Exam -- Fall Term 000 Page of 3 pages QUEE'S UIVERSITY AT KIGSTO Department of Economcs ECOOMICS 35* - Secton A Introductory Econometrcs Fall Term 000 MID-TERM EAM ASWERS MG Abbott
ECOOMICS 35*-A Md-Term Exam -- Fall Term 000 Page of 3 pages QUEE'S UIVERSITY AT KIGSTO Department of Economcs ECOOMICS 35* - Secton A Introductory Econometrcs Fall Term 000 MID-TERM EAM ASWERS MG Abbott
Composite Hypotheses testing
 Composte ypotheses testng In many hypothess testng problems there are many possble dstrbutons that can occur under each of the hypotheses. The output of the source s a set of parameters (ponts n a parameter
Composte ypotheses testng In many hypothess testng problems there are many possble dstrbutons that can occur under each of the hypotheses. The output of the source s a set of parameters (ponts n a parameter
Here is the rationale: If X and y have a strong positive relationship to one another, then ( x x) will tend to be positive when ( y y)
 Secton 1.5 Correlaton In the prevous sectons, we looked at regresson and the value r was a measurement of how much of the varaton n y can be attrbuted to the lnear relatonshp between y and x. In ths secton,
Secton 1.5 Correlaton In the prevous sectons, we looked at regresson and the value r was a measurement of how much of the varaton n y can be attrbuted to the lnear relatonshp between y and x. In ths secton,
Estimation: Part 2. Chapter GREG estimation
 Chapter 9 Estmaton: Part 2 9. GREG estmaton In Chapter 8, we have seen that the regresson estmator s an effcent estmator when there s a lnear relatonshp between y and x. In ths chapter, we generalzed the
Chapter 9 Estmaton: Part 2 9. GREG estmaton In Chapter 8, we have seen that the regresson estmator s an effcent estmator when there s a lnear relatonshp between y and x. In ths chapter, we generalzed the
4.3 Poisson Regression
 of teratvely reweghted least squares regressons (the IRLS algorthm). We do wthout gvng further detals, but nstead focus on the practcal applcaton. > glm(survval~log(weght)+age, famly="bnomal", data=baby)
of teratvely reweghted least squares regressons (the IRLS algorthm). We do wthout gvng further detals, but nstead focus on the practcal applcaton. > glm(survval~log(weght)+age, famly="bnomal", data=baby)
ANOMALIES OF THE MAGNITUDE OF THE BIAS OF THE MAXIMUM LIKELIHOOD ESTIMATOR OF THE REGRESSION SLOPE
 P a g e ANOMALIES OF THE MAGNITUDE OF THE BIAS OF THE MAXIMUM LIKELIHOOD ESTIMATOR OF THE REGRESSION SLOPE Darmud O Drscoll ¹, Donald E. Ramrez ² ¹ Head of Department of Mathematcs and Computer Studes
P a g e ANOMALIES OF THE MAGNITUDE OF THE BIAS OF THE MAXIMUM LIKELIHOOD ESTIMATOR OF THE REGRESSION SLOPE Darmud O Drscoll ¹, Donald E. Ramrez ² ¹ Head of Department of Mathematcs and Computer Studes
UNIVERSITY OF TORONTO Faculty of Arts and Science. December 2005 Examinations STA437H1F/STA1005HF. Duration - 3 hours
 UNIVERSITY OF TORONTO Faculty of Arts and Scence December 005 Examnatons STA47HF/STA005HF Duraton - hours AIDS ALLOWED: (to be suppled by the student) Non-programmable calculator One handwrtten 8.5'' x
UNIVERSITY OF TORONTO Faculty of Arts and Scence December 005 Examnatons STA47HF/STA005HF Duraton - hours AIDS ALLOWED: (to be suppled by the student) Non-programmable calculator One handwrtten 8.5'' x
Durban Watson for Testing the Lack-of-Fit of Polynomial Regression Models without Replications
 Durban Watson for Testng the Lack-of-Ft of Polynomal Regresson Models wthout Replcatons Ruba A. Alyaf, Maha A. Omar, Abdullah A. Al-Shha ralyaf@ksu.edu.sa, maomar@ksu.edu.sa, aalshha@ksu.edu.sa Department
Durban Watson for Testng the Lack-of-Ft of Polynomal Regresson Models wthout Replcatons Ruba A. Alyaf, Maha A. Omar, Abdullah A. Al-Shha ralyaf@ksu.edu.sa, maomar@ksu.edu.sa, aalshha@ksu.edu.sa Department
Department of Statistics University of Toronto STA305H1S / 1004 HS Design and Analysis of Experiments Term Test - Winter Solution
 Department of Statstcs Unversty of Toronto STA35HS / HS Desgn and Analyss of Experments Term Test - Wnter - Soluton February, Last Name: Frst Name: Student Number: Instructons: Tme: hours. Ads: a non-programmable
Department of Statstcs Unversty of Toronto STA35HS / HS Desgn and Analyss of Experments Term Test - Wnter - Soluton February, Last Name: Frst Name: Student Number: Instructons: Tme: hours. Ads: a non-programmable
Chapter 13: Multiple Regression
 Chapter 13: Multple Regresson 13.1 Developng the multple-regresson Model The general model can be descrbed as: It smplfes for two ndependent varables: The sample ft parameter b 0, b 1, and b are used to
Chapter 13: Multple Regresson 13.1 Developng the multple-regresson Model The general model can be descrbed as: It smplfes for two ndependent varables: The sample ft parameter b 0, b 1, and b are used to
Comments on Detecting Outliers in Gamma Distribution by M. Jabbari Nooghabi et al. (2010)
 Comments on Detectng Outlers n Gamma Dstrbuton by M. Jabbar Nooghab et al. (21) M. Magdalena Lucn Alejandro C. Frery September 17, 215 arxv:159.55v1 [stat.co] 16 Sep 215 Ths note shows that the results
Comments on Detectng Outlers n Gamma Dstrbuton by M. Jabbar Nooghab et al. (21) M. Magdalena Lucn Alejandro C. Frery September 17, 215 arxv:159.55v1 [stat.co] 16 Sep 215 Ths note shows that the results
Chapter 5. Solution of System of Linear Equations. Module No. 6. Solution of Inconsistent and Ill Conditioned Systems
 Numercal Analyss by Dr. Anta Pal Assstant Professor Department of Mathematcs Natonal Insttute of Technology Durgapur Durgapur-713209 emal: anta.bue@gmal.com 1 . Chapter 5 Soluton of System of Lnear Equatons
Numercal Analyss by Dr. Anta Pal Assstant Professor Department of Mathematcs Natonal Insttute of Technology Durgapur Durgapur-713209 emal: anta.bue@gmal.com 1 . Chapter 5 Soluton of System of Lnear Equatons
Hidden Markov Models & The Multivariate Gaussian (10/26/04)
 CS281A/Stat241A: Statstcal Learnng Theory Hdden Markov Models & The Multvarate Gaussan (10/26/04) Lecturer: Mchael I. Jordan Scrbes: Jonathan W. Hu 1 Hdden Markov Models As a bref revew, hdden Markov models
CS281A/Stat241A: Statstcal Learnng Theory Hdden Markov Models & The Multvarate Gaussan (10/26/04) Lecturer: Mchael I. Jordan Scrbes: Jonathan W. Hu 1 Hdden Markov Models As a bref revew, hdden Markov models
An (almost) unbiased estimator for the S-Gini index
 An (almost unbased estmator for the S-Gn ndex Thomas Demuynck February 25, 2009 Abstract Ths note provdes an unbased estmator for the absolute S-Gn and an almost unbased estmator for the relatve S-Gn for
An (almost unbased estmator for the S-Gn ndex Thomas Demuynck February 25, 2009 Abstract Ths note provdes an unbased estmator for the absolute S-Gn and an almost unbased estmator for the relatve S-Gn for
See Book Chapter 11 2 nd Edition (Chapter 10 1 st Edition)
 Count Data Models See Book Chapter 11 2 nd Edton (Chapter 10 1 st Edton) Count data consst of non-negatve nteger values Examples: number of drver route changes per week, the number of trp departure changes
Count Data Models See Book Chapter 11 2 nd Edton (Chapter 10 1 st Edton) Count data consst of non-negatve nteger values Examples: number of drver route changes per week, the number of trp departure changes
NUMERICAL DIFFERENTIATION
 NUMERICAL DIFFERENTIATION 1 Introducton Dfferentaton s a method to compute the rate at whch a dependent output y changes wth respect to the change n the ndependent nput x. Ths rate of change s called the
NUMERICAL DIFFERENTIATION 1 Introducton Dfferentaton s a method to compute the rate at whch a dependent output y changes wth respect to the change n the ndependent nput x. Ths rate of change s called the
Module 3 LOSSY IMAGE COMPRESSION SYSTEMS. Version 2 ECE IIT, Kharagpur
 Module 3 LOSSY IMAGE COMPRESSION SYSTEMS Verson ECE IIT, Kharagpur Lesson 6 Theory of Quantzaton Verson ECE IIT, Kharagpur Instructonal Objectves At the end of ths lesson, the students should be able to:
Module 3 LOSSY IMAGE COMPRESSION SYSTEMS Verson ECE IIT, Kharagpur Lesson 6 Theory of Quantzaton Verson ECE IIT, Kharagpur Instructonal Objectves At the end of ths lesson, the students should be able to:
Chapter 20 Duration Analysis
 Chapter 20 Duraton Analyss Duraton: tme elapsed untl a certan event occurs (weeks unemployed, months spent on welfare). Survval analyss: duraton of nterest s survval tme of a subject, begn n an ntal state
Chapter 20 Duraton Analyss Duraton: tme elapsed untl a certan event occurs (weeks unemployed, months spent on welfare). Survval analyss: duraton of nterest s survval tme of a subject, begn n an ntal state
Generalized Linear Methods
 Generalzed Lnear Methods 1 Introducton In the Ensemble Methods the general dea s that usng a combnaton of several weak learner one could make a better learner. More formally, assume that we have a set
Generalzed Lnear Methods 1 Introducton In the Ensemble Methods the general dea s that usng a combnaton of several weak learner one could make a better learner. More formally, assume that we have a set
A new Approach for Solving Linear Ordinary Differential Equations
 , ISSN 974-57X (Onlne), ISSN 974-5718 (Prnt), Vol. ; Issue No. 1; Year 14, Copyrght 13-14 by CESER PUBLICATIONS A new Approach for Solvng Lnear Ordnary Dfferental Equatons Fawz Abdelwahd Department of
, ISSN 974-57X (Onlne), ISSN 974-5718 (Prnt), Vol. ; Issue No. 1; Year 14, Copyrght 13-14 by CESER PUBLICATIONS A new Approach for Solvng Lnear Ordnary Dfferental Equatons Fawz Abdelwahd Department of
2016 Wiley. Study Session 2: Ethical and Professional Standards Application
 6 Wley Study Sesson : Ethcal and Professonal Standards Applcaton LESSON : CORRECTION ANALYSIS Readng 9: Correlaton and Regresson LOS 9a: Calculate and nterpret a sample covarance and a sample correlaton
6 Wley Study Sesson : Ethcal and Professonal Standards Applcaton LESSON : CORRECTION ANALYSIS Readng 9: Correlaton and Regresson LOS 9a: Calculate and nterpret a sample covarance and a sample correlaton
A Note on Test of Homogeneity Against Umbrella Scale Alternative Based on U-Statistics
 J Stat Appl Pro No 3 93- () 93 NSP Journal of Statstcs Applcatons & Probablty --- An Internatonal Journal @ NSP Natural Scences Publshng Cor A Note on Test of Homogenety Aganst Umbrella Scale Alternatve
J Stat Appl Pro No 3 93- () 93 NSP Journal of Statstcs Applcatons & Probablty --- An Internatonal Journal @ NSP Natural Scences Publshng Cor A Note on Test of Homogenety Aganst Umbrella Scale Alternatve
2E Pattern Recognition Solutions to Introduction to Pattern Recognition, Chapter 2: Bayesian pattern classification
 E395 - Pattern Recognton Solutons to Introducton to Pattern Recognton, Chapter : Bayesan pattern classfcaton Preface Ths document s a soluton manual for selected exercses from Introducton to Pattern Recognton
E395 - Pattern Recognton Solutons to Introducton to Pattern Recognton, Chapter : Bayesan pattern classfcaton Preface Ths document s a soluton manual for selected exercses from Introducton to Pattern Recognton
COMPARISON OF SOME RELIABILITY CHARACTERISTICS BETWEEN REDUNDANT SYSTEMS REQUIRING SUPPORTING UNITS FOR THEIR OPERATIONS
 Avalable onlne at http://sck.org J. Math. Comput. Sc. 3 (3), No., 6-3 ISSN: 97-537 COMPARISON OF SOME RELIABILITY CHARACTERISTICS BETWEEN REDUNDANT SYSTEMS REQUIRING SUPPORTING UNITS FOR THEIR OPERATIONS
Avalable onlne at http://sck.org J. Math. Comput. Sc. 3 (3), No., 6-3 ISSN: 97-537 COMPARISON OF SOME RELIABILITY CHARACTERISTICS BETWEEN REDUNDANT SYSTEMS REQUIRING SUPPORTING UNITS FOR THEIR OPERATIONS
LOW BIAS INTEGRATED PATH ESTIMATORS. James M. Calvin
 Proceedngs of the 007 Wnter Smulaton Conference S G Henderson, B Bller, M-H Hseh, J Shortle, J D Tew, and R R Barton, eds LOW BIAS INTEGRATED PATH ESTIMATORS James M Calvn Department of Computer Scence
Proceedngs of the 007 Wnter Smulaton Conference S G Henderson, B Bller, M-H Hseh, J Shortle, J D Tew, and R R Barton, eds LOW BIAS INTEGRATED PATH ESTIMATORS James M Calvn Department of Computer Scence
Linear Approximation with Regularization and Moving Least Squares
 Lnear Approxmaton wth Regularzaton and Movng Least Squares Igor Grešovn May 007 Revson 4.6 (Revson : March 004). 5 4 3 0.5 3 3.5 4 Contents: Lnear Fttng...4. Weghted Least Squares n Functon Approxmaton...
Lnear Approxmaton wth Regularzaton and Movng Least Squares Igor Grešovn May 007 Revson 4.6 (Revson : March 004). 5 4 3 0.5 3 3.5 4 Contents: Lnear Fttng...4. Weghted Least Squares n Functon Approxmaton...
A Generalization of the Weibull Distribution with Applications
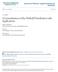 Journal of Modern Appled Statstcal Methods Volume 5 Issue 2 Artcle 47 --26 A Generalzaton of the Webull Dstrbuton wth Applcatons Maalee Almhedat Unversty of Petra, Amman, Jordan, malmhedat@uop.edu.jo Carl
Journal of Modern Appled Statstcal Methods Volume 5 Issue 2 Artcle 47 --26 A Generalzaton of the Webull Dstrbuton wth Applcatons Maalee Almhedat Unversty of Petra, Amman, Jordan, malmhedat@uop.edu.jo Carl
CIS526: Machine Learning Lecture 3 (Sept 16, 2003) Linear Regression. Preparation help: Xiaoying Huang. x 1 θ 1 output... θ M x M
 CIS56: achne Learnng Lecture 3 (Sept 6, 003) Preparaton help: Xaoyng Huang Lnear Regresson Lnear regresson can be represented by a functonal form: f(; θ) = θ 0 0 +θ + + θ = θ = 0 ote: 0 s a dummy attrbute
CIS56: achne Learnng Lecture 3 (Sept 6, 003) Preparaton help: Xaoyng Huang Lnear Regresson Lnear regresson can be represented by a functonal form: f(; θ) = θ 0 0 +θ + + θ = θ = 0 ote: 0 s a dummy attrbute
Statistics for Economics & Business
 Statstcs for Economcs & Busness Smple Lnear Regresson Learnng Objectves In ths chapter, you learn: How to use regresson analyss to predct the value of a dependent varable based on an ndependent varable
Statstcs for Economcs & Busness Smple Lnear Regresson Learnng Objectves In ths chapter, you learn: How to use regresson analyss to predct the value of a dependent varable based on an ndependent varable
New Extended Weibull Distribution
 Crculaton n Computer Scence Vol No6 pp: (4-9) July 7 https:doorg6ccs-7-5- New Extended Webull Dstrbuton Zubar Ahmad Research Scholar: Department of Statstcs Quad--Aam Unversty 45 Islamabad 44 Pastan Zawar
Crculaton n Computer Scence Vol No6 pp: (4-9) July 7 https:doorg6ccs-7-5- New Extended Webull Dstrbuton Zubar Ahmad Research Scholar: Department of Statstcs Quad--Aam Unversty 45 Islamabad 44 Pastan Zawar
DERIVATION OF THE PROBABILITY PLOT CORRELATION COEFFICIENT TEST STATISTICS FOR THE GENERALIZED LOGISTIC DISTRIBUTION
 Internatonal Worshop ADVANCES IN STATISTICAL HYDROLOGY May 3-5, Taormna, Italy DERIVATION OF THE PROBABILITY PLOT CORRELATION COEFFICIENT TEST STATISTICS FOR THE GENERALIZED LOGISTIC DISTRIBUTION by Sooyoung
Internatonal Worshop ADVANCES IN STATISTICAL HYDROLOGY May 3-5, Taormna, Italy DERIVATION OF THE PROBABILITY PLOT CORRELATION COEFFICIENT TEST STATISTICS FOR THE GENERALIZED LOGISTIC DISTRIBUTION by Sooyoung
MATH 829: Introduction to Data Mining and Analysis The EM algorithm (part 2)
 1/16 MATH 829: Introducton to Data Mnng and Analyss The EM algorthm (part 2) Domnque Gullot Departments of Mathematcal Scences Unversty of Delaware Aprl 20, 2016 Recall 2/16 We are gven ndependent observatons
1/16 MATH 829: Introducton to Data Mnng and Analyss The EM algorthm (part 2) Domnque Gullot Departments of Mathematcal Scences Unversty of Delaware Aprl 20, 2016 Recall 2/16 We are gven ndependent observatons
DISCRETE GENERALIZED RAYLEIGH DISTRIBUTION
 Pak. J. Statst. 06 Vol. 3(), -0 DISCRETE GENERALIZED RAYLEIGH DISTRIBUTION M.H. Alamatsaz, S. Dey, T. Dey 3 and S. Shams Harand 4 Department of Statstcs, Unversty of Isfahan, Isfahan, Iran Naghshejahan
Pak. J. Statst. 06 Vol. 3(), -0 DISCRETE GENERALIZED RAYLEIGH DISTRIBUTION M.H. Alamatsaz, S. Dey, T. Dey 3 and S. Shams Harand 4 Department of Statstcs, Unversty of Isfahan, Isfahan, Iran Naghshejahan
PARAMETRIC CONFIDENCE INTERVALS FOR THE RENEWAL FUNCTION VIA COUPLED INTEGRAL EQUATIONS. Michael Tortorella
 PARAMETRIC CONFIDENCE INTERVAS FOR THE RENEWA FUNCTION VIA COUPED INTEGRA EQUATIONS Mchael Tortorella and Steve. G. From Department of Mathematcs Unversty of Nebraska Omaha, NE 68182-0243 INDUSTRIA & SYSTEMS
PARAMETRIC CONFIDENCE INTERVAS FOR THE RENEWA FUNCTION VIA COUPED INTEGRA EQUATIONS Mchael Tortorella and Steve. G. From Department of Mathematcs Unversty of Nebraska Omaha, NE 68182-0243 INDUSTRIA & SYSTEMS
Journal of Biostatistics and Epidemiology
 Journal of Bostatstcs Epdemology J Bostat Epdemol 07; 3(: 65-75 Orgnal Artcle Generalzed Topp-Leone famly of dstrbutons Abbas Mahdav * Department of Statstcs School of Mathematcal Scences Val-e-Asr Unversty
Journal of Bostatstcs Epdemology J Bostat Epdemol 07; 3(: 65-75 Orgnal Artcle Generalzed Topp-Leone famly of dstrbutons Abbas Mahdav * Department of Statstcs School of Mathematcal Scences Val-e-Asr Unversty
Modeling and Simulation NETW 707
 Modelng and Smulaton NETW 707 Lecture 5 Tests for Random Numbers Course Instructor: Dr.-Ing. Magge Mashaly magge.ezzat@guc.edu.eg C3.220 1 Propertes of Random Numbers Random Number Generators (RNGs) must
Modelng and Smulaton NETW 707 Lecture 5 Tests for Random Numbers Course Instructor: Dr.-Ing. Magge Mashaly magge.ezzat@guc.edu.eg C3.220 1 Propertes of Random Numbers Random Number Generators (RNGs) must
Global Sensitivity. Tuesday 20 th February, 2018
 Global Senstvty Tuesday 2 th February, 28 ) Local Senstvty Most senstvty analyses [] are based on local estmates of senstvty, typcally by expandng the response n a Taylor seres about some specfc values
Global Senstvty Tuesday 2 th February, 28 ) Local Senstvty Most senstvty analyses [] are based on local estmates of senstvty, typcally by expandng the response n a Taylor seres about some specfc values
Efficient nonresponse weighting adjustment using estimated response probability
 Effcent nonresponse weghtng adjustment usng estmated response probablty Jae Kwang Km Department of Appled Statstcs, Yonse Unversty, Seoul, 120-749, KOREA Key Words: Regresson estmator, Propensty score,
Effcent nonresponse weghtng adjustment usng estmated response probablty Jae Kwang Km Department of Appled Statstcs, Yonse Unversty, Seoul, 120-749, KOREA Key Words: Regresson estmator, Propensty score,
Stat260: Bayesian Modeling and Inference Lecture Date: February 22, Reference Priors
 Stat60: Bayesan Modelng and Inference Lecture Date: February, 00 Reference Prors Lecturer: Mchael I. Jordan Scrbe: Steven Troxler and Wayne Lee In ths lecture, we assume that θ R; n hgher-dmensons, reference
Stat60: Bayesan Modelng and Inference Lecture Date: February, 00 Reference Prors Lecturer: Mchael I. Jordan Scrbe: Steven Troxler and Wayne Lee In ths lecture, we assume that θ R; n hgher-dmensons, reference
Population Design in Nonlinear Mixed Effects Multiple Response Models: extension of PFIM and evaluation by simulation with NONMEM and MONOLIX
 Populaton Desgn n Nonlnear Mxed Effects Multple Response Models: extenson of PFIM and evaluaton by smulaton wth NONMEM and MONOLIX May 4th 007 Carolne Bazzol, Sylve Retout, France Mentré Inserm U738 Unversty
Populaton Desgn n Nonlnear Mxed Effects Multple Response Models: extenson of PFIM and evaluaton by smulaton wth NONMEM and MONOLIX May 4th 007 Carolne Bazzol, Sylve Retout, France Mentré Inserm U738 Unversty
Lecture 4: September 12
 36-755: Advanced Statstcal Theory Fall 016 Lecture 4: September 1 Lecturer: Alessandro Rnaldo Scrbe: Xao Hu Ta Note: LaTeX template courtesy of UC Berkeley EECS dept. Dsclamer: These notes have not been
36-755: Advanced Statstcal Theory Fall 016 Lecture 4: September 1 Lecturer: Alessandro Rnaldo Scrbe: Xao Hu Ta Note: LaTeX template courtesy of UC Berkeley EECS dept. Dsclamer: These notes have not been
Influence Diagnostics on Competing Risks Using Cox s Model with Censored Data. Jalan Gombak, 53100, Kuala Lumpur, Malaysia.
 Proceedngs of the 8th WSEAS Internatonal Conference on APPLIED MAHEMAICS, enerfe, Span, December 16-18, 5 (pp14-138) Influence Dagnostcs on Competng Rsks Usng Cox s Model wth Censored Data F. A. M. Elfak
Proceedngs of the 8th WSEAS Internatonal Conference on APPLIED MAHEMAICS, enerfe, Span, December 16-18, 5 (pp14-138) Influence Dagnostcs on Competng Rsks Usng Cox s Model wth Censored Data F. A. M. Elfak
Lecture Notes on Linear Regression
 Lecture Notes on Lnear Regresson Feng L fl@sdueducn Shandong Unversty, Chna Lnear Regresson Problem In regresson problem, we am at predct a contnuous target value gven an nput feature vector We assume
Lecture Notes on Lnear Regresson Feng L fl@sdueducn Shandong Unversty, Chna Lnear Regresson Problem In regresson problem, we am at predct a contnuous target value gven an nput feature vector We assume
CS 2750 Machine Learning. Lecture 5. Density estimation. CS 2750 Machine Learning. Announcements
 CS 750 Machne Learnng Lecture 5 Densty estmaton Mlos Hauskrecht mlos@cs.ptt.edu 539 Sennott Square CS 750 Machne Learnng Announcements Homework Due on Wednesday before the class Reports: hand n before
CS 750 Machne Learnng Lecture 5 Densty estmaton Mlos Hauskrecht mlos@cs.ptt.edu 539 Sennott Square CS 750 Machne Learnng Announcements Homework Due on Wednesday before the class Reports: hand n before
Rockefeller College University at Albany
 Rockefeller College Unverst at Alban PAD 705 Handout: Maxmum Lkelhood Estmaton Orgnal b Davd A. Wse John F. Kenned School of Government, Harvard Unverst Modfcatons b R. Karl Rethemeer Up to ths pont n
Rockefeller College Unverst at Alban PAD 705 Handout: Maxmum Lkelhood Estmaton Orgnal b Davd A. Wse John F. Kenned School of Government, Harvard Unverst Modfcatons b R. Karl Rethemeer Up to ths pont n
Numerical Heat and Mass Transfer
 Master degree n Mechancal Engneerng Numercal Heat and Mass Transfer 06-Fnte-Dfference Method (One-dmensonal, steady state heat conducton) Fausto Arpno f.arpno@uncas.t Introducton Why we use models and
Master degree n Mechancal Engneerng Numercal Heat and Mass Transfer 06-Fnte-Dfference Method (One-dmensonal, steady state heat conducton) Fausto Arpno f.arpno@uncas.t Introducton Why we use models and
The Multiple Classical Linear Regression Model (CLRM): Specification and Assumptions. 1. Introduction
 ECONOMICS 5* -- NOTE (Summary) ECON 5* -- NOTE The Multple Classcal Lnear Regresson Model (CLRM): Specfcaton and Assumptons. Introducton CLRM stands for the Classcal Lnear Regresson Model. The CLRM s also
ECONOMICS 5* -- NOTE (Summary) ECON 5* -- NOTE The Multple Classcal Lnear Regresson Model (CLRM): Specfcaton and Assumptons. Introducton CLRM stands for the Classcal Lnear Regresson Model. The CLRM s also
The Order Relation and Trace Inequalities for. Hermitian Operators
 Internatonal Mathematcal Forum, Vol 3, 08, no, 507-57 HIKARI Ltd, wwwm-hkarcom https://doorg/0988/mf088055 The Order Relaton and Trace Inequaltes for Hermtan Operators Y Huang School of Informaton Scence
Internatonal Mathematcal Forum, Vol 3, 08, no, 507-57 HIKARI Ltd, wwwm-hkarcom https://doorg/0988/mf088055 The Order Relaton and Trace Inequaltes for Hermtan Operators Y Huang School of Informaton Scence
ASYMPTOTIC PROPERTIES OF ESTIMATES FOR THE PARAMETERS IN THE LOGISTIC REGRESSION MODEL
 Asymptotc Asan-Afrcan Propertes Journal of Estmates Economcs for and the Econometrcs, Parameters n Vol. the Logstc, No., Regresson 20: 65-74 Model 65 ASYMPTOTIC PROPERTIES OF ESTIMATES FOR THE PARAMETERS
Asymptotc Asan-Afrcan Propertes Journal of Estmates Economcs for and the Econometrcs, Parameters n Vol. the Logstc, No., Regresson 20: 65-74 Model 65 ASYMPTOTIC PROPERTIES OF ESTIMATES FOR THE PARAMETERS
System in Weibull Distribution
 Internatonal Matheatcal Foru 4 9 no. 9 94-95 Relablty Equvalence Factors of a Seres-Parallel Syste n Webull Dstrbuton M. A. El-Dacese Matheatcs Departent Faculty of Scence Tanta Unversty Tanta Egypt eldacese@yahoo.co
Internatonal Matheatcal Foru 4 9 no. 9 94-95 Relablty Equvalence Factors of a Seres-Parallel Syste n Webull Dstrbuton M. A. El-Dacese Matheatcs Departent Faculty of Scence Tanta Unversty Tanta Egypt eldacese@yahoo.co
LINEAR REGRESSION ANALYSIS. MODULE IX Lecture Multicollinearity
 LINEAR REGRESSION ANALYSIS MODULE IX Lecture - 30 Multcollnearty Dr. Shalabh Department of Mathematcs and Statstcs Indan Insttute of Technology Kanpur 2 Remedes for multcollnearty Varous technques have
LINEAR REGRESSION ANALYSIS MODULE IX Lecture - 30 Multcollnearty Dr. Shalabh Department of Mathematcs and Statstcs Indan Insttute of Technology Kanpur 2 Remedes for multcollnearty Varous technques have
Conjugacy and the Exponential Family
 CS281B/Stat241B: Advanced Topcs n Learnng & Decson Makng Conjugacy and the Exponental Famly Lecturer: Mchael I. Jordan Scrbes: Bran Mlch 1 Conjugacy In the prevous lecture, we saw conjugate prors for the
CS281B/Stat241B: Advanced Topcs n Learnng & Decson Makng Conjugacy and the Exponental Famly Lecturer: Mchael I. Jordan Scrbes: Bran Mlch 1 Conjugacy In the prevous lecture, we saw conjugate prors for the
Dr. Shalabh Department of Mathematics and Statistics Indian Institute of Technology Kanpur
 Analyss of Varance and Desgn of Experment-I MODULE VIII LECTURE - 34 ANALYSIS OF VARIANCE IN RANDOM-EFFECTS MODEL AND MIXED-EFFECTS EFFECTS MODEL Dr Shalabh Department of Mathematcs and Statstcs Indan
Analyss of Varance and Desgn of Experment-I MODULE VIII LECTURE - 34 ANALYSIS OF VARIANCE IN RANDOM-EFFECTS MODEL AND MIXED-EFFECTS EFFECTS MODEL Dr Shalabh Department of Mathematcs and Statstcs Indan
Lecture 9: Linear regression: centering, hypothesis testing, multiple covariates, and confounding
 Recall: man dea of lnear regresson Lecture 9: Lnear regresson: centerng, hypothess testng, multple covarates, and confoundng Sandy Eckel seckel@jhsph.edu 6 May 8 Lnear regresson can be used to study an
Recall: man dea of lnear regresson Lecture 9: Lnear regresson: centerng, hypothess testng, multple covarates, and confoundng Sandy Eckel seckel@jhsph.edu 6 May 8 Lnear regresson can be used to study an
CS-433: Simulation and Modeling Modeling and Probability Review
 CS-433: Smulaton and Modelng Modelng and Probablty Revew Exercse 1. (Probablty of Smple Events) Exercse 1.1 The owner of a camera shop receves a shpment of fve cameras from a camera manufacturer. Unknown
CS-433: Smulaton and Modelng Modelng and Probablty Revew Exercse 1. (Probablty of Smple Events) Exercse 1.1 The owner of a camera shop receves a shpment of fve cameras from a camera manufacturer. Unknown
Hydrological statistics. Hydrological statistics and extremes
 5--0 Stochastc Hydrology Hydrologcal statstcs and extremes Marc F.P. Berkens Professor of Hydrology Faculty of Geoscences Hydrologcal statstcs Mostly concernes wth the statstcal analyss of hydrologcal
5--0 Stochastc Hydrology Hydrologcal statstcs and extremes Marc F.P. Berkens Professor of Hydrology Faculty of Geoscences Hydrologcal statstcs Mostly concernes wth the statstcal analyss of hydrologcal
Joint Statistical Meetings - Biopharmaceutical Section
 Iteratve Ch-Square Test for Equvalence of Multple Treatment Groups Te-Hua Ng*, U.S. Food and Drug Admnstraton 1401 Rockvlle Pke, #200S, HFM-217, Rockvlle, MD 20852-1448 Key Words: Equvalence Testng; Actve
Iteratve Ch-Square Test for Equvalence of Multple Treatment Groups Te-Hua Ng*, U.S. Food and Drug Admnstraton 1401 Rockvlle Pke, #200S, HFM-217, Rockvlle, MD 20852-1448 Key Words: Equvalence Testng; Actve
Department of Quantitative Methods & Information Systems. Time Series and Their Components QMIS 320. Chapter 6
 Department of Quanttatve Methods & Informaton Systems Tme Seres and Ther Components QMIS 30 Chapter 6 Fall 00 Dr. Mohammad Zanal These sldes were modfed from ther orgnal source for educatonal purpose only.
Department of Quanttatve Methods & Informaton Systems Tme Seres and Ther Components QMIS 30 Chapter 6 Fall 00 Dr. Mohammad Zanal These sldes were modfed from ther orgnal source for educatonal purpose only.
Lecture 9: Linear regression: centering, hypothesis testing, multiple covariates, and confounding
 Lecture 9: Lnear regresson: centerng, hypothess testng, multple covarates, and confoundng Sandy Eckel seckel@jhsph.edu 6 May 008 Recall: man dea of lnear regresson Lnear regresson can be used to study
Lecture 9: Lnear regresson: centerng, hypothess testng, multple covarates, and confoundng Sandy Eckel seckel@jhsph.edu 6 May 008 Recall: man dea of lnear regresson Lnear regresson can be used to study
Statistics for Managers Using Microsoft Excel/SPSS Chapter 13 The Simple Linear Regression Model and Correlation
 Statstcs for Managers Usng Mcrosoft Excel/SPSS Chapter 13 The Smple Lnear Regresson Model and Correlaton 1999 Prentce-Hall, Inc. Chap. 13-1 Chapter Topcs Types of Regresson Models Determnng the Smple Lnear
Statstcs for Managers Usng Mcrosoft Excel/SPSS Chapter 13 The Smple Lnear Regresson Model and Correlaton 1999 Prentce-Hall, Inc. Chap. 13-1 Chapter Topcs Types of Regresson Models Determnng the Smple Lnear
On mutual information estimation for mixed-pair random variables
 On mutual nformaton estmaton for mxed-par random varables November 3, 218 Aleksandr Beknazaryan, Xn Dang and Haln Sang 1 Department of Mathematcs, The Unversty of Msssspp, Unversty, MS 38677, USA. E-mal:
On mutual nformaton estmaton for mxed-par random varables November 3, 218 Aleksandr Beknazaryan, Xn Dang and Haln Sang 1 Department of Mathematcs, The Unversty of Msssspp, Unversty, MS 38677, USA. E-mal:
MATH 281A: Homework #6
 MATH 28A: Homework #6 Jongha Ryu Due date: November 8, 206 Problem. (Problem 2..2. Soluton. If X,..., X n Bern(p, then T = X s a complete suffcent statstc. Our target s g(p = p, and the nave guess suggested
MATH 28A: Homework #6 Jongha Ryu Due date: November 8, 206 Problem. (Problem 2..2. Soluton. If X,..., X n Bern(p, then T = X s a complete suffcent statstc. Our target s g(p = p, and the nave guess suggested
Small Area Interval Estimation
 .. Small Area Interval Estmaton Partha Lahr Jont Program n Survey Methodology Unversty of Maryland, College Park (Based on jont work wth Masayo Yoshmor, Former JPSM Vstng PhD Student and Research Fellow
.. Small Area Interval Estmaton Partha Lahr Jont Program n Survey Methodology Unversty of Maryland, College Park (Based on jont work wth Masayo Yoshmor, Former JPSM Vstng PhD Student and Research Fellow
