CSE 417, Winter Greedy Algorithms
|
|
|
- Noel Fletcher
- 5 years ago
- Views:
Transcription
1 CSE 417, Witer 2012 Greedy Algorithms Be Birbaum Widad Machmouchi Slides adapted from Larry Ruzzo, Steve Taimoto, ad Kevi Waye 1
2 Chapter 4 Greedy Algorithms Slides by Kevi Waye. Copyright 2005 Pearso-Addiso Wesley. All rights reserved. 2
3 4.1 Iterval Schedulig
4 Iterval Schedulig Iterval schedulig. Job j starts at s j ad fiishes at f j. Two jobs compatible if they do't overlap. Goal: fid maximum subset of mutually compatible jobs. a b c d e f g h Time 4
5 Iterval Schedulig: Greedy Algorithms Greedy template. Cosider jobs i some atural order. Take each job provided it's compatible with the oes already take. [Earliest start time] Cosider jobs i ascedig order of s j. [Earliest fiish time] Cosider jobs i ascedig order of f j. [Shortest iterval] Cosider jobs i ascedig order of f j - s j. [Fewest coflicts] For each job j, cout the umber of coflictig jobs c j. Schedule i ascedig order of c j. 5
6 Iterval Schedulig: Greedy Algorithms Greedy template. Cosider jobs i some atural order. Take each job provided it's compatible with the oes already take. couterexample for earliest start time couterexample for shortest iterval couterexample for fewest coflicts 6
7 Iterval Schedulig: Greedy Algorithm Greedy algorithm. Cosider jobs i icreasig order of fiish time. Take each job provided it's compatible with the oes already take. Sort jobs by fiish times so that f 1 f 2... f. set of jobs selected A φ for j = 1 to { if (job j compatible with A) A A {j} } retur A Implemetatio. O( log ). Remember job j* that was added last to A. Job j is compatible with A if s j f j*. 7
8 Iterval Schedulig: Aalysis Theorem. Greedy algorithm is optimal. Pf. (by cotradictio) Assume greedy is ot optimal, ad let's see what happes. Let i 1, i 2,... i k deote set of jobs selected by greedy. Let j 1, j 2,... j m deote set of jobs i the optimal solutio with i 1 = j 1, i 2 = j 2,..., i r = j r for the largest possible value of r. job i r+1 fiishes before j r+1 Greedy: i 1 i 2 i r i r+1 OPT: j 1 j 2 j r j r+1... why ot replace job j r+1 with job i r+1? 8
9 Iterval Schedulig: Aalysis Theorem. Greedy algorithm is optimal. Pf. (by cotradictio) Assume greedy is ot optimal, ad let's see what happes. Let i 1, i 2,... i k deote set of jobs selected by greedy. Let j 1, j 2,... j m deote set of jobs i the optimal solutio with i 1 = j 1, i 2 = j 2,..., i r = j r for the largest possible value of r. job i r+1 fiishes before j r+1 Greedy: i 1 i 2 i r i r+1 OPT: j 1 j 2 j r i r+1... solutio still feasible ad optimal, but cotradicts maximality of r. 9
10 4.1 Iterval Partitioig
11 Iterval Partitioig Iterval partitioig. Lecture j starts at s j ad fiishes at f j. Goal: fid miimum umber of classrooms to schedule all lectures so that o two occur at the same time i the same room. Ex: This schedule uses 4 classrooms to schedule 10 lectures. 4 e j 3 c d g 2 b h 1 a f i 9 9: : : :30 1 1:30 2 2:30 3 3:30 4 4:30 Time 11
12 Iterval Partitioig Iterval partitioig. Lecture j starts at s j ad fiishes at f j. Goal: fid miimum umber of classrooms to schedule all lectures so that o two occur at the same time i the same room. Ex: This schedule uses oly 3. 3 c d f j 2 b g i 1 a e h 9 9: : : :30 1 1:30 2 2:30 3 3:30 4 4:30 Time 12
13 Iterval Partitioig: Lower Boud o Optimal Solutio Def. The depth of a set of ope itervals is the maximum umber that cotai ay give time. Key observatio. Number of classrooms eeded depth. Ex: Depth of schedule below = 3 schedule below is optimal. a, b, c all cotai 9:30 Q. Does there always exist a schedule equal to depth of itervals? 3 c d f j 2 b g i 1 a e h 9 9: : : :30 1 1:30 2 2:30 3 3:30 4 4:30 Time 13
14 Iterval Partitioig: Greedy Algorithm Greedy algorithm. Cosider lectures i icreasig order of start time: assig lecture to ay compatible classroom. Sort itervals by startig time so that s 1 s 2... s. d 0 umber of allocated classrooms for j = 1 to { if (lecture j is compatible with some classroom k) schedule lecture j i classroom k else allocate a ew classroom d + 1 schedule lecture j i classroom d + 1 d d + 1 } Implemetatio. O( log ). For each classroom k, maitai the fiish time of the last job added. Keep the classrooms i a priority queue. 14
15 Iterval Partitioig: Greedy Aalysis Observatio. Greedy algorithm ever schedules two icompatible lectures i the same classroom. Theorem. Greedy algorithm is optimal. Pf. Let d = umber of classrooms that the greedy algorithm allocates. Classroom d is opeed because we eeded to schedule a job, say j, that is icompatible with all d-1 other classrooms. These d jobs each ed after s j. Sice we sorted by start time, all these icompatibilities are caused by lectures that start o later tha s j. Thus, we have d lectures overlappig at time s j + ε. Key observatio all schedules use d classrooms. 15
16 4.2 Schedulig to Miimize Lateess
17 Schedulig to Miimizig Lateess Miimizig lateess problem. Sigle resource processes oe job at a time. Job j requires t j uits of processig time ad is due at time d j. If j starts at time s j, it fiishes at time f j = s j + t j. Lateess: l j = max { 0, f j - d j }. Goal: schedule all jobs to miimize maximum lateess L = max l j. Ex: t j d j lateess = 2 lateess = 0 max lateess = 6 d 3 = 9 d 2 = 8 d 6 = 15 d 1 = 6 d 5 = 14 d 4 =
18 Miimizig Lateess: Greedy Algorithms Greedy template. Cosider jobs i some order. [Shortest processig time first] Cosider jobs i ascedig order of processig time t j. [Earliest deadlie first] Cosider jobs i ascedig order of deadlie d j. [Smallest slack] Cosider jobs i ascedig order of slack d j - t j. 18
19 Miimizig Lateess: Greedy Algorithms Greedy template. Cosider jobs i some order. [Shortest processig time first] Cosider jobs i ascedig order of processig time t j. d j 1 t j couterexample [Smallest slack] Cosider jobs i ascedig order of slack d j - t j. 1 t j 1 2 d j couterexample 19
20 Miimizig Lateess: Greedy Algorithm Greedy algorithm. Earliest deadlie first. Sort jobs by deadlie so that d 1 d 2 d t 0 for j = 1 to Assig job j to iterval [t, t + t j ] s j t, f j t + t j t t + t j output itervals [s j, f j ] max lateess = 1 d 1 = 6 d 2 = 8 d 3 = 9 d 4 = 9 d 5 = 14 d 6 =
21 Miimizig Lateess: No Idle Time Observatio. There exists a optimal schedule with o idle time. d = 4 d = d = d = 4 d = 6 d = Observatio. The greedy schedule has o idle time. 21
22 Miimizig Lateess: Iversios Def. Give a schedule S, a iversio is a pair of jobs i ad j such that: i < j but j scheduled before i. iversio f i before swap j i [ as before, we assume jobs are umbered so that d 1 d 2 d ] Observatio. Greedy schedule has o iversios. Observatio. If a schedule (with o idle time) has a iversio, it has oe with a pair of iverted jobs scheduled cosecutively. 22
23 Miimizig Lateess: Iversios Def. Give a schedule S, a iversio is a pair of jobs i ad j such that: i < j but j scheduled before i. iversio f i before swap j i after swap i j f' j Claim. Swappig two cosecutive, iverted jobs reduces the umber of iversios by oe ad does ot icrease the max lateess. Pf. Let l be the lateess before the swap, ad let l ' be it afterwards. l ' k = l k for all k i, j l ' i l i If job j is late: l j = f j d j (defiitio) = f i d j ( j fiishes at time f i ) f i d i (i < j) l i (defiitio) 23
24 Miimizig Lateess: Aalysis of Greedy Algorithm Theorem. Greedy schedule S is optimal. Pf. Defie S* to be a optimal schedule that has the fewest umber of iversios, ad let's see what happes. Ca assume S* has o idle time. If S* has o iversios, the S = S*. If S* has a iversio, let i-j be a adjacet iversio. swappig i ad j does ot icrease the maximum lateess ad strictly decreases the umber of iversios this cotradicts defiitio of S* 24
25 Greedy Aalysis Strategies Greedy algorithm stays ahead. Show that after each step of the greedy algorithm, its solutio is at least as good as ay other algorithm's. Structural. Discover a simple "structural" boud assertig that every possible solutio must have a certai value. The show that your algorithm always achieves this boud. Exchage argumet. Gradually trasform ay solutio to the oe foud by the greedy algorithm without hurtig its quality. Other greedy algorithms. Kruskal, Prim, Dijkstra, Huffma, 25
26 4.5 Miimum Spaig Tree
27 Miimum Spaig Tree Miimum spaig tree. Give a coected graph G = (V, E) with realvalued edge weights c e, a MST is a subset of the edges T E such that T is a spaig tree whose sum of edge weights is miimized G = (V, E) T, Σ e T c e = 50 Cayley's Theorem. There are -2 spaig trees of K. ca't solve by brute force 27
28 Applicatios MST is fudametal problem with diverse applicatios. Network desig. telephoe, electrical, hydraulic, TV cable, computer, road Approximatio algorithms for NP-hard problems. travelig salesperso problem, Steier tree Idirect applicatios. max bottleeck paths LDPC codes for error correctio image registratio with Reyi etropy learig saliet features for real-time face verificatio reducig data storage i sequecig amio acids i a protei model locality of particle iteractios i turbulet fluid flows autocofig protocol for Etheret bridgig to avoid cycles i a etwork 28
29 Greedy Algorithms Kruskal's algorithm. Start with T = φ. Cosider edges i ascedig order of cost. Isert edge e i T uless doig so would create a cycle. Prim's algorithm. Start with some root ode s ad greedily grow a tree T from s outward. At each step, add the cheapest edge e to T that has exactly oe edpoit i T. Uses the same approach as Dijkistra s algorithm that you ve see before. Remark. All these algorithms produce a MST. 29
30 Greedy Algorithms Simplifyig assumptio. All edge costs c e are distict. Cut property. Let S be ay subset of odes, ad let e be the mi cost edge with exactly oe edpoit i S. The the MST cotais e. Cycle property. Let C be ay cycle, ad let f be the max cost edge belogig to C. The the MST does ot cotai f. f C S e e is i the MST f is ot i the MST 30
31 Cycles ad Cuts Cycle. Set of edges the form a-b, b-c, c-d,, y-z, z-a Cycle C = 1-2, 2-3, 3-4, 4-5, 5-6, Cutset. A cut is a subset of odes S. The correspodig cutset D is the subset of edges with exactly oe edpoit i S Cut S = { 4, 5, 8 } Cutset D = 5-6, 5-7, 3-4, 3-5,
32 Cycle-Cut Itersectio Claim. A cycle ad a cutset itersect i a eve umber of edges Cycle C = 1-2, 2-3, 3-4, 4-5, 5-6, 6-1 Cutset D = 3-4, 3-5, 5-6, 5-7, 7-8 Itersectio = 3-4, Pf. (by picture) C S V - S 32
33 Greedy Algorithms Simplifyig assumptio. All edge costs c e are distict. Cut property. Let S be ay subset of odes, ad let e be the mi cost edge with exactly oe edpoit i S. The the MST T* cotais e. Pf. (exchage argumet) Suppose e does ot belog to T*, ad let's see what happes. Addig e to T* creates a cycle C i T*. Edge e is both i the cycle C ad i the cutset D correspodig to S there exists aother edge, say f, that is i both C ad D. T' = T* { e } - { f } is also a spaig tree. Sice c e < c f, cost(t') < cost(t*). This is a cotradictio. S f e T* 33
34 Greedy Algorithms Simplifyig assumptio. All edge costs c e are distict. Cycle property. Let C be ay cycle i G, ad let f be the max cost edge belogig to C. The the MST T* does ot cotai f. Pf. (exchage argumet) Suppose f belogs to T*, ad let's see what happes. Deletig f from T* creates a cut S i T*. Edge f is both i the cycle C ad i the cutset D correspodig to S there exists aother edge, say e, that is i both C ad D. T' = T* { e } - { f } is also a spaig tree. Sice c e < c f, cost(t') < cost(t*). This is a cotradictio. S f e T* 34
35 Kruskal's Algorithm: Proof of Correctess Kruskal's algorithm. [Kruskal, 1956] Cosider edges i ascedig order of weight. Case 1: If addig e to T creates a cycle, discard e accordig to cycle property. Case 2: Otherwise, isert e = (u, v) ito T accordig to cut property where S = set of odes i u's coected compoet. v e S e u Case 1 Case 2 35
36 Lexicographic Tiebreakig To remove the assumptio that all edge costs are distict: perturb all edge costs by tiy amouts to break ay ties. Impact. Kruskal ad Prim oly iteract with costs via pairwise comparisos. If perturbatios are sufficietly small, MST with perturbed costs is MST with origial costs. e.g., if all edge costs are itegers, perturbig cost of edge e i by i / 2 Implemetatio. Ca hadle arbitrarily small perturbatios implicitly by breakig ties lexicographically, accordig to idex. Ruig Time: O(m log ) 36
37 MST Algorithms: Theory Determiistic compariso based algorithms. O(m log ) [Jarík, Prim, Dijkstra, Kruskal, Boruvka] O(m log log ). [Cherito-Tarja 1976, Yao 1975] O(m β(m, )). [Fredma-Tarja 1987] O(m log β(m, )). [Gabow-Galil-Specer-Tarja 1986] O(m α (m, )). [Chazelle 2000] Holy grail. O(m). Notable. O(m) radomized. [Karger-Klei-Tarja 1995] O(m) verificatio. [Dixo-Rauch-Tarja 1992] Euclidea. 2-d: O( log ). compute MST of edges i Delauay k-d: O(k 2 ). dese Prim 37
CS 580: Algorithm Design and Analysis
 CS 580: Algorithm Design and Analysis Jeremiah Blocki Purdue University Spring 2018 Reminder: Homework 1 due tonight at 11:59PM! Recap: Greedy Algorithms Interval Scheduling Goal: Maximize number of meeting
CS 580: Algorithm Design and Analysis Jeremiah Blocki Purdue University Spring 2018 Reminder: Homework 1 due tonight at 11:59PM! Recap: Greedy Algorithms Interval Scheduling Goal: Maximize number of meeting
Chapter 4. Greedy Algorithms. Slides by Kevin Wayne. Copyright 2005 Pearson-Addison Wesley. All rights reserved.
 Chapter 4 Greedy Algorithms Slides by Kevin Wayne. Copyright 2005 Pearson-Addison Wesley. All rights reserved. 1 4.1 Interval Scheduling Interval Scheduling Interval scheduling. Job j starts at s j and
Chapter 4 Greedy Algorithms Slides by Kevin Wayne. Copyright 2005 Pearson-Addison Wesley. All rights reserved. 1 4.1 Interval Scheduling Interval Scheduling Interval scheduling. Job j starts at s j and
w (1) ˆx w (1) x (1) /ρ and w (2) ˆx w (2) x (2) /ρ.
 2 5. Weighted umber of late jobs 5.1. Release dates ad due dates: maximimizig the weight of o-time jobs Oce we add release dates, miimizig the umber of late jobs becomes a sigificatly harder problem. For
2 5. Weighted umber of late jobs 5.1. Release dates ad due dates: maximimizig the weight of o-time jobs Oce we add release dates, miimizig the umber of late jobs becomes a sigificatly harder problem. For
Solutions for the Exam 9 January 2012
 Mastermath ad LNMB Course: Discrete Optimizatio Solutios for the Exam 9 Jauary 2012 Utrecht Uiversity, Educatorium, 15:15 18:15 The examiatio lasts 3 hours. Gradig will be doe before Jauary 23, 2012. Studets
Mastermath ad LNMB Course: Discrete Optimizatio Solutios for the Exam 9 Jauary 2012 Utrecht Uiversity, Educatorium, 15:15 18:15 The examiatio lasts 3 hours. Gradig will be doe before Jauary 23, 2012. Studets
Algorithm Design and Analysis
 Algorithm Design and Analysis LECTURE 6 Greedy Algorithms Interval Scheduling Interval Partitioning Scheduling to Minimize Lateness Sofya Raskhodnikova S. Raskhodnikova; based on slides by E. Demaine,
Algorithm Design and Analysis LECTURE 6 Greedy Algorithms Interval Scheduling Interval Partitioning Scheduling to Minimize Lateness Sofya Raskhodnikova S. Raskhodnikova; based on slides by E. Demaine,
Chapter 4. Greedy Algorithms. Slides by Kevin Wayne. Copyright 2005 Pearson-Addison Wesley. All rights reserved.
 Chapter 4 Greedy Algorithms Slides by Kevin Wayne. Copyright 2005 Pearson-Addison Wesley. All rights reserved. 1 4.1 Interval Scheduling Interval Scheduling Interval scheduling. Job j starts at s j and
Chapter 4 Greedy Algorithms Slides by Kevin Wayne. Copyright 2005 Pearson-Addison Wesley. All rights reserved. 1 4.1 Interval Scheduling Interval Scheduling Interval scheduling. Job j starts at s j and
Greedy Algorithms. Kleinberg and Tardos, Chapter 4
 Greedy Algorithms Kleinberg and Tardos, Chapter 4 1 Selecting breakpoints Road trip from Fort Collins to Durango on a given route. Fuel capacity = C. Goal: makes as few refueling stops as possible. Greedy
Greedy Algorithms Kleinberg and Tardos, Chapter 4 1 Selecting breakpoints Road trip from Fort Collins to Durango on a given route. Fuel capacity = C. Goal: makes as few refueling stops as possible. Greedy
CS781 Lecture 3 January 27, 2011
 CS781 Lecture 3 January 7, 011 Greedy Algorithms Topics: Interval Scheduling and Partitioning Dijkstra s Shortest Path Algorithm Minimum Spanning Trees Single-Link k-clustering Interval Scheduling Interval
CS781 Lecture 3 January 7, 011 Greedy Algorithms Topics: Interval Scheduling and Partitioning Dijkstra s Shortest Path Algorithm Minimum Spanning Trees Single-Link k-clustering Interval Scheduling Interval
CSE 417. Chapter 4: Greedy Algorithms. Many Slides by Kevin Wayne. Copyright 2005 Pearson-Addison Wesley. All rights reserved.
 CSE 417 Chapter 4: Greedy Algorithms Many Slides by Kevin Wayne. Copyright 2005 Pearson-Addison Wesley. All rights reserved. 1 Greed is good. Greed is right. Greed works. Greed clarifies, cuts through,
CSE 417 Chapter 4: Greedy Algorithms Many Slides by Kevin Wayne. Copyright 2005 Pearson-Addison Wesley. All rights reserved. 1 Greed is good. Greed is right. Greed works. Greed clarifies, cuts through,
CSE 421 Greedy Algorithms / Interval Scheduling
 CSE 421 Greedy Algorithms / Interval Scheduling Yin Tat Lee 1 Interval Scheduling Job j starts at s(j) and finishes at f(j). Two jobs compatible if they don t overlap. Goal: find maximum subset of mutually
CSE 421 Greedy Algorithms / Interval Scheduling Yin Tat Lee 1 Interval Scheduling Job j starts at s(j) and finishes at f(j). Two jobs compatible if they don t overlap. Goal: find maximum subset of mutually
Chapter 4. Greedy Algorithms. Slides by Kevin Wayne. Copyright 2005 Pearson-Addison Wesley. All rights reserved.
 Chapter 4 Greedy Algorithms Slides by Kevin Wayne. Copyright Pearson-Addison Wesley. All rights reserved. 4 4.1 Interval Scheduling Interval Scheduling Interval scheduling. Job j starts at s j and finishes
Chapter 4 Greedy Algorithms Slides by Kevin Wayne. Copyright Pearson-Addison Wesley. All rights reserved. 4 4.1 Interval Scheduling Interval Scheduling Interval scheduling. Job j starts at s j and finishes
Algorithm Design and Analysis
 Algorithm Design and Analysis LECTURE 5 Greedy Algorithms Interval Scheduling Interval Partitioning Guest lecturer: Martin Furer Review In a DFS tree of an undirected graph, can there be an edge (u,v)
Algorithm Design and Analysis LECTURE 5 Greedy Algorithms Interval Scheduling Interval Partitioning Guest lecturer: Martin Furer Review In a DFS tree of an undirected graph, can there be an edge (u,v)
CS / MCS 401 Homework 3 grader solutions
 CS / MCS 401 Homework 3 grader solutios assigmet due July 6, 016 writte by Jāis Lazovskis maximum poits: 33 Some questios from CLRS. Questios marked with a asterisk were ot graded. 1 Use the defiitio of
CS / MCS 401 Homework 3 grader solutios assigmet due July 6, 016 writte by Jāis Lazovskis maximum poits: 33 Some questios from CLRS. Questios marked with a asterisk were ot graded. 1 Use the defiitio of
On Algorithm for the Minimum Spanning Trees Problem with Diameter Bounded Below
 O Algorithm for the Miimum Spaig Trees Problem with Diameter Bouded Below Edward Kh. Gimadi 1,2, Alexey M. Istomi 1, ad Ekateria Yu. Shi 2 1 Sobolev Istitute of Mathematics, 4 Acad. Koptyug aveue, 630090
O Algorithm for the Miimum Spaig Trees Problem with Diameter Bouded Below Edward Kh. Gimadi 1,2, Alexey M. Istomi 1, ad Ekateria Yu. Shi 2 1 Sobolev Istitute of Mathematics, 4 Acad. Koptyug aveue, 630090
Sorting Algorithms. Algorithms Kyuseok Shim SoEECS, SNU.
 Sortig Algorithms Algorithms Kyuseo Shim SoEECS, SNU. Desigig Algorithms Icremetal approaches Divide-ad-Coquer approaches Dyamic programmig approaches Greedy approaches Radomized approaches You are ot
Sortig Algorithms Algorithms Kyuseo Shim SoEECS, SNU. Desigig Algorithms Icremetal approaches Divide-ad-Coquer approaches Dyamic programmig approaches Greedy approaches Radomized approaches You are ot
Analysis of Algorithms. Introduction. Contents
 Itroductio The focus of this module is mathematical aspects of algorithms. Our mai focus is aalysis of algorithms, which meas evaluatig efficiecy of algorithms by aalytical ad mathematical methods. We
Itroductio The focus of this module is mathematical aspects of algorithms. Our mai focus is aalysis of algorithms, which meas evaluatig efficiecy of algorithms by aalytical ad mathematical methods. We
Application to Random Graphs
 A Applicatio to Radom Graphs Brachig processes have a umber of iterestig ad importat applicatios. We shall cosider oe of the most famous of them, the Erdős-Réyi radom graph theory. 1 Defiitio A.1. Let
A Applicatio to Radom Graphs Brachig processes have a umber of iterestig ad importat applicatios. We shall cosider oe of the most famous of them, the Erdős-Réyi radom graph theory. 1 Defiitio A.1. Let
Davenport-Schinzel Sequences and their Geometric Applications
 Advaced Computatioal Geometry Sprig 2004 Daveport-Schizel Sequeces ad their Geometric Applicatios Prof. Joseph Mitchell Scribe: Mohit Gupta 1 Overview I this lecture, we itroduce the cocept of Daveport-Schizel
Advaced Computatioal Geometry Sprig 2004 Daveport-Schizel Sequeces ad their Geometric Applicatios Prof. Joseph Mitchell Scribe: Mohit Gupta 1 Overview I this lecture, we itroduce the cocept of Daveport-Schizel
Optimization Methods: Linear Programming Applications Assignment Problem 1. Module 4 Lecture Notes 3. Assignment Problem
 Optimizatio Methods: Liear Programmig Applicatios Assigmet Problem Itroductio Module 4 Lecture Notes 3 Assigmet Problem I the previous lecture, we discussed about oe of the bech mark problems called trasportatio
Optimizatio Methods: Liear Programmig Applicatios Assigmet Problem Itroductio Module 4 Lecture Notes 3 Assigmet Problem I the previous lecture, we discussed about oe of the bech mark problems called trasportatio
CS 580: Algorithm Design and Analysis
 CS 580: Algorithm Design and Analysis Jeremiah Blocki Purdue University Spring 2018 Announcement: Homework 1 due soon! Due: January 25 th at midnight (Blackboard) Recap: Graphs Bipartite Graphs Definition
CS 580: Algorithm Design and Analysis Jeremiah Blocki Purdue University Spring 2018 Announcement: Homework 1 due soon! Due: January 25 th at midnight (Blackboard) Recap: Graphs Bipartite Graphs Definition
ACO Comprehensive Exam 9 October 2007 Student code A. 1. Graph Theory
 1. Graph Theory Prove that there exist o simple plaar triagulatio T ad two distict adjacet vertices x, y V (T ) such that x ad y are the oly vertices of T of odd degree. Do ot use the Four-Color Theorem.
1. Graph Theory Prove that there exist o simple plaar triagulatio T ad two distict adjacet vertices x, y V (T ) such that x ad y are the oly vertices of T of odd degree. Do ot use the Four-Color Theorem.
Skip Lists. Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015 S 3 S S 1
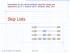 Presetatio for use with the textbook, Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 2015 Skip Lists S 3 15 15 23 10 15 23 36 Skip Lists 1 What is a Skip List A skip list for
Presetatio for use with the textbook, Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 2015 Skip Lists S 3 15 15 23 10 15 23 36 Skip Lists 1 What is a Skip List A skip list for
(A sequence also can be thought of as the list of function values attained for a function f :ℵ X, where f (n) = x n for n 1.) x 1 x N +k x N +4 x 3
 MATH 337 Sequeces Dr. Neal, WKU Let X be a metric space with distace fuctio d. We shall defie the geeral cocept of sequece ad limit i a metric space, the apply the results i particular to some special
MATH 337 Sequeces Dr. Neal, WKU Let X be a metric space with distace fuctio d. We shall defie the geeral cocept of sequece ad limit i a metric space, the apply the results i particular to some special
Optimization Methods MIT 2.098/6.255/ Final exam
 Optimizatio Methods MIT 2.098/6.255/15.093 Fial exam Date Give: December 19th, 2006 P1. [30 pts] Classify the followig statemets as true or false. All aswers must be well-justified, either through a short
Optimizatio Methods MIT 2.098/6.255/15.093 Fial exam Date Give: December 19th, 2006 P1. [30 pts] Classify the followig statemets as true or false. All aswers must be well-justified, either through a short
Disjoint set (Union-Find)
 CS124 Lecture 7 Fall 2018 Disjoit set (Uio-Fid) For Kruskal s algorithm for the miimum spaig tree problem, we foud that we eeded a data structure for maitaiig a collectio of disjoit sets. That is, we eed
CS124 Lecture 7 Fall 2018 Disjoit set (Uio-Fid) For Kruskal s algorithm for the miimum spaig tree problem, we foud that we eeded a data structure for maitaiig a collectio of disjoit sets. That is, we eed
CHAPTER 2 NEIGHBORHOOD CONNECTED PERFECT DOMINATION IN GRAPHS
 22 CHAPTER 2 NEIGHBORHOOD CONNECTED PERFECT DOMINATION IN GRAPHS 2.1 INTRODUCTION Various types of domiatio have bee studied by several authors ad more tha 75 models of domiatio are listed i the appedix
22 CHAPTER 2 NEIGHBORHOOD CONNECTED PERFECT DOMINATION IN GRAPHS 2.1 INTRODUCTION Various types of domiatio have bee studied by several authors ad more tha 75 models of domiatio are listed i the appedix
Advanced Analysis. Min Yan Department of Mathematics Hong Kong University of Science and Technology
 Advaced Aalysis Mi Ya Departmet of Mathematics Hog Kog Uiversity of Sciece ad Techology September 3, 009 Cotets Limit ad Cotiuity 7 Limit of Sequece 8 Defiitio 8 Property 3 3 Ifiity ad Ifiitesimal 8 4
Advaced Aalysis Mi Ya Departmet of Mathematics Hog Kog Uiversity of Sciece ad Techology September 3, 009 Cotets Limit ad Cotiuity 7 Limit of Sequece 8 Defiitio 8 Property 3 3 Ifiity ad Ifiitesimal 8 4
Design and Analysis of ALGORITHM (Topic 2)
 DR. Gatot F. Hertoo, MSc. Desig ad Aalysis of ALGORITHM (Topic 2) Algorithms + Data Structures = Programs Lessos Leared 1 Our Machie Model: Assumptios Geeric Radom Access Machie (RAM) Executes operatios
DR. Gatot F. Hertoo, MSc. Desig ad Aalysis of ALGORITHM (Topic 2) Algorithms + Data Structures = Programs Lessos Leared 1 Our Machie Model: Assumptios Geeric Radom Access Machie (RAM) Executes operatios
Lecture 14: Graph Entropy
 15-859: Iformatio Theory ad Applicatios i TCS Sprig 2013 Lecture 14: Graph Etropy March 19, 2013 Lecturer: Mahdi Cheraghchi Scribe: Euiwoog Lee 1 Recap Bergma s boud o the permaet Shearer s Lemma Number
15-859: Iformatio Theory ad Applicatios i TCS Sprig 2013 Lecture 14: Graph Etropy March 19, 2013 Lecturer: Mahdi Cheraghchi Scribe: Euiwoog Lee 1 Recap Bergma s boud o the permaet Shearer s Lemma Number
PARETO-OPTIMAL SOLUTION OF A SCHEDULING PROBLEM ON A SINGLE MACHINE WITH PERIODIC MAINTENANCE AND NON-PRE-EMPTIVE JOBS
 Proceedigs of the Iteratioal Coferece o Mechaical Egieerig 2007 (ICME2007) 2-3 December 2007, Dhaka, Bagladesh ICME07-AM-6 PARETO-OPTIMAL SOLUTION OF A SCHEDULING PROBLEM ON A SINGLE MACHINE WITH PERIODIC
Proceedigs of the Iteratioal Coferece o Mechaical Egieerig 2007 (ICME2007) 2-3 December 2007, Dhaka, Bagladesh ICME07-AM-6 PARETO-OPTIMAL SOLUTION OF A SCHEDULING PROBLEM ON A SINGLE MACHINE WITH PERIODIC
Math 220A Fall 2007 Homework #2. Will Garner A
 Math 0A Fall 007 Homewor # Will Garer Pg 3 #: Show that {cis : a o-egative iteger} is dese i T = {z œ : z = }. For which values of q is {cis(q): a o-egative iteger} dese i T? To show that {cis : a o-egative
Math 0A Fall 007 Homewor # Will Garer Pg 3 #: Show that {cis : a o-egative iteger} is dese i T = {z œ : z = }. For which values of q is {cis(q): a o-egative iteger} dese i T? To show that {cis : a o-egative
MA131 - Analysis 1. Workbook 3 Sequences II
 MA3 - Aalysis Workbook 3 Sequeces II Autum 2004 Cotets 2.8 Coverget Sequeces........................ 2.9 Algebra of Limits......................... 2 2.0 Further Useful Results........................
MA3 - Aalysis Workbook 3 Sequeces II Autum 2004 Cotets 2.8 Coverget Sequeces........................ 2.9 Algebra of Limits......................... 2 2.0 Further Useful Results........................
Disjoint Systems. Abstract
 Disjoit Systems Noga Alo ad Bey Sudaov Departmet of Mathematics Raymod ad Beverly Sacler Faculty of Exact Scieces Tel Aviv Uiversity, Tel Aviv, Israel Abstract A disjoit system of type (,,, ) is a collectio
Disjoit Systems Noga Alo ad Bey Sudaov Departmet of Mathematics Raymod ad Beverly Sacler Faculty of Exact Scieces Tel Aviv Uiversity, Tel Aviv, Israel Abstract A disjoit system of type (,,, ) is a collectio
CSE 202 Homework 1 Matthias Springer, A Yes, there does always exist a perfect matching without a strong instability.
 CSE 0 Homework 1 Matthias Spriger, A9950078 1 Problem 1 Notatio a b meas that a is matched to b. a < b c meas that b likes c more tha a. Equality idicates a tie. Strog istability Yes, there does always
CSE 0 Homework 1 Matthias Spriger, A9950078 1 Problem 1 Notatio a b meas that a is matched to b. a < b c meas that b likes c more tha a. Equality idicates a tie. Strog istability Yes, there does always
Optimally Sparse SVMs
 A. Proof of Lemma 3. We here prove a lower boud o the umber of support vectors to achieve geeralizatio bouds of the form which we cosider. Importatly, this result holds ot oly for liear classifiers, but
A. Proof of Lemma 3. We here prove a lower boud o the umber of support vectors to achieve geeralizatio bouds of the form which we cosider. Importatly, this result holds ot oly for liear classifiers, but
4/9/13. Fibonacci Heaps. H.min. H.min. Priority Queues Performance Cost Summary. COMP 160 Algorithms - Tufts University
 4/9/ Priority Queues Performace Cost Summary Fiboacci Heas Oeratio Liked List Biary Hea Biomial Hea Fiboacci Hea Relaed Hea make-hea COMP 60 Algorithms - Tufts Uiversity is-emty isert Origial Slides from
4/9/ Priority Queues Performace Cost Summary Fiboacci Heas Oeratio Liked List Biary Hea Biomial Hea Fiboacci Hea Relaed Hea make-hea COMP 60 Algorithms - Tufts Uiversity is-emty isert Origial Slides from
Matrix Multiplication. Data Structures and Algorithms Andrei Bulatov
 Matrix Multiplicatio Data Structures ad Algorithms Adrei Bulatov Algorithms Matrix Multiplicatio 7- Matrix Multiplicatio Matrix multiplicatio. Give two -by- matrices A ad B, compute A B. k kj ik ij b a
Matrix Multiplicatio Data Structures ad Algorithms Adrei Bulatov Algorithms Matrix Multiplicatio 7- Matrix Multiplicatio Matrix multiplicatio. Give two -by- matrices A ad B, compute A B. k kj ik ij b a
page Suppose that S 0, 1 1, 2.
 page 10 1. Suppose that S 0, 1 1,. a. What is the set of iterior poits of S? The set of iterior poits of S is 0, 1 1,. b. Give that U is the set of iterior poits of S, evaluate U. 0, 1 1, 0, 1 1, S. The
page 10 1. Suppose that S 0, 1 1,. a. What is the set of iterior poits of S? The set of iterior poits of S is 0, 1 1,. b. Give that U is the set of iterior poits of S, evaluate U. 0, 1 1, 0, 1 1, S. The
Math 61CM - Solutions to homework 3
 Math 6CM - Solutios to homework 3 Cédric De Groote October 2 th, 208 Problem : Let F be a field, m 0 a fixed oegative iteger ad let V = {a 0 + a x + + a m x m a 0,, a m F} be the vector space cosistig
Math 6CM - Solutios to homework 3 Cédric De Groote October 2 th, 208 Problem : Let F be a field, m 0 a fixed oegative iteger ad let V = {a 0 + a x + + a m x m a 0,, a m F} be the vector space cosistig
4.3 Growth Rates of Solutions to Recurrences
 4.3. GROWTH RATES OF SOLUTIONS TO RECURRENCES 81 4.3 Growth Rates of Solutios to Recurreces 4.3.1 Divide ad Coquer Algorithms Oe of the most basic ad powerful algorithmic techiques is divide ad coquer.
4.3. GROWTH RATES OF SOLUTIONS TO RECURRENCES 81 4.3 Growth Rates of Solutios to Recurreces 4.3.1 Divide ad Coquer Algorithms Oe of the most basic ad powerful algorithmic techiques is divide ad coquer.
CS 332: Algorithms. Linear-Time Sorting. Order statistics. Slide credit: David Luebke (Virginia)
 1 CS 332: Algorithms Liear-Time Sortig. Order statistics. Slide credit: David Luebke (Virgiia) Quicksort: Partitio I Words Partitio(A, p, r): Select a elemet to act as the pivot (which?) Grow two regios,
1 CS 332: Algorithms Liear-Time Sortig. Order statistics. Slide credit: David Luebke (Virgiia) Quicksort: Partitio I Words Partitio(A, p, r): Select a elemet to act as the pivot (which?) Grow two regios,
Problem Set 2 Solutions
 CS271 Radomess & Computatio, Sprig 2018 Problem Set 2 Solutios Poit totals are i the margi; the maximum total umber of poits was 52. 1. Probabilistic method for domiatig sets 6pts Pick a radom subset S
CS271 Radomess & Computatio, Sprig 2018 Problem Set 2 Solutios Poit totals are i the margi; the maximum total umber of poits was 52. 1. Probabilistic method for domiatig sets 6pts Pick a radom subset S
A sequence of numbers is a function whose domain is the positive integers. We can see that the sequence
 Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece,, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet as
Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece,, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet as
Sequences A sequence of numbers is a function whose domain is the positive integers. We can see that the sequence
 Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece 1, 1, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet
Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece 1, 1, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet
Linear chord diagrams with long chords
 Liear chord diagrams with log chords Everett Sulliva Departmet of Mathematics Dartmouth College Haover New Hampshire, U.S.A. everett..sulliva@dartmouth.edu Submitted: Feb 7, 2017; Accepted: Oct 7, 2017;
Liear chord diagrams with log chords Everett Sulliva Departmet of Mathematics Dartmouth College Haover New Hampshire, U.S.A. everett..sulliva@dartmouth.edu Submitted: Feb 7, 2017; Accepted: Oct 7, 2017;
MA131 - Analysis 1. Workbook 2 Sequences I
 MA3 - Aalysis Workbook 2 Sequeces I Autum 203 Cotets 2 Sequeces I 2. Itroductio.............................. 2.2 Icreasig ad Decreasig Sequeces................ 2 2.3 Bouded Sequeces..........................
MA3 - Aalysis Workbook 2 Sequeces I Autum 203 Cotets 2 Sequeces I 2. Itroductio.............................. 2.2 Icreasig ad Decreasig Sequeces................ 2 2.3 Bouded Sequeces..........................
2. ALGORITHM ANALYSIS
 2. ALGORITHM ANALYSIS computatioal tractability survey of commo ruig times 2. ALGORITHM ANALYSIS computatioal tractability survey of commo ruig times Lecture slides by Kevi Waye Copyright 2005 Pearso-Addiso
2. ALGORITHM ANALYSIS computatioal tractability survey of commo ruig times 2. ALGORITHM ANALYSIS computatioal tractability survey of commo ruig times Lecture slides by Kevi Waye Copyright 2005 Pearso-Addiso
Sequences I. Chapter Introduction
 Chapter 2 Sequeces I 2. Itroductio A sequece is a list of umbers i a defiite order so that we kow which umber is i the first place, which umber is i the secod place ad, for ay atural umber, we kow which
Chapter 2 Sequeces I 2. Itroductio A sequece is a list of umbers i a defiite order so that we kow which umber is i the first place, which umber is i the secod place ad, for ay atural umber, we kow which
# fixed points of g. Tree to string. Repeatedly select the leaf with the smallest label, write down the label of its neighbour and remove the leaf.
 Combiatorics Graph Theory Coutig labelled ad ulabelled graphs There are 2 ( 2) labelled graphs of order. The ulabelled graphs of order correspod to orbits of the actio of S o the set of labelled graphs.
Combiatorics Graph Theory Coutig labelled ad ulabelled graphs There are 2 ( 2) labelled graphs of order. The ulabelled graphs of order correspod to orbits of the actio of S o the set of labelled graphs.
62. Power series Definition 16. (Power series) Given a sequence {c n }, the series. c n x n = c 0 + c 1 x + c 2 x 2 + c 3 x 3 +
 62. Power series Defiitio 16. (Power series) Give a sequece {c }, the series c x = c 0 + c 1 x + c 2 x 2 + c 3 x 3 + is called a power series i the variable x. The umbers c are called the coefficiets of
62. Power series Defiitio 16. (Power series) Give a sequece {c }, the series c x = c 0 + c 1 x + c 2 x 2 + c 3 x 3 + is called a power series i the variable x. The umbers c are called the coefficiets of
Algebra of Least Squares
 October 19, 2018 Algebra of Least Squares Geometry of Least Squares Recall that out data is like a table [Y X] where Y collects observatios o the depedet variable Y ad X collects observatios o the k-dimesioal
October 19, 2018 Algebra of Least Squares Geometry of Least Squares Recall that out data is like a table [Y X] where Y collects observatios o the depedet variable Y ad X collects observatios o the k-dimesioal
Infinite Sequences and Series
 Chapter 6 Ifiite Sequeces ad Series 6.1 Ifiite Sequeces 6.1.1 Elemetary Cocepts Simply speakig, a sequece is a ordered list of umbers writte: {a 1, a 2, a 3,...a, a +1,...} where the elemets a i represet
Chapter 6 Ifiite Sequeces ad Series 6.1 Ifiite Sequeces 6.1.1 Elemetary Cocepts Simply speakig, a sequece is a ordered list of umbers writte: {a 1, a 2, a 3,...a, a +1,...} where the elemets a i represet
DATA STRUCTURES I, II, III, AND IV
 Data structures DATA STRUCTURES I, II, III, AND IV I. Amortized Aalysis II. Biary ad Biomial Heaps III. Fiboacci Heaps IV. Uio Fid Static problems. Give a iput, produce a output. Ex. Sortig, FFT, edit
Data structures DATA STRUCTURES I, II, III, AND IV I. Amortized Aalysis II. Biary ad Biomial Heaps III. Fiboacci Heaps IV. Uio Fid Static problems. Give a iput, produce a output. Ex. Sortig, FFT, edit
Linear regression. Daniel Hsu (COMS 4771) (y i x T i β)2 2πσ. 2 2σ 2. 1 n. (x T i β y i ) 2. 1 ˆβ arg min. β R n d
 Liear regressio Daiel Hsu (COMS 477) Maximum likelihood estimatio Oe of the simplest liear regressio models is the followig: (X, Y ),..., (X, Y ), (X, Y ) are iid radom pairs takig values i R d R, ad Y
Liear regressio Daiel Hsu (COMS 477) Maximum likelihood estimatio Oe of the simplest liear regressio models is the followig: (X, Y ),..., (X, Y ), (X, Y ) are iid radom pairs takig values i R d R, ad Y
Solutions. tan 2 θ(tan 2 θ + 1) = cot6 θ,
 Solutios 99. Let A ad B be two poits o a parabola with vertex V such that V A is perpedicular to V B ad θ is the agle betwee the chord V A ad the axis of the parabola. Prove that V A V B cot3 θ. Commet.
Solutios 99. Let A ad B be two poits o a parabola with vertex V such that V A is perpedicular to V B ad θ is the agle betwee the chord V A ad the axis of the parabola. Prove that V A V B cot3 θ. Commet.
Definitions and Theorems. where x are the decision variables. c, b, and a are constant coefficients.
 Defiitios ad Theorems Remember the scalar form of the liear programmig problem, Miimize, Subject to, f(x) = c i x i a 1i x i = b 1 a mi x i = b m x i 0 i = 1,2,, where x are the decisio variables. c, b,
Defiitios ad Theorems Remember the scalar form of the liear programmig problem, Miimize, Subject to, f(x) = c i x i a 1i x i = b 1 a mi x i = b m x i 0 i = 1,2,, where x are the decisio variables. c, b,
If a subset E of R contains no open interval, is it of zero measure? For instance, is the set of irrationals in [0, 1] is of measure zero?
![If a subset E of R contains no open interval, is it of zero measure? For instance, is the set of irrationals in [0, 1] is of measure zero? If a subset E of R contains no open interval, is it of zero measure? For instance, is the set of irrationals in [0, 1] is of measure zero?](/thumbs/89/99848926.jpg) 2 Lebesgue Measure I Chapter 1 we defied the cocept of a set of measure zero, ad we have observed that every coutable set is of measure zero. Here are some atural questios: If a subset E of R cotais a
2 Lebesgue Measure I Chapter 1 we defied the cocept of a set of measure zero, ad we have observed that every coutable set is of measure zero. Here are some atural questios: If a subset E of R cotais a
Bertrand s Postulate
 Bertrad s Postulate Lola Thompso Ross Program July 3, 2009 Lola Thompso (Ross Program Bertrad s Postulate July 3, 2009 1 / 33 Bertrad s Postulate I ve said it oce ad I ll say it agai: There s always a
Bertrad s Postulate Lola Thompso Ross Program July 3, 2009 Lola Thompso (Ross Program Bertrad s Postulate July 3, 2009 1 / 33 Bertrad s Postulate I ve said it oce ad I ll say it agai: There s always a
CSE 4095/5095 Topics in Big Data Analytics Spring 2017; Homework 1 Solutions
 CSE 09/09 Topics i ig Data Aalytics Sprig 2017; Homework 1 Solutios Note: Solutios to problems,, ad 6 are due to Marius Nicolae. 1. Cosider the followig algorithm: for i := 1 to α log e do Pick a radom
CSE 09/09 Topics i ig Data Aalytics Sprig 2017; Homework 1 Solutios Note: Solutios to problems,, ad 6 are due to Marius Nicolae. 1. Cosider the followig algorithm: for i := 1 to α log e do Pick a radom
Square-Congruence Modulo n
 Square-Cogruece Modulo Abstract This paper is a ivestigatio of a equivalece relatio o the itegers that was itroduced as a exercise i our Discrete Math class. Part I - Itro Defiitio Two itegers are Square-Cogruet
Square-Cogruece Modulo Abstract This paper is a ivestigatio of a equivalece relatio o the itegers that was itroduced as a exercise i our Discrete Math class. Part I - Itro Defiitio Two itegers are Square-Cogruet
6.3 Testing Series With Positive Terms
 6.3. TESTING SERIES WITH POSITIVE TERMS 307 6.3 Testig Series With Positive Terms 6.3. Review of what is kow up to ow I theory, testig a series a i for covergece amouts to fidig the i= sequece of partial
6.3. TESTING SERIES WITH POSITIVE TERMS 307 6.3 Testig Series With Positive Terms 6.3. Review of what is kow up to ow I theory, testig a series a i for covergece amouts to fidig the i= sequece of partial
Applications of Yao s Minimax Principle
 Applicatios of Yao s Miimax Priciple Game Tree evaluatio We study the problem of evaluatig a game tree, which is a rooted tree of the type T d,k, where the root ad every iteral ode (i.e. all odes except
Applicatios of Yao s Miimax Priciple Game Tree evaluatio We study the problem of evaluatig a game tree, which is a rooted tree of the type T d,k, where the root ad every iteral ode (i.e. all odes except
Seunghee Ye Ma 8: Week 5 Oct 28
 Week 5 Summary I Sectio, we go over the Mea Value Theorem ad its applicatios. I Sectio 2, we will recap what we have covered so far this term. Topics Page Mea Value Theorem. Applicatios of the Mea Value
Week 5 Summary I Sectio, we go over the Mea Value Theorem ad its applicatios. I Sectio 2, we will recap what we have covered so far this term. Topics Page Mea Value Theorem. Applicatios of the Mea Value
NICK DUFRESNE. 1 1 p(x). To determine some formulas for the generating function of the Schröder numbers, r(x) = a(x) =
 AN INTRODUCTION TO SCHRÖDER AND UNKNOWN NUMBERS NICK DUFRESNE Abstract. I this article we will itroduce two types of lattice paths, Schröder paths ad Ukow paths. We will examie differet properties of each,
AN INTRODUCTION TO SCHRÖDER AND UNKNOWN NUMBERS NICK DUFRESNE Abstract. I this article we will itroduce two types of lattice paths, Schröder paths ad Ukow paths. We will examie differet properties of each,
Riemann Sums y = f (x)
 Riema Sums Recall that we have previously discussed the area problem I its simplest form we ca state it this way: The Area Problem Let f be a cotiuous, o-egative fuctio o the closed iterval [a, b] Fid
Riema Sums Recall that we have previously discussed the area problem I its simplest form we ca state it this way: The Area Problem Let f be a cotiuous, o-egative fuctio o the closed iterval [a, b] Fid
Some special clique problems
 Some special clique problems Reate Witer Istitut für Iformatik Marti-Luther-Uiversität Halle-Witteberg Vo-Seckedorff-Platz, D 0620 Halle Saale Germay Abstract: We cosider graphs with cliques of size k
Some special clique problems Reate Witer Istitut für Iformatik Marti-Luther-Uiversität Halle-Witteberg Vo-Seckedorff-Platz, D 0620 Halle Saale Germay Abstract: We cosider graphs with cliques of size k
Complex Numbers Solutions
 Complex Numbers Solutios Joseph Zoller February 7, 06 Solutios. (009 AIME I Problem ) There is a complex umber with imagiary part 64 ad a positive iteger such that Fid. [Solutio: 697] 4i + + 4i. 4i 4i
Complex Numbers Solutios Joseph Zoller February 7, 06 Solutios. (009 AIME I Problem ) There is a complex umber with imagiary part 64 ad a positive iteger such that Fid. [Solutio: 697] 4i + + 4i. 4i 4i
BI-INDUCED SUBGRAPHS AND STABILITY NUMBER *
 Yugoslav Joural of Operatios Research 14 (2004), Number 1, 27-32 BI-INDUCED SUBGRAPHS AND STABILITY NUMBER * I E ZVEROVICH, O I ZVEROVICH RUTCOR Rutgers Ceter for Operatios Research, Rutgers Uiversity,
Yugoslav Joural of Operatios Research 14 (2004), Number 1, 27-32 BI-INDUCED SUBGRAPHS AND STABILITY NUMBER * I E ZVEROVICH, O I ZVEROVICH RUTCOR Rutgers Ceter for Operatios Research, Rutgers Uiversity,
CHAPTER 10 INFINITE SEQUENCES AND SERIES
 CHAPTER 10 INFINITE SEQUENCES AND SERIES 10.1 Sequeces 10.2 Ifiite Series 10.3 The Itegral Tests 10.4 Compariso Tests 10.5 The Ratio ad Root Tests 10.6 Alteratig Series: Absolute ad Coditioal Covergece
CHAPTER 10 INFINITE SEQUENCES AND SERIES 10.1 Sequeces 10.2 Ifiite Series 10.3 The Itegral Tests 10.4 Compariso Tests 10.5 The Ratio ad Root Tests 10.6 Alteratig Series: Absolute ad Coditioal Covergece
Section 5.1 The Basics of Counting
 1 Sectio 5.1 The Basics of Coutig Combiatorics, the study of arragemets of objects, is a importat part of discrete mathematics. I this chapter, we will lear basic techiques of coutig which has a lot of
1 Sectio 5.1 The Basics of Coutig Combiatorics, the study of arragemets of objects, is a importat part of discrete mathematics. I this chapter, we will lear basic techiques of coutig which has a lot of
Linear Programming! References! Introduction to Algorithms.! Dasgupta, Papadimitriou, Vazirani. Algorithms.! Cormen, Leiserson, Rivest, and Stein.
 Liear Programmig! Refereces! Dasgupta, Papadimitriou, Vazirai. Algorithms.! Corme, Leiserso, Rivest, ad Stei. Itroductio to Algorithms.! Slack form! For each costrait i, defie a oegative slack variable
Liear Programmig! Refereces! Dasgupta, Papadimitriou, Vazirai. Algorithms.! Corme, Leiserso, Rivest, ad Stei. Itroductio to Algorithms.! Slack form! For each costrait i, defie a oegative slack variable
Randomized Algorithms I, Spring 2018, Department of Computer Science, University of Helsinki Homework 1: Solutions (Discussed January 25, 2018)
 Radomized Algorithms I, Sprig 08, Departmet of Computer Sciece, Uiversity of Helsiki Homework : Solutios Discussed Jauary 5, 08). Exercise.: Cosider the followig balls-ad-bi game. We start with oe black
Radomized Algorithms I, Sprig 08, Departmet of Computer Sciece, Uiversity of Helsiki Homework : Solutios Discussed Jauary 5, 08). Exercise.: Cosider the followig balls-ad-bi game. We start with oe black
(b) What is the probability that a particle reaches the upper boundary n before the lower boundary m?
 MATH 529 The Boudary Problem The drukard s walk (or boudary problem) is oe of the most famous problems i the theory of radom walks. Oe versio of the problem is described as follows: Suppose a particle
MATH 529 The Boudary Problem The drukard s walk (or boudary problem) is oe of the most famous problems i the theory of radom walks. Oe versio of the problem is described as follows: Suppose a particle
Spectral Partitioning in the Planted Partition Model
 Spectral Graph Theory Lecture 21 Spectral Partitioig i the Plated Partitio Model Daiel A. Spielma November 11, 2009 21.1 Itroductio I this lecture, we will perform a crude aalysis of the performace of
Spectral Graph Theory Lecture 21 Spectral Partitioig i the Plated Partitio Model Daiel A. Spielma November 11, 2009 21.1 Itroductio I this lecture, we will perform a crude aalysis of the performace of
Fundamental Theorem of Algebra. Yvonne Lai March 2010
 Fudametal Theorem of Algebra Yvoe Lai March 010 We prove the Fudametal Theorem of Algebra: Fudametal Theorem of Algebra. Let f be a o-costat polyomial with real coefficiets. The f has at least oe complex
Fudametal Theorem of Algebra Yvoe Lai March 010 We prove the Fudametal Theorem of Algebra: Fudametal Theorem of Algebra. Let f be a o-costat polyomial with real coefficiets. The f has at least oe complex
The minimum value and the L 1 norm of the Dirichlet kernel
 The miimum value ad the L orm of the Dirichlet kerel For each positive iteger, defie the fuctio D (θ + ( cos θ + cos θ + + cos θ e iθ + + e iθ + e iθ + e + e iθ + e iθ + + e iθ which we call the (th Dirichlet
The miimum value ad the L orm of the Dirichlet kerel For each positive iteger, defie the fuctio D (θ + ( cos θ + cos θ + + cos θ e iθ + + e iθ + e iθ + e + e iθ + e iθ + + e iθ which we call the (th Dirichlet
On Random Line Segments in the Unit Square
 O Radom Lie Segmets i the Uit Square Thomas A. Courtade Departmet of Electrical Egieerig Uiversity of Califoria Los Ageles, Califoria 90095 Email: tacourta@ee.ucla.edu I. INTRODUCTION Let Q = [0, 1] [0,
O Radom Lie Segmets i the Uit Square Thomas A. Courtade Departmet of Electrical Egieerig Uiversity of Califoria Los Ageles, Califoria 90095 Email: tacourta@ee.ucla.edu I. INTRODUCTION Let Q = [0, 1] [0,
Machine Learning. Ilya Narsky, Caltech
 Machie Learig Ilya Narsky, Caltech Lecture 4 Multi-class problems. Multi-class versios of Neural Networks, Decisio Trees, Support Vector Machies ad AdaBoost. Reductio of a multi-class problem to a set
Machie Learig Ilya Narsky, Caltech Lecture 4 Multi-class problems. Multi-class versios of Neural Networks, Decisio Trees, Support Vector Machies ad AdaBoost. Reductio of a multi-class problem to a set
The multiplicative structure of finite field and a construction of LRC
 IERG6120 Codig for Distributed Storage Systems Lecture 8-06/10/2016 The multiplicative structure of fiite field ad a costructio of LRC Lecturer: Keeth Shum Scribe: Zhouyi Hu Notatios: We use the otatio
IERG6120 Codig for Distributed Storage Systems Lecture 8-06/10/2016 The multiplicative structure of fiite field ad a costructio of LRC Lecturer: Keeth Shum Scribe: Zhouyi Hu Notatios: We use the otatio
Recursive Algorithms. Recurrences. Recursive Algorithms Analysis
 Recursive Algorithms Recurreces Computer Sciece & Egieerig 35: Discrete Mathematics Christopher M Bourke cbourke@cseuledu A recursive algorithm is oe i which objects are defied i terms of other objects
Recursive Algorithms Recurreces Computer Sciece & Egieerig 35: Discrete Mathematics Christopher M Bourke cbourke@cseuledu A recursive algorithm is oe i which objects are defied i terms of other objects
2 DD2458 Popup HT Solution: Choose the activity which ends first and does not conflict with earlier chosen activities.
 DD2458, Problem Solvig ad Programmig Uder Pressure Lecture 1: Greedy algorithms ad dyamic programmig Date: 2008-09-01 Scribe(s: Marti Wedi ad Nilas Wagre Lecturer: Douglas Wiström This lecture cotais basic
DD2458, Problem Solvig ad Programmig Uder Pressure Lecture 1: Greedy algorithms ad dyamic programmig Date: 2008-09-01 Scribe(s: Marti Wedi ad Nilas Wagre Lecturer: Douglas Wiström This lecture cotais basic
Lecture Notes for Analysis Class
 Lecture Notes for Aalysis Class Topological Spaces A topology for a set X is a collectio T of subsets of X such that: (a) X ad the empty set are i T (b) Uios of elemets of T are i T (c) Fiite itersectios
Lecture Notes for Aalysis Class Topological Spaces A topology for a set X is a collectio T of subsets of X such that: (a) X ad the empty set are i T (b) Uios of elemets of T are i T (c) Fiite itersectios
Lecture 2: April 3, 2013
 TTIC/CMSC 350 Mathematical Toolkit Sprig 203 Madhur Tulsiai Lecture 2: April 3, 203 Scribe: Shubhedu Trivedi Coi tosses cotiued We retur to the coi tossig example from the last lecture agai: Example. Give,
TTIC/CMSC 350 Mathematical Toolkit Sprig 203 Madhur Tulsiai Lecture 2: April 3, 203 Scribe: Shubhedu Trivedi Coi tosses cotiued We retur to the coi tossig example from the last lecture agai: Example. Give,
Weakly Connected Closed Geodetic Numbers of Graphs
 Iteratioal Joural of Mathematical Aalysis Vol 10, 016, o 6, 57-70 HIKARI Ltd, wwwm-hikaricom http://dxdoiorg/101988/ijma01651193 Weakly Coected Closed Geodetic Numbers of Graphs Rachel M Pataga 1, Imelda
Iteratioal Joural of Mathematical Aalysis Vol 10, 016, o 6, 57-70 HIKARI Ltd, wwwm-hikaricom http://dxdoiorg/101988/ijma01651193 Weakly Coected Closed Geodetic Numbers of Graphs Rachel M Pataga 1, Imelda
Balanced coloring of bipartite graphs
 Balaced colorig of bipartite graphs Uriel Feige Shimo Koga Departmet of Computer Sciece ad Applied Mathematics Weizma Istitute, Rehovot 76100, Israel uriel.feige@weizma.ac.il Jue 16, 009 Abstract Give
Balaced colorig of bipartite graphs Uriel Feige Shimo Koga Departmet of Computer Sciece ad Applied Mathematics Weizma Istitute, Rehovot 76100, Israel uriel.feige@weizma.ac.il Jue 16, 009 Abstract Give
Markov Decision Processes
 Markov Decisio Processes Defiitios; Statioary policies; Value improvemet algorithm, Policy improvemet algorithm, ad liear programmig for discouted cost ad average cost criteria. Markov Decisio Processes
Markov Decisio Processes Defiitios; Statioary policies; Value improvemet algorithm, Policy improvemet algorithm, ad liear programmig for discouted cost ad average cost criteria. Markov Decisio Processes
Geometry of LS. LECTURE 3 GEOMETRY OF LS, PROPERTIES OF σ 2, PARTITIONED REGRESSION, GOODNESS OF FIT
 OCTOBER 7, 2016 LECTURE 3 GEOMETRY OF LS, PROPERTIES OF σ 2, PARTITIONED REGRESSION, GOODNESS OF FIT Geometry of LS We ca thik of y ad the colums of X as members of the -dimesioal Euclidea space R Oe ca
OCTOBER 7, 2016 LECTURE 3 GEOMETRY OF LS, PROPERTIES OF σ 2, PARTITIONED REGRESSION, GOODNESS OF FIT Geometry of LS We ca thik of y ad the colums of X as members of the -dimesioal Euclidea space R Oe ca
4.1 Sigma Notation and Riemann Sums
 0 the itegral. Sigma Notatio ad Riema Sums Oe strategy for calculatig the area of a regio is to cut the regio ito simple shapes, calculate the area of each simple shape, ad the add these smaller areas
0 the itegral. Sigma Notatio ad Riema Sums Oe strategy for calculatig the area of a regio is to cut the regio ito simple shapes, calculate the area of each simple shape, ad the add these smaller areas
It is often useful to approximate complicated functions using simpler ones. We consider the task of approximating a function by a polynomial.
 Taylor Polyomials ad Taylor Series It is ofte useful to approximate complicated fuctios usig simpler oes We cosider the task of approximatig a fuctio by a polyomial If f is at least -times differetiable
Taylor Polyomials ad Taylor Series It is ofte useful to approximate complicated fuctios usig simpler oes We cosider the task of approximatig a fuctio by a polyomial If f is at least -times differetiable
Merge and Quick Sort
 Merge ad Quick Sort Merge Sort Merge Sort Tree Implemetatio Quick Sort Pivot Item Radomized Quick Sort Adapted from: Goodrich ad Tamassia, Data Structures ad Algorithms i Java, Joh Wiley & So (1998). Ruig
Merge ad Quick Sort Merge Sort Merge Sort Tree Implemetatio Quick Sort Pivot Item Radomized Quick Sort Adapted from: Goodrich ad Tamassia, Data Structures ad Algorithms i Java, Joh Wiley & So (1998). Ruig
4.1 SIGMA NOTATION AND RIEMANN SUMS
 .1 Sigma Notatio ad Riema Sums Cotemporary Calculus 1.1 SIGMA NOTATION AND RIEMANN SUMS Oe strategy for calculatig the area of a regio is to cut the regio ito simple shapes, calculate the area of each
.1 Sigma Notatio ad Riema Sums Cotemporary Calculus 1.1 SIGMA NOTATION AND RIEMANN SUMS Oe strategy for calculatig the area of a regio is to cut the regio ito simple shapes, calculate the area of each
Sets and Probabilistic Models
 ets ad Probabilistic Models Berli Che Departmet of Computer ciece & Iformatio Egieerig Natioal Taiwa Normal Uiversity Referece: - D. P. Bertsekas, J. N. Tsitsiklis, Itroductio to Probability, ectios 1.1-1.2
ets ad Probabilistic Models Berli Che Departmet of Computer ciece & Iformatio Egieerig Natioal Taiwa Normal Uiversity Referece: - D. P. Bertsekas, J. N. Tsitsiklis, Itroductio to Probability, ectios 1.1-1.2
The Interval of Convergence for a Power Series Examples
 The Iterval of Covergece for a Power Series Examples To review the process: How to Test a Power Series for Covergece. Fid the iterval where the series coverges absolutely. We have to use the Ratio or Root
The Iterval of Covergece for a Power Series Examples To review the process: How to Test a Power Series for Covergece. Fid the iterval where the series coverges absolutely. We have to use the Ratio or Root
( ) = p and P( i = b) = q.
 MATH 540 Radom Walks Part 1 A radom walk X is special stochastic process that measures the height (or value) of a particle that radomly moves upward or dowward certai fixed amouts o each uit icremet of
MATH 540 Radom Walks Part 1 A radom walk X is special stochastic process that measures the height (or value) of a particle that radomly moves upward or dowward certai fixed amouts o each uit icremet of
Recursive Algorithm for Generating Partitions of an Integer. 1 Preliminary
 Recursive Algorithm for Geeratig Partitios of a Iteger Sug-Hyuk Cha Computer Sciece Departmet, Pace Uiversity 1 Pace Plaza, New York, NY 10038 USA scha@pace.edu Abstract. This article first reviews the
Recursive Algorithm for Geeratig Partitios of a Iteger Sug-Hyuk Cha Computer Sciece Departmet, Pace Uiversity 1 Pace Plaza, New York, NY 10038 USA scha@pace.edu Abstract. This article first reviews the
Introduction to Machine Learning DIS10
 CS 189 Fall 017 Itroductio to Machie Learig DIS10 1 Fu with Lagrage Multipliers (a) Miimize the fuctio such that f (x,y) = x + y x + y = 3. Solutio: The Lagragia is: L(x,y,λ) = x + y + λ(x + y 3) Takig
CS 189 Fall 017 Itroductio to Machie Learig DIS10 1 Fu with Lagrage Multipliers (a) Miimize the fuctio such that f (x,y) = x + y x + y = 3. Solutio: The Lagragia is: L(x,y,λ) = x + y + λ(x + y 3) Takig
Spectral Graph Theory and its Applications. Lillian Dai Oct. 20, 2004
 Spectral raph Theory ad its Applicatios Lillia Dai 6.454 Oct. 0, 004 Outlie Basic spectral graph theory raph partitioig usig spectral methods D. Spielma ad S. Teg, Spectral Partitioig Works: Plaar raphs
Spectral raph Theory ad its Applicatios Lillia Dai 6.454 Oct. 0, 004 Outlie Basic spectral graph theory raph partitioig usig spectral methods D. Spielma ad S. Teg, Spectral Partitioig Works: Plaar raphs
Integer Linear Programming
 Iteger Liear Programmig Itroductio Iteger L P problem (P) Mi = s. t. a = b i =,, m = i i 0, iteger =,, c Eemple Mi z = 5 s. t. + 0 0, 0, iteger F(P) = feasible domai of P Itroductio Iteger L P problem
Iteger Liear Programmig Itroductio Iteger L P problem (P) Mi = s. t. a = b i =,, m = i i 0, iteger =,, c Eemple Mi z = 5 s. t. + 0 0, 0, iteger F(P) = feasible domai of P Itroductio Iteger L P problem
THE ASYMPTOTIC COMPLEXITY OF MATRIX REDUCTION OVER FINITE FIELDS
 THE ASYMPTOTIC COMPLEXITY OF MATRIX REDUCTION OVER FINITE FIELDS DEMETRES CHRISTOFIDES Abstract. Cosider a ivertible matrix over some field. The Gauss-Jorda elimiatio reduces this matrix to the idetity
THE ASYMPTOTIC COMPLEXITY OF MATRIX REDUCTION OVER FINITE FIELDS DEMETRES CHRISTOFIDES Abstract. Cosider a ivertible matrix over some field. The Gauss-Jorda elimiatio reduces this matrix to the idetity
Chapter Vectors
 Chapter 4. Vectors fter readig this chapter you should be able to:. defie a vector. add ad subtract vectors. fid liear combiatios of vectors ad their relatioship to a set of equatios 4. explai what it
Chapter 4. Vectors fter readig this chapter you should be able to:. defie a vector. add ad subtract vectors. fid liear combiatios of vectors ad their relatioship to a set of equatios 4. explai what it
