Learning from Sensor Data: Set II. Behnaam Aazhang J.S. Abercombie Professor Electrical and Computer Engineering Rice University
|
|
|
- Susan Long
- 5 years ago
- Views:
Transcription
1 Learning from Sensor Data: Set II Behnaam Aazhang J.S. Abercombie Professor Electrical and Computer Engineering Rice University 1
2 6. Data Representation The approach for learning from data Probabilistic modeling and algebraic manipulation Diagrammatic representation is often extremely useful Probabilistic graphical modeling Visualize the structure Infer dependence based on inspection of the graph Simplify complex computations 2
3 Examples of graphical modeling in engineering problems Circuit diagrams Signal flow diagrams Trellis diagrams Block diagrams 3
4 A graph can be viewed as the simplest way to represent a complex system where vertices are simplest units of the system edges represent their mutual interactions 4
5 Elements Nodes or vertices X 4 X 5 A random variable (data) or a group of random variables X 6 X 7 Links or edges Probabilistic relationships between the variables 5
6 Examples of graphs C X1, I( ; ) I(! ) 6
7 A typical graph representing data RAH1 RPBT1 LAH12 RPH4 RMOF10 RAH13 LAH8 RPBT11 RMOF5 RAMY7 LAH5 RAH5 RAINS4 RAMY6 RAH2 RAMY12 RPH3 RAMY5 RAH3 RPH2 RAMY11 RPH10 RAH10 RAH6 RAMY10 RAMY9 RAMY2 RAINS3 RAMY4 RAMY3 7
8 RAH2 node is influencing several nodes RAH1 RPBT1 RPH4 RMOF10 LAH12 RAH13 LAH8 RPBT11 RMOF5 RAMY7 LAH5 RAH5 RAINS4 RAMY6 RAH2 RAMY12 RPH3 RAMY5 RAH3 RPH2 RAMY11 RPH10 RAH10 RAH6 RAMY10 RAMY9 RAMY2 RAINS3 RAMY4 RAMY3 8
9 Another example 9
10 10
11 neurons spike
12 does neuron 3 excite neuron 8?
13 does neuron 3 excite neuron 8?
14 did neuron 3 causally influence firing of neuron 8? Neuron 3 Neuron
15 I(! X 8 ) 15
16 Learning from graphs Identifying important features of data from graphs A graph G = (V,E) with V as the set of vertices and E as the set of edges A graph is simple if it has no parallel edges and no loops Adjacent edges and adjacent vertices are defined as the terms suggest The degree of vertex v is d(v) as the number of edges with v as the end A pendant vertex is a vertex with degree 1. 16
17 A graph is called regular if all vertices have the same degree In an undirected graph each edge is an unordered pair of vertices ( u, v ) In a directed graph each edge is an ordered pair of vertices ( u, v ) 17
18 In degree of vertex v in a directed graph is the number of edges with v as the end Out degree of vertex v in a directed graph is the number of edges with as the tail An isolated vertex is one with degree 0. In degree and out degree 0 in a directed graph. 18
19 For undirected graph we define the following concepts and properties Some definitions can be extended to directed graphs Minimum degree of a graph Maximum degree of a graph (G) (G) 19
20 It can be shown that for a graph G = ( V, E ) with n vertices and m edges then nx d(v i )=2m i=1 A graph G = ( V, E ) is a subgraph of graph H = ( W, F ) if V is a subset of W and every edge in E is also an edge in F. A complete graph is a simple graph with all the possible edges A complete subgraph of graph G is called a clique. 20
21 The density of a graph G = ( V, E ) is defined as where n 2 = (G) = m n 2 n! 2!(n 2)! for n 2 The density of a complete graph is 1 The adjacency matrix of graph G is a n x n matrix 21
22 The spectrum of graph G = ( V, E ) is the set of eigenvalues of the adjacency matrix and their eigenvectors. The Laplacian matrix of graph G = ( V, E ) is defined as where the diagonal degree matrix, D is defined as 22
23 The normalized Laplacian is The Laplacian matrix carries some of the key properties of a graph. Since the adjacency and Laplacian matrices are symmetric their eigenvalues are real. The eigenvalues of the normalized Laplacian are in [0, 2]. This fact makes it convenient to compare the spectral properties of two graphs. 23
24 Two graphs are isomorphic if any two vertices of one are adjacent if and only if the equivalent vertices in the other graph are also adjacent f(a) = 1 f(b) = 6 f(c) = 8 f(d) = 3 f(g) = 5 f(h) = 2 f(i) = 4 f(j) = 7 24
25 Graphs that have the same spectrum are referred to as cospectral ( or isospectral) If two graphs have the same eigenvalues but different eigenvectors they are referred to as weakly cospectral. Although adjacency matrix of a graph depends on the labeling of the vertices, the spectrum of a graph is independent of labeling. Isomorphic graphs are cospectral but not all cospectral graphs are isomorphic 25
26 The complement of graph G = ( V, E ) is Ḡ =(V,Ē) where the edges in complement graph are the ones not in E Common binary and linear operations can be defined for graphs Complement, union, intersection, ring sum, examples of commutative and associative operations. 26
27 A community is a group of vertices that belong together according to some criterion that could be measured An example, a group of vertices where the density of edges between the vertices in the group is higher than the average edge density in the graph In some literature a community is also referred to as a module or a cluster. 27
28 Examples Figure 2.4 Bipartite Graph 28
29 <latexit sha1_base64="xys+jdtlh65oyskhfer6en2tb7a=">aaacbnicbvdlssnafj3uv62vqetbbotqqutsbhvxdooygrgfnptjdnioth7o3agldofgx3hjqswt3+dov3gabthww71woodezu7xysevwnaxuzibx1hcki6xvlbx1jfmza0bfswsmodgipitjygmemgc4cbyk5ambj5gte/2yuw375lupaqvyrgznyd9kpucetbs19yt4i66k5dwrofyyuror8ehxbnsva0mejbyosmjhi2u+dnprtqjwahuekxathwdmxijnao2knusxwjcb0mfttunsccum2z3jpc+vnryj6tuehcm/t5isadumpd0zebgoka9sfif107ap3vthsyjsjbohvitgshc41bwj0tgqqw1ivry/vdmb0qscjq6kg7bnj55lji16lnvujou18/znipob+2hcrlrcaqjs9radqloat2hf/rqpbrpxpvxphktgpnonvod4+mbbtiwba==</latexit> <latexit sha1_base64="x7ulc+u1qtnmk88yvbshzn/ptrq=">aaab83icbvbns8naej3ur1q/qh69lbahgpskcuqt6mvjbwmlbsib7azdutne3u2hhp4olx5uvppnvplv3ky5aotjbh7vzbczz485u9q2v63cyura+kzxs7s1vbo7v94/efrrigl1scqj2faxopwj6mqmow3hkulq57tlj25nfmtmpwkrenctmhohhggwmik1kbwqoj9dtlb2aa9cswt2brrmnjxuieezv/7q9ioshfrowrfshceotzdiqrnhdfrqjorgmizwghymftikykuzo6foxch9fetstnaou39vpdhuahl6zjleeqgwvzn4n9djdhdlpuzeiaaczb8keo50hgyjod6tlgg+mqqtycytiayxxesbneombgfxy8verdeua/b9ravxk6drhcm4hio4caknuimmuedgcz7hfd6ssfvivvsf89gcle8cwh9ynz+ugi7p</latexit> Example 6.1. D = A = L = The eigenvalues of adjacency matrix ( p 2, 0, 0, p 2) The eigenvalues of the Laplacian matrix (3, 1, 1, 0) One isolated vertex and two pendent vertices 29
30 <latexit sha1_base64="carub333yfojvhul+htsh+ofpq8=">aaacthicbzblswmxemez9v1fvy9egkxxvdyi6ewoevgoyb/qxuo2o63bbhzjsmjz+gg9epdmp/diqrhbdltqfqwm+fobmwtydxlbtxhdr6c0nt0zoze/uf5cwl5zraytn3wckgynfotytqoqqxajdconghaigeabgfzwftqqt25aar7lszniwi9ox/iez9ry1k2wy3yevqd6xgzbri3it0ps4p08sx563hdwpwgzagsyoxgbgx5f161u3zqbb/4rscgqqijzbuxbc2owriane1trdnet42dugc4edmteqigh7jr2owolpbfop8vngojts0lci5vnaxbojycygmk9ialbare80r9ri/hfrzoa3qgfczmkbiqbp9rlbtyxhjmlq66agtgwgjlf7a6yxvffmbh+l60j5pex/4rmxo24nxkxx62ffhbmo020hxyrqqeojs7qowoghu7qe3pbr8698+y8oe/j1pjtzgygh1ga/qbbxkcu</latexit> <latexit sha1_base64="carub333yfojvhul+htsh+ofpq8=">aaacthicbzblswmxemez9v1fvy9egkxxvdyi6ewoevgoyb/qxuo2o63bbhzjsmjz+gg9epdmp/diqrhbdltqfqwm+fobmwtydxlbtxhdr6c0nt0zoze/uf5cwl5zraytn3wckgynfotytqoqqxajdconghaigeabgfzwftqqt25aar7lszniwi9ox/iez9ry1k2wy3yevqd6xgzbri3it0ps4p08sx563hdwpwgzagsyoxgbgx5f161u3zqbb/4rscgqqijzbuxbc2owriane1trdnet42dugc4edmteqigh7jr2owolpbfop8vngojts0lci5vnaxbojycygmk9ialbare80r9ri/hfrzoa3qgfczmkbiqbp9rlbtyxhjmlq66agtgwgjlf7a6yxvffmbh+l60j5pex/4rmxo24nxkxx62ffhbmo020hxyrqqeojs7qowoghu7qe3pbr8698+y8oe/j1pjtzgygh1ga/qbbxkcu</latexit> <latexit sha1_base64="carub333yfojvhul+htsh+ofpq8=">aaacthicbzblswmxemez9v1fvy9egkxxvdyi6ewoevgoyb/qxuo2o63bbhzjsmjz+gg9epdmp/diqrhbdltqfqwm+fobmwtydxlbtxhdr6c0nt0zoze/uf5cwl5zraytn3wckgynfotytqoqqxajdconghaigeabgfzwftqqt25aar7lszniwi9ox/iez9ry1k2wy3yevqd6xgzbri3it0ps4p08sx563hdwpwgzagsyoxgbgx5f161u3zqbb/4rscgqqijzbuxbc2owriane1trdnet42dugc4edmteqigh7jr2owolpbfop8vngojts0lci5vnaxbojycygmk9ialbare80r9ri/hfrzoa3qgfczmkbiqbp9rlbtyxhjmlq66agtgwgjlf7a6yxvffmbh+l60j5pex/4rmxo24nxkxx62ffhbmo020hxyrqqeojs7qowoghu7qe3pbr8698+y8oe/j1pjtzgygh1ga/qbbxkcu</latexit> <latexit sha1_base64="hp+6lruf2d3tzaldqaqqvekmxyw=">aaab2xicbzdnsgmxfixv1l86vq1rn8eiucozbnqpuhfzwbzco5rm5k4bmskmyr2hdh0bf25efc93vo3pz0jbdwq+zknivscullqubn9ebwd3b/+gfugfnfzjk9nmo2fz0gjsilzl5jnmfpxu2cvjcp8lgzylffbj6f0i77+gstlxtzqrmmr4wmtuck7o6oyaraadlmw2ivxdc9yanb+gss7kddujxa0dhefbucunsafw7g9liwuxuz7ggupnm7rrtrxzzi6dk7a0n+5oykv394ukz9bostjdzdhn7ga2mp/lbiwlt1eldvesarh6kc0vo5wtdmajnchizrxwyasblykjn1yqa8z3hysbg29d77odbu3wmya6nmmfxeein3ahd9cblghi4bxevyn35n2suqp569lo4i+8zx84xio4</latexit> <latexit sha1_base64="bnjuhgqqtpwptzarpln0okiplhe=">aaacqxicbzbnswmxeizn/az1q3r1ehtfu0m86evqvhisyfxolpjnp21onrskwbes/yfephjzv3jxoihgulathwndxp6zsszvlcpphaupwdt0zozcfgmhvli0vljawvu6selmbnzfohjzfxglsmqso+kuxqugerwpviz6j6p65tuakxn97gypnmpe1bijbxcetsrimbysmmku1hkuc2fkzzbqslmkk84w/al0e7ajwcy7xioo29/xtspbteqlih8fg4stgeetvbkp24niytrokg5tg9hunxnunbqkh+uws5hy0eddbhipeyy2mrdmdmm2j23ssyxp7uhbjydyhls7icpf6rfs2d+1efyv1shc56czs51mdrx4ekitkeismnkwtkvb4dtacy6m9lss0eogc+f9l3st2o8v/xuxe1vgq+ymqgk2ybn2gce+hmep1kaoam7hez7hjbglnolxd7umgrfv6/ajgrd3lokmdg==</latexit> <latexit sha1_base64="bnjuhgqqtpwptzarpln0okiplhe=">aaacqxicbzbnswmxeizn/az1q3r1ehtfu0m86evqvhisyfxolpjnp21onrskwbes/yfephjzv3jxoihgulathwndxp6zsszvlcpphaupwdt0zozcfgmhvli0vljawvu6selmbnzfohjzfxglsmqso+kuxqugerwpviz6j6p65tuakxn97gypnmpe1bijbxcetsrimbysmmku1hkuc2fkzzbqslmkk84w/al0e7ajwcy7xioo29/xtspbteqlih8fg4stgeetvbkp24niytrokg5tg9hunxnunbqkh+uws5hy0eddbhipeyy2mrdmdmm2j23ssyxp7uhbjydyhls7icpf6rfs2d+1efyv1shc56czs51mdrx4ekitkeismnkwtkvb4dtacy6m9lss0eogc+f9l3st2o8v/xuxe1vgq+ymqgk2ybn2gce+hmep1kaoam7hez7hjbglnolxd7umgrfv6/ajgrd3lokmdg==</latexit> <latexit sha1_base64="w5pnd980xs2d1eagrsirntfe8co=">aaacthicbzblswmxemez9v1fvy9egkxxvbivehf8xdxwsa/olpjnpzwyzs5jvixlp6axd978ff48kckyblet1oehf34zk0z+qsyfsyq8eywz2bn5hcwl4vlk6tp6awozbqjec6jxsea6gtaduiiowwelngmnlawknikb81g9cqvaiehd2uem7zd1legjzqxdnri/xcfyd6avvbqezgpxn8qe72vjs9p3vwh5anqc0mmofaru9+e6tqlmkiqlpc1olsooj2qn9oh3i56eocyxzjgwjbftp0xbwsumi35iigb8hvwh5ariizh2mpkxxluodhev0i6vxrmdnehzamwgdfynw/da/k2n4h+1vmj7r+1uqdixopj4ov4isy3wyfncfrq4lqmngnfc7yr5ndomw+d/0zla/355wtqpkpru6cupn5zldiyibbsd9hffh+gexaaqqigo7tezekvv3op34r17h+pwgpfpbkffuzj/bfocpyo=</latexit> <latexit sha1_base64="carub333yfojvhul+htsh+ofpq8=">aaacthicbzblswmxemez9v1fvy9egkxxvdyi6ewoevgoyb/qxuo2o63bbhzjsmjz+gg9epdmp/diqrhbdltqfqwm+fobmwtydxlbtxhdr6c0nt0zoze/uf5cwl5zraytn3wckgynfotytqoqqxajdconghaigeabgfzwftqqt25aar7lszniwi9ox/iez9ry1k2wy3yevqd6xgzbri3it0ps4p08sx563hdwpwgzagsyoxgbgx5f161u3zqbb/4rscgqqijzbuxbc2owriane1trdnet42dugc4edmteqigh7jr2owolpbfop8vngojts0lci5vnaxbojycygmk9ialbare80r9ri/hfrzoa3qgfczmkbiqbp9rlbtyxhjmlq66agtgwgjlf7a6yxvffmbh+l60j5pex/4rmxo24nxkxx62ffhbmo020hxyrqqeojs7qowoghu7qe3pbr8698+y8oe/j1pjtzgygh1ga/qbbxkcu</latexit> <latexit sha1_base64="carub333yfojvhul+htsh+ofpq8=">aaacthicbzblswmxemez9v1fvy9egkxxvdyi6ewoevgoyb/qxuo2o63bbhzjsmjz+gg9epdmp/diqrhbdltqfqwm+fobmwtydxlbtxhdr6c0nt0zoze/uf5cwl5zraytn3wckgynfotytqoqqxajdconghaigeabgfzwftqqt25aar7lszniwi9ox/iez9ry1k2wy3yevqd6xgzbri3it0ps4p08sx563hdwpwgzagsyoxgbgx5f161u3zqbb/4rscgqqijzbuxbc2owriane1trdnet42dugc4edmteqigh7jr2owolpbfop8vngojts0lci5vnaxbojycygmk9ialbare80r9ri/hfrzoa3qgfczmkbiqbp9rlbtyxhjmlq66agtgwgjlf7a6yxvffmbh+l60j5pex/4rmxo24nxkxx62ffhbmo020hxyrqqeojs7qowoghu7qe3pbr8698+y8oe/j1pjtzgygh1ga/qbbxkcu</latexit> <latexit sha1_base64="carub333yfojvhul+htsh+ofpq8=">aaacthicbzblswmxemez9v1fvy9egkxxvdyi6ewoevgoyb/qxuo2o63bbhzjsmjz+gg9epdmp/diqrhbdltqfqwm+fobmwtydxlbtxhdr6c0nt0zoze/uf5cwl5zraytn3wckgynfotytqoqqxajdconghaigeabgfzwftqqt25aar7lszniwi9ox/iez9ry1k2wy3yevqd6xgzbri3it0ps4p08sx563hdwpwgzagsyoxgbgx5f161u3zqbb/4rscgqqijzbuxbc2owriane1trdnet42dugc4edmteqigh7jr2owolpbfop8vngojts0lci5vnaxbojycygmk9ialbare80r9ri/hfrzoa3qgfczmkbiqbp9rlbtyxhjmlq66agtgwgjlf7a6yxvffmbh+l60j5pex/4rmxo24nxkxx62ffhbmo020hxyrqqeojs7qowoghu7qe3pbr8698+y8oe/j1pjtzgygh1ga/qbbxkcu</latexit> <latexit sha1_base64="carub333yfojvhul+htsh+ofpq8=">aaacthicbzblswmxemez9v1fvy9egkxxvdyi6ewoevgoyb/qxuo2o63bbhzjsmjz+gg9epdmp/diqrhbdltqfqwm+fobmwtydxlbtxhdr6c0nt0zoze/uf5cwl5zraytn3wckgynfotytqoqqxajdconghaigeabgfzwftqqt25aar7lszniwi9ox/iez9ry1k2wy3yevqd6xgzbri3it0ps4p08sx563hdwpwgzagsyoxgbgx5f161u3zqbb/4rscgqqijzbuxbc2owriane1trdnet42dugc4edmteqigh7jr2owolpbfop8vngojts0lci5vnaxbojycygmk9ialbare80r9ri/hfrzoa3qgfczmkbiqbp9rlbtyxhjmlq66agtgwgjlf7a6yxvffmbh+l60j5pex/4rmxo24nxkxx62ffhbmo020hxyrqqeojs7qowoghu7qe3pbr8698+y8oe/j1pjtzgygh1ga/qbbxkcu</latexit> <latexit sha1_base64="carub333yfojvhul+htsh+ofpq8=">aaacthicbzblswmxemez9v1fvy9egkxxvdyi6ewoevgoyb/qxuo2o63bbhzjsmjz+gg9epdmp/diqrhbdltqfqwm+fobmwtydxlbtxhdr6c0nt0zoze/uf5cwl5zraytn3wckgynfotytqoqqxajdconghaigeabgfzwftqqt25aar7lszniwi9ox/iez9ry1k2wy3yevqd6xgzbri3it0ps4p08sx563hdwpwgzagsyoxgbgx5f161u3zqbb/4rscgqqijzbuxbc2owriane1trdnet42dugc4edmteqigh7jr2owolpbfop8vngojts0lci5vnaxbojycygmk9ialbare80r9ri/hfrzoa3qgfczmkbiqbp9rlbtyxhjmlq66agtgwgjlf7a6yxvffmbh+l60j5pex/4rmxo24nxkxx62ffhbmo020hxyrqqeojs7qowoghu7qe3pbr8698+y8oe/j1pjtzgygh1ga/qbbxkcu</latexit> <latexit sha1_base64="carub333yfojvhul+htsh+ofpq8=">aaacthicbzblswmxemez9v1fvy9egkxxvdyi6ewoevgoyb/qxuo2o63bbhzjsmjz+gg9epdmp/diqrhbdltqfqwm+fobmwtydxlbtxhdr6c0nt0zoze/uf5cwl5zraytn3wckgynfotytqoqqxajdconghaigeabgfzwftqqt25aar7lszniwi9ox/iez9ry1k2wy3yevqd6xgzbri3it0ps4p08sx563hdwpwgzagsyoxgbgx5f161u3zqbb/4rscgqqijzbuxbc2owriane1trdnet42dugc4edmteqigh7jr2owolpbfop8vngojts0lci5vnaxbojycygmk9ialbare80r9ri/hfrzoa3qgfczmkbiqbp9rlbtyxhjmlq66agtgwgjlf7a6yxvffmbh+l60j5pex/4rmxo24nxkxx62ffhbmo020hxyrqqeojs7qowoghu7qe3pbr8698+y8oe/j1pjtzgygh1ga/qbbxkcu</latexit> <latexit sha1_base64="xys+jdtlh65oyskhfer6en2tb7a=">aaacbnicbvdlssnafj3uv62vqetbbotqqutsbhvxdooygrgfnptjdnioth7o3agldofgx3hjqswt3+dov3gabthww71woodezu7xysevwnaxuzibx1hcki6xvlbx1jfmza0bfswsmodgipitjygmemgc4cbyk5ambj5gte/2yuw375lupaqvyrgznyd9kpucetbs19yt4i66k5dwrofyyuror8ehxbnsva0mejbyosmjhi2u+dnprtqjwahuekxathwdmxijnao2knusxwjcb0mfttunsccum2z3jpc+vnryj6tuehcm/t5isadumpd0zebgoka9sfif107ap3vthsyjsjbohvitgshc41bwj0tgqqw1ivry/vdmb0qscjq6kg7bnj55lji16lnvujou18/znipob+2hcrlrcaqjs9radqloat2hf/rqpbrpxpvxphktgpnonvod4+mbbtiwba==</latexit> <latexit sha1_base64="xxavqn/qwpfxnofue80g0cmwka4=">aaacuhicbvhlsgmxfl1tx7w+rl26crbftctmexqjig5cukhgq9apjzpe1mammyqzsqz9rdfu/a43lhrnpy0+6ovlts45ez2eiedaen6lu5ibx1hcki6xvlbx1jfcza2mjlpfsmfieavbkgouxgldccpwnlfio1dgtxh/ptjvhlbphstrm0iwhdg+5d3oqlfux+1fkhmshnjnmgsjahr/hbkf7bppdmumgicffbclklnpbez74ckly6dsfm/zccte1culzaj/asowqxrhfq66musjliyjqnxl9xltzqgynakclojuy0lzpe1jy0jji9ttla9kspys0yw9wnmwhutszxuzjbqerkf12gve6b/aipxpa6wmd9zouexsg5knd+qlgpiyjnilxa6qgtgwgdlf7v0ju6okmmp/ogrd8p8+ery0a1xfq/pxh+xts0kcrdibxtgah47gfc6gdg1g8asv8a4fzrpz5nwwnlf1osi2/kpc6qtsykca</latexit> <latexit sha1_base64="xxavqn/qwpfxnofue80g0cmwka4=">aaacuhicbvhlsgmxfl1tx7w+rl26crbftctmexqjig5cukhgq9apjzpe1mammyqzsqz9rdfu/a43lhrnpy0+6ovlts45ez2eiedaen6lu5ibx1hcki6xvlbx1jfcza2mjlpfsmfieavbkgouxgldccpwnlfio1dgtxh/ptjvhlbphstrm0iwhdg+5d3oqlfux+1fkhmshnjnmgsjahr/hbkf7bppdmumgicffbclklnpbez74ckly6dsfm/zccte1culzaj/asowqxrhfq66musjliyjqnxl9xltzqgynakclojuy0lzpe1jy0jji9ttla9kspys0yw9wnmwhutszxuzjbqerkf12gve6b/aipxpa6wmd9zouexsg5knd+qlgpiyjnilxa6qgtgwgdlf7v0ju6okmmp/ogrd8p8+ery0a1xfq/pxh+xts0kcrdibxtgah47gfc6gdg1g8asv8a4fzrpz5nwwnlf1osi2/kpc6qtsykca</latexit> <latexit sha1_base64="xxavqn/qwpfxnofue80g0cmwka4=">aaacuhicbvhlsgmxfl1tx7w+rl26crbftctmexqjig5cukhgq9apjzpe1mammyqzsqz9rdfu/a43lhrnpy0+6ovlts45ez2eiedaen6lu5ibx1hcki6xvlbx1jfcza2mjlpfsmfieavbkgouxgldccpwnlfio1dgtxh/ptjvhlbphstrm0iwhdg+5d3oqlfux+1fkhmshnjnmgsjahr/hbkf7bppdmumgicffbclklnpbez74ckly6dsfm/zccte1culzaj/asowqxrhfq66musjliyjqnxl9xltzqgynakclojuy0lzpe1jy0jji9ttla9kspys0yw9wnmwhutszxuzjbqerkf12gve6b/aipxpa6wmd9zouexsg5knd+qlgpiyjnilxa6qgtgwgdlf7v0ju6okmmp/ogrd8p8+ery0a1xfq/pxh+xts0kcrdibxtgah47gfc6gdg1g8asv8a4fzrpz5nwwnlf1osi2/kpc6qtsykca</latexit> <latexit sha1_base64="xxavqn/qwpfxnofue80g0cmwka4=">aaacuhicbvhlsgmxfl1tx7w+rl26crbftctmexqjig5cukhgq9apjzpe1mammyqzsqz9rdfu/a43lhrnpy0+6ovlts45ez2eiedaen6lu5ibx1hcki6xvlbx1jfcza2mjlpfsmfieavbkgouxgldccpwnlfio1dgtxh/ptjvhlbphstrm0iwhdg+5d3oqlfux+1fkhmshnjnmgsjahr/hbkf7bppdmumgicffbclklnpbez74ckly6dsfm/zccte1culzaj/asowqxrhfq66musjliyjqnxl9xltzqgynakclojuy0lzpe1jy0jji9ttla9kspys0yw9wnmwhutszxuzjbqerkf12gve6b/aipxpa6wmd9zouexsg5knd+qlgpiyjnilxa6qgtgwgdlf7v0ju6okmmp/ogrd8p8+ery0a1xfq/pxh+xts0kcrdibxtgah47gfc6gdg1g8asv8a4fzrpz5nwwnlf1osi2/kpc6qtsykca</latexit> <latexit sha1_base64="x7ulc+u1qtnmk88yvbshzn/ptrq=">aaab83icbvbns8naej3ur1q/qh69lbahgpskcuqt6mvjbwmlbsib7azdutne3u2hhp4olx5uvppnvplv3ky5aotjbh7vzbczz485u9q2v63cyura+kzxs7s1vbo7v94/efrrigl1scqj2faxopwj6mqmow3hkulq57tlj25nfmtmpwkrenctmhohhggwmik1kbwqoj9dtlb2aa9cswt2brrmnjxuieezv/7q9ioshfrowrfshceotzdiqrnhdfrqjorgmizwghymftikykuzo6foxch9fetstnaou39vpdhuahl6zjleeqgwvzn4n9djdhdlpuzeiaaczb8keo50hgyjod6tlgg+mqqtycytiayxxesbneombgfxy8verdeua/b9ravxk6drhcm4hio4caknuimmuedgcz7hfd6ssfvivvsf89gcle8cwh9ynz+ugi7p</latexit> Example 6.1 Alternative adjacency and Laplacian matrices are A = L = Eigenvalues of A and L are ( p 2, 0, 0, p 2) (3, 1, 1, 0) 30
31 Example 6.2 The bipartite graph Figure 2.4 Bipartite Graph 31
32 <latexit sha1_base64="uiq7n4v+vb4qn7doovuctgcxtye=">aaac+hicdzjnb9naeibxlh8lfdsfi5creagcinytussbqyilbw5firrshexrzthzdb22dseviiv/hespgljyu7jxb1i7pk2tmtksxs37znqzu0mhlspo/wthxq3bd+5u3uvcf/dw0vz3+/exl5dw4kdmorcnixcolcebkdj4ulguwalxodl9x/vhz2idys1nmhc4ystuqfrjqb403g62psjbidwmtnobjuiep8puwloxx1syiuxraezbc+btvoqulji+rgprdw3hsilugs1j14jlxqvt/onccns3mnwli/g3kppjoyjevk1n9hlc7fe+bwlwrdskhmvjanz9hu9ywwzosgrh3ddiby38rqskxkunlh0wqp6kkq69ncjdn6qam1vac1+zqjpbn4agqs53vcjzbp4lnswezdyqvxdv8oylpqejspmijdty4knpqyfyqj8btjrfsxruhzbw+x8fornwspkppempivodev0mdvtv+vzt697hu/y0ntlt9oztsijts0p2gr2xazpbwfa1+bz8d6vwppwr/rxaw6dteckurfjrl5xfwt8=</latexit> <latexit sha1_base64="f5wptdrwxa28ujjvn9zkp7hsrku=">aaac7nicfvlbbhmxepvuwyih0lqcuywauzvl5k0qaqekfg5wlbjpk2wjyovmjla93swerypw+qkupqdiyvdw429wtlta0tanjfq0743hm3zsaowi899bulk6du/++opww41hjzfbw9snli+txj7mdw7peufqk4m9uqtxrlaosktjaxl+dq6ffkbrvg4+0rtaqsbgrqvkcvkp4vawdjr8b68h1pjsxgtqxamolametwi6q2snwambcnj9g9fvxpgdoof/gpgyw3xvzvhiio4yllbhcduemlezhmrwjsf0fnju8c6vabdj1jaoa3a8bp+kr7ksmzqktxcuh/gcbv5uulljrbwxdgshz8uy+54akaebvpv7zeczz4wgza0pq1bnb1zuinnumixemqmauevtnlym9utkxw4qzyqs0mjlrmmpgxkypz6mlevjeuqjkfb5u4kcccsk+s/s8kuifke+txr73vdd/uggc/im2cy6e8p22b6l2at2yn6zy9zjmtdbl+br8c38ff6e38mfl9ywagqesh8q/vwdaeq/tg==</latexit> Figure 2.4 Bipartite Graph Example 6.2 The bipartite graph The adjacency metric The Laplacian L = 0 A G = C A 1 C A 32
33 <latexit sha1_base64="pvyggdenq5wcprfrm8comekf++c=">aaacy3icdzhbt9swfmadwkb0gwv23mwiyoidvyiqdq6tqu3cjdr10gpitvu57ktr1xei+wwrzt3uh9yn8/6ruwk2sry+ydgn7/1sv/hfmrqgff/bctc2x2xtn3aal1/t7r329g+utzprdn2eyltfrsyafar6kfdcbaabjzgem2j2avg/uqntrkq+yzhbmgetjwlbgdpo5p2+oh9okchg4yatfeyweapkwrnixvjk87pgaye+o6fb6icm/wfvteatamvuk8bj6nmgpv62d2pcn09dlsztpbl5lb/tv6lrjqhni9tqjbxf4tjleqikuwtgdai/w6e9fqwxmg+guygm8rmbwmbaxriww7iaxpwe2wrm41tbpzbw6emdjuumkzlikgndqvmtlcknaomc4/nhkvswiyi+vcjojcwulizlx0idr1lyw7gwtlfkp0wzjnb+tfsiweovr5v+wfui7x/ttlof69doklfkkbytglwnxxjjeqrpuppzsz17p3c/uoh+d38sudep97wh/8n9+qc3tbom</latexit> Example 6.3 A complete graph The diagonal degree matrix is D = 4xI where I is a 5x5 identity matrix The Laplacian is L = C A 33
34 Example 6.4 A regular graph with D = 2xI where I is a 4x4 identity matrix
35 Graphs can be used to efficiently compute different functions of data represent data identify which vertices-data are significant reduce dimensionality and only focus on important vertices-data 35
36 Defining a suitable centrality metric (or index of significance) is important Centrality Closeness Betweenness Degree Eigenvector Katz PageRank 36
37 Degree centrality The degree vector d = Ae where A is the adjacency matrix of the graph and e is the all 1 vector. Degree'Centrality' CD = 0.16 CD = /5*4' /4*3=1/6' /6*5=5/30' ' 37
38 Degree centrality For directed graphs In degree centrality Out degree centrality 38
39 Degree centrality For directed graphs In degree centrality Out degree centrality 39
40 Degree centrality For directed graphs In degree centrality Out degree centrality 40
41 Eigenvector centrality Identifying important vertices in a large network is critical problem with numerous applications. Degree'Centrality' A vertex is important if its adjacent vertices are important CD = 0.16 CD = /5*4' /4*3=1/6' /6*5=5/30' ' 41
42 Eigenvector centrality Identifying important vertices in a large network is critical problem with numerous applications. Degree'Centrality' A vertex is important if its adjacent vertices are important CD = 0.16 CD = 1.0 which one is more important? /5*4' /4*3=1/6' /6*5=5/30' ' 42
43 <latexit sha1_base64="cb/yf6ymhrl/nadclzc3qyrgc80=">aaacl3icbvdnsgmxgmzwv1r/vj16crbbu9mkob6eooiepijrc92yzno0tzvnhirbkms+khcfrs8kkl59c7ptilodcawz8/hlm0awqrtjvfifufmfxaxicmlldw19w97culnrldfxccqi2qyqioxy4mqqgwkksvaymniihuez3xgrqwjeb/vykhaiepx2kubasl59eeeni5+m0bmyejqcnopdpxlaj3kyebgxej1m/iq3sohpndgaye/o4fv37bjtcsaaf0k1j2wqo+7bj14nwnfiumymkdwqokk3eyq1xyykjs9wrca8rd3smpsjkkh2mjk4hxtg6cbujm3jgk7unxmjcpuah4fjhkj31ayxif95rvh3j9sj5slwhoppom7mockmaw92qcrys7ehcetq/gpxh0metem4zeqozp78l7ghlzokc3nyrp3lbrtbdtgf+6akjkanxie6caeg9+ajvii368f6tt6tj2m0youz2+axrm8vroeplq==</latexit> Eigenvector centrality Identifying important vertices in a large network is critical problem with numerous applications. A vertex is important if its adjacent vertices are important Centrality is proportional to the centrality of adjacent vertices E vi / X j2n i E vj = X A system of equations with n unknowns j a ij E vj 43
44 <latexit sha1_base64="p8uvqdbzqejvr9e6+xnfnbvogaw=">aaadkxicfzjnbxmxeia9w6bt+erhygvebcqxyfshqq9iaq5wlbkhlbjr5hvme6te78qerypw+t1c+cu99mdxlt9sj9lw6ayw0kiv5n08tsdocq0ccf47cldu3b6zvbpbunvv/ooh7b1hx1xewol9mevcnitcovyg+6ri40lhuwsjxupk9p3cp/6k1qncfkzzgcnmtixklrtks6o9opd29aheqkwxpf0wlcnockjmjawvs3klvzgvtqaozyhyyrszxfevc+k3uxvm3b/onaamgp0l2uj4h+zqx8apb7ozh8vjobnxc4hyqsmuxozahd7ly4bnedwiw+o4grxp43euywwnss2cg0s8okhvskpqnlfi0meh5kmy4mblizj0w2r51hn45itjshpr0xasq+srkpe5n8sst2acpq7plyo3eyos0tfdspmijdrytvfaaqacfv8gxsqijd3zqkir/flbtouvkvzvavkhrm0rb4r+qfewyz+97pte1dpyyu/yu7bpivak9dhhdst6tabfgrpgr/az/b6eh7/cpys0doo1j9m1cp9eaix2yr0=</latexit> <latexit sha1_base64="w0rwl5ut/zgnrm+fy6fdhfjih7m=">aaacanicbvdlsgmxfl3js9bxqdvdbivgqsyioc6eqogukzi20a5djpnpqzmpkkyhdau3/oobfypu/qp3/o1powttpra4oedcknv8ldoplovbmjtfwfxalq2uv9fwnzbnre0hmwscuickpbfnh0vkwuwdxrsnzvrqhpmcnvze1chv9kmqlinv1sclboq7mqszwuplnrnb5jocyhtt5f0hokfowruzxdyzylwtmdassqtsgqj1z/xqbwnjihorwrguldtklztjorjhdfhuz5kmmprwh7y0jxfepzupdxiia60ekeyeprfcy/x3ri4jkqerr5mrvl057y3e/7xwpsjtn2dxmikak8ldycarstcoebqwqynia00weuz/fzeufpgoxvtzl2bprzxlnkpqwdw6o67ulos2srah+3ainpxadw6hdg4qeirneiu348l4md6nj0l0zihmduapjm8fnm2wjw==</latexit> <latexit sha1_base64="cb/yf6ymhrl/nadclzc3qyrgc80=">aaacl3icbvdnsgmxgmzwv1r/vj16crbbu9mkob6eooiepijrc92yzno0tzvnhirbkms+khcfrs8kkl59c7ptilodcawz8/hlm0awqrtjvfifufmfxaxicmlldw19w97culnrldfxccqi2qyqioxy4mqqgwkksvaymniihuez3xgrqwjeb/vykhaiepx2kubasl59eeeni5+m0bmyejqcnopdpxlaj3kyebgxej1m/iq3sohpndgaye/o4fv37bjtcsaaf0k1j2wqo+7bj14nwnfiumymkdwqokk3eyq1xyykjs9wrca8rd3smpsjkkh2mjk4hxtg6cbujm3jgk7unxmjcpuah4fjhkj31ayxif95rvh3j9sj5slwhoppom7mockmaw92qcrys7ehcetq/gpxh0metem4zeqozp78l7ghlzokc3nyrp3lbrtbdtgf+6akjkanxie6caeg9+ajvii368f6tt6tj2m0youz2+axrm8vroeplq==</latexit> E vi / X j2n i E vj = X j a ij E vj Eigenvector centrality E v = A G E v The eigenvector of the adjacency matrix A G = C A
45 <latexit sha1_base64="p8uvqdbzqejvr9e6+xnfnbvogaw=">aaadkxicfzjnbxmxeia9w6bt+erhygvebcqxyfshqq9iaq5wlbkhlbjr5hvme6te78qerypw+t1c+cu99mdxlt9sj9lw6ayw0kiv5n08tsdocq0ccf47cldu3b6zvbpbunvv/ooh7b1hx1xewol9mevcnitcovyg+6ri40lhuwsjxupk9p3cp/6k1qncfkzzgcnmtixklrtks6o9opd29aheqkwxpf0wlcnockjmjawvs3klvzgvtqaozyhyyrszxfevc+k3uxvm3b/onaamgp0l2uj4h+zqx8apb7ozh8vjobnxc4hyqsmuxozahd7ly4bnedwiw+o4grxp43euywwnss2cg0s8okhvskpqnlfi0meh5kmy4mblizj0w2r51hn45itjshpr0xasq+srkpe5n8sst2acpq7plyo3eyos0tfdspmijdrytvfaaqacfv8gxsqijd3zqkir/flbtouvkvzvavkhrm0rb4r+qfewyz+97pte1dpyyu/yu7bpivak9dhhdst6tabfgrpgr/az/b6eh7/cpys0doo1j9m1cp9eaix2yr0=</latexit> <latexit sha1_base64="w0rwl5ut/zgnrm+fy6fdhfjih7m=">aaacanicbvdlsgmxfl3js9bxqdvdbivgqsyioc6eqogukzi20a5djpnpqzmpkkyhdau3/oobfypu/qp3/o1powttpra4oedcknv8ldoplovbmjtfwfxalq2uv9fwnzbnre0hmwscuickpbfnh0vkwuwdxrsnzvrqhpmcnvze1chv9kmqlinv1sclboq7mqszwuplnrnb5jocyhtt5f0hokfowruzxdyzylwtmdassqtsgqj1z/xqbwnjihorwrguldtklztjorjhdfhuz5kmmprwh7y0jxfepzupdxiia60ekeyeprfcy/x3ri4jkqerr5mrvl057y3e/7xwpsjtn2dxmikak8ldycarstcoebqwqynia00weuz/fzeufpgoxvtzl2bprzxlnkpqwdw6o67ulos2srah+3ainpxadw6hdg4qeirneiu348l4md6nj0l0zihmduapjm8fnm2wjw==</latexit> <latexit sha1_base64="cb/yf6ymhrl/nadclzc3qyrgc80=">aaacl3icbvdnsgmxgmzwv1r/vj16crbbu9mkob6eooiepijrc92yzno0tzvnhirbkms+khcfrs8kkl59c7ptilodcawz8/hlm0awqrtjvfifufmfxaxicmlldw19w97culnrldfxccqi2qyqioxy4mqqgwkksvaymniihuez3xgrqwjeb/vykhaiepx2kubasl59eeeni5+m0bmyejqcnopdpxlaj3kyebgxej1m/iq3sohpndgaye/o4fv37bjtcsaaf0k1j2wqo+7bj14nwnfiumymkdwqokk3eyq1xyykjs9wrca8rd3smpsjkkh2mjk4hxtg6cbujm3jgk7unxmjcpuah4fjhkj31ayxif95rvh3j9sj5slwhoppom7mockmaw92qcrys7ehcetq/gpxh0metem4zeqozp78l7ghlzokc3nyrp3lbrtbdtgf+6akjkanxie6caeg9+ajvii368f6tt6tj2m0youz2+axrm8vroeplq==</latexit> E vi / X j2n i E vj = X j a ij E vj Eigenvector centrality E v = A G E v The eigenvector of the adjacency matrix A G = C A
46 Intuition starts with degree centrality Degree vector Incorporating the degree of the neighbors 46 X = 0 B B B B B B B C C C C C C C C A <latexit sha1_base64="pmazh83mzka9fqedbef0pork0iy=">aaacfxicdvhbsgmxem2u93qr+uhltcjeknsqqa9c0rcffawwuqvk09k2njtdklmhlp0mf8w3v8ux03yv6+va4mw5m5lkjkikmoh5b447mzs3v7c4vfhewv1bl25sppo41rzqpjaxbgtmgbqk6ihqqiprwkjawlpqvxn5t8+gjyjvaw4saewsq0qooemrtysvdxpffqkhhhtogh4axaeypjubddm+zgvkq9t3v4lt70gv/m9npu3xfdye1cnbuv+lbg8p28wsv/bgol9jjsclkuouxxz1ozfpi1dijtomwfesbnlbuxajw4kfgkgy77munc1vlaltysbjg9i9q3roggt7fnkx+r0iy5exgyiwmrhdnvnpjcs/vgak4uureypjersfnaptstgmo13qjtdauq4syvwl+1bke0wzjnzjbtueys8v/yb1avmy7n2flwrx+tqwytbzjqekqs5jjdyso1innlw7o86rc+wsd989ccutvnfja7bifnzzd+brqyy=</latexit> <latexit sha1_base64="pmazh83mzka9fqedbef0pork0iy=">aaacfxicdvhbsgmxem2u93qr+uhltcjeknsqqa9c0rcffawwuqvk09k2njtdklmhlp0mf8w3v8ux03yv6+va4mw5m5lkjkikmoh5b447mzs3v7c4vfhewv1bl25sppo41rzqpjaxbgtmgbqk6ihqqiprwkjawlpqvxn5t8+gjyjvaw4saewsq0qooemrtysvdxpffqkhhhtogh4axaeypjubddm+zgvkq9t3v4lt70gv/m9npu3xfdye1cnbuv+lbg8p28wsv/bgol9jjsclkuouxxz1ozfpi1dijtomwfesbnlbuxajw4kfgkgy77munc1vlaltysbjg9i9q3roggt7fnkx+r0iy5exgyiwmrhdnvnpjcs/vgak4uureypjersfnaptstgmo13qjtdauq4syvwl+1bke0wzjnzjbtueys8v/yb1avmy7n2flwrx+tqwytbzjqekqs5jjdyso1innlw7o86rc+wsd989ccutvnfja7bifnzzd+brqyy=</latexit> <latexit sha1_base64="pmazh83mzka9fqedbef0pork0iy=">aaacfxicdvhbsgmxem2u93qr+uhltcjeknsqqa9c0rcffawwuqvk09k2njtdklmhlp0mf8w3v8ux03yv6+va4mw5m5lkjkikmoh5b447mzs3v7c4vfhewv1bl25sppo41rzqpjaxbgtmgbqk6ihqqiprwkjawlpqvxn5t8+gjyjvaw4saewsq0qooemrtysvdxpffqkhhhtogh4axaeypjubddm+zgvkq9t3v4lt70gv/m9npu3xfdye1cnbuv+lbg8p28wsv/bgol9jjsclkuouxxz1ozfpi1dijtomwfesbnlbuxajw4kfgkgy77munc1vlaltysbjg9i9q3roggt7fnkx+r0iy5exgyiwmrhdnvnpjcs/vgak4uureypjersfnaptstgmo13qjtdauq4syvwl+1bke0wzjnzjbtueys8v/yb1avmy7n2flwrx+tqwytbzjqekqs5jjdyso1innlw7o86rc+wsd989ccutvnfja7bifnzzd+brqyy=</latexit> A G X = 0 B B B B B B B C C C C C C C C A 0 B B B B B B B C C C C C C C C A = 0 B B B B B B B C C C C C C C C A <latexit sha1_base64="undxforystuarjtjjbqmapfhkjg=">aaaevhicjvrnj9mwehwtakubpqthlimq0hkpki7lx2glbq5wxctkvmqqynenrvxhiwwhqyr6j/ec+cdckhdb7jkk24qrrhrpezmep2kcpojr43m/go7bvhp33sh91oohjw4ft4+efndjphj2wsisnqiprsel9g03agepqhqhai/d+acvfvkdleaj/gywky5iopu84owamxofofmp488wgdmibebmuavrc0kccpltpehimbonlqsqwiox4fv3au4hwq3ngq/zypwyxuxvshwiv4u01xep5+bg2ts3vcyda2vqtgpdifb8ojovwnu1+6darzzwsfnqg91qhvat2tpsgfznukflnm+qh53qatmuahuhgrc7xtdbg2whfhf0sgex4/zvmelyfqm0tfcth76xmpftazgtugwfmcausjmd4tcgksaor/l6k5bwwmymecxkujswzpyrchprvyhdy4ypmek6tkrehg0ze70b5vymmuhjnhdfmqctwgrfymivmimwnqbmctsrsblvlbm7icsr/pqtt4n+r/u+63193tn/wkhxqj6r5+sy+oqtosdfyaxpe+zcob/dhuu4p90/tftlbkhoo6h5sirwppwlqwoixa==</latexit> <latexit sha1_base64="undxforystuarjtjjbqmapfhkjg=">aaaevhicjvrnj9mwehwtakubpqthlimq0hkpki7lx2glbq5wxctkvmqqynenrvxhiwwhqyr6j/ec+cdckhdb7jkk24qrrhrpezmep2kcpojr43m/go7bvhp33sh91oohjw4ft4+efndjphj2wsisnqiprsel9g03agepqhqhai/d+acvfvkdleaj/gywky5iopu84owamxofofmp488wgdmibebmuavrc0kccpltpehimbonlqsqwiox4fv3au4hwq3ngq/zypwyxuxvshwiv4u01xep5+bg2ts3vcyda2vqtgpdifb8ojovwnu1+6darzzwsfnqg91qhvat2tpsgfznukflnm+qh53qatmuahuhgrc7xtdbg2whfhf0sgex4/zvmelyfqm0tfcth76xmpftazgtugwfmcausjmd4tcgksaor/l6k5bwwmymecxkujswzpyrchprvyhdy4ypmek6tkrehg0ze70b5vymmuhjnhdfmqctwgrfymivmimwnqbmctsrsblvlbm7icsr/pqtt4n+r/u+63193tn/wkhxqj6r5+sy+oqtosdfyaxpe+zcob/dhuu4p90/tftlbkhoo6h5sirwppwlqwoixa==</latexit> <latexit sha1_base64="undxforystuarjtjjbqmapfhkjg=">aaaevhicjvrnj9mwehwtakubpqthlimq0hkpki7lx2glbq5wxctkvmqqynenrvxhiwwhqyr6j/ec+cdckhdb7jkk24qrrhrpezmep2kcpojr43m/go7bvhp33sh91oohjw4ft4+efndjphj2wsisnqiprsel9g03agepqhqhai/d+acvfvkdleaj/gywky5iopu84owamxofofmp488wgdmibebmuavrc0kccpltpehimbonlqsqwiox4fv3au4hwq3ngq/zypwyxuxvshwiv4u01xep5+bg2ts3vcyda2vqtgpdifb8ojovwnu1+6darzzwsfnqg91qhvat2tpsgfznukflnm+qh53qatmuahuhgrc7xtdbg2whfhf0sgex4/zvmelyfqm0tfcth76xmpftazgtugwfmcausjmd4tcgksaor/l6k5bwwmymecxkujswzpyrchprvyhdy4ypmek6tkrehg0ze70b5vymmuhjnhdfmqctwgrfymivmimwnqbmctsrsblvlbm7icsr/pqtt4n+r/u+63193tn/wkhxqj6r5+sy+oqtosdfyaxpe+zcob/dhuu4p90/tftlbkhoo6h5sirwppwlqwoixa==</latexit>
47 <latexit sha1_base64="y840c6ung8/1cwkq3ko/hcq6nwo=">aaaevnicjvppa9swffztd+2yx2l33eusbhsxijv1aw+dsl127gbzc3eisvkcimqykercmpknyy79v3rzlmttbkc1e/dg8/s+vffpguwzfmyscrpl+ch2k53dp51nz1+8fnxd2/9l0lxzgpbupvoiygakudcwwkq4ydswjjjwhl1+w/lnv6cnsnvpo89gllcperhgzlrsem9lqgmxpejgvyqrtiuqmnzsvij4ohylithb7zf1srpjw/bec8c3dvvnla/rgqkmkd4m2ujyormf2hd90m0ivtsmqem5fxxqmz3zd45pw96/tr1vhx+qfzxkhvvxjcbtnr448v9cuvrtsmvd6sfuiwu/u96ftprrjls90ierwjualqchyjgbd6/dscrzbjtlkhkzpcszi9fxci5h0qlzaxnjl2wkqwcvs8cmitw7wob3rjlbcapdkotx1eqjgixgzjpikrnmz6bjlyspccpcxsejqqgst6d4elccs2xtvhxkeci0ccvndjcuhfok+yxpxq17issl0oavn8hgsh/sjz8+9k6/ltvyrw/qw3sakpqmttf3diygihu/vvvf9wp/xv8tbac7a6m3vz55jwordp8criiiiq==</latexit> <latexit sha1_base64="w0rwl5ut/zgnrm+fy6fdhfjih7m=">aaacanicbvdlsgmxfl3js9bxqdvdbivgqsyioc6eqogukzi20a5djpnpqzmpkkyhdau3/oobfypu/qp3/o1powttpra4oedcknv8ldoplovbmjtfwfxalq2uv9fwnzbnre0hmwscuickpbfnh0vkwuwdxrsnzvrqhpmcnvze1chv9kmqlinv1sclboq7mqszwuplnrnb5jocyhtt5f0hokfowruzxdyzylwtmdassqtsgqj1z/xqbwnjihorwrguldtklztjorjhdfhuz5kmmprwh7y0jxfepzupdxiia60ekeyeprfcy/x3ri4jkqerr5mrvl057y3e/7xwpsjtn2dxmikak8ldycarstcoebqwqynia00weuz/fzeufpgoxvtzl2bprzxlnkpqwdw6o67ulos2srah+3ainpxadw6hdg4qeirneiu348l4md6nj0l0zihmduapjm8fnm2wjw==</latexit> The process of adjusting the significance of a node based on the significance of neighbors can continue till the adjustment settles Leading to an eigenvector of the matrix A 1 0 C B C A = C A E v = A G E v 47
48 <latexit sha1_base64="xnylzn9er7rtcfqz1fnuxnjzkek=">aaaclhichvfnsynbeo0zxvezfmt14mflyrdcs5gyzbmhwq8et6jgvietqk+njmns0zn01whhyd/y13jz39iji2gufndw6r2q7uqqkfpsuha8e/7c4o+ln8srlv+ra+sb1d+b/22ag4ftkaru3efcopia2yrj4x1mkcerwrtodd717x7qwjnqwxpn2e34qmtyck5o6lufl3opcayhwpj2kzbdgofa6oibw8etqkxkgscon5sqhu/iw6opcbmf3yq058j5g+ctc9t9sgcijrwm6u+vwgvqwqzwmtrkummlrnvvp7cfijxbtujxazunikouu5wkudiphlnfjisrh2dhuc0ttn1intuj7dmld3fq3neem/v9rceta8dj5dittkm7703fr7xotngrw0id5yravd4u5woohemkoc8ncljjr7gw0vukysgnf+qwwxfdamx/+tnph9t/1yobw9rjwtmnzbbddtk+a7c/7irdsmvwzslb9freqxfmb/vh/rl/8zrqe2xnfvsa/+ofl42v1g==</latexit> The set of eigenvalues are The eigenvector corresponding to the largest eigenvalue will have nonnegative elements since the adjacency matrix has non-negative elements ( from the Perron-Frobenius theorem) That is also the best lower rank approximation of the matrix A Eigenvalue 2.34 and the corresponding eigenvector E v = C A 48
49 <latexit sha1_base64="xnylzn9er7rtcfqz1fnuxnjzkek=">aaaclhichvfnsynbeo0zxvezfmt14mflyrdcs5gyzbmhwq8et6jgvietqk+njmns0zn01whhyd/y13jz39iji2gufndw6r2q7uqqkfpsuha8e/7c4o+ln8srlv+ra+sb1d+b/22ag4ftkaru3efcopia2yrj4x1mkcerwrtodd717x7qwjnqwxpn2e34qmtyck5o6lufl3opcayhwpj2kzbdgofa6oibw8etqkxkgscon5sqhu/iw6opcbmf3yq058j5g+ctc9t9sgcijrwm6u+vwgvqwqzwmtrkummlrnvvp7cfijxbtujxazunikouu5wkudiphlnfjisrh2dhuc0ttn1intuj7dmld3fq3neem/v9rceta8dj5dittkm7703fr7xotngrw0id5yravd4u5woohemkoc8ncljjr7gw0vukysgnf+qwwxfdamx/+tnph9t/1yobw9rjwtmnzbbddtk+a7c/7irdsmvwzslb9freqxfmb/vh/rl/8zrqe2xnfvsa/+ofl42v1g==</latexit> E v = C A
50 Eigenvalue 2.34 and the corresponding eigenvector The average degree of vertices is 2.28 It can be shown that 2.28 < 2.34 < 3, that is, the value of the largest eigenvalue of A is between the average degree and the maximum degree of the vertices The consequence of eigenvector centrality is to only focus on critical vertices and reduce the dimensionality of the problem. 50
51 A graph can also capture the way joint probability distributions of all variables can be decomposed and then computed Different graphical models for inference Bayesian networks Markov random fields Factor graph 51
52 Example 6.5 A common motivating example Difficulty of an exam, intelligence of the student, grade in a class, student s SAT exam results, professor s letter of recommendation Denoted as D, i, g, S, l, respectively How is the dependency structure of all these variables? 52
53 Example 6.5 How is the dependency structure of all these variables? Intuitively Difficulty Intelligence grade SAT letter 53
54 Example 6.5 Difficulty Intelligence The joint probability grade SAT Lets find out how letter 54
55 Example 6.6 Some basic concepts for two random variables, that is, two data sets F X1, (a, b) =Pr{ apple a, apple b}, (a, b) =Pr{ apple a, apple b} = Pr{A = {w 2 (w) apple a} \ B = {w 2 (w) apple b}} = Pr{B A}Pr{A} 55
56 Example 6.6 Some basic concepts for two random variables, that is, two data sets F X1, (a, b) =Pr{ apple a, apple b} F X1, (a, b) =F X2 (b a)f X1 (a) = Pr{ apple a, apple b} = Pr{ apple b apple a}pr{ apple a} F X2 (b) = lim F,X (a, b) = 2 a!+1 lim Pr{ apple a, apple b} a!+1 56
57 If the data sets are discrete valued then probability mass functions (pmf s) are defined and we will have similar implications p X1, (a, b) =Pr{ = a, = b} p X1, (a, b) =p X2 (b a)p X1 (a) = Pr{ = a, = b} = Pr{ = b = a}pr{ = a} p X2 (b) = X a p X1, (a, b) = X a Pr{ = a, = b} 57
58 If the data sets were continuous valued then probability density functions (pdf s) will be defined and we will have similar implications Z b Z a F X1, (a, b) =Pr{ apple a, apple b} = 1 1 f X1, (x 1,x 2 )dx 1 dx 2 f X1, (x 1,x 2 )=f X2 (x 2 x 1 )f X1 (x 1 ) f X2 (x 2 )= Z +1 1 f X1, (x 1,x 2 )dx 1 = Z +1 1 f X2 (x 2 x 1 )f X1 (x 1 )dx 1 58
59 Efficient graphical models Compute joint distribution of data global function of multiple variables F X = F X1,,,X 4,X 5 Marginalize F X3 (x 3 )= lim x 1!+1 lim x 2!+1 lim x 4!+1 lim x 5!+1 F,,,X 4,X 5 59
60 Efficient graphical models Compute joint distribution of data global function of multiple variables f X = f X1,,,X 4,X 5 Marginalize f X3 (x 3 )= Z +1 1 Z +1 1 Z +1 1 Z +1 1 f X1,,,X 4,X 5 (x 1,x 2,x 3,x 4,x 5 )dx 1 dx 2 dx 4 dx 5 60
61 Efficient graphical models Compute joint distribution of data global function of multiple variables p X (x) =p X1,,,X 4,X 5 Marginalize X p (x X3 3 )= x 1 X x 2 X x 4 X x 5 p X1,,,X 4,X 5 (x 1,x 2,x 3,x 4,x 5 ) 61
62 Critical for inference problems The global function factorizing into local functions F X1, (a, b) =F X2 (b a)f X1 (a) f X1, (x 1,x 2 )=f X2 (x 2 x 1 )f X1 (x 1 ) p X1, (a, b) =p X2 (b a)p X1 (a) Graphical models are powerful tools in representing these expressions 62
63 Bayesian network directed graphs Consider three variables and their joint distribution F X1,, (x 1,x 2,x 3 )=F X3, (x 3 x 1,x 2 )F X1, (x 1,x 2 ) = F X3, (x 3 x 1,x 2 )F X2 (x 2 x 1 )F X1 (x 1 ) 63
64 Bayesian network directed graphs Consider three variables and their joint distribution F X1,, (x 1,x 2,x 3 )=F X3, (x 3 x 1,x 2 )F X1, (x 1,x 2 ) = F X3, (x 3 x 1,x 2 )F X2 (x 2 x 1 )F X1 (x 1 ) 64
65 Bayesian network directed graphs Consider three variables and their joint distribution F X1,, (x 1,x 2,x 3 )=F X3, (x 3 x 1,x 2 )F X1, (x 1,x 2 ) = F X3, (x 3 x 1,x 2 )F X2 (x 2 x 1 )F X1 (x 1 ) 65
66 Bayesian network directed graphs Consider three variables and their joint distribution F X1,, (x 1,x 2,x 3 )=F X3, (x 3 x 1,x 2 )F X1, (x 1,x 2 ) = F X3, (x 3 x 1,x 2 )F X2 (x 2 x 1 )F X1 (x 1 ) 66
67 Bayesian network directed graphs Consider three variables and their joint distribution F X1,, (x 1,x 2,x 3 )=F X3, (x 3 x 1,x 2 )F X1, (x 1,x 2 ) = F X3, (x 3 x 1,x 2 )F X2 (x 2 x 1 )F X1 (x 1 ) 67
68 If and are independent F X1,, (x 1,x 2,x 3 )=F X3, (x 3 x 1,x 2 )F X2 (x 2 )F X1 (x 1 ) 68
69 If and are independent F X1,, (x 1,x 2,x 3 )=F X3, (x 3 x 1,x 2 )F X2 (x 2 )F X1 (x 1 ) Here, are the parents of The computation of joint density Decomposed Tractable 69
70 An alternative order of conditioning would lead to F X1,, = F X1, F X2, = F X1, F X2 F X3 70
71 If and are independent This graph will not be reduced F X1,, = F X1, F X2, = F X1, F X2 F X3 71
72 If and are independent This graph will not be reduced Since and may not be independent conditioned on F X1,, = F X1, F X2, = F X1, F X2 F X3 72
73 If and are independent This graph will not be reduced Since and may not be independent conditioned on Can we construct a counter example to show? F X1,, = F X1, F X2, = F X1, F X2 F X3 73
74 However, if and were independent then The graph will be reduced F X1,, = F X1, F X2, = F X1, F X2 F X3 F X1,, = F X1, F X2 F X3 74
75 If the graph is X 4 X 5 X 6 X 7 75
76 If the graph is X 4 X 5 X 6 X 7 Then, F X1,,...,X 7 = F X1 F X2 F X3 F X4,, F X5, F X6 X 4 F X7 X 4,X 5 76
77 If the graph is Y X n 77
78 If the graph is Y X n Then, F X1,,...,X n,y = F Y F X1 Y F X2 Y...F Xn Y 78
79 The repetition could be simplified by defining a plate Y X i n 79
80 Graphical probabilistic model with deterministic parameters F X,Y s,. 2 = F Y n Y i=1 F Xi Y,s i, 2 Y 2 X i s i n 80
81 Graphical probabilistic model with deterministic parameters F X,Y s,. 2 = F Y n Y i=1 F Xi Y,s i, 2 For example, F Xi Y,s i, 2 Gaussian Y 2 X i s i n 81
82 Graphical probabilistic model with observed variables F X,Y s,. 2 = F Y n Y i=1 F Xi Y,s i, 2 Y 2 X i observed variables s i n 82
83 Graphical probabilistic model with observed variables F X,Y s,. 2 = F Y n Y i=1 F Xi Y,s i, 2 latent variable Y 2 X i s i n 83
84 Can we infer independence or conditional independence from Bayesian graphs? Let us investigate via a few simple examples. The joint pmf of these variables using the graph is p X1,, = p X3 p X1 p X2 84
85 Can we infer independence or conditional independence from Bayesian graphs? Let us investigate via a few simple examples. p X1,, = p X3 p X1 p X2 p X1, = p,, p X3 = p X1 p X2 They are independent conditioned on Node is tail-to-tail with respect to path from to 85
86 Can we infer independence or conditional independence from Bayesian graphs? Let us investigate via a few simple examples. The joint pmf of these variables using the graph p X1,, = p X3 p X1 p X2 and are independent conditioned on Are, independent? 86
87 Can we infer independence or conditional independence from Bayesian graphs? Let us investigate via a few simple examples. p X1,, = p X3 p X1 p X2 p X1, = X x 3 p X1,, = X x 3 p X3 p X1 p X2 6= p X1 p X2 They are not independent unless and as well as and are independent 87
88 Another example p X1,, = p X1 p X3 p X2 p X1, = X x 3 p X1,, = p X1 X x 3 p X3 p X2 6= p X1 p X2 They are not independent 88
89 Another example p X1,, = p X1 p X3 p X2 p X1, = p,, p X3 = p p X3 p X2 p X3 = p X1 p X2 They are independent conditioned on Node is head-to-tail with respect to path from to 89
90 Another example p X1,, = p X1 p X2 p X3, Are, independent? 90
91 Another example p X1,, = p X1 p X2 p X3, Are, independent? X X p X1,X = p 2 X1,,X = p p 3 X1 X2 x 3 Yes they are independent p X3, = p p X1 X2 91
92 Another example p X1,, = p X1 p X2 p X3, Are, conditioned on independent? p X1, = p,, p X3 = p p X2 p X3, p X3 6= p X1 p X2 They are not independent conditioned on Node is head-to-head with respect to path from to 92
93 Example 6.7 Two random variable are independent Conditioned on a third random variable then they are not. Assume X and Y are independent random binary data (that is basically a coin flip experiment). Equally likely to 0 or 1. 93
94 Example 6.7 Then by assumption they are independent. Define Z to be another random variable as Z = X+Y X and Y are dependent conditioned on Z = 1 P (X =1,Y =1 Z = 1) = 0 however P (X =1 Z = 1)P (Y =1 Z = 1) = 1/2 1/2 =1/4 94
95 Summary of and independence Conditionally independent but not independent not blocked unless the node on the path is observed Conditionally independent but not independent not blocked unless the node on the path is observed Independent but not conditionally independent blocked unless the blocking node is observed 95
96 Bayesian networks A tail-to-tail node or head-to-tail node leaves a path unblocked unless the node is observed (that is, the distribution is conditioned on that variable). In that case it blocks the path Conditionally independent but not independent 96
97 Bayesian networks A tail-to-tail node or head-to-tail node leaves a path unblocked unless the node is observed (that is, it is conditioned on that variable). In that case it blocks the path A head-to-head node blocks the path if it is unobserved If the node, and/or at least one of its descendants, is observed then the path becomes unblocked Independent but not conditionally independent 97
98 Bayesian networks A tail-to-tail node or head-to-tail node leaves a path unblocked unless the node is observed (that is, it is conditioned on that variable). In that case it blocks the path A head-to-head node blocks the path if it is unobserved If the node, and/or at least one of its descendants, is observed then the path becomes unblocked When the path between two nodes is blocked then the two nodes (the variables) are independent 98
99 These rules apply to larger networks and to sets of nodes The path between and Unblocked by X 5 Tail-to-tail X 5 Blocked by Head-to-head and are independent X 4 99
100 If the path between two nodes is blocked then the nodes are independent conditioned on the variable that blocked the path 100
101 These rules apply to larger networks and to sets of nodes The path between and Blocked by X 5 Conditioned X 5 Tail-to-tail Blocked by Head-to-head and are independent X 4 101
102 These rules apply to larger networks and to sets of nodes The path between and Unblocked by Head-to-head X 5 Conditioned on its descendent Unblocked byx 5 Tail-to-tail and are not independent X 4 102
103 In general, Bayesian networks can be represented as p X = KY k=1 p Xk p a (k) where p a (k) is the set of parent s of node k Note that Bayesian graphs do not have cycles Directed acyclic graph Invalid p X1 p X2 p X3 103
104 Graphical modeling for inference Bayesian networks Markov random fields Factor graphs 104
105 Conditional independence is often difficult to infer from directed graphs. Undirected graphs are also powerful tools Markov undirected networks Clique A group of nodes fully connected Maximal clique Cliques that can not be expanded 105
106 Cliques X 4 106
107 Cliques X 4 107
108 Cliques X 4 108
109 Maximal clique X 4 109
110 Maximal clique X 4 110
111 Not a clique X 4 111
112 The probability distribution can be written as F X = 1 Z Y C C(X) where C is the potential function of clique An example, X n 1 X n F X = F X1,,...,X n = F X1 F X2 F X3...F Xn X n 1 F X = 1 Z 1,2 (, ) 2,3 (, )... n 1,n (X n 1,X n ) 112
113 The network X n 1 X n... 1,2(, )=F X1 F X2 2,3(, )=F X3 n 1,n(X n 1,X n )=F Xn X n 1 F X = 1 Z 1,2 (, ) 2,3 (, )... n 1,n (X n 1,X n ) 113
114 A less obvious example F X = F X1,,,X 4,X 5 = F X1 F X2 F X3, F X4 F X5 X 5 X 4 114
115 <latexit sha1_base64="ogep1qiwgh7wefqptgar9csmc3a=">aaachnicbvdlsgmxfm3uv62vqks3wsk4kjnsx7gpunfzwdpcw4zm5rynzwsg5i5ysv/ejb/ixowk4er/xvsx0nydcsfn3ppknicrwqdrfjuzhcwl5zxsam5tfwnzk7+9c2fivhoo8ljguh4wa1ioqkjacfvea4sccbwgdzwq1+5bgxgrw+wn0ipyr4m24ayt5odp6n6jni9oe+ebb0yfw9gp7h//ejvqfsmvkoqe7kzw6oclbtedg84tb0okziqkn/9shjfpi2vmkhnt8nwew/zuffzcmndmdssm91ghgpyqfofpdcbzdembvulajrvdculy/e0ysmiyfhtyzohh18zwruj/tuak7bpwqkgkrvb88la7lrrjogqlhkidr9m3hhet7f8p7zlnonpiczyeb3bkevi9kp4xvztsoxw5tsnl9sg+osqeosvlck0qpeo4estp5jw8ou/oi/pufexam87us0v+wpn6aywwobm=</latexit> <latexit sha1_base64="ogep1qiwgh7wefqptgar9csmc3a=">aaachnicbvdlsgmxfm3uv62vqks3wsk4kjnsx7gpunfzwdpcw4zm5rynzwsg5i5ysv/ejb/ixowk4er/xvsx0nydcsfn3ppknicrwqdrfjuzhcwl5zxsam5tfwnzk7+9c2fivhoo8ljguh4wa1ioqkjacfvea4sccbwgdzwq1+5bgxgrw+wn0ipyr4m24ayt5odp6n6jni9oe+ebb0yfw9gp7h//ejvqfsmvkoqe7kzw6oclbtedg84tb0okziqkn/9shjfpi2vmkhnt8nwew/zuffzcmndmdssm91ghgpyqfofpdcbzdembvulajrvdculy/e0ysmiyfhtyzohh18zwruj/tuak7bpwqkgkrvb88la7lrrjogqlhkidr9m3hhet7f8p7zlnonpiczyeb3bkevi9kp4xvztsoxw5tsnl9sg+osqeosvlck0qpeo4estp5jw8ou/oi/pufexam87us0v+wpn6aywwobm=</latexit> <latexit sha1_base64="ogep1qiwgh7wefqptgar9csmc3a=">aaachnicbvdlsgmxfm3uv62vqks3wsk4kjnsx7gpunfzwdpcw4zm5rynzwsg5i5ysv/ejb/ixowk4er/xvsx0nydcsfn3ppknicrwqdrfjuzhcwl5zxsam5tfwnzk7+9c2fivhoo8ljguh4wa1ioqkjacfvea4sccbwgdzwq1+5bgxgrw+wn0ipyr4m24ayt5odp6n6jni9oe+ebb0yfw9gp7h//ejvqfsmvkoqe7kzw6oclbtedg84tb0okziqkn/9shjfpi2vmkhnt8nwew/zuffzcmndmdssm91ghgpyqfofpdcbzdembvulajrvdculy/e0ysmiyfhtyzohh18zwruj/tuak7bpwqkgkrvb88la7lrrjogqlhkidr9m3hhet7f8p7zlnonpiczyeb3bkevi9kp4xvztsoxw5tsnl9sg+osqeosvlck0qpeo4estp5jw8ou/oi/pufexam87us0v+wpn6aywwobm=</latexit> <latexit sha1_base64="ogep1qiwgh7wefqptgar9csmc3a=">aaachnicbvdlsgmxfm3uv62vqks3wsk4kjnsx7gpunfzwdpcw4zm5rynzwsg5i5ysv/ejb/ixowk4er/xvsx0nydcsfn3ppknicrwqdrfjuzhcwl5zxsam5tfwnzk7+9c2fivhoo8ljguh4wa1ioqkjacfvea4sccbwgdzwq1+5bgxgrw+wn0ipyr4m24ayt5odp6n6jni9oe+ebb0yfw9gp7h//ejvqfsmvkoqe7kzw6oclbtedg84tb0okziqkn/9shjfpi2vmkhnt8nwew/zuffzcmndmdssm91ghgpyqfofpdcbzdembvulajrvdculy/e0ysmiyfhtyzohh18zwruj/tuak7bpwqkgkrvb88la7lrrjogqlhkidr9m3hhet7f8p7zlnonpiczyeb3bkevi9kp4xvztsoxw5tsnl9sg+osqeosvlck0qpeo4estp5jw8ou/oi/pufexam87us0v+wpn6aywwobm=</latexit> <latexit sha1_base64="pf/7dqf0u+btz4vaovag9vrfopc=">aaacgnicbvdlsgmxfm34rpvvdekmwarxzayikm6kblxwcgyhlummc9ugzjjdckcspf/hxl9x40lfnbjxb0wfi9p6iohk3hus3bomuhh03r9naxlldw09t5hf3nre2s3s7d+bjnmcfj7irnddzkakbt4klfbpnba4lfale9ejeu0btbgjusn+cq2ydzroc87qskghxa882ryktyrhhdavduenelceetvqosjiww4kh0gh6jbcmegi8aakskaobowvzptwllzmlpkxdc9nswxvrceldppnzedkei91oggpyjgy1ma825aewywi7utbpzco1vnhgmxg9opqdsymu2a+nhl/qzuybj+3bkklgylik4famasy0ffqnbiaomq+jyxryf9kezdpxthgmbchepmjlxk/xlooebenxcrvni0cosrh5ir45ixuya2pep9w8kreybt5d56dv+fd+zy0ljltzwh5a+f7f3hpobq=</latexit> <latexit sha1_base64="pf/7dqf0u+btz4vaovag9vrfopc=">aaacgnicbvdlsgmxfm34rpvvdekmwarxzayikm6kblxwcgyhlummc9ugzjjdckcspf/hxl9x40lfnbjxb0wfi9p6iohk3hus3bomuhh03r9naxlldw09t5hf3nre2s3s7d+bjnmcfj7irnddzkakbt4klfbpnba4lfale9ejeu0btbgjusn+cq2ydzroc87qskghxa882ryktyrhhdavduenelceetvqosjiww4kh0gh6jbcmegi8aakskaobowvzptwllzmlpkxdc9nswxvrceldppnzedkei91oggpyjgy1ma825aewywi7utbpzco1vnhgmxg9opqdsymu2a+nhl/qzuybj+3bkklgylik4famasy0ffqnbiaomq+jyxryf9kezdpxthgmbchepmjlxk/xlooebenxcrvni0cosrh5ir45ixuya2pep9w8kreybt5d56dv+fd+zy0ljltzwh5a+f7f3hpobq=</latexit> <latexit sha1_base64="pf/7dqf0u+btz4vaovag9vrfopc=">aaacgnicbvdlsgmxfm34rpvvdekmwarxzayikm6kblxwcgyhlummc9ugzjjdckcspf/hxl9x40lfnbjxb0wfi9p6iohk3hus3bomuhh03r9naxlldw09t5hf3nre2s3s7d+bjnmcfj7irnddzkakbt4klfbpnba4lfale9ejeu0btbgjusn+cq2ydzroc87qskghxa882ryktyrhhdavduenelceetvqosjiww4kh0gh6jbcmegi8aakskaobowvzptwllzmlpkxdc9nswxvrceldppnzedkei91oggpyjgy1ma825aewywi7utbpzco1vnhgmxg9opqdsymu2a+nhl/qzuybj+3bkklgylik4famasy0ffqnbiaomq+jyxryf9kezdpxthgmbchepmjlxk/xlooebenxcrvni0cosrh5ir45ixuya2pep9w8kreybt5d56dv+fd+zy0ljltzwh5a+f7f3hpobq=</latexit> <latexit sha1_base64="pf/7dqf0u+btz4vaovag9vrfopc=">aaacgnicbvdlsgmxfm34rpvvdekmwarxzayikm6kblxwcgyhlummc9ugzjjdckcspf/hxl9x40lfnbjxb0wfi9p6iohk3hus3bomuhh03r9naxlldw09t5hf3nre2s3s7d+bjnmcfj7irnddzkakbt4klfbpnba4lfale9ejeu0btbgjusn+cq2ydzroc87qskghxa882ryktyrhhdavduenelceetvqosjiww4kh0gh6jbcmegi8aakskaobowvzptwllzmlpkxdc9nswxvrceldppnzedkei91oggpyjgy1ma825aewywi7utbpzco1vnhgmxg9opqdsymu2a+nhl/qzuybj+3bkklgylik4famasy0ffqnbiaomq+jyxryf9kezdpxthgmbchepmjlxk/xlooebenxcrvni0cosrh5ir45ixuya2pep9w8kreybt5d56dv+fd+zy0ljltzwh5a+f7f3hpobq=</latexit> F X = F X1 F X2 F X3, F X4 F X5 Lets recall the rules on independence and are independent X 4 and X 5 are not independent X 5 X 4 115
116 <latexit sha1_base64="xbon6ondbb9h94lhsysynq7coza=">aaacnhicbva9t8mwehx4pnwvgfkskismkiligfgqlawmiffaqa0ix7lsc8eo7auiqvqnwpgftdawaglln+cudea5ydbzu3t3vhelulj0/wdvynjqemz2br60sli0vfjexbuyojmc6lxlbzorsycfgjoklnbmdbakktcibk7yfomwjbvaxwi/hu7crpxocs7quwh5rbkgth1i2wh3ogaqhuavzlj7qrqgsimvkoyu3kwqcq1ikxeamgpvahbccswv+qog4yaoqiuucr6wh9ux5lniwnljrg0ffoodnxeflzasttmlkem37bpadiqwgo0mrlsp6zzjytrvxp3rlxz7uzfgibx9jhkvccoe/zvlyf9yrqy7+52bugmgopj3og4mkwqaw0hjyycj7dvauhe2cmp7zdcozuismyh4u/i4qneqb9xgyrdydfy4muc2ycbzjghzi0fkljytouhknjyrv/lmpxgv3rv38v064rwadfirvm8v5n+p9w==</latexit> <latexit sha1_base64="xbon6ondbb9h94lhsysynq7coza=">aaacnhicbva9t8mwehx4pnwvgfkskismkiligfgqlawmiffaqa0ix7lsc8eo7auiqvqnwpgftdawaglln+cudea5ydbzu3t3vhelulj0/wdvynjqemz2br60sli0vfjexbuyojmc6lxlbzorsycfgjoklnbmdbakktcibk7yfomwjbvaxwi/hu7crpxocs7quwh5rbkgth1i2wh3ogaqhuavzlj7qrqgsimvkoyu3kwqcq1ikxeamgpvahbccswv+qog4yaoqiuucr6wh9ux5lniwnljrg0ffoodnxeflzasttmlkem37bpadiqwgo0mrlsp6zzjytrvxp3rlxz7uzfgibx9jhkvccoe/zvlyf9yrqy7+52bugmgopj3og4mkwqaw0hjyycj7dvauhe2cmp7zdcozuismyh4u/i4qneqb9xgyrdydfy4muc2ycbzjghzi0fkljytouhknjyrv/lmpxgv3rv38v064rwadfirvm8v5n+p9w==</latexit> <latexit sha1_base64="xbon6ondbb9h94lhsysynq7coza=">aaacnhicbva9t8mwehx4pnwvgfkskismkiligfgqlawmiffaqa0ix7lsc8eo7auiqvqnwpgftdawaglln+cudea5ydbzu3t3vhelulj0/wdvynjqemz2br60sli0vfjexbuyojmc6lxlbzorsycfgjoklnbmdbakktcibk7yfomwjbvaxwi/hu7crpxocs7quwh5rbkgth1i2wh3ogaqhuavzlj7qrqgsimvkoyu3kwqcq1ikxeamgpvahbccswv+qog4yaoqiuucr6wh9ux5lniwnljrg0ffoodnxeflzasttmlkem37bpadiqwgo0mrlsp6zzjytrvxp3rlxz7uzfgibx9jhkvccoe/zvlyf9yrqy7+52bugmgopj3og4mkwqaw0hjyycj7dvauhe2cmp7zdcozuismyh4u/i4qneqb9xgyrdydfy4muc2ycbzjghzi0fkljytouhknjyrv/lmpxgv3rv38v064rwadfirvm8v5n+p9w==</latexit> <latexit sha1_base64="xbon6ondbb9h94lhsysynq7coza=">aaacnhicbva9t8mwehx4pnwvgfkskismkiligfgqlawmiffaqa0ix7lsc8eo7auiqvqnwpgftdawaglln+cudea5ydbzu3t3vhelulj0/wdvynjqemz2br60sli0vfjexbuyojmc6lxlbzorsycfgjoklnbmdbakktcibk7yfomwjbvaxwi/hu7crpxocs7quwh5rbkgth1i2wh3ogaqhuavzlj7qrqgsimvkoyu3kwqcq1ikxeamgpvahbccswv+qog4yaoqiuucr6wh9ux5lniwnljrg0ffoodnxeflzasttmlkem37bpadiqwgo0mrlsp6zzjytrvxp3rlxz7uzfgibx9jhkvccoe/zvlyf9yrqy7+52bugmgopj3og4mkwqaw0hjyycj7dvauhe2cmp7zdcozuismyh4u/i4qneqb9xgyrdydfy4muc2ycbzjghzi0fkljytouhknjyrv/lmpxgv3rv38v064rwadfirvm8v5n+p9w==</latexit> <latexit sha1_base64="tc2t4mepq0e6w/vhwzpkfq+khmo=">aaacmhicbvbntwixeo36ififevtssew8kv3fqpfc9mirexesijtud4dgbrtpu0zc+ete/cfgcwc1xv0vdmepce7s5vxnm5noc2lothhdsbo0vlk6tp7byg9ube/sfvb2h7rmfiu6lvyqzka0ccagbpjh0iwvkcjg0ageb9n84wmuzllcm0emnyj0bosysoyl/ek16zdx+xq3dtybirhhkh01/fmzugfmioqy7cumplkelk2geeur6c/8qtetuzpai8dlqbflufmlb+1q0isylsknwrc8nzydo80wymgubycaykifsq9afgosge4mjxup8lflqtyvyp7jlyw7wzekkdadkldkiji+ns+l5h+5vmk6l50he3fiqndpog7csze4tq+htae1fgabocraqdhte0wossbnrqne/mqloh5auip5d+vi5szzi4co0re6qr66qbvurtvurxs9ohf0gt6dv2fsfdnfu+msk9ucod/h/pwcxq6oza==</latexit> <latexit sha1_base64="tc2t4mepq0e6w/vhwzpkfq+khmo=">aaacmhicbvbntwixeo36ififevtssew8kv3fqpfc9mirexesijtud4dgbrtpu0zc+ete/cfgcwc1xv0vdmepce7s5vxnm5noc2lothhdsbo0vlk6tp7byg9ube/sfvb2h7rmfiu6lvyqzka0ccagbpjh0iwvkcjg0ageb9n84wmuzllcm0emnyj0bosysoyl/ek16zdx+xq3dtybirhhkh01/fmzugfmioqy7cumplkelk2geeur6c/8qtetuzpai8dlqbflufmlb+1q0isylsknwrc8nzydo80wymgubycaykifsq9afgosge4mjxup8lflqtyvyp7jlyw7wzekkdadkldkiji+ns+l5h+5vmk6l50he3fiqndpog7csze4tq+htae1fgabocraqdhte0wossbnrqne/mqloh5auip5d+vi5szzi4co0re6qr66qbvurtvurxs9ohf0gt6dv2fsfdnfu+msk9ucod/h/pwcxq6oza==</latexit> <latexit sha1_base64="tc2t4mepq0e6w/vhwzpkfq+khmo=">aaacmhicbvbntwixeo36ififevtssew8kv3fqpfc9mirexesijtud4dgbrtpu0zc+ete/cfgcwc1xv0vdmepce7s5vxnm5noc2lothhdsbo0vlk6tp7byg9ube/sfvb2h7rmfiu6lvyqzka0ccagbpjh0iwvkcjg0ageb9n84wmuzllcm0emnyj0bosysoyl/ek16zdx+xq3dtybirhhkh01/fmzugfmioqy7cumplkelk2geeur6c/8qtetuzpai8dlqbflufmlb+1q0isylsknwrc8nzydo80wymgubycaykifsq9afgosge4mjxup8lflqtyvyp7jlyw7wzekkdadkldkiji+ns+l5h+5vmk6l50he3fiqndpog7csze4tq+htae1fgabocraqdhte0wossbnrqne/mqloh5auip5d+vi5szzi4co0re6qr66qbvurtvurxs9ohf0gt6dv2fsfdnfu+msk9ucod/h/pwcxq6oza==</latexit> <latexit sha1_base64="tc2t4mepq0e6w/vhwzpkfq+khmo=">aaacmhicbvbntwixeo36ififevtssew8kv3fqpfc9mirexesijtud4dgbrtpu0zc+ete/cfgcwc1xv0vdmepce7s5vxnm5noc2lothhdsbo0vlk6tp7byg9ube/sfvb2h7rmfiu6lvyqzka0ccagbpjh0iwvkcjg0ageb9n84wmuzllcm0emnyj0bosysoyl/ek16zdx+xq3dtybirhhkh01/fmzugfmioqy7cumplkelk2geeur6c/8qtetuzpai8dlqbflufmlb+1q0isylsknwrc8nzydo80wymgubycaykifsq9afgosge4mjxup8lflqtyvyp7jlyw7wzekkdadkldkiji+ns+l5h+5vmk6l50he3fiqndpog7csze4tq+htae1fgabocraqdhte0wossbnrqne/mqloh5auip5d+vi5szzi4co0re6qr66qbvurtvurxs9ohf0gt6dv2fsfdnfu+msk9ucod/h/pwcxq6oza==</latexit> F X = F X1 F X2 F X3, F X4 F X5 Lets recall the rules on independence and are not independent conditioned on X 4 and X 5 are independent conditioned on X 5 X 4 116
Chris Bishop s PRML Ch. 8: Graphical Models
 Chris Bishop s PRML Ch. 8: Graphical Models January 24, 2008 Introduction Visualize the structure of a probabilistic model Design and motivate new models Insights into the model s properties, in particular
Chris Bishop s PRML Ch. 8: Graphical Models January 24, 2008 Introduction Visualize the structure of a probabilistic model Design and motivate new models Insights into the model s properties, in particular
Chapter 16. Structured Probabilistic Models for Deep Learning
 Peng et al.: Deep Learning and Practice 1 Chapter 16 Structured Probabilistic Models for Deep Learning Peng et al.: Deep Learning and Practice 2 Structured Probabilistic Models way of using graphs to describe
Peng et al.: Deep Learning and Practice 1 Chapter 16 Structured Probabilistic Models for Deep Learning Peng et al.: Deep Learning and Practice 2 Structured Probabilistic Models way of using graphs to describe
Lecture 4 October 18th
 Directed and undirected graphical models Fall 2017 Lecture 4 October 18th Lecturer: Guillaume Obozinski Scribe: In this lecture, we will assume that all random variables are discrete, to keep notations
Directed and undirected graphical models Fall 2017 Lecture 4 October 18th Lecturer: Guillaume Obozinski Scribe: In this lecture, we will assume that all random variables are discrete, to keep notations
Part I. C. M. Bishop PATTERN RECOGNITION AND MACHINE LEARNING CHAPTER 8: GRAPHICAL MODELS
 Part I C. M. Bishop PATTERN RECOGNITION AND MACHINE LEARNING CHAPTER 8: GRAPHICAL MODELS Probabilistic Graphical Models Graphical representation of a probabilistic model Each variable corresponds to a
Part I C. M. Bishop PATTERN RECOGNITION AND MACHINE LEARNING CHAPTER 8: GRAPHICAL MODELS Probabilistic Graphical Models Graphical representation of a probabilistic model Each variable corresponds to a
4.1 Notation and probability review
 Directed and undirected graphical models Fall 2015 Lecture 4 October 21st Lecturer: Simon Lacoste-Julien Scribe: Jaime Roquero, JieYing Wu 4.1 Notation and probability review 4.1.1 Notations Let us recall
Directed and undirected graphical models Fall 2015 Lecture 4 October 21st Lecturer: Simon Lacoste-Julien Scribe: Jaime Roquero, JieYing Wu 4.1 Notation and probability review 4.1.1 Notations Let us recall
CS 2750: Machine Learning. Bayesian Networks. Prof. Adriana Kovashka University of Pittsburgh March 14, 2016
 CS 2750: Machine Learning Bayesian Networks Prof. Adriana Kovashka University of Pittsburgh March 14, 2016 Plan for today and next week Today and next time: Bayesian networks (Bishop Sec. 8.1) Conditional
CS 2750: Machine Learning Bayesian Networks Prof. Adriana Kovashka University of Pittsburgh March 14, 2016 Plan for today and next week Today and next time: Bayesian networks (Bishop Sec. 8.1) Conditional
Graphical Models and Kernel Methods
 Graphical Models and Kernel Methods Jerry Zhu Department of Computer Sciences University of Wisconsin Madison, USA MLSS June 17, 2014 1 / 123 Outline Graphical Models Probabilistic Inference Directed vs.
Graphical Models and Kernel Methods Jerry Zhu Department of Computer Sciences University of Wisconsin Madison, USA MLSS June 17, 2014 1 / 123 Outline Graphical Models Probabilistic Inference Directed vs.
{ p if x = 1 1 p if x = 0
 Discrete random variables Probability mass function Given a discrete random variable X taking values in X = {v 1,..., v m }, its probability mass function P : X [0, 1] is defined as: P (v i ) = Pr[X =
Discrete random variables Probability mass function Given a discrete random variable X taking values in X = {v 1,..., v m }, its probability mass function P : X [0, 1] is defined as: P (v i ) = Pr[X =
CPSC 540: Machine Learning
 CPSC 540: Machine Learning Undirected Graphical Models Mark Schmidt University of British Columbia Winter 2016 Admin Assignment 3: 2 late days to hand it in today, Thursday is final day. Assignment 4:
CPSC 540: Machine Learning Undirected Graphical Models Mark Schmidt University of British Columbia Winter 2016 Admin Assignment 3: 2 late days to hand it in today, Thursday is final day. Assignment 4:
Graphical models and causality: Directed acyclic graphs (DAGs) and conditional (in)dependence
 Graphical models and causality: Directed acyclic graphs (DAGs) and conditional (in)dependence General overview Introduction Directed acyclic graphs (DAGs) and conditional independence DAGs and causal effects
Graphical models and causality: Directed acyclic graphs (DAGs) and conditional (in)dependence General overview Introduction Directed acyclic graphs (DAGs) and conditional independence DAGs and causal effects
MATH 829: Introduction to Data Mining and Analysis Graphical Models I
 MATH 829: Introduction to Data Mining and Analysis Graphical Models I Dominique Guillot Departments of Mathematical Sciences University of Delaware May 2, 2016 1/12 Independence and conditional independence:
MATH 829: Introduction to Data Mining and Analysis Graphical Models I Dominique Guillot Departments of Mathematical Sciences University of Delaware May 2, 2016 1/12 Independence and conditional independence:
Machine Learning 4771
 Machine Learning 4771 Instructor: Tony Jebara Topic 16 Undirected Graphs Undirected Separation Inferring Marginals & Conditionals Moralization Junction Trees Triangulation Undirected Graphs Separation
Machine Learning 4771 Instructor: Tony Jebara Topic 16 Undirected Graphs Undirected Separation Inferring Marginals & Conditionals Moralization Junction Trees Triangulation Undirected Graphs Separation
CSC 412 (Lecture 4): Undirected Graphical Models
 CSC 412 (Lecture 4): Undirected Graphical Models Raquel Urtasun University of Toronto Feb 2, 2016 R Urtasun (UofT) CSC 412 Feb 2, 2016 1 / 37 Today Undirected Graphical Models: Semantics of the graph:
CSC 412 (Lecture 4): Undirected Graphical Models Raquel Urtasun University of Toronto Feb 2, 2016 R Urtasun (UofT) CSC 412 Feb 2, 2016 1 / 37 Today Undirected Graphical Models: Semantics of the graph:
Probabilistic Graphical Models
 Probabilistic Graphical Models Brown University CSCI 295-P, Spring 213 Prof. Erik Sudderth Lecture 11: Inference & Learning Overview, Gaussian Graphical Models Some figures courtesy Michael Jordan s draft
Probabilistic Graphical Models Brown University CSCI 295-P, Spring 213 Prof. Erik Sudderth Lecture 11: Inference & Learning Overview, Gaussian Graphical Models Some figures courtesy Michael Jordan s draft
Undirected Graphical Models
 Undirected Graphical Models 1 Conditional Independence Graphs Let G = (V, E) be an undirected graph with vertex set V and edge set E, and let A, B, and C be subsets of vertices. We say that C separates
Undirected Graphical Models 1 Conditional Independence Graphs Let G = (V, E) be an undirected graph with vertex set V and edge set E, and let A, B, and C be subsets of vertices. We say that C separates
Directed Graphical Models
 CS 2750: Machine Learning Directed Graphical Models Prof. Adriana Kovashka University of Pittsburgh March 28, 2017 Graphical Models If no assumption of independence is made, must estimate an exponential
CS 2750: Machine Learning Directed Graphical Models Prof. Adriana Kovashka University of Pittsburgh March 28, 2017 Graphical Models If no assumption of independence is made, must estimate an exponential
Directed and Undirected Graphical Models
 Directed and Undirected Davide Bacciu Dipartimento di Informatica Università di Pisa bacciu@di.unipi.it Machine Learning: Neural Networks and Advanced Models (AA2) Last Lecture Refresher Lecture Plan Directed
Directed and Undirected Davide Bacciu Dipartimento di Informatica Università di Pisa bacciu@di.unipi.it Machine Learning: Neural Networks and Advanced Models (AA2) Last Lecture Refresher Lecture Plan Directed
1 T 1 = where 1 is the all-ones vector. For the upper bound, let v 1 be the eigenvector corresponding. u:(u,v) E v 1(u)
 CME 305: Discrete Mathematics and Algorithms Instructor: Reza Zadeh (rezab@stanford.edu) Final Review Session 03/20/17 1. Let G = (V, E) be an unweighted, undirected graph. Let λ 1 be the maximum eigenvalue
CME 305: Discrete Mathematics and Algorithms Instructor: Reza Zadeh (rezab@stanford.edu) Final Review Session 03/20/17 1. Let G = (V, E) be an unweighted, undirected graph. Let λ 1 be the maximum eigenvalue
Independencies. Undirected Graphical Models 2: Independencies. Independencies (Markov networks) Independencies (Bayesian Networks)
 (Bayesian Networks) Undirected Graphical Models 2: Use d-separation to read off independencies in a Bayesian network Takes a bit of effort! 1 2 (Markov networks) Use separation to determine independencies
(Bayesian Networks) Undirected Graphical Models 2: Use d-separation to read off independencies in a Bayesian network Takes a bit of effort! 1 2 (Markov networks) Use separation to determine independencies
Message Passing and Junction Tree Algorithms. Kayhan Batmanghelich
 Message Passing and Junction Tree Algorithms Kayhan Batmanghelich 1 Review 2 Review 3 Great Ideas in ML: Message Passing Each soldier receives reports from all branches of tree 3 here 7 here 1 of me 11
Message Passing and Junction Tree Algorithms Kayhan Batmanghelich 1 Review 2 Review 3 Great Ideas in ML: Message Passing Each soldier receives reports from all branches of tree 3 here 7 here 1 of me 11
Directed Graphical Models or Bayesian Networks
 Directed Graphical Models or Bayesian Networks Le Song Machine Learning II: Advanced Topics CSE 8803ML, Spring 2012 Bayesian Networks One of the most exciting recent advancements in statistical AI Compact
Directed Graphical Models or Bayesian Networks Le Song Machine Learning II: Advanced Topics CSE 8803ML, Spring 2012 Bayesian Networks One of the most exciting recent advancements in statistical AI Compact
Machine Learning Lecture Notes
 Machine Learning Lecture Notes Predrag Radivojac January 3, 25 Random Variables Until now we operated on relatively simple sample spaces and produced measure functions over sets of outcomes. In many situations,
Machine Learning Lecture Notes Predrag Radivojac January 3, 25 Random Variables Until now we operated on relatively simple sample spaces and produced measure functions over sets of outcomes. In many situations,
MATH 829: Introduction to Data Mining and Analysis Clustering II
 his lecture is based on U. von Luxburg, A Tutorial on Spectral Clustering, Statistics and Computing, 17 (4), 2007. MATH 829: Introduction to Data Mining and Analysis Clustering II Dominique Guillot Departments
his lecture is based on U. von Luxburg, A Tutorial on Spectral Clustering, Statistics and Computing, 17 (4), 2007. MATH 829: Introduction to Data Mining and Analysis Clustering II Dominique Guillot Departments
Probabilistic Graphical Models (I)
 Probabilistic Graphical Models (I) Hongxin Zhang zhx@cad.zju.edu.cn State Key Lab of CAD&CG, ZJU 2015-03-31 Probabilistic Graphical Models Modeling many real-world problems => a large number of random
Probabilistic Graphical Models (I) Hongxin Zhang zhx@cad.zju.edu.cn State Key Lab of CAD&CG, ZJU 2015-03-31 Probabilistic Graphical Models Modeling many real-world problems => a large number of random
STATISTICAL METHODS IN AI/ML Vibhav Gogate The University of Texas at Dallas. Bayesian networks: Representation
 STATISTICAL METHODS IN AI/ML Vibhav Gogate The University of Texas at Dallas Bayesian networks: Representation Motivation Explicit representation of the joint distribution is unmanageable Computationally:
STATISTICAL METHODS IN AI/ML Vibhav Gogate The University of Texas at Dallas Bayesian networks: Representation Motivation Explicit representation of the joint distribution is unmanageable Computationally:
Conditional Independence
 Conditional Independence Sargur Srihari srihari@cedar.buffalo.edu 1 Conditional Independence Topics 1. What is Conditional Independence? Factorization of probability distribution into marginals 2. Why
Conditional Independence Sargur Srihari srihari@cedar.buffalo.edu 1 Conditional Independence Topics 1. What is Conditional Independence? Factorization of probability distribution into marginals 2. Why
Based on slides by Richard Zemel
 CSC 412/2506 Winter 2018 Probabilistic Learning and Reasoning Lecture 3: Directed Graphical Models and Latent Variables Based on slides by Richard Zemel Learning outcomes What aspects of a model can we
CSC 412/2506 Winter 2018 Probabilistic Learning and Reasoning Lecture 3: Directed Graphical Models and Latent Variables Based on slides by Richard Zemel Learning outcomes What aspects of a model can we
Prof. Dr. Lars Schmidt-Thieme, L. B. Marinho, K. Buza Information Systems and Machine Learning Lab (ISMLL), University of Hildesheim, Germany, Course
 Course on Bayesian Networks, winter term 2007 0/31 Bayesian Networks Bayesian Networks I. Bayesian Networks / 1. Probabilistic Independence and Separation in Graphs Prof. Dr. Lars Schmidt-Thieme, L. B.
Course on Bayesian Networks, winter term 2007 0/31 Bayesian Networks Bayesian Networks I. Bayesian Networks / 1. Probabilistic Independence and Separation in Graphs Prof. Dr. Lars Schmidt-Thieme, L. B.
Recall from last time. Lecture 3: Conditional independence and graph structure. Example: A Bayesian (belief) network.
 ecall from last time Lecture 3: onditional independence and graph structure onditional independencies implied by a belief network Independence maps (I-maps) Factorization theorem The Bayes ball algorithm
ecall from last time Lecture 3: onditional independence and graph structure onditional independencies implied by a belief network Independence maps (I-maps) Factorization theorem The Bayes ball algorithm
Cheng Soon Ong & Christian Walder. Canberra February June 2018
 Cheng Soon Ong & Christian Walder Research Group and College of Engineering and Computer Science Canberra February June 2018 Outlines Overview Introduction Linear Algebra Probability Linear Regression
Cheng Soon Ong & Christian Walder Research Group and College of Engineering and Computer Science Canberra February June 2018 Outlines Overview Introduction Linear Algebra Probability Linear Regression
A lower bound for the Laplacian eigenvalues of a graph proof of a conjecture by Guo
 A lower bound for the Laplacian eigenvalues of a graph proof of a conjecture by Guo A. E. Brouwer & W. H. Haemers 2008-02-28 Abstract We show that if µ j is the j-th largest Laplacian eigenvalue, and d
A lower bound for the Laplacian eigenvalues of a graph proof of a conjecture by Guo A. E. Brouwer & W. H. Haemers 2008-02-28 Abstract We show that if µ j is the j-th largest Laplacian eigenvalue, and d
Spectra of Adjacency and Laplacian Matrices
 Spectra of Adjacency and Laplacian Matrices Definition: University of Alicante (Spain) Matrix Computing (subject 3168 Degree in Maths) 30 hours (theory)) + 15 hours (practical assignment) Contents 1. Spectra
Spectra of Adjacency and Laplacian Matrices Definition: University of Alicante (Spain) Matrix Computing (subject 3168 Degree in Maths) 30 hours (theory)) + 15 hours (practical assignment) Contents 1. Spectra
CS Lecture 4. Markov Random Fields
 CS 6347 Lecture 4 Markov Random Fields Recap Announcements First homework is available on elearning Reminder: Office hours Tuesday from 10am-11am Last Time Bayesian networks Today Markov random fields
CS 6347 Lecture 4 Markov Random Fields Recap Announcements First homework is available on elearning Reminder: Office hours Tuesday from 10am-11am Last Time Bayesian networks Today Markov random fields
Basic graph theory 18.S995 - L26.
 Basic graph theory 18.S995 - L26 dunkel@math.mit.edu http://java.dzone.com/articles/algorithm-week-graphs-and no cycles Isomorphic graphs f(a) = 1 f(b) = 6 f(c) = 8 f(d) = 3 f(g) = 5 f(h) = 2 f(i) = 4
Basic graph theory 18.S995 - L26 dunkel@math.mit.edu http://java.dzone.com/articles/algorithm-week-graphs-and no cycles Isomorphic graphs f(a) = 1 f(b) = 6 f(c) = 8 f(d) = 3 f(g) = 5 f(h) = 2 f(i) = 4
Data Mining 2018 Bayesian Networks (1)
 Data Mining 2018 Bayesian Networks (1) Ad Feelders Universiteit Utrecht Ad Feelders ( Universiteit Utrecht ) Data Mining 1 / 49 Do you like noodles? Do you like noodles? Race Gender Yes No Black Male 10
Data Mining 2018 Bayesian Networks (1) Ad Feelders Universiteit Utrecht Ad Feelders ( Universiteit Utrecht ) Data Mining 1 / 49 Do you like noodles? Do you like noodles? Race Gender Yes No Black Male 10
Graph fundamentals. Matrices associated with a graph
 Graph fundamentals Matrices associated with a graph Drawing a picture of a graph is one way to represent it. Another type of representation is via a matrix. Let G be a graph with V (G) ={v 1,v,...,v n
Graph fundamentals Matrices associated with a graph Drawing a picture of a graph is one way to represent it. Another type of representation is via a matrix. Let G be a graph with V (G) ={v 1,v,...,v n
Multivariate random variables
 Multivariate random variables DS GA 1002 Statistical and Mathematical Models http://www.cims.nyu.edu/~cfgranda/pages/dsga1002_fall16 Carlos Fernandez-Granda Joint distributions Tool to characterize several
Multivariate random variables DS GA 1002 Statistical and Mathematical Models http://www.cims.nyu.edu/~cfgranda/pages/dsga1002_fall16 Carlos Fernandez-Granda Joint distributions Tool to characterize several
3 : Representation of Undirected GM
 10-708: Probabilistic Graphical Models 10-708, Spring 2016 3 : Representation of Undirected GM Lecturer: Eric P. Xing Scribes: Longqi Cai, Man-Chia Chang 1 MRF vs BN There are two types of graphical models:
10-708: Probabilistic Graphical Models 10-708, Spring 2016 3 : Representation of Undirected GM Lecturer: Eric P. Xing Scribes: Longqi Cai, Man-Chia Chang 1 MRF vs BN There are two types of graphical models:
Graphical Models - Part I
 Graphical Models - Part I Oliver Schulte - CMPT 726 Bishop PRML Ch. 8, some slides from Russell and Norvig AIMA2e Outline Probabilistic Models Bayesian Networks Markov Random Fields Inference Outline Probabilistic
Graphical Models - Part I Oliver Schulte - CMPT 726 Bishop PRML Ch. 8, some slides from Russell and Norvig AIMA2e Outline Probabilistic Models Bayesian Networks Markov Random Fields Inference Outline Probabilistic
Recitation 2: Probability
 Recitation 2: Probability Colin White, Kenny Marino January 23, 2018 Outline Facts about sets Definitions and facts about probability Random Variables and Joint Distributions Characteristics of distributions
Recitation 2: Probability Colin White, Kenny Marino January 23, 2018 Outline Facts about sets Definitions and facts about probability Random Variables and Joint Distributions Characteristics of distributions
Massachusetts Institute of Technology Department of Electrical Engineering and Computer Science Algorithms For Inference Fall 2014
 Massachusetts Institute of Technology Department of Electrical Engineering and Computer Science 6.438 Algorithms For Inference Fall 2014 Recitation 3 1 Gaussian Graphical Models: Schur s Complement Consider
Massachusetts Institute of Technology Department of Electrical Engineering and Computer Science 6.438 Algorithms For Inference Fall 2014 Recitation 3 1 Gaussian Graphical Models: Schur s Complement Consider
Review of Probability Theory
 Review of Probability Theory Arian Maleki and Tom Do Stanford University Probability theory is the study of uncertainty Through this class, we will be relying on concepts from probability theory for deriving
Review of Probability Theory Arian Maleki and Tom Do Stanford University Probability theory is the study of uncertainty Through this class, we will be relying on concepts from probability theory for deriving
Probabilistic Graphical Models
 Probabilistic Graphical Models Lecture 4 Learning Bayesian Networks CS/CNS/EE 155 Andreas Krause Announcements Another TA: Hongchao Zhou Please fill out the questionnaire about recitations Homework 1 out.
Probabilistic Graphical Models Lecture 4 Learning Bayesian Networks CS/CNS/EE 155 Andreas Krause Announcements Another TA: Hongchao Zhou Please fill out the questionnaire about recitations Homework 1 out.
Massachusetts Institute of Technology Department of Electrical Engineering and Computer Science Algorithms For Inference Fall 2014
 Massachusetts Institute of Technology Department of Electrical Engineering and Computer Science 6.438 Algorithms For Inference Fall 2014 Problem Set 3 Issued: Thursday, September 25, 2014 Due: Thursday,
Massachusetts Institute of Technology Department of Electrical Engineering and Computer Science 6.438 Algorithms For Inference Fall 2014 Problem Set 3 Issued: Thursday, September 25, 2014 Due: Thursday,
Markov Independence (Continued)
 Markov Independence (Continued) As an Undirected Graph Basic idea: Each variable V is represented as a vertex in an undirected graph G = (V(G), E(G)), with set of vertices V(G) and set of edges E(G) the
Markov Independence (Continued) As an Undirected Graph Basic idea: Each variable V is represented as a vertex in an undirected graph G = (V(G), E(G)), with set of vertices V(G) and set of edges E(G) the
1. what conditional independencies are implied by the graph. 2. whether these independecies correspond to the probability distribution
 NETWORK ANALYSIS Lourens Waldorp PROBABILITY AND GRAPHS The objective is to obtain a correspondence between the intuitive pictures (graphs) of variables of interest and the probability distributions of
NETWORK ANALYSIS Lourens Waldorp PROBABILITY AND GRAPHS The objective is to obtain a correspondence between the intuitive pictures (graphs) of variables of interest and the probability distributions of
Intelligent Systems:
 Intelligent Systems: Undirected Graphical models (Factor Graphs) (2 lectures) Carsten Rother 15/01/2015 Intelligent Systems: Probabilistic Inference in DGM and UGM Roadmap for next two lectures Definition
Intelligent Systems: Undirected Graphical models (Factor Graphs) (2 lectures) Carsten Rother 15/01/2015 Intelligent Systems: Probabilistic Inference in DGM and UGM Roadmap for next two lectures Definition
Undirected Graphical Models
 Outline Hong Chang Institute of Computing Technology, Chinese Academy of Sciences Machine Learning Methods (Fall 2012) Outline Outline I 1 Introduction 2 Properties Properties 3 Generative vs. Conditional
Outline Hong Chang Institute of Computing Technology, Chinese Academy of Sciences Machine Learning Methods (Fall 2012) Outline Outline I 1 Introduction 2 Properties Properties 3 Generative vs. Conditional
ECE521 Tutorial 11. Topic Review. ECE521 Winter Credits to Alireza Makhzani, Alex Schwing, Rich Zemel and TAs for slides. ECE521 Tutorial 11 / 4
 ECE52 Tutorial Topic Review ECE52 Winter 206 Credits to Alireza Makhzani, Alex Schwing, Rich Zemel and TAs for slides ECE52 Tutorial ECE52 Winter 206 Credits to Alireza / 4 Outline K-means, PCA 2 Bayesian
ECE52 Tutorial Topic Review ECE52 Winter 206 Credits to Alireza Makhzani, Alex Schwing, Rich Zemel and TAs for slides ECE52 Tutorial ECE52 Winter 206 Credits to Alireza / 4 Outline K-means, PCA 2 Bayesian
Spectral Graph Theory and You: Matrix Tree Theorem and Centrality Metrics
 Spectral Graph Theory and You: and Centrality Metrics Jonathan Gootenberg March 11, 2013 1 / 19 Outline of Topics 1 Motivation Basics of Spectral Graph Theory Understanding the characteristic polynomial
Spectral Graph Theory and You: and Centrality Metrics Jonathan Gootenberg March 11, 2013 1 / 19 Outline of Topics 1 Motivation Basics of Spectral Graph Theory Understanding the characteristic polynomial
Graphical Models and Independence Models
 Graphical Models and Independence Models Yunshu Liu ASPITRG Research Group 2014-03-04 References: [1]. Steffen Lauritzen, Graphical Models, Oxford University Press, 1996 [2]. Christopher M. Bishop, Pattern
Graphical Models and Independence Models Yunshu Liu ASPITRG Research Group 2014-03-04 References: [1]. Steffen Lauritzen, Graphical Models, Oxford University Press, 1996 [2]. Christopher M. Bishop, Pattern
STA 4273H: Statistical Machine Learning
 STA 4273H: Statistical Machine Learning Russ Salakhutdinov Department of Statistics! rsalakhu@utstat.toronto.edu! http://www.utstat.utoronto.ca/~rsalakhu/ Sidney Smith Hall, Room 6002 Lecture 3 Linear
STA 4273H: Statistical Machine Learning Russ Salakhutdinov Department of Statistics! rsalakhu@utstat.toronto.edu! http://www.utstat.utoronto.ca/~rsalakhu/ Sidney Smith Hall, Room 6002 Lecture 3 Linear
Sistemi Cognitivi per le
 Università degli Studi di Genova Dipartimento di Ingegneria Biofisica ed Elettronica Sistemi Cognitivi per le Telecomunicazioni Prof. Carlo Regazzoni DIBE An Introduction to Bayesian Networks Markov random
Università degli Studi di Genova Dipartimento di Ingegneria Biofisica ed Elettronica Sistemi Cognitivi per le Telecomunicazioni Prof. Carlo Regazzoni DIBE An Introduction to Bayesian Networks Markov random
Implementing Machine Reasoning using Bayesian Network in Big Data Analytics
 Implementing Machine Reasoning using Bayesian Network in Big Data Analytics Steve Cheng, Ph.D. Guest Speaker for EECS 6893 Big Data Analytics Columbia University October 26, 2017 Outline Introduction Probability
Implementing Machine Reasoning using Bayesian Network in Big Data Analytics Steve Cheng, Ph.D. Guest Speaker for EECS 6893 Big Data Analytics Columbia University October 26, 2017 Outline Introduction Probability
The Signless Laplacian Spectral Radius of Graphs with Given Degree Sequences. Dedicated to professor Tian Feng on the occasion of his 70 birthday
 The Signless Laplacian Spectral Radius of Graphs with Given Degree Sequences Xiao-Dong ZHANG Ü À Shanghai Jiao Tong University xiaodong@sjtu.edu.cn Dedicated to professor Tian Feng on the occasion of his
The Signless Laplacian Spectral Radius of Graphs with Given Degree Sequences Xiao-Dong ZHANG Ü À Shanghai Jiao Tong University xiaodong@sjtu.edu.cn Dedicated to professor Tian Feng on the occasion of his
Spectral Clustering. Guokun Lai 2016/10
 Spectral Clustering Guokun Lai 2016/10 1 / 37 Organization Graph Cut Fundamental Limitations of Spectral Clustering Ng 2002 paper (if we have time) 2 / 37 Notation We define a undirected weighted graph
Spectral Clustering Guokun Lai 2016/10 1 / 37 Organization Graph Cut Fundamental Limitations of Spectral Clustering Ng 2002 paper (if we have time) 2 / 37 Notation We define a undirected weighted graph
Preliminaries and Complexity Theory
 Preliminaries and Complexity Theory Oleksandr Romanko CAS 746 - Advanced Topics in Combinatorial Optimization McMaster University, January 16, 2006 Introduction Book structure: 2 Part I Linear Algebra
Preliminaries and Complexity Theory Oleksandr Romanko CAS 746 - Advanced Topics in Combinatorial Optimization McMaster University, January 16, 2006 Introduction Book structure: 2 Part I Linear Algebra
A New Spectral Technique Using Normalized Adjacency Matrices for Graph Matching 1
 CHAPTER-3 A New Spectral Technique Using Normalized Adjacency Matrices for Graph Matching Graph matching problem has found many applications in areas as diverse as chemical structure analysis, pattern
CHAPTER-3 A New Spectral Technique Using Normalized Adjacency Matrices for Graph Matching Graph matching problem has found many applications in areas as diverse as chemical structure analysis, pattern
Algebraic Representation of Networks
 Algebraic Representation of Networks 0 1 2 1 1 0 0 1 2 0 0 1 1 1 1 1 Hiroki Sayama sayama@binghamton.edu Describing networks with matrices (1) Adjacency matrix A matrix with rows and columns labeled by
Algebraic Representation of Networks 0 1 2 1 1 0 0 1 2 0 0 1 1 1 1 1 Hiroki Sayama sayama@binghamton.edu Describing networks with matrices (1) Adjacency matrix A matrix with rows and columns labeled by
Multivariate random variables
 DS-GA 002 Lecture notes 3 Fall 206 Introduction Multivariate random variables Probabilistic models usually include multiple uncertain numerical quantities. In this section we develop tools to characterize
DS-GA 002 Lecture notes 3 Fall 206 Introduction Multivariate random variables Probabilistic models usually include multiple uncertain numerical quantities. In this section we develop tools to characterize
Bayes Nets: Independence
 Bayes Nets: Independence [These slides were created by Dan Klein and Pieter Abbeel for CS188 Intro to AI at UC Berkeley. All CS188 materials are available at http://ai.berkeley.edu.] Bayes Nets A Bayes
Bayes Nets: Independence [These slides were created by Dan Klein and Pieter Abbeel for CS188 Intro to AI at UC Berkeley. All CS188 materials are available at http://ai.berkeley.edu.] Bayes Nets A Bayes
Markov Chains and Spectral Clustering
 Markov Chains and Spectral Clustering Ning Liu 1,2 and William J. Stewart 1,3 1 Department of Computer Science North Carolina State University, Raleigh, NC 27695-8206, USA. 2 nliu@ncsu.edu, 3 billy@ncsu.edu
Markov Chains and Spectral Clustering Ning Liu 1,2 and William J. Stewart 1,3 1 Department of Computer Science North Carolina State University, Raleigh, NC 27695-8206, USA. 2 nliu@ncsu.edu, 3 billy@ncsu.edu
Alternative Parameterizations of Markov Networks. Sargur Srihari
 Alternative Parameterizations of Markov Networks Sargur srihari@cedar.buffalo.edu 1 Topics Three types of parameterization 1. Gibbs Parameterization 2. Factor Graphs 3. Log-linear Models Features (Ising,
Alternative Parameterizations of Markov Networks Sargur srihari@cedar.buffalo.edu 1 Topics Three types of parameterization 1. Gibbs Parameterization 2. Factor Graphs 3. Log-linear Models Features (Ising,
Exact Inference I. Mark Peot. In this lecture we will look at issues associated with exact inference. = =
 Exact Inference I Mark Peot In this lecture we will look at issues associated with exact inference 10 Queries The objective of probabilistic inference is to compute a joint distribution of a set of query
Exact Inference I Mark Peot In this lecture we will look at issues associated with exact inference 10 Queries The objective of probabilistic inference is to compute a joint distribution of a set of query
Basics on Probability. Jingrui He 09/11/2007
 Basics on Probability Jingrui He 09/11/2007 Coin Flips You flip a coin Head with probability 0.5 You flip 100 coins How many heads would you expect Coin Flips cont. You flip a coin Head with probability
Basics on Probability Jingrui He 09/11/2007 Coin Flips You flip a coin Head with probability 0.5 You flip 100 coins How many heads would you expect Coin Flips cont. You flip a coin Head with probability
Undirected Graphical Models: Markov Random Fields
 Undirected Graphical Models: Markov Random Fields 40-956 Advanced Topics in AI: Probabilistic Graphical Models Sharif University of Technology Soleymani Spring 2015 Markov Random Field Structure: undirected
Undirected Graphical Models: Markov Random Fields 40-956 Advanced Topics in AI: Probabilistic Graphical Models Sharif University of Technology Soleymani Spring 2015 Markov Random Field Structure: undirected
1 Undirected Graphical Models. 2 Markov Random Fields (MRFs)
 Machine Learning (ML, F16) Lecture#07 (Thursday Nov. 3rd) Lecturer: Byron Boots Undirected Graphical Models 1 Undirected Graphical Models In the previous lecture, we discussed directed graphical models.
Machine Learning (ML, F16) Lecture#07 (Thursday Nov. 3rd) Lecturer: Byron Boots Undirected Graphical Models 1 Undirected Graphical Models In the previous lecture, we discussed directed graphical models.
A graph contains a set of nodes (vertices) connected by links (edges or arcs)
 BOLTZMANN MACHINES Generative Models Graphical Models A graph contains a set of nodes (vertices) connected by links (edges or arcs) In a probabilistic graphical model, each node represents a random variable,
BOLTZMANN MACHINES Generative Models Graphical Models A graph contains a set of nodes (vertices) connected by links (edges or arcs) In a probabilistic graphical model, each node represents a random variable,
Representation of undirected GM. Kayhan Batmanghelich
 Representation of undirected GM Kayhan Batmanghelich Review Review: Directed Graphical Model Represent distribution of the form ny p(x 1,,X n = p(x i (X i i=1 Factorizes in terms of local conditional probabilities
Representation of undirected GM Kayhan Batmanghelich Review Review: Directed Graphical Model Represent distribution of the form ny p(x 1,,X n = p(x i (X i i=1 Factorizes in terms of local conditional probabilities
8.1 Concentration inequality for Gaussian random matrix (cont d)
 MGMT 69: Topics in High-dimensional Data Analysis Falll 26 Lecture 8: Spectral clustering and Laplacian matrices Lecturer: Jiaming Xu Scribe: Hyun-Ju Oh and Taotao He, October 4, 26 Outline Concentration
MGMT 69: Topics in High-dimensional Data Analysis Falll 26 Lecture 8: Spectral clustering and Laplacian matrices Lecturer: Jiaming Xu Scribe: Hyun-Ju Oh and Taotao He, October 4, 26 Outline Concentration
Machine Learning Summer School
 Machine Learning Summer School Lecture 1: Introduction to Graphical Models Zoubin Ghahramani zoubin@eng.cam.ac.uk http://learning.eng.cam.ac.uk/zoubin/ epartment of ngineering University of ambridge, UK
Machine Learning Summer School Lecture 1: Introduction to Graphical Models Zoubin Ghahramani zoubin@eng.cam.ac.uk http://learning.eng.cam.ac.uk/zoubin/ epartment of ngineering University of ambridge, UK
Probability & Computing
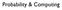 Probability & Computing Stochastic Process time t {X t t 2 T } state space Ω X t 2 state x 2 discrete time: T is countable T = {0,, 2,...} discrete space: Ω is finite or countably infinite X 0,X,X 2,...
Probability & Computing Stochastic Process time t {X t t 2 T } state space Ω X t 2 state x 2 discrete time: T is countable T = {0,, 2,...} discrete space: Ω is finite or countably infinite X 0,X,X 2,...
Linear algebra and applications to graphs Part 1
 Linear algebra and applications to graphs Part 1 Written up by Mikhail Belkin and Moon Duchin Instructor: Laszlo Babai June 17, 2001 1 Basic Linear Algebra Exercise 1.1 Let V and W be linear subspaces
Linear algebra and applications to graphs Part 1 Written up by Mikhail Belkin and Moon Duchin Instructor: Laszlo Babai June 17, 2001 1 Basic Linear Algebra Exercise 1.1 Let V and W be linear subspaces
Undirected graphical models
 Undirected graphical models Semantics of probabilistic models over undirected graphs Parameters of undirected models Example applications COMP-652 and ECSE-608, February 16, 2017 1 Undirected graphical
Undirected graphical models Semantics of probabilistic models over undirected graphs Parameters of undirected models Example applications COMP-652 and ECSE-608, February 16, 2017 1 Undirected graphical
Semidefinite and Second Order Cone Programming Seminar Fall 2001 Lecture 5
 Semidefinite and Second Order Cone Programming Seminar Fall 2001 Lecture 5 Instructor: Farid Alizadeh Scribe: Anton Riabov 10/08/2001 1 Overview We continue studying the maximum eigenvalue SDP, and generalize
Semidefinite and Second Order Cone Programming Seminar Fall 2001 Lecture 5 Instructor: Farid Alizadeh Scribe: Anton Riabov 10/08/2001 1 Overview We continue studying the maximum eigenvalue SDP, and generalize
Lecture 1: Basics of Probability
 Lecture 1: Basics of Probability (Luise-Vitetta, Chapter 8) Why probability in data science? Data acquisition is noisy Sampling/quantization external factors: If you record your voice saying machine learning
Lecture 1: Basics of Probability (Luise-Vitetta, Chapter 8) Why probability in data science? Data acquisition is noisy Sampling/quantization external factors: If you record your voice saying machine learning
Lecture 15. Probabilistic Models on Graph
 Lecture 15. Probabilistic Models on Graph Prof. Alan Yuille Spring 2014 1 Introduction We discuss how to define probabilistic models that use richly structured probability distributions and describe how
Lecture 15. Probabilistic Models on Graph Prof. Alan Yuille Spring 2014 1 Introduction We discuss how to define probabilistic models that use richly structured probability distributions and describe how
6.047 / Computational Biology: Genomes, Networks, Evolution Fall 2008
 MIT OpenCourseWare http://ocw.mit.edu 6.047 / 6.878 Computational Biology: Genomes, Networks, Evolution Fall 2008 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms.
MIT OpenCourseWare http://ocw.mit.edu 6.047 / 6.878 Computational Biology: Genomes, Networks, Evolution Fall 2008 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms.
Markov Chains and MCMC
 Markov Chains and MCMC Markov chains Let S = {1, 2,..., N} be a finite set consisting of N states. A Markov chain Y 0, Y 1, Y 2,... is a sequence of random variables, with Y t S for all points in time
Markov Chains and MCMC Markov chains Let S = {1, 2,..., N} be a finite set consisting of N states. A Markov chain Y 0, Y 1, Y 2,... is a sequence of random variables, with Y t S for all points in time
CSE 473: Artificial Intelligence Autumn 2011
 CSE 473: Artificial Intelligence Autumn 2011 Bayesian Networks Luke Zettlemoyer Many slides over the course adapted from either Dan Klein, Stuart Russell or Andrew Moore 1 Outline Probabilistic models
CSE 473: Artificial Intelligence Autumn 2011 Bayesian Networks Luke Zettlemoyer Many slides over the course adapted from either Dan Klein, Stuart Russell or Andrew Moore 1 Outline Probabilistic models
Part I Qualitative Probabilistic Networks
 Part I Qualitative Probabilistic Networks In which we study enhancements of the framework of qualitative probabilistic networks. Qualitative probabilistic networks allow for studying the reasoning behaviour
Part I Qualitative Probabilistic Networks In which we study enhancements of the framework of qualitative probabilistic networks. Qualitative probabilistic networks allow for studying the reasoning behaviour
Lecture 19: NP-Completeness 1
 Lecture 19: NP-Completeness 1 Revised Sun May 25, 2003 Outline of this Lecture Polynomial-time reductions. CLRS pp.984-5 The class N PC. CLRS p. 986 Proving that problems are N PC. SAT, CLIQUE, INDEPENDENT
Lecture 19: NP-Completeness 1 Revised Sun May 25, 2003 Outline of this Lecture Polynomial-time reductions. CLRS pp.984-5 The class N PC. CLRS p. 986 Proving that problems are N PC. SAT, CLIQUE, INDEPENDENT
Lecture 9: PGM Learning
 13 Oct 2014 Intro. to Stats. Machine Learning COMP SCI 4401/7401 Table of Contents I Learning parameters in MRFs 1 Learning parameters in MRFs Inference and Learning Given parameters (of potentials) and
13 Oct 2014 Intro. to Stats. Machine Learning COMP SCI 4401/7401 Table of Contents I Learning parameters in MRFs 1 Learning parameters in MRFs Inference and Learning Given parameters (of potentials) and
Fiedler s Theorems on Nodal Domains
 Spectral Graph Theory Lecture 7 Fiedler s Theorems on Nodal Domains Daniel A Spielman September 9, 202 7 About these notes These notes are not necessarily an accurate representation of what happened in
Spectral Graph Theory Lecture 7 Fiedler s Theorems on Nodal Domains Daniel A Spielman September 9, 202 7 About these notes These notes are not necessarily an accurate representation of what happened in
Causality in Econometrics (3)
 Graphical Causal Models References Causality in Econometrics (3) Alessio Moneta Max Planck Institute of Economics Jena moneta@econ.mpg.de 26 April 2011 GSBC Lecture Friedrich-Schiller-Universität Jena
Graphical Causal Models References Causality in Econometrics (3) Alessio Moneta Max Planck Institute of Economics Jena moneta@econ.mpg.de 26 April 2011 GSBC Lecture Friedrich-Schiller-Universität Jena
CS 5522: Artificial Intelligence II
 CS 5522: Artificial Intelligence II Bayes Nets: Independence Instructor: Alan Ritter Ohio State University [These slides were adapted from CS188 Intro to AI at UC Berkeley. All materials available at http://ai.berkeley.edu.]
CS 5522: Artificial Intelligence II Bayes Nets: Independence Instructor: Alan Ritter Ohio State University [These slides were adapted from CS188 Intro to AI at UC Berkeley. All materials available at http://ai.berkeley.edu.]
Machine Learning Lecture 14
 Many slides adapted from B. Schiele, S. Roth, Z. Gharahmani Machine Learning Lecture 14 Undirected Graphical Models & Inference 23.06.2015 Bastian Leibe RWTH Aachen http://www.vision.rwth-aachen.de/ leibe@vision.rwth-aachen.de
Many slides adapted from B. Schiele, S. Roth, Z. Gharahmani Machine Learning Lecture 14 Undirected Graphical Models & Inference 23.06.2015 Bastian Leibe RWTH Aachen http://www.vision.rwth-aachen.de/ leibe@vision.rwth-aachen.de
Alternative Parameterizations of Markov Networks. Sargur Srihari
 Alternative Parameterizations of Markov Networks Sargur srihari@cedar.buffalo.edu 1 Topics Three types of parameterization 1. Gibbs Parameterization 2. Factor Graphs 3. Log-linear Models with Energy functions
Alternative Parameterizations of Markov Networks Sargur srihari@cedar.buffalo.edu 1 Topics Three types of parameterization 1. Gibbs Parameterization 2. Factor Graphs 3. Log-linear Models with Energy functions
6.867 Machine learning, lecture 23 (Jaakkola)
 Lecture topics: Markov Random Fields Probabilistic inference Markov Random Fields We will briefly go over undirected graphical models or Markov Random Fields (MRFs) as they will be needed in the context
Lecture topics: Markov Random Fields Probabilistic inference Markov Random Fields We will briefly go over undirected graphical models or Markov Random Fields (MRFs) as they will be needed in the context
CS6220: DATA MINING TECHNIQUES
 CS6220: DATA MINING TECHNIQUES Matrix Data: Classification: Part 2 Instructor: Yizhou Sun yzsun@ccs.neu.edu September 21, 2014 Methods to Learn Matrix Data Set Data Sequence Data Time Series Graph & Network
CS6220: DATA MINING TECHNIQUES Matrix Data: Classification: Part 2 Instructor: Yizhou Sun yzsun@ccs.neu.edu September 21, 2014 Methods to Learn Matrix Data Set Data Sequence Data Time Series Graph & Network
Product rule. Chain rule
 Probability Recap CS 188: Artificial Intelligence ayes Nets: Independence Conditional probability Product rule Chain rule, independent if and only if: and are conditionally independent given if and only
Probability Recap CS 188: Artificial Intelligence ayes Nets: Independence Conditional probability Product rule Chain rule, independent if and only if: and are conditionally independent given if and only
Statistical Approaches to Learning and Discovery
 Statistical Approaches to Learning and Discovery Graphical Models Zoubin Ghahramani & Teddy Seidenfeld zoubin@cs.cmu.edu & teddy@stat.cmu.edu CALD / CS / Statistics / Philosophy Carnegie Mellon University
Statistical Approaches to Learning and Discovery Graphical Models Zoubin Ghahramani & Teddy Seidenfeld zoubin@cs.cmu.edu & teddy@stat.cmu.edu CALD / CS / Statistics / Philosophy Carnegie Mellon University
Codes on graphs. Chapter Elementary realizations of linear block codes
 Chapter 11 Codes on graphs In this chapter we will introduce the subject of codes on graphs. This subject forms an intellectual foundation for all known classes of capacity-approaching codes, including
Chapter 11 Codes on graphs In this chapter we will introduce the subject of codes on graphs. This subject forms an intellectual foundation for all known classes of capacity-approaching codes, including
p L yi z n m x N n xi
 y i z n x n N x i Overview Directed and undirected graphs Conditional independence Exact inference Latent variables and EM Variational inference Books statistical perspective Graphical Models, S. Lauritzen
y i z n x n N x i Overview Directed and undirected graphs Conditional independence Exact inference Latent variables and EM Variational inference Books statistical perspective Graphical Models, S. Lauritzen
Markov properties for undirected graphs
 Graphical Models, Lecture 2, Michaelmas Term 2011 October 12, 2011 Formal definition Fundamental properties Random variables X and Y are conditionally independent given the random variable Z if L(X Y,
Graphical Models, Lecture 2, Michaelmas Term 2011 October 12, 2011 Formal definition Fundamental properties Random variables X and Y are conditionally independent given the random variable Z if L(X Y,
CS281A/Stat241A Lecture 19
 CS281A/Stat241A Lecture 19 p. 1/4 CS281A/Stat241A Lecture 19 Junction Tree Algorithm Peter Bartlett CS281A/Stat241A Lecture 19 p. 2/4 Announcements My office hours: Tuesday Nov 3 (today), 1-2pm, in 723
CS281A/Stat241A Lecture 19 p. 1/4 CS281A/Stat241A Lecture 19 Junction Tree Algorithm Peter Bartlett CS281A/Stat241A Lecture 19 p. 2/4 Announcements My office hours: Tuesday Nov 3 (today), 1-2pm, in 723
9 Forward-backward algorithm, sum-product on factor graphs
 Massachusetts Institute of Technology Department of Electrical Engineering and Computer Science 6.438 Algorithms For Inference Fall 2014 9 Forward-backward algorithm, sum-product on factor graphs The previous
Massachusetts Institute of Technology Department of Electrical Engineering and Computer Science 6.438 Algorithms For Inference Fall 2014 9 Forward-backward algorithm, sum-product on factor graphs The previous
ACO Comprehensive Exam March 17 and 18, Computability, Complexity and Algorithms
 1. Computability, Complexity and Algorithms (a) Let G(V, E) be an undirected unweighted graph. Let C V be a vertex cover of G. Argue that V \ C is an independent set of G. (b) Minimum cardinality vertex
1. Computability, Complexity and Algorithms (a) Let G(V, E) be an undirected unweighted graph. Let C V be a vertex cover of G. Argue that V \ C is an independent set of G. (b) Minimum cardinality vertex
Graphical Model Inference with Perfect Graphs
 Graphical Model Inference with Perfect Graphs Tony Jebara Columbia University July 25, 2013 joint work with Adrian Weller Graphical models and Markov random fields We depict a graphical model G as a bipartite
Graphical Model Inference with Perfect Graphs Tony Jebara Columbia University July 25, 2013 joint work with Adrian Weller Graphical models and Markov random fields We depict a graphical model G as a bipartite
Introduction to Graphical Models
 Introduction to Graphical Models The 15 th Winter School of Statistical Physics POSCO International Center & POSTECH, Pohang 2018. 1. 9 (Tue.) Yung-Kyun Noh GENERALIZATION FOR PREDICTION 2 Probabilistic
Introduction to Graphical Models The 15 th Winter School of Statistical Physics POSCO International Center & POSTECH, Pohang 2018. 1. 9 (Tue.) Yung-Kyun Noh GENERALIZATION FOR PREDICTION 2 Probabilistic
