A THESIS SUBMITTED TO THE GRADUATE SCHOOL OF APPLIED AND NATURAL SCIENCES OF MIDDLE EAST TECHNICAL UNIVERSITY SERDAR ASLAN
|
|
|
- Janel Jackson
- 5 years ago
- Views:
Transcription
1 NONLINEAR ESTIMATION TECHNIQUES APPLIED TO ECONOMETRIC PROBLEMS A THESIS SUBMITTED TO THE GRADUATE SCHOOL OF APPLIED AND NATURAL SCIENCES OF MIDDLE EAST TECHNICAL UNIVERSITY BY SERDAR ASLAN IN PARTIAL FULFILMENT OF THE REQUIREMENTS FOR THE DEGREE OF MASTER OF SCIENCE IN ELECTRICAL AND ELECTRONICS ENGINEERING NOVEMBER 004
2 Aroval of Gradua School of Naural and Ald Scncs. Prof. Dr. Canan ÖZGEN Drcor I crfy ha hs hss sasfs all h rqurmns as a hss for h dgr of Masr of Scnc. Prof. Dr. İSMET ERKMEN Had of Darmn Ths s o crfy ha w hav rad hs hss and ha n our onon s fully adqua, n sco and qualy, as a hss for h dgr of Masr of Scnc. Prof. Dr. Krm DEMİRBAŞ Survsor Eamnng Comm Mmbrs Prof. Dr. Mübccl DEMİREKLER METU,EEE Prof. Dr. Krm DEMİRBAŞ METU,EEE Prof. Dr. Kmal LEBLEBİCİOĞLU METU,EEE Asss. Prof. Dr. Üm Özlal BİLKENT,ECON Asss. Prof. Dr. Çağaay CANDAN METU,EEE
3 I hrby dclar ha all nformaon n hs documn has bn oband and rsnd n accordanc wh acadmc ruls and hcal conduc. I also dclar ha, as rqurd by hs ruls and conduc, I hav fully cd and rfrncd all maral and rsuls ha ar no orgnal o hs wor. Nam, Las Nam : Srdar Aslan Sgnaur :
4 ABSTRACT NONLINEAR ESTIMATION TECHNIQUES APPLIED TO ECONOMETRIC Aslan, Srdar M. Sc., Darmn of Elcrcal and Elcroncs Engnrng Survsor: Prof. Dr. Krm Dmrbaş Novmbr 004, 6 ags Ths hss consdrs h flrng and rdcon roblms of nonlnar nosy conomrc sysms. As a flr/rdcor, h sandard ool Endd Kalman Flr and nw aroachs Dscr Quanzaon Flr and Squnal Imoranc Rsamlng Flr ar usd. Th algorhms ar comard by usng Mon Carlo Smulaon chnqu. Th advanags of h nw algorhms ovr Endd Kalman Flr ar shown. Kywords: Dscr Quanzaon Flr, Squnal Imoranc Rsamlng Flr, Endd Kalman Flr, Sochasc Calculus, Mon Carlo v
5 ÖZ DOĞRUSAL OLMAYAN KESTİRME ALGORİTMALARININ EKONOMETRİK PROBLEMLERE UYGULANMASI Aslan, Srdar M. Sc., Darmn of Elcrcal and Elcroncs Engnrng Survsor: Prof. Dr. Krm Dmrbaş Novmbr 004, 6 sayfa Bu z doğrusal olmayan onomr gürülülü ssmlrd gürülüdn arındırma v ahmn yama üzrndr. Flr v öngörücü olara sandar grç olan Glşrlmş Kalman Algorması v yn yalaşımlar olan Zamanda Ayrı Ncmlm Flrs v Ardışı Önm Trarlı Örnlm Flrs ullanıldı. Algormalar brbryl Mon Carlo Smlasyon nğyl arşılaşırıldı. Algormaların Glşrlmş Kalman Algormasından avanajlı yanları gösrld. Anahar Klmlr: Glşrlmş Kalman Flrs, Zamanda Ayrı Ncmlm Flrs, Ardışı Önm Trarlı Örnlm Flrs, Olasılısal Analz, Mon Carlo. v
6 ACKNOWLEDGEMENTS I would l o han o my advsor, Profssor Krm Dmrbaş, for hs asssanc hroughou h hss. My hss was a combnaon of dffrn scnc branchs. In hs rsc I hav an clln fdbac from dffrn darmns such as: Mahmacs, Economcs, and Sascs. In hs rsc, I would l o han Profssor Hayr Körzloğlu for hs suggsons on sochasc calculus. H also drcd m hrough choosng h nonlnar dynamc sysms from h fld of conomcs. I am also graful o Asssan Profssor Üm Özlal for hs varous advcs on h conomc sysms bng usd. Rgardng h Malab cods, I would l o han Mura Tgöz, Hüsyn Yğlr and Srdar Suay for hr nd hl. Mura Tgöz hld o m o summarz h cods. Hüsyn Yğlr and Srdar Suay wro h cods n an alrnav way such ha I could comar my rogram ouu wh hrs. I am also graful o Umu Orgunr for asssng m n h hory of Endd Kalman Flr and n Mon Carlo Smulaons. I would also l o han Asssan Profssor Çağaay Candan and Asaf Bhza Şahn for hr valuabl advcs. Asssan Profssor Candan and Assoca Profssor Sncr Koç also hld m on h numrcal comuaon chnqus of solvng nonlnar quaons. Scal hans go o Prof. Dr. Mübccl Dmrlr for hr hl o connu my masr sudy. v
7 TABLE OF CONTENTS ABSTRACT v ACKNOWLEDGEMENTS v TABLE OF CONTENTS v LIST OF TABLES LIST OF FIGURES. INTRODUCTION. FIRST MODEL FROM CONTINUOUS TIME TO DISCRETE TIME 4. Dscrzaon of h Modl 5 3. STOCHASTIC CALCULUS and APPLICATION TO THE CASE STUDY 7 3. STOCHASTIC DIFFERENTIAL EQUATIONS 8 3. Th Rmann Ingral Th Rmann-Sljs Ingral L P Convrgnc and Convrgnc n Man Squar 3.5 Sml Procsss 3.6 Ouln for h Dfnon of h Io Sochasc Ingral 3.7 Th Io Sochasc Ingral of Sml Procsss 3.8 Th Io Sochasc Ingral of Gnral Procsss Io s Lmma Soluon of h Sochasc Dffrnal Equaon 6 3. Unqunss of h Soluon of h Sochasc Dffrnal Equaon 9 4. DQF ALGORITHM 4. DQF 4.. Obanng a Trlls Dagram 4.. Assgnng Mrcs o h Nods of h Trlls Dagram 4..3 Choosng h Hghs Mrc for h Drmnaon of h Bs Pah 4 4. Quanzaon of h random varabl 5 5. EKF 7 6. APPLICATION OF EKF TO ECONOMETRICS 9 7. PARTICLE FILTERS-SIR ALGORITHM 3 7. Drvaon of h SIS and SIR algorhm SIMULATIONS OF FILTERING AND PREDICTION EXPERIMENTS Gnral Ouln Flrng Tools Prdcon Tools Error Crra and Mon Carlo Smulaons 38 v
8 8.4. Flrng Error Error n R N Sacs: Errors n h Ermns Prdcon Error Smulaons Flrng Prdcon SIMULATIONS OF FILTERING EXPERIMENTS FOR STOCHASTIC GROWTH MODELS CONCLUSION 5. REFERENCES 54. APPENDIX 57 v
9 LIST OF TABLES TABLES Tabl Mon Carlo rsuls-errors of h algorhms vrsus chang of h varanc of w 43 Tabl Mon Carlo rsuls-errors of h algorhms vrsus chang of h varanc of w 44 Tabl 3 Mon Carlo rsuls-errors of h algorhms vrsus chang of h varanc of w 44 Tabl 4 Mon Carlo rsuls-errors of h algorhms for h varanc of w=5 46 Tabl 5 Mon Carlo rsuls-errors of h algorhms SIR and EKF 48 Tabl 6 Mon Carlo rsuls-errors of h algorhms SIR and EKF 5
10 LIST OF FIGURES Fgur... 45
11 CHAPTER INTRODUCTION In lcrcal and lcroncs ngnrng, hr ar many dynamcal sysm rrsnaons, whch nclud nos comonns. In such cass, on of h rmary goals s o rmov h nos comonn from h masurmn and/or ry o rdc h n sa of h sysm. If h roblm a hand can b wrn n a lnar Gaussan sysm form, hn h Kalman Flr mrgs as h omal mhodology. Howvr, whn h sysm has nonlnar characrscs, hn h Endd Kalman Flr EKF hncforh should b mloyd. Howvr, h smaon of nonlnar sysms should by no mans rsrcd o usng only EKF. As dscussd n [3] and [5] n dals, Dscr Quanzaon Flr and Squnal Imoranc Rsamlng SIR flrs can convnnly b usd Basd on h abov dscusson, hr ar hr faurs of hs sudy: Conrol hory aroachs ar ald o h fld of conomrcs: Sochasc Calculus has bn nroducd whn h con of a sochasc Io rocss, whch s usd bascally n h ass rcng modls 3 Two rlavly unnown algorhms, DQF and SIR flr ar nroducd and comard wh h EKF. As wll b clar, som cass whr hs wo alrnavs ar suror o EKF ar rsnd. To bgn wh, sa sac rrsnaons ar convnn o dscrb h dynamcal sysms. I s sraghforward o oban h dynamcs of h modl from h dffrnal quaon rrsnaon of h nonnosy sysms. [4] Howvr, n nosy sysms, h dscron of h sysm s gnrally s nroducd whn h sa sac rrsnaon. In such sysms, h nos s assumd o b gnrally addv. Bu hans o h sochasc calculus, w hav a mor gnral rscv. For a dald dscusson on Kalman Flr s [] and []
12 Th assumons of h nos srucur can b mad drcly n a dffrnal quaon form. Thn, h dffrnal quaons wh nos ar solvd by mloyng sochasc calculus. For a gnral ramn of h subjc sochasc calculus, h radr s rfrrd o [5]. Consqunly, h sudy brfly dscrbd abov s comosd of h followng ars: Inroducon Frs Modl From Connuous Tm o Dscr Tm 3 Sochasc Calculus and Alcaon o h Cas Sudy 4 DQF Algorhm 5 EKF Algorhm 6 Alcaon of EKF o h Economrc Problm 7 Parcl Flrs-SIR Algorhm 8 Smulaons of h Frs modl 9 Smulaons of h Scond Modl Th scond scon lans how h dscr-m nonlnar nosy sysm rrsnaon of h frs modl s oband from connuous m rrsnaon. Th dynamcal sysm s basd on obanng h rsson for h rc of on rsy ass soc. Snc h rmary goal of hs sudy s no o focus on h dals of h drvaon, jus a succnc nroducon s gvn n hs scon. In h hrd scon namd Sochasc Calculus and Alcaon o h Cas Sudy, h ncssary bacground o undrsand h bascs of Sochasc Calculus s land. Thn s shown, how h connuous m soluon has bn oband from h sochasc dffrnal quaons. In h fourh scon, namd DQF Algorhm, h bascs of h algorhms roosd by Dmrbaş [3] ar land. Alhough no wdly nown, hs algorhm s caabl o lad o br rsuls han h sandard EKF algorhm. Th n wo scons brfly dscuss h EKF algorhm. In h formr, EKF for dscr m cass s land. In h lar scon, h algorhm s ald o h nonlnar dynamc sysm of h modl drv n h rvous scons. Th svnh scon laboras h arcl flrs. I gvs h drvaon of h Squnal Imoranc Samlng SIS flr along wh s roof. Thn, h SIR flr, whch s also mloyd n hs sudy, s asly drvd from SIS flr.
13 Th ghh scon dslays h smulaon rsuls of h flrng and rdcon algorhms of h bnchmar modl nroducd bfor. Th n scon rsns h smulaon rsuls of h flrng algorhm of h scond modl, whch bascally amns roducvy shocs and caal accumulaon whn a sochasc growh modl. Th fnal scon concluds. 3
14 CHAPTER FIRST MODEL FROM CONTINUOUS TIME TO DISCRETE TIME In a convnonal ass rcng modl, h rc of on shar of h rsy ass soc s dscrbd by h followng sochasc dffrnal quaon.. dx = c X d + X db. X : Th rc X s calld rsy ass. I s also namd as soc. c : Th consan c s h man ra of rurn. : Th aramr dnos volaly. B : B = B, 0 rrsns h Brownan moon. [6] Th dffrnal formula n quaon. s smlar o h rssons usd n dffrnal calculus wh h moran con ha hr s a rm db, whch rrsns h sochasc ar. Such a rm mas h usag of h sochasc calculus ncssary, whch has also bn wdly usd n h fld of conomrcs. In h hrd scon, a ncssary bacground for a horough undrsandng of h abov mnond subjc s gvn. As h hrd scon shows n dals, h soluon o h abov gvn formula for X s gvn by: X c0.5 +B = f, B = X 0.. s an onnal funcon whch s randomly rurbd. I s also namd as Gomrc Brownan Moon. X 0 s assumd o b ndndn of B. If h 4
15 5 volaly rm 0 =, hn. rducs o h usual drmnsc onnal funcon, whch s gvn by.3: c X X 0 =.3. Dscrzaon of h Modl In hs scon, h connuous m rsson scfd n. s ransformd no h dscr m doman. On basc aroach s o saml. wh unform m nrval T. Thn a rcursv rlaon bwn T X + and X s oband as follows:.5 0 T B T o c X T X = T B T o c X + + = * T B T c c X + = * T B T c c X + = B -B * B T B T c B c X + = * ] [ B T B T c B c X + = * ] [ B T B T c B c X + + = 0.5 ] [ B T B T c X + = 0.5 B T B T c X + = 0.5 B T B T c X + = ] [ 0.5 B T B T c X + = 0.5 T w T c X = Whr T w rrsns Gaussan nos wh varanc T. Hnc.4 can b wrn as.
16 X + T = c0.5 T w T.4 X In ordr o oban.4, h fac ha h random varabls B B s hav a normal dsrbuon N 0, s for s <, s usd n h las quaon. [8] Summarzng h soluon.4, quaon.5 can b oband as: X + T = LX w T.5 whr L = c0.5 T, whch s assumd o b consan. Hnc sarng a X 0 and usng.5 s ossbl o oban h valus of { X T, X T, X 3 T, X T, }. Th noaons X T, X T, X 3 T, X T ar wrn as X, X, X 3, X rscvly. As a rsul.5 has h alrna rrsnaon as: X LX w + =.6 whr w sll hav L = c0.5 T. Snc h n sa of h sysm s calculad accordng o.6, mrgs as h sa quaon of h sysm. Th masurmn quaon, on h ohr hand s gvn by.7: Z = X + v.7 whr v rrsns h sculaors nos or radrs nos. Th abov drvaon and rsnaon of h ass rcng modl s farly sandard and can b convnnly usd o valua h rformancs of svral flrs dsgnd o b usd n non-lnar cass. 6
17 CHAPTER 3 STOCHASTIC CALCULUS and APPLICATION TO THE CASE STUDY Ths scon brfly nroducs sochasc dffrnal calculus. Bfor dscussng h mlcaons should b mnond ha, h radr, who s no famlar wh sochasc rocsss s rfrrd o [9]. Frs, s moran o rmnd h dfnon and h nrraon of sochasc dffrnal quaons. Th ngral ha s wrn n h form of 3. 0 b s, X s db s 3. s calld Io Ingral. Ths ngral rrsnaon dffrs n wo ways from s counrars: W hav dbs nsad of ds. B s no a drmnsc funcon bu a sochasc on. Th formal dfnon of 3. s gvn n h subscon 3.8. Th subscon 3. Th Rmann Ingral rmnds h radr h formal dfnon of Rmann Ingral. Th subscon 3.3 namd Th Rmann-Sljs Ingral s a sml nson of Rmann Ingral. Th rason o nroduc hs ngral y s h conncon bwn h Io Ingral and Rmann-Sljs Ingral Th subscons 3.4 and 3.5, whch ar L Convrgnc and Man Squar Convrgnc and Sml Procsss rscvly, dfn convrgnc ys of sochasc rocsss, whch ar usd n h dfnon of Io ngral, 7
18 Th subscon 3.7, namly h Io Ingral of Sml Procsss frs dfns h Io Ingral for a rsrcd class of rocsss. Thn h subscon 3.8 Io Ingral of Gnral Procsss nlargs h dfnon of h Io Ingral for a wdr class of rocsss. A hs sag, h horcal mlcaon of h Io ngral s concludd wh a brf dscusson. Afr hs scon, raccal ascs of sochasc calculus ar nroducd and ald o conomrcs, whch was land n h scond scon. Th subscon 3.9 Io Lmma s h basc ool, whch s ndd o solv h sochasc dffrnal quaons. Th subscon 3.0 s an alcaon of h Io Lmma o h cas sudy, whch s a sandard sochasc growh modl. Fnally, h subscon 3. dscusss h unqunss roblm of h soluon, whch s oband n h scon STOCHASTIC DIFFERENTIAL EQUATIONS In sochasc calculus, a basc rsson as h followng form: dx = a, X d + b, db 3. whr s h ndndn varabl, a, and b, ar drmnsc funcons, and B = B, 0 s h Brownan moon. I s asy o s ha, for b, = 0, 3. rducs o h usual drmnsc dffrnal quaon. In h sochasc calculus 3., can also b nrrd as: X = X 0 + a s, X s ds + b s, X s db s, 0 T In hs noaon, 0 a s, X s ds s h usual Rmann ngral. Th ngrand funcon b s, X s and h ngrang funcon B s ar sochasc rocsss. 8
19 Ingrals of h form 0 b s, X s db s should b nrrd dffrnly. Io rocss offrs such an nrraon. Snc Io nrraon s h mos commonly usd rocss, wll b mloyd hroughou h sudy. Howvr, should b rmndd ha hr ar also ohr nrraons l h Sraonovch nrraon. In som cass, s br o us Sraonovch nrraon, as rssd n [0] Th n scon Rmann ngral s dfnd formally. 3. Th Rmann Ingral Th classcal ngraon chnqu s h Rmann ngral. Th sandard noaon s shown n 3.4. = T =0 f d 3.4 whr dnos h ndndn varabl. f s h funcon o b ngrad. 0 and T ar h lms of ngraon. Th dfnon of Rmann Ingral s as follows: Frs h nrval [ 0, T ] s arond as: L τ n : 0 = 0 < <... < n < n = T b h mnond aron of h nrval [ 0, T ]. Choos y, y for =,..., n. n 3 L S = f y n = 4 If lm = S S n n ss, for som S and for ach ossbl aron τ n and yas 0, hn S = f d. = T = 0 Whl Rmann ngraon chnqu s usd nsvly n svral aras s no arora for analyzng h dynamcs of h sysms wh random rms. For ha uros, Io s Sochasc Ingral offrs a soluon. 9
20 Th Rmann-Sljs Ingral, whch s a sml nson of Rmann Ingral, s dscussd n h n scon. 3.3 Th Rmann-Sljs Ingral Dfnon [] L τ n : 0 = 0 < <... < n < n = T b a aron of h nrval [0,]. Choos y, y for =,..., n. 3 L f and g b wo ral-valud funcons on [0,] and dfn 3.5 g = g g, =,,n Th Rmann-Sljs sum corrsondng o τ n and s gvn by 3.6 n S n = S n τ n = f y g = f y [ g g ]. = n = If h lm lm S n ss and S s ndndn of h choc of h n arons τ n and yas 0, hn S s calld h Rmann-Sljs ngral of f wh rsc o g on [0,]. Symbolcally, s wrn as 3.7. S = 0 f dg. 3.7 Rmann-Sljs ngral s jus an nson of h classcal Rmann ngral. I s rducd o h Rmann ngral for g=. Ths ngraon chnqu s also usd n h robably hory. In hs cass g s o b chosn as F, whch s h dsrbuon funcon of a random varabl. For aml, 3.8 rrsns such a form: P { A} = df 3.8 A 0
21 Alhough Io s sochasc ngral s dffrn from h Rmann-Sljs ngral, as h rocdng scons wll show, hr ar conncons as wll. Ths conncons ar shown afr h dfnon of h Io sochasc ngral. In h n scon, som mahmacal rms, whch ar ncssary o undrsand h dfnon of h Io ngral, ar nroducd. 3.4 L P Convrgnc and Convrgnc n Man Squar If X n and X blong o L and X n X 0 E, hn X } s sad o { n convrg n h man o X. For =, s smly calld convrgnc n man; for =, on h ohr hand, h rocss s gnrally rmd as convrgnc n man squar or n quadrac man.[] Ths rocss s mloyd for h dfnon of Io Ingral. In h abov dfnon, E s h usual caons oraor whl sac of funcons, for whch h L norm s fn. L s h
22 3.5 Sml Procsss Th sochasc rocss C = C, [0, T] s sad o b sml rocss f sasfs h followng rors: Thr ss a aron: τ n : 0 = 0 < <... < n < n = Z, =,..., n of random varabls such ha: [3] C = f = T, Z n C = f <, Z =,..., n. T, and a squnc 3.6 Ouln for h Dfnon of h Io Sochasc Ingral As mnond bfor, h Io Ingral mloys h man squar convrgnc. For h dfnon of h Io sochasc ngral, h followng way wll b racd:. Th ngrand funcon s frs assumd o b a sml rocss.. Th Io ngral of h sml rocsss s gvn. 3. Th ngrand funcon s assumd o b a gnral rocss. 4. Th Io ngral of h gnral rocss s dfnd va h sml rocsss. 3.7 Th Io Sochasc Ingral of Sml Procsss Th Io sochasc ngral of a sml rocss C on [ 0, T ] s gvn by 3.9. T n C s db s : = C B B = = = 0 n Z B 3.9 whr Z C and B = B B. =
23 Th Io sochasc ngral of a sml rocss C on [0,],, s gvn by T C s db s : = C s I[0, ] s db s = Z B + Z B B 0 = 3.0 whr, s I for s [ 0,] [ 0, ] = and I s 0 ohrws. [ 0, ] = Whn comarng 3.9 wh h Rmann-Sljs sum noaon 3.6, s asly sn ha y =. Furhrmor, g corrsonds o Brownan moon. Hnc h Io sochasc ngral s h Rmann-Sljs sum, whr h nrmda ons y ar chosn a h lf nd ons of h nrvals, ]. 0 = Z B = 0 [ Ths concluds h dfnon of h Io ngral for sml rocsss, whch can b rgardd as h cornr son for h gnral sochasc ngraon. 3.8 Th Io Sochasc Ingral of Gnral Procsss Th Io sochasc ngral s dfnd for sml rocsss n scon 3.7. In hs scon, howvr, h ngrand rocss wll b from a wdr class of funcon sac. Bu h followng rsrcons ar u for hs class: Assumons on h Ingrand Procss C:. C s adad o Brownan moon on [0,T],.. C s a funcon of Bs s.. Th ngral 3. s fn. T 0 EC s ds 3. L C b a rocss sasfyng h abov addonal assumons. Thn, on can fnd a squnc C n of sml rocsss such ha h followng samn holds. S [4], for h roof of hs samn. 3
24 T 0 E[ C s C s n ] ds 0 3. Hnc, h sml rocsss n C convrg n man squar sns o h n ngrand rocss C. Usng 3.0, w can calcula h Io ngrals I C of hs sml rocsss. Hnc w hav a nw squnc { I C, C, }. Ths nw squnc convrgs o a unqu rocss, whch van b convnnly calld as I C on [0,T] Thn, w can wr 3.3 as[5]: I n E su[ I C I C ] T Th man squar lm I C s calld h Io sochasc ngral of C. I s dnod by 3.4[4] I C = C s db s, [ 0, T ]. o 3.4 Ths nds h formal dfnon for h Io sochasc ngral. In ordr o aly h ngral, howvr, h Io Lmma should b nroducd. 3.9 Io s Lmma In hs subscon, h Io s Lmma s nroducd n ordr o aly h sochasc ngral ha s dfnd abov. Io s Lmma: L f, b a funcon whos scond ordr aral drvavs ar connuous. Thn 3.5 s ru. f, B f s, B s = [ f, B + f, B ] d + f s s 4, B db 3.5
25 whr s <. For h dals of h lmma, las rfr o [6]. [ f, B + f s, B ] d 3.6 s f, B db 3.7 Th frs ngral 3.6 s a sml drmnsc ngral. Th scond ngral 3.7 s h aformnond sochasc ngral n scon 3.8. Furhrmor f, f and f ar h aral drvavs. 5
26 3.0 Soluon of h Sochasc Dffrnal Equaon In subscon 3., s land ha 3.8 s quvaln o h followng rrsnaon of 3.9. dx = a, X d + b, X db 3.8 X = X 0 + a s, X s ds + b s, X s db s, 0 T Tha s, 3.8 s nrrd as 3.9 n sochasc calculus. As s mnond n h scond char, h rc of on shar of h rsy ass soc s dscrbd by h sochasc dffrnal quaon 3.0. dx = cx d + X db 3.0 whr X : Th rc X s calld rsy ass. I s also calld as soc. c : Th consan c s calld man ra of rurn : Th s calld volaly. B : B = B, 0 s Brownan moon. Whn h quaons 3.0 and 3.8 ar comard, s sn ha 3.0 s a scal cas of 3.8 wh a, X = cx and b, X = X. Hnc 3.0 s quvaln o h followng: X = X 0 + c X s ds + X s db s, 0 T Mor gnrally, h sochasc dffrnal quaons n h followng form of 3., whr c and σ =, ar consans, can b rmd as lnar sochasc dffrnal quaons. Hnc 3.0 s from h famly of lnar sochasc dffrnal quaons. 6
27 c X s + c ds + X s + X = X 0 + σ σ db s, 0 T Th nroducd sochasc ngral n 3. can b solvd accordng o h Io s Lmma, whr h soluon s gvn n [7]. Soluon: Suos X s dscrbd as 3.3. X = f, B = c 0.5 +B 3.3 whr c and > 0 ar consans. I s rovd blow ha 3.3 s ndd a soluon. Accordng o 3.3, quaons 3.4 o 3.7 ar vald. f, B = c 0.5 +B 3.4 f, B = c 0.5 f, 3.5 B f f, B = f, 3.6 B, B = f, 3.7 B whr f, f and f ar agan h aral drvavs wh rsc o frs and scond varabls. L f, b a funcon whos scond ordr aral drvavs ar connuous. Thn 3.8 s ru. f, B f s, B s = [ f, B + f, B ] d + f s s, s <, B db 3.8 7
28 Usng h quaons 3.4 o 3.7, quaon 3.9 s oband. f, B f s, B s = c X y dy + X y db y s s 3.9 If on subsus s = 0 n 3.9, and uss X = f, B, 3.30 s oband, whch s nohng bu 3.. X = X 0 + c X y dy X y db y 3.30 Hnc o summarz, s shown ha c0.5 +B X = s a soluon for 3.. 8
29 3. Unqunss of h Soluon of h Sochasc Dffrnal Equaon In h soluon of h sochasc dffrnal quaon, was rovn ha 3.3 s a soluon for h sochasc ngral quaon 3.3. X c0.5 +B = 3.3 X = X 0 + c X s ds X s db s 3.3 Ths scon rovs ha 3.3 s also h unqu soluon. Th followng Lmma s gvn whch can b ald o our cas. Lmma Assum ha h gnral sochasc ngral quaon s dscrbd by X = X 0 + a s, X s ds b s, X s db s 3.33 Assum ha h nal condon X0 has a fn scond momn: E[X0 ] <, and s ndndn of B, 0. Assum ha, for all ε [ 0, T ] and,y ε R, h coffcn funcons a, and b, sasfy h followng condons: Thy ar connuous. Thy sasfy a Lschz condon 3.34 wh rsc o h scond varabl: a, a, y + b, b, y K y 3.34 Thn h Io sochasc dffrnal quaon 3.33 has a unqu srong soluon X on [ 0, T ]. [8] For mor nformaon on h srongnss of h soluon, h radr can rfr o [9]. 9
30 Alcaon of h Lmma Afr dfnng h Io s Lmma, s sraghforward o aly h abov samn o 3.3 Snc a, = c and b, =, hn a, and b, ar connuous. Furhrmor: a, a, y b, b, y = c = y y a, a, y + b, b, y = c + y 3.35 Comarng 3.34 and 3.35, for K = c + +, a, and b, sasfy h Lschz condon. As a rsul, 3.3 has a unqu srong soluon X on [0,T]. Ths unqu srong soluon s gvn n
31 CHAPTER 4 DQF ALGORITHM 4. DQF L h sysm b rrsnd by 4. and 4.. X + = f X,, w 4. Z = g X,, v 4. whr X s sa, X + s n sa, Z s masurmn, v, w ar noss. Fnally, f and g ar nonlnar funcons n gnral. Th roblm can b sad as: Gvn Z,.., Z, fnd X,.., X n h flrng algorhm Gvn Z,.., Z, fnd X + n h rdcon algorhm Ths roblm dos no hav omal soluons. Howvr, h EKF mrgs as a subomal soluon o h roblms gvn abov. Th da of DQF algorhm roosd by Dmrbaş [3] s o quanz h sa sac and quanz h connuous random varabls. Th quanzd sa sac rrsnaon s analyzd n ordr o fnd an omal soluon. Two aromaon chnqus ar usd: Th sac wll b sarad by gas. All h lmns n h gas wll b aromad wh h cnr of h gas. X 0, w 0, w, wll b aromad by dscr random varabls. Usng hs wo assumons, Dmrbaş obans a rlls dagram for h sas. Th algorhm comoss of 3 man ss.
32 Obanng a rlls dagram Assgnng mrcs o h nods of h rlls dagram 3 Choosng h hghs mrc for h drmnaon of h bs ah 4.. Obanng a Trlls Dagram Th abov mnond algorhm sas ha h frs s s o oban a Trlls Dagram. No ha h algorhm uss dscr random varabls nsad of h connuous random varabls. Tha s X 0, w, w,... ar h dscr vrsons of h orgnal connuous random varabls. Th rlls dagram s h s of all ossbl valus of { X, X, }. X = f X 0,0, w0 4.3 Pung all ossbl valus X 0 and w 0 o 4.3, all ossbl valus of X ar oband. Th n s s smlar: X = f X,, w 4.4 Smlarly ung all ossbl valus X and w o 4.4, all ossbl valus of X ar oband. As a rsul, all ossbl valus of X, X,, X N ar oband va 4.4. Th rlls dagram s jus h comoson of hs valus. Th dagram consss of columns, ach of whch ndcas h m 0,,... N. Also, ach column comoss from h ossbl valus of h sa X 0, X,.., X N 4.. Assgnng Mrcs o h Nods of h Trlls Dagram Th scond s of h algorhm s h mos crucal on. Frs, h mrcs of h frs column ar assgnd. L h ossbl valus of X 0 b X q0, X q0, X q30,.., X qm0
33 L M X q0, M X q0, M X q30,, M X qm0 mrcs of X q0, X q0, X qm0 rscvly. Th valus of h Mrcs ar calculad accordng o 4.5. dno h M X q 0 = ln P X 0 X 0 whr {,,, m } 4.5 q Th n s s o drmn h mrcs of h scond column nods. Thr ar manly hr ss o b followd o fnd hs mrcs. Transon mrcs wll b calculad from ach nod of h frs column o ach nod of h n column. For aml, M X q 0 X q dnos h ranson mrc from h h nod of h frs column o h l h nod of h scond column. Th calculaon of hs ranson mrc s accordng o 4.9, whch s land n h subscon 4... For h drmnaon of h mrcs of h scond column nods, h followng rocdur mus b followd: L X q dno h l h nod of h n column. Th sum 4.6 mus b calculad for ach nod of h frs column. M X q = M X q 0 + M X q 0 X q Th ral Mrc M s h largs among h calculad mrcs X q accordng o 4.6. Th calculaon of h mrcs of h hrd column jus rqurs h ulzaon of h sam rocdur Calculaon of h ranson mrc: L h sysm b dscrbd as 4.7 and 4.8. X + = f, X, w 4.7 Z = g, X + v 4.8 3
34 whr X 0 s a Gaussan random vcor wh man m0and covaranc R 0 ; Z s h masurmn daa; w s a Gaussan dsurbanc nos vcor wh zro man and varancσ ; f and g ar nonlnar funcons n gnral; v s a Gaussan w nos wh zro man and varanc σ. Morovr, h random varabls X 0, v w j, w, v l and v m ar assumd o b ndndn for all j,, l and m. Thn h ranson mrc s calculad accordng o h followng samn 4.9: M{ X X } = InΠ q [ z g, X q In{ π v } v q ] 4.9 whr Π s h ranson robably from h nod. For h calculaon of ranson mrc of h muldmnsonal sysm, s [0] Choosng h Hghs Mrc for h Drmnaon of h Bs Pah Usng h rocdur dscrbd n scon 4.., h followng ls s oband. A rlls dagram,. Each nods mrcs has bn calculad 3. Th rvous nod from whch w cam o ha nod Thn h ouu of h algorhm s found as follows:. Loo a h las column. Fnd h largs mrc 3. Loong a h assocad rvous nod, rac on s bac 4. Go u o h frs column 5. Th ouu s jus h comoson of hs nods. 4
35 4. Quanzaon of h random varabl DQF algorhm uss h quanzd vrson of connuous random varabls. In hs sudy, snc h noss ar assumd o b Gaussan, h robably dnsy funcon of h Gaussan random varabl wh man µ and varanc s dscrbd by 4.0: f µ = π 4.0 Whr 4.0 s aromad accordng o 4.. f y n = P y = 4. whr y s ar h dscr ossbl valus of h connuous random varabl and P s ar h assocad robably valus. L F and F y dno h robably dsrbuon funcons of h connuous and dscr m random varabls. Thn F = y for < y+ y, whr = P =. In ordr o fnd y and, h followng cos funcon s dfnd: [ F a Fy a ] J F. = da y 4. Th bs dscr candda for h robably dsrbuon funcon s assumd o mnmz h cos funcon dscrbd n 4.. 5
36 Accordng o Dmrbaş [6], mnmzaon of 4. s quvaln o solvng h sysm of nonlnar quaons from 4.3 o 4.6. = F 4.3 y F y, =,,3,..., n = + n n + = F y y y = F a da =,,3,..., n + y y 4.6 whr F dnos h robably dsrbuon funcon. In hs sudy, a rcursv Malab rogram s wrn n ordr o fnd y and. Th algorhm of h rogram s as follows: Assum an nal s of robabls Us 4.3 o 4.5 o fnd y 3 Uda usng Go o s Ingral n h quaon 4.6 s calculad numrcally usng h razodal rul. Usng hs algorhm, h sysm s solvd u o n = 40. 6
37 CHAPTER 5 EKF Th Kalman Flr aroach o h flrng and smaon roblms s on of h sandard ools n smaon hory. In h lnar cas, Kalman Flr wors n h omal sns. Bu n nonlnar roblms, whr h n sa s a nonlnar funcon of currn sa and nos, Endd Kalman Flr s usd. L h sysm b dscrbd as: X + = Φ, + Γ, w 5. Z = h, + v 5. L E X 0 = µ 0, Varanc { X 0} = V 0 Cov{ w, w j} = Vw [ j] Ew = Ev = 0 Cov{ v, v j} = Vv [ j] Cov { v, w j} = Cov{ v, X } = Cov{ w, X 0} = 0 In hs sag + and z wll b aromad accordng o 5.3 and 5.4. φ X, 5.3 X + Φ X P, + [ X ] + Γ X, w X h X, Z h X P, + [ X ] + v X 5.4 7
38 Snc 5.3 and 5.4 consu a lnar sysm, h sandard KF can b ulzd. As a rsul h followng quaons ar usd for flrng and rdcon []: V~ + = φ X X, T φ X, ~ + X V 5.5 Τ Γ X, V Γ X, w X + = Φ [, ] 5.6 X 3 V~ + = V~ + - V~ + h X T X + +, { h X X +, + + h * ~ + * V T X X +, V v + } - * h X X +, + + V + 4 K + = V~ + T h X +, + [ V v + ] X X + = X + + K + { z + h X +, +} 5.9 In h abov quaons, h nal condons ar E X 0 = µ 0 and V ~ 0 = V0. 8
39 CHAPTER 6 APPLICATION OF EKF TO ECONOMETRICS Th nonlnar sysm s dscrbd wh h followng wo quaons, whch ar 6. and 6.. X w + = LX 6. whr L = c0.5 T, whch s a consan. Z = X + v 6. In h ffh scon, h sysm rrsnaon of EKF was: X + = Φ X + Γ X, w 6.3 Z = h X, + v 6.4 Comarng 6.3 and 6.4 wh 6. and 6.,w g h followng rsul: h X, = X 6.5 Equaon 6. and 6.3 canno b qual for any choc of Γ and Φ. In ordr o us EKF, h lnarzaon chnqu wll b usd for 6.. w s rrsnd n h Taylor anson form
40 LX w [ w ] 6.6 = + w w T LX [ w ] = LX [ + w + w +...] = LX + LX w +... srs Equaon 6.7 s oband by ang a frs ordr aromaon for Taylor LX w T LX + L w T X 6.7 Insad 6., quaon 6.7 s usd o b abl o aly EKF. Comarng 6.7 wh 6.3, quaons 6.8 and 6.9 ar oband. Φ X, = LX 6.8 Γ X, = L X 6.9 Rlacng h valus of h, φ, Γ quaons s oband. n 5.5 o 5.9, h followng s of V~ + = L V~ L + [ L X ] V w [ L X ] 6.0 X + = LX 6. 3 ~ + = ~ + - ~ + * { ~ + + V V V V V v +} - * 6. V + 4 K + = V + [ V v + ] X + = X + + K + { z + X + } 6.4 Fnally, wh h hl of h quaons 6.0 o 6.4, s ossbl o smooh h nosy daa and ma a rdcon. 30
41 CHAPTER 7 PARTICLE FILTERS-SIR ALGORITHM SIR algorhm s drvd from a grou of algorhms, whch ar nown as arcl flrs. Th algorhm s a Mon Carlo mhod ha can b ald o rcursv Baysan flrng roblms. I s frs roosd by Gordon.al. [3]. SIR algorhm can b ald o sysms rrsnd by 7., 7. + = f, w 7. z = h, v 7. Th condons for h sa and masurmn quaons ar wa. Th sa and masurmn noss ar wh nos squncs, whr f and h ar nonlnar funcons n gnral. Th as s o uda 7.3 rcursvly. z,..., z 7.3 Th man da s o aroma h condonal robably dnsy funcon accordng o 7.4. N s : ω = z 7.4 3
42 Hr, rrsns h randomly gnrad arcls and w s ar h assocad robably valus. s h usual muls funcon. z : dnos h s {, z,..., z } : z. Also dnos h s {,,..., } Th SIR flr s comosd of hr ss:. Prdcon Uda 3 Rsamlng Prdcon A h rdcon s, gvn, z h as s o oban z : Each arcl wll b udad usng h followng quaon 7.5. : = f, w 7.5 Each w s drawn from h robably dnsy funcon df of. w Uda Th wghs of n 7.4 ar calculad accordng o 7.6. w = N s j= z z j 7.6 3
43 Rsamlng arcls Whn h uda s comld, z : from z: s achvd. Th and h assocad robably valus w rrsn h condonal valu n h sns of 7.4. If h rsamlng s was o b sd, hn w would bcom mor and mor swd. Afr a whl, only on arcl wh nonzro robably valu wll s [5]. To avod hs dgnracy, h rsamlng s s roosd. As a rsul, h nw df s rrsnd by 7.7. z N : = N N = 7.7 whr N = N = N 7.8 For mor nformaon abou h rsamlng sag, h radr s rfrrd o [4]. 7. Drvaon of h SIS and SIR algorhm Th squnal moranc samlng SIS algorhm s a Mon Carlo MC mhod ha forms h bass for mos squnal MC flrs dvlod ovr h as dcads. SIR s also on of hs flrs. Suos π, s a robably dnsy funcon from whch s dffcul o draw samls, bu for whch π can b valuad [as wll as u o rooronaly]. In addon, l q,,.., ~ = N b samls ha ar asly s gnrad from a roosal q calld moranc dnsy. Thn, a wghd aromaon o h dnsy s gvn by N s w =
44 whr w π q s h normalzd wgh of h h arcl [4]. If h samls ar drawn from q, hn h wghs wll b 7.. z 0: : w q 0: 0: z z : : 7. L h moranc dnsy b chosn as: q z q, z q z 7. 0: : = 0: : 0: : Usng h Bays rul: 0: z : = z 0:, z z : z : 0: z : 7.3 0: z : = z 0:, z : z 0: z, z : : 0: z : 7.4 nos Snc h sa s acually a Marov rocss du o whnss of h rocss, z 7.5 0: : = 34
45 35 and snc h masurmns ar a sac funcon of h las sa and h masurmn nos s wh, : : 0 z z z = 7.6 : : 0: : 0: = z z z z z 7.7 : 0: : : 0 z z z 7.8 Pung 7. and 7.8 no 7., h rsulng quaons 7.9 and 7.0 ar oband., : 0: : 0: : 0: z q z q z z w 7.9, : 0: z q z w w 7.0 Hnc, h gnral framwor for SIS flrs s concludd. Th SIR flr s asly drvd by choosng, : 0: z q = 7. Thn, z w w 7.
46 Hnc h wghs ar udad accordng o h 7. and accordng o h 7.. s ar udad 36
47 CHAPTER 8 SIMULATIONS OF FILTERING AND PREDICTION EXPERIMENTS 8. Gnral Ouln In hs scon, h conomrc sysm s analyzd from svral ascs. Th sysm was dscrbd by 8. and 8.. X w + = LX 8. whr L = c0.5 T, whch s a consan. 8. s h sandard sa quaon. In ral world alcaons, corrsonds o h ral rc uda n rms of currn ral rc and nos. Th obsrvaon quaon s dfnd by 8.. Z = X + v 8. whr v s h masurmn nos or sculaors nos or, alrnavly, h radrs nos. 8. and 8. consu oghr h dynamc sysm rrsnaon. In hs scon, s assumd ha h masurmn daa s gvn and h as s o flr h nos and c h currn and h n ral rc 37
48 8. Flrng Tools Th rvous lraur on flrng gnrally vws h Endd Kalman Flr as a, sandard analyss ool for flrng of nos for nonlnar dynamc sysms. In hs sudy, an alrnav mhod DQF, as mnond bfor n dals, s usd. Alhough h hory of DQF s dscussd n scon 4., h alcaons of DQF o svral cass nd o b word ou. Thrfor, hs sudy s an am o aly DQF o a nw ara, Mahmacal Fnanc, whch bcam ncrasngly oular n h rcn yars. 8.3 Prdcon Tools Ndlss o mnon, rdcon s crucally moran n conomc sysms. In hs con, rdcng h mos robabl n valu of h soc mrgs as an nrsng quson o answr. In ordr o rdc h n valu of h soc, whch s dscrbd by h sysm rrsnaon 8. and 8., SIR flr and EKF ar usd. 8.4 Error Crra and Mon Carlo Smulaons Whn hr s gra dal of dffculy n analyzng h sysms n svral branchs of scnc, Mon Carlo smulaons ar mloyd. Thrfor, n hs sudy, o comar h rformancs of EKF and DQF, hs mhod s rfrrd. Th mhod can smly b summarzd as mang many rmns and usng h rsuls of hs rmns o rdc h rformanc of h sysm. In ach smulaon rmn, h followd rocdur s smlar: On aramr s vard or chosn a scfc valu. For ach valu of h aramr, 0 rmns ar don. 3 Errors for ach rmn ar calculad for o EKF ouu 38
49 o DQF ouu 4 Avrag Error EKF and DQF ar calculad Flrng Error Error n R N Sacs: L N R b dfnd by 8.3. = [,,..., N] 8.3 L norm of s calculad accordng o 8.4 N = [ ] = 8.4 L N, y R, hn h dsanc bwn h vcors and y s gvn by 8.6 y 8.6 Th dsanc conc dfnd n 8.6 s usd for h dfnon of rror. L b h ru valu hn h rror y s dfnd by 8.7 rror y = y Errors n h Ermns In ordr o calcula h rrors, h noaons 8.8 o 8. ar usd o rrsn ral daa, EKF ouu, and DQF ouu rscvly. 39
50 X = [ X, X,, X N] 8.8 EKF = [EKF, EKF,, EKF N] 8.0 DQF = [DQF, DQF,, DQF N] 8. Th corrsondng rror valus of EKF and DQF ar calculad accordng o 8. and 8.3 rror EKF = EKF X = N [ EKF = X ] 8. rror DQF = DQF X = N [ DQF = X ] 8.3 Havng oband h rrors for ach rmn, h avrag of h rrors of boh EKF and DQF ar calculad accordng o h followng formula n 8.4. avrag _ rror = K rror 8.4 K = whr K s h numbr of rmns don n h Mon Carlo smulaon Prdcon Error For a sngl rmn, h rror calculaons of rdcon algorhms of nrs, whch ar EKF and SIR arcl flr, ar 8.5 and 8.6. rror EKF = EKF N + X N rror SIR = SIR N + X N Havng oband h rrors for ach rmn, hn h avrag of h rrors of boh EKF and SIR arcl flr ar calculad accordng o h formula
51 avrag _ rror = K rror 8.7 K = whr K s h numbr of rmns don n on Mon Carlo smulaon. 8.5 Smulaons Afr h smulaon rsuls ar oband, h followng rgulars hav bn obsrvd: Th rncl of EKF algorhm s h lnarzaon of h sysm quaons. Whn h lnarzaon condon s volad, h rror rformanc of EKF bcoms oor. In ordr o oban good rror rformanc for DQF algorhm, h quanzaon lvls mus b adqualy chosn. Whn hs condon s sasfd, DQF rforms br comard o EKF. 3 Th comuaon m rformanc of h DQF algorhm s bad whn s comard o EKF. Quanzaon Lvl As mld abov and h rsuls show, h DQF algorhm has onnal comly, whch sands ou as s bggs dsadvanag. I s hard o mlmn n ral m alcaons, whr h comuaon m rformanc s h crucal on. In conomrcs, hr ar svral cass whr h comuaon m s no h rmary concrn. Thrfor, f h sac mus s adqualy quanzd, hn h DQF algorhm may b rfrrd. Howvr, h sa quaon 8. conans an onnal rm 8.8 ω 8.8 Wh h rm 8.8, s mor dffcul o adqualy dscrb h sysm n h quanzd doman. I rqurs a hug numbr of quanzaon lvl. 4
52 Lnarzaon Condon 8.8 s rssd n Taylor anson form as 8.9. w = + w ] w + [ ] Thn, a frs ordr aromaon 8.0 has bn mad. w + w 8.0 In ordr 8.0 o b an adqua aromaon of 8.9, 8. mus b sasfd. [ w ] << w s also quvaln o 8.. w << 8. 4
53 8.5. Flrng Whn h smulaons ar run and h rsuls ar oband, Tabl shows h rror rformancs vrsus h chang of varanc of h sa quaon nos. For ach varanc valu, 0 rmns ar don. Inal condons ar: quanzaon lvl of X 0 and w ar 3, Varanc of v s 4, s, man of X0 s, Varanc of X0 s 0., and m nd N s. Th varanc of w s changd from o 6. c s 0.. Tabl Mon Carlo rsuls-errors of h algorhms vrsus chang of h varanc of w EKF DQF I s clar from Tabl ha whl h varanc of w s ncrasd, h rrors of EKF and DQF algorhms ar ncrasd. Ths s cd, snc accordng o 8., h aromaon of h onnal funcon by frs ordr rms s no rgh. Hnc h lnarzaon of h sysm wh h frs ordr s no adqua. Th lnarzaon of h sysm s h basc assumon of EKF, whch s smly fals. DQF s assumd o b an omal soluon whn h ga sz aroachs o zro and quanzaon lvl aroachs o nfny. From h rrors, s also concludd ha h quanzaon lvl s no hgh nough Th rsuls ha ar dslayd n h rcdng scon s no sasfacory n rms of h h rrors of h DQF. I was assumd ha h quanzaon lvls wr no hgh nough. For ha uros, n hs rmn, h numbr of quanzaon lvl of w s an as 40 and h quanzaon lvl of X0 s an as 0. Th rrors of DQF algorhm ar dcrasd drascally, bu h crucal on s ha, rformd br han h EKF. For aml, whn h varanc of w s 5, rformd 43
54 aromaly 8 ms br han EKF. Tabl shows h rmnal rsuls of h scond Mon Carlo smulaon. Th scond obsrvaon from Tabl s ha, wh h ncras of varanc of w, h rror of DQF s also ncrasd. Ths s also cd snc h rang of ossbl valus of w s ncrasd, bu for ach varanc valu of w, h sam quanzaon lvl s usd. Tabl Mon Carlo rsuls-errors of h algorhms vrsus chang of h varanc of w EKF DQF In hs rmn, h rror rformancs of h algorhms ar shown whn h volaly consan s dcrasd o 0.. All nal condons ar sam wh h rvous rmn c h consan volaly. Agan h varanc of w s vard bwn and 6. Tabl 3 shows h Mon Carlo Smulaon rsuls. Tabl 3 Mon Carlo rsuls-errors of h algorhms vrsus chang of h varanc of w DQF EKF As s sn from Tabl 3, EKF s sabl n hs rmn. Ths s also cd, snc h rm w s dcrasd 0 ms for h sam valus of w comard o h rmn DQF s also sabl. Ths s also cd snc h ncras du o onnal rm s now lmd. Th rang of ossbl valus of X s dcrasd. Ths rang s also adqualy quanzd wh h chosn quanzaon lvls. 44
55 In h rmn 8.5.., was shown ha wh h ncras of h quanzaon lvl, h rror rformanc of DQF ncrasd subsanally. In hs rmn, h ncras of rformanc s sudd n dals. Inal condons ar sam wh h scond rmn, bu h quanzaon lvl of w s vard from o 40. Th quanzaon lvl of X 0 s assumd o b 0 n all smulaons. Th nos varancs ar assumd o b 5 and 4, for w and v rscvly. Fgur, whch dslays h lo of quanzaon lvl vrsus h rror rms shows h mrovmn of rrors whn h quanzaon lvl s ncrasd. I aroachs o a lmng valu as can b asly sn from h fgur. Fgur 45
56 As mnond abov, on moran roblm wh h DQF and DQP was h comly of h algorhms. Comard o EKF, comuaon m rformanc of h algorhm s also wors for larg quanzaon lvls. In hs rmn h m nd wll b ncrmnd on lvl. To a rasonabl rror rformanc and comuaon m, quanzaon lvl s chosn as 0 for w and 0 for X0. All ohr nal condons ar sam as h scond rmn bu N s. Conssn wh h rvous rmn, 0 rmns ar rformd for Mon Carlo smulaon. Tabl 4 Mon Carlo rsuls-errors of h algorhms for h varanc of w=5 EKF DQF.7439 Th rsuls ar rmarabl, whch ndca ha h rror rformanc of h algorhm s aromaly 5 ms br han h convnonal EKF. Bu should b nod ha comuaon m of DQF ncrass. 46
57 8.5. Prdcon Th rdcon ar dffrs from h smoohng ar. Th sysm dscrbd by 8.3 and 8.4 s ransformd o anohr quvaln form. Th rason for ha s h numbr of rmns n h Mon Carlo smulaon rqurd o comar DQP and EKF s oo hgh. Howvr, afr ransformng o h nw quvaln form, br rsuls hav bn oband. Furhrmor, h m nd could b ncrmnd o vn hghr numbrs, whch was no ossbl bfor for h cas of DQF algorhm. X w + = LX 8.3 Z = X + v 8.4 Whn ang logarhm of boh sds, 8.3 s rwrn as 8.5 ln X + = ln L + ln + w 8.5 Furhrmor f Y = ln X 8.6 Y + = ln L + Y + w 8.7 As a rsul h nw s of quaons ar 8.7 and 8.8. Y Z = + v 8.8 Th quaon 7.7 s lnar, bu h quaon 7.8 s nonlnar. Furhrmor h robably dnsy funcon of Y 0 s no Gaussan. In fac, s oband from h Gaussan nos by h ransformaon 8.6. Hnc h sandard assumon of EKF for h nal nos dos no hold.evn n hs cas, h nw s of nonlnar quaon s mlmnd by SIR and EKF algorhm. 47
58 Man and Varanc of Y0 Y can a valus 0 and ngav, so Y 0 can hav coml valus accordng o 8.6. For ha rason, all h valus for Y 0 s aromad by Y = Ths mas sns, snc h man of X 0 s and s varanc s an as 0.. Undr hs assumons, man and varanc of Y 0 s oband rmnally. For ha uros 8.9 and 8.30 ar usd. s Y 0 µ = Y 0 N = N = = N Y Y µ N Y whr Y s h randomly gnrad numbr. Ths smas ar nown o convrg o h ru man and varanc valus as N. Ermns In hs rmn, s, h man of X0 s, h varanc of X0 s 0., and h m nd N s 5. Th varanc of w and v ar s o uny. For hs smulaon, 000 rmns ar don. Tabl 5 Mon Carlo rsuls-errors of h algorhms SIR and EKF EKF SIR.976 As can b sn from Tabl 5, SIR rror rformanc s br han h on for EKF. 48
59 CHAPTER 9 SIMULATIONS OF FILTERING EXPERIMENTS FOR STOCHASTIC GROWTH MODELS Bgnnng wh h sandard sochasc growh modls, for whch h ycal soluons ar offrd n Hansn [7],[8], modlng boh roducvy shocs and caal soc accumulaon bcam crcal ssus. Alhough, h rlaonsh bwn h wo varabls can b land n a sandard way by usng h Solow rsduals, hr ar also som rcn suds, whch lan h dynamcs whn h con of mor comac modls. Howvr, hr ar only a fw of hs suds ha am o lor h ssu n a non-lnar framwor. Howvr, as s vdnly dscussd n Novals al [9], h roducvy shocs may carry a non-lnar naur, for whch h sandard Kalman flrng algorhms fal o b arora. In hs con, h non-lnar sa sac modl can b solvd hr by ndd Kalman flr or Parcl flr. Followng Novals al [9], h sa sac modl can b wrn as: log θ = ρ log θ + ε 9. = c + αθ + N 9. Th frs quaon 9. modls h roducvy shocs as bng frs ordr auorgrssv rocss, whr h dsurbanc rm s assumd o b ndndn and dncally dsrbud. If h aramr rho gs closr o uny, hn h roducvy shocs follow random wal rocsss, whr any shoc o h quaon wll hav rmann ffcs. Th scond quaon 9. rlas h moranc of hs roducvy shocs on h chang of h caal soc. Basd on h no-classcal growh modls, an ncras n h roducvy wll ncras h rurn o h caal, whch wll cra 49
60 an ra ncnv for h frms o accumula furhr caal. Usng h aramrs ha ar oband from h calbraon of h mcro-basd fundamnals, h followng valus for h aramrs ar usd. c = α = ρ = 9.5 In rms of smaon, h frs quaon, whch s h sa quaon n h modl, has a non-lnar naur, whr h rformanc of ndd Kalman flr and Parcl flr can b sd. By us of h ransformaon 9.6, h quaons 9.7 and 9.8 ar oband. X = ln θ 9.6 X = X + ε 9.7 X = c + α + N 9.8 Th man and varanc ar calculad rmnally. Man and Varanc of X0 As bfor, θ 0 can a valus 0 and ngav, so X 0 can hav coml valus accordng o 9.6. For ha rason, all h valus for θ 0 0 s aromad by θ 0 = Ths mas sns, snc h man of θ 0 s and s varanc s an as 0.. Undr hs assumons, h man and h varanc of X 0 s oband rmnally. µ X 0 N = = N X
61 s X 0 = N = X µ N X whr X s h randomly gnrad numbr. Ths smas ar nown o convrg o h ru man and varanc valus as N. Ermn In hs rmn, flrng rformanc of h algorhms of SIR and EKF ar comard. Man of X0 s, varanc of X0 s 0., and h m nd N s 5. Th varanc of w s. Th varanc of v s. For hs smulaon, agan, 000 rmns ar don. Tabl 6 Mon Carlo rsuls-errors of h algorhms SIR and EKF EKF.0875 SIR.836 As sn from Tabl 6, rror rformanc of h SIR algorhm s br han h EKF algorhm. Thrfor, h las wo rmns clarly show ha whn h SIR algorhm s comard wh h convnonally usd Endd Kalman Flr, has br rformancs. Such a concluson ndcas ha SIR can b a comng alrnav o EKF n comuaon rocss of h conomrcs roblm. 5
62 CHAPTER 0 CONCLUSION Ths sudy nds h rvous wor on h nonlnar smaon roblms. For ha uros, Endd Kalman Flr EKF, Dscr Quanzaon Flr and Squnal Imoranc Rsamlng SIR Flr ar mloyd.. Snc h alrady dns lraur on nonlnar smaon has no valuad h las wo flrs, hs sudy can b vwd as a conrbuon n offrng wo alrnav algorhms. Anohr rmary concrn n hs hss s o show h advanags of hs wo algorhms ovr EKF, whch s h convnonally usd algorhm n h fld. Th man da of DQF s o quanz h random varabls. If suffcn quanzaon of h random varabls ar mad, hn DQF rforms br han h EKF. Howvr, s major dsadvanag s h comuaon m. Hnc hr s a rad-off for rformanc vrsus comuaon m. SIR flr s from a grou of flrs ha ar nown as arcl flrs. I s h mlmnaon of Mon Carlo chnqus o smaon roblms. Error rformancs of h SIR flr wr br comard o EKF. Th comuaon m rformanc was also rasonabl comard o DQF. Thrfor, h flr can b sn as a good alrnav o hekf. Th cas suds wr chosn from h fld of conomrcs. Hnc, h conrol hory chnqus hav bn ald o a dffrn scnc branch. Ohr han valuang h rformanc of h abov mnond algorhms, anohr rmary concrn n hs sudy s o romo h us of sochasc calculus, whch nabls us o hav a mor gnral rscv for nonlnar dynamcal sysms wh nos. Th classcal aroach n h sysm hory s o ma assumons for nos drcly n h sa sac form. Howvr, wh h us of sochasc calculus, w can ma assumons also n h dffrnal quaons form. 5
63 Alhough h hory bhnd hs subjc rqurs undrsandng advancd mahmacal concs, s usag s farly sml. 53
64 REFERENCES [] Mohndr S.Grwal and Angus P. Andrws, Kalman Flrng Thory and Pracc usng Malab,John Wly,Nw Yor, 00 [] C.K.Chu and G.Chn, Kalman Flrng wh Ral-Tm Alcaons, Srngr, Brln; Nw Yor, 999 [3] Krm Dmrbaş, Informaon Thorc Smoohng Algorhms for Dynamc Sysms wh or whou Inrfrnc, Conrol and Dynamc Sysms, [4] Thomas Kalah, Lnar Sysms, Prnc Hall, Englwood Clffs, N. J., 980 [5] Zdzslaw Brzzna and Tomasz Zasawna, Basc Sochasc Procsss, Srngr-Vrlag, London Lmd, 999,.79- [6] Thomas Mosch, Elmnary Sochasc Calculus, World Scnfc, Sngaor; Rvr Edg, N. J.,. 80, 998 [7] Thomas Mosch, Elmnary Sochasc Calculus, World Scnfc, Sngaor; Rvr Edg, N. J.,. 68, 998 [8] Thomas Mosch, Elmnary Sochasc Calculus, World Scnfc, Sngaor; Rvr Edg, N. J.,. 35, 998 [9] Hayr Körzloğlu, Azz Basıyalı Hayfav, Elmns of Probably Thory, ODTÜ, Anara, 00 [0] Brn Osndal, Sochasc Dffrnal Equaons, An Inroducon wh Alcaons, Srngr, Brln; Nw Yor,. 36, 995 [] Thomas Mosch, Elmnary Sochasc Calculus, World Scnfc, Sngaor; Rvr Edg, N. J.,. 93, 998 [] Ludwg Arnold, Sochasc Dffrnal Equaons Thory and Alcaons, Wly, Nw Yor,. 3, 974 [3] Thomas Mosch, Elmnary Sochasc Calculus, World Scnfc, Sngaor; Rvr Edg, N. J.,. 0, 998 [4] Thomas Mosch, Elmnary Sochasc Calculus, World Scnfc, Sngaor; Rvr Edg, N. J.,. 90,
65 [5] Thomas Mosch, Elmnary Sochasc Calculus, World Scnfc, Sngaor; Rvr Edg, N. J., , 998 [6] Thomas Mosch, Elmnary Sochasc Calculus, World Scnfc, Sngaor; Rvr Edg, N. J.,. 7, 998 [7] Thomas Mosch, Elmnary Sochasc Calculus, World Scnfc, Sngaor; Rvr Edg, N. J.,. 8-9, 998 [8] Thomas Mosch, Elmnary Sochasc Calculus, World Scnfc, Sngaor; Rvr Edg, N. J.,. 38, 998 [9] Thomas Mosch, Elmnary Sochasc Calculus, World Scnfc, Sngaor; Rvr Edg, N. J.,. 37, 998 [0] Krm Dmrbaş, Informaon Thorc Smoohng Algorhms for Dynamc Sysms wh or whou Inrfrnc, Conrol and Dynamc Sysms,. 48 [] Krm Dmrbaş, Informaon Thorc Smoohng Algorhms for Dynamc Sysms wh or whou Inrfrnc, Conrol and Dynamc Sysms,. 9 [] A.P. Sag and J.L. Mlsa, Esmaon Thory wh Alcaons o Communcaons and Conrol, McGraw-Hll, Nw Yor,. 97 [3] N.Gordon, D. Salmond, and A.F.M. Smh, Novl Aroach o nonlnar and non-gaussan Baysan sa smaon, Proc. Ins. Elc. Eng., F, vol. 40,.07-3,993 [4] M. Sanjv Arulamalam, Smon Masll, Nl Gordon, and Tm Cla, A Tuoral on Parcl Flrs for Onln Nonlnar/Non-Gaussan Baysan Tracng, IEEE Transacons On Sgnal Procssng, Vol. 50, No., Fbruary 00 [5] Arnoud Douc, Nando d Fras, Nl Gordon, Squnal Mon Carlo Mhods n Pracc, Srngr-Vrlag 00,.0 [6] Krm Dmrbaş, Informaon Thorc Smoohng Algorhms for Dynamc Sysms wh or whou Inrfrnc, Conrol and Dynamc Sysms,.9 [7] Hansn, G.D. 985, "Indvsbl Labor and Th Busnss Cycl", Journal of Monary Economcs, 6, [8] Hansn, G.D. 997, "Tchncal Progrss and Aggrga Flucuaons", Journal of Economc Dynamcs and Conrol,,
66 [9] Novals A., E. Domnguz, J.J. Prz and J. Ruz 999, "Solvng Nonlnar Raonal Ecaons Modls By Egnvalu-Egnvcor Dcomosons", n R. Marmon and A. Sco ds., Comuaonal Mhods For Th Sudy Of Dynamc Economs, Oford Unvrsy Prss, Oford, UK. 56
67 APPENDIX Comma Srad Form for h quanzaon of h Gaussan random varabl uo 40 ons. Quanzd valus for h random varabl wh man 0 and varanc. :0 :-0.675, ,0, :.90, ,0.3550,.90 5:.3760,-0.590,0,0.590, :-.4990, ,-0.40,0.40,0.7670, :.5990, ,-0.430,0,0.430,0.9050, :-.6830,-.080, ,-0.830,0.830,0.5670,.080, :-.758,-.73, ,-0.330,-0.000,0.3309,0.688,.7, :-.8,-.005, , ,-0.48,0.480,0.453,0.7898,.003,.89 :-.8790,-.736, , ,-0.79,-0.000,0.76,0.5575,0.8778,.733,.8788 :-.930,-.3385, , , ,-0.43,0.39,0.3773,0.648,0.955,.338,.999 3:-.9765,-.3969,-.045,-0.785, ,-0.308,-0.000,0.303,0.4694,0.780,.04,.3966,.976 4:-.089,-.4499,-.0867, ,-0.555,-0.339,-0.07,0.065,0.333,0.5509, ,.086,.4495,.086 5:-.0580,-.4984,-.43, ,-0.645, ,-0.007, ,0.999,0.4058, 0.638,0.8638,.46,.4978, :-.094,-.5430,-.949,-0.93, , ,-0.838,-0.094,0.0933, 0.89,0.4797,0.6897,0.93,.94,.543, :-.77,-.584,-.45, , , , ,-0.776, ,0.766, ,0.5465,0.7497,0.9759,.46,.5834,.7 8:-.59,-.66,-.865,-.064, , ,-0.46,-0.57,-0.084, 0.089,0.55,0.449,0.6075,0.8047,.053,.856,.67,.584 9:-.886,-.6584,-.375,-.073, , , ,-0.308,-0.594, , 0.580,0.394,0.4866,0.6634,0.8554,.07,.364,.6573,.877 0:-.64,-.690,-.3659,-.5, ,-0.767, ,-0.383,-0.78, , ,0.6,0.385,0.543,0.75,0.904,.36,.3645,.6908,.53 :-.46,-.736,-.408,-.55, , , , ,-0.905, ,-0.000,0.48,0.886,0.4386,0.5956,0.7630,0.946,.534,.4003,.7,.43 :-.674,-.7534,-.4356,-.96,-0.989, , , ,-0.348, , ,0.0675,0.054,0.346,0.495,0.644,0.8077,0.987,.907,.4339,.758,
68 3:-.909,-.787,-.4675,-.79,-.077,-0.858,-0.699, ,-0.407, ,-0.36,-0.00,0.30,0.63,0.3993,0.5406,0.6896,0.8496,.056,.58,.4656,.7799,.894 4:-.333,-.8085,-.4978,-.63,-.064,-0.894, ,-0.589,-0.455, ,-0.908, ,0.065,0.880,0.366,0.4488,0.5865,0.730,0.8888,.067,.589,.4956,.8065,.36 5:-.3347,-.8339,-.565,-.99,-.0986,-0.986, ,-0.634,-0.498, ,-0.448,-0.6,-0.006,0.94,0.47,0.3664,0.4950,0.695,0.770,0.958,.0959,.903,.540,.838,.338 6:-.355,-.858,-.5537,-.38,-.3, ,-0.88,-0.673,-0.548, ,-0.95,-0.767, ,0.0564,0.73,0.97,0.49,0.5384,0.6699,0.8096,0.9607,.8,.300,.55,.8558, :-.3747,-.884,-.5797,-.354,-.6,-0.997, ,-0.76,-0.589, ,-0.34,-0.7,-0.4, ,0.0,0.33,0.3384,0.4565,0.579,0.7079,0.845,0.9938,.589,.348,.5768,.8788,.374 8:-.3934,-.9036,-.6046,-.3786,-.97,-.090,-0.887, ,-0.67, , ,-0.744,-0.647, ,0.059,0.604,0.70,0.38,0.4976,0.676,0.7439,0.8788,.05,.880,.375,.603,.9007, :-.44,-.949,-.684,-.4046,-.98,-.059,-0.950,-0.784, , ,-0.48,-0.389,-0.,-0.068, ,0.0,0.074,0.343,0.436,0.5364,0.654,0.778,0.907,.055,.58,.4008,.648,.97, :-.488,-.9453,-.65,-.495,-.466,-.0880, ,-0.853, , , , ,-0.566,-0.543, ,0.0479,0.49,0.56,0.3557,0.466,0.573,0.6886,0.805,0.94,.0836,.44,.454,.6473,.949,.458, 3:-.4454,-.9650,-.6730,-.4533,-.73,-.55,-0.975, ,-0.766,- 0.63, , ,-0.987,-0.990,-0.006,-0.008,0.0950,0.935,0.93,0.3950,0.4996,0.6080,0.74,0.844,0.970,.07,.677,.4489,.6689,.96,.44 3:-.465,-.9838,-.6940,-.476,-.970,-.49,-.003, ,-0.758, , , , ,-0.4,-0.453, ,0.0444,0.394,0.35,0.336, 0.43,0.5346,0.64,0.756,0.8709,0.9979,.367,.90,.474,.6895,.9798, :-.4770,-.000,-.74,-.498,-.306,-.67,-.030, , , ,-0.574, ,-0.376,-0.8,-0.876,-0.095, ,0.0887,0.8,0.746,
Consider a system of 2 simultaneous first order linear equations
 Soluon of sysms of frs ordr lnar quaons onsdr a sysm of smulanous frs ordr lnar quaons a b c d I has h alrna mar-vcor rprsnaon a b c d Or, n shorhand A, f A s alrady known from con W know ha h abov sysm
Soluon of sysms of frs ordr lnar quaons onsdr a sysm of smulanous frs ordr lnar quaons a b c d I has h alrna mar-vcor rprsnaon a b c d Or, n shorhand A, f A s alrady known from con W know ha h abov sysm
Frequency Response. Response of an LTI System to Eigenfunction
 Frquncy Rsons Las m w Rvsd formal dfnons of lnary and m-nvaranc Found an gnfuncon for lnar m-nvaran sysms Found h frquncy rsons of a lnar sysm o gnfuncon nu Found h frquncy rsons for cascad, fdbac, dffrnc
Frquncy Rsons Las m w Rvsd formal dfnons of lnary and m-nvaranc Found an gnfuncon for lnar m-nvaran sysms Found h frquncy rsons of a lnar sysm o gnfuncon nu Found h frquncy rsons for cascad, fdbac, dffrnc
Summary: Solving a Homogeneous System of Two Linear First Order Equations in Two Unknowns
 Summary: Solvng a Homognous Sysm of Two Lnar Frs Ordr Equaons n Two Unknowns Gvn: A Frs fnd h wo gnvalus, r, and hr rspcv corrspondng gnvcors, k, of h coffcn mar A Dpndng on h gnvalus and gnvcors, h gnral
Summary: Solvng a Homognous Sysm of Two Lnar Frs Ordr Equaons n Two Unknowns Gvn: A Frs fnd h wo gnvalus, r, and hr rspcv corrspondng gnvcors, k, of h coffcn mar A Dpndng on h gnvalus and gnvcors, h gnral
The Variance-Covariance Matrix
 Th Varanc-Covaranc Marx Our bggs a so-ar has bn ng a lnar uncon o a s o daa by mnmzng h las squars drncs rom h o h daa wh mnsarch. Whn analyzng non-lnar daa you hav o us a program l Malab as many yps o
Th Varanc-Covaranc Marx Our bggs a so-ar has bn ng a lnar uncon o a s o daa by mnmzng h las squars drncs rom h o h daa wh mnsarch. Whn analyzng non-lnar daa you hav o us a program l Malab as many yps o
Advanced Queueing Theory. M/G/1 Queueing Systems
 Advand Quung Thory Ths slds ar rad by Dr. Yh Huang of Gorg Mason Unvrsy. Sudns rgsrd n Dr. Huang's ourss a GMU an ma a sngl mahn-radabl opy and prn a sngl opy of ah sld for hr own rfrn, so long as ah sld
Advand Quung Thory Ths slds ar rad by Dr. Yh Huang of Gorg Mason Unvrsy. Sudns rgsrd n Dr. Huang's ourss a GMU an ma a sngl mahn-radabl opy and prn a sngl opy of ah sld for hr own rfrn, so long as ah sld
Wave Superposition Principle
 Physcs 36: Was Lcur 5 /7/8 Wa Suroson Prncl I s qu a common suaon for wo or mor was o arr a h sam on n sac or o xs oghr along h sam drcon. W wll consdr oday sral moran cass of h combnd ffcs of wo or mor
Physcs 36: Was Lcur 5 /7/8 Wa Suroson Prncl I s qu a common suaon for wo or mor was o arr a h sam on n sac or o xs oghr along h sam drcon. W wll consdr oday sral moran cass of h combnd ffcs of wo or mor
Supplementary Figure 1. Experiment and simulation with finite qudit. anharmonicity. (a), Experimental data taken after a 60 ns three-tone pulse.
 Supplmnar Fgur. Eprmn and smulaon wh fn qud anharmonc. a, Eprmnal daa akn afr a 6 ns hr-on puls. b, Smulaon usng h amlonan. Supplmnar Fgur. Phagoran dnamcs n h m doman. a, Eprmnal daa. Th hr-on puls s
Supplmnar Fgur. Eprmn and smulaon wh fn qud anharmonc. a, Eprmnal daa akn afr a 6 ns hr-on puls. b, Smulaon usng h amlonan. Supplmnar Fgur. Phagoran dnamcs n h m doman. a, Eprmnal daa. Th hr-on puls s
innovations shocks white noise
 Innovaons Tm-srs modls ar consrucd as lnar funcons of fundamnal forcasng rrors, also calld nnovaons or shocks Ths basc buldng blocks sasf var σ Srall uncorrlad Ths rrors ar calld wh nos In gnral, f ou
Innovaons Tm-srs modls ar consrucd as lnar funcons of fundamnal forcasng rrors, also calld nnovaons or shocks Ths basc buldng blocks sasf var σ Srall uncorrlad Ths rrors ar calld wh nos In gnral, f ou
State Observer Design
 Sa Obsrvr Dsgn A. Khak Sdgh Conrol Sysms Group Faculy of Elcrcal and Compur Engnrng K. N. Toos Unvrsy of Tchnology Fbruary 2009 1 Problm Formulaon A ky assumpon n gnvalu assgnmn and sablzng sysms usng
Sa Obsrvr Dsgn A. Khak Sdgh Conrol Sysms Group Faculy of Elcrcal and Compur Engnrng K. N. Toos Unvrsy of Tchnology Fbruary 2009 1 Problm Formulaon A ky assumpon n gnvalu assgnmn and sablzng sysms usng
9. Simple Rules for Monetary Policy
 9. Smpl Ruls for Monar Polc John B. Talor, Ma 0, 03 Woodford, AR 00 ovrvw papr Purpos s o consdr o wha xn hs prscrpon rsmbls h sor of polc ha conomc hor would rcommnd Bu frs, l s rvw how hs sor of polc
9. Smpl Ruls for Monar Polc John B. Talor, Ma 0, 03 Woodford, AR 00 ovrvw papr Purpos s o consdr o wha xn hs prscrpon rsmbls h sor of polc ha conomc hor would rcommnd Bu frs, l s rvw how hs sor of polc
RELATIONSHIPS BETWEEN SPECTRAL PEAK FREQUENCIES OF A CAUSAL AR(P) PROCESS AND ARGUMENTS OF ROOTS OF THE ASSOCIATED AR POLYNOMIAL.
 RELATIONSHIPS BETWEEN SPECTRAL PEAK FREQUENCIES OF A CAUSAL AR(P) PROCESS AND ARGUMENTS OF ROOTS OF THE ASSOCIATED AR POLYNOMIAL A Wrng Proc Prsnd o T Faculy of Darmn of Mamacs San Jos Sa Unvrsy In Paral
RELATIONSHIPS BETWEEN SPECTRAL PEAK FREQUENCIES OF A CAUSAL AR(P) PROCESS AND ARGUMENTS OF ROOTS OF THE ASSOCIATED AR POLYNOMIAL A Wrng Proc Prsnd o T Faculy of Darmn of Mamacs San Jos Sa Unvrsy In Paral
t=0 t>0: + vr - i dvc Continuation
 hapr Ga Dlay and rcus onnuaon s rcu Equaon >: S S Ths dffrnal quaon, oghr wh h nal condon, fully spcfs bhaor of crcu afr swch closs Our n challng: larn how o sol such quaons TUE/EE 57 nwrk analys 4/5 NdM
hapr Ga Dlay and rcus onnuaon s rcu Equaon >: S S Ths dffrnal quaon, oghr wh h nal condon, fully spcfs bhaor of crcu afr swch closs Our n challng: larn how o sol such quaons TUE/EE 57 nwrk analys 4/5 NdM
CIVL 8/ D Boundary Value Problems - Triangular Elements (T6) 1/8
 CIVL 8/7 -D Boundar Valu Problm - rangular Elmn () /8 SI-ODE RIAGULAR ELEMES () A quadracall nrpolad rangular lmn dfnd b nod, hr a h vrc and hr a h mddl a ach d. h mddl nod, dpndng on locaon, ma dfn a
CIVL 8/7 -D Boundar Valu Problm - rangular Elmn () /8 SI-ODE RIAGULAR ELEMES () A quadracall nrpolad rangular lmn dfnd b nod, hr a h vrc and hr a h mddl a ach d. h mddl nod, dpndng on locaon, ma dfn a
Chapter 9 Transient Response
 har 9 Transn sons har 9: Ouln N F n F Frs-Ordr Transns Frs-Ordr rcus Frs ordr crcus: rcus conan onl on nducor or on caacor gornd b frs-ordr dffrnal quaons. Zro-nu rsons: h crcu has no ald sourc afr a cran
har 9 Transn sons har 9: Ouln N F n F Frs-Ordr Transns Frs-Ordr rcus Frs ordr crcus: rcus conan onl on nducor or on caacor gornd b frs-ordr dffrnal quaons. Zro-nu rsons: h crcu has no ald sourc afr a cran
Theoretical Seismology
 Thorcal Ssmology Lcur 9 Sgnal Procssng Fourr analyss Fourr sudd a h Écol Normal n Pars, augh by Lagrang, who Fourr dscrbd as h frs among Europan mn of scnc, Laplac, who Fourr rad lss hghly, and by Mong.
Thorcal Ssmology Lcur 9 Sgnal Procssng Fourr analyss Fourr sudd a h Écol Normal n Pars, augh by Lagrang, who Fourr dscrbd as h frs among Europan mn of scnc, Laplac, who Fourr rad lss hghly, and by Mong.
Boosting and Ensemble Methods
 Boosng and Ensmbl Mhods PAC Larnng modl Som dsrbuon D ovr doman X Eampls: c* s h arg funcon Goal: Wh hgh probably -d fnd h n H such ha rrorh,c* < d and ar arbrarly small. Inro o ML 2 Wak Larnng
Boosng and Ensmbl Mhods PAC Larnng modl Som dsrbuon D ovr doman X Eampls: c* s h arg funcon Goal: Wh hgh probably -d fnd h n H such ha rrorh,c* < d and ar arbrarly small. Inro o ML 2 Wak Larnng
FAULT TOLERANT SYSTEMS
 FAULT TOLERANT SYSTEMS hp://www.cs.umass.du/c/orn/faultolransysms ar 4 Analyss Mhods Chapr HW Faul Tolranc ar.4.1 Duplx Sysms Boh procssors xcu h sam as If oupus ar n agrmn - rsul s assumd o b corrc If
FAULT TOLERANT SYSTEMS hp://www.cs.umass.du/c/orn/faultolransysms ar 4 Analyss Mhods Chapr HW Faul Tolranc ar.4.1 Duplx Sysms Boh procssors xcu h sam as If oupus ar n agrmn - rsul s assumd o b corrc If
SIMEON BALL AND AART BLOKHUIS
 A BOUND FOR THE MAXIMUM WEIGHT OF A LINEAR CODE SIMEON BALL AND AART BLOKHUIS Absrac. I s shown ha h paramrs of a lnar cod ovr F q of lngh n, dmnson k, mnmum wgh d and maxmum wgh m sasfy a cran congrunc
A BOUND FOR THE MAXIMUM WEIGHT OF A LINEAR CODE SIMEON BALL AND AART BLOKHUIS Absrac. I s shown ha h paramrs of a lnar cod ovr F q of lngh n, dmnson k, mnmum wgh d and maxmum wgh m sasfy a cran congrunc
Safety and Reliability of Embedded Systems. (Sicherheit und Zuverlässigkeit eingebetteter Systeme) Stochastic Reliability Analysis
 (Schrh und Zuvrlässgk ngbr Sysm) Sochasc Rlably Analyss Conn Dfnon of Rlably Hardwar- vs. Sofwar Rlably Tool Asssd Rlably Modlng Dscrpons of Falurs ovr Tm Rlably Modlng Exampls of Dsrbuon Funcons Th xponnal
(Schrh und Zuvrlässgk ngbr Sysm) Sochasc Rlably Analyss Conn Dfnon of Rlably Hardwar- vs. Sofwar Rlably Tool Asssd Rlably Modlng Dscrpons of Falurs ovr Tm Rlably Modlng Exampls of Dsrbuon Funcons Th xponnal
Chapter 13 Laplace Transform Analysis
 Chapr aplac Tranorm naly Chapr : Ouln aplac ranorm aplac Tranorm -doman phaor analy: x X σ m co ω φ x X X m φ x aplac ranorm: [ o ] d o d < aplac Tranorm Thr condon Unlaral on-dd aplac ranorm: aplac ranorm
Chapr aplac Tranorm naly Chapr : Ouln aplac ranorm aplac Tranorm -doman phaor analy: x X σ m co ω φ x X X m φ x aplac ranorm: [ o ] d o d < aplac Tranorm Thr condon Unlaral on-dd aplac ranorm: aplac ranorm
Homework: Introduction to Motion
 Homwork: Inroducon o Moon Dsanc vs. Tm Graphs Nam Prod Drcons: Answr h foowng qusons n h spacs provdd. 1. Wha do you do o cra a horzona n on a dsancm graph? 2. How do you wak o cra a sragh n ha sops up?
Homwork: Inroducon o Moon Dsanc vs. Tm Graphs Nam Prod Drcons: Answr h foowng qusons n h spacs provdd. 1. Wha do you do o cra a horzona n on a dsancm graph? 2. How do you wak o cra a sragh n ha sops up?
NDC Dynamic Equilibrium model with financial and
 9 July 009 NDC Dynamc Equlbrum modl wh fnancal and dmograhc rsks rr DEVOLDER, Inmaculada DOMÍNGUEZ-FABIÁN, Aurél MILLER ABSTRACT Classcal socal scury nson schms, combnng a dfnd bnf hlosohy and a ay as
9 July 009 NDC Dynamc Equlbrum modl wh fnancal and dmograhc rsks rr DEVOLDER, Inmaculada DOMÍNGUEZ-FABIÁN, Aurél MILLER ABSTRACT Classcal socal scury nson schms, combnng a dfnd bnf hlosohy and a ay as
Safety and Reliability of Embedded Systems. (Sicherheit und Zuverlässigkeit eingebetteter Systeme) Stochastic Reliability Analysis
 Safy and Rlably of Embddd Sysms (Schrh und Zuvrlässgk ngbr Sysm) Sochasc Rlably Analyss Safy and Rlably of Embddd Sysms Conn Dfnon of Rlably Hardwar- vs. Sofwar Rlably Tool Asssd Rlably Modlng Dscrpons
Safy and Rlably of Embddd Sysms (Schrh und Zuvrlässgk ngbr Sysm) Sochasc Rlably Analyss Safy and Rlably of Embddd Sysms Conn Dfnon of Rlably Hardwar- vs. Sofwar Rlably Tool Asssd Rlably Modlng Dscrpons
10.5 Linear Viscoelasticity and the Laplace Transform
 Scn.5.5 Lnar Vclacy and h Lalac ranfrm h Lalac ranfrm vry uful n cnrucng and analyng lnar vclac mdl..5. h Lalac ranfrm h frmula fr h Lalac ranfrm f h drvav f a funcn : L f f L f f f f f c..5. whr h ranfrm
Scn.5.5 Lnar Vclacy and h Lalac ranfrm h Lalac ranfrm vry uful n cnrucng and analyng lnar vclac mdl..5. h Lalac ranfrm h frmula fr h Lalac ranfrm f h drvav f a funcn : L f f L f f f f f c..5. whr h ranfrm
8. Queueing systems. Contents. Simple teletraffic model. Pure queueing system
 8. Quug sysms Cos 8. Quug sysms Rfrshr: Sml lraffc modl Quug dscl M/M/ srvr wag lacs Alcao o ack lvl modllg of daa raffc M/M/ srvrs wag lacs lc8. S-38.45 Iroduco o Tlraffc Thory Srg 5 8. Quug sysms 8.
8. Quug sysms Cos 8. Quug sysms Rfrshr: Sml lraffc modl Quug dscl M/M/ srvr wag lacs Alcao o ack lvl modllg of daa raffc M/M/ srvrs wag lacs lc8. S-38.45 Iroduco o Tlraffc Thory Srg 5 8. Quug sysms 8.
Gauge Theories. Elementary Particle Physics Strong Interaction Fenomenology. Diego Bettoni Academic year
 Gau Thors Elmary Parcl Physcs Sro Iraco Fomoloy o Bo cadmc yar - Gau Ivarac Gau Ivarac Whr do Laraas or Hamloas com from? How do w kow ha a cra raco should dscrb a acual hyscal sysm? Why s h lcromac raco
Gau Thors Elmary Parcl Physcs Sro Iraco Fomoloy o Bo cadmc yar - Gau Ivarac Gau Ivarac Whr do Laraas or Hamloas com from? How do w kow ha a cra raco should dscrb a acual hyscal sysm? Why s h lcromac raco
ELEN E4830 Digital Image Processing
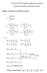 ELEN E48 Dgal Imag Procssng Mrm Eamnaon Sprng Soluon Problm Quanzaon and Human Encodng r k u P u P u r r 6 6 6 6 5 6 4 8 8 4 P r 6 6 P r 4 8 8 6 8 4 r 8 4 8 4 7 8 r 6 6 6 6 P r 8 4 8 P r 6 6 8 5 P r /
ELEN E48 Dgal Imag Procssng Mrm Eamnaon Sprng Soluon Problm Quanzaon and Human Encodng r k u P u P u r r 6 6 6 6 5 6 4 8 8 4 P r 6 6 P r 4 8 8 6 8 4 r 8 4 8 4 7 8 r 6 6 6 6 P r 8 4 8 P r 6 6 8 5 P r /
Conventional Hot-Wire Anemometer
 Convnonal Ho-Wr Anmomr cro Ho Wr Avanag much mallr prob z mm o µm br paal roluon array o h nor hghr rquncy rpon lowr co prormanc/co abrcaon roc I µm lghly op p layr 8µm havly boron op ch op layr abrcaon
Convnonal Ho-Wr Anmomr cro Ho Wr Avanag much mallr prob z mm o µm br paal roluon array o h nor hghr rquncy rpon lowr co prormanc/co abrcaon roc I µm lghly op p layr 8µm havly boron op ch op layr abrcaon
Lecture 1: Numerical Integration The Trapezoidal and Simpson s Rule
 Lcur : Numrical ngraion Th Trapzoidal and Simpson s Rul A problm Th probabiliy of a normally disribud (man µ and sandard dviaion σ ) vn occurring bwn h valus a and b is B A P( a x b) d () π whr a µ b -
Lcur : Numrical ngraion Th Trapzoidal and Simpson s Rul A problm Th probabiliy of a normally disribud (man µ and sandard dviaion σ ) vn occurring bwn h valus a and b is B A P( a x b) d () π whr a µ b -
Black-Scholes Partial Differential Equation In The Mellin Transform Domain
 INTRNATIONAL JOURNAL OF SCINTIFIC & TCHNOLOGY RSARCH VOLUM 3, ISSU, Dcmbr 4 ISSN 77-866 Blac-Schols Paral Dffrnal qaon In Th Mlln Transform Doman Fadgba Snday mmanl, Ognrnd Rosln Bosd Absrac: Ths ar rsns
INTRNATIONAL JOURNAL OF SCINTIFIC & TCHNOLOGY RSARCH VOLUM 3, ISSU, Dcmbr 4 ISSN 77-866 Blac-Schols Paral Dffrnal qaon In Th Mlln Transform Doman Fadgba Snday mmanl, Ognrnd Rosln Bosd Absrac: Ths ar rsns
Chapter 7 Stead St y- ate Errors
 Char 7 Say-Sa rror Inroucon Conrol ym analy an gn cfcaon a. rann ron b. Sably c. Say-a rror fnon of ay-a rror : u c a whr u : nu, c: ouu Val only for abl ym chck ym ably fr! nu for ay-a a nu analy U o
Char 7 Say-Sa rror Inroucon Conrol ym analy an gn cfcaon a. rann ron b. Sably c. Say-a rror fnon of ay-a rror : u c a whr u : nu, c: ouu Val only for abl ym chck ym ably fr! nu for ay-a a nu analy U o
Published in: Proceedings of the Twenty Second Nordic Seminar on Computational Mechanics
 Downloadd from vbn.aau.dk on: aprl 09, 019 Aalborg Unvrs Implmnaon of Moldng Consrans n Topology Opmzaon Marx, S.; Krsnsn, Andrs Schmd Publshd n: Procdngs of h Twny Scond Nordc Smnar on Compuaonal Mchancs
Downloadd from vbn.aau.dk on: aprl 09, 019 Aalborg Unvrs Implmnaon of Moldng Consrans n Topology Opmzaon Marx, S.; Krsnsn, Andrs Schmd Publshd n: Procdngs of h Twny Scond Nordc Smnar on Compuaonal Mchancs
Lecture 4 : Backpropagation Algorithm. Prof. Seul Jung ( Intelligent Systems and Emotional Engineering Laboratory) Chungnam National University
 Lcur 4 : Bacpropagaon Algorhm Pro. Sul Jung Inllgn Sm and moonal ngnrng Laboraor Chungnam Naonal Unvr Inroducon o Bacpropagaon algorhm 969 Mn and Papr aac. 980 Parr and Wrbo dcovrd bac propagaon algorhm.
Lcur 4 : Bacpropagaon Algorhm Pro. Sul Jung Inllgn Sm and moonal ngnrng Laboraor Chungnam Naonal Unvr Inroducon o Bacpropagaon algorhm 969 Mn and Papr aac. 980 Parr and Wrbo dcovrd bac propagaon algorhm.
Problem 1: Consider the following stationary data generation process for a random variable y t. e t ~ N(0,1) i.i.d.
 A/CN C m Sr Anal Profor Òcar Jordà Wnr conomc.c. Dav POBLM S SOLIONS Par I Analcal Quon Problm : Condr h followng aonar daa gnraon proc for a random varabl - N..d. wh < and N -. a Oban h populaon man varanc
A/CN C m Sr Anal Profor Òcar Jordà Wnr conomc.c. Dav POBLM S SOLIONS Par I Analcal Quon Problm : Condr h followng aonar daa gnraon proc for a random varabl - N..d. wh < and N -. a Oban h populaon man varanc
( r) E (r) Phasor. Function of space only. Fourier series Synthesis equations. Sinusoidal EM Waves. For complex periodic signals
 Inoducon Snusodal M Was.MB D Yan Pllo Snusodal M.3MB 3. Snusodal M.3MB 3. Inoducon Inoducon o o dsgn h communcaons sd of a sall? Fqunc? Oms oagaon? Oms daa a? Annnas? Dc? Gan? Wa quaons Sgnal analss Wa
Inoducon Snusodal M Was.MB D Yan Pllo Snusodal M.3MB 3. Snusodal M.3MB 3. Inoducon Inoducon o o dsgn h communcaons sd of a sall? Fqunc? Oms oagaon? Oms daa a? Annnas? Dc? Gan? Wa quaons Sgnal analss Wa
OUTLINE FOR Chapter 2-2. Basic Laws
 0//8 OUTLINE FOR Chapr - AERODYNAMIC W-- Basc Laws Analss of an problm n fld mchancs ncssarl nclds samn of h basc laws gornng h fld moon. Th basc laws, whch applcabl o an fld, ar: Consraon of mass Conn
0//8 OUTLINE FOR Chapr - AERODYNAMIC W-- Basc Laws Analss of an problm n fld mchancs ncssarl nclds samn of h basc laws gornng h fld moon. Th basc laws, whch applcabl o an fld, ar: Consraon of mass Conn
Comparative Study of Finite Element and Haar Wavelet Correlation Method for the Numerical Solution of Parabolic Type Partial Differential Equations
 ISS 746-7659, England, UK Journal of Informaon and Compung Scnc Vol., o. 3, 6, pp.88-7 Comparav Sudy of Fn Elmn and Haar Wavl Corrlaon Mhod for h umrcal Soluon of Parabolc Typ Paral Dffrnal Equaons S.
ISS 746-7659, England, UK Journal of Informaon and Compung Scnc Vol., o. 3, 6, pp.88-7 Comparav Sudy of Fn Elmn and Haar Wavl Corrlaon Mhod for h umrcal Soluon of Parabolc Typ Paral Dffrnal Equaons S.
Guaranteed Cost Control for a Class of Uncertain Delay Systems with Actuator Failures Based on Switching Method
 49 Inrnaonal Journal of Conrol, Ru Wang Auomaon, and Jun and Zhao Sysms, vol. 5, no. 5, pp. 49-5, Ocobr 7 Guarand Cos Conrol for a Class of Uncran Dlay Sysms wh Acuaor Falurs Basd on Swchng Mhod Ru Wang
49 Inrnaonal Journal of Conrol, Ru Wang Auomaon, and Jun and Zhao Sysms, vol. 5, no. 5, pp. 49-5, Ocobr 7 Guarand Cos Conrol for a Class of Uncran Dlay Sysms wh Acuaor Falurs Basd on Swchng Mhod Ru Wang
Adaptive Neural Network Flight Control Using both Current and Recorded Data
 AIAA Gudanc Navgaon and Conrol Confrnc and Eh - 3 Augus 7 Hlon H Souh Carolna AIAA 7-655 Adav Nural Nork Flgh Conrol Usng oh Currn and Rcordd Daa Grsh Chodhary * and Erc N. Johnson Darmn of Arosac Engnrng
AIAA Gudanc Navgaon and Conrol Confrnc and Eh - 3 Augus 7 Hlon H Souh Carolna AIAA 7-655 Adav Nural Nork Flgh Conrol Usng oh Currn and Rcordd Daa Grsh Chodhary * and Erc N. Johnson Darmn of Arosac Engnrng
A Differential Game Approach to Adoption of Conservation Practices
 A Dffrnal Gam Aroach o Adoon of Consrvaon Praccs Jo L. Parcll Profssor Darmn of Agrculural and Ald Economcs Unvrsy of Mssour Columba, MO 65211 arcll@mssour.du and Halu Gdoglu Asssan Profssor of Agrculural
A Dffrnal Gam Aroach o Adoon of Consrvaon Praccs Jo L. Parcll Profssor Darmn of Agrculural and Ald Economcs Unvrsy of Mssour Columba, MO 65211 arcll@mssour.du and Halu Gdoglu Asssan Profssor of Agrculural
Boyce/DiPrima 9 th ed, Ch 2.1: Linear Equations; Method of Integrating Factors
 Boc/DiPrima 9 h d, Ch.: Linar Equaions; Mhod of Ingraing Facors Elmnar Diffrnial Equaions and Boundar Valu Problms, 9 h diion, b William E. Boc and Richard C. DiPrima, 009 b John Wil & Sons, Inc. A linar
Boc/DiPrima 9 h d, Ch.: Linar Equaions; Mhod of Ingraing Facors Elmnar Diffrnial Equaions and Boundar Valu Problms, 9 h diion, b William E. Boc and Richard C. DiPrima, 009 b John Wil & Sons, Inc. A linar
EE243 Advanced Electromagnetic Theory Lec # 10: Poynting s Theorem, Time- Harmonic EM Fields
 Appl M Fall 6 Nuruhr Lcur # r 9/6/6 4 Avanc lcromagnc Thory Lc # : Poynng s Thorm Tm- armonc M Fls Poynng s Thorm Consrvaon o nrgy an momnum Poynng s Thorm or Lnar sprsv Ma Poynng s Thorm or Tm-armonc
Appl M Fall 6 Nuruhr Lcur # r 9/6/6 4 Avanc lcromagnc Thory Lc # : Poynng s Thorm Tm- armonc M Fls Poynng s Thorm Consrvaon o nrgy an momnum Poynng s Thorm or Lnar sprsv Ma Poynng s Thorm or Tm-armonc
A Note on Estimability in Linear Models
 Intrnatonal Journal of Statstcs and Applcatons 2014, 4(4): 212-216 DOI: 10.5923/j.statstcs.20140404.06 A Not on Estmablty n Lnar Modls S. O. Adymo 1,*, F. N. Nwob 2 1 Dpartmnt of Mathmatcs and Statstcs,
Intrnatonal Journal of Statstcs and Applcatons 2014, 4(4): 212-216 DOI: 10.5923/j.statstcs.20140404.06 A Not on Estmablty n Lnar Modls S. O. Adymo 1,*, F. N. Nwob 2 1 Dpartmnt of Mathmatcs and Statstcs,
Transient Analysis of Two-dimensional State M/G/1 Queueing Model with Multiple Vacations and Bernoulli Schedule
 Inrnaonal Journal of Compur Applcaons (975 8887) Volum 4 No.3, Fbruary 22 Transn Analyss of Two-dmnsonal Sa M/G/ Quung Modl wh Mulpl Vacaons and Brnoull Schdul Indra Assoca rofssor Dparmn of Sascs and
Inrnaonal Journal of Compur Applcaons (975 8887) Volum 4 No.3, Fbruary 22 Transn Analyss of Two-dmnsonal Sa M/G/ Quung Modl wh Mulpl Vacaons and Brnoull Schdul Indra Assoca rofssor Dparmn of Sascs and
EXERCISE - 01 CHECK YOUR GRASP
 DIFFERENTIAL EQUATION EXERCISE - CHECK YOUR GRASP 7. m hn D() m m, D () m m. hn givn D () m m D D D + m m m m m m + m m m m + ( m ) (m ) (m ) (m + ) m,, Hnc numbr of valus of mn will b. n ( ) + c sinc
DIFFERENTIAL EQUATION EXERCISE - CHECK YOUR GRASP 7. m hn D() m m, D () m m. hn givn D () m m D D D + m m m m m m + m m m m + ( m ) (m ) (m ) (m + ) m,, Hnc numbr of valus of mn will b. n ( ) + c sinc
Applying Software Reliability Techniques to Low Retail Demand Estimation
 Applyng Sofwar Rlably Tchnqus o Low Ral Dmand Esmaon Ma Lndsy Unvrsy of Norh Txas ITDS Dp P.O. Box 30549 Dnon, TX 7603-549 940 565 3174 lndsym@un.du Robr Pavur Unvrsy of Norh Txas ITDS Dp P.O. Box 30549
Applyng Sofwar Rlably Tchnqus o Low Ral Dmand Esmaon Ma Lndsy Unvrsy of Norh Txas ITDS Dp P.O. Box 30549 Dnon, TX 7603-549 940 565 3174 lndsym@un.du Robr Pavur Unvrsy of Norh Txas ITDS Dp P.O. Box 30549
Double Slits in Space and Time
 Doubl Slis in Sac an Tim Gorg Jons As has bn ror rcnly in h mia, a am l by Grhar Paulus has monsra an inrsing chniqu for ionizing argon aoms by using ulra-shor lasr ulss. Each lasr uls is ffcivly on an
Doubl Slis in Sac an Tim Gorg Jons As has bn ror rcnly in h mia, a am l by Grhar Paulus has monsra an inrsing chniqu for ionizing argon aoms by using ulra-shor lasr ulss. Each lasr uls is ffcivly on an
Reliability analysis of time - dependent stress - strength system when the number of cycles follows binomial distribution
 raoal Joural of Sascs ad Ssms SSN 97-675 Volum, Numbr 7,. 575-58 sarch da Publcaos h://www.rublcao.com labl aalss of m - dd srss - srgh ssm wh h umbr of ccls follows bomal dsrbuo T.Sumah Umamahswar, N.Swah,
raoal Joural of Sascs ad Ssms SSN 97-675 Volum, Numbr 7,. 575-58 sarch da Publcaos h://www.rublcao.com labl aalss of m - dd srss - srgh ssm wh h umbr of ccls follows bomal dsrbuo T.Sumah Umamahswar, N.Swah,
Two-Dimensional Quantum Harmonic Oscillator
 D Qa Haroc Oscllaor Two-Dsoal Qa Haroc Oscllaor 6 Qa Mchacs Prof. Y. F. Ch D Qa Haroc Oscllaor D Qa Haroc Oscllaor ch5 Schrödgr cosrcd h cohr sa of h D H.O. o dscrb a classcal arcl wh a wav ack whos cr
D Qa Haroc Oscllaor Two-Dsoal Qa Haroc Oscllaor 6 Qa Mchacs Prof. Y. F. Ch D Qa Haroc Oscllaor D Qa Haroc Oscllaor ch5 Schrödgr cosrcd h cohr sa of h D H.O. o dscrb a classcal arcl wh a wav ack whos cr
4.1 The Uniform Distribution Def n: A c.r.v. X has a continuous uniform distribution on [a, b] when its pdf is = 1 a x b
![4.1 The Uniform Distribution Def n: A c.r.v. X has a continuous uniform distribution on [a, b] when its pdf is = 1 a x b 4.1 The Uniform Distribution Def n: A c.r.v. X has a continuous uniform distribution on [a, b] when its pdf is = 1 a x b](/thumbs/71/65779443.jpg) 4. Th Uniform Disribuion Df n: A c.r.v. has a coninuous uniform disribuion on [a, b] whn is pdf is f x a x b b a Also, b + a b a µ E and V Ex4. Suppos, h lvl of unblivabiliy a any poin in a Transformrs
4. Th Uniform Disribuion Df n: A c.r.v. has a coninuous uniform disribuion on [a, b] whn is pdf is f x a x b b a Also, b + a b a µ E and V Ex4. Suppos, h lvl of unblivabiliy a any poin in a Transformrs
UNIT #5 EXPONENTIAL AND LOGARITHMIC FUNCTIONS
 Answr Ky Nam: Da: UNIT # EXPONENTIAL AND LOGARITHMIC FUNCTIONS Par I Qusions. Th prssion is quivaln o () () 6 6 6. Th ponnial funcion y 6 could rwrin as y () y y 6 () y y (). Th prssion a is quivaln o
Answr Ky Nam: Da: UNIT # EXPONENTIAL AND LOGARITHMIC FUNCTIONS Par I Qusions. Th prssion is quivaln o () () 6 6 6. Th ponnial funcion y 6 could rwrin as y () y y 6 () y y (). Th prssion a is quivaln o
Engineering Circuit Analysis 8th Edition Chapter Nine Exercise Solutions
 Engnrng rcu naly 8h Eon hapr Nn Exrc Soluon. = KΩ, = µf, an uch ha h crcu rpon oramp. a For Sourc-fr paralll crcu: For oramp or b H 9V, V / hoo = H.7.8 ra / 5..7..9 9V 9..9..9 5.75,.5 5.75.5..9 . = nh,
Engnrng rcu naly 8h Eon hapr Nn Exrc Soluon. = KΩ, = µf, an uch ha h crcu rpon oramp. a For Sourc-fr paralll crcu: For oramp or b H 9V, V / hoo = H.7.8 ra / 5..7..9 9V 9..9..9 5.75,.5 5.75.5..9 . = nh,
Charging of capacitor through inductor and resistor
 cur 4&: R circui harging of capacior hrough inducor and rsisor us considr a capacior of capacianc is conncd o a D sourc of.m.f. E hrough a rsisr of rsisanc R, an inducor of inducanc and a y K in sris.
cur 4&: R circui harging of capacior hrough inducor and rsisor us considr a capacior of capacianc is conncd o a D sourc of.m.f. E hrough a rsisr of rsisanc R, an inducor of inducanc and a y K in sris.
CONTINUOUS TIME DYNAMIC PROGRAMMING
 Eon. 511b Sprng 1993 C. Sms I. Th Opmaon Problm CONTINUOUS TIME DYNAMIC PROGRAMMING W onsdr h problm of maxmng subj o and EU(C, ) d (1) j ^ d = (C, ) d + σ (C, ) dw () h(c, ), (3) whr () and (3) hold for
Eon. 511b Sprng 1993 C. Sms I. Th Opmaon Problm CONTINUOUS TIME DYNAMIC PROGRAMMING W onsdr h problm of maxmng subj o and EU(C, ) d (1) j ^ d = (C, ) d + σ (C, ) dw () h(c, ), (3) whr () and (3) hold for
FI 3103 Quantum Physics
 /9/4 FI 33 Quanum Physcs Aleander A. Iskandar Physcs of Magnesm and Phooncs Research Grou Insu Teknolog Bandung Basc Conces n Quanum Physcs Probably and Eecaon Value Hesenberg Uncerany Prncle Wave Funcon
/9/4 FI 33 Quanum Physcs Aleander A. Iskandar Physcs of Magnesm and Phooncs Research Grou Insu Teknolog Bandung Basc Conces n Quanum Physcs Probably and Eecaon Value Hesenberg Uncerany Prncle Wave Funcon
MEM 355 Performance Enhancement of Dynamical Systems A First Control Problem - Cruise Control
 MEM 355 Prformanc Enhancmn of Dynamical Sysms A Firs Conrol Problm - Cruis Conrol Harry G. Kwany Darmn of Mchanical Enginring & Mchanics Drxl Univrsiy Cruis Conrol ( ) mv = F mg sinθ cv v +.2v= u 9.8θ
MEM 355 Prformanc Enhancmn of Dynamical Sysms A Firs Conrol Problm - Cruis Conrol Harry G. Kwany Darmn of Mchanical Enginring & Mchanics Drxl Univrsiy Cruis Conrol ( ) mv = F mg sinθ cv v +.2v= u 9.8θ
Bethe-Salpeter Equation Green s Function and the Bethe-Salpeter Equation for Effective Interaction in the Ladder Approximation
 Bh-Salp Equaon n s Funcon and h Bh-Salp Equaon fo Effcv Inacon n h Ladd Appoxmaon Csa A. Z. Vasconcllos Insuo d Físca-UFRS - upo: Físca d Hadons Sngl-Pacl Popagao. Dagam xpanson of popagao. W consd as
Bh-Salp Equaon n s Funcon and h Bh-Salp Equaon fo Effcv Inacon n h Ladd Appoxmaon Csa A. Z. Vasconcllos Insuo d Físca-UFRS - upo: Físca d Hadons Sngl-Pacl Popagao. Dagam xpanson of popagao. W consd as
CHAPTER CHAPTER14. Expectations: The Basic Tools. Prepared by: Fernando Quijano and Yvonn Quijano
 Expcaions: Th Basic Prpard by: Frnando Quijano and Yvonn Quijano CHAPTER CHAPTER14 2006 Prnic Hall Businss Publishing Macroconomics, 4/ Olivir Blanchard 14-1 Today s Lcur Chapr 14:Expcaions: Th Basic Th
Expcaions: Th Basic Prpard by: Frnando Quijano and Yvonn Quijano CHAPTER CHAPTER14 2006 Prnic Hall Businss Publishing Macroconomics, 4/ Olivir Blanchard 14-1 Today s Lcur Chapr 14:Expcaions: Th Basic Th
Dynamic modeling, simulation and control of a hybrid driven press mechanism
 INTERNTIONL JOURNL OF MECHNICS Volum 1 16 Dynamc modlng smulaon and conrol of a hybrd drvn prss mchansm Mhm Erkan Küük Lal Canan Dülgr bsrac Hybrd drvn mchansm combns h moon of a larg consan vlocy moor
INTERNTIONL JOURNL OF MECHNICS Volum 1 16 Dynamc modlng smulaon and conrol of a hybrd drvn prss mchansm Mhm Erkan Küük Lal Canan Dülgr bsrac Hybrd drvn mchansm combns h moon of a larg consan vlocy moor
Neutron electric dipole moment on the lattice
 ron lcrc dol on on h lac go Shnan Unv. of Tkba 3/6/006 ron lcrc dol on fro lac QCD Inrodcon arar Boh h ha of CKM arx and QCD vac ffc conrb o CP volaon P and T volaon arar. CP odd QCD 4 L arg d CKM f f
ron lcrc dol on on h lac go Shnan Unv. of Tkba 3/6/006 ron lcrc dol on fro lac QCD Inrodcon arar Boh h ha of CKM arx and QCD vac ffc conrb o CP volaon P and T volaon arar. CP odd QCD 4 L arg d CKM f f
Economics 600: August, 2007 Dynamic Part: Problem Set 5. Problems on Differential Equations and Continuous Time Optimization
 THE UNIVERSITY OF MARYLAND COLLEGE PARK, MARYLAND Economcs 600: August, 007 Dynamc Part: Problm St 5 Problms on Dffrntal Equatons and Contnuous Tm Optmzaton Quston Solv th followng two dffrntal quatons.
THE UNIVERSITY OF MARYLAND COLLEGE PARK, MARYLAND Economcs 600: August, 007 Dynamc Part: Problm St 5 Problms on Dffrntal Equatons and Contnuous Tm Optmzaton Quston Solv th followng two dffrntal quatons.
Chap 2: Reliability and Availability Models
 Chap : lably ad valably Modls lably = prob{s s fully fucog [,]} Suppos from [,] m prod, w masur ou of N compos, of whch N : # of compos oprag corrcly a m N f : # of compos whch hav fald a m rlably of h
Chap : lably ad valably Modls lably = prob{s s fully fucog [,]} Suppos from [,] m prod, w masur ou of N compos, of whch N : # of compos oprag corrcly a m N f : # of compos whch hav fald a m rlably of h
Ergodic Capacity of a SIMO System Over Nakagami-q Fading Channel
 DUET Journal Vol., Issu, Jun Ergodc apac of a SIO Ssm Ovr Nakagam-q Fadng hannl d. Sohdul Islam * and ohammad akbul Islam Dp. of Elcrcal and Elcronc Engnrng, Islamc Unvrs of Tchnolog (IUT, Gazpur, Bangladsh
DUET Journal Vol., Issu, Jun Ergodc apac of a SIO Ssm Ovr Nakagam-q Fadng hannl d. Sohdul Islam * and ohammad akbul Islam Dp. of Elcrcal and Elcronc Engnrng, Islamc Unvrs of Tchnolog (IUT, Gazpur, Bangladsh
Institute of Actuaries of India
 Insiu of Acuaris of India ubjc CT3 Probabiliy and Mahmaical aisics Novmbr Examinaions INDICATIVE OLUTION Pag of IAI CT3 Novmbr ol. a sampl man = 35 sampl sandard dviaion = 36.6 b for = uppr bound = 35+*36.6
Insiu of Acuaris of India ubjc CT3 Probabiliy and Mahmaical aisics Novmbr Examinaions INDICATIVE OLUTION Pag of IAI CT3 Novmbr ol. a sampl man = 35 sampl sandard dviaion = 36.6 b for = uppr bound = 35+*36.6
Diffusivity scaling on shear flow
 Amrcan Journal of Modrn Physcs 4; 3(5: -6 Pulshd onln Smr 3, 4 (h://www.scnculshnggrou.com/j/ajm do:.648/j.ajm.435. ISSN: 36-8867 (Prn; ISSN: 36-889 (Onln Dffusvy scalng on shar flow hong-tan Wang,, h-xong
Amrcan Journal of Modrn Physcs 4; 3(5: -6 Pulshd onln Smr 3, 4 (h://www.scnculshnggrou.com/j/ajm do:.648/j.ajm.435. ISSN: 36-8867 (Prn; ISSN: 36-889 (Onln Dffusvy scalng on shar flow hong-tan Wang,, h-xong
Dynamic Power Allocation in MIMO Fading Systems Without Channel Distribution Information
 PROC. IEEE INFOCOM 06 Dynamc Powr Allocaon n MIMO Fadng Sysms Whou Channl Dsrbuon Informaon Hao Yu and Mchal J. Nly Unvrsy of Souhrn Calforna Absrac Ths papr consdrs dynamc powr allocaon n MIMO fadng sysms
PROC. IEEE INFOCOM 06 Dynamc Powr Allocaon n MIMO Fadng Sysms Whou Channl Dsrbuon Informaon Hao Yu and Mchal J. Nly Unvrsy of Souhrn Calforna Absrac Ths papr consdrs dynamc powr allocaon n MIMO fadng sysms
Convergence of Quintic Spline Interpolation
 Inrnaonal Journal o ompur Applcaons 97 8887 Volum 7 No., Aprl onvrgnc o Qunc Spln Inrpolaon Y.P. Dub Dparmn O Mamacs, L.N..T. Jabalpur 8 Anl Sukla Dparmn O Mamacs Gan Ganga ollg O Tcnog, Jabalpur 8 ASTRAT
Inrnaonal Journal o ompur Applcaons 97 8887 Volum 7 No., Aprl onvrgnc o Qunc Spln Inrpolaon Y.P. Dub Dparmn O Mamacs, L.N..T. Jabalpur 8 Anl Sukla Dparmn O Mamacs Gan Ganga ollg O Tcnog, Jabalpur 8 ASTRAT
(heat loss divided by total enthalpy flux) is of the order of 8-16 times
 16.51, Rok Prolson Prof. Manl Marnz-Sanhz r 8: Convv Ha ransfr: Ohr Effs Ovrall Ha oss and Prforman Effs of Ha oss (1) Ovrall Ha oss h loal ha loss r n ara s q = ρ ( ) ngrad ha loss s a S, and sng m =
16.51, Rok Prolson Prof. Manl Marnz-Sanhz r 8: Convv Ha ransfr: Ohr Effs Ovrall Ha oss and Prforman Effs of Ha oss (1) Ovrall Ha oss h loal ha loss r n ara s q = ρ ( ) ngrad ha loss s a S, and sng m =
Thermodynamic Properties of the Harmonic Oscillator and a Four Level System
 www.ccsn.org/apr Appld Physcs Rsarch Vol. 3, No. ; May Thrmodynamc Proprs of h Harmonc Oscllaor and a Four Lvl Sysm Oladunjoy A. Awoga Thorcal Physcs Group, Dparmn of Physcs, Unvrsy of Uyo, Uyo, Ngra E-mal:
www.ccsn.org/apr Appld Physcs Rsarch Vol. 3, No. ; May Thrmodynamc Proprs of h Harmonc Oscllaor and a Four Lvl Sysm Oladunjoy A. Awoga Thorcal Physcs Group, Dparmn of Physcs, Unvrsy of Uyo, Uyo, Ngra E-mal:
Implementation of the Extended Conjugate Gradient Method for the Two- Dimensional Energized Wave Equation
 Lonardo Elcronc Jornal of raccs and Tchnolos ISSN 58-078 Iss 9 Jl-Dcmbr 006 p. -4 Implmnaon of h Endd Cona Gradn Mhod for h Two- Dmnsonal Enrd Wav Eqaon Vcor Onoma WAZIRI * Snda Ass REJU Mahmacs/Compr
Lonardo Elcronc Jornal of raccs and Tchnolos ISSN 58-078 Iss 9 Jl-Dcmbr 006 p. -4 Implmnaon of h Endd Cona Gradn Mhod for h Two- Dmnsonal Enrd Wav Eqaon Vcor Onoma WAZIRI * Snda Ass REJU Mahmacs/Compr
Klein-Gordon Equation
 Inroducon o lnar Parcl Phscs. Lcur 5 Pag of 5 Kln-Gordon quaon 96 Schrodngr: Quanu chancal quaon for non-rlavsc chancs: V,, V V 96 Kln Rlavsc chancs (fr arcl):,, Soluons ar: ( r), whr ( r), whr ) Soluons
Inroducon o lnar Parcl Phscs. Lcur 5 Pag of 5 Kln-Gordon quaon 96 Schrodngr: Quanu chancal quaon for non-rlavsc chancs: V,, V V 96 Kln Rlavsc chancs (fr arcl):,, Soluons ar: ( r), whr ( r), whr ) Soluons
Analysis of decentralized potential field based multi-agent navigation via primal-dual Lyapunov theory
 Analyss of dcnralzd ponal fld basd mul-agn navgaon va prmal-dual Lyapunov hory Th MIT Faculy has mad hs arcl opnly avalabl. Plas shar how hs accss bnfs you. Your sory mars. Caon As Publshd Publshr Dmarogonas,
Analyss of dcnralzd ponal fld basd mul-agn navgaon va prmal-dual Lyapunov hory Th MIT Faculy has mad hs arcl opnly avalabl. Plas shar how hs accss bnfs you. Your sory mars. Caon As Publshd Publshr Dmarogonas,
Oscillations of Hyperbolic Systems with Functional Arguments *
 Avll ://vmd/gs/9/s Vol Iss Dcmr 6 95 Prvosly Vol No Alcons nd Ald mcs AA: An Inrnonl Jornl Asrc Oscllons of Hyrolc Sysms w Fnconl Argmns * Y So Fcly of Engnrng nzw Unvrsy Isw 9-9 Jn E-ml: so@nzw-c Noro
Avll ://vmd/gs/9/s Vol Iss Dcmr 6 95 Prvosly Vol No Alcons nd Ald mcs AA: An Inrnonl Jornl Asrc Oscllons of Hyrolc Sysms w Fnconl Argmns * Y So Fcly of Engnrng nzw Unvrsy Isw 9-9 Jn E-ml: so@nzw-c Noro
Gaussian Random Process and Its Application for Detecting the Ionospheric Disturbances Using GPS
 Journal of Global Posonng Sysms (005) Vol. 4, No. 1-: 76-81 Gaussan Random Procss and Is Applcaon for Dcng h Ionosphrc Dsurbancs Usng GPS H.. Zhang 1,, J. Wang 3, W. Y. Zhu 1, C. Huang 1 (1) Shangha Asronomcal
Journal of Global Posonng Sysms (005) Vol. 4, No. 1-: 76-81 Gaussan Random Procss and Is Applcaon for Dcng h Ionosphrc Dsurbancs Usng GPS H.. Zhang 1,, J. Wang 3, W. Y. Zhu 1, C. Huang 1 (1) Shangha Asronomcal
Folding of Regular CW-Complexes
 Ald Mathmatcal Scncs, Vol. 6,, no. 83, 437-446 Foldng of Rgular CW-Comlxs E. M. El-Kholy and S N. Daoud,3. Dartmnt of Mathmatcs, Faculty of Scnc Tanta Unvrsty,Tanta,Egyt. Dartmnt of Mathmatcs, Faculty
Ald Mathmatcal Scncs, Vol. 6,, no. 83, 437-446 Foldng of Rgular CW-Comlxs E. M. El-Kholy and S N. Daoud,3. Dartmnt of Mathmatcs, Faculty of Scnc Tanta Unvrsty,Tanta,Egyt. Dartmnt of Mathmatcs, Faculty
The Matrix Exponential
 Th Matrix Exponntial (with xrciss) by D. Klain Vrsion 207.0.05 Corrctions and commnts ar wlcom. Th Matrix Exponntial For ach n n complx matrix A, dfin th xponntial of A to b th matrix A A k I + A + k!
Th Matrix Exponntial (with xrciss) by D. Klain Vrsion 207.0.05 Corrctions and commnts ar wlcom. Th Matrix Exponntial For ach n n complx matrix A, dfin th xponntial of A to b th matrix A A k I + A + k!
Solutions of the linearized Richards equation with arbitrary boundary and initial conditions: flux and soil moisture respectively
 Hydrology ays Soluons of h lnard Rchards uaon wh arbrary boundary and nal condons: flux and sol mosur rspcvly M. Mnan S. Pugnagh Unvrsà dgl Sud d Modna Rggo Emla p. Inggnra d Maral dllambn Va Vgnols 95
Hydrology ays Soluons of h lnard Rchards uaon wh arbrary boundary and nal condons: flux and sol mosur rspcvly M. Mnan S. Pugnagh Unvrsà dgl Sud d Modna Rggo Emla p. Inggnra d Maral dllambn Va Vgnols 95
Advanced time-series analysis (University of Lund, Economic History Department)
 Advanced me-seres analss (Unvers of Lund, Economc Hsor Dearmen) 3 Jan-3 Februar and 6-3 March Lecure 4 Economerc echnues for saonar seres : Unvarae sochasc models wh Box- Jenns mehodolog, smle forecasng
Advanced me-seres analss (Unvers of Lund, Economc Hsor Dearmen) 3 Jan-3 Februar and 6-3 March Lecure 4 Economerc echnues for saonar seres : Unvarae sochasc models wh Box- Jenns mehodolog, smle forecasng
arxiv: v1 [math.ap] 16 Apr 2016
![arxiv: v1 [math.ap] 16 Apr 2016 arxiv: v1 [math.ap] 16 Apr 2016](/thumbs/91/106796584.jpg) Th Cauchy problm for a combuson modl n porous mda J. C. da Moa M. M. Sanos. A. Sanos arxv:64.4798v [mah.ap] 6 Apr 6 Absrac W prov h xsnc of a global soluon o h Cauchy problm for a nonlnar racon-dffuson
Th Cauchy problm for a combuson modl n porous mda J. C. da Moa M. M. Sanos. A. Sanos arxv:64.4798v [mah.ap] 6 Apr 6 Absrac W prov h xsnc of a global soluon o h Cauchy problm for a nonlnar racon-dffuson
Group Codes Define Over Dihedral Groups of Small Order
 Malaysan Journal of Mathmatcal Scncs 7(S): 0- (0) Spcal Issu: Th rd Intrnatonal Confrnc on Cryptology & Computr Scurty 0 (CRYPTOLOGY0) MALAYSIA JOURAL OF MATHEMATICAL SCIECES Journal hompag: http://nspm.upm.du.my/ournal
Malaysan Journal of Mathmatcal Scncs 7(S): 0- (0) Spcal Issu: Th rd Intrnatonal Confrnc on Cryptology & Computr Scurty 0 (CRYPTOLOGY0) MALAYSIA JOURAL OF MATHEMATICAL SCIECES Journal hompag: http://nspm.upm.du.my/ournal
Control Systems (Lecture note #6)
 6.5 Corol Sysms (Lcur o #6 Las Tm: Lar algbra rw Lar algbrac quaos soluos Paramrzao of all soluos Smlary rasformao: compao form Egalus ad gcors dagoal form bg pcur: o brach of h cours Vcor spacs marcs
6.5 Corol Sysms (Lcur o #6 Las Tm: Lar algbra rw Lar algbrac quaos soluos Paramrzao of all soluos Smlary rasformao: compao form Egalus ad gcors dagoal form bg pcur: o brach of h cours Vcor spacs marcs
Valuation and Analysis of Basket Credit Linked Notes with Issuer Default Risk
 Valuaon and Analy of Ba Crd Lnd o wh ur Dfaul R Po-Chng Wu * * Dparmn of Banng and Fnanc Kanan Unvry Addr: o. Kanan Rd. Luchu Shang aoyuan 33857 awan R.O.C. E-mal: pcwu@mal.nu.du.w l.: 886-3-34500 x. 67
Valuaon and Analy of Ba Crd Lnd o wh ur Dfaul R Po-Chng Wu * * Dparmn of Banng and Fnanc Kanan Unvry Addr: o. Kanan Rd. Luchu Shang aoyuan 33857 awan R.O.C. E-mal: pcwu@mal.nu.du.w l.: 886-3-34500 x. 67
One dimensional steady state heat transfer of composite slabs
 BUILDING PHYSICS On dmnsonal sady sa a ransfr of compos slas Par 2 Ass. Prof. Dr. Norr Harmay Budaps Unvrsy of Tcnology and Economcs Dparmn of Buldng Enrgcs and Buldng Srvc Engnrng Inroducon - Buldng Pyscs
BUILDING PHYSICS On dmnsonal sady sa a ransfr of compos slas Par 2 Ass. Prof. Dr. Norr Harmay Budaps Unvrsy of Tcnology and Economcs Dparmn of Buldng Enrgcs and Buldng Srvc Engnrng Inroducon - Buldng Pyscs
Elementary Differential Equations and Boundary Value Problems
 Elmnar Diffrnial Equaions and Boundar Valu Problms Boc. & DiPrima 9 h Ediion Chapr : Firs Ordr Diffrnial Equaions 00600 คณ ตศาสตร ว ศวกรรม สาขาว ชาว ศวกรรมคอมพ วเตอร ป การศ กษา /55 ผศ.ดร.อร ญญา ผศ.ดร.สมศ
Elmnar Diffrnial Equaions and Boundar Valu Problms Boc. & DiPrima 9 h Ediion Chapr : Firs Ordr Diffrnial Equaions 00600 คณ ตศาสตร ว ศวกรรม สาขาว ชาว ศวกรรมคอมพ วเตอร ป การศ กษา /55 ผศ.ดร.อร ญญา ผศ.ดร.สมศ
8-node quadrilateral element. Numerical integration
 Fnt Elmnt Mthod lctur nots _nod quadrlatral lmnt Pag of 0 -nod quadrlatral lmnt. Numrcal ntgraton h tchnqu usd for th formulaton of th lnar trangl can b formall tndd to construct quadrlatral lmnts as wll
Fnt Elmnt Mthod lctur nots _nod quadrlatral lmnt Pag of 0 -nod quadrlatral lmnt. Numrcal ntgraton h tchnqu usd for th formulaton of th lnar trangl can b formall tndd to construct quadrlatral lmnts as wll
AR(1) Process. The first-order autoregressive process, AR(1) is. where e t is WN(0, σ 2 )
 AR() Procss Th firs-ordr auorgrssiv procss, AR() is whr is WN(0, σ ) Condiional Man and Varianc of AR() Condiional man: Condiional varianc: ) ( ) ( Ω Ω E E ) var( ) ) ( var( ) var( σ Ω Ω Ω Ω E Auocovarianc
AR() Procss Th firs-ordr auorgrssiv procss, AR() is whr is WN(0, σ ) Condiional Man and Varianc of AR() Condiional man: Condiional varianc: ) ( ) ( Ω Ω E E ) var( ) ) ( var( ) var( σ Ω Ω Ω Ω E Auocovarianc
Searching for pairing interactions with coherent charge fluctuations spectroscopy
 Sarchng for parng nracons wh cohrn charg flucuaons spcroscopy J. Lornzana ISC-CNR, Sapnza, Unvrsy of Rom B. Mansar, A. Mann, A. Odh, M. Scaronglla, M. Chrgu, F. Carbon EPFL, Lausann Ouln Raman scarng Cohrn
Sarchng for parng nracons wh cohrn charg flucuaons spcroscopy J. Lornzana ISC-CNR, Sapnza, Unvrsy of Rom B. Mansar, A. Mann, A. Odh, M. Scaronglla, M. Chrgu, F. Carbon EPFL, Lausann Ouln Raman scarng Cohrn
On One Analytic Method of. Constructing Program Controls
 Appled Mahemacal Scences, Vol. 9, 05, no. 8, 409-407 HIKARI Ld, www.m-hkar.com hp://dx.do.org/0.988/ams.05.54349 On One Analyc Mehod of Consrucng Program Conrols A. N. Kvko, S. V. Chsyakov and Yu. E. Balyna
Appled Mahemacal Scences, Vol. 9, 05, no. 8, 409-407 HIKARI Ld, www.m-hkar.com hp://dx.do.org/0.988/ams.05.54349 On One Analyc Mehod of Consrucng Program Conrols A. N. Kvko, S. V. Chsyakov and Yu. E. Balyna
Solution in semi infinite diffusion couples (error function analysis)
 Soluon n sem nfne dffuson couples (error funcon analyss) Le us consder now he sem nfne dffuson couple of wo blocks wh concenraon of and I means ha, n a A- bnary sysem, s bondng beween wo blocks made of
Soluon n sem nfne dffuson couples (error funcon analyss) Le us consder now he sem nfne dffuson couple of wo blocks wh concenraon of and I means ha, n a A- bnary sysem, s bondng beween wo blocks made of
Lucas Test is based on Euler s theorem which states that if n is any integer and a is coprime to n, then a φ(n) 1modn.
 Modul 10 Addtonal Topcs 10.1 Lctur 1 Prambl: Dtrmnng whthr a gvn ntgr s prm or compost s known as prmalty tstng. Thr ar prmalty tsts whch mrly tll us whthr a gvn ntgr s prm or not, wthout gvng us th factors
Modul 10 Addtonal Topcs 10.1 Lctur 1 Prambl: Dtrmnng whthr a gvn ntgr s prm or compost s known as prmalty tstng. Thr ar prmalty tsts whch mrly tll us whthr a gvn ntgr s prm or not, wthout gvng us th factors
Robust decentralized control with scalar output of multivariable structurally uncertain plants with state delay 1
 rprns of h 8h IFAC World Congrss lano Ial Augus 8 - Spmbr obus dcnralzd conrol wh scalar oupu of mulvarabl srucurall uncran plans wh sa dla Elzava arshva Absrac h problm of a robus conrol ssm dsgn for
rprns of h 8h IFAC World Congrss lano Ial Augus 8 - Spmbr obus dcnralzd conrol wh scalar oupu of mulvarabl srucurall uncran plans wh sa dla Elzava arshva Absrac h problm of a robus conrol ssm dsgn for
a dt a dt a dt dt If 1, then the poles in the transfer function are complex conjugates. Let s look at f t H t f s / s. So, for a 2 nd order system:
 Undrdamd Sysms Undrdamd Sysms nd Ordr Sysms Ouu modld wih a nd ordr ODE: d y dy a a1 a0 y b f If a 0 0, hn: whr: a d y a1 dy b d y dy y f y f a a a 0 0 0 is h naural riod of oscillaion. is h daming facor.
Undrdamd Sysms Undrdamd Sysms nd Ordr Sysms Ouu modld wih a nd ordr ODE: d y dy a a1 a0 y b f If a 0 0, hn: whr: a d y a1 dy b d y dy y f y f a a a 0 0 0 is h naural riod of oscillaion. is h daming facor.
Foundations of State Estimation Part II
 Foundaons of Sae Esmaon Par II Tocs: Hdden Markov Models Parcle Flers Addonal readng: L.R. Rabner, A uoral on hdden Markov models," Proceedngs of he IEEE, vol. 77,. 57-86, 989. Sequenal Mone Carlo Mehods
Foundaons of Sae Esmaon Par II Tocs: Hdden Markov Models Parcle Flers Addonal readng: L.R. Rabner, A uoral on hdden Markov models," Proceedngs of he IEEE, vol. 77,. 57-86, 989. Sequenal Mone Carlo Mehods
CSE 245: Computer Aided Circuit Simulation and Verification
 CSE 45: Compur Aidd Circui Simulaion and Vrificaion Fall 4, Sp 8 Lcur : Dynamic Linar Sysm Oulin Tim Domain Analysis Sa Equaions RLC Nwork Analysis by Taylor Expansion Impuls Rspons in im domain Frquncy
CSE 45: Compur Aidd Circui Simulaion and Vrificaion Fall 4, Sp 8 Lcur : Dynamic Linar Sysm Oulin Tim Domain Analysis Sa Equaions RLC Nwork Analysis by Taylor Expansion Impuls Rspons in im domain Frquncy
The Matrix Exponential
 Th Matrix Exponntial (with xrciss) by Dan Klain Vrsion 28928 Corrctions and commnts ar wlcom Th Matrix Exponntial For ach n n complx matrix A, dfin th xponntial of A to b th matrix () A A k I + A + k!
Th Matrix Exponntial (with xrciss) by Dan Klain Vrsion 28928 Corrctions and commnts ar wlcom Th Matrix Exponntial For ach n n complx matrix A, dfin th xponntial of A to b th matrix () A A k I + A + k!
DISTRIBUTION OF DIFFERENCE BETWEEN INVERSES OF CONSECUTIVE INTEGERS MODULO P
 DISTRIBUTION OF DIFFERENCE BETWEEN INVERSES OF CONSECUTIVE INTEGERS MODULO P Tsz Ho Chan Dartmnt of Mathmatics, Cas Wstrn Rsrv Univrsity, Clvland, OH 4406, USA txc50@cwru.du Rcivd: /9/03, Rvisd: /9/04,
DISTRIBUTION OF DIFFERENCE BETWEEN INVERSES OF CONSECUTIVE INTEGERS MODULO P Tsz Ho Chan Dartmnt of Mathmatics, Cas Wstrn Rsrv Univrsity, Clvland, OH 4406, USA txc50@cwru.du Rcivd: /9/03, Rvisd: /9/04,
Partition Functions for independent and distinguishable particles
 0.0J /.77J / 5.60J hrodynacs of oolcular Syss Insrucors: Lnda G. Grffh, Kbrly Haad-Schffrl, Moung G. awnd, Robr W. Fld Lcur 5 5.60/0.0/.77 vs. q for dsngushabl vs ndsngushabl syss Drvaon of hrodynac Proprs
0.0J /.77J / 5.60J hrodynacs of oolcular Syss Insrucors: Lnda G. Grffh, Kbrly Haad-Schffrl, Moung G. awnd, Robr W. Fld Lcur 5 5.60/0.0/.77 vs. q for dsngushabl vs ndsngushabl syss Drvaon of hrodynac Proprs
Grand Canonical Ensemble
 Th nsmbl of systms mmrsd n a partcl-hat rsrvor at constant tmpratur T, prssur P, and chmcal potntal. Consdr an nsmbl of M dntcal systms (M =,, 3,...M).. Thy ar mutually sharng th total numbr of partcls
Th nsmbl of systms mmrsd n a partcl-hat rsrvor at constant tmpratur T, prssur P, and chmcal potntal. Consdr an nsmbl of M dntcal systms (M =,, 3,...M).. Thy ar mutually sharng th total numbr of partcls
Economics 302 (Sec. 001) Intermediate Macroeconomic Theory and Policy (Spring 2011) 4/25/2011. UW Madison
 conomics 302 (Sc. 001) Inrmdia Macroconomic Thory and Policy (Spring 2011) 4/25/2011 Insrucor: Prof. Mnzi Chinn Insrucor: Prof. Mnzi Chinn UW Madison 21 1 Th Mdium Run ε = P * P Thr ar wo ways in which
conomics 302 (Sc. 001) Inrmdia Macroconomic Thory and Policy (Spring 2011) 4/25/2011 Insrucor: Prof. Mnzi Chinn Insrucor: Prof. Mnzi Chinn UW Madison 21 1 Th Mdium Run ε = P * P Thr ar wo ways in which
Dynamic Controllability with Overlapping Targets: Or Why Target Independence May Not be Good for You
 Dynamc Conrollably wh Ovrlappng Targs: Or Why Targ Indpndnc May No b Good for You Ncola Acoclla Unvrsy of Rom La Sapnza Govann D Barolomo Unvrsy of Rom La Sapnza and Unvrsy of Tramo Andrw Hughs Hall Vandrbl
Dynamc Conrollably wh Ovrlappng Targs: Or Why Targ Indpndnc May No b Good for You Ncola Acoclla Unvrsy of Rom La Sapnza Govann D Barolomo Unvrsy of Rom La Sapnza and Unvrsy of Tramo Andrw Hughs Hall Vandrbl
