Lecture 4 : Backpropagation Algorithm. Prof. Seul Jung ( Intelligent Systems and Emotional Engineering Laboratory) Chungnam National University

The Variance-Covariance Matrix

Th Varanc-Covaranc Marx Our bggs a so-ar has bn ng a lnar uncon o a s o daa by mnmzng h las squars drncs rom h o h daa wh mnsarch. Whn analyzng non-lnar daa you hav o us a program l Malab as many yps o

CIVL 8/ D Boundary Value Problems - Triangular Elements (T6) 1/8

CIVL 8/7 -D Boundar Valu Problm - rangular Elmn () /8 SI-ODE RIAGULAR ELEMES () A quadracall nrpolad rangular lmn dfnd b nod, hr a h vrc and hr a h mddl a ach d. h mddl nod, dpndng on locaon, ma dfn a

innovations shocks white noise

Innovaons Tm-srs modls ar consrucd as lnar funcons of fundamnal forcasng rrors, also calld nnovaons or shocks Ths basc buldng blocks sasf var σ Srall uncorrlad Ths rrors ar calld wh nos In gnral, f ou

Final Exam : Solutions

Comp : Algorihm and Daa Srucur Final Exam : Soluion. Rcuriv Algorihm. (a) To bgin ind h mdian o {x, x,... x n }. Sinc vry numbr xcp on in h inrval [0, n] appar xacly onc in h li, w hav ha h mdian mu b

Boosting and Ensemble Methods

Boosng and Ensmbl Mhods PAC Larnng modl Som dsrbuon D ovr doman X Eampls: c* s h arg funcon Goal: Wh hgh probably -d fnd h n H such ha rrorh,c* < d and ar arbrarly small. Inro o ML 2 Wak Larnng

Conventional Hot-Wire Anemometer

Convnonal Ho-Wr Anmomr cro Ho Wr Avanag much mallr prob z mm o µm br paal roluon array o h nor hghr rquncy rpon lowr co prormanc/co abrcaon roc I µm lghly op p layr 8µm havly boron op ch op layr abrcaon

Chapter 13 Laplace Transform Analysis

Chapr aplac Tranorm naly Chapr : Ouln aplac ranorm aplac Tranorm -doman phaor analy: x X σ m co ω φ x X X m φ x aplac ranorm: [ o ] d o d < aplac Tranorm Thr condon Unlaral on-dd aplac ranorm: aplac ranorm

Computational Element. What are the Neural Networks?

Copuaonal Eln Copuaonalprocssng ln or nod fors a ghd su of d npus and passs h rsul hrough a non-lnar. Chapr 6 Mullar ural ors Bac Propagaon Algorh Th os popular hod for ranng ulplar ors n basd on gradn

Chapter 5 The Laplace Transform. x(t) input y(t) output Dynamic System

EE 422G No: Chapr 5 Inrucor: Chung Chapr 5 Th Laplac Tranform 5- Inroducion () Sym analyi inpu oupu Dynamic Sym Linar Dynamic ym: A procor which proc h inpu ignal o produc h oupu dy ( n) ( n dy ( n) +

Problem 1: Consider the following stationary data generation process for a random variable y t. e t ~ N(0,1) i.i.d.

A/CN C m Sr Anal Profor Òcar Jordà Wnr conomc.c. Dav POBLM S SOLIONS Par I Analcal Quon Problm : Condr h followng aonar daa gnraon proc for a random varabl - N..d. wh < and N -. a Oban h populaon man varanc

Consider a system of 2 simultaneous first order linear equations

Soluon of sysms of frs ordr lnar quaons onsdr a sysm of smulanous frs ordr lnar quaons a b c d I has h alrna mar-vcor rprsnaon a b c d Or, n shorhand A, f A s alrady known from con W know ha h abov sysm

Lecture 11 SVM cont

Lecure SVM con. 0 008 Wha we have done so far We have esalshed ha we wan o fnd a lnear decson oundary whose margn s he larges We know how o measure he margn of a lnear decson oundary Tha s: he mnmum geomerc

CHAPTER 10: LINEAR DISCRIMINATION

CHAPER : LINEAR DISCRIMINAION Dscrmnan-based Classfcaon 3 In classfcaon h K classes (C,C,, C k ) We defned dscrmnan funcon g j (), j=,,,k hen gven an es eample, e chose (predced) s class label as C f g

Advanced Queueing Theory. M/G/1 Queueing Systems

Advand Quung Thory Ths slds ar rad by Dr. Yh Huang of Gorg Mason Unvrsy. Sudns rgsrd n Dr. Huang's ourss a GMU an ma a sngl mahn-radabl opy and prn a sngl opy of ah sld for hr own rfrn, so long as ah sld

Lecture 1: Numerical Integration The Trapezoidal and Simpson s Rule

Lcur : Numrical ngraion Th Trapzoidal and Simpson s Rul A problm Th probabiliy of a normally disribud (man µ and sandard dviaion σ ) vn occurring bwn h valus a and b is B A P( a x b) d () π whr a µ b -

ELEN E4830 Digital Image Processing

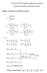ELEN E48 Dgal Imag Procssng Mrm Eamnaon Sprng Soluon Problm Quanzaon and Human Encodng r k u P u P u r r 6 6 6 6 5 6 4 8 8 4 P r 6 6 P r 4 8 8 6 8 4 r 8 4 8 4 7 8 r 6 6 6 6 P r 8 4 8 P r 6 6 8 5 P r /

FAULT TOLERANT SYSTEMS

FAULT TOLERANT SYSTEMS hp://www.cs.umass.du/c/orn/faultolransysms ar 4 Analyss Mhods Chapr HW Faul Tolranc ar.4.1 Duplx Sysms Boh procssors xcu h sam as If oupus ar n agrmn - rsul s assumd o b corrc If

Transfer function and the Laplace transformation

Lab No PH-35 Porland Sa Univriy A. La Roa Tranfr funcion and h Laplac ranformaion. INTRODUTION. THE LAPLAE TRANSFORMATION L 3. TRANSFER FUNTIONS 4. ELETRIAL SYSTEMS Analyi of h hr baic paiv lmn R, and

An introduction to Support Vector Machine

An nroducon o Suppor Vecor Machne 報告者 : 黃立德 References: Smon Haykn, "Neural Neworks: a comprehensve foundaon, second edon, 999, Chaper 2,6 Nello Chrsann, John Shawe-Tayer, An Inroducon o Suppor Vecor Machnes,

Lecture VI Regression

Lecure VI Regresson (Lnear Mehods for Regresson) Conens: Lnear Mehods for Regresson Leas Squares, Gauss Markov heorem Recursve Leas Squares Lecure VI: MLSC - Dr. Sehu Vjayakumar Lnear Regresson Model M

CPSC 211 Data Structures & Implementations (c) Texas A&M University [ 259] B-Trees

CPSC 211 Daa Srucurs & Implmnaions (c) Txas A&M Univrsiy [ 259] B-Trs Th AVL r and rd-black r allowd som variaion in h lnghs of h diffrn roo-o-laf pahs. An alrnaiv ida is o mak sur ha all roo-o-laf pahs

Statistical Analysis of Environmental Data - Academic Year Prof. Fernando Sansò

Scl nly of nvronmnl D - cdmc r 8-9 Prof. Frnndo Snò XRISS - PR 5 bl of onn Inroducon... xrc (D mprcl covrnc m)...7 xrc (D mprcl covrnc m)... xrc 3 (D mprcl covrnc m)... xrc 4 (D mprcl covrnc m)...3 xrc

State Observer Design

Sa Obsrvr Dsgn A. Khak Sdgh Conrol Sysms Group Faculy of Elcrcal and Compur Engnrng K. N. Toos Unvrsy of Tchnology Fbruary 2009 1 Problm Formulaon A ky assumpon n gnvalu assgnmn and sablzng sysms usng

DEPARTMENT OF ELECTRICAL &ELECTRONICS ENGINEERING SIGNALS AND SYSTEMS. Assoc. Prof. Dr. Burak Kelleci. Spring 2018

DEPARTMENT OF ELECTRICAL &ELECTRONICS ENGINEERING SIGNALS AND SYSTEMS Aoc. Prof. Dr. Burak Kllci Spring 08 OUTLINE Th Laplac Tranform Rgion of convrgnc for Laplac ranform Invr Laplac ranform Gomric valuaion

Chapter 12 Introduction To The Laplace Transform

Chapr Inroducion To Th aplac Tranorm Diniion o h aplac Tranorm - Th Sp & Impul uncion aplac Tranorm o pciic uncion 5 Opraional Tranorm Applying h aplac Tranorm 7 Invr Tranorm o Raional uncion 8 Pol and

Summary: Solving a Homogeneous System of Two Linear First Order Equations in Two Unknowns

Summary: Solvng a Homognous Sysm of Two Lnar Frs Ordr Equaons n Two Unknowns Gvn: A Frs fnd h wo gnvalus, r, and hr rspcv corrspondng gnvcors, k, of h coffcn mar A Dpndng on h gnvalus and gnvcors, h gnral

Convergence of Quintic Spline Interpolation

Inrnaonal Journal o ompur Applcaons 97 8887 Volum 7 No., Aprl onvrgnc o Qunc Spln Inrpolaon Y.P. Dub Dparmn O Mamacs, L.N..T. Jabalpur 8 Anl Sukla Dparmn O Mamacs Gan Ganga ollg O Tcnog, Jabalpur 8 ASTRAT

Calculus II (MAC )

Calculus II (MAC232-2) Tst 2 (25/6/25) Nam (PRINT): Plas show your work. An answr with no work rcivs no crdit. You may us th back of a pag if you nd mor spac for a problm. You may not us any calculators.

Poisson process Markov process

E2200 Quuing hory and lraffic 2nd lcur oion proc Markov proc Vikoria Fodor KTH Laboraory for Communicaion nwork, School of Elcrical Enginring 1 Cour oulin Sochaic proc bhind quuing hory L2-L3 oion proc

Variants of Pegasos. December 11, 2009

Inroducon Varans of Pegasos SooWoong Ryu bshboy@sanford.edu December, 009 Youngsoo Cho yc344@sanford.edu Developng a new SVM algorhm s ongong research opc. Among many exng SVM algorhms, we wll focus on

Theoretical Seismology

Thorcal Ssmology Lcur 9 Sgnal Procssng Fourr analyss Fourr sudd a h Écol Normal n Pars, augh by Lagrang, who Fourr dscrbd as h frs among Europan mn of scnc, Laplac, who Fourr rad lss hghly, and by Mong.

Implementation of the Extended Conjugate Gradient Method for the Two- Dimensional Energized Wave Equation

Lonardo Elcronc Jornal of raccs and Tchnolos ISSN 58-078 Iss 9 Jl-Dcmbr 006 p. -4 Implmnaon of h Endd Cona Gradn Mhod for h Two- Dmnsonal Enrd Wav Eqaon Vcor Onoma WAZIRI * Snda Ass REJU Mahmacs/Compr

Frequency Response. Response of an LTI System to Eigenfunction

Frquncy Rsons Las m w Rvsd formal dfnons of lnary and m-nvaranc Found an gnfuncon for lnar m-nvaran sysms Found h frquncy rsons of a lnar sysm o gnfuncon nu Found h frquncy rsons for cascad, fdbac, dffrnc

8-node quadrilateral element. Numerical integration

Fnt Elmnt Mthod lctur nots _nod quadrlatral lmnt Pag of 0 -nod quadrlatral lmnt. Numrcal ntgraton h tchnqu usd for th formulaton of th lnar trangl can b formall tndd to construct quadrlatral lmnts as wll

Introduction to Laplace Transforms October 25, 2017

Iroduco o Lplc Trform Ocobr 5, 7 Iroduco o Lplc Trform Lrr ro Mchcl Egrg 5 Smr Egrg l Ocobr 5, 7 Oul Rvw l cl Wh Lplc rform fo of Lplc rform Gg rform b gro Fdg rform d vr rform from bl d horm pplco o dffrl

Chapter 4. Neural Networks Based on Competition

Chaper 4. Neural Neworks Based on Compeon Compeon s mporan for NN Compeon beween neurons has been observed n bologcal nerve sysems Compeon s mporan n solvng many problems To classfy an npu paern _1 no

Microscopic Flow Characteristics Time Headway - Distribution

CE57: Traffic Flow Thory Spring 20 Wk 2 Modling Hadway Disribuion Microscopic Flow Characrisics Tim Hadway - Disribuion Tim Hadway Dfiniion Tim Hadway vrsus Gap Ahmd Abdl-Rahim Civil Enginring Dparmn,

Lecture 6: Learning for Control (Generalised Linear Regression)

Lecure 6: Learnng for Conrol (Generalsed Lnear Regresson) Conens: Lnear Mehods for Regresson Leas Squares, Gauss Markov heorem Recursve Leas Squares Lecure 6: RLSC - Prof. Sehu Vjayakumar Lnear Regresson

Central University of Finance and Economics, Beijing, China. *Corresponding author

016 Jon Inrnaonal Confrnc on Arfcal Inllgnc and Copur Engnrng (AICE 016) and Inrnaonal Confrnc on Nwork and Councaon Scury (NCS 016) ISBN: 978-1-60595-36-5 AdaBoos Arfcal Nural Nwork for Sock Mark Prdcng

The Analysis of the Thickness-predictive Model Based on the SVM Xiu-ming Zhao1,a,Yan Wang2,band Zhimin Bi3,c

h Naonal Conference on Elecrcal, Elecroncs and Compuer Engneerng (NCEECE The Analyss of he Thcknesspredcve Model Based on he SVM Xumng Zhao,a,Yan Wang,band Zhmn B,c School of Conrol Scence and Engneerng,

y = 2xe x + x 2 e x at (0, 3). solution: Since y is implicitly related to x we have to use implicit differentiation: 3 6y = 0 y = 1 2 x ln(b) ln(b)

4. y = y = + 5. Find th quation of th tangnt lin for th function y = ( + ) 3 whn = 0. solution: First not that whn = 0, y = (1 + 1) 3 = 8, so th lin gos through (0, 8) and thrfor its y-intrcpt is 8. y

EE243 Advanced Electromagnetic Theory Lec # 10: Poynting s Theorem, Time- Harmonic EM Fields

Appl M Fall 6 Nuruhr Lcur # r 9/6/6 4 Avanc lcromagnc Thory Lc # : Poynng s Thorm Tm- armonc M Fls Poynng s Thorm Consrvaon o nrgy an momnum Poynng s Thorm or Lnar sprsv Ma Poynng s Thorm or Tm-armonc

Chapter 9 Transient Response

har 9 Transn sons har 9: Ouln N F n F Frs-Ordr Transns Frs-Ordr rcus Frs ordr crcus: rcus conan onl on nducor or on caacor gornd b frs-ordr dffrnal quaons. Zro-nu rsons: h crcu has no ald sourc afr a cran

Introduction to Boosting

Inroducon o Boosng Cynha Rudn PACM, Prnceon Unversy Advsors Ingrd Daubeches and Rober Schapre Say you have a daabase of news arcles, +, +, -, -, +, +, -, -, +, +, -, -, +, +, -, + where arcles are labeled

Elementary Differential Equations and Boundary Value Problems

Elmnar Diffrnial Equaions and Boundar Valu Problms Boc. & DiPrima 9 h Ediion Chapr : Firs Ordr Diffrnial Equaions 00600 คณ ตศาสตร ว ศวกรรม สาขาว ชาว ศวกรรมคอมพ วเตอร ป การศ กษา /55 ผศ.ดร.อร ญญา ผศ.ดร.สมศ

LQR based Speed Control of BLDC Motors

G Inrnaonal ournal o Elcrcal and Elcronc Engnrng (G-IEEE) volu 3 Iu 6 un 6 Q bad pd Conrol o BDC Moor Mha M., Awn.B.G udn, Aan proor Elcrcal & Elcronc Dp. Mar Balo collg o Engnrng, hruvananhapura, rala,

t=0 t>0: + vr - i dvc Continuation

hapr Ga Dlay and rcus onnuaon s rcu Equaon >: S S Ths dffrnal quaon, oghr wh h nal condon, fully spcfs bhaor of crcu afr swch closs Our n challng: larn how o sol such quaons TUE/EE 57 nwrk analys 4/5 NdM

9. Simple Rules for Monetary Policy

9. Smpl Ruls for Monar Polc John B. Talor, Ma 0, 03 Woodford, AR 00 ovrvw papr Purpos s o consdr o wha xn hs prscrpon rsmbls h sor of polc ha conomc hor would rcommnd Bu frs, l s rvw how hs sor of polc

1 Finite Automata and Regular Expressions

1 Fini Auom nd Rgulr Exprion Moivion: Givn prn (rgulr xprion) for ring rching, w migh wn o convr i ino drminiic fini uomon or nondrminiic fini uomon o mk ring rching mor fficin; drminiic uomon only h o

(,,, ) (,,, ). In addition, there are three other consumers, -2, -1, and 0. Consumer -2 has the utility function

MACROECONOMIC THEORY T J KEHOE ECON 87 SPRING 5 PROBLEM SET # Conder an overlappng generaon economy le ha n queon 5 on problem e n whch conumer lve for perod The uly funcon of he conumer born n perod,

Computing Relevance, Similarity: The Vector Space Model

Compung Relevance, Smlary: The Vecor Space Model Based on Larson and Hears s sldes a UC-Bereley hp://.sms.bereley.edu/courses/s0/f00/ aabase Managemen Sysems, R. Ramarshnan ocumen Vecors v ocumens are

Inversion of Complex Valued Neural Networks Using Complex Back-propagation Algorithm

ITERATIOAL JOURAL OF ATHEATICS AD COPUTERS I SIULATIO Inverson of Complex Valued eural ewors Usng Complex Bac-propagaon Algorhm Ana S. Gangal, P.K. Kalra, and D.S.Chauhan Absrac Ths paper presens he nverson

u x v x dx u x v x v x u x dx d u x v x u x v x dx u x v x dx Integration by Parts Formula

7. Intgration by Parts Each drivativ formula givs ris to a corrsponding intgral formula, as w v sn many tims. Th drivativ product rul yilds a vry usful intgration tchniqu calld intgration by parts. Starting

SIMEON BALL AND AART BLOKHUIS

A BOUND FOR THE MAXIMUM WEIGHT OF A LINEAR CODE SIMEON BALL AND AART BLOKHUIS Absrac. I s shown ha h paramrs of a lnar cod ovr F q of lngh n, dmnson k, mnmum wgh d and maxmum wgh m sasfy a cran congrunc

Supplementary Figure 1. Experiment and simulation with finite qudit. anharmonicity. (a), Experimental data taken after a 60 ns three-tone pulse.

Supplmnar Fgur. Eprmn and smulaon wh fn qud anharmonc. a, Eprmnal daa akn afr a 6 ns hr-on puls. b, Smulaon usng h amlonan. Supplmnar Fgur. Phagoran dnamcs n h m doman. a, Eprmnal daa. Th hr-on puls s

The Method of Steepest Descent for Feedforward Artificial Neural Networks

IOSR Joural o Mahac (IOSR-JM) -ISSN: 78-578, p-issn:39-765x. Volu, Iu Vr. II. (F. 4), PP 53-6.oroural.org Th Mhod o Sp Dc or Fdorard Arcal Nural Nor Muhaad Ha, Md. Jah Udd ad Md Adul Al 3 Aoca Proor, Dpar

EXERCISE - 01 CHECK YOUR GRASP

DIFFERENTIAL EQUATION EXERCISE - CHECK YOUR GRASP 7. m hn D() m m, D () m m. hn givn D () m m D D D + m m m m m m + m m m m + ( m ) (m ) (m ) (m + ) m,, Hnc numbr of valus of mn will b. n ( ) + c sinc

Propositional Logic. Combinatorial Problem Solving (CPS) Albert Oliveras Enric Rodríguez-Carbonell. May 17, 2018

Propositional Logic Combinatorial Problm Solving (CPS) Albrt Olivras Enric Rodríguz-Carbonll May 17, 2018 Ovrviw of th sssion Dfinition of Propositional Logic Gnral Concpts in Logic Rduction to SAT CNFs

Engineering Circuit Analysis 8th Edition Chapter Nine Exercise Solutions

Engnrng rcu naly 8h Eon hapr Nn Exrc Soluon. = KΩ, = µf, an uch ha h crcu rpon oramp. a For Sourc-fr paralll crcu: For oramp or b H 9V, V / hoo = H.7.8 ra / 5..7..9 9V 9..9..9 5.75,.5 5.75.5..9 . = nh,

10.5 Linear Viscoelasticity and the Laplace Transform

Scn.5.5 Lnar Vclacy and h Lalac ranfrm h Lalac ranfrm vry uful n cnrucng and analyng lnar vclac mdl..5. h Lalac ranfrm h frmula fr h Lalac ranfrm f h drvav f a funcn : L f f L f f f f f c..5. whr h ranfrm

CSE 245: Computer Aided Circuit Simulation and Verification

CSE 45: Compur Aidd Circui Simulaion and Vrificaion Fall 4, Sp 8 Lcur : Dynamic Linar Sysm Oulin Tim Domain Analysis Sa Equaions RLC Nwork Analysis by Taylor Expansion Impuls Rspons in im domain Frquncy

LaPlace Transform in Circuit Analysis

LaPlac Tranform in Circui Analyi Obciv: Calcula h Laplac ranform of common funcion uing h dfiniion and h Laplac ranform abl Laplac-ranform a circui, including componn wih non-zro iniial condiion. Analyz

Chapter 7 Stead St y- ate Errors

Char 7 Say-Sa rror Inroucon Conrol ym analy an gn cfcaon a. rann ron b. Sably c. Say-a rror fnon of ay-a rror : u c a whr u : nu, c: ouu Val only for abl ym chck ym ably fr! nu for ay-a a nu analy U o

T h e C S E T I P r o j e c t

T h e P r o j e c t T H E P R O J E C T T A B L E O F C O N T E N T S A r t i c l e P a g e C o m p r e h e n s i v e A s s es s m e n t o f t h e U F O / E T I P h e n o m e n o n M a y 1 9 9 1 1 E T

Chap.3 Laplace Transform

Chap. aplac Tranorm Tranorm: An opraion ha ranorm a uncion ino anohr uncion i Dirniaion ranorm: ii x: d dx x x Ingraion ranorm: x: x dx x c Now, conidr a dind ingral k, d,ha ranorm ino a uncion o variabl

First Lecture of Machine Learning. Hung-yi Lee

Firs Lcur of Machin Larning Hung-yi L Larning o say ys/no Binary Classificaion Larning o say ys/no Sam filring Is an -mail sam or no? Rcommndaion sysms rcommnd h roduc o h cusomr or no? Malwar dcion Is

CHAPTER 10: LINEAR DISCRIMINATION

HAPER : LINEAR DISRIMINAION Dscmnan-based lassfcaon 3 In classfcaon h K classes ( k ) We defned dsmnan funcon g () = K hen gven an es eample e chose (pedced) s class label as f g () as he mamum among g

[ ] 1+ lim G( s) 1+ s + s G s s G s Kacc SYSTEM PERFORMANCE. Since. Lecture 10: Steady-state Errors. Steady-state Errors. Then

SYSTEM PERFORMANCE Lctur 0: Stady-tat Error Stady-tat Error Lctur 0: Stady-tat Error Dr.alyana Vluvolu Stady-tat rror can b found by applying th final valu thorm and i givn by lim ( t) lim E ( ) t 0 providd

Outline. Probabilistic Model Learning. Probabilistic Model Learning. Probabilistic Model for Time-series Data: Hidden Markov Model

Probablsc Model for Tme-seres Daa: Hdden Markov Model Hrosh Mamsuka Bonformacs Cener Kyoo Unversy Oulne Three Problems for probablsc models n machne learnng. Compung lkelhood 2. Learnng 3. Parsng (predcon

CHAPTER 2: Supervised Learning

HATER 2: Supervsed Learnng Learnng a lass from Eamples lass of a famly car redcon: Is car a famly car? Knowledge eracon: Wha do people epec from a famly car? Oupu: osve (+) and negave ( ) eamples Inpu

On the Speed of Heat Wave. Mihály Makai

On h Spd of Ha Wa Mihály Maai maai@ra.bm.hu Conns Formulaion of h problm: infini spd? Local hrmal qulibrium (LTE hypohsis Balanc quaion Phnomnological balanc Spd of ha wa Applicaion in plasma ranspor 1.

Control Systems (Lecture note #6)

6.5 Corol Sysms (Lcur o #6 Las Tm: Lar algbra rw Lar algbrac quaos soluos Paramrzao of all soluos Smlary rasformao: compao form Egalus ad gcors dagoal form bg pcur: o brach of h cours Vcor spacs marcs

Lecture 37 (Schrödinger Equation) Physics Spring 2018 Douglas Fields

Lctur 37 (Schrödingr Equation) Physics 6-01 Spring 018 Douglas Filds Rducd Mass OK, so th Bohr modl of th atom givs nrgy lvls: E n 1 k m n 4 But, this has on problm it was dvlopd assuming th acclration

2. The Laplace Transform

Th aac Tranorm Inroucion Th aac ranorm i a unamna an vry uu oo or uying many nginring robm To in h aac ranorm w conir a comx variab σ, whr σ i h ra ar an i h imaginary ar or ix vau o σ an w viw a a oin

Multilayer neural networks

Topic 3 Artificial nural ntwors: Suprvisd larning Multi nural ntwors Acclratd larning in multi nural ntwors Multi nural ntwors A multi prcptron is a fdforward nural ntwor with on or mor hiddn s. Th ntwor

Robust and Accurate Cancer Classification with Gene Expression Profiling

Robus and Accurae Cancer Classfcaon wh Gene Expresson Proflng (Compuaonal ysems Bology, 2005) Auhor: Hafeng L, Keshu Zhang, ao Jang Oulne Background LDA (lnear dscrmnan analyss) and small sample sze problem

Improved Exponential Estimator for Population Variance Using Two Auxiliary Variables

Improvd Epoal Emaor for Populao Varac Ug Two Aular Varabl Rajh gh Dparm of ac,baara Hdu Uvr(U.P., Ida (rgha@ahoo.com Pakaj Chauha ad rmala awa chool of ac, DAVV, Idor (M.P., Ida Flor maradach Dparm of

Aperiodic and Sporadic Jobs. Scheduling Aperiodic and Sporadic Jobs

CPSC-663: Ral-Tm Sym Arodc and Soradc Job Schdulng Arodc and Soradc Job Dfnon Comaron o radonal chdulng of aynchronou vn Pollng Srvr Dfrrabl Srvr Soradc Srvr Gnralzd Procor Sharng Conan Ulzaon Srvr Toal

Homework: Introduction to Motion

Homwork: Inroducon o Moon Dsanc vs. Tm Graphs Nam Prod Drcons: Answr h foowng qusons n h spacs provdd. 1. Wha do you do o cra a horzona n on a dsancm graph? 2. How do you wak o cra a sragh n ha sops up?

Math 266, Practice Midterm Exam 2

Mh 66, Prcic Midrm Exm Nm: Ground Rul. Clculor i NOT llowd.. Show your work for vry problm unl ohrwi d (pril crdi r vilbl). 3. You my u on 4-by-6 indx crd, boh id. 4. Th bl of Lplc rnform i vilbl h l pg.

On the Derivatives of Bessel and Modified Bessel Functions with Respect to the Order and the Argument

Inrnaional Rsarch Journal of Applid Basic Scincs 03 Aailabl onlin a wwwirjabscom ISSN 5-838X / Vol 4 (): 47-433 Scinc Eplorr Publicaions On h Driais of Bssl Modifid Bssl Funcions wih Rspc o h Ordr h Argumn

Robust decentralized control with scalar output of multivariable structurally uncertain plants with state delay 1

rprns of h 8h IFAC World Congrss lano Ial Augus 8 - Spmbr obus dcnralzd conrol wh scalar oupu of mulvarabl srucurall uncran plans wh sa dla Elzava arshva Absrac h problm of a robus conrol ssm dsgn for

Single-loop System Reliability-Based Design & Topology Optimization (SRBDO/SRBTO): A Matrix-based System Reliability (MSR) Method

10 h US Naonal Congress on Compuaonal Mechancs Columbus, Oho 16-19, 2009 Sngle-loop Sysem Relably-Based Desgn & Topology Opmzaon (SRBDO/SRBTO): A Marx-based Sysem Relably (MSR) Mehod Tam Nguyen, Junho

Adaptive Neural Network Flight Control Using both Current and Recorded Data

AIAA Gudanc Navgaon and Conrol Confrnc and Eh - 3 Augus 7 Hlon H Souh Carolna AIAA 7-655 Adav Nural Nork Flgh Conrol Usng oh Currn and Rcordd Daa Grsh Chodhary * and Erc N. Johnson Darmn of Arosac Engnrng

Advanced Engineering Mathematics, K.A. Stroud, Dexter J. Booth Engineering Mathematics, H.K. Dass Higher Engineering Mathematics, Dr. B.S.

Rfrc: (i) (ii) (iii) Advcd Egirig Mhmic, K.A. Sroud, Dxr J. Booh Egirig Mhmic, H.K. D Highr Egirig Mhmic, Dr. B.S. Grwl Th mhod of m Thi coi of h followig xm wih h giv coribuio o h ol. () Mid-rm xm : 3%

Generalized Half Linear Canonical Transform And Its Properties

Gnrlz Hl Lnr Cnoncl Trnorm An I Propr A S Guh # A V Joh* # Gov Vrh Inu o Scnc n Humn, Amrv M S * Shnkrll Khnlwl Collg, Akol - 444 M S Arc: A gnrlzon o h Frconl Fourr rnorm FRFT, h lnr cnoncl rnorm LCT

Valuing Credit Derivatives Using Gaussian Quadrature : A Stochastic Volatility Framework

alung Cr rvav Ung Gauan uaraur : A Sochac olaly Framwork Nabl AHANI * Fr vron: Jun h vron: January 3 Conac normaon Nabl ahan HC Monréal parmn o Fnanc Oc 4-455 3 Chmn la Cô-San-Cahrn Monral ubc Canaa H3

Journal of Theoretical and Applied Information Technology 10 th January Vol. 47 No JATIT & LLS. All rights reserved.

Journal o Thortcal and Appld Inormaton Tchnology th January 3. Vol. 47 No. 5-3 JATIT & LLS. All rghts rsrvd. ISSN: 99-8645 www.att.org E-ISSN: 87-395 RESEARCH ON PROPERTIES OF E-PARTIAL DERIVATIVE OF LOGIC

Boyce/DiPrima 9 th ed, Ch 2.1: Linear Equations; Method of Integrating Factors

Boc/DiPrima 9 h d, Ch.: Linar Equaions; Mhod of Ingraing Facors Elmnar Diffrnial Equaions and Boundar Valu Problms, 9 h diion, b William E. Boc and Richard C. DiPrima, 009 b John Wil & Sons, Inc. A linar

Wave Superposition Principle

Physcs 36: Was Lcur 5 /7/8 Wa Suroson Prncl I s qu a common suaon for wo or mor was o arr a h sam on n sac or o xs oghr along h sam drcon. W wll consdr oday sral moran cass of h combnd ffcs of wo or mor

CSCE 478/878 Lecture 5: Artificial Neural Networks and Support Vector Machines. Stephen Scott. Introduction. Outline. Linear Threshold Units

(Adaped from Ehem Alpaydn and Tom Mchell) Consder humans: Toal number of neurons Neuron schng me 3 second (vs ) Connecons per neuron 4 5 Scene recognon me second nference seps doesn seem lke enough ) much

Mor Tutorial at www.dumblittldoctor.com Work th problms without a calculator, but us a calculator to chck rsults. And try diffrntiating your answrs in part III as a usful chck. I. Applications of Intgration

PSS Tuning of the Combined Cycle Power Station by Neural Network

Procngs of h Worl Congrss on Engnrng an Compur Scnc 7 WCECS 7, Ocobr 46, 7, San Francsco, USA PSS Tunng of h Combn Cycl Powr Saon by Nural Nwork E. L. F. Danl, F. M. F. Souza, J. N. R. a Slva Jr, J. A.

Gradient Descent for General Reinforcement Learning

To appar n M. S. Karns, S. A. Solla, and D. A. Cohn, dors, Advancs n Nral Informaon Procssng Sysms, MIT Prss, Cambrdg, MA, 999. Gradn Dscn for Gnral Rnforcmn Larnng Lmon Bard Andrw Moor lmon@cs.cm.d awm@cs.cm.d

4.1 The Uniform Distribution Def n: A c.r.v. X has a continuous uniform distribution on [a, b] when its pdf is = 1 a x b

4. Th Uniform Disribuion Df n: A c.r.v. has a coninuous uniform disribuion on [a, b] whn is pdf is f x a x b b a Also, b + a b a µ E and V Ex4. Suppos, h lvl of unblivabiliy a any poin in a Transformrs

An N-Component Series Repairable System with Repairman Doing Other Work and Priority in Repair

Mor ppl Novmbr 8 N-Compo r Rparabl m h Rparma Dog Ohr ork a ror Rpar Jag Yag E-mal: jag_ag7@6om Xau Mg a uo hg ollag arb Normal Uvr Yaq ua Taoao ag uppor b h Fouao or h aural o b prov o Cha 5 uppor b h

FL/VAL ~RA1::1. Professor INTERVI of. Professor It Fr recru. sor Social,, first of all, was. Sys SDC? Yes, as a. was a. assumee.

B Pror NTERV FL/VAL ~RA1::1 1 21,, 1989 i n or Socil,, fir ll, Pror Fr rcru Sy Ar you lir SDC? Y, om um SM: corr n 'd m vry ummr yr. Now, y n y, f pr my ry for ummr my 1 yr Un So vr ummr cour d rr o l

S.Y. B.Sc. (IT) : Sem. III. Applied Mathematics. Q.1 Attempt the following (any THREE) [15]

S.Y. B.Sc. (IT) : Sm. III Applid Mahmaics Tim : ½ Hrs.] Prlim Qusion Papr Soluion [Marks : 75 Q. Amp h following (an THREE) 3 6 Q.(a) Rduc h mari o normal form and find is rank whr A 3 3 5 3 3 3 6 Ans.:

P a g e 5 1 of R e p o r t P B 4 / 0 9

P a g e 5 1 of R e p o r t P B 4 / 0 9 J A R T a l s o c o n c l u d e d t h a t a l t h o u g h t h e i n t e n t o f N e l s o n s r e h a b i l i t a t i o n p l a n i s t o e n h a n c e c o n n e

OUTLINE FOR Chapter 2-2. Basic Laws

0//8 OUTLINE FOR Chapr - AERODYNAMIC W-- Basc Laws Analss of an problm n fld mchancs ncssarl nclds samn of h basc laws gornng h fld moon. Th basc laws, whch applcabl o an fld, ar: Consraon of mass Conn