The Condition of Linear Barycentric Rational Interpolation from Equispaced Samples
|
|
|
- Wilfrid McDowell
- 5 years ago
- Views:
Transcription
1 The Condition of Linear Barycentric Rational Interpolation from Equispaced Samples Georges Klein University of Fribourg (Switzerland) homeweb.unifr.ch/kleing/pub Vancouver, ICIAM, July 21, 2011 G. Klein Condition of LBRI from equispaced samples 1/23
2 Outline 1 Barycentric rational interpolation 2 3 G. Klein Condition of LBRI from equispaced samples 2/23
3 Introduction and notation One-dimensional interpolation Floater Hormann interpolation Barycentric rational interpolation G. Klein Condition of LBRI from equispaced samples 3/23
4 One-dimensional interpolation One-dimensional interpolation Floater Hormann interpolation Given: a x 0 < x 1 <... < x n b, f(x 0 ),f(x 1 ),...,f(x n ), n+1 distinct nodes and corresponding values. Aim: find a function g from a finite-dimensional linear subspace of (C[a,b], ) such that g interpolates f at the nodes, g(x j ) = f(x j ) = f j, j = 0,...,n. G. Klein Condition of LBRI from equispaced samples 4/23
5 One-dimensional interpolation Floater Hormann interpolation Construction presented by Floater and Hormann - Choose an integer d {0,1,...,n}, - for j = 0,...,n d, define p j (x), the polynomial of degree d interpolating f j,f j+1,...,f j+d. The d-th interpolant of the family is given by r n [f](x) = n d λ j (x)p j (x) j=0 n d λ j (x) j=0, where λ j (x) = ( 1) j (x x j )...(x x j+d ). G. Klein Condition of LBRI from equispaced samples 5/23
6 One-dimensional interpolation Floater Hormann interpolation Construction presented by Floater and Hormann - Choose an integer d {0,1,...,n}, - for j = 0,...,n d, define p j (x), the polynomial of degree d interpolating f j,f j+1,...,f j+d. The d-th interpolant of the family is given by r n [f](x) = n d λ j (x)p j (x) j=0 n d λ j (x) j=0, where λ j (x) = ( 1) j (x x j )...(x x j+d ). G. Klein Condition of LBRI from equispaced samples 5/23
7 One-dimensional interpolation Floater Hormann interpolation Construction presented by Floater and Hormann - Choose an integer d {0,1,...,n}, - for j = 0,...,n d, define p j (x), the polynomial of degree d interpolating f j,f j+1,...,f j+d. The d-th interpolant of the family is given by r n [f](x) = n d λ j (x)p j (x) j=0 n d λ j (x) j=0, where λ j (x) = ( 1) j (x x j )...(x x j+d ). G. Klein Condition of LBRI from equispaced samples 5/23
8 One-dimensional interpolation Floater Hormann interpolation Lemma (Berrut Baltensperger Mittelmann (2005)) Let {x j } n j=0 be a set of n+1 distinct nodes, {f j} n j=0 corresponding real numbers and let {v j } n j=0 be any non-zero real numbers. Then (a) the barycentric rational function R(x) = n j=0 n j=0 v j x x j f j v j x x j, interpolates f k at x k : lim x xk R(x) = f k ; (b) conversely, every rational interpolant of the f j may be written in barycentric form for some weights v j. G. Klein Condition of LBRI from equispaced samples 6/23
9 Barycentric weights One-dimensional interpolation Floater Hormann interpolation Write r n [f] in barycentric form r n [f](x) = n j=0 n j=0 w j x x j f j w j x x j For equispaced nodes, the weights w j oscillate in sign with absolute values 1,1,...,1,1, d = 0, (Berrut) 1 2,1,1,...,1,1, 1 2, d = 1, (Berrut) 1 4, 3 4,1,1,...,1,1, 3 4, 1 4, d = 2, (Floater Hormann) 1 8, 4 8, 7 8,1,1,...,1,1, 7 8, 4 8, 1 8, d = 3. (Floater Hormann). G. Klein Condition of LBRI from equispaced samples 7/23
10 One-dimensional interpolation Floater Hormann interpolation Theorem (Floater Hormann (2007)) Let 0 d n and f C d+2 [a,b], h = max 0 i n 1 (x i+1 x i ), then the rational function r n [f] has no poles in lr, if d 1, r n [f] f = max a x b r n[f](x) f(x) Ch d+1, if d = 0, r n [f] f Cβh, where β is a mesh ratio and C is a generic constant, independent of n. G. Klein Condition of LBRI from equispaced samples 8/23
11 Lebesgue function and constant Lower and upper bound Condition of Floater Hormann interpolation in equispaced nodes G. Klein Condition of LBRI from equispaced samples 9/23
12 Lebesgue function and constant Lebesgue function and constant Lower and upper bound The Lebesgue constant n w j x x j Λ n = max Λ j=0 n(x) = max, a x b a x b n w j x x j is the condition number of the interpolation method. It is the maximum of the Lebesgue function Λ n (x) in [a,b]. j=0 G. Klein Condition of LBRI from equispaced samples 10/23
13 Lebesgue function and constant Lower and upper bound Lebesgue function for Floater Hormann interpolation Figure: Lebesgue function for Floater Hormann interpolation in equispaced nodes in [ 1,1] with d = 2,3,4,5 and n = 40 G. Klein Condition of LBRI from equispaced samples 11/23
14 Lebesgue function and constant Lower and upper bound Lebesgue constant for Floater Hormann interpolation Theorem (Bos De Marchi Hormann K. (2011)) Let 0 d n and the nodes x j, j = 0,...,n, be equispaced. Then 2 d 2 ( n ) d +1 ln d 1 Λ n 2 d 1 (2+ln(n)). Logarithmic growth with n but exponential growth with d. G. Klein Condition of LBRI from equispaced samples 12/23
15 Lebesgue function and constant Lower and upper bound Lebesgue constant for Floater Hormann interpolation Theorem (Bos De Marchi Hormann K. (2011)) Let 0 d n and the nodes x j, j = 0,...,n, be equispaced. Then 2 d 2 ( n ) d +1 ln d 1 Λ n 2 d 1 (2+ln(n)). Logarithmic growth with n but exponential growth with d. G. Klein Condition of LBRI from equispaced samples 12/23
16 Construction of EFH Examples Extended Floater Hormann interpolation G. Klein Condition of LBRI from equispaced samples 13/23
17 Construction of EFH Examples It turns out that for given d, Λ n (x) has at most d high oscillations at the ends and is much smaller in the remaining part of the interval if the nodes are equispaced. Idea: we add 2d new data values f d,..., f 1 and f n+1,..., f n+d, corresponding to additional nodes x d,...,x 1 and x n+1,...,x n+d. The global data set is then interpolated and evaluated only in the interval [a, b]. To be precise, we choose positive integers ñ n and d ñ, and compute r (k) ñ [f](x 0) and r (k) ñ [f](x n), k = 1,..., d, where rñ[f](x 0 ) is the rational interpolant of the values f 0,...,fñ, evaluated in x 0, and rñ[f](x n ) is the rational interpolant of the values f n ñ,...,f n, evaluated in x n, both with parameter d. G. Klein Condition of LBRI from equispaced samples 14/23
18 Construction of EFH Examples It turns out that for given d, Λ n (x) has at most d high oscillations at the ends and is much smaller in the remaining part of the interval if the nodes are equispaced. Idea: we add 2d new data values f d,..., f 1 and f n+1,..., f n+d, corresponding to additional nodes x d,...,x 1 and x n+1,...,x n+d. The global data set is then interpolated and evaluated only in the interval [a, b]. To be precise, we choose positive integers ñ n and d ñ, and compute r (k) ñ [f](x 0) and r (k) ñ [f](x n), k = 1,..., d, where rñ[f](x 0 ) is the rational interpolant of the values f 0,...,fñ, evaluated in x 0, and rñ[f](x n ) is the rational interpolant of the values f n ñ,...,f n, evaluated in x n, both with parameter d. G. Klein Condition of LBRI from equispaced samples 14/23
19 Construction of EFH Examples It turns out that for given d, Λ n (x) has at most d high oscillations at the ends and is much smaller in the remaining part of the interval if the nodes are equispaced. Idea: we add 2d new data values f d,..., f 1 and f n+1,..., f n+d, corresponding to additional nodes x d,...,x 1 and x n+1,...,x n+d. The global data set is then interpolated and evaluated only in the interval [a, b]. To be precise, we choose positive integers ñ n and d ñ, and compute r (k) ñ [f](x 0) and r (k) ñ [f](x n), k = 1,..., d, where rñ[f](x 0 ) is the rational interpolant of the values f 0,...,fñ, evaluated in x 0, and rñ[f](x n ) is the rational interpolant of the values f n ñ,...,f n, evaluated in x n, both with parameter d. G. Klein Condition of LBRI from equispaced samples 14/23
20 Construction of EFH Examples We set f 0 + r (k) ñ [f](x 0) (x j x 0 ) k, d j 1, k! k=1 fj := f j, 0 j n, f n + d d r (k) k=1 ñ [f](x n) (x j x n ) k, n+1 j n+d. k! Our extension of the Floater Hormann family then is r n [f](x) := n+d j= d n+d j= d w j x x j fj w j x x j. G. Klein Condition of LBRI from equispaced samples 15/23
21 Construction of EFH Examples We set f 0 + r (k) ñ [f](x 0) (x j x 0 ) k, d j 1, k! k=1 fj := f j, 0 j n, f n + d d r (k) k=1 ñ [f](x n) (x j x n ) k, n+1 j n+d. k! Our extension of the Floater Hormann family then is r n [f](x) := n+d j= d n+d j= d w j x x j fj w j x x j. G. Klein Condition of LBRI from equispaced samples 15/23
22 Construction of EFH Examples Convergence of extended Floater Hormann interpolation Notation: D := min{d, d}. Theorem (K. (2011)) Suppose n, d, ñ < n and d ñ are positive integers and assume that f C d+2 [a dh,b +dh] C 2 d+1 ([a,a+ñh] [b ñh,b]) is sampled at n+1 equispaced nodes in [a,b]. Then r n [f] f = max a x b r n[f](x) f(x) Ch D+1. r n has no poles in lr. G. Klein Condition of LBRI from equispaced samples 16/23
23 Construction of EFH Examples Lebesgue constant for extended FH interpolation Theorem (K. (2011)) For positive integers n and d, the Lebesgue constant Λ n associated with extended Floater Hormann interpolation is bounded as Λ n 2+ln(n+2d). Logarithmic growth with n and d. G. Klein Condition of LBRI from equispaced samples 17/23
24 Construction of EFH Examples Lebesgue constant for extended FH interpolation Theorem (K. (2011)) For positive integers n and d, the Lebesgue constant Λ n associated with extended Floater Hormann interpolation is bounded as Λ n 2+ln(n+2d). Logarithmic growth with n and d. G. Klein Condition of LBRI from equispaced samples 17/23
25 Lebesgue functions Construction of EFH Examples Figure: Lebesgue function with n = 50 for extended FH interpolation in equispaced nodes with d = 3 (left), for polynomial interpolation in Chebyshev points of the second kind (center) and first kind (right) G. Klein Condition of LBRI from equispaced samples 18/23
26 Lebesgue constants and bound Construction of EFH Examples FH EFH bound for EFH Figure: Lebesgue constants associated with FH and EFH interpolation with d = 8 and 8 n 1000, together with the upper bound on the EFH Lebesgue constant G. Klein Condition of LBRI from equispaced samples 19/23
27 Lebesgue constants Construction of EFH Examples 10 6 FH EFH Figure: Lebesgue constants associated with FH and EFH interpolation in equispaced nodes with n = 200 and 1 d 25 G. Klein Condition of LBRI from equispaced samples 20/23
28 Construction of EFH Examples Interpolation of Runge s example 1/(1+x 2 ) in [ 5,5] 10 2 spline FH EFH Figure: Error behaviour of spline, FH and EFH interpolation of 1/(1+x 2 ) with d = 4 and 20 n 1000 G. Klein Condition of LBRI from equispaced samples 21/23
29 Construction of EFH Examples Perturbed Runge s example 1/(1+x 2 ) in [ 5,5] 10 4 spline FH EFH Figure: Error behaviour of spline, FH and EFH interpolation of 1/(1+x 2 ) with sign alternating perturbation of the data, n = 1000 and 1 d 50 G. Klein Condition of LBRI from equispaced samples 22/23
30 Thank you for your attention! G. Klein Condition of LBRI from equispaced samples 23/23
Convergence rates of derivatives of a family of barycentric rational interpolants
 Convergence rates of derivatives of a family of barycentric rational interpolants J.-P. Berrut, M. S. Floater and G. Klein University of Fribourg (Switzerland) CMA / IFI, University of Oslo jean-paul.berrut@unifr.ch
Convergence rates of derivatives of a family of barycentric rational interpolants J.-P. Berrut, M. S. Floater and G. Klein University of Fribourg (Switzerland) CMA / IFI, University of Oslo jean-paul.berrut@unifr.ch
On the Lebesgue constant of barycentric rational interpolation at equidistant nodes
 On the Lebesgue constant of barycentric rational interpolation at equidistant nodes by Len Bos, Stefano De Marchi, Kai Hormann and Georges Klein Report No. 0- May 0 Université de Fribourg (Suisse Département
On the Lebesgue constant of barycentric rational interpolation at equidistant nodes by Len Bos, Stefano De Marchi, Kai Hormann and Georges Klein Report No. 0- May 0 Université de Fribourg (Suisse Département
Chebfun and equispaced data
 Chebfun and equispaced data Georges Klein University of Oxford SIAM Annual Meeting, San Diego, July 12, 2013 Outline 1 1D Interpolation, Chebfun and equispaced data 2 3 (joint work with R. Platte) G. Klein
Chebfun and equispaced data Georges Klein University of Oxford SIAM Annual Meeting, San Diego, July 12, 2013 Outline 1 1D Interpolation, Chebfun and equispaced data 2 3 (joint work with R. Platte) G. Klein
Barycentric rational interpolation with no poles and high rates of approximation
 Barycentric rational interpolation with no poles and high rates of approximation Michael S. Floater Kai Hormann Abstract It is well known that rational interpolation sometimes gives better approximations
Barycentric rational interpolation with no poles and high rates of approximation Michael S. Floater Kai Hormann Abstract It is well known that rational interpolation sometimes gives better approximations
Mathematical Economics: Lecture 2
 Mathematical Economics: Lecture 2 Yu Ren WISE, Xiamen University September 25, 2012 Outline 1 Number Line The number line, origin (Figure 2.1 Page 11) Number Line Interval (a, b) = {x R 1 : a < x < b}
Mathematical Economics: Lecture 2 Yu Ren WISE, Xiamen University September 25, 2012 Outline 1 Number Line The number line, origin (Figure 2.1 Page 11) Number Line Interval (a, b) = {x R 1 : a < x < b}
Chapter 2 Interpolation
 Chapter 2 Interpolation Experiments usually produce a discrete set of data points (x i, f i ) which represent the value of a function f (x) for a finite set of arguments {x 0...x n }. If additional data
Chapter 2 Interpolation Experiments usually produce a discrete set of data points (x i, f i ) which represent the value of a function f (x) for a finite set of arguments {x 0...x n }. If additional data
(0, 0), (1, ), (2, ), (3, ), (4, ), (5, ), (6, ).
 1 Interpolation: The method of constructing new data points within the range of a finite set of known data points That is if (x i, y i ), i = 1, N are known, with y i the dependent variable and x i [x
1 Interpolation: The method of constructing new data points within the range of a finite set of known data points That is if (x i, y i ), i = 1, N are known, with y i the dependent variable and x i [x
A rational interpolation scheme with super-polynomial rate of convergence
 Center for Turbulence Research Annual Research Briefs 2008 31 A rational interpolation scheme with super-polynomial rate of convergence By Q. Wang, P. Moin AND G. Iaccarino 1. Motivation and objectives
Center for Turbulence Research Annual Research Briefs 2008 31 A rational interpolation scheme with super-polynomial rate of convergence By Q. Wang, P. Moin AND G. Iaccarino 1. Motivation and objectives
Limits at Infinity. Horizontal Asymptotes. Definition (Limits at Infinity) Horizontal Asymptotes
 Limits at Infinity If a function f has a domain that is unbounded, that is, one of the endpoints of its domain is ±, we can determine the long term behavior of the function using a it at infinity. Definition
Limits at Infinity If a function f has a domain that is unbounded, that is, one of the endpoints of its domain is ±, we can determine the long term behavior of the function using a it at infinity. Definition
Scientific Computing
 2301678 Scientific Computing Chapter 2 Interpolation and Approximation Paisan Nakmahachalasint Paisan.N@chula.ac.th Chapter 2 Interpolation and Approximation p. 1/66 Contents 1. Polynomial interpolation
2301678 Scientific Computing Chapter 2 Interpolation and Approximation Paisan Nakmahachalasint Paisan.N@chula.ac.th Chapter 2 Interpolation and Approximation p. 1/66 Contents 1. Polynomial interpolation
10.1 Sequences. Example: A sequence is a function f(n) whose domain is a subset of the integers. Notation: *Note: n = 0 vs. n = 1.
 10.1 Sequences Example: A sequence is a function f(n) whose domain is a subset of the integers. Notation: *Note: n = 0 vs. n = 1 Examples: EX1: Find a formula for the general term a n of the sequence,
10.1 Sequences Example: A sequence is a function f(n) whose domain is a subset of the integers. Notation: *Note: n = 0 vs. n = 1 Examples: EX1: Find a formula for the general term a n of the sequence,
7.4* General logarithmic and exponential functions
 7.4* General logarithmic and exponential functions Mark Woodard Furman U Fall 2010 Mark Woodard (Furman U) 7.4* General logarithmic and exponential functions Fall 2010 1 / 9 Outline 1 General exponential
7.4* General logarithmic and exponential functions Mark Woodard Furman U Fall 2010 Mark Woodard (Furman U) 7.4* General logarithmic and exponential functions Fall 2010 1 / 9 Outline 1 General exponential
11.6: Ratio and Root Tests Page 1. absolutely convergent, conditionally convergent, or divergent?
 .6: Ratio and Root Tests Page Questions ( 3) n n 3 ( 3) n ( ) n 5 + n ( ) n e n ( ) n+ n2 2 n Example Show that ( ) n n ln n ( n 2 ) n + 2n 2 + converges for all x. Deduce that = 0 for all x. Solutions
.6: Ratio and Root Tests Page Questions ( 3) n n 3 ( 3) n ( ) n 5 + n ( ) n e n ( ) n+ n2 2 n Example Show that ( ) n n ln n ( n 2 ) n + 2n 2 + converges for all x. Deduce that = 0 for all x. Solutions
OBJECTIVE Find limits of functions, if they exist, using numerical or graphical methods.
 1.1 Limits: A Numerical and Graphical Approach OBJECTIVE Find limits of functions, if they exist, using numerical or graphical methods. 1.1 Limits: A Numerical and Graphical Approach DEFINITION: As x approaches
1.1 Limits: A Numerical and Graphical Approach OBJECTIVE Find limits of functions, if they exist, using numerical or graphical methods. 1.1 Limits: A Numerical and Graphical Approach DEFINITION: As x approaches
DIFFERENTIATION RULES
 3 DIFFERENTIATION RULES DIFFERENTIATION RULES We have: Seen how to interpret derivatives as slopes and rates of change Seen how to estimate derivatives of functions given by tables of values Learned how
3 DIFFERENTIATION RULES DIFFERENTIATION RULES We have: Seen how to interpret derivatives as slopes and rates of change Seen how to estimate derivatives of functions given by tables of values Learned how
University of Houston, Department of Mathematics Numerical Analysis, Fall 2005
 4 Interpolation 4.1 Polynomial interpolation Problem: LetP n (I), n ln, I := [a,b] lr, be the linear space of polynomials of degree n on I, P n (I) := { p n : I lr p n (x) = n i=0 a i x i, a i lr, 0 i
4 Interpolation 4.1 Polynomial interpolation Problem: LetP n (I), n ln, I := [a,b] lr, be the linear space of polynomials of degree n on I, P n (I) := { p n : I lr p n (x) = n i=0 a i x i, a i lr, 0 i
H 2, Numerical Algorithms 5 (1993)
 List of publications Jean Paul Berrut Refereed: [1] Baryzentrische Formeln zur trigonometrischen Interpolation (I), J. Appl. Math. Phys. (ZAMP) 35 (1984) 91 105. [2] Baryzentrische Formeln zur trigonometrischen
List of publications Jean Paul Berrut Refereed: [1] Baryzentrische Formeln zur trigonometrischen Interpolation (I), J. Appl. Math. Phys. (ZAMP) 35 (1984) 91 105. [2] Baryzentrische Formeln zur trigonometrischen
8.1 Sequences. Example: A sequence is a function f(n) whose domain is a subset of the integers. Notation: *Note: n = 0 vs. n = 1.
 8. Sequences Example: A sequence is a function f(n) whose domain is a subset of the integers. Notation: *Note: n = 0 vs. n = Examples: 6. Find a formula for the general term a n of the sequence, assuming
8. Sequences Example: A sequence is a function f(n) whose domain is a subset of the integers. Notation: *Note: n = 0 vs. n = Examples: 6. Find a formula for the general term a n of the sequence, assuming
3 a = 3 b c 2 = a 2 + b 2 = 2 2 = 4 c 2 = 3b 2 + b 2 = 4b 2 = 4 b 2 = 1 b = 1 a = 3b = 3. x 2 3 y2 1 = 1.
 MATH 222 LEC SECOND MIDTERM EXAM THU NOV 8 PROBLEM ( 5 points ) Find the standard-form equation for the hyperbola which has its foci at F ± (±2, ) and whose asymptotes are y ± 3 x The calculations b a
MATH 222 LEC SECOND MIDTERM EXAM THU NOV 8 PROBLEM ( 5 points ) Find the standard-form equation for the hyperbola which has its foci at F ± (±2, ) and whose asymptotes are y ± 3 x The calculations b a
Math 651 Introduction to Numerical Analysis I Fall SOLUTIONS: Homework Set 1
 ath 651 Introduction to Numerical Analysis I Fall 2010 SOLUTIONS: Homework Set 1 1. Consider the polynomial f(x) = x 2 x 2. (a) Find P 1 (x), P 2 (x) and P 3 (x) for f(x) about x 0 = 0. What is the relation
ath 651 Introduction to Numerical Analysis I Fall 2010 SOLUTIONS: Homework Set 1 1. Consider the polynomial f(x) = x 2 x 2. (a) Find P 1 (x), P 2 (x) and P 3 (x) for f(x) about x 0 = 0. What is the relation
80 Wyner PreCalculus Spring 2017
 80 Wyner PreCalculus Spring 2017 CHAPTER NINE: DERIVATIVES Review May 16 Test May 23 Calculus begins with the study of rates of change, called derivatives. For example, the derivative of velocity is acceleration
80 Wyner PreCalculus Spring 2017 CHAPTER NINE: DERIVATIVES Review May 16 Test May 23 Calculus begins with the study of rates of change, called derivatives. For example, the derivative of velocity is acceleration
Lecture 10 Polynomial interpolation
 Lecture 10 Polynomial interpolation Weinan E 1,2 and Tiejun Li 2 1 Department of Mathematics, Princeton University, weinan@princeton.edu 2 School of Mathematical Sciences, Peking University, tieli@pku.edu.cn
Lecture 10 Polynomial interpolation Weinan E 1,2 and Tiejun Li 2 1 Department of Mathematics, Princeton University, weinan@princeton.edu 2 School of Mathematical Sciences, Peking University, tieli@pku.edu.cn
Lecture Note 3: Polynomial Interpolation. Xiaoqun Zhang Shanghai Jiao Tong University
 Lecture Note 3: Polynomial Interpolation Xiaoqun Zhang Shanghai Jiao Tong University Last updated: October 24, 2013 1.1 Introduction We first look at some examples. Lookup table for f(x) = 2 π x 0 e x2
Lecture Note 3: Polynomial Interpolation Xiaoqun Zhang Shanghai Jiao Tong University Last updated: October 24, 2013 1.1 Introduction We first look at some examples. Lookup table for f(x) = 2 π x 0 e x2
Vectors in Function Spaces
 Jim Lambers MAT 66 Spring Semester 15-16 Lecture 18 Notes These notes correspond to Section 6.3 in the text. Vectors in Function Spaces We begin with some necessary terminology. A vector space V, also
Jim Lambers MAT 66 Spring Semester 15-16 Lecture 18 Notes These notes correspond to Section 6.3 in the text. Vectors in Function Spaces We begin with some necessary terminology. A vector space V, also
Interpolation Theory
 Numerical Analysis Massoud Malek Interpolation Theory The concept of interpolation is to select a function P (x) from a given class of functions in such a way that the graph of y P (x) passes through the
Numerical Analysis Massoud Malek Interpolation Theory The concept of interpolation is to select a function P (x) from a given class of functions in such a way that the graph of y P (x) passes through the
SMOOTH APPROXIMATION OF DATA WITH APPLICATIONS TO INTERPOLATING AND SMOOTHING. Karel Segeth Institute of Mathematics, Academy of Sciences, Prague
 SMOOTH APPROXIMATION OF DATA WITH APPLICATIONS TO INTERPOLATING AND SMOOTHING Karel Segeth Institute of Mathematics, Academy of Sciences, Prague CONTENTS The problem of interpolating and smoothing Smooth
SMOOTH APPROXIMATION OF DATA WITH APPLICATIONS TO INTERPOLATING AND SMOOTHING Karel Segeth Institute of Mathematics, Academy of Sciences, Prague CONTENTS The problem of interpolating and smoothing Smooth
ON A WEIGHTED INTERPOLATION OF FUNCTIONS WITH CIRCULAR MAJORANT
 ON A WEIGHTED INTERPOLATION OF FUNCTIONS WITH CIRCULAR MAJORANT Received: 31 July, 2008 Accepted: 06 February, 2009 Communicated by: SIMON J SMITH Department of Mathematics and Statistics La Trobe University,
ON A WEIGHTED INTERPOLATION OF FUNCTIONS WITH CIRCULAR MAJORANT Received: 31 July, 2008 Accepted: 06 February, 2009 Communicated by: SIMON J SMITH Department of Mathematics and Statistics La Trobe University,
Lecture Note 3: Interpolation and Polynomial Approximation. Xiaoqun Zhang Shanghai Jiao Tong University
 Lecture Note 3: Interpolation and Polynomial Approximation Xiaoqun Zhang Shanghai Jiao Tong University Last updated: October 10, 2015 2 Contents 1.1 Introduction................................ 3 1.1.1
Lecture Note 3: Interpolation and Polynomial Approximation Xiaoqun Zhang Shanghai Jiao Tong University Last updated: October 10, 2015 2 Contents 1.1 Introduction................................ 3 1.1.1
APPROXIMATING CONTINUOUS FUNCTIONS: WEIERSTRASS, BERNSTEIN, AND RUNGE
 APPROXIMATING CONTINUOUS FUNCTIONS: WEIERSTRASS, BERNSTEIN, AND RUNGE WILLIE WAI-YEUNG WONG. Introduction This set of notes is meant to describe some aspects of polynomial approximations to continuous
APPROXIMATING CONTINUOUS FUNCTIONS: WEIERSTRASS, BERNSTEIN, AND RUNGE WILLIE WAI-YEUNG WONG. Introduction This set of notes is meant to describe some aspects of polynomial approximations to continuous
Jim Lambers MAT 460/560 Fall Semester Practice Final Exam
 Jim Lambers MAT 460/560 Fall Semester 2009-10 Practice Final Exam 1. Let f(x) = sin 2x + cos 2x. (a) Write down the 2nd Taylor polynomial P 2 (x) of f(x) centered around x 0 = 0. (b) Write down the corresponding
Jim Lambers MAT 460/560 Fall Semester 2009-10 Practice Final Exam 1. Let f(x) = sin 2x + cos 2x. (a) Write down the 2nd Taylor polynomial P 2 (x) of f(x) centered around x 0 = 0. (b) Write down the corresponding
Jim Lambers MAT 169 Fall Semester Lecture 6 Notes. a n. n=1. S = lim s k = lim. n=1. n=1
 Jim Lambers MAT 69 Fall Semester 2009-0 Lecture 6 Notes These notes correspond to Section 8.3 in the text. The Integral Test Previously, we have defined the sum of a convergent infinite series to be the
Jim Lambers MAT 69 Fall Semester 2009-0 Lecture 6 Notes These notes correspond to Section 8.3 in the text. The Integral Test Previously, we have defined the sum of a convergent infinite series to be the
Sec 4.1 Limits, Informally. When we calculated f (x), we first started with the difference quotient. f(x + h) f(x) h
 1 Sec 4.1 Limits, Informally When we calculated f (x), we first started with the difference quotient f(x + h) f(x) h and made h small. In other words, f (x) is the number f(x+h) f(x) approaches as h gets
1 Sec 4.1 Limits, Informally When we calculated f (x), we first started with the difference quotient f(x + h) f(x) h and made h small. In other words, f (x) is the number f(x+h) f(x) approaches as h gets
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
 Calculus I - Homework Chapter 2 Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Determine whether the graph is the graph of a function. 1) 1)
Calculus I - Homework Chapter 2 Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Determine whether the graph is the graph of a function. 1) 1)
A. Evaluate log Evaluate Logarithms
 A. Evaluate log 2 16. Evaluate Logarithms Evaluate Logarithms B. Evaluate. C. Evaluate. Evaluate Logarithms D. Evaluate log 17 17. Evaluate Logarithms Evaluate. A. 4 B. 4 C. 2 D. 2 A. Evaluate log 8 512.
A. Evaluate log 2 16. Evaluate Logarithms Evaluate Logarithms B. Evaluate. C. Evaluate. Evaluate Logarithms D. Evaluate log 17 17. Evaluate Logarithms Evaluate. A. 4 B. 4 C. 2 D. 2 A. Evaluate log 8 512.
Aim: How do we prepare for AP Problems on limits, continuity and differentiability? f (x)
 Name AP Calculus Date Supplemental Review 1 Aim: How do we prepare for AP Problems on limits, continuity and differentiability? Do Now: Use the graph of f(x) to evaluate each of the following: 1. lim x
Name AP Calculus Date Supplemental Review 1 Aim: How do we prepare for AP Problems on limits, continuity and differentiability? Do Now: Use the graph of f(x) to evaluate each of the following: 1. lim x
y2 + 4y - 5 c a + b 27 i C) ) (16, ) B) (16 3 3, )
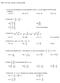 MAT 107 Final, Version A, Spring 2008 1) If (4, 4) is the endpoint of a line segment, and (2, 1) is its midpoint, find the other endpoint. A) (0, 7) B) (-2, 0) C) (8, 10) D) (0, -2) 2) Solve for x: A)
MAT 107 Final, Version A, Spring 2008 1) If (4, 4) is the endpoint of a line segment, and (2, 1) is its midpoint, find the other endpoint. A) (0, 7) B) (-2, 0) C) (8, 10) D) (0, -2) 2) Solve for x: A)
JUST THE MATHS UNIT NUMBER DIFFERENTIATION APPLICATIONS 5 (Maclaurin s and Taylor s series) A.J.Hobson
 JUST THE MATHS UNIT NUMBER.5 DIFFERENTIATION APPLICATIONS 5 (Maclaurin s and Taylor s series) by A.J.Hobson.5. Maclaurin s series.5. Standard series.5.3 Taylor s series.5.4 Exercises.5.5 Answers to exercises
JUST THE MATHS UNIT NUMBER.5 DIFFERENTIATION APPLICATIONS 5 (Maclaurin s and Taylor s series) by A.J.Hobson.5. Maclaurin s series.5. Standard series.5.3 Taylor s series.5.4 Exercises.5.5 Answers to exercises
Lectures 9-10: Polynomial and piecewise polynomial interpolation
 Lectures 9-1: Polynomial and piecewise polynomial interpolation Let f be a function, which is only known at the nodes x 1, x,, x n, ie, all we know about the function f are its values y j = f(x j ), j
Lectures 9-1: Polynomial and piecewise polynomial interpolation Let f be a function, which is only known at the nodes x 1, x,, x n, ie, all we know about the function f are its values y j = f(x j ), j
1 + lim. n n+1. f(x) = x + 1, x 1. and we check that f is increasing, instead. Using the quotient rule, we easily find that. 1 (x + 1) 1 x (x + 1) 2 =
 Chapter 5 Sequences and series 5. Sequences Definition 5. (Sequence). A sequence is a function which is defined on the set N of natural numbers. Since such a function is uniquely determined by its values
Chapter 5 Sequences and series 5. Sequences Definition 5. (Sequence). A sequence is a function which is defined on the set N of natural numbers. Since such a function is uniquely determined by its values
International Competition in Mathematics for Universtiy Students in Plovdiv, Bulgaria 1994
 International Competition in Mathematics for Universtiy Students in Plovdiv, Bulgaria 1994 1 PROBLEMS AND SOLUTIONS First day July 29, 1994 Problem 1. 13 points a Let A be a n n, n 2, symmetric, invertible
International Competition in Mathematics for Universtiy Students in Plovdiv, Bulgaria 1994 1 PROBLEMS AND SOLUTIONS First day July 29, 1994 Problem 1. 13 points a Let A be a n n, n 2, symmetric, invertible
EQ: What are limits, and how do we find them? Finite limits as x ± Horizontal Asymptote. Example Horizontal Asymptote
 Finite limits as x ± The symbol for infinity ( ) does not represent a real number. We use to describe the behavior of a function when the values in its domain or range outgrow all finite bounds. For example,
Finite limits as x ± The symbol for infinity ( ) does not represent a real number. We use to describe the behavior of a function when the values in its domain or range outgrow all finite bounds. For example,
Lecture 32: Taylor Series and McLaurin series We saw last day that some functions are equal to a power series on part of their domain.
 Lecture 32: Taylor Series and McLaurin series We saw last day that some functions are equal to a power series on part of their domain. For example f(x) = 1 1 x = 1 + x + x2 + x 3 + = ln(1 + x) = x x2 2
Lecture 32: Taylor Series and McLaurin series We saw last day that some functions are equal to a power series on part of their domain. For example f(x) = 1 1 x = 1 + x + x2 + x 3 + = ln(1 + x) = x x2 2
10/22/16. 1 Math HL - Santowski SKILLS REVIEW. Lesson 15 Graphs of Rational Functions. Lesson Objectives. (A) Rational Functions
 Lesson 15 Graphs of Rational Functions SKILLS REVIEW! Use function composition to prove that the following two funtions are inverses of each other. 2x 3 f(x) = g(x) = 5 2 x 1 1 2 Lesson Objectives! The
Lesson 15 Graphs of Rational Functions SKILLS REVIEW! Use function composition to prove that the following two funtions are inverses of each other. 2x 3 f(x) = g(x) = 5 2 x 1 1 2 Lesson Objectives! The
INTERPOLATION. and y i = cos x i, i = 0, 1, 2 This gives us the three points. Now find a quadratic polynomial. p(x) = a 0 + a 1 x + a 2 x 2.
 INTERPOLATION Interpolation is a process of finding a formula (often a polynomial) whose graph will pass through a given set of points (x, y). As an example, consider defining and x 0 = 0, x 1 = π/4, x
INTERPOLATION Interpolation is a process of finding a formula (often a polynomial) whose graph will pass through a given set of points (x, y). As an example, consider defining and x 0 = 0, x 1 = π/4, x
MAT 107 College Algebra Fall 2013 Name. Final Exam, Version X
 MAT 107 College Algebra Fall 013 Name Final Exam, Version X EKU ID Instructor Part 1: No calculators are allowed on this section. Show all work on your paper. Circle your answer. Each question is worth
MAT 107 College Algebra Fall 013 Name Final Exam, Version X EKU ID Instructor Part 1: No calculators are allowed on this section. Show all work on your paper. Circle your answer. Each question is worth
AP Calculus Summer Homework
 Class: Date: AP Calculus Summer Homework Show your work. Place a circle around your final answer. 1. Use the properties of logarithms to find the exact value of the expression. Do not use a calculator.
Class: Date: AP Calculus Summer Homework Show your work. Place a circle around your final answer. 1. Use the properties of logarithms to find the exact value of the expression. Do not use a calculator.
Convergence of sequences and series
 Convergence of sequences and series A sequence f is a map from N the positive integers to a set. We often write the map outputs as f n rather than f(n). Often we just list the outputs in order and leave
Convergence of sequences and series A sequence f is a map from N the positive integers to a set. We often write the map outputs as f n rather than f(n). Often we just list the outputs in order and leave
3.4 Introduction to power series
 3.4 Introduction to power series Definition 3.4.. A polynomial in the variable x is an expression of the form n a i x i = a 0 + a x + a 2 x 2 + + a n x n + a n x n i=0 or a n x n + a n x n + + a 2 x 2
3.4 Introduction to power series Definition 3.4.. A polynomial in the variable x is an expression of the form n a i x i = a 0 + a x + a 2 x 2 + + a n x n + a n x n i=0 or a n x n + a n x n + + a 2 x 2
Cubic Splines MATH 375. J. Robert Buchanan. Fall Department of Mathematics. J. Robert Buchanan Cubic Splines
 Cubic Splines MATH 375 J. Robert Buchanan Department of Mathematics Fall 2006 Introduction Given data {(x 0, f(x 0 )), (x 1, f(x 1 )),...,(x n, f(x n ))} which we wish to interpolate using a polynomial...
Cubic Splines MATH 375 J. Robert Buchanan Department of Mathematics Fall 2006 Introduction Given data {(x 0, f(x 0 )), (x 1, f(x 1 )),...,(x n, f(x n ))} which we wish to interpolate using a polynomial...
CH 2: Limits and Derivatives
 2 The tangent and velocity problems CH 2: Limits and Derivatives the tangent line to a curve at a point P, is the line that has the same slope as the curve at that point P, ie the slope of the tangent
2 The tangent and velocity problems CH 2: Limits and Derivatives the tangent line to a curve at a point P, is the line that has the same slope as the curve at that point P, ie the slope of the tangent
Topic 3 Outline. What is a Limit? Calculating Limits Infinite Limits Limits at Infinity Continuity. 1 Limits and Continuity
 Topic 3 Outline 1 Limits and Continuity What is a Limit? Calculating Limits Infinite Limits Limits at Infinity Continuity D. Kalajdzievska (University of Manitoba) Math 1520 Fall 2015 1 / 27 Topic 3 Learning
Topic 3 Outline 1 Limits and Continuity What is a Limit? Calculating Limits Infinite Limits Limits at Infinity Continuity D. Kalajdzievska (University of Manitoba) Math 1520 Fall 2015 1 / 27 Topic 3 Learning
Math 113: Quiz 6 Solutions, Fall 2015 Chapter 9
 Math 3: Quiz 6 Solutions, Fall 05 Chapter 9 Keep in mind that more than one test will wor for a given problem. I chose one that wored. In addition, the statement lim a LR b means that L Hôpital s rule
Math 3: Quiz 6 Solutions, Fall 05 Chapter 9 Keep in mind that more than one test will wor for a given problem. I chose one that wored. In addition, the statement lim a LR b means that L Hôpital s rule
Analysis II: Basic knowledge of real analysis: Part V, Power Series, Differentiation, and Taylor Series
 .... Analysis II: Basic knowledge of real analysis: Part V, Power Series, Differentiation, and Taylor Series Kenichi Maruno Department of Mathematics, The University of Texas - Pan American March 4, 20
.... Analysis II: Basic knowledge of real analysis: Part V, Power Series, Differentiation, and Taylor Series Kenichi Maruno Department of Mathematics, The University of Texas - Pan American March 4, 20
Numerical Methods. King Saud University
 Numerical Methods King Saud University Aims In this lecture, we will... find the approximate solutions of derivative (first- and second-order) and antiderivative (definite integral only). Numerical Differentiation
Numerical Methods King Saud University Aims In this lecture, we will... find the approximate solutions of derivative (first- and second-order) and antiderivative (definite integral only). Numerical Differentiation
function independent dependent domain range graph of the function The Vertical Line Test
 Functions A quantity y is a function of another quantity x if there is some rule (an algebraic equation, a graph, a table, or as an English description) by which a unique value is assigned to y by a corresponding
Functions A quantity y is a function of another quantity x if there is some rule (an algebraic equation, a graph, a table, or as an English description) by which a unique value is assigned to y by a corresponding
Review I: Interpolation
 Review I: Interpolation Varun Shankar January, 206 Introduction In this document, we review interpolation by polynomials. Unlike many reviews, we will not stop there: we will discuss how to differentiate
Review I: Interpolation Varun Shankar January, 206 Introduction In this document, we review interpolation by polynomials. Unlike many reviews, we will not stop there: we will discuss how to differentiate
Section 5.1 Determine if a function is a polynomial function. State the degree of a polynomial function.
 Test Instructions Objectives Section 5.1 Section 5.1 Determine if a function is a polynomial function. State the degree of a polynomial function. Form a polynomial whose zeros and degree are given. Graph
Test Instructions Objectives Section 5.1 Section 5.1 Determine if a function is a polynomial function. State the degree of a polynomial function. Form a polynomial whose zeros and degree are given. Graph
Applied Math 205. Full office hour schedule:
 Applied Math 205 Full office hour schedule: Rui: Monday 3pm 4:30pm in the IACS lounge Martin: Monday 4:30pm 6pm in the IACS lounge Chris: Tuesday 1pm 3pm in Pierce Hall, Room 305 Nao: Tuesday 3pm 4:30pm
Applied Math 205 Full office hour schedule: Rui: Monday 3pm 4:30pm in the IACS lounge Martin: Monday 4:30pm 6pm in the IACS lounge Chris: Tuesday 1pm 3pm in Pierce Hall, Room 305 Nao: Tuesday 3pm 4:30pm
Calculus. Central role in much of modern science Physics, especially kinematics and electrodynamics Economics, engineering, medicine, chemistry, etc.
 Calculus Calculus - the study of change, as related to functions Formally co-developed around the 1660 s by Newton and Leibniz Two main branches - differential and integral Central role in much of modern
Calculus Calculus - the study of change, as related to functions Formally co-developed around the 1660 s by Newton and Leibniz Two main branches - differential and integral Central role in much of modern
Limits at Infinity. Use algebraic techniques to help with indeterminate forms of ± Use substitutions to evaluate limits of compositions of functions.
 SUGGESTED REFERENCE MATERIAL: Limits at Infinity As you work through the problems listed below, you should reference Chapter. of the recommended textbook (or the equivalent chapter in your alternative
SUGGESTED REFERENCE MATERIAL: Limits at Infinity As you work through the problems listed below, you should reference Chapter. of the recommended textbook (or the equivalent chapter in your alternative
A Library of Functions
 LibraryofFunctions.nb 1 A Library of Functions Any study of calculus must start with the study of functions. Functions are fundamental to mathematics. In its everyday use the word function conveys to us
LibraryofFunctions.nb 1 A Library of Functions Any study of calculus must start with the study of functions. Functions are fundamental to mathematics. In its everyday use the word function conveys to us
1. If 1, ω, ω 2, -----, ω 9 are the 10 th roots of unity, then (1 + ω) (1 + ω 2 ) (1 + ω 9 ) is A) 1 B) 1 C) 10 D) 0
 4 INUTES. If, ω, ω, -----, ω 9 are the th roots of unity, then ( + ω) ( + ω ) ----- ( + ω 9 ) is B) D) 5. i If - i = a + ib, then a =, b = B) a =, b = a =, b = D) a =, b= 3. Find the integral values for
4 INUTES. If, ω, ω, -----, ω 9 are the th roots of unity, then ( + ω) ( + ω ) ----- ( + ω 9 ) is B) D) 5. i If - i = a + ib, then a =, b = B) a =, b = a =, b = D) a =, b= 3. Find the integral values for
b n x n + b n 1 x n b 1 x + b 0
 Math Partial Fractions Stewart 7.4 Integrating basic rational functions. For a function f(x), we have examined several algebraic methods for finding its indefinite integral (antiderivative) F (x) = f(x)
Math Partial Fractions Stewart 7.4 Integrating basic rational functions. For a function f(x), we have examined several algebraic methods for finding its indefinite integral (antiderivative) F (x) = f(x)
Legendre s Equation. PHYS Southern Illinois University. October 18, 2016
 Legendre s Equation PHYS 500 - Southern Illinois University October 18, 2016 PHYS 500 - Southern Illinois University Legendre s Equation October 18, 2016 1 / 11 Legendre s Equation Recall We are trying
Legendre s Equation PHYS 500 - Southern Illinois University October 18, 2016 PHYS 500 - Southern Illinois University Legendre s Equation October 18, 2016 1 / 11 Legendre s Equation Recall We are trying
be the set of complex valued 2π-periodic functions f on R such that
 . Fourier series. Definition.. Given a real number P, we say a complex valued function f on R is P -periodic if f(x + P ) f(x) for all x R. We let be the set of complex valued -periodic functions f on
. Fourier series. Definition.. Given a real number P, we say a complex valued function f on R is P -periodic if f(x + P ) f(x) for all x R. We let be the set of complex valued -periodic functions f on
SPLINE INTERPOLATION
 Spline Background SPLINE INTERPOLATION Problem: high degree interpolating polynomials often have extra oscillations. Example: Runge function f(x = 1 1+4x 2, x [ 1, 1]. 1 1/(1+4x 2 and P 8 (x and P 16 (x
Spline Background SPLINE INTERPOLATION Problem: high degree interpolating polynomials often have extra oscillations. Example: Runge function f(x = 1 1+4x 2, x [ 1, 1]. 1 1/(1+4x 2 and P 8 (x and P 16 (x
NUMERICAL ANALYSIS I. MARTIN LOTZ School of Mathematics The University of Manchester. May 2016
 NUMERICAL ANALYSIS I by MARTIN LOTZ School of Mathematics The University of Manchester May 06 Contents Contents ii Week. Computational Complexity....................... Accuracy...............................
NUMERICAL ANALYSIS I by MARTIN LOTZ School of Mathematics The University of Manchester May 06 Contents Contents ii Week. Computational Complexity....................... Accuracy...............................
An idea how to solve some of the problems. diverges the same must hold for the original series. T 1 p T 1 p + 1 p 1 = 1. dt = lim
 An idea how to solve some of the problems 5.2-2. (a) Does not converge: By multiplying across we get Hence 2k 2k 2 /2 k 2k2 k 2 /2 k 2 /2 2k 2k 2 /2 k. As the series diverges the same must hold for the
An idea how to solve some of the problems 5.2-2. (a) Does not converge: By multiplying across we get Hence 2k 2k 2 /2 k 2k2 k 2 /2 k 2 /2 2k 2k 2 /2 k. As the series diverges the same must hold for the
AP Calculus (BC) Chapter 9 Test No Calculator Section Name: Date: Period:
 WORKSHEET: Series, Taylor Series AP Calculus (BC) Chapter 9 Test No Calculator Section Name: Date: Period: 1 Part I. Multiple-Choice Questions (5 points each; please circle the correct answer.) 1. The
WORKSHEET: Series, Taylor Series AP Calculus (BC) Chapter 9 Test No Calculator Section Name: Date: Period: 1 Part I. Multiple-Choice Questions (5 points each; please circle the correct answer.) 1. The
Three hours THE UNIVERSITY OF MANCHESTER. 24th January
 Three hours MATH41011 THE UNIVERSITY OF MANCHESTER FOURIER ANALYSIS AND LEBESGUE INTEGRATION 24th January 2013 9.45 12.45 Answer ALL SIX questions in Section A (25 marks in total). Answer THREE of the
Three hours MATH41011 THE UNIVERSITY OF MANCHESTER FOURIER ANALYSIS AND LEBESGUE INTEGRATION 24th January 2013 9.45 12.45 Answer ALL SIX questions in Section A (25 marks in total). Answer THREE of the
2.6 Logarithmic Functions. Inverse Functions. Question: What is the relationship between f(x) = x 2 and g(x) = x?
 Inverse Functions Question: What is the relationship between f(x) = x 3 and g(x) = 3 x? Question: What is the relationship between f(x) = x 2 and g(x) = x? Definition (One-to-One Function) A function f
Inverse Functions Question: What is the relationship between f(x) = x 3 and g(x) = 3 x? Question: What is the relationship between f(x) = x 2 and g(x) = x? Definition (One-to-One Function) A function f
Math Section Bekki George: 01/16/19. University of Houston. Bekki George (UH) Math /16/19 1 / 31
 Math 1431 Section 12200 Bekki George: bekki@math.uh.edu University of Houston 01/16/19 Bekki George (UH) Math 1431 01/16/19 1 / 31 Office Hours: Mondays 1-2pm, Tuesdays 2:45-3:30pm (also available by appointment)
Math 1431 Section 12200 Bekki George: bekki@math.uh.edu University of Houston 01/16/19 Bekki George (UH) Math 1431 01/16/19 1 / 31 Office Hours: Mondays 1-2pm, Tuesdays 2:45-3:30pm (also available by appointment)
Note on Newton Interpolation Formula
 Int. Journal of Math. Analysis, Vol. 6, 2012, no. 50, 2459-2465 Note on Newton Interpolation Formula Ramesh Kumar Muthumalai Department of Mathematics D.G. Vaishnav College, Arumbaam Chennai-600106, Tamilnadu,
Int. Journal of Math. Analysis, Vol. 6, 2012, no. 50, 2459-2465 Note on Newton Interpolation Formula Ramesh Kumar Muthumalai Department of Mathematics D.G. Vaishnav College, Arumbaam Chennai-600106, Tamilnadu,
The final is cumulative, but with more emphasis on chapters 3 and 4. There will be two parts.
 Math 141 Review for Final The final is cumulative, but with more emphasis on chapters 3 and 4. There will be two parts. Part 1 (no calculator) graphing (polynomial, rational, linear, exponential, and logarithmic
Math 141 Review for Final The final is cumulative, but with more emphasis on chapters 3 and 4. There will be two parts. Part 1 (no calculator) graphing (polynomial, rational, linear, exponential, and logarithmic
Engg. Math. II (Unit-IV) Numerical Analysis
 Dr. Satish Shukla of 33 Engg. Math. II (Unit-IV) Numerical Analysis Syllabus. Interpolation and Curve Fitting: Introduction to Interpolation; Calculus of Finite Differences; Finite Difference and Divided
Dr. Satish Shukla of 33 Engg. Math. II (Unit-IV) Numerical Analysis Syllabus. Interpolation and Curve Fitting: Introduction to Interpolation; Calculus of Finite Differences; Finite Difference and Divided
Numerical Analysis: Interpolation Part 1
 Numerical Analysis: Interpolation Part 1 Computer Science, Ben-Gurion University (slides based mostly on Prof. Ben-Shahar s notes) 2018/2019, Fall Semester BGU CS Interpolation (ver. 1.00) AY 2018/2019,
Numerical Analysis: Interpolation Part 1 Computer Science, Ben-Gurion University (slides based mostly on Prof. Ben-Shahar s notes) 2018/2019, Fall Semester BGU CS Interpolation (ver. 1.00) AY 2018/2019,
Constructing Approximations to Functions
 Constructing Approximations to Functions Given a function, f, if is often useful to it is often useful to approximate it by nicer functions. For example give a continuous function, f, it can be useful
Constructing Approximations to Functions Given a function, f, if is often useful to it is often useful to approximate it by nicer functions. For example give a continuous function, f, it can be useful
x x 1 x 2 + x 2 1 > 0. HW5. Text defines:
 Lecture 15: Last time: MVT. Special case: Rolle s Theorem (when f(a) = f(b)). Recall: Defn: Let f be defined on an interval I. f is increasing (or strictly increasing) if whenever x 1, x 2 I and x 2 >
Lecture 15: Last time: MVT. Special case: Rolle s Theorem (when f(a) = f(b)). Recall: Defn: Let f be defined on an interval I. f is increasing (or strictly increasing) if whenever x 1, x 2 I and x 2 >
Degree Master of Science in Mathematical Modelling and Scientific Computing Mathematical Methods I Thursday, 12th January 2012, 9:30 a.m.- 11:30 a.m.
 Degree Master of Science in Mathematical Modelling and Scientific Computing Mathematical Methods I Thursday, 12th January 2012, 9:30 a.m.- 11:30 a.m. Candidates should submit answers to a maximum of four
Degree Master of Science in Mathematical Modelling and Scientific Computing Mathematical Methods I Thursday, 12th January 2012, 9:30 a.m.- 11:30 a.m. Candidates should submit answers to a maximum of four
Power series solutions for 2nd order linear ODE s (not necessarily with constant coefficients) a n z n. n=0
 Lecture 22 Power series solutions for 2nd order linear ODE s (not necessarily with constant coefficients) Recall a few facts about power series: a n z n This series in z is centered at z 0. Here z can
Lecture 22 Power series solutions for 2nd order linear ODE s (not necessarily with constant coefficients) Recall a few facts about power series: a n z n This series in z is centered at z 0. Here z can
Interpolation. Chapter Interpolation. 7.2 Existence, Uniqueness and conditioning
 76 Chapter 7 Interpolation 7.1 Interpolation Definition 7.1.1. Interpolation of a given function f defined on an interval [a,b] by a polynomial p: Given a set of specified points {(t i,y i } n with {t
76 Chapter 7 Interpolation 7.1 Interpolation Definition 7.1.1. Interpolation of a given function f defined on an interval [a,b] by a polynomial p: Given a set of specified points {(t i,y i } n with {t
Review all the activities leading to Midterm 3. Review all the problems in the previous online homework sets (8+9+10).
 MA109, Activity 34: Review (Sections 3.6+3.7+4.1+4.2+4.3) Date: Objective: Additional Assignments: To prepare for Midterm 3, make sure that you can solve the types of problems listed in Activities 33 and
MA109, Activity 34: Review (Sections 3.6+3.7+4.1+4.2+4.3) Date: Objective: Additional Assignments: To prepare for Midterm 3, make sure that you can solve the types of problems listed in Activities 33 and
TAYLOR AND MACLAURIN SERIES
 TAYLOR AND MACLAURIN SERIES. Introduction Last time, we were able to represent a certain restricted class of functions as power series. This leads us to the question: can we represent more general functions
TAYLOR AND MACLAURIN SERIES. Introduction Last time, we were able to represent a certain restricted class of functions as power series. This leads us to the question: can we represent more general functions
Worksheet 7, Math 10560
 Worksheet 7, Math 0560 You must show all of your work to receive credit!. Determine whether the following series and sequences converge or diverge, and evaluate if they converge. If they diverge, you must
Worksheet 7, Math 0560 You must show all of your work to receive credit!. Determine whether the following series and sequences converge or diverge, and evaluate if they converge. If they diverge, you must
Chapter-2 Relations and Functions. Miscellaneous
 1 Chapter-2 Relations and Functions Miscellaneous Question 1: The relation f is defined by The relation g is defined by Show that f is a function and g is not a function. The relation f is defined as It
1 Chapter-2 Relations and Functions Miscellaneous Question 1: The relation f is defined by The relation g is defined by Show that f is a function and g is not a function. The relation f is defined as It
2 the maximum/minimum value is ( ).
 Math 60 Ch3 practice Test The graph of f(x) = 3(x 5) + 3 is with its vertex at ( maximum/minimum value is ( ). ) and the The graph of a quadratic function f(x) = x + x 1 is with its vertex at ( the maximum/minimum
Math 60 Ch3 practice Test The graph of f(x) = 3(x 5) + 3 is with its vertex at ( maximum/minimum value is ( ). ) and the The graph of a quadratic function f(x) = x + x 1 is with its vertex at ( the maximum/minimum
Chapter 4: Interpolation and Approximation. October 28, 2005
 Chapter 4: Interpolation and Approximation October 28, 2005 Outline 1 2.4 Linear Interpolation 2 4.1 Lagrange Interpolation 3 4.2 Newton Interpolation and Divided Differences 4 4.3 Interpolation Error
Chapter 4: Interpolation and Approximation October 28, 2005 Outline 1 2.4 Linear Interpolation 2 4.1 Lagrange Interpolation 3 4.2 Newton Interpolation and Divided Differences 4 4.3 Interpolation Error
Announcements. Topics: Homework: - sections 4.5 and * Read these sections and study solved examples in your textbook!
 Announcements Topics: - sections 4.5 and 5.1-5.5 * Read these sections and study solved examples in your textbook! Homework: - review lecture notes thoroughly - work on practice problems from the textbook
Announcements Topics: - sections 4.5 and 5.1-5.5 * Read these sections and study solved examples in your textbook! Homework: - review lecture notes thoroughly - work on practice problems from the textbook
EXAMPLES OF PROOFS BY INDUCTION
 EXAMPLES OF PROOFS BY INDUCTION KEITH CONRAD 1. Introduction In this handout we illustrate proofs by induction from several areas of mathematics: linear algebra, polynomial algebra, and calculus. Becoming
EXAMPLES OF PROOFS BY INDUCTION KEITH CONRAD 1. Introduction In this handout we illustrate proofs by induction from several areas of mathematics: linear algebra, polynomial algebra, and calculus. Becoming
Continuity. The Continuity Equation The equation that defines continuity at a point is called the Continuity Equation.
 Continuity A function is continuous at a particular x location when you can draw it through that location without picking up your pencil. To describe this mathematically, we have to use limits. Recall
Continuity A function is continuous at a particular x location when you can draw it through that location without picking up your pencil. To describe this mathematically, we have to use limits. Recall
11.5. The Chain Rule. Introduction. Prerequisites. Learning Outcomes
 The Chain Rule 11.5 Introduction In this Section we will see how to obtain the derivative of a composite function (often referred to as a function of a function ). To do this we use the chain rule. This
The Chain Rule 11.5 Introduction In this Section we will see how to obtain the derivative of a composite function (often referred to as a function of a function ). To do this we use the chain rule. This
Preliminary Examination, Part I Tuesday morning, August 31, 2004
 Preliminary Examination, Part I Tuesday morning, August 31, 24 This part of the examination consists of six problems. You should work all of the problems. Show all of your work in your workbook. Try to
Preliminary Examination, Part I Tuesday morning, August 31, 24 This part of the examination consists of six problems. You should work all of the problems. Show all of your work in your workbook. Try to
Dividing Polynomials: Remainder and Factor Theorems
 Dividing Polynomials: Remainder and Factor Theorems When we divide one polynomial by another, we obtain a quotient and a remainder. If the remainder is zero, then the divisor is a factor of the dividend.
Dividing Polynomials: Remainder and Factor Theorems When we divide one polynomial by another, we obtain a quotient and a remainder. If the remainder is zero, then the divisor is a factor of the dividend.
MATH 118, LECTURES 27 & 28: TAYLOR SERIES
 MATH 8, LECTURES 7 & 8: TAYLOR SERIES Taylor Series Suppose we know that the power series a n (x c) n converges on some interval c R < x < c + R to the function f(x). That is to say, we have f(x) = a 0
MATH 8, LECTURES 7 & 8: TAYLOR SERIES Taylor Series Suppose we know that the power series a n (x c) n converges on some interval c R < x < c + R to the function f(x). That is to say, we have f(x) = a 0
Final Exam A Name. 20 i C) Solve the equation by factoring. 4) x2 = x + 30 A) {-5, 6} B) {5, 6} C) {1, 30} D) {-5, -6} -9 ± i 3 14
 Final Exam A Name First, write the value(s) that make the denominator(s) zero. Then solve the equation. 1 1) x + 3 + 5 x - 3 = 30 (x + 3)(x - 3) 1) A) x -3, 3; B) x -3, 3; {4} C) No restrictions; {3} D)
Final Exam A Name First, write the value(s) that make the denominator(s) zero. Then solve the equation. 1 1) x + 3 + 5 x - 3 = 30 (x + 3)(x - 3) 1) A) x -3, 3; B) x -3, 3; {4} C) No restrictions; {3} D)
Function: exactly Functions as equations:
 Function: - a connection between sets in which each element of the first set corresponds with exactly one element of the second set o the reverse is not necessarily true, but if it is, the function is
Function: - a connection between sets in which each element of the first set corresponds with exactly one element of the second set o the reverse is not necessarily true, but if it is, the function is
Introduction and Review of Power Series
 Introduction and Review of Power Series Definition: A power series in powers of x a is an infinite series of the form c n (x a) n = c 0 + c 1 (x a) + c 2 (x a) 2 +...+c n (x a) n +... If a = 0, this is
Introduction and Review of Power Series Definition: A power series in powers of x a is an infinite series of the form c n (x a) n = c 0 + c 1 (x a) + c 2 (x a) 2 +...+c n (x a) n +... If a = 0, this is
Completion Date: Monday February 11, 2008
 MATH 4 (R) Winter 8 Intermediate Calculus I Solutions to Problem Set #4 Completion Date: Monday February, 8 Department of Mathematical and Statistical Sciences University of Alberta Question. [Sec..9,
MATH 4 (R) Winter 8 Intermediate Calculus I Solutions to Problem Set #4 Completion Date: Monday February, 8 Department of Mathematical and Statistical Sciences University of Alberta Question. [Sec..9,
 Student: Date: Instructor: kumnit nong Course: MATH 105 by Nong https://xlitemprodpearsoncmgcom/api/v1/print/math Assignment: CH test review 1 Find the transformation form of the quadratic function graphed
Student: Date: Instructor: kumnit nong Course: MATH 105 by Nong https://xlitemprodpearsoncmgcom/api/v1/print/math Assignment: CH test review 1 Find the transformation form of the quadratic function graphed
Lecture 4 : General Logarithms and Exponentials. a x = e x ln a, a > 0.
 For a > 0 an x any real number, we efine Lecture 4 : General Logarithms an Exponentials. a x = e x ln a, a > 0. The function a x is calle the exponential function with base a. Note that ln(a x ) = x ln
For a > 0 an x any real number, we efine Lecture 4 : General Logarithms an Exponentials. a x = e x ln a, a > 0. The function a x is calle the exponential function with base a. Note that ln(a x ) = x ln
