STABILITY AND OSCILLATIONS OF A CATENOID SOAP FILM SURFACE
|
|
|
- Millicent Marilynn Gilmore
- 5 years ago
- Views:
Transcription
1 STABILITY AND OSCILLATIONS OF A CATENOID SOAP FILM SURFACE Interpretable quantities and equations of motion derived from Sturm-Liouville theory for a minimized surface Sweden, Edited by ANDREAS ASKER Karlstad University
2 Abstract The system of a soap lm conguration suspended between two coaxial rings is considered. By perturbing the surface for the kinetic and potential energy functional, one obtains a second variational term. This contains information about the stability and oscillations of the extremal surface. Approaching the problem as a Sturm-Liouville problem, eigenvalues and eigenfunctions are obtained. These in turn provide interpretable result for the stability and oscillation of the extremal surface. One should therefore investigate further whether this mathematical formulation for a variational problem is applicable for more complicated problems in physics.
3 Contents 1 Introduction 4 Background Theory 4 3 Minimal surface 7 4 Stability of a soap lm Variational problem Perturbed surface and second variation Sturm-Liouville problem formulation Oscillations of a soap lm Oscillations about an extremal surface Conclusions 16 Appendix A The Catenoid equation 17 Appendix B Second variation in terms of ξ's 18
4 1 Introduction There are some physical phenomena in classical mechanics that are variational problems. A standard example is to determine the equilibrium conguration of a soap lm suspended between two coaxial rings. When considering a variational problem one obtain information about the shape of the conguration for the given system. It however does not present any information about stability of the extremal surface or about oscillations. These issues have been studied in Loyal Durand's paper [1], where the problem has been treated as an eigenfunction problem within the frame of Sturm-Liouville theory. The author of the present paper will demonstrate the analytic approach of determining the stability and oscillations for the system treated in [1]. Some background theory and additional steps, that were not included in [1], will be conducted. The considered system is the soap lm suspended between two parallel coaxial rings. Background Theory In order to describe a catenoid soap lm there are some mathematical concepts that are required. The author recommends the reader to be familiar with some of these concepts in order to be able to fully appreciate the content of this report. For example, the theory of variational principles and Lagrange's equations from the calculus of variations. However, some theory about second ordered partial dierential equation and Sturm-Liouville problems will be treated in this section. Second-order partial dierential equations arise in many areas of physics. Some examples of partial dierential equations are the heat equation, the wave equation and Laplace equation [, Page: 755,768,786]. Many partial dierential equations can be solved by a method called seperation of variables [, Page: 756]. Denition.1. Consider a linear partial dierential equation of a function T. The function T = T x, y) is said to be seperable if it factors into a function of x only times a function of y only, T x, y) = Xx)Y y) [, Page: ]. Remark.. The separation of variables method is not excluded to second order partial dierential equations only, but it is also relevant for higher order dierential equations. Example.3. A brief example, consider the time-dependent Schrödinger equation 4
5 with a time-independent potential V i Ψr, t) = t m Ψr, t) + V r)ψr, t). 1) To show that Equation 1) indeed admits a solution of the form Ψr, t) = ψr)ft), one must test it in the following way. Substituting Ψr, t) = ψr)ft) into Equation 1) and rearrange it, one nds that i 1 dft) ft) dt = 1 ψr) [ ] m ψr) + V r)ψr). ) Since the left-hand side depends only on t, and the right-hand side only on r, both sides must be equal to a constant. Therefore, Equation 1) is separable. Let this constant be E, which is referred to as a separation constant. From Equation ) one then obtains the two equations and i dft) dt = Eft), 3) m ψr) + V r)ψr) = Eψr). 4) Equation 3) has the solution ft) = Cexp iet/ ), where C is an arbitrary constant and Equation 4) is called the time-independent Schrödinger equation [3]. The time-independent Schrödinger equation in Example.3 is a central part of quantum mechanics when describing important physical systems. Furthermore, the resulting dierential equations for these systems are solved as an eigenfunction problem. This is due to a mathematical formulation of quantum mechanics which originates from Sturm-Liouville theory. Denition.4. Consider a dierential equation of the form [ px)y x) ] + [ qx) + λrx) ] yx) = 0, 5) where λ is a parameter and the prime-notation means derivative with respect to x. Assume that the functions px), p x), qx) and rx) are continuous on the interval [a, b] and px) 0 and rx) 0 everywhere in [a, b]. Then this, together with the boundary conditions α 1 ya) + α y a) = 0, and β 1 yb) + β y b) = 0, 6) where the coecients are assumed real and at least one α i and one β i are non-zero, is called a Sturm-Liouville problem [, Page: 687]. 5
6 By general conditions on px), qx) and rx), it turns out that there are special values of λ for which non-trivial solutions are obtained. These values of λ are called eigenvalues and the corresponding solutions are called eigenfunctions [, page:688]. By introducing the dierential operator L Equation 5) becomes Lyx) = [ px)y x) ] qx)yx), 7) Lyx) = λrx)yx). 8) Equation 8) is called a generalized eigenvalue problem and rx) is called a weight [, Page: 678, 688]. Lemma.5. Let px), qx) and rx) be real functions. Then L is a Hermitian operator. Proof. Allow λ and yx) to be complex. From Equation 8) one obtains for y n x) and y m x) Ly n x) = λ n rx)y n x), and Ly mx) = λ mrx)y mx), 9) where the equation for y m x) have been complex conjugated. By multiplying the rst equation by y mx) and the second equation by y n x), one then integrates both from a to b. Subtracting these two results yields b a y mx)ly n x) dx b a y n x)lymx) dx = ) b λ n λ m rx)ymx)y n x) dx. Using the denition of L given by Equation 7) and the boundary conditions in Equation 6), one can show that the left-hand side of Equation 10) equals zero for a Sturm-Liouville problem. Equation 10) becomes b a y mx)ly n x) dx = b a a 10) y n x)ly mx) dx. 11) An operator that satises this equation is said to be a hermitian operator. Theorem.6. The eigenvalues of a Sturm-Liouville problem are real [, Page: 690]. 6
7 Proof. From Equation 11) and Equation 10) one has ) b λ m λ n rx)ymx)y n x) dx = 0. 1) a Let m = n and use the fact that rx) > 0 in the interval a, b). Since the integrand is everywhere greater than or equal to zero the integral cannot equal zero. This implies that λ n = λ n. Theorem.7. The eigenfunctions corresponding to dierent eigenvalues of a Sturm-Liouville system are orthogonal [, Page: 691]. Proof. If λ m = λ m λ n in Equation 1), then the integral must equal zero: b a rx)y mx)y n x) dx = 0. 13) When an equation such as Equation 13) is satised, the set of functions y n is said to be orthogonal [, Page: 678]. 3 Minimal surface In this section, the main concepts of a minimal surface are treated. Let the surface be dened by z = fx, y), where fx, y) is the height of the surface above the point x, y) in the plane. The surface area is given by the functional [4, Page: 4] A[f] = 1 + fx + fy dxdy, 14) where S is the region of the plane on which the area is dened. S Denition 3.1. A surface S R 3 is minimal if and only if its mean curvature vanishes identically [5, Page: 1]. After suitable rotation, any regular surface S R 3 can be locally expressed as the graph of a function f = fx, y). The variation of Equation 14) implies that the function fx, y) satises the Euler- Lagrange equation for two independent variables) L f x L f x y 7 L f y = 0, 15)
8 where L is L = 1 + f x + f y. 16) One obtains the following relation from Equation 15) 1 + f x)f yy f x f y f xy f y )f xx = 0, 17) which is a second order nonlinear elliptic partial dierential equation [5, Page: 1]. It has been shown that the condition that the mean curvature vanishes for a minimal S is satised if the graph fx, y) satises Equation 17). Denition 3.. A surface S R 3 is minimal if and only if it can be locally expressed as the graph of a solution of Equation 17) [5, Page: 1]. An example of a minimal surface that satises Equation 17) is the catenoid [4, Page: 6]. 4 Stability of a soap lm In this section, the stability for a soap lm suspended between two parallel coaxial rings is examined see Figure 1). Figure 1: Soap lm. r, φ and z are the cylindrical coordinates. It will be shown that the stability may be treated as Sturm-Liouville problem. From this method the range of parameters for which the solutions are stable may be determined. 8
9 4.1 Variational problem Let S be the surface of the soap lm, σ the surface tension and neglect gravitational eects to the surface. The potential energy functional for an ideal soap lm is given by [1, Page: 1] V [S] = σ ds. 18) S The possible equilibrium shapes of the lm are determined by evaluating those surfaces where the quantity 18) has a local minimum. For the system described in Figure 1, Equation 18) becomes V [S] = 4πσ r 1 + rz dz, 19) where r z dr. It should be noted that from now on, if nothing else is explicitly dz stated, a subscript means derivative with respect to the indicated variable. The variation of Equation 19) must be zero in order for a surface S to be an extremal, that is δv [S] = 0. The integrand is identied to be the Lagrangian and must satisfy the Euler-Lagrange equation ) d L = L dz r z r. 0) The calculation of δv [S] will lead to the result ) z b rz) = a cosh, 1) a where a and b are constants. Equation 1) is called the catenoid equation. The derivation of the catenoid equation is shown in Appendix A. Restricting the attention to two coaxial rings of equal radii r0) = rh) r 0, the constant of integration b becomes b = h. Thus z rz) = a cosh a h ), ) a and the boundary value problem reduces to determining a from Equation ) for the case ) h r0) r 0 = a cosh a > 0. 3) a 9
10 The variation of Equation 19) provides information about the shape of the minimized surface. Furthermore, critical ratios between h and r 0 may be obtained. However, in order to examine stability and oscillations of the minimized surface one have to consider a dierent variation. 4. Perturbed surface and second variation If V [S] has a local minimum for the surface S, then a soap lm described by Equation ) and Equation 3) will be stable by any small perturbation [1, Page: 3]. Therefore, in order to see whether this is the case the second variation must be examined. Consider a perturbed surface described by rz) = fz) + gz), 4) where rz) = fz) describes an initial surface S 0 it is not necessary for S 0 to be a minimum) and let gz) be an innitesimal twice-dierential function that satises the boundary condition g0) = gh) = 0. Assume further that the derivative of gz), g z, is innitesimal for 0 z h. Then, V [S] can be expanded in a power series of g and g z as V [S] = 4πσ = 4πσ h 0 h 0 r 1 + rz dz = f 1 + fz + g 1 + fz + ff zg z 1 + f z + + gf ) zg z fgz + ) 1 + f z 1 + f 3/ + Og 3 ) dz = z = V [S 0 ] + 4πσ h + πσ 0 h 0 1 g + f z d ) ff z dz + dz 1 + f z fg z f zz g ) 1 + f z ) 3/ dz + Og 3 ) = V [S 0 ] + δv [S 0 ] + δ V [S 0 ] + Og 3 ), 5) where integration by parts has been performed to eliminate g z and gg z. The last term in Equation 5), δ V [S 0 ], is the second variation and is calculated in the same way as an ordinary variation. V [S 0 ] in Equation 5) satises Equation 0). Therefore δv [S 0 ] = 0 and f is compare Equation )) fz) = a cosh 10 z a h a ), 6)
11 where, again, the analysis has been limited to the case of symmetrical rings. Inserting Equation 6) into the second variation yields δ V [S 0 ] = πσa = πσ h 0 g z 1 a g) cosh z a h a ) dz g u g ) cosh u) du, 7) where the substitution u = z h a, with u 0 = h, has been implemented in the a second line. From Equation 7), it is not immediately clear whether the extremal will be a minimum or a maximum of V [S] due to the indenite sign of the integrand. However, it has been shown that a sucient condition for the extremal curve to give a minimum for V [S] is that the second derivative of the integrand in Equation 19) with respect to r z all nite) is positive for all z and r in a neighborhood of the curve [1, Page: 4]. The condition is satised for this problem and it can be further relaxed because both the innitesimals g and g z, for a smooth surface S, require the coecient of g z in δ V to be positive [1, Page: 4]. There is a second condition for the extremal to be a minimum [1, Page: 4]. However, the signicance of this condition is not obvious and it is not interpreted easily. By adopting a dierent approach, both conditions will be capsuled in the formalism very naturally. Particularly, by formulating the dynamical stability of a soap lm as a Sturm-Liouville problem the rst condition will be converted into determining the sign of the lowest eigenvalue of an appropriate operator. The second condition is interchanged into the necessity of having a positive lowest eigenvalue [1, Page: 4]. For simplicity of future discussion, the radial displacement gz) will be changed into an equivalent innitesimal displacement ξz) that is perpendicular to the initial surface of the soap lm. The innitesimal displacement satises the boundary condition ξ ) = ξu 0 ) = 0. The associated vector displacement of a point r = r, z) is given by where ˆnz) is the surface normal at r, z) = fz), z): r r = ˆnz)ξz), 8) ˆn = ˆr f z ẑ ) 1 + f z. 9) 11
12 One then obtains r z ) = fz) + ξz) f, and z = z z ξz). 30) 1 + f z 1 + f z Inserting z into r z ), expanding up to rst order in ξ and compare to Equation 4) one nds that g = ξ coshu). 31) Inserting Equation 31) into Equation 7) gives the result ) δ V [S 0 ] = πσ ξ ξ uu cosh u) ξ du. 3) For the detailed derivation of Equation 3), refer to Appendix B. 4.3 Sturm-Liouville problem formulation As mentioned in the last section, to determine the stability of the soap lm for a given value u 0 one treat this as a Sturm-Liouville problem. Let L be the Sturm- Liouville operator dened as L = d du cosh u). 33) If L is a positive operator, that is, if the integral in Equation 3) is positive for any ξ, then δ V is positive for any variation and the soap lm is stable [1, Page: 5]. The operator will only be positive if the lowest eigenvalue is positive. The Sturm-Liouville problem is dened by d ψ n u) du + Lψ n u) = λ n wu)ψ n u), 34) with the boundary conditions ψ n u 0 ) = ψ n ) = 0. The weight function in Equation 34) must be positive within the entire interval of u. As long as this condition holds the choice of weight function is arbitrary. It turns out that a natural choice is wu) = cosh u) [1, Page:5]. Equation 34) then becomes ) λ n cosh u) + ψ n u) = 0, 35) cosh u) 1
13 where the eigenfunctions ψ n u), where n = 1,,..., are chosen to be real, assumed normalized and satisfy the orthogonality relation compare Equation 13)) ψ m u)ψ n u) cosh u) du = δ mn. 36) The eigenvalues λ n are real and discrete. Furthermore, they can be ordered in such a way that λ 1 < λ < λ 3 <... < λ n <.... This is a consequence of a theorem for regular Sturm-Liouville problems [, Page: 694]. If ξ is expanded into a complete set of eigenfunctions ψ n as ξu) = c n ψ n, 37) then, using Equation 35) and Equation 36), Equation 3) is found to be n=1 δ V [S 0 ] = πσ λ n c n. 38) From Equation 38) and the assumptions mentioned above, one can see whether a given extremal soap lm conguration is stable or unstable by examining the lowest eigenvalue λ 1. For λ 1 > 0, all the eigenvalues are positive and δ V [S 0 ] > 0 for any choice of c n. This means that for any innitesimal displacement ξu) that satises the given boundary conditions, the area of the soap lm is increasing. This is the condition for stability. If λ 1 < 0, then for c 1 0 and c n = 0 for n > 1 one obtains a ξ for which the area of the lm decreases, δ V [S 0 ] < 0. This means that the conguration is unstable. n=1 5 Oscillations of a soap lm In this section, one considers the oscillation motions of a soap lm. The motion about an extremal surface is of interest. 13
14 5.1 Oscillations about an extremal surface For an innitesimal displacement ξz, t) that is perpendicular to the surface S, the kinetic energy is given by the following functional [1, Page: 6] T [S] = 1 ρ ξt ds, 39) where ρ is the mass surface density of the soap lm. In this analysis, the subscript in Equation 39) means partial derivative with respect to time t. From now on, ρ is assumed to be a constant. Considering a symmetric lm with the radii of the coaxial rings r0) = rh) r 0, Equation 39) becomes T [S] = πρ h 0 = πρa S ξ t r 1 + r z dz = ξ t cosh u) du, 40) where r = rz) is given by Equation 6). The substitution u = z h a, with u 0 = h, has been used in the second line. a The potential energy functional is given by Equation 3). Since ξ satisfy the boundary conditions ξ ) = ξu 0 ) = 0 the integrand will be expressed in terms of ξ in second order. Therefore compare the calculation in Appendix B) V [S] = πσ ξu The Lagrangian functional is dened as cosh u) ξ ) du. 41) L[S] = T [S] V [S]. 4) The second order Lagrangian functional to the system of a displaced soap lm is given by ) 1 L[S] = π ρ a ξt cosh u) σξu σ + cosh u) ξ du. 43) The variation of Equation 43), δl[s] = 0, suggests that the expression in the integral will satisfy the Euler-Lagrange equation ) d L = L du ξ u ξ, 44) 14
15 where L is the integrand in Equation 44). After some calculation one obtains ρ a cosh u)ξ tt + σξ uu + 4σ cosh ξ = 0. 45) u) The expression in Equation 45) is a hyperbolic partial dierential equation for wavelike displacements of the surface [1, Page: 6]. To nd solutions to Equation 45) one rst implements the method of separation of variables described in section ). Inserting ξu, t) = ζu)t t) into Equation 45) one nds that the dierential equation for T t) is or T tt + σλ T = 0, 46) ρa T tt + ω T = 0, 47) where the separation constant λ has been chosen to λ = ρa ω and ω is interpreted σ as angular frequency. The solutions to Equation 47) are trigonometric functions. The dierential equation for ζu) becomes λ cosh u) + d ζu) du + ) cosh ζ = 0, 48) u) with the boundary conditions ζ ) = ζu 0 ) = 0. By comparing Equation 48) and Equation 35), the normal modes of the system will be treated as a Sturm- Liouville problem with the operator L dened as Equation 33) and eigenfunctions ψ n. The weight function is, again, chosen to be wu) = cosh u). The angular frequencies of the normal modes may be written as ) 1/ ) σλn σ ω n = = 1/ ω ρa ρh n, n = 1,,..., 49) ) 1/ σ where the constant is the systems characteristic angular frequency and ρh ω n is a dimensionless reduced frequency which is related to λ by ω n = 4u 0λ n. Since each ξ n u, t) are solutions to Equation 45), their superposition is also a solution and is the general solution [, Page: 769]. Therefore, for a general initial displacement and velocity, ξu, 0) respectively ξ t u, 0), one obtains ξ n u, t) = a n cosω n t) + b ) n sinω n t) ψ n u), 50) ω n n=1 15
16 where the coecients a n and b n are determined by and a n = b n = ψ n u) ξu, 0) cosh u) du, 51) ψ n u) ξ t u, 0) cosh u) du. 5) From Equation 51) and Equation 5), one may obtain interesting results when considering the relation between u 0 and a critical value u c. Since u 0 contains a ratio between the distance h and ring diameter r 0, one may obtain u c for some critical value h c from Equation 3). If u 0 < u c, then ω n is positive and all frequencies ω n are real. This means that the motions described by Equation 5) are bounded small-amplitude oscillations about a stable equilibrium conguration of the soap lm. For the case when u 0 > u c, ω n is negative and all frequencies ω n are imaginary. This means that the trigonometric functions are replaced by hyperbolic functions. As a consequence, a small perturbation in the n = 1 mode would grow exponentially over time. Thus, the initial surface is unstable. 6 Conclusions By formulating the second variation of a perturbed surface as a Sturm-Liouville problem one could obtain interpretable parameters and solutions. Furthermore, the derived eigenvalues and eigenfunction provides information about the stability of the surface and the nature of the motion about the given conguration, respectively. After this study of the catenoid soap lm one may ask if this mathematical formulation, for a variational problem, may be used for dierent problems that arise in physics. For example, if it could be used for more complicated systems of soap lm congurations and for non-idealized soap lms. Furthermore, whether it is possible to apply the formulation for a variational problem in a dierent area of physics. These are interesting ideas that should be further investigated. 16
17 Appendix A The Catenoid equation Consider a cylindrical coordinate system with z-axial symmetry. Then, the surface S has the following parametric representation [6, Page: 6] r = rz) cosφ), rz) sinφ), z ), 53) where φ is the angle around the z-axis. The surface area of revolution around the z-axis is given by the following surface integral A = da = r z r φ dφdz. 54) S From the parametrization given in Equation 53), using the notation r z dr dz, the length of the surface normal becomes r z r φ = rz cosφ), r z sinφ), 1 ) r sinφ), r cosφ), 0 ) = ) = r cosφ), r sinφ), rrz = s = r 1 + r z. 55) The surface integral in Equation 54) is evaluated to be A = da = π r 1 + rz dz. 56) S To nd the minimal surface of revolutions the variation of the functional A[r] equals zero, δa[r] = 0 [7, Page: 38]. From Equation 56) the Lagrangian is identied to be L = r 1 + rz and it is required that the Lagrangian satises the Euler-Lagrange equation [7, Page: 38] ) d L = L dz r z r. 57) Inserting L into Equation 57) yields ) d rrz = 1 + r dz 1 + r z, 58) z which can be further simplied into the following form ) 1 d r = 0. 59) dz 1 + r z r z 17
18 Integrating Equation 59) and arranging the result, one have r z = dr dz = r a, 60) a where a is an integration constant. The solution to the dierential equation is ) dr r z = a r a + b = a arccosh + b, 61) a or ) z b rz) = a cosh, 6) a where b is an integration constant. Equation 6) is called the catenoid equation [6, Page: 7]. Appendix B Second variation in terms of ξ's The derivation of Equation 3) starts from Equation 7), which is δ V [S 0 ] = πσ Using the acquired expression for gu) g u in Equation 63) is determined to be and g u g ) cosh u) du. 63) g = ξ coshu), 64) g u = ξ u coshu) + ξ sinhu), 65) g u g = ξ u cosh u) + ξξ u coshu) sinhu) + ξ sinh u) cosh u) ) = = ξu cosh u) + ξξ u coshu) sinhu) ξ = ) = cosh u) ξu ξ + ξξ u tanhu) cosh, 66) u) where the identity cosh u) sinh u) = 1 has been used. Inserting Equation 66) into Equation 63) yields ) δ V [S 0 ] = πσ ξu ξ + ξξ u tanhu) cosh du. 67) u) 18
19 Since ξu) satises the boundary conditions ξ ) = ξu 0 ) = 0, the terms with ξ u and ξξ u in Equation 67) may be eliminated via integration by parts and the fact that Thus δ V [S 0 ] = πσ = πσ d ) ξξu = ξ du u + ξξ uu, 68) ξu du + 4πσ ξξ u tanhu) du πσ cosh u) du = d ) u0 [ ] u0 ξξu du πσ ξξ uu du + πσξ tanhu) du ξ πσ cosh du πσ u) ] u0 = [πσξξ u + πσ ξ ξ uu u 0 u0 = πσ ξ ξ uu ξ cosh u) du = cosh u) ξ) du + ξ [ ] u0 πσξ tanhu) = cosh u) ξ) du. 69) 19
20 References [1] Loyal Durand. Stability and oscillations of a soap lm: An analytic treatment. American Journal of Physics, 494):334343, [] Donald A. McQuarrie. Mathematical methods for scientists and engineers [3] B.H. Bransden and C.J. Joachain. Quantum Mechanics. Prentice Hall, 000. [4] Frederik Brasz. Soap lms: Statics and dynamics stonelab/teaching/fredbraszfinalpaper.pdf. [5] William Meeks III and Joaquín Pérez. The classical theory of minimal surfaces. Bulletin of the American Mathematical Society, 483):35407, 011. [6] Masato Ito and Taku Sato. In situ observation of a soap-lm catenoida simple educational physics experiment. European Journal of Physics, 31):357, 010. [7] H. Goldstein. Classical Mechanics. A-W series in advanced physics. Addison- Wesley,
Equations (3) and (6) form a complete solution as long as the set of functions fy n (x)g exist that satisfy the Properties One and Two given by equati
 PHYS/GEOL/APS 661 Earth and Planetary Physics I Eigenfunction Expansions, Sturm-Liouville Problems, and Green's Functions 1. Eigenfunction Expansions In seismology in general, as in the simple oscillating
PHYS/GEOL/APS 661 Earth and Planetary Physics I Eigenfunction Expansions, Sturm-Liouville Problems, and Green's Functions 1. Eigenfunction Expansions In seismology in general, as in the simple oscillating
In situ observation of a soap-film catenoid a simple educational physics experiment
 Home Search Collections Journals About Contact us My IOPscience In situ observation of a soap-film catenoid a simple educational physics experiment This article has been downloaded from IOPscience. Please
Home Search Collections Journals About Contact us My IOPscience In situ observation of a soap-film catenoid a simple educational physics experiment This article has been downloaded from IOPscience. Please
DIFFERENTIAL EQUATIONS
 DIFFERENTIAL EQUATIONS Chapter 1 Introduction and Basic Terminology Most of the phenomena studied in the sciences and engineering involve processes that change with time. For example, it is well known
DIFFERENTIAL EQUATIONS Chapter 1 Introduction and Basic Terminology Most of the phenomena studied in the sciences and engineering involve processes that change with time. For example, it is well known
MODELLING OF FLEXIBLE MECHANICAL SYSTEMS THROUGH APPROXIMATED EIGENFUNCTIONS L. Menini A. Tornambe L. Zaccarian Dip. Informatica, Sistemi e Produzione
 MODELLING OF FLEXIBLE MECHANICAL SYSTEMS THROUGH APPROXIMATED EIGENFUNCTIONS L. Menini A. Tornambe L. Zaccarian Dip. Informatica, Sistemi e Produzione, Univ. di Roma Tor Vergata, via di Tor Vergata 11,
MODELLING OF FLEXIBLE MECHANICAL SYSTEMS THROUGH APPROXIMATED EIGENFUNCTIONS L. Menini A. Tornambe L. Zaccarian Dip. Informatica, Sistemi e Produzione, Univ. di Roma Tor Vergata, via di Tor Vergata 11,
Ordinary Differential Equations II
 Ordinary Differential Equations II February 23 2017 Separation of variables Wave eq. (PDE) 2 u t (t, x) = 2 u 2 c2 (t, x), x2 c > 0 constant. Describes small vibrations in a homogeneous string. u(t, x)
Ordinary Differential Equations II February 23 2017 Separation of variables Wave eq. (PDE) 2 u t (t, x) = 2 u 2 c2 (t, x), x2 c > 0 constant. Describes small vibrations in a homogeneous string. u(t, x)
Before you begin read these instructions carefully:
 NATURAL SCIENCES TRIPOS Part IB & II (General) Friday, 27 May, 2016 9:00 am to 12:00 pm MATHEMATICS (2) Before you begin read these instructions carefully: You may submit answers to no more than six questions.
NATURAL SCIENCES TRIPOS Part IB & II (General) Friday, 27 May, 2016 9:00 am to 12:00 pm MATHEMATICS (2) Before you begin read these instructions carefully: You may submit answers to no more than six questions.
Final Exam May 4, 2016
 1 Math 425 / AMCS 525 Dr. DeTurck Final Exam May 4, 2016 You may use your book and notes on this exam. Show your work in the exam book. Work only the problems that correspond to the section that you prepared.
1 Math 425 / AMCS 525 Dr. DeTurck Final Exam May 4, 2016 You may use your book and notes on this exam. Show your work in the exam book. Work only the problems that correspond to the section that you prepared.
Separation of Variables in Linear PDE: One-Dimensional Problems
 Separation of Variables in Linear PDE: One-Dimensional Problems Now we apply the theory of Hilbert spaces to linear differential equations with partial derivatives (PDE). We start with a particular example,
Separation of Variables in Linear PDE: One-Dimensional Problems Now we apply the theory of Hilbert spaces to linear differential equations with partial derivatives (PDE). We start with a particular example,
LEGENDRE POLYNOMIALS AND APPLICATIONS. We construct Legendre polynomials and apply them to solve Dirichlet problems in spherical coordinates.
 LEGENDRE POLYNOMIALS AND APPLICATIONS We construct Legendre polynomials and apply them to solve Dirichlet problems in spherical coordinates.. Legendre equation: series solutions The Legendre equation is
LEGENDRE POLYNOMIALS AND APPLICATIONS We construct Legendre polynomials and apply them to solve Dirichlet problems in spherical coordinates.. Legendre equation: series solutions The Legendre equation is
! 4 4! o! +! h 4 o=0! ±= ± p i And back-substituting into the linear equations gave us the ratios of the amplitudes of oscillation:.»» = A p e i! +t»»
 Topic 6: Coupled Oscillators and Normal Modes Reading assignment: Hand and Finch Chapter 9 We are going to be considering the general case of a system with N degrees of freedome close to one of its stable
Topic 6: Coupled Oscillators and Normal Modes Reading assignment: Hand and Finch Chapter 9 We are going to be considering the general case of a system with N degrees of freedome close to one of its stable
is conserved, calculating E both at θ = 0 and θ = π/2 we find that this happens for a value ω = ω given by: 2g
 UNIVERSITETET I STAVANGER Institutt for matematikk og naturvitenskap Suggested solutions, FYS 500 Classical Mechanics Theory 2016 fall Set 5 for 23. September 2016 Problem 27: A string can only support
UNIVERSITETET I STAVANGER Institutt for matematikk og naturvitenskap Suggested solutions, FYS 500 Classical Mechanics Theory 2016 fall Set 5 for 23. September 2016 Problem 27: A string can only support
Welcome to Math 257/316 - Partial Differential Equations
 Welcome to Math 257/316 - Partial Differential Equations Instructor: Mona Rahmani email: mrahmani@math.ubc.ca Office: Mathematics Building 110 Office hours: Mondays 2-3 pm, Wednesdays and Fridays 1-2 pm.
Welcome to Math 257/316 - Partial Differential Equations Instructor: Mona Rahmani email: mrahmani@math.ubc.ca Office: Mathematics Building 110 Office hours: Mondays 2-3 pm, Wednesdays and Fridays 1-2 pm.
Two special equations: Bessel s and Legendre s equations. p Fourier-Bessel and Fourier-Legendre series. p
 LECTURE 1 Table of Contents Two special equations: Bessel s and Legendre s equations. p. 259-268. Fourier-Bessel and Fourier-Legendre series. p. 453-460. Boundary value problems in other coordinate system.
LECTURE 1 Table of Contents Two special equations: Bessel s and Legendre s equations. p. 259-268. Fourier-Bessel and Fourier-Legendre series. p. 453-460. Boundary value problems in other coordinate system.
Before you begin read these instructions carefully.
 MATHEMATICAL TRIPOS Part IB Tuesday, 5 June, 2012 9:00 am to 12:00 pm PAPER 1 Before you begin read these instructions carefully. Each question in Section II carries twice the number of marks of each question
MATHEMATICAL TRIPOS Part IB Tuesday, 5 June, 2012 9:00 am to 12:00 pm PAPER 1 Before you begin read these instructions carefully. Each question in Section II carries twice the number of marks of each question
Aero III/IV Conformal Mapping
 Aero III/IV Conformal Mapping View complex function as a mapping Unlike a real function, a complex function w = f(z) cannot be represented by a curve. Instead it is useful to view it as a mapping. Write
Aero III/IV Conformal Mapping View complex function as a mapping Unlike a real function, a complex function w = f(z) cannot be represented by a curve. Instead it is useful to view it as a mapping. Write
Degree Master of Science in Mathematical Modelling and Scientific Computing Mathematical Methods I Thursday, 12th January 2012, 9:30 a.m.- 11:30 a.m.
 Degree Master of Science in Mathematical Modelling and Scientific Computing Mathematical Methods I Thursday, 12th January 2012, 9:30 a.m.- 11:30 a.m. Candidates should submit answers to a maximum of four
Degree Master of Science in Mathematical Modelling and Scientific Computing Mathematical Methods I Thursday, 12th January 2012, 9:30 a.m.- 11:30 a.m. Candidates should submit answers to a maximum of four
Sturm-Liouville Theory
 More on Ryan C. Trinity University Partial Differential Equations April 19, 2012 Recall: A Sturm-Liouville (S-L) problem consists of A Sturm-Liouville equation on an interval: (p(x)y ) + (q(x) + λr(x))y
More on Ryan C. Trinity University Partial Differential Equations April 19, 2012 Recall: A Sturm-Liouville (S-L) problem consists of A Sturm-Liouville equation on an interval: (p(x)y ) + (q(x) + λr(x))y
Chapter 3 Second Order Linear Equations
 Partial Differential Equations (Math 3303) A Ë@ Õæ Aë áöß @. X. @ 2015-2014 ú GA JË@ É Ë@ Chapter 3 Second Order Linear Equations Second-order partial differential equations for an known function u(x,
Partial Differential Equations (Math 3303) A Ë@ Õæ Aë áöß @. X. @ 2015-2014 ú GA JË@ É Ë@ Chapter 3 Second Order Linear Equations Second-order partial differential equations for an known function u(x,
Calculus of Variations Summer Term 2014
 Calculus of Variations Summer Term 2014 Lecture 2 25. April 2014 c Daria Apushkinskaya 2014 () Calculus of variations lecture 2 25. April 2014 1 / 20 Purpose of Lesson Purpose of Lesson: To discuss the
Calculus of Variations Summer Term 2014 Lecture 2 25. April 2014 c Daria Apushkinskaya 2014 () Calculus of variations lecture 2 25. April 2014 1 / 20 Purpose of Lesson Purpose of Lesson: To discuss the
LECTURE 15 + C+F. = A 11 x 1x1 +2A 12 x 1x2 + A 22 x 2x2 + B 1 x 1 + B 2 x 2. xi y 2 = ~y 2 (x 1 ;x 2 ) x 2 = ~x 2 (y 1 ;y 2 1
 LECTURE 5 Characteristics and the Classication of Second Order Linear PDEs Let us now consider the case of a general second order linear PDE in two variables; (5.) where (5.) 0 P i;j A ij xix j + P i,
LECTURE 5 Characteristics and the Classication of Second Order Linear PDEs Let us now consider the case of a general second order linear PDE in two variables; (5.) where (5.) 0 P i;j A ij xix j + P i,
Congurations of periodic orbits for equations with delayed positive feedback
 Congurations of periodic orbits for equations with delayed positive feedback Dedicated to Professor Tibor Krisztin on the occasion of his 60th birthday Gabriella Vas 1 MTA-SZTE Analysis and Stochastics
Congurations of periodic orbits for equations with delayed positive feedback Dedicated to Professor Tibor Krisztin on the occasion of his 60th birthday Gabriella Vas 1 MTA-SZTE Analysis and Stochastics
Lecture 9: Eigenvalues and Eigenvectors in Classical Mechanics (See Section 3.12 in Boas)
 Lecture 9: Eigenvalues and Eigenvectors in Classical Mechanics (See Section 3 in Boas) As suggested in Lecture 8 the formalism of eigenvalues/eigenvectors has many applications in physics, especially in
Lecture 9: Eigenvalues and Eigenvectors in Classical Mechanics (See Section 3 in Boas) As suggested in Lecture 8 the formalism of eigenvalues/eigenvectors has many applications in physics, especially in
Before you begin read these instructions carefully.
 MATHEMATICAL TRIPOS Part IB Thursday, 9 June, 2011 9:00 am to 12:00 pm PAPER 3 Before you begin read these instructions carefully. Each question in Section II carries twice the number of marks of each
MATHEMATICAL TRIPOS Part IB Thursday, 9 June, 2011 9:00 am to 12:00 pm PAPER 3 Before you begin read these instructions carefully. Each question in Section II carries twice the number of marks of each
Solutions to Laplace s Equation in Cylindrical Coordinates and Numerical solutions. ρ + (1/ρ) 2 V
 Solutions to Laplace s Equation in Cylindrical Coordinates and Numerical solutions Lecture 8 1 Introduction Solutions to Laplace s equation can be obtained using separation of variables in Cartesian and
Solutions to Laplace s Equation in Cylindrical Coordinates and Numerical solutions Lecture 8 1 Introduction Solutions to Laplace s equation can be obtained using separation of variables in Cartesian and
Name: Math Homework Set # 5. March 12, 2010
 Name: Math 4567. Homework Set # 5 March 12, 2010 Chapter 3 (page 79, problems 1,2), (page 82, problems 1,2), (page 86, problems 2,3), Chapter 4 (page 93, problems 2,3), (page 98, problems 1,2), (page 102,
Name: Math 4567. Homework Set # 5 March 12, 2010 Chapter 3 (page 79, problems 1,2), (page 82, problems 1,2), (page 86, problems 2,3), Chapter 4 (page 93, problems 2,3), (page 98, problems 1,2), (page 102,
Lecture IX. Definition 1 A non-singular Sturm 1 -Liouville 2 problem consists of a second order linear differential equation of the form.
 Lecture IX Abstract When solving PDEs it is often necessary to represent the solution in terms of a series of orthogonal functions. One way to obtain an orthogonal family of functions is by solving a particular
Lecture IX Abstract When solving PDEs it is often necessary to represent the solution in terms of a series of orthogonal functions. One way to obtain an orthogonal family of functions is by solving a particular
1. Solve the boundary-value problems or else show that no solutions exist. y (x) = c 1 e 2x + c 2 e 3x. (3)
 Diff. Eqns. Problem Set 6 Solutions. Solve the boundary-value problems or else show that no solutions exist. a y + y 6y, y, y 4 b y + 9y x + e x, y, yπ a Assuming y e rx is a solution, we get the characteristic
Diff. Eqns. Problem Set 6 Solutions. Solve the boundary-value problems or else show that no solutions exist. a y + y 6y, y, y 4 b y + 9y x + e x, y, yπ a Assuming y e rx is a solution, we get the characteristic
Consider an ideal pendulum as shown below. l θ is the angular acceleration θ is the angular velocity
 1 Second Order Ordinary Differential Equations 1.1 The harmonic oscillator Consider an ideal pendulum as shown below. θ l Fr mg l θ is the angular acceleration θ is the angular velocity A point mass m
1 Second Order Ordinary Differential Equations 1.1 The harmonic oscillator Consider an ideal pendulum as shown below. θ l Fr mg l θ is the angular acceleration θ is the angular velocity A point mass m
INTRODUCTION TO PDEs
 INTRODUCTION TO PDEs In this course we are interested in the numerical approximation of PDEs using finite difference methods (FDM). We will use some simple prototype boundary value problems (BVP) and initial
INTRODUCTION TO PDEs In this course we are interested in the numerical approximation of PDEs using finite difference methods (FDM). We will use some simple prototype boundary value problems (BVP) and initial
An Introduction to Partial Differential Equations
 An Introduction to Partial Differential Equations Ryan C. Trinity University Partial Differential Equations Lecture 1 Ordinary differential equations (ODEs) These are equations of the form where: F(x,y,y,y,y,...)
An Introduction to Partial Differential Equations Ryan C. Trinity University Partial Differential Equations Lecture 1 Ordinary differential equations (ODEs) These are equations of the form where: F(x,y,y,y,y,...)
SOLUTIONS, PROBLEM SET 11
 SOLUTIONS, PROBLEM SET 11 1 In this problem we investigate the Lagrangian formulation of dynamics in a rotating frame. Consider a frame of reference which we will consider to be inertial. Suppose that
SOLUTIONS, PROBLEM SET 11 1 In this problem we investigate the Lagrangian formulation of dynamics in a rotating frame. Consider a frame of reference which we will consider to be inertial. Suppose that
Our goal is to solve a general constant coecient linear second order. this way but that will not always happen). Once we have y 1, it will always
 October 5 Relevant reading: Section 2.1, 2.2, 2.3 and 2.4 Our goal is to solve a general constant coecient linear second order ODE a d2 y dt + bdy + cy = g (t) 2 dt where a, b, c are constants and a 0.
October 5 Relevant reading: Section 2.1, 2.2, 2.3 and 2.4 Our goal is to solve a general constant coecient linear second order ODE a d2 y dt + bdy + cy = g (t) 2 dt where a, b, c are constants and a 0.
Equations of linear stellar oscillations
 Chapter 4 Equations of linear stellar oscillations In the present chapter the equations governing small oscillations around a spherical equilibrium state are derived. The general equations were presented
Chapter 4 Equations of linear stellar oscillations In the present chapter the equations governing small oscillations around a spherical equilibrium state are derived. The general equations were presented
Before you begin read these instructions carefully:
 NATURAL SCIENCES TRIPOS Part IB & II (General Friday, 30 May, 2014 9:00 am to 12:00 pm MATHEMATICS (2 Before you begin read these instructions carefully: You may submit answers to no more than six questions.
NATURAL SCIENCES TRIPOS Part IB & II (General Friday, 30 May, 2014 9:00 am to 12:00 pm MATHEMATICS (2 Before you begin read these instructions carefully: You may submit answers to no more than six questions.
Dynamic Green Function Solution of Beams Under a Moving Load with Dierent Boundary Conditions
 Transaction B: Mechanical Engineering Vol. 16, No. 3, pp. 273{279 c Sharif University of Technology, June 2009 Research Note Dynamic Green Function Solution of Beams Under a Moving Load with Dierent Boundary
Transaction B: Mechanical Engineering Vol. 16, No. 3, pp. 273{279 c Sharif University of Technology, June 2009 Research Note Dynamic Green Function Solution of Beams Under a Moving Load with Dierent Boundary
Minimal Surfaces: Nonparametric Theory. Andrejs Treibergs. January, 2016
 USAC Colloquium Minimal Surfaces: Nonparametric Theory Andrejs Treibergs University of Utah January, 2016 2. USAC Lecture: Minimal Surfaces The URL for these Beamer Slides: Minimal Surfaces: Nonparametric
USAC Colloquium Minimal Surfaces: Nonparametric Theory Andrejs Treibergs University of Utah January, 2016 2. USAC Lecture: Minimal Surfaces The URL for these Beamer Slides: Minimal Surfaces: Nonparametric
expression that describes these corrections with the accuracy of the order of 4. frame usually connected with extragalactic objects.
 RUSSIAN JOURNAL OF EARTH SCIENCES, English Translation, VOL, NO, DECEMBER 998 Russian Edition: JULY 998 On the eects of the inertia ellipsoid triaxiality in the theory of nutation S. M. Molodensky Joint
RUSSIAN JOURNAL OF EARTH SCIENCES, English Translation, VOL, NO, DECEMBER 998 Russian Edition: JULY 998 On the eects of the inertia ellipsoid triaxiality in the theory of nutation S. M. Molodensky Joint
The Rotating Spring. ω Rotating spring. Spring at rest. x L. x' L' Jacob Gade Koefoed
 The Rotating Spring A spring of mass m, which is uniformly distributed along the spring, spring constant k and unstretched length L is rotated about an ais perpendicular to the spring at a constant angular
The Rotating Spring A spring of mass m, which is uniformly distributed along the spring, spring constant k and unstretched length L is rotated about an ais perpendicular to the spring at a constant angular
Contents. 2 Partial Derivatives. 2.1 Limits and Continuity. Calculus III (part 2): Partial Derivatives (by Evan Dummit, 2017, v. 2.
 Calculus III (part 2): Partial Derivatives (by Evan Dummit, 2017, v 260) Contents 2 Partial Derivatives 1 21 Limits and Continuity 1 22 Partial Derivatives 5 23 Directional Derivatives and the Gradient
Calculus III (part 2): Partial Derivatives (by Evan Dummit, 2017, v 260) Contents 2 Partial Derivatives 1 21 Limits and Continuity 1 22 Partial Derivatives 5 23 Directional Derivatives and the Gradient
Monte Carlo Methods for Statistical Inference: Variance Reduction Techniques
 Monte Carlo Methods for Statistical Inference: Variance Reduction Techniques Hung Chen hchen@math.ntu.edu.tw Department of Mathematics National Taiwan University 3rd March 2004 Meet at NS 104 On Wednesday
Monte Carlo Methods for Statistical Inference: Variance Reduction Techniques Hung Chen hchen@math.ntu.edu.tw Department of Mathematics National Taiwan University 3rd March 2004 Meet at NS 104 On Wednesday
Contents. MATH 32B-2 (18W) (L) G. Liu / (TA) A. Zhou Calculus of Several Variables. 1 Multiple Integrals 3. 2 Vector Fields 9
 MATH 32B-2 (8W) (L) G. Liu / (TA) A. Zhou Calculus of Several Variables Contents Multiple Integrals 3 2 Vector Fields 9 3 Line and Surface Integrals 5 4 The Classical Integral Theorems 9 MATH 32B-2 (8W)
MATH 32B-2 (8W) (L) G. Liu / (TA) A. Zhou Calculus of Several Variables Contents Multiple Integrals 3 2 Vector Fields 9 3 Line and Surface Integrals 5 4 The Classical Integral Theorems 9 MATH 32B-2 (8W)
Dynamical Systems & Scientic Computing: Homework Assignments
 Fakultäten für Informatik & Mathematik Technische Universität München Dr. Tobias Neckel Summer Term Dr. Florian Rupp Exercise Sheet 3 Dynamical Systems & Scientic Computing: Homework Assignments 3. [ ]
Fakultäten für Informatik & Mathematik Technische Universität München Dr. Tobias Neckel Summer Term Dr. Florian Rupp Exercise Sheet 3 Dynamical Systems & Scientic Computing: Homework Assignments 3. [ ]
d 1 µ 2 Θ = 0. (4.1) consider first the case of m = 0 where there is no azimuthal dependence on the angle φ.
 4 Legendre Functions In order to investigate the solutions of Legendre s differential equation d ( µ ) dθ ] ] + l(l + ) m dµ dµ µ Θ = 0. (4.) consider first the case of m = 0 where there is no azimuthal
4 Legendre Functions In order to investigate the solutions of Legendre s differential equation d ( µ ) dθ ] ] + l(l + ) m dµ dµ µ Θ = 0. (4.) consider first the case of m = 0 where there is no azimuthal
for changing independent variables. Most simply for a function f(x) the Legendre transformation f(x) B(s) takes the form B(s) = xs f(x) with s = df
 Physics 106a, Caltech 1 November, 2018 Lecture 10: Hamiltonian Mechanics I The Hamiltonian In the Hamiltonian formulation of dynamics each second order ODE given by the Euler- Lagrange equation in terms
Physics 106a, Caltech 1 November, 2018 Lecture 10: Hamiltonian Mechanics I The Hamiltonian In the Hamiltonian formulation of dynamics each second order ODE given by the Euler- Lagrange equation in terms
(You may need to make a sin / cos-type trigonometric substitution.) Solution.
 MTHE 7 Problem Set Solutions. As a reminder, a torus with radii a and b is the surface of revolution of the circle (x b) + z = a in the xz-plane about the z-axis (a and b are positive real numbers, with
MTHE 7 Problem Set Solutions. As a reminder, a torus with radii a and b is the surface of revolution of the circle (x b) + z = a in the xz-plane about the z-axis (a and b are positive real numbers, with
Introduction to Differential Equations
 Chapter 1 Introduction to Differential Equations 1.1 Basic Terminology Most of the phenomena studied in the sciences and engineering involve processes that change with time. For example, it is well known
Chapter 1 Introduction to Differential Equations 1.1 Basic Terminology Most of the phenomena studied in the sciences and engineering involve processes that change with time. For example, it is well known
Lecture Notes on Partial Dierential Equations (PDE)/ MaSc 221+MaSc 225
 Lecture Notes on Partial Dierential Equations (PDE)/ MaSc 221+MaSc 225 Dr. Asmaa Al Themairi Assistant Professor a a Department of Mathematical sciences, University of Princess Nourah bint Abdulrahman,
Lecture Notes on Partial Dierential Equations (PDE)/ MaSc 221+MaSc 225 Dr. Asmaa Al Themairi Assistant Professor a a Department of Mathematical sciences, University of Princess Nourah bint Abdulrahman,
6.7 Hyperbolic Functions
 6.7 6.7 Hyperbolic Functions Even and Odd Parts of an Exponential Function We recall that a function f is called even if f( x) = f(x). f is called odd if f( x) = f(x). The sine function is odd while the
6.7 6.7 Hyperbolic Functions Even and Odd Parts of an Exponential Function We recall that a function f is called even if f( x) = f(x). f is called odd if f( x) = f(x). The sine function is odd while the
Homework 1. Due Tuesday, January 29.
 Homework 1. Due Tuesday, January 29. Problem 1. An ideal rope (no friction) lying on a table slides from its edge down to a scales lying on the floor. The table s height is h. Find a stationary velocity
Homework 1. Due Tuesday, January 29. Problem 1. An ideal rope (no friction) lying on a table slides from its edge down to a scales lying on the floor. The table s height is h. Find a stationary velocity
Physics 6010, Fall 2016 Constraints and Lagrange Multipliers. Relevant Sections in Text:
 Physics 6010, Fall 2016 Constraints and Lagrange Multipliers. Relevant Sections in Text: 1.3 1.6 Constraints Often times we consider dynamical systems which are defined using some kind of restrictions
Physics 6010, Fall 2016 Constraints and Lagrange Multipliers. Relevant Sections in Text: 1.3 1.6 Constraints Often times we consider dynamical systems which are defined using some kind of restrictions
QM1 - Tutorial 2 Schrodinger Equation, Hamiltonian and Free Particle
 QM - Tutorial Schrodinger Equation, Hamiltonian and Free Particle Yaakov Yuin November 07 Contents Hamiltonian. Denition...................................................... Example: Hamiltonian of a
QM - Tutorial Schrodinger Equation, Hamiltonian and Free Particle Yaakov Yuin November 07 Contents Hamiltonian. Denition...................................................... Example: Hamiltonian of a
LOWELL WEEKLY JOURNAL.
 Y 5 ; ) : Y 3 7 22 2 F $ 7 2 F Q 3 q q 6 2 3 6 2 5 25 2 2 3 $2 25: 75 5 $6 Y q 7 Y Y # \ x Y : { Y Y Y : ( \ _ Y ( ( Y F [ F F ; x Y : ( : G ( ; ( ~ x F G Y ; \ Q ) ( F \ Q / F F \ Y () ( \ G Y ( ) \F
Y 5 ; ) : Y 3 7 22 2 F $ 7 2 F Q 3 q q 6 2 3 6 2 5 25 2 2 3 $2 25: 75 5 $6 Y q 7 Y Y # \ x Y : { Y Y Y : ( \ _ Y ( ( Y F [ F F ; x Y : ( : G ( ; ( ~ x F G Y ; \ Q ) ( F \ Q / F F \ Y () ( \ G Y ( ) \F
A Fourier-Bessel Expansion for Solving Radial Schrödinger Equation in Two Dimensions
 A Fourier-Bessel Expansion for Solving Radial Schrödinger Equation in Two Dimensions H. TAŞELI and A. ZAFER Department of Mathematics, Middle East Technical University, 06531 Ankara, Turkey ABSTRACT The
A Fourier-Bessel Expansion for Solving Radial Schrödinger Equation in Two Dimensions H. TAŞELI and A. ZAFER Department of Mathematics, Middle East Technical University, 06531 Ankara, Turkey ABSTRACT The
L = 1 2 a(q) q2 V (q).
 Physics 3550, Fall 2011 Motion near equilibrium - Small Oscillations Relevant Sections in Text: 5.1 5.6 Motion near equilibrium 1 degree of freedom One of the most important situations in physics is motion
Physics 3550, Fall 2011 Motion near equilibrium - Small Oscillations Relevant Sections in Text: 5.1 5.6 Motion near equilibrium 1 degree of freedom One of the most important situations in physics is motion
The Simple Harmonic Oscillator
 The Simple Harmonic Oscillator Asaf Pe er 1 November 4, 215 This part of the course is based on Refs [1] [3] 1 Introduction We return now to the study of a 1-d stationary problem: that of the simple harmonic
The Simple Harmonic Oscillator Asaf Pe er 1 November 4, 215 This part of the course is based on Refs [1] [3] 1 Introduction We return now to the study of a 1-d stationary problem: that of the simple harmonic
752 Final. April 16, Fadeev Popov Ghosts and Non-Abelian Gauge Fields. Tim Wendler BYU Physics and Astronomy. The standard model Lagrangian
 752 Final April 16, 2010 Tim Wendler BYU Physics and Astronomy Fadeev Popov Ghosts and Non-Abelian Gauge Fields The standard model Lagrangian L SM = L Y M + L W D + L Y u + L H The rst term, the Yang Mills
752 Final April 16, 2010 Tim Wendler BYU Physics and Astronomy Fadeev Popov Ghosts and Non-Abelian Gauge Fields The standard model Lagrangian L SM = L Y M + L W D + L Y u + L H The rst term, the Yang Mills
Free Boundary Minimal Surfaces in the Unit 3-Ball
 Free Boundary Minimal Surfaces in the Unit 3-Ball T. Zolotareva (joint work with A. Folha and F. Pacard) CMLS, Ecole polytechnique December 15 2015 Free boundary minimal surfaces in B 3 Denition : minimal
Free Boundary Minimal Surfaces in the Unit 3-Ball T. Zolotareva (joint work with A. Folha and F. Pacard) CMLS, Ecole polytechnique December 15 2015 Free boundary minimal surfaces in B 3 Denition : minimal
Elliptical-like orbits on a warped spandex fabric
 Elliptical-like orbits on a warped spandex fabric Prof. Chad A. Middleton CMU Physics Seminar September 3, 2015 Submitted to the American Journal of Physics Kepler s 3 Laws of planetary motion Kepler s
Elliptical-like orbits on a warped spandex fabric Prof. Chad A. Middleton CMU Physics Seminar September 3, 2015 Submitted to the American Journal of Physics Kepler s 3 Laws of planetary motion Kepler s
Partial Differential Equations for Engineering Math 312, Fall 2012
 Partial Differential Equations for Engineering Math 312, Fall 2012 Jens Lorenz July 17, 2012 Contents Department of Mathematics and Statistics, UNM, Albuquerque, NM 87131 1 Second Order ODEs with Constant
Partial Differential Equations for Engineering Math 312, Fall 2012 Jens Lorenz July 17, 2012 Contents Department of Mathematics and Statistics, UNM, Albuquerque, NM 87131 1 Second Order ODEs with Constant
V (r,t) = i ˆ u( x, y,z,t) + ˆ j v( x, y,z,t) + k ˆ w( x, y, z,t)
 IV. DIFFERENTIAL RELATIONS FOR A FLUID PARTICLE This chapter presents the development and application of the basic differential equations of fluid motion. Simplifications in the general equations and common
IV. DIFFERENTIAL RELATIONS FOR A FLUID PARTICLE This chapter presents the development and application of the basic differential equations of fluid motion. Simplifications in the general equations and common
Prancing Through Quantum Fields
 November 23, 2009 1 Introduction Disclaimer Review of Quantum Mechanics 2 Quantum Theory Of... Fields? Basic Philosophy 3 Field Quantization Classical Fields Field Quantization 4 Intuitive Field Theory
November 23, 2009 1 Introduction Disclaimer Review of Quantum Mechanics 2 Quantum Theory Of... Fields? Basic Philosophy 3 Field Quantization Classical Fields Field Quantization 4 Intuitive Field Theory
First order Partial Differential equations
 First order Partial Differential equations 0.1 Introduction Definition 0.1.1 A Partial Deferential equation is called linear if the dependent variable and all its derivatives have degree one and not multiple
First order Partial Differential equations 0.1 Introduction Definition 0.1.1 A Partial Deferential equation is called linear if the dependent variable and all its derivatives have degree one and not multiple
Mathematical Methods of Physics I ChaosBook.org/ predrag/courses/phys Homework 1
 PHYS 6124 Handout 6 23 August 2012 Mathematical Methods of Physics I ChaosBook.org/ predrag/courses/phys-6124-12 Homework 1 Prof. P. Goldbart School of Physics Georgia Tech Homework assignments are posted
PHYS 6124 Handout 6 23 August 2012 Mathematical Methods of Physics I ChaosBook.org/ predrag/courses/phys-6124-12 Homework 1 Prof. P. Goldbart School of Physics Georgia Tech Homework assignments are posted
Stabilization and Passivity-Based Control
 DISC Systems and Control Theory of Nonlinear Systems, 2010 1 Stabilization and Passivity-Based Control Lecture 8 Nonlinear Dynamical Control Systems, Chapter 10, plus handout from R. Sepulchre, Constructive
DISC Systems and Control Theory of Nonlinear Systems, 2010 1 Stabilization and Passivity-Based Control Lecture 8 Nonlinear Dynamical Control Systems, Chapter 10, plus handout from R. Sepulchre, Constructive
Applied Mathematics 505b January 22, Today Denitions, survey of applications. Denition A PDE is an equation of the form F x 1 ;x 2 ::::;x n ;~u
 Applied Mathematics 505b January 22, 1998 1 Applied Mathematics 505b Partial Dierential Equations January 22, 1998 Text: Sobolev, Partial Dierentail Equations of Mathematical Physics available at bookstore
Applied Mathematics 505b January 22, 1998 1 Applied Mathematics 505b Partial Dierential Equations January 22, 1998 Text: Sobolev, Partial Dierentail Equations of Mathematical Physics available at bookstore
Some Explicit Solutions of the Cable Equation
 Some Explicit Solutions of the Cable Equation Marco Herrera-Valdéz and Sergei K. Suslov Mathematical, Computational and Modeling Sciences Center, Arizona State University, Tempe, AZ 85287 1904, U.S.A.
Some Explicit Solutions of the Cable Equation Marco Herrera-Valdéz and Sergei K. Suslov Mathematical, Computational and Modeling Sciences Center, Arizona State University, Tempe, AZ 85287 1904, U.S.A.
Derivatives and Integrals
 Derivatives and Integrals Definition 1: Derivative Formulas d dx (c) = 0 d dx (f ± g) = f ± g d dx (kx) = k d dx (xn ) = nx n 1 (f g) = f g + fg ( ) f = f g fg g g 2 (f(g(x))) = f (g(x)) g (x) d dx (ax
Derivatives and Integrals Definition 1: Derivative Formulas d dx (c) = 0 d dx (f ± g) = f ± g d dx (kx) = k d dx (xn ) = nx n 1 (f g) = f g + fg ( ) f = f g fg g g 2 (f(g(x))) = f (g(x)) g (x) d dx (ax
Appendix C. Modal Analysis of a Uniform Cantilever with a Tip Mass. C.1 Transverse Vibrations. Boundary-Value Problem
 Appendix C Modal Analysis of a Uniform Cantilever with a Tip Mass C.1 Transverse Vibrations The following analytical modal analysis is given for the linear transverse vibrations of an undamped Euler Bernoulli
Appendix C Modal Analysis of a Uniform Cantilever with a Tip Mass C.1 Transverse Vibrations The following analytical modal analysis is given for the linear transverse vibrations of an undamped Euler Bernoulli
M2A2 Problem Sheet 3 - Hamiltonian Mechanics
 MA Problem Sheet 3 - Hamiltonian Mechanics. The particle in a cone. A particle slides under gravity, inside a smooth circular cone with a vertical axis, z = k x + y. Write down its Lagrangian in a) Cartesian,
MA Problem Sheet 3 - Hamiltonian Mechanics. The particle in a cone. A particle slides under gravity, inside a smooth circular cone with a vertical axis, z = k x + y. Write down its Lagrangian in a) Cartesian,
Tutorial Exercises: Geometric Connections
 Tutorial Exercises: Geometric Connections 1. Geodesics in the Isotropic Mercator Projection When the surface of the globe is projected onto a flat map some aspects of the map are inevitably distorted.
Tutorial Exercises: Geometric Connections 1. Geodesics in the Isotropic Mercator Projection When the surface of the globe is projected onto a flat map some aspects of the map are inevitably distorted.
Math 115 ( ) Yum-Tong Siu 1. Euler-Lagrange Equations for Many Functions and Variables and High-Order Derivatives
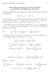 Math 115 006-007 Yum-Tong Siu 1 Euler-Lagrange Equations for Many Functions and Variables and High-Order Derivatives The Case of High-Order Derivatives. The context is to find the extremal for the functional
Math 115 006-007 Yum-Tong Siu 1 Euler-Lagrange Equations for Many Functions and Variables and High-Order Derivatives The Case of High-Order Derivatives. The context is to find the extremal for the functional
Physics 70007, Fall 2009 Answers to Final Exam
 Physics 70007, Fall 009 Answers to Final Exam December 17, 009 1. Quantum mechanical pictures a Demonstrate that if the commutation relation [A, B] ic is valid in any of the three Schrodinger, Heisenberg,
Physics 70007, Fall 009 Answers to Final Exam December 17, 009 1. Quantum mechanical pictures a Demonstrate that if the commutation relation [A, B] ic is valid in any of the three Schrodinger, Heisenberg,
Boundary value problems
 1 Introduction Boundary value problems Lecture 5 We have found that the electric potential is a solution of the partial differential equation; 2 V = ρ/ǫ 0 The above is Poisson s equation where ρ is the
1 Introduction Boundary value problems Lecture 5 We have found that the electric potential is a solution of the partial differential equation; 2 V = ρ/ǫ 0 The above is Poisson s equation where ρ is the
Chapter 4. Series Solutions. 4.1 Introduction to Power Series
 Series Solutions Chapter 4 In most sciences one generation tears down what another has built and what one has established another undoes. In mathematics alone each generation adds a new story to the old
Series Solutions Chapter 4 In most sciences one generation tears down what another has built and what one has established another undoes. In mathematics alone each generation adds a new story to the old
MTH4101 CALCULUS II REVISION NOTES. 1. COMPLEX NUMBERS (Thomas Appendix 7 + lecture notes) ax 2 + bx + c = 0. x = b ± b 2 4ac 2a. i = 1.
 MTH4101 CALCULUS II REVISION NOTES 1. COMPLEX NUMBERS (Thomas Appendix 7 + lecture notes) 1.1 Introduction Types of numbers (natural, integers, rationals, reals) The need to solve quadratic equations:
MTH4101 CALCULUS II REVISION NOTES 1. COMPLEX NUMBERS (Thomas Appendix 7 + lecture notes) 1.1 Introduction Types of numbers (natural, integers, rationals, reals) The need to solve quadratic equations:
Introduction to Sturm-Liouville Theory and the Theory of Generalized Fourier Series
 CHAPTER 5 Introduction to Sturm-Liouville Theory and the Theory of Generalized Fourier Series We start with some introductory examples. 5.. Cauchy s equation The homogeneous Euler-Cauchy equation (Leonhard
CHAPTER 5 Introduction to Sturm-Liouville Theory and the Theory of Generalized Fourier Series We start with some introductory examples. 5.. Cauchy s equation The homogeneous Euler-Cauchy equation (Leonhard
Non-Linear Response of Test Mass to External Forces and Arbitrary Motion of Suspension Point
 LASER INTERFEROMETER GRAVITATIONAL WAVE OBSERVATORY -LIGO- CALIFORNIA INSTITUTE OF TECHNOLOGY MASSACHUSETTS INSTITUTE OF TECHNOLOGY Technical Note LIGO-T980005-01- D 10/28/97 Non-Linear Response of Test
LASER INTERFEROMETER GRAVITATIONAL WAVE OBSERVATORY -LIGO- CALIFORNIA INSTITUTE OF TECHNOLOGY MASSACHUSETTS INSTITUTE OF TECHNOLOGY Technical Note LIGO-T980005-01- D 10/28/97 Non-Linear Response of Test
( ) = 9φ 1, ( ) = 4φ 2.
 Chemistry 46 Dr Jean M Standard Homework Problem Set 6 Solutions The Hermitian operator A ˆ is associated with the physical observable A Two of the eigenfunctions of A ˆ are and These eigenfunctions are
Chemistry 46 Dr Jean M Standard Homework Problem Set 6 Solutions The Hermitian operator A ˆ is associated with the physical observable A Two of the eigenfunctions of A ˆ are and These eigenfunctions are
Partial Differential Equations (PDEs)
 C H A P T E R Partial Differential Equations (PDEs) 5 A PDE is an equation that contains one or more partial derivatives of an unknown function that depends on at least two variables. Usually one of these
C H A P T E R Partial Differential Equations (PDEs) 5 A PDE is an equation that contains one or more partial derivatives of an unknown function that depends on at least two variables. Usually one of these
Two-Body Problem. Central Potential. 1D Motion
 Two-Body Problem. Central Potential. D Motion The simplest non-trivial dynamical problem is the problem of two particles. The equations of motion read. m r = F 2, () We already know that the center of
Two-Body Problem. Central Potential. D Motion The simplest non-trivial dynamical problem is the problem of two particles. The equations of motion read. m r = F 2, () We already know that the center of
3 Stability and Lyapunov Functions
 CDS140a Nonlinear Systems: Local Theory 02/01/2011 3 Stability and Lyapunov Functions 3.1 Lyapunov Stability Denition: An equilibrium point x 0 of (1) is stable if for all ɛ > 0, there exists a δ > 0 such
CDS140a Nonlinear Systems: Local Theory 02/01/2011 3 Stability and Lyapunov Functions 3.1 Lyapunov Stability Denition: An equilibrium point x 0 of (1) is stable if for all ɛ > 0, there exists a δ > 0 such
r 2 i(x; y; z; t) =0for 1<x<1; h <y<0and b<z<b; 2 =0 at y =0; =0 at y = =0 at z = (4) and appropriate
 Forced Dispersive Waves Along a Narrow Channel. January 22, 2002 Linear surface gravity waves propagating along a narrow channel display interesting phenomena. At first we consider free waves propagating
Forced Dispersive Waves Along a Narrow Channel. January 22, 2002 Linear surface gravity waves propagating along a narrow channel display interesting phenomena. At first we consider free waves propagating
Applied Mathematics Masters Examination Fall 2016, August 18, 1 4 pm.
 Applied Mathematics Masters Examination Fall 16, August 18, 1 4 pm. Each of the fifteen numbered questions is worth points. All questions will be graded, but your score for the examination will be the
Applied Mathematics Masters Examination Fall 16, August 18, 1 4 pm. Each of the fifteen numbered questions is worth points. All questions will be graded, but your score for the examination will be the
On reaching head-to-tail ratios for balanced and unbalanced coins
 Journal of Statistical Planning and Inference 0 (00) 0 0 www.elsevier.com/locate/jspi On reaching head-to-tail ratios for balanced and unbalanced coins Tamas Lengyel Department of Mathematics, Occidental
Journal of Statistical Planning and Inference 0 (00) 0 0 www.elsevier.com/locate/jspi On reaching head-to-tail ratios for balanced and unbalanced coins Tamas Lengyel Department of Mathematics, Occidental
Coordinate systems and vectors in three spatial dimensions
 PHYS2796 Introduction to Modern Physics (Spring 2015) Notes on Mathematics Prerequisites Jim Napolitano, Department of Physics, Temple University January 7, 2015 This is a brief summary of material on
PHYS2796 Introduction to Modern Physics (Spring 2015) Notes on Mathematics Prerequisites Jim Napolitano, Department of Physics, Temple University January 7, 2015 This is a brief summary of material on
An Exactly Solvable 3 Body Problem
 An Exactly Solvable 3 Body Problem The most famous n-body problem is one where particles interact by an inverse square-law force. However, there is a class of exactly solvable n-body problems in which
An Exactly Solvable 3 Body Problem The most famous n-body problem is one where particles interact by an inverse square-law force. However, there is a class of exactly solvable n-body problems in which
Physics 129a Calculus of Variations Frank Porter Revision
 Physics 129a Calculus of Variations 71113 Frank Porter Revision 171116 1 Introduction Many problems in physics have to do with extrema. When the problem involves finding a function that satisfies some
Physics 129a Calculus of Variations 71113 Frank Porter Revision 171116 1 Introduction Many problems in physics have to do with extrema. When the problem involves finding a function that satisfies some
f(z)dz = 0. P dx + Qdy = D u dx v dy + i u dy + v dx. dxdy + i x = v
 MA525 ON CAUCHY'S THEOREM AND GREEN'S THEOREM DAVID DRASIN (EDITED BY JOSIAH YODER) 1. Introduction No doubt the most important result in this course is Cauchy's theorem. Every critical theorem in the
MA525 ON CAUCHY'S THEOREM AND GREEN'S THEOREM DAVID DRASIN (EDITED BY JOSIAH YODER) 1. Introduction No doubt the most important result in this course is Cauchy's theorem. Every critical theorem in the
Section 9 Variational Method. Page 492
 Section 9 Variational Method Page 492 Page 493 Lecture 27: The Variational Method Date Given: 2008/12/03 Date Revised: 2008/12/03 Derivation Section 9.1 Variational Method: Derivation Page 494 Motivation
Section 9 Variational Method Page 492 Page 493 Lecture 27: The Variational Method Date Given: 2008/12/03 Date Revised: 2008/12/03 Derivation Section 9.1 Variational Method: Derivation Page 494 Motivation
Surfaces of Revolution with Constant Mean Curvature H = c in Hyperbolic 3-Space H 3 ( c 2 )
 Surfaces of Revolution with Constant Mean Curvature H = c in Hyerbolic 3-Sace H 3 ( c 2 Kinsey-Ann Zarske Deartment of Mathematics, University of Southern Mississii, Hattiesburg, MS 39406, USA E-mail:
Surfaces of Revolution with Constant Mean Curvature H = c in Hyerbolic 3-Sace H 3 ( c 2 Kinsey-Ann Zarske Deartment of Mathematics, University of Southern Mississii, Hattiesburg, MS 39406, USA E-mail:
Consider a particle in 1D at position x(t), subject to a force F (x), so that mẍ = F (x). Define the kinetic energy to be.
 Chapter 4 Energy and Stability 4.1 Energy in 1D Consider a particle in 1D at position x(t), subject to a force F (x), so that mẍ = F (x). Define the kinetic energy to be T = 1 2 mẋ2 and the potential energy
Chapter 4 Energy and Stability 4.1 Energy in 1D Consider a particle in 1D at position x(t), subject to a force F (x), so that mẍ = F (x). Define the kinetic energy to be T = 1 2 mẋ2 and the potential energy
Math 4263 Homework Set 1
 Homework Set 1 1. Solve the following PDE/BVP 2. Solve the following PDE/BVP 2u t + 3u x = 0 u (x, 0) = sin (x) u x + e x u y = 0 u (0, y) = y 2 3. (a) Find the curves γ : t (x (t), y (t)) such that that
Homework Set 1 1. Solve the following PDE/BVP 2. Solve the following PDE/BVP 2u t + 3u x = 0 u (x, 0) = sin (x) u x + e x u y = 0 u (0, y) = y 2 3. (a) Find the curves γ : t (x (t), y (t)) such that that
Viscous Fluids. Amanda Meier. December 14th, 2011
 Viscous Fluids Amanda Meier December 14th, 2011 Abstract Fluids are represented by continuous media described by mass density, velocity and pressure. An Eulerian description of uids focuses on the transport
Viscous Fluids Amanda Meier December 14th, 2011 Abstract Fluids are represented by continuous media described by mass density, velocity and pressure. An Eulerian description of uids focuses on the transport
4. Complex Oscillations
 4. Complex Oscillations The most common use of complex numbers in physics is for analyzing oscillations and waves. We will illustrate this with a simple but crucially important model, the damped harmonic
4. Complex Oscillations The most common use of complex numbers in physics is for analyzing oscillations and waves. We will illustrate this with a simple but crucially important model, the damped harmonic
1 Assignment 1: Nonlinear dynamics (due September
 Assignment : Nonlinear dynamics (due September 4, 28). Consider the ordinary differential equation du/dt = cos(u). Sketch the equilibria and indicate by arrows the increase or decrease of the solutions.
Assignment : Nonlinear dynamics (due September 4, 28). Consider the ordinary differential equation du/dt = cos(u). Sketch the equilibria and indicate by arrows the increase or decrease of the solutions.
2. The Schrödinger equation for one-particle problems. 5. Atoms and the periodic table of chemical elements
 1 Historical introduction The Schrödinger equation for one-particle problems 3 Mathematical tools for quantum chemistry 4 The postulates of quantum mechanics 5 Atoms and the periodic table of chemical
1 Historical introduction The Schrödinger equation for one-particle problems 3 Mathematical tools for quantum chemistry 4 The postulates of quantum mechanics 5 Atoms and the periodic table of chemical
Before you begin read these instructions carefully:
 NATURAL SCIENCES TRIPOS Part IB & II (General) Tuesday, 29 May, 2012 9:00 am to 12:00 pm MATHEMATICS (1) Before you begin read these instructions carefully: You may submit answers to no more than six questions.
NATURAL SCIENCES TRIPOS Part IB & II (General) Tuesday, 29 May, 2012 9:00 am to 12:00 pm MATHEMATICS (1) Before you begin read these instructions carefully: You may submit answers to no more than six questions.
Advanced Mathematics Support Programme OCR Year 2 Pure Core Suggested Scheme of Work ( )
 OCR Year 2 Pure Core Suggested Scheme of Work (2018-2019) This template shows how Integral Resources and FMSP FM videos can be used to support Further Mathematics students and teachers. This template is
OCR Year 2 Pure Core Suggested Scheme of Work (2018-2019) This template shows how Integral Resources and FMSP FM videos can be used to support Further Mathematics students and teachers. This template is
1 Solutions in cylindrical coordinates: Bessel functions
 1 Solutions in cylindrical coordinates: Bessel functions 1.1 Bessel functions Bessel functions arise as solutions of potential problems in cylindrical coordinates. Laplace s equation in cylindrical coordinates
1 Solutions in cylindrical coordinates: Bessel functions 1.1 Bessel functions Bessel functions arise as solutions of potential problems in cylindrical coordinates. Laplace s equation in cylindrical coordinates

 Y G q G Y Y 29 8 $ 29 G 6 q )
Y G q G Y Y 29 8 $ 29 G 6 q )