Surfaces of Revolution with Constant Mean Curvature H = c in Hyperbolic 3-Space H 3 ( c 2 )
|
|
|
- Rosalind Charles
- 6 years ago
- Views:
Transcription
1 Surfaces of Revolution with Constant Mean Curvature H = c in Hyerbolic 3-Sace H 3 ( c 2 Kinsey-Ann Zarske Deartment of Mathematics, University of Southern Mississii, Hattiesburg, MS 39406, USA kinseyann.zarske@eagles.usm.edu Abstract In this article, we construct surfaces of revolution with constant mean curvature H = c in hyerbolic 3- sace H 3 ( c 2 of constant curvature c 2. It is shown that the limit of the surfaces of revolution with H = c in H 3 ( c 2 is catenoid, the minimal surface of revolution in Euclidean 3-sace as c aroaches 0. Introduction Let R 3 be equied with the metric ds 2 = (dt 2 + e 2ct {(dx 2 + (dy 2 }. (1 The sace (R 3, g c has constant curvature c 2. It is denoted by H 3 ( c 2 and is called the seudosherical model of hyerbolic 3-sace. From the metric (1, one can easily see that H 3 ( c 2 attens out to E 3, Euclidean 3-sace as c 0. In H 3 ( c 2, surfaces of constant mean curvature H = c are articularly interesting, because they exhibit many geometric roerties in common with minimal surfaces in E 3. This is not a coincidence. There is a one-to-one corresondence, so-called Lawson corresondence, between surfaces of constant mean curvature H h in H 3 ( c 2 and surfaces of constant mean curvature H e = Hh 2 c2 [Lawson]. Those corresonding constant mean curvature surfaces satisfy the same Gauss-Codazzi equations, so they share many geometric roerties in common, even though they live in dierent saces. In this article, we are articularly interested in constructing surfaces of revolution with H = c in H 3 ( c 2. Hyerbolic 3-sace does not have rotational symmetry as much as Euclidean 3-sace does. From the metric (1, we see that rotations on the xy-lane i.e. rotations about the t-axis may be considered in H 3 ( c 2. Surfaces of constant mean curvature H = c in H 3 ( c 2 can be in general constructed by Bryant's reresentation formula which is an analogue of Weierstrass reresentation formula for minimal surfaces in E 3 [Bryant]. But it is not suitable to use to construct surfaces of revolution with H = c. We calculate directly the mean curvature H of the surface obtained by rotating an unknown role curve about the t axis. This results a second order non-linear dierential equation of the role curve. We unfortunately cannot solve the dierential equation analytically but are able to solve it numerically with the aid of MAPLE software. Once we obtain the role curve, we then construct surface of revolution with H = c simly by rotating the role curve about the t-axis. From the dierential equation of role curves, it can be seen that the limit of the surfaces of revolution with H = c in H 3 ( c 2 is a catenoid, the minimal surface of revolution in Euclidean 3-sace as c aroaches 0. This limiting behavior of the surfaces of revolution with H = c in H 3 ( c 2 is also illustrated with grahics. The author is a junior mathematics and hysics major of the University of Southern Mississii. This research has been conducted under the direction of Dr. Sungwook Lee in the Deartment of Mathematics at the University of Southern Mississii. 1 Parametric Surfaces in H 3 ( c 2 Let M be a domain and ϕ : M H 3 ( c 2 a arametric surface. The metric (1 induces an inner roduct on each tangent sace T H 3 ( c 2. This inner roduct can be used to dene conformal surfaces in H 3 ( c 2. Denition 1. ϕ : M H 3 ( c 2 is said to be conformal if ϕ u, ϕ v = 0, ϕ u = ϕ v = e ω/2, (2 1
2 where (u, v is a local coordinate system in M and ω : M R is a real-valued function in M. The induced metric on the conformal arametric surface is given by ds 2 ϕ = e ω {(du 2 + (dv 2 }. (3 In order to calculate the mean curvature of ϕ, we need to nd a unit normal vector eld N of ϕ. For that, we need something like cross roduct. H 3 ( c 2 is not a vector sace but we can dene an analogue 1 of cross roduct locally on each tangent sace ( T H 3 ( c 2. Let v = v 1 t + v ( ( 2 x + v 3 y, ( w = w 1 t + w ( ( 2 x + w 3 y T H 3 ( c 2, { ( where t, ( ( } x, y denote the canonical basis for T H 3 ( c 2. then dened to be v w = (v 2 w 3 v 3 w 2 where = (t, x, y H 3 ( c 2. Let The cross roduct v w is ( t ( + e 2ct (v 3 w 1 v 1 w 3 x ( + e 2ct (v 1 w 2 v 2 w 1 y E := ϕ u, ϕ u, F := ϕ u, ϕ v, G := ϕ v, ϕ v. Then by a direct calculation we obatin (4 Proosition 2. Let ϕ : M H 3 ( c 2 be a arametric surface. Then on each tangent lane T ϕ(m, we have ϕ u ϕ v 2 = e 4ct(u,v (EG F 2 (5 where = (t(u, v, x(u, v, y(u, v H 3 ( c 2. Remark 3. If c 0, (5 becomes the familiar formula from the Euclidean case. ϕ u ϕ v 2 = EG F 2 2 The Mean curvature of a Parametric Surface in H 3 ( c 2 In the Euclidean case, the mean curvature of a arametric surface ϕ(u, v may be calculated by Gauss' formula Gl + En 2F m H = (6 2(EG F 2 1 We will simly call it cross rodcut. where l = ϕ uu, N, m = ϕ uv, N, n = ϕ vv, N and N is a unit normal vector eld of ϕ. It is not certain, but (6 does not aear to be valid for arametric surfaces in H 3 ( c 2 in general. The derivation of (6 requires the use of Lagrange's identity, but it is no longer valid in the tangent saces of H 3 ( c 2. However, (6 is still valid for conformal surfaces in H 3 ( c 2. It is well-known that: Proosition 4. Let ϕ : M H 3 ( c 2 be a conformal surface satisfying (2. The mean curvature H of ϕ is then comuted to be H = 1 2 e ω ϕ, N. (7 One can then easily see that the the formulas (6 and (7 coincide for conformal surfaces. 3 Surfaces of Revolution with Constant Mean Curvature H = c in H 3 ( c 2 In this section, we construct a surface of revolution with constant mean curvature H = c in H 3 ( c 2. As mentioned in Introduction, rotations about the t-axis are the only tye of Euclidean rotations that can be considered in H 3 ( c 2. Consider a role curve α(u = (u, h(u, 0 in the tx-lane. Denote ϕ(u, v as the rotation of α(u about the t-axis through an angle v. Then, ϕ(u, v = (u, h(u cos v, h(u sin v. (8 The quantities E, F, and G are calculated to be E = e 2cu {e 2cu + (h (u 2 }, F = 0, G = e 2cu h(u. If we require ϕ(u, v to be conformal, then e 2cu + (h (u 2 = (h(u 2. (9 The quantities l, m, n are calculated to be h (uh(u l = (h(u2 (e 2cu + (h (u 2, m = 0, n = (h(u 2 (h(u2 (e 2cu + (h (u 2. 2
3 The mean curvature H is comuted to be 2. H = Gl + En 2F m 2(EG F 2 = 1 h(uh (u + e 2cu + (h (u 2 2 e 2cu (e 2cu + (h (u 2 (h(u 2 (e 2cu + (h (u 2. If we aly the conformality condition (9, H becomes H = h (u + h(u 2e 2cu (h(u 3. (10 Let H = c. Then (10 can be written as h (u h(u + 2ce 2cu (h(u 3 = 0. (11 Hence, constructing a surface of revolution with H = c comes down to solving the second order nonlinear dierential equation (11. If c 0, then (11 becomes h (u h(u = 0 (12 which is a harmonic oscillator. This is the role curve for a surface of revolution in E 3. (12 has the general solution h(u = c 1 cosh u + c 2 sinh u. For c 1 = 1, c 2 = 0, ϕ(u, v is given by ϕ(u, v = (u, cosh u cos v, cosh u sin v (13 This is a minimal surface of revolution in E 3, which is called a catenoid since it is obtained by rotating a catenary h(u = cosh u. See Figure 1. Unfortunately, the author cannot solve (11 analytically, so we solve it numerically with the aid of MAPLE. References Figure 1: Catenoid in E 3 [Lawson] H. Blaine Lawson, Jr., Comlete minimal surfaces in S 3, Ann. of Math. 92, (1970 [Bryant] Robert L. Bryant, Surfaces of mean curvature one in hyerbolic 3-sace, Astérisque 12, No , ( The Illustration of the Limit of Surfaces of Revolution with H = c in H 3 ( c 2 as c 0 In section 3, it is shown that the limit of surfaces of revolution with constant mean curvature H = c in H 3 ( c 2 is a catenoid, a minimal surface of revolution in E 3. Such limiting behavior of surfaces of revolution with H = c in H 3 ( c 2 is illustrated with grahics in Figure 2 (H = 1, Figure 3 (H = 1 2, Figure 4 (H = 1 4, Figure 5 (H = 1 8, Figure 6 (H = 1 64, Figure 7 (H = Figure 7 (b already looks retty close to the catenoid in Figure 1. 2 The validity of this formula should not be a concern since we assume that the surface is conformal. 3
4 (a Prole curve h(u (a Prole Curve h(u (b Surface of Revolution in H 3 ( 1 Figure 2: Constant Mean Curvature H = 1 (b Surface of Revolution in H 3 ( 1 4 Figure 3: Constant Mean Curvature H = 1 2 4
5 (a Prole Curve h(u (a Prole Curve h(u (b Surface of Revolution in H 3 ( 1 16 Figure 4: Constant Mean Curvature H = 1 4 (b Surface of Revolution in H 3 ( 1 64 Figure 5: Constant Mean Curvature H = 1 8 5
6 (a Prole Curve h(u (a Prole Curve h(u (b Surface of Revolution in H 3 ( Figure 6: ConstSurface of Revolution in H 3 ( c 2 ant Mean Curvature H = 1 64 (b Surface of Revolution in H 3 ( Figure 7: Constant Mean Curvature H =
Surfaces of Revolution with Constant Mean Curvature in Hyperbolic 3-Space
Surfaces of Revolution with Constant Mean Curvature in Hyerbolic 3-Sace Sungwook Lee Deartment of Mathematics, University of Southern Mississii, Hattiesburg, MS 39401, USA sunglee@usm.edu Kinsey-Ann Zarske
Isothermal parameters
MTH.B402; Sect. 3 (20180626) 26 Isothermal parameters A Review of Complex Analysis. Let C be the complex plane. A C 1 -function 7 f : C D z w = f(z) C defined on a domain D is said to be holomorphic if
Lectures 12: The Second Fundamental Form. Table of contents
ectures 1: The Second Fundamental Form Disclaimer. As we have a textbook, this lecture note is for guidance sulement only. It should not be relied on when rearing for exams. In this lecture we introduce
Chapter 14. Basics of The Differential Geometry of Surfaces. Introduction. Parameterized Surfaces. The First... Home Page. Title Page.
Chapter 14 Basics of The Differential Geometry of Surfaces Page 649 of 681 14.1. Almost all of the material presented in this chapter is based on lectures given by Eugenio Calabi in an upper undergraduate
DIFFERENTIAL GEOMETRY HW 4. Show that a catenoid and helicoid are locally isometric.
DIFFERENTIAL GEOMETRY HW 4 CLAY SHONKWILER Show that a catenoid and helicoid are locally isometric. 3 Proof. Let X(u, v) = (a cosh v cos u, a cosh v sin u, av) be the parametrization of the catenoid and
Lectures 15: Parallel Transport. Table of contents
Lectures 15: Parallel Transport Disclaimer. As we have a textbook, this lecture note is for guidance and supplement only. It should not be relied on when preparing for exams. In this lecture we study the
THE GAUSS MAP OF TIMELIKE SURFACES IN R n Introduction
Chin. Ann. of Math. 16B: 3(1995),361-370. THE GAUSS MAP OF TIMELIKE SURFACES IN R n 1 Hong Jianqiao* Abstract Gauss maps of oriented timelike 2-surfaces in R1 n are characterized, and it is shown that
Math 20E Midterm II(ver. a)
Name: olutions tudent ID No.: Discussion ection: Math 20E Midterm IIver. a) Fall 2018 Problem core 1 /24 2 /25 3 /26 4 /25 Total /100 1. 24 Points.) Consider the force field F 5y ı + 3y 2 j. Compute the
Geometric Modelling Summer 2016
Geometric Modelling Summer 2016 Exercises Benjamin Karer M.Sc. http://gfx.uni-kl.de/~gm Benjamin Karer M.Sc. Geometric Modelling Summer 2016 1 Dierential Geometry Benjamin Karer M.Sc. Geometric Modelling
Minimal timelike surfaces in a certain homogeneous Lorentzian 3-manifold II
Minimal timelike surfaces in a certain homogeneous Lorentzian 3-manifold II Sungwook Lee Abstract The 2-parameter family of certain homogeneous Lorentzian 3-manifolds which includes Minkowski 3-space and
Surface x(u, v) and curve α(t) on it given by u(t) & v(t). Math 4140/5530: Differential Geometry
Surface x(u, v) and curve α(t) on it given by u(t) & v(t). α du dv (t) x u dt + x v dt Surface x(u, v) and curve α(t) on it given by u(t) & v(t). α du dv (t) x u dt + x v dt ( ds dt )2 Surface x(u, v)
Lecture 8: The First Fundamental Form Table of contents
Math 38 Fall 2016 Lecture 8: The First Fundamental Form Disclaimer. As we have a textbook, this lecture note is for guidance and sulement only. It should not be relied on when rearing for exams. In this
ν(u, v) = N(u, v) G(r(u, v)) E r(u,v) 3.
5. The Gauss Curvature Beyond doubt, the notion of Gauss curvature is of paramount importance in differential geometry. Recall two lessons we have learned so far about this notion: first, the presence
Math 5378, Differential Geometry Solutions to practice questions for Test 2
Math 5378, Differential Geometry Solutions to practice questions for Test 2. Find all possible trajectories of the vector field w(x, y) = ( y, x) on 2. Solution: A trajectory would be a curve (x(t), y(t))
d F = (df E 3 ) E 3. (4.1)
4. The Second Fundamental Form In the last section we developed the theory of intrinsic geometry of surfaces by considering the covariant differential d F, that is, the tangential component of df for a
Arc Length and Surface Area in Parametric Equations
Arc Length and Surface Area in Parametric Equations MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2011 Background We have developed definite integral formulas for arc length
Minimal Surfaces in R 3
Minimal Suaces in R 3 AJ Vargas May 10, 018 1 Introduction The goal of this note is to give a brief introduction to the theory of minimal suaces in R 3, and to show how one would go about generalizing
Hyperbolic Geometry on Geometric Surfaces
Mathematics Seminar, 15 September 2010 Outline Introduction Hyperbolic geometry Abstract surfaces The hemisphere model as a geometric surface The Poincaré disk model as a geometric surface Conclusion Introduction
Inner Product Spaces 6.1 Length and Dot Product in R n
Inner Product Spaces 6.1 Length and Dot Product in R n Summer 2017 Goals We imitate the concept of length and angle between two vectors in R 2, R 3 to define the same in the n space R n. Main topics are:
Lecture Notes on Minimal Surfaces January 27, 2006 by Michael Dorff
Lecture Notes on Minimal Surfaces January 7, 6 by Michael Dorff 1 Some Background in Differential Geometry Our goal is to develop the mathematics necessary to investigate minimal surfaces in R 3. Every
ε i (E j )=δj i = 0, if i j, form a basis for V, called the dual basis to (E i ). Therefore, dim V =dim V.
Covectors Definition. Let V be a finite-dimensional vector sace. A covector on V is real-valued linear functional on V, that is, a linear ma ω : V R. The sace of all covectors on V is itself a real vector
ON THE SYMMETRY OF ANNULAR BRYANT SURFACE WITH CONSTANT CONTACT ANGLE. Sung-Ho Park
Korean J. Math. 22 (201), No. 1, pp. 133 138 http://dx.doi.org/10.11568/kjm.201.22.1.133 ON THE SYMMETRY OF ANNULAR BRYANT SURFACE WITH CONSTANT CONTACT ANGLE Sung-Ho Park Abstract. We show that a compact
Curves I: Curvature and Torsion. Table of contents
Math 48 Fall 07 Curves I: Curvature and Torsion Disclaimer. As we have a textbook, this lecture note is for guidance and sulement only. It should not be relied on when rearing for exams. In this lecture
Minimal Surfaces. December 13, Alex Verzea. MATH 580: Partial Dierential Equations 1. Professor: Gantumur Tsogtgerel
Minimal Surfaces December 13, 2012 Alex Verzea 260324472 MATH 580: Partial Dierential Equations 1 Professor: Gantumur Tsogtgerel 1 Intuitively, a Minimal Surface is a surface that has minimal area, locally.
Sharp gradient estimate and spectral rigidity for p-laplacian
Shar gradient estimate and sectral rigidity for -Lalacian Chiung-Jue Anna Sung and Jiaing Wang To aear in ath. Research Letters. Abstract We derive a shar gradient estimate for ositive eigenfunctions of
HEAT AND LAPLACE TYPE EQUATIONS WITH COMPLEX SPATIAL VARIABLES IN WEIGHTED BERGMAN SPACES
Electronic Journal of ifferential Equations, Vol. 207 (207), No. 236,. 8. ISSN: 072-669. URL: htt://ejde.math.txstate.edu or htt://ejde.math.unt.edu HEAT AN LAPLACE TYPE EQUATIONS WITH COMPLEX SPATIAL
Generic Singularities of Solutions to some Nonlinear Wave Equations
Generic Singularities of Solutions to some Nonlinear Wave Equations Alberto Bressan Deartment of Mathematics, Penn State University (Oberwolfach, June 2016) Alberto Bressan (Penn State) generic singularities
The Jacobian. v y u y v (see exercise 46). The total derivative is also known as the Jacobian Matrix of the transformation T (u; v) :
The Jacobian The Jacobian of a Transformation In this section, we explore the concept of a "derivative" of a coordinate transformation, which is known as the Jacobian of the transformation. However, in
Non-Relativistic Quantum Mechanics as a Gauge Theory
Non-Relativistic Quantum Mechanics as a Gauge Theory Sungwook Lee Department of Mathematics, University of Southern Mississippi LA/MS Section of MAA Meeting, March 1, 2013 Outline Lifted Quantum Mechanics
Conformally flat hypersurfaces with cyclic Guichard net
Conformally flat hypersurfaces with cyclic Guichard net (Udo Hertrich-Jeromin, 12 August 2006) Joint work with Y. Suyama A geometrical Problem Classify conformally flat hypersurfaces f : M n 1 S n. Def.
Math 265H: Calculus III Practice Midterm II: Fall 2014
Name: Section #: Math 65H: alculus III Practice Midterm II: Fall 14 Instructions: This exam has 7 problems. The number of points awarded for each question is indicated in the problem. Answer each question
jf 00 (x)j ds (x) = [1 + (f 0 (x)) 2 ] 3=2 (t) = jjr0 (t) r 00 (t)jj jjr 0 (t)jj 3
![jf 00 (x)j ds (x) = [1 + (f 0 (x)) 2 ] 3=2 (t) = jjr0 (t) r 00 (t)jj jjr 0 (t)jj 3](/thumbs/78/77303345.jpg "jf 00 (x)j ds (x) = [1 + (f 0 (x)) 2 ] 3=2 (t) = jjr0 (t) r 00 (t)jj jjr 0 (t)jj 3")
M73Q Multivariable Calculus Fall 7 Review Problems for Exam The formulas in the box will be rovided on the exam. (s) dt jf (x)j ds (x) [ + (f (x)) ] 3 (t) jjt (t)jj jjr (t)jj (t) jjr (t) r (t)jj jjr (t)jj
Solutions to Homework #05 MATH ln z 2 + x 2 1 = 2x2 z 2 + x 2 + ln z2 + x 2. = x. ln z 2 + x 2 2z z 2 + x 2 = 2xz
Solutions to Homeork #05 MATH Kaai Section. (I) Exercise #. g x and g z : Product Rule: g x = x @ ln z + x + ln z + x @ [x] = x x z + x + ln z + x = x z + x + ln z + x x is eld constant. g z = x @ ln z
Practice Final Solutions
Practice Final Solutions Math 1, Fall 17 Problem 1. Find a parameterization for the given curve, including bounds on the parameter t. Part a) The ellipse in R whose major axis has endpoints, ) and 6, )
Totally quasi-umbilic timelike surfaces in R 1,2
Totally quasi-umbilic timelike surfaces in R 1,2 Jeanne N. Clelland, University of Colorado AMS Central Section Meeting Macalester College April 11, 2010 Definition: Three-dimensional Minkowski space R
Rule ST1 (Symmetry). α β = β α for 1-forms α and β. Like the exterior product, the symmetric tensor product is also linear in each slot :
2. Metrics as Symmetric Tensors So far we have studied exterior products of 1-forms, which obey the rule called skew symmetry: α β = β α. There is another operation for forming something called the symmetric
CMSC 425: Lecture 4 Geometry and Geometric Programming
CMSC 425: Lecture 4 Geometry and Geometric Programming Geometry for Game Programming and Grahics: For the next few lectures, we will discuss some of the basic elements of geometry. There are many areas
MATH 220: PROBLEM SET 1, SOLUTIONS DUE FRIDAY, OCTOBER 2, 2015
MATH 220: PROBLEM SET 1, SOLUTIONS DUE FRIDAY, OCTOBER 2, 2015 Problem 1 Classify the following PDEs by degree of non-linearity (linear, semilinear, quasilinear, fully nonlinear: (1 (cos x u x + u y =
Past Exam Problems in Integrals, Solutions
Past Exam Problems in Integrals, olutions Prof. Qiao Zhang ourse 11.22 December 7, 24 Note: These problems do not imply, in any sense, my taste or preference for our own exam. ome of the problems here
Multiplicative group law on the folium of Descartes
Multilicative grou law on the folium of Descartes Steluţa Pricoie and Constantin Udrişte Abstract. The folium of Descartes is still studied and understood today. Not only did it rovide for the roof of
LEIBNIZ SEMINORMS IN PROBABILITY SPACES
LEIBNIZ SEMINORMS IN PROBABILITY SPACES ÁDÁM BESENYEI AND ZOLTÁN LÉKA Abstract. In this aer we study the (strong) Leibniz roerty of centered moments of bounded random variables. We shall answer a question
Molding surfaces and Liouville s equation
Molding surfaces and Liouville s equation Naoya Ando Abstract According to [9], a molding surface has a property that a family of lines of curvature consists of geodesics. In the present paper, we will
SINGULAR CURVES OF AFFINE MAXIMAL MAPS
Fundamental Journal of Mathematics and Mathematical Sciences Vol. 1, Issue 1, 014, Pages 57-68 This paper is available online at http://www.frdint.com/ Published online November 9, 014 SINGULAR CURVES
Report submitted to Prof. P. Shipman for Math 641, Spring 2012
Dynamics at the Horsetooth Volume 4, 2012. The Weierstrass-Enneper Representations Department of Mathematics Colorado State University mylak@rams.colostate.edu drpackar@rams.colostate.edu Report submitted
CHAPTER 3: TANGENT SPACE
CHAPTER 3: TANGENT SPACE DAVID GLICKENSTEIN 1. Tangent sace We shall de ne the tangent sace in several ways. We rst try gluing them together. We know vectors in a Euclidean sace require a baseoint x 2
Dierential Geometry Curves and surfaces Local properties Geometric foundations (critical for visual modeling and computing) Quantitative analysis Algo
Dierential Geometry Curves and surfaces Local properties Geometric foundations (critical for visual modeling and computing) Quantitative analysis Algorithm development Shape control and interrogation Curves
Math 115 ( ) Yum-Tong Siu 1. Euler-Lagrange Equations for Many Functions and Variables and High-Order Derivatives
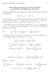Math 115 006-007 Yum-Tong Siu 1 Euler-Lagrange Equations for Many Functions and Variables and High-Order Derivatives The Case of High-Order Derivatives. The context is to find the extremal for the functional
SELECTED SAMPLE FINAL EXAM SOLUTIONS - MATH 5378, SPRING 2013
SELECTED SAMPLE FINAL EXAM SOLUTIONS - MATH 5378, SPRING 03 Problem (). This problem is perhaps too hard for an actual exam, but very instructional, and simpler problems using these ideas will be on the
Dependence on Initial Conditions of Attainable Sets of Control Systems with p-integrable Controls
Nonlinear Analysis: Modelling and Control, 2007, Vol. 12, No. 3, 293 306 Deendence on Initial Conditions o Attainable Sets o Control Systems with -Integrable Controls E. Akyar Anadolu University, Deartment
Lectures 18: Gauss's Remarkable Theorem II. Table of contents
Math 348 Fall 27 Lectures 8: Gauss's Remarkable Theorem II Disclaimer. As we have a textbook, this lecture note is for guidance and supplement only. It should not be relied on when preparing for exams.
A QUATERNIONIC APPROACH to GEOMETRY of CURVES on SPACES of CONSTANT CURVATURE
INTERNATIONAL JOURNAL OF GEOMETRY Vol. 3 (2014), No. 1, 53-65 A QUATERNIONIC APPROACH to GEOMETRY of CURVES on SPACES of CONSTANT CURVATURE TUNA BAYRAKDAR and A. A. ERG IN Abstract. We construct the Frenet-Serret
j=1 ωj k E j. (3.1) j=1 θj E j, (3.2)
3. Cartan s Structural Equations and the Curvature Form Let E,..., E n be a moving (orthonormal) frame in R n and let ωj k its associated connection forms so that: de k = n ωj k E j. (3.) Recall that ωj
Minimal Surfaces. Clay Shonkwiler
Minimal Surfaces Clay Shonkwiler October 18, 2006 Soap Films A soap film seeks to minimize its surface energy, which is proportional to area. Hence, a soap film achieves a minimum area among all surfaces
UNICITY RESULTS FOR GAUSS MAPS OF MNINIMAL. SURFACES IMMERSED IN R m
UNICITY RESULTS FOR GAUSS MAPS OF MNINIMAL SURFACES IMMERSED IN R m A Dissertation Presented to the Faculty of the Department of Mathematics University of Houston In Partial Fulllment of the Requirements
On the Weierstrass-Enneper Representation of Minimal Surfaces
On the Weierstrass-Enneper Representation of Minimal Surfaces Albin Ingelström Bachelor s thesis 2017:K15 Faculty of Science Centre for Mathematical Sciences Mathematics CENTRUM SCIENTIARUM MATHEMATICARUM
Volume-Preserving Diffeomorphisms with Periodic Shadowing
Int. Journal of Math. Analysis, Vol. 7, 2013, no. 48, 2379-2383 HIKARI Ltd, www.m-hikari.com htt://dx.doi.org/10.12988/ijma.2013.37187 Volume-Preserving Diffeomorhisms with Periodic Shadowing Manseob Lee
An Existence Theorem for a Class of Nonuniformly Nonlinear Systems
Australian Journal of Basic and Alied Sciences, 5(7): 1313-1317, 11 ISSN 1991-8178 An Existence Theorem for a Class of Nonuniformly Nonlinear Systems G.A. Afrouzi and Z. Naghizadeh Deartment of Mathematics,
Alexei F. Cheviakov. University of Saskatchewan, Saskatoon, Canada. INPL seminar June 09, 2011
Direct Method of Construction of Conservation Laws for Nonlinear Differential Equations, its Relation with Noether s Theorem, Applications, and Symbolic Software Alexei F. Cheviakov University of Saskatchewan,
Chapter 4. The First Fundamental Form (Induced Metric)
Chapter 4. The First Fundamental Form (Induced Metric) We begin with some definitions from linear algebra. Def. Let V be a vector space (over IR). A bilinear form on V is a map of the form B : V V IR which
Bi-quartic parametric polynomial minimal surfaces
arxiv:1503.09159v1 [math.dg] 31 Mar 015 Bi-quartic parametric polynomial minimal surfaces Ognian Kassabov Abstract Krassimira Vlachkova Minimal surfaces with isothermal parameters admitting Bézier representation
Differential Sandwich Theorem for Multivalent Meromorphic Functions associated with the Liu-Srivastava Operator
KYUNGPOOK Math. J. 512011, 217-232 DOI 10.5666/KMJ.2011.51.2.217 Differential Sandwich Theorem for Multivalent Meromorhic Functions associated with the Liu-Srivastava Oerator Rosihan M. Ali, R. Chandrashekar
Math 23b Practice Final Summer 2011
Math 2b Practice Final Summer 211 1. (1 points) Sketch or describe the region of integration for 1 x y and interchange the order to dy dx dz. f(x, y, z) dz dy dx Solution. 1 1 x z z f(x, y, z) dy dx dz
HILBERT S THEOREM ON THE HYPERBOLIC PLANE
HILBET S THEOEM ON THE HYPEBOLIC PLANE MATTHEW D. BOWN Abstract. We recount a proof of Hilbert s result that a complete geometric surface of constant negative Gaussian curvature cannot be isometrically
A local characterization for constant curvature metrics in 2-dimensional Lorentz manifolds
A local characterization for constant curvature metrics in -dimensional Lorentz manifolds Ivo Terek Couto Alexandre Lymberopoulos August 9, 8 arxiv:65.7573v [math.dg] 4 May 6 Abstract In this paper we
GENERICITY OF INFINITE-ORDER ELEMENTS IN HYPERBOLIC GROUPS
GENERICITY OF INFINITE-ORDER ELEMENTS IN HYPERBOLIC GROUPS PALLAVI DANI 1. Introduction Let Γ be a finitely generated grou and let S be a finite set of generators for Γ. This determines a word metric on
Inequalities for the generalized trigonometric and hyperbolic functions with two parameters
Available online at www.tjnsa.com J. Nonlinear Sci. Al. 8 5, 35 33 Research Article Inequalities for the generalized trigonometric and hyerbolic functions with two arameters Li Yin a,, Li-Guo Huang a a
MTH234 Chapter 15 - Multiple Integrals Michigan State University
MTH24 Chater 15 - Multile Integrals Michigan State University 6 Surface Area Just as arc length is an alication of a single integral, surface area is an alication of double integrals. In 15.6 we comute
Name: SOLUTIONS Date: 11/9/2017. M20550 Calculus III Tutorial Worksheet 8
Name: SOLUTIONS Date: /9/7 M55 alculus III Tutorial Worksheet 8. ompute R da where R is the region bounded by x + xy + y 8 using the change of variables given by x u + v and y v. Solution: We know R is
Part IB Geometry. Theorems. Based on lectures by A. G. Kovalev Notes taken by Dexter Chua. Lent 2016
Part IB Geometry Theorems Based on lectures by A. G. Kovalev Notes taken by Dexter Chua Lent 2016 These notes are not endorsed by the lecturers, and I have modified them (often significantly) after lectures.
Helicoidal surfaces with J r = Ar in 3-dimensional Euclidean space
Stud. Univ. Babeş-Bolyai Math. 60(2015), No. 3, 437 448 Helicoidal surfaces with J r = Ar in 3-dimensional Euclidean space Bendehiba Senoussi and Mohammed Bekkar Abstract. In this paper we study the helicoidal
Introduction to Algebraic and Geometric Topology Week 14
Introduction to Algebraic and Geometric Topology Week 14 Domingo Toledo University of Utah Fall 2016 Computations in coordinates I Recall smooth surface S = {f (x, y, z) =0} R 3, I rf 6= 0 on S, I Chart
F(p) y + 3y + 2y = δ(t a) y(0) = 0 and y (0) = 0.
Page 5- Chater 5: Lalace Transforms The Lalace Transform is a useful tool that is used to solve many mathematical and alied roblems. In articular, the Lalace transform is a technique that can be used to
The First Fundamental Form
The First Fundamental Form Outline 1. Bilinear Forms Let V be a vector space. A bilinear form on V is a function V V R that is linear in each variable separately. That is,, is bilinear if αu + β v, w αu,
Math 1270 Honors ODE I Fall, 2008 Class notes # 14. x 0 = F (x; y) y 0 = G (x; y) u 0 = au + bv = cu + dv
Math 1270 Honors ODE I Fall, 2008 Class notes # 1 We have learned how to study nonlinear systems x 0 = F (x; y) y 0 = G (x; y) (1) by linearizing around equilibrium points. If (x 0 ; y 0 ) is an equilibrium
AN INTRODUCTION TO CURVILINEAR ORTHOGONAL COORDINATES
AN INTRODUCTION TO CURVILINEAR ORTHOGONAL COORDINATES Overview Throughout the first few weeks of the semester, we have studied vector calculus using almost exclusively the familiar Cartesian x,y,z coordinate
Dr. Allen Back. Dec. 3, 2014
Dr. Allen Back Dec. 3, 2014 forms are sums of wedge products of the basis 1-forms dx, dy, and dz. They are kinds of tensors generalizing ordinary scalar functions and vector fields. They have a skew-symmetry
Calculus of Variations Summer Term 2014
Calculus of Variations Summer Term 2014 Lecture 5 7. Mai 2014 c Daria Apushkinskaya 2014 () Calculus of variations lecture 5 7. Mai 2014 1 / 25 Purpose of Lesson Purpose of Lesson: To discuss catenary
On Isoperimetric Functions of Probability Measures Having Log-Concave Densities with Respect to the Standard Normal Law
On Isoerimetric Functions of Probability Measures Having Log-Concave Densities with Resect to the Standard Normal Law Sergey G. Bobkov Abstract Isoerimetric inequalities are discussed for one-dimensional
FFTs in Graphics and Vision. Rotational and Reflective Symmetry Detection
FFTs in Grahics and Vision Rotational and Relectie Symmetry Detection Outline Reresentation Theory Symmetry Detection Rotational Symmetry Relectie Symmetry Reresentation Theory Recall: A rou is a set o
Generalized exterior forms, geometry and space-time
Generalized exterior forms, geometry and sace-time P Nurowski Instytut Fizyki Teoretycznej Uniwersytet Warszawski ul. Hoza 69, Warszawa nurowski@fuw.edu.l D C Robinson Mathematics Deartment King s College
Math 212-Lecture 8. The chain rule with one independent variable
Math 212-Lecture 8 137: The multivariable chain rule The chain rule with one independent variable w = f(x, y) If the particle is moving along a curve x = x(t), y = y(t), then the values that the particle
A Numerical Radius Version of the Arithmetic-Geometric Mean of Operators
Filomat 30:8 (2016), 2139 2145 DOI 102298/FIL1608139S Published by Faculty of Sciences and Mathematics, University of Niš, Serbia vailable at: htt://wwwmfniacrs/filomat Numerical Radius Version of the
Mathematics II. Tutorial 2 First order differential equations. Groups: B03 & B08
Tutorial 2 First order differential equations Groups: B03 & B08 February 1, 2012 Department of Mathematics National University of Singapore 1/15 : First order linear differential equations In this question,
Lecture No 1 Introduction to Diffusion equations The heat equat
Lecture No 1 Introduction to Diffusion equations The heat equation Columbia University IAS summer program June, 2009 Outline of the lectures We will discuss some basic models of diffusion equations and
Prolongation structure for nonlinear integrable couplings of a KdV soliton hierarchy
Prolongation structure for nonlinear integrable couplings of a KdV soliton hierarchy Yu Fa-Jun School of Mathematics and Systematic Sciences, Shenyang Normal University, Shenyang 110034, China Received
Hölder s and Minkowski s Inequality
Hölder s and Minkowski s Inequality James K. Peterson Deartment of Biological Sciences and Deartment of Mathematical Sciences Clemson University Setember 10, 2018 Outline 1 Conjugate Exonents 2 Hölder
Surfaces with zero mean curvature vector in 4-dimensional space forms
Surfaces with zero mean curvature vector in 4-dimensional space forms Naoya Ando Abstract Equations for minimal surfaces in 4-dimensional Riemannian space forms and space-like surfaces in 4-dimensional
8.7 Associated and Non-associated Flow Rules
8.7 Associated and Non-associated Flow Rules Recall the Levy-Mises flow rule, Eqn. 8.4., d ds (8.7.) The lastic multilier can be determined from the hardening rule. Given the hardening rule one can more
The Gauss map and second fundamental form of surfaces in R 3
The Gauss map and second fundamental form of surfaces in R 3 J. A. Gálvez A. Martínez Departamento de Geometría y Topoloía, Facultad de Ciencias, Universidad de Granada, 18071 GRANADA. SPAIN. e-mail: jaalvez@oliat.ur.es;
The oerators a and a obey the commutation relation Proof: [a a ] = (7) aa ; a a = ((q~ i~)(q~ ; i~) ; ( q~ ; i~)(q~ i~)) = i ( ~q~ ; q~~) = (8) As a s
![The oerators a and a obey the commutation relation Proof: [a a ] = (7) aa ; a a = ((q~ i~)(q~ ; i~) ; ( q~ ; i~)(q~ i~)) = i ( ~q~ ; q~~) = (8) As a s](/thumbs/78/77678205.jpg "The oerators a and a obey the commutation relation Proof: [a a ] = (7) aa ; a a = ((q~ i~)(q~ ; i~) ; ( q~ ; i~)(q~ i~)) = i ( ~q~ ; q~~) = (8) As a s")
They can b e used to exress q, and H as follows: 8.54: Many-body henomena in condensed matter and atomic hysics Last modied: Setember 4, 3 Lecture. Coherent States. We start the course with the discussion
Final Exam May 4, 2016
1 Math 425 / AMCS 525 Dr. DeTurck Final Exam May 4, 2016 You may use your book and notes on this exam. Show your work in the exam book. Work only the problems that correspond to the section that you prepared.
A Quadratic Cumulative Production Model for the Material Balance of Abnormally-Pressured Gas Reservoirs
A Quadratic Cumulative Production Model for the Material Balance of Abnormally-Pressured as Reservoirs F.E. onale, M.S. Thesis Defense 7 October 2003 Deartment of Petroleum Engineering Texas A&M University
MATHS 267 Answers to Stokes Practice Dr. Jones
MATH 267 Answers to tokes Practice Dr. Jones 1. Calculate the flux F d where is the hemisphere x2 + y 2 + z 2 1, z > and F (xz + e y2, yz, z 2 + 1). Note: the surface is open (doesn t include any of the
Supergeometry of Three Dimensional Black Holes. Alan R. Steif.
UCD-PHY-95- Suergeometry of Three Dimensional Black Holes PostScrit rocessed by the SLAC/DESY Libraries on 4 Ar 995. Alan R. Steif Deartment of Physics University of California Davis, CA 9566 steif@dirac.ucdavis.edu
On the approximation of a polytope by its dual L p -centroid bodies
On the aroximation of a olytoe by its dual L -centroid bodies Grigoris Paouris and Elisabeth M. Werner Abstract We show that the rate of convergence on the aroximation of volumes of a convex symmetric
. Consider the linear system dx= =! = " a b # x y! : (a) For what values of a and b do solutions oscillate (i.e., do both x(t) and y(t) pass through z
Preliminary Exam { 1999 Morning Part Instructions: No calculators or crib sheets are allowed. Do as many problems as you can. Justify your answers as much as you can but very briey. 1. For positive real
A PROOF OF THE GAUSS-BONNET THEOREM. Contents. 1. Introduction. 2. Regular Surfaces
A PROOF OF THE GAUSS-BONNET THEOREM AARON HALPER Abstract. In this paper I will provide a proof of the Gauss-Bonnet Theorem. I will start by briefly explaining regular surfaces and move on to the first
MATH 361: NUMBER THEORY ELEVENTH LECTURE
MATH 361: NUMBER THEORY ELEVENTH LECTURE The subjects of this lecture are characters, Gauss sums, Jacobi sums, and counting formulas for olynomial equations over finite fields. 1. Definitions, Basic Proerties
, where s is the arclength parameter. Prove that. κ = w = 1 κ (θ) + 1. k (θ + π). dγ dθ. = 1 κ T. = N dn dθ. = T, N T = 0, N = T =1 T (θ + π) = T (θ)
Here is a collection of old exam problems: 1. Let β (t) :I R 3 be a regular curve with speed = dβ, where s is the arclength parameter. Prove that κ = d β d β d s. Let β (t) :I R 3 be a regular curve such
L 2 Geometry of the Symplectomorphism Group
University of Notre Dame Workshop on Innite Dimensional Geometry, Vienna 2015 Outline 1 The Exponential Map on D s ω(m) 2 Existence of Multiplicity of Outline 1 The Exponential Map on D s ω(m) 2 Existence