Journal of Computational and Applied Mathematics
|
|
|
- Laurel Harper
- 5 years ago
- Views:
Transcription
1 Journl of Compuionl n Applie Mhemis 245 (23) Conens liss ville SiVerse SieneDire Journl of Compuionl n Applie Mhemis journl homepge: On exponenil men-squre siliy of wo-sep Mruym mehos for sohsi ely ifferenil equions Wnrong Co,,, Zhongqing Zhng Deprmen of Mhemis, Souhes Universiy, Nnjing 296, PR Chin Division of Applie Mhemis, Brown Universiy, Proviene, RI 292, USA r i l e i n f o s r Arile hisory: Reeive 5 July 2 Reeive in revise form 29 Deemer 22 Keywors: Sohsi moeling Exponenil men-squre siliy Two-sep Mruym mehos We re onerne wih he exponenil men-squre siliy of wo-sep Mruym mehos for sohsi ifferenil equions wih ime ely. We propose fmily of shemes n prove h i n minin he exponenil men-squre siliy of he liner sohsi ely ifferenil equion for every sep size of inegrl frion of he ely in he equion. Numeril resuls for liner n nonliner equions show h his fmily of wo-sep Mruym mehos exhiis eer siliy hn previous wo-sep Mruym mehos. 23 Elsevier B.V. All righs reserve.. Inrouion Sohsi ely ifferenil equions (SDDEs) hve een inresingly use o moel he effes of noise n ime ely on vrious ypes of omplex sysems, suh s elye visul feek sysems [], onrol prolems [2,3] n he ynmis of noisy i-sle sysems wih ely [4]. SDDEs re lso use in moeling iseses, for exmple, epiemi iseses [5], neurologil iseses [6], e., n lso in finne SDDEs pper in moels of sok mrkes [7]. Some numeril mehos n heir onvergene n siliy properies hve een eslishe [8 4] reenly, u mos of hem re on one-sep mehos. Inse of one-sep mehos we here fous on sohsi muli-sep mehos for SDDEs, whih hve een wiely suie for solving sohsi orinry ifferenil equions (SODEs), i.e. wih no ime ely. To exen he muli-sep mehos for SODEs o hose for SDDEs is nonrivil sk n hese exensions hve no een invesige unil reenly. For review of muli-sep mehos for SODEs, we refer o [5,6]. Some more reen suies re s follows. In [7], erin sohsi liner muli-sep mehos re onsrue; n men-squre onvergene res re oine; n onsiseny oniions in he men-squre sense re given for wo-sep Mruym mehos. Ewl n Témm [8] suie he onvergene of sohsi Ams Bshforh sheme wih ppliion o geophysil ppliions. Ams-ype mehos for SODEs re lso nlyze in [9], where firs-orer srong onvergene oniions re given. For some speil SODEs wih iive noise, high orer muli-sep mehos hve een isusse in [2]. In his pper, we follow [2] n suy wo-sep Mruym shemes for he slr equion X() = f, X(), X( τ) + g, X(), X( τ) W(), J, X() = ξ(), [ τ, ], where τ is posiive fixe ely, J = [, T], W() is one-imensionl snr Wiener proess n he funions f : J R R R, g : J R R R. We noe h [2] is perhps he only work on muli-sep mehos for SDDEs, wherein (.) Corresponing uhor : Deprmen of Mhemis, Souhes Universiy, Nnjing 296, PR Chin. Tel.: E-mil resses: wro@seu.eu.n, seu_wr@sin.om (W. Co), Zhongqing_zhng@rown.eu (Z. Zhng) /$ see fron mer 23 Elsevier B.V. All righs reserve. oi:.6/j.m
2 W. Co, Z. Zhng / Journl of Compuionl n Applie Mhemis 245 (23) muli-sep mehos re propose for m-imensionl sysems of Iô SDDEs wih riving Wiener proesses n muli-ely, n heir properies re suie onerning onsiseny, numeril siliy n onvergene. Inse of working wih he generl SDDE (.), we suy he liner es moel (.2), whih n she some insigh on he generl SDDE (.), X() = [X() + X( τ)] + [X() + X( τ)]w(),, X() = ξ(), [ τ, ], (.2) where,,, R, τ is posiive fixe ely, W() is one-imensionl snr Wiener proess n ξ() is C([ τ, ]; R)-vlue iniil segmen. In his work, we im o erive men-squre sle wo-sep Mruym mehos for he SDDE (.2). The pper is orgnize in he following wy. In Seion 2 we provie some neessry noions n preliminries on SDDEs, inluing some properies of nlyil soluions o Eq. (.2). Also, in his seion he wo-sep Mruym mehos n heir onvergene properies re inroue. In Seion 3 we erive series of wo-sep Mruym mehos n prove h he numeril soluion is exponenilly sle for he exponenilly eying liner SDDE in men-squre sense. Seion 4 illusres he men-squre siliy of hese wo-sep Mruym mehos wih numeril exmples for he es moel (.2) n nonliner equion. 2. Noions n preliminries Le (Ω, F, P) e proiliy spe wih filrion (F ), whih sisfies he usul oniions (inresing n righoninuous; eh {F }, onins ll P-null ses in F ). Le W(), in Eq. (.2) e F -pe n inepenen of F. Assume ξ(), [ τ, ] o e F -mesurle n righ oninuous, n E ξ 2 <. Here ξ is efine y ξ = sup τ ξ() n is he Eulien norm in R. Throughou he pper, Eqs. (.) n (.2) re inerpree in he Iô sense. Uner hese usul oniions, Eq. (.2) hs unique srong soluion X() : [ τ, + ) R, whih sisfies Eq. (.2) n X() is mesurle, smple-oninuous n F -pe proess; see [22,23]. Definiion ([24]). The rivil soluion of Eq. (.) is si o e exponenilly men-squre sle, if here exiss pir of onsns λ > n C >, suh h, whenever E ξ 2 <, E X(, ξ) 2 CE ξ 2 e λ,. (2.) The inequliy (2.) implies h E X() 2 goes o exponenilly in s we ssume E ξ 2 <. Lemm 2 ([25]). If he oniion < ( + ) 2 (2.2) hols, hen he rivil soluion of Eq. (.2) is exponenilly men-squre sle. Applying he wo-sep Mruym mehos o Eq. (.) les o he following α j X i j = h j= β j f ( i j, X i j, X i m j ) + j= γ j g( i j, X i j, X i m j )W i j, i = 2, 3,..., N, (2.3) j= where α j, β j, γ j, (j {,, }) re prmeers; h > is he sepsize in ime whih sisfies τ = mh for posiive ineger m, n n = nh, N = T/h. The inremens W i := W( i+ ) W( i ), re inepenen N (, h)-isriue Gussin rnom vriles. Suppose h X i is F i -mesurle he mesh-poin i. Then X i is n pproximion o X( i ), where for i, X i re given y he iniil funion. Definiion 3. The funion u : R + R R R is si o e uniform Lipshiz oninuous if here exiss posiive onsn L u, suh h he funion u sisfies u(, x, x 2 ) u(, y, y 2 ) L u ( x y + x 2 y 2 ) (2.4) for every x, x 2, y, y 2 R n, When here exiss posiive onsn K, suh h u(, x, y) K( + x 2 + y 2 ) 2 (2.5) for x, y R n, we sy h u sisfies liner growh oniion.
3 84 W. Co, Z. Zhng / Journl of Compuionl n Applie Mhemis 245 (23) The hrerisi polynomil of (2.3) is given y ρ(λ) = α λ 2 + α λ + α. Definiion 4. The meho (2.3) is si o fulfill Dhlquis s roo oniion if (i) he roos of ρ(λ) lie on or wihin he uni irle; (ii) he roos on he uni irle re simple. Here re he onsiseny n onvergene properies of numeril mehos (2.3). Lemm 5 ([2]). Assume h he oeffiiens f n g of he SDDE (.) re Lipshiz oninuous in he sense of (2.4) n hve firs-orer oninuous pril erivives wih respe o he firs vrile n seon-orer oninuous pril erivives wih respe o he seon n hir vriles; hese pril erivives sisfy he liner growh oniion (2.5); he oeffiiens of he sohsi liner wo-sep Mruym sheme (2.3) sisfy Dhlquis s roo oniion, n he onsiseny oniions α j =, 2α + α = j= β j, α = γ, α + α = γ. (2.6) j= Then he glol error of he sheme (2.3) pplie o (.) sisfies mx E X( i ) X i 2 = O(h /2 ). i=2,...,n 3. Men-squre-siliy of he wo-sep Mruym mehos In his seion, we will erive he shemes in he lss of wo-sep Mruym mehos for Eq. (.2) n eermine series of wo-sep Mruym shemes, whih re exponenilly men-squre sle, see Theorem 7. Bse on he resuls in [8,26,27], we give he following efiniion. Definiion 6. A numeril meho is si o e exponenilly men-squre sle, if here exis onsn C > n λ h >, suh h, whenever E ξ 2 <, he numeril soluion X n of Eq. (.2), whih hs n exponenilly men-squre sle rivil soluion, he mesh n = nh, n, sisfies E(X n ) 2 CE ξ 2 e λ h n, s n, for fixe sep size h uner he onsrin h = τ/m, where m is posiive ineger. Applying he wo-sep Mruym mehos (2.3) o Eq. (.2) gives α j X i j = h j= β j [X i j + X i m j ] + j= γ j [X i j + X i m j ]W i j, i = 2, 3,... ; (3.) j= for i, we hve X i = ξ( i ). For eer ury, we ompue X using he Milsein meho wih smll sep size, whih hs onvergene re O(h) in men-squre sense (see []). We lso suppose h X is F -mesurle he mesh-poin. By hoosing he prmeers of he wo-sep Mruym meho o sisfy he onsiseny oniion (2.6) n hen we ge α =, α <, β = β =, (3.2) α = α, β = 2 + α, γ =, γ = + α. (3.3) Thus, we oin fmily of wo-sep Mruym shemes from (3.): X i+ + α X i + ( α )X i = h(2 + α )(X i+ + X i m+ ) + (X i + X i m )W i + ( + α )(X i + X i m )W i, (3.4) where prmeer α <. Nex we eermine he oniions on he prmeers for men squre siliy. I n e heke h he shemes (3.4) sisfy Dhlquis s roo oniion n ll ssumpions in Lemm 5. Thus, we hve he following onlusion on men-squre exponenil siliy. Theorem 7. Assume h he oniion (2.2) hols. If he prmeers of he wo-sep Mruym meho (3.) sisfy he resrie oniions (3.2) n (3.3), hen he meho is exponenilly men-squre sle.
4 W. Co, Z. Zhng / Journl of Compuionl n Applie Mhemis 245 (23) The proof of his heorem nees he following lemm. Lemm 8. Uner oniion (2.2), he numeril soluions {X i, i 2} proue y he wo-sep Mruym meho (3.4) sisfy E(X i X i W i ) < he(x 2 i ) + he( X i X i m ), E(X i X i m W i ) < he( X i X i m ) + he(x 2 i m ). (3.5) (3.5) Proof. Noe h E(W k ) =, E (W k ) 2 = h n X j is F i -mesurle n inepenen of W i if j i. Hene from properies of oniionl expeion we n ge E(X i X j W k ) =, i, j k, E(X i X j W k W k ) =, i, j k, E(X i X j W 2 k ) = he(x ix j ), i, j k. (3.6) (3.7) (3.8) Now we prove he inequliy (3.5). From he sheme (3.4) we hve X i+ = (2 + α )hx i m+ + ( + α )X i α X i ( (2 + α )h) + (X i + X i m )W i + ( + α )(X i + X i m )W i n hen X i = ( (2 + α )h) (2 + α )hx i m + ( + α )X i 2 α X i + (X i + X i m )W i + ( + α )(X i 2 + X i m 2 )W i 2. Due o he oniion (2.2) n α <, we ge (2 + α )h >. Using (3.6) (3.8), i hols h E(X i X i W i ) = (2 + α )he(x i m X i W i ) + ( + α )E(X i 2 X i W i ) ( (2 + α )h) α E(X 2 i W i ) + E(X 2 i W 2 ) + i E(X i m X i W 2 ) i + ( + α )E(X i 2 W i 2 X i W i ) + ( + α )E(X i m 2 W i 2 X i W i ) = he(x 2 i ( (2 + α )h) ) + he(x i m X i ) < he(x 2 i ) + he( X i m X i ). Inequliy (3.5) n e prove in he sme wy. This proves he lemm. Proof of Theorem 7. The explii form of he sheme (3.4) is (2 + α )h X i+ = (2 + α )hx i m+ + ( + α )X i α X i + (X i + X i m )W i + ( + α )(X i + X i m )W i. We squre oh sies of he ls ifferene equion o oin 2 ( (2 + α )h) 2 X 2 = i+ (2 + α ) 2 2 h 2 X 2 + i m+ ( + α )X i α X i + (Xi + X i m ) 2 W 2 i + ( + α ) 2 (X i + X i m ) 2 W 2 + i 2(2 + α )hx i m+ ( + α )X i α X i + 2(2 + α )hx i m+ (X i + X i m )W i + 2(2 + α )hx i m+ ( + α )(X i + X i m )W i + 2 ( + α )X i α X i (X i + X i m )W i + 2 ( + α )X i α X i ( + α )(X i + X i m )W i + 2( + α )(X i + X i m )(X i + X i m )W i W i.
5 86 W. Co, Z. Zhng / Journl of Compuionl n Applie Mhemis 245 (23) Then ( (2 + α )h) 2 X 2 = i+ α2 X 2 i + 2 W 2 i X 2 i + ( + α ) 2 X 2 + i ( + α ) 2 2 W 2 i X 2 + i (2 + α ) 2 h 2 2 X 2 i m+ + 2 W 2 i X 2 + i m ( + α ) 2 2 W 2 i X 2 2α i m ( + α )X i X i 2α ( + α )W i X i X i 2α (2 + α )hx i X i m+ 2α ( + α )W i X i X i m + 2( + α )(2 + α )hx i X i m+ where we efine + 2W 2 i X ix i m + 2( + α ) 2 W 2 i X i X i m + O i (W i, W i ), (3.9) O i (W i, W i ) = 2( + α ) 2 (X i + X i m )X i W i + 2(2 + α )hx i m+ (X i + X i m )W i + 2(2 + α )hx i m+ ( + α )(X i + X i m )W i + 2 ( + α )X i α X i (X i + X i m )W i + 2( + α )(X i + X i m )(X i + X i m )W i W i. By he lineriy of expeion n (3.6) (3.7) in Lemm 8, we ge E (O i (W i, W i )) =. Le Y i = E(X 2 i ), i =,, 2,.... Tking he expeion over oh sies of (3.9), n using he inequliy n (3.5), (3.5) n (3.8) in Lemm 8, i follows h where P Y i+ P Y i + P 2 Y i + P 3 Y i m+ + P 4 Y i m + P 5 Y i m, i = 2, 3,..., (3.) P = ( (2 + α )h) 2, P = α h α ( + α ) α (2 + α ) h + h, P 2 = ( + α ) 2 2 h + ( + α ) 2 α ( + α ) 2α ( + α ) 2 h 2α ( + α ) h + ( + α )(2 + α ) h + ( + α ) 2 h, P 3 = (2 + α ) 2 2 h 2 α (2 + α ) h + ( + α )(2 + α ) h, P 4 = 2 h + h, P 5 = ( + α ) 2 ( 2 + )h 2α ( + α ) 2 h 2α ( + α ) h. Le P = P(,,,, α, h) = P + P 2 + P 3 + P 4 + P 5 /P. I is ovious h Y i+ P mx Y i, Y i, Y i m+, Y i m, Y i m, i = 2, 3,.... (3.) We now lim h, for ny sepsize h = τ/m, i m Y i+ mx P i+, P i +,..., P E ξ 2. (3.2) Thus, if P <, hen we n ge lim i Y i =, s E ξ 2 <. In f, we use reurrene meho o inequliy (3.) n ge Y i+ P mx{y i, Y i, Y i m+, Y i m, Y i m } P 2 mx{y i, Y i 2,..., Y i 2m 3 } P P i m + mx i m +2 mx P i+ mx mx Y i i m,..., Y, E ξ 2 Y,..., i i m E ξ 2, P E ξ 2 E ξ 2, P E ξ 2,..., P i+, P i,..., P P i i m E ξ 2 i m + E ξ 2. (3.3)
6 W. Co, Z. Zhng / Journl of Compuionl n Applie Mhemis 245 (23) Tle Prmeers for ifferen wo-sep Mruym shemes. Sheme α β β Two-sep meho (TS) /2 /4 5/4 Two-sep meho 2 (TS2) 3/2 /2 Two-sep meho 3 (TS3) /2 3/2 Two-sep meho 4 (TS4) /3 /3 4/3 Two-sep meho 5 (TS5) 2/3 4/3 Two-sep meho 6 (TS6) 4/3 2/3 The hir inequliy is oine euse he inex of Y i m in (3.) keeps reuing y m 2 fer eh reurrene proess. The fifh inequliy hols sine he inex of Y i in (3.) elines y fer eh reurrene. For he reson h E ξ 2 is elimine from he reurrene proess, we ivie i y P for eh ime n evenully we ge i [ i m E ξ 2. P ] In he proess of ierion, Y i m (i m + ) will e he firs erm own o Y = E ξ 2 n i lls for is previous ] + seps, where [z] mens he lrges ineger no more hn rel numer z. This proves he lim (3.2). [ i m I is essenil o verify h P <, i.e. P + P 2 + P 3 + P 4 + P 5 < P. Rell h α < n hus 2 α 2 2(2 + α ), hen from (3.), we hve P + P 2 + P 3 + P 4 + P 5 P = + 2(2 + α ) + (2 α 2 )( + )2 h + (2 + α ) 2 2 h 2 ( (2 + α )h) 2 (2 + α ) + (2 + α ) + 2 (2 α2 )( + )2 = (2 + α ) 2 ( 2 2 )h (2 + α ) 2 ( 2 2 )h 2 + 2(2 + α ) + + ( + ) 2 h. (3.4) Bse on oniion (2.2), we oin h P + P 2 + P 3 + P 4 + P 5 P < hols for eh sepsize h = τ/m. Due o P <, we oin Y i+ P [ i m ]+ E ξ 2 from (3.3) n hus i m + Y i+ P E ξ 2 P i+ E ξ 2 = e λ h i+ E ξ 2, h where λ h = ln P >. The proof ens. ()h 4. Numeril exmples In ll our numeril exmples, E(X 2 ) = 2 n X n (ω i ) 2, 2 i= re he smple verge over 2 rjeories in Ml. Tle liss numer of wo-sep Mruym shemes wih ifferen prmeers uner es here. Noe h only he shemes in ol (TS3 n TS5) sisfy he require oniions in Theorem 7 n hene re exponenilly men-squre sle. However, he oher Mruym shemes TS, TS2, TS4, TS6 o no sisfy he oniions in Theorem 7 n hus my e only oniionlly sle n even no sle s we show ler on. Exmple. We onsier he liner es moel X() = [X() + X( τ)] + [X() + X( τ)]w(),, X() = + τ, [ τ, ] (4.) o illusre he men-squre siliy of he wo-sep Mruym shemes in Tle. We hoose he prmeers s = 4, = 2, =.5, =.5 n τ =, whih ensures h he ex soluion of he Eq. (4.) is men-squre sle y Lemm 2. From Fig., we oserve h TS is no men-squre sle for oh lrge sepsize h = /4 n smll sepsize h = /64. From Figs. 2 n 3, we see h TS3 n TS5 re men-squre sle even for lrge sepsize h = /4; Fig. 2 illusres h TS4 is oniionlly men-squre sle; TS4 is men squre sle if he sepsize h is smll enough (like h = /64 here). In Fig. 3, we fix he sepsize h = /8 n show h o gre exen he men squre siliy of he implii sheme TS3 is eer hn he explii wo-sep sheme TS6. If we es TS6 for rher long ime inervl, hen he numeril soluion
7 88 W. Co, Z. Zhng / Journl of Compuionl n Applie Mhemis 245 (23) Fig.. Simulions wih TS n TS3. (): TS, h = /4; (): TS3, h = /4; (): TS, h = /64; (): TS3, h = / Fig. 2. Simulions wih TS4 n TS5. (): TS4, h = /4; (): TS5, h = /4; (): TS4, h = /64; (): TS5, h = /64. will osille n will finlly iverge. From Figs. 3, we oserve h he numeril soluion from TS6 lows up erlier hn ny oher unsle implii mehos shown in Figs. n 2. On he oher hn, numeril soluions of oh TS3 n TS5 onverge. o zero very fs.
8 W. Co, Z. Zhng / Journl of Compuionl n Applie Mhemis 245 (23) Fig. 3. Simulions wih TS3 n he explii meho TS6. (): TS6; (): TS3. h = / TS3 TS2 TS Fig. 4. Simulions wih TS, TS2 n TS3 for fixe sepsize h = /2. In Fig. 4 we hoose ifferen prmeers for he Eq. (4.): = 3, =, =.5, =.5 n τ = when (4.) is men squre sle. Here we use very lrge sepsize h = /2 for TS, TS2 n TS3. The resuls show h he sheme TS3 minins he men-squre siliy even wih lrge sepsize h. Exmple 2. We es he propose wo-sep Mruym mehos for he following nonliner SDDE (Exmple 5.2., [28]): X() = + X() + X() sin(x( τ))w(),, + X() = + τ, [ τ, ]. (4.2) The soluion of Eq. (4.2) is men squre sle if 2 2 n [28].
9 9 W. Co, Z. Zhng / Journl of Compuionl n Applie Mhemis 245 (23) e f Fig. 5. Simulions wih TS n TS3. (): TS, h = /2; (): TS3, h = /2; (): TS, h = /6; (): TS3, h = /6; (e): TS, h = /64; (f): TS3, h = / e f Fig. 6. Simulions wih TS4 n TS5. (): TS4, h = /2; (): TS5, h = /2; (): TS4, h = /6; (): TS5, h = /6; (e): TS4, h = /64; (f): TS5, h = /64.
10 W. Co, Z. Zhng / Journl of Compuionl n Applie Mhemis 245 (23) X n X n X n X n Fig. 7. Simulions wih TS2 n TS5. (): TS2, h = /4; (): TS5, h = /4; (): TS2, h = /6; (): TS5, h = /6. 4 X n X n X n X n Fig. 8. Simulions wih TS3 n TS4. (): TS4, h = /6; (): TS3, h = /4; (): TS4, h = /64; (): TS3, h = /64. We ke =, = n τ =. I is shown from Figs. 5 n 6 h he shemes TS3 n TS5 minin heir men-squre siliy for nonliner SDDE (4.2); TS n TS4 re oniionlly men-squre sle. In some rnge of sepsize h, smller h les o greer insiliy, ompring o (), () in Fig. 5 n (), () in Fig. 6.
11 92 W. Co, Z. Zhng / Journl of Compuionl n Applie Mhemis 245 (23) TS,Xn TS,X2n TS4,Xn TS4,X2n TS6,Xn TS6,X2n TS6 TS TS4 5 5 TS,Xn TS,X2n TS4,Xn TS4,X2n TS6,Xn TS6,X2n TS TS6 TS Fig. 9. Simulions wih TS, TS4 n TS6. (): h = /4; (): h = /8. X n X n X n X n Fig.. Simulions wih TS3 n TS5. (): TS3, h = /2; (): TS5, h = /2; (): TS3, h = ; (): TS5, h =. Exmple 3. We es he propose wo-sep Mruym mehos for he following nonliner sohsi ely ifferenil 2-imensionl sysem: X () X () sin(x ( τ)) X () W () = A + B + C, (4.3) X 2 () X 2 () os(x 2 ( τ)) X 2 () W 2 () where A = 28, B = 3 2 /2 3/2, C =. /4 5/2 /2 When [ τ, ], X () = + τ n X 2 () = e. Bse on Corollry 2.2 [24], we know h soluions of sysem (4.3) re exponenilly men-squre sle. From Fig. 7, we oserve h he soluions oine y sheme TS2 low up for h = /4 n re exponenilly mensqure sle when h = /6 (() n ()) n he soluions oine from exponenilly men-squre sle sheme TS5 re men-squre sle for oh h = /4 n h = /6, see Fig. 7() n (). I is shown from Fig. 8 h TS3 performs goo exponenilly men-squre siliy. Menwhile, TS4 is oniionlly men-squre sle, n he smller sep size h = /64 is neee (ompre o TS2).
12 W. Co, Z. Zhng / Journl of Compuionl n Applie Mhemis 245 (23) We ompre soluions oine y he shemes TS, TS4 n TS6 in Fig. 9. Fig. 9() shows h neiher of hem re mensqure sle for h = /4, n he soluion from he explii sheme TS6 lows up fser hn h from implii sheme TS n TS4. On he oher hn, he explii sheme TS6 performs eer hn he sheme TS n TS4 when h = /8 s we n see from Fig. 9() h TS6 is men-squre sle for h = /8 u TS n TS4 re no. Fig. 9 inies h he explii sheme TS6 requires less resrie ime sep size h for men-squre siliy hn he implii sheme TS n TS4 o. In Fig., we es he propose shemes TS3 n TS5 wih very lrge sep size h = /2 n h =, he shemes TS3 n TS5 re minining heir exponenil siliy in men-squre sense for nonliner sohsi ely ifferenil sysem (4.3). 5. Conlusion We hve propose fmily of exponenilly men-squre sle wo-sep Mruym shemes. I hs een prove h he propose shemes n minin he exponenil men-squre siliy of he liner SDDE for every sep size of inegrl frion of he ely in he equion. Numeril exmples show h his fmily of numeril mehos exhiis exponenil men-squre siliy for oh liner n some priulr nonliner SDDE n 2-imensionl SDDEs. The numeril resuls sugges h our propose sheme n e ope for generl nonliner SDDEs, u furher numeril suies re require. Aknowlegmens The uhors hnk he referees n Dr. Tkeomo Misui for heir helpful suggesions for improving he pper. The firs uhor lso woul like o hnk Professor George Em Krnikis for his hospiliy when she ws visiing Division of Applie Mhemis Brown Universiy. Firs uhor s work ws suppore y he NSF of Chin (No. 936). Seon uhor s work ws suppore y AIRFORCE MURI. Referenes [] A. Beuer, K. Vsilkos, Effes of noise on elye visul feek sysem, J. Theore. Biol. 65 (993) [2] M. Grigoriu, Conrol of ime ely liner sysems wih Gussin whie noise, Pro. Eng. Meh. 2 (997) [3] M.D. Pol, A. Pirro, Time ely inue effes on onrol of liner sysems uner rnom exiion, Pro. Eng. Meh. 6 (2) [4] L.S. Tsimring, A. Pikovsky, Noise-inue ynmis in isle sysems wih ely, Phys. Rev. Le. 87 (2) 2562 [4 pges]. [5] E. Bere, V.B. Kolmnovskii, L. Shikhe, Siliy of epiemi moel wih ime elys influene y sohsi perurions, Mh. Compu. Simul. 45 (998) [6] A. Beuer, J. Belir, Feek n elys in neurologil iseses: moeling suy using ynmil sysems, Bull. Mh. Biol. 55 (993) [7] D.G. Hoson, L.C.G. Rogers, Complee moels wih sohsi liliy, Mh. Finne 8 (998) [8] C.T.H. Bker, E. Bukwr, Exponenil siliy in p-h men of soluions, n of onvergen Euler-ype soluions, of sohsi ely ifferenil equions, J. Compu. Appl. Mh. 84 (25) [9] Z. Fn, Wveform relxion meho for sohsi ifferenil equions wih onsn ely, Appl. Numer. Mh. 6 (2) [] Y. Hu, S.A. Mohmme, F. Yn, Disree-ime pproximions of sohsi ely equions: he Milsein sheme, Ann. Pro. 32 (24) [] R. Li, Convergene n siliy of numeril soluions o SDDEs wih Mrkovin swihing, Appl. Mh. Compu. 75 (26) 8 9. [2] M. Liu, W. Co, Z. Fn, Convergene n siliy of he semi-implii Euler meho for liner sohsi ifferenil ely equion, J. Compu. Appl. Mh. 7 (24) [3] X. Mo, Numeril soluions of sohsi ifferenil ely equions uner he generlize Khsminskii-ype oniions, Appl. Mh. Compu. 27 (2) [4] S. Zhou, F. Wu, Convergene of numeril soluions o neurl sohsi ely ifferenil equions wih Mrkovin swihing, J. Compu. Appl. Mh. 229 (29) [5] P.E. Kloeen, E. Plen, Numeril Soluion of Sohsi Differenil Equions, Springer, Berlin, 992. [6] G.N. Milsein, Numeril Inegrion of Sohsi Differenil Equions, Kluwer Aemi Pulishers Group, Dorreh, 995. [7] E. Bukwr, R. Winkler, Muli-sep mehos for SDEs n heir ppliion o prolems wih smll noise, SIAM J. Numer. Anl. 44 (26) [8] B.D. Ewl, R. Témm, Numeril nlysis of sohsi shemes in geophysis, SIAM J. Numer. Anl. 42 (25) [9] L. Brugnno, K. Burrge, P.M. Burrge, Ams-ype mehos for he numeril soluion of sohsi orinry ifferenil equions, BIT 4 (2) [2] G. Denk, S. Shäffler, Ams mehos for he effiien soluion of sohsi ifferenil equions wih iive noise, Compuing 59 (996) [2] E. Bukwr, R. Winkler, Muli-sep Mruym mehos for sohsi ely ifferenil equions, Soh. Anl. Appl. 25 (27) [22] X. Mo, Sohsi Differenil Equions n Appliions, Horwoo, 997. [23] S.E.A. Mohmme, Sohsi Funionl Differenil Equions, in: Reserh Noes in Mhemis, vol. 99, Pimn, Lonon, 984. [24] X. Mo, Exponenil Siliy of Sohsi Differenil Equions, Mrel Dekker, In., New York, 994. [25] X. Mo, Rzumikhin-ype heorems on exponenil siliy of sohsi funionl ifferenil equions, Soh. Pro. Appl. 65 (996) [26] V.K. Brwell, Speil siliy prolems for funionl equions, BIT 5 (975) [27] L. Shikhe, Lypunov Funionls n Siliy of Sohsi Differene Equions, Springer, Lonon, Dorreh, Heielerg, New York, 2. [28] X. Mo, Siliy of Sohsi Differenil Equions wih Respe o Semimringles, Longmn Sienifi & Tehnil, 99.
Generalized Projective Synchronization Using Nonlinear Control Method
 ISSN 79-3889 (prin), 79-3897 (online) Inernionl Journl of Nonliner Siene Vol.8(9) No.,pp.79-85 Generlized Projeive Synhronizion Using Nonliner Conrol Mehod Xin Li Deprmen of Mhemis, Chngshu Insiue of Tehnology
ISSN 79-3889 (prin), 79-3897 (online) Inernionl Journl of Nonliner Siene Vol.8(9) No.,pp.79-85 Generlized Projeive Synhronizion Using Nonliner Conrol Mehod Xin Li Deprmen of Mhemis, Chngshu Insiue of Tehnology
Contraction Mapping Principle Approach to Differential Equations
 epl Journl of Science echnology 0 (009) 49-53 Conrcion pping Principle pproch o Differenil Equions Bishnu P. Dhungn Deprmen of hemics, hendr Rn Cmpus ribhuvn Universiy, Khmu epl bsrc Using n eension of
epl Journl of Science echnology 0 (009) 49-53 Conrcion pping Principle pproch o Differenil Equions Bishnu P. Dhungn Deprmen of hemics, hendr Rn Cmpus ribhuvn Universiy, Khmu epl bsrc Using n eension of
ON A METHOD FOR FINDING THE NUMERICAL SOLUTION OF CAUCHY PROBLEM FOR 2D BURGERS EQUATION
 Europen Sienifi Journl Augus 05 /SPECIAL/ eiion ISSN: 857 788 Prin e - ISSN 857-743 ON A MEHOD FOR FINDING HE NUMERICAL SOLUION OF CAUCHY PROBLEM FOR D BURGERS EQUAION Mir Rsulo Prof. Been Uniersi Deprmen
Europen Sienifi Journl Augus 05 /SPECIAL/ eiion ISSN: 857 788 Prin e - ISSN 857-743 ON A MEHOD FOR FINDING HE NUMERICAL SOLUION OF CAUCHY PROBLEM FOR D BURGERS EQUAION Mir Rsulo Prof. Been Uniersi Deprmen
5.1-The Initial-Value Problems For Ordinary Differential Equations
 5.-The Iniil-Vlue Problems For Ordinry Differenil Equions Consider solving iniil-vlue problems for ordinry differenil equions: (*) y f, y, b, y. If we know he generl soluion y of he ordinry differenil
5.-The Iniil-Vlue Problems For Ordinry Differenil Equions Consider solving iniil-vlue problems for ordinry differenil equions: (*) y f, y, b, y. If we know he generl soluion y of he ordinry differenil
e t dt e t dt = lim e t dt T (1 e T ) = 1
 Improper Inegrls There re wo ypes of improper inegrls - hose wih infinie limis of inegrion, nd hose wih inegrnds h pproch some poin wihin he limis of inegrion. Firs we will consider inegrls wih infinie
Improper Inegrls There re wo ypes of improper inegrls - hose wih infinie limis of inegrion, nd hose wih inegrnds h pproch some poin wihin he limis of inegrion. Firs we will consider inegrls wih infinie
Hermite-Hadamard-Fejér type inequalities for convex functions via fractional integrals
 Sud. Univ. Beş-Bolyi Mh. 6(5, No. 3, 355 366 Hermie-Hdmrd-Fejér ype inequliies for convex funcions vi frcionl inegrls İmd İşcn Asrc. In his pper, firsly we hve eslished Hermie Hdmrd-Fejér inequliy for
Sud. Univ. Beş-Bolyi Mh. 6(5, No. 3, 355 366 Hermie-Hdmrd-Fejér ype inequliies for convex funcions vi frcionl inegrls İmd İşcn Asrc. In his pper, firsly we hve eslished Hermie Hdmrd-Fejér inequliy for
Convergence of Singular Integral Operators in Weighted Lebesgue Spaces
 EUROPEAN JOURNAL OF PURE AND APPLIED MATHEMATICS Vol. 10, No. 2, 2017, 335-347 ISSN 1307-5543 www.ejpm.com Published by New York Business Globl Convergence of Singulr Inegrl Operors in Weighed Lebesgue
EUROPEAN JOURNAL OF PURE AND APPLIED MATHEMATICS Vol. 10, No. 2, 2017, 335-347 ISSN 1307-5543 www.ejpm.com Published by New York Business Globl Convergence of Singulr Inegrl Operors in Weighed Lebesgue
EXISTENCE AND UNIQUENESS OF SOLUTIONS FOR A SECOND-ORDER ITERATIVE BOUNDARY-VALUE PROBLEM
 Elecronic Journl of Differenil Equions, Vol. 208 (208), No. 50, pp. 6. ISSN: 072-669. URL: hp://ejde.mh.xse.edu or hp://ejde.mh.un.edu EXISTENCE AND UNIQUENESS OF SOLUTIONS FOR A SECOND-ORDER ITERATIVE
Elecronic Journl of Differenil Equions, Vol. 208 (208), No. 50, pp. 6. ISSN: 072-669. URL: hp://ejde.mh.xse.edu or hp://ejde.mh.un.edu EXISTENCE AND UNIQUENESS OF SOLUTIONS FOR A SECOND-ORDER ITERATIVE
ANSWERS TO EVEN NUMBERED EXERCISES IN CHAPTER 2
 ANSWERS TO EVEN NUMBERED EXERCISES IN CHAPTER Seion Eerise -: Coninuiy of he uiliy funion Le λ ( ) be he monooni uiliy funion defined in he proof of eisene of uiliy funion If his funion is oninuous y hen
ANSWERS TO EVEN NUMBERED EXERCISES IN CHAPTER Seion Eerise -: Coninuiy of he uiliy funion Le λ ( ) be he monooni uiliy funion defined in he proof of eisene of uiliy funion If his funion is oninuous y hen
4.8 Improper Integrals
 4.8 Improper Inegrls Well you ve mde i hrough ll he inegrion echniques. Congrs! Unforunely for us, we sill need o cover one more inegrl. They re clled Improper Inegrls. A his poin, we ve only del wih inegrls
4.8 Improper Inegrls Well you ve mde i hrough ll he inegrion echniques. Congrs! Unforunely for us, we sill need o cover one more inegrl. They re clled Improper Inegrls. A his poin, we ve only del wih inegrls
3. Renewal Limit Theorems
 Virul Lborories > 14. Renewl Processes > 1 2 3 3. Renewl Limi Theorems In he inroducion o renewl processes, we noed h he rrivl ime process nd he couning process re inverses, in sens The rrivl ime process
Virul Lborories > 14. Renewl Processes > 1 2 3 3. Renewl Limi Theorems In he inroducion o renewl processes, we noed h he rrivl ime process nd he couning process re inverses, in sens The rrivl ime process
Characteristic Function for the Truncated Triangular Distribution., Myron Katzoff and Rahul A. Parsa
 Secion on Survey Reserch Mehos JSM 009 Chrcerisic Funcion for he Trunce Tringulr Disriuion Jy J. Kim 1 1, Myron Kzoff n Rhul A. Prs 1 Nionl Cener for Helh Sisics, 11Toleo Ro, Hysville, MD. 078 College
Secion on Survey Reserch Mehos JSM 009 Chrcerisic Funcion for he Trunce Tringulr Disriuion Jy J. Kim 1 1, Myron Kzoff n Rhul A. Prs 1 Nionl Cener for Helh Sisics, 11Toleo Ro, Hysville, MD. 078 College
CSC 373: Algorithm Design and Analysis Lecture 9
 CSC 373: Algorihm Deign n Anlyi Leure 9 Alln Boroin Jnury 28, 2013 1 / 16 Leure 9: Announemen n Ouline Announemen Prolem e 1 ue hi Friy. Term Te 1 will e hel nex Mony, Fe in he uoril. Two nnounemen o follow
CSC 373: Algorihm Deign n Anlyi Leure 9 Alln Boroin Jnury 28, 2013 1 / 16 Leure 9: Announemen n Ouline Announemen Prolem e 1 ue hi Friy. Term Te 1 will e hel nex Mony, Fe in he uoril. Two nnounemen o follow
Lecture 2: Network Flow. c 14
 Comp 260: Avne Algorihms Tufs Universiy, Spring 2016 Prof. Lenore Cowen Srie: Alexner LeNil Leure 2: Nework Flow 1 Flow Neworks s 16 12 13 10 4 20 14 4 Imgine some nework of pipes whih rry wer, represene
Comp 260: Avne Algorihms Tufs Universiy, Spring 2016 Prof. Lenore Cowen Srie: Alexner LeNil Leure 2: Nework Flow 1 Flow Neworks s 16 12 13 10 4 20 14 4 Imgine some nework of pipes whih rry wer, represene
Green s Functions and Comparison Theorems for Differential Equations on Measure Chains
 Green s Funcions nd Comprison Theorems for Differenil Equions on Mesure Chins Lynn Erbe nd Alln Peerson Deprmen of Mhemics nd Sisics, Universiy of Nebrsk-Lincoln Lincoln,NE 68588-0323 lerbe@@mh.unl.edu
Green s Funcions nd Comprison Theorems for Differenil Equions on Mesure Chins Lynn Erbe nd Alln Peerson Deprmen of Mhemics nd Sisics, Universiy of Nebrsk-Lincoln Lincoln,NE 68588-0323 lerbe@@mh.unl.edu
Minimum Squared Error
 Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > for ll smples y i solve sysem of liner inequliies MSE procedure y i = i for ll smples
Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > for ll smples y i solve sysem of liner inequliies MSE procedure y i = i for ll smples
Minimum Squared Error
 Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > 0 for ll smples y i solve sysem of liner inequliies MSE procedure y i i for ll smples
Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > 0 for ll smples y i solve sysem of liner inequliies MSE procedure y i i for ll smples
ENGR 1990 Engineering Mathematics The Integral of a Function as a Function
 ENGR 1990 Engineering Mhemics The Inegrl of Funcion s Funcion Previously, we lerned how o esime he inegrl of funcion f( ) over some inervl y dding he res of finie se of rpezoids h represen he re under
ENGR 1990 Engineering Mhemics The Inegrl of Funcion s Funcion Previously, we lerned how o esime he inegrl of funcion f( ) over some inervl y dding he res of finie se of rpezoids h represen he re under
Positive and negative solutions of a boundary value problem for a
 Invenion Journl of Reerch Technology in Engineering & Mngemen (IJRTEM) ISSN: 2455-3689 www.ijrem.com Volume 2 Iue 9 ǁ Sepemer 28 ǁ PP 73-83 Poiive nd negive oluion of oundry vlue prolem for frcionl, -difference
Invenion Journl of Reerch Technology in Engineering & Mngemen (IJRTEM) ISSN: 2455-3689 www.ijrem.com Volume 2 Iue 9 ǁ Sepemer 28 ǁ PP 73-83 Poiive nd negive oluion of oundry vlue prolem for frcionl, -difference
Integral Transform. Definitions. Function Space. Linear Mapping. Integral Transform
 Inegrl Trnsform Definiions Funcion Spce funcion spce A funcion spce is liner spce of funcions defined on he sme domins & rnges. Liner Mpping liner mpping Le VF, WF e liner spces over he field F. A mpping
Inegrl Trnsform Definiions Funcion Spce funcion spce A funcion spce is liner spce of funcions defined on he sme domins & rnges. Liner Mpping liner mpping Le VF, WF e liner spces over he field F. A mpping
Application on Inner Product Space with. Fixed Point Theorem in Probabilistic
 Journl of Applied Mhemics & Bioinformics, vol.2, no.2, 2012, 1-10 ISSN: 1792-6602 prin, 1792-6939 online Scienpress Ld, 2012 Applicion on Inner Produc Spce wih Fixed Poin Theorem in Probbilisic Rjesh Shrivsv
Journl of Applied Mhemics & Bioinformics, vol.2, no.2, 2012, 1-10 ISSN: 1792-6602 prin, 1792-6939 online Scienpress Ld, 2012 Applicion on Inner Produc Spce wih Fixed Poin Theorem in Probbilisic Rjesh Shrivsv
On Hadamard and Fejér-Hadamard inequalities for Caputo k-fractional derivatives
 In J Nonliner Anl Appl 9 8 No, 69-8 ISSN: 8-68 elecronic hp://dxdoiorg/75/ijn8745 On Hdmrd nd Fejér-Hdmrd inequliies for Cpuo -frcionl derivives Ghulm Frid, Anum Jved Deprmen of Mhemics, COMSATS Universiy
In J Nonliner Anl Appl 9 8 No, 69-8 ISSN: 8-68 elecronic hp://dxdoiorg/75/ijn8745 On Hdmrd nd Fejér-Hdmrd inequliies for Cpuo -frcionl derivives Ghulm Frid, Anum Jved Deprmen of Mhemics, COMSATS Universiy
A LOG IS AN EXPONENT.
 Ojeives: n nlze nd inerpre he ehvior of rihmi funions, inluding end ehvior nd smpoes. n solve rihmi equions nlill nd grphill. n grph rihmi funions. n deermine he domin nd rnge of rihmi funions. n deermine
Ojeives: n nlze nd inerpre he ehvior of rihmi funions, inluding end ehvior nd smpoes. n solve rihmi equions nlill nd grphill. n grph rihmi funions. n deermine he domin nd rnge of rihmi funions. n deermine
Released Assessment Questions, 2017 QUESTIONS
 Relese Assessmen Quesions, 17 QUESTIONS Gre 9 Assessmen of Mhemis Aemi Re he insruions elow. Along wih his ookle, mke sure ou hve he Answer Bookle n he Formul Shee. You m use n spe in his ook for rough
Relese Assessmen Quesions, 17 QUESTIONS Gre 9 Assessmen of Mhemis Aemi Re he insruions elow. Along wih his ookle, mke sure ou hve he Answer Bookle n he Formul Shee. You m use n spe in his ook for rough
Problem Set 9 Due December, 7
 EE226: Random Proesses in Sysems Leurer: Jean C. Walrand Problem Se 9 Due Deember, 7 Fall 6 GSI: Assane Gueye his problem se essenially reviews Convergene and Renewal proesses. No all exerises are o be
EE226: Random Proesses in Sysems Leurer: Jean C. Walrand Problem Se 9 Due Deember, 7 Fall 6 GSI: Assane Gueye his problem se essenially reviews Convergene and Renewal proesses. No all exerises are o be
Chapter Introduction. 2. Linear Combinations [4.1]
![Chapter Introduction. 2. Linear Combinations [4.1] Chapter Introduction. 2. Linear Combinations [4.1]](/thumbs/95/126023605.jpg) Chper 4 Inrouion Thi hper i ou generlizing he onep you lerne in hper o pe oher n hn R Mny opi in hi hper re heoreil n MATLAB will no e le o help you ou You will ee where MATLAB i ueful in hper 4 n how
Chper 4 Inrouion Thi hper i ou generlizing he onep you lerne in hper o pe oher n hn R Mny opi in hi hper re heoreil n MATLAB will no e le o help you ou You will ee where MATLAB i ueful in hper 4 n how
0 for t < 0 1 for t > 0
 8.0 Sep nd del funcions Auhor: Jeremy Orloff The uni Sep Funcion We define he uni sep funcion by u() = 0 for < 0 for > 0 I is clled he uni sep funcion becuse i kes uni sep = 0. I is someimes clled he Heviside
8.0 Sep nd del funcions Auhor: Jeremy Orloff The uni Sep Funcion We define he uni sep funcion by u() = 0 for < 0 for > 0 I is clled he uni sep funcion becuse i kes uni sep = 0. I is someimes clled he Heviside
MTH 146 Class 11 Notes
 8.- Are of Surfce of Revoluion MTH 6 Clss Noes Suppose we wish o revolve curve C round n is nd find he surfce re of he resuling solid. Suppose f( ) is nonnegive funcion wih coninuous firs derivive on he
8.- Are of Surfce of Revoluion MTH 6 Clss Noes Suppose we wish o revolve curve C round n is nd find he surfce re of he resuling solid. Suppose f( ) is nonnegive funcion wih coninuous firs derivive on he
FURTHER GENERALIZATIONS. QI Feng. The value of the integral of f(x) over [a; b] can be estimated in a variety ofways. b a. 2(M m)
![FURTHER GENERALIZATIONS. QI Feng. The value of the integral of f(x) over [a; b] can be estimated in a variety ofways. b a. 2(M m) FURTHER GENERALIZATIONS. QI Feng. The value of the integral of f(x) over [a; b] can be estimated in a variety ofways. b a. 2(M m)](/thumbs/75/72845579.jpg) Univ. Beogrd. Pul. Elekroehn. Fk. Ser. M. 8 (997), 79{83 FUTHE GENEALIZATIONS OF INEQUALITIES FO AN INTEGAL QI Feng Using he Tylor's formul we prove wo inegrl inequliies, h generlize K. S. K. Iyengr's
Univ. Beogrd. Pul. Elekroehn. Fk. Ser. M. 8 (997), 79{83 FUTHE GENEALIZATIONS OF INEQUALITIES FO AN INTEGAL QI Feng Using he Tylor's formul we prove wo inegrl inequliies, h generlize K. S. K. Iyengr's
Title: On mean-square-stability of two-step Maruyama methods for stochastic delay differential equations
 Elsevier Ediorial Sysem(m) for Journal of Compuaional and Applied Mahemaics Manuscrip Draf Manuscrip Number: Tile: On mean-square-sabiliy of wo-sep Maruyama mehods for sochasic delay differenial equaions
Elsevier Ediorial Sysem(m) for Journal of Compuaional and Applied Mahemaics Manuscrip Draf Manuscrip Number: Tile: On mean-square-sabiliy of wo-sep Maruyama mehods for sochasic delay differenial equaions
Boyce/DiPrima 9 th ed, Ch 6.1: Definition of. Laplace Transform. In this chapter we use the Laplace transform to convert a
 Boye/DiPrima 9 h ed, Ch 6.: Definiion of Laplae Transform Elemenary Differenial Equaions and Boundary Value Problems, 9 h ediion, by William E. Boye and Rihard C. DiPrima, 2009 by John Wiley & Sons, In.
Boye/DiPrima 9 h ed, Ch 6.: Definiion of Laplae Transform Elemenary Differenial Equaions and Boundary Value Problems, 9 h ediion, by William E. Boye and Rihard C. DiPrima, 2009 by John Wiley & Sons, In.
( ) ( ) ( ) ( ) ( ) ( y )
 8. Lengh of Plne Curve The mos fmous heorem in ll of mhemics is he Pyhgoren Theorem. I s formulion s he disnce formul is used o find he lenghs of line segmens in he coordine plne. In his secion you ll
8. Lengh of Plne Curve The mos fmous heorem in ll of mhemics is he Pyhgoren Theorem. I s formulion s he disnce formul is used o find he lenghs of line segmens in he coordine plne. In his secion you ll
A LIMIT-POINT CRITERION FOR A SECOND-ORDER LINEAR DIFFERENTIAL OPERATOR IAN KNOWLES
 A LIMIT-POINT CRITERION FOR A SECOND-ORDER LINEAR DIFFERENTIAL OPERATOR j IAN KNOWLES 1. Inroducion Consider he forml differenil operor T defined by el, (1) where he funcion q{) is rel-vlued nd loclly
A LIMIT-POINT CRITERION FOR A SECOND-ORDER LINEAR DIFFERENTIAL OPERATOR j IAN KNOWLES 1. Inroducion Consider he forml differenil operor T defined by el, (1) where he funcion q{) is rel-vlued nd loclly
SOME USEFUL MATHEMATICS
 SOME USEFU MAHEMAICS SOME USEFU MAHEMAICS I is esy o mesure n preic he behvior of n elecricl circui h conins only c volges n currens. However, mos useful elecricl signls h crry informion vry wih ime. Since
SOME USEFU MAHEMAICS SOME USEFU MAHEMAICS I is esy o mesure n preic he behvior of n elecricl circui h conins only c volges n currens. However, mos useful elecricl signls h crry informion vry wih ime. Since
Three Dimensional Coordinate Geometry
 HKCWCC dvned evel Pure Mhs. / -D Co-Geomer Three Dimensionl Coordine Geomer. Coordine of Poin in Spe Z XOX, YOY nd ZOZ re he oordine-es. P,, is poin on he oordine plne nd is lled ordered riple. P,, X Y
HKCWCC dvned evel Pure Mhs. / -D Co-Geomer Three Dimensionl Coordine Geomer. Coordine of Poin in Spe Z XOX, YOY nd ZOZ re he oordine-es. P,, is poin on he oordine plne nd is lled ordered riple. P,, X Y
1.0 Electrical Systems
 . Elecricl Sysems The ypes of dynmicl sysems we will e sudying cn e modeled in erms of lgeric equions, differenil equions, or inegrl equions. We will egin y looking fmilir mhemicl models of idel resisors,
. Elecricl Sysems The ypes of dynmicl sysems we will e sudying cn e modeled in erms of lgeric equions, differenil equions, or inegrl equions. We will egin y looking fmilir mhemicl models of idel resisors,
Solutions to assignment 3
 D Sruure n Algorihm FR 6. Informik Sner, Telikeplli WS 03/04 hp://www.mpi-.mpg.e/~ner/oure/lg03/inex.hml Soluion o ignmen 3 Exerie Arirge i he ue of irepnie in urreny exhnge re o rnform one uni of urreny
D Sruure n Algorihm FR 6. Informik Sner, Telikeplli WS 03/04 hp://www.mpi-.mpg.e/~ner/oure/lg03/inex.hml Soluion o ignmen 3 Exerie Arirge i he ue of irepnie in urreny exhnge re o rnform one uni of urreny
Analysis of Constant Deteriorating Inventory Management with Quadratic Demand Rate
 Amerin Journl of Operionl Reserh, (): 98- DOI:.9/j.jor.. Anlysis of onsn Deerioring Invenory Mngemen wih Qudri Demnd Re Goind hndr Pnd,*, Syji Shoo, Prv Kumr Sukl Dep of Mhemis,Mhvir Insiue of Engineering
Amerin Journl of Operionl Reserh, (): 98- DOI:.9/j.jor.. Anlysis of onsn Deerioring Invenory Mngemen wih Qudri Demnd Re Goind hndr Pnd,*, Syji Shoo, Prv Kumr Sukl Dep of Mhemis,Mhvir Insiue of Engineering
REAL ANALYSIS I HOMEWORK 3. Chapter 1
 REAL ANALYSIS I HOMEWORK 3 CİHAN BAHRAN The quesions re from Sein nd Shkrchi s e. Chper 1 18. Prove he following sserion: Every mesurble funcion is he limi.e. of sequence of coninuous funcions. We firs
REAL ANALYSIS I HOMEWORK 3 CİHAN BAHRAN The quesions re from Sein nd Shkrchi s e. Chper 1 18. Prove he following sserion: Every mesurble funcion is he limi.e. of sequence of coninuous funcions. We firs
Graduate Algorithms CS F-18 Flow Networks
 Grue Algorihm CS673-2016F-18 Flow Nework Dvi Glle Deprmen of Compuer Siene Univeriy of Sn Frnio 18-0: Flow Nework Diree Grph G Eh ege weigh i piy Amoun of wer/eon h n flow hrough pipe, for inne Single
Grue Algorihm CS673-2016F-18 Flow Nework Dvi Glle Deprmen of Compuer Siene Univeriy of Sn Frnio 18-0: Flow Nework Diree Grph G Eh ege weigh i piy Amoun of wer/eon h n flow hrough pipe, for inne Single
ON NEW INEQUALITIES OF SIMPSON S TYPE FOR FUNCTIONS WHOSE SECOND DERIVATIVES ABSOLUTE VALUES ARE CONVEX.
 ON NEW INEQUALITIES OF SIMPSON S TYPE FOR FUNCTIONS WHOSE SECOND DERIVATIVES ABSOLUTE VALUES ARE CONVEX. MEHMET ZEKI SARIKAYA?, ERHAN. SET, AND M. EMIN OZDEMIR Asrc. In his noe, we oin new some ineuliies
ON NEW INEQUALITIES OF SIMPSON S TYPE FOR FUNCTIONS WHOSE SECOND DERIVATIVES ABSOLUTE VALUES ARE CONVEX. MEHMET ZEKI SARIKAYA?, ERHAN. SET, AND M. EMIN OZDEMIR Asrc. In his noe, we oin new some ineuliies
Mathematics 805 Final Examination Answers
 . 5 poins Se he Weiersrss M-es. Mhemics 85 Finl Eminion Answers Answer: Suppose h A R, nd f n : A R. Suppose furher h f n M n for ll A, nd h Mn converges. Then f n converges uniformly on A.. 5 poins Se
. 5 poins Se he Weiersrss M-es. Mhemics 85 Finl Eminion Answers Answer: Suppose h A R, nd f n : A R. Suppose furher h f n M n for ll A, nd h Mn converges. Then f n converges uniformly on A.. 5 poins Se
CS 491G Combinatorial Optimization Lecture Notes
 CS 491G Comintoril Optimiztion Leture Notes Dvi Owen July 30, August 1 1 Mthings Figure 1: two possile mthings in simple grph. Definition 1 Given grph G = V, E, mthing is olletion of eges M suh tht e i,
CS 491G Comintoril Optimiztion Leture Notes Dvi Owen July 30, August 1 1 Mthings Figure 1: two possile mthings in simple grph. Definition 1 Given grph G = V, E, mthing is olletion of eges M suh tht e i,
LAPLACE TRANSFORMS. 1. Basic transforms
 LAPLACE TRANSFORMS. Bic rnform In hi coure, Lplce Trnform will be inroduced nd heir properie exmined; ble of common rnform will be buil up; nd rnform will be ued o olve ome dierenil equion by rnforming
LAPLACE TRANSFORMS. Bic rnform In hi coure, Lplce Trnform will be inroduced nd heir properie exmined; ble of common rnform will be buil up; nd rnform will be ued o olve ome dierenil equion by rnforming
FM Applications of Integration 1.Centroid of Area
 FM Applicions of Inegrion.Cenroid of Are The cenroid of ody is is geomeric cenre. For n ojec mde of uniform meril, he cenroid coincides wih he poin which he ody cn e suppored in perfecly lnced se ie, is
FM Applicions of Inegrion.Cenroid of Are The cenroid of ody is is geomeric cenre. For n ojec mde of uniform meril, he cenroid coincides wih he poin which he ody cn e suppored in perfecly lnced se ie, is
Linear Quadratic Regulator (LQR) - State Feedback Design
 Linear Quadrai Regulaor (LQR) - Sae Feedbak Design A sysem is expressed in sae variable form as x = Ax + Bu n m wih x( ) R, u( ) R and he iniial ondiion x() = x A he sabilizaion problem using sae variable
Linear Quadrai Regulaor (LQR) - Sae Feedbak Design A sysem is expressed in sae variable form as x = Ax + Bu n m wih x( ) R, u( ) R and he iniial ondiion x() = x A he sabilizaion problem using sae variable
CS3510 Design & Analysis of Algorithms Fall 2017 Section A. Test 3 Solutions. Instructor: Richard Peng In class, Wednesday, Nov 15, 2017
 Uer ID (NOT he 9 igi numer): gurell4 CS351 Deign & Anlyi of Algorihm Fll 17 Seion A Te 3 Soluion Inruor: Rihr Peng In l, Weney, Nov 15, 17 Do no open hi quiz ookle unil you re iree o o o. Re ll he inruion
Uer ID (NOT he 9 igi numer): gurell4 CS351 Deign & Anlyi of Algorihm Fll 17 Seion A Te 3 Soluion Inruor: Rihr Peng In l, Weney, Nov 15, 17 Do no open hi quiz ookle unil you re iree o o o. Re ll he inruion
More on Magnetically C Coupled Coils and Ideal Transformers
 Appenix ore on gneiclly C Couple Coils Iel Trnsformers C. Equivlen Circuis for gneiclly Couple Coils A imes, i is convenien o moel mgneiclly couple coils wih n equivlen circui h oes no involve mgneic coupling.
Appenix ore on gneiclly C Couple Coils Iel Trnsformers C. Equivlen Circuis for gneiclly Couple Coils A imes, i is convenien o moel mgneiclly couple coils wih n equivlen circui h oes no involve mgneic coupling.
DIFFERENCE BETWEEN TWO RIEMANN-STIELTJES INTEGRAL MEANS
 Krgujev Journl of Mthemtis Volume 38() (204), Pges 35 49. DIFFERENCE BETWEEN TWO RIEMANN-STIELTJES INTEGRAL MEANS MOHAMMAD W. ALOMARI Abstrt. In this pper, severl bouns for the ifferene between two Riemn-
Krgujev Journl of Mthemtis Volume 38() (204), Pges 35 49. DIFFERENCE BETWEEN TWO RIEMANN-STIELTJES INTEGRAL MEANS MOHAMMAD W. ALOMARI Abstrt. In this pper, severl bouns for the ifferene between two Riemn-
SOME INTEGRAL INEQUALITIES FOR HARMONICALLY CONVEX STOCHASTIC PROCESSES ON THE CO-ORDINATES
 Avne Mth Moels & Applitions Vol3 No 8 pp63-75 SOME INTEGRAL INEQUALITIES FOR HARMONICALLY CONVE STOCHASTIC PROCESSES ON THE CO-ORDINATES Nurgül Okur * Imt Işn Yusuf Ust 3 3 Giresun University Deprtment
Avne Mth Moels & Applitions Vol3 No 8 pp63-75 SOME INTEGRAL INEQUALITIES FOR HARMONICALLY CONVE STOCHASTIC PROCESSES ON THE CO-ORDINATES Nurgül Okur * Imt Işn Yusuf Ust 3 3 Giresun University Deprtment
An Explicit Method for Geometrically Nonlinear Dynamic Analysis of Spatial Beams
 An Eplii Meho or eomerilly Nonliner ynmi Anlysis o pil Bems hu hng Hung Wen Yi Lin umio uii n Kuo Mo Hsio Asr An eplii meho se on he enrl ierene meho or nonliner rnsien ynmi nlysis o spil ems wih inie
An Eplii Meho or eomerilly Nonliner ynmi Anlysis o pil Bems hu hng Hung Wen Yi Lin umio uii n Kuo Mo Hsio Asr An eplii meho se on he enrl ierene meho or nonliner rnsien ynmi nlysis o spil ems wih inie
A Kalman filtering simulation
 A Klmn filering simulion The performnce of Klmn filering hs been esed on he bsis of wo differen dynmicl models, ssuming eiher moion wih consn elociy or wih consn ccelerion. The former is epeced o beer
A Klmn filering simulion The performnce of Klmn filering hs been esed on he bsis of wo differen dynmicl models, ssuming eiher moion wih consn elociy or wih consn ccelerion. The former is epeced o beer
A new model for solving fuzzy linear fractional programming problem with ranking function
 J. ppl. Res. Ind. Eng. Vol. 4 No. 07 89 96 Journl of pplied Reserch on Indusril Engineering www.journl-prie.com new model for solving fuzzy liner frcionl progrmming prolem wih rning funcion Spn Kumr Ds
J. ppl. Res. Ind. Eng. Vol. 4 No. 07 89 96 Journl of pplied Reserch on Indusril Engineering www.journl-prie.com new model for solving fuzzy liner frcionl progrmming prolem wih rning funcion Spn Kumr Ds
Factorising FACTORISING.
 Ftorising FACTORISING www.mthletis.om.u Ftorising FACTORISING Ftorising is the opposite of expning. It is the proess of putting expressions into rkets rther thn expning them out. In this setion you will
Ftorising FACTORISING www.mthletis.om.u Ftorising FACTORISING Ftorising is the opposite of expning. It is the proess of putting expressions into rkets rther thn expning them out. In this setion you will
defines eigenvectors and associated eigenvalues whenever there are nonzero solutions ( 0
 Chper 7. Inroduion In his hper we ll explore eigeneors nd eigenlues from geomeri perspeies, lern how o use MATLAB o lgerilly idenify hem, nd ulimely see how hese noions re fmously pplied o he digonlizion
Chper 7. Inroduion In his hper we ll explore eigeneors nd eigenlues from geomeri perspeies, lern how o use MATLAB o lgerilly idenify hem, nd ulimely see how hese noions re fmously pplied o he digonlizion
Production Inventory Model with Weibull Deterioration Rate, Time Dependent Quadratic Demand and Variable Holding Cost
 roduion nvenory Model wih Weiull Deeriorion Re Time Dependen Qudri Demnd nd Vrile Holding Cos BN: 978--9495-5- R Venkeswrlu GTAM Universiy rngvjhlv@yhoooin M Reddy BVR Engineering College nveensrinu@gmilom
roduion nvenory Model wih Weiull Deeriorion Re Time Dependen Qudri Demnd nd Vrile Holding Cos BN: 978--9495-5- R Venkeswrlu GTAM Universiy rngvjhlv@yhoooin M Reddy BVR Engineering College nveensrinu@gmilom
Solutions for Nonlinear Partial Differential Equations By Tan-Cot Method
 IOSR Journl of Mhemics (IOSR-JM) e-issn: 78-578. Volume 5, Issue 3 (Jn. - Feb. 13), PP 6-11 Soluions for Nonliner Pril Differenil Equions By Tn-Co Mehod Mhmood Jwd Abdul Rsool Abu Al-Sheer Al -Rfidin Universiy
IOSR Journl of Mhemics (IOSR-JM) e-issn: 78-578. Volume 5, Issue 3 (Jn. - Feb. 13), PP 6-11 Soluions for Nonliner Pril Differenil Equions By Tn-Co Mehod Mhmood Jwd Abdul Rsool Abu Al-Sheer Al -Rfidin Universiy
How to Prove the Riemann Hypothesis Author: Fayez Fok Al Adeh.
 How o Prove he Riemnn Hohesis Auhor: Fez Fok Al Adeh. Presiden of he Srin Cosmologicl Socie P.O.Bo,387,Dmscus,Sri Tels:963--77679,735 Emil:hf@scs-ne.org Commens: 3 ges Subj-Clss: Funcionl nlsis, comle
How o Prove he Riemnn Hohesis Auhor: Fez Fok Al Adeh. Presiden of he Srin Cosmologicl Socie P.O.Bo,387,Dmscus,Sri Tels:963--77679,735 Emil:hf@scs-ne.org Commens: 3 ges Subj-Clss: Funcionl nlsis, comle
1. Introduction. 1 b b
 Journl of Mhemicl Inequliies Volume, Number 3 (007), 45 436 SOME IMPROVEMENTS OF GRÜSS TYPE INEQUALITY N. ELEZOVIĆ, LJ. MARANGUNIĆ AND J. PEČARIĆ (communiced b A. Čižmešij) Absrc. In his pper some inequliies
Journl of Mhemicl Inequliies Volume, Number 3 (007), 45 436 SOME IMPROVEMENTS OF GRÜSS TYPE INEQUALITY N. ELEZOVIĆ, LJ. MARANGUNIĆ AND J. PEČARIĆ (communiced b A. Čižmešij) Absrc. In his pper some inequliies
Research Article New General Integral Inequalities for Lipschitzian Functions via Hadamard Fractional Integrals
 Hindwi Pulishing orporion Inernionl Journl of Anlysis, Aricle ID 35394, 8 pges hp://d.doi.org/0.55/04/35394 Reserch Aricle New Generl Inegrl Inequliies for Lipschizin Funcions vi Hdmrd Frcionl Inegrls
Hindwi Pulishing orporion Inernionl Journl of Anlysis, Aricle ID 35394, 8 pges hp://d.doi.org/0.55/04/35394 Reserch Aricle New Generl Inegrl Inequliies for Lipschizin Funcions vi Hdmrd Frcionl Inegrls
GENERALIZATION OF SOME INEQUALITIES VIA RIEMANN-LIOUVILLE FRACTIONAL CALCULUS
 - TAMKANG JOURNAL OF MATHEMATICS Volume 5, Number, 7-5, June doi:5556/jkjm555 Avilble online hp://journlsmhkueduw/ - - - GENERALIZATION OF SOME INEQUALITIES VIA RIEMANN-LIOUVILLE FRACTIONAL CALCULUS MARCELA
- TAMKANG JOURNAL OF MATHEMATICS Volume 5, Number, 7-5, June doi:5556/jkjm555 Avilble online hp://journlsmhkueduw/ - - - GENERALIZATION OF SOME INEQUALITIES VIA RIEMANN-LIOUVILLE FRACTIONAL CALCULUS MARCELA
Cylindrically Symmetric Marder Universe and Its Proper Teleparallel Homothetic Motions
 J. Bsi. Appl. i. Res. 4-5 4 4 TeRod Publiion IN 9-44 Journl of Bsi nd Applied ienifi Reserh www.erod.om Clindrill mmeri Mrder Universe nd Is Proper Teleprllel Homohei Moions Amjd Ali * Anwr Ali uhil Khn
J. Bsi. Appl. i. Res. 4-5 4 4 TeRod Publiion IN 9-44 Journl of Bsi nd Applied ienifi Reserh www.erod.om Clindrill mmeri Mrder Universe nd Is Proper Teleprllel Homohei Moions Amjd Ali * Anwr Ali uhil Khn
EOQ Inventory Models for Deteriorating Item with Weibull Deterioration and Time-Varying Quadratic Holding Cost
 ISSN (e): 50 005 Volume, 06 Issue, 0 Jnury 06 Inernionl Journl of Compuionl Engineering Reserh (IJCER) EOQ Invenory Models for eerioring Iem wih Weiull eeriorion nd ime-vrying Qudri Holding Cos Nresh Kumr
ISSN (e): 50 005 Volume, 06 Issue, 0 Jnury 06 Inernionl Journl of Compuionl Engineering Reserh (IJCER) EOQ Invenory Models for eerioring Iem wih Weiull eeriorion nd ime-vrying Qudri Holding Cos Nresh Kumr
Motion. Part 2: Constant Acceleration. Acceleration. October Lab Physics. Ms. Levine 1. Acceleration. Acceleration. Units for Acceleration.
 Moion Accelerion Pr : Consn Accelerion Accelerion Accelerion Accelerion is he re of chnge of velociy. = v - vo = Δv Δ ccelerion = = v - vo chnge of velociy elpsed ime Accelerion is vecor, lhough in one-dimensionl
Moion Accelerion Pr : Consn Accelerion Accelerion Accelerion Accelerion is he re of chnge of velociy. = v - vo = Δv Δ ccelerion = = v - vo chnge of velociy elpsed ime Accelerion is vecor, lhough in one-dimensionl
THE EXTENDED TANH METHOD FOR SOLVING THE -DIMENSION NONLINEAR DISPERSIVE LONG WAVE EQUATION
 Jornl of Mhemil Sienes: Adnes nd Appliions Volme Nmer 8 Pes 99- THE EXTENDED TANH METHOD FOR SOLVING THE ( ) -DIMENSION NONLINEAR DISPERSIVE LONG WAVE EQUATION SHENGQIANG TANG KELEI ZHANG nd JIHONG RONG
Jornl of Mhemil Sienes: Adnes nd Appliions Volme Nmer 8 Pes 99- THE EXTENDED TANH METHOD FOR SOLVING THE ( ) -DIMENSION NONLINEAR DISPERSIVE LONG WAVE EQUATION SHENGQIANG TANG KELEI ZHANG nd JIHONG RONG
How to prove the Riemann Hypothesis
 Scholrs Journl of Phsics, Mhemics nd Sisics Sch. J. Phs. Mh. S. 5; (B:5-6 Scholrs Acdemic nd Scienific Publishers (SAS Publishers (An Inernionl Publisher for Acdemic nd Scienific Resources *Corresonding
Scholrs Journl of Phsics, Mhemics nd Sisics Sch. J. Phs. Mh. S. 5; (B:5-6 Scholrs Acdemic nd Scienific Publishers (SAS Publishers (An Inernionl Publisher for Acdemic nd Scienific Resources *Corresonding
Some Inequalities variations on a common theme Lecture I, UL 2007
 Some Inequliies vriions on common heme Lecure I, UL 2007 Finbrr Hollnd, Deprmen of Mhemics, Universiy College Cork, fhollnd@uccie; July 2, 2007 Three Problems Problem Assume i, b i, c i, i =, 2, 3 re rel
Some Inequliies vriions on common heme Lecure I, UL 2007 Finbrr Hollnd, Deprmen of Mhemics, Universiy College Cork, fhollnd@uccie; July 2, 2007 Three Problems Problem Assume i, b i, c i, i =, 2, 3 re rel
can be viewed as a generalized product, and one for which the product of f and g. That is, does
 Boyce/DiPrim 9 h e, Ch 6.6: The Convoluion Inegrl Elemenry Differenil Equion n Bounry Vlue Problem, 9 h eiion, by Willim E. Boyce n Richr C. DiPrim, 9 by John Wiley & Son, Inc. Someime i i poible o wrie
Boyce/DiPrim 9 h e, Ch 6.6: The Convoluion Inegrl Elemenry Differenil Equion n Bounry Vlue Problem, 9 h eiion, by Willim E. Boyce n Richr C. DiPrim, 9 by John Wiley & Son, Inc. Someime i i poible o wrie
On The Hermite- Hadamard-Fejér Type Integral Inequality for Convex Function
 Turkish Journl o Anlysis nd Numer Theory, 4, Vol., No. 3, 85-89 Aville online h://us.scieu.com/jn//3/6 Science nd Educion Pulishing DOI:.69/jn--3-6 On The Hermie- Hdmrd-Fejér Tye Inegrl Ineuliy or Convex
Turkish Journl o Anlysis nd Numer Theory, 4, Vol., No. 3, 85-89 Aville online h://us.scieu.com/jn//3/6 Science nd Educion Pulishing DOI:.69/jn--3-6 On The Hermie- Hdmrd-Fejér Tye Inegrl Ineuliy or Convex
ON NEW INEQUALITIES OF SIMPSON S TYPE FOR FUNCTIONS WHOSE SECOND DERIVATIVES ABSOLUTE VALUES ARE CONVEX
 Journl of Applied Mhemics, Sisics nd Informics JAMSI), 9 ), No. ON NEW INEQUALITIES OF SIMPSON S TYPE FOR FUNCTIONS WHOSE SECOND DERIVATIVES ABSOLUTE VALUES ARE CONVEX MEHMET ZEKI SARIKAYA, ERHAN. SET
Journl of Applied Mhemics, Sisics nd Informics JAMSI), 9 ), No. ON NEW INEQUALITIES OF SIMPSON S TYPE FOR FUNCTIONS WHOSE SECOND DERIVATIVES ABSOLUTE VALUES ARE CONVEX MEHMET ZEKI SARIKAYA, ERHAN. SET
September 20 Homework Solutions
 College of Engineering nd Compuer Science Mechnicl Engineering Deprmen Mechnicl Engineering A Seminr in Engineering Anlysis Fll 7 Number 66 Insrucor: Lrry Creo Sepember Homework Soluions Find he specrum
College of Engineering nd Compuer Science Mechnicl Engineering Deprmen Mechnicl Engineering A Seminr in Engineering Anlysis Fll 7 Number 66 Insrucor: Lrry Creo Sepember Homework Soluions Find he specrum
ON DIFFERENTIATION OF A LEBESGUE INTEGRAL WITH RESPECT TO A PARAMETER
 Mh. Appl. 1 (2012, 91 116 ON DIFFERENTIATION OF A LEBESGUE INTEGRAL WITH RESPECT TO A PARAMETER JIŘÍ ŠREMR Abr. The im of hi pper i o diu he bolue oninuiy of erin ompoie funion nd differeniion of Lebegue
Mh. Appl. 1 (2012, 91 116 ON DIFFERENTIATION OF A LEBESGUE INTEGRAL WITH RESPECT TO A PARAMETER JIŘÍ ŠREMR Abr. The im of hi pper i o diu he bolue oninuiy of erin ompoie funion nd differeniion of Lebegue
Asymptotic relationship between trajectories of nominal and uncertain nonlinear systems on time scales
 Asympoic relionship beween rjecories of nominl nd uncerin nonliner sysems on ime scles Fim Zohr Tousser 1,2, Michel Defoor 1, Boudekhil Chfi 2 nd Mohmed Djemï 1 Absrc This pper sudies he relionship beween
Asympoic relionship beween rjecories of nominl nd uncerin nonliner sysems on ime scles Fim Zohr Tousser 1,2, Michel Defoor 1, Boudekhil Chfi 2 nd Mohmed Djemï 1 Absrc This pper sudies he relionship beween
Mathematical Modeling
 ME pplie Engineering nlsis Chper Mhemicl Moeling Professor Ti-Rn Hsu, Ph.D. Deprmen of Mechnicl n erospce Engineering Sn Jose Se Universi Sn Jose, Cliforni, US Jnur Chper Lerning Ojecives Mhemicl moeling
ME pplie Engineering nlsis Chper Mhemicl Moeling Professor Ti-Rn Hsu, Ph.D. Deprmen of Mechnicl n erospce Engineering Sn Jose Se Universi Sn Jose, Cliforni, US Jnur Chper Lerning Ojecives Mhemicl moeling
Necessary and sucient conditions for some two. Abstract. Further we show that the necessary conditions for the existence of an OD(44 s 1 s 2 )
 Neessry n suient onitions for some two vrile orthogonl esigns in orer 44 C. Koukouvinos, M. Mitrouli y, n Jennifer Seerry z Deite to Professor Anne Penfol Street Astrt We give new lgorithm whih llows us
Neessry n suient onitions for some two vrile orthogonl esigns in orer 44 C. Koukouvinos, M. Mitrouli y, n Jennifer Seerry z Deite to Professor Anne Penfol Street Astrt We give new lgorithm whih llows us
Second-Order Boundary Value Problems of Singular Type
 JOURNAL OF MATEMATICAL ANALYSIS AND APPLICATIONS 226, 4443 998 ARTICLE NO. AY98688 Seond-Order Boundary Value Probles of Singular Type Ravi P. Agarwal Deparen of Maheais, Naional Uniersiy of Singapore,
JOURNAL OF MATEMATICAL ANALYSIS AND APPLICATIONS 226, 4443 998 ARTICLE NO. AY98688 Seond-Order Boundary Value Probles of Singular Type Ravi P. Agarwal Deparen of Maheais, Naional Uniersiy of Singapore,
The solution is often represented as a vector: 2xI + 4X2 + 2X3 + 4X4 + 2X5 = 4 2xI + 4X2 + 3X3 + 3X4 + 3X5 = 4. 3xI + 6X2 + 6X3 + 3X4 + 6X5 = 6.
 [~ o o :- o o ill] i 1. Mrices, Vecors, nd Guss-Jordn Eliminion 1 x y = = - z= The soluion is ofen represened s vecor: n his exmple, he process of eliminion works very smoohly. We cn elimine ll enries
[~ o o :- o o ill] i 1. Mrices, Vecors, nd Guss-Jordn Eliminion 1 x y = = - z= The soluion is ofen represened s vecor: n his exmple, he process of eliminion works very smoohly. We cn elimine ll enries
The Forming Theory and Computer Simulation of the Rotary Cutting Tools with Helical Teeth and Complex Surfaces
 Compuer nd Informion Siene The Forming Theory nd Compuer Simulion of he Rory Cuing Tools wih Helil Teeh nd Comple Surfes Hurn Liu Deprmen of Mehnil Engineering Zhejing Universiy of Siene nd Tehnology Hngzhou
Compuer nd Informion Siene The Forming Theory nd Compuer Simulion of he Rory Cuing Tools wih Helil Teeh nd Comple Surfes Hurn Liu Deprmen of Mehnil Engineering Zhejing Universiy of Siene nd Tehnology Hngzhou
white strictly far ) fnf regular [ with f fcs)8( hs ) as function Preliminary question jointly speaking does not exist! Brownian : APA Lecture 1.
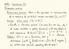 Am : APA Lecure 13 Brownin moion Preliminry quesion : Wh is he equivlen in coninuous ime of sequence of? iid Ncqe rndom vribles ( n nzn noise ( 4 e Re whie ( ie se every fm ( xh o + nd covrince E ( xrxs
Am : APA Lecure 13 Brownin moion Preliminry quesion : Wh is he equivlen in coninuous ime of sequence of? iid Ncqe rndom vribles ( n nzn noise ( 4 e Re whie ( ie se every fm ( xh o + nd covrince E ( xrxs
A Structural Approach to the Enforcement of Language and Disjunctive Constraints
 A Srucurl Aroch o he Enforcemen of Lnguge nd Disjuncive Consrins Mrin V. Iordche School of Engineering nd Eng. Tech. LeTourneu Universiy Longview, TX 7607-700 Pnos J. Ansklis Dermen of Elecricl Engineering
A Srucurl Aroch o he Enforcemen of Lnguge nd Disjuncive Consrins Mrin V. Iordche School of Engineering nd Eng. Tech. LeTourneu Universiy Longview, TX 7607-700 Pnos J. Ansklis Dermen of Elecricl Engineering
Properties of Logarithms. Solving Exponential and Logarithmic Equations. Properties of Logarithms. Properties of Logarithms. ( x)
 Properies of Logrihms Solving Eponenil nd Logrihmic Equions Properies of Logrihms Produc Rule ( ) log mn = log m + log n ( ) log = log + log Properies of Logrihms Quoien Rule log m = logm logn n log7 =
Properies of Logrihms Solving Eponenil nd Logrihmic Equions Properies of Logrihms Produc Rule ( ) log mn = log m + log n ( ) log = log + log Properies of Logrihms Quoien Rule log m = logm logn n log7 =
Global alignment in linear space
 Globl linmen in liner spe 1 2 Globl linmen in liner spe Gol: Find n opiml linmen of A[1..n] nd B[1..m] in liner spe, i.e. O(n) Exisin lorihm: Globl linmen wih bkrkin O(nm) ime nd spe, bu he opiml os n
Globl linmen in liner spe 1 2 Globl linmen in liner spe Gol: Find n opiml linmen of A[1..n] nd B[1..m] in liner spe, i.e. O(n) Exisin lorihm: Globl linmen wih bkrkin O(nm) ime nd spe, bu he opiml os n
Harmonic Balance Solution of Mulholland Equation
 Hrmoni Bne Souion of Muhon Equion M. Sifur Rhmn M. A Hosen n M. Shmsu Am Absr oowing new hrmoni bne meho pproime souions of vn er Po s equion hve been eermine ner he imi ye. The meho is eenbe o higher
Hrmoni Bne Souion of Muhon Equion M. Sifur Rhmn M. A Hosen n M. Shmsu Am Absr oowing new hrmoni bne meho pproime souions of vn er Po s equion hve been eermine ner he imi ye. The meho is eenbe o higher
PAIR OF LINEAR EQUATIONS IN TWO VARIABLES
 PAIR OF LINEAR EQUATIONS IN TWO VARIABLES. Two liner equtions in the sme two vriles re lled pir of liner equtions in two vriles. The most generl form of pir of liner equtions is x + y + 0 x + y + 0 where,,,,,,
PAIR OF LINEAR EQUATIONS IN TWO VARIABLES. Two liner equtions in the sme two vriles re lled pir of liner equtions in two vriles. The most generl form of pir of liner equtions is x + y + 0 x + y + 0 where,,,,,,
Solutions to Problems from Chapter 2
 Soluions o Problems rom Chper Problem. The signls u() :5sgn(), u () :5sgn(), nd u h () :5sgn() re ploed respecively in Figures.,b,c. Noe h u h () :5sgn() :5; 8 including, bu u () :5sgn() is undeined..5
Soluions o Problems rom Chper Problem. The signls u() :5sgn(), u () :5sgn(), nd u h () :5sgn() re ploed respecively in Figures.,b,c. Noe h u h () :5sgn() :5; 8 including, bu u () :5sgn() is undeined..5
New Inequalities in Fractional Integrals
 ISSN 1749-3889 (prin), 1749-3897 (online) Inernionl Journl of Nonliner Science Vol.9(21) No.4,pp.493-497 New Inequliies in Frcionl Inegrls Zoubir Dhmni Zoubir DAHMANI Lborory of Pure nd Applied Mhemics,
ISSN 1749-3889 (prin), 1749-3897 (online) Inernionl Journl of Nonliner Science Vol.9(21) No.4,pp.493-497 New Inequliies in Frcionl Inegrls Zoubir Dhmni Zoubir DAHMANI Lborory of Pure nd Applied Mhemics,
D.I. Survival models and copulas
 D- D. SURVIVAL COPULA D.I. Survival moels an copulas Definiions, relaionships wih mulivariae survival isribuion funcions an relaionships beween copulas an survival copulas. D.II. Fraily moels Use of a
D- D. SURVIVAL COPULA D.I. Survival moels an copulas Definiions, relaionships wih mulivariae survival isribuion funcions an relaionships beween copulas an survival copulas. D.II. Fraily moels Use of a
rank Additionally system of equation only independent atfect Gawp (A) possible ( Alb ) easily process form rang A. Proposition with Definition
 Defiion nexivnol numer ler dependen rows mrix sid row Gwp elimion mehod does no fec h numer end process i possile esily red rng fc for mrix form der zz rn rnk wih m dcussion i holds rr o Proposiion ler
Defiion nexivnol numer ler dependen rows mrix sid row Gwp elimion mehod does no fec h numer end process i possile esily red rng fc for mrix form der zz rn rnk wih m dcussion i holds rr o Proposiion ler
2k 1. . And when n is odd number, ) The conclusion is when n is even number, an. ( 1) ( 2 1) ( k 0,1,2 L )
 Scholrs Journl of Engineering d Technology SJET) Sch. J. Eng. Tech., ; A):8-6 Scholrs Acdemic d Scienific Publisher An Inernionl Publisher for Acdemic d Scienific Resources) www.sspublisher.com ISSN -X
Scholrs Journl of Engineering d Technology SJET) Sch. J. Eng. Tech., ; A):8-6 Scholrs Acdemic d Scienific Publisher An Inernionl Publisher for Acdemic d Scienific Resources) www.sspublisher.com ISSN -X
POSITIVE IMPLICATIVE AND ASSOCIATIVE FILTERS OF LATTICE IMPLICATION ALGEBRAS
 Bull. Koren Mth. So. 35 (998), No., pp. 53 6 POSITIVE IMPLICATIVE AND ASSOCIATIVE FILTERS OF LATTICE IMPLICATION ALGEBRAS YOUNG BAE JUN*, YANG XU AND KEYUN QIN ABSTRACT. We introue the onepts of positive
Bull. Koren Mth. So. 35 (998), No., pp. 53 6 POSITIVE IMPLICATIVE AND ASSOCIATIVE FILTERS OF LATTICE IMPLICATION ALGEBRAS YOUNG BAE JUN*, YANG XU AND KEYUN QIN ABSTRACT. We introue the onepts of positive
Designing A Fanlike Structure
 Designing A Fnlike Sruure To proeed wih his lesson, lik on he Nex buon here or he op of ny pge. When you re done wih his lesson, lik on he Conens buon here or he op of ny pge o reurn o he lis of lessons.
Designing A Fnlike Sruure To proeed wih his lesson, lik on he Nex buon here or he op of ny pge. When you re done wih his lesson, lik on he Conens buon here or he op of ny pge o reurn o he lis of lessons.
T b a(f) [f ] +. P b a(f) = Conclude that if f is in AC then it is the difference of two monotone absolutely continuous functions.
![T b a(f) [f ] +. P b a(f) = Conclude that if f is in AC then it is the difference of two monotone absolutely continuous functions. T b a(f) [f ] +. P b a(f) = Conclude that if f is in AC then it is the difference of two monotone absolutely continuous functions.](/thumbs/78/77085178.jpg) Rel Vribles, Fll 2014 Problem set 5 Solution suggestions Exerise 1. Let f be bsolutely ontinuous on [, b] Show tht nd T b (f) P b (f) f (x) dx [f ] +. Conlude tht if f is in AC then it is the differene
Rel Vribles, Fll 2014 Problem set 5 Solution suggestions Exerise 1. Let f be bsolutely ontinuous on [, b] Show tht nd T b (f) P b (f) f (x) dx [f ] +. Conlude tht if f is in AC then it is the differene
1. Find a basis for the row space of each of the following matrices. Your basis should consist of rows of the original matrix.
 Mh 7 Exm - Prcice Prolem Solions. Find sis for he row spce of ech of he following mrices. Yor sis shold consis of rows of he originl mrix. 4 () 7 7 8 () Since we wn sis for he row spce consising of rows
Mh 7 Exm - Prcice Prolem Solions. Find sis for he row spce of ech of he following mrices. Yor sis shold consis of rows of he originl mrix. 4 () 7 7 8 () Since we wn sis for he row spce consising of rows
Existence of positive solutions for fractional q-difference. equations involving integral boundary conditions with p- Laplacian operator
 Invenion Journal of Researh Tehnology in Engineering & Managemen IJRTEM) ISSN: 455-689 www.ijrem.om Volume Issue 7 ǁ July 8 ǁ PP 5-5 Exisene of osiive soluions for fraional -differene euaions involving
Invenion Journal of Researh Tehnology in Engineering & Managemen IJRTEM) ISSN: 455-689 www.ijrem.om Volume Issue 7 ǁ July 8 ǁ PP 5-5 Exisene of osiive soluions for fraional -differene euaions involving
S Radio transmission and network access Exercise 1-2
 S-7.330 Rdio rnsmission nd nework ccess Exercise 1 - P1 In four-symbol digil sysem wih eqully probble symbols he pulses in he figure re used in rnsmission over AWGN-chnnel. s () s () s () s () 1 3 4 )
S-7.330 Rdio rnsmission nd nework ccess Exercise 1 - P1 In four-symbol digil sysem wih eqully probble symbols he pulses in he figure re used in rnsmission over AWGN-chnnel. s () s () s () s () 1 3 4 )
Journal of Mathematical Analysis and Applications. Two normality criteria and the converse of the Bloch principle
 J. Mh. Anl. Appl. 353 009) 43 48 Conens liss vilble ScienceDirec Journl of Mhemicl Anlysis nd Applicions www.elsevier.com/loce/jm Two normliy crieri nd he converse of he Bloch principle K.S. Chrk, J. Rieppo
J. Mh. Anl. Appl. 353 009) 43 48 Conens liss vilble ScienceDirec Journl of Mhemicl Anlysis nd Applicions www.elsevier.com/loce/jm Two normliy crieri nd he converse of he Bloch principle K.S. Chrk, J. Rieppo
The order of reaction is defined as the number of atoms or molecules whose concentration change during the chemical reaction.
 www.hechemisryguru.com Re Lw Expression Order of Recion The order of recion is defined s he number of oms or molecules whose concenrion chnge during he chemicl recion. Or The ol number of molecules or
www.hechemisryguru.com Re Lw Expression Order of Recion The order of recion is defined s he number of oms or molecules whose concenrion chnge during he chemicl recion. Or The ol number of molecules or
Abstract. W.W. Memudu 1 and O.A. Taiwo, 2
 Theoreicl Mhemics & Applicions, vol. 6, no., 06, 3-50 ISS: 79-9687 prin, 79-9709 online Scienpress d, 06 Eponenilly fied collocion pproimion mehod for he numericl soluions of Higher Order iner Fredholm
Theoreicl Mhemics & Applicions, vol. 6, no., 06, 3-50 ISS: 79-9687 prin, 79-9709 online Scienpress d, 06 Eponenilly fied collocion pproimion mehod for he numericl soluions of Higher Order iner Fredholm
Counting Paths Between Vertices. Isomorphism of Graphs. Isomorphism of Graphs. Isomorphism of Graphs. Isomorphism of Graphs. Isomorphism of Graphs
 Isomorphism of Grphs Definition The simple grphs G 1 = (V 1, E 1 ) n G = (V, E ) re isomorphi if there is ijetion (n oneto-one n onto funtion) f from V 1 to V with the property tht n re jent in G 1 if
Isomorphism of Grphs Definition The simple grphs G 1 = (V 1, E 1 ) n G = (V, E ) re isomorphi if there is ijetion (n oneto-one n onto funtion) f from V 1 to V with the property tht n re jent in G 1 if
Homework 5 for BST 631: Statistical Theory I Solutions, 09/21/2006
 Homewok 5 fo BST 63: Sisicl Theoy I Soluions, 9//6 Due Time: 5:PM Thusy, on 9/8/6. Polem ( oins). Book olem.8. Soluion: E = x f ( x) = ( x) f ( x) + ( x ) f ( x) = xf ( x) + xf ( x) + f ( x) f ( x) Accoing
Homewok 5 fo BST 63: Sisicl Theoy I Soluions, 9//6 Due Time: 5:PM Thusy, on 9/8/6. Polem ( oins). Book olem.8. Soluion: E = x f ( x) = ( x) f ( x) + ( x ) f ( x) = xf ( x) + xf ( x) + f ( x) f ( x) Accoing
