QS 015/1 Matriculation Programme Examination Semester I Session 2013/2014
|
|
|
- Randall Sutton
- 5 years ago
- Views:
Transcription
1 QS 015/1 Matriculation Programme Examination Semester I Session KANG KOOI WEI
2 5 3 0 c Given matrices A = [ 3 1 0] and B = [ 3 d 0]. Find the values of c, d and e e such that AB = 14I, where I is the identity matrix. Hence, determine A Consider the function f(x) = 1 + ln(x), x 1. Determine f 1 (x) and state its range. Hence, evaluate f 1 (3). 3. Find the value of x which satisfies the equation log 9 x = (log 3 x) 2, x > Solve the equation 2 2x 2 2 x+1 = 2 x Given g(x) = kx+8, x 5 where k is a constant. 4x 5 4 a. Find the value of k if (g g)(x) = x. b. Find the value of k so that g(x) is not a one-to-one function. 6. Given f(x) = e 3x + 4, x R. a. Find f 1 (x). b. On the same axes, sketch the graphs of f(x) and f 1 (x). State the domain of f(x) and f 1 (x). 7. a. Find the values of p and q if p 4 2i + q 4+2i = i. b. Given log 10 2 = m and log 10 7 = n. Express x in terms of m and n if (14 3x+1 )(8 2x+3 ) = 7. Kang Kooi Wei Page 2
3 8. An osteoprorosis patient was advised by a doctor to take enough magnesium, vitamin D and calcium to improve bone density. In a week, the patient has to take 8 units magnesium, 11 units vitamin D and 17 units calcium. The following are three types of capsule that contains the three essential nutrients for the bone: Capsule of type P: 2 units magnesium, 1 unit vitamin D and 1 unit calcium. Capsule of type Q: 1 unit magnesium, 2 units vitamin D and 3 units calcium. Capsule of type R: 4 units magnesium, 6 units vitamin D and 10 units calcium. Let x, y and z represent the number of capsule of types P, Q and R respectively that the patient has to take in a week. (a) Obtain a system of linear equation to represent the given information and write x the system in the form of matrix equation AX = B, where X = ( y). z (b) Find the inverse of matrix A from part (a) by using the adjoint method. Hence, find the values of x, y and z. (c) The cost for each capsule of type P, Q and R are RM10, RM15 and RM17 respectively. How much will the expenses be for 4 weeks if the patient follws the doctor s advice? 9. a. In an arithmetic progression, the sum of the first four terms is 46 and the seventh term exceeds twice of the second term by 5. Obtain the first term and the common difference for the progression. Hence, calculate the sum of the first ten even terms of the progression. b. A ball is dropped from a height of 2m. Each time the ball hits the floor, it bounces vertically to a height that is 3 of its previous height. 4 i. Find the height of the ball at the tenth bounce. ii. Find the total distance that the ball will travel before the eleventh bounce. 10 a. Find the solution set of 2 3x < x + 3. b. If x + 1 < 0, show that i. 2x 1 < 0 2x 1 ii. > 2 x+1 Kang Kooi Wei Page 3
4 5 3 0 c Given matrices A = [ 3 1 0] and B = [ 3 d 0]. Find the values of c, d and e e such that AB = 14I, where I is the identity matrix. Hence, determine A 1. AB = 14I c [ 3 1 0] [ 3 d 0] = [ ] e c d [ 3c 3 9 d 0 ] = [ ] 0 0 2e c + 9 = 14 c = d = 0 d = 5 2e = 14 e = 7 c = 1, d = 5, e = 7 AB = 14I A 1 = 1 14 B A 1 = [ 3 5 0] A 1 = A 1 = [ [ ] ] Kang Kooi Wei Page 4
5 2. Consider the function f(x) = 1 + ln(x), x 1. Determine f 1 (x) and state its range. Hence, evaluate f 1 (3). Method I y = ln x + 1, x 1 ln x = y 1 x = e y 1 f 1 (x) = e x 1 R f 1 = {y: y 1} f 1 (3) = e 3 1 = e 2 Method II f(x) = 1 + ln(x) f(f 1 (x)) = x 1 + ln(f 1 (x)) = x ln(f 1 (x)) = x 1 f 1 (x) = e x 1 R f 1 = {y: y 1} f 1 (3) = e 3 1 = e 2 Kang Kooi Wei Page 5
6 3. Find the value of x which satisfies the equation log 9 x = (log 3 x) 2, x > 1. log 9 x = (log 3 x) 2 log 3 x log 3 9 = (log 3x) 2 log 3 x log = (log 3x) 2 log 3 x 2log 3 3 = (log 3x) 2 log 3 x 2 = (log 3 x) 2 log 3 x = 2(log 3 x) 2 Let u = log 3 x u = 2u 2 2u 2 u = 0 u(2u 1) = 0 u = 0 or (2u 1) = 0 u = 0 or u = 1 2 log 3 x = 0 or log 3 x = 1 2 x = 3 0 or x = x = 1 or x = 3 Since x > 1, the solution is x = 3 Kang Kooi Wei Page 6
7 4. Solve the equation 2 2x 2 2 x+1 = 2 x x 2 2 x+1 = 2 x x x 2 1 = 2 x 2 3 (2 x ) 2 2(2 x ) = 2 x 8 4 Let u = 2 x (u) 2 2(u) = u 8 4 u 2 8u = 4u 32 u 2 8u 4u + 32 = 0 u 2 12u + 32 = 0 (u 8)(u 4) = 0 u 8 = 0 or u 4 = 0 u = 8 or u = 4 2 x = 8 or 2 x = 4 x = 3 or x = 2 Kang Kooi Wei Page 7
8 5. Given g(x) = kx+8, x 5 where k is a constant. 4x 5 4 a. Find the value of k if (g g)(x) = x. b. Find the value of k so that g(x) is not a one-to-one function. 5a. g(x) = kx + 8 4x 5 (g g)(x) = x g[g(x)] = x k ( kx + 8 4x 5 ) ( kx + 8 = x 4x 5 ) 5 k ( kx + 8 8(4x 5) ) + 4x 5 (4x 5) 4 ( kx + 8 = x 5(4x 5) ) 4x 5 (4x 5) k(kx + 8) + 8(4x 5) 4x 5 = x 4(kx + 8) 5 (4x 5) 4x 5 k(kx + 8) + 8(4x 5) 4(kx + 8) 5 (4x 5) = x (k 2 x + 8k) + (32x 40) = x[(4kx + 32) (20x 25)] k 2 x + 8k + 32x 40 = x[4kx x + 25] (k )x + (8k 40) = 4kx x 20x x (k )x + (8k 40) = (4k 20)x x Compare the coeeficient of x 2 4k 20 = 0 k = 5 Kang Kooi Wei Page 8
9 5b. g(x) = kx + 8 4x 5 Let x 2 x 1, but g(x 2 ) = g(x 1 ) kx x 2 5 = kx x 1 5 (kx 2 + 8)(4x 1 5) = (kx 1 + 8)(4x 2 5) 4kx 1 x 2 5kx x 1 40 = 4kx 1 x 2 5kx x x 1 5kx 2 32x 2 + 5kx 1 = 0 32x 1 32x 2 + 5kx 1 5kx 2 = 0 32(x 1 x 2 ) + 5k(x 1 x 2 ) = 0 (x 1 x 2 )(32 + 5k) = 0 x 1 x k = 0 k = 32 5 Kang Kooi Wei Page 9
10 6. Given f(x) = e 3x + 4, x R. a. Find f 1 (x). b. On the same axes, sketch the graphs of f(x) and f 1 (x). State the domain of f(x) and f 1 (x). 6a f(x) = e 3x + 4 Method I Method II Let y = e 3x + 4 e 3x = y 4 ln( e 3x ) = ln (y 4) 3x ln e = ln (y 4) 3x = ln (y 4) x = 1 ln (y 4) 3 f 1 (x) = 1 ln (x 4) 3 f[f 1 (x)] = x e 3f 1 (x) + 4 = x e 3f 1 (x) = x 4 ln e 3f 1 (x) = ln(x 4) 3f 1 (x) ln e = ln(x 4) 3f 1 (x) = ln(x 4) f 1 (x) = 1 ln (x 4) 3 6b y f(x) y = x f 1 (x) x Domain f(x): {, } Domain f 1 (x): {4, } Kang Kooi Wei Page 10
11 7. a. Find the values of p and q if p 4 2i + q 4+2i = i. b. Given log 10 2 = m and log 10 7 = n. Express x in terms of m and n if (14 3x+1 )(8 2x+3 ) = 7. 7a p 4 2i + q 4 + 2i = i p(4 + 2i) + q(4 2i) (4 2i)(4 + 2i) = 2 + 5i 2 4p + 2pi + 4q 2qi i 8i 4i 2 = 2 + 5i 2 4p + 4q + 2pi 2qi 16 4( 1) (4p + 4q) + (2p 2q)i 20 = 2 + 5i 2 = 2 + 5i 2 2[(4p + 4q) + (2p 2q)i] = 20[2 + 5i] [(4p + 4q) + (2p 2q)i] = 20 2 [2 + 5i] [(4p + 4q) + (2p 2q)i] = 10[2 + 5i] [(4p + 4q) + (2p 2q)i] = [ i] (4p + 4q) = 20 p + q = 5... (1) 2p 2q = 50 p q = (2) (1) + (2) 2p = 30 p = 15 q = 10 Kang Kooi Wei Page 11
12 7b log 10 2 = m, log 10 7 = n (14 3x+1 )(8 2x+3 ) = 7 [(2 x 7) 3x+1 ][(2 3 ) 2x+3 ] = 7 [2 3x+1 x 7 3x+1 ][(2) 6x+9 ] = 7 [2 3x+1 x(2) 6x+9 ][7 3x+1 ] = 7 [2 3x+1+6x+9 ][7 3x+1 ] = 7 [2 9x+10 ][7 3x+1 ] = 7 log{[2 9x+10 ][7 3x+1 ]} = log 7 log2 9x+10 + log7 3x+1 = log 7 (9x + 10) log 2 + (3x + 1) log 7 = log 7 (9x + 10)m + (3x + 1)n = n 9xm + 10m + 3xn + n = n 9xm + 3xn = n n 10m x(9m + 3n) = 10m x = 10m 9m + 3n Kang Kooi Wei Page 12
13 8. An osteoprorosis patient was advised by a doctor to take enough magnesium, vitamin D and calcium to improve bone density. In a week, the patient has to take 8 units magnesium, 11 units vitamin D and 17 units calcium. The following are three types of capsule that contains the three essential nutrients for the bone: Capsule of type P: 2 units magnesium, 1 unit vitamin D and 1 unit calcium. Capsule of type Q: 1 unit magnesium, 2 units vitamin D and 3 units calcium. Capsule of type R: 4 units magnesium, 6 units vitamin D and 10 units calcium. Let x, y and z represent the number of capsule of types P, Q and R respectively that the patient has to take in a week. (a) Obtain a system of linear equation to represent the given information and write x the system in the form of matrix equation AX = B, where X = ( y). z (b) Find the inverse of matrix A from part (a) by using the adjoint method. Hence, find the values of x, y and z. (c) The cost for each capsule of type P, Q and R are RM10, RM15 and RM17 respectively. How much will the expenses be for 4 weeks if the patient follws the doctor s advice? 8a 8b 2x + y + 4z = 8 x + 2y + 6z = 11 x + 3y + 10z = x 8 [ ] [ y] = [ 11] z A = [ ] A = (2) 2 6 (1) (4) A = (2)[20 18] (1)[10 6] + (4)[3 2] A = (2)[2] (1)[4] + (4)[1] A = 4 Kang Kooi Wei Page 13
14 Cofactor of A = [ ] +(20 18) (10 6) +(3 2) Cofactor of A = [ (10 12) +(20 4) (6 1) ] +(6 8) (12 4) +(4 1) Cofactor of A = [ ] A 1 = Adjoin of A = C T Adjoin of A = [ ] Adj A A A 1 = [ ] AX = B A 1 AX = A 1 B X = A 1 B X = [ ] [ 11] X = [ 2] 1 x = 1, y = 2, z = 1 8c P = 10, Q = 15, R = 17 Expenses for 4 weeks = 4[10(1) + 15(2) + 17(1)] Expenses for 4 weeks = 4[57] Kang Kooi Wei Page 14
15 Expenses for 4 weeks = RM a. In an arithmetic progression, the sum of the first four terms is 46 and the seventh term exceeds twice of the second term by 5. Obtain the first term and the common difference for the progression. Hence, calculate the sum of the first ten even terms of the progression. 9a b. A ball is dropped from a height of 2m. Each time the ball hits the floor, it bounces vertically to a height that is 3 of its previous height. 4 i. Find the height of the ball at the tenth bounce. ii. Find the total distance that the ball will travel before the eleventh bounce. Arithmetic progression S n = n 2 [2a + (n 1)d], T n = a + (n 1)d S 4 = 46 4 [2a + (4 1)d] = [2a + 3d] = 46 4a + 6d = 46 2a + 3d = (1) T 7 = 2T a + (7 1)d = 2[a + (2 1)d] + 5 a + 6d = 2[a + d] + 5 a + 6d = 2a + 2d + 5 a 4d = 5 2a 8d = 10...(2) (1) (2) 11d = 33 d = 3 a = 7 Kang Kooi Wei Page 15
16 9b(i) 1 st bounce T 1 = 2 ( 3 4 ) 2 nd bounce T 2 = 2 ( 3 4 ) (3 4 ) = 2 (3 4 )2 3 rd bounce T 3 = 2 ( 3 4 )3 a = 2 ( 3 4 ), r = (3 4 ) T r = ar n 1 T 10 = [2 ( 3 4 )] [(3 4 ) 10 1] T 10 = [2 ( 3 4 )] [(3 4 ) 9] T 10 = 2 ( 3 4 ) 10 9b(ii) 2 [2 ( 3 4 )] 2 [2 ( 3 4 ) 2] 2m 2 [2 ( 3 4 ) 10] Total distance = [2 ( 3 4 )] + 2 [2 (3 4 ) 2 ] [2 ( 3 4 ) 10] = 2 [1 + 2 ( ) + 2 (3 4 ) ( 3 10] 4 ) = 2 {1 + 2 [( 3 4 ) + (3 4 )2 + + ( 3 4 )10 ]} a = ( 3 4 ), r = (3 4 ) S n = a(1 rn ) 1 r Kang Kooi Wei Page 16
17 = ( 3 4 ) [1 (3 4 ) 10] { = [ 1 ( 3 4 ) ]} 10 a. Find the solution set of 2 3x < x a b. If x + 1 < 0, show that 2 3x < x + 3 (2 3x) 2 < (x + 3) 2 i. 2x 1 < 0 2x 1 ii. > 2 x x + 9x 2 < x 2 + 6x + 9 9x 2 x 2 12x 6x < 0 8x 2 18x 5 < 0 (2x 5)(4x + 1) < 0 x = 5 2, Solution set is {x: 1 4 < x < 5 2 } 10b(i) 2x 1 = 2x = 2(x + 1) 3 x + 1 < 0 2(x + 1) 3 < 0 Kang Kooi Wei Page 17
18 2x 1 < 0 Kang Kooi Wei Page 18
19 10b(ii) 2x 1 x + 1 > 2 2x 1 x > 0 2x 1 x + 1 x + 1 < 0 2 = (2x 1) 2(x + 1) x + 1 = 2x 1 2x 2 x + 1 = 3 x x + 1 > 0 2x 1 x > 0 2x 1 x + 1 > 2 Kang Kooi Wei Page 19
Semester I Session 2013/2014 Sesi 2013/ hours 2iam BAHAGIAN MATRIKULASI KEMENTERIAN PENDIDIKAN MALAYSIA MATRICUATION DIVBION MATEMATIK.
 Mathemalix QS015/1 Matematik Paprl Kertas 1 Semester 1 Semester I Session 2013/2014 Sesi 2013/2014 2 hours 2iam BAHAGIAN MATRIKULASI KEMENTERIAN PENDIDIKAN MALAYSIA MATRICUATION DIVBION MINNIRY OF EDUCATION
Mathemalix QS015/1 Matematik Paprl Kertas 1 Semester 1 Semester I Session 2013/2014 Sesi 2013/2014 2 hours 2iam BAHAGIAN MATRIKULASI KEMENTERIAN PENDIDIKAN MALAYSIA MATRICUATION DIVBION MINNIRY OF EDUCATION
April 9, 2009 Name The problems count as marked. The total number of points available is 160. Throughout this test, show your work.
 April 9, 009 Name The problems count as marked The total number of points available is 160 Throughout this test, show your work 1 (15 points) Consider the cubic curve f(x) = x 3 + 3x 36x + 17 (a) Build
April 9, 009 Name The problems count as marked The total number of points available is 160 Throughout this test, show your work 1 (15 points) Consider the cubic curve f(x) = x 3 + 3x 36x + 17 (a) Build
Algebra II Honors Final Exam Review
 Class: Date: Algebra II Honors Final Exam Review Short Answer. Evaluate the series 5n. 8 n =. Evaluate the series (n + ). n = What is the sum of the finite arithmetic series?. 9+ + 5+ 8+ + + 59. 6 + 9
Class: Date: Algebra II Honors Final Exam Review Short Answer. Evaluate the series 5n. 8 n =. Evaluate the series (n + ). n = What is the sum of the finite arithmetic series?. 9+ + 5+ 8+ + + 59. 6 + 9
GRADE 12 SEPTEMBER 2012 MATHEMATICS P1
 Province of the EASTERN CAPE EDUCATION NATIONAL SENIOR CERTIFICATE GRADE 12 SEPTEMBER 2012 MATHEMATICS P1 MARKS: 150 TIME: 3 hours *MATHE1* This question paper consists of 8 pages, 3 diagram sheets and
Province of the EASTERN CAPE EDUCATION NATIONAL SENIOR CERTIFICATE GRADE 12 SEPTEMBER 2012 MATHEMATICS P1 MARKS: 150 TIME: 3 hours *MATHE1* This question paper consists of 8 pages, 3 diagram sheets and
Math RE - Calculus II Antiderivatives and the Indefinite Integral Page 1 of 5
 Math 201-203-RE - Calculus II Antiderivatives and the Indefinite Integral Page 1 of 5 What is the Antiderivative? In a derivative problem, a function f(x) is given and you find the derivative f (x) using
Math 201-203-RE - Calculus II Antiderivatives and the Indefinite Integral Page 1 of 5 What is the Antiderivative? In a derivative problem, a function f(x) is given and you find the derivative f (x) using
2. If the discriminant of a quadratic equation is zero, then there (A) are 2 imaginary roots (B) is 1 rational root
 Academic Algebra II 1 st Semester Exam Mr. Pleacher Name I. Multiple Choice 1. Which is the solution of x 1 3x + 7? (A) x -4 (B) x 4 (C) x -4 (D) x 4. If the discriminant of a quadratic equation is zero,
Academic Algebra II 1 st Semester Exam Mr. Pleacher Name I. Multiple Choice 1. Which is the solution of x 1 3x + 7? (A) x -4 (B) x 4 (C) x -4 (D) x 4. If the discriminant of a quadratic equation is zero,
Skill 6 Exponential and Logarithmic Functions
 Skill 6 Exponential and Logarithmic Functions Skill 6a: Graphs of Exponential Functions Skill 6b: Solving Exponential Equations (not requiring logarithms) Skill 6c: Definition of Logarithms Skill 6d: Graphs
Skill 6 Exponential and Logarithmic Functions Skill 6a: Graphs of Exponential Functions Skill 6b: Solving Exponential Equations (not requiring logarithms) Skill 6c: Definition of Logarithms Skill 6d: Graphs
f and radius , where is the angle between a and b sin A B sin Acos B cos Asin cos A B cos Acos B msin Asin sin 2A 2sin Acos cos 2 cos sin A A A
 FORMULAE LIST Circle: The equation 2 2 x y gx fy c 2 2 0 represents a circle centre g, f and radius 2 2 2 x a y b r The equation represents a circle centre ab, and radius r. 2 2 g f c. Scalar Product:
FORMULAE LIST Circle: The equation 2 2 x y gx fy c 2 2 0 represents a circle centre g, f and radius 2 2 2 x a y b r The equation represents a circle centre ab, and radius r. 2 2 g f c. Scalar Product:
Intermediate Algebra Study Guide
 Chapter 1 Intermediate Algebra Study Guide 1. Simplify the following. (a) ( 6) + ( 4) ( 9) (b) ( 7) ( 6)( )( ) (c) 8 5 9 (d) 6x(xy x ) x (y 6x ) (e) 7x {6 [8 (x ) (6 x)]} (f) Evaluate x y for x =, y =.
Chapter 1 Intermediate Algebra Study Guide 1. Simplify the following. (a) ( 6) + ( 4) ( 9) (b) ( 7) ( 6)( )( ) (c) 8 5 9 (d) 6x(xy x ) x (y 6x ) (e) 7x {6 [8 (x ) (6 x)]} (f) Evaluate x y for x =, y =.
Example. Determine the inverse of the given function (if it exists). f(x) = 3
 Example. Determine the inverse of the given function (if it exists). f(x) = g(x) = p x + x We know want to look at two di erent types of functions, called logarithmic functions and exponential functions.
Example. Determine the inverse of the given function (if it exists). f(x) = g(x) = p x + x We know want to look at two di erent types of functions, called logarithmic functions and exponential functions.
Algebra 2, Spring Semester Review
 Class: Date: Algebra, Spring Semester Review 1. (1 point) Graph the relation and its inverse. Use open circles to graph the points of the inverse. x 0 4 9 10 y 3 7 1 a. c. b. d. 1 . (1 point) Is relation
Class: Date: Algebra, Spring Semester Review 1. (1 point) Graph the relation and its inverse. Use open circles to graph the points of the inverse. x 0 4 9 10 y 3 7 1 a. c. b. d. 1 . (1 point) Is relation
Skill 6 Exponential and Logarithmic Functions
 Skill 6 Exponential and Logarithmic Functions Skill 6a: Graphs of Exponential Functions Skill 6b: Solving Exponential Equations (not requiring logarithms) Skill 6c: Definition of Logarithms Skill 6d: Graphs
Skill 6 Exponential and Logarithmic Functions Skill 6a: Graphs of Exponential Functions Skill 6b: Solving Exponential Equations (not requiring logarithms) Skill 6c: Definition of Logarithms Skill 6d: Graphs
Name Advanced Math Functions & Statistics. Non- Graphing Calculator Section A. B. C.
 1. Compare and contrast the following graphs. Non- Graphing Calculator Section A. B. C. 2. For R, S, and T as defined below, which of the following products is undefined? A. RT B. TR C. TS D. ST E. RS
1. Compare and contrast the following graphs. Non- Graphing Calculator Section A. B. C. 2. For R, S, and T as defined below, which of the following products is undefined? A. RT B. TR C. TS D. ST E. RS
ln(9 4x 5 = ln(75) (4x 5) ln(9) = ln(75) 4x 5 = ln(75) ln(9) ln(75) ln(9) = 1. You don t have to simplify the exact e x + 4e x
 Math 11. Exponential and Logarithmic Equations Fall 016 Instructions. Work in groups of 3 to solve the following problems. Turn them in at the end of class for credit. Names. 1. Find the (a) exact solution
Math 11. Exponential and Logarithmic Equations Fall 016 Instructions. Work in groups of 3 to solve the following problems. Turn them in at the end of class for credit. Names. 1. Find the (a) exact solution
(a) Write down the value of q and of r. (2) Write down the equation of the axis of symmetry. (1) (c) Find the value of p. (3) (Total 6 marks)
 1. Let f(x) = p(x q)(x r). Part of the graph of f is shown below. The graph passes through the points ( 2, 0), (0, 4) and (4, 0). (a) Write down the value of q and of r. (b) Write down the equation of
1. Let f(x) = p(x q)(x r). Part of the graph of f is shown below. The graph passes through the points ( 2, 0), (0, 4) and (4, 0). (a) Write down the value of q and of r. (b) Write down the equation of
The final is cumulative, but with more emphasis on chapters 3 and 4. There will be two parts.
 Math 141 Review for Final The final is cumulative, but with more emphasis on chapters 3 and 4. There will be two parts. Part 1 (no calculator) graphing (polynomial, rational, linear, exponential, and logarithmic
Math 141 Review for Final The final is cumulative, but with more emphasis on chapters 3 and 4. There will be two parts. Part 1 (no calculator) graphing (polynomial, rational, linear, exponential, and logarithmic
Logarithms Dr. Laura J. Pyzdrowski
 1 Names: (8 communication points) About this Laboratory An exponential function of the form f(x) = a x, where a is a positive real number not equal to 1, is an example of a one-to-one function. This means
1 Names: (8 communication points) About this Laboratory An exponential function of the form f(x) = a x, where a is a positive real number not equal to 1, is an example of a one-to-one function. This means
Math 121, Practice Questions for Final (Hints/Answers)
 Math 11, Practice Questions for Final Hints/Answers) 1. The graphs of the inverse functions are obtained by reflecting the graph of the original function over the line y = x. In each graph, the original
Math 11, Practice Questions for Final Hints/Answers) 1. The graphs of the inverse functions are obtained by reflecting the graph of the original function over the line y = x. In each graph, the original
Without fully opening the exam, check that you have pages 1 through 13.
 MTH 33 Solutions to Exam November th, 08 Name: Section: Recitation Instructor: INSTRUCTIONS Fill in your name, etc. on this first page. Without fully opening the exam, check that you have pages through
MTH 33 Solutions to Exam November th, 08 Name: Section: Recitation Instructor: INSTRUCTIONS Fill in your name, etc. on this first page. Without fully opening the exam, check that you have pages through
Antiderivatives and Indefinite Integrals
 Antiderivatives and Indefinite Integrals MATH 151 Calculus for Management J. Robert Buchanan Department of Mathematics Fall 2018 Objectives After completing this lesson we will be able to use the definition
Antiderivatives and Indefinite Integrals MATH 151 Calculus for Management J. Robert Buchanan Department of Mathematics Fall 2018 Objectives After completing this lesson we will be able to use the definition
Name Class. (a) (b) (c) 4 t4 3 C
 Chapter 4 Test Bank 77 Test Form A Chapter 4 Name Class Date Section. Evaluate the integral: t dt. t C (a) (b) 4 t4 C t C C t. Evaluate the integral: 5 sec x tan x dx. (a) 5 sec x tan x C (b) 5 sec x C
Chapter 4 Test Bank 77 Test Form A Chapter 4 Name Class Date Section. Evaluate the integral: t dt. t C (a) (b) 4 t4 C t C C t. Evaluate the integral: 5 sec x tan x dx. (a) 5 sec x tan x C (b) 5 sec x C
(a) Show that (5) The function f is defined by. (b) Differentiate g(x) to show that g '(x) = (3) (c) Find the exact values of x for which g '(x) = 1
 Q1. The function f is defined by (a) Show that (5) The function g is defined by (b) Differentiate g(x) to show that g '(x) = (c) Find the exact values of x for which g '(x) = 1 (Total 12 marks) Q2. (a)
Q1. The function f is defined by (a) Show that (5) The function g is defined by (b) Differentiate g(x) to show that g '(x) = (c) Find the exact values of x for which g '(x) = 1 (Total 12 marks) Q2. (a)
, g : x x 6, Sketch, in a single diagram, the graphs of y = f(x) and y = f -1 (x), making clear the
 PAST QUESTION ON FUNCTIONS 1. Express x + 4x in the form (x + a) + b, stating the numerical values of a and b. The functions f and g are defined as follows : f : x x 4x, x, g : x x 6, x R (ii) (iii) Show
PAST QUESTION ON FUNCTIONS 1. Express x + 4x in the form (x + a) + b, stating the numerical values of a and b. The functions f and g are defined as follows : f : x x 4x, x, g : x x 6, x R (ii) (iii) Show
Answer all the questions
 SECTION A ( 38 marks) Answer all the questions 1 The following information refer to the set A and set B. Set A = { -3, -2, 2, 3 } Set B = { 4, 9 } The relations between set A and set B is defined by the
SECTION A ( 38 marks) Answer all the questions 1 The following information refer to the set A and set B. Set A = { -3, -2, 2, 3 } Set B = { 4, 9 } The relations between set A and set B is defined by the
Power, Taylor, & Maclaurin Series Page 1
 Power, Taylor, & Maclaurin Series Page 1 Directions: Solve the following problems using the available space for scratchwork. Indicate your answers on the front page. Do not spend too much time on any one
Power, Taylor, & Maclaurin Series Page 1 Directions: Solve the following problems using the available space for scratchwork. Indicate your answers on the front page. Do not spend too much time on any one
in terms of p, q and r.
 Logarithms and Exponents 1. Let ln a = p, ln b = q. Write the following expressions in terms of p and q. ln a 3 b ln a b 2. Let log 10 P = x, log 10 Q = y and log 10 R = z. Express P log 10 QR 3 2 in terms
Logarithms and Exponents 1. Let ln a = p, ln b = q. Write the following expressions in terms of p and q. ln a 3 b ln a b 2. Let log 10 P = x, log 10 Q = y and log 10 R = z. Express P log 10 QR 3 2 in terms
Book 4. June 2013 June 2014 June Name :
 Book 4 June 2013 June 2014 June 2015 Name : June 2013 1. Given that 4 3 2 2 ax bx c 2 2 3x 2x 5x 4 dxe x 4 x 4, x 2 find the values of the constants a, b, c, d and e. 2. Given that f(x) = ln x, x > 0 sketch
Book 4 June 2013 June 2014 June 2015 Name : June 2013 1. Given that 4 3 2 2 ax bx c 2 2 3x 2x 5x 4 dxe x 4 x 4, x 2 find the values of the constants a, b, c, d and e. 2. Given that f(x) = ln x, x > 0 sketch
d. What are the steps for finding the y intercepts algebraically?(hint: what is equal to 0?)
 st Semester Pre Calculus Exam Review You will not receive hints on your exam. Make certain you know how to answer each of the following questions. This is a test grade. Your WORK and EXPLANATIONS are graded
st Semester Pre Calculus Exam Review You will not receive hints on your exam. Make certain you know how to answer each of the following questions. This is a test grade. Your WORK and EXPLANATIONS are graded
y2 + 4y - 5 c a + b 27 i C) ) (16, ) B) (16 3 3, )
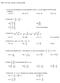 MAT 107 Final, Version A, Spring 2008 1) If (4, 4) is the endpoint of a line segment, and (2, 1) is its midpoint, find the other endpoint. A) (0, 7) B) (-2, 0) C) (8, 10) D) (0, -2) 2) Solve for x: A)
MAT 107 Final, Version A, Spring 2008 1) If (4, 4) is the endpoint of a line segment, and (2, 1) is its midpoint, find the other endpoint. A) (0, 7) B) (-2, 0) C) (8, 10) D) (0, -2) 2) Solve for x: A)
C3 PAPER JUNE 2014 *P43164A0232* 1. The curve C has equation y = f (x) where + 1. (a) Show that 9 f (x) = (3)
 PMT C3 papers from 2014 and 2013 C3 PAPER JUNE 2014 1. The curve C has equation y = f (x) where 4x + 1 f( x) =, x 2 x > 2 (a) Show that 9 f (x) = ( x ) 2 2 Given that P is a point on C such that f (x)
PMT C3 papers from 2014 and 2013 C3 PAPER JUNE 2014 1. The curve C has equation y = f (x) where 4x + 1 f( x) =, x 2 x > 2 (a) Show that 9 f (x) = ( x ) 2 2 Given that P is a point on C such that f (x)
What is on today. 1 Linear approximation. MA 123 (Calculus I) Lecture 17: November 2, 2017 Section A2. Professor Jennifer Balakrishnan,
 Professor Jennifer Balakrishnan, jbala@bu.edu What is on today 1 Linear approximation 1 1.1 Linear approximation and concavity....................... 2 1.2 Change in y....................................
Professor Jennifer Balakrishnan, jbala@bu.edu What is on today 1 Linear approximation 1 1.1 Linear approximation and concavity....................... 2 1.2 Change in y....................................
MATHEMATICS A2/M/P1 A LEVEL PAPER 1
 Surname Other Names Candidate Signature Centre Number Candidate Number Examiner Comments Total Marks MATHEMATICS A LEVEL PAPER 1 Bronze Set B (Edexcel Version) CM Time allowed: 2 hours Instructions to
Surname Other Names Candidate Signature Centre Number Candidate Number Examiner Comments Total Marks MATHEMATICS A LEVEL PAPER 1 Bronze Set B (Edexcel Version) CM Time allowed: 2 hours Instructions to
Multiple-Choice Questions
 Multiple-Choice Questions 1. A rock is thrown straight up from the edge of a cliff. The rock reaches the maximum height of 15 m above the edge and then falls down to the bottom of the cliff 35 m below
Multiple-Choice Questions 1. A rock is thrown straight up from the edge of a cliff. The rock reaches the maximum height of 15 m above the edge and then falls down to the bottom of the cliff 35 m below
f(x) = 2x + 5 3x 1. f 1 (x) = x + 5 3x 2. f(x) = 102x x
 1. Let f(x) = x 3 + 7x 2 x 2. Use the fact that f( 1) = 0 to factor f completely. (2x-1)(3x+2)(x+1). 2. Find x if log 2 x = 5. x = 1/32 3. Find the vertex of the parabola given by f(x) = 2x 2 + 3x 4. (Give
1. Let f(x) = x 3 + 7x 2 x 2. Use the fact that f( 1) = 0 to factor f completely. (2x-1)(3x+2)(x+1). 2. Find x if log 2 x = 5. x = 1/32 3. Find the vertex of the parabola given by f(x) = 2x 2 + 3x 4. (Give
g 0 (x) = u(x)v0 (x) v(x)u 0 (x) u (x) A g 0 ( 1) 1(3) (3) = = 5 4 : c) What can be said about the number and location of solutions to the equation f(
 1A (10) 1. Suppose f(x) =x 3x. Use the definition of derivative to find f 0 (x). f 0 f(x + h) f(x) (x) h (x + h) 3(x + h) (x 3x) h x +4xh +h 3x 3h x +3x h 4xh +h 3h h 4x +h 3=4x 3 (9). Find an equation
1A (10) 1. Suppose f(x) =x 3x. Use the definition of derivative to find f 0 (x). f 0 f(x + h) f(x) (x) h (x + h) 3(x + h) (x 3x) h x +4xh +h 3x 3h x +3x h 4xh +h 3h h 4x +h 3=4x 3 (9). Find an equation
Math 1120 Calculus Final Exam
 May 4, 2001 Name The first five problems count 7 points each (total 35 points) and rest count as marked. There are 195 points available. Good luck. 1. Consider the function f defined by: { 2x 2 3 if x
May 4, 2001 Name The first five problems count 7 points each (total 35 points) and rest count as marked. There are 195 points available. Good luck. 1. Consider the function f defined by: { 2x 2 3 if x
FUNCTIONS AND MODELS
 1 FUNCTIONS AND MODELS FUNCTIONS AND MODELS 1.6 Inverse Functions and Logarithms In this section, we will learn about: Inverse functions and logarithms. INVERSE FUNCTIONS The table gives data from an experiment
1 FUNCTIONS AND MODELS FUNCTIONS AND MODELS 1.6 Inverse Functions and Logarithms In this section, we will learn about: Inverse functions and logarithms. INVERSE FUNCTIONS The table gives data from an experiment
Without fully opening the exam, check that you have pages 1 through 12.
 MTH 33 Exam 2 November 4th, 208 Name: Section: Recitation Instructor: INSTRUCTIONS Fill in your name, etc. on this first page. Without fully opening the exam, check that you have pages through 2. Show
MTH 33 Exam 2 November 4th, 208 Name: Section: Recitation Instructor: INSTRUCTIONS Fill in your name, etc. on this first page. Without fully opening the exam, check that you have pages through 2. Show
4 Exponential and Logarithmic Functions
 4 Exponential and Logarithmic Functions 4.1 Exponential Functions Definition 4.1 If a > 0 and a 1, then the exponential function with base a is given by fx) = a x. Examples: fx) = x, gx) = 10 x, hx) =
4 Exponential and Logarithmic Functions 4.1 Exponential Functions Definition 4.1 If a > 0 and a 1, then the exponential function with base a is given by fx) = a x. Examples: fx) = x, gx) = 10 x, hx) =
2. (12 points) Find an equation for the line tangent to the graph of f(x) =
 November 23, 2010 Name The total number of points available is 153 Throughout this test, show your work Throughout this test, you are expected to use calculus to solve problems Graphing calculator solutions
November 23, 2010 Name The total number of points available is 153 Throughout this test, show your work Throughout this test, you are expected to use calculus to solve problems Graphing calculator solutions
Math 1310 Lab 10. (Sections )
 Math 131 Lab 1. (Sections 5.1-5.3) Name/Unid: Lab section: 1. (Properties of the integral) Use the properties of the integral in section 5.2 for answering the following question. (a) Knowing that 2 2f(x)
Math 131 Lab 1. (Sections 5.1-5.3) Name/Unid: Lab section: 1. (Properties of the integral) Use the properties of the integral in section 5.2 for answering the following question. (a) Knowing that 2 2f(x)
1. The graph of a quadratic function is shown. Each square is one unit.
 1. The graph of a quadratic function is shown. Each square is one unit. a. What is the vertex of the function? b. If the lead coefficient (the value of a) is 1, write the formula for the function in vertex
1. The graph of a quadratic function is shown. Each square is one unit. a. What is the vertex of the function? b. If the lead coefficient (the value of a) is 1, write the formula for the function in vertex
2. (10 points) Find an equation for the line tangent to the graph of y = e 2x 3 at the point (3/2, 1). Solution: y = 2(e 2x 3 so m = 2e 2 3
 November 24, 2009 Name The total number of points available is 145 work Throughout this test, show your 1 (10 points) Find an equation for the line tangent to the graph of y = ln(x 2 +1) at the point (1,
November 24, 2009 Name The total number of points available is 145 work Throughout this test, show your 1 (10 points) Find an equation for the line tangent to the graph of y = ln(x 2 +1) at the point (1,
You must have: Ruler graduated in centimetres and millimetres, pair of compasses, pen, HB pencil, eraser.
 Write your name here Surname Other names Pearson Edexcel Award Algebra Level 3 Calculator NOT allowed Centre Number Candidate Number Thursday 12 January 2017 Morning Time: 2 hours Paper Reference AAL30/01
Write your name here Surname Other names Pearson Edexcel Award Algebra Level 3 Calculator NOT allowed Centre Number Candidate Number Thursday 12 January 2017 Morning Time: 2 hours Paper Reference AAL30/01
MATH 140 Practice Final Exam Semester 20XX Version X
 MATH 140 Practice Final Exam Semester 20XX Version X Name ID# Instructor Section Do not open this booklet until told to do so. On the separate answer sheet, fill in your name and identification number
MATH 140 Practice Final Exam Semester 20XX Version X Name ID# Instructor Section Do not open this booklet until told to do so. On the separate answer sheet, fill in your name and identification number
Summer Math Packet for AP Calculus BC
 Class: Date: Summer Math Packet for AP Calculus BC 018-19 1. Find the smallest value in the range of the function f (x) = x + 4x + 40. a. 4 b. 5 c. 6 d. 7 e. 8 f. 16 g. 4 h. 40. Find the smallest value
Class: Date: Summer Math Packet for AP Calculus BC 018-19 1. Find the smallest value in the range of the function f (x) = x + 4x + 40. a. 4 b. 5 c. 6 d. 7 e. 8 f. 16 g. 4 h. 40. Find the smallest value
Section 4.2 Logarithmic Functions & Applications
 34 Section 4.2 Logarithmic Functions & Applications Recall that exponential functions are one-to-one since every horizontal line passes through at most one point on the graph of y = b x. So, an exponential
34 Section 4.2 Logarithmic Functions & Applications Recall that exponential functions are one-to-one since every horizontal line passes through at most one point on the graph of y = b x. So, an exponential
Learning Target: I can sketch the graphs of rational functions without a calculator. a. Determine the equation(s) of the asymptotes.
 Learning Target: I can sketch the graphs of rational functions without a calculator Consider the graph of y= f(x), where f(x) = 3x 3 (x+2) 2 a. Determine the equation(s) of the asymptotes. b. Find the
Learning Target: I can sketch the graphs of rational functions without a calculator Consider the graph of y= f(x), where f(x) = 3x 3 (x+2) 2 a. Determine the equation(s) of the asymptotes. b. Find the
A car travels at a constant speed of 110 Km/hour between Montreal and Toronto. Determine the independent variable for this functional situation.
 Question 1 A car travels at a constant speed of 110 Km/hour between Montreal and Toronto. Determine the independent variable for this functional situation. Answer: Question 2 A function is described by
Question 1 A car travels at a constant speed of 110 Km/hour between Montreal and Toronto. Determine the independent variable for this functional situation. Answer: Question 2 A function is described by
SECTION A. f(x) = ln(x). Sketch the graph of y = f(x), indicating the coordinates of any points where the graph crosses the axes.
 SECTION A 1. State the maximal domain and range of the function f(x) = ln(x). Sketch the graph of y = f(x), indicating the coordinates of any points where the graph crosses the axes. 2. By evaluating f(0),
SECTION A 1. State the maximal domain and range of the function f(x) = ln(x). Sketch the graph of y = f(x), indicating the coordinates of any points where the graph crosses the axes. 2. By evaluating f(0),
y+2 x 1 is in the range. We solve x as x =
 Dear Students, Here are sample solutions. The most fascinating thing about mathematics is that you can solve the same problem in many different ways. The correct answer will always be the same. Be creative
Dear Students, Here are sample solutions. The most fascinating thing about mathematics is that you can solve the same problem in many different ways. The correct answer will always be the same. Be creative
2013 Bored of Studies Trial Examinations. Mathematics SOLUTIONS
 03 Bored of Studies Trial Examinations Mathematics SOLUTIONS Section I. B 3. B 5. A 7. B 9. C. D 4. B 6. A 8. D 0. C Working/Justification Question We can eliminate (A) and (C), since they are not to 4
03 Bored of Studies Trial Examinations Mathematics SOLUTIONS Section I. B 3. B 5. A 7. B 9. C. D 4. B 6. A 8. D 0. C Working/Justification Question We can eliminate (A) and (C), since they are not to 4
3. (12 points) Find an equation for the line tangent to the graph of f(x) =
 April 8, 2015 Name The total number of points available is 168 Throughout this test, show your work Throughout this test, you are expected to use calculus to solve problems Graphing calculator solutions
April 8, 2015 Name The total number of points available is 168 Throughout this test, show your work Throughout this test, you are expected to use calculus to solve problems Graphing calculator solutions
Polynomial Review Problems
 Polynomial Review Problems 1. Find polynomial function formulas that could fit each of these graphs. Remember that you will need to determine the value of the leading coefficient. The point (0,-3) is on
Polynomial Review Problems 1. Find polynomial function formulas that could fit each of these graphs. Remember that you will need to determine the value of the leading coefficient. The point (0,-3) is on
Final Exam Review Problems
 Final Exam Review Problems Name: Date: June 23, 2013 P 1.4. 33. Determine whether the line x = 4 represens y as a function of x. P 1.5. 37. Graph f(x) = 3x 1 x 6. Find the x and y-intercepts and asymptotes
Final Exam Review Problems Name: Date: June 23, 2013 P 1.4. 33. Determine whether the line x = 4 represens y as a function of x. P 1.5. 37. Graph f(x) = 3x 1 x 6. Find the x and y-intercepts and asymptotes
Core Mathematics C4 Advanced Level
 Paper Reference(s) 6666/0 Edexcel GCE Core Mathematics C4 Advanced Level Thursday June 0 Afternoon Time: hour 0 minutes Materials required for examination Mathematical Formulae (Pink) Items included with
Paper Reference(s) 6666/0 Edexcel GCE Core Mathematics C4 Advanced Level Thursday June 0 Afternoon Time: hour 0 minutes Materials required for examination Mathematical Formulae (Pink) Items included with
*P43632A0120* Algebra Level 3 Calculator NOT allowed. Pearson Edexcel Award AAL30/01. P43632A 2014 Pearson Education Ltd.
 Write your name here Surname Other names Pearson Edexcel Award Algebra Level 3 Calculator NOT allowed Centre Number Candidate Number Monday 12 May 2014 Morning Time: 2 hours Paper Reference AAL30/01 You
Write your name here Surname Other names Pearson Edexcel Award Algebra Level 3 Calculator NOT allowed Centre Number Candidate Number Monday 12 May 2014 Morning Time: 2 hours Paper Reference AAL30/01 You
Lecture 32: Taylor Series and McLaurin series We saw last day that some functions are equal to a power series on part of their domain.
 Lecture 32: Taylor Series and McLaurin series We saw last day that some functions are equal to a power series on part of their domain. For example f(x) = 1 1 x = 1 + x + x2 + x 3 + = ln(1 + x) = x x2 2
Lecture 32: Taylor Series and McLaurin series We saw last day that some functions are equal to a power series on part of their domain. For example f(x) = 1 1 x = 1 + x + x2 + x 3 + = ln(1 + x) = x x2 2
Sample Final Exam. Math S o l u t i o n s. 1. Three points are given: A = ( 2, 2), B = (2, 4), C = ( 4, 0)
 Math 0031 Sample Final Exam S o l u t i o n s 1. Three points are given: A = ( 2, 2), B = (2, 4), C = ( 4, 0) (a) (5 points) Find the midpoint D of the segment with endpoints B and C. ( 2 + ( 4) D =, 4
Math 0031 Sample Final Exam S o l u t i o n s 1. Three points are given: A = ( 2, 2), B = (2, 4), C = ( 4, 0) (a) (5 points) Find the midpoint D of the segment with endpoints B and C. ( 2 + ( 4) D =, 4
ISLAMIYA ENGLISH SCHOOL ABU DHABI U. A. E.
 ISLAMIYA ENGLISH SCHOOL ABU DHABI U. A. E. MATHEMATICS ASSIGNMENT-1 GRADE-A/L-II(Sci) CHAPTER.NO.1,2,3(C3) Algebraic fractions,exponential and logarithmic functions DATE:18/3/2017 NAME.------------------------------------------------------------------------------------------------
ISLAMIYA ENGLISH SCHOOL ABU DHABI U. A. E. MATHEMATICS ASSIGNMENT-1 GRADE-A/L-II(Sci) CHAPTER.NO.1,2,3(C3) Algebraic fractions,exponential and logarithmic functions DATE:18/3/2017 NAME.------------------------------------------------------------------------------------------------
Algebra 2, Spring Semester Review 2013
 Class: Date: Algebra, Spring Semester Review 01 1. (1 point) Find the annual percent increase or decrease that y = 0.5(.) x models. 0% increase 0% decrease 10% increase d. 5% decrease. (1 point) An initial
Class: Date: Algebra, Spring Semester Review 01 1. (1 point) Find the annual percent increase or decrease that y = 0.5(.) x models. 0% increase 0% decrease 10% increase d. 5% decrease. (1 point) An initial
for every x in the gomain of g
 Section.7 Definition of Inverse Function Let f and g be two functions such that f(g(x)) = x for every x in the gomain of g and g(f(x)) = x for every x in the gomain of f Under these conditions, the function
Section.7 Definition of Inverse Function Let f and g be two functions such that f(g(x)) = x for every x in the gomain of g and g(f(x)) = x for every x in the gomain of f Under these conditions, the function
4x 2-5x+3. 7x-1 HOMEWORK 1-1
 HOMEWORK 1-1 As it is always the case that correct answers without sufficient mathematical justification may not receive full credit, make sure that you show all your work. Please circle, draw a box around,
HOMEWORK 1-1 As it is always the case that correct answers without sufficient mathematical justification may not receive full credit, make sure that you show all your work. Please circle, draw a box around,
Advanced Math Quiz Review Name: Dec Use Synthetic Division to divide the first polynomial by the second polynomial.
 Advanced Math Quiz 3.1-3.2 Review Name: Dec. 2014 Use Synthetic Division to divide the first polynomial by the second polynomial. 1. 5x 3 + 6x 2 8 x + 1, x 5 1. Quotient: 2. x 5 10x 3 + 5 x 1, x + 4 2.
Advanced Math Quiz 3.1-3.2 Review Name: Dec. 2014 Use Synthetic Division to divide the first polynomial by the second polynomial. 1. 5x 3 + 6x 2 8 x + 1, x 5 1. Quotient: 2. x 5 10x 3 + 5 x 1, x + 4 2.
11.10a Taylor and Maclaurin Series
 11.10a 1 11.10a Taylor and Maclaurin Series Let y = f(x) be a differentiable function at x = a. In first semester calculus we saw that (1) f(x) f(a)+f (a)(x a), for all x near a The right-hand side of
11.10a 1 11.10a Taylor and Maclaurin Series Let y = f(x) be a differentiable function at x = a. In first semester calculus we saw that (1) f(x) f(a)+f (a)(x a), for all x near a The right-hand side of
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
 Calculus 1 Instructor: James Lee Practice Exam 3 Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Determine from the graph whether the function
Calculus 1 Instructor: James Lee Practice Exam 3 Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Determine from the graph whether the function
If a function has an inverse then we can determine the input if we know the output. For example if the function
 1 Inverse Functions We know what it means for a relation to be a function. Every input maps to only one output, it passes the vertical line test. But not every function has an inverse. A function has no
1 Inverse Functions We know what it means for a relation to be a function. Every input maps to only one output, it passes the vertical line test. But not every function has an inverse. A function has no
UNIVERSITY OF HOUSTON HIGH SCHOOL MATHEMATICS CONTEST Spring 2018 Calculus Test
 UNIVERSITY OF HOUSTON HIGH SCHOOL MATHEMATICS CONTEST Spring 2018 Calculus Test NAME: SCHOOL: 1. Let f be some function for which you know only that if 0 < x < 1, then f(x) 5 < 0.1. Which of the following
UNIVERSITY OF HOUSTON HIGH SCHOOL MATHEMATICS CONTEST Spring 2018 Calculus Test NAME: SCHOOL: 1. Let f be some function for which you know only that if 0 < x < 1, then f(x) 5 < 0.1. Which of the following
Name. 3) f(x) = -x2-2. Sketch the graph of the function and find the domain and range. 1) f(x) = x2-4. 4) f(x) = x ) f(x) = -3(x + 3)2-2
 Exam 3 Final Preparation Ch 7, 9, etal v0 There will be 5 questions on Exam 3 (Final). Twenty questions from chapters 7 & 9. Five questions from chapter 5. No Book/No Notes/No Ipod/ No Phone/Yes Calculator/55
Exam 3 Final Preparation Ch 7, 9, etal v0 There will be 5 questions on Exam 3 (Final). Twenty questions from chapters 7 & 9. Five questions from chapter 5. No Book/No Notes/No Ipod/ No Phone/Yes Calculator/55
Algebra II Unit #2 4.6 NOTES: Solving Quadratic Equations (More Methods) Block:
 Algebra II Unit # Name: 4.6 NOTES: Solving Quadratic Equations (More Methods) Block: (A) Background Skills - Simplifying Radicals To simplify a radical that is not a perfect square: 50 8 300 7 7 98 (B)
Algebra II Unit # Name: 4.6 NOTES: Solving Quadratic Equations (More Methods) Block: (A) Background Skills - Simplifying Radicals To simplify a radical that is not a perfect square: 50 8 300 7 7 98 (B)
The graph shows how the resultant force on the car varies with displacement.
 1 (a) A car is moving at constant velocity when the driver applies the brakes. The graph shows how the resultant force on the car varies with displacement. Resultant force 0 A B Displacement (i) State
1 (a) A car is moving at constant velocity when the driver applies the brakes. The graph shows how the resultant force on the car varies with displacement. Resultant force 0 A B Displacement (i) State
Final exam (practice) UCLA: Math 31B, Spring 2017
 Instructor: Noah White Date: Final exam (practice) UCLA: Math 3B, Spring 207 This exam has 8 questions, for a total of 80 points. Please print your working and answers neatly. Write your solutions in the
Instructor: Noah White Date: Final exam (practice) UCLA: Math 3B, Spring 207 This exam has 8 questions, for a total of 80 points. Please print your working and answers neatly. Write your solutions in the
New test - November 03, 2015 [79 marks]
![New test - November 03, 2015 [79 marks] New test - November 03, 2015 [79 marks]](/thumbs/80/81606672.jpg) New test - November 03, 05 [79 marks] Let f(x) = e x cosx, x. a. Show that f (x) = e x ( cosx sin x). correctly finding the derivative of e x, i.e. e x correctly finding the derivative of cosx, i.e. sin
New test - November 03, 05 [79 marks] Let f(x) = e x cosx, x. a. Show that f (x) = e x ( cosx sin x). correctly finding the derivative of e x, i.e. e x correctly finding the derivative of cosx, i.e. sin
Chapter 5: Quadratic Functions
 Section 5.1: Square Root Property #1-20: Solve the equations using the square root property. 1) x 2 = 16 2) y 2 = 25 3) b 2 = 49 4) a 2 = 16 5) m 2 = 98 6) d 2 = 24 7) x 2 = 75 8) x 2 = 54 9) (x 3) 2 =
Section 5.1: Square Root Property #1-20: Solve the equations using the square root property. 1) x 2 = 16 2) y 2 = 25 3) b 2 = 49 4) a 2 = 16 5) m 2 = 98 6) d 2 = 24 7) x 2 = 75 8) x 2 = 54 9) (x 3) 2 =
DEPARTMENT OF MATHEMATICS
 DEPARTMENT OF MATHEMATICS A2 level Mathematics Core 3 course workbook 2015-2016 Name: Welcome to Core 3 (C3) Mathematics. We hope that you will use this workbook to give you an organised set of notes for
DEPARTMENT OF MATHEMATICS A2 level Mathematics Core 3 course workbook 2015-2016 Name: Welcome to Core 3 (C3) Mathematics. We hope that you will use this workbook to give you an organised set of notes for
Solutionbank Edexcel AS and A Level Modular Mathematics
 Page of Exercise A, Question The curve C, with equation y = x ln x, x > 0, has a stationary point P. Find, in terms of e, the coordinates of P. (7) y = x ln x, x > 0 Differentiate as a product: = x + x
Page of Exercise A, Question The curve C, with equation y = x ln x, x > 0, has a stationary point P. Find, in terms of e, the coordinates of P. (7) y = x ln x, x > 0 Differentiate as a product: = x + x
Polynomial Approximations and Power Series
 Polynomial Approximations and Power Series June 24, 206 Tangent Lines One of the first uses of the derivatives is the determination of the tangent as a linear approximation of a differentiable function
Polynomial Approximations and Power Series June 24, 206 Tangent Lines One of the first uses of the derivatives is the determination of the tangent as a linear approximation of a differentiable function
LOWELL WEEKLY JOURNAL. ^Jberxy and (Jmott Oao M d Ccmsparftble. %m >ai ruv GEEAT INDUSTRIES
 ? (») /»» 9 F ( ) / ) /»F»»»»»# F??»»» Q ( ( »»» < 3»» /» > > } > Q ( Q > Z F 5
? (») /»» 9 F ( ) / ) /»F»»»»»# F??»»» Q ( ( »»» < 3»» /» > > } > Q ( Q > Z F 5
PART A: Solve the following equations/inequalities. Give all solutions. x 3 > x + 3 x
 CFHS Honors Precalculus Calculus BC Review PART A: Solve the following equations/inequalities. Give all solutions. 1. 2x 3 + 3x 2 8x = 3 2. 3 x 1 + 4 = 8 3. 1 x + 1 2 x 4 = 5 x 2 3x 4 1 4. log 2 2 + log
CFHS Honors Precalculus Calculus BC Review PART A: Solve the following equations/inequalities. Give all solutions. 1. 2x 3 + 3x 2 8x = 3 2. 3 x 1 + 4 = 8 3. 1 x + 1 2 x 4 = 5 x 2 3x 4 1 4. log 2 2 + log
2.5 SOME APPLICATIONS OF THE CHAIN RULE
 2.5 SOME APPLICATIONS OF THE CHAIN RULE The Chain Rule will help us etermine the erivatives of logarithms an exponential functions a x. We will also use it to answer some applie questions an to fin slopes
2.5 SOME APPLICATIONS OF THE CHAIN RULE The Chain Rule will help us etermine the erivatives of logarithms an exponential functions a x. We will also use it to answer some applie questions an to fin slopes
Study Guide for Benchmark #1 Window of Opportunity: March 4-11
 Study Guide for Benchmark #1 Window of Opportunity: March -11 Benchmark testing is the department s way of assuring that students have achieved minimum levels of computational skill. While partial credit
Study Guide for Benchmark #1 Window of Opportunity: March -11 Benchmark testing is the department s way of assuring that students have achieved minimum levels of computational skill. While partial credit
Chapter 3. Exponential and Logarithmic Functions. 3.2 Logarithmic Functions
 Chapter 3 Exponential and Logarithmic Functions 3.2 Logarithmic Functions 1/23 Chapter 3 Exponential and Logarithmic Functions 3.2 4, 8, 14, 16, 18, 20, 22, 30, 31, 32, 33, 34, 39, 42, 54, 56, 62, 68,
Chapter 3 Exponential and Logarithmic Functions 3.2 Logarithmic Functions 1/23 Chapter 3 Exponential and Logarithmic Functions 3.2 4, 8, 14, 16, 18, 20, 22, 30, 31, 32, 33, 34, 39, 42, 54, 56, 62, 68,
Integrated Calculus II Exam 1 Solutions 2/6/4
 Integrated Calculus II Exam Solutions /6/ Question Determine the following integrals: te t dt. We integrate by parts: u = t, du = dt, dv = e t dt, v = dv = e t dt = e t, te t dt = udv = uv vdu = te t (
Integrated Calculus II Exam Solutions /6/ Question Determine the following integrals: te t dt. We integrate by parts: u = t, du = dt, dv = e t dt, v = dv = e t dt = e t, te t dt = udv = uv vdu = te t (
3. Solve the following inequalities and express your answer in interval notation.
 Youngstown State University College Algebra Final Exam Review (Math 50). Find all Real solutions for the following: a) x 2 + 5x = 6 b) 9 x2 x 8 = 0 c) (x 2) 2 = 6 d) 4x = 8 x 2 e) x 2 + 4x = 5 f) 36x 3
Youngstown State University College Algebra Final Exam Review (Math 50). Find all Real solutions for the following: a) x 2 + 5x = 6 b) 9 x2 x 8 = 0 c) (x 2) 2 = 6 d) 4x = 8 x 2 e) x 2 + 4x = 5 f) 36x 3
Exponential Functions Dr. Laura J. Pyzdrowski
 1 Names: (4 communication points) About this Laboratory An exponential function is an example of a function that is not an algebraic combination of polynomials. Such functions are called trancendental
1 Names: (4 communication points) About this Laboratory An exponential function is an example of a function that is not an algebraic combination of polynomials. Such functions are called trancendental
PRE-LEAVING CERTIFICATE EXAMINATION, 2010
 L.7 PRE-LEAVING CERTIFICATE EXAMINATION, 00 MATHEMATICS HIGHER LEVEL PAPER (300 marks) TIME : ½ HOURS Attempt SIX QUESTIONS (50 marks each). WARNING: Marks will be lost if all necessary work is not clearly
L.7 PRE-LEAVING CERTIFICATE EXAMINATION, 00 MATHEMATICS HIGHER LEVEL PAPER (300 marks) TIME : ½ HOURS Attempt SIX QUESTIONS (50 marks each). WARNING: Marks will be lost if all necessary work is not clearly
ADVANCED PROGRAMME MATHEMATICS MARKING GUIDELINES
 GRADE EXAMINATION NOVEMBER ADVANCED PROGRAMME MATHEMATICS MARKING GUIDELINES Time: hours marks These marking guidelines are prepared for use by examiners and sub-examiners, all of whom are required to
GRADE EXAMINATION NOVEMBER ADVANCED PROGRAMME MATHEMATICS MARKING GUIDELINES Time: hours marks These marking guidelines are prepared for use by examiners and sub-examiners, all of whom are required to
Chapter 6: Exponential and Logarithmic Functions
 Section 6.1: Algebra and Composition of Functions #1-9: Let f(x) = 2x + 3 and g(x) = 3 x. Find each function. 1) (f + g)(x) 2) (g f)(x) 3) (f/g)(x) 4) ( )( ) 5) ( g/f)(x) 6) ( )( ) 7) ( )( ) 8) (g+f)(x)
Section 6.1: Algebra and Composition of Functions #1-9: Let f(x) = 2x + 3 and g(x) = 3 x. Find each function. 1) (f + g)(x) 2) (g f)(x) 3) (f/g)(x) 4) ( )( ) 5) ( g/f)(x) 6) ( )( ) 7) ( )( ) 8) (g+f)(x)
1 The distributive law
 THINGS TO KNOW BEFORE GOING INTO DISCRETE MATHEMATICS The distributive law The distributive law is this: a(b + c) = ab + bc This can be generalized to any number of terms between parenthesis; for instance:
THINGS TO KNOW BEFORE GOING INTO DISCRETE MATHEMATICS The distributive law The distributive law is this: a(b + c) = ab + bc This can be generalized to any number of terms between parenthesis; for instance:
Section 6.1: Composite Functions
 Section 6.1: Composite Functions Def: Given two function f and g, the composite function, which we denote by f g and read as f composed with g, is defined by (f g)(x) = f(g(x)). In other words, the function
Section 6.1: Composite Functions Def: Given two function f and g, the composite function, which we denote by f g and read as f composed with g, is defined by (f g)(x) = f(g(x)). In other words, the function
Calculus I Homework: Linear Approximation and Differentials Page 1
 Calculus I Homework: Linear Approximation and Differentials Page Example (3..8) Find the linearization L(x) of the function f(x) = (x) /3 at a = 8. The linearization is given by which approximates the
Calculus I Homework: Linear Approximation and Differentials Page Example (3..8) Find the linearization L(x) of the function f(x) = (x) /3 at a = 8. The linearization is given by which approximates the
HORIZONTAL AND VERTICAL TRANSLATIONS
 MCR3U Sections 1.6 1.8 Transformations HORIZONTAL AND VERTICAL TRANSLATIONS A change made to a figure or a relation such that the figure or graph of the relation is shifted or changed in shape. Translations,
MCR3U Sections 1.6 1.8 Transformations HORIZONTAL AND VERTICAL TRANSLATIONS A change made to a figure or a relation such that the figure or graph of the relation is shifted or changed in shape. Translations,
Introduction to Decision Sciences Lecture 6
 Introduction to Decision Sciences Lecture 6 Andrew Nobel September 21, 2017 Functions Functions Given: Sets A and B, possibly different Definition: A function f : A B is a rule that assigns every element
Introduction to Decision Sciences Lecture 6 Andrew Nobel September 21, 2017 Functions Functions Given: Sets A and B, possibly different Definition: A function f : A B is a rule that assigns every element
Core Mathematics C3. You must have: Mathematical Formulae and Statistical Tables (Pink)
 Write your name here Surname Other names Pearson Edexcel GCE Centre Number Core Mathematics C3 Advanced Candidate Number Tuesday 20 June 2017 Afternoon Time: 1 hour 30 minutes Paper Reference 6665/01 You
Write your name here Surname Other names Pearson Edexcel GCE Centre Number Core Mathematics C3 Advanced Candidate Number Tuesday 20 June 2017 Afternoon Time: 1 hour 30 minutes Paper Reference 6665/01 You
Core 3 (A2) Practice Examination Questions
 Core 3 (A) Practice Examination Questions Trigonometry Mr A Slack Trigonometric Identities and Equations I know what secant; cosecant and cotangent graphs look like and can identify appropriate restricted
Core 3 (A) Practice Examination Questions Trigonometry Mr A Slack Trigonometric Identities and Equations I know what secant; cosecant and cotangent graphs look like and can identify appropriate restricted
Content Standard Geometric Series. What number 0, 1, 2, 3, 4, 5, 6, 7, 8, or 9
 9-5 Content Standard Geometric Series A.SSE.4 Derive the formula for the sum of a geometric series (when the common ratio is not 1), and use the formula to solve problems. Objective To define geometric
9-5 Content Standard Geometric Series A.SSE.4 Derive the formula for the sum of a geometric series (when the common ratio is not 1), and use the formula to solve problems. Objective To define geometric
1 FUNCTIONS _ 5 _ 1.0 RELATIONS
 1 FUNCTIONS 1.0 RELATIONS Notes : (i) Four types of relations : one-to-one many-to-one one-to-many many-to-many. (ii) Three ways to represent relations : arrowed diagram set of ordered pairs graph. (iii)
1 FUNCTIONS 1.0 RELATIONS Notes : (i) Four types of relations : one-to-one many-to-one one-to-many many-to-many. (ii) Three ways to represent relations : arrowed diagram set of ordered pairs graph. (iii)
2018 AP PHYSICS 1 FREE-RESPONSE QUESTIONS. PHYSICS 1 Section II 1 Questions Time 25 minutes
 2018 AP FREE-RESPONSE QUESTIONS Time 25 minutes Directions: Question 1 is a long free-response question that requires about 25 minutes to answer and is worth 12 points. Show your work for each part in
2018 AP FREE-RESPONSE QUESTIONS Time 25 minutes Directions: Question 1 is a long free-response question that requires about 25 minutes to answer and is worth 12 points. Show your work for each part in
The highest degree term is x $, therefore the function is degree 4 (quartic) c) What are the x-intercepts?
 L3 1.3 Factored Form Polynomial Functions Lesson MHF4U Jensen In this section, you will investigate the relationship between the factored form of a polynomial function and the x-intercepts of the corresponding
L3 1.3 Factored Form Polynomial Functions Lesson MHF4U Jensen In this section, you will investigate the relationship between the factored form of a polynomial function and the x-intercepts of the corresponding
AP Calculus AB Summer Packet 2018
 AP Calculus AB Summer Packet 2018 Dear Calculus Student: To be successful in AP Calculus AB, you must be proficient at solving and simplifying each type of problem in this packet. This is a review of Algebra
AP Calculus AB Summer Packet 2018 Dear Calculus Student: To be successful in AP Calculus AB, you must be proficient at solving and simplifying each type of problem in this packet. This is a review of Algebra
