Homework 1 2/7/2018 SOLUTIONS Exercise 1. (a) Graph the following sets (i) C = {x R x in Z} Answer:
|
|
|
- Tyrone Joseph
- 5 years ago
- Views:
Transcription
1 Homework 1 2/7/2018 SOLTIONS Eercise 1. (a) Graph the following sets (i) C = { R in Z} nswer: 0 R (ii) D = {(, y), y in R,, y 2}. nswer: = 2 y y = 2 (iii) C C nswer: y 1
2 2 (iv) (C C) D nswer: = 2 y y = 2 (v) (C C) D nswer: = 2 y y = 2
3 3 (vi) (C C) D, where = R 2. nswer: Since (C C) looks like y D looks like = 2 y y = 2 we have (C C) D looks like = 2 y y = 2 (vii) ((C C) D), where = R 2. nswer: From the picture of (C C) D in part (v), we can see that the picture of ((C C) D) is the same as the one in part (vi). (b) Pick a set two universal sets 1 2 that illustrate that Ā depends on the choice of universal set. nswer: Let = {1}, 1 = {1} 2 = {1, 2, 3}. Then in 1, =, in 2, = {2, 3}.
4 4 (c) Let be sets contained in a universal set. Decide whether the following identities are true or false. If false, give an eample where the identity doesn t hold. If true, eplain why (in complete sentences). (i) = nswer: TRE. The set is the set elements that are in both, which does not depend on the order of sets considered. (ii) = nswer: TRE. The set is the set elements that are in either or (or both), which does not depend on the order of sets considered. (iii) = nswer: FLSE. For eample, if = {1, 2} = {2, 3}, then = {1} = {3}. (iv) = nswer: FLSE. For eample, if = {1} = {2}, then = {(1, 2)} = {(2, 1)}. (v) = nswer: FLSE. See part (iii) for eample. (vi) If is finite, then so is P() nswer: TRE. If is finite, then P() = 2 < (see the bonus problem). (vii) = ( ) nswer: TRE. If is in in, then is neither in nor in, so is in the complement of, vice versa.
5 (ONS) se what we learned about Pascal s triangle to eplain why 2 n = n k=0 ( n k) by counting the size of the power set of a set of size n in two ways (the cardinality of a power set of only depends on the cardinality of ). nswer: Let be a set of size n. Step 1: Show P() = 2 n. For each element a, eactly half of the subsets include a: P() = P( {a}) {S {a} S P( {a})}. So P() = 2 P( {a}). Similarly, do the same thing for any element of {a} until you ve ehausted the elements of. For eample, the subsets of = {, y, z} are 5 {S {a} S P( {})} all subsets P( {}) subsets with subsets without with y without y with y without y with z: {, y, z} without z: {, y} with z: {, z} without z: {} with z: {y, z} without z: {y} with z: {z} without z: So P() = } 2 2 {{ 2} = 2 n. terms Step 2: Show P() = n k=0 ( n k). The set of subsets of can be broken into the disjoint union of { subsets of size 0 } (of which there are ( n 0) ), { subsets of size 1 } (of which there are ( n 1) ), { subsets of size 2 } (of which there are ( n 2) ),. { subsets of size n } (of which there are ( n n) ). So there are n k=0 ( n k) subsets of in total. Step 3: conclusion. So for a set of size n, 2 n = P() = n k=0 ( ) n. k.
6 6 Eercise 2. Fi two sets a universal set. Draw shade in diagrams to decide whether the following identities are true or false. For those that are false, give a concrete eample illustrating the failure of the identity. (a) ( ) = looks like so looks like which is the same as the union of : :
7 7 (b) ( ) = looks like so looks like which is the same as the intersection of as drawn in part (a). (c) ( ) = ( ( )) ( ) is as drawn in part (b), so ( ) = looks like ( ) On the other h, looks like so ( ) looks like Then subtracting ( ) (drawn in part (b)) gets us back to the picture in ( ).
8 8 Eercise 3. Let i = {1, 2,..., i} for i = 1, 2, 3,.... Calculate n i n i for n = 2, 4, 5. Make a hypothesis about what n i n i are for general n. Make a hypothesis about what i i are. Eplain in words why. We have 2 i = 1 2 = {1} {1, 2} = {1, 2} = 2, 3 i = = {1} {1, 2} {1, 2, 3} = {1, 2, 3} = 3, 4 i = 1 4 = {1} {1, 2, 3, 4} = {1, 2, 3, 4} = 4. From this we can conjecture that n i = n. Since for every integer in Z >0, there is a big enough n such that n contains it, we hypothesize that i = Z >0. Net, we have 2 i = 1 2 = {1} {1, 2} = {1} = a 3 i = = {1} {1, 2} {1, 2, 3} = {1} = 1 4 i = 1 4 = {1} {1, 2, 3, 4} = {1} = 1 From this we can conjecture that n i = 1. ut since 1 is a subset of every finite intersection, we conjecture that i = 1.
9 Eercise 4. Show that if i = {1, 2,..., i} for i = 1, 2, 3,..., then i = {1}. [Hint: Call i = for brevity. First argue that {1}. For the reverse, eplain why = 1 i=2 i, use that epression to show that {1}.] 9 Proof. Let i =. Since 1 i for all i, we have 1, so that {1}. Net, by the associative identity, we have = i = 1 i. i=2 ut = 1 i=2 i 1. In summary {1} {1}. So = {1}. Eercise 5. rgue formally that =. Proof. First, we ll show that : Let. This equivalent to /. This means that is not in (so that ) is not in (so that ). So. Thus. Net, show that : Let. This equivalent to / /. So is in neither nor, so. Thus. Therefore =.
10 10 2.1#4 For each of these pairs of sets, determine whether the first is a subset of the second, the second is a subset of the first, or neither is a subset of the other. (a) the set of people who speak English, the set of people who speak English with an ustralian accent: { people who speak English } { people who speak English with an ustralian accent } (b) the set of fruits, the set of citrus fruits: { fruits } { citrus fruits } (c) the set of students studying discrete mathematics, the set of students studying data structures: Normally, neither is a subset of the other. 2.1#10 Determine whether these statements are true or false. (a) { } TRE (b) {, { }} TRE (c) { } { } FLSE (the only element of the RHS is ) (d) { } {{ }} TRE (e) { } {, { }} TRE (f) {{ }} {, { }} TRE (g) {{ }} {{ }, { }} FLSE. e careful: {{ }} = {{ }, { }}, but the symbol means subset but not equal. This is a small bit of trickiness. 2.1#23 How many elements does each of these sets have where a b are distinct elements? (a) P ({a, b, {a, b}}) nswer: {a, b, {a, b}} = 3, so P({a, b, {a, b}}) = 2 3 = 8. (b) P ({, a, {a}, {{a}}}) nswer: {, a, {a}, {{a}}} = 4, so P({, a, {a}, {{a}}}) = 2 4 = 16. (c) P (P ( )) nswer: P ( ) = 1, so P( ) = #30 Suppose that =, where are sets. What can you conclude? nswer: If both are nonempty, then this isn t possible. So at least one of or must be empty. nd in fact, if is empty, then so is ; similarly so when is empty. 2.2 #1 Let be the set of students who live within one mile of school let be the set of students who walk to classes. Describe the students in each of these sets. (a) ns: Students who both live within a mile of school walk to classes. (b) ns: Students who live within a mile of school /or who walk to classes. (c) ns: Students who live within a mile of school but don t walk to classes. (d) ns: Students who live farther that a mile away from school but who walk to classes anyway.
11 2.2 #14 Find the sets if = {1, 5, 7, 8}, = {2, 10}, { = {3, 6, 9}. ns: = ( ) ( ) = {1, 3, 5, 6, 7, 8, 9}, = ( ) ( ) = {2, 3, 6, 9, 10} #50 Find for the following. i (a) i = {i, i + 1, i + 2,... }: Claim: i = Z >0 i i = Proof. Let = i I = i. To show = Z >0, first we show Z >0 : For each i = 1, 2,..., i Z >0. So their union is also a subset of Z >0. Net, we show Z >0 : For each n Z >0, we have n n. So Z >0. So = Z >0. To show I =, we note that I 1 = Z 1. ut for each n Z 1, we have n is not an element of n+1. So n is not an element of I. Thus I =. (b) i = {0, i}: Claim: i = Z 0 i = {0} Proof. Let = i I = i. To show = Z 0, first we show Z 0 : For each i = 1, 2,..., we have i Z 0. So their union is also a subset of Z 0. Net, we show Z 0 : For each n Z 0, we have n n. Thus Z 0. So = Z >0. To show I = {0}, first we show I {0}: We have that I = 1 2 ( 3 4 ) 1 2. So since 1 2 = {0, 1} {0, 2} = {0}, we have I {0}. Net, we show I {0}: For each i = 1, 2,..., we have 0 i. Thus 0 I, so that I {0}. So I = {0}.
12 12 (c) i = (0, i): Claim: i = (0, ) i = (0, 1) Proof. Let = i I = i. To show = (0, ), first we show (0, ): For each i = 1, 2, 3,..., we have i (0, ). So the union is also a subset of (0, ). Net, we show (0, ): For each (0, ), let n be an integer greater than. Then n. Thus (0, ). So = (0, ). To show I = (0, 1), first we show I (0, 1): We have that I = 1 2 ( 3 4 ) 1 2. So since 1 2 = (0, 1) (0, 2) = (0, 1), we have I (0, 1). Net, we show I (0, 1): For each i = 1, 2, 3,..., we have (0, 1) i. So (0, 1) I. So I = (0, 1). (d) i = (i, ): Claim: i = (1, ) Proof. Let = i I = i. To show = Z >0, first we show (1, ): For each i = 1, 2, 3,..., we have i (1, ). subset of (1, ). Net, we show (1, ): This is because (1, ) = 1. So = (1, ). i = Therefore their union is also a To show I =, we note that I 1 = (1, ). ut for any (1, ), any integer n greater than, we have / n. So is not in the intersection I.
MATH 215 DISCRETE MATHEMATICS INSTRUCTOR: P. WENG
 MATH 215 DISCRETE MATHEMATICS INSTRUCTOR: P. WENG Suggested Problems for Sets and Functions The following problems are from Discrete Mathematics and Its Applications by Kenneth H. Rosen. 1. Define the
MATH 215 DISCRETE MATHEMATICS INSTRUCTOR: P. WENG Suggested Problems for Sets and Functions The following problems are from Discrete Mathematics and Its Applications by Kenneth H. Rosen. 1. Define the
ACCUPLACER MATH 0311 OR MATH 0120
 The University of Teas at El Paso Tutoring and Learning Center ACCUPLACER MATH 0 OR MATH 00 http://www.academics.utep.edu/tlc MATH 0 OR MATH 00 Page Factoring Factoring Eercises 8 Factoring Answer to Eercises
The University of Teas at El Paso Tutoring and Learning Center ACCUPLACER MATH 0 OR MATH 00 http://www.academics.utep.edu/tlc MATH 0 OR MATH 00 Page Factoring Factoring Eercises 8 Factoring Answer to Eercises
MGF 1106: Exam 1 Solutions
 MGF 1106: Exam 1 Solutions 1. (15 points total) True or false? Explain your answer. a) A A B Solution: Drawn as a Venn diagram, the statement says: This is TRUE. The union of A with any set necessarily
MGF 1106: Exam 1 Solutions 1. (15 points total) True or false? Explain your answer. a) A A B Solution: Drawn as a Venn diagram, the statement says: This is TRUE. The union of A with any set necessarily
2.4 Graphing Inequalities
 .4 Graphing Inequalities Why We Need This Our applications will have associated limiting values - and either we will have to be at least as big as the value or no larger than the value. Why We Need This
.4 Graphing Inequalities Why We Need This Our applications will have associated limiting values - and either we will have to be at least as big as the value or no larger than the value. Why We Need This
Chapter 1 Review of Equations and Inequalities
 Chapter 1 Review of Equations and Inequalities Part I Review of Basic Equations Recall that an equation is an expression with an equal sign in the middle. Also recall that, if a question asks you to solve
Chapter 1 Review of Equations and Inequalities Part I Review of Basic Equations Recall that an equation is an expression with an equal sign in the middle. Also recall that, if a question asks you to solve
2. Sets. 2.1&2.2: Sets and Subsets. Combining Sets. c Dr Oksana Shatalov, Spring
 c Dr Oksana Shatalov, Spring 2015 1 2. Sets 2.1&2.2: Sets and Subsets. Combining Sets. Set Terminology and Notation DEFINITIONS: Set is well-defined collection of objects. Elements are objects or members
c Dr Oksana Shatalov, Spring 2015 1 2. Sets 2.1&2.2: Sets and Subsets. Combining Sets. Set Terminology and Notation DEFINITIONS: Set is well-defined collection of objects. Elements are objects or members
One-to-one functions and onto functions
 MA 3362 Lecture 7 - One-to-one and Onto Wednesday, October 22, 2008. Objectives: Formalize definitions of one-to-one and onto One-to-one functions and onto functions At the level of set theory, there are
MA 3362 Lecture 7 - One-to-one and Onto Wednesday, October 22, 2008. Objectives: Formalize definitions of one-to-one and onto One-to-one functions and onto functions At the level of set theory, there are
Sets. your school. A group of odd natural numbers less than 25.
 1 Sets The set theory was developed by German Mathematician Georg Cantor (1845-1918). He first encountered sets while working on problems on trigonometric series. This concept is used in every branch of
1 Sets The set theory was developed by German Mathematician Georg Cantor (1845-1918). He first encountered sets while working on problems on trigonometric series. This concept is used in every branch of
Sets. A set is a collection of objects without repeats. The size or cardinality of a set S is denoted S and is the number of elements in the set.
 Sets A set is a collection of objects without repeats. The size or cardinality of a set S is denoted S and is the number of elements in the set. If A and B are sets, then the set of ordered pairs each
Sets A set is a collection of objects without repeats. The size or cardinality of a set S is denoted S and is the number of elements in the set. If A and B are sets, then the set of ordered pairs each
In this initial chapter, you will be introduced to, or more than likely be reminded of, a
 1 Sets In this initial chapter, you will be introduced to, or more than likely be reminded of, a fundamental idea that occurs throughout mathematics: sets. Indeed, a set is an object from which every mathematical
1 Sets In this initial chapter, you will be introduced to, or more than likely be reminded of, a fundamental idea that occurs throughout mathematics: sets. Indeed, a set is an object from which every mathematical
15.4 Equation of a Circle
 Name Class Date 1.4 Equation of a Circle Essential Question: How can ou write the equation of a circle if ou know its radius and the coordinates of its center? Eplore G.1.E Show the equation of a circle
Name Class Date 1.4 Equation of a Circle Essential Question: How can ou write the equation of a circle if ou know its radius and the coordinates of its center? Eplore G.1.E Show the equation of a circle
3.4 Set Operations Given a set A, the complement (in the Universal set U) A c is the set of all elements of U that are not in A. So A c = {x x / A}.
 3.4 Set Operations Given a set, the complement (in the niversal set ) c is the set of all elements of that are not in. So c = {x x /. (This type of picture is called a Venn diagram.) Example 39 Let = {1,
3.4 Set Operations Given a set, the complement (in the niversal set ) c is the set of all elements of that are not in. So c = {x x /. (This type of picture is called a Venn diagram.) Example 39 Let = {1,
A CURL-FREE VECTOR FIELD THAT IS NOT A GRADIENT. Robert L. Foote. Math 225
 A URL-FREE VETOR FIELD THAT IS NOT A GRADIENT Robert L. Foote Math 225 Recall our main theorem about vector fields. Theorem. Let R be an open region in E 2 and let F be a vector field on R. The following
A URL-FREE VETOR FIELD THAT IS NOT A GRADIENT Robert L. Foote Math 225 Recall our main theorem about vector fields. Theorem. Let R be an open region in E 2 and let F be a vector field on R. The following
CM10196 Topic 2: Sets, Predicates, Boolean algebras
 CM10196 Topic 2: Sets, Predicates, oolean algebras Guy McCusker 1W2.1 Sets Most of the things mathematicians talk about are built out of sets. The idea of a set is a simple one: a set is just a collection
CM10196 Topic 2: Sets, Predicates, oolean algebras Guy McCusker 1W2.1 Sets Most of the things mathematicians talk about are built out of sets. The idea of a set is a simple one: a set is just a collection
What can I tell from a survey?
 CCA Ch 10: Solving Comple Equations Name Team # 10.1.1 What can I tell from a survey? Association in Two-Way Tables 10-1. a. c. d. d. 10-. a. Complete the following two-way table: Laptop No Laptop TOTAL
CCA Ch 10: Solving Comple Equations Name Team # 10.1.1 What can I tell from a survey? Association in Two-Way Tables 10-1. a. c. d. d. 10-. a. Complete the following two-way table: Laptop No Laptop TOTAL
Sets, Induction, Counting
 1 Sets and Relations Sets, Induction, Counting Using the basic definition of subsets, show that the empty set is a subset of every set. 1. Subset definition: A B : A B. 2. Empty set definition: an empty
1 Sets and Relations Sets, Induction, Counting Using the basic definition of subsets, show that the empty set is a subset of every set. 1. Subset definition: A B : A B. 2. Empty set definition: an empty
9. TRANSFORMING TOOL #2 (the Multiplication Property of Equality)
 9 TRANSFORMING TOOL # (the Multiplication Property of Equality) a second transforming tool THEOREM Multiplication Property of Equality In the previous section, we learned that adding/subtracting the same
9 TRANSFORMING TOOL # (the Multiplication Property of Equality) a second transforming tool THEOREM Multiplication Property of Equality In the previous section, we learned that adding/subtracting the same
NIT #7 CORE ALGE COMMON IALS
 UN NIT #7 ANSWER KEY POLYNOMIALS Lesson #1 Introduction too Polynomials Lesson # Multiplying Polynomials Lesson # Factoring Polynomials Lesson # Factoring Based on Conjugate Pairs Lesson #5 Factoring Trinomials
UN NIT #7 ANSWER KEY POLYNOMIALS Lesson #1 Introduction too Polynomials Lesson # Multiplying Polynomials Lesson # Factoring Polynomials Lesson # Factoring Based on Conjugate Pairs Lesson #5 Factoring Trinomials
MATH2206 Prob Stat/20.Jan Weekly Review 1-2
 MATH2206 Prob Stat/20.Jan.2017 Weekly Review 1-2 This week I explained the idea behind the formula of the well-known statistic standard deviation so that it is clear now why it is a measure of dispersion
MATH2206 Prob Stat/20.Jan.2017 Weekly Review 1-2 This week I explained the idea behind the formula of the well-known statistic standard deviation so that it is clear now why it is a measure of dispersion
We are going to discuss what it means for a sequence to converge in three stages: First, we define what it means for a sequence to converge to zero
 Chapter Limits of Sequences Calculus Student: lim s n = 0 means the s n are getting closer and closer to zero but never gets there. Instructor: ARGHHHHH! Exercise. Think of a better response for the instructor.
Chapter Limits of Sequences Calculus Student: lim s n = 0 means the s n are getting closer and closer to zero but never gets there. Instructor: ARGHHHHH! Exercise. Think of a better response for the instructor.
AP Calculus AB Summer Assignment
 AP Calculus AB Summer Assignment Name: When you come back to school, it is my epectation that you will have this packet completed. You will be way behind at the beginning of the year if you haven t attempted
AP Calculus AB Summer Assignment Name: When you come back to school, it is my epectation that you will have this packet completed. You will be way behind at the beginning of the year if you haven t attempted
MATH 220 (all sections) Homework #12 not to be turned in posted Friday, November 24, 2017
 MATH 220 (all sections) Homework #12 not to be turned in posted Friday, November 24, 2017 Definition: A set A is finite if there exists a nonnegative integer c such that there exists a bijection from A
MATH 220 (all sections) Homework #12 not to be turned in posted Friday, November 24, 2017 Definition: A set A is finite if there exists a nonnegative integer c such that there exists a bijection from A
SET THEORY. 1. Roster or Tabular form In this form the elements of the set are enclosed in curly braces { } after separating them by commas.
 SETS: set is a well-defined collection of objects. SET THEORY The objects in a set are called elements or members of the set. If x is an object of set, we write x and is read as x is an element of set
SETS: set is a well-defined collection of objects. SET THEORY The objects in a set are called elements or members of the set. If x is an object of set, we write x and is read as x is an element of set
Show Your Work! Point values are in square brackets. There are 35 points possible. Some facts about sets are on the last page.
 Formal Methods Name: Key Midterm 2, Spring, 2007 Show Your Work! Point values are in square brackets. There are 35 points possible. Some facts about sets are on the last page.. Determine whether each of
Formal Methods Name: Key Midterm 2, Spring, 2007 Show Your Work! Point values are in square brackets. There are 35 points possible. Some facts about sets are on the last page.. Determine whether each of
Introduction to Set Operations
 Introduction to Set Operations CIS008-2 Logic and Foundations of Mathematics David Goodwin david.goodwin@perisic.com 12:00, Friday 21 st October 2011 Outline 1 Recap 2 Introduction to sets 3 Class Exercises
Introduction to Set Operations CIS008-2 Logic and Foundations of Mathematics David Goodwin david.goodwin@perisic.com 12:00, Friday 21 st October 2011 Outline 1 Recap 2 Introduction to sets 3 Class Exercises
Chapter 2 Analysis of Graphs of Functions
 Chapter Analysis of Graphs of Functions Chapter Analysis of Graphs of Functions Covered in this Chapter:.1 Graphs of Basic Functions and their Domain and Range. Odd, Even Functions, and their Symmetry..
Chapter Analysis of Graphs of Functions Chapter Analysis of Graphs of Functions Covered in this Chapter:.1 Graphs of Basic Functions and their Domain and Range. Odd, Even Functions, and their Symmetry..
AP Calculus AB Summer Assignment
 AP Calculus AB Summer Assignment Name: When you come back to school, you will be epected to have attempted every problem. These skills are all different tools that you will pull out of your toolbo this
AP Calculus AB Summer Assignment Name: When you come back to school, you will be epected to have attempted every problem. These skills are all different tools that you will pull out of your toolbo this
Lecture 9. The Principle of Inclusion/Exclusion. 9.1 Introduction: a familiar example
 Lecture 9 he Principle of Inclusion/Exclusion hese notes are based on a pair of lectures originally written by (Manchester s own) Prof. Nige Ray. Reading: he Principle of Inclusion/Exclusion appears in
Lecture 9 he Principle of Inclusion/Exclusion hese notes are based on a pair of lectures originally written by (Manchester s own) Prof. Nige Ray. Reading: he Principle of Inclusion/Exclusion appears in
1 Chapter 1: SETS. 1.1 Describing a set
 1 Chapter 1: SETS set is a collection of objects The objects of the set are called elements or members Use capital letters :, B, C, S, X, Y to denote the sets Use lower case letters to denote the elements:
1 Chapter 1: SETS set is a collection of objects The objects of the set are called elements or members Use capital letters :, B, C, S, X, Y to denote the sets Use lower case letters to denote the elements:
MODEL ANSWERS TO THE SEVENTH HOMEWORK. (b) We proved in homework six, question 2 (c) that. But we also proved homework six, question 2 (a) that
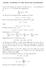 MODEL ANSWERS TO THE SEVENTH HOMEWORK 1. Let X be a finite set, and let A, B and A 1, A 2,..., A n be subsets of X. Let A c = X \ A denote the complement. (a) χ A (x) = A. x X (b) We proved in homework
MODEL ANSWERS TO THE SEVENTH HOMEWORK 1. Let X be a finite set, and let A, B and A 1, A 2,..., A n be subsets of X. Let A c = X \ A denote the complement. (a) χ A (x) = A. x X (b) We proved in homework
Combinatorics. But there are some standard techniques. That s what we ll be studying.
 Combinatorics Problem: How to count without counting. How do you figure out how many things there are with a certain property without actually enumerating all of them. Sometimes this requires a lot of
Combinatorics Problem: How to count without counting. How do you figure out how many things there are with a certain property without actually enumerating all of them. Sometimes this requires a lot of
SET THEORY. Disproving an Alleged Set Property. Disproving an Alleged Set. Example 1 Solution CHAPTER 6
 CHAPTER 6 SET THEORY SECTION 6.3 Disproofs, Algebraic Proofs, and Boolean Algebras Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. Disproving an Alleged
CHAPTER 6 SET THEORY SECTION 6.3 Disproofs, Algebraic Proofs, and Boolean Algebras Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. Disproving an Alleged
Understanding Part 2 of The Fundamental Theorem of Calculus
 Understanding Part of The Fundamental Theorem of Calculus Worksheet 8: The Graph of F () What is an Anti-Derivative? Give an eample that is algebraic: and an eample that is graphical: eample : Below is
Understanding Part of The Fundamental Theorem of Calculus Worksheet 8: The Graph of F () What is an Anti-Derivative? Give an eample that is algebraic: and an eample that is graphical: eample : Below is
Set theory. Math 304 Spring 2007
 Math 304 Spring 2007 Set theory Contents 1. Sets 2 1.1. Objects and set formation 2 1.2. Unions and intersections 3 1.3. Differences 4 1.4. Power sets 4 1.5. Ordered pairs and binary,amscdcartesian products
Math 304 Spring 2007 Set theory Contents 1. Sets 2 1.1. Objects and set formation 2 1.2. Unions and intersections 3 1.3. Differences 4 1.4. Power sets 4 1.5. Ordered pairs and binary,amscdcartesian products
Chapter 12 Practice Test
 hapter 12 Practice Test Multiple hoice Identify the choice that best completes the statement or answers the question. ssume that lines that appear to be tangent are tangent. is the center of the circle.
hapter 12 Practice Test Multiple hoice Identify the choice that best completes the statement or answers the question. ssume that lines that appear to be tangent are tangent. is the center of the circle.
Lecture 3: Sizes of Infinity
 Math/CS 20: Intro. to Math Professor: Padraic Bartlett Lecture 3: Sizes of Infinity Week 2 UCSB 204 Sizes of Infinity On one hand, we know that the real numbers contain more elements than the rational
Math/CS 20: Intro. to Math Professor: Padraic Bartlett Lecture 3: Sizes of Infinity Week 2 UCSB 204 Sizes of Infinity On one hand, we know that the real numbers contain more elements than the rational
M17 MAT25-21 HOMEWORK 6
 M17 MAT25-21 HOMEWORK 6 DUE 10:00AM WEDNESDAY SEPTEMBER 13TH 1. To Hand In Double Series. The exercises in this section will guide you to complete the proof of the following theorem: Theorem 1: Absolute
M17 MAT25-21 HOMEWORK 6 DUE 10:00AM WEDNESDAY SEPTEMBER 13TH 1. To Hand In Double Series. The exercises in this section will guide you to complete the proof of the following theorem: Theorem 1: Absolute
7.12 The student will represent relationships with tables, graphs, rules, and words.
 7.12 The student will represent relationships with tables, graphs, rules, and words. HINTS & NOTES Relation- is a set of ordered pairs. Remember to always start from the origin. Origin is (0,0) Move horizontally
7.12 The student will represent relationships with tables, graphs, rules, and words. HINTS & NOTES Relation- is a set of ordered pairs. Remember to always start from the origin. Origin is (0,0) Move horizontally
Equations and Solutions
 Section 2.1 Solving Equations: The Addition Principle 1 Equations and Solutions ESSENTIALS An equation is a number sentence that says that the expressions on either side of the equals sign, =, represent
Section 2.1 Solving Equations: The Addition Principle 1 Equations and Solutions ESSENTIALS An equation is a number sentence that says that the expressions on either side of the equals sign, =, represent
Chapter 9: Relations Relations
 Chapter 9: Relations 9.1 - Relations Definition 1 (Relation). Let A and B be sets. A binary relation from A to B is a subset R A B, i.e., R is a set of ordered pairs where the first element from each pair
Chapter 9: Relations 9.1 - Relations Definition 1 (Relation). Let A and B be sets. A binary relation from A to B is a subset R A B, i.e., R is a set of ordered pairs where the first element from each pair
SETS. Chapter Overview
 Chapter 1 SETS 1.1 Overview This chapter deals with the concept of a set, operations on sets.concept of sets will be useful in studying the relations and functions. 1.1.1 Set and their representations
Chapter 1 SETS 1.1 Overview This chapter deals with the concept of a set, operations on sets.concept of sets will be useful in studying the relations and functions. 1.1.1 Set and their representations
Appalachian State University. Outline
 Discrete Mathematics: Venn Diagrams and Logic 2 February 11, 2003 Jeff Hirst Appalachian State University 1 Outline Venn Diagrams: Representing unions and intersections Venn diagrams and Eulerian diagrams
Discrete Mathematics: Venn Diagrams and Logic 2 February 11, 2003 Jeff Hirst Appalachian State University 1 Outline Venn Diagrams: Representing unions and intersections Venn diagrams and Eulerian diagrams
11.4 Polar Coordinates
 11. Polar Coordinates 917 11. Polar Coordinates In Section 1.1, we introduced the Cartesian coordinates of a point in the plane as a means of assigning ordered pairs of numbers to points in the plane.
11. Polar Coordinates 917 11. Polar Coordinates In Section 1.1, we introduced the Cartesian coordinates of a point in the plane as a means of assigning ordered pairs of numbers to points in the plane.
Can that be Axl, your author s yellow lab, sharing a special
 46 Chapter P Prerequisites: Fundamental Concepts Algebra Objectives Section Understand the vocabulary polynomials. Add and subtract polynomials. Multiply polynomials. Use FOIL in polynomial multiplication.
46 Chapter P Prerequisites: Fundamental Concepts Algebra Objectives Section Understand the vocabulary polynomials. Add and subtract polynomials. Multiply polynomials. Use FOIL in polynomial multiplication.
1 Continuity and Limits of Functions
 Week 4 Summary This week, we will move on from our discussion of sequences and series to functions. Even though sequences and functions seem to be very different things, they very similar. In fact, we
Week 4 Summary This week, we will move on from our discussion of sequences and series to functions. Even though sequences and functions seem to be very different things, they very similar. In fact, we
PGSS Discrete Math Solutions to Problem Set #4. Note: signifies the end of a problem, and signifies the end of a proof.
 PGSS Discrete Math Solutions to Problem Set #4 Note: signifies the end of a problem, and signifies the end of a proof. 1. Prove that for any k N, there are k consecutive composite numbers. (Hint: (k +
PGSS Discrete Math Solutions to Problem Set #4 Note: signifies the end of a problem, and signifies the end of a proof. 1. Prove that for any k N, there are k consecutive composite numbers. (Hint: (k +
Seminaar Abstrakte Wiskunde Seminar in Abstract Mathematics Lecture notes in progress (27 March 2010)
 http://math.sun.ac.za/amsc/sam Seminaar Abstrakte Wiskunde Seminar in Abstract Mathematics 2009-2010 Lecture notes in progress (27 March 2010) Contents 2009 Semester I: Elements 5 1. Cartesian product
http://math.sun.ac.za/amsc/sam Seminaar Abstrakte Wiskunde Seminar in Abstract Mathematics 2009-2010 Lecture notes in progress (27 March 2010) Contents 2009 Semester I: Elements 5 1. Cartesian product
Math Theory of Number Homework 1
 Math 4050 Theory of Number Homework 1 Due Wednesday, 015-09-09, in class Do 5 of the following 7 problems. Please only attempt 5 because I will only grade 5. 1. Find all rational numbers and y satisfying
Math 4050 Theory of Number Homework 1 Due Wednesday, 015-09-09, in class Do 5 of the following 7 problems. Please only attempt 5 because I will only grade 5. 1. Find all rational numbers and y satisfying
Math 13, Spring 2013, Lecture B: Midterm
 Math 13, Spring 2013, Lecture B: Midterm Name Signature UCI ID # E-mail address Each numbered problem is worth 12 points, for a total of 84 points. Present your work, especially proofs, as clearly as possible.
Math 13, Spring 2013, Lecture B: Midterm Name Signature UCI ID # E-mail address Each numbered problem is worth 12 points, for a total of 84 points. Present your work, especially proofs, as clearly as possible.
Inequalities - Solve and Graph Inequalities
 3.1 Inequalities - Solve and Graph Inequalities Objective: Solve, graph, and give interval notation for the solution to linear inequalities. When we have an equation such as x = 4 we have a specific value
3.1 Inequalities - Solve and Graph Inequalities Objective: Solve, graph, and give interval notation for the solution to linear inequalities. When we have an equation such as x = 4 we have a specific value
EQUIVALENCE RELATIONS (NOTES FOR STUDENTS) 1. RELATIONS
 EQUIVALENCE RELATIONS (NOTES FOR STUDENTS) LIOR SILBERMAN Version 1.0 compiled September 9, 2015. 1.1. List of examples. 1. RELATIONS Equality of real numbers: for some x,y R we have x = y. For other pairs
EQUIVALENCE RELATIONS (NOTES FOR STUDENTS) LIOR SILBERMAN Version 1.0 compiled September 9, 2015. 1.1. List of examples. 1. RELATIONS Equality of real numbers: for some x,y R we have x = y. For other pairs
LECTURE 1. 1 Introduction. 1.1 Sample spaces and events
 LECTURE 1 1 Introduction The first part of our adventure is a highly selective review of probability theory, focusing especially on things that are most useful in statistics. 1.1 Sample spaces and events
LECTURE 1 1 Introduction The first part of our adventure is a highly selective review of probability theory, focusing especially on things that are most useful in statistics. 1.1 Sample spaces and events
Chapter 3. Cartesian Products and Relations. 3.1 Cartesian Products
 Chapter 3 Cartesian Products and Relations The material in this chapter is the first real encounter with abstraction. Relations are very general thing they are a special type of subset. After introducing
Chapter 3 Cartesian Products and Relations The material in this chapter is the first real encounter with abstraction. Relations are very general thing they are a special type of subset. After introducing
Math 3361-Modern Algebra Lecture 08 9/26/ Cardinality
 Math 336-Modern Algebra Lecture 08 9/26/4. Cardinality I started talking about cardinality last time, and you did some stuff with it in the Homework, so let s continue. I said that two sets have the same
Math 336-Modern Algebra Lecture 08 9/26/4. Cardinality I started talking about cardinality last time, and you did some stuff with it in the Homework, so let s continue. I said that two sets have the same
CS 301. Lecture 18 Decidable languages. Stephen Checkoway. April 2, 2018
 CS 301 Lecture 18 Decidable languages Stephen Checkoway April 2, 2018 1 / 26 Decidable language Recall, a language A is decidable if there is some TM M that 1 recognizes A (i.e., L(M) = A), and 2 halts
CS 301 Lecture 18 Decidable languages Stephen Checkoway April 2, 2018 1 / 26 Decidable language Recall, a language A is decidable if there is some TM M that 1 recognizes A (i.e., L(M) = A), and 2 halts
Distance in the Plane
 Distance in the Plane The absolute value function is defined as { x if x 0; and x = x if x < 0. If the number a is positive or zero, then a = a. If a is negative, then a is the number you d get by erasing
Distance in the Plane The absolute value function is defined as { x if x 0; and x = x if x < 0. If the number a is positive or zero, then a = a. If a is negative, then a is the number you d get by erasing
With Question/Answer Animations. Chapter 2
 With Question/Answer Animations Chapter 2 Chapter Summary Sets The Language of Sets Set Operations Set Identities Functions Types of Functions Operations on Functions Sequences and Summations Types of
With Question/Answer Animations Chapter 2 Chapter Summary Sets The Language of Sets Set Operations Set Identities Functions Types of Functions Operations on Functions Sequences and Summations Types of
Study skills for mathematicians
 PART I Study skills for mathematicians CHAPTER 1 Sets and functions Everything starts somewhere, although many physicists disagree. Terry Pratchett, Hogfather, 1996 To think like a mathematician requires
PART I Study skills for mathematicians CHAPTER 1 Sets and functions Everything starts somewhere, although many physicists disagree. Terry Pratchett, Hogfather, 1996 To think like a mathematician requires
Focusing on Linear Functions and Linear Equations
 Focusing on Linear Functions and Linear Equations In grade, students learn how to analyze and represent linear functions and solve linear equations and systems of linear equations. They learn how to represent
Focusing on Linear Functions and Linear Equations In grade, students learn how to analyze and represent linear functions and solve linear equations and systems of linear equations. They learn how to represent
Adding Integers. Adding Integers.notebook. September 22, Symbols. Addition: A walk on the number line. Let's do on the number line.
 Symbols Adding Integers We will use "+" to indicate addition and " " for subtraction. Parentheses will also be used to show things more clearly. For instance, if we want to add 3 to 4 we will write: 4
Symbols Adding Integers We will use "+" to indicate addition and " " for subtraction. Parentheses will also be used to show things more clearly. For instance, if we want to add 3 to 4 we will write: 4
Unit 1: Equations & Inequalities in One Variable
 Date Period Unit 1: Equations & Inequalities in One Variable Day Topic 1 Properties of Real Numbers Algebraic Expressions Solving Equations 3 Solving Inequalities 4 QUIZ 5 Absolute Value Equations 6 Double
Date Period Unit 1: Equations & Inequalities in One Variable Day Topic 1 Properties of Real Numbers Algebraic Expressions Solving Equations 3 Solving Inequalities 4 QUIZ 5 Absolute Value Equations 6 Double
Research Methods in Mathematics Extended assignment 1
 Research Methods in Mathematics Extended assignment 1 T. PERUTZ Due: at the beginning of class, October 5. Choose one of the following assignments: (1) The circle problem (2) Complete ordered fields 2
Research Methods in Mathematics Extended assignment 1 T. PERUTZ Due: at the beginning of class, October 5. Choose one of the following assignments: (1) The circle problem (2) Complete ordered fields 2
1. (B) The union of sets A and B is the set whose elements belong to at least one of A
 1. (B) The union of sets A and B is the set whose elements belong to at least one of A or B. Thus, A B = { 2, 1, 0, 1, 2, 5}. 2. (A) The intersection of sets A and B is the set whose elements belong to
1. (B) The union of sets A and B is the set whose elements belong to at least one of A or B. Thus, A B = { 2, 1, 0, 1, 2, 5}. 2. (A) The intersection of sets A and B is the set whose elements belong to
Lecture 4: Constructing the Integers, Rationals and Reals
 Math/CS 20: Intro. to Math Professor: Padraic Bartlett Lecture 4: Constructing the Integers, Rationals and Reals Week 5 UCSB 204 The Integers Normally, using the natural numbers, you can easily define
Math/CS 20: Intro. to Math Professor: Padraic Bartlett Lecture 4: Constructing the Integers, Rationals and Reals Week 5 UCSB 204 The Integers Normally, using the natural numbers, you can easily define
ACCUPLACER MATH 0310
 The University of Teas at El Paso Tutoring and Learning Center ACCUPLACER MATH 00 http://www.academics.utep.edu/tlc MATH 00 Page Linear Equations Linear Equations Eercises 5 Linear Equations Answer to
The University of Teas at El Paso Tutoring and Learning Center ACCUPLACER MATH 00 http://www.academics.utep.edu/tlc MATH 00 Page Linear Equations Linear Equations Eercises 5 Linear Equations Answer to
Chapter Summary. Sets (2.1) Set Operations (2.2) Functions (2.3) Sequences and Summations (2.4) Cardinality of Sets (2.5) Matrices (2.
 Chapter 2 Chapter Summary Sets (2.1) Set Operations (2.2) Functions (2.3) Sequences and Summations (2.4) Cardinality of Sets (2.5) Matrices (2.6) Section 2.1 Section Summary Definition of sets Describing
Chapter 2 Chapter Summary Sets (2.1) Set Operations (2.2) Functions (2.3) Sequences and Summations (2.4) Cardinality of Sets (2.5) Matrices (2.6) Section 2.1 Section Summary Definition of sets Describing
Solving Equations with Variables on Both Sides
 1. Solving Equations with Variables on Both Sides Essential Question How can you solve an equation that has variables on both sides? Perimeter Work with a partner. The two polygons have the same perimeter.
1. Solving Equations with Variables on Both Sides Essential Question How can you solve an equation that has variables on both sides? Perimeter Work with a partner. The two polygons have the same perimeter.
Theorem. For every positive integer n, the sum of the positive integers from 1 to n is n(n+1)
 Week 1: Logic Lecture 1, 8/1 (Sections 1.1 and 1.3) Examples of theorems and proofs Theorem (Pythagoras). Let ABC be a right triangle, with legs of lengths a and b, and hypotenuse of length c. Then a +
Week 1: Logic Lecture 1, 8/1 (Sections 1.1 and 1.3) Examples of theorems and proofs Theorem (Pythagoras). Let ABC be a right triangle, with legs of lengths a and b, and hypotenuse of length c. Then a +
Bridging the gap between GCSE and A level mathematics
 Bridging the gap between GCSE and A level mathematics This booklet is designed to help you revise important algebra topics from GCSE and make the transition from GCSE to A level a smooth one. You are advised
Bridging the gap between GCSE and A level mathematics This booklet is designed to help you revise important algebra topics from GCSE and make the transition from GCSE to A level a smooth one. You are advised
Fundamentals of Algebra, Geometry, and Trigonometry. (Self-Study Course)
 Fundamentals of Algebra, Geometry, and Trigonometry (Self-Study Course) This training is offered eclusively through the Pennsylvania Department of Transportation, Business Leadership Office, Technical
Fundamentals of Algebra, Geometry, and Trigonometry (Self-Study Course) This training is offered eclusively through the Pennsylvania Department of Transportation, Business Leadership Office, Technical
31. TRANSFORMING TOOL #2 (the Multiplication Property of Equality)
 3 TRANSFORMING TOOL # (the Multiplication Property of Equality) a second transforming tool THEOREM Multiplication Property of Equality In the previous section, we learned that adding/subtracting the same
3 TRANSFORMING TOOL # (the Multiplication Property of Equality) a second transforming tool THEOREM Multiplication Property of Equality In the previous section, we learned that adding/subtracting the same
Homework 12; Due Monday, 4/9/2018
 Homework 2; Due Monday, 4/9/28 Answer-Only Questions Credit based solely on the answer Question For each of the following relations, determine whether each one is symmetric, transitive, or refleive If
Homework 2; Due Monday, 4/9/28 Answer-Only Questions Credit based solely on the answer Question For each of the following relations, determine whether each one is symmetric, transitive, or refleive If
Homework 5. Solutions
 Homework 5. Solutions 1. Let (X,T) be a topological space and let A,B be subsets of X. Show that the closure of their union is given by A B = A B. Since A B is a closed set that contains A B and A B is
Homework 5. Solutions 1. Let (X,T) be a topological space and let A,B be subsets of X. Show that the closure of their union is given by A B = A B. Since A B is a closed set that contains A B and A B is
WUCT121. Discrete Mathematics. Logic. Tutorial Exercises
 WUCT11 Discrete Mathematics Logic Tutorial Exercises 1 Logic Predicate Logic 3 Proofs 4 Set Theory 5 Relations and Functions WUCT11 Logic Tutorial Exercises 1 Section 1: Logic Question1 For each of the
WUCT11 Discrete Mathematics Logic Tutorial Exercises 1 Logic Predicate Logic 3 Proofs 4 Set Theory 5 Relations and Functions WUCT11 Logic Tutorial Exercises 1 Section 1: Logic Question1 For each of the
In last semester, we have seen some examples about it (See Tutorial Note #13). Try to have a look on that. Here we try to show more technique.
 MATH202 Introduction to Analysis (2007 Fall and 2008 Spring) Tutorial Note #4 Part I: Cauchy Sequence Definition (Cauchy Sequence): A sequence of real number { n } is Cauchy if and only if for any ε >
MATH202 Introduction to Analysis (2007 Fall and 2008 Spring) Tutorial Note #4 Part I: Cauchy Sequence Definition (Cauchy Sequence): A sequence of real number { n } is Cauchy if and only if for any ε >
Lesson 3-2: Solving Linear Systems Algebraically
 Yesterday we took our first look at solving a linear system. We learned that a linear system is two or more linear equations taken at the same time. Their solution is the point that all the lines have
Yesterday we took our first look at solving a linear system. We learned that a linear system is two or more linear equations taken at the same time. Their solution is the point that all the lines have
Connectedness. Proposition 2.2. The following are equivalent for a topological space (X, T ).
 Connectedness 1 Motivation Connectedness is the sort of topological property that students love. Its definition is intuitive and easy to understand, and it is a powerful tool in proofs of well-known results.
Connectedness 1 Motivation Connectedness is the sort of topological property that students love. Its definition is intuitive and easy to understand, and it is a powerful tool in proofs of well-known results.
Name: Block: Unit 2 Inequalities
 Name: Block: Unit 2 Inequalities 2.1 Graphing and Writing Inequalities 2.2 Solving by Adding and Subtracting 2.3 Solving by Multiplying and Dividing 2.4 Solving Two Step and Multi Step Inequalities 2.5
Name: Block: Unit 2 Inequalities 2.1 Graphing and Writing Inequalities 2.2 Solving by Adding and Subtracting 2.3 Solving by Multiplying and Dividing 2.4 Solving Two Step and Multi Step Inequalities 2.5
Section 20: Arrow Diagrams on the Integers
 Section 0: Arrow Diagrams on the Integers Most of the material we have discussed so far concerns the idea and representations of functions. A function is a relationship between a set of inputs (the leave
Section 0: Arrow Diagrams on the Integers Most of the material we have discussed so far concerns the idea and representations of functions. A function is a relationship between a set of inputs (the leave
Summer HSSP Lecture Notes Week 1. Lane Gunderman, Victor Lopez, James Rowan
 Summer HSSP Lecture Notes Week 1 Lane Gunderman, Victor Lopez, James Rowan July 6, 014 First Class: proofs and friends 1 Contents 1 Glossary of symbols 4 Types of numbers 5.1 Breaking it down...........................
Summer HSSP Lecture Notes Week 1 Lane Gunderman, Victor Lopez, James Rowan July 6, 014 First Class: proofs and friends 1 Contents 1 Glossary of symbols 4 Types of numbers 5.1 Breaking it down...........................
Chapter VI. Relations. Assumptions are the termites of relationships. Henry Winkler
 Chapter VI Relations Assumptions are the termites of relationships. Henry Winkler Studying relationships between objects can yield important information about the objects themselves. In the real numbers,
Chapter VI Relations Assumptions are the termites of relationships. Henry Winkler Studying relationships between objects can yield important information about the objects themselves. In the real numbers,
PACKET Unit 4 Honors ICM Functions and Limits 1
 PACKET Unit 4 Honors ICM Functions and Limits 1 Day 1 Homework For each of the rational functions find: a. domain b. -intercept(s) c. y-intercept Graph #8 and #10 with at least 5 EXACT points. 1. f 6.
PACKET Unit 4 Honors ICM Functions and Limits 1 Day 1 Homework For each of the rational functions find: a. domain b. -intercept(s) c. y-intercept Graph #8 and #10 with at least 5 EXACT points. 1. f 6.
MATH 2200 Final LC Review
 MATH 2200 Final LC Review Thomas Goller April 25, 2013 1 Final LC Format The final learning celebration will consist of 12-15 claims to be proven or disproven. It will take place on Wednesday, May 1, from
MATH 2200 Final LC Review Thomas Goller April 25, 2013 1 Final LC Format The final learning celebration will consist of 12-15 claims to be proven or disproven. It will take place on Wednesday, May 1, from
Binomial Coefficient Identities/Complements
 Binomial Coefficient Identities/Complements CSE21 Fall 2017, Day 4 Oct 6, 2017 https://sites.google.com/a/eng.ucsd.edu/cse21-fall-2017-miles-jones/ permutation P(n,r) = n(n-1) (n-2) (n-r+1) = Terminology
Binomial Coefficient Identities/Complements CSE21 Fall 2017, Day 4 Oct 6, 2017 https://sites.google.com/a/eng.ucsd.edu/cse21-fall-2017-miles-jones/ permutation P(n,r) = n(n-1) (n-2) (n-r+1) = Terminology
Summer HSSP Week 1 Homework. Lane Gunderman, Victor Lopez, James Rowan
 Summer HSSP Week 1 Homework Lane Gunderman, Victor Lopez, James Rowan July 9, 2014 Questions 1 Chapter 1 Homework Questions These are the questions that should be turned in as homework. As mentioned in
Summer HSSP Week 1 Homework Lane Gunderman, Victor Lopez, James Rowan July 9, 2014 Questions 1 Chapter 1 Homework Questions These are the questions that should be turned in as homework. As mentioned in
In this unit we will study exponents, mathematical operations on polynomials, and factoring.
 GRADE 0 MATH CLASS NOTES UNIT E ALGEBRA In this unit we will study eponents, mathematical operations on polynomials, and factoring. Much of this will be an etension of your studies from Math 0F. This unit
GRADE 0 MATH CLASS NOTES UNIT E ALGEBRA In this unit we will study eponents, mathematical operations on polynomials, and factoring. Much of this will be an etension of your studies from Math 0F. This unit
F6 Solving Inequalities
 UNIT F6 Solving Inequalities: Tet F6 Solving Inequalities F6. Inequalities on a Number Line An inequalit involves one of the four smbols >,, < or The following statements illustrate the meaning of each
UNIT F6 Solving Inequalities: Tet F6 Solving Inequalities F6. Inequalities on a Number Line An inequalit involves one of the four smbols >,, < or The following statements illustrate the meaning of each
Worksheet on Relations
 Worksheet on Relations Recall the properties that relations can have: Definition. Let R be a relation on the set A. R is reflexive if for all a A we have ara. R is irreflexive or antireflexive if for all
Worksheet on Relations Recall the properties that relations can have: Definition. Let R be a relation on the set A. R is reflexive if for all a A we have ara. R is irreflexive or antireflexive if for all
CISC 1100: Structures of Computer Science
 CISC 1100: Structures of Computer Science Chapter 2 Sets and Sequences Fordham University Department of Computer and Information Sciences Fall, 2010 CISC 1100/Fall, 2010/Chapter 2 1 / 49 Outline Sets Basic
CISC 1100: Structures of Computer Science Chapter 2 Sets and Sequences Fordham University Department of Computer and Information Sciences Fall, 2010 CISC 1100/Fall, 2010/Chapter 2 1 / 49 Outline Sets Basic
CITS2211 Discrete Structures (2017) Cardinality and Countability
 CITS2211 Discrete Structures (2017) Cardinality and Countability Highlights What is cardinality? Is it the same as size? Types of cardinality and infinite sets Reading Sections 45 and 81 84 of Mathematics
CITS2211 Discrete Structures (2017) Cardinality and Countability Highlights What is cardinality? Is it the same as size? Types of cardinality and infinite sets Reading Sections 45 and 81 84 of Mathematics
Solutions Quiz 9 Nov. 8, Prove: If a, b, m are integers such that 2a + 3b 12m + 1, then a 3m + 1 or b 2m + 1.
 Solutions Quiz 9 Nov. 8, 2010 1. Prove: If a, b, m are integers such that 2a + 3b 12m + 1, then a 3m + 1 or b 2m + 1. Answer. We prove the contrapositive. Suppose a, b, m are integers such that a < 3m
Solutions Quiz 9 Nov. 8, 2010 1. Prove: If a, b, m are integers such that 2a + 3b 12m + 1, then a 3m + 1 or b 2m + 1. Answer. We prove the contrapositive. Suppose a, b, m are integers such that a < 3m
STA111 - Lecture 1 Welcome to STA111! 1 What is the difference between Probability and Statistics?
 STA111 - Lecture 1 Welcome to STA111! Some basic information: Instructor: Víctor Peña (email: vp58@duke.edu) Course Website: http://stat.duke.edu/~vp58/sta111. 1 What is the difference between Probability
STA111 - Lecture 1 Welcome to STA111! Some basic information: Instructor: Víctor Peña (email: vp58@duke.edu) Course Website: http://stat.duke.edu/~vp58/sta111. 1 What is the difference between Probability
Lesson 2-6: Graphs of Absolute Value Equations
 Where we re headed today Today we re going to take the net graphing step we ll learn how to graph absolute value equations. Here are the three things you are going to need to be able to do: 1. Match an
Where we re headed today Today we re going to take the net graphing step we ll learn how to graph absolute value equations. Here are the three things you are going to need to be able to do: 1. Match an
Discrete Mathematics and Probability Theory Spring 2016 Rao and Walrand Note 14
 CS 70 Discrete Mathematics and Probability Theory Spring 2016 Rao and Walrand Note 14 Introduction One of the key properties of coin flips is independence: if you flip a fair coin ten times and get ten
CS 70 Discrete Mathematics and Probability Theory Spring 2016 Rao and Walrand Note 14 Introduction One of the key properties of coin flips is independence: if you flip a fair coin ten times and get ten
CS1800: Strong Induction. Professor Kevin Gold
 CS1800: Strong Induction Professor Kevin Gold Mini-Primer/Refresher on Unrelated Topic: Limits This is meant to be a problem about reasoning about quantifiers, with a little practice of other skills, too
CS1800: Strong Induction Professor Kevin Gold Mini-Primer/Refresher on Unrelated Topic: Limits This is meant to be a problem about reasoning about quantifiers, with a little practice of other skills, too
Functions and cardinality (solutions) sections A and F TA: Clive Newstead 6 th May 2014
 Functions and cardinality (solutions) 21-127 sections A and F TA: Clive Newstead 6 th May 2014 What follows is a somewhat hastily written collection of solutions for my review sheet. I have omitted some
Functions and cardinality (solutions) 21-127 sections A and F TA: Clive Newstead 6 th May 2014 What follows is a somewhat hastily written collection of solutions for my review sheet. I have omitted some
Senior Math Circles November 19, 2008 Probability II
 University of Waterloo Faculty of Mathematics Centre for Education in Mathematics and Computing Senior Math Circles November 9, 2008 Probability II Probability Counting There are many situations where
University of Waterloo Faculty of Mathematics Centre for Education in Mathematics and Computing Senior Math Circles November 9, 2008 Probability II Probability Counting There are many situations where
Unit 1 Day 1. Set Operations & Venn Diagrams
 Unit 1 Day 1 Set Operations & Venn Diagrams Honors ICM Get out your signed syllabus form Get out paper and a pencil for notes! Has everyone accessed the website? Math Riddles Mr. Smith has 4 daughters.
Unit 1 Day 1 Set Operations & Venn Diagrams Honors ICM Get out your signed syllabus form Get out paper and a pencil for notes! Has everyone accessed the website? Math Riddles Mr. Smith has 4 daughters.
2 Generating Functions
 2 Generating Functions In this part of the course, we re going to introduce algebraic methods for counting and proving combinatorial identities. This is often greatly advantageous over the method of finding
2 Generating Functions In this part of the course, we re going to introduce algebraic methods for counting and proving combinatorial identities. This is often greatly advantageous over the method of finding
the time it takes until a radioactive substance undergoes a decay
 1 Probabilities 1.1 Experiments with randomness Wewillusethetermexperimentinaverygeneralwaytorefertosomeprocess that produces a random outcome. Examples: (Ask class for some first) Here are some discrete
1 Probabilities 1.1 Experiments with randomness Wewillusethetermexperimentinaverygeneralwaytorefertosomeprocess that produces a random outcome. Examples: (Ask class for some first) Here are some discrete
