A Divide-and-Conquer Method for the Takagi Factorization
|
|
|
- Silas Poole
- 5 years ago
- Views:
Transcription
1 A Divide-and-Conquer Method for the Takagi Factorization Wei Xu 1 and Sanzheng Qiao 1, Department of Computing and Software, McMaster University Hamilton, Ont, L8S 4K1, Canada. 1 xuw5@mcmaster.ca qiao@mcmaster.ca Abstract This paper presents a divide-and-conquer method for computing the Takagi factorization, or symmetric singular value decomposition, of a complex symmetric and tridiagonal matrix. An analysis of accuracy shows that our method produces accurate Takagi values and orthogonal Takagi vectors. Our preliminary numerical experiments have confirmed our analysis and demonstrated that our divide-and-conquer method is much more efficient than the implicit QR method even for moderately large matrices. 1 Introduction The Takagi factorization of a complex symmetric n n matrix A can be written as A = V ΣV T, where V is a unitary matrix, V T is the transpose of V and Σ is a diagonal matrix with non-negative diagonal elements. The columns of V are called the Takagi vectors of A and the diagonal elements of Σ are its Takagi values. Since V T = V H, where V denotes the complex conjugate of V, the Takagi factorization is a symmetric form of the singular value decomposition (SVD). The Takagi values are the singular values, the Takagi vectors are the left singular vectors and the complex conjugates of the Takagi vectors are the right singular vectors. A standard algorithm for computing the Takagi factorization consists of two stages. The first stage reduces a complex symmetric matrix A to a complex symmetric tridiagonal matrix through Lanczos method with partial orthogonalization 5, 8 as the following a 1 b 1 0. A = PTP T b..... P P T, (1).. bn 1 0 b n 1 a n where P is a unitary matrix of order n and T is an n n tridiagonal matrix. The second stage computes the Takagi factorization of T = QΣQ T. The combination of the two stages 1
2 gives A = P(QΣQ T )P T = V ΣV T, where V = PQ. In this paper, we focus on the computation of the Takagi factorization of a complex symmetric tridiagonal matrix T by the divide-and-conquer method based on rank-one tearings of TT H. It is known that the divide-and-conquer method is the most efficient method for computing the eigenvalues and eigenvectors of a Hermitian matrix. The Takagi vectors of T, that is the columns of Q, are the eigenvectors of the semi-positive definite Hermitian matrix TT H, since TT H = QΣQ T QΣQ H = QΣ Q H. However, it is not always true that an eigenvector of TT H is a Takagi vector of T. For example, let 1 1 T =, 1 1 It is easy to see that the eigenvalue decomposition of TT H is TT H = Obviously, the unit vectors are not the Takagi vectors of T since T is not diagonal. In fact, using the algorithm in 6, we can get the Takagi factorization: T = QΣQ T = The basic idea of our method is to apply the divide-and-conquer method to TT H to get its eigenvectors and eigenvalues. The square roots of the eigenvalues of TT H are the Takagi values of T. We then transform the eigenvectors of TT H into the Takagi vectors of T. However, explicitly computing TT H is too expensive and also destroys the tridiagonal structure of T. We will introduce an implicit method for computing the eigenvalue decomposition of TT H. The rest of the paper is organized as follows. Section describes a divide-and-conquer method for computing the eigenvalue decomposition of TT H without explicitly forming TT H. However, as mentioned above, the eigenvectors of TT H may not be the Takagi vectors of T. In Section 3, We will propose a method for transforming the eigenvectors of TT H into the Takagi vectors of T. We analyze the sensitivity of Takagi vectors of T in Section 4. Finally, the results of our preliminary numerical experiments are given in Section 5 to show the stability, accuracy, and efficiency of our algorithm..
3 Divide-and-Conquer Scheme.1 Dividing the matrix Let the Takagi factorization of the complex symmetric tridiagonal matrix T in (1) be Q H T Q = Σ = diag(σ 1,,σ n ) or T = QΣQ T. In the first step, we tear the tridiagonal matrix T into two tridiagonal submatrices of half size. For simplicity, we assume that n is a power of and m = n/, then T T = 1 b m e m e T 1 b m e 1 e T () m T where a 1 b 1 0 a m+1 b m+1 0. b T 1 = 1 b , T.. = m+1. bm bn 1 0 b m 1 a m 0 b n 1 a n and e 1 and e m are unit vectors, 1,0,,0 and 0,,0,1 respectively. Now, we establish the relations between the eigenvalues and eigenvectors of T i Ti H and those of TT H as follows. From (), we get TT H T = 1 b m e m e T 1 T b m e 1 e T 1 H bm e m e T 1 m T bm e 1 e T m T H T = 1 T1 H + b m e m e T m b m e m e T 1 T H + b m T 1 e m e T 1 bm T e 1 e T m + b me 1 e T m T 1 H T T H + b m e 1 e T 1 T1 T = 1 H 0 bm 0 T T H + e m e T m b m e m e T 1 T H bm T e 1 e T m 0 0 bm T + 1 e m e T 1 b m e 1 e T mt1 H b m e 1 e T 1 T1 T1 = H 0 bm e 0 T (I m e 1 e T 1 )T H + m bm e T e T m e T 1 T H 1 0 bm T + 1 e m e T 1 b m e 1 e T mt1 H b m e 1 e T 1 T1 (I = m e m e T m)t1 H 0 bm e 0 T (I m e 1 e T 1 )T H + m bm e T e T m et 1 T H 1 T1 e + m e b m e T mt1 H bm e T 1 1 T1 (I = m e m e T m )T 1 H 0 0 T (I m e 1 e T 1 )T H + z 1 z H 1 + z z H, (3) 3
4 where bm e z 1 = m T e 1 From (3), if the eigenvalue decompositions and z = T1 e m b m e 1. T 1 T H 1 = U 1 Σ 1U H 1 and T T H = U Σ U H (4) of the semi-positive definite Hermitian matrices T 1 T H 1 and T T H are available, we can find the eigenvalue decomposition of TT H by four rank-one modifications. Thus, if the Takagi factorizations of T 1 and T are available, we can compute the Takagi values of T and the eigenvectors of TT H by four rank-one modifications. Later in Section 3, we will show how to transform the eigenvectors into the Takagi vectors. Theorem.1 in characterizes the eigenvalues and eigenvectors of the real rank-one modification. We generalize it to the complex case. The proof is similar to the proof in. Theorem.1 Suppose D = diag(d 1,,d n), d 1 > d > > d n, z C n is a vector with no zero entries, and ρ > 0, then the eigenvalues of the matrix D + ρzz H are the n roots δ 1 > δ > > δ n of the rational function w(δ ) = 1 + ρz H (D δ I) 1 z = 1 + ρ d j z j The corresponding eigenvectors, g 1, g,, g n of D + ρzz H are given by and d j strictly separate the eigenvalues δ j : δ. (5) g j = (D δ I) 1 z/ (D δ I) 1 z, (6) d n < δ n < d n 1 < δ n 1 < < d 1 < δ 1 < d 1 + ρz H z. Proof. Let (δ,g) be an eigenpair of D + ρzz H, then it satisfies (D + ρzz H )g = δ g, which implies that (D δ I)g = ρzz H g. We will show that D δ I is nonsingular. Suppose it is singular, then we can find δ = d i, for some i. Consequently, the ith component (D δ I)g i = z i z H g = 0, implying that z H g = 0. It then follows that (D δ I)g = ρzz H g = 0, that is, (d j δ )g j = 0 for all j i. Thus, we have z H g = z i g i = 0, which shows that z i = 0. It contradicts the assumption. Therefore, we have z H g 0 and g = ρz H g(d δ I) 1 z. The rest of the proof is the same as the proof of Theorem.1 in. The above theorem shows that if all diagonal entries of D are nonnegative and satisfy the assumptions in Theorem.1, then the eigenvalues computed by this rank-one modification 4
5 are also nonnegative and satisfy the strict interlacing property. For now, we assume that all entries in Σ 1 and Σ are distinct and there is no zero entry in the rank-one modification vector z. In the next subsection, we will remove these assumptions. Now, from Theorem.1, we can get the eigenvalues of TT H from (4) via four rankone modifications. First, we compute the rank-one modifications T 1 T1 H T 1e m e T m T 1 H and T T H T e 1 e T 1 T H to obtain the eigenvalue decompositions T 1 T1 H T 1e m e T m T 1 H = Û1ˆΣ 1ÛH 1 and T T H T e 1 e T 1 T H = ÛˆΣ ÛH. (7) Applying the above equations to (3), we have = TT H Û1 Û ˆΣ 1 ˆΣ + û1 û û1 û H + ˆv1 ˆv ˆv1 ˆv H Û1 Û H,(8) where û 1 = b m Û1 He m, û = ÛH T e 1, ˆv 1 = Û1H T1 e m, and ˆv = b m Û He 1. We then do the rank-one modification using the first two terms in the parenthesis to get the eigenvalue decomposition: H ˆΣ 1 û1 û1 + = G GH (9) ˆΣ û û Thus, we can rewrite (8) as TT H = Û1 Û ( G + ṽṽ H) Û1 GH Û H (10) where ṽ H = ˆv 1 ˆv H GH. Finally, applying the rank-one modification to the matrices in the parenthesis in (10), we get the eigenvalue decomposition:. Deflation TT H = Û1 Û GGΣ G H Û1 GH Û H UΣ U H. (11) In this subsection, we remove the assumptions of distinct diagonal entries d i and no zero entries in the modification vector z. We first consider the case when z has zero entries. It can be easily verified that (d i,e i) is an eigenpair of D + ρzz H if z i = 0. In this case, the problem can be deflated by one for each zero entry in z. Next, we consider the case when there are two equal diagonal elements in D, say, d i = d j. Let P be a Givens rotation such that di P =, 0 d j 5
6 then P d i 0 0 d j + zi z j zi z j H P H = P d i 0 0 d j H P H Thus, when d i = d j for some i j, we can assume z i = 0 or z j = 0. So, the case of equal diagonal elements in D is reduced to the case of zero entries in z. The procedure is described in the following algorithm. Algorithm. Assume that D is a diagonal matrix with nonnegative elements sorted in decreasing order, z C n and ρ > 0, then this algorithm computes the eigenvalues and eigenvectors of D + ρzz H. 1. Check the diagonal elements of D, for each pair (i,j) such that d i = d j and i j, find a Givens matrix to transform z i, z j T to, 0 T ; 0 D1. Order z into the form and order D into accordingly; ẑ 3. Apply the rank-one update to D + ρẑẑh to get the eigenvalue decomposition (D + ρẑẑ H ) = G GH ; D 4. The eigenvalue decomposition of D + ρzz H is given by D + ρzz H Ip D = 1 Ip G G H, where p is the number of zero entries in z after step 1. Due to the rounding errors, we regard two elements d i and d j equal if they are sufficiently close. In other words, if the difference between d i and d j is less than a predetermined tolerance, tol, then we set them equal. How do we determine the tolerance? In our deflation procedure, when d i and d j are numerically equal, we find a Givens rotation to transform z i,z j T into,0 T. Let c = z i / z i + z j and s = z j / z i + z j, then where c s d i s c d j E = (d i d j) c s s c = d i s cs c s s We set the tolerance tol so that E F ɛ diag(d i,d j ) F when d i d j tol, where ɛ is the machine precision. Taking the Frobenius norm on E and diag(d i,d j ), we get. d j + E E F = s d i d j and diag(d i,d j ) F d max, 6
7 where d max = max(d i,d j ), and then set the tolerance 3 Takagi Factorization tol = d max ɛ. s As described in the previous section, given the Takagi factorizations of T 1 and T in (), we can compute the eigenvalue decomposition TT H = UΣ U H through four rank-one modifications. Let T = QΣQ T be the Takagi factorization of T. It is obvious that the Takagi values of T are the square roots of the eigenvalues of TT H. What remains is to convert the eigenvectors of TT H into the Takagi vectors of T. First, in the case when the eigenvalues are distinct, the eigenvectors of TT H are uniquely defined up to a scalar, which implies that the Takagi vector q i is a scalar multiple of u i. Let Tū i = ξσ i u i for some scalar ξ such that ξ = 1, and define q i sign(ξ)u i = ξu i, (1) where sign(x) = x/ x if x 0, otherwise sign(x) = 1. Then T q i = sign(ξ) Tū i = ξ ξσi u i = ξ ξσi ξ qi = ξ σ i q i = σ i q i as desired. Specifically, ξ can be obtained by ξ = sign(u H i Tū i). Next, in the case of multiple eigenvalues, Tū i may not equal ξσ i u i. We construct where α i = 1/ Tū i + σ i u i. Then q i = α i (Tū i + σ i u i ), (13) T q i = α i T(Tū i + σ i u i ) = α i (T Tu i + σ i Tū i ) = α i (σ i u i + σ i Tū i ) = σ i q i. Finally, we check the orthogonality of the Takagi vectors of T converted from the eigenvectors of TT H. It is obvious that the orthogonality is maintained among the Takagi vectors corresponding to distinct Takagi values because of the orthogonality of the eigenvectors corresponding to distinct eigenvalues. Now, assume that q i,,q i+k are the Takagi vectors corresponding to a multiple Takagi value σ i of multiplicity k. The construction of q i shows that the subspace spanned by q i,,q i+k is same as the one spanned by u i,,u i+k since q i,,q i+k are the eigenvectors associated with σ i. Thus, q i+t (t = 1,,k) are orthogonal to q j, the Takagi vector corresponding to σ j, if σ j σ i. However, the Takagi vectors corresponding to the same Takagi value may lose their orthogonality. So, the modified Grand-Schmidt orthogonalization is applied to these vectors to restore the orthogonality. Suppose that q i+t is one of the Takagi vectors corresponding to σ i computed from (13), then we orthogonalize it against the previous t 1 vectors q i,,q i+t 1 as follows: for j = 1 : t 1 q i+t = q i+t q H i+j q i+tq i+j ; end 7
8 Now, we give the divide-and-conquer algorithm for computing the Takagi factorization of a complex symmetric tridiagonal matrix. Algorithm 3.1 Given a complex symmetric and tridiagonal matrix T, this algorithm computes the Takagi factorization T = QΣQ T. There are two stages in this algorithm. The first stage computes the eigenvalue decomposition TT H = UΣ U H ; the second stage computes the Takagi vectors q i of T from the eigenvectors u i of TT H. 1. Partition T as (). If T 1 and T are small enough, directly compute the eigenvalue decompositions T 1 T H 1 = U 1Σ 1 U H 1 and T T H = U Σ U H. If T 1 and T are large, apply this algorithm to T 1 and T ;. Apply the rank-one modification Algorithm. to T 1 T1 H T 1e m e T mt1 H and T T H T e 1 e T 1 T H to obtain their eigenvalue decompositions (7). Thus, TT H has the form (8); 3. Compute the eigenvalue decomposition (9) using Algorithm.. Then, TT H has the form (10); 4. Apply Algorithm. again to the rank-one modification in the parenthesis in (10) to compute the eigenvalue decomposition + ṽṽ H = GΣ G H. 5. At this point, we get the eigenvalue decomposition TT H = UΣ U H. The Takagi values of T are the square roots of the eigenvalues of TT H ; 6. For a single Takagi value, its corresponding Takagi vector q i is computed using (1); for a multiple Takagi value, its Takagi vector q i is computed using (13) and then orthogonalized against the previously computed Takagi vectors corresponding to the same Takagi value by the modified Gram-Schmidt orthorgonalization. 4 Orthogonality of Takagi Vectors In the previous section, we presented a divide-and-conquer algorithm for computing the Takagi factorization of T. It is based on the rank-one update of the eigenvalue decomposition of a Hermitian matrix. Rank-one modification Theorem.1 is applied four times to get the eigenvalue decomposition if we have the decompositions of T 1 T1 H and T T H. Due to the rounding errors, the orthogonality of the eigenvectors may be lost after rank-one modifications. In this section, we present an analysis of the orthogonality of the computed eigenvectors and discuss the circumstances under which the orthogonality can be maintained. For simplicity, we assume that the given matrix in the rank-one modification is already deflated. 8
9 First, we derive a formula for the eigenvectors g j in Theorem.1. Differentiating the both sides of the function w(t) in (5) with respect to t, we get Then (6) can be rewritten as (D δ I) 1 = g j = ( z1 z d 1, δ j d,..., δ j d n δ j z j (d j δ ) = 1 ρ w (δ ). z n ) ρ (14) w (δj ). Let ˆδ i be a computed root of w in (5). In the following, by extending the results in 4, we show that if the relative error in d j ˆδ i is small for all i and j, then the computed eigenvectors g i have good orthogonality. Theorem 4.1 Denote ˆδ i and ˆδ k as the computed roots of w in (5). Let the relative errors in d j ˆδ i and d j ˆδ k be θ i and θ k respectively, that is, d j ˆδ i = (d j δ i )(1 + θ i ) and d j ˆδ k = (d j δ k)(1 + θ k ), and θ i, θ k τ 1 for all j, then ĝ H i ĝ k = g H i Eg k τ( + τ) ( ) 1 + τ, 1 τ where ĝ i and ĝ k are computed eigenvectors using (14) and E is a diagonal matrix whose ith diagonal entry is E ii = θ ( i + θ k + θ i θ k w (δi )w (δk ) ) 1/ (1 + θ i )(1 + θ k ) w (ˆδ i )w (ˆδ k ). Proof. From (14), we have ĝi H ĝ k z = j ρ (d j δ k )(d j δ i )(1 + θ i)(1 + θ k ) (w (ˆδ i )w (ˆδ k ))1/ z = j n (d j δ k )(d j δ i ) z j ρ (d j δ k )(d j δ i )(1 + θ i)(1 + θ k ) (w (ˆδ i )w (ˆδ k ))1/ since g H i g k = 0. Thus, we have ĝ H i ĝ k 9
10 = = ( ( z j (d j δ k )(d j δ i ) z j (d j δ k )(d j δ i ) = g H i Eg k E, ) ( 1 ) 1 (1 + θ i )(1 + θ k ) ) ( θi + θ k + θ i θ k (1 + θ i )(1 + θ k ) where E is a diagonal matrix, whose diagonal elements are E ii = θ i + θ k + θ i θ k (1 + θ i )(1 + θ k ) On the other hand, it is easy to show that w (δ i ) w (ˆδ i ) = n z j Subsituting w (δi )/w (ˆδ i ) in (15) with (16), we have ρ (w (ˆδ i )w (ˆδ k ))1/ ) ( w (δi )w (δk ) ) 1/ ρ w (ˆδ i )w (ˆδ k ) (w (δi )w (δk ))1/ ( w (δi )w (δk ) ) 1/. (15) w (ˆδ i )w (ˆδ k ) (d j δ i ) n z j (d j δ i ) (1+θ i ) (1 + τ). (16) max(e ii ) τ + τ + ( ) τ 1 + τ (1 τ) (1 + τ) = τ( + τ). 1 τ It completes the proof. Apparently, if the roots δi of w are computed in high accuracy, then the relative errors in d j ˆδ i are small, provided that the eigenvalues δi are not clustered. Consequently, from the above theorem, the computed eigenvectors ĝ i have good orthogonality. In the following, we show how to compute the roots δi accurately. From Theorem.1, the eigenvalues of a rank-one modification are the zeros of the function w(t) in (5). There are many zero finding methods, for example, the rational interpolation strategy in 1 and bisection and its variations 7, 9. We adopt the rational interpolation strategy in our algorithm. In a zero finding method, accurate function evaluation is crucial. In the following, we reformulate the function w(t) in (5) into a new function, which can be evaluated accurately. Theorem.1 shows that each root δi of the function w(δ ) is located in (d i, d i 1 ). First, we consider the case when δ (d i, (d i 1 + d i )/) and let ζ j = (d j d i )/ρ, ψ i (µ) = i 1 z j ζ j µ and ϕ i(µ) = j=i z j ζ j µ where µ = (δ d i )/ρ (0,ζ i 1/). Thus, the equation w(δ ) = 0 can be rewritten as w(ρµ + d i ) = 1 + ψ i(µ) + ϕ i (µ) f i (µ) = 0. 10
11 An important property of f i (µ) is that the difference ζ j µ can be computed to high relative accuracy for any µ (0,ζ i 1 /) 3. It then assures that the function f i (µ) can be evaluated for any µ (0,ζ i 1 /) and d j δ = d j d i (δ d i ) = ρ(ζ j µ) is in high relative accuracy, which guarantees the good orthogonality of the computed eigenvectors. Now we consider the case when δ (d i 1 + d i )/, d i 1 ) and let ζ j = (d j d i 1 )/ρ, ψ i (µ) = i 1 z j ζ j µ and ϕ i(µ) = j=i z j ζ j µ where µ = (δ d i 1 )/ρ ζ i/, 0). So, the equation w(δ ) = 0 can be rewritten as w(ρµ + d i 1) = 1 + ψ i (µ) + ϕ i (µ) f i (µ) = 0. Also, the difference ζ j µ can be computed to high relative accuracy. Finally, we consider the case when i = 1. Let ζ j = (d j d 1 )/ρ, ψ 1 (µ) = 0, and ϕ 1 (µ) = z j ζ j µ. We want to find a root µ = (δ d 1 )/ρ in (0, z ). Similar to the previous cases, for any µ (0, z ), the ratio z i /(ζ j µ) can be computed to high relative accuracy. So far, we have reformulated the problem of finding the zeros of w(t) into the problem of finding the zeros of f i (µ) which can be accurately evaluated. Now, we propose a stopping criterion for f i (µ) so that using this stopping criterion we can obtain accurate computed eigenvalues ˆδ i. From the definitions of ψ i (µ) and ϕ i (µ), we have ψ i (µ) 0 and ϕ i (µ) 0. We define the stopping criterion as f i (µ) ɛn( ψ i (µ) + ϕ i (µ) + 1). (17) In the following, we show that using this criterion, the computed roots ˆδ i of w(δ ) are accurate. Since w(δi ) = 0, we have w(ˆδ i ) = w(ˆδ i ) w(δ i ) = ρ n = ρ(ˆδ i δ i ) z j d j ˆδ i z j (d j ˆδ i )(d j δ i ) ρ z j d j δ i According to the stopping criterion, since f i (µ) can be evaluated accurately, we have w(ˆδ i ) ɛn 1 + ρ z j d j ˆδ z i ρɛn j d j ˆδ i + z j d j δ i 11
12 since 1 = ρ n z j. Without loss of generality, we assume δ d j δ i and ˆδ i are in the same i interval, say (d i, d i 1 ). It follows that (d j δ i )(d j ˆδ i ) > 0. So, w(ˆδ i ) = ρ ˆδ i δi z j z (d j ˆδ i )(d j ρɛn j δ i ) d j ˆδ i + z j d j δ i ρɛn(4 D + ρzz H + ˆδ i δ i ) n z j (d j ˆδ i )(d j δ i ), since d j ˆδ i + d j δ i d j δ i + ˆδ i δ i 4 D + ρzz H + ˆδ i δ i. From the above equation, we can get the upper bound for ˆδ i δ i : ˆδ i δ i 4ɛn D + ρzz H. (18) 1 ɛn In conclusion, we apply the rational interpolation zero finding method to f i (µ) using the stopping criterion (17). We then can obtain accurate eigenvalues δi. Provided that the eigenvalues are not clustered, it results the high relative accuracy of the difference d i ˆδ i, which implies good orthogonality of the computed eigenvectors of TT H. 5 Numerical Examples We programmed our divide-and-conquer Algorithm 3.1 in Matlab and tested it on three types of complex symmetric and tridiagonal matrices. Our experiments were carried out on a SUN SPARC Ultra 10. The complex symmetric and tridiagonal matrices with predetermined Takagi values were generated as follows. First, a random vector uniformly distributed on (0,1 was generated and sorted in descending order as a Takagi value vector d. Then a random unitary matrix was generated as a Takagi vector matrix V. The product A = V ΣV T, where Σ = diag(d), was computed as a complex symmetric matrix. Finally, a complex symmetric and tridiagonal T was obtained by applying the Lanczos method with partial orthogonalization 8 to A. Denoting ˆQ and ˆd as the computed Takagi vector matrix and Takagi value vector respectively, the error in the computed Takagi factorization was measured by γ t = ˆQˆΣ ˆQ T T, where ˆΣ = diag( ˆd). The error in the computed Takagi values was measured by γ v = d ˆd and the orthogonality of the computed Takagi vector matrix ˆQ was measured by γ o = ˆQ ˆQ H I. 1
13 Example γ o γ v γ t e e e e e e e e e e e e e e e-13 Table 1: The Takagi factorization of five testing matrices with distinct Takagi values Example γ o γ v γ t e e e e e e e e e e e e e e e-13 Table : The Takagi factorization of five testing matrices with multiple Takagi values of small multiplicity Example 1 Five random complex symmetric and tridiagonal matrices of order 64 were generated as described above. In this example, the Takagi values of each matrix were distinct. Table 1 shows that the computed Takagi values and Takagi vectors are accurate. Example Five random complex symmetric and tridiagonal matrices of order 64 were generated. In this example, we set the three largest Takagi values equal and the four smallest Takagi values equal. Table shows the results. Example 3 Five random T of order 64 were generated. In this example, however, we set the 15 largest Takagi values equal. As expected, when the Takagi values are clustered, the computed Takagi vectors may lose orthogonality as shown in the third matrix. For performance, we tested our algorithm on random complex symmetric and tridiagonal matrices of five different sizes. For each size, we generated five matrices and ran our divideand-conquer (DAC) method and the implicit QR (IQR) method 6. In our method, when the size of the submatrix T i, for i = 1,, in () is less than or equal to 4, its Takagi factorization is computed directly by the implicit QR method. Table 4 shows the average running time and the average factorization error γ t of the five matrices of same size. The results in Table 4 demonstrate that our method is significantly more efficient than the implicit QR method even for matrices of moderately large size. We expect the improvement in efficiency is more significant for large matrices. 13
14 Example γ o γ v γ t e e e e e e e e e e e e e e-14 Table 3: The Takagi factorization of five testing matrices with multiple Takagi values of large multiplicity Running time (sec) γ t matrix size DAC method IQR method DAC method IQR method e e e e e e e e e e-13 Table 4: The performance and accuracy comparison of the divide-and-conquer (DAC) method and the implicit QR (IQR) method Conclusion We have proposed a divide-and-conquer method for the Takagi factorization of a complex symmetric and tridiagonal matrix and presented an analysis, which shows that our method computes accurate Takagi values and vectors provided that the Takagi values are not clustered. Our preliminary experiments have demonstrated that our method produced accurate results even for matrices with Takagi values of moderate multiplicities and is much more efficient than the implicit QR method 6. References 1 J.R. Bunch, C.P. Nielsen, and D.C. Sorensen. Rank-one modification of the symmetric eigenproblems. Numer. Math., 1978(31), J.J.M. Cuppen. A divide and conquer method for the symmetric tridiagonal eigenproblem. Numer. Math. 1981(36), M. Gu and S.C. Eisenstat. A divide-and-conquer algorithm for the symmetric tridiagonal eigenproblem. SIAM J. Matrix Anal. Appl. 1995(16), E.R. Jessup and D.C. Sorensen. A parallel algorithm for computing the singular value decomposition of a matrix. SIAM J. Matrix Anal. Appl. 1994(15),
15 5 Guohong Liu, Wei Xu and Sanzheng Qiao. Block Lanczos tridiagonalization of complex symmetric matrices. Technical Report No. CAS SQ, Department of Computing and Software, McMaster University, Hamilton, Ontario, Canada. L8S 4K1. September F.T. Luk and S. Qiao. A fast singular value algorithm for Hankel matrices. Fast Algorithms for Structured Matrices: Theory and Applications. Contemporary Mathematics 33, Editor V. Olshevsky. American Mathematical Society. 003, D.P. O Leary and G.W. Stewart. Computing the eigencalues and eigenvectors of symmetric arrowhead matrices. J. Comput. Phys. 1990(90), Sanzheng Qiao. Orthogonalization techniques for the Lanczos tridiagonalization of complex symmetric matrices. Advanced Signal Processing Algorithms, Architectures, and Implementations XIV, edited by Franklin T. Luk, Proc. of SPIE Vol , W.E.Shreve and M.R. Stabnow. An eigenvalue algorithm for symmetric bordered diagonal matrices. Current Trends in Matrix Theory, F. Uhling and R. Grone, eds., Elsevier Science Publishing Co., Inc., New York, 1987,
A DIVIDE-AND-CONQUER METHOD FOR THE TAKAGI FACTORIZATION
 SIAM J MATRIX ANAL APPL Vol 0, No 0, pp 000 000 c XXXX Society for Industrial and Applied Mathematics A DIVIDE-AND-CONQUER METHOD FOR THE TAKAGI FACTORIZATION WEI XU AND SANZHENG QIAO Abstract This paper
SIAM J MATRIX ANAL APPL Vol 0, No 0, pp 000 000 c XXXX Society for Industrial and Applied Mathematics A DIVIDE-AND-CONQUER METHOD FOR THE TAKAGI FACTORIZATION WEI XU AND SANZHENG QIAO Abstract This paper
Block Lanczos Tridiagonalization of Complex Symmetric Matrices
 Block Lanczos Tridiagonalization of Complex Symmetric Matrices Sanzheng Qiao, Guohong Liu, Wei Xu Department of Computing and Software, McMaster University, Hamilton, Ontario L8S 4L7 ABSTRACT The classic
Block Lanczos Tridiagonalization of Complex Symmetric Matrices Sanzheng Qiao, Guohong Liu, Wei Xu Department of Computing and Software, McMaster University, Hamilton, Ontario L8S 4L7 ABSTRACT The classic
Total least squares. Gérard MEURANT. October, 2008
 Total least squares Gérard MEURANT October, 2008 1 Introduction to total least squares 2 Approximation of the TLS secular equation 3 Numerical experiments Introduction to total least squares In least squares
Total least squares Gérard MEURANT October, 2008 1 Introduction to total least squares 2 Approximation of the TLS secular equation 3 Numerical experiments Introduction to total least squares In least squares
Integer Least Squares: Sphere Decoding and the LLL Algorithm
 Integer Least Squares: Sphere Decoding and the LLL Algorithm Sanzheng Qiao Department of Computing and Software McMaster University 28 Main St. West Hamilton Ontario L8S 4L7 Canada. ABSTRACT This paper
Integer Least Squares: Sphere Decoding and the LLL Algorithm Sanzheng Qiao Department of Computing and Software McMaster University 28 Main St. West Hamilton Ontario L8S 4L7 Canada. ABSTRACT This paper
Exponentials of Symmetric Matrices through Tridiagonal Reductions
 Exponentials of Symmetric Matrices through Tridiagonal Reductions Ya Yan Lu Department of Mathematics City University of Hong Kong Kowloon, Hong Kong Abstract A simple and efficient numerical algorithm
Exponentials of Symmetric Matrices through Tridiagonal Reductions Ya Yan Lu Department of Mathematics City University of Hong Kong Kowloon, Hong Kong Abstract A simple and efficient numerical algorithm
Exponential Decomposition and Hankel Matrix
 Exponential Decomposition and Hankel Matrix Franklin T Luk Department of Computer Science and Engineering, Chinese University of Hong Kong, Shatin, NT, Hong Kong luk@csecuhkeduhk Sanzheng Qiao Department
Exponential Decomposition and Hankel Matrix Franklin T Luk Department of Computer Science and Engineering, Chinese University of Hong Kong, Shatin, NT, Hong Kong luk@csecuhkeduhk Sanzheng Qiao Department
Efficient and Accurate Rectangular Window Subspace Tracking
 Efficient and Accurate Rectangular Window Subspace Tracking Timothy M. Toolan and Donald W. Tufts Dept. of Electrical Engineering, University of Rhode Island, Kingston, RI 88 USA toolan@ele.uri.edu, tufts@ele.uri.edu
Efficient and Accurate Rectangular Window Subspace Tracking Timothy M. Toolan and Donald W. Tufts Dept. of Electrical Engineering, University of Rhode Island, Kingston, RI 88 USA toolan@ele.uri.edu, tufts@ele.uri.edu
13-2 Text: 28-30; AB: 1.3.3, 3.2.3, 3.4.2, 3.5, 3.6.2; GvL Eigen2
 The QR algorithm The most common method for solving small (dense) eigenvalue problems. The basic algorithm: QR without shifts 1. Until Convergence Do: 2. Compute the QR factorization A = QR 3. Set A :=
The QR algorithm The most common method for solving small (dense) eigenvalue problems. The basic algorithm: QR without shifts 1. Until Convergence Do: 2. Compute the QR factorization A = QR 3. Set A :=
arxiv: v1 [cs.lg] 26 Jul 2017
![arxiv: v1 [cs.lg] 26 Jul 2017 arxiv: v1 [cs.lg] 26 Jul 2017](/thumbs/94/121875314.jpg) Updating Singular Value Decomposition for Rank One Matrix Perturbation Ratnik Gandhi, Amoli Rajgor School of Engineering & Applied Science, Ahmedabad University, Ahmedabad-380009, India arxiv:70708369v
Updating Singular Value Decomposition for Rank One Matrix Perturbation Ratnik Gandhi, Amoli Rajgor School of Engineering & Applied Science, Ahmedabad University, Ahmedabad-380009, India arxiv:70708369v
Numerical Methods in Matrix Computations
 Ake Bjorck Numerical Methods in Matrix Computations Springer Contents 1 Direct Methods for Linear Systems 1 1.1 Elements of Matrix Theory 1 1.1.1 Matrix Algebra 2 1.1.2 Vector Spaces 6 1.1.3 Submatrices
Ake Bjorck Numerical Methods in Matrix Computations Springer Contents 1 Direct Methods for Linear Systems 1 1.1 Elements of Matrix Theory 1 1.1.1 Matrix Algebra 2 1.1.2 Vector Spaces 6 1.1.3 Submatrices
Notes on Eigenvalues, Singular Values and QR
 Notes on Eigenvalues, Singular Values and QR Michael Overton, Numerical Computing, Spring 2017 March 30, 2017 1 Eigenvalues Everyone who has studied linear algebra knows the definition: given a square
Notes on Eigenvalues, Singular Values and QR Michael Overton, Numerical Computing, Spring 2017 March 30, 2017 1 Eigenvalues Everyone who has studied linear algebra knows the definition: given a square
University of Maryland Department of Computer Science TR-5009 University of Maryland Institute for Advanced Computer Studies TR April 2012
 University of Maryland Department of Computer Science TR-5009 University of Maryland Institute for Advanced Computer Studies TR-202-07 April 202 LYAPUNOV INVERSE ITERATION FOR COMPUTING A FEW RIGHTMOST
University of Maryland Department of Computer Science TR-5009 University of Maryland Institute for Advanced Computer Studies TR-202-07 April 202 LYAPUNOV INVERSE ITERATION FOR COMPUTING A FEW RIGHTMOST
Chapter 3 Transformations
 Chapter 3 Transformations An Introduction to Optimization Spring, 2014 Wei-Ta Chu 1 Linear Transformations A function is called a linear transformation if 1. for every and 2. for every If we fix the bases
Chapter 3 Transformations An Introduction to Optimization Spring, 2014 Wei-Ta Chu 1 Linear Transformations A function is called a linear transformation if 1. for every and 2. for every If we fix the bases
The QR Factorization
 The QR Factorization How to Make Matrices Nicer Radu Trîmbiţaş Babeş-Bolyai University March 11, 2009 Radu Trîmbiţaş ( Babeş-Bolyai University) The QR Factorization March 11, 2009 1 / 25 Projectors A projector
The QR Factorization How to Make Matrices Nicer Radu Trîmbiţaş Babeş-Bolyai University March 11, 2009 Radu Trîmbiţaş ( Babeş-Bolyai University) The QR Factorization March 11, 2009 1 / 25 Projectors A projector
Preliminary/Qualifying Exam in Numerical Analysis (Math 502a) Spring 2012
 Instructions Preliminary/Qualifying Exam in Numerical Analysis (Math 502a) Spring 2012 The exam consists of four problems, each having multiple parts. You should attempt to solve all four problems. 1.
Instructions Preliminary/Qualifying Exam in Numerical Analysis (Math 502a) Spring 2012 The exam consists of four problems, each having multiple parts. You should attempt to solve all four problems. 1.
4.8 Arnoldi Iteration, Krylov Subspaces and GMRES
 48 Arnoldi Iteration, Krylov Subspaces and GMRES We start with the problem of using a similarity transformation to convert an n n matrix A to upper Hessenberg form H, ie, A = QHQ, (30) with an appropriate
48 Arnoldi Iteration, Krylov Subspaces and GMRES We start with the problem of using a similarity transformation to convert an n n matrix A to upper Hessenberg form H, ie, A = QHQ, (30) with an appropriate
The Singular Value Decomposition and Least Squares Problems
 The Singular Value Decomposition and Least Squares Problems Tom Lyche Centre of Mathematics for Applications, Department of Informatics, University of Oslo September 27, 2009 Applications of SVD solving
The Singular Value Decomposition and Least Squares Problems Tom Lyche Centre of Mathematics for Applications, Department of Informatics, University of Oslo September 27, 2009 Applications of SVD solving
On the Modification of an Eigenvalue Problem that Preserves an Eigenspace
 Purdue University Purdue e-pubs Department of Computer Science Technical Reports Department of Computer Science 2009 On the Modification of an Eigenvalue Problem that Preserves an Eigenspace Maxim Maumov
Purdue University Purdue e-pubs Department of Computer Science Technical Reports Department of Computer Science 2009 On the Modification of an Eigenvalue Problem that Preserves an Eigenspace Maxim Maumov
The Singular Value Decomposition
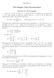 CHAPTER 6 The Singular Value Decomposition Exercise 67: SVD examples (a) For A =[, 4] T we find a matrixa T A =5,whichhastheeigenvalue =5 Thisprovidesuswiththesingularvalue =+ p =5forA Hence the matrix
CHAPTER 6 The Singular Value Decomposition Exercise 67: SVD examples (a) For A =[, 4] T we find a matrixa T A =5,whichhastheeigenvalue =5 Thisprovidesuswiththesingularvalue =+ p =5forA Hence the matrix
The Singular Value Decomposition
 The Singular Value Decomposition Philippe B. Laval KSU Fall 2015 Philippe B. Laval (KSU) SVD Fall 2015 1 / 13 Review of Key Concepts We review some key definitions and results about matrices that will
The Singular Value Decomposition Philippe B. Laval KSU Fall 2015 Philippe B. Laval (KSU) SVD Fall 2015 1 / 13 Review of Key Concepts We review some key definitions and results about matrices that will
Accurate eigenvalue decomposition of arrowhead matrices and applications
 Accurate eigenvalue decomposition of arrowhead matrices and applications Nevena Jakovčević Stor FESB, University of Split joint work with Ivan Slapničar and Jesse Barlow IWASEP9 June 4th, 2012. 1/31 Introduction
Accurate eigenvalue decomposition of arrowhead matrices and applications Nevena Jakovčević Stor FESB, University of Split joint work with Ivan Slapničar and Jesse Barlow IWASEP9 June 4th, 2012. 1/31 Introduction
Math 408 Advanced Linear Algebra
 Math 408 Advanced Linear Algebra Chi-Kwong Li Chapter 4 Hermitian and symmetric matrices Basic properties Theorem Let A M n. The following are equivalent. Remark (a) A is Hermitian, i.e., A = A. (b) x
Math 408 Advanced Linear Algebra Chi-Kwong Li Chapter 4 Hermitian and symmetric matrices Basic properties Theorem Let A M n. The following are equivalent. Remark (a) A is Hermitian, i.e., A = A. (b) x
arxiv: v1 [math.na] 1 Sep 2018
![arxiv: v1 [math.na] 1 Sep 2018 arxiv: v1 [math.na] 1 Sep 2018](/thumbs/85/92407263.jpg) On the perturbation of an L -orthogonal projection Xuefeng Xu arxiv:18090000v1 [mathna] 1 Sep 018 September 5 018 Abstract The L -orthogonal projection is an important mathematical tool in scientific computing
On the perturbation of an L -orthogonal projection Xuefeng Xu arxiv:18090000v1 [mathna] 1 Sep 018 September 5 018 Abstract The L -orthogonal projection is an important mathematical tool in scientific computing
Chapter 12 Solving secular equations
 Chapter 12 Solving secular equations Gérard MEURANT January-February, 2012 1 Examples of Secular Equations 2 Secular equation solvers 3 Numerical experiments Examples of secular equations What are secular
Chapter 12 Solving secular equations Gérard MEURANT January-February, 2012 1 Examples of Secular Equations 2 Secular equation solvers 3 Numerical experiments Examples of secular equations What are secular
Last Time. Social Network Graphs Betweenness. Graph Laplacian. Girvan-Newman Algorithm. Spectral Bisection
 Eigenvalue Problems Last Time Social Network Graphs Betweenness Girvan-Newman Algorithm Graph Laplacian Spectral Bisection λ 2, w 2 Today Small deviation into eigenvalue problems Formulation Standard eigenvalue
Eigenvalue Problems Last Time Social Network Graphs Betweenness Girvan-Newman Algorithm Graph Laplacian Spectral Bisection λ 2, w 2 Today Small deviation into eigenvalue problems Formulation Standard eigenvalue
be a Householder matrix. Then prove the followings H = I 2 uut Hu = (I 2 uu u T u )u = u 2 uut u
 MATH 434/534 Theoretical Assignment 7 Solution Chapter 7 (71) Let H = I 2uuT Hu = u (ii) Hv = v if = 0 be a Householder matrix Then prove the followings H = I 2 uut Hu = (I 2 uu )u = u 2 uut u = u 2u =
MATH 434/534 Theoretical Assignment 7 Solution Chapter 7 (71) Let H = I 2uuT Hu = u (ii) Hv = v if = 0 be a Householder matrix Then prove the followings H = I 2 uut Hu = (I 2 uu )u = u 2 uut u = u 2u =
Lecture notes: Applied linear algebra Part 1. Version 2
 Lecture notes: Applied linear algebra Part 1. Version 2 Michael Karow Berlin University of Technology karow@math.tu-berlin.de October 2, 2008 1 Notation, basic notions and facts 1.1 Subspaces, range and
Lecture notes: Applied linear algebra Part 1. Version 2 Michael Karow Berlin University of Technology karow@math.tu-berlin.de October 2, 2008 1 Notation, basic notions and facts 1.1 Subspaces, range and
The Lanczos and conjugate gradient algorithms
 The Lanczos and conjugate gradient algorithms Gérard MEURANT October, 2008 1 The Lanczos algorithm 2 The Lanczos algorithm in finite precision 3 The nonsymmetric Lanczos algorithm 4 The Golub Kahan bidiagonalization
The Lanczos and conjugate gradient algorithms Gérard MEURANT October, 2008 1 The Lanczos algorithm 2 The Lanczos algorithm in finite precision 3 The nonsymmetric Lanczos algorithm 4 The Golub Kahan bidiagonalization
Structured Condition Numbers of Symmetric Algebraic Riccati Equations
 Proceedings of the 2 nd International Conference of Control Dynamic Systems and Robotics Ottawa Ontario Canada May 7-8 2015 Paper No. 183 Structured Condition Numbers of Symmetric Algebraic Riccati Equations
Proceedings of the 2 nd International Conference of Control Dynamic Systems and Robotics Ottawa Ontario Canada May 7-8 2015 Paper No. 183 Structured Condition Numbers of Symmetric Algebraic Riccati Equations
RITZ VALUE BOUNDS THAT EXPLOIT QUASI-SPARSITY
 RITZ VALUE BOUNDS THAT EXPLOIT QUASI-SPARSITY ILSE C.F. IPSEN Abstract. Absolute and relative perturbation bounds for Ritz values of complex square matrices are presented. The bounds exploit quasi-sparsity
RITZ VALUE BOUNDS THAT EXPLOIT QUASI-SPARSITY ILSE C.F. IPSEN Abstract. Absolute and relative perturbation bounds for Ritz values of complex square matrices are presented. The bounds exploit quasi-sparsity
Eigenvalue Problems and Singular Value Decomposition
 Eigenvalue Problems and Singular Value Decomposition Sanzheng Qiao Department of Computing and Software McMaster University August, 2012 Outline 1 Eigenvalue Problems 2 Singular Value Decomposition 3 Software
Eigenvalue Problems and Singular Value Decomposition Sanzheng Qiao Department of Computing and Software McMaster University August, 2012 Outline 1 Eigenvalue Problems 2 Singular Value Decomposition 3 Software
The Singular Value Decomposition
 The Singular Value Decomposition An Important topic in NLA Radu Tiberiu Trîmbiţaş Babeş-Bolyai University February 23, 2009 Radu Tiberiu Trîmbiţaş ( Babeş-Bolyai University)The Singular Value Decomposition
The Singular Value Decomposition An Important topic in NLA Radu Tiberiu Trîmbiţaş Babeş-Bolyai University February 23, 2009 Radu Tiberiu Trîmbiţaş ( Babeş-Bolyai University)The Singular Value Decomposition
ON ORTHOGONAL REDUCTION TO HESSENBERG FORM WITH SMALL BANDWIDTH
 ON ORTHOGONAL REDUCTION TO HESSENBERG FORM WITH SMALL BANDWIDTH V. FABER, J. LIESEN, AND P. TICHÝ Abstract. Numerous algorithms in numerical linear algebra are based on the reduction of a given matrix
ON ORTHOGONAL REDUCTION TO HESSENBERG FORM WITH SMALL BANDWIDTH V. FABER, J. LIESEN, AND P. TICHÝ Abstract. Numerous algorithms in numerical linear algebra are based on the reduction of a given matrix
MATH 581D FINAL EXAM Autumn December 12, 2016
 MATH 58D FINAL EXAM Autumn 206 December 2, 206 NAME: SIGNATURE: Instructions: there are 6 problems on the final. Aim for solving 4 problems, but do as much as you can. Partial credit will be given on all
MATH 58D FINAL EXAM Autumn 206 December 2, 206 NAME: SIGNATURE: Instructions: there are 6 problems on the final. Aim for solving 4 problems, but do as much as you can. Partial credit will be given on all
Bindel, Fall 2016 Matrix Computations (CS 6210) Notes for
 1 Algorithms Notes for 2016-10-31 There are several flavors of symmetric eigenvalue solvers for which there is no equivalent (stable) nonsymmetric solver. We discuss four algorithmic ideas: the workhorse
1 Algorithms Notes for 2016-10-31 There are several flavors of symmetric eigenvalue solvers for which there is no equivalent (stable) nonsymmetric solver. We discuss four algorithmic ideas: the workhorse
AMS526: Numerical Analysis I (Numerical Linear Algebra)
 AMS526: Numerical Analysis I (Numerical Linear Algebra) Lecture 1: Course Overview & Matrix-Vector Multiplication Xiangmin Jiao SUNY Stony Brook Xiangmin Jiao Numerical Analysis I 1 / 20 Outline 1 Course
AMS526: Numerical Analysis I (Numerical Linear Algebra) Lecture 1: Course Overview & Matrix-Vector Multiplication Xiangmin Jiao SUNY Stony Brook Xiangmin Jiao Numerical Analysis I 1 / 20 Outline 1 Course
A Cholesky LR algorithm for the positive definite symmetric diagonal-plus-semiseparable eigenproblem
 A Cholesky LR algorithm for the positive definite symmetric diagonal-plus-semiseparable eigenproblem Bor Plestenjak Department of Mathematics University of Ljubljana Slovenia Ellen Van Camp and Marc Van
A Cholesky LR algorithm for the positive definite symmetric diagonal-plus-semiseparable eigenproblem Bor Plestenjak Department of Mathematics University of Ljubljana Slovenia Ellen Van Camp and Marc Van
Foundations of Matrix Analysis
 1 Foundations of Matrix Analysis In this chapter we recall the basic elements of linear algebra which will be employed in the remainder of the text For most of the proofs as well as for the details, the
1 Foundations of Matrix Analysis In this chapter we recall the basic elements of linear algebra which will be employed in the remainder of the text For most of the proofs as well as for the details, the
Math 102, Winter Final Exam Review. Chapter 1. Matrices and Gaussian Elimination
 Math 0, Winter 07 Final Exam Review Chapter. Matrices and Gaussian Elimination { x + x =,. Different forms of a system of linear equations. Example: The x + 4x = 4. [ ] [ ] [ ] vector form (or the column
Math 0, Winter 07 Final Exam Review Chapter. Matrices and Gaussian Elimination { x + x =,. Different forms of a system of linear equations. Example: The x + 4x = 4. [ ] [ ] [ ] vector form (or the column
Eigenvalue Problems. Eigenvalue problems occur in many areas of science and engineering, such as structural analysis
 Eigenvalue Problems Eigenvalue problems occur in many areas of science and engineering, such as structural analysis Eigenvalues also important in analyzing numerical methods Theory and algorithms apply
Eigenvalue Problems Eigenvalue problems occur in many areas of science and engineering, such as structural analysis Eigenvalues also important in analyzing numerical methods Theory and algorithms apply
AN ITERATIVE METHOD WITH ERROR ESTIMATORS
 AN ITERATIVE METHOD WITH ERROR ESTIMATORS D. CALVETTI, S. MORIGI, L. REICHEL, AND F. SGALLARI Abstract. Iterative methods for the solution of linear systems of equations produce a sequence of approximate
AN ITERATIVE METHOD WITH ERROR ESTIMATORS D. CALVETTI, S. MORIGI, L. REICHEL, AND F. SGALLARI Abstract. Iterative methods for the solution of linear systems of equations produce a sequence of approximate
ELA THE OPTIMAL PERTURBATION BOUNDS FOR THE WEIGHTED MOORE-PENROSE INVERSE. 1. Introduction. Let C m n be the set of complex m n matrices and C m n
 Electronic Journal of Linear Algebra ISSN 08-380 Volume 22, pp. 52-538, May 20 THE OPTIMAL PERTURBATION BOUNDS FOR THE WEIGHTED MOORE-PENROSE INVERSE WEI-WEI XU, LI-XIA CAI, AND WEN LI Abstract. In this
Electronic Journal of Linear Algebra ISSN 08-380 Volume 22, pp. 52-538, May 20 THE OPTIMAL PERTURBATION BOUNDS FOR THE WEIGHTED MOORE-PENROSE INVERSE WEI-WEI XU, LI-XIA CAI, AND WEN LI Abstract. In this
arxiv: v2 [math.na] 21 Sep 2015
![arxiv: v2 [math.na] 21 Sep 2015 arxiv: v2 [math.na] 21 Sep 2015](/thumbs/85/92873052.jpg) Forward stable eigenvalue decomposition of rank-one modifications of diagonal matrices arxiv:1405.7537v2 [math.na] 21 Sep 2015 N. Jakovčević Stor a,1,, I. Slapničar a,1, J. L. Barlow b,2 a Faculty of Electrical
Forward stable eigenvalue decomposition of rank-one modifications of diagonal matrices arxiv:1405.7537v2 [math.na] 21 Sep 2015 N. Jakovčević Stor a,1,, I. Slapničar a,1, J. L. Barlow b,2 a Faculty of Electrical
Maths for Signals and Systems Linear Algebra in Engineering
 Maths for Signals and Systems Linear Algebra in Engineering Lectures 13 15, Tuesday 8 th and Friday 11 th November 016 DR TANIA STATHAKI READER (ASSOCIATE PROFFESOR) IN SIGNAL PROCESSING IMPERIAL COLLEGE
Maths for Signals and Systems Linear Algebra in Engineering Lectures 13 15, Tuesday 8 th and Friday 11 th November 016 DR TANIA STATHAKI READER (ASSOCIATE PROFFESOR) IN SIGNAL PROCESSING IMPERIAL COLLEGE
Chap 3. Linear Algebra
 Chap 3. Linear Algebra Outlines 1. Introduction 2. Basis, Representation, and Orthonormalization 3. Linear Algebraic Equations 4. Similarity Transformation 5. Diagonal Form and Jordan Form 6. Functions
Chap 3. Linear Algebra Outlines 1. Introduction 2. Basis, Representation, and Orthonormalization 3. Linear Algebraic Equations 4. Similarity Transformation 5. Diagonal Form and Jordan Form 6. Functions
Applied Mathematics 205. Unit V: Eigenvalue Problems. Lecturer: Dr. David Knezevic
 Applied Mathematics 205 Unit V: Eigenvalue Problems Lecturer: Dr. David Knezevic Unit V: Eigenvalue Problems Chapter V.4: Krylov Subspace Methods 2 / 51 Krylov Subspace Methods In this chapter we give
Applied Mathematics 205 Unit V: Eigenvalue Problems Lecturer: Dr. David Knezevic Unit V: Eigenvalue Problems Chapter V.4: Krylov Subspace Methods 2 / 51 Krylov Subspace Methods In this chapter we give
Arnoldi Methods in SLEPc
 Scalable Library for Eigenvalue Problem Computations SLEPc Technical Report STR-4 Available at http://slepc.upv.es Arnoldi Methods in SLEPc V. Hernández J. E. Román A. Tomás V. Vidal Last update: October,
Scalable Library for Eigenvalue Problem Computations SLEPc Technical Report STR-4 Available at http://slepc.upv.es Arnoldi Methods in SLEPc V. Hernández J. E. Román A. Tomás V. Vidal Last update: October,
Singular Value Decomposition
 Chapter 5 Singular Value Decomposition We now reach an important Chapter in this course concerned with the Singular Value Decomposition of a matrix A. SVD, as it is commonly referred to, is one of the
Chapter 5 Singular Value Decomposition We now reach an important Chapter in this course concerned with the Singular Value Decomposition of a matrix A. SVD, as it is commonly referred to, is one of the
Jordan Journal of Mathematics and Statistics (JJMS) 5(3), 2012, pp A NEW ITERATIVE METHOD FOR SOLVING LINEAR SYSTEMS OF EQUATIONS
 Jordan Journal of Mathematics and Statistics JJMS) 53), 2012, pp.169-184 A NEW ITERATIVE METHOD FOR SOLVING LINEAR SYSTEMS OF EQUATIONS ADEL H. AL-RABTAH Abstract. The Jacobi and Gauss-Seidel iterative
Jordan Journal of Mathematics and Statistics JJMS) 53), 2012, pp.169-184 A NEW ITERATIVE METHOD FOR SOLVING LINEAR SYSTEMS OF EQUATIONS ADEL H. AL-RABTAH Abstract. The Jacobi and Gauss-Seidel iterative
MATH36001 Generalized Inverses and the SVD 2015
 MATH36001 Generalized Inverses and the SVD 201 1 Generalized Inverses of Matrices A matrix has an inverse only if it is square and nonsingular. However there are theoretical and practical applications
MATH36001 Generalized Inverses and the SVD 201 1 Generalized Inverses of Matrices A matrix has an inverse only if it is square and nonsingular. However there are theoretical and practical applications
Matrix Algorithms. Volume II: Eigensystems. G. W. Stewart H1HJ1L. University of Maryland College Park, Maryland
 Matrix Algorithms Volume II: Eigensystems G. W. Stewart University of Maryland College Park, Maryland H1HJ1L Society for Industrial and Applied Mathematics Philadelphia CONTENTS Algorithms Preface xv xvii
Matrix Algorithms Volume II: Eigensystems G. W. Stewart University of Maryland College Park, Maryland H1HJ1L Society for Industrial and Applied Mathematics Philadelphia CONTENTS Algorithms Preface xv xvii
The Singular Value Decomposition (SVD) and Principal Component Analysis (PCA)
 Chapter 5 The Singular Value Decomposition (SVD) and Principal Component Analysis (PCA) 5.1 Basics of SVD 5.1.1 Review of Key Concepts We review some key definitions and results about matrices that will
Chapter 5 The Singular Value Decomposition (SVD) and Principal Component Analysis (PCA) 5.1 Basics of SVD 5.1.1 Review of Key Concepts We review some key definitions and results about matrices that will
Using semiseparable matrices to compute the SVD of a general matrix product/quotient
 Using semiseparable matrices to compute the SVD of a general matrix product/quotient Marc Van Barel Yvette Vanberghen Paul Van Dooren Report TW 508, November 007 n Katholieke Universiteit Leuven Department
Using semiseparable matrices to compute the SVD of a general matrix product/quotient Marc Van Barel Yvette Vanberghen Paul Van Dooren Report TW 508, November 007 n Katholieke Universiteit Leuven Department
Applied Linear Algebra in Geoscience Using MATLAB
 Applied Linear Algebra in Geoscience Using MATLAB Contents Getting Started Creating Arrays Mathematical Operations with Arrays Using Script Files and Managing Data Two-Dimensional Plots Programming in
Applied Linear Algebra in Geoscience Using MATLAB Contents Getting Started Creating Arrays Mathematical Operations with Arrays Using Script Files and Managing Data Two-Dimensional Plots Programming in
Principal Component Analysis
 Machine Learning Michaelmas 2017 James Worrell Principal Component Analysis 1 Introduction 1.1 Goals of PCA Principal components analysis (PCA) is a dimensionality reduction technique that can be used
Machine Learning Michaelmas 2017 James Worrell Principal Component Analysis 1 Introduction 1.1 Goals of PCA Principal components analysis (PCA) is a dimensionality reduction technique that can be used
Review of some mathematical tools
 MATHEMATICAL FOUNDATIONS OF SIGNAL PROCESSING Fall 2016 Benjamín Béjar Haro, Mihailo Kolundžija, Reza Parhizkar, Adam Scholefield Teaching assistants: Golnoosh Elhami, Hanjie Pan Review of some mathematical
MATHEMATICAL FOUNDATIONS OF SIGNAL PROCESSING Fall 2016 Benjamín Béjar Haro, Mihailo Kolundžija, Reza Parhizkar, Adam Scholefield Teaching assistants: Golnoosh Elhami, Hanjie Pan Review of some mathematical
Linear Algebra Review. Vectors
 Linear Algebra Review 9/4/7 Linear Algebra Review By Tim K. Marks UCSD Borrows heavily from: Jana Kosecka http://cs.gmu.edu/~kosecka/cs682.html Virginia de Sa (UCSD) Cogsci 8F Linear Algebra review Vectors
Linear Algebra Review 9/4/7 Linear Algebra Review By Tim K. Marks UCSD Borrows heavily from: Jana Kosecka http://cs.gmu.edu/~kosecka/cs682.html Virginia de Sa (UCSD) Cogsci 8F Linear Algebra review Vectors
Multiplicative Perturbation Bounds of the Group Inverse and Oblique Projection
 Filomat 30: 06, 37 375 DOI 0.98/FIL67M Published by Faculty of Sciences Mathematics, University of Niš, Serbia Available at: http://www.pmf.ni.ac.rs/filomat Multiplicative Perturbation Bounds of the Group
Filomat 30: 06, 37 375 DOI 0.98/FIL67M Published by Faculty of Sciences Mathematics, University of Niš, Serbia Available at: http://www.pmf.ni.ac.rs/filomat Multiplicative Perturbation Bounds of the Group
Scientific Computing: An Introductory Survey
 Scientific Computing: An Introductory Survey Chapter 4 Eigenvalue Problems Prof. Michael T. Heath Department of Computer Science University of Illinois at Urbana-Champaign Copyright c 2002. Reproduction
Scientific Computing: An Introductory Survey Chapter 4 Eigenvalue Problems Prof. Michael T. Heath Department of Computer Science University of Illinois at Urbana-Champaign Copyright c 2002. Reproduction
Math 411 Preliminaries
 Math 411 Preliminaries Provide a list of preliminary vocabulary and concepts Preliminary Basic Netwon s method, Taylor series expansion (for single and multiple variables), Eigenvalue, Eigenvector, Vector
Math 411 Preliminaries Provide a list of preliminary vocabulary and concepts Preliminary Basic Netwon s method, Taylor series expansion (for single and multiple variables), Eigenvalue, Eigenvector, Vector
Multiplicative Perturbation Analysis for QR Factorizations
 Multiplicative Perturbation Analysis for QR Factorizations Xiao-Wen Chang Ren-Cang Li Technical Report 011-01 http://www.uta.edu/math/preprint/ Multiplicative Perturbation Analysis for QR Factorizations
Multiplicative Perturbation Analysis for QR Factorizations Xiao-Wen Chang Ren-Cang Li Technical Report 011-01 http://www.uta.edu/math/preprint/ Multiplicative Perturbation Analysis for QR Factorizations
EIGENVALUE PROBLEMS. EIGENVALUE PROBLEMS p. 1/4
 EIGENVALUE PROBLEMS EIGENVALUE PROBLEMS p. 1/4 EIGENVALUE PROBLEMS p. 2/4 Eigenvalues and eigenvectors Let A C n n. Suppose Ax = λx, x 0, then x is a (right) eigenvector of A, corresponding to the eigenvalue
EIGENVALUE PROBLEMS EIGENVALUE PROBLEMS p. 1/4 EIGENVALUE PROBLEMS p. 2/4 Eigenvalues and eigenvectors Let A C n n. Suppose Ax = λx, x 0, then x is a (right) eigenvector of A, corresponding to the eigenvalue
Linear Algebra Massoud Malek
 CSUEB Linear Algebra Massoud Malek Inner Product and Normed Space In all that follows, the n n identity matrix is denoted by I n, the n n zero matrix by Z n, and the zero vector by θ n An inner product
CSUEB Linear Algebra Massoud Malek Inner Product and Normed Space In all that follows, the n n identity matrix is denoted by I n, the n n zero matrix by Z n, and the zero vector by θ n An inner product
MATH 350: Introduction to Computational Mathematics
 MATH 350: Introduction to Computational Mathematics Chapter V: Least Squares Problems Greg Fasshauer Department of Applied Mathematics Illinois Institute of Technology Spring 2011 fasshauer@iit.edu MATH
MATH 350: Introduction to Computational Mathematics Chapter V: Least Squares Problems Greg Fasshauer Department of Applied Mathematics Illinois Institute of Technology Spring 2011 fasshauer@iit.edu MATH
Krylov Subspace Methods for Large/Sparse Eigenvalue Problems
 Krylov Subspace Methods for Large/Sparse Eigenvalue Problems Tsung-Ming Huang Department of Mathematics National Taiwan Normal University, Taiwan April 17, 2012 T.-M. Huang (Taiwan Normal University) Krylov
Krylov Subspace Methods for Large/Sparse Eigenvalue Problems Tsung-Ming Huang Department of Mathematics National Taiwan Normal University, Taiwan April 17, 2012 T.-M. Huang (Taiwan Normal University) Krylov
Katholieke Universiteit Leuven Department of Computer Science
 Orthogonal similarity transformation of a symmetric matrix into a diagonal-plus-semiseparable one with free choice of the diagonal Raf Vandebril, Ellen Van Camp, Marc Van Barel, Nicola Mastronardi Report
Orthogonal similarity transformation of a symmetric matrix into a diagonal-plus-semiseparable one with free choice of the diagonal Raf Vandebril, Ellen Van Camp, Marc Van Barel, Nicola Mastronardi Report
1 Singular Value Decomposition and Principal Component
 Singular Value Decomposition and Principal Component Analysis In these lectures we discuss the SVD and the PCA, two of the most widely used tools in machine learning. Principal Component Analysis (PCA)
Singular Value Decomposition and Principal Component Analysis In these lectures we discuss the SVD and the PCA, two of the most widely used tools in machine learning. Principal Component Analysis (PCA)
Applied Mathematics 205. Unit II: Numerical Linear Algebra. Lecturer: Dr. David Knezevic
 Applied Mathematics 205 Unit II: Numerical Linear Algebra Lecturer: Dr. David Knezevic Unit II: Numerical Linear Algebra Chapter II.3: QR Factorization, SVD 2 / 66 QR Factorization 3 / 66 QR Factorization
Applied Mathematics 205 Unit II: Numerical Linear Algebra Lecturer: Dr. David Knezevic Unit II: Numerical Linear Algebra Chapter II.3: QR Factorization, SVD 2 / 66 QR Factorization 3 / 66 QR Factorization
ON THE QR ITERATIONS OF REAL MATRICES
 Unspecified Journal Volume, Number, Pages S????-????(XX- ON THE QR ITERATIONS OF REAL MATRICES HUAJUN HUANG AND TIN-YAU TAM Abstract. We answer a question of D. Serre on the QR iterations of a real matrix
Unspecified Journal Volume, Number, Pages S????-????(XX- ON THE QR ITERATIONS OF REAL MATRICES HUAJUN HUANG AND TIN-YAU TAM Abstract. We answer a question of D. Serre on the QR iterations of a real matrix
Lecture 3: Review of Linear Algebra
 ECE 83 Fall 2 Statistical Signal Processing instructor: R Nowak Lecture 3: Review of Linear Algebra Very often in this course we will represent signals as vectors and operators (eg, filters, transforms,
ECE 83 Fall 2 Statistical Signal Processing instructor: R Nowak Lecture 3: Review of Linear Algebra Very often in this course we will represent signals as vectors and operators (eg, filters, transforms,
Linear Algebra. Session 12
 Linear Algebra. Session 12 Dr. Marco A Roque Sol 08/01/2017 Example 12.1 Find the constant function that is the least squares fit to the following data x 0 1 2 3 f(x) 1 0 1 2 Solution c = 1 c = 0 f (x)
Linear Algebra. Session 12 Dr. Marco A Roque Sol 08/01/2017 Example 12.1 Find the constant function that is the least squares fit to the following data x 0 1 2 3 f(x) 1 0 1 2 Solution c = 1 c = 0 f (x)
p q m p q p q m p q p Σ q 0 I p Σ 0 0, n 2p q
 A NUMERICAL METHOD FOR COMPUTING AN SVD-LIKE DECOMPOSITION HONGGUO XU Abstract We present a numerical method to compute the SVD-like decomposition B = QDS 1 where Q is orthogonal S is symplectic and D
A NUMERICAL METHOD FOR COMPUTING AN SVD-LIKE DECOMPOSITION HONGGUO XU Abstract We present a numerical method to compute the SVD-like decomposition B = QDS 1 where Q is orthogonal S is symplectic and D
Recycling Bi-Lanczos Algorithms: BiCG, CGS, and BiCGSTAB
 Recycling Bi-Lanczos Algorithms: BiCG, CGS, and BiCGSTAB Kapil Ahuja Thesis submitted to the Faculty of the Virginia Polytechnic Institute and State University in partial fulfillment of the requirements
Recycling Bi-Lanczos Algorithms: BiCG, CGS, and BiCGSTAB Kapil Ahuja Thesis submitted to the Faculty of the Virginia Polytechnic Institute and State University in partial fulfillment of the requirements
AMS526: Numerical Analysis I (Numerical Linear Algebra for Computational and Data Sciences)
 AMS526: Numerical Analysis I (Numerical Linear Algebra for Computational and Data Sciences) Lecture 1: Course Overview; Matrix Multiplication Xiangmin Jiao Stony Brook University Xiangmin Jiao Numerical
AMS526: Numerical Analysis I (Numerical Linear Algebra for Computational and Data Sciences) Lecture 1: Course Overview; Matrix Multiplication Xiangmin Jiao Stony Brook University Xiangmin Jiao Numerical
Lecture 3: Review of Linear Algebra
 ECE 83 Fall 2 Statistical Signal Processing instructor: R Nowak, scribe: R Nowak Lecture 3: Review of Linear Algebra Very often in this course we will represent signals as vectors and operators (eg, filters,
ECE 83 Fall 2 Statistical Signal Processing instructor: R Nowak, scribe: R Nowak Lecture 3: Review of Linear Algebra Very often in this course we will represent signals as vectors and operators (eg, filters,
REORTHOGONALIZATION FOR GOLUB KAHAN LANCZOS BIDIAGONAL REDUCTION: PART II SINGULAR VECTORS
 REORTHOGONALIZATION FOR GOLUB KAHAN LANCZOS BIDIAGONAL REDUCTION: PART II SINGULAR VECTORS JESSE L. BARLOW Department of Computer Science and Engineering, The Pennsylvania State University, University
REORTHOGONALIZATION FOR GOLUB KAHAN LANCZOS BIDIAGONAL REDUCTION: PART II SINGULAR VECTORS JESSE L. BARLOW Department of Computer Science and Engineering, The Pennsylvania State University, University
A HARMONIC RESTARTED ARNOLDI ALGORITHM FOR CALCULATING EIGENVALUES AND DETERMINING MULTIPLICITY
 A HARMONIC RESTARTED ARNOLDI ALGORITHM FOR CALCULATING EIGENVALUES AND DETERMINING MULTIPLICITY RONALD B. MORGAN AND MIN ZENG Abstract. A restarted Arnoldi algorithm is given that computes eigenvalues
A HARMONIC RESTARTED ARNOLDI ALGORITHM FOR CALCULATING EIGENVALUES AND DETERMINING MULTIPLICITY RONALD B. MORGAN AND MIN ZENG Abstract. A restarted Arnoldi algorithm is given that computes eigenvalues
DELFT UNIVERSITY OF TECHNOLOGY
 DELFT UNIVERSITY OF TECHNOLOGY REPORT 10-12 Large-Scale Eigenvalue Problems in Trust-Region Calculations Marielba Rojas, Bjørn H. Fotland, and Trond Steihaug ISSN 1389-6520 Reports of the Department of
DELFT UNIVERSITY OF TECHNOLOGY REPORT 10-12 Large-Scale Eigenvalue Problems in Trust-Region Calculations Marielba Rojas, Bjørn H. Fotland, and Trond Steihaug ISSN 1389-6520 Reports of the Department of
AN INVERSE EIGENVALUE PROBLEM AND AN ASSOCIATED APPROXIMATION PROBLEM FOR GENERALIZED K-CENTROHERMITIAN MATRICES
 AN INVERSE EIGENVALUE PROBLEM AND AN ASSOCIATED APPROXIMATION PROBLEM FOR GENERALIZED K-CENTROHERMITIAN MATRICES ZHONGYUN LIU AND HEIKE FAßBENDER Abstract: A partially described inverse eigenvalue problem
AN INVERSE EIGENVALUE PROBLEM AND AN ASSOCIATED APPROXIMATION PROBLEM FOR GENERALIZED K-CENTROHERMITIAN MATRICES ZHONGYUN LIU AND HEIKE FAßBENDER Abstract: A partially described inverse eigenvalue problem
Elementary linear algebra
 Chapter 1 Elementary linear algebra 1.1 Vector spaces Vector spaces owe their importance to the fact that so many models arising in the solutions of specific problems turn out to be vector spaces. The
Chapter 1 Elementary linear algebra 1.1 Vector spaces Vector spaces owe their importance to the fact that so many models arising in the solutions of specific problems turn out to be vector spaces. The
Institute for Computational Mathematics Hong Kong Baptist University
 Institute for Computational Mathematics Hong Kong Baptist University ICM Research Report 08-0 How to find a good submatrix S. A. Goreinov, I. V. Oseledets, D. V. Savostyanov, E. E. Tyrtyshnikov, N. L.
Institute for Computational Mathematics Hong Kong Baptist University ICM Research Report 08-0 How to find a good submatrix S. A. Goreinov, I. V. Oseledets, D. V. Savostyanov, E. E. Tyrtyshnikov, N. L.
A Randomized Algorithm for the Approximation of Matrices
 A Randomized Algorithm for the Approximation of Matrices Per-Gunnar Martinsson, Vladimir Rokhlin, and Mark Tygert Technical Report YALEU/DCS/TR-36 June 29, 2006 Abstract Given an m n matrix A and a positive
A Randomized Algorithm for the Approximation of Matrices Per-Gunnar Martinsson, Vladimir Rokhlin, and Mark Tygert Technical Report YALEU/DCS/TR-36 June 29, 2006 Abstract Given an m n matrix A and a positive
QR-decomposition. The QR-decomposition of an n k matrix A, k n, is an n n unitary matrix Q and an n k upper triangular matrix R for which A = QR
 QR-decomposition The QR-decomposition of an n k matrix A, k n, is an n n unitary matrix Q and an n k upper triangular matrix R for which In Matlab A = QR [Q,R]=qr(A); Note. The QR-decomposition is unique
QR-decomposition The QR-decomposition of an n k matrix A, k n, is an n n unitary matrix Q and an n k upper triangular matrix R for which In Matlab A = QR [Q,R]=qr(A); Note. The QR-decomposition is unique
Notes on Householder QR Factorization
 Notes on Householder QR Factorization Robert A van de Geijn Department of Computer Science he University of exas at Austin Austin, X 7872 rvdg@csutexasedu September 2, 24 Motivation A fundamental problem
Notes on Householder QR Factorization Robert A van de Geijn Department of Computer Science he University of exas at Austin Austin, X 7872 rvdg@csutexasedu September 2, 24 Motivation A fundamental problem
Applied Linear Algebra in Geoscience Using MATLAB
 Applied Linear Algebra in Geoscience Using MATLAB Contents Getting Started Creating Arrays Mathematical Operations with Arrays Using Script Files and Managing Data Two-Dimensional Plots Programming in
Applied Linear Algebra in Geoscience Using MATLAB Contents Getting Started Creating Arrays Mathematical Operations with Arrays Using Script Files and Managing Data Two-Dimensional Plots Programming in
We will discuss matrix diagonalization algorithms in Numerical Recipes in the context of the eigenvalue problem in quantum mechanics, m A n = λ m
 Eigensystems We will discuss matrix diagonalization algorithms in umerical Recipes in the context of the eigenvalue problem in quantum mechanics, A n = λ n n, (1) where A is a real, symmetric Hamiltonian
Eigensystems We will discuss matrix diagonalization algorithms in umerical Recipes in the context of the eigenvalue problem in quantum mechanics, A n = λ n n, (1) where A is a real, symmetric Hamiltonian
Cuppen s Divide and Conquer Algorithm
 Chapter 4 Cuppen s Divide and Conquer Algorithm In this chapter we deal with an algorithm that is designed for the efficient solution of the symmetric tridiagonal eigenvalue problem a b (4) x λx, b a bn
Chapter 4 Cuppen s Divide and Conquer Algorithm In this chapter we deal with an algorithm that is designed for the efficient solution of the symmetric tridiagonal eigenvalue problem a b (4) x λx, b a bn
Permutation transformations of tensors with an application
 DOI 10.1186/s40064-016-3720-1 RESEARCH Open Access Permutation transformations of tensors with an application Yao Tang Li *, Zheng Bo Li, Qi Long Liu and Qiong Liu *Correspondence: liyaotang@ynu.edu.cn
DOI 10.1186/s40064-016-3720-1 RESEARCH Open Access Permutation transformations of tensors with an application Yao Tang Li *, Zheng Bo Li, Qi Long Liu and Qiong Liu *Correspondence: liyaotang@ynu.edu.cn
Numerical Solution of Linear Eigenvalue Problems
 Numerical Solution of Linear Eigenvalue Problems Jessica Bosch and Chen Greif Abstract We review numerical methods for computing eigenvalues of matrices We start by considering the computation of the dominant
Numerical Solution of Linear Eigenvalue Problems Jessica Bosch and Chen Greif Abstract We review numerical methods for computing eigenvalues of matrices We start by considering the computation of the dominant
Analysis of Block LDL T Factorizations for Symmetric Indefinite Matrices
 Analysis of Block LDL T Factorizations for Symmetric Indefinite Matrices Haw-ren Fang August 24, 2007 Abstract We consider the block LDL T factorizations for symmetric indefinite matrices in the form LBL
Analysis of Block LDL T Factorizations for Symmetric Indefinite Matrices Haw-ren Fang August 24, 2007 Abstract We consider the block LDL T factorizations for symmetric indefinite matrices in the form LBL
Homework 1. Yuan Yao. September 18, 2011
 Homework 1 Yuan Yao September 18, 2011 1. Singular Value Decomposition: The goal of this exercise is to refresh your memory about the singular value decomposition and matrix norms. A good reference to
Homework 1 Yuan Yao September 18, 2011 1. Singular Value Decomposition: The goal of this exercise is to refresh your memory about the singular value decomposition and matrix norms. A good reference to
INTERLACING PROPERTIES FOR HERMITIAN MATRICES WHOSE GRAPH IS A GIVEN TREE
 INTERLACING PROPERTIES FOR HERMITIAN MATRICES WHOSE GRAPH IS A GIVEN TREE C M DA FONSECA Abstract We extend some interlacing properties of the eigenvalues of tridiagonal matrices to Hermitian matrices
INTERLACING PROPERTIES FOR HERMITIAN MATRICES WHOSE GRAPH IS A GIVEN TREE C M DA FONSECA Abstract We extend some interlacing properties of the eigenvalues of tridiagonal matrices to Hermitian matrices
Introduction. Chapter One
 Chapter One Introduction The aim of this book is to describe and explain the beautiful mathematical relationships between matrices, moments, orthogonal polynomials, quadrature rules and the Lanczos and
Chapter One Introduction The aim of this book is to describe and explain the beautiful mathematical relationships between matrices, moments, orthogonal polynomials, quadrature rules and the Lanczos and
5 Selected Topics in Numerical Linear Algebra
 5 Selected Topics in Numerical Linear Algebra In this chapter we will be concerned mostly with orthogonal factorizations of rectangular m n matrices A The section numbers in the notes do not align with
5 Selected Topics in Numerical Linear Algebra In this chapter we will be concerned mostly with orthogonal factorizations of rectangular m n matrices A The section numbers in the notes do not align with
1 Eigenvalues and eigenvectors
 1 Eigenvalues and eigenvectors 1.1 Introduction A non-zero column-vector v is called the eigenvector of a matrix A with the eigenvalue λ, if Av = λv. (1) If an n n matrix A is real and symmetric, A T =
1 Eigenvalues and eigenvectors 1.1 Introduction A non-zero column-vector v is called the eigenvector of a matrix A with the eigenvalue λ, if Av = λv. (1) If an n n matrix A is real and symmetric, A T =
On Powers of General Tridiagonal Matrices
 Applied Mathematical Sciences, Vol. 9, 5, no., 583-59 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/.988/ams.5.49 On Powers of General Tridiagonal Matrices Qassem M. Al-Hassan Department of Mathematics
Applied Mathematical Sciences, Vol. 9, 5, no., 583-59 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/.988/ams.5.49 On Powers of General Tridiagonal Matrices Qassem M. Al-Hassan Department of Mathematics
The Solvability Conditions for the Inverse Eigenvalue Problem of Hermitian and Generalized Skew-Hamiltonian Matrices and Its Approximation
 The Solvability Conditions for the Inverse Eigenvalue Problem of Hermitian and Generalized Skew-Hamiltonian Matrices and Its Approximation Zheng-jian Bai Abstract In this paper, we first consider the inverse
The Solvability Conditions for the Inverse Eigenvalue Problem of Hermitian and Generalized Skew-Hamiltonian Matrices and Its Approximation Zheng-jian Bai Abstract In this paper, we first consider the inverse
THE PERTURBATION BOUND FOR THE SPECTRAL RADIUS OF A NON-NEGATIVE TENSOR
 THE PERTURBATION BOUND FOR THE SPECTRAL RADIUS OF A NON-NEGATIVE TENSOR WEN LI AND MICHAEL K. NG Abstract. In this paper, we study the perturbation bound for the spectral radius of an m th - order n-dimensional
THE PERTURBATION BOUND FOR THE SPECTRAL RADIUS OF A NON-NEGATIVE TENSOR WEN LI AND MICHAEL K. NG Abstract. In this paper, we study the perturbation bound for the spectral radius of an m th - order n-dimensional
Matrix Theory, Math6304 Lecture Notes from October 25, 2012
 Matrix Theory, Math6304 Lecture Notes from October 25, 2012 taken by John Haas Last Time (10/23/12) Example of Low Rank Perturbation Relationship Between Eigenvalues and Principal Submatrices: We started
Matrix Theory, Math6304 Lecture Notes from October 25, 2012 taken by John Haas Last Time (10/23/12) Example of Low Rank Perturbation Relationship Between Eigenvalues and Principal Submatrices: We started
Performance Evaluation of Some Inverse Iteration Algorithms on PowerXCell T M 8i Processor
 Performance Evaluation of Some Inverse Iteration Algorithms on PowerXCell T M 8i Processor Masami Takata 1, Hiroyuki Ishigami 2, Kini Kimura 2, and Yoshimasa Nakamura 2 1 Academic Group of Information
Performance Evaluation of Some Inverse Iteration Algorithms on PowerXCell T M 8i Processor Masami Takata 1, Hiroyuki Ishigami 2, Kini Kimura 2, and Yoshimasa Nakamura 2 1 Academic Group of Information
