(U) vanishes. A special case of system (1.1), (1.2) is given by the equations for compressible flow in a variable area duct, a ρv2,
|
|
|
- Juniper Stevenson
- 5 years ago
- Views:
Transcription
1 MEHODS AND APPLICAIONS OF ANALYSIS. c 2003 Intenational Pe Vol. 10, No. 2, pp , June HE GENERIC SOLUION OF HE RIEMANN PROBLEM IN A NEIGHBORHOOD OF A POIN OF RESONANCE FOR SYSEMS OF NONLINEAR BALANCE LAWS JOHN HONG AND BLAKE EMPLE Abtact. We decibe the geneic olution of the Riemann poblem nea a point of eonance in a geneal 2x2 ytem of balance law coupled to a tationay ouce. he ouce i teated a a coneved quantity in an augmented 3x3 ytem, and Reonance i between a nonlinea wave family and the tationay ouce. anonic compeible Eule flow in a vaiable aea duct, a well a pheically ymmetic flow, ae hown to be pecial cae of the geneal cla of equation tudied hee. 1. Intoduction. We conide a geneal 3x3 ytem of balance law of the fom (1.1) (1.2) a t = 0, w t + f(a,w) x = a g(a,w), whee (1.2) i a 2 2 ytem of conevation law, w = (u,v) (w 1,w 2 ), f = (f 1,f 2 ), g = (g 1,g 2 ) and (1.1) i incopoated to model eonance between a tationay ouce a(x) R and one of the nonlinea wave familie of (1.2). Letting U = (a,u,v), ytem (1.1), (1.2) i equivalent to the 3 3 ytem (1.3) U t + F(U) x = a G(U), whee F = (0,f 1,f 2 ) and G = (0,g 1,g 2 ). Reonance occu at tate U = (a,w ) whee an eigenvalue of Df Dw (U) vanihe. A pecial cae of ytem (1.1), (1.2) i given by the equation fo compeible flow in a vaiable aea duct, (1.4) (1.5) (1.6) a t = 0, ρ t + (ρv) x = a a ρv, (ρv) t + (ρv 2 + p) x = a a ρv2, whee ρ i the denity, p i the peue, v i the velocity, and a(x) i the diamete of the duct at poition x. Sytem (1.4)-(1.6) eult unde the aumption that p i a function of ρ alone, in which cae the enegy equation (ρe) t + (ρev + pv) x = a a (ρev + pv) uncouple fom the ma and momentum equation (1.5) and (1.6). Spheically ymmetic n-dimenional flow aie when a a = n 1 x. Sytem (1.4)-(1.6) i a 2 2 ytem with ouce of fom (1.1), (1.2), and the condition of eonance Received Febuay 18, 2003; accepted fo publication Augut 15, Depatment of Mathematic, UCLA, Lo Angele, CA , USA (jhong@math.ucla.edu). Depatment of Mathematic, Univeity of Califonia, Davi, Davi CA 95616, USA (jbtemple@ucdavi.edu). Suppoted in pat by NSF Applied Mathematic Gant Numbe DMS and by the Intitute of heoetical Dynamic, UC-Davi. 279
2 280 J. HONG AND B. EMPLE fo ytem (1.4)-(1.6) tanlate into the tatement that the flow i tanonic in a neighbohood of U, [2]. Hee we identify natual geneic condition on f and g at a point of eonance U in ytem (1.1), (1.2) that guaantee a canonical olution of the Riemann poblem in a neighbohood of U, and we then peent the olution. A a pecial cae we how that thee condition ae met by ytem (1.4)-(1.6) howeve, with a diffeent choice of ign, qualitatively diffeent olution ae poible. By identifying the geneic local tuctue of the Riemann poblem nea a point of eonance, we accomplih a peliminay tep in ou pogam to extend the eult in [7] to ytem; that i, ou pogam i to obtain a time independent etimate fo the total vaiation of the coneved quantitie nea a point of eonance by analyzing appoximate Glimm cheme olution of ytem (1.3). Note that becaue of the peence of the a tem in (1.2), the Riemann poblem, (the initial value poblem when the data i given by piecewie contant tate), appea to be ingula when a i dicontinuou. Howeve, becaue of a e-caling popety of tanding wave fo ytem of fom (1.2), the Riemann poblem eally doe give the elementay wave that povide the building block fo moe geneal olution. Fo example, in [6] it wa hown that Glimm analyi of wave inteaction and the local total vaiation bound extend to thee ingula Riemann poblem fo n n tictly hypebolic ytem of fom (1.2), and convegence of the Glimm Scheme i poven fo Lipchitz continuou a, (the cae when the weak fomulation of (1.2) applie). Inteetingly, the eidual convege weakly, by ocillation, athe than by L 1 convegence a in Glimm oiginal pape. hee eult wee extended to eonant cala balance law in [7]. 2. Geneic Condition. We dicu geneic condition on the function f(u), g(u) fo ytem (1.1), (1.2), that guaantee a canonical olution of the Riemann poblem nea a point of eonance U. hi i pepaatoy to the peentation of the olution of the Riemann poblem in the next ection. o tat, let λ i λ i (a,w) denote the eigenvalue, and R i R i (a,w), L i L i (a,w) coeponding ight and left eigenvecto, epectively, fo the 2 2 matix Df Dw ( fi w j ) at fixed a, i,j = 1,2. Let Dg Dw ( gi w j ), the diffeential holding a contant. (We will nomalize R i, L i below, but the condition to follow ae independent of nomalization). We aume the following fou geneic condition hold at the tate U : (2.1) 0 = λ 1 (U ) < λ 2 (U ), (2.2) λ i R i U=U 0, i = 1,2, (2.3) L i (g f a ) U=U 0, i = 1,2, (2.4) [ L1 (g f Det a ), L 1 Dg Dw R 1 L 2 (g f a ), L 2 Dg Dw R 1. ] 0.
3 RESONAN NONLINEAR SYSEMS OF CONSERVAION LAWS 281 Ou main eult can be tated a follow: heoem 1. Aume that ytem (1.1), (1.2) atifie (2.1)-(2.4) at the tate U = U. hen the olution of the Riemann poblem ha a unique canonical tuctue in a neighbohood of the tate U, thi being explicitly given in the Figue below. Befoe we contuct the olution of the Riemann poblem fo ytem (1.1), (1.2) in a neighbohood of U, unde aumption (2.1)-(2.3), we fit veify (2.1)-(2.4) fo the ga dynamic example (1.5), (1.6) when U = (a,u,v) (a,ρ,ρv), f(u) = (ρv,ρv 2 +p), and g(u) = ( ρv a, ρv2 a ). he eigenvalue and ight eigenvecto fo ytem (1.5), (1.6) at fixed a ae given by, (2.5) λ 1 = v σ, λ 2 = v + σ, (2.6) R 1 = (1,λ 1 ) t, R 2 = (1,λ 2 ) t, whee the ound peed σ i given by (2.7) σ = p (ρ). Since the left eigenvecto atify L i R j = 0, i j, we can chooe (2.8) L 1 = 1 ρ ( λ 2,1), L 2 = 1 ρ ( λ 1,1). he coodinate ytem of Riemann invaiant (,) can be defined in tem of L 1 and L 2 by (2.9) = L 1, = L 2, which yield (2.10) = v = v + ρ ρ p ρ, p ρ. Fom (2.5)-(2.7) it follow that aumption (2.1)-(2.4) epectively tanlate into the following condition at U = (a,u,v ), (we aume equation of tate p = p(ρ), p (ρ) > 0, p (ρ) > 0): (2.11) u = σ = p (ρ ), (2.12) { p λ i R i = 2σ + σ } > 0, i = 1,2, ρ
4 282 J. HONG AND B. EMPLE (2.13) (2.14) L 1 (g f a ) = 1 ρ ( λ 2,1) ( ρv a, ρv2 a ) = vσ a > 0, L 2 (g f a ) = 1 ρ ( λ 1,1) ( ρv a, ρv2 a ) = vσ a < 0. Finally, to veify (2.4), wite (2.15) (2.16) L 1 Dg Dw = 1 ρ ( λ 2,1) L 2 Dg Dw = 1 ρ ( λ 1,1) [ 0 1 a v 2 a 2v a [ 0 1 a v 2 a 2v a It follow that at U = U, λ 1 = 0, and o we have ] ] = 1 aρ (v2,λ 2 2v), = 1 aρ (v2,λ 1 2v). (2.17) (2.18) L 1 Dg Dw R 1 = 1 aρ ( v2 + λ 2 1) = v2 aρ < 0, L 2 Dg Dw R 1 = 1 aρ ( v2 + λ 1 λ 2 ) = v2 aρ < 0. he condition (2.4) now follow fom (2.13), (2.14) and (2.15), (2.18). 3. he Riemann Poblem. he Riemann poblem i the initial value poblem with initial data given at t = 0 by the jump dicontinuity (3.1) U 0 (x) = { UL = (a L,u L ) if x < 0, U R = (a R,u R ) if x > 0. We deive the olution of (3.1) fo ytem (1.1), (1.2) within the cla of elementay wave, hock wave, aefaction wave and tanding wave. It i eaiet to diplay the olution in a coodinate ytem of Riemann invaiant, whee, with convenient convention fo R i, L i, the olution ha a unique local tuctue. At each fixed a, ytem (1.2) i a 2 2 ytem of conevation law, and thu, ince the tate pace i the plane, thee exit a coodinate ytem of Riemann invaiant (,). Chooe (,) uch that L 1 = ( u, v ), and imilaly, L 2 =. Alo, let {U : λ 1 (U) = 0} denote the tanition uface. hi i the uface whee the peed of 1-aefaction wave change thei ign elative to the local peed of tanding wave, c.f. [8]. Since λ 1 0, it follow that i a mooth one dimenional uface paing though the bae point U = U and tanveal to R 1 at that point, and hence the one wave cuve cut the tanition uface tanveally in a neighbohood of U. Fo convenience, chooe the ign in (2.1)-(2.3) o that they agee with the ign in the ga dynamic example (2.11)-(2.13). hat i, aume (3.2) λ 1 R 1 > 0, (3.3) L 1 (g f a ) U=U > 0,
5 RESONAN NONLINEAR SYSEMS OF CONSERVAION LAWS 283 (3.4) L 2 (g f a ) U=U < 0. Unde thee aumption, the olution of the Riemann poblem i diagammed in the figue below. Befoe dicuing the olution of the Riemann poblem, we fit how that thee i no lo of geneality in the choice of ign (3.2)-(3.4), and dicu the ignificance of the ign in (2.4). o tat, note that we can fix the ign in (3.2) by chooing the oientation of R 1. We next how that the ign in (3.3) and (3.4) fix the convexity of tanding wave cuve elative to the and coodinate axe, and the ign in (2.4) then detemine whethe the zeo peed hock cuve, (c.f. [7]), lie inide o outide the coeponding tanding wave cuve, both of which eminate fom the ame point on the tanition uface. Moe peciely, we how that (3.3) fixe the ign of d2 a d, and then (3.4) 2 fixe the ign of d2 d at the point whee a tanding wave cuve U 2 () coe the tanition uface λ 1 = 0. hen, with the choice of ign in (3.2)-(3.4), we how that the negative, [epectively poitive], ign in (2.4) implie that zeo peed hock cuve, which emanate fom point on the tanition uface, beak to the inide, [epectively outide], of the coeponding tanding wave cuve that emanate fom the ame point on the tanition uface, in a neighbohood of U = U, c.f. [7]. o thi end, let U (x) (a (x),w (x)) denote a tanding wave cuve, obtained fom (1.3) by auming no tempoal dependence. hat i, U atifie (3.5) Df Dw dw = (g f a)da. Multiplying by L i on the left, i = 1,2, we obtain (3.6) (3.7) λ 1 L 1 dw = L 1 (g f a )da, λ 2 L 2 dw = L 2 (g f a )da. Uing L 1 dw = d, L 2 dw = d, we obtain (3.8) (3.9) λ 1 d = L 1 (g f a )da, λ 2 d = L 2 (g f a )da, which lead to (3.10) (3.11) da d = λ 1 L 1 (g f a ), d d = λ 1 {L 2 (g f a )} λ 2 {L 1 (g f a )}. Note that (3.10) implie that tanding wave cuve ae tangent to 1-wave cuve at the tanition uface λ 1 = 0. We now how that (3.4) implie that thi tangency i quadatic. (Since hock wave cuve have cubic tangency with aefaction cuve, thi implie that hock cuve emanating fom left tate on U and coing into
6 284 J. HONG AND B. EMPLE the convex ide of the tanding wave cuve, mut co the tanding wave cuve at a unique point on the oppoite ide of ). So conide the tanding wave cuve at a point on the tanition uface. hen (3.10), (3.11) and (3.3) imply that (3.12) (3.13) d 2 a d 2 = 1 dλ 1 L 1 (g f a ) d > 0, d 2 d 2 = L 2 (g f a ) dλ 1 λ 2 L 1 (g f a ) d < 0, give the cuvatue in a and of the tanding wave cuve at a point on the tanition uface. By (3.12), we have hown that (3.3) detemine the ign of d2 a d, and (3.4) 2 detemine the ign of d2 d along a tanding wave cuve at the point whee it coe 2 the tanition uface, a claimed. We can now how that (2.4) detemine whethe the zeo peed hock cuve beak to the left o to the ight of the tanding wave cuve at the point on the tanition uface at which they emanate. o define the zeo peed hock cuve, tat with a fixed tanding wave cuve U (). hi cuve coe the tanition uface at a unique point in a neighbohood of U, and o a not to intoduce moe notation, aume without lo of geneality that thi point i U itelf. By ou ign convention, the wave peed λ 1 inceae moving to the ight though the tanition uface, (that i, towad inceaing ), along the tanding wave cuve U () in the (,)-plane. Conide the potion of a tanding wave cuve that lie to the ight of the tanition uface; that i, conide U () = (a (),u (),v ()) fo >, whee U ( ) = U. hen λ 1 inceae fom λ 1 (U ) = 0 a inceae fom = along U (), and thu it follow that fo each >, thee i a unique tate Ũ() on the left of the tanition uface uch that the hock [U (),Ũ()] i a zeo peed hock when the left tate of the hock i U () and the ight tate i Ũ(). We call the cuve Ũ() the zeo peed hock cuve aociated with the tanding wave cuve U (). (hi i diagammed in Figue 1 and 2, in the cae when the tanding wave cuve lie to the left and ight of the zeo peed hock cuve, epectively, auming nomalization (3.2)-(3.4). he dotted line denote the zeo peed hock cuve, and it aociated tanding wave cuve i dawn a the paabolic cuve though tate U U. Ou convention i that the zeo peed hock cuve i paameteized by value of > that paameteize U on the ight of, and obeve that U () and Ũ() ae cuve that lie at the ame value of a. A a paameteized cuve, Ũ () lie to the left of, and emanate fom the tate U = U, whee it i tangent to R 1.) Note that ince hock cuve have thid ode tangency with = cont at the tate U L, and the tanding wave cuve have quadatic tangency, it follow that the hock cuve emanating fom left tate on U () fo >, alway beak tanveally into the egion below the tanding wave cuve, and hence, in a ufficiently mall neighbohood, uch hock cuve inteect the tanding wave cuve U at exactly two point: at the left tate U L = U () on the ight of, and at a unique point U R on the left of. We now how that, (with the choice of ign in (3.2)-(3.4)), the point Ũ() on the zeo peed hock cuve alway lie on the hock cuve emanating fom U L between U L and U R when the ign in (2.4) i negative, (that i, the hock wave [U L,U R ] ha negative peed), while the point U R lie on the hock cuve emanating fom U L between U L and Ũ() when the ign in (2.4) i poitive, (o that the hock wave [U L,U R ] ha poitive peed in thi cae). o thi end, conide the zeo peed hock [U ( ),Ũ( )], >. (We ue in thi agument to indicate the -paameteization of U on the ight of.)
7 RESONAN NONLINEAR SYSEMS OF CONSERVAION LAWS 285 Since the hock ha zeo peed, the Rankine-Hugoniot jump condition imply that f(u ( )) = f(ũ( )), and a ( ) = ã ( ), o we can wite (3.14) f(a ( ),ũ ( ),ṽ ( )) = f(a ( ),u ( ),v ( )). Uing the condition fo a tanding wave df = gda, we can expe the incement df on the left and ight ide of (3.14), coeponding to an incement d, by (3.15) df = f a (Ũ)da + D Dw f(ũ)d w = g(u )da, which lead to (3.16) But D Dw f(ũ)d w = [g(ũ) f a (Ũ)]da + [g(u ) g(ũ)]da. (3.17) [g(u ) g(ũ)] = D Dw g(ũ) (W W ) + O( W W 2 ), and (3.18) W W = ǫr 1 (Ũ) + O( W W 2 ), whee (3.19) ǫ = O( W W ). Multiplying (3.16) by L i, i = 1,2, uing L 1 Df Dw = λ 1 L 1 = λ 1, L 2 Df Dw = λ 2 L 2 = λ 2, and uing (3.17) and (3.18), we obtain the deivative of a and with epect to the value of on the zeo peed hock cuve to the left of, (3.20) (3.21) da d = λ 1 ( ) + O(ǫ 2 ), L 1 (g f a )da + ǫ L 1 Dg Dw R 1 ( ) d d = λ L 2 (g f a ) + ǫ L 2 Dg 1 Dw R 1 ( ) + O(ǫ 2 ). λ 2 L 1 (g f a ) + ǫ L 1 Dg Dw R 1 Note that etting ǫ = 0 in (3.20), (3.21) give the fomula (3.10), (3.11) fo the coeponding deivative of the tanding wave cuve at U = U. Futhemoe, taking the deivative of (3.21) with epect to ǫ at ǫ = 0, we ee that the zeo peed hock cuve will beak tanveally to one ide o the othe of the tanding wave cuve at U = U if the deteminant in (2.4) i non-zeo. Uing the choice of ign in (3.2)- (3.4), it follow that Ũ() lie to the ight, [epectively left], of U () fo < if the deteminant in (2.4) i poitive, [epectively negative], (diagammed in Figue 1 and 2, epectively), a claimed.
8 286 J. HONG AND B. EMPLE he olution of the Riemann poblem i diagammed in Figue 3-10, auming the nomalization (3.2)-(3.4). A an entopy condition we take the condition that the change in a i monotone along tanding wave in a olution. hi allow fo what we call tiple compoite tanding wave, and alo entail a non-uniquene of olution, and a coeponding lack of continuou dependence of the olution on U L and U R. hi wa obeved in the cala cae in [14, 7], and epeent an inteeting complication in the tuctue of the poible time aymptotic wave patten. Even o, the analyi hee how that thi inteeting tuctue i canonical in a neighbohood of a tate of eonance. he analyi of the Glimm cheme fo the cala cae teated in [14, 7] lead to additional entopy condition that futhe etict the admiible olution of the Riemann poblem. In paticula, the L w minimization pinciple intoduced in [7], detemined a unique olution of the Riemann poblem, except fo an inheent duplicity of olution at boundaie whee the qualitative wave tuctue of olution change. Fo ou pupoe hee, we make no futhe entopy etiction, c.f. [7]. Figue 3-6 give the olution of the Riemann poblem in the cae when the zeo peed hock cuve, (dawn a a dahed, downwad paabolic cuve to the left of in each diagam), lie to the ight of the tanding wave cuve, (the cae of a poitive ign in (2.4)), and Figue 7-10 give the cae when the zeo peed hock cuve lie to the ight of the tanding wave cuve, (the cae of a negative ign in (2.4)), accoding to the fou cae a L le than o geate than a R, and U L left o ight of. (he ga dynamic ytem (1.4)-(1.6) i of the type diagammed in Figue 3-6.) o keep the diagam a imple a poible, we make the following idealization. Fit, the 1- wave cuve and 2-wave cuve ae dawn a hoizontal and vetical line, epectively. Moe pecifically, the thid ode tangency of hock cuve and aefaction cuve i neglected a a highe ode effect elative to the quadatic tangency of tanding wave cuve and 1-wave cuve in each diagam. Alo, the tate at level a = a R ae dawn along a ingle hoizontal line. In fact, the 1- and 2-wave cuve lie at contant a, o the change in a in a Riemann poblem ente a a jump aco the tanding wave. hu, the tate at level a = a R would actually be a cuve of tate obtained by maintaining the condition a=a R a L along the tanding wave in the olution. he value of a change quadatically along tanding wave cuve, and by ou convention, a take a minimum at the point of inteection of the tanding wave with the tanition uface. he dak cuve in Figue 3 10 epeent tate that can be eached by a 1-wave, o by 1-wave and the citical tanding wave that mak the place whee the 1-wave and tanding wave change thei elative peed. In each diagam, the olution i a combination of 1-wave and tanding wave, followed by a 2-wave, whee the ode of 1-wave and tanding wave i detemined by taking the lowe wave fit. In paticula, by (3.2)-(3.4), 1-wave with left tate U L to the ight of have poitive peed, (and hence come afte the zeo peed tanding wave moving fom left to ight in the xt-plane), unle the 1-wave i a hock wave with a left tate to the left of the zeo peed hock cuve. In the cae of Figue 3-10 excluding the cae of Figue 5 and 9, the olution of the Riemann poblem can contain what we call tiple compoite tanding wave. hi i a tanding wave that conit of a tanding wave to the ight of, followed by a zeo peed hock wave, followed by a diffeent tanding wave to the left of, whee the um of the change in a along the tanding wave i a = a R a L. Since all wave move with zeo peed, a tiple compoite tanding wave can be teated a a ingle wave. In each diagam, the egion between the two vetical dahed line,
9 RESONAN NONLINEAR SYSEMS OF CONSERVAION LAWS 287 (which actually epeent 2-wave cuve), define the value of U R fo which thee i a olution [U L,U R ] that contain a tiple compoite tanding wave. We now dicu the diagam individually. Dicuion of Figue 3: he dahed line emanating fom tate U i the zeo peed hock wave. he coeponding tanding wave cuve i dawn to the ight of a the dak, downwad paabolic cuve emanating fom the tate U, continuing to the left of a the olid paabolic cuve emanating fom U. o obtain the olution fo given ight tate U R that lie to the ight of tate D in the figue 3, tat at U L, take the 1-wave cuve, (the hoizontal line though U L ), to an intemediate tate left of U, follow thi by the tanding wave cuve to the level a = a R, (dawn a a hoizontal line), and then take a two wave cuve at level a R to U R. When U R lie between the 2-wave cuve though D and E, take the 1-wave to U, (a aefaction wave), take the tiple compoite tanding wave to C, and then the two wave fom C to U R ; that i, the olution i U L U A B C U R. he tiple compoite tanding wave i the tanding wave fom U to A followed by the zeo peed hock fom A to B followed by the tanding wave fom B to C. Finally, if U R lie to the ight of tate E, take the aefaction wave fom U L to U, the citical tanding wave fom U to level a R, and then a poitive peed 1-wave at level a R to a tate ight of E that connect by a 2-wave to the tate U R. In thi cae the olution of the Riemann poblem i unique. Dicuion of Figue 4: he olution i a negative peed 1-hock followed by a tanding wave followed by a two wave when the tate U R lie to the left of tate D. When U R lie between D and E, the olution conit of a tiple compoite wave to a tate between D and E, followed by a 2-wave to U L, fo example, U L A B C U R, diagammed in the figue. Fo U R to the ight of tate E, the olution conit of a tanding wave followed by a poitive peed 1-wave followed by a 2-wave. In thi cae the olution of the Riemann poblem i unique. Dicuion of Figue 5: he olution conit of a 1-wave followed by a tanding wave followed by a 2-wave. In thi cae the olution of the Riemann poblem i unique. Dicuion of Figue 6 : he olution conit of a negative peed hock wave, (to a tate left of D), followed by a tanding wave fo tate U R which lie to the left of tate F. Howeve, tate between F and G can alo be olved by a tiple compoite tanding wave followed by a 2-wave, a in the olution U L A B C U R, o by a negative peed hock to a tate left of E, followed by a tanding wave, and then a 2-wave. When U R lie to the ight of tate G, the olution conit of a tanding wave followed by a poitive peed 1-wave followed by a 2-wave. In thi cae thee i a tiple non-uniquene of olution when U R lie between tate F and G. Dicuion of Figue 7: Fo tate U R to the left of tate D, the olution conit of a negavive peed 1-wave followed by a tanding wave to level a = a R, followed by a 2-wave. Fo tate U R between D and F, the olution ha a tiple multiplicity: a 1-wave followed by a tanding wave followed by a 2-wave; o a 1-aefaction wave to U followed by the citical tanding wave to B followed by a poitive peed 1-wave to tate between D and F, followed by a 2-wave to U R ; o ele olution with a tiple compoite tanding wave like the olution U L U A C E U R. When U R lie to the ight of tate F, the olution educe to the ingle olution U L U B 3 We ay the tate lie to the ight of a tate if it lie to the ight of the 2-wave cuve though that tate, dawn a a vetical line in the diagam.
10 288 J. HONG AND B. EMPLE followed by a poitive peed 1-wave followed by a 2-wave. In thi cae thee i a tiple multiplicity of olution when U R lie between tate D and F. Dicuion of Figue 8: Fo tate U R to the left of tate D, the olution conit of a negative peed 1-wave followed by a tanding wave to level a = a R, followed by a 2-wave. Fo tate U R between D and E, the olution ha a tiple multiplicity: a negative peed 1-hock followed by a tanding wave followed by a 2-wave; o the citical tanding wave fom U L to E followed by a poitive peed 1-wave to a tate between D and E, followed by a 2-wave to U R ; o ele a olution with a tiple compoite tanding wave like the olution U L A B C U R. When U R lie to the ight of tate E, the olution educe to the ingle olution U L H followed by a poitive peed 1-wave followed by a 2-wave. In thi cae thee i a tiple multiplicity of olution when U R lie between tate D and E. Dicuion of Figue 9: hi agee with Figue 5. Dicuion of Figue 10: Fo tate U R to the left of tate F, the olution conit of a negavive peed 1-wave followed by a tanding wave to level a = a R, followed by a 2-wave. Fo tate U R between F and G, the olution conit of a tiple compoite tanding wave to a tate between F and G, followed by a 2-wave. And fo ight tate U R to the ight of G, the olution conit of a citical tanding wave to level a = a R, followed by a poitive peed 1-wave, followed by a 2-wave to U R. In thi cae the olution of the Riemann poblem i unique. REFERENCES [1] G. Chen and J. Glimm, Global olution to the compeible Eule equation with geometical tuctue, Comm. Math. Phy., 179 (1996), pp [2] R. Couant and K.O. Fiedich, Supeonic flow and hock wave, John Wiley & Son, New Yok, [3] G. Dal Mao, P.G. LeFloch, and F. Muat, Definition and weak tability of nonconevative poduct, J. Math. Pue Appl., 74 (1995), pp [4] J. Glimm, Solution in the lage fo nonlinea hypebolic ytem of equation, Comm. Pue Appl. Math., 18 (1965), pp [5] S.K. Godunov, A diffeence method fo numeical calculation of dicontinuou olution of the equation of hydodynamic, Mat. Sb., 47 (1959), in Ruion, pp [6] J. Hong, he Glimm cheme extended to inhomogeneou ytem, Doctoal hei, UC-Davi. [7] J. Hong and B. emple, A bound on the total vaiation of the coneved quantitie fo olution of a geneal eonant nonlinea balance law, SIAM J. Appl. Math., to appea. [8] E. Iaacon, Global olution of a Riemann poblem fo a non-tictly hypebolic ytem of conevation law aiing in enhanced oil ecovey, Rockefelle Univeity pepint. [9] E. Iaacon, D. Machein, B. Ploh, and B. emple, he Riemann poblem nea a hypebolic ingulaity: the claification of olution of quadatic Riemann poblem I, SIAM J. Appl. Math., 48 (1988), pp [10] E. Iaacon, B. emple, he tuctue of aymptotic tate in a ingula ytem of conevation law, Adv. Appl. Math., 11 (1990), pp [11] E. Iaacon, B. emple, Analyi of a ingula hypebolic ytem of conevation law, Jou. Diff. Equn., 65 (1986), pp [12] E. Iaacon, B. emple, Example and claification of non-tictly hypebolic ytem of conevation law, Abtact of AMS, Januay [13] E. Iaacon, B. emple, Nonlinea eonance in ytem of conevation law, with E. Iaacon, SIAM Jou. Appl. Anal., 52 (1992), pp [14] E. Iaacon, B. emple, Convegence of the 2 2 Godunov method fo a geneal eonant nonlinea balance law, SIAM Jou. Appl. Math., 55:3 (1995), pp [15] B. Keyfitz and H. Kanze, A ytem of non-tictly hypebolic conevation law aiing in elaticity theoy, Ach. Rat. Mech. Anal., 72 (1980), pp
11 RESONAN NONLINEAR SYSEMS OF CONSERVAION LAWS 289 [16] S.N. Kuzkov, Fit ode quailinea equation with eveal pace vaiable, Mat. USSR Sb., 10 (1970), pp [17] P.D. Lax, Hypebolic ytem of conevation law, II, Comm. Pue Appl. Math., 10 (1957), pp [18] P.D. Lax and B. Wendoff, Sytem of Conevation law, Comm. Pue Appl. Math., 13 (1960), pp [19] L. Lin, J. Wang and B. emple, A compaion of convegence ate fo Godunov method and Glimm method in eonant nonlinea ytem of conevation law, with L.Lin and J. Wang., SIAM J. Nume. Anal., 32:3, pp [20] L. Lin, J. Wang and B. emple, Suppeion of ocillation in Godunov method fo a eonant non-tictly hypebolic ytem, SIAM J. Nume. Anal., 32:3, June [21].P. Liu, Quailinea hypebolic ytem, Comm. Math. Phy., 68 (1979), pp [22].P. Liu, Reonance fo a quailinea hypebolic equation, J. Math. Phy., 28:11 (1987), pp [23] D. Machein and P.J. Pae-Leme, A Riemann poblem in ga dynamic with bifucation, Compute and Mathematic with Application, 12A (1986), pp [24] O.A. Oleinik, Dicontinuou olution of non-linea diffeential equation, Upekhi Mat. Nauk (N.S.), 12 (1957), no.3 (75), pp (Am. Math. Soc. an., Se. 2, 26, pp ). [25] J. Smolle, Shock wave and eaction diffuion equation, Spinge-Velag, Belin, New Yok, [26] B. emple, Global olution of the Cauchy poblem fo a cla of 2 2 nontictly hypebolic conevation law, Adv. in Appl. Math., 3 (1982), pp [27] A. veito and R. Winthe, Exitence, uniquene and continuou dependence fo a ytem of hypebolic conevation law modelling polyme flooding, Pepint, Depatment of Infomatic, Univeity of Olo, Noway, Januay, 1990.
12 290 J. HONG AND B. EMPLE U * U * R 1 (a R S, u R S,vR S) R 1 (a R S,uR S,vR S ) ( a ~ S, u~ S,v ~ S) (a ~ S,u ~ S,v ~ S ) Figue 1 Figue 2 UL U * a=a L B A D C E a=a R Figue 3 ( a > a, U < ) R L L
13 RESONAN NONLINEAR SYSEMS OF CONSERVAION LAWS 291 F U L a =a L B A D C E a =a R Figue 4 (a > a,u >) R L L a=a R a=a L UL Figue 5 (a < a, U < ) R L L
14 292 J. HONG AND B. EMPLE U R F C G a =a R B A D E U L a =a L Figue 6 (a < a, U > ) R L L U L U * a=a L U R C A D E F B a=a R Figue 7 (a > a, U < ) R L L
15 RESONAN NONLINEAR SYSEMS OF CONSERVAION LAWS 293 F G UL a=a L B A D C E H a=a R U R Figue 8 (a > a, U > ) R L L U * a=a R U L a=a L Figue 9 (a < a, U < ) R L L
16 294 J. HONG AND B. EMPLE F G a=a R D E U L a=a L Figue 10 ( a < a, U > ) R L L
Chapter 19 Webassign Help Problems
 Chapte 9 Webaign Help Poblem 4 5 6 7 8 9 0 Poblem 4: The pictue fo thi poblem i a bit mileading. They eally jut give you the pictue fo Pat b. So let fix that. Hee i the pictue fo Pat (a): Pat (a) imply
Chapte 9 Webaign Help Poblem 4 5 6 7 8 9 0 Poblem 4: The pictue fo thi poblem i a bit mileading. They eally jut give you the pictue fo Pat b. So let fix that. Hee i the pictue fo Pat (a): Pat (a) imply
Gravity. David Barwacz 7778 Thornapple Bayou SE, Grand Rapids, MI David Barwacz 12/03/2003
 avity David Bawacz 7778 Thonapple Bayou, and Rapid, MI 495 David Bawacz /3/3 http://membe.titon.net/daveb Uing the concept dicued in the peceding pape ( http://membe.titon.net/daveb ), I will now deive
avity David Bawacz 7778 Thonapple Bayou, and Rapid, MI 495 David Bawacz /3/3 http://membe.titon.net/daveb Uing the concept dicued in the peceding pape ( http://membe.titon.net/daveb ), I will now deive
FI 2201 Electromagnetism
 FI Electomagnetim Aleande A. Ikanda, Ph.D. Phyic of Magnetim and Photonic Reeach Goup ecto Analyi CURILINEAR COORDINAES, DIRAC DELA FUNCION AND HEORY OF ECOR FIELDS Cuvilinea Coodinate Sytem Cateian coodinate:
FI Electomagnetim Aleande A. Ikanda, Ph.D. Phyic of Magnetim and Photonic Reeach Goup ecto Analyi CURILINEAR COORDINAES, DIRAC DELA FUNCION AND HEORY OF ECOR FIELDS Cuvilinea Coodinate Sytem Cateian coodinate:
ASTR 3740 Relativity & Cosmology Spring Answers to Problem Set 4.
 ASTR 3740 Relativity & Comology Sping 019. Anwe to Poblem Set 4. 1. Tajectoie of paticle in the Schwazchild geomety The equation of motion fo a maive paticle feely falling in the Schwazchild geomety ae
ASTR 3740 Relativity & Comology Sping 019. Anwe to Poblem Set 4. 1. Tajectoie of paticle in the Schwazchild geomety The equation of motion fo a maive paticle feely falling in the Schwazchild geomety ae
Inference for A One Way Factorial Experiment. By Ed Stanek and Elaine Puleo
 Infeence fo A One Way Factoial Expeiment By Ed Stanek and Elaine Puleo. Intoduction We develop etimating equation fo Facto Level mean in a completely andomized one way factoial expeiment. Thi development
Infeence fo A One Way Factoial Expeiment By Ed Stanek and Elaine Puleo. Intoduction We develop etimating equation fo Facto Level mean in a completely andomized one way factoial expeiment. Thi development
Then the number of elements of S of weight n is exactly the number of compositions of n into k parts.
 Geneating Function In a geneal combinatoial poblem, we have a univee S of object, and we want to count the numbe of object with a cetain popety. Fo example, if S i the et of all gaph, we might want to
Geneating Function In a geneal combinatoial poblem, we have a univee S of object, and we want to count the numbe of object with a cetain popety. Fo example, if S i the et of all gaph, we might want to
Solutions Practice Test PHYS 211 Exam 2
 Solution Pactice Tet PHYS 11 Exam 1A We can plit thi poblem up into two pat, each one dealing with a epaate axi. Fo both the x- and y- axe, we have two foce (one given, one unknown) and we get the following
Solution Pactice Tet PHYS 11 Exam 1A We can plit thi poblem up into two pat, each one dealing with a epaate axi. Fo both the x- and y- axe, we have two foce (one given, one unknown) and we get the following
Passive Pressure on Retaining Wall supporting c-φ Backfill using Horizontal Slices Method
 Cloud Publication Intenational Jounal of Advanced Civil Engineeing and Achitectue Reeach 2013, Volume 2, Iue 1, pp. 42-52, Aticle ID Tech-106 Reeach Aticle Open Acce Paive Peue on Retaining Wall uppoting
Cloud Publication Intenational Jounal of Advanced Civil Engineeing and Achitectue Reeach 2013, Volume 2, Iue 1, pp. 42-52, Aticle ID Tech-106 Reeach Aticle Open Acce Paive Peue on Retaining Wall uppoting
one primary direction in which heat transfers (generally the smallest dimension) simple model good representation for solving engineering problems
 CHAPTER 3: One-Dimenional Steady-State Conduction one pimay diection in which heat tanfe (geneally the mallet dimenion) imple model good epeentation fo olving engineeing poblem 3. Plane Wall 3.. hot fluid
CHAPTER 3: One-Dimenional Steady-State Conduction one pimay diection in which heat tanfe (geneally the mallet dimenion) imple model good epeentation fo olving engineeing poblem 3. Plane Wall 3.. hot fluid
Theorem 2: Proof: Note 1: Proof: Note 2:
 A New 3-Dimenional Polynomial Intepolation Method: An Algoithmic Appoach Amitava Chattejee* and Rupak Bhattachayya** A new 3-dimenional intepolation method i intoduced in thi pape. Coeponding to the method
A New 3-Dimenional Polynomial Intepolation Method: An Algoithmic Appoach Amitava Chattejee* and Rupak Bhattachayya** A new 3-dimenional intepolation method i intoduced in thi pape. Coeponding to the method
22.615, MHD Theory of Fusion Systems Prof. Freidberg Lecture 18
 .65, MHD Theoy of Fuion Sytem Pof. Feidbeg Lectue 8. Deive δw fo geneal cew pinch. Deive Suydam citeion Scew Pinch Equilibia μ p + + ( ) = μ J = μ J= Stability ( ) m k ξ=ξ e ι +ι ξ=ξ e +ξ e +ξ e =ξ +ξ
.65, MHD Theoy of Fuion Sytem Pof. Feidbeg Lectue 8. Deive δw fo geneal cew pinch. Deive Suydam citeion Scew Pinch Equilibia μ p + + ( ) = μ J = μ J= Stability ( ) m k ξ=ξ e ι +ι ξ=ξ e +ξ e +ξ e =ξ +ξ
TRAVELING WAVES. Chapter Simple Wave Motion. Waves in which the disturbance is parallel to the direction of propagation are called the
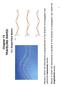 Chapte 15 RAVELING WAVES 15.1 Simple Wave Motion Wave in which the ditubance i pependicula to the diection of popagation ae called the tanvee wave. Wave in which the ditubance i paallel to the diection
Chapte 15 RAVELING WAVES 15.1 Simple Wave Motion Wave in which the ditubance i pependicula to the diection of popagation ae called the tanvee wave. Wave in which the ditubance i paallel to the diection
ON A SINGULAR PERTURBED PROBLEM IN AN ANNULUS
 ON A SINGULAR PERTURBE PROBLEM IN AN ANNULUS SANJIBAN SANTRA AN JUNCHENG WEI Abtact. In thi pape, we extend the eult obtained by Ruf Sikanth 8. We pove the exitence of poitive olution unde iichlet and
ON A SINGULAR PERTURBE PROBLEM IN AN ANNULUS SANJIBAN SANTRA AN JUNCHENG WEI Abtact. In thi pape, we extend the eult obtained by Ruf Sikanth 8. We pove the exitence of poitive olution unde iichlet and
Impulse and Momentum
 Impule and Momentum 1. A ca poee 20,000 unit of momentum. What would be the ca' new momentum if... A. it elocity wee doubled. B. it elocity wee tipled. C. it ma wee doubled (by adding moe paenge and a
Impule and Momentum 1. A ca poee 20,000 unit of momentum. What would be the ca' new momentum if... A. it elocity wee doubled. B. it elocity wee tipled. C. it ma wee doubled (by adding moe paenge and a
Lecture No. 6 (Waves) The Doppler Effect
 Lectue No. 6 (Wave) The Dopple Eect 1) A ound ouce i moving at 80 m/ towad a tationay litene that i tanding in till ai. (a) Find the wavelength o the ound in the egion between the ouce and the litene.
Lectue No. 6 (Wave) The Dopple Eect 1) A ound ouce i moving at 80 m/ towad a tationay litene that i tanding in till ai. (a) Find the wavelength o the ound in the egion between the ouce and the litene.
Symmetry of Lagrangians of holonomic systems in terms of quasi-coordinates
 Vol 18 No 8, Augut 009 c 009 Chin. Phy. Soc. 1674-1056/009/1808/3145-05 Chinee Phyic B an IOP Publihing Lt Symmety of Lagangian of holonomic ytem in tem of quai-cooinate Wu Hui-Bin an Mei Feng-Xiang School
Vol 18 No 8, Augut 009 c 009 Chin. Phy. Soc. 1674-1056/009/1808/3145-05 Chinee Phyic B an IOP Publihing Lt Symmety of Lagangian of holonomic ytem in tem of quai-cooinate Wu Hui-Bin an Mei Feng-Xiang School
SIMPLE LOW-ORDER AND INTEGRAL-ACTION CONTROLLER SYNTHESIS FOR MIMO SYSTEMS WITH TIME DELAYS
 Appl. Comput. Math., V.10, N.2, 2011, pp.242-249 SIMPLE LOW-ORDER AND INTEGRAL-ACTION CONTROLLER SYNTHESIS FOR MIMO SYSTEMS WITH TIME DELAYS A.N. GÜNDEŞ1, A.N. METE 2 Abtact. A imple finite-dimenional
Appl. Comput. Math., V.10, N.2, 2011, pp.242-249 SIMPLE LOW-ORDER AND INTEGRAL-ACTION CONTROLLER SYNTHESIS FOR MIMO SYSTEMS WITH TIME DELAYS A.N. GÜNDEŞ1, A.N. METE 2 Abtact. A imple finite-dimenional
Fall 2004/05 Solutions to Assignment 5: The Stationary Phase Method Provided by Mustafa Sabri Kilic. I(x) = e ixt e it5 /5 dt (1) Z J(λ) =
 8.35 Fall 24/5 Solution to Aignment 5: The Stationay Phae Method Povided by Mutafa Sabi Kilic. Find the leading tem fo each of the integal below fo λ >>. (a) R eiλt3 dt (b) R e iλt2 dt (c) R eiλ co t dt
8.35 Fall 24/5 Solution to Aignment 5: The Stationay Phae Method Povided by Mutafa Sabi Kilic. Find the leading tem fo each of the integal below fo λ >>. (a) R eiλt3 dt (b) R e iλt2 dt (c) R eiλ co t dt
MATERIAL SPREADING AND COMPACTION IN POWDER-BASED SOLID FREEFORM FABRICATION METHODS: MATHEMATICAL MODELING
 MATERIAL SPREADING AND COMPACTION IN POWDER-BASED SOLID FREEFORM FABRICATION METHODS: MATHEMATICAL MODELING Yae Shanjani and Ehan Toyekani Depatment of Mechanical and Mechatonic Engineeing, Univeity of
MATERIAL SPREADING AND COMPACTION IN POWDER-BASED SOLID FREEFORM FABRICATION METHODS: MATHEMATICAL MODELING Yae Shanjani and Ehan Toyekani Depatment of Mechanical and Mechatonic Engineeing, Univeity of
On the quadratic support of strongly convex functions
 Int. J. Nonlinea Anal. Appl. 7 2016 No. 1, 15-20 ISSN: 2008-6822 electonic http://dx.doi.og/10.22075/ijnaa.2015.273 On the quadatic uppot of tongly convex function S. Abbazadeh a,b,, M. Ehaghi Godji a
Int. J. Nonlinea Anal. Appl. 7 2016 No. 1, 15-20 ISSN: 2008-6822 electonic http://dx.doi.og/10.22075/ijnaa.2015.273 On the quadatic uppot of tongly convex function S. Abbazadeh a,b,, M. Ehaghi Godji a
Determining the Best Linear Unbiased Predictor of PSU Means with the Data. included with the Random Variables. Ed Stanek
 Detemining te Bet Linea Unbiaed Pedicto of PSU ean wit te Data included wit te andom Vaiable Ed Stanek Intoduction We develop te equation fo te bet linea unbiaed pedicto of PSU mean in a two tage andom
Detemining te Bet Linea Unbiaed Pedicto of PSU ean wit te Data included wit te andom Vaiable Ed Stanek Intoduction We develop te equation fo te bet linea unbiaed pedicto of PSU mean in a two tage andom
V V The circumflex (^) tells us this is a unit vector
 Vecto Vecto have Diection and Magnitude Mike ailey mjb@c.oegontate.edu Magnitude: V V V V x y z vecto.pptx Vecto Can lo e Defined a the oitional Diffeence etween Two oint 3 Unit Vecto have a Magnitude
Vecto Vecto have Diection and Magnitude Mike ailey mjb@c.oegontate.edu Magnitude: V V V V x y z vecto.pptx Vecto Can lo e Defined a the oitional Diffeence etween Two oint 3 Unit Vecto have a Magnitude
QUADRATIC DEPENDENCE MEASURE FOR NONLINEAR BLIND SOURCES SEPARATION
 QUADRATI DPNDN MASUR FR NNLINAR BLIND SURS SPARATIN Sophie Achad Dinh Tuan Pham Univ. of Genoble Laboatoy of Modeling and omputation IMAG.N.R.S. B.P. 5X 84 Genoble edex Fance Sophie.Achad@imag.f Dinh-Tuan.Pham@imag.f
QUADRATI DPNDN MASUR FR NNLINAR BLIND SURS SPARATIN Sophie Achad Dinh Tuan Pham Univ. of Genoble Laboatoy of Modeling and omputation IMAG.N.R.S. B.P. 5X 84 Genoble edex Fance Sophie.Achad@imag.f Dinh-Tuan.Pham@imag.f
LECTURE 14. m 1 m 2 b) Based on the second law of Newton Figure 1 similarly F21 m2 c) Based on the third law of Newton F 12
 CTU 4 ] NWTON W O GVITY -The gavity law i foulated fo two point paticle with ae and at a ditance between the. Hee ae the fou tep that bing to univeal law of gavitation dicoveed by NWTON. a Baed on expeiental
CTU 4 ] NWTON W O GVITY -The gavity law i foulated fo two point paticle with ae and at a ditance between the. Hee ae the fou tep that bing to univeal law of gavitation dicoveed by NWTON. a Baed on expeiental
γ from B D(Kπ)K and B D(KX)K, X=3π or ππ 0
 fom and X, X= o 0 Jim Libby, Andew Powell and Guy Wilkinon Univeity of Oxfod 8th Januay 007 Gamma meeting 1 Outline The AS technique to meaue Uing o 0 : intoducing the coheence facto Meauing the coheence
fom and X, X= o 0 Jim Libby, Andew Powell and Guy Wilkinon Univeity of Oxfod 8th Januay 007 Gamma meeting 1 Outline The AS technique to meaue Uing o 0 : intoducing the coheence facto Meauing the coheence
Section 25 Describing Rotational Motion
 Section 25 Decibing Rotational Motion What do object do and wh do the do it? We have a ve thoough eplanation in tem of kinematic, foce, eneg and momentum. Thi include Newton thee law of motion and two
Section 25 Decibing Rotational Motion What do object do and wh do the do it? We have a ve thoough eplanation in tem of kinematic, foce, eneg and momentum. Thi include Newton thee law of motion and two
Simulation of Spatially Correlated Large-Scale Parameters and Obtaining Model Parameters from Measurements
 Simulation of Spatially Coelated Lage-Scale Paamete and Obtaining Model Paamete fom PER ZETTERBERG Stockholm Septembe 8 TRITA EE 8:49 Simulation of Spatially Coelated Lage-Scale Paamete and Obtaining Model
Simulation of Spatially Coelated Lage-Scale Paamete and Obtaining Model Paamete fom PER ZETTERBERG Stockholm Septembe 8 TRITA EE 8:49 Simulation of Spatially Coelated Lage-Scale Paamete and Obtaining Model
Rotational Kinetic Energy
 Add Impotant Rotational Kinetic Enegy Page: 353 NGSS Standad: N/A Rotational Kinetic Enegy MA Cuiculum Famewok (006):.1,.,.3 AP Phyic 1 Leaning Objective: N/A, but olling poblem have appeaed on peviou
Add Impotant Rotational Kinetic Enegy Page: 353 NGSS Standad: N/A Rotational Kinetic Enegy MA Cuiculum Famewok (006):.1,.,.3 AP Phyic 1 Leaning Objective: N/A, but olling poblem have appeaed on peviou
Several new identities involving Euler and Bernoulli polynomials
 Bull. Math. Soc. Sci. Math. Roumanie Tome 9107 No. 1, 016, 101 108 Seveal new identitie involving Eule and Benoulli polynomial by Wang Xiaoying and Zhang Wenpeng Abtact The main pupoe of thi pape i uing
Bull. Math. Soc. Sci. Math. Roumanie Tome 9107 No. 1, 016, 101 108 Seveal new identitie involving Eule and Benoulli polynomial by Wang Xiaoying and Zhang Wenpeng Abtact The main pupoe of thi pape i uing
On the integration of the equations of hydrodynamics
 Uebe die Integation de hydodynamischen Gleichungen J f eine u angew Math 56 (859) -0 On the integation of the equations of hydodynamics (By A Clebsch at Calsuhe) Tanslated by D H Delphenich In a pevious
Uebe die Integation de hydodynamischen Gleichungen J f eine u angew Math 56 (859) -0 On the integation of the equations of hydodynamics (By A Clebsch at Calsuhe) Tanslated by D H Delphenich In a pevious
Momentum and the Flow of Mass Challenge Problems Solutions
 Poblem 1: Steam Bouncing off Wall Momentum and the Flow of Ma Challenge Poblem Solution A team of paticle of ma m and epaation d hit a pependicula uface with peed v. The team ebound along the oiginal line
Poblem 1: Steam Bouncing off Wall Momentum and the Flow of Ma Challenge Poblem Solution A team of paticle of ma m and epaation d hit a pependicula uface with peed v. The team ebound along the oiginal line
Non-Linear Dynamics Homework Solutions Week 2
 Non-Linea Dynamics Homewok Solutions Week Chis Small Mach, 7 Please email me at smach9@evegeen.edu with any questions o concens eguading these solutions. Fo the ececises fom section., we sketch all qualitatively
Non-Linea Dynamics Homewok Solutions Week Chis Small Mach, 7 Please email me at smach9@evegeen.edu with any questions o concens eguading these solutions. Fo the ececises fom section., we sketch all qualitatively
RE 7.a. RE 7.b Energy Dissipation & Resonance RE 7.c EP7, HW7: Ch 7 Pr s 31, 32, 45, 62 & CP
 Wed. Lab Fi. Mon. Tue. 7.-.4 Macocopic Enegy Quiz 6 4pm, hee Math & Phy Reeach L6 Wok and Enegy 7.5-.9 Enegy Tanfe RE 7.a RE 7.b 7.0-. Enegy Diipation & Reonance RE 7.c EP7, HW7: Ch 7 P 3, 3, 45, 6 & CP
Wed. Lab Fi. Mon. Tue. 7.-.4 Macocopic Enegy Quiz 6 4pm, hee Math & Phy Reeach L6 Wok and Enegy 7.5-.9 Enegy Tanfe RE 7.a RE 7.b 7.0-. Enegy Diipation & Reonance RE 7.c EP7, HW7: Ch 7 P 3, 3, 45, 6 & CP
Supplemental Materials. Advanced Thermoelectrics Governed by Single Parabolic Band Model:
 Electonic Supplementay Mateial (ESI) fo Phyical Chemity Chemical Phyic. Thi jounal i The Royal Society of Chemity 04 Supplemental Mateial Advanced Themoelectic Govened by Single Paabolic and Model: Mg
Electonic Supplementay Mateial (ESI) fo Phyical Chemity Chemical Phyic. Thi jounal i The Royal Society of Chemity 04 Supplemental Mateial Advanced Themoelectic Govened by Single Paabolic and Model: Mg
Noether Theorem, Noether Charge and All That
 Noethe Theoem, Noethe Chage and All That Ceated fo PF by Samalkhaiat 10 Tanfomation Let G be a Lie goup whoe action on Minkowki pace-time fomally ealized by coodinate tanfomation ( ) ( 1,3,η) M i Infiniteimally,
Noethe Theoem, Noethe Chage and All That Ceated fo PF by Samalkhaiat 10 Tanfomation Let G be a Lie goup whoe action on Minkowki pace-time fomally ealized by coodinate tanfomation ( ) ( 1,3,η) M i Infiniteimally,
AE 245 homework #9 solutions
 AE 245 homewok #9 olution Tim Smith 13 Apil 2000 1 Poblem1 In the Apollo miion fom the Eath to the Moon, the Satun thid tage povided the tan-luna inetion bun that tanfeed the Apollo pacecaft fom a low
AE 245 homewok #9 olution Tim Smith 13 Apil 2000 1 Poblem1 In the Apollo miion fom the Eath to the Moon, the Satun thid tage povided the tan-luna inetion bun that tanfeed the Apollo pacecaft fom a low
Precision Spectrophotometry
 Peciion Spectophotomety Pupoe The pinciple of peciion pectophotomety ae illutated in thi expeiment by the detemination of chomium (III). ppaatu Spectophotomete (B&L Spec 20 D) Cuvette (minimum 2) Pipet:
Peciion Spectophotomety Pupoe The pinciple of peciion pectophotomety ae illutated in thi expeiment by the detemination of chomium (III). ppaatu Spectophotomete (B&L Spec 20 D) Cuvette (minimum 2) Pipet:
1 Similarity Analysis
 ME43A/538A/538B Axisymmetic Tubulent Jet 9 Novembe 28 Similaity Analysis. Intoduction Conside the sketch of an axisymmetic, tubulent jet in Figue. Assume that measuements of the downsteam aveage axial
ME43A/538A/538B Axisymmetic Tubulent Jet 9 Novembe 28 Similaity Analysis. Intoduction Conside the sketch of an axisymmetic, tubulent jet in Figue. Assume that measuements of the downsteam aveage axial
An annotated English translation of Kinetics of stationary reactions [M. I. Temkin, Dolk. Akad. Nauk SSSR. 152, 156 (1963)]
![An annotated English translation of Kinetics of stationary reactions [M. I. Temkin, Dolk. Akad. Nauk SSSR. 152, 156 (1963)] An annotated English translation of Kinetics of stationary reactions [M. I. Temkin, Dolk. Akad. Nauk SSSR. 152, 156 (1963)]](/thumbs/87/96010656.jpg) An annotated Englih tanlation of Kinetic of tationay eaction [M. I. Temkin, Dolk. Akad. Nauk R. 52, 56 (963)] Vladilav V. Levchenko *, Ronan Fleming, Hong Qian #, and Daniel A. Bead * * Depatment of hyiology,
An annotated Englih tanlation of Kinetic of tationay eaction [M. I. Temkin, Dolk. Akad. Nauk R. 52, 56 (963)] Vladilav V. Levchenko *, Ronan Fleming, Hong Qian #, and Daniel A. Bead * * Depatment of hyiology,
you of a spring. The potential energy for a spring is given by the parabola U( x)
 Small oscillations The theoy of small oscillations is an extemely impotant topic in mechanics. Conside a system that has a potential enegy diagam as below: U B C A x Thee ae thee points of stable equilibium,
Small oscillations The theoy of small oscillations is an extemely impotant topic in mechanics. Conside a system that has a potential enegy diagam as below: U B C A x Thee ae thee points of stable equilibium,
Honors Classical Physics I
 Hono Claical Phyic I PHY141 Lectue 9 Newton Law of Gavity Pleae et you Clicke Channel to 1 9/15/014 Lectue 9 1 Newton Law of Gavity Gavitational attaction i the foce that act between object that have a
Hono Claical Phyic I PHY141 Lectue 9 Newton Law of Gavity Pleae et you Clicke Channel to 1 9/15/014 Lectue 9 1 Newton Law of Gavity Gavitational attaction i the foce that act between object that have a
Absorption Rate into a Small Sphere for a Diffusing Particle Confined in a Large Sphere
 Applied Mathematics, 06, 7, 709-70 Published Online Apil 06 in SciRes. http://www.scip.og/jounal/am http://dx.doi.og/0.46/am.06.77065 Absoption Rate into a Small Sphee fo a Diffusing Paticle Confined in
Applied Mathematics, 06, 7, 709-70 Published Online Apil 06 in SciRes. http://www.scip.og/jounal/am http://dx.doi.og/0.46/am.06.77065 Absoption Rate into a Small Sphee fo a Diffusing Paticle Confined in
AERODYNAMIC DESIGN METHOD FOR SUPERSONIC SLENDER BODY USING AN INVERSE PROBLEM
 AERODYNAMIC DESIGN METHOD FOR SUPERSONIC SLENDER BODY Kia Matuhima*, Ikki Yamamichi**, Naoko Tokugawa*** * Dept. Engineeing, Univeity of Toyama, Gofuku 3190, Toyama 930-8555, JAPAN. Phone: +81-76-445-6796,
AERODYNAMIC DESIGN METHOD FOR SUPERSONIC SLENDER BODY Kia Matuhima*, Ikki Yamamichi**, Naoko Tokugawa*** * Dept. Engineeing, Univeity of Toyama, Gofuku 3190, Toyama 930-8555, JAPAN. Phone: +81-76-445-6796,
Boise State University Department of Electrical and Computer Engineering ECE470 Electric Machines
 Boie State Univeity Depatment of Electical and Compute Engineeing ECE470 Electic Machine Deivation of the Pe-Phae Steady-State Equivalent Cicuit of a hee-phae Induction Machine Nomenclatue θ: oto haft
Boie State Univeity Depatment of Electical and Compute Engineeing ECE470 Electic Machine Deivation of the Pe-Phae Steady-State Equivalent Cicuit of a hee-phae Induction Machine Nomenclatue θ: oto haft
Eddy Currents in Permanent Magnets of a Multi-pole Direct Drive Motor
 Acta Technica Jauineni Vol. 6. No. 1. 2013 Eddy Cuent in Pemanent Magnet of a Multi-pole Diect Dive Moto G. Gotovac 1, G. Lampic 1, D. Miljavec 2 Elaphe Ltd. 1, Univeity of Ljubljana, Faculty of Electical
Acta Technica Jauineni Vol. 6. No. 1. 2013 Eddy Cuent in Pemanent Magnet of a Multi-pole Diect Dive Moto G. Gotovac 1, G. Lampic 1, D. Miljavec 2 Elaphe Ltd. 1, Univeity of Ljubljana, Faculty of Electical
arxiv: v1 [math.cv] 7 Nov 2018
![arxiv: v1 [math.cv] 7 Nov 2018 arxiv: v1 [math.cv] 7 Nov 2018](/thumbs/90/101586781.jpg) INTERMEDIATE HANKEL OPERATORS ON THE FOCK SPACE OLIVIA CONSTANTIN axiv:181103137v1 [mathcv] 7 Nov 2018 Abtact We contuct a natual equence of middle Hankel opeato on the Fock pace, ie opeato which ae intemediate
INTERMEDIATE HANKEL OPERATORS ON THE FOCK SPACE OLIVIA CONSTANTIN axiv:181103137v1 [mathcv] 7 Nov 2018 Abtact We contuct a natual equence of middle Hankel opeato on the Fock pace, ie opeato which ae intemediate
Theory. Single Soil Layer. ProShake User s Manual
 PoShake Ue Manual Theoy PoShake ue a fequency domain appoach to olve the gound epone poblem. In imple tem, the input motion i epeented a the um of a eie of ine wave of diffeent amplitude, fequencie, and
PoShake Ue Manual Theoy PoShake ue a fequency domain appoach to olve the gound epone poblem. In imple tem, the input motion i epeented a the um of a eie of ine wave of diffeent amplitude, fequencie, and
Geometry Contest 2013
 eomety ontet 013 1. One pizza ha a diamete twice the diamete of a malle pizza. What i the atio of the aea of the lage pizza to the aea of the malle pizza? ) to 1 ) to 1 ) to 1 ) 1 to ) to 1. In ectangle
eomety ontet 013 1. One pizza ha a diamete twice the diamete of a malle pizza. What i the atio of the aea of the lage pizza to the aea of the malle pizza? ) to 1 ) to 1 ) to 1 ) 1 to ) to 1. In ectangle
Equations of 2-body motion
 Equation of -body motion The fundamental eqn. of claical atodynamic i Newton Law of Univeal Gavitation: F g = Gm i i i ˆ i (1) We ae inteeted in atellite in obit about ingle planet, o (1) educe to the
Equation of -body motion The fundamental eqn. of claical atodynamic i Newton Law of Univeal Gavitation: F g = Gm i i i ˆ i (1) We ae inteeted in atellite in obit about ingle planet, o (1) educe to the
Shot-geophone migration for seismic data
 Shot-geophone migation fo eimic data Chi Stolk Depatment of Applied Mathematic, Univeity of Twente, The Netheland ouce x Seimic data poceing eceive x h time... ubuface Contempoay pimaie only poceing: Body
Shot-geophone migation fo eimic data Chi Stolk Depatment of Applied Mathematic, Univeity of Twente, The Netheland ouce x Seimic data poceing eceive x h time... ubuface Contempoay pimaie only poceing: Body
A FORMULATION AND PRELIMINARY RESULTS FOR SIMULATION OF SHIP MOTIONS COUPLED HEAVE, PITCH AND ROLL
 8 th Intenational Confeence on the Stability of Ship and Ocean Vehicle Ecuela Técnica Supeio de Ingenieo Navale A FORMUATION AND PREIMINARY RESUTS FOR SIMUATION OF SHIP MOTIONS COUPED HEAVE, PITCH AND
8 th Intenational Confeence on the Stability of Ship and Ocean Vehicle Ecuela Técnica Supeio de Ingenieo Navale A FORMUATION AND PREIMINARY RESUTS FOR SIMUATION OF SHIP MOTIONS COUPED HEAVE, PITCH AND
Second Order Fuzzy S-Hausdorff Spaces
 Inten J Fuzzy Mathematical Achive Vol 1, 013, 41-48 ISSN: 30-34 (P), 30-350 (online) Publihed on 9 Febuay 013 wwweeachmathciog Intenational Jounal o Second Ode Fuzzy S-Haudo Space AKalaichelvi Depatment
Inten J Fuzzy Mathematical Achive Vol 1, 013, 41-48 ISSN: 30-34 (P), 30-350 (online) Publihed on 9 Febuay 013 wwweeachmathciog Intenational Jounal o Second Ode Fuzzy S-Haudo Space AKalaichelvi Depatment
Static Electric Fields. Coulomb s Law Ε = 4πε. Gauss s Law. Electric Potential. Electrical Properties of Materials. Dielectrics. Capacitance E.
 Coulomb Law Ε Gau Law Electic Potential E Electical Popetie of Mateial Conducto J σe ielectic Capacitance Rˆ V q 4πε R ρ v 2 Static Electic Field εe E.1 Intoduction Example: Electic field due to a chage
Coulomb Law Ε Gau Law Electic Potential E Electical Popetie of Mateial Conducto J σe ielectic Capacitance Rˆ V q 4πε R ρ v 2 Static Electic Field εe E.1 Intoduction Example: Electic field due to a chage
New Analysis for The FGM Thick Cylinders Under Combined Pressure and Temperature Loading
 Ameican Jounal of Applied Science 5 (7): 85-859, 008 ISSN 546-939 008 Science Publication New Analyi fo The FGM Thick Cylinde Unde Combined Peue and Tempeatue Loading K. Abinia, H. Naee, F. Sadeghi and
Ameican Jounal of Applied Science 5 (7): 85-859, 008 ISSN 546-939 008 Science Publication New Analyi fo The FGM Thick Cylinde Unde Combined Peue and Tempeatue Loading K. Abinia, H. Naee, F. Sadeghi and
On Locally Convex Topological Vector Space Valued Null Function Space c 0 (S,T, Φ, ξ, u) Defined by Semi Norm and Orlicz Function
 Jounal of Intitute of Science and Technology, 204, 9(): 62-68, Intitute of Science and Technology, T.U. On Locally Convex Topological Vecto Space Valued Null Function Space c 0 (S,T, Φ, ξ, u) Defined by
Jounal of Intitute of Science and Technology, 204, 9(): 62-68, Intitute of Science and Technology, T.U. On Locally Convex Topological Vecto Space Valued Null Function Space c 0 (S,T, Φ, ξ, u) Defined by
Thin-Walled Tube Extension by Rigid Curved Punch
 Engineeing,, 3, 45-46 doi:.436/eng..355 Publihed Online May (http://www.scirp.og/jounal/eng) Thin-Walled Tube Extenion by Rigid Cuved Punch Abtact Rotilav I. Nepehin Platic Defomation Sytem Depatment,
Engineeing,, 3, 45-46 doi:.436/eng..355 Publihed Online May (http://www.scirp.og/jounal/eng) Thin-Walled Tube Extenion by Rigid Cuved Punch Abtact Rotilav I. Nepehin Platic Defomation Sytem Depatment,
Point defects in nematic gels: The case for hedgehogs
 Point defect in nematic gel: The cae fo hedgehog John Dolbow, Eliot Fied and Amy Q. Shen 3 Depatment of Civil and Envionmental Engineeing Duke Univeity, Duham, NC 778-87, USA Depatment of Theoetical and
Point defect in nematic gel: The cae fo hedgehog John Dolbow, Eliot Fied and Amy Q. Shen 3 Depatment of Civil and Envionmental Engineeing Duke Univeity, Duham, NC 778-87, USA Depatment of Theoetical and
A Neural Network for the Travelling Salesman Problem with a Well Behaved Energy Function
 A Neual Netwok fo the Tavelling Saleman Poblem with a Well Behaved Enegy Function Maco Budinich and Babaa Roaio Dipatimento di Fiica & INFN, Via Valeio, 347 Tiete, Italy E-mail: mbh@tiete.infn.it (Contibuted
A Neual Netwok fo the Tavelling Saleman Poblem with a Well Behaved Enegy Function Maco Budinich and Babaa Roaio Dipatimento di Fiica & INFN, Via Valeio, 347 Tiete, Italy E-mail: mbh@tiete.infn.it (Contibuted
MATH 415, WEEK 3: Parameter-Dependence and Bifurcations
 MATH 415, WEEK 3: Paamete-Dependence and Bifucations 1 A Note on Paamete Dependence We should pause to make a bief note about the ole played in the study of dynamical systems by the system s paametes.
MATH 415, WEEK 3: Paamete-Dependence and Bifucations 1 A Note on Paamete Dependence We should pause to make a bief note about the ole played in the study of dynamical systems by the system s paametes.
How can you find the dimensions of a square or a circle when you are given its area? When you multiply a number by itself, you square the number.
 7. Finding Squae Root How can you find the dimenion of a quae o a cicle when you ae given it aea? When you multiply a numbe by itelf, you quae the numbe. Symbol fo quaing i the exponent. = = 6 quaed i
7. Finding Squae Root How can you find the dimenion of a quae o a cicle when you ae given it aea? When you multiply a numbe by itelf, you quae the numbe. Symbol fo quaing i the exponent. = = 6 quaed i
Mathematical Modeling of Metabolic Processes in a Living Organism in Relation to Nutrition
 Mathematical Modeling of Metabolic Pocee in a Living Oganim in Relation to Nutition Dimitova N., Makov S. Depatment Biomathematic Intitute of Mathematic and Infomatic Bulgaian Academy of Science 8 Acad.
Mathematical Modeling of Metabolic Pocee in a Living Oganim in Relation to Nutition Dimitova N., Makov S. Depatment Biomathematic Intitute of Mathematic and Infomatic Bulgaian Academy of Science 8 Acad.
ψ - exponential type orbitals, Frictional
 ew develoment in theoy of Laguee olynomial I. I. Gueinov Deatment of Phyic, Faculty of At and Science, Onekiz Mat Univeity, Çanakkale, Tukey Abtact The new comlete othonomal et of L -Laguee tye olynomial
ew develoment in theoy of Laguee olynomial I. I. Gueinov Deatment of Phyic, Faculty of At and Science, Onekiz Mat Univeity, Çanakkale, Tukey Abtact The new comlete othonomal et of L -Laguee tye olynomial
A generalization of the Bernstein polynomials
 A genealization of the Benstein polynomials Halil Ouç and Geoge M Phillips Mathematical Institute, Univesity of St Andews, Noth Haugh, St Andews, Fife KY16 9SS, Scotland Dedicated to Philip J Davis This
A genealization of the Benstein polynomials Halil Ouç and Geoge M Phillips Mathematical Institute, Univesity of St Andews, Noth Haugh, St Andews, Fife KY16 9SS, Scotland Dedicated to Philip J Davis This
arxiv: v2 [quant-ph] 29 Sep 2017
![arxiv: v2 [quant-ph] 29 Sep 2017 arxiv: v2 [quant-ph] 29 Sep 2017](/thumbs/77/76346489.jpg) A duality pinciple fo the multi-block entanglement entopy of fee femion ytem J.A. Caaco 1,+, F. Finkel 1,+, A. González-López 1,+,*, and P. Tempeta 1,,+ 1 Depatamento de Fíica Teóica II, Univeidad Complutene
A duality pinciple fo the multi-block entanglement entopy of fee femion ytem J.A. Caaco 1,+, F. Finkel 1,+, A. González-López 1,+,*, and P. Tempeta 1,,+ 1 Depatamento de Fíica Teóica II, Univeidad Complutene
AIRCRAFT ENGINE RESPONSE DUE TO FAN UNBALANCE AND TO THE PRESENCE OF CONSUMED GAPS IN THE ENGINE DURING THE PHASE OF WINDMILLING
 ICAS CONGRESS AIRCRAF ENGINE RESPONSE DUE O FAN UNBALANCE AND O HE PRESENCE OF CONSUMED GAPS IN HE ENGINE DURING HE PHASE OF WINDMILLING B. Benay AEROSPAIALE MARA AIRBUS 316 ouloue Cedex 3 Fance Abtact
ICAS CONGRESS AIRCRAF ENGINE RESPONSE DUE O FAN UNBALANCE AND O HE PRESENCE OF CONSUMED GAPS IN HE ENGINE DURING HE PHASE OF WINDMILLING B. Benay AEROSPAIALE MARA AIRBUS 316 ouloue Cedex 3 Fance Abtact
Vectors, Vector Calculus, and Coordinate Systems
 Apil 5, 997 A Quick Intoduction to Vectos, Vecto Calculus, and Coodinate Systems David A. Randall Depatment of Atmospheic Science Coloado State Univesity Fot Collins, Coloado 80523. Scalas and vectos Any
Apil 5, 997 A Quick Intoduction to Vectos, Vecto Calculus, and Coodinate Systems David A. Randall Depatment of Atmospheic Science Coloado State Univesity Fot Collins, Coloado 80523. Scalas and vectos Any
RIGID-ROTOR VLASOV EQUILIBRIUM FOR AN INTENSE CHARGED-PARTICLE BEAM PROPAGATING THROUGH A PERIODIC SOLENOIDAL MAGNETIC FIELD
 RIGID-ROTOR VLASOV EQUILIBRIUM FOR AN INTENSE CHARGED-PARTICLE BEAM PROPAGATING THROUGH A PERIODIC SOLENOIDAL MAGNETIC FIELD Chiping Chen and Renato Pakte Plama Science and Fuion Cente Maachuett Intitute
RIGID-ROTOR VLASOV EQUILIBRIUM FOR AN INTENSE CHARGED-PARTICLE BEAM PROPAGATING THROUGH A PERIODIC SOLENOIDAL MAGNETIC FIELD Chiping Chen and Renato Pakte Plama Science and Fuion Cente Maachuett Intitute
Determination of Excitation Capacitance of a Three Phase Self Excited Induction Generator
 ISSN (Online): 78 8875 (An ISO 397: 007 Cetified Oganization) Detemination of Excitation Capacitance of a Thee Phae Self Excited Induction Geneato Anamika Kumai, D. A. G. Thoa, S. S. Mopai 3 PG Student
ISSN (Online): 78 8875 (An ISO 397: 007 Cetified Oganization) Detemination of Excitation Capacitance of a Thee Phae Self Excited Induction Geneato Anamika Kumai, D. A. G. Thoa, S. S. Mopai 3 PG Student
Analytical evaluation of 3D BEM integral representations using complex analysis
 BIR Wokshop 5w5052 Moden Applications of Complex Vaiables: Modeling, Theoy and Computation Analytical evaluation of 3D BEM integal epesentations using complex analysis onia Mogilevskaya Depatment of Civil,
BIR Wokshop 5w5052 Moden Applications of Complex Vaiables: Modeling, Theoy and Computation Analytical evaluation of 3D BEM integal epesentations using complex analysis onia Mogilevskaya Depatment of Civil,
Chapter 2: Basic Physics and Math Supplements
 Chapte 2: Basic Physics and Math Supplements Decembe 1, 215 1 Supplement 2.1: Centipetal Acceleation This supplement expands on a topic addessed on page 19 of the textbook. Ou task hee is to calculate
Chapte 2: Basic Physics and Math Supplements Decembe 1, 215 1 Supplement 2.1: Centipetal Acceleation This supplement expands on a topic addessed on page 19 of the textbook. Ou task hee is to calculate
PHYS 705: Classical Mechanics. Small Oscillations
 PHYS 705: Classical Mechanics Small Oscillations Fomulation of the Poblem Assumptions: V q - A consevative system with depending on position only - The tansfomation equation defining does not dep on time
PHYS 705: Classical Mechanics Small Oscillations Fomulation of the Poblem Assumptions: V q - A consevative system with depending on position only - The tansfomation equation defining does not dep on time
Markscheme May 2017 Calculus Higher level Paper 3
 M7/5/MATHL/HP3/ENG/TZ0/SE/M Makscheme May 07 Calculus Highe level Pape 3 pages M7/5/MATHL/HP3/ENG/TZ0/SE/M This makscheme is the popety of the Intenational Baccalaueate and must not be epoduced o distibuted
M7/5/MATHL/HP3/ENG/TZ0/SE/M Makscheme May 07 Calculus Highe level Pape 3 pages M7/5/MATHL/HP3/ENG/TZ0/SE/M This makscheme is the popety of the Intenational Baccalaueate and must not be epoduced o distibuted
The Normal Stress Dıstribution in an Infinite. Elastic Body with a Locally Curved and Hollow. Fiber under Geometrical Nonlinear Statement
 Nonlinea Analyi and Diffeential quation Vol. 4 06 no. 6 95-04 HIKARI td www.m-hikai.com htt://dx.doi.og/0.988/nade.06.656 The Nomal Ste Dıtibution in an Infinite latic Body with a ocally Cuved and Hollow
Nonlinea Analyi and Diffeential quation Vol. 4 06 no. 6 95-04 HIKARI td www.m-hikai.com htt://dx.doi.og/0.988/nade.06.656 The Nomal Ste Dıtibution in an Infinite latic Body with a ocally Cuved and Hollow
Vectors, Vector Calculus, and Coordinate Systems
 ! Revised Apil 11, 2017 1:48 PM! 1 Vectos, Vecto Calculus, and Coodinate Systems David Randall Physical laws and coodinate systems Fo the pesent discussion, we define a coodinate system as a tool fo descibing
! Revised Apil 11, 2017 1:48 PM! 1 Vectos, Vecto Calculus, and Coodinate Systems David Randall Physical laws and coodinate systems Fo the pesent discussion, we define a coodinate system as a tool fo descibing
AE 423 Space Technology I Chapter 2 Satellite Dynamics
 AE 43 Space Technology I Chapte Satellite Dynamic.1 Intoduction In thi chapte we eview ome dynamic elevant to atellite dynamic and we etablih ome of the baic popetie of atellite dynamic.. Dynamic of a
AE 43 Space Technology I Chapte Satellite Dynamic.1 Intoduction In thi chapte we eview ome dynamic elevant to atellite dynamic and we etablih ome of the baic popetie of atellite dynamic.. Dynamic of a
Limit Analysis of Stability of Circular Foundation Pit
 5t WSEAS Int. Conf. on ENIRONMENT, ECOSYSTEMS and DEELOPMENT, Teneife, Spain, Decembe 14-16, 27 13 Limit Analyi of Stability of Cicula Foundation Pit CUI XINZHUANG, YAO ZHANYONG, JIN QING, WU SHIMEI Scool
5t WSEAS Int. Conf. on ENIRONMENT, ECOSYSTEMS and DEELOPMENT, Teneife, Spain, Decembe 14-16, 27 13 Limit Analyi of Stability of Cicula Foundation Pit CUI XINZHUANG, YAO ZHANYONG, JIN QING, WU SHIMEI Scool
Research Article On Alzer and Qiu s Conjecture for Complete Elliptic Integral and Inverse Hyperbolic Tangent Function
 Abstact and Applied Analysis Volume 011, Aticle ID 697547, 7 pages doi:10.1155/011/697547 Reseach Aticle On Alze and Qiu s Conjectue fo Complete Elliptic Integal and Invese Hypebolic Tangent Function Yu-Ming
Abstact and Applied Analysis Volume 011, Aticle ID 697547, 7 pages doi:10.1155/011/697547 Reseach Aticle On Alze and Qiu s Conjectue fo Complete Elliptic Integal and Invese Hypebolic Tangent Function Yu-Ming
Geometry of the homogeneous and isotropic spaces
 Geomety of the homogeneous and isotopic spaces H. Sonoda Septembe 2000; last evised Octobe 2009 Abstact We summaize the aspects of the geomety of the homogeneous and isotopic spaces which ae most elevant
Geomety of the homogeneous and isotopic spaces H. Sonoda Septembe 2000; last evised Octobe 2009 Abstact We summaize the aspects of the geomety of the homogeneous and isotopic spaces which ae most elevant
EN40: Dynamics and Vibrations. Midterm Examination Thursday March
 EN40: Dynamics and Vibations Midtem Examination Thusday Mach 9 2017 School of Engineeing Bown Univesity NAME: Geneal Instuctions No collaboation of any kind is pemitted on this examination. You may bing
EN40: Dynamics and Vibations Midtem Examination Thusday Mach 9 2017 School of Engineeing Bown Univesity NAME: Geneal Instuctions No collaboation of any kind is pemitted on this examination. You may bing
Physics 161 Fall 2011 Extra Credit 2 Investigating Black Holes - Solutions The Following is Worth 50 Points!!!
 Physics 161 Fall 011 Exta Cedit Investigating Black Holes - olutions The Following is Woth 50 Points!!! This exta cedit assignment will investigate vaious popeties of black holes that we didn t have time
Physics 161 Fall 011 Exta Cedit Investigating Black Holes - olutions The Following is Woth 50 Points!!! This exta cedit assignment will investigate vaious popeties of black holes that we didn t have time
Stress, Cauchy s equation and the Navier-Stokes equations
 Chapte 3 Stess, Cauchy s equation and the Navie-Stokes equations 3. The concept of taction/stess Conside the volume of fluid shown in the left half of Fig. 3.. The volume of fluid is subjected to distibuted
Chapte 3 Stess, Cauchy s equation and the Navie-Stokes equations 3. The concept of taction/stess Conside the volume of fluid shown in the left half of Fig. 3.. The volume of fluid is subjected to distibuted
Above Flux Estimation Issues in Induction Generators with Application at Energy Conversion Systems
 Acta Polytechnica Hungaica Vol. 3, No. 3, 2006 Above Flux Etimation Iue in Induction Geneato with Application at Enegy Conveion Sytem Ioif Szeidet, Octavian Potean, Ioan Filip, Vaa Citian Depatment of
Acta Polytechnica Hungaica Vol. 3, No. 3, 2006 Above Flux Etimation Iue in Induction Geneato with Application at Enegy Conveion Sytem Ioif Szeidet, Octavian Potean, Ioan Filip, Vaa Citian Depatment of
Two figures are similar fi gures when they have the same shape but not necessarily the same size.
 NDIN O PIION. o be poficient in math, ou need to ue clea definition in dicuion with othe and in ou own eaoning. imilait and anfomation ential uetion When a figue i tanlated, eflected, otated, o dilated
NDIN O PIION. o be poficient in math, ou need to ue clea definition in dicuion with othe and in ou own eaoning. imilait and anfomation ential uetion When a figue i tanlated, eflected, otated, o dilated
Topic 4a Introduction to Root Finding & Bracketing Methods
 /8/18 Couse Instucto D. Raymond C. Rumpf Office: A 337 Phone: (915) 747 6958 E Mail: cumpf@utep.edu Topic 4a Intoduction to Root Finding & Backeting Methods EE 4386/531 Computational Methods in EE Outline
/8/18 Couse Instucto D. Raymond C. Rumpf Office: A 337 Phone: (915) 747 6958 E Mail: cumpf@utep.edu Topic 4a Intoduction to Root Finding & Backeting Methods EE 4386/531 Computational Methods in EE Outline
Multivariable Control Systems
 Multivaiable Contol Sytem Ali Kaimpou Aociate ofeo Fedowi Univeity of Mahhad Refeence ae appeaed in the lat lide. Stability of Multivaiable Feedback Contol Sytem Topic to be coveed include: Well - oedne
Multivaiable Contol Sytem Ali Kaimpou Aociate ofeo Fedowi Univeity of Mahhad Refeence ae appeaed in the lat lide. Stability of Multivaiable Feedback Contol Sytem Topic to be coveed include: Well - oedne
On Sextic Equation With Five Unknowns
 Intenational Jounal of Scientific and Reeach ublication, Volume 7, Iue 8, Augut 017 ISSN 50-15 On Setic Equation With Five Unknown ( )( ) = 8( w ) S.Vidhalakhmi 1, S. Aath Thangam, G. Dhanalakhmi 1 ofeo,
Intenational Jounal of Scientific and Reeach ublication, Volume 7, Iue 8, Augut 017 ISSN 50-15 On Setic Equation With Five Unknown ( )( ) = 8( w ) S.Vidhalakhmi 1, S. Aath Thangam, G. Dhanalakhmi 1 ofeo,
Bogoliubov Transformation in Classical Mechanics
 Bogoliubov Tranformation in Claical Mechanic Canonical Tranformation Suppoe we have a et of complex canonical variable, {a j }, and would like to conider another et of variable, {b }, b b ({a j }). How
Bogoliubov Tranformation in Claical Mechanic Canonical Tranformation Suppoe we have a et of complex canonical variable, {a j }, and would like to conider another et of variable, {b }, b b ({a j }). How
The Morning Commute Problem with Coarse Toll and Nonidentical Commuters
 Netw Spat Econ (2011) 11:343 369 DOI 10.1007/11067-010-9141-8 The Moning Commute Poblem with Coae Toll and Nonidentical Commute Feng (Evan) Xiao & Zhen (Sean) Qian & H. Michael Zhang Publihed online: 12
Netw Spat Econ (2011) 11:343 369 DOI 10.1007/11067-010-9141-8 The Moning Commute Poblem with Coae Toll and Nonidentical Commute Feng (Evan) Xiao & Zhen (Sean) Qian & H. Michael Zhang Publihed online: 12
Considerations Regarding the Flux Estimation in Induction Generator with Application at the Control of Unconventional Energetic Conversion Systems
 Conideation Regading the Flux Etimation in Induction Geneato with Application at the Contol of Unconventional Enegetic Conveion Sytem Ioif Szeidet, Octavian Potean, Ioan Filip, Vaa Citian Depatment of
Conideation Regading the Flux Etimation in Induction Geneato with Application at the Contol of Unconventional Enegetic Conveion Sytem Ioif Szeidet, Octavian Potean, Ioan Filip, Vaa Citian Depatment of
arxiv: v1 [math.ap] 30 Jul 2013
![arxiv: v1 [math.ap] 30 Jul 2013 arxiv: v1 [math.ap] 30 Jul 2013](/thumbs/76/73798630.jpg) BOUNDAY CONCENTATION OF A GAUGED NONLINEA SCHÖDINGE EQUATION ON LAGE BALLS ALESSIO POMPONIO 1 AND DAVID UIZ axiv:137815v1 [mathap] 3 Jul 13 ABSTACT Thi pape i motivated by a gauged Schödinge equation in
BOUNDAY CONCENTATION OF A GAUGED NONLINEA SCHÖDINGE EQUATION ON LAGE BALLS ALESSIO POMPONIO 1 AND DAVID UIZ axiv:137815v1 [mathap] 3 Jul 13 ABSTACT Thi pape i motivated by a gauged Schödinge equation in
Development of Model Reduction using Stability Equation and Cauer Continued Fraction Method
 Intenational Jounal of Electical and Compute Engineeing. ISSN 0974-90 Volume 5, Numbe (03), pp. -7 Intenational Reeach Publication Houe http://www.iphoue.com Development of Model Reduction uing Stability
Intenational Jounal of Electical and Compute Engineeing. ISSN 0974-90 Volume 5, Numbe (03), pp. -7 Intenational Reeach Publication Houe http://www.iphoue.com Development of Model Reduction uing Stability
PHYS833 Astrophysics of Compact Objects Notes Part 12
 1 PHYS833 Atophyic of Compact Object Note Pat 1 Black Hole If the coe of a maive ta gow too lage to fom a neuton ta then thee i nothing that can top it collaping to vey high denity The gavitational field
1 PHYS833 Atophyic of Compact Object Note Pat 1 Black Hole If the coe of a maive ta gow too lage to fom a neuton ta then thee i nothing that can top it collaping to vey high denity The gavitational field
2 x 8 2 x 2 SKILLS Determine whether the given value is a solution of the. equation. (a) x 2 (b) x 4. (a) x 2 (b) x 4 (a) x 4 (b) x 8
 5 CHAPTER Fundamentals When solving equations that involve absolute values, we usually take cases. EXAMPLE An Absolute Value Equation Solve the equation 0 x 5 0 3. SOLUTION By the definition of absolute
5 CHAPTER Fundamentals When solving equations that involve absolute values, we usually take cases. EXAMPLE An Absolute Value Equation Solve the equation 0 x 5 0 3. SOLUTION By the definition of absolute
PHYSICS 151 Notes for Online Lecture 2.6
 PHYSICS 151 Note fo Online Lectue.6 Toque: The whole eaon that we want to woy about cente of ma i that we ae limited to lookin at point mae unle we know how to deal with otation. Let eviit the metetick.
PHYSICS 151 Note fo Online Lectue.6 Toque: The whole eaon that we want to woy about cente of ma i that we ae limited to lookin at point mae unle we know how to deal with otation. Let eviit the metetick.
Computational Methods of Solid Mechanics. Project report
 Computational Methods of Solid Mechanics Poject epot Due on Dec. 6, 25 Pof. Allan F. Bowe Weilin Deng Simulation of adhesive contact with molecula potential Poject desciption In the poject, we will investigate
Computational Methods of Solid Mechanics Poject epot Due on Dec. 6, 25 Pof. Allan F. Bowe Weilin Deng Simulation of adhesive contact with molecula potential Poject desciption In the poject, we will investigate
1D2G - Numerical solution of the neutron diffusion equation
 DG - Numeical solution of the neuton diffusion equation Y. Danon Daft: /6/09 Oveview A simple numeical solution of the neuton diffusion equation in one dimension and two enegy goups was implemented. Both
DG - Numeical solution of the neuton diffusion equation Y. Danon Daft: /6/09 Oveview A simple numeical solution of the neuton diffusion equation in one dimension and two enegy goups was implemented. Both
Exceptional regular singular points of second-order ODEs. 1. Solving second-order ODEs
 (May 14, 2011 Exceptional egula singula points of second-ode ODEs Paul Gaett gaett@math.umn.edu http://www.math.umn.edu/ gaett/ 1. Solving second-ode ODEs 2. Examples 3. Convegence Fobenius method fo solving
(May 14, 2011 Exceptional egula singula points of second-ode ODEs Paul Gaett gaett@math.umn.edu http://www.math.umn.edu/ gaett/ 1. Solving second-ode ODEs 2. Examples 3. Convegence Fobenius method fo solving
Shrinkage Estimation of Reliability Function for Some Lifetime Distributions
 Ameican Jounal of Computational and Applied Mathematic 4, 4(3): 9-96 DOI:.593/j.ajcam.443.4 Shinkage Etimation of eliability Function fo Some Lifetime Ditibution anjita Pandey Depatment of Statitic, niveity
Ameican Jounal of Computational and Applied Mathematic 4, 4(3): 9-96 DOI:.593/j.ajcam.443.4 Shinkage Etimation of eliability Function fo Some Lifetime Ditibution anjita Pandey Depatment of Statitic, niveity
Estimation and Confidence Intervals: Additional Topics
 Chapte 8 Etimation and Confidence Inteval: Additional Topic Thi chapte imply follow the method in Chapte 7 fo foming confidence inteval The text i a bit dioganized hee o hopefully we can implify Etimation:
Chapte 8 Etimation and Confidence Inteval: Additional Topic Thi chapte imply follow the method in Chapte 7 fo foming confidence inteval The text i a bit dioganized hee o hopefully we can implify Etimation:
Two-Body Problem with Varying Mass in Case. of Isotropic Mass Loss
 Adv Theo Appl Mech Vol no 69-8 Two-Body Poblem with Vaying Ma in Cae of Iotopic Ma o W A Rahoma M K Ahmed and I A El-Tohamy Caio Univeity Faculty of Science Dept of Atonomy Caio 6 Egypt FA Abd El-Salam
Adv Theo Appl Mech Vol no 69-8 Two-Body Poblem with Vaying Ma in Cae of Iotopic Ma o W A Rahoma M K Ahmed and I A El-Tohamy Caio Univeity Faculty of Science Dept of Atonomy Caio 6 Egypt FA Abd El-Salam
