Songklanakarin Journal of Science and Technology SJST R1 Akram. N-Fuzzy BiΓ -Ternary Semigroups
|
|
|
- Willis Singleton
- 5 years ago
- Views:
Transcription
1 ongklnkrin Journl of cience nd Technology JT-0-0.R Akrm N-Fuzzy Bi -Ternry emigroups Journl: ongklnkrin Journl of cience nd Technology Mnuscript ID JT-0-0.R Mnuscript Type: Originl Article Dte ubmitted by the Author: -Apr-0 Complete List of Authors: Akrm, Muhmmd; University Tun Hussein Onn Mlysi, Mthemtics nd ttistic; University of Gujrt, Mthemtics Jcob, Kvikumr; University Tun Hussein Onn Mlysi, Mthemtics nd ttistic Khmis, Azme; University Tun Hussein Onn Mlysi, Mthemtics nd ttistic Iqbl, Zffr; University of Gujrt, Mthemtics hmsidh, Nor; University Tun Hussein Onn Mlysi, Mthemtics nd ttistic Keyword: Bi -ternry smigroup, N-fuzzy set, N-fuzzy bi -ternry subsmigroup, N-fuzzy bi -idel.
2 Pge of ongklnkrin Journl of cience nd Technology JT-0-0.R Akrm N-Fuzzy Bi -Ternry emigroups Muhmmd Akrm ; ; Jcob Kvikumr, Azme Bin Khmis, Zffr Iqbl nd A.H. Nor hmsidh Deprtment of Mthemtics nd ttistics, Fculty of cience, Technology nd Humn Development, Universiti Tun Hussein Onn Mlysi, Btu Pht, Mlysi Deprtment of Mthemtics, University of Gujrt, Gujrt, Pkistn Corresponding uthor emil: Abstrct The notion of N-fuzzy sets (NF) hs been pplied to newly defined lgebric structure bi-ternry semigroup. The notions of N-fuzzy bi-ternry subsemigroups nd N-fuzzy bi-left (right, lterl, qusi, nd bi) idels hve been defined nd relted properties hve been investigted. The chrcteriztion of bi-ternry semigroup under these idels hve been estblished. 00 AM Clssifictions: 0A, 0N0, 0M Keywords: Bi -ternry semigroup, N-fuzzy set, N-fuzzy bi -ternry subsemigroup, N- fuzzy bi-idel.
3 ongklnkrin Journl of cience nd Technology JT-0-0.R Akrm Pge of Introduction Zdeh () introduced the concept of fuzzy set. The fuzzy set theories developed by Zdeh nd others hve been found mny pplictions in the domin of mthemtics nd elsewhere. Rosenfeld () strted the study of fuzzy lgebric structures nd introduced fuzzy subgroup (subgroupoid) nd fuzzy (left, right) idel in his pioneering pper. The concept of intuitionistic fuzzy set ws introduced by Atnssov () s generliztion of fuzzy set. Bisws (), introduced the concept of intuitionistic fuzzy subgroupoids. Kim nd Jun (00) pplied the concept of intuitionistic fuzzy sets to the idel theory of semigroup nd defined severl idels of semigroup. Mny other uthors pplied the concept of fuzzy set nd intuitionistic fuzzy set to the lgebric structures. A crisp set A in universe X cn be defined in the form of its chrcteristics function : X {0,}. o fr most of the generliztions of the crisp set hve been A conducted on the unit intervl [ 0,] nd they re consistent with the symmetry observtion. the generliztion of the crisp set to fuzzy set nd fuzzy set to intuitionistic fuzzy set relied on spreding positive informtion. Jun et l. (00) first time used the negtive mening of informtion nd introduced new function which is clled negtivevlued function (or negtive fuzzy set, briefly, N -fuzzy set) nd constructed N - structures. Khn et l. (00) used the ide of N -fuzzy sets to chrcterized ordered semigroups by their N -fuzzy idels. Akrm et l. (0) worked on the N -fuzzy idels of -AG-groupoids. Recently Akrm et l. (0) proposed new lgebric structure clled bi-ternry
4 Pge of ongklnkrin Journl of cience nd Technology JT-0-0.R Akrm semigroup s generliztion of -semigroup nd ternry semigroup. They introduced the notions of bi-ternry subsemigroup, bi-left (right, lterl) idel, bi-qusi idel nd bi-bi-idels for this structure nd discussed the reltionship between these substructures. They lso defined the regulr bi-ternry semigroup nd chrcterized it by these idels. In this pper, we hve pplied the concept of N -fuzzy set to the idel theory of bi - ternry semigroup. The notions of N -fuzzy bi -ternry subsemigroup, N -fuzzy bi - left (right, lterl, qusi nd bi) idels hve been defined nd the reltionship between them hve been investigted. The chrcteriztions of bi-ternry semigroup by these idels hve been discussed here.. Preliminry Concepts Definition. (Akrm et l., 0 ) Let T = { x, y, z,...} nd = { α, β, γ,...} be two nonempty sets. Then T is clled bi-ternry semigroup if it stisfies (i) xα yβz T (ii) ( xα yβz) γuδv = xα( yβzγu) δv= xαyβ ( zγuδv), for ll x, y, z, u, v nd α, β, γ, δ. Exmple. (Akrm et l., 0) Let T = { n+, n N} nd = { n+, n N}. Define the mpping T T T T s x α yβz= x+ α+ y+ β + z. Then T is bi-ternry semigroup.
5 ongklnkrin Journl of cience nd Technology JT-0-0.R Akrm Pge of Exmple. ( Akrm et l., 0) Let T = Z nd Z. Define xγ yδz, for x, y, z T nd γ, δ s the usul multipliction of integers. Then T is bi-ternry semigroup but not -semigroup. Exmple. (Akrm et l., 0) Let T = ir, where, i = nd R is the set of rel numbers. If R nd xα yβz is defined s the usul multipliction of complex numbers T is bi-ternry semigroup but not -semigroup. Definition. (Akrm et l., 0) A nonempty subset A of bi-ternry semigroup T is clled bi -ternry subsemigroup of T if A AA A. Exmple. (Akrm et l., 0) Let T = N = {,,,...} nd = { n+, n N}. Define x α yβz= x+ α+ y+ β + z. Then T is bi-ternry semigroup. Let A= { n, n N} be nonempty subset of T. Then A is bi-ternry subsemigroup of T. Definition. (Akrm et l., 0) A nonempty subset A of bi-ternry semigroup T is clled bi-left idel of T if T TA A. Definition. (Akrm et l., 0) A nonempty subset A of bi-ternry semigroup T is clled bi-right idel of T if A TT A.
6 Pge of ongklnkrin Journl of cience nd Technology JT-0-0.R Akrm Definition. (Akrm et l., 0) A nonempty subset A of bi-ternry semigroup T is clled bi -lterl idel of T if T AT A. Definition.0 (Akrm et l., 0) A nonempty subset A of bi-ternry semigroup T is clled bi-idel of T if it is bi-left, bi-right nd bi-lterl idel of T. Definition. (Akrm et l., 0) Let T be bi-ternry semigroup. A nonempty subset Q of T is clled bi-qusi-idel of T if QTT TQT TTQ Q QTT TTQTT TTQ Q. Definition. (Akrm et l., 0) Let T be bi-ternry semigroup. A bi-ternry subsemigroup B of T is clled bi -bi-idel of T if B TBTB B. Definition. (Akrm et l., 0) Let T = { n, n N}, = { α, β, γ,...} nd A= { n, n N}. Define, x α yβz= x+ y+ z, for x, y, z T nd α, β. Then T is bi-ternry semigroup nd A is bi-left idel of T but neither bi-right nor bi-lterl idel of T. If we define, nd xα yβz= x+ y+ z nd xα yβz= x+ y+ z respectively, then A is bi -right nd bi -lterl idel of T. Exmple. In the bove exmple if we define, x α yβz= x+ y+ z, then A is bi-left, bi-right nd bi-lterl idel of T. Hence A is bi -idel of T. Proposition. (Akrm et l., 0) Let T be bi-ternry semigroup nd
7 ongklnkrin Journl of cience nd Technology JT-0-0.R Akrm Pge of φ X T. Then (i) (ii) (iii) T TX is bi-left idel of T. X TT is bi-right idel of T. TXT TTXT T is bi-lterl idel of T.. N-fuzzy bi -ternry subsemigroup nd N-fuzzy bi -idels Definition. (Khn, 00) A negtive fuzzy set (briefly, N -fuzzy set or NF) in nonempty set X is function : X [, 0]. Here we re using fuzzy function. " " for the negtive Jun et l. ( Jun et l., 00) used the term negtive-vlued function nd N -function for negtive fuzzy set nd N -fuzzy set. Definition. Let be n NF in X nd t [,0]. Then the set N( ; t) = { x X ( x) t} is clled n N -level subset of. Definition. Let nd be two NFs in X. If for ll x X, ( x ) ( x) then is clled n N -fuzzy subset (NF) of nd is written s. We sy tht = if nd only if nd. Definition. Let nd be two NFs in X. Then their union nd intersection is
8 Pge of ongklnkrin Journl of cience nd Technology JT-0-0.R Akrm lso n N -fuzzy set in X, defined s, for ll x X, ( ) = { x, min{ ( x), ( x)}} = ( ( x) ( x)), nd ( ) = { x, mx{ ( x), ( x)}} = ( ( x) ( x)). Definition. Let X = {, b, c, d} be nonempty set. Define : X [,0] s, ( ) = 0., ( b) = 0., ( c) = 0., ( d) = 0.. Then = { <, 0.>, < b, 0.>, < c, 0.>, < d, 0.> }, obviously, is n N -fuzzy set in X. Now, let = { <, >, < b, 0.>, < c, 0.>, < d, 0. } nd > = { <,.>, < b, 0.>, < c, 0.>, < d, 0.> }. Then nd re N -fuzzy sets in X. Esily we cn verify tht. If, we tke = { <, 0.>, < b, 0.>, < c, 0.>, < d, 0.> } = { <, 0.>, < b, 0.>, < c, 0.>, < d, 0.> }. Then nd re N -fuzzy sets in X nd = { <, 0.>, < b, 0.>, < c, 0.>, < d, 0.> } = { <, 0.>, < b, 0.>, < c, 0.>, < d, 0.> }. Obviously, nd re N -fuzzy sets in X. In wht follows, let T denotes bi-ternry semigroup unless otherwise specified. Definition. Let be nonempty subset of T. Then the N - chrcteristic function of
9 ongklnkrin Journl of cience nd Technology JT-0-0.R Akrm Pge of is function χ defined s, for ny x T, χ, if x ( x) = 0, if x. We denotes the N -chrcteristic function of T by χ. Definition. Let, nd be the three NFs in T. Then their product is given s,, o ( o where for ny x T, o o )( = = α β x x b c ) { ( ) ( b) ( c)}, if 0, x= αbβc, for, b, c T, α, β otherwise. Definition. Let be n NF in T. Then is clled n N -fuzzy bi-ternry subsemigroup of T if ( x αyβz) mx{ ( x), ( y), ( z)}for ll x, y, z T, α, β. Definition. Let be n NF in T. Then is clled n N -fuzzy bi-left idel of T if ( x αyβz) ( z), for ll x, y, z T, α, β. Definition.0 Let be n NF in T. Then is clled n N -fuzzy bi-right idel oft if ( x αyβz) ( x), for ll x, y, z T, α, β. Definition. Let be n NF in T. Then is clled n N -fuzzy bi-lterl idel oft if ( x αyβz) ( y), for ll x, y, z T, α, β.
10 Pge of ongklnkrin Journl of cience nd Technology JT-0-0.R Akrm Definition. Let be n NF in T. Then is clled n N -fuzzy bi-idel oft if it is bi-left, bi-right nd bi-lterl idel of T. + Exmple. Let T = Z nd = Z. ThenT is bi-ternry semigroup but not semigroup under the usul multipliction of integers i.e. for x, y, z T, α, β, ( xα yβz) = xαyβz. Now define, : T [,0] s, for x T, 0., if x is even ( x) = 0., otherwise. Then is n N -fuzzy set in T. By simple clcultions we cn verify tht is n N -fuzzy bi -ternry subsemigroup of T. Exmple. Let T = {, b, c} nd = {α }. ThenT is bi-ternry semigroup under the opertion defined in the following tble, α b c b b c c b c. Define, : T [,0] such tht = { <, 0.>, < b, 0.>, < c, 0.> }. Then is n N -fuzzy set in T which is n N -fuzzy bi -ternry subsemigroup of T. Further we cn verify tht A is not n N -fuzzy bi -left (bi -right, bi -lterl) idel of T. If we tke = { <, 0.>, < b, 0.>, < c, 0.> }, then is n N -fuzzy bi-left, bi -right nd bi-lterl idel of T, hence N -fuzzy bi -idel of T. Obviously it is
11 ongklnkrin Journl of cience nd Technology JT-0-0.R Akrm Pge 0 of n N -fuzzy bi -ternry subsemigroup of T. Exmple. Let T = { n, n N} nd = { α, β, γ,...}. Define x α yβz= x+ y+ z, for x, y, z T, α, β, then T is bi-ternry semigroup. Now define, : T [,0] s 0., if ( x) = 0., x= n for some n N Then is n N -fuzzy bi-left idel of T. otherwise. Now, for,, T, α, β, ( α ) β = () + () + = 0= (). Thus ( α β ) = (()) = 0. nd ( ) = 0. implies tht ( α β ) (). Hence is not n N -fuzzy bi -right idel of T. imilrly, we cn verify tht is not n N -fuzzy bi-lterl idel of T. If we define xα yβz= x+ y+ z nd x αyβz = x+ y+ z, then is n N -fuzzy bi-right idel oft nd N -fuzzy bi-lterl idel of T, respectively. Further more if x αyβz = x+ y+ z, then is n N -fuzzy biidel of T. From Exmple. &., we cn write the following remrk. Remrk. In bi-ternry semigroup T, (i) An N -fuzzy bi-left (right, lterl ) idel of T is n N -fuzzy bi-ternry subsemigroup of T but the converse is not true. 0
12 Pge of ongklnkrin Journl of cience nd Technology JT-0-0.R Akrm (ii) An N -fuzzy bi-left idel of T my not be n N -fuzzy bi-right (lterl) idel of T nd vice vers. Lemm. LetT be bi-ternry semigroup then, (i) The intersection of ny collection of N -fuzzy bi-ternry subsemigroups oft is n N -fuzzy bi -ternry subsemigroup of T. (ii) The intersection of ny collection of N -fuzzy bi-left (right, lterl) idels of T is n N -fuzzy bi -left (right, lterl) idel of T. Proof. (i) Let { i, i I} be collection of N -fuzzy bi-ternry subsemigroups of T, then ( xαyβz) mx{ ( x), ( y), ( z)}, for ll i I, x, y, z T, α, β. Now, for i i i i ll for i I, x, y, z T, α, β. ( i i I )(xαyβz) = (( xαyβz)) (mx{ ( x), ( y), ( z)}) Hence i I i i I i = mx{ ( x), ( y), ( z)} = mx{( )( x),( )( y),( )( z)}. i I i i I is n N -fuzzy bi-ternry subsemigroup oft. i I i (ii) Proof is similr s (i). i i I Proposition. Let be n NF in T then (i) is n N -fuzzy bi-ternry subsemigroup oft if nd only if, i i i i I i i I i i I i
13 ongklnkrin Journl of cience nd Technology JT-0-0.R Akrm Pge of o. o (ii) is n N -fuzzy bi-left idel oft if nd only if, χ o χ. o (iii) is n N -fuzzy bi-lterl idel oft if nd only if, χ o χ. o (iv) is n N -fuzzy bi -right idel oft if nd only If, o χ χ. o Proof. (i) Let be n N -fuzzy bi -ternry subsemigroup oft nd x T. Cse. If x αbβc, forα, β,, b, c T then ( o )( x ) = 0 ( )( x). Cse. If x= αbβc, forα, β nd, b, c T, then o ( o o )( x) min {mx( ( ), ( b), ( c))} min ( αbβc) ( x), x T. = x= αbβc This implies tht o. o x= αbβc Conversely, we suppose tht o. Let, α, β,, b, c T nd x= αbβc then, o ( αbβc ) = ( x) ( o o )( x) = min {mx( ( u), ( v), ( w))} mx( ( ), ( b), ( c)). x= uδvθw Hence is n N -fuzzy bi -ternry subsemigroup of T. Proof of imilrly, we cn prove (ii), (iii) nd (iv). Lemm. Let be n NF in T. Then (i) χ o χ o is n N -fuzzy bi -left idel of T. (ii) o χ o χ is n N -fuzzy bi -right idel of T. (iii) χ o o χ is n N -fuzzy bi -lterl idel of T.
14 Pge of ongklnkrin Journl of cience nd Technology JT-0-0.R Akrm Proof. (i) Let L = χ o χ o. Then χ o χ o L χ o χ o χ o χ o χ o χ o = L. Hence L = χ o χ o is n N - = fuzzy bi -left idel of T. imilrly, we cn prove (ii) nd (iii). Theorem.0 Let be n NF in T. Then is n N -fuzzy bi-ternry subsemigroup of T if nd only if N ( ; t) is bi-ternry subsemigroup of T, for ll t [,0]. Proof. Let be n N -fuzzy bi -ternry subsemigroup of T. Let x, y, z N( ; t), where t [,0] then ( x) t, ( y) t nd ( z) t. Now for α, β ( xαyβz) mx{ ( x), ( y), ( z)} t. This implies tht x αyβz N( ; t), for ll x, y, z N ( ; t) nd α, β. Hence N ( ; t) is bi -ternry subsemigroup of T. Conversely, we suppose tht N ( ; t) is bi -ternry subsemigroup of T, for ll t [,0]. Let x, y, z T such tht ( x ) = tx, ( y ) = t y nd ( z ) = tz with t, t, t [,0] then x N ; t ), y N ; t ) nd z N ; t ). We my ssume tht t x x y y z z ( x A ( y ( z t t then N ; t ) N ( ; t ) N( ; t ), which implies tht x y, z N( ; t ). ( x y z, z ince, N ; t ) is bi -ternry subsemigroup of T implies tht x αyβz N ; t ), for ( z α, β. Then ( xαyβz) t = mx( t, t, t ) = mx( ( x), ( y), ( z) ), z x y z ( z for ll x, y, z T nd α, β. Hence is n N -fuzzy bi-ternry subsemigroup of T.
15 ongklnkrin Journl of cience nd Technology JT-0-0.R Akrm Pge of Theorem. Let be n NF in T. Then is n N -fuzzy bi-left (right, lterl) idel of T if nd only if N ( ; t) is bi-left (right, lterl) idel of T, for ll t [,0]. Proof. trightforwrd. Theorem. A nonempty subset of T is bi-ternry subsemigroup of T if nd only if χ is n N -fuzzy bi -ternry subsemigroup of T. Proof. Let be bi-ternry subsemigroup of T then. Let x, y, z T, α, β then we hve following cses. Cse. If x, y, z then xα yβz nd hence χ ( x) = χ ( y) = χ ( z) = χ ( xαyβz) = implies tht χ ( xαyβz) = mx{ χ ( x), χ ( y), χ ( z)}. Cse. If either x or y or z then either χ ( x) = 0 or χ ( y) = 0 or χ ( z) = 0. This implies tht, mx{ χ ( x), χ ( y), χ ( z)} = 0 but χ ( xαyβz) 0 implies tht χ ( xαyβz) mx{ χ ( x), χ ( y), χ ( z)}, for ll x, y, z T, α, β. Cse. When ny two of Cse. When ll x, y, z re not in. x, y, z re not in. Above both cses gives the sme results s in Cse. Hence χ is n N -fuzzy biternry subsemigroup of T. Conversely, we suppose tht χ is n N -fuzzy bi -ternry subsemigroup of T. Let
16 Pge of ongklnkrin Journl of cience nd Technology JT-0-0.R Akrm x, y, z nd α, β then xα yβz. By definition of χ, χ ( x) = χ ( y) = χ ( z) = implies tht mx{ χ ( x), χ ( y), χ ( z)} =. ince χ is n N -fuzzy bi -ternry subsemigroup of T, χ ( xαyβz) mx{ χ ( x), χ ( y), χ ( z)} = implies tht χ ( xαyβz) but by definition χ ( xαyβz), which implies tht χ ( xαyβz) =. This gives tht xα yβz implies tht. Hence is bi-ternry subsemigroup of T. Theorem. A nonempty subset of T is bi-left (right, lterl) idel of T if nd only if χ is n N -fuzzy bi -left (right, lterl) idel of T. Proof. trightforwrd. Definition. Let be nonempty subset of T nd, b [,0] with b. Define N -fuzzy set C in T s for ll x T, C if x ( x) = b if x. Lemm. A nonempty subset of T is bi-ternry subsemigroup (left idel, right idel, lterl idel) of T if nd only if idel, right idel, lterl idel) of T. C is n N -fuzzy bi-ternry subsemigroup (left Proof. We prove this result for bi-right idels. Let be bi- right idel of T nd x, y, z T. If x then xα yβz implies tht C ( x) = = C ( xαyβz). If x then
17 ongklnkrin Journl of cience nd Technology JT-0-0.R Akrm Pge of C ( x) = b C ( xαyβz). Hence C is n N -fuzzy bi -right idel of T. Conversely, we suppose tht C is n N -fuzzy bi -right idel of T. Let x then C ( x) =. For y, z T nd α, β, C ( xαyβz) C ( x) = but C ( xα yβz) implies tht C ( xα yβz) = implies tht xα yβz TT. Hence is biright idel of T. The result for other cses is similr.. N-fuzzy bi-qusi idels nd N-fuzzy bi-bi-idels Definition. Let be n NF in T. Then is clled n N -fuzzy bi-qusi idel of T if for ll x T, ( x) mx{( o ( x) mx{( o Alterntively, o o χo χo χ o χ o χ)( x),( χ o χ)( x),( χ o χ χ o χ χ o o χ o o χo o χ)( x),( χ o o χ χ o χ o χ o χ o χ o χ)( x),( χ o χ χ o )( x)}, χ o χ o. )( x)}. Proposition. Every N -fuzzy bi-qusi idel of T is n N -fuzzy bi-ternry subsemigroup of T. Proof. Let be n N -fuzzy bi -qusi idel of T. ince, o χ o χ o o, χ o o χ o o nd χ o χ o o o implies tht o χ o χ χ o o χ χ o χ o o o. Also, since is N -fuzzy
18 Pge of ongklnkrin Journl of cience nd Technology JT-0-0.R Akrm bi-qusi idel of T, so o χ o χ χ o o χ χ o χ o. This implies tht o o. Hence by Proposition., is n N -fuzzy bi-ternry subsemigroup of T. Lemm. Let { i, i I} be collection of N -fuzzy bi -qusi idels of T then is lso n N -fuzzy bi -qusi idel of T. Proof. trightforwrd. Lemm. Every N -fuzzy bi-left (right, lterl) idel of T is n N -fuzzy bi-qusi idel of T. Proof. trightforwrd. i I Theorem. Let be n NF in T. Then is n N -fuzzy bi-qusi idel of T if nd only if N ( ; t) is bi-qusi idel of T, for ll t [,0]. Proof. We suppose tht is n N -fuzzy bi-qusi idel of T then Let o χ o χ χ o o χ χ o χ o. m N( ; t)tt then m= nαyβz for n N( ; t), y, z T nd α, β. ince n N( ; t) implies tht ( n) t. Now, ( o χ o χ)( m) min {mx( ( n), χ( y), χ( z)} mx( t,, ) t = x= nαyβz i
19 ongklnkrin Journl of cience nd Technology JT-0-0.R Akrm Pge of imilrly, ( χ o o χ)( m t nd ( χ o χ o )( m t implies tht ) ) mx{( o χ o χ)( m),( χ o o χ)( m),( χ o χ o )( m)} t i.e. ( o χ o χ χ o o χ χ o χ o )( m) t, nd by supposition, ( m ) ( o χ o χ χ o o χ χ o χ o )( m) implies tht ( m) t. This gives tht m = nαyβz N( ; t) implies tht N ( ; t) TT N ( ; t). o, N ( ; t) TT TN ( ; t) T TTN ( ; t) N ( ; t) nd N ( ; t) TT TTN ( ; t) TT TTN ( ; t) N ( ; t). Hence N ( ; t) is bi -qusi idel of T. Conversely, we suppose tht N ( ; t) is bi-qusi idel of T, for ll t [,0]. We hve to prove tht is n N -fuzzy bi -qusi idel of T. On contrry, we suppose tht there exist some m T such tht ( o χ o χ χ o o χ χ o χ o )( m ) < ( m), i.e. ( o χ o χ)( m ) ( χ o o χ)( m) ( χ o χ o )( m) < ( m). Now, choose t [,0] such tht ince, implies tht ( o χ o χ χ o o χ χ o χ o )( m ) t < ( m), ( o χ o χ)( m t implies tht m N( ; t)tt nd ( χ o o χ)( m t This gives tht ) ) m TN (; t) T nd ( χ o χ o )( m t implies tht m TTN( ; t). ) m N( ; t) TT TN ( ; t) T TTN ( ; t) N( ; t) m N( ; t) ( m) t, which is contrdiction. o ( o χo χ χo o χ χo χo )( m) ( m), m T.
20 Pge of ongklnkrin Journl of cience nd Technology JT-0-0.R Akrm i.e. ( o χ o χ χ o o χ χ o χ o ). imilrly, we cn verify tht o χ o χ χ o χ o o χ o χ χ o χ o. Hence is n N -fuzzy bi-qusi idel of T. Theorem. A nonempty subset of T is bi-qusi idel of T if nd only if χ is n N -fuzzy bi -qusi idel of T. Proof. Let be bi-qusi idel of T. For m T either then χ ( m) = nd ( χ o o )( m) implies tht T T ( χ o χ χ)( m) χ ( m) implies tht If o m or m. If ( χ o χ o χ )( m) χ o χ o χ )( m) χ o χ o χ )( m) χ ( m) i.e. ( χ o χ o χ χ o χ o χ χ o χ o χ )( m) χ ( m). m then either m m= αbβc or m αbβc, for, b, c T nd α, β. When m αbβc, for, b, c T then ( χ o χ o χ )( m) = 0. Also χ ( m) = 0 implies tht ( χ o χ χ)( m) = χ ( m). When m= αbβc, for, b, c T then mximum two of o, b, c my contined in otherwise if, b, c then m= α bβc TT TT TT (ince is bi-qusi idel of T ) m, which is contrdiction. We hve following cses, (i) m= αbβc nd, b, c. In this cse ( χ o χ o χ )( m) = ( χ o χ o χ )( αbβc) = min{mx( χ ( ), χ( b), χ( c)) = mx{( 0,, )} = 0.
21 ongklnkrin Journl of cience nd Technology JT-0-0.R Akrm Pge 0 of This implies tht ( χ o χ o χ )( m) = 0. imilrly, ( χ o χ o χ )( m) = 0 nd ( χ o χ o )( m) = 0. ince χ ( m) = 0, which implies tht (ii) χ ( χ o χ o χ χ o χ o χ χ o χ o χ )( m) = χ ( m). m= αbβc nd exctly one of, b, c contined in. Let then χ ( m) = 0 nd χ ( ) =. Also, b nd c ( χ o χ o χ )( m) = ( χ o χ o χ )( αbβc) = min{mx( χ ( ), χ( b), χ( c)) = mx{(,, )} =. imilrly, ( χ o χ o χ )( m) = 0 nd ( χ o χ o )( m) = 0 implies tht (iii) χ ( χ o χ o χ )( m) ( χ o χ o χ )( m) ( χ o χ o χ )( m) = 0= χ ( m). m= αbβc nd exctly two of, b, c contined in. Let, b nd c then χ ( m) = 0 nd χ ( ) =, χ ( b) =. In this cse ( χ o χ o )( m) =, T ( o χ o χ)( m) = nd ( χ o χ o )( m) = 0, which implies tht T χ ( χ o χ o χ )( m) ( χ o χ o χ )( m) ( χ o χ o χ )( m) = χ ( m). Hence, for ll m T, ( χ o χo χ)( m) ( χo χ o χ)( m) ( χo χo χ )( m) χ ( m). This implies tht χ o χ o χ χ o χ o χ χ o χ o χ χ. imilrly, we cn verify tht χ o χ o χ χ o χ o χ o χ o χ χ o χ o χ χ. Hence, χ is n N -fuzzy bi-qusi idel of T. Conversely, we suppose tht χ is n N -fuzzy bi-qusi idel of T. Let x TT TT TT. Then x TT, x TT nd x TT implies 0
22 Pge of ongklnkrin Journl of cience nd Technology JT-0-0.R Akrm tht x= α bβ c = α b β c = α b β, where c b, c, b, c,, c, b T nd α β, α, β, α, β. Then,, ( χ o χ o χ)( x) = ( χ o χ o χ)( α bβ c) =, ( χo χ o χ)( x) = ( χo χ o χ)( αbβ c) =, ( χo χo χ )( x) = ( χo χo χ )( αbβ c) =., This implies tht ( ( χ o χ o χ χ o χ o χ χ o χ o χ )( x) =. ince, χ is n N -fuzzy bi-qusi idel of T, ( χ o χ o χ χ o χ o χ χ o χ o χ )( x) χ ( x). This implies tht ( x) but χ ( x) implies tht χ ( x) = implies tht χ x tht is TT TT TT. Likewise, we cn verify tht TT TTTT TT. Hence, is bi-qusi idel of T. Lemm. A nonempty subset of T is bi-qusi-idel of T if nd only if N -fuzzy bi -qusi idel of T. Proof. trightforwrd. The following Exmples. &., shows tht the converses of Proposition. nd Lemm. re not true in generl. C is n Exmple. Let T = {, b, c} nd = {α }. Then T is bi-ternry semigroup long with the opertion defined in the tble below.
23 ongklnkrin Journl of cience nd Technology JT-0-0.R Akrm Pge of α b c Let A= { b, c} then A is bi-ternry subsemigroup of T but not bi-qusi idel of T. Now, define : T [,0] s ( ) = 0., ( b) = ( c) = 0.. Then T if N (, t) = { b, c} if Φ if b b c c b c. t [ 0., 0] t [ 0., 0.) t [, 0.). Obviously, N (, t) is bi-ternry subsemigroup of T but not bi-qusi idel of T, for ll t [,0]. Then by Proposition. nd Theorem., is n N -fuzzy bi - ternry subsemigroup of T but not n N -fuzzy bi -qusi idel of T. Exmple. In bove exmple if we tke, A = {, c} then A is bi -qusi idel of T. Further more A is bi-left idel of T but neither bi-right idel nor bi-lterl idel of T. Now, define : T [,0] s ( ) = ( c) = 0., ( b) = 0.. Then T if N (, t) = {, c} if Φ if t [ 0., 0] t [ 0., 0.) t [, 0.). Obviously, N (, t) is bi-qusi idel of T, for ll t [,0] but neither bi-right idel nor bi-lterl idel of T for t [ 0., 0.). Hence by Theorem., is n N -fuzzy bi-qusi idel of T nd by Theorem., is neither n N -fuzzy bi-right idel nor n N -fuzzy bi -lterl idel of T. imilrly, we cn construct exmples of
24 Pge of ongklnkrin Journl of cience nd Technology JT-0-0.R Akrm N -fuzzy bi -qusi idel of T, which re not N -fuzzy bi -left idel of T. Definition.0 Let be n NF in T. Then is clled n N -fuzzy bi-bi-idel of T if (i) is n N -fuzzy bi -ternry subsemigroup of T. (ii) For ll x, y, z T, α, β, η, δ, ( xαuβyηvδz) mx( ( x), ( y), ( z)). B B B Proposition. Let be n NF in T. Then is n N -fuzzy bi-bi-idel of T if nd only if (i) o nd o (ii) o χ o o χ o. Proof. We suppose tht is n N -fuzzy bi-bi-idel of T then it is bi-ternry subsemigroup of T nd by Proposition., condition (i) holds. Now for (ii), let m T. If m xαyβz, for x, y, z T nd α, β then ( o χ o o χ o )( m ) = 0 ( m). If m= xαyβz nd x = uδvθw, for u, v, w T nd δ, θ then ( o χ o o χ o )( m) = min {mx{( o χ o = = = m= xαyβz )( x), χ( y), ( z)}} min {mx{ min {mx( ( u), χ( v), ( w))}, χ( y), ( z)}} m= xα yβz x= uδvθw min {mx{ min {mx( ( u),, ( w))},, ( z)}} m= xαyβz x= uδvθw min { min {mx{mx( ( u), ( w))}, ( z)}} m= xα yβz x= uδvθw
25 ongklnkrin Journl of cience nd Technology JT-0-0.R Akrm Pge of = = min { min {mx( ( u), ( w), ( z)}} m= xα yβz x= uδvθw min m= uδvθwαyβz {mx( ( u), ( w))}, ( z)}} min ( uδvθwαyβz) = (m ). m= uδvθwαyβz This implies tht o χ o o χ o. Conversely, we suppose tht (i) nd (ii) holds for ny N -fuzzy subset of T. Let m= xαuβyδvθz, for x, y, z, u, v T, α, β, δ, θ. As by (ii), o χ o o χ o implies tht ( x αuβyδvθz) = ( m) ( o χ o o χ o )( m) = min {mx{( o χ o m= xαuβyδvθz )( xαuβy), χ( v), ( z)}} mx{ min {mx( ( x), χ( u), ( y))}, χ( v), ( z)} n= xαuβy min {mx{mx( ( x),, ( y))},, ( z)} = n = xαuβy mx( ( x ), ( y), ( z)). Hence is n N -fuzzy bi-bi-idel of T. Lemm. Let nd be two NFs in T. Then o χ o is lso n N -fuzzy bi -bi-idel of T. Proof. trightforwrd.
26 Pge of ongklnkrin Journl of cience nd Technology JT-0-0.R Akrm Theorem. Let, nd be three NFs in T. Then o o is lso n N -fuzzy bi -bi-idel of T if ny one of, or is either n N -fuzzy bi-left idel or n N -fuzzy bi -right idel or n N -fuzzy bi -lterl idel of T. Proof. trightforwrd. Lemm. Every N -fuzzy bi -qusi idel of T is n N -fuzzy bi -bi-idel of T. Proof. trightforwrd. Lemm. Every N -fuzzy bi -left (right, lterl) idel of T is n N -fuzzy bi -biidel of T. Proof. trightforwrd. Lemm. Let { i, i I} be collection of N -fuzzy bi -bi-idels of T then lso n N -fuzzy bi -bi-idel of T. Proof. trightforwrd. is Theorem. Let be n NF in T. Then is n N -fuzzy bi-bi-idel of T if nd only if N ( ; t) is bi-bi-idel of T, for ll t [,0]. i I i
27 ongklnkrin Journl of cience nd Technology JT-0-0.R Akrm Pge of Proof. We suppose tht is n N -fuzzy bi-bi-idel of T nd m N( ; t) TN ( ; t) TN ( ; t). Then m= nαxβoδyθq for n, o, q N( ; t), x, y T nd α, β, δ, θ. ince n, o, q N ( ; t) implies tht ( n), ( o), ( q) t. Now, since is N -fuzzy bi-bi-idel of T so ( m) = ( nαxβoδyθq) mx( ( n ), ( o), ( q)) mx( t, t, t) = t implies tht ( m) t. This implies tht m N( ; t) tht is N ( ; t) TN ( ; t) TN ( ; t) N( ; t). Hence N ( ; t) is bi-bi-idel of T. Conversely, we suppose tht N ( ; t) is bi-bi-idel of T, for ll t [,0]. Let x, y, z T such tht ( x ) = tx, ( y) = t y nd ( z ) = tz with t x, t y, tz [,0]. Then x N ; t ), y N ( ; t ) nd z N ; t ). We my ssume tht tx t y tz nd ( x y ( z then N ; t ) N ( ; t ) N ; t ). This implies tht x y, z N( ; t ). ince N ; t ) ( x y ( z, z ( z is bi-bi-idel of T then for u, v T, α β, η, θ, x αuβyδvθz N( ; t ), so we hve, z x αuβyδvθz) t = mx( t, t, t ) = mx( ( x ), ( y), ( z)). ( z x y z Above holds for ll x, y, z, u, v T nd α, β, η, θ. Hence is n N -fuzzy bi-biidel of T. Theorem. A nonempty subset of T is bi-bi-idel of T if nd only if χ is n N -fuzzy bi -bi-idel of T.
28 Pge of ongklnkrin Journl of cience nd Technology JT-0-0.R Akrm Proof. We suppose tht is bi-bi-idel of T then it is bi -ternry subsemigroup of T nd by Theorem., χ is n N -fuzzy bi -ternry subsemigroup of T. Also TT. Now for ny x, y, z, u, v T, α, β, η, θ, xαuβyηvθz T. We hve following cses, (i) If x, y, z then xα uβyηvθz TT implies tht χ ( x) = χ ( y) = χ ( z) = = χ ( xαuβyηvθz). Hence χ ( xαuβyηvθz) = = mx( χ ( x), χ ( y), χ ( z)). (ii) If either x or y or z then either χ ( x) = 0 or χ ( y) = 0 or χ ( z) = 0 implies tht mx( χ ( x), χ ( y), χ ( z)) = 0. But χ ( xαuβyηvθz) 0. This implies tht χ ( xαuβyηvθz) mx( χ ( x), χ ( y), χ ( z)). (iii) If ny two of (iv) If x A nd x, y, z re not in. It is sme like (ii). y A nd z A. It is lso sme like (ii). Hence χ is n N -fuzzy bi-bi-idel of T. Conversely, we suppose tht χ is n N -fuzzy bi-bi-idel of T. For ny t TT there exists x, y, z, u, v T nd α, β, η, θ such tht t= xαuβyηvθz. Then χ ( x) = χ ( y) = χ ( z) = implies tht mx( χ ( x), χ ( y), χ ( z)) =. ince χ is n N -fuzzy bi-bi-idel of T implies tht χ ( xαuβyηvθz) mx( χ ( x), χ ( y), χ ( z)) =. But by definition χ ( xαuβyηvθz). This gives tht χ ( xαuβyηvθz) = implies tht t= xα uβyηvθz. Which shows tht TT. Hence is bi-bi-idel of T.
29 ongklnkrin Journl of cience nd Technology JT-0-0.R Akrm Pge of Lemm. A nonempty subset of T is bi-bi-idel of T if nd only if N -fuzzy bi -bi-idel of T. Proof. trightforwrd. C is n Exmple.0 Let T = {, b, c} nd = {α }. Then T is bi-ternry semigroup long with the opertion defined in the bellow tble. α b c Define, : T [,0] such tht = { <, 0.>, < b, 0.>, < c, 0.> }. Then is n N -fuzzy bi -bi-idel of T. Also, ( c αcαb) = ( c) = 0. 0.= ( b) nd ( cαbαc) = ( c) = 0. 0.= ( b). This implies tht is neither N -fuzzy bi -left nor N -fuzzy bi -lterl idel of T. + Exmple. Let T = Z nd = Z. Then T is bi -ternry semigroup but not - semigroup under the usul multipliction of integers i.e. for x, y, z T, α, β, ( xα yβz) = xαyβz. Define, : T [,0] s, for x T, 0., if x is even ( x) = 0., otherwise. b b c c b c.
30 Pge of ongklnkrin Journl of cience nd Technology JT-0-0.R Akrm Then is n N -fuzzy set in T. By simple clcultions we cn verify tht is n N - fuzzy bi-bi-idel of T s well s N -fuzzy bi-idel T. Exmple. Let where b c T = 0 0 d,, b, c, d, e Z 0 nd = Z 0 0 e Z 0 is the set of ll non-positive integers. Then T is bi-ternry semigroup under the usul nd sclr multipliction of mtrices. Now consider 0 B = 0 0 m m, 0 m Z0. Then B is bi-bi-idel of T but not bi-qusi idel of T, s we cn see below, for s B, x, y, z T nd α, β, where s = 0 0, x= 0 0, y= 0 0 0, z= , nd 0 α =, β =, then sαxβy = z BTT, xαsβy = z TBT nd xαyβs = z TTB. This implies tht z BTT TBT TTB but z B implies tht B TT TBT TTB B. Hence, B is not bi-bi-idel of T. Then by Theorem., χ is not n N -fuzzy bi -qusi idel of T but by Theorem., χ is n N -fuzzy bi -bi-idel of T. If, we define
31 ongklnkrin Journl of cience nd Technology JT-0-0.R Akrm Pge 0 of C B 0. if x B ( x) = 0. if x B. Then by Lemm., C B (x) is not n N -fuzzy bi-qusi idel of T but by Lemm., C B (x) is n N -fuzzy bi-bi-idel of T. References Akrm, M., Kvikumr, J. nd Khmis, A. 0. On N --idels in-ag**- Groupoids. Anlele Universittii Orde Fscicol Mtemtic. Tom XXI, Issue No., -. Akrm, M., Kvikumr, J. nd Khmis, A. 0. Chrcteriztion of bi-ternry semigroups by their idels. Itlin Journl of Pure nd Applied Mthemtics. N-(), -. Atnssov, K.. Intuitionistic fuzzy sets, VII, ITKR's ession, ofi, June (Deposed in Centrl cience nd Technicl, Librry of Bulgrin Acdemy of cience, /) (in Bulg.). Bisws, R.. Intuitionistic fuzzy subgroupoids. Mthemticl Forum x, -. Jun, Y.B., Lee, K.J. nd ong,.z. 00. N -idels of BCK/BCI-lgebrs. Journl Chungcheong Mthemticl ociety., -. Khn, A., Jun, Y.B. nd hbir, M. 00. N -fuzzy idels in ordered semigroups. Interntionl Journl of Mthemtics nd Mthemticl ciences. 00, Article ID, pges. Khn, A., Jun, Y.B. nd hbir, M. 00. N -fuzzy qusi-idels in ordered semigroups. 0
32 Pge of ongklnkrin Journl of cience nd Technology JT-0-0.R Akrm Qusigroups nd Relted ystems., -. Kim, K.H. nd Jun, Y.B. 00. Intuitionistic fuzzy idels of semigroups. Indin Journl of Pure nd Applied Mthemtics. (), -. Rosenfeld, A.. Fuzzy groups. Journl of Mthemticl Anlysis nd Applictions., -. Zdeh, L.A.. Fuzzy sets. Informtion & Control., -.
Results on Planar Near Rings
 Interntionl Mthemticl Forum, Vol. 9, 2014, no. 23, 1139-1147 HIKARI Ltd, www.m-hikri.com http://dx.doi.org/10.12988/imf.2014.4593 Results on Plnr Ner Rings Edurd Domi Deprtment of Mthemtics, University
Interntionl Mthemticl Forum, Vol. 9, 2014, no. 23, 1139-1147 HIKARI Ltd, www.m-hikri.com http://dx.doi.org/10.12988/imf.2014.4593 Results on Plnr Ner Rings Edurd Domi Deprtment of Mthemtics, University
Hermite-Hadamard type inequalities for harmonically convex functions
 Hcettepe Journl o Mthemtics nd Sttistics Volume 43 6 4 935 94 Hermite-Hdmrd type ineulities or hrmoniclly convex unctions İmdt İşcn Abstrct The uthor introduces the concept o hrmoniclly convex unctions
Hcettepe Journl o Mthemtics nd Sttistics Volume 43 6 4 935 94 Hermite-Hdmrd type ineulities or hrmoniclly convex unctions İmdt İşcn Abstrct The uthor introduces the concept o hrmoniclly convex unctions
The Hadamard s inequality for quasi-convex functions via fractional integrals
 Annls of the University of Criov, Mthemtics nd Computer Science Series Volume (), 3, Pges 67 73 ISSN: 5-563 The Hdmrd s ineulity for usi-convex functions vi frctionl integrls M E Özdemir nd Çetin Yildiz
Annls of the University of Criov, Mthemtics nd Computer Science Series Volume (), 3, Pges 67 73 ISSN: 5-563 The Hdmrd s ineulity for usi-convex functions vi frctionl integrls M E Özdemir nd Çetin Yildiz
Intuitionistic Fuzzy Lattices and Intuitionistic Fuzzy Boolean Algebras
 Intuitionistic Fuzzy Lttices nd Intuitionistic Fuzzy oolen Algebrs.K. Tripthy #1, M.K. Stpthy *2 nd P.K.Choudhury ##3 # School of Computing Science nd Engineering VIT University Vellore-632014, TN, Indi
Intuitionistic Fuzzy Lttices nd Intuitionistic Fuzzy oolen Algebrs.K. Tripthy #1, M.K. Stpthy *2 nd P.K.Choudhury ##3 # School of Computing Science nd Engineering VIT University Vellore-632014, TN, Indi
IN GAUSSIAN INTEGERS X 3 + Y 3 = Z 3 HAS ONLY TRIVIAL SOLUTIONS A NEW APPROACH
 INTEGERS: ELECTRONIC JOURNAL OF COMBINATORIAL NUMBER THEORY 8 (2008), #A2 IN GAUSSIAN INTEGERS X + Y = Z HAS ONLY TRIVIAL SOLUTIONS A NEW APPROACH Elis Lmpkis Lmpropoulou (Term), Kiprissi, T.K: 24500,
INTEGERS: ELECTRONIC JOURNAL OF COMBINATORIAL NUMBER THEORY 8 (2008), #A2 IN GAUSSIAN INTEGERS X + Y = Z HAS ONLY TRIVIAL SOLUTIONS A NEW APPROACH Elis Lmpkis Lmpropoulou (Term), Kiprissi, T.K: 24500,
Solution to Fredholm Fuzzy Integral Equations with Degenerate Kernel
 Int. J. Contemp. Mth. Sciences, Vol. 6, 2011, no. 11, 535-543 Solution to Fredholm Fuzzy Integrl Equtions with Degenerte Kernel M. M. Shmivnd, A. Shhsvrn nd S. M. Tri Fculty of Science, Islmic Azd University
Int. J. Contemp. Mth. Sciences, Vol. 6, 2011, no. 11, 535-543 Solution to Fredholm Fuzzy Integrl Equtions with Degenerte Kernel M. M. Shmivnd, A. Shhsvrn nd S. M. Tri Fculty of Science, Islmic Azd University
New Integral Inequalities of the Type of Hermite-Hadamard Through Quasi Convexity
 Punjb University Journl of Mthemtics (ISSN 116-56) Vol. 45 (13) pp. 33-38 New Integrl Inequlities of the Type of Hermite-Hdmrd Through Qusi Convexity S. Hussin Deprtment of Mthemtics, College of Science,
Punjb University Journl of Mthemtics (ISSN 116-56) Vol. 45 (13) pp. 33-38 New Integrl Inequlities of the Type of Hermite-Hdmrd Through Qusi Convexity S. Hussin Deprtment of Mthemtics, College of Science,
Some estimates on the Hermite-Hadamard inequality through quasi-convex functions
 Annls of University of Criov, Mth. Comp. Sci. Ser. Volume 3, 7, Pges 8 87 ISSN: 13-693 Some estimtes on the Hermite-Hdmrd inequlity through qusi-convex functions Dniel Alexndru Ion Abstrct. In this pper
Annls of University of Criov, Mth. Comp. Sci. Ser. Volume 3, 7, Pges 8 87 ISSN: 13-693 Some estimtes on the Hermite-Hdmrd inequlity through qusi-convex functions Dniel Alexndru Ion Abstrct. In this pper
KRASNOSEL SKII TYPE FIXED POINT THEOREM FOR NONLINEAR EXPANSION
 Fixed Point Theory, 13(2012), No. 1, 285-291 http://www.mth.ubbcluj.ro/ nodecj/sfptcj.html KRASNOSEL SKII TYPE FIXED POINT THEOREM FOR NONLINEAR EXPANSION FULI WANG AND FENG WANG School of Mthemtics nd
Fixed Point Theory, 13(2012), No. 1, 285-291 http://www.mth.ubbcluj.ro/ nodecj/sfptcj.html KRASNOSEL SKII TYPE FIXED POINT THEOREM FOR NONLINEAR EXPANSION FULI WANG AND FENG WANG School of Mthemtics nd
New Expansion and Infinite Series
 Interntionl Mthemticl Forum, Vol. 9, 204, no. 22, 06-073 HIKARI Ltd, www.m-hikri.com http://dx.doi.org/0.2988/imf.204.4502 New Expnsion nd Infinite Series Diyun Zhng College of Computer Nnjing University
Interntionl Mthemticl Forum, Vol. 9, 204, no. 22, 06-073 HIKARI Ltd, www.m-hikri.com http://dx.doi.org/0.2988/imf.204.4502 New Expnsion nd Infinite Series Diyun Zhng College of Computer Nnjing University
Parametrized inequality of Hermite Hadamard type for functions whose third derivative absolute values are quasi convex
 Wu et l. SpringerPlus (5) 4:83 DOI.8/s44-5-33-z RESEARCH Prmetrized inequlity of Hermite Hdmrd type for functions whose third derivtive bsolute vlues re qusi convex Shn He Wu, Bnyt Sroysng, Jin Shn Xie
Wu et l. SpringerPlus (5) 4:83 DOI.8/s44-5-33-z RESEARCH Prmetrized inequlity of Hermite Hdmrd type for functions whose third derivtive bsolute vlues re qusi convex Shn He Wu, Bnyt Sroysng, Jin Shn Xie
Theoretical foundations of Gaussian quadrature
 Theoreticl foundtions of Gussin qudrture 1 Inner product vector spce Definition 1. A vector spce (or liner spce) is set V = {u, v, w,...} in which the following two opertions re defined: (A) Addition of
Theoreticl foundtions of Gussin qudrture 1 Inner product vector spce Definition 1. A vector spce (or liner spce) is set V = {u, v, w,...} in which the following two opertions re defined: (A) Addition of
Zero-Sum Magic Graphs and Their Null Sets
 Zero-Sum Mgic Grphs nd Their Null Sets Ebrhim Slehi Deprtment of Mthemticl Sciences University of Nevd Ls Vegs Ls Vegs, NV 89154-4020. ebrhim.slehi@unlv.edu Abstrct For ny h N, grph G = (V, E) is sid to
Zero-Sum Mgic Grphs nd Their Null Sets Ebrhim Slehi Deprtment of Mthemticl Sciences University of Nevd Ls Vegs Ls Vegs, NV 89154-4020. ebrhim.slehi@unlv.edu Abstrct For ny h N, grph G = (V, E) is sid to
Journal of Inequalities in Pure and Applied Mathematics
 Journl of Inequlities in Pure nd Applied Mthemtics GENERALIZATIONS OF THE TRAPEZOID INEQUALITIES BASED ON A NEW MEAN VALUE THEOREM FOR THE REMAINDER IN TAYLOR S FORMULA volume 7, issue 3, rticle 90, 006.
Journl of Inequlities in Pure nd Applied Mthemtics GENERALIZATIONS OF THE TRAPEZOID INEQUALITIES BASED ON A NEW MEAN VALUE THEOREM FOR THE REMAINDER IN TAYLOR S FORMULA volume 7, issue 3, rticle 90, 006.
Introduction to Group Theory
 Introduction to Group Theory Let G be n rbitrry set of elements, typiclly denoted s, b, c,, tht is, let G = {, b, c, }. A binry opertion in G is rule tht ssocites with ech ordered pir (,b) of elements
Introduction to Group Theory Let G be n rbitrry set of elements, typiclly denoted s, b, c,, tht is, let G = {, b, c, }. A binry opertion in G is rule tht ssocites with ech ordered pir (,b) of elements
Realistic Method for Solving Fully Intuitionistic Fuzzy. Transportation Problems
 Applied Mthemticl Sciences, Vol 8, 201, no 11, 6-69 HKAR Ltd, wwwm-hikricom http://dxdoiorg/10988/ms20176 Relistic Method for Solving Fully ntuitionistic Fuzzy Trnsporttion Problems P Pndin Deprtment of
Applied Mthemticl Sciences, Vol 8, 201, no 11, 6-69 HKAR Ltd, wwwm-hikricom http://dxdoiorg/10988/ms20176 Relistic Method for Solving Fully ntuitionistic Fuzzy Trnsporttion Problems P Pndin Deprtment of
Binding Numbers for all Fractional (a, b, k)-critical Graphs
 Filomt 28:4 (2014), 709 713 DOI 10.2298/FIL1404709Z Published by Fculty of Sciences nd Mthemtics, University of Niš, Serbi Avilble t: http://www.pmf.ni.c.rs/filomt Binding Numbers for ll Frctionl (, b,
Filomt 28:4 (2014), 709 713 DOI 10.2298/FIL1404709Z Published by Fculty of Sciences nd Mthemtics, University of Niš, Serbi Avilble t: http://www.pmf.ni.c.rs/filomt Binding Numbers for ll Frctionl (, b,
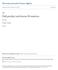
f (a) + f (b) f (λx + (1 λ)y) max {f (x),f (y)}, x, y [a, b]. (1.1)
![f (a) + f (b) f (λx + (1 λ)y) max {f (x),f (y)}, x, y [a, b]. (1.1) f (a) + f (b) f (λx + (1 λ)y) max {f (x),f (y)}, x, y [a, b]. (1.1)](/thumbs/82/86576045.jpg) TAMKANG JOURNAL OF MATHEMATICS Volume 41, Number 4, 353-359, Winter 1 NEW INEQUALITIES OF HERMITE-HADAMARD TYPE FOR FUNCTIONS WHOSE SECOND DERIVATIVES ABSOLUTE VALUES ARE QUASI-CONVEX M. ALOMARI, M. DARUS
TAMKANG JOURNAL OF MATHEMATICS Volume 41, Number 4, 353-359, Winter 1 NEW INEQUALITIES OF HERMITE-HADAMARD TYPE FOR FUNCTIONS WHOSE SECOND DERIVATIVES ABSOLUTE VALUES ARE QUASI-CONVEX M. ALOMARI, M. DARUS
A New Grey-rough Set Model Based on Interval-Valued Grey Sets
 Proceedings of the 009 IEEE Interntionl Conference on Systems Mn nd Cybernetics Sn ntonio TX US - October 009 New Grey-rough Set Model sed on Intervl-Vlued Grey Sets Wu Shunxing Deprtment of utomtion Ximen
Proceedings of the 009 IEEE Interntionl Conference on Systems Mn nd Cybernetics Sn ntonio TX US - October 009 New Grey-rough Set Model sed on Intervl-Vlued Grey Sets Wu Shunxing Deprtment of utomtion Ximen
A General Dynamic Inequality of Opial Type
 Appl Mth Inf Sci No 3-5 (26) Applied Mthemtics & Informtion Sciences An Interntionl Journl http://dxdoiorg/2785/mis/bos7-mis A Generl Dynmic Inequlity of Opil Type Rvi Agrwl Mrtin Bohner 2 Donl O Regn
Appl Mth Inf Sci No 3-5 (26) Applied Mthemtics & Informtion Sciences An Interntionl Journl http://dxdoiorg/2785/mis/bos7-mis A Generl Dynmic Inequlity of Opil Type Rvi Agrwl Mrtin Bohner 2 Donl O Regn
Semigroup of generalized inverses of matrices
 Semigroup of generlized inverses of mtrices Hnif Zekroui nd Sid Guedjib Abstrct. The pper is divided into two principl prts. In the first one, we give the set of generlized inverses of mtrix A structure
Semigroup of generlized inverses of mtrices Hnif Zekroui nd Sid Guedjib Abstrct. The pper is divided into two principl prts. In the first one, we give the set of generlized inverses of mtrix A structure
The Hadamard s Inequality for s-convex Function
 Int. Journl o Mth. Anlysis, Vol., 008, no. 3, 639-646 The Hdmrd s Inequlity or s-conve Function M. Alomri nd M. Drus School o Mthemticl Sciences Fculty o Science nd Technology Universiti Kebngsn Mlysi
Int. Journl o Mth. Anlysis, Vol., 008, no. 3, 639-646 The Hdmrd s Inequlity or s-conve Function M. Alomri nd M. Drus School o Mthemticl Sciences Fculty o Science nd Technology Universiti Kebngsn Mlysi
Research Article Moment Inequalities and Complete Moment Convergence
 Hindwi Publishing Corportion Journl of Inequlities nd Applictions Volume 2009, Article ID 271265, 14 pges doi:10.1155/2009/271265 Reserch Article Moment Inequlities nd Complete Moment Convergence Soo Hk
Hindwi Publishing Corportion Journl of Inequlities nd Applictions Volume 2009, Article ID 271265, 14 pges doi:10.1155/2009/271265 Reserch Article Moment Inequlities nd Complete Moment Convergence Soo Hk
RELATIONS ON BI-PERIODIC JACOBSTHAL SEQUENCE
 TJMM 10 018, No., 141-151 RELATIONS ON BI-PERIODIC JACOBSTHAL SEQUENCE S. UYGUN, H. KARATAS, E. AKINCI Abstrct. Following the new generliztion of the Jcobsthl sequence defined by Uygun nd Owusu 10 s ĵ
TJMM 10 018, No., 141-151 RELATIONS ON BI-PERIODIC JACOBSTHAL SEQUENCE S. UYGUN, H. KARATAS, E. AKINCI Abstrct. Following the new generliztion of the Jcobsthl sequence defined by Uygun nd Owusu 10 s ĵ
WENJUN LIU AND QUÔ C ANH NGÔ
 AN OSTROWSKI-GRÜSS TYPE INEQUALITY ON TIME SCALES WENJUN LIU AND QUÔ C ANH NGÔ Astrct. In this pper we derive new inequlity of Ostrowski-Grüss type on time scles nd thus unify corresponding continuous
AN OSTROWSKI-GRÜSS TYPE INEQUALITY ON TIME SCALES WENJUN LIU AND QUÔ C ANH NGÔ Astrct. In this pper we derive new inequlity of Ostrowski-Grüss type on time scles nd thus unify corresponding continuous
Integral points on the rational curve
 Integrl points on the rtionl curve y x bx c x ;, b, c integers. Konstntine Zeltor Mthemtics University of Wisconsin - Mrinette 750 W. Byshore Street Mrinette, WI 5443-453 Also: Konstntine Zeltor P.O. Box
Integrl points on the rtionl curve y x bx c x ;, b, c integers. Konstntine Zeltor Mthemtics University of Wisconsin - Mrinette 750 W. Byshore Street Mrinette, WI 5443-453 Also: Konstntine Zeltor P.O. Box
A NOTE ON PREPARACOMPACTNESS
 Volume 1, 1976 Pges 253 260 http://topology.uburn.edu/tp/ A NOTE ON PREPARACOMPACTNE by J. C. mith Topology Proceedings Web: http://topology.uburn.edu/tp/ Mil: Topology Proceedings Deprtment of Mthemtics
Volume 1, 1976 Pges 253 260 http://topology.uburn.edu/tp/ A NOTE ON PREPARACOMPACTNE by J. C. mith Topology Proceedings Web: http://topology.uburn.edu/tp/ Mil: Topology Proceedings Deprtment of Mthemtics
Improvement of Ostrowski Integral Type Inequalities with Application
 Filomt 30:6 06), 56 DOI 098/FIL606Q Published by Fculty of Sciences nd Mthemtics, University of Niš, Serbi Avilble t: http://wwwpmfnicrs/filomt Improvement of Ostrowski Integrl Type Ineulities with Appliction
Filomt 30:6 06), 56 DOI 098/FIL606Q Published by Fculty of Sciences nd Mthemtics, University of Niš, Serbi Avilble t: http://wwwpmfnicrs/filomt Improvement of Ostrowski Integrl Type Ineulities with Appliction
DYNAMICAL SYSTEMS SUPPLEMENT 2007 pp Natalija Sergejeva. Department of Mathematics and Natural Sciences Parades 1 LV-5400 Daugavpils, Latvia
 DISCRETE AND CONTINUOUS Website: www.aimsciences.org DYNAMICAL SYSTEMS SUPPLEMENT 2007 pp. 920 926 ON THE UNUSUAL FUČÍK SPECTRUM Ntlij Sergejev Deprtment of Mthemtics nd Nturl Sciences Prdes 1 LV-5400
DISCRETE AND CONTINUOUS Website: www.aimsciences.org DYNAMICAL SYSTEMS SUPPLEMENT 2007 pp. 920 926 ON THE UNUSUAL FUČÍK SPECTRUM Ntlij Sergejev Deprtment of Mthemtics nd Nturl Sciences Prdes 1 LV-5400
FUNCTIONS OF α-slow INCREASE
 Bulletin of Mthemticl Anlysis nd Applictions ISSN: 1821-1291, URL: http://www.bmth.org Volume 4 Issue 1 (2012), Pges 226-230. FUNCTIONS OF α-slow INCREASE (COMMUNICATED BY HÜSEYIN BOR) YILUN SHANG Abstrct.
Bulletin of Mthemticl Anlysis nd Applictions ISSN: 1821-1291, URL: http://www.bmth.org Volume 4 Issue 1 (2012), Pges 226-230. FUNCTIONS OF α-slow INCREASE (COMMUNICATED BY HÜSEYIN BOR) YILUN SHANG Abstrct.
arxiv: v1 [math.ra] 1 Nov 2014
![arxiv: v1 [math.ra] 1 Nov 2014 arxiv: v1 [math.ra] 1 Nov 2014](/thumbs/85/92740375.jpg) CLASSIFICATION OF COMPLEX CYCLIC LEIBNIZ ALGEBRAS DANIEL SCOFIELD AND S MCKAY SULLIVAN rxiv:14110170v1 [mthra] 1 Nov 2014 Abstrct Since Leibniz lgebrs were introduced by Lody s generliztion of Lie lgebrs,
CLASSIFICATION OF COMPLEX CYCLIC LEIBNIZ ALGEBRAS DANIEL SCOFIELD AND S MCKAY SULLIVAN rxiv:14110170v1 [mthra] 1 Nov 2014 Abstrct Since Leibniz lgebrs were introduced by Lody s generliztion of Lie lgebrs,
13.3 CLASSICAL STRAIGHTEDGE AND COMPASS CONSTRUCTIONS
 33 CLASSICAL STRAIGHTEDGE AND COMPASS CONSTRUCTIONS As simple ppliction of the results we hve obtined on lgebric extensions, nd in prticulr on the multiplictivity of extension degrees, we cn nswer (in
33 CLASSICAL STRAIGHTEDGE AND COMPASS CONSTRUCTIONS As simple ppliction of the results we hve obtined on lgebric extensions, nd in prticulr on the multiplictivity of extension degrees, we cn nswer (in
Extensions of Chebyshev inequality for fuzzy integral and applications
 Extensions of Chebyshev inequlity for fuzzy integrl nd pplictions H. Román-Flores, Y. Chlco-Cno, nd. Flores-Frnulič Instituto de lt Investigción, Universidd de Trpcá {hromn,ychlco,flores}@ut.cl bstrct.
Extensions of Chebyshev inequlity for fuzzy integrl nd pplictions H. Román-Flores, Y. Chlco-Cno, nd. Flores-Frnulič Instituto de lt Investigción, Universidd de Trpcá {hromn,ychlco,flores}@ut.cl bstrct.
N 0 completions on partial matrices
 N 0 completions on prtil mtrices C. Jordán C. Mendes Arújo Jun R. Torregros Instituto de Mtemátic Multidisciplinr / Centro de Mtemátic Universidd Politécnic de Vlenci / Universidde do Minho Cmino de Ver
N 0 completions on prtil mtrices C. Jordán C. Mendes Arújo Jun R. Torregros Instituto de Mtemátic Multidisciplinr / Centro de Mtemátic Universidd Politécnic de Vlenci / Universidde do Minho Cmino de Ver
New general integral inequalities for quasiconvex functions
 NTMSCI 6, No 1, 1-7 18 1 New Trends in Mthemticl Sciences http://dxdoiorg/185/ntmsci1739 New generl integrl ineulities for usiconvex functions Cetin Yildiz Atturk University, K K Eduction Fculty, Deprtment
NTMSCI 6, No 1, 1-7 18 1 New Trends in Mthemticl Sciences http://dxdoiorg/185/ntmsci1739 New generl integrl ineulities for usiconvex functions Cetin Yildiz Atturk University, K K Eduction Fculty, Deprtment
Linearly Similar Polynomials
 Linerly Similr Polynomils rthur Holshouser 3600 Bullrd St. Chrlotte, NC, US Hrold Reiter Deprtment of Mthemticl Sciences University of North Crolin Chrlotte, Chrlotte, NC 28223, US hbreiter@uncc.edu stndrd
Linerly Similr Polynomils rthur Holshouser 3600 Bullrd St. Chrlotte, NC, US Hrold Reiter Deprtment of Mthemticl Sciences University of North Crolin Chrlotte, Chrlotte, NC 28223, US hbreiter@uncc.edu stndrd
Multidimensional. MOD Planes. W. B. Vasantha Kandasamy Ilanthenral K Florentin Smarandache
 Multidimensionl MOD Plnes W. B. Vsnth Kndsmy Ilnthenrl K Florentin Smrndche 2015 This book cn be ordered from: EuropNov ASBL Clos du Prnsse, 3E 1000, Bruxelles Belgium E-mil: info@europnov.be URL: http://www.europnov.be/
Multidimensionl MOD Plnes W. B. Vsnth Kndsmy Ilnthenrl K Florentin Smrndche 2015 This book cn be ordered from: EuropNov ASBL Clos du Prnsse, 3E 1000, Bruxelles Belgium E-mil: info@europnov.be URL: http://www.europnov.be/
A Convergence Theorem for the Improper Riemann Integral of Banach Space-valued Functions
 Interntionl Journl of Mthemticl Anlysis Vol. 8, 2014, no. 50, 2451-2460 HIKARI Ltd, www.m-hikri.com http://dx.doi.org/10.12988/ijm.2014.49294 A Convergence Theorem for the Improper Riemnn Integrl of Bnch
Interntionl Journl of Mthemticl Anlysis Vol. 8, 2014, no. 50, 2451-2460 HIKARI Ltd, www.m-hikri.com http://dx.doi.org/10.12988/ijm.2014.49294 A Convergence Theorem for the Improper Riemnn Integrl of Bnch
Set Integral Equations in Metric Spaces
 Mthemtic Morvic Vol. 13-1 2009, 95 102 Set Integrl Equtions in Metric Spces Ion Tişe Abstrct. Let P cp,cvr n be the fmily of ll nonempty compct, convex subsets of R n. We consider the following set integrl
Mthemtic Morvic Vol. 13-1 2009, 95 102 Set Integrl Equtions in Metric Spces Ion Tişe Abstrct. Let P cp,cvr n be the fmily of ll nonempty compct, convex subsets of R n. We consider the following set integrl
arxiv:math/ v2 [math.ho] 16 Dec 2003
![arxiv:math/ v2 [math.ho] 16 Dec 2003 arxiv:math/ v2 [math.ho] 16 Dec 2003](/thumbs/92/109668180.jpg) rxiv:mth/0312293v2 [mth.ho] 16 Dec 2003 Clssicl Lebesgue Integrtion Theorems for the Riemnn Integrl Josh Isrlowitz 244 Ridge Rd. Rutherford, NJ 07070 jbi2@njit.edu Februry 1, 2008 Abstrct In this pper,
rxiv:mth/0312293v2 [mth.ho] 16 Dec 2003 Clssicl Lebesgue Integrtion Theorems for the Riemnn Integrl Josh Isrlowitz 244 Ridge Rd. Rutherford, NJ 07070 jbi2@njit.edu Februry 1, 2008 Abstrct In this pper,
Self-similarity and symmetries of Pascal s triangles and simplices mod p
 Sn Jose Stte University SJSU ScholrWorks Fculty Publictions Mthemtics nd Sttistics Februry 2004 Self-similrity nd symmetries of Pscl s tringles nd simplices mod p Richrd P. Kubelk Sn Jose Stte University,
Sn Jose Stte University SJSU ScholrWorks Fculty Publictions Mthemtics nd Sttistics Februry 2004 Self-similrity nd symmetries of Pscl s tringles nd simplices mod p Richrd P. Kubelk Sn Jose Stte University,
WHEN IS A FUNCTION NOT FLAT? 1. Introduction. {e 1 0, x = 0. f(x) =
 WHEN IS A FUNCTION NOT FLAT? YIFEI PAN AND MEI WANG Abstrct. In this pper we prove unique continution property for vector vlued functions of one vrible stisfying certin differentil inequlity. Key words:
WHEN IS A FUNCTION NOT FLAT? YIFEI PAN AND MEI WANG Abstrct. In this pper we prove unique continution property for vector vlued functions of one vrible stisfying certin differentil inequlity. Key words:
Frobenius numbers of generalized Fibonacci semigroups
 Frobenius numbers of generlized Fiboncci semigroups Gretchen L. Mtthews 1 Deprtment of Mthemticl Sciences, Clemson University, Clemson, SC 29634-0975, USA gmtthe@clemson.edu Received:, Accepted:, Published:
Frobenius numbers of generlized Fiboncci semigroups Gretchen L. Mtthews 1 Deprtment of Mthemticl Sciences, Clemson University, Clemson, SC 29634-0975, USA gmtthe@clemson.edu Received:, Accepted:, Published:
Positive Solutions of Operator Equations on Half-Line
 Int. Journl of Mth. Anlysis, Vol. 3, 29, no. 5, 211-22 Positive Solutions of Opertor Equtions on Hlf-Line Bohe Wng 1 School of Mthemtics Shndong Administrtion Institute Jinn, 2514, P.R. Chin sdusuh@163.com
Int. Journl of Mth. Anlysis, Vol. 3, 29, no. 5, 211-22 Positive Solutions of Opertor Equtions on Hlf-Line Bohe Wng 1 School of Mthemtics Shndong Administrtion Institute Jinn, 2514, P.R. Chin sdusuh@163.com
The Algebra (al-jabr) of Matrices
 Section : Mtri lgebr nd Clculus Wshkewicz College of Engineering he lgebr (l-jbr) of Mtrices lgebr s brnch of mthemtics is much broder thn elementry lgebr ll of us studied in our high school dys. In sense
Section : Mtri lgebr nd Clculus Wshkewicz College of Engineering he lgebr (l-jbr) of Mtrices lgebr s brnch of mthemtics is much broder thn elementry lgebr ll of us studied in our high school dys. In sense
A BRIEF INTRODUCTION TO UNIFORM CONVERGENCE. In the study of Fourier series, several questions arise naturally, such as: c n e int
 A BRIEF INTRODUCTION TO UNIFORM CONVERGENCE HANS RINGSTRÖM. Questions nd exmples In the study of Fourier series, severl questions rise nturlly, such s: () (2) re there conditions on c n, n Z, which ensure
A BRIEF INTRODUCTION TO UNIFORM CONVERGENCE HANS RINGSTRÖM. Questions nd exmples In the study of Fourier series, severl questions rise nturlly, such s: () (2) re there conditions on c n, n Z, which ensure
Research Article On Existence and Uniqueness of Solutions of a Nonlinear Integral Equation
 Journl of Applied Mthemtics Volume 2011, Article ID 743923, 7 pges doi:10.1155/2011/743923 Reserch Article On Existence nd Uniqueness of Solutions of Nonliner Integrl Eqution M. Eshghi Gordji, 1 H. Bghni,
Journl of Applied Mthemtics Volume 2011, Article ID 743923, 7 pges doi:10.1155/2011/743923 Reserch Article On Existence nd Uniqueness of Solutions of Nonliner Integrl Eqution M. Eshghi Gordji, 1 H. Bghni,
Expected Value of Function of Uncertain Variables
 Journl of Uncertin Systems Vol.4, No.3, pp.8-86, 2 Online t: www.jus.org.uk Expected Vlue of Function of Uncertin Vribles Yuhn Liu, Minghu H College of Mthemtics nd Computer Sciences, Hebei University,
Journl of Uncertin Systems Vol.4, No.3, pp.8-86, 2 Online t: www.jus.org.uk Expected Vlue of Function of Uncertin Vribles Yuhn Liu, Minghu H College of Mthemtics nd Computer Sciences, Hebei University,
Exponentials - Grade 10 [CAPS] *
![Exponentials - Grade 10 [CAPS] * Exponentials - Grade 10 [CAPS] *](/thumbs/88/115984632.jpg) OpenStx-CNX module: m859 Exponentils - Grde 0 [CAPS] * Free High School Science Texts Project Bsed on Exponentils by Rory Adms Free High School Science Texts Project Mrk Horner Hether Willims This work
OpenStx-CNX module: m859 Exponentils - Grde 0 [CAPS] * Free High School Science Texts Project Bsed on Exponentils by Rory Adms Free High School Science Texts Project Mrk Horner Hether Willims This work
Rectangular group congruences on an epigroup
 cholrs Journl of Engineering nd Technology (JET) ch J Eng Tech, 015; 3(9):73-736 cholrs Acdemic nd cientific Pulisher (An Interntionl Pulisher for Acdemic nd cientific Resources) wwwsspulishercom IN 31-435X
cholrs Journl of Engineering nd Technology (JET) ch J Eng Tech, 015; 3(9):73-736 cholrs Acdemic nd cientific Pulisher (An Interntionl Pulisher for Acdemic nd cientific Resources) wwwsspulishercom IN 31-435X
arxiv: v1 [math.ca] 28 Jan 2013
![arxiv: v1 [math.ca] 28 Jan 2013 arxiv: v1 [math.ca] 28 Jan 2013](/thumbs/75/71517898.jpg) ON NEW APPROACH HADAMARD-TYPE INEQUALITIES FOR s-geometrically CONVEX FUNCTIONS rxiv:3.9v [mth.ca 8 Jn 3 MEVLÜT TUNÇ AND İBRAHİM KARABAYIR Astrct. In this pper we chieve some new Hdmrd type ineulities
ON NEW APPROACH HADAMARD-TYPE INEQUALITIES FOR s-geometrically CONVEX FUNCTIONS rxiv:3.9v [mth.ca 8 Jn 3 MEVLÜT TUNÇ AND İBRAHİM KARABAYIR Astrct. In this pper we chieve some new Hdmrd type ineulities
IST 4 Information and Logic
 IST 4 Informtion nd Logic T = tody x= hw#x out x= hw#x due mon tue wed thr fri 31 M1 1 7 oh M1 14 oh 1 oh 2M2 21 oh oh 2 oh Mx= MQx out Mx= MQx due 28 oh M2 oh oh = office hours 5 3 12 oh 3 T 4 oh oh 19
IST 4 Informtion nd Logic T = tody x= hw#x out x= hw#x due mon tue wed thr fri 31 M1 1 7 oh M1 14 oh 1 oh 2M2 21 oh oh 2 oh Mx= MQx out Mx= MQx due 28 oh M2 oh oh = office hours 5 3 12 oh 3 T 4 oh oh 19
1.9 C 2 inner variations
 46 CHAPTER 1. INDIRECT METHODS 1.9 C 2 inner vritions So fr, we hve restricted ttention to liner vritions. These re vritions of the form vx; ǫ = ux + ǫφx where φ is in some liner perturbtion clss P, for
46 CHAPTER 1. INDIRECT METHODS 1.9 C 2 inner vritions So fr, we hve restricted ttention to liner vritions. These re vritions of the form vx; ǫ = ux + ǫφx where φ is in some liner perturbtion clss P, for
Simple Gamma Rings With Involutions.
 IOSR Journl of Mthemtics (IOSR-JM) ISSN: 2278-5728. Volume 4, Issue (Nov. - Dec. 2012), PP 40-48 Simple Gmm Rings With Involutions. 1 A.C. Pul nd 2 Md. Sbur Uddin 1 Deprtment of Mthemtics University of
IOSR Journl of Mthemtics (IOSR-JM) ISSN: 2278-5728. Volume 4, Issue (Nov. - Dec. 2012), PP 40-48 Simple Gmm Rings With Involutions. 1 A.C. Pul nd 2 Md. Sbur Uddin 1 Deprtment of Mthemtics University of
Numerical Linear Algebra Assignment 008
 Numericl Liner Algebr Assignment 008 Nguyen Qun B Hong Students t Fculty of Mth nd Computer Science, Ho Chi Minh University of Science, Vietnm emil. nguyenqunbhong@gmil.com blog. http://hongnguyenqunb.wordpress.com
Numericl Liner Algebr Assignment 008 Nguyen Qun B Hong Students t Fculty of Mth nd Computer Science, Ho Chi Minh University of Science, Vietnm emil. nguyenqunbhong@gmil.com blog. http://hongnguyenqunb.wordpress.com
Here we study square linear systems and properties of their coefficient matrices as they relate to the solution set of the linear system.
 Section 24 Nonsingulr Liner Systems Here we study squre liner systems nd properties of their coefficient mtrices s they relte to the solution set of the liner system Let A be n n Then we know from previous
Section 24 Nonsingulr Liner Systems Here we study squre liner systems nd properties of their coefficient mtrices s they relte to the solution set of the liner system Let A be n n Then we know from previous
A product convergence theorem for Henstock Kurzweil integrals
 A product convergence theorem for Henstock Kurzweil integrls Prsr Mohnty Erik Tlvil 1 Deprtment of Mthemticl nd Sttisticl Sciences University of Albert Edmonton AB Cnd T6G 2G1 pmohnty@mth.ulbert.c etlvil@mth.ulbert.c
A product convergence theorem for Henstock Kurzweil integrls Prsr Mohnty Erik Tlvil 1 Deprtment of Mthemticl nd Sttisticl Sciences University of Albert Edmonton AB Cnd T6G 2G1 pmohnty@mth.ulbert.c etlvil@mth.ulbert.c
Chapter 3 MATRIX. In this chapter: 3.1 MATRIX NOTATION AND TERMINOLOGY
 Chpter 3 MTRIX In this chpter: Definition nd terms Specil Mtrices Mtrix Opertion: Trnspose, Equlity, Sum, Difference, Sclr Multipliction, Mtrix Multipliction, Determinnt, Inverse ppliction of Mtrix in
Chpter 3 MTRIX In this chpter: Definition nd terms Specil Mtrices Mtrix Opertion: Trnspose, Equlity, Sum, Difference, Sclr Multipliction, Mtrix Multipliction, Determinnt, Inverse ppliction of Mtrix in
Rough Lattice: A Combination with the Lattice Theory and the Rough Set Theory
 06 Interntionl Conference on Mechtronics, Control nd Automtion Engineering (MCAE 06) ough Lttice: A Combintion with the Lttice Theory nd the ough Set Theory Yingcho Sho,*, Li Fu, Fei Ho 3 nd Keyun Qin
06 Interntionl Conference on Mechtronics, Control nd Automtion Engineering (MCAE 06) ough Lttice: A Combintion with the Lttice Theory nd the ough Set Theory Yingcho Sho,*, Li Fu, Fei Ho 3 nd Keyun Qin
SUPERSTABILITY OF DIFFERENTIAL EQUATIONS WITH BOUNDARY CONDITIONS
 Electronic Journl of Differentil Equtions, Vol. 01 (01), No. 15, pp. 1. ISSN: 107-6691. URL: http://ejde.mth.txstte.edu or http://ejde.mth.unt.edu ftp ejde.mth.txstte.edu SUPERSTABILITY OF DIFFERENTIAL
Electronic Journl of Differentil Equtions, Vol. 01 (01), No. 15, pp. 1. ISSN: 107-6691. URL: http://ejde.mth.txstte.edu or http://ejde.mth.unt.edu ftp ejde.mth.txstte.edu SUPERSTABILITY OF DIFFERENTIAL
p-adic Egyptian Fractions
 p-adic Egyptin Frctions Contents 1 Introduction 1 2 Trditionl Egyptin Frctions nd Greedy Algorithm 2 3 Set-up 3 4 p-greedy Algorithm 5 5 p-egyptin Trditionl 10 6 Conclusion 1 Introduction An Egyptin frction
p-adic Egyptin Frctions Contents 1 Introduction 1 2 Trditionl Egyptin Frctions nd Greedy Algorithm 2 3 Set-up 3 4 p-greedy Algorithm 5 5 p-egyptin Trditionl 10 6 Conclusion 1 Introduction An Egyptin frction
Generalized Fano and non-fano networks
 Generlized Fno nd non-fno networks Nildri Ds nd Brijesh Kumr Ri Deprtment of Electronics nd Electricl Engineering Indin Institute of Technology Guwhti, Guwhti, Assm, Indi Emil: {d.nildri, bkri}@iitg.ernet.in
Generlized Fno nd non-fno networks Nildri Ds nd Brijesh Kumr Ri Deprtment of Electronics nd Electricl Engineering Indin Institute of Technology Guwhti, Guwhti, Assm, Indi Emil: {d.nildri, bkri}@iitg.ernet.in
TRAPEZOIDAL TYPE INEQUALITIES FOR n TIME DIFFERENTIABLE FUNCTIONS
 TRAPEZOIDAL TYPE INEQUALITIES FOR n TIME DIFFERENTIABLE FUNCTIONS S.S. DRAGOMIR AND A. SOFO Abstrct. In this pper by utilising result given by Fink we obtin some new results relting to the trpezoidl inequlity
TRAPEZOIDAL TYPE INEQUALITIES FOR n TIME DIFFERENTIABLE FUNCTIONS S.S. DRAGOMIR AND A. SOFO Abstrct. In this pper by utilising result given by Fink we obtin some new results relting to the trpezoidl inequlity
Math 61CM - Solutions to homework 9
 Mth 61CM - Solutions to homework 9 Cédric De Groote November 30 th, 2018 Problem 1: Recll tht the left limit of function f t point c is defined s follows: lim f(x) = l x c if for ny > 0 there exists δ
Mth 61CM - Solutions to homework 9 Cédric De Groote November 30 th, 2018 Problem 1: Recll tht the left limit of function f t point c is defined s follows: lim f(x) = l x c if for ny > 0 there exists δ
Introduction To Matrices MCV 4UI Assignment #1
 Introduction To Mtrices MCV UI Assignment # INTRODUCTION: A mtrix plurl: mtrices) is rectngulr rry of numbers rrnged in rows nd columns Exmples: ) b) c) [ ] d) Ech number ppering in the rry is sid to be
Introduction To Mtrices MCV UI Assignment # INTRODUCTION: A mtrix plurl: mtrices) is rectngulr rry of numbers rrnged in rows nd columns Exmples: ) b) c) [ ] d) Ech number ppering in the rry is sid to be
ON THE EXCEPTIONAL SET IN THE PROBLEM OF DIOPHANTUS AND DAVENPORT
 ON THE EXCEPTIONAL SET IN THE PROBLEM OF DIOPHANTUS AND DAVENPORT Andrej Dujell Deprtment of Mthemtics, University of Zgreb, 10000 Zgreb, CROATIA The Greek mthemticin Diophntus of Alexndri noted tht the
ON THE EXCEPTIONAL SET IN THE PROBLEM OF DIOPHANTUS AND DAVENPORT Andrej Dujell Deprtment of Mthemtics, University of Zgreb, 10000 Zgreb, CROATIA The Greek mthemticin Diophntus of Alexndri noted tht the
The Regulated and Riemann Integrals
 Chpter 1 The Regulted nd Riemnn Integrls 1.1 Introduction We will consider severl different pproches to defining the definite integrl f(x) dx of function f(x). These definitions will ll ssign the sme vlue
Chpter 1 The Regulted nd Riemnn Integrls 1.1 Introduction We will consider severl different pproches to defining the definite integrl f(x) dx of function f(x). These definitions will ll ssign the sme vlue
On the degree of regularity of generalized van der Waerden triples
 On the degree of regulrity of generlized vn der Werden triples Jcob Fox Msschusetts Institute of Technology, Cmbridge, MA 02139, USA Rdoš Rdoičić Deprtment of Mthemtics, Rutgers, The Stte University of
On the degree of regulrity of generlized vn der Werden triples Jcob Fox Msschusetts Institute of Technology, Cmbridge, MA 02139, USA Rdoš Rdoičić Deprtment of Mthemtics, Rutgers, The Stte University of
Fredholm Integral Equations of the First Kind Solved by Using the Homotopy Perturbation Method
 Int. Journl of Mth. Anlysis, Vol. 5, 211, no. 19, 935-94 Fredholm Integrl Equtions of the First Kind Solved by Using the Homotopy Perturbtion Method Seyyed Mhmood Mirzei Deprtment of Mthemtics, Fculty
Int. Journl of Mth. Anlysis, Vol. 5, 211, no. 19, 935-94 Fredholm Integrl Equtions of the First Kind Solved by Using the Homotopy Perturbtion Method Seyyed Mhmood Mirzei Deprtment of Mthemtics, Fculty
INEQUALITIES FOR GENERALIZED WEIGHTED MEAN VALUES OF CONVEX FUNCTION
 INEQUALITIES FOR GENERALIZED WEIGHTED MEAN VALUES OF CONVEX FUNCTION BAI-NI GUO AND FENG QI Abstrct. In the rticle, using the Tchebycheff s integrl inequlity, the suitble properties of double integrl nd
INEQUALITIES FOR GENERALIZED WEIGHTED MEAN VALUES OF CONVEX FUNCTION BAI-NI GUO AND FENG QI Abstrct. In the rticle, using the Tchebycheff s integrl inequlity, the suitble properties of double integrl nd
ON THE GENERALIZED SUPERSTABILITY OF nth ORDER LINEAR DIFFERENTIAL EQUATIONS WITH INITIAL CONDITIONS
 PUBLICATIONS DE L INSTITUT MATHÉMATIQUE Nouvelle série, tome 9811 015, 43 49 DOI: 10.98/PIM15019019H ON THE GENERALIZED SUPERSTABILITY OF nth ORDER LINEAR DIFFERENTIAL EQUATIONS WITH INITIAL CONDITIONS
PUBLICATIONS DE L INSTITUT MATHÉMATIQUE Nouvelle série, tome 9811 015, 43 49 DOI: 10.98/PIM15019019H ON THE GENERALIZED SUPERSTABILITY OF nth ORDER LINEAR DIFFERENTIAL EQUATIONS WITH INITIAL CONDITIONS
ON THE C-INTEGRAL BENEDETTO BONGIORNO
 ON THE C-INTEGRAL BENEDETTO BONGIORNO Let F : [, b] R be differentible function nd let f be its derivtive. The problem of recovering F from f is clled problem of primitives. In 1912, the problem of primitives
ON THE C-INTEGRAL BENEDETTO BONGIORNO Let F : [, b] R be differentible function nd let f be its derivtive. The problem of recovering F from f is clled problem of primitives. In 1912, the problem of primitives
AQA Further Pure 1. Complex Numbers. Section 1: Introduction to Complex Numbers. The number system
 Complex Numbers Section 1: Introduction to Complex Numbers Notes nd Exmples These notes contin subsections on The number system Adding nd subtrcting complex numbers Multiplying complex numbers Complex
Complex Numbers Section 1: Introduction to Complex Numbers Notes nd Exmples These notes contin subsections on The number system Adding nd subtrcting complex numbers Multiplying complex numbers Complex
The Modified Heinz s Inequality
 Journl of Applied Mthemtics nd Physics, 03,, 65-70 Pulished Online Novemer 03 (http://wwwscirporg/journl/jmp) http://dxdoiorg/0436/jmp03500 The Modified Heinz s Inequlity Tkshi Yoshino Mthemticl Institute,
Journl of Applied Mthemtics nd Physics, 03,, 65-70 Pulished Online Novemer 03 (http://wwwscirporg/journl/jmp) http://dxdoiorg/0436/jmp03500 The Modified Heinz s Inequlity Tkshi Yoshino Mthemticl Institute,
A PROOF OF THE FUNDAMENTAL THEOREM OF CALCULUS USING HAUSDORFF MEASURES
 INROADS Rel Anlysis Exchnge Vol. 26(1), 2000/2001, pp. 381 390 Constntin Volintiru, Deprtment of Mthemtics, University of Buchrest, Buchrest, Romni. e-mil: cosv@mt.cs.unibuc.ro A PROOF OF THE FUNDAMENTAL
INROADS Rel Anlysis Exchnge Vol. 26(1), 2000/2001, pp. 381 390 Constntin Volintiru, Deprtment of Mthemtics, University of Buchrest, Buchrest, Romni. e-mil: cosv@mt.cs.unibuc.ro A PROOF OF THE FUNDAMENTAL
Binding Number and Connected (g, f + 1)-Factors in Graphs
 Binding Number nd Connected (g, f + 1)-Fctors in Grphs Jinsheng Ci, Guizhen Liu, nd Jinfeng Hou School of Mthemtics nd system science, Shndong University, Jinn 50100, P.R.Chin helthci@163.com Abstrct.
Binding Number nd Connected (g, f + 1)-Fctors in Grphs Jinsheng Ci, Guizhen Liu, nd Jinfeng Hou School of Mthemtics nd system science, Shndong University, Jinn 50100, P.R.Chin helthci@163.com Abstrct.
GENERALIZATIONS OF WEIGHTED TRAPEZOIDAL INEQUALITY FOR MONOTONIC MAPPINGS AND ITS APPLICATIONS. (b a)3 [f(a) + f(b)] f x (a,b)
![GENERALIZATIONS OF WEIGHTED TRAPEZOIDAL INEQUALITY FOR MONOTONIC MAPPINGS AND ITS APPLICATIONS. (b a)3 [f(a) + f(b)] f x (a,b) GENERALIZATIONS OF WEIGHTED TRAPEZOIDAL INEQUALITY FOR MONOTONIC MAPPINGS AND ITS APPLICATIONS. (b a)3 [f(a) + f(b)] f x (a,b)](/thumbs/94/119230441.jpg) GENERALIZATIONS OF WEIGHTED TRAPEZOIDAL INEQUALITY FOR MONOTONIC MAPPINGS AND ITS APPLICATIONS KUEI-LIN TSENG, GOU-SHENG YANG, AND SEVER S. DRAGOMIR Abstrct. In this pper, we estblish some generliztions
GENERALIZATIONS OF WEIGHTED TRAPEZOIDAL INEQUALITY FOR MONOTONIC MAPPINGS AND ITS APPLICATIONS KUEI-LIN TSENG, GOU-SHENG YANG, AND SEVER S. DRAGOMIR Abstrct. In this pper, we estblish some generliztions
RIEMANN-LIOUVILLE AND CAPUTO FRACTIONAL APPROXIMATION OF CSISZAR S f DIVERGENCE
 SARAJEVO JOURNAL OF MATHEMATICS Vol.5 (17 (2009, 3 12 RIEMANN-LIOUVILLE AND CAPUTO FRACTIONAL APPROIMATION OF CSISZAR S f DIVERGENCE GEORGE A. ANASTASSIOU Abstrct. Here re estblished vrious tight probbilistic
SARAJEVO JOURNAL OF MATHEMATICS Vol.5 (17 (2009, 3 12 RIEMANN-LIOUVILLE AND CAPUTO FRACTIONAL APPROIMATION OF CSISZAR S f DIVERGENCE GEORGE A. ANASTASSIOU Abstrct. Here re estblished vrious tight probbilistic
Riemann Sums and Riemann Integrals
 Riemnn Sums nd Riemnn Integrls Jmes K. Peterson Deprtment of Biologicl Sciences nd Deprtment of Mthemticl Sciences Clemson University August 26, 2013 Outline 1 Riemnn Sums 2 Riemnn Integrls 3 Properties
Riemnn Sums nd Riemnn Integrls Jmes K. Peterson Deprtment of Biologicl Sciences nd Deprtment of Mthemticl Sciences Clemson University August 26, 2013 Outline 1 Riemnn Sums 2 Riemnn Integrls 3 Properties
Review of Riemann Integral
 1 Review of Riemnn Integrl In this chpter we review the definition of Riemnn integrl of bounded function f : [, b] R, nd point out its limittions so s to be convinced of the necessity of more generl integrl.
1 Review of Riemnn Integrl In this chpter we review the definition of Riemnn integrl of bounded function f : [, b] R, nd point out its limittions so s to be convinced of the necessity of more generl integrl.
An inequality related to η-convex functions (II)
 Int. J. Nonliner Anl. Appl. 6 (15) No., 7-33 ISSN: 8-68 (electronic) http://d.doi.org/1.75/ijn.15.51 An inequlity relted to η-conve functions (II) M. Eshghi Gordji, S. S. Drgomir b, M. Rostmin Delvr, Deprtment
Int. J. Nonliner Anl. Appl. 6 (15) No., 7-33 ISSN: 8-68 (electronic) http://d.doi.org/1.75/ijn.15.51 An inequlity relted to η-conve functions (II) M. Eshghi Gordji, S. S. Drgomir b, M. Rostmin Delvr, Deprtment
Path product and inverse M-matrices
 Electronic Journl of Liner Algebr Volume 22 Volume 22 (2011) Article 42 2011 Pth product nd inverse M-mtrices Yn Zhu Cheng-Yi Zhng Jun Liu Follow this nd dditionl works t: http://repository.uwyo.edu/el
Electronic Journl of Liner Algebr Volume 22 Volume 22 (2011) Article 42 2011 Pth product nd inverse M-mtrices Yn Zhu Cheng-Yi Zhng Jun Liu Follow this nd dditionl works t: http://repository.uwyo.edu/el
NEW HERMITE HADAMARD INEQUALITIES VIA FRACTIONAL INTEGRALS, WHOSE ABSOLUTE VALUES OF SECOND DERIVATIVES IS P CONVEX
 Journl of Mthemticl Ineulities Volume 1, Number 3 18, 655 664 doi:1.7153/jmi-18-1-5 NEW HERMITE HADAMARD INEQUALITIES VIA FRACTIONAL INTEGRALS, WHOSE ABSOLUTE VALUES OF SECOND DERIVATIVES IS P CONVEX SHAHID
Journl of Mthemticl Ineulities Volume 1, Number 3 18, 655 664 doi:1.7153/jmi-18-1-5 NEW HERMITE HADAMARD INEQUALITIES VIA FRACTIONAL INTEGRALS, WHOSE ABSOLUTE VALUES OF SECOND DERIVATIVES IS P CONVEX SHAHID
Theory of Computation Regular Languages
 Theory of Computtion Regulr Lnguges Bow-Yw Wng Acdemi Sinic Spring 2012 Bow-Yw Wng (Acdemi Sinic) Regulr Lnguges Spring 2012 1 / 38 Schemtic of Finite Automt control 0 0 1 0 1 1 1 0 Figure: Schemtic of
Theory of Computtion Regulr Lnguges Bow-Yw Wng Acdemi Sinic Spring 2012 Bow-Yw Wng (Acdemi Sinic) Regulr Lnguges Spring 2012 1 / 38 Schemtic of Finite Automt control 0 0 1 0 1 1 1 0 Figure: Schemtic of
Chapter 14. Matrix Representations of Linear Transformations
 Chpter 4 Mtrix Representtions of Liner Trnsformtions When considering the Het Stte Evolution, we found tht we could describe this process using multipliction by mtrix. This ws nice becuse computers cn
Chpter 4 Mtrix Representtions of Liner Trnsformtions When considering the Het Stte Evolution, we found tht we could describe this process using multipliction by mtrix. This ws nice becuse computers cn
ON A CONVEXITY PROPERTY. 1. Introduction Most general class of convex functions is defined by the inequality
 Krgujevc Journl of Mthemtics Volume 40( (016, Pges 166 171. ON A CONVEXITY PROPERTY SLAVKO SIMIĆ Abstrct. In this rticle we proved n interesting property of the clss of continuous convex functions. This
Krgujevc Journl of Mthemtics Volume 40( (016, Pges 166 171. ON A CONVEXITY PROPERTY SLAVKO SIMIĆ Abstrct. In this rticle we proved n interesting property of the clss of continuous convex functions. This
The asymptotic behavior of the real roots of Fibonacci-like polynomials
 Act Acdemie Pedgogice Agriensis, Sectio Mthemtice, 4. 997) pp. 55 6 The symptotic behvior of the rel roots of Fiboncci-like polynomils FERENC MÁTYÁS Abstrct. The Fiboncci-like polynomils G n x) re defined
Act Acdemie Pedgogice Agriensis, Sectio Mthemtice, 4. 997) pp. 55 6 The symptotic behvior of the rel roots of Fiboncci-like polynomils FERENC MÁTYÁS Abstrct. The Fiboncci-like polynomils G n x) re defined
Riemann Sums and Riemann Integrals
 Riemnn Sums nd Riemnn Integrls Jmes K. Peterson Deprtment of Biologicl Sciences nd Deprtment of Mthemticl Sciences Clemson University August 26, 203 Outline Riemnn Sums Riemnn Integrls Properties Abstrct
Riemnn Sums nd Riemnn Integrls Jmes K. Peterson Deprtment of Biologicl Sciences nd Deprtment of Mthemticl Sciences Clemson University August 26, 203 Outline Riemnn Sums Riemnn Integrls Properties Abstrct
Hermite-Hadamard Type Inequalities for the Functions whose Second Derivatives in Absolute Value are Convex and Concave
 Applied Mthemticl Sciences Vol. 9 05 no. 5-36 HIKARI Ltd www.m-hikri.com http://d.doi.org/0.988/ms.05.9 Hermite-Hdmrd Type Ineulities for the Functions whose Second Derivtives in Absolute Vlue re Conve
Applied Mthemticl Sciences Vol. 9 05 no. 5-36 HIKARI Ltd www.m-hikri.com http://d.doi.org/0.988/ms.05.9 Hermite-Hdmrd Type Ineulities for the Functions whose Second Derivtives in Absolute Vlue re Conve
On New Inequalities of Hermite-Hadamard-Fejer Type for Harmonically Quasi-Convex Functions Via Fractional Integrals
 X th Interntionl Sttistics Dys Conference ISDC 6), Giresun, Turkey On New Ineulities of Hermite-Hdmrd-Fejer Type for Hrmoniclly Qusi-Convex Functions Vi Frctionl Integrls Mehmet Kunt * nd İmdt İşcn Deprtment
X th Interntionl Sttistics Dys Conference ISDC 6), Giresun, Turkey On New Ineulities of Hermite-Hdmrd-Fejer Type for Hrmoniclly Qusi-Convex Functions Vi Frctionl Integrls Mehmet Kunt * nd İmdt İşcn Deprtment
Research Article On The Hadamard s Inequality for Log-Convex Functions on the Coordinates
 Hindwi Publishing Corportion Journl of Inequlities nd Applictions Volume 29, Article ID 28347, 3 pges doi:.55/29/28347 Reserch Article On The Hdmrd s Inequlity for Log-Convex Functions on the Coordintes
Hindwi Publishing Corportion Journl of Inequlities nd Applictions Volume 29, Article ID 28347, 3 pges doi:.55/29/28347 Reserch Article On The Hdmrd s Inequlity for Log-Convex Functions on the Coordintes
Farey Fractions. Rickard Fernström. U.U.D.M. Project Report 2017:24. Department of Mathematics Uppsala University
 U.U.D.M. Project Report 07:4 Frey Frctions Rickrd Fernström Exmensrete i mtemtik, 5 hp Hledre: Andres Strömergsson Exmintor: Jörgen Östensson Juni 07 Deprtment of Mthemtics Uppsl University Frey Frctions
U.U.D.M. Project Report 07:4 Frey Frctions Rickrd Fernström Exmensrete i mtemtik, 5 hp Hledre: Andres Strömergsson Exmintor: Jörgen Östensson Juni 07 Deprtment of Mthemtics Uppsl University Frey Frctions
Research Article On Hermite-Hadamard Type Inequalities for Functions Whose Second Derivatives Absolute Values Are s-convex
 ISRN Applied Mthemtics, Article ID 8958, 4 pges http://dx.doi.org/.55/4/8958 Reserch Article On Hermite-Hdmrd Type Inequlities for Functions Whose Second Derivtives Absolute Vlues Are s-convex Feixing
ISRN Applied Mthemtics, Article ID 8958, 4 pges http://dx.doi.org/.55/4/8958 Reserch Article On Hermite-Hdmrd Type Inequlities for Functions Whose Second Derivtives Absolute Vlues Are s-convex Feixing
HERMITE-HADAMARD TYPE INEQUALITIES OF CONVEX FUNCTIONS WITH RESPECT TO A PAIR OF QUASI-ARITHMETIC MEANS
 HERMITE-HADAMARD TYPE INEQUALITIES OF CONVEX FUNCTIONS WITH RESPECT TO A PAIR OF QUASI-ARITHMETIC MEANS FLAVIA CORINA MITROI nd CĂTĂLIN IRINEL SPIRIDON In this pper we estblish some integrl inequlities
HERMITE-HADAMARD TYPE INEQUALITIES OF CONVEX FUNCTIONS WITH RESPECT TO A PAIR OF QUASI-ARITHMETIC MEANS FLAVIA CORINA MITROI nd CĂTĂLIN IRINEL SPIRIDON In this pper we estblish some integrl inequlities
TANDEM QUEUE WITH THREE MULTISERVER UNITS AND BULK SERVICE WITH ACCESSIBLE AND NON ACCESSBLE BATCH IN UNIT III WITH VACATION
 Indin Journl of Mthemtics nd Mthemticl Sciences Vol. 7, No., (June ) : 9-38 TANDEM QUEUE WITH THREE MULTISERVER UNITS AND BULK SERVICE WITH ACCESSIBLE AND NON ACCESSBLE BATCH IN UNIT III WITH VACATION
Indin Journl of Mthemtics nd Mthemticl Sciences Vol. 7, No., (June ) : 9-38 TANDEM QUEUE WITH THREE MULTISERVER UNITS AND BULK SERVICE WITH ACCESSIBLE AND NON ACCESSBLE BATCH IN UNIT III WITH VACATION
Research Article On New Inequalities via Riemann-Liouville Fractional Integration
 Abstrct nd Applied Anlysis Volume 202, Article ID 428983, 0 pges doi:0.55/202/428983 Reserch Article On New Inequlities vi Riemnn-Liouville Frctionl Integrtion Mehmet Zeki Sriky nd Hsn Ogunmez 2 Deprtment
Abstrct nd Applied Anlysis Volume 202, Article ID 428983, 0 pges doi:0.55/202/428983 Reserch Article On New Inequlities vi Riemnn-Liouville Frctionl Integrtion Mehmet Zeki Sriky nd Hsn Ogunmez 2 Deprtment
Dually quasi-de Morgan Stone semi-heyting algebras II. Regularity
 Volume 2, Number, July 204, 65-82 ISSN Print: 2345-5853 Online: 2345-586 Dully qusi-de Morgn Stone semi-heyting lgebrs II. Regulrity Hnmntgoud P. Snkppnvr Abstrct. This pper is the second of two prt series.
Volume 2, Number, July 204, 65-82 ISSN Print: 2345-5853 Online: 2345-586 Dully qusi-de Morgn Stone semi-heyting lgebrs II. Regulrity Hnmntgoud P. Snkppnvr Abstrct. This pper is the second of two prt series.
NEW INEQUALITIES OF SIMPSON S TYPE FOR s CONVEX FUNCTIONS WITH APPLICATIONS. := f (4) (x) <. The following inequality. 2 b a
 NEW INEQUALITIES OF SIMPSON S TYPE FOR s CONVEX FUNCTIONS WITH APPLICATIONS MOHAMMAD ALOMARI A MASLINA DARUS A AND SEVER S DRAGOMIR B Abstrct In terms of the first derivtive some ineulities of Simpson
NEW INEQUALITIES OF SIMPSON S TYPE FOR s CONVEX FUNCTIONS WITH APPLICATIONS MOHAMMAD ALOMARI A MASLINA DARUS A AND SEVER S DRAGOMIR B Abstrct In terms of the first derivtive some ineulities of Simpson
Research Article Fejér and Hermite-Hadamard Type Inequalities for Harmonically Convex Functions
 Hindwi Pulishing Corportion Journl of Applied Mthemtics Volume 4, Article ID 38686, 6 pges http://dx.doi.org/.55/4/38686 Reserch Article Fejér nd Hermite-Hdmrd Type Inequlities for Hrmoniclly Convex Functions
Hindwi Pulishing Corportion Journl of Applied Mthemtics Volume 4, Article ID 38686, 6 pges http://dx.doi.org/.55/4/38686 Reserch Article Fejér nd Hermite-Hdmrd Type Inequlities for Hrmoniclly Convex Functions
A unified generalization of perturbed mid-point and trapezoid inequalities and asymptotic expressions for its error term
 An. Ştiinţ. Univ. Al. I. Cuz Işi. Mt. (N.S. Tomul LXIII, 07, f. A unified generliztion of perturbed mid-point nd trpezoid inequlities nd symptotic expressions for its error term Wenjun Liu Received: 7.XI.0
An. Ştiinţ. Univ. Al. I. Cuz Işi. Mt. (N.S. Tomul LXIII, 07, f. A unified generliztion of perturbed mid-point nd trpezoid inequlities nd symptotic expressions for its error term Wenjun Liu Received: 7.XI.0
