THEORY OF COMPUTATION
|
|
|
- Madeleine Elliott
- 5 years ago
- Views:
Transcription
1 THEORY OF COMPUTATION There are four sorts of men: He who knows not and knows not he knows not: he is a fool - shun him; He who knows not and knows he knows not: he is simple teach him; He who knows and knows not he knows: he is asleep wake him; He who knows and knows he knows: he is wise follows him Arabian proverb
2 Chapter 1: Sets, Relations and Languages Recommended Readings: Textbook + A Basis for Theoretical Computer Science by M. A. Arbib, A. J. Kfoury, R N. Moll. A set is a collection of objects. Examples of sets are: the set of integers, denoted by Z, the set of nonnegative integers, also called natural numbers, denoted by N, the set of truth values B = {T, F } the set of students taking the theory of computation course The elements or members of a set are the objects comprising it. If b is an element of a set L, then we write b L. There are two ways to display a set: either explicitly listing the elements belonging to it like in the case of the set of truth values B = {T, F }, or by specifying the properties that characterize the elements of this set like: the set of even integers
3 {x x Z and x mod 2 = 0} Two sets are equal if they have the same elements A set without any element is called the empty set A set with infinitely many elements is said to be infinite A set with finitely many elements is said to be finite A set X is a subset of a set Y, written X Y, if each element of X is also an element of Y. X is a proper subset of Y if X is a subset of Y and X and Y are not equal. For example, the set of nonnegative integers is a proper subset of the set of integers, N Z. Basic facts: For any set A, the empty set is a subset of A, A, and A is a subset of A, A A. If A B and B A then A = B.
4 Set operations: Union, Difference, Intersection The union of two sets A,B is the set of elements which belongs to at least one of them. The intersection of two sets A,B is the set of elements which belongs to both of them. We say two sets are disjoint if their intersection is empty. The set difference A \ B of two sets A,B is the set of those elements in A that are not in B. Laws for set operations: Idempotency A A = A A A = A Commutativity A B = B A A B = B A Associativity (A B) C = A (B C) (A B) C = A (B C) Suppose now that there is a big set U such that both A, and B are subsets of U. Let B = U \ B,
5 B = U \ B. Then A \ B = A B A B = A B A B = A B Exercises Prove the above equalities. Distributivity (A C) C) A (B C) = (A B) A (B C) = (A B) (A Proof 1. To show A (B C) = (A B) (A C), we show A (B C) (A B) (A C) and (A B) (A C) A (B C). (a) Let x A (B C). From x A (B C), it follows: x A or x B C. If x A then x A B and x A C. Hence x (A B) (A C). If x B C then x B and x C. If x B then x A B. If x C then x A C. Therefore if x B C then x (A B) (A C).
6 Hence from x A or x B C we can conclude x (A B) (A C). Therefore we have proved that if x A (B C) then x (A B) (A C). (b) Let x (A B) (A C). To show x A (B C). From x (A B) (A C), it follows: x A B and x A C. Hence (x A or x B) and (x A or x C). Hence there are four cases: (x A) or (x A and x B) or (x A and x C) or (x B and x C). It follows that x A or (x B and x C). That means x A (B C). 2. Exercise. Absorption A (A B) = A A (A B) = A Proof Exercise. DeMorgan s Laws Proof A\(B C) = (A\B) (A\C) A\(B C) = (A\B) (A\C)
7 1. Suppose there is a set U such that all sets A,B,C are subsets of U. Hence A \ (B C) = A (B C) = A (B C) = (A B) (A C) = (A \ B) (A \ C) 2. Exercise. If S is a collection of sets then S is the set whose elements are the elements of the sets in S. Example: S = {{a, b}, {c}, {a, d}} S = {a, b, c, d} S = { {a, b}, {c}, {a, {d, a} } } S = {a, b, c, {d, a} } The power set of a set S, denoted by 2 S, is the set of all subsets of S. Example: S = {a}, 2 S = {, {a} } S = {a, b}, 2 S = {, {a}, {b}, {a, b} }
8 A partition of a set S is a set Π of subsets of S, i.e. Π 2 S, such that 1. Each element of Π is nonempty 2. Distinct members of Π are disjoint 3. Π = S Example S = {a, b, c} Π = { {a}, {b, c} } is a partition of S. A = { {a}, {a, b}, {c} } is not a partition. B = { {a}, {b, c}, } is not a partition.
9 Functions or Maps Ordered pairs are written as (a,b) where a is the first component and b the second. The Cartesian product of two sets A,B, denoted by A B, is the set of all ordered pairs (a,b) with a A, b B. Example {a, b} {a} = {(a, a), (b, a)} The plane could be represented as a Cartesian product R R where R is the set of all real numbers. A map or function from a set A to a set B, denoted f : A B, is an assignment to each element a in A a single element, denoted by f(a), in B. A is called the domain of f and B is the codomain of f. f(a) is called the image of a under f. The range of f is denoted by f(a) = {b there is a in A such that b = f(a)}
10 For A A, f(a ) = {f(a) : a A } is called the image of A under f. Example of functions: The integer addition +: N N N is a function from N N to N Exercises 1) If A is empty, how many functions are there from A to B? 2) If B is empty, how many functions are there from A to B? 3) If A contains exactly one element, how many functions are there from A to B? A function f : A B is one to one if for any two distinct elements a, a A, f(a) f(a ). A function f : A B is onto B if B = f(a).
11 A function f : A B is a bijection between A and B if it is both one-to-one and onto B. Let A and B be two finite sets. A and B have the same number of elements iff there is a bijection between A and B Given a function f : A B and g : B C, the composition f g : A C is defined by: f g(a) = g(f(a))
12 Relations A binary relation on two sets A,B is a subset of A B. An example of binary relation is the greater or equal relation in the set of integers R = {(n, m) n m} Z Z. An ordered n-tuple is written as (a 1,..., a n ) where a i is the ith component of (a 1,..., a n ). The n-fold Cartesian product of the sets A 1,..., A n, denoted by A 1... A n, is the set of all ordered n-tuples with a i A i for i = 1,..., n. An n-ary relation on sets A 1,..., A n is a subset of A 1... A n.
13 Property (A function is a special relation) A function from a set A to a set B is a binary relation R on A,B such that following property is satisfied: For each a A there is exactly one ordered pair in R with first component a. A binary relation R A B has an inverse R 1 B A defined by: (b, a) R 1 iff (a, b) R. For binary relations Q A B and R B C, the composition Q R is defined by Q R = {(a, c) : b B s.t. (a, b) Q and (b, c) R} Note that for two functions f : A B and g : B C, f g : A C. Exercise Show that if f : A B is a bijection, then f 1 is also a bijection from B to A.
14 Special Types of Relations A relation R A A can be represented as a directed graph. A relation R A A is reflexive if for each a A, (a, a) R. A relation R A A is symmetric if (a, b) R whenever (b, a) R. Symmetric relation can be represented by undirected graph. A relation R A A is transitive if whenever (a, b) R and (b, c) R then (a, c) R A relation R A A is an equivalent relation if it is reflexive, transitive and symmetric. Let R be an equivalent relation on a set A. Then for each a in A, the equivalence class of a with respect to R is denoted by [a] R and is defined formally by [a] R = {b (a, b) R} When the context R is clear, we simply write [a] for [a] R A representation of an equivalent relation R A A as an undirected graph consists of a num-
15 ber of clusters where within clusters each pair is connected by a line. The set of nodes in a cluster is an equivalence class. Property Let R be an equivalent relation on a set A. Then for any two elements a,b in A, either [a] R = [b] R or [a] R, [b] R are disjoint. Proof Exercise. Let R be an equivalent relation on a set A. Define A modulo R to be the set A/R = {[a] R a A} Theorem 1. Let R A A be an equivalent relation. Then A modulo R is a partition of A. Proof Exercise. Example of Partition and equivalence relation: Let Z + be the set of positive integers. Define an equivalent relation Z + Z + as follows: (p, q) (r, s) iff ps = qr The is an equivalent relation characterizing the rational numbers, i.e.
16 The set Z + Z + modulo is the set of rational numbers. A relation R A A is antisymmetric whenever (a, b) R and a b then (b, a) R if A relation that is reflexive, transitive and antisymmetric is called a partial order. A partial order R A A is called a total order if for all a, b A, either (a, b) R or (b, a) R. A path from a to b in a binary relation R A A is a sequence (a 1,..., a n ), n 1 such that a = a 1, b = a n, for each i = 1,... n 1, (a i, a i+1 ) R. A path (a 1,..., a n ) is a cycle if a 1 = a n and all a i s are distinct.
17 Two sets A, B are equinumerous if there is a bijection f : A B. We say that the cardinality of A is n if A is equinumeruos with the set {1,...,n}. A is countably infinite if it is equinumerous with the set of natural numbers N. A is uncountable if it is not equinumerous with the set of natural numbers N. Exercise Every subset of a finite set is finite. Exercise Every subset of a countably infinite set is finite or countably infinite. Exercise The set N N is countably infinite. Theorem 2. The union of countably infinite collection of countably infinite sets is again countable infinite. Exercixe Is the set of all finite subsets of N countably infinite?
18 Three Fundamental Proof Techniques Principle of Mathematical Induction: Let A be a set of natural number such that 1. 0 A, and 2. for each natural number n, if {0, 1,..., n} A then n + 1 A. Then A = N. Exercise Prove that for each natural number n n(n + 1) n = 2 Exercise Suppose f, g : N (N {0}) satisfy following properties: 1. g(0) f(0), and 2. for each n 0, g(n + 1) g(n) f(n + 1) f(n) Then for any n 0: g(n) f(n).
19 The pigeon principle If A, B are finite sets and A > B. Then there is no one-to-one function from A to B. Exercise Suppose there are 100 new students for the august semester at AIT and only 97 vacant rooms. Is it possible to give each student a separate room? Prove it. Exercise If there are 10 scholarships and 50 applicants. Is it possible that each applicant get a scholarship. (Note that scholarship can not be shared). Exercise Could you try to prove the pigeon principle using mathematical induction?
20 The Diagonalization Principle Let R be a binary relation on a set A, and let D = {a a A and (a, a) R} D is called the diagonal set of R. for each a A, R a = {b b A and (a, b) R} Then for each a A, D R a. Exercise Let A = {1, 2, 3, 4, 5} and R = {(1, 3), (2, 4), (3, 5), (5, 1), (2, 3), (1, 1), (4, 2), (4, 4)}. Determine the sets D, R 1, R 2, R 3, R 4, R 5. Check whethere the diagonal principle holds in this case. Exercise Would the diagonal principle still holds if the sets R a are replaced by the sets R a = {b b A and (b, a) R} Exercise Would the diagonal principle still holds if the sets D is replaced by the set C = {a a A and (a, a) R}.
21 Theorem 3. The set 2 N is uncountably infinite Proof (Sketch) Suppose the theorem is not correct. Therefore, the set 2 N is countably infinite, i.e. there is a bijection (i.e. one-one and onto) function f : N 2 N. Define R = {(n, m) m f(n) }. Apply the diagonal principle on R and show a contradiction to the assumption that f is a bijection. Exercice Is the set of all infinite subsets of N countably infinite?
22 Algorithms Definition Let R A 2 be a directed graph on a set A. The reflexive transitive closure of R is the relation R = {(a, b) a, b A and there is a path from a to b in R} Algorithms The question we interested in this course is: What is an algorithm Example of an algorithm: Initially S := for i = 1,..., n do for each i-tuple (b 1,..., b i ) A i do if (b 1,..., b i ) is a path in R then add (b 1, b i ) to S How much time the algorithm needs to terminate?
23 The total number of operations can be no more than n + n n n that belongs to O(n n+1 ) where n is the number of elements of A. This algorithm is therefore not efficient. An efficient algorithm: Initially S = R {(a i, a i ) a i A} for each j = 1,2,...,n do for each i = 1,2,...,n and k = 1,2,...,n do If (a i, a j ), (a j, a k ) S but (a i, a k ) S then add (a i, a k ) to S. The algorithm terminate after no more than n 3 steps. Is this algorithm correct, i.e. S = R after termination of the algorithm. (Could you use mathematical induction to show it correctness?)
24 Definition Rate of Growth of Functions 1. Let f be a function from N into N. The order of f, denoted by O(f) is the set of all functions g : N N such that there are positive natural numbers c, d > 0 such that for each n N g(n) c.f(n) + d 2. We write f g iff f O(g) and g O(f). Lemma is a equivalence relation. Proof Exercise. Definition The equivalence class of a function f : N N with respect to is called the rate of growth of f.
25 Lemma Let f(n) = a 0 + a 1.n a k.n k be a polynomial of degree k with nonnegative coefficients. Then 1. f n k 2. n k O(n k+1 ) 3. n k+1 O(n k ) Proof 1. Let c = a 0 + a a k and d = 0. It is easy to see: f(n) c.n k. 2. Obviously n k n k Suppose n k+1 O(n k ). Hence, there is c, d > 0: n k+1 c.n k + d. Let n = c + d. It follows (c + d).n k = c.n k + d.n k > c.n k + d. Contradiction. That means that assuming n k+1 O(n k ) leads to a contradiction. Therefore n k+1 O(n k ).
26 Lemma 1. Let f, g : N N be monotonic, i.e. for all m n: f(m) f(n) and g(m) g(n). Further let n 0 N be a natural number such that for each n n 0, g(n + 1) g(n) Then g O(f) f(n + 1) f(n) Proof Let c be a number such that g(n 0 ) cf(n 0 ) From an earlier exercise: n n 0 : g(n) c.f(n) Let d = g(n 0 ). We can prove that for each n N: g(n) cf(n) + d
27 Theorem Let r > 1. Then 1. n i O(r n ) 2. r n O(n i ) Proof 1. It follows immediately from lemma 1. (Elaborate) 2. Suppose r n O(n i ). Hence n i r n n i+1. Contradiction to lemma 1. (Elaborate)
28 Alphabet and Languages An alphabet is a finite set of symbols. A string over an alphabet is a finite sequence of symbols from this alphabet. The empty string is denoted by e. The length of a string is its length as a sequence. The concatenation of two strings x,y, denoted by x y or simply xy, is the string x followed by string y. The concatenation is associative, i.e (x y) z = x (y z). A string v is a substring of a string w if there are strings x, y such that w = xvy. For each string w, each natural number i, define w 0 = e w n+1 = w n w This is an example of inductive definition.
29 The reversal of a string is defined inductively as follows: e R = e (ua) R = au R Exercise Prove (w v) R = v R w R The set of all strings over an alphabet Σ is denoted by Σ. Any set of strings over an alphabet Σ is a language. Question: Is Σ countably infinite?
30 Language Operations Complement The complement of a language A over Σ is Σ A Concatenation Let L 1, L 2 be two languages over Σ. The concatenation of L 1, L 2, denoted by L 1 L 2 is defined by: L 1 L 2 = {x y x L 1, y L 2 } Denote 1. L 0 = {e}, 2. L 1 = L 3. L 2 = L L 4. L n+1 = L n L The Kleen star of a language L, denoted by L, is L = {w 1 w 2... w n w i L, n 0} = L 0 L 1 L 2... L n... Notes = {e} Define L + = {w 1 w 2... w n w i L, n 1}
31 Regular Languages The class of regular languages is the least set of languages satisfying the following properties: The emptyset is regular For each character a Σ, the language {a} is regular If A, B are regular languages then A, A B, A B are also regular.
32 Finite Representation of Languages If we want to study languages, we need to represent them. For example, a context-free language could be represented by a context-free grammar. Such a representation must be finite even if the represented language is infinite, otherwise it would be useless (just imagine an infinite set of grammar for Thai, Chinese or English. Would you be able to learn such a set of grammar?). On the other handside, different languages should have different representations. Could we have enough representations for every possible language over a nonempty alphabet Σ? How many languages there are over an nonempty alphabet Σ? Since Σ is countable infinite, 2 Σ is uncountable infinite. The representation of languages must be again some form of language. hence every finite representation can be viewed as a finite string over some alphabet Σ. Since Σ is countable infinite, we can
33 not find a finite representation for each langauge over Σ.
34 Finte representation of regular languages The set of regular expresions over Σ is the least language over Σ {, (, ),,, } satisfying the following properties: a regular expression Every symbol in Σ is a regular expression If α, β are regular expressions, then so are (αβ), α, α β Any regular expression represents a language as follows: L( ) = empty set Every symbol a Σ, L(a) = {a} If α, β are regular expressions, then L(αβ) = L(α) L(β), L(α ) = L(α), L(α β) = L(α) L(β) Theorem 4. A language A is regular iff there exists a regular expression α such that A = L(α) Proof Exercise.
35 Exercise Show that the Kleen star, concatenation and union operators are monotonic, i.e. for languages L 0, L 1, L, followings hold: 1. If L 0 L 1 then L 0 L 1 2. If L 0 L 1 then L 0 L L 1 L 3. If L 0 L 1 then L 0 L L 1 L Exercise Check whether the following equations are correct. 1. ((a b) ) = (a b) 2. (a b) (a b) = (a b) 3. (a b) = a (a b) 4. (a b) = (a b) 5. (a b) = (b a) (a b) Exercise Exercise in text book.
36 Question Given a regular language L, and a string w, how could we check whether w L? Example Let L = (a b a) w = aababa. Question: w L? Algorithm: s : q : x := get-next-symbol; if x := end-of-file then accept; else if x := a then goto s; else if x := b then goto q; x := get-next-symbol; if x := end-of-file then reject; else if x := a then goto s; else if x := b then goto q;
37 s : q : x := get-next-symbol; if x := end-of-file then accept; else if x := a then goto s; else if x := b then goto q; x := get-next-symbol; if x := end-of-file then reject; else if x := a then goto s; else if x := b then goto q; Fig. 1. Fig. 2.
38 Fig. 3. A shortened representation of the algorithm in above figure is M = (K, Σ, δ, s, F ): 1. K = {s, q} 2. Σ = {a, b} 3. F = {s} 4. δ : K Σ K δ = {(s, a, s), (s, b, q), (q, a, s), (q, b, q)}
39 Chapter 2: Finite Automata Chapter 2.1: Deterministic Finite Automata Definition 1. A deterministic finite automaton is a quintuple M = (K, Σ, δ, s, F ) where K is a finite set of states Σ is an alphabet s K is the initial state F K is the set of final states δ, the transition function, is a function from K Σ to K. An example of finite automata is given in figure 3.
40 A configuration of a finite automaton M = (K, Σ, δ, s, F ) is a pair (q, w) where q K and w Σ We say that a configuration (q,w) yields another configuration (q, w ) in one step, denoted by (q, w) M (q, w ), if there is a symbol σ Σ such that w = σw and q = δ(q, σ). M is the reflexive and transitive closure of M, i.e. we write (q 0, w 0 ) M (q n, w n ) iff there are (q 1, w 1 ),..., (q n1, w n 1 ) such that (q 0, w 0 ) M (q 1, w 1 ) M... M (q n1, w n 1 ) M (q n, w n ) A string w is said to be accepted by M = (K, Σ, δ, s, F ) if and only if there exists a state q F such that (s, w) M (q, e) The language accepted by M, L(M), is the set of all strings accepted by M. Exercise Design an automaton for recognizing the language a ba b.
41 Chapter 2.2: Nondeterministic Finite Automata Definition 2. A nondeterministic finite automaton is a quintuple M = (K, Σ,, s, F ) where K is a finite set of states Σ is an alphabet s K is the initial state F K is the set of final states, the transition relation, is a finite subset of K (Σ {e}) K. Examples A nondeterministic machine for (a ab). Fig. 4.
42 Fig. 5. M = (K, Σ, δ, s, F ): K = {s, q} Σ = {a, b} F = {s} K (Σ {e}) K: = {(s, a, q), (q, e, s), (q, b, s)} Exercise Design a deterministic machine for (a ab). Exercise Could you design a nondeterministic machine for (a ab) without using e.
43 A configuration of a nondeterministic finite automata M = (K, Σ,, s, F ) is a pair (q, w) where q K and w Σ We say that a configuration (q,w) yields another configuration (q, w ) in one step, denoted by (q, w) M (q, w ), if there is u Σ {e} such that w = uw and (q, u, q ). M is the reflexive and transitive closure of M, i.e. we write (q 0, w 0 ) M (q n, w n ) iff there are (q 1, w 1 ),..., (q n1, w n 1 ) such that (q 0, w 0 ) M (q 1, w 1 ) M... M (q n1, w n 1 ) M (q n, w n ) A string w is said to be accepted by M = (K, Σ, δ, s, F ) if and only if there exists a state q F such that (s, w) M (q, e) The language accepted by M, L(M), is the set of all strings accepted by M. Exercise Design a deterministic and a nondeterministic automaton for recognizing the language (ab aba).
44 Chapter 2.3: Equivalence of Deterministic and Nondeterministic Finite Automata Two finite automata M, M are equivalent iff L(M) = L(M ). Theorem 5. For each nondeterministic finite automaton there exists an equivalent deterministic finite automaton. Proof Let M = (K, Σ,, s, F ) be a nondeterministic automata. For each q K, define E(q) = {p K (q, e) M (p, e) } Define M = (K, Σ, δ, s, F ). K = 2 K s = E(s) δ : K Σ K δ (Q, σ) = q Q{E(p) p K and (q, σ, p) } F = {Q K Q F }
45 Property For each w Σ : (q, w) M (p, e) iff (E(q), w) M (P, e) for some P K such that p P. Therefore, it follows that w L(M) iff (s, w) M (p, e) for some p F iff (s, w) M (P, e) and P F iff w L(M ).
46 Example Let Σ = {a 1,..., a n }, n 2 and L = {w there is one symbol in Σ not appearing in w } A nondeterministic finite automaton accepting L: M = (K, Σ,, s, F ) where K = {s, q 1,..., q n } F = {q 1,..., q n } = {(s, e, q i ) 1 i n} {(q i, σ, q i ) 1 i n, σ a i } Translate M into an equivalent deterministic finite automaton.
47 Chapter 2.4: Properties of Languages Accepted by Finite Automata Theorem 6. The class of languages accepted by finte automata is closed under 1. union 2. concatenation 3. Kleen star 4. complementation 5. intersection
48 Theorem 7. A language is regular iff it is accepted by a finite automata Proof From the definition of regular languages, it is clear that every regular language is accepted by a finite automata (exercise). It remains to prove that every language accepted by a finite automata is also regular. M = (K, Σ,, s, F ) be a deterministic finite automaton. Let K = {q 1,..., q n } with s = q 1 and Σ = {a 1,..., a n }. R(i, j, k) = { σ 1... σ m Σ (q i, σ 1... σ m ) M (q k1, σ 2... σ m ) M... M (q km 1, σ m ) M (q j, e) and max{k 1,..., k m 1 } k } It is clear L(M) = q j F R(1, j, n)
49 Now we want to show that R(i, j, k) are regular. We prove this by induction on k. Base case: k = 0. Obvious from the definition of R(i, j, 0) Inductive Step: Follows from the following equation R(i, j, k) = R(i, j, k 1) R(i, k, k 1) R(k, k, k 1) R(k, j, k 1)
50 Pumping Theorem Theorem 8. Let L be a regular language. There is an integer n > 0 such that any string w L with w n can be rewritten as w = xyz such that y e, xy n and xy k z L for any k 0. Example L = {a i b i i 0 } is not regular. Example L = {w {a, b} w has an equal number of a s and b s } is not regular.
51 STATE MINIMIZATION Problem: Given a regular language L, design a finite automaton M such that L = L(M) and M has as few states as possible, i.e. for each finite automaton M that accepts L, the number of states of M is greater or equal the number of states of M Definition 3. Let M = (K, Σ, δ, s, F ) be a deterministic automaton. We say that two strings x, y Σ are equivalent wrt M, denoted by x M y, if there is a state q such that (s, x) M (q, e) and (s, y) M (q, e) Definition 4. Let L Σ and x, y Σ. We say that x and y are equivalent wrt to L, denoted by x L y if for all z Σ,. xz L iff yz L It is obvious that for all x, y Σ and a Σ, x L y implies xa L ya
52 Theorem 9. For any deterministic finite automaton M = (K, Σ, δ, s, F ) and for any string x, y Σ, if x M y then x L(M) y. Let M = (K, Σ, δ, s, F ) be a deterministic finite automaton and q K and L q be the set of all strings x such that (s, x) M (q, e). Further for each x Σ, let [x] M be the equivalent class of x wrt M. It is obvious that for each x L q following assertions hold: L q = [x] M. The mapping µ(q) = L q is a bijection from K onto {[x] M x Σ } such that for all p, q K, δ(q, a) = p iff [xa] M = L p Therefore M is equivalent to the following automaton M = (K, Σ, δ, s, F ) where K = {[x] M x Σ } s = [e] M δ ([x] m, a) = [xa] M F = {[x] M (s, x) M (q, e), and q F }
53 Let L Σ be a regular language. Define a deterministic finite automaton M = (K, Σ, δ, s, F ) as follows: K = {[x] L x Σ } where [x] L is the equivalent class of x wrt L s = [e] L F = {[x] L x L} δ([x] L, a) = [xa] L Theorem 10. L = L(M)
54 Question Given a deterministic finite automaton M = (K, Σ, δ, s, F ), how to construct a deterministic finite automaton M such that L(M) = L(M ) and M has a minimal number of states. Define L p = {w f F : (p, w) M (f, e)} L p,n = {w w L p, w n} For p, q K, define p q iff L p = L q For p, q K, define p n q iff L p,n = L q,n
55 It is obvious that n... Because K is finite, there is n such that n = n+1 = Lemma 2. For any two states p,q and any number n 0, p n+1 q iff following conditions hold: p n q for each a Σ: δ(p, a) n δ(q, a)
56 ALGORITHMS FOR FINITE AUTOMATA Theorem There is an exponential algorithm which given a nondeterministic finite automaton, constructs an equivalent deterministic finite automaton. 2. There is a polynomial algorithm which given a deterministic finite automaton, constructs an equivalent deterministic finite automaton with a minimal number of states. 3. There is a polynomial algorithm which given two deterministic finite automata, decides whether they are equivalent. Theorem 12. Given a deterministic finite automaton M = (K, Σ, δ, s, F ) and a string w, there is an algorithm to decide whether w is accepted by M in O( w ) time.
57 Theorem 13. Given a nondeterministic finite automaton M = (K, Σ, δ, s, F ) and a string w, there is a polynomial algorithm to decide whether w is accepted by M. Proof The algorithm is given below: S 0 := E(s); n := 0; repeat the following { n := n + 1; σ := the n-th input symbol; if σ end-of-file then S n := { E(q) p S n 1 : (p, σ, q) } } until σ = end-of-file if S n 1 F then accept else reject The algorithm is polynomial.
58 Context Free Languages Definition 5. A context-free grammar G is a quadruple (V, Σ, R, S) where V is an alphabet Σ (the set of terminals) is a subset of V R (the set of rules) is a finite subset of (V Σ) V S (the start symbol) is an element of V Σ. The elements of V Σ are called nonterminals. We write A G u for any rule (A, u) R. For any strings w, v V, we write iff there is a rule A and v = xuy. w G = v G u in R and w = xay
59 A sequence w 0 G G G = w1 =... = wn, n 0 is called a derivation of w n from w 0. We write w G = v iff there is a derivation of v from w. The language generated by G is L(G) = {w Σ S G = w } A context-free language is a language generated by some context free grammar.
60 Example A grammar for arithmetic expressions: Σ = {x, +,, (, )} V = Σ {T, F, E} R = { E E + T E T T T F T F F (E) F x } Give a derivation for (x), (x + x) x.
61 Regular Languages are Context-free Theorem 14. Any regular language is context free Proof Let L be a regular language accepted by a deterministic finite automaton M = (K, Σ, δ, S, F ). Construct a grammar G = (V, Σ, R, S) as follows: V = K Σ R consists of rules of the forms P aq where δ(p, a) = Q, and P e for P F We show by induction on n that (S, a 1... a n ) M (Q 1, a 2... a n ) M... M (Q n, e) iff S = G G G a 1 Q 1 =... = a1... a n Q n Basic step: n = 0. Obvious. Inductive Step: Suppose the assertion holds for n. We show that it holds for n + 1. Let (S, a 1... a n a n+1 ) M (Q 1, a 2... a n ) M... M (Q n+1, e) be a computation in M. Hence, (S, a 1... a n ) M (Q 1, a 2... a n ) M... M (Q n, e) is also a computation in M. From induction hypothesis, S G = a 1 Q 1 G =... G = a1... a n Q n
62 is a derivation wrt G. From (Q n, a n+1 ) M (Q n+1, e), it follows δ(q n, a n+1 ) = Q n+1. Hence Q n G a n+1 Q n+1 is a rule in R. Therefore a 1... a n Q n = a 1... a n a n+1 Q n+1. The other direction holds obviously. Hence for any string w Σ, w L iff (S, w) G M (P, e) and P F iff S = wp and P e in R iff S = G w.
63 Let G = (V, Σ, R, S) Parse Trees 1. For each a Σ, the tree a is a parse tree. The root of this tree is a which is also its only leaf. The yield of this tree is also a. 2. If A e is a rule in G, then Fig If is a parse tree whose root is A, whose only leaf is e and whose yield is e. Fig. 7. are parse trees (n 1), with roots A 1,..., A n and yields y 1,..., y n respectively, and A A 1... A n is a rule in R then
64 Fig. 8. is also a parse tree whose root is A, whose leafs are the leaves of T 1,..., T n and whose yield is y 1... y n. 4. Nothing else is a parse tree Examples Construct parse trees yielding (x), (x + x) x wrt the grammar for arithmetic expressions.
65 Lemma 3. Let G = (V, Σ, R, S) be a contextfree grammar, and let A V Σ, and w Σ. Then the following statements are equivalent 1. A w 2. There is a parse tree with root A and yield w. We write x L = y if the nonterminal symbol being replaced is the leftmost nonterminal symbol in the string, i.e x = wav, y = wuv where w Σ, v V, A u R. A leftmost derivation is of the form x 1 L L = x 2 =... L = x n We write x R = y if the nonterminal symbol being replaced is the rightmost nonterminal symbol in the string, i.e x = wav, y = wuv where v Σ, w V, A u R. A rightmost derivation is of the form x 1 R R R = x2 =... = xn Theorem 15. Let G = (V, Σ, R, S) be a contextfree grammar, and let A V Σ, and w Σ.
66 Then the following statements are equivalent: 1. A w 2. There is a parse tree with root A and yield w 3. There is a leftmost derivation A L = w 4. There is a rightmost derivation A R = w
67 AMBIGUITY Let Σ = {x, +,, (, )}. Consider the following two grammars: G 1 = (V 1, Σ, R 1, E) V 1 = Σ {T, F, E} R 1 = { E E + T E T T T F T F F (E) F x } G 2 = (V 2, Σ, R 2, E) V 2 = Σ {E} R 2 = { E E + E E E E E (E) E x } G 1 is unambiguous in the sense that for each string w L(G 1 ), there is exactly one parse tree that yields w. On the contrary, G 2 is ambiguous as there are distinct parse trees yielding the same string. Exercise Could we use the following grammar as the generator of arithmetic expressions in programming languages:
68 Σ = {x, +,, (, )} V = Σ {T, F, E} R = { E E T E T T T + F T F F (E) F x }
69 Pushdown Automata Definition 6. A pushdown automata is a sixtuple M = (K, Σ,, Γ,, s, F ) where K is a finite set of states Σ is an alphabet (the input symbols) Γ is an alphabet (the stack symbols) s K is the initial state F K is the set of final states, the transition relation, is a finite subset of (K (Σ {e}) Γ ) (K Γ ) For ease of undertsanding, we often write (p, a, α) (q, β) for ((p, a, α), (q, β))
70 Let L = { wcw R w {a, b} }. L is accepted by pushdown automaton M = (K, Σ, Γ,, s, F ) K = {s, p, f}, F = {f} Σ = {a, b, c}, Γ = {a, b} consists of the following rules (s, a, e) (p, a) (s, b, e) (p, b) (s, c, e) (f, e) (p, a, e) (p, a) (p, b, e) (p, b) (p, c, e) (f, e) (f, a, a) (f, e) (f, b, b) (f, e) Fig. 9.
71 A configuration of a pushdown automata is a triple (q, w, v) where q K, w Σ and v Γ A configuration (q,w,v) yields another configuration (q, w, v ) in one step, denoted by (q, w, v) M (q, w, v ) if there is a rule (q, a, α) (q, β) in such that w = aw, v = αv 0, v = βv 0. We write if there is a sequence (q, w, v) M (q, w, v ) (q 1, w 1, v 1 ) M... M (q n, w n, v n ) such that (q, w, v) = (q 1, w 1, v 1 ), (q n, w n, v n ) = (q, w, v ).
72 A string w is said to be accepted by M = (K, Σ, δ, s, F ) if and only if there exists a state q F such that (s, w, e) M (q, e, e) The language accepted by M, L(M), is the set of all strings accepted by M.
73 Theorem 16. A language is context-free iff it is accepted by a pushdown automaton. Lemma 4. Each context-free language is accepted by some pushdown automaton. Proof Let G = (V, Σ, R, S) be a context-free grammar. The language generated by G is accepted by the pushdown automaton M = (K, Σ, Γ,, s, F ): K = {s, q}, F = {q} Γ = V consists of the following transitions: (s, e, e) (q, S) (q, e, A) (q, x) for each rule A x in R (q, a, a) (q, e) for each a Σ. Exercise Construct a pushdown automaton accepting the language generated by the following grammar G = (V, Σ, R, S) where V = {S, a, b}, Σ = {a, b} R consists of rules S asa S bsb, S e
74 A pushdown automata M = (K, Σ, Γ,, s, F ) is called simple if following conditions are satisfied: For each ((q, a, β)(p, γ)) such that q s: β Γ and γ 2 Claim For every pushdown automaton there exists an equivalent simple pushdown automata. Proof Let M = (K, Σ, Γ,, s, F ) be a push down automaton. Construct a simple PA M = (K, Σ, Γ {Z},, s, {f }) as follows: Add to the transitions: ((s, e, e)(s, Z)) ((f, e, Z)(f, e)) for each f F Replace transitions with β 2. Let ((q, a, β)(p, γ)) be a transition with β = B 1... B n with n > 1. Replace this transition by the following transitions ((q, e, B 1 )(q B1, e)) ((q B1, e, B 2 )(q B1 B 2, e)) ((q B1 B 2...B n 2, e, B n 1 )(q B1 B 2...B n 1, e)) ((q B1 B 2...B n 1, a, B n )(p, γ)) Get rid of transition with γ > 2
75 Let ((q, a, β)(p, γ)) be a transition with γ = C 1... C n with m > 1. Replace this transition by the following transitions ((q, a, β)(r 1, C m )) ((r 1, e, e)(r 2, C m 1 )) ((r m 2, e, e)(r m 1, C 2 )) ((r m 1, e, e)(p, C 1 )) Get rid of transition with β = e Replace all transitions of the form ((q, a, e)(p, γ)) with q s by all transitions of the form ((q, a, A)(p, γa))
76 Lemma 5. Any language accepted by a simple pushdown automata is context-free. Proof Let M = (K, Σ, Γ,, s, F ) be a pushdown automata and M be constructed as above. Define G = (V, Σ, R, S) as follows: V = {S} Σ K (Γ {e}) K R consists of the following rules: S s, Z, f for each transtition ((q, a, B), (r, C)) and for each p K : q, B, p a r, C, p for each transition ((q, a, B), (r, C 1 C 2 )), for all p, p K q, B, p a r, C 1, p p, C 2, p q, e, q e for each q K
77 Properties of Context-free Languages Theorem 17. The context-free languages are closed under union, concatenation and Kleen star. Proof Let L, L be context-free languages generated by context-free grammars G = (V, Σ, R, S), G = (V, Σ, R, S ) where we assume that V Σ and V Σ are disjoint. Construct new grammars from G, G to generate L L, L L, L. Theorem 18. The intersection of a context-free language with a regular language is a contextfree language. Proof Let L be a context-free language accepted by pushdown automaton M = (K, Σ, Γ,, s, F ) and L be a regular language accepted by a deterministic finite automaton M = (K, Σ, δ, s, F ) where K, K are disjoint. Construct a new pushdown automaton from M, M to accept L L.
78 Theorem 19. The intersection of two context free languages is not always context-free. The complementation of a context free language is not always context-free. Proof Let L 0 = {a m b n c n m, n 0 }, L 1 = {a m b m c n m, n 0 }. Both L 0, L 1 are context free (exercise). L = L 0 L 1 = {a n b n c n n 0 }. We show below that L is not context-free. We use the equation L 0 L 1 = L 0 L 1 to show that the complementation of a context free language is not always context-free (exercise).
79 Theorem 20. (Pumping Theorem) Let G = (V, Σ, R, S) be a context-free grammar. Then there is a number n such that for any string w L(G) of length greater than n can be rewritten as w = uvxyz in such a way that either v or y is nonempty and uv k xy k z is in L(G) for any k. Proof The fanout of a grammar G = (V, Σ, R, S), denoted by φ(g) is the largest number ofsymbols on the right handsid of any rule in G. A path in the parse tree is a sequence of distinct nodes each connected to the previous one by a line segment; the first node is the root and the last node is a leaf. The length of a path is the number of line segments in it. The height of the parse tree is the length of the longest path in it. Lemma 6. The yield of any parse tree of G with the height h has length at most φ(g) h. Lemma 7. Let G = (V, Σ, R, S) be a contextfree grammar. Then any string w L(G) of length greater than φ(g) V Σ can be rewritten as w = uvxyz in such a way that either v or y is nonempty and uv k xy k z is in L(G) for any k.
80 Algorithmic Properties Definition 7. A context-free grammar G = (V, Σ, R, S) is said to be in Chomsky normal form if all rules are of the form where A, B, C V A BC Theorem 21. There is a polynomial algorithm which given a context-free grammar G and a string w, decides whether w L(G)? Proof The proof consists of three main steps: A polynomial translation of G into an grammar G in Chomsky normal form such that L(G) (Σ {e}) = L(G ). A polynomial algorithm to decide whether w L(G ) for w 2. A polynomial algorithm to decide whether a L(G) for a Σ {e}.
81 Lemma 8. For every context-free grammar G = (V, Σ, R, S) there is a context-free grammar G in Chomsky normal form such that L(G ) = L(G) ({e} Σ). G could be constructed in time polynomial to the size of G. Proof Replace each rule A B 1 B 2... B n by A B 1 A 1 A 1 B 2 A 2... A n 2 B n 1 B n where A 1,..., A n 2 are new nonterminals. Construct E = {A A e} as follows: E := While there is a rule A α with α E and A E do E := E {A}. Removing e-rules: Delete all rules of the form A e For each rule of the form A BC or A CB where B E add the rule A C Construct for each A, D(A) = {B A B} as follows:
82 D(A) = {A} While there is a rule B C with B D(A) and C D(A) do D(A) := D(A) {C}. Removing rules containing only one symbol on the right hand side: Delete all rules of the form A B Replace each rule of the form A BC by all possible rules of the form A B C where B D(B), C D(C) Add the rule S BC for each rule A BC such that A D(S) {S}.
83 Lemma 9. Let G be a grammar in Chomski normal form. There is a polynomial algorithm to decide whether w L(G) for w 2. Proof Let w = x 1... x n. Define N[i, j] = {A A x i... x j } The sets N[i, j] could be computed by N[i, i] = {x i } N[i, j] = {A A BC, B N[i, s], C N[s + 1, j] } w L(G) iff w N[1, n].
84 Example Translate the grammar S (S) S SS S e into Chomski normal form S SS S () S (S 1 S 1 S) Check whether the string ( ( ) ( ( ) ) ) is generated by the Chomski normal form grammar. Fig. 10.
85 TURING MACHINES Definition 8. A Turing machine is a 5-tuple M = (K, Σ, δ, s, H) where K is a finite set of states, Σ is an alphabet containing the blank symbol and the left end symbol, but not containing the symbols and s K is the initial state H K is the set of halting states δ, the transition function, is a function from (K H) Σ to K (Σ {, }) such that for all q K H there exists p such that δ(q, ) = (p, ) for all q K H, and a Σ, if δ(q, a) = (p, b) then b
86 Example Design a Turing machine for accepting L = {w w {a, b}, w is even }. M = (K, Σ, δ, s, H) with K = {s, q 0, q 1, y, n}, H = {y, n} Σ = {a, b} δ : (K H) Σ K (Σ {, }) q σ δ(q, r) s q 0, q 0 y, q 0 a or b q 1, q 1 n, q 1 a or b q 0, M accepts aa: (s, aa) M (q 0, aa) M (q 1, aa) M (q 0, aa ) M (y, aa ) M rejects a: (s, a) M (q 0, a) M (q 1, a ) M (n, a )
87 A configuration of a Turing machine M = (K, Σ, δ, s, H) is a member of K Σ (Σ (Σ { }) {e}) Definition 9. Let M = (K, Σ, δ, s, H) and let (q 1, w 1 a 1 u 1 ) and (q 2, w 2 a 2 u 2 ) be configurations of M. Then (q 1, w 1 a 1 u 1 ) M (q 2, w 2 a 2 u 2 ) iff for some b Σ {, }, δ(q 1, a 1 ) = (q 2, b) and either 1. b Σ, w 1 = w 2, u 1 = u 2 and a 2 = b or 2. b =, w 1 = w 2 a 2, and either (a) u 2 = a 1 u 1, if a 1 or u 1 e or (b) u 2 = e, if a 1 = and u 1 = e or 3. b =, w 2 = w 1 a 1, and either (a) u 1 = a 2 u 2 or (b) u 1 = u 2 = e and a 2 =
88 A halted configuration is of the form (h, w 1 aw 2 ) with h H. A computation is a sequence of configurations C 1, C 2,..., C n such that C 1 M C 2 M... M C n. We say that the computation has length n and C 1 yields C n. M is said to halt on input w iff (s, w) yields some halted configuration.
89 COMBINING TURING MACHINES Symbol writing machine: For each symbol a Σ {, } { }, M a is a Turing machine which write the symbol a into the scanned tape square. M a = ({s, h}, Σ, δ, s, {h}): δ(s, b) = (h, a) for each b Σ { } Notations: We often write a for M a L for M R for M L : Finds the first blank square to the left of the currently scanned symbol R : Finds the first blank square to the right of the currently scanned symbol
90 An initial configuration is of the form (s, w) Definition 10. Given is a Turing machine M = (K, Σ, δ, s, H) with H = {y, n}. Any halting configuration whose state is y is said to be an accepting state while a halting configuration whose state is n is said to be a rejecting state. We say that M accepts an input w (Σ {, }) if (s, w) yields an accepting configuration. We say that M rejects an input w (Σ {, }) if (s, w) yields a rejecting configuration. Let Σ 0 Σ {, } be an alphabet, called input alphabet. We say that M decides a language L Σ 0 if for any string w Σ 0 If w L then M accepts w If w L then M rejects w A language L is called recursive if it is decided by some Turing machine.
91 Example Show that L 0 = {a n b n n 0 } and L 1 = {a n b n c n n 0 } are recursive. Fig. 11. Fig. 12.
92 Example Eeach deterministic finite automaton could be simulated by a TM. Let M = (K, Σ, δ, s, F ) be a DFA. Define a TM M = (K {y, n}, Σ, δ, s, {y, n}) with Σ = Σ {, } and δ : K Σ (K {y, n}) (Σ {, }) δ(s, ) = (s, ) δ (p, a) = (δ(p), ) for p K, a Σ δ (p, ) = (y, ) for p F δ (p, ) = (n, ) for p F It holds: w Σ : w L(M) iff (s, w) M w Σ : w L(M) iff (s, w) M (y, w ) (n, w )
93 Recursive Functions Definition 11. Let M = (K, Σ, δ, s, {h}). Let Σ 0 (Σ {, } and w Σ 0. Suppose (s, w) M (h, u) Then u is called the output of M on input w and denoted by M(w). 1. We say that M computes function f : Σ 0 Σ 0 if for all w Σ 0, M(w) = f(w). 2. We say that M computes function f : N k N, (k 1) if for all binary numbers w 1,..., w k, M(w;... ; w k ) = f(w 1,..., w k ) where f(w 1,..., w k ) is also in binary representation. A function f is recursive if there is a Turing machine that computes f. Example Show that g(n) = 2n and f(n) = n + 1 are recursive functions.
94 Recursively Enumerable Languages Definition 12. Let M = (K, Σ, δ, s, H) be a Turing machine. Let Σ 0 Σ {, } be an alphabet, and L Σ0. We say that M semidecides L if for any string w Σ0: w L iff M halts on input w A language L is called recursively enumerable if it is semidecided by some Turing machine. Theorem 22. If a language is recursive then it is also recursively enumerable. If a language is recursive then its complement is also recursive.
95 Extensions of Turing Machines We study two important extensions of Turing machines: 1. Allowing several tapes instead of one 2. Allowing nondeterministism Multi-tape Turing Machines A k-tape Turing machine consists of a finite control together with k infinite tapes. Each tape is scanned by a read/write head. The machine can in one step sense the symbols scanned by all its heads and then depending on those symbols and it s current state, rewrite some of those scanned squares or move some of the heads to the left or right. Definition 13. A k-tape Turing machine is a 5-tuple M = (K, Σ, δ, s, H) where K, Σ, s, H are as in the definition of ordinary Turing machine δ, the transition function, is a function δ : (K H) Σ k K (Σ {, }) k Example Design a two-tapes machine to decide L = { wcw w {a, b} } where c {a, b}.
96 w c w q r 1 r 2 δ(q, r 1, r 2 ) s p,, p n,, p σ p,, σ p σ p,, p c r 2,, r 2 x σ r 2, x, r 2 x f, x, f σ σ f,, f y,, f x y n, x, y if x y σ stands for a or b x stands for a or b or y stands for a or b or
97 Extending Turing machines with more than one tape does not increase the power of the machines. Theorem 23. Let k > 1 and M = (K, Σ, δ, s, H) be a k-tape Turing machine. Then there is a standard Turing machine M = (K, Σ, δ, s, H) where Σ Σ, and such that for any w (Σ {, }) : M halts on input w with output y on its first tape after t steps if and only if M halts on input x with the same output after a polynomial number of steps of t and the size of x.
98 Nondeterministic Turing machines Definition 14. A nondeterministic Turing machine is a quintuple M = (K, Σ,, s, H) where K, Σ, s, H are as for standard Turing machines, and, the transition relation, is a subset of ((K H) Σ) ( K (Σ {, }) ) Definition 15. Let M = (K, Σ,, s) and let (q 1, w 1 a 1 u 1 ) and (q 2, w 2 a 2 u 2 ) be configurations of M. Then (q 1, w 1 a 1 u 1 ) M (q 2, w 2 a 2 u 2 ) iff for some b Σ {, }, ((q 1, a 1 ), (q 2, b)) and 1. either b Σ, w 1 = w 2, u 1 = u 2 and a 2 = b 2. or b =, w 1 = w 2 a 2, and (a) either u 2 = a 1 u 1, if a 1 or u 1 e (b) or u 2 = e, if a 1 = and u 1 = e 3. or b =, w 2 = w 1 a 1, and (a) either u 1 = a 2 u 2 (b) or u 1 = u 2 = e and a 2 =
99 Definition 16. Let M = (K, Σ, δ, s, H) be a nondeterministic Turing machine. We say that M accepts w (Σ {, }) if (s, w) M (h, uav) for some h H, a Σ, u, v Σ. We say that M semidecides L (Σ {, }) if for any string w (Σ {, }) : w L iff M halts on input w. Definition 17. Let M = (K, Σ, δ, s, {y, n}) be a nondeterministic Turing machine. We say that M decides L (Σ {, }) if the following conditions hold for any string w (Σ {, }) : 1. There is a number N depending on M and w such that no computation starting from (s, w) has a length greater than N 2. w L iff (s, w) M (y, uav) for some a Σ, u, v Σ. We say that M computes a function f : (Σ {, }) (Σ {, }) if the following conditions hold for any string w (Σ {, }) : 1. There is a number N depending on M and w such that no computation starting from (s, w) has a length greater than N 2. (s, w) M (h, uav) iff ua =, v = f(w).
100 Theorem 24. If a nondeterministic Turing machine semidecides or decides a language or computes a function then there is a standard one that semidecides or decides the same language or computes the same function.
101 Unrestricted Grammars Definition 18. A unrestricted grammar G is a quadruple (V, Σ, R, S) where V is an alphabet Σ (the set of terminals) is a subset of V R (the set of rules) is a finite subset of V (V Σ)V V S (the start symbol) is an element of V Σ. We write u G v for any rule (u, v) R. For any strings w, w V, we write iff there is a rule u w = xvy. w G = w G v and w = xuy and
102 A sequence w 0 G G G = w1 =... = wn, n 0 is called a derivation of w n from w 0. We write w G = v iff there is a derivation of v from w. The language generated by G is L(G) = {w Σ S G = w }
103 Example Design an unrestricted grammar for L = {a n b n c n n 1 } G = (V, Σ, R, S) where V = {S, A, B, C, T a, T b, T c, a, b, c} Σ = {a, b, c} R consists of the following rules: S ABCS S T c CA AC BA AB CB BC CT c T c c BT c T b b AT b T a a BT b T b b AT a T a a T a e Theorem 25. A language is generated by an unrestricted grammar if and only if it is recursively enumerable.
104 UNDECIDABILITY The Church - Turing Thesis An algorithm is anything that can be viewed as corresponding to a Turing machine that halts on all inputs. Nothing is considered to be an algorithm if it cannot be rendered as a Turing machine that is guaranteed to halt on all inputs.
105 Universal Turing Machine Let M = (K, Σ, δ, s, H) be a Turing machine. M is now encoded over the alphabet {a, q, 0, 1} as follows: Let i, j be smallest integer such that 2 i K and 2 j Σ + 2 each state in K is represented by a string from q{0, 1} i each symbol in Σ is represented by a string from a{0, 1} j The representation of the special symbols is as follows: a0 j a0 j 1 1 a0 j 2 10 a0 j 2 11 The start state is represented by q0 i The representation of a Turing machine M, denoted by M, consists of a sequence of strings of the form (p,b,r,c) with p,r representations of states and b,c representations of symbols.
106 Example Let M = (K, Σ, δ, {h}) be a TM where K = {s, p, q, h}, Σ = {0, 1,, } and δ(s, ) = (p, ), δ(p, 0) = (p, ), δ(p, 1) = (p, ), δ(p, ) = (q, 0), δ(q, 0) = (q, ), δ(q, 1) = (q, ), δ(q, ) = (h, ). s q00 p q01 q q10 h q11 a000 a001 a010 a011 0 a100 1 a101 The representation M is the following string: (q00, a000, q01, a011)(q01, a100, q01, a011)(q01, a101, q01, a011) (q01, a000, q10, a100)(q10, a100, q10, a011)(q10, a101, q10, a011) (q10, a000, q11, a000)
107 The universal Turing machine U is a machine which uses the encodings of other machine to direct its operations. Intuitively U takes two arguments: a description of a Turing machine M, M, and a description of an input string w, w. U has the following property: U halts on M w iff M halts on w U is constructed in two steps: 1. A three-tape universal machine U is constructed. 2. Transform U into an equivalent single tape machine U.
108 U simulates a TM M as follows: 1. The first tape contains the encoding of the tape of M 2. The second tape contains the encoding of M 3. The third tape contains the encoding of the state of M at the current point in the simulated computation U starts with the string M w on its first tape and the other tapes blank. M is moved onto the second tape, and w is shifted down to the left end of the first tape, preceding it by U extracts the coding of the initial state of M and puts it on the third tape.
109 Halting Problem: The halting problem Given an arbitrary Turing machine M and an input w, is there an algorithm which can decide whether M accepts w? Let H = { M w Turing machine M accepts input string w }. From the Church-Turing thesis, Yes answer to the halting problem iff the language H is recursive. It is clear that the universal Turing machine accepts H. Hence H recursively enumerable.
110 Theorem 26. H is not recursive. Proof Suppose H is recursive. Let H 1 = {w w = M for some TM M and M accepts w } Because H is recursive, H 1 is also recursive. Let Σ U = {a, q, 0, 1, (, ),, } be the alphabet of the universal TM. Define R Σ U Σ U by (u, w) R iff u = M for some TM machine M accepting w For each string u, R u = {w (u, w) R } Therefore, for each language L, L is r.e. iff u = M : L = R u = L(M). Let D = {w (w, w) R } From the diagonalization principle, there is no u such that D = R u. Therefore D is not r.e. It is not difficult (exercise) to see that H 1 = {w (w, w) R } = D Since H 1 is recursive and D = H 1, D is also recursive, hence r.e. Contradiction because we have showed that D is not r.e. Hence, the assumption that H is recursive leads to a contradiction. H is hence not recursive.
THEORY OF COMPUTATION (AUBER) EXAM CRIB SHEET
 THEORY OF COMPUTATION (AUBER) EXAM CRIB SHEET Regular Languages and FA A language is a set of strings over a finite alphabet Σ. All languages are finite or countably infinite. The set of all languages
THEORY OF COMPUTATION (AUBER) EXAM CRIB SHEET Regular Languages and FA A language is a set of strings over a finite alphabet Σ. All languages are finite or countably infinite. The set of all languages
DM17. Beregnelighed. Jacob Aae Mikkelsen
 DM17 Beregnelighed Jacob Aae Mikkelsen January 12, 2007 CONTENTS Contents 1 Introduction 2 1.1 Operations with languages...................... 2 2 Finite Automata 3 2.1 Regular expressions/languages....................
DM17 Beregnelighed Jacob Aae Mikkelsen January 12, 2007 CONTENTS Contents 1 Introduction 2 1.1 Operations with languages...................... 2 2 Finite Automata 3 2.1 Regular expressions/languages....................
Functions on languages:
 MA/CSSE 474 Final Exam Notation and Formulas page Name (turn this in with your exam) Unless specified otherwise, r,s,t,u,v,w,x,y,z are strings over alphabet Σ; while a, b, c, d are individual alphabet
MA/CSSE 474 Final Exam Notation and Formulas page Name (turn this in with your exam) Unless specified otherwise, r,s,t,u,v,w,x,y,z are strings over alphabet Σ; while a, b, c, d are individual alphabet
FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY
 15-453 FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY REVIEW for MIDTERM 1 THURSDAY Feb 6 Midterm 1 will cover everything we have seen so far The PROBLEMS will be from Sipser, Chapters 1, 2, 3 It will be
15-453 FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY REVIEW for MIDTERM 1 THURSDAY Feb 6 Midterm 1 will cover everything we have seen so far The PROBLEMS will be from Sipser, Chapters 1, 2, 3 It will be
CPSC 421: Tutorial #1
 CPSC 421: Tutorial #1 October 14, 2016 Set Theory. 1. Let A be an arbitrary set, and let B = {x A : x / x}. That is, B contains all sets in A that do not contain themselves: For all y, ( ) y B if and only
CPSC 421: Tutorial #1 October 14, 2016 Set Theory. 1. Let A be an arbitrary set, and let B = {x A : x / x}. That is, B contains all sets in A that do not contain themselves: For all y, ( ) y B if and only
CS 455/555: Finite automata
 CS 455/555: Finite automata Stefan D. Bruda Winter 2019 AUTOMATA (FINITE OR NOT) Generally any automaton Has a finite-state control Scans the input one symbol at a time Takes an action based on the currently
CS 455/555: Finite automata Stefan D. Bruda Winter 2019 AUTOMATA (FINITE OR NOT) Generally any automaton Has a finite-state control Scans the input one symbol at a time Takes an action based on the currently
Computational Models - Lecture 4
 Computational Models - Lecture 4 Regular languages: The Myhill-Nerode Theorem Context-free Grammars Chomsky Normal Form Pumping Lemma for context free languages Non context-free languages: Examples Push
Computational Models - Lecture 4 Regular languages: The Myhill-Nerode Theorem Context-free Grammars Chomsky Normal Form Pumping Lemma for context free languages Non context-free languages: Examples Push
Final exam study sheet for CS3719 Turing machines and decidability.
 Final exam study sheet for CS3719 Turing machines and decidability. A Turing machine is a finite automaton with an infinite memory (tape). Formally, a Turing machine is a 6-tuple M = (Q, Σ, Γ, δ, q 0,
Final exam study sheet for CS3719 Turing machines and decidability. A Turing machine is a finite automaton with an infinite memory (tape). Formally, a Turing machine is a 6-tuple M = (Q, Σ, Γ, δ, q 0,
CS 455/555: Mathematical preliminaries
 CS 455/555: Mathematical preliminaries Stefan D. Bruda Winter 2019 SETS AND RELATIONS Sets: Operations: intersection, union, difference, Cartesian product Big, powerset (2 A ) Partition (π 2 A, π, i j
CS 455/555: Mathematical preliminaries Stefan D. Bruda Winter 2019 SETS AND RELATIONS Sets: Operations: intersection, union, difference, Cartesian product Big, powerset (2 A ) Partition (π 2 A, π, i j
Pushdown Automata. We have seen examples of context-free languages that are not regular, and hence can not be recognized by finite automata.
 Pushdown Automata We have seen examples of context-free languages that are not regular, and hence can not be recognized by finite automata. Next we consider a more powerful computation model, called a
Pushdown Automata We have seen examples of context-free languages that are not regular, and hence can not be recognized by finite automata. Next we consider a more powerful computation model, called a
Introduction to Theory of Computing
 CSCI 2670, Fall 2012 Introduction to Theory of Computing Department of Computer Science University of Georgia Athens, GA 30602 Instructor: Liming Cai www.cs.uga.edu/ cai 0 Lecture Note 3 Context-Free Languages
CSCI 2670, Fall 2012 Introduction to Theory of Computing Department of Computer Science University of Georgia Athens, GA 30602 Instructor: Liming Cai www.cs.uga.edu/ cai 0 Lecture Note 3 Context-Free Languages
cse303 ELEMENTS OF THE THEORY OF COMPUTATION Professor Anita Wasilewska
 cse303 ELEMENTS OF THE THEORY OF COMPUTATION Professor Anita Wasilewska LECTURE 1 Course Web Page www3.cs.stonybrook.edu/ cse303 The webpage contains: lectures notes slides; very detailed solutions to
cse303 ELEMENTS OF THE THEORY OF COMPUTATION Professor Anita Wasilewska LECTURE 1 Course Web Page www3.cs.stonybrook.edu/ cse303 The webpage contains: lectures notes slides; very detailed solutions to
FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY
 15-453 FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY Chomsky Normal Form and TURING MACHINES TUESDAY Feb 4 CHOMSKY NORMAL FORM A context-free grammar is in Chomsky normal form if every rule is of the form:
15-453 FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY Chomsky Normal Form and TURING MACHINES TUESDAY Feb 4 CHOMSKY NORMAL FORM A context-free grammar is in Chomsky normal form if every rule is of the form:
Automata and Computability. Solutions to Exercises
 Automata and Computability Solutions to Exercises Spring 27 Alexis Maciel Department of Computer Science Clarkson University Copyright c 27 Alexis Maciel ii Contents Preface vii Introduction 2 Finite Automata
Automata and Computability Solutions to Exercises Spring 27 Alexis Maciel Department of Computer Science Clarkson University Copyright c 27 Alexis Maciel ii Contents Preface vii Introduction 2 Finite Automata
Decidability (What, stuff is unsolvable?)
 University of Georgia Fall 2014 Outline Decidability Decidable Problems for Regular Languages Decidable Problems for Context Free Languages The Halting Problem Countable and Uncountable Sets Diagonalization
University of Georgia Fall 2014 Outline Decidability Decidable Problems for Regular Languages Decidable Problems for Context Free Languages The Halting Problem Countable and Uncountable Sets Diagonalization
Automata and Computability. Solutions to Exercises
 Automata and Computability Solutions to Exercises Fall 28 Alexis Maciel Department of Computer Science Clarkson University Copyright c 28 Alexis Maciel ii Contents Preface vii Introduction 2 Finite Automata
Automata and Computability Solutions to Exercises Fall 28 Alexis Maciel Department of Computer Science Clarkson University Copyright c 28 Alexis Maciel ii Contents Preface vii Introduction 2 Finite Automata
CSE 105 THEORY OF COMPUTATION. Spring 2018 review class
 CSE 105 THEORY OF COMPUTATION Spring 2018 review class Today's learning goals Summarize key concepts, ideas, themes from CSE 105. Approach your final exam studying with confidence. Identify areas to focus
CSE 105 THEORY OF COMPUTATION Spring 2018 review class Today's learning goals Summarize key concepts, ideas, themes from CSE 105. Approach your final exam studying with confidence. Identify areas to focus
FORMAL LANGUAGES, AUTOMATA AND COMPUTATION
 FORMAL LANGUAGES, AUTOMATA AND COMPUTATION DECIDABILITY ( LECTURE 15) SLIDES FOR 15-453 SPRING 2011 1 / 34 TURING MACHINES-SYNOPSIS The most general model of computation Computations of a TM are described
FORMAL LANGUAGES, AUTOMATA AND COMPUTATION DECIDABILITY ( LECTURE 15) SLIDES FOR 15-453 SPRING 2011 1 / 34 TURING MACHINES-SYNOPSIS The most general model of computation Computations of a TM are described
Part I: Definitions and Properties
 Turing Machines Part I: Definitions and Properties Finite State Automata Deterministic Automata (DFSA) M = {Q, Σ, δ, q 0, F} -- Σ = Symbols -- Q = States -- q 0 = Initial State -- F = Accepting States
Turing Machines Part I: Definitions and Properties Finite State Automata Deterministic Automata (DFSA) M = {Q, Σ, δ, q 0, F} -- Σ = Symbols -- Q = States -- q 0 = Initial State -- F = Accepting States
Chomsky Normal Form and TURING MACHINES. TUESDAY Feb 4
 Chomsky Normal Form and TURING MACHINES TUESDAY Feb 4 CHOMSKY NORMAL FORM A context-free grammar is in Chomsky normal form if every rule is of the form: A BC A a S ε B and C aren t start variables a is
Chomsky Normal Form and TURING MACHINES TUESDAY Feb 4 CHOMSKY NORMAL FORM A context-free grammar is in Chomsky normal form if every rule is of the form: A BC A a S ε B and C aren t start variables a is
NODIA AND COMPANY. GATE SOLVED PAPER Computer Science Engineering Theory of Computation. Copyright By NODIA & COMPANY
 No part of this publication may be reproduced or distributed in any form or any means, electronic, mechanical, photocopying, or otherwise without the prior permission of the author. GATE SOLVED PAPER Computer
No part of this publication may be reproduced or distributed in any form or any means, electronic, mechanical, photocopying, or otherwise without the prior permission of the author. GATE SOLVED PAPER Computer
Foundations of Informatics: a Bridging Course
 Foundations of Informatics: a Bridging Course Week 3: Formal Languages and Semantics Thomas Noll Lehrstuhl für Informatik 2 RWTH Aachen University noll@cs.rwth-aachen.de http://www.b-it-center.de/wob/en/view/class211_id948.html
Foundations of Informatics: a Bridging Course Week 3: Formal Languages and Semantics Thomas Noll Lehrstuhl für Informatik 2 RWTH Aachen University noll@cs.rwth-aachen.de http://www.b-it-center.de/wob/en/view/class211_id948.html
Automata Theory and Formal Grammars: Lecture 1
 Automata Theory and Formal Grammars: Lecture 1 Sets, Languages, Logic Automata Theory and Formal Grammars: Lecture 1 p.1/72 Sets, Languages, Logic Today Course Overview Administrivia Sets Theory (Review?)
Automata Theory and Formal Grammars: Lecture 1 Sets, Languages, Logic Automata Theory and Formal Grammars: Lecture 1 p.1/72 Sets, Languages, Logic Today Course Overview Administrivia Sets Theory (Review?)
MA/CSSE 474 Theory of Computation
 MA/CSSE 474 Theory of Computation CFL Hierarchy CFL Decision Problems Your Questions? Previous class days' material Reading Assignments HW 12 or 13 problems Anything else I have included some slides online
MA/CSSE 474 Theory of Computation CFL Hierarchy CFL Decision Problems Your Questions? Previous class days' material Reading Assignments HW 12 or 13 problems Anything else I have included some slides online
Lecture 17: Language Recognition
 Lecture 17: Language Recognition Finite State Automata Deterministic and Non-Deterministic Finite Automata Regular Expressions Push-Down Automata Turing Machines Modeling Computation When attempting to
Lecture 17: Language Recognition Finite State Automata Deterministic and Non-Deterministic Finite Automata Regular Expressions Push-Down Automata Turing Machines Modeling Computation When attempting to
CSE 105 THEORY OF COMPUTATION
 CSE 105 THEORY OF COMPUTATION Spring 2017 http://cseweb.ucsd.edu/classes/sp17/cse105-ab/ Today's learning goals Summarize key concepts, ideas, themes from CSE 105. Approach your final exam studying with
CSE 105 THEORY OF COMPUTATION Spring 2017 http://cseweb.ucsd.edu/classes/sp17/cse105-ab/ Today's learning goals Summarize key concepts, ideas, themes from CSE 105. Approach your final exam studying with
Computational Models - Lecture 3
 Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p. 1 Computational Models - Lecture 3 Equivalence of regular expressions and regular languages (lukewarm leftover
Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p. 1 Computational Models - Lecture 3 Equivalence of regular expressions and regular languages (lukewarm leftover
CISC4090: Theory of Computation
 CISC4090: Theory of Computation Chapter 2 Context-Free Languages Courtesy of Prof. Arthur G. Werschulz Fordham University Department of Computer and Information Sciences Spring, 2014 Overview In Chapter
CISC4090: Theory of Computation Chapter 2 Context-Free Languages Courtesy of Prof. Arthur G. Werschulz Fordham University Department of Computer and Information Sciences Spring, 2014 Overview In Chapter
The View Over The Horizon
 The View Over The Horizon enumerable decidable context free regular Context-Free Grammars An example of a context free grammar, G 1 : A 0A1 A B B # Terminology: Each line is a substitution rule or production.
The View Over The Horizon enumerable decidable context free regular Context-Free Grammars An example of a context free grammar, G 1 : A 0A1 A B B # Terminology: Each line is a substitution rule or production.
Theory of Computation
 Thomas Zeugmann Hokkaido University Laboratory for Algorithmics http://www-alg.ist.hokudai.ac.jp/ thomas/toc/ Lecture 3: Finite State Automata Motivation In the previous lecture we learned how to formalize
Thomas Zeugmann Hokkaido University Laboratory for Algorithmics http://www-alg.ist.hokudai.ac.jp/ thomas/toc/ Lecture 3: Finite State Automata Motivation In the previous lecture we learned how to formalize
DD2371 Automata Theory
 KTH CSC VT 2008 DD2371 Automata Theory Dilian Gurov Lecture Outline 1. The lecturer 2. Introduction to automata theory 3. Course syllabus 4. Course objectives 5. Course organization 6. First definitions
KTH CSC VT 2008 DD2371 Automata Theory Dilian Gurov Lecture Outline 1. The lecturer 2. Introduction to automata theory 3. Course syllabus 4. Course objectives 5. Course organization 6. First definitions
Computational Theory
 Computational Theory Finite Automata and Regular Languages Curtis Larsen Dixie State University Computing and Design Fall 2018 Adapted from notes by Russ Ross Adapted from notes by Harry Lewis Curtis Larsen
Computational Theory Finite Automata and Regular Languages Curtis Larsen Dixie State University Computing and Design Fall 2018 Adapted from notes by Russ Ross Adapted from notes by Harry Lewis Curtis Larsen
CSCE 551: Chin-Tser Huang. University of South Carolina
 CSCE 551: Theory of Computation Chin-Tser Huang huangct@cse.sc.edu University of South Carolina Church-Turing Thesis The definition of the algorithm came in the 1936 papers of Alonzo Church h and Alan
CSCE 551: Theory of Computation Chin-Tser Huang huangct@cse.sc.edu University of South Carolina Church-Turing Thesis The definition of the algorithm came in the 1936 papers of Alonzo Church h and Alan
V Honors Theory of Computation
 V22.0453-001 Honors Theory of Computation Problem Set 3 Solutions Problem 1 Solution: The class of languages recognized by these machines is the exactly the class of regular languages, thus this TM variant
V22.0453-001 Honors Theory of Computation Problem Set 3 Solutions Problem 1 Solution: The class of languages recognized by these machines is the exactly the class of regular languages, thus this TM variant
BASIC MATHEMATICAL TECHNIQUES
 CHAPTER 1 ASIC MATHEMATICAL TECHNIQUES 1.1 Introduction To understand automata theory, one must have a strong foundation about discrete mathematics. Discrete mathematics is a branch of mathematics dealing
CHAPTER 1 ASIC MATHEMATICAL TECHNIQUES 1.1 Introduction To understand automata theory, one must have a strong foundation about discrete mathematics. Discrete mathematics is a branch of mathematics dealing
Theory of Computation Turing Machine and Pushdown Automata
 Theory of Computation Turing Machine and Pushdown Automata 1. What is a Turing Machine? A Turing Machine is an accepting device which accepts the languages (recursively enumerable set) generated by type
Theory of Computation Turing Machine and Pushdown Automata 1. What is a Turing Machine? A Turing Machine is an accepting device which accepts the languages (recursively enumerable set) generated by type
Undecidability COMS Ashley Montanaro 4 April Department of Computer Science, University of Bristol Bristol, UK
 COMS11700 Undecidability Department of Computer Science, University of Bristol Bristol, UK 4 April 2014 COMS11700: Undecidability Slide 1/29 Decidability We are particularly interested in Turing machines
COMS11700 Undecidability Department of Computer Science, University of Bristol Bristol, UK 4 April 2014 COMS11700: Undecidability Slide 1/29 Decidability We are particularly interested in Turing machines
SYLLABUS. Introduction to Finite Automata, Central Concepts of Automata Theory. CHAPTER - 3 : REGULAR EXPRESSIONS AND LANGUAGES
 Contents i SYLLABUS UNIT - I CHAPTER - 1 : AUT UTOMA OMATA Introduction to Finite Automata, Central Concepts of Automata Theory. CHAPTER - 2 : FINITE AUT UTOMA OMATA An Informal Picture of Finite Automata,
Contents i SYLLABUS UNIT - I CHAPTER - 1 : AUT UTOMA OMATA Introduction to Finite Automata, Central Concepts of Automata Theory. CHAPTER - 2 : FINITE AUT UTOMA OMATA An Informal Picture of Finite Automata,
Context-Free and Noncontext-Free Languages
 Examples: Context-Free and Noncontext-Free Languages a*b* is regular. A n B n = {a n b n : n 0} is context-free but not regular. A n B n C n = {a n b n c n : n 0} is not context-free The Regular and the
Examples: Context-Free and Noncontext-Free Languages a*b* is regular. A n B n = {a n b n : n 0} is context-free but not regular. A n B n C n = {a n b n c n : n 0} is not context-free The Regular and the
T (s, xa) = T (T (s, x), a). The language recognized by M, denoted L(M), is the set of strings accepted by M. That is,
 Recall A deterministic finite automaton is a five-tuple where S is a finite set of states, M = (S, Σ, T, s 0, F ) Σ is an alphabet the input alphabet, T : S Σ S is the transition function, s 0 S is the
Recall A deterministic finite automaton is a five-tuple where S is a finite set of states, M = (S, Σ, T, s 0, F ) Σ is an alphabet the input alphabet, T : S Σ S is the transition function, s 0 S is the
Introduction to Languages and Computation
 Introduction to Languages and Computation George Voutsadakis 1 1 Mathematics and Computer Science Lake Superior State University LSSU Math 400 George Voutsadakis (LSSU) Languages and Computation July 2014
Introduction to Languages and Computation George Voutsadakis 1 1 Mathematics and Computer Science Lake Superior State University LSSU Math 400 George Voutsadakis (LSSU) Languages and Computation July 2014
Section 1 (closed-book) Total points 30
 CS 454 Theory of Computation Fall 2011 Section 1 (closed-book) Total points 30 1. Which of the following are true? (a) a PDA can always be converted to an equivalent PDA that at each step pops or pushes
CS 454 Theory of Computation Fall 2011 Section 1 (closed-book) Total points 30 1. Which of the following are true? (a) a PDA can always be converted to an equivalent PDA that at each step pops or pushes
MA/CSSE 474 Theory of Computation
 MA/CSSE 474 Theory of Computation Bottom-up parsing Pumping Theorem for CFLs Recap: Going One Way Lemma: Each context-free language is accepted by some PDA. Proof (by construction): The idea: Let the stack
MA/CSSE 474 Theory of Computation Bottom-up parsing Pumping Theorem for CFLs Recap: Going One Way Lemma: Each context-free language is accepted by some PDA. Proof (by construction): The idea: Let the stack
Finite Automata Theory and Formal Languages TMV027/DIT321 LP4 2018
 Finite Automata Theory and Formal Languages TMV027/DIT321 LP4 2018 Lecture 14 Ana Bove May 14th 2018 Recap: Context-free Grammars Simplification of grammars: Elimination of ǫ-productions; Elimination of
Finite Automata Theory and Formal Languages TMV027/DIT321 LP4 2018 Lecture 14 Ana Bove May 14th 2018 Recap: Context-free Grammars Simplification of grammars: Elimination of ǫ-productions; Elimination of
Decidability. William Chan
 Decidability William Chan Preface : In 1928, David Hilbert gave a challenge known as the Entscheidungsproblem, which is German for Decision Problem. Hilbert s problem asked for some purely mechanical procedure
Decidability William Chan Preface : In 1928, David Hilbert gave a challenge known as the Entscheidungsproblem, which is German for Decision Problem. Hilbert s problem asked for some purely mechanical procedure
Finite Automata and Regular languages
 Finite Automata and Regular languages Huan Long Shanghai Jiao Tong University Acknowledgements Part of the slides comes from a similar course in Fudan University given by Prof. Yijia Chen. http://basics.sjtu.edu.cn/
Finite Automata and Regular languages Huan Long Shanghai Jiao Tong University Acknowledgements Part of the slides comes from a similar course in Fudan University given by Prof. Yijia Chen. http://basics.sjtu.edu.cn/
COMP/MATH 300 Topics for Spring 2017 June 5, Review and Regular Languages
 COMP/MATH 300 Topics for Spring 2017 June 5, 2017 Review and Regular Languages Exam I I. Introductory and review information from Chapter 0 II. Problems and Languages A. Computable problems can be expressed
COMP/MATH 300 Topics for Spring 2017 June 5, 2017 Review and Regular Languages Exam I I. Introductory and review information from Chapter 0 II. Problems and Languages A. Computable problems can be expressed
Introduction to Turing Machines. Reading: Chapters 8 & 9
 Introduction to Turing Machines Reading: Chapters 8 & 9 1 Turing Machines (TM) Generalize the class of CFLs: Recursively Enumerable Languages Recursive Languages Context-Free Languages Regular Languages
Introduction to Turing Machines Reading: Chapters 8 & 9 1 Turing Machines (TM) Generalize the class of CFLs: Recursively Enumerable Languages Recursive Languages Context-Free Languages Regular Languages
Languages, regular languages, finite automata
 Notes on Computer Theory Last updated: January, 2018 Languages, regular languages, finite automata Content largely taken from Richards [1] and Sipser [2] 1 Languages An alphabet is a finite set of characters,
Notes on Computer Theory Last updated: January, 2018 Languages, regular languages, finite automata Content largely taken from Richards [1] and Sipser [2] 1 Languages An alphabet is a finite set of characters,
Recap DFA,NFA, DTM. Slides by Prof. Debasis Mitra, FIT.
 Recap DFA,NFA, DTM Slides by Prof. Debasis Mitra, FIT. 1 Formal Language Finite set of alphabets Σ: e.g., {0, 1}, {a, b, c}, { {, } } Language L is a subset of strings on Σ, e.g., {00, 110, 01} a finite
Recap DFA,NFA, DTM Slides by Prof. Debasis Mitra, FIT. 1 Formal Language Finite set of alphabets Σ: e.g., {0, 1}, {a, b, c}, { {, } } Language L is a subset of strings on Σ, e.g., {00, 110, 01} a finite
Undecidable Problems and Reducibility
 University of Georgia Fall 2014 Reducibility We show a problem decidable/undecidable by reducing it to another problem. One type of reduction: mapping reduction. Definition Let A, B be languages over Σ.
University of Georgia Fall 2014 Reducibility We show a problem decidable/undecidable by reducing it to another problem. One type of reduction: mapping reduction. Definition Let A, B be languages over Σ.
Theory of computation: initial remarks (Chapter 11)
 Theory of computation: initial remarks (Chapter 11) For many purposes, computation is elegantly modeled with simple mathematical objects: Turing machines, finite automata, pushdown automata, and such.
Theory of computation: initial remarks (Chapter 11) For many purposes, computation is elegantly modeled with simple mathematical objects: Turing machines, finite automata, pushdown automata, and such.
Homework 8. a b b a b a b. two-way, read/write
 Homework 8 309 Homework 8 1. Describe a TM that accepts the set {a n n is a power of 2}. Your description should be at the level of the descriptions in Lecture 29 of the TM that accepts {ww w Σ } and the
Homework 8 309 Homework 8 1. Describe a TM that accepts the set {a n n is a power of 2}. Your description should be at the level of the descriptions in Lecture 29 of the TM that accepts {ww w Σ } and the
AC68 FINITE AUTOMATA & FORMULA LANGUAGES DEC 2013
 Q.2 a. Prove by mathematical induction n 4 4n 2 is divisible by 3 for n 0. Basic step: For n = 0, n 3 n = 0 which is divisible by 3. Induction hypothesis: Let p(n) = n 3 n is divisible by 3. Induction
Q.2 a. Prove by mathematical induction n 4 4n 2 is divisible by 3 for n 0. Basic step: For n = 0, n 3 n = 0 which is divisible by 3. Induction hypothesis: Let p(n) = n 3 n is divisible by 3. Induction
} Some languages are Turing-decidable A Turing Machine will halt on all inputs (either accepting or rejecting). No infinite loops.
 and their languages } Some languages are Turing-decidable A Turing Machine will halt on all inputs (either accepting or rejecting). No infinite loops. } Some languages are Turing-recognizable, but not
and their languages } Some languages are Turing-decidable A Turing Machine will halt on all inputs (either accepting or rejecting). No infinite loops. } Some languages are Turing-recognizable, but not
3130CIT Theory of Computation
 GRIFFITH UNIVERSITY School of Computing and Information Technology 3130CIT Theory of Computation Final Examination, Semester 2, 2006 Details Total marks: 120 (40% of the total marks for this subject) Perusal:
GRIFFITH UNIVERSITY School of Computing and Information Technology 3130CIT Theory of Computation Final Examination, Semester 2, 2006 Details Total marks: 120 (40% of the total marks for this subject) Perusal:
Harvard CS 121 and CSCI E-207 Lecture 10: CFLs: PDAs, Closure Properties, and Non-CFLs
 Harvard CS 121 and CSCI E-207 Lecture 10: CFLs: PDAs, Closure Properties, and Non-CFLs Harry Lewis October 8, 2013 Reading: Sipser, pp. 119-128. Pushdown Automata (review) Pushdown Automata = Finite automaton
Harvard CS 121 and CSCI E-207 Lecture 10: CFLs: PDAs, Closure Properties, and Non-CFLs Harry Lewis October 8, 2013 Reading: Sipser, pp. 119-128. Pushdown Automata (review) Pushdown Automata = Finite automaton
Pushdown Automata. Notes on Automata and Theory of Computation. Chia-Ping Chen
 Pushdown Automata Notes on Automata and Theory of Computation Chia-Ping Chen Department of Computer Science and Engineering National Sun Yat-Sen University Kaohsiung, Taiwan ROC Pushdown Automata p. 1
Pushdown Automata Notes on Automata and Theory of Computation Chia-Ping Chen Department of Computer Science and Engineering National Sun Yat-Sen University Kaohsiung, Taiwan ROC Pushdown Automata p. 1
TURING MAHINES
 15-453 TURING MAHINES TURING MACHINE FINITE STATE q 10 CONTROL AI N P U T INFINITE TAPE read write move 0 0, R, R q accept, R q reject 0 0, R 0 0, R, L read write move 0 0, R, R q accept, R 0 0, R 0 0,
15-453 TURING MAHINES TURING MACHINE FINITE STATE q 10 CONTROL AI N P U T INFINITE TAPE read write move 0 0, R, R q accept, R q reject 0 0, R 0 0, R, L read write move 0 0, R, R q accept, R 0 0, R 0 0,
CSE355 SUMMER 2018 LECTURES TURING MACHINES AND (UN)DECIDABILITY
 CSE355 SUMMER 2018 LECTURES TURING MACHINES AND (UN)DECIDABILITY RYAN DOUGHERTY If we want to talk about a program running on a real computer, consider the following: when a program reads an instruction,
CSE355 SUMMER 2018 LECTURES TURING MACHINES AND (UN)DECIDABILITY RYAN DOUGHERTY If we want to talk about a program running on a real computer, consider the following: when a program reads an instruction,
Introduction to Formal Languages, Automata and Computability p.1/42
 Introduction to Formal Languages, Automata and Computability Pushdown Automata K. Krithivasan and R. Rama Introduction to Formal Languages, Automata and Computability p.1/42 Introduction We have considered
Introduction to Formal Languages, Automata and Computability Pushdown Automata K. Krithivasan and R. Rama Introduction to Formal Languages, Automata and Computability p.1/42 Introduction We have considered
ACS2: Decidability Decidability
 Decidability Bernhard Nebel and Christian Becker-Asano 1 Overview An investigation into the solvable/decidable Decidable languages The halting problem (undecidable) 2 Decidable problems? Acceptance problem
Decidability Bernhard Nebel and Christian Becker-Asano 1 Overview An investigation into the solvable/decidable Decidable languages The halting problem (undecidable) 2 Decidable problems? Acceptance problem
What Is a Language? Grammars, Languages, and Machines. Strings: the Building Blocks of Languages
 Do Homework 2. What Is a Language? Grammars, Languages, and Machines L Language Grammar Accepts Machine Strings: the Building Blocks of Languages An alphabet is a finite set of symbols: English alphabet:
Do Homework 2. What Is a Language? Grammars, Languages, and Machines L Language Grammar Accepts Machine Strings: the Building Blocks of Languages An alphabet is a finite set of symbols: English alphabet:
Computational Models: Class 5
 Computational Models: Class 5 Benny Chor School of Computer Science Tel Aviv University March 27, 2019 Based on slides by Maurice Herlihy, Brown University, and modifications by Iftach Haitner and Yishay
Computational Models: Class 5 Benny Chor School of Computer Science Tel Aviv University March 27, 2019 Based on slides by Maurice Herlihy, Brown University, and modifications by Iftach Haitner and Yishay
Pushdown automata. Twan van Laarhoven. Institute for Computing and Information Sciences Intelligent Systems Radboud University Nijmegen
 Pushdown automata Twan van Laarhoven Institute for Computing and Information Sciences Intelligent Systems Version: fall 2014 T. van Laarhoven Version: fall 2014 Formal Languages, Grammars and Automata
Pushdown automata Twan van Laarhoven Institute for Computing and Information Sciences Intelligent Systems Version: fall 2014 T. van Laarhoven Version: fall 2014 Formal Languages, Grammars and Automata
Computational Models - Lecture 5 1
 Computational Models - Lecture 5 1 Handout Mode Iftach Haitner and Yishay Mansour. Tel Aviv University. April 10/22, 2013 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice
Computational Models - Lecture 5 1 Handout Mode Iftach Haitner and Yishay Mansour. Tel Aviv University. April 10/22, 2013 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice
Turing Machines. 22c:135 Theory of Computation. Tape of a Turing Machine (TM) TM versus FA, PDA
 Turing Machines A Turing machine is similar to a finite automaton with supply of unlimited memory. A Turing machine can do everything that any computing device can do. There exist problems that even a
Turing Machines A Turing machine is similar to a finite automaton with supply of unlimited memory. A Turing machine can do everything that any computing device can do. There exist problems that even a
Computational Models Lecture 8 1
 Computational Models Lecture 8 1 Handout Mode Ronitt Rubinfeld and Iftach Haitner. Tel Aviv University. May 11/13, 2015 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice
Computational Models Lecture 8 1 Handout Mode Ronitt Rubinfeld and Iftach Haitner. Tel Aviv University. May 11/13, 2015 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice
Before We Start. The Pumping Lemma. Languages. Context Free Languages. Plan for today. Now our picture looks like. Any questions?
 Before We Start The Pumping Lemma Any questions? The Lemma & Decision/ Languages Future Exam Question What is a language? What is a class of languages? Context Free Languages Context Free Languages(CFL)
Before We Start The Pumping Lemma Any questions? The Lemma & Decision/ Languages Future Exam Question What is a language? What is a class of languages? Context Free Languages Context Free Languages(CFL)
Models of Computation. by Costas Busch, LSU
 Models of Computation by Costas Busch, LSU 1 Computation CPU memory 2 temporary memory input memory CPU output memory Program memory 3 Example: f ( x) x 3 temporary memory input memory Program memory compute
Models of Computation by Costas Busch, LSU 1 Computation CPU memory 2 temporary memory input memory CPU output memory Program memory 3 Example: f ( x) x 3 temporary memory input memory Program memory compute
CS21 Decidability and Tractability
 CS21 Decidability and Tractability Lecture 8 January 24, 2018 Outline Turing Machines and variants multitape TMs nondeterministic TMs Church-Turing Thesis So far several models of computation finite automata
CS21 Decidability and Tractability Lecture 8 January 24, 2018 Outline Turing Machines and variants multitape TMs nondeterministic TMs Church-Turing Thesis So far several models of computation finite automata
Automata and Languages
 Automata and Languages Prof. Mohamed Hamada Software Engineering Lab. The University of Aizu Japan Mathematical Background Mathematical Background Sets Relations Functions Graphs Proof techniques Sets
Automata and Languages Prof. Mohamed Hamada Software Engineering Lab. The University of Aizu Japan Mathematical Background Mathematical Background Sets Relations Functions Graphs Proof techniques Sets
Finite Automata and Regular Languages
 Finite Automata and Regular Languages Topics to be covered in Chapters 1-4 include: deterministic vs. nondeterministic FA, regular expressions, one-way vs. two-way FA, minimization, pumping lemma for regular
Finite Automata and Regular Languages Topics to be covered in Chapters 1-4 include: deterministic vs. nondeterministic FA, regular expressions, one-way vs. two-way FA, minimization, pumping lemma for regular
CS243, Logic and Computation Nondeterministic finite automata
 CS243, Prof. Alvarez NONDETERMINISTIC FINITE AUTOMATA (NFA) Prof. Sergio A. Alvarez http://www.cs.bc.edu/ alvarez/ Maloney Hall, room 569 alvarez@cs.bc.edu Computer Science Department voice: (67) 552-4333
CS243, Prof. Alvarez NONDETERMINISTIC FINITE AUTOMATA (NFA) Prof. Sergio A. Alvarez http://www.cs.bc.edu/ alvarez/ Maloney Hall, room 569 alvarez@cs.bc.edu Computer Science Department voice: (67) 552-4333
Decision Problems with TM s. Lecture 31: Halting Problem. Universe of discourse. Semi-decidable. Look at following sets: CSCI 81 Spring, 2012
 Decision Problems with TM s Look at following sets: Lecture 31: Halting Problem CSCI 81 Spring, 2012 Kim Bruce A TM = { M,w M is a TM and w L(M)} H TM = { M,w M is a TM which halts on input w} TOTAL TM
Decision Problems with TM s Look at following sets: Lecture 31: Halting Problem CSCI 81 Spring, 2012 Kim Bruce A TM = { M,w M is a TM and w L(M)} H TM = { M,w M is a TM which halts on input w} TOTAL TM
Uses of finite automata
 Chapter 2 :Finite Automata 2.1 Finite Automata Automata are computational devices to solve language recognition problems. Language recognition problem is to determine whether a word belongs to a language.
Chapter 2 :Finite Automata 2.1 Finite Automata Automata are computational devices to solve language recognition problems. Language recognition problem is to determine whether a word belongs to a language.
Solution Scoring: SD Reg exp.: a(a
 MA/CSSE 474 Exam 3 Winter 2013-14 Name Solution_with explanations Section: 02(3 rd ) 03(4 th ) 1. (28 points) For each of the following statements, circle T or F to indicate whether it is True or False.
MA/CSSE 474 Exam 3 Winter 2013-14 Name Solution_with explanations Section: 02(3 rd ) 03(4 th ) 1. (28 points) For each of the following statements, circle T or F to indicate whether it is True or False.
UNIT-VIII COMPUTABILITY THEORY
 CONTEXT SENSITIVE LANGUAGE UNIT-VIII COMPUTABILITY THEORY A Context Sensitive Grammar is a 4-tuple, G = (N, Σ P, S) where: N Set of non terminal symbols Σ Set of terminal symbols S Start symbol of the
CONTEXT SENSITIVE LANGUAGE UNIT-VIII COMPUTABILITY THEORY A Context Sensitive Grammar is a 4-tuple, G = (N, Σ P, S) where: N Set of non terminal symbols Σ Set of terminal symbols S Start symbol of the
ECS 120: Theory of Computation UC Davis Phillip Rogaway February 16, Midterm Exam
 ECS 120: Theory of Computation Handout MT UC Davis Phillip Rogaway February 16, 2012 Midterm Exam Instructions: The exam has six pages, including this cover page, printed out two-sided (no more wasted
ECS 120: Theory of Computation Handout MT UC Davis Phillip Rogaway February 16, 2012 Midterm Exam Instructions: The exam has six pages, including this cover page, printed out two-sided (no more wasted
CS 121, Section 2. Week of September 16, 2013
 CS 121, Section 2 Week of September 16, 2013 1 Concept Review 1.1 Overview In the past weeks, we have examined the finite automaton, a simple computational model with limited memory. We proved that DFAs,
CS 121, Section 2 Week of September 16, 2013 1 Concept Review 1.1 Overview In the past weeks, we have examined the finite automaton, a simple computational model with limited memory. We proved that DFAs,
CSCE 551 Final Exam, Spring 2004 Answer Key
 CSCE 551 Final Exam, Spring 2004 Answer Key 1. (10 points) Using any method you like (including intuition), give the unique minimal DFA equivalent to the following NFA: 0 1 2 0 5 1 3 4 If your answer is
CSCE 551 Final Exam, Spring 2004 Answer Key 1. (10 points) Using any method you like (including intuition), give the unique minimal DFA equivalent to the following NFA: 0 1 2 0 5 1 3 4 If your answer is
Finite Automata. Mahesh Viswanathan
 Finite Automata Mahesh Viswanathan In this lecture, we will consider different models of finite state machines and study their relative power. These notes assume that the reader is familiar with DFAs,
Finite Automata Mahesh Viswanathan In this lecture, we will consider different models of finite state machines and study their relative power. These notes assume that the reader is familiar with DFAs,
CSE 105 THEORY OF COMPUTATION
 CSE 105 THEORY OF COMPUTATION Spring 2016 http://cseweb.ucsd.edu/classes/sp16/cse105-ab/ Today's learning goals Sipser Ch 3.3, 4.1 State and use the Church-Turing thesis. Give examples of decidable problems.
CSE 105 THEORY OF COMPUTATION Spring 2016 http://cseweb.ucsd.edu/classes/sp16/cse105-ab/ Today's learning goals Sipser Ch 3.3, 4.1 State and use the Church-Turing thesis. Give examples of decidable problems.
Discrete Mathematics: Lectures 6 and 7 Sets, Relations, Functions and Counting Instructor: Arijit Bishnu Date: August 4 and 6, 2009
 Discrete Mathematics: Lectures 6 and 7 Sets, Relations, Functions and Counting Instructor: Arijit Bishnu Date: August 4 and 6, 2009 Our main goal is here is to do counting using functions. For that, we
Discrete Mathematics: Lectures 6 and 7 Sets, Relations, Functions and Counting Instructor: Arijit Bishnu Date: August 4 and 6, 2009 Our main goal is here is to do counting using functions. For that, we
SCHEME FOR INTERNAL ASSESSMENT TEST 3
 SCHEME FOR INTERNAL ASSESSMENT TEST 3 Max Marks: 40 Subject& Code: Automata Theory & Computability (15CS54) Sem: V ISE (A & B) Note: Answer any FIVE full questions, choosing one full question from each
SCHEME FOR INTERNAL ASSESSMENT TEST 3 Max Marks: 40 Subject& Code: Automata Theory & Computability (15CS54) Sem: V ISE (A & B) Note: Answer any FIVE full questions, choosing one full question from each
Most General computer?
 Turing Machines Most General computer? DFAs are simple model of computation. Accept only the regular languages. Is there a kind of computer that can accept any language, or compute any function? Recall
Turing Machines Most General computer? DFAs are simple model of computation. Accept only the regular languages. Is there a kind of computer that can accept any language, or compute any function? Recall
cse303 ELEMENTS OF THE THEORY OF COMPUTATION Professor Anita Wasilewska
 cse303 ELEMENTS OF THE THEORY OF COMPUTATION Professor Anita Wasilewska LECTURE 6 CHAPTER 2 FINITE AUTOMATA 2. Nondeterministic Finite Automata NFA 3. Finite Automata and Regular Expressions 4. Languages
cse303 ELEMENTS OF THE THEORY OF COMPUTATION Professor Anita Wasilewska LECTURE 6 CHAPTER 2 FINITE AUTOMATA 2. Nondeterministic Finite Automata NFA 3. Finite Automata and Regular Expressions 4. Languages
CS Lecture 29 P, NP, and NP-Completeness. k ) for all k. Fall The class P. The class NP
 CS 301 - Lecture 29 P, NP, and NP-Completeness Fall 2008 Review Languages and Grammars Alphabets, strings, languages Regular Languages Deterministic Finite and Nondeterministic Automata Equivalence of
CS 301 - Lecture 29 P, NP, and NP-Completeness Fall 2008 Review Languages and Grammars Alphabets, strings, languages Regular Languages Deterministic Finite and Nondeterministic Automata Equivalence of
Computational Models Lecture 8 1
 Computational Models Lecture 8 1 Handout Mode Nachum Dershowitz & Yishay Mansour. Tel Aviv University. May 17 22, 2017 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice
Computational Models Lecture 8 1 Handout Mode Nachum Dershowitz & Yishay Mansour. Tel Aviv University. May 17 22, 2017 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice
3515ICT: Theory of Computation. Regular languages
 3515ICT: Theory of Computation Regular languages Notation and concepts concerning alphabets, strings and languages, and identification of languages with problems (H, 1.5). Regular expressions (H, 3.1,
3515ICT: Theory of Computation Regular languages Notation and concepts concerning alphabets, strings and languages, and identification of languages with problems (H, 1.5). Regular expressions (H, 3.1,
Definition: Let S and T be sets. A binary relation on SxT is any subset of SxT. A binary relation on S is any subset of SxS.
 4 Functions Before studying functions we will first quickly define a more general idea, namely the notion of a relation. A function turns out to be a special type of relation. Definition: Let S and T be
4 Functions Before studying functions we will first quickly define a more general idea, namely the notion of a relation. A function turns out to be a special type of relation. Definition: Let S and T be
Computational Models - Lecture 4 1
 Computational Models - Lecture 4 1 Handout Mode Iftach Haitner and Yishay Mansour. Tel Aviv University. April 3/8, 2013 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice
Computational Models - Lecture 4 1 Handout Mode Iftach Haitner and Yishay Mansour. Tel Aviv University. April 3/8, 2013 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice
Finite Automata Theory and Formal Languages TMV027/DIT321 LP4 2018
 Finite Automata Theory and Formal Languages TMV027/DIT321 LP4 2018 Lecture 15 Ana Bove May 17th 2018 Recap: Context-free Languages Chomsky hierarchy: Regular languages are also context-free; Pumping lemma
Finite Automata Theory and Formal Languages TMV027/DIT321 LP4 2018 Lecture 15 Ana Bove May 17th 2018 Recap: Context-free Languages Chomsky hierarchy: Regular languages are also context-free; Pumping lemma
Introduction to Automata
 Introduction to Automata Seungjin Choi Department of Computer Science and Engineering Pohang University of Science and Technology 77 Cheongam-ro, Nam-gu, Pohang 37673, Korea seungjin@postech.ac.kr 1 /
Introduction to Automata Seungjin Choi Department of Computer Science and Engineering Pohang University of Science and Technology 77 Cheongam-ro, Nam-gu, Pohang 37673, Korea seungjin@postech.ac.kr 1 /
Homework Assignment 6 Answers
 Homework Assignment 6 Answers CSCI 2670 Introduction to Theory of Computing, Fall 2016 December 2, 2016 This homework assignment is about Turing machines, decidable languages, Turing recognizable languages,
Homework Assignment 6 Answers CSCI 2670 Introduction to Theory of Computing, Fall 2016 December 2, 2016 This homework assignment is about Turing machines, decidable languages, Turing recognizable languages,
CS20a: summary (Oct 24, 2002)
 CS20a: summary (Oct 24, 2002) Context-free languages Grammars G = (V, T, P, S) Pushdown automata N-PDA = CFG D-PDA < CFG Today What languages are context-free? Pumping lemma (similar to pumping lemma for
CS20a: summary (Oct 24, 2002) Context-free languages Grammars G = (V, T, P, S) Pushdown automata N-PDA = CFG D-PDA < CFG Today What languages are context-free? Pumping lemma (similar to pumping lemma for
Theory of Computation
 Fall 2002 (YEN) Theory of Computation Midterm Exam. Name:... I.D.#:... 1. (30 pts) True or false (mark O for true ; X for false ). (Score=Max{0, Right- 1 2 Wrong}.) (1) X... If L 1 is regular and L 2 L
Fall 2002 (YEN) Theory of Computation Midterm Exam. Name:... I.D.#:... 1. (30 pts) True or false (mark O for true ; X for false ). (Score=Max{0, Right- 1 2 Wrong}.) (1) X... If L 1 is regular and L 2 L
Theory Bridge Exam Example Questions
 Theory Bridge Exam Example Questions Annotated version with some (sometimes rather sketchy) answers and notes. This is a collection of sample theory bridge exam questions. This is just to get some idea
Theory Bridge Exam Example Questions Annotated version with some (sometimes rather sketchy) answers and notes. This is a collection of sample theory bridge exam questions. This is just to get some idea
Lecture Notes On THEORY OF COMPUTATION MODULE -1 UNIT - 2
 BIJU PATNAIK UNIVERSITY OF TECHNOLOGY, ODISHA Lecture Notes On THEORY OF COMPUTATION MODULE -1 UNIT - 2 Prepared by, Dr. Subhendu Kumar Rath, BPUT, Odisha. UNIT 2 Structure NON-DETERMINISTIC FINITE AUTOMATA
BIJU PATNAIK UNIVERSITY OF TECHNOLOGY, ODISHA Lecture Notes On THEORY OF COMPUTATION MODULE -1 UNIT - 2 Prepared by, Dr. Subhendu Kumar Rath, BPUT, Odisha. UNIT 2 Structure NON-DETERMINISTIC FINITE AUTOMATA
PUSHDOWN AUTOMATA (PDA)
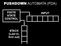 PUSHDOWN AUTOMATA (PDA) FINITE STATE CONTROL INPUT STACK (Last in, first out) input pop push ε,ε $ 0,ε 0 1,0 ε ε,$ ε 1,0 ε PDA that recognizes L = { 0 n 1 n n 0 } Definition: A (non-deterministic) PDA
PUSHDOWN AUTOMATA (PDA) FINITE STATE CONTROL INPUT STACK (Last in, first out) input pop push ε,ε $ 0,ε 0 1,0 ε ε,$ ε 1,0 ε PDA that recognizes L = { 0 n 1 n n 0 } Definition: A (non-deterministic) PDA
