Inverse problems Total Variation Regularization Mark van Kraaij Casa seminar 23 May 2007 Technische Universiteit Eindh ove n University of Technology
|
|
|
- Frederica York
- 5 years ago
- Views:
Transcription
1 Inverse problems Total Variation Regularization Mark van Kraaij Casa seminar 23 May 27
2 Introduction Fredholm first kind integral equation of convolution type in one space dimension: g(x) = 1 k(x x )f(x )dx = (Kf)(x), < x < 1, k(x) = C exp( x 2 /2γ 2 ). (Gaussian kernel)
3 Introduction Fredholm first kind integral equation of convolution type in one space dimension: g(x) = 1 k(x x )f(x )dx = (Kf)(x), < x < 1, k(x) = C exp( x 2 /2γ 2 ). (Gaussian kernel) Direct problem: Given the source f and the kernel k, determine the blurred image g. For a piecewise smooth source and smooth kernel, an accurate approximation of g = Kf is found using standard numerical quadrature.
4 Introduction Fredholm first kind integral equation of convolution type in one space dimension: g(x) = 1 k(x x )f(x )dx = (Kf)(x), < x < 1, k(x) = C exp( x 2 /2γ 2 ). (Gaussian kernel) Inverse problem: Given the blurred image g and the kernel k, determine the source f. Discretize equation using collocation in the independent variable x and quadrature in x to obtain a discrete linear system Kf = d.
5 Introduction Composite midpoint quadrature with h = 1/n: ( f = K 1 ((i ) j)h)2 d, where K ij = h C exp. 2γ 2 To obtain an accurate quadrature approximation, n must be relatively large. Unfortunately, matrix K becomes increasingly ill-conditioned for large n.
6 Introduction Composite midpoint quadrature with h = 1/n: ( f = K 1 ((i ) j)h)2 d, where K ij = h C exp. 2γ 2 To obtain an accurate quadrature approximation, n must be relatively large. Unfortunately, matrix K becomes increasingly ill-conditioned for large n. Errors due to quadrature can be controlled, errors in d may be amplified! Source function f Blurred image g Discrete noisy data d Figure 1: γ =.5, C = 1 γ 2π, n = 8
7 Regularization by filtering Assume a discrete data model for the discrete linear system Kf = d, i.e. d = Kf true + η, with δ := η > the error level. Assuming K is invertible the SVD (K = U diag(s i )V T ) gives n K 1 d = f true + s 1 i (u T i η)v i. i=1
8 Regularization by filtering Assume a discrete data model for the discrete linear system Kf = d, i.e. d = Kf true + η, with δ := η > the error level. Assuming K is invertible the SVD (K = U diag(s i )V T ) gives n K 1 d = f true + s 1 i (u T i η)v i. i=1 Instabilities arise due to division by small singular values. Use regularizing filter function w α (s 2 i ) for which the product w α (s 2 )s 1 as s. Approximate solution n f α = w α (s 2 i )s 1 i (u T i d)v i. i=1
9 Regularization by filtering TSVD Tikhonov w α (s 2 ) = { 1 if s2 > α, if s 2 α. w α (s 2 ) = s2 s 2 + α f α = s 2 i >α s 1 i (u T i d)v i f α = (K T K + αi) 1 K T d 1 TSVD Tikhonov.8 w α (s 2 ) Figure 2: Regularization parameter α = 1 2 s 2
10 Regularization by filtering 5 Norm of TSVD Solution Error α = e α = f α f true α f α (x) α = α = f α (x).4 f α (x) Figure 3: TSVD regularized solutions with 2% error level
11 Regularization by filtering Choose regularization parameter α such that e α = e trunc α + e noise α for δ. For both TSVD and Tikhonov filter e noise α α 1 2 δ, for α = δ p and p < 2, e trunc α, for α thus p >.
12 Regularization by filtering Choose regularization parameter α such that e α = e trunc α + e noise α for δ. For both TSVD and Tikhonov filter e noise α α 1 2 δ, for α = δ p and p < 2, e trunc α, for α thus p >. For TSVD assume δ s min and f true = K T z for z R n then e α α 1 2 z + α 1 2 δ. Minimizing w.r.t. α gives α = δ/ z and e α 2 z 1 2 δ 1 2 = O( δ).
13 Variational regularization methods For very large ill-conditioned systems regularization by filtering is impractical since it requires the SVD of a large matrix. Alternative, Tikhonov variational representation f α = arg min f R n Kf d 2 + α f 2, might be easier to compute incorporate constraints, e.g. nonnegativity of f replace least squares term Kf d 2 by other fit-to-data functionals replace penalty term f 2 by other functionals incorporating a priori information Total Variation Regularization
14 Variational regularization methods For very large ill-conditioned systems regularization by filtering is impractical since it requires the SVD of a large matrix. Alternative, Tikhonov variational representation f α = arg min f R n Kf d 2 + αtv(f), with the discrete one-dimensional total variation function n 1 TV(f) = f i+1 f i = i=1 n 1 f i+1 f i x. x i=1 This penalizes highly oscillatory solutions while allowing jumps in the regularized solution.
15 Variational regularization methods 2 Norm of TV Solution Error 1.2 α = e α = f α f true f α (x) α α = 1e α = f α (x).4 f α (x) Figure 4: TV regularized solutions with 2% error level
16 Definition total variation Definition. The total variation of a function f L 1 (Ω) is defined by TV(f) = sup f div v dx, v V where Ω Ω denotes a simply connected, nonempty, open subset of R d, d = 1, 2,..., with Lipschitz continuous boundary. the space of test functions V = {v C 1 (Ω; R d ) v(x) 1 for all x Ω}. C 1 (Ω; R d ) denotes the space of vector valued functions v = (v 1,..., v d ) whose component functions v i are each continuously differentiable and compactly supported on Ω, i.e., each v i vanishes outside some compact subset of Ω.
17 Definition total variation Example. Let Ω = [, 1] R, and define { f, x < 1, 2 f(x) = f 1 x > 1 2, where f, f 1 are constants. For any v C 1 [, 1], 1 f(x)v (x) dx = 1/2 f(x)v (x) dx + = (f f 1 )v(1/2). 1 1/2 f(x)v (x) dx This quantity is maximized over all v V when v(1/2) = sign(f f 1 ), thus TV(f) = f 1 f.
18 Definition total variation Definition. The total variation of a function f defined on [, 1] is defined by TV(f) = sup i f(x i ) f(x i 1 ), where the supremum is taken over all partitions = x < < x n = 1. Proposition. If f is smooth (f W 1,1 (Ω)) then TV(f) = f dx. Ω
19 Definition total variation Definition. The total variation of a function f defined on [, 1] is defined by TV(f) = sup i f(x i ) f(x i 1 ), where the supremum is taken over all partitions = x < < x n = 1. Proposition. If f is smooth (f W 1,1 (Ω)) then TV(f) = f dx. Ω TV(f) can be interpreted geometrically as the lateral surface area of the graph of f. If f has many large amplitude oscillations f has large lateral surface area TV(f) is large
20 Numerical methods for total variation Find regularized solutions to operator equations Kf = g by minimizing Tikhonov-TV functional T α (f) = 1 2 Kf g 2 + αtv(f), where TV(f) = TV(f) = 1 df 1 1 dx, in 1D, dx f dx dy, in 2D. Standard methods requiring gradient and/or hessian info (e.g. Steepest descent, Newton s method) are not suitable due to the non-differentiability of the Euclidean norm at the origin.
21 Numerical methods for total variation Find regularized solutions to operator equations Kf = g by minimizing approximate Tikhonov-TV functional T α (f) = 1 2 Kf g 2 + αj β (f), where J β (f) = J β (f) = ( df ) 2 + β2 dx, in 1D, dx ( f ) 2 ( f ) β2 dx dy, in 2D. x y Now the standard techniques can be used to minimize the discretized approximate Tikhonov-TV functional T (f) = 1 2 Kf d 2 + αj(f).
22 Numerical methods for total variation A one-dimensional discretization Using a composite midpoint quadrature, central difference approximation for the derivative, the approximation to the one-dimensional TV functional becomes J(f) = 1 n ψ ( (D i f) 2) x, 2 i=1 where f = (f,..., f n ) T, with f i = f(x i ), x i = i x, x = 1/n, D i = [,...,, 1/ x, 1/ x,,..., ] 1 (n+1), ψ(t) = 2 t + β 2.
23 Numerical methods for total variation From the directional derivative the gradient is derived d dτ J(f + τv) τ= n = ψ ( (D i f) 2) (D i f)(d i v) x where i=1 [diag(ψ (f))] i,i = ψ ( (D i f) 2 ) ), = x (Dv) T diag(ψ (f)) (Df) = x D T diag(ψ (f)) Df, v = grad J(f), v =: L(f)f, v, D = [D 1 ;... ; D n ] n (n+1). The matrix L(f) is symmetric and positive semidefinite.
24 Numerical methods for total variation In a similar way the hessian is derived Hess J(f) = L(f) + L (f)f, where L (f)f = x D T diag(2(df) 2 ψ (f))d, [diag(2(df) 2 ψ (f))] i,i = 2(D i f) 2 ψ ((D i f) 2 ).
25 Numerical methods for total variation In a similar way the hessian is derived Hess J(f) = L(f) + L (f)f, where L (f)f = x D T diag(2(df) 2 ψ (f))d, [diag(2(df) 2 ψ (f))] i,i = 2(D i f) 2 ψ ((D i f) 2 ). The gradient and hessian of the discretized approximate Tikhonov-TV functional are now simply given by grad T (f) = K T (Kf d) + αl(f)f, Hess T (f) = K T K + αl(f) + αl (f)f.
26 Numerical methods for total variation 1. Steepest descent with line search for total variation f ν+1 = f ν τ grad T (f ν ) Algorithm: ν := ; f := initial guess; while no convergence g ν := K T (Kf ν d) + αl(f ν )f ν ; % gradient τ ν := arg min τ> T (fν τg ν ); % line search f ν+1 := f ν τ ν g ν ; % update approximate solution ν := ν + 1;
27 Numerical methods for total variation 2. Newton s method with line search for total variation f ν+1 = f ν τ (Hess T (f ν )) 1 grad T (f ν ) Algorithm: ν := ; f := initial guess; while no convergence g ν := K T (Kf ν d) + αl(f ν )f ν ; % gradient H J := L(f ν ) + L (f ν )f ν ; % hessian of penalty functional H := K T K + αh J ; % hessian of cost functional s ν := H 1 g ν ; % newton step τ ν := arg min τ> T (fν + τs ν ); % line search f ν+1 := f ν + τ ν s ν ; % update approximate solution ν := ν + 1;
28 Numerical methods for total variation 3. Lagged diffusivity fixed point iteration f ν+1 = (K T K + αl(f ν )) 1 K T d = f ν (K T K + αl(f ν )) 1 grad T (f ν ). Fixed point form can be derived by setting grad T (f) =. The matrix L(f) can be viewed as a discretization of a steady-state diffusion operator and is evaluated at f ν, hence the name. The equivalent quasi-newton iteration can also be derived by dropping the term αl (f)f from the Hessian. The quasi Newton form tends to be less sensitive to roundoff error.
29 Numerical methods for total variation 3. Lagged diffusivity fixed point iteration Algorithm: ν := ; f := initial guess; while no convergence g ν := K T (Kf ν d) + αl(f ν )f ν ; % gradient H := K T K + αl(f ν ); % approximate hessian of cost functional s ν := H 1 g ν ; % quasi-newton step f ν+1 := f ν + s ν ; % update approximate solution ν := ν + 1; If K T K is positive definite, then this fixed point iteration converges globally and no line-search is needed. Because the Hessian is approximated, only linear convergence is expected.
30 Numerical methods for total variation Results for one-dimensional test problem All three methods give essentially the same reconstruction. Measure for numerical performance is relative iterative solution error e ν α = f α ν f α, f α with f α the minimizer of the approximate Tikhonov-TV functional (use accurate approximation obtained with Primal-Dual Newton method) True solution Approximate TV regularized solution Figure 5: α =.1, β =.1
31 Numerical methods for total variation Results for one-dimensional test problem Steepest Descent: Hessian ill-conditioned slow (linear) convergence Newton: Line search restricts stepsize local quadratic convergence attained late (α small, β small) Cost per iteration is about the same for Newton, Fixed point and Primal- Dual Newton Norm of gradient Steepest Descent Newton Fixed point Primal Dual Newton 1 Norm of solution error Iteration Iteration
32 Summary Variational representation of Tikhonov functional TV is a penalty functional which penalizes oscillatory solutions Approximate TV functional needed for standard optimization tools References [Vog2] Curtis R. Vogel. Computational Methods for Inverse Problems. Society for Industrial and Applied Mathematics, 22.
A Two-Stage Method for Piecewise-Constant Solution for Fredholm Integral Equations of the First Kind
 mathematics Article A Two-Stage Method for Piecewise-Constant Solution for Fredholm Integral Equations of the First Kind Fu-Rong Lin * and Shi-Wei Yang Department of Mathematics, Shantou University, Shantou
mathematics Article A Two-Stage Method for Piecewise-Constant Solution for Fredholm Integral Equations of the First Kind Fu-Rong Lin * and Shi-Wei Yang Department of Mathematics, Shantou University, Shantou
Optimization with nonnegativity constraints
 Optimization with nonnegativity constraints Arie Verhoeven averhoev@win.tue.nl CASA Seminar, May 30, 2007 Seminar: Inverse problems 1 Introduction Yves van Gennip February 21 2 Regularization strategies
Optimization with nonnegativity constraints Arie Verhoeven averhoev@win.tue.nl CASA Seminar, May 30, 2007 Seminar: Inverse problems 1 Introduction Yves van Gennip February 21 2 Regularization strategies
PDEs in Image Processing, Tutorials
 PDEs in Image Processing, Tutorials Markus Grasmair Vienna, Winter Term 2010 2011 Direct Methods Let X be a topological space and R: X R {+ } some functional. following definitions: The mapping R is lower
PDEs in Image Processing, Tutorials Markus Grasmair Vienna, Winter Term 2010 2011 Direct Methods Let X be a topological space and R: X R {+ } some functional. following definitions: The mapping R is lower
Algorithms for Nonsmooth Optimization
 Algorithms for Nonsmooth Optimization Frank E. Curtis, Lehigh University presented at Center for Optimization and Statistical Learning, Northwestern University 2 March 2018 Algorithms for Nonsmooth Optimization
Algorithms for Nonsmooth Optimization Frank E. Curtis, Lehigh University presented at Center for Optimization and Statistical Learning, Northwestern University 2 March 2018 Algorithms for Nonsmooth Optimization
One Picture and a Thousand Words Using Matrix Approximtions October 2017 Oak Ridge National Lab Dianne P. O Leary c 2017
 One Picture and a Thousand Words Using Matrix Approximtions October 2017 Oak Ridge National Lab Dianne P. O Leary c 2017 1 One Picture and a Thousand Words Using Matrix Approximations Dianne P. O Leary
One Picture and a Thousand Words Using Matrix Approximtions October 2017 Oak Ridge National Lab Dianne P. O Leary c 2017 1 One Picture and a Thousand Words Using Matrix Approximations Dianne P. O Leary
Math 5630: Image Restoration April 29, 2018
 Math 5630: Image Restoration April 29, 208 Image Restoration in D We consider the -dimensional image model d Kf true + η, where the received image d is resulted from a distortion of the true image f true
Math 5630: Image Restoration April 29, 208 Image Restoration in D We consider the -dimensional image model d Kf true + η, where the received image d is resulted from a distortion of the true image f true
Lecture 15 Newton Method and Self-Concordance. October 23, 2008
 Newton Method and Self-Concordance October 23, 2008 Outline Lecture 15 Self-concordance Notion Self-concordant Functions Operations Preserving Self-concordance Properties of Self-concordant Functions Implications
Newton Method and Self-Concordance October 23, 2008 Outline Lecture 15 Self-concordance Notion Self-concordant Functions Operations Preserving Self-concordance Properties of Self-concordant Functions Implications
Iteration-complexity of first-order penalty methods for convex programming
 Iteration-complexity of first-order penalty methods for convex programming Guanghui Lan Renato D.C. Monteiro July 24, 2008 Abstract This paper considers a special but broad class of convex programing CP)
Iteration-complexity of first-order penalty methods for convex programming Guanghui Lan Renato D.C. Monteiro July 24, 2008 Abstract This paper considers a special but broad class of convex programing CP)
Oslo Class 4 Early Stopping and Spectral Regularization
 RegML2017@SIMULA Oslo Class 4 Early Stopping and Spectral Regularization Lorenzo Rosasco UNIGE-MIT-IIT June 28, 2016 Learning problem Solve min w E(w), E(w) = dρ(x, y)l(w x, y) given (x 1, y 1 ),..., (x
RegML2017@SIMULA Oslo Class 4 Early Stopping and Spectral Regularization Lorenzo Rosasco UNIGE-MIT-IIT June 28, 2016 Learning problem Solve min w E(w), E(w) = dρ(x, y)l(w x, y) given (x 1, y 1 ),..., (x
Optimization. Escuela de Ingeniería Informática de Oviedo. (Dpto. de Matemáticas-UniOvi) Numerical Computation Optimization 1 / 30
 Optimization Escuela de Ingeniería Informática de Oviedo (Dpto. de Matemáticas-UniOvi) Numerical Computation Optimization 1 / 30 Unconstrained optimization Outline 1 Unconstrained optimization 2 Constrained
Optimization Escuela de Ingeniería Informática de Oviedo (Dpto. de Matemáticas-UniOvi) Numerical Computation Optimization 1 / 30 Unconstrained optimization Outline 1 Unconstrained optimization 2 Constrained
Convex Optimization. Newton s method. ENSAE: Optimisation 1/44
 Convex Optimization Newton s method ENSAE: Optimisation 1/44 Unconstrained minimization minimize f(x) f convex, twice continuously differentiable (hence dom f open) we assume optimal value p = inf x f(x)
Convex Optimization Newton s method ENSAE: Optimisation 1/44 Unconstrained minimization minimize f(x) f convex, twice continuously differentiable (hence dom f open) we assume optimal value p = inf x f(x)
Spring 2014: Computational and Variational Methods for Inverse Problems CSE 397/GEO 391/ME 397/ORI 397 Assignment 4 (due 14 April 2014)
 Spring 2014: Computational and Variational Methods for Inverse Problems CSE 397/GEO 391/ME 397/ORI 397 Assignment 4 (due 14 April 2014) The first problem in this assignment is a paper-and-pencil exercise
Spring 2014: Computational and Variational Methods for Inverse Problems CSE 397/GEO 391/ME 397/ORI 397 Assignment 4 (due 14 April 2014) The first problem in this assignment is a paper-and-pencil exercise
1 Sparsity and l 1 relaxation
 6.883 Learning with Combinatorial Structure Note for Lecture 2 Author: Chiyuan Zhang Sparsity and l relaxation Last time we talked about sparsity and characterized when an l relaxation could recover the
6.883 Learning with Combinatorial Structure Note for Lecture 2 Author: Chiyuan Zhang Sparsity and l relaxation Last time we talked about sparsity and characterized when an l relaxation could recover the
Optimization. Benjamin Recht University of California, Berkeley Stephen Wright University of Wisconsin-Madison
 Optimization Benjamin Recht University of California, Berkeley Stephen Wright University of Wisconsin-Madison optimization () cost constraints might be too much to cover in 3 hours optimization (for big
Optimization Benjamin Recht University of California, Berkeley Stephen Wright University of Wisconsin-Madison optimization () cost constraints might be too much to cover in 3 hours optimization (for big
On the interior of the simplex, we have the Hessian of d(x), Hd(x) is diagonal with ith. µd(w) + w T c. minimize. subject to w T 1 = 1,
 Math 30 Winter 05 Solution to Homework 3. Recognizing the convexity of g(x) := x log x, from Jensen s inequality we get d(x) n x + + x n n log x + + x n n where the equality is attained only at x = (/n,...,
Math 30 Winter 05 Solution to Homework 3. Recognizing the convexity of g(x) := x log x, from Jensen s inequality we get d(x) n x + + x n n log x + + x n n where the equality is attained only at x = (/n,...,
Lecture 3. Optimization Problems and Iterative Algorithms
 Lecture 3 Optimization Problems and Iterative Algorithms January 13, 2016 This material was jointly developed with Angelia Nedić at UIUC for IE 598ns Outline Special Functions: Linear, Quadratic, Convex
Lecture 3 Optimization Problems and Iterative Algorithms January 13, 2016 This material was jointly developed with Angelia Nedić at UIUC for IE 598ns Outline Special Functions: Linear, Quadratic, Convex
Tikhonov Regularization in General Form 8.1
 Tikhonov Regularization in General Form 8.1 To introduce a more general formulation, let us return to the continuous formulation of the first-kind Fredholm integral equation. In this setting, the residual
Tikhonov Regularization in General Form 8.1 To introduce a more general formulation, let us return to the continuous formulation of the first-kind Fredholm integral equation. In this setting, the residual
Variational Image Restoration
 Variational Image Restoration Yuling Jiao yljiaostatistics@znufe.edu.cn School of and Statistics and Mathematics ZNUFE Dec 30, 2014 Outline 1 1 Classical Variational Restoration Models and Algorithms 1.1
Variational Image Restoration Yuling Jiao yljiaostatistics@znufe.edu.cn School of and Statistics and Mathematics ZNUFE Dec 30, 2014 Outline 1 1 Classical Variational Restoration Models and Algorithms 1.1
arxiv: v1 [math.oc] 3 Jul 2014
![arxiv: v1 [math.oc] 3 Jul 2014 arxiv: v1 [math.oc] 3 Jul 2014](/thumbs/84/91153454.jpg) SIAM J. IMAGING SCIENCES Vol. xx, pp. x c xxxx Society for Industrial and Applied Mathematics x x Solving QVIs for Image Restoration with Adaptive Constraint Sets F. Lenzen, J. Lellmann, F. Becker, and
SIAM J. IMAGING SCIENCES Vol. xx, pp. x c xxxx Society for Industrial and Applied Mathematics x x Solving QVIs for Image Restoration with Adaptive Constraint Sets F. Lenzen, J. Lellmann, F. Becker, and
Investigating the Influence of Box-Constraints on the Solution of a Total Variation Model via an Efficient Primal-Dual Method
 Article Investigating the Influence of Box-Constraints on the Solution of a Total Variation Model via an Efficient Primal-Dual Method Andreas Langer Department of Mathematics, University of Stuttgart,
Article Investigating the Influence of Box-Constraints on the Solution of a Total Variation Model via an Efficient Primal-Dual Method Andreas Langer Department of Mathematics, University of Stuttgart,
Variational Methods in Image Denoising
 Variational Methods in Image Denoising Jamylle Carter Postdoctoral Fellow Mathematical Sciences Research Institute (MSRI) MSRI Workshop for Women in Mathematics: Introduction to Image Analysis 22 January
Variational Methods in Image Denoising Jamylle Carter Postdoctoral Fellow Mathematical Sciences Research Institute (MSRI) MSRI Workshop for Women in Mathematics: Introduction to Image Analysis 22 January
WHY DUALITY? Gradient descent Newton s method Quasi-newton Conjugate gradients. No constraints. Non-differentiable ???? Constrained problems? ????
 DUALITY WHY DUALITY? No constraints f(x) Non-differentiable f(x) Gradient descent Newton s method Quasi-newton Conjugate gradients etc???? Constrained problems? f(x) subject to g(x) apple 0???? h(x) =0
DUALITY WHY DUALITY? No constraints f(x) Non-differentiable f(x) Gradient descent Newton s method Quasi-newton Conjugate gradients etc???? Constrained problems? f(x) subject to g(x) apple 0???? h(x) =0
THE SINGULAR VALUE DECOMPOSITION MARKUS GRASMAIR
 THE SINGULAR VALUE DECOMPOSITION MARKUS GRASMAIR 1. Definition Existence Theorem 1. Assume that A R m n. Then there exist orthogonal matrices U R m m V R n n, values σ 1 σ 2... σ p 0 with p = min{m, n},
THE SINGULAR VALUE DECOMPOSITION MARKUS GRASMAIR 1. Definition Existence Theorem 1. Assume that A R m n. Then there exist orthogonal matrices U R m m V R n n, values σ 1 σ 2... σ p 0 with p = min{m, n},
Line Search Methods for Unconstrained Optimisation
 Line Search Methods for Unconstrained Optimisation Lecture 8, Numerical Linear Algebra and Optimisation Oxford University Computing Laboratory, MT 2007 Dr Raphael Hauser (hauser@comlab.ox.ac.uk) The Generic
Line Search Methods for Unconstrained Optimisation Lecture 8, Numerical Linear Algebra and Optimisation Oxford University Computing Laboratory, MT 2007 Dr Raphael Hauser (hauser@comlab.ox.ac.uk) The Generic
Convex Optimization Algorithms for Machine Learning in 10 Slides
 Convex Optimization Algorithms for Machine Learning in 10 Slides Presenter: Jul. 15. 2015 Outline 1 Quadratic Problem Linear System 2 Smooth Problem Newton-CG 3 Composite Problem Proximal-Newton-CD 4 Non-smooth,
Convex Optimization Algorithms for Machine Learning in 10 Slides Presenter: Jul. 15. 2015 Outline 1 Quadratic Problem Linear System 2 Smooth Problem Newton-CG 3 Composite Problem Proximal-Newton-CD 4 Non-smooth,
17 Solution of Nonlinear Systems
 17 Solution of Nonlinear Systems We now discuss the solution of systems of nonlinear equations. An important ingredient will be the multivariate Taylor theorem. Theorem 17.1 Let D = {x 1, x 2,..., x m
17 Solution of Nonlinear Systems We now discuss the solution of systems of nonlinear equations. An important ingredient will be the multivariate Taylor theorem. Theorem 17.1 Let D = {x 1, x 2,..., x m
Sparsity Regularization
 Sparsity Regularization Bangti Jin Course Inverse Problems & Imaging 1 / 41 Outline 1 Motivation: sparsity? 2 Mathematical preliminaries 3 l 1 solvers 2 / 41 problem setup finite-dimensional formulation
Sparsity Regularization Bangti Jin Course Inverse Problems & Imaging 1 / 41 Outline 1 Motivation: sparsity? 2 Mathematical preliminaries 3 l 1 solvers 2 / 41 problem setup finite-dimensional formulation
10. Unconstrained minimization
 Convex Optimization Boyd & Vandenberghe 10. Unconstrained minimization terminology and assumptions gradient descent method steepest descent method Newton s method self-concordant functions implementation
Convex Optimization Boyd & Vandenberghe 10. Unconstrained minimization terminology and assumptions gradient descent method steepest descent method Newton s method self-concordant functions implementation
ECE580 Exam 1 October 4, Please do not write on the back of the exam pages. Extra paper is available from the instructor.
 ECE580 Exam 1 October 4, 2012 1 Name: Solution Score: /100 You must show ALL of your work for full credit. This exam is closed-book. Calculators may NOT be used. Please leave fractions as fractions, etc.
ECE580 Exam 1 October 4, 2012 1 Name: Solution Score: /100 You must show ALL of your work for full credit. This exam is closed-book. Calculators may NOT be used. Please leave fractions as fractions, etc.
Statistical Machine Learning from Data
 Samy Bengio Statistical Machine Learning from Data 1 Statistical Machine Learning from Data Support Vector Machines Samy Bengio IDIAP Research Institute, Martigny, Switzerland, and Ecole Polytechnique
Samy Bengio Statistical Machine Learning from Data 1 Statistical Machine Learning from Data Support Vector Machines Samy Bengio IDIAP Research Institute, Martigny, Switzerland, and Ecole Polytechnique
EE 367 / CS 448I Computational Imaging and Display Notes: Image Deconvolution (lecture 6)
 EE 367 / CS 448I Computational Imaging and Display Notes: Image Deconvolution (lecture 6) Gordon Wetzstein gordon.wetzstein@stanford.edu This document serves as a supplement to the material discussed in
EE 367 / CS 448I Computational Imaging and Display Notes: Image Deconvolution (lecture 6) Gordon Wetzstein gordon.wetzstein@stanford.edu This document serves as a supplement to the material discussed in
On semilinear elliptic equations with measure data
 On semilinear elliptic equations with measure data Andrzej Rozkosz (joint work with T. Klimsiak) Nicolaus Copernicus University (Toruń, Poland) Controlled Deterministic and Stochastic Systems Iasi, July
On semilinear elliptic equations with measure data Andrzej Rozkosz (joint work with T. Klimsiak) Nicolaus Copernicus University (Toruń, Poland) Controlled Deterministic and Stochastic Systems Iasi, July
Written Examination
 Division of Scientific Computing Department of Information Technology Uppsala University Optimization Written Examination 202-2-20 Time: 4:00-9:00 Allowed Tools: Pocket Calculator, one A4 paper with notes
Division of Scientific Computing Department of Information Technology Uppsala University Optimization Written Examination 202-2-20 Time: 4:00-9:00 Allowed Tools: Pocket Calculator, one A4 paper with notes
Numerical Optimization
 Numerical Optimization Unit 2: Multivariable optimization problems Che-Rung Lee Scribe: February 28, 2011 (UNIT 2) Numerical Optimization February 28, 2011 1 / 17 Partial derivative of a two variable function
Numerical Optimization Unit 2: Multivariable optimization problems Che-Rung Lee Scribe: February 28, 2011 (UNIT 2) Numerical Optimization February 28, 2011 1 / 17 Partial derivative of a two variable function
Introduction to Alternating Direction Method of Multipliers
 Introduction to Alternating Direction Method of Multipliers Yale Chang Machine Learning Group Meeting September 29, 2016 Yale Chang (Machine Learning Group Meeting) Introduction to Alternating Direction
Introduction to Alternating Direction Method of Multipliers Yale Chang Machine Learning Group Meeting September 29, 2016 Yale Chang (Machine Learning Group Meeting) Introduction to Alternating Direction
A VARIATIONAL METHOD FOR THE ANALYSIS OF A MONOTONE SCHEME FOR THE MONGE-AMPÈRE EQUATION 1. INTRODUCTION
 A VARIATIONAL METHOD FOR THE ANALYSIS OF A MONOTONE SCHEME FOR THE MONGE-AMPÈRE EQUATION GERARD AWANOU AND LEOPOLD MATAMBA MESSI ABSTRACT. We give a proof of existence of a solution to the discrete problem
A VARIATIONAL METHOD FOR THE ANALYSIS OF A MONOTONE SCHEME FOR THE MONGE-AMPÈRE EQUATION GERARD AWANOU AND LEOPOLD MATAMBA MESSI ABSTRACT. We give a proof of existence of a solution to the discrete problem
Numerical Optimization Professor Horst Cerjak, Horst Bischof, Thomas Pock Mat Vis-Gra SS09
 Numerical Optimization 1 Working Horse in Computer Vision Variational Methods Shape Analysis Machine Learning Markov Random Fields Geometry Common denominator: optimization problems 2 Overview of Methods
Numerical Optimization 1 Working Horse in Computer Vision Variational Methods Shape Analysis Machine Learning Markov Random Fields Geometry Common denominator: optimization problems 2 Overview of Methods
Functional Analysis HW 2
 Brandon Behring Functional Analysis HW 2 Exercise 2.6 The space C[a, b] equipped with the L norm defined by f = b a f(x) dx is incomplete. If f n f with respect to the sup-norm then f n f with respect
Brandon Behring Functional Analysis HW 2 Exercise 2.6 The space C[a, b] equipped with the L norm defined by f = b a f(x) dx is incomplete. If f n f with respect to the sup-norm then f n f with respect
PhD Course: Introduction to Inverse Problem. Salvatore Frandina Siena, August 19, 2012
 PhD Course: to Inverse Problem salvatore.frandina@gmail.com theory Department of Information Engineering, Siena, Italy Siena, August 19, 2012 1 / 68 An overview of the - - - theory 2 / 68 Direct and Inverse
PhD Course: to Inverse Problem salvatore.frandina@gmail.com theory Department of Information Engineering, Siena, Italy Siena, August 19, 2012 1 / 68 An overview of the - - - theory 2 / 68 Direct and Inverse
CS-E4830 Kernel Methods in Machine Learning
 CS-E4830 Kernel Methods in Machine Learning Lecture 3: Convex optimization and duality Juho Rousu 27. September, 2017 Juho Rousu 27. September, 2017 1 / 45 Convex optimization Convex optimisation This
CS-E4830 Kernel Methods in Machine Learning Lecture 3: Convex optimization and duality Juho Rousu 27. September, 2017 Juho Rousu 27. September, 2017 1 / 45 Convex optimization Convex optimisation This
Numerical optimization
 Numerical optimization Lecture 4 Alexander & Michael Bronstein tosca.cs.technion.ac.il/book Numerical geometry of non-rigid shapes Stanford University, Winter 2009 2 Longest Slowest Shortest Minimal Maximal
Numerical optimization Lecture 4 Alexander & Michael Bronstein tosca.cs.technion.ac.il/book Numerical geometry of non-rigid shapes Stanford University, Winter 2009 2 Longest Slowest Shortest Minimal Maximal
Convex Optimization Theory. Athena Scientific, Supplementary Chapter 6 on Convex Optimization Algorithms
 Convex Optimization Theory Athena Scientific, 2009 by Dimitri P. Bertsekas Massachusetts Institute of Technology Supplementary Chapter 6 on Convex Optimization Algorithms This chapter aims to supplement
Convex Optimization Theory Athena Scientific, 2009 by Dimitri P. Bertsekas Massachusetts Institute of Technology Supplementary Chapter 6 on Convex Optimization Algorithms This chapter aims to supplement
Proximal methods. S. Villa. October 7, 2014
 Proximal methods S. Villa October 7, 2014 1 Review of the basics Often machine learning problems require the solution of minimization problems. For instance, the ERM algorithm requires to solve a problem
Proximal methods S. Villa October 7, 2014 1 Review of the basics Often machine learning problems require the solution of minimization problems. For instance, the ERM algorithm requires to solve a problem
Linear Diffusion and Image Processing. Outline
 Outline Linear Diffusion and Image Processing Fourier Transform Convolution Image Restoration: Linear Filtering Diffusion Processes for Noise Filtering linear scale space theory Gauss-Laplace pyramid for
Outline Linear Diffusion and Image Processing Fourier Transform Convolution Image Restoration: Linear Filtering Diffusion Processes for Noise Filtering linear scale space theory Gauss-Laplace pyramid for
2 Tikhonov Regularization and ERM
 Introduction Here we discusses how a class of regularization methods originally designed to solve ill-posed inverse problems give rise to regularized learning algorithms. These algorithms are kernel methods
Introduction Here we discusses how a class of regularization methods originally designed to solve ill-posed inverse problems give rise to regularized learning algorithms. These algorithms are kernel methods
Total Variation-Penalized Poisson Likelihood Estimation for Ill-Posed Problems
 Total Variation-Penalized Poisson Likelihood Estimation for Ill-Posed Problems Johnathan M. Bardsley Department of Mathematical Sciences, University of Montana, Missoula, MT. Email: bardsleyj@mso.umt.edu
Total Variation-Penalized Poisson Likelihood Estimation for Ill-Posed Problems Johnathan M. Bardsley Department of Mathematical Sciences, University of Montana, Missoula, MT. Email: bardsleyj@mso.umt.edu
Numerical optimization. Numerical optimization. Longest Shortest where Maximal Minimal. Fastest. Largest. Optimization problems
 1 Numerical optimization Alexander & Michael Bronstein, 2006-2009 Michael Bronstein, 2010 tosca.cs.technion.ac.il/book Numerical optimization 048921 Advanced topics in vision Processing and Analysis of
1 Numerical optimization Alexander & Michael Bronstein, 2006-2009 Michael Bronstein, 2010 tosca.cs.technion.ac.il/book Numerical optimization 048921 Advanced topics in vision Processing and Analysis of
Optimal control as a regularization method for. an ill-posed problem.
 Optimal control as a regularization method for ill-posed problems Stefan Kindermann, Carmeliza Navasca Department of Mathematics University of California Los Angeles, CA 995-1555 USA {kinder,navasca}@math.ucla.edu
Optimal control as a regularization method for ill-posed problems Stefan Kindermann, Carmeliza Navasca Department of Mathematics University of California Los Angeles, CA 995-1555 USA {kinder,navasca}@math.ucla.edu
Erkut Erdem. Hacettepe University February 24 th, Linear Diffusion 1. 2 Appendix - The Calculus of Variations 5.
 LINEAR DIFFUSION Erkut Erdem Hacettepe University February 24 th, 2012 CONTENTS 1 Linear Diffusion 1 2 Appendix - The Calculus of Variations 5 References 6 1 LINEAR DIFFUSION The linear diffusion (heat)
LINEAR DIFFUSION Erkut Erdem Hacettepe University February 24 th, 2012 CONTENTS 1 Linear Diffusion 1 2 Appendix - The Calculus of Variations 5 References 6 1 LINEAR DIFFUSION The linear diffusion (heat)
Network Newton. Aryan Mokhtari, Qing Ling and Alejandro Ribeiro. University of Pennsylvania, University of Science and Technology (China)
 Network Newton Aryan Mokhtari, Qing Ling and Alejandro Ribeiro University of Pennsylvania, University of Science and Technology (China) aryanm@seas.upenn.edu, qingling@mail.ustc.edu.cn, aribeiro@seas.upenn.edu
Network Newton Aryan Mokhtari, Qing Ling and Alejandro Ribeiro University of Pennsylvania, University of Science and Technology (China) aryanm@seas.upenn.edu, qingling@mail.ustc.edu.cn, aribeiro@seas.upenn.edu
A memory gradient algorithm for l 2 -l 0 regularization with applications to image restoration
 A memory gradient algorithm for l 2 -l 0 regularization with applications to image restoration E. Chouzenoux, A. Jezierska, J.-C. Pesquet and H. Talbot Université Paris-Est Lab. d Informatique Gaspard
A memory gradient algorithm for l 2 -l 0 regularization with applications to image restoration E. Chouzenoux, A. Jezierska, J.-C. Pesquet and H. Talbot Université Paris-Est Lab. d Informatique Gaspard
Regularization and Inverse Problems
 Regularization and Inverse Problems Caroline Sieger Host Institution: Universität Bremen Home Institution: Clemson University August 5, 2009 Caroline Sieger (Bremen and Clemson) Regularization and Inverse
Regularization and Inverse Problems Caroline Sieger Host Institution: Universität Bremen Home Institution: Clemson University August 5, 2009 Caroline Sieger (Bremen and Clemson) Regularization and Inverse
Convex Optimization. Problem set 2. Due Monday April 26th
 Convex Optimization Problem set 2 Due Monday April 26th 1 Gradient Decent without Line-search In this problem we will consider gradient descent with predetermined step sizes. That is, instead of determining
Convex Optimization Problem set 2 Due Monday April 26th 1 Gradient Decent without Line-search In this problem we will consider gradient descent with predetermined step sizes. That is, instead of determining
8 Numerical methods for unconstrained problems
 8 Numerical methods for unconstrained problems Optimization is one of the important fields in numerical computation, beside solving differential equations and linear systems. We can see that these fields
8 Numerical methods for unconstrained problems Optimization is one of the important fields in numerical computation, beside solving differential equations and linear systems. We can see that these fields
MATH 411 NOTES (UNDER CONSTRUCTION)
 MATH 411 NOTES (NDE CONSTCTION 1. Notes on compact sets. This is similar to ideas you learned in Math 410, except open sets had not yet been defined. Definition 1.1. K n is compact if for every covering
MATH 411 NOTES (NDE CONSTCTION 1. Notes on compact sets. This is similar to ideas you learned in Math 410, except open sets had not yet been defined. Definition 1.1. K n is compact if for every covering
5 Handling Constraints
 5 Handling Constraints Engineering design optimization problems are very rarely unconstrained. Moreover, the constraints that appear in these problems are typically nonlinear. This motivates our interest
5 Handling Constraints Engineering design optimization problems are very rarely unconstrained. Moreover, the constraints that appear in these problems are typically nonlinear. This motivates our interest
Constrained Optimization and Lagrangian Duality
 CIS 520: Machine Learning Oct 02, 2017 Constrained Optimization and Lagrangian Duality Lecturer: Shivani Agarwal Disclaimer: These notes are designed to be a supplement to the lecture. They may or may
CIS 520: Machine Learning Oct 02, 2017 Constrained Optimization and Lagrangian Duality Lecturer: Shivani Agarwal Disclaimer: These notes are designed to be a supplement to the lecture. They may or may
2 Two-Point Boundary Value Problems
 2 Two-Point Boundary Value Problems Another fundamental equation, in addition to the heat eq. and the wave eq., is Poisson s equation: n j=1 2 u x 2 j The unknown is the function u = u(x 1, x 2,..., x
2 Two-Point Boundary Value Problems Another fundamental equation, in addition to the heat eq. and the wave eq., is Poisson s equation: n j=1 2 u x 2 j The unknown is the function u = u(x 1, x 2,..., x
Krylov subspace iterative methods for nonsymmetric discrete ill-posed problems in image restoration
 Krylov subspace iterative methods for nonsymmetric discrete ill-posed problems in image restoration D. Calvetti a, B. Lewis b and L. Reichel c a Department of Mathematics, Case Western Reserve University,
Krylov subspace iterative methods for nonsymmetric discrete ill-posed problems in image restoration D. Calvetti a, B. Lewis b and L. Reichel c a Department of Mathematics, Case Western Reserve University,
Chapter 2. Optimization. Gradients, convexity, and ALS
 Chapter 2 Optimization Gradients, convexity, and ALS Contents Background Gradient descent Stochastic gradient descent Newton s method Alternating least squares KKT conditions 2 Motivation We can solve
Chapter 2 Optimization Gradients, convexity, and ALS Contents Background Gradient descent Stochastic gradient descent Newton s method Alternating least squares KKT conditions 2 Motivation We can solve
Laplace-distributed increments, the Laplace prior, and edge-preserving regularization
 J. Inverse Ill-Posed Probl.? (????), 1 15 DOI 1.1515/JIIP.????.??? de Gruyter???? Laplace-distributed increments, the Laplace prior, and edge-preserving regularization Johnathan M. Bardsley Abstract. For
J. Inverse Ill-Posed Probl.? (????), 1 15 DOI 1.1515/JIIP.????.??? de Gruyter???? Laplace-distributed increments, the Laplace prior, and edge-preserving regularization Johnathan M. Bardsley Abstract. For
Inverse problems in statistics
 Inverse problems in statistics Laurent Cavalier (Université Aix-Marseille 1, France) Yale, May 2 2011 p. 1/35 Introduction There exist many fields where inverse problems appear Astronomy (Hubble satellite).
Inverse problems in statistics Laurent Cavalier (Université Aix-Marseille 1, France) Yale, May 2 2011 p. 1/35 Introduction There exist many fields where inverse problems appear Astronomy (Hubble satellite).
Reproducing Kernel Hilbert Spaces
 Reproducing Kernel Hilbert Spaces Lorenzo Rosasco 9.520 Class 03 February 9, 2011 About this class Goal To introduce a particularly useful family of hypothesis spaces called Reproducing Kernel Hilbert
Reproducing Kernel Hilbert Spaces Lorenzo Rosasco 9.520 Class 03 February 9, 2011 About this class Goal To introduce a particularly useful family of hypothesis spaces called Reproducing Kernel Hilbert
Two-parameter regularization method for determining the heat source
 Global Journal of Pure and Applied Mathematics. ISSN 0973-1768 Volume 13, Number 8 (017), pp. 3937-3950 Research India Publications http://www.ripublication.com Two-parameter regularization method for
Global Journal of Pure and Applied Mathematics. ISSN 0973-1768 Volume 13, Number 8 (017), pp. 3937-3950 Research India Publications http://www.ripublication.com Two-parameter regularization method for
Laplace s Equation. Chapter Mean Value Formulas
 Chapter 1 Laplace s Equation Let be an open set in R n. A function u C 2 () is called harmonic in if it satisfies Laplace s equation n (1.1) u := D ii u = 0 in. i=1 A function u C 2 () is called subharmonic
Chapter 1 Laplace s Equation Let be an open set in R n. A function u C 2 () is called harmonic in if it satisfies Laplace s equation n (1.1) u := D ii u = 0 in. i=1 A function u C 2 () is called subharmonic
Spectral Regularization
 Spectral Regularization Lorenzo Rosasco 9.520 Class 07 February 27, 2008 About this class Goal To discuss how a class of regularization methods originally designed for solving ill-posed inverse problems,
Spectral Regularization Lorenzo Rosasco 9.520 Class 07 February 27, 2008 About this class Goal To discuss how a class of regularization methods originally designed for solving ill-posed inverse problems,
A Limited Memory, Quasi-Newton Preconditioner. for Nonnegatively Constrained Image. Reconstruction
 A Limited Memory, Quasi-Newton Preconditioner for Nonnegatively Constrained Image Reconstruction Johnathan M. Bardsley Department of Mathematical Sciences, The University of Montana, Missoula, MT 59812-864
A Limited Memory, Quasi-Newton Preconditioner for Nonnegatively Constrained Image Reconstruction Johnathan M. Bardsley Department of Mathematical Sciences, The University of Montana, Missoula, MT 59812-864
Convex Optimization. Convex Analysis - Functions
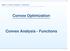 Convex Optimization Convex Analsis - Functions p. 1 A function f : K R n R is convex, if K is a convex set and x, K,x, λ (,1) we have f(λx+(1 λ)) λf(x)+(1 λ)f(). (x, f(x)) (,f()) x - strictl convex,
Convex Optimization Convex Analsis - Functions p. 1 A function f : K R n R is convex, if K is a convex set and x, K,x, λ (,1) we have f(λx+(1 λ)) λf(x)+(1 λ)f(). (x, f(x)) (,f()) x - strictl convex,
Lecture No 2 Degenerate Diffusion Free boundary problems
 Lecture No 2 Degenerate Diffusion Free boundary problems Columbia University IAS summer program June, 2009 Outline We will discuss non-linear parabolic equations of slow diffusion. Our model is the porous
Lecture No 2 Degenerate Diffusion Free boundary problems Columbia University IAS summer program June, 2009 Outline We will discuss non-linear parabolic equations of slow diffusion. Our model is the porous
Regularization via Spectral Filtering
 Regularization via Spectral Filtering Lorenzo Rosasco MIT, 9.520 Class 7 About this class Goal To discuss how a class of regularization methods originally designed for solving ill-posed inverse problems,
Regularization via Spectral Filtering Lorenzo Rosasco MIT, 9.520 Class 7 About this class Goal To discuss how a class of regularization methods originally designed for solving ill-posed inverse problems,
Scaled gradient projection methods in image deblurring and denoising
 Scaled gradient projection methods in image deblurring and denoising Mario Bertero 1 Patrizia Boccacci 1 Silvia Bonettini 2 Riccardo Zanella 3 Luca Zanni 3 1 Dipartmento di Matematica, Università di Genova
Scaled gradient projection methods in image deblurring and denoising Mario Bertero 1 Patrizia Boccacci 1 Silvia Bonettini 2 Riccardo Zanella 3 Luca Zanni 3 1 Dipartmento di Matematica, Università di Genova
2.098/6.255/ Optimization Methods Practice True/False Questions
 2.098/6.255/15.093 Optimization Methods Practice True/False Questions December 11, 2009 Part I For each one of the statements below, state whether it is true or false. Include a 1-3 line supporting sentence
2.098/6.255/15.093 Optimization Methods Practice True/False Questions December 11, 2009 Part I For each one of the statements below, state whether it is true or false. Include a 1-3 line supporting sentence
Parameter Identification
 Lecture Notes Parameter Identification Winter School Inverse Problems 25 Martin Burger 1 Contents 1 Introduction 3 2 Examples of Parameter Identification Problems 5 2.1 Differentiation of Data...............................
Lecture Notes Parameter Identification Winter School Inverse Problems 25 Martin Burger 1 Contents 1 Introduction 3 2 Examples of Parameter Identification Problems 5 2.1 Differentiation of Data...............................
2 Nonlinear least squares algorithms
 1 Introduction Notes for 2017-05-01 We briefly discussed nonlinear least squares problems in a previous lecture, when we described the historical path leading to trust region methods starting from the
1 Introduction Notes for 2017-05-01 We briefly discussed nonlinear least squares problems in a previous lecture, when we described the historical path leading to trust region methods starting from the
1 Newton s Method. Suppose we want to solve: x R. At x = x, f (x) can be approximated by:
 Newton s Method Suppose we want to solve: (P:) min f (x) At x = x, f (x) can be approximated by: n x R. f (x) h(x) := f ( x)+ f ( x) T (x x)+ (x x) t H ( x)(x x), 2 which is the quadratic Taylor expansion
Newton s Method Suppose we want to solve: (P:) min f (x) At x = x, f (x) can be approximated by: n x R. f (x) h(x) := f ( x)+ f ( x) T (x x)+ (x x) t H ( x)(x x), 2 which is the quadratic Taylor expansion
Gauge optimization and duality
 1 / 54 Gauge optimization and duality Junfeng Yang Department of Mathematics Nanjing University Joint with Shiqian Ma, CUHK September, 2015 2 / 54 Outline Introduction Duality Lagrange duality Fenchel
1 / 54 Gauge optimization and duality Junfeng Yang Department of Mathematics Nanjing University Joint with Shiqian Ma, CUHK September, 2015 2 / 54 Outline Introduction Duality Lagrange duality Fenchel
Selected Methods for Modern Optimization in Data Analysis Department of Statistics and Operations Research UNC-Chapel Hill Fall 2018
 Selected Methods for Modern Optimization in Data Analysis Department of Statistics and Operations Research UNC-Chapel Hill Fall 08 Instructor: Quoc Tran-Dinh Scriber: Quoc Tran-Dinh Lecture 4: Selected
Selected Methods for Modern Optimization in Data Analysis Department of Statistics and Operations Research UNC-Chapel Hill Fall 08 Instructor: Quoc Tran-Dinh Scriber: Quoc Tran-Dinh Lecture 4: Selected
Inverse problem and optimization
 Inverse problem and optimization Laurent Condat, Nelly Pustelnik CNRS, Gipsa-lab CNRS, Laboratoire de Physique de l ENS de Lyon Decembre, 15th 2016 Inverse problem and optimization 2/36 Plan 1. Examples
Inverse problem and optimization Laurent Condat, Nelly Pustelnik CNRS, Gipsa-lab CNRS, Laboratoire de Physique de l ENS de Lyon Decembre, 15th 2016 Inverse problem and optimization 2/36 Plan 1. Examples
Due Giorni di Algebra Lineare Numerica (2GALN) Febbraio 2016, Como. Iterative regularization in variable exponent Lebesgue spaces
 Due Giorni di Algebra Lineare Numerica (2GALN) 16 17 Febbraio 2016, Como Iterative regularization in variable exponent Lebesgue spaces Claudio Estatico 1 Joint work with: Brigida Bonino 1, Fabio Di Benedetto
Due Giorni di Algebra Lineare Numerica (2GALN) 16 17 Febbraio 2016, Como Iterative regularization in variable exponent Lebesgue spaces Claudio Estatico 1 Joint work with: Brigida Bonino 1, Fabio Di Benedetto
ICS-E4030 Kernel Methods in Machine Learning
 ICS-E4030 Kernel Methods in Machine Learning Lecture 3: Convex optimization and duality Juho Rousu 28. September, 2016 Juho Rousu 28. September, 2016 1 / 38 Convex optimization Convex optimisation This
ICS-E4030 Kernel Methods in Machine Learning Lecture 3: Convex optimization and duality Juho Rousu 28. September, 2016 Juho Rousu 28. September, 2016 1 / 38 Convex optimization Convex optimisation This
Numerisches Rechnen. (für Informatiker) M. Grepl P. Esser & G. Welper & L. Zhang. Institut für Geometrie und Praktische Mathematik RWTH Aachen
 Numerisches Rechnen (für Informatiker) M. Grepl P. Esser & G. Welper & L. Zhang Institut für Geometrie und Praktische Mathematik RWTH Aachen Wintersemester 2011/12 IGPM, RWTH Aachen Numerisches Rechnen
Numerisches Rechnen (für Informatiker) M. Grepl P. Esser & G. Welper & L. Zhang Institut für Geometrie und Praktische Mathematik RWTH Aachen Wintersemester 2011/12 IGPM, RWTH Aachen Numerisches Rechnen
Markov Random Fields
 Markov Random Fields Umamahesh Srinivas ipal Group Meeting February 25, 2011 Outline 1 Basic graph-theoretic concepts 2 Markov chain 3 Markov random field (MRF) 4 Gauss-Markov random field (GMRF), and
Markov Random Fields Umamahesh Srinivas ipal Group Meeting February 25, 2011 Outline 1 Basic graph-theoretic concepts 2 Markov chain 3 Markov random field (MRF) 4 Gauss-Markov random field (GMRF), and
Mumford-Shah Level-Set Ideas for Problems in Medical Imaging Paris Dauphine 2005
 1/26 Mumford-Shah Level-Set Ideas for Problems in Medical Imaging Paris Dauphine 2005 Wolfgang Ring, Marc Droske, Ronny Ramlau Institut für Mathematik, Universität Graz General Mumford-Shah like 2/26 functionals
1/26 Mumford-Shah Level-Set Ideas for Problems in Medical Imaging Paris Dauphine 2005 Wolfgang Ring, Marc Droske, Ronny Ramlau Institut für Mathematik, Universität Graz General Mumford-Shah like 2/26 functionals
Discrete Ill Posed and Rank Deficient Problems. Alistair Boyle, Feb 2009, SYS5906: Directed Studies Inverse Problems 1
 Discrete Ill Posed and Rank Deficient Problems Alistair Boyle, Feb 2009, SYS5906: Directed Studies Inverse Problems 1 Definitions Overview Inversion, SVD, Picard Condition, Rank Deficient, Ill-Posed Classical
Discrete Ill Posed and Rank Deficient Problems Alistair Boyle, Feb 2009, SYS5906: Directed Studies Inverse Problems 1 Definitions Overview Inversion, SVD, Picard Condition, Rank Deficient, Ill-Posed Classical
Insights into the Geometry of the Gaussian Kernel and an Application in Geometric Modeling
 Insights into the Geometry of the Gaussian Kernel and an Application in Geometric Modeling Master Thesis Michael Eigensatz Advisor: Joachim Giesen Professor: Mark Pauly Swiss Federal Institute of Technology
Insights into the Geometry of the Gaussian Kernel and an Application in Geometric Modeling Master Thesis Michael Eigensatz Advisor: Joachim Giesen Professor: Mark Pauly Swiss Federal Institute of Technology
Parameter Identification in Partial Differential Equations
 Parameter Identification in Partial Differential Equations Differentiation of data Not strictly a parameter identification problem, but good motivation. Appears often as a subproblem. Given noisy observation
Parameter Identification in Partial Differential Equations Differentiation of data Not strictly a parameter identification problem, but good motivation. Appears often as a subproblem. Given noisy observation
Optimization and Root Finding. Kurt Hornik
 Optimization and Root Finding Kurt Hornik Basics Root finding and unconstrained smooth optimization are closely related: Solving ƒ () = 0 can be accomplished via minimizing ƒ () 2 Slide 2 Basics Root finding
Optimization and Root Finding Kurt Hornik Basics Root finding and unconstrained smooth optimization are closely related: Solving ƒ () = 0 can be accomplished via minimizing ƒ () 2 Slide 2 Basics Root finding
NONLINEAR DIFFUSION PDES
 NONLINEAR DIFFUSION PDES Erkut Erdem Hacettepe University March 5 th, 0 CONTENTS Perona-Malik Type Nonlinear Diffusion Edge Enhancing Diffusion 5 References 7 PERONA-MALIK TYPE NONLINEAR DIFFUSION The
NONLINEAR DIFFUSION PDES Erkut Erdem Hacettepe University March 5 th, 0 CONTENTS Perona-Malik Type Nonlinear Diffusion Edge Enhancing Diffusion 5 References 7 PERONA-MALIK TYPE NONLINEAR DIFFUSION The
Sequential Unconstrained Minimization: A Survey
 Sequential Unconstrained Minimization: A Survey Charles L. Byrne February 21, 2013 Abstract The problem is to minimize a function f : X (, ], over a non-empty subset C of X, where X is an arbitrary set.
Sequential Unconstrained Minimization: A Survey Charles L. Byrne February 21, 2013 Abstract The problem is to minimize a function f : X (, ], over a non-empty subset C of X, where X is an arbitrary set.
Scientific Computing: Optimization
 Scientific Computing: Optimization Aleksandar Donev Courant Institute, NYU 1 donev@courant.nyu.edu 1 Course MATH-GA.2043 or CSCI-GA.2112, Spring 2012 March 8th, 2011 A. Donev (Courant Institute) Lecture
Scientific Computing: Optimization Aleksandar Donev Courant Institute, NYU 1 donev@courant.nyu.edu 1 Course MATH-GA.2043 or CSCI-GA.2112, Spring 2012 March 8th, 2011 A. Donev (Courant Institute) Lecture
The Proximal Gradient Method
 Chapter 10 The Proximal Gradient Method Underlying Space: In this chapter, with the exception of Section 10.9, E is a Euclidean space, meaning a finite dimensional space endowed with an inner product,
Chapter 10 The Proximal Gradient Method Underlying Space: In this chapter, with the exception of Section 10.9, E is a Euclidean space, meaning a finite dimensional space endowed with an inner product,
Preconditioning. Noisy, Ill-Conditioned Linear Systems
 Preconditioning Noisy, Ill-Conditioned Linear Systems James G. Nagy Emory University Atlanta, GA Outline 1. The Basic Problem 2. Regularization / Iterative Methods 3. Preconditioning 4. Example: Image
Preconditioning Noisy, Ill-Conditioned Linear Systems James G. Nagy Emory University Atlanta, GA Outline 1. The Basic Problem 2. Regularization / Iterative Methods 3. Preconditioning 4. Example: Image
Numerical Methods for Separable Nonlinear Inverse Problems with Constraint and Low Rank
 Numerical Methods for Separable Nonlinear Inverse Problems with Constraint and Low Rank Taewon Cho Thesis submitted to the Faculty of the Virginia Polytechnic Institute and State University in partial
Numerical Methods for Separable Nonlinear Inverse Problems with Constraint and Low Rank Taewon Cho Thesis submitted to the Faculty of the Virginia Polytechnic Institute and State University in partial
Optimality Conditions for Constrained Optimization
 72 CHAPTER 7 Optimality Conditions for Constrained Optimization 1. First Order Conditions In this section we consider first order optimality conditions for the constrained problem P : minimize f 0 (x)
72 CHAPTER 7 Optimality Conditions for Constrained Optimization 1. First Order Conditions In this section we consider first order optimality conditions for the constrained problem P : minimize f 0 (x)
Accelerated Block-Coordinate Relaxation for Regularized Optimization
 Accelerated Block-Coordinate Relaxation for Regularized Optimization Stephen J. Wright Computer Sciences University of Wisconsin, Madison October 09, 2012 Problem descriptions Consider where f is smooth
Accelerated Block-Coordinate Relaxation for Regularized Optimization Stephen J. Wright Computer Sciences University of Wisconsin, Madison October 09, 2012 Problem descriptions Consider where f is smooth
Total Variation Theory and Its Applications
 Total Variation Theory and Its Applications 2nd UCC Annual Research Conference, Kingston, Jamaica Peter Ndajah University of the Commonwealth Caribbean, Kingston, Jamaica September 27, 2018 Peter Ndajah
Total Variation Theory and Its Applications 2nd UCC Annual Research Conference, Kingston, Jamaica Peter Ndajah University of the Commonwealth Caribbean, Kingston, Jamaica September 27, 2018 Peter Ndajah
Multi-Linear Mappings, SVD, HOSVD, and the Numerical Solution of Ill-Conditioned Tensor Least Squares Problems
 Multi-Linear Mappings, SVD, HOSVD, and the Numerical Solution of Ill-Conditioned Tensor Least Squares Problems Lars Eldén Department of Mathematics, Linköping University 1 April 2005 ERCIM April 2005 Multi-Linear
Multi-Linear Mappings, SVD, HOSVD, and the Numerical Solution of Ill-Conditioned Tensor Least Squares Problems Lars Eldén Department of Mathematics, Linköping University 1 April 2005 ERCIM April 2005 Multi-Linear
Uncertainty principles for far field patterns and applications to inverse source problems
 for far field patterns and applications to inverse source problems roland.griesmaier@uni-wuerzburg.de (joint work with J. Sylvester) Paris, September 17 Outline Source problems and far field patterns AregularizedPicardcriterion
for far field patterns and applications to inverse source problems roland.griesmaier@uni-wuerzburg.de (joint work with J. Sylvester) Paris, September 17 Outline Source problems and far field patterns AregularizedPicardcriterion
Computing regularization paths for learning multiple kernels
 Computing regularization paths for learning multiple kernels Francis Bach Romain Thibaux Michael Jordan Computer Science, UC Berkeley December, 24 Code available at www.cs.berkeley.edu/~fbach Computing
Computing regularization paths for learning multiple kernels Francis Bach Romain Thibaux Michael Jordan Computer Science, UC Berkeley December, 24 Code available at www.cs.berkeley.edu/~fbach Computing
Algorithms for constrained local optimization
 Algorithms for constrained local optimization Fabio Schoen 2008 http://gol.dsi.unifi.it/users/schoen Algorithms for constrained local optimization p. Feasible direction methods Algorithms for constrained
Algorithms for constrained local optimization Fabio Schoen 2008 http://gol.dsi.unifi.it/users/schoen Algorithms for constrained local optimization p. Feasible direction methods Algorithms for constrained
