Functional equations 1.
|
|
|
- Patience Thornton
- 5 years ago
- Views:
Transcription
1 Functional equations. What is a function? Technically speaking, it would be rather impossible to give a proper notion of a function. We will need to use other words, such as 'relation', 'map' or other, which are just synonyms of a word function and need to be properly dened. Question: What we can do? We will get understanding of not what the object is, but how we can work with it. Assume, we have two sets, call them A and B, and the aim is to describe a function, which maps A on B. We will just say, that for eery from set A there is a choice of an element y from set B. This element y we will denote as f, it's called the image of. Notation: f : A B; y = f or f : y Composition of functions. Denition. Let us have two functions y = f, g : A B and z = gy, f : B C. Then a function z = F = gf, F : A C is called a composition of functions g and f. Notation: F = g f. Remark. There can be a composition of more than two functions, i. e. : z = F = f f... f n = f f f 3... f n.... Remark. Note, that g f and f g are dierent functions. Eample. Let g =, fy = cos y.then F = f g = cos. Eample. Let ϕ = 3. Then ϕ ϕ = 3 3 = 9. Eample 3. Let ψ = Then ψ ψ = = Let f = +, g = +. Find f g.. Let ϕ = , [ 5; ]. Find ϕ ϕ. 3. Let f = +. Find: a f f; b f f f; c f f f f; d f f f f f. Homework 4. Find ϕ ϕ, if a ϕ = ; b ϕ = ; c ϕ = ; d ϕ =. 5. Let ϕ =. Find ϕ ϕ ϕ. 6. Let ϕ =. Find } ϕ ϕ {{... ϕ. } n times
2 The simplest functional equations Functional equations are equations where unknown is a function. Generally, those functions are connected with well-known functions using composition. Eamples of functional equations: f + 5 f f3 = 0 or f y = f + fy, where f is unknown, and the aim is to nd f. Denition. Function f is called a soultion of a functional equation on set M, if it satises this equation for all values of variable in the set M. Problems. Prove that a function f = A + B 3, where A and B some constant numbers, is a solution of f + 5 f f = 0.. Proof, that a function f = C, where C is some constant, is a solution of f + y = f + fy. 3. Prove, that f = α for any α is a solution of f y = f fy. 4. Prove, that f = sgn is a solution of f y = f fy. Remark. Last two tasks show, that dierent functions may be solutions of the same equation. To solve a functional equation means to nd all of the solutions or prove that they do not eist Prove, that f = g, where g is any function, is a solution of 6. Find all functions f dened on the set of real numbers, such that 3 f f +5 = 0 for any real. 7. Find all functions f and g satisfying net condition for all 0 f + g = + +, f + g = Find all functions f dened on the set of all real numbers, such that for all real and y this function satises sin + cos y = f + fy + g gy. Homework 9. Prove, that a function f = a for any a > 0 is a solution of f + y = f fy. 0. Find all functions f dened on real numberssatisfying for any real π f = f0 sin f cos +.. Find all functions f and g dened on real numbers, such that for any real numbers and y the following holds f + fy + g gy = y.. A function fn from integers to integers satises the condition: { n 0, if n > 00, fn = f f n +, if n 00. Prove that fn = 9 for all n 00.
3 Functional equations-3. Substituion in equations without free variables. Find all functions f, such that for every ± it satises f =. +. Find all functions f, such that for every 0 it satises f f =. 3. Find all functions f, such that for every, 0 it satises f + f =. 4. Find all functions f, such that for every it satises f + f + = Let a, b, c be some constant numbers, a b. Find all functions f satisfying af + bf = c. 6. Find all functions f, such that for every 0 it satises 3f + f + f =. 7. Find all functions f, such that for every 0, it satises f + f + f = Homework 8. Find all functions f, satisfying f + =. 9. Let a, c, k be some constant numbers and a c. Find all functions f, such that for a + every c, it satises f = k. c + 0. Let a ±. Find all functions f, such that for every 0 it satises af + f = a.. Find all functions f, such that for every 0 it satises + f + f =.. Let a ± and let g be some function. Find all functions f, such that for every it satises f af = g. 3. Find all functions f, such that for every 5 it satises f f =. 4. Let a 0 be some constant number. Find all functions f, such that for every 0, a it satises a f + f =. a
4 5. Find all functions f, such that for every ± it satises 3 + f + f = Let a and b be some constant numbers, a 0, a b. Find all functions f, such that for every ± it satises + af + + bf = Let a and b be some constant real numbers, a ±, and let n be a natural number. Find all functions f, satisfying af n + f n = b n. 8. Let a be some constant number, a ±. Find all functions f, such that for every 0 è ± it satises + f + af = +. +
5 Rules Setup. The board consists of a grid of 8 8 squares.. Squares are adjacent horizontally, vertically or diagonally. 3. The game is played by two or four players. 4. Each of the player has his own camp: a 3 3 square adjoint to a corner of the whole board. 5. Each player has a set of pieces in a distinct color, of the same number as squares in each camp. 6. The board starts with all the squares of each player's camp occupied by a piece of that player's color. Objective The winning objective is to be the rst player to race all one's pieces into the opposing camp the camp diagonally opposite one's own. Play sequence. Players randomly determine who will move rst.. Pieces can move in eight possible directions up, down, left, right and diagonally. 3. Each player's turn consists of moving a single piece of one's own color in one of the following plays: 3a. One move to an empty square: Place the piece in an empty adjacent square. This move ends the play. 3b. One or more jumps over adjacent pieces: An adjacent piece of any color can be jumped if there is an adjacent empty square on the directly opposite side of that piece. Place the piece in the empty square on the opposite side of the jumped piece. The piece which was jumped over is unaected and remains on the board. After any jump, one may make further jumps using the same piece, or end the play. 4. Then the other player makes his step in the same way. First set of tasks 0. Play as many as possible games, to understand game mechanics and simplest rules of the game. Try to see logical connections, and try to distinguish somehow good moves and bad moves. The more you play, the deeper you understand how to play this game.. To nish the rules you need to write down when the game ends.. To make the game proper you need to add up etra rules, so the game will always end up somehow one of the players winning or draw. Also you need to epress properly the winning conditions. 3. Find ways to measure moves of each player to describe which move sequence of moves is better. Can you do it numerically?
6 Symmetric polynomials variables case Theorem Vieta. Let, be roots of polynomial + p + q. Then { + = p; = q. Both + and are polynomials over variables and and moreover those polynomials do not change, if one replace with and with. We will study such polynomials. Denition. Polynomial f, y, which does not change if one echange variables and y are called symmetric Eample. Polynomial f, y = y + y is symmetric, while f, y = 3 3y is not. Denition. Polynomials σ = + y and σ = y are called elementary symmetric polynomials over two variables. Aside of σ and σ we will be using polynomials + y, 3 + y 3,..., n + y n, which are called power sums and we will denote them as S n : S n = n + y n. We will try to epress rst several of S n using σ and σ : S = + y = + y y = σ σ ; S 3 = 3 + y 3 = + y y + y = σ 3 3σ σ ; S 4 = 4 + y 4 = + y y = σ 4 4σ σ + σ. From that you may assume, that it will hold for any n, which is your rst task: Lemma. Every power sum S n = n + y n can be represented as a polynomial over σ and σ. I hope your soultion for the rst task was constructive so it gives you way to construct that polynomial over sigma and sigma, so you will easily show us such representation for S 5, S 6 and S 7. Etra task: There also direct formulas for S n, which you may try to prove or at least to show that those formulas are equal to each other: S n = n + y n = σ + σ 4σ n + σ σ 4σ n S n = n S n = n [ n ] m=0 [ n ] m=0 n m σ n m σ 4σ m. m n m! σ n m σ m, 3 m! n m! where [ ] n means the biggest integer less than n. The third formula was constructed by Edward Waring in 779. Using the proven lemma, one can etend it to the proof of the main theorem about symmetric polynomials
7 Theorem Main. Any symmetric plynomial over two variables can be represented as a polynomial over σ, σ. This the main task to prove the main theorem. Aso one can show that such representaion is unique it does not depend on the way we obtain this representation, we will always end up with the same thing.
Syllabus. + + x + n 1 n. + x + 2
 1. Special Functions This class will cover problems involving algebraic functions other than polynomials, such as square roots, the floor function, and logarithms. Example Problem: Let n be a positive
1. Special Functions This class will cover problems involving algebraic functions other than polynomials, such as square roots, the floor function, and logarithms. Example Problem: Let n be a positive
Linear Algebra, 4th day, Thursday 7/1/04 REU Info:
 Linear Algebra, 4th day, Thursday 7/1/04 REU 004. Info http//people.cs.uchicago.edu/laci/reu04. Instructor Laszlo Babai Scribe Nick Gurski 1 Linear maps We shall study the notion of maps between vector
Linear Algebra, 4th day, Thursday 7/1/04 REU 004. Info http//people.cs.uchicago.edu/laci/reu04. Instructor Laszlo Babai Scribe Nick Gurski 1 Linear maps We shall study the notion of maps between vector
Define a rational expression: a quotient of two polynomials. ..( 3 10) (3 2) Rational expressions have the same properties as rational numbers:
 1 UNIT 7 RATIONAL EXPRESSIONS & EQUATIONS Simplifying Rational Epressions Define a rational epression: a quotient of two polynomials. A rational epression always indicates division EX: 10 means..( 10)
1 UNIT 7 RATIONAL EXPRESSIONS & EQUATIONS Simplifying Rational Epressions Define a rational epression: a quotient of two polynomials. A rational epression always indicates division EX: 10 means..( 10)
Fractional Roman Domination
 Chapter 6 Fractional Roman Domination It is important to discuss minimality of Roman domination functions before we get into the details of fractional version of Roman domination. Minimality of domination
Chapter 6 Fractional Roman Domination It is important to discuss minimality of Roman domination functions before we get into the details of fractional version of Roman domination. Minimality of domination
Solutions to Problem Sheet for Week 11
 THE UNIVERSITY OF SYDNEY SCHOOL OF MATHEMATICS AND STATISTICS Solutions to Problem Sheet for Week MATH9: Differential Calculus (Advanced) Semester, 7 Web Page: sydney.edu.au/science/maths/u/ug/jm/math9/
THE UNIVERSITY OF SYDNEY SCHOOL OF MATHEMATICS AND STATISTICS Solutions to Problem Sheet for Week MATH9: Differential Calculus (Advanced) Semester, 7 Web Page: sydney.edu.au/science/maths/u/ug/jm/math9/
Homework 12; Due Monday, 4/9/2018
 Homework 2; Due Monday, 4/9/28 Answer-Only Questions Credit based solely on the answer Question For each of the following relations, determine whether each one is symmetric, transitive, or refleive If
Homework 2; Due Monday, 4/9/28 Answer-Only Questions Credit based solely on the answer Question For each of the following relations, determine whether each one is symmetric, transitive, or refleive If
Unit 4 Day 8 Symmetry & Compositions
 Unit 4 Day 8 Symmetry & Compositions Warm Up Day 8 1. f ( ) 4 3. g( ) 4 a. f(-1)= a. -g()= b. f(3)= b. g(+y)= c. f(-y)= c. g(-)= 3. Write and graph an equation that has the following: -Nonremovable discontinuity
Unit 4 Day 8 Symmetry & Compositions Warm Up Day 8 1. f ( ) 4 3. g( ) 4 a. f(-1)= a. -g()= b. f(3)= b. g(+y)= c. f(-y)= c. g(-)= 3. Write and graph an equation that has the following: -Nonremovable discontinuity
Calculus Problem Sheet Prof Paul Sutcliffe. 2. State the domain and range of each of the following functions
 f() 8 6 4 8 6-3 - - 3 4 5 6 f().9.8.7.6.5.4.3.. -4-3 - - 3 f() 7 6 5 4 3-3 - - Calculus Problem Sheet Prof Paul Sutcliffe. By applying the vertical line test, or otherwise, determine whether each of the
f() 8 6 4 8 6-3 - - 3 4 5 6 f().9.8.7.6.5.4.3.. -4-3 - - 3 f() 7 6 5 4 3-3 - - Calculus Problem Sheet Prof Paul Sutcliffe. By applying the vertical line test, or otherwise, determine whether each of the
PUTNAM PROBLEM SOLVING SEMINAR WEEK 7 This is the last meeting before the Putnam. The Rules. These are way too many problems to consider. Just pick a
 PUTNAM PROBLEM SOLVING SEMINAR WEEK 7 This is the last meeting before the Putnam The Rules These are way too many problems to consider Just pick a few problems in one of the sections and play around with
PUTNAM PROBLEM SOLVING SEMINAR WEEK 7 This is the last meeting before the Putnam The Rules These are way too many problems to consider Just pick a few problems in one of the sections and play around with
In last semester, we have seen some examples about it (See Tutorial Note #13). Try to have a look on that. Here we try to show more technique.
 MATH202 Introduction to Analysis (2007 Fall and 2008 Spring) Tutorial Note #4 Part I: Cauchy Sequence Definition (Cauchy Sequence): A sequence of real number { n } is Cauchy if and only if for any ε >
MATH202 Introduction to Analysis (2007 Fall and 2008 Spring) Tutorial Note #4 Part I: Cauchy Sequence Definition (Cauchy Sequence): A sequence of real number { n } is Cauchy if and only if for any ε >
Section 7.2: One-to-One, Onto and Inverse Functions
 Section 7.2: One-to-One, Onto and Inverse Functions In this section we shall developed the elementary notions of one-to-one, onto and inverse functions, similar to that developed in a basic algebra course.
Section 7.2: One-to-One, Onto and Inverse Functions In this section we shall developed the elementary notions of one-to-one, onto and inverse functions, similar to that developed in a basic algebra course.
Section 4.4 The Fundamental Theorem of Calculus
 Section 4.4 The Fundamental Theorem of Calculus The First Fundamental Theorem of Calculus If f is continuous on the interval [a,b] and F is any function that satisfies F '() = f() throughout this interval
Section 4.4 The Fundamental Theorem of Calculus The First Fundamental Theorem of Calculus If f is continuous on the interval [a,b] and F is any function that satisfies F '() = f() throughout this interval
Individual Round CHMMC November 20, 2016
 Individual Round CHMMC 20 November 20, 20 Problem. We say that d k d k d d 0 represents the number n in base 2 if each d i is either 0 or, and n d k ( 2) k + d k ( 2) k + + d ( 2) + d 0. For example, 0
Individual Round CHMMC 20 November 20, 20 Problem. We say that d k d k d d 0 represents the number n in base 2 if each d i is either 0 or, and n d k ( 2) k + d k ( 2) k + + d ( 2) + d 0. For example, 0
Functions If (x, y 1 ), (x, y 2 ) S, then y 1 = y 2
 Functions 4-3-2008 Definition. A function f from a set X to a set Y is a subset S of the product X Y such that if (, y 1 ), (, y 2 ) S, then y 1 = y 2. Instead of writing (, y) S, you usually write f()
Functions 4-3-2008 Definition. A function f from a set X to a set Y is a subset S of the product X Y such that if (, y 1 ), (, y 2 ) S, then y 1 = y 2. Instead of writing (, y) S, you usually write f()
Horizontal asymptotes
 Roberto s Notes on Differential Calculus Chapter : Limits and continuity Section 5 Limits at infinity and Horizontal asymptotes What you need to know already: The concept, notation and terminology of its.
Roberto s Notes on Differential Calculus Chapter : Limits and continuity Section 5 Limits at infinity and Horizontal asymptotes What you need to know already: The concept, notation and terminology of its.
10.7 Polynomial and Rational Inequalities
 10.7 Polynomial and Rational Inequalities In this section we want to turn our attention to solving polynomial and rational inequalities. That is, we want to solve inequalities like 5 4 0. In order to do
10.7 Polynomial and Rational Inequalities In this section we want to turn our attention to solving polynomial and rational inequalities. That is, we want to solve inequalities like 5 4 0. In order to do
MATH section 3.4 Curve Sketching Page 1 of 29
 MATH section. Curve Sketching Page of 9 The step by step procedure below is for regular rational and polynomial functions. If a function contains radical or trigonometric term, then proceed carefully because
MATH section. Curve Sketching Page of 9 The step by step procedure below is for regular rational and polynomial functions. If a function contains radical or trigonometric term, then proceed carefully because
211 Real Analysis. f (x) = x2 1. x 1. x 2 1
 Part. Limits of functions. Introduction 2 Real Analysis Eample. What happens to f : R \ {} R, given by f () = 2,, as gets close to? If we substitute = we get f () = 0 which is undefined. Instead we 0 might
Part. Limits of functions. Introduction 2 Real Analysis Eample. What happens to f : R \ {} R, given by f () = 2,, as gets close to? If we substitute = we get f () = 0 which is undefined. Instead we 0 might
Analysis on Graphs. Alexander Grigoryan Lecture Notes. University of Bielefeld, WS 2011/12
 Analysis on Graphs Alexander Grigoryan Lecture Notes University of Bielefeld, WS 0/ Contents The Laplace operator on graphs 5. The notion of a graph............................. 5. Cayley graphs..................................
Analysis on Graphs Alexander Grigoryan Lecture Notes University of Bielefeld, WS 0/ Contents The Laplace operator on graphs 5. The notion of a graph............................. 5. Cayley graphs..................................
Unit #3 Rules of Differentiation Homework Packet
 Unit #3 Rules of Differentiation Homework Packet In the table below, a function is given. Show the algebraic analysis that leads to the derivative of the function. Find the derivative by the specified
Unit #3 Rules of Differentiation Homework Packet In the table below, a function is given. Show the algebraic analysis that leads to the derivative of the function. Find the derivative by the specified
Midterm 1 Solutions. Monday, 10/24/2011
 Midterm Solutions Monday, 0/24/20. (0 points) Consider the function y = f() = e + 2e. (a) (2 points) What is the domain of f? Epress your answer using interval notation. Solution: We must eclude the possibility
Midterm Solutions Monday, 0/24/20. (0 points) Consider the function y = f() = e + 2e. (a) (2 points) What is the domain of f? Epress your answer using interval notation. Solution: We must eclude the possibility
Finite and Infinite Sets
 Chapter 9 Finite and Infinite Sets 9. Finite Sets Preview Activity (Equivalent Sets, Part ). Let A and B be sets and let f be a function from A to B..f W A! B/. Carefully complete each of the following
Chapter 9 Finite and Infinite Sets 9. Finite Sets Preview Activity (Equivalent Sets, Part ). Let A and B be sets and let f be a function from A to B..f W A! B/. Carefully complete each of the following
Answers. Investigation 3. ACE Assignment Choices. Applications. = = 210 (Note: students
 Answers Investigation ACE Assignment Choices Problem. Core,,, Other Applications ; Connections, ; Etensions 7, ; unassigned choices from previous problems Problem. Core, Other Connections 7; Etensions
Answers Investigation ACE Assignment Choices Problem. Core,,, Other Applications ; Connections, ; Etensions 7, ; unassigned choices from previous problems Problem. Core, Other Connections 7; Etensions
Contents. 2 Partial Derivatives. 2.1 Limits and Continuity. Calculus III (part 2): Partial Derivatives (by Evan Dummit, 2017, v. 2.
 Calculus III (part 2): Partial Derivatives (by Evan Dummit, 2017, v 260) Contents 2 Partial Derivatives 1 21 Limits and Continuity 1 22 Partial Derivatives 5 23 Directional Derivatives and the Gradient
Calculus III (part 2): Partial Derivatives (by Evan Dummit, 2017, v 260) Contents 2 Partial Derivatives 1 21 Limits and Continuity 1 22 Partial Derivatives 5 23 Directional Derivatives and the Gradient
Denition and some Properties of Generalized Elementary Functions of a Real Variable
 Denition and some Properties of Generalized Elementary Functions of a Real Variable I. Introduction The term elementary function is very often mentioned in many math classes and in books, e.g. Calculus
Denition and some Properties of Generalized Elementary Functions of a Real Variable I. Introduction The term elementary function is very often mentioned in many math classes and in books, e.g. Calculus
USA Mathematical Talent Search Round 2 Solutions Year 27 Academic Year
 1/2/27. In the grid to the right, the shortest path through unit squares between the pair of 2 s has length 2. Fill in some of the unit squares in the grid so that (i) exactly half of the squares in each
1/2/27. In the grid to the right, the shortest path through unit squares between the pair of 2 s has length 2. Fill in some of the unit squares in the grid so that (i) exactly half of the squares in each
A BRIEF REVIEW OF ALGEBRA AND TRIGONOMETRY
 A BRIEF REVIEW OF ALGEBRA AND TRIGONOMETR Some Key Concepts:. The slope and the equation of a straight line. Functions and functional notation. The average rate of change of a function and the DIFFERENCE-
A BRIEF REVIEW OF ALGEBRA AND TRIGONOMETR Some Key Concepts:. The slope and the equation of a straight line. Functions and functional notation. The average rate of change of a function and the DIFFERENCE-
Algebra 2 Summer Work Packet
 Algebra Summer Work Packet Covering Prerequisite Concepts for Incoming Algebra 1 Students This workbook contains problems designed to ensure the student's readiness for Algebra. The nine topics covered
Algebra Summer Work Packet Covering Prerequisite Concepts for Incoming Algebra 1 Students This workbook contains problems designed to ensure the student's readiness for Algebra. The nine topics covered
Partial Fractions. June 27, In this section, we will learn to integrate another class of functions: the rational functions.
 Partial Fractions June 7, 04 In this section, we will learn to integrate another class of functions: the rational functions. Definition. A rational function is a fraction of two polynomials. For example,
Partial Fractions June 7, 04 In this section, we will learn to integrate another class of functions: the rational functions. Definition. A rational function is a fraction of two polynomials. For example,
CSCI 150 Discrete Mathematics Homework 5 Solution
 CSCI 150 Discrete Mathematics Homework 5 Solution Saad Mneimneh Computer Science Hunter College of CUNY Problem 1: Happy Birthday (if it applies to you)! Based on the size of the class, there is approximately
CSCI 150 Discrete Mathematics Homework 5 Solution Saad Mneimneh Computer Science Hunter College of CUNY Problem 1: Happy Birthday (if it applies to you)! Based on the size of the class, there is approximately
INDEPENDENCE OF THE CONTINUUM HYPOTHESIS
 INDEPENDENCE OF THE CONTINUUM HYPOTHESIS CAPSTONE MATT LUTHER 1 INDEPENDENCE OF THE CONTINUUM HYPOTHESIS 2 1. Introduction This paper will summarize many of the ideas from logic and set theory that are
INDEPENDENCE OF THE CONTINUUM HYPOTHESIS CAPSTONE MATT LUTHER 1 INDEPENDENCE OF THE CONTINUUM HYPOTHESIS 2 1. Introduction This paper will summarize many of the ideas from logic and set theory that are
NIT #7 CORE ALGE COMMON IALS
 UN NIT #7 ANSWER KEY POLYNOMIALS Lesson #1 Introduction too Polynomials Lesson # Multiplying Polynomials Lesson # Factoring Polynomials Lesson # Factoring Based on Conjugate Pairs Lesson #5 Factoring Trinomials
UN NIT #7 ANSWER KEY POLYNOMIALS Lesson #1 Introduction too Polynomials Lesson # Multiplying Polynomials Lesson # Factoring Polynomials Lesson # Factoring Based on Conjugate Pairs Lesson #5 Factoring Trinomials
PUTNAM TRAINING MATHEMATICAL INDUCTION. Exercises
 PUTNAM TRAINING MATHEMATICAL INDUCTION (Last updated: December 11, 017) Remark. This is a list of exercises on mathematical induction. Miguel A. Lerma 1. Prove that n! > n for all n 4. Exercises. Prove
PUTNAM TRAINING MATHEMATICAL INDUCTION (Last updated: December 11, 017) Remark. This is a list of exercises on mathematical induction. Miguel A. Lerma 1. Prove that n! > n for all n 4. Exercises. Prove
MATH 250 TOPIC 11 LIMITS. A. Basic Idea of a Limit and Limit Laws. Answers to Exercises and Problems
 Math 5 T-Limits Page MATH 5 TOPIC LIMITS A. Basic Idea of a Limit and Limit Laws B. Limits of the form,, C. Limits as or as D. Summary for Evaluating Limits Answers to Eercises and Problems Math 5 T-Limits
Math 5 T-Limits Page MATH 5 TOPIC LIMITS A. Basic Idea of a Limit and Limit Laws B. Limits of the form,, C. Limits as or as D. Summary for Evaluating Limits Answers to Eercises and Problems Math 5 T-Limits
MAC1105-College Algebra
 MAC1105-College Algebra Chapter -Polynomial Division & Rational Functions. Polynomial Division;The Remainder and Factor Theorems I. Long Division of Polynomials A. For f ( ) 6 19 16, a zero of f ( ) occurs
MAC1105-College Algebra Chapter -Polynomial Division & Rational Functions. Polynomial Division;The Remainder and Factor Theorems I. Long Division of Polynomials A. For f ( ) 6 19 16, a zero of f ( ) occurs
Ch. 7.1 Polynomial Degree & Finite Differences
 Ch. 7.1 Polynomial Degree & Finite Differences Learning Intentions: Define terminology associated with polynomials: term, monomial, binomial & trinomial. Use the finite differences method to determine
Ch. 7.1 Polynomial Degree & Finite Differences Learning Intentions: Define terminology associated with polynomials: term, monomial, binomial & trinomial. Use the finite differences method to determine
Modelling with cellular automata
 Modelling with cellular automata Shan He School for Computational Science University of Birmingham Module 06-23836: Computational Modelling with MATLAB Outline Outline of Topics Concepts about cellular
Modelling with cellular automata Shan He School for Computational Science University of Birmingham Module 06-23836: Computational Modelling with MATLAB Outline Outline of Topics Concepts about cellular
Math 2414 Activity 1 (Due by end of class July 23) Precalculus Problems: 3,0 and are tangent to the parabola axis. Find the other line.
 Math 44 Activity (Due by end of class July 3) Precalculus Problems: 3, and are tangent to the parabola ais. Find the other line.. One of the two lines that pass through y is the - {Hint: For a line through
Math 44 Activity (Due by end of class July 3) Precalculus Problems: 3, and are tangent to the parabola ais. Find the other line.. One of the two lines that pass through y is the - {Hint: For a line through
Daily Lessons and Assessments for AP* Calculus AB, A Complete Course Page 584 Mark Sparks 2012
 The Second Fundamental Theorem of Calculus Functions Defined by Integrals Given the functions, f(t), below, use F( ) f ( t) dt to find F() and F () in terms of.. f(t) = 4t t. f(t) = cos t Given the functions,
The Second Fundamental Theorem of Calculus Functions Defined by Integrals Given the functions, f(t), below, use F( ) f ( t) dt to find F() and F () in terms of.. f(t) = 4t t. f(t) = cos t Given the functions,
Section 7.1: Functions Defined on General Sets
 Section 7.1: Functions Defined on General Sets In this chapter, we return to one of the most primitive and important concepts in mathematics - the idea of a function. Functions are the primary object of
Section 7.1: Functions Defined on General Sets In this chapter, we return to one of the most primitive and important concepts in mathematics - the idea of a function. Functions are the primary object of
DISCOVERING THE PYTHAGOREAN IDENTITIES LEARNING TASK:
 Name: Class Period: DISCOVERING THE PYTHAGOREAN IDENTITIES LEARNING TASK: An identity is an equation that is valid for all values of the variable for which the epressions in the equation are defined. You
Name: Class Period: DISCOVERING THE PYTHAGOREAN IDENTITIES LEARNING TASK: An identity is an equation that is valid for all values of the variable for which the epressions in the equation are defined. You
Basic Proof Techniques
 Basic Proof Techniques Joshua Wilde, revised by Isabel Tecu, Takeshi Suzuki and María José Boccardi August 13, 2013 1 Basic Notation The following is standard notation for proofs: A B. A implies B. A B.
Basic Proof Techniques Joshua Wilde, revised by Isabel Tecu, Takeshi Suzuki and María José Boccardi August 13, 2013 1 Basic Notation The following is standard notation for proofs: A B. A implies B. A B.
Lecture 9 : PPAD and the Complexity of Equilibrium Computation. 1 Complexity Class PPAD. 1.1 What does PPAD mean?
 CS 599: Algorithmic Game Theory October 20, 2010 Lecture 9 : PPAD and the Complexity of Equilibrium Computation Prof. Xi Chen Scribes: Cheng Lu and Sasank Vijayan 1 Complexity Class PPAD 1.1 What does
CS 599: Algorithmic Game Theory October 20, 2010 Lecture 9 : PPAD and the Complexity of Equilibrium Computation Prof. Xi Chen Scribes: Cheng Lu and Sasank Vijayan 1 Complexity Class PPAD 1.1 What does
10.4: WORKING WITH TAYLOR SERIES
 04: WORKING WITH TAYLOR SERIES Contributed by OpenSta Mathematics at OpenSta CNX In the preceding section we defined Taylor series and showed how to find the Taylor series for several common functions
04: WORKING WITH TAYLOR SERIES Contributed by OpenSta Mathematics at OpenSta CNX In the preceding section we defined Taylor series and showed how to find the Taylor series for several common functions
Upper and Lower Bounds on the Number of Faults. a System Can Withstand Without Repairs. Cambridge, MA 02139
 Upper and Lower Bounds on the Number of Faults a System Can Withstand Without Repairs Michel Goemans y Nancy Lynch z Isaac Saias x Laboratory for Computer Science Massachusetts Institute of Technology
Upper and Lower Bounds on the Number of Faults a System Can Withstand Without Repairs Michel Goemans y Nancy Lynch z Isaac Saias x Laboratory for Computer Science Massachusetts Institute of Technology
The nite submodel property and ω-categorical expansions of pregeometries
 The nite submodel property and ω-categorical expansions of pregeometries Marko Djordjevi bstract We prove, by a probabilistic argument, that a class of ω-categorical structures, on which algebraic closure
The nite submodel property and ω-categorical expansions of pregeometries Marko Djordjevi bstract We prove, by a probabilistic argument, that a class of ω-categorical structures, on which algebraic closure
3.3 Limits and Infinity
 Calculus Maimus. Limits Infinity Infinity is not a concrete number, but an abstract idea. It s not a destination, but a really long, never-ending journey. It s one of those mind-warping ideas that is difficult
Calculus Maimus. Limits Infinity Infinity is not a concrete number, but an abstract idea. It s not a destination, but a really long, never-ending journey. It s one of those mind-warping ideas that is difficult
8.2 Graphing More Complicated Rational Functions
 1 Locker LESSON 8. Graphing More Complicated Rational Functions PAGE 33 Name Class Date 8. Graphing More Complicated Rational Functions Essential Question: What features of the graph of a rational function
1 Locker LESSON 8. Graphing More Complicated Rational Functions PAGE 33 Name Class Date 8. Graphing More Complicated Rational Functions Essential Question: What features of the graph of a rational function
18.303: Introduction to Green s functions and operator inverses
 8.33: Introduction to Green s functions and operator inverses S. G. Johnson October 9, 2 Abstract In analogy with the inverse A of a matri A, we try to construct an analogous inverse  of differential
8.33: Introduction to Green s functions and operator inverses S. G. Johnson October 9, 2 Abstract In analogy with the inverse A of a matri A, we try to construct an analogous inverse  of differential
Introduction to Real Analysis
 Introduction to Real Analysis Joshua Wilde, revised by Isabel Tecu, Takeshi Suzuki and María José Boccardi August 13, 2013 1 Sets Sets are the basic objects of mathematics. In fact, they are so basic that
Introduction to Real Analysis Joshua Wilde, revised by Isabel Tecu, Takeshi Suzuki and María José Boccardi August 13, 2013 1 Sets Sets are the basic objects of mathematics. In fact, they are so basic that
Unofficial Solutions
 Canadian Open Mathematics Challenge 2016 Unofficial Solutions COMC exams from other years, with or without the solutions included, are free to download online. Please visit http://comc.math.ca/2016/practice.html
Canadian Open Mathematics Challenge 2016 Unofficial Solutions COMC exams from other years, with or without the solutions included, are free to download online. Please visit http://comc.math.ca/2016/practice.html
2 Generating Functions
 2 Generating Functions In this part of the course, we re going to introduce algebraic methods for counting and proving combinatorial identities. This is often greatly advantageous over the method of finding
2 Generating Functions In this part of the course, we re going to introduce algebraic methods for counting and proving combinatorial identities. This is often greatly advantageous over the method of finding
Announcements. Read Section 2.1 (Sets), 2.2 (Set Operations) and 5.1 (Mathematical Induction) Existence Proofs. Non-constructive
 Announcements Homework 2 Due Homework 3 Posted Due next Monday Quiz 2 on Wednesday Read Section 2.1 (Sets), 2.2 (Set Operations) and 5.1 (Mathematical Induction) Exam 1 in two weeks Monday, February 19
Announcements Homework 2 Due Homework 3 Posted Due next Monday Quiz 2 on Wednesday Read Section 2.1 (Sets), 2.2 (Set Operations) and 5.1 (Mathematical Induction) Exam 1 in two weeks Monday, February 19
Math 1314 Lesson 4 Limits
 Math 1314 Lesson 4 Limits What is calculus? Calculus is the study of change, particularly, how things change over time. It gives us a framework for measuring change using some fairly simple models. In
Math 1314 Lesson 4 Limits What is calculus? Calculus is the study of change, particularly, how things change over time. It gives us a framework for measuring change using some fairly simple models. In
Reading and Writing. Mathematical Proofs. Slides by Arthur van Goetham
 Reading and Writing Mathematical Proofs Slides by Arthur van Goetham What is a proof? Why explanations are not proofs What is a proof? A method for establishing truth What establishes truth depends on
Reading and Writing Mathematical Proofs Slides by Arthur van Goetham What is a proof? Why explanations are not proofs What is a proof? A method for establishing truth What establishes truth depends on
Applications of Statics, Including Problem-Solving Strategies
 OpenStax-CNX module: m42173 1 Applications of Statics, Including Problem-Solving Strategies OpenStax College This work is produced by OpenStax-CNX and licensed under the Creative Commons Attribution License
OpenStax-CNX module: m42173 1 Applications of Statics, Including Problem-Solving Strategies OpenStax College This work is produced by OpenStax-CNX and licensed under the Creative Commons Attribution License
3.7 Indeterminate Forms - l Hôpital s Rule
 3.7. INDETERMINATE FORMS - L HÔPITAL S RULE 4 3.7 Indeterminate Forms - l Hôpital s Rule 3.7. Introduction An indeterminate form is a form for which the answer is not predictable. From the chapter on lits,
3.7. INDETERMINATE FORMS - L HÔPITAL S RULE 4 3.7 Indeterminate Forms - l Hôpital s Rule 3.7. Introduction An indeterminate form is a form for which the answer is not predictable. From the chapter on lits,
Exam EDAF May 2011, , Vic1. Thore Husfeldt
 Exam EDAF05 25 May 2011, 8.00 13.00, Vic1 Thore Husfeldt Instructions What to bring. You can bring any written aid you want. This includes the course book and a dictionary. In fact, these two things are
Exam EDAF05 25 May 2011, 8.00 13.00, Vic1 Thore Husfeldt Instructions What to bring. You can bring any written aid you want. This includes the course book and a dictionary. In fact, these two things are
COM S 330 Lecture Notes Week of Feb 9 13
 Monday, February 9. Rosen.4 Sequences Reading: Rosen.4. LLM 4.. Ducks 8., 8., Def: A sequence is a function from a (usually infinite) subset of the integers (usually N = {0,,, 3,... } or Z + = {,, 3, 4,...
Monday, February 9. Rosen.4 Sequences Reading: Rosen.4. LLM 4.. Ducks 8., 8., Def: A sequence is a function from a (usually infinite) subset of the integers (usually N = {0,,, 3,... } or Z + = {,, 3, 4,...
Sec. 1 Simplifying Rational Expressions: +
 Chapter 9 Rational Epressions Sec. Simplifying Rational Epressions: + The procedure used to add and subtract rational epressions in algebra is the same used in adding and subtracting fractions in 5 th
Chapter 9 Rational Epressions Sec. Simplifying Rational Epressions: + The procedure used to add and subtract rational epressions in algebra is the same used in adding and subtracting fractions in 5 th
Limits and Continuity
 Limits and Continuity Philippe B. Laval Kennesaw State University January 2, 2005 Contents Abstract Notes and practice problems on its and continuity. Limits 2. Introduction... 2.2 Theory:... 2.2. GraphicalMethod...
Limits and Continuity Philippe B. Laval Kennesaw State University January 2, 2005 Contents Abstract Notes and practice problems on its and continuity. Limits 2. Introduction... 2.2 Theory:... 2.2. GraphicalMethod...
Notes for Recitation 14
 6.04/18.06J Mathematics for Computer Science October 7, 006 Tom Leighton and Ronitt Rubinfeld Notes for Recitation 14 Guessing a Particular Solution A general linear recurrence has the form: fn) = b 1
6.04/18.06J Mathematics for Computer Science October 7, 006 Tom Leighton and Ronitt Rubinfeld Notes for Recitation 14 Guessing a Particular Solution A general linear recurrence has the form: fn) = b 1
Linear Algebra (part 1) : Vector Spaces (by Evan Dummit, 2017, v. 1.07) 1.1 The Formal Denition of a Vector Space
 Linear Algebra (part 1) : Vector Spaces (by Evan Dummit, 2017, v. 1.07) Contents 1 Vector Spaces 1 1.1 The Formal Denition of a Vector Space.................................. 1 1.2 Subspaces...................................................
Linear Algebra (part 1) : Vector Spaces (by Evan Dummit, 2017, v. 1.07) Contents 1 Vector Spaces 1 1.1 The Formal Denition of a Vector Space.................................. 1 1.2 Subspaces...................................................
CANADIAN MATHEMATICAL OLYMPIAD 2010 PROBLEMS AND SOLUTIONS
 CANADIAN MATHEMATICAL OLYMPIAD 2010 PROBLEMS AND SOLUTIONS (1) For a positive integer n, an n-staircase is a figure consisting of unit squares, with one square in the first row, two squares in the second
CANADIAN MATHEMATICAL OLYMPIAD 2010 PROBLEMS AND SOLUTIONS (1) For a positive integer n, an n-staircase is a figure consisting of unit squares, with one square in the first row, two squares in the second
Contents. 2.1 Vectors in R n. Linear Algebra (part 2) : Vector Spaces (by Evan Dummit, 2017, v. 2.50) 2 Vector Spaces
 Linear Algebra (part 2) : Vector Spaces (by Evan Dummit, 2017, v 250) Contents 2 Vector Spaces 1 21 Vectors in R n 1 22 The Formal Denition of a Vector Space 4 23 Subspaces 6 24 Linear Combinations and
Linear Algebra (part 2) : Vector Spaces (by Evan Dummit, 2017, v 250) Contents 2 Vector Spaces 1 21 Vectors in R n 1 22 The Formal Denition of a Vector Space 4 23 Subspaces 6 24 Linear Combinations and
4 Inverse function theorem
 Tel Aviv University, 2014/15 Analysis-III,IV 71 4 Inverse function theorem 4a What is the problem................ 71 4b Simple observations before the theorem..... 72 4c The theorem.....................
Tel Aviv University, 2014/15 Analysis-III,IV 71 4 Inverse function theorem 4a What is the problem................ 71 4b Simple observations before the theorem..... 72 4c The theorem.....................
Discrete Mathematics. Spring 2017
 Discrete Mathematics Spring 2017 Previous Lecture Principle of Mathematical Induction Mathematical Induction: Rule of Inference Mathematical Induction: Conjecturing and Proving Mathematical Induction:
Discrete Mathematics Spring 2017 Previous Lecture Principle of Mathematical Induction Mathematical Induction: Rule of Inference Mathematical Induction: Conjecturing and Proving Mathematical Induction:
21.1 Solving Equations by Factoring
 Name Class Date 1.1 Solving Equations by Factoring x + bx + c Essential Question: How can you use factoring to solve quadratic equations in standard form for which a = 1? Resource Locker Explore 1 Using
Name Class Date 1.1 Solving Equations by Factoring x + bx + c Essential Question: How can you use factoring to solve quadratic equations in standard form for which a = 1? Resource Locker Explore 1 Using
MATH 1010E University Mathematics Lecture Notes (week 8) Martin Li
 MATH 1010E University Mathematics Lecture Notes (week 8) Martin Li 1 L Hospital s Rule Another useful application of mean value theorems is L Hospital s Rule. It helps us to evaluate its of indeterminate
MATH 1010E University Mathematics Lecture Notes (week 8) Martin Li 1 L Hospital s Rule Another useful application of mean value theorems is L Hospital s Rule. It helps us to evaluate its of indeterminate
Horizontal asymptotes
 Roberto s Notes on Differential Calculus Chapter 1: Limits and continuity Section 5 Limits at infinity and Horizontal asymptotes What you need to know already: The concept, notation and terminology of
Roberto s Notes on Differential Calculus Chapter 1: Limits and continuity Section 5 Limits at infinity and Horizontal asymptotes What you need to know already: The concept, notation and terminology of
Taylor and Maclaurin Series. Approximating functions using Polynomials.
 Taylor and Maclaurin Series Approximating functions using Polynomials. Approximating f x = e x near x = 0 In order to approximate the function f x = e x near x = 0, we can use the tangent line (The Linear
Taylor and Maclaurin Series Approximating functions using Polynomials. Approximating f x = e x near x = 0 In order to approximate the function f x = e x near x = 0, we can use the tangent line (The Linear
1 I A Q E B A I E Q 1 A ; E Q A I A (2) A : (3) A : (4)
 Latin Squares Denition and examples Denition. (Latin Square) An n n Latin square, or a latin square of order n, is a square array with n symbols arranged so that each symbol appears just once in each row
Latin Squares Denition and examples Denition. (Latin Square) An n n Latin square, or a latin square of order n, is a square array with n symbols arranged so that each symbol appears just once in each row
7.3 Adding and Subtracting Rational Expressions
 7.3 Adding and Subtracting Rational Epressions LEARNING OBJECTIVES. Add and subtract rational epressions with common denominators. 2. Add and subtract rational epressions with unlike denominators. 3. Add
7.3 Adding and Subtracting Rational Epressions LEARNING OBJECTIVES. Add and subtract rational epressions with common denominators. 2. Add and subtract rational epressions with unlike denominators. 3. Add
Grades ALGEBRA TILES. Don Balka and Laurie Boswell. Rowley, MA didax.com
 Grades 6 12 ALGEBRA TILES Don Balka and Laurie Boswell Rowley, MA 01969 didax.com CONTENTS Introduction Correlation to the h Standards Unit 1: Introduction to Algebra Tiles 1 Overview and Answers 2 Activity
Grades 6 12 ALGEBRA TILES Don Balka and Laurie Boswell Rowley, MA 01969 didax.com CONTENTS Introduction Correlation to the h Standards Unit 1: Introduction to Algebra Tiles 1 Overview and Answers 2 Activity
Section 5.3 The Newton Form of the Interpolating Polynomial
 Section 5.3 The Newton Form of the Interpolating Polynomial Key terms Divided Difference basis Add-on feature Divided Difference Table The Lagrange form is not very efficient if we have to evaluate the
Section 5.3 The Newton Form of the Interpolating Polynomial Key terms Divided Difference basis Add-on feature Divided Difference Table The Lagrange form is not very efficient if we have to evaluate the
Integration by substitution
 Roberto s Notes on Integral Calculus Chapter : Integration methods Section 1 Integration by substitution or by change of variable What you need to know already: What an indefinite integral is. The chain
Roberto s Notes on Integral Calculus Chapter : Integration methods Section 1 Integration by substitution or by change of variable What you need to know already: What an indefinite integral is. The chain
Monte Carlo Methods for Statistical Inference: Variance Reduction Techniques
 Monte Carlo Methods for Statistical Inference: Variance Reduction Techniques Hung Chen hchen@math.ntu.edu.tw Department of Mathematics National Taiwan University 3rd March 2004 Meet at NS 104 On Wednesday
Monte Carlo Methods for Statistical Inference: Variance Reduction Techniques Hung Chen hchen@math.ntu.edu.tw Department of Mathematics National Taiwan University 3rd March 2004 Meet at NS 104 On Wednesday
ECE 440 Lecture 12 : Diffusion of Carriers Class Outline:
 ECE 440 Lecture 12 : Diffusion of Carriers Class Outline: Band Bending Diffusion Processes Diffusion and Drift of Carriers Things you should know when you leave Key Questions How do I calculate kinetic
ECE 440 Lecture 12 : Diffusion of Carriers Class Outline: Band Bending Diffusion Processes Diffusion and Drift of Carriers Things you should know when you leave Key Questions How do I calculate kinetic
CHMMC 2015 Individual Round Problems
 CHMMC 05 Individual Round Problems November, 05 Problem 0.. The following number is the product of the divisors of n. What is n? 6 3 3 Solution.. In general, the product of the divisors of n is n # of
CHMMC 05 Individual Round Problems November, 05 Problem 0.. The following number is the product of the divisors of n. What is n? 6 3 3 Solution.. In general, the product of the divisors of n is n # of
QUIZ ON CHAPTERS 1 AND 2 - SOLUTIONS REVIEW / LIMITS AND CONTINUITY; MATH 150 SPRING 2017 KUNIYUKI 105 POINTS TOTAL, BUT 100 POINTS = 100%
 QUIZ ON CHAPTERS AND 2 - SOLUTIONS REVIEW / LIMITS AND CONTINUITY; MATH 50 SPRING 207 KUNIYUKI 05 POINTS TOTAL, BUT 00 POINTS = 00% ) For a), b), and c) below, bo in the correct answer. (6 points total;
QUIZ ON CHAPTERS AND 2 - SOLUTIONS REVIEW / LIMITS AND CONTINUITY; MATH 50 SPRING 207 KUNIYUKI 05 POINTS TOTAL, BUT 00 POINTS = 00% ) For a), b), and c) below, bo in the correct answer. (6 points total;
Math 42, Discrete Mathematics
 c Fall 2018 last updated 12/05/2018 at 15:47:21 For use by students in this class only; all rights reserved. Note: some prose & some tables are taken directly from Kenneth R. Rosen, and Its Applications,
c Fall 2018 last updated 12/05/2018 at 15:47:21 For use by students in this class only; all rights reserved. Note: some prose & some tables are taken directly from Kenneth R. Rosen, and Its Applications,
Homework 1 Solutions ECEn 670, Fall 2013
 Homework Solutions ECEn 670, Fall 03 A.. Use the rst seven relations to prove relations (A.0, (A.3, and (A.6. Prove (F G c F c G c (A.0. (F G c ((F c G c c c by A.6. (F G c F c G c by A.4 Prove F (F G
Homework Solutions ECEn 670, Fall 03 A.. Use the rst seven relations to prove relations (A.0, (A.3, and (A.6. Prove (F G c F c G c (A.0. (F G c ((F c G c c c by A.6. (F G c F c G c by A.4 Prove F (F G
On the Chvatál-Complexity of Binary Knapsack Problems. Gergely Kovács 1 Béla Vizvári College for Modern Business Studies, Hungary
 On the Chvatál-Complexity of Binary Knapsack Problems Gergely Kovács 1 Béla Vizvári 2 1 College for Modern Business Studies, Hungary 2 Eastern Mediterranean University, TRNC 2009. 1 Chvátal Cut and Complexity
On the Chvatál-Complexity of Binary Knapsack Problems Gergely Kovács 1 Béla Vizvári 2 1 College for Modern Business Studies, Hungary 2 Eastern Mediterranean University, TRNC 2009. 1 Chvátal Cut and Complexity
Basic methods to solve equations
 Roberto s Notes on Prerequisites for Calculus Chapter 1: Algebra Section 1 Basic methods to solve equations What you need to know already: How to factor an algebraic epression. What you can learn here:
Roberto s Notes on Prerequisites for Calculus Chapter 1: Algebra Section 1 Basic methods to solve equations What you need to know already: How to factor an algebraic epression. What you can learn here:
13 Lecture 13 L Hospital s Rule and Taylor s Theorem
 3 Lecture 3 L Hospital s Rule and Taylor s Theorem 3 L Hospital s Rule Theorem 3 L Hospital s Rule) Let a R or a = and functions f,g : a,b) R satisfy the following properties ) f,g are differentiable on
3 Lecture 3 L Hospital s Rule and Taylor s Theorem 3 L Hospital s Rule Theorem 3 L Hospital s Rule) Let a R or a = and functions f,g : a,b) R satisfy the following properties ) f,g are differentiable on
Problem 1. Solve the equation 3 x + 9 x = 27 x. Solution: 3 x + 3 2x = 3 3x. Denote: y = 3 x, then. y + y 2 = y 3. y 3 y 2 y = 0. y(y 2 y 1) = 0.
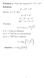 Problem 1. Solve the equation 3 x + 9 x = 7 x. Solution: 3 x + 3 x = 3 3x. Denote: y = 3 x, then Therefore, y + y = y 3. y 3 y y = 0. y(y y 1) = 0. y = 0 or y = 1 ± 5. i) 3 x = 0 has no solutions, ii)
Problem 1. Solve the equation 3 x + 9 x = 7 x. Solution: 3 x + 3 x = 3 3x. Denote: y = 3 x, then Therefore, y + y = y 3. y 3 y y = 0. y(y y 1) = 0. y = 0 or y = 1 ± 5. i) 3 x = 0 has no solutions, ii)
David Sagan. The standard analysis for a coupled lattice is based upon the formalism of Edwards
 Twiss Analysis With a Mobius Lattice David Sagan CBN 98{14 July 10, 1998 1 Introduction The standard analysis for a coupled lattice is based upon the formalism of Edwards and Teng[1]. This is ne for weak
Twiss Analysis With a Mobius Lattice David Sagan CBN 98{14 July 10, 1998 1 Introduction The standard analysis for a coupled lattice is based upon the formalism of Edwards and Teng[1]. This is ne for weak
Maths A Level Summer Assignment & Transition Work
 Maths A Level Summer Assignment & Transition Work The summer assignment element should take no longer than hours to complete. Your summer assignment for each course must be submitted in the relevant first
Maths A Level Summer Assignment & Transition Work The summer assignment element should take no longer than hours to complete. Your summer assignment for each course must be submitted in the relevant first
Understanding Part 2 of The Fundamental Theorem of Calculus
 Understanding Part of The Fundamental Theorem of Calculus Worksheet 8: The Graph of F () What is an Anti-Derivative? Give an eample that is algebraic: and an eample that is graphical: eample : Below is
Understanding Part of The Fundamental Theorem of Calculus Worksheet 8: The Graph of F () What is an Anti-Derivative? Give an eample that is algebraic: and an eample that is graphical: eample : Below is
2.5 Absolute Value Equations and Inequalities
 5 Absolute Value Equations Inequalities We begin this section by recalling the following definition Definition: Absolute Value The absolute value of a number is the distance that the number is from zero
5 Absolute Value Equations Inequalities We begin this section by recalling the following definition Definition: Absolute Value The absolute value of a number is the distance that the number is from zero
Taylor and Maclaurin Series. Approximating functions using Polynomials.
 Taylor and Maclaurin Series Approximating functions using Polynomials. Approximating f x = e x near x = 0 In order to approximate the function f x = e x near x = 0, we can use the tangent line (The Linear
Taylor and Maclaurin Series Approximating functions using Polynomials. Approximating f x = e x near x = 0 In order to approximate the function f x = e x near x = 0, we can use the tangent line (The Linear
Systems of Linear Equations
 Systems of Linear Equations Linear Equation Definition Any equation that is equivalent to the following format a a ann b (.) where,,, n are unknown variables and a, a,, an, b are known numbers (the so
Systems of Linear Equations Linear Equation Definition Any equation that is equivalent to the following format a a ann b (.) where,,, n are unknown variables and a, a,, an, b are known numbers (the so
Math 2414 Activity 1 (Due by end of class Jan. 26) Precalculus Problems: 3,0 and are tangent to the parabola axis. Find the other line.
 Math Activity (Due by end of class Jan. 6) Precalculus Problems: 3, and are tangent to the parabola ais. Find the other line.. One of the two lines that pass through y is the - {Hint: For a line through
Math Activity (Due by end of class Jan. 6) Precalculus Problems: 3, and are tangent to the parabola ais. Find the other line.. One of the two lines that pass through y is the - {Hint: For a line through
CSC 8301 Design & Analysis of Algorithms: Lower Bounds
 CSC 8301 Design & Analysis of Algorithms: Lower Bounds Professor Henry Carter Fall 2016 Recap Iterative improvement algorithms take a feasible solution and iteratively improve it until optimized Simplex
CSC 8301 Design & Analysis of Algorithms: Lower Bounds Professor Henry Carter Fall 2016 Recap Iterative improvement algorithms take a feasible solution and iteratively improve it until optimized Simplex
Single Pile (Move Size) Dynamic Blocking Nim
 Single Pile (Move Size) Dynamic Blocking Nim Abstract: Several authors have written papers dealing with a class of combinatorial games consisting of one-pile counter pickup games for which the maximum
Single Pile (Move Size) Dynamic Blocking Nim Abstract: Several authors have written papers dealing with a class of combinatorial games consisting of one-pile counter pickup games for which the maximum
CMPSCI 250: Introduction to Computation. Lecture 11: Proof Techniques David Mix Barrington 5 March 2013
 CMPSCI 250: Introduction to Computation Lecture 11: Proof Techniques David Mix Barrington 5 March 2013 Proof Techniques Review: The General Setting for Proofs Types of Proof: Direct, Contraposition, Contradiction
CMPSCI 250: Introduction to Computation Lecture 11: Proof Techniques David Mix Barrington 5 March 2013 Proof Techniques Review: The General Setting for Proofs Types of Proof: Direct, Contraposition, Contradiction
AP Calculus Notes: Unit 1 Limits & Continuity. Syllabus Objective: 1.1 The student will calculate limits using the basic limit theorems.
 Syllabus Objective:. The student will calculate its using the basic it theorems. LIMITS how the outputs o a unction behave as the inputs approach some value Finding a Limit Notation: The it as approaches
Syllabus Objective:. The student will calculate its using the basic it theorems. LIMITS how the outputs o a unction behave as the inputs approach some value Finding a Limit Notation: The it as approaches
Essential Question: How can you solve equations involving variable exponents? Explore 1 Solving Exponential Equations Graphically
 6 7 6 y 7 8 0 y 7 8 0 Locker LESSON 1 1 Using Graphs and Properties to Solve Equations with Eponents Common Core Math Standards The student is epected to: A-CED1 Create equations and inequalities in one
6 7 6 y 7 8 0 y 7 8 0 Locker LESSON 1 1 Using Graphs and Properties to Solve Equations with Eponents Common Core Math Standards The student is epected to: A-CED1 Create equations and inequalities in one
Math 19, Homework-1 Solutions
 SSEA Summer 207 Math 9, Homework- Solutions. Consider the graph of function f shown below. Find the following its or eplain why they do not eist: (a) t 2 f(t). = 0. (b) t f(t). =. (c) t 0 f(t). (d) Does
SSEA Summer 207 Math 9, Homework- Solutions. Consider the graph of function f shown below. Find the following its or eplain why they do not eist: (a) t 2 f(t). = 0. (b) t f(t). =. (c) t 0 f(t). (d) Does
