DIFFERENTIAL GEOMETRY
|
|
|
- Rolf Walker
- 5 years ago
- Views:
Transcription
1 DIFFERENTIAL GEOMETRY MUZAMMIL TANVEER Available at :
2 Lecture # 1 Curvature: Centre, Radius of Curvature: y More bending less curvature. Less bending more curvature. Q A P + x Let AP s QP s PNQ If P Q then N C Also 0 C is the Centre of curvature. lim K (Kappa) Radius of Curvature 1 P a g e
3 The curvature, radius of curvature, Centre of curvature, circle of curvature is different at any points on the curve. If we change the points. Then these all can be change. If the curvature is constant at every point then it is called Circle. Radius of Curvature Formula for Radius of Curvature: Let tangent of curve at point makes angle with x-axis then by the definition of the derivative tan sec (1+tan ) [1+ ] K [ ] length of the curve [ ] Radius of Curvature Centre of Curvature: Let y f(x) be the given curve. And (, ) be the Centre of the curvature. Then at point P (x, y ) of the curve the values of and given as x - [ ] y + [ ] Circle of Curvature: (x ) + (y ) If sometime parametric equations of the curve y f(t), x g(t) then. 2 P a g e
4 Question: Prove that curvature of the circle x + y a is constant. Given x + y a 2x + 2y 0 x + y 0 - [ ] [ ] [ ] Question: -a Prove that Radius of the curvature at point x p then y 4sinx-sin2x is 4cosx-2cos2x at x p, 2-4sinx+4sin2x at x p, -4 [ ] [ ] - Note: Here (-) is neglected because radius cannot be negative. 3 P a g e
5 Question: Find the Centre of curvature at point x, y of parabola y 4ax. Solution Given y 4ax. 2y 4a 2ay -4a y x - [ ] x - [ ] x - [ ] x - [ ] x + + 3x + 2a y + [ ] y - [ ] y - [ ] y [ + ] y - y - or - 4 P a g e
6 Question: Find the radius of curvature for the curve. y 3asint-asin3t x 3acost-acos3t 3acost-3acos3t, -3asint+3asin3t -3asint+9asin3t, -3acost+9acos3t., cosa-cosb -2sin sin sina-sinb 2cos sin sina-sinb cos2t.sint, cosa-cosb sin2t.sint tan2t 2sec 2t. [ ] [ ] 3asint (3acos2t.sint) (sec2t) 5 P a g e
7 Question: If and be the radii of curvature at the Extremities of two conjugate diameters then prove that + (ab ) a + b Solution: Use an equation of Ellipse + 1 (1) (-a,0) (0,b) (a,0) (a,0) + 0 or (0,-b) [ ] [ ] y a [y 2 a 4 x 2 b 4 ] y 2 a 4 y a [y2 a 4 x 2 b 4 ] [y 2 a 4 x 2 b 4 ] At (a,0), At (0,b) + (ab ) a + b + (ab ) a + b (ab ) + a + b a + b a + b 6 P a g e
8 Lecture # 2 Curvature and Radius of Curvature in Polar Form: Let r f () Let x rcos, y rsin cos rsin sin + rcos (ii) (i) rcos sin sin+cos cos 2 sin rcos (iii) rsin+cos + sin + cos sin+2 cos rsin (iv) Squaring and Adding (i) and (ii) + cos rsin + sin + rcos + (cos + sin )+r (sin + cos ) r (1)+ (1) + r + Formula for curvature if x f(), y g() (v) K.. K. Replace r, r 7 P a g e
9 K K [( ).( ) ( )( )] [ ] ( ) ( ) K ( ) ( ) ( ) K K K or ( ) ( ) Question: For curve r a cosm then prove that Solution: r a cosm Taking ln on both side ln r ln a cosm m lnr ln (a ) + ln (cosm) Differentiate w.r.t m. 0 + ( sinm. m). - m. -tanm or -rtanm Again, differentiating w.r.t rsec m. m-tanm mrsec m. m-tanm(-rtanm) rtan m mrsec m 8 P a g e
10 We know that ( ) ( ) [ ( ) ] ( ) ( ) [ ] [ ] [] since r a cosm or cosm Question: Prove that If r a (1+cos) then is constant. Solution: r a (1+cos) r a+acos -asin -acos ( ) ( ) [ ] [ ] [ ] ( ) [ ] [ ] [ ] Taking square on both sides which is constant 9 P a g e
11 For Parametric Equations: Question:.. If x a(t+sint), y a(1-cost) then show that 4acos Solution: x a(t+sint) y a(1-cost) a(1+cost) or (a+accost) asint -asint accost We know that.. [ ]. [ )] [ )] [ )] [ )] [ )] 2 a 2cos 2 acos 4acos Question: Find the curvature at (, ) of x +y 3axy Solution: Let f(x, y) x +y 3axy f (x, y) 3x 3ay f (x, y)/(, ) 3 3a 10 P a g e
12 f (x, y) 3y 3ax f (x,y)/(, ) 3 3a f (x, y) 6x f (x,y)/(, ) 6 9a f (x, y) 6y f (x,y)/(, ) 6 9a f (x, y) 3a Now formula for Curvature K [ ] Question: K Show that the radius of curvature at point x acos, y asin is equal to three times length of perpendicular from origin to the tangent. Solution: x acos, y asin -3acos sin, 3asin cos. -tan 11 P a g e
13 sec. -sec. We Know [ ] [ ] [1 + tan ]. 3acos sin [sec ]. 3acos sin sec. 3acos sin 3asincos (i) Now we find the equation of tangent. Equation of tangent at (acos,asin ) Since y y m(x x ) y asin tan (x acos ) y asin (x acos ) ycos asin cos xsin + asincos xsin + ycos asin cos + asincos 0 xsin + ycos asincos(cos + sin ) 0 xsin + ycos asincos 0 (ii) Let d be the length of perpendicular from (0,0) to the tangent line. Since d d ( q) ( q) q q d asincos q q d q q from (i) 3asincos 3d Hence radius of curvature is equal to three times length of perpendicular from origin to tangent. 12 P a g e
14 Lecture # 3 Space curve or Twisted curve or Skew curve: When all the points denoted the curve lies in the same plane is said to be a plain curve otherwise is called space curve or twisted curve or skew curve. Tangent line: The line which cut the curve at one point is called tangent line. Normal line: The line which is perpendicular to the tangent line is called Normal line. Secant line: The line which cut the curve at two points is called secant line. Equation of tangent of a point: Let P and a be any two points on the curve c whose position vector are and +. a t We note that the limiting value if is a unit vector and parallel to the tangent to the curve at point P. s P Let tangent lim, Let be the position vector of any point on the tangent line. If u is the variable number +ve or -ve then we know that is parallel to then + + which is equation of tangent. Similarly, equation of normal is + and equation of binomial is +. The line which is perpendicular on both tangent and normal line is called binomial line. 13 P a g e
15 Question: Find the equation of tangent to the curve whose coordinates are x acos, y asin and z 0 Let And + + -asin.q, acos.q, 0 We know the equation of tangent u Question: u.q.q.q.q cos( acos) sin( asin) Xcos-a q -Ysin+a q Xcos + Ysin a Find the equation of tangent whose coordinates are x -bcos, y bsin and z 0 Solution: Given the coordinates are x -bcos, y bsin and z 0 Let And + + bsin.q, bcos.q, 0 14 P a g e
16 We know the equation of tangent u.q.q.q u.q Xcos+b q Ysin q Ysin-Xcos b Normal plane: A plane passing through the point P and perpendicular to the tangent at point P is called normal plane. Equation of Normal plane: Let be the position vector of point on the curve is the position vector at any line in the plane. According to the definition of normal plane and are perpendicular to each other. c t. 0 Which is the equation of normal plane. P Oscillating plane or plane of Curvature: The plane parallel to the and normal at a point P on the curve c. If be the position vector of any point on the plane the, and are coplanar vector. [,, ] 0 (1) N P t // to or. 0 which is the equation of oscillating plane. It can also be expressed as // to N K K 15 P a g e
17 So, Equation (1) [,, ] 0 Which is the equation of oscillating plane in terms of and its derivative. In Cartesian form the equation of oscillating plane is 0 Question: For the curve x 3t, y 3 and z 2. Find the equation of oscillating plane. Solution: Since [ x, y, z] [ 3t, 3, 2 ] [ 3, 6t, 6 ] [ 0, 6, 12t] Now (X-3t)[72 36 ] ( 3 )[36 0] + ( 2 )[18 0] 0 0 (X-3t)[36 ] ( 3 )[36 ] + ( 2 )[18] [ ] P a g e
18 Question: Find the equation of oscillating plane if (s) (s) (s) + 0 We know the equation of oscillating plane is (X-acosx)(0-0)-(Y-asins)(0-0)+Z( + ) 0 z ( + ) 0 z 0 z 0 17 P a g e
19 Lecture # 4 Frenet-Serret Formula: (i) (ii) (iii) K τ K τ The vector, and are perpendicular to each other. From the right-handed system. And. 0,. 0,. 0. 1,. 1,. 1 or 1, 1, 1 1, 1, 1 Proof: τ Consider. 1 Diff. w.r.t s Now. 0 Diff. w.r.t s. 0 and are to each other As in (i) K. + K P a g e
20 . + K(0) is to. is to and is to. But is to tangent and. is parallel to τ Where τ measure the magnitude of arc rate of rotation of binomial and -ve sign indicate that vector along the normal but opposite direction. τ K Consider Diff. w.r.t s. +. Torsion:. +.. (K ) + ( τ ). K( ) τ( ) K( ) τ( ) -, τ K Rate of turning of binormal is called torsion of the curve at point P. Question: Prove that tangent (i) + Kτ (ii) ( Kτ ) 3K + (2 τ+kτ ) Proof: Since 19 P a g e
21 (1) K + K(τ K) + τ K + Kτ Now again diff. w.r.t s + 2K + τ + Kτ + Kτ (τ K) + 2K (K )+ τ + Kτ + Kτ( τ ) τ K + 2K + τ + Kτ Kτ ( Kτ ) 3K + (2 τ+kτ ) Question: (i) If τ find and (ii) If τ K find and Solution: (i) τ τ τ τ τ(τ K) τ τ +Kτ Kτ τ τ Again diff. w.r.t s τ+ Kτ + Kτ τ τ 2ττ τ τ + Kτ + Kτ(K ) τ τ (τ K) 2ττ τ ( τ ) τ + Kτ + τ τ τ τ + τ K 2ττ + τ 2 Kτ + τ + τ τ + τ 3ττ (2 Kτ + τ) + ( τ τ +τ ) 3ττ 20 P a g e
22 Solution: (ii) τ K τ + τ K K τ + τ( τ ) K K(K ) τ τ K K Diff. w.r.t s τ + τ 2ττ τ K K 2 K K τ + τ ( τ ) 2ττ τ (τ K) K K (K ) 2 K K (τ K) τ 3ττ τ +τ K K 3KK τk + K (τ τ K τ) + (Kτ +K K )+( 3ττ 3KK ) Question: Prove that τ [,, ] Solution: Since K K + K(τ K) + + K τ Now [,, ]. K. + K τ K ( ). [ + K τ ] K. [ + K τ ] K. + K.Kτ.. [,, ] K (0) + K.Kτ(1) (0) τ τ [,, ] 21 P a g e
23 Question: Prove that position vector on the curve satisfied the differential equation. [ ( )]+ [ ] + 0 Solution: Since K L.H.S [ ( K )]+ [ ] + K Since K, τ [ ]+ [ ] + τ [ ]+ [ ] + τ [ (τ K)]+ [ ] + τ [ (1) K)]+ [ ] + τ τ τ τ + τ 0 R.H.S τ Theorem: If tangent and binormal at a point P of a curve make angle and with a fix direction then prove that c Proof: q q Let c be the curve with point P on it and be a fixed direction with magnitude making angle and with tangent and normal respectively. P 22 P a g e
24 Consider. cos 1.1 cos. cos (1) Diff. w.r.t s. +. -sin q sin q 0 as is fixed K. -sin q (2) K Now. cos 1.1 cos. cos Diff. w.r.t s sin since 0 as is fixed τ. -sin Divide (2) by (3).. q q q Question: Prove that if K 0 at all points then that curve is straight line. Proof: We know that K (0) 0 On integrating a (tangent is fix which is possible only when curve is straight line. Question: Prove that if τ 0 at all points then that curve is plane curve. Proof: We know that τ (0) 0 On integrating a Binormal is fix which is possible only when curve is plane curve. 23 P a g e
25 Lecture # 5 Parameters other than s If the position vector r is a function of any other parameter u then prove that (i) (iii) K (v) τ [,, ] Solution: Since (ii) (iv) ( ).. (1) and K. +. (2) K Again differentiating w.r.t. u. +K. + K K. + 2K K. + 2K. +K K(τ K). + 2K. +K. +. since τ K, K Now +Kτ +3K. + (i) (. ) K + K ( ) + ( ) 24 P a g e
26 K + (0) since 0, (ii) ( K. +. ) (. ) K K + (iii) K K K K since 1 K (iv) ( ) ( ) ( K. +. ). ( K. +. ) (. ) (1) + (0)+ (0) + (1) + ( ) ( ) (v) τ [,, ] [,, ]. K.[ K +Kτ K +3K + ] K (. )+ τ (. ) (. )+ 3 (. )+K (. ) As. 1,. 0, P a g e
27 K (0)+ τ (1) (0)+ 3 (0)+K (0) Theorem: [,, ] τ τ [,, ] For x a(3u ) 3au-, y 3a, z a(3u+ ) 3au+ Then prove that K τ. Solution: We know that K And τ [,, ] τ [,, ] ( ) Now (x,y,z) τ [,, ] (3au-, 3a, 3au+ ) Diff. w.r.t u (3a-3a, 6au, 3a+3a ) (-6au, 6a, 6au) (-6a, 0, 6a) Now (3a 3a ) + (6 ) + (3a + 3a ) Now Note: ( ) 18 (1 + ) 3 2 a(1+ ) (1)... since 1 3a 3a 6 3a + 3a 6au 6a 6au 26 P a g e
28 18 {( 1) 2 + ( + 1) } (18 ) {( 1) + ( 2 ) + ( + 1) } 18 { } 18 2(1+ ) K K Now [,, ]. (2) 18 {( 1) 2 + ( + 1) }.(-6a +0 +6a ) 18 { 6 ( 1) 2 (0) + ( + 1)6 } 18 (12a) a(1 + ) (1 + ) 29 (2 ) (1 + ) 5832 (1 + ) τ [,, ]. τ From (2) and (3) K τ (3) Hence proved 27 P a g e
29 Lecture # 6 Question: For x 4a, y 4a, z 3ccos2u Then prove that (sinu, cosu, 0) and K Solution: (x, y, z) (4a, 4a, 3ccos2u) Diff. w.r.t s. since ((,, ). ( 12, 12a, 6 2 ). ( 6 (2 ), 6a(2 ), 6 2 ). ( 6 ( 2 ), 6a( 2 ), 6 2 ). 6 2 (, a, ). (1) Taking magnitude on both sides (6 2 ) ( + + ) 1 6sin2u ( + ) sin2u +. Put in (1) 6 2 (, a, ). (, a, ). Diff. w.r.t s. since 28 P a g e
30 [(, a, ). ]. K (,, ). (2) K Put the value of in eq (2) K (,, ). K (,, ) Taking Magnitude of both sides (3) K ( ) K ( )6sin2u 1, K From (3) K (,, ) K K(, co, 0) (, co, 0) Question: For a point of curve of intersection of surfaces and y xtanh Then prove that Solution: As given that (i) y xtanh (ii) (1) (cosh q h q) 29 P a g e
31 On comparing cosh q h q cosh q, h q x ccosh, y csinh cosh, sinh tanh (iii) From (ii) tanh tanh tanh We know z c (x, y, z) (c cosh, c sinh, c) (c sinh, c cosh, c) (c cos, c sinh, 0) (c sinh, c cosh, 0) As K Now c sinh hq c c cosh c sinh hq 0 2 hq + 2 sinh 2 q 2 cosh 2 q 2 hq + 2 hq + 2 (iv) 4 sinh 2 q + 4 cosh 2 q P a g e
32 4 h 2 q + 4 (sinh 2 q + 1) 4 h 2 q + 4 cosh 2 q 2 4 cosh 2 q 2 coshq 2 sinh 2 q + 2 cosh 2 q h 2 q + 2 (sinh 2 q + 1) 2 h 2 q + 2 cosh 2 q 2 2 cosh 2 q 2 coshq K q ( q) q ( ) q q 2c osh q And τ [,, ] 2 c 2c (v) since cosh. ( 2 hq + 2 hq + 2 ). (c sinh +c cosh +0 ) sinh q + osh q + 0. τ 3 1 ( 2 cosh 2 ) ( 2 coshq) q 4 2 cosh 4 q cosh 6 q q 2 cosh q 2c since cosh Proved 31 P a g e
33 Prove that (i). 0 (ii). 2 (iii). 3 (iv). (v). ( τ ) (vi). τ + ττ +2 + Solution: We know that τ 2 + ( Kτ ) 3K + (2 τ+kτ ) (i). 0 L.H.S.. K(0). 0 0 R.H.S (ii).. ( τ 2 + ) Kτ(. ). + (. ) Kτ(0) (1) + (0) (iii)..[ ( Kτ ) 3K + (2 τ+kτ ) ] 3. 3 (iv).. ( τ 2 + ) (. ) 3. + τ. (v).. [( Kτ ) 3K + (2 τ+kτ ) ] K( Kτ ) (. ) 3 Tanget. +K(2 τ+kτ ). K( Kτ ) since. 1,. 0, P a g e
34 (vi). ( τ + ). [( Kτ ) 3K + (2 τ+kτ ) ] τ( Kτ ). + τ( 3 ). + τ(2 τ+kτ ). ( Kτ ). +3. (2 τ+kτ ). + ( Kτ ) (. ) + ( 3 ). + (2 τ+kτ ). Since (. ).. 1 And... 0 τ(2 τ+kτ )(1) +3 (1) + ( Kτ )(1) 2 τ + ττ +3 + τ. τ + ττ +2 + Question: Prove that [,, ] [,, ] Solution: We know that τ 3K +( Kτ ) + (2 τ+kτ ) [,, ] [,, ] τ 3K Kτ 2 τ + Kτ 0 K[ 2 τ 3 τ ] + 0 K[ τ 3 τ ] K. [ τ τ] 2. 3 [ 2 ] d ds Hence proved. τ 33 P a g e
35 Question: Prove that [,, ] τ Solution: We know that τ 0 τ + 0 τ τ τ 2 [,, ] (2Kτ + τ) +( τ τ + τ ) 3ττ 0 τ 0 τ τ τ 2Kτ + τ τ τ + τ 3ττ 0 τ [ 3 τ τ + 2 τ 2 τ + τ 3 ] + 0 τ [ τ τ + τ 3 ] τ [ τ τ 2 τ ] τ. τ 2 [ τ τ ] 2. 3 [ ] 2 τ d ds Hence proved. K τ 34 P a g e
36 Lecture # 7 Equation of the Centre of Curvature: τ Let be the position vector of Centre of curvature. And be the position vector of point p on the curve with respect to Centre O. Then + Theorem: Prove that tangent to its locus lies in the normal plane. Proof: We know that equation of center of curvature Diff. w.r.t s + (1) (τ K ) + + τ K τ. K + + τ + τ lies in normal plane proved 35 P a g e
37 Moving Trihedral: The triplet (,, ) of unit tangent, unit principle normal and unit binormal are called Moving trihedral. Equation of binormal + + ( ) + ( ) Theorem: + ( ) + ( ) + ( ) If the radius of curvature is a constant for a given curve C then prove that (i) The tangent to its locus of its center is parallel to the binormal at point P on C. (ii) Curvature of locus is same as curvature of the given curve. (iii) Torsion of locus of centre of curvature vary inversely as the torsion of the given curve c. τ Proof: (i) As we know that + (1) Diff. w.r.t s (0). given radius is constant + (τ K) + τ K + τ. K 36 P a g e
38 + τ τ l τ l // // l (ii) As we know that + Diff. w.r.t s. ( + ). τ (1) Taking magnitude both side τ 1 τ 1, 1 Put eq (2) in eq (1) τ (2) (3) Now diff. (3) w.r.t s.. τ. τ, K K K, K Taking magnitude on both sides K K K K Proved 37 P a g e
39 (iii) As we know (1) (2) Taking cross product of (1) and (2) ( ) ( ) ( ) Diff. w.r.t s.. τ K. τ, K, K. τ K τ ( ). ( ) τ is constant Hence proved Theorem: If s is the arc length of locus of centre of curvature then show that τ + Or + Proof: As we know that + Diff. w.r.t s. ( + ). 38 P a g e
40 ( + + ) ( + (τ K) + ) ( + τ K + ) ( + + τ. ) K ( + + τ ) ( + τ ) Taking magnitude on both sides + ( τ) 1 + ( τ) + ( τ) (1) Taking derivative Put in (1) + ( τ) + τ + Proved 39 P a g e
41 Lecture # 8 Helix: A curve traced on the surface of a cylinder and cutting the generator at a constant angle is called Helix. Thus, the tangent to the Helix is inclined at a constant angle to a fix direction. If is on its tangent to the Helix and is a constant vector parallel to the generator of the Helix then. constant. cos 1.1 cos. cos tangent Since is fixed so the. is constant Question: Prove that necessary and sufficient condition for the curve to be Helix is that Constant angle constant Solution: Let the curve is helix. Then we have to prove that constant Since for a helix we know that tangent at any point to the curve makes a constant angle with the fix direction of the cylinder. Let be the unit constant vector along the direction (generator). Then. cos 1. cos is constant Diff. w.r.t s is constant P a g e
42 K. 0 K K 0,. 0 but will lies in the plane formed by the tangent and binormal. Then cos + sin cos + sin Diff. w.r.t s cos + sin is constant sin cos 0 K cos + ( ) sin K, 0 (Kcos sin) Taking dot product with both sides 0.. (Kcos sin) 0 (1) (Kcos sin) 0 Kcos sin a a tan constant is constant Sufficient Condition: Let constant We have to prove that curve is helix. For this it is sufficient to prove that. constant or K (1) c is constant Now we consider K (2) 41 P a g e
43 Put eq (1) in eq (2) (3) As Divide both sides by c (4) Adding (3) and (4) c + 0 (c + ) 0 Integrate both sides (c + ) 0 c + a is constant of integration Taking dot product with c ,. 1 c(1) c. constant Spherical indicatrices: When we move all unit tangent of a curve c to points their extremities then describe a curve on the unit sphere. This curve is called spherical images (indicatrices). There is on-one corresponding between c and. We can similarly obtain image of c when its normal and binormal move to a point to construct the spherical indicatrices of tangent line parallel to the positive 42 P a g e
44 direction. If the tangent at the points of the given curve from the center o of unit sphere. Let,,, where those line meets are spherical indicatrices of the tangent. Definition: (i) (ii) (iii) Spherical Indicatrices of tangent: The locus of point where position vector is equal to unit tangent at any point of the given curve. Spherical Indicatrices of Normal: The locus of point where position vector is equal to unit normal at any point of the given curve. Spherical Indicatrices of Binormal: The locus of point where position vector is equal to unit binormal at any point of the given curve. 43 P a g e
45 Lecture # 9 Question: Let x 3cosh2t, y 3sinh2t, z 6t Find arc length from 0 to p. Solution: Diff. the above w.r.t t 6sinh2t 6cosh2t 6 Formula for arc length + + dt Now (6sinh2t) + (6cosh2t) + (6) (6) ( h 2 + h 2 + 1) 6 ( h 2 + 1) + h 2 6 h 2 + h h 2 6 2cosh2t Taking integration from 0 to p. p p 6 2 cosh2t p (sinh2p sinh2(0)) (sinh2p 0) 3 2 sinh2p 44 P a g e
46 Question: Given that x (a+b)cos bcos, y (a+b)sin bsin, z 0 Find arc length from 0 to Solution: Diff the above equation w.r.t (a+b)sin bsin. q (a+b)sin+(a+b)sin (a+b) ( sin + sin) (a+b)cos bcos. q (a+b)cos (a+b)cos (a+b) (cos cos) q 0 Formula for arc length q q q + q + q d Now q (a + b) ( sin + sin) + (a + b) (cos cos) + (0) (a + b) ( sin + sin) + (a + b) (cos cos) ( + ) sin + sin( + ) 2 + cos cos( + ) 2 (a+b) q + 2sinθsin + q + 2cosθcos (a+b) cos (q + q) 45 P a g e
47 (a+b) 2 2cos ( q q+ q ) (a+b) 2(1 cos ( q )) cos(-) cos (a+b) 2(1 cos ( q)) 1-cos 2 q (a+b) 2(2 ( q)) (a+b) 4 ( q) 2(a+b)sin( q) Now integrate from 0 to q q q q 2(a + b)sin( q) q 2(a+b) ( q) ( q) 0 2(a+b). ( cos q ( cos 0 ) 2(a+b). ( cos q + 1) 4(a+b). {1 cos q } Question: x 2a( + t 1 ), y 2a and z 4at find arc length from 0 to t. Solution: Diff. above w.r.t t 2a [ ( ( 2 )] 2a [ + 1 ] 2a[ + 1 ] 2a [ ] 46 P a g e
48 2a(2 1 ) 4a 1 4at 4a Now Formula for arc length + + dt 4a 1 + ( 4at) + ( 4a) ( )( 4a) 4a 2 Integrate from 0 to t 4a 2 Theorem: 4a 2(t 0) 4a 2t Show that the curvature of spherical indicatrices of the tangent is the ratio of skew curvature to circular curvature of the curve that is also prove that Proof: Let be the position vector of a point of the spherical indicatrices of the tangent to the curve then (1) 47 P a g e
49 Diff. eq (1) w.r.t s. K. K So that K (2) Diff. eq (2) w.r.t s.. (K) τ K τ K ( ).K τ K Divide by K Taking square (. ).. Now equation of osculating sphere R + (3) As the indicatrices lies on the sphere of unit radius since R P a g e
50 1 + (. ), τ, 1 +. τ τ Also Diff. w.r.t s (4) s 1. K K 3 Put the value of K in equation (4) τ 3 49 P a g e
51 τ. 3 ) τ. τ proved P a g e
52 Lecture # 10 Theorem: Prove that the curvature and torsion of the spherical indicatrices of the binormal is and τ Proof: The equation of spherical indicatrices of the binormal is Diff. eq (1) w.r.t......(1) Diff. eq (1) w.r.t τ K ( ) (τ K). Taking square on both sides P a g e
53 (2) As the indicatrices lies on the sphere of unit sphere ( R 1) R (. ), τ, 1 +. τ τ Also Diff. w.r.t s (3) s 1. K τ P a g e
54 3 K 3 Put the value of K in equation (3) τ τ τ 3. 3 ) 2. τ Question: proved Find out spherical indicatrices of circular helix. Solution: As (acos, asin, c) ; c 0 Diff. w.r.t s q ( q. q q, asin,c). q (-asin, acos, c). q (1) Squaring both sides. ( q+ q+ ) ( q ) 1 ( ( + )+ ) ( ) 1 ( + ) ( ) ( ) 53 P a g e
55 l (say) l + q l Put in (1) (-asin, acos, c). l Diff. w.r.t s. q q ( asin, acos, c). l 1 1 dq 1 K n ( acos q, asin q,0). l l ds l 1 Kn ( acos q, asin q,0)...(4) 2 l Squaring both sides K ( n. n) ( a cos q a sin q ). l K ( a (cos q sin q )). 4 l a K put in (4) 2 l a 1 ( cos, sin,0). 2 n a q q 2 l l n ( cos q, sin q, 0) (5) Now b t n i j k asinq acosq c l l l cosq sinq 0 c c a 2 a 2 i 0 sinq i0 cosq k sin q cos q l l l l c c a 2 2 sinqi cosq j sin q cos q k l l l 54 P a g e
56 Question: c c a b sin q, cos q, l l l Spherical indicatrices for tangent is asinq x l acosq y l c z l Spherical indicatrices for normal is x cosq y sinq z 0 Spherical indicatrices for binormal is csinq x l c cosq y l a z l Find the equation of tangent plane and normal to the surfaces z + at point (1, 1,2) Solution Given that z + Let F[x,y,z] z [x,y,z] 2x At (1, 1,2) [x,y,z] 2(1) 2 [x,y,z] 2y At (1, 1,2) [x,y,z] 2( 1) 2 [x,y,z] 1 At (1, 1,2) [x,y,z] 1 55 P a g e
57 As equation of tangent is (X x) +(Y y) +(Z z) 0 (X 1) ( 2)+(Y+1) (2)+(Z 2) (1) 0 2X+2+2Y+2+Z 2 0 2X+2Y+Z X+2Y+Z 2 Now equation of Normal is Question: Find the equation of tangent plane and normal to the surfaces / / + / + / at point (1,2,2) Solution Given that / / + / + / AT (1,2,2) Let F[x,y,z] / + / + / / [x,y,z], [x,y,z], [x,y,z] [x,y,z] (1), [x,y,z] (2), [x,y,z] (2) As equation of tangent is (X x) +(Y y) +(Z z) 0 (X 1) +(Y 2) +(Z 2) 0 [2(X-1)+ 2 (Y-2)+ 2 (Z-2)] 0 2(X-1)+ 2 (Y-2)+ 2 (Z-2) 0 56 P a g e
58 Now equation of Normal is Surface: is the equation of normal. A surface is said to be a locus of a point whose cartesian coordinate (x,y,z) are function of independent parameter u and v i.e. x f(u,v) y g(u,v) z h(u,v) Another definition of Surface: A surface S is locus of point whose coordinates can be expressed as the function of two independent variables i.e. (, ) (, ) (, ) (1) where a ub and c v d In vector form u,v) denotes the equation of surfaces. Equation (1) called Gaussian form of the surface. Sometimes it is possible to eliminate u and v to get functional relation f(x,y,z) c (2) which is called implicit form of surface. It is possible only if the matrix M has rank 2 those points where matrix M has rank 0 or 1 is called singular point. The implicit form of eq (2) can be written as z f(x,y)..(3) Which is called as Monge s form of surface 57 P a g e
59 Example: x acossin find matrix Solution:, y acoscos, z asin -asinsin, acoscos -asincos, -acossin acos, 0 M asinsin asincos acos acoscos acossin 0 58 P a g e
60 Lecture # 11 Tangent plane: Let (u,v) be the equation of surface in terms of parameters u,v. Then where, Equation of Normal N,, forms right handed system Parametric curves: Let (u,v) be the equation of surface. Now by keeping u c (constant) or v c (constant) we get curves of spherical importance and are called parametric curves. U-curves: If v c and u varies the points (u,c) describe a parametric curve called u-curve or parametric curve at v c. V-curves: If u c and v varies the points (c,v) describe a parametric curve called u-curve or parametric curve at u c. Family of curves u constant Family of curves v constant 59 P a g e
61 First order Fundamental magnitude: As, And, The vector is tangential to the curve v constant at the point. Its direction is that the displacement dr due to the variation du in the first parameter. We take the positive direction along the parametric curve v constant i.e. for which u increases. Similarly, vector is the tangent to the curve when u constant which correspond to the increase of v. Consider the neighbouring point on the surface which position vector r and r+dr corresponding to the parametric to the parametric value u,v and u+du, v+dv respectively Then d. du +.. du +. Since the two points are adjacent point on the curve passing through them. The length ds of the element of arc joining them is equal to their actual distance. d d. du +.. du dudv As E, F., G E +2Fdudv+G..(1) The quantities denoted by E,F,G are called Fundamental magnitude of first order. The quantity EG is positive on real surface in u and v are real and are the modulus of and and if it denotes the angle between these vectors. Let EG and He be the positive square root to this quantity. 60 P a g e
62 Question: Calculate the 1 st fundamental magnitude as x ucos, y sin, z c Sol. Let (x,y,z) (ucos, usin, c) (x,y,z) (cos, sin, 0) (x,y,z) (0,0,0) f (x,y,z) (-usin, ucos, c) (x,y,z) (-ucos, -usin, 0) (x,y,z) (-sin, cos, 0) Now for first order fundamental magnitude E (cos, sin, 0). (cos, sin, 0) E 1 F (cos, sin, 0). (-usin, ucos, c) -ucossin+ucossin+0 0 G (-usin, ucos, c). (-usin, ucos, c) Question: Take x,y as parameters. Calculate the first fundamental magnitude of 2z +2hxy+ Solution: 61 P a g e
63 Given 2z +2hxy+ z (x,y,z) (x, y, ) (x,y,z) (1, 0, ) (1,0, ax+hy) (x,y,z) (0,0,a) (x,y,z) (0, 1, ) (0,1, by+hx) (x,y,z) (0, 0, b) (x,y,z) (0, 0, h) Now for first order fundamental magnitude E (1,0, ax+hy). (1,0, ax+hy) 1+ ( + h ) F (1,0, ax+hy). (0,1, by+hx) (ax+hy) (by+hx) G (0,1, by+hx). (0,1, by+hx) 1+ (h + ) Question: For the surface x ucos, y sin, z f(u). Find first fundamental magnitude. Solution: Let (x,y,z) (ucos, usin, f(u)) (x,y,z) (cos, sin, ) 62 P a g e
64 (x,y,z) (0,0, ) f (x,y,z) (-usin, ucos, 0) (x,y,z) (-ucos, -usin, 0) (x,y,z) (-sin, cos, 0) Now for first order fundamental magnitude E (cos, sin, ). (cos, sin, ) E 1 F (cos, sin, ). (-usin, ucos, 0) -ucossin+ucossin+0 0 G (-usin, ucos, 0). (-usin, ucos, 0) + +0 G 63 P a g e
65 Lecture # 12 Second order Fundamental form and second order Fundamental magnitude: Let (u,v) be the equation of surface and N be the normal to this surface at the point (u,v).(a) where H As we know that, And, If L., M., N. Then the quadratic equation form L +2Mdudv+M where du,dv is called second order fundamental form. The quantities L,M,N are called the second Fundamental magnitude Alternative form for L,M,N since the vector are tangential to the surface at point. So unit vector N is perpendicular to both vectors Then we have. 0. (1) &. 0. (2) Diff. (1) w.r.t u Diff. (2) w.r.t v L.. N.. Diff. (1) w.r.t v M.. 64 P a g e
66 In the case of three vectors [,, ]. H. From (A) H HL. L [,, ]. H. From (A) H HN. N Question: Calculate the 2 nd fundamental magnitude as x ucos, y sin, z c Sol. Let (x,y,z) (ucos, usin, c) (x,y,z) (cos, sin, 0) (x,y,z) (0,0,0) (x,y,z) (-usin, ucos, c) f (x,y,z) (-ucos, -usin, 0) (x,y,z) (-sin, cos, 0) Now cos sin 0 usin ucos (csin-0) (ccos f f csin c cos u (csin, -c cos, u) f + f P a g e
67 (,, ) L. (0,0,0). (,, ) 0 M. (-sin, cos, 0). (,, ) Question: N. (-ucos, -usin, 0). (,, ) 0 ) Take x,y as parameters. Calculate the 2 nd fundamental magnitude of Solution: 2z +2hxy+ Given 2z +2hxy+ z (x,y,z) (x, y, ) (x,y,z) (1, 0, ) (1,0, ax+hy) (x,y,z) (0,0,a) (x,y,z) (0, 1, ) (0,1, by+hx) (x,y,z) (0, 0, b) (x,y,z) (0, 0, h) Now for 2 nd order fundamental magnitude 66 P a g e
68 Now h h (0-(ax+hy)) (hx+by -(ax+hy) (hx+by) (-(ax+hy), -(hx+by), 1) (ax + hy) + (by + hx) + (1) (ax + hy) + (by + hx) + 1 (,, ) L. (0,0,a). (,, ) M. (0, 0, h). (,, ) N. (0, 0, b). (,, ) Question: For the surface x ucos, y usin, z f(u). Find 2 nd fundamental magnitude. Solution: Let (x,y,z) (ucos, usin, f(u)) (x,y,z) (cos, sin, ) (x,y,z) (0,0, ) (x,y,z) (-usin, ucos, 0) f (x,y,z) (-ucos, -usin, 0) 67 P a g e
69 (x,y,z) (-sin, cos, 0) Now for 2 nd order fundamental magnitude Now cos sin usin ucos 0 (0-ucos ) (usin ) f f (ucos ) (usin ) u (( ucos ), ( usin )u) (( ucos ), ( usin )u) (( ucos ) + (( usin ) + (u) u + u f (,, ) L. (0,0, ). (,, ) M. (-sin, cos, 0). (,, ) 0 N. (-ucos, -usin, 0). (,, ) 68 P a g e
CURVATURE AND RADIUS OF CURVATURE
 CHAPTER 5 CURVATURE AND RADIUS OF CURVATURE 5.1 Introduction: Curvature is a numerical measure of bending of the curve. At a particular point on the curve, a tangent can be drawn. Let this line makes an
CHAPTER 5 CURVATURE AND RADIUS OF CURVATURE 5.1 Introduction: Curvature is a numerical measure of bending of the curve. At a particular point on the curve, a tangent can be drawn. Let this line makes an
STRAIGHT LINES EXERCISE - 3
 STRAIGHT LINES EXERCISE - 3 Q. D C (3,4) E A(, ) Mid point of A, C is B 3 E, Point D rotation of point C(3, 4) by angle 90 o about E. 3 o 3 3 i4 cis90 i 5i 3 i i 5 i 5 D, point E mid point of B & D. So
STRAIGHT LINES EXERCISE - 3 Q. D C (3,4) E A(, ) Mid point of A, C is B 3 E, Point D rotation of point C(3, 4) by angle 90 o about E. 3 o 3 3 i4 cis90 i 5i 3 i i 5 i 5 D, point E mid point of B & D. So
Vectors, dot product, and cross product
 MTH 201 Multivariable calculus and differential equations Practice problems Vectors, dot product, and cross product 1. Find the component form and length of vector P Q with the following initial point
MTH 201 Multivariable calculus and differential equations Practice problems Vectors, dot product, and cross product 1. Find the component form and length of vector P Q with the following initial point
MATHEMATICS PAPER IB COORDINATE GEOMETRY(2D &3D) AND CALCULUS. Note: This question paper consists of three sections A,B and C.
 MATHEMATICS PAPER IB COORDINATE GEOMETRY(D &3D) AND CALCULUS. TIME : 3hrs Ma. Marks.75 Note: This question paper consists of three sections A,B and C. SECTION A VERY SHORT ANSWER TYPE QUESTIONS. 0X =0.
MATHEMATICS PAPER IB COORDINATE GEOMETRY(D &3D) AND CALCULUS. TIME : 3hrs Ma. Marks.75 Note: This question paper consists of three sections A,B and C. SECTION A VERY SHORT ANSWER TYPE QUESTIONS. 0X =0.
Section Arclength and Curvature. (1) Arclength, (2) Parameterizing Curves by Arclength, (3) Curvature, (4) Osculating and Normal Planes.
 Section 10.3 Arclength and Curvature (1) Arclength, (2) Parameterizing Curves by Arclength, (3) Curvature, (4) Osculating and Normal Planes. MATH 127 (Section 10.3) Arclength and Curvature The University
Section 10.3 Arclength and Curvature (1) Arclength, (2) Parameterizing Curves by Arclength, (3) Curvature, (4) Osculating and Normal Planes. MATH 127 (Section 10.3) Arclength and Curvature The University
DRAFT - Math 101 Lecture Note - Dr. Said Algarni
 3 Differentiation Rules 3.1 The Derivative of Polynomial and Exponential Functions In this section we learn how to differentiate constant functions, power functions, polynomials, and exponential functions.
3 Differentiation Rules 3.1 The Derivative of Polynomial and Exponential Functions In this section we learn how to differentiate constant functions, power functions, polynomials, and exponential functions.
Equations of Ellipse Conics HSC Maths Extension 2
 Equations of Ellipse HSC Maths Extension 1 Question 1 Find the equation of the ellipse whose foci on the y-axis, centre 0,0, a, b. Question Find the equation of the ellipse whose foci 4,0, b. Question
Equations of Ellipse HSC Maths Extension 1 Question 1 Find the equation of the ellipse whose foci on the y-axis, centre 0,0, a, b. Question Find the equation of the ellipse whose foci 4,0, b. Question
a Write down the coordinates of the point on the curve where t = 2. b Find the value of t at the point on the curve with coordinates ( 5 4, 8).
 Worksheet A 1 A curve is given by the parametric equations x = t + 1, y = 4 t. a Write down the coordinates of the point on the curve where t =. b Find the value of t at the point on the curve with coordinates
Worksheet A 1 A curve is given by the parametric equations x = t + 1, y = 4 t. a Write down the coordinates of the point on the curve where t =. b Find the value of t at the point on the curve with coordinates
Differential Geometry of Curves
 Differential Geometry of Curves Cartesian coordinate system René Descartes (1596-165) (lat. Renatus Cartesius) French philosopher, mathematician, and scientist. Rationalism y Ego cogito, ergo sum (I think,
Differential Geometry of Curves Cartesian coordinate system René Descartes (1596-165) (lat. Renatus Cartesius) French philosopher, mathematician, and scientist. Rationalism y Ego cogito, ergo sum (I think,
MATH 332: Vector Analysis Summer 2005 Homework
 MATH 332, (Vector Analysis), Summer 2005: Homework 1 Instructor: Ivan Avramidi MATH 332: Vector Analysis Summer 2005 Homework Set 1. (Scalar Product, Equation of a Plane, Vector Product) Sections: 1.9,
MATH 332, (Vector Analysis), Summer 2005: Homework 1 Instructor: Ivan Avramidi MATH 332: Vector Analysis Summer 2005 Homework Set 1. (Scalar Product, Equation of a Plane, Vector Product) Sections: 1.9,
Mixed exercise 3. x y. cosh t sinh t 1 Substituting the values for cosh t and sinht in the equation for the hyperbola H. = θ =
 Mixed exercise x x a Parametric equations: cosθ and sinθ 9 cos θ + sin θ Substituting the values for cos θ and sinθ in the equation for ellipse E gives the Cartesian equation: + 9 b Comparing with the
Mixed exercise x x a Parametric equations: cosθ and sinθ 9 cos θ + sin θ Substituting the values for cos θ and sinθ in the equation for ellipse E gives the Cartesian equation: + 9 b Comparing with the
 Q.1. Which one of the following is scalar quantity? Displacement Option Electric field Acceleration Work Correct Answer 4 w = F.ds; it does not have any direction, it s a scalar quantity. Q.. Which one
Q.1. Which one of the following is scalar quantity? Displacement Option Electric field Acceleration Work Correct Answer 4 w = F.ds; it does not have any direction, it s a scalar quantity. Q.. Which one
FIRST SEMESTER DIPLOMA EXAMINATION IN ENGINEERING/ TECHNOLIGY- MARCH, 2013
 TED (10)-1002 (REVISION-2010) Reg. No.. Signature. FIRST SEMESTER DIPLOMA EXAMINATION IN ENGINEERING/ TECHNOLIGY- MARCH, 2013 TECHNICAL MATHEMATICS- I (Common Except DCP and CABM) (Maximum marks: 100)
TED (10)-1002 (REVISION-2010) Reg. No.. Signature. FIRST SEMESTER DIPLOMA EXAMINATION IN ENGINEERING/ TECHNOLIGY- MARCH, 2013 TECHNICAL MATHEMATICS- I (Common Except DCP and CABM) (Maximum marks: 100)
Vector-Valued Functions
 Vector-Valued Functions 1 Parametric curves 8 ' 1 6 1 4 8 1 6 4 1 ' 4 6 8 Figure 1: Which curve is a graph of a function? 1 4 6 8 1 8 1 6 4 1 ' 4 6 8 Figure : A graph of a function: = f() 8 ' 1 6 4 1 1
Vector-Valued Functions 1 Parametric curves 8 ' 1 6 1 4 8 1 6 4 1 ' 4 6 8 Figure 1: Which curve is a graph of a function? 1 4 6 8 1 8 1 6 4 1 ' 4 6 8 Figure : A graph of a function: = f() 8 ' 1 6 4 1 1
ANSWER KEY 1. [A] 2. [C] 3. [B] 4. [B] 5. [C] 6. [A] 7. [B] 8. [C] 9. [A] 10. [A] 11. [D] 12. [A] 13. [D] 14. [C] 15. [B] 16. [C] 17. [D] 18.
![ANSWER KEY 1. [A] 2. [C] 3. [B] 4. [B] 5. [C] 6. [A] 7. [B] 8. [C] 9. [A] 10. [A] 11. [D] 12. [A] 13. [D] 14. [C] 15. [B] 16. [C] 17. [D] 18. ANSWER KEY 1. [A] 2. [C] 3. [B] 4. [B] 5. [C] 6. [A] 7. [B] 8. [C] 9. [A] 10. [A] 11. [D] 12. [A] 13. [D] 14. [C] 15. [B] 16. [C] 17. [D] 18.](/thumbs/89/97771760.jpg) ANSWER KEY. [A]. [C]. [B] 4. [B] 5. [C] 6. [A] 7. [B] 8. [C] 9. [A]. [A]. [D]. [A]. [D] 4. [C] 5. [B] 6. [C] 7. [D] 8. [B] 9. [C]. [C]. [D]. [A]. [B] 4. [D] 5. [A] 6. [D] 7. [B] 8. [D] 9. [D]. [B]. [A].
ANSWER KEY. [A]. [C]. [B] 4. [B] 5. [C] 6. [A] 7. [B] 8. [C] 9. [A]. [A]. [D]. [A]. [D] 4. [C] 5. [B] 6. [C] 7. [D] 8. [B] 9. [C]. [C]. [D]. [A]. [B] 4. [D] 5. [A] 6. [D] 7. [B] 8. [D] 9. [D]. [B]. [A].
for 2 1/3 < t 3 1/3 parametrizes
 Solution to Set 4, due Friday April 1) Section 5.1, Problem ) Explain why the path parametrized by ft) = t, t 1 ) is not smooth. Note this is true more specifically if the interval of t contains t = 1
Solution to Set 4, due Friday April 1) Section 5.1, Problem ) Explain why the path parametrized by ft) = t, t 1 ) is not smooth. Note this is true more specifically if the interval of t contains t = 1
Part r A A A 1 Mark Part r B B B 2 Marks Mark P t ar t t C C 5 Mar M ks Part r E 4 Marks Mark Tot To a t l
 Part Part P t Part Part Total A B C E 1 Mark 2 Marks 5 Marks M k 4 Marks CIRCLES 12 Marks approximately Definition ; A circle is defined as the locus of a point which moves such that its distance from
Part Part P t Part Part Total A B C E 1 Mark 2 Marks 5 Marks M k 4 Marks CIRCLES 12 Marks approximately Definition ; A circle is defined as the locus of a point which moves such that its distance from
More Final Practice Problems
 8.0 Calculus Jason Starr Final Exam at 9:00am sharp Fall 005 Tuesday, December 0, 005 More 8.0 Final Practice Problems Here are some further practice problems with solutions for the 8.0 Final Exam. Many
8.0 Calculus Jason Starr Final Exam at 9:00am sharp Fall 005 Tuesday, December 0, 005 More 8.0 Final Practice Problems Here are some further practice problems with solutions for the 8.0 Final Exam. Many
Math 153 Calculus III Notes
 Math 153 Calculus III Notes 10.1 Parametric Functions A parametric function is a where x and y are described by a function in terms of the parameter t: Example 1 (x, y) = {x(t), y(t)}, or x = f(t); y =
Math 153 Calculus III Notes 10.1 Parametric Functions A parametric function is a where x and y are described by a function in terms of the parameter t: Example 1 (x, y) = {x(t), y(t)}, or x = f(t); y =
MAS153/MAS159. MAS153/MAS159 1 Turn Over SCHOOL OF MATHEMATICS AND STATISTICS hours. Mathematics (Materials) Mathematics For Chemists
 Data provided: Formula sheet MAS53/MAS59 SCHOOL OF MATHEMATICS AND STATISTICS Mathematics (Materials Mathematics For Chemists Spring Semester 203 204 3 hours All questions are compulsory. The marks awarded
Data provided: Formula sheet MAS53/MAS59 SCHOOL OF MATHEMATICS AND STATISTICS Mathematics (Materials Mathematics For Chemists Spring Semester 203 204 3 hours All questions are compulsory. The marks awarded
2016 SPECIALIST MATHEMATICS
 2016 SPECIALIST MATHEMATICS External Examination 2016 FOR OFFICE USE ONLY SUPERVISOR CHECK ATTACH SACE REGISTRATION NUMBER LABEL TO THIS BOX Graphics calculator Brand Model Computer software RE-MARKED
2016 SPECIALIST MATHEMATICS External Examination 2016 FOR OFFICE USE ONLY SUPERVISOR CHECK ATTACH SACE REGISTRATION NUMBER LABEL TO THIS BOX Graphics calculator Brand Model Computer software RE-MARKED
Chapter 14: Vector Calculus
 Chapter 14: Vector Calculus Introduction to Vector Functions Section 14.1 Limits, Continuity, Vector Derivatives a. Limit of a Vector Function b. Limit Rules c. Component By Component Limits d. Continuity
Chapter 14: Vector Calculus Introduction to Vector Functions Section 14.1 Limits, Continuity, Vector Derivatives a. Limit of a Vector Function b. Limit Rules c. Component By Component Limits d. Continuity
Jim Lambers MAT 169 Fall Semester Practice Final Exam
 Jim Lambers MAT 169 Fall Semester 2010-11 Practice Final Exam 1. A ship is moving northwest at a speed of 50 mi/h. A passenger is walking due southeast on the deck at 4 mi/h. Find the speed of the passenger
Jim Lambers MAT 169 Fall Semester 2010-11 Practice Final Exam 1. A ship is moving northwest at a speed of 50 mi/h. A passenger is walking due southeast on the deck at 4 mi/h. Find the speed of the passenger
+ 2gx + 2fy + c = 0 if S
 CIRCLE DEFINITIONS A circle is the locus of a point which moves in such a way that its distance from a fixed point, called the centre, is always a constant. The distance r from the centre is called the
CIRCLE DEFINITIONS A circle is the locus of a point which moves in such a way that its distance from a fixed point, called the centre, is always a constant. The distance r from the centre is called the
Lecture D4 - Intrinsic Coordinates
 J. Peraire 16.07 Dynamics Fall 2004 Version 1.1 Lecture D4 - Intrinsic Coordinates In lecture D2 we introduced the position, velocity and acceleration vectors and referred them to a fixed cartesian coordinate
J. Peraire 16.07 Dynamics Fall 2004 Version 1.1 Lecture D4 - Intrinsic Coordinates In lecture D2 we introduced the position, velocity and acceleration vectors and referred them to a fixed cartesian coordinate
MATH 32A: MIDTERM 2 REVIEW. sin 2 u du z(t) = sin 2 t + cos 2 2
 MATH 3A: MIDTERM REVIEW JOE HUGHES 1. Curvature 1. Consider the curve r(t) = x(t), y(t), z(t), where x(t) = t Find the curvature κ(t). 0 cos(u) sin(u) du y(t) = Solution: The formula for curvature is t
MATH 3A: MIDTERM REVIEW JOE HUGHES 1. Curvature 1. Consider the curve r(t) = x(t), y(t), z(t), where x(t) = t Find the curvature κ(t). 0 cos(u) sin(u) du y(t) = Solution: The formula for curvature is t
H I G H E R S T I L L. Extended Unit Tests Higher Still Higher Mathematics. (more demanding tests covering all levels)
 M A T H E M A T I C S H I G H E R S T I L L Higher Still Higher Mathematics Extended Unit Tests 00-0 (more demanding tests covering all levels) Contents Unit Tests (at levels A, B and C) Detailed marking
M A T H E M A T I C S H I G H E R S T I L L Higher Still Higher Mathematics Extended Unit Tests 00-0 (more demanding tests covering all levels) Contents Unit Tests (at levels A, B and C) Detailed marking
Review Exercise 2. , æ. ç ø. ç ø. ç ø. ç ø. = -0.27, 0 x 2p. 1 Crosses y-axis when x = 0 at sin 3p 4 = 1 2. ö ø. æ Crosses x-axis when sin x + 3p è
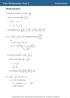 Review Exercise 1 Crosses y-axis when x 0 at sin p 4 1 Crosses x-axis when sin x + p 4 ö 0 x + p 4 -p, 0, p, p x - 7p 4, - p 4, p 4, 5p 4 So coordinates are 0, 1 ö, - 7p 4,0 ö, - p 4,0 ö, p 4,0 ö, 5p 4,0
Review Exercise 1 Crosses y-axis when x 0 at sin p 4 1 Crosses x-axis when sin x + p 4 ö 0 x + p 4 -p, 0, p, p x - 7p 4, - p 4, p 4, 5p 4 So coordinates are 0, 1 ö, - 7p 4,0 ö, - p 4,0 ö, p 4,0 ö, 5p 4,0
SOLVED SUBJECTIVE EXAMPLES
 Example 1 : SOLVED SUBJECTIVE EXAMPLES Find the locus of the points of intersection of the tangents to the circle x = r cos, y = r sin at points whose parametric angles differ by /3. All such points P
Example 1 : SOLVED SUBJECTIVE EXAMPLES Find the locus of the points of intersection of the tangents to the circle x = r cos, y = r sin at points whose parametric angles differ by /3. All such points P
Dierential Geometry Curves and surfaces Local properties Geometric foundations (critical for visual modeling and computing) Quantitative analysis Algo
 Dierential Geometry Curves and surfaces Local properties Geometric foundations (critical for visual modeling and computing) Quantitative analysis Algorithm development Shape control and interrogation Curves
Dierential Geometry Curves and surfaces Local properties Geometric foundations (critical for visual modeling and computing) Quantitative analysis Algorithm development Shape control and interrogation Curves
JUST THE MATHS UNIT NUMBER INTEGRATION APPLICATIONS 10 (Second moments of an arc) A.J.Hobson
 JUST THE MATHS UNIT NUMBER 13.1 INTEGRATION APPLICATIONS 1 (Second moments of an arc) by A.J.Hobson 13.1.1 Introduction 13.1. The second moment of an arc about the y-axis 13.1.3 The second moment of an
JUST THE MATHS UNIT NUMBER 13.1 INTEGRATION APPLICATIONS 1 (Second moments of an arc) by A.J.Hobson 13.1.1 Introduction 13.1. The second moment of an arc about the y-axis 13.1.3 The second moment of an
Week 3: Differential Geometry of Curves
 Week 3: Differential Geometry of Curves Introduction We now know how to differentiate and integrate along curves. This week we explore some of the geometrical properties of curves that can be addressed
Week 3: Differential Geometry of Curves Introduction We now know how to differentiate and integrate along curves. This week we explore some of the geometrical properties of curves that can be addressed
Practice problems for Exam 1. a b = (2) 2 + (4) 2 + ( 3) 2 = 29
 Practice problems for Exam.. Given a = and b =. Find the area of the parallelogram with adjacent sides a and b. A = a b a ı j k b = = ı j + k = ı + 4 j 3 k Thus, A = 9. a b = () + (4) + ( 3)
Practice problems for Exam.. Given a = and b =. Find the area of the parallelogram with adjacent sides a and b. A = a b a ı j k b = = ı j + k = ı + 4 j 3 k Thus, A = 9. a b = () + (4) + ( 3)
π π π π Trigonometry Homework Booklet 1. Convert 5.3 radians to degrees. A B C D Determine the period of 15
 Trigonometry Homework Booklet 1. Convert 5.3 radians to degrees. A. 0.09 B. 0.18 C. 151.83 D. 303.67. Determine the period of y = 6cos x + 8. 15 15 A. B. C. 15 D. 30 15 3. Determine the exact value of
Trigonometry Homework Booklet 1. Convert 5.3 radians to degrees. A. 0.09 B. 0.18 C. 151.83 D. 303.67. Determine the period of y = 6cos x + 8. 15 15 A. B. C. 15 D. 30 15 3. Determine the exact value of
MATH 2433 Homework 1
 MATH 433 Homework 1 1. The sequence (a i ) is defined recursively by a 1 = 4 a i+1 = 3a i find a closed formula for a i in terms of i.. In class we showed that the Fibonacci sequence (a i ) defined by
MATH 433 Homework 1 1. The sequence (a i ) is defined recursively by a 1 = 4 a i+1 = 3a i find a closed formula for a i in terms of i.. In class we showed that the Fibonacci sequence (a i ) defined by
MAT 272 Test 1 Review. 1. Let P = (1,1) and Q = (2,3). Find the unit vector u that has the same
 11.1 Vectors in the Plane 1. Let P = (1,1) and Q = (2,3). Find the unit vector u that has the same direction as. QP a. u =< 1, 2 > b. u =< 1 5, 2 5 > c. u =< 1, 2 > d. u =< 1 5, 2 5 > 2. If u has magnitude
11.1 Vectors in the Plane 1. Let P = (1,1) and Q = (2,3). Find the unit vector u that has the same direction as. QP a. u =< 1, 2 > b. u =< 1 5, 2 5 > c. u =< 1, 2 > d. u =< 1 5, 2 5 > 2. If u has magnitude
Sec 4 Maths SET D PAPER 2
 S4MA Set D Paper Sec 4 Maths Exam papers with worked solutions SET D PAPER Compiled by THE MATHS CAFE P a g e Answer all questions. Write your answers and working on the separate Answer Paper provided.
S4MA Set D Paper Sec 4 Maths Exam papers with worked solutions SET D PAPER Compiled by THE MATHS CAFE P a g e Answer all questions. Write your answers and working on the separate Answer Paper provided.
CALCULUS PROBLEMS Courtesy of Prof. Julia Yeomans. Michaelmas Term
 CALCULUS PROBLEMS Courtesy of Prof. Julia Yeomans Michaelmas Term The problems are in 5 sections. The first 4, A Differentiation, B Integration, C Series and limits, and D Partial differentiation follow
CALCULUS PROBLEMS Courtesy of Prof. Julia Yeomans Michaelmas Term The problems are in 5 sections. The first 4, A Differentiation, B Integration, C Series and limits, and D Partial differentiation follow
Practice problems. 1. Given a = 3i 2j and b = 2i + j. Write c = i + j in terms of a and b.
 Practice problems 1. Given a = 3i 2j and b = 2i + j. Write c = i + j in terms of a and b. 1, 1 = c 1 3, 2 + c 2 2, 1. Solve c 1, c 2. 2. Suppose a is a vector in the plane. If the component of the a in
Practice problems 1. Given a = 3i 2j and b = 2i + j. Write c = i + j in terms of a and b. 1, 1 = c 1 3, 2 + c 2 2, 1. Solve c 1, c 2. 2. Suppose a is a vector in the plane. If the component of the a in
Power Series. x n. Using the ratio test. n n + 1. x n+1 n 3. = lim x. lim n + 1. = 1 < x < 1. Then r = 1 and I = ( 1, 1) ( 1) n 1 x n.
 .8 Power Series. n x n x n n Using the ratio test. lim x n+ n n + lim x n n + so r and I (, ). By the ratio test. n Then r and I (, ). n x < ( ) n x n < x < n lim x n+ n (n + ) x n lim xn n (n + ) x
.8 Power Series. n x n x n n Using the ratio test. lim x n+ n n + lim x n n + so r and I (, ). By the ratio test. n Then r and I (, ). n x < ( ) n x n < x < n lim x n+ n (n + ) x n lim xn n (n + ) x
CO-ORDINATE GEOMETRY
 CO-ORDINATE GEOMETRY 1 To change from Cartesian coordinates to polar coordinates, for X write r cos θ and for y write r sin θ. 2 To change from polar coordinates to cartesian coordinates, for r 2 write
CO-ORDINATE GEOMETRY 1 To change from Cartesian coordinates to polar coordinates, for X write r cos θ and for y write r sin θ. 2 To change from polar coordinates to cartesian coordinates, for r 2 write
y mx 25m 25 4 circle. Then the perpendicular distance of tangent from the centre (0, 0) is the radius. Since tangent
 Mathematics. The sides AB, BC and CA of ABC have, 4 and 5 interior points respectively on them as shown in the figure. The number of triangles that can be formed using these interior points is () 80 ()
Mathematics. The sides AB, BC and CA of ABC have, 4 and 5 interior points respectively on them as shown in the figure. The number of triangles that can be formed using these interior points is () 80 ()
13.3 Arc Length and Curvature
 13 Vector Functions 13.3 Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. We have defined the length of a plane curve with parametric equations x = f(t),
13 Vector Functions 13.3 Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. We have defined the length of a plane curve with parametric equations x = f(t),
a 2 = 5 Þ 2cos y + sin y = Þ 2cos y = sin y 5-1 Þ tan y = 3 a
 Trigonometry and Modelling Mixed Exercise a i ii sin40 cos0 - cos40 sin0 sin(40-0 ) sin0 cos - sin cos 4 cos - sin 4 sin As cos(x - y) sin y cos xcos y + sin xsin y sin y () Draw a right-angled triangle,
Trigonometry and Modelling Mixed Exercise a i ii sin40 cos0 - cos40 sin0 sin(40-0 ) sin0 cos - sin cos 4 cos - sin 4 sin As cos(x - y) sin y cos xcos y + sin xsin y sin y () Draw a right-angled triangle,
Final Examination 201-NYA-05 May 18, 2018
 . ( points) Evaluate each of the following limits. 3x x + (a) lim x x 3 8 x + sin(5x) (b) lim x sin(x) (c) lim x π/3 + sec x ( (d) x x + 5x ) (e) lim x 5 x lim x 5 + x 6. (3 points) What value of c makes
. ( points) Evaluate each of the following limits. 3x x + (a) lim x x 3 8 x + sin(5x) (b) lim x sin(x) (c) lim x π/3 + sec x ( (d) x x + 5x ) (e) lim x 5 x lim x 5 + x 6. (3 points) What value of c makes
Lecture Wise Questions from 23 to 45 By Virtualians.pk. Q105. What is the impact of double integration in finding out the area and volume of Regions?
 Lecture Wise Questions from 23 to 45 By Virtualians.pk Q105. What is the impact of double integration in finding out the area and volume of Regions? Ans: It has very important contribution in finding the
Lecture Wise Questions from 23 to 45 By Virtualians.pk Q105. What is the impact of double integration in finding out the area and volume of Regions? Ans: It has very important contribution in finding the
Spherical trigonometry
 Spherical trigonometry 1 The spherical Pythagorean theorem Proposition 1.1 On a sphere of radius, any right triangle AC with C being the right angle satisfies cos(c/) = cos(a/) cos(b/). (1) Proof: Let
Spherical trigonometry 1 The spherical Pythagorean theorem Proposition 1.1 On a sphere of radius, any right triangle AC with C being the right angle satisfies cos(c/) = cos(a/) cos(b/). (1) Proof: Let
f dr. (6.1) f(x i, y i, z i ) r i. (6.2) N i=1
 hapter 6 Integrals In this chapter we will look at integrals in more detail. We will look at integrals along a curve, and multi-dimensional integrals in 2 or more dimensions. In physics we use these integrals
hapter 6 Integrals In this chapter we will look at integrals in more detail. We will look at integrals along a curve, and multi-dimensional integrals in 2 or more dimensions. In physics we use these integrals
ECM Calculus and Geometry. Revision Notes
 ECM1702 - Calculus and Geometry Revision Notes Joshua Byrne Autumn 2011 Contents 1 The Real Numbers 1 1.1 Notation.................................................. 1 1.2 Set Notation...............................................
ECM1702 - Calculus and Geometry Revision Notes Joshua Byrne Autumn 2011 Contents 1 The Real Numbers 1 1.1 Notation.................................................. 1 1.2 Set Notation...............................................
JEE-ADVANCED MATHEMATICS. Paper-1. SECTION 1: (One or More Options Correct Type)
 JEE-ADVANCED MATHEMATICS Paper- SECTION : (One or More Options Correct Type) This section contains 8 multiple choice questions. Each question has four choices (A), (B), (C) and (D) out of which ONE OR
JEE-ADVANCED MATHEMATICS Paper- SECTION : (One or More Options Correct Type) This section contains 8 multiple choice questions. Each question has four choices (A), (B), (C) and (D) out of which ONE OR
2014 HSC Mathematics Extension 2 Marking Guidelines
 04 HSC Mathematics Extension Marking Guidelines Section I Multiple-choice Answer Key Question Answer D A 3 B 4 C 5 C 6 D 7 B 8 B 9 A 0 D BOSTES 04 HSC Mathematics Extension Marking Guidelines Section II
04 HSC Mathematics Extension Marking Guidelines Section I Multiple-choice Answer Key Question Answer D A 3 B 4 C 5 C 6 D 7 B 8 B 9 A 0 D BOSTES 04 HSC Mathematics Extension Marking Guidelines Section II
CIRCLES. ii) P lies in the circle S = 0 s 11 = 0
 CIRCLES 1 The set of points in a plane which are at a constant distance r ( 0) from a given point C is called a circle The fixed point C is called the centre and the constant distance r is called the radius
CIRCLES 1 The set of points in a plane which are at a constant distance r ( 0) from a given point C is called a circle The fixed point C is called the centre and the constant distance r is called the radius
Parametric Equations and Polar Coordinates
 Parametric Equations and Polar Coordinates Parametrizations of Plane Curves In previous chapters, we have studied curves as the graphs of functions or equations involving the two variables x and y. Another
Parametric Equations and Polar Coordinates Parametrizations of Plane Curves In previous chapters, we have studied curves as the graphs of functions or equations involving the two variables x and y. Another
MATH Final Review
 MATH 1592 - Final Review 1 Chapter 7 1.1 Main Topics 1. Integration techniques: Fitting integrands to basic rules on page 485. Integration by parts, Theorem 7.1 on page 488. Guidelines for trigonometric
MATH 1592 - Final Review 1 Chapter 7 1.1 Main Topics 1. Integration techniques: Fitting integrands to basic rules on page 485. Integration by parts, Theorem 7.1 on page 488. Guidelines for trigonometric
C3 Revision Questions. (using questions from January 2006, January 2007, January 2008 and January 2009)
 C3 Revision Questions (using questions from January 2006, January 2007, January 2008 and January 2009) 1 2 1. f(x) = 1 3 x 2 + 3, x 2. 2 ( x 2) (a) 2 x x 1 Show that f(x) =, x 2. 2 ( x 2) (4) (b) Show
C3 Revision Questions (using questions from January 2006, January 2007, January 2008 and January 2009) 1 2 1. f(x) = 1 3 x 2 + 3, x 2. 2 ( x 2) (a) 2 x x 1 Show that f(x) =, x 2. 2 ( x 2) (4) (b) Show
IMPORTANT QUESTIONS FOR INTERMEDIATE PUBLIC EXAMINATIONS IN MATHS-IB
 ` KUKATPALLY CENTRE IMPORTANT QUESTIONS FOR INTERMEDIATE PUBLIC EXAMINATIONS IN MATHS-IB 017-18 FIITJEE KUKATPALLY CENTRE: # -97, Plot No1, Opp Patel Kunta Huda Park, Vijaynagar Colony, Hyderabad - 500
` KUKATPALLY CENTRE IMPORTANT QUESTIONS FOR INTERMEDIATE PUBLIC EXAMINATIONS IN MATHS-IB 017-18 FIITJEE KUKATPALLY CENTRE: # -97, Plot No1, Opp Patel Kunta Huda Park, Vijaynagar Colony, Hyderabad - 500
Tangent and Normal Vectors
 Tangent and Normal Vectors MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Navigation When an observer is traveling along with a moving point, for example the passengers in
Tangent and Normal Vectors MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Navigation When an observer is traveling along with a moving point, for example the passengers in
1 + f 2 x + f 2 y dy dx, where f(x, y) = 2 + 3x + 4y, is
 1. The value of the double integral (a) 15 26 (b) 15 8 (c) 75 (d) 105 26 5 4 0 1 1 + f 2 x + f 2 y dy dx, where f(x, y) = 2 + 3x + 4y, is 2. What is the value of the double integral interchange the order
1. The value of the double integral (a) 15 26 (b) 15 8 (c) 75 (d) 105 26 5 4 0 1 1 + f 2 x + f 2 y dy dx, where f(x, y) = 2 + 3x + 4y, is 2. What is the value of the double integral interchange the order
The Frenet Serret formulas
 The Frenet Serret formulas Attila Máté Brooklyn College of the City University of New York January 19, 2017 Contents Contents 1 1 The Frenet Serret frame of a space curve 1 2 The Frenet Serret formulas
The Frenet Serret formulas Attila Máté Brooklyn College of the City University of New York January 19, 2017 Contents Contents 1 1 The Frenet Serret frame of a space curve 1 2 The Frenet Serret formulas
MA 351 Fall 2007 Exam #1 Review Solutions 1
 MA 35 Fall 27 Exam # Review Solutions THERE MAY BE TYPOS in these solutions. Please let me know if you find any.. Consider the two surfaces ρ 3 csc θ in spherical coordinates and r 3 in cylindrical coordinates.
MA 35 Fall 27 Exam # Review Solutions THERE MAY BE TYPOS in these solutions. Please let me know if you find any.. Consider the two surfaces ρ 3 csc θ in spherical coordinates and r 3 in cylindrical coordinates.
PhysicsAndMathsTutor.com
 PhysicsAndMathsTutor.com physicsandmathstutor.com June 2005 1. (a) Given that sin 2 θ + cos 2 θ 1, show that 1 + tan 2 θ sec 2 θ. (b) Solve, for 0 θ < 360, the equation 2 tan 2 θ + secθ = 1, giving your
PhysicsAndMathsTutor.com physicsandmathstutor.com June 2005 1. (a) Given that sin 2 θ + cos 2 θ 1, show that 1 + tan 2 θ sec 2 θ. (b) Solve, for 0 θ < 360, the equation 2 tan 2 θ + secθ = 1, giving your
ENGI 4430 Surface Integrals Page and 0 2 r
 ENGI 4430 Surface Integrals Page 9.01 9. Surface Integrals - Projection Method Surfaces in 3 In 3 a surface can be represented by a vector parametric equation r x u, v ˆi y u, v ˆj z u, v k ˆ where u,
ENGI 4430 Surface Integrals Page 9.01 9. Surface Integrals - Projection Method Surfaces in 3 In 3 a surface can be represented by a vector parametric equation r x u, v ˆi y u, v ˆj z u, v k ˆ where u,
Indefinite Integration
 Indefinite Integration 1 An antiderivative of a function y = f(x) defined on some interval (a, b) is called any function F(x) whose derivative at any point of this interval is equal to f(x): F'(x) = f(x)
Indefinite Integration 1 An antiderivative of a function y = f(x) defined on some interval (a, b) is called any function F(x) whose derivative at any point of this interval is equal to f(x): F'(x) = f(x)
n4 + 1 n 4 1 ] [5] (b) Find the interval of convergence of the following series 1
![n4 + 1 n 4 1 ] [5] (b) Find the interval of convergence of the following series 1 n4 + 1 n 4 1 ] [5] (b) Find the interval of convergence of the following series 1](/thumbs/82/84773531.jpg) ode No: R05010102 Set No. 1 I B.Tech Supplimentary Examinations, February 2008 MATHEMATIS-I ( ommon to ivil Engineering, Electrical & Electronic Engineering, Mechanical Engineering, Electronics & ommunication
ode No: R05010102 Set No. 1 I B.Tech Supplimentary Examinations, February 2008 MATHEMATIS-I ( ommon to ivil Engineering, Electrical & Electronic Engineering, Mechanical Engineering, Electronics & ommunication
Engineering Mechanics Prof. U. S. Dixit Department of Mechanical Engineering Indian Institute of Technology, Guwahati Kinematics
 Engineering Mechanics Prof. U. S. Dixit Department of Mechanical Engineering Indian Institute of Technology, Guwahati Kinematics Module 10 - Lecture 24 Kinematics of a particle moving on a curve Today,
Engineering Mechanics Prof. U. S. Dixit Department of Mechanical Engineering Indian Institute of Technology, Guwahati Kinematics Module 10 - Lecture 24 Kinematics of a particle moving on a curve Today,
SOLUTIONS TO HOMEWORK ASSIGNMENT #2, Math 253
 SOLUTIONS TO HOMEWORK ASSIGNMENT #, Math 5. Find the equation of a sphere if one of its diameters has end points (, 0, 5) and (5, 4, 7). The length of the diameter is (5 ) + ( 4 0) + (7 5) = =, so the
SOLUTIONS TO HOMEWORK ASSIGNMENT #, Math 5. Find the equation of a sphere if one of its diameters has end points (, 0, 5) and (5, 4, 7). The length of the diameter is (5 ) + ( 4 0) + (7 5) = =, so the
CONTINUITY AND DIFFERENTIABILITY
 CONTINUITY AND DIFFERENTIABILITY Revision Assignment Class 1 Chapter 5 QUESTION1: Check the continuity of the function f given by f () = 7 + 5at = 1. The function is efine at the given point = 1 an its
CONTINUITY AND DIFFERENTIABILITY Revision Assignment Class 1 Chapter 5 QUESTION1: Check the continuity of the function f given by f () = 7 + 5at = 1. The function is efine at the given point = 1 an its
Lesson-3 TRIGONOMETRIC RATIOS AND IDENTITIES
 Lesson- TRIGONOMETRIC RATIOS AND IDENTITIES Angle in trigonometry In trigonometry, the measure of an angle is the amount of rotation from B the direction of one ray of the angle to the other ray. Angle
Lesson- TRIGONOMETRIC RATIOS AND IDENTITIES Angle in trigonometry In trigonometry, the measure of an angle is the amount of rotation from B the direction of one ray of the angle to the other ray. Angle
Edexcel GCE A Level Maths. Further Maths 3 Coordinate Systems
 Edecel GCE A Level Maths Further Maths 3 Coordinate Sstems Edited b: K V Kumaran kumarmaths.weebl.com 1 kumarmaths.weebl.com kumarmaths.weebl.com 3 kumarmaths.weebl.com 4 kumarmaths.weebl.com 5 1. An ellipse
Edecel GCE A Level Maths Further Maths 3 Coordinate Sstems Edited b: K V Kumaran kumarmaths.weebl.com 1 kumarmaths.weebl.com kumarmaths.weebl.com 3 kumarmaths.weebl.com 4 kumarmaths.weebl.com 5 1. An ellipse
Created by T. Madas LINE INTEGRALS. Created by T. Madas
 LINE INTEGRALS LINE INTEGRALS IN 2 DIMENSIONAL CARTESIAN COORDINATES Question 1 Evaluate the integral ( x + 2y) dx, C where C is the path along the curve with equation y 2 = x + 1, from ( ) 0,1 to ( )
LINE INTEGRALS LINE INTEGRALS IN 2 DIMENSIONAL CARTESIAN COORDINATES Question 1 Evaluate the integral ( x + 2y) dx, C where C is the path along the curve with equation y 2 = x + 1, from ( ) 0,1 to ( )
3.4 The Chain Rule. F (x) = f (g(x))g (x) Alternate way of thinking about it: If y = f(u) and u = g(x) where both are differentiable functions, then
 3.4 The Chain Rule To find the derivative of a function that is the composition of two functions for which we already know the derivatives, we can use the Chain Rule. The Chain Rule: Suppose F (x) = f(g(x)).
3.4 The Chain Rule To find the derivative of a function that is the composition of two functions for which we already know the derivatives, we can use the Chain Rule. The Chain Rule: Suppose F (x) = f(g(x)).
*P46958A0244* IAL PAPER JANUARY 2016 DO NOT WRITE IN THIS AREA DO NOT WRITE IN THIS AREA DO NOT WRITE IN THIS AREA. 1. f(x) = (3 2x) 4, x 3 2
 Edexcel "International A level" "C3/4" papers from 016 and 015 IAL PAPER JANUARY 016 Please use extra loose-leaf sheets of paper where you run out of space in this booklet. 1. f(x) = (3 x) 4, x 3 Find
Edexcel "International A level" "C3/4" papers from 016 and 015 IAL PAPER JANUARY 016 Please use extra loose-leaf sheets of paper where you run out of space in this booklet. 1. f(x) = (3 x) 4, x 3 Find
Exercises for Multivariable Differential Calculus XM521
 This document lists all the exercises for XM521. The Type I (True/False) exercises will be given, and should be answered, online immediately following each lecture. The Type III exercises are to be done
This document lists all the exercises for XM521. The Type I (True/False) exercises will be given, and should be answered, online immediately following each lecture. The Type III exercises are to be done
Exercise: concepts from chapter 3
 Reading:, Ch 3 1) The natural representation of a curve, c = c(s), satisfies the condition dc/ds = 1, where s is the natural parameter for the curve. a) Describe in words and a sketch what this condition
Reading:, Ch 3 1) The natural representation of a curve, c = c(s), satisfies the condition dc/ds = 1, where s is the natural parameter for the curve. a) Describe in words and a sketch what this condition
11.6. Parametric Differentiation. Introduction. Prerequisites. Learning Outcomes
 Parametric Differentiation 11.6 Introduction Sometimes the equation of a curve is not be given in Cartesian form y f(x) but in parametric form: x h(t), y g(t). In this Section we see how to calculate the
Parametric Differentiation 11.6 Introduction Sometimes the equation of a curve is not be given in Cartesian form y f(x) but in parametric form: x h(t), y g(t). In this Section we see how to calculate the
Practice Problems for the Final Exam
 Math 114 Spring 2017 Practice Problems for the Final Exam 1. The planes 3x + 2y + z = 6 and x + y = 2 intersect in a line l. Find the distance from the origin to l. (Answer: 24 3 ) 2. Find the area of
Math 114 Spring 2017 Practice Problems for the Final Exam 1. The planes 3x + 2y + z = 6 and x + y = 2 intersect in a line l. Find the distance from the origin to l. (Answer: 24 3 ) 2. Find the area of
Ordinary Differential Equations (ODE)
 ++++++++++ Ordinary Differential Equations (ODE) Previous year Questions from 07 to 99 Ramanasri Institute W E B S I T E : M A T H E M A T I C S O P T I O N A L. C O M C O N T A C T : 8 7 5 0 7 0 6 6 /
++++++++++ Ordinary Differential Equations (ODE) Previous year Questions from 07 to 99 Ramanasri Institute W E B S I T E : M A T H E M A T I C S O P T I O N A L. C O M C O N T A C T : 8 7 5 0 7 0 6 6 /
Week beginning Videos Page
 1 M Week beginning Videos Page June/July C3 Algebraic Fractions 3 June/July C3 Algebraic Division 4 June/July C3 Reciprocal Trig Functions 5 June/July C3 Pythagorean Identities 6 June/July C3 Trig Consolidation
1 M Week beginning Videos Page June/July C3 Algebraic Fractions 3 June/July C3 Algebraic Division 4 June/July C3 Reciprocal Trig Functions 5 June/July C3 Pythagorean Identities 6 June/July C3 Trig Consolidation
Mark Scheme (Results) Summer Pearson Edexcel GCE In Further Pure Mathematics FP2 (6668/01)
 Mark Scheme (Results) Summer 017 Pearson Edexcel GCE In Further Pure Mathematics FP (6668/01) Edexcel and BTEC Qualifications Edexcel and BTEC qualifications are awarded by Pearson, the UK s largest awarding
Mark Scheme (Results) Summer 017 Pearson Edexcel GCE In Further Pure Mathematics FP (6668/01) Edexcel and BTEC Qualifications Edexcel and BTEC qualifications are awarded by Pearson, the UK s largest awarding
INTEGRAL CALCULUS DIFFERENTIATION UNDER THE INTEGRAL SIGN: Consider an integral involving one parameter and denote it as
 INTEGRAL CALCULUS DIFFERENTIATION UNDER THE INTEGRAL SIGN: Consider an integral involving one parameter and denote it as, where a and b may be constants or functions of. To find the derivative of when
INTEGRAL CALCULUS DIFFERENTIATION UNDER THE INTEGRAL SIGN: Consider an integral involving one parameter and denote it as, where a and b may be constants or functions of. To find the derivative of when
Lecture 4: Partial and Directional derivatives, Differentiability
 Lecture 4: Partial and Directional derivatives, Differentiability Rafikul Alam Department of Mathematics IIT Guwahati Differential Calculus Task: Extend differential calculus to the functions: Case I:
Lecture 4: Partial and Directional derivatives, Differentiability Rafikul Alam Department of Mathematics IIT Guwahati Differential Calculus Task: Extend differential calculus to the functions: Case I:
Chapter 10. Additional Topics in Trigonometry
 Chapter 10 Additional Topics in Trigonometry 1 Right Triangle applications Law of Sines and Cosines Parametric equations Polar coordinates Curves in polar coordinates Summary 2 Chapter 10.1 Right Triangle
Chapter 10 Additional Topics in Trigonometry 1 Right Triangle applications Law of Sines and Cosines Parametric equations Polar coordinates Curves in polar coordinates Summary 2 Chapter 10.1 Right Triangle
Ordinary Differential Equations
 ++++++++++ Ordinary Differential Equations Previous year Questions from 016 to 199 Ramanasri 016 S H O P NO- 4, 1 S T F L O O R, N E A R R A P I D F L O U R M I L L S, O L D R A J E N D E R N A G A R,
++++++++++ Ordinary Differential Equations Previous year Questions from 016 to 199 Ramanasri 016 S H O P NO- 4, 1 S T F L O O R, N E A R R A P I D F L O U R M I L L S, O L D R A J E N D E R N A G A R,
PRACTICE PAPER 6 SOLUTIONS
 PRACTICE PAPER 6 SOLUTIONS SECTION A I.. Find the value of k if the points (, ) and (k, 3) are conjugate points with respect to the circle + y 5 + 8y + 6. Sol. Equation of the circle is + y 5 + 8y + 6
PRACTICE PAPER 6 SOLUTIONS SECTION A I.. Find the value of k if the points (, ) and (k, 3) are conjugate points with respect to the circle + y 5 + 8y + 6. Sol. Equation of the circle is + y 5 + 8y + 6
Find the indicated derivative. 1) Find y(4) if y = 3 sin x. A) y(4) = 3 cos x B) y(4) = 3 sin x C) y(4) = - 3 cos x D) y(4) = - 3 sin x
 Assignment 5 Name Find the indicated derivative. ) Find y(4) if y = sin x. ) A) y(4) = cos x B) y(4) = sin x y(4) = - cos x y(4) = - sin x ) y = (csc x + cot x)(csc x - cot x) ) A) y = 0 B) y = y = - csc
Assignment 5 Name Find the indicated derivative. ) Find y(4) if y = sin x. ) A) y(4) = cos x B) y(4) = sin x y(4) = - cos x y(4) = - sin x ) y = (csc x + cot x)(csc x - cot x) ) A) y = 0 B) y = y = - csc
Contents. MATH 32B-2 (18W) (L) G. Liu / (TA) A. Zhou Calculus of Several Variables. 1 Multiple Integrals 3. 2 Vector Fields 9
 MATH 32B-2 (8W) (L) G. Liu / (TA) A. Zhou Calculus of Several Variables Contents Multiple Integrals 3 2 Vector Fields 9 3 Line and Surface Integrals 5 4 The Classical Integral Theorems 9 MATH 32B-2 (8W)
MATH 32B-2 (8W) (L) G. Liu / (TA) A. Zhou Calculus of Several Variables Contents Multiple Integrals 3 2 Vector Fields 9 3 Line and Surface Integrals 5 4 The Classical Integral Theorems 9 MATH 32B-2 (8W)
e x3 dx dy. 0 y x 2, 0 x 1.
 Problem 1. Evaluate by changing the order of integration y e x3 dx dy. Solution:We change the order of integration over the region y x 1. We find and x e x3 dy dx = y x, x 1. x e x3 dx = 1 x=1 3 ex3 x=
Problem 1. Evaluate by changing the order of integration y e x3 dx dy. Solution:We change the order of integration over the region y x 1. We find and x e x3 dy dx = y x, x 1. x e x3 dx = 1 x=1 3 ex3 x=
Higher Mathematics Course Notes
 Higher Mathematics Course Notes Equation of a Line (i) Collinearity: (ii) Gradient: If points are collinear then they lie on the same straight line. i.e. to show that A, B and C are collinear, show that
Higher Mathematics Course Notes Equation of a Line (i) Collinearity: (ii) Gradient: If points are collinear then they lie on the same straight line. i.e. to show that A, B and C are collinear, show that
2. (i) Find the equation of the circle which passes through ( 7, 1) and has centre ( 4, 3).
 Circle 1. (i) Find the equation of the circle with centre ( 7, 3) and of radius 10. (ii) Find the centre of the circle 2x 2 + 2y 2 + 6x + 8y 1 = 0 (iii) What is the radius of the circle 3x 2 + 3y 2 + 5x
Circle 1. (i) Find the equation of the circle with centre ( 7, 3) and of radius 10. (ii) Find the centre of the circle 2x 2 + 2y 2 + 6x + 8y 1 = 0 (iii) What is the radius of the circle 3x 2 + 3y 2 + 5x
MAHARASHTRA STATE BOARD OF TECHNICAL EDUCATION (Autonomous) (ISO/IEC Certified)
 SUMMER 8 EXAMINATION Important Instructions to eaminers: ) The answers should be eamined by key words and not as word-to-word as given in the model answer scheme. ) The model answer and the answer written
SUMMER 8 EXAMINATION Important Instructions to eaminers: ) The answers should be eamined by key words and not as word-to-word as given in the model answer scheme. ) The model answer and the answer written
e 2 = e 1 = e 3 = v 1 (v 2 v 3 ) = det(v 1, v 2, v 3 ).
 3. Frames In 3D space, a sequence of 3 linearly independent vectors v 1, v 2, v 3 is called a frame, since it gives a coordinate system (a frame of reference). Any vector v can be written as a linear combination
3. Frames In 3D space, a sequence of 3 linearly independent vectors v 1, v 2, v 3 is called a frame, since it gives a coordinate system (a frame of reference). Any vector v can be written as a linear combination
MTH 277 Test 4 review sheet Chapter , 14.7, 14.8 Chalmeta
 MTH 77 Test 4 review sheet Chapter 13.1-13.4, 14.7, 14.8 Chalmeta Multiple Choice 1. Let r(t) = 3 sin t i + 3 cos t j + αt k. What value of α gives an arc length of 5 from t = 0 to t = 1? (a) 6 (b) 5 (c)
MTH 77 Test 4 review sheet Chapter 13.1-13.4, 14.7, 14.8 Chalmeta Multiple Choice 1. Let r(t) = 3 sin t i + 3 cos t j + αt k. What value of α gives an arc length of 5 from t = 0 to t = 1? (a) 6 (b) 5 (c)
Vectors and Geometry
 Vectors and Geometry Vectors In the context of geometry, a vector is a triplet of real numbers. In applications to a generalized parameters space, such as the space of random variables in a reliability
Vectors and Geometry Vectors In the context of geometry, a vector is a triplet of real numbers. In applications to a generalized parameters space, such as the space of random variables in a reliability
Calculus Vector Principia Mathematica. Lynne Ryan Associate Professor Mathematics Blue Ridge Community College
 Calculus Vector Principia Mathematica Lynne Ryan Associate Professor Mathematics Blue Ridge Community College Defining a vector Vectors in the plane A scalar is a quantity that can be represented by a
Calculus Vector Principia Mathematica Lynne Ryan Associate Professor Mathematics Blue Ridge Community College Defining a vector Vectors in the plane A scalar is a quantity that can be represented by a
School of Distance Education UNIVERSITY OF CALICUT SCHOOL OF DISTANCE EDUCATION. B Sc Mathematics. (2011 Admission Onwards) IV Semester.
 School of Dtance Education UNIVERSITY OF CALICUT SCHOOL OF DISTANCE EDUCATION B Sc Mathematics 0 Admsion Onwards IV Semester Core Course CALCULUS AND ANALYTIC GEOMETRY QUESTION BANK The natural logarithm
School of Dtance Education UNIVERSITY OF CALICUT SCHOOL OF DISTANCE EDUCATION B Sc Mathematics 0 Admsion Onwards IV Semester Core Course CALCULUS AND ANALYTIC GEOMETRY QUESTION BANK The natural logarithm
Functions, Graphs, Equations and Inequalities
 CAEM DPP Learning Outcomes per Module Module Functions, Graphs, Equations and Inequalities Learning Outcomes 1. Functions, inverse functions and composite functions 1.1. concepts of function, domain and
CAEM DPP Learning Outcomes per Module Module Functions, Graphs, Equations and Inequalities Learning Outcomes 1. Functions, inverse functions and composite functions 1.1. concepts of function, domain and
MATHEMATICS LEARNING AREA. Methods Units 1 and 2 Course Outline. Week Content Sadler Reference Trigonometry
 MATHEMATICS LEARNING AREA Methods Units 1 and 2 Course Outline Text: Sadler Methods and 2 Week Content Sadler Reference Trigonometry Cosine and Sine rules Week 1 Trigonometry Week 2 Radian Measure Radian
MATHEMATICS LEARNING AREA Methods Units 1 and 2 Course Outline Text: Sadler Methods and 2 Week Content Sadler Reference Trigonometry Cosine and Sine rules Week 1 Trigonometry Week 2 Radian Measure Radian
Find the slope of the curve at the given point P and an equation of the tangent line at P. 1) y = x2 + 11x - 15, P(1, -3)
 Final Exam Review AP Calculus AB Find the slope of the curve at the given point P and an equation of the tangent line at P. 1) y = x2 + 11x - 15, P(1, -3) Use the graph to evaluate the limit. 2) lim x
Final Exam Review AP Calculus AB Find the slope of the curve at the given point P and an equation of the tangent line at P. 1) y = x2 + 11x - 15, P(1, -3) Use the graph to evaluate the limit. 2) lim x
Sets. 1.2 Find the set of all x R satisfying > = > = > = - > 0 = [x- 3 (x -2)] > 0. = - (x 1) (x 2) (x 3) > 0. Test x = 0, 5
![Sets. 1.2 Find the set of all x R satisfying > = > = > = - > 0 = [x- 3 (x -2)] > 0. = - (x 1) (x 2) (x 3) > 0. Test x = 0, 5 Sets. 1.2 Find the set of all x R satisfying > = > = > = - > 0 = [x- 3 (x -2)] > 0. = - (x 1) (x 2) (x 3) > 0. Test x = 0, 5](/thumbs/94/120119838.jpg) Sets 1.2 Find the set of all x R satisfying > > Test x 0, 5 > - > 0 [x- 3 (x -2)] > 0 - (x 1) (x 2) (x 3) > 0 At x0: y - (-1)(-2)(-3) 6 > 0 x < 1 At x5: y - (4)(3)(2) -24 < 0 2 < x < 3 Hence, {x R: x
Sets 1.2 Find the set of all x R satisfying > > Test x 0, 5 > - > 0 [x- 3 (x -2)] > 0 - (x 1) (x 2) (x 3) > 0 At x0: y - (-1)(-2)(-3) 6 > 0 x < 1 At x5: y - (4)(3)(2) -24 < 0 2 < x < 3 Hence, {x R: x
Specialist Mathematics 2017 Sample paper
 South Australian Certificate of Education Specialist Mathematics 07 Sample paper Question Booklet Part (Questions to 9) 75 marks Answer all questions in Part Write your answers in this question booklet
South Australian Certificate of Education Specialist Mathematics 07 Sample paper Question Booklet Part (Questions to 9) 75 marks Answer all questions in Part Write your answers in this question booklet
