Forecasting in functional regressive or autoregressive models
|
|
|
- Samuel Goodwin
- 5 years ago
- Views:
Transcription
1 Forcasing in funcional rgrssiv or auorgrssiv modls Ann Philipp 1 and Mari-Claud Viano 2 Univrsié d Nans Univrsié d Lill Laboraoir d mahémaiqus Jan Lray, 2 ru d la Houssinièr Nans, Franc Ann.Philipp@univ-nans.fr 2 Laboraoir Paul Painlvé, Villnuv d Ascq, Cd, Franc viano@mah.univ-lill1.fr
2
3 Conns Chapr 1. Inroducion 5 1. Gnral modl 5 2. Opimal prdicor 5 3. Difficulis 6 Chapr 2. Linar modls 7 1. Assumpions 7 2. Paramr simaion 8 3. Forcasing Erciss 12 Chapr 3. Prliminaris on krnl mhods in funcional rgrssion simaion Hurisic approach Naiv inrpraion Erciss 16 Chapr 4. Mor on funcional rgrssion simaion Inroducion Uniform almos sur convrgnc Ingrad quadraic rror Illusraion Forcasing Incrasing h mmory Erciss 35 Chapr 5. Funcional auorgrssion modls Inroducion Wak dpndnc of non-linar auorgrssions Propris of srong miing squncs, and hir consquncs Esimaion of a Illusraion Forcasing Incrasing h mmory Erciss 60 Chapr 6. Mid modls Inroducion 63 3
4 4 CONTENTS 2. Assumpions and firs consquncs Convrgnc rsuls Illusraion Forcasing Ohr mhods Erciss 73 Bibliography 75
5 CHAPTER 1 Inroducion This documn is dvod o qusions rlad o forcasing im sris modls, a opic which has now a growing imporanc in various domains lik signal and imag procssing, agro-indusry, conomrics, gophysics and all socio-conomics aras whr good forcass can graly improv h gains and limi h wasing. W ar inrsd in modls lik 1. Gnral modl (1) X k = a(x k 1,..., X k p ) + b( k,..., k q ) + ε k k, whr h obsrvd variabls ar (X n,..., X 1 ) and ( n+1,..., 1 ) and whr h squnc (ε j ) is an unobsrvd whi nois. Th goal is o prdic h valu of X n+h for h = 1, 2,... from h obsrvd variabls. For convninc, in mos cass, w shall ak h forcasing horizon h = 1. Bu i should b clar o h radr ha his is a ral loss of gnraliy. Ohr valus of h shall b rad in rciss. Noic in (1) h simulanous prsnc, in h righ hand sid, of an auorgrssiv summand and of a purly rgrssiv on. h auorgrssiv par a(x k 1,..., X k p ) mans ha h pas valus of h im sris, up o a lag of lngh p, affc h valu X k+h. h rgrssiv par b( k,..., k q ) summarizs h acion of an ognous squnc ( j ). For ampl imagin ha h lcriciy consumpion X k a im k dpnds on h consumpion a h p insans jus bfor and on h mpraur k,..., k q a h momns k,..., k q. 2. Opimal prdicor Th mos usual forcasing mhod consiss in minimizing a quadraic cririon (assuming ha h scond ordr momns ar fini). Namly X n+h = Argmin{(X n+h Z) 2 Z F n }, whr F n is h σ-algbra gnrad by (X n,..., X 1 ), ( n+1,..., 1 ). Wih his cririon, X n+h is nohing ls han h condiional pcaion X n+h = E(X n+h F n ) 5
6 6 A. Philipp & M.-C. Viano Considr h cas h = 1. In all h siuaions sudid blow, ε n is indpndn of F n, so ha h on sp ahad opimal prdicor is X n+1 = a(x n,..., X n p+1 ) + b( n+1,..., n q+1 ), and consqunly, ε n+1 is h forcasing rror a horizon h = 1. Unforunaly, h funcions a and b ar gnrally unknown, so h saisician has o plug in an simaion of h funcions. Consqunly, h forcasing rror includs boh h horical rror ε n and h simaion rror. Mor prcisly, w hav o rplac X n+1 by (2) ˆXn+1 = â(x n,..., X n p+1 ) + ˆb( n+1,..., n q+1 ), implying ha X n+1 ˆX n+1 = ε n + (a(x n,..., X n p+1 ) â(x n,..., X n p+1 )) ( + b( n+1,..., n q+1 ) ˆb( ) n+1,..., n q+1 ). 3. Difficulis Th horical ramns of h gnral modl (1) ar difficul for svral rasons. Th firs rason is h fac hs wo rgrssions hav a funcional form: in ordr o prdic X n+1, on has o sima wo funcions a and b. Esimaing funcions is always mor ricky han o sima fini-dimnsional paramrs. Th scond on is h simulanous prsnc of rgrssion and auorgrssion. Rgrssion is asy o ra, bing a rlaivly wll known siuaion. Auorgrssion, which inducs sochasic dpndnc bwn h X js, is much mor difficul o handl, cp in h familiar cas of linar auorgrssion. W shall procd sp by sp. Firsly, in scion 2 w dal wih a linar vrsion of (1). Thn w ra in scions 3 and 4 simpl rgrssion modls, and a simpl auorgrssion on in scion 5. In hs wo cass, w shall ak p = q = 1 in (1), kping in mind ha h gnral cas can b rad as wll, dspi a ncssary mulivaria ramn (s scion 6 for ampl).
7 CHAPTER 2 Linar modls W bgin wih h linar vrsion of (1) (3) X k = a 0 + a 1 X k a p X k p + b 0 k b q k q + ε k k. 1. Assumpions Th nois (ε n ) is a Gaussian zro-man i.i.d squnc, wih varianc σ 2 0. Th ognous squnc ( n ) is i.i.d, Gaussian, wih zro man and Var( n ) = 1. Indpndnc: Th wo squncs (ε n ) and ( n ) ar indpndn. Saionariy: a p 0 and h polynomial A(z) = z p a 1 z p 1... a p dos no vanish on h domain z 1. Minimaliy: h wo polynomials A(z) and B(z) = b 0 z q + b 1 z q b q hav no common roo. Saionariy again: Th procss (X n ) is h uniqu saionary soluion of (3). Rmark 1. Whinss assumpion of h inpu nois (ε n ) is rahr naural, a las in a firs approach. So is h indpndnc of (ε n ) and of ( n ). Rmark 2. Th Gaussian assumpion is convnin, bu could asily b rlad. Rmark 3. Assuming ha ( n ) is i.i.d. is no ralisic in mos cass (for ampl whn n rprsns h mpraur!), and should b rlad. Howvr, his siuaion is chosn hr bcaus i maks h dvlopmns mor asy. Indd, in his cas, quaions (3) hav a uniqu Gaussian saionary soluion ha saisfis h ARMA(p,q) rprsnaion (4) (5) Y k a 1 Y k 1... a p Y k p = η k + c 1 η k c q η k q Y k = X k E(X k ) wih = a 0 X k =: X k m 0. 1 a 1... a p whr (η k ) is a zro-man Gaussian whi nois (s rcis 1 for h proof of his rsul in a simpl cas). This soluion also wris (6) Y k = u k + d 1 u k d l u k l... whr (7) u k = b 0 k b q k q + ε k, 7
8 8 A. Philipp & M.-C. Viano and whr h d js ar h cofficins of h pansion of h auorgrssiv par (1 a 1 z... a p z p ) 1 = 1 + d 1 z d l z l +... Rmark 4. Th minimaliy assumpion implis ha i is impossibl o find for h sam modl a shorr rprsnaion lik X k = c 0 + c 1 X k c p 1 X k p+1 + d 0 k d q 1 k q+1 + ε k k. 2. Paramr simaion In h ARMA rprsnaion (4), w know ha h maimum liklihood sima ˆθ n of h vcor paramr θ = (a 1,..., a p, c 1,..., c q ) (hrafr, v is wrin for h ranspos of vcor v) is almos surly convrgn and ha n 1/2 (ˆθ n θ) is asympoically normally disribud (s for ampl [4], chapr 8). Howvr, his is no a vry usful rsul, for wo rasons. Th firs on is ha h vcor w wan o sima is no θ, bu θ = (a 1,..., a p, b 0,..., b q ), h link bwn h wo vcors bing highly non linar (s rcis 1). Th scond rason is ha in h classical ARMA hory, h inpu nois (η n ) is unobsrvd, whil in modl (3), h ognous par k,..., k q is obsrvd. Th only unobsrvd rm bing ε k. Esimaor ˆθ n is no fid o his siuaion. For hos rasons, i is br o sima θ by a dirc las man squar mhod ( ) 2 n p q (8) ˆθn = Argmin X k α 0 α j X k j β j k j, k=1+p q h minimum bing akn ovr (α 0, α 1,..., α p, β 0,..., β q ). Dnoing k 0 = 1 + p q j=1 j=0 φ k = (1, X k 1,..., X k p, k,..., k q ) n M n = φ k φ k k=k 0 i is asy o chck ha, if M n is invribl, (8) has a uniqu soluion givn by n (9) ˆθn = Mn 1 X k φ k. k=k 0 For his simaor h following rsul holds. Proposiion 1. As n, wih ˆθ n dfind as in (8), (i) ˆθ n θ = o as (n α ) for vry α < 1/2 (ii) n (ˆθn θ) L N (0, σ 2 M 1 ) whr σ 2 = Var(ε n ) and whr M = E(φ k φ k ), is invribl.
9 Forcasing in funcional rgrssiv or auorgrssiv modls 9 Proof. Rcall ha u n = o as (v n ) mans ha u n vn 1 a.s. 0. Bfor procding, i is usful o s ha h vcor squnc (φ k ) k k0 saionary and rgodic. Indd, using (7), φ k = 1 a 0 + u k 1 + j=1 d ju k 1 j. a 0 + u k p + j=1 d ju k p j k. k q is Gaussian, so ha, inroducing h backward shif opraor B (dfind by B m z n = z n m ), w can wri a 0 B + j=1 d jb j 0 φ k =. a B p + j=1 d jb p+j 0 0 B B q ( uk k ) so ha h squnc (φ k ) k k0 is clarly consrucd by linar filring from h Gaussian squnc (u k, k ) k 1. Finally, aking (7) ino accoun, (φ k ) k k0 is obaind from ( k, ε k ) k 1 by linar filring. Now w rcall wo rsuls: If a saionary squnc (w k ) has a spcral dnsiy, i is also h cas for vry squnc (w k ) obaind from w by linar filring (i.. w k = 0 γ jw k j, wih γj 2 < ). A saionary Gaussian squnc having a spcral dnsiy is rgodic. For rgodiciy and rlad propris s for ampl [5]). Firs sp: considr h mari M n. Sinc (φ k ) k k0 is rgodic, h law of larg numbrs applis, lading o (10) n 1 M n a.s. M = E(φ kφ k ). Now, suppos ha E(φ k φ k) is no invribl. This mans ha hr iss a non zro vcor v such ha E( vφ kφ k v) = 0 k Hnc, vφ k = a.s 0 for all k. This implis ha hr iss cofficins such ha v 0 + v 1 X k v p X k p + w 0 k +... w q k q = 0 k.
10 10 A. Philipp & M.-C. Viano As k is indpndn of h ohr variabls in h prssion abov, his implis ha w 0 = 0, so ha v 1 X k v p X k p + w 1 k 1... w q k q = v 0 k. Bu in urn his conradics h hypohsis of minimaliy (s h assumpion 4 in subscion 1). Consqunly, M is invribl, so ha, almos surly, M n is invribl for n sufficinly larg, and formula (9) is hn valid. Scond sp: l us prov h almos sur convrgnc. From (9), and from h fac ha X k = φ k θ + ε k, wri n n α (ˆθ n θ) = Mn 1 X k φ k θ k=k 0 ( ) n = n α Mn 1 φ k ( φ k θ + ε k ) θ k=k 0 ( ) n = n α Mn 1 φ k ε k = ( ) ( n ) nmn 1 k=k 0 φ k ε k (11) n 1 α k=k 0 Now, ε k is indpndn of all h coordinas of φ k, so ha E(φ k ε k F k 1 ) = 0. In ohr words, (φ k ε k ) k k0 is a (vcor) maringal diffrnc squnc wih rspc o h squnc (F k ) k 1. Morovr, for β > 1/2 ( E φk ε k 2) = σ 2 E ( φ k 2β k 2) 1 k < 2β k k 0 k k 0 Hnc, applying Thorm in [16], Finally, as was sn abov, nmn 1 provd. Third sp: w prov now ha n β n k=k 0 φ k ε k a.s. 0. a.s. M 1. Using (10), h almos sur convrgnc is (12) n k=k 0 φ k ε k n L N (0, σ 2 M) To prov his rsul, l T b a fid ingr, and considr h runcad pansion T X (T ) k = m 0 + u k + d j u k j, and h corrsponding vcor j=1 φ (T ) k = (1, X (T ) k 1,..., X(T ) k p, k,..., k q ).
11 Forcasing in funcional rgrssiv or auorgrssiv modls 11 I is asy o chck ha h squnc (ε k φ (T ) k ) k k 0 is T + p + q-dpndn (ha is o say: ε k φ (T ) k and ε k+h φ (T ) k+h ar indpndn as soon as h > T + p + q). Hnc h cnral limi horm holds. In ordr o find h covarianc mari of h limiing law, noic ha E(ε k ε k+h φ k φ k+h ) = 0 if h 0. Hnc, n k=k 0 φ k ε k L N (0, σ 2 M T ) n ( ) whr M T = E φ (T ) k φ (T ) k. Finally, as T, M T M and Var(φ (T ) k φ k ) 0. To prov (11) i rmains o apply h following lmma whos proof is lf as an rcis. Lmma 2. Suppos ha, Z n = Z T,n,1 + Z T,n,2 n, T whr for fid T, as n, Z T,n,1 L N (0, V T ) V T V as T Var(Z T,n,2 ) 0 uniformly wih rspc o n, as T hn Z n L N (0, V ) whn n. 3. Forcasing As was sn in h inroducion, w choos ˆX n+1 = θ ˆ n φ n+1, and, consqunly, h forcasing rror a horizon 1 is X n+1 ˆX n+1 = (θ θ ˆ n )φ n+1 + ε n+1, whr h wo summands in h righ hand sid ar indpndn. From Proposiion 1, for vry α < 1/2, n α (θ θ ˆ n ) a.s. 0. Morovr h disribuion of φ n dos no dpnd on n. To summariz, Proposiion 3. Wih h sam assumpions as in Proposiion 1, X n+1 ˆX n+1 = ε n+1 + T n, whr ε n+1 and T n ar indpndn and whr, as n, T n = o P (n α ) for vry α < 1/2.
12 12 A. Philipp & M.-C. Viano 4. Erciss Ercis 1. Prov rprsnaion (4) for h simpl modl X k a 1 X k 1 = b 0 k + b 1 k 1 + ε k, and giv a hin for h proof in h gnral cas (3). Ercis 2. Prov Lmma 2. Ercis 3. Giv h prssion of h opimal forcas X n+2 a horizon h = 2 in h modl of rcis 1. Ercis 4. Considr now h linar modl X k+1 = ax k + b k+1 + ε k+1, and suppos ha now ha ( k ) is an auorgrssiv squnc k+1 = c k + η k+1 whr (η k ) is a zro man whi nois. (1) Show ha, if a < 1 and c < 1, hr is a saionary soluion (X k, k ). (2) Working wih his saionary soluion, propos an simaor of h paramrs a, b and c.
13 CHAPTER 3 Prliminaris on krnl mhods in funcional rgrssion simaion Krnl mhods ar old and popular mhods usd in all aras whr h saisician has o sima a funcional paramr. As ampls, l h daa (Z 1,..., Z n ) rprsn a sampl from an i.i.d. squnc, h qusion bing o sima h dnsiy of h marginal disribuion. Or l [(Y 1, Z 1 ),..., (Y n, Z n )] b a sampl of an i.i.d. squnc, h problm bing hn o sima E(Z 1 Y 1 = y). Th firs ampl is h problm of dnsiy simaion, for which krnl mhods wr proposd by Parzn in Th scond is h problm of rgrssion simaion, for which krnl mhods wr proposd by Nadaraya and Wason in Hr w concnra on rgrssion simaion, and h so-calld Nadaraya-Wason simaor. 1. Hurisic approach 1.1. Sp 1. In h cas of discr daa, whn h dnominaor dos no vanish (13) r(y) := E(Z 1 Y 1 = y) = E(Z 1 I Y1 =y) P (Y 1 = y). hnc, from h sampl (Y 1, Z 1 ),..., (Y n, Z n ), i is naural sima r(y) by ˆr n (y) = n 1 n j=1 Z j I n Yj =y n j=1 1 n j=1 I = Z j I Yj =y n Y j =y j=1 I Y j =y which, hanks o h law of larg numbrs, convrgs owards h condiional pcaion. Now, whn h daa ar no discr, formula (12) no longr holds, boh numraor and dnominaor gnrally bing zro Sp 2. Howvr, h sam mhod could b applid o sima (if h dnominaor is non zro) (14) E (Z 1 Y 1 [y h, y + h]) = E(Z 1 I Y1 [y h,y+h]) P (Y 1 [y h, y + h]) 13
14 14 A. Philipp & M.-C. Viano by n j=1 Z j I Yj [y h,y+h] n j=1 I. Y j [y h,y+h] 1.3. Sp 3. As vry on knows, if h 0 in (13), h lf hand sid nds o E(Z 1 Y 1 = y), a las undr suiabl smoohnss assumpions. From his, i sms naural o rplac h by a squnc h n nding o zro as n, and ak (15) ˆr n (y) = n j=1 Z j I Yj [y h n,y+h n] n j=1 I, Y j [y h n,y+h n] whr h n has o dcras whn h sampl siz incrass. This las poin has o b dvlopd. From now on, in ordr o hav a wll dfind simaor, w ak 0/0 = Sp 4. Fas nough, bu no oo fas! Wriing Z j = E(Z j Y j ) + (Z j E(Z j Y j )) = r(y j ) + η j whr Y j and Z j E(Z j Y j ) =: η j ar uncorrlad, w g ˆr n (y) r(y) = n j=1 (Z j r(y)) I Yj [y h n,y+h n] n j=1 I Y j [y h n,y+h n] = n j=1 (r(y j) r(y)) I Yj [y h n,y+h n] n j=1 I Y j [y h n,y+h n] + n j=1 η j I Yj [y h n,y+h n] n j=1 I Y j [y h n,y+h n] = A n + B n. Firs considr A n. If r is coninuous, i is clar ha his rm nds o zro if h n 0. In fac, h smallr h n is, h smallr A n. Now considr B n. For h sak of simpliciy, suppos ha (Y j, Z j ) is Gaussian. Thn for vry j, η j is indpndn from all h indicaors I Yl [y h n,y+h n], so ha n B n = η j u j j=1 whr, for vry j, η j and u j ar indpndn and E(η j = 0). This implis ha E(B n ) = 0 and ha, wih p n = P (Y j [y h n, y + h n ]) ( n ) Var(B n ) = E(Var(B n u 1,..., u n )) = Var(η 1 )E (16) ( ) 1 = Var(η 1 )E n j=1 I Y j [y h n,y+h n] j=1 u 2 j Var(η 1 ) 1 np n. This provs ha np n is ncssary for Var(B n ) 0. From his i is clar ha for h convrgnc of B n o zro, h n has o nd o zro no oo fas. For ampl, if h Y j ar
15 Forcasing in funcional rgrssiv or auorgrssiv modls 15 uniformly disribud, w hav p n ch n, and hn w s ha h wo condiions ar h n 0 and nh n. Mor gnrally, w shall s ha i is a gnral faur whn a krnl mhod is usd for simaing a funcion ha h sam kind of anagonis consrains hold. Th consqunc for h praciionr is ha h smoohing paramr has o b carfully rgulad Sp 5. Choic of h krnl. Th simaor in (14) also wris ( ) Yj y n K h n (17) ˆr n (y) = Z j ( ), n j=1 j=1 K Yj y h n whr K() = I [ 1,1] (). This krnl is ofn rfrd o as h rcangular krnl. Ohr ons ar commonly proposd. Wha is askd is som smoohnss a = 0, symmry and som ingrabiliy condiions. As formula (14) shows, K is dfind up o a muliplicaiv consan. As ampls (up o muliplicaiv consans): Triangular krnl: K() = (1 ) I [ 1,1] () Epanchnikov krnl Biwigh krnl Gaussian krnl K() = (1 2 ) I [ 1,1] () K() = (1 2 ) 2 I [ 1,1] () K() = 2 2 gaussian panchnikov rcangular Dnsiy Dnsiy Dnsiy riangular biwigh Dnsiy Dnsiy Figur 1. Graph of h krnls: [Top] Gaussian, Epanchnikov and Rcangular. [Boom] Triangular and Biwigh. Ecp h rcangular krnl, hy all ar vrywhr coninuous. This is h rason why h rcangular krnl is rarly usd. Noic also ha all hs krnls ar non ngaiv. In chapr 4 w us non posiiv krnls in ordr o g br ras (s rcis 10).
16 16 A. Philipp & M.-C. Viano Th simaor, in (16), wris also 2. Naiv inrpraion ˆr n (y) = n Z j W j, j=1 so i is clar ha h simaor is a wighd sum of h Z j s. Th wighs W j ar random posiiv variabls and n W j = 1. Now, for all h krnls proposd abov, h wigh W j = j=1 K Yj y hn P n j=1 K Yj y hn indicas whhr Y j is clos or no o y. Th closr Y j and y ar, h largr is h wigh. For h rcangular krnl, h wighs simply ar 0 (if h disanc is oo larg), or 1. To summariz, h simaor of E(Z 1 Y 1 = y) is a wighd sum of h Z j s, wih wighs calculad according h disanc bwn h Y j s and y. 3. Erciss Ercis 5. Prov h las inqualiy in formula (15). Ercis 6. How h abov mhod can b usd o prdic Z n from h obsrvaion of Y n and of h (Y j, Z j ) s for j n 1? Could you giv a naiv inrpraion of his prdicor? Ercis 7. Esimaion of a disribuion dnsiy. L X 1,, X n n b i.i.d. variabls having a dnsiy f. L K b a krnl such ha K(u)du = 1 K 2 (u)du <, uk(u) du < Considr h simaor of f givn by ˆf n () = 1 n n k=1 1 h n K Suppos ha f is C 1 and ha f and f ar boundd. 1) Prov ha ( ) Xk h n 0 whn n + hn, for all, E ˆf n () f() h n
17 Forcasing in funcional rgrssiv or auorgrssiv modls 17 and ha if nh n + hn for all, ( ) Var ˆf 1 n () = O nh n 2) Prov ha for all, E ˆf n () f() 2 c 1 h 2 n + c 2 nh n and conclud ha, if h n n α, hr is a valu of α for which h ra of convrgnc of h quadraic risk is opimal. This rsul shall b improvd in h n chapr (s rcis 10). Ercis 8. In rcis 7, ak h rcangular krnl, and compar h obaind simaor wih h familiar hisogram. Ercis 9. Discuss h rsuls givn by Figur 2 and Figur 3? Wha is h snsiiviy of h krnl sima o h choic of h krnls and of h bandwidhs? Eplain why you could hav gussd your conclusions from h rsuls of his chapr (and of h following ons!). sam bandwidh, 6 diffrn krnls Frquncy Dnsiy gau pa rc rian biw prcip N = 70 Bandwidh = 3.9 Figur 2. [Lf] Hisogram of h avrag amoun of prcipiaion (rainfall) in inchs for ach of 70 Unid Sas, [Righ] Krnl dnsiy simas wih 5 diffrn krnls
18 18 A. Philipp & M.-C. Viano bandwidhs = 1 bandwidhs = 2 Dnsiy Dnsiy N = 70 Bandwidh = 1 N = 70 Bandwidh = 2 bandwidhs = 3 bandwidhs = 4 Dnsiy Dnsiy N = 70 Bandwidh = 3 N = 70 Bandwidh = 4 Figur 3. Sam daa s as Figur 2. Krnl dnsiy simas wih Gaussian krnl and 4 diffrn bandwidhs.
19 CHAPTER 4 Mor on funcional rgrssion simaion 1. Inroducion W considr hr modl (1) whr only h purly rgrssiv par is prsn, and whr q = 0. Namly (18) X k = b( k ) + ε k, and w suppos ha h nois (ε n ) n 1 and h ognous squnc ( n ) n 1 ar wo indpndn i.i.d. squncs. Rcall ha h qusion is o prdic X n+1 from h obsrvaion of n+1,..., Th simaor. Noic firs ha, undr h abov hypohss, h squnc ( k, X k ) k 1 is i.i.d. Hnc, h siuaion is acly h sam as in h prcding chapr. Hr, E(X n n = ) = b(), and h funcion b() is simad by ( ) n j=1 X j jk h n (19) ˆbn () = ( ) n j=1 K j h n and h prdicor is (20) ˆXn+1 = ˆb n ( n+1 ) Th aim is o compl h hurisic rsuls of chapr 3. Two yps of convrgnc shall b invsigad. Scion 2 is dvod o uniform almos sur convrgnc (21) sup ˆb n () b() a.s. 0, and scion 3 o h ingrad quadraic rror ( ) E (ˆb n () b()) 2 w()d. In boh cass, ras of convrgnc ar givn Assumpions. Among h following hypohss, som ar only chnical (such as bounddnss of b and of h nois) and could asily b rlasd. Thy ar chosn o shorn som proofs. Ohr ons (lik smoohnss of b) ar mor fundamnal, as can b sn from som simulaions. Th nois and h variabls j ar wo i.i.d. indpndn squncs 19
20 20 A. Philipp & M.-C. Viano hr iss a drminisic consan m such ha n m and ε n m n (22) (23) (24) h ognous variabl 1 has a dnsiy f, sricly posiiv on [ m, m] and C 2. b is C 2 On h krnl: K is boundd, compacdly suppord and K(u)du = 1 uk(u)du = 0, u 2 K(u)du 0. Suppos also ha hr iss β > 0 and a consan γ such ha (25) K( 1 ) K( 2 ) γ 1 2 β if m 1, 2 m. Noic ha, from h bounddnss hypohss, (26) X n sup b() + m m m Noic also ha h nois can b Gaussian. n. 2. Uniform almos sur convrgnc Thorm 4. W considr h simaor ˆb n dfind in (18), wih a krnl saisfying assumpions (22), (23) and (24). Undr h hypohss abov, and if hn, h n 0 and nh n ln n ( ) ln n sup ˆb n () b() = O as (h 2 n) + O as nh n L u n and v n b random squncs. Rcall ha v n = O as (u n ) mans ha v n /u n is almos surly boundd. Of cours h bound may b a random variabl. L us bgin wih h proof of h horm. Thn w shall giv som rmarks. W choos a proof largly inspird by [9]. Firs rwri h simaor as: ( ) n j=1 X j P n j=1 jk jk X j hn h n nh ˆbn () = ( ) = n ĝ n j=1 K j P n j=1 K j n () (27) hn ˆf n () h n nh n =:
21 Forcasing in funcional rgrssiv or auorgrssiv modls 21 I should b clar (s chapr 3 and rcis 7) ha ˆf n () simas h dnsiy f() and ha ĝ n () simas g() := b()f(). Now, dcompos h simaion rror in implying ha ˆbn () b() = ĝn() ˆf n () g() f() = ĝn() g() ˆf n () + (f() ˆf n ()) b() ˆf n () sup ˆb n () b() sup ĝ n () g() sup inf ˆf + b f() ˆf n () n () inf ˆf n () and w ra sparaly h wo numraors and h dnominaor in h following subscions Ra of convrgnc of sup ĝ n () g(). W ar going o prov ha Lmma 5. Wih h hypohss of Thorm 4, ( ) ln n (28) sup ĝ n () g() = O as nh n Proof. Sinc + O(h 2 n) ĝ n () g() = ĝ n () E(ĝ n ()) + E(ĝ n ()) g(), w shall giv a bound for sup ĝ n () E(ĝ n ()), and for sup E(ĝ n ()) g(). W sar wih ĝ n () E(ĝ n ()) for fid. Dfin h i.i.d variabls U j by (29) U j = 1 ( ) ( ( ))) j j (X j K E X j K j = 1,..., n h n h n From (25) and sinc K is boundd, i is clar ha hr is a consan C such ha U j C 1 /h n. Scondly, E(U 2 j ) C 2 /h n, bcaus E(Uj 2 ) = 1 ( ( )) j Var X h 2 j K 1 ( ( )) 2 j E X n h n h 2 j K n h n = 1 ( ( ) E K 2 j E ( ) ) X h 2 j 2 j = 1 ( ( E K 2 j n h n h 2 n h n = 1 ( ) u (σ 2 + b 2 (u))k 2 f(u)du h 2 n h n = 1 h n h n (σ 2 + b 2 (vh n + ))K 2 (v)f(vh n + )dv C 2 h n, ) ) (σ 2 + b 2 ( j ))
22 22 A. Philipp & M.-C. Viano whr h las ingral is obaind via h chang of variabls v = (u )/h n, and h las bound from bounddnss assumpions on K, b and f. Thn i is possibl o apply h following ky ponnial inqualiy of Hoffding Lmma 6. L U 1,..., U n b i.i.d. variabls such ha Thn, for vry ε ]0, δ 2 /d[, ( n j=1 P U j n E(U j ) = 0 and U j d. ) > ε 2 nε2 4δ 2 whr δ 2 is any ral numbr such ha E(U 2 i ) δ 2 Applying his lmma o h variabls U j dfind in (28), wih d = δ 2 = C h n givs, for 0 < ε < 1, ( n j=1 (30) P ( ĝ n () E(ĝ n ()) > ε)) = P U ) j n > ε 2 nhnε2 4C (31) Th rsul (29) concrns a fid valu of. W hav now o considr h suprmum ovr. Th mhod is simpl. Covr [ m, m] by J n inrvals of lngh 2m/J n, rspcivly cnrd in 1,..., Jn. For any funcion φ, wri φ() = φ( j() ) + φ() φ( j() ) whr j() is h nars nighbour of among 1,..., Jn. So, sup φ() m m which in urn implis ha ma φ( j ) + j=1,...,j n sup φ() φ( j() ), m m sup φ() ε = { ma φ( j ) ε/2 or sup φ() φ( j() ) ε/2} m m j=1,...,j n m m L s apply his o φ() = ĝ n () E(ĝ n ()). W hav, using inqualiy (6) ( ) J n P ma ĝ n ( j ) E(ĝ n ( j )) ε/2 P ( ĝ n ( j ) E(ĝ n ( j )) ε/2) j=1,...,j n sup m m j=1 2J n nhnε 2 C 1. Thn, noicing ha for vry, j() m/j n and using h Lipschiz propry of h krnl (s (24)), ĝ n () E(ĝ n ()) ĝ n ( j() ) + E(ĝ n ( j() )) C 2 J β n h 1+β n
23 (32) P ( + P = P Now, chos J n such ha Forcasing in funcional rgrssiv or auorgrssiv modls 23 nhn ln n 1 h 1+β n = o(j β n ) ln n For such a choic, h firs mmbr of (30) is smallr han ε 0 nh n, a las for n larg nough. So, for n larg nough, sup m m ( ( sup m m ĝ n () E(ĝ n ()) > ε 0 ln n nh n ) P ( ma ĝ n ( j ) E(ĝ n ( j )) > ε 0 j=1,...,j n ) ĝn () E(ĝ n ()) ĝ n ( j() ) + E(ĝ n ( j() )) ln n > ε0 nh n ) ln n ma j=1,...,j n ĝ n ( j ) E(ĝ n ( j )) > ε 0 nh n 2J n ε 2 0 ln n C 1 = 2J n n ε2 0 C 1 ) ln n To finish wih, ak J n = n β, and ε 0 larg nough in ordr o obain n β ε 2 0 C 1 <, implying, via Borl Canlli lmma, ha almos surly, ln n sup ĝ n () E(ĝ n ()) ε 0 m m nh n holds for n larg nough. This provs ha ( ) ln n (33) sup ĝ n () E(ĝ n ()) = O as m m nh n which is h firs par in h righ hand mmbr of (27). W urn now o E(ĝ n ()) g(), h so-calld bias rm. From h dfiniion of ĝ n and from saionariy, E(ĝ n ()) g() = 1 [ ( )] 1 E X 1 K b()f(). h n Thn rplacing X 1 by is condiional pcaion E(X 1 1 ) = b( 1 ), E(ĝ n ()) g() = 1 [ ( )] 1 E b( 1 )K b()f() h n h n = 1 ( ) u b(u)k f(u)du b()f() h n h n = (b(vh n + )f(vh n + ) b()f())k(v)dv h n nh n
24 24 A. Philipp & M.-C. Viano whr h las lin coms via h chang of variabl (u )/h n = v and from (21). Now, sinc b and f ar C 2, so is h produc bf and b(vh n + )f(vh n + ) = b()f() + vh n [bf] () + (vh n ) 2 ψ n (v, ) whr ψ n (v, ) is uniformly boundd wih rspc o n, and v, bcaus h scond drivaiv of bf is coninuous and h domain of h variabls is compac. Finally, rmmbring (22) sup E(ĝ n ()) g() = h 2 n sup ψ n (v, )v 2 K(v)dv Ch2 n Ra of convrgnc of sup m m ˆfn () E( ˆf n ()). v 2 K(v)dv. Sinc ˆf n () has h sam form as ĝ n () (simply rplac X i by 1), i is no so difficul o undrsand ha h sam sor of chnical proof as for (27) abov lads o h following rsul, whos proof is lf o h radr. Lmma 7. Undr h hypohss of horm 4, as n ( ) (34) sup ˆf ln n n () f() = O as + O(h 2 nh n) n A lowr bound for inf ˆf n (). Bing C 2 and sricly posiiv on [ m, m], f has a non zro lowr bound inf f() = i > 0. Thn, wriing f() = ˆf n () + f() ˆf n () givs, for all i f() = f() ˆf n () + sup ˆf n () f() and consqunly from (33), ( ) inf ˆf ln n n () i O as O(h 2 nh n) n proving ha almos surly inf ˆf n () i/2 for n larg nough. Collcing h rsuls of h hr subscions concluds h proof of Thorm 4. Rmark 5. Forging h chnical dails, h radr can noic ha wo yps of ras ar obaind all along his proof ras lik h 2 n aris from bias rms E(ĝ n ) g or E( ˆf n ) f ln n nh n ras lik aris from ĝ n E(ĝ n ) or ˆf n E( ˆf n ), disprsions of h simaors from hir pcaions.
25 Forcasing in funcional rgrssiv or auorgrssiv modls 25 I is inrsing o no again ha (s also chapr 3, scion1.4) h smoohing paramr h n plays anagonisic rols in h bias and in h disprsion. Larg h n incrass h bias and dcrass h disprsion Opimal ra. Suppos ha h n c ( n β lnn) for som ngaiv β. Thn, h bs ra of convrgnc o zro of h bound O as (h 2 n) + O as ( ln n nh n ) = O as ( ln n ) 2β + O as ( ln n n ) (1+β)/2 is obaind for 2β = (β + 1)/2, ha is for β = 1/5. This is summarizd in h n corollary hn Corollary 8. Wih h hypohss of Thorm 4, if ( ) 1/5 ln n h n c, n ( ) 2/5 ln n sup ˆb n () b() = O as, n which happns o b opimal for h uniform convrgnc in his funcional siuaion and whn h krnl is posiiv (s [10]). Rmark 6. Now l us compar wih h rsuls obaind in h linar cas (chapr 2). In Proposiion 1, h ra of convrgnc of h cofficin s simaor is 1/n α for all α < 1/2. So, roughly spaking, in h linar cas h ra is n 1/2 whil in h non linar cas i is n 2/5. Comparing 1/2 and 2/5 givs a good ida of h pric o pay whn passing from a paramric o a non paramric simaion. 3. Ingrad quadraic rror I is also inrsing o considr h ingrad quadraic rror ( ) (35) E (ˆb n () b()) 2 w()d, whr w is a posiiv funcion (for ampl i can b h dnsiy f). W jus giv h rsul: Proposiion 9. Undr h assumpions of Thorm 4, if h wigh w is boundd and compacdly suppord ( ) ( ) 1 E (ˆb n () b()) 2 w()d = O(h 4 n) + O nh n Rmark 7. Compard o Thorm 4, hr is no logarihmic facor in h scond rm. Th rsul is br han wha is obaind by dircly rplacing (ˆb n () b()) 2 by sup ˆb n () b() 2 in h ingral, and using h bound in Thorm 4.
26 26 A. Philipp & M.-C. Viano Rmark 8. I is worh noicing ha, if h n n β, h opimal valu of β is 1/5, h opimal ra of h righ hand sid is n 4/5. Hnc, up o a logarihmic facor, w obain h sam opimal ra of h rror as in h prcding rmark. 4. Illusraion W illusra h propris of h sima (18) on diffrn simulad daa ss. c= 1 h= 0.37,n= 1000 sima of a() ru funcion b KERNEL : Gauss riang. Epan. biw. Rc. 6 6 Figur 1. Th modl is dfind by b() = sin(), ( n ) ar iid from a Gaussian N (0, 4) and a Gaussian nois N (0, 1). Th sampl siz is n = 1000 and h bandwidh h n = 0.37 As shown Fig 1, h choic of h krnl has fw ffcs on h convrgnc propris of h sima of b, cp h rcancular krnl which provid a lss rgular sima. Hrafr W only considr h cas of h Gaussian krnl and w valua h ffcs of h bandwidh h n. According o h horical rsul w ak h n of h form C(log(n)/n) 1/5 for diffrn valus of C Prsnaion. Th following picurs provid Th s of poin ( i, X i ) and h hisogram of boh sris (X i ) and ( i ) Th krnl sima for h sampl siz n = 500, 5000 and h consan C = 0.1, 0.5, 1, 2. Figurs 2, 3 and 4 : h modl is dfind by b() = sin() Fig. 2 and Fig.3 : h random variabls ( n ) ar iid from h Gaussian N (0, 2) and h nois is Gaussian wih varianc qual o 1 (Fig. 2) and 4 (Fig. 3) Fig. 4: h random variabls ( n ) ar iid from h uniform disribuion on [ 2, 2] and h nois is Gaussian N (0, 1)
27 Forcasing in funcional rgrssiv or auorgrssiv modls 27 Figur 5 : h modl is dfind by b() = 2 sign(), ( n ) ar iid from a uniform disribuion on ( 2π, 2π) and a Gaussian nois N (0, 9). Figur 6 : h modl is dfind by b() = 2I [0,1] () + 2I [ 1,0] (), ( n ) ar iid from a uniform disribuion on ( 2π, 2π) and a Gaussian nois N (0, 1) Commns. Th main faurs o b noicd as illusraing h hory ar h following: Influnc of h n. Too small valus of h smoohing paramr lad o small bias and larg varianc, whil oo larg valus lad o ovrsmoohing, ha is small varianc and bad bias Influnc of h consan. In all h ampls h chosn ra is h opimal ra (ln n/n) 2/5, muliplid by a consan c. In viw of h prcding commn, for a fid n, h valu of c is imporan Influnc of h law of X n. Th hisogram of h valus X j is dpicd on h op graphic in ach pag. Sinc hr ar lss obsrvaions on h ails of h hisogram, h funcion b is badly simad in hs zons. Kping his in mind, compar Figurs 1 and 2 wih h ohr ons Smoohnss of b. S rcis 14 blow.
28 28 A. Philipp & M.-C. Viano c= 0.1 h= 0.042,n= 500 sima of a() c= 0.5 h= 0.21,n= 500 sima of a() c= 1 h= 0.42,n= 500 sima of a() c= 3 h= 1.2,n= 500 sima of a() c= 0.1 h= 0.028,n= 5000 sima of a() c= 0.5 h= 0.14,n= 5000 sima of a() c= 1 h= 0.28,n= 5000 sima of a() c= 3 h= 0.84,n= 5000 sima of a() Figur 2. Th modl is dfind by b() = sin(), ( n ) ar iid from a Gaussian N (0, 4) and a Gaussian nois N (0, 1).
29 Forcasing in funcional rgrssiv or auorgrssiv modls c= 0.1 h= 0.042,n= 500 sima of a() c= 0.5 h= 0.21,n= 500 sima of a() c= 1 h= 0.42,n= 500 sima of a() c= 3 h= 1.2,n= 500 sima of a() c= 0.1 h= 0.028,n= 5000 sima of a() c= 0.5 h= 0.14,n= 5000 sima of a() c= 1 h= 0.28,n= 5000 sima of a() c= 3 h= 0.84,n= 5000 sima of a() Figur 3. Th modl is dfind by b() = sin(), ( n ) ar iid from a Gaussian N (0, 4) and a Gaussian nois N (0, 4).
30 30 A. Philipp & M.-C. Viano c= 0.1 h= 0.042,n= 500 sima of a() c= 0.5 h= 0.21,n= 500 sima of a() c= 1 h= 0.42,n= 500 sima of a() c= 3 h= 1.2,n= 500 sima of a() c= 0.1 h= 0.028,n= 5000 sima of a() c= 0.5 h= 0.14,n= 5000 sima of a() c= 1 h= 0.28,n= 5000 sima of a() c= 3 h= 0.84,n= 5000 sima of a() Figur 4. Th modl is dfind by b() = sin(), ( n ) ar iid from a uniform disribuion on ( 2π, 2π) and a Gaussian nois N (0, 1).
31 Forcasing in funcional rgrssiv or auorgrssiv modls c= 0.1 h= 0.042,n= 500 sima of a() c= 0.5 h= 0.21,n= 500 sima of a() c= 1 h= 0.42,n= 500 sima of a() c= 3 h= 1.2,n= 500 sima of a() c= 0.1 h= 0.028,n= 5000 sima of a() c= 0.5 h= 0.14,n= 5000 sima of a() c= 1 h= 0.28,n= 5000 sima of a() c= 3 h= 0.84,n= 5000 sima of a() Figur 5. Th modl is dfind by b() = 2 sign(), ( n ) ar iid from a uniform disribuion on ( 2π, 2π) and a Gaussian nois N (0, 9).
32 32 A. Philipp & M.-C. Viano c= 0.1 h= 0.042,n= 500 sima of a() c= 0.5 h= 0.21,n= 500 sima of a() c= 1 h= 0.42,n= 500 sima of a() c= 3 h= 1.2,n= 500 sima of a() c= 0.1 h= 0.028,n= 5000 sima of a() c= 0.5 h= 0.14,n= 5000 sima of a() c= 1 h= 0.28,n= 5000 sima of a() c= 3 h= 0.84,n= 5000 sima of a() Figur 6. Th modl is dfind by b() = 2I [0,1] () + 2I [ 1,0] (), ( n ) ar iid from a uniform disribuion on ( 2π, 2π) and a Gaussian nois N (0, 1).
33 Forcasing in funcional rgrssiv or auorgrssiv modls Forcasing Rcall ha h problm consiss in prdicing X n+1 from h obsrvd valus (X n,..., X 1, n+1,..., 1 ). In h modl (17), aking ino accoun h fac ha n+1 is indpndn of (X n,..., X 1, n,..., 1 ), E(X n+1 X n,..., X 1, n+1,..., 1 ) = E(X n+1 n+1 ) = b( n+1 ). So, h opimal prdicor is b( n ). As in gnral h funcion b is unknown, w rplac i by h simaor (18), and ak ˆX n+1 = ˆb n ( n+1 ). Th forcasing rror is X n+1 ˆX n+1 = ε n+1 + b( n+1 ) ˆb n ( n+1 ) Thorical forcasing rror. From h uniform convrgnc rsul of Thorm 4: Proposiion 10. Wih h sam assumpions as in Thorm 4, X n+1 ˆX n+1 = ε n+1 + T n, whr ε n+1 and T n ar indpndn and whr, as n, ( ) ln n T n = O as (h 2 n) + O as. nh n 5.2. How o build h forcasing inrval? Proposiion10 implis ha h disribuion of forcasing rror convrgs o h law of h nois. If h saisician knows his law, h can, nglcing h simaion rror T n, ak as forcasing inrval [ ˆX n+1 + Q α, ˆXn+1 + Q 1 α ] whr Q α and Q 1 α ar h wo quanils of ordr α and 1 α of h law of ε 1. Unforunaly, h disribuion of ε 1 is gnrally unknown and h quanils ar o b simad. Th following consqunc of Corollary 8 and of Proposiion 10 givs a mhod Corollary 11. Undr assumpions of Proposiion 10, dnoing by F ε h marginal disribuion funcion of ε, n j=1 sup I ],u](x j ˆb n ( j )) a.s. F ε (u) 0. u n Proof. For vry fid j and u, from Proposiion 10, X j+1 ˆb n ( j+1 ) a.s. 0 as n. Sinc h nois has a marginal dnsiy, P (ε j = u) = 0. Hnc, I ],u] (X j ˆb n ( j )) I ],u] (ε j ) a.s. 0, which in urn implis ha n j=1 I ],u](x j ˆb n ( j )) I ],u] (ε j ) a.s. 0. n
34 34 A. Philipp & M.-C. Viano Thn, by h law of larg numbrs applid o h nois, n j=1 I ],u](ε j ) a.s. F ε (u), n lading o n j=1 I ],u](x j ˆb n ( j )) a.s. F ε (u). n Th uniform convrgnc is a consqunc of h fac ha w dal wih disribuion funcions. This corollary mans ha h saisician can ra h sampl of prdicion rrors as a sampl of simad ε j and us i o sima h law of h nois. As his law is also h limi law of h forcasing rror, h simad quanils ˆQ n,α and ˆQ n,1 α can b usd o build a forcas inrval of asympoic lvl α [ ˆX n+1 + ˆQ n,α, ˆXn+1 + ˆQ n,1 α ]. W now considr modls of h form 6. Incrasing h mmory X k = b( k,..., k q+1 ) + ε k. Now w hav o sima a funcion of q variabls b( (1),..., (q) ). Th mor naural ida is o rplac in (18) h ind masuring h disanc bwn j and by h disanc bwn h wo vcors and sima b( 1,..., q ) = b() by j j q+1 := ( j,..., j q+1 ) and := ( (1),..., (q) ), ˆbn () = ( ) n j=1 X jk j j q+1 2 h n n j=1 K ( j j q+1 h n 2 ). Rmark 9. Rcall h naiv inrpraion of h prcding chapr (scion2). Th simaor is a wighd sum of h obsrvaions, ach X j having a small or larg wigh according o h disanc of is immdia pas of lngh q from h fid block ( 1,..., q ). In his siuaion, and wih h sam hypohss as in h prvious scions (som of hm hav o b adapd bcaus now b is a funcion of svral variabls) if h smoohing paramr has h form h n L 1 (n)n 1/(q+4) whr L 1 is a logarihmic funcion, hn ( L2 (n) (36) sup ˆb n () b() = O as n 2/(q+4) )
35 Forcasing in funcional rgrssiv or auorgrssiv modls 35 whr L 2 is anohr logarihmic funcion. For h proof, for dails on h hypohss and on h funcions L 1 and L 2 s [2]. Rmark 10. For q = 1 w g back o h prvious scions. As q incrass, 2/(q + 4) dcrass and, sinc h bound in (35) is opimal, h ra of convrgnc rally dcrass. As a rsul, h qualiy of simaion is rapidly drioraing for dimnsions q > 1. On of h mhods aiming o rmdy his so-calld curs of dimnsionaliy consiss in adoping addiiv modls such as q X k = b j ( k j+1 ) + ε k, j=1 modls for which w hav o sima q funcions of on variabl insad of on funcion of q variabls (s[11]). 7. Erciss Ercis 10. Suppos ha b and f ar C k (for som k > 2) and ha u j K(u)du = 0 j = 1,..., k 1 u k K(u)du 0, (which implis of cours ha K can ak ngaiv valus). Prov ha E(ĝ n ()) g() = O(h k n), and giv h bs ra of convrgnc of h simaor ˆb n whn h n cn β. Ercis 11. Find symmric, boundd and compacly suppord krnls saisfying assumpions of rcis abov. Ercis 12. Us h ida of rcis 10 o improv h rsul of rcis 7. Compar h ras o wha obains Proposiion 9. Could you giv on rason for prfrring posiiv krnls? Ercis 13. Try o prov (a las giv h main lins) h rsul of scion 6 for h modl X k = b( k, k 1 ) + ε k
36 36 A. Philipp & M.-C. Viano Ercis 14. Commn Figurs 4 and 5 whr h funcion b dos no saisfy hypohss of Thorm 4. Ercis 15. For h modls of Figurs 2 o 5, giv h dnsiy of X n and commn h hisograms dpicd on h op of ach corrsponding pag. Ercis 16. Considr h addiiv modl X k = b 1 ( k ) + b 2 ( k 1 ) + ε k, wih i.i.d nois and i.i.d ( k ). (1) Noic ha you hav o suppos ha ihr E(b 1 ( k )) = 0 or E(b 2 ( k )) = 0 for h modl o b idnifiabl. Why? (2) Suppos ha E(b 2 ( k 1 )) = 0. Giv h prssion of E(X k k ). (3) Us his rsul o propos a mhod o sima b 1 (). (4) And now, us h sam ida o build an simaor of b 2 (). (5) Wha do you hink of your simaors (ry o giv h main lins of a proof). (6) Wha happns if h k ar no indpndn?
37 CHAPTER 5 Funcional auorgrssion modls 1. Inroducion In his chapr w urn o funcional auorgrssiv modls (37) X k = a(x k 1,..., X k p ) + ε k ha is modls (1) whr h ognous par is missing. Th problm rmains h sam as prviously: find a good forcasing mhod for X n+1 basd on h passd valus X n,..., X 1. In fac, for h sak of simpliciy, w shall suppos ha p = 1. In ohr words, w dal wih h modl (38) X k = a(x k 1 ) + ε k, k 2 whr (ε k ) is an i.i.d. squnc. Suppos for h momn ha X 1 is indpndn from h nois (ε k ). I should b clar ha h squnc (X k ) is a Markov procss, and ha E(X k X k 1,..., X 1 ) = E(X k X k 1 ) = a(x k 1 ), implying ha h opimal forcas consiss in aking X n+1 = a(x n ). Thn, why no sima a by a krnl mhod analogously o wha was don in (18), and ak ( ) n 1 j=1 X Xj j+1k h n (39) â n () = ( ) n 1 j=1 K Xj h n and hn plug in h valu of X n o obain ˆX n+1 = â n (X n ) Hurisic inrpraion. Th sam naiv inrpraion as for h pur auorgrssion can b dvlopd. For ach X j+1, h simaor calculas a wigh masuring h viciniy of h obsrvaion X j jus bfor from h fid valu. Thn h simaor is h wighd sum of h X j s. 37
38 38 A. Philipp & M.-C. Viano 1.2. Thorical difficulis. Thr is an imporan diffrnc bwn h prsn chapr and chaprs 3 and 4. Formally, h problm is h sam in all h cass: sima E(Z n+1 Y n+1 = y), using h availabl obsrvaions. In h wo prcding chaprs, h (Z j, Y j ) s ar i.i.d. For ampl in h pur rgrssion siuaion, w hav Z j = Y j and X j = j and h (X j, j ) s ar indpndn. Hr, Z j = X j+1 and Y j = X j, and h (X j+1, X j ) s ar crainly no indpndn. So i should b vidn ha som knowldg on h dpndnc bwn h X j s is ncssary for sudying h propris of h simaor (38). Whn a() = a 1 + a 2, you rcogniz h usual linar AR 1 (non cnrd) modl, X k = a 1 X k 1 + a 2 + ε k, abou which narly vry hing is known. In paricular, i is wll known ha h linar quaions abov admi a sricly saionary soluion iff a 1 < 1. In h ohr cass, w giv in h following scion som rsuls on h isnc of a saionary soluion and on is dpndnc srucur. 2. Wak dpndnc of non-linar auorgrssions Wihou giving any proof, w rfr hr o svral paprs or books, whr dails and proofs can b found. For ampl: [6] is dvod o miing propris, [7] ras prcisly markov procsss lik (37) and [10] and [17] includ rviws on h qusion of wak dpndnc of squncs and paricularly of Markov squncs. Th main rsul is ha, modulo ad hoc assumpions on h funcion a and on h nois squnc, (37) has a saionary soluion, and ha, for his soluion, h X j s ar no dpndn nough o modify h rsuls of h prcding chapr. Th mos imporan noion o quanify waknss of dpndncis is h noion of srongmiing. Givn a squnc (U n ) n of saionary random variabls (or random vcors), dno by h sigma-algbra gnrad by U l,..., U k U k l by Dfiniion 1. Th srong-miing cofficins α n of h squnc (U k ) k 1 ar dfind α n = sup k sup A U k 0,B U k+n P (A B) P (A)P (B) Dfiniion 2. Th squnc (U n ) n is srong miing if α n 0 whn n. Th squnc is gomrically srong miing if h convrgnc o zro is as fas as h convrgnc of a gomric squnc, maning ha hr iss τ ]0, 1[ such ha α n cτ n for n n 0
39 Forcasing in funcional rgrssiv or auorgrssiv modls 39 Rmark 11. Clarly, for an i.i.d. squnc, α n = 0 for vry n 1. Rmark 12. Roughly spaking, in a srong miing squnc (U n ) n 1, h dpndnc bwn U j and U k disappars whn j k incrass. Rmark 13. If (U n ) n Z is saionary, h dpndnc bwn X k and X k+n only dpnds on n, so ha α n can b rdfind by α n = sup A U 0,B U n P (A B) P (A)P (B) Rmark 14. If (U n ) n is a saionary Markov squnc, α n = sup P (A B) P (A)P (B) A U 0,B U n whr U k = U k k is h sigma algbra gnrad by X k. Concrning modl (37) w shall us h following rsul (s for ampl [6], or [7], or [17]) Thorm 12. If (ε k ) k 1 is an i.i.d. squnc having a sricly posiiv marginal dnsiy, and if h funcion a is boundd hn Markov modl (37) has a sricly saionary soluion (X k ) k 1, and his soluion is gomrically srongly miing. 3. Propris of srong miing squncs, and hir consquncs 3.1. Invarianc. Th miing propry is invarian by simpl ransformaions. For ampl Lmma 13. If (U n ) n 1 is srong miing, so is h squnc (V n = φ(u n k1,..., U n+k2 )) n 1, whr k 1 and k 2 ar fid ingrs and φ any R p -valud funcion. Th ra of convrgnc o 0 of h miing cofficin is h sam for h wo squncs. For ampl, i is asy o dduc from his Lmma ha, undr h assumpion of Thorm 12, h squnc (X k+1, X k ) k 1 is gomrically srongly miing Eponnial inqualiy. As miing is a kind of wak dpndnc, i is no surprising ha mos classical rsuls for i.i.d. squncs sill hold wih minor changs for miing ons undr a suiabl ra of convrgnc of h miing squnc. As an ampl, ak Lmma 6, which plays a ky rol in h proof of Thorm 4. This lmma is sad for i.i.d. squncs. Thr ar many analogous rsuls for miing squncs. Th following on is wll fid o our problm. S [15] for h proof.
40 40 A. Philipp & M.-C. Viano Lmma 14. L V j b a gomrically srong miing squnc of cnrd boundd random variabls. For any a > 1, r > 1 and ε > 0, ( ) n ) r/2 P V j > 4ε 4 (1 + ε2 + 2c n ( ) a 2r r ε j=1 whr s 2 n = 1 j,k n Cov(V j, V k ) rs 2 n 3.3. Covariancs. In ordr o us his inqualiy, w shall nd o valua s 2 n. Th ky rsul o do ha concrns h link bwn h covarianc squnc and h squnc of miing cofficins (s [6] for ohr rsuls of h sam yp). Lmma 15. L (V n ) n 1 b a saionary squnc, and (α n ) is squnc of miing cofficins dfind in 1. Suppos ha hr iss a consan m such ha V j m for all j. Thn Cov(V j, V k ) 4m 2 α j k This inqualiy can b usd for ampl o prov ha, if α n 0 fasly nough, s 2 n n as n, ha is o say ha is asympoic bhaviour is (up o a muliplicaiv consan) h sam as if h variabls wr i.i.d. (s rcis 18 for dails). j, k 4. Esimaion of a W procd acly as in chapr 4, only changing ( k, X k ) for (X k, X k+1 ), as mniond in h inroducion. So, w sima a() by â n () dfind in (38) Assumpions. Th nois is i.i.d. and hr iss a drminisic consan m such ha ε n m n a is boundd and C 2 Th marginal disribuion of h saionary soluion X n has a dnsiy φ, sricly posiiv on [ m, m] and C 2. For vry j, k, h disribuion of (X j, X k ) has a boundd dnsiy φ j,k On h krnl: K is boundd, compacdly suppord and saisfis h condiions (21),(22),(23) and (24) Rmark 15. From hs hypohss X k a + m k
41 Forcasing in funcional rgrssiv or auorgrssiv modls Convrgnc rsul. Th rsul of Thorm 4 bcoms now: Thorm 16. Undr assumpions abov, ( ) ln n sup â n () a() = O as nh n â n () = + O(h 2 n). Proof. Th proof follows h sam lins as ha of Thorm 4, modulo h chang indicad abov. W rwri h simaor: ( ) n 1 j=1 X Xj P n 1 j=1 j+1k X Xj j+1k hn h n (40) n 1 j=1 K ( Xj h n ) = nh P n n 1 j=1 K Xj =: hn nh n ˆψ n () ˆφ n (), whr ˆφ n () simas h marginal dnsiy φ() of X j and whr ˆψ n () simas So, h simaion rror is splid ino ψ() := E(X 2 I X1 =) = a()φ(). â n () a() = ˆψ n () ˆφ n () ψ() φ() = ˆψ n () ψ() ˆφ n () + (φ() ˆφ n ()) a() ˆφ n () implying ha sup â n () a() sup ˆψ n () ψ() inf ˆφ n () sup + a φ() ˆφ n () inf ˆφ. n () From his poin, h only modificaions from h proof of horm 4 concrn inqualiis (29) and (32). Th basic Lmma 6 is now rplacd by Lmma 14 which w apply o h variabls ( ) Xj (41) V j := X j+1 K h n ( E X j+1 K ( Xj h n )). Ths variabls ar boundd by a consan C (s wha concrns variabls U j in h proof of Lmma 27). Morovr, applying Thorm 12 and Lmma 13 shows ha h squnc (V j ) j 1 is gomrically srong miing. Thn w apply Lmma 14. Firsly w nd an simaion of s 2 n = 1 j,k n Cov(V j, V k ). Lmma 17. If, as n, h n cn β 1 (ln n) β 2 (42) s 2 n = O(nh n ) L us prov h lmma. Wih h sam kind of proofs as for h variabls U j (s again proof of Lmma 27) w obain hn (43) Var(V j ) Ch n j,
42 42 A. Philipp & M.-C. Viano (44) Cov(V j, V k ) ( ) u K K h n ( v h n ) 2 ) φ j,k (u, v)dudv ( ( ) u + K φ(u)du h n = h 2 n K(u)K(v)φ j,k (h n u, h n v )dudv ( ) 2 + h 2 n K(u)φ(h n u )du = O(h 2 n) j k and, from Lmma 15 (45) Cov(V j, V k ) 4C 2 α j k C 1 τ j k W us inqualiy (44) for larg valus of j k, inqualiy (42) for h variancs and inqualiy (43) ohrwis. For a squnc δ n o b prcisd, s 2 n = j k δ n Cov(V j, V k ) + = nvar(x 1 ) + j k >δ n Cov(V j, V k ) 1< j k δ n Cov(V j, V k ) + C 2 (nh n + nδ n h 2 n + n 2 α δn ). j k >δ n Cov(V j, V k ) Thn w ak δ n = 1/(h n ln n) and obain s 2 n = O(nh n + n 2 τ 1/(hn ln n) ) Taking h n cn β 1 (ln n) β 2 and using h fac ha τ = o( k ) for vry k > 0, i is asy o s ha h scond rm is ngligibl compard wih h firs on, and h lmma is provd. Now, from Lmma 14, oghr wih h bound (41), w dduc for any a > 1, r > 1 and ε > 0, P ( ) n V j > 4ε j=1 4 (1 + C ) 3ε 2 r/2 + 2c n rnh n r ( ) a 2r, ε
43 Forcasing in funcional rgrssiv or auorgrssiv modls 43 lading o ( ( P ˆψ ln n ) n j=1 n () ψ() ε 0 = P V ) j ln n ε 0 = nh n nh n nh n ( ) n ( = P V j ε 0 nhn ln n C ) 3ε 2 r/2 0nh n ln n + 16rnh j=1 n + 2c n ( ) a 2r 4 C 4 r ε 2 0 ln n 2 16r + 2c n ( ) a 2r r ε 0 nhn ln n r ε 0 nhn ln n = 4 C 4 ε 2 0 ln n c n ( ) a 2r = 4n C 4 ε c n ( ) a 2r. r ε 0 nhn ln n r ε 0 nhn ln n Thn, ak r = n β. Rmmbring ha h n cn β 1 ln n β 2 ( P ˆψ ln n ) n () ψ() ε 0 4n C 4 ε 2 0 nh n givs a+1 c ε a 0 n 1/2+b(1 a) β 1/2 (ln n) (1+β 1)/2. Thn, i rmains o chos ε 0 larg nough o hav C 4 ε 2 0 > 16, and a and b larg nough o hav 1/2 + b(1 a) β 1 /2 < 1. Thn h sris ( n P ˆψ ) ln n n () ψ() ε 0 nh n convrgs, which implis ha ( ) ln n ˆψ n () ψ() = O as. nh n Th rs of h proof gos similarly as for horm 4 and is omid. Rmark 16. Noic ha h ra of convrgnc is h sam as in h pur rgrssion problm. Th rason is, as was alrady poind ou in h inroducion, h waknss of dpndnc bwn h X j s Opimal ra. From Proposiion 16, wih smoohing paramr h n cn β 1 ln n β 2, ( sup â n () a() = O as n (1 β 1 )/2 ln n ) (1+β 2)/2 + O(n 2β 1 ln n 2β 2 ). Th opimal ra is obaind for β 2 = β 1 = 1/5. Hnc Corollary 18. For smoohing paramrs having h form h n cn β 1 ln n β 2, h opimal ra of convrgnc, obaind for ( ) 1/5 ln n h n c, n is ( ) 2/5 ln n sup â n () a() = O as n
44 44 A. Philipp & M.-C. Viano 5. Illusraion W illusra h propris of h sima (38) on diffrn simulad daa ss. W only considr h cas of h Gaussian krnl and w valua h ffcs of h bandwidh h n. According o h horical rsul w ak h n of h form C(log(n)/n) 1/5 for diffrn valus of C Prsnaion. Th following picurs provid Th im sris (X i ) wih is auo corrlaions funcion and h s of poins (X i, X i+1 ) Th krnl sima for h sampl siz n = 500, 5000 and h consan C = 0.1, 0.5, 1, 2. Figurs 4, 1 and 2 : h modl is dfind by a() = sin() Fig. 4 : Fig. 1 : Fig. 2 Figur 3 : h modl is dfind by a() = 1/(1 + 2 ) and a Gaussian nois N (0, 1) Figur 5 : h modl is dfind by a() = 2 sign() and a Gaussian nois N (0, 1) Figur 6 : h modl is dfind by a() = 2I [0,1] ()+2I [ 1,0] () and a Gaussian nois N (0, 1) 5.2. Commns. Th sam commns as in Chapr 4 can b givn. W lav hm o h radr. I may b inrsing o look a h mpirical auocorrlaions givn on h firs lin of ach pag, and o hink of h ARMA (linar) modls which could b adapd o h daa.
45 Forcasing in funcional rgrssiv or auorgrssiv modls 45 h simulad sris Tim Lag ACF acf of h sris h firs valus of h sris Tim s of poins ((i),(i+1)) (i) (i+1) c= 0.1 h= 0.042,n= 500 sima of a() c= 0.5 h= 0.21,n= 500 sima of a() c= 1 h= 0.42,n= 500 sima of a() c= 2 h= 0.83,n= 500 sima of a() c= 0.1 h= 0.028,n= 5000 sima of a() c= 0.5 h= 0.14,n= 5000 sima of a() c= 1 h= 0.28,n= 5000 sima of a() c= 2 h= 0.56,n= 5000 sima of a() Figur 1. Th modl is dfind by a() = sin() and a Gaussian nois N (0, 1).
46 46 A. Philipp & M.-C. Viano h simulad sris Tim Lag ACF acf of h sris h firs valus of h sris Tim s of poins ((i),(i+1)) (i) (i+1) c= 0.1 h= 0.042,n= 500 sima of a() c= 0.5 h= 0.21,n= 500 sima of a() c= 1 h= 0.42,n= 500 sima of a() c= 2 h= 0.83,n= 500 sima of a() c= 0.1 h= 0.028,n= 5000 sima of a() c= 0.5 h= 0.14,n= 5000 sima of a() c= 1 h= 0.28,n= 5000 sima of a() c= 2 h= 0.56,n= 5000 sima of a() Figur 2. Th modl is dfind by a() = sin() and a uniform nois on ( π, π).
47 Forcasing in funcional rgrssiv or auorgrssiv modls 47 h simulad sris Tim Lag ACF acf of h sris h firs valus of h sris Tim s of poins ((i),(i+1)) (i) (i+1) 6 6 c= 0.1 h= 0.042,n= 500 sima of a() c= 0.5 h= 0.21,n= 500 sima of a() c= 1 h= 0.42,n= 500 sima of a() c= 2 h= 0.83,n= 500 sima of a() c= 0.1 h= 0.028,n= 5000 sima of a() c= 0.5 h= 0.14,n= 5000 sima of a() c= 1 h= 0.28,n= 5000 sima of a() c= 2 h= 0.56,n= 5000 sima of a() Figur 3. Th modl is dfind by a() = sin() and a uniform nois on ( 2π, 2π).
Elementary Differential Equations and Boundary Value Problems
 Elmnar Diffrnial Equaions and Boundar Valu Problms Boc. & DiPrima 9 h Ediion Chapr : Firs Ordr Diffrnial Equaions 00600 คณ ตศาสตร ว ศวกรรม สาขาว ชาว ศวกรรมคอมพ วเตอร ป การศ กษา /55 ผศ.ดร.อร ญญา ผศ.ดร.สมศ
Elmnar Diffrnial Equaions and Boundar Valu Problms Boc. & DiPrima 9 h Ediion Chapr : Firs Ordr Diffrnial Equaions 00600 คณ ตศาสตร ว ศวกรรม สาขาว ชาว ศวกรรมคอมพ วเตอร ป การศ กษา /55 ผศ.ดร.อร ญญา ผศ.ดร.สมศ
AR(1) Process. The first-order autoregressive process, AR(1) is. where e t is WN(0, σ 2 )
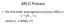 AR() Procss Th firs-ordr auorgrssiv procss, AR() is whr is WN(0, σ ) Condiional Man and Varianc of AR() Condiional man: Condiional varianc: ) ( ) ( Ω Ω E E ) var( ) ) ( var( ) var( σ Ω Ω Ω Ω E Auocovarianc
AR() Procss Th firs-ordr auorgrssiv procss, AR() is whr is WN(0, σ ) Condiional Man and Varianc of AR() Condiional man: Condiional varianc: ) ( ) ( Ω Ω E E ) var( ) ) ( var( ) var( σ Ω Ω Ω Ω E Auocovarianc
On the Derivatives of Bessel and Modified Bessel Functions with Respect to the Order and the Argument
 Inrnaional Rsarch Journal of Applid Basic Scincs 03 Aailabl onlin a wwwirjabscom ISSN 5-838X / Vol 4 (): 47-433 Scinc Eplorr Publicaions On h Driais of Bssl Modifid Bssl Funcions wih Rspc o h Ordr h Argumn
Inrnaional Rsarch Journal of Applid Basic Scincs 03 Aailabl onlin a wwwirjabscom ISSN 5-838X / Vol 4 (): 47-433 Scinc Eplorr Publicaions On h Driais of Bssl Modifid Bssl Funcions wih Rspc o h Ordr h Argumn
UNIT #5 EXPONENTIAL AND LOGARITHMIC FUNCTIONS
 Answr Ky Nam: Da: UNIT # EXPONENTIAL AND LOGARITHMIC FUNCTIONS Par I Qusions. Th prssion is quivaln o () () 6 6 6. Th ponnial funcion y 6 could rwrin as y () y y 6 () y y (). Th prssion a is quivaln o
Answr Ky Nam: Da: UNIT # EXPONENTIAL AND LOGARITHMIC FUNCTIONS Par I Qusions. Th prssion is quivaln o () () 6 6 6. Th ponnial funcion y 6 could rwrin as y () y y 6 () y y (). Th prssion a is quivaln o
Lecture 1: Numerical Integration The Trapezoidal and Simpson s Rule
 Lcur : Numrical ngraion Th Trapzoidal and Simpson s Rul A problm Th probabiliy of a normally disribud (man µ and sandard dviaion σ ) vn occurring bwn h valus a and b is B A P( a x b) d () π whr a µ b -
Lcur : Numrical ngraion Th Trapzoidal and Simpson s Rul A problm Th probabiliy of a normally disribud (man µ and sandard dviaion σ ) vn occurring bwn h valus a and b is B A P( a x b) d () π whr a µ b -
Spring 2006 Process Dynamics, Operations, and Control Lesson 2: Mathematics Review
 Spring 6 Procss Dynamics, Opraions, and Conrol.45 Lsson : Mahmaics Rviw. conx and dircion Imagin a sysm ha varis in im; w migh plo is oupu vs. im. A plo migh imply an quaion, and h quaion is usually an
Spring 6 Procss Dynamics, Opraions, and Conrol.45 Lsson : Mahmaics Rviw. conx and dircion Imagin a sysm ha varis in im; w migh plo is oupu vs. im. A plo migh imply an quaion, and h quaion is usually an
Boyce/DiPrima 9 th ed, Ch 2.1: Linear Equations; Method of Integrating Factors
 Boc/DiPrima 9 h d, Ch.: Linar Equaions; Mhod of Ingraing Facors Elmnar Diffrnial Equaions and Boundar Valu Problms, 9 h diion, b William E. Boc and Richard C. DiPrima, 009 b John Wil & Sons, Inc. A linar
Boc/DiPrima 9 h d, Ch.: Linar Equaions; Mhod of Ingraing Facors Elmnar Diffrnial Equaions and Boundar Valu Problms, 9 h diion, b William E. Boc and Richard C. DiPrima, 009 b John Wil & Sons, Inc. A linar
Chapter 3: Fourier Representation of Signals and LTI Systems. Chih-Wei Liu
 Chapr 3: Fourir Rprsnaion of Signals and LTI Sysms Chih-Wi Liu Oulin Inroducion Complx Sinusoids and Frquncy Rspons Fourir Rprsnaions for Four Classs of Signals Discr-im Priodic Signals Fourir Sris Coninuous-im
Chapr 3: Fourir Rprsnaion of Signals and LTI Sysms Chih-Wi Liu Oulin Inroducion Complx Sinusoids and Frquncy Rspons Fourir Rprsnaions for Four Classs of Signals Discr-im Priodic Signals Fourir Sris Coninuous-im
DEPARTMENT OF ELECTRICAL &ELECTRONICS ENGINEERING SIGNALS AND SYSTEMS. Assoc. Prof. Dr. Burak Kelleci. Spring 2018
 DEPARTMENT OF ELECTRICAL &ELECTRONICS ENGINEERING SIGNALS AND SYSTEMS Aoc. Prof. Dr. Burak Kllci Spring 08 OUTLINE Th Laplac Tranform Rgion of convrgnc for Laplac ranform Invr Laplac ranform Gomric valuaion
DEPARTMENT OF ELECTRICAL &ELECTRONICS ENGINEERING SIGNALS AND SYSTEMS Aoc. Prof. Dr. Burak Kllci Spring 08 OUTLINE Th Laplac Tranform Rgion of convrgnc for Laplac ranform Invr Laplac ranform Gomric valuaion
Institute of Actuaries of India
 Insiu of Acuaris of India ubjc CT3 Probabiliy and Mahmaical aisics Novmbr Examinaions INDICATIVE OLUTION Pag of IAI CT3 Novmbr ol. a sampl man = 35 sampl sandard dviaion = 36.6 b for = uppr bound = 35+*36.6
Insiu of Acuaris of India ubjc CT3 Probabiliy and Mahmaical aisics Novmbr Examinaions INDICATIVE OLUTION Pag of IAI CT3 Novmbr ol. a sampl man = 35 sampl sandard dviaion = 36.6 b for = uppr bound = 35+*36.6
I) Title: Rational Expectations and Adaptive Learning. II) Contents: Introduction to Adaptive Learning
 I) Til: Raional Expcaions and Adapiv Larning II) Conns: Inroducion o Adapiv Larning III) Documnaion: - Basdvan, Olivir. (2003). Larning procss and raional xpcaions: an analysis using a small macroconomic
I) Til: Raional Expcaions and Adapiv Larning II) Conns: Inroducion o Adapiv Larning III) Documnaion: - Basdvan, Olivir. (2003). Larning procss and raional xpcaions: an analysis using a small macroconomic
Midterm exam 2, April 7, 2009 (solutions)
 Univrsiy of Pnnsylvania Dparmn of Mahmaics Mah 26 Honors Calculus II Spring Smsr 29 Prof Grassi, TA Ashr Aul Midrm xam 2, April 7, 29 (soluions) 1 Wri a basis for h spac of pairs (u, v) of smooh funcions
Univrsiy of Pnnsylvania Dparmn of Mahmaics Mah 26 Honors Calculus II Spring Smsr 29 Prof Grassi, TA Ashr Aul Midrm xam 2, April 7, 29 (soluions) 1 Wri a basis for h spac of pairs (u, v) of smooh funcions
2.1. Differential Equations and Solutions #3, 4, 17, 20, 24, 35
 MATH 5 PS # Summr 00.. Diffrnial Equaions and Soluions PS.# Show ha ()C #, 4, 7, 0, 4, 5 ( / ) is a gnral soluion of h diffrnial quaion. Us a compur or calculaor o skch h soluions for h givn valus of h
MATH 5 PS # Summr 00.. Diffrnial Equaions and Soluions PS.# Show ha ()C #, 4, 7, 0, 4, 5 ( / ) is a gnral soluion of h diffrnial quaion. Us a compur or calculaor o skch h soluions for h givn valus of h
4.1 The Uniform Distribution Def n: A c.r.v. X has a continuous uniform distribution on [a, b] when its pdf is = 1 a x b
![4.1 The Uniform Distribution Def n: A c.r.v. X has a continuous uniform distribution on [a, b] when its pdf is = 1 a x b 4.1 The Uniform Distribution Def n: A c.r.v. X has a continuous uniform distribution on [a, b] when its pdf is = 1 a x b](/thumbs/71/65779443.jpg) 4. Th Uniform Disribuion Df n: A c.r.v. has a coninuous uniform disribuion on [a, b] whn is pdf is f x a x b b a Also, b + a b a µ E and V Ex4. Suppos, h lvl of unblivabiliy a any poin in a Transformrs
4. Th Uniform Disribuion Df n: A c.r.v. has a coninuous uniform disribuion on [a, b] whn is pdf is f x a x b b a Also, b + a b a µ E and V Ex4. Suppos, h lvl of unblivabiliy a any poin in a Transformrs
Let s look again at the first order linear differential equation we are attempting to solve, in its standard form:
 Th Ingraing Facor Mhod In h prvious xampls of simpl firs ordr ODEs, w found h soluions by algbraically spara h dpndn variabl- and h indpndn variabl- rms, and wri h wo sids of a givn quaion as drivaivs,
Th Ingraing Facor Mhod In h prvious xampls of simpl firs ordr ODEs, w found h soluions by algbraically spara h dpndn variabl- and h indpndn variabl- rms, and wri h wo sids of a givn quaion as drivaivs,
Applied Statistics and Probability for Engineers, 6 th edition October 17, 2016
 Applid Saisics and robabiliy for Enginrs, 6 h diion Ocobr 7, 6 CHATER Scion - -. a d. 679.. b. d. 88 c d d d. 987 d. 98 f d.. Thn, = ln. =. g d.. Thn, = ln.9 =.. -7. a., by symmry. b.. d...6. 7.. c...
Applid Saisics and robabiliy for Enginrs, 6 h diion Ocobr 7, 6 CHATER Scion - -. a d. 679.. b. d. 88 c d d d. 987 d. 98 f d.. Thn, = ln. =. g d.. Thn, = ln.9 =.. -7. a., by symmry. b.. d...6. 7.. c...
1. Inverse Matrix 4[(3 7) (02)] 1[(0 7) (3 2)] Recall that the inverse of A is equal to:
![1. Inverse Matrix 4[(3 7) (02)] 1[(0 7) (3 2)] Recall that the inverse of A is equal to: 1. Inverse Matrix 4[(3 7) (02)] 1[(0 7) (3 2)] Recall that the inverse of A is equal to:](/thumbs/84/89365453.jpg) Rfrncs Brnank, B. and I. Mihov (1998). Masuring monary policy, Quarrly Journal of Economics CXIII, 315-34. Blanchard, O. R. Proi (00). An mpirical characrizaion of h dynamic ffcs of changs in govrnmn spnding
Rfrncs Brnank, B. and I. Mihov (1998). Masuring monary policy, Quarrly Journal of Economics CXIII, 315-34. Blanchard, O. R. Proi (00). An mpirical characrizaion of h dynamic ffcs of changs in govrnmn spnding
CSE 245: Computer Aided Circuit Simulation and Verification
 CSE 45: Compur Aidd Circui Simulaion and Vrificaion Fall 4, Sp 8 Lcur : Dynamic Linar Sysm Oulin Tim Domain Analysis Sa Equaions RLC Nwork Analysis by Taylor Expansion Impuls Rspons in im domain Frquncy
CSE 45: Compur Aidd Circui Simulaion and Vrificaion Fall 4, Sp 8 Lcur : Dynamic Linar Sysm Oulin Tim Domain Analysis Sa Equaions RLC Nwork Analysis by Taylor Expansion Impuls Rspons in im domain Frquncy
An Indian Journal FULL PAPER. Trade Science Inc. A stage-structured model of a single-species with density-dependent and birth pulses ABSTRACT
 [Typ x] [Typ x] [Typ x] ISSN : 974-7435 Volum 1 Issu 24 BioTchnology 214 An Indian Journal FULL PAPE BTAIJ, 1(24), 214 [15197-1521] A sag-srucurd modl of a singl-spcis wih dnsiy-dpndn and birh pulss LI
[Typ x] [Typ x] [Typ x] ISSN : 974-7435 Volum 1 Issu 24 BioTchnology 214 An Indian Journal FULL PAPE BTAIJ, 1(24), 214 [15197-1521] A sag-srucurd modl of a singl-spcis wih dnsiy-dpndn and birh pulss LI
CHAPTER CHAPTER14. Expectations: The Basic Tools. Prepared by: Fernando Quijano and Yvonn Quijano
 Expcaions: Th Basic Prpard by: Frnando Quijano and Yvonn Quijano CHAPTER CHAPTER14 2006 Prnic Hall Businss Publishing Macroconomics, 4/ Olivir Blanchard 14-1 Today s Lcur Chapr 14:Expcaions: Th Basic Th
Expcaions: Th Basic Prpard by: Frnando Quijano and Yvonn Quijano CHAPTER CHAPTER14 2006 Prnic Hall Businss Publishing Macroconomics, 4/ Olivir Blanchard 14-1 Today s Lcur Chapr 14:Expcaions: Th Basic Th
7.4 QUANTUM MECHANICAL TREATMENT OF FLUCTUATIONS *
 Andri Tokmakoff, MIT Dparmn of Chmisry, 5/19/5 7-11 7.4 QUANTUM MECANICAL TREATMENT OF FLUCTUATIONS * Inroducion and Prviw Now h origin of frquncy flucuaions is inracions of our molcul (or mor approprialy
Andri Tokmakoff, MIT Dparmn of Chmisry, 5/19/5 7-11 7.4 QUANTUM MECANICAL TREATMENT OF FLUCTUATIONS * Inroducion and Prviw Now h origin of frquncy flucuaions is inracions of our molcul (or mor approprialy
3(8 ) (8 x x ) 3x x (8 )
 Scion - CHATER -. a d.. b. d.86 c d 8 d d.9997 f g 6. d. d. Thn, = ln. =. =.. d Thn, = ln.9 =.7 8 -. a d.6 6 6 6 6 8 8 8 b 9 d 6 6 6 8 c d.8 6 6 6 6 8 8 7 7 d 6 d.6 6 6 6 6 6 6 8 u u u u du.9 6 6 6 6 6
Scion - CHATER -. a d.. b. d.86 c d 8 d d.9997 f g 6. d. d. Thn, = ln. =. =.. d Thn, = ln.9 =.7 8 -. a d.6 6 6 6 6 8 8 8 b 9 d 6 6 6 8 c d.8 6 6 6 6 8 8 7 7 d 6 d.6 6 6 6 6 6 6 8 u u u u du.9 6 6 6 6 6
Voltage v(z) ~ E(z)D. We can actually get to this wave behavior by using circuit theory, w/o going into details of the EM fields!
 Considr a pair of wirs idal wirs ngh >, say, infinily long olag along a cabl can vary! D olag v( E(D W can acually g o his wav bhavior by using circui hory, w/o going ino dails of h EM filds! Thr
Considr a pair of wirs idal wirs ngh >, say, infinily long olag along a cabl can vary! D olag v( E(D W can acually g o his wav bhavior by using circui hory, w/o going ino dails of h EM filds! Thr
Ali Karimpour Associate Professor Ferdowsi University of Mashhad. Reference: System Identification Theory For The User Lennart Ljung
 SYSEM IDEIFICAIO Ali Karimpour Associa Prossor Frdowsi Univrsi o Mashhad Rrnc: Ssm Idniicaion hor For h Usr Lnnar Ljung Lcur 7 lcur 7 Paramr Esimaion Mhods opics o b covrd includ: Guiding Principls Bhind
SYSEM IDEIFICAIO Ali Karimpour Associa Prossor Frdowsi Univrsi o Mashhad Rrnc: Ssm Idniicaion hor For h Usr Lnnar Ljung Lcur 7 lcur 7 Paramr Esimaion Mhods opics o b covrd includ: Guiding Principls Bhind
Phys463.nb Conductivity. Another equivalent definition of the Fermi velocity is
 39 Anohr quival dfiniion of h Fri vlociy is pf vf (6.4) If h rgy is a quadraic funcion of k H k L, hs wo dfiniions ar idical. If is NOT a quadraic funcion of k (which could happ as will b discussd in h
39 Anohr quival dfiniion of h Fri vlociy is pf vf (6.4) If h rgy is a quadraic funcion of k H k L, hs wo dfiniions ar idical. If is NOT a quadraic funcion of k (which could happ as will b discussd in h
A MATHEMATICAL MODEL FOR NATURAL COOLING OF A CUP OF TEA
 MTHEMTICL MODEL FOR NTURL COOLING OF CUP OF TE 1 Mrs.D.Kalpana, 2 Mr.S.Dhvarajan 1 Snior Lcurr, Dparmn of Chmisry, PSB Polychnic Collg, Chnnai, India. 2 ssisan Profssor, Dparmn of Mahmaics, Dr.M.G.R Educaional
MTHEMTICL MODEL FOR NTURL COOLING OF CUP OF TE 1 Mrs.D.Kalpana, 2 Mr.S.Dhvarajan 1 Snior Lcurr, Dparmn of Chmisry, PSB Polychnic Collg, Chnnai, India. 2 ssisan Profssor, Dparmn of Mahmaics, Dr.M.G.R Educaional
Chapter 17 Handout: Autocorrelation (Serial Correlation)
 Chapr 7 Handou: Auocorrlaion (Srial Corrlaion Prviw Rviw o Rgrssion Modl o Sandard Ordinary Las Squars Prmiss o Esimaion Procdurs Embddd wihin h Ordinary Las Squars (OLS Esimaion Procdur o Covarianc and
Chapr 7 Handou: Auocorrlaion (Srial Corrlaion Prviw Rviw o Rgrssion Modl o Sandard Ordinary Las Squars Prmiss o Esimaion Procdurs Embddd wihin h Ordinary Las Squars (OLS Esimaion Procdur o Covarianc and
Wave Equation (2 Week)
 Rfrnc Wav quaion ( Wk 6.5 Tim-armonic filds 7. Ovrviw 7. Plan Wavs in Losslss Mdia 7.3 Plan Wavs in Loss Mdia 7.5 Flow of lcromagnic Powr and h Poning Vcor 7.6 Normal Incidnc of Plan Wavs a Plan Boundaris
Rfrnc Wav quaion ( Wk 6.5 Tim-armonic filds 7. Ovrviw 7. Plan Wavs in Losslss Mdia 7.3 Plan Wavs in Loss Mdia 7.5 Flow of lcromagnic Powr and h Poning Vcor 7.6 Normal Incidnc of Plan Wavs a Plan Boundaris
The transition:transversion rate ratio vs. the T-ratio.
 PhyloMah Lcur 8 by Dan Vandrpool March, 00 opics of Discussion ransiion:ransvrsion ra raio Kappa vs. ransiion:ransvrsion raio raio alculaing h xpcd numbr of subsiuions using marix algbra Why h nral im
PhyloMah Lcur 8 by Dan Vandrpool March, 00 opics of Discussion ransiion:ransvrsion ra raio Kappa vs. ransiion:ransvrsion raio raio alculaing h xpcd numbr of subsiuions using marix algbra Why h nral im
Chapter 5 The Laplace Transform. x(t) input y(t) output Dynamic System
 EE 422G No: Chapr 5 Inrucor: Chung Chapr 5 Th Laplac Tranform 5- Inroducion () Sym analyi inpu oupu Dynamic Sym Linar Dynamic ym: A procor which proc h inpu ignal o produc h oupu dy ( n) ( n dy ( n) +
EE 422G No: Chapr 5 Inrucor: Chung Chapr 5 Th Laplac Tranform 5- Inroducion () Sym analyi inpu oupu Dynamic Sym Linar Dynamic ym: A procor which proc h inpu ignal o produc h oupu dy ( n) ( n dy ( n) +
H is equal to the surface current J S
 Chapr 6 Rflcion and Transmission of Wavs 6.1 Boundary Condiions A h boundary of wo diffrn mdium, lcromagnic fild hav o saisfy physical condiion, which is drmind by Maxwll s quaion. This is h boundary condiion
Chapr 6 Rflcion and Transmission of Wavs 6.1 Boundary Condiions A h boundary of wo diffrn mdium, lcromagnic fild hav o saisfy physical condiion, which is drmind by Maxwll s quaion. This is h boundary condiion
whereby we can express the phase by any one of the formulas cos ( 3 whereby we can express the phase by any one of the formulas
 Third In-Class Exam Soluions Mah 6, Profssor David Lvrmor Tusday, 5 April 07 [0] Th vrical displacmn of an unforcd mass on a spring is givn by h 5 3 cos 3 sin a [] Is his sysm undampd, undr dampd, criically
Third In-Class Exam Soluions Mah 6, Profssor David Lvrmor Tusday, 5 April 07 [0] Th vrical displacmn of an unforcd mass on a spring is givn by h 5 3 cos 3 sin a [] Is his sysm undampd, undr dampd, criically
The Matrix Exponential
 Th Matrix Exponntial (with xrciss) by D. Klain Vrsion 207.0.05 Corrctions and commnts ar wlcom. Th Matrix Exponntial For ach n n complx matrix A, dfin th xponntial of A to b th matrix A A k I + A + k!
Th Matrix Exponntial (with xrciss) by D. Klain Vrsion 207.0.05 Corrctions and commnts ar wlcom. Th Matrix Exponntial For ach n n complx matrix A, dfin th xponntial of A to b th matrix A A k I + A + k!
A Condition for Stability in an SIR Age Structured Disease Model with Decreasing Survival Rate
 A Condiion for abiliy in an I Ag rucurd Disas Modl wih Dcrasing urvival a A.K. upriana, Edy owono Dparmn of Mahmaics, Univrsias Padjadjaran, km Bandung-umng 45363, Indonsia fax: 6--7794696, mail: asupria@yahoo.com.au;
A Condiion for abiliy in an I Ag rucurd Disas Modl wih Dcrasing urvival a A.K. upriana, Edy owono Dparmn of Mahmaics, Univrsias Padjadjaran, km Bandung-umng 45363, Indonsia fax: 6--7794696, mail: asupria@yahoo.com.au;
The Matrix Exponential
 Th Matrix Exponntial (with xrciss) by Dan Klain Vrsion 28928 Corrctions and commnts ar wlcom Th Matrix Exponntial For ach n n complx matrix A, dfin th xponntial of A to b th matrix () A A k I + A + k!
Th Matrix Exponntial (with xrciss) by Dan Klain Vrsion 28928 Corrctions and commnts ar wlcom Th Matrix Exponntial For ach n n complx matrix A, dfin th xponntial of A to b th matrix () A A k I + A + k!
Microscopic Flow Characteristics Time Headway - Distribution
 CE57: Traffic Flow Thory Spring 20 Wk 2 Modling Hadway Disribuion Microscopic Flow Characrisics Tim Hadway - Disribuion Tim Hadway Dfiniion Tim Hadway vrsus Gap Ahmd Abdl-Rahim Civil Enginring Dparmn,
CE57: Traffic Flow Thory Spring 20 Wk 2 Modling Hadway Disribuion Microscopic Flow Characrisics Tim Hadway - Disribuion Tim Hadway Dfiniion Tim Hadway vrsus Gap Ahmd Abdl-Rahim Civil Enginring Dparmn,
Double Slits in Space and Time
 Doubl Slis in Sac an Tim Gorg Jons As has bn ror rcnly in h mia, a am l by Grhar Paulus has monsra an inrsing chniqu for ionizing argon aoms by using ulra-shor lasr ulss. Each lasr uls is ffcivly on an
Doubl Slis in Sac an Tim Gorg Jons As has bn ror rcnly in h mia, a am l by Grhar Paulus has monsra an inrsing chniqu for ionizing argon aoms by using ulra-shor lasr ulss. Each lasr uls is ffcivly on an
5. An object moving along an x-coordinate axis with its scale measured in meters has a velocity of 6t
 AP CALCULUS FINAL UNIT WORKSHEETS ACCELERATION, VELOCTIY AND POSITION In problms -, drmin h posiion funcion, (), from h givn informaion.. v (), () = 5. v ()5, () = b g. a (), v() =, () = -. a (), v() =
AP CALCULUS FINAL UNIT WORKSHEETS ACCELERATION, VELOCTIY AND POSITION In problms -, drmin h posiion funcion, (), from h givn informaion.. v (), () = 5. v ()5, () = b g. a (), v() =, () = -. a (), v() =
On the Speed of Heat Wave. Mihály Makai
 On h Spd of Ha Wa Mihály Maai maai@ra.bm.hu Conns Formulaion of h problm: infini spd? Local hrmal qulibrium (LTE hypohsis Balanc quaion Phnomnological balanc Spd of ha wa Applicaion in plasma ranspor 1.
On h Spd of Ha Wa Mihály Maai maai@ra.bm.hu Conns Formulaion of h problm: infini spd? Local hrmal qulibrium (LTE hypohsis Balanc quaion Phnomnological balanc Spd of ha wa Applicaion in plasma ranspor 1.
Economics 302 (Sec. 001) Intermediate Macroeconomic Theory and Policy (Spring 2011) 3/28/2012. UW Madison
 Economics 302 (Sc. 001) Inrmdia Macroconomic Thory and Policy (Spring 2011) 3/28/2012 Insrucor: Prof. Mnzi Chinn Insrucor: Prof. Mnzi Chinn UW Madison 16 1 Consumpion Th Vry Forsighd dconsumr A vry forsighd
Economics 302 (Sc. 001) Inrmdia Macroconomic Thory and Policy (Spring 2011) 3/28/2012 Insrucor: Prof. Mnzi Chinn Insrucor: Prof. Mnzi Chinn UW Madison 16 1 Consumpion Th Vry Forsighd dconsumr A vry forsighd
FIRST-ORDER SYSTEMS OF ORDINARY DIFFERENTIAL EQUATIONS I: Introduction and Linear Systems
 FIRST-ORDER SYSTEMS OF ORDINARY DIFFERENTIAL EQUATIONS I: Inroducion and Linar Sysms David Lvrmor Dparmn of Mahmaics Univrsiy of Maryland 9 Dcmbr 0 Bcaus h prsnaion of his marial in lcur will diffr from
FIRST-ORDER SYSTEMS OF ORDINARY DIFFERENTIAL EQUATIONS I: Inroducion and Linar Sysms David Lvrmor Dparmn of Mahmaics Univrsiy of Maryland 9 Dcmbr 0 Bcaus h prsnaion of his marial in lcur will diffr from
DE Dr. M. Sakalli
 DE-0 Dr. M. Sakalli DE 55 M. Sakalli a n n 0 a Lh.: an Linar g Equaions Hr if g 0 homognous non-homognous ohrwis driving b a forc. You know h quaions blow alrad. A linar firs ordr ODE has h gnral form
DE-0 Dr. M. Sakalli DE 55 M. Sakalli a n n 0 a Lh.: an Linar g Equaions Hr if g 0 homognous non-homognous ohrwis driving b a forc. You know h quaions blow alrad. A linar firs ordr ODE has h gnral form
CPSC 211 Data Structures & Implementations (c) Texas A&M University [ 259] B-Trees
![CPSC 211 Data Structures & Implementations (c) Texas A&M University [ 259] B-Trees CPSC 211 Data Structures & Implementations (c) Texas A&M University [ 259] B-Trees](/thumbs/74/70718364.jpg) CPSC 211 Daa Srucurs & Implmnaions (c) Txas A&M Univrsiy [ 259] B-Trs Th AVL r and rd-black r allowd som variaion in h lnghs of h diffrn roo-o-laf pahs. An alrnaiv ida is o mak sur ha all roo-o-laf pahs
CPSC 211 Daa Srucurs & Implmnaions (c) Txas A&M Univrsiy [ 259] B-Trs Th AVL r and rd-black r allowd som variaion in h lnghs of h diffrn roo-o-laf pahs. An alrnaiv ida is o mak sur ha all roo-o-laf pahs
Transfer function and the Laplace transformation
 Lab No PH-35 Porland Sa Univriy A. La Roa Tranfr funcion and h Laplac ranformaion. INTRODUTION. THE LAPLAE TRANSFORMATION L 3. TRANSFER FUNTIONS 4. ELETRIAL SYSTEMS Analyi of h hr baic paiv lmn R, and
Lab No PH-35 Porland Sa Univriy A. La Roa Tranfr funcion and h Laplac ranformaion. INTRODUTION. THE LAPLAE TRANSFORMATION L 3. TRANSFER FUNTIONS 4. ELETRIAL SYSTEMS Analyi of h hr baic paiv lmn R, and
Discussion 06 Solutions
 STAT Discussion Soluions Spring 8. Th wigh of fish in La Paradis follows a normal disribuion wih man of 8. lbs and sandard dviaion of. lbs. a) Wha proporion of fish ar bwn 9 lbs and lbs? æ 9-8. - 8. P
STAT Discussion Soluions Spring 8. Th wigh of fish in La Paradis follows a normal disribuion wih man of 8. lbs and sandard dviaion of. lbs. a) Wha proporion of fish ar bwn 9 lbs and lbs? æ 9-8. - 8. P
University of Kansas, Department of Economics Economics 911: Applied Macroeconomics. Problem Set 2: Multivariate Time Series Analysis
 Univrsiy of Kansas, Dparmn of Economics Economics 9: Applid Macroconomics Problm S : Mulivaria Tim Sris Analysis Unlss sad ohrwis, assum ha shocks (.g. g and µ) ar whi nois in h following qusions.. Considr
Univrsiy of Kansas, Dparmn of Economics Economics 9: Applid Macroconomics Problm S : Mulivaria Tim Sris Analysis Unlss sad ohrwis, assum ha shocks (.g. g and µ) ar whi nois in h following qusions.. Considr
S.Y. B.Sc. (IT) : Sem. III. Applied Mathematics. Q.1 Attempt the following (any THREE) [15]
![S.Y. B.Sc. (IT) : Sem. III. Applied Mathematics. Q.1 Attempt the following (any THREE) [15] S.Y. B.Sc. (IT) : Sem. III. Applied Mathematics. Q.1 Attempt the following (any THREE) [15]](/thumbs/92/108666103.jpg) S.Y. B.Sc. (IT) : Sm. III Applid Mahmaics Tim : ½ Hrs.] Prlim Qusion Papr Soluion [Marks : 75 Q. Amp h following (an THREE) 3 6 Q.(a) Rduc h mari o normal form and find is rank whr A 3 3 5 3 3 3 6 Ans.:
S.Y. B.Sc. (IT) : Sm. III Applid Mahmaics Tim : ½ Hrs.] Prlim Qusion Papr Soluion [Marks : 75 Q. Amp h following (an THREE) 3 6 Q.(a) Rduc h mari o normal form and find is rank whr A 3 3 5 3 3 3 6 Ans.:
Final Exam : Solutions
 Comp : Algorihm and Daa Srucur Final Exam : Soluion. Rcuriv Algorihm. (a) To bgin ind h mdian o {x, x,... x n }. Sinc vry numbr xcp on in h inrval [0, n] appar xacly onc in h li, w hav ha h mdian mu b
Comp : Algorihm and Daa Srucur Final Exam : Soluion. Rcuriv Algorihm. (a) To bgin ind h mdian o {x, x,... x n }. Sinc vry numbr xcp on in h inrval [0, n] appar xacly onc in h li, w hav ha h mdian mu b
SOLUTIONS. 1. Consider two continuous random variables X and Y with joint p.d.f. f ( x, y ) = = = 15. Stepanov Dalpiaz
 STAT UIUC Pracic Problms #7 SOLUTIONS Spanov Dalpiaz Th following ar a numbr of pracic problms ha ma b hlpful for compling h homwor, and will lil b vr usful for suding for ams.. Considr wo coninuous random
STAT UIUC Pracic Problms #7 SOLUTIONS Spanov Dalpiaz Th following ar a numbr of pracic problms ha ma b hlpful for compling h homwor, and will lil b vr usful for suding for ams.. Considr wo coninuous random
EXERCISE - 01 CHECK YOUR GRASP
 DIFFERENTIAL EQUATION EXERCISE - CHECK YOUR GRASP 7. m hn D() m m, D () m m. hn givn D () m m D D D + m m m m m m + m m m m + ( m ) (m ) (m ) (m + ) m,, Hnc numbr of valus of mn will b. n ( ) + c sinc
DIFFERENTIAL EQUATION EXERCISE - CHECK YOUR GRASP 7. m hn D() m m, D () m m. hn givn D () m m D D D + m m m m m m + m m m m + ( m ) (m ) (m ) (m + ) m,, Hnc numbr of valus of mn will b. n ( ) + c sinc
4.3 Design of Sections for Flexure (Part II)
 Prsrssd Concr Srucurs Dr. Amlan K Sngupa and Prof. Dvdas Mnon 4. Dsign of Scions for Flxur (Par II) This scion covrs h following opics Final Dsign for Typ Mmrs Th sps for Typ 1 mmrs ar xplaind in Scion
Prsrssd Concr Srucurs Dr. Amlan K Sngupa and Prof. Dvdas Mnon 4. Dsign of Scions for Flxur (Par II) This scion covrs h following opics Final Dsign for Typ Mmrs Th sps for Typ 1 mmrs ar xplaind in Scion
Midterm Examination (100 pts)
 Econ 509 Spring 2012 S.L. Parn Midrm Examinaion (100 ps) Par I. 30 poins 1. Dfin h Law of Diminishing Rurns (5 ps.) Incrasing on inpu, call i inpu x, holding all ohr inpus fixd, on vnuall runs ino h siuaion
Econ 509 Spring 2012 S.L. Parn Midrm Examinaion (100 ps) Par I. 30 poins 1. Dfin h Law of Diminishing Rurns (5 ps.) Incrasing on inpu, call i inpu x, holding all ohr inpus fixd, on vnuall runs ino h siuaion
Chapter 12 Introduction To The Laplace Transform
 Chapr Inroducion To Th aplac Tranorm Diniion o h aplac Tranorm - Th Sp & Impul uncion aplac Tranorm o pciic uncion 5 Opraional Tranorm Applying h aplac Tranorm 7 Invr Tranorm o Raional uncion 8 Pol and
Chapr Inroducion To Th aplac Tranorm Diniion o h aplac Tranorm - Th Sp & Impul uncion aplac Tranorm o pciic uncion 5 Opraional Tranorm Applying h aplac Tranorm 7 Invr Tranorm o Raional uncion 8 Pol and
Lecture 2: Current in RC circuit D.K.Pandey
 Lcur 2: urrn in circui harging of apacior hrough Rsisr L us considr a capacior of capacianc is conncd o a D sourc of.m.f. E hrough a rsisr of rsisanc R and a ky K in sris. Whn h ky K is swichd on, h charging
Lcur 2: urrn in circui harging of apacior hrough Rsisr L us considr a capacior of capacianc is conncd o a D sourc of.m.f. E hrough a rsisr of rsisanc R and a ky K in sris. Whn h ky K is swichd on, h charging
Copyright 2012 Pearson Education, Inc. Publishing as Prentice Hall.
 Chapr Rviw 0 6. ( a a ln a. This will qual a if an onl if ln a, or a. + k an (ln + c. Thrfor, a an valu of, whr h wo curvs inrsc, h wo angn lins will b prpnicular. 6. (a Sinc h lin passs hrough h origin
Chapr Rviw 0 6. ( a a ln a. This will qual a if an onl if ln a, or a. + k an (ln + c. Thrfor, a an valu of, whr h wo curvs inrsc, h wo angn lins will b prpnicular. 6. (a Sinc h lin passs hrough h origin
Lecture 4: Laplace Transforms
 Lur 4: Lapla Transforms Lapla and rlad ransformaions an b usd o solv diffrnial quaion and o rdu priodi nois in signals and imags. Basially, hy onvr h drivaiv opraions ino mulipliaion, diffrnial quaions
Lur 4: Lapla Transforms Lapla and rlad ransformaions an b usd o solv diffrnial quaion and o rdu priodi nois in signals and imags. Basially, hy onvr h drivaiv opraions ino mulipliaion, diffrnial quaions
14.02 Principles of Macroeconomics Problem Set 5 Fall 2005
 40 Principls of Macroconomics Problm S 5 Fall 005 Posd: Wdnsday, Novmbr 6, 005 Du: Wdnsday, Novmbr 3, 005 Plas wri your nam AND your TA s nam on your problm s Thanks! Exrcis I Tru/Fals? Explain Dpnding
40 Principls of Macroconomics Problm S 5 Fall 005 Posd: Wdnsday, Novmbr 6, 005 Du: Wdnsday, Novmbr 3, 005 Plas wri your nam AND your TA s nam on your problm s Thanks! Exrcis I Tru/Fals? Explain Dpnding
LaPlace Transform in Circuit Analysis
 LaPlac Tranform in Circui Analyi Obciv: Calcula h Laplac ranform of common funcion uing h dfiniion and h Laplac ranform abl Laplac-ranform a circui, including componn wih non-zro iniial condiion. Analyz
LaPlac Tranform in Circui Analyi Obciv: Calcula h Laplac ranform of common funcion uing h dfiniion and h Laplac ranform abl Laplac-ranform a circui, including componn wih non-zro iniial condiion. Analyz
A Simple Procedure to Calculate the Control Limit of Z Chart
 Inrnaional Journal of Saisics and Applicaions 214, 4(6): 276-282 DOI: 1.5923/j.saisics.21446.4 A Simpl Procdur o Calcula h Conrol Limi of Z Char R. C. Loni 1, N. A. S. Sampaio 2, J. W. J. Silva 2,3,*,
Inrnaional Journal of Saisics and Applicaions 214, 4(6): 276-282 DOI: 1.5923/j.saisics.21446.4 A Simpl Procdur o Calcula h Conrol Limi of Z Char R. C. Loni 1, N. A. S. Sampaio 2, J. W. J. Silva 2,3,*,
On Ψ-Conditional Asymptotic Stability of First Order Non-Linear Matrix Lyapunov Systems
 In. J. Nonlinar Anal. Appl. 4 (213) No. 1, 7-2 ISSN: 28-6822 (lcronic) hp://www.ijnaa.smnan.ac.ir On Ψ-Condiional Asympoic Sabiliy of Firs Ordr Non-Linar Marix Lyapunov Sysms G. Sursh Kumar a, B. V. Appa
In. J. Nonlinar Anal. Appl. 4 (213) No. 1, 7-2 ISSN: 28-6822 (lcronic) hp://www.ijnaa.smnan.ac.ir On Ψ-Condiional Asympoic Sabiliy of Firs Ordr Non-Linar Marix Lyapunov Sysms G. Sursh Kumar a, B. V. Appa
Boyce/DiPrima 9 th ed, Ch 7.8: Repeated Eigenvalues
 Boy/DiPrima 9 h d Ch 7.8: Rpad Eignvalus Elmnary Diffrnial Equaions and Boundary Valu Problms 9 h diion by William E. Boy and Rihard C. DiPrima 9 by John Wily & Sons In. W onsidr again a homognous sysm
Boy/DiPrima 9 h d Ch 7.8: Rpad Eignvalus Elmnary Diffrnial Equaions and Boundary Valu Problms 9 h diion by William E. Boy and Rihard C. DiPrima 9 by John Wily & Sons In. W onsidr again a homognous sysm
Charging of capacitor through inductor and resistor
 cur 4&: R circui harging of capacior hrough inducor and rsisor us considr a capacior of capacianc is conncd o a D sourc of.m.f. E hrough a rsisr of rsisanc R, an inducor of inducanc and a y K in sris.
cur 4&: R circui harging of capacior hrough inducor and rsisor us considr a capacior of capacianc is conncd o a D sourc of.m.f. E hrough a rsisr of rsisanc R, an inducor of inducanc and a y K in sris.
46. Let y = ln r. Then dy = dr, and so. = [ sin (ln r) cos (ln r)
 98 Scion 7.. L w. Thn dw d, so d dw w dw. sin d (sin w)( wdw) w sin w dw L u w dv sin w dw du dw v cos w w sin w dw w cos w + cos w dw w cos w+ sin w+ sin d wsin wdw w cos w+ sin w+ cos + sin +. L w +
98 Scion 7.. L w. Thn dw d, so d dw w dw. sin d (sin w)( wdw) w sin w dw L u w dv sin w dw du dw v cos w w sin w dw w cos w + cos w dw w cos w+ sin w+ sin d wsin wdw w cos w+ sin w+ cos + sin +. L w +
Introduction to Arithmetic Geometry Fall 2013 Lecture #20 11/14/2013
 18.782 Introduction to Arithmtic Gomtry Fall 2013 Lctur #20 11/14/2013 20.1 Dgr thorm for morphisms of curvs Lt us rstat th thorm givn at th nd of th last lctur, which w will now prov. Thorm 20.1. Lt φ:
18.782 Introduction to Arithmtic Gomtry Fall 2013 Lctur #20 11/14/2013 20.1 Dgr thorm for morphisms of curvs Lt us rstat th thorm givn at th nd of th last lctur, which w will now prov. Thorm 20.1. Lt φ:
Impulsive Differential Equations. by using the Euler Method
 Applid Mahmaical Scincs Vol. 4 1 no. 65 19 - Impulsiv Diffrnial Equaions by using h Eulr Mhod Nor Shamsidah B Amir Hamzah 1 Musafa bin Mama J. Kaviumar L Siaw Chong 4 and Noor ani B Ahmad 5 1 5 Dparmn
Applid Mahmaical Scincs Vol. 4 1 no. 65 19 - Impulsiv Diffrnial Equaions by using h Eulr Mhod Nor Shamsidah B Amir Hamzah 1 Musafa bin Mama J. Kaviumar L Siaw Chong 4 and Noor ani B Ahmad 5 1 5 Dparmn
Review Lecture 5. The source-free R-C/R-L circuit Step response of an RC/RL circuit. The time constant = RC The final capacitor voltage v( )
 Rviw Lcur 5 Firs-ordr circui Th sourc-fr R-C/R-L circui Sp rspons of an RC/RL circui v( ) v( ) [ v( 0) v( )] 0 Th i consan = RC Th final capacior volag v() Th iniial capacior volag v( 0 ) Volag/currn-division
Rviw Lcur 5 Firs-ordr circui Th sourc-fr R-C/R-L circui Sp rspons of an RC/RL circui v( ) v( ) [ v( 0) v( )] 0 Th i consan = RC Th final capacior volag v() Th iniial capacior volag v( 0 ) Volag/currn-division
Revisiting what you have learned in Advanced Mathematical Analysis
 Fourir sris Rvisiing wh you hv lrnd in Advncd Mhmicl Anlysis L f x b priodic funcion of priod nd is ingrbl ovr priod. f x cn b rprsnd by rigonomric sris, f x n cos nx bn sin nx n cos x b sin x cosx b whr
Fourir sris Rvisiing wh you hv lrnd in Advncd Mhmicl Anlysis L f x b priodic funcion of priod nd is ingrbl ovr priod. f x cn b rprsnd by rigonomric sris, f x n cos nx bn sin nx n cos x b sin x cosx b whr
Fourier Transforms and the Wave Equation. Key Mathematics: More Fourier transform theory, especially as applied to solving the wave equation.
 Lur 7 Fourir Transforms and th Wav Euation Ovrviw and Motivation: W first discuss a fw faturs of th Fourir transform (FT), and thn w solv th initial-valu problm for th wav uation using th Fourir transform
Lur 7 Fourir Transforms and th Wav Euation Ovrviw and Motivation: W first discuss a fw faturs of th Fourir transform (FT), and thn w solv th initial-valu problm for th wav uation using th Fourir transform
22/ Breakdown of the Born-Oppenheimer approximation. Selection rules for rotational-vibrational transitions. P, R branches.
 Subjct Chmistry Papr No and Titl Modul No and Titl Modul Tag 8/ Physical Spctroscopy / Brakdown of th Born-Oppnhimr approximation. Slction ruls for rotational-vibrational transitions. P, R branchs. CHE_P8_M
Subjct Chmistry Papr No and Titl Modul No and Titl Modul Tag 8/ Physical Spctroscopy / Brakdown of th Born-Oppnhimr approximation. Slction ruls for rotational-vibrational transitions. P, R branchs. CHE_P8_M
Chapter 10. The singular integral Introducing S(n) and J(n)
 Chaptr Th singular intgral Our aim in this chaptr is to rplac th functions S (n) and J (n) by mor convnint xprssions; ths will b calld th singular sris S(n) and th singular intgral J(n). This will b don
Chaptr Th singular intgral Our aim in this chaptr is to rplac th functions S (n) and J (n) by mor convnint xprssions; ths will b calld th singular sris S(n) and th singular intgral J(n). This will b don
symmetric/hermitian matrices, and similarity transformations
 Linar lgbra for Wirlss Communicaions Lcur: 6 Diffrnial quaions, Grschgorin's s circl horm, symmric/hrmiian marics, and similariy ransformaions Ov Edfors Dparmn of Elcrical and Informaion Tchnology Lund
Linar lgbra for Wirlss Communicaions Lcur: 6 Diffrnial quaions, Grschgorin's s circl horm, symmric/hrmiian marics, and similariy ransformaions Ov Edfors Dparmn of Elcrical and Informaion Tchnology Lund
Real time estimation of traffic flow and travel time Based on time series analysis
 TNK084 Traffic Thory sris Vol.4, numbr.1 May 008 Ral im simaion of raffic flow and ravl im Basd on im sris analysis Wi Bao Absrac In his papr, h auhor sudy h raffic parn and im sris. Afr ha, a im sris
TNK084 Traffic Thory sris Vol.4, numbr.1 May 008 Ral im simaion of raffic flow and ravl im Basd on im sris analysis Wi Bao Absrac In his papr, h auhor sudy h raffic parn and im sris. Afr ha, a im sris
Chapter 2 The Derivative Business Calculus 99
 Chapr Th Drivaiv Businss Calculus 99 Scion 5: Drivaivs of Formulas In his scion, w ll g h rivaiv ruls ha will l us fin formulas for rivaivs whn our funcion coms o us as a formula. This is a vry algbraic
Chapr Th Drivaiv Businss Calculus 99 Scion 5: Drivaivs of Formulas In his scion, w ll g h rivaiv ruls ha will l us fin formulas for rivaivs whn our funcion coms o us as a formula. This is a vry algbraic
The Optimal Timing of Transition to New Environmental Technology in Economic Growth
 h Opimal iming of ransiion o Nw Environmnal chnology in Economic Growh h IAEE Europan Confrnc 7- Spmbr, 29 Vinna, Ausria Akira AEDA and akiko NAGAYA yoo Univrsiy Background: Growh and h Environmn Naural
h Opimal iming of ransiion o Nw Environmnal chnology in Economic Growh h IAEE Europan Confrnc 7- Spmbr, 29 Vinna, Ausria Akira AEDA and akiko NAGAYA yoo Univrsiy Background: Growh and h Environmn Naural
Instructors Solution for Assignment 3 Chapter 3: Time Domain Analysis of LTIC Systems
 Inrucor Soluion for Aignmn Chapr : Tim Domain Anali of LTIC Sm Problm i a 8 x x wih x u,, an Zro-inpu rpon of h m: Th characriic quaion of h LTIC m i i 8, which ha roo a ± j Th zro-inpu rpon i givn b zi
Inrucor Soluion for Aignmn Chapr : Tim Domain Anali of LTIC Sm Problm i a 8 x x wih x u,, an Zro-inpu rpon of h m: Th characriic quaion of h LTIC m i i 8, which ha roo a ± j Th zro-inpu rpon i givn b zi
Economics 302 (Sec. 001) Intermediate Macroeconomic Theory and Policy (Spring 2011) 4/25/2011. UW Madison
 conomics 302 (Sc. 001) Inrmdia Macroconomic Thory and Policy (Spring 2011) 4/25/2011 Insrucor: Prof. Mnzi Chinn Insrucor: Prof. Mnzi Chinn UW Madison 21 1 Th Mdium Run ε = P * P Thr ar wo ways in which
conomics 302 (Sc. 001) Inrmdia Macroconomic Thory and Policy (Spring 2011) 4/25/2011 Insrucor: Prof. Mnzi Chinn Insrucor: Prof. Mnzi Chinn UW Madison 21 1 Th Mdium Run ε = P * P Thr ar wo ways in which
ANSWERS TO EVEN NUMBERED EXERCISES IN CHAPTER 11
 8 Jun ANSWERS TO EVEN NUMBERED EXERCISES IN CHAPTER SECTION : INCENTIVE COMPATABILITY Exrcis - Educaional Signaling A yp consulan has a marginal produc of m( ) = whr Θ = {,, 3} Typs ar uniformly disribud
8 Jun ANSWERS TO EVEN NUMBERED EXERCISES IN CHAPTER SECTION : INCENTIVE COMPATABILITY Exrcis - Educaional Signaling A yp consulan has a marginal produc of m( ) = whr Θ = {,, 3} Typs ar uniformly disribud
MEM 355 Performance Enhancement of Dynamical Systems A First Control Problem - Cruise Control
 MEM 355 Prformanc Enhancmn of Dynamical Sysms A Firs Conrol Problm - Cruis Conrol Harry G. Kwany Darmn of Mchanical Enginring & Mchanics Drxl Univrsiy Cruis Conrol ( ) mv = F mg sinθ cv v +.2v= u 9.8θ
MEM 355 Prformanc Enhancmn of Dynamical Sysms A Firs Conrol Problm - Cruis Conrol Harry G. Kwany Darmn of Mchanical Enginring & Mchanics Drxl Univrsiy Cruis Conrol ( ) mv = F mg sinθ cv v +.2v= u 9.8θ
First derivative analysis
 Robrto s Nots on Dirntial Calculus Chaptr 8: Graphical analysis Sction First drivativ analysis What you nd to know alrady: How to us drivativs to idntiy th critical valus o a unction and its trm points
Robrto s Nots on Dirntial Calculus Chaptr 8: Graphical analysis Sction First drivativ analysis What you nd to know alrady: How to us drivativs to idntiy th critical valus o a unction and its trm points
cycle that does not cross any edges (including its own), then it has at least
 W prov th following thorm: Thorm If a K n is drawn in th plan in such a way that it has a hamiltonian cycl that dos not cross any dgs (including its own, thn it has at last n ( 4 48 π + O(n crossings Th
W prov th following thorm: Thorm If a K n is drawn in th plan in such a way that it has a hamiltonian cycl that dos not cross any dgs (including its own, thn it has at last n ( 4 48 π + O(n crossings Th
Consider a system of 2 simultaneous first order linear equations
 Soluon of sysms of frs ordr lnar quaons onsdr a sysm of smulanous frs ordr lnar quaons a b c d I has h alrna mar-vcor rprsnaon a b c d Or, n shorhand A, f A s alrady known from con W know ha h abov sysm
Soluon of sysms of frs ordr lnar quaons onsdr a sysm of smulanous frs ordr lnar quaons a b c d I has h alrna mar-vcor rprsnaon a b c d Or, n shorhand A, f A s alrady known from con W know ha h abov sysm
Mundell-Fleming I: Setup
 Mundll-Flming I: Sup In ISLM, w had: E ( ) T I( i π G T C Y ) To his, w now add n xpors, which is a funcion of h xchang ra: ε E P* P ( T ) I( i π ) G T NX ( ) C Y Whr NX is assumd (Marshall Lrnr condiion)
Mundll-Flming I: Sup In ISLM, w had: E ( ) T I( i π G T C Y ) To his, w now add n xpors, which is a funcion of h xchang ra: ε E P* P ( T ) I( i π ) G T NX ( ) C Y Whr NX is assumd (Marshall Lrnr condiion)
fiziks Institute for NET/JRF, GATE, IIT JAM, JEST, TIFR and GRE in PHYSICAL SCIENCES MATEMATICAL PHYSICS SOLUTIONS are
 MTEMTICL PHYSICS SOLUTIONS GTE- Q. Considr an ani-symmric nsor P ij wih indics i and j running from o 5. Th numbr of indpndn componns of h nsor is 9 6 ns: Soluion: Th numbr of indpndn componns of h nsor
MTEMTICL PHYSICS SOLUTIONS GTE- Q. Considr an ani-symmric nsor P ij wih indics i and j running from o 5. Th numbr of indpndn componns of h nsor is 9 6 ns: Soluion: Th numbr of indpndn componns of h nsor
Poisson process Markov process
 E2200 Quuing hory and lraffic 2nd lcur oion proc Markov proc Vikoria Fodor KTH Laboraory for Communicaion nwork, School of Elcrical Enginring 1 Cour oulin Sochaic proc bhind quuing hory L2-L3 oion proc
E2200 Quuing hory and lraffic 2nd lcur oion proc Markov proc Vikoria Fodor KTH Laboraory for Communicaion nwork, School of Elcrical Enginring 1 Cour oulin Sochaic proc bhind quuing hory L2-L3 oion proc
10. The Discrete-Time Fourier Transform (DTFT)
 Th Discrt-Tim Fourir Transform (DTFT Dfinition of th discrt-tim Fourir transform Th Fourir rprsntation of signals plays an important rol in both continuous and discrt signal procssing In this sction w
Th Discrt-Tim Fourir Transform (DTFT Dfinition of th discrt-tim Fourir transform Th Fourir rprsntation of signals plays an important rol in both continuous and discrt signal procssing In this sction w
1 General boundary conditions in diffusion
 Gnral boundary conditions in diffusion Πρόβλημα 4.8 : Δίνεται μονοδιάτατη πλάκα πάχους, που το ένα άκρο της κρατιέται ε θερμοκραία T t και το άλλο ε θερμοκραία T 2 t. Αν η αρχική θερμοκραία της πλάκας
Gnral boundary conditions in diffusion Πρόβλημα 4.8 : Δίνεται μονοδιάτατη πλάκα πάχους, που το ένα άκρο της κρατιέται ε θερμοκραία T t και το άλλο ε θερμοκραία T 2 t. Αν η αρχική θερμοκραία της πλάκας
Availability Analysis of Repairable Computer Systems and Stationarity Detection
 1166 IEEE TRANSACTIONS ON COMPUTERS, VOL. 48, NO. 11, NOVEMBER 1999 Availabiliy Analysis of Rpairabl Compur Sysms and Saionariy Dcion Bruno Sricola AbsracÐPoin availabiliy and xpcd inrval availabiliy ar
1166 IEEE TRANSACTIONS ON COMPUTERS, VOL. 48, NO. 11, NOVEMBER 1999 Availabiliy Analysis of Rpairabl Compur Sysms and Saionariy Dcion Bruno Sricola AbsracÐPoin availabiliy and xpcd inrval availabiliy ar
XV Exponential and Logarithmic Functions
 MATHEMATICS 0-0-RE Dirnial Calculus Marin Huard Winr 08 XV Eponnial and Logarihmic Funcions. Skch h graph o h givn uncions and sa h domain and rang. d) ) ) log. Whn Sarah was born, hr parns placd $000
MATHEMATICS 0-0-RE Dirnial Calculus Marin Huard Winr 08 XV Eponnial and Logarihmic Funcions. Skch h graph o h givn uncions and sa h domain and rang. d) ) ) log. Whn Sarah was born, hr parns placd $000
UNSTEADY FLOW OF A FLUID PARTICLE SUSPENSION BETWEEN TWO PARALLEL PLATES SUDDENLY SET IN MOTION WITH SAME SPEED
 006-0 Asian Rsarch Publishing work (ARP). All righs rsrvd. USTEADY FLOW OF A FLUID PARTICLE SUSPESIO BETWEE TWO PARALLEL PLATES SUDDELY SET I MOTIO WITH SAME SPEED M. suniha, B. Shankr and G. Shanha 3
006-0 Asian Rsarch Publishing work (ARP). All righs rsrvd. USTEADY FLOW OF A FLUID PARTICLE SUSPESIO BETWEE TWO PARALLEL PLATES SUDDELY SET I MOTIO WITH SAME SPEED M. suniha, B. Shankr and G. Shanha 3
A THREE COMPARTMENT MATHEMATICAL MODEL OF LIVER
 A THREE COPARTENT ATHEATICAL ODEL OF LIVER V. An N. Ch. Paabhi Ramacharyulu Faculy of ahmaics, R D collgs, Hanamonda, Warangal, India Dparmn of ahmaics, Naional Insiu of Tchnology, Warangal, India E-ail:
A THREE COPARTENT ATHEATICAL ODEL OF LIVER V. An N. Ch. Paabhi Ramacharyulu Faculy of ahmaics, R D collgs, Hanamonda, Warangal, India Dparmn of ahmaics, Naional Insiu of Tchnology, Warangal, India E-ail:
Chapter 6 Differential Equations and Mathematical Modeling
 6 Scion 6. hapr 6 Diffrnial Equaions and Mahmaical Modling Scion 6. Slop Filds and Eulr s Mhod (pp. ) Eploraion Sing h Slops. Sinc rprsns a lin wih a slop of, w should d pc o s inrvals wih no chang in.
6 Scion 6. hapr 6 Diffrnial Equaions and Mahmaical Modling Scion 6. Slop Filds and Eulr s Mhod (pp. ) Eploraion Sing h Slops. Sinc rprsns a lin wih a slop of, w should d pc o s inrvals wih no chang in.
A Propagating Wave Packet Group Velocity Dispersion
 Lctur 8 Phys 375 A Propagating Wav Packt Group Vlocity Disprsion Ovrviw and Motivation: In th last lctur w lookd at a localizd solution t) to th 1D fr-particl Schrödingr quation (SE) that corrsponds to
Lctur 8 Phys 375 A Propagating Wav Packt Group Vlocity Disprsion Ovrviw and Motivation: In th last lctur w lookd at a localizd solution t) to th 1D fr-particl Schrödingr quation (SE) that corrsponds to
Fourier Series and Parseval s Relation Çağatay Candan Dec. 22, 2013
 Fourir Sris nd Prsvl s Rlion Çğy Cndn Dc., 3 W sudy h m problm EE 3 M, Fll3- in som dil o illusr som conncions bwn Fourir sris, Prsvl s rlion nd RMS vlus. Q. ps h signl sin is h inpu o hlf-wv rcifir circui
Fourir Sris nd Prsvl s Rlion Çğy Cndn Dc., 3 W sudy h m problm EE 3 M, Fll3- in som dil o illusr som conncions bwn Fourir sris, Prsvl s rlion nd RMS vlus. Q. ps h signl sin is h inpu o hlf-wv rcifir circui
Higher order derivatives
 Robrto s Nots on Diffrntial Calculus Chaptr 4: Basic diffrntiation ruls Sction 7 Highr ordr drivativs What you nd to know alrady: Basic diffrntiation ruls. What you can larn hr: How to rpat th procss of
Robrto s Nots on Diffrntial Calculus Chaptr 4: Basic diffrntiation ruls Sction 7 Highr ordr drivativs What you nd to know alrady: Basic diffrntiation ruls. What you can larn hr: How to rpat th procss of
EE 350 Signals and Systems Spring 2005 Sample Exam #2 - Solutions
 EE 35 Signals an Sysms Spring 5 Sampl Exam # - Soluions. For h following signal x( cos( sin(3 - cos(5 - T, /T x( j j 3 j 3 j j 5 j 5 j a -, a a -, a a - ½, a 3 /j-j -j/, a -3 -/jj j/, a 5 -½, a -5 -½,
EE 35 Signals an Sysms Spring 5 Sampl Exam # - Soluions. For h following signal x( cos( sin(3 - cos(5 - T, /T x( j j 3 j 3 j j 5 j 5 j a -, a a -, a a - ½, a 3 /j-j -j/, a -3 -/jj j/, a 5 -½, a -5 -½,
Logistic equation of Human population growth (generalization to the case of reactive environment).
 Logisic quaion of Human populaion growh gnralizaion o h cas of raciv nvironmn. Srg V. Ershkov Insiu for Tim aur Exploraions M.V. Lomonosov's Moscow Sa Univrsi Lninski gor - Moscow 999 ussia -mail: srgj-rshkov@andx.ru
Logisic quaion of Human populaion growh gnralizaion o h cas of raciv nvironmn. Srg V. Ershkov Insiu for Tim aur Exploraions M.V. Lomonosov's Moscow Sa Univrsi Lninski gor - Moscow 999 ussia -mail: srgj-rshkov@andx.ru
EE 434 Lecture 22. Bipolar Device Models
 EE 434 Lcur 22 Bipolar Dvic Modls Quiz 14 Th collcor currn of a BJT was masurd o b 20mA and h bas currn masurd o b 0.1mA. Wha is h fficincy of injcion of lcrons coming from h mir o h collcor? 1 And h numbr
EE 434 Lcur 22 Bipolar Dvic Modls Quiz 14 Th collcor currn of a BJT was masurd o b 20mA and h bas currn masurd o b 0.1mA. Wha is h fficincy of injcion of lcrons coming from h mir o h collcor? 1 And h numbr
Likelihood Ratio Based Tests for Markov Regime Switching
 Liklihood Raio Basd ss for Markov Rgim Swiching Zhongjun Qu y Boson Univrsiy Fan Zhuo z Boson Univrsiy Fbruary 4, 07 Absrac Markov rgim swiching modls ar widly considrd in conomics and nanc. Alhough hr
Liklihood Raio Basd ss for Markov Rgim Swiching Zhongjun Qu y Boson Univrsiy Fan Zhuo z Boson Univrsiy Fbruary 4, 07 Absrac Markov rgim swiching modls ar widly considrd in conomics and nanc. Alhough hr
Circuits and Systems I
 Circuis and Sysms I LECTURE #3 Th Spcrum, Priodic Signals, and h Tim-Varying Spcrum lions@pfl Prof. Dr. Volan Cvhr LIONS/Laboraory for Informaion and Infrnc Sysms Licns Info for SPFirs Slids This wor rlasd
Circuis and Sysms I LECTURE #3 Th Spcrum, Priodic Signals, and h Tim-Varying Spcrum lions@pfl Prof. Dr. Volan Cvhr LIONS/Laboraory for Informaion and Infrnc Sysms Licns Info for SPFirs Slids This wor rlasd
Recall that by Theorems 10.3 and 10.4 together provide us the estimate o(n2 ), S(q) q 9, q=1
 Chaptr 11 Th singular sris Rcall that by Thorms 10 and 104 togthr provid us th stimat 9 4 n 2 111 Rn = SnΓ 2 + on2, whr th singular sris Sn was dfind in Chaptr 10 as Sn = q=1 Sq q 9, with Sq = 1 a q gcda,q=1
Chaptr 11 Th singular sris Rcall that by Thorms 10 and 104 togthr provid us th stimat 9 4 n 2 111 Rn = SnΓ 2 + on2, whr th singular sris Sn was dfind in Chaptr 10 as Sn = q=1 Sq q 9, with Sq = 1 a q gcda,q=1
