Tail effects in the 3PN gravitational wave angular momentum flux of compact binaries in quasi-elliptical orbits
|
|
|
- Jesse Joshua Todd
- 5 years ago
- Views:
Transcription
1 Chapr 5 Tail ffcs in h 3PN graviaional wav angular momnum flux of compac binaris in quasi-llipical orbis 5.1 Inroducion Asrophysical compac binaris in quasi-llipical orbis In h prvious hr chaprs w hav sudid h daa-analysis and compuaion of graviaional wav (GW) polarisaions from inspiralling compac binaris, bu wih orbis which wr quasi-circular. Indd, hs ar h mos plausibl sourcs for dcing GW wih h hlp of lasr inrfromrs lik LIGO, VIRGO and h plannd LISA. I has bn sablishd long ago, in a sminal work by Prs [47], ha compac binaris moving in llipical orbis wih larg rlaiv sparaion circularis undr radiaion racion du o loss of nrgy hrough mission of GW. Moivad by his, h 3.5PN phasing of inspiralling compac binaris moving in quasi-circular orbis is now compl and availabl for us in GW daa analysis [32, 163]. Rcn progrss in incrasing h snsiiviy of LIGO by an ordr of magniud o rach Advancd LIGO snsiiviy rndrs h complion of h highly accura phasing formula vry imly. This is bcaus prooyp binary sourcs of GW for ground-basd inrfromric GW dcors ar nuron sar (NS) or black hol (BH) binaris clos o hir mrgr phas and consqunly hav los all hir ccnriciy by h im h GW from hm nr h dcor bandwidh. Howvr, asrophysical invsigaions indicas h possibiliy of dcing binaris wih ccnriciy in h snsiiv bandwidh of boh rrsrial and spac-basd graviaional wav dcors. On such scnario is h Kozai oscillaions [48]. This occurs in h cors of dns globular clusrs whr graviaional inracions bwn pairs of binary BH sysms ar likly. Ths inracions can lad o an vnual jcion of on of h BH rsuling in h formaion of a sabl hirarchical ripl. This is a hr-body configuraion, whr wo closly bound BH orbi ach ohr whil h hird orbis h cnr-of-mass of h firs wo. Whn h wo orbial plans hav a larg inclinaion angl bwn hm, idal forcs from h our body incrass h ccnriciy of h innr sabl binary by causing an orbial 13
2 rsonanc. Th Kozai mchanism dscribd abov can lad o ccnriciis grar han.1 a h im GW from h innr binary nrs h bandwidh of Advancd LIGO [49]. Binaris comprising sllar mass BH ar simad o possss a hrmal disribuion of ccnriciis [164]. Eccnric binaris wih highr masss siuad in globular clusrs ar also ponial sourcs for LISA. Inrmdia mass ( 1 3 M ) BH binaris wih ccnriciis bwn.1 and.2 ar also xpcd o b gnrad by h Kozai mchanism [165]. Ths sysms will li in h bandwidh of LISA. Suprmassiv BH binaris, which ar h mos promising sourcs for LISA, can also mrg wihin Hubbl im wih high ccnriciis if h Kozai mchanism is in opraion [166]. Anohr asrophysical siuaion whr GW from ccnric binaris can b obsrvabl has bn dscribd by Davis, Lvan and King [167]. A NS-BH binary can bcom ccnric in h la sags of is inspiral. During h firs phas of mass ransfr, numrical sudis [167] show ha h NS is no disrupd and orbis h BH in a high ccnriciy orbi. Th rsuling sysm loss angular momnum via mission of GW which fall in h bandwidh of dcors lik Advancd LIGO. Evoluion undr radiaion racion drivs h wo bodis o conac which is followd by furhr phass of mass-ransfr. Rcnly, his mchanism was succssful in xplaining h ligh curv of h shor gamma-ray-burs GRB 5911 [168]. Rcnly, Grindlay. al [169] hav proposd ha shor GRBs ar producd by NS-NS binary mrgrs which ar formd in globular clusrs. Ths sysms hav h disinc faur ha hy possss high ccnriciis a shor orbial sparaions (s Figur 2 of [169]). Apar from globular clusrs, galaxis can also hos compac binaris which hav rsidual ccnriciy in hir la-inspiral phas. Asymmric kicks impard o NS a h im of hir birh will rsul in highly ccnric NS-NS binaris [17]. Th sam conclusion also applis o NS-BH and BH-BH binaris [17] Tmpla consrucion for ccnric binaris and daa analysis All h abov asrophysical paradigms clarly shows ha inspiralling compac binaris in quasi-llipic orbis ar also qui plausibl sourcs for boh ground and spac basd inrfromric GW dcors. Consrucion of mplas for ccnric binaris rquir an accura knowldg of h scular voluion of h GW phas and h voluion of h orbial lmns (lik smi-major axis, ccnriciy) undr radiaion racion. Th firs amp in his dircion was h classic works of Prs and Mahws [171, 47]. Afr compuing h imavragd (ovr an orbi) far-zon nrgy and angular momnum flux in h Nwonian limi, Prs and Mahws balancd hm wih h loss of binding nrgy and angular momnum of h Kplrian orbi. This allowd hm o obain h ra of dcay of h orbial lmns and showd ha ccnriciy dcays roughly by a facor of hr whn h smi-major axis of h orbi is halvd. Afr Prs and Mahws h voluion of h orbial lmns by his procdur was progrssivly xndd by Blanch and Schäfr o 1PN in [172] and 1.5PN in [172, 173] and finally o 2PN by Gopakumar and Iyr [174]. Whil [175, 173] rquir h 1PN accura orbial dscripion of Damour and Drull [176], [174] crucially mploys h gnralisd 2PN quasi-kplrian paramrizaion of h binary s orbial moion in ADM coordinas as givn in [177, 178, 179]. Mor rcnly, Damour, Gopakumar and Iyr [18] discussd an analyic mhod for consrucing high accuracy mplas for h GW signals from compac binaris in quasillipical orbis in hir inspiral phas. Thy go byond h compuaion of h slow scular 14
3 ffcs by h sandard avraging ovr h orbial priod and compu h addiional fas oscillaory conribuions byond h avrag scular conribuions. Using an improvd mhod of variaion of consans and working up o h lading radiaion racion ordr of 2.5PN, hy combin h hr im scals involvd in h llipical orbi cas -h orbial priod, priasron prcssion and radiaion racion im scals - wihou making h usual approximaion of raing h radiaiv im scal as an adiabaic procss. This was xndd o 3.5PN ordr in Rf [181]. Thr hav bn rlaivly fw xrciss in daa-analysis aspcs of GW from ccnric binaris. This is primarily bcaus inclusion of ccnriciy in h paramr spac lads o a larg incras in h numbr of mplas rquird o sarch for signals [182], which is consqunly accompanid by highr compuaional coss. To circumvn his issu, Marl and Poisson [183] compud h loss in vn ra if ccnric binaris ar sarchd wih circular mplas. Thy found ha vn hough h circular mplas ar no opimal filrs, hy will b fficin in dcing ccnric binaris. Furhr, h loss in signal-o-nois-raio incurrd incrass wih incrasing ccnriciy for a givn oal mass of h binary. Rcnly Tssmr and Gopakumar [184] rvisid h sam problm, bu usd a 2.5PN accura orbial voluion and adopd h phasing formalism dvlopd in [18] mniond abov. Th rsul of hir analysis (wih dcor Iniial LIGO) was ha mplas which modlld GW from binaris volving undr quadrupolar radiaion racion and whos orbis ar 2PN accura circular orbis ar vry fficin in sarching for ccnric binaris PN angular momnum flux: hrdiary rms Th gnraion problm of graviaional wavs for inspiralling compac binaris has bn compld a h hird pos-nwonian (3PN) ordr boh for h quaion of moion of h binary and for is far-zon radiaion fild. Rcnly, in a sris of wo rlad paprs [185, 186], h compuaion of h nrgy flux of graviaional wavs (GW) from inspiralling compac binaris moving in gnral non-circular orbis up o 3PN ordr was discussd. For non-circular orbis, in addiion o h consrvd nrgy and graviaional wav nrgy flux, h angular momnum flux nds o b known o drmin h phasing of quasi-ccnric binaris. As mniond bfor, a knowldg of h angular momnum flux of h sysm avragd ovr an orbi is mandaory o calcula h voluion of h orbial lmns of non-circular, in paricular, llipic orbis undr GW radiaion racion. In his chapr, w compu all h hrdiary rms in h angular momnum flux of inspiralling compac binaris moving in non-circular orbis up o 3PN ordr gnralising arlir work a 1.5PN ordr (ails and spin-orbi) by Scha fr and Rih [173]. Th hrdiary rms, unlik h insananous rms which ar funcions of h rardd im, dpnd on h dynamics of h sysm in is nir pas. Th 3PN hrdiary conribuion o angular momnum flux coms, apar from h ail rms, h ails of ails and ail-squard rms [135, 134]. Unlik h nrgy flux cas, h angular momnum flux also conains an inrsing mmory conribuion a 2.5PN. Using h angular momnum flux xprssion in conjuncion wih h 3PN accura hrdiary par of h nrgy flux obaind in Rf. [187, 185], w compu h hrdiary par of h voluion of h orbial lmns, smi-major axis a r, ccnriciy, man moion n and h priasron advanc paramr k. Evoluion of ohr rlad paramrs such as orbial priod P can b drivd from hs xprssions. W also provid h xprssions for h fluxs and voluion of orbial lmns in h limi of small ccnriciy up o 15
4 scond ordr in. All h rsuls of his chapr ar providd in rms of h PN paramr x = ( Gmω ) 2/3, rlad o h orbial frquncy ω, which hlps on o rcovr h circular orbi c 3 limi sraighforwardly. Th insananous rms in h 3PN angular momnum flux wr compud by Arun in [188]. Th rs of his chapr is organisd as follows. In Scion 5.2, w provid h gnral xprssion for h angular momnum flux in rms of radiaiv momns and rlaions bwn h radiaiv and sourc momns, kping only rms rlvan for compuaion of h hrdiary rms upo 3PN accuracy. Scion 5.3 rviws h soluion of h quaions of moion of compac binaris upo h accuracy w rquir for his chapr. In Scion 5.4, w provid h Fourir domain rprsnaions of h sourc mulipol momns and hir us in avraging h flux ovr h orbial im-scal. Scion 5.5 provids xplici xprssions of h hrdiary conribuions in rms of h Fourir ampliuds. In Scion 5.6 w giv dails of h numrical valuaion of hs conribuions. W provid h compl 3PN hrdiary rms in Scion 5.7 along wih rlvan chcks. In Scion 5.8, voluion of h orbial lmns du o hrdiary rms ar providd. Scion 5.9 compriss h conclusion and discussion of h rsuls of his chapr. Finally, in Scion 5.1, a lis of h Fourir cofficins of h Nwonian momns ar givn in rms of Bssl funcions. 5.2 Srucur of h hrdiary rms in h angular momnum flux Th compl 3PN accura angular momnum flux in h sourc s far-zon, wrin in rms of h symmric rac-fr (STF) mass and currn yp radiaiv mulipol momns (U L s and V L s) [13] can b found in Rf. [188]. Blow w provid h far zon angular momnum flux F J i upo 1PN ordr which will b sufficin o conrol h hrdiary par of F J i upo 3PN. F J i = G { 2 c ɛ 5 i jk 5 U jau (1) ka + 1 [ 1 c 2 63 U jabu (1) kab + 32 ]} 45 V jav (1) ka +. (5.1) Th dos indica rms which conribu o h 3PN insananous rms in F J i and w do no wri hm xplicily. U L and V L (wih L = i jk... a muli-indx composd of l indics, ach indx running from 1 o 3) ar h mass and currn yp radiaiv mulipol momns rspcivly and U (l) L and V(l) L dno hir lh im drivaivs. Th momns ar funcions of rardd im T R T R in radiaiv coordinas. ε c ipq is h usual Lvi-Civia symbol such ha ε 123 = +1. Th shorhand O(n) indicas ha h pos-nwonian rmaindr is of ordr of O(c n ). Using h mulipolar Pos-Minkowskian (MPM) formalism oulind in h prvious chapr, w r-xprss h radiaiv momns in Eq. (5.1) in rms of h sourc momns o an accuracy sufficin for h compuaion of h hrdiary par of h angular momnum flux up o 3PN. Th compl xprssions rquird o calcula h insananous rms wr alrady givn in h prvious chapr. Th rlaions conncing h diffrn radiaiv momns U L and V L o h corrsponding sourc momns I L and J L [124, 135, 134] rquird for his chapr ar givn blow. 16
5 For h mass yp momns w hav U i j (T R ) = I (2) i j (T R ) + 2GM c 3 ( GM ) 2 TR +2 c 3 +O(7), U i jk (T R ) = I (3) i jk (T R) + 2GM c 3 TR dvi (5) i j TR dv [ ( TR V ln [ (V) dv 2b ln 2 ( TR V 2b [ ( TR V ln 2b ) ) ) ] I (4) i j (V) 2 G 7 c ( 7 ln TR V 2b + 97 ] 6 ) I (5) i jk (V) + O(5), (5.2b) TR dvi (3) a<i (V)I(3) ] whr h brack <> dnos STF projcion. In h abov formulas, M is h oal ADM mass of h binary sysm. Th I L s and J L s ar h mass and currn-yp sourc momns, and I L, J L dno hir p-h im drivaivs. For h currn-yp momns, on h ohr hand, w find V i j (T R ) = J (2) i j (T R ) + 2GM TR [ ( TR V ) dv ln + 7 ] J (4) c 3 i j (V) + O(5). (5.3) 2b 6 Th radiaiv momns hav wo disinc conribuions. Th firs par which is a funcion only of h rardd im, T R = T R, ar h insananous rms. Th scond par ha c dpnds on h dynamics of h sysm in is nir pas [124] is rfrrd o as hrdiary conribuions and forms h subjc mar of his chapr. Th paramr b apparing in h logarihms of Eqs. (5.2) and (5.3) is a frly spcifiabl consan, having h dimnsion of im, nring h rlaion bwn h rardd im T R = T R/c in radiaiv coordinas and h corrsponding im ρ/c in harmonic coordinas (whr ρ is h disanc of h sourc in harmonic coordinas). Mor prcisly, w hav T R = ρ c 2 G M ( ) ρ ln. (5.4) c 3 c r W choos h consan b scaling h logarihm o b r o mach wih h choic mad in h c compuaion of ails-of-ails in [135]. From h xprssions for U L s and V L s, on can schmaically spli h oal conribuion o h angular momnum flux as h sum of h insananous and hrdiary rms. F J i = ( ) F J i + ( ) F J i. (5.5) ins hrd Sinc w do no discuss h insananous rms in h angular momnum flux hr, hy ar no givn byond h Nwonian ordr hr hough i is asy o wri hm down using h xprssions, Eqs (5.2) and (5.3) for h radiaiv momns. Th Nwonian insananous rm in F J i which will b calculad lar in his chapr for illusraing h Fourir dcomposiion mhod for calculaing h hrdiary rms is j>a (V) (5.2a) ( ) F J Nwonian i () = 2 G ins 5 c ε ipqi (2) 5 p j ()I(3) q j () (5.6) 17
6 Th hrdiary par can b dcomposd, as mniond in h arlir Scion, as (F J i) hrd = (F J i) ail + (F J i) ail(ail) + (F J i) (ail) 2 + (F J i) mmory, (5.7) Th quadraic-ordr ail ingrals ar xplicily givn by (using Eqs 5.2 and 5.3 in Eq 5.1) (F J i) ail () = G { 4GM + ε c 5 5c 3 i jk dτ ( ( ) I (2) ja () I(5) ka ( τ) I(3) ja () I(4) ka [ln ( τ)) τ + 11 ] 2r /c GM + 63c ε 5 i jk dτ ( ( ) I (3) jab () I(6) kab ( τ) I(4) jab () I(5) kab [ln ( τ)) τ + 97 ] 2r /c GM + ε 45c 5 i jk dτ ( ( ) J (2) ja () J(5) ka ( τ) J(3) ja () J(4) ka [ln ( τ)) τ + 7 ]}, 2r /c 6 (5.8) whil h cubic-ordr ails (proporional o M 2 ) ar + (F J i) ail(ail) () = G 4G 2 M 2 ε c 5 5c 6 i jk dτ ( I (2) ja ()I(6) ka ( τ) I(3) ja ()I(5) ka ( τ)) (5.9a) ( ) [ln 2 τ + 57 ( ) 2r /c 7 ln τ ], 2r /c 441 (F J i) (ail) 2() = G ( 8G 2 M 2 + ( ) ε c 5 5c 6 i jk dτ I (4) ja [ln ( τ) τ + 11 ]) 2r /c 12 ( + ( ) dτ I (5) ka [ln ( τ) τ + 11 ]), 2r /c 12 (5.9b) and finally, h mmory ingral is ( F J i )mmory () = G c 5 4G 35c 5 ε i jk I (3) ja () ( [ ] ) I (3) b<k I(3) a>b [ τ] dτ. (5.1) No ha in Eq. (5.1), a rm of h form G 4G ε c 5 35c 5 i jk I (2) ja () ( d [ ) d I (3) b<k a>b] I(3) [ τ] dτ has bn lf ou. This rm simply rducs o G 4G ε c 5 35c 5 i jk I (2) ja ()I(3) b<k ()I(3) a>b (), i.., an insananous rm. This rm, hrfor, has bn incorporad in h insananous par of h angular momnum flux and has bn compud in Rf. [188]. For h nrgy flux cas, h nir mmory conribuion bcoms insananous (s Rf. [185]). In h quaions Eq. (5.8), (5.9) rcall ha M is h consrvd mass monopol or oal ADM mass of h sourc. Th firs rm in (5.8) is h dominan ail a ordr 1.5PN whil h scond and hird rprsn h sub-dominan ails apparing boh a ordr 2.5PN. Th highr-ordr ails ar no givn sinc hy ar a las a 3.5PN ordr (s [135] for hir xprssions). Th wo cubic-ordr ails givn in Eqs. (5.9) ar boh a 3PN ordr. Th mmory rm appars a 2.5PN ordr. No ha h consan b scaling h logarihms in h ail ingrals in h radiaiv momns Eqs (5.2) & (5.3) has bn rplacd in h abov ail, ail-of-ail c. ingrals as (r /c). For simpliciy, w hav rplacd h symbol for h rardd im T R in radiaiv coordinas by. 18
7 5.3 Soluion of h quaions of moion of compac binaris Doubly-priodic srucur of h soluion To compu h ingrals apparing in Eqs. (5.8), (5.9) and (5.1), a knowldg of h voluion of h sourc is rquird. For his purpos, w nd o consruc h soluion of h quaion-of-moion of compac binaris. For his purpos, w rviw in his Scion, h gnral doubly-priodic srucur of h PN soluion, and h quasi-kplrian rprsnaion of h 1PN binary moion by mans of diffrn yps of ccnriciis. Th works [31, 189, 176] ar closly followd hr. If w nglc h radiaion racion rm a h 2.5PN ordr, h quaions of moion of a compac binary sysm up o h 3PN ordr admi n firs ingrals of h moion. Ths corrspond o h consrvd nrgy, angular and linar momna, and posiion of h cnr of mass [145, 146]. Whn rsricd o h fram of h cnr of mass, h quaions admi four firs ingrals associad wih h nrgy E and h angular momnum vcor J, givn a 3PN ordr by Eqs. (4.8) (4.9) of Rf. [149]. Th moion aks plac in a plan orhogonal o J. W dno by r = x h binary s orbial sparaion, and by v = v 1 v 2 h rlaiv vlociy (boh x and v li in h plan of moion). Th consrvd E and J ar funcions of r, ṙ 2, v 2 and x v (for dfininss w mploy h harmonic coordina sysm of [149] 1 ), and dpnd on h oal mass m = m 1 +m 2 and rducd mass µ = m 1 m 2 /m. Polar coordinas r, φ in h orbial plan ar usd o xprss E and h norm J = J as som xplici funcions of r, ṙ 2 and φ (v 2 = ṙ 2 + r 2 φ 2 ). Th lar funcions can b invrd (by mans of sraighforward PN iraion) o giv ṙ 2 and φ in rms of r and h consans of moion E and J. Thus, ṙ 2 = R[r; E, J], (5.11a) φ = G[r; E, J], (5.11b) whr R and G ar polynomials in 1/r, h dgr of which dpnds on h PN approximaion in qusion. A 3PN ordr, i is svnh dgr for boh R and G [19]. Th various cofficins of h powrs of 1/r ar hmslvs polynomials in E and J, and also, of cours, dpnd on m and h dimnsionlss rducd mass raio ν µ/m. For bound llipic-lik orbis, on can prov [189] ha h funcion R admis wo ral roos, r P and r A such ha r P < r A, which admi som non-zro fini Nwonian limis whn c, and rprsn rspcivly h radii of h orbi s priasron and apasron. Th ohr roos nd o zro in h limi c. Th binary s orbial priod, or im of rurn o h priasron, is obaind by ingraing h radial moion (w drop h dpndnc on E and J in h following, for simpliciy). P = 2 ra r P dr R[r]. (5.12) L us inroduc h man anomaly l and h man moion n by l = n( P ) (5.13) 1 All calculaions in his chapr will b don a h rlaiv 1PN ordr, and a ha ordr hr is no diffrnc bwn h harmonic and ADM coordinas. 19
8 n = 2π P, (5.14) whr P dnos h insan of passag o h priasron. For a givn valu of h man anomaly l, h orbial sparaion r is obaind by invrsion of h ingral quaion l = n r dr r P R [r ]. (5.15) This dfins h funcion r(l) which is a priodic funcion in l wih priod 2π. Using his in Eq. (5.11), h orbial phas φ can b obaind in rms of h man anomaly l by ingraing h angular moion as φ(l) = φ P + 1 n l dl G [ r(l ) ], (5.16) whr φ P dnos h valu of h phas a h insan P. Formally, h funcions r(l) and φ(l) compl h soluion bu dos no ak ino accoun h doubly-priodic naur of h problm. For his purpos, considr h advanc of priasron pr priod, i.., h incras in h orbial phas φ (modulo 2π) during a singl rurn o h priasron φ + 2π = 2 ra r P dr G[r] R[r], (5.17) L us dfin h fracional angl (i.. h angl dividd by 2π) of h oal advanc of h priasron pr orbial rvoluion, 2πK = 2π + φ. (5.18) Thus h prcssion of h priasron pr priod is givn by φ = 2π(K 1). As K nds o on in h limi c (as is chckd from h Nwonian limi), i is ofn convnin o dfin k K 1, which will hn nirly consiu h rlaivisic prcssion. If, lik h radial moion, w inroduc anohr man anomaly l φ and a man angular moion ω φ givn by l φ = ω φ ( P ) (5.19) ω φ = 2π P/K, (5.2) w find ha h wo man moions and man anomalis ar rlad by ω φ = K n (5.21) l φ = K l (5.22) In h cas of a circular orbi, whr h phas volvs linarly wih im, φ = G [r] = ω, whr ω is h orbial frquncy of h circular orbi givn by ω = K n = (1 + k) n. (5.23) In h gnral cas of a non-circular orbi w us h man angular moion ω = Kn (w 11
9 drop h subscrip φ) and o xplicily inroduc h linarly growing par of h orbial phas (5.16) by dcomposing i in h form φ = φ P + ω ( P ) + W(l) = φ P + K l + W(l). (5.24) Hr W(l) dnos a paricular funcion which is priodic in l (hnc, priodic in im wih priod P). From Eq (5.16), his funcion is givn in rms of h man anomaly l by W(l) = 1 n l dl [ G [ r(l ) ] ω ]. (5.25) Finally, h dcomposiion (5.24) xhibis clarly h doubly priodic naur of h binary moion, in rms of h man anomaly l wih priod 2π, and in rms of h priasron advanc K l wih priod 2π K. I is worh noing ha in Rfs. [191, 18] h noaion λ is usd; i corrsponds o λ = K l and will also occasionally b usd hr Quasi-Kplrian rprsnaion of h moion of compac binaris In our calculaions w shall also rquir h xplici soluion of h moion a 1PN ordr, in h form du o Damour & Drull [176]. Th soluion is givn in paramric form in rms of h ccnric anomaly u. Th radius r and h man anomaly l ar xprssd as r = a r (1 r cos u), l = u sin u. (5.26a) (5.26b) Th phas angl φ is givn by (h addiiv consan φ P has bn s qual o zro) whr h ru anomaly V is dfind by 2 φ = K V, (5.27) [( ) 1/2 1 + φ V = 2 arcan an u ]. (5.28) 1 φ 2 In h abov, K is h priasron advanc givn in gnral rms by Eq. (5.18), and a r is h smi-major axis of h orbi. No ha hr ar, in his paramrizaion a 1PN ordr, hr kinds of ccnriciis r, and φ (lablld afr h coordinas r, and φ). All hs ccnriciis diffr from on anohr by 1PN rms, whil h advanc of h priasron pr orbial rvoluion appars also saring a h 1PN ordr. Du o hs faurs, his rprsnaion is rfrrd o as h quasi-kplrian (QK) paramrizaion for h 1PN orbial moion of h binary. Th priodic funcion W of Eq. (5.25) now rads W = K (V l). (5.29) 2 W hav dnod h ru anomaly by V rahr han by h symbol v of arlir paprs o avoid confusion wih h rlaiv spd v. 111
10 Th abov soluion is closd by h xplici dpndnc of h orbial lmns in rms of h 1PN consrvd nrgy E and angular momnum J in h cnr-of-mass fram (akn as usual pr uni of h rducd mass µ). This is givn in Rf. [176]. No ha h smi-major axis a r and man moion n dpnd a 1PN ordr only on h consan of nrgy hrough a r = G m { ( E 2 ν ) } E, (5.3a) 2 c { ( 2 ( 2 E)3/2 15 n = 1 + G m 4 ν ) } E. (5.3b) 4 c 2 Posing h J/(Gm), h 1PN priasron prcssion simply rads whil h hr diffrn ccnriciis ar givn by r = = φ = K = c 2 h 2, (5.31) [ ( {1 + 2 E h ) E 2 ν c ν ]} 1/2, (5.32a) 2 c 2 h 2 [ ( 17 {1 + 2 E h ) E 2 ν c + 2 2ν ]} 1/2, (5.32b) 2 c 2 h 2 [ ( {1 + 2 E h ν ) E 2 c 6 ]} 1/2. (5.32c) 2 c 2 h 2 Noic h following simpl raios (valid a 1PN ordr) r = 1 + (8 3ν) E c, 2 (5.33a) φ = 1 + (8 2ν) E c, 2 (5.33b) r φ = 1 + ν E c. 2 (5.33c) Th binary orbi can b characrisd by ihr (E, J) or any wo of h quasi-kplrian orbial lmns. W choos (n, ) and lis h 1PN accura xprssions for h ohr orbial lmns in rms of n and, which w will rquir lar in h work. For his purpos w firs invr Eq. (5.3b) o obain h 1PN consrvd nrgy in rms of n. E = 1 ( G m n ) 2/3} {1 2 (G m n)2/3 + (15 ν), (5.34) c 3 Using his in Eq. (5.3a), w g a r = ( ) G m 1/3 { ( ) G m n 2/3} 1 + ( 3 + ν), (5.35) n 2 c 3 which is a 1PN xnsion of Kplr s law. From Eqs (5.33) w obain r and φ in rms of n 112
11 and. { r = 1 + (4 3 ( G m n ) 2/3} 2 ν), (5.36a) c 3 ( G m n ) 2/3} φ = {1 + (4 ν). (5.36b) c 3 Th priasron prcssion, givn by Eq. (5.31), also nds o b xprssd as a funcion of n and. To obain i, w us h following xprssion, asily obaind from Eq. (5.32b). 2E h 2 = (1 ) 2 {1 + Th abov rlaion, along wih Eq. (5.34) yilds ( G m n ) 2/3 1 ( ) } 9 + ν (17 7 ν) 2 c 3 4 (1 2 ) (5.37) K = (1 2 ) ( G m n c 3 ) 2/3 (5.38) 5.4 Fourir dcomposiion of h binary s mulipol momns Nwonian Angular Momnum flux Th mhod w shall us in his chapr is illusrad by h compuaion of h avragd angular momnum flux of compac binaris a Nwonian ordr using a Fourir dcomposiion of h Kplrian moion [171]. Th GW angular momnum flux rducs a Nwonian ordr o (from Eq. 5.6) 3 (F J i) = 2 5 ε (2) i jk I ja () I (3) ka (), (5.39) whr mans h Nwonian limi, h suprscrip (n) rfrs o im diffrniaions. I i j is, by consrucion, h symmric-rac-fr (STF) quadrupol momn a Nwonian ordr givn by I i j = µ x <i x j>. x i is h binary s orbial sparaion, and h angular bracks around indics indica h STF projcion: x <i x j> x i x j 1 3 δi j r 2. Howvr, h prsnc of h Lvi-Civia symbol nsurs ha h rac par of h symmrizd quadrupol momn cancls ou. Hnc, unlik h nrgy-flux calculaion in Rf. [185], in his chapr w will ignor h rac of h quadrupol momn. Thus I i j = µ x i x j. (5.4) Prs & Mahws [171, 47] obaind h xprssion of h (avragd) Nwonian flux for compac binaris on ccnric orbis by wo mhods. Th firs mhod was o dircly avrag in im Eq. (5.39) using h xprssion (5.4) compud for h Kplrian llips; h scond mhod was o dcompos h componns of h quadrupol momn ino discr Fourir sris using h known Fourir dcomposiion of h Kplr orbi (h wo mhods, 3 From now on w s c = 1 and G =
12 as xpcd, agrd on h rsul). In h scond mhod h quadrupol momn, which is a priodic funcion of im a Nwonian ordr, is hus dcomposd ino a Fourir sris I i j () = wih I i j = p= 2π Ii j i p l, (5.41a) dl 2π I i j i p l, (5.41b) whr l is h man anomaly of h binary moion, Eq. (5.13). Sinc I i j cofficins clarly saisfy I i j Eqs. (5.41) ino (5.39) w obain (F J i) = 2 5 = ( p) I i j p= q= is ral h Fourir ( dnos h complx conjuga). Insring (ip n) 2 (iq n) 3 ε i jk I ja I (q) ka i(p+q)l. (5.42) Afr his, w prform an avrag ovr on priod P. This mans h avrag ovr l = n ( P ) which is asily prformd wih h following ipl 2π dl 2π i p l = δ p,. (5.43) This immdialy yilds h avragd angular momnum flux in h form of h Fourir sris (F J i) = 4 5 i (p n) 5 ε i jk I ja I ka. (5.44) p=1 Using dimnsional analysis (and h known circular orbi limi) his flux is ncssarily of h form (F J i) = 32 m9/2 ν2 5 a f J() z 7/2 i, (5.45) whr ν = µ/m and a is h smi-major axis of h Kplr orbi, z i is an uni vcor paralll o h angular momnum of h binary (and prpndicular o h orbi lying in h x-y plan) and h funcion f J () is a dimnsionlss funcion dpnding only on h binary s ccnriciy. Th cofficin in fron of (5.45) is chosn in such a way ha f J () rducs o on in h circular orbi limi ( ). Thrfor, f J () = i 8 µ 2 a 4 p=1 p 5 ε i jk I ja I ka z i. (5.46) Th Fourir cofficins of h quadrupol momn ar xplicily givn by Eqs. (5.128) in Scion 5.1. f J () admis an algbraically closd-form xprssion which is crucial for h iming of h binary pulsar PSR [5], and givn by f J () = (1 2 ) 2. (5.47) 114
13 Th mhod of dcomposing h Nwonian momn of compac binaris as discr Fourir sris was usd in Rf. [173] o compu h ail a h dominan 1.5PN ordr. To xnd his rsul w nd o b mor sysmaic abou h Fourir dcomposiion of h (no ncssarily Nwonian) sourc mulipol momns Gnral srucur of h Fourir dcomposiion Th wo ss of sourc momns of h compac binary ar dnod by I L () and J L () following Rf. [126]. Th muli-indx noaion mans L i 1 i 2 i l, whr l is h numbr of indics or mulipolariy (which should no b confusd wih h man anomaly l). In his Scion w sudy h srucur of h mass and currn momns I L and say J L 1 (whr L 1 i 1 i 2 i l 1 is chosn in h currn momn for convninc rahr han L), a any PN ordr and for a compac binary sysm moving on a gnral non-circular orbi 4. Thir gnral srucur can b wrin as I L () = J L 1 () = l F k [r, ṙ, v 2 ] x <i 1 i k v i k+1 i l >, k= l 2 k= G k [r, ṙ, v 2 ] x <i 1 i k v i k+1 i l 2 ε i l 1>ab x a v b, (5.48a) (5.48b) whr x i = y i 1 yi 2 and vi = dx i /d = v i 1 vi 2 dno h rlaiv posiion and vlociy of h wo bodis (in a harmonic coordina sysm). In (5.48) w pos for insanc x i 1 i k x i1 x i k, and h angular bracks surrounding indics rfr o h usual symmric-rac-fr (STF) projcion wih rspc o hos indics. Using polar coordinas r, φ in h orbial plan (as in Sc ), h abov inroducd cofficins F k and G k dpnd on h masss and on r, ṙ and v 2 = ṙ 2 + r 2 φ 2. For quasi-llipic moion on can xplicily facoriz ou h dpndnc on h orbial phas φ by insring x = r cos φ, y = r sin φ, and v x = ṙ cos φ r φ sin φ, v y = ṙ sin φ + r φ cos φ. Furhrmor, using h xplici soluion of h moion (Sc ) r, ṙ and v 2, and hnc h F k s and G k s can b xprssd as priodic funcions of h man anomaly l = n ( P ), whr n = 2π/P. W hn find ha h abov gnral srucur of h mulipol momns can b xprssd in rms of h phas angl φ, as h following fini sum ovr som magnicyp indx m ranging from l o +l, I L () = J L 1 () = l m= l l m= l A (m) L (l) i m φ, B (m) L 1 (l) i m φ, (5.49a) (5.49b) involving som cofficins (m) A L and (m) B L 1 dpnding on h man anomaly l and which ar complx ( C). (Som of hs cofficins could b vanishing in paricular cass.) Th poin for our purpos is ha hs cofficins ar priodic funcions of l wih priod 2π. As plan. 4 Howvr h inrinsic spins of h compac objcs ar nglcd, so h moion aks plac in a fixd orbial 115
14 w can s, h srucur of h mass and currn momns I L and J L 1 is basically h sam, bu hir cofficins (m) A L and (m) B L 1 will hav a diffrn pariy, bcaus of h Lvi-Civia symbol nring h currn momn J L 1. To procd furhr, l us xploi h doubly priodic naur of h dynamics in h wo variabls λ K l and l (as rviwd in Sc ). Th phas is givn in full gnraliy by Eq. (5.24) whr W(l) is priodic in l. In h following i will b mor convnin o singl ou in h xprssion of h phas h purly rlaivisic prcssion of h priasron, namly λ l = k l whr k = K 1. W insr h xprssion of h phas variabl ino Eqs. (5.49) which yilds many facors modifying h cofficins of (5.49), bu in such a way ha hy rain h priodiciy in l. Hnc I L () = J L 1 () = l m= l l m= l I (m) L (l) i m k l, J (m) L 1 (l) i m k l, (5.5a) (5.5b) whr h cofficins (m) I L (l) and (m) J L 1 (l) ar 2π-priodic. This allows us o us a discr Fourir sris xpansion in h inrval l [, 2π] for ach of hs cofficins, i.., I (m) L (l) = J (m) L 1 (l) = p= p= I (p,m) L i p l, J (p,m) L 1 i p l, (5.51a) (5.51b) and h invrs rlaions ar I (p,m) L = J (p,m) L 1 = 2π 2π dl 2π I (m) L (l) i p l, dl 2π J (m) L 1 (l) i p l. (5.52a) (5.52b) W now hav h following final dcomposiions of h mulipol momns, I L () = J L 1 () = l p= m= l l p= m= l I (p,m) L i (p+m k) l, J (p,m) L 1 i (p+m k) l. (5.53a) (5.53b) Th momns I L and J L 1 bing ral, hir Fourir cofficins saisfy (p,m) I L = ( p, m) I L and (p,m)j L 1 = ( p, m) J L 1. Th prvious dcomposiions wr gnral, bu i is sill usful o inroduc a spcial noaion for h paricular cas of h Nwonian ordr, for which h rlaivisic prcssion k. In his limi, h usual priodic Fourir dcomposiion of h momns is rcovrd 116
15 [gnralizing Eqs. (5.41)], wih only on Fourir summaion ovr h indx p, so ha I L () = p= J L 1 () = IL i p l, (5.54a) JL 1 i p l. p= (5.54b) Th Nwonian Fourir cofficins ar qual o h sums ovr m of h doubly-priodic Fourir cofficins in Eqs. (5.53) whn akn in h Nwonian limi, namly IL = JL 1 = l (p,m) m= l l I L, (5.55a) J L 1. (p,m) m= l (5.55b) 5.5 Hrdiary conribuions in h angular momnum flux Th chniqu of h prvious Scion is applid o h compuaion of h ail ingrals in h angular momnum flux of compac binaris. Alhough h compuaions ar ffcivly don up o h 3PN lvl, h mhod w propos could in principl b implmnd a any PN ordr. W shall compu all h ail and ail-of-ail rms (5.8) (5.9) [i.. up o h 3PN ordr] avragd ovr h man anomaly l. Toghr wih h insananous rms rpord in Rf. [188] w shall obain h compl xprssion of h 3PN angular momnum flux. I is clar from Eqs. (5.8) (5.9) ha all h rms ncssia an valuaion a h rlaiv Nwonian ordr xcp h mass-yp quadrupolar ail rm firs rm in (5.8) which mus crucially includ h 1PN corrcions. W sar wih all h rms rquird a rlaiv Nwonian ordr and hn ackl h mor difficul 1PN quadrupolar ail rm Tails a rlaiv Nwonian ordr In his scion w considr h mass-yp quadrupolar ail rm in h angular momnum flux, h firs rm in Eq. (5.8). Howvr, w will no compu his rm a h PN ordr rquird for his chapr, bu a h rlaiv Nwonian ordr 5. This will srv as a simpl illusraion of h mhod w will us for compuing h highr-ordr ails. Th 1.5PN mass-quadrupol ail conribuion is, from Eq. (5.8) (F J i) mass quad ail = 4M 5 ε i jk [ ln + dτ ( ) τ 2r 5 W shall compu his rm a 1PN rlaiv ordr in Sc ( (2) I ja () (5) I ka ( τ) (3) I ja () (4) I ka ( τ) + 11 ], (5.56) 12 ) 117
16 whr h bracks rfr o h avrag ovr h man anomaly l as dfind by Eq. (5.43). Th rm (5.56) was alrady compud using a Fourir sris a Nwonian ordr in Rf. [173]; no ha h mhod of [173] is valid only for priodic moion and hus is applicabl only a h Nwonian lvl. In his Scion w rcovr h Nwonian rsul of [173]. Th Fourir dcomposiion of h Nwonian quadrupol momn was alrady givn in gnral form by Eqs. (5.41). Insring ha ino h flux (5.56), w valua h ail ingral by using h fac ha if l() = n ( P ) corrsponds o h currn im, hn l( τ) = l() n τ corrsponds o h rardd im τ. Nx w prform h avrag ovr h currn valu l() wih h hlp of h formula (5.43). W g (F J i) mass quad ail = 8M 5 i p= (p n) 7 ε i jk I ja I ka ( p) + ( ) τ dτ [ln ip n τ 2r + 11 ]. (5.57) 12 No h crucial rplacmn of h Fourir dcomposiion of h quadrupol momn I ka ( τ) a h rardd im τ in h ail ingral in Eq. (5.56) by h Fourir cofficins a h currn im, dfind by Eq. (5.41). This prmis us o ak h Fourir cofficins of I ka ousid h ail ingral. This rplacmn maks h rsul drivd blow xac only in a PN sns, as w hav nglcd h ffc of h binary s adiabaic voluion by radiaion racion in h pas. Consqunly, his rplacmn inroducs a rmaindr rm in Eq. (5.57) givn by h ordr of magniud of h adiabaic paramr ξ rad ω/ω 2. From Rfs. [124, 158], w know ha h abov rplacmn of h currn moion in h ail ingral is valid only modulo som rmaindr O(ξ rad ) or, mor prcisly, O(ξ rad ln ξ rad ). This rmaindr corrsponds o a corrcion rm of rlaiv 2.5PN ordr which is always ngligibl for our purposs (h 1.5PN ordr of h ails maks h corrcion rms du o h influnc of h binary s pas a 4PN ordr). To ackl h las facor in (5.57) which is h ail ingral in h Fourir domain, w us h closd-form formula + ( ) τ dτ i σ τ ln = 1 [ π 2r σ 2 sign(σ) + i( ln(2 σ r ) + C ) ], (5.58) whr σ p n, sign(σ) = ±1 and C =.577 dnos h Eulr consan. Insring Eq. (5.58) ino (5.57) w hav (F J i) mass quad ail = 8π M i (p n) 6 ε i jk I ja I ka 5. (5.59) p=1 No ha h rang of p s corrsponds o posiiv frquncis only. Th rmaining ail ingrals, givn by h scond and hird rms in Eq. (5.8), ar valuad in xacly h sam way. Wih h PN accuracy of h prsn calculaion hs ingrals ar ruly Nwonian so h mass ocupol momn I i jk and currn quadrupol momn J i j ar rquird a Nwonian ordr only. For simpliciy, w drop h suprcrip bcaus hr can b no confusion wih ohr rsuls. W hus nd o valua h im-avragd fluxs (F J i) mass oc ail = 2M 63 ε i jk + dτ ( I (3) jab () I(6) kab ( τ) I(4) jab () I(5) kab ( τ)) 118
17 (F J i) curr quad ail = 64M + 45 ε i jk [ ( τ ln 2r [ ln ) dτ ( J (2) ja ( ) τ 2r + 97 ], (5.6) 6 () J(5) ka ( τ) J(3) ja () J(4) ka ( τ)) ]. (5.61) No ha, as in h cas of h mass-quadrupol momn, h rac of J i j also dos no conribu o h angular momnum flux (s h argumn afr Eq. (5.39)). Howvr, for I i jk, w do hav o ak ino accoun is rac. Insring h Fourir dcomposiion of h momns, prforming h avrag using Eq. (5.43) and using h ingraion formula (5.58) givs us (F J i) mass oc ail = 4πM 63 i (p n) 8 ε i jk I (F J i) curr quad ail = 128πM 45 p=1 i p=1 (p n) 6 ε i jk J jab I kab ja J (5.62a) ka. (5.62b) In Sc. 5.6 w shall provid som numrical plos for h nhancmn ccnriciydpndn facors associad wih Eqs. (5.62), sinc hy do no hav a closd-form xprssion Tails-of-ails and ails squard A h 3PN ordr (i.. 1.5PN byond h dominan ail) h firs cubic non-linar inracion, bwn h quadrupol momn I i j and wo mass monopol facors M, appars. From Eqs. (5.9) w hav o compu h ail-of-ail conribuion and h so-calld ail squard on, + (F J i) ail(ail) = 4M2 5 ε i jk dτ ( I (2) ja ()I(6) ka ( τ) I(3) ja ()I(5) ka ( τ)) [ ( ) τ ln ( ) τ 2r 7 ln ], (5.63a) 2r 441 ( + ( ) (F J i) (ail) 2 = 8M2 τ 5 ε i jk dτ I (4) ja [ln ( τ) + 11 ]) 2r 12 ( + ( ) τ dτ I (5) ka [ln ( τ) + 11 ]). (5.63b) 2r 12 (5.63c) Boh rms ar valuad a rlaiv Nwonian ordr. W insr h Fourir dcomposiion of h Nwonian quadrupol momn (5.41) [again supprssing h suprscrip for simpliciy]. Th nw faur wih rspc o h ails is h apparanc of a logarihm squard in h ail-of-ail ingral (5.63). W hav again rplacd h moion in h infini pas of 119
18 h binary by h moion in h currn im (s h argumn following Eq. (5.57)). Th closd-form formula rquird o dal wih his rm is [compar wih Eq. (5.58)] + ( ) τ dτ i σ τ ln 2 = i { π 2 [ π 2r σ 6 2 sign(σ) + i( ln(2 σ r ) + C ) ] 2 }, (5.64) and wih his formula, oghr wih (5.58), w obain h rsul (F J i) ail(ail) = 8M2 5 i (p n) 7 ε i jk I ja I ka p=1 { π 2 6 2( ln(2p n r ) + C ) 2 57( + ln(2p n r ) + C ) } Th ail squard rm is radily compud wih (5.58) and is (F J i) (ail) 2 = 8M2 5 i (p n) 7 ε i jk I ja p=1 I ka { π ( Adding h wo rsuls (5.65a) and (5.66) w finally g ln(2p n r ) + C (5.65a) ) 2 }. (5.66) (F J i) ail(ail)+(ail) 2 = 8M2 5 i (p n) 7 ε i jk I ja p=1 I ka { 2π ln(2p n r ) C }. 294 (5.67a) No ha h conribuion from logarihms squard has canclld ou bwn h wo rms (5.65a) (5.66). Such cancllaion is known o occur for gnral sourcs [135]. No also ha h rsul (5.67a) sill dpnds on h arbirary lngh scal r. I is imporan o rac ou h fa of his consan and chck ha h compl angular momnum flux w obain a h nd (including all h insananous conribuions compud in [188]) is indpndn of r Th mass quadrupol ail a 1PN ordr In his subscion, w calcula h mass quadrupol ail a h rlaiv 1PN ordr, namly (F J i) mass quad ail = 4M 5 ε i jk + [ ln ( τ dτ ( I (2) ja ) 2r () I(5) ka ( τ) I(3) ja () I(4) ka ( τ)) ], (5.68) A h 1PN ordr (and similarly a any highr PN ordrs), w mus ak car of h doubly-priodic srucur of h soluion of h moion [Sc ], and dcompos h mulipol momns according o h gnral formulas (5.53). Hnc h 1PN mass quadrupol 12
19 momn I i j nring Eq. (5.68) is dcomposd as I i j () = 2 p= m= 2 I (p,m) i j i (p+m k) l, (5.69) wih doubly-indxd Fourir cofficins (p,m) I i j which ar valid hrough ordr 1PN. Th harmonics for which m = ±1 ar zro a h 1PN ordr, so Eq. (5.69) rducs o I i j () = p= { } I (p, 2) i j i (p 2k) l + I i j i p l + I i j i (p+2k) l, (5.7) (p,) (p,2) bu for our purposs, Eq. (5.69) is mor convnin, kping in mind ha h rms wih m = ±1 ar absn. As bfor w insr Eq. (5.69) ino Eq. (5.68) o obain [afr nglcing 2.5PN radiaion racion rms O (ξ rad ) mniond bfor] (F J i) mass quad ail = 4M 5 i ε i jk I (p,m) ja p,p ;m,m n 7 ( (p + mk) 2 (p + m k) 5 (p + mk) 3 (p + m k) 4) I (p,m ) ka i(p+p +(m+m )k)l + [ ( ) dτ i (p +m k) n τ τ ln + 11 ], 2r 12 (5.71) whr h summaions rang from o + for p and p, and from 2 o 2 for m and m. Th facors (p + mk) 2, (p + m k) 5 c. com from h im-drivaivs of h quadrupol momn. W lav h las wo facors in Eq. (5.71) as hy ar, namly h avrag ovr l of an lmnary doubly-priodic complx xponnial, and h Fourir ransform of h ail ingral. Th xprssion in Eq. (5.71) is o b calculad a h 1PN ordr. Sinc h rlaivisic advanc of h priasron k is a small 1PN quaniy, w firs valua Eq. (5.71) a linar ordr in k [i.., nglcing O(k 2 ) which is a las 2PN]. Afrwards w shall insr h xplici PN xprssions for h 1PN quadrupol momn and ADM mass. Th ncssary formulas for prforming h linar-ordr xpansion in k of h las wo facors in Eq. (5.71) ar providd blow. Th avrag w prform is ovr h orbial priod (im o rurn o h priasron) and so is dfind by 2π i (p+m k) l dl 2π i (p+m k) l. (5.72) Using h fac ha m k 1 sinc w ar in h limi whr k (hnc p + m k is nvr an ingr unlss k = ), w radily find m k if p i (p+m k) l p = + O(k 2 ). (5.73) 1 + i π m k if p = Th abov rsul dpnds only on whhr p is zro or no, and is ru for any ingr m, xcp ha whn m = h rsul (5.73) bcoms xac as hr is no rmaindr rm O(k 2 ) in his cas. 121
20 To compu h ail ingral givn by h las facor in Eq. (5.71), w xpand i a firs ordr in k, obaining + ( ) ( τ dτ i (p+m k) n τ ln = 1 m k ) + ( ) τ dτ ip n τ ln i m k 2r p 2r p 2 n + O(k2 ), (5.74) and w apply for h rmaining ingral in Eq (5.74) h formula Eq. (5.58). Using Eqs. (5.73) and (5.74) w can xplicily compu h ail xprssion Eq. (5.71) a firs ordr in k (h xnsion o highr ordr in k would in principl b sraighforward). Th rsul is lf in h form of h mulipl Fourir sris Eq. (5.71), ino which h rsuls (5.73) (5.74) hav bn insrd (w do no giv a mor xplici form for his rsul which is givn by a complicad Mahmaica xprssion). In h nx Scion w shall rxprss his sris in rms of som lmnary nhancmn funcions which w valua numrically Mmory Ingral a 2.5PN ordr Th mmory conribuion is, from Eq. (5.1), ( F J i )mm = 4 35 ε i jk I (3) ja () ( [ ] ) I (3) b<k I(3) a>b [ τ] dτ (5.75) in which h symmrisaion ovr k & a in h ingrand can b rmovd bcaus i is manifsly symmric and h raclssnss condiion can also b rmovd bcaus of h prsnc of ε i jk and h symmry of I i j. Fourir dcomposing I i j w g ( F J i )mm = 4 35 ε i jk (i p n) 3 I ja ipl p= ( ) i(q+r)n τ dτ q= (i q n) 3 I bk iql r= (i r n) 3 I ab irl (5.76) whr, lik in h ail ingrals w hav nglcd h adiabaic orbial voluion of h binary and rplacd i by h moion a h currn im. Th ingrand for h mmory dos no conain h log krnl, bu i bing highly oscillaory h crss and roughs cancl ou and h only conribuion coms from h boundaris. Howvr h infini pas conribuion (corrsponding o τ ) is zro if w assum saionariy in h pas. On prforming an avrag ovr an orbi w g using i(p+q+r)l = δ p+q+r,. (5.77) ( F J i )mm = 4 35 n8 ε i jk p= q= p 2 q 3 (p + q) 3 I ja I bk I (p+q) ab (5.78) 122
21 This, on simplificaion, rducs o ( F J i )mm = 8 35 n8 ε i jk p=1 q=1 p 2 q ((p 3 + q) 3 R[I ja I bk I ab ] (q) (p+q) ) (p q) 3 R[I ja I bk I ab ] (q) (p q) (5.79) whr R[x] sands for ral par of x. Th angular momnum flux conribuion from h mmory, in rms of h PN paramr x = (m ω) 2/3, bcoms ( F J i )mm = 32 ( ) 1 5 ν2 m x 7/2 28 x5/2 ρ J () z i (5.8) whr ρ J () is h nhancmn funcion corrsponding o h mmory and gos o zro as. I is givn by ρ J () = ε i jk p=1 q=1 ) p 2 q ((p 3 + q) 3 R[I ja I bk I ab ] (p q)3 R[I ja I bk I ab ] z i (5.81) (q) (p+q) (q) (p q) W find ha h funcions of h quadrupol momn Fourir cofficins apparing in ach of h wo rms in Eq. (5.81) ar pur imaginary and hrfor, w hav, lik h circular orbi cas, ρ J () =. (5.82) In h fuur, w would lik o look a his rsul in mor dail, spcially a proof of h vanishing of his rm in a im-domain calculaion. Also, h validiy of h assumpion of h rplacmn of h pas moion by h currn moion insid h mmory ingral nds o b rad mor rigorously, prhaps by h us of Fourir ransforms rahr han Fourir sris. 5.6 Numrical calculaion of h ail ingrals Dfiniion of h ccnriciy nhancmn facors W dfin hr som funcions of h ccnriciy by crain Fourir sris of h componns of h Nwonian mulipol momns I L and J L 1 for a Kplrian llips wih ccnriciy, smi-major axis a, frquncy n = 2π/P (such ha Kplr s law n 2 a 3 = m holds a Nwonian ordr). In h cnr of mass fram I L = µs l (ν)x <L> and J L 1 = µs l(ν)x <L 2 ε il 1>ab x a v b whr µ = m 1 m 2 /m = ν m. W pos s l (ν) X l ( ) l X l 1 1, whr, X 1 m 1 = ( ) 1 m ν, and, X 2 m 2 = ( ) 1 m ν. L us rscal h lar Nwonian momns in ordr o mak hm dimnsionlss I L µ a l s l (ν) Î L, (5.83a) J L 1 µ a l n s l (ν) Jˆ L 1. (5.83b) 123
22 φ J ( ) Figur 5.1: Variaion of ϕ J () wih h ccnriciy. In h circular orbi limi w hav ϕ J () = 1. Our firs nhancmn funcion is h Prs & Mahws [171, 47] funcion which w hav alrady xprssd in Eq. (5.46) as a Fourir sris [and which urns ou o admi h analyically closd form (5.47)]. This sris bcoms, in rms of h Fourir componns of h rscald quadrupol momn Î i j f J () = i 8 p=1 p 5 ε i jk Î jb Î kb zi, (5.84) and is such ha h avragd Nwonian angular momnum flux of compac binaris rads (F J i) = 32 5 ν2 m x 7/2 f J () z i. (5.85) In h abov w hav dfind, for fuur convninc, h frquncy-rlad PN paramr x = (m ω) 2/3 whr ω is h binary s orbial frquncy dfind for gnral orbis by Eq. (5.23). No ha in Eq. (5.85) (which is Nwonian) w can rplac ω by n (hnc x rducs o m/a). Nx, w dfin svral ohr nhancmn funcions of h ccnriciy which will prmi o usfully paramriz h ail rms a Nwonian ordr. Firs w pos ϕ J () = i 16 p=1 p 6 ε i jk Î jb Î kb zi. (5.86) Lik for f J () his funcion is dfind in such a way ha i nds o on in h circular orbi limi, whn. Howvr, unlik f J (), i dos no admi a closd-form xprssion, and w lav i in h form of a Fourir sris. Th funcion ϕ J () paramrizs h mass quadrupol ail a Nwonian ordr, in h sns ha w hav, from Eq. (5.59), (F J i) mass quad = 32 5 ν2 m x 7/2 [ 4π x 3/2 ϕ J () ] z i. (5.87) For circular orbis, ϕ J () = 1 and w rcogniz h cofficin 4π of h 1.5PN ail rm ( x 3/2 ) as compud analyically in Rfs. [173]. Th funcion ϕ J () has alrady bn compud 124
23 β J ( ) γ J ( ) Figur 5.2: Variaion of β J () (lf panl) and γ J () (righ panl) wih h ccnriciy. In h circular orbi limi w hav β J () = γ J () = 1. numrically from is Fourir sris (5.86) in Rf. [173]. Hr w show h plo of ϕ J () in Fig. 5.1 (s Sc for dails on h numrical compuaion) 6. W nx provid similar xprssions for h 2.5PN mass ocupol and currn quadrupol ails by posing β J () = 2 i 1643 γ J () = 8 i p=1 p=1 p 6 ε i jk p 8 ε i jk Î jab Î ˆ J ja J ˆ ka zi. kab zi, (5.88a) (5.88b) Ths funcions also nd o on whn (as will b chckd lar) and mos probably do no admi any closd-form xprssions. Th ail rms ( x 5/2 ) of Eqs. (5.6) rduc o (F J i) mass oc ail = 32 [ ] ν2 m x 7/2 216 π (1 4 ν) x5/2 β J () z i, (5.89) (F J i) curr quad ail = 32 [ π ] 5 ν2 m x 7/2 18 (1 4 ν) x5/2 γ J () z i. (5.9) Th numrical graphs of h funcions β J () and γ J () ar shown in Fig Two furhr nhancmn facors ar ndd for h ail-of-ail and ail squard ingrals (which ar Nwonian). Th firs of hs funcions looks vry much lik f J (), Eq. (5.84), in h sns ha is Fourir sris involvs odd powrs of h mods p. Namly w dfin F J () = i 32 p=1 p 7 ε i jk Î ja Î ka zi. (5.91) Thanks o his odd powr p 7 w find ha F J () admis lik for f J () an analyic closd 6 Our noaion is diffrn from h on in Rih & Schäfr [173]; h funcion ϕ RS () hr is rlad o our dfiniion by ϕ RS () = ϕ J ()/ f J (). In h prsn work i is br no o divid h various funcions by h Prs & Mahws funcion f J (). 125
24 χ J ( ) F J ( ) Figur 5.3: Variaion of χ J () (lf panl) and F J () (righ panl) wih h ccnriciy. In h righ panl, h xac xprssion of F J () givn by Eq. (5.92) is usd. In h circular orbi limi w hav χ J () = and F J () = 1. form which is F J () = (1 2 ) 5. (5.92) W nd anohr funcion whos Fourir ransform diffrs from h on of F J () by h prsnc of h logarihm of mods, namly χ J () = i 32 p=1 ( p ) p 7 ln ε i jk 2 Î ja Î ka zi. (5.93) Mos probably χ J () dos no admi any analyic form [hnc w nam i using h Grk alphab in conras o f J () and F J ()]. No ha χ J () has bn xcpionally dfind in such a way ha i vanishs whn. This is asily chckd sinc in h circular orbi posssss only on harmonic, which is h on for which p = 2, and consqunly h log-rm in χ J () bcoms zro. In Fig. 5.3 w show h numrical plo of h funcion χ J () [and also h on for F J ()]. In Fig. 5.3 w show h numrical plo of h funcion χ J () [and also h on for F J ()]. Wih h abov dfiniions h sum of ail-of-ail and ail squard conribuions obaind in Eq. (5.67a) bcoms limi (and a Nwonian ordr) h quadrupol momn I i j (F J i) ail(ail)+(ail) 2 = 32 {[ 5 ν2 m x 13/ π C 1712 ] 15 ln (4 ω r ) F J () 1712 } 15 χ J() z i. (5.94) (5.95) Th circular-orbi limi is rad off and sn o agr wih Eq. (5.9) in Rf. [135] or Eq. (12.7) in Rf. [116]. Finally w provid h mass quadrupol ail a 1PN ordr, whos compuaion is much mor involvd (s Sc ) as h Fourir sris Eq. (5.71) conains svral summaions, and dpnd on h inrmdia rsuls (5.73) and (5.74). Th compuaion mus also incor- 126
25 α J ( ) θ J ( ) Figur 5.4: Variaion of α J () (lf panl) and θ J () (righ panl) wih h ccnriciy. In h circular orbi limi w hav α J () = and θ J () = 1. pora h 1PN rlaivisic corrcion in h mass quadrupol momn and ADM mass; w provid hm in Eqs. (5.98) and (5.99) blow. Probably no simpl way xiss [i.. no simpl Fourir sris lik for insanc (5.93)] for xprssing h nw nhancmn funcions of ccnriciy which appar a h 1PN ordr. Howvr i can b asily chckd ha h 1PN rm is a linar funcion of h symmric mass raio ν, hnc w mus inroduc wo nhancmn funcions, dnod blow α J and θ J. As usual, w normaliz hm so ha α J () = 1 and θ J () = 1. W hus hav [xnding Eq. (5.87) a h 1PN ordr] (F J i) mass quad = 32 [ 5 ν2 m x {4π 5 ϕ J ( ) + π x α J( ) ]} 21 ν θ J( ) z i. (5.96) This quaion dfins h wo nhancmn funcions α J and θ J, and w us Mahmaica o compu hm as complicad Fourir dcomposiions, which will hn b dircly compud numrically using h mhod oulind in Sc Noic ha sinc w ar a h 1PN ordr w mus b spcific abou ccnriciy w us. W adopd hr h im ccnriciy nring h Kplr quaion (5.26b) in Sc Th ohr ccnriciis ar rlad o i by Eqs. (5.33) a h 1PN ordr. On h ohr hand, h frquncy-rlad PN paramr, givn by x = (m ω) 2/3, (5.97) crucially includs h 1PN rlaivisic corrcion coming from h priasron advanc K = 1 + k, hrough h dfiniion ω = n K of Sc All h 1PN corrcions arising from h formulas (5.73) and (5.74), h mulipol momns M and I i j, h us of h im ccnriciy and h spcific PN variabl x, ar incorporad in a Mahmaica program daling wih h dcomposiion (5.71) and usd o obain (5.96). Th plos of h nhancmn funcions α() and θ() ar givn in Fig Numrical valuaion of h Fourir cofficins L us now dscrib h numrical implmnaion of h compuaion of h Fourir cofficins of h mulipol momns ha lad o h numrical plos of h prvious Scion. W focus on h compuaion of h crucial cofficins (p,m) I i j a 1PN ordr which ar h mor difficul o obain. Th mass quadrupol momn wih 1PN accuracy is givn by [compar 127
26 wih h gnral srucur (5.48a)] { [ ( 29 I i j = µ 1 + v ) 14 ν + m ( 57 r + 87 )] ν x i x j ( ) 7 ν r 2 v i v j + ( ) } ν r ṙ x i v j, (5.98) whr x i and v i = dx i /d ar h rlaiv posiion and vlociy in harmonic coordinas, and r = x i (lik in Sc ). Equaion (5.98) is valid for non-spinning compac binaris on an arbirary quasi-kplrian orbi in h cnr-of-mass fram (s.g. [132]). Sinc w calcula ails wih 1PN rlaiv accuracy w nd o know how h ADM mass M rlas o h oal mass m = m 1 + m 2 a 1PN ordr, ( v 2 M = m [ 1 + ν 2 m r )]. (5.99) Wih h hlp of h quasi-kplrian rprsnaion [Sc ], h dpndnc of I i j on x i, v i, r, v 2 and ṙ is paramrizd by h ccnric anomaly u. Howvr, as xplaind prviously w rquir I i j (l) in h im domain o procd. Th sps of our numrical implmnaion can b schmaically xprssd as : 1. Firsly, ach componn of h 1PN mass quadrupol is xprssd in rms of h quasi-kplrian paramrs using Eqs. (5.26) (5.28). Th componns of h mass quadrupol bcom funcions of h ccnric anomaly u, and ar paramrizd by h man moion n and by on of h ccnriciis (w chos o b h im ccnriciy in Kplr s quaion (5.26b) 7 ) 2. Now w numrically invr h quaion for h man anomaly l = u sin u o obain h funcion u(l). This can b don ihr by using h sris rprsnaion in rms of Bssl funcions, 1 u = l + 2 s J s(s ) sin(s l), (5.1) (5.33). s=1 or numrically by finding h roo of l = u sin u. W find h lar mhod o b mor fficin and accura mhod and mploy i using h FindRoo rouin in Mahmaica. A abl of 2 poins of u and l bwn and 2π (for ach valu of ) was gnrad for his purpos. Th abov invrsion allows us o r-xprss all funcions of h ccnric anomaly u as funcions of h man anomaly l. If rquird, on can amp a mor accura implmnaion, in h fuur, for solving Kplr s quaion along h lins of [192]. 3. Thr is a disconinuiy in h u dpndnc of V in Eq. (5.28). To avoid i w us ( V(u) = u + 2 arcan β φ sin u 1 β φ cos u ), (5.11) 7 Th smi-major axis a r and h ohr ccnriciis r and φ ar dducd from n and using Eqs. (5.3) 128
CSE 245: Computer Aided Circuit Simulation and Verification
 CSE 45: Compur Aidd Circui Simulaion and Vrificaion Fall 4, Sp 8 Lcur : Dynamic Linar Sysm Oulin Tim Domain Analysis Sa Equaions RLC Nwork Analysis by Taylor Expansion Impuls Rspons in im domain Frquncy
CSE 45: Compur Aidd Circui Simulaion and Vrificaion Fall 4, Sp 8 Lcur : Dynamic Linar Sysm Oulin Tim Domain Analysis Sa Equaions RLC Nwork Analysis by Taylor Expansion Impuls Rspons in im domain Frquncy
Spring 2006 Process Dynamics, Operations, and Control Lesson 2: Mathematics Review
 Spring 6 Procss Dynamics, Opraions, and Conrol.45 Lsson : Mahmaics Rviw. conx and dircion Imagin a sysm ha varis in im; w migh plo is oupu vs. im. A plo migh imply an quaion, and h quaion is usually an
Spring 6 Procss Dynamics, Opraions, and Conrol.45 Lsson : Mahmaics Rviw. conx and dircion Imagin a sysm ha varis in im; w migh plo is oupu vs. im. A plo migh imply an quaion, and h quaion is usually an
Boyce/DiPrima 9 th ed, Ch 2.1: Linear Equations; Method of Integrating Factors
 Boc/DiPrima 9 h d, Ch.: Linar Equaions; Mhod of Ingraing Facors Elmnar Diffrnial Equaions and Boundar Valu Problms, 9 h diion, b William E. Boc and Richard C. DiPrima, 009 b John Wil & Sons, Inc. A linar
Boc/DiPrima 9 h d, Ch.: Linar Equaions; Mhod of Ingraing Facors Elmnar Diffrnial Equaions and Boundar Valu Problms, 9 h diion, b William E. Boc and Richard C. DiPrima, 009 b John Wil & Sons, Inc. A linar
Lecture 1: Numerical Integration The Trapezoidal and Simpson s Rule
 Lcur : Numrical ngraion Th Trapzoidal and Simpson s Rul A problm Th probabiliy of a normally disribud (man µ and sandard dviaion σ ) vn occurring bwn h valus a and b is B A P( a x b) d () π whr a µ b -
Lcur : Numrical ngraion Th Trapzoidal and Simpson s Rul A problm Th probabiliy of a normally disribud (man µ and sandard dviaion σ ) vn occurring bwn h valus a and b is B A P( a x b) d () π whr a µ b -
Chapter 3: Fourier Representation of Signals and LTI Systems. Chih-Wei Liu
 Chapr 3: Fourir Rprsnaion of Signals and LTI Sysms Chih-Wi Liu Oulin Inroducion Complx Sinusoids and Frquncy Rspons Fourir Rprsnaions for Four Classs of Signals Discr-im Priodic Signals Fourir Sris Coninuous-im
Chapr 3: Fourir Rprsnaion of Signals and LTI Sysms Chih-Wi Liu Oulin Inroducion Complx Sinusoids and Frquncy Rspons Fourir Rprsnaions for Four Classs of Signals Discr-im Priodic Signals Fourir Sris Coninuous-im
Elementary Differential Equations and Boundary Value Problems
 Elmnar Diffrnial Equaions and Boundar Valu Problms Boc. & DiPrima 9 h Ediion Chapr : Firs Ordr Diffrnial Equaions 00600 คณ ตศาสตร ว ศวกรรม สาขาว ชาว ศวกรรมคอมพ วเตอร ป การศ กษา /55 ผศ.ดร.อร ญญา ผศ.ดร.สมศ
Elmnar Diffrnial Equaions and Boundar Valu Problms Boc. & DiPrima 9 h Ediion Chapr : Firs Ordr Diffrnial Equaions 00600 คณ ตศาสตร ว ศวกรรม สาขาว ชาว ศวกรรมคอมพ วเตอร ป การศ กษา /55 ผศ.ดร.อร ญญา ผศ.ดร.สมศ
Let s look again at the first order linear differential equation we are attempting to solve, in its standard form:
 Th Ingraing Facor Mhod In h prvious xampls of simpl firs ordr ODEs, w found h soluions by algbraically spara h dpndn variabl- and h indpndn variabl- rms, and wri h wo sids of a givn quaion as drivaivs,
Th Ingraing Facor Mhod In h prvious xampls of simpl firs ordr ODEs, w found h soluions by algbraically spara h dpndn variabl- and h indpndn variabl- rms, and wri h wo sids of a givn quaion as drivaivs,
Wave Equation (2 Week)
 Rfrnc Wav quaion ( Wk 6.5 Tim-armonic filds 7. Ovrviw 7. Plan Wavs in Losslss Mdia 7.3 Plan Wavs in Loss Mdia 7.5 Flow of lcromagnic Powr and h Poning Vcor 7.6 Normal Incidnc of Plan Wavs a Plan Boundaris
Rfrnc Wav quaion ( Wk 6.5 Tim-armonic filds 7. Ovrviw 7. Plan Wavs in Losslss Mdia 7.3 Plan Wavs in Loss Mdia 7.5 Flow of lcromagnic Powr and h Poning Vcor 7.6 Normal Incidnc of Plan Wavs a Plan Boundaris
Lecture 2: Current in RC circuit D.K.Pandey
 Lcur 2: urrn in circui harging of apacior hrough Rsisr L us considr a capacior of capacianc is conncd o a D sourc of.m.f. E hrough a rsisr of rsisanc R and a ky K in sris. Whn h ky K is swichd on, h charging
Lcur 2: urrn in circui harging of apacior hrough Rsisr L us considr a capacior of capacianc is conncd o a D sourc of.m.f. E hrough a rsisr of rsisanc R and a ky K in sris. Whn h ky K is swichd on, h charging
H is equal to the surface current J S
 Chapr 6 Rflcion and Transmission of Wavs 6.1 Boundary Condiions A h boundary of wo diffrn mdium, lcromagnic fild hav o saisfy physical condiion, which is drmind by Maxwll s quaion. This is h boundary condiion
Chapr 6 Rflcion and Transmission of Wavs 6.1 Boundary Condiions A h boundary of wo diffrn mdium, lcromagnic fild hav o saisfy physical condiion, which is drmind by Maxwll s quaion. This is h boundary condiion
DEPARTMENT OF ELECTRICAL &ELECTRONICS ENGINEERING SIGNALS AND SYSTEMS. Assoc. Prof. Dr. Burak Kelleci. Spring 2018
 DEPARTMENT OF ELECTRICAL &ELECTRONICS ENGINEERING SIGNALS AND SYSTEMS Aoc. Prof. Dr. Burak Kllci Spring 08 OUTLINE Th Laplac Tranform Rgion of convrgnc for Laplac ranform Invr Laplac ranform Gomric valuaion
DEPARTMENT OF ELECTRICAL &ELECTRONICS ENGINEERING SIGNALS AND SYSTEMS Aoc. Prof. Dr. Burak Kllci Spring 08 OUTLINE Th Laplac Tranform Rgion of convrgnc for Laplac ranform Invr Laplac ranform Gomric valuaion
Charging of capacitor through inductor and resistor
 cur 4&: R circui harging of capacior hrough inducor and rsisor us considr a capacior of capacianc is conncd o a D sourc of.m.f. E hrough a rsisr of rsisanc R, an inducor of inducanc and a y K in sris.
cur 4&: R circui harging of capacior hrough inducor and rsisor us considr a capacior of capacianc is conncd o a D sourc of.m.f. E hrough a rsisr of rsisanc R, an inducor of inducanc and a y K in sris.
CPSC 211 Data Structures & Implementations (c) Texas A&M University [ 259] B-Trees
![CPSC 211 Data Structures & Implementations (c) Texas A&M University [ 259] B-Trees CPSC 211 Data Structures & Implementations (c) Texas A&M University [ 259] B-Trees](/thumbs/74/70718364.jpg) CPSC 211 Daa Srucurs & Implmnaions (c) Txas A&M Univrsiy [ 259] B-Trs Th AVL r and rd-black r allowd som variaion in h lnghs of h diffrn roo-o-laf pahs. An alrnaiv ida is o mak sur ha all roo-o-laf pahs
CPSC 211 Daa Srucurs & Implmnaions (c) Txas A&M Univrsiy [ 259] B-Trs Th AVL r and rd-black r allowd som variaion in h lnghs of h diffrn roo-o-laf pahs. An alrnaiv ida is o mak sur ha all roo-o-laf pahs
Midterm exam 2, April 7, 2009 (solutions)
 Univrsiy of Pnnsylvania Dparmn of Mahmaics Mah 26 Honors Calculus II Spring Smsr 29 Prof Grassi, TA Ashr Aul Midrm xam 2, April 7, 29 (soluions) 1 Wri a basis for h spac of pairs (u, v) of smooh funcions
Univrsiy of Pnnsylvania Dparmn of Mahmaics Mah 26 Honors Calculus II Spring Smsr 29 Prof Grassi, TA Ashr Aul Midrm xam 2, April 7, 29 (soluions) 1 Wri a basis for h spac of pairs (u, v) of smooh funcions
On the Derivatives of Bessel and Modified Bessel Functions with Respect to the Order and the Argument
 Inrnaional Rsarch Journal of Applid Basic Scincs 03 Aailabl onlin a wwwirjabscom ISSN 5-838X / Vol 4 (): 47-433 Scinc Eplorr Publicaions On h Driais of Bssl Modifid Bssl Funcions wih Rspc o h Ordr h Argumn
Inrnaional Rsarch Journal of Applid Basic Scincs 03 Aailabl onlin a wwwirjabscom ISSN 5-838X / Vol 4 (): 47-433 Scinc Eplorr Publicaions On h Driais of Bssl Modifid Bssl Funcions wih Rspc o h Ordr h Argumn
4.1 The Uniform Distribution Def n: A c.r.v. X has a continuous uniform distribution on [a, b] when its pdf is = 1 a x b
![4.1 The Uniform Distribution Def n: A c.r.v. X has a continuous uniform distribution on [a, b] when its pdf is = 1 a x b 4.1 The Uniform Distribution Def n: A c.r.v. X has a continuous uniform distribution on [a, b] when its pdf is = 1 a x b](/thumbs/71/65779443.jpg) 4. Th Uniform Disribuion Df n: A c.r.v. has a coninuous uniform disribuion on [a, b] whn is pdf is f x a x b b a Also, b + a b a µ E and V Ex4. Suppos, h lvl of unblivabiliy a any poin in a Transformrs
4. Th Uniform Disribuion Df n: A c.r.v. has a coninuous uniform disribuion on [a, b] whn is pdf is f x a x b b a Also, b + a b a µ E and V Ex4. Suppos, h lvl of unblivabiliy a any poin in a Transformrs
Phys463.nb Conductivity. Another equivalent definition of the Fermi velocity is
 39 Anohr quival dfiniion of h Fri vlociy is pf vf (6.4) If h rgy is a quadraic funcion of k H k L, hs wo dfiniions ar idical. If is NOT a quadraic funcion of k (which could happ as will b discussd in h
39 Anohr quival dfiniion of h Fri vlociy is pf vf (6.4) If h rgy is a quadraic funcion of k H k L, hs wo dfiniions ar idical. If is NOT a quadraic funcion of k (which could happ as will b discussd in h
Part I: Short Answer [50 points] For each of the following, give a short answer (2-3 sentences, or a formula). [5 points each]
![Part I: Short Answer [50 points] For each of the following, give a short answer (2-3 sentences, or a formula). [5 points each] Part I: Short Answer [50 points] For each of the following, give a short answer (2-3 sentences, or a formula). [5 points each]](/thumbs/92/109815505.jpg) Soluions o Midrm Exam Nam: Paricl Physics Fall 0 Ocobr 6 0 Par I: Shor Answr [50 poins] For ach of h following giv a shor answr (- snncs or a formula) [5 poins ach] Explain qualiaivly (a) how w acclra
Soluions o Midrm Exam Nam: Paricl Physics Fall 0 Ocobr 6 0 Par I: Shor Answr [50 poins] For ach of h following giv a shor answr (- snncs or a formula) [5 poins ach] Explain qualiaivly (a) how w acclra
whereby we can express the phase by any one of the formulas cos ( 3 whereby we can express the phase by any one of the formulas
 Third In-Class Exam Soluions Mah 6, Profssor David Lvrmor Tusday, 5 April 07 [0] Th vrical displacmn of an unforcd mass on a spring is givn by h 5 3 cos 3 sin a [] Is his sysm undampd, undr dampd, criically
Third In-Class Exam Soluions Mah 6, Profssor David Lvrmor Tusday, 5 April 07 [0] Th vrical displacmn of an unforcd mass on a spring is givn by h 5 3 cos 3 sin a [] Is his sysm undampd, undr dampd, criically
7.4 QUANTUM MECHANICAL TREATMENT OF FLUCTUATIONS *
 Andri Tokmakoff, MIT Dparmn of Chmisry, 5/19/5 7-11 7.4 QUANTUM MECANICAL TREATMENT OF FLUCTUATIONS * Inroducion and Prviw Now h origin of frquncy flucuaions is inracions of our molcul (or mor approprialy
Andri Tokmakoff, MIT Dparmn of Chmisry, 5/19/5 7-11 7.4 QUANTUM MECANICAL TREATMENT OF FLUCTUATIONS * Inroducion and Prviw Now h origin of frquncy flucuaions is inracions of our molcul (or mor approprialy
Transfer function and the Laplace transformation
 Lab No PH-35 Porland Sa Univriy A. La Roa Tranfr funcion and h Laplac ranformaion. INTRODUTION. THE LAPLAE TRANSFORMATION L 3. TRANSFER FUNTIONS 4. ELETRIAL SYSTEMS Analyi of h hr baic paiv lmn R, and
Lab No PH-35 Porland Sa Univriy A. La Roa Tranfr funcion and h Laplac ranformaion. INTRODUTION. THE LAPLAE TRANSFORMATION L 3. TRANSFER FUNTIONS 4. ELETRIAL SYSTEMS Analyi of h hr baic paiv lmn R, and
UNIT #5 EXPONENTIAL AND LOGARITHMIC FUNCTIONS
 Answr Ky Nam: Da: UNIT # EXPONENTIAL AND LOGARITHMIC FUNCTIONS Par I Qusions. Th prssion is quivaln o () () 6 6 6. Th ponnial funcion y 6 could rwrin as y () y y 6 () y y (). Th prssion a is quivaln o
Answr Ky Nam: Da: UNIT # EXPONENTIAL AND LOGARITHMIC FUNCTIONS Par I Qusions. Th prssion is quivaln o () () 6 6 6. Th ponnial funcion y 6 could rwrin as y () y y 6 () y y (). Th prssion a is quivaln o
Voltage v(z) ~ E(z)D. We can actually get to this wave behavior by using circuit theory, w/o going into details of the EM fields!
 Considr a pair of wirs idal wirs ngh >, say, infinily long olag along a cabl can vary! D olag v( E(D W can acually g o his wav bhavior by using circui hory, w/o going ino dails of h EM filds! Thr
Considr a pair of wirs idal wirs ngh >, say, infinily long olag along a cabl can vary! D olag v( E(D W can acually g o his wav bhavior by using circui hory, w/o going ino dails of h EM filds! Thr
The transition:transversion rate ratio vs. the T-ratio.
 PhyloMah Lcur 8 by Dan Vandrpool March, 00 opics of Discussion ransiion:ransvrsion ra raio Kappa vs. ransiion:ransvrsion raio raio alculaing h xpcd numbr of subsiuions using marix algbra Why h nral im
PhyloMah Lcur 8 by Dan Vandrpool March, 00 opics of Discussion ransiion:ransvrsion ra raio Kappa vs. ransiion:ransvrsion raio raio alculaing h xpcd numbr of subsiuions using marix algbra Why h nral im
UNSTEADY FLOW OF A FLUID PARTICLE SUSPENSION BETWEEN TWO PARALLEL PLATES SUDDENLY SET IN MOTION WITH SAME SPEED
 006-0 Asian Rsarch Publishing work (ARP). All righs rsrvd. USTEADY FLOW OF A FLUID PARTICLE SUSPESIO BETWEE TWO PARALLEL PLATES SUDDELY SET I MOTIO WITH SAME SPEED M. suniha, B. Shankr and G. Shanha 3
006-0 Asian Rsarch Publishing work (ARP). All righs rsrvd. USTEADY FLOW OF A FLUID PARTICLE SUSPESIO BETWEE TWO PARALLEL PLATES SUDDELY SET I MOTIO WITH SAME SPEED M. suniha, B. Shankr and G. Shanha 3
Applied Statistics and Probability for Engineers, 6 th edition October 17, 2016
 Applid Saisics and robabiliy for Enginrs, 6 h diion Ocobr 7, 6 CHATER Scion - -. a d. 679.. b. d. 88 c d d d. 987 d. 98 f d.. Thn, = ln. =. g d.. Thn, = ln.9 =.. -7. a., by symmry. b.. d...6. 7.. c...
Applid Saisics and robabiliy for Enginrs, 6 h diion Ocobr 7, 6 CHATER Scion - -. a d. 679.. b. d. 88 c d d d. 987 d. 98 f d.. Thn, = ln. =. g d.. Thn, = ln.9 =.. -7. a., by symmry. b.. d...6. 7.. c...
Double Slits in Space and Time
 Doubl Slis in Sac an Tim Gorg Jons As has bn ror rcnly in h mia, a am l by Grhar Paulus has monsra an inrsing chniqu for ionizing argon aoms by using ulra-shor lasr ulss. Each lasr uls is ffcivly on an
Doubl Slis in Sac an Tim Gorg Jons As has bn ror rcnly in h mia, a am l by Grhar Paulus has monsra an inrsing chniqu for ionizing argon aoms by using ulra-shor lasr ulss. Each lasr uls is ffcivly on an
On the Speed of Heat Wave. Mihály Makai
 On h Spd of Ha Wa Mihály Maai maai@ra.bm.hu Conns Formulaion of h problm: infini spd? Local hrmal qulibrium (LTE hypohsis Balanc quaion Phnomnological balanc Spd of ha wa Applicaion in plasma ranspor 1.
On h Spd of Ha Wa Mihály Maai maai@ra.bm.hu Conns Formulaion of h problm: infini spd? Local hrmal qulibrium (LTE hypohsis Balanc quaion Phnomnological balanc Spd of ha wa Applicaion in plasma ranspor 1.
Lecture 1: Growth and decay of current in RL circuit. Growth of current in LR Circuit. D.K.Pandey
 cur : Growh and dcay of currn in circui Growh of currn in Circui us considr an inducor of slf inducanc is conncd o a DC sourc of.m.f. E hrough a rsisr of rsisanc and a ky K in sris. Whn h ky K is swichd
cur : Growh and dcay of currn in circui Growh of currn in Circui us considr an inducor of slf inducanc is conncd o a DC sourc of.m.f. E hrough a rsisr of rsisanc and a ky K in sris. Whn h ky K is swichd
AR(1) Process. The first-order autoregressive process, AR(1) is. where e t is WN(0, σ 2 )
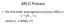 AR() Procss Th firs-ordr auorgrssiv procss, AR() is whr is WN(0, σ ) Condiional Man and Varianc of AR() Condiional man: Condiional varianc: ) ( ) ( Ω Ω E E ) var( ) ) ( var( ) var( σ Ω Ω Ω Ω E Auocovarianc
AR() Procss Th firs-ordr auorgrssiv procss, AR() is whr is WN(0, σ ) Condiional Man and Varianc of AR() Condiional man: Condiional varianc: ) ( ) ( Ω Ω E E ) var( ) ) ( var( ) var( σ Ω Ω Ω Ω E Auocovarianc
2.1. Differential Equations and Solutions #3, 4, 17, 20, 24, 35
 MATH 5 PS # Summr 00.. Diffrnial Equaions and Soluions PS.# Show ha ()C #, 4, 7, 0, 4, 5 ( / ) is a gnral soluion of h diffrnial quaion. Us a compur or calculaor o skch h soluions for h givn valus of h
MATH 5 PS # Summr 00.. Diffrnial Equaions and Soluions PS.# Show ha ()C #, 4, 7, 0, 4, 5 ( / ) is a gnral soluion of h diffrnial quaion. Us a compur or calculaor o skch h soluions for h givn valus of h
fiziks Institute for NET/JRF, GATE, IIT JAM, JEST, TIFR and GRE in PHYSICAL SCIENCES MATEMATICAL PHYSICS SOLUTIONS are
 MTEMTICL PHYSICS SOLUTIONS GTE- Q. Considr an ani-symmric nsor P ij wih indics i and j running from o 5. Th numbr of indpndn componns of h nsor is 9 6 ns: Soluion: Th numbr of indpndn componns of h nsor
MTEMTICL PHYSICS SOLUTIONS GTE- Q. Considr an ani-symmric nsor P ij wih indics i and j running from o 5. Th numbr of indpndn componns of h nsor is 9 6 ns: Soluion: Th numbr of indpndn componns of h nsor
EXERCISE - 01 CHECK YOUR GRASP
 DIFFERENTIAL EQUATION EXERCISE - CHECK YOUR GRASP 7. m hn D() m m, D () m m. hn givn D () m m D D D + m m m m m m + m m m m + ( m ) (m ) (m ) (m + ) m,, Hnc numbr of valus of mn will b. n ( ) + c sinc
DIFFERENTIAL EQUATION EXERCISE - CHECK YOUR GRASP 7. m hn D() m m, D () m m. hn givn D () m m D D D + m m m m m m + m m m m + ( m ) (m ) (m ) (m + ) m,, Hnc numbr of valus of mn will b. n ( ) + c sinc
Economics 302 (Sec. 001) Intermediate Macroeconomic Theory and Policy (Spring 2011) 3/28/2012. UW Madison
 Economics 302 (Sc. 001) Inrmdia Macroconomic Thory and Policy (Spring 2011) 3/28/2012 Insrucor: Prof. Mnzi Chinn Insrucor: Prof. Mnzi Chinn UW Madison 16 1 Consumpion Th Vry Forsighd dconsumr A vry forsighd
Economics 302 (Sc. 001) Inrmdia Macroconomic Thory and Policy (Spring 2011) 3/28/2012 Insrucor: Prof. Mnzi Chinn Insrucor: Prof. Mnzi Chinn UW Madison 16 1 Consumpion Th Vry Forsighd dconsumr A vry forsighd
A MATHEMATICAL MODEL FOR NATURAL COOLING OF A CUP OF TEA
 MTHEMTICL MODEL FOR NTURL COOLING OF CUP OF TE 1 Mrs.D.Kalpana, 2 Mr.S.Dhvarajan 1 Snior Lcurr, Dparmn of Chmisry, PSB Polychnic Collg, Chnnai, India. 2 ssisan Profssor, Dparmn of Mahmaics, Dr.M.G.R Educaional
MTHEMTICL MODEL FOR NTURL COOLING OF CUP OF TE 1 Mrs.D.Kalpana, 2 Mr.S.Dhvarajan 1 Snior Lcurr, Dparmn of Chmisry, PSB Polychnic Collg, Chnnai, India. 2 ssisan Profssor, Dparmn of Mahmaics, Dr.M.G.R Educaional
5. An object moving along an x-coordinate axis with its scale measured in meters has a velocity of 6t
 AP CALCULUS FINAL UNIT WORKSHEETS ACCELERATION, VELOCTIY AND POSITION In problms -, drmin h posiion funcion, (), from h givn informaion.. v (), () = 5. v ()5, () = b g. a (), v() =, () = -. a (), v() =
AP CALCULUS FINAL UNIT WORKSHEETS ACCELERATION, VELOCTIY AND POSITION In problms -, drmin h posiion funcion, (), from h givn informaion.. v (), () = 5. v ()5, () = b g. a (), v() =, () = -. a (), v() =
1. Inverse Matrix 4[(3 7) (02)] 1[(0 7) (3 2)] Recall that the inverse of A is equal to:
![1. Inverse Matrix 4[(3 7) (02)] 1[(0 7) (3 2)] Recall that the inverse of A is equal to: 1. Inverse Matrix 4[(3 7) (02)] 1[(0 7) (3 2)] Recall that the inverse of A is equal to:](/thumbs/84/89365453.jpg) Rfrncs Brnank, B. and I. Mihov (1998). Masuring monary policy, Quarrly Journal of Economics CXIII, 315-34. Blanchard, O. R. Proi (00). An mpirical characrizaion of h dynamic ffcs of changs in govrnmn spnding
Rfrncs Brnank, B. and I. Mihov (1998). Masuring monary policy, Quarrly Journal of Economics CXIII, 315-34. Blanchard, O. R. Proi (00). An mpirical characrizaion of h dynamic ffcs of changs in govrnmn spnding
CHAPTER CHAPTER14. Expectations: The Basic Tools. Prepared by: Fernando Quijano and Yvonn Quijano
 Expcaions: Th Basic Prpard by: Frnando Quijano and Yvonn Quijano CHAPTER CHAPTER14 2006 Prnic Hall Businss Publishing Macroconomics, 4/ Olivir Blanchard 14-1 Today s Lcur Chapr 14:Expcaions: Th Basic Th
Expcaions: Th Basic Prpard by: Frnando Quijano and Yvonn Quijano CHAPTER CHAPTER14 2006 Prnic Hall Businss Publishing Macroconomics, 4/ Olivir Blanchard 14-1 Today s Lcur Chapr 14:Expcaions: Th Basic Th
A THREE COMPARTMENT MATHEMATICAL MODEL OF LIVER
 A THREE COPARTENT ATHEATICAL ODEL OF LIVER V. An N. Ch. Paabhi Ramacharyulu Faculy of ahmaics, R D collgs, Hanamonda, Warangal, India Dparmn of ahmaics, Naional Insiu of Tchnology, Warangal, India E-ail:
A THREE COPARTENT ATHEATICAL ODEL OF LIVER V. An N. Ch. Paabhi Ramacharyulu Faculy of ahmaics, R D collgs, Hanamonda, Warangal, India Dparmn of ahmaics, Naional Insiu of Tchnology, Warangal, India E-ail:
Lecture 4: Laplace Transforms
 Lur 4: Lapla Transforms Lapla and rlad ransformaions an b usd o solv diffrnial quaion and o rdu priodi nois in signals and imags. Basially, hy onvr h drivaiv opraions ino mulipliaion, diffrnial quaions
Lur 4: Lapla Transforms Lapla and rlad ransformaions an b usd o solv diffrnial quaion and o rdu priodi nois in signals and imags. Basially, hy onvr h drivaiv opraions ino mulipliaion, diffrnial quaions
AN INTRODUCTION TO FOURIER ANALYSIS PROF. VEDAT TAVSANOĞLU
 A IRODUCIO O FOURIER AALYSIS PROF. VEDA AVSAOĞLU 994 A IRODUCIO O FOURIER AALYSIS ABLE OF COES. HE FOURIER SERIES ---------------------------------------------------------------------3.. Priodic Funcions-----------------------------------------------------------------------3..
A IRODUCIO O FOURIER AALYSIS PROF. VEDA AVSAOĞLU 994 A IRODUCIO O FOURIER AALYSIS ABLE OF COES. HE FOURIER SERIES ---------------------------------------------------------------------3.. Priodic Funcions-----------------------------------------------------------------------3..
Chapter 12 Introduction To The Laplace Transform
 Chapr Inroducion To Th aplac Tranorm Diniion o h aplac Tranorm - Th Sp & Impul uncion aplac Tranorm o pciic uncion 5 Opraional Tranorm Applying h aplac Tranorm 7 Invr Tranorm o Raional uncion 8 Pol and
Chapr Inroducion To Th aplac Tranorm Diniion o h aplac Tranorm - Th Sp & Impul uncion aplac Tranorm o pciic uncion 5 Opraional Tranorm Applying h aplac Tranorm 7 Invr Tranorm o Raional uncion 8 Pol and
Circuits and Systems I
 Circuis and Sysms I LECTURE #3 Th Spcrum, Priodic Signals, and h Tim-Varying Spcrum lions@pfl Prof. Dr. Volan Cvhr LIONS/Laboraory for Informaion and Infrnc Sysms Licns Info for SPFirs Slids This wor rlasd
Circuis and Sysms I LECTURE #3 Th Spcrum, Priodic Signals, and h Tim-Varying Spcrum lions@pfl Prof. Dr. Volan Cvhr LIONS/Laboraory for Informaion and Infrnc Sysms Licns Info for SPFirs Slids This wor rlasd
I) Title: Rational Expectations and Adaptive Learning. II) Contents: Introduction to Adaptive Learning
 I) Til: Raional Expcaions and Adapiv Larning II) Conns: Inroducion o Adapiv Larning III) Documnaion: - Basdvan, Olivir. (2003). Larning procss and raional xpcaions: an analysis using a small macroconomic
I) Til: Raional Expcaions and Adapiv Larning II) Conns: Inroducion o Adapiv Larning III) Documnaion: - Basdvan, Olivir. (2003). Larning procss and raional xpcaions: an analysis using a small macroconomic
Review Lecture 5. The source-free R-C/R-L circuit Step response of an RC/RL circuit. The time constant = RC The final capacitor voltage v( )
 Rviw Lcur 5 Firs-ordr circui Th sourc-fr R-C/R-L circui Sp rspons of an RC/RL circui v( ) v( ) [ v( 0) v( )] 0 Th i consan = RC Th final capacior volag v() Th iniial capacior volag v( 0 ) Volag/currn-division
Rviw Lcur 5 Firs-ordr circui Th sourc-fr R-C/R-L circui Sp rspons of an RC/RL circui v( ) v( ) [ v( 0) v( )] 0 Th i consan = RC Th final capacior volag v() Th iniial capacior volag v( 0 ) Volag/currn-division
A Condition for Stability in an SIR Age Structured Disease Model with Decreasing Survival Rate
 A Condiion for abiliy in an I Ag rucurd Disas Modl wih Dcrasing urvival a A.K. upriana, Edy owono Dparmn of Mahmaics, Univrsias Padjadjaran, km Bandung-umng 45363, Indonsia fax: 6--7794696, mail: asupria@yahoo.com.au;
A Condiion for abiliy in an I Ag rucurd Disas Modl wih Dcrasing urvival a A.K. upriana, Edy owono Dparmn of Mahmaics, Univrsias Padjadjaran, km Bandung-umng 45363, Indonsia fax: 6--7794696, mail: asupria@yahoo.com.au;
General Article Application of differential equation in L-R and C-R circuit analysis by classical method. Abstract
 Applicaion of Diffrnial... Gnral Aricl Applicaion of diffrnial uaion in - and C- circui analysis by classical mhod. ajndra Prasad gmi curr, Dparmn of Mahmaics, P.N. Campus, Pokhara Email: rajndraprasadrgmi@yahoo.com
Applicaion of Diffrnial... Gnral Aricl Applicaion of diffrnial uaion in - and C- circui analysis by classical mhod. ajndra Prasad gmi curr, Dparmn of Mahmaics, P.N. Campus, Pokhara Email: rajndraprasadrgmi@yahoo.com
Boyce/DiPrima 9 th ed, Ch 7.8: Repeated Eigenvalues
 Boy/DiPrima 9 h d Ch 7.8: Rpad Eignvalus Elmnary Diffrnial Equaions and Boundary Valu Problms 9 h diion by William E. Boy and Rihard C. DiPrima 9 by John Wily & Sons In. W onsidr again a homognous sysm
Boy/DiPrima 9 h d Ch 7.8: Rpad Eignvalus Elmnary Diffrnial Equaions and Boundary Valu Problms 9 h diion by William E. Boy and Rihard C. DiPrima 9 by John Wily & Sons In. W onsidr again a homognous sysm
Chapter 5 The Laplace Transform. x(t) input y(t) output Dynamic System
 EE 422G No: Chapr 5 Inrucor: Chung Chapr 5 Th Laplac Tranform 5- Inroducion () Sym analyi inpu oupu Dynamic Sym Linar Dynamic ym: A procor which proc h inpu ignal o produc h oupu dy ( n) ( n dy ( n) +
EE 422G No: Chapr 5 Inrucor: Chung Chapr 5 Th Laplac Tranform 5- Inroducion () Sym analyi inpu oupu Dynamic Sym Linar Dynamic ym: A procor which proc h inpu ignal o produc h oupu dy ( n) ( n dy ( n) +
Lagrangian for RLC circuits using analogy with the classical mechanics concepts
 Lagrangian for RLC circuis using analogy wih h classical mchanics concps Albrus Hariwangsa Panuluh and Asan Damanik Dparmn of Physics Educaion, Sanaa Dharma Univrsiy Kampus III USD Paingan, Maguwoharjo,
Lagrangian for RLC circuis using analogy wih h classical mchanics concps Albrus Hariwangsa Panuluh and Asan Damanik Dparmn of Physics Educaion, Sanaa Dharma Univrsiy Kampus III USD Paingan, Maguwoharjo,
S.Y. B.Sc. (IT) : Sem. III. Applied Mathematics. Q.1 Attempt the following (any THREE) [15]
![S.Y. B.Sc. (IT) : Sem. III. Applied Mathematics. Q.1 Attempt the following (any THREE) [15] S.Y. B.Sc. (IT) : Sem. III. Applied Mathematics. Q.1 Attempt the following (any THREE) [15]](/thumbs/92/108666103.jpg) S.Y. B.Sc. (IT) : Sm. III Applid Mahmaics Tim : ½ Hrs.] Prlim Qusion Papr Soluion [Marks : 75 Q. Amp h following (an THREE) 3 6 Q.(a) Rduc h mari o normal form and find is rank whr A 3 3 5 3 3 3 6 Ans.:
S.Y. B.Sc. (IT) : Sm. III Applid Mahmaics Tim : ½ Hrs.] Prlim Qusion Papr Soluion [Marks : 75 Q. Amp h following (an THREE) 3 6 Q.(a) Rduc h mari o normal form and find is rank whr A 3 3 5 3 3 3 6 Ans.:
Revisiting what you have learned in Advanced Mathematical Analysis
 Fourir sris Rvisiing wh you hv lrnd in Advncd Mhmicl Anlysis L f x b priodic funcion of priod nd is ingrbl ovr priod. f x cn b rprsnd by rigonomric sris, f x n cos nx bn sin nx n cos x b sin x cosx b whr
Fourir sris Rvisiing wh you hv lrnd in Advncd Mhmicl Anlysis L f x b priodic funcion of priod nd is ingrbl ovr priod. f x cn b rprsnd by rigonomric sris, f x n cos nx bn sin nx n cos x b sin x cosx b whr
Institute of Actuaries of India
 Insiu of Acuaris of India ubjc CT3 Probabiliy and Mahmaical aisics Novmbr Examinaions INDICATIVE OLUTION Pag of IAI CT3 Novmbr ol. a sampl man = 35 sampl sandard dviaion = 36.6 b for = uppr bound = 35+*36.6
Insiu of Acuaris of India ubjc CT3 Probabiliy and Mahmaical aisics Novmbr Examinaions INDICATIVE OLUTION Pag of IAI CT3 Novmbr ol. a sampl man = 35 sampl sandard dviaion = 36.6 b for = uppr bound = 35+*36.6
A HAMILTON-JACOBI TREATMENT OF DISSIPATIVE SYSTEMS
 Europan Scinific Journal Ocobr 13 diion vol9, No3 ISSN: 1857 7881 (Prin) - ISSN 1857-7431 A AMILTON-JACOBI TREATMENT OF DISSIPATIVE SYSTEMS Ola A Jarab'ah Tafila Tchnical Univrsiy, Tafila, Jordan Khald
Europan Scinific Journal Ocobr 13 diion vol9, No3 ISSN: 1857 7881 (Prin) - ISSN 1857-7431 A AMILTON-JACOBI TREATMENT OF DISSIPATIVE SYSTEMS Ola A Jarab'ah Tafila Tchnical Univrsiy, Tafila, Jordan Khald
A Propagating Wave Packet Group Velocity Dispersion
 Lctur 8 Phys 375 A Propagating Wav Packt Group Vlocity Disprsion Ovrviw and Motivation: In th last lctur w lookd at a localizd solution t) to th 1D fr-particl Schrödingr quation (SE) that corrsponds to
Lctur 8 Phys 375 A Propagating Wav Packt Group Vlocity Disprsion Ovrviw and Motivation: In th last lctur w lookd at a localizd solution t) to th 1D fr-particl Schrödingr quation (SE) that corrsponds to
Control System Engineering (EE301T) Assignment: 2
 Conrol Sysm Enginring (EE0T) Assignmn: PART-A (Tim Domain Analysis: Transin Rspons Analysis). Oain h rspons of a uniy fdack sysm whos opn-loop ransfr funcion is (s) s ( s 4) for a uni sp inpu and also
Conrol Sysm Enginring (EE0T) Assignmn: PART-A (Tim Domain Analysis: Transin Rspons Analysis). Oain h rspons of a uniy fdack sysm whos opn-loop ransfr funcion is (s) s ( s 4) for a uni sp inpu and also
MEM 355 Performance Enhancement of Dynamical Systems A First Control Problem - Cruise Control
 MEM 355 Prformanc Enhancmn of Dynamical Sysms A Firs Conrol Problm - Cruis Conrol Harry G. Kwany Darmn of Mchanical Enginring & Mchanics Drxl Univrsiy Cruis Conrol ( ) mv = F mg sinθ cv v +.2v= u 9.8θ
MEM 355 Prformanc Enhancmn of Dynamical Sysms A Firs Conrol Problm - Cruis Conrol Harry G. Kwany Darmn of Mchanical Enginring & Mchanics Drxl Univrsiy Cruis Conrol ( ) mv = F mg sinθ cv v +.2v= u 9.8θ
Final Exam : Solutions
 Comp : Algorihm and Daa Srucur Final Exam : Soluion. Rcuriv Algorihm. (a) To bgin ind h mdian o {x, x,... x n }. Sinc vry numbr xcp on in h inrval [0, n] appar xacly onc in h li, w hav ha h mdian mu b
Comp : Algorihm and Daa Srucur Final Exam : Soluion. Rcuriv Algorihm. (a) To bgin ind h mdian o {x, x,... x n }. Sinc vry numbr xcp on in h inrval [0, n] appar xacly onc in h li, w hav ha h mdian mu b
4.3 Design of Sections for Flexure (Part II)
 Prsrssd Concr Srucurs Dr. Amlan K Sngupa and Prof. Dvdas Mnon 4. Dsign of Scions for Flxur (Par II) This scion covrs h following opics Final Dsign for Typ Mmrs Th sps for Typ 1 mmrs ar xplaind in Scion
Prsrssd Concr Srucurs Dr. Amlan K Sngupa and Prof. Dvdas Mnon 4. Dsign of Scions for Flxur (Par II) This scion covrs h following opics Final Dsign for Typ Mmrs Th sps for Typ 1 mmrs ar xplaind in Scion
Section 5 Exercises, Problems, and Solutions. Exercises:
 Scion 5 Exrciss, Problms, and Soluions Exrciss: 1. Tim dpndn prurbaion hory provids an xprssion for h radiaiv lifim of an xcid lcronic sa, givn by τ R : τ h- R 4 c 4(E i - E f ) µ fi, whr i rfrs o h xcid
Scion 5 Exrciss, Problms, and Soluions Exrciss: 1. Tim dpndn prurbaion hory provids an xprssion for h radiaiv lifim of an xcid lcronic sa, givn by τ R : τ h- R 4 c 4(E i - E f ) µ fi, whr i rfrs o h xcid
Logistic equation of Human population growth (generalization to the case of reactive environment).
 Logisic quaion of Human populaion growh gnralizaion o h cas of raciv nvironmn. Srg V. Ershkov Insiu for Tim aur Exploraions M.V. Lomonosov's Moscow Sa Univrsi Lninski gor - Moscow 999 ussia -mail: srgj-rshkov@andx.ru
Logisic quaion of Human populaion growh gnralizaion o h cas of raciv nvironmn. Srg V. Ershkov Insiu for Tim aur Exploraions M.V. Lomonosov's Moscow Sa Univrsi Lninski gor - Moscow 999 ussia -mail: srgj-rshkov@andx.ru
3(8 ) (8 x x ) 3x x (8 )
 Scion - CHATER -. a d.. b. d.86 c d 8 d d.9997 f g 6. d. d. Thn, = ln. =. =.. d Thn, = ln.9 =.7 8 -. a d.6 6 6 6 6 8 8 8 b 9 d 6 6 6 8 c d.8 6 6 6 6 8 8 7 7 d 6 d.6 6 6 6 6 6 6 8 u u u u du.9 6 6 6 6 6
Scion - CHATER -. a d.. b. d.86 c d 8 d d.9997 f g 6. d. d. Thn, = ln. =. =.. d Thn, = ln.9 =.7 8 -. a d.6 6 6 6 6 8 8 8 b 9 d 6 6 6 8 c d.8 6 6 6 6 8 8 7 7 d 6 d.6 6 6 6 6 6 6 8 u u u u du.9 6 6 6 6 6
14.02 Principles of Macroeconomics Problem Set 5 Fall 2005
 40 Principls of Macroconomics Problm S 5 Fall 005 Posd: Wdnsday, Novmbr 6, 005 Du: Wdnsday, Novmbr 3, 005 Plas wri your nam AND your TA s nam on your problm s Thanks! Exrcis I Tru/Fals? Explain Dpnding
40 Principls of Macroconomics Problm S 5 Fall 005 Posd: Wdnsday, Novmbr 6, 005 Du: Wdnsday, Novmbr 3, 005 Plas wri your nam AND your TA s nam on your problm s Thanks! Exrcis I Tru/Fals? Explain Dpnding
Microscopic Flow Characteristics Time Headway - Distribution
 CE57: Traffic Flow Thory Spring 20 Wk 2 Modling Hadway Disribuion Microscopic Flow Characrisics Tim Hadway - Disribuion Tim Hadway Dfiniion Tim Hadway vrsus Gap Ahmd Abdl-Rahim Civil Enginring Dparmn,
CE57: Traffic Flow Thory Spring 20 Wk 2 Modling Hadway Disribuion Microscopic Flow Characrisics Tim Hadway - Disribuion Tim Hadway Dfiniion Tim Hadway vrsus Gap Ahmd Abdl-Rahim Civil Enginring Dparmn,
FIRST-ORDER SYSTEMS OF ORDINARY DIFFERENTIAL EQUATIONS I: Introduction and Linear Systems
 FIRST-ORDER SYSTEMS OF ORDINARY DIFFERENTIAL EQUATIONS I: Inroducion and Linar Sysms David Lvrmor Dparmn of Mahmaics Univrsiy of Maryland 9 Dcmbr 0 Bcaus h prsnaion of his marial in lcur will diffr from
FIRST-ORDER SYSTEMS OF ORDINARY DIFFERENTIAL EQUATIONS I: Inroducion and Linar Sysms David Lvrmor Dparmn of Mahmaics Univrsiy of Maryland 9 Dcmbr 0 Bcaus h prsnaion of his marial in lcur will diffr from
An Indian Journal FULL PAPER. Trade Science Inc. A stage-structured model of a single-species with density-dependent and birth pulses ABSTRACT
 [Typ x] [Typ x] [Typ x] ISSN : 974-7435 Volum 1 Issu 24 BioTchnology 214 An Indian Journal FULL PAPE BTAIJ, 1(24), 214 [15197-1521] A sag-srucurd modl of a singl-spcis wih dnsiy-dpndn and birh pulss LI
[Typ x] [Typ x] [Typ x] ISSN : 974-7435 Volum 1 Issu 24 BioTchnology 214 An Indian Journal FULL PAPE BTAIJ, 1(24), 214 [15197-1521] A sag-srucurd modl of a singl-spcis wih dnsiy-dpndn and birh pulss LI
Midterm Examination (100 pts)
 Econ 509 Spring 2012 S.L. Parn Midrm Examinaion (100 ps) Par I. 30 poins 1. Dfin h Law of Diminishing Rurns (5 ps.) Incrasing on inpu, call i inpu x, holding all ohr inpus fixd, on vnuall runs ino h siuaion
Econ 509 Spring 2012 S.L. Parn Midrm Examinaion (100 ps) Par I. 30 poins 1. Dfin h Law of Diminishing Rurns (5 ps.) Incrasing on inpu, call i inpu x, holding all ohr inpus fixd, on vnuall runs ino h siuaion
DE Dr. M. Sakalli
 DE-0 Dr. M. Sakalli DE 55 M. Sakalli a n n 0 a Lh.: an Linar g Equaions Hr if g 0 homognous non-homognous ohrwis driving b a forc. You know h quaions blow alrad. A linar firs ordr ODE has h gnral form
DE-0 Dr. M. Sakalli DE 55 M. Sakalli a n n 0 a Lh.: an Linar g Equaions Hr if g 0 homognous non-homognous ohrwis driving b a forc. You know h quaions blow alrad. A linar firs ordr ODE has h gnral form
Fourier Series and Parseval s Relation Çağatay Candan Dec. 22, 2013
 Fourir Sris nd Prsvl s Rlion Çğy Cndn Dc., 3 W sudy h m problm EE 3 M, Fll3- in som dil o illusr som conncions bwn Fourir sris, Prsvl s rlion nd RMS vlus. Q. ps h signl sin is h inpu o hlf-wv rcifir circui
Fourir Sris nd Prsvl s Rlion Çğy Cndn Dc., 3 W sudy h m problm EE 3 M, Fll3- in som dil o illusr som conncions bwn Fourir sris, Prsvl s rlion nd RMS vlus. Q. ps h signl sin is h inpu o hlf-wv rcifir circui
Physics 160 Lecture 3. R. Johnson April 6, 2015
 Physics 6 Lcur 3 R. Johnson April 6, 5 RC Circui (Low-Pass Filr This is h sam RC circui w lookd a arlir h im doma, bu hr w ar rsd h frquncy rspons. So w pu a s wav sad of a sp funcion. whr R C RC Complx
Physics 6 Lcur 3 R. Johnson April 6, 5 RC Circui (Low-Pass Filr This is h sam RC circui w lookd a arlir h im doma, bu hr w ar rsd h frquncy rspons. So w pu a s wav sad of a sp funcion. whr R C RC Complx
Decline Curves. Exponential decline (constant fractional decline) Harmonic decline, and Hyperbolic decline.
 Dlin Curvs Dlin Curvs ha lo flow ra vs. im ar h mos ommon ools for forasing roduion and monioring wll rforman in h fild. Ths urvs uikly show by grahi mans whih wlls or filds ar roduing as xd or undr roduing.
Dlin Curvs Dlin Curvs ha lo flow ra vs. im ar h mos ommon ools for forasing roduion and monioring wll rforman in h fild. Ths urvs uikly show by grahi mans whih wlls or filds ar roduing as xd or undr roduing.
CHAPTER. Linear Systems of Differential Equations. 6.1 Theory of Linear DE Systems. ! Nullcline Sketching. Equilibrium (unstable) at (0, 0)
 CHATER 6 inar Sysms of Diffrnial Equaions 6 Thory of inar DE Sysms! ullclin Skching = y = y y υ -nullclin Equilibrium (unsabl) a (, ) h nullclin y = υ nullclin = h-nullclin (S figur) = + y y = y Equilibrium
CHATER 6 inar Sysms of Diffrnial Equaions 6 Thory of inar DE Sysms! ullclin Skching = y = y y υ -nullclin Equilibrium (unsabl) a (, ) h nullclin y = υ nullclin = h-nullclin (S figur) = + y y = y Equilibrium
LaPlace Transform in Circuit Analysis
 LaPlac Tranform in Circui Analyi Obciv: Calcula h Laplac ranform of common funcion uing h dfiniion and h Laplac ranform abl Laplac-ranform a circui, including componn wih non-zro iniial condiion. Analyz
LaPlac Tranform in Circui Analyi Obciv: Calcula h Laplac ranform of common funcion uing h dfiniion and h Laplac ranform abl Laplac-ranform a circui, including componn wih non-zro iniial condiion. Analyz
Copyright 2012 Pearson Education, Inc. Publishing as Prentice Hall.
 Chapr Rviw 0 6. ( a a ln a. This will qual a if an onl if ln a, or a. + k an (ln + c. Thrfor, a an valu of, whr h wo curvs inrsc, h wo angn lins will b prpnicular. 6. (a Sinc h lin passs hrough h origin
Chapr Rviw 0 6. ( a a ln a. This will qual a if an onl if ln a, or a. + k an (ln + c. Thrfor, a an valu of, whr h wo curvs inrsc, h wo angn lins will b prpnicular. 6. (a Sinc h lin passs hrough h origin
Introduction to Fourier Transform
 EE354 Signals and Sysms Inroducion o Fourir ransform Yao Wang Polychnic Univrsiy Som slids includd ar xracd from lcur prsnaions prpard y McClllan and Schafr Licns Info for SPFirs Slids his work rlasd undr
EE354 Signals and Sysms Inroducion o Fourir ransform Yao Wang Polychnic Univrsiy Som slids includd ar xracd from lcur prsnaions prpard y McClllan and Schafr Licns Info for SPFirs Slids his work rlasd undr
SECTION where P (cos θ, sin θ) and Q(cos θ, sin θ) are polynomials in cos θ and sin θ, provided Q is never equal to zero.
 SETION 6. 57 6. Evaluation of Dfinit Intgrals Exampl 6.6 W hav usd dfinit intgrals to valuat contour intgrals. It may com as a surpris to larn that contour intgrals and rsidus can b usd to valuat crtain
SETION 6. 57 6. Evaluation of Dfinit Intgrals Exampl 6.6 W hav usd dfinit intgrals to valuat contour intgrals. It may com as a surpris to larn that contour intgrals and rsidus can b usd to valuat crtain
Chapter 4 Longitudinal static stability and control Effect of acceleration (Lecture 15)
 Chapr 4 Longiudinal saic sabiliy and conrol Effc of acclraion (Lcur 15) Kywords : Elvaor rquird in pull-up; sick-fixd manuvr poin; sick forc gradin in pull-up; manuvr poin sick-fr; ovrall limis on c.g.
Chapr 4 Longiudinal saic sabiliy and conrol Effc of acclraion (Lcur 15) Kywords : Elvaor rquird in pull-up; sick-fixd manuvr poin; sick forc gradin in pull-up; manuvr poin sick-fr; ovrall limis on c.g.
EE 529 Remote Sensing Techniques. Review
 59 Rmo Snsing Tchniqus Rviw Oulin Annna array Annna paramrs RCS Polariaion Signals CFT DFT Array Annna Shor Dipol l λ r, R[ r ω ] r H φ ηk Ilsin 4πr η µ - Prmiiviy ε - Prmabiliy
59 Rmo Snsing Tchniqus Rviw Oulin Annna array Annna paramrs RCS Polariaion Signals CFT DFT Array Annna Shor Dipol l λ r, R[ r ω ] r H φ ηk Ilsin 4πr η µ - Prmiiviy ε - Prmabiliy
The Optimal Timing of Transition to New Environmental Technology in Economic Growth
 h Opimal iming of ransiion o Nw Environmnal chnology in Economic Growh h IAEE Europan Confrnc 7- Spmbr, 29 Vinna, Ausria Akira AEDA and akiko NAGAYA yoo Univrsiy Background: Growh and h Environmn Naural
h Opimal iming of ransiion o Nw Environmnal chnology in Economic Growh h IAEE Europan Confrnc 7- Spmbr, 29 Vinna, Ausria Akira AEDA and akiko NAGAYA yoo Univrsiy Background: Growh and h Environmn Naural
EE 350 Signals and Systems Spring 2005 Sample Exam #2 - Solutions
 EE 35 Signals an Sysms Spring 5 Sampl Exam # - Soluions. For h following signal x( cos( sin(3 - cos(5 - T, /T x( j j 3 j 3 j j 5 j 5 j a -, a a -, a a - ½, a 3 /j-j -j/, a -3 -/jj j/, a 5 -½, a -5 -½,
EE 35 Signals an Sysms Spring 5 Sampl Exam # - Soluions. For h following signal x( cos( sin(3 - cos(5 - T, /T x( j j 3 j 3 j j 5 j 5 j a -, a a -, a a - ½, a 3 /j-j -j/, a -3 -/jj j/, a 5 -½, a -5 -½,
Instructors Solution for Assignment 3 Chapter 3: Time Domain Analysis of LTIC Systems
 Inrucor Soluion for Aignmn Chapr : Tim Domain Anali of LTIC Sm Problm i a 8 x x wih x u,, an Zro-inpu rpon of h m: Th characriic quaion of h LTIC m i i 8, which ha roo a ± j Th zro-inpu rpon i givn b zi
Inrucor Soluion for Aignmn Chapr : Tim Domain Anali of LTIC Sm Problm i a 8 x x wih x u,, an Zro-inpu rpon of h m: Th characriic quaion of h LTIC m i i 8, which ha roo a ± j Th zro-inpu rpon i givn b zi
22/ Breakdown of the Born-Oppenheimer approximation. Selection rules for rotational-vibrational transitions. P, R branches.
 Subjct Chmistry Papr No and Titl Modul No and Titl Modul Tag 8/ Physical Spctroscopy / Brakdown of th Born-Oppnhimr approximation. Slction ruls for rotational-vibrational transitions. P, R branchs. CHE_P8_M
Subjct Chmistry Papr No and Titl Modul No and Titl Modul Tag 8/ Physical Spctroscopy / Brakdown of th Born-Oppnhimr approximation. Slction ruls for rotational-vibrational transitions. P, R branchs. CHE_P8_M
10. If p and q are the lengths of the perpendiculars from the origin on the tangent and the normal to the curve
 0. If p and q ar h lnghs of h prpndiculars from h origin on h angn and h normal o h curv + Mahmaics y = a, hn 4p + q = a a (C) a (D) 5a 6. Wha is h diffrnial quaion of h family of circls having hir cnrs
0. If p and q ar h lnghs of h prpndiculars from h origin on h angn and h normal o h curv + Mahmaics y = a, hn 4p + q = a a (C) a (D) 5a 6. Wha is h diffrnial quaion of h family of circls having hir cnrs
Lecture 37 (Schrödinger Equation) Physics Spring 2018 Douglas Fields
 Lctur 37 (Schrödingr Equation) Physics 6-01 Spring 018 Douglas Filds Rducd Mass OK, so th Bohr modl of th atom givs nrgy lvls: E n 1 k m n 4 But, this has on problm it was dvlopd assuming th acclration
Lctur 37 (Schrödingr Equation) Physics 6-01 Spring 018 Douglas Filds Rducd Mass OK, so th Bohr modl of th atom givs nrgy lvls: E n 1 k m n 4 But, this has on problm it was dvlopd assuming th acclration
Mundell-Fleming I: Setup
 Mundll-Flming I: Sup In ISLM, w had: E ( ) T I( i π G T C Y ) To his, w now add n xpors, which is a funcion of h xchang ra: ε E P* P ( T ) I( i π ) G T NX ( ) C Y Whr NX is assumd (Marshall Lrnr condiion)
Mundll-Flming I: Sup In ISLM, w had: E ( ) T I( i π G T C Y ) To his, w now add n xpors, which is a funcion of h xchang ra: ε E P* P ( T ) I( i π ) G T NX ( ) C Y Whr NX is assumd (Marshall Lrnr condiion)
Chemistry 988 Part 1
 Chmisry 988 Par 1 Radiaion Dcion & Masurmn Dp. of Chmisry --- Michigan Sa Univ. aional Suprconducing Cycloron Lab DJMorrissy Spring/2oo9 Cours informaion can b found on h wbsi: hp://www.chmisry.msu.du/courss/cm988uclar/indx.hml
Chmisry 988 Par 1 Radiaion Dcion & Masurmn Dp. of Chmisry --- Michigan Sa Univ. aional Suprconducing Cycloron Lab DJMorrissy Spring/2oo9 Cours informaion can b found on h wbsi: hp://www.chmisry.msu.du/courss/cm988uclar/indx.hml
Solutions to FINAL JEE MAINS/IITJEE
 Soluions o FINAL JEE MAINS/IIJEE - [CHEMISRY].(C By consrvaion of mols PV P V P V + R R R P + P am..(a.(d.(b KMnO will rac wih FSO only. mols 5 mols χ FSO / N (g + H (g NH (g a a a a q a a P PNH P. a AgNO
Soluions o FINAL JEE MAINS/IIJEE - [CHEMISRY].(C By consrvaion of mols PV P V P V + R R R P + P am..(a.(d.(b KMnO will rac wih FSO only. mols 5 mols χ FSO / N (g + H (g NH (g a a a a q a a P PNH P. a AgNO
a dt a dt a dt dt If 1, then the poles in the transfer function are complex conjugates. Let s look at f t H t f s / s. So, for a 2 nd order system:
 Undrdamd Sysms Undrdamd Sysms nd Ordr Sysms Ouu modld wih a nd ordr ODE: d y dy a a1 a0 y b f If a 0 0, hn: whr: a d y a1 dy b d y dy y f y f a a a 0 0 0 is h naural riod of oscillaion. is h daming facor.
Undrdamd Sysms Undrdamd Sysms nd Ordr Sysms Ouu modld wih a nd ordr ODE: d y dy a a1 a0 y b f If a 0 0, hn: whr: a d y a1 dy b d y dy y f y f a a a 0 0 0 is h naural riod of oscillaion. is h daming facor.
Voltage v(z) ~ E(z)D. We can actually get to this wave behavior by using circuit theory, w/o going into details of the EM fields!
 Considr a pair of wirs idal wirs ngh >, say, infinily long olag along a cabl can vary! D olag v( E(D W can acually g o his wav bhavior by using circui hory, w/o going ino dails of h EM filds! Thr
Considr a pair of wirs idal wirs ngh >, say, infinily long olag along a cabl can vary! D olag v( E(D W can acually g o his wav bhavior by using circui hory, w/o going ino dails of h EM filds! Thr
Homework #2: CMPT-379 Distributed on Oct 2; due on Oct 16 Anoop Sarkar
 Homwork #2: CMPT-379 Disribud on Oc 2 du on Oc 16 Anoop Sarkar anoop@cs.su.ca Rading or his homwork includs Chp 4 o h Dragon book. I ndd, rr o: hp://ldp.org/howto/lx-yacc-howto.hml Only submi answrs or
Homwork #2: CMPT-379 Disribud on Oc 2 du on Oc 16 Anoop Sarkar anoop@cs.su.ca Rading or his homwork includs Chp 4 o h Dragon book. I ndd, rr o: hp://ldp.org/howto/lx-yacc-howto.hml Only submi answrs or
Modelling of three dimensional liquid steel flow in continuous casting process
 AMME 2003 12h Modlling of hr dimnsional liquid sl flow in coninuous casing procss M. Jani, H. Dyja, G. Banasz, S. Brsi Insiu of Modlling and Auomaion of Plasic Woring Procsss, Faculy of Marial procssing
AMME 2003 12h Modlling of hr dimnsional liquid sl flow in coninuous casing procss M. Jani, H. Dyja, G. Banasz, S. Brsi Insiu of Modlling and Auomaion of Plasic Woring Procsss, Faculy of Marial procssing
REPETITION before the exam PART 2, Transform Methods. Laplace transforms: τ dτ. L1. Derive the formulas : L2. Find the Laplace transform F(s) if.
 Tranform Mhod and Calculu of Svral Variabl H7, p Lcurr: Armin Halilovic KTH, Campu Haning E-mail: armin@dkh, wwwdkh/armin REPETITION bfor h am PART, Tranform Mhod Laplac ranform: L Driv h formula : a L[
Tranform Mhod and Calculu of Svral Variabl H7, p Lcurr: Armin Halilovic KTH, Campu Haning E-mail: armin@dkh, wwwdkh/armin REPETITION bfor h am PART, Tranform Mhod Laplac ranform: L Driv h formula : a L[
Lecture 26: Leapers and Creepers
 Lcur 6: Lapr and Crpr Scrib: Grain Jon (and Marin Z. Bazan) Dparmn of Economic, MIT May, 005 Inroducion Thi lcur conidr h analyi of h non-parabl CTRW in which h diribuion of p iz and im bwn p ar dpndn.
Lcur 6: Lapr and Crpr Scrib: Grain Jon (and Marin Z. Bazan) Dparmn of Economic, MIT May, 005 Inroducion Thi lcur conidr h analyi of h non-parabl CTRW in which h diribuion of p iz and im bwn p ar dpndn.
Fourier Transforms and the Wave Equation. Key Mathematics: More Fourier transform theory, especially as applied to solving the wave equation.
 Lur 7 Fourir Transforms and th Wav Euation Ovrviw and Motivation: W first discuss a fw faturs of th Fourir transform (FT), and thn w solv th initial-valu problm for th wav uation using th Fourir transform
Lur 7 Fourir Transforms and th Wav Euation Ovrviw and Motivation: W first discuss a fw faturs of th Fourir transform (FT), and thn w solv th initial-valu problm for th wav uation using th Fourir transform
Economics 302 (Sec. 001) Intermediate Macroeconomic Theory and Policy (Spring 2011) 4/25/2011. UW Madison
 conomics 302 (Sc. 001) Inrmdia Macroconomic Thory and Policy (Spring 2011) 4/25/2011 Insrucor: Prof. Mnzi Chinn Insrucor: Prof. Mnzi Chinn UW Madison 21 1 Th Mdium Run ε = P * P Thr ar wo ways in which
conomics 302 (Sc. 001) Inrmdia Macroconomic Thory and Policy (Spring 2011) 4/25/2011 Insrucor: Prof. Mnzi Chinn Insrucor: Prof. Mnzi Chinn UW Madison 21 1 Th Mdium Run ε = P * P Thr ar wo ways in which
k (but not necessarily much larger).
 Dolgopolov Sanislav dolgopolov-s@lis.ru Russian Fdraion Sank-rsburg Inracion bwn lcrons as wav packs and suprconduciviy In h work h suprconduciviy is plaind using h rprsnaion of valnc lcrons as packs of
Dolgopolov Sanislav dolgopolov-s@lis.ru Russian Fdraion Sank-rsburg Inracion bwn lcrons as wav packs and suprconduciviy In h work h suprconduciviy is plaind using h rprsnaion of valnc lcrons as packs of
Arturo R. Samana* in collaboration with Carlos Bertulani*, & FranjoKrmpotic(UNLP-Argentina) *Department of Physics Texas A&M University -Commerce 07/
 Comparison of RPA-lik modls in Nurino-Nuclus Nuclus Procsss Aruro R. Samana* in collaboraion wih Carlos Brulani* & FranjoKrmpoicUNLP-Argnina *Dparmn of Physics Txas A&M Univrsiy -Commrc 07/ 0/008 Aomic
Comparison of RPA-lik modls in Nurino-Nuclus Nuclus Procsss Aruro R. Samana* in collaboraion wih Carlos Brulani* & FranjoKrmpoicUNLP-Argnina *Dparmn of Physics Txas A&M Univrsiy -Commrc 07/ 0/008 Aomic
10. The Discrete-Time Fourier Transform (DTFT)
 Th Discrt-Tim Fourir Transform (DTFT Dfinition of th discrt-tim Fourir transform Th Fourir rprsntation of signals plays an important rol in both continuous and discrt signal procssing In this sction w
Th Discrt-Tim Fourir Transform (DTFT Dfinition of th discrt-tim Fourir transform Th Fourir rprsntation of signals plays an important rol in both continuous and discrt signal procssing In this sction w
The Science of Monetary Policy
 Th Scinc of Monary Policy. Inroducion o Topics of Sminar. Rviw: IS-LM, AD-AS wih an applicaion o currn monary policy in Japan 3. Monary Policy Sragy: Inrs Ra Ruls and Inflaion Targing (Svnsson EER) 4.
Th Scinc of Monary Policy. Inroducion o Topics of Sminar. Rviw: IS-LM, AD-AS wih an applicaion o currn monary policy in Japan 3. Monary Policy Sragy: Inrs Ra Ruls and Inflaion Targing (Svnsson EER) 4.
Effects of ion motion on linear Landau damping
 Effcs of ion moion on linar Landau damping Hui Xu 1**, Zhng-Ming Shng 2,3,4, Xiang-Mu Kong 1, Fu-Fang Su 1 1 Shandong Provincial Ky Laboraory of Lasr Polarizaion and Informaion Tchnology, Dparmn of Physics,
Effcs of ion moion on linar Landau damping Hui Xu 1**, Zhng-Ming Shng 2,3,4, Xiang-Mu Kong 1, Fu-Fang Su 1 1 Shandong Provincial Ky Laboraory of Lasr Polarizaion and Informaion Tchnology, Dparmn of Physics,
