Nonlocal gradient-dependent modeling of plasticity with anisotropic hardening
|
|
|
- Lily Booth
- 5 years ago
- Views:
Transcription
1 Louisiana State University LSU Digital Commons LSU Master's Theses Graduate School 2008 Nonlocal gradient-deendent modeling of lasticity with anisotroic hardening Gerald Pekmezi Louisiana State University and Agricultural and Mechanical College Follow this and additional works at: htts://digitalcommons.lsu.edu/gradschool_theses Part of the Civil and Environmental Engineering Commons Recommended Citation Pekmezi, Gerald, "Nonlocal gradient-deendent modeling of lasticity with anisotroic hardening" (2008). LSU Master's Theses htts://digitalcommons.lsu.edu/gradschool_theses/1920 This Thesis is brought to you for free and oen access by the Graduate School at LSU Digital Commons. It has been acceted for inclusion in LSU Master's Theses by an authorized graduate school editor of LSU Digital Commons. For more information, lease contact
2 NONLOCAL GRADIENT-DEPENDENT MODELING OF PLASTICITY WITH ANISOTROPIC HARDENING A Thesis Submitted to the Graduate Faculty of the Louisiana State University and Agricultural and Mechanical College in artial fulfillment of the requirements for the degree of Master of Science In Civil Engineering in The Deartment of Civil Engineering by Gerald Pekmezi B.S., Louisiana State University, 2002 December 2008
3 ACKNOWLEDGMENTS I would like to exress my gratitude and areciation to my advisor, Dr. George Z. Voyiadjis, for his valuable suggestions, helful guidance, and encouragement. I would also like to exress my most sincere gratefulness to my beloved wife, Dr. Dori Pekmezi. Her hard work set a recious examle and her words of encouragement gave me the strength to ress on with my research. Last, but not least, I would like to thank my family for all the sacrifices they ve made over the years. ii
4 TABLE OF CONTENTS Acknowledgements ii Abstract iv 1 Introduction Literature Review Crystallograhic Basis for Use of Strain Gradients in Nonlocal Plasticity 13 4 Thermodynamic Formulation in Local/Classical Plasticity Thermodynamic Formulation in Local Plasticity with Anisotroic Hardening Thermodynamic Formulation with Higher-Order Gradients and Anisotroic Hardening Numerical Alications in Thin Films Conclusions References Aendix: Mathcad File Vita iii
5 ABSTRACT This work is concerned with the formulation of the thermodynamics of nonlocal lasticity using the gradient theory. The formulation is based on the nonlocality energy residual introduced by Eringen and Edelen (1972). Gradients are introduced for those variables associated with isotroic and kinematic hardening. The formulation alies to small strain gradient lasticity and makes use of the evanescent memory model for kinematic hardening. This is accomlished using the kinematic flux evolution as develoed by Zbib and Aifantis (1987). Therefore, the resent theory is a four nonlocal arameter-based theory that accounts for the influence of large variations in the lastic strain, accumulated lastic strain, accumulated lastic strain gradients, and the micromechanical evolution of the kinematic flux. Using the rincile of virtual ower and the laws of thermodynamics, thermodynamically-consistent equations are derived for the nonlocal lastic yield criterion and associated flow rule. The resence of higher-order gradients in the lastic strain is shown to enhance a corresonding history variable which arises from the accumulation of the lastic strain gradients. Furthermore, anisotroy is introduced by lastic strain gradients in the form of kinematic hardening. Plastic strain gradients can be attributed to the net Burgers vector, while gradients in the accumulation of lastic strain are resonsible for the introduction of isotroic hardening. The equilibrium between internal Cauchy stress and the microstresses conjugate to the higherorder gradients frames the yield criterion, which is obtained from the rincile of virtual ower. Microscoic boundary conditions, associated with lastic flow, are introduced to sulement the macroscoic boundary conditions of classical lasticity. The nonlocal formulation develoed here reserves the classical assumtion of local lasticity, wherein iv
6 lastic flow direction is governed by the deviatoric Cauchy stress. The theory is alied to the roblems of thin films on both soft and hard substrates. Numerical solutions are resented for bi-axial tension and simle shear loading of thin films on substrates. v
7 1 INTRODUCTION In the 1850s, the introduction of the Bessemer rocess facilitated construction using a material that until then had been considered too exensive to roduce and use en masse. That material was steel and its availability sarked a structural revolution, whereby grander and grander scale structures became feasible. Since then, material engineering has advanced at an ever increasing ace, and today we have reached the oint where we can engineer materials at scales aroaching the atomic scale. However, in solid mechanics, as in most other branches of hysics, we have found that mathematical models conceived for the visible or macro scale, become increasingly insufficient as we aroach the discrete microstructure of the material. The need has therefore become evident for new models to cature relevant effects in the behavior of the material. The comlexity of such models is key to their adequacy in describing the material behavior. However, the comlexity of the models must also be limited to what is necessary, since increased comlexity leads to increased cost (e.g. comutational cost). One aroach, favored in the resent model, is to maintain the general framework of the macro-scale model (continuum mechanics), but to embed into it micromechanical characteristics which enable the comosite model to describe the observed micro-scale effects. The articular roblem this model aims to address, is the introduction at the continuum lasticity level of the so-called size effect. Exerimental observations reveal that, in many cases, the size of the material secimen and grain size significantly imacts deformation and failure. For examle, it has been observed that, in the bending of thin films, decreasing the thickness of the films roduces a strengthening effect on the film material. Similarly, micro-torsion tests of thin wires exhibit increased strength for smaller 1
8 diameters of the wires. Other effects of a similar nature include increased strength of article-reinforced comosites for decreased article size, and increased hardness for smaller indentation size in micro-indentation tests. These effects are not comatible with the classical aroach of continuum lasticity, where the material behavior is assumed to be the same even if its size is reduced ad infinitum. It seems, therefore, necessary to formulate a coarse model, one that has an embedded length scale to identify that scale where discrete events that occur in the microstructure are relevant to the material behavior in the hysical scale. The aforementioned roblem has been tackled by a number of researchers using a range of models, which can be collectively laced under the umbrella of nonlocal models. A nonlocal model is one where the evolution of a state variable (or tensor) at a articular oint in the material, is deendent not only on the internal state of the oint itself, but also on the state of the neighboring oints. In general, this influence is weighed satially, whereby the magnitude of the influence of a neighboring oint is related to the roximity of the oint. Examles of micro, meso and macro models that deal with the size effect in lasticity include molecular dynamics, discrete dislocation dynamics, and higher-order extension of classical lasticity. The first two tyes involve comletely different hysics than those used in local (classical) lasticity; atoms/molecules/dislocations are modeled individually and their interactions simulated. This means that the models are incaable of modeling materials in hysical scales, as the comutational effort necessary is beyond what is available. By contrast, higher-order models such as the gradient model, maintain the framework of continuum mechanics, but introduce effects from higher order derivatives 2
9 or integrals of constitutive variables. A model that contains higher-order variables is inherently nonlocal, since its constitutive equations result in having one oint in the continuum influence the other. The realization of higher-order modeling is varied. The formulation strategy can be to either heuristically introduce higher-order deendence directly into the constitutive equations, or to derive the constitutive equations by means of suitable energy arguments. The second strategy involves higher-order stresses in addition to higher-order strains, which means that additional boundary conditions are required. The first strategy is easier to imlement, since it does not involve higher-order stresses. The means by which the higher order strains are introduced is either through integral-tye models, exlicit gradient models, or imlicit gradient models which are in essence equivalent to integral-tye models. The exlicit gradient models are essentially weak forms of the integral-tye models and are most suitable for imlementation in numerical comutations. The formulation resented here is based on the nonlocality energy residual introduced by Eringen and Edelen (1972). The model alies to small strain gradient lasticity and makes use of the Armstrong-Frederick-tye model for kinematic hardening roosed by Voyiadjis and Abu Al-Rub (2003). 3
10 2 LITERATURE REVIEW A number of theoretical and numerical models have been roosed to overcome the lack of a length scale in the classical theory of lasticity. These include discrete dislocation dynamics simulations (Nicola et al., 2001, 2003), molecular dynamics simulations (Schiotz et al., 1998), crystal lasticity theories (Voyiadjis and Huang, 1996, Bittencourt et al., 2003), and strain gradient lasticity theories such as the one roosed here. These models have been termed nonlocal models (Nilsson, 1998, Stromberg and Ristinmaa, 1996). The common thread in these models is that a nonlocal quantity is incororated as the average of the corresonding local field quantity weighted satially over an aroriate, finite volume surrounding the oint under consideration. Oftentimes, this nonlocal quantity is resolved through the use of an integral format. In this format the associated intrinsic length scale influences the weight amlitude in roximity to a material oint. Then there are lasticity formulations that make use of a gradient-enhanced model (De Borst and Muhlhaus, 1992). The benefit rovided by these formulations, is that the integral format is avoided by aroximating the nonlocal kernel with a Taylor series exansion. This yields a differential rather than integral, format. The gradient formulation may be considered a higher-order extension of the local lasticity theory. The introduction of strain gradients into the local theory formulations leads to boundary value roblems governed by artial differential equations of higher order with non-standard boundary conditions. There are essentially two strategies for the strain gradient theory formulations: one consists in heuristically introducing the gradient deendence directly into the constitutive equations of the local-tye material. This 4
11 framework of strain gradient lasticity theories does not involve the higher-order stress, and requires no additional boundary conditions. The lastic strain gradient (or inverse elastic strain gradient) comes into lay through the incremental lastic modulus. Examles in this class include the works by (Acharya, 2000, Acharya and Beaudoin, 2000, Acharya, et al., 2004, Dai and Parks, 1997)). In the aforementioned works, strain gradient hardening is assumed to be accounted for but not the work erformed by the strain gradients in the material interior. It was concluded that the only ossible formulation is a flow theory with strain gradient effects reresented as an internal variable which acts to increase the current tangent hardening modulus. These theories are straightforward to imlement in standard Finite Element (FE) codes. This articular aroach was used in redicting olycrystal size effect and cleavage/orientation deendence in the fracture of ductile single crystals. However, criticism has been directed on the model s caability due to the nonstandard boundary conditions (Niordson and Hutchinson, 2003, Volokh and Hutchinson, 2002) and the lack of systematic construction of the tangent modulus (Gao, et al., 1999). In another class of strain gradient theory, formulations are derived by means of suitable energy arguments. A classical examle of this strategy is the second strain gradient elasticity theory by Mindlin (1964) in which the higher order stresses are defined as the work conjugate of strain gradient by imlying the virtual work rincile and a strain energy otential incororating the strain gradients. Along with the standard equilibrium equations, higher order nonlocal micro force balance equations are retrieved from the variational formulation of the virtual work rincile. This additional equation requires the extra boundary conditions. Examles in this class include the works of Fleck 5
12 and Hutchinson (1997), Fleck and Hutchinson (2001) and Fleck, et al. (1994) where exerimentally observed size effects have been modeled successfully. From a dimensional, consideration of an internal constitutive length arameter was introduced to scale the rotational gradient terms in the coule stress theory of the strain gradient lasticity. The hysical basis of the length scale is connected to the storage of geometrically necessary dislocations (Ashby, 1970, Nye, 1953). They found in the twisting of thin coer wires that the scaled shear strength increases by a factor of three as the wire diameter decreases from 170 to 20 microns, while the increase of work hardening in simle tension is negligible. Chen and Wang (2002) roosed the so-called new strain gradient theory, based on the general concet of coule stress theory. They imlemented their new formulation to solve thin metallic wires in torsion and ultra thin metallic beam bending roblems. It was concluded that if the boundary conditions are roerly taken in their new theory, the results of the solution will redict the exerimental findings rovided by Fleck et al. (1994) and Stolken and Evans (1998). Xiang et al.(2006) used Fleck et al. (1994) strain gradient theory in order to cature the Bauschinger effect that is observed in the exerimental investigations on Cu thin films with a assivation layer. From these exeriments they found that thin films yield strength increased significantly with decreasing film thickness if one or both surfaces are assivated. By contrast, unassivated thin films are relatively indeendent of film thickness and yield strength increases mainly as a result of grain size strengthening. Gao et al.(1999), and Huang et al. (2000) roosed a Taylor based nonlocal theory of lasticity to account for the size deendency of the lastic deformation at the micron and 6
13 submicron scales. The length scale is related to the density of the geometrically necessary dislocations as introduced into the constitutive equations via the nonlocal variables which are exressed as an integral of local variables over all material oints in the body. Gao and Huang (2001), Zhang et al. (2007), and Shi et al. (2008) alied this theory to microbending, micro tension, void growth, cavitations instabilities and article reinforced comosites. Their analyses results in identical redictions as in the mechanism-based strain gradient (MSG) lasticity. This higher order strain gradient theory is established from a multiscale, hierarchical framework to connect with the Taylor model in dislocation mechanics (Taylor, 1934, 1938). Results obtained using the MSG model agrees well with the work of McElhaney et al. (1998) on micro-indentation exeriments of bulk coer, Gao et al. (1999) and Saha et al. (2001) on indentation exeriments of aluminum thin film on a glass substrate, Fleck et al. (1994) on micro-torsion, Stolken and Evans (1998) on micro-bending exeriments (see Gao, et al., 1999), and on metalmatrix comosites (Xue, et al., 2002). It has also been successfully alied to study a few imortant roblems at the micron and submicron scales, including microelectromechanical systems (Saha, et al., 2001), lastic flow localization (Shi, et al., 2000), and fracture (Jiang, 2001, Lu, et al., 2000). Shi and Gao (2001) recently used the singular erturbation method to investigate a solid subjected to a constant body force, and showed that the effect of the higher-order stresses is significant only within a thin layer near the boundary of the material. Comaring the material length scale used in strain gradient theories, the thickness of the boundary layer is much smaller and is on the order of 10 nm., These results are interreted by Huang et al. (2000) and Saha et al. (2001) as the higher-order stress has 7
14 little or essentially no effect on material roerties that reresent an average over the micron scale and above, such as the micro-indentation hardness. Therefore, they distinguished the effect of higher-order stress from the strain gradient effect by defining the former is within a thin boundary layer (thickness on the order of 10 nm) and the latter comes from the Taylor dislocation model and is imortant at the micron scale. As art of this searation they concluded that the effect of higher-order stress is negligible away from the thin boundary layer, and argued the ossibility to develo a strain gradient lasticity theory based on the dislocation model to incororate the strain gradient effects without the higher-order stress. The reason to eliminate the effect of higher order stress from the governing equations in such a theory is to avoid from the additional boundary conditions and to have essentially the same boundary conditions as in the conventional lasticity theories. Gurtin (2004) develoed a gradient theory of small deformation viscolasticity based on the system of micro forces consistent with its eculiar balance, a mechanical version of the second law and a constitutive theory that includes Burgers vector through a free energy deendence on where reresents the lastic art of the elastic lastic decomosition of the dislacement gradient. Later Anand et al. (2005) studied the one dimensional theory of the strain gradient lasticity by erforming analytical and numerical analyses by means of nonlocal finite element on three distinct hysical henomena such as internal variable hardening, energetic hardening with back stress associated with lastic strain gradient and dissiative strengthening associated with lastic strain rate and resulting in a size deendent increase in yield strength. 8
15 The Dislocation Dynamics (DD) and the molecular dynamics simulations are the alternative aroaches to study small scale henomena (Benzerga and Shaver, 2006, Devincre, et al., 1997, Nicola, et al., 2003, Shu, et al., 2001, Zbib, et al., 2002). Shizawa and Zbib (1999) develoed a thermodynamic theory of gradient elastolasticity by introducing microstress which is conjugate to the dislocation density tensor. One of the drawbacks of these theories is that an additional set of arameters is required in order to secify the fundamental behavior of a single dislocation and the generation of new dislocations along with their interactions. Shen and Wang (2003) for 2D and Schiotz (2004) for 3D studied the influence of boundaries on dislocations from a continuum oint of view. However, there are certain vital considerations that need to be addressed on the molecular dynamics simulations in the sense of the choice of the interatomic otential. The most commonly used otentials are emirical or semi-emirical. Furthermore there are limitations concerning dimensions as well as time. For instance, due to comutational costs the simulations are limited to very short time intervals and high strain rates in order to reach interesting strain levels (Wolf et al., 2005, Lidorikis et al., 2001, Nakano et al., 2001). Gudmundson (2004) formulated the small strain gradient lasticity for isotroic materials based on the balance law and dissiation inequality. He addressed boundary conditions and concluded that there is a close connection between surface energy of an interface and boundary conditions in terms of lastic strain and moment stress. A simle version of the theory was alied to a few examles such as biaxial loading of a thin film on thick substrate, torsion of thin wire and sherical void under remote hydrostatic tension in order to investigate the effect of varying length scales. This formulation is later 9
16 used to analyze the size deendent yield strength of thin films by Fredriksson and Gudmundson (2005). The results of their numerical analysis from these studies reveals that boundary layer is develoed in the thin film for both biaxial and shear loading giving rise to size effects. These size effects are strongly connected to the buildu of surface energy at the interface. These effects of interface surface energy on the lastic deformation at the micron scale were motivated by Fredriksson and Gudmundson (2007) in order to conduct a detailed study on modeling of the interface between a thin film and a substrate. They addressed this issue within the framework of strain gradient lasticity and roosed two kinds of interface models for isotroic materials. Fist kind is based on the assumtion that lastic work at the interface is comletely stored as a surface energy and no dissiation occurred due to lasticity at the interface. In the second tye it is assumed that the lastic work is comletely dissiated and there is no build u of a surface energy. Two tyes of length scales are introduced one is for the behavior of the bulk material the other one is for the interface. Their model can be considered in the same class of the existing interface models roosed by Cermelli and Gurtin (2002), Gurtin and Needleman (2005), Sun et al. (2000), Gurtin (2008), and Borg and Fleck (2007). Gurtin and Needleman (2005) and Cermelli and Gurtin (2002) addressed in their work the alication of strain gradient lasticity for the case of crystal lasticity. In the case of Gurtin and Needleman (2005) they assumed continuity of the conjugate higher-order stresses on both sides of the interface. However, Cermelli and Gurtin (2002) assumed a jum at the interface of the conjugate higher order stresses. Both Gurtin and Needleman (2005) and Cermelli and Gurtin (2002) used dissiative mechanisms to model the interface (grain boundaries) 10
17 using a viscolastic model that involved lastic sli rates at both sides of the interface as well as conjugate higher order stresses on both sides of the interface. In both cases they included discontinuities in lastic strains over the interface. Willis and co-workers (Aifantis, et al., 2006, Aifantis and Willis, 2005, 2006) modeled the interface by a surface contribution to the strain energy that deends on the lastic strain at the interface. The distinct feature of this formulation is to introduce an interfacial yield stress that allows the interface to follow its own yield behavior. This interfacial yield stress is then described via dislocation transfer henomena where its hysical justification is made from observations of the nanoindentation near grain boundaries of body-centered cubic (bcc) metals. The main distinction of the work of Willis and co-workers from that of Gurtin and coworkers is that Willis and co-workers assumed a continuity in the lastic strain over the interface with a jum in the conjugate higher-order stresses. Abu Al-Rub (2008) investigated the interfacial effect in arallel to the work of Willis and coworkers by using the higher order gradient deendent lasticity theory (Abu Al- Rub, et al., 2007, Voyiadjis and Abu Al-Rub, 2007) where microstress boundary conditions at the interface and free surfaces are enforced. In these works (Voyiadjis and Abu Al-Rub, 2007; Abu Al-Rub, 2008) they assumed that the total strain energy stored at the interface can be exressed in terms of the global nonlocality residual (Borino and Polizzotto, 1999, Borino and Polizzotto, 2003, Polizzotto, 2007, Polizzotto, et al., 2004). Gudmundson (2004) resented a quite general discussion on the formulation of interface conditions within a strain gradient theory. He assumed discontinuity of both lastic strains and conjugate moment stresses over the interface. Fredriksson and 11
18 Gudmundson (2007) further discussed the distinctions among the above mentioned the interface models by resenting a mechanical analogy for the interface model. 12
19 3 CRYSTALLOGRAPHIC BASIS FOR USE OF HIGHER-ORDER GRADIENTS IN NONLOCAL PLASTICITY As aforementioned, the imetus for the current research is rovided by exerimental results in the emerging areas of micro- and nanotechnology. These results exhibit distinct size deendence in the behavior of materials at the micron and submicron level. Secifically, strength differences have been observed to arise from continuous modification of the microstructural characteristics with changing size, whereby the smaller the size the higher the material strength aears to be. In order to construct a mathematical formulation that roerly models the observed effects, it is necessary to understand the behavior of the material at the most basic level that is relevant to lastic deformation. In this section, we review the hysical mechanism by which lastic deformation occurs. Physically, a dislocation is a crystallograhic defect or irregularity in the crystal structure. Mathematically, the dislocation is a toological defect or a soliton. The mathematical descrition imlies that dislocations behave as stable articles; they can move, grow and annihilate each other. At the microscoic level, lastic deformation in metallic materials is the end result of the collective behavior of a vast number of dislocations. Hence, crystallograhic dislocation densities are aroriate metrics of lastic deformation in metals. These densities can be defined by their magnitude ρ and are tyically measured in line length er unit volume. Plastic strain is directly related to the motion of dislocations. Meanwhile, hardening in metals is attributed to the interaction among dislocations and the interaction with the crystal microstructure nearby. These henomena are driven by dislocation multilication mechanisms: cross-sli and double cross-sli, glide, climb etc. Dislocations can also form 13
20 loos, aggregate at grain boundaries, and arrange themselves into varied tyes of substructures commonly called dislocation networks. These networks in turn constitute obstacles to the motion of other dislocations. This effect rovides the mechanism by which hardening occurs. It may therefore be said that the ease with which dislocation are able to move, determines the degree of hardening in the material. Hence, there are two tyes of dislocations which should be distinguished by even the simlest dislocation model: mobile and immobile dislocations. These basic tyes of dislocations corresond to the basic mechanics of lastic deformation, whereby lastic strain is carried by the motion of mobile dislocations, while lastic hardening is related to the resistance from immobile dislocations. As immobile dislocations accumulate, the mobile dislocations interact to an increasing degree with immobile dislocations and movement becomes more difficult. Consequently the threshold of stress required to roduce additional lastic strain is continuously raised. This may be recognized as the very effect that has been named hardening of a material. That critical shear stress which is required to untangle the interacting dislocations and to induce a significant lastic deformation, is defined as the Taylor flow stress τ (Taylor, 1938). The Taylor flow stress may also be viewed as the assing stress for a mobile dislocation to glide through a forest of immobile dislocation without being traed or inned. The related hardening law, the Taylor hardening law relates the shear strength to the dislocation density, and reresents the genesis and basis of the so-called mechanism-based strain gradient (MSG) lasticity theory (Nix and Gao, 1998; Gao et al., 1999a; Huang et al., 2000a; Hwang et al., 2002; Qiu et al., 2003; Hwang et al., 2003; Huang et al., 2004) as well as the Taylor-based nonlocal theory (TNT) of lasticity (Gao 14
21 and Huang, 2001; Guo et al., 2001). The hardening law rovides a simle descrition of the dislocation interaction rocess at the microscale. One form of Taylor s hardening law which is generally acceted in literature is τ = τ + αgb ρ (1) 0 i where ρ i is the immobile forest dislocation density, G is the shear modulus, b is the magnitude of the Burgers vector, and α is a material constant related to the crystal and grain structure and tyically ranging from 0.1 to 0.5 (Ashby, 1970). Meanwhile, τ 0 reresents the stress extraolated to a dislocation density of zero. The immobile or forest dislocation density is generally assumed to reresent the total couling between two tyes of dislocations that lay significant roles in the hardening mechanism. Deformation in metals enhances the formation, motion, and storage of dislocations. Storage of dislocations in turn is the cause of hardening in the material. Stored dislocations which are generated by traing each other in a random way are commonly referred to as statistically stored dislocations (SSDs), while stored dislocations that maintain the lastic deformation incomatibilities within the olycrystal caused by nonuniform dislocation sli are called geometrically necessary dislocations (GNDs). The resence of GNDs causes additional storage of defects and increases the resistance to deformation by acting as an obstacle to the SSDs (Ashby, 1970). 15
22 Statistically Stored Dislocations Geometrically Necessary Dislocations Square Lattice in Pure Shear (Homogenous Plastic Strain) Square Lattice in Pure Bending (Non-homogenous Plastic Strain) Figure 1: Illustration of SSDs and GNDs Figure 2: Transmission Electron Micrograhs Showing Dislocations (URL: TEM) 16
23 4 THERMODYNAMIC FORMULATION OF LOCAL/CLASSICAL PLASTICITY In order to formulate a continuum-based lasticity model, it is necessary to satisfy the axioms of equilibrium and thermodynamics. Herein is resented the rincile of virtual ower and the fundamental statements of irreversible thermodynamics that are used commonly in the mathematical modeling of the thermo-mechanical behavior of the material. Henceforth, is the Euclidean norm of second rank tensors, (:) stands for tensor contraction, the suerimosed dot () indicates the differentiation with resect to time t, and a comma followed by an index j (e.g. x i, j) denotes differentiation with resect to x i. The first-order gradient, divergence, curl, and Lalacian of a tensor field A are defined by (div A ) i = A, j, (curl A ) = e iq A jq,, A, and ( A) k = A, k, 2 ( ) = A, kk resectively. Princile of Virtual Power The rincile of virtual ower may be defined as the assertion that, given any subbody Γ, the virtual ower exended on Γ by exterior materials of bodies (i.e. external ower) must be identical to the virtual ower exended within Γ (i.e. internal ower). It may be stated that the rincile of virtual ower is the cornerstone of the Finite Element Method. Let n denote the outward unit normal of Γ. The exenditure of external ower is assumed to arise from a macroscoic surface traction t, a macroscoic body force b, and inertia forces whose virtual work is associated with the macroscoic motion of the body. This motion is defined by the virtual velocity vector v. The external ower may therefore be written in the following form: 17
24 (2) Pext = bv i idv + tv i ida ρvv i idv Γ Γ Γ where ρ is the mass density and v is the acceleration vector. The external ower is balanced by an internal exenditure of ower. The internal exenditure of ower is characterized by an elastic stress σ defined over Γ for all time, the back-stress X associated with kinematic hardening, and the drag-stress R associated with isotroic hardening. The internal ower is assumed to have the following form e ( σε ε ) Pint = + X + R dv (3) Γ and is also assumed to balance external ower P ext such that P ext = P (4) int strain The energetic balance is better characterized by a deendence of P int on the lastic ε rather than on the (scalar) accumulation of the lastic strain (internal history variable), since a deendence of P int on deendence of P int on gives rise to isotroic hardening. ε gives rise to kinematic hardening; while a The second-order tensor σ introduced above will be shown to be the symmetric Cauchy stress tensor. Meanwhile, the second-order tensor, ε, is the rate of deformation which is defined by the symmetric art of the velocity gradient v i, j ( v, v, ) ε = + (5) 1 2 i j j i The classical theory of small deformation isotroic lasticity is based on the additive decomosition of the total strain rate into elastic and lastic arts, with e ε being the elastic comonent and ε being the corresonding lastic comonent such that: 18
25 ε = ε + ε, ε = 0 (6) e kk where the suerscrits e and denote the elastic and lastic arts, resectively. The second term in Eq. (3) reresents the internal ower associated with the back-stress X, which is attributed to kinematic hardening. The kinematic variable used most commonly in classical nonlocal lasticity is the lastic strain itself ( ε ). An examle of this is Prager s hardening model, which is a linear kinematic hardening model. A more general flux tensor associated with back-stress, the Frederick-Armstrong evanescent memory kinematic flux, will be used in the following section and in the higher-order nonlocal formulation. The third term in Eq. (3) reresents the internal ower associated with the drag-stress R which causes isotroic hardening. The variable is defined as the accumulated or effective lastic strain and its rate is defined by the exression = ε = ε ε (7) Furthermore, the unit direction of the lastic strain may be defined as N = ε ε ε = (8) In this way one may write N ε = N N = 1 N = 1 N ε = ε = N (9) with the last exression corresonding to the definition of the flow rule in classical lasticity theory. If the axiom of equilibrium of the rincile of virtual ower is alied to the region Γ, Eq.(4), the following equilibrium equation is obtained 19
26 e i i + i i ρ i i = ( σ ε+ ε+ ) bvdv tvda vv dv X R dv (10) Γ Γ Γ Γ Substituting both Eq. (9) 3 and Eq. (6) 1 e ε = ε ε into the above exression yields + = ( ) bvd d d i i V tv i i A ρvv i i V σε τ X RN ε dv (11) Γ Γ Γ Γ where, due to lastic incomressibility, it can easily be roven that σ : ε = τ: ε where τ = σ σ δ is the deviatoric comonent of the Cauchy stress tensor, σ. By 1 3 kk alying the divergence theorem (also known as Gauss theorem or integration by arts), the following exression may be derived = = ( ), j σεdv σv dv σv dv σ vdv i, j i, j i Γ Γ Γ Γ = σ nvda Γ σ j i, j i Γ vdv (12) and Eq. (11)may be rewritten as ( ) ( ) ( ) (13) σ, j + bi ρvi vdv i + ti σnj vda i + τ X RN ε dv = 0 Γ Γ Γ Γ, v, and σ, j i i ε may be arbitrarily secified if and only if + b = ρv (macro-force balance) (14) t = σ n (macro-traction condition) (15) i j and τ X RN = 0 (micro-force balance) (16) In the first of these three equations, the local static or dynamic equilibrium or the macro-force balance is exressed according to the notion of Gurtin (2003). In the second one the stress vector is defined as the surface density of the forces introduced. It is shown that σ is really the Cauchy stress tensor, which is a second-order symmetric tensor. It 20
27 also rovides the local macro-traction boundary conditions on forces if the axiom of equilibrium of virtual ower is alied to the whole region under consideration as oosed to arbitrarily sub-regions. Local Yield Criterion Meanwhile the third of the equations above, Eq.(16), reresents the micro-force balance. It can easily be shown that this micro-force balance is nothing more than the yield criterion of classical lasticity theory. Substituting Eq. (8) into Eq. (16), one can write the following exression for the flow rule, Eq. (9) 4 : N τ X = R τ X = (17) ε R Furthermore, by taking the Euclidean norm of Eq. (16) one can write τ X N R = 0 (18) However, since N = 1 and R = R, the following exression can be written τ X R= 0 (19) This equation constitutes the von-mises yield criterion of local lasticity. Therefore, the micro-force balance, Eq. (18), may be set as the yield criterion or the lasticity loading surface f f = τ X R= 0 (20) such that the flow rule in Eq. (17) can also be exressed by τ X ε = (21) τ mn X mn 21
28 Comaring Eq. (21) with Eq. (8), it is ossible to reformulate the direction of the lastic flow as N = τ X τ mn X mn (22) It is obvious that Eq. (20) reresents a shere in deviatoric stress-sace of radius R centered at X. The radius R reresents isotroic hardening while the backstress X reresents kinematic hardening. Furthermore, the flow rule in Eq. (21) dictates that the flow direction N in Eq. (22) is normal to the yield surface and directed outward from the yield surface. Remark: The micro-force balance from the rincial of virtual ower reresents the yield criterion or the yield function in the theory of lasticity. Local Clausius-Duhem Inequality Using the conclusion above, it can easily be roved that the internal virtual ower in Eq.(3), after substituting Eqs. (6) 1, (9) 3, and (16), can be rewritten as P int = σε dv (23) Γ This exression coincides with the classical definition by Green and Naghdi (1971). The macro-force balance equation, Eq. (14), can be interreted as a form of the law of conservation of momentum. By integrating it over Γ and alying the divergence theorem along with Eq. (15), the global mechanical conservation law is obtained as d tida+ bidv = ρvidv dt (24) Γ Γ Γ with d dt denoting the material derivative. 22
29 Similarly, the symmetry of the Cauchy stress tensor, σ = σ ji, which results directly from the rincile of virtual ower, can be considered to be a consequence of the equation of momentum balance equation. Furthermore, the conservation of mass law can be obtained as d ρdv = 0 dt (25) Γ The main consideration here is a urely mechanical theory (isothermal conditions are assumed) based on the requirement that the rate of change in the total free energy should be less than or equal to the work of external forces (Gurtin, 2002). If the secific free energy is denoted as ρψ, this requirement takes the form of a free energy inequality Γ i ρψdv P ext (26) From Eq. (25) it is ossible to write ρψ dv = ρψ dv Γ i Γ. Furthermore, substituting the virtual work balance equation, Eq. (4), into Eq. (26) along with the new form of the internal ower resented in Eq.(23), one can write the following thermodynamic restriction σε ρψ 0 (27) The reader will recognize this as the classical (local) Clausius-Duhem inequality. The degree of recision with which material lasticity can be described is deendent uon the choice of the nature and the number of state variables. The rocesses of lasticity will be admissible if, at any instant of the evolution, the Clausius-Duhem inequality is satisfied. The state variables, also called thermodynamic or indeendent 23
30 variables, are the observable and the internal variables. The articular state variables to use are chosen based on the alication and urose of the model. Local State Variables Hardening in lasticity is introduced by hidden indeendent internal state variables in the thermodynamic state otential. The Helmholtz free secific energy can be considered as the thermodynamic state otential which deends on both observable and internal state variables. In order to define the Helmholtz free secific energy, it is necessary to choose the nature of the state variables. The choice made here is a classical form of this otential in terms of the elastic strain, ε e, and n int - of henomenological dissiative internal state variables ( ℵ, k k = 1,..., nint int ; n 1): Ψ=Ψ ( ε e, ℵ k ) (28) In order to incororate the lasticity isotroic and kinematic hardening effects, a finite set of internal state variables ℵ ( k = 1,..., n ) reresenting either scalars or k int tensorial variables are assumed such that ℵ =ℵ ( ε, ) k k (29) where ε and are internal variables characterize the kinematic and isotroic and hardening flux variables in classical lasticity, resectively. Moreover, the free energy in Eq. (28) is assumed to have the following decouled form ( ε ) (, ) e e Ψ=Ψ +Ψ ε (30) where e Ψ is the elastic energy and Ψ is the lastic energy. This assumtion classifies the material as a searable material (Gurtin, 2003) whereby there is no interaction between the stretching of the material structure as characterized by the elastic strain ε e 24
31 and the evolution and interaction of dislocations and other defects as characterized by and. The time derivative of Eq. (28) with resect to its internal state variables in Eq. (29) is given by the exression: ε e e Ψ ε e Ψ e ε Ψ Ψ e e N ε ε ε ε Ψ Ψ Ψ= + + = + + ε ε (31) where Eq. (8) is used. Substitution of Eq. (31) into the Clausius-Duhem inequality, Eq. (27), yields the following exression: e Ψ e Ψ Ψ σ ρ ε + τ ρ ρ N ε 0 (32) e ε ε A classical hyothesis ermits the cancellation of some terms in this inequality indeendently from which the following thermodynamic state laws are obtained = Ψ e σ ρ e ε (33) J Ψ Ψ = τ ρ ρ ε N (34) Local Plastic Flow Rule By substituting the thermodynamic state laws, Eqs. (33) and (34), back into the Clausius-Duhem inequality, Eq. (32), one obtains Π= J ε 0 (35) where Π is the dissiation energy er unit volume. Substituting the exression for ε from Eq. (9) 4 into Eq. (35) and defining γ = JN 0 (36) 25
32 yields the following Π= γ 0 (37) where γ =Π > 0 for > 0 can be interreted as the dissiation modulus (Gurtin, 2003). Further, one obtains γ = 0 for = 0. Equating Eqs. (35) and (37) yields γ J ε JN = γ = γ = J N γ = J (38) Thus one can write the lastic flow direction N from Eq. (38) 4 and Eq. (36) as N J = (39) J Therefore from Eqs. (39), (38), and (34) one can write the flow direction as Ψ τ ρ ε N = Ψ γ + ρ (40) Comaring Eqs. (39) and (22), one can write J = τ X J = τ X (41) Equating Eqs. (41) 1 and (34), or equivalently comaring Eqs. (40) and (17) 1, yields the following exression for the back-stress X Ψ X = ρ ε (42) Moreover, comaring Eqs. (41) 2, (38), and (20) 1 gives the micro-force R as R = γ + ρ Ψ (43) From the above equation it aears that the isotroic hardening/softening function R is the sum of a dissiative term γ > 0 and an energetic term ρ Ψ. The conjugate 26
33 force R has a hardening or softening effect as ρ Ψ > 0 or < 0, resectively. A direct consequence of the above formalism is that the yield function in Eq. (20) can be derived from the rincile of virtual ower. This yield surface is sherical in the deviatoric stress sace of radius R and centered at the back-stress X. Moreover, the direction of the lastic flow N is normal to the yield surface and directed outward. The Princile of Maximum Dissiation The maximum dissiation rincile (also rincile of maximum entroy roduction) states that the hysical state of the thermodynamic forces is the one that maximizes the dissiation function over all other ossible admissible states. This rincile is a central illar of the mathematical formulation of lasticity (Duvat and Lions, 1972). From the revious discussion it can be observed that the thermodynamic otential Ψ allows one to write relations between internal variables and the corresonding conjugate forces. However, in order to describe the dissiation rocess the evolution of the internal variables is needed, which can be obtained through the use of the generalized normality rule of thermodynamics which is a consequence of the maximum dissiation rincile. In this regard the evolution laws for the lastic strain rate, ε, and the rate of the isotroic hardening flux,, can be obtained by utilizing the calculus of function of several variables with the Lagrange multilier, λ, and subjected to a constrain f = 0 from Eq. (20). Formulating this rincile, the objective function Ω can be constructed in the following form: Ω= Π+ λ f (44) In order to obtain ε and, the following conditions are used to maximize the objective function, Ω, resectively: 27
34 Ω = J 0 Ω Ω = 0, = 0 σ X Ω, = 0 R (45) By Substituting Eq. (35) into the above relations along with Eq. (34) and Eqs. (42) and (43), the corresonding flow rules of ε and are obtained, resectively, as follows: ε f = λ J f ε = λ, σ f ε = λ, X f = λ = λ (46) R where λ is the lastic multilier which can be determined from the Kuhn-Tucker loading/unloading conditions f 0, λ 0, λ f = 0 and λ f = 0 (47) It can be noted that the whole roblem of modeling the lasticity henomenon lies in the determination of the analytical exressions for the Helmholtz free energy function Ψ and its identification from exeriments. 28
35 5 THERMODYNAMIC FORMULATION IN LOCAL PLASTICITY WITH ANISOTROPIC HARDENING Kinematic Flux Exression Zbib and Aifantis (1988) indicated that the lastic sin is a consequence of standard kinematic arguments in conjunction with the constitutive equation for the rate of lastic deformation ε. Aifantis (1984) and Zbib and Aifantis (1988) used the single sli theory and showed that the evolution equation for the back stress flux α is given by t t t t α ( m n m ) ( n = ) γ t γ ε + t α n n (48) where t and m t n are scalar functions of γ, and γ is the rate of shearing of the sli system. Based on the growth law in Eq. (48), several evolution equations for the back stress were derived by Zbib and Aifantis (1988). The first tye is obtained by setting 1 tn = = cons tan t (49) ζ Equation (48) along with Equation (49) lead to the well-known Prager kinematic hardening rule. The corresonding lastic sin in this case is obtained from Eq. (48) by using the constant value of l in Eq. (49). A second tye of evolution is obtained from Equation (48) by assuming 1 c t n n = e γ (50) ζ t n k 1 c e n γ = (51) c ζ n 0 where c and k are constants. These equations will lead to the Armstrong-Frederick evanescent memory kinematic hardening evolution equation for the backstress 29
36 (52) α = kε cα In this case the resulting equation for the lastic sin contains an exonential term as follows: W cn = ζ e ( αε ε α) (53) Exression (49), which is used in conjunction with Eq. (6) may be further generalized such that it may be used with the more general exression (5) for the lastic sin tensor. Princile of Virtual Power The external ower is written as before (54) Pext = bv i idv + tv i ida ρvv i idv Γ Γ Γ where, again, ρ is the mass density and v is the acceleration vector. The external ower is balanced by the internal exenditure of ower. The internal exenditure of ower is characterized by the elastic stress σ defined over Γ for all time, the back-stress X associated with kinematic hardening, and the drag-stress R associated with isotroic hardening. The internal ower is now assumed to have the following form e ( σε α ) Pint = + X + R dv (55) Γ where the kinematic flux α is defined by the exression from Equation (52), that is. Internal ower is balanced by external ower P ext such that α = kε cα P ext = P (56) int As before, the rate of deformation is defined by ( v, v, ) ε = + (57) 1 2 i j j i 30
37 Also the additive decomosition of the total strain rate into elastic and lastic arts, is assumed, such that: ε = ε + ε, ε = 0 (58) e kk The more general flux tensor used here, the Frederick-Armstrong evanescent memory kinematic flux, introduces anisotroy to the hardening formulation. The rate of the accumulated lastic strain is still defined using lastic strain = ε = ε ε (59) also the unit direction of the lastic strain is defined as N = ε ε ε = (60) So that one may still write N ε = N N = 1 N = 1 N ε = ε = N (61) The axiom of equilibrium of the rincile of virtual ower is alied to the region Γ, Eq. (56), and the equilibrium equation becomes e + = ( + + i i i i i i ) bvdv tvda ρvvdv σ ε X α R dv (62) Γ Γ Γ Γ Substituting both Eq. (61) 3 and from Eq. (58) 1 e ε = ε ε into the above exression yields bvdv + tvda ρvv dv = i i i i i i Γ Γ Γ Γ { σε τ ( α ) ε } mn mn kx R cx N dv (63) 31
38 where, due to lastic incomressibility σ : ε = τ: ε with τ = σ σ δ is the 1 3 kk deviatoric comonent of the Cauchy stress tensor, σ. Alying the divergence theorem, the following exression is derived = = ( ), j σεdv σv dv σv dv σ vdv i, j i, j i Γ Γ Γ Γ = σ nvda Γ σ j i, j i Γ vdv (64) and Eq. (63) may be rewritten as ( σ, + ρ ) + ( σ ) Γ b v vdv t n vda j i i i i j i Γ ( ) + τ kx R cx mnαmn N ε dv = 0 Γ (65) Γ, v, and σ, j i i ε may be arbitrarily secified if and only if + b = ρv (macro-force balance) (66) t = σ n (macro-traction condition) (67) i j and τ kx RN + cx α N =0 (micro-force balance) (68) mn mn Local Yield Criterion Once again, the micro-force balance can be shown to be nothing more than the yield criterion of classical lasticity theory. Substituting Eq. (60) into Eq. (68), it is ossible to write the following exression for the flow rule, Eq. (61) 4 : N = τ kx R cx mn α mn ε = τ kx R cx α mn mn (69) Taking the Euclidean norm of Eq. (68) one can write τ kx R cx α N =0 (70) mn mn 32
39 And, since N = 1 and R = R, the von-mises yield criterion can be written τ kx mr =0 (71) Therefore, the micro-force balance, Eq. (70), may be set as the yield criterion or the lasticity loading surface f f = τ kx mr=0 (72) such that the flow rule in Eq. (69) can also be exressed by ε = τ kx τ mn kx mn (73) Comaring Eq. (73) with Eq. (60), it is ossible to reformulate the direction of the lastic flow as N = τ kx τ mn kx mn (74) It is obvious that Eq. (72) reresents a shere in deviatoric stress-sace of radius R centered at kx. The radius mr reresents isotroic hardening while the backstress kx reresents kinematic hardening. Furthermore, the flow rule in Eq. (73) dictates that the flow direction N in Eq. (74) is normal to the yield surface and directed outward from the yield surface. Clausius-Duhem Inequality The internal virtual ower in Eq.(55), after substituting Eqs. (58) 1, (61) 3, and (68), is rewritten as P int = σε dv (75) Γ 33
40 Integrating the macro-force balance equation, Eq. (66) over Γ and alying the divergence theorem along with Eq. (67) d tida+ bidv = ρvidv dt (76) Γ Γ Γ The conservation of mass law is obtained as d ρdv = 0 dt (77) Γ The rate of change in the total free energy should be less than or equal to the work of external forces (Gurtin, 2002). The secific free energy is denoted as ρψ so that the free energy inequality is written as Γ i ρψdv P ext (78) From Eq. (77) it is ossible to write ρψ dv = ρψ dv Γ i Γ. Substituting the virtual work balance equation, Eq. (56), into Eq. (78) along with the new form of the internal ower resented in Eq. (75), one can write the following thermodynamic restriction σε ρψ 0 (79) Local State Variables As before, the choice with regard to the Helmholtz free energy is a classical form of the thermodynamic state otential in terms of the elastic strain, ε e, and n int - of henomenological dissiative internal state variables ( ℵ, k k = 1,..., nint int ; n 1): Ψ=Ψ ( ε e, ℵ k ) (80) 34
41 The lasticity isotroic and kinematic hardening effects are incororated using the finite set of internal state variables ℵ ( k = 1,..., n ) reresenting either scalars or k int tensorial variables as below ℵ =ℵ α, (81) ( ) k k where α characterizes the kinematic hardening flux variable and the hardening flux variable in classical lasticity. Therefore the free energy in Eq. (80) can be assumed to have the following decouled form ( ) (, ) e e Ψ=Ψ ε +Ψ α (82) where, using the searable material characterization, Ψ is the elastic energy and the lastic energy. e Ψ is The time derivative of Eq. (80) with resect to its internal state variables in Eq. (81) is now given by the exression: e e ε e α Ψ Ψ Ψ Ψ= + α + ε Ψ Ψ Ψ Ψ = + + α ε e e ε k e c q N ε α α q (83) where Eq. (60) is used. Substitution of Eq. (83) into the Clausius-Duhem inequality, Eq. (79), yields the following exression: e Ψ Ψ Ψ Ψ e σ ρ ε + τ ρ k + c α 0 α q N α ε e ε q (84) A classical hyothesis ermits the cancellation of some terms in this inequality indeendently from which the following thermodynamic state laws are obtained 35
42 = Ψ e σ ρ e ε (85) Ψ Ψ Ψ J = τ ρ k + c α α q N α (86) q Local Plastic Flow Rule By substituting the thermodynamic state laws, Eqs. (85) and (86), back into the Clausius-Duhem inequality, Eq. (84), the following exression is obtained Π= J ε 0 (87) where Π is the dissiation energy er unit volume. Substituting the exression for ε from Eq. (61) 4 into Eq. (87) and defining γ = JN 0 (88) yields the following Π= γ 0 (89) where γ =Π > 0 for > 0 can be interreted as the dissiation modulus (Gurtin, 2003). Further, one obtains γ = 0 for = 0. Equating Eqs. (87) and (89) yields ε JN γ = J γ = γ = J N γ = J (90) Thus it is ossible to write the lastic flow direction N from Eq. (90) 4 and Eq. (88) as N J = (91) J Therefore from Eqs. (91), (90), and (86) the flow direction may now be written as 36
43 N Ψ τ ρ ε = Ψ Ψ γ + ρ c α q α q (92) Comaring Eqs. (91) and (74), the following exression may be written J = τ kx J = τ kx (93) Equating Eqs. (93) 1 and (86), or comaring Eqs. (92) and (69) 1, yields this new exression for the back-stress X Ψ X = ρ (94) α Furthermore, comarison of Eqs. (93) 2, (90), and (72) 1 yields the new micro-force R as R = γ + ρ Ψ (95) γ ρ Ψ Ψ R= + c m m α q α q (96) From the above equation it aears that the isotroic hardening/softening function R is the sum of a dissiative term γ > 0 and an energetic term ρ Ψ m Ψ c α q α q. The ρ Ψ Ψ conjugate force R has a hardening or softening effect as c α q > 0 m α q or < 0, resectively. As a consequence of the above, the yield function in Eq. (72) may be derived from the rincile of virtual ower. This yield surface is sherical in the deviatoric stress sace of radius mr and centered at the back-stress kx. Additionally, the direction of the 37
44 lastic flow N is normal to the yield surface and outwardly directed. The Princile of Maximum Dissiation Formulating the rincile as before, the objective function Ω can be constructed in the following form: Ω= Π+ λ f (97) In order to obtain function, Ω, resectively: ε and, the following conditions are used to maximize the objective Ω = J 0 Ω Ω = 0, = 0 σ X Ω, = 0 R (98) Substituting Eq. (87) into the above relations along with Eq. (86) and Eqs. (94) and (95), the corresonding flow rules of ε, α, and are obtained, resectively, as follows: ε f = λ J ε f λ σ =, α λ f =, k X f = λ = λ (99) R where λ is the lastic multilier which can be determined from the Kuhn-Tucker loading/unloading conditions f 0, λ 0, λ f = 0 and λ f = 0 (100) The determination of the analytical exressions for the Helmholtz free energy function Ψ and its identification from exeriments is essential to the whole roblem of modeling the lasticity henomenon. 38
45 6 THERMODYNAMIC FORMULATION WITH HIGHER-ORDER GRADIENTS AND ANISOTROPIC HARDENING An attemt is made to account for the effect of non-uniform distribution of microdefects on the homogenized resonse of the material. This is done in order to be able to model small-scale henomena, such as the effect of relative size on the mechanical roerties of the material or the width of localization zones in softening media. The issue that necessitates resolution here is that classical lasticity theory as resented in the revious sections does not osses an intrinsic material length scale. This makes it incaable of redicting small-scale henomena. However, by assuming that the internal energy deends not only on the internal state variables ε and, but also on its satial higher-order gradients ε and, the aforementioned henomena can be catured mathematically. The third-order tensor ( ) = ε, ε introduces kinematic hardening which is k k attributed to the net Burgers vector being not equal to zero at the microscale. The firstorder gradient ( ) =,k introduces isotroic hardening or internal history which is k attributed to the accumulation of the so-called geometrically necessary dislocations. The third order flux gradient tensor ( ), α = introduces anisotroy through kinematic k α k hardening as well as internal history. The lastic strain gradient, ε, is related to the geometrically necessary dislocation density tensor, G, through the following relation (Arsenlis and Parks, 1999): G = e ε (101) irq jq, r 39
46 where e irq is the ermutation tensor. Additionally, the gradient of the effective lastic strain,, can be related to the effective density of geometrically necessary dislocation, ρ G, through the following relation (Ashby, 1970): r ρ G =, k, k (102) b where r is the Nye factor introduced by Arsenlis and Parks (1999) to reflect the scalar measure of GND density resultant from macroscoic lastic strain gradients. For FCC olycrystals, Arsenlis and Parks (1999) reorted a value of r = 1.85 in bending and a value of r = 1.93 in torsion for the Nye factor. Therefore, the resence of higher-order gradients through the lastic strain tensor (i.e. accumulation of lastic strain (i.e. Because of the resence of both lastic strain gradients ε ) leads to higher-order gradients in the ) such that one cannot exist without the other. ε and the total rate of accumulation of the with 2 2 e= +, k, k t e= e dt (103) 0 should also be taken into account in the constitutive descrition since it introduces additional isotroic hardening. In obtaining the equality in Eq. (103) 1, the gradient of the lastic strain direction, N, is neglected. This assumtion is suorted by the lastic deformation localization, whereby the lastic flow direction is almost the same within the localized zone. Moreover, adoting this assumtion greatly simlifies the subsequent derivations. Hence, the generalized rate of total accumulation of the lastic strain and lastic strain gradients can be defined as (e.g. Fleck and Hutchinson, 2001; Gurtin, 2003; Gudmundson, 2004): 40
47 E = ε ε + ε ε (104) 2 2, k, k where is the material length scale arameter and E = E dt is the nonlocal effective 0 t lastic strain, intended to measure the total dislocation density. It must be noted that the hysical justification of Eq. (104) is that E rovides an overall scalar measure of the density of dislocations, with giving a measure of statistically stored dislocation density and e roviding a measure of the geometrically necessary dislocation density. If lastic strain gradients are absent, E can be reduced to the local effective lastic strain. It follows that for a comlete constitutive descrition at small length scales, the internal ower and the Helmholtz free energy should include not only the effects of should also include the effects of ε and but α,, and e. These variables may have a common origin in dislocation storage and motion, but they will be treated indeendent of each other. This gives different hysical interretations that lead to different evolution equations and allowing one the comutational introduction of the influence of one scale on the other (e.g. mesoscale on macroscale). For examle, dislocation interactions are observed on a mesolevel with length-scale µ m and strongly affect the material behavior on the macrolevel with length-scale 100µ m. In this model however, those variables are considered mathematically related to their local counterarts. Therefore, secial care must be taken to roerly account for their couling. It is imortant to note that some authors have considered in their thermodynamics formulation only the gradient of the lastic strain ε or the gradient of the kinematic flux α, while others have considered only the gradient of the effective lastic strain. But no one seems to have really considered the effect of both α and together. 41
48 For examle, Fleck and Hutchinson (2001), Gao et al. (1999), Gurtin (2003, 2004), Gudmundson (2004) develoed gradient theories that allow deendences on lastic strain gradients only. However, the theories of Fleck and Hutchinson and Gao introduce gradients in the lastic strain that only affect the isotroic hardening art with no kinematic hardening. Gurtin (2003, 2004) did not incororate in his variational formulation, but was incororated in the functional definition of the Helmholtz free energy. Aifantis (1984), Mühlhaus and Aifantis (1991), Acharya and Bassani (2000), Liebe and Steinmann (2001), and Polizzotto and Borino (1998) develoed gradient theories that allow deendences on the accumulation of the lastic strain such that only the isotroic hardening art is affected by the resence of these gradients. Voyiadjis et al. (2001, 2003, 2004) introduced first and second order gradients in both isotroic and kinematic hardening. However, the kinematic hardening was introduced through an arbitrary flux variable. It must be emhasized that this model is develoed on the conviction that both α and should enter the definitions of the internal virtual ower and the Helmholtz free energy. Therefore, one can anticiate from the formulation in the revious sections that the conjugate force of the conjugate force of Princile of Virtual Power α is the nonlocal back-stress while is the nonlocal drag stress. This will be shown subsequently. It follows from the discussion above, that the deendence of the internal ower on α,, and e through the internal variable E is the essential ingredient of the resent strain gradient lasticity model. Therefore, the internal and external ower exenditures are assumed to have the following forms, resectively, 42
49 e ( σε α kα k k k ) P X R S Q Ke V (105) int = + + +, +, + d Γ i i i i ρ i i ( α ) Pext = bvdv + tvda vv dv + m + q da (106) Γ Γ Γ Γ Pint and P ext balance each other in the sense of Eq. (4). The kinematical fields in the exressions above are considered as virtual. Eq. (105) is based on the concet that the ower exended by each kinematical field be exressible in terms of an associated force system consistent with its own balance (Gurtin, 2000). However, these kinematical fields are no longer indeendent. Therefore, secial care is taken in the following sections to roerly account for their couling. The nature of this couling can be determined using the rincile of virtual ower. In Eq. (106) m is the microtraction tensor conjugate to ε, defined for each unit vector n normal on the boundary Γ of Γ, and is symmetric and deviatoric since ε is symmetric and deviatoric. q is the microtraction force associated with the history variable. The force q is recisely that introduced by Fleck and Hutchinson (2001) in their reresentation of a variational rincile governing the one-arameter theory,. The last integral term in Eq. (106) results in higher-order boundary conditions generally consistent with the framework of a gradient theory. The first three terms in Eq. (105) constitute the definition of the local internal virtual ower as resented in Eq. (3). The last three terms in Eq. (105) are meant to take into account the large satial variations in ε at small length scales. The first of the last three terms reresents the internal ower generated by the nonlocal backstress S such that it introduces kinematic hardening through the net Burgers vector. The third-order tensor S also follows recisely that introduced by Gurtin (2000, 2002, 2003, 2004) in his thermodynamics of one-arameter 43
50 theory ε. The last two terms in Eq. (105) reresent the internal ower generated by the nonlocal drag vector Q and drag force K which account for the additional isotroic hardening from the accumulation of geometrically necessary dislocations. As aforementioned, if the gradients in the lastic strain tensor are considered then the corresonding history variable e defined in Eq. (103) 2 must also be considered. The last term in Eq. (105), therefore, introduces the history in the accumulation of ε and. This comletes the consideration of the large variations in lasticity defects at the microscale. Referring to the definition in Eq. (8) of the direction of the lastic strain, N, one can similarly define the directions of the lastic strain gradient, effective lastic strain,, resectively, as ε, and the gradient of the M k = ε ε ε = e, k, k, k, k = = e, k, k, k (107) where M and define the unit tensors of ε and, resectively, such that the M: M = : = 1. Therefore, it can easily be shown from Eqs. (107) that N, M, and are related by the following identity: NM = 1 (108) k k Moreover, from Eqs. (8) and (107) one can easily write ε N,, k ε, kn = =, e = ε, kmk (109) Utilizing Eq. (108) one can write Eq. (109) 3 as e = ε N (110), k k 44
51 Substituting the relation ε e = ε ε and Eqs. (109) 1, (109) 2, and (110) into Eq. (105) yields P int (, ) σε τ kx cαmn X mn R csmnkαmn k N ε + + = dv Γ + ksk ( csmnkαmn Qk + K k ) N ε, k (111) Making use of Eq. (12) and alying the divergence theorem, Eq. (111) can be rewritten as follows: P = σ v dv int, j i Γ τ kx + ksk, k Γ ( R cα X + cs, α Q, + K, + K, ) N mn mn mnk k mn k k k k k k ( ) + σnjvi da+ ksk + Qk + K k csmnk N n kε da Γ Γ ε dv (112) Moreover, Eq. (106) can be rewritten by substituting Eq. (109) 1 as Pext = bv i idv + tv i ida ρvv i idv + m εda (113) Γ Γ Γ Γ such that = k + ( q c ) m m mα N. Alying the axiom of equilibrium of the rincile of virtual ower to the region Γ, Eq. (4), one obtains the following equilibrium equation ( ti σnj ) vi da+ m ( ksk ( Qk K k csmnk ) N ) n + + k ε da Γ Γ + ( σ, j + bi ρv i ) vi dv Γ, (,,,, ) + τ kx + kskk R Qkk cx mnαmn+ csmnkkαmn K kk K k k N ε dv = 0 Γ Γ, v, and (114) ε may be arbitrarily secified such that the classical macro-force balance and the macro-traction condition remain the same as resented, resectively, in Eqs. (14) and 45
52 (15), while the micro-force balance condition undergoes a major change. Secifically, the micro-force balance takes the form τ kx + ks k, k ( α α ) R Q cx + cs K K N = k, k mn mn mnk, k mn k, k, k k 0 (microforce balance) (115) which is sulemented by a micro-traction condition given by (, ) m = + + ksk Qk K k csmnk kα mn N nk (microtraction condition) (116) As concluded reviously, the micro-force balance, Eq. (115), can be viewed as the lasticity yield condition. Thus, the micro-traction condition, Eq. (116), may be viewed as a higher-order condition (or internal boundary condition) augmented by the interaction of dislocations across interfaces (Gurtin, 2003; Gudmundson, 2004). Moreover, it is noticed from Eq. (114) that since ε is deviatoric, then m and div( S ) = S, are deviatoric while S is deviatoric in its first two arguments (i.e., S iik = 0 ). Nonlocal Yield Criterion Subsequently, it will be shown that the micro-force balance resented in Eq. (115) is nothing more than the nonlocal yield condition. Substituting Eq. (8) into Eq. (115), one can easily write the following exression for the flow rule in Eq. (9) 4 : k k k N k, k = R Qk, k cxmnαmn + csmnk, kαmn K k, k K, k k ε = τ kx + ks τ X + S k, k R Q k, k cx mnαmn + cs mnk, kαmn K k, k K, k k (117) Moreover, by taking the Euclidean norm of Eq. (115) one can also write kx + ksk, k R Qk, k cx mn mn + csmnk, k mn K k, k K, k k N = 0 τ α α (118) Since N = 1 and 46
53 R Q cx α + cs α K K = R Q cx α + cs α K K k, k mn mn mnk, k mn k, k, k k k, k mn mn mnk, k mn k, k, k k one can then rewrite the above exression as kx + ksk, k R + Qk, k + cxmn mn csmnk, k mn + K k, k + K, k k = 0 τ α α (119) Therefore, micro-force balance, Eq. (115) can be set as the nonlocal yield criterion or the nonlocal lasticity loading surface f f = τ kx + ks R+ Q + cx α cs α + K + K = (120) k, k k, k mn mn mnk, k mn k, k, k k 0 such that the flow rule in Eq. (117) 2 can also be exressed by ε = τ τ kx + ks k, k kx + ks mn mn mnk, k (121) Comaring Eq. (121) with Eq. (8), one can rewrite the direction of the lastic flow as N = τ τ kx + ks k, k kx + ks mn mn mnk, k (122) It may be noticed that higher-order stress div( S ) is a backstress quantity giving rise to kinematic hardening, while the stresses div( Q ) = Qkk, and ( K ) = K, + K, div k k k k k give rise to isotroic hardening. Furthermore, if the higher-order gradients are neglected, one can easily retrieve from Eqs. (120), (121), and (122), resectively, the classical yield criterion, Eq. (72), flow rule, Eq. (73), and flow direction, Eq. (74). Nonlocal Clausius-Duhem Inequality Utilizing the derived micro-force balance, Eq. (115), and the micro-traction condition, Eq. (116), into Eq. (112), the exression for the internal ower defined in Eq. (105) can be rewritten as follows: Pint = σε dv + m ε da (123) Γ Γ 47
54 Comaring the above equation with its corresonding local exression, Eq. (23), imlies that the nonlocal energy interactions can be non-vanishing only within the lastic zone. Hence, the energy term Γ m ε da may be described as the nonlocality energy residual that results from microstructural interactions between the material oints in the active lastic zone (Eringen and Edelen, 1972). Similar arguments have been resented by Polizzotto and Borino (1998). They assumed m ε da= 0 and described it as the insulation condition, imlying that nonlocal energy is not allowed to flow from any oint in Γ to the exterior of the body. However, their arguments were based on hysical justifications rather than mathematically derived. Furthermore, Eq. (123) coincides with the classical definition in Eq. (23) if the Γ micro-traction term Γ m ε da is set to zero. This yields the standard definition of the internal ower resented in Eq. (23) and ostulated by Green and Naghdi (1971), which has also been used by numerous researchers over the last three decades. Therefore, the alication of the following internal micro-boundary conditions on the lastic interfaces may be required m ε = 0 on Γ (124) where Γ Γ is the lastic boundary. The above equation gives two different conditions according to a slit of the lastic subdomain boundary into external and internal arts such that Γ = Γint Γext (Polizzotto and Borino, 1998). Thereby one boundary condition is imosed on the external lastic boundary Γext Γ m = 0 on Γ ext (125) 48
55 which corresonds to the so-called Neumann tye boundary. This microtraction-free boundary condition is the simlest form of Eq. (116) and assumes that the moment tractions m vanish at the external surfaces Γ ext = Γ Γ (i.e. unmovable external surfaces). Moreover, Eq. (125) laces no constraint on the lastic flow and could characterize free dislocation movements across the boundaries. If external surface tractions exist, the macro-traction t in Eq. (15) has a value whereas the micro-traction m vanishes. The other condition is imosed on the internal lastic boundary Γ int such that on int ε = 0 Γ (126) which corresonds to a continuity boundary condition of Dirichlet tye. This condition arises from the consideration that, in general, the stress rate σ is continuous across Γ int. Therefore, the related elastic strain rate, ε e, and lastic strain rate, ε, must be continuous. Moreover, this microlastic-clamed boundary condition laces a constraint on the lastic flow and could characterize the dislocation blocking at the interface. Meanwhile, Γ int characterizes the movable elastic-lastic boundary. However, m is meant to be the driving force at the material internal boundaries such that generally m 0. Hence, for an intermediate (i.e. not free and not clamed) kind of boundary condition (i.e. m 0 on Γ ext and the nonlocality energy residual,, as follows Γ Γ Γ int ε 0 ), one can define the density of dv = m ε da (127) Therefore, if one neglects the interior surface energy that results from dislocation interactions at the internal boundaries (e.g. internal boundaries at inclusions), the 49
56 insulation condition of Polizzotto (e.g. Polizzotto and Borino, 1998; Polizzotto, 2003) can be exressed as Γ dv = 0 (128) By substituting the exression for m from Eq. (116) into Eq. (127) and alying the divergence theorem, one obtains ( ( ) k k k mnk mn ), dv = ks + Q + K cs α N ε dv (129) Γ Γ As mentioned reviously, the consideration here is a urely mechanical theory (i.e. rocesses are isothermal) based on the requirement that the rate of change in the total free energy should be less than or equal to the ower done be external forces (Gurtin, 2000). Consequently, by substituting Eqs. (123) and (127) into Eq. (26), the following thermodynamic restriction is obtained in a oint wise form: σε ρψ+ 0 (130) k where is given by ( ks ( Q K cs α ) N ε ) k k k mnk mn = + + ( ) = ks Q K K cs α cs α N ε k, k k, k k, k, k k mnk mn, k mnk, k mn ( α ) + ks + Q + K cs N ε k k k mnk mn, k, k (131) The inequality in Eq. (130) may be described as the nonlocal Clausius-Duhem inequality. This differs from its classical counterart, Eq. (27), only because of the resence of the nonlocality residual. This inequality holds everywhere in Γ, but = 0 at material oints in the elastic zone. Moreover, it can be obtained from Eq. (131) that for a homogeneous strain distribution = 0 and one retains the classical Clausius- Duhem inequality. 50
57 Next the nonlocal Clausius-Duhem inequality in Eq. (130) will be emloyed for deriving the thermodynamic restrictions uon the inherent constitutive equations, to be satisfied for any admissible deformation mechanism. Nonlocal State Variables Now it is ossible to continue considering constitutive equations of the form resented in Section 2.3, but with the higher-order gradients, α,, and e added to the list of internal state variables. Secifically, the definition of the state ℵ ( k = 1,..., n ) in Eq. (81)can be generalized to include the nonlocal internal variables from the internal ower exression, Eq. (105), such that ℵ =ℵ α,, α,, e (132) (,, ) k k k k Therefore, it is art of this model s hilosohy that the nonlocal variables k int α,, and e must aear in the secific free energy Ψ since they contribute to the internal ower exression. Assuming a searable material, the Helmholtz free energy otential can be written as ( ) (,,, k,, k, e) e e Ψ=Ψ ε +Ψ α α (133) Taking the time derivative of Eq. (133) with resect to its internal state variables yields e e ε e, k, k α α, k, k e Ψ Ψ Ψ Ψ Ψ Ψ Ψ= + α + + α + + e ε (134) Making use of Eqs. (109) and (110) in Eq. (134), yields Ψ Ψ Ψ Ψ Ψ Ψ= + + α α ε e e ε k c mn c mn, k N ε e α αmn αmn, k Ψ Ψ Ψ Ψ + k + + c α N α α k mn ε, k, k, k e mn, k (135) 51
58 The nonlocal Clausius-Duhem inequality from Eq. (130) can now be alied to the resent case along the exanded time derivative in Eq. (135) such that e Ψ σ ρ ε e ε e + τ ρ ρ α α ε Ψ Ψ Ψ Ψ k c mn c mn, k N α α mn αmn, k Ψ Ψ Ψ Ψ ρk + ρ + k c α mn N ε, k + 0 α, k, k e α mn, k (136) A classical hyothesis ermits the canceling of the first term in this inequality. Indeendently from the inequality the thermodynamic laws in Eqs. (85) and (86) are obtained along with the following nonlocal thermodynamic state law Ψ Ψ Ψ Ψ = ρk + ρ + α c N (137) k k mn α, k, k e αmn, k From Eqs. (136), (86), and (137), one can rewrite the nonlocal Clausius-Duhem inequality in Eq. (136) as k ε, k 0 Π= J ε + (138) where Π is the nonlocal dissiation energy er unit volume. Nonlocal Plastic Flow Rule By making use of the Onsager recirocity rincile (Malvern, 1969), which is assumed to hold also in the case of nonlocal material behavior, the secific dissiation energy in Eq. (138) can be exressed in a linear form in terms of the driving flux, related thermodynamic force, similar to the exression in Eq. (87), such that ε, and Π= J ε 0 (139) 52
59 where J denotes the unknown total quasi-nonlocal thermodynamic force. By comaring Eqs. (138) and (139), the nonlocality residual can be exressed by = J ε J ε + ε (140) k, k On imosing the insulation condition in Eq. (128) with setting Γ=Γ such that Γ Γ is the region of Γ where the lastic deformation is taking lace, one can write from Eq. (140) J ε J ε + k ε, k dv = 0 (141) Γ Uon alying the divergence theorem to the last term in Eq. (141), one can write J J k, k ε dv + kn kε da= 0 (142) ( ) Γ Γ Since Eq. (142) must hold for any lastic deformation mechanism, and for any ossible evolution law as well; hence, for any arbitrary choice of ε in Γ Γ, the necessary and sufficient conditions rove to be the following: J = J + in k, k and n ε = 0 on k k Γ (143) Γ (144) It is obvious that Eq. (143), after substitution of Eqs. (86) and (137), identifies the total quasi-nonlocal thermodynamic force J in Γ and, therefore, it is the force that must be introduced into the evolution equations as the ertinent hardening/softening driving force. J is a quasi-nonlocal force since it is decomosed into a local art, J, and a nonlocal art, div( ). Eq. (144) rovides the nonstandard boundary conditions. Substitution of Eq. (143) into Eq. (140) gives 53
60 ( ) k, k k ε, k k, k = ε + = ε (145) such that 0 in Γ, but = 0 out of Γ or for a homogeneous lastic deformation. Now substituting Eq. (137) into Eq. (145) and comaring the result with Eq. (131) yields the following exressions for the nonlocal thermodynamic conjugate forces Ψ Sk = ρ, α, k Q k = ρ Ψ, K, k = ρ Ψ e (146) Hence, one can rewrite in Eq. (137), after substituting Eqs. (146), as ( ) = ks + Q + K cs α N (147) k k k k mnk mn Moreover, substituting Eq. (147) into Eq. (144) yields the same micro-traction boundary condition derived from the rincile of virtual ower, Eq. (116) or (124), such that the corresonding thermodynamic conjugate force is m = n (148) k k which in turn yields the same non-standard boundary conditions resented in Eqs. (125) and (126). Substitution of Eq. (143) into Eq. (139) yields the following exression for Π ( J ) Π= + (149) k, k ε 0 That is, has disaeared from Π in Eq. (138), but its nonlocality has been relaced by div( ). Substituting the exression for ( J ) k, k N 0 ε from Eq. (9) 4 into Eq. (149) and defining γ = + (150) yields Eq. (37) (i.e. Π= γ 0 ), where γ is interreted here as the nonlocal dissiation modulus. Furthermore, equating Eqs. (37) and (149) gives Eqs. (38) and (39), but with J is given by Eq. (143) instead of Eq. (86), such that the lastic flow direction N is exressed 54
61 as N J = = J k, k mn J J mn + + mnk, k (151) By substituting Eqs. (86) and (147) into the above exression, Eq. (151) can be rewritten as N Ψ τ ρk + ks α = Ψ γ + ρ Q k, k ( K ) kk, k, k (152) Comaring Eqs. (152) and (122), one can write J = kx + ks τ J = kx + ks = R Q ( K ) k, k τ (153) k, k k, k k, k such that the back-stress X and the micro-force R are given by Eqs. (94) and (95), resectively. Therefore, one can exress the nonlocal lastic flow rule as resented reviously in Eq. (121) with the thermodynamic conjugate forces σ, X, S, R, Q, and K as given by Eqs. (85), (94), (95), (146) 1, (146) 2, (146) 3, resectively. Thus, the essential change in the classical lasticity theory is that here the size of the yield surface deends on the gradient of the effective lastic strain and effective lastic strain gradient e ; while the center of the yield surface deends on the kinematic flux gradient Nonlocal Evolution Equations α. Equation (139), which holds with Eqs. (125) and (126), exresses the lastic dissiation density, Π, through the local evolution of ε and the related thermodynamic force J. Therefore, in case of associative lasticity, as is the case here, a consistent way to establish the lastic evolution laws is by making use of the maximum lastic dissiation rincile introduced in Section 2.5. This can be also used to find the evolution 55
62 equations of the nonlocal internal variables α,, and e. Therefore, substituting Eq. (139) into Eq. (96) and alying the calculus of several variables, one can write Ω = 0 J Ω 0 Ω =, = 0, σ X Ω = 0 S k, k (154) Ω = 0, R Ω = 0, Q kk, Ω = 0 ( K ), k k (155) and Ω Ω Ω = 0, = 0, = 0 S k Q k K (156) By making use of Eqs. (86), (143), and (137) along with Eqs. (94), (95), and (146) the lastic flow rule, ε, can then be obtained from any of the conditions in Eq. (154), such that ε f = λ J f λ f λ f ε = λ = = (157) σ k X k S k, k which agrees with the classical assumtion that the lastic flow direction N is governed by the Cauchy stress σ. However, Eq. (157) suggests that similarly N is governed by the nonlocal microstress div( S ), such that N f f f = = = σ X S k, k (158) or equivalently N can be exressed by Eqs. (117) 1 or (122). The evolution of can be obtained from any of the conditions in Eq. (155) along with Eq. (120) such that f f f = λ = λ = λ = λ R Q K ( ) kk, k, k (159) 56
63 where λ is the lastic multilier which can be determined by the nonlocal consistency condition similar to that in Eq. (99). Moreover, the exressions in Eqs. (157) and (158) agree well with the reviously derived exressions, namely those in Eqs. (121) and (122). By substituting Eq. (159) into Eq. (109) 2, one can write the flow rule of lastic strain gradient as ε = λ N (160), k, k such that = λ, while the evolution equation of e can be obtained from Eqs. (107) 2 and (120) such that e = λ,k k with f k = (161) K, k Moreover, one can rewrite an evolution law for ε, other than Eq. (160), from Eq. (107) 1 as ε = em with, k k M f f = N = (162) S K k k m, m, k The three conditions in Eq. (156) give, resectively, f S k = 0, f Q k f = 0, = 0 K (163) which does not agree with the roosition of Gurtin (2000, 2003) and Gudmundson (2004) who argued that the lastic flow direction N is governed by the microstress S and not the Cauchy stress σ. However, in this model the classical assumtion is reiterated that N is governed by σ or equivalently by the microstress, div( S ). 57
64 7 NUMERICAL APPLICATIONS IN THIN FILMS Gradient-Deendence of the Helmholtz Free Energy In order to develo equations amenable to the analysis and comutation, some consideration is give to the definition of the Helmholtz free energy function. One can assume decouling between the elastic behavior and lasticity hardening (i.e. searable material) such that both e Ψ and Ψ that aear in Eq. (133) can be assumed to have the following quadratic analytical form: e 1 e e ρψ = εeklεkl (164) ρψ = a1ε ε + a2 + a3αα + a5, k, k + a6e + a7 α, kα, k (165) where E is the symmetric fourth-order elastic stiffness tensor and a i ( i = 1 5) are material constants. However, utilizing the following relations = ε ε, 2 e 2 = ε ε = (166), k, k, k, k resectively, from Eqs. (60) and (103), one can equivalently write Eq. (165) as ρψ = ( a1+ a2) + ( a3+ a4 + a5) e (167) 2 2 Moreover, by assuming that the hardening moduli h= a1+ a2 and can rewrite Eq. (167) as 2 h = a3+ a4 + a5, one ρψ = h( + e ) = he (168) 2 2 where the generalized effective lastic strain E is given by Eq. (104). Now, one can obtain the Cauchy stress from Eqs. (85) and (164) such that ( ) σ = E ε = E ε ε (169) e kl kl kl kl kl 58
65 and the local and nonlocal conjugate forces by making use of Eqs. (94), (95), (146), resectively, as follows: X = hα (170) R = γ + h (171) 2 Sk h ε, k = (172) 2 Qk h, k = (173) 2 K = h e (174) where γ coincides with the initial coarse-grain yield strength for rate and temerature indeendent materials. Moreover, substituting Eqs. (172)-(174) into the yield function f, Eq. (120), one can then write ( ) 2 2 f = τ X + Sk, k γ h i k, k e + +, k k = 0 (175) with 2 2 Sk, k = h ε (176) where 2 designates the Lalacian oerator and k designates the first gradient vector. For monotonic and roortional loading (in the case of isotroic hardening) one can easily show by using Eqs. (103) and (107) 2 that the last two terms in the left-hand-side of Eq. (175) can be reduced to + = (177) 2 i k, k e, k k such that f can be given by k, k effective von-mises stress f = τ X + S γ h+ h = isotroic hardening function (178) 59
66 Thus this theory shows that the Lalacian of the effective lastic strain contributes to the size of the yield surface (isotroic hardening) and the Lalacian of the lastic strain contributes to the movement of the center of the yield surface (kinematic hardening). It is also noteworthy that the resent formulation links hardening to the gradients of lastic strain ε and the effective lastic strain and, resectively, not to 2 ε and 2, consistent with basic notions of the role of the net Burgers vector and the geometrically necessary dislocations. Instead, 2 ε and 2 emerges in the resulting field equations as a byroduct of the more fundamental role of the lastic strain gradients. The next sections resent some alications of the gradient lasticity model. Of articular interest is the model s ability to describe size effects observed in metals. The roosed gradient lasticity theory is used to investigate the size deendent behavior in biaxial loading of a lastic thin film on an elastic substrate and shear loading of a thin film fixed to a rigid substrate. In the following alications the exression of the yield surface f in Eq. (178) is emloyed. Biaxial Loading of a Thin Film on a Substrate A biaxially loaded isotroic elasto-lastic thin film of thickness T on a thick semiinfinite elastic substrate is considered as shown in Figure 3. Let x 3 be the erendicular axis to the film with x 3 = 0 corresonding to the film-substrate interface. The loading is defined by a monotonically increasing biaxial strain ε o such that ε11 = ε22 = εo. 60
67 ε o x 3 ε o ε o ε o Figure 3: Biaxial Loading of a Thin Film on an Elastic Substrate A lane stress situation is assumed such that the non-vanishing stress comonents are ( ) σ = σ = σ o x (179) From the lastic incomressibility assumtion and the symmetry, one can write the nonvanishing lastic strain comonents as ( ) ε = ε = ε = ε o x (180) Therefore the total and lastic strain tensors may be written in matrix format as ε ε ( x ) = 0 ε0( x3) and ε ε ( x ) = 0 ε0 ( x3) ε 0 ( x3) (181) Meanwhile, using the conditions of lastic incomressibility and symmetry, the lane and deviatoric stress tensors may be written in matrix format as 61
68 σ σ ( x ) = 0 σ0( x3) and τ σ 0( x3) σ ( x ) = σ 0( x3) 3 (182) Finally, the kinematic flux and deviatoric art of the microstress (backstress) may be written in matrix format as α α ( x ) = 0 α22( x3) α33( x3) X11( x3) 0 0 and X = 0 X22( x3) X 33( x3) (183) The effective lastic strain = ε ε and its Lalacian 2 are given as = 6ε o and 2 = 6ε o,33 (184) where εo,33 εo x3 x3 =. The stress-strain relationshi can be obtained from the generalized Hooke s law as E σ = ε ε ( x ) ( 1 ν ) ( ( x )) o 3 o o 3 (185) Substituting Eqs. (179), (184), and (185) into the yield condition, Eq. (178), yields the imlicit differential equation below: 62
69 { 2 2E 2 2ka3E ( ε0 ε0 ) ( α11 + α22 2 α33)( ε0 ε0 ) 3(1 ν) 3(1 ν) 2 2khl E `` `` `` ( α11 + α22 2 α33)( ε0 ε0 ) + ka3( α11 + α22 + α33) 3(1 ν ) `` `` `` `` 2 `` 2 `` α11α11 α22α22 α33α33 hkl α11 α22 α 33 2 ahkl ( + + ) + ( ) + ( ) + ( ) γ 6h 2 `` 1+ m ε0 + 6 hl ε0 ca3( α11+ α22 + α33) m m m ` `` ` ` ` `` 2 `` `` `` 2 α11α11 + α22α22 + α33α33 chl ( α11α11 + α22α22 + α33α33) + hl 0 1 = ` 2 ` 2 ` 2 ( α 2 11) + ( α22) + ( α33) } (186) It is obvious that a closed-form solution is not feasible for such a comlex equation. A numerical aroximation method must therefore be used to obtain results. However, even a numerical solution requires additional arameters to be established before an aroximation method may be executed. It is worthwhile to note that α and ε 0 are related by Equation (52). For monotonic loading, and at any given oint i along x 3, the kinematic flux may be related to the lastic strain by solving Equation (52) as a differential equation. This yields the following relations 6k α11() i = α22() i = 1 e 6c 6k α33() i = 2 6c 6 cε 0 ( i) ( ) 6 cε 0 ( i) ( e ) (187) Use of these exressions requires discretization of Equation (186) along x 3. Discretizing Equation (186), substituting Equations (187) into the resulting exression, and using the Central Finite Difference Method, yields a set of n equations, where n reresents the number of oints along x 3 in the mesh. However, the Central Finite 63
70 Difference Method roduces n+2 unknowns, where two of the unknowns reresent the fictional lastic strain at the virtual oints outside the hysical bounds of the thin film. This is where the boundary conditions at either edge of the film come in. The micro-boundary conditions can be utilized as resented by Eqs. (125) and (126). The microtraction-free boundary condition is imosed at the free surface (i.e. x3 = t ) and the microlastic-clamed boundary condition is imosed at the film-substrate interface ε o such tha = 0 z at z = 1 and ε = 0 at z = 0 (188) o The n equations from the Finite Difference formulation, along with these micro-boundary condition exressions are solved using the comuter mathematics ackage Mathcad. 4 ε ε y 3 2 /t z Figure 4: Biaxial Plastic Strain through the Film Thickness 64
71 The stress along the film can be found by using the lastic strain results with Eq. (185). 6 σ 0 σ y 4 2 /t z Figure 5: Biaxial Stress through the Film Thickness Furthermore the average stress in the thin-film, σ ave o, can be determined from an integration of from 0 to 1 8 σ σ ave y 6 4 /t ε / ε 0 y Figure 6: Average Biaxial Strain versus Biaxial Strain 65
72 Results in Figure 4, 5, and 6 are resented for h( 1 ν ) E=0.05 and ν =0.3. Different film thicknesses are reresented by / t =0.1, 0.5, 1, 1.5, 2. In Figure 6, normalized results for average film stress versus alied biaxial strain ε o are resented. It is clearly seen that the hardening tangent modulus increases with decreasing the film thickness, which agrees qualitatively with the exerimental observations. Figures 4 and 5 show the variation of the biaxial stress and lastic strain across the film thickness. Instead of a uniform distribution of stress and lastic strain across the film thickness, according to classical local lasticity, the stress increases and the lastic strain decreases as the film-substrate interface is aroached. Moreover, the results clearly show that the biaxial stress and lastic strain rofiles tend to become homogeneous with increased thickness due to smaller gradient effects. This means that gradients eventually disaear for large thicknesses. As shown in Figure 4, the increase of lastic strain at x3 = t overwhelms the increase as the substrate is aroached due to the distribution of gradients, which is lower as the free boundary is aroached and higher at the substrate. The elimination of gradients sreads from the free boundary, roagating through the entire thickness. Finally, the lastic strain becomes uniform across the thickness. Shear Loading of a Thin Film on a Substrate An elasto-lastic thin film is bonded to a rigid substrate under ure shear loading as shown in Figure 7. Thereafter, the bottom surface of the film is held fixed and a shear traction is alied to the to surface in the x 1 -direction. The film is assumed to be infinitely long in the x 1 -direction and initially homogeneous and, therefore, the solution deends only on x 3. 66
73 x 3 x 1 γ o Figure 7: Shear Loading of a Thin Film on a Substrate Shu et al. (2001) simulated this roblem in a discrete dislocation calculation of constrained lastic flow within a crystalline layer. The only non-vanishing stress and lastic strain comonents are σ 1 = τ, ε = γ o ( x ) (189) 31 o where τ o is homogeneous across the film thickness since the macroscoic force balance, Eq. (66), yields τ o x3 = 0 if body forces and inertia are neglected. According to these assumtions the total and lastic strain tensors may be written in matrix format as ε 0 0 γ 0( x3) = γ 0( x3) 0 0 and γ 0 0 γ 0 ( x3) = γ 0 ( x3) 0 0 (190) Meanwhile, using the conditions of lastic incomressibility and symmetry, the lane and deviatoric stress tensors are identical and may be written in matrix format as 67
8.7 Associated and Non-associated Flow Rules
 8.7 Associated and Non-associated Flow Rules Recall the Levy-Mises flow rule, Eqn. 8.4., d ds (8.7.) The lastic multilier can be determined from the hardening rule. Given the hardening rule one can more
8.7 Associated and Non-associated Flow Rules Recall the Levy-Mises flow rule, Eqn. 8.4., d ds (8.7.) The lastic multilier can be determined from the hardening rule. Given the hardening rule one can more
FE FORMULATIONS FOR PLASTICITY
 G These slides are designed based on the book: Finite Elements in Plasticity Theory and Practice, D.R.J. Owen and E. Hinton, 1970, Pineridge Press Ltd., Swansea, UK. 1 Course Content: A INTRODUCTION AND
G These slides are designed based on the book: Finite Elements in Plasticity Theory and Practice, D.R.J. Owen and E. Hinton, 1970, Pineridge Press Ltd., Swansea, UK. 1 Course Content: A INTRODUCTION AND
A SIMPLE PLASTICITY MODEL FOR PREDICTING TRANSVERSE COMPOSITE RESPONSE AND FAILURE
 THE 19 TH INTERNATIONAL CONFERENCE ON COMPOSITE MATERIALS A SIMPLE PLASTICITY MODEL FOR PREDICTING TRANSVERSE COMPOSITE RESPONSE AND FAILURE K.W. Gan*, M.R. Wisnom, S.R. Hallett, G. Allegri Advanced Comosites
THE 19 TH INTERNATIONAL CONFERENCE ON COMPOSITE MATERIALS A SIMPLE PLASTICITY MODEL FOR PREDICTING TRANSVERSE COMPOSITE RESPONSE AND FAILURE K.W. Gan*, M.R. Wisnom, S.R. Hallett, G. Allegri Advanced Comosites
THE INFLUENCE OF DISLOCATION DENSITY ON THE BEHAVIOUR OF CRYSTALLINE MATERIALS
 THE PUBLISHING HOUSE PROCEEDINGS OF THE ROMANIAN ACADEMY, Series A, OF THE ROMANIAN ACADEMY Volume 7, Number 4/6, 358 365 THE INFLUENCE OF DISLOCATION DENSITY ON THE BEHAVIOUR OF CRYSTALLINE MATERIALS
THE PUBLISHING HOUSE PROCEEDINGS OF THE ROMANIAN ACADEMY, Series A, OF THE ROMANIAN ACADEMY Volume 7, Number 4/6, 358 365 THE INFLUENCE OF DISLOCATION DENSITY ON THE BEHAVIOUR OF CRYSTALLINE MATERIALS
Churilova Maria Saint-Petersburg State Polytechnical University Department of Applied Mathematics
 Churilova Maria Saint-Petersburg State Polytechnical University Deartment of Alied Mathematics Technology of EHIS (staming) alied to roduction of automotive arts The roblem described in this reort originated
Churilova Maria Saint-Petersburg State Polytechnical University Deartment of Alied Mathematics Technology of EHIS (staming) alied to roduction of automotive arts The roblem described in this reort originated
Computational Solid Mechanics Computational Plasticity
 Comutational Solid Mechanics Comutational Plasticity Chater 3. J Plasticity Models C. Agelet de Saracibar ETS Ingenieros de Caminos, Canales y Puertos, Universidad Politécnica de Cataluña (UPC), Barcelona,
Comutational Solid Mechanics Comutational Plasticity Chater 3. J Plasticity Models C. Agelet de Saracibar ETS Ingenieros de Caminos, Canales y Puertos, Universidad Politécnica de Cataluña (UPC), Barcelona,
Lower bound solutions for bearing capacity of jointed rock
 Comuters and Geotechnics 31 (2004) 23 36 www.elsevier.com/locate/comgeo Lower bound solutions for bearing caacity of jointed rock D.J. Sutcliffe a, H.S. Yu b, *, S.W. Sloan c a Deartment of Civil, Surveying
Comuters and Geotechnics 31 (2004) 23 36 www.elsevier.com/locate/comgeo Lower bound solutions for bearing caacity of jointed rock D.J. Sutcliffe a, H.S. Yu b, *, S.W. Sloan c a Deartment of Civil, Surveying
Adam Paweł Zaborski. 8 Plasticity. reloading. 1. Bauschinger s effect. 2. unchanged yielding limit. 3. isotropic hardening
 8 lasticity Introduction Definitions loading/unloading/reloading words commonly used in lasticity lastic strain a ermanent strain that doesn t vanish after unloading, lastically assive rocess a rocess
8 lasticity Introduction Definitions loading/unloading/reloading words commonly used in lasticity lastic strain a ermanent strain that doesn t vanish after unloading, lastically assive rocess a rocess
Geo-E2010 Advanced Soil Mechanics L Wojciech Sołowski. 07 March 2017
 Geo-E2010 Advanced Soil Mechanics L Wojciech Sołowski 07 March 2017 Soil modeling: critical state soil mechanics and Modified Cam Clay model Outline 1. Refresh of the theory of lasticity 2. Critical state
Geo-E2010 Advanced Soil Mechanics L Wojciech Sołowski 07 March 2017 Soil modeling: critical state soil mechanics and Modified Cam Clay model Outline 1. Refresh of the theory of lasticity 2. Critical state
The effect of dynamic bending moments on the ratchetting behavior of stainless steel pressurized piping elbows
 International Journal of echanical Engineering and Alications 2014; 2(2): 31-37 Published online ay 30, 2014 (htt://www.scienceublishinggrou.com/j/ijmea) doi: 10.11648/j.ijmea.20140202.12 The effect of
International Journal of echanical Engineering and Alications 2014; 2(2): 31-37 Published online ay 30, 2014 (htt://www.scienceublishinggrou.com/j/ijmea) doi: 10.11648/j.ijmea.20140202.12 The effect of
A General Damage Initiation and Evolution Model (DIEM) in LS-DYNA
 9th Euroean LS-YNA Conference 23 A General amage Initiation and Evolution Model (IEM) in LS-YNA Thomas Borrvall, Thomas Johansson and Mikael Schill, YNAmore Nordic AB Johan Jergéus, Volvo Car Cororation
9th Euroean LS-YNA Conference 23 A General amage Initiation and Evolution Model (IEM) in LS-YNA Thomas Borrvall, Thomas Johansson and Mikael Schill, YNAmore Nordic AB Johan Jergéus, Volvo Car Cororation
Pressure-sensitivity Effects on Toughness Measurements of Compact Tension Specimens for Strain-hardening Solids
 American Journal of Alied Sciences (9): 19-195, 5 ISSN 1546-939 5 Science Publications Pressure-sensitivity Effects on Toughness Measurements of Comact Tension Secimens for Strain-hardening Solids Abdulhamid
American Journal of Alied Sciences (9): 19-195, 5 ISSN 1546-939 5 Science Publications Pressure-sensitivity Effects on Toughness Measurements of Comact Tension Secimens for Strain-hardening Solids Abdulhamid
Characterization of Material Parameters
 Proceedings of the World Congress on Engineering 29 Vol II WCE 29, July 1-3, 29, London, U.K. Characterization of Material Parameters S. M. Humayun Kabir, Tae-In Yeo, Sang-Ho Kim Abstract The resent work
Proceedings of the World Congress on Engineering 29 Vol II WCE 29, July 1-3, 29, London, U.K. Characterization of Material Parameters S. M. Humayun Kabir, Tae-In Yeo, Sang-Ho Kim Abstract The resent work
Implementation and Validation of Finite Volume C++ Codes for Plane Stress Analysis
 CST0 191 October, 011, Krabi Imlementation and Validation of Finite Volume C++ Codes for Plane Stress Analysis Chakrit Suvanjumrat and Ekachai Chaichanasiri* Deartment of Mechanical Engineering, Faculty
CST0 191 October, 011, Krabi Imlementation and Validation of Finite Volume C++ Codes for Plane Stress Analysis Chakrit Suvanjumrat and Ekachai Chaichanasiri* Deartment of Mechanical Engineering, Faculty
Driving Forces and Boundary Conditions in Continuum Dislocation Mechanics
 Driving Forces and Boundary Conditions in Continuum Dislocation Mechanics Amit Acharya Det. of Civil and Environmental Engineering Carnegie Mellon University, Pittsburgh, PA 1513, U.S.A. Summary As a guide
Driving Forces and Boundary Conditions in Continuum Dislocation Mechanics Amit Acharya Det. of Civil and Environmental Engineering Carnegie Mellon University, Pittsburgh, PA 1513, U.S.A. Summary As a guide
On the Prediction of Material Failure in LS-DYNA : A Comparison Between GISSMO and DIEM
 13 th International LS-YNA Users Conference Session: Constitutive Modeling On the Prediction of Material Failure in LS-YNA : A Comarison Between GISSMO and IEM Filie Andrade¹, Markus Feucht², Andre Haufe¹
13 th International LS-YNA Users Conference Session: Constitutive Modeling On the Prediction of Material Failure in LS-YNA : A Comarison Between GISSMO and IEM Filie Andrade¹, Markus Feucht², Andre Haufe¹
ANALYSIS OF ULTRA LOW CYCLE FATIGUE PROBLEMS WITH THE BARCELONA PLASTIC DAMAGE MODEL
 XII International Conerence on Comutational Plasticity. Fundamentals and Alications COMPLAS XII E. Oñate, D.R.J. Owen, D. Peric and B. Suárez (Eds) ANALYSIS OF ULTRA LOW CYCLE FATIGUE PROBLEMS WITH THE
XII International Conerence on Comutational Plasticity. Fundamentals and Alications COMPLAS XII E. Oñate, D.R.J. Owen, D. Peric and B. Suárez (Eds) ANALYSIS OF ULTRA LOW CYCLE FATIGUE PROBLEMS WITH THE
Chapter 1 Fundamentals
 Chater Fundamentals. Overview of Thermodynamics Industrial Revolution brought in large scale automation of many tedious tasks which were earlier being erformed through manual or animal labour. Inventors
Chater Fundamentals. Overview of Thermodynamics Industrial Revolution brought in large scale automation of many tedious tasks which were earlier being erformed through manual or animal labour. Inventors
Numerical simulation of bird strike in aircraft leading edge structure using a new dynamic failure model
 Numerical simulation of bird strike in aircraft leading edge structure using a new dynamic failure model Q. Sun, Y.J. Liu, R.H, Jin School of Aeronautics, Northwestern Polytechnical University, Xi an 710072,
Numerical simulation of bird strike in aircraft leading edge structure using a new dynamic failure model Q. Sun, Y.J. Liu, R.H, Jin School of Aeronautics, Northwestern Polytechnical University, Xi an 710072,
Paper C Exact Volume Balance Versus Exact Mass Balance in Compositional Reservoir Simulation
 Paer C Exact Volume Balance Versus Exact Mass Balance in Comositional Reservoir Simulation Submitted to Comutational Geosciences, December 2005. Exact Volume Balance Versus Exact Mass Balance in Comositional
Paer C Exact Volume Balance Versus Exact Mass Balance in Comositional Reservoir Simulation Submitted to Comutational Geosciences, December 2005. Exact Volume Balance Versus Exact Mass Balance in Comositional
Adiabatic Shear Bands in Simple and Dipolar Plastic Materials
 Adiabatic Shear Bands in Simle and Diolar Plastic Materials T W \-1RIGHT us Army Ballistic Research Laboratory Aberdeen Proving Ground, MD 215 R C BATRA University of Missouri-Rolla Rolla, Missouri 6541
Adiabatic Shear Bands in Simle and Diolar Plastic Materials T W \-1RIGHT us Army Ballistic Research Laboratory Aberdeen Proving Ground, MD 215 R C BATRA University of Missouri-Rolla Rolla, Missouri 6541
Week 8 lectures. ρ t +u ρ+ρ u = 0. where µ and λ are viscosity and second viscosity coefficients, respectively and S is the strain tensor:
 Week 8 lectures. Equations for motion of fluid without incomressible assumtions Recall from week notes, the equations for conservation of mass and momentum, derived generally without any incomressibility
Week 8 lectures. Equations for motion of fluid without incomressible assumtions Recall from week notes, the equations for conservation of mass and momentum, derived generally without any incomressibility
dn i where we have used the Gibbs equation for the Gibbs energy and the definition of chemical potential
 Chem 467 Sulement to Lectures 33 Phase Equilibrium Chemical Potential Revisited We introduced the chemical otential as the conjugate variable to amount. Briefly reviewing, the total Gibbs energy of a system
Chem 467 Sulement to Lectures 33 Phase Equilibrium Chemical Potential Revisited We introduced the chemical otential as the conjugate variable to amount. Briefly reviewing, the total Gibbs energy of a system
Keywords: pile, liquefaction, lateral spreading, analysis ABSTRACT
 Key arameters in seudo-static analysis of iles in liquefying sand Misko Cubrinovski Deartment of Civil Engineering, University of Canterbury, Christchurch 814, New Zealand Keywords: ile, liquefaction,
Key arameters in seudo-static analysis of iles in liquefying sand Misko Cubrinovski Deartment of Civil Engineering, University of Canterbury, Christchurch 814, New Zealand Keywords: ile, liquefaction,
Characteristics of Beam-Based Flexure Modules
 Shorya Awtar e-mail: shorya@mit.edu Alexander H. Slocum e-mail: slocum@mit.edu Precision Engineering Research Grou, Massachusetts Institute of Technology, Cambridge, MA 039 Edi Sevincer Omega Advanced
Shorya Awtar e-mail: shorya@mit.edu Alexander H. Slocum e-mail: slocum@mit.edu Precision Engineering Research Grou, Massachusetts Institute of Technology, Cambridge, MA 039 Edi Sevincer Omega Advanced
INTRODUCING THE SHEAR-CAP MATERIAL CRITERION TO AN ICE RUBBLE LOAD MODEL
 Symosium on Ice (26) INTRODUCING THE SHEAR-CAP MATERIAL CRITERION TO AN ICE RUBBLE LOAD MODEL Mohamed O. ElSeify and Thomas G. Brown University of Calgary, Calgary, Canada ABSTRACT Current ice rubble load
Symosium on Ice (26) INTRODUCING THE SHEAR-CAP MATERIAL CRITERION TO AN ICE RUBBLE LOAD MODEL Mohamed O. ElSeify and Thomas G. Brown University of Calgary, Calgary, Canada ABSTRACT Current ice rubble load
Hydrogen-assisted stress corrosion cracking simulation using the stress-modified fracture strain model
 Journal of Mechanical Science and Technology 26 (8) (2012) 2631~2638 www.sringerlink.com/content/1738-494x DOI 10.1007/s12206-012-0642-x Hydrogen-assisted stress corrosion cracking simulation using the
Journal of Mechanical Science and Technology 26 (8) (2012) 2631~2638 www.sringerlink.com/content/1738-494x DOI 10.1007/s12206-012-0642-x Hydrogen-assisted stress corrosion cracking simulation using the
MODELING THE RELIABILITY OF C4ISR SYSTEMS HARDWARE/SOFTWARE COMPONENTS USING AN IMPROVED MARKOV MODEL
 Technical Sciences and Alied Mathematics MODELING THE RELIABILITY OF CISR SYSTEMS HARDWARE/SOFTWARE COMPONENTS USING AN IMPROVED MARKOV MODEL Cezar VASILESCU Regional Deartment of Defense Resources Management
Technical Sciences and Alied Mathematics MODELING THE RELIABILITY OF CISR SYSTEMS HARDWARE/SOFTWARE COMPONENTS USING AN IMPROVED MARKOV MODEL Cezar VASILESCU Regional Deartment of Defense Resources Management
On the Fluid Dependence of Rock Compressibility: Biot-Gassmann Refined
 Downloaded 0/9/3 to 99.86.4.8. Redistribution subject to SEG license or coyright; see Terms of Use at htt://library.seg.org/ On the luid Deendence of Rock Comressibility: Biot-Gassmann Refined Leon Thomsen,
Downloaded 0/9/3 to 99.86.4.8. Redistribution subject to SEG license or coyright; see Terms of Use at htt://library.seg.org/ On the luid Deendence of Rock Comressibility: Biot-Gassmann Refined Leon Thomsen,
Session 5: Review of Classical Astrodynamics
 Session 5: Review of Classical Astrodynamics In revious lectures we described in detail the rocess to find the otimal secific imulse for a articular situation. Among the mission requirements that serve
Session 5: Review of Classical Astrodynamics In revious lectures we described in detail the rocess to find the otimal secific imulse for a articular situation. Among the mission requirements that serve
Domain Dynamics in a Ferroelastic Epilayer on a Paraelastic Substrate
 Y. F. Gao Z. Suo Mechanical and Aerosace Engineering Deartment and Princeton Materials Institute, Princeton University, Princeton, NJ 08544 Domain Dynamics in a Ferroelastic Eilayer on a Paraelastic Substrate
Y. F. Gao Z. Suo Mechanical and Aerosace Engineering Deartment and Princeton Materials Institute, Princeton University, Princeton, NJ 08544 Domain Dynamics in a Ferroelastic Eilayer on a Paraelastic Substrate
SAMARIS. Draft report
 SAMARIS Work Package 5 - Performance based secifications Selection and evaluation of models for rediction of ermanent deformations of unbound granular materials in road avements Draft reort Pierre Hornych
SAMARIS Work Package 5 - Performance based secifications Selection and evaluation of models for rediction of ermanent deformations of unbound granular materials in road avements Draft reort Pierre Hornych
Chapter 6. Thermodynamics and the Equations of Motion
 Chater 6 hermodynamics and the Equations of Motion 6.1 he first law of thermodynamics for a fluid and the equation of state. We noted in chater 4 that the full formulation of the equations of motion required
Chater 6 hermodynamics and the Equations of Motion 6.1 he first law of thermodynamics for a fluid and the equation of state. We noted in chater 4 that the full formulation of the equations of motion required
Finite Element Analysis of V-Bending of Polypropylene Using Hydrostatic-Pressure-Dependent Plastic Constitutive Equation*
 Materials Transactions, Vol. 48, No. 1 (7). 6 to 664 #7 The Jaan Society for Technology of Plasticity Finite Element Analysis of V-Bending of Polyroylene Using Hydrostatic-Pressure-Deendent Plastic onstitutive
Materials Transactions, Vol. 48, No. 1 (7). 6 to 664 #7 The Jaan Society for Technology of Plasticity Finite Element Analysis of V-Bending of Polyroylene Using Hydrostatic-Pressure-Deendent Plastic onstitutive
A Simple And Efficient FEM-Implementation Of The Modified Mohr-Coulomb Criterion Clausen, Johan Christian; Damkilde, Lars
 Aalborg Universitet A Simle And Efficient FEM-Imlementation Of The Modified Mohr-Coulomb Criterion Clausen, Johan Christian; Damkilde, Lars Published in: Proceedings of the 9th Nordic Seminar on Comutational
Aalborg Universitet A Simle And Efficient FEM-Imlementation Of The Modified Mohr-Coulomb Criterion Clausen, Johan Christian; Damkilde, Lars Published in: Proceedings of the 9th Nordic Seminar on Comutational
GBT (GENERALISED BEAM THEORY)-BASED ELASTIC - PLASTIC POST-BUCKLING ANALYSIS OF STAINLESS STEEL THIN-WALLED MEMBERS
 4 TH INTERNATIONAL EXERTS SEMINAR STAINLESS STEEL IN STRUCTURES ASCOT, UK, 6-7 DECEMBER 2012 (GENERALISED BEAM THEORY)-BASED ELASTIC - LASTIC OST-BUCKLING ANALYSIS OF STAINLESS STEEL THIN-WALLED MEMBERS
4 TH INTERNATIONAL EXERTS SEMINAR STAINLESS STEEL IN STRUCTURES ASCOT, UK, 6-7 DECEMBER 2012 (GENERALISED BEAM THEORY)-BASED ELASTIC - LASTIC OST-BUCKLING ANALYSIS OF STAINLESS STEEL THIN-WALLED MEMBERS
Elementary Analysis in Q p
 Elementary Analysis in Q Hannah Hutter, May Szedlák, Phili Wirth November 17, 2011 This reort follows very closely the book of Svetlana Katok 1. 1 Sequences and Series In this section we will see some
Elementary Analysis in Q Hannah Hutter, May Szedlák, Phili Wirth November 17, 2011 This reort follows very closely the book of Svetlana Katok 1. 1 Sequences and Series In this section we will see some
Feedback-error control
 Chater 4 Feedback-error control 4.1 Introduction This chater exlains the feedback-error (FBE) control scheme originally described by Kawato [, 87, 8]. FBE is a widely used neural network based controller
Chater 4 Feedback-error control 4.1 Introduction This chater exlains the feedback-error (FBE) control scheme originally described by Kawato [, 87, 8]. FBE is a widely used neural network based controller
Meshless Methods for Scientific Computing Final Project
 Meshless Methods for Scientific Comuting Final Project D0051008 洪啟耀 Introduction Floating island becomes an imortant study in recent years, because the lands we can use are limit, so eole start thinking
Meshless Methods for Scientific Comuting Final Project D0051008 洪啟耀 Introduction Floating island becomes an imortant study in recent years, because the lands we can use are limit, so eole start thinking
SHAPE OPTOMIZATION OF H-BEAM FLANGE FOR MAXIMUM PLASTIC ENERGY DISSIPATION
 The Fourth China-Jaan-Korea Joint Symosium on Otimization of Structural and Mechanical Systems Kunming, Nov. 6-9, 2006, China SHAPE OPTOMIZATION OF H-BEAM FLANGE FOR MAXIMUM PLASTIC ENERGY DISSIPATION
The Fourth China-Jaan-Korea Joint Symosium on Otimization of Structural and Mechanical Systems Kunming, Nov. 6-9, 2006, China SHAPE OPTOMIZATION OF H-BEAM FLANGE FOR MAXIMUM PLASTIC ENERGY DISSIPATION
Application of Automated Ball Indentation for Property Measurement of Degraded Zr2.5Nb
 Journal of Minerals & Materials Characterization & Engineering, Vol. 10, No.7,.661-669, 011 jmmce.org Printed in the USA. All rights reserved Alication of Automated Ball Indentation for Proerty Measurement
Journal of Minerals & Materials Characterization & Engineering, Vol. 10, No.7,.661-669, 011 jmmce.org Printed in the USA. All rights reserved Alication of Automated Ball Indentation for Proerty Measurement
Multiscale Surfaces and Amontons Law of Friction
 Tribol Lett (23) 49:539 543 DOI.7/s249-2-94-6 ORIGINAL PAPER Multiscale Surfaces and Amontons Law of Friction J. R. Barber Received: 4 December 22 / Acceted: 24 December 22 / Published online: 26 January
Tribol Lett (23) 49:539 543 DOI.7/s249-2-94-6 ORIGINAL PAPER Multiscale Surfaces and Amontons Law of Friction J. R. Barber Received: 4 December 22 / Acceted: 24 December 22 / Published online: 26 January
Combining Logistic Regression with Kriging for Mapping the Risk of Occurrence of Unexploded Ordnance (UXO)
 Combining Logistic Regression with Kriging for Maing the Risk of Occurrence of Unexloded Ordnance (UXO) H. Saito (), P. Goovaerts (), S. A. McKenna (2) Environmental and Water Resources Engineering, Deartment
Combining Logistic Regression with Kriging for Maing the Risk of Occurrence of Unexloded Ordnance (UXO) H. Saito (), P. Goovaerts (), S. A. McKenna (2) Environmental and Water Resources Engineering, Deartment
A Comparison between Biased and Unbiased Estimators in Ordinary Least Squares Regression
 Journal of Modern Alied Statistical Methods Volume Issue Article 7 --03 A Comarison between Biased and Unbiased Estimators in Ordinary Least Squares Regression Ghadban Khalaf King Khalid University, Saudi
Journal of Modern Alied Statistical Methods Volume Issue Article 7 --03 A Comarison between Biased and Unbiased Estimators in Ordinary Least Squares Regression Ghadban Khalaf King Khalid University, Saudi
MATHEMATICAL MODELLING OF THE WIRELESS COMMUNICATION NETWORK
 Comuter Modelling and ew Technologies, 5, Vol.9, o., 3-39 Transort and Telecommunication Institute, Lomonosov, LV-9, Riga, Latvia MATHEMATICAL MODELLIG OF THE WIRELESS COMMUICATIO ETWORK M. KOPEETSK Deartment
Comuter Modelling and ew Technologies, 5, Vol.9, o., 3-39 Transort and Telecommunication Institute, Lomonosov, LV-9, Riga, Latvia MATHEMATICAL MODELLIG OF THE WIRELESS COMMUICATIO ETWORK M. KOPEETSK Deartment
Numerical and experimental investigation on shot-peening induced deformation. Application to sheet metal forming.
 Coyright JCPDS-International Centre for Diffraction Data 29 ISSN 197-2 511 Numerical and exerimental investigation on shot-eening induced deformation. Alication to sheet metal forming. Florent Cochennec
Coyright JCPDS-International Centre for Diffraction Data 29 ISSN 197-2 511 Numerical and exerimental investigation on shot-eening induced deformation. Alication to sheet metal forming. Florent Cochennec
Various Proofs for the Decrease Monotonicity of the Schatten s Power Norm, Various Families of R n Norms and Some Open Problems
 Int. J. Oen Problems Comt. Math., Vol. 3, No. 2, June 2010 ISSN 1998-6262; Coyright c ICSRS Publication, 2010 www.i-csrs.org Various Proofs for the Decrease Monotonicity of the Schatten s Power Norm, Various
Int. J. Oen Problems Comt. Math., Vol. 3, No. 2, June 2010 ISSN 1998-6262; Coyright c ICSRS Publication, 2010 www.i-csrs.org Various Proofs for the Decrease Monotonicity of the Schatten s Power Norm, Various
VIBRATION ANALYSIS OF BEAMS WITH MULTIPLE CONSTRAINED LAYER DAMPING PATCHES
 Journal of Sound and Vibration (998) 22(5), 78 85 VIBRATION ANALYSIS OF BEAMS WITH MULTIPLE CONSTRAINED LAYER DAMPING PATCHES Acoustics and Dynamics Laboratory, Deartment of Mechanical Engineering, The
Journal of Sound and Vibration (998) 22(5), 78 85 VIBRATION ANALYSIS OF BEAMS WITH MULTIPLE CONSTRAINED LAYER DAMPING PATCHES Acoustics and Dynamics Laboratory, Deartment of Mechanical Engineering, The
KEY ISSUES IN THE ANALYSIS OF PILES IN LIQUEFYING SOILS
 4 th International Conference on Earthquake Geotechnical Engineering June 2-28, 27 KEY ISSUES IN THE ANALYSIS OF PILES IN LIQUEFYING SOILS Misko CUBRINOVSKI 1, Hayden BOWEN 1 ABSTRACT Two methods for analysis
4 th International Conference on Earthquake Geotechnical Engineering June 2-28, 27 KEY ISSUES IN THE ANALYSIS OF PILES IN LIQUEFYING SOILS Misko CUBRINOVSKI 1, Hayden BOWEN 1 ABSTRACT Two methods for analysis
Finite Element Analysis of Concrete Structures Using PlasticDamage Model in 3-D Implementation
 Finite Element Analysis of Concrete Structures Using PlasticDamage Model in 3-D Imlementation O. Omidi1 and V. Lotfi,* Received: October 009 Acceted: August 010 Abstract: Neither damage mechanics model
Finite Element Analysis of Concrete Structures Using PlasticDamage Model in 3-D Imlementation O. Omidi1 and V. Lotfi,* Received: October 009 Acceted: August 010 Abstract: Neither damage mechanics model
Design of Isolated Bridges from the Viewpoint of Collapse under Extreme Earthquakes
 Design of Isolated Bridges from the Viewoint of Collase under Extreme Earthquakes D.W. Chang, Y.T. Lin, C.H. Peng, C.Y. Liou CECI Engineering Consultants, Inc., Taiwan T.Y. Lee National Central University,
Design of Isolated Bridges from the Viewoint of Collase under Extreme Earthquakes D.W. Chang, Y.T. Lin, C.H. Peng, C.Y. Liou CECI Engineering Consultants, Inc., Taiwan T.Y. Lee National Central University,
Hidden Predictors: A Factor Analysis Primer
 Hidden Predictors: A Factor Analysis Primer Ryan C Sanchez Western Washington University Factor Analysis is a owerful statistical method in the modern research sychologist s toolbag When used roerly, factor
Hidden Predictors: A Factor Analysis Primer Ryan C Sanchez Western Washington University Factor Analysis is a owerful statistical method in the modern research sychologist s toolbag When used roerly, factor
SIMULATION OF DIFFUSION PROCESSES IN LABYRINTHIC DOMAINS BY USING CELLULAR AUTOMATA
 SIMULATION OF DIFFUSION PROCESSES IN LABYRINTHIC DOMAINS BY USING CELLULAR AUTOMATA Udo Buschmann and Thorsten Rankel and Wolfgang Wiechert Deartment of Simulation University of Siegen Paul-Bonatz-Str.
SIMULATION OF DIFFUSION PROCESSES IN LABYRINTHIC DOMAINS BY USING CELLULAR AUTOMATA Udo Buschmann and Thorsten Rankel and Wolfgang Wiechert Deartment of Simulation University of Siegen Paul-Bonatz-Str.
On the rotation of orthotropic axes under uniaxial off-axis tension in sheet metals
 64 ISSN 39-07. MECHANIKA. 03 Volume 9(3): 64-68 On the rotation of orthotroic axes under uniaxial off-axis tension in sheet metals Mohammad Zehsaz*, Hadi Mehdiour**, Alireza Alimohammadi*** *Deartment
64 ISSN 39-07. MECHANIKA. 03 Volume 9(3): 64-68 On the rotation of orthotroic axes under uniaxial off-axis tension in sheet metals Mohammad Zehsaz*, Hadi Mehdiour**, Alireza Alimohammadi*** *Deartment
arxiv: v1 [physics.data-an] 26 Oct 2012
![arxiv: v1 [physics.data-an] 26 Oct 2012 arxiv: v1 [physics.data-an] 26 Oct 2012](/thumbs/93/114154382.jpg) Constraints on Yield Parameters in Extended Maximum Likelihood Fits Till Moritz Karbach a, Maximilian Schlu b a TU Dortmund, Germany, moritz.karbach@cern.ch b TU Dortmund, Germany, maximilian.schlu@cern.ch
Constraints on Yield Parameters in Extended Maximum Likelihood Fits Till Moritz Karbach a, Maximilian Schlu b a TU Dortmund, Germany, moritz.karbach@cern.ch b TU Dortmund, Germany, maximilian.schlu@cern.ch
REFINED STRAIN ENERGY OF THE SHELL
 REFINED STRAIN ENERGY OF THE SHELL Ryszard A. Walentyński Deartment of Building Structures Theory, Silesian University of Technology, Gliwice, PL44-11, Poland ABSTRACT The aer rovides information on evaluation
REFINED STRAIN ENERGY OF THE SHELL Ryszard A. Walentyński Deartment of Building Structures Theory, Silesian University of Technology, Gliwice, PL44-11, Poland ABSTRACT The aer rovides information on evaluation
Quantitative estimates of propagation of chaos for stochastic systems with W 1, kernels
 oname manuscrit o. will be inserted by the editor) Quantitative estimates of roagation of chaos for stochastic systems with W, kernels Pierre-Emmanuel Jabin Zhenfu Wang Received: date / Acceted: date Abstract
oname manuscrit o. will be inserted by the editor) Quantitative estimates of roagation of chaos for stochastic systems with W, kernels Pierre-Emmanuel Jabin Zhenfu Wang Received: date / Acceted: date Abstract
International Journal of Plasticity
 International Journal of lasticity 26 (2010) 141 148 Contents lists available at ScienceDirect International Journal of lasticity journal homepage: www.elsevier.com/locate/ijplas The equivalent axisymmetric
International Journal of lasticity 26 (2010) 141 148 Contents lists available at ScienceDirect International Journal of lasticity journal homepage: www.elsevier.com/locate/ijplas The equivalent axisymmetric
Shadow Computing: An Energy-Aware Fault Tolerant Computing Model
 Shadow Comuting: An Energy-Aware Fault Tolerant Comuting Model Bryan Mills, Taieb Znati, Rami Melhem Deartment of Comuter Science University of Pittsburgh (bmills, znati, melhem)@cs.itt.edu Index Terms
Shadow Comuting: An Energy-Aware Fault Tolerant Comuting Model Bryan Mills, Taieb Znati, Rami Melhem Deartment of Comuter Science University of Pittsburgh (bmills, znati, melhem)@cs.itt.edu Index Terms
A Qualitative Event-based Approach to Multiple Fault Diagnosis in Continuous Systems using Structural Model Decomposition
 A Qualitative Event-based Aroach to Multile Fault Diagnosis in Continuous Systems using Structural Model Decomosition Matthew J. Daigle a,,, Anibal Bregon b,, Xenofon Koutsoukos c, Gautam Biswas c, Belarmino
A Qualitative Event-based Aroach to Multile Fault Diagnosis in Continuous Systems using Structural Model Decomosition Matthew J. Daigle a,,, Anibal Bregon b,, Xenofon Koutsoukos c, Gautam Biswas c, Belarmino
Guidelines for Constructing Strain Gradient Plasticity Theories
 . A. Fleck Deartment of Engineering, Cambridge University, Trumington Street, Cambridge CB2 1Z, UK J. W. Hutchinson School of Engineering and Alied Sciences, Harvard University, Cambridge, MA 2138 J. R.
. A. Fleck Deartment of Engineering, Cambridge University, Trumington Street, Cambridge CB2 1Z, UK J. W. Hutchinson School of Engineering and Alied Sciences, Harvard University, Cambridge, MA 2138 J. R.
Single Crystal Gradient Plasticity Part I
 Chair for Continuum Mechanics Institute of Engineering Mechanics (Prof. Böhlke) Department of Mechanical Engineering S. Wulfinghoff, T. Böhlke, E. Bayerschen Single Crystal Gradient Plasticity Part I Chair
Chair for Continuum Mechanics Institute of Engineering Mechanics (Prof. Böhlke) Department of Mechanical Engineering S. Wulfinghoff, T. Böhlke, E. Bayerschen Single Crystal Gradient Plasticity Part I Chair
The. Consortium. Continuum Mechanics. Original notes by Professor Mike Gunn, South Bank University, London, UK Produced by the CRISP Consortium Ltd
 The C R I S P Consortium Continuum Mechanics Original notes b Professor Mike Gunn, South Bank Universit, London, UK Produced b the CRISP Consortium Ltd THOR OF STRSSS In a three dimensional loaded bod,
The C R I S P Consortium Continuum Mechanics Original notes b Professor Mike Gunn, South Bank Universit, London, UK Produced b the CRISP Consortium Ltd THOR OF STRSSS In a three dimensional loaded bod,
MATH 2710: NOTES FOR ANALYSIS
 MATH 270: NOTES FOR ANALYSIS The main ideas we will learn from analysis center around the idea of a limit. Limits occurs in several settings. We will start with finite limits of sequences, then cover infinite
MATH 270: NOTES FOR ANALYSIS The main ideas we will learn from analysis center around the idea of a limit. Limits occurs in several settings. We will start with finite limits of sequences, then cover infinite
Conference Paper A Finite Element Approach for the Elastic-Plastic Behavior of a Steel Pipe Used to Transport Natural Gas
 Conference Paers in Energy, Article ID 267095, 10 ages htt://dx.doi.org/10.1155/2013/267095 Conference Paer A Finite Element Aroach for the Elastic-Plastic Behavior of a Steel Pie Used to Transort Natural
Conference Paers in Energy, Article ID 267095, 10 ages htt://dx.doi.org/10.1155/2013/267095 Conference Paer A Finite Element Aroach for the Elastic-Plastic Behavior of a Steel Pie Used to Transort Natural
Statics and dynamics: some elementary concepts
 1 Statics and dynamics: some elementary concets Dynamics is the study of the movement through time of variables such as heartbeat, temerature, secies oulation, voltage, roduction, emloyment, rices and
1 Statics and dynamics: some elementary concets Dynamics is the study of the movement through time of variables such as heartbeat, temerature, secies oulation, voltage, roduction, emloyment, rices and
Buckling of Spherical Shells Revisited. John W. Hutchinson. School of Engineering and Applied Sciences, Harvard University.
 Buckling of Sherical Shells Revisited John W. Hutchinson School of Engineering and Alied Sciences, Harvard University Abstract A study is resented of the ost-buckling behavior and imerfection-sensitivity
Buckling of Sherical Shells Revisited John W. Hutchinson School of Engineering and Alied Sciences, Harvard University Abstract A study is resented of the ost-buckling behavior and imerfection-sensitivity
RE-ORIENTATION OF ORTHOTROPIC AXES IN SHEET METAL USING A DEVELOPED METHOD BASED ON A SIMPLE SEMI GEOMETRICAL MODEL
 U.P.B. Sci. Bull., Series D, Vol. 75, Iss. 4, 2013 ISSN 1454-2358 RE-ORIENTATION OF ORTHOTROPIC AXES IN SHEET META USING A DEVEOPED METHOD BASED ON A SIMPE SEMI GEOMETRICA MODE Mohammad ZEHSAZ 1, Hadi
U.P.B. Sci. Bull., Series D, Vol. 75, Iss. 4, 2013 ISSN 1454-2358 RE-ORIENTATION OF ORTHOTROPIC AXES IN SHEET META USING A DEVEOPED METHOD BASED ON A SIMPE SEMI GEOMETRICA MODE Mohammad ZEHSAZ 1, Hadi
LECTURE 3 BASIC QUANTUM THEORY
 LECTURE 3 BASIC QUANTUM THEORY Matter waves and the wave function In 194 De Broglie roosed that all matter has a wavelength and exhibits wave like behavior. He roosed that the wavelength of a article of
LECTURE 3 BASIC QUANTUM THEORY Matter waves and the wave function In 194 De Broglie roosed that all matter has a wavelength and exhibits wave like behavior. He roosed that the wavelength of a article of
Identification of the source of the thermoelastic response from orthotropic laminated composites
 Identification of the source of the thermoelastic resonse from orthotroic laminated comosites S. Sambasivam, S. Quinn and J.M. Dulieu-Barton School of Engineering Sciences, University of Southamton, Highfield,
Identification of the source of the thermoelastic resonse from orthotroic laminated comosites S. Sambasivam, S. Quinn and J.M. Dulieu-Barton School of Engineering Sciences, University of Southamton, Highfield,
1 University of Edinburgh, 2 British Geological Survey, 3 China University of Petroleum
 Estimation of fluid mobility from frequency deendent azimuthal AVO a synthetic model study Yingrui Ren 1*, Xiaoyang Wu 2, Mark Chaman 1 and Xiangyang Li 2,3 1 University of Edinburgh, 2 British Geological
Estimation of fluid mobility from frequency deendent azimuthal AVO a synthetic model study Yingrui Ren 1*, Xiaoyang Wu 2, Mark Chaman 1 and Xiangyang Li 2,3 1 University of Edinburgh, 2 British Geological
Chapter 2 Introductory Concepts of Wave Propagation Analysis in Structures
 Chater 2 Introductory Concets of Wave Proagation Analysis in Structures Wave roagation is a transient dynamic henomenon resulting from short duration loading. Such transient loadings have high frequency
Chater 2 Introductory Concets of Wave Proagation Analysis in Structures Wave roagation is a transient dynamic henomenon resulting from short duration loading. Such transient loadings have high frequency
Numerical simulation of sheet metal forming using anisotropic strain-rate potentials
 Numerical simulation of sheet metal forming using anisotroic strain-rate otentials Meziane Rabahallah, Salima Bouvier, Tudor Balan, Brigitte Bacroix To cite this version: Meziane Rabahallah, Salima Bouvier,
Numerical simulation of sheet metal forming using anisotroic strain-rate otentials Meziane Rabahallah, Salima Bouvier, Tudor Balan, Brigitte Bacroix To cite this version: Meziane Rabahallah, Salima Bouvier,
PARAMETER IDENTIFICATION OF ADVANCED PLASTIC POTENTIALS AND IMPACT ON PLASTIC ANISOTROPY PREDICTION
 PARAMETER IDENTIFICATION OF ADVANCED PLASTIC POTENTIALS AND IMPACT ON PLASTIC ANISOTROPY PREDICTION Meziane Rabahallah, Tudor Balan, Salima Bouvier, Brigitte Bacroix, Frédéric Barlat, Kwansoo Chung, Cristian
PARAMETER IDENTIFICATION OF ADVANCED PLASTIC POTENTIALS AND IMPACT ON PLASTIC ANISOTROPY PREDICTION Meziane Rabahallah, Tudor Balan, Salima Bouvier, Brigitte Bacroix, Frédéric Barlat, Kwansoo Chung, Cristian
4. Score normalization technical details We now discuss the technical details of the score normalization method.
 SMT SCORING SYSTEM This document describes the scoring system for the Stanford Math Tournament We begin by giving an overview of the changes to scoring and a non-technical descrition of the scoring rules
SMT SCORING SYSTEM This document describes the scoring system for the Stanford Math Tournament We begin by giving an overview of the changes to scoring and a non-technical descrition of the scoring rules
Modified Quasi-Static, Elastic-Plastic Analysis for Blast Walls with Partially Fixed Support
 Article Modified Quasi-Static, Elastic-Plastic Analysis for Blast Walls with Partially Fixed Suort Pattamad Panedojaman Deartment of Civil Engineering, Faculty of Engineering, Prince of Songkla University,
Article Modified Quasi-Static, Elastic-Plastic Analysis for Blast Walls with Partially Fixed Suort Pattamad Panedojaman Deartment of Civil Engineering, Faculty of Engineering, Prince of Songkla University,
Kinetics of Protein Adsorption and Desorption on Surfaces with Grafted Polymers
 1516 Biohysical Journal Volume 89 Setember 2005 1516 1533 Kinetics of Protein Adsortion and Desortion on Surfaces with Grafted Polymers Fang Fang,* Javier Satulovsky, y and Igal Szleifer* *Deartment of
1516 Biohysical Journal Volume 89 Setember 2005 1516 1533 Kinetics of Protein Adsortion and Desortion on Surfaces with Grafted Polymers Fang Fang,* Javier Satulovsky, y and Igal Szleifer* *Deartment of
Engineering Fracture Mechanics
 Engineering Fracture Mechanics 90 (2012) 172 179 Contents lists available at SciVerse ScienceDirect Engineering Fracture Mechanics journal homeage: www.elsevier.com/locate/engfracmech Discussion of: Mode
Engineering Fracture Mechanics 90 (2012) 172 179 Contents lists available at SciVerse ScienceDirect Engineering Fracture Mechanics journal homeage: www.elsevier.com/locate/engfracmech Discussion of: Mode
Time Domain Calculation of Vortex Induced Vibration of Long-Span Bridges by Using a Reduced-order Modeling Technique
 2017 2nd International Conference on Industrial Aerodynamics (ICIA 2017) ISBN: 978-1-60595-481-3 Time Domain Calculation of Vortex Induced Vibration of Long-San Bridges by Using a Reduced-order Modeling
2017 2nd International Conference on Industrial Aerodynamics (ICIA 2017) ISBN: 978-1-60595-481-3 Time Domain Calculation of Vortex Induced Vibration of Long-San Bridges by Using a Reduced-order Modeling
Chapter 5. Transient Conduction. Islamic Azad University
 Chater 5 Transient Conduction Islamic Azad University Karaj Branch 1 Transient Conduction Many heat transfer roblems are time deendent Changes in oerating conditions in a system cause temerature variation
Chater 5 Transient Conduction Islamic Azad University Karaj Branch 1 Transient Conduction Many heat transfer roblems are time deendent Changes in oerating conditions in a system cause temerature variation
Introduction to Landau s Fermi Liquid Theory
 Introduction to Landau s Fermi Liquid Theory Erkki Thuneberg Deartment of hysical sciences University of Oulu 29 1. Introduction The rincial roblem of hysics is to determine how bodies behave when they
Introduction to Landau s Fermi Liquid Theory Erkki Thuneberg Deartment of hysical sciences University of Oulu 29 1. Introduction The rincial roblem of hysics is to determine how bodies behave when they
2. Keywords Topology optimization, stress constraints, Raghava criterion, Ishai criterion.
 oology Otimization with Different Stress Limits in ension and Comression P. Duysinx Robotics and Automation, Institute of Mechanics, C3, University of Liège, 1 Rue Solvay, B-4 Liège, Belgium, el: +3.4.366.91.94,
oology Otimization with Different Stress Limits in ension and Comression P. Duysinx Robotics and Automation, Institute of Mechanics, C3, University of Liège, 1 Rue Solvay, B-4 Liège, Belgium, el: +3.4.366.91.94,
Phase transition. Asaf Pe er Background
 Phase transition Asaf Pe er 1 November 18, 2013 1. Background A hase is a region of sace, throughout which all hysical roerties (density, magnetization, etc.) of a material (or thermodynamic system) are
Phase transition Asaf Pe er 1 November 18, 2013 1. Background A hase is a region of sace, throughout which all hysical roerties (density, magnetization, etc.) of a material (or thermodynamic system) are
SYMPLECTIC STRUCTURES: AT THE INTERFACE OF ANALYSIS, GEOMETRY, AND TOPOLOGY
 SYMPLECTIC STRUCTURES: AT THE INTERFACE OF ANALYSIS, GEOMETRY, AND TOPOLOGY FEDERICA PASQUOTTO 1. Descrition of the roosed research 1.1. Introduction. Symlectic structures made their first aearance in
SYMPLECTIC STRUCTURES: AT THE INTERFACE OF ANALYSIS, GEOMETRY, AND TOPOLOGY FEDERICA PASQUOTTO 1. Descrition of the roosed research 1.1. Introduction. Symlectic structures made their first aearance in
Sums of independent random variables
 3 Sums of indeendent random variables This lecture collects a number of estimates for sums of indeendent random variables with values in a Banach sace E. We concentrate on sums of the form N γ nx n, where
3 Sums of indeendent random variables This lecture collects a number of estimates for sums of indeendent random variables with values in a Banach sace E. We concentrate on sums of the form N γ nx n, where
integral invariant relations is not limited to one or two such
 The Astronomical Journal, 126:3138 3142, 2003 December # 2003. The American Astronomical Society. All rights reserved. Printed in U.S.A. EFFICIENT ORBIT INTEGRATION BY SCALING AND ROTATION FOR CONSISTENCY
The Astronomical Journal, 126:3138 3142, 2003 December # 2003. The American Astronomical Society. All rights reserved. Printed in U.S.A. EFFICIENT ORBIT INTEGRATION BY SCALING AND ROTATION FOR CONSISTENCY
A Continuum/Discontinuum Micro Plane Damage Model for Concrete
 A Continuum/Discontinuum icro Plane Damage odel for Concrete Downloaded from ce.iust.ac.ir at 17:17 IRST on Sunday January 6th 2019 1.Introduction S. A. Sadrnejad 1 and. abibzadeh 2 Deartment of Civil
A Continuum/Discontinuum icro Plane Damage odel for Concrete Downloaded from ce.iust.ac.ir at 17:17 IRST on Sunday January 6th 2019 1.Introduction S. A. Sadrnejad 1 and. abibzadeh 2 Deartment of Civil
Evaluating Circuit Reliability Under Probabilistic Gate-Level Fault Models
 Evaluating Circuit Reliability Under Probabilistic Gate-Level Fault Models Ketan N. Patel, Igor L. Markov and John P. Hayes University of Michigan, Ann Arbor 48109-2122 {knatel,imarkov,jhayes}@eecs.umich.edu
Evaluating Circuit Reliability Under Probabilistic Gate-Level Fault Models Ketan N. Patel, Igor L. Markov and John P. Hayes University of Michigan, Ann Arbor 48109-2122 {knatel,imarkov,jhayes}@eecs.umich.edu
FEM simulation of a crack propagation in a round bar under combined tension and torsion fatigue loading
 FEM simulation of a crack roagation in a round bar under combined tension and torsion fatigue loading R.Citarella, M.Leore Det. of Industrial Engineering University of Salerno - Fisciano (SA), Italy. rcitarella@unisa.it
FEM simulation of a crack roagation in a round bar under combined tension and torsion fatigue loading R.Citarella, M.Leore Det. of Industrial Engineering University of Salerno - Fisciano (SA), Italy. rcitarella@unisa.it
A compression line for soils with evolving particle and pore size distributions due to particle crushing
 Russell, A. R. (2011) Géotechnique Letters 1, 5 9, htt://dx.doi.org/10.1680/geolett.10.00003 A comression line for soils with evolving article and ore size distributions due to article crushing A. R. RUSSELL*
Russell, A. R. (2011) Géotechnique Letters 1, 5 9, htt://dx.doi.org/10.1680/geolett.10.00003 A comression line for soils with evolving article and ore size distributions due to article crushing A. R. RUSSELL*
CONCRETE MATERIAL MODELING IN EXPLICIT COMPUTATIONS ABSTRACT
 Worksho on Recent Advances in Comutational Structural Dynamics and High Performance Comuting USAE Waterways Exeriment Station Aril 24-26 1996 CONCRETE MATERIAL MODELING IN EXPLICIT COMPUTATIONS L. Javier
Worksho on Recent Advances in Comutational Structural Dynamics and High Performance Comuting USAE Waterways Exeriment Station Aril 24-26 1996 CONCRETE MATERIAL MODELING IN EXPLICIT COMPUTATIONS L. Javier
Equivalence of Wilson actions
 Prog. Theor. Ex. Phys. 05, 03B0 7 ages DOI: 0.093/te/tv30 Equivalence of Wilson actions Physics Deartment, Kobe University, Kobe 657-850, Jaan E-mail: hsonoda@kobe-u.ac.j Received June 6, 05; Revised August
Prog. Theor. Ex. Phys. 05, 03B0 7 ages DOI: 0.093/te/tv30 Equivalence of Wilson actions Physics Deartment, Kobe University, Kobe 657-850, Jaan E-mail: hsonoda@kobe-u.ac.j Received June 6, 05; Revised August
An elasto-plastic model to describe the undrained cyclic behavior of saturated sand with initial static shear
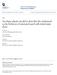 University of Wollongong Research Online Faculty of Engineering - Paers (Archive) Faculty of Engineering and Information Sciences 211 An elasto-lastic model to describe the undrained cyclic behavior of
University of Wollongong Research Online Faculty of Engineering - Paers (Archive) Faculty of Engineering and Information Sciences 211 An elasto-lastic model to describe the undrained cyclic behavior of
Effective conductivity in a lattice model for binary disordered media with complex distributions of grain sizes
 hys. stat. sol. b 36, 65-633 003 Effective conductivity in a lattice model for binary disordered media with comlex distributions of grain sizes R. PIASECKI Institute of Chemistry, University of Oole, Oleska
hys. stat. sol. b 36, 65-633 003 Effective conductivity in a lattice model for binary disordered media with comlex distributions of grain sizes R. PIASECKI Institute of Chemistry, University of Oole, Oleska
VI. Electrokinetics. Lecture 31: Electrokinetic Energy Conversion
 VI. Electrokinetics Lecture 31: Electrokinetic Energy Conversion MIT Student 1 Princiles 1.1 General Theory We have the following equation for the linear electrokinetic resonse of a nanochannel: ( ) (
VI. Electrokinetics Lecture 31: Electrokinetic Energy Conversion MIT Student 1 Princiles 1.1 General Theory We have the following equation for the linear electrokinetic resonse of a nanochannel: ( ) (
VISCOELASTIC PROPERTIES OF INHOMOGENEOUS NANOCOMPOSITES
 VISCOELASTIC PROPERTIES OF INHOMOGENEOUS NANOCOMPOSITES V. V. Novikov ), K.W. Wojciechowski ) ) Odessa National Polytechnical University, Shevchenko Prosekt, 6544 Odessa, Ukraine; e-mail: novikov@te.net.ua
VISCOELASTIC PROPERTIES OF INHOMOGENEOUS NANOCOMPOSITES V. V. Novikov ), K.W. Wojciechowski ) ) Odessa National Polytechnical University, Shevchenko Prosekt, 6544 Odessa, Ukraine; e-mail: novikov@te.net.ua
Scaling Multiple Point Statistics for Non-Stationary Geostatistical Modeling
 Scaling Multile Point Statistics or Non-Stationary Geostatistical Modeling Julián M. Ortiz, Steven Lyster and Clayton V. Deutsch Centre or Comutational Geostatistics Deartment o Civil & Environmental Engineering
Scaling Multile Point Statistics or Non-Stationary Geostatistical Modeling Julián M. Ortiz, Steven Lyster and Clayton V. Deutsch Centre or Comutational Geostatistics Deartment o Civil & Environmental Engineering
ε(ω,k) =1 ω = ω'+kv (5) ω'= e2 n 2 < 0, where f is the particle distribution function and v p f v p = 0 then f v = 0. For a real f (v) v ω (kv T
 High High Power Power Laser Laser Programme Programme Theory Theory and Comutation and Asects of electron acoustic wave hysics in laser backscatter N J Sircombe, T D Arber Deartment of Physics, University
High High Power Power Laser Laser Programme Programme Theory Theory and Comutation and Asects of electron acoustic wave hysics in laser backscatter N J Sircombe, T D Arber Deartment of Physics, University
Maximum Entropy and the Stress Distribution in Soft Disk Packings Above Jamming
 Maximum Entroy and the Stress Distribution in Soft Disk Packings Above Jamming Yegang Wu and S. Teitel Deartment of Physics and Astronomy, University of ochester, ochester, New York 467, USA (Dated: August
Maximum Entroy and the Stress Distribution in Soft Disk Packings Above Jamming Yegang Wu and S. Teitel Deartment of Physics and Astronomy, University of ochester, ochester, New York 467, USA (Dated: August
Wave Drift Force in a Two-Layer Fluid of Finite Depth
 Wave Drift Force in a Two-Layer Fluid of Finite Deth Masashi Kashiwagi Research Institute for Alied Mechanics, Kyushu University, Jaan Abstract Based on the momentum and energy conservation rinciles, a
Wave Drift Force in a Two-Layer Fluid of Finite Deth Masashi Kashiwagi Research Institute for Alied Mechanics, Kyushu University, Jaan Abstract Based on the momentum and energy conservation rinciles, a
