ADVANCED PROBLEMS AND SOLUTIONS
|
|
|
- Kelley Carson
- 5 years ago
- Views:
Transcription
1 ADVANCED PROBLEMS AND SOLUTIONS EDITED BY FLORIAN LUCA Please send all communications concerning ADVANCED PROBLEMS AND SOLUTIONS to FLORIAN LUCA, MATHEMATICAL INSTITUTE, UNAM, CP 0450, MEXICO DF, MEXICO or by at as files of the type tex, dvi, ps, doc, html, pdf, etc. This department especially welcomes problems believed to be new or extending old results. Proposers should submit solutions or other information that will assist the editor. To facilitate their consideration, all solutions sent by regular mail should be submitted on separate signed sheets within two months after publication of the problems. PROBLEMS PROPOSED IN THIS ISSUE H-75 Proposed by D. M. Bătineţu-Giurgiu, Bucharest and Neculai Stanciu, Buzău, Romania. Prove that F 2n m+ + 2n+ F 2n m+ F m + + 2n+ n F n m+ Fm n + 2n+ n+ F m F n m+ F n m + + 2n+ 2n F m+ Fm+ F 2n m p+ p+ F 2n+ p+ m+2 2 p F m F m+ holds for any p 0 and positive integers m and n, and that the same inequality holds with all the F s replaced by L s. H-752 Proposed by D. M. Bătineţu-Giurgiu, Bucharest and Neculai Stanciu, Buzău, Romania. Prove that 2n+ 2n+ p 2m+ p 2m+ p p 5 m L 2m+ F 5 n L 2n+ F, p p p0 2n+ 2 5 m F 2m+ p0 0 p 2n+ p 0 p p0 0 2m+ p 2m+ L 5 n F 2n+ p p0 0 p L. H-753 Proposed by H. Ohtsua, Saitama, Japan. For integers n, m, a 0 and b, prove that n 2m Fa+b 4m 4m an+b+r F anr L an+a+2br 2mr 25 m + F ar r 4m n 2m 25 m. MAY
2 THE FIBONACCI QUARTERLY H-754 Proposed by H. Ohtsua, Saitama, Japan. Let a, b and n be integers. The two sequences {T n } and {S n } satisfy T n+3 T n+2 +T n+ +T n with arbitrary T 0, T, T 2, S n+3 S n+2 +S n+ +S n with S 0 3, S, S 2 3 for all integers n. Let R n S n +. For n, prove that n Ra 2 R2 a Ta+b 2 A n A 0, where A n 2T an+b R a T an+a+b +R a T ana+b T an+a+b T ana+b 2 R a T an+b 2. SOLUTIONS Infinite Sums With Reciprocals of Squares of Fibonacci and Lucas Numbers H-724 Proposed by H. Ohtsua, Saitama, Japan. Vol. 50, No. 3, August 202 Determine Solution by the proposer. F 2 4 The following identity is easily verified. L L 2 2 5F 2 n L2 n 4n. If n 0, dividing both sides of the identity by F 2 2n, 2 5 L 2 n F 2 n 4n F2n 2. F 2 2. Using the above identity, we have F 2 L 2 + L 2 F F L 2 + L 2 F F 2 F F F F 2 + F 2 4 F F 2 4 F VOLUME 52, NUMBER 2
3 ADVANCED PROBLEMS AND SOLUTIONS Thus, we have Therefore, 5 F 2 4 F 2 4 L L L 2 2 L 2 2 F 2 2 F Also solved by Paul S. Brucman and Dmitry Fleishman. Sums With Powers of 3, 4 and Binomial Coefficients H-725 Proposed by Paul S. Brucman, Nanaimo, BC. Vol. 50, No. 4, November 202 Prove the following identities valid for n 0,,2,... n3 a n4 6 0 where sinθ 2/3; n b n4 8 3n+53 n n 3 n/2sinnθ sinθ, 9n+7+3 3n/2 cosnρ+sinnρ/ 2, where sinρ 2/27; n2 pqp 2 q 2 2 c 2 p 2 +q 2 2 pp+qn+ qq p n+ 2p 2 +2pq q 2 p 2 +q 2 n 0 + ppqn+ qq +p n+ 2p 2 2pq q 2 p 2 +q 2, where p > q > 0 are integers. n Solution by G. C. Greubel. a The process for the three series will be to consider the generating function of the given relations and compare the final results. For the first series in question consider From this, we have Sn tn n,0 0 S n n+ 0 n n t n n t t 4 4t 4t 27t 4 0 4t + n 4t n n! 4t+27t4. MAY
4 THE FIBONACCI QUARTERLY Alternatively, let φ n be given by for which φ n 6 [ φ n tn 6 3n+53 n n 3 n/2sinnθ, sinθ 56t 3t 2 ] 3t n sinnθ. sinθ The summation on the right-hand side can be evaluated as follows. 3t n sinnθ e inθ e inθ 3t n 2i e iθ 2i + 3e e iθ iθt cosθt sinθ 3e iθ t +2. 3cosθt+3t 2 From this, we have [ φ nt n ] 56t 6 3t cosθt +2. 3cosθt+3t 2 In order to reduce this expression use sinθ 2/3 or cosθ /3 to obtain φ n tn [ ] 56t 6 6t+9t t +2t+3t 2 By comparing equations and 2, we are led to the desired result 0 n3 where sinθ 2/ n4 6 4t+27t2. 2 3n+53 n n 3 n/2sinnθ, sinθ b Let Sn 2 be the series to be summed. As before, consider the generating function for this series. Snt 2 n [n/4] 0 n t n4 t n n,0 3 + n 4t n n! 4t n n t n+3 27t 4 0 4t 3 4t 2 4t 3 +27t VOLUME 52, NUMBER 2
5 ADVANCED PROBLEMS AND SOLUTIONS Now that we have the desired generating function to compare to, let φ 2 n be the right-hand side of the desired result and proceed to find its generating function. φ 2 n tn 7+9n+ 33n/2 2cosnρ+sinnρ t n 8 2 where Υ,2 are the series Υ 8 7+2t t 2 + Υ + Υ 2, cosnρ3 3/2 t n, and Υ 2 Evaluating Υ yields Υ [ ] 2 3 3/2 e iρ t + 3 3/2 e iρ t The result for Υ 2 is similar and is given by Υ 2 sinnρ3 3/2 t n. 3 3/2 cosρ t 2 3 3/2 cosρ t+27t /2 sinρ t 2 3 3/2 cosρ t+27t2. 6 By combining 4, 5 and 6, the resulting series taes the form φ 2 n tn 7+2t 8 t /2 2cosρsinρt /2 cosρt+27t 2 Now using the provided value sinρ 2/27, which also provides cosρ 25/27, leads to the reduction φ 2 nt n [ ] 7+2t 8 t t 0t+27t 3 [ 844t+268t 2 ] 8 2t+48t 2 64t 3 +27t 4 4t 2 4t 3 +27t4. 8 Since 3 and 8 have the same generating function, then we conclude that 0 n 3 where sinρ 2/ n n+ 33n/2 2cosnρ+sinnρ, 9 2 c Let x pqp2 q 2 p 2 +q 2 2, 0 MAY
6 THE FIBONACCI QUARTERLY and let Sn 3 be the series in question, then [n/4] n2 Sn 3 tn 2 0 n,0 x 2 t n n,0 2 + n x 2 t 4 t n n! t n+2 2 x 2 t 4 0 x 2 t 4 t n t 2 t t 2 x 2 t4. Alternatively, let φ 3 n be the right-hand side of the third series in question and see the generating function. where Υ 3 φ 3 nt n 2p 2 +2pq q 2 Υ 3 + pp+q n+ qq p n+ p 2 +q 2 n t n, and Υ 4 2p 2 2pq q 2 Υ 4, 2 ppq n+ qp+q n+ p 2 +q 2 n t n. Consider the evaluation of Υ 3. This is done in the following way. pp+q n+ qq p n+ Υ 3 p 2 +q 2 n t n pp+qp2 +q 2 p 2 +q 2 pp+qt qq pp2 +q 2 p 2 +q 2 qq pt p 2 +2pq q 2 p 2 +q 2 2 p 2 +q 2 2 tpqp 2 q 2 t 2 p2 +2pq q 2 txt 2, 3 where x is given by 0. The same process may be applied to evaluating Υ 4 and we are led to the result Υ 4 p2 2pq q 2 t+xt 2. 4 From these expressions equation 2 is reduced to φ 3 n tn 2 txt 2 + t+xt 2 t t 2 x 2 t 4. This is the same generating function as that of equation. Thus leading to the statement n2 pqp 2 q p 2 +q 2 2 pp+qn+ qq p n+ 2p 2 +2pq q 2 p 2 +q 2 n 0 where p > q > 0 are integers. + ppqn+ qq +p n+ 2p 2 2pq q 2 p 2 +q 2 n, 5 Also solved by Paul S. Brucman and Kenneth B. Davenport. 90 VOLUME 52, NUMBER 2
7 ADVANCED PROBLEMS AND SOLUTIONS Sums of Sums of Reciprocals of Fibonacci Numbers H-726 Proposed by Hideyui Ohtsua, Saitama, Japan. Vol. 50, No. 4, November 202 Prove that F 2 F 4 F 8 F 6 F 2 n F 2 F 2. Solution by the proposer. First, we will prove the following lemma. Lemma. F n F n+ α n + F n α n+ ; F n+ 2 F 2n α n n F n α 2n. F 2n Proof of Lemma. We have Thus, 5αFn+ +F n αα n+ β n+ +α n β n α n+2 +α n α n α 2 + 5α n+. α n+ αf n+ +F n. Dividing both sides of this identity by α n+ F n F n+, we get identity. 2 We have Thus, α n L n α n α n +β n α 2n + n. α 2n α n L n n. Dividing both sides of this identity by α 2n F 2n, we get identity 2. Using Lemma, we have F 2 F 2 Using Lemma 2, we have F 4 α 2 + F 2 α 2 F 2 α 2 F 2 α 4 F 4 α F. α 42 F MAY 204 9
8 THE FIBONACCI QUARTERLY Using Lemma 2, we have We have Thus, we obtain, F n3 2 n lim N F 2 lim N n3 α 4 F 4 F 2 F 2 F 2 F 2 F 2 α F N α 2n F 2 n α 2n F 2 n α 2N F 2 N α 4 F 4 + F n3 2 n F 4 + Also solved by Paul S. Brucman. α 4 F 4. 3 α 2 F 2 by Lemma 2 + F n3 2 n α 42 F 42 by F 4. by 2 and 3. F 2 F VOLUME 52, NUMBER 2
ADVANCED PROBLEMS AND SOLUTIONS PROBLEMS PROPOSED IN THIS ISSUE
 ADVANCED PROBLEMS AND SOLUTIONS EDITED BY LORIAN LUCA Please sen all communications concerning ADVANCED PROBLEMS AND SOLUTIONS to LORIAN LUCA, SCHOOL O MATHEMATICS, UNIVERSITY O THE WITWA- TERSRAND, PRIVATE
ADVANCED PROBLEMS AND SOLUTIONS EDITED BY LORIAN LUCA Please sen all communications concerning ADVANCED PROBLEMS AND SOLUTIONS to LORIAN LUCA, SCHOOL O MATHEMATICS, UNIVERSITY O THE WITWA- TERSRAND, PRIVATE
ELEMENTARY PROBLEMS AND SOLUTIONS
 EDITED BY RUSS EULER AND JAWAD SADEK Please submit all new problem proposals their solutions to the Problems Editor, DR. RUSS EULER, Department of Mathematics Statistics, Northwest Missouri State University,
EDITED BY RUSS EULER AND JAWAD SADEK Please submit all new problem proposals their solutions to the Problems Editor, DR. RUSS EULER, Department of Mathematics Statistics, Northwest Missouri State University,
ELEMENTARY PROBLEMS AND SOLUTIONS
 EDITED BY RUSS EULER AND JAWAD SADEK Please submit all new problem proposals and their solutions to the Problems Editor, DR. RUSS EULER, Department of Mathematics and Statistics, Northwest Missouri State
EDITED BY RUSS EULER AND JAWAD SADEK Please submit all new problem proposals and their solutions to the Problems Editor, DR. RUSS EULER, Department of Mathematics and Statistics, Northwest Missouri State
ELEMENTARY PROBLEMS AND SOLUTIONS
 EDITED BY RUSS EULER AND JAWAD SADEK Please submit all new problem proposals their solutions to the Problems Editor, DR. RUSS EULER, Department of Mathematics Statistics, Northwest Missouri State University,
EDITED BY RUSS EULER AND JAWAD SADEK Please submit all new problem proposals their solutions to the Problems Editor, DR. RUSS EULER, Department of Mathematics Statistics, Northwest Missouri State University,
ADVANCED PROBLEMS AND SOLUTIONS
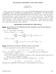 ADVANCED PROBLEMS AND SOLUTIONS EDITED BY FLORIAN LUCA Please sed all commuicatios cocerig ADVANCED PROBLEMS AND SOLUTIONS to FLORIAN LUCA, SCHOOL OF MATHEMATICS, UNIVERSITY OF THE WITWA- TERSRAND, WITS
ADVANCED PROBLEMS AND SOLUTIONS EDITED BY FLORIAN LUCA Please sed all commuicatios cocerig ADVANCED PROBLEMS AND SOLUTIONS to FLORIAN LUCA, SCHOOL OF MATHEMATICS, UNIVERSITY OF THE WITWA- TERSRAND, WITS
ADVANCED PROBLEMS AND SOLUTIONS
 Edited by Florian Luca Please send all communications concerning ADVANCED PROBLEMS AND SOLU- TIONS to FLORIAN LUCA, IMATE, UNAM, AP. POSTAL 61-3 (XANGARI),CP 58 089, MORELIA, MICHOACAN, MEXICO, or by e-mail
Edited by Florian Luca Please send all communications concerning ADVANCED PROBLEMS AND SOLU- TIONS to FLORIAN LUCA, IMATE, UNAM, AP. POSTAL 61-3 (XANGARI),CP 58 089, MORELIA, MICHOACAN, MEXICO, or by e-mail
ELEMENTARY PROBLEMS AND SOLUTIONS
 EDITED BY RUSS EULER AND JAWAD SADEK Please submit all new problem proposals and their solutions to the Problems Editor, DR RUSS EULER, Department of Mathematics and Statistics, Northwest Missouri State
EDITED BY RUSS EULER AND JAWAD SADEK Please submit all new problem proposals and their solutions to the Problems Editor, DR RUSS EULER, Department of Mathematics and Statistics, Northwest Missouri State
ELEMENTARY PROBLEMS AND SOLUTIONS
 ELEMENTARY PROBLEMS AND SOLUTIONS EDITED BY HARRIS KWONG Please submit solutions and problem proposals to Dr Harris Kwong, Department of Mathematical Sciences, SUNY Fredonia, Fredonia, NY 4063, or by email
ELEMENTARY PROBLEMS AND SOLUTIONS EDITED BY HARRIS KWONG Please submit solutions and problem proposals to Dr Harris Kwong, Department of Mathematical Sciences, SUNY Fredonia, Fredonia, NY 4063, or by email
ADVANCED PROBLEMS AND SOLUTIONS PROBLEMS PROPOSED IN THIS ISSUE
 EDITED BY LORIAN LUCA Please sed all commuicatios cocerig to LORIAN LUCA, SCHOOL O MATHEMATICS, UNIVERSITY O THE WITWA- TERSRAND, PRIVATE BAG X3, WITS 00, JOHANNESBURG, SOUTH ARICA or by e-mail at the
EDITED BY LORIAN LUCA Please sed all commuicatios cocerig to LORIAN LUCA, SCHOOL O MATHEMATICS, UNIVERSITY O THE WITWA- TERSRAND, PRIVATE BAG X3, WITS 00, JOHANNESBURG, SOUTH ARICA or by e-mail at the
ADVANCED PROBLEMS AND SOLUTIONS
 ADVANCED PROBLEMS AND SOLUTIONS EDITED BY FLORIAN LUCA Please sed all couicatios cocerig ADVANCED PROBLEMS AND SOLUTIONS to FLORIAN LUCA, SCHOOL OF MATHEMATICS, UNIVERSITY OF THE WITWA- TERSRAND, PRIVATE
ADVANCED PROBLEMS AND SOLUTIONS EDITED BY FLORIAN LUCA Please sed all couicatios cocerig ADVANCED PROBLEMS AND SOLUTIONS to FLORIAN LUCA, SCHOOL OF MATHEMATICS, UNIVERSITY OF THE WITWA- TERSRAND, PRIVATE
ELEMENTARY PROBLEMS AND SOLUTIONS
 EDITED BY HARRIS KWONG Please submit solutions and problem proposals to Dr Harris Kwong, Department of Mathematical Sciences, SUNY Fredonia, Fredonia, NY, 4063, or by email at kwong@fredoniaedu If you
EDITED BY HARRIS KWONG Please submit solutions and problem proposals to Dr Harris Kwong, Department of Mathematical Sciences, SUNY Fredonia, Fredonia, NY, 4063, or by email at kwong@fredoniaedu If you
ELEMENTARY PROBLEMS AND SOLUTIONS
 ELEMENTARY PROBLEMS AND SOLUTIONS EDITED BY HARRIS KWONG Please submit solutions and problem proposals to Dr Harris Kwong, Department of Mathematical Sciences, SUNY Fredonia, Fredonia, NY, 4063, or by
ELEMENTARY PROBLEMS AND SOLUTIONS EDITED BY HARRIS KWONG Please submit solutions and problem proposals to Dr Harris Kwong, Department of Mathematical Sciences, SUNY Fredonia, Fredonia, NY, 4063, or by
ADVANCED PROBLEMS AND SOLUTIONS. Edited by Florian Luca
 Edited by Floria Luca Please sed all commuicatios cocerig ADVANCED PROBLEMS AND SOLU- TIONS to FLORIAN LUCA, IMATE, UNAM, AP. POSTAL 6-3 (XANGARI), CP 58 089, MORELIA, MICHOACAN, MEXICO, or by e-mail at
Edited by Floria Luca Please sed all commuicatios cocerig ADVANCED PROBLEMS AND SOLU- TIONS to FLORIAN LUCA, IMATE, UNAM, AP. POSTAL 6-3 (XANGARI), CP 58 089, MORELIA, MICHOACAN, MEXICO, or by e-mail at
ELEMENTARY PROBLEMS AND SOLUTIONS
 ELEMENTARY PROBLEMS AND SOLUTIONS EDITED BY HARRIS KWONG Please submit solutions and problem proposals to Dr. Harris Kwong, Department of Mathematical Sciences, SUNY Fredonia, Fredonia, NY, 4063, or by
ELEMENTARY PROBLEMS AND SOLUTIONS EDITED BY HARRIS KWONG Please submit solutions and problem proposals to Dr. Harris Kwong, Department of Mathematical Sciences, SUNY Fredonia, Fredonia, NY, 4063, or by
ELEMENTARY PROBLEMS AND SOLUTIONS
 ELEMENTARY PROBLEMS AND SOLUTIONS EDITED BY HARRIS KWONG Please submit solutios ad problem proposals to Dr. Harris Kwog Departmet of Mathematical Scieces SUNY Fredoia Fredoia NY 14063 or by email at wog@fredoia.edu.
ELEMENTARY PROBLEMS AND SOLUTIONS EDITED BY HARRIS KWONG Please submit solutios ad problem proposals to Dr. Harris Kwog Departmet of Mathematical Scieces SUNY Fredoia Fredoia NY 14063 or by email at wog@fredoia.edu.
Edited by Russ Euler and Jawad Sadek
 Edited by Russ Euler and Jawad Sade Please submit all new problem proposals and corresponding solutions to the Problems Editor, DR RUSS EULER, Department of Mathematics and Statistics, Northwest Missouri
Edited by Russ Euler and Jawad Sade Please submit all new problem proposals and corresponding solutions to the Problems Editor, DR RUSS EULER, Department of Mathematics and Statistics, Northwest Missouri
ELEMENTARY PROBLEMS AND SOLUTIONS
 ELEMENTARY PROBLEMS AND SOLUTIONS EDITED BY RUSS EULER AND JAWAD SADEK Please submit all new problem proposals and their solutions to the Problems Editor, DR RUSS EULER, Department of Mathematics and Statistics,
ELEMENTARY PROBLEMS AND SOLUTIONS EDITED BY RUSS EULER AND JAWAD SADEK Please submit all new problem proposals and their solutions to the Problems Editor, DR RUSS EULER, Department of Mathematics and Statistics,
ADVANCED PROBLEMS AND SOLUTIONS
 Edited by Raymond E. Whitney Please send all communications concerning ADVANCED PROBLEMS AND SOLUTIONS to RAYMOND E. WHITNEY, MATHEMATICS DEPARTMENT, LOCK HAVEN UNIVERSITY, LOCK HA VEN, PA 17745. This
Edited by Raymond E. Whitney Please send all communications concerning ADVANCED PROBLEMS AND SOLUTIONS to RAYMOND E. WHITNEY, MATHEMATICS DEPARTMENT, LOCK HAVEN UNIVERSITY, LOCK HA VEN, PA 17745. This
ADVANCED PROBLEMS AND SOLUTIONS
 Edited by RAYMOND E. WHITNEY Please send all communications concerning to RAYMOND E. WHITNEY, MATHEMATICS DEPARTMENT, LOCK HAVEN UNIVERSITY, LOCK HAVEN, PA 17745. This department especially welcomes problems
Edited by RAYMOND E. WHITNEY Please send all communications concerning to RAYMOND E. WHITNEY, MATHEMATICS DEPARTMENT, LOCK HAVEN UNIVERSITY, LOCK HAVEN, PA 17745. This department especially welcomes problems
ADVANCED PROBLEMS AND SOLUTIONS
 Edited by RAYMOND E. WHITNEY Please send all communications concerning ADVANCED PROBLEMS AND SOLUTIONS to RAYMOND E. WHITNEY, MATHEMATICS DEPARTMENT, LOCK HAVEN UNIVERSITY, LOCK HA PA 17745, This department
Edited by RAYMOND E. WHITNEY Please send all communications concerning ADVANCED PROBLEMS AND SOLUTIONS to RAYMOND E. WHITNEY, MATHEMATICS DEPARTMENT, LOCK HAVEN UNIVERSITY, LOCK HA PA 17745, This department
ADVANCED PEOBLEMS AND SOLUTIONS
 ADVANCED PEOBLEMS AND SOLUTIONS Edited by Raymond E* Whitney Please send all communications concerning to RAYMOND K WHITNEY, MATHEMATICS DEPARTMENT, LOCK HAVEN UNIVERSITY, LOCK HAVEN, PA 7745. This department
ADVANCED PEOBLEMS AND SOLUTIONS Edited by Raymond E* Whitney Please send all communications concerning to RAYMOND K WHITNEY, MATHEMATICS DEPARTMENT, LOCK HAVEN UNIVERSITY, LOCK HAVEN, PA 7745. This department
ADVANCED PROBLEMS AND SOLUTIONS. Edited by Raymond E. Whitney
 Edited by Raymond E. Whitney Please send all communications concerning ADVANCED PROBLEMS AND SOLUTIONS to RAYMOND E. WHITNEY, MATHEMATICS DEPARTMENT, LOCK HAVEN UNIVERSITY, LOCK HAVEN, PA 7745. This department
Edited by Raymond E. Whitney Please send all communications concerning ADVANCED PROBLEMS AND SOLUTIONS to RAYMOND E. WHITNEY, MATHEMATICS DEPARTMENT, LOCK HAVEN UNIVERSITY, LOCK HAVEN, PA 7745. This department
Cullen Numbers in Binary Recurrent Sequences
 Cullen Numbers in Binary Recurrent Sequences Florian Luca 1 and Pantelimon Stănică 2 1 IMATE-UNAM, Ap. Postal 61-3 (Xangari), CP 58 089 Morelia, Michoacán, Mexico; e-mail: fluca@matmor.unam.mx 2 Auburn
Cullen Numbers in Binary Recurrent Sequences Florian Luca 1 and Pantelimon Stănică 2 1 IMATE-UNAM, Ap. Postal 61-3 (Xangari), CP 58 089 Morelia, Michoacán, Mexico; e-mail: fluca@matmor.unam.mx 2 Auburn
ADVANCED PROBLEMS AND SOLUTIONS
 ADVANCED PROBLEMS AND SOLUTIONS Edited by RAYMOND E.WHITNEY Lk Haven State College, Lock Haven, Pennsylvania 17745 Send all communications concerning Advanced Problems and Solutions to Raymond E. Whitney,
ADVANCED PROBLEMS AND SOLUTIONS Edited by RAYMOND E.WHITNEY Lk Haven State College, Lock Haven, Pennsylvania 17745 Send all communications concerning Advanced Problems and Solutions to Raymond E. Whitney,
ADVANCED PROBLEMS AND SOLUTIONS
 Edited by Raymond E* Whitney Please send all communications concerning ADVANCED PROBLEMS AND SOLUTIONS to RAYMOND E. WHITNEY, MATHEMATICS DEPARTMENT, LOCK HAVEN UNIVERSITY, LOCK HAVEN, PA 775. This department
Edited by Raymond E* Whitney Please send all communications concerning ADVANCED PROBLEMS AND SOLUTIONS to RAYMOND E. WHITNEY, MATHEMATICS DEPARTMENT, LOCK HAVEN UNIVERSITY, LOCK HAVEN, PA 775. This department
ADVANCED PROBLEMS AND SOLUTIONS
 ADVANCED PROBLEMS AND SOLUTIONS Edited by RAYMOND E. WHITNEY Lock Haven State College, Lock Haven, Pennsylvania Send all communications concerning Advanced Problems and Solutions to Raymond E. Whitney,
ADVANCED PROBLEMS AND SOLUTIONS Edited by RAYMOND E. WHITNEY Lock Haven State College, Lock Haven, Pennsylvania Send all communications concerning Advanced Problems and Solutions to Raymond E. Whitney,
Fibonacci and Lucas Identities the Golden Way
 Fibonacci Lucas Identities the Golden Way Kunle Adegoe adegoe00@gmail.com arxiv:1810.12115v1 [math.nt] 25 Oct 2018 Department of Physics Engineering Physics, Obafemi Awolowo University, 220005 Ile-Ife,
Fibonacci Lucas Identities the Golden Way Kunle Adegoe adegoe00@gmail.com arxiv:1810.12115v1 [math.nt] 25 Oct 2018 Department of Physics Engineering Physics, Obafemi Awolowo University, 220005 Ile-Ife,
ADVANCED PROBLEMS AND SOLUTIONS Edited By RAYMOND E.WHITNEY Lock Haven State College, Lock Haven, Pennsylvania
 ADVANCED PROBLEMS AND SOLUTIONS Edited By RAYMOND E.WHITNEY Loc Haven State College, Loc Haven, Pennsylvania Send all communications concerning Advanced Problems and Solutions to Raymond E. Whitney, Mathematics
ADVANCED PROBLEMS AND SOLUTIONS Edited By RAYMOND E.WHITNEY Loc Haven State College, Loc Haven, Pennsylvania Send all communications concerning Advanced Problems and Solutions to Raymond E. Whitney, Mathematics
SOME FORMULAE FOR THE FIBONACCI NUMBERS
 SOME FORMULAE FOR THE FIBONACCI NUMBERS Brian Curtin Department of Mathematics, University of South Florida, 4202 E Fowler Ave PHY4, Tampa, FL 33620 e-mail: bcurtin@mathusfedu Ena Salter Department of
SOME FORMULAE FOR THE FIBONACCI NUMBERS Brian Curtin Department of Mathematics, University of South Florida, 4202 E Fowler Ave PHY4, Tampa, FL 33620 e-mail: bcurtin@mathusfedu Ena Salter Department of
ELEMENTARY PROBLEMS AND SOLUTIONS
 ELEMENTARY PROBLEMS AND SOLUTIONS EDITED BY HARRIS KWONG Please submit solutios ad problem proposals to Dr Harris Kwog, Departmet of Mathematical Scieces, SUNY Fredoia, Fredoia, NY, 4063, or by email at
ELEMENTARY PROBLEMS AND SOLUTIONS EDITED BY HARRIS KWONG Please submit solutios ad problem proposals to Dr Harris Kwog, Departmet of Mathematical Scieces, SUNY Fredoia, Fredoia, NY, 4063, or by email at
ADVANCED PROBLEMS AND SOLUTIONS Edited by RAYMOND E.WHITNEY Lock Haven State College, Lock Haven, Pennsylvania
 ADVANCED PROBLEMS AND SOLUTIONS Edited by RAYMOND E.WHITNEY Lock Haven State College, Lock Haven, Pennsylvania Send all communications concerning Advanced Problems and Solutions to Raymond E. Whitney,
ADVANCED PROBLEMS AND SOLUTIONS Edited by RAYMOND E.WHITNEY Lock Haven State College, Lock Haven, Pennsylvania Send all communications concerning Advanced Problems and Solutions to Raymond E. Whitney,
Journal of Number Theory
 Journal of Number Theory 132 2012) 324 331 Contents lists available at SciVerse ScienceDirect Journal of Number Theory www.elsevier.com/locate/jnt Digit sums of binomial sums Arnold Knopfmacher a,florianluca
Journal of Number Theory 132 2012) 324 331 Contents lists available at SciVerse ScienceDirect Journal of Number Theory www.elsevier.com/locate/jnt Digit sums of binomial sums Arnold Knopfmacher a,florianluca
In memoriam Péter Kiss
 Kálmán Liptai Eszterházy Károly Collage, Leányka út 4, 3300 Eger, Hungary e-mail: liptaik@gemini.ektf.hu (Submitted March 2002-Final Revision October 2003) In memoriam Péter Kiss ABSTRACT A positive integer
Kálmán Liptai Eszterházy Károly Collage, Leányka út 4, 3300 Eger, Hungary e-mail: liptaik@gemini.ektf.hu (Submitted March 2002-Final Revision October 2003) In memoriam Péter Kiss ABSTRACT A positive integer
Edited by Russ Euler and Jawad Sadek
 Edited by Russ Euler and Jawad Sadek Please submit all new problem proposals and corresponding solutions to the Problems Editor, DR RUSS EULER, Department of Mathematics and Statistics, Northwest Missouri
Edited by Russ Euler and Jawad Sadek Please submit all new problem proposals and corresponding solutions to the Problems Editor, DR RUSS EULER, Department of Mathematics and Statistics, Northwest Missouri
K th -order linear difference equation (Normal Form)
 The standard form of the general K th -order difference equation is x n + 1 = F(x n, x n - 1, x n - 2,..., x n - K + 1, P) where P is a vector of parameters. However, linear equations are normally expressed
The standard form of the general K th -order difference equation is x n + 1 = F(x n, x n - 1, x n - 2,..., x n - K + 1, P) where P is a vector of parameters. However, linear equations are normally expressed
Winter 2014 Practice Final 3/21/14 Student ID
 Math 4C Winter 2014 Practice Final 3/21/14 Name (Print): Student ID This exam contains 5 pages (including this cover page) and 20 problems. Check to see if any pages are missing. Enter all requested information
Math 4C Winter 2014 Practice Final 3/21/14 Name (Print): Student ID This exam contains 5 pages (including this cover page) and 20 problems. Check to see if any pages are missing. Enter all requested information
A LINEAR BINOMIAL RECURRENCE AND THE BELL NUMBERS AND POLYNOMIALS
 Applicable Analysis and Discrete Mathematics, 1 (27, 371 385. Available electronically at http://pefmath.etf.bg.ac.yu A LINEAR BINOMIAL RECURRENCE AND THE BELL NUMBERS AND POLYNOMIALS H. W. Gould, Jocelyn
Applicable Analysis and Discrete Mathematics, 1 (27, 371 385. Available electronically at http://pefmath.etf.bg.ac.yu A LINEAR BINOMIAL RECURRENCE AND THE BELL NUMBERS AND POLYNOMIALS H. W. Gould, Jocelyn
HIGHER-ORDER DIFFERENCES AND HIGHER-ORDER PARTIAL SUMS OF EULER S PARTITION FUNCTION
 ISSN 2066-6594 Ann Acad Rom Sci Ser Math Appl Vol 10, No 1/2018 HIGHER-ORDER DIFFERENCES AND HIGHER-ORDER PARTIAL SUMS OF EULER S PARTITION FUNCTION Mircea Merca Dedicated to Professor Mihail Megan on
ISSN 2066-6594 Ann Acad Rom Sci Ser Math Appl Vol 10, No 1/2018 HIGHER-ORDER DIFFERENCES AND HIGHER-ORDER PARTIAL SUMS OF EULER S PARTITION FUNCTION Mircea Merca Dedicated to Professor Mihail Megan on
ADVANCED PROBLEMS AND SOLUTIONS
 Edited by Raymond E. Whitney Please send all communications concerning ADVANCED PROBLEMS AND SOLUTIONS to RAYMOND E. WHITNEY, MATHEMATICS DEPARTMENT, LOCK HAVEN UNIVERSITY, LOCK HA VEN, PA 17745. This
Edited by Raymond E. Whitney Please send all communications concerning ADVANCED PROBLEMS AND SOLUTIONS to RAYMOND E. WHITNEY, MATHEMATICS DEPARTMENT, LOCK HAVEN UNIVERSITY, LOCK HA VEN, PA 17745. This
Course 2BA1: Hilary Term 2006 Section 7: Trigonometric and Exponential Functions
 Course 2BA1: Hilary Term 2006 Section 7: Trigonometric and Exponential Functions David R. Wilkins Copyright c David R. Wilkins 2005 Contents 7 Trigonometric and Exponential Functions 1 7.1 Basic Trigonometric
Course 2BA1: Hilary Term 2006 Section 7: Trigonometric and Exponential Functions David R. Wilkins Copyright c David R. Wilkins 2005 Contents 7 Trigonometric and Exponential Functions 1 7.1 Basic Trigonometric
ELEMENTARY PROBLEMS AND SOLUTIONS. Edited by Russ Euler and Jawad Sadek
 Edited by Russ Euler and Jawad Sadek Please submit all new problem proposals and corresponding solutions to the Problems Editor, DR. RUSS EULER, Department of Mathematics and Statistics, Northwest Missouri
Edited by Russ Euler and Jawad Sadek Please submit all new problem proposals and corresponding solutions to the Problems Editor, DR. RUSS EULER, Department of Mathematics and Statistics, Northwest Missouri
Summation of certain infinite Fibonacci related series
 arxiv:52.09033v (30 Dec 205) Summation of certain infinite Fibonacci related series Bakir Farhi Laboratoire de Mathématiques appliquées Faculté des Sciences Exactes Université de Bejaia 06000 Bejaia Algeria
arxiv:52.09033v (30 Dec 205) Summation of certain infinite Fibonacci related series Bakir Farhi Laboratoire de Mathématiques appliquées Faculté des Sciences Exactes Université de Bejaia 06000 Bejaia Algeria
Some Generalized Fibonomial Sums related with the Gaussian q Binomial sums
 Bull. Math. Soc. Sci. Math. Roumanie Tome 55(103 No. 1, 01, 51 61 Some Generalized Fibonomial Sums related with the Gaussian q Binomial sums by Emrah Kilic, Iler Aus and Hideyui Ohtsua Abstract In this
Bull. Math. Soc. Sci. Math. Roumanie Tome 55(103 No. 1, 01, 51 61 Some Generalized Fibonomial Sums related with the Gaussian q Binomial sums by Emrah Kilic, Iler Aus and Hideyui Ohtsua Abstract In this
A SUMMATION FORMULA FOR SEQUENCES INVOLVING FLOOR AND CEILING FUNCTIONS
 ROCKY MOUNTAIN JOURNAL OF MATHEMATICS Volume 36, Number 5, 006 A SUMMATION FORMULA FOR SEQUENCES INVOLVING FLOOR AND CEILING FUNCTIONS M.A. NYBLOM ABSTRACT. A closed form expression for the Nth partial
ROCKY MOUNTAIN JOURNAL OF MATHEMATICS Volume 36, Number 5, 006 A SUMMATION FORMULA FOR SEQUENCES INVOLVING FLOOR AND CEILING FUNCTIONS M.A. NYBLOM ABSTRACT. A closed form expression for the Nth partial
17 Advancement Operator Equations
 November 14, 2017 17 Advancement Operator Equations William T. Trotter trotter@math.gatech.edu Review of Recurrence Equations (1) Problem Let r(n) denote the number of regions determined by n lines that
November 14, 2017 17 Advancement Operator Equations William T. Trotter trotter@math.gatech.edu Review of Recurrence Equations (1) Problem Let r(n) denote the number of regions determined by n lines that
uniform distribution theory
 Uniform Distribution Theory 9 204 no. 2 25 uniform distribution theory ON THE FIRST DIGITS OF THE FIBONACCI NUMBERS AND THEIR EULER FUNCTION Florian Luca Pantelimon Stănică ABSTRACT. Here we show that
Uniform Distribution Theory 9 204 no. 2 25 uniform distribution theory ON THE FIRST DIGITS OF THE FIBONACCI NUMBERS AND THEIR EULER FUNCTION Florian Luca Pantelimon Stănică ABSTRACT. Here we show that
8. Sequences, Series, and Probability 8.1. SEQUENCES AND SERIES
 8. Sequences, Series, and Probability 8.1. SEQUENCES AND SERIES What You Should Learn Use sequence notation to write the terms of sequences. Use factorial notation. Use summation notation to write sums.
8. Sequences, Series, and Probability 8.1. SEQUENCES AND SERIES What You Should Learn Use sequence notation to write the terms of sequences. Use factorial notation. Use summation notation to write sums.
O N P O S I T I V E N U M B E R S n F O R W H I C H Q(n) D I V I D E S F n
 O N P O S I T I V E N U M B E R S n F O R W H I C H Q(n) D I V I D E S F n Florian Luca IMATE de la UNAM, Ap. Postal 61-3 (Xangari), CP 58 089, Morelia, Michoacan, Mexico e-mail: fluca@matmor.unain.inx
O N P O S I T I V E N U M B E R S n F O R W H I C H Q(n) D I V I D E S F n Florian Luca IMATE de la UNAM, Ap. Postal 61-3 (Xangari), CP 58 089, Morelia, Michoacan, Mexico e-mail: fluca@matmor.unain.inx
arxiv: v1 [math.co] 26 Sep 2017
![arxiv: v1 [math.co] 26 Sep 2017 arxiv: v1 [math.co] 26 Sep 2017](/thumbs/74/70856286.jpg) SPECTRAL RADIUS OF A STAR WITH ONE LONG ARM arxiv:170908871v1 [mathco] 26 Sep 2017 HYUNSHIK SHIN Abstract A tree is said to be starlike if exactly one vertex has degree greater than two In this paper,
SPECTRAL RADIUS OF A STAR WITH ONE LONG ARM arxiv:170908871v1 [mathco] 26 Sep 2017 HYUNSHIK SHIN Abstract A tree is said to be starlike if exactly one vertex has degree greater than two In this paper,
ABSTRACT. In this note, we find all the solutions of the Diophantine equation x k = y n, 1, y 1, k N, n INTRODUCTION
 Florian Luca Instituto de Matemáticas UNAM, Campus Morelia Apartado Postal 27-3 (Xangari), C.P. 58089, Morelia, Michoacán, Mexico e-mail: fluca@matmor.unam.mx Alain Togbé Mathematics Department, Purdue
Florian Luca Instituto de Matemáticas UNAM, Campus Morelia Apartado Postal 27-3 (Xangari), C.P. 58089, Morelia, Michoacán, Mexico e-mail: fluca@matmor.unam.mx Alain Togbé Mathematics Department, Purdue
Florian Luca Instituto de Matemáticas, Universidad Nacional Autonoma de México, C.P , Morelia, Michoacán, México
 Florian Luca Instituto de Matemáticas, Universidad Nacional Autonoma de México, C.P. 8180, Morelia, Michoacán, México e-mail: fluca@matmor.unam.mx Laszlo Szalay Department of Mathematics and Statistics,
Florian Luca Instituto de Matemáticas, Universidad Nacional Autonoma de México, C.P. 8180, Morelia, Michoacán, México e-mail: fluca@matmor.unam.mx Laszlo Szalay Department of Mathematics and Statistics,
Solutions I.N. Herstein- Second Edition
 Solutions I.N. Herstein- Second Edition Sadiah Zahoor Please email me if any corrections at sadiahzahoor@cantab.net. R is a ring in all problems. Problem 0.1. If a, b, c, d R, evaluate (a + b)(c + d).
Solutions I.N. Herstein- Second Edition Sadiah Zahoor Please email me if any corrections at sadiahzahoor@cantab.net. R is a ring in all problems. Problem 0.1. If a, b, c, d R, evaluate (a + b)(c + d).
Products of Factorials Modulo p
 Products of Factorials Modulo p Florian Luca and Pantelimon Stănică IMATE, UNAM, Ap. Postal 6-3 Xangari, CP. 58 089 Morelia, Michoacán, Mexico; e-mail: fluca@matmor.unam.mx Auburn University Montgomery,
Products of Factorials Modulo p Florian Luca and Pantelimon Stănică IMATE, UNAM, Ap. Postal 6-3 Xangari, CP. 58 089 Morelia, Michoacán, Mexico; e-mail: fluca@matmor.unam.mx Auburn University Montgomery,
THE EULER FUNCTION OF FIBONACCI AND LUCAS NUMBERS AND FACTORIALS
 Annales Univ. Sci. Budapest., Sect. Comp. 41 (2013) 119 124 THE EULER FUNCTION OF FIBONACCI AND LUCAS NUMBERS AND FACTORIALS Florian Luca (Morelia, Mexico) Pantelimon Stănică (Monterey, USA) Dedicated
Annales Univ. Sci. Budapest., Sect. Comp. 41 (2013) 119 124 THE EULER FUNCTION OF FIBONACCI AND LUCAS NUMBERS AND FACTORIALS Florian Luca (Morelia, Mexico) Pantelimon Stănică (Monterey, USA) Dedicated
Linear recurrence relations with the coefficients in progression
 Annales Mathematicae et Informaticae 4 (013) pp. 119 17 http://ami.ektf.hu Linear recurrence relations with the coefficients in progression Mircea I. Cîrnu Department of Mathematics, Faculty of Applied
Annales Mathematicae et Informaticae 4 (013) pp. 119 17 http://ami.ektf.hu Linear recurrence relations with the coefficients in progression Mircea I. Cîrnu Department of Mathematics, Faculty of Applied
UWO CS2214 Feb. 4, Assignment #1 Due: Feb. 12, 2017, by 23:55 Submission: on the OWL web site of the course
 UWO CS2214 Feb. 4, 2019 Assignment #1 Due: Feb. 12, 2017, by 23:55 Submission: on the OWL web site of the course Format of the submission. You must submit a single file which must be in PDF format. All
UWO CS2214 Feb. 4, 2019 Assignment #1 Due: Feb. 12, 2017, by 23:55 Submission: on the OWL web site of the course Format of the submission. You must submit a single file which must be in PDF format. All
Partial Sums of Powers of Prime Factors
 1 3 47 6 3 11 Journal of Integer Sequences, Vol. 10 (007), Article 07.1.6 Partial Sums of Powers of Prime Factors Jean-Marie De Koninck Département de Mathématiques et de Statistique Université Laval Québec
1 3 47 6 3 11 Journal of Integer Sequences, Vol. 10 (007), Article 07.1.6 Partial Sums of Powers of Prime Factors Jean-Marie De Koninck Département de Mathématiques et de Statistique Université Laval Québec
#A2 INTEGERS 12A (2012): John Selfridge Memorial Issue ON A CONJECTURE REGARDING BALANCING WITH POWERS OF FIBONACCI NUMBERS
 #A2 INTEGERS 2A (202): John Selfridge Memorial Issue ON A CONJECTURE REGARDING BALANCING WITH POWERS OF FIBONACCI NUMBERS Saúl Díaz Alvarado Facultad de Ciencias, Universidad Autónoma del Estado de México,
#A2 INTEGERS 2A (202): John Selfridge Memorial Issue ON A CONJECTURE REGARDING BALANCING WITH POWERS OF FIBONACCI NUMBERS Saúl Díaz Alvarado Facultad de Ciencias, Universidad Autónoma del Estado de México,
z = a + ib (4.1) i 2 = 1. (4.2) <(z) = a, (4.3) =(z) = b. (4.4)
 Chapter 4 Complex Numbers 4.1 Definition of Complex Numbers A complex number is a number of the form where a and b are real numbers and i has the property that z a + ib (4.1) i 2 1. (4.2) a is called the
Chapter 4 Complex Numbers 4.1 Definition of Complex Numbers A complex number is a number of the form where a and b are real numbers and i has the property that z a + ib (4.1) i 2 1. (4.2) a is called the
uniform distribution theory
 Uniform Distribution Theory 9 (2014), no.1, 21 25 uniform distribution theory ON THE FIRST DIGITS OF THE FIBONACCI NUMBERS AND THEIR EULER FUNCTION Florian Luca Pantelimon Stănică ABSTRACT. Here, we show
Uniform Distribution Theory 9 (2014), no.1, 21 25 uniform distribution theory ON THE FIRST DIGITS OF THE FIBONACCI NUMBERS AND THEIR EULER FUNCTION Florian Luca Pantelimon Stănică ABSTRACT. Here, we show
ADVANCED PROBLEMS AND SOLUTIONS Edited by Raymond E. Whitney
 Edited by Raymond E. Whitney Please send all communications concerning to RAYMOND E. WHITNEY, MATHEMATICS DEPARTMENT, LOCK HAVEN UNIVERSITY, LOCK HA VEN, PA 7745. This department especially welcomes problems
Edited by Raymond E. Whitney Please send all communications concerning to RAYMOND E. WHITNEY, MATHEMATICS DEPARTMENT, LOCK HAVEN UNIVERSITY, LOCK HA VEN, PA 7745. This department especially welcomes problems
FIFTH ROOTS OF FIBONACCI FRACTIONS. Christopher P. French Grinnell College, Grinnell, IA (Submitted June 2004-Final Revision September 2004)
 Christopher P. French Grinnell College, Grinnell, IA 0112 (Submitted June 2004-Final Revision September 2004) ABSTRACT We prove that when n is odd, the continued fraction expansion of Fn+ begins with a
Christopher P. French Grinnell College, Grinnell, IA 0112 (Submitted June 2004-Final Revision September 2004) ABSTRACT We prove that when n is odd, the continued fraction expansion of Fn+ begins with a
Real Variables: Solutions to Homework 9
 Real Variables: Solutions to Homework 9 Theodore D Drivas November, 20 xercise 0 Chapter 8, # : For complex-valued, measurable f, f = f + if 2 with f i real-valued and measurable, we have f = f + i f 2
Real Variables: Solutions to Homework 9 Theodore D Drivas November, 20 xercise 0 Chapter 8, # : For complex-valued, measurable f, f = f + if 2 with f i real-valued and measurable, we have f = f + i f 2
Examples of Finite Sequences (finite terms) Examples of Infinite Sequences (infinite terms)
 Math 120 Intermediate Algebra Sec 10.1: Sequences Defn A sequence is a function whose domain is the set of positive integers. The formula for the nth term of a sequence is called the general term. Examples
Math 120 Intermediate Algebra Sec 10.1: Sequences Defn A sequence is a function whose domain is the set of positive integers. The formula for the nth term of a sequence is called the general term. Examples
ELEMENTARY PROBLEMS AND SOLUTIONS. Edited by Russ Euler and Jawad Sadek
 Edited by Russ Euler and Jawad Sadek Please submit all new problem proposals and corresponding solutions to the Problems Editor, DR. RUSS EULER, Department of Mathematics and Statistics, Northwest Missouri
Edited by Russ Euler and Jawad Sadek Please submit all new problem proposals and corresponding solutions to the Problems Editor, DR. RUSS EULER, Department of Mathematics and Statistics, Northwest Missouri
ELEMENTARY PROBLEMS AND SOLUTIONS. Edited by Stanley Rabinowitz
 Edited by Stanley Rabinowitz Please send all material for to Dr. STANLEY RABINOWITZ; 12 VINE BROOK RD; WESTFORD, MA 01886-4212 USA. Correspondence may also be sent to the problem editor by electronic mail
Edited by Stanley Rabinowitz Please send all material for to Dr. STANLEY RABINOWITZ; 12 VINE BROOK RD; WESTFORD, MA 01886-4212 USA. Correspondence may also be sent to the problem editor by electronic mail
Manual for SOA Exam MLC.
 Chapter 10. Poisson processes. Section 10.5. Nonhomogenous Poisson processes Extract from: Arcones Fall 2009 Edition, available at http://www.actexmadriver.com/ 1/14 Nonhomogenous Poisson processes Definition
Chapter 10. Poisson processes. Section 10.5. Nonhomogenous Poisson processes Extract from: Arcones Fall 2009 Edition, available at http://www.actexmadriver.com/ 1/14 Nonhomogenous Poisson processes Definition
COM S 330 Homework 05 Solutions. Type your answers to the following questions and submit a PDF file to Blackboard. One page per problem.
 Type your answers to the following questions and submit a PDF file to Blackboard. One page per problem. Problem 1. [5pts] Consider our definitions of Z, Q, R, and C. Recall that A B means A is a subset
Type your answers to the following questions and submit a PDF file to Blackboard. One page per problem. Problem 1. [5pts] Consider our definitions of Z, Q, R, and C. Recall that A B means A is a subset
Section 11.1 Sequences
 Math 152 c Lynch 1 of 8 Section 11.1 Sequences A sequence is a list of numbers written in a definite order: a 1, a 2, a 3,..., a n,... Notation. The sequence {a 1, a 2, a 3,...} can also be written {a
Math 152 c Lynch 1 of 8 Section 11.1 Sequences A sequence is a list of numbers written in a definite order: a 1, a 2, a 3,..., a n,... Notation. The sequence {a 1, a 2, a 3,...} can also be written {a
arxiv: v1 [math.ca] 15 Jan 2018
![arxiv: v1 [math.ca] 15 Jan 2018 arxiv: v1 [math.ca] 15 Jan 2018](/thumbs/82/85242988.jpg) Preprint submitted to arxiv.org Accurate estimates of 1 + x 1/x Involved in Carleman Inequality and Keller Limit arxiv:1801.04963v1 [math.ca] 15 Jan 2018 Branko Malešević 1, Yue Hu 2 and Cristinel Mortici
Preprint submitted to arxiv.org Accurate estimates of 1 + x 1/x Involved in Carleman Inequality and Keller Limit arxiv:1801.04963v1 [math.ca] 15 Jan 2018 Branko Malešević 1, Yue Hu 2 and Cristinel Mortici
Mathematics 324 Riemann Zeta Function August 5, 2005
 Mathematics 324 Riemann Zeta Function August 5, 25 In this note we give an introduction to the Riemann zeta function, which connects the ideas of real analysis with the arithmetic of the integers. Define
Mathematics 324 Riemann Zeta Function August 5, 25 In this note we give an introduction to the Riemann zeta function, which connects the ideas of real analysis with the arithmetic of the integers. Define
Applications. More Counting Problems. Complexity of Algorithms
 Recurrences Applications More Counting Problems Complexity of Algorithms Part I Recurrences and Binomial Coefficients Paths in a Triangle P(0, 0) P(1, 0) P(1,1) P(2, 0) P(2,1) P(2, 2) P(3, 0) P(3,1) P(3,
Recurrences Applications More Counting Problems Complexity of Algorithms Part I Recurrences and Binomial Coefficients Paths in a Triangle P(0, 0) P(1, 0) P(1,1) P(2, 0) P(2,1) P(2, 2) P(3, 0) P(3,1) P(3,
Sums of fourth powers of Fibonacci and Lucas numbers
 Sums of fourth powers of Fibonacci Lucas numbers arxiv:1706.00407v1 [math.nt] 28 May 2017 Kunle Adegoke Department of Physics Engineering Physics, Obafemi Awolowo University, Ile-Ife, Nigeria Abstract
Sums of fourth powers of Fibonacci Lucas numbers arxiv:1706.00407v1 [math.nt] 28 May 2017 Kunle Adegoke Department of Physics Engineering Physics, Obafemi Awolowo University, Ile-Ife, Nigeria Abstract
198 VOLUME 46/47, NUMBER 3
 LAWRENCE SOMER Abstract. Rotkiewicz has shown that there exist Fibonacci pseudoprimes having the forms p(p + 2), p(2p 1), and p(2p + 3), where all the terms in the products are odd primes. Assuming Dickson
LAWRENCE SOMER Abstract. Rotkiewicz has shown that there exist Fibonacci pseudoprimes having the forms p(p + 2), p(2p 1), and p(2p + 3), where all the terms in the products are odd primes. Assuming Dickson
#A12 INTEGERS 11 (2011) ON THE NUMBER OF FACTORIZATIONS OF AN INTEGER
 #A12 INTEGERS 11 (2011) ON THE NUMBER OF FACTORIZATIONS OF AN INTEGER R. Balasubramanian The Institute of Mathematical Sciences, Chennai, India balu@imsc.res.in Florian Luca 1 Instituto de Matemáticas,
#A12 INTEGERS 11 (2011) ON THE NUMBER OF FACTORIZATIONS OF AN INTEGER R. Balasubramanian The Institute of Mathematical Sciences, Chennai, India balu@imsc.res.in Florian Luca 1 Instituto de Matemáticas,
GAPS IN BINARY EXPANSIONS OF SOME ARITHMETIC FUNCTIONS, AND THE IRRATIONALITY OF THE EULER CONSTANT
 Journal of Prime Research in Mathematics Vol. 8 202, 28-35 GAPS IN BINARY EXPANSIONS OF SOME ARITHMETIC FUNCTIONS, AND THE IRRATIONALITY OF THE EULER CONSTANT JORGE JIMÉNEZ URROZ, FLORIAN LUCA 2, MICHEL
Journal of Prime Research in Mathematics Vol. 8 202, 28-35 GAPS IN BINARY EXPANSIONS OF SOME ARITHMETIC FUNCTIONS, AND THE IRRATIONALITY OF THE EULER CONSTANT JORGE JIMÉNEZ URROZ, FLORIAN LUCA 2, MICHEL
MTH4101 CALCULUS II REVISION NOTES. 1. COMPLEX NUMBERS (Thomas Appendix 7 + lecture notes) ax 2 + bx + c = 0. x = b ± b 2 4ac 2a. i = 1.
 MTH4101 CALCULUS II REVISION NOTES 1. COMPLEX NUMBERS (Thomas Appendix 7 + lecture notes) 1.1 Introduction Types of numbers (natural, integers, rationals, reals) The need to solve quadratic equations:
MTH4101 CALCULUS II REVISION NOTES 1. COMPLEX NUMBERS (Thomas Appendix 7 + lecture notes) 1.1 Introduction Types of numbers (natural, integers, rationals, reals) The need to solve quadratic equations:
Introduction to Abstract Mathematics
 Introduction to Abstract Mathematics Notation: Z + or Z >0 denotes the set {1, 2, 3,...} of positive integers, Z 0 is the set {0, 1, 2,...} of nonnegative integers, Z is the set {..., 1, 0, 1, 2,...} of
Introduction to Abstract Mathematics Notation: Z + or Z >0 denotes the set {1, 2, 3,...} of positive integers, Z 0 is the set {0, 1, 2,...} of nonnegative integers, Z is the set {..., 1, 0, 1, 2,...} of
3 a = 3 b c 2 = a 2 + b 2 = 2 2 = 4 c 2 = 3b 2 + b 2 = 4b 2 = 4 b 2 = 1 b = 1 a = 3b = 3. x 2 3 y2 1 = 1.
 MATH 222 LEC SECOND MIDTERM EXAM THU NOV 8 PROBLEM ( 5 points ) Find the standard-form equation for the hyperbola which has its foci at F ± (±2, ) and whose asymptotes are y ± 3 x The calculations b a
MATH 222 LEC SECOND MIDTERM EXAM THU NOV 8 PROBLEM ( 5 points ) Find the standard-form equation for the hyperbola which has its foci at F ± (±2, ) and whose asymptotes are y ± 3 x The calculations b a
CONGRUENCES FOR BERNOULLI - LUCAS SUMS
 CONGRUENCES FOR BERNOULLI - LUCAS SUMS PAUL THOMAS YOUNG Abstract. We give strong congruences for sums of the form N BnVn+1 where Bn denotes the Bernoulli number and V n denotes a Lucas sequence of the
CONGRUENCES FOR BERNOULLI - LUCAS SUMS PAUL THOMAS YOUNG Abstract. We give strong congruences for sums of the form N BnVn+1 where Bn denotes the Bernoulli number and V n denotes a Lucas sequence of the
EXTENDING THE DOMAINS OF DEFINITION OF SOME FIBONACCI IDENTITIES
 EXTENDING THE DOMAINS OF DEFINITION OF SOME FIBONACCI IDENTITIES MARTIN GRIFFITHS Abstract. In this paper we consider the possibility for extending the domains of definition of particular Fibonacci identities
EXTENDING THE DOMAINS OF DEFINITION OF SOME FIBONACCI IDENTITIES MARTIN GRIFFITHS Abstract. In this paper we consider the possibility for extending the domains of definition of particular Fibonacci identities
MATH 117 LECTURE NOTES
 MATH 117 LECTURE NOTES XIN ZHOU Abstract. This is the set of lecture notes for Math 117 during Fall quarter of 2017 at UC Santa Barbara. The lectures follow closely the textbook [1]. Contents 1. The set
MATH 117 LECTURE NOTES XIN ZHOU Abstract. This is the set of lecture notes for Math 117 during Fall quarter of 2017 at UC Santa Barbara. The lectures follow closely the textbook [1]. Contents 1. The set
Sequences and Series. Copyright Cengage Learning. All rights reserved.
 Sequences and Series Copyright Cengage Learning. All rights reserved. 12.1 Sequences and Summation Notation Copyright Cengage Learning. All rights reserved. Objectives Sequences Recursively Defined Sequences
Sequences and Series Copyright Cengage Learning. All rights reserved. 12.1 Sequences and Summation Notation Copyright Cengage Learning. All rights reserved. Objectives Sequences Recursively Defined Sequences
On Two New Classes of Fibonacci and Lucas Reciprocal Sums with Subscripts in Arithmetic Progression
 Applied Mathematical Sciences Vol. 207 no. 25 2-29 HIKARI Ltd www.m-hikari.com https://doi.org/0.2988/ams.207.7392 On Two New Classes of Fibonacci Lucas Reciprocal Sums with Subscripts in Arithmetic Progression
Applied Mathematical Sciences Vol. 207 no. 25 2-29 HIKARI Ltd www.m-hikari.com https://doi.org/0.2988/ams.207.7392 On Two New Classes of Fibonacci Lucas Reciprocal Sums with Subscripts in Arithmetic Progression
Summation of Certain Infinite Lucas-Related Series
 J. Integer Sequences 22 (209) Article 9..6. Summation of Certain Infinite Lucas-Related Series arxiv:90.04336v [math.nt] Jan 209 Bakir Farhi Laboratoire de Mathématiques appliquées Faculté des Sciences
J. Integer Sequences 22 (209) Article 9..6. Summation of Certain Infinite Lucas-Related Series arxiv:90.04336v [math.nt] Jan 209 Bakir Farhi Laboratoire de Mathématiques appliquées Faculté des Sciences
GENERATING FUNCTIONS OF CENTRAL VALUES IN GENERALIZED PASCAL TRIANGLES. CLAUDIA SMITH and VERNER E. HOGGATT, JR.
 GENERATING FUNCTIONS OF CENTRAL VALUES CLAUDIA SMITH and VERNER E. HOGGATT, JR. San Jose State University, San Jose, CA 95. INTRODUCTION In this paper we shall examine the generating functions of the central
GENERATING FUNCTIONS OF CENTRAL VALUES CLAUDIA SMITH and VERNER E. HOGGATT, JR. San Jose State University, San Jose, CA 95. INTRODUCTION In this paper we shall examine the generating functions of the central
16.4. Power Series. Introduction. Prerequisites. Learning Outcomes
 Power Series 6.4 Introduction In this Section we consider power series. These are examples of infinite series where each term contains a variable, x, raised to a positive integer power. We use the ratio
Power Series 6.4 Introduction In this Section we consider power series. These are examples of infinite series where each term contains a variable, x, raised to a positive integer power. We use the ratio
Preliminary check: are the terms that we are adding up go to zero or not? If not, proceed! If the terms a n are going to zero, pick another test.
 Throughout these templates, let series. be a series. We hope to determine the convergence of this Divergence Test: If lim is not zero or does not exist, then the series diverges. Preliminary check: are
Throughout these templates, let series. be a series. We hope to determine the convergence of this Divergence Test: If lim is not zero or does not exist, then the series diverges. Preliminary check: are
ftz]}]z .tt#t*qtmjfi aiii } { n } or [ n ] I anianforn 1+2=2+-5 an = n 11.1 Sequences A sequence is a list of numbers in a certain order:
![ftz]}]z .tt#t*qtmjfi aiii } { n } or [ n ] I anianforn 1+2=2+-5 an = n 11.1 Sequences A sequence is a list of numbers in a certain order: ftz]}]z .tt#t*qtmjfi aiii } { n } or [ n ] I anianforn 1+2=2+-5 an = n 11.1 Sequences A sequence is a list of numbers in a certain order:](/thumbs/84/89678078.jpg) . 11.1 Sequences A sequence is a list of numbers in a certain order: a 1 a 2 a 3 a 4 a n1 a n (In this book all the sequences will be infinite.) The number a 1 is called the first term of the sequence.
. 11.1 Sequences A sequence is a list of numbers in a certain order: a 1 a 2 a 3 a 4 a n1 a n (In this book all the sequences will be infinite.) The number a 1 is called the first term of the sequence.
On strings of consecutive economical numbers of arbitrary length
 INTEGERS: ELECTRONIC JOURNAL OF COMBINATORIAL NUMBER THEORY 5(2) (2005), #A05 1 On strings of consecutive economical numbers of arbitrary length Jean-Marie De Koninck 1 and Florian Luca 2 Received: 11/5/03,
INTEGERS: ELECTRONIC JOURNAL OF COMBINATORIAL NUMBER THEORY 5(2) (2005), #A05 1 On strings of consecutive economical numbers of arbitrary length Jean-Marie De Koninck 1 and Florian Luca 2 Received: 11/5/03,
LONGEST SUCCESS RUNS AND FIBONACCI-TYPE POLYNOMIALS
 LONGEST SUCCESS RUNS AND FIBONACCI-TYPE POLYNOMIALS ANDREAS N. PHILIPPOU & FROSSO S. MAKRI University of Patras, Patras, Greece (Submitted January 1984; Revised April 1984) 1. INTRODUCTION AND SUMMARY
LONGEST SUCCESS RUNS AND FIBONACCI-TYPE POLYNOMIALS ANDREAS N. PHILIPPOU & FROSSO S. MAKRI University of Patras, Patras, Greece (Submitted January 1984; Revised April 1984) 1. INTRODUCTION AND SUMMARY
Introduction to Series and Sequences Math 121 Calculus II Spring 2015
 Introduction to Series and Sequences Math Calculus II Spring 05 The goal. The main purpose of our study of series and sequences is to understand power series. A power series is like a polynomial of infinite
Introduction to Series and Sequences Math Calculus II Spring 05 The goal. The main purpose of our study of series and sequences is to understand power series. A power series is like a polynomial of infinite
Fibonacci numbers. Chapter The Fibonacci sequence. The Fibonacci numbers F n are defined recursively by
 Chapter Fibonacci numbers The Fibonacci sequence The Fibonacci numbers F n are defined recursively by F n+ = F n + F n, F 0 = 0, F = The first few Fibonacci numbers are n 0 5 6 7 8 9 0 F n 0 5 8 55 89
Chapter Fibonacci numbers The Fibonacci sequence The Fibonacci numbers F n are defined recursively by F n+ = F n + F n, F 0 = 0, F = The first few Fibonacci numbers are n 0 5 6 7 8 9 0 F n 0 5 8 55 89
ELEMENTARY PROBLEMS AND SOLUTIONS. Edited by Stanley Rabinowitz
 Edited by Stanley Rabinowitz IMPORTANT NOTICE: There is a new editor of this department and a new address for all submissions. Please send all material for ELEMENTARY PROBLEMS AND SOLUTIONS to DR. STANLEY
Edited by Stanley Rabinowitz IMPORTANT NOTICE: There is a new editor of this department and a new address for all submissions. Please send all material for ELEMENTARY PROBLEMS AND SOLUTIONS to DR. STANLEY
^ ) = ^ : g ' f ^4(x)=a(xr + /xxr,
 Edited by Stanley Rablnowitz Please send all material for ELEMENTARY PROBLEMS AND SOLUTIONS to Dr. STANLEY RABINOWITZ; 12 VINE BROOK RD; WESTFORD, MA 01886-4212 USA. Correspondence may also be sent to
Edited by Stanley Rablnowitz Please send all material for ELEMENTARY PROBLEMS AND SOLUTIONS to Dr. STANLEY RABINOWITZ; 12 VINE BROOK RD; WESTFORD, MA 01886-4212 USA. Correspondence may also be sent to
THE EULER FUNCTION OF FIBONACCI AND LUCAS NUMBERS AND FACTORIALS
 Annales Univ. Sci. Budapest., Sect. Comp. 40 (2013) nn nnn THE EULER FUNCTION OF FIBONACCI AND LUCAS NUMBERS AND FACTORIALS Florian Luca (Morelia, Mexico) Pantelimon Stănică (Monterey, USA) Dedicated to
Annales Univ. Sci. Budapest., Sect. Comp. 40 (2013) nn nnn THE EULER FUNCTION OF FIBONACCI AND LUCAS NUMBERS AND FACTORIALS Florian Luca (Morelia, Mexico) Pantelimon Stănică (Monterey, USA) Dedicated to
7-7 Multiplying Polynomials
 Example 1: Multiplying Monomials A. (6y 3 )(3y 5 ) (6y 3 )(3y 5 ) (6 3)(y 3 y 5 ) 18y 8 Group factors with like bases together. B. (3mn 2 ) (9m 2 n) Example 1C: Multiplying Monomials Group factors with
Example 1: Multiplying Monomials A. (6y 3 )(3y 5 ) (6y 3 )(3y 5 ) (6 3)(y 3 y 5 ) 18y 8 Group factors with like bases together. B. (3mn 2 ) (9m 2 n) Example 1C: Multiplying Monomials Group factors with
Partition of Integers into Distinct Summands with Upper Bounds. Partition of Integers into Even Summands. An Example
 Partition of Integers into Even Summands We ask for the number of partitions of m Z + into positive even integers The desired number is the coefficient of x m in + x + x 4 + ) + x 4 + x 8 + ) + x 6 + x
Partition of Integers into Even Summands We ask for the number of partitions of m Z + into positive even integers The desired number is the coefficient of x m in + x + x 4 + ) + x 4 + x 8 + ) + x 6 + x
ADVANCED PROBLEMS AND SOLUTIONS
 Edited by Raymond E 0 Whitney Please send all communications concerning to RAYMOND E. WHITNEY, MATHEMATICS DEPARTMENT, LOCK HAVEN UNIVERSITY, LOCK HAVEN, PA 17745. This department especially welcomes problems
Edited by Raymond E 0 Whitney Please send all communications concerning to RAYMOND E. WHITNEY, MATHEMATICS DEPARTMENT, LOCK HAVEN UNIVERSITY, LOCK HAVEN, PA 17745. This department especially welcomes problems
CS Data Structures and Algorithm Analysis
 CS 483 - Data Structures and Algorithm Analysis Lecture II: Chapter 2 R. Paul Wiegand George Mason University, Department of Computer Science February 1, 2006 Outline 1 Analysis Framework 2 Asymptotic
CS 483 - Data Structures and Algorithm Analysis Lecture II: Chapter 2 R. Paul Wiegand George Mason University, Department of Computer Science February 1, 2006 Outline 1 Analysis Framework 2 Asymptotic
