Lecture 2 - Learning Binary & Multi-class Classifiers from Labelled Training Data
|
|
|
- Garry Sutton
- 5 years ago
- Views:
Transcription
1 Lecture 2 - Learning Binary & Multi-class Classifiers from Labelled Training Data DD2424 March 23, 2017
2 Binary classification problem given labelled training data Have labelled training examples? Given a test example how do we decide its class?
3 High level solution Decision Boundary Learn a decision boundary from the labelled training data. Compare the test example to the decision boundary.
4 Technical description of the binary problem Have a set of labelled training examples D = {(x 1, y 1 ),..., (x n, y n )} with each x i R d, y i { 1, 1}. Want to learn from D a classification function Usually g : R d input space R p parameter space { 1, 1} g(x; θ) = sign(f(x; θ)) where f : R d R p R Have to decide on 1. Form of f (a hyperplane?) and 2. How to estimate f s parameters ˆθ from D.
5 Learn decision boundary discriminatively Set up an optimization of the form (usually) arg min θ training error { }}{ l(y, f(x; θ)) + λ R(θ) }{{} (x,y) D regularization term where - l(y, f(x θ)) is the loss function and measures how well (and robustly) f(x; θ) predicts the label y. - The training error term measures how well and robustly the function f( ; θ) predicts the labels over all the training data. - The regularization term measures the complexity of the function f( ; θ). Usually want to learn simpler functions = less risk of over-fitting.
6 Comment on Over- and Under-fitting
7 Example of Over and Under fitting Bayes Optimal Under-fitting Over-fitting
8 Overfitting Overview of Supervised Learning High Bias Low Variance Low Bias High Variance Prediction Error Test Sample Training Sample Low Model Complexity High FIGURE Test and training error as a function of model complexity. Too much fitting = adapt too closely to the training data. be close to f(x 0 ). As k grows, the neighbors are further away, and then anything can happen. The variance term is simply the variance of an average here, and decreases as the inverse of k. So as k varies, there is a bias variance tradeoff. More generally, as the model complexity of our procedure is increased, the variance tends to increase and the squared bias tends to decrease. The opposite behavior occurs as the model complexity is decreased. For k-nearest neighbors, the model complexity is controlled by k. Have a high variance predictor. This scenario is termed overfitting. In such cases predictor loses the ability to generalize.
9 Underfitting Overview of Supervised Learning High Bias Low Variance Low Bias High Variance Prediction Error Test Sample Training Sample Low Model Complexity High FIGURE Test and training error as a function of model complexity. Low complexity model = predictor may have large bias be close to f(x 0 ). As k grows, the neighbors are further away, and then anything can happen. The variance term is simply the variance of an average here, and decreases as the inverse of k. So as k varies, there is a bias variance tradeoff. More generally, as the model complexity of our procedure is increased, the variance tends to increase and the squared bias tends to decrease. The opposite behavior occurs as the model complexity is decreased. For k-nearest Therefore predictor has poor generalization.
10 Linear Decision Boundaries
11 Linear discriminant functions Linear function for the binary classification problem: f(x; w, b) = w T x + b where model parameters are w the weight vector and b the bias. x 2 w w d w T x + b > 0 d = b w w T x + b < 0 w T x + b = 0 g(x; w, b) = x 1 { 1 if f(x; w, b) > 0 1 if f(x; w, b) < 0
12 Pros & Cons of Linear classifiers Pros Low variance classifier Easy to estimate. Frequently can set up training so that have an easy optimization problem. For high dimensional input data a linear decision boundary can sometimes be sufficient. Cons High bias classifier Often the decision boundary is not well-described by a linear classifier.
13 Optimal h training examples will have better generalization capabil How do we choose & learn the linear classifier? " Therefore, the optimal separating hyperplane will be th margin, which is defined as the minimum distance of a surface x 2 x 2 Introduction to Pattern Analysis Ricardo Gutierrez-Osuna Texas A&M University Given labelled training data: how do we choose and learn the best hyperplane to separate the two classes? x 1 From [Cherkassky
14 Have a linear classifier next need to decide: Supervised learning of my classifier 1. How to measure the quality of the classifier w.r.t. labelled training data? - Choose/Define a loss function.
15 Most intuitive loss function , 1 Loss function For a single example (x, y) the 0-1 loss is defined as { 0 if y = sgn(f(x; θ)) l(y, f(x; θ)) = 1 if y sgn(f(x; θ)) 0, 1 Loss y * f(x) = { 0 if y f(x; θ) > 0 1 if y f(x; θ) < 0 (assuming y { 1, 1}) Applied to all training data = count the number of misclassifications. Not really used in practice as has lots of problems! What are some?
16 Have a linear classifier next need to decide: Supervised learning of my classifier 1. How to measure the quality of the classifier w.r.t. labelled training data? - Choose/Define a loss function. 2. How to measure the complexity of the classifier? - Choose/Define a regularization term.
17 Most common regularization function L 2 regularization R(w) = w 2 = d i=1 w 2 i Adding this form of regularization: - Encourages w not to contain entries with large absolute values. - or want small absolute values in all entries of w.
18 Have a linear classifier next need to decide: Supervised learning of my classifier 1. How to measure the quality of the classifier w.r.t. labelled training data? - Choose/Define a loss function. 2. How to measure the complexity of the classifier? - Choose/Define a regularization term. 3. How to do estimate the classifier s parameters by optimizing relative to the above factors?
19 Example: Squared Error loss
20 Squared error loss & no regularization Learn w, b from D. Find the w, b that minimizes: L(D, w, b) = 1 2 = 1 2 (x,y) D (x,y) D l sq (y, f(x; w, b)) ( (w T x + b) y ) 2 } {{ } Squared error loss L is known as the sum-of-squares error function. The w, b that minimizes L(D, w, b) is known as the Minimum Squared Error solution. This minimum is found as follows...
21 Technical interlude: Matrix Calculus
22 Matrix Calculus Have a function f : R d R that is f(x) = b We use the notation f x = f x 1. f x d Example: If f(x) = a T x = d i=1 a ix i then f x i = a i = f x = a 1. a d = a
23 Matrix Calculus Have a function f : R d d R that is f(x) = b with X R d d We use the notation f X = f x 11 f x 21. f x d1 f f x 1d f x 2d x f x f x d2... f x dd Example: If f(x) = a T Xb = d i=1 a d i j=1 x ijb j then f = a i b j = f a 1 b 1 a 1 b 2... a 1 b d x ij X =.... = ab T a d b 1 a d b 2... a d b d
24 Matrix Calculus Derivative of a linear function x T a x = a (1) a T x x = a (2) a T Xb X = abt (3) a T X T b X = ba T (4)
25 Matrix Calculus Derivative of a quadratic function x T Bx x b T X T Xc X (Bx + b) T C(Dx + d) x = (B + B T )x (5) = X(bc T + cb T ) (6) = B T C(Dx + d) + D T C T (Bx + b) (7) b T X T DXc X = D T Xbc T + DXcb T (8)
26 End of Technical interlude
27 Pseudo-Inverse solution Can write the cost function as L(D, w, b) = 1 ( w T x + b y ) 2 1 = 2 2 (x,y) D where x = (x T, 1) T, w 1 = (w T, b) T (x,y) D ( w T 1 x y ) 2 Writing in matrix notation this becomes L(D, w 1 ) = 1 2 Xw 1 y 2 = 1 2 (Xw 1 y) T (Xw 1 y) = 1 ( w T 2 1 X T Xw 1 2y T Xw 1 + y T y ) where x T 1 1 y = (y 1,..., y n ) T, w = (w 1,..., w d+1 ) T, X =.. x T n 1
28 Pseudo-Inverse solution The gradient of L(D, w 1 ) w.r.t. w 1 : w1 L(D, w 1 ) = X T Xw 1 X T y Setting this equal to zero yields X T Xw 1 = X T y and w 1 = X y where X ( X T X ) 1 X T X is called the pseudo-inverse of X. Note that X X = I but in general XX I.
29 Simple 2D Example Decision boundary found by minimizing L squared error (D, w, b) = ( y (w T x + b) ) 2 (x,y) D
30 Pseudo-Inverse solution The gradient of L(D, w 1 ) w.r.t. w 1 : w1 L(D, w 1 ) = X T Xw 1 X T y Setting this equal to zero yields X T Xw 1 = X T y and where w 1 = X y X ( X T X ) 1 X T X is called the pseudo-inverse of X. Note that X X = I but in general XX I. If X T X singular = no unique solution to X T Xw = X T y.
31 Technical interlude: Iterative Optimization
32 Iterative Optimization Common approach to solving such unconstrained optimization problem is iterative non-linear optimization. Start with an estimate x (0). x = arg min x f(x) Try to improve it by finding successive new estimates x (1), x (2), x (3),... s.t. f(x (1) ) f(x (2) ) f(x (3) ) until convergence. To find a better estimate at each iteration: Perform the search locally around the current estimate. Such iterative approaches will find a local minima.
33 Iterative Optimization Iterative optimization methods alternate between these two steps: Decide search direction Choose a search direction based on the local properties of the cost function. Line Search Perform an intensive search to find the minimum along the chosen direction.
34 Choosing a search direction: The gradient The gradient is defined as: x f(x) f(x) x = f(x) x 1 f(x) x 2. f(x) x d The gradient points in the direction of the greatest increase of f(x).
35 Gradient descent: Method for function minimization nction minimization defined by the zeros of the gradient (x) $ 0 Gradient descent finds the minimum in an iterative fashion by unction moving has a closed in the form direction solution of steepest descent. ay exist, but is numerically illents) Gradient Descent Minimization iterative fashion by moving 2 1. Start with an arbitrary solution Local x (0). x 2 0 minimum Initial guess Global minimum x Compute the gradient x f(x (k) ). 3. Move in the direction of steepest descent: x (k+1) = x (k) η (k) x f(x (k) ). where η (k) is the step size. 4. Go to 2 (until convergence).
36 nction minimization defined by the zeros of the gradient Gradient descent: Method for function minimization (x) $ 0 Gradient descent finds the minimum in an iterative fashion by unction has a closed form solution moving in the direction of steepest descent. ay exist, but is numerically illents) iterative fashion by moving Gradient Descent Minimization Properties x Local minimum Initial guess Global minimum x Will converge to a local minimum. 2. The local minimum found depends on the initialization x (0). But this is okay 1. For convex optimization problems: local minimum global minimum 2. For deep networks most parameter setting corresponding to a local minimum are fine.
37 nction minimization defined by the zeros of the gradient Gradient descent: Method for function minimization (x) $ 0 Gradient descent finds the minimum in an iterative fashion by unction has a closed form solution moving in the direction of steepest descent. ay exist, but is numerically illents) iterative fashion by moving Gradient Descent Minimization Properties x Local minimum Initial guess Global minimum x Will converge to a local minimum. 2. The local minimum found depends on the initialization x (0). But this is okay 1. For convex optimization problems: local minimum global minimum 2. For deep networks most parameter setting corresponding to a local minimum are fine.
38 End of Technical interlude
39 Gradient descent solution The error function L(D, w 1 ) could also be minimized wrt w 1 by using a gradient descent procedure. Why? This avoids the numerical problems that arise when X T X is (nearly) singular. It also avoids the need for working with large matrices. How 1. Begin with an initial guess w (0) 1 for w Update the weight vector by moving a small distance in the direction w1 L.
40 Gradient descent solution Solution w (t+1) 1 = w (t) 1 η (t) X T (Xw (t) 1 y) If η (t) = η 0 /t, where η 0 > 0, then w (0) 1, w(1) 1, w(2) 1,... converges to a solution of X T (Xw 1 y) = 0 Irrespective of whether X T X is singular or not.
41 Stochastic gradient descent solution Increase the number of updates per computation by considering each training sample sequentially w (t+1) 1 = w (t) 1 η (t) (x T i w (t) 1 y i )x i This is known as the Widrow-Hoff, least-mean-squares (LMS) or delta rule [Mitchell, 1997]. More generally this is an application of Stochastic Gradient Descent.
42 Technical interlude: Stochastic Gradient Descent
43 Common Optimization Problem in Machine Learning Form of the optimization problem: J(D, θ) = 1 D (x,y) D l(y, f(x; θ)) + λr(θ) θ = arg min θ J(D, θ) Solution with gradient descent 1. Start with a random guess θ (0) for the parameters. 2. Then iterate until convergence θ (t+1) = θ (t) η (t) θ J(D, θ) θ (t)
44 If D is large = computing θ J(θ, D) θ (t) is time consuming = each update of θ (t) takes lots of computations Given large scale data Gradient descent needs lots of iterations to converge as η usually small = GD takes an age to find a local optimum.
45 Work around: Stochastic Gradient Descent Start with a random solution θ (0). Until convergence for t = 1, Randomly select (x, y) D. 2. Set D (t) = {(x, y)}. 3. Update parameter estimate with θ (t+1) = θ (t) η (t) θ J(D (t), θ) θ (t)
46 Comments about SGD When D (t) = 1: θ J(D (t), θ) θ (t) a noisy estimate of θ J(D, θ) θ (t) Therefore D noisy update steps in SGD 1 correct update step in GD. In practice SGD converges a lot faster then GD. Given lots of labelled training data: Quantity of updates more important than quality of updates!
47 Best practices for SGD Preparing the data - Randomly shuffle the training examples and zip sequentially through D. - Use preconditioning techniques. Monitoring and debugging - Monitor both the training cost and the validation error. - Check the gradients using finite differences. - Experiment with learning rates η (t) using a small sample of the training set.
48 Mini-Batch Gradient Descent Start with a random guess θ (0) for the parameters. Until convergence for t = 1, Randomly select a subset D (t) D s.t. D (t) = n b (typically n b 150.) 2. Update parameter estimate with θ (t+1) = θ (t) η (t) θ J(D (t), θ) θ (t)
49 Benefits of mini-batch gradient descent Obtain a more accurate estimate of θ J(D, θ) θ (t) SGD. than in Still get lots of updates per epoch (one iteration through all the training data).
50 What learning rate? Issues with setting the learning rate η (t)? - Larger η s = potentially faster learning but with the risk of less stable convergence. - Smaller η s = slow learning but stable convergence. Strategies - Constant: η (t) =.01 - Decreasing: η (t) = 1/ t Lots of recent algorithms dealing with this issue Will describe these algorithms in the near future.
51 End of Technical interlude
52 Squared Error loss + L 2 regularization
53 Add an L 2 regularization term (a.k.a. ridge regression) Add a regularization term to the loss function J ridge (D, w, b) = 1 2 (x,y) D l sq (y, w T x + b) + λ w 2 = 1 2 Xw + b1 y 2 + λ w 2 where λ > 0 and small and X is the data matrix x T 1 x T 2 X =. x T n
54 Solving Ridge Regression: Centre the data to simplify Add a regularization term to the loss function J ridge (D, w, b) = 1 2 Xw + b1 y 2 + λ w 2 Let s centre the input data = X T c 1 = 0. x T c,1 x T c,2 X c =. x T c,n where xc,i = xi µ x Optimal bias with centered input X c (does not depend on w ) is: J ridge b = b = 1/n n i=1 y i = ȳ. = b1 T 1 + w T X T c 1 1 T y = b1 T 1 1 T y
55 Solving ridge regression: Optimal weight vector Add a regularization term to the loss function J ridge (D, w) = 1 2 X cw + ȳ1 y 2 + λ w 2 Compute the gradient of J ridge w.r.t. w J ridge w = ( X T c X c + λi d ) w X T c y Set to zero to get w = ( X T c X c + λi d ) 1 X T c y (X T c X c + λi d ) has a unique inverse even if X T c X c is singular.
56 Ridge Regression decision boundaries as λ is varied Simple 2D Example λ = 1 λ = 10 λ = 100 λ = 1000
57 Solving ridge regression: Optimal weight vector Add a regularization term to the loss function J ridge (D, w) = 1 2 X cw + ȳ1 y 2 + λ w 2 Compute the gradient of J ridge w.r.t. w J ridge w = ( X T c X c + λi d ) w X T c y Set to zero to get w = ( X T c X c + λi d ) 1 X T c y (X T c X c + λi d ) has a unique inverse even if X T c X c is singular. If d is large = have to invert a very large matrix.
58 Solving ridge regression: Iteratively The gradient-descent update step is [ (X w (t+1) = w (t) ) ] T η c X c + λi d w (t) Xc T y The SGD update step for sample (x, y) is ) ] w (t+1) = w (t) η [((x µ x )(x µ x ) T + λi d w (t) (x µ x )y
59 Hinge Loss
60 The Hinge loss l(x, y; w, b) = max { 0, 1 y(w T x + b) } 12 hinge loss y g(x; θ)) This loss is not differentiable but is convex. Correctly classified examples sufficiently far from the decision boundary have zero loss. = have a way of choosing between classifiers that correctly classify all the training examples.
61 Technical interlude: Sub-gradient
62 g is a subgradient Subgradient of f at x ifof a function g is a subgradient of f (not necessarily f(y) f(x) + g T convex) at x if (y x) y Subgradient of a function f(y) f(x) + g T (y x) ( 1D (g, example: 1) supports epi f at (x, f(x))) PSfrag replacements f(x 1 ) + g T 1 (x x 1) for all y f(x) f(x 2 ) + g T 2 (x x 2) f(x 2 ) + g T 3 (x x 2) x 1 x 2 g 2, g 3 are - g subgradients at x 2 ; g 1 is a subgradient at x 1 2, g 3 are subgradients at x 2 ; - g 1 is a subgradient at x 1. Prof. S. Boyd, EE392o, Stanford University 2
63 Subgradient of a function Set of all subgradients of f at x is called the subdifferential of example: f at x, f(x) written = x f(x) 1D example: frag replacements f(x) = x f(x) 1 x 1 x If f is convex and differentiable: f(x) a subgradient of f at x.
64 End of Technical interlude
65 The Hinge loss Find w, b that minimize L hinge (D, w, b) = (x,y) D max { 0, 1 y(w T x + b) } }{{} Hinge Loss Can use stochastic gradient descent to do the optimization. The (sub-)gradients of the hinge-loss are { y x if y(w T x + b) < 1 w l(x, y; w, b) = 0 otherwise. { l(x, y; w, b) y if y(w T x + b) < 1 = b 0 otherwise.
66 Example of decision boundary found Decision boundary found by minimizing with SGD L hinge (D, w, b) = max { 0, 1 y(w T x + b) } (x,y) D
67 L 2 Regularization + Hinge Loss
68 L 2 regularization + Hinge loss Find w, b that minimize J svm (D, w, b) = λ 2 w 2 + (x,y) D max { 0, 1 y(w T x + b) } }{{} Hinge Loss Can use stochastic gradient descent to do the optimization. The sub-gradients of this cost function { λw y x if y(w T x + b) < 1 w l(x, y; w, b) = λw otherwise. { l(x, y; w, b) y if y(w T x + b) < 1 = b 0 otherwise.
69 Example of decision boundary found Decision boundary found with SGD by minimizing (λ =.01) J hinge (D, w, b) = λ 2 w 2 + max { 0, 1 y(w T x + b) } (x,y) D
70 Regularization reduces the influence of outliers Decision boundaries found by minimizing Hinge Loss L 2 Regularization + Hinge Loss
71 L 2 Regularization + Hinge Loss SVM
72 SVM s constrained optimization problem SVM solves this constrained optimization problem: ( ) 1 n min w,b 2 wt w + C ξ i subject to 12. Flexible Discriminants i=1 y i (w T x i + b) 1 ξ i for i = 1,..., n and ξ i 0 for i = 1,..., n. T β + β 0 =0 M = 1 β M = 1 β margin x T β + β 0 =0 ξ 4 ξ5 ξ ξ 3 1 ξ 2 M = 1 β M = 1 β margin
73 Alternative formulation of SVM optimization SVM solves this constrained optimization problem: ( ) 1 n min w,b 2 wt w + C ξ i subject to i=1 y i (w T x i + b) 1 ξ i for i = 1,..., n and ξ i 0 for i = 1,..., n. Let s look at the constraints: y i (w T x i + b) 1 ξ i = ξ i 1 y i (w T x i + b) But ξ i 0 also, therefore ξ i max { 0, 1 y i (w T x i + b) }
74 Alternative formulation of the SVM optimization Thus the original constrained optimization problem can be restated as an unconstrained optimization problem: min 1 n w,b 2 w 2 + C max { 0, 1 y i (w T x i + b) } }{{}}{{} i=1 Regularization term Hinge loss and corresponds to the L 2 regularization + Hinge loss formulation! = can train SVMs with SGD/mini-batch gradient descent.
75 Alternative formulation of the SVM optimization Thus the original constrained optimization problem can be restated as an unconstrained optimization problem: min 1 n w,b 2 w 2 + C max { 0, 1 y i (w T x i + b) } }{{}}{{} i=1 Regularization term Hinge loss and corresponds to the L 2 regularization + Hinge loss formulation! = can train SVMs with SGD/mini-batch gradient descent.
76 From binary to multi-class classification
77 Example dataset: CIFAR-10 airplane automobile bird cat deer dog frog horse ship truck
78 Example dataset: CIFAR-10 airplane automobile bird cat deer dog frog horse ship CIFAR classes 50,000 training images 10,000 test images Each image has size truck
79 Technical description of the multi-class problem Have a set of labelled training examples D = {(x 1, y 1 ),..., (x n, y n )} with each x i R d, y i {1,..., C}. Want to learn from D a classification function Usually g : R d input space where for j = 1,..., C: and Θ = (θ 1, θ 2,..., θ C ). R P parameter space {1,..., C} g(x; Θ) = arg max 1 j C f j(x; θ j ) f j : R d R p R
80 Multi-class linear classifier Let each f j be a linear function that is Define then where f j (x; θ j ) = w T j x + b j f 1 (x) f(x; Θ) =. f C (x) f(x; Θ) = f(x; W, b) = W x + b W = w T 1. w T C, b = Note W has size C d and b is C 1. b 1. b C
81 Apply a multi-class linear classifier to an image Have a 2D colour image but can flatten it into a 1D vector x flatten image Apply classifier: W x + b to get a score for each class. + = W x b class scores airplane car bird cat deer dog frog horse ship truck
82 Interpreting a multi-class linear classifier Learn W, b to classify the images in a dataset. Can interpret each row, w j, of W as a template for class j. Below is the visualization of each learnt w j for CIFAR-10 airplane car bird cat deer dog frog horse ship truck
83 Interpreting a multi-class linear classifier Each w T j x + b j = 0 corresponds to a hyperplane, H j, in R d. sign(w T j x + b j) tells us which side of H j the point x lies. The score w T j x + b j the distance of x to H j. 0 car classifier airplane classifier deer classifier
84 How do we learn W and b? As before need to Specify a loss function (+ a regularization term). Set up the optimization problem. Perform the optimization.
85 How do we learn W and b? As before need to Specify a loss function - must quantify the quality of all the class scores across all the training data. Set up the optimization problem. Perform the optimization.
86 Multi-class loss functions
87 Multi-class SVM Loss Remember have training data D = {(x 1, y 1 ),..., (x n, y n )} with each x i R d, y i {1,..., C}. Let s j be the score of function f j applied to x s j = f j (x; w j, b j ) = w T j x + b j The SVM loss for training example x with label y is l = C max(0, s j s y + 1) j=1 j y
88 Multi-class SVM Loss s j is the score of function f j applied to x s j = f j (x; w j, b j ) = w T j x + b j max(0, s i s y + 1) s i s y SVM loss for training example x with label y is l = C max(0, s j s y + 1) j=1 j y
89 Calculate the multi-class SVM loss for a CIFAR image input: x output label loss s = W x + b y = 8 l = 10 j=1 j y max(0, s j s y + 1) Scores airplane car bird cat deer dog frog horse ship truck s = W x + b
90 Calculate the multi-class SVM loss for a CIFAR image input: x output label loss s = W x + b y = 8 l = 10 j=1 j y max(0, s j s y + 1) Scores Compare to horse score airplane car bird cat deer dog frog horse ship truck s = W x + b s s 8 + 1
91 Calculate the multi-class SVM loss for a CIFAR image input: x output label loss s = W x + b y = 8 l = 10 j=1 j y max(0, s j s y + 1) Scores Compare to horse score Keep badly performing classes airplane car bird cat deer dog frog horse ship truck Loss for x: s = W x + b s s max(0, s s 8 + 1)
92 Problem with the SVM loss Given W and b then Response for one training example f(x; W, b) = W x + b = s loss for x l(x, y, W, x) = C max(0, s j s y + 1) j=1 j y Loss over all the training data L(D, W, b) = 1 D (x,y) D Have found a W s.t. L = 0. Is this W unique? l(x, y, W, b)
93 No Let W 1 = αw and b 1 = αb where α > 1 then Response for one training example f(x; W 1, b) = W 1 x + b 1 = s = α(w x + b) Loss for (x, y) w.r.t. W 1 and b 1 l(x, y, W 1, b 1 ) = C max(0, s j s y + 1) j=1 j y = max(0, α(w T j x + b j w T y x b y ) + 1) = max(0, α(s j s y ) + 1) = 0 as by definition s j s y < 1 and α > 1 Thus the total loss L(D, W 1, b 1 ) is 0.
94 Solution: Weight regularization L(D, W, b) = 1 D (x,y) D C max(0, f j (x; W, b) f y (x; W, b) + 1) + λr(w ) j=1 j y Commonly used Regularization Name of regularization Mathematical def. of R(W ) L 2 k l W k,l 2 L 1 k Elastic Net k l l W k,l ( βw 2 k,l + W k,l )
95 Cross-entropy Loss
96 Probabilistic interpretation of scores Let p j be the probability that input x has label j: P Y X (j x) = p j For x our linear classifier outputs scores for each class: s = W x + b Can interpret scores, s, as: unnormalized log probability for each class. = s j = log p j where αp j = p j and α = p j. = P Y X (j x) = p j = exp(s j) k exp(s k)
97 Softmax operation This transformation is known as Softmax(s) = exp(s j) k exp(s k) x Softmax(x)
98 Softmax operation This transformation is known as Softmax(s) = exp(s j) k exp(s k) x Softmax(x)
99 Softmax classifier: Log likelihood of the training data Given probabilistic model: Estimate its parameters by maximizing the log-likelihood of the training data. θ = arg max θ 1 D = arg min θ 1 D (x,y) D (x,y) D log P Y X (y x; θ) log P Y X (y x; θ) Given probabilistic interpretation of our classifier, the negative log-likelihood of the training data is ( ) 1 exp(s y ) log D C k=1 exp(s k) where s = W x + b. (x,y) D
100 Softmax classifier: Log likelihood of the training data Given probabilistic model: Estimate its parameters by maximizing the log-likelihood of the training data. θ = arg max θ 1 D = arg min θ 1 D (x,y) D (x,y) D log P Y X (y x; θ) log P Y X (y x; θ) Given probabilistic interpretation of our classifier, the negative log-likelihood of the training data is ( ) 1 exp(s y ) log D C k=1 exp(s k) where s = W x + b. (x,y) D
101 Softmax classifier + cross-entropy loss Given the probabilistic interpretation of our classifier, the negative log-likelihood of the training data is ( ) L(D, W, b) = 1 exp(s y ) log D C k=1 exp(s k) where s = W x + b. (x,y) D Can also interpret this in terms of the cross-entropy loss: ( ) L(D, W, b) = 1 exp(s y ) log D C (x,y) D k=1 exp(s k) }{{} cross-entropy loss for (x, y) = 1 l(x, y, W, b) D (x,y) D
102 Cross-entropy loss p the probability vector the network assigns to x for each class p = SOFTMAX (W x + b) log(p y ) Cross-entropy loss for training example x with label y is l = log(p y ) p y
103 Calculate the cross-entropy loss for a CIFAR image input: x output label loss ( ) s = W x + b y = 8 exp(sy) l = log exp(sk ) Scores airplane car bird cat deer dog frog horse ship truck s = W x + b
104 Calculate the cross-entropy loss for a CIFAR image input: x output label loss ( ) s = W x + b y = 8 exp(sy) l = log exp(sk ) Scores exp(scores) airplane car bird cat deer dog frog horse ship truck s = W x + b exp(s)
105 Calculate the cross-entropy loss for a CIFAR image input: x output label loss ( ) s = W x + b y = 8 exp(sy) l = log exp(sk ) Scores exp(scores) Normalized scores airplane car bird cat deer dog frog horse ship truck Loss for x: s = W x + b exp(s) exp(s) k exp(s k)
106 Cross-entropy loss ( ) exp(s y ) l(x, y, W, b) = log C k=1 exp(s k) Cross-entropy loss Questions What is the minimum possible value of l(x, y, W, b)? What is the max possible value of l(x, y, W, b)? At initialization all the entries of W are small = all s k 0. What is the loss? A training point s input value is changed slightly. What happens to the loss? The log of zero is not defined. Could this be a problem?
107 Learning the parameters: W, b Have training data D. Have scoring function: s = f(x; W, b) = W x + b We have a choice of loss functions ( ) exp(s y ) l softmax (x, y, W, b) = log C k=1 exp(s k) l svm (x, y, W, b) = Complete training loss L(W, b; D) = 1 D (x,y) D C max(0, s j s y + 1) j=1 j y l softmax(svm) (W, b; x, y) + λr(w )
108 Learning the parameters: W, b Learning W, b corresponds to solving the optimization problem where L(D, W, b) = 1 D W, b = arg min L(D, W, b) W,b (x,y) D l softmax(svm) (x, y, W, b) + λr(w ) Know how to solve this! Mini-batch gradient descent. To implement mini-batch gradient descent need - to compute gradient of the loss l softmax(svm) (x, y, W, b) and R(W ) - Set the hyper-parameters of the mini-batch gradient descent procedure.
109 Learning the parameters: W, b Learning W, b corresponds to solving the optimization problem where L(D, W, b) = 1 D W, b = arg min L(D, W, b) W,b (x,y) D l softmax(svm) (x, y, W, b) + λr(w ) Know how to solve this! Mini-batch gradient descent. To implement mini-batch gradient descent need - to compute gradient of the loss l softmax(svm) (x, y, W, b) and R(W ) - Set the hyper-parameters of the mini-batch gradient descent procedure.
110 Learning the parameters: W, b Learning W, b corresponds to solving the optimization problem where L(D, W, b) = 1 D W, b = arg min L(D, W, b) W,b (x,y) D l softmax(svm) (x, y, W, b) + λr(w ) Know how to solve this! Mini-batch gradient descent. To implement mini-batch gradient descent need - to compute gradient of the loss l softmax(svm) (x, y, W, b) and R(W ) - Set the hyper-parameters of the mini-batch gradient descent procedure.
111 We will cover how to compute these gradients using back-propagation. Next Lecture
Linear Regression (continued)
 Linear Regression (continued) Professor Ameet Talwalkar Professor Ameet Talwalkar CS260 Machine Learning Algorithms February 6, 2017 1 / 39 Outline 1 Administration 2 Review of last lecture 3 Linear regression
Linear Regression (continued) Professor Ameet Talwalkar Professor Ameet Talwalkar CS260 Machine Learning Algorithms February 6, 2017 1 / 39 Outline 1 Administration 2 Review of last lecture 3 Linear regression
Overfitting, Bias / Variance Analysis
 Overfitting, Bias / Variance Analysis Professor Ameet Talwalkar Professor Ameet Talwalkar CS260 Machine Learning Algorithms February 8, 207 / 40 Outline Administration 2 Review of last lecture 3 Basic
Overfitting, Bias / Variance Analysis Professor Ameet Talwalkar Professor Ameet Talwalkar CS260 Machine Learning Algorithms February 8, 207 / 40 Outline Administration 2 Review of last lecture 3 Basic
Machine Learning for NLP
 Machine Learning for NLP Linear Models Joakim Nivre Uppsala University Department of Linguistics and Philology Slides adapted from Ryan McDonald, Google Research Machine Learning for NLP 1(26) Outline
Machine Learning for NLP Linear Models Joakim Nivre Uppsala University Department of Linguistics and Philology Slides adapted from Ryan McDonald, Google Research Machine Learning for NLP 1(26) Outline
Max Margin-Classifier
 Max Margin-Classifier Oliver Schulte - CMPT 726 Bishop PRML Ch. 7 Outline Maximum Margin Criterion Math Maximizing the Margin Non-Separable Data Kernels and Non-linear Mappings Where does the maximization
Max Margin-Classifier Oliver Schulte - CMPT 726 Bishop PRML Ch. 7 Outline Maximum Margin Criterion Math Maximizing the Margin Non-Separable Data Kernels and Non-linear Mappings Where does the maximization
Linear discriminant functions
 Andrea Passerini passerini@disi.unitn.it Machine Learning Discriminative learning Discriminative vs generative Generative learning assumes knowledge of the distribution governing the data Discriminative
Andrea Passerini passerini@disi.unitn.it Machine Learning Discriminative learning Discriminative vs generative Generative learning assumes knowledge of the distribution governing the data Discriminative
Applied Machine Learning Lecture 5: Linear classifiers, continued. Richard Johansson
 Applied Machine Learning Lecture 5: Linear classifiers, continued Richard Johansson overview preliminaries logistic regression training a logistic regression classifier side note: multiclass linear classifiers
Applied Machine Learning Lecture 5: Linear classifiers, continued Richard Johansson overview preliminaries logistic regression training a logistic regression classifier side note: multiclass linear classifiers
CSCI567 Machine Learning (Fall 2014)
 CSCI567 Machine Learning (Fall 24) Drs. Sha & Liu {feisha,yanliu.cs}@usc.edu October 2, 24 Drs. Sha & Liu ({feisha,yanliu.cs}@usc.edu) CSCI567 Machine Learning (Fall 24) October 2, 24 / 24 Outline Review
CSCI567 Machine Learning (Fall 24) Drs. Sha & Liu {feisha,yanliu.cs}@usc.edu October 2, 24 Drs. Sha & Liu ({feisha,yanliu.cs}@usc.edu) CSCI567 Machine Learning (Fall 24) October 2, 24 / 24 Outline Review
CENG 793. On Machine Learning and Optimization. Sinan Kalkan
 CENG 793 On Machine Learning and Optimization Sinan Kalkan 2 Now Introduction to ML Problem definition Classes of approaches K-NN Support Vector Machines Softmax classification / logistic regression Parzen
CENG 793 On Machine Learning and Optimization Sinan Kalkan 2 Now Introduction to ML Problem definition Classes of approaches K-NN Support Vector Machines Softmax classification / logistic regression Parzen
Linear Discrimination Functions
 Laurea Magistrale in Informatica Nicola Fanizzi Dipartimento di Informatica Università degli Studi di Bari November 4, 2009 Outline Linear models Gradient descent Perceptron Minimum square error approach
Laurea Magistrale in Informatica Nicola Fanizzi Dipartimento di Informatica Università degli Studi di Bari November 4, 2009 Outline Linear models Gradient descent Perceptron Minimum square error approach
Lecture 2 Machine Learning Review
 Lecture 2 Machine Learning Review CMSC 35246: Deep Learning Shubhendu Trivedi & Risi Kondor University of Chicago March 29, 2017 Things we will look at today Formal Setup for Supervised Learning Things
Lecture 2 Machine Learning Review CMSC 35246: Deep Learning Shubhendu Trivedi & Risi Kondor University of Chicago March 29, 2017 Things we will look at today Formal Setup for Supervised Learning Things
Machine learning comes from Bayesian decision theory in statistics. There we want to minimize the expected value of the loss function.
 Bayesian learning: Machine learning comes from Bayesian decision theory in statistics. There we want to minimize the expected value of the loss function. Let y be the true label and y be the predicted
Bayesian learning: Machine learning comes from Bayesian decision theory in statistics. There we want to minimize the expected value of the loss function. Let y be the true label and y be the predicted
Machine Learning and Data Mining. Linear classification. Kalev Kask
 Machine Learning and Data Mining Linear classification Kalev Kask Supervised learning Notation Features x Targets y Predictions ŷ = f(x ; q) Parameters q Program ( Learner ) Learning algorithm Change q
Machine Learning and Data Mining Linear classification Kalev Kask Supervised learning Notation Features x Targets y Predictions ŷ = f(x ; q) Parameters q Program ( Learner ) Learning algorithm Change q
MLCC 2017 Regularization Networks I: Linear Models
 MLCC 2017 Regularization Networks I: Linear Models Lorenzo Rosasco UNIGE-MIT-IIT June 27, 2017 About this class We introduce a class of learning algorithms based on Tikhonov regularization We study computational
MLCC 2017 Regularization Networks I: Linear Models Lorenzo Rosasco UNIGE-MIT-IIT June 27, 2017 About this class We introduce a class of learning algorithms based on Tikhonov regularization We study computational
Machine Learning. Support Vector Machines. Fabio Vandin November 20, 2017
 Machine Learning Support Vector Machines Fabio Vandin November 20, 2017 1 Classification and Margin Consider a classification problem with two classes: instance set X = R d label set Y = { 1, 1}. Training
Machine Learning Support Vector Machines Fabio Vandin November 20, 2017 1 Classification and Margin Consider a classification problem with two classes: instance set X = R d label set Y = { 1, 1}. Training
Gaussian and Linear Discriminant Analysis; Multiclass Classification
 Gaussian and Linear Discriminant Analysis; Multiclass Classification Professor Ameet Talwalkar Slide Credit: Professor Fei Sha Professor Ameet Talwalkar CS260 Machine Learning Algorithms October 13, 2015
Gaussian and Linear Discriminant Analysis; Multiclass Classification Professor Ameet Talwalkar Slide Credit: Professor Fei Sha Professor Ameet Talwalkar CS260 Machine Learning Algorithms October 13, 2015
Logistic Regression. COMP 527 Danushka Bollegala
 Logistic Regression COMP 527 Danushka Bollegala Binary Classification Given an instance x we must classify it to either positive (1) or negative (0) class We can use {1,-1} instead of {1,0} but we will
Logistic Regression COMP 527 Danushka Bollegala Binary Classification Given an instance x we must classify it to either positive (1) or negative (0) class We can use {1,-1} instead of {1,0} but we will
Linear Regression. S. Sumitra
 Linear Regression S Sumitra Notations: x i : ith data point; x T : transpose of x; x ij : ith data point s jth attribute Let {(x 1, y 1 ), (x, y )(x N, y N )} be the given data, x i D and y i Y Here D
Linear Regression S Sumitra Notations: x i : ith data point; x T : transpose of x; x ij : ith data point s jth attribute Let {(x 1, y 1 ), (x, y )(x N, y N )} be the given data, x i D and y i Y Here D
Machine Learning. Lecture 04: Logistic and Softmax Regression. Nevin L. Zhang
 Machine Learning Lecture 04: Logistic and Softmax Regression Nevin L. Zhang lzhang@cse.ust.hk Department of Computer Science and Engineering The Hong Kong University of Science and Technology This set
Machine Learning Lecture 04: Logistic and Softmax Regression Nevin L. Zhang lzhang@cse.ust.hk Department of Computer Science and Engineering The Hong Kong University of Science and Technology This set
Machine Learning Practice Page 2 of 2 10/28/13
 Machine Learning 10-701 Practice Page 2 of 2 10/28/13 1. True or False Please give an explanation for your answer, this is worth 1 pt/question. (a) (2 points) No classifier can do better than a naive Bayes
Machine Learning 10-701 Practice Page 2 of 2 10/28/13 1. True or False Please give an explanation for your answer, this is worth 1 pt/question. (a) (2 points) No classifier can do better than a naive Bayes
Linear Regression. CSL603 - Fall 2017 Narayanan C Krishnan
 Linear Regression CSL603 - Fall 2017 Narayanan C Krishnan ckn@iitrpr.ac.in Outline Univariate regression Multivariate regression Probabilistic view of regression Loss functions Bias-Variance analysis Regularization
Linear Regression CSL603 - Fall 2017 Narayanan C Krishnan ckn@iitrpr.ac.in Outline Univariate regression Multivariate regression Probabilistic view of regression Loss functions Bias-Variance analysis Regularization
Linear Regression. CSL465/603 - Fall 2016 Narayanan C Krishnan
 Linear Regression CSL465/603 - Fall 2016 Narayanan C Krishnan ckn@iitrpr.ac.in Outline Univariate regression Multivariate regression Probabilistic view of regression Loss functions Bias-Variance analysis
Linear Regression CSL465/603 - Fall 2016 Narayanan C Krishnan ckn@iitrpr.ac.in Outline Univariate regression Multivariate regression Probabilistic view of regression Loss functions Bias-Variance analysis
Warm up: risk prediction with logistic regression
 Warm up: risk prediction with logistic regression Boss gives you a bunch of data on loans defaulting or not: {(x i,y i )} n i= x i 2 R d, y i 2 {, } You model the data as: P (Y = y x, w) = + exp( yw T
Warm up: risk prediction with logistic regression Boss gives you a bunch of data on loans defaulting or not: {(x i,y i )} n i= x i 2 R d, y i 2 {, } You model the data as: P (Y = y x, w) = + exp( yw T
Linear classifiers selecting hyperplane maximizing separation margin between classes (large margin classifiers)
 Support vector machines In a nutshell Linear classifiers selecting hyperplane maximizing separation margin between classes (large margin classifiers) Solution only depends on a small subset of training
Support vector machines In a nutshell Linear classifiers selecting hyperplane maximizing separation margin between classes (large margin classifiers) Solution only depends on a small subset of training
Least Mean Squares Regression
 Least Mean Squares Regression Machine Learning Spring 2018 The slides are mainly from Vivek Srikumar 1 Lecture Overview Linear classifiers What functions do linear classifiers express? Least Squares Method
Least Mean Squares Regression Machine Learning Spring 2018 The slides are mainly from Vivek Srikumar 1 Lecture Overview Linear classifiers What functions do linear classifiers express? Least Squares Method
Machine Learning And Applications: Supervised Learning-SVM
 Machine Learning And Applications: Supervised Learning-SVM Raphaël Bournhonesque École Normale Supérieure de Lyon, Lyon, France raphael.bournhonesque@ens-lyon.fr 1 Supervised vs unsupervised learning Machine
Machine Learning And Applications: Supervised Learning-SVM Raphaël Bournhonesque École Normale Supérieure de Lyon, Lyon, France raphael.bournhonesque@ens-lyon.fr 1 Supervised vs unsupervised learning Machine
ESS2222. Lecture 4 Linear model
 ESS2222 Lecture 4 Linear model Hosein Shahnas University of Toronto, Department of Earth Sciences, 1 Outline Logistic Regression Predicting Continuous Target Variables Support Vector Machine (Some Details)
ESS2222 Lecture 4 Linear model Hosein Shahnas University of Toronto, Department of Earth Sciences, 1 Outline Logistic Regression Predicting Continuous Target Variables Support Vector Machine (Some Details)
Apprentissage, réseaux de neurones et modèles graphiques (RCP209) Neural Networks and Deep Learning
 Apprentissage, réseaux de neurones et modèles graphiques (RCP209) Neural Networks and Deep Learning Nicolas Thome Prenom.Nom@cnam.fr http://cedric.cnam.fr/vertigo/cours/ml2/ Département Informatique Conservatoire
Apprentissage, réseaux de neurones et modèles graphiques (RCP209) Neural Networks and Deep Learning Nicolas Thome Prenom.Nom@cnam.fr http://cedric.cnam.fr/vertigo/cours/ml2/ Département Informatique Conservatoire
Support Vector Machine
 Andrea Passerini passerini@disi.unitn.it Machine Learning Support vector machines In a nutshell Linear classifiers selecting hyperplane maximizing separation margin between classes (large margin classifiers)
Andrea Passerini passerini@disi.unitn.it Machine Learning Support vector machines In a nutshell Linear classifiers selecting hyperplane maximizing separation margin between classes (large margin classifiers)
Machine Learning 2017
 Machine Learning 2017 Volker Roth Department of Mathematics & Computer Science University of Basel 21st March 2017 Volker Roth (University of Basel) Machine Learning 2017 21st March 2017 1 / 41 Section
Machine Learning 2017 Volker Roth Department of Mathematics & Computer Science University of Basel 21st March 2017 Volker Roth (University of Basel) Machine Learning 2017 21st March 2017 1 / 41 Section
Statistical Data Mining and Machine Learning Hilary Term 2016
 Statistical Data Mining and Machine Learning Hilary Term 2016 Dino Sejdinovic Department of Statistics Oxford Slides and other materials available at: http://www.stats.ox.ac.uk/~sejdinov/sdmml Naïve Bayes
Statistical Data Mining and Machine Learning Hilary Term 2016 Dino Sejdinovic Department of Statistics Oxford Slides and other materials available at: http://www.stats.ox.ac.uk/~sejdinov/sdmml Naïve Bayes
Support Vector Machines: Training with Stochastic Gradient Descent. Machine Learning Fall 2017
 Support Vector Machines: Training with Stochastic Gradient Descent Machine Learning Fall 2017 1 Support vector machines Training by maximizing margin The SVM objective Solving the SVM optimization problem
Support Vector Machines: Training with Stochastic Gradient Descent Machine Learning Fall 2017 1 Support vector machines Training by maximizing margin The SVM objective Solving the SVM optimization problem
Linear Models in Machine Learning
 CS540 Intro to AI Linear Models in Machine Learning Lecturer: Xiaojin Zhu jerryzhu@cs.wisc.edu We briefly go over two linear models frequently used in machine learning: linear regression for, well, regression,
CS540 Intro to AI Linear Models in Machine Learning Lecturer: Xiaojin Zhu jerryzhu@cs.wisc.edu We briefly go over two linear models frequently used in machine learning: linear regression for, well, regression,
Linear models: the perceptron and closest centroid algorithms. D = {(x i,y i )} n i=1. x i 2 R d 9/3/13. Preliminaries. Chapter 1, 7.
 Preliminaries Linear models: the perceptron and closest centroid algorithms Chapter 1, 7 Definition: The Euclidean dot product beteen to vectors is the expression d T x = i x i The dot product is also
Preliminaries Linear models: the perceptron and closest centroid algorithms Chapter 1, 7 Definition: The Euclidean dot product beteen to vectors is the expression d T x = i x i The dot product is also
Engineering Part IIB: Module 4F10 Statistical Pattern Processing Lecture 5: Single Layer Perceptrons & Estimating Linear Classifiers
 Engineering Part IIB: Module 4F0 Statistical Pattern Processing Lecture 5: Single Layer Perceptrons & Estimating Linear Classifiers Phil Woodland: pcw@eng.cam.ac.uk Michaelmas 202 Engineering Part IIB:
Engineering Part IIB: Module 4F0 Statistical Pattern Processing Lecture 5: Single Layer Perceptrons & Estimating Linear Classifiers Phil Woodland: pcw@eng.cam.ac.uk Michaelmas 202 Engineering Part IIB:
Neural Network Training
 Neural Network Training Sargur Srihari Topics in Network Training 0. Neural network parameters Probabilistic problem formulation Specifying the activation and error functions for Regression Binary classification
Neural Network Training Sargur Srihari Topics in Network Training 0. Neural network parameters Probabilistic problem formulation Specifying the activation and error functions for Regression Binary classification
Midterm exam CS 189/289, Fall 2015
 Midterm exam CS 189/289, Fall 2015 You have 80 minutes for the exam. Total 100 points: 1. True/False: 36 points (18 questions, 2 points each). 2. Multiple-choice questions: 24 points (8 questions, 3 points
Midterm exam CS 189/289, Fall 2015 You have 80 minutes for the exam. Total 100 points: 1. True/False: 36 points (18 questions, 2 points each). 2. Multiple-choice questions: 24 points (8 questions, 3 points
Machine Learning Lecture 7
 Course Outline Machine Learning Lecture 7 Fundamentals (2 weeks) Bayes Decision Theory Probability Density Estimation Statistical Learning Theory 23.05.2016 Discriminative Approaches (5 weeks) Linear Discriminant
Course Outline Machine Learning Lecture 7 Fundamentals (2 weeks) Bayes Decision Theory Probability Density Estimation Statistical Learning Theory 23.05.2016 Discriminative Approaches (5 weeks) Linear Discriminant
Machine Learning Basics Lecture 4: SVM I. Princeton University COS 495 Instructor: Yingyu Liang
 Machine Learning Basics Lecture 4: SVM I Princeton University COS 495 Instructor: Yingyu Liang Review: machine learning basics Math formulation Given training data x i, y i : 1 i n i.i.d. from distribution
Machine Learning Basics Lecture 4: SVM I Princeton University COS 495 Instructor: Yingyu Liang Review: machine learning basics Math formulation Given training data x i, y i : 1 i n i.i.d. from distribution
Stochastic Gradient Descent
 Stochastic Gradient Descent Machine Learning CSE546 Carlos Guestrin University of Washington October 9, 2013 1 Logistic Regression Logistic function (or Sigmoid): Learn P(Y X) directly Assume a particular
Stochastic Gradient Descent Machine Learning CSE546 Carlos Guestrin University of Washington October 9, 2013 1 Logistic Regression Logistic function (or Sigmoid): Learn P(Y X) directly Assume a particular
Midterm. Introduction to Machine Learning. CS 189 Spring Please do not open the exam before you are instructed to do so.
 CS 89 Spring 07 Introduction to Machine Learning Midterm Please do not open the exam before you are instructed to do so. The exam is closed book, closed notes except your one-page cheat sheet. Electronic
CS 89 Spring 07 Introduction to Machine Learning Midterm Please do not open the exam before you are instructed to do so. The exam is closed book, closed notes except your one-page cheat sheet. Electronic
Kernel Methods and Support Vector Machines
 Kernel Methods and Support Vector Machines Oliver Schulte - CMPT 726 Bishop PRML Ch. 6 Support Vector Machines Defining Characteristics Like logistic regression, good for continuous input features, discrete
Kernel Methods and Support Vector Machines Oliver Schulte - CMPT 726 Bishop PRML Ch. 6 Support Vector Machines Defining Characteristics Like logistic regression, good for continuous input features, discrete
Machine Learning Basics
 Security and Fairness of Deep Learning Machine Learning Basics Anupam Datta CMU Spring 2019 Image Classification Image Classification Image classification pipeline Input: A training set of N images, each
Security and Fairness of Deep Learning Machine Learning Basics Anupam Datta CMU Spring 2019 Image Classification Image Classification Image classification pipeline Input: A training set of N images, each
Linear classifiers selecting hyperplane maximizing separation margin between classes (large margin classifiers)
 Support vector machines In a nutshell Linear classifiers selecting hyperplane maximizing separation margin between classes (large margin classifiers) Solution only depends on a small subset of training
Support vector machines In a nutshell Linear classifiers selecting hyperplane maximizing separation margin between classes (large margin classifiers) Solution only depends on a small subset of training
Least Mean Squares Regression. Machine Learning Fall 2018
 Least Mean Squares Regression Machine Learning Fall 2018 1 Where are we? Least Squares Method for regression Examples The LMS objective Gradient descent Incremental/stochastic gradient descent Exercises
Least Mean Squares Regression Machine Learning Fall 2018 1 Where are we? Least Squares Method for regression Examples The LMS objective Gradient descent Incremental/stochastic gradient descent Exercises
Deep Learning for Computer Vision
 Deep Learning for Computer Vision Lecture 4: Curse of Dimensionality, High Dimensional Feature Spaces, Linear Classifiers, Linear Regression, Python, and Jupyter Notebooks Peter Belhumeur Computer Science
Deep Learning for Computer Vision Lecture 4: Curse of Dimensionality, High Dimensional Feature Spaces, Linear Classifiers, Linear Regression, Python, and Jupyter Notebooks Peter Belhumeur Computer Science
Linear Models for Classification: Discriminative Learning (Perceptron, SVMs, MaxEnt)
 Linear Models for Classification: Discriminative Learning (Perceptron, SVMs, MaxEnt) Nathan Schneider (some slides borrowed from Chris Dyer) ENLP 12 February 2018 23 Outline Words, probabilities Features,
Linear Models for Classification: Discriminative Learning (Perceptron, SVMs, MaxEnt) Nathan Schneider (some slides borrowed from Chris Dyer) ENLP 12 February 2018 23 Outline Words, probabilities Features,
Linear Models for Regression CS534
 Linear Models for Regression CS534 Prediction Problems Predict housing price based on House size, lot size, Location, # of rooms Predict stock price based on Price history of the past month Predict the
Linear Models for Regression CS534 Prediction Problems Predict housing price based on House size, lot size, Location, # of rooms Predict stock price based on Price history of the past month Predict the
Statistical Machine Learning Hilary Term 2018
 Statistical Machine Learning Hilary Term 2018 Pier Francesco Palamara Department of Statistics University of Oxford Slide credits and other course material can be found at: http://www.stats.ox.ac.uk/~palamara/sml18.html
Statistical Machine Learning Hilary Term 2018 Pier Francesco Palamara Department of Statistics University of Oxford Slide credits and other course material can be found at: http://www.stats.ox.ac.uk/~palamara/sml18.html
Lecture 14 : Online Learning, Stochastic Gradient Descent, Perceptron
 CS446: Machine Learning, Fall 2017 Lecture 14 : Online Learning, Stochastic Gradient Descent, Perceptron Lecturer: Sanmi Koyejo Scribe: Ke Wang, Oct. 24th, 2017 Agenda Recap: SVM and Hinge loss, Representer
CS446: Machine Learning, Fall 2017 Lecture 14 : Online Learning, Stochastic Gradient Descent, Perceptron Lecturer: Sanmi Koyejo Scribe: Ke Wang, Oct. 24th, 2017 Agenda Recap: SVM and Hinge loss, Representer
Linear Models for Regression. Sargur Srihari
 Linear Models for Regression Sargur srihari@cedar.buffalo.edu 1 Topics in Linear Regression What is regression? Polynomial Curve Fitting with Scalar input Linear Basis Function Models Maximum Likelihood
Linear Models for Regression Sargur srihari@cedar.buffalo.edu 1 Topics in Linear Regression What is regression? Polynomial Curve Fitting with Scalar input Linear Basis Function Models Maximum Likelihood
EXAM IN STATISTICAL MACHINE LEARNING STATISTISK MASKININLÄRNING
 EXAM IN STATISTICAL MACHINE LEARNING STATISTISK MASKININLÄRNING DATE AND TIME: August 30, 2018, 14.00 19.00 RESPONSIBLE TEACHER: Niklas Wahlström NUMBER OF PROBLEMS: 5 AIDING MATERIAL: Calculator, mathematical
EXAM IN STATISTICAL MACHINE LEARNING STATISTISK MASKININLÄRNING DATE AND TIME: August 30, 2018, 14.00 19.00 RESPONSIBLE TEACHER: Niklas Wahlström NUMBER OF PROBLEMS: 5 AIDING MATERIAL: Calculator, mathematical
Machine Learning and Computational Statistics, Spring 2017 Homework 2: Lasso Regression
 Machine Learning and Computational Statistics, Spring 2017 Homework 2: Lasso Regression Due: Monday, February 13, 2017, at 10pm (Submit via Gradescope) Instructions: Your answers to the questions below,
Machine Learning and Computational Statistics, Spring 2017 Homework 2: Lasso Regression Due: Monday, February 13, 2017, at 10pm (Submit via Gradescope) Instructions: Your answers to the questions below,
CS60021: Scalable Data Mining. Large Scale Machine Learning
 J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 1 CS60021: Scalable Data Mining Large Scale Machine Learning Sourangshu Bhattacharya Example: Spam filtering Instance
J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 1 CS60021: Scalable Data Mining Large Scale Machine Learning Sourangshu Bhattacharya Example: Spam filtering Instance
Topics we covered. Machine Learning. Statistics. Optimization. Systems! Basics of probability Tail bounds Density Estimation Exponential Families
 Midterm Review Topics we covered Machine Learning Optimization Basics of optimization Convexity Unconstrained: GD, SGD Constrained: Lagrange, KKT Duality Linear Methods Perceptrons Support Vector Machines
Midterm Review Topics we covered Machine Learning Optimization Basics of optimization Convexity Unconstrained: GD, SGD Constrained: Lagrange, KKT Duality Linear Methods Perceptrons Support Vector Machines
Non-Bayesian Classifiers Part II: Linear Discriminants and Support Vector Machines
 Non-Bayesian Classifiers Part II: Linear Discriminants and Support Vector Machines Selim Aksoy Department of Computer Engineering Bilkent University saksoy@cs.bilkent.edu.tr CS 551, Fall 2018 CS 551, Fall
Non-Bayesian Classifiers Part II: Linear Discriminants and Support Vector Machines Selim Aksoy Department of Computer Engineering Bilkent University saksoy@cs.bilkent.edu.tr CS 551, Fall 2018 CS 551, Fall
NONLINEAR CLASSIFICATION AND REGRESSION. J. Elder CSE 4404/5327 Introduction to Machine Learning and Pattern Recognition
 NONLINEAR CLASSIFICATION AND REGRESSION Nonlinear Classification and Regression: Outline 2 Multi-Layer Perceptrons The Back-Propagation Learning Algorithm Generalized Linear Models Radial Basis Function
NONLINEAR CLASSIFICATION AND REGRESSION Nonlinear Classification and Regression: Outline 2 Multi-Layer Perceptrons The Back-Propagation Learning Algorithm Generalized Linear Models Radial Basis Function
Machine Learning and Data Mining. Linear regression. Kalev Kask
 Machine Learning and Data Mining Linear regression Kalev Kask Supervised learning Notation Features x Targets y Predictions ŷ Parameters q Learning algorithm Program ( Learner ) Change q Improve performance
Machine Learning and Data Mining Linear regression Kalev Kask Supervised learning Notation Features x Targets y Predictions ŷ Parameters q Learning algorithm Program ( Learner ) Change q Improve performance
CSC 411: Lecture 04: Logistic Regression
 CSC 411: Lecture 04: Logistic Regression Raquel Urtasun & Rich Zemel University of Toronto Sep 23, 2015 Urtasun & Zemel (UofT) CSC 411: 04-Prob Classif Sep 23, 2015 1 / 16 Today Key Concepts: Logistic
CSC 411: Lecture 04: Logistic Regression Raquel Urtasun & Rich Zemel University of Toronto Sep 23, 2015 Urtasun & Zemel (UofT) CSC 411: 04-Prob Classif Sep 23, 2015 1 / 16 Today Key Concepts: Logistic
ECS171: Machine Learning
 ECS171: Machine Learning Lecture 3: Linear Models I (LFD 3.2, 3.3) Cho-Jui Hsieh UC Davis Jan 17, 2018 Linear Regression (LFD 3.2) Regression Classification: Customer record Yes/No Regression: predicting
ECS171: Machine Learning Lecture 3: Linear Models I (LFD 3.2, 3.3) Cho-Jui Hsieh UC Davis Jan 17, 2018 Linear Regression (LFD 3.2) Regression Classification: Customer record Yes/No Regression: predicting
CSC 411 Lecture 17: Support Vector Machine
 CSC 411 Lecture 17: Support Vector Machine Ethan Fetaya, James Lucas and Emad Andrews University of Toronto CSC411 Lec17 1 / 1 Today Max-margin classification SVM Hard SVM Duality Soft SVM CSC411 Lec17
CSC 411 Lecture 17: Support Vector Machine Ethan Fetaya, James Lucas and Emad Andrews University of Toronto CSC411 Lec17 1 / 1 Today Max-margin classification SVM Hard SVM Duality Soft SVM CSC411 Lec17
Linear Models for Classification
 Linear Models for Classification Oliver Schulte - CMPT 726 Bishop PRML Ch. 4 Classification: Hand-written Digit Recognition CHINE INTELLIGENCE, VOL. 24, NO. 24, APRIL 2002 x i = t i = (0, 0, 0, 1, 0, 0,
Linear Models for Classification Oliver Schulte - CMPT 726 Bishop PRML Ch. 4 Classification: Hand-written Digit Recognition CHINE INTELLIGENCE, VOL. 24, NO. 24, APRIL 2002 x i = t i = (0, 0, 0, 1, 0, 0,
Need for Deep Networks Perceptron. Can only model linear functions. Kernel Machines. Non-linearity provided by kernels
 Need for Deep Networks Perceptron Can only model linear functions Kernel Machines Non-linearity provided by kernels Need to design appropriate kernels (possibly selecting from a set, i.e. kernel learning)
Need for Deep Networks Perceptron Can only model linear functions Kernel Machines Non-linearity provided by kernels Need to design appropriate kernels (possibly selecting from a set, i.e. kernel learning)
Neural Networks Learning the network: Backprop , Fall 2018 Lecture 4
 Neural Networks Learning the network: Backprop 11-785, Fall 2018 Lecture 4 1 Recap: The MLP can represent any function The MLP can be constructed to represent anything But how do we construct it? 2 Recap:
Neural Networks Learning the network: Backprop 11-785, Fall 2018 Lecture 4 1 Recap: The MLP can represent any function The MLP can be constructed to represent anything But how do we construct it? 2 Recap:
Support Vector Machine (SVM) and Kernel Methods
 Support Vector Machine (SVM) and Kernel Methods CE-717: Machine Learning Sharif University of Technology Fall 2016 Soleymani Outline Margin concept Hard-Margin SVM Soft-Margin SVM Dual Problems of Hard-Margin
Support Vector Machine (SVM) and Kernel Methods CE-717: Machine Learning Sharif University of Technology Fall 2016 Soleymani Outline Margin concept Hard-Margin SVM Soft-Margin SVM Dual Problems of Hard-Margin
Optimization Methods for Machine Learning
 Optimization Methods for Machine Learning Sathiya Keerthi Microsoft Talks given at UC Santa Cruz February 21-23, 2017 The slides for the talks will be made available at: http://www.keerthis.com/ Introduction
Optimization Methods for Machine Learning Sathiya Keerthi Microsoft Talks given at UC Santa Cruz February 21-23, 2017 The slides for the talks will be made available at: http://www.keerthis.com/ Introduction
Mark your answers ON THE EXAM ITSELF. If you are not sure of your answer you may wish to provide a brief explanation.
 CS 189 Spring 2015 Introduction to Machine Learning Midterm You have 80 minutes for the exam. The exam is closed book, closed notes except your one-page crib sheet. No calculators or electronic items.
CS 189 Spring 2015 Introduction to Machine Learning Midterm You have 80 minutes for the exam. The exam is closed book, closed notes except your one-page crib sheet. No calculators or electronic items.
Online Videos FERPA. Sign waiver or sit on the sides or in the back. Off camera question time before and after lecture. Questions?
 Online Videos FERPA Sign waiver or sit on the sides or in the back Off camera question time before and after lecture Questions? Lecture 1, Slide 1 CS224d Deep NLP Lecture 4: Word Window Classification
Online Videos FERPA Sign waiver or sit on the sides or in the back Off camera question time before and after lecture Questions? Lecture 1, Slide 1 CS224d Deep NLP Lecture 4: Word Window Classification
Machine Learning Lecture 5
 Machine Learning Lecture 5 Linear Discriminant Functions 26.10.2017 Bastian Leibe RWTH Aachen http://www.vision.rwth-aachen.de leibe@vision.rwth-aachen.de Course Outline Fundamentals Bayes Decision Theory
Machine Learning Lecture 5 Linear Discriminant Functions 26.10.2017 Bastian Leibe RWTH Aachen http://www.vision.rwth-aachen.de leibe@vision.rwth-aachen.de Course Outline Fundamentals Bayes Decision Theory
Machine Learning A Geometric Approach
 Machine Learning A Geometric Approach CIML book Chap 7.7 Linear Classification: Support Vector Machines (SVM) Professor Liang Huang some slides from Alex Smola (CMU) Linear Separator Ham Spam From Perceptron
Machine Learning A Geometric Approach CIML book Chap 7.7 Linear Classification: Support Vector Machines (SVM) Professor Liang Huang some slides from Alex Smola (CMU) Linear Separator Ham Spam From Perceptron
Kernelized Perceptron Support Vector Machines
 Kernelized Perceptron Support Vector Machines Emily Fox University of Washington February 13, 2017 What is the perceptron optimizing? 1 The perceptron algorithm [Rosenblatt 58, 62] Classification setting:
Kernelized Perceptron Support Vector Machines Emily Fox University of Washington February 13, 2017 What is the perceptron optimizing? 1 The perceptron algorithm [Rosenblatt 58, 62] Classification setting:
Classification CE-717: Machine Learning Sharif University of Technology. M. Soleymani Fall 2012
 Classification CE-717: Machine Learning Sharif University of Technology M. Soleymani Fall 2012 Topics Discriminant functions Logistic regression Perceptron Generative models Generative vs. discriminative
Classification CE-717: Machine Learning Sharif University of Technology M. Soleymani Fall 2012 Topics Discriminant functions Logistic regression Perceptron Generative models Generative vs. discriminative
Support Vector Machines and Bayes Regression
 Statistical Techniques in Robotics (16-831, F11) Lecture #14 (Monday ctober 31th) Support Vector Machines and Bayes Regression Lecturer: Drew Bagnell Scribe: Carl Doersch 1 1 Linear SVMs We begin by considering
Statistical Techniques in Robotics (16-831, F11) Lecture #14 (Monday ctober 31th) Support Vector Machines and Bayes Regression Lecturer: Drew Bagnell Scribe: Carl Doersch 1 1 Linear SVMs We begin by considering
Linear Models for Regression CS534
 Linear Models for Regression CS534 Example Regression Problems Predict housing price based on House size, lot size, Location, # of rooms Predict stock price based on Price history of the past month Predict
Linear Models for Regression CS534 Example Regression Problems Predict housing price based on House size, lot size, Location, # of rooms Predict stock price based on Price history of the past month Predict
Introduction to Machine Learning
 Introduction to Machine Learning Linear Regression Varun Chandola Computer Science & Engineering State University of New York at Buffalo Buffalo, NY, USA chandola@buffalo.edu Chandola@UB CSE 474/574 1
Introduction to Machine Learning Linear Regression Varun Chandola Computer Science & Engineering State University of New York at Buffalo Buffalo, NY, USA chandola@buffalo.edu Chandola@UB CSE 474/574 1
Classification Logistic Regression
 Announcements: Classification Logistic Regression Machine Learning CSE546 Sham Kakade University of Washington HW due on Friday. Today: Review: sub-gradients,lasso Logistic Regression October 3, 26 Sham
Announcements: Classification Logistic Regression Machine Learning CSE546 Sham Kakade University of Washington HW due on Friday. Today: Review: sub-gradients,lasso Logistic Regression October 3, 26 Sham
1 Machine Learning Concepts (16 points)
 CSCI 567 Fall 2018 Midterm Exam DO NOT OPEN EXAM UNTIL INSTRUCTED TO DO SO PLEASE TURN OFF ALL CELL PHONES Problem 1 2 3 4 5 6 Total Max 16 10 16 42 24 12 120 Points Please read the following instructions
CSCI 567 Fall 2018 Midterm Exam DO NOT OPEN EXAM UNTIL INSTRUCTED TO DO SO PLEASE TURN OFF ALL CELL PHONES Problem 1 2 3 4 5 6 Total Max 16 10 16 42 24 12 120 Points Please read the following instructions
Linear smoother. ŷ = S y. where s ij = s ij (x) e.g. s ij = diag(l i (x))
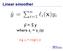 Linear smoother ŷ = S y where s ij = s ij (x) e.g. s ij = diag(l i (x)) 2 Online Learning: LMS and Perceptrons Partially adapted from slides by Ryan Gabbard and Mitch Marcus (and lots original slides by
Linear smoother ŷ = S y where s ij = s ij (x) e.g. s ij = diag(l i (x)) 2 Online Learning: LMS and Perceptrons Partially adapted from slides by Ryan Gabbard and Mitch Marcus (and lots original slides by
CSE 417T: Introduction to Machine Learning. Final Review. Henry Chai 12/4/18
 CSE 417T: Introduction to Machine Learning Final Review Henry Chai 12/4/18 Overfitting Overfitting is fitting the training data more than is warranted Fitting noise rather than signal 2 Estimating! "#$
CSE 417T: Introduction to Machine Learning Final Review Henry Chai 12/4/18 Overfitting Overfitting is fitting the training data more than is warranted Fitting noise rather than signal 2 Estimating! "#$
Support Vector Machine (SVM) and Kernel Methods
 Support Vector Machine (SVM) and Kernel Methods CE-717: Machine Learning Sharif University of Technology Fall 2014 Soleymani Outline Margin concept Hard-Margin SVM Soft-Margin SVM Dual Problems of Hard-Margin
Support Vector Machine (SVM) and Kernel Methods CE-717: Machine Learning Sharif University of Technology Fall 2014 Soleymani Outline Margin concept Hard-Margin SVM Soft-Margin SVM Dual Problems of Hard-Margin
SVAN 2016 Mini Course: Stochastic Convex Optimization Methods in Machine Learning
 SVAN 2016 Mini Course: Stochastic Convex Optimization Methods in Machine Learning Mark Schmidt University of British Columbia, May 2016 www.cs.ubc.ca/~schmidtm/svan16 Some images from this lecture are
SVAN 2016 Mini Course: Stochastic Convex Optimization Methods in Machine Learning Mark Schmidt University of British Columbia, May 2016 www.cs.ubc.ca/~schmidtm/svan16 Some images from this lecture are
Optimization and Gradient Descent
 Optimization and Gradient Descent INFO-4604, Applied Machine Learning University of Colorado Boulder September 12, 2017 Prof. Michael Paul Prediction Functions Remember: a prediction function is the function
Optimization and Gradient Descent INFO-4604, Applied Machine Learning University of Colorado Boulder September 12, 2017 Prof. Michael Paul Prediction Functions Remember: a prediction function is the function
ECS171: Machine Learning
 ECS171: Machine Learning Lecture 4: Optimization (LFD 3.3, SGD) Cho-Jui Hsieh UC Davis Jan 22, 2018 Gradient descent Optimization Goal: find the minimizer of a function min f (w) w For now we assume f
ECS171: Machine Learning Lecture 4: Optimization (LFD 3.3, SGD) Cho-Jui Hsieh UC Davis Jan 22, 2018 Gradient descent Optimization Goal: find the minimizer of a function min f (w) w For now we assume f
CSE 417T: Introduction to Machine Learning. Lecture 11: Review. Henry Chai 10/02/18
 CSE 417T: Introduction to Machine Learning Lecture 11: Review Henry Chai 10/02/18 Unknown Target Function!: # % Training data Formal Setup & = ( ), + ),, ( -, + - Learning Algorithm 2 Hypothesis Set H
CSE 417T: Introduction to Machine Learning Lecture 11: Review Henry Chai 10/02/18 Unknown Target Function!: # % Training data Formal Setup & = ( ), + ),, ( -, + - Learning Algorithm 2 Hypothesis Set H
CMU-Q Lecture 24:
 CMU-Q 15-381 Lecture 24: Supervised Learning 2 Teacher: Gianni A. Di Caro SUPERVISED LEARNING Hypotheses space Hypothesis function Labeled Given Errors Performance criteria Given a collection of input
CMU-Q 15-381 Lecture 24: Supervised Learning 2 Teacher: Gianni A. Di Caro SUPERVISED LEARNING Hypotheses space Hypothesis function Labeled Given Errors Performance criteria Given a collection of input
Regression with Numerical Optimization. Logistic
 CSG220 Machine Learning Fall 2008 Regression with Numerical Optimization. Logistic regression Regression with Numerical Optimization. Logistic regression based on a document by Andrew Ng October 3, 204
CSG220 Machine Learning Fall 2008 Regression with Numerical Optimization. Logistic regression Regression with Numerical Optimization. Logistic regression based on a document by Andrew Ng October 3, 204
Evaluation requires to define performance measures to be optimized
 Evaluation Basic concepts Evaluation requires to define performance measures to be optimized Performance of learning algorithms cannot be evaluated on entire domain (generalization error) approximation
Evaluation Basic concepts Evaluation requires to define performance measures to be optimized Performance of learning algorithms cannot be evaluated on entire domain (generalization error) approximation
Support Vector Machines and Kernel Methods
 2018 CS420 Machine Learning, Lecture 3 Hangout from Prof. Andrew Ng. http://cs229.stanford.edu/notes/cs229-notes3.pdf Support Vector Machines and Kernel Methods Weinan Zhang Shanghai Jiao Tong University
2018 CS420 Machine Learning, Lecture 3 Hangout from Prof. Andrew Ng. http://cs229.stanford.edu/notes/cs229-notes3.pdf Support Vector Machines and Kernel Methods Weinan Zhang Shanghai Jiao Tong University
Gradient Descent. Sargur Srihari
 Gradient Descent Sargur srihari@cedar.buffalo.edu 1 Topics Simple Gradient Descent/Ascent Difficulties with Simple Gradient Descent Line Search Brent s Method Conjugate Gradient Descent Weight vectors
Gradient Descent Sargur srihari@cedar.buffalo.edu 1 Topics Simple Gradient Descent/Ascent Difficulties with Simple Gradient Descent Line Search Brent s Method Conjugate Gradient Descent Weight vectors
Linear Models for Regression CS534
 Linear Models for Regression CS534 Example Regression Problems Predict housing price based on House size, lot size, Location, # of rooms Predict stock price based on Price history of the past month Predict
Linear Models for Regression CS534 Example Regression Problems Predict housing price based on House size, lot size, Location, # of rooms Predict stock price based on Price history of the past month Predict
ORIE 4741 Final Exam
 ORIE 4741 Final Exam December 15, 2016 Rules for the exam. Write your name and NetID at the top of the exam. The exam is 2.5 hours long. Every multiple choice or true false question is worth 1 point. Every
ORIE 4741 Final Exam December 15, 2016 Rules for the exam. Write your name and NetID at the top of the exam. The exam is 2.5 hours long. Every multiple choice or true false question is worth 1 point. Every
Neural Networks: Backpropagation
 Neural Networks: Backpropagation Seung-Hoon Na 1 1 Department of Computer Science Chonbuk National University 2018.10.25 eung-hoon Na (Chonbuk National University) Neural Networks: Backpropagation 2018.10.25
Neural Networks: Backpropagation Seung-Hoon Na 1 1 Department of Computer Science Chonbuk National University 2018.10.25 eung-hoon Na (Chonbuk National University) Neural Networks: Backpropagation 2018.10.25
Discriminative Models
 No.5 Discriminative Models Hui Jiang Department of Electrical Engineering and Computer Science Lassonde School of Engineering York University, Toronto, Canada Outline Generative vs. Discriminative models
No.5 Discriminative Models Hui Jiang Department of Electrical Engineering and Computer Science Lassonde School of Engineering York University, Toronto, Canada Outline Generative vs. Discriminative models
DATA MINING AND MACHINE LEARNING. Lecture 4: Linear models for regression and classification Lecturer: Simone Scardapane
 DATA MINING AND MACHINE LEARNING Lecture 4: Linear models for regression and classification Lecturer: Simone Scardapane Academic Year 2016/2017 Table of contents Linear models for regression Regularized
DATA MINING AND MACHINE LEARNING Lecture 4: Linear models for regression and classification Lecturer: Simone Scardapane Academic Year 2016/2017 Table of contents Linear models for regression Regularized
Computational statistics
 Computational statistics Lecture 3: Neural networks Thierry Denœux 5 March, 2016 Neural networks A class of learning methods that was developed separately in different fields statistics and artificial
Computational statistics Lecture 3: Neural networks Thierry Denœux 5 March, 2016 Neural networks A class of learning methods that was developed separately in different fields statistics and artificial
Logistic Regression Review Fall 2012 Recitation. September 25, 2012 TA: Selen Uguroglu
 Logistic Regression Review 10-601 Fall 2012 Recitation September 25, 2012 TA: Selen Uguroglu!1 Outline Decision Theory Logistic regression Goal Loss function Inference Gradient Descent!2 Training Data
Logistic Regression Review 10-601 Fall 2012 Recitation September 25, 2012 TA: Selen Uguroglu!1 Outline Decision Theory Logistic regression Goal Loss function Inference Gradient Descent!2 Training Data
Machine Learning Basics III
 Machine Learning Basics III Benjamin Roth CIS LMU München Benjamin Roth (CIS LMU München) Machine Learning Basics III 1 / 62 Outline 1 Classification Logistic Regression 2 Gradient Based Optimization Gradient
Machine Learning Basics III Benjamin Roth CIS LMU München Benjamin Roth (CIS LMU München) Machine Learning Basics III 1 / 62 Outline 1 Classification Logistic Regression 2 Gradient Based Optimization Gradient
Machine Learning. Lecture 2: Linear regression. Feng Li. https://funglee.github.io
 Machine Learning Lecture 2: Linear regression Feng Li fli@sdu.edu.cn https://funglee.github.io School of Computer Science and Technology Shandong University Fall 2017 Supervised Learning Regression: Predict
Machine Learning Lecture 2: Linear regression Feng Li fli@sdu.edu.cn https://funglee.github.io School of Computer Science and Technology Shandong University Fall 2017 Supervised Learning Regression: Predict
Optimization and (Under/over)fitting
 Optimization and (Under/over)fitting EECS 442 Prof. David Fouhey Winter 2019, University of Michigan http://web.eecs.umich.edu/~fouhey/teaching/eecs442_w19/ Administrivia We re grading HW2 and will try
Optimization and (Under/over)fitting EECS 442 Prof. David Fouhey Winter 2019, University of Michigan http://web.eecs.umich.edu/~fouhey/teaching/eecs442_w19/ Administrivia We re grading HW2 and will try
Support Vector Machine (SVM) and Kernel Methods
 Support Vector Machine (SVM) and Kernel Methods CE-717: Machine Learning Sharif University of Technology Fall 2015 Soleymani Outline Margin concept Hard-Margin SVM Soft-Margin SVM Dual Problems of Hard-Margin
Support Vector Machine (SVM) and Kernel Methods CE-717: Machine Learning Sharif University of Technology Fall 2015 Soleymani Outline Margin concept Hard-Margin SVM Soft-Margin SVM Dual Problems of Hard-Margin
